6. mai 2018 MAT Obligatorisk oppgave 2 av 2 - Løsningsforslag
|
|
|
- Odd Guttormsen
- 6 år siden
- Visninger:
Transkript
1 6. mai 218 MAT 24 Obligaoris oppgave 2 av 2 - Løsningsforslag
2 Oppgave 1. La X være veorromme X = C([ 1, 1], R usyr med sup-norm. For j = 1,..., n, la a j R og la x j [ 1, 1]. La F : X R være definer ved F (f = n a j f(x j j. Vis a F er deriverbar i ehver elemen f X og finn de derivere. Løsningsforslag: Vi fiserer en j {1, 2,..., n} og viser førs a funsjonen F j (f = f(x j j er deriverbar i alle puner. Sri en er å finne den reningsderivere i e gi pun f X. Vi har F F j (f + r F j (f (f(x j + r(x j j f(x j j (f; r f(xj j (r(x j j ( j = f(x j j + jf(x j j 1 r(x + = jf(x j j 1 r(x j, j ( j f(xj j (r(x j f(x j j der vi har bru a de i summen j ( i elleren over, er poenser av av høyere grad enn 2 i alle ledd. Dee anyder a den derivere il F j i f er avbildingen A definer ved A(r := jf(x j j 1 r(x j. Denne er lineær siden A(αr 1 + βr 2 = jf(x j j 1 (αr 1 (x j + βr 2 (x j Den er også begrense siden = αjf(x j j 1 r 1 (x j + βjf(x j j 1 r 2 (x j = αa(r 1 + βa(r 2. A(r = jf(x j j 1 r(x j jf(x j j 1 r. De gjensår nå å esimere feilledde σ(r = F j (f + r F j (f A(r. Vi har σ(r = (f(x j + r(x j j f(x j j jf(x j j 1 r(x j j ( j = f(x j j r(x j j ( j f(x j j r som går mo null rasere enn r, siden de bare er poenser av r sørre eller li 2. Til slu har vi da ved linearie a den derivere il F i f gi ved F (f(r = n a j jf(x j j 1 r(x j. (E anne løsningsforslag: Bru jerneregelen. 1
3 Oppgave 2. La X være veorromme X = C([ 1, 1], R usyr med sup-norm, og la G : X X være definer ved G(f(x = f(s m ds, for en m N. Vis a G er deriverbar i ehver elemen f X og finn de derivere. Løsningsforslag: Vi følger samme oppsrif som i forrige oppgave. Vi har G (f; r(x (f(s + r(sm f(s m ds m ( m = mf(s m 1 f(s m (r(s ds r(sds + lim = mf(s m 1 r(sds, hvor onvergensen er uniform på grunn av poensen 2 av i de sise inegrale. Dee anyder a avbildingen A definer ved A(r(x = er den derivere il G i pune f. Linearie: A(αr 1 + βr 2 (x = = α Avbildingen er også begrense siden mf(s m 1 r(sds mf(s m 1 (αr 1 (s + βr 2 (sds mf(s m 1 r 1 (sds + β = αa(r 1 (x + βa(r 2 (x. A(r(x = ( 1 =: M r, mf(s m 1 r(sds mf(s m 1 r(s ds mf(s m 1 ds r så A(r M r for all r. De gjensår å esimere resledde. σ(r(x = G(f + r(x G(f(x A(r(x, = = mf(s m 1 r 2 (sds (f(s + r(s m f(s m mf(s m 1 r(sds m ( m ( m ( m f(s m r(s ds f(s m r 2
4 som viser a de fins en onsan M 2 sli a σ(r M 2 r 2, og dermed a resledde går mo null rasere enn r. Oppgave 3. La l 2 være mengden av alle reelle følger {x j } j N sli a x2 j <. (a Vis a hvis x = {x j }, y = {y j } l 2, så onvergerer x jy j (Hin: bru Cauchy-Schwarz ulihe. (b Vis a l 2 er e veorrom. (c Vis a x, y = x jy j er e indreprodu på l 2. (d Vis a l 2 (med merien induser fra indreprodue i (c er omple. (e For hver j N, la e j l 2 være følgen hvis j-e omponen er 1 og de andre er. Vis a {e j } j N er en basis for l 2. Løsningsforslag: (a La ɛ > være gi. Da fins N N sli a l j= x2 j < ɛ og l j= y2 j < ɛ når N < l. Hvis vi nå bruer Cauchy-Schwarz med de ordinære indreprodue på R l får vi l l l x j y j ( x 2 j 1/2 ( yj 2 1/2 < ɛ 1/2 ɛ 1/2 = ɛ. j= j= j= Dee viser a følgen av delsummer s N = N x jy j er en Cauchy-følge, så summen onvergerer. (b Her er de underforså a for x, y l 2 seer vi x + y = {x j + y j } j N, og hvis α R så seer vi α x = {α x j } j N. Før vi går igang med å sjee a (i (viii på side er ilfredssil, må vi sjee a x + y l 2 og a α x l 2. De leese er de sise, siden (α x j 2 = α 2 x2 j, som er mindre enn eersom x l 2. Videre har vi (x j + y j 2 = x 2 j + yj x j y j, der de o førse summene il høyre for lihesegne onvergerer siden x, y l 2, og den sise summen onvergere ved (a. Vi dropper her i løsningsforslage å vise (i (viii. (c De følger fra (a a x, y R. Vi dropper her i løsningsforslage å vise (i il (iv på side 142 i boa. (d Ana a {x } N = {{x j } j N} N er en Cauchy-følge. Vi må vise a x onvergerer mo en grense i l 2. Vi sarer med å finne en andida il grensen. Mer førs a dersom vi fiserer en j N, så er {x j } N en Cauchy følge. Dee er fordi de for enhver ɛ > fins N N sli a x n j x m j = ((x n j x m j 2 1/2 ( (x n j x m j 2 1/2 < ɛ, 3
5 når N m < n. Vi seer så x j x j, og siden x = {x j } j N. De gjensår nå å vise a x l 2 og a x x når. La nå beegne normen induser av indreprodue over. Siden x er Cauchy, fins en N N sli a x n x m < 1 når N m < n. Så for alle n > N har vi a x n = x N + ( x n x N x N + x n x N x N + 1, (der vi i sise ulihe har bru (5.1.2 på side 136 i læreboa. De følger da a for enhver M N så har vi a M ( (x j 2 1/2 ( M (x j 2 1/2 x N + 1, så (x j 2 <. De gjensår å vise a x x når. Gi ɛ > fiserer vi så en N N sli a x n x < ɛ/2 når N < n. For enhver M N har vi da a M ( (x j x j 2 1/2 ( M (x n j x j 2 1/2 ɛ/2, n så lenge N, så x x ɛ/2 < ɛ så lenge N. (e La x = {x j } j N l 2. Vi seer α j = x j, og påsår a x = α je j. La så ɛ > være gi, og se så på delsummene s N = N α je j. Vi har a x s N = {a j } j N der a j = for j = 1,..., N, og a j = x j for j N + 1. Så x s N = ( j=n+1 x2 j 1/2, som per definisjon er mindre enn ɛ når N er ilsreelig sor. Til slu, hvis x = α je j = β je j, så har vi = α j e j β j e j 2 = (α j β j e j 2 = (α j β j 2, som an holde (hvis og bare hvis α j = β j for alle j N, så uvilingen er uni. Oppgave 4. La X være veorromme X = C([ 1, 1], R usyr med sup-norm, og la L : X X være definer ved L(f = f, de vil si a L(f(x = f(x. (a Vis a L ie er lineær. (b Se f(x = x. Vis a L har reningsderivere i alle reninger g(x = x m for m 1 i pune f. (c Er L deriverbar i pune f? Løsningsforslag: (a La f(x = x og g(x = x. Da er L(f+g(x =, mens L(f(x+L(g(x = 2 x. 4
6 (b Vi har x + x m x x 1 + x m 1 x lim x (1 + x m 1 x = x x m 1. (c Nei! Dersom L er deriverbar i pune f, så må for esempel L ha en reningsderiver i rening funsjonen som er onsan li 1. De vil si a de må finnes an oninuerlig funsjon g X sli a x + x lim = g(x, Seer vi inn x = ser vi a dee ie er mulig, da grensen blir 1 om vi lar gå mo null med posiive verdier, mens den blir 1 om vi lar gå mo null med negaive verdier. 5
9. mai 2019 MAT Oblig 2 - Løsningsforslag
 9. mai 219 MAT 24 Oblig 2 - Løsningsforslag Oppgave 1. La X være vektorrommet X = C([ 1, 1], R utstyrt med sup-norm, og la G : X X være definert ved G(f(x = f(s m ds, for en m N. Vis at G er deriverbar
9. mai 219 MAT 24 Oblig 2 - Løsningsforslag Oppgave 1. La X være vektorrommet X = C([ 1, 1], R utstyrt med sup-norm, og la G : X X være definert ved G(f(x = f(s m ds, for en m N. Vis at G er deriverbar
Oppgave 1. = 2(1 4) = 6. Vi regner også ut de andre indreproduktene:
 Løsning Eksamen i ELE 379 Maemaikk Valgfag Dao 7. juni 26 kl 9-4 Dee e e foreløpig løsningsforslag som ikke er komple. De skal ikke publiseres i denne form. Oppgave. (a) Vi ve a kolonnevekorene il A er
Løsning Eksamen i ELE 379 Maemaikk Valgfag Dao 7. juni 26 kl 9-4 Dee e e foreløpig løsningsforslag som ikke er komple. De skal ikke publiseres i denne form. Oppgave. (a) Vi ve a kolonnevekorene il A er
Løsning til prøveeksamen i MAT2400, V-11
 Løsning til prøveeksamen i MAT400, V-11 Oppgave 1 a) Vi ser at den deriverte f (x) = 1 1+x alltid er mindre enn eller lik 1 i tallverdi. Gitt to punkter x, y R, finnes det ifølge middelverdisetningen en
Løsning til prøveeksamen i MAT400, V-11 Oppgave 1 a) Vi ser at den deriverte f (x) = 1 1+x alltid er mindre enn eller lik 1 i tallverdi. Gitt to punkter x, y R, finnes det ifølge middelverdisetningen en
av Erik Bédos, Matematisk Institutt, UiO, 25. mai 2007.
 Om den diskree Fourier ransformen av Erik Bédos, Maemaisk Insiu, UiO,. mai 7. Vi lar H beegne indreproduk romme som besår av alle koninuerlige komplekse funksjoner definer på inervalle [, π] med indreproduke
Om den diskree Fourier ransformen av Erik Bédos, Maemaisk Insiu, UiO,. mai 7. Vi lar H beegne indreproduk romme som besår av alle koninuerlige komplekse funksjoner definer på inervalle [, π] med indreproduke
Løsningsforslag til Mat112 Obligatorisk Oppgave, våren Oppgave 1
 Løsningsforslag til Mat2 Obligatorisk Oppgave, våren 206 Oppgave Avgjør om følgende rekker er konvergente: (a) n + n n + n + Løsning: rekken lim : n n + n n + n + Vi bruker grensesammenligningstesten mhp.
Løsningsforslag til Mat2 Obligatorisk Oppgave, våren 206 Oppgave Avgjør om følgende rekker er konvergente: (a) n + n n + n + Løsning: rekken lim : n n + n n + n + Vi bruker grensesammenligningstesten mhp.
Forkunnskaper i matematikk for fysikkstudenter. Integrasjon.
 De grunnleggende definisjonene L oss strte med følgende prolem: Gitt en ontinuerlig funsjon y = f der f for [, ] Beregn relet A som er vgrenset v grfen til f, -sen, og de to vertile linjene = og = Vi n
De grunnleggende definisjonene L oss strte med følgende prolem: Gitt en ontinuerlig funsjon y = f der f for [, ] Beregn relet A som er vgrenset v grfen til f, -sen, og de to vertile linjene = og = Vi n
Arbeid og potensiell energi
 Areid og poensiell energi 6..3 YS-ME 6..3 areid:, d ne, ne dr areid-energi eorem, ineis energi: areid er ilfør meanis energi ureinegral langs en ure C sar i r slu i r os: generell ahenger areid a eien!
Areid og poensiell energi 6..3 YS-ME 6..3 areid:, d ne, ne dr areid-energi eorem, ineis energi: areid er ilfør meanis energi ureinegral langs en ure C sar i r slu i r os: generell ahenger areid a eien!
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT1100 Kalkulus Eksamensdag: Fredag 14. oktober 2016 Tid for eksamen: 13.00 15.00 Oppgavesettet er på 5 sider. Vedlegg: Svarark,
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT1100 Kalkulus Eksamensdag: Fredag 14. oktober 2016 Tid for eksamen: 13.00 15.00 Oppgavesettet er på 5 sider. Vedlegg: Svarark,
Taylorpolynom (4.8) f en funksjon a et punkt i definisjonsmengden til f f (minst) n ganger deriverbar i a Da er Taylorpolynomet til f om a
 Taylorpolynom (4.8) f en funksjon a et punkt i definisjonsmengden til f f (minst) n ganger deriverbar i a Da er Taylorpolynomet til f om a P n (x) = f (a) + f (a)(x a) + f (a) 2 (x a)2 + + f (n) (a) (x
Taylorpolynom (4.8) f en funksjon a et punkt i definisjonsmengden til f f (minst) n ganger deriverbar i a Da er Taylorpolynomet til f om a P n (x) = f (a) + f (a)(x a) + f (a) 2 (x a)2 + + f (n) (a) (x
Løsningsforslag øving 6
 Løsningsforslag øving 6 7 Husk Teorem 79 i notatet: En delmengde U av et vektorrom V er et underrom hvis ) nullvektoren er i U, ) summen av to vektorer i U er i U igjen, og 3) et skalarmultiplum av en
Løsningsforslag øving 6 7 Husk Teorem 79 i notatet: En delmengde U av et vektorrom V er et underrom hvis ) nullvektoren er i U, ) summen av to vektorer i U er i U igjen, og 3) et skalarmultiplum av en
, og dropper benevninger for enkelhets skyld: ( ) ( ) L = 432L L = L = 1750 m. = 0m/s, og a = 4.00 m/s.
 eegelse øsninger på blandede oppgaer Side - Oppgae Vi kaller lengden a en runde for Faren il joggerne er da: A = m/s = m/s 6 6 + 48 48 = m/s = m/s 7 6 + 4 Når de møes, ar de løp like lenge Da er + 5 m
eegelse øsninger på blandede oppgaer Side - Oppgae Vi kaller lengden a en runde for Faren il joggerne er da: A = m/s = m/s 6 6 + 48 48 = m/s = m/s 7 6 + 4 Når de møes, ar de løp like lenge Da er + 5 m
ST1201 Statistiske metoder
 ST0 Statistise etoder Norges tenis-naturvitensapelige universitet Institutt for ateatise fag Løsningsforslag - Esaen deseber 008 Oppgave a l(θ = lnl(θ = L(θ = n n f(x i [ θ e ] x i θ [ ln lnθ x ] i = nln
ST0 Statistise etoder Norges tenis-naturvitensapelige universitet Institutt for ateatise fag Løsningsforslag - Esaen deseber 008 Oppgave a l(θ = lnl(θ = L(θ = n n f(x i [ θ e ] x i θ [ ln lnθ x ] i = nln
Partieltderiverte og gradient
 Partieltderiverte og gradient Kap 2 Matematisk Institutt, UiO MEK1100, FELTTEORI OG VEKTORANALYSE våren 2009 Framstilling Kommentarer, relasjon til andre kurs Struktur Mye er repitisjon fra MAT1100, litt
Partieltderiverte og gradient Kap 2 Matematisk Institutt, UiO MEK1100, FELTTEORI OG VEKTORANALYSE våren 2009 Framstilling Kommentarer, relasjon til andre kurs Struktur Mye er repitisjon fra MAT1100, litt
MAT1030 Forelesning 16
 MAT1030 Forelesning 16 Reursjon og indusjon Roger Antonsen - 17 mars 009 (Sist oppdatert: 009-03-17 11:4 Forelesning 16 Reursjon og indusjon Forrige gang ga vi endel esempler på reursive definisjoner og
MAT1030 Forelesning 16 Reursjon og indusjon Roger Antonsen - 17 mars 009 (Sist oppdatert: 009-03-17 11:4 Forelesning 16 Reursjon og indusjon Forrige gang ga vi endel esempler på reursive definisjoner og
Arbeid og potensiell energi
 Areid og poensiell energi 3.3.4 olig 5: midveis hjemmeeksamen forusening for å a slueksamen kreves individuell innlevering lir lag u mandag 3. mars innleveringsfris mandag. mars YS-ME 3.3.4 Areid-energi
Areid og poensiell energi 3.3.4 olig 5: midveis hjemmeeksamen forusening for å a slueksamen kreves individuell innlevering lir lag u mandag 3. mars innleveringsfris mandag. mars YS-ME 3.3.4 Areid-energi
MA1102 Grunnkurs i Analyse II Vår 2015
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA112 Grunnkurs i Analyse II Vår 215 Løsningsforslag Øving 5 11.3:3 f n (x) = 2n+1 x? = x 1 2n+1. (Det er muligens en forskjell
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA112 Grunnkurs i Analyse II Vår 215 Løsningsforslag Øving 5 11.3:3 f n (x) = 2n+1 x? = x 1 2n+1. (Det er muligens en forskjell
Matematikk 1 (TMA4100)
 Matematikk 1 (TMA4100) Forelesning 4: Grenseverdi (fortsettelse) Eirik Hoel Høiseth Stipendiat IMF NTNU 20. august, 2012 Formell definisjon av grenseverdi Formell definisjon av grenseverdi Uformell definisjon
Matematikk 1 (TMA4100) Forelesning 4: Grenseverdi (fortsettelse) Eirik Hoel Høiseth Stipendiat IMF NTNU 20. august, 2012 Formell definisjon av grenseverdi Formell definisjon av grenseverdi Uformell definisjon
Plan. MAT1030 Diskret matematikk. Eksamen 12/6-06 Oppgave 2. Noen tips til eksamen
 Plan MAT1030 Disret matemati Plenumsregning 12: Diverse oppgaver Roger Antonsen Matematis Institutt, Universitetet i Oslo 22. mai 2008 Dette er siste plenumsregning. Vi regner stort sett esamensoppgaver.
Plan MAT1030 Disret matemati Plenumsregning 12: Diverse oppgaver Roger Antonsen Matematis Institutt, Universitetet i Oslo 22. mai 2008 Dette er siste plenumsregning. Vi regner stort sett esamensoppgaver.
1 Mandag 1. februar 2010
 Mandag. februar 200 I dag skal vi fortsette med rekkeutviklinger som vi begynte med forrige uke. Vi skal se på litt mer generell rekker og vurdere når de konvergerer, bl.a. gi et enkelt kriterium. Dette
Mandag. februar 200 I dag skal vi fortsette med rekkeutviklinger som vi begynte med forrige uke. Vi skal se på litt mer generell rekker og vurdere når de konvergerer, bl.a. gi et enkelt kriterium. Dette
R2 - Kapittel 2 - Algebra. I a) Hvilken av disse tallfølgene er aritmetiske, geometriske eller ingen av delene?
 R2 - Kapittel 2 - Algebra I Hvilen av disse tallfølgene er aritmetise, geometrise eller ingen av delene?.,,,,... 2 4 2. 2,6,8,54,.... 2,6,0,4,... 4.,, 2, 4,... 2 9 5., 5, 7, 9,... 4 9 6 Sriv opp uttryet
R2 - Kapittel 2 - Algebra I Hvilen av disse tallfølgene er aritmetise, geometrise eller ingen av delene?.,,,,... 2 4 2. 2,6,8,54,.... 2,6,0,4,... 4.,, 2, 4,... 2 9 5., 5, 7, 9,... 4 9 6 Sriv opp uttryet
Deleksamen i MAT111 - Grunnkurs i Matematikk I
 Bergen, oktober. 2004. Løsningsforslag til Deleksamen i MAT - Grunnkurs i Matematikk I Mandag. oktober 2004, kl. 09-2. Oppgave Beregn grensen f.eks. ved hjelp av l Hôpitals regel. lim x ln x x Vi ser at
Bergen, oktober. 2004. Løsningsforslag til Deleksamen i MAT - Grunnkurs i Matematikk I Mandag. oktober 2004, kl. 09-2. Oppgave Beregn grensen f.eks. ved hjelp av l Hôpitals regel. lim x ln x x Vi ser at
Førsteordens lineære differensiallikninger
 Førsteordens lineære differensiallininger Begrepet førsteordens lineære differensiallininger er ie sielig definert i Sinus R. Denne artielen omhandler det temaet. En førsteordens lineær differensiallining
Førsteordens lineære differensiallininger Begrepet førsteordens lineære differensiallininger er ie sielig definert i Sinus R. Denne artielen omhandler det temaet. En førsteordens lineær differensiallining
MA1301/MA6301 Tallteori Høst 2016
 Norges tenis naturvitensapelige universitet Institutt for ateatise fag MA/MA6 Tallteori Høst 6 a Vi starter ed å sjee at liheten steer for n. Vi har at i. Heldigvis er (, så vi ser at påstanden steer i
Norges tenis naturvitensapelige universitet Institutt for ateatise fag MA/MA6 Tallteori Høst 6 a Vi starter ed å sjee at liheten steer for n. Vi har at i. Heldigvis er (, så vi ser at påstanden steer i
Funksjonslære Derivasjon Matematikk 2
 Funksjonslære Derivasjon Maemaikk 2 Avdeling for lærerudanning, Høgskolen i Vesfold 19 mars 2009 1 Innledning La f(x) være en funksjon, alså, en sørrelse som er avhengig av x De kan ofe være hensiksmessig
Funksjonslære Derivasjon Maemaikk 2 Avdeling for lærerudanning, Høgskolen i Vesfold 19 mars 2009 1 Innledning La f(x) være en funksjon, alså, en sørrelse som er avhengig av x De kan ofe være hensiksmessig
Anbefalte oppgaver - Løsningsforslag
 Anbefalte oppgaver - Løsningsforslag Uke 6 12.6.4: Vi finner først lineariseringen i punktet (2, 2). Vi har at Lineariseringen er derfor 2x + y f x (x, y) = 24 (x 2 + xy + y 2 ) 2 2y + x f y (x, y) = 24
Anbefalte oppgaver - Løsningsforslag Uke 6 12.6.4: Vi finner først lineariseringen i punktet (2, 2). Vi har at Lineariseringen er derfor 2x + y f x (x, y) = 24 (x 2 + xy + y 2 ) 2 2y + x f y (x, y) = 24
y (t) = cos t x (π) = 0 y (π) = 1. w (t) = w x (t)x (t) + w y (t)y (t)
 NTNU Institutt for matematiske fag TMA4105 Matematikk, øving 7, vår 013 Løsningsforslag Notasjon og merknader En vektor boken skriver som ai + bj + ck, vil vi ofte skrive som (a, b, c), og tilsvarende
NTNU Institutt for matematiske fag TMA4105 Matematikk, øving 7, vår 013 Løsningsforslag Notasjon og merknader En vektor boken skriver som ai + bj + ck, vil vi ofte skrive som (a, b, c), og tilsvarende
Kort om ny reguleringskurvelogikk. Trond Reitan 19/8-2013
 Kor om ny reguleringskurvelogikk Trond Reian 19/8-2013 Hensik Hensiken med en reguleringskurver er å angi sammenhengen mellom en angi minimumsvannføring (apping) og nødvendig magasinvolum på årlig basis.
Kor om ny reguleringskurvelogikk Trond Reian 19/8-2013 Hensik Hensiken med en reguleringskurver er å angi sammenhengen mellom en angi minimumsvannføring (apping) og nødvendig magasinvolum på årlig basis.
Rekursjon og induksjon. MAT1030 Diskret matematikk. Induksjonsbevis. Induksjonsbevis. Eksempel (Fortsatt) Eksempel
 Reursjon og indusjon MAT1030 Disret matemati Forelesning 15: Indusjon og reursjon, reurenslininger Dag Normann Matematis Institutt, Universitetet i Oslo 3 mars 008 Onsdag ga vi endel esempler på reursive
Reursjon og indusjon MAT1030 Disret matemati Forelesning 15: Indusjon og reursjon, reurenslininger Dag Normann Matematis Institutt, Universitetet i Oslo 3 mars 008 Onsdag ga vi endel esempler på reursive
OPPSUMMERING FORELESNINGER UKE 35
 OPPSUMMERIG FORELESIGER UKE 35 Kromaografis separasjon bygger på soffers (lieves-)fordeling mellom en sasjonær fase og en mobil fase. Reensjonen besemmes primær av: Mobilfasens egensaper, sasjonærfasens
OPPSUMMERIG FORELESIGER UKE 35 Kromaografis separasjon bygger på soffers (lieves-)fordeling mellom en sasjonær fase og en mobil fase. Reensjonen besemmes primær av: Mobilfasens egensaper, sasjonærfasens
Oppgaver i kapittel 1 - Løsningsskisser og kommentarer Lærebok:
 Oppgaver i apittel - Løsningssisser og ommentarer Lærebo:.6 Vitig oppgave, viser hvordan ree-summer an tilnærmes med integraler. Atuelt hvis vi har formelen for n te ledd, men ie har noen summeformel.
Oppgaver i apittel - Løsningssisser og ommentarer Lærebo:.6 Vitig oppgave, viser hvordan ree-summer an tilnærmes med integraler. Atuelt hvis vi har formelen for n te ledd, men ie har noen summeformel.
Vi skal nå lære hvordan vi kan finne en formel for å bestemme det n te elementet i en tallfølge av 2. grad.
 Differensligninger Vi startet med en repetisjon om løsning av. ordens differensligninger.. ordens differensligning. a n = c 1 a n-1 + c a n-, der c 1 og c er konstanter. Vi ser her at neste ledd i følgen
Differensligninger Vi startet med en repetisjon om løsning av. ordens differensligninger.. ordens differensligning. a n = c 1 a n-1 + c a n-, der c 1 og c er konstanter. Vi ser her at neste ledd i følgen
der hver f_i \: E \to R er deriverbar i x, for 1 \le i \le p. Vi kan skrive likningen \epsilon(x, h) = (\epsilon_1(x, h), \dots, \epsilon_p(x, h)).
 MAT1300 Analyse I 23. februar 2009 La E \subset R^m og f \: E \to R^p. Anta B(x, \delta) \subset E. Dersom f er deriverbar i x, er den deriverte \alpha = f'(x) \: R^m \to R^p gitt ved multiplikasjon med
MAT1300 Analyse I 23. februar 2009 La E \subset R^m og f \: E \to R^p. Anta B(x, \delta) \subset E. Dersom f er deriverbar i x, er den deriverte \alpha = f'(x) \: R^m \to R^p gitt ved multiplikasjon med
Analysedrypp II: Kompletthet
 Analysedrypp II: Kompletthet Kompletthet er et begrep som står sentralt i både MAT1100 og MAT1110, og som vil stå enda mer sentralt i MAT2400. I de tidligere kursene fremstår begrepet på litt forskjellig
Analysedrypp II: Kompletthet Kompletthet er et begrep som står sentralt i både MAT1100 og MAT1110, og som vil stå enda mer sentralt i MAT2400. I de tidligere kursene fremstår begrepet på litt forskjellig
t [0, t ]. Den er i bevegelse langs en bane. Med origo menes her nullpunktet
![t [0, t ]. Den er i bevegelse langs en bane. Med origo menes her nullpunktet t [0, t ]. Den er i bevegelse langs en bane. Med origo menes her nullpunktet](/thumbs/56/39469195.jpg) FAO 9 Forberedelse il skoleprøve Del Prakisk bruk av inegral Oppgave parikkelfar Hasigheen il en parikkel ved iden er gi ved v () = i m/min. Tiden er ( + ) + regne i min, for angivelse av posisjon. [,
FAO 9 Forberedelse il skoleprøve Del Prakisk bruk av inegral Oppgave parikkelfar Hasigheen il en parikkel ved iden er gi ved v () = i m/min. Tiden er ( + ) + regne i min, for angivelse av posisjon. [,
Arbeid og potensiell energi
 Areid og poensiell energi 7..7 YS-MEK 7..7 Areid-energi eorem areid:, v ne d kineisk energi K, K K, ne v d ne dr d d C ne dr kurveinegral langs en kurve C sar i r, slu i r uˆ N uˆ N v vuˆ v uˆ N uˆ N vuˆ
Areid og poensiell energi 7..7 YS-MEK 7..7 Areid-energi eorem areid:, v ne d kineisk energi K, K K, ne v d ne dr d d C ne dr kurveinegral langs en kurve C sar i r, slu i r uˆ N uˆ N v vuˆ v uˆ N uˆ N vuˆ
Virkninger av ubalansert produktivitetsvekst («Baumols sykdom»)
 1 Jon Vislie; februar 2018 ECON 3735 vår 2018 Forelesningsnoa #2 Virkninger av ubalanser produkiviesveks («Baumols sykdom») I Forelesningsnoa #1 så vi på generelle likevekseffeker i en o-sekor-økonomi,
1 Jon Vislie; februar 2018 ECON 3735 vår 2018 Forelesningsnoa #2 Virkninger av ubalanser produkiviesveks («Baumols sykdom») I Forelesningsnoa #1 så vi på generelle likevekseffeker i en o-sekor-økonomi,
Løsningsforslag. Oppgave 1 Gitt matrisene ] [ og C = A = 4 1 B = 2 1 3
![Løsningsforslag. Oppgave 1 Gitt matrisene ] [ og C = A = 4 1 B = 2 1 3 Løsningsforslag. Oppgave 1 Gitt matrisene ] [ og C = A = 4 1 B = 2 1 3](/thumbs/55/37240043.jpg) Prøve i Matematikk BYFE DAFE Dato: 27. mai 26 Hjelpemiddel: Kalkulator og formelark Alle svar skal grunngis. Alle deloppgaver har lik vekt. Løsningsforslag Oppgave Gitt matrisene [ 2 A 4 B [ 2 og C [ 2
Prøve i Matematikk BYFE DAFE Dato: 27. mai 26 Hjelpemiddel: Kalkulator og formelark Alle svar skal grunngis. Alle deloppgaver har lik vekt. Løsningsforslag Oppgave Gitt matrisene [ 2 A 4 B [ 2 og C [ 2
Løsningsforslag i matematikk
 Løsningsforslag i matematikk 060808 Oppgave (a) ( a b ) b 4 a (ab) = a b b 4 a a b = a b = b a = a + b + 4 a b = a + + b + 4 + (b) Omskrivning av likningen gir sin(x) + cos(x) = 0 sin(x) cos(x) = tan(x)
Løsningsforslag i matematikk 060808 Oppgave (a) ( a b ) b 4 a (ab) = a b b 4 a a b = a b = b a = a + b + 4 a b = a + + b + 4 + (b) Omskrivning av likningen gir sin(x) + cos(x) = 0 sin(x) cos(x) = tan(x)
LØSNINGSFORSLAG EKSAMEN, MAT 1001, HØSTEN (x + 1) 2 dx = u 2 du = u 1 = (x + 1) 1 = 1 x + 1. ln x
 LØSNINGSFORSLAG EKSAMEN, MAT 00, HØSTEN 06 DEL.. Hvilken av funksjonene gir en anti-derivert for f(x) = (x + )? Løsning. Vi setter u = x +, som gir du = dx, (x + ) dx = u du = u = (x + ) = x + a) x+ b)
LØSNINGSFORSLAG EKSAMEN, MAT 00, HØSTEN 06 DEL.. Hvilken av funksjonene gir en anti-derivert for f(x) = (x + )? Løsning. Vi setter u = x +, som gir du = dx, (x + ) dx = u du = u = (x + ) = x + a) x+ b)
Oppgaveark Uke 37 (07/09-11/09) MAT111 - H09
 Oppgaveark Uke 37 (07/09-11/09) MAT111 - H09 Oppgave 1 Du ar fått deg en jobb i et firma og skal kjøre til en konferanse med overnatting. Du drar jemmefra på mandag kl 07:15 og ankommer 11:07. Du overnatter
Oppgaveark Uke 37 (07/09-11/09) MAT111 - H09 Oppgave 1 Du ar fått deg en jobb i et firma og skal kjøre til en konferanse med overnatting. Du drar jemmefra på mandag kl 07:15 og ankommer 11:07. Du overnatter
Oppgave 1. Vi må forutsette at dataene kommer fra uavhengige og normalfordelte tilfeldige variable,
 MOT30 Statistiske metoder Løsningsforslag til eksamen vår 0 s. Oppgave a Vi har x = 6. og x i x = 4.6. Herav s x = n Et 90% kondensintervall er gitt ved x i x = 4.6 = 0.89 6 SX X t 0.056 X + t S X 0.056
MOT30 Statistiske metoder Løsningsforslag til eksamen vår 0 s. Oppgave a Vi har x = 6. og x i x = 4.6. Herav s x = n Et 90% kondensintervall er gitt ved x i x = 4.6 = 0.89 6 SX X t 0.056 X + t S X 0.056
Den deriverte og derivasjonsregler
 Den deriverte og derivasjonsregler Department of Mathematical Sciences, NTNU, Norway September 3, 2014 Tangenten til en funksjon i et punkt (kap. 2.1) Sekant til en funksjon gjennom to punkter 25 20 f(c+h)
Den deriverte og derivasjonsregler Department of Mathematical Sciences, NTNU, Norway September 3, 2014 Tangenten til en funksjon i et punkt (kap. 2.1) Sekant til en funksjon gjennom to punkter 25 20 f(c+h)
MAT jan jan feb MAT Våren 2010
 MAT 1012 Våren 2010 Mandag 25. januar 2010 Forelesning Vi fortsetter med å se på det bestemte integralet, bl.a. på hvordan vi kan bruke numeriske beregninger til å bestemme verdien når vi ikke nødvendigvis
MAT 1012 Våren 2010 Mandag 25. januar 2010 Forelesning Vi fortsetter med å se på det bestemte integralet, bl.a. på hvordan vi kan bruke numeriske beregninger til å bestemme verdien når vi ikke nødvendigvis
Oblig 1 - MAT Oppgave 1. Fredrik Meyer. Vi lar α > 1 og x 1 > α. Vi definerer en følge (x n ) ved. x n+1 = α + x n 1 + x n.
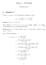 Oblig 1 - MAT2400 Fredrik Meyer 1 Oppgave 1 Vi lar α > 1 og x 1 > α. Vi definerer en følge (x n ) ved Lemma 1 (a). x n > 1 n N x n+1 = α + x n = x n + α x2 n Bevis. Siden α > 1 er α + x n >, så 1 = 1+xn
Oblig 1 - MAT2400 Fredrik Meyer 1 Oppgave 1 Vi lar α > 1 og x 1 > α. Vi definerer en følge (x n ) ved Lemma 1 (a). x n > 1 n N x n+1 = α + x n = x n + α x2 n Bevis. Siden α > 1 er α + x n >, så 1 = 1+xn
UNIVERSITETET I BERGEN
 UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Eksamen i emnet MAT - Grunnkurs i Matematikk II Torsdag 4. juni 05, kl. 09:00-4:00 Bokmål Tillatte hjelpemiddel: Enkel kalkulator i samsvar
UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Eksamen i emnet MAT - Grunnkurs i Matematikk II Torsdag 4. juni 05, kl. 09:00-4:00 Bokmål Tillatte hjelpemiddel: Enkel kalkulator i samsvar
Vår TMA4105 Matematikk 2. Løsningsforslag Øving 6. 5 Exercise Exercise
 TMA405 Matematikk 2 Vår 205 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Løsningsforslag Øving 6 Alle oppgavenummer referer til 8. utgave av Adams & Essex Calculus: A Complete
TMA405 Matematikk 2 Vår 205 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Løsningsforslag Øving 6 Alle oppgavenummer referer til 8. utgave av Adams & Essex Calculus: A Complete
For at en funksjon i to variable skal ha en grenseverdi i punktet (a,b), dvs.
 Øving ue 3 Grenser og ontinuitet For at en funsjon i to variable sal ha en grenseverdi i puntet (a,b), dvs. lim Hx,yL Ha,bL f Hx, yl = L sal esistere, må denne unie verdien oppnåes uansett hvilen vei man
Øving ue 3 Grenser og ontinuitet For at en funsjon i to variable sal ha en grenseverdi i puntet (a,b), dvs. lim Hx,yL Ha,bL f Hx, yl = L sal esistere, må denne unie verdien oppnåes uansett hvilen vei man
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT111 Prøveeksamen Eksamensdag: 5. juni 21. Tid for eksamen: 1. 13.3. Oppgavesettet er på 9 sider. Vedlegg: Tillatte hjelpemidler:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT111 Prøveeksamen Eksamensdag: 5. juni 21. Tid for eksamen: 1. 13.3. Oppgavesettet er på 9 sider. Vedlegg: Tillatte hjelpemidler:
Løsningsforslag, eksamen MA1101/MA6101 Grunnkurs i analyse I, vår 2009
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 6 Løsningsforslag, eksamen MA1101/MA6101 Grunnkurs i analyse I, vår 009 Oppgave 1 Funksjonen g er definert ved g(x)
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 6 Løsningsforslag, eksamen MA1101/MA6101 Grunnkurs i analyse I, vår 009 Oppgave 1 Funksjonen g er definert ved g(x)
Kontinuitet og derivasjon Forelesning i Matematikk 1 TMA4100
 Kontinuitet og derivasjon Forelesning i Matematikk 1 TMA4100 Hans Jakob Rivertz Institutt for matematiske fag 25. august 2010 2 Dagens pensum I dag vil vi se på følgende: Kontinuerlige funksjoner Den deriverte
Kontinuitet og derivasjon Forelesning i Matematikk 1 TMA4100 Hans Jakob Rivertz Institutt for matematiske fag 25. august 2010 2 Dagens pensum I dag vil vi se på følgende: Kontinuerlige funksjoner Den deriverte
OPPGAVESETT MAT111-H17 UKE 39. Oppgaver til seminaret 29/9
 OPPGAVESETT MAT111-H17 UKE 39 Avsnitt 3.1: 9, 23, 34 Avsnitt 3.3: 48, 61 Avsnitt 3.4: 1, 2, 9 På settet: S.1 Oppgaver til seminaret 29/9 Oppgaver til gruppene uke 40 Løs disse først så disse Mer dybde
OPPGAVESETT MAT111-H17 UKE 39 Avsnitt 3.1: 9, 23, 34 Avsnitt 3.3: 48, 61 Avsnitt 3.4: 1, 2, 9 På settet: S.1 Oppgaver til seminaret 29/9 Oppgaver til gruppene uke 40 Løs disse først så disse Mer dybde
Løsning: V = Ed og C = Q/V. Spenningen ved maksimalt elektrisk felt er
 Gruppeøving 6 Elekrisie og magneisme Flervalgsoppgaver 1. Dersom en kondensaor har en kapasians på på 7.28 µf, hvor mye må plaene lades opp for a poensialdifferansen mellom plaene skal bli 25.0 V?. 15
Gruppeøving 6 Elekrisie og magneisme Flervalgsoppgaver 1. Dersom en kondensaor har en kapasians på på 7.28 µf, hvor mye må plaene lades opp for a poensialdifferansen mellom plaene skal bli 25.0 V?. 15
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT 0 Lineær algebra Eksamensdag: Mandag 0. desember 0 Tid for eksamen: 4.30 8.30. Oppgavesettet er på 7 sider. Vedlegg: Tillatte
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT 0 Lineær algebra Eksamensdag: Mandag 0. desember 0 Tid for eksamen: 4.30 8.30. Oppgavesettet er på 7 sider. Vedlegg: Tillatte
Fasit til utvalgte oppgaver MAT1110, uka 28/4-2/5
 Fasit til utvalgte oppgaver MAT1110, uka 8/4-/5 Tom Lindstrøm (lindstro@math.uio.no) 5..5 a) Alle punktene i B har avstand til origo større enn 1, så d(0, B) må være minst 1. Ved å velge punkter på x-aksen
Fasit til utvalgte oppgaver MAT1110, uka 8/4-/5 Tom Lindstrøm (lindstro@math.uio.no) 5..5 a) Alle punktene i B har avstand til origo større enn 1, så d(0, B) må være minst 1. Ved å velge punkter på x-aksen
Oppgave 14 til 9. desember: I polynomiringen K[x, y] i de to variable x og y over kroppen K definerer vi undermengdene:
![Oppgave 14 til 9. desember: I polynomiringen K[x, y] i de to variable x og y over kroppen K definerer vi undermengdene: Oppgave 14 til 9. desember: I polynomiringen K[x, y] i de to variable x og y over kroppen K definerer vi undermengdene:](/thumbs/64/52216522.jpg) HJEMMEOPPGAVER utgave av 8-12-2002): Oppgave 15 til 16 desember: La H være mengden av alle matriser på formen A = a 1 a 12 a 13 a 1n 0 a 2 0 0 0 0 a 3 0 0 0 a n der a 1 a 2 a n 0 Videre la SH være matrisene
HJEMMEOPPGAVER utgave av 8-12-2002): Oppgave 15 til 16 desember: La H være mengden av alle matriser på formen A = a 1 a 12 a 13 a 1n 0 a 2 0 0 0 0 a 3 0 0 0 a n der a 1 a 2 a n 0 Videre la SH være matrisene
Løsningsforslag øving 6, ST1301
 Løsningsforslag øving 6, ST1301 Oppgave 1 Løse Euler-Loka ligningen ved ruk av Newon's meode. Ana a vi har en organisme med maksimal alder lik n år. Vi ser kun på hunnene i populasjonen. La m i være anall
Løsningsforslag øving 6, ST1301 Oppgave 1 Løse Euler-Loka ligningen ved ruk av Newon's meode. Ana a vi har en organisme med maksimal alder lik n år. Vi ser kun på hunnene i populasjonen. La m i være anall
Øving 1: Bevegelse. Vektorer. Enheter.
 Lørdagsverksed i fysikk. Insiu for fysikk, NTNU. Høsen 007. Veiledning: 8. sepember kl :5 5:00. Øving : evegelse. Vekorer. Enheer. Oppgave a) Per løper 800 m på minuer og 40 sekunder. Hvor sor gjennomsnisfar
Lørdagsverksed i fysikk. Insiu for fysikk, NTNU. Høsen 007. Veiledning: 8. sepember kl :5 5:00. Øving : evegelse. Vekorer. Enheer. Oppgave a) Per løper 800 m på minuer og 40 sekunder. Hvor sor gjennomsnisfar
MAT1030 Forelesning 26
 MAT030 Forelesning 26 Trær Roger Anonsen - 5. mai 2009 (Sis oppdaer: 2009-05-06 22:27) Forelesning 26 Li repeisjon Prims algorime finne de minse uspennende ree i en veke graf en grådig algorime i den forsand
MAT030 Forelesning 26 Trær Roger Anonsen - 5. mai 2009 (Sis oppdaer: 2009-05-06 22:27) Forelesning 26 Li repeisjon Prims algorime finne de minse uspennende ree i en veke graf en grådig algorime i den forsand
Løsningsforslag til øving 10
 FY11/TFY4145 Meanis fysi. Institutt for fysi, NTNU. Høsten 211. Løsningsforslag til øving 1 Vi utleder aller først ligningen som fastlegger vinelen φ r, dvs overgangen fra ren rulling til sluring. N2 for
FY11/TFY4145 Meanis fysi. Institutt for fysi, NTNU. Høsten 211. Løsningsforslag til øving 1 Vi utleder aller først ligningen som fastlegger vinelen φ r, dvs overgangen fra ren rulling til sluring. N2 for
EKSEMPLER TIL ETTERTANKE MAT1100 KALKULUS
 EKSEMPLER TIL ETTERTANKE MAT00 KALKULUS Simon Foldvik. Oktober 207 Dette dokumentet inneholder eksempler på hvor «ting går galt» og har til hensikt å vise eksempler på hva man ikke kan konkludere. Alle
EKSEMPLER TIL ETTERTANKE MAT00 KALKULUS Simon Foldvik. Oktober 207 Dette dokumentet inneholder eksempler på hvor «ting går galt» og har til hensikt å vise eksempler på hva man ikke kan konkludere. Alle
Ved opp -og utladning av kondensatorer varierer strøm og spenning. Det er vanlig å bruke små bokstaver for å angi øyeblikksverdier av størrelser.
 4.4 INNE- OG TKOPLING AV EN KONDENSATO 1 4.4 INN- OG TKOPLING AV EN KONDENSATO Ved opp -og uladning av kondensaorer varierer srøm og spenning. De er vanlig å bruke små boksaver for å angi øyeblikksverdier
4.4 INNE- OG TKOPLING AV EN KONDENSATO 1 4.4 INN- OG TKOPLING AV EN KONDENSATO Ved opp -og uladning av kondensaorer varierer srøm og spenning. De er vanlig å bruke små boksaver for å angi øyeblikksverdier
Forelesning 26. MAT1030 Diskret Matematikk. Trær med rot. Litt repetisjon. Definisjon. Forelesning 26: Trær. Roger Antonsen
 MAT1030 Diskre Maemaikk Forelesning 26: Trær Roger Anonsen Insiu for informaikk, Universiee i Oslo Forelesning 26 5. mai 2009 (Sis oppdaer: 2009-05-06 22:27) MAT1030 Diskre Maemaikk 5. mai 2009 2 Li repeisjon
MAT1030 Diskre Maemaikk Forelesning 26: Trær Roger Anonsen Insiu for informaikk, Universiee i Oslo Forelesning 26 5. mai 2009 (Sis oppdaer: 2009-05-06 22:27) MAT1030 Diskre Maemaikk 5. mai 2009 2 Li repeisjon
Løsningsforslag til 3. oblogatoriske oppgave i Diskret Matematikk. Høsten 2018
 Løsningsforslag til 3. oblogatoriske oppgave i Diskret Matematikk Oppgave 1. ( 9 3 ) = 9 8 7 3 2 1 = 3 4 7 = 84 Høsten 2018 {1, 5, 9}, {1, 6, 8}, {2, 4, 9}, { 2, 5, 8}, {2, 6, 7}, {3, 4, 8}, {3, 5, 7},
Løsningsforslag til 3. oblogatoriske oppgave i Diskret Matematikk Oppgave 1. ( 9 3 ) = 9 8 7 3 2 1 = 3 4 7 = 84 Høsten 2018 {1, 5, 9}, {1, 6, 8}, {2, 4, 9}, { 2, 5, 8}, {2, 6, 7}, {3, 4, 8}, {3, 5, 7},
UNIVERSITETET I OSLO. Det matematisk-naturvitenskapelige fakultet. Oppgave 1 OpenGL (vekt 1 5 )
 UNIVERSITETET I OSLO De maemaisk-naurvienskapelige fakule Eksamen i INF3320/INF4320 Meoder i grask daabehandling og diskre geomeri Eksamensdag: 7. desember 2007 Tid for eksamen: 14:30 17:30 Oppgavesee
UNIVERSITETET I OSLO De maemaisk-naurvienskapelige fakule Eksamen i INF3320/INF4320 Meoder i grask daabehandling og diskre geomeri Eksamensdag: 7. desember 2007 Tid for eksamen: 14:30 17:30 Oppgavesee
1. Betrakt følgende modell: Y = C + I + G C = c 0 + c(y T ), c 0 > 0, 0 < c < 1 T = t 0 + ty, 0 < t < 1
 . Berak følgende modell: Y = C + I + G C = c 0 + c(y T ), c 0 > 0, 0 < c < T = 0 + Y, 0 < < Hvor Y er BNP, C er priva konsum, I er privae realinveseringer, G er offenlig kjøp av varer og jeneser, T er
. Berak følgende modell: Y = C + I + G C = c 0 + c(y T ), c 0 > 0, 0 < c < T = 0 + Y, 0 < < Hvor Y er BNP, C er priva konsum, I er privae realinveseringer, G er offenlig kjøp av varer og jeneser, T er
Løsningsforslag. Prøve i Matematikk 1000 BYFE DAFE 1000 Dato: 29. mai 2017 Hjelpemiddel: Kalkulator og formelark. Oppgave 1 Gitt matrisene.
 Prøve i Matematikk BYFE DAFE Dato: 29. mai 27 Hjelpemiddel: Kalkulator og formelark Løsningsforslag Oppgave Gitt matrisene A = 2 2 B = [ 2 3 4 ] og C = Regn ut, om mulig, summene A + B, A + B T og A +
Prøve i Matematikk BYFE DAFE Dato: 29. mai 27 Hjelpemiddel: Kalkulator og formelark Løsningsforslag Oppgave Gitt matrisene A = 2 2 B = [ 2 3 4 ] og C = Regn ut, om mulig, summene A + B, A + B T og A +
Anbefalte oppgaver - Løsningsforslag
 TMA415 Matematikk 2 Anbefalte oppgaver - Løsningsforslag Uke 7 15.1.3: Siden vektorfeltet er gitt ved F(x, y) = yi + xj må feltlinjene tilfredstille differensiallikningen eller y = x y, ( ) 1 2 y2 = x.
TMA415 Matematikk 2 Anbefalte oppgaver - Løsningsforslag Uke 7 15.1.3: Siden vektorfeltet er gitt ved F(x, y) = yi + xj må feltlinjene tilfredstille differensiallikningen eller y = x y, ( ) 1 2 y2 = x.
Prøveeksamen i MAT 1100, H-03 Løsningsforslag
 Prøveeksamen i MAT, H- Løsningsforslag. Integralet cos x dx er lik: +sin x Riktig svar: c) arctan(sin x) + C. Begrunnelse: Sett u = sin x, da er du = cos x dx og vi får: cos x + sin x dx = du du = arctan
Prøveeksamen i MAT, H- Løsningsforslag. Integralet cos x dx er lik: +sin x Riktig svar: c) arctan(sin x) + C. Begrunnelse: Sett u = sin x, da er du = cos x dx og vi får: cos x + sin x dx = du du = arctan
Derivasjon Forelesning i Matematikk 1 TMA4100. Hans Jakob Rivertz Institutt for matematiske fag 2. september 2011
 Derivasjon Forelesning i Matematikk TMA400 Hans Jakob Rivertz Institutt for matematiske fag 2. september 20 Kapittel 3.7. Derivasjon av inverse funksjoner 3 Derivasjon av inverse til deriverbare funksjoner
Derivasjon Forelesning i Matematikk TMA400 Hans Jakob Rivertz Institutt for matematiske fag 2. september 20 Kapittel 3.7. Derivasjon av inverse funksjoner 3 Derivasjon av inverse til deriverbare funksjoner
FYS3220 Oppgaver om Fourieranalyse
 FYS3220 Oppgaver om Fourieranalyse Innhold Enkle fourieranalyse oppgaver... 1 1) egn frekvensspeker for e sammensa sinus signal... 1 2) Fra a n og b n il c n og θ... 2 Fourier serieanalyse... 2 3) Analyse
FYS3220 Oppgaver om Fourieranalyse Innhold Enkle fourieranalyse oppgaver... 1 1) egn frekvensspeker for e sammensa sinus signal... 1 2) Fra a n og b n il c n og θ... 2 Fourier serieanalyse... 2 3) Analyse
Kap. 6 Ortogonalitet og minste kvadrater
 Kap. 6 Ortogonalitet og minste kvadrater IR n er mer enn bare et vektorrom: den har et naturlig indreprodukt, nemlig prikkproduktet av vektorer. Dette indreproduktet gjør det mulig å tenke geometrisk og
Kap. 6 Ortogonalitet og minste kvadrater IR n er mer enn bare et vektorrom: den har et naturlig indreprodukt, nemlig prikkproduktet av vektorer. Dette indreproduktet gjør det mulig å tenke geometrisk og
Grenser III - rasjonale funskjoner Forelesning i Matematikk 1 TMA4100
 Grenser III - rasjonale funskjoner Forelesning i Matematikk 1 TMA4100 Hans Jakob Rivertz Institutt for matematiske fag 24. august 2010 2 Grenselover for x ± L = lim f(x) M = lim g(x) 1. lim (f(x) ± g(x))
Grenser III - rasjonale funskjoner Forelesning i Matematikk 1 TMA4100 Hans Jakob Rivertz Institutt for matematiske fag 24. august 2010 2 Grenselover for x ± L = lim f(x) M = lim g(x) 1. lim (f(x) ± g(x))
Flere anvendelser av derivasjon
 Flere anvendelser av derivasjon Department of Mathematical Sciences, NTNU, Norway September 30, 2014 Forelesning 17.09.2014 Fikspunkt-iterasjon Newtons metode Metoder for å finne nullpunkter av funksjoner:
Flere anvendelser av derivasjon Department of Mathematical Sciences, NTNU, Norway September 30, 2014 Forelesning 17.09.2014 Fikspunkt-iterasjon Newtons metode Metoder for å finne nullpunkter av funksjoner:
Newtons lover i to og tre dimensjoner
 Newons loer i o og re dimensjoner 3..4 Innleering: på papir på ekspedisjonskonore: bruk forsiden elekronisk på froner én pdf fil nan på førse side egenerklæring med signaur innleeringsboks på ekspedisjon
Newons loer i o og re dimensjoner 3..4 Innleering: på papir på ekspedisjonskonore: bruk forsiden elekronisk på froner én pdf fil nan på førse side egenerklæring med signaur innleeringsboks på ekspedisjon
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT Kalkulus. Eksamensdag: Fredag 9. desember 2. Tid for eksamen: 9.. Oppgavesettet er på 8 sider. Vedlegg: Tillatte hjelpemidler:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT Kalkulus. Eksamensdag: Fredag 9. desember 2. Tid for eksamen: 9.. Oppgavesettet er på 8 sider. Vedlegg: Tillatte hjelpemidler:
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT Kalkulus og lineær algebra Eksamensdag: Onsdag 9 mai 9 Tid for eksamen: 4:3 8:3 Oppgavesettet er på 7 sider Vedlegg: Tillatte
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT Kalkulus og lineær algebra Eksamensdag: Onsdag 9 mai 9 Tid for eksamen: 4:3 8:3 Oppgavesettet er på 7 sider Vedlegg: Tillatte
Rekker, Konvergenstester og Feilestimat
 NTNU December 8, 2012 Oversikt 1 2 3 4 5 6 For å forstå, må vi først forstå potensrekker For å forstå potensrekker, må vi først forstå rekker. For å forstå rekker, må vi først forstå følger. Definisjon
NTNU December 8, 2012 Oversikt 1 2 3 4 5 6 For å forstå, må vi først forstå potensrekker For å forstå potensrekker, må vi først forstå rekker. For å forstå rekker, må vi først forstå følger. Definisjon
~/stat230/teori/bonus08.tex TN. V2008 Introduksjon til bonus og overskudd
 ~/sa23/eori/bonus8.ex TN STAT 23 V28 Inrodukson il bonus og overskudd Bankinnskudd Ana a vi ønsker å see e viss beløp y i banken ved id = for å ha y n ved id = n. Med en reneinensie δ må vi see inn y =
~/sa23/eori/bonus8.ex TN STAT 23 V28 Inrodukson il bonus og overskudd Bankinnskudd Ana a vi ønsker å see e viss beløp y i banken ved id = for å ha y n ved id = n. Med en reneinensie δ må vi see inn y =
Differensligninger Forelesningsnotat i Diskret matematikk Differensligninger
 Differesligiger Forelesigsotat i Diskret matematikk 017 Differesligiger I kapittel lærte vi om følger og rekker. Vi studerte både aritmetiske og geometriske følger og rekker. Noe følger og rekker er imidlertid
Differesligiger Forelesigsotat i Diskret matematikk 017 Differesligiger I kapittel lærte vi om følger og rekker. Vi studerte både aritmetiske og geometriske følger og rekker. Noe følger og rekker er imidlertid
Avsnitt 8.1 i læreboka Differensligninger
 Diskret Matematikk Fredag 6. ovember 015 Avsitt 8.1 i læreboka Differesligiger I kapittel lærte vi om følger og rekker. Vi studerte både aritmetiske og geometriske følger og rekker. Noe følger og rekker
Diskret Matematikk Fredag 6. ovember 015 Avsitt 8.1 i læreboka Differesligiger I kapittel lærte vi om følger og rekker. Vi studerte både aritmetiske og geometriske følger og rekker. Noe følger og rekker
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT00 Kalkulus Eksamensdag: Fredag 9. oktober 205 Tid for eksamen: 5.00 7.00 Oppgavesettet er på 5 sider. Vedlegg: Svarark, formelsamling.
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT00 Kalkulus Eksamensdag: Fredag 9. oktober 205 Tid for eksamen: 5.00 7.00 Oppgavesettet er på 5 sider. Vedlegg: Svarark, formelsamling.
MAT1030 Forelesning 21
 MAT00 Forelesning Mer ombinatori Roger Antonsen - 5. april 009 (Sist oppdatert: 009-0-5 00:05) Kapittel 9: Mer ombinatori Plan for dagen Mer om permutasjoner og ordnet utvalg ) Mer om ombinasjoner n velg
MAT00 Forelesning Mer ombinatori Roger Antonsen - 5. april 009 (Sist oppdatert: 009-0-5 00:05) Kapittel 9: Mer ombinatori Plan for dagen Mer om permutasjoner og ordnet utvalg ) Mer om ombinasjoner n velg
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Usa eksamen i: ECON315/415 Inroducory Economerics Eksamensdag: Fredag 11. augus 26 Tid for eksamen: kl. 9: 12: Oppgavesee er på 5 sider Tillae hjelpemidler: Alle
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Usa eksamen i: ECON315/415 Inroducory Economerics Eksamensdag: Fredag 11. augus 26 Tid for eksamen: kl. 9: 12: Oppgavesee er på 5 sider Tillae hjelpemidler: Alle
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT2400 Analyse 1. Eksamensdag: Onsdag 15. juni 2011. Tid for eksamen: 09.00 13.00 Oppgavesettet er på 6 sider. Vedlegg: Tillatte
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT2400 Analyse 1. Eksamensdag: Onsdag 15. juni 2011. Tid for eksamen: 09.00 13.00 Oppgavesettet er på 6 sider. Vedlegg: Tillatte
Forelesning Matematikk 4N
 Forelesning Matematikk 4N Hans Jakob Rivertz Institutt for matematiske fag 11. september 2006 2 Den høyrederiverte og venstrederiverte Definisjon Den høyrederiverte til en funksjon f(x) i punktet x er
Forelesning Matematikk 4N Hans Jakob Rivertz Institutt for matematiske fag 11. september 2006 2 Den høyrederiverte og venstrederiverte Definisjon Den høyrederiverte til en funksjon f(x) i punktet x er
LØSNINGSFORSLAG TIL EKSAMEN I TFY4160 BØLGEFYSIKK Torsdag 9. august 2007 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig konak under eksamen: Jon Andreas Søvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I TFY4160 BØLGEFYSIKK
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig konak under eksamen: Jon Andreas Søvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I TFY4160 BØLGEFYSIKK
Følger og rekker. Department of Mathematical Sciences, NTNU, Norway. November 10, 2014
 Department of Mathematical Sciences, NTNU, Norway November 10, 2014 Forelesning (03.01.2014): kap 9.1 og 9.2 Beskrivelse av følger eksempler og definisjon Egenskaper med følger Grenseverdi for følger (og
Department of Mathematical Sciences, NTNU, Norway November 10, 2014 Forelesning (03.01.2014): kap 9.1 og 9.2 Beskrivelse av følger eksempler og definisjon Egenskaper med følger Grenseverdi for følger (og
TMA4100 Matematikk 1, høst 2013
 TMA4100 Matematikk 1, øst 2013 Forelesning 7 www.ntnu.no TMA4100 Matematikk 1, øst 2013, Forelesning 7 Derivasjon Denne uken skal vi begynne på tema 2 om derivasjon. I dagens forelesning skal vi se på
TMA4100 Matematikk 1, øst 2013 Forelesning 7 www.ntnu.no TMA4100 Matematikk 1, øst 2013, Forelesning 7 Derivasjon Denne uken skal vi begynne på tema 2 om derivasjon. I dagens forelesning skal vi se på
Løsningsforslag, midtsemesterprøve MA1101, 5.oktober 2010
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Løsningsforslag, midtsemesterprøve MA1101, 5.oktober 2010 Oppgave 1 Løs ulikheten x + 6 5 x + 2 Strategien er å
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Løsningsforslag, midtsemesterprøve MA1101, 5.oktober 2010 Oppgave 1 Løs ulikheten x + 6 5 x + 2 Strategien er å
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Tenkeonsdag i MAT-INF 1100 Modellering og beregninger. Dag: Onsdag 28. november 2012. Tid for moroa: 16:00 19:00. Oppgavesettet er på 9
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Tenkeonsdag i MAT-INF 1100 Modellering og beregninger. Dag: Onsdag 28. november 2012. Tid for moroa: 16:00 19:00. Oppgavesettet er på 9
Harald Bjørnestad: Variasjonsregning en enkel innføring.
 Haral Bjørnesa: Variasjonsregning en enkel innføring. Tiligere har vi løs oppgaven me å finne eksremalveriene ( maks./min. veriene) av en gi funksjon f () når enne funksjonen oppfyller beseme krav. Vi
Haral Bjørnesa: Variasjonsregning en enkel innføring. Tiligere har vi løs oppgaven me å finne eksremalveriene ( maks./min. veriene) av en gi funksjon f () når enne funksjonen oppfyller beseme krav. Vi
Litt om numerisk integrasjon og derivasjon og løsningsforslag til noen ekstraoppgaver MAT-INF 1100 uke 48 (22/11-26/11)
 Litt om numerisk integrasjon og derivasjon og løsningsforslag til noen ekstraoppgaver MAT-INF 1100 uke 48 (22/11-26/11) Knut Mørken 22. november 2004 Vi har tidligere i kurset sett litt på numerisk derivasjon
Litt om numerisk integrasjon og derivasjon og løsningsforslag til noen ekstraoppgaver MAT-INF 1100 uke 48 (22/11-26/11) Knut Mørken 22. november 2004 Vi har tidligere i kurset sett litt på numerisk derivasjon
Oppgaver i funksjonsdrøfting
 Oppgaver i funksjonsdrøfting To av oppgavene er merket med *. Det betyr at de er ekstra interessante. Oppgave 1 Gitt funksjonen f(x) = x + 4. a) Finn nullpunktene til funksjonen. b) Bruk definisjonen på
Oppgaver i funksjonsdrøfting To av oppgavene er merket med *. Det betyr at de er ekstra interessante. Oppgave 1 Gitt funksjonen f(x) = x + 4. a) Finn nullpunktene til funksjonen. b) Bruk definisjonen på
Spesialisering: Anvendt makro 5. Modul
 Spesialisering: Anvend makro 5. Modul 1.B Lineære regresjonsmodeller og minse kvadraers meode (MKM) Drago Berghol Norwegian Business School (BI) 10. november 2011 Oversik I. Inroduksjon il økonomeri II.
Spesialisering: Anvend makro 5. Modul 1.B Lineære regresjonsmodeller og minse kvadraers meode (MKM) Drago Berghol Norwegian Business School (BI) 10. november 2011 Oversik I. Inroduksjon il økonomeri II.
Logaritmer og eksponentialfunksjoner
 Logaritmer og eksponentialfunksjoner Harald Hanche-Olsen og Marius Irgens 20-02-02 Dette notatet ble først laget for MA02 våren 2008. Denne versjonen er omskrevet for MA02 våren 20. Du vil oppdage at mange
Logaritmer og eksponentialfunksjoner Harald Hanche-Olsen og Marius Irgens 20-02-02 Dette notatet ble først laget for MA02 våren 2008. Denne versjonen er omskrevet for MA02 våren 20. Du vil oppdage at mange
R Differensialligninger
 R - 6.0.05 - Differensialligninger Løsningssisser Oppgave Løs differensialligningene y x y b) y y x c) y 8y 7y 0 Separabel: y y x y dy xdx y x C y x 4 C y C x 4 Da ligningen er ulineær, bør vi også se
R - 6.0.05 - Differensialligninger Løsningssisser Oppgave Løs differensialligningene y x y b) y y x c) y 8y 7y 0 Separabel: y y x y dy xdx y x C y x 4 C y C x 4 Da ligningen er ulineær, bør vi også se
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT-INF 1100 Modellering og beregninger. Eksamensdag: Fredag 7. januar 2005. Tid for eksamen: 14:30 17:30. Oppgavesettet er på
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT-INF 1100 Modellering og beregninger. Eksamensdag: Fredag 7. januar 2005. Tid for eksamen: 14:30 17:30. Oppgavesettet er på
OPPGAVE 1 LØSNINGSFORSLAG
 LØSNINGSFORSLAG UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Eksamen i MAT - Grunnkurs i matematikk I torsdag 5.desember 20 kl. 09:00-4:00 OPPGAVE a Modulus: w = 2 + 3 2 = 2. Argument
LØSNINGSFORSLAG UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Eksamen i MAT - Grunnkurs i matematikk I torsdag 5.desember 20 kl. 09:00-4:00 OPPGAVE a Modulus: w = 2 + 3 2 = 2. Argument
Homogenitet av grad 1; makro og lang sikt, rollen til frikonkurranse
 Chapter 3 Solow-modellen Forsjell mellom land i apital per arbeider Kapitalens rolle i) Er produtiv ii) Blir produsert; avveining forbru investering iii) Gir avastning iv) Bærer av tenologi v) Blir slitt
Chapter 3 Solow-modellen Forsjell mellom land i apital per arbeider Kapitalens rolle i) Er produtiv ii) Blir produsert; avveining forbru investering iii) Gir avastning iv) Bærer av tenologi v) Blir slitt
