Kap. 24 Kapasitans og dielektrika
|
|
|
- Pål Eriksson
- 6 år siden
- Visninger:
Transkript
1 Kap. 4 Kapasitans og ielektrika Grunnleggene forståelse for HA en konensator er, HORFOR en virker som en gjør, hvilke BEGRENSINGER en har og hvorfor et DIELEKTRIKUM er påkrev i en konensator. Kapasitans Energi i konensatorer og laningssamlinger generelt Beskrive et ielektrikum: polarisering, elektrisk flukstetthet D, relativ permittivitet ε r Gauss lov for ielektrika. Små konensatorer og store konensatorer.. Fra Wikipeia: Øving 3, opg. 1 Coronautlaning ve > 30 k/cm Kap. 4 Kapasitans og ielektrika Konensatorer = to leere som kan lagre laning Kapasitans: C = Q/ (enhet F = fara) er = 1 for to leere (Type A) eller = for enkeltleer (Type B) Eks. 1: Enkeltkule: C = 4πε 0 R Eks. : arallellplatekonensator Eks. 3: Kulekonensator Eks. 4: Sylinerkonensator (koakskabel) Seriekopling og parallellkopling Uttrykk for energi i konensatorer og laningssamlinger I ag Fra Corona ischarge on insulator string of a 500 k overhea power line. Corona ischarges represent a significant power loss for electric utilities. Dielektriske materialer: Elektrisk polarisering Elektrisk flukstetthetsvektor: D Gauss lov for ielektrika. 1
2 an e Graaff generator Y&F fig.7 Se også Wikipeia Oppgitt overslagsspenning k ,5 ve cm Coronautlaning ve E max = 30 k/cm på overflata max = E max R = 300 k Q max = max C = 3,3 μc an e Graaffgenerator i Gamle fysikk, 195 Forskning i kjernefysikk. Opptil 000 k Kuleiameter ca 60 cm høytrykkskammer runt sett fra ITbygg sør (Au F1) Jorkloen: Laning og felt arallellplatekonensator C = ε 0 A/ E = 130 /m (neover) C = 4πε 0 R = 0,71 mf = ER = 0,83 G Hvor stort areal for 1F konensator hvis f.eks. = 0,1 mm? R = 6400 km Q = C = 0,59 MC A = C / ε 0 = 1 F 0,1 mm / F/m = 11 km!!
3 Eks. 1: Enkeltkule (laning q) Type B Eks. 3: Kulekonensator Type A = to kuleskall me laning Q og Q =Ex. 4.3 Eks. 4: Sylinerkonensator = Y&F Ex. 4.4 Type A = to sylinerskall me laning λ og λ (C/m) = koaksialkabel Utregnes helt tilsvarene som kulekonensator. Fra labhefte 016: C = 4πε 0 R (Fig 4.5) C = 4πε 0 r b r a /(r b r a ) 4πε 0 r b r a /r b = 4πε 0 r a når r b (Fig 4.6) 1) Finn E r ) integrer og finn (r) (Metoe ) ( Eks 9 Kap 3) 3) finn kapasitansen C = Q/ ab Metoe 1: 1 qi ( r) 4 0 i ri 1 q ( r) 4 r Metoe : E l b a 0 b a Uttrykk kapasitans i parallell Konensatorer: i serie korreksjonsfaktor i ielektrika (anna enn luft) Koaksialkonensator: C = ε r ε 0 (geometrifaktor) enhet: meter C r0 ln r / r b a l C 1 Q 1 C Q C 1 Q Q C Q Q 1 arallellplatekonensator: Kulekonensator: A C r0 rb ra C r 0 4 r r b 4 r når r r 0 a b a Q = Q 1 Q C = C 1 C lik for alle => C = C 1 C = Σ C i C Q C Q Q = 1 Q/C = Q/C 1 Q/C Q lik for alle => 1/C = 1/C 1 1/C = Σ 1/C i kon: C = C 1 C /(C 1 C ) 3
4 Kap. 4 Kapasitans og ielektrika Konensatorer = to leere som kan lagre laning Kapasitans: C = Q/ (enhet F = fara) er = 1 for to leere (Type A) eller = for enkeltleer (Type B) Eks. 1: Enkeltkule: C = 4πε 0 R Eks. : arallellplatekonensator C = ε 0 A/ Eks. 3: Kulekonensator C = 4πε 0 r b r a /(r b r a ) 4πε 0 r a når r b Eks. 4: Sylinerkonensator (koakskabel) arallellkopling: C = Σ C i ; Seriekopling: 1/C = Σ 1/C i Uttrykk for energi i konensatorer Uttrykk for energi i laningssamling Dielektriske materialer: Elektrisk polarisering Elektrisk flukstetthetsvektor: D Gauss lov for ielektrika. Øking av avstan i platekonensator: 1. Tilkopla batteri: konstant Q = C avtar E avtar U = ½ Q avtar (gis til batteriet). Frakopla batteri: Q konstant = Q/C øker E konstant U = ½ Q øker (tilføres fra ytre kraft) => C = ε 0 A/ avtar Q Q Q Q F = QE Elektrisk energi 1. Uttrykt me laning og potensial: U = ½ Q = ½ C = ½ Q /C (4.9) (utleet for konenstor; all Q på samme ) Kap 3, eks.. To laninger A. Energiberegning uner oppbygging: q 1 først, så q : U = U 1 U = 0 q kq 1 /a U = ½ Σ i Q i (ulike Q i på ulike i ) U = ½ q (ulike q på ulike ) (4.9C) (4.9C) q først, så q 1 : U = U U 1 = 0 q 1 kq /a B. Ferig oppbyg: ve potensial energi q 1 1 =kq /a q 1 1 = q 1 kq /a q =kq 1 /a q = q kq 1 /a Sum: Σ q i i = q kq 1 /a Regnet obbelt! Konklusjon: C. Energi beregnet fra potensial i ferig oppbyg laning: U = ½ Σq i i 4
5 Elektrisk energi Beregning for sum av punktlaninger: Au R: Hvor mye energi for å plassere inn mange 1C laninger? A. Sette inn én og én laning: A. Setter inn én og én laning me energi for hver: U = q 1 0 q 1 q 3 ( 3 31 ) etc. B. Sum over parvise laninger, men hvert par bare én gang: U = Σ i<j k Q i Q j /r ij C. Sum over ferig oppbyg laning U = ½ Σ i Q i (4.9C) U = 1 Q 1 1= U 1 =0 U 3 =( 31 3 )Q Anbefaler C. o.s.v. Øving 5, oppgave a): Fire punktlaninger Eks.6: Energi for homogent la kule Energi U uttrykt me Efeltet Beregna i Eks.8 kap. 3: ~ 1/r k Q r ( r) 3 R R inni kula 1 U ( ) r q (4.9C) 1 3 kq ( r) 5 R iealisert areal A volum = A U = ½ ε 0 E A (Y&F Fig.) OBS: q = 0 utenfor kula Kulesymmetri: τ = 4π r r = kuleareal tykkelse u = U/τ = ½ ε 0 E 5
6 Elektrisk energi Eks. 7: Energi på leerkule me laning q 1. Uttrykt me laning og potensial: U = ½ q (= ½ Q = ½ C ) (4.9C). Uttrykt me elektrisk felt: U = u τ = ½ ε 0 E τ Hvor er energien lagra: I laningene eller i et elektriske feltet? å platene eller mellom platene? To uttrykk for SAMME energi! (4.11B) U fra E: U = ½ ε 0 E τ U fra : U = ½ q = ½ (R) q (R) Eks.67 U = ½ (r) q Eks.7: La leerkule: U = ½ kq /R Eks.6B: Energi for homogent la kule ve U = u τ = ½ ε 0 E τ Heimelekse (4.11B) (R) Eks. 6: Homogent la kule: U = 3/5 kq /R = 6/5 U la leerkule ~ 1/r (Y&F Fig.) 6
7 Dielektrika og elektrisk polarisering Materialer: akuum Leere Dielektrikum Mellom plater i konensator brukes allti et ielektrikum Kapasitansen øker a me en faktor ε r. Kap. 4 Kapasitans og ielektrika Gjennomgått: Konensatorer = to leere som kan ta opp laning Kapasitans: C = Q/ (fara), me eksempler:» Enkeltkule:» arallellplate:» Kulekonensator: Seriekopling og parallellkopling Energi i konensatorer Energi i laningssamlinger iere: Dielektriske materialer: Elektrisk polarisering =χ e ε 0 E Elektrisk flukstetthetsvektor: D = ε 0 E Gauss lov for ielektrika: Noen anvenelser/eksempler C = 4πε 0 r a C = ε 0 A/ C = 4πε 0 r b r a /(r b r a ) σ i U = ½ Q = ½ C U = ½ q U = ½ ε 0 E τ p σ i (fig 4.0) Kraftmoment ipol: a/ qe ( a/) ( qe) qae pe p Kraftmoment reier p til å bli (om mulig) parallell me E p Leere i ytre Efelt Laninger forskyves, inntil E = 0 σ σ E = 0 (fig.8a) 7
8 Dipolinnretting (polarisering) gir flatelaning σ i (i = inusert laning) σ i σ i D = ε 0 E 0 = χ e ε 0 E (1) E D = ε 0 E () Resulterene E minre enn E 0 p Definisjon: = p/volum El. nøytralt innenfor her Observasjon: = χ e ε 0 E D = ε 0 E er uenra. Men «spiser opp» noe av E relativ permittivitet ε r ( ) ε r χ e = ε r D = ε r ε 0 E = χ e ε 0 E ε r χ e = ε r σ Gaussflate S 0 Gaussflate S 1 σ i σ i σ Relative permittivity ε r Luft: 0,3 X
9 Gauss lov: Gauss lov for fri laning Q: eller Gauss lov for inusert laning Q i : (11) A Qi Gauss lov for totallaning Q tot : (10) Q tot = Q Q i I alle tiligere formler kan ε 0 E erstattes av ε r ε 0 E =ε E = D og la Q = fri laning Eks.: Gauss lov (ovenfor) og Coulombs lov: D A Q E A Q / (1) Mest praktiske 1 Q 1 Q E r E r 40 r 4r0 r 1 Q D r 4 r Kap. 4. Dielektrika og polarisering. Oppsummering så langt Dielektriske materialer: Elektrisk polarisering = ipoltetthet: = χ e ε 0 E er χ e er elektrisk susceptibilitet. Relativ permittivitet ε r = χ e 1 (ielektrisitetskonstant) Elektrisk flukstetthetsvektor: D = ε 0 E = ε r ε 0 E (forskyvningsvektor) D og ikke presentert i Y&F. Kort sammenfatta i Notat 1 Øving 7 sentral! Eks. 8 arallellplatekonensator uten og me ielektrikum A. Frakopla batteri: Konstant: σ = D = Q/A Avtar: 1 = 0 /ε r Øker: C 1 = Q/ 1 = ε r C 0 = ε r ε 0 A/ Energi: U 1 = ½ Q 1 avtar B. Tilkopla batteri: Konstant: 1 = 0 Øker: σ 1 = D 1 = Q 1 /A = ε r D 0 Øker: C 1 = Q/ 1 = ε r C 0 = ε r ε 0 A/ Energi: U 1 = ½ Q 1 øker (tilføres fra batteriet) Q Q Integralform: Differensialform: Gauss lov Kap. Kap. 4 1 E E A q 0 S 1 ive ivd ivergensen til D iv D D [ / x, / y, / z] D 0 DA q = elektrisk fluks ivd 9
10 ivergens = kile = pos.laning = kile = Efelt iv D > 0 Kap. 4: Oppsummering 1 Konensatorer og kapasitans Konensatorer = to leere som kan ta opp laning Kapasitans: C = Q/ (fara) Enkeltkulekonensator: C = 4πε 0 R (Eks. 1) arallellplatekonensator: C = ε 0 A/ (Eks. ) Kule(skall)konensator: C = 4πε 0 r a r b (r b r a ) (Eks. 3) Sylinerkonensator (koakskabel): C = πε 0 /lnr b /r a (Eks. 4) iv D = 0 Uttrykk ivergens, se formelark arallellkopling: C = C 1 C Seriekopling: 1/C = 1/C 1 1/C Energi ve laning og potensial: U = ½ q Energi ve elektrisk felt: u = ½ ε 0 E vs. U = ½ ε 0 E τ For konensator gir ette: U = ½ Q = ½ C = ½ Q /C Kap. 4: Oppsummering Dielektrika og polarisering. Mer utfyllene i Notat1: Dielektriske materialer. Dielektriske materialer: Elektrisk polarisering = ipoltetthet: = χ e ε 0 E er χ e er elektrisk susceptibilitet. Relativ permittivitet ε r = χ e 1 (ielektrisitetskonstant) Elektrisk flukstetthetsvektor: D = ε 0 E = ε r ε 0 E (forskyvningsvektor) Elektrisk fluks: D A Gauss lov for fri laning Q = Q tot Q i : E Gauss lov for inusert laning Q i : D A Q eller A Q / A Qi Gauss lov for totallaning Q tot : I alle tiligere formler kan ε 0 E erstattes av ε r ε 0 E =ε E = D me Q = fri laning Konensator me ielektrikum: Alle ε 0 erstattes av ε r ε 0 Uttrykk kapasitans Koaksialkonensator: arallellplatekonensator: Kulekonensator: C = ε r ε 0 (geometrifaktor) enhet: meter C r0 l ln r / r A C r0 rb ra C r 0 4 r r b b a 4 r når r r 0 a b a 10
11 Dielektrika i konensatorer: 1. Kapasitansen øker me faktor ε r.. Overslag ( breakown, «ielectric strength») ve høyere grense. Høyere max spenning! Spesielle ielektrika. (ikke pensum) iezoelektriske materialer: Mekanisk strekk eller trykk polarisasjon (eller motsatt:) Efelt felt eformasjon Bruk: Kvartskrystaller, mikrofoner, pickup (platespillere vinyl ) ε r Dielectric strength Ferroelektriske materialer (ipolelectrets): Materialer me permanent polarisasjon (tilsvarer permanente magneter) Luft: 3 X 10 6 Skjematisk om E, og D: Dielektrisk materiale i homogent Efelt Skjematisk om E, og D: Dielektrisk materiale i homogent Efelt ε r = χ e ε 0 E ε 0 E χ e ε r = χ e 1 1/3 4/3 D = ε 0 E 0 = D = ε 0 E = D = ε 0 E 0 avtar øker 1 D = 1 ε 0 E = D = ε r ε 0 E = D = 1 ε 0 E 3 4 D = ε 0 E enres ikke (ingen frie lan. i ielektriet) = χ e ε 0 E er E er inni ielektriket, ikke ytre (# flukslinjer ) = χ e (# flukslinjer ε 0 E) 11
12 Øking av avstan i platekonensator: => C = ε 0 A/ avtar Flervalgsoppgaver fra «Thinking physics»: ng/tfy4155/iverse/thinkingphysics/ 1. Tilkopla batteri: konstant Q = C avtar E avtar U = ½ Q avtar (gis til batteriet). Frakopla batteri: Q konstant = Q/C øker E konstant U = ½ Q øker (tilføres fra ytre kraft) Q Q Q F = QE Q Beregning fra arbei: ΔU = F Δ = QE Δ Svar: a) Konstant laning Q Lavere kapasitans C = ε 0 A/ => Høyere spenning = Q/C => Mer energi U = ½ Q! eller: Konstant laning Q => Konstant felt E = σ/ε 0 => Konstant energitetthet u = ½ ε 0 E => U = u (volum) øker! = E øker også Noen av Støvnengs flervalgsoppgaver Svar: a) Konstant laning Q Lavere ε r =>Lavere kapasitans C = ε r ε 0 A/ => Høyere spenning = Q/C => Mer energi U = ½ Q! E uenret. eller: Konstant laning Q Lavere ε r => Økene felt E = σ/ε r ε 0 => Økene energitetthet u = ½ ε 0 E = E øker også 1
Kap. 24 Kapasitans og dielektrika
 Kap. 24 Kapasitans og dielektrika Grunnleggende forståelse for HVA en kondensator er, HVORFOR den virker som den gjør, hvilke BEGRENSINGER den har og hvorfor et DIELEKTRIKUM er påkrevd i en kondensator.
Kap. 24 Kapasitans og dielektrika Grunnleggende forståelse for HVA en kondensator er, HVORFOR den virker som den gjør, hvilke BEGRENSINGER den har og hvorfor et DIELEKTRIKUM er påkrevd i en kondensator.
Kap. 24 Kapasitans og dielektrika. Van de Graaff generator. Kap 24 15.05.2015. Van de Graaff-generator i Gamle fysikk, 1952
 Kap. 4 Kapasitans og dielektrika Grunnleggende forståelse for HA en kondensator er, HORFOR den virker som den gjør, hvilke BEGRENSINGER den har og hvorfor et DIELEKTRIKUM er påkrevd i en kondensator. Kapasitans
Kap. 4 Kapasitans og dielektrika Grunnleggende forståelse for HA en kondensator er, HORFOR den virker som den gjør, hvilke BEGRENSINGER den har og hvorfor et DIELEKTRIKUM er påkrevd i en kondensator. Kapasitans
Kap. 24 Kapasitans og dielektrika. Van de Graaf generator. Kap 24. Van de Graaf-generator i Gamle fysikk, 1952
 Kap. 4 Kapasitans og dielektrika Grunnleggende forståelse for HVA en kondensator er, HVORFOR den virker som den gjør, hvilke BEGRENSINGER den har og hvorfor et DIELEKTRIKUM er påkrevd i en kondensator.
Kap. 4 Kapasitans og dielektrika Grunnleggende forståelse for HVA en kondensator er, HVORFOR den virker som den gjør, hvilke BEGRENSINGER den har og hvorfor et DIELEKTRIKUM er påkrevd i en kondensator.
Kap. 22. Gauss lov. Vi skal se på: Fluksen til elektrisk felt E Gauss lov. Elektrisk ledere. Integralform og differensialform
 Kap. 22. Gauss lov Vi skal se på: Fluksen til elektrisk felt E Gauss lov Integralform og differensialform Elektrisk ledere. E-felt fra Coulombs lov: E k q r 2 r E k n q r n 2 0n r 0n dq E k r 2 r tot.
Kap. 22. Gauss lov Vi skal se på: Fluksen til elektrisk felt E Gauss lov Integralform og differensialform Elektrisk ledere. E-felt fra Coulombs lov: E k q r 2 r E k n q r n 2 0n r 0n dq E k r 2 r tot.
Gauss lov. Kap. 22. Gauss lov. Gauss lov skjematisk. Vi skal se på: Fluksen til elektrisk felt E Gauss lov Integralform og differensialform
 Kap. 5..6 Kap.. Gauss lov Vi skal se på: Fluksen til elektrisk felt E Gauss lov Integralform og differensialform Elektrisk ledere. Efelt fra Coulombs lov: q E k r r E k n q r n n r n dq E k r r tot. ladn.
Kap. 5..6 Kap.. Gauss lov Vi skal se på: Fluksen til elektrisk felt E Gauss lov Integralform og differensialform Elektrisk ledere. Efelt fra Coulombs lov: q E k r r E k n q r n n r n dq E k r r tot. ladn.
FYS1120 Elektromagnetisme, vekesoppgåvesett 3
 FYS20 Elektromagnetisme, vekesoppgåvesett 3 7. september 206 I FYS20-unervisninga legg vi meir vekt på matematikk og numeriske metoer enn et oppgåvene i læreboka gjer. Det gjel òg oppgåvene som vert gitt
FYS20 Elektromagnetisme, vekesoppgåvesett 3 7. september 206 I FYS20-unervisninga legg vi meir vekt på matematikk og numeriske metoer enn et oppgåvene i læreboka gjer. Det gjel òg oppgåvene som vert gitt
LØSNINGSFORSLAG TIL EKSAMEN I FY1003 ELEKTRISITET OG MAGNETISME I Mandag 5. desember 2005 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt uner eksamen: Jon Anreas Støvneng Telefon: 7 59 6 6 / 41 4 9 0 LØSNINGSFORSLAG TIL EKSAMEN I FY100 ELEKTRISITET OG MAGNETISME
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt uner eksamen: Jon Anreas Støvneng Telefon: 7 59 6 6 / 41 4 9 0 LØSNINGSFORSLAG TIL EKSAMEN I FY100 ELEKTRISITET OG MAGNETISME
Frivillig test 5. april Flervalgsoppgaver.
 Inst for fysikk 2013 TFY4155/FY1003 Elektr & magnetisme Frivillig test 5 april 2013 Flervalgsoppgaver Kun ett av svarene rett Du skal altså svare A, B, C, D eller E (stor bokstav) eller du kan svare blankt
Inst for fysikk 2013 TFY4155/FY1003 Elektr & magnetisme Frivillig test 5 april 2013 Flervalgsoppgaver Kun ett av svarene rett Du skal altså svare A, B, C, D eller E (stor bokstav) eller du kan svare blankt
Løsningsforslag. b) Hva er den totale admittansen til parallellkoblingen i figuren over? Oppgi både modul og fasevinkel.
 Løsningsforslag FYS / FY / FYS Elektromagnetisme, torsag 8. esember Ve sensurering vil alle elspørsmål i utgangspunktet bli gitt samme vekt (uavhengig av oppgavenummer), men vi forbeholer oss retten til
Løsningsforslag FYS / FY / FYS Elektromagnetisme, torsag 8. esember Ve sensurering vil alle elspørsmål i utgangspunktet bli gitt samme vekt (uavhengig av oppgavenummer), men vi forbeholer oss retten til
Oppgave 4 : FYS linjespesifikk del
 Oppgave 4 : FYS 10 - linjespesifikk del Fysiske konstanter og definisjoner: Vakuumpermittiviteten: = 8,854 10 1 C /Nm a) Hva er det elektriske potensialet i sentrum av kvadratet (punktet P)? Anta at q
Oppgave 4 : FYS 10 - linjespesifikk del Fysiske konstanter og definisjoner: Vakuumpermittiviteten: = 8,854 10 1 C /Nm a) Hva er det elektriske potensialet i sentrum av kvadratet (punktet P)? Anta at q
Midtsemesterprøve fredag 10. mars kl
 Institutt for fysikk, NTNU FY1003 Elektrisitet og magnetisme TFY4155 Elektromagnetisme Vår 2006 Midtsemesterprøve fredag 10. mars kl 0830 1130. Løsningsforslag 1) A. (Andel som svarte riktig: 83%) Det
Institutt for fysikk, NTNU FY1003 Elektrisitet og magnetisme TFY4155 Elektromagnetisme Vår 2006 Midtsemesterprøve fredag 10. mars kl 0830 1130. Løsningsforslag 1) A. (Andel som svarte riktig: 83%) Det
TFY4104 Fysikk. Institutt for fysikk, NTNU. Høsten Løsningsforslag til øving 10.
 TFY4104 Fysikk. Institutt for fysikk, NTNU. Høsten 015. Løsningsforslag til øving 10. Oppgave A B C D 1 x x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11 x 1 x 13 x 14 x 15 x 16 x 17 x 18 x 9 x 0 x 1) Glass-staven
TFY4104 Fysikk. Institutt for fysikk, NTNU. Høsten 015. Løsningsforslag til øving 10. Oppgave A B C D 1 x x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11 x 1 x 13 x 14 x 15 x 16 x 17 x 18 x 9 x 0 x 1) Glass-staven
KONTINUASJONSEKSAMEN TFY4155 ELEKTROMAGNETISME Onsdag 17. august 2005 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 KONTINUASJONSEKSAMEN TFY4155 ELEKTROMAGNETISME
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 KONTINUASJONSEKSAMEN TFY4155 ELEKTROMAGNETISME
D i e l e ktri ku m (i s o l a s j o n s s to ff) L a d n i n g i e t e l e ktri s k fe l t. E l e ktri s ke fe l tl i n j e r
 1 4.1 FELTVIRKNINGER I ET ELEKTRISK FELT Mellom to ledere eller to plater med forskjellig potensial vil det virke krefter. Når ladningen i platene eller lederne er forskjellige vil platene tiltrekke hverandre
1 4.1 FELTVIRKNINGER I ET ELEKTRISK FELT Mellom to ledere eller to plater med forskjellig potensial vil det virke krefter. Når ladningen i platene eller lederne er forskjellige vil platene tiltrekke hverandre
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME I Mandag 5. desember 2005 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME
Mandag qq 4πε 0 r 2 ˆr F = Elektrisk felt fra punktladning q (følger av definisjonen kraft pr ladningsenhet ): F dl
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007, uke 6 Mandag 05.02.07 Oppsummering til nå, og møte med Maxwell-ligning nr 1 Coulombs lov (empirisk lov for kraft mellom to
Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007, uke 6 Mandag 05.02.07 Oppsummering til nå, og møte med Maxwell-ligning nr 1 Coulombs lov (empirisk lov for kraft mellom to
LØSNINGSFORSLAG TIL KONTINUASJONSEKSAMEN I TFY4155 ELEKTROMAGNETISME Onsdag 17. august 2005 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 LØSNINGSFORSLAG TIL KONTINUASJONSEKSAMEN I TFY4155
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 LØSNINGSFORSLAG TIL KONTINUASJONSEKSAMEN I TFY4155
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME I Mandag 17. desember 2007 kl K. Rottmann: Matematisk formelsamling (eller tilsvarende).
 NOGES TEKNSK- NATUVTENSKAPELGE UNVESTET NSTTUTT FO FYSKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTSTET OG MAGNETSME Mandag 17. desember
NOGES TEKNSK- NATUVTENSKAPELGE UNVESTET NSTTUTT FO FYSKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTSTET OG MAGNETSME Mandag 17. desember
EKSAMEN I FAG SIF 4012 ELEKTROMAGNETISME (SIF 4012 FYSIKK 2) Onsdag 11. desember kl Bokmål
 Side av 6 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 4 43 39 3 EKSAMEN I FAG SIF 42 ELEKTROMAGNETISME
Side av 6 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 4 43 39 3 EKSAMEN I FAG SIF 42 ELEKTROMAGNETISME
Mandag Ledere: Metaller. Atomenes ytterste elektron(er) er fri til å bevege seg gjennom lederen. Eksempler: Cu, Al, Ag etc.
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007, uke 7 Mandag 12.02.07 Materialer og elektriske egenskaper Hovedinndeling av materialer med hensyn på deres elektriske egenskaper:
Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007, uke 7 Mandag 12.02.07 Materialer og elektriske egenskaper Hovedinndeling av materialer med hensyn på deres elektriske egenskaper:
Overflateladningstetthet på metalloverflate
 0.0.08: Rettet opp feil i oppgave 4 og løsningsforslag til oppgave 8b. Overflateladningstetthet på metalloverflate. Ei metallkule med diameter 0.0 m har ei netto ladning på 0.50 nc. Hvor stort er det elektriske
0.0.08: Rettet opp feil i oppgave 4 og løsningsforslag til oppgave 8b. Overflateladningstetthet på metalloverflate. Ei metallkule med diameter 0.0 m har ei netto ladning på 0.50 nc. Hvor stort er det elektriske
Onsdag og fredag
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2009, uke 7 Onsdag 11.02.09 og fredag 13.02.09 Gauss lov [FGT 23.2; YF 22.3; TM 22.2, 22.6; AF 25.4; LHL 19.7; DJG 2.2.1] Gauss
Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2009, uke 7 Onsdag 11.02.09 og fredag 13.02.09 Gauss lov [FGT 23.2; YF 22.3; TM 22.2, 22.6; AF 25.4; LHL 19.7; DJG 2.2.1] Gauss
a) Bruk en passende Gaussflate og bestem feltstyrken E i rommet mellom de 2 kuleskallene.
 Oppgave 1 Bestem løsningen av differensialligningen Oppgave 2 dy dx + y = e x, y(1) = 1 e Du skal beregne en kulekondensator som består av 2 kuleskall av metall med samme sentrum. Det indre skallet har
Oppgave 1 Bestem løsningen av differensialligningen Oppgave 2 dy dx + y = e x, y(1) = 1 e Du skal beregne en kulekondensator som består av 2 kuleskall av metall med samme sentrum. Det indre skallet har
EKSAMENSOPPGAVE I SIF4029- FYSIKK
 Sie 1 av 1 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk EKSMENSOPPGVE I SIF49- FYSIKK Faglig kontakt uner eksamen: Rani Holmesta Tlf. 9388 Eksamensato: Manag 6. mai Eksamensti: 9.
Sie 1 av 1 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk EKSMENSOPPGVE I SIF49- FYSIKK Faglig kontakt uner eksamen: Rani Holmesta Tlf. 9388 Eksamensato: Manag 6. mai Eksamensti: 9.
LØSNINGSFORSLAG TIL EKSAMEN I TFY4155 ELEKTROMAGNETISME FY1003 ELEKTRISITET OG MAGNETISME Tirsdag 30. mai 2006 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I TFY4155 ELEKTROMAGNETISME
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I TFY4155 ELEKTROMAGNETISME
EKSAMENSOPPGAVE. Eksamen i: FYS- 1002 Elektromagnetisme Fredag 31. august 2012 Kl 09:00 13:00 adm. Bygget, rom B154
 side 1 av 6 sider FAKULTET FOR NATURVITENSKAP OG TEKNOLOGI EKSAMENSOPPGAVE Eksamen i: FYS- 1002 Elektromagnetisme Dato: Tid: Sted: Fredag 31. august 2012 Kl 09:00 13:00 adm. Bygget, rom B154 Tillatte hjelpemidler:
side 1 av 6 sider FAKULTET FOR NATURVITENSKAP OG TEKNOLOGI EKSAMENSOPPGAVE Eksamen i: FYS- 1002 Elektromagnetisme Dato: Tid: Sted: Fredag 31. august 2012 Kl 09:00 13:00 adm. Bygget, rom B154 Tillatte hjelpemidler:
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Ola Hunderi, tlf (mobil: )
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Ola Hunderi, tlf. 93411 (mobil: 95143671) Eksamen TFY 4240: Elektromagnetisk teori Torsdag 1 desember
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Ola Hunderi, tlf. 93411 (mobil: 95143671) Eksamen TFY 4240: Elektromagnetisk teori Torsdag 1 desember
EKSAMEN TFY4155 ELEKTROMAGNETISME FY1003 ELEKTRISITET OG MAGNETISME Tirsdag 31. mai 2005 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 EKSAMEN TFY4155 ELEKTROMAGNETISME FY1003
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 EKSAMEN TFY4155 ELEKTROMAGNETISME FY1003
Løsningsforslag til øving 14
 Institutt for fysikk, NTNU TFY4155/FY13 Elektromagnetisme Vår 29 Løsningsforslag til øving 14 Oppgave 1 Den påtrykte strømmen I genererer et H-felt H ni på langs overalt inne i spolen (pga Amperes lov
Institutt for fysikk, NTNU TFY4155/FY13 Elektromagnetisme Vår 29 Løsningsforslag til øving 14 Oppgave 1 Den påtrykte strømmen I genererer et H-felt H ni på langs overalt inne i spolen (pga Amperes lov
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME Mandag 4. desember 2006 kl
 NOGES TEKNSK- NATUVTENSKAPELGE UNVESTET NSTTUTT FO FYSKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTSTET OG MAGNETSME Mandag 4. desember
NOGES TEKNSK- NATUVTENSKAPELGE UNVESTET NSTTUTT FO FYSKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTSTET OG MAGNETSME Mandag 4. desember
Kap. 8 Bevegelsesmengde. Kollisjoner. Massesenter.
 Kap. 8 Bevegelsesmengde. Kollisjoner. Massesenter. Vi skal se på: Newtons 2. lov på ny: Definisjon bevegelsesmengde Kollisjoner: Kraftstøt, impuls. Impulsloven Elastisk, uelastisk, fullstendig uelastisk
Kap. 8 Bevegelsesmengde. Kollisjoner. Massesenter. Vi skal se på: Newtons 2. lov på ny: Definisjon bevegelsesmengde Kollisjoner: Kraftstøt, impuls. Impulsloven Elastisk, uelastisk, fullstendig uelastisk
Midtsemesterprøve fredag 11. mars kl
 Institutt for fysikk, NTNU FY1003 Elektrisitet og magnetisme TFY4155 Elektromagnetisme Vår 2005 Midtsemesterprøve fredag 11. mars kl 1030 1330. Løsningsforslag 1) B. Newtons 3. lov: Kraft = motkraft. (Andel
Institutt for fysikk, NTNU FY1003 Elektrisitet og magnetisme TFY4155 Elektromagnetisme Vår 2005 Midtsemesterprøve fredag 11. mars kl 1030 1330. Løsningsforslag 1) B. Newtons 3. lov: Kraft = motkraft. (Andel
Tirsdag r r
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2008, uke 6 Tirsdag 05.02.08 Gauss lov [FGT 23.2; YF 22.3; TM 22.2, 22.6; AF 25.4; LHL 19.7; DJG 2.2.1] Fra forrige uke; Gauss
Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2008, uke 6 Tirsdag 05.02.08 Gauss lov [FGT 23.2; YF 22.3; TM 22.2, 22.6; AF 25.4; LHL 19.7; DJG 2.2.1] Fra forrige uke; Gauss
KONTINUASJONSEKSAMEN TFY4155 ELEKTROMAGNETISME Fredag 11. august 2006 kl
 NOGES TEKNSK- NATUVTENSKAPELGE UNVESTET NSTTUTT FO FYSKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 KONTNUASJONSEKSAMEN TFY4155 ELEKTOMAGNETSME Fredag 11.
NOGES TEKNSK- NATUVTENSKAPELGE UNVESTET NSTTUTT FO FYSKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 KONTNUASJONSEKSAMEN TFY4155 ELEKTOMAGNETSME Fredag 11.
EKSAMENSOPPGAVE. 7 (6 sider med oppgaver + 1 side med formler)
 Fakultet for naturvitenskap og teknologi EKSAMENSOPPGAE Eksamen i: FYS-1002 (elektromagnetisme) Dato: 9. juni 2017 Klokkeslett: 09.00-13.00 Sted: Åsgårdvegen 9 Tillatte hjelpemidler: ü Kalkulator med tomt
Fakultet for naturvitenskap og teknologi EKSAMENSOPPGAE Eksamen i: FYS-1002 (elektromagnetisme) Dato: 9. juni 2017 Klokkeslett: 09.00-13.00 Sted: Åsgårdvegen 9 Tillatte hjelpemidler: ü Kalkulator med tomt
Kap. 8 Bevegelsesmengde. Kollisjoner. Massesenter.
 Kap. 8 Bevegelsesmengde. Kollisjoner. Massesenter. Vi skal se på: Newtons 2. lov på ny: Definisjon bevegelsesmengde Kollisjoner: Kraftstøt, impuls. Impulsloven Elastisk, uelastisk, fullstendig uelastisk
Kap. 8 Bevegelsesmengde. Kollisjoner. Massesenter. Vi skal se på: Newtons 2. lov på ny: Definisjon bevegelsesmengde Kollisjoner: Kraftstøt, impuls. Impulsloven Elastisk, uelastisk, fullstendig uelastisk
Kondensator - Capacitor. Kondensator - en komponent som kan lagre elektrisk ladning. Symbol. Kapasitet, C = 1volt
 Kondensator - apacitor Lindem jan.. 008 Kondensator - en komponent som kan lagre elektrisk ladning. Symbol Kapasiteten ( - capacity ) til en kondensator måles i Farad. Som en teknisk definisjon kan vi
Kondensator - apacitor Lindem jan.. 008 Kondensator - en komponent som kan lagre elektrisk ladning. Symbol Kapasiteten ( - capacity ) til en kondensator måles i Farad. Som en teknisk definisjon kan vi
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME TFY4155 ELEKTROMAGNETISME Tirsdag 27. mai 2008 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS1120 Elektromagnetisme Eksamensdag: Prøveeksamen 2017 Oppgavesettet er på 9 sider Vedlegg: Tillatte hjelpemidler: Formelark
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS1120 Elektromagnetisme Eksamensdag: Prøveeksamen 2017 Oppgavesettet er på 9 sider Vedlegg: Tillatte hjelpemidler: Formelark
EKSAMENSOPPGAVE. Adm.bygget, Aud.max. ü Kalkulator med tomt dataminne ü Rottmann: Matematisk Formelsamling. rute
 Fakultet for naturvitenskap og teknologi EKSAMENSOPPGAE Eksamen i: Fys-1002 Dato: 30. september 2016 Klokkeslett: 09.00-13.00 Sted: Tillatte hjelpemidler: Adm.bygget, Aud.max ü Kalkulator med tomt dataminne
Fakultet for naturvitenskap og teknologi EKSAMENSOPPGAE Eksamen i: Fys-1002 Dato: 30. september 2016 Klokkeslett: 09.00-13.00 Sted: Tillatte hjelpemidler: Adm.bygget, Aud.max ü Kalkulator med tomt dataminne
EKSAMEN i TFY4155/FY1003 ELEKTRISITET OG MAGNETISME
 Side 1 av 7 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk BOKMÅL EKSAMEN i TFY4155/FY1003 ELEKTRISITET OG MAGNETISME Eksamensdato: Tirsdag 24 mai 2011 Eksamenstid: 09:00-13:00 Faglig
Side 1 av 7 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk BOKMÅL EKSAMEN i TFY4155/FY1003 ELEKTRISITET OG MAGNETISME Eksamensdato: Tirsdag 24 mai 2011 Eksamenstid: 09:00-13:00 Faglig
FYS1120 Elektromagnetisme H10 Midtveiseksamen
 FYS1120 Elektromagnetisme H10 Midtveiseksamen Oppgave 1 a) Vi ser i denne oppgave på elektroner som akselereres gjennom et elektrisk potensial slik at de oppnår en hastighet 1.410. Som vist på figuren
FYS1120 Elektromagnetisme H10 Midtveiseksamen Oppgave 1 a) Vi ser i denne oppgave på elektroner som akselereres gjennom et elektrisk potensial slik at de oppnår en hastighet 1.410. Som vist på figuren
UKE 5. Kondensatorer, kap. 12, s RC kretser, kap. 13, s Frekvensfilter, kap. 15, s kap. 16, s
 UKE 5 Kondensatorer, kap. 2, s. 364-382 R kretser, kap. 3, s. 389-43 Frekvensfilter, kap. 5, s. 462-500 kap. 6, s. 50-528 Kondensator Lindem 22. jan. 202 Kondensator (apacitor) er en komponent som kan
UKE 5 Kondensatorer, kap. 2, s. 364-382 R kretser, kap. 3, s. 389-43 Frekvensfilter, kap. 5, s. 462-500 kap. 6, s. 50-528 Kondensator Lindem 22. jan. 202 Kondensator (apacitor) er en komponent som kan
LØSNINGSFORSLAG TIL EKSAMEN I TFY4155 ELEKTROMAGNETISME FY1003 ELEKTRISITET OG MAGNETISME Tirsdag 31. mai 2005 kl
 NORGES TEKNISK- NATURVITENSKAPEIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 ØSNINGSFORSAG TI EKSAMEN I TFY4155 EEKTROMAGNETISME
NORGES TEKNISK- NATURVITENSKAPEIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 ØSNINGSFORSAG TI EKSAMEN I TFY4155 EEKTROMAGNETISME
EKSAMEN TFY4155 ELEKTROMAGNETISME FY1003 ELEKTRISITET OG MAGNETISME Tirsdag 30. mai 2006 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN TFY4155 ELEKTROMAGNETISME FY1003
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN TFY4155 ELEKTROMAGNETISME FY1003
TFY4104 Fysikk. Institutt for fysikk, NTNU. Lsningsforslag til ving 10.
 TFY404 Fysikk. Institutt for fysikk, NTNU. Lsningsforslag til ving 0. Oppgave A B C D x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 0 x x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 29 x 20 x ) Glass-staven er ikke i berring med
TFY404 Fysikk. Institutt for fysikk, NTNU. Lsningsforslag til ving 0. Oppgave A B C D x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 0 x x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 29 x 20 x ) Glass-staven er ikke i berring med
EKSAMEN I EMNE SIF4005 FYSIKK For kjemi og materialteknologi Onsdag 13. desember 2000 kl
 Sie 1 av 7 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt uner eksamen: Inst. for fsikk, Gløshaugen Professor Bjørn Torger Stokke 735 93434 BOKMÅL EKSAMEN I EMNE SIF45
Sie 1 av 7 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt uner eksamen: Inst. for fsikk, Gløshaugen Professor Bjørn Torger Stokke 735 93434 BOKMÅL EKSAMEN I EMNE SIF45
NORGES TEKNISKNATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK EKSAMEN I EMNE TFY4120 FYSIKK. Fredag 9. desember 2005 Tid: kl
 Bokmål Side 1 av 1 Studentnummer: Studieretning: NORGES TEKNISKNATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK EKSAMEN I EMNE TFY4120 FYSIKK Fredag 9. desember 2005 Tid: kl 09.00-13.00 Faglig kontakt
Bokmål Side 1 av 1 Studentnummer: Studieretning: NORGES TEKNISKNATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK EKSAMEN I EMNE TFY4120 FYSIKK Fredag 9. desember 2005 Tid: kl 09.00-13.00 Faglig kontakt
Kap. 22. Gauss lov. Gauss lov skjematisk. Eks.1: Homogent ladd kule =Y&F Ex = LHL Vi skal se på: Fluksen til elektrisk felt E Gauss lov
 Kap.. Gauss lov Vi skal se på: Fluksen til elektisk felt E Gauss lov Integalfom og diffeensialfom Elektisk ledee. Efelt fa Coulombs lov: q E = k E = k å n q n n n dq E= k ò tot. ladn. Punktladn Flee punktladn.
Kap.. Gauss lov Vi skal se på: Fluksen til elektisk felt E Gauss lov Integalfom og diffeensialfom Elektisk ledee. Efelt fa Coulombs lov: q E = k E = k å n q n n n dq E= k ò tot. ladn. Punktladn Flee punktladn.
TFY4104 Fysikk. Institutt for fysikk, NTNU. ving 11.
 TFY0 Fysikk. Institutt for fysikk, NTNU. ving. Opplysninger: Noe av dette kan du fa bruk for: =" 0 = 9 0 9 Nm /, e = :6 0 9, m e = 9: 0 kg, m p = :67 0 7 kg, g = 9:8 m/s Symboler angis i kursiv (f.eks
TFY0 Fysikk. Institutt for fysikk, NTNU. ving. Opplysninger: Noe av dette kan du fa bruk for: =" 0 = 9 0 9 Nm /, e = :6 0 9, m e = 9: 0 kg, m p = :67 0 7 kg, g = 9:8 m/s Symboler angis i kursiv (f.eks
EKSAMEN I EMNE TFE 4120 ELEKTROMAGNETISME
 Norges teknisk naturvitenskapelige universitet Institutt for elektronikk og telekommunikasjon ide 1 av 7 Bokmål/Nynorsk Faglig/fagleg kontakt under eksamen: Guro vendsen (73592773) Hjelpemidler: C - pesifiserte
Norges teknisk naturvitenskapelige universitet Institutt for elektronikk og telekommunikasjon ide 1 av 7 Bokmål/Nynorsk Faglig/fagleg kontakt under eksamen: Guro vendsen (73592773) Hjelpemidler: C - pesifiserte
EKSAMENSOPPGAVE. Fys-1002 Elektromagnetisme. Adm.bygget B154 Kalkulator med tomt dataminne, Rottmann: Matematisk formelsamling
 Fakultet for naturvitenskap og teknologi EKSAMENSOPPGAE Eksamen i: Fys-1002 Elektromagnetisme Dato: Onsdag 26. september 2018 Klokkeslett: Kl. 9:00-13:00 Sted: Tillatte hjelpemidler: Adm.bygget B154 Kalkulator
Fakultet for naturvitenskap og teknologi EKSAMENSOPPGAE Eksamen i: Fys-1002 Elektromagnetisme Dato: Onsdag 26. september 2018 Klokkeslett: Kl. 9:00-13:00 Sted: Tillatte hjelpemidler: Adm.bygget B154 Kalkulator
To sider med formler blir delt ut i eksamenslokalet. Denne formelsamlingen finnes også på første side i oppgavesettet.
 Forside Midtveiseksamen i FYS 1120 Elektromagnetisme Torsdag 12. oktober kl. 09:00-12:00 (3 timer) Alle 18 oppgaver skal besvares. Lik vekt på alle oppgavene. Ikke minuspoeng for galt svar. Maksimum poengsum
Forside Midtveiseksamen i FYS 1120 Elektromagnetisme Torsdag 12. oktober kl. 09:00-12:00 (3 timer) Alle 18 oppgaver skal besvares. Lik vekt på alle oppgavene. Ikke minuspoeng for galt svar. Maksimum poengsum
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS1120 Elektromagnetisme Eksamensdag: 10. oktober 2016 Tid for eksamen: 10.00 13.00 Oppgavesettet er på 8 sider. Vedlegg: Tillatte
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS1120 Elektromagnetisme Eksamensdag: 10. oktober 2016 Tid for eksamen: 10.00 13.00 Oppgavesettet er på 8 sider. Vedlegg: Tillatte
EKSAMENSOPPGAVE. ü Kalkulator med tomt dataminne ü Rottmann: Matematisk Formelsamling. rute
 Fakultet for naturvitenskap og teknologi EKSAMENSOPPGAE Eksamen i: FYS-1002 Dato: 26. september 2017 Klokkeslett: 09.00-13.00 Sted: Åsgårdvegen 9 Tillatte hjelpemidler: ü Kalkulator med tomt dataminne
Fakultet for naturvitenskap og teknologi EKSAMENSOPPGAE Eksamen i: FYS-1002 Dato: 26. september 2017 Klokkeslett: 09.00-13.00 Sted: Åsgårdvegen 9 Tillatte hjelpemidler: ü Kalkulator med tomt dataminne
EKSAMENSOPPGAVE. Tillatte hjelpemidler: Kalkulator med tomt dataminne Rottmann: Matematisk Formelsamling A.T. Surenovna: Norsk russisk ordbok
 EKSAMENSOPPGAVE Eksamen i: FYS-1002 Dato: Fredag 12.juni 2015 Tid: Kl 09:00 13:00 Sted: Åsgårdvegen 9 Tillatte hjelpemidler: Kalkulator med tomt dataminne Rottmann: Matematisk Formelsamling A.T. Surenovna:
EKSAMENSOPPGAVE Eksamen i: FYS-1002 Dato: Fredag 12.juni 2015 Tid: Kl 09:00 13:00 Sted: Åsgårdvegen 9 Tillatte hjelpemidler: Kalkulator med tomt dataminne Rottmann: Matematisk Formelsamling A.T. Surenovna:
EKSAMEN i TFY4155/FY1003 ELEKTRISITET OG MAGNETISME
 Side 1 av 8 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk BOKMÅL EKSAMEN i TFY4155/FY1003 ELEKTRISITET OG MAGNETISME Eksamensdato: Tirsdag 22 mai 2012 Eksamenstid: 09:00-13:00 Faglig
Side 1 av 8 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk BOKMÅL EKSAMEN i TFY4155/FY1003 ELEKTRISITET OG MAGNETISME Eksamensdato: Tirsdag 22 mai 2012 Eksamenstid: 09:00-13:00 Faglig
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME I TFY4155 ELEKTROMAGNETISME Fredag 8. juni 2007 kl
 NOGES TEKNISK- NATUVITENSKAPELIGE UNIVESITET INSTITUTT FO FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTISITET OG MAGNETISME I TFY4155
NOGES TEKNISK- NATUVITENSKAPELIGE UNIVESITET INSTITUTT FO FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTISITET OG MAGNETISME I TFY4155
KONTIUNASJONSEKSAMEN I EMNE TFE 4120 ELEKTROMAGNETISME
 NTNU Norges teknisk-naturvitenskapelige universitet ide 1 av 7 Fakultet for informatikk, matematikk og elektroteknikk Institutt for elektronikk og telekommunikasjon Bokmål/Nynorsk Faglig/fagleg kontakt
NTNU Norges teknisk-naturvitenskapelige universitet ide 1 av 7 Fakultet for informatikk, matematikk og elektroteknikk Institutt for elektronikk og telekommunikasjon Bokmål/Nynorsk Faglig/fagleg kontakt
1. En tynn stav med lengde L har uniform ladning λ per lengdeenhet. Hvor mye ladning dq er det på en liten lengde dx av staven?
 Ladet stav 1 En tynn stav med lengde L har uniform ladning per lengdeenhet Hvor mye ladning d er det på en liten lengde d av staven? A /d B d C 2 d D d/ E L d Løsning: Med linjeladning (dvs ladning per
Ladet stav 1 En tynn stav med lengde L har uniform ladning per lengdeenhet Hvor mye ladning d er det på en liten lengde d av staven? A /d B d C 2 d D d/ E L d Løsning: Med linjeladning (dvs ladning per
KONTINUASJONSEKSAMEN I EMNE SIE 4010 ELEKTROMAGNETISME
 NTNU Norges teknisk-naturvitenskapelige universitet Side 1 av 6 Fakultet for informatikk, matematikk og elektroteknikk Institutt for fysikalsk elektronikk Bokmål/Nynorsk Faglig/fagleg kontakt under eksamen:
NTNU Norges teknisk-naturvitenskapelige universitet Side 1 av 6 Fakultet for informatikk, matematikk og elektroteknikk Institutt for fysikalsk elektronikk Bokmål/Nynorsk Faglig/fagleg kontakt under eksamen:
UKE 5. Kondensatorer, kap. 12, s RC kretser, kap. 13, s Frekvensfilter, kap. 15, s og kap. 16, s.
 UKE 5 Kondensatorer, kap. 12, s. 364-382 R kretser, kap. 13, s. 389-413 Frekvensfilter, kap. 15, s. 462-500 og kap. 16, s. 510-528 1 Kondensator Lindem 22. jan. 2012 Kondensator (apacitor) er en komponent
UKE 5 Kondensatorer, kap. 12, s. 364-382 R kretser, kap. 13, s. 389-413 Frekvensfilter, kap. 15, s. 462-500 og kap. 16, s. 510-528 1 Kondensator Lindem 22. jan. 2012 Kondensator (apacitor) er en komponent
Kondensator - Capacitor. Kondensator - en komponent som kan lagre elektrisk ladning. Symbol. Kapasitet, C. 1volt
 Kondensator - apacitor Lindem. mai 00 Kondensator - en komponent som kan lagre elektrisk ladning. Symbol Kapasiteten ( - capacity ) til en kondensator måles i Farad. Som en teknisk definisjon kan vi si
Kondensator - apacitor Lindem. mai 00 Kondensator - en komponent som kan lagre elektrisk ladning. Symbol Kapasiteten ( - capacity ) til en kondensator måles i Farad. Som en teknisk definisjon kan vi si
TFY4104 Fysikk. Institutt for fysikk, NTNU. Høsten 2015. Øving 11. Veiledning: 9. - 13. november.
 TFY0 Fysikk. Institutt for fysikk, NTNU. Høsten 05. Øving. Veiledning: 9. -. november. Opplysninger: Noe av dette kan du få bruk for: /πε 0 = 9 0 9 Nm /, e =.6 0 9, m e = 9. 0 kg, m p =.67 0 7 kg, g =
TFY0 Fysikk. Institutt for fysikk, NTNU. Høsten 05. Øving. Veiledning: 9. -. november. Opplysninger: Noe av dette kan du få bruk for: /πε 0 = 9 0 9 Nm /, e =.6 0 9, m e = 9. 0 kg, m p =.67 0 7 kg, g =
UNIVERSITETET I TROMSØ. EKSAMENSOPPGAVE i FYS-1002
 UNIVERSITETET I T R O M S Ø UNIVERSITETET I TROMSØ Intitutt for fysikk og teknologi EKSAMENSOPPGAVE i FYS-1002 Eksamen i: Fys-1002 Elektromagnetisme Eksamensdato: 10. juni, 2013 Tid: 09:00 13:00 Sted:
UNIVERSITETET I T R O M S Ø UNIVERSITETET I TROMSØ Intitutt for fysikk og teknologi EKSAMENSOPPGAVE i FYS-1002 Eksamen i: Fys-1002 Elektromagnetisme Eksamensdato: 10. juni, 2013 Tid: 09:00 13:00 Sted:
Elektrisk potensial/potensiell energi
 Elektrisk potensial/potensiell energi. Figuren viser et uniformt elektrisk felt E heltrukne linjer. Langs hvilken stiplet linje endrer potensialet seg ikke? A. B. C. 3 D. 4 E. Det endrer seg langs alle
Elektrisk potensial/potensiell energi. Figuren viser et uniformt elektrisk felt E heltrukne linjer. Langs hvilken stiplet linje endrer potensialet seg ikke? A. B. C. 3 D. 4 E. Det endrer seg langs alle
FYS1120 Elektromagnetisme
 Det matematisk-naturvitenskapelige fakultet Universitetet i Oslo FYS1120 Elektromagnetisme J. Skaar: Øvingsoppgaver til midtveiseksamen (med fasit) Her er 46 flervalgsoppgaver som kanskje kan være nyttige
Det matematisk-naturvitenskapelige fakultet Universitetet i Oslo FYS1120 Elektromagnetisme J. Skaar: Øvingsoppgaver til midtveiseksamen (med fasit) Her er 46 flervalgsoppgaver som kanskje kan være nyttige
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME TFY4155 ELEKTROMAGNETISME Onsdag 3. juni 2009 kl
 NOGES TEKNISK- NATUVITENSKAPEIGE UNIVESITET INSTITUTT FO FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 EEKTISITET OG MAGNETISME TFY4155
NOGES TEKNISK- NATUVITENSKAPEIGE UNIVESITET INSTITUTT FO FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 EEKTISITET OG MAGNETISME TFY4155
Kondensator. Symbol. Lindem 22. jan. 2012
 UKE 5 Kondensatorer, kap. 12, s. 364-382 RC kretser, kap. 13, s. 389-413 Frekvensfilter, kap. 15, s. 462-500 og kap. 16, s. 510-528 Spoler, kap. 10, s. 289-304 1 Kondensator Lindem 22. jan. 2012 Kondensator
UKE 5 Kondensatorer, kap. 12, s. 364-382 RC kretser, kap. 13, s. 389-413 Frekvensfilter, kap. 15, s. 462-500 og kap. 16, s. 510-528 Spoler, kap. 10, s. 289-304 1 Kondensator Lindem 22. jan. 2012 Kondensator
NORGES LANDBRUKSHØGSKOLE Institutt for matematiske realfag og teknologi LØSNING TIL PRØVE 2 I FYS135 - ELEKTRO- MAGNETISME, 2004.
 NOGES LANDBUKSHØGSKOLE Institutt for matematiske realfag og teknologi LØSNING TIL PØVE 2 I FYS3 - ELEKTO- MAGNETISME, 2004. Dato: 20. oktober 2004. Prøvens varighet: 08:4-09:4 ( time) Informasjon: Alle
NOGES LANDBUKSHØGSKOLE Institutt for matematiske realfag og teknologi LØSNING TIL PØVE 2 I FYS3 - ELEKTO- MAGNETISME, 2004. Dato: 20. oktober 2004. Prøvens varighet: 08:4-09:4 ( time) Informasjon: Alle
EKSAMEN I TFY4155 ELEKTROMAGNETISME OG FY1003 ELEKTRISITET OG MAGNETISME
 TFY4155/FY1003 31. mai 2010 Side 1 av 8 NOGS TKNSK-NATUVTNSKAPLG UNVSTT NSTTUTT FO FYSKK Kontakt under eksamen: Jon Andreas Støvneng, telefon: 45 45 55 33 / 73 59 36 63 KSAMN TFY4155 LKTOMAGNTSM OG FY1003
TFY4155/FY1003 31. mai 2010 Side 1 av 8 NOGS TKNSK-NATUVTNSKAPLG UNVSTT NSTTUTT FO FYSKK Kontakt under eksamen: Jon Andreas Støvneng, telefon: 45 45 55 33 / 73 59 36 63 KSAMN TFY4155 LKTOMAGNTSM OG FY1003
Mandag 7. mai. Elektromagnetisk induksjon (fortsatt) [FGT ; YF ; TM ; AF ; LHL 24.1; DJG 7.
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007, uke19 Mandag 7. mai Elektromagnetisk induksjon (fortsatt) [FGT 30.1-30.6; YF 29.1-29.5; TM 28.2-28.3; AF 27.1-27.3; LHL 24.1;
Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007, uke19 Mandag 7. mai Elektromagnetisk induksjon (fortsatt) [FGT 30.1-30.6; YF 29.1-29.5; TM 28.2-28.3; AF 27.1-27.3; LHL 24.1;
TFY4104 Fysikk. Institutt for fysikk, NTNU. Høsten Løsningsforslag til øving 9. E dl = 0. q i q j 4πε 0 r ij. U = i<j
 TFY404 Fysikk. Institutt for fysikk, NTNU. Høsten 207. Løsningsforslag til øving 9. Oppgave. a) C V = E dl = 0 dersom dl E b) B U = e2 4πε 0 r = e e 4πε 0 r = e.6 0 9 9 0 9 0 0 = 4.4 ev c) D Total potensiell
TFY404 Fysikk. Institutt for fysikk, NTNU. Høsten 207. Løsningsforslag til øving 9. Oppgave. a) C V = E dl = 0 dersom dl E b) B U = e2 4πε 0 r = e e 4πε 0 r = e.6 0 9 9 0 9 0 0 = 4.4 ev c) D Total potensiell
Eksamensoppgave i TFY4155 ELEKTRISITET OG MAGNETISME FY1003 ELEKTRISITET OG MAGNETISME
 Side 1 av 8 Institutt for fysikk Eksamensoppgave i TFY4155 ELEKTRISITET OG MAGNETISME FY1003 ELEKTRISITET OG MAGNETISME Faglig kontakt under eksamen: Institutt for fysikk v/arne Mikkelsen, Tlf: 486 05
Side 1 av 8 Institutt for fysikk Eksamensoppgave i TFY4155 ELEKTRISITET OG MAGNETISME FY1003 ELEKTRISITET OG MAGNETISME Faglig kontakt under eksamen: Institutt for fysikk v/arne Mikkelsen, Tlf: 486 05
Kap. 3 Arbeid og energi. Energibevaring.
 Kap. 3 Arbeid og energi. Energibevaring. Definisjon arbeid, W Kinetisk energi, E k Potensiell energi, E p. Konservative krefter Energibevaring Energibevaring når friksjon. Arbeid = areal under kurve F(x)
Kap. 3 Arbeid og energi. Energibevaring. Definisjon arbeid, W Kinetisk energi, E k Potensiell energi, E p. Konservative krefter Energibevaring Energibevaring når friksjon. Arbeid = areal under kurve F(x)
LØSNINGSFORSLAG TIL EKSAMEN I FY1003 ELEKTRISITET OG MAGNETISME I Mandag 17. desember 2007 kl
 NOGES TEKNISK- NATUVITENSKAPELIGE UNIVESITET INSTITUTT FO FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFOSLAG TIL EKSAMEN I FY1003 ELEKTISITET OG
NOGES TEKNISK- NATUVITENSKAPELIGE UNIVESITET INSTITUTT FO FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFOSLAG TIL EKSAMEN I FY1003 ELEKTISITET OG
b) Vi legger en uendelig lang, rett stav langs y-aksen. Staven har linjeladningen λ = [C/m].
![b) Vi legger en uendelig lang, rett stav langs y-aksen. Staven har linjeladningen λ = [C/m]. b) Vi legger en uendelig lang, rett stav langs y-aksen. Staven har linjeladningen λ = [C/m].](/thumbs/54/33413684.jpg) Oppgave 1 a) Punktladningen q 1 = 1.0 10 9 [C] ligger fast i punktet (2.0, 0, 0) [m]. Punktladningen q 2 = 4.0 10 9 [C] ligger i punktet ( 1.0, 0, 0) [m]. I) Finnes det punkt(er) i rommet med elektrisk
Oppgave 1 a) Punktladningen q 1 = 1.0 10 9 [C] ligger fast i punktet (2.0, 0, 0) [m]. Punktladningen q 2 = 4.0 10 9 [C] ligger i punktet ( 1.0, 0, 0) [m]. I) Finnes det punkt(er) i rommet med elektrisk
EKSAMENSOPPGAVE. ü Kalkulator med tomt dataminne ü Rottmann: Matematisk Formelsamling. rute
 Fakultet for naturvitenskap og teknologi EKSAMENSOPPGAE Eksamen i: Fys-1002 Dato: 10.juni 2016 Klokkeslett: 09.00-13.00 Sted: Åsgårdveien 9 Tillatte hjelpemidler: ü Kalkulator med tomt dataminne ü Rottmann:
Fakultet for naturvitenskap og teknologi EKSAMENSOPPGAE Eksamen i: Fys-1002 Dato: 10.juni 2016 Klokkeslett: 09.00-13.00 Sted: Åsgårdveien 9 Tillatte hjelpemidler: ü Kalkulator med tomt dataminne ü Rottmann:
OPPGAVESETT 1. PS: Spørsmål 1a) og 1b) har ingenting med hverandre å gjøre. 1b) refererer til to nøytrale kuler, ikke kulene i 1a)
 Fasit for FYS1120-oppgaver H2010. OPPGAVESETT 1 1a) 9.88 10-7 C 1b) 891 PS: Spørsmål 1a) og 1b) har ingenting med hverandre å gjøre. 1b) refererer til to nøytrale kuler, ikke kulene i 1a) 2a) 7.25 10 24
Fasit for FYS1120-oppgaver H2010. OPPGAVESETT 1 1a) 9.88 10-7 C 1b) 891 PS: Spørsmål 1a) og 1b) har ingenting med hverandre å gjøre. 1b) refererer til to nøytrale kuler, ikke kulene i 1a) 2a) 7.25 10 24
Den franske fysikeren Charles de Columb er opphavet til Colombs lov.
 4.5 KREFTER I ET ELEKTRISK FELT ELEKTRISK FELT - COLOMBS LOV Den franske fysikeren Charles de Columb er opphavet til Colombs lov. Kraften mellom to punktladninger er proporsjonal med produktet av kulenes
4.5 KREFTER I ET ELEKTRISK FELT ELEKTRISK FELT - COLOMBS LOV Den franske fysikeren Charles de Columb er opphavet til Colombs lov. Kraften mellom to punktladninger er proporsjonal med produktet av kulenes
Kondensator - Capacitor. Kondensator - en komponent som kan lagre elektrisk ladning. Symbol. Kapasitet, C = 1volt
 Kondensator - apacitor Lindem 3. feb.. 007 Kondensator - en komponent som kan lagre elektrisk ladning. Symbol Kapasiteten ( - capacity ) til en kondensator måles i arad. Som en teknisk definisjon kan vi
Kondensator - apacitor Lindem 3. feb.. 007 Kondensator - en komponent som kan lagre elektrisk ladning. Symbol Kapasiteten ( - capacity ) til en kondensator måles i arad. Som en teknisk definisjon kan vi
Flervalgsoppgaver. Gruppeøving 5 Elektrisitet og magnetisme
 Flervalgsoppgaver. Hvis en positiv ladning Q blir plassert i origo i figuren (i krysningspunktet mellom vertikal og horisontal linje), mot hvilken kvadrant vil den føle ei netto kraft? A. A B. B C. C D.
Flervalgsoppgaver. Hvis en positiv ladning Q blir plassert i origo i figuren (i krysningspunktet mellom vertikal og horisontal linje), mot hvilken kvadrant vil den føle ei netto kraft? A. A B. B C. C D.
Øving 15. H j B j M j
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007 Veiledning: Uke 17 Innleveringsfrist: Mandag 30. april Øving 15 Oppgave 1 H j j M j H 0 0 M 0 I En sylinderformet jernstav
Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007 Veiledning: Uke 17 Innleveringsfrist: Mandag 30. april Øving 15 Oppgave 1 H j j M j H 0 0 M 0 I En sylinderformet jernstav
FYS1120 Elektromagnetisme
 Det matematisk-naturvitenskapelige fakultet Universitetet i Oslo FYS112 Elektromagnetisme Løsningsforslag til ukesoppgave 2 Oppgave 1 a) Gauss lov sier at den elektriske fluksen Φ er lik den totale ladningen
Det matematisk-naturvitenskapelige fakultet Universitetet i Oslo FYS112 Elektromagnetisme Løsningsforslag til ukesoppgave 2 Oppgave 1 a) Gauss lov sier at den elektriske fluksen Φ er lik den totale ladningen
Fysikkk. Støvneng Tlf.: 45. Andreas Eksamensdato: Rottmann, boksen 1 12) Dato. Sign
 Instituttt for fysikk Eksamensoppgave i TFY4104 Fysikkk Faglig kontakt under eksamen: Jon Andreas Støvneng Tlf.: 45 45 55 33 Eksamensdato: 18. desember 2013 Eksamenstid (fra-til): 0900-1300 Hjelpemiddelkode/Tillattee
Instituttt for fysikk Eksamensoppgave i TFY4104 Fysikkk Faglig kontakt under eksamen: Jon Andreas Støvneng Tlf.: 45 45 55 33 Eksamensdato: 18. desember 2013 Eksamenstid (fra-til): 0900-1300 Hjelpemiddelkode/Tillattee
Vi skal se på: Lineær bevegelsesmengde, kollisjoner (Kap. 8)
 kap8.ppt 03.0.203 TFY445/FY00 ekanisk fysikk Størrelser og enheter (Kap ) Kinematikk i en, to og tre dimensjoner (Kap. 2+3) Posisjon, hastighet, akselerasjon. Sirkelbevegelse. Dynamikk (krefter): Newtons
kap8.ppt 03.0.203 TFY445/FY00 ekanisk fysikk Størrelser og enheter (Kap ) Kinematikk i en, to og tre dimensjoner (Kap. 2+3) Posisjon, hastighet, akselerasjon. Sirkelbevegelse. Dynamikk (krefter): Newtons
KONTINUASJONSEKSAMEN I EMNE SIF4005 FYSIKK Mandag 7. august 2000 kl. kl
 Side 1 av 6 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Inst. for fysikk, Gløshaugen Professor Bjørn Torger Stokke 735 93434 KONTINUASJONSEKSAMEN
Side 1 av 6 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Inst. for fysikk, Gløshaugen Professor Bjørn Torger Stokke 735 93434 KONTINUASJONSEKSAMEN
OBLIGATORISK MIDTSEMESTERØVING I EMNE TFE 4120 ELEKTROMAGNETISME
 ide 1 av 6 NTNU Norges teknisk-naturvitenskapelige universitet Fakultet for informatikk, matematikk og elektroteknikk Institutt for elektronikk og telekommunikasjon OBLIGATORIK MIDTEMETERØVING I EMNE TFE
ide 1 av 6 NTNU Norges teknisk-naturvitenskapelige universitet Fakultet for informatikk, matematikk og elektroteknikk Institutt for elektronikk og telekommunikasjon OBLIGATORIK MIDTEMETERØVING I EMNE TFE
EKSAMENSOPPGAVE. Tillatte hjelpemidler: Kalkulator med tomt dataminne, Rottmann: Matematisk formelsamling.
 EKSAMENSOPPGAE Eksamen i: FYS-1002 Dato: Mandag 4. juni, 2018 Klokkeslett: 9:00 13:00 Sted: ADM B154 Tillatte hjelpemidler: Kalkulator med tomt dataminne, Rottmann: Matematisk formelsamling. Eksamenoppgaven
EKSAMENSOPPGAE Eksamen i: FYS-1002 Dato: Mandag 4. juni, 2018 Klokkeslett: 9:00 13:00 Sted: ADM B154 Tillatte hjelpemidler: Kalkulator med tomt dataminne, Rottmann: Matematisk formelsamling. Eksamenoppgaven
Løysingsframlegg TFY 4104 Fysikk Kontinuasjonseksamen august 2010
 NTNU Fakultet for Naturvitskap og Teknologi Institutt for Fysikk Løysingsframlegg TFY 404 Fysikk Kontinuasjonseksamen august 200 Faglærar: Professor Jens O Andersen Institutt for Fysikk, NTNU Telefon:
NTNU Fakultet for Naturvitskap og Teknologi Institutt for Fysikk Løysingsframlegg TFY 404 Fysikk Kontinuasjonseksamen august 200 Faglærar: Professor Jens O Andersen Institutt for Fysikk, NTNU Telefon:
Løsningsforslag TFE4120 Elektromagnetisme 13. mai 2004
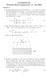 Løsningsforslag TFE4120 Elektromagnetisme 13. mai 2004 Oppgae 1 a) Speilladningsmetoden gir at potensialet for z > 0 er summen a potensialet pga ladningen Q i posisjon z = h og potensialet pga en speillanding
Løsningsforslag TFE4120 Elektromagnetisme 13. mai 2004 Oppgae 1 a) Speilladningsmetoden gir at potensialet for z > 0 er summen a potensialet pga ladningen Q i posisjon z = h og potensialet pga en speillanding
Eksamensoppgave i TFY4155 ELEKTRISITET OG MAGNETISME FY1003 ELEKTRISITET OG MAGNETISME
 Institutt for fysikk Eksamensoppgave i TFY455 ELEKTRISITET OG MAGNETISME FY003 ELEKTRISITET OG MAGNETISME Faglig kontakt under eksamen: Institutt for fysikk v/arne Mikkelsen, Tlf: 486 05 392 / 7359 3433
Institutt for fysikk Eksamensoppgave i TFY455 ELEKTRISITET OG MAGNETISME FY003 ELEKTRISITET OG MAGNETISME Faglig kontakt under eksamen: Institutt for fysikk v/arne Mikkelsen, Tlf: 486 05 392 / 7359 3433
Kap. 27 Kjapp historie. Kap. 27 Magnetisk felt og magnetiske krefter. Kap. 27 Magnetisme. Kraft på ledningsbit. Kap 27
 Kap. 27 Magnetisk felt og magnetiske krefter Kortfatta målsetning: Forstå at magnetiske monopoler ikke fins, kun dipoler. (mens elektriske monopoler fins, dvs. +q, -q) Lære at permanente magneter og elektromagneter
Kap. 27 Magnetisk felt og magnetiske krefter Kortfatta målsetning: Forstå at magnetiske monopoler ikke fins, kun dipoler. (mens elektriske monopoler fins, dvs. +q, -q) Lære at permanente magneter og elektromagneter
Eksamensoppgåve i TFY4155 ELEKTRISITET OG MAGNETISME FY1003 ELEKTRISITET OG MAGNETISME
 Side 1 av 6 Institutt for fysikk Eksamensoppgåve i TFY4155 ELEKTRISITET OG MAGNETISME FY1003 ELEKTRISITET OG MAGNETISME Faglig kontakt under eksamen: Institutt for fysikk v/arne Mikkelsen, Tlf: 486 05
Side 1 av 6 Institutt for fysikk Eksamensoppgåve i TFY4155 ELEKTRISITET OG MAGNETISME FY1003 ELEKTRISITET OG MAGNETISME Faglig kontakt under eksamen: Institutt for fysikk v/arne Mikkelsen, Tlf: 486 05
Løsningsforslag, Midtsemesterprøve torsdag 6. mars 2008 kl Oppgavene med kort løsningsskisse
 Institutt for fysikk, NTNU FY1003 Elektrisitet og mgnetisme TFY4155 Elektromgnetisme Vår 2008 Løsningsforslg, Midtsemesterprøve torsdg 6. mrs 2008 kl 1000 1200. Fsit side 12. Oppgvene med kort løsningsskisse
Institutt for fysikk, NTNU FY1003 Elektrisitet og mgnetisme TFY4155 Elektromgnetisme Vår 2008 Løsningsforslg, Midtsemesterprøve torsdg 6. mrs 2008 kl 1000 1200. Fsit side 12. Oppgvene med kort løsningsskisse
NORGES TEKNISKNATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK EKSAMEN I EMNE TFY4120 FYSIKK. Fredag 9. desember 2005 Tid: kl 09.00-13.
 Bokmål Side 1 av 1 Studentnummer: Studieretning: NORGES TEKNISKNATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK EKSAMEN I EMNE TFY4120 FYSIKK Fredag 9. desember 2005 Tid: kl 09.00-13.00 Faglig kontakt
Bokmål Side 1 av 1 Studentnummer: Studieretning: NORGES TEKNISKNATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK EKSAMEN I EMNE TFY4120 FYSIKK Fredag 9. desember 2005 Tid: kl 09.00-13.00 Faglig kontakt
EKSAMEN I EMNE TFE 4120 ELEKTROMAGNETISME
 NTNU Norges teknisk-naturvitenskapelige universitet ide 1 av 7 Fakultet for informatikk, matematikk og elektroteknikk Institutt for elektronikk og telekommunikasjon Bokmål/Nynorsk Faglig/fagleg kontakt
NTNU Norges teknisk-naturvitenskapelige universitet ide 1 av 7 Fakultet for informatikk, matematikk og elektroteknikk Institutt for elektronikk og telekommunikasjon Bokmål/Nynorsk Faglig/fagleg kontakt
Kap. 27 Kjapp historie. Kap. 27 Magnetisk felt og magnetiske krefter. Kap. 27 Magnetisme. Kraft på ledningsbit. Kap 27
 Kap. 27 Magnetisk felt og magnetiske krefter Kortfatta målsetning: Forstå at magnetiske monopoler ikke fins, kun dipoler. (mens elektriske monopoler fins, dvs. +q, -q) Lære at permanente magneter og elektromagneter
Kap. 27 Magnetisk felt og magnetiske krefter Kortfatta målsetning: Forstå at magnetiske monopoler ikke fins, kun dipoler. (mens elektriske monopoler fins, dvs. +q, -q) Lære at permanente magneter og elektromagneter
LØSNINGSFORSLAG TIL EKSAMEN I FY1003 ELEKTRISITET OG MAGNETISME TFY4155 ELEKTROMAGNETISME Onsdag 3. juni 2009 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY003 ELEKTRISITET
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY003 ELEKTRISITET
Løysingsforslag Kontinuasjonseksamen TFE4120 Elektromagnetisme 13. august 2004
 Løysinsforsla Kontinuasjonseksamen TFE4120 Elektromanetisme 13. auust 2004 Oppåve 1 a) Fiure 1: Ei telefonlinje som år parallelt med ei straumlinje. Det skraverte området er definert av kurva C 2. Innbyrdes
Løysinsforsla Kontinuasjonseksamen TFE4120 Elektromanetisme 13. auust 2004 Oppåve 1 a) Fiure 1: Ei telefonlinje som år parallelt med ei straumlinje. Det skraverte området er definert av kurva C 2. Innbyrdes
