1. En tynn stav med lengde L har uniform ladning λ per lengdeenhet. Hvor mye ladning dq er det på en liten lengde dx av staven?
|
|
|
- Torild Haaland
- 6 år siden
- Visninger:
Transkript
1 Ladet stav 1 En tynn stav med lengde L har uniform ladning per lengdeenhet Hvor mye ladning d er det på en liten lengde d av staven? A /d B d C 2 d D d/ E L d Løsning: Med linjeladning (dvs ladning per lengdeenhet) må ladningen d på en liten lengde d bli d = d 2 Vi legger staven på aksen, slik at punktet P har koordinater (, y) = (0, R) Vi betrakter også et lite lengdeelement d av staven som har avstand r til P Hva er riktig uttrykk for det elektriske feltet fra lengdeelementet d E i P? A d E = k d r ˆr B d E = d kr ˆr C d E = d kr 2 ˆr D d E = k d r 2 ˆr E d E = k d r 2 ˆr P θ 1 R y L Løsning: Elektrisk felt i punkt P i avstand r fra lengdeelement d i posisjon (som vist i figuren) er d E = k d r 2 ˆr da d = d (jf forrige oppgave) de P θ θ 1 2 θ r R y 2 0 d 1 L
2 3 Hva er komponenten E av det elektriske feltet i P, i avstand R fra staven? (Tips: I figuren er det definert to vinkler θ 1 og som dannes mellom linjene fra P til stavens endepunkter og normalen til staven gjennom P (dvs yaksen) Fortegnet til vinklene er som indikert i figuren, dvs θ er negativ når < 0) A E = 4πε (cos θ 0R 1cos ) B E = 4πε (cos θ 0R 1 cos ) C E = 4πε (sin θ 0R 1cos ) D E = 4πε (cos θ 0R 1 sin ) E E = 4πε (sin θ 0R 1 sin ) Løsning: Vi ser fra figuren over at vektoren d E har komponent k d de = de sin θ = r 2 sin θ Her har vi valgt = 0 når θ = 0, og fortegnet stemmer med oppgaveteksten, dvs θ > 0 når > 0 Vi uttrykker d og 1/r 2 ved vinkelen θ: = R tan θ d = R dθ cos 2 θ r = R 1 cos θ r 2 = cos2 θ R 2 d r 2 = dθ R Vi får komponenten E av feltet E i punktet P fra hele staven ved å integrere de : E = staven de = k R θ1 sin θ dθ = k θ 1 R cos θ = 4πε 0 R (cos θ 1 cos ) 4 Hva med E y? A E y = 4πε (sin θ 0R 1 sin ) B E y = 4πε (sin θ 0R 1 sin ) C E y = 4πε (cos θ 0R 1 sin ) D E y = 4πε (sin θ 0R 1 cos ) E E y = 4πε (sin θ 0R 1 cos ) Løsning: Vi bruker samme metode som over Vi har ykomponenten de y = de cos θ = Vi integrerer over hele staven igjen og får E y = staven de y = k R θ1 k d r 2 cos θ cos θ dθ = k θ 1 R sin θ = 4πε 0 R (sin θ 1 sin ) 5 Hva er det elektriske feltet dersom P er like langt fra stavens to ender? A E = ĵ B E = î C E = î 4πε 0R R 2 L 2 /4 4πε 0R R 2 L 2 /4 8πε 0R R 2 L 2 /4 D E = 4πε ĵ E 0R R 2 L E = 2 2 4πε 0R(R 2 L 2 ) ĵ Her er î og ĵ enhetsvektorer i og yretning 8πε 0R R 2 L 2 /4 ĵ Løsning: Med P like langt fra stavens to ender er θ 1 = og følgelig er cos θ 1 cos = 0 og sin θ 1 sin = 2 sin θ 1 = L/ R 2 L 2 /4 Dermed får vi E = 0 Page 2
3 og E = E y ĵ = 4πε 0 R ĵ R 2 L 2 /4 6 Hva blir E når R << L, dvs når P er langt unna staven? A E 4πε 0R B E 4πε 0R 2 C E 2πε 0 RL D E 2πε 0R R/L E E 4πε 0R Løsning: Når P er langt unna staven kan vi neglisjere L 2 /4 i forhold til R 2 i kvadratrota, slik at R 2 L 2 /4 R 2 = R, slik at E 4πε 0 R 2 = Q 4πε 0 R 2 Dette er det samme feltet som fra en punktladning Q i avstand R Ikke uventet; langt unna ser staven essensielt ut som en punktladning med total ladning Q = 7 Hva ville det elektriske feltet blitt i avstand R dersom staven var uendelig lang? A E = E y = 4πε 0R 2 B E = E y = 2πε 0R 2 C E = E y = 4πε 0R D E = E y = 2πε 0 R E E = E y = 2πε 0R Løsning: En uendelig lang stang oppnår vi ved å la π/2 og θ 1 π/2 Da blir igjen E = 0 og følgelig E = E y = 2πε 0 R Med andre ord: Feltet fra en uendelig lang linjeladning faller av omvendt proporsjonalt med R Elektrisk dipol 8 Finn det elektriske feltet fra en elektrisk dipol i punktet P (se figur), som ligger langs midtlinja på dipolen Uttrykk svaret ved dipolmomentet p = L og avstanden r Page 3
4 Løsning: Totalt Efelt i punktet P er gitt ved E 1 fra og E 2 fra Størrelsen på E 1 og E 2 er den samme, men E 1 er i retning fra og E 2 i retning mot ykomponentene vil kansellere hverandre, og for komponenten får vi: E = (E 1 E 2 ) î = 2E 1, E 1 = E 1 cos θ = k cos θ r2 hvor Fra figuren har vi at cos θ = L/2 r, som gir E = 2 k L r 2 2r î = k L r 3 î = k p r 3, der vi har brukt at den elektriske dipol (som peker fra negativ til positiv ladning) er gitt ved p = L = L( î ) Merk at det elektriske feltet synker med r som 1/r 3 Dette er rett for alle punkter (i alle retninger) langt unna en dipol, der det altså er 1/r 2 for en punktladning Feltlinjer 9 I denne oppgaven skal dere vise skissene i hvert av tilfellene både i stor og i liten målestokk, slik at de gir et kvalitativt bilde av feltet både nærme og svært langt unna (a) Skissér elektriske feltlinjer for disse to systemene av punktladninger: (i) (ii) 2 (b) For staven i flervalgsoppgavene, skissér i de elektriske feltlinjer i et plan normalt på staven gjennom dets midtpunkt, ii de elektriske feltlinjer i et plan som inneholder staven Page 4
5 Løsning: a) i) Feltlinjer rundt to like store positive punktladninger: Nærbilde Like mange feltlinjer ut fra hver ladning siden de er like Her valgt 18 feltlinjer fra hver, og feltlinjene går ut til uendelig Riktig langt unna Riktig langt unna ser vi de to ladningene som én punktladning 2 Her valgt kun 8 feltlinjer totalt, og de går til uendelig a) ii) Feltlinjer rundt punktladninger 2 og : Nærbilde Like mange feltlinjer ut per positiv ladning som inn per negativ ladning, derfor dobbelt så mange inn mot 2 som ut fra De resterende må komme fra uendelig Det er en feil i figuren: 7 linjer ut fra og 16 linjer inn til 2 Finner du en løsning på problemet? Riktig langt unna ser vi essensielt en punktladning 2 =, dvs feltlinjene går radielt inn mot ladningen: b) i) stav, plan normalt på, nært stav, plan normalt på, langt unna b) ii) stav, plan inneholder staven, nært stav, plan inneholder staven, langt unna Page 5
6 Kommentar til disse oppgavene: Skissene vist er bare kvalitative, ikke kvantitative Legg spesielt merke til at langt unna ser alt ut som en punktladning På nært hold kan en som regel benytte symmetribetraktninger kombinert med det en vet om feltet i umiddelbar nærhet av eventuelle punktladninger til å tegne opp et temmelig korrekt bilde av feltlinjene Ladning på leder 10 Figuren viser et snitt gjennom ei elektrisk ledende kule med et hulrom inni Kula er elektrisk nøytral, hulrommet er sfærisk men ikke konsentrisk med metallkula I hulrommet er det plassert en punktladning, punktladningen ligger ikke i sentrum av verken hulrommet eller kula Hvordan vil (fri) ladning i lederen være fordelt når systemet er i elektrostatisk likevekt? Skissér feltlinjer for det elektrostatiske feltet E Finn uttrykk for E utenfor kula Ingen regning er påkrevd i denne oppgaven, bare elektrostatiske betraktninger med bruk av regler for feltlinjer og Efelt på overflata og inni metaller Løsning: Venstre figur under viser 16 feltlinjer fra punktladningen Når denne plasseres i hulrommet i lederen vil i første omgang feltlinjene stråle i samme retning og ende opp på indre metalloverflate For å opprettholde E = 0 overalt inne i lederen, vil det induseres negative motladninger fordelt som vist på figuren i midten Det må bli størst indusert ladningstetthet på den delen av hulrommets overflate som ligger nærmest punktladningen, lavere ladningstetthet på den delen av hulrommets overflate som ligger lengst unna punktladningen Den totale induserte ladning på hulrommets overflate er, ifølge Gauss lov Vi kan nemlig legge inn ei Gaussflate i lederen og som omslutter hulrommet men vilkårlig nær hulrommets overflate Fordi E = 0 i lederen må total nettoladning innenfor Gaussflata være lik null Skal dette være oppfylt må vi ha en indusert ladning på hulrommets overflate Med denne ladningsfordelingen forsvinner det elektriske feltet overalt inne i lederen, dvs bidraget til feltet inne i lederen fra punktladningen kanselleres av bidraget fra den induserte ladningsfordelingen Men feltlinjene i hulrommet i midtre figur oppfyller ikke kravet om at feltlinjer skal gå normalt inn på en lederoverflate Vi må derfor justere feltlinjene slik at de blir i figuren til høyre Ladningstettheten forblir uendret Page 6
7 Lederen var oppgitt å være elektrisk nøytral Det betyr at vi må ha fått indusert ladning på lederens ytre overflate, slik at total ladning på lederen blir = 0 Denne ladningen vil fordele seg jamt på den ytre overflata, fordi asymmetrien som skyldes punktladningen inne i hulrommet presis kanselleres av den induserte ladningen på hulrommets overflate Fra utsida ser vi altså rett og slett en kulesymmetrisk overflateladning med 16 radielt fordelte feltlinjer Dvs E(r) = der r er avstanden fra metallkulas sentrum 4πε 0 r 2 ˆr Fluks 11 Ei Gaussflate S er formet som en kube med sidekant a og har det ene hjørnet i origo (se figuren) Flata er plassert i et område hver det er en elektrisk feltstyrke E(, y, z) For hvert tilfelle iiv, finn (a) total (netto) fluks Φ E for E ut gjennom flata S, og (b) total ladning Q innenfor S i E = E î = C î = C [1, 0, 0] (uniformt og parallelt med aksen) ii E = E î = C î = C [, 0, 0] (parallelt med aksen og lineært økende) iii E = E î = C 2 î = C [2, 0, 0] (parallelt med aksen og kvadratisk økende) iv E = E î E y ĵ = C y î C ĵ = C [y,, 0] (i yplanet og økende) Her er C en konstant (ulik i hvert tilfelle) Løsning: Den lukkede flata S har sideflater med areal A i = a 2, der i =, y, z Retningen på d A er normalt på sideflata som figuren viser Når vi beregner flusken vil sideflater hvor E d A ikke gi noe bidrag (prikkproduktet er null) da a z da z E = C î a a d A y y Page 7
8 i) E = E î = C î = konstant medfører at Φ E = E d A = C a 2 ( C a 2 ) = 0 Det første leddet er fra flate = a, det andre fra flate = 0 og de fire siste er andre flater der E d A Altså bidrar bare 2 av de 6 flatene, og siden Efeltet er uavhengig av, blir fluks inn lik fluks ut og total fluks blir lik null Ladning innefor S blir da ifølge Gauss lov: Q = ε 0 Φ E = 0 ii) E = E î = C î gir at fluksen inn ved = 0 er lik null, mens den er positiv ut ved = a: Φ E = E d A = Ca a 2 C 0 a = Ca 3 og Q = ε 0 Φ E = ε 0 Ca 3 iii) E 2 = E î = C î gir videre Φ E = E d A = Ca 2 a 2 C 0 a = Ca 4 og Q = ε 0 Ca 4 iv) Når E ikke er avhengig av vil fluks ut ved flata = a være lik fluks inn ved flata = 0, slik at netto fluks blir 0, som vist i figuren under Tilsvarende argument gjelder for fluks i yretning (ikke vist i figuren) og i zretning er det ingen felt slik at fluks i denne retning er null Totalt: Φ E = 0 Om man vil, uttrykt matematisk oppdelt på hver koordinatretning: Φ E, = y=0 z=0 Cy dy dz y=0 z=0 Likedan er Φ E,y = 0 og som i alle tilfeller Φ E,z = 0 Konklusjon: Φ E = 0 og Q = 0 Cy dy dz = C a 2 a2 C a 2 a2 = 0, da a z d A z E = Cy î a a d A y y En alternativ måte å finne Q på er å bruke Gauss lov på differensialform: ρ(, y, z) = ε 0 E(, y, z), Page 8
9 altså beregne divergensen til E og så integrere ρ over kuben med volum τ = a 3 Dette gir mindre arbeid: i) ρ = ε 0 E = ε 0 E = 0 Q = ρa3 = 0 a 3 = 0 ii) ρ = ε 0 E = ε 0 E = ε 0C Q = ρa 3 = ε 0 Ca 3 iii) ρ = ε 0 E E = ε 0 = ε 0 2C Q = kube iv) ρ d dy dz = ε 0 2C 0 d 0 dy 0 dz = ε 0 C ( a 2 0 2) a a = ε 0 Ca 4 ( ρ = ε 0 E E = ε 0 E ) y = 0 Q = 0 a 3 = 0 y Merk at når rommet er divergensfritt i E er det også ladningsfritt Page 9
Elektrisk potensial/potensiell energi
 Elektrisk potensial/potensiell energi. Figuren viser et uniformt elektrisk felt E heltrukne linjer. Langs hvilken stiplet linje endrer potensialet seg ikke? A. B. C. 3 D. 4 E. Det endrer seg langs alle
Elektrisk potensial/potensiell energi. Figuren viser et uniformt elektrisk felt E heltrukne linjer. Langs hvilken stiplet linje endrer potensialet seg ikke? A. B. C. 3 D. 4 E. Det endrer seg langs alle
Mandag qq 4πε 0 r 2 ˆr F = Elektrisk felt fra punktladning q (følger av definisjonen kraft pr ladningsenhet ): F dl
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007, uke 6 Mandag 05.02.07 Oppsummering til nå, og møte med Maxwell-ligning nr 1 Coulombs lov (empirisk lov for kraft mellom to
Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007, uke 6 Mandag 05.02.07 Oppsummering til nå, og møte med Maxwell-ligning nr 1 Coulombs lov (empirisk lov for kraft mellom to
Tirsdag r r
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2008, uke 6 Tirsdag 05.02.08 Gauss lov [FGT 23.2; YF 22.3; TM 22.2, 22.6; AF 25.4; LHL 19.7; DJG 2.2.1] Fra forrige uke; Gauss
Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2008, uke 6 Tirsdag 05.02.08 Gauss lov [FGT 23.2; YF 22.3; TM 22.2, 22.6; AF 25.4; LHL 19.7; DJG 2.2.1] Fra forrige uke; Gauss
Onsdag og fredag
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2009, uke 7 Onsdag 11.02.09 og fredag 13.02.09 Gauss lov [FGT 23.2; YF 22.3; TM 22.2, 22.6; AF 25.4; LHL 19.7; DJG 2.2.1] Gauss
Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2009, uke 7 Onsdag 11.02.09 og fredag 13.02.09 Gauss lov [FGT 23.2; YF 22.3; TM 22.2, 22.6; AF 25.4; LHL 19.7; DJG 2.2.1] Gauss
Overflateladningstetthet på metalloverflate
 0.0.08: Rettet opp feil i oppgave 4 og løsningsforslag til oppgave 8b. Overflateladningstetthet på metalloverflate. Ei metallkule med diameter 0.0 m har ei netto ladning på 0.50 nc. Hvor stort er det elektriske
0.0.08: Rettet opp feil i oppgave 4 og løsningsforslag til oppgave 8b. Overflateladningstetthet på metalloverflate. Ei metallkule med diameter 0.0 m har ei netto ladning på 0.50 nc. Hvor stort er det elektriske
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS1120 Elektromagnetisme Eksamensdag: 10. oktober 2016 Tid for eksamen: 10.00 13.00 Oppgavesettet er på 8 sider. Vedlegg: Tillatte
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS1120 Elektromagnetisme Eksamensdag: 10. oktober 2016 Tid for eksamen: 10.00 13.00 Oppgavesettet er på 8 sider. Vedlegg: Tillatte
Gauss lov. Kap. 22. Gauss lov. Gauss lov skjematisk. Vi skal se på: Fluksen til elektrisk felt E Gauss lov Integralform og differensialform
 Kap. 5..6 Kap.. Gauss lov Vi skal se på: Fluksen til elektrisk felt E Gauss lov Integralform og differensialform Elektrisk ledere. Efelt fra Coulombs lov: q E k r r E k n q r n n r n dq E k r r tot. ladn.
Kap. 5..6 Kap.. Gauss lov Vi skal se på: Fluksen til elektrisk felt E Gauss lov Integralform og differensialform Elektrisk ledere. Efelt fra Coulombs lov: q E k r r E k n q r n n r n dq E k r r tot. ladn.
FYS1120 Elektromagnetisme, Ukesoppgavesett 1
 FYS1120 Elektromagnetisme, Ukesoppgavesett 1 22. august 2016 I FYS1120-undervisningen legg vi mer vekt på matematikk og numeriske metoder enn det oppgavene i læreboka gjør. Det gjelder også oppgavene som
FYS1120 Elektromagnetisme, Ukesoppgavesett 1 22. august 2016 I FYS1120-undervisningen legg vi mer vekt på matematikk og numeriske metoder enn det oppgavene i læreboka gjør. Det gjelder også oppgavene som
Kap. 22. Gauss lov. Vi skal se på: Fluksen til elektrisk felt E Gauss lov. Elektrisk ledere. Integralform og differensialform
 Kap. 22. Gauss lov Vi skal se på: Fluksen til elektrisk felt E Gauss lov Integralform og differensialform Elektrisk ledere. E-felt fra Coulombs lov: E k q r 2 r E k n q r n 2 0n r 0n dq E k r 2 r tot.
Kap. 22. Gauss lov Vi skal se på: Fluksen til elektrisk felt E Gauss lov Integralform og differensialform Elektrisk ledere. E-felt fra Coulombs lov: E k q r 2 r E k n q r n 2 0n r 0n dq E k r 2 r tot.
Øving 3. Oppgave 1 (oppvarming med noen enkle oppgaver fra tidligere midtsemesterprøver)
 Institutt for fysikk, NTNU TFY455/FY003: Elektrisitet og magnetisme Vår 2008 Veiledning: Fredag 25. og mandag 28. januar Innleveringsfrist: Fredag. februar kl 2.00 Øving 3 Oppgave (oppvarming med noen
Institutt for fysikk, NTNU TFY455/FY003: Elektrisitet og magnetisme Vår 2008 Veiledning: Fredag 25. og mandag 28. januar Innleveringsfrist: Fredag. februar kl 2.00 Øving 3 Oppgave (oppvarming med noen
Løsningsforslag til øving 4
 Institutt for fysikk, NTNU TFY455/FY003 Elektrisitet og magnetisme Vår 2007 Veiledning uke 5 Løsningsforslag til øving 4 Oppgave a) Vi benytter oss av tipsene gitt i oppgaveteksten og tar utgangspunkt
Institutt for fysikk, NTNU TFY455/FY003 Elektrisitet og magnetisme Vår 2007 Veiledning uke 5 Løsningsforslag til øving 4 Oppgave a) Vi benytter oss av tipsene gitt i oppgaveteksten og tar utgangspunkt
Løsningsforslag til øving 3
 Institutt for fysikk, NTNU TFY455/FY003 Elektromagnetisme Vår 2009 Løsningsforslag til øving 3 Oppgave a) C V = E dl = 0 dersom dl E b) B På samme måte som et legeme med null starthastighet faller i gravitasjonsfeltet
Institutt for fysikk, NTNU TFY455/FY003 Elektromagnetisme Vår 2009 Løsningsforslag til øving 3 Oppgave a) C V = E dl = 0 dersom dl E b) B På samme måte som et legeme med null starthastighet faller i gravitasjonsfeltet
Midtsemesterprøve fredag 10. mars kl
 Institutt for fysikk, NTNU FY1003 Elektrisitet og magnetisme TFY4155 Elektromagnetisme Vår 2006 Midtsemesterprøve fredag 10. mars kl 0830 1130. Løsningsforslag 1) A. (Andel som svarte riktig: 83%) Det
Institutt for fysikk, NTNU FY1003 Elektrisitet og magnetisme TFY4155 Elektromagnetisme Vår 2006 Midtsemesterprøve fredag 10. mars kl 0830 1130. Løsningsforslag 1) A. (Andel som svarte riktig: 83%) Det
Tirsdag E = F q. q 4πε 0 r 2 ˆr E = E j = 1 4πε 0. 2 j. r 1. r n
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2008, uke 3 Tirsdag 15.01.07 Elektrisk felt [FGT 22.1; YF 21.4; TM 21.4; AF 21.5; LHL 19.4; DJG 2.1.3] = kraft pr ladningsenhet
Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2008, uke 3 Tirsdag 15.01.07 Elektrisk felt [FGT 22.1; YF 21.4; TM 21.4; AF 21.5; LHL 19.4; DJG 2.1.3] = kraft pr ladningsenhet
TFY4104 Fysikk. Institutt for fysikk, NTNU. Høsten Løsningsforslag til øving 10.
 TFY4104 Fysikk. Institutt for fysikk, NTNU. Høsten 015. Løsningsforslag til øving 10. Oppgave A B C D 1 x x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11 x 1 x 13 x 14 x 15 x 16 x 17 x 18 x 9 x 0 x 1) Glass-staven
TFY4104 Fysikk. Institutt for fysikk, NTNU. Høsten 015. Løsningsforslag til øving 10. Oppgave A B C D 1 x x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11 x 1 x 13 x 14 x 15 x 16 x 17 x 18 x 9 x 0 x 1) Glass-staven
Onsdag og fredag
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2009, uke 4 Onsdag 21.01.09 og fredag 23.01.09 Elektrisk felt fra punktladning [FGT 22.1; YF 21.4; TM 21.4; AF 21.6; LHL 19.5;
Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2009, uke 4 Onsdag 21.01.09 og fredag 23.01.09 Elektrisk felt fra punktladning [FGT 22.1; YF 21.4; TM 21.4; AF 21.6; LHL 19.5;
Midtsemesterprøve fredag 11. mars kl
 Institutt for fysikk, NTNU FY1003 Elektrisitet og magnetisme TFY4155 Elektromagnetisme Vår 2005 Midtsemesterprøve fredag 11. mars kl 1030 1330. Løsningsforslag 1) B. Newtons 3. lov: Kraft = motkraft. (Andel
Institutt for fysikk, NTNU FY1003 Elektrisitet og magnetisme TFY4155 Elektromagnetisme Vår 2005 Midtsemesterprøve fredag 11. mars kl 1030 1330. Løsningsforslag 1) B. Newtons 3. lov: Kraft = motkraft. (Andel
Mandag Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007, uke 4
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007, uke 4 Mandag 22.01.07 Elektriske feltlinjer [FGT 22.2; YF 21.6; TM 21.5; F 21.6; LHL 19.6; DJG 2.2.1] gir en visuell framstilling
Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007, uke 4 Mandag 22.01.07 Elektriske feltlinjer [FGT 22.2; YF 21.6; TM 21.5; F 21.6; LHL 19.6; DJG 2.2.1] gir en visuell framstilling
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME Mandag 4. desember 2006 kl
 NOGES TEKNSK- NATUVTENSKAPELGE UNVESTET NSTTUTT FO FYSKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTSTET OG MAGNETSME Mandag 4. desember
NOGES TEKNSK- NATUVTENSKAPELGE UNVESTET NSTTUTT FO FYSKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTSTET OG MAGNETSME Mandag 4. desember
Flervalgsoppgaver. Gruppeøving 1 Elektrisitet og magnetisme
 Gruppeøving Elektrisitet og magnetisme Flervalgsoppgaver Ei svært tynn sirkulær skive av kobber har radius R = 000 m og tykkelse d = 00 mm Hva er total masse? A 0560 kg B 0580 kg C 0630 kg D 0650 kg E
Gruppeøving Elektrisitet og magnetisme Flervalgsoppgaver Ei svært tynn sirkulær skive av kobber har radius R = 000 m og tykkelse d = 00 mm Hva er total masse? A 0560 kg B 0580 kg C 0630 kg D 0650 kg E
KONTINUASJONSEKSAMEN TFY4155 ELEKTROMAGNETISME Onsdag 17. august 2005 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 KONTINUASJONSEKSAMEN TFY4155 ELEKTROMAGNETISME
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 KONTINUASJONSEKSAMEN TFY4155 ELEKTROMAGNETISME
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME I Mandag 17. desember 2007 kl K. Rottmann: Matematisk formelsamling (eller tilsvarende).
 NOGES TEKNSK- NATUVTENSKAPELGE UNVESTET NSTTUTT FO FYSKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTSTET OG MAGNETSME Mandag 17. desember
NOGES TEKNSK- NATUVTENSKAPELGE UNVESTET NSTTUTT FO FYSKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTSTET OG MAGNETSME Mandag 17. desember
Frivillig test 5. april Flervalgsoppgaver.
 Inst for fysikk 2013 TFY4155/FY1003 Elektr & magnetisme Frivillig test 5 april 2013 Flervalgsoppgaver Kun ett av svarene rett Du skal altså svare A, B, C, D eller E (stor bokstav) eller du kan svare blankt
Inst for fysikk 2013 TFY4155/FY1003 Elektr & magnetisme Frivillig test 5 april 2013 Flervalgsoppgaver Kun ett av svarene rett Du skal altså svare A, B, C, D eller E (stor bokstav) eller du kan svare blankt
LØSNINGSFORSLAG TIL EKSAMEN I FY1003 ELEKTRISITET OG MAGNETISME TFY4155 ELEKTROMAGNETISME Onsdag 3. juni 2009 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY003 ELEKTRISITET
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY003 ELEKTRISITET
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME I Mandag 5. desember 2005 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME
FYS1120 Elektromagnetisme
 Det matematisk-naturvitenskapelige fakultet Universitetet i Oslo FYS1120 Elektromagnetisme J. Skaar: Øvingsoppgaver til midtveiseksamen (med fasit) Her er 46 flervalgsoppgaver som kanskje kan være nyttige
Det matematisk-naturvitenskapelige fakultet Universitetet i Oslo FYS1120 Elektromagnetisme J. Skaar: Øvingsoppgaver til midtveiseksamen (med fasit) Her er 46 flervalgsoppgaver som kanskje kan være nyttige
Kontinuasjonseksamensoppgave i TFY4120 Fysikk
 Side 1 av 10 Bokmål Institutt for fysikk Kontinuasjonseksamensoppgave i TFY4120 Fysikk Faglig kontakt under eksamen: Ragnvald Mathiesen Tlf.: 97692132 Eksamensdato: 13.08.2014 Eksamenstid (fra-til): 09:00-13:00
Side 1 av 10 Bokmål Institutt for fysikk Kontinuasjonseksamensoppgave i TFY4120 Fysikk Faglig kontakt under eksamen: Ragnvald Mathiesen Tlf.: 97692132 Eksamensdato: 13.08.2014 Eksamenstid (fra-til): 09:00-13:00
Oppgave 4 : FYS linjespesifikk del
 Oppgave 4 : FYS 10 - linjespesifikk del Fysiske konstanter og definisjoner: Vakuumpermittiviteten: = 8,854 10 1 C /Nm a) Hva er det elektriske potensialet i sentrum av kvadratet (punktet P)? Anta at q
Oppgave 4 : FYS 10 - linjespesifikk del Fysiske konstanter og definisjoner: Vakuumpermittiviteten: = 8,854 10 1 C /Nm a) Hva er det elektriske potensialet i sentrum av kvadratet (punktet P)? Anta at q
TFY4104 Fysikk. Institutt for fysikk, NTNU. Lsningsforslag til ving 10.
 TFY404 Fysikk. Institutt for fysikk, NTNU. Lsningsforslag til ving 0. Oppgave A B C D x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 0 x x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 29 x 20 x ) Glass-staven er ikke i berring med
TFY404 Fysikk. Institutt for fysikk, NTNU. Lsningsforslag til ving 0. Oppgave A B C D x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 0 x x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 29 x 20 x ) Glass-staven er ikke i berring med
Løsningsforslag til øving 4: Coulombs lov. Elektrisk felt. Magnetfelt.
 Lørdagsverksted i fysikk. Institutt for fysikk, NTNU. Høsten 27. Veiledning: 29. september kl 12:15 15:. Løsningsforslag til øving 4: Coulombs lov. Elektrisk felt. Magnetfelt. Oppgave 1 a) C. Elektrisk
Lørdagsverksted i fysikk. Institutt for fysikk, NTNU. Høsten 27. Veiledning: 29. september kl 12:15 15:. Løsningsforslag til øving 4: Coulombs lov. Elektrisk felt. Magnetfelt. Oppgave 1 a) C. Elektrisk
KONTINUASJONSEKSAMEN TFY4155 ELEKTROMAGNETISME Fredag 11. august 2006 kl
 NOGES TEKNSK- NATUVTENSKAPELGE UNVESTET NSTTUTT FO FYSKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 KONTNUASJONSEKSAMEN TFY4155 ELEKTOMAGNETSME Fredag 11.
NOGES TEKNSK- NATUVTENSKAPELGE UNVESTET NSTTUTT FO FYSKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 KONTNUASJONSEKSAMEN TFY4155 ELEKTOMAGNETSME Fredag 11.
Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen Q ligger i punktet ( 3, 0) [mm].
![Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen Q ligger i punktet ( 3, 0) [mm]. Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen Q ligger i punktet ( 3, 0) [mm].](/thumbs/58/41840831.jpg) Oppgave 1 Finn løsningen til følgende 1.ordens differensialligninger: a) y = x e y, y(0) = 0 b) dy dt + a y = b, a og b er konstanter. Oppgave 2 Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen
Oppgave 1 Finn løsningen til følgende 1.ordens differensialligninger: a) y = x e y, y(0) = 0 b) dy dt + a y = b, a og b er konstanter. Oppgave 2 Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen
LØSNINGSFORSLAG TIL KONTINUASJONSEKSAMEN I FAG SIF 4012 ELEKTROMAGNETISME (SIF 4012 FYSIKK 2) Mandag 29. juli kl
 Side av 9 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng LØSNINGSFORSLAG TIL KONTINUASJONSEKSAMEN I FAG SIF 4 ELEKTROMAGNETISME
Side av 9 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng LØSNINGSFORSLAG TIL KONTINUASJONSEKSAMEN I FAG SIF 4 ELEKTROMAGNETISME
TFY4104 Fysikk. Institutt for fysikk, NTNU. Høsten Løsningsforslag til øving 9. E dl = 0. q i q j 4πε 0 r ij. U = i<j
 TFY404 Fysikk. Institutt for fysikk, NTNU. Høsten 207. Løsningsforslag til øving 9. Oppgave. a) C V = E dl = 0 dersom dl E b) B U = e2 4πε 0 r = e e 4πε 0 r = e.6 0 9 9 0 9 0 0 = 4.4 ev c) D Total potensiell
TFY404 Fysikk. Institutt for fysikk, NTNU. Høsten 207. Løsningsforslag til øving 9. Oppgave. a) C V = E dl = 0 dersom dl E b) B U = e2 4πε 0 r = e e 4πε 0 r = e.6 0 9 9 0 9 0 0 = 4.4 ev c) D Total potensiell
LØSNINGSFORSLAG TIL EKSAMEN I FY1003 ELEKTRISITET OG MAGNETISME Mandag 4. desember 2006 kl
 NOGES TEKNISK- NATUVITENSKAPEIGE UNIVESITET INSTITUTT FO FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 ØSNINGSFOSAG TI EKSAMEN I FY1003 EEKTISITET OG MAGNETISME
NOGES TEKNISK- NATUVITENSKAPEIGE UNIVESITET INSTITUTT FO FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 ØSNINGSFOSAG TI EKSAMEN I FY1003 EEKTISITET OG MAGNETISME
TFY4104 Fysikk. Institutt for fysikk, NTNU. Høsten 2015. Øving 11. Veiledning: 9. - 13. november.
 TFY0 Fysikk. Institutt for fysikk, NTNU. Høsten 05. Øving. Veiledning: 9. -. november. Opplysninger: Noe av dette kan du få bruk for: /πε 0 = 9 0 9 Nm /, e =.6 0 9, m e = 9. 0 kg, m p =.67 0 7 kg, g =
TFY0 Fysikk. Institutt for fysikk, NTNU. Høsten 05. Øving. Veiledning: 9. -. november. Opplysninger: Noe av dette kan du få bruk for: /πε 0 = 9 0 9 Nm /, e =.6 0 9, m e = 9. 0 kg, m p =.67 0 7 kg, g =
OPPGAVESETT 1. PS: Spørsmål 1a) og 1b) har ingenting med hverandre å gjøre. 1b) refererer til to nøytrale kuler, ikke kulene i 1a)
 Fasit for FYS1120-oppgaver H2010. OPPGAVESETT 1 1a) 9.88 10-7 C 1b) 891 PS: Spørsmål 1a) og 1b) har ingenting med hverandre å gjøre. 1b) refererer til to nøytrale kuler, ikke kulene i 1a) 2a) 7.25 10 24
Fasit for FYS1120-oppgaver H2010. OPPGAVESETT 1 1a) 9.88 10-7 C 1b) 891 PS: Spørsmål 1a) og 1b) har ingenting med hverandre å gjøre. 1b) refererer til to nøytrale kuler, ikke kulene i 1a) 2a) 7.25 10 24
Løsningsforslag til øving 13
 Institutt for fysikk, NTNU TFY4155/FY1003 Elektromagnetisme Vår 2009 Løsningsforslag til øving 13 Oppgave 1 a) Sløyfas magnetiske dipolmoment: m = IA ˆn = Ia 2 ˆn Sløyfa består av 4 rette ledere med lengde
Institutt for fysikk, NTNU TFY4155/FY1003 Elektromagnetisme Vår 2009 Løsningsforslag til øving 13 Oppgave 1 a) Sløyfas magnetiske dipolmoment: m = IA ˆn = Ia 2 ˆn Sløyfa består av 4 rette ledere med lengde
Midtsemesterprøve torsdag 7. mai 2009 kl
 Institutt for fysikk, NTNU FY1003 Elektrisitet og magnetisme TFY4155 Elektromagnetisme Våren 2009 Tillatte hjelpemidler: Midtsemesterprøve torsdag 7. mai 2009 kl 09.15 11.15. Oppgaver på side 5 10. Svartabell
Institutt for fysikk, NTNU FY1003 Elektrisitet og magnetisme TFY4155 Elektromagnetisme Våren 2009 Tillatte hjelpemidler: Midtsemesterprøve torsdag 7. mai 2009 kl 09.15 11.15. Oppgaver på side 5 10. Svartabell
EKSAMEN I FAG SIF 4012 ELEKTROMAGNETISME (SIF 4012 FYSIKK 2) Onsdag 11. desember kl Bokmål
 Side av 6 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 4 43 39 3 EKSAMEN I FAG SIF 42 ELEKTROMAGNETISME
Side av 6 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 4 43 39 3 EKSAMEN I FAG SIF 42 ELEKTROMAGNETISME
UNIVERSITETET I OSLO
 UNIVESITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS1120 Elektromagnetisme Eksamensdag: 29. November 2016 Tid for eksamen: 14.30 18.30 Oppgavesettet er på 3 sider. Vedlegg: Tillatte
UNIVESITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS1120 Elektromagnetisme Eksamensdag: 29. November 2016 Tid for eksamen: 14.30 18.30 Oppgavesettet er på 3 sider. Vedlegg: Tillatte
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME I TFY4155 ELEKTROMAGNETISME Fredag 8. juni 2007 kl
 NOGES TEKNISK- NATUVITENSKAPELIGE UNIVESITET INSTITUTT FO FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTISITET OG MAGNETISME I TFY4155
NOGES TEKNISK- NATUVITENSKAPELIGE UNIVESITET INSTITUTT FO FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTISITET OG MAGNETISME I TFY4155
Løsningsforslag til øving
 1 FY1002/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 2012. Løsningsforslag til øving 11-2012 Oppgave 1 a) Forplantning i z-retning betyr at E og B begge ligger i xy-planet. La oss for eksempel
1 FY1002/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 2012. Løsningsforslag til øving 11-2012 Oppgave 1 a) Forplantning i z-retning betyr at E og B begge ligger i xy-planet. La oss for eksempel
LØSNINGSFORSLAG TIL EKSAMEN I TFY4155 ELEKTROMAGNETISME FY1003 ELEKTRISITET OG MAGNETISME Tirsdag 30. mai 2006 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I TFY4155 ELEKTROMAGNETISME
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I TFY4155 ELEKTROMAGNETISME
Øving 1. Institutt for fysikk, NTNU TFY4155/FY1003: Elektromagnetisme. Veiledning: Mandag 19. januar Innleveringsfrist: Fredag 23. januar kl 12.
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektromagnetisme Vår 2009 Veiledning: Mandag 19. januar Innleveringsfrist: Fredag 23. januar kl 12.00 Øving 1 Oppgave 1 a) Komponentene av en vektor A er A =
Institutt for fysikk, NTNU TFY4155/FY1003: Elektromagnetisme Vår 2009 Veiledning: Mandag 19. januar Innleveringsfrist: Fredag 23. januar kl 12.00 Øving 1 Oppgave 1 a) Komponentene av en vektor A er A =
Flervalgsoppgaver. Gruppeøving 5 Elektrisitet og magnetisme
 Flervalgsoppgaver. Hvis en positiv ladning Q blir plassert i origo i figuren (i krysningspunktet mellom vertikal og horisontal linje), mot hvilken kvadrant vil den føle ei netto kraft? A. A B. B C. C D.
Flervalgsoppgaver. Hvis en positiv ladning Q blir plassert i origo i figuren (i krysningspunktet mellom vertikal og horisontal linje), mot hvilken kvadrant vil den føle ei netto kraft? A. A B. B C. C D.
LØSNINGSFORSLAG TIL EKSAMEN I TFY4155 ELEKTROMAGNETISME FY1003 ELEKTRISITET OG MAGNETISME Tirsdag 31. mai 2005 kl
 NORGES TEKNISK- NATURVITENSKAPEIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 ØSNINGSFORSAG TI EKSAMEN I TFY4155 EEKTROMAGNETISME
NORGES TEKNISK- NATURVITENSKAPEIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 ØSNINGSFORSAG TI EKSAMEN I TFY4155 EEKTROMAGNETISME
Mandag Ledere: Metaller. Atomenes ytterste elektron(er) er fri til å bevege seg gjennom lederen. Eksempler: Cu, Al, Ag etc.
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007, uke 7 Mandag 12.02.07 Materialer og elektriske egenskaper Hovedinndeling av materialer med hensyn på deres elektriske egenskaper:
Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007, uke 7 Mandag 12.02.07 Materialer og elektriske egenskaper Hovedinndeling av materialer med hensyn på deres elektriske egenskaper:
LØSNINGSFORSLAG TIL KONTINUASJONSEKSAMEN I TFY4155 ELEKTROMAGNETISME Onsdag 17. august 2005 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 LØSNINGSFORSLAG TIL KONTINUASJONSEKSAMEN I TFY4155
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 LØSNINGSFORSLAG TIL KONTINUASJONSEKSAMEN I TFY4155
LØSNINGSFORSLAG TIL EKSAMEN I FY1003 ELEKTRISITET OG MAGNETISME I Mandag 17. desember 2007 kl
 NOGES TEKNISK- NATUVITENSKAPELIGE UNIVESITET INSTITUTT FO FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFOSLAG TIL EKSAMEN I FY1003 ELEKTISITET OG
NOGES TEKNISK- NATUVITENSKAPELIGE UNIVESITET INSTITUTT FO FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFOSLAG TIL EKSAMEN I FY1003 ELEKTISITET OG
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME TFY4155 ELEKTROMAGNETISME Tirsdag 27. mai 2008 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME
TFY4104 Fysikk. Institutt for fysikk, NTNU. ving 11.
 TFY0 Fysikk. Institutt for fysikk, NTNU. ving. Opplysninger: Noe av dette kan du fa bruk for: =" 0 = 9 0 9 Nm /, e = :6 0 9, m e = 9: 0 kg, m p = :67 0 7 kg, g = 9:8 m/s Symboler angis i kursiv (f.eks
TFY0 Fysikk. Institutt for fysikk, NTNU. ving. Opplysninger: Noe av dette kan du fa bruk for: =" 0 = 9 0 9 Nm /, e = :6 0 9, m e = 9: 0 kg, m p = :67 0 7 kg, g = 9:8 m/s Symboler angis i kursiv (f.eks
To sider med formler blir delt ut i eksamenslokalet. Denne formelsamlingen finnes også på første side i oppgavesettet.
 Forside Midtveiseksamen i FYS 1120 Elektromagnetisme Torsdag 12. oktober kl. 09:00-12:00 (3 timer) Alle 18 oppgaver skal besvares. Lik vekt på alle oppgavene. Ikke minuspoeng for galt svar. Maksimum poengsum
Forside Midtveiseksamen i FYS 1120 Elektromagnetisme Torsdag 12. oktober kl. 09:00-12:00 (3 timer) Alle 18 oppgaver skal besvares. Lik vekt på alle oppgavene. Ikke minuspoeng for galt svar. Maksimum poengsum
Elektrisk og Magnetisk felt
 Elektrisk og Magnetisk felt Kjetil Liestøl Nielsen 1 Emner for i dag Coulombs lov Elektrisk felt Ladet partikkel i elektrisk felt Magnetisk felt Magnetisk kraft på elektrisk eladninger Elektromagnetiske
Elektrisk og Magnetisk felt Kjetil Liestøl Nielsen 1 Emner for i dag Coulombs lov Elektrisk felt Ladet partikkel i elektrisk felt Magnetisk felt Magnetisk kraft på elektrisk eladninger Elektromagnetiske
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME TFY4155 ELEKTROMAGNETISME Onsdag 3. juni 2009 kl
 NOGES TEKNISK- NATUVITENSKAPEIGE UNIVESITET INSTITUTT FO FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 EEKTISITET OG MAGNETISME TFY4155
NOGES TEKNISK- NATUVITENSKAPEIGE UNIVESITET INSTITUTT FO FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 EEKTISITET OG MAGNETISME TFY4155
Løsningsforslag, eksamen MA1103 Flerdimensjonal analyse, vår 2009
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 8 Løsningsforslag, eksamen MA1103 Flerdimensjonal analyse, vår 2009 Oppgave 1 Avgjør om grenseverdiene eksisterer:
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 8 Løsningsforslag, eksamen MA1103 Flerdimensjonal analyse, vår 2009 Oppgave 1 Avgjør om grenseverdiene eksisterer:
A. positiv x-retning B. negativ z-retning C. positiv y-retning D. negativ y-retning E. krafta er null
 Flervalgsoppgaver En lang, rett ledning langs x-aksen fører en strøm i positiv x-retning. En positiv punktladning beveger seg langs z-aksen i positiv z- 1. retning (opp av papirplanet). Den magnetiske
Flervalgsoppgaver En lang, rett ledning langs x-aksen fører en strøm i positiv x-retning. En positiv punktladning beveger seg langs z-aksen i positiv z- 1. retning (opp av papirplanet). Den magnetiske
Flervalgsoppgaver. Gruppeøving 8 Elektrisitet og magnetisme. 1. SI-enheten til magnetisk flukstetthet er tesla, som er ekvivalent med A. E.
 Flervalgsoppgaver 1. SI-enheten til magnetisk flukstetthet er tesla, som er ekvivalent med A. N s C m B. N C s m C. N m s 2 D. C A s E. Wb m 2 Løsning: F = q v B gir [B] = N Cm/s = N s C m. 2. Et elektron
Flervalgsoppgaver 1. SI-enheten til magnetisk flukstetthet er tesla, som er ekvivalent med A. N s C m B. N C s m C. N m s 2 D. C A s E. Wb m 2 Løsning: F = q v B gir [B] = N Cm/s = N s C m. 2. Et elektron
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MEK 11 Feltteori og vektoranalyse. Eksamensdag: Torsdag 1 desember 29. Tid for eksamen: 14:3 17:3. Oppgavesettet er på 7 sider.
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MEK 11 Feltteori og vektoranalyse. Eksamensdag: Torsdag 1 desember 29. Tid for eksamen: 14:3 17:3. Oppgavesettet er på 7 sider.
LØSNINGSFORSLAG TIL EKSAMEN I TFY4155 ELEKTROMAGNETISME Fredag 11. august 2006 kl
 NOGES TEKNISK- NATUVITENSKAPELIGE UNIVESITET INSTITUTT FO FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFOSLAG TIL EKSAMEN I TFY4155 ELEKTOMAGNETISME
NOGES TEKNISK- NATUVITENSKAPELIGE UNIVESITET INSTITUTT FO FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFOSLAG TIL EKSAMEN I TFY4155 ELEKTOMAGNETISME
EKSAMEN TFY4155 ELEKTROMAGNETISME FY1003 ELEKTRISITET OG MAGNETISME Tirsdag 30. mai 2006 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN TFY4155 ELEKTROMAGNETISME FY1003
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN TFY4155 ELEKTROMAGNETISME FY1003
Onsdag og fredag
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2009, uke 13 Onsdag 25.03.09 og fredag 27.03.09 Amperes lov [FGT 30.1, 30.3; YF 28.6, 28.7; AF 26.2; H 23.6; G 5.3] B dl = µ 0
Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2009, uke 13 Onsdag 25.03.09 og fredag 27.03.09 Amperes lov [FGT 30.1, 30.3; YF 28.6, 28.7; AF 26.2; H 23.6; G 5.3] B dl = µ 0
EKSAMEN I TFY4155 ELEKTROMAGNETISME OG FY1003 ELEKTRISITET OG MAGNETISME
 TFY4155/FY1003 31. mai 2010 Side 1 av 8 NOGS TKNSK-NATUVTNSKAPLG UNVSTT NSTTUTT FO FYSKK Kontakt under eksamen: Jon Andreas Støvneng, telefon: 45 45 55 33 / 73 59 36 63 KSAMN TFY4155 LKTOMAGNTSM OG FY1003
TFY4155/FY1003 31. mai 2010 Side 1 av 8 NOGS TKNSK-NATUVTNSKAPLG UNVSTT NSTTUTT FO FYSKK Kontakt under eksamen: Jon Andreas Støvneng, telefon: 45 45 55 33 / 73 59 36 63 KSAMN TFY4155 LKTOMAGNTSM OG FY1003
FYS1120 Elektromagnetisme H10 Midtveiseksamen
 FYS1120 Elektromagnetisme H10 Midtveiseksamen Oppgave 1 a) Vi ser i denne oppgave på elektroner som akselereres gjennom et elektrisk potensial slik at de oppnår en hastighet 1.410. Som vist på figuren
FYS1120 Elektromagnetisme H10 Midtveiseksamen Oppgave 1 a) Vi ser i denne oppgave på elektroner som akselereres gjennom et elektrisk potensial slik at de oppnår en hastighet 1.410. Som vist på figuren
Maxwell s ligninger og elektromagnetiske bølger
 Maxwell s ligninger og elektromagnetiske bølger I forelesningene og i læreboken er Coulombs lov for the elektriske felt E formulert på følgende form: v da E = Q/ε 0 (1) Integralet til venstre går over
Maxwell s ligninger og elektromagnetiske bølger I forelesningene og i læreboken er Coulombs lov for the elektriske felt E formulert på følgende form: v da E = Q/ε 0 (1) Integralet til venstre går over
Løsningsforslag TFE4120 Elektromagnetisme 13. mai 2004
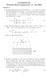 Løsningsforslag TFE4120 Elektromagnetisme 13. mai 2004 Oppgae 1 a) Speilladningsmetoden gir at potensialet for z > 0 er summen a potensialet pga ladningen Q i posisjon z = h og potensialet pga en speillanding
Løsningsforslag TFE4120 Elektromagnetisme 13. mai 2004 Oppgae 1 a) Speilladningsmetoden gir at potensialet for z > 0 er summen a potensialet pga ladningen Q i posisjon z = h og potensialet pga en speillanding
FYS1120 Elektromagnetisme
 Det matematisk-naturvitenskapelige fakultet Universitetet i Oslo FY112 Elektromagnetisme Løsningsforslag til ukesoppgave 1 Oppgave 1 a i Her er alternativ 1 riktig. Hvis massetettheten er F, vil et linjestykke
Det matematisk-naturvitenskapelige fakultet Universitetet i Oslo FY112 Elektromagnetisme Løsningsforslag til ukesoppgave 1 Oppgave 1 a i Her er alternativ 1 riktig. Hvis massetettheten er F, vil et linjestykke
b) Vi legger en uendelig lang, rett stav langs y-aksen. Staven har linjeladningen λ = [C/m].
![b) Vi legger en uendelig lang, rett stav langs y-aksen. Staven har linjeladningen λ = [C/m]. b) Vi legger en uendelig lang, rett stav langs y-aksen. Staven har linjeladningen λ = [C/m].](/thumbs/54/33413684.jpg) Oppgave 1 a) Punktladningen q 1 = 1.0 10 9 [C] ligger fast i punktet (2.0, 0, 0) [m]. Punktladningen q 2 = 4.0 10 9 [C] ligger i punktet ( 1.0, 0, 0) [m]. I) Finnes det punkt(er) i rommet med elektrisk
Oppgave 1 a) Punktladningen q 1 = 1.0 10 9 [C] ligger fast i punktet (2.0, 0, 0) [m]. Punktladningen q 2 = 4.0 10 9 [C] ligger i punktet ( 1.0, 0, 0) [m]. I) Finnes det punkt(er) i rommet med elektrisk
EKSAMENSOPPGAVE. Fys-1002 Elektromagnetisme. Adm.bygget B154 Kalkulator med tomt dataminne, Rottmann: Matematisk formelsamling
 Fakultet for naturvitenskap og teknologi EKSAMENSOPPGAE Eksamen i: Fys-1002 Elektromagnetisme Dato: Onsdag 26. september 2018 Klokkeslett: Kl. 9:00-13:00 Sted: Tillatte hjelpemidler: Adm.bygget B154 Kalkulator
Fakultet for naturvitenskap og teknologi EKSAMENSOPPGAE Eksamen i: Fys-1002 Elektromagnetisme Dato: Onsdag 26. september 2018 Klokkeslett: Kl. 9:00-13:00 Sted: Tillatte hjelpemidler: Adm.bygget B154 Kalkulator
EKSAMEN i TFY4155/FY1003 ELEKTRISITET OG MAGNETISME
 Side 1 av 8 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk BOKMÅL EKSAMEN i TFY4155/FY1003 ELEKTRISITET OG MAGNETISME Eksamensdato: Tirsdag 22 mai 2012 Eksamenstid: 09:00-13:00 Faglig
Side 1 av 8 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk BOKMÅL EKSAMEN i TFY4155/FY1003 ELEKTRISITET OG MAGNETISME Eksamensdato: Tirsdag 22 mai 2012 Eksamenstid: 09:00-13:00 Faglig
a) Bruk en passende Gaussflate og bestem feltstyrken E i rommet mellom de 2 kuleskallene.
 Oppgave 1 Bestem løsningen av differensialligningen Oppgave 2 dy dx + y = e x, y(1) = 1 e Du skal beregne en kulekondensator som består av 2 kuleskall av metall med samme sentrum. Det indre skallet har
Oppgave 1 Bestem løsningen av differensialligningen Oppgave 2 dy dx + y = e x, y(1) = 1 e Du skal beregne en kulekondensator som består av 2 kuleskall av metall med samme sentrum. Det indre skallet har
Fasit til eksamen i MEK1100 høst 2006
 Fasit til eksamen i MEK11 høst 26 Det er tilsammen 1 delspørsmål. Hvert delspørsmål honoreres med poengsum fra til 1 (1 for fullstendig svar, for blank). Maksimal oppnåelig poengsum er 1. Kontroller at
Fasit til eksamen i MEK11 høst 26 Det er tilsammen 1 delspørsmål. Hvert delspørsmål honoreres med poengsum fra til 1 (1 for fullstendig svar, for blank). Maksimal oppnåelig poengsum er 1. Kontroller at
EKSAMEN TFY4155 ELEKTROMAGNETISME FY1003 ELEKTRISITET OG MAGNETISME Tirsdag 31. mai 2005 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 EKSAMEN TFY4155 ELEKTROMAGNETISME FY1003
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 EKSAMEN TFY4155 ELEKTROMAGNETISME FY1003
Løsningsforslag TFE4120 Elektromagnetisme 29. mai 2017
 Norges teknisk naturvitenskapelige universitet Institutt for elektroniske systemer Side 1 av 6 Løsningsforslag TFE4120 Elektromagnetisme 29. mai 2017 Oppgave 1 a) Start med å tegne figur! Tegn inn en Gauss-flate
Norges teknisk naturvitenskapelige universitet Institutt for elektroniske systemer Side 1 av 6 Løsningsforslag TFE4120 Elektromagnetisme 29. mai 2017 Oppgave 1 a) Start med å tegne figur! Tegn inn en Gauss-flate
TFY4104 Fysikk. Institutt for fysikk, NTNU. Høsten Løsningsforslag til øving 8. a = e m E
 TFY414 Fysikk. Institutt for fysikk, NTNU. Høsten 16. Løsningsforslg til øving 8. Oppgve 1. ) C F = E = m Newtons. lov. Her er = e, så elektronets kselersjon blir = e m E ltså mot venstre. b) C Totlt elektrisk
TFY414 Fysikk. Institutt for fysikk, NTNU. Høsten 16. Løsningsforslg til øving 8. Oppgve 1. ) C F = E = m Newtons. lov. Her er = e, så elektronets kselersjon blir = e m E ltså mot venstre. b) C Totlt elektrisk
EKSAMEN i TFY4155/FY1003 ELEKTRISITET OG MAGNETISME
 Side 1 av 7 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk BOKMÅL EKSAMEN i TFY4155/FY1003 ELEKTRISITET OG MAGNETISME Eksamensdato: Tirsdag 24 mai 2011 Eksamenstid: 09:00-13:00 Faglig
Side 1 av 7 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk BOKMÅL EKSAMEN i TFY4155/FY1003 ELEKTRISITET OG MAGNETISME Eksamensdato: Tirsdag 24 mai 2011 Eksamenstid: 09:00-13:00 Faglig
FYS1120 Elektromagnetisme
 Det matematisk-naturvitenskapelige fakultet Universitetet i Oslo FYS112 Elektromagnetisme Løsningsforslag til ukesoppgave 2 Oppgave 1 a) Gauss lov sier at den elektriske fluksen Φ er lik den totale ladningen
Det matematisk-naturvitenskapelige fakultet Universitetet i Oslo FYS112 Elektromagnetisme Løsningsforslag til ukesoppgave 2 Oppgave 1 a) Gauss lov sier at den elektriske fluksen Φ er lik den totale ladningen
TFY4104 Fysikk. Institutt for fysikk, NTNU. Høsten Øving 12.
 TFY0 Fsikk. nstitutt for fsikk, NTNU. Høsten 06. Øving. Oppgave Partikler med masse m, ladning q og hastighet v kommer inn i et område med krsset elektrisk og magnetisk felt, E og, som vist i figuren.
TFY0 Fsikk. nstitutt for fsikk, NTNU. Høsten 06. Øving. Oppgave Partikler med masse m, ladning q og hastighet v kommer inn i et område med krsset elektrisk og magnetisk felt, E og, som vist i figuren.
3. Hvilken av Maxwells ligninger beskriver hvordan en leder som fører en jevn strøm genererer et magnetisk felt?
 Flervalgsoppgaver 1. En stavmagnet slippes gjennom ei strømsløyfe som vist i venstre del av figuren under. Pilene i sløyfa viser valgt positiv strømretning. Husk at magnetiske feltlinjer går ut fra nordpol
Flervalgsoppgaver 1. En stavmagnet slippes gjennom ei strømsløyfe som vist i venstre del av figuren under. Pilene i sløyfa viser valgt positiv strømretning. Husk at magnetiske feltlinjer går ut fra nordpol
Løsningsforslag til øving 9
 FY1002/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 2010. Løsningsforslag til øving 9 Oppgave 1 a) Forplantning i z-retning betyr at E og B begge ligger i xy-planet. La oss for eksempel velge
FY1002/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 2010. Løsningsforslag til øving 9 Oppgave 1 a) Forplantning i z-retning betyr at E og B begge ligger i xy-planet. La oss for eksempel velge
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS1120 Elektromagnetisme Eksamensdag: Prøveeksamen 2017 Oppgavesettet er på 9 sider Vedlegg: Tillatte hjelpemidler: Formelark
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS1120 Elektromagnetisme Eksamensdag: Prøveeksamen 2017 Oppgavesettet er på 9 sider Vedlegg: Tillatte hjelpemidler: Formelark
Fjæra i a) kobles sammen med massen m = 100 [kg] og et dempeledd med dempningskoeffisient b til en harmonisk oscillator.
![Fjæra i a) kobles sammen med massen m = 100 [kg] og et dempeledd med dempningskoeffisient b til en harmonisk oscillator. Fjæra i a) kobles sammen med massen m = 100 [kg] og et dempeledd med dempningskoeffisient b til en harmonisk oscillator.](/thumbs/34/17139427.jpg) Oppgave 1 a) Ei ideell fjær har fjærkonstant k = 2.60 10 3 [N/m]. Finn hvilken kraft en må bruke for å trykke sammen denne fjæra 0.15 [m]. Fjæra i a) kobles sammen med massen m = 100 [kg] og et dempeledd
Oppgave 1 a) Ei ideell fjær har fjærkonstant k = 2.60 10 3 [N/m]. Finn hvilken kraft en må bruke for å trykke sammen denne fjæra 0.15 [m]. Fjæra i a) kobles sammen med massen m = 100 [kg] og et dempeledd
LØSNINGSFORSLAG EKSAMEN TMA4105 MATEMATIKK 2 Lørdag 14. aug 2004
 Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag ide av LØNINGFOLAG EKAMEN TMA4 MATEMATIKK 2 Lørdag 4. aug 24 Oppgave Grenseverdien eksisterer ikke. For eksempel er grenseverdien
Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag ide av LØNINGFOLAG EKAMEN TMA4 MATEMATIKK 2 Lørdag 4. aug 24 Oppgave Grenseverdien eksisterer ikke. For eksempel er grenseverdien
Løsningsforslag, Midtsemesterprøve torsdag 6. mars 2008 kl Oppgavene med kort løsningsskisse
 Institutt for fysikk, NTNU FY1003 Elektrisitet og mgnetisme TFY4155 Elektromgnetisme Vår 2008 Løsningsforslg, Midtsemesterprøve torsdg 6. mrs 2008 kl 1000 1200. Fsit side 12. Oppgvene med kort løsningsskisse
Institutt for fysikk, NTNU FY1003 Elektrisitet og mgnetisme TFY4155 Elektromgnetisme Vår 2008 Løsningsforslg, Midtsemesterprøve torsdg 6. mrs 2008 kl 1000 1200. Fsit side 12. Oppgvene med kort løsningsskisse
FYS1120 Elektromagnetisme - Ukesoppgavesett 2
 FYS1120 Elektromagnetisme - Ukesoppgavesett 2 7. september 2016 I FYS1120-undervisningen legger vi mer vekt på matematikk og numeriske metoder enn det oppgavene i læreboka gjør. Det gjelder også oppgavene
FYS1120 Elektromagnetisme - Ukesoppgavesett 2 7. september 2016 I FYS1120-undervisningen legger vi mer vekt på matematikk og numeriske metoder enn det oppgavene i læreboka gjør. Det gjelder også oppgavene
Ma Flerdimensjonal Analyse II Øving 9
 Ma23 - Flerdimensjonal Analyse II Øving 9 Øistein Søvik 2.3.22 Oppgaver 4.5 Evaluate the triple integrals over the indicated region. Be alert for simplifications and auspicious orders of integration 3.
Ma23 - Flerdimensjonal Analyse II Øving 9 Øistein Søvik 2.3.22 Oppgaver 4.5 Evaluate the triple integrals over the indicated region. Be alert for simplifications and auspicious orders of integration 3.
Fysikkolympiaden Norsk finale 2017
 Norsk fysikklærerforening Fysikkolympiaden Norsk finale 7 Fredag. mars kl. 8. til. Hjelpemidler: abell/formelsamling, lommeregner og utdelt formelark Oppgavesettet består av 6 oppgaver på sider Lykke til!
Norsk fysikklærerforening Fysikkolympiaden Norsk finale 7 Fredag. mars kl. 8. til. Hjelpemidler: abell/formelsamling, lommeregner og utdelt formelark Oppgavesettet består av 6 oppgaver på sider Lykke til!
Bølgeledere. Figur 1: Eksempler på bølgeledere. (a) parallell to-leder (b) koaksial (c) hul rektangulær (d) hul sirkulær (e) hul, generell form
 Bølgeledere Vi skal se hvordan elektromagnetiske bølger forplanter seg gjennom såkalte bølgeledere. Eksempel på bølgeledere vi kjenner fra tidligere som transportrerer elektromagnetiske bølger er fiberoptiske
Bølgeledere Vi skal se hvordan elektromagnetiske bølger forplanter seg gjennom såkalte bølgeledere. Eksempel på bølgeledere vi kjenner fra tidligere som transportrerer elektromagnetiske bølger er fiberoptiske
EKSAMENSOPPGAVE. Tillatte hjelpemidler: Kalkulator med tomt dataminne, Rottmann: Matematisk formelsamling.
 EKSAMENSOPPGAE Eksamen i: FYS-1002 Dato: Mandag 4. juni, 2018 Klokkeslett: 9:00 13:00 Sted: ADM B154 Tillatte hjelpemidler: Kalkulator med tomt dataminne, Rottmann: Matematisk formelsamling. Eksamenoppgaven
EKSAMENSOPPGAE Eksamen i: FYS-1002 Dato: Mandag 4. juni, 2018 Klokkeslett: 9:00 13:00 Sted: ADM B154 Tillatte hjelpemidler: Kalkulator med tomt dataminne, Rottmann: Matematisk formelsamling. Eksamenoppgaven
Øving 15. H j B j M j
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007 Veiledning: Uke 17 Innleveringsfrist: Mandag 30. april Øving 15 Oppgave 1 H j j M j H 0 0 M 0 I En sylinderformet jernstav
Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007 Veiledning: Uke 17 Innleveringsfrist: Mandag 30. april Øving 15 Oppgave 1 H j j M j H 0 0 M 0 I En sylinderformet jernstav
Eksamensoppgave i TFY4155 ELEKTRISITET OG MAGNETISME FY1003 ELEKTRISITET OG MAGNETISME
 Institutt for fysikk Eksamensoppgave i TFY455 ELEKTRISITET OG MAGNETISME FY003 ELEKTRISITET OG MAGNETISME Faglig kontakt under eksamen: Institutt for fysikk v/arne Mikkelsen, Tlf: 486 05 392 / 7359 3433
Institutt for fysikk Eksamensoppgave i TFY455 ELEKTRISITET OG MAGNETISME FY003 ELEKTRISITET OG MAGNETISME Faglig kontakt under eksamen: Institutt for fysikk v/arne Mikkelsen, Tlf: 486 05 392 / 7359 3433
E, B. q m. TFY4104 Fysikk. Institutt for fysikk, NTNU. ving 12.
 TFY4104 Fsikk. nstitutt for fsikk, NTNU. ving 12. Oppgave 1 Partikler med masse m, ladning q og hastighet v kommer inn i et omrade med "krsset" elektrisk og magnetisk felt, E og, som vist i guren. E har
TFY4104 Fsikk. nstitutt for fsikk, NTNU. ving 12. Oppgave 1 Partikler med masse m, ladning q og hastighet v kommer inn i et omrade med "krsset" elektrisk og magnetisk felt, E og, som vist i guren. E har
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Ola Hunderi, tlf (mobil: )
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Ola Hunderi, tlf. 93411 (mobil: 95143671) Eksamen TFY 4240: Elektromagnetisk teori Torsdag 1 desember
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Ola Hunderi, tlf. 93411 (mobil: 95143671) Eksamen TFY 4240: Elektromagnetisk teori Torsdag 1 desember
MA1102 Grunnkurs i analyse II Vår 2019
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA1102 Grunnkurs i analyse II Vår 2019 Først en kommentar. I læreboka møter man kjeglesnitt på standardform, som ellipser x
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA1102 Grunnkurs i analyse II Vår 2019 Først en kommentar. I læreboka møter man kjeglesnitt på standardform, som ellipser x
Magnetisme som relativistisk fenomen
 Magnetisme som relativistisk fenomen Øystein Marøy Lars Kyllingstad 23. april 2004 Sammendrag I denne oppgaven har vi sett på magnetisme som et resultat av elektrostatikk og relativitetsteori. Vi har regnet
Magnetisme som relativistisk fenomen Øystein Marøy Lars Kyllingstad 23. april 2004 Sammendrag I denne oppgaven har vi sett på magnetisme som et resultat av elektrostatikk og relativitetsteori. Vi har regnet
FY2045/TFY4250 Kvantemekanikk I, løsning øving 14 1 LØSNING ØVING 14. ψ 210 z ψ 100 d 3 r a.
 FY45/TFY45 Kvantemekanikk I, løsning øving 14 1 LØSNING ØVING 14 Løsning Oppgave 14 1 Fra oppg 3, eksamen august 1 a. Med Y = 1/ 4π og zy = ry 1 / 3 kan vi skrive matrise-elementene av z på formen (z)
FY45/TFY45 Kvantemekanikk I, løsning øving 14 1 LØSNING ØVING 14 Løsning Oppgave 14 1 Fra oppg 3, eksamen august 1 a. Med Y = 1/ 4π og zy = ry 1 / 3 kan vi skrive matrise-elementene av z på formen (z)
Løsningsforslag eksamen TMA4105 matematikk 2, 25. mai 2005
 Løsningsforslag eksamen TMA5 matematikk, 5. mai 5 Oppgave Vi finner de partiellderiverte av første og annen orden av f, ) = sin : f = sin, f = cos, f =, f = cos, f = sin. Finner de kritiske punktene ved
Løsningsforslag eksamen TMA5 matematikk, 5. mai 5 Oppgave Vi finner de partiellderiverte av første og annen orden av f, ) = sin : f = sin, f = cos, f =, f = cos, f = sin. Finner de kritiske punktene ved
Kap. 22. Gauss lov. Gauss lov skjematisk. Eks.1: Homogent ladd kule =Y&F Ex = LHL Vi skal se på: Fluksen til elektrisk felt E Gauss lov
 Kap.. Gauss lov Vi skal se på: Fluksen til elektisk felt E Gauss lov Integalfom og diffeensialfom Elektisk ledee. Efelt fa Coulombs lov: q E = k E = k å n q n n n dq E= k ò tot. ladn. Punktladn Flee punktladn.
Kap.. Gauss lov Vi skal se på: Fluksen til elektisk felt E Gauss lov Integalfom og diffeensialfom Elektisk ledee. Efelt fa Coulombs lov: q E = k E = k å n q n n n dq E= k ò tot. ladn. Punktladn Flee punktladn.
LØSNINGSFORSLAG TIL ØVING 11, TMA4105, V2008. x = r cos θ, y = r sin θ, z = 2r for 0 θ 2π, 2 2r 6. i j k. 5 r dr dθ = 8
 LØNINGFORLAG TIL ØVING, TMA45, V8 Oppgave 4.5.9. Parametrisering: x = r cos θ, y = r sin θ, z = r for θ π, r 6. r(r, θ) = r cos θ, r sin θ, r. N = r r r θ = cos θ sin θ = r cos θ, r sin θ, r. r sin θ r
LØNINGFORLAG TIL ØVING, TMA45, V8 Oppgave 4.5.9. Parametrisering: x = r cos θ, y = r sin θ, z = r for θ π, r 6. r(r, θ) = r cos θ, r sin θ, r. N = r r r θ = cos θ sin θ = r cos θ, r sin θ, r. r sin θ r
Kap. 6 Ortogonalitet og minste kvadrater
 Kap. 6 Ortogonalitet og minste kvadrater IR n er mer enn bare et vektorrom: den har et naturlig indreprodukt, nemlig prikkproduktet av vektorer. Dette indreproduktet gjør det mulig å tenke geometrisk og
Kap. 6 Ortogonalitet og minste kvadrater IR n er mer enn bare et vektorrom: den har et naturlig indreprodukt, nemlig prikkproduktet av vektorer. Dette indreproduktet gjør det mulig å tenke geometrisk og
