Løsningsforslag til øving 4
|
|
|
- Maria Isaksen
- 7 år siden
- Visninger:
Transkript
1 Institutt for fysikk, NTNU TFY455/FY003 Elektrisitet og magnetisme Vår 2007 Veiledning uke 5 Løsningsforslag til øving 4 Oppgave a) Vi benytter oss av tipsene gitt i oppgaveteksten og tar utgangspunkt i figuren fra ukentlig sammendrag uke 3 : Volumelement dv i kulekoordinater: z d dl dr r^ ϕ^ ^ r d r sin dϕ r r cos y r^ ^ dv ϕ^ d r d ϕ ϕ dϕ d x ρ = r sin ρ dϕ = r sin dϕ dv = (dr) (r d ) (r sin d ϕ) I figuren har vi tegnet inn et veielement dl, som i kulekoordinater, i sin mest generelle form, består av en forflytning langs de tre ortogonale retningene spesifisert ved de ovenfor nevnte enhetsvektorer. Vi ser at en slik forflytning, fra punktet (r,, φ) til punktet (r+dr, +d, φ+dφ), nettopp tilsvarer vektoren dl diagonalt gjennom volumelementet dv. Vi ser av figuren at denne vektoren har komponenter dr langs ˆr, r d langs ˆ og r sin dφ langs ˆφ. ltså: dl = dr ˆr + r d ˆ + r sin dφ ˆφ Legg merke til at mens komponentene til vektoren dl i kartesiske koordinater alltid er de samme (dx, dy, dz), avhenger to av dem av hvor vi er i kulekoordinater: Komponenten langs ˆ er proporsjonal med r, dvs avstanden til origo, mens komponenten langs ˆφ i tillegg avhenger av vinkelen (dvs breddegraden, hvis vi tenker oss z-aksen gjennom polene og ekvator i xyplanet). F.eks. er dl φ = r sin 0 = 0 hvis vi starter i = 0. Ikke urimelig: Står vi på en av polene, vil et lite skritt alltid bli i retning sørover (evt nordover), aldri østover eller vestover. Står vi på ekvator, derimot, dvs i = π/2, blir dl φ = r sin π/2 dφ = r dφ. Ikke urimelig det
2 heller: Her er øst, vest, sør og nord likeverdige retninger, så dl = r d og dl φ = r dφ bør her være på samme form. Fra figuren finner vi videre de tre flateelementene med flatenormaler henholdsvis langs ˆr, ˆ og ˆφ: d r d d φ = (r d)(r sin dφ)ˆr = r 2 sin d dφ ˆr = (dr)(r sin dφ)ˆ = r dr sin dφ ˆ = (dr)(r d)ˆφ = r dr d ˆφ Merk at disse tre er vektorer, med absoluttverdi lik arealet av flateelementet (f.eks. d r ) og retning normalt på flaten (f.eks. ˆr). Vi trenger både størrelse og orientering for å gi en presis beskrivelse av en flate! Endelig ser vi at volumelementet må bli dv = (dr)(r d)(r sin dφ) = r 2 dr sin d dφ b) Volumet av ei kule med radius R finner vi ved å integrere volumelementet dv over alle verdier av og φ og r fra 0 til R: V (R) = r<r dv = R = 3 R3 2 2π = 4π 3 R3 0 π 2π r 2 dr sin d dφ 0 0 Merk at når vi integrerer over φ fra 0 til 2π, må vi integrere over fra 0 til π, og ikke 2π, for å dekke alle romvinkler ( retninger ) en gang, og ikke to. realet av ei kuleflate med radius R finner vi ved å integrere flateelementet d r (altså absoluttverdien av d r ) over alle verdier av og φ med r = R: (R) = r=r d r = R 2 π 0 2π sin d dφ = R 2 2 2π = 4πR 2 0 c) Den oppgitte ladningstettheten er positiv (eller null) overalt inne i kula. Den vokser lineært med avstanden fra kulas sentrum. Videre fører leddet cos 2 til størst ladningstetthet på de to polene (dvs = 0 eller = π) og minst ladningstetthet (null) i ekvatorplanet (dvs = π/2). Et lite volumelement dv av kula inneholder en ladning d = ρ dv Kulas totale ladning får vi ved å integrere d over kulas volum. Vi bruker uttrykket for dv fra punkt a) og får: 2
3 Q = = R d r=0 π =0 = ρ 0 ( R = ρ 0 R 0 r=0 2π r ρ 0 R cos2 r 2 dr sin d dφ φ=0 ) ( π r 3 R dr r 4 4R π 0 = ρ 0 R π = ρ 0πR 3 3 cos 2 sin d =0 ) ( 3 cos3 2π 0 φ ) ( 2π Har vi regnet riktig? Vel, vi har i hvert fall riktig dimensjon: Ladning pr volumenhet ρ 0 ganget med en faktor R 3, som har dimensjon som et volum. Med andre ord: Intet mystisk med slike flerdimensjonale integraler: Det er bare å integrere over hver integrasjonsvariabel for seg. Her var integranden hele tiden uavhengig av vinkelen φ, så integralet over den gav bare en faktor 2π. Videre var selvsagt -avhengigheten i ρ i den siste oppgaven valgt med omhu, slik at vi fikk et enkelt løsbart integral over variabelen. Legg videre merke til at vi som regel ikke gidder å skrive dv, men simpelthen dv, selv om det altså er tre integrasjoner involvert. Det vil alltid gå fram av sammenhengen om det er en linje, en flate eller et volum vi skal integrere over. Oppgave 2 Potensialforskjellen V mellom to punkter er gitt ved V = V B V = E dl φ=0 ) dφ I denne oppgaven har vi et uniformt elektrisk felt E = E 0 ˆx, så vi kan skrive V = E 0 ˆx der punktet er origo, (0, 0) og B er de tre punktene gitt i oppgaveteksten. Vi får: (i) slik at dl = (a,0) (0,0) dl dl = a ˆx V = E 0 ˆx a ˆx = E 0 a (ii) dl = (0,a) (0,0) dl = a ŷ 3
4 slik at (iii) slik at V = E 0 ˆx a ŷ = 0 dl = (a,a) (0,0) dl = a ˆx + a ŷ V = E 0 ˆx (a ˆx + a ŷ) = E 0 a Oppgave 3 a) Med vårt valg av polarvinkel ser vi fra figuren at x = r sin z = r cos r = x 2 + z 2 b) Vi bruker superposisjonsprinsippet for å bestemme potensialet fra de to punktladningene. Med punktet (x, z) i en avstand r fra og en avstand r 2 fra får vi V (x, z) = = 4πε 0 r 4πε 0 r 2 4πε 0 x 2 + (z a/2) 2 x 2 + (z + a/2) 2 vstandene r og r 2 uttrykt ved x og z ser vi direkte fra figuren. Potensialet på x-aksen blir V (x, 0) = 4πε 0 x 2 + a 2 /4 = 0 x 2 + a 2 /4 Potensialet på z-aksen blir V (0, z) = ( ) 4πε 0 z a/2 z + a/2 Legg merke til at vi her må bruke absoluttverditegn hvis vi vil ha ett uttrykk som gjelder på hele z-aksen. Med z > a/2: Med z < a/2: z a/2 z + a/2 = z a/2 z + a/2 = a z 2 a 2 /4 z a/2 z + a/2 = z a/2 + z + a/2 = a z 2 a 2 /4 4
5 Med a/2 < z < a/2: Skisse av V (0, z): z a/2 z + a/2 = z a/2 z + a/2 = 2z z 2 a 2 /4 = 2z a 2 /4 z 2 V(0,z) a/2 a/2 z c) Vi bruker tipset gitt i oppgaveteksten, samt betraktning av følgende figur, og får: z V =? r p r^ a r r 2 x a cos r 2 r ( V (r, ) = ) 4πε 0 r r 2 = r2 r 4πε 0 r r 2 a cos 4πε 0 r 2 = p cos 4πε 0 r 2 pr cos = 4πε 0 r 3 = p r 4πε 0 r 3 5
6 Vi kan alternativt gå litt saktere fram: Fra figuren ser vi at r r a 2 cos r 2 r + a 2 cos Når r a kan vi rekkeutvikle både /r og /r 2 omkring /r og får: r r 2 r a cos r + a cos 2 2 = ( a cos ) ( + a cos ) r [ + a cos + a cos ] r = a cos r 2 Er det så rimelig at potensialet fra en elektrisk dipol faller av raskere enn potensialet fra en punktladning (dvs en elektrisk monopol )? Det er det, fordi dipolens negative og positive ladning bidrar med motsatt fortegn til det totale potensialet. Dermed vil bidragene til potensialet fra de to punktladningene delvis oppheve hverandre. (På x-aksen vil de to bidragene eksakt oppheve hverandre.) Ekstranøtten (ikke så viktig, mest for moro skyld ): I første omgang kunne en kanskje tenke seg å fortsette rekkeutviklingen ovenfor, og ta med så mange ledd at vi får tak i dominerende korreksjon. Tar vi med ett ledd til, får vi ingenting nytt, i og med at det neste leddet vil opptre to ganger og med motsatt fortegn og dermed kansellere. Vi må ta med to ledd til: r = r ( = a cos r 2 = a cos r 2 a cos + a cos ) ( + a cos ) ( ) 2 ( ) 3 a cos a cos a3 cos ( 4r 4 a2 cos 2 ) r 2 a cos ( ) 2 ( ) 3 a cos a cos Her brukte vi rekkeutviklingen ( + x) = x + x 2 x (som gjelder når x < ). Ikke noe dårlig forsøk dette, men det er en liten hake ved det hele: Utgangspunktet for hele rekkeutviklingen var i seg selv en tilnærmelse, nemlig r r a 2 cos r 2 r + a 2 cos 6
7 Og feilen vi gjør i disse tilnærmelsene er av samme størrelsesorden som det korreksjonsleddet vi er på jakt etter! Løsningen ligger i å gå helt tilbake til det eksakte uttrykket for V, med r og r 2 uttrykt ved de kartesiske koordinatene x og z. Regningen er ikke direkte vanskelig, men såpass kronglete at jeg ikke tror jeg tar med noen flere detaljer her. Hvis jeg har regnet riktig, hvilket på ingen måte er sikkert, blir svaret = a cos [ ( 3a2 5 ) ] r r 2 r 2 8r 2 3 cos Her har vi tatt med alle korreksjoner som er en størrelsesorden a 2 /r 2 mindre enn det dominerende bidraget. Neste ledd i rekken vil bli ytterligere redusert, med en eller annen potens av den lille størrelsen a/r. Det første leddet som vi ikke tar med vil alltid være neglisjerbart i forhold til det siste leddet som vi tar med. (I vårt spesielle tilfelle, med unntak av retninger gitt ved cos 2 3/5, der vi ser at første korreksjonsledd faktisk forsvinner.) 7
Løsningsforslag til øving 3
 Institutt for fysikk, NTNU TFY455/FY003 Elektromagnetisme Vår 2009 Løsningsforslag til øving 3 Oppgave a) C V = E dl = 0 dersom dl E b) B På samme måte som et legeme med null starthastighet faller i gravitasjonsfeltet
Institutt for fysikk, NTNU TFY455/FY003 Elektromagnetisme Vår 2009 Løsningsforslag til øving 3 Oppgave a) C V = E dl = 0 dersom dl E b) B På samme måte som et legeme med null starthastighet faller i gravitasjonsfeltet
Øving 3. Oppgave 1 (oppvarming med noen enkle oppgaver fra tidligere midtsemesterprøver)
 Institutt for fysikk, NTNU TFY455/FY003: Elektrisitet og magnetisme Vår 2008 Veiledning: Fredag 25. og mandag 28. januar Innleveringsfrist: Fredag. februar kl 2.00 Øving 3 Oppgave (oppvarming med noen
Institutt for fysikk, NTNU TFY455/FY003: Elektrisitet og magnetisme Vår 2008 Veiledning: Fredag 25. og mandag 28. januar Innleveringsfrist: Fredag. februar kl 2.00 Øving 3 Oppgave (oppvarming med noen
Elektrisk potensial/potensiell energi
 Elektrisk potensial/potensiell energi. Figuren viser et uniformt elektrisk felt E heltrukne linjer. Langs hvilken stiplet linje endrer potensialet seg ikke? A. B. C. 3 D. 4 E. Det endrer seg langs alle
Elektrisk potensial/potensiell energi. Figuren viser et uniformt elektrisk felt E heltrukne linjer. Langs hvilken stiplet linje endrer potensialet seg ikke? A. B. C. 3 D. 4 E. Det endrer seg langs alle
Onsdag og fredag
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2009, uke 4 Onsdag 21.01.09 og fredag 23.01.09 Elektrisk felt fra punktladning [FGT 22.1; YF 21.4; TM 21.4; AF 21.6; LHL 19.5;
Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2009, uke 4 Onsdag 21.01.09 og fredag 23.01.09 Elektrisk felt fra punktladning [FGT 22.1; YF 21.4; TM 21.4; AF 21.6; LHL 19.5;
TFY4104 Fysikk. Institutt for fysikk, NTNU. Høsten Løsningsforslag til øving 9. E dl = 0. q i q j 4πε 0 r ij. U = i<j
 TFY404 Fysikk. Institutt for fysikk, NTNU. Høsten 207. Løsningsforslag til øving 9. Oppgave. a) C V = E dl = 0 dersom dl E b) B U = e2 4πε 0 r = e e 4πε 0 r = e.6 0 9 9 0 9 0 0 = 4.4 ev c) D Total potensiell
TFY404 Fysikk. Institutt for fysikk, NTNU. Høsten 207. Løsningsforslag til øving 9. Oppgave. a) C V = E dl = 0 dersom dl E b) B U = e2 4πε 0 r = e e 4πε 0 r = e.6 0 9 9 0 9 0 0 = 4.4 ev c) D Total potensiell
Mandag qq 4πε 0 r 2 ˆr F = Elektrisk felt fra punktladning q (følger av definisjonen kraft pr ladningsenhet ): F dl
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007, uke 6 Mandag 05.02.07 Oppsummering til nå, og møte med Maxwell-ligning nr 1 Coulombs lov (empirisk lov for kraft mellom to
Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007, uke 6 Mandag 05.02.07 Oppsummering til nå, og møte med Maxwell-ligning nr 1 Coulombs lov (empirisk lov for kraft mellom to
Tirsdag E = F q. q 4πε 0 r 2 ˆr E = E j = 1 4πε 0. 2 j. r 1. r n
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2008, uke 3 Tirsdag 15.01.07 Elektrisk felt [FGT 22.1; YF 21.4; TM 21.4; AF 21.5; LHL 19.4; DJG 2.1.3] = kraft pr ladningsenhet
Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2008, uke 3 Tirsdag 15.01.07 Elektrisk felt [FGT 22.1; YF 21.4; TM 21.4; AF 21.5; LHL 19.4; DJG 2.1.3] = kraft pr ladningsenhet
Mandag Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007, uke 4
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007, uke 4 Mandag 22.01.07 Elektriske feltlinjer [FGT 22.2; YF 21.6; TM 21.5; F 21.6; LHL 19.6; DJG 2.2.1] gir en visuell framstilling
Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007, uke 4 Mandag 22.01.07 Elektriske feltlinjer [FGT 22.2; YF 21.6; TM 21.5; F 21.6; LHL 19.6; DJG 2.2.1] gir en visuell framstilling
1. En tynn stav med lengde L har uniform ladning λ per lengdeenhet. Hvor mye ladning dq er det på en liten lengde dx av staven?
 Ladet stav 1 En tynn stav med lengde L har uniform ladning per lengdeenhet Hvor mye ladning d er det på en liten lengde d av staven? A /d B d C 2 d D d/ E L d Løsning: Med linjeladning (dvs ladning per
Ladet stav 1 En tynn stav med lengde L har uniform ladning per lengdeenhet Hvor mye ladning d er det på en liten lengde d av staven? A /d B d C 2 d D d/ E L d Løsning: Med linjeladning (dvs ladning per
Midtsemesterprøve fredag 10. mars kl
 Institutt for fysikk, NTNU FY1003 Elektrisitet og magnetisme TFY4155 Elektromagnetisme Vår 2006 Midtsemesterprøve fredag 10. mars kl 0830 1130. Løsningsforslag 1) A. (Andel som svarte riktig: 83%) Det
Institutt for fysikk, NTNU FY1003 Elektrisitet og magnetisme TFY4155 Elektromagnetisme Vår 2006 Midtsemesterprøve fredag 10. mars kl 0830 1130. Løsningsforslag 1) A. (Andel som svarte riktig: 83%) Det
FYS1120 Elektromagnetisme
 Det matematisk-naturvitenskapelige fakultet Universitetet i Oslo FY112 Elektromagnetisme Løsningsforslag til ukesoppgave 1 Oppgave 1 a i Her er alternativ 1 riktig. Hvis massetettheten er F, vil et linjestykke
Det matematisk-naturvitenskapelige fakultet Universitetet i Oslo FY112 Elektromagnetisme Løsningsforslag til ukesoppgave 1 Oppgave 1 a i Her er alternativ 1 riktig. Hvis massetettheten er F, vil et linjestykke
Tirsdag r r
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2008, uke 6 Tirsdag 05.02.08 Gauss lov [FGT 23.2; YF 22.3; TM 22.2, 22.6; AF 25.4; LHL 19.7; DJG 2.2.1] Fra forrige uke; Gauss
Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2008, uke 6 Tirsdag 05.02.08 Gauss lov [FGT 23.2; YF 22.3; TM 22.2, 22.6; AF 25.4; LHL 19.7; DJG 2.2.1] Fra forrige uke; Gauss
Onsdag og fredag
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2009, uke 7 Onsdag 11.02.09 og fredag 13.02.09 Gauss lov [FGT 23.2; YF 22.3; TM 22.2, 22.6; AF 25.4; LHL 19.7; DJG 2.2.1] Gauss
Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2009, uke 7 Onsdag 11.02.09 og fredag 13.02.09 Gauss lov [FGT 23.2; YF 22.3; TM 22.2, 22.6; AF 25.4; LHL 19.7; DJG 2.2.1] Gauss
Løsningsforslag til øving
 1 FY1002/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 2012. Løsningsforslag til øving 11-2012 Oppgave 1 a) Forplantning i z-retning betyr at E og B begge ligger i xy-planet. La oss for eksempel
1 FY1002/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 2012. Løsningsforslag til øving 11-2012 Oppgave 1 a) Forplantning i z-retning betyr at E og B begge ligger i xy-planet. La oss for eksempel
LØSNINGSFORSLAG TIL EKSAMEN I FY1003 ELEKTRISITET OG MAGNETISME Mandag 4. desember 2006 kl
 NOGES TEKNISK- NATUVITENSKAPEIGE UNIVESITET INSTITUTT FO FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 ØSNINGSFOSAG TI EKSAMEN I FY1003 EEKTISITET OG MAGNETISME
NOGES TEKNISK- NATUVITENSKAPEIGE UNIVESITET INSTITUTT FO FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 ØSNINGSFOSAG TI EKSAMEN I FY1003 EEKTISITET OG MAGNETISME
LØSNINGSFORSLAG TIL EKSAMEN I FY1003 ELEKTRISITET OG MAGNETISME TFY4155 ELEKTROMAGNETISME Onsdag 3. juni 2009 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY003 ELEKTRISITET
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY003 ELEKTRISITET
Løsningsforslag til øving 4: Coulombs lov. Elektrisk felt. Magnetfelt.
 Lørdagsverksted i fysikk. Institutt for fysikk, NTNU. Høsten 27. Veiledning: 29. september kl 12:15 15:. Løsningsforslag til øving 4: Coulombs lov. Elektrisk felt. Magnetfelt. Oppgave 1 a) C. Elektrisk
Lørdagsverksted i fysikk. Institutt for fysikk, NTNU. Høsten 27. Veiledning: 29. september kl 12:15 15:. Løsningsforslag til øving 4: Coulombs lov. Elektrisk felt. Magnetfelt. Oppgave 1 a) C. Elektrisk
TFE4120 Elektromagnetisme
 NTNU IET, IME-fakultetet, Norge teknisk-naturitenskapelige uniersitet TFE412 Elektromagnetisme Løsningsforslag repetisjonsøing Oppgae 1 a) i) Her er alternati 1) riktig. His massetettheten er F, il et
NTNU IET, IME-fakultetet, Norge teknisk-naturitenskapelige uniersitet TFE412 Elektromagnetisme Løsningsforslag repetisjonsøing Oppgae 1 a) i) Her er alternati 1) riktig. His massetettheten er F, il et
LØSNINGSFORSLAG TIL ØVING 11, TMA4105, V2008. x = r cos θ, y = r sin θ, z = 2r for 0 θ 2π, 2 2r 6. i j k. 5 r dr dθ = 8
 LØNINGFORLAG TIL ØVING, TMA45, V8 Oppgave 4.5.9. Parametrisering: x = r cos θ, y = r sin θ, z = r for θ π, r 6. r(r, θ) = r cos θ, r sin θ, r. N = r r r θ = cos θ sin θ = r cos θ, r sin θ, r. r sin θ r
LØNINGFORLAG TIL ØVING, TMA45, V8 Oppgave 4.5.9. Parametrisering: x = r cos θ, y = r sin θ, z = r for θ π, r 6. r(r, θ) = r cos θ, r sin θ, r. N = r r r θ = cos θ sin θ = r cos θ, r sin θ, r. r sin θ r
KONTINUASJONSEKSAMEN TFY4155 ELEKTROMAGNETISME Fredag 11. august 2006 kl
 NOGES TEKNSK- NATUVTENSKAPELGE UNVESTET NSTTUTT FO FYSKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 KONTNUASJONSEKSAMEN TFY4155 ELEKTOMAGNETSME Fredag 11.
NOGES TEKNSK- NATUVTENSKAPELGE UNVESTET NSTTUTT FO FYSKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 KONTNUASJONSEKSAMEN TFY4155 ELEKTOMAGNETSME Fredag 11.
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME Mandag 4. desember 2006 kl
 NOGES TEKNSK- NATUVTENSKAPELGE UNVESTET NSTTUTT FO FYSKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTSTET OG MAGNETSME Mandag 4. desember
NOGES TEKNSK- NATUVTENSKAPELGE UNVESTET NSTTUTT FO FYSKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTSTET OG MAGNETSME Mandag 4. desember
LØSNINGSFORSLAG TIL EKSAMEN I TFY4155 ELEKTROMAGNETISME FY1003 ELEKTRISITET OG MAGNETISME Tirsdag 31. mai 2005 kl
 NORGES TEKNISK- NATURVITENSKAPEIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 ØSNINGSFORSAG TI EKSAMEN I TFY4155 EEKTROMAGNETISME
NORGES TEKNISK- NATURVITENSKAPEIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 ØSNINGSFORSAG TI EKSAMEN I TFY4155 EEKTROMAGNETISME
TFY4104 Fysikk. Institutt for fysikk, NTNU. Høsten Løsningsforslag til øving 10.
 TFY4104 Fysikk. Institutt for fysikk, NTNU. Høsten 015. Løsningsforslag til øving 10. Oppgave A B C D 1 x x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11 x 1 x 13 x 14 x 15 x 16 x 17 x 18 x 9 x 0 x 1) Glass-staven
TFY4104 Fysikk. Institutt for fysikk, NTNU. Høsten 015. Løsningsforslag til øving 10. Oppgave A B C D 1 x x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11 x 1 x 13 x 14 x 15 x 16 x 17 x 18 x 9 x 0 x 1) Glass-staven
Oppgavene er hentet fra fagets lærebok, Hass, Weir og Thomas, samt gamle eksamener.
 NTNU Institutt for matematiske fag TMA45 Matematikk, øving, vår Løsningsforslag Notasjon og merknader Oppgavene er hentet fra fagets lærebok, Hass, Weir og Thomas, samt gamle eksamener. Oppgaver fra kapittel
NTNU Institutt for matematiske fag TMA45 Matematikk, øving, vår Løsningsforslag Notasjon og merknader Oppgavene er hentet fra fagets lærebok, Hass, Weir og Thomas, samt gamle eksamener. Oppgaver fra kapittel
Overflateladningstetthet på metalloverflate
 0.0.08: Rettet opp feil i oppgave 4 og løsningsforslag til oppgave 8b. Overflateladningstetthet på metalloverflate. Ei metallkule med diameter 0.0 m har ei netto ladning på 0.50 nc. Hvor stort er det elektriske
0.0.08: Rettet opp feil i oppgave 4 og løsningsforslag til oppgave 8b. Overflateladningstetthet på metalloverflate. Ei metallkule med diameter 0.0 m har ei netto ladning på 0.50 nc. Hvor stort er det elektriske
Midtsemesterprøve fredag 11. mars kl
 Institutt for fysikk, NTNU FY1003 Elektrisitet og magnetisme TFY4155 Elektromagnetisme Vår 2005 Midtsemesterprøve fredag 11. mars kl 1030 1330. Løsningsforslag 1) B. Newtons 3. lov: Kraft = motkraft. (Andel
Institutt for fysikk, NTNU FY1003 Elektrisitet og magnetisme TFY4155 Elektromagnetisme Vår 2005 Midtsemesterprøve fredag 11. mars kl 1030 1330. Løsningsforslag 1) B. Newtons 3. lov: Kraft = motkraft. (Andel
Løsningsforslag til øving 8
 FY12/TFY416 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 21. Løsningsforslag til øving 8 Oppgave 1 Helt generelt vil vi ha, for en elektromagnetisk bølge som forplanter seg i retning ˆk og som er polarisert
FY12/TFY416 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 21. Løsningsforslag til øving 8 Oppgave 1 Helt generelt vil vi ha, for en elektromagnetisk bølge som forplanter seg i retning ˆk og som er polarisert
NTNU. MA1103 Flerdimensjonal Analyse våren Maple-øving 2. Viktig informasjon. Institutt for matematiske fag. maple02 28.
 NTNU Institutt for matematiske fag MA1103 Flerdimensjonal Analyse våren 2011 Maple-øving 2 Fyll inn studieprogram: Fyll inn navn: 1. 2. 3. 4. Viktig informasjon Besvarelsen kan leveres som gruppearbeid
NTNU Institutt for matematiske fag MA1103 Flerdimensjonal Analyse våren 2011 Maple-øving 2 Fyll inn studieprogram: Fyll inn navn: 1. 2. 3. 4. Viktig informasjon Besvarelsen kan leveres som gruppearbeid
LØSNINGSFORSLAG TIL EKSAMEN I TFY4155 ELEKTROMAGNETISME Fredag 11. august 2006 kl
 NOGES TEKNISK- NATUVITENSKAPELIGE UNIVESITET INSTITUTT FO FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFOSLAG TIL EKSAMEN I TFY4155 ELEKTOMAGNETISME
NOGES TEKNISK- NATUVITENSKAPELIGE UNIVESITET INSTITUTT FO FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFOSLAG TIL EKSAMEN I TFY4155 ELEKTOMAGNETISME
Løsningsforslag, eksamen MA1103 Flerdimensjonal analyse, vår 2009
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 8 Løsningsforslag, eksamen MA1103 Flerdimensjonal analyse, vår 2009 Oppgave 1 Avgjør om grenseverdiene eksisterer:
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 8 Løsningsforslag, eksamen MA1103 Flerdimensjonal analyse, vår 2009 Oppgave 1 Avgjør om grenseverdiene eksisterer:
Anbefalte oppgaver - Løsningsforslag
 TMA415 Matematikk 2 Anbefalte oppgaver - Løsningsforslag Uke 14 1.4.5: Vi skal finne fluksen ut overflaten til den solide ballen B med sentrum = (2,, 3) og radius r = 3, av vektorfeltet F = x 2 i + y 2
TMA415 Matematikk 2 Anbefalte oppgaver - Løsningsforslag Uke 14 1.4.5: Vi skal finne fluksen ut overflaten til den solide ballen B med sentrum = (2,, 3) og radius r = 3, av vektorfeltet F = x 2 i + y 2
LØSNINGSFORSLAG TIL KONTINUASJONSEKSAMEN I TFY4155 ELEKTROMAGNETISME Onsdag 17. august 2005 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 LØSNINGSFORSLAG TIL KONTINUASJONSEKSAMEN I TFY4155
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 LØSNINGSFORSLAG TIL KONTINUASJONSEKSAMEN I TFY4155
Løsning, Trippelintegraler
 Ukeoppgaver, uke 7 Matematikk, rippelintegraler Løsning, rippelintegraler Oppgave a) b) c) 6 x + + ) d d dx x + +/) d dx x) d d dx x + + /] d dx x + /+/] dx x +6)dx 8 6 d ) ) d xdx 6 ) ) ) d d xdx 6 8
Ukeoppgaver, uke 7 Matematikk, rippelintegraler Løsning, rippelintegraler Oppgave a) b) c) 6 x + + ) d d dx x + +/) d dx x) d d dx x + + /] d dx x + /+/] dx x +6)dx 8 6 d ) ) d xdx 6 ) ) ) d d xdx 6 8
FYS1120 Elektromagnetisme, Ukesoppgavesett 1
 FYS1120 Elektromagnetisme, Ukesoppgavesett 1 22. august 2016 I FYS1120-undervisningen legg vi mer vekt på matematikk og numeriske metoder enn det oppgavene i læreboka gjør. Det gjelder også oppgavene som
FYS1120 Elektromagnetisme, Ukesoppgavesett 1 22. august 2016 I FYS1120-undervisningen legg vi mer vekt på matematikk og numeriske metoder enn det oppgavene i læreboka gjør. Det gjelder også oppgavene som
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME I Mandag 5. desember 2005 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME
KONTINUASJONSEKSAMEN TFY4155 ELEKTROMAGNETISME Onsdag 17. august 2005 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 KONTINUASJONSEKSAMEN TFY4155 ELEKTROMAGNETISME
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 KONTINUASJONSEKSAMEN TFY4155 ELEKTROMAGNETISME
a 2 x 2 dy dx = e r r dr dθ =
 NTNU Institutt for matematiske fag TMA4 Matematikk, øving, vår Løsningsforslag Notasjon og merknader Som vanlig er enkelte oppgaver kopiert fra tidligere års løsningsforslag. Derfor kan notasjon, språk
NTNU Institutt for matematiske fag TMA4 Matematikk, øving, vår Løsningsforslag Notasjon og merknader Som vanlig er enkelte oppgaver kopiert fra tidligere års løsningsforslag. Derfor kan notasjon, språk
LØSNINGSFORSLAG TIL KONTINUASJONSEKSAMEN I FAG SIF 4012 ELEKTROMAGNETISME (SIF 4012 FYSIKK 2) Mandag 29. juli kl
 Side av 9 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng LØSNINGSFORSLAG TIL KONTINUASJONSEKSAMEN I FAG SIF 4 ELEKTROMAGNETISME
Side av 9 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng LØSNINGSFORSLAG TIL KONTINUASJONSEKSAMEN I FAG SIF 4 ELEKTROMAGNETISME
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME I Mandag 17. desember 2007 kl K. Rottmann: Matematisk formelsamling (eller tilsvarende).
 NOGES TEKNSK- NATUVTENSKAPELGE UNVESTET NSTTUTT FO FYSKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTSTET OG MAGNETSME Mandag 17. desember
NOGES TEKNSK- NATUVTENSKAPELGE UNVESTET NSTTUTT FO FYSKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTSTET OG MAGNETSME Mandag 17. desember
Oppgavesettet har 10 punkter 1, 2ab, 3ab, 4ab, 5abc som teller likt ved bedømmelsen.
 NTNU Institutt for matematiske fag SIF55 Matematikk 2 4. mai 999 Løsningsforslag Oppgavesettet har punkter, 2ab, 3ab, 4ab, 5abc som teller likt ved bedømmelsen. i alternativ (3, ii alternativ (2. 2 a For
NTNU Institutt for matematiske fag SIF55 Matematikk 2 4. mai 999 Løsningsforslag Oppgavesettet har punkter, 2ab, 3ab, 4ab, 5abc som teller likt ved bedømmelsen. i alternativ (3, ii alternativ (2. 2 a For
LØSNINGSFORSLAG TIL EKSAMEN I TFY4155 ELEKTROMAGNETISME FY1003 ELEKTRISITET OG MAGNETISME Tirsdag 30. mai 2006 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I TFY4155 ELEKTROMAGNETISME
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I TFY4155 ELEKTROMAGNETISME
Anbefalte oppgaver - Løsningsforslag
 TMA45 Matematikk Anbefalte oppgaver - Løsningsforslag Uke 5.5.: Kulen er grafen til rφ, θ) asinφ) cosθ)i + sin φ sinθ)j + cosφ)k), φ π, θ < π. Vi har slik at φ θ acosφ) cosθ)i + sinφ) sinθ)j + cosφ)k)
TMA45 Matematikk Anbefalte oppgaver - Løsningsforslag Uke 5.5.: Kulen er grafen til rφ, θ) asinφ) cosθ)i + sin φ sinθ)j + cosφ)k), φ π, θ < π. Vi har slik at φ θ acosφ) cosθ)i + sinφ) sinθ)j + cosφ)k)
Løsningsforslag, eksamen MA1103 Flerdimensjonal analyse, 8.juni 2010
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 7 Løsningsforslag, eksamen MA11 Flerdimensjonal analyse, 8.juni 21 Oppgave 1 a) Finn og klassifiser alle kritiske
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 7 Løsningsforslag, eksamen MA11 Flerdimensjonal analyse, 8.juni 21 Oppgave 1 a) Finn og klassifiser alle kritiske
EKSAMEN I FAG SIF 4012 ELEKTROMAGNETISME (SIF 4012 FYSIKK 2) Onsdag 11. desember kl Bokmål
 Side av 6 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 4 43 39 3 EKSAMEN I FAG SIF 42 ELEKTROMAGNETISME
Side av 6 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 4 43 39 3 EKSAMEN I FAG SIF 42 ELEKTROMAGNETISME
Ma Flerdimensjonal Analyse II Øving 9
 Ma23 - Flerdimensjonal Analyse II Øving 9 Øistein Søvik 2.3.22 Oppgaver 4.5 Evaluate the triple integrals over the indicated region. Be alert for simplifications and auspicious orders of integration 3.
Ma23 - Flerdimensjonal Analyse II Øving 9 Øistein Søvik 2.3.22 Oppgaver 4.5 Evaluate the triple integrals over the indicated region. Be alert for simplifications and auspicious orders of integration 3.
EKSAMEN TFY4155 ELEKTROMAGNETISME FY1003 ELEKTRISITET OG MAGNETISME Tirsdag 31. mai 2005 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 EKSAMEN TFY4155 ELEKTROMAGNETISME FY1003
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 EKSAMEN TFY4155 ELEKTROMAGNETISME FY1003
TFY4115: Løsningsforslag til oppgaver gitt
 Institutt for fysikk, NTNU. Høsten. TFY45: Løsningsforslag til oppgaver gitt 6.8.9. OPPGAVER 6.8. Vi skal estemme Taylorrekkene til noen kjente funksjoner: a c d sin x sin + x cos x sin 3 x3 cos +... x
Institutt for fysikk, NTNU. Høsten. TFY45: Løsningsforslag til oppgaver gitt 6.8.9. OPPGAVER 6.8. Vi skal estemme Taylorrekkene til noen kjente funksjoner: a c d sin x sin + x cos x sin 3 x3 cos +... x
Løsningsforslag til øving 13
 Institutt for fysikk, NTNU TFY4155/FY1003 Elektromagnetisme Vår 2009 Løsningsforslag til øving 13 Oppgave 1 a) Sløyfas magnetiske dipolmoment: m = IA ˆn = Ia 2 ˆn Sløyfa består av 4 rette ledere med lengde
Institutt for fysikk, NTNU TFY4155/FY1003 Elektromagnetisme Vår 2009 Løsningsforslag til øving 13 Oppgave 1 a) Sløyfas magnetiske dipolmoment: m = IA ˆn = Ia 2 ˆn Sløyfa består av 4 rette ledere med lengde
Løsningsforslag til øving 9
 FY1002/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 2010. Løsningsforslag til øving 9 Oppgave 1 a) Forplantning i z-retning betyr at E og B begge ligger i xy-planet. La oss for eksempel velge
FY1002/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 2010. Løsningsforslag til øving 9 Oppgave 1 a) Forplantning i z-retning betyr at E og B begge ligger i xy-planet. La oss for eksempel velge
Øving 1. Institutt for fysikk, NTNU TFY4155/FY1003: Elektromagnetisme. Veiledning: Mandag 19. januar Innleveringsfrist: Fredag 23. januar kl 12.
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektromagnetisme Vår 2009 Veiledning: Mandag 19. januar Innleveringsfrist: Fredag 23. januar kl 12.00 Øving 1 Oppgave 1 a) Komponentene av en vektor A er A =
Institutt for fysikk, NTNU TFY4155/FY1003: Elektromagnetisme Vår 2009 Veiledning: Mandag 19. januar Innleveringsfrist: Fredag 23. januar kl 12.00 Øving 1 Oppgave 1 a) Komponentene av en vektor A er A =
FYS1120 Elektromagnetisme - Ukesoppgavesett 2
 FYS1120 Elektromagnetisme - Ukesoppgavesett 2 7. september 2016 I FYS1120-undervisningen legger vi mer vekt på matematikk og numeriske metoder enn det oppgavene i læreboka gjør. Det gjelder også oppgavene
FYS1120 Elektromagnetisme - Ukesoppgavesett 2 7. september 2016 I FYS1120-undervisningen legger vi mer vekt på matematikk og numeriske metoder enn det oppgavene i læreboka gjør. Det gjelder også oppgavene
Kap. 22. Gauss lov. Vi skal se på: Fluksen til elektrisk felt E Gauss lov. Elektrisk ledere. Integralform og differensialform
 Kap. 22. Gauss lov Vi skal se på: Fluksen til elektrisk felt E Gauss lov Integralform og differensialform Elektrisk ledere. E-felt fra Coulombs lov: E k q r 2 r E k n q r n 2 0n r 0n dq E k r 2 r tot.
Kap. 22. Gauss lov Vi skal se på: Fluksen til elektrisk felt E Gauss lov Integralform og differensialform Elektrisk ledere. E-felt fra Coulombs lov: E k q r 2 r E k n q r n 2 0n r 0n dq E k r 2 r tot.
Mandag E = V. y ŷ + V ẑ (kartesiske koordinater) r sin θ φ ˆφ (kulekoordinater)
 Institutt fo fysikk, NTNU TFY4155/FY13: Elektisitet og magnetisme Vå 26, uke 6 Mandag 6.2.6 Beegning av E fa V [FGT 24.4; YF 23.5; TM 23.3; F 21.1; LHL 19.9; DJG 2.3.1, 1.2.2] Gadientopeatoen : V = V V
Institutt fo fysikk, NTNU TFY4155/FY13: Elektisitet og magnetisme Vå 26, uke 6 Mandag 6.2.6 Beegning av E fa V [FGT 24.4; YF 23.5; TM 23.3; F 21.1; LHL 19.9; DJG 2.3.1, 1.2.2] Gadientopeatoen : V = V V
5 z ds = x 2 +4y 2 4
 TMA45 Matematikk 2 Vår 25 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Løsningsforslag Øving Alle oppgavenummer referer til 8. utgave av Adams & Essex Calculus: A Complete
TMA45 Matematikk 2 Vår 25 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Løsningsforslag Øving Alle oppgavenummer referer til 8. utgave av Adams & Essex Calculus: A Complete
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME TFY4155 ELEKTROMAGNETISME Onsdag 3. juni 2009 kl
 NOGES TEKNISK- NATUVITENSKAPEIGE UNIVESITET INSTITUTT FO FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 EEKTISITET OG MAGNETISME TFY4155
NOGES TEKNISK- NATUVITENSKAPEIGE UNIVESITET INSTITUTT FO FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 EEKTISITET OG MAGNETISME TFY4155
TFY4104 Fysikk. Institutt for fysikk, NTNU. Høsten Øving 12.
 TFY0 Fsikk. nstitutt for fsikk, NTNU. Høsten 06. Øving. Oppgave Partikler med masse m, ladning q og hastighet v kommer inn i et område med krsset elektrisk og magnetisk felt, E og, som vist i figuren.
TFY0 Fsikk. nstitutt for fsikk, NTNU. Høsten 06. Øving. Oppgave Partikler med masse m, ladning q og hastighet v kommer inn i et område med krsset elektrisk og magnetisk felt, E og, som vist i figuren.
Vektorkalkulus Introduksjonsforelesninger
 Vektorkalkulus Introduksjonsforelesninger Jørgen Eriksson Midtbø og Henrik Andersen veinsson 19. september 217 Dette er et forelesningsnotat i ordets strengeste forstand: Et notat som brukes til å forelese.
Vektorkalkulus Introduksjonsforelesninger Jørgen Eriksson Midtbø og Henrik Andersen veinsson 19. september 217 Dette er et forelesningsnotat i ordets strengeste forstand: Et notat som brukes til å forelese.
LØSNINGSFORSLAG TIL EKSAMEN I FY1003 ELEKTRISITET OG MAGNETISME I Mandag 17. desember 2007 kl
 NOGES TEKNISK- NATUVITENSKAPELIGE UNIVESITET INSTITUTT FO FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFOSLAG TIL EKSAMEN I FY1003 ELEKTISITET OG
NOGES TEKNISK- NATUVITENSKAPELIGE UNIVESITET INSTITUTT FO FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFOSLAG TIL EKSAMEN I FY1003 ELEKTISITET OG
Maxwell s ligninger og elektromagnetiske bølger
 Maxwell s ligninger og elektromagnetiske bølger I forelesningene og i læreboken er Coulombs lov for the elektriske felt E formulert på følgende form: v da E = Q/ε 0 (1) Integralet til venstre går over
Maxwell s ligninger og elektromagnetiske bølger I forelesningene og i læreboken er Coulombs lov for the elektriske felt E formulert på følgende form: v da E = Q/ε 0 (1) Integralet til venstre går over
Gauss lov. Kap. 22. Gauss lov. Gauss lov skjematisk. Vi skal se på: Fluksen til elektrisk felt E Gauss lov Integralform og differensialform
 Kap. 5..6 Kap.. Gauss lov Vi skal se på: Fluksen til elektrisk felt E Gauss lov Integralform og differensialform Elektrisk ledere. Efelt fra Coulombs lov: q E k r r E k n q r n n r n dq E k r r tot. ladn.
Kap. 5..6 Kap.. Gauss lov Vi skal se på: Fluksen til elektrisk felt E Gauss lov Integralform og differensialform Elektrisk ledere. Efelt fra Coulombs lov: q E k r r E k n q r n n r n dq E k r r tot. ladn.
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME I TFY4155 ELEKTROMAGNETISME Fredag 8. juni 2007 kl
 NOGES TEKNISK- NATUVITENSKAPELIGE UNIVESITET INSTITUTT FO FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTISITET OG MAGNETISME I TFY4155
NOGES TEKNISK- NATUVITENSKAPELIGE UNIVESITET INSTITUTT FO FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTISITET OG MAGNETISME I TFY4155
Onsdag og fredag
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2009, uke 13 Onsdag 25.03.09 og fredag 27.03.09 Amperes lov [FGT 30.1, 30.3; YF 28.6, 28.7; AF 26.2; H 23.6; G 5.3] B dl = µ 0
Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2009, uke 13 Onsdag 25.03.09 og fredag 27.03.09 Amperes lov [FGT 30.1, 30.3; YF 28.6, 28.7; AF 26.2; H 23.6; G 5.3] B dl = µ 0
TFY4104 Fysikk. Institutt for fysikk, NTNU. Lsningsforslag til ving 10.
 TFY404 Fysikk. Institutt for fysikk, NTNU. Lsningsforslag til ving 0. Oppgave A B C D x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 0 x x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 29 x 20 x ) Glass-staven er ikke i berring med
TFY404 Fysikk. Institutt for fysikk, NTNU. Lsningsforslag til ving 0. Oppgave A B C D x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 0 x x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 29 x 20 x ) Glass-staven er ikke i berring med
(1 + x 2 + y 2 ) 2 = 1 x2 + y 2. (1 + x 2 + y 2 ) 2, x 2y
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA45 Matematikk vår 9 Løsningsforslag til eksamen.5.9 Gitt f(, y) = + +y. a) Vi regner ut f = f y = + + y ( + + y ) = + + y
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA45 Matematikk vår 9 Løsningsforslag til eksamen.5.9 Gitt f(, y) = + +y. a) Vi regner ut f = f y = + + y ( + + y ) = + + y
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME TFY4155 ELEKTROMAGNETISME Tirsdag 27. mai 2008 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME
Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen Q ligger i punktet ( 3, 0) [mm].
![Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen Q ligger i punktet ( 3, 0) [mm]. Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen Q ligger i punktet ( 3, 0) [mm].](/thumbs/58/41840831.jpg) Oppgave 1 Finn løsningen til følgende 1.ordens differensialligninger: a) y = x e y, y(0) = 0 b) dy dt + a y = b, a og b er konstanter. Oppgave 2 Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen
Oppgave 1 Finn løsningen til følgende 1.ordens differensialligninger: a) y = x e y, y(0) = 0 b) dy dt + a y = b, a og b er konstanter. Oppgave 2 Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen
Løsningsforslag til øving 4
 1 FY100/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 01. Løsningsforslag til øving 4 Oppgave 1 a) D = D 0 [ cos (kx ωt) + sin (kx ωt) ] 1/ = D 0 for alle x og t. Med andre ord, vi har overalt
1 FY100/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 01. Løsningsforslag til øving 4 Oppgave 1 a) D = D 0 [ cos (kx ωt) + sin (kx ωt) ] 1/ = D 0 for alle x og t. Med andre ord, vi har overalt
Løsningsforslag TFE4120 Elektromagnetisme 13. mai 2004
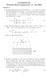 Løsningsforslag TFE4120 Elektromagnetisme 13. mai 2004 Oppgae 1 a) Speilladningsmetoden gir at potensialet for z > 0 er summen a potensialet pga ladningen Q i posisjon z = h og potensialet pga en speillanding
Løsningsforslag TFE4120 Elektromagnetisme 13. mai 2004 Oppgae 1 a) Speilladningsmetoden gir at potensialet for z > 0 er summen a potensialet pga ladningen Q i posisjon z = h og potensialet pga en speillanding
Løsningsforslag til øving 4
 Institutt for fysikk, NTNU FY3 Elektrisitet og magnetisme II Høst 25 Løsningsforslag til øving 4 Veiledning mandag 9. og onsdag 2. september Likeretter a) Strømmen som leveres av spenningskilden må gå
Institutt for fysikk, NTNU FY3 Elektrisitet og magnetisme II Høst 25 Løsningsforslag til øving 4 Veiledning mandag 9. og onsdag 2. september Likeretter a) Strømmen som leveres av spenningskilden må gå
Flervalgsoppgaver. Gruppeøving 1 Elektrisitet og magnetisme
 Gruppeøving Elektrisitet og magnetisme Flervalgsoppgaver Ei svært tynn sirkulær skive av kobber har radius R = 000 m og tykkelse d = 00 mm Hva er total masse? A 0560 kg B 0580 kg C 0630 kg D 0650 kg E
Gruppeøving Elektrisitet og magnetisme Flervalgsoppgaver Ei svært tynn sirkulær skive av kobber har radius R = 000 m og tykkelse d = 00 mm Hva er total masse? A 0560 kg B 0580 kg C 0630 kg D 0650 kg E
LØSNINGSFORSLAG TIL EKSAMEN I FY1003 ELEKTRISITET OG MAGNETISME I Mandag 5. desember 2005 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt uner eksamen: Jon Anreas Støvneng Telefon: 7 59 6 6 / 41 4 9 0 LØSNINGSFORSLAG TIL EKSAMEN I FY100 ELEKTRISITET OG MAGNETISME
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt uner eksamen: Jon Anreas Støvneng Telefon: 7 59 6 6 / 41 4 9 0 LØSNINGSFORSLAG TIL EKSAMEN I FY100 ELEKTRISITET OG MAGNETISME
dg = ( g P0 u)ds = ( ) = 0
 NTNU Institutt for matematiske fag TMA4105 Matematikk 2, øving 8, vår 2011 Løsningsforslag Notasjon og merknader Som vanlig er enkelte oppgaver kopiert fra tidligere års løsningsforslag. Derfor kan notasjon,
NTNU Institutt for matematiske fag TMA4105 Matematikk 2, øving 8, vår 2011 Løsningsforslag Notasjon og merknader Som vanlig er enkelte oppgaver kopiert fra tidligere års løsningsforslag. Derfor kan notasjon,
E, B. q m. TFY4104 Fysikk. Institutt for fysikk, NTNU. ving 12.
 TFY4104 Fsikk. nstitutt for fsikk, NTNU. ving 12. Oppgave 1 Partikler med masse m, ladning q og hastighet v kommer inn i et omrade med "krsset" elektrisk og magnetisk felt, E og, som vist i guren. E har
TFY4104 Fsikk. nstitutt for fsikk, NTNU. ving 12. Oppgave 1 Partikler med masse m, ladning q og hastighet v kommer inn i et omrade med "krsset" elektrisk og magnetisk felt, E og, som vist i guren. E har
EKSAMEN TFY4155 ELEKTROMAGNETISME FY1003 ELEKTRISITET OG MAGNETISME Tirsdag 30. mai 2006 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN TFY4155 ELEKTROMAGNETISME FY1003
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN TFY4155 ELEKTROMAGNETISME FY1003
NTNU. MA1103 Flerdimensjonal analyse våren Maple/Matlab-øving 2. Viktig informasjon. Institutt for matematiske fag
 NTNU Institutt for matematiske fag MA1103 Flerdimensjonal analyse våren 2012 Maple/Matlab-øving 2 Fyll inn studieprogram: Fyll inn navn: 1. 2. 3. 4. Viktig informasjon Besvarelsen kan leveres som gruppearbeid
NTNU Institutt for matematiske fag MA1103 Flerdimensjonal analyse våren 2012 Maple/Matlab-øving 2 Fyll inn studieprogram: Fyll inn navn: 1. 2. 3. 4. Viktig informasjon Besvarelsen kan leveres som gruppearbeid
A. positiv x-retning B. negativ z-retning C. positiv y-retning D. negativ y-retning E. krafta er null
 Flervalgsoppgaver En lang, rett ledning langs x-aksen fører en strøm i positiv x-retning. En positiv punktladning beveger seg langs z-aksen i positiv z- 1. retning (opp av papirplanet). Den magnetiske
Flervalgsoppgaver En lang, rett ledning langs x-aksen fører en strøm i positiv x-retning. En positiv punktladning beveger seg langs z-aksen i positiv z- 1. retning (opp av papirplanet). Den magnetiske
Løsningsforslag TFE4120 Elektromagnetisme 29. mai 2017
 Norges teknisk naturvitenskapelige universitet Institutt for elektroniske systemer Side 1 av 6 Løsningsforslag TFE4120 Elektromagnetisme 29. mai 2017 Oppgave 1 a) Start med å tegne figur! Tegn inn en Gauss-flate
Norges teknisk naturvitenskapelige universitet Institutt for elektroniske systemer Side 1 av 6 Løsningsforslag TFE4120 Elektromagnetisme 29. mai 2017 Oppgave 1 a) Start med å tegne figur! Tegn inn en Gauss-flate
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MEK 11 Feltteori og vektoranalyse. Eksamensdag: Torsdag 1 desember 29. Tid for eksamen: 14:3 17:3. Oppgavesettet er på 7 sider.
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MEK 11 Feltteori og vektoranalyse. Eksamensdag: Torsdag 1 desember 29. Tid for eksamen: 14:3 17:3. Oppgavesettet er på 7 sider.
SIF5005 Matematikk 2, 13. mai 2002 Løsningsforslag
 SIF55 Matematikk, 3. mai Oppgave Alternativ : At de to ligningene skjærer hverandre vil si at det finnes parameterverdier u og v som, innsatt i de to parametriseringene, gir samme punkt: Vi løser hver
SIF55 Matematikk, 3. mai Oppgave Alternativ : At de to ligningene skjærer hverandre vil si at det finnes parameterverdier u og v som, innsatt i de to parametriseringene, gir samme punkt: Vi løser hver
Løsningsforslag til prøveeksamen i MAT 1110, våren 2006
 Løsningsforslag til prøveeksamen i MAT, våren 6 Oppgave : a) Vi har C 5 3 II+( )I a + 3a 3a III+I 3 II 3 3 3 3 a + 3a 3a 3 a + 3a 3a III+II I+( ))II 3 3 3 a + 3a 3a 3 3 3 a + 3a 4 3 3a a + 3a 4 3 3a b)
Løsningsforslag til prøveeksamen i MAT, våren 6 Oppgave : a) Vi har C 5 3 II+( )I a + 3a 3a III+I 3 II 3 3 3 3 a + 3a 3a 3 a + 3a 3a III+II I+( ))II 3 3 3 a + 3a 3a 3 3 3 a + 3a 4 3 3a a + 3a 4 3 3a b)
Løsningsforslag, eksamen MA1101/MA6101 Grunnkurs i analyse I, vår 2009
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 6 Løsningsforslag, eksamen MA1101/MA6101 Grunnkurs i analyse I, vår 009 Oppgave 1 Funksjonen g er definert ved g(x)
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 6 Løsningsforslag, eksamen MA1101/MA6101 Grunnkurs i analyse I, vår 009 Oppgave 1 Funksjonen g er definert ved g(x)
EKSAMEN i TFY4155/FY1003 ELEKTRISITET OG MAGNETISME
 Side 1 av 7 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk BOKMÅL EKSAMEN i TFY4155/FY1003 ELEKTRISITET OG MAGNETISME Eksamensdato: Tirsdag 24 mai 2011 Eksamenstid: 09:00-13:00 Faglig
Side 1 av 7 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk BOKMÅL EKSAMEN i TFY4155/FY1003 ELEKTRISITET OG MAGNETISME Eksamensdato: Tirsdag 24 mai 2011 Eksamenstid: 09:00-13:00 Faglig
I C Q R. Øving 11. Institutt for fysikk, NTNU TFY4155/FY1003: Elektromagnetisme
 nstitutt for fsikk, NTNU TFY4155/FY1003: Elektromagnetisme Vår 2009 Øving 11 Veiledning: Mandag 23. mars og fredag 27. mars nnleveringsfrist: Fredag 27. mars Oppgave 1 nnledning (dvs vi rekapitulerer fra
nstitutt for fsikk, NTNU TFY4155/FY1003: Elektromagnetisme Vår 2009 Øving 11 Veiledning: Mandag 23. mars og fredag 27. mars nnleveringsfrist: Fredag 27. mars Oppgave 1 nnledning (dvs vi rekapitulerer fra
FYS1120 Elektromagnetisme
 Det matematisk-naturvitenskapelige fakultet Universitetet i Oslo FYS112 Elektromagnetisme Løsningsforslag til ukesoppgave 2 Oppgave 1 a) Gauss lov sier at den elektriske fluksen Φ er lik den totale ladningen
Det matematisk-naturvitenskapelige fakultet Universitetet i Oslo FYS112 Elektromagnetisme Løsningsforslag til ukesoppgave 2 Oppgave 1 a) Gauss lov sier at den elektriske fluksen Φ er lik den totale ladningen
Tillegg om flateintegraler
 Kapittel 6 Tillegg om flateintegraler 6.1 Litt ekstra om flateintegraler I kompendiet har vi definert flateintegraler som grenseoverganger for diskretiseringer. Har vi en flate kan vi representere den
Kapittel 6 Tillegg om flateintegraler 6.1 Litt ekstra om flateintegraler I kompendiet har vi definert flateintegraler som grenseoverganger for diskretiseringer. Har vi en flate kan vi representere den
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS1120 Elektromagnetisme Eksamensdag: 10. oktober 2016 Tid for eksamen: 10.00 13.00 Oppgavesettet er på 8 sider. Vedlegg: Tillatte
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS1120 Elektromagnetisme Eksamensdag: 10. oktober 2016 Tid for eksamen: 10.00 13.00 Oppgavesettet er på 8 sider. Vedlegg: Tillatte
Fasit for eksamen i MEK1100 torsdag 13. desember 2007 Hvert delspørsmål honoreres med poengsum fra 0 til 10 (10 for perfekt svar).
 Fasit for eksamen i MEK torsdag 3. desember 27 Hvert delspørsmål honoreres med poengsum fra til ( for perfekt svar). Oppgave Vi har gitt to vektorfelt i kartesiske koordinater (x,y,z) A = yi+coszj +xy
Fasit for eksamen i MEK torsdag 3. desember 27 Hvert delspørsmål honoreres med poengsum fra til ( for perfekt svar). Oppgave Vi har gitt to vektorfelt i kartesiske koordinater (x,y,z) A = yi+coszj +xy
a) Bruk en passende Gaussflate og bestem feltstyrken E i rommet mellom de 2 kuleskallene.
 Oppgave 1 Bestem løsningen av differensialligningen Oppgave 2 dy dx + y = e x, y(1) = 1 e Du skal beregne en kulekondensator som består av 2 kuleskall av metall med samme sentrum. Det indre skallet har
Oppgave 1 Bestem løsningen av differensialligningen Oppgave 2 dy dx + y = e x, y(1) = 1 e Du skal beregne en kulekondensator som består av 2 kuleskall av metall med samme sentrum. Det indre skallet har
Midtsemesterprøve torsdag 7. mai 2009 kl
 Institutt for fysikk, NTNU FY1003 Elektrisitet og magnetisme TFY4155 Elektromagnetisme Våren 2009 Tillatte hjelpemidler: Midtsemesterprøve torsdag 7. mai 2009 kl 09.15 11.15. Oppgaver på side 5 10. Svartabell
Institutt for fysikk, NTNU FY1003 Elektrisitet og magnetisme TFY4155 Elektromagnetisme Våren 2009 Tillatte hjelpemidler: Midtsemesterprøve torsdag 7. mai 2009 kl 09.15 11.15. Oppgaver på side 5 10. Svartabell
TMA4105 Matematikk 2 vår 2013
 TMA4105 Matematikk vår 013 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Løsningsforslag Øving Alle oppgavene er fra læreboka Merk: I løsningene til alle oppgavene fra seksjon
TMA4105 Matematikk vår 013 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Løsningsforslag Øving Alle oppgavene er fra læreboka Merk: I løsningene til alle oppgavene fra seksjon
Elektrisk og Magnetisk felt
 Elektrisk og Magnetisk felt Kjetil Liestøl Nielsen 1 Emner for i dag Coulombs lov Elektrisk felt Ladet partikkel i elektrisk felt Magnetisk felt Magnetisk kraft på elektrisk eladninger Elektromagnetiske
Elektrisk og Magnetisk felt Kjetil Liestøl Nielsen 1 Emner for i dag Coulombs lov Elektrisk felt Ladet partikkel i elektrisk felt Magnetisk felt Magnetisk kraft på elektrisk eladninger Elektromagnetiske
Eksamensoppgave i MA1103 Flerdimensjonal analyse
 Institutt for matematiske fag Eksamensoppgave i MA3 Flerdimensjonal analyse Faglig kontakt under eksamen: Mats Ehrnstrøm Tlf: 735 97 44 Eksamensdato: 22. mai 28 Eksamenstid (fra til): 9: 3: Hjelpemiddelkode/Tillatte
Institutt for matematiske fag Eksamensoppgave i MA3 Flerdimensjonal analyse Faglig kontakt under eksamen: Mats Ehrnstrøm Tlf: 735 97 44 Eksamensdato: 22. mai 28 Eksamenstid (fra til): 9: 3: Hjelpemiddelkode/Tillatte
SIF5005 MATEMATIKK 2 VÅR r5 drdθ = 1 m. zrdzdrdθ = 1 m. zrdzdrdθ =
 SIF55 MAEMAIKK Å 3 Løsningsforslag Hjemmeøving 5 Oppgave. Ser at massen fordeler seg symetrisk om z-aksen, derfor vil tyngdepunktet ligge på z-aksen. Det eneste vi da trenger å regne ut er z. zδd = m π
SIF55 MAEMAIKK Å 3 Løsningsforslag Hjemmeøving 5 Oppgave. Ser at massen fordeler seg symetrisk om z-aksen, derfor vil tyngdepunktet ligge på z-aksen. Det eneste vi da trenger å regne ut er z. zδd = m π
Integralsatser: Green, Stokes og Gauss
 Kapittel 7 Integralsatser: Green, tokes og Gauss Oppgave 1 Vi har gitt strømfeltet v = ωyi+ωxj der ω er en konstant. a) trømfarten: v = ω 2 y 2 +ω 2 x 2 = ωr, r = x 2 +y 2. Langs sirkelen r 2 = x 2 +y
Kapittel 7 Integralsatser: Green, tokes og Gauss Oppgave 1 Vi har gitt strømfeltet v = ωyi+ωxj der ω er en konstant. a) trømfarten: v = ω 2 y 2 +ω 2 x 2 = ωr, r = x 2 +y 2. Langs sirkelen r 2 = x 2 +y
Løsningsforslag til eksamen i TMA4105 matematikk 2,
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av Løsningsforslag til eksamen i TMA45 matematikk, 9.5.4 Oppgave La fx, y, z) xy + arctanxz). La P være punktet,, ). a)
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av Løsningsforslag til eksamen i TMA45 matematikk, 9.5.4 Oppgave La fx, y, z) xy + arctanxz). La P være punktet,, ). a)
FY2045/TFY4250 Kvantemekanikk I, løsning øving 14 1 LØSNING ØVING 14. ψ 210 z ψ 100 d 3 r a.
 FY45/TFY45 Kvantemekanikk I, løsning øving 14 1 LØSNING ØVING 14 Løsning Oppgave 14 1 Fra oppg 3, eksamen august 1 a. Med Y = 1/ 4π og zy = ry 1 / 3 kan vi skrive matrise-elementene av z på formen (z)
FY45/TFY45 Kvantemekanikk I, løsning øving 14 1 LØSNING ØVING 14 Løsning Oppgave 14 1 Fra oppg 3, eksamen august 1 a. Med Y = 1/ 4π og zy = ry 1 / 3 kan vi skrive matrise-elementene av z på formen (z)
LØSNINGSFORSLAG TIL EKSAMEN I FY1003 ELEKTRISITET OG MAGNETISME TFY4155 ELEKTROMAGNETISME Tirsdag 27. mai 2008 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY003 ELEKTRISITET
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY003 ELEKTRISITET
Velkommen til MA1103 Flerdimensjonal analyse
 Velkommen til MA1103 Flerdimensjonal analyse Foreleser: 14. januar 2013 Kursinformasjon Nettside: wiki.math.ntnu.no/ma1103/2013v/start Foreleser: (mariusi@math.ntnu.no) Start emne i epost med MA1103 Treffetid:
Velkommen til MA1103 Flerdimensjonal analyse Foreleser: 14. januar 2013 Kursinformasjon Nettside: wiki.math.ntnu.no/ma1103/2013v/start Foreleser: (mariusi@math.ntnu.no) Start emne i epost med MA1103 Treffetid:
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MEK 1100 Feltteori og vektoranalyse. Eksamensdag: Torsdag 11 desember 2008. Tid for eksamen: 14:30 17:30. Oppgavesettet er på
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MEK 1100 Feltteori og vektoranalyse. Eksamensdag: Torsdag 11 desember 2008. Tid for eksamen: 14:30 17:30. Oppgavesettet er på
Øving 6, løsningsskisse.
 Inst for fysikk 202 TFY455/FY003 Elektr & magnetisme Øving 6, løsningsskisse Diol Platekondensatorer Ogave Potensial rundt diol Vi skriver først V a om til en funksjon av x og z ved å bruke relasjonene
Inst for fysikk 202 TFY455/FY003 Elektr & magnetisme Øving 6, løsningsskisse Diol Platekondensatorer Ogave Potensial rundt diol Vi skriver først V a om til en funksjon av x og z ved å bruke relasjonene
