Litt matematikk som er nyttig for teorien bak spillteorien.
|
|
|
- Victoria Hermansen
- 8 år siden
- Visninger:
Transkript
1 Litt matematikk som er nyttig for teorien bak spillteorien.. John von Neumanns min-max teorem For å vise dette resultatet trenger vi et lite hjelperesultat. For p R m så sier vi at p er en sannsynlighetsvektor hvis m p 0 og p i =. Vi kaller mengden av sannsynlighetsvektorer i R m for m. Lemma. La A være en m n matrise. Da er enten Aq 0 for en q n eller p T A < 0 for en p m. Bevis. Anta at Aq < 0 for alle q n. Det vil si at A n ligger i den negative oktanten i R m, m.a.o. for alle q n så vil Aq) i < 0 for i =,...,m. Det vil si at det fins et hyperplan som er slik at m og A n ligger på hver sin side. Hvis u er en normalvektor til dette planet, så kan vi velge u slik at u i 0, siden vi skal ha at i= p T u 0 for alle p m, og u T A n < 0. Siden u 0, så kan vi velge lengden på u slik at u m. Siden vektorer i n har minst en positiv komponent, så betyr dette at u T A < 0. Teorem Von Neumann s min-max teorem). La A være en m n matrise. Da er max p m min q n pt Aq = min q n max p m pt Aq. Bevis. Vi viser først den svake versjonen. La u n og v m. Da har vi at min q vt Aq v T Au max n p pt Au. m Nå kan vi ta max over m til venstre og min over m til høyre. Dette gir ) max p m min q n pt Aq min q n max p m pt Aq. Anta nå at dette er en streng ulikhet. Da kan vi finne en r som passer imellom, altså 2) max p m min q n pt Aq < r < min q n max p m pt Aq. La nå A være definert ved Vi har at a ij = a ij r. p T A q = p T A r)q,
2 2 der... = Siden p og q er sannsynlighetsvektorer så har vi at q + q q n p T q = p,..., p m ). = p,...,p m ). = p + + p n =. q + q q n Altså er p T A q = p T Aq r. Nå kan vi bruke Lemma på A, og konkludere at enten 3) A u 0, for en u n, eller 4) v T A 0, for en v m. Anta at 3) holder. Da har vi at p T A u 0 for alle p m. Dette medfører at eller max p pt A u 0 min max m q n p pt A q 0, m min max q n p pt Aq r, m som strider mot 2). Hvis 4) gjelder så vil v T A q 0 for alle q n. Dette gir at som medfører som også strider imot 2). min q vt A q 0 max min n p m q pt A q 0, n max p m min q n pt Aq r, Dette beviset er ikke konstruktivt, og simplexalgoritmen gir et konstruktivt bevis for samme teorem. Oppgaver: : La f : X Y R være en funksjon, der X og Y er vilkårlige mengder. Vis at sup inf fx, y) inf x X y Y sup y Y x X fx, y). 2: For u R n vis max q n u q = max i=,...,n u i
3 2. Alle N-spiller spill har en Nash likevekt. Von Neumann s min-max teorem gir at alle to spiller null sum spill har en Nash likevekt. Nå skal vi vise det samme for spill med N spillere. Siden vi har N spillere blir notasjonen litt mer komplisert. For i =,..., N har spiller nr. i strategien p i = p i,..., p i n i ) T n i. Sett Spiller i vil nå få utbetalingen 5) E i p) = p = p, p 2,...,p N) n n 2 n N =: S N. n n 2 i = i 2 = n N i N = b i i i 2...i N p i p 2 i 2 p N i N, her er b i i i 2...i N utbetalingen spiller i får dersom alle spillerne velger de rene) strategiene e i,...,e in. Merk at avbildningen p i E i p,...,p i,...,p N) er lineær. Nå bruker vi notasjonen p i = p,...,p i, p i+,...,p N), dvs. p i er p der p i er tatt vekk. Gitt p i, så vil spiller i prøve å få størst mulig utbetaling. H-n vil derfor velge p i slik at 6) E i p) = max E i p,...,p i,...,p N) =: Ê p i). p i n i Nå kan vi definere Nash likevekt, Definisjon. En Nash likevekt er en p S N som er slik at Ê i p i ) E i p,...,q i,...,p N), i =,..., N, og for alle q S N. Mao. p i er det beste svar på p i for alle spillere. En rettferdiggjøring for begrepet Nash likevekt er tolkningen om at dette er en selvforsterkende avtale. Anta at du og jeg har anledningen til å gjøre en ikke bindende) avtale om hvordan vi skal spille før vi velger strategier. Hvis vi gjør en avtale, så bør dette være en Nash likevekt. Grunnen til dette er at hvis vi tror den andre spilleren vil holde seg til avtalen, lønner det seg å holde seg til avtalen dersom den er en Nash likevekt. Hvis vi ikke hadde avtalt en Nash likevekt, ville en av oss kunne tjene på å bryte avtalen. For å vise at en Nash likevekt alltid fins må vi introdusere litt matematikk. En korrespondanse er en funksjon som kan ta flere verdier. Hvis f er en korrespondanse fra X til Y så er fx) en delmengde av Y for x X. Vi skriver f : X Y for dette. En korrespondanse f kalles kontinuerlig hvis det for alle følger Kjønnsnøytral betegnelse, sett inn u eller a. {x n } n X, og {y n } n 0 Y, 3
4 4 som er slik at gjelder at x n x 0, y n y 0, og y n f x n ), y 0 f x 0 ). En korrepondanse f : X Y kalles konveks hvis fx) er konveks for alle x X.. Vi sier at x er et fikspunkt for korrespondansen f : X X hvis x fx). For de av dere som har glemt det, kalles en mengde A konveks dersom for alle y og y 2 i A gjelder at den rette linjen mellom y og y 2 ligger i A. Dette kan utrykkes ved at τy + τ)y 2 A, for alle τ [0, ]. Vi må også vite hva kompakthet er. En mengde A R n kalles kompakt hvis den er begrenset og lukket. Hvis en mengde A er kompakt, så vil alle følger {x n } n A ha en konvergent delfølge. Videre vil alle kontinuerlige funksjoner f : A R anta sitt maksimum og mimimum på A. Spesiellt vil k være kompakt for alle endelige k. Av samme grunn vil også S N være kompakt. Oppgaver 3: La X = [, ] og la Fx) = { y x 2 + y 2 /4 }. Tegn grafen x X, y Fx). Vis at G er lukket. Hvilke av mengdene F ), F0), F/2), F/3), F3/4) er konvekse? Nå kan vi definere spiller i s beste svar som korrspondansen ψ i : S N n i definert ved { 7) ψ i p) = p i n i E i p,...,p i,...,p N) = Ê p i)}. Siden S N er kompakt er ψ i veldefinert. Nash likevekter er karakterisert ved at alle spilleres strategi er det beste svar på de andre spillernes strategier. For å karakterisere dette la ψ : S N S N være 8) ψp) = ψ p) ψ 2 p) ψ N p). Nå har vi at p er en Nash likevekt hvis og bare hvis p ψp). Altså er Nash likevekter det samme som fikspunkter for ψ. Oppgaver 4: Per, Pål og Espen spiller følgende spill: Alle skriver et heltall fra til 0 på en lapp. Hvis Per skriver i, Pål j og Espen k blir utbetalingen til hver Finn en Nash likevekt for dette spillet. Per: i j, Pål: j k, Espen: k i.
5 5: Per, Pål og Espen spiller Flertallet vinner. Dette er et spill der alle spillerne på likt roper Blå! eller Rød!. De som har flertall vinner, og taperen må betale vinnerne en daler. Hvis alle roper samme farge blir det ingen utbetaling. Vis at dette er et nullsumspill og finn en Nash løsning. For å komme videre bruker vi Teorem 2 Kakutanis teorem). Hvis X er kompakt og konveks, og f : X X er en kontinuerlig og konveks korrespondanse slik at fx) for alle x X, så fins x X s.a. x fx). M.a.o. f har et fikspunkt. Dette teoremet skal vi forløpig ta for gitt. For å vise eksistens av en Nash likevekt, så må vi sjekke om ψ : S N S N og S N oppfyller kravene i Kakutanis teorem. Vi har allerede etablert at S N er konveks og kompakt, siden n i er det, og at ψp). Vi må vise at ψ er kontinuerlig og konveks. Det er lettest å vise at ψ er konveks. Først observerer vi at det direkte produktet av konvekse mengder blir konvekst, så for å vise at ψ er konveks, så holder det å vise at ψ i er konveks. Anta derfor at x og y er i ψ i p). Det vil si at Ê i p i ) = E i p,...,p i, x, p i+,...,p N) = E i p,...,p i, y, p i+,..., p N). Vi må vise at q = τx + τ)y ψ i p) for alle τ [0, ]. Siden p i E i p) er lineær, har vi E i p,...,p i, q, p i+,...,p N) = E i p,...,p i, τx + τ)y, p i+,...,p N) = τe i p,...,p i, x, p i+,...,p N) + τ)e i p,..., p i, y, p i+,...,p N) = ) τêi p i + ) τ)êi p i = Êi p i ). Altså er q ψ i p) og dermed blir ψ i, og også ψ, konveks. For å vise at ψ blir kontinurelig, viser vi først at ψ i er kontinuerlig. La {p n } S N og {q i n} n i være følger slik at p n p 0 og qn i q, når n. Videre antar vi at q i n ψ i p n ) for alle n. At ψ i er kontinuerlig betyr at q ψ i p 0 ), m.a.o. at Ê ) ) p i 0 = Ei p 0,..., q,...,p N 0. Siden ψ i p 0 ) velger vi w ψ i p 0 ), og lar ɛ være gitt ved ) ) ɛ = E i p 0,..., w,..., p N 0 Ei p 0,..., q,...,p N 0. 5
6 6 Siden w maksimerer E i så er ɛ 0. Ved å trekke fra og legge til samme ledd kan vi skrive ɛ som ) ) ɛ = E i p 0,...,w,..., p N 0 Ei p n,...,w,..., p N n } {{ } a ) ) + E i p n,...,w,..., p N n Ei p n,..., qn, i...,p N n } {{ } b + E i p n,...,qn i,.. ) ).,pn n Ei p 0,...,q,..., p N 0. } {{ } c Siden q i n ψ ip n ) så maksimerer q i n E ip i ) og derfor er b 0. Vi har altså etablert at 0 ɛ a + c. Nå har vi at p n p 0, og at qn i q. Derfor vil ) ) p n,..., w,..., p N n p 0,...,w,..., p N 0 og p n,..., qn i,.. ) ).,pn n p n,...,q,..., p N n. Siden E i : S N R er kontinuerlig, så kan vi få a og c vilkårlig små ved å velge n stor. Altså må ɛ = 0, og ψ i blir kontinuerlig. Antå nå at vi har en følge {q n } slik at q n ψp n ) og q n q 0. Vi må vise at q 0 ψp 0 ). Siden ψ i er kontinuerlig, så har vi at q i 0 ψ i p 0 ) for alle i, og dermed blir q 0 ψp). Altså er også ψ kontiuerlig. Ved Kakutanis teorem har ψ et fikspunkt. Dermed har spillet minst) en Nash likevekt. Å finne en Nash likevekt er et komplisert problem, for de av dere som synes slikt er interessant, er det ikke kjent om dette er P eller NP. 3. Brouwers og Kakutanis fikspunktsteoremer Nå gjør vi et forsøk på å forklare disse viktige teoremene. I dagligspråk sier Brouwers fikspunktsteorem følgende: Ta en kopp kaffe. Rør rolig rundt med en teskje. Ta ut skjeen og vent til kaffen igjen er i ro. Da sier Brouwer at det minst er ett punkt i kaffen som har kommet tilbake der det var før du rørte. Matematisk erstatter vi koppen med I N, gitt ved Nå lyder Brouwers teorem I N = { x R N x i, i =,..., N }. Teorem 3 Brouwers fikspunktsteorem). Hvis f : I N I N er en kontinuerlig funksjon, så fins det minst en x I N slik at fx) = x. Bevis. I første omgang presenterer jeg et overbevis for å overbevise eventuelle lesere om at dette er riktig. For N = så er teoremet lett å vise. La hx) = fx) x, siden f[, ]) [, ], så er f ) og f). Altså blir h ) 0 h). Videre er h kontinuerlig. Da sier skjæringssetningen at hx) = 0 for en x [, ].
7 Nå bruker vi induksjon, altså vi antar at teoremet gjelder for I N, og la f : I N I N, m.a.o. fx) = f x,..., x N ),f 2 x,...,x N ),..., f N x,...,x N )). Vi har også at f i x,..., x N ), for i =,...,N. Se nå på funksjonen h x N ) gitt ved x N f N x,...,x N, x N ) x N. Vi har at h ) 0 h) for alle x,...,x N ) I N. Da fins det minst en x N = x N x,...,x N ) [, ] slik at hx N ) = 0. Men vi vet mer, det må finnes en N dimensjonal hyperflate som deler I N i to, slik at h > 0 til venstre og h < 0 til høyre. Hvis ikke, ville vi kunne finne en kontinuerlig kurve ϕs) som gikk fra x N = til x N = slik at f N ϕs)) skiftet fortegn uten å ta verdien null. Altså fins det en kontinuerlig N 7 R Tx) R h < 0 h > 0 R N- - T y) h < 0 h > 0 R N- Figur. Hyperflaten der h = 0 dimensional flate Ψ gitt ved at h = 0 på denne flaten. Det kan selvfølgelig finnes flere. Dersom Ψ ikke er en funksjon av x,...,x N ) så kan vi finne en kontinuerlig og invertibel funksjon T : I N I N som retter ut Ψ. Vi kan også velge T slik at T N x) = x N, dvs. T forandrer ikke den Nte koordinaten til et punkt. Sett y = Tx) = T x),...,t N x)) I N, og observer at flaten Ψ kan skrives som y, ψy)) for en kontinuerlig funksjon ψ. La Fy) = T f T y, ψy)) )). Nå er F : I N I N og kontinunerlig, ved induksjonshypotesen har F et fikspunkt y 0. Sett x 0 = T y 0, ψy 0 )), vi har nå at y 0 = F y 0 ), = T f T y 0, ψy 0 )) )), vi bruker T på y 0, ψy 0 )) og får x 0 = f x 0 ), siden T og T ikke forandrer på den Nte komponenten. Altså har f et fikspunkt. Dette beviset må bygges litt på for å bli vanntett, men det fins bevis som bruker denne strategien. Vi kan imidlertid merke oss at dersom Brouwers teorem holder for f : I N I N, så holder det for alle kontinuerlige funksjoner som tar en konveks begrenset mengde inn i seg
8 8 selv. Dette kan lett vises ved å transformere den gitte konvekse mengden inn i I N. Derfor spiller det ingen rolle hvilken konveks mengde vi viser Brouwers teorem i. Holder teoremet for én slik mengde, holder det for alle. Vi skal vise Brouwers teorem på ordentlig til slutt i dette notatet, forløpig får vi klare oss med det overbeviset jeg har gitt. La nå { v 0,...,v N} være vektorer i R n. Det er n+ stykker av dem, så de kan ikke være lineært uavhengige. Sett v 0,...,v N til å være mengden av vektorer x som kan skrives der x i R slik at x = x 0 v 0 + x v + + x N v N, x i 0, og x 0 + x + + x N =. Mengden v 0,...,v N kalles et simpleks, og x 0,..., x N kalles de barysentriske koordinatene til x relativt til simplekset v 0,...,v N. I en dimensjon er et simplex en linje, og i to dimensjoner en trekant, i tre dimensjoner et tetraeder osv. Et simpleks kalles ikke-degenerert hvis v v 0, v 2 v 0,...,v N v 0 er lineært uavhengige. Fra definisjonen er det opplagt?) at et simpleks er konvekst. Derfor gjelder Brouwers teorem for simplekset, altså hvis f : v 0,..., v N v 0,..., v N er kontinuerlig, så fins det et punkt x v 0,...,v N slik at f x) = x. Vi kan nå definere den nte barysentriske oppdelingen av v 0,...,v N. Dette er de punktene som har barysentriske koordinater der 0 k i N er heltall, og x = n k 0,...,k N ), k 0 + k + + k N = n. Dette gir et slage gitter på v 0,...,v N, og deler opp simplekset i mange mindre simplekser som er skalerte versjoner av v 0,...,v N. Hver av disse små simpleksene kaller vi en celle. Oppgaver 6: La v 0, v, v 2 være simplekset bestemt av v 0 = 3, 2), v =, 5), v 2 = 7, ). Dersom x har Kartesiske koordinater c, c 2 ), finn de barysentriske koordinatene x 0, x, x 2 ). Vis at v 0, v, v 2 er ikke-degenerert. Tegn simplekset, og de fem linjene x = 0, x = /5, x = 2/5, x = 3/5, x = 4/5. Tegn den sjette barysentriske oppdelingen av v 0, v, v 2. Merk av punktet med barysentriske koordinater 3,, 2)/6.
9 Teorem 4 Kakutanis teorem for simplekser). Hvis X = v 0,..., v N er ikke-degenerert og f : X X er en kontinuerlig og konveks korrespondanse slik at fx) for alle x X, så fins x X s.a. x fx). M.a.o. f har et fikspunkt. Bevis. Vi starter med å lage den nte barysentriske oppdelingen av X. Nå kan vi lage en kontinuerlig funksjon g n : X X som følger. Hvis x er et hjørne i oppdelingen, så definerer vi g n x) = y, der y er et punkt i fx). Hvis x ikke er et hjørnepunkt, så ligger x i en celle som selv er et simpleks x x 0, x,...,x N. Her er x 0,...,x N hjørnene i cellen. Altså har x barysentriske koordinater relativt til x 0, x,...,x N gitt ved θ 0,...,θ N, Da kan vi definere x = θ 0 x θ N x N. g n x) = N θ j f x j). j=0 Dette er en lineær interpolasjon i mellom hjørneverdiene i cellen, derfor blir g n kontinuerlig. Ved Brouwers teorem har g n et fikspunkt x n = g n x n ) X. Hvis x n er et hjørne i en celle, så er teoremet bevist. Derfor antar vi at x n ikke er et hjørne, og at x n ligger i cellen x 0 n, x n,...,xn n, slik at x n har barysentriske koordinater Ved definisjonen av g n får vi at x n = θ 0,n x 0 n + θ,nx n + + θ N,nx N n. 9) x n = g n x n ) = θ 0,n y 0 n + θ,ny n + + θ N,ny N n, der 0) y j n f x j n), j = 0,...,N. Siden alle følgene våre {x n } n>0, {θn j } n>0, {yj n } n>0 ) ligger i begrensede og lukkede mengder, så finnes det delfølger slik at alle konvergerer. Ved å ta videre delfølger kan vi få alle til å konvergere for samme delfølge {n l }. For å spare blekk, nummererer vi om og fortsetter å indeksere alle følgene med n. Nå har vi altså følger {x n } n>0, x n x, {θ j,n } n>0 θ j,n θ j, { y j n } n>0 y j n yj. 9
10 0 Siden cellene krymper til ett punkt når n, så må cellehjørnene i x 0 n, x n,...,xn n alle konvergere mot det samme punktet, m.a.o. Ved å gå til grensen i 9) får vi at x j n x, for j = 0,...,N. x = θ 0 y 0 + θ y + + θ N y N. Siden korrespondansen f kontinuerlig, så kan vi gå til grensen i 0) og konkludere at y j f x) for j = 0,...,N. Men f er konveks, og x er en konvekskombinasjon av punkter i f x), altså er x f x). Hvis Kakutanis teorem holder for simplekser, så holder det for alle konvekse, lukkede og begrensede mengder X R n. Her følger argumentasjonen for det. La X være konveks, lukket og begrenset og f : X X være kontinuerlig og konveks. Velg et simplex S = v 0,...,v N slik at X S, og et punkt a X. Nå kan vi definere en korrespondanse g : S S som følger. For s S \X la xs) være skjæringspunktet mellom v 2 a X xs) v 0 s v Figur 2 linjen fra a til s og X. Siden X er konveks, så fins det bare ett skjæringspunkt. For alle s X sett xs) = s, og definer gs) = fxs)) X S. Nå blir g konveks, siden f er det. For å sjekke at g blir kontinuerlig, la Siden s xs) er kontinuerlig, har vi at Nå er f kontinuerlig, og derfor blir s i s, y i g s i ), og y i ȳ. x s i ) x s), y i f x s i )) og y i ȳ. ȳ fx s)) = g s).
11 Derfor blir også g kontinuerlig. Ved Kakutanis teorem for simplekser vet vi at det fins et punkt s S slik at s g s). Men gs) X for alle s, derfor er x s) = s, og g s) = f s). Altså har f et fikspunkt. Tilslutt kommer et ordentlig bevis for Brouwers fikspunktsteorem. Vi har sett at det er det samme hvilken konveks mengde vi velger når vi skal vise dette teoremet. Det beviset vi skal bruke stammer fra Milnor som publiserte det i 978. Som den konvekse mengden bruker vi kula i n dimensjoner. Vi bruker notasjonen B n = { x R n x }, B n = { x R n x = }, for kula og kuleskallet. Milnors bevis for Brouwers teorem støtter seg på at you can t comb the hair on a sphere. På matematisk betyr dette Teorem 5. For odde n så fins det ingen kontinuerlige tangentvektorfelt på B n som ikke tar verdien null i minst ett punkt. Bevis. Hvis det fins et slikt vektorfelt wx), så fins det et vektorfelt vx) slik at vx) = v = w/ w ). Så derfor antar vi at for u B n, har vi u vu) = 0, vu) =. Antå også foreløpig at v er kontinuerlig deriverbar. Definer nå A som A = { x R n /2 x 3/2 }. Vi kan utvide definisjonsmengden til v ved å sette ) x vx) = x v, x A. x Nå er v kontinuerlig deriverbar og vi har Velg nå et lite tall t og definer funksjonen x vx) = 0, og vx) = x. η t x) = x + tvx). Denne funksjonen avbilder A på en annen mengde A t = η t A). Vi påstår at for tilstrekkelig små t er η t. Siden v er kontinuerlig deriverbar har vi at vx) vy) λ x y, for alle x og y i A og en konstant λ. Anta at η t x) = η t y), da blir x + tvx) = y + tvy), og dermed x y = t vx) vy) t λ x y. Dette medfører at x = y dersom t λ <. Videre har vi at siden x vx) blir η t x) = x + tvx) = x + t 2) /2.
12 2 Derfor avbilder η t kulskallet med radius r på kuleskallet med radius r + t 2 ) /2. For å gå videre må vi forsikre oss om at bildet av kuleskallet med radius r er hele kuleskallet med radius r + t 2 ) /2. Det er det samme som at ligningen x + tvx) = z alltid har en løsning, for /2 x 3/2 og z = x + t 2 ) /2. For å vise dette antar vi først at z =. En løsning vil tilfredstille ligningen x = h t x) = z tvx), m.a.o. den er et fikspunkt for h t. Ved å bruke trekantulikhetene får vi a b a b a + b, t h t x) + t, slik at dersom t /2 så avbilder h t A inn i A. Hvis t λ < så blir h t x) h t y) λ t x y < x y. Det betyr at h t er en kontraksjon av A inn i seg selv. Nå kan vi bruke kontraksjonsprinsippet 2 og konkludere at h t har et fikspunkt. For z, sett z = z/ z, da kan vi løse ligningen x + tv x) = z. Multipliser denne ligningen med z, sett x = z x, dette gir x + t z v x) = x + tv z x) = t + tvx) = z. Nå har vi vist at for tilstrekkelig små t avbilder η t A på A t, og at A t = { x R n /2 + t 2 ) /2 x 3/2 + t 2 ) /2}. Siden A t er similær med A, så skalerer volumet med størrelsen, d.v.s., A t = + t 2) n/2 A, der A er volumet av A. Vi kan også bruke kalkulus for å beregne volumet av A t, siden η t tar A på A t har vi at ) A t = det ηt ) i dx...dx n, A x j der ) ηt ) i betegner Jacobideterminanten til η t. x j Vi har at η t ) i = δ ij + t v i. x j x j 2 Ikke fortvil! Kontraksonsprinsippet er et mye enklere fikspunkresultat som blir vist etterpå. Det er det siste som blir vist i dette notatet.
13 Vi ser at Jacobimatrisen går mot identitetsmatrisen når t 0. Derfor er determinanten positiv for små t, og absoluttverdiene er unødvendige. Hvis vi ser på Jacobideterminanten som en funksjon av t, så ser vi at den blir et polynom på formen ) ηt ) i det = a 0 x) + a x)t + + a n x)t n. x j Derfor blir integralet også et nte gradspolynom, altså vi får vi at Men vi har at funksjonen + t 2 ) n/2 A t = b 0 + b t + + b n t n = A + t 2) n/2. ikke er et polynom dersom n er odd. Dersom vi ikke har gjort noen andre feil, så må forutsetningen for regningen være feil, altså fins det ikke noe kontinuerlig deriverbart vektorfelt på B n som er forskjellig fra null i alle punkter. For å fullføre beviset må vi fjerne antagelsen om deriverbarhet. Hvis nå v er et kontinuerlig vektorfelt på B n slik at v 0, kan vi utvide v til enhetskuben ved å sette vx) = x vx/ x ). Deretter kan vi finne en uendelig) deriverbar approximasjon p slik at v p blir vilkårlig liten. Siden vu) u = 0 så vil wu) = p p u)u 0 for u =. Vi har at w er deriverbar, at w er tangent til B n. Derfor vil ṽu) = wu) wu) være et kontinuerlig deriverbart enehetstangentvektorfelt. Men det fins ikke siden n er odd. Nå kan bevise Teorem 6 Brouwers fikspunktsteorem). La f : B n B n være kontinuerlig. Da har f et fikspunkt. Bevis. Vi antar at f ikke har et fikspunkt, og håper på å oppnå en selvmotsigelse. La x B n, sett y = fx) og z = x y. Da er z 0, og på B n peker z utover siden og vi har at x z = x x x y = x y, 0 < x y 2 = x x 2x y + y y 2 x y). Altså er x y > 0 og z peker utorver på B n. Nå definerer vi wx) til å være wx) = x λy, λ = x x x y. 3
14 4 Dette veldefinert og kontinuerlig, siden x y > 0. For x B n har vi at λ = 0, og derfor er wx) = x. Hvis wx) = 0 for en x i det indre av B n så har vi at ) 0 = x y)x x x)y. Men hvis wx) = 0, så er x = λy, og Derfor gir ) at x y)x = λ 2 y y)y = x x)y. 0 = x x x)y y + x x)y = x y 0. Altså er wx) 0 for alle x B n. Kula B n er ekvatorialdisken i kula B n+, vi bruker dette til å konstruere et tangentialvektorfelt til kuleskallet B n+. Vi konstruerer først vektorfeltet på den sørlige havlkule. N B n sørlige halvkule av x B n+ w u v Figur 3 For x B n, la u B n+ være skjæringspunktet mellom B n+ og linja som går gjennom nordpolen i B n+ og x denne linja går gjennom planeten ). Siden x ligger mellom N og u så har vi x = θ)n + θu, for en θ [0, ]. Vi kan regne ut at 2) θ = x + ). 2 Ved å bruke denne stereografiske projeksjonen kan vi overføre vektorfeltet wx) til et vektorfelt på den sørlige halvkule. La først og sett deretter xt) = x + twx), 3) vx) = d dt uxt)) t=0.
15 For å se at v 0 deriverer vi identiteten xt) = θt))n + θt)ut) og setter t = 0. Da får vi at w = θ 0)N + θ 0)u0) + θ0)v, og løser vi denne for v får vi at v = θ0) w + θ 0)N u)). Hvis θ 0) = 0 så er v 0 siden w 0. Hvis θ 0) 0 kan vi se på den siste n + )te) kompontenten til v, v n+ = θ 0 + θ 0) u n+ )) 0 siden w n+ = 0 og u n+ < 0. Hva med vx) når x B n? Her har vi at wx) x, u x 0 og θ. Vii har også at θ 0) = d 2 dt + xt) xt)) t=0 = x wx) = x x =. Nå får vi altså at v x = = x + N x) = N. Ved ekvator peker vektorfeltet vu) rett mot nord, og vu) 0 i hele den sørlige halvkule. Nå kan vi gjøre nesten) det samme ved å projisere fra sørpolen, den enenste forskjellen blir at vi bytter fortegn i defininsjonen av v i ligning 3), slik at v + x) = d dt u+ xt)) t=0, hvor u + er den stereografiske projeksjonen av x fra sørpolen på den nordlige halvkule. Ved ekvator vil v + = N) = N og v + 0 i hele den nordlige halvkule. Nå kan vi skjøte sammen v og v + til et vektorfelt som aldri er null på hele B n+. Slike finnes ikke dersom n + er odd. Altså fins heller ikke en kontinuerlig funksjon f : B n B n uten fikspunkter hvis n er et partall. Hva om n er et oddetall og f : B n B n er kontinuerlig? Ved å skrive et punkt z R n+ som z = x, x n+ ) der x R n kan vi betrakte B n B n+ og definere g : B n+ B n+ ved at g x, x n+ ) = fx). Da er g kontinuerlig og siden n + er et partall har g et fikspunkt x. Siden gb n+ ) B n må x B n også være et fikspunkt for f. Oppgaver 7: Et berømt teorem navngitt etter Oscar Perron sier at en n n matrise med bare positive elementer må ha minst en positiv egenverdi, med tilhørende egenvektor med bare positive elementer. M.a.o., det fins en vektor x med x i > 0 for i =,..., n og λ > 0 slik at Ax = λx. La x n, sett λx) = i Ax) i, og definer fx) = Ax λx). 5
16 6 Vis at f : n n er kontinuerlig, dermed Perrons teorem. For å gjøre dette notatet mest mulig komplett, viser vi kontraksjonsprinsippet til slutt. En funksjon kalles en kontraksjon hvis fx) fy) < x y. Lemma 2 Kontraksjonsprinsippet). Anta at f : X Y X er kontinuerlig, der X R n og Y er begrenset. Hvis f er en kontraksjon så fins det en entydig x Y s.a. fx) = x. Bevis. Siden f er en kontraksjon, så fins det et tall r < slik at fx) fy) r x y. Velg en x 0 Y og sett x n+ = fx n ) for n. Da har vi at x n+ x n = f x n ) f x n ) r x n x n r n f x ) x 0 Cr n, siden Y er begrenset. Nå kan vi vise at {x n } n>0 er en Cauchyfølge og derfor konvergent. For m > n har vi x m x n x m x m + x m x m x n+ x n Cr m + Cr m Cr n = Cr n rm n r 0 når n blir stor. Altså har vi at x n x Y. Nå har vi at x = lim n f x n ) = f ) lim x n n = fx), siden f er kontinuerlig. For å vise at vi kun har ett fikspunkt anta at vi har to, x og y. Da får vi at som er en selvmotsigelse hvis x y. x y = fx) fy) < x y, Oppgaver 8: For x R la fx) = sinλx) der λ er en konstant. For hvilke λ er f en kontraksjon?
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT111 Prøveeksamen Eksamensdag: 5. juni 21. Tid for eksamen: 1. 13.3. Oppgavesettet er på 9 sider. Vedlegg: Tillatte hjelpemidler:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT111 Prøveeksamen Eksamensdag: 5. juni 21. Tid for eksamen: 1. 13.3. Oppgavesettet er på 9 sider. Vedlegg: Tillatte hjelpemidler:
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Ny/utsatt eksamen i Eksamensdag: 9. august 2. Tid for eksamen: 9 2. Oppgavesettet er på 8 sider. Vedlegg: Tillatte hjelpemidler: MAT Kalkulus
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Ny/utsatt eksamen i Eksamensdag: 9. august 2. Tid for eksamen: 9 2. Oppgavesettet er på 8 sider. Vedlegg: Tillatte hjelpemidler: MAT Kalkulus
Løsningsforslag øving 6
 Løsningsforslag øving 6 7 Husk Teorem 79 i notatet: En delmengde U av et vektorrom V er et underrom hvis ) nullvektoren er i U, ) summen av to vektorer i U er i U igjen, og 3) et skalarmultiplum av en
Løsningsforslag øving 6 7 Husk Teorem 79 i notatet: En delmengde U av et vektorrom V er et underrom hvis ) nullvektoren er i U, ) summen av to vektorer i U er i U igjen, og 3) et skalarmultiplum av en
Fasit til utvalgte oppgaver MAT1110, uka 28/4-2/5
 Fasit til utvalgte oppgaver MAT1110, uka 8/4-/5 Tom Lindstrøm (lindstro@math.uio.no) 5..5 a) Alle punktene i B har avstand til origo større enn 1, så d(0, B) må være minst 1. Ved å velge punkter på x-aksen
Fasit til utvalgte oppgaver MAT1110, uka 8/4-/5 Tom Lindstrøm (lindstro@math.uio.no) 5..5 a) Alle punktene i B har avstand til origo større enn 1, så d(0, B) må være minst 1. Ved å velge punkter på x-aksen
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i Eksamensdag: 11. juni 21. Tid for eksamen: 14.3 17.3. Oppgavesettet er på 7 sider. Vedlegg: Tillatte hjelpemidler: MAT111 Kalkulus
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i Eksamensdag: 11. juni 21. Tid for eksamen: 14.3 17.3. Oppgavesettet er på 7 sider. Vedlegg: Tillatte hjelpemidler: MAT111 Kalkulus
Løsninger for eksamen i MAT Lineær algebra og M102 - Lineær algebra, fredag 28. mai 2004, Oppgave 1. M s = = 1 2 (cofm 2) T.
 Løsninger for eksamen i MAT - Lineær algebra og M - Lineær algebra, fredag 8. mai 4, (a) Finn determinanten til matrisen M s = Oppgave s uttrykt ved s, og bruk dette til å avgjøre for hvilke s matrisen
Løsninger for eksamen i MAT - Lineær algebra og M - Lineær algebra, fredag 8. mai 4, (a) Finn determinanten til matrisen M s = Oppgave s uttrykt ved s, og bruk dette til å avgjøre for hvilke s matrisen
MAT1120 Notat 2 Tillegg til avsnitt 5.4
 MAT1120 Notat 2 Tillegg til avsnitt 54 Dette notatet utfyller bokas avsnitt 54 om matriserepresentasjonen (også kalt koordinatmatrisen) til en lineær avbildning mellom to endeligdimensjonale vektorrom
MAT1120 Notat 2 Tillegg til avsnitt 54 Dette notatet utfyller bokas avsnitt 54 om matriserepresentasjonen (også kalt koordinatmatrisen) til en lineær avbildning mellom to endeligdimensjonale vektorrom
MAT1120 Notat 2 Tillegg til avsnitt 5.4
 MAT1120 Notat 2 Tillegg til avsnitt 54 Dette notatet utfyller bokas avsnitt 54 om matriserepresentasjoner (også kalt koordinatmatriser) av lineære avbildninger mellom endeligdimensjonale vektorrom En slik
MAT1120 Notat 2 Tillegg til avsnitt 54 Dette notatet utfyller bokas avsnitt 54 om matriserepresentasjoner (også kalt koordinatmatriser) av lineære avbildninger mellom endeligdimensjonale vektorrom En slik
Løsningsforslag. e n. n=0. 3 n 2 2n 1. n=1
 Eksamen i BYPE2000 - Matematikk 2000 Dato: 6. juni 2014 Målform: Bokmål Antall oppgaver: 7 (20 deloppgaver) Antall sider: 4 Vedlegg: Noen formler Hjelpemiddel: Ingen Alle svarene skal grunngis. Alle deloppgavene
Eksamen i BYPE2000 - Matematikk 2000 Dato: 6. juni 2014 Målform: Bokmål Antall oppgaver: 7 (20 deloppgaver) Antall sider: 4 Vedlegg: Noen formler Hjelpemiddel: Ingen Alle svarene skal grunngis. Alle deloppgavene
MAT Prøveeksamen 29. mai - Løsningsforslag
 MAT0 - Prøveeksamen 9 mai - Løsningsforslag Oppgave Sett A = 4 4 0 x 0, x = x, b =, x 0 og la v, v, v betegne kolonnevektorene til A a) Skriv A x = y som en vektorlikning x Svar : Siden A x = [v v v ]
MAT0 - Prøveeksamen 9 mai - Løsningsforslag Oppgave Sett A = 4 4 0 x 0, x = x, b =, x 0 og la v, v, v betegne kolonnevektorene til A a) Skriv A x = y som en vektorlikning x Svar : Siden A x = [v v v ]
Løsningsforslag til eksamen i TMA4105 matematikk 2,
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av Løsningsforslag til eksamen i TMA45 matematikk, 9.5.4 Oppgave La fx, y, z) xy + arctanxz). La P være punktet,, ). a)
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av Løsningsforslag til eksamen i TMA45 matematikk, 9.5.4 Oppgave La fx, y, z) xy + arctanxz). La P være punktet,, ). a)
= x lim n n 2 + 2n + 4
 NTNU Institutt for matematiske fag TMA400 Matematikk høsten 20 Løsningsforslag - Øving Avsnitt 8.7 6 Potensrekken konvergerer opplagt for x = 0, så i drøftingen nedenfor antar vi x 0. Vi vil bruke forholdstesten
NTNU Institutt for matematiske fag TMA400 Matematikk høsten 20 Løsningsforslag - Øving Avsnitt 8.7 6 Potensrekken konvergerer opplagt for x = 0, så i drøftingen nedenfor antar vi x 0. Vi vil bruke forholdstesten
Matematikk 1 (TMA4100)
 Matematikk 1 (TMA4100) Forelesning 6: Derivasjon Eirik Hoel Høiseth Stipendiat IMF NTNU 22. august, 2012 Stigningstallet i et punkt Stigningstallet i et punkt Vi vender nå tilbake til problemet med å finne
Matematikk 1 (TMA4100) Forelesning 6: Derivasjon Eirik Hoel Høiseth Stipendiat IMF NTNU 22. august, 2012 Stigningstallet i et punkt Stigningstallet i et punkt Vi vender nå tilbake til problemet med å finne
Notater nr 9: oppsummering for uke 45-46
 Notater nr 9: oppsummering for uke 45-46 Bøkene B (læreboken): Tor Gulliksen og Arne Hole, Matematikk i Praksis, 5. utgave. K (kompendium): Amir M. Hashemi, Brukerkurs i matematikk MAT, høsten. Oppsummering
Notater nr 9: oppsummering for uke 45-46 Bøkene B (læreboken): Tor Gulliksen og Arne Hole, Matematikk i Praksis, 5. utgave. K (kompendium): Amir M. Hashemi, Brukerkurs i matematikk MAT, høsten. Oppsummering
n=0 n=1 n + 1 Vi får derfor at summen er lik 1/2. c)
 Eksamen i BYPE2000 - Matematikk 2000 Dato: 204 Målform: Bokmål Antall oppgaver: 7 (20 deloppgaver) Antall sider: 4 Vedlegg: Noen formler Hjelpemiddel: Ingen Alle svarene skal grunngis. Alle deloppgavene
Eksamen i BYPE2000 - Matematikk 2000 Dato: 204 Målform: Bokmål Antall oppgaver: 7 (20 deloppgaver) Antall sider: 4 Vedlegg: Noen formler Hjelpemiddel: Ingen Alle svarene skal grunngis. Alle deloppgavene
Vær OBS på at svarene på mange av oppgavene kan skrives på flere ulike måter!
 Vær OBS på at svarene på mange av oppgavene kan skrives på flere ulike måter! Oppgave.. a x y = x + y = r r r +r r x y = y fri x y = y fri Vi får én fri variabel, og løsningens har følgelig dimensjon.
Vær OBS på at svarene på mange av oppgavene kan skrives på flere ulike måter! Oppgave.. a x y = x + y = r r r +r r x y = y fri x y = y fri Vi får én fri variabel, og løsningens har følgelig dimensjon.
Løsningsforslag til eksamen i MAT 1100, H06
 Løsningsforslag til eksamen i MAT, H6 DEL. poeng Hva er den partiellderiverte f z xyz cosxyz x sinyz + xyz cosyz xy cosyz x sinyz + xz cosyz cosyz xyz sinyz når fx, y, z = xz sinyz? Riktig svar b: x sinyz
Løsningsforslag til eksamen i MAT, H6 DEL. poeng Hva er den partiellderiverte f z xyz cosxyz x sinyz + xyz cosyz xy cosyz x sinyz + xz cosyz cosyz xyz sinyz når fx, y, z = xz sinyz? Riktig svar b: x sinyz
MAT1100 - Grublegruppen Uke 36
 MAT - Grublegruppen Uke 36 Jørgen O. Lye Partiell derivasjon Hvis f : R 2 R er en kontinuerlig funksjon, så kaller man følgende dens partiellderiverte (gitt at de finnes!) f f(x + h, y) f(x, y) (x, y)
MAT - Grublegruppen Uke 36 Jørgen O. Lye Partiell derivasjon Hvis f : R 2 R er en kontinuerlig funksjon, så kaller man følgende dens partiellderiverte (gitt at de finnes!) f f(x + h, y) f(x, y) (x, y)
Litt om evolusjonær spillteori.
 Litt om evolusjonær spillteori 1 ESS: Evolusjonært Stabile Strategier I klassisk spillteori har spillere strategier, i biologi har arter strategier (genotypiske varianter som arves, modulo mutasjoner,
Litt om evolusjonær spillteori 1 ESS: Evolusjonært Stabile Strategier I klassisk spillteori har spillere strategier, i biologi har arter strategier (genotypiske varianter som arves, modulo mutasjoner,
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT 0 Lineær algebra Eksamensdag: Mandag 0. desember 0 Tid for eksamen: 4.30 8.30. Oppgavesettet er på 7 sider. Vedlegg: Tillatte
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT 0 Lineær algebra Eksamensdag: Mandag 0. desember 0 Tid for eksamen: 4.30 8.30. Oppgavesettet er på 7 sider. Vedlegg: Tillatte
TMA4100 Matematikk 1, høst 2013
 TMA4100 Matematikk 1, høst 2013 Teknostart forelesning 6 www.ntnu.no TMA4100 Matematikk 1, høst 2013, Teknostart forelesning 6 Grenseverdier I dagens forelesning skal vi se på følgende: 1 En formell definisjon
TMA4100 Matematikk 1, høst 2013 Teknostart forelesning 6 www.ntnu.no TMA4100 Matematikk 1, høst 2013, Teknostart forelesning 6 Grenseverdier I dagens forelesning skal vi se på følgende: 1 En formell definisjon
Løsningsforslag til prøveeksamen i MAT 1110, våren 2006
 Løsningsforslag til prøveeksamen i MAT, våren 6 Oppgave : a) Vi har C 5 3 II+( )I a + 3a 3a III+I 3 II 3 3 3 3 a + 3a 3a 3 a + 3a 3a III+II I+( ))II 3 3 3 a + 3a 3a 3 3 3 a + 3a 4 3 3a a + 3a 4 3 3a b)
Løsningsforslag til prøveeksamen i MAT, våren 6 Oppgave : a) Vi har C 5 3 II+( )I a + 3a 3a III+I 3 II 3 3 3 3 a + 3a 3a 3 a + 3a 3a III+II I+( ))II 3 3 3 a + 3a 3a 3 3 3 a + 3a 4 3 3a a + 3a 4 3 3a b)
Analysedrypp II: Kompletthet
 Analysedrypp II: Kompletthet Kompletthet er et begrep som står sentralt i både MAT1100 og MAT1110, og som vil stå enda mer sentralt i MAT2400. I de tidligere kursene fremstår begrepet på litt forskjellig
Analysedrypp II: Kompletthet Kompletthet er et begrep som står sentralt i både MAT1100 og MAT1110, og som vil stå enda mer sentralt i MAT2400. I de tidligere kursene fremstår begrepet på litt forskjellig
Oppgave 1 (25 %) - Flervalgsoppgaver
 Oppgaver og løsningsforslag for 4t eksamen 10.mai 006 i LO510D Lineær algebra med grafiske anvendelser. Fra og med oppgave skal alle svar begrunnes. Oppgave 1 (5 %) - Flervalgsoppgaver Denne oppgaven består
Oppgaver og løsningsforslag for 4t eksamen 10.mai 006 i LO510D Lineær algebra med grafiske anvendelser. Fra og med oppgave skal alle svar begrunnes. Oppgave 1 (5 %) - Flervalgsoppgaver Denne oppgaven består
3x + 2y 8, 2x + 4y 8.
 Oppgave En møbelfabrikk produserer bord og stoler Produksjonen av møbler skjer i to avdelinger, avdeling I og avdeling II Alle møbler må innom både avdeling I og avdeling II Det å produsere et bord tar
Oppgave En møbelfabrikk produserer bord og stoler Produksjonen av møbler skjer i to avdelinger, avdeling I og avdeling II Alle møbler må innom både avdeling I og avdeling II Det å produsere et bord tar
TMA4105 Matematikk 2 Vår 2014
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA4105 Matematikk 2 Vår 2014 Løsningsforslag Øving 7 10.4.7 Vi skal finne likningen til et plan gitt to punkter P = (1, 1,
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA4105 Matematikk 2 Vår 2014 Løsningsforslag Øving 7 10.4.7 Vi skal finne likningen til et plan gitt to punkter P = (1, 1,
Løsningsforslag, midtsemesterprøve MA1103, 2.mars 2010
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 5 Løsningsforslag, midtsemesterprøve MA03,.mars 00 Oppgave Tegn figur og finn en parametrisering for skjæringskurven
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 5 Løsningsforslag, midtsemesterprøve MA03,.mars 00 Oppgave Tegn figur og finn en parametrisering for skjæringskurven
MAT1120 Notat 1 Tillegg til avsnitt 4.4
 MAT1120 Notat 1 Tillegg til avsnitt 4.4 Vi tar utgangspunkt i Teorem 8 fra avsn. 4.4 i boka. For ordens skyld gjentar vi teoremet her: Teorem 8 [Avsn. 4.4]: Anta at B = {b 1,..., b n } er en (ordnet) basis
MAT1120 Notat 1 Tillegg til avsnitt 4.4 Vi tar utgangspunkt i Teorem 8 fra avsn. 4.4 i boka. For ordens skyld gjentar vi teoremet her: Teorem 8 [Avsn. 4.4]: Anta at B = {b 1,..., b n } er en (ordnet) basis
Løsningsforslag MAT 120B, høsten 2001
 Løsningsforslag MAT B, høsten Sett A = ( ) (a) Finn egenverdiene og egenvektorene til A ( ) λ =, e = ( λ =, e = ) (b) Finn matrisen e ta og den generelle løsningen på initialverdiproblemet Ẋ = AX, X()
Løsningsforslag MAT B, høsten Sett A = ( ) (a) Finn egenverdiene og egenvektorene til A ( ) λ =, e = ( λ =, e = ) (b) Finn matrisen e ta og den generelle løsningen på initialverdiproblemet Ẋ = AX, X()
MA0002 Brukerkurs i matematikk B Vår 2017
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA0002 Brukerkurs i matematikk B Vår 2017 Løsningsforslag Øving 11 Oppgaver fra boken: 10.6 :, 8, 12, 19, 1, (valgfritt - 9,
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA0002 Brukerkurs i matematikk B Vår 2017 Løsningsforslag Øving 11 Oppgaver fra boken: 10.6 :, 8, 12, 19, 1, (valgfritt - 9,
MA0002 Brukerkurs i matematikk B Vår 2014
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA0002 Brukerkurs i matematikk B Vår 2014 Løsningsforslag Øving 10 Oppgaver fra boken: 10.6 : 1, 8, 9, 12, 19, 26, 29,, 4 Det
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA0002 Brukerkurs i matematikk B Vår 2014 Løsningsforslag Øving 10 Oppgaver fra boken: 10.6 : 1, 8, 9, 12, 19, 26, 29,, 4 Det
LØSNINGSFORSLAG EKSAMEN I GRUNNKURS I ANALYSE I (MA1101/MA6101)
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 6 LØSNINGSFORSLAG EKSAMEN I GRUNNKURS I ANALYSE I (MA0/MA60) Fredag 2. desember 202 Tid: 09:00 3:00 Hjelpemidler: Kode
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 6 LØSNINGSFORSLAG EKSAMEN I GRUNNKURS I ANALYSE I (MA0/MA60) Fredag 2. desember 202 Tid: 09:00 3:00 Hjelpemidler: Kode
Oblig 1 - MAT Oppgave 1. Fredrik Meyer. Vi lar α > 1 og x 1 > α. Vi definerer en følge (x n ) ved. x n+1 = α + x n 1 + x n.
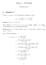 Oblig 1 - MAT2400 Fredrik Meyer 1 Oppgave 1 Vi lar α > 1 og x 1 > α. Vi definerer en følge (x n ) ved Lemma 1 (a). x n > 1 n N x n+1 = α + x n = x n + α x2 n Bevis. Siden α > 1 er α + x n >, så 1 = 1+xn
Oblig 1 - MAT2400 Fredrik Meyer 1 Oppgave 1 Vi lar α > 1 og x 1 > α. Vi definerer en følge (x n ) ved Lemma 1 (a). x n > 1 n N x n+1 = α + x n = x n + α x2 n Bevis. Siden α > 1 er α + x n >, så 1 = 1+xn
Anbefalte oppgaver - Løsningsforslag
 TMA405 Matematikk Anbefalte oppgaver - Løsningsforslag Uke 6 3..9: Vi starter med å finne de kritiske punktene. De deriverte blir T x (x, y) = ( x xy)e x y T y (x, y) = ( y xy)e x y, slik at de kritiske
TMA405 Matematikk Anbefalte oppgaver - Løsningsforslag Uke 6 3..9: Vi starter med å finne de kritiske punktene. De deriverte blir T x (x, y) = ( x xy)e x y T y (x, y) = ( y xy)e x y, slik at de kritiske
Kontinuitet og derivasjon Forelesning i Matematikk 1 TMA4100
 Kontinuitet og derivasjon Forelesning i Matematikk 1 TMA4100 Hans Jakob Rivertz Institutt for matematiske fag 25. august 2010 2 Dagens pensum I dag vil vi se på følgende: Kontinuerlige funksjoner Den deriverte
Kontinuitet og derivasjon Forelesning i Matematikk 1 TMA4100 Hans Jakob Rivertz Institutt for matematiske fag 25. august 2010 2 Dagens pensum I dag vil vi se på følgende: Kontinuerlige funksjoner Den deriverte
MA0002 Brukerkurs i matematikk B Vår 2016
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA0002 Brukerkurs i matematikk B Vår 2016 Løsningsforslag Øving 11 Oppgaver fra boken: 10.6 : 1, 8, 9, 12, 19, 26, 29,, 4 Det
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA0002 Brukerkurs i matematikk B Vår 2016 Løsningsforslag Øving 11 Oppgaver fra boken: 10.6 : 1, 8, 9, 12, 19, 26, 29,, 4 Det
Lineære likningssystemer og matriser
 Kapittel 3 Lineære likningssystemer og matriser I dette kapittelet skal vi sette sammen Kapittel 1 og 2. 3.1 Den utvidede matrisen til et likningssystem Vi starter med et lineært likningssystem med m likninger
Kapittel 3 Lineære likningssystemer og matriser I dette kapittelet skal vi sette sammen Kapittel 1 og 2. 3.1 Den utvidede matrisen til et likningssystem Vi starter med et lineært likningssystem med m likninger
4.1 Vektorrom og underrom
 4.1 Vektorrom og underrom Vektorrom er en abstraksjon av R n. De kan brukes til å utlede egenskaper, resultater og metoder for tilsynelatende svært ulike klasser av objekter : n-tupler, følger, funksjoner,
4.1 Vektorrom og underrom Vektorrom er en abstraksjon av R n. De kan brukes til å utlede egenskaper, resultater og metoder for tilsynelatende svært ulike klasser av objekter : n-tupler, følger, funksjoner,
LP. Leksjon Spillteori
 LP. Leksjon Spillteori Kapittel 11: spillteori matrisespill optimale strategier von Neumann s minmax teorem forbindelse til LP nyttig LP modellering av (visse) minmax and maxmin problemer 1 / 11 Eksempel:
LP. Leksjon Spillteori Kapittel 11: spillteori matrisespill optimale strategier von Neumann s minmax teorem forbindelse til LP nyttig LP modellering av (visse) minmax and maxmin problemer 1 / 11 Eksempel:
Litt topologi. Harald Hanche-Olsen
 MA2104 2006 Litt topologi Harald Hanche-Olsen hanche@math.ntnu.no De reelle tall En grunnleggende egenskap ved de reelle tall, som skiller dem fra de rasjonale tall, er kompletthetsaksiomet. Det har flere
MA2104 2006 Litt topologi Harald Hanche-Olsen hanche@math.ntnu.no De reelle tall En grunnleggende egenskap ved de reelle tall, som skiller dem fra de rasjonale tall, er kompletthetsaksiomet. Det har flere
TMA4100 Matematikk 1, høst 2013
 TMA4100 Matematikk 1, høst 2013 Forelesning 9 www.ntnu.no TMA4100 Matematikk 1, høst 2013, Forelesning 9 Derivasjon I dagens forelesning skal vi se på følgende: 1 Tilnærminger til små endringer. 2 Vekstfart.
TMA4100 Matematikk 1, høst 2013 Forelesning 9 www.ntnu.no TMA4100 Matematikk 1, høst 2013, Forelesning 9 Derivasjon I dagens forelesning skal vi se på følgende: 1 Tilnærminger til små endringer. 2 Vekstfart.
Løsningsforslag. Prøve i Matematikk 1000 BYFE DAFE 1000 Dato: 29. mai 2017 Hjelpemiddel: Kalkulator og formelark. Oppgave 1 Gitt matrisene.
 Prøve i Matematikk BYFE DAFE Dato: 29. mai 27 Hjelpemiddel: Kalkulator og formelark Løsningsforslag Oppgave Gitt matrisene A = 2 2 B = [ 2 3 4 ] og C = Regn ut, om mulig, summene A + B, A + B T og A +
Prøve i Matematikk BYFE DAFE Dato: 29. mai 27 Hjelpemiddel: Kalkulator og formelark Løsningsforslag Oppgave Gitt matrisene A = 2 2 B = [ 2 3 4 ] og C = Regn ut, om mulig, summene A + B, A + B T og A +
LØSNINGSFORSLAG TMA4105 Matematikk 2 8. August 2005
 LØSNINGSFORSLAG TMA45 Matematikk 8. August 5 Oppgave Vi introduserer funksjonen g(x, y, z) x +y z slik at flaten z x + y er gitt ved g(x, y, z). I dette tilfellet utgjør gradienten til g en normalvektor
LØSNINGSFORSLAG TMA45 Matematikk 8. August 5 Oppgave Vi introduserer funksjonen g(x, y, z) x +y z slik at flaten z x + y er gitt ved g(x, y, z). I dette tilfellet utgjør gradienten til g en normalvektor
Analysedrypp IV: Metriske rom
 Analysedrypp IV: Metriske rom Vi har tidligere sett at begreper som konvergens og kontinuitet har med avstand å gjøre at f er kontinuerlig i punktet a, betyr f. eks. at det for enhver ɛ > 0, finnes en
Analysedrypp IV: Metriske rom Vi har tidligere sett at begreper som konvergens og kontinuitet har med avstand å gjøre at f er kontinuerlig i punktet a, betyr f. eks. at det for enhver ɛ > 0, finnes en
The full and long title of the presentation
 The full and long title of the presentation Subtitle if you want Øistein Søvik Mai 207 Ø. Søvik Short title Mai 207 / 4 Innholdsfortegnelse Introduksjon Nyttige tips før eksamen Nyttige tips under eksamen
The full and long title of the presentation Subtitle if you want Øistein Søvik Mai 207 Ø. Søvik Short title Mai 207 / 4 Innholdsfortegnelse Introduksjon Nyttige tips før eksamen Nyttige tips under eksamen
Den deriverte og derivasjonsregler
 Den deriverte og derivasjonsregler Department of Mathematical Sciences, NTNU, Norway September 3, 2014 Tangenten til en funksjon i et punkt (kap. 2.1) Sekant til en funksjon gjennom to punkter 25 20 f(c+h)
Den deriverte og derivasjonsregler Department of Mathematical Sciences, NTNU, Norway September 3, 2014 Tangenten til en funksjon i et punkt (kap. 2.1) Sekant til en funksjon gjennom to punkter 25 20 f(c+h)
MA1102 Grunnkurs i analyse II Vår 2019
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA1102 Grunnkurs i analyse II Vår 2019 10.2.27 a) Vi skal vise at u + v 2 = u 2 + 2u v + v 2. (1) Som boka nevner på side 581,
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA1102 Grunnkurs i analyse II Vår 2019 10.2.27 a) Vi skal vise at u + v 2 = u 2 + 2u v + v 2. (1) Som boka nevner på side 581,
Analysedrypp I: Bevis, mengder og funksjoner
 Analysedrypp I: Bevis, mengder og funksjoner Hensikten med Analysedrypp er å bygge en bro mellom MAT1100 og MAT1110 på den ene siden og MAT2400 på den andre. Egentlig burde det være unødvendig med en slik
Analysedrypp I: Bevis, mengder og funksjoner Hensikten med Analysedrypp er å bygge en bro mellom MAT1100 og MAT1110 på den ene siden og MAT2400 på den andre. Egentlig burde det være unødvendig med en slik
1 Mandag 22. februar 2010
 1 Mandag 22. februar 2010 Vi begynner med litt repetisjon fra forrige gang, med å sjekke om et vektorfelt er konservativt og dersom svaret er ja, regne ut potensialfunksjonen. Videre skal vi se på en variant
1 Mandag 22. februar 2010 Vi begynner med litt repetisjon fra forrige gang, med å sjekke om et vektorfelt er konservativt og dersom svaret er ja, regne ut potensialfunksjonen. Videre skal vi se på en variant
Flere anvendelser av derivasjon
 Flere anvendelser av derivasjon Department of Mathematical Sciences, NTNU, Norway September 30, 2014 Forelesning 17.09.2014 Fikspunkt-iterasjon Newtons metode Metoder for å finne nullpunkter av funksjoner:
Flere anvendelser av derivasjon Department of Mathematical Sciences, NTNU, Norway September 30, 2014 Forelesning 17.09.2014 Fikspunkt-iterasjon Newtons metode Metoder for å finne nullpunkter av funksjoner:
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Deleksamen i Eksamensdag: 9. april,. Tid for eksamen: : :. Oppgavesettet er på 9 sider. Vedlegg: Tillatte hjelpemidler: MAT Kalkulus og
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Deleksamen i Eksamensdag: 9. april,. Tid for eksamen: : :. Oppgavesettet er på 9 sider. Vedlegg: Tillatte hjelpemidler: MAT Kalkulus og
Karakteriseringen av like mengder. Mengder definert ved en egenskap.
 Notat 2 for MAT1140 2 Bevis La oss si at vi er overbevist om at utsagn P er sant, og at vi ønsker å kommunisere denne innsikten. Eller la oss si vi er ganske sikre på at P er sant, men ønsker, overfor
Notat 2 for MAT1140 2 Bevis La oss si at vi er overbevist om at utsagn P er sant, og at vi ønsker å kommunisere denne innsikten. Eller la oss si vi er ganske sikre på at P er sant, men ønsker, overfor
Løsningsforslag MAT102 Vår 2018
 Løsningsforslag MAT102 Vår 2018 Universitetet i Bergen Det matematisk-naturvitenskapelige fakultet Eksamen i emnet MAT102 Tirsdag 12 juni 2018, kl 0900-1400 Oppgavesettet har fem oppgaver Hver deloppgave
Løsningsforslag MAT102 Vår 2018 Universitetet i Bergen Det matematisk-naturvitenskapelige fakultet Eksamen i emnet MAT102 Tirsdag 12 juni 2018, kl 0900-1400 Oppgavesettet har fem oppgaver Hver deloppgave
MAT feb feb mars 2010 MAT Våren 2010
 MAT 1012 Våren 2010 Mandag 22. februar 2010 Forelesning Vi begynner med litt repetisjon fra forrige gang, med å sjekke om et vektorfelt er konservativt og dersom svaret er ja, regne ut potensialfunksjonen.
MAT 1012 Våren 2010 Mandag 22. februar 2010 Forelesning Vi begynner med litt repetisjon fra forrige gang, med å sjekke om et vektorfelt er konservativt og dersom svaret er ja, regne ut potensialfunksjonen.
Oppgaveark Uke 37 (07/09-11/09) MAT111 - H09
 Oppgaveark Uke 37 (07/09-11/09) MAT111 - H09 Oppgave 1 Du ar fått deg en jobb i et firma og skal kjøre til en konferanse med overnatting. Du drar jemmefra på mandag kl 07:15 og ankommer 11:07. Du overnatter
Oppgaveark Uke 37 (07/09-11/09) MAT111 - H09 Oppgave 1 Du ar fått deg en jobb i et firma og skal kjøre til en konferanse med overnatting. Du drar jemmefra på mandag kl 07:15 og ankommer 11:07. Du overnatter
Notat2 - MAT Om matriserepresentasjoner av lineære avbildninger
 Notat2 - MAT1120 - Om matriserepresentasjoner av lineære avbildninger Dette notatet uftfyller bokas avsn 54 om matriserepresentasjoner av lineære avbildninger mellom endelig dimensjonale vektorrom En matriserepresentasjon
Notat2 - MAT1120 - Om matriserepresentasjoner av lineære avbildninger Dette notatet uftfyller bokas avsn 54 om matriserepresentasjoner av lineære avbildninger mellom endelig dimensjonale vektorrom En matriserepresentasjon
Løsningsforslag. Oppgave 1 Gitt matrisene ] [ og C = A = 4 1 B = 2 1 3
![Løsningsforslag. Oppgave 1 Gitt matrisene ] [ og C = A = 4 1 B = 2 1 3 Løsningsforslag. Oppgave 1 Gitt matrisene ] [ og C = A = 4 1 B = 2 1 3](/thumbs/55/37240043.jpg) Prøve i Matematikk BYFE DAFE Dato: 27. mai 26 Hjelpemiddel: Kalkulator og formelark Alle svar skal grunngis. Alle deloppgaver har lik vekt. Løsningsforslag Oppgave Gitt matrisene [ 2 A 4 B [ 2 og C [ 2
Prøve i Matematikk BYFE DAFE Dato: 27. mai 26 Hjelpemiddel: Kalkulator og formelark Alle svar skal grunngis. Alle deloppgaver har lik vekt. Løsningsforslag Oppgave Gitt matrisene [ 2 A 4 B [ 2 og C [ 2
MAT1120 Notat 1 Tillegg til avsnitt 4.4
 MAT1120 Notat 1 Tillegg til avsnitt 4.4 Dette notatet tar utgangspunkt i Teorem 8 fra avsnitt 4.4 i boka. For ordens skyld gjentar vi dette teoremet her: Teorem 8 [Avsn. 4.4]: Anta at B = {b 1,..., b n
MAT1120 Notat 1 Tillegg til avsnitt 4.4 Dette notatet tar utgangspunkt i Teorem 8 fra avsnitt 4.4 i boka. For ordens skyld gjentar vi dette teoremet her: Teorem 8 [Avsn. 4.4]: Anta at B = {b 1,..., b n
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT 00 Kalkulus. Eksamensdag: Mandag,. desember 006. Tid for eksamen:.30 8.30. Oppgavesettet er på sider. Vedlegg: Tillatte hjelpemidler:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT 00 Kalkulus. Eksamensdag: Mandag,. desember 006. Tid for eksamen:.30 8.30. Oppgavesettet er på sider. Vedlegg: Tillatte hjelpemidler:
Notat om Peanos aksiomer for MAT1140
 Notat om Peanos aksiomer for MAT1140 1 Tall Hva er egentlig tall? Tanken her, er ikke å si hva tall er, hva deres interne struktur muligens kan være, men å si hva vi kan gjøre med dem, sett utenifra. Vi
Notat om Peanos aksiomer for MAT1140 1 Tall Hva er egentlig tall? Tanken her, er ikke å si hva tall er, hva deres interne struktur muligens kan være, men å si hva vi kan gjøre med dem, sett utenifra. Vi
BYFE DAFE Matematikk 1000 HIOA Obligatorisk innlevering 5 Innleveringsfrist Fredag 15. april 2016 kl 14 Antall oppgaver: 8
 Innlevering BYFE DAFE Matematikk HIOA Obligatorisk innlevering 5 Innleveringsfrist Fredag 5. april 6 kl Antall oppgaver: 8 Funksjonen ft) er vist i guren over. Funksjonen F x) er denert som for x. F x)
Innlevering BYFE DAFE Matematikk HIOA Obligatorisk innlevering 5 Innleveringsfrist Fredag 5. april 6 kl Antall oppgaver: 8 Funksjonen ft) er vist i guren over. Funksjonen F x) er denert som for x. F x)
TMA4123/TMA4125 Matematikk 4M/4N Vår 2013
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA4123/TMA4125 Matematikk 4M/4N Vår 2013 Løsningsforslag Øving 4 1 a) Bølgeligningen er definert ved u tt c 2 u xx = 0. Sjekk
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA4123/TMA4125 Matematikk 4M/4N Vår 2013 Løsningsforslag Øving 4 1 a) Bølgeligningen er definert ved u tt c 2 u xx = 0. Sjekk
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT Kalkulus og lineær algebra Eksamensdag: Lørdag 25. Mai 29. Tid for eksamen: :5 4:5. Oppgavesettet er på 7 sider. Vedlegg:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT Kalkulus og lineær algebra Eksamensdag: Lørdag 25. Mai 29. Tid for eksamen: :5 4:5. Oppgavesettet er på 7 sider. Vedlegg:
5.5 Komplekse egenverdier
 5.5 Komplekse egenverdier Mange reelle n n matriser har komplekse egenverdier. Vi skal tolke slike matriser når n = 2. Ved å bytte ut R med C kan man snakke om komplekse vektorrom, komplekse matriser,
5.5 Komplekse egenverdier Mange reelle n n matriser har komplekse egenverdier. Vi skal tolke slike matriser når n = 2. Ved å bytte ut R med C kan man snakke om komplekse vektorrom, komplekse matriser,
(ii) g = (f B)^{-1} \: V \to B \subset R^m er deriverbar med Dg(f(u)) = (Df(u))^{-1} \: R^m \to R^m for alle u i B.
 MAT1300 Analyse I 5. mai 2009 13.3. Det inverse funksjonsteoremet Vi vil bruke kontraksjonsprinsippet for å bevise følgende teorem: Teorem 13.13 (Det inverse funksjonsteoremet): La U \subset R^m være åpen,
MAT1300 Analyse I 5. mai 2009 13.3. Det inverse funksjonsteoremet Vi vil bruke kontraksjonsprinsippet for å bevise følgende teorem: Teorem 13.13 (Det inverse funksjonsteoremet): La U \subset R^m være åpen,
dg = ( g P0 u)ds = ( ) = 0
 NTNU Institutt for matematiske fag TMA4105 Matematikk 2, øving 8, vår 2011 Løsningsforslag Notasjon og merknader Som vanlig er enkelte oppgaver kopiert fra tidligere års løsningsforslag. Derfor kan notasjon,
NTNU Institutt for matematiske fag TMA4105 Matematikk 2, øving 8, vår 2011 Løsningsforslag Notasjon og merknader Som vanlig er enkelte oppgaver kopiert fra tidligere års løsningsforslag. Derfor kan notasjon,
Institutt for Samfunnsøkonomi
 Institutt for Samfunnsøkonomi Løsninger i: ELE 379 Matematikk valgfag Dato: 6.6., 9: 4: Tillatte hjelpemidler: Alle hjelpemidler + Eksamenskalkulator: TEXAS INSTRUMENTS BA II Plus TM Innføringsark: Ruter
Institutt for Samfunnsøkonomi Løsninger i: ELE 379 Matematikk valgfag Dato: 6.6., 9: 4: Tillatte hjelpemidler: Alle hjelpemidler + Eksamenskalkulator: TEXAS INSTRUMENTS BA II Plus TM Innføringsark: Ruter
Eksamen R2, Våren 2011 Løsning
 R Eksamen, Våren 0 Løsning Eksamen R, Våren 0 Løsning Del Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave (8 poeng) a) Deriver funksjonene
R Eksamen, Våren 0 Løsning Eksamen R, Våren 0 Løsning Del Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave (8 poeng) a) Deriver funksjonene
Arne B. Sletsjøe. Oppgaver, MAT 1012
 Arne B. Sletsjøe Oppgaver, MAT 101 1 En-variabel kalkulus 1.1 I de følgende oppgavene, i) finn alle kritiske punkter til f(x), ii) beskriv monotoniegenskapene til funksjonene ved å se på fortegnet til
Arne B. Sletsjøe Oppgaver, MAT 101 1 En-variabel kalkulus 1.1 I de følgende oppgavene, i) finn alle kritiske punkter til f(x), ii) beskriv monotoniegenskapene til funksjonene ved å se på fortegnet til
Oppgave 1. e rt = 120e. = 240 e
 Løsning MET 803 Matematikk Dato 5. desember 05 kl 0900-00 Oppgave. (a) Dersom vi selger eiendommen etter t år, med t > 0, så er nåverdien av salgssummen med r = 0,0. Da får vi N(t) = V (t)e rt = 0 e e
Løsning MET 803 Matematikk Dato 5. desember 05 kl 0900-00 Oppgave. (a) Dersom vi selger eiendommen etter t år, med t > 0, så er nåverdien av salgssummen med r = 0,0. Da får vi N(t) = V (t)e rt = 0 e e
Notat 05 for MAT Relasjoner, operasjoner, ringer. 5.1 Relasjoner
 Notat 05 for MAT1140 5 Relasjoner, operasjoner, ringer 5.1 Relasjoner Når R er en relasjon som er veldefinert på A B, slik at R(x, y) er en påstand når x A og B B, tenker vi på relasjonen som noe som lever
Notat 05 for MAT1140 5 Relasjoner, operasjoner, ringer 5.1 Relasjoner Når R er en relasjon som er veldefinert på A B, slik at R(x, y) er en påstand når x A og B B, tenker vi på relasjonen som noe som lever
Løsningsforslag, eksamen MA1103 Flerdimensjonal analyse, vår 2009
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 8 Løsningsforslag, eksamen MA1103 Flerdimensjonal analyse, vår 2009 Oppgave 1 Avgjør om grenseverdiene eksisterer:
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 8 Løsningsforslag, eksamen MA1103 Flerdimensjonal analyse, vår 2009 Oppgave 1 Avgjør om grenseverdiene eksisterer:
Populærvitenskapelig kilde: Robin Wilson, Four Colours Suffice/How the Map Problem was Solved, Penguin Books 2003, ISBN 0-141-00908-X.
 Om Fargelegging av Kart og Grafer i Planet Populærvitenskapelig kilde: Robin Wilson, Four Colours Suffice/How the Map Problem was Solved, Penguin Books 2003, ISBN 0-141-00908-X. 1. Firefargeteoremet Et
Om Fargelegging av Kart og Grafer i Planet Populærvitenskapelig kilde: Robin Wilson, Four Colours Suffice/How the Map Problem was Solved, Penguin Books 2003, ISBN 0-141-00908-X. 1. Firefargeteoremet Et
Fasit til eksamen i emnet MAT102 - Brukerkurs i matematikk II Mandag 21.september 2015
 Fasit til eksamen i emnet MAT02 - Brukerkurs i matematikk II Mandag 2.september 205 Fasit. (a) Løs ligningssystemene. i) 5x + 7y = 4 3x + 2y = ii) 3x + 4y + z = 2 2x + 3y + 3z = 7 Svar: i) x = 85/, y =
Fasit til eksamen i emnet MAT02 - Brukerkurs i matematikk II Mandag 2.september 205 Fasit. (a) Løs ligningssystemene. i) 5x + 7y = 4 3x + 2y = ii) 3x + 4y + z = 2 2x + 3y + 3z = 7 Svar: i) x = 85/, y =
Løsningsforslag til Eksamen i MAT111
 Universitetet i Bergen Matematisk institutt Bergen, 9. desember 25. Bokmål Løsningsforslag til Eksamen i MAT Mandag 9. desember 25, kl. 9-. Dette er kun et løsningsforslag. Oppgave a) Betrakt de to komplekse
Universitetet i Bergen Matematisk institutt Bergen, 9. desember 25. Bokmål Løsningsforslag til Eksamen i MAT Mandag 9. desember 25, kl. 9-. Dette er kun et løsningsforslag. Oppgave a) Betrakt de to komplekse
4.4 Koordinatsystemer
 4.4 Koordinatsystemer Minner om at B = { b 1, b 2,..., b n } V kalles en basis for et vektorrom V dersom B er lineært uavhengig og B utspenner V. I samme vektorrom kan vi innføre ulike koordinatsystemer
4.4 Koordinatsystemer Minner om at B = { b 1, b 2,..., b n } V kalles en basis for et vektorrom V dersom B er lineært uavhengig og B utspenner V. I samme vektorrom kan vi innføre ulike koordinatsystemer
EKSAMEN I NUMERISK LØSNING AV DIFFERENSIALLIGNINGER MED DIFFERANSEMETODER (TMA4212)
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren (964) EKSAMEN I NUMERISK LØSNING AV DIFFERENSIALLIGNINGER MED DIFFERANSEMETODER
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren (964) EKSAMEN I NUMERISK LØSNING AV DIFFERENSIALLIGNINGER MED DIFFERANSEMETODER
MAT1120 Oppgaver til plenumsregningen torsdag 25/9
 MAT1120 Oppgaver til plenumsregningen torsdag 25/9 Øyvind Ryan (oyvindry@i.uio.no) September 2008 Oppgaver fra 5.1 Denisjon av egenverdier, egenvektorer, egenrom. Teorem 1 s. 306: Egenverdiene til en triangulær
MAT1120 Oppgaver til plenumsregningen torsdag 25/9 Øyvind Ryan (oyvindry@i.uio.no) September 2008 Oppgaver fra 5.1 Denisjon av egenverdier, egenvektorer, egenrom. Teorem 1 s. 306: Egenverdiene til en triangulær
y (t) = cos t x (π) = 0 y (π) = 1. w (t) = w x (t)x (t) + w y (t)y (t)
 NTNU Institutt for matematiske fag TMA4105 Matematikk, øving 7, vår 013 Løsningsforslag Notasjon og merknader En vektor boken skriver som ai + bj + ck, vil vi ofte skrive som (a, b, c), og tilsvarende
NTNU Institutt for matematiske fag TMA4105 Matematikk, øving 7, vår 013 Løsningsforslag Notasjon og merknader En vektor boken skriver som ai + bj + ck, vil vi ofte skrive som (a, b, c), og tilsvarende
Et forsøk på et oppslagsverk for TMA4145 Lineære metoder
 Et forsøk på et oppslagsverk for TMA4145 Lineære metoder Ruben Spaans May 21, 2009 1 Oppslagsverk Adjungert Ball, la (X, d) være et metrisk rom og la ɛ > 0. Da er for x 0 X: 1. B(x 0 ; ɛ) = {x x X d(x,
Et forsøk på et oppslagsverk for TMA4145 Lineære metoder Ruben Spaans May 21, 2009 1 Oppslagsverk Adjungert Ball, la (X, d) være et metrisk rom og la ɛ > 0. Da er for x 0 X: 1. B(x 0 ; ɛ) = {x x X d(x,
Matriser. Kapittel 4. Definisjoner og notasjon
 Kapittel Matriser Vi har lært å løse et lineært ligningssystem ved å sette opp totalmatrisen til systemet gausseliminere den ved hjelp av radoperasjoner på matrisen Vi skal nå se nærmere på egenskaper
Kapittel Matriser Vi har lært å løse et lineært ligningssystem ved å sette opp totalmatrisen til systemet gausseliminere den ved hjelp av radoperasjoner på matrisen Vi skal nå se nærmere på egenskaper
Eksamensoppgavehefte 1. MAT1012 Matematikk 2: Mer funksjonsteori i en og flere variabler
 Eksamensoppgavehefte 1 MAT1012 Matematikk 2: Mer funksjonsteori i en og flere variabler Matematisk institutt, UiO, våren 2010 I dette heftet er det samlet et utvalg av tidligere eksamensoppgaver innenfor
Eksamensoppgavehefte 1 MAT1012 Matematikk 2: Mer funksjonsteori i en og flere variabler Matematisk institutt, UiO, våren 2010 I dette heftet er det samlet et utvalg av tidligere eksamensoppgaver innenfor
Logaritmer og eksponentialfunksjoner
 Logaritmer og eksponentialfunksjoner Harald Hanche-Olsen og Marius Irgens 20-02-02 Dette notatet ble først laget for MA02 våren 2008. Denne versjonen er omskrevet for MA02 våren 20. Du vil oppdage at mange
Logaritmer og eksponentialfunksjoner Harald Hanche-Olsen og Marius Irgens 20-02-02 Dette notatet ble først laget for MA02 våren 2008. Denne versjonen er omskrevet for MA02 våren 20. Du vil oppdage at mange
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT Kalkulus og lineær algebra Eksamensdag: Onsdag 9 mai 9 Tid for eksamen: 4:3 8:3 Oppgavesettet er på 7 sider Vedlegg: Tillatte
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT Kalkulus og lineær algebra Eksamensdag: Onsdag 9 mai 9 Tid for eksamen: 4:3 8:3 Oppgavesettet er på 7 sider Vedlegg: Tillatte
Tiden går og alt forandres, selv om vi stopper klokka. Stoffet i dette kapittelet vil være en utømmelig kilde med tanke på eksamensoppgaver.
 Kapittel 4 Anvendelser av lineære likningssystemer Tiden går og alt forandres, selv om vi stopper klokka Stoffet i dette kapittelet vil være en utømmelig kilde med tanke på eksamensoppgaver 4 Populasjonsdynamikk
Kapittel 4 Anvendelser av lineære likningssystemer Tiden går og alt forandres, selv om vi stopper klokka Stoffet i dette kapittelet vil være en utømmelig kilde med tanke på eksamensoppgaver 4 Populasjonsdynamikk
Løsningsforslag. og B =
 Prøve i Matte EMFE DAFE ELFE BYFE Dato: august 25 Hjelpemiddel: Kalkulator og formelark Alle svar skal grunngis. Alle deloppgaver har lik vekt. Oppgave a) Gitt matrisene A = 2 3 2 4 2 Løsningsforslag og
Prøve i Matte EMFE DAFE ELFE BYFE Dato: august 25 Hjelpemiddel: Kalkulator og formelark Alle svar skal grunngis. Alle deloppgaver har lik vekt. Oppgave a) Gitt matrisene A = 2 3 2 4 2 Løsningsforslag og
MA1301 Tallteori Høsten 2014
 MA1301 Tallteori Høsten 014 Richard Williamson 1. august 015 Innhold Forord 7 1 Induksjon og rekursjon 9 1.1 Naturlige tall og heltall............................ 9 1. Bevis.......................................
MA1301 Tallteori Høsten 014 Richard Williamson 1. august 015 Innhold Forord 7 1 Induksjon og rekursjon 9 1.1 Naturlige tall og heltall............................ 9 1. Bevis.......................................
Løsningsforslag, midtsemesterprøve MA1101, 5.oktober 2010
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Løsningsforslag, midtsemesterprøve MA1101, 5.oktober 2010 Oppgave 1 Løs ulikheten x + 6 5 x + 2 Strategien er å
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Løsningsforslag, midtsemesterprøve MA1101, 5.oktober 2010 Oppgave 1 Løs ulikheten x + 6 5 x + 2 Strategien er å
Løsningsforslag til eksamen i MAT111 - Grunnkurs i Matematikk I
 Universitetet i Bergen Matematisk institutt Bokmål Løsningsforslag til eksamen i MAT111 - Grunnkurs i Matematikk I Mandag 17. desember 2007, kl. 09-14. Oppgave 1 Gitt f(x) = x + x 2 1, 1 x 1. a) Finn og
Universitetet i Bergen Matematisk institutt Bokmål Løsningsforslag til eksamen i MAT111 - Grunnkurs i Matematikk I Mandag 17. desember 2007, kl. 09-14. Oppgave 1 Gitt f(x) = x + x 2 1, 1 x 1. a) Finn og
Notat om kardinalitet for MAT1140 (litt uferdig)
 Notat om kardinalitet for MAT1140 (litt uferdig) Poenget med tall kan man kanskje si er det å telle. In mengdeteorien ønsker man å telle antall elementer i en mengde, og det tallet man oppnår kalles da
Notat om kardinalitet for MAT1140 (litt uferdig) Poenget med tall kan man kanskje si er det å telle. In mengdeteorien ønsker man å telle antall elementer i en mengde, og det tallet man oppnår kalles da
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: Eksamensdag: Torsdag 8. juni 07 Tid for eksamen: 09.00 3.00 Oppgavesettet er på 7 sider. Vedlegg: Tillatte hjelpemidler: MAT-INF360
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: Eksamensdag: Torsdag 8. juni 07 Tid for eksamen: 09.00 3.00 Oppgavesettet er på 7 sider. Vedlegg: Tillatte hjelpemidler: MAT-INF360
Notasjon i rettingen:
 UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Løsningsforslag med kommentarer) til Innlevering /4 i emnet MAT, høsten 207 Notasjon i rettingen: R Rett R Rett, men med liten tulle)feil
UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Løsningsforslag med kommentarer) til Innlevering /4 i emnet MAT, høsten 207 Notasjon i rettingen: R Rett R Rett, men med liten tulle)feil
Universitetet i Agder Fakultetet for teknologi og realfag Institutt for matematiske fag. Eksamen MA desember Lykke til!
 Universitetet i Agder Fakultetet for teknologi og realfag Institutt for matematiske fag Eksamen Emnekode: Emnenavn: MA-2 Lineær algebra Dato: Varighet:. desember 2 9. - 4. Antall sider: Tillatte hjelpemidler:
Universitetet i Agder Fakultetet for teknologi og realfag Institutt for matematiske fag Eksamen Emnekode: Emnenavn: MA-2 Lineær algebra Dato: Varighet:. desember 2 9. - 4. Antall sider: Tillatte hjelpemidler:
13 Oppsummering til Ch. 5.1, 5.2 og 8.5
 3 Oppsummering til Ch. 5. 5. og 8.5 3. Motivasjon Det er veldig viktig å kunne beregne funksjonsverdier f (A) for kvadratiske matriser A. I kalkulus (teori av differensiallikninger) er det viktig å beregne
3 Oppsummering til Ch. 5. 5. og 8.5 3. Motivasjon Det er veldig viktig å kunne beregne funksjonsverdier f (A) for kvadratiske matriser A. I kalkulus (teori av differensiallikninger) er det viktig å beregne
Deleksamen i MAT111 - Grunnkurs i Matematikk I
 Bergen, oktober. 2004. Løsningsforslag til Deleksamen i MAT - Grunnkurs i Matematikk I Mandag. oktober 2004, kl. 09-2. Oppgave Beregn grensen f.eks. ved hjelp av l Hôpitals regel. lim x ln x x Vi ser at
Bergen, oktober. 2004. Løsningsforslag til Deleksamen i MAT - Grunnkurs i Matematikk I Mandag. oktober 2004, kl. 09-2. Oppgave Beregn grensen f.eks. ved hjelp av l Hôpitals regel. lim x ln x x Vi ser at
Grublegruppe 19. sept. 2011: Algebra I
 Grublegruppe 19. sept. 2011: Algebra I Ivar Staurseth ivarsta@math.uio.no Innledning, definisjoner Vi har så langt jobbet med mengder, X, hvor vi har hatt et avstandsbegrep og hvor vi har vært i stand
Grublegruppe 19. sept. 2011: Algebra I Ivar Staurseth ivarsta@math.uio.no Innledning, definisjoner Vi har så langt jobbet med mengder, X, hvor vi har hatt et avstandsbegrep og hvor vi har vært i stand
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: Eksamensdag: Mandag. mai Tid for eksamen: 9. 4. Oppgavesettet er på sider. Vedlegg: Tillatte hjelpemidler: MAT-INF36 Anvendelser
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: Eksamensdag: Mandag. mai Tid for eksamen: 9. 4. Oppgavesettet er på sider. Vedlegg: Tillatte hjelpemidler: MAT-INF36 Anvendelser
