Seismisk inversjon ved bruk av genetiske algoritmer
|
|
|
- Vibeke Jensen
- 10 år siden
- Visninger:
Transkript
1 Seismisk inversjon ved bruk av genetiske algoritmer Fredrik Helland Master i elektronikk Oppgaven levert: Juni 2006 Hovedveileder: Åge Kristensen, IET Norges teknisk-naturvitenskapelige universitet Institutt for elektronikk og telekommunikasjon
2
3 Oppgavetekst Oppgaven sikter på: 1. Lage et system som utfører global inversion ved å bruke genetiske algoritmer som optimaliseringsmetode. 2. Teste inversjonskoden ved å invertere seismoakustiske parametere. - Når inversjonssystemet er oppe å går, testes det mot syntetiske data for en enkel geologisk modell for å undersøke om koden klarer å estimere parametere som kompresjonshastighet og sjærbølgehastighet i havbunnen. Oppgaven gitt: 16. januar 2006 Hovedveileder: Åge Kristensen, IET
4
5 Forord Denne rapporten er skrevet i i forbindelse med masteroppgaven min ved institutt for elektronikk og telekommunikasjon (IET) ved Norges teknisk-naturvitenskaplige universitet, NTNU. Oppgaven er delvis blitt utført på Statoil forskningssenter Rotvoll. Oppgaven tar utgangspunkt i min prosjektoppgave fra høsten 2005 som hadde tittelen: Bruk av genetiske algoritmer i optimalisering. Jeg vil gjerne rette en takk til min hovedveileder Åge Kristensen og til Statoil for at jeg fikk kontorplass og datatilgang på forskningssenteret på Rotvoll, Trondheim. Jeg vil også takke institutt for elektronikk og telekommunikasjon for lån av bærbar pc hele siste året ved NTNU. En siste takk går til mine medstudenter for en fin tid ved NTNU. Fredrik Helland Trondheim, i
6 Sammendrag Det er ønskelig med nøyaktig informasjon om fysiske egenskaper som beskriver havbunnen for å kunne modellere akustisk utbredelse i vannet. Det har i denne oppgaven blitt sett på global inversjon av geoakustiske parametere. Inversjonen blir sett på som et optimaliseringsproblem, som blir løst ved hjelp av genetiske algoritmer. Med genetiske algoritmer blir responsen fra en rekke forskjellige parametersett som beskriver miljøet beregnet parallelt for å estimere løsningen. En inversjonskode er skrevet i Matlab som bruker genetiske algoritmer som optimaliseringsmetode og en forovermodell for å kalkulere data tilhørende et sett geoakustiske parametere som beskriver havbunnen. Inversjonen ble utført ved å bruke syntetiske data og to eksempler ble gjennomført. Resultatet indikerer at det er mulig å utføre inversjon av geoakustiske parametere ved å bruke genetiske algoritmer. ii
7 Innhold 1 Innledning 1 2 Genetiske algoritmer Optimalisering med bruk av genetiske algoritmer Analogi og virkemåte for genetiske algoritmer Diskretisering av miljøet Genetiske operatorer Terminering av genetiske algoritmer Inversjon Forovermodell Begrensinger i Osiris Inversjon med bruk av genetiske algoritmer Inversjonskode Beskrivelse av koden Testing av inversjonskoden Syntetiske data og innstillinger i Osiris Diskretisering av parametere Innstillinger for genetiske algoritmer Resultater og diskusjon Eksempel 1 - Inversjon av hastighet og lagtykkelse Resultater fra eksempel Eksempel 2 - Inversjon av P-hastighet og S-hastighet Resultater fra eksempel Konklusjon og endelige tanker 42 A Figurer 46 A.1 Eksempel A.2 Eksempel iii
8 B Oversikt over filer 53 B.1 M-fil skript i matlab B.2 M-fil funksjoner i matlab B.3 Unix C-Shell skript B.4 Diverse Osiris filer iv
9 Kapittel 1 Innledning Det har i denne masteroppgaven blitt sett på global inversjon av lydfelt i vannet for å bestemme ukjente fysiske egenskaper i havbunnen. En viktig del av inversjonsproblemet er å finne en geologisk modell som ved hjelp av en forovermodell kan generere data som svarer godt til et sett med observerte data. Det velges et miljø og flere parametere m, settes som ukjent. Inversjonsproblemet sees på som et optimaliseringsproblem og vi vil benytte genetiske algoritmer for å optimalisere modellparameterne. Genetiske algoritmer er en robust global optimaliseringsmetode som baserer seg på metoder om naturlig utvelging og evolusjon. Det defineres en kostfunksjon som finner et avvik mellom observert felt og kalkulert felt. Deretter blir det utført optimalisering for å finne den modellvektoren ˆm som minimaliser den definerte kostfunksjonen. I dette tilfelle er det blitt benyttet syntetiske data generert av en enkel geologsik modell ved å bruke modelleringsverktøyet Osiris. Rapporten er organisert som følger: I kapittel 2 er det sett på genetiske algoritmer som optimaliseringsprosedyre. Det blir beskrevet hvordan genetiske algoritmer prøver å finne best mulig løsninig på inversjonsproblemet.det beskrives også hvordan miljøet må diskretiseres. I kapittel 3 blir det sett nærmere på hvordan inversjon med genetiske algoritmer og en valgt forovermodell fungerer, og det nevnes hvilke begrensninger som ligger i forovermodellen. I kapittel 4 beskrives virkemåten til inversjonskoden. 1
10 1. Innledning 2 Deretter blir innstillinger som ligger til grunn for testen av koden presentert i kapittel 5. I kapittel 6 blir resultater fra testen av inversjonskoden presentert og diskutert.
11 Kapittel 2 Genetiske algoritmer Genetiske algoritmer (GA) er en stokastisk global søkemetode som etterligner seleksjon fra naturlig evolusjon. Formålet er enten å finne globalt minimum eller globalt maksimum i en kostfunksjon. GA opererer med en flere potensielle løsninger parallelt og benytter prinsippet med at den sterkeste overlever (survival of the fittest), for forhåpentligvis å produsere bedre og bedre approksimasjoner til en løsning. I hver generasjon (iterasjon), blir et sett mulige løsninger generert ved hjelp av kombinasjon av forskjellige biter fra de beste individene fra forrige generasjon. Denne prosessen fører til en utvikling av befolkninger med individer, som er bedre enn individene som de ble dannet av. Genetiske algoritmer er forskjellig fra tradisjonelle optimaliserings- og søkemetoder på fire basisområder: GA søker gjennom en befolkning av punkter parallelt istedenfor et enkelt punkt GA bruker kun verdien til kost funksjonen, ikke derivater eller annen tilleggs informasjon. 3
12 2. Genetiske algoritmer 4 GA bruker probabilistiske regler, ikke deterministiske. GA jobber med en koding av hele parametersettet istedenfor de enkelte parameterverdiene 2.1 Optimalisering med bruk av genetiske algoritmer Det ikke-linære inversjonsproblemet kan sees som et optimaliseringsproblem. Vi ønsker å finne modellvektoren, eller et sett med parametere, som minimerer avviket φ(m) = d p(m), (2.1) der φ er kostfunksjonen. Her er d er observert data, p er det kalkulerte datasettet og m er modellvektoren som består av de fysiske parameterne. De kalkulerte feltene blir beregnet ved hjelp av en forovermodell. I denne oppgaven er det modelleringsverktøyet Osiris som er benyttet. Genetiske algoritmer og globale metoder aksepterer at kostfunksjonen er uregelmessig og prøver og finne globalt minimum uten å gjøre et fullstendig søk i søkerommet. Fordelen med GA er at den kun trenger verdier av kostfunksjonen på vilkårlige punkter i søkerommet, og optimaliseringsproblemet kan løses uten at GA trenger noen inngående kunnskap om hva kostfunksjonen består av. Dette medfører blant annet at hvilken som helst forovermodell kan benyttes.
13 2. Genetiske algoritmer Analogi og virkemåte for genetiske algoritmer I genetiske algoritmer benyttes en analogi som er hentet fra biologisk evolusjon. Virkemåten er relativt grei og vist i figur 2.1: ut i fra alle mulige modeller blir en initial befolkning med q individer valgt tilfeldig. En befolkning er et sett med mulige løsninger til inversjonsproblemet og et individ er en modellvektor som består av de parametere som vi ønsker å estimere, for eksempel de fysiske parameterne til en geologisk modell og/eller kilde- og mottakerparametere. Større befolkningstørrelse øker mulighetene for å finne globalt minimum, men vil også øke beregningstiden. Vanligvis brukes en befolkningstørrelse på mellom 20 og 100 individer. For hver modellvektor i befolkningen blir det så beregnet såkalt fitness. Dette er verdien fra kostfunksjonen, ligning 2.1. Jo lavere verdien er, jo bedre er tilpasningen mellom observert og kalkulert data. Det er viktig at kostfunksjonen defineres best mulig, slik at fitnessverdien faktisk samsvarer med hvor god tilpasningen er i forhold til obsertvert felt. Figur 2.1: Struktur for en genetisk algoritme [1] Neste steg i GA er å benytte et sett med genetiske operatorer på initialbefolkningen slik at denne utvikler seg til å bli bedre. De genetiske operatorene er:
14 2. Genetiske algoritmer 6 Utvelging Crossover Mutasjon Ved utvelgelsesprosessen velges det ut en rekke individer fra den nåværende generasjonen. De utvalgte individene blir kalt foreldre og velges ut i fra hvor god fitness de har. Dette vil si at individer med god fitness (lavere verdi av kostfunksjonen), har bedre sjanse for å bli valgt som foreldre enn individer med dårlig fitness. Det finnes en del forskjellige metoder å velge ut foreldre på. Etter at foreldre er valgt ut, blir to og to foreldre kombinert for å danne to nye individer. De nye individene kalles avkom eller barn. Disse dannes ved å utføre crossover med en gitt sannsynlighet, P x. Avkommet fra to foreldre kan da enten være en eksakt kopi av foreldrene, med sannsynlighet 1 P x, eller de kan være en kombinasjon av de to, med sannsynlighet P x. Vanligvis velges crossover sannsynlighet som P x = Det finnes flere typer crossover. Etter at de nye individene er dannet ved hjelp av crossover, blir det utført mutasjon med sannsynlighet P m. Mutasjon fungerer slik at et bit i et individ kan bli permutert, med mutasjonssannsynlighet P m. Mutasjonssansynligheten er vanligvis liten, P m = Mutasjon hjelper til at optimaliseringen ikke setter seg fast i lokale minimum. Tilslutt erstatter de nye individene deler eller hele befolkningen for danne en ny og bedre befolkning i neste generasjon. Hvor mange individer som erstattes bestemmes av parameteren G (generation gap), der 0 < G 1. G er betegnelse for reproduskjonsfaktor for befolkningen. G = 1 ikke-overlappende befolkninger 0 <G<1 overlappende befolkninger
15 2. Genetiske algoritmer 7 Hvis G < 1, blir så Gq antall individer erstattet av nye individer. De individene som blir erstattet kan velges ut på flere måter. Det kan velges tilfeldig eller velges ved hjelp av fitness verdien, slik at de beste individene ikke blir erstattet. Hvis G =1, blir hele befolkningen erstattet av nye individer hver gang, og man erstatter da også det beste individet. Det er vanlig og beholde en del av de beste individene. Stegene som er vist i figur 2.1 og beskrevet ovenfor blir gjentatt helt til et termineringskrav er oppfylt. Befolkningen utvikler seg gjennom iterasjoner som kalles generasjoner, etterhvert vil forhåpentligvis befolkningen konvergere mot det globale minimum Diskretisering av miljøet Miljøet blir diskretisert i M parametere vi ønsker å estimere. Disse lagres i en modellvektor m. Den vanligste tallrepresentasjonen i genetiske algoritmer er binær kode. Hver parameter m j, der j =1,..., M, kan da ta 2 n j diskret verdier, n j er antall bits i parameter m j. Det brukes en rektangulær inndeling på parameterne der hver parameter kan variere mellom en nedre og en øvre grense, [m min j,m max j ], som blir bestemt av a priori informasjon. m j = m min j + m j i j, i j =0,..., 2 n j 1 (2.2) m j = mmax j m min j (2.3) 2 n j 1 Sammenhengen mellom de diskret verdiene som GA jobber med og de numeriske verdiene av parameterne er gitt av ligning 2.2. Ligning 2.3 viser avstanden mellom to nærliggende diskret verdier. Sammenhengen mellom binær koding og de numeriske parameterverdiene er også illustrert i figur 2.2.
16 2. Genetiske algoritmer 8 Figur 2.2: Binær koding av modellparametere Genetiske operatorer Hovedvirkemåten til genetiske algoritmer består som sagt av operatorene utvelging, crossover og mutasjon. Utvelging Ved utviklingsprosessen velger man ut et antall individer i nåverende generasjon som skal produsere nye individer til neste generasjon. Før utvelgingen kan skje, blir hver modellvektor tilegnet en sannsynlighet som er direkte basert på fitnessverdien til individet. Sansynligheten sier noe om hvor stor sjanse et individ har for å bli valgt som forelder. Jo bedre fitness verdi, jo høyere blir sannsynligheten. Ligning 2.4 kan brukes for å beregne denne verdien [2]. p k = exp[ φ(m k)/t ], k =1,..., q (2.4) q exp[ φ(m l )/T ] l=1 T er en kontrollparameter som kalles temperatur og er hentet fra optimaliseringsmetoden simulated annealing. Ved lav verdi av T, vil ligning 2.4 skille mer mellom gode og middels gode individer, mens en høy verdi av T vil skille mindre mellom jevngode
17 2. Genetiske algoritmer 9 individer. Ved å sette T lik den beste fitnessverdien i hver generasjon vil vi få en relativt høy verdi av temperaturen i begynnelsen, mens den vil synke etter hvert som algoritmen konvergerer [2]. Andre måter å tilegne sannsynlighet kan gjøres ved å sortere alle individene i befolkningen etter fitness. Deretter tilegnes individene en ny verdi ettersom hvor de er i rangeringen. Dette kan gjøres med såkalt lineær fitness rangering og ikke-lineær fitness rangering, figur 2.3. (a) (b) Figur 2.3: Linear og ikke-linear fitness rangering Etter at sannsynlighet har blitt tilegnet, kan selve utvelgingen starte. En av de vanligste måtene å velge ut individer på er ved rulletthjul utvelging. Det blir definert en et intervall, Sum, som er bestemt som enten summen av en skalert fitness over alle individene i en befolkning, eller summen av alle sannsynlighetene. Individene blir deretter mappet en etter en til et kontinuerlig intervall mellom [0, Sum]. Størrelsen til hvert individ samsvarer med fitness verdien assosiert med individet. Figur 2.4 viser en illustrasjon over rulletthjul utvelging med seks individer. Individ 5 har det største intervallet og har derfor best fitness, mens individene 4 og 6 har det minste intervallet som korresponderer til dårligst fitness. For å velge et individ blir det generert et tilfeldig tall i intervallet [0, Sum] og det individet hvis segment spenner seg over det genererte tallet, blir valgt. Denne prosessen blir repetert helt til ønsket antall individer er valgt.
18 2. Genetiske algoritmer 10 Figur 2.4: Ruletthjul utvelging [3] Andre metoder for å utføre utvelging av foreldre er: Stochastic universal sampling Remainder stochastic sampling uten tilbakelegging Remainder stochastic sampling med tilbakelegging) Deterministic sampling Stochastic tournament Crossover Den grunnleggende operatoren for å produsere ny individer i GA er crossover. Dette er prosessen der to foreldre blir kombinert for å danne nye individer. Den enkleste formen for crossover er single-point crossover. Et krysningspunkt k blir valgt tilfeldig i intervallet k {1,..., N ind 1}, der N ind er lengden på individene.
19 2. Genetiske algoritmer 11 Innholdet av de to foreldrene blir så byttet om rundt krysningspunktet, og to nye individer blir dannet. Figur 2.5 illustrerer denne prosessen: Figur 2.5: Singlepoint crossover Resultatet er en kombinasjon av de to foreldrene. Offspring 1 har den første delen til Parent 1, mens den siste delen kommer fra slutten av Parent 2. Offspring 2 derimot er bygget opp av begynnelsen av Parent 2 og slutten av Parent 1. For multi-point crossover blir det valgt m krysningsposisjoner, k i {1,..., N ind 1}, der k i er krysningspunktene. Disse posisjonene velges ut tilfeldig. Deretter blir bitene mellom de etterfølgende krysningspunktene vekslet mellom de to foreldrene for å produsere to nye individer, som vist i figur 2.6: Figur 2.6: Multipoint crossover [3] Seksjonen frem til det første krysningspunktet er ikke vekslet mellom individene. Ved singlepoint crossover er det kun en parameter som får en helt ny verdi. De andre parameterne vil få verdien fra en av foreldrene. Ved multipoint crossover vil sannsynligvis flere parametere få nye verdier alt etter som hvor mange krysningspunkter det er og hvor de befinner seg i modellvektoren.
20 2. Genetiske algoritmer 12 Mutasjon Etter at crossover er utført må de nye modellvektorene gjennomgå mutasjon. I naturlig evolusjon er mutasjon en prosess der en del av et gen blir erstattet for å produsere en ny genetisk struktur. Mutasjon er vanligvis sett på som en bakgrunnsoperator som skal sørge for at sannsynligheten for å prøve ut en tilfeldig kombinasjon av parametere aldri er null. På denne måten kan gode løsninger finnes som ellers kan være tapt ved utvelging og crossover. Ved binær representasjon blir mutasjon implementert ved at hvert bit har en sannsynlighet P m for å flippes fra 0 til 1 og omvendt. I figuren under er det vist et eksempel på mutasjon for et en parameter bestående av 10 bit, kodet over intervallet [0,10]. Mutasjonspunktet er det 3.bit-et i den binære strengen. Her blir verdien av bitet snudd fra 0 til 1. Figur 2.7: Binær mutasjon Siden mutasjon vanligvis blir utført uniformt på hele befolkningen, kan det i utgangspunkter bli utført mutasjon på flere steder i et individ Terminering av genetiske algoritmer Siden genetiske algoritmer er en stokastisk søkeprosess, er det vanskelig å spesifisere et generelt konvergeringskriterium. Fitnessen for en befolkning kan gjerne være statisk i en rekke generasjoner før et bedre individ blir funnet. Dette fører til at det er vanskelig å vite hvor lenge inversjonen vil pågå og konvensjonelle stopp kriterier lett problematiske. En vanlig praksis er å terminere GA etter et spesifikt antall generasjoner og deretter teste kvaliteten til det beste medlemmet mot problem definisjonen. Hvis ingen akseptable løsninger er funnet, kan den genetiske algoritmen re-startes og et nytt søk initialiseres.
21 Kapittel 3 Inversjon Generelt i inversjon ønsker man å estimere fysiske parametere til en geologisk modell som kan generere data med best mulig match til et sett med observerte data. Figur 3.1: Blokkskjema for inversjon I et inversjonsskjema som i figur 3.1 defineres det en geologisk modell, ut i fra denne blir det i en forovermodell beregnet et akustisk felt. Dette blir så sammenlignet med et sett med målte data ved hjelp av en kostfunksjon. Ved å bruke en optimaliseringsmetode vil man så prøve å forbedre den aktuelle modellen ved å finne nye geoakustiske 13
22 3. Inversjon 14 parametere som kan generere data som har større likhet til de målte. 3.1 Forovermodell Forovermodellen som er brukt i inversjonen er modelleringsverktøyet Osiris. Ved å sette fysiske parametere i en geologisk modell samt kilde- og mottakerparametere, kan Osiris blant annet beregne akustisk trykk på hydrofoner i vannsøylen ved hjelp av bølgetallsintegrasjon. Figur 3.2: Skjermbilde av Osiris Osiris er delt i tre deler: Osipre, Osical og Osipos (figur 3.2). Osipre er forprossesseringsdelen. Her definerer man den geologiske modellen, geometri for kilden og mottakere, samt annen nødvendige informasjon. Dette blir lagret i en pre-fil. Deretter kjører man Osical som beregner selve feltet på bakgrunn av informasjonen i pre-filen. Etter at Osical er kjørt, får man en out-fil som beskriver frekvensresponsen på hver mottaker. Osipos kan deretter kjøres som en etterprosessering og resultatet kan vises i form av et seismogram. Frekvensresponsen som man får ut fra Osical kan betraktes som en overføringsfunksjon for hver mottaker. For å vise trykket som funksjon av tid må det defineres en wavelet som representerer kilden. Denne må multipliseres med overføringsfunksjonen i frekvensplanet og deretter må det taes invers fourier transformasjon. Det kan velges mellom en rekke forskjellig typer impulser som kan brukes som kilder i Osipos. I inversjonskoden som senere blir beskrevet i, blir ikke brukergrensesnittet av Osiris brukt. I stedet blir kalkuleringsdelen av Osiris kalt opp ved hjelp av et unix skript.
23 3. Inversjon Begrensinger i Osiris Når de fysiske egenskapene i den geologiske modellen settes, er det to hovedbegrensinger som må være oppfylt for at Osiris kan beregne akustisk felt. V s V p < 3 2 (3.1) a s <a p 3 4 ( Vp V s ) 2 (3.2) V p, V s, a p og a s er henholdsvis P-hastighet, S-hastighet, dempning av p-bølger og dempning av s-bølger for hvert lag. Ligning 3.1 sier at sjær hastigheten må være mindre enn ca. 86,7 % av P-hastigheten. Dette er en fysisk begrensning som kommer av den nedre grensen til poisson forholdet, v> 1 som også kan forklares med at sjærmodulen må være positiv, G>0. Ligning 3.2 må også være oppfylt for at man skal unngå feilmeldinger fra Osiris. Disse begrensningene setter en grense for hvilke verdier hver parameter i modellvektoren kan variere mellom under inversjonen. Dette må regnes ut på forhånd ellers vil Osiris sannsynligvis stoppe med feilmeldinger.
24 3. Inversjon Inversjon med bruk av genetiske algoritmer Ved å bruke genetiske algoritmer som optimalisering i inversjon, opereres det med en befolkning med modellvektorer. Det beregnes akustisk felt for alle disse i Osiris og de blir deretter sammenlignet med syntetiske data som også er generert av Osiris. Man får så en fitnessverdi for hver modellvektor etter sammenligning i kostfunksjonen. I tilbakekoblingssløyfen blir de genetiske operatorene benyttet på hele befolkningen av modellvektorer for å generere nye modellvektorer. Figur 3.3 viser virkemåten for inversjon med genetiske algoritmer og Osiris som forovermodell. Figur 3.3: Blokkskjema for inversjon ved bruk av genetiske algoritmer Et punkt som kan gjøre inversjonen vanskelig er at mange av modellparameterne kan være avhengige av hverandre. For at det skal finnes en modellvektor med bedre fitness enn i nåverende generasjon, er inversjonen avhengig av at flere parametere forandrer seg mot riktig minimum samtidig. En av fordelene til genetiske algoritmer er den nettopp kan forandre på flere parametere samtidig, men siden GA i stor grad er basert på sannsynlighet og statistikk er dette ikke alltid så lett som en skulle håpe. Crossover og mutasjon må skje på riktige punkter og med riktige foreldre for å komme ut av det lokale minimum. Det er vanlig at fitness kan holde seg konstant i flere generasjoner før en bedre modellvektor blir funnet.
25 3. Inversjon 17 Siden vi har frekvensresponsen (overføringsfunksjonen) for både syntetiske- og kalkulerte data, da begge er generert av Osiris, kan vi sammenligne direkte på disse. Kostfunksjonene kan da skrives, φ(m) = h w(m), (3.3) der h er overføringsfunksjonene for syntetiske data og w(m) er overføringsfunksjonen for en predikert geologisk modell. Hvis det skal utføres inversjon med reelle data, må kostfunksjonene modifiseres litt. Det må da taes hensyn til kilden. Kostfunksjonene kan da bli som i ligning 3.4. φ(m) = d w(m)s, (3.4) S er signalet fra kilden og d er komplekst akustisk trykk observert på hydrofonene.
26 Kapittel 4 Inversjonskode For å implementere genetiske algoritmer i et inversjonsskjema, må det skrives en kode. Dette er gjort hovedsakelig i Matlab, men to C Shell skriptfiler blir også benyttet for å kalle opp forovermodellen. Virkemåten til inversjonskoden vil i dette kapittelet bli beskrevet. Koden består av en hovedfil og en rekke funksjonsfiler som kalles opp inne i hovedfilen. I tillegg er den en del matlab skript som kan kjøres etter selve inversjonen er ferdig for å vise diverse resultater. Koden må kjøres på maskiner hos Statoil forskningssenter siden forovermodellen Osiris er installert der. Osiris kjører i Unix som fører til at også Matlab kjøres i Unix. 4.1 Beskrivelse av koden Før koden kan kjøres må de syntetiske dataene genereres i Osiris. Det må defineres en geologisk modell, kilde- og mottakerinformasjon og andre parametere. Dette blir lagret i fil som er kalt observed.pre. Deretter blir feltet beregnet ved å kjøre Osical og filen observed.out blir generert. Denne inneholder frekvensresponsen for hver mottaker som er definert. Hvilke parametere det er ønskelig å estimere, kan beskrives i matlabskriptet presga.m. Her må det også spesifiseres øvre- og nedre grenseverdi og antall bit til hver parameter 18
27 4. Inversjonskode 19 Figur 4.1: Blokkskjema over inversjonskoden
28 4. Inversjonskode 20 i hvert lag. Koden kjøres ved å starte skriptfilen GA inversion.m som er hovedfilen. Blokkskjema i figur 4.1 viser de viktigste punktene for virkemåten til koden. Til høyre i figuren vises hvilke filer som kalles opp for å utføre det som står i den tilhørende blokken. I initialiseringsdelen blir det satt variabler og konstanter. Deretter importeres deler av filen observed.pre som skal brukes senere for å generere pre-filer på en korrekt måte slik at de kan leses av Osiris. Overføringsfunksjonen for det syntetiske datasettet i observed.out importeres og lagres i en vektor. Funksjonen initialize.m blir kalt opp og ut i fra grenseverdiene for hvert parameter genereres den første generasjonen i befolkningen tilfeldig i matrisen OldChrom på binær form: OldChrom = g 1,1 g 1,2 g 1,3... g 1,Lind g 2,1 g 2,2 g 2,3... g 2,Lind g 3,1 g 3,2 g 3,3... g 2,Lind g Nind,1 g Nind,2 g Nind,3... g Nind,Lind individual 1 individual 2 individual 3. individual Nind Her er g verdien av et bit, Nind er befolkningsstørrelsen og Lind er den totale lengden av alle bitene i en modellvektor. Deretter kalles funksjonen decode.m og befolkningen blir dekodet til de numeriske verdiene og lagret i matrisen P henold. Nvar er antall parametere som skal estimeres, mens x er de forskjellige parameterne.
29 4. Inversjonskode 21 P henold = x 1,1 x 1,2 x 1,3... x 1,Nvar x 2,1 x 2,2 x 2,3... x 2,Nvar x 3,1 x 3,2 x 3,3... x 3,Nvar x 1,Nind x 2,Nind x 3,Nind... x Nind,Nvar individual 1 individual 2 individual 3. individual Nind Neste steg er å generere en pre-fil for hver modellvektor i befolkningen. Dette gjøres med funksjonen write file.m. For å beregne feltet brukes et C-Shell skript, gaosiris, som kaller opp Osical, beregningsdelen av Osiris. Etter at alle modellene er beregnet er neste punkt å importere den delen av de nylig genererte out-filene som inneholder frekvensresponsen. Funksjonen importdata.m tar seg av dette. For å bestemme fitness for hver modellvektor, må kostfunksjonene beregnes. Funksjonen objectfunc2.m inneholder kostfunksjonen, ligning 3.3. Koden går nå inn i løkken ved punktene 7 12 i figur 4.1 og optimaliseringen starter. For å velge ut hvilke individer som skal være foreldre, må det tilegnes en sannsynlighet til hvert individ som er direkte basert på fitness. Dette blir gjort med filen prob.m som beregner sannsynlighet basert på ligning 2.4. Kontrollparameteren T er valgt som verdien av kostfunksjonen til den beste modellen i hver generasjon. En kan også kjøre filene ranking.m eller scale.m for å beregne sannsynligheten med henholdsvis ulineær fitness rangering og lineær fitness rangering beskrevet i kapittel 2. Velgingen av foreldre gjøres med funksjonen sel roulette.m som utfører ruletthjul utvelging, sus.m og stochastic selection.m kan også brukes for andre metoder. Etter at foreldre er valgt ut, blir det dannet nye modellvektorer med crossover funksjonen. Enten singlepoint crossover med funksjonen crossover.m eller multipoint crossover med xovermulti.m. De nye modellene blir lagret i matrisen NewChrom. Deretter blir det utført mutasjon på de nye individene med filen mutation.m. Individene blir så dekodet med decode.m og lagret i matrisen P hennew. Deretter blir pre-filene som tidligere ble generert oppdatert parameterne til de nye modellvektorene med funksjo-
30 4. Inversjonskode 22 nen o write.m. Igjen blir frekvensresponsen beregnet på samme måte som tidligere beskrevet og etter at Osiris er ferdig, blir resultatet importert og fitness blir beregnet. De nye individene erstatter nå de dårligste fra forrige generasjon og generasjonstellerenen øker med én. Punktene 7 12 blir utført helt til termineringskravet er oppfylt, som er her er etter et visst antall iterasjoner. Når inversjonen er ferdig, kan det kjøres en del Matlab skript for å vise resultater. Det finnes også en del filer utenom de som er beskrevet her. I tillegg B er alle filene som koden består av ramset opp med kort beskrivelse.
31 Kapittel 5 Testing av inversjonskoden 5.1 Syntetiske data og innstillinger i Osiris Det første som gjøres når inversjonskoden skal testes, er å derfinere en geologisk modell og kilde- og mottakerparametere. Dette kan så brukes til å generer syntetiske data med Osiris. Den geologiske modellen består av flere horisontalt flate lag, der hvert lag er definert av seks fysiske egenskaper: dybde fra havoverflaten til toppen av laget, P-bølge hastighet, S-bølge hastighet, tetthet og P- og S-bølge dempning. Lagene er antatt å være isotropisk homogene, altså parameterne er konstant innenfor laget. Modellen som er brukt under testingen av inversjonskoden er vist i tabell 5.1 og figur 5.1. Det øverste laget representerer vannet. Her er det ingen sjærbølgehastighet siden sjærbølger ikke forplanter seg i væsker. Havbunnen består av to sedimentere lag av tykkelse 50 meter hver, og et hardt substrat nederst som regnes som uendelig Tabell 5.1: Geologisk modell for inversjon Dybde P-hastighet S-hastighet P-dempning S-dempning Tetthet [m] [m/s] [m/s] [db/λ] [db/λ]] [kg/m 3 ] Lag Lag Lag Lag
32 5. Testing av inversjonskoden 24 dypt. Lydhastigheten i vannet er satt konstant til 1500 m/s. Figur 5.1: Geoakustiske parametere som funksjon av dybde. Tabell 5.2: Informasjon om kilde/mottakere og utregningsvindu Parameter Verdi Kildetype Punktkilde Kildedybde 7 m Avstand til mottakere 2000 m Dybde til første mottaker 20 m Antall mottakere vertikalt i vannet 4 Avstand mellom mottakere 6 m Tidsdomene Traselengde s samplingstid s Maks senter frekv. for kilde wavelet 35.7 Hz Frekvensdomene Nedre frekvens 0 Hz Øvre frekvens 125 Hz Delta f Hz
33 5. Testing av inversjonskoden 25 I tillegg til de geoakustiske parameterene, må det også settes geometriske parametere for kilde og mottakere og det må defineres et beregnings vindu enten i frekvens eller i tid. Disse parameterene er vist i tabell 5.2. En punktkilde blir plassert 7 meter under havflaten. 2 km unna er det plassert 4 hydrofoner i et vertikalt array i vannsøylen. Avstanden mellom hver hydrofon er 6 meter og første hydrofon er ved 20 meters dyp. Hydrofonene er satt til å måle akustisk trykk. Figur 5.2 illustrerer den geologiske modellen, med posisjon for kilde og mottakere, antall lag og tykkelse på lagene. Ved hjelp av Osiris blir det beregnet akustisk felt tilhørende denne modellen. Dette vil representere observerte data under inversjonen. Figur 5.2: Illustrasjon av Geologisk modell med kilde og mottaker Frekvensene som Osiris skal utføre bølgetallsintergrasjon på må spesifiseres. Dette kan enten gjøres i tidsdomenet eller i frekvensdomenet. Tabell 5.2 viser trase lengde er valgt som til sekunder og samplingstiden er satt til Dette fører til at vi får /0.002 = 4096 samplinger i tid. I tidsdomenet må det også spesifiseres en maks senterfrekvens for kildeimpulsen. Dette vil være den største senterfrekvensen
34 5. Testing av inversjonskoden 26 en kilde kan ha når vi etterhvert skal regne ut tidsresponsen på hydrofonene. Denne ble anbefalt av Osiris til å settes til 35.7 Hz. Når vi velger innstillingene i tid regner Osiris ut parameterne i frekvensdomenet. Med de verdiene vi har valgt fører det til at frekvensresponsen beregnes fra 0 til 125 Hz på 1025 frekvenser. Beregningstiden for én modell avhenger sterkt av trase tiden og maks senterfrekvens. Den avhenger også av antall mottakere og plasseringen til disse. Andre innstillinger som kan settes i Osiris går på hvordan selve beregningen av feltet skjer. Vi velger å bruke standardinnstillinger på fasehastigheten for bølgetallsintegrasjonen, som er 900 integrasjonspunkter og lar Osiris bestemme maks og min fasehastighet automatisk. Vi velger at kalkuleringen skal foregå i bølgetallsdomenet fremfor slowness domene. Bølgeforplantningen blir satt til 2-D fremfor 3-D for å lette beregningstiden litt per modell. Et anti-aliaseringsfilter, et såkalt kompleks-omega, kan benyttes på frekvensresponsen for å glatte ut spekteret. Dette skal gjøre utregningen litt raskere og skal gjøre at resultatene ser bedre ut når de vises i tid. Vi velger å bruke vanlig besselfunksjon i beregningen. Hankel eller modifisert Hankel kan også brukes. Besselfunksjonen er kostbar i beregningstid, men gir et nøyaktig resultat. Hankel funksjonene kan brukes som en tilnærming til Bessel og er vanligvis mer numerisk effektiv. Hankel funksjonene er ikke like nøyaktig som Bessel, og inkluderer ikke nær-felt løsningen. Mesteparten av CPU-tiden som går med på å kjøre inversjonen, blir brukt under forrover modelleringen. CPU-tiden er proporsjonal med antall forover beregninger. Derfor er det her begrensningen sitter på hvor mange iterasjoner vi kan ha og hvor stor befolkning vi bør bruke under inversjonen. Med de parameterne som er valgt i Osiris, tar det ca. 8-9 sekunder å kjøre en forrover løsning. 5.2 Diskretisering av parametere Testingen av inversjonskoden foregår ved at vi lar noen parametere i tabell 5.1 være konstant mens andre varierer. De parameterne vi ønsker å estimere, vil variere mellom en øvre og nedre grense definert av a priori informasjon. I tillegg blir hver parameter som skal estimeres diskretisert i et vist antall verdier. Med dette kan vi bestemme viktigheten av en parameter og hvor nøyaktig den kan estimeres. Forskjellige parametere har forskjellig betydning for hvordan feltet på mottakerne ser ut. Derfor er det
35 5. Testing av inversjonskoden 27 naturlig å bruke forskjellig oppløsning på forskjellige parametere. P-hastigheten i det øverste laget har for eksempel svært mye og si og denne er ofte lettere å finne. Derfor kan vi gjerne ha større diskretisering her enn på p-hastigheten lenger nede. 5.3 Innstillinger for genetiske algoritmer I genetiske algoritmer er det noen få parametere som må bestemmes på forhånd: Befolkningstørrelsen q bør være såpass stor at modellvektorene kan representere flere lokale minimum, men samtidig liten nok til at nok iterasjoner kan utføres. Vi har valgt q = 54. Reproduksjonsfaktoren G bør være stor nok til at de beste modellvektorene forblir i befolkningen i flere generasjoner. G Bør være mindre enn 0.9. Vi velger her 0.5. En annen fordel med dette er vi da bruker halvparten av modellvektorene som vi beregnet i forrige generasjon og altså slipper å sende disse i forovermodellen igjen. Altså sparer vi cpu-tid til sammenligning til at vi hadde brukt høyere G. Bestemmelse av Crossover sannsynligheten kommer an på av hvor uavhengig parameterne er. For uavhengig parametere, bør P x være nær 1.0, for avhengige parametere bør den være lavere [5]. Vanligvis velges P x mellom 0.5 og 0.9. Her velges den til P x =0.8. Vi velger å bruke multipoint crossover med 3 og 4 crossover punkter. Mutasjonsfaktoren P m, velges vanligvis mellom 0.01 og 0.1. Her velges en relativt høy mutasjonsrate, P m =0.05, som syns å være bra i dette tilfelle [5]. Antall foroverberegninger bør ikke være for stor da dette er tidkrevende. Hvis vi velger 60 iterasjoner får vi totalt 1648 modeller som må beregnes i forovermodellen.
36 Kapittel 6 Resultater og diskusjon Testresultatene har utgangspunkt i innstillingene som ble beskrevet i kapittel 5. Miljøet i tabell 5.1 ble brukt til å generere det syntetiske datasettet ved hjelp av Osiris. Det er i hovedsak kompresjonshastigheten og sjærhastigheten samt tykkelsen til de to sedimentene som vi ønsker å finne. Parametere som tetthet og dempning i havbunnen har svært lite å si for hvordan signalet på mottakerne blir. Det har liten nytte og prøve å invertere på disse parameterne sammen med P- og S-hastighet. Først har det blitt utført inversjon på P- og S-hastighet og tykkelse. Deretter prøver vi å estimere kun P- og S-hastighet. 6.1 Eksempel 1 - Inversjon av hastighet og lagtykkelse I det første eksempelet har vi prøvd å estimere P-hastighet, S-hastighet og tykkelse på lagene. De andre parameterne i modellen er satt fast under inversjonen i henhold til tabell 5.1. Tabell 6.1 viser diskretiseringen av parametere som vil vil estimere. På grunn av begrensningene i ligning 3.1 og 3.2, kan ikke grensene til P- og S-hastigheten settes vilkårlig. Dette fører til at det blir det en nedre grense på hvilke for hvilke verdier vi gi til kompresjonshastigheten i hvert lag og en øvre grense på sjærhastigheten i hvert lag. 28
37 6. Resultater og diskusjon 29 Tabell 6.1: Diskretisering av inversjonsparametere P-hasitighet S-hastighet Lagtykkelse m/s Diskret verdier m/s Diskret verdier m Diskret verdier Lag (9 bit) (9 bit) (7 bit) Lag (8 bit) (8 bit) (7 bit) Lag (8 bit) (8 bit) Tykkelsen til lagene er satt til å kunne varierer mellom 20 og 80 meter. Kompresjonshastigheten og sjærhastigheten i det øverste laget har mest og si for hvordan feltet ser ut, og har derfor høyere oppløsning. De tar hver 512 diskret verdier. I lagene lenger nede tar disse parameterene 256 diskret verdier. Utfallserommet for tykkelsen på lagene er mindre og derfor tar disse bare 128 diskret verdier. Med den valgte diskretiseringen blir det et totalt søkerom på = mulige modeller. Med de innstillingene som er satt fra kapittel 5, blir det beregnet 1648 forovermodeller Resultater fra eksempel 1 For å vise utviklingen til inversjonen kan vi plotte kostfunksjonen til den beste modellvektoren som funksjon av tiden. Cpu tid er proporsjonalt med antall forovermodeller som er proporsjonalt med generasjoner. Siden genetiske algoritmer er en stokastisk metode, vil inversjonen så og si aldri få nøyaktig det samme resultatet. Noen ganger kan vi få et veldig bra resultat, mens andre ganger kan den konvergere mot et lokalt minimum. Inversjonen bør kjøres flere ganger for å få en pekepinn på hva som er riktig. Figur 6.1 er basert på en midling av 10 uavhengige inversjoner av det gjeldende problemet. Vi ser at etterhvert som interasjonene øker, blir fitness lavere og inversjonen konvergerer. En kjøring av inversjonen med de gjeldene innstillinger tar ca. 3 timer. I tabell 6.2 vises parameterne til den beste modellvektoren som ble funnet og differansen til de korrekte verdiene. I det beste tilfelle ble alle parameterne funnet ganske korrekt. Figur 6.2 viser den beste modellen funnet i hver av de 10 inversjonene. Den modellen med best fitness er vist i rødt, mens de øvrige er vist i blått. Man kan se at parame-
38 6. Resultater og diskusjon Fitness generasjon Figur 6.1: Konvergens av fitness som funksjon av generajoner Tabell 6.2: Beste modell og differanse i forhold til korrekte verdier Parameter Estimert verdi Differanse P-hastighet lag m/s P-hastighet lag m/s P-hastighet lag m/s S-hastighet lag m/s S-hastighet lag m/s S-hastighet lag m/s Tykkelse lag m Tykkelse lag m
39 6. Resultater og diskusjon 31 1 Layer P velocity (m/s) 1 Layer S velocity (m/s) 1 Layer Layer thickness (m) Figur 6.2: Beste modellvektor fra hver inversjon terne, spesielt i lavere lag, varierer en del fra gang til gang. Kompresjonshastigheten og sjærhastigheten i det øverste laget er som forventet best estimert og blir funnet nesten korrekt ved hver inversjon. Spesielt kompresjonshastigheten i det øverste laget blir nøyaktig estimert, da denne har mye å si for forplantningen av bølger i vannet. Lenger nede er det mer usikkerhet rundt riktig verdi, disse parameterne er også mer korrelerte. Det er lettere å invertere ukorrelerte parametere siden man da kan bedre fitness ved å stille på kun en parameter av gangen. Allikevel kan de sies å være rimelig nært det de korrekte verdiene. Dette går også frem av figur 6.3. Her plottes de ti beste modellvektorene i hver inver-
40 6. Resultater og diskusjon 32 1 Layer P velocity (m/s) 1 Layer S velocity (m/s) 1 Layer Layer thickness (m) Figur 6.3: 10 beste modellvektorer fra hver inversjon sjon, totalt 100 modellvektorer. Vi ser igjen at kompresjonshastigheten i det øverste laget er godt estimert. Det samme gjelder for sjærbølgehastigheten i samme lag, men med noe mer spredning. Jo lenger ned man kommer jo større er usikkerheten og det fører til mer spredning rundt de korrekte verdiene. Figur 6.4 viser utviklingen til parameterne for den beste modellen gjennom inversjonsprosessen. P-hastigheten i det øverste laget er alltid den første parameteren som blir funnet. Dette er den viktigste parameteren og må finnes noenlunde riktig før at de andre parameterne kan finnes. Med de grenseverdiene som er valgt for modellparame-
41 6. Resultater og diskusjon 33 P vel Final = P vel Final = P vel Final = S vel Final = S vel Final = S vel Final = Layer thickness 1 65 Final = Layer thickness 2 70 Final = Figur 6.4: Parameterutvikling for beste modell i hver generasjon
42 6. Resultater og diskusjon Modelled frequency response hydrophone #4 True model Best calculated model Magnitude (db) frequency (Hz) Figur 6.5: Frekvensrespons for beste estimert modell og korrekt modell terne vil noen av parameterne vanligvis være i nærheten av globalt minimum allerede ved første generasjonen. Ofte vil parametere som er mindre viktige gå fra en god verdi til en dårligere verdi hvis en parameter som er viktigere plutselig får en bedre verdi. I figur 6.5 vises frekvenseresponsen for observerte data og den beste modellen som ble funnet i inversjonene på hydrofon 4 som er den nederste hydrofonen. Dette er det vi sammenligner med i kostfunksjonen. Den estimerte frekvensresponsen er her veldig god tilnærming til den korrekte responsen. I figur A.1, A.2 og A.3 under tillegg A vises responsen fra de øvrige hydrofonene. Også her er det god tilnærming mellom estimert og korrekt respons. Hvis en kildeimpuls multipliseres med frekvensresponsen og det utføres en invers fourier transformasjon, kan trykket som funksjon av tiden på hver hydrofon vises. Dette er gjort i figur 6.7. Kilden som er brukt her er en såkalt Ricker Impuls 3-loops
43 6. Resultater og diskusjon 35 delayed. Den har en en senterfrekvens på 25 Hz, vist i figur 6.6. Den er generert og eksportert fra Osiris. Det estimerte signalet i figur 6.7 blir rimelig likt som det estimerte, siden frekvensresponsen er så godt estimert. 3 x 10 3 Frequency spectrum of source x timesignal of source Frequency (Hz) Time (s) Figur 6.6: Delayed Ricker 3 impuls x 10 7 Acoustic pressure on hydrophone #1 Amplitude 5 0 Observed signal Best calculated model Amplitude Time (s) x 10 7 Acoustic pressure on hydrophone #2 5 0 Observed signal Best calculated model Amplitude Time (s) x 10 7 Acoustic pressure on hydrophone #3 5 0 Observed signal Best calculated model Amplitude Time (s) x 10 7 Acoustic pressure on hydrophone #4 5 0 Observed signal Best calculated model Time (s) Figur 6.7: Trykk som funksjon av tid på hydrofonene
44 6. Resultater og diskusjon 36 Figur 6.8 viser kostfunksjonen som funksjon av P-hastighet og S-hastighet i det øverste laget. Alle de andre parameterne er satt konstant. Av figuren kan det sees at P- hastigheten er relativt uavhengig, mens S-hastigheten er avhengig av at P-hastigheten finnes før S-hastigheten kan estimeres. Verdien av kostfunksjonen varier mye når det forandres på P-hastigheten, mens det er mindre variasjon når sjærhastigheten forandres. Lignende figurer er vist i tillegg A. I figur A.4 er det P- og S-hastigheten i lag nummer 2 som varierer mens de andre parameterne er satt konstant. Det kan sees et lokalt minimum omtrent ved V p = 2100 og V s = 850. Dette er en kombinasjon som P- og S-hastighetene som regel alltid er innom under inversjonen. I forhold til parameterne fra det øverste laget, forandrer verdien av kostfunksjonen seg mye mindre når P- og S- hastighetene varieres. Det globale minimum er også mye smalere enn for parameterne i det øverste laget. Figur A.5 viser kostfunksjonen som funksjon av P- og S-hastighet i det nederste laget. Verdien av kostfunksjonen er enda mindre her når parameterne varierer. For at riktig P-hastighet her skal finnes må først S-hastigheten komme seg inn rett spor i figuren.
45 6. Resultater og diskusjon 37 Shear vel P vel. vs. S vel. in layer Comp. vel. (a) 2D visning P vel. vs. S vel. in layer Shear vel. [m/s] Comp. vel. [m/s] (b) 3D visning Figur 6.8: Kostfunksjonen som funksjon av P-hastighet og S-hastighet i det øverste laget.
46 6. Resultater og diskusjon Eksempel 2 - Inversjon av P-hastighet og S- hastighet I dette eksempelet er det P-hastighet og S-hastighet i de tre lagene det inverteres på. Parameterne er diskretisert i henhold til tabell 6.3. Her er noen av grensene økt i forhold til det første eksempelet siden det nå er færre ukjente parametere. Med verdiene fra tabell 6.3, får vi et søkerom på = Under inversjonen er ellers brukt samme innstillinger som i eksempel 1. Tabell 6.3: Diskretisering av inversjonsparametere P-hasitighet S-hastighet m/s Diskret verdier m/s Diskret verdier Lag (9 bit) (9 bit) Lag (8 bit) (8 bit) Lag (8 bit) (8 bit) Resultater fra eksempel 2 Figur 6.9 viser inversjonen konvergerer. Denne figuren er basert på 10 uavhengige inversjoner som er midlet. I forhold til eksempel 1 kan en se av figur 6.9 at kostfunksjo- Tabell 6.4: Beste estimerte parameterverdier Parameter Estimert verdi Differanse P-hastighet lag m/s P-hastighet lag m/s P-hastighet lag m/s S-hastighet lag m/s S-hastighet lag m/s S-hastighet lag m/s
47 6. Resultater og diskusjon Fitness generasjon Figur 6.9: Fitness som funksjon av iterasjoner nen kommer nærmerer null, altså en bedre tilpasning mellom observert og kalkulert felt. Det kan se ut som fitness kunne blitt enda bedre hvis inversjonen hadde fått kjøre litt lengre. Den modellen med best fitness er vist i tabell 6.4. P-hastighet og S-hastigheten i det øverste laget er best estimert, men generelt sett så er parameterne veldig nær de korrekte verdiene i dette tilfelle. Dette vil variere fra fra gang til gang ettersom hvilken verdi kostfunksjonen har når inversjonen er ferdig. I figur 6.10a vises den beste modellen som er funnet i hver av de ti inversjonene. I forhold til eksempel 1 er parameterne nå bedre estimert ved hver inversjon. Det har med at det er færre ukjente parametere, noe som gjør inversjonen lettere. I figur 6.10b er det plottet de ti beste modellvektorene i hver inversjon, totalt 100 modeller. Tendensen er den samme som i eksempel 1, nemlig at jo lengre ned en kommer jo større blir usikkerheten i henhold til riktig verdi av parameteren. Frekvensresponsen til den beste modellen er vist i figur A.6 A.9 i tillegg A. Med de parameterne fra tabell 6.4 er den estimerte responsen veldig lik den observerte. Dette fører også til at estimert tidsrespons i figur A.10 er nesten identisk med den observerte.
48 6. Resultater og diskusjon 40 1 Layer P velocity (m/s) 1 Layer S velocity (m/s) (a) Beste modell fra hver inversjon 1 Layer P velocity (m/s) 1 Layer S velocity (m/s) (b) 10 beste modeller fra hver inversjon Figur 6.10: Modellparametere gruppert etter parameter
49 6. Resultater og diskusjon 41 Figur 6.11 viser utviklingen til den beste modellen gjennom inversjonen. Ingen av de andre parameterne blir funnet før P-hastigheten i det øverste laget er ganske nær riktig verdi, noe som i dette tilfelle tar litt tid. P vel Final = P vel. 2 Final = P vel Final = S vel. 1 Final = S vel Final = S vel. 3 Final = Figur 6.11: Parameterutvikling for beste modell i hver generasjon
50 Kapittel 7 Konklusjon og endelige tanker Global inversjon av fysiske parameterne i havbunnen som kompresjonshastighet, sjærhastighet og tykkelse på lagene har blitt gjennomført. For å optimalisere parameterne ble det benyttet genetiske algoritmer. Man ser på inversjonsproblemet som et optimaliseringsproblem der vi ønsker å finne minimum av en kostfunksjon som er avviket mellom et observert og estimert felt. Genetiske algoritmer prøver å finne globalt minimum uansett om kostfunksjonen er ulineær og inneholder lokale minimum. Begrensninger i forovermodellen gjør at vi trenger a priori informasjon om inversjonsproblemet når grensene for parameterne settes. En inversjonskode har blitt skrevet i Matlab som kaller opp en forovermodell og bergener frekvensrespons tilhørende en geologisk modell. Det har blitt benyttet syntetiske data under inversjonen. Deretter har inversjonskoden blitt testet med to eksempler: først på P-hastighet, S-hastighet og tykkelse, deretter kun på P- og S- hastighet. Inversjonen fant parameterne lettere og mer nøyaktig når det kun ble invertert på P- og S-hastighet. Jo mer forhåndsinformasjon en har jo lettere blir det for inversjonen. Det er også viktig at diskretiseringen av miljøet er utført så godt som mulig for at ikke inversjonen skal konvergere i et lokalt minimum. Det er tydelig at for begge eksemplene så konvergerer systemet og vi kan konkludere med at global inversjon ved å bruke genetiske algoritmer er fullt mulig. Men det bør gjennomføres flere uavhengige inversjoner av samme problem for å være sikker på at riktig løsning er funnet. 42
51 7. Konklusjon og endelige tanker 43 Siden vi har benyttet syntetiske data, gjør det at inversjonen har kunnet estimere parameterne relativt nøyaktig. Vi har sammenlignet direkte på frekvensresponsen til kalkulert og observert felt. Hvis det hadde blitt benyttet virkelige data i stedenfor syntetiske, hadde inversjonsproblemet blitt en del vanskeligere. Miljøet som da måtte beskrives hadde blitt mye mer komplisert og i tillegg hadde støy på mottakerne kommet inn i bildet. Det hadde også vært fordelaktig med informansjon om kilden som hadde blitt benyttet, både fase og amplitude. Kostfunksjonen hadde nok også måtte skrives om. Videre arbeid kan være å teste koden på reelle data. Koden må sikkert forandres litt hvis dette skal gjøres.
52 Bibliografi [1] H. Pohlheim, Genetic and Evolutionary Algorithms: Principles, Methods and Algorithms, ilmenau.de/ pohlheim/ga Toolbox/algindex.html, Germany, [2] P. Gerstoft, Inversion of seismoacoustic data using genetic algorithms and a posteriori probability distributions, J. Acoust. Soc. Am. 95, place, (1994), p [3] A. Chipperfield, P. Fleming, H. Pohlheim, C. Fonseca, Genetic Algorithm Toolbox Tutorial, University of Sheffield, [4] P. Gerstoft and C. F. Mecklendbräuker, Ocean acoustic inversion with estimation of a posteriori probability distribution, J. Acoust. Soc. Am 104, No. 2, Pt. 1, (1998), pp [5] P. Gerstoft, Global inversjon by genetic algorithms for both source position and environmental parameters, Journal of Computationl Acoustics, Vol. 2, No. 3, (1994), pp [6] C. F. Mecklenbräuker and P. Gerstoft, Objective functions for ocean acoustic inversion derived by likelihood methods, Journal of Computational Acoustics, Vol. 8, No. 2, (2000), pp [7] T. Bäck, Optimal Mutation Rates in Genetic Search, Morgan Kaufmann Publishers, San Mateo, California, USA, (1993), pp [8] O. Diachok, A. Caiti, P. Gerstoft, H. Schmidt, Full field inversion methods in ocean and seismo-acoustics, Kluwe Academic Publishers, Dordrecht, The Nederlands, (1995). pp ,
53 BIBLIOGRAFI 45 [9] David E. Goldberg, Genetic Algorithms in Search, Optimization & Machine Learning, Addison-Wesley, Reading, Massachusetts, (1989).
54 Tillegg A Figurer A.1 Eksempel 1 10 Modelled frequency response hydrophone #1 True model Best calculated model Magnitude (db) frequency (Hz) Figur A.1: Frekvensrespons for beste modell og korrekt modell på hydrofon 2 46
55 A. Figurer Modelled frequency response hydrophone #2 True model Best calculated model Magnitude (db) frequency (Hz) Figur A.2: Frekvensrespons for beste modell og korrekt modell på hydrofon 3 10 Modelled frequency response hydrophone #3 True model Best calculated model Magnitude (db) frequency (Hz) Figur A.3: Frekvensrespons for beste modell og korrekt modell på hydrofon 4
56 A. Figurer P vel. vs. S vel. in layer Shear vel Comp. vel. (a) 2D visning P vel. vs. S vel. in layer Shear vel. [m/s] Comp. vel. [m/s] (b) 3D visning Figur A.4: Fitness som funksjon av P- og S-hastighet i lag 2.
57 A. Figurer P vel. vs. S vel. in layer 3 Shear vel Comp. vel. (a) 2D visning P vel. vs. S vel. in layer Shear vel. [m/s] Comp. vel. [m/s] (b) 3D visning Figur A.5: Fitness som funksjon av P- og S-hastighet i lag 3.
58 A. Figurer 50 A.2 Eksempel 2 10 Modelled frequency response hydrophone #1 True model Best calculated model Magnitude (db) frequency (Hz) Figur A.6: Frekvensrespons for beste modell og korrekt modell på hydrofon 1 10 Modelled frequency response hydrophone #2 True model Best calculated model Magnitude (db) frequency (Hz) Figur A.7: Frekvensrespons for beste modell og korrekt modell på hydrofon 2
59 A. Figurer Modelled frequency response hydrophone #3 True model Best calculated model Magnitude (db) frequency (Hz) Figur A.8: Frekvensrespons for beste modell og korrekt modell på hydrofon 3 10 Modelled frequency response hydrophone #4 True model Best calculated model Magnitude (db) frequency (Hz) Figur A.9: Frekvensrespons for beste modell og korrekt modell på hydrofon 3
60 A. Figurer 52 x 10 7 Acoustic pressure on hydrophone #1 Amplitude 5 0 Observed signal Best calculated model Amplitude Time (s) x 10 7 Acoustic pressure on hydrophone #2 5 0 Observed signal Best calculated model Amplitude Time (s) x 10 7 Acoustic pressure on hydrophone #3 5 0 Observed signal Best calculated model Amplitude Time (s) x 10 7 Acoustic pressure on hydrophone #4 5 0 Observed signal Best calculated model Time (s) Figur A.10: Trykk som funksjon av tid på hver mottaker
61 Tillegg B Oversikt over filer B.1 M-fil skript i matlab GA inversion.m presga.m divplots.m plotfreq.m plottime.m plotsource.m postplot.m Hovedfil for kjøring av inversjonen. Kaller opp alle andre nødvendige funksjoner. Intialisering av inversjonen. Her settes hvilke parametere man ønsker å estimere. Øvre og nedre grense og antall bit for hver parameter i hvert lag settes også. Skript for å plotte utviklingen til den beste modellvektoren. Plotter også parameterne for de 20 beste modellene funnet gjennom inversjonen. Kaller opp plot best.m. Skriptfil for å plotte frekvensresponsen for beste predikerte modell og den virkelige modellen. Plotter for hver hydrofon. Skript for å plotte det akustiske trykket som funksjon av tid for på hver hydrofon. Plotter den beste modellen og den virkelige modellen. Skriptfil for å plotte impulsen som er brukt som kilde. Plotter både i tid og frekvens. Plotter utviklingen av parameterne og konvergens av fitness etter at inversjon er ferdig. 53
62 B. Oversikt over filer 54 B.2 M-fil funksjoner i matlab bin2int.m crossover.m decode.m fitsrank.m importdata.m initialize.m konverterer binære tall til det tilsvarende heltall. utfører singlepoint crossover på en befolkning med crossoversansynlighet Px. dekoder alle parametere i en befolkning til sine desimaltall verdier. Kaller opp bin2int.m. utfører ikke-lineær rank basert fitness skalering. importerer frekvensresponsen av filer som er generert av OSICAL. genererer initialbefolkningen helt tilfeldig. multipointxover2.m utfører såkalt mulitple point crossover med kryssnigssansynlighet Px. mutation.m utfører binær mutasjon på en befolkning med mutasjonssansynlighet Pm. o write.m skriver til inputfiler til OSICAL. Erstatter kun den delen som involverer de geologiske parameterne. objfunc2.m kostfunksjonen der observerte og predikerte data blir sammenlignet. plot best.m funksjon som plotter de 20 beste modellene som er funnet gjennom inversjonsprosessen. prob.m Beregner sansynligheten for å bli valgt som foreldre. readfile.m leser diverse informasjon av en osiris generet pre-fil, for å siden og kunne generere en tilsvarende fil. savevar.m genererer automatisk et filnavn på formen data #n dd mm som kan brukes for å lagre alle matlabvariabler i en binær mat-fil. scale.m utfører lineær fitness skalering. sel roulette.m velg foreldre med rulletthjul uvelginsprosedyre. stochastic selection.m velg foreldre med såkalt stokastisk remainder uvelginsprosedyre. storebest.m Lagrer kontinuerlig de 20 beste modellvektorene som er funnet sålangt i inversjonen
63 B. Oversikt over filer 55 sus.m writefile.m xovermulti.m velg foreldre med såkalt stokastisk universal uvelginsprosedyre. skriver pre filer på bakgrunn av informasjonen fra readfile funksjonen og de geologiske parameterne GA har kommet fram til. utfører multi point crossover med crossoversansynlighet Px og med M antall krysningspunkter. B.3 Unix C-Shell skript sgaosical sgaosiris unix skript som kjører osical med en pre-fil som input. unix skript som setter miljøvariabler og lisenspath for OSIRIS og kaller opp sgaosical* med en definert pre-fil som input. B.4 Diverse Osiris filer ricker.wlt *.pre filer *.out filer Filen inneholder informasjon om kilden, her en såkalt Delayed Ricker 3 impulse. Inneholder informasjon som tidsampling, antall sampler og tissignalet til kilden. Dette er filer som brukes som input til OSIRIS. Inneholder all informasjon som er nødvendig for å beregne det akustiske feltet. Dette inkulderer den geologiske modellen, kildeinformasjon, mottakerinformasjon. I tillegg settes diverse parametre som bestemmer på hvilken måte osiris skal beregne feltet. Dette er resultatet av kalkuleringen osiris gjør. Denne består av en modellert frekvensrespons eller overføringsfunksjonen, dvs. at kilden ikke er inkludert. Det er to vektorer som representerer komplekst trykk.
64 Figurer 2.1 Struktur for en genetisk algoritme [1] Binær koding av modellparametere Linear og ikke-linear fitness rangering Ruletthjul utvelging [3] Singlepoint crossover Multipoint crossover [3] Binær mutasjon Blokkskjema for inversjon Skjermbilde av Osiris Blokkskjema for inversjon ved bruk av genetiske algoritmer Blokkskjema over inversjonskoden Geoakustiske parametere som funksjon av dybde Illustrasjon av Geologisk modell med kilde og mottaker Konvergens av fitness som funksjon av generajoner Beste modellvektor fra hver inversjon beste modellvektorer fra hver inversjon Parameterutvikling for beste modell i hver generasjon Frekvensrespons for beste estimert modell og korrekt modell Delayed Ricker 3 impuls Trykk som funksjon av tid på hydrofonene Kostfunksjonen som funksjon av P-hastighet og S-hastighet i det øverste laget Fitness som funksjon av iterasjoner Modellparametere gruppert etter parameter Parameterutvikling for beste modell i hver generasjon A.1 Frekvensrespons for beste modell og korrekt modell på hydrofon A.2 Frekvensrespons for beste modell og korrekt modell på hydrofon A.3 Frekvensrespons for beste modell og korrekt modell på hydrofon A.4 Fitness som funksjon av P- og S-hastighet i lag
65 FIGURER 57 A.5 Fitness som funksjon av P- og S-hastighet i lag A.6 Frekvensrespons for beste modell og korrekt modell på hydrofon A.7 Frekvensrespons for beste modell og korrekt modell på hydrofon A.8 Frekvensrespons for beste modell og korrekt modell på hydrofon A.9 Frekvensrespons for beste modell og korrekt modell på hydrofon A.10 Trykk som funksjon av tid på hver mottaker
Universitetet i Stavanger Institutt for petroleumsteknologi
 Universitetet i Stavanger Institutt for petroleumsteknologi Side 1 av 6 Faglig kontakt under eksamen: Professor Ingve Simonsen Telefon: 470 76 416 Eksamen i PET110 Geofysikk og brønnlogging Mar. 09, 2015
Universitetet i Stavanger Institutt for petroleumsteknologi Side 1 av 6 Faglig kontakt under eksamen: Professor Ingve Simonsen Telefon: 470 76 416 Eksamen i PET110 Geofysikk og brønnlogging Mar. 09, 2015
Reelle tall på datamaskin
 Reelle tall på datamaskin Knut Mørken 5. september 2007 1 Innledning Tirsdag 4/9 var tema for forelesningen hvordan reelle tall representeres på datamaskin og noen konsekvenser av dette, særlig med tanke
Reelle tall på datamaskin Knut Mørken 5. september 2007 1 Innledning Tirsdag 4/9 var tema for forelesningen hvordan reelle tall representeres på datamaskin og noen konsekvenser av dette, særlig med tanke
Lineære likningssystemer og matriser
 Kapittel 3 Lineære likningssystemer og matriser I dette kapittelet skal vi sette sammen Kapittel 1 og 2. 3.1 Den utvidede matrisen til et likningssystem Vi starter med et lineært likningssystem med m likninger
Kapittel 3 Lineære likningssystemer og matriser I dette kapittelet skal vi sette sammen Kapittel 1 og 2. 3.1 Den utvidede matrisen til et likningssystem Vi starter med et lineært likningssystem med m likninger
Heuristisk søk 1. Prinsipper og metoder
 Heuristisk søk Prinsipper og metoder Oversikt Kombinatorisk optimering Lokalt søk og simulert størkning Populasjonsbasert søk Traveling sales person (TSP) Tromsø Bergen Stavanger Trondheim Oppdal Oslo
Heuristisk søk Prinsipper og metoder Oversikt Kombinatorisk optimering Lokalt søk og simulert størkning Populasjonsbasert søk Traveling sales person (TSP) Tromsø Bergen Stavanger Trondheim Oppdal Oslo
Oversikt. Heuristisk søk 1. Kombinatorisk optimering Lokalt søk og simulert størkning Populasjonsbasert søk. Prinsipper og metoder
 Oversikt Heuristisk søk Kombinatorisk optimering Lokalt søk og simulert størkning Populasjonsbasert søk Prinsipper og metoder Pål Sætrom Traveling sales person (TSP) Kombinatorisk optimering Trondheim
Oversikt Heuristisk søk Kombinatorisk optimering Lokalt søk og simulert størkning Populasjonsbasert søk Prinsipper og metoder Pål Sætrom Traveling sales person (TSP) Kombinatorisk optimering Trondheim
Noen presiseringer mhp Diskret Fourier Transform. Relevant for oblig 1.
 FYS2130 Våren 2008 Noen presiseringer mhp Diskret Fourier Transform. Relevant for oblig 1. Vi har på forelesning gått gjennom foldingsfenomenet ved diskret Fourier transform, men ikke vært pinlig nøyaktige
FYS2130 Våren 2008 Noen presiseringer mhp Diskret Fourier Transform. Relevant for oblig 1. Vi har på forelesning gått gjennom foldingsfenomenet ved diskret Fourier transform, men ikke vært pinlig nøyaktige
Vektorligninger. Kapittel 3. Vektorregning
 Kapittel Vektorligninger I denne uken skal vi bruke enkel vektorregning til å analysere lineære ligningssystemer. Vi skal ha et spesielt fokus på R, for det går an å visualisere; klarer man det, går det
Kapittel Vektorligninger I denne uken skal vi bruke enkel vektorregning til å analysere lineære ligningssystemer. Vi skal ha et spesielt fokus på R, for det går an å visualisere; klarer man det, går det
Ikke lineære likninger
 Ikke lineære likninger Opp til nå har vi studert lineære likninger og lineære likningsystemer. 1/19 Ax = b Ax b = 0. I en dimensjon, lineære likninger kan alltid løses ved hjelp av formler: ax + b = 0
Ikke lineære likninger Opp til nå har vi studert lineære likninger og lineære likningsystemer. 1/19 Ax = b Ax b = 0. I en dimensjon, lineære likninger kan alltid løses ved hjelp av formler: ax + b = 0
Forelesning nr.14 INF 1410
 Forelesning nr.14 INF 1410 Frekvensrespons 1 Oversikt dagens temaer Generell frekvensrespons Resonans Kvalitetsfaktor Dempning Frekvensrespons Oppførselen For I Like til elektriske kretser i frekvensdomenet
Forelesning nr.14 INF 1410 Frekvensrespons 1 Oversikt dagens temaer Generell frekvensrespons Resonans Kvalitetsfaktor Dempning Frekvensrespons Oppførselen For I Like til elektriske kretser i frekvensdomenet
år i 1 2 3 4 5 6 7 8 9 alder x i 37 38 39 40 41 42 43 44 45 tid y i 45.54 41.38 42.50 38.80 41.26 37.20 38.19 38.05 37.45 i=1 (x i x) 2 = 60, 9
 TMA424 Statistikk Vår 214 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 11, blokk II Oppgave 1 Matlabkoden linearreg.m, tilgjengelig fra emnets hjemmeside, utfører
TMA424 Statistikk Vår 214 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 11, blokk II Oppgave 1 Matlabkoden linearreg.m, tilgjengelig fra emnets hjemmeside, utfører
Ghost amplitude spectrum. d=6 m V=1500 m/s c= 1
 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR PETROLEUMSTEKNOLOGI OG ANVENDT GEOFYSIKK Oppgave SIG445 Geofysisk Signalanalyse ving 5 En seismisk kilde er plassert pa endybde d ivann, hvor
NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR PETROLEUMSTEKNOLOGI OG ANVENDT GEOFYSIKK Oppgave SIG445 Geofysisk Signalanalyse ving 5 En seismisk kilde er plassert pa endybde d ivann, hvor
Tallfølger er noe av det første vi treffer i matematikken, for eksempel når vi lærer å telle.
 Kapittel 1 Tallfølger 1, 2, 3, 4, 5, 6, 7, 8,... Det andre temaet i kurset MAT1001 er differenslikninger. I en differenslikning er den ukjente en tallfølge. I dette kapittelet skal vi legge grunnlaget
Kapittel 1 Tallfølger 1, 2, 3, 4, 5, 6, 7, 8,... Det andre temaet i kurset MAT1001 er differenslikninger. I en differenslikning er den ukjente en tallfølge. I dette kapittelet skal vi legge grunnlaget
TDT4105 IT Grunnkurs Høst 2014
 TDT4105 IT Grunnkurs Høst 2014 Norges teknisknaturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap Øving 6 1 Teori a) Hva er 2-komplement? b) Hva er en sample innen digital
TDT4105 IT Grunnkurs Høst 2014 Norges teknisknaturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap Øving 6 1 Teori a) Hva er 2-komplement? b) Hva er en sample innen digital
Simulering i MATLAB og SIMULINK
 Simulering i MATLAB og SIMULINK Av Finn Haugen ([email protected]) TechTeach (http://techteach.no) 13. november 2004 1 2 TechTeach Innhold 1 Simulering av differensiallikningsmodeller 7 1.1 Innledning...
Simulering i MATLAB og SIMULINK Av Finn Haugen ([email protected]) TechTeach (http://techteach.no) 13. november 2004 1 2 TechTeach Innhold 1 Simulering av differensiallikningsmodeller 7 1.1 Innledning...
MAT Oblig 1. Halvard Sutterud. 22. september 2016
 MAT1110 - Oblig 1 Halvard Sutterud 22. september 2016 Sammendrag I dette prosjektet skal vi se på anvendelsen av lineær algebra til å generere rangeringer av nettsider i et web basert på antall hyperlinker
MAT1110 - Oblig 1 Halvard Sutterud 22. september 2016 Sammendrag I dette prosjektet skal vi se på anvendelsen av lineær algebra til å generere rangeringer av nettsider i et web basert på antall hyperlinker
INF1010 notat: Binærsøking og quicksort
 INF1010 notat: Binærsøking og quicksort Ragnhild Kobro Runde Februar 2004 I dette notatet skal vi ta for oss ytterligere to eksempler der rekursjon har en naturlig anvendelse, nemlig binærsøking og quicksort.
INF1010 notat: Binærsøking og quicksort Ragnhild Kobro Runde Februar 2004 I dette notatet skal vi ta for oss ytterligere to eksempler der rekursjon har en naturlig anvendelse, nemlig binærsøking og quicksort.
= 5, forventet inntekt er 26
 Eksempel på optimal risikodeling Hevdet forrige gang at i en kontrakt mellom en risikonøytral og en risikoavers person burde den risikonøytrale bære all risiko Kan illustrere dette i en enkel situasjon,
Eksempel på optimal risikodeling Hevdet forrige gang at i en kontrakt mellom en risikonøytral og en risikoavers person burde den risikonøytrale bære all risiko Kan illustrere dette i en enkel situasjon,
MAT1030 Diskret Matematikk
 MAT1030 Diskret Matematikk Forelesning 29: Kompleksitetsteori Roger Antonsen Institutt for informatikk, Universitetet i Oslo 13. mai 2009 (Sist oppdatert: 2009-05-17 22:38) Forelesning 29: Kompleksitetsteori
MAT1030 Diskret Matematikk Forelesning 29: Kompleksitetsteori Roger Antonsen Institutt for informatikk, Universitetet i Oslo 13. mai 2009 (Sist oppdatert: 2009-05-17 22:38) Forelesning 29: Kompleksitetsteori
Forelesning 29: Kompleksitetsteori
 MAT1030 Diskret Matematikk Forelesning 29: Kompleksitetsteori Roger Antonsen Institutt for informatikk, Universitetet i Oslo Forelesning 29: Kompleksitetsteori 13. mai 2009 (Sist oppdatert: 2009-05-17
MAT1030 Diskret Matematikk Forelesning 29: Kompleksitetsteori Roger Antonsen Institutt for informatikk, Universitetet i Oslo Forelesning 29: Kompleksitetsteori 13. mai 2009 (Sist oppdatert: 2009-05-17
Mer om Markov modeller
 Høyere ordens Markov modeller Mer om Markov modeller p h mnr = Pr( Y j+ 3 = ah Y j+ 2 = am, Y j+ 1 = an, Y j = a : r For en k-te ordens Markov modell som modellerer en DNA prosess vil det være 3*4 k mulige
Høyere ordens Markov modeller Mer om Markov modeller p h mnr = Pr( Y j+ 3 = ah Y j+ 2 = am, Y j+ 1 = an, Y j = a : r For en k-te ordens Markov modell som modellerer en DNA prosess vil det være 3*4 k mulige
4 Matriser TMA4110 høsten 2018
 Matriser TMA høsten 8 Nå har vi fått erfaring med å bruke matriser i et par forskjellige sammenhenger Vi har lært å løse et lineært likningssystem ved å sette opp totalmatrisen til systemet og gausseliminere
Matriser TMA høsten 8 Nå har vi fått erfaring med å bruke matriser i et par forskjellige sammenhenger Vi har lært å løse et lineært likningssystem ved å sette opp totalmatrisen til systemet og gausseliminere
TDT4102 Prosedyre og Objektorientert programmering Vår 2014
 Norges teknisk naturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap TDT4102 Prosedyre og Objektorientert programmering Vår 2014 Øving 10 Frist: 2014-04-11 Mål for denne øvinga:
Norges teknisk naturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap TDT4102 Prosedyre og Objektorientert programmering Vår 2014 Øving 10 Frist: 2014-04-11 Mål for denne øvinga:
TMA Matlab Oppgavesett 2
 TMA4123 - Matlab Oppgavesett 2 18.02.2013 1 Fast Fourier Transform En matematisk observasjon er at data er tall, og ofte opptrer med en implisitt rekkefølge, enten i rom eller tid. Da er det naturlig å
TMA4123 - Matlab Oppgavesett 2 18.02.2013 1 Fast Fourier Transform En matematisk observasjon er at data er tall, og ofte opptrer med en implisitt rekkefølge, enten i rom eller tid. Da er det naturlig å
Matlab-tips til Oppgave 2
 Matlab-tips til Oppgave 2 Numerisk integrasjon (a) Velg ut maks 10 passende punkter fra øvre og nedre del av hysteresekurven. Bruk punktene som input til Matlab og lag et plot. Vi definerer tre vektorer
Matlab-tips til Oppgave 2 Numerisk integrasjon (a) Velg ut maks 10 passende punkter fra øvre og nedre del av hysteresekurven. Bruk punktene som input til Matlab og lag et plot. Vi definerer tre vektorer
Eksamen - INF 283 Maskinlæring
 Eksamen - INF 283 Maskinlæring 23 feb. 2016 Tid: 3 timer Eksamen inneholder 15 oppgaver, som vil bli vektet likt ved evaluering. 1 Table 1 attributt antall personer forsørget av låntaker månedlig inntekt
Eksamen - INF 283 Maskinlæring 23 feb. 2016 Tid: 3 timer Eksamen inneholder 15 oppgaver, som vil bli vektet likt ved evaluering. 1 Table 1 attributt antall personer forsørget av låntaker månedlig inntekt
Oblig 2 - MAT1120. Fredrik Meyer 23. september 2009 A =
 Oblig - MAT Fredrik Meyer. september 9 Oppgave Linkmatrise: A = En basis til nullrommet til matrisen A I kan finnes ved å bruke MATLAB. Jeg kjører kommandoen rref(a-i) og får følge: >> rref(a-i). -.875.
Oblig - MAT Fredrik Meyer. september 9 Oppgave Linkmatrise: A = En basis til nullrommet til matrisen A I kan finnes ved å bruke MATLAB. Jeg kjører kommandoen rref(a-i) og får følge: >> rref(a-i). -.875.
TMA4122/TMA4130 Matematikk 4M/4N Høsten 2010
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA4122/TMA410 Matematikk 4M/4N Høsten 2010 1 Oppgave: Løs følgende ligningssystemer ved hjelp av Gauss-eliminasjon med delvis
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA4122/TMA410 Matematikk 4M/4N Høsten 2010 1 Oppgave: Løs følgende ligningssystemer ved hjelp av Gauss-eliminasjon med delvis
UTVIDET TEST AV PROGRAM
 Tid : 16.2.99, kl. 153 Til : Ole Meyer og prøvenemda Fra : Anders Sak : Fagprøve våren 1999, utvidet test av program Denne oppgaven var tre-delt. UTVIDET TEST AV PROGRAM Først skulle jeg påtrykke AD-kortet
Tid : 16.2.99, kl. 153 Til : Ole Meyer og prøvenemda Fra : Anders Sak : Fagprøve våren 1999, utvidet test av program Denne oppgaven var tre-delt. UTVIDET TEST AV PROGRAM Først skulle jeg påtrykke AD-kortet
Løsningsforslag ECON 2130 Obligatorisk semesteroppgave 2017 vår
 Løsningsforslag ECON 130 Obligatorisk semesteroppgave 017 vår Andreas Myhre Oppgave 1 1. (i) Siden X og Z er uavhengige, vil den simultane fordelingen mellom X og Z kunne skrives som: f(x, z) = P(X = x
Løsningsforslag ECON 130 Obligatorisk semesteroppgave 017 vår Andreas Myhre Oppgave 1 1. (i) Siden X og Z er uavhengige, vil den simultane fordelingen mellom X og Z kunne skrives som: f(x, z) = P(X = x
Steg 1: Lag en figur som bytter drakt
 Enarmet banditt Skrevet av: Oversatt fra Code Club UK (//codeclub.org.uk) Oversatt av: Gudbrand Tandberg og Anne-Marit Gravem Kurs: Scratch Tema: Blokkbasert, Spill, Animasjon Fag: Matematikk, Programmering
Enarmet banditt Skrevet av: Oversatt fra Code Club UK (//codeclub.org.uk) Oversatt av: Gudbrand Tandberg og Anne-Marit Gravem Kurs: Scratch Tema: Blokkbasert, Spill, Animasjon Fag: Matematikk, Programmering
Dynamisk programmering
 Dynamisk programmering Metoden ble formalisert av Richard Bellmann (RAND Corporation) på 50-tallet. Programmering i betydningen planlegge, ta beslutninger. (Har ikke noe med kode eller å skrive kode å
Dynamisk programmering Metoden ble formalisert av Richard Bellmann (RAND Corporation) på 50-tallet. Programmering i betydningen planlegge, ta beslutninger. (Har ikke noe med kode eller å skrive kode å
L12-Dataanalyse. Introduksjon. Nelson Aalen plott. Page 76 of Introduksjon til dataanalyse. Levetider og sensurerte tider
 Page 76 of 80 L12-Dataanalyse Introduksjon Introduksjon til dataanalyse Presentasjonen her fokuserer på dataanalyseteknikker med formål å estimere parametere (MTTF,, osv) i modeller vi benytter for vedlikeholdsoptimering
Page 76 of 80 L12-Dataanalyse Introduksjon Introduksjon til dataanalyse Presentasjonen her fokuserer på dataanalyseteknikker med formål å estimere parametere (MTTF,, osv) i modeller vi benytter for vedlikeholdsoptimering
Notat 4 - ST februar 2005
 Notat 4 - ST1301 8. februar 2005 1 While- og repeat-løkker Vi har tidligere sett på bruk av før-løkker. Slike løkker er hensiktsmessig å bruke når vi skal gjenta visse beregninger (løkke-kroppen) et antall
Notat 4 - ST1301 8. februar 2005 1 While- og repeat-løkker Vi har tidligere sett på bruk av før-løkker. Slike løkker er hensiktsmessig å bruke når vi skal gjenta visse beregninger (løkke-kroppen) et antall
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT-INF 1100 Modellering og beregninger. Eksamensdag: Mandag 5. desember 2011. Tid for eksamen: 9:00 13:00. Oppgavesettet er på
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT-INF 1100 Modellering og beregninger. Eksamensdag: Mandag 5. desember 2011. Tid for eksamen: 9:00 13:00. Oppgavesettet er på
Matriser. Kapittel 4. Definisjoner og notasjon
 Kapittel Matriser Vi har lært å løse et lineært ligningssystem ved å sette opp totalmatrisen til systemet gausseliminere den ved hjelp av radoperasjoner på matrisen Vi skal nå se nærmere på egenskaper
Kapittel Matriser Vi har lært å løse et lineært ligningssystem ved å sette opp totalmatrisen til systemet gausseliminere den ved hjelp av radoperasjoner på matrisen Vi skal nå se nærmere på egenskaper
Kanter, kanter, mange mangekanter. Introduksjon: Steg 1: Enkle firkanter. Sjekkliste. Skrevet av: Sigmund Hansen
 Kanter, kanter, mange mangekanter Skrevet av: Sigmund Hansen Kurs: Processing Tema: Tekstbasert, Animasjon Fag: Matematikk, Programmering, Kunst og håndverk Klassetrinn: 8.-10. klasse, Videregående skole
Kanter, kanter, mange mangekanter Skrevet av: Sigmund Hansen Kurs: Processing Tema: Tekstbasert, Animasjon Fag: Matematikk, Programmering, Kunst og håndverk Klassetrinn: 8.-10. klasse, Videregående skole
Repetisjon: LTI-systemer
 Forelesning, 11. mars 4 Tilhørende pensum er 6.1-6.4 i læreboken. repetisjon av FIR-filtre frekvensresponsen til et FIR-filter beregne utgangen fra FIR-filtret ved hjelp av frekvensresponsen steady-state
Forelesning, 11. mars 4 Tilhørende pensum er 6.1-6.4 i læreboken. repetisjon av FIR-filtre frekvensresponsen til et FIR-filter beregne utgangen fra FIR-filtret ved hjelp av frekvensresponsen steady-state
Experiment Norwegian (Norway) Hoppende frø - En modell for faseoverganger og ustabilitet (10 poeng)
 Q2-1 Hoppende frø - En modell for faseoverganger og ustabilitet (10 poeng) Vennligst les de generelle instruksjonene som ligger i egen konvolutt, før du begynner på denne oppgaven. Introduksjon Faseoverganger
Q2-1 Hoppende frø - En modell for faseoverganger og ustabilitet (10 poeng) Vennligst les de generelle instruksjonene som ligger i egen konvolutt, før du begynner på denne oppgaven. Introduksjon Faseoverganger
Illustrasjon av regel 5.19 om sentralgrenseteoremet og litt om heltallskorreksjon (som i eksempel 5.20).
 Econ 130 HG mars 017 Supplement til forelesningen 7. februar Illustrasjon av regel 5.19 om sentralgrenseteoremet og litt om heltallskorreksjon (som i eksempel 5.0). Regel 5.19 sier at summer, Y X1 X X
Econ 130 HG mars 017 Supplement til forelesningen 7. februar Illustrasjon av regel 5.19 om sentralgrenseteoremet og litt om heltallskorreksjon (som i eksempel 5.0). Regel 5.19 sier at summer, Y X1 X X
Bioberegninger - notat 4: Mer om sannsynlighetsmaksimering
 Bioberegninger - notat 4: Mer om sannsynlighetsmaksimering 8. mars 2004 1 Kort om Newton s metode i flere dimensjoner Newton s metode kan generaliseres til å løse sett av n ligninger med n ukjente. Skal
Bioberegninger - notat 4: Mer om sannsynlighetsmaksimering 8. mars 2004 1 Kort om Newton s metode i flere dimensjoner Newton s metode kan generaliseres til å løse sett av n ligninger med n ukjente. Skal
Forelesning, 23.februar INF2400 Sampling II. Øyvind Ryan. Februar 2006
 INF2400 Februar 2006 INF2400 Innhold Delkapitlene 4.4-4.6 fra læreboken, 4.3 er til selvstudium. Repetisjon om sampling og aliasing Diskret-til-kontinuerlig omforming Interpolasjon med pulser Oversamling
INF2400 Februar 2006 INF2400 Innhold Delkapitlene 4.4-4.6 fra læreboken, 4.3 er til selvstudium. Repetisjon om sampling og aliasing Diskret-til-kontinuerlig omforming Interpolasjon med pulser Oversamling
MATLABs brukergrensesnitt
 Kapittel 3 MATLABs brukergrensesnitt 3.1 Brukergrensesnittets vinduer Ved oppstart av MATLAB åpnes MATLAB-vinduet, se figur 1.1. MATLAB-vinduet inneholder forskjellige (under-)vinduer. De ulike vinduene
Kapittel 3 MATLABs brukergrensesnitt 3.1 Brukergrensesnittets vinduer Ved oppstart av MATLAB åpnes MATLAB-vinduet, se figur 1.1. MATLAB-vinduet inneholder forskjellige (under-)vinduer. De ulike vinduene
FFT. Prosessering i frekvensdomenet. Digital signalprosessering Øyvind Brandtsegg
 FFT Prosessering i frekvensdomenet Digital signalprosessering Øyvind Brandtsegg Representasjonsmåter Tidsdomene: Amplityde over tid Frekvensdomene: Amplityde over frekvens Hvorfor? Prosessering i frekvensdomenet
FFT Prosessering i frekvensdomenet Digital signalprosessering Øyvind Brandtsegg Representasjonsmåter Tidsdomene: Amplityde over tid Frekvensdomene: Amplityde over frekvens Hvorfor? Prosessering i frekvensdomenet
Mandag 04.09.06. Institutt for fysikk, NTNU TFY4160/FY1002: Bølgefysikk Høsten 2006, uke 36
 Institutt for fsikk, NTNU TFY4160/FY1002: Bølgefsikk Høsten 2006, uke 36 Mandag 04.09.06 Del II: BØLGER Innledning Bølger er forplantning av svingninger. Når en bølge forplanter seg i et materielt medium,
Institutt for fsikk, NTNU TFY4160/FY1002: Bølgefsikk Høsten 2006, uke 36 Mandag 04.09.06 Del II: BØLGER Innledning Bølger er forplantning av svingninger. Når en bølge forplanter seg i et materielt medium,
11. september Institutt for geofag Universitetet i Oslo. GEO En Introduksjon til MatLab. Kapittel 5 (del 2) Ada Gjermundsen
 , Institutt for geofag Universitetet i Oslo 11. september 2012 Litt repetisjon: Array, En array er en variabel som inneholder flere objekter (verdier) En endimensjonal array er en vektor En array med to
, Institutt for geofag Universitetet i Oslo 11. september 2012 Litt repetisjon: Array, En array er en variabel som inneholder flere objekter (verdier) En endimensjonal array er en vektor En array med to
Prosjekt 2 - Introduksjon til Vitenskapelige Beregninger
 Prosjekt - Introduksjon til Vitenskapelige Beregninger Studentnr: 755, 759 og 7577 Mars 6 Oppgave Feltlinjene for en kvadrupol med positive punktladninger Q lang x-aksen i x = ±r og negative punktladninger
Prosjekt - Introduksjon til Vitenskapelige Beregninger Studentnr: 755, 759 og 7577 Mars 6 Oppgave Feltlinjene for en kvadrupol med positive punktladninger Q lang x-aksen i x = ±r og negative punktladninger
Forelesning, 17.februar INF2400 Sampling II. Øyvind Ryan. Februar 2005
 INF2400 Februar 2005 INF2400 Innhold Delkapitlene 4.4-4.6 fra læreboken, 4.3 er til selvstudium. Repetisjon om sampling og aliasing Diskret-til-kontinuerlig omforming Interpolasjon med pulser Oversamling
INF2400 Februar 2005 INF2400 Innhold Delkapitlene 4.4-4.6 fra læreboken, 4.3 er til selvstudium. Repetisjon om sampling og aliasing Diskret-til-kontinuerlig omforming Interpolasjon med pulser Oversamling
Matematikk Øvingsoppgaver i numerikk leksjon 9. Løsningsforslag
 Matematikk 000 Øvingsoppgaver i numerikk leksjon 9 Løsningsforslag Oppgave Integral som en sum av rektangler a) 3 f(x) dx = 3 x 3 dx = [ ] 3 3 + x3+ = [ x 4 ] 3 4 = 34 = 20. 4 b) 0.5 f() + 0.5 f(.5) +
Matematikk 000 Øvingsoppgaver i numerikk leksjon 9 Løsningsforslag Oppgave Integral som en sum av rektangler a) 3 f(x) dx = 3 x 3 dx = [ ] 3 3 + x3+ = [ x 4 ] 3 4 = 34 = 20. 4 b) 0.5 f() + 0.5 f(.5) +
Prosjektoppgaver om diusjonsprosesser og diusjonstilnærmelse
 Prosjektoppgaver om diusjonsprosesser og diusjonstilnærmelse February 13, 2006 I alle oppgavene skal det skrives litt om hva diusjonsprosesser er, hvilke spesielle resultater fra diusjonsteorien man skal
Prosjektoppgaver om diusjonsprosesser og diusjonstilnærmelse February 13, 2006 I alle oppgavene skal det skrives litt om hva diusjonsprosesser er, hvilke spesielle resultater fra diusjonsteorien man skal
TMA4240 Statistikk Høst 2016
 TMA4240 Statistikk Høst 2016 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 11 Oppgavene i denne øvingen dreier seg om hypotesetesting og sentrale begreper
TMA4240 Statistikk Høst 2016 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 11 Oppgavene i denne øvingen dreier seg om hypotesetesting og sentrale begreper
TMA4240 Statistikk 2014
 TMA4240 Statistikk 2014 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 12, blokk II Oppgave 1 På ein av vegane inn til Trondheim er UP interessert i å måle effekten
TMA4240 Statistikk 2014 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 12, blokk II Oppgave 1 På ein av vegane inn til Trondheim er UP interessert i å måle effekten
Introduksjon til Algoritmeanalyse
 Introduksjon til Algoritmeanalyse 26. August, 2019 Institutt for Informatikk 1 Hvordan skal vi tenke i IN2010? Effektive løsninger Hvordan skalérer problemet og løsningen? 2 Terminologi Betegnelse Problem
Introduksjon til Algoritmeanalyse 26. August, 2019 Institutt for Informatikk 1 Hvordan skal vi tenke i IN2010? Effektive løsninger Hvordan skalérer problemet og løsningen? 2 Terminologi Betegnelse Problem
EKSAMEN Løsningsforslag
 5..7 EKSAMEN Løsningsforslag Emnekode: ITD5 Dato:. desember 7 Hjelpemidler: - To A-ark med valgfritt innhold på begge sider. - Formelhefte. - Kalkulator som deles ut samtidig med oppgaven. Emnenavn: Matematikk
5..7 EKSAMEN Løsningsforslag Emnekode: ITD5 Dato:. desember 7 Hjelpemidler: - To A-ark med valgfritt innhold på begge sider. - Formelhefte. - Kalkulator som deles ut samtidig med oppgaven. Emnenavn: Matematikk
Representasjon av tall på datamaskin Kort innføring for MAT-INF1100L
 Representasjon av tall på datamaskin Kort innføring for MAT-INF00L Knut Mørken 3. desember 204 Det er noen få prinsipper fra den første delen av MAT-INF00 om tall som studentene i MAT-INF00L bør kjenne
Representasjon av tall på datamaskin Kort innføring for MAT-INF00L Knut Mørken 3. desember 204 Det er noen få prinsipper fra den første delen av MAT-INF00 om tall som studentene i MAT-INF00L bør kjenne
INF2220: Time 12 - Sortering
 INF0: Time 1 - Sortering Mathias Lohne mathialo Noen algoritmer Vi skal nå se på noen konkrete sorteringsalgoritmer. Gjennomgående i alle eksempler vil vi sortere tall etter tallverdi, men som diskutert
INF0: Time 1 - Sortering Mathias Lohne mathialo Noen algoritmer Vi skal nå se på noen konkrete sorteringsalgoritmer. Gjennomgående i alle eksempler vil vi sortere tall etter tallverdi, men som diskutert
Steg 1: Streken. Steg 2: En hoppende helt. Sjekkliste. Sjekkliste. Introduksjon. Hei der! Hoppehelt
 Hei der! Hoppehelt Ser ut som dette er ditt første besøk, vil du ha en omvisning? Ekspert Scratch PDF Introduksjon Hoppehelt er litt inspirert av musikkspillet Guitar Hero. I Hoppehelt skal man kontrollere
Hei der! Hoppehelt Ser ut som dette er ditt første besøk, vil du ha en omvisning? Ekspert Scratch PDF Introduksjon Hoppehelt er litt inspirert av musikkspillet Guitar Hero. I Hoppehelt skal man kontrollere
i x i
 TMA4245 Statistikk Vår 2016 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalte oppgaver 11, blokk II Oppgavene i denne øvingen dreier seg om hypotesetesting og sentrale
TMA4245 Statistikk Vår 2016 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalte oppgaver 11, blokk II Oppgavene i denne øvingen dreier seg om hypotesetesting og sentrale
Repetisjon: Sampling. Repetisjon: Diskretisering. Repetisjon: Diskret vs kontinuerlig. Forelesning, 12.februar 2004
 Repetisjon: Diskret vs kontinuerlig Forelesning,.februar 4 Kap. 4.-4. i læreboken. Anta variabelen t slik at a < t < b, (a, b) R sampling og rekonstruksjon, i tids- og frekvensdomenet Nyquist-Shannons
Repetisjon: Diskret vs kontinuerlig Forelesning,.februar 4 Kap. 4.-4. i læreboken. Anta variabelen t slik at a < t < b, (a, b) R sampling og rekonstruksjon, i tids- og frekvensdomenet Nyquist-Shannons
TMA4240 Statistikk 2014
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 5, blokk I Løsningsskisse Oppgave 1 X og Y er uavhengige Poisson-fordelte stokastiske variable, X p(x;5 og Y p(y;1.
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 5, blokk I Løsningsskisse Oppgave 1 X og Y er uavhengige Poisson-fordelte stokastiske variable, X p(x;5 og Y p(y;1.
ST0103 Brukerkurs i statistikk Høst 2014
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag ST0103 Brukerkurs i statistikk Høst 2014 Løsningsforslag Øving 1 2.1 Frekvenstabell For å lage en frekvenstabell må vi telle
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag ST0103 Brukerkurs i statistikk Høst 2014 Løsningsforslag Øving 1 2.1 Frekvenstabell For å lage en frekvenstabell må vi telle
Oppsummering av Uke 3. MAT1030 Diskret matematikk. Binære tall. Oppsummering av Uke 3
 Oppsummering av Uke 3 MAT1030 Diskret matematikk Forelesning 3: Mer om representasjon av tall Dag Normann Matematisk Institutt, Universitetet i Oslo 21. januar 2008 Mandag 14.01 og delvis onsdag 16.01
Oppsummering av Uke 3 MAT1030 Diskret matematikk Forelesning 3: Mer om representasjon av tall Dag Normann Matematisk Institutt, Universitetet i Oslo 21. januar 2008 Mandag 14.01 og delvis onsdag 16.01
a. Hva er de inverse transformasjonene avfølgende tre transformasjoner T, R og S: θ θ sin( ) cos( ) Fasit: 1 s x cos( θ) sin( θ) 0 0 y y z
 Kommentar: Svar kort og konsist. Husk at eksamen har tre oppgaver. Poengene for hver (del-) oppgave bør gi en indikasjon på hvor me tid som bør benttes per oppgave. Oppgave 1: Forskjellige emner (40 poeng)
Kommentar: Svar kort og konsist. Husk at eksamen har tre oppgaver. Poengene for hver (del-) oppgave bør gi en indikasjon på hvor me tid som bør benttes per oppgave. Oppgave 1: Forskjellige emner (40 poeng)
LØSNINGSFORSLAG ØVING 2 - APPROKSIMERING AV TSP
 LØSNINGSFORSLAG ØVING 2 - APPROKSIMERING AV TSP Approksimering av Travling Salesman Problem er her illustrert vha. en genetisk algoritme (GA). Den grunnlegge metaforen for en genetisk algoritme er evolusjon
LØSNINGSFORSLAG ØVING 2 - APPROKSIMERING AV TSP Approksimering av Travling Salesman Problem er her illustrert vha. en genetisk algoritme (GA). Den grunnlegge metaforen for en genetisk algoritme er evolusjon
UNIVERSAL TENNIS RATING SPØRSMÅL OG SVAR
 Introduksjon UNIVERSAL TENNIS RATING SPØRSMÅL OG SVAR UTR er et ratingsystem som skal fremme rettferdig og konkurransedyktige kamper i tennis. Spillerne blir ratet etter faktiske resultater og ikke etter
Introduksjon UNIVERSAL TENNIS RATING SPØRSMÅL OG SVAR UTR er et ratingsystem som skal fremme rettferdig og konkurransedyktige kamper i tennis. Spillerne blir ratet etter faktiske resultater og ikke etter
ST0202 Statistikk for samfunnsvitere
 ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag 2 Statistisk inferens (kap. 8) Statistisk inferens er å tolke/analysere resultater fra utvalget for å finne ut mest mulig
ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag 2 Statistisk inferens (kap. 8) Statistisk inferens er å tolke/analysere resultater fra utvalget for å finne ut mest mulig
Eksamensoppgave i TMA4275 Levetidsanalyse
 Institutt for matematiske fag Eksamensoppgave i TMA4275 Levetidsanalyse Faglig kontakt under eksamen: Jacopo Paglia Tlf: 967 03 414 Eksamensdato: Fredag 7. juni 2019 Eksamenstid (fra til): 09:00 13:00
Institutt for matematiske fag Eksamensoppgave i TMA4275 Levetidsanalyse Faglig kontakt under eksamen: Jacopo Paglia Tlf: 967 03 414 Eksamensdato: Fredag 7. juni 2019 Eksamenstid (fra til): 09:00 13:00
Om plotting. Knut Mørken. 31. oktober 2003
 Om plotting Knut Mørken 31. oktober 2003 1 Innledning Dette lille notatet tar for seg primitiv plotting av funksjoner og visualisering av Newtons metode ved hjelp av Java-klassen PlotDisplayer. Merk at
Om plotting Knut Mørken 31. oktober 2003 1 Innledning Dette lille notatet tar for seg primitiv plotting av funksjoner og visualisering av Newtons metode ved hjelp av Java-klassen PlotDisplayer. Merk at
MAT-INF 2360: Obligatorisk oppgave 1
 6. februar, MAT-INF 36: Obligatorisk oppgave Oppgave I denne oppgaven skal vi sammenligne effektiviteten av FFT-algoritmen med en mer rett frem algoritme for DFT. Deloppgave a Lag en funksjon y=dftimpl(x)
6. februar, MAT-INF 36: Obligatorisk oppgave Oppgave I denne oppgaven skal vi sammenligne effektiviteten av FFT-algoritmen med en mer rett frem algoritme for DFT. Deloppgave a Lag en funksjon y=dftimpl(x)
Strøm av olje og vann i berggrunnen matematisk model, simulering og visualisering
 Strøm av olje og vann i berggrunnen matematisk model, simulering og visualisering Hans Fredrik Nordhaug Matematisk institutt Faglig-pedagogisk dag, 01.02.2000. Oversikt 1 Oversikt Introduksjon. Hva er
Strøm av olje og vann i berggrunnen matematisk model, simulering og visualisering Hans Fredrik Nordhaug Matematisk institutt Faglig-pedagogisk dag, 01.02.2000. Oversikt 1 Oversikt Introduksjon. Hva er
Gruvedrift. Institutt for matematiske fag, NTNU. Notat for TMA4240/TMA4245 Statistikk
 Gruvedrift Notat for TMA/TMA Statistikk Institutt for matematiske fag, NTNU I forbindelse med planlegging av gruvedrift i et område er det mange hensyn som må tas når en skal vurdere om prosjektet er lønnsomt.
Gruvedrift Notat for TMA/TMA Statistikk Institutt for matematiske fag, NTNU I forbindelse med planlegging av gruvedrift i et område er det mange hensyn som må tas når en skal vurdere om prosjektet er lønnsomt.
Lineære ligningssystemer og gausseliminasjon
 Kapittel Lineære ligningssystemer og gausseliminasjon Vi skal lære en metode for å finne og beskrive alle løsninger av systemer av m lineære ligninger med n ukjente Oppvarming Her er et eksempel på et
Kapittel Lineære ligningssystemer og gausseliminasjon Vi skal lære en metode for å finne og beskrive alle løsninger av systemer av m lineære ligninger med n ukjente Oppvarming Her er et eksempel på et
Tall. Posisjons-tallsystemer. Representasjon av heltall. Tall positive, negative heltall, flytende tall. Tekst ASCII, UNICODE XML, CSS
 Tall jfr. Cyganski & Orr 3..3, 3..5 se også http://courses.cs.vt.edu/~csonline/numbersystems/lessons/index.html Tekst ASCII, UNICODE XML, CSS Konverteringsrutiner Tall positive, negative heltall, flytende
Tall jfr. Cyganski & Orr 3..3, 3..5 se også http://courses.cs.vt.edu/~csonline/numbersystems/lessons/index.html Tekst ASCII, UNICODE XML, CSS Konverteringsrutiner Tall positive, negative heltall, flytende
Snøtetthet. Institutt for matematiske fag, NTNU 15. august Notat for TMA4240/TMA4245 Statistikk
 Snøtetthet Notat for TMA424/TMA4245 Statistikk Institutt for matematiske fag, NTNU 5. august 22 I forbindelse med varsling av om, klimaforskning og særlig kraftproduksjon er det viktig å kunne anslå hvor
Snøtetthet Notat for TMA424/TMA4245 Statistikk Institutt for matematiske fag, NTNU 5. august 22 I forbindelse med varsling av om, klimaforskning og særlig kraftproduksjon er det viktig å kunne anslå hvor
TTK4180 Stokastiske og adaptive systemer. Datamaskinøving 2 - Parameterestimering
 Institutt for teknisk kybernetikk Norges teknisk-naturvitenskapelige universitet 27.10.98 EWR TTK4180 Stokastiske og adaptive systemer Datamaskinøving 2 - Parameterestimering Tid og sted: -Utdeling av
Institutt for teknisk kybernetikk Norges teknisk-naturvitenskapelige universitet 27.10.98 EWR TTK4180 Stokastiske og adaptive systemer Datamaskinøving 2 - Parameterestimering Tid og sted: -Utdeling av
ENC - 100. ENKEL AKSE og KLIPPE LENGDE KONTROLLER for PLATESAKSER
 ENC - 100 ENKEL AKSE og KLIPPE LENGDE KONTROLLER for PLATESAKSER 1. GENERELLE SPESIFIKASJONER Membran tastatur med lang levetid. Klart og lett lesbart display. Viser hver av de 6 sifrene for aktuell og
ENC - 100 ENKEL AKSE og KLIPPE LENGDE KONTROLLER for PLATESAKSER 1. GENERELLE SPESIFIKASJONER Membran tastatur med lang levetid. Klart og lett lesbart display. Viser hver av de 6 sifrene for aktuell og
Dataøvelse 3 Histogram og normalplott
 Matematisk institutt STAT200 Anvendt statistikk Universitetet i Bergen 18. februar 2004 Dataøvelse 3 Histogram og normalplott A. Formål med øvelsen Denne øvelsen skal vise hvordan man med SAS-systemet
Matematisk institutt STAT200 Anvendt statistikk Universitetet i Bergen 18. februar 2004 Dataøvelse 3 Histogram og normalplott A. Formål med øvelsen Denne øvelsen skal vise hvordan man med SAS-systemet
Kanter, kanter, mange mangekanter
 Kanter, kanter, mange mangekanter Nybegynner Processing PDF Introduksjon: Her skal vi se på litt mer avansert opptegning og bevegelse. Vi skal ta utgangspunkt i oppgaven om den sprettende ballen, men bytte
Kanter, kanter, mange mangekanter Nybegynner Processing PDF Introduksjon: Her skal vi se på litt mer avansert opptegning og bevegelse. Vi skal ta utgangspunkt i oppgaven om den sprettende ballen, men bytte
Obligatorisk oppgave nr 4 FYS-2130. Lars Kristian Henriksen UiO
 Obligatorisk oppgave nr 4 FYS-2130 Lars Kristian Henriksen UiO 23. februar 2015 Diskusjonsoppgaver: 3 Ved tordenvær ser vi oftest lynet før vi hører tordenen. Forklar dette. Det finnes en enkel regel
Obligatorisk oppgave nr 4 FYS-2130 Lars Kristian Henriksen UiO 23. februar 2015 Diskusjonsoppgaver: 3 Ved tordenvær ser vi oftest lynet før vi hører tordenen. Forklar dette. Det finnes en enkel regel
Dagens temaer. Endelig lengde data. Tema. Time 11: Diskret Fourier Transform, del 2. Spektral glatting pga endelig lengde data.
 Dagens temaer Time : Diskret Fourier Transform, del Andreas [email protected], INF37 Institutt for informatikk, Universitetet i Oslo Spektral glatting pga endelig lengde data Bruk av en Frekvensestimering
Dagens temaer Time : Diskret Fourier Transform, del Andreas [email protected], INF37 Institutt for informatikk, Universitetet i Oslo Spektral glatting pga endelig lengde data Bruk av en Frekvensestimering
Prosjektoppgave, FYS-MEK1110 V06 ROBERT JACOBSEN
 Prosjektoppgave, FYS-MEK1110 V06 ROBERT JACOBSEN Innledning Prosjektet i FYS-MEK1110 v06 handler om å forske litt på hvordan Jupiters bane er, og hvordan denne kan sammenliknes ved andre baner i solsystemet.
Prosjektoppgave, FYS-MEK1110 V06 ROBERT JACOBSEN Innledning Prosjektet i FYS-MEK1110 v06 handler om å forske litt på hvordan Jupiters bane er, og hvordan denne kan sammenliknes ved andre baner i solsystemet.
Matematikk 1000. Øvingsoppgaver i numerikk leksjon 3. Løsningsforslag
 Matematikk 1000 Øvingsoppgaver i numerikk leksjon 3 Løsningsforslag Oppgave 1 Flo og fjære a) >> x=0:.1:24; >> y=3.2*sin(pi/6*(x-3)); Disse linjene burde vel være forståelige nå. >> plot(x,y,'linewidth',3)
Matematikk 1000 Øvingsoppgaver i numerikk leksjon 3 Løsningsforslag Oppgave 1 Flo og fjære a) >> x=0:.1:24; >> y=3.2*sin(pi/6*(x-3)); Disse linjene burde vel være forståelige nå. >> plot(x,y,'linewidth',3)
TMA4240 Statistikk Høst 2016
 TMA4240 Statistikk Høst 2016 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 12 Denne øvingen består av oppgaver om enkel lineær regresjon. De handler blant
TMA4240 Statistikk Høst 2016 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 12 Denne øvingen består av oppgaver om enkel lineær regresjon. De handler blant
Statistisk inferens (kap. 8) Hovedtyper av statistisk inferens. ST0202 Statistikk for samfunnsvitere
 2 Statistisk inferens (kap. 8) Statistisk inferens er å tolke/analysere resultater fra utvalget for å finne ut mest mulig om populasjonen. Konkret: Analysere en observator for å finne ut noe om korresponderende
2 Statistisk inferens (kap. 8) Statistisk inferens er å tolke/analysere resultater fra utvalget for å finne ut mest mulig om populasjonen. Konkret: Analysere en observator for å finne ut noe om korresponderende
Oppsummering TMA4100. Kristian Seip. 26./28. november 2013
 Oppsummering TMA4100 Kristian Seip 26./28. november 2013 Forelesningene 26./28. november Disse forelesningene er et forsøk på å se de store linjer og sammenhengen mellom de ulike deltemaene i TMA4100 delvis
Oppsummering TMA4100 Kristian Seip 26./28. november 2013 Forelesningene 26./28. november Disse forelesningene er et forsøk på å se de store linjer og sammenhengen mellom de ulike deltemaene i TMA4100 delvis
Beregning av HLR- poeng. Oppdatert 19. November 2013
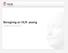 Beregning av HLR- poeng Oppdatert 19. November 2013 Introduksjon Når du tar i bruk din treningsdukke med QCPR fra Laerdal blir dine hjertelungeredningsferdigheter målt med en poengsum fra 0% til 100%.
Beregning av HLR- poeng Oppdatert 19. November 2013 Introduksjon Når du tar i bruk din treningsdukke med QCPR fra Laerdal blir dine hjertelungeredningsferdigheter målt med en poengsum fra 0% til 100%.
Simulerings-eksperiment - Fysikk/Matematikk
 Simulerings-eksperiment - Fysikk/Matematikk Tidligere dette semesteret er det gjennomført et såkalt Tracker-eksperiment i fysikk ved UiA. Her sammenlignes data fra et kast-eksperiment med data fra en tilhørende
Simulerings-eksperiment - Fysikk/Matematikk Tidligere dette semesteret er det gjennomført et såkalt Tracker-eksperiment i fysikk ved UiA. Her sammenlignes data fra et kast-eksperiment med data fra en tilhørende
Tilstandsestimering Oppgaver
 University College of Southeast Norway Tilstandsestimering Oppgaver HANS-PETTER HALVORSEN http://home.hit.no/~hansha Innholdsfortegnelse 1 Grunnlag... 3 1.1 Statistikk og Stokastiske systemer... 3 1.2
University College of Southeast Norway Tilstandsestimering Oppgaver HANS-PETTER HALVORSEN http://home.hit.no/~hansha Innholdsfortegnelse 1 Grunnlag... 3 1.1 Statistikk og Stokastiske systemer... 3 1.2
TMA4140 Diskret Matematikk Høst 2016
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA4140 Diskret Matematikk Høst 2016 Seksjon 10.2 18 La G = (V,E) være en enkel graf med V 2. Ettersom G er enkel er de mulige
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA4140 Diskret Matematikk Høst 2016 Seksjon 10.2 18 La G = (V,E) være en enkel graf med V 2. Ettersom G er enkel er de mulige
Oblig 1 FYS2130. Elling Hauge-Iversen
 Oblig 1 FYS2130 Elling Hauge-Iversen February 9, 2009 Oppgave 1 For å estimere kvalitetsfaktoren til basilarmembranen for ulike frekvenser har jeg laget et program som generer et rent sinussignal. Ideen
Oblig 1 FYS2130 Elling Hauge-Iversen February 9, 2009 Oppgave 1 For å estimere kvalitetsfaktoren til basilarmembranen for ulike frekvenser har jeg laget et program som generer et rent sinussignal. Ideen
Hvor i All Verden? Del 3 Erfaren Scratch PDF
 Hvor i All Verden? Del 3 Erfaren Scratch PDF Introduksjon Hvor i All Verden? er et reise- og geografispill hvor man raskest mulig skal fly innom reisemål spredt rundt i Europa. Dette er den siste av tre
Hvor i All Verden? Del 3 Erfaren Scratch PDF Introduksjon Hvor i All Verden? er et reise- og geografispill hvor man raskest mulig skal fly innom reisemål spredt rundt i Europa. Dette er den siste av tre
Lineære ligningssystemer og gausseliminasjon
 Kapittel Lineære ligningssystemer og gausseliminasjon Vi skal lære en metode for å finne og beskrive alle løsninger av systemer av m lineære ligninger med n ukjente. Oppvarming Her er et eksempel på et
Kapittel Lineære ligningssystemer og gausseliminasjon Vi skal lære en metode for å finne og beskrive alle løsninger av systemer av m lineære ligninger med n ukjente. Oppvarming Her er et eksempel på et
