Nabla, elektromagnetisme, vektorpotensial og superledning for FYS1120
|
|
|
- Hildur Slettebakk
- 6 år siden
- Visninger:
Transkript
1 Nabla, elektromagnetisme, vektorpotensial og superledning for FYS1120 Den differensielle vektoroperatoren = e x x + e y y + e z z (1) kalles vanligvis for nabla eller del hvis man er mer engelsk orientert. Her er e x, e y og e z ortogonale enhetsvektorer i henholdsvis x-, y- og z-retning i et kartesisk koordinatsystem. Et punkt i dette systemet kan derved angis ved posisjonsvektoren r = xe x + ye y + ze z. Tilsvarende kan en skalar funksjon F = F (x, y, z) skrives mer kompakt som F (r). Hvis denne operatoren nå virker på en slik funksjon F (r), så får vi en ny vektor F = F x e x + F y e y + F z e z (2) Dette kalles for gradienten til funksjonen F og sier noe om hvordan funksjonen forandrer seg i forskjellige retninger. Det ser vi ved å beregne forskjellen i funksjonsverdien i to nærliggende punkter r og r + dr ved å gjøre bruk av en vanlig Taylor-utvikling, df = F (r + dr) F (r) = F F F dx + dy + x y z dz Siden den differensielle posisjonsvektoren er dr = e x dx + e y dy + e z dz, kan vi derfor skrive denne forskjellen som df = F dr. Ligger vektoren dr i en flate F (x, y, z) = konst, vil df = 0. Gradienten F står derfor normalt på slike ekvipotensialflater. Den peker i den retning hvor funksjonen F (r) øker mest. Fra regelen for den deriverte av et produkt, ser vi nå fra (2) at gradienten av et produkt av to funksjoner F og G er (F G) = ( F )G + F ( G) (3) I elektromagnetismen er vektorfelt viktigere enn skalare felt. Et slikt felt V = V(r) angir derfor en vektor med størrelse og retning i hvert punkt r. I mer detalj kan vi skrive V(r) = V x (r)e x + V y (r)e y + V z (r)e z På samme måte som to vektorer kan kombineres enten ved skalar (prikk) eller vektoriell (kryss) multiplikasjon, kan også nabla anvendes på vektorfeltet V(r) på to forskjellige måter. Med skalar multiplikasjon får vi divergensen til vektorfeltet V = V x x + V y y + V z z, (4) 1
2 mens vektoriell multiplikasjon gir curl eller virvlingen av feltet: e x e y e z V = / x / y / z V x V y V z ( Vz = y V ) ( y Vx e x + z z V ) ( z Vy e y + x x V ) x e z y (5) Fra disse to definisjonene har vi nå med en gang den viktige identiteten ( V) = 0 (6) som sier at divergensen av en curl alltid er null. Like viktig er identiteten F = 0 (7) som sier at curl til en gradient alltid er identisk lik null. Derimot er divergensen av en gradient ikke null. For vektoren V = F med komponenter V i = F/ x i i (4) finner vi F = 2 F. Her er den viktige Laplace-operatoren. Ved hjelp av den kan vi også skrive en curl av en curl som 2 = 2 x y z 2 (8) ( V) = ( V) 2 V (9) Dette følger direkte fra definisjonen (5). I elektromagnetisk teori blir denne ofte brukt. Produktet av et skalart felt F (r) og et vektorfelt V(r) er et nytt vektor felt U = F V med komponenter U i (r) = F (r)v i (r). Produktregelen for derivasjon gir nå direkte for U mens U blir (F V) = ( F ) V + F ( V), (10) (F V) = ( F ) V + F ( V). (11) Tilsvarende formler for nabla virkende på produkt av to vektorer kan også utledes. 1 Symmetriske felt Ofte vil vi møte situasjoner hvor det er sfærisk symmetri i problemet vi er opptatt av. Da vil vi kunne ha skalare felt F = F (r) og vektorfelt R = R(r)ˆr hvor ˆr = r/r er 2
3 en enhetsvektor i radiell retning. Siden r = (x 2 + y 2 + z 2 ) 1/2, vil vi måtte regne ut gradienten av r. Nå er r/ x = x/r og tilsvarende for de andre komponentene slik at r = (x/r)e x + (y/r)e y + (z/r)e z = ˆr. Derfor har vi at F (r) = F ˆr (12) r Skal vi beregne divergensen av et radielt vektorfelt R = R(r)ˆr, trenger vi først r = ( x/ x) + ( y/ y) + ( z/ z) = = 3 som følger direkte fra definisjonen. Bruker vi nå (10), får vi for divergensen ((R/r)r) = (R/r) r + (R/r) r For gradienten i første ledd finner vi fra resultatet over at (R/r) = r ( ) ( R R ˆr = r r R ) r 2 ˆr Dermed blir R = R R/r + 3R/r = R + 2R/r når vi benytter at r = 3. Dette resultatet kan vi skrive på en litt mer kompakt og generell form som R = 1 ( ) r 2 r 2 R r På samme måte finner vi at r = 0 slik at curl av et radielt vektorfelt er null, i.e. (R(r)ˆr) = 0. Tilsvarende resultat kan utledes for vektorfelt med sylindrisk symmetri. (13) 2 Elektriske felt En elektrisk ladningsfordeling med tetthet ρ(r) gir opphav til et elektrisk felt E(r) = 1 d 3 r ρ(r )(r r ) 4πε 0 r r 3 (14) Dette er i grunnen bare en mer generell utgave av Coulombs lov. Vi kan nå lett skrive om dette integralet ved bruk av (12). Derav følger at (1/r) = (1/r 2 )ˆr = (1/r 3 )r som lar oss skrive 1 r r = r r r r 3 (15) da bare virker på komponentene til r og ikke komponentene til r. Derfor kan vi skrive E(r) = 1 d 3 r ρ(r ) 1 4πε 0 r r = 1 4πε 0 3 d 3 r ρ(r 1 ) r r
4 av samme grunn. Vi har dermed vist at for statiske felt er det elektriske feltet gitt ved gradienten E = V hvor nå den skalare funksjonen V (r) = 1 4πε 0 d 3 r ρ(r 1 ) r r er det elektriske potensialet i punktet r. Fra (7) vil vi nå ha E = 0 som er Maxwells 2. ligning i en slik statisk situasjon. Maxwells første ligning sier at E(r) = ρ(r)/ε 0. Bruker vi nå her at E = V, ser vi at det elektriske potensialet må tilfredsstille (16) 2 V (r) = ρ(r)/ε 0 (17) Dette er en 2. ordens, partiell differensialligning og spiller en viktig rolle i elektromagnetisk teori. I vårt tilfelle kjenner vi allerede den generelle løsningen (16). Feltet fra en punktladning kan vi nå finne tilbake til fra (14). En slik ladning Q har en ladningstetthet som er null overalt bortsett fra i det punktet r hvor ladningen er lokalisert. Dette kan vi beskrive matematisk ved å innføre δ-funksjon δ(r) brukt av Dirac i kvantemekanikken. Den er null i alle punkt bort sett fra punktet r = 0. Tilsvarende er δ(r r ) null i alle punkt bortsett fra punktet r = r. Singulariteten i dette punktet er definert ved at integralet d 3 r F (r )δ(r r ) = F (r) (18) for alle funksjoner F = F (r). Ladningstettheten for en punktladning Q plassert i punktet r 0 kan dermed skrives ρ(r) = Qδ(r r 0 ). Fra den generelle formelen (14) gir denne punktladningen opphav til feltet E(r) = 1 d 3 r Qδ(r r 0 ) r r 4πε 0 r r 3 = Q r r 0 4πε 0 r r 0 3 når vi benytter egenskapen (18) til δ-funksjonen. Dette er jo akkurat hva vi gikk ut fra da vi formulerte Coulombs lov for kraften mellom to punktladninger. Tar vi nå divergensen av dette feltet og sammenligner med Maxwells 1. ligning E(r) = ρ(r)/ε 0, får vi det matematiske resulatet r r 0 r r 0 3 = 4πδ(r r 0) (19) Kombineres dette med (15), føger at 2 (1/r) = 4πδ(r) når vi setter r 0 = 0. Dette er ikke noe annet enn Poissons ligning (17) for potensialet fra en punktladning plassert i origo. 4
5 3 Magnetiske felt Under stasjonære forhold skapes magnetiske felt av elektriske strømmer. Generelt er disse gitt av en strømtetthet J(r) som er bevart, det vil si at elektriske ladninger ikke kan oppstå eller forsvinne. Den totale ladning Q i et volum V med ladningstetthet ρ er Q = d 3 rρ(r, t) V hvor vi har helt generelt antatt at den også kan variere med tiden. Forandringen dq dt V = d 3 ρ(r, t) r må opptre som ladning som strømmer ut av volumet gjennom dets overflate og er gitt ved Vda J. Her er da er et differensielt flateelement på overflaten V til dette volumet. Derfor må vi ha d 3 r ρ V V = da J Dette siste integralet kan skrives om ved hjelp av Gauss divergensteorem som sier at V da J = V d3 r J. Flytter vi nå disse to romlige integral over på samme side av likhetstegnet, får vi [ ρ ] d 3 r + J = 0 V Siden det valgte volumet V kan være ganske vilkårlig, må vi ha at inneholdet i parantesen er null, i.e. ρ + J = 0 (20) Dette er den matematiske utgave av loven for ladning/strømbevarelse. Siden vi er foreløbig opptatt av stasjonære forhold, vil ρ/ = 0 slik at vi da må ha J = 0. En mer direkte måte å innse at J = 0 under stasjonære forhold, kommer fra J = σe hvor σ er materialets ledningsevne. Da er J = σ E = 0 siden den totale, elektriske ladningstetthet i en leder er null. Det magnetiske felt fra en slik strømtetthet er gitt ved Biot-Savarts lov B(r) = µ 0 d 3 r J(r ) (r r ) 4π r r 3 (21) som har en tilsvarende matematisk struktur som Coulombs lov (14). Igjen kan vi benytte (15) til å omskrive dette som B(r) = µ 0 d 3 r J(r ) 1 4π r r 5
6 Vi bytter om de to vektorene i kryssproduktet og får B(r) = µ 0 d 3 r J(r ) 4π r r Her kan igjen nabla-operatoren taes utenfor integralet da den bare virker på r. Vi ser da at B = A hvor A(r) = µ 0 d 3 r J(r ) 4π r r kalles det magnetiske vektorpotensialet. Det spiller en tilsvarende rolle for det magnetiske feltet som det skalare potensialet gjør for det elektriske feltet E = V. Det er ofte viktig å kjenne divergensen av dette vektorfeltet. Vi finner A(r) = µ 0 d 3 r J(r ) 1 4π r r hvor virker på koordinatene i vektoren r. Men nå er (1/ r r ) = (1/ r r ) hvor nå virker på kordinatene i r. Vi kan dermed foreta en partiell integrasjon hvor overflateleddet kan settes lik null. Dermed blir A(r) = µ 0 4π d 3 r 1 r r J(r ) Men under slike statiske forhold som vi her tenker oss, har vi sett at J = 0. Derfor vil vi også ha at A = 0. (22) 4 Gauge transformasjoner Dette resultatet for divergensen av vektorpotensialet er i virkeligheten mer generelt. Også når vi har tidsvariasjoner, kan vi velge at A = 0. Dette skyldes at vi kan erstatte A med et nytt vektorpotensial A uten at det magnetiske feltet B forandrer seg. Hvis nemlig forskjellen mellom A og A er en gradient av en funksjon og da curl av en gradient alltid er null, ser vi at dette er mulig. Denne spesielle forandringen av vektorpotensialet, A A = A + Λ (23) hvor Λ = Λ(r) er en vilkårlig funksjon, kaller vi en gaugetransformasjon. Magnetfeltet vil da transformere som B B = A = A + Λ = A = B (24) da Λ = 0. Det er derfor invariant under transformasjonen. Vi har en tilsvarende invarians for det elektriske potensialet V (r) hvor vi alltid kan addere til en konstant uten 6
7 at det elektriske feltet E = V forandrer sin verdi. Ofte velger vi denne konstanten slik at potensialet i det uendelige er null. Som et enkelt eksempel på en slik gaugetransformasjon, la oss betrakte et konstant magnetfelt B = Be z langs z-aksen. Da er det lett å se ved direkte utregning at vektorpotensial A = Bx e y vil beskrive dette. Hvis vi nå velger transformasjonsfunksjonen Λ = Bxy, får vi fra (23) ved enkel derivasjon et nytt potensial A = Bx e y +( By e x Bx e y ) = By e x. Hadde vi istedet valgt Λ = Bxy/2, ville vi fått A = Bx e y ( By e x Bx e y ) = 1 2 Bx e y 1 2 By e x Dette kan mer kompakt skrives som A = 1 2 B r (25) og brukes ofte i kvantemekanikken. Det magnetiske vektorpotensialet spiller der en meget viktig rolle i beskrivelsen av elektromagnetiske prosesser. Invarians under gauge transformasjoner spiller en meget viktig rolle i dagens elementrpartikkelfysikk. 5 Maxwell s ligninger Som vist i forelesningene, er de fire fundamentale ligningene til Maxwell som følger: 1) D = ρ 2) E = B 3) B = 0 4) H = J + D Disse gjelder helt gjenerelt, også for elektromagnetiske felt som varierer med tiden. Som Einstein viste, er ligningene i overensstemmelse med hans spesielle relativitetsteori og gjelder derfor for ladning- og strømkilder som beveger seg vilkårlig hurtig. Benytter vi at B = A i den andre ligningen, kan vi på høyre side skrive B/ = /( A) = ( A/) da derivasjoner med hensyn på tid og rom kan ombyttes. Flytter vi dette leddet nå over på høyresiden av ligningen, får vi (E + A ) = 0 Inneholdet i parantesen må derfor være en gradient for alltid å være sant. Sammenholder vi dette med hva vi hadde under statiske forhold, må denne gradienten derfor være V hvor V er det elektriske potensial. Derfor har vi at det elektriske feltet kan alltid skrives som E = V A 7 (26) (27) (28)
8 Det siste leddet er ikke-konservativt og tilsvarerer den elektromotoriske spenning som beskrives i Faraday s induksjonslov. Under gaugetransformasjonen (23) kan det nå se ut til at det elektriske feltet E vil forandres. Vi unngår det ved at det elektriske potensialet samtidig transformeres til V V = V Λ Da må også transformasjonsfunksjonen avhenge av tiden, i.e. Λ = Λ(r, t). Disse to kombinerte transformasjonene utgjør en full gaugetransformasjon som nå vil være en invarians også for tidsvariable elektriske og magnetiske felt. Tar vi divergensen av fjerde ligning, får vi på samme måte at 0 = J + ( D) hvor vi i siste ledd igjen har byttet om på tid og rom-derivasjon. Fra Maxwell s første ligning har vi nå at D = ρ slik at vi får strømbevaringsloven (20) som resultat. Den er nå en konsekvens av Maxwell s ligninger. Eller vi kan si at den er automatisk bygget inn i dem. (29) 6 Elektromagnetiske bølger I vakum et det hverken elektriske ladninger eller strømmer. Her er D = ε 0 E og B = ε 0 H. Maxwell s fjerde ligning blir da B = ε 0 µ 0 ( E/). Deriverer denne partielt med hensyn på tiden, får vi B = ε 2 E 0µ 0 2 På venstre side kan vi her sette inn for B/ fra Maxwell s andre ligning. Det gir ( E) = ε 0 µ 0 2 E 2 Bruker vi nå identiteten (9) kombinert med E = 0, finner vi 2 E = ε 0 µ 0 2 E 2 (30) Dette er bølgeligningen for det elektriske feltet. Den tilsvarende ligningen for det magnetiske feltet finner vi på samme måte ved å først tidsderivere Maxwell s andre ligning og så sette inn E/ fra den fjerde ligningen. Gjør vi så bruk av (9) igjen kombinert med B = 0, blir resultatet 2 B = ε 0 µ 0 2 B 2 (31) 8
9 I begge disse bølgeligningene ser vi at forplantningshastigheten er 1 c = (32) ε 0 µ 0 Setter vi inn de kjente verdiene for konstantene ε 0 og µ 0, gir dette c = m/s. Dette er det samme som lyshastigheten i vakum. Med denne oppdagelsen skjønte Maxwell at lysbølger er et rent elektromagnetisk fenomen beskrevet ved hans ligninger. En plan bølge med frekvens ω = 2πf som forplanter seg langs enhetsvektoren n og med amplitude E 0, er beskrevet ved E(x, t) = E 0 cos(k x ωt) (33) hvor bølgetallet k = (ω/c)n. Man ser at dette er en løsning ved direkte innsettelse i (30). Da vi må ha oppfylt at E = 0, betyr det at k E 0 = 0. På samme måte finner vi for det magnetiske feltet i (31) at k B 0 = 0 som nå følger fra B = 0. Begge feltvektorene står derfor normalt på forplantningsretningen n. Bølgebevegelsen sies å være transvers. Dette ser vi også ved å ta i bruk den andre Maxwell-ligningene. Setter vi inn her løsningene (30) og (31), finner vi at k E 0 = ωb 0. Dette betyr at vi vil ha n E = cb for bølgen. De tre vektorene E, B og n danner derfor hele tiden et høyre-orientert aksekors. Energitettheten i bølgen følger fra det vanlige uttrykket u = 1 (E D + B H) (34) 2 som gir den instantane verdi u = E D for en plan bølge. I alminnelighet vil denne variere med tiden. Fra Maxwell s ligninger kan vi nå undersøke dette nærmere. Vi multipliserer Maxwell s fjerde ligning med E og den andre med H og trekker så de to ligningene fra hverandre. Det gir D E + B H = E ( H) H ( E) J E etter å ha flyttet alle tidsderiverte ledd over på venstre side. Siden B = µ 0 H og D = ε 0 E, ser vi at den dermed blir den tidsderiverte u/ av energitettheten (34). Høyresiden kan tilsvarende forenkles ved å bruke nabla-identiteten (E H) = H ( E) E ( H) Innfører vi her den såkalte Poynting s vektor S = E H, kan vi derfor skrive den resultererende ligning som u + S = J E (35) Her representerer høyresiden ohmsk energitap og vil være null der det ikke er noen strømmer, det vil si utenfor alle ledere. På samme måte som bevaringsligningen for 9
10 elektrisk ladning i (20), har vi dermed etablert en tilsvarende ligning for energi. Her representerer nå Poynting s vektor strømmen av energi. For den plane bølgen (33) skjer den med lysets hastighet i retning n. Elektromagnetiske bølger i media beskrives på nøyaktig samme måte ved de mer generelle Maxwell-ligninger (26) og (27). De resulterende bølgeligningene vil da ble de samme som i vakum, bare med ε 0 µ 0 erstattet med material-verdiene εµ. Vanligvis er ε = εε r og µ = µ r µ 0. Derfor vil materialet ha en lyshastighet v = c/n hvor n = ε r µ r > 1 er brytningsindeksen. 7 Superledere og Meissner-effekt Den spesifikke, elektriske motstand ρ i de fleste materialer avtar langsomt med avtagende temperatur T. I noen få tilfeller går den så plutselig til null som vist i figuren. Slike materialer sies å bli superledende. I alle superledere finnes det nesten frie ledningselektroner. På grunn av den elektriske vekselvirkningen med de faste ionene i gitteret, går ρ T c Figure 1: Den elektriske motsand blir null i en superleder for temperaturer lavere enn den kritiske. elektronene i en superleder ved tilstrekkelige lave temperaturer inn i en kvantemekanisk tilstand hvor de effektivt parer seg to og to. Slike par kalles Cooper-par etter han som foreslo denne mekanismen første gangen - og som senere fikk Nobel-prisen for sitt bidrag. Antall slike par n s per volumenhet varierer med temperaturen til materialet som vist i figuren. For temperaturer T > T c finnes det ingen slike par lenger og T c kalles den kritiske temperaturen. Hvert slikt par satt sammen av to fermioner blir da på et vis en ny bosonisk partikkel. Det er derfor alle parene kan være i samme kvantetilstand. De vil dermed alle ha samme impuls og hastighet. Dette er mulig i kvantemekanikken, men vanskelig å forestille seg i klassisk T 10
11 n s T T c Figure 2: Superledende Cooper-par finnes bare for temperaturer under den kritiske. fysikk. Når superlederen befinner seg i et magnetfelt beskrevet ved vektorpotensialet A, er ikke lenger impulsen p og bevegelsesmengden mv for hver slik partikkel den samme som i klassisk mekanikk. Derimot er det en direkte konsekvens av gauge-invarians at hvor q = 2e er den elektriske ladning for et Cooper-par. p = mv + qa (36) Vi sier ofte at alle partikkelparene i samme kvantetilstand inngår i et kondensat i analogi med hva vi har i klassisk fysikk. Er kondensatet uniformt i rommet, kan det ikke ha noen impuls. Men likevel vil hvert Cooper-par ha en hastighet gitt ved mv = qa som nå er et meget overraskende resultat av gauge-invarians. Det vil derfor være en elektrisk strøm J s = qn s v i superlederen som kan skrives som J s = n sq 2 m A (37) Dette er London s ligning, funnet før ideen om Cooper-par var foreslått. Et enda mer nyttig resultat får vi når vi kombinerer denne ligning med Maxwell s fjerde ligning. Denne skriver vi som B = µ 0 J hvor strømmen J nå inneholder alle strømmer, frie, bundne og superledende. I vårt tilfelle med superstrømmen J s finner vi dermed den viktige relasjonen B = (µ 0 n s q 2 /m)a. Dens fysiske betydning blir klar når vi så tar curl av begge sider. Venstre side av ligningen forenkles ved å benytte identiteten (9) kombinert med Maxwell s tredje ligning B = 0. På høyre side bruker vi at A = B. Dermed får vi 2 B = κ 2 B (38) hvor nå κ 2 = µ 0 n s q 2 /m. konsekvens av (37). Dette kalles også for London s ligning da den er en direkte 11
12 Denne ligningen forklarer nå en av de viktigste egenskapene til superledere, nemlig Meissnereffekten. Tenk deg at du har en superleder som er plassert slik at materialet ligger helt B B 0 x λ Figure 3: Når T < T c trenger et ytre magnetfelt bare litt inn i en superleder. i områet x > 0. Befinner den seg nå i et ytre magnetfelt B 0 langs z-aksen, vil dette inni superlederen være beskrevet av London s ligning (38). Da vi bare har variasjon i x-retningen, forenkles den nå til d 2 B dx 2 = κ2 B Den har enkle løsninger i form av eksponentialfunksjoner. Da det er fysisk umulig at T > T c T < T c c Figure 4: Meissner-effekten består i at magnetfeltet blir presset ut av en superleder når temperaturen T < T c. magnetfeltet vokser inni superlederen, ser vi at den akseptable løsningen er B = B 0 e κx (39) 12
13 hvor B 0 er feltet utenfor superlederen. Dette er vist i figuren. Magnetfeltet trenger bare inn i superlederen et lite stykke gitt ved penetrasjonslengden λ = 1/κ. Desto mindre antall n s Cooper-par vi har, desto lengre inn trenger feltet. For T > T c er n s = 0 og magnetfeltet trenger uhindret inn. Dette er Meissner effekten som vanligvis fremstilles med en superledende sylinder som vist i den siste figuren. Oslo 11/ , Finn Ravndal 13
Maxwell s ligninger og elektromagnetiske bølger
 Maxwell s ligninger og elektromagnetiske bølger I forelesningene og i læreboken er Coulombs lov for the elektriske felt E formulert på følgende form: v da E = Q/ε 0 (1) Integralet til venstre går over
Maxwell s ligninger og elektromagnetiske bølger I forelesningene og i læreboken er Coulombs lov for the elektriske felt E formulert på følgende form: v da E = Q/ε 0 (1) Integralet til venstre går over
Øving 3. Oppgave 1 (oppvarming med noen enkle oppgaver fra tidligere midtsemesterprøver)
 Institutt for fysikk, NTNU TFY455/FY003: Elektrisitet og magnetisme Vår 2008 Veiledning: Fredag 25. og mandag 28. januar Innleveringsfrist: Fredag. februar kl 2.00 Øving 3 Oppgave (oppvarming med noen
Institutt for fysikk, NTNU TFY455/FY003: Elektrisitet og magnetisme Vår 2008 Veiledning: Fredag 25. og mandag 28. januar Innleveringsfrist: Fredag. februar kl 2.00 Øving 3 Oppgave (oppvarming med noen
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME Mandag 4. desember 2006 kl
 NOGES TEKNSK- NATUVTENSKAPELGE UNVESTET NSTTUTT FO FYSKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTSTET OG MAGNETSME Mandag 4. desember
NOGES TEKNSK- NATUVTENSKAPELGE UNVESTET NSTTUTT FO FYSKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTSTET OG MAGNETSME Mandag 4. desember
Mandag qq 4πε 0 r 2 ˆr F = Elektrisk felt fra punktladning q (følger av definisjonen kraft pr ladningsenhet ): F dl
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007, uke 6 Mandag 05.02.07 Oppsummering til nå, og møte med Maxwell-ligning nr 1 Coulombs lov (empirisk lov for kraft mellom to
Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007, uke 6 Mandag 05.02.07 Oppsummering til nå, og møte med Maxwell-ligning nr 1 Coulombs lov (empirisk lov for kraft mellom to
KONTINUASJONSEKSAMEN TFY4155 ELEKTROMAGNETISME Onsdag 17. august 2005 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 KONTINUASJONSEKSAMEN TFY4155 ELEKTROMAGNETISME
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 KONTINUASJONSEKSAMEN TFY4155 ELEKTROMAGNETISME
KONTINUASJONSEKSAMEN TFY4155 ELEKTROMAGNETISME Fredag 11. august 2006 kl
 NOGES TEKNSK- NATUVTENSKAPELGE UNVESTET NSTTUTT FO FYSKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 KONTNUASJONSEKSAMEN TFY4155 ELEKTOMAGNETSME Fredag 11.
NOGES TEKNSK- NATUVTENSKAPELGE UNVESTET NSTTUTT FO FYSKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 KONTNUASJONSEKSAMEN TFY4155 ELEKTOMAGNETSME Fredag 11.
KORT INTRODUKSJON TIL TENSORER
 KORT INTRODUKSJON TIL TENSORER Tensorer har vi allerede møtt i form av skalarer (tall) og vektorer. En skalar kan betraktes som en tensor av rang null (en komponent), mens en vektor er en tensor av rang
KORT INTRODUKSJON TIL TENSORER Tensorer har vi allerede møtt i form av skalarer (tall) og vektorer. En skalar kan betraktes som en tensor av rang null (en komponent), mens en vektor er en tensor av rang
EKSAMEN TFY4155 ELEKTROMAGNETISME FY1003 ELEKTRISITET OG MAGNETISME Tirsdag 31. mai 2005 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 EKSAMEN TFY4155 ELEKTROMAGNETISME FY1003
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 EKSAMEN TFY4155 ELEKTROMAGNETISME FY1003
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME TFY4155 ELEKTROMAGNETISME Tirsdag 27. mai 2008 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME I Mandag 17. desember 2007 kl K. Rottmann: Matematisk formelsamling (eller tilsvarende).
 NOGES TEKNSK- NATUVTENSKAPELGE UNVESTET NSTTUTT FO FYSKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTSTET OG MAGNETSME Mandag 17. desember
NOGES TEKNSK- NATUVTENSKAPELGE UNVESTET NSTTUTT FO FYSKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTSTET OG MAGNETSME Mandag 17. desember
Løsningsforslag til øving 3
 Institutt for fysikk, NTNU TFY455/FY003 Elektromagnetisme Vår 2009 Løsningsforslag til øving 3 Oppgave a) C V = E dl = 0 dersom dl E b) B På samme måte som et legeme med null starthastighet faller i gravitasjonsfeltet
Institutt for fysikk, NTNU TFY455/FY003 Elektromagnetisme Vår 2009 Løsningsforslag til øving 3 Oppgave a) C V = E dl = 0 dersom dl E b) B På samme måte som et legeme med null starthastighet faller i gravitasjonsfeltet
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME I Mandag 5. desember 2005 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME
Elektrisk potensial/potensiell energi
 Elektrisk potensial/potensiell energi. Figuren viser et uniformt elektrisk felt E heltrukne linjer. Langs hvilken stiplet linje endrer potensialet seg ikke? A. B. C. 3 D. 4 E. Det endrer seg langs alle
Elektrisk potensial/potensiell energi. Figuren viser et uniformt elektrisk felt E heltrukne linjer. Langs hvilken stiplet linje endrer potensialet seg ikke? A. B. C. 3 D. 4 E. Det endrer seg langs alle
Løsningsforslag til eksamen i TFY4170 Fysikk august 2004
 NTNU Side 1av7 Institutt for fysikk Fakultet for naturvitenskap og teknologi Dette løsningsforslaget er på 7 sider. Løsningsforslag til eksamen i TFY4170 Fysikk 1. august 004 Oppgave 1. Interferens a)
NTNU Side 1av7 Institutt for fysikk Fakultet for naturvitenskap og teknologi Dette løsningsforslaget er på 7 sider. Løsningsforslag til eksamen i TFY4170 Fysikk 1. august 004 Oppgave 1. Interferens a)
Felttur 2016 Elektromagnetisme
 Felttur 2016 Elektromagnetisme August Geelmuyden Universitetet i Oslo Teori I. Påvirkning uten berøring Når to objekter påvirker hverandre uten å være i berøring er det ofte naturlig å introdusere konseptet
Felttur 2016 Elektromagnetisme August Geelmuyden Universitetet i Oslo Teori I. Påvirkning uten berøring Når to objekter påvirker hverandre uten å være i berøring er det ofte naturlig å introdusere konseptet
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Ola Hunderi, tlf (mobil: )
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Ola Hunderi, tlf. 93411 (mobil: 95143671) Eksamen TFY 4240: Elektromagnetisk teori Torsdag 1 desember
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Ola Hunderi, tlf. 93411 (mobil: 95143671) Eksamen TFY 4240: Elektromagnetisk teori Torsdag 1 desember
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME TFY4155 ELEKTROMAGNETISME Onsdag 3. juni 2009 kl
 NOGES TEKNISK- NATUVITENSKAPEIGE UNIVESITET INSTITUTT FO FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 EEKTISITET OG MAGNETISME TFY4155
NOGES TEKNISK- NATUVITENSKAPEIGE UNIVESITET INSTITUTT FO FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 EEKTISITET OG MAGNETISME TFY4155
Løsningsforslag til øving
 1 FY1002/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 2012. Løsningsforslag til øving 11-2012 Oppgave 1 a) Forplantning i z-retning betyr at E og B begge ligger i xy-planet. La oss for eksempel
1 FY1002/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 2012. Løsningsforslag til øving 11-2012 Oppgave 1 a) Forplantning i z-retning betyr at E og B begge ligger i xy-planet. La oss for eksempel
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS1120 Elektromagnetisme Eksamensdag: 10. oktober 2016 Tid for eksamen: 10.00 13.00 Oppgavesettet er på 8 sider. Vedlegg: Tillatte
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS1120 Elektromagnetisme Eksamensdag: 10. oktober 2016 Tid for eksamen: 10.00 13.00 Oppgavesettet er på 8 sider. Vedlegg: Tillatte
Tirsdag E = F q. q 4πε 0 r 2 ˆr E = E j = 1 4πε 0. 2 j. r 1. r n
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2008, uke 3 Tirsdag 15.01.07 Elektrisk felt [FGT 22.1; YF 21.4; TM 21.4; AF 21.5; LHL 19.4; DJG 2.1.3] = kraft pr ladningsenhet
Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2008, uke 3 Tirsdag 15.01.07 Elektrisk felt [FGT 22.1; YF 21.4; TM 21.4; AF 21.5; LHL 19.4; DJG 2.1.3] = kraft pr ladningsenhet
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME I TFY4155 ELEKTROMAGNETISME Fredag 8. juni 2007 kl
 NOGES TEKNISK- NATUVITENSKAPELIGE UNIVESITET INSTITUTT FO FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTISITET OG MAGNETISME I TFY4155
NOGES TEKNISK- NATUVITENSKAPELIGE UNIVESITET INSTITUTT FO FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTISITET OG MAGNETISME I TFY4155
Onsdag og fredag
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2009, uke 7 Onsdag 11.02.09 og fredag 13.02.09 Gauss lov [FGT 23.2; YF 22.3; TM 22.2, 22.6; AF 25.4; LHL 19.7; DJG 2.2.1] Gauss
Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2009, uke 7 Onsdag 11.02.09 og fredag 13.02.09 Gauss lov [FGT 23.2; YF 22.3; TM 22.2, 22.6; AF 25.4; LHL 19.7; DJG 2.2.1] Gauss
EKSAMEN TFY4155 ELEKTROMAGNETISME FY1003 ELEKTRISITET OG MAGNETISME Tirsdag 30. mai 2006 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN TFY4155 ELEKTROMAGNETISME FY1003
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN TFY4155 ELEKTROMAGNETISME FY1003
Onsdag og fredag
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2009, uke 4 Onsdag 21.01.09 og fredag 23.01.09 Elektrisk felt fra punktladning [FGT 22.1; YF 21.4; TM 21.4; AF 21.6; LHL 19.5;
Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2009, uke 4 Onsdag 21.01.09 og fredag 23.01.09 Elektrisk felt fra punktladning [FGT 22.1; YF 21.4; TM 21.4; AF 21.6; LHL 19.5;
EKSAMENSOPPGAVE. 7 (6 sider med oppgaver + 1 side med formler)
 Fakultet for naturvitenskap og teknologi EKSAMENSOPPGAE Eksamen i: FYS-1002 (elektromagnetisme) Dato: 9. juni 2017 Klokkeslett: 09.00-13.00 Sted: Åsgårdvegen 9 Tillatte hjelpemidler: ü Kalkulator med tomt
Fakultet for naturvitenskap og teknologi EKSAMENSOPPGAE Eksamen i: FYS-1002 (elektromagnetisme) Dato: 9. juni 2017 Klokkeslett: 09.00-13.00 Sted: Åsgårdvegen 9 Tillatte hjelpemidler: ü Kalkulator med tomt
Løsningsforslag til øving 4
 Institutt for fysikk, NTNU TFY455/FY003 Elektrisitet og magnetisme Vår 2007 Veiledning uke 5 Løsningsforslag til øving 4 Oppgave a) Vi benytter oss av tipsene gitt i oppgaveteksten og tar utgangspunkt
Institutt for fysikk, NTNU TFY455/FY003 Elektrisitet og magnetisme Vår 2007 Veiledning uke 5 Løsningsforslag til øving 4 Oppgave a) Vi benytter oss av tipsene gitt i oppgaveteksten og tar utgangspunkt
EKSAMENSOPPGAVE. Tillatte hjelpemidler: Kalkulator med tomt dataminne, Rottmann: Matematisk formelsamling.
 EKSAMENSOPPGAE Eksamen i: FYS-1002 Dato: Mandag 4. juni, 2018 Klokkeslett: 9:00 13:00 Sted: ADM B154 Tillatte hjelpemidler: Kalkulator med tomt dataminne, Rottmann: Matematisk formelsamling. Eksamenoppgaven
EKSAMENSOPPGAE Eksamen i: FYS-1002 Dato: Mandag 4. juni, 2018 Klokkeslett: 9:00 13:00 Sted: ADM B154 Tillatte hjelpemidler: Kalkulator med tomt dataminne, Rottmann: Matematisk formelsamling. Eksamenoppgaven
1. En tynn stav med lengde L har uniform ladning λ per lengdeenhet. Hvor mye ladning dq er det på en liten lengde dx av staven?
 Ladet stav 1 En tynn stav med lengde L har uniform ladning per lengdeenhet Hvor mye ladning d er det på en liten lengde d av staven? A /d B d C 2 d D d/ E L d Løsning: Med linjeladning (dvs ladning per
Ladet stav 1 En tynn stav med lengde L har uniform ladning per lengdeenhet Hvor mye ladning d er det på en liten lengde d av staven? A /d B d C 2 d D d/ E L d Løsning: Med linjeladning (dvs ladning per
Tirsdag r r
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2008, uke 6 Tirsdag 05.02.08 Gauss lov [FGT 23.2; YF 22.3; TM 22.2, 22.6; AF 25.4; LHL 19.7; DJG 2.2.1] Fra forrige uke; Gauss
Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2008, uke 6 Tirsdag 05.02.08 Gauss lov [FGT 23.2; YF 22.3; TM 22.2, 22.6; AF 25.4; LHL 19.7; DJG 2.2.1] Fra forrige uke; Gauss
FYS1120 Elektromagnetisme
 Det matematisk-naturvitenskapelige fakultet Universitetet i Oslo FY112 Elektromagnetisme Løsningsforslag til ukesoppgave 1 Oppgave 1 a i Her er alternativ 1 riktig. Hvis massetettheten er F, vil et linjestykke
Det matematisk-naturvitenskapelige fakultet Universitetet i Oslo FY112 Elektromagnetisme Løsningsforslag til ukesoppgave 1 Oppgave 1 a i Her er alternativ 1 riktig. Hvis massetettheten er F, vil et linjestykke
Elektromagnetiske bølger
 Elektromagnetiske bølger. Bølgeligningen I læreboka er det vist hvordan bølgeligningen kan utledes fra Maxwells ligninger på integralform. Vi skal her vise at bølgeligningen kan utledes fra Maxwells ligninger
Elektromagnetiske bølger. Bølgeligningen I læreboka er det vist hvordan bølgeligningen kan utledes fra Maxwells ligninger på integralform. Vi skal her vise at bølgeligningen kan utledes fra Maxwells ligninger
Midtsemesterprøve fredag 10. mars kl
 Institutt for fysikk, NTNU FY1003 Elektrisitet og magnetisme TFY4155 Elektromagnetisme Vår 2006 Midtsemesterprøve fredag 10. mars kl 0830 1130. Løsningsforslag 1) A. (Andel som svarte riktig: 83%) Det
Institutt for fysikk, NTNU FY1003 Elektrisitet og magnetisme TFY4155 Elektromagnetisme Vår 2006 Midtsemesterprøve fredag 10. mars kl 0830 1130. Løsningsforslag 1) A. (Andel som svarte riktig: 83%) Det
FYS 3120: Klassisk mekanikk og elektrodynamikk
 FYS 3120: Klassisk mekanikk og elektrodynamikk Formelsamling (bokmål) Våren 2014 1 Analytisk mekanikk Lagrangefunksjonen L = L(q, q, t), (1) er en funksjon av systemets generaliserte koordinater q = {q
FYS 3120: Klassisk mekanikk og elektrodynamikk Formelsamling (bokmål) Våren 2014 1 Analytisk mekanikk Lagrangefunksjonen L = L(q, q, t), (1) er en funksjon av systemets generaliserte koordinater q = {q
FYS 3120: Klassisk mekanikk og elektrodynamikk
 FYS 3120: Klassisk mekanikk og elektrodynamikk 1 Analytisk mekanikk Lagrangefunksjonen Formelsamling (bokmål) L = L(q, q, t), (1) er en funksjon av systemets generaliserte koordinater q = {q i ; i = 1,
FYS 3120: Klassisk mekanikk og elektrodynamikk 1 Analytisk mekanikk Lagrangefunksjonen Formelsamling (bokmål) L = L(q, q, t), (1) er en funksjon av systemets generaliserte koordinater q = {q i ; i = 1,
LØSNINGSFORSLAG TIL KONTINUASJONSEKSAMEN I TFY4155 ELEKTROMAGNETISME Onsdag 17. august 2005 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 LØSNINGSFORSLAG TIL KONTINUASJONSEKSAMEN I TFY4155
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 LØSNINGSFORSLAG TIL KONTINUASJONSEKSAMEN I TFY4155
FYS1120 Elektromagnetisme, Ukesoppgavesett 1
 FYS1120 Elektromagnetisme, Ukesoppgavesett 1 22. august 2016 I FYS1120-undervisningen legg vi mer vekt på matematikk og numeriske metoder enn det oppgavene i læreboka gjør. Det gjelder også oppgavene som
FYS1120 Elektromagnetisme, Ukesoppgavesett 1 22. august 2016 I FYS1120-undervisningen legg vi mer vekt på matematikk og numeriske metoder enn det oppgavene i læreboka gjør. Det gjelder også oppgavene som
TFY4104 Fysikk. Institutt for fysikk, NTNU. Høsten Løsningsforslag til øving 10.
 TFY4104 Fysikk. Institutt for fysikk, NTNU. Høsten 015. Løsningsforslag til øving 10. Oppgave A B C D 1 x x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11 x 1 x 13 x 14 x 15 x 16 x 17 x 18 x 9 x 0 x 1) Glass-staven
TFY4104 Fysikk. Institutt for fysikk, NTNU. Høsten 015. Løsningsforslag til øving 10. Oppgave A B C D 1 x x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11 x 1 x 13 x 14 x 15 x 16 x 17 x 18 x 9 x 0 x 1) Glass-staven
Onsdag isolator => I=0
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2008, uke 13 Onsdag 26.03.08 RC-kretser [FGT 27.5; YF 26.4; TM 25.6; AF Note 25.1; LHL 22.4; DJG Problem 7.2] Rommet mellom de
Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2008, uke 13 Onsdag 26.03.08 RC-kretser [FGT 27.5; YF 26.4; TM 25.6; AF Note 25.1; LHL 22.4; DJG Problem 7.2] Rommet mellom de
LØSNINGSFORSLAG TIL EKSAMEN I FY1003 ELEKTRISITET OG MAGNETISME Mandag 4. desember 2006 kl
 NOGES TEKNISK- NATUVITENSKAPEIGE UNIVESITET INSTITUTT FO FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 ØSNINGSFOSAG TI EKSAMEN I FY1003 EEKTISITET OG MAGNETISME
NOGES TEKNISK- NATUVITENSKAPEIGE UNIVESITET INSTITUTT FO FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 ØSNINGSFOSAG TI EKSAMEN I FY1003 EEKTISITET OG MAGNETISME
Skinndybde. FYS 2130
 Skinndybde. FYS 130 Vi skal se hvordan en elektromagnetisk bølge oppfører seg i et ledende medium. ølgeligningen for E-feltet i vakuum ble utledet i notatet om elektromagnetiske bølger: E E =εµ 0 0 Denne
Skinndybde. FYS 130 Vi skal se hvordan en elektromagnetisk bølge oppfører seg i et ledende medium. ølgeligningen for E-feltet i vakuum ble utledet i notatet om elektromagnetiske bølger: E E =εµ 0 0 Denne
Felttur 2017 Elektromagnetisme
 Felttur 2017 Elektromagnetisme August Geelmuyden Universitetet i Oslo Teori I. Påvirkning uten berøring Når to objekter påvirker hverandre uten å være i berøring er det ofte naturlig å introdusere konseptet
Felttur 2017 Elektromagnetisme August Geelmuyden Universitetet i Oslo Teori I. Påvirkning uten berøring Når to objekter påvirker hverandre uten å være i berøring er det ofte naturlig å introdusere konseptet
Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen Q ligger i punktet ( 3, 0) [mm].
![Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen Q ligger i punktet ( 3, 0) [mm]. Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen Q ligger i punktet ( 3, 0) [mm].](/thumbs/58/41840831.jpg) Oppgave 1 Finn løsningen til følgende 1.ordens differensialligninger: a) y = x e y, y(0) = 0 b) dy dt + a y = b, a og b er konstanter. Oppgave 2 Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen
Oppgave 1 Finn løsningen til følgende 1.ordens differensialligninger: a) y = x e y, y(0) = 0 b) dy dt + a y = b, a og b er konstanter. Oppgave 2 Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen
FYS1120 Elektromagnetisme - Ukesoppgavesett 2
 FYS1120 Elektromagnetisme - Ukesoppgavesett 2 7. september 2016 I FYS1120-undervisningen legger vi mer vekt på matematikk og numeriske metoder enn det oppgavene i læreboka gjør. Det gjelder også oppgavene
FYS1120 Elektromagnetisme - Ukesoppgavesett 2 7. september 2016 I FYS1120-undervisningen legger vi mer vekt på matematikk og numeriske metoder enn det oppgavene i læreboka gjør. Det gjelder også oppgavene
LØSNINGSFORSLAG TIL EKSAMEN I TFY4155 ELEKTROMAGNETISME FY1003 ELEKTRISITET OG MAGNETISME Tirsdag 31. mai 2005 kl
 NORGES TEKNISK- NATURVITENSKAPEIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 ØSNINGSFORSAG TI EKSAMEN I TFY4155 EEKTROMAGNETISME
NORGES TEKNISK- NATURVITENSKAPEIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 ØSNINGSFORSAG TI EKSAMEN I TFY4155 EEKTROMAGNETISME
Kap. 22. Gauss lov. Vi skal se på: Fluksen til elektrisk felt E Gauss lov. Elektrisk ledere. Integralform og differensialform
 Kap. 22. Gauss lov Vi skal se på: Fluksen til elektrisk felt E Gauss lov Integralform og differensialform Elektrisk ledere. E-felt fra Coulombs lov: E k q r 2 r E k n q r n 2 0n r 0n dq E k r 2 r tot.
Kap. 22. Gauss lov Vi skal se på: Fluksen til elektrisk felt E Gauss lov Integralform og differensialform Elektrisk ledere. E-felt fra Coulombs lov: E k q r 2 r E k n q r n 2 0n r 0n dq E k r 2 r tot.
EKSAMENSOPPGAVE. Fys-1002 Elektromagnetisme. Adm.bygget B154 Kalkulator med tomt dataminne, Rottmann: Matematisk formelsamling
 Fakultet for naturvitenskap og teknologi EKSAMENSOPPGAE Eksamen i: Fys-1002 Elektromagnetisme Dato: Onsdag 26. september 2018 Klokkeslett: Kl. 9:00-13:00 Sted: Tillatte hjelpemidler: Adm.bygget B154 Kalkulator
Fakultet for naturvitenskap og teknologi EKSAMENSOPPGAE Eksamen i: Fys-1002 Elektromagnetisme Dato: Onsdag 26. september 2018 Klokkeslett: Kl. 9:00-13:00 Sted: Tillatte hjelpemidler: Adm.bygget B154 Kalkulator
Mandag dq dt. I = Q t + + x (tverrsnitt av leder) Med n = N/ V ladningsbærere pr volumenhet, med midlere driftshastighet v og ladning q:
 Institutt for fysikk, NTNU TFY455/FY003: Elektrisitet og magnetisme Vår 2007, uke Mandag 2.03.07 Elektrisk strøm. [FGT 26.; YF 25.; TM 25.; AF 24., 24.2; LHL 2.; DJG 5..3] Elektrisk strømstyrke = (positiv)
Institutt for fysikk, NTNU TFY455/FY003: Elektrisitet og magnetisme Vår 2007, uke Mandag 2.03.07 Elektrisk strøm. [FGT 26.; YF 25.; TM 25.; AF 24., 24.2; LHL 2.; DJG 5..3] Elektrisk strømstyrke = (positiv)
LØSNINGSFORSLAG TIL EKSAMEN I TFY4155 ELEKTROMAGNETISME Fredag 11. august 2006 kl
 NOGES TEKNISK- NATUVITENSKAPELIGE UNIVESITET INSTITUTT FO FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFOSLAG TIL EKSAMEN I TFY4155 ELEKTOMAGNETISME
NOGES TEKNISK- NATUVITENSKAPELIGE UNIVESITET INSTITUTT FO FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFOSLAG TIL EKSAMEN I TFY4155 ELEKTOMAGNETISME
Løsningsforslag til øving 9
 FY1002/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 2010. Løsningsforslag til øving 9 Oppgave 1 a) Forplantning i z-retning betyr at E og B begge ligger i xy-planet. La oss for eksempel velge
FY1002/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 2010. Løsningsforslag til øving 9 Oppgave 1 a) Forplantning i z-retning betyr at E og B begge ligger i xy-planet. La oss for eksempel velge
Mandag Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007, uke12
 nstitutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007, uke12 Mandag 19.03.07 Likestrømkretser [FGT 27; YF 26; TM 25; AF 24.7; LHL 22] Eksempel: lommelykt + a d b c + m Likespenningskilde
nstitutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007, uke12 Mandag 19.03.07 Likestrømkretser [FGT 27; YF 26; TM 25; AF 24.7; LHL 22] Eksempel: lommelykt + a d b c + m Likespenningskilde
Enkel introduksjon til kvantemekanikken
 Kapittel Enkel introduksjon til kvantemekanikken. Kort oppsummering. Elektromagnetiske bølger med bølgelengde og frekvens f opptrer også som partikler eller fotoner med energi E = hf, der h er Plancks
Kapittel Enkel introduksjon til kvantemekanikken. Kort oppsummering. Elektromagnetiske bølger med bølgelengde og frekvens f opptrer også som partikler eller fotoner med energi E = hf, der h er Plancks
Overflateladningstetthet på metalloverflate
 0.0.08: Rettet opp feil i oppgave 4 og løsningsforslag til oppgave 8b. Overflateladningstetthet på metalloverflate. Ei metallkule med diameter 0.0 m har ei netto ladning på 0.50 nc. Hvor stort er det elektriske
0.0.08: Rettet opp feil i oppgave 4 og løsningsforslag til oppgave 8b. Overflateladningstetthet på metalloverflate. Ei metallkule med diameter 0.0 m har ei netto ladning på 0.50 nc. Hvor stort er det elektriske
LØSNINGSFORSLAG TIL EKSAMEN I TFY4155 ELEKTROMAGNETISME FY1003 ELEKTRISITET OG MAGNETISME Tirsdag 30. mai 2006 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I TFY4155 ELEKTROMAGNETISME
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I TFY4155 ELEKTROMAGNETISME
Mandag Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007, uke 4
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007, uke 4 Mandag 22.01.07 Elektriske feltlinjer [FGT 22.2; YF 21.6; TM 21.5; F 21.6; LHL 19.6; DJG 2.2.1] gir en visuell framstilling
Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007, uke 4 Mandag 22.01.07 Elektriske feltlinjer [FGT 22.2; YF 21.6; TM 21.5; F 21.6; LHL 19.6; DJG 2.2.1] gir en visuell framstilling
Gauss lov. Kap. 22. Gauss lov. Gauss lov skjematisk. Vi skal se på: Fluksen til elektrisk felt E Gauss lov Integralform og differensialform
 Kap. 5..6 Kap.. Gauss lov Vi skal se på: Fluksen til elektrisk felt E Gauss lov Integralform og differensialform Elektrisk ledere. Efelt fra Coulombs lov: q E k r r E k n q r n n r n dq E k r r tot. ladn.
Kap. 5..6 Kap.. Gauss lov Vi skal se på: Fluksen til elektrisk felt E Gauss lov Integralform og differensialform Elektrisk ledere. Efelt fra Coulombs lov: q E k r r E k n q r n n r n dq E k r r tot. ladn.
LØSNINGSFORSLAG TIL EKSAMEN I FY1003 ELEKTRISITET OG MAGNETISME TFY4155 ELEKTROMAGNETISME Onsdag 3. juni 2009 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY003 ELEKTRISITET
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY003 ELEKTRISITET
Formelsamling. ξ(r, t) = ξ 0 sin(k r ωt + φ) 2 ξ(x, t) = 1 2 ξ(x, t) t 2. 2 ξ. x ξ. z 2. y ξ. v = ω k. v g = dω dk
 Formelsamling Side 7 av 16 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk plan bølge: Bølgeligning:
Formelsamling Side 7 av 16 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk plan bølge: Bølgeligning:
Oppgave 2 Vi ser på et éndimensjonalt system hvor en av de stasjonære tilstandene ψ(x) er gitt som { 0 for x < 0, ψ(x) = Ne ax (1 e ax (1)
 Oppgave Gjør kort rede for hva den fotoelektriske effekt er, hva slags konklusjoner man kunne trekke fra observasjoner av denne i kvantefysikkens fødsel, og beskriv et eksperiment som kan observere og
Oppgave Gjør kort rede for hva den fotoelektriske effekt er, hva slags konklusjoner man kunne trekke fra observasjoner av denne i kvantefysikkens fødsel, og beskriv et eksperiment som kan observere og
Sammendrag, uke 13 (30. mars)
 nstitutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2005 Sammendrag, uke 13 (30. mars) Likestrømkretser [FGT 27; YF 26; TM 25; AF 24.7; LHL 22] Eksempel: lommelykt + a d b c + m Spenningskilde
nstitutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2005 Sammendrag, uke 13 (30. mars) Likestrømkretser [FGT 27; YF 26; TM 25; AF 24.7; LHL 22] Eksempel: lommelykt + a d b c + m Spenningskilde
Onsdag og fredag
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2009, uke 13 Onsdag 25.03.09 og fredag 27.03.09 Amperes lov [FGT 30.1, 30.3; YF 28.6, 28.7; AF 26.2; H 23.6; G 5.3] B dl = µ 0
Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2009, uke 13 Onsdag 25.03.09 og fredag 27.03.09 Amperes lov [FGT 30.1, 30.3; YF 28.6, 28.7; AF 26.2; H 23.6; G 5.3] B dl = µ 0
TFY4104 Fysikk. Institutt for fysikk, NTNU. Høsten Øving 12.
 TFY0 Fsikk. nstitutt for fsikk, NTNU. Høsten 06. Øving. Oppgave Partikler med masse m, ladning q og hastighet v kommer inn i et område med krsset elektrisk og magnetisk felt, E og, som vist i figuren.
TFY0 Fsikk. nstitutt for fsikk, NTNU. Høsten 06. Øving. Oppgave Partikler med masse m, ladning q og hastighet v kommer inn i et område med krsset elektrisk og magnetisk felt, E og, som vist i figuren.
Formelsamling Bølgefysikk Desember 2006
 Vedlegg 1 av 9 Formelsamling Bølgefysikk Desember 2006 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk
Vedlegg 1 av 9 Formelsamling Bølgefysikk Desember 2006 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk
Løsningsforslag til eksamen i TFY4170 Fysikk 2 Tirsdag 9. desember 2003
 NTNU Side 1av7 Institutt for fysikk Fakultet for naturvitenskap og teknologi Dette løsningsforslaget er på 7 sider. Løsningsforslag til eksamen i TFY4170 Fysikk Tirsdag 9. desember 003 Oppgave 1. a) Amplituden
NTNU Side 1av7 Institutt for fysikk Fakultet for naturvitenskap og teknologi Dette løsningsforslaget er på 7 sider. Løsningsforslag til eksamen i TFY4170 Fysikk Tirsdag 9. desember 003 Oppgave 1. a) Amplituden
b) Vi legger en uendelig lang, rett stav langs y-aksen. Staven har linjeladningen λ = [C/m].
![b) Vi legger en uendelig lang, rett stav langs y-aksen. Staven har linjeladningen λ = [C/m]. b) Vi legger en uendelig lang, rett stav langs y-aksen. Staven har linjeladningen λ = [C/m].](/thumbs/54/33413684.jpg) Oppgave 1 a) Punktladningen q 1 = 1.0 10 9 [C] ligger fast i punktet (2.0, 0, 0) [m]. Punktladningen q 2 = 4.0 10 9 [C] ligger i punktet ( 1.0, 0, 0) [m]. I) Finnes det punkt(er) i rommet med elektrisk
Oppgave 1 a) Punktladningen q 1 = 1.0 10 9 [C] ligger fast i punktet (2.0, 0, 0) [m]. Punktladningen q 2 = 4.0 10 9 [C] ligger i punktet ( 1.0, 0, 0) [m]. I) Finnes det punkt(er) i rommet med elektrisk
Eksamen i Klassisk feltteori, fag TFY 4270 Onsdag 26. mai 2004 Løsninger
 Eksamen i Klassisk feltteori, fag TFY 470 Onsdag 6. mai 004 Løsninger 1a) Sammenhengen mellom koordinattiden t og egentiden τ er at Den relativistiske impulsen er Hamiltonfunksjonen er Siden har vi at
Eksamen i Klassisk feltteori, fag TFY 470 Onsdag 6. mai 004 Løsninger 1a) Sammenhengen mellom koordinattiden t og egentiden τ er at Den relativistiske impulsen er Hamiltonfunksjonen er Siden har vi at
FYS1120 Elektromagnetisme
 Det matematisk-naturvitenskapelige fakultet Universitetet i Oslo FYS112 Elektromagnetisme Løsningsforslag til ukesoppgave 2 Oppgave 1 a) Gauss lov sier at den elektriske fluksen Φ er lik den totale ladningen
Det matematisk-naturvitenskapelige fakultet Universitetet i Oslo FYS112 Elektromagnetisme Løsningsforslag til ukesoppgave 2 Oppgave 1 a) Gauss lov sier at den elektriske fluksen Φ er lik den totale ladningen
FYS 3120: Klassisk mekanikk og elektrodynamikk
 FYS 3120: Klassisk mekanikk og elektrodynamikk 1 Analytisk mekanikk Lagrangefunksjonen Formelsamling (nynorsk) L = L(q, q, t), (1) til eit fysisk system er ein funksjon av dei generaliserte koordinatane
FYS 3120: Klassisk mekanikk og elektrodynamikk 1 Analytisk mekanikk Lagrangefunksjonen Formelsamling (nynorsk) L = L(q, q, t), (1) til eit fysisk system er ein funksjon av dei generaliserte koordinatane
FYS1120 Elektromagnetisme
 Det matematisk-naturvitenskapelige fakultet Universitetet i Oslo FYS1120 Elektromagnetisme J. Skaar: Øvingsoppgaver til midtveiseksamen (med fasit) Her er 46 flervalgsoppgaver som kanskje kan være nyttige
Det matematisk-naturvitenskapelige fakultet Universitetet i Oslo FYS1120 Elektromagnetisme J. Skaar: Øvingsoppgaver til midtveiseksamen (med fasit) Her er 46 flervalgsoppgaver som kanskje kan være nyttige
Løsningsforslag til øving 8
 FY12/TFY416 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 21. Løsningsforslag til øving 8 Oppgave 1 Helt generelt vil vi ha, for en elektromagnetisk bølge som forplanter seg i retning ˆk og som er polarisert
FY12/TFY416 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 21. Løsningsforslag til øving 8 Oppgave 1 Helt generelt vil vi ha, for en elektromagnetisk bølge som forplanter seg i retning ˆk og som er polarisert
Mandag 04.09.06. Institutt for fysikk, NTNU TFY4160/FY1002: Bølgefysikk Høsten 2006, uke 36
 Institutt for fsikk, NTNU TFY4160/FY1002: Bølgefsikk Høsten 2006, uke 36 Mandag 04.09.06 Del II: BØLGER Innledning Bølger er forplantning av svingninger. Når en bølge forplanter seg i et materielt medium,
Institutt for fsikk, NTNU TFY4160/FY1002: Bølgefsikk Høsten 2006, uke 36 Mandag 04.09.06 Del II: BØLGER Innledning Bølger er forplantning av svingninger. Når en bølge forplanter seg i et materielt medium,
Formelsamling. ξ(r, t) = ξ 0 sin(k r ωt + φ) 2 ξ(x, t) = 1 2 ξ(x, t) t 2. 2 ξ. x ξ. z 2. y ξ. v = ω k. v g = dω dk
 Formelsamling Side 7 av 15 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk plan bølge: Bølgeligning:
Formelsamling Side 7 av 15 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk plan bølge: Bølgeligning:
EKSAMENSOPPGAVE. Adm.bygget, Aud.max. ü Kalkulator med tomt dataminne ü Rottmann: Matematisk Formelsamling. rute
 Fakultet for naturvitenskap og teknologi EKSAMENSOPPGAE Eksamen i: Fys-1002 Dato: 30. september 2016 Klokkeslett: 09.00-13.00 Sted: Tillatte hjelpemidler: Adm.bygget, Aud.max ü Kalkulator med tomt dataminne
Fakultet for naturvitenskap og teknologi EKSAMENSOPPGAE Eksamen i: Fys-1002 Dato: 30. september 2016 Klokkeslett: 09.00-13.00 Sted: Tillatte hjelpemidler: Adm.bygget, Aud.max ü Kalkulator med tomt dataminne
LØSNINGSFORSLAG TIL EKSAMEN I FY1003 ELEKTRISITET OG MAGNETISME I TFY4155 ELEKTROMAGNETISME Fredag 8. juni 2007 kl
 NOGES TEKNISK- NATUVITENSKAPELIGE UNIVESITET INSTITUTT FO FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFOSLAG TIL EKSAMEN I FY1003 ELEKTISITET OG
NOGES TEKNISK- NATUVITENSKAPELIGE UNIVESITET INSTITUTT FO FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFOSLAG TIL EKSAMEN I FY1003 ELEKTISITET OG
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet
 UNVERTETET OLO Det matematisk-naturitenskapelige fakultet Eksamen i: Fys1120 Eksamensdag: Onsdag 12. desember 2018 Tid for eksamen: 0900 1300 Oppgaesettet er på: 5 sider Vedlegg: Formelark Tilatte hjelpemidler
UNVERTETET OLO Det matematisk-naturitenskapelige fakultet Eksamen i: Fys1120 Eksamensdag: Onsdag 12. desember 2018 Tid for eksamen: 0900 1300 Oppgaesettet er på: 5 sider Vedlegg: Formelark Tilatte hjelpemidler
LØSNINGSFORSLAG TIL EKSAMEN I FY1003 ELEKTRISITET OG MAGNETISME I Mandag 17. desember 2007 kl
 NOGES TEKNISK- NATUVITENSKAPELIGE UNIVESITET INSTITUTT FO FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFOSLAG TIL EKSAMEN I FY1003 ELEKTISITET OG
NOGES TEKNISK- NATUVITENSKAPELIGE UNIVESITET INSTITUTT FO FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFOSLAG TIL EKSAMEN I FY1003 ELEKTISITET OG
FY2045/TFY4250 Kvantemekanikk I, løsning øving 4 1 LØSNING ØVING 4
 FY2045/TFY4250 Kvantemekanikk I, løsning øving 4 1 Løsning oppgave 4 1 LØSNING ØVING 4 Elektron i potensial med to δ-funksjoner a En delta-brønn er grensen av en veldig dyp og veldig trang brønn Inne i
FY2045/TFY4250 Kvantemekanikk I, løsning øving 4 1 Løsning oppgave 4 1 LØSNING ØVING 4 Elektron i potensial med to δ-funksjoner a En delta-brønn er grensen av en veldig dyp og veldig trang brønn Inne i
EKSAMEN I EMNE TFE 4120 ELEKTROMAGNETISME
 NTNU Norges teknisk-naturvitenskapelige universitet ide 1 av 7 Fakultet for informatikk, matematikk og elektroteknikk Institutt for fysikalsk elektronikk Bokmål/Nynorsk Faglig/fagleg kontakt under eksamen:
NTNU Norges teknisk-naturvitenskapelige universitet ide 1 av 7 Fakultet for informatikk, matematikk og elektroteknikk Institutt for fysikalsk elektronikk Bokmål/Nynorsk Faglig/fagleg kontakt under eksamen:
FYS1120 Elektromagnetisme ukesoppgavesett 7
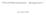 FYS1120 Elektromagnetisme ukesoppgavesett 7 25. november 2016 Figur 1: En Wheatstone-bro I FYS1120-undervisningen legger vi mer vekt på matematikk og numeriske metoder enn det oppgavene i læreboka gjør.
FYS1120 Elektromagnetisme ukesoppgavesett 7 25. november 2016 Figur 1: En Wheatstone-bro I FYS1120-undervisningen legger vi mer vekt på matematikk og numeriske metoder enn det oppgavene i læreboka gjør.
a) Bruk en passende Gaussflate og bestem feltstyrken E i rommet mellom de 2 kuleskallene.
 Oppgave 1 Bestem løsningen av differensialligningen Oppgave 2 dy dx + y = e x, y(1) = 1 e Du skal beregne en kulekondensator som består av 2 kuleskall av metall med samme sentrum. Det indre skallet har
Oppgave 1 Bestem løsningen av differensialligningen Oppgave 2 dy dx + y = e x, y(1) = 1 e Du skal beregne en kulekondensator som består av 2 kuleskall av metall med samme sentrum. Det indre skallet har
FYS1120 Elektromagnetisme H10 Midtveiseksamen
 FYS1120 Elektromagnetisme H10 Midtveiseksamen Oppgave 1 a) Vi ser i denne oppgave på elektroner som akselereres gjennom et elektrisk potensial slik at de oppnår en hastighet 1.410. Som vist på figuren
FYS1120 Elektromagnetisme H10 Midtveiseksamen Oppgave 1 a) Vi ser i denne oppgave på elektroner som akselereres gjennom et elektrisk potensial slik at de oppnår en hastighet 1.410. Som vist på figuren
Løsningsforslag TFE4120 Elektromagnetisme 29. mai 2017
 Norges teknisk naturvitenskapelige universitet Institutt for elektroniske systemer Side 1 av 6 Løsningsforslag TFE4120 Elektromagnetisme 29. mai 2017 Oppgave 1 a) Start med å tegne figur! Tegn inn en Gauss-flate
Norges teknisk naturvitenskapelige universitet Institutt for elektroniske systemer Side 1 av 6 Løsningsforslag TFE4120 Elektromagnetisme 29. mai 2017 Oppgave 1 a) Start med å tegne figur! Tegn inn en Gauss-flate
I C Q R. Øving 11. Institutt for fysikk, NTNU TFY4155/FY1003: Elektromagnetisme
 nstitutt for fsikk, NTNU TFY4155/FY1003: Elektromagnetisme Vår 2009 Øving 11 Veiledning: Mandag 23. mars og fredag 27. mars nnleveringsfrist: Fredag 27. mars Oppgave 1 nnledning (dvs vi rekapitulerer fra
nstitutt for fsikk, NTNU TFY4155/FY1003: Elektromagnetisme Vår 2009 Øving 11 Veiledning: Mandag 23. mars og fredag 27. mars nnleveringsfrist: Fredag 27. mars Oppgave 1 nnledning (dvs vi rekapitulerer fra
FY2045/TFY4250 Kvantemekanikk I, løsning øving 13 1 LØSNING ØVING 13. V (x, t) = xf (t) = xf 0 e t2 /τ 2.
 FY045/TFY450 Kvantemekanikk I, løsning øving 13 1 Løsning Oppgave 13 1 LØSNING ØVING 13 Transient perturbasjon av harmonisk oscillator a. Med kraften F (t) = qe(t) = F 0 exp( t /τ ) og sammenhengen F (t)
FY045/TFY450 Kvantemekanikk I, løsning øving 13 1 Løsning Oppgave 13 1 LØSNING ØVING 13 Transient perturbasjon av harmonisk oscillator a. Med kraften F (t) = qe(t) = F 0 exp( t /τ ) og sammenhengen F (t)
FY2045/TFY4250 Kvantemekanikk I, øving 6 1 ØVING 6. Fermi-impulser og -energier
 FY2045/TFY4250 Kvantemekanikk I, 2012 - øving 6 1 ØVING 6 Oppgave 6 1 Fermi-impulser og -energier a. Anta at en ideell gass av N (ikke-vekselvirkende) spinn- 1 -fermioner befinner seg i grunntilstanden
FY2045/TFY4250 Kvantemekanikk I, 2012 - øving 6 1 ØVING 6 Oppgave 6 1 Fermi-impulser og -energier a. Anta at en ideell gass av N (ikke-vekselvirkende) spinn- 1 -fermioner befinner seg i grunntilstanden
Frivillig test 5. april Flervalgsoppgaver.
 Inst for fysikk 2013 TFY4155/FY1003 Elektr & magnetisme Frivillig test 5 april 2013 Flervalgsoppgaver Kun ett av svarene rett Du skal altså svare A, B, C, D eller E (stor bokstav) eller du kan svare blankt
Inst for fysikk 2013 TFY4155/FY1003 Elektr & magnetisme Frivillig test 5 april 2013 Flervalgsoppgaver Kun ett av svarene rett Du skal altså svare A, B, C, D eller E (stor bokstav) eller du kan svare blankt
1 I mengdeteori er kontinuumshypotesen en antakelse om at det ikke eksisterer en mengde som
 Forelesning 12/3 2019 ved Karsten Trulsen Fluid- og kontinuumsmekanikk Som eksempel på anvendelse av vektor feltteori og flervariabel kalkulus, og som illustrasjon av begrepene vi har gått igjennom så
Forelesning 12/3 2019 ved Karsten Trulsen Fluid- og kontinuumsmekanikk Som eksempel på anvendelse av vektor feltteori og flervariabel kalkulus, og som illustrasjon av begrepene vi har gått igjennom så
OPPGAVESETT 1. PS: Spørsmål 1a) og 1b) har ingenting med hverandre å gjøre. 1b) refererer til to nøytrale kuler, ikke kulene i 1a)
 Fasit for FYS1120-oppgaver H2010. OPPGAVESETT 1 1a) 9.88 10-7 C 1b) 891 PS: Spørsmål 1a) og 1b) har ingenting med hverandre å gjøre. 1b) refererer til to nøytrale kuler, ikke kulene i 1a) 2a) 7.25 10 24
Fasit for FYS1120-oppgaver H2010. OPPGAVESETT 1 1a) 9.88 10-7 C 1b) 891 PS: Spørsmål 1a) og 1b) har ingenting med hverandre å gjøre. 1b) refererer til to nøytrale kuler, ikke kulene i 1a) 2a) 7.25 10 24
Eksamen i fag FY1004 Innføring i kvantemekanikk Tirsdag 22. mai 2007 Tid:
 Side 1 av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 51 72) Sensurfrist: Tirsdag 12. juni 2007
Side 1 av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 51 72) Sensurfrist: Tirsdag 12. juni 2007
Obligatorisk oppgave nr 4 FYS Lars Kristian Henriksen UiO
 Obligatorisk oppgave nr 4 FYS-13 Lars Kristian Henriksen UiO. februar 15 Oppgave 1 Vi betrakter bølgefunksjonen Ψ(x, t) Ae λ x e iωt hvor A, λ og ω er positive reelle konstanter. a) Finn normaliseringen
Obligatorisk oppgave nr 4 FYS-13 Lars Kristian Henriksen UiO. februar 15 Oppgave 1 Vi betrakter bølgefunksjonen Ψ(x, t) Ae λ x e iωt hvor A, λ og ω er positive reelle konstanter. a) Finn normaliseringen
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MEK 11 Feltteori og vektoranalyse. Eksamensdag: Torsdag 1 desember 29. Tid for eksamen: 14:3 17:3. Oppgavesettet er på 7 sider.
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MEK 11 Feltteori og vektoranalyse. Eksamensdag: Torsdag 1 desember 29. Tid for eksamen: 14:3 17:3. Oppgavesettet er på 7 sider.
FY2045/TFY4250 Kvantemekanikk I, øving 5 1 LØSNING ØVING 5. Kvantekraft. L x. L 2 x. = A sin n xπx. sin n yπy. 2 y + 2.
 FY045/TFY450 Kvantemekanikk I, øving 5 1 øsning oppgave 5 1 a Med finner vi energien til egenfunksjonen ØSNING ØVING 5 Kvantekraft nπx sin = n xπ x x x ψ nx,n y,n z = A sin n xπx x sin nπx x, sin n yπy
FY045/TFY450 Kvantemekanikk I, øving 5 1 øsning oppgave 5 1 a Med finner vi energien til egenfunksjonen ØSNING ØVING 5 Kvantekraft nπx sin = n xπ x x x ψ nx,n y,n z = A sin n xπx x sin nπx x, sin n yπy
LØSNINGSFORSLAG TIL EKSAMEN I FY1003 ELEKTRISITET OG MAGNETISME TFY4155 ELEKTROMAGNETISME Tirsdag 27. mai 2008 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY003 ELEKTRISITET
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY003 ELEKTRISITET
dg = ( g P0 u)ds = ( ) = 0
 NTNU Institutt for matematiske fag TMA4105 Matematikk 2, øving 8, vår 2011 Løsningsforslag Notasjon og merknader Som vanlig er enkelte oppgaver kopiert fra tidligere års løsningsforslag. Derfor kan notasjon,
NTNU Institutt for matematiske fag TMA4105 Matematikk 2, øving 8, vår 2011 Løsningsforslag Notasjon og merknader Som vanlig er enkelte oppgaver kopiert fra tidligere års løsningsforslag. Derfor kan notasjon,
EKSAMEN I FAG SIF 4012 ELEKTROMAGNETISME (SIF 4012 FYSIKK 2) Onsdag 11. desember kl Bokmål
 Side av 6 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 4 43 39 3 EKSAMEN I FAG SIF 42 ELEKTROMAGNETISME
Side av 6 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 4 43 39 3 EKSAMEN I FAG SIF 42 ELEKTROMAGNETISME
FYS2140 Kvantefysikk, Løsningsforslag for Oblig 1
 FYS4 Kvantefysikk, Løsningsforslag for Oblig. januar 8 Her er løsningsforslag for Oblig som dreide seg om å friske opp en del grunnleggende matematikk. I tillegg finner dere til slutt et løsningsforslag
FYS4 Kvantefysikk, Løsningsforslag for Oblig. januar 8 Her er løsningsforslag for Oblig som dreide seg om å friske opp en del grunnleggende matematikk. I tillegg finner dere til slutt et løsningsforslag
EKSAMEN I EMNE TFE 4120 ELEKTROMAGNETISME
 Norges teknisk naturvitenskapelige universitet Institutt for elektronikk og telekommunikasjon ide 1 av 7 Bokmål/Nynorsk Faglig/fagleg kontakt under eksamen: Guro vendsen (73592773) Hjelpemidler: C - pesifiserte
Norges teknisk naturvitenskapelige universitet Institutt for elektronikk og telekommunikasjon ide 1 av 7 Bokmål/Nynorsk Faglig/fagleg kontakt under eksamen: Guro vendsen (73592773) Hjelpemidler: C - pesifiserte
OBLIGATORISK MIDTSEMESTERØVING I EMNE TFE 4120 ELEKTROMAGNETISME
 ide 1 av 6 NTNU Norges teknisk-naturvitenskapelige universitet Fakultet for informatikk, matematikk og elektroteknikk Institutt for elektronikk og telekommunikasjon OBLIGATORIK MIDTEMETERØVING I EMNE TFE
ide 1 av 6 NTNU Norges teknisk-naturvitenskapelige universitet Fakultet for informatikk, matematikk og elektroteknikk Institutt for elektronikk og telekommunikasjon OBLIGATORIK MIDTEMETERØVING I EMNE TFE
Mandag 7. mai. Elektromagnetisk induksjon (fortsatt) [FGT ; YF ; TM ; AF ; LHL 24.1; DJG 7.
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007, uke19 Mandag 7. mai Elektromagnetisk induksjon (fortsatt) [FGT 30.1-30.6; YF 29.1-29.5; TM 28.2-28.3; AF 27.1-27.3; LHL 24.1;
Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007, uke19 Mandag 7. mai Elektromagnetisk induksjon (fortsatt) [FGT 30.1-30.6; YF 29.1-29.5; TM 28.2-28.3; AF 27.1-27.3; LHL 24.1;
FY2045/TFY4250 Kvantemekanikk I, løsning øving 14 1 LØSNING ØVING 14. ψ 210 z ψ 100 d 3 r a.
 FY45/TFY45 Kvantemekanikk I, løsning øving 14 1 LØSNING ØVING 14 Løsning Oppgave 14 1 Fra oppg 3, eksamen august 1 a. Med Y = 1/ 4π og zy = ry 1 / 3 kan vi skrive matrise-elementene av z på formen (z)
FY45/TFY45 Kvantemekanikk I, løsning øving 14 1 LØSNING ØVING 14 Løsning Oppgave 14 1 Fra oppg 3, eksamen august 1 a. Med Y = 1/ 4π og zy = ry 1 / 3 kan vi skrive matrise-elementene av z på formen (z)
