Julenøtter til gruppe 5&7! (IKKE eksamensrelevant, bare for gøy gjerne i romjulen)
|
|
|
- Karsten Rønningen
- 7 år siden
- Visninger:
Transkript
1 Julenøtter til gruppe 5&7! (IKKE eksamensrelevant, bare for gøy gjerne i romjulen) Dette er smakebiter på ting som dukker opp i videregående emner (MAT2400 og MAT2200). Del I og II kan gjøres uavhengig av hverandre. Hvis oppgavene er vanskelige betyr det ikke noe annet enn at juleferien er for kort. DEL I: Analyse DEFINISJON: Vi sier at en følge {x n } er en Cauchy-følge dersom gitt en ε >0 så finnes en N slik at for alle m,n > N vil x m - x n < ε 1. Vis at en konvergent følge er en Cauchy-følge. 2. Vis at en Cauchy-følge i R må være begrenset (dvs. det finnes en M slik at x n < M for alle n) 3. Vis at en begrenset følge må ha en konvergent delfølge. (En delfølge betyr at vi plukker ut uendelig mange ledd, f.eks. x 1, x 2, x 4, x 5, x 7, x 33, x 77,, slik at indeksene hele tiden øker, vi hopper bare over noen i den opprinnelige følgen) Hint: Kall delfølgen {y n } og sett y 1 = x 1. Se på intervallet [-M, M], som inneholder alle de uendelig mange elementene i følgen {x n }. Del intervallet i to på midten. Minst ett av de to nye intervallene må inneholde uendelig mange elementer i følgen, og dermed inneholde en x k hvor k >1. Sett y 2 = x k. og kall det halve intervallet du velger [a 2,b 2 ] Del dette intervallet i to på nytt, velg en halvpart som inneholder uendelig mange elementer, kall det [a 3, b 3 ], og sett y 3 = x m, hvor m>k og x m er med i [a 3,b 3 ] og fortsett. a n <y n <b n hele tiden og gi et argument for at y n må konvergere. 4. La {x n } være en reell Cauchy-følge, altså begrenset (iflg. 1). La {y n } være en konvergent delfølge av {x n } med grense y. Vis at når {x n } er Cauchy må {x n } selv være konvergent med grense y. Konkluder med at alle reelle Cauchy-følger er konvergente. I oppgave 1 viste vi at alle konvergente følger er Cauchy, og 2-4 viser at for reelle følger er alle Cauchy-følger konvergente. Dette gjelder ikke generelt. I noen metriske rom finnes det Cauchyfølger som ikke er konvergente. Dersom alle Cauchy-følger i et metrisk rom X er konvergente med grense i X, sier vi at det metriske rommet er komplett. Mer om metriske rom på neste side. EKSEMPEL: Legg merke til at vi presiserer at grensen skal være i rommet. Hvis vi ser på det åpne intervallet I = (0,1) følgen {x n } gitt ved x n = 1/(n+1), så er det klart at følgen er i I, dvs. at alle leddene, uansett hvor langt ut vi går, ligger i intervallet (0,1). Den er også Cauchy, for gitt en ε >0 kan vi sette N = 1/ε og for alle m,n > 1/ε, vil x m - x n < ε ettersom de begge vil ligge i intervallet (0, ε). Men er den konvergent?
2 Tja, hvis vi tenker på følgen som en følge i hele R, er den konvergent med grense 0. Men siden 0 ligger utenfor I, er ikke {x n } konvergent i I. Derfor er ikke I komplett! Metriske rom Metrikk er en generalisering av avstandsbegrepet. En metrikk på en mengde X er en funksjon d som tar to elementer i X og returnerer et positivt reelt tall. Det tallet kan vi tenke på som avstanden mellom punktene. d(x,y) må være definert for ALLE par av punkter (x,y) i X. Dessuten må den tilfredsstille: d(x,y) 0 for alle x og y i X d(x,y) = 0 hvis og bare hvis x = y d(x,y) = d(y,x) d(x,z) d(x,y) + d(y,z) (Trekantulikheten!) En mengde X sammen med en metrikk (en slik funksjon) d kalles et metrisk rom, og vi skriver det gjerne som et par (X,d). Dette gjør vi fordi vi kan definere ulike metrikker på én og samme mengde. To slike metrikker, d og q, gir opphav til to ulike metriske rom (X,d) og (X,q), selv om mengden X skulle være den samme. 5. Vis at i R n er d(x,y) := (x 1 y 1 ) 2 + (x 2 y 2 ) (x n y n ) 2 en metrikk. (Dvs. at den tilfredsstiller betingelsene på forrige side). Dette er den standard euklidske metrikken som du har brukt hele livet. 6. La d være som over. Vis at d(x, y) = min{d(x, y),1} er en metrikk på R n 7. La d(x, y) = 0, x = y 1, x y Vis at dette er en metrikk. Dette kalles den diskrete metrikken Kontinuitet La (X,d) og (Y,q) være to metriske rom, og la f være en funksjon fra X til Y. La a være et punkt i X. Da sier vi at f er kontinuerlig i a hvis vi for hver ε >0 kan finne en δ >0 slik at d(a,x) < δ => q( f(a), f(x) ) < ε Konvergens: La (x n ) være en følge i et metrisk rom (X,d). Følgen er konvergent med grense x hvis vi for hver ε >0 kan finne en N slik at for alle n > N har vi d(x n, x) < ε. Vi ser at kontinuitet og konvergens har med avstanden mellom elementer å gjøre. Med en gang vi har en ide om avstanden mellom elementene i en mengde, kan vi snakke om kontinuitet og konvergens. Definisjonen av kontinuitet og konvergens er helt lik den du er vant med den har bare fått en litt mer generell form. Andre metriske rom: Vi kan også definere metrikker på andre mengder enn R n. La C[0,1] være mengden av alle kontinuerlige funksjoner på intervallet [0,1]. La f(x) og g(x) være to slike funksjoner.
3 Da kan vi definere en funksjon d(f,g) = sup f (x) g(x). Avstanden mellom to funksjoner er her x [0,1] definert som største avstand mellom f(x) og g(x) når x løper over alle verdier i intervallet. d(f,g) = 4 betyr at f(x) g(x) aldri blir større enn 4 for noen x i intervallet. Denne metrikken kalles supmetrikken. OPPGAVER 8. Vis sup-metrikken er en metrikk (At den tilfredsstiller betingelsene nederst på forrige side). 9. La {f n } være en følge i C[0,1], hvor f n (x) = 4sin(x) + (1/n)cos(x). Bruk definisjonen av konvergens i metriske rom til å vise at {f n } konvergerer mor grensa f(x) = 4sin(x) *** Litt gruppeteori DEL II: Algebra Gruppeteori er en del av matematikken (algebra) som har stor anvendelse, ikke bare i matematikk, men også i fysikk, kjemi, Rubiks kube med mer Gruppeteori kan se veldig abstrakt og unyttig ut her, men er veldig spennende når man får mer kjøtt på beina. Denne lille introduksjonen skal vekke appetitten på sånn kjøtt! La G være en mengde. En binær operasjon på G er en funksjon * som tar to elementer i G og returnerer et tredje element i G. Hvis vi holder oss i de hele tallene (Z), ser vi at + er en slik funksjon. 5+3 = (-2) = 110 osv. Hvis G er en mengde og * en binær operasjon, sier vi at e er et identitetselement hvis a*e = e*a = a for alle a. I de hele tallene, sammen med den binære operasjonen +, er det 0 som er identitetselement, for z + 0 = 0 + z = z for alle z i Z. Vi sier at h er en invers av g dersom h*g = g*h = e (identitetselementet). I heltallene (sammen med +) er z den inverse til z fordi (-z) + z = z + (-z) = 0. DEFINISJON: En gruppe er en mengde G sammen med en binær operasjon *, slik at følgende holder: Hvis g 1 og g 2 er elementer i G, så er også g 1 *g 2 med i G g 1 *(g 2 *g 3 ) = (g 1 *g 2 )*g 3 Det finnes et identitetselement e slik at e*g = g*e = g, for alle g i G Alle elementer g skal ha en invers g -1 slik at g*g -1 = g -1 *g = e NB! MERK at det IKKE er noe krav om at operasjonen skal være kommutativ. a*b trenger ikke være lik b*a. DERSOM dette er tilfelle sier vi at gruppen er abelsk. (Oppkalt etter Niels Henrik Abel!) Vi bruker gjerne notasjonen (G,*) for å presisere hvilken mengde det er snakk om og hvilken binær operasjon.
4 Vi har i innledningen brukt (Z,+) som eksempel. De hele tallene, sammen med den binære operasjonen +, er en gruppe fordi den tilfredsstiller alle de fire aksiomene. Addisjon av heltall er dessuten kommutativt: z 1 + z 2 = z 2 + z 1 for alle z 1,z 2 i Z. Dermed er heltallene, sammen med +, en abelsk gruppe. Undergrupper En gruppe er en mengde, sammen med en binær operasjon *, hvor de fire punktene over er oppfylt. Vi er vant med at mengder har delmengder, og da er det eneste kravet at alle elementene i delmengden må høre til den opprinnelige mengden. {1,2,3} er en delmengde av de hele tallene. De hele tallene er en delmengde av de rasjonale tallene, osv. For at en delmengde skal være en undergruppe må følgende være oppfylt: DEFINISJON: La G være en gruppe (med binær operasjon *). H er en undergruppe av G (H < G) dersom H er en delmengde av G som selv er en gruppe under den samme binære operasjonen *. Det betyr at identiteten e i G også må ligge i H. Videre må H være lukket under den binære operasjonen *., dvs. at hvis vi tar to elementer h 1 og h 2, som begge er i H, så må også h 1 *h 2 ligge i H. Og alle elementer h i H må ha sin invers h -1 i H. EKSEMPEL: Hvis vi ser på (Z,+) vil H = {5z z er i Z} = {, -15, -10, -5, 0, 5, 10, 15, } være en undergruppe fordi: 0 er med i H hvis a og b er med i H, la a = 5k, b = 5m, så er a + b = 5k + 5l = 5(k+l) = 5s for en s i Z. dvs. at a+b er med i H a + (b + c) = (a + b) + c fordi vi kan tenke på disse som elementer i Z, hvor dette gjelder fordi Z er en gruppe. Det samme må gjelde om vi tenker på dem som elementer i undergruppa H Alle elementer i H har en invers i H. La a = 5k for en k i Z, Lar vi b = 5(-k), har vi a + b = 5k + 5(-k) = 5k 5k = 0. Dvs. at b er a sin invers, og b = 5(-k) er med i H siden (-k) er med i Z. (Jfr. def. av H) 10. Forklar hvorfor (Z, ) (Heltallene sammen med multiplikasjon) IKKE er en gruppe. Er (Q, ) en gruppe? 11. Vis at identitetselementet i en gruppe (G,*) må være unikt. (Hint: anta at det finnes to identiteter e 1 og e 2, slik at e 1 *x = x og e 2 x = x for alle x. Utled at de må være like) 12. Forklar hvorfor mengden av alle invertible 2x2-matriser med reelle elementer, sammen med matrisemultiplikasjon, er en gruppe. Hvorfor trenger vi betingelsen om at matrisene er invertible? (Kommentar: Denne gruppa kalles gjerne GL(2, R) )
5 13. I hvilke tilfeller er H en undergruppe av G? (C = komplekse tall, R = reelle tall, Q rasjonale osv ) a. G = (R, ) H = (Z, +) b. G = (C, ) H = { z : z = 1} 1 z c. G = GL(2,R) (se forrige oppgave) H = : z Z 0 1 (vedr. c: Ser du noen algebraiske likheter mellom (H, *) og (Z, +)? (* står for matrisemultiplikasjon) Takk for en givende høst! God jul og godt nytt år! Ta kontakt hvis du har spørsmål eller kommentarer til oppgavene! ivarsta@student.uio.no
Grublegruppe 19. sept. 2011: Algebra I
 Grublegruppe 19. sept. 2011: Algebra I Ivar Staurseth ivarsta@math.uio.no Innledning, definisjoner Vi har så langt jobbet med mengder, X, hvor vi har hatt et avstandsbegrep og hvor vi har vært i stand
Grublegruppe 19. sept. 2011: Algebra I Ivar Staurseth ivarsta@math.uio.no Innledning, definisjoner Vi har så langt jobbet med mengder, X, hvor vi har hatt et avstandsbegrep og hvor vi har vært i stand
Analysedrypp IV: Metriske rom
 Analysedrypp IV: Metriske rom Vi har tidligere sett at begreper som konvergens og kontinuitet har med avstand å gjøre at f er kontinuerlig i punktet a, betyr f. eks. at det for enhver ɛ > 0, finnes en
Analysedrypp IV: Metriske rom Vi har tidligere sett at begreper som konvergens og kontinuitet har med avstand å gjøre at f er kontinuerlig i punktet a, betyr f. eks. at det for enhver ɛ > 0, finnes en
Løsningsforslag øving 6
 Løsningsforslag øving 6 7 Husk Teorem 79 i notatet: En delmengde U av et vektorrom V er et underrom hvis ) nullvektoren er i U, ) summen av to vektorer i U er i U igjen, og 3) et skalarmultiplum av en
Løsningsforslag øving 6 7 Husk Teorem 79 i notatet: En delmengde U av et vektorrom V er et underrom hvis ) nullvektoren er i U, ) summen av to vektorer i U er i U igjen, og 3) et skalarmultiplum av en
Definisjon 10.14: La V være et reelt vektorrom og N \: V \to R en funksjon. Vi skriver x = N(x) og sier at N er en norm på V dersom følgende holder:
 MAT1300 Analyse I 23. mars 2009 10.3 Metriske rom Har gjort analyse for funksjoner på R ved hjelp av avstandsbegrepet y-x gitt ved absoluttverdien til differansen mellom to punkter, og i R^m ved hjelp
MAT1300 Analyse I 23. mars 2009 10.3 Metriske rom Har gjort analyse for funksjoner på R ved hjelp av avstandsbegrepet y-x gitt ved absoluttverdien til differansen mellom to punkter, og i R^m ved hjelp
En rekke av definisjoner i algebra
 En rekke av definisjoner i algebra Martin Strand, martin.strand@math.ntnu.no 11. november 2010 Definisjonene som er gitt her, kommer i MA2201 Algebra og MA3201 Ringer og moduler. Forhåpentligvis blir det
En rekke av definisjoner i algebra Martin Strand, martin.strand@math.ntnu.no 11. november 2010 Definisjonene som er gitt her, kommer i MA2201 Algebra og MA3201 Ringer og moduler. Forhåpentligvis blir det
MAUMAT644 ALGEBRA vår 2016 Første samling Runar Ile
 MAUMAT644 ALGEBRA vår 2016 Første samling Runar Ile 1 Introduksjon: Grupper og ringer Ringer En ring er et sted hvor du kan addere, subtrahere og multiplisere. Hvis du også kan dividere kalles ringen for
MAUMAT644 ALGEBRA vår 2016 Første samling Runar Ile 1 Introduksjon: Grupper og ringer Ringer En ring er et sted hvor du kan addere, subtrahere og multiplisere. Hvis du også kan dividere kalles ringen for
Litt topologi. Harald Hanche-Olsen
 MA2104 2006 Litt topologi Harald Hanche-Olsen hanche@math.ntnu.no De reelle tall En grunnleggende egenskap ved de reelle tall, som skiller dem fra de rasjonale tall, er kompletthetsaksiomet. Det har flere
MA2104 2006 Litt topologi Harald Hanche-Olsen hanche@math.ntnu.no De reelle tall En grunnleggende egenskap ved de reelle tall, som skiller dem fra de rasjonale tall, er kompletthetsaksiomet. Det har flere
Oppgaver MAT2500. Fredrik Meyer. 29. august 2014
 Oppgaver MAT500 Fredrik Meyer 9. august 04 Oppgave. Bruk cosinus-setningen til å se at definisjonen av vinkel i planet blir riktig. Løsning. Dette er en litt rar oppgave. Husk at cosinus-setningen sier
Oppgaver MAT500 Fredrik Meyer 9. august 04 Oppgave. Bruk cosinus-setningen til å se at definisjonen av vinkel i planet blir riktig. Løsning. Dette er en litt rar oppgave. Husk at cosinus-setningen sier
Matriser. Kapittel 4. Definisjoner og notasjon
 Kapittel Matriser Vi har lært å løse et lineært ligningssystem ved å sette opp totalmatrisen til systemet gausseliminere den ved hjelp av radoperasjoner på matrisen Vi skal nå se nærmere på egenskaper
Kapittel Matriser Vi har lært å løse et lineært ligningssystem ved å sette opp totalmatrisen til systemet gausseliminere den ved hjelp av radoperasjoner på matrisen Vi skal nå se nærmere på egenskaper
7 Ordnede ringer, hele tall, induksjon
 Notat 07 for MAT1140 7 Ordnede ringer, hele tall, induksjon Definition 7.1. La R være utstyrt med addisjon og multiplikasjon slik at vi har å gjøre med en kommutativ ring. Anta videre at R er utstyrt med
Notat 07 for MAT1140 7 Ordnede ringer, hele tall, induksjon Definition 7.1. La R være utstyrt med addisjon og multiplikasjon slik at vi har å gjøre med en kommutativ ring. Anta videre at R er utstyrt med
For å vise at et metrisk rom (X, d) er komplett må vi vise at enhver Cauchy-følge (x_n)_n i (X, d) konvergerer mot en grense x i X.
 MAT1300 Analyse I 20. april 2009 For å vise at et metrisk rom (X, d) er komplett må vi vise at enhver Cauchy-følge (x_n)_n i (X, d) konvergerer mot en grense x i X. Da kan vi (A) finne en kandidat x for
MAT1300 Analyse I 20. april 2009 For å vise at et metrisk rom (X, d) er komplett må vi vise at enhver Cauchy-følge (x_n)_n i (X, d) konvergerer mot en grense x i X. Da kan vi (A) finne en kandidat x for
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF1080 Logiske metoder for informatikk Eksamensdag: 27. desember 2015 Tid for eksamen: 08.15 12:15 Oppgave 1 Grunnleggende mengdelære
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF1080 Logiske metoder for informatikk Eksamensdag: 27. desember 2015 Tid for eksamen: 08.15 12:15 Oppgave 1 Grunnleggende mengdelære
Notat 05 for MAT Relasjoner, operasjoner, ringer. 5.1 Relasjoner
 Notat 05 for MAT1140 5 Relasjoner, operasjoner, ringer 5.1 Relasjoner Når R er en relasjon som er veldefinert på A B, slik at R(x, y) er en påstand når x A og B B, tenker vi på relasjonen som noe som lever
Notat 05 for MAT1140 5 Relasjoner, operasjoner, ringer 5.1 Relasjoner Når R er en relasjon som er veldefinert på A B, slik at R(x, y) er en påstand når x A og B B, tenker vi på relasjonen som noe som lever
Oppgave 14 til 9. desember: I polynomiringen K[x, y] i de to variable x og y over kroppen K definerer vi undermengdene:
![Oppgave 14 til 9. desember: I polynomiringen K[x, y] i de to variable x og y over kroppen K definerer vi undermengdene: Oppgave 14 til 9. desember: I polynomiringen K[x, y] i de to variable x og y over kroppen K definerer vi undermengdene:](/thumbs/64/52216522.jpg) HJEMMEOPPGAVER utgave av 8-12-2002): Oppgave 15 til 16 desember: La H være mengden av alle matriser på formen A = a 1 a 12 a 13 a 1n 0 a 2 0 0 0 0 a 3 0 0 0 a n der a 1 a 2 a n 0 Videre la SH være matrisene
HJEMMEOPPGAVER utgave av 8-12-2002): Oppgave 15 til 16 desember: La H være mengden av alle matriser på formen A = a 1 a 12 a 13 a 1n 0 a 2 0 0 0 0 a 3 0 0 0 a n der a 1 a 2 a n 0 Videre la SH være matrisene
x A e x = x e = x. (2)
 Notat om Algebra for MAT1140 1 Algebra 1.1 Operasjoner Definisjon 1.1. En operasjon på en mengde A er en avbildning fra A A til A. Bemerkning 1.1. Mer generelt kan man snakke om n-ære operasjoner på A,
Notat om Algebra for MAT1140 1 Algebra 1.1 Operasjoner Definisjon 1.1. En operasjon på en mengde A er en avbildning fra A A til A. Bemerkning 1.1. Mer generelt kan man snakke om n-ære operasjoner på A,
4 Matriser TMA4110 høsten 2018
 Matriser TMA høsten 8 Nå har vi fått erfaring med å bruke matriser i et par forskjellige sammenhenger Vi har lært å løse et lineært likningssystem ved å sette opp totalmatrisen til systemet og gausseliminere
Matriser TMA høsten 8 Nå har vi fått erfaring med å bruke matriser i et par forskjellige sammenhenger Vi har lært å løse et lineært likningssystem ved å sette opp totalmatrisen til systemet og gausseliminere
En (reell) funksjon f fra en (reell) mengde D er en regel som til hvert element x D tilordner en unik verdi y = f (x).
 Funksjoner En (reell) funksjon f fra en (reell) mengde D er en regel som til hvert element x D tilordner en unik verdi y = f (x). Mengden D kalles definisjonsmengden (eng.: domain) til f. Merknad Dersom
Funksjoner En (reell) funksjon f fra en (reell) mengde D er en regel som til hvert element x D tilordner en unik verdi y = f (x). Mengden D kalles definisjonsmengden (eng.: domain) til f. Merknad Dersom
Oblig 1 - MAT2400. Fredrik Meyer
 Oblig 1 - MAT2400 Fredrik Meyer 1 Oppgave 1 Påstand 1 a). Z 5 har fire generatorer og AutZ 5 ) Z 4 Bevis. Hvert ikke-null-element i Z 5 genererer en undergruppe. Siden 5 er et primtall, må denne undergruppen
Oblig 1 - MAT2400 Fredrik Meyer 1 Oppgave 1 Påstand 1 a). Z 5 har fire generatorer og AutZ 5 ) Z 4 Bevis. Hvert ikke-null-element i Z 5 genererer en undergruppe. Siden 5 er et primtall, må denne undergruppen
MAT Grublegruppen Notat 6
 MAT00 - Grublegruppen Notat 6 Jørgen O. Lye Vektorrom og indreprodukt Vektorrom Vi trenger å si litt om vektorrom og indreprodukt for å formulere Fourierrekker. Denisjonen av vektorrom kan man tenke på
MAT00 - Grublegruppen Notat 6 Jørgen O. Lye Vektorrom og indreprodukt Vektorrom Vi trenger å si litt om vektorrom og indreprodukt for å formulere Fourierrekker. Denisjonen av vektorrom kan man tenke på
UNIVERSITETET I BERGEN
 BOKMÅL UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Eksamen i emnet MAT220/MAUMAT44 - Algebra Fredag. juni 204, kl. 09-4 Tillatte hjelpemidler: Kalkulator i samsvar med fakultetets
BOKMÅL UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Eksamen i emnet MAT220/MAUMAT44 - Algebra Fredag. juni 204, kl. 09-4 Tillatte hjelpemidler: Kalkulator i samsvar med fakultetets
Analysedrypp II: Kompletthet
 Analysedrypp II: Kompletthet Kompletthet er et begrep som står sentralt i både MAT1100 og MAT1110, og som vil stå enda mer sentralt i MAT2400. I de tidligere kursene fremstår begrepet på litt forskjellig
Analysedrypp II: Kompletthet Kompletthet er et begrep som står sentralt i både MAT1100 og MAT1110, og som vil stå enda mer sentralt i MAT2400. I de tidligere kursene fremstår begrepet på litt forskjellig
Analysedrypp III: ɛ-δ og alt det der
 Analysedrypp III: ɛ-δ og alt det der Mange strever med ɛ-δ-argumenter. Det er flere grunner til dette: Noen har problemer med å forstå den underliggende tankegangen, mens andre sliter med de grunnleggende
Analysedrypp III: ɛ-δ og alt det der Mange strever med ɛ-δ-argumenter. Det er flere grunner til dette: Noen har problemer med å forstå den underliggende tankegangen, mens andre sliter med de grunnleggende
Vektorrom. Kapittel 7. Hva kan vi gjøre med vektorer?
 Kapittel 7 Vektorrom Vårt mål i dette kapitlet og det neste er å generalisere og abstrahere ideene vi har jobbet med til nå Især skal vi stille spørsmålet Hva er en vektor? Svaret vi skal gi, vil virke
Kapittel 7 Vektorrom Vårt mål i dette kapitlet og det neste er å generalisere og abstrahere ideene vi har jobbet med til nå Især skal vi stille spørsmålet Hva er en vektor? Svaret vi skal gi, vil virke
Mer om mengder: Tillegg til Kapittel 1. 1 Regneregler for Booleske operasjoner
 MAT1140, H-16 Mer om mengder: Tillegg til Kapittel 1 Vi trenger å vite litt mer om mengder enn det som omtales i første kapittel av læreboken. I dette tillegget skal vi først se på regneregler for Booleske
MAT1140, H-16 Mer om mengder: Tillegg til Kapittel 1 Vi trenger å vite litt mer om mengder enn det som omtales i første kapittel av læreboken. I dette tillegget skal vi først se på regneregler for Booleske
8 Vektorrom TMA4110 høsten 2018
 8 Vektorrom TMA4 høsten 8 I de foregående kapitlene har vi tatt en lang vandring gjennom den lineære algebraens jungel. Nå skal vi gå opp på en fjelltopp og skue ut over landskapet vi har vandret gjennom.
8 Vektorrom TMA4 høsten 8 I de foregående kapitlene har vi tatt en lang vandring gjennom den lineære algebraens jungel. Nå skal vi gå opp på en fjelltopp og skue ut over landskapet vi har vandret gjennom.
(a) R n defineres som mengden av kolonnevektorer. a 1 a 2. a n. (b) R n defineres som mengden av radvektorer
 5 Vektorrom Et vektorrom er en mengde V med tre algebraiske operasjoner (addisjon, negasjon og skalærmultiplikasjon) som tilfredsstiller de 10 betingelsene fra Def. 4.1.1. Jeg vil ikke gi en eksamensoppgave
5 Vektorrom Et vektorrom er en mengde V med tre algebraiske operasjoner (addisjon, negasjon og skalærmultiplikasjon) som tilfredsstiller de 10 betingelsene fra Def. 4.1.1. Jeg vil ikke gi en eksamensoppgave
Iterasjon og optimering
 Innhold 5 Iterasjon og optimering 3 5.1 Litt topologi i R m........................ 4 5. Kompletthet av R m....................... 13 5.3 Noen konsekvenser av kompletthet............... 18 5.4 Iterasjon
Innhold 5 Iterasjon og optimering 3 5.1 Litt topologi i R m........................ 4 5. Kompletthet av R m....................... 13 5.3 Noen konsekvenser av kompletthet............... 18 5.4 Iterasjon
Fraktaler og kaos Harald Hanche-Olsen
 TMA4165 Dynamiske systemer 2007 Fraktaler og kaos 2 Fraktaler og kaos Harald Hanche-Olsen hanche@math.ntnu.no Sammendrag. Tillegg til dynamiske systemer 2007. Etter notater av Nils A. Baas. Notatet gir
TMA4165 Dynamiske systemer 2007 Fraktaler og kaos 2 Fraktaler og kaos Harald Hanche-Olsen hanche@math.ntnu.no Sammendrag. Tillegg til dynamiske systemer 2007. Etter notater av Nils A. Baas. Notatet gir
Direkte produkter. (a, b)(a 0,b 0 )=(ab, a 0 b 0 ).
 Direkte produkter Vi kjenner det kartesiske produktet av to mengder Y.Detbeståravallepar(x, y) av elementer x 2 og y 2 Y.OrdetkartesiskerdannetavegennavnetRenéDécartes, en fransk filosof og matematiker
Direkte produkter Vi kjenner det kartesiske produktet av to mengder Y.Detbeståravallepar(x, y) av elementer x 2 og y 2 Y.OrdetkartesiskerdannetavegennavnetRenéDécartes, en fransk filosof og matematiker
Hint til oppgavene. Uke 34. Uke 35. Fullstendige løsningsforslag finnes på emnesidene for 2017.
 Hint til oppgavene Fullstendige løsningsforslag finnes på emnesidene for 2017. Uke 34 Oppgave 1, 2, 3 og 4 kan alle løses ved å tegne sannhetstabeller, men i flere tilfeller kan man like gjerne manipulere
Hint til oppgavene Fullstendige løsningsforslag finnes på emnesidene for 2017. Uke 34 Oppgave 1, 2, 3 og 4 kan alle løses ved å tegne sannhetstabeller, men i flere tilfeller kan man like gjerne manipulere
TMA4100 Matematikk 1, høst 2013
 TMA4100 Matematikk 1, høst 2013 Teknostart forelesning 6 www.ntnu.no TMA4100 Matematikk 1, høst 2013, Teknostart forelesning 6 Grenseverdier I dagens forelesning skal vi se på følgende: 1 En formell definisjon
TMA4100 Matematikk 1, høst 2013 Teknostart forelesning 6 www.ntnu.no TMA4100 Matematikk 1, høst 2013, Teknostart forelesning 6 Grenseverdier I dagens forelesning skal vi se på følgende: 1 En formell definisjon
Velkommen til oversiktsforelesninger i Matematikk 1. med Jørgen Endal
 Velkommen til oversiktsforelesninger i Matematikk 1 med Jørgen Endal Nytt tema: Følger, rekker, og potensrekker (kap. 9.1 9.7) Nytt tema: Følger, rekker, og potensrekker (kap. 9.1 9.7) Forelesning 1 (kap.
Velkommen til oversiktsforelesninger i Matematikk 1 med Jørgen Endal Nytt tema: Følger, rekker, og potensrekker (kap. 9.1 9.7) Nytt tema: Følger, rekker, og potensrekker (kap. 9.1 9.7) Forelesning 1 (kap.
QED 1 7. Matematikk for grunnskolelærerutdanningen. Bind 2. Fasit kapittel 1 Tallenes hemmeligheter
 QED 1 7 Matematikk for grunnskolelærerutdanningen Bind 2 Fasit kapittel 1 Tallenes hemmeligheter Kapittel 1 Oppgave 8. Nei Oppgave 9. Det nnes ikke nødvendigvis et minste element i mengden. Et eksempel
QED 1 7 Matematikk for grunnskolelærerutdanningen Bind 2 Fasit kapittel 1 Tallenes hemmeligheter Kapittel 1 Oppgave 8. Nei Oppgave 9. Det nnes ikke nødvendigvis et minste element i mengden. Et eksempel
Eksamen i MNFMA205/SIF5021, 19. mai 1999-Løsningsforslag a b Oppgave 2. (a) Vi skal vise at H = 0 a b under matrisemultiplikasjon. Vi har at det.
 Eksamen i MNFMA205/SIF5021 19. mai 1999-Løsningsforslag { } Oppgave 2. a Vi skal vise at H 0 a C er en gruppe under matrisemultiplikasjon. Vi har at det aā + a 2 + 2 > 0 da enten a 0 eller 0. Dette fører
Eksamen i MNFMA205/SIF5021 19. mai 1999-Løsningsforslag { } Oppgave 2. a Vi skal vise at H 0 a C er en gruppe under matrisemultiplikasjon. Vi har at det aā + a 2 + 2 > 0 da enten a 0 eller 0. Dette fører
Begreper i analyse. Olav Nygaard
 Begreper i analyse Olav Nygaard 27. april 2007 Litt om dette heftet Analyse er et sentralt emne, nesten uansett hvilke retninger en vil studere i matematikk. I dette heftet har jeg plukka ut noen temaer
Begreper i analyse Olav Nygaard 27. april 2007 Litt om dette heftet Analyse er et sentralt emne, nesten uansett hvilke retninger en vil studere i matematikk. I dette heftet har jeg plukka ut noen temaer
MA2201/TMA4150 Vår 2018
 MA2201/TMA4150 Vår 2018 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Løsningsforslag Øving 6 Seksjon 14 34 La G = n < og la H G være eneste undergruppe av G av orden m.
MA2201/TMA4150 Vår 2018 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Løsningsforslag Øving 6 Seksjon 14 34 La G = n < og la H G være eneste undergruppe av G av orden m.
9 Lineærtransformasjoner TMA4110 høsten 2018
 9 Lineærtransformasjoner MA4 høsten 8 I forrige kapittel begynte vi å formulere lineær algebra på en generell måte, ved å gi en abstrakt definisjon av vektorrom For å beskrive sammenhenger mellom forskjellige
9 Lineærtransformasjoner MA4 høsten 8 I forrige kapittel begynte vi å formulere lineær algebra på en generell måte, ved å gi en abstrakt definisjon av vektorrom For å beskrive sammenhenger mellom forskjellige
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT1100 Kalkulus Eksamensdag: Fredag 11. desember 2015 Tid for eksamen: 09.00 13.00. Oppgavesettet er på 5 sider. Vedlegg: Svarark,
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT1100 Kalkulus Eksamensdag: Fredag 11. desember 2015 Tid for eksamen: 09.00 13.00. Oppgavesettet er på 5 sider. Vedlegg: Svarark,
MAT Grublegruppen Notat 9
 MAT1100 - Grublegruppen Notat 9 Jørgen O. Lye Gruppeteori Oppvarmingseksempel La oss som vanlig ta en historisk vinkling. En klassisk måte grupper (som jeg straks skal denere) oppstod er gjennom å lete
MAT1100 - Grublegruppen Notat 9 Jørgen O. Lye Gruppeteori Oppvarmingseksempel La oss som vanlig ta en historisk vinkling. En klassisk måte grupper (som jeg straks skal denere) oppstod er gjennom å lete
TOPOLOGI. Dan Laksov
 Forum för matematiklärare TOPOLOGI Dan Laksov Institutionen för Matematik, 2009 Finansierat av Marianne och Marcus Wallenbergs Stiftelse Topologi Dan Laksov Notater for Forum för Matematiklärare. Høst
Forum för matematiklärare TOPOLOGI Dan Laksov Institutionen för Matematik, 2009 Finansierat av Marianne och Marcus Wallenbergs Stiftelse Topologi Dan Laksov Notater for Forum för Matematiklärare. Høst
TMA4100 Matematikk 1, høst 2013
 TMA4100 Matematikk 1, høst 2013 Forelesning 11 www.ntnu.no TMA4100 Matematikk 1, høst 2013, Forelesning 11 Transcendentale funksjoner Vi begynner nå på temaet transcendentale funksjoner. I dagens forelesning
TMA4100 Matematikk 1, høst 2013 Forelesning 11 www.ntnu.no TMA4100 Matematikk 1, høst 2013, Forelesning 11 Transcendentale funksjoner Vi begynner nå på temaet transcendentale funksjoner. I dagens forelesning
DISKRET MATEMATIKK FINNES IKKE. Dan Laksov KTH, Stockholm
 DISKRET MATEMATIKK FINNES IKKE Dan Laksov KTH, Stockholm matematikk/thorup/dlbook/april 11, 2005 DISKRET MATEMATIKK FINNES IKKE Diskret matematikk finnes ikke Dan Laksov Notater for Forum för Matematiklärare.
DISKRET MATEMATIKK FINNES IKKE Dan Laksov KTH, Stockholm matematikk/thorup/dlbook/april 11, 2005 DISKRET MATEMATIKK FINNES IKKE Diskret matematikk finnes ikke Dan Laksov Notater for Forum för Matematiklärare.
TMA4165 Dynamiske systemer 2007. Fraktaler og kaos. Harald Hanche-Olsen. hanche@math.ntnu.no
 TMA4165 Dynamiske systemer 2007 Fraktaler og kaos Harald Hanche-Olsen hanche@math.ntnu.no Sammendrag. Tillegg til dynamiske systemer 2007. Etter notater av Nils A. Baas. Notatet gir et kort og meget konsist
TMA4165 Dynamiske systemer 2007 Fraktaler og kaos Harald Hanche-Olsen hanche@math.ntnu.no Sammendrag. Tillegg til dynamiske systemer 2007. Etter notater av Nils A. Baas. Notatet gir et kort og meget konsist
ANALYSEDRYPP. Et forkurs til MAT2400. av Tom Lindstrøm. Matematisk insitutt og CMA Universitetet i Oslo 2011
 1 ANALYSEDRYPP Et forkurs til MAT2400 av Tom Lindstrøm Matematisk insitutt og CMA Universitetet i Oslo 2011 2 Forord Hensikten med dette heftet er å bygge en bro mellom kalkuluskursene og det første kurset
1 ANALYSEDRYPP Et forkurs til MAT2400 av Tom Lindstrøm Matematisk insitutt og CMA Universitetet i Oslo 2011 2 Forord Hensikten med dette heftet er å bygge en bro mellom kalkuluskursene og det første kurset
Oblig 1 - MAT Oppgave 1. Fredrik Meyer. Vi lar α > 1 og x 1 > α. Vi definerer en følge (x n ) ved. x n+1 = α + x n 1 + x n.
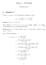 Oblig 1 - MAT2400 Fredrik Meyer 1 Oppgave 1 Vi lar α > 1 og x 1 > α. Vi definerer en følge (x n ) ved Lemma 1 (a). x n > 1 n N x n+1 = α + x n = x n + α x2 n Bevis. Siden α > 1 er α + x n >, så 1 = 1+xn
Oblig 1 - MAT2400 Fredrik Meyer 1 Oppgave 1 Vi lar α > 1 og x 1 > α. Vi definerer en følge (x n ) ved Lemma 1 (a). x n > 1 n N x n+1 = α + x n = x n + α x2 n Bevis. Siden α > 1 er α + x n >, så 1 = 1+xn
MA1102 Grunnkurs i Analyse II Vår 2015
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA112 Grunnkurs i Analyse II Vår 215 Løsningsforslag Øving 5 11.3:3 f n (x) = 2n+1 x? = x 1 2n+1. (Det er muligens en forskjell
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA112 Grunnkurs i Analyse II Vår 215 Løsningsforslag Øving 5 11.3:3 f n (x) = 2n+1 x? = x 1 2n+1. (Det er muligens en forskjell
Lineærtransformasjoner
 Kapittel 8 Lineærtransformasjoner I forrige kapittel begynte vi å formulere lineær algebra på en generell måte, ved å gi en abstrakt definisjon av vektorrom For å beskrive sammenhenger mellom forskjellige
Kapittel 8 Lineærtransformasjoner I forrige kapittel begynte vi å formulere lineær algebra på en generell måte, ved å gi en abstrakt definisjon av vektorrom For å beskrive sammenhenger mellom forskjellige
Notater fra forelesning i MAT1100 mandag
 Notater fra forelesning i MAT00 mandag 3.08.09 Amandip Sangha, amandips@math.uio.no 8. august 009 Følger og konvergens (seksjon 4.3 i Kalkulus) Definisjon.. En følge er en uendelig sekvens av tall {a,a,a
Notater fra forelesning i MAT00 mandag 3.08.09 Amandip Sangha, amandips@math.uio.no 8. august 009 Følger og konvergens (seksjon 4.3 i Kalkulus) Definisjon.. En følge er en uendelig sekvens av tall {a,a,a
Gauss-Jordan eliminasjon; redusert echelonform. Forelesning, TMA4110 Fredag 18/9. Reduserte echelonmatriser. Reduserte echelonmatriser (forts.
 Gauss-Jordan eliminasjon; redusert echelonform Forelesning, TMA4110 Fredag 18/9 Martin Wanvik, IMF MartinWanvik@mathntnuno En matrise vil normalt være radekvivalent med flere echelonmatriser; med andre
Gauss-Jordan eliminasjon; redusert echelonform Forelesning, TMA4110 Fredag 18/9 Martin Wanvik, IMF MartinWanvik@mathntnuno En matrise vil normalt være radekvivalent med flere echelonmatriser; med andre
Karakterer. Kapittel Homomorfier av grupper. 8.2 Representasjoner
 Kapittel 8 Karakterer 8. Homomorfier av grupper I forrige kapittel definerte vi begrepet abstrakt gruppe, som en abstrakt versjon av begrepet symmetrigruppe. For å studere forbindelsen mellom abstrakte
Kapittel 8 Karakterer 8. Homomorfier av grupper I forrige kapittel definerte vi begrepet abstrakt gruppe, som en abstrakt versjon av begrepet symmetrigruppe. For å studere forbindelsen mellom abstrakte
Et noget ukomplett oppslagsverk for TMA4150 Algebra og tallteori. Ruben Spaans
 Et noget ukomplett oppslagsverk for TMA4150 Algebra og tallteori Ruben Spaans August 19, 2007 2 Part I Leksikon 3 Chapter 1 Alfabetisk oppslagsverk, for alle, kvantifikator. Brukes i forbindelse med utsagn,
Et noget ukomplett oppslagsverk for TMA4150 Algebra og tallteori Ruben Spaans August 19, 2007 2 Part I Leksikon 3 Chapter 1 Alfabetisk oppslagsverk, for alle, kvantifikator. Brukes i forbindelse med utsagn,
Matematikk 1 (TMA4100)
 Matematikk 1 (TMA4100) Forelesning 4: Grenseverdi (fortsettelse) Eirik Hoel Høiseth Stipendiat IMF NTNU 20. august, 2012 Formell definisjon av grenseverdi Formell definisjon av grenseverdi Uformell definisjon
Matematikk 1 (TMA4100) Forelesning 4: Grenseverdi (fortsettelse) Eirik Hoel Høiseth Stipendiat IMF NTNU 20. august, 2012 Formell definisjon av grenseverdi Formell definisjon av grenseverdi Uformell definisjon
Kontinuitet og derivasjon Forelesning i Matematikk 1 TMA4100
 Kontinuitet og derivasjon Forelesning i Matematikk 1 TMA4100 Hans Jakob Rivertz Institutt for matematiske fag 25. august 2010 2 Dagens pensum I dag vil vi se på følgende: Kontinuerlige funksjoner Den deriverte
Kontinuitet og derivasjon Forelesning i Matematikk 1 TMA4100 Hans Jakob Rivertz Institutt for matematiske fag 25. august 2010 2 Dagens pensum I dag vil vi se på følgende: Kontinuerlige funksjoner Den deriverte
4.1 Vektorrom og underrom
 4.1 Vektorrom og underrom Vektorrom er en abstraksjon av R n. De kan brukes til å utlede egenskaper, resultater og metoder for tilsynelatende svært ulike klasser av objekter : n-tupler, følger, funksjoner,
4.1 Vektorrom og underrom Vektorrom er en abstraksjon av R n. De kan brukes til å utlede egenskaper, resultater og metoder for tilsynelatende svært ulike klasser av objekter : n-tupler, følger, funksjoner,
Forelesning 2. Boolsk algebra og logiske porter
 Forelesning 2 Boolsk algebra og logiske porter Hovedpunkter Toverdi Boolsk algebra Huntington s postulater Diverse teorem Boolske funksjoner med sannhetstabell Forenkling av uttrykk (port implementasjon)
Forelesning 2 Boolsk algebra og logiske porter Hovedpunkter Toverdi Boolsk algebra Huntington s postulater Diverse teorem Boolske funksjoner med sannhetstabell Forenkling av uttrykk (port implementasjon)
Løsningsforslag til Mat112 Obligatorisk Oppgave, våren Oppgave 1
 Løsningsforslag til Mat2 Obligatorisk Oppgave, våren 206 Oppgave Avgjør om følgende rekker er konvergente: (a) n + n n + n + Løsning: rekken lim : n n + n n + n + Vi bruker grensesammenligningstesten mhp.
Løsningsforslag til Mat2 Obligatorisk Oppgave, våren 206 Oppgave Avgjør om følgende rekker er konvergente: (a) n + n n + n + Løsning: rekken lim : n n + n n + n + Vi bruker grensesammenligningstesten mhp.
MAT jan jan feb MAT Våren 2010
 MAT 1012 Våren 2010 Mandag 25. januar 2010 Forelesning Vi fortsetter med å se på det bestemte integralet, bl.a. på hvordan vi kan bruke numeriske beregninger til å bestemme verdien når vi ikke nødvendigvis
MAT 1012 Våren 2010 Mandag 25. januar 2010 Forelesning Vi fortsetter med å se på det bestemte integralet, bl.a. på hvordan vi kan bruke numeriske beregninger til å bestemme verdien når vi ikke nødvendigvis
Velkommen til eksamenskurs i matematikk 1
 Velkommen til eksamenskurs i matematikk 1 Haakon C. Bakka Institutt for matematiske fag 4.-5. desember 2010 Program I dag og i morgen skal vi holde på fra 10-16 med en pause fra 13-14. Vi skal gjennom:
Velkommen til eksamenskurs i matematikk 1 Haakon C. Bakka Institutt for matematiske fag 4.-5. desember 2010 Program I dag og i morgen skal vi holde på fra 10-16 med en pause fra 13-14. Vi skal gjennom:
Høgskolen i Agder Avdeling for realfag Institutt for matematiske fag. Emne: MA 2410: Reell analyse Dato: Våren 2000 Tema: Grenser og kontinuitet i R n
 Høgskolen i Agder Avdeling for realfag Institutt for matematiske fag Emne: MA 2410: Reell analyse Dato: Våren 2000 Tema: Grenser og kontinuitet i R n I kursbeskrivelsen står det... Topologiske omgrep i
Høgskolen i Agder Avdeling for realfag Institutt for matematiske fag Emne: MA 2410: Reell analyse Dato: Våren 2000 Tema: Grenser og kontinuitet i R n I kursbeskrivelsen står det... Topologiske omgrep i
Analyse og metodikk i Calculus 1
 Analyse og metodikk i Calculus 1 Fredrik Göthner og Raymi Eldby Norges teknisk-naturvitenskapelige universitet 3. desember 01 1 Innhold Forord 3 1 Vurdering av grafer og funksjoner 4 1.1 Hva er en funksjon?.........................
Analyse og metodikk i Calculus 1 Fredrik Göthner og Raymi Eldby Norges teknisk-naturvitenskapelige universitet 3. desember 01 1 Innhold Forord 3 1 Vurdering av grafer og funksjoner 4 1.1 Hva er en funksjon?.........................
Kapittel 3: Stokastiske variable og sannsynlighetsfordelinger
 Kapittel 3: Stokastiske variable og sannsynlighetsfordelinger TMA4245 Statistikk (B, K1, I) 3.1, 3.2, 3.3 foreleses torsdag 15.januar 0.00 0.02 0.04 0.06 0.08 160 170 180 190 hoyde i cm Mette.Langaas@math.ntnu.no
Kapittel 3: Stokastiske variable og sannsynlighetsfordelinger TMA4245 Statistikk (B, K1, I) 3.1, 3.2, 3.3 foreleses torsdag 15.januar 0.00 0.02 0.04 0.06 0.08 160 170 180 190 hoyde i cm Mette.Langaas@math.ntnu.no
Løsningsforslag. Oppgave 1 Gitt matrisene ] [ og C = A = 4 1 B = 2 1 3
![Løsningsforslag. Oppgave 1 Gitt matrisene ] [ og C = A = 4 1 B = 2 1 3 Løsningsforslag. Oppgave 1 Gitt matrisene ] [ og C = A = 4 1 B = 2 1 3](/thumbs/55/37240043.jpg) Prøve i Matematikk BYFE DAFE Dato: 27. mai 26 Hjelpemiddel: Kalkulator og formelark Alle svar skal grunngis. Alle deloppgaver har lik vekt. Løsningsforslag Oppgave Gitt matrisene [ 2 A 4 B [ 2 og C [ 2
Prøve i Matematikk BYFE DAFE Dato: 27. mai 26 Hjelpemiddel: Kalkulator og formelark Alle svar skal grunngis. Alle deloppgaver har lik vekt. Løsningsforslag Oppgave Gitt matrisene [ 2 A 4 B [ 2 og C [ 2
Et forsøk på et oppslagsverk for TMA4145 Lineære metoder
 Et forsøk på et oppslagsverk for TMA4145 Lineære metoder Ruben Spaans May 21, 2009 1 Oppslagsverk Adjungert Ball, la (X, d) være et metrisk rom og la ɛ > 0. Da er for x 0 X: 1. B(x 0 ; ɛ) = {x x X d(x,
Et forsøk på et oppslagsverk for TMA4145 Lineære metoder Ruben Spaans May 21, 2009 1 Oppslagsverk Adjungert Ball, la (X, d) være et metrisk rom og la ɛ > 0. Da er for x 0 X: 1. B(x 0 ; ɛ) = {x x X d(x,
Potensrekker Forelesning i Matematikk 1 TMA4100
 Potensrekker Forelesning i Matematikk 1 TMA4100 Hans Jakob Rivertz Institutt for matematiske fag 11. november 2011 Kapittel 8.8. Taylorrekker og Maclaurinrekker 3 Taylor-polynomer Definisjon (Taylorpolynomet
Potensrekker Forelesning i Matematikk 1 TMA4100 Hans Jakob Rivertz Institutt for matematiske fag 11. november 2011 Kapittel 8.8. Taylorrekker og Maclaurinrekker 3 Taylor-polynomer Definisjon (Taylorpolynomet
MAT Grublegruppen Notat 10
 MAT1100 - Grublegruppen Notat 10 Jørgen O. Lye Ringer Vi fortsetter i et lynkurs i algebraiske dyr. Først ut er ringer. En ring A (også kalt R) er en abelsk gruppe med addisjon + som operasjon. I tillegg
MAT1100 - Grublegruppen Notat 10 Jørgen O. Lye Ringer Vi fortsetter i et lynkurs i algebraiske dyr. Først ut er ringer. En ring A (også kalt R) er en abelsk gruppe med addisjon + som operasjon. I tillegg
EKSEMPLER TIL ETTERTANKE MAT1100 KALKULUS
 EKSEMPLER TIL ETTERTANKE MAT00 KALKULUS Simon Foldvik. Oktober 207 Dette dokumentet inneholder eksempler på hvor «ting går galt» og har til hensikt å vise eksempler på hva man ikke kan konkludere. Alle
EKSEMPLER TIL ETTERTANKE MAT00 KALKULUS Simon Foldvik. Oktober 207 Dette dokumentet inneholder eksempler på hvor «ting går galt» og har til hensikt å vise eksempler på hva man ikke kan konkludere. Alle
TMA 4140 Diskret Matematikk, 4. forelesning
 TMA 4140 Diskret Matematikk, 4. forelesning Haaken Annfelt Moe Department of Mathematical Sciences Norwegian University of Science and Technology (NTNU) September 9, 2011 Haaken Annfelt Moe (NTNU) TMA
TMA 4140 Diskret Matematikk, 4. forelesning Haaken Annfelt Moe Department of Mathematical Sciences Norwegian University of Science and Technology (NTNU) September 9, 2011 Haaken Annfelt Moe (NTNU) TMA
TMA4100 Matematikk 1, høst 2013
 TMA4100 Matematikk 1, høst 2013 Teknostart Forelesning 3 www.ntnu.no TMA4100 Matematikk 1, høst 2013, Teknostart Forelesning 3 Tema Logikk Definisjoner og Teoremer Mengder og Egenskaper ved de Reelle Tall
TMA4100 Matematikk 1, høst 2013 Teknostart Forelesning 3 www.ntnu.no TMA4100 Matematikk 1, høst 2013, Teknostart Forelesning 3 Tema Logikk Definisjoner og Teoremer Mengder og Egenskaper ved de Reelle Tall
Lineær Algebra og Vektorrom. Eivind Eriksen. Høgskolen i Oslo, Avdeling for Ingeniørutdanning
 Lineær Algebra og Vektorrom Eivind Eriksen Høgskolen i Oslo, Avdeling for Ingeniørutdanning c Eivind Eriksen 2005. Innhold Kapittel 1. Lineære likningssystemer 1 1.1. Lineære likningssystemer i to variable
Lineær Algebra og Vektorrom Eivind Eriksen Høgskolen i Oslo, Avdeling for Ingeniørutdanning c Eivind Eriksen 2005. Innhold Kapittel 1. Lineære likningssystemer 1 1.1. Lineære likningssystemer i to variable
MA1102 Grunnkurs i analyse II Vår 2019
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA112 Grunnkurs i analyse II Vår 219 8.4.1 Vi skal finne lengden til kurven x = 3t 2, y = 2t 3 der t 1. Som boka beskriver på
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA112 Grunnkurs i analyse II Vår 219 8.4.1 Vi skal finne lengden til kurven x = 3t 2, y = 2t 3 der t 1. Som boka beskriver på
De hele tall har addisjon, multiplikasjon, subtraksjon og lineær ordning, men ikke divisjon.
 Innledning til Matematikk Hans Petter Hornæs, hans.hornaes@hig.no Det er ofte vanskelig å komme i gang et fag. Innledningsvis er det gjerne en del grunnleggende begreper som må på plass. Mange studenter
Innledning til Matematikk Hans Petter Hornæs, hans.hornaes@hig.no Det er ofte vanskelig å komme i gang et fag. Innledningsvis er det gjerne en del grunnleggende begreper som må på plass. Mange studenter
Løsningsforslag til eksamen i MA0002, Brukerkurs i matematikk B
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 7 Løsningsforslag til eksamen i MA000, Brukerkurs i matematikk B 9. mai 01 Oppgave 1 a) Et plan i rommet har ligning
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 7 Løsningsforslag til eksamen i MA000, Brukerkurs i matematikk B 9. mai 01 Oppgave 1 a) Et plan i rommet har ligning
En følge i en lukket delmengde av R^m kan altså ikke konvergere mot en vektor utenfor den lukkede delmengden.
 MAT1300 Analyse I 2. februar 2009 For analyse i R spiller delmengder E \subset R på formen E = (a,b) og E= [a,b] ofte en spesiell rolle. Dette er de åpne og de lukkede intervallene. For analyse i R^m er
MAT1300 Analyse I 2. februar 2009 For analyse i R spiller delmengder E \subset R på formen E = (a,b) og E= [a,b] ofte en spesiell rolle. Dette er de åpne og de lukkede intervallene. For analyse i R^m er
Matriseoperasjoner. E.Malinnikova, NTNU, Institutt for matematiske fag. September 22, 2009
 Matriseoperasjoner E.Malinnikova, NTNU, Institutt for matematiske fag September 22, 2009 Addisjon av matriser Hvis A = [a ij ] og B = [b ij ] er matriser med samme størrelse, så er summen A + B matrisen
Matriseoperasjoner E.Malinnikova, NTNU, Institutt for matematiske fag September 22, 2009 Addisjon av matriser Hvis A = [a ij ] og B = [b ij ] er matriser med samme størrelse, så er summen A + B matrisen
Fasit MAT102 juni 2016
 Fasit MAT02 juni 206. (a) Finn egenverdiene og egenvektorene til matrisen ( ) 6 A = 2 7 Svar: λ = 8 og ( ) x = y y ( ) /2, λ = 5 og ( ) x = y y ( ) for alle y 0. (b) Finn den generelle løsningen på systemet
Fasit MAT02 juni 206. (a) Finn egenverdiene og egenvektorene til matrisen ( ) 6 A = 2 7 Svar: λ = 8 og ( ) x = y y ( ) /2, λ = 5 og ( ) x = y y ( ) for alle y 0. (b) Finn den generelle løsningen på systemet
Funksjoner Forelesning i Matematikk 1 TMA4100. Hans Jakob Rivertz Institutt for matematiske fag 18. august 2011
 Funksjoner Forelesning i Matematikk TMA400 Hans Jakob Rivertz Institutt for matematiske fag 8. august 20 2 Definisjon av funksjon Definisjon En funksjon er en regel f som til et hvert tall i definisjonsmengden
Funksjoner Forelesning i Matematikk TMA400 Hans Jakob Rivertz Institutt for matematiske fag 8. august 20 2 Definisjon av funksjon Definisjon En funksjon er en regel f som til et hvert tall i definisjonsmengden
Underveiseksamen i MAT-INF 1100, 17. oktober 2003 Tid: Oppgave- og svarark
 Underveiseksamen i MAT-INF 1100, 17. oktober 003 Tid: 9.00 11.00 Kandidatnummer: De 15 første oppgavene teller poeng hver, de siste 5 teller 4 poeng hver. Den totale poengsummen er altså 50. Det er 5 svaralternativer
Underveiseksamen i MAT-INF 1100, 17. oktober 003 Tid: 9.00 11.00 Kandidatnummer: De 15 første oppgavene teller poeng hver, de siste 5 teller 4 poeng hver. Den totale poengsummen er altså 50. Det er 5 svaralternativer
Emne 12 Mengdelære. ( bokstaven g er ikke et element i mengden B ) Betyr: B er mengden av alle positive oddetall.
 Emne 12 Mengdelære En mengde er en samling elementer. Mengden er veldefinert hvis vi entydig kan avgjøre om et vilkårlig element tilhører mengden eller ikke. Mengder på listeform. Endelige mengder:, Uendelige
Emne 12 Mengdelære En mengde er en samling elementer. Mengden er veldefinert hvis vi entydig kan avgjøre om et vilkårlig element tilhører mengden eller ikke. Mengder på listeform. Endelige mengder:, Uendelige
Obligatorisk oppgave MAT2200 VÅREN 2011
 Obligatorisk oppgave MAT2200 VÅREN 2011 Alle punkter teller likt. Det kreves at 50% er riktig (som betyr 10 av 19 punkter) for at oppgaven skal godkjennes. Den skal leveres i egen innleveringsboks i 7.
Obligatorisk oppgave MAT2200 VÅREN 2011 Alle punkter teller likt. Det kreves at 50% er riktig (som betyr 10 av 19 punkter) for at oppgaven skal godkjennes. Den skal leveres i egen innleveringsboks i 7.
Hans Petter Hornæs,
 Innledning til Matematikk Hans Petter Hornæs, hans.hornaes@hig.no Det er ofte vanskelig å komme i gang et fag. Innledningsvis er det gjerne en del grunnleggende begreper som må på plass. Mange studenter
Innledning til Matematikk Hans Petter Hornæs, hans.hornaes@hig.no Det er ofte vanskelig å komme i gang et fag. Innledningsvis er det gjerne en del grunnleggende begreper som må på plass. Mange studenter
OPPGAVE 1 LØSNINGSFORSLAG
 LØSNINGSFORSLAG UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Eksamen i MAT - Grunnkurs i matematikk I torsdag 5.desember 20 kl. 09:00-4:00 OPPGAVE a Modulus: w = 2 + 3 2 = 2. Argument
LØSNINGSFORSLAG UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Eksamen i MAT - Grunnkurs i matematikk I torsdag 5.desember 20 kl. 09:00-4:00 OPPGAVE a Modulus: w = 2 + 3 2 = 2. Argument
Eneboerspillet del 2. Håvard Johnsbråten, januar 2014
 Eneboerspillet del 2 Håvard Johnsbråten, januar 2014 I Johnsbråten (2013) løste jeg noen problemer omkring eneboerspillet vha partall/oddetall. I denne parallellversjonen av artikkelen i vil jeg i stedet
Eneboerspillet del 2 Håvard Johnsbråten, januar 2014 I Johnsbråten (2013) løste jeg noen problemer omkring eneboerspillet vha partall/oddetall. I denne parallellversjonen av artikkelen i vil jeg i stedet
OPPGAVER FOR FORUM
 OPPGAVER FOR FORUM 2006-2007 MERK!: Du skal først skrive hele oppgaveteksten for hver oppgave, og deretter svaret på oppgaven. Hvert svar skal være detajert, og skrevet i et klart og tydelig matematisk
OPPGAVER FOR FORUM 2006-2007 MERK!: Du skal først skrive hele oppgaveteksten for hver oppgave, og deretter svaret på oppgaven. Hvert svar skal være detajert, og skrevet i et klart og tydelig matematisk
Potensrekker Forelesning i Matematikk 1 TMA4100
 Potensrekker Forelesning i Matematikk 1 TMA4100 Hans Jakob Rivertz Institutt for matematiske fag 1. november 2011 Kapittel 8.7. Potensrekker (fra konvergens av) 3 Konvergens av potensrekker Eksempel For
Potensrekker Forelesning i Matematikk 1 TMA4100 Hans Jakob Rivertz Institutt for matematiske fag 1. november 2011 Kapittel 8.7. Potensrekker (fra konvergens av) 3 Konvergens av potensrekker Eksempel For
Sammensetningen h = f g er en funksjon fra A til C, h: A -> C og er definert ved h(a) = f(g(a)) Viktig: f g g f
 Sammensetningen av to funksjoner. Gitt mengdene A, B og C. La f og g være funksjonene der g: A -> B f: B -> C Da kan vi lage sammensetningen h av f og g. Den betegnes som h = f g (lese som «f ring g»).
Sammensetningen av to funksjoner. Gitt mengdene A, B og C. La f og g være funksjonene der g: A -> B f: B -> C Da kan vi lage sammensetningen h av f og g. Den betegnes som h = f g (lese som «f ring g»).
I dette kapittelet skal vi studerer noen matematiske objekter som kalles matriser. Disse kan blant annet brukes for å løse lineære likningssystemer.
 Kapittel 2 Matriser I dette kapittelet skal vi studerer noen matematiske objekter som kalles matriser. Disse kan blant annet brukes for å løse lineære likningssystemer. 2.1 Definisjoner og regneoperasjoner
Kapittel 2 Matriser I dette kapittelet skal vi studerer noen matematiske objekter som kalles matriser. Disse kan blant annet brukes for å løse lineære likningssystemer. 2.1 Definisjoner og regneoperasjoner
UNIVERSITETET I BERGEN
 BOKMÅL MAT - Høst 03 UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Eksamen i emnet MAT Grunnkurs i Matematikk I Mandag 6. desember 03, kl. 09- Tillatte hjelpemidler: Lærebok ( Calculus
BOKMÅL MAT - Høst 03 UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Eksamen i emnet MAT Grunnkurs i Matematikk I Mandag 6. desember 03, kl. 09- Tillatte hjelpemidler: Lærebok ( Calculus
INF1080 Logiske metoder for informatikk. 1 Små oppgaver [70 poeng] 1.1 Grunnleggende mengdelære [3 poeng] 1.2 Utsagnslogikk [3 poeng]
![INF1080 Logiske metoder for informatikk. 1 Små oppgaver [70 poeng] 1.1 Grunnleggende mengdelære [3 poeng] 1.2 Utsagnslogikk [3 poeng] INF1080 Logiske metoder for informatikk. 1 Små oppgaver [70 poeng] 1.1 Grunnleggende mengdelære [3 poeng] 1.2 Utsagnslogikk [3 poeng]](/thumbs/60/44567099.jpg) INF1080 Logiske metoder for informatikk Digital eksamen (med løsningsforslag) Dette er et utkast til løsningsforslag til eksamen i INF1080, og feil kan forekomme. Hvis du finner noen feil, si ifra til
INF1080 Logiske metoder for informatikk Digital eksamen (med løsningsforslag) Dette er et utkast til løsningsforslag til eksamen i INF1080, og feil kan forekomme. Hvis du finner noen feil, si ifra til
INF1080 Logiske metoder for informatikk. 1 Små oppgaver [70 poeng] 1.1 Grunnleggende mengdelære [3 poeng] 1.2 Utsagnslogikk [3 poeng]
![INF1080 Logiske metoder for informatikk. 1 Små oppgaver [70 poeng] 1.1 Grunnleggende mengdelære [3 poeng] 1.2 Utsagnslogikk [3 poeng] INF1080 Logiske metoder for informatikk. 1 Små oppgaver [70 poeng] 1.1 Grunnleggende mengdelære [3 poeng] 1.2 Utsagnslogikk [3 poeng]](/thumbs/57/40971904.jpg) INF1080 Logiske metoder for informatikk Digital eksamen Tid: Onsdag 7. desember 2016 kl. 14.30 18.30 (4 timer) Tillatte hjelpemidler: Ingen Eksamen består av to deler som er verdt omtrent like mye. Den
INF1080 Logiske metoder for informatikk Digital eksamen Tid: Onsdag 7. desember 2016 kl. 14.30 18.30 (4 timer) Tillatte hjelpemidler: Ingen Eksamen består av to deler som er verdt omtrent like mye. Den
Eksamensoppgave i MA1101 Grunnkurs i analyse
 Institutt for matematiske fag Eksamensoppgave i MA1101 Grunnkurs i analyse Faglig kontakt under eksamen: Kari Hag Tlf: 48 30 19 88 Eksamensdato: 15. oktober 018 Eksamenstid (fra til): 17:30 19:00 Hjelpemiddelkode/Tillatte
Institutt for matematiske fag Eksamensoppgave i MA1101 Grunnkurs i analyse Faglig kontakt under eksamen: Kari Hag Tlf: 48 30 19 88 Eksamensdato: 15. oktober 018 Eksamenstid (fra til): 17:30 19:00 Hjelpemiddelkode/Tillatte
MAT-INF 2360: Obligatorisk oppgave 2
 6. mars, 13 MAT-INF 36: Obligatorisk oppgave Innleveringsfrist: 4/4-13, kl. 14:3 Informasjon Den skriftlige besvarelsen skal leveres i obligkassa som står i gangen utenfor ekspedisjonen i 7. et. i Niels
6. mars, 13 MAT-INF 36: Obligatorisk oppgave Innleveringsfrist: 4/4-13, kl. 14:3 Informasjon Den skriftlige besvarelsen skal leveres i obligkassa som står i gangen utenfor ekspedisjonen i 7. et. i Niels
Konvergenstester Forelesning i Matematikk 1 TMA4100
 Konvergenstester Forelesning i Matematikk 1 TMA4100 Hans Jakob Rivertz Institutt for matematiske fag 1. november 2011 Kapittel 8.6. Alternerende rekker Absolutt og betinget konvergens 3 Alternerende rekker
Konvergenstester Forelesning i Matematikk 1 TMA4100 Hans Jakob Rivertz Institutt for matematiske fag 1. november 2011 Kapittel 8.6. Alternerende rekker Absolutt og betinget konvergens 3 Alternerende rekker
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Deleksamen i Eksamensdag: 9. april,. Tid for eksamen: : :. Oppgavesettet er på 9 sider. Vedlegg: Tillatte hjelpemidler: MAT Kalkulus og
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Deleksamen i Eksamensdag: 9. april,. Tid for eksamen: : :. Oppgavesettet er på 9 sider. Vedlegg: Tillatte hjelpemidler: MAT Kalkulus og
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT111 Prøveeksamen Eksamensdag: 5. juni 21. Tid for eksamen: 1. 13.3. Oppgavesettet er på 9 sider. Vedlegg: Tillatte hjelpemidler:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT111 Prøveeksamen Eksamensdag: 5. juni 21. Tid for eksamen: 1. 13.3. Oppgavesettet er på 9 sider. Vedlegg: Tillatte hjelpemidler:
Oppfriskningskurs i matematikk Dag 3
 Oppfriskningskurs i matematikk Dag 3 Petter Nyland Institutt for matematiske fag Onsdag 8. august 2018 Dagen i dag Tema 4 Polynomer: Faktorisering, røtter, polynomdivisjon, kvadratiske ligninger og rasjonale
Oppfriskningskurs i matematikk Dag 3 Petter Nyland Institutt for matematiske fag Onsdag 8. august 2018 Dagen i dag Tema 4 Polynomer: Faktorisering, røtter, polynomdivisjon, kvadratiske ligninger og rasjonale
Institutionen för Matematik, KTH
 Institutionen för Matematik, KTH Lösningsforslag till tentamen, 200-2-7, kl. 8.00-.00. 5B04, Envariabel. Uppgift. Den karakteristiske ligningen r 2 r + 2 0 kan omskrives som (r )(r 2) 0. Den generelle
Institutionen för Matematik, KTH Lösningsforslag till tentamen, 200-2-7, kl. 8.00-.00. 5B04, Envariabel. Uppgift. Den karakteristiske ligningen r 2 r + 2 0 kan omskrives som (r )(r 2) 0. Den generelle
MAT1030 Forelesning 14
 MAT1030 Forelesning 14 Mer om funksjoner Roger Antonsen - 10. mars 2009 (Sist oppdatert: 2009-03-10 11:34) Kapittel 6: Funksjoner Surjektive funksjoner Den neste gruppen av funksjoner vi skal se på er
MAT1030 Forelesning 14 Mer om funksjoner Roger Antonsen - 10. mars 2009 (Sist oppdatert: 2009-03-10 11:34) Kapittel 6: Funksjoner Surjektive funksjoner Den neste gruppen av funksjoner vi skal se på er
Grunnleggende notasjon ℕ = 1, 2, 3, 4, 5, 6, ℤ =, 3, 2, 1, 0, 1, 2, 3,
 Grunnleggende notasjon ℕ,, 3, 4, 5, 6, ℤ, 3,,, 0,,, 3, ℝ 𝑎𝑙𝑙𝑒 𝑟𝑒𝑒𝑙𝑒 𝑡𝑎𝑙𝑙 ℚ 𝑎𝑙𝑙𝑒 𝑟𝑎𝑠𝑗𝑜𝑛𝑎𝑙𝑒 𝑡𝑎𝑙𝑙 𝑎 𝑎, ℤ, 0 Induksjonsprinsippet Anta at for hver 𝑛 ℕ har vi gitt et utsagn 𝑃. Anta videre at vi vet at følgende
Grunnleggende notasjon ℕ,, 3, 4, 5, 6, ℤ, 3,,, 0,,, 3, ℝ 𝑎𝑙𝑙𝑒 𝑟𝑒𝑒𝑙𝑒 𝑡𝑎𝑙𝑙 ℚ 𝑎𝑙𝑙𝑒 𝑟𝑎𝑠𝑗𝑜𝑛𝑎𝑙𝑒 𝑡𝑎𝑙𝑙 𝑎 𝑎, ℤ, 0 Induksjonsprinsippet Anta at for hver 𝑛 ℕ har vi gitt et utsagn 𝑃. Anta videre at vi vet at følgende
x 1 x 2 x = x n b 1 b 2 b = b m Det kan være vanskelig (beregningsmessig) og bearbeide utrykk som inneholder
 4 Noen merknader 4. Lineære systemer Ax = b Gitt systemet Ax = b, A = [a i,j ] i=,,...,m, j=,,...,n x = b = Det kan være vanskelig (beregningsmessig) og bearbeide utrykk som inneholder b i. Med det finnes
4 Noen merknader 4. Lineære systemer Ax = b Gitt systemet Ax = b, A = [a i,j ] i=,,...,m, j=,,...,n x = b = Det kan være vanskelig (beregningsmessig) og bearbeide utrykk som inneholder b i. Med det finnes
