TMA 4140 Diskret Matematikk, 2. forelesning
|
|
|
- Edvin Eskil Espeland
- 7 år siden
- Visninger:
Transkript
1 TMA 4140 Diskret Matematikk, 2. forelesning Haaken Annfelt Moe Department of Mathematical Sciences Norwegian University of Science and Technology (NTNU) September 2, 2011 Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
2 Outline 1 Generell informasjon 2 Repetisjon Predikater og kvantorer Nøstede kvantorer Slutningsregler Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
3 Outline 1 Generell informasjon 2 Repetisjon Predikater og kvantorer Nøstede kvantorer Slutningsregler Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
4 Midtsemesterprøve Midtsemesterprøve blir onsdag 12. Oktober, , samme tid som øvingsforelesningene. Sted er ikke avklart ennå. Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
5 Outline 1 Generell informasjon 2 Repetisjon Predikater og kvantorer Nøstede kvantorer Slutningsregler Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
6 Repetisjon fra 1.1, 1.2 En proposisjon er en deklarativ setning som en enten er sann eller usann. Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
7 Repetisjon fra 1.1, 1.2 En proposisjon er en deklarativ setning som en enten er sann eller usann. Sannhetsverdien til en proposisjon er T (true/sann) eller F (false/usann). Representeres ofte med 0 (usann) og 1 (sann). Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
8 Repetisjon fra 1.1, 1.2 En proposisjon er en deklarativ setning som en enten er sann eller usann. Sannhetsverdien til en proposisjon er T (true/sann) eller F (false/usann). Representeres ofte med 0 (usann) og 1 (sann). Proposisjoner dannet med eksisterende proposisjoner og operatorer (f.eks ) kalles sammensatte proposisjoner. Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
9 Repetisjon fra 1.1, 1.2 En proposisjon er en deklarativ setning som en enten er sann eller usann. Sannhetsverdien til en proposisjon er T (true/sann) eller F (false/usann). Representeres ofte med 0 (usann) og 1 (sann). Proposisjoner dannet med eksisterende proposisjoner og operatorer (f.eks ) kalles sammensatte proposisjoner. Operatorer som brukes til å danne sammensatte proposisjoner er,,,,,. Vi definerte disse ved bruk av sannhetsverditabeller. Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
10 Repetisjon fra 1.2, 1.3 En tautologi er en proposisjon som alltid er sann, en kontradiksjon er en proposisjon som aldri er sann. Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
11 Repetisjon fra 1.2, 1.3 En tautologi er en proposisjon som alltid er sann, en kontradiksjon er en proposisjon som aldri er sann. To proposisjoner er logisk ekvivalente,, om de alltid tar samme sannhetsverdi. Sett fra et logikk-synspunkt er disse to proposisjonene like. Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
12 Repetisjon fra 1.2, 1.3 En tautologi er en proposisjon som alltid er sann, en kontradiksjon er en proposisjon som aldri er sann. To proposisjoner er logisk ekvivalente,, om de alltid tar samme sannhetsverdi. Sett fra et logikk-synspunkt er disse to proposisjonene like. En proposisjonell funksjon er en funksjon som tar en bestemt sannhetsverdi avhengig av verdien på en eller flere sannhetsverdier. Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
13 Repetisjon fra 1.2, 1.3 En tautologi er en proposisjon som alltid er sann, en kontradiksjon er en proposisjon som aldri er sann. To proposisjoner er logisk ekvivalente,, om de alltid tar samme sannhetsverdi. Sett fra et logikk-synspunkt er disse to proposisjonene like. En proposisjonell funksjon er en funksjon som tar en bestemt sannhetsverdi avhengig av verdien på en eller flere sannhetsverdier. Systemspesifikasjon. Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
14 Outline 1 Generell informasjon 2 Repetisjon Predikater og kvantorer Nøstede kvantorer Slutningsregler Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
15 Predikater Utsagn som x < 7 og x y = 5 er ikke sanne eller gale før det er bestemt verdier for x og y. Dvs de får en sannhetsverdi som varierer ettersom hva x og y er. Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
16 Predikater Utsagn som x < 7 og x y = 5 er ikke sanne eller gale før det er bestemt verdier for x og y. Dvs de får en sannhetsverdi som varierer ettersom hva x og y er. Definition (Proposisjonell funksjon) Et utsagn P(x 1, x 2,...) som er enten sant eller usant avhengig av verdien på variablene x 1, x 2,... kalles en proposisjonell funksjon. Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
17 Predikater Utsagn som x < 7 og x y = 5 er ikke sanne eller gale før det er bestemt verdier for x og y. Dvs de får en sannhetsverdi som varierer ettersom hva x og y er. Definition (Proposisjonell funksjon) Et utsagn P(x 1, x 2,...) som er enten sant eller usant avhengig av verdien på variablene x 1, x 2,... kalles en proposisjonell funksjon. Det som skal oppfylles, som < 7, kalles predikatet. Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
18 Predikater Utsagn som x < 7 og x y = 5 er ikke sanne eller gale før det er bestemt verdier for x og y. Dvs de får en sannhetsverdi som varierer ettersom hva x og y er. Definition (Proposisjonell funksjon) Et utsagn P(x 1, x 2,...) som er enten sant eller usant avhengig av verdien på variablene x 1, x 2,... kalles en proposisjonell funksjon. Det som skal oppfylles, som < 7, kalles predikatet. Hvis vi bestemmer at variablene tar verdier fra en bestemt samling U, et univers, kan man spørre hvordan predikatet oppfører seg på hele universet. Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
19 Kvantorer Definition (Allkvantor) Den universelle kvantifiseringen av P(x), xp(x), er proposisjonen P(x) er sann for alle x fra U. Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
20 Kvantorer Definition (Allkvantor) Den universelle kvantifiseringen av P(x), xp(x), er proposisjonen P(x) er sann for alle x fra U. Definition (Eksistenskvantor) Den eksistensielle kvantifiseringen av P(x), xp(x), er proposisjonen det finnes minst en x i U slik at P(x) er sann. Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
21 Kvantorer Definition (Allkvantor) Den universelle kvantifiseringen av P(x), xp(x), er proposisjonen P(x) er sann for alle x fra U. Definition (Eksistenskvantor) Den eksistensielle kvantifiseringen av P(x), xp(x), er proposisjonen det finnes minst en x i U slik at P(x) er sann. I et utsagn med variabler sier vi at en variabel er bundet hvis den er kvantifisert og at den er fri hvis den ikke er kvantifisert. Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
22 Kvantorer Definition (Allkvantor) Den universelle kvantifiseringen av P(x), xp(x), er proposisjonen P(x) er sann for alle x fra U. Definition (Eksistenskvantor) Den eksistensielle kvantifiseringen av P(x), xp(x), er proposisjonen det finnes minst en x i U slik at P(x) er sann. I et utsagn med variabler sier vi at en variabel er bundet hvis den er kvantifisert og at den er fri hvis den ikke er kvantifisert. Merk at en proposisjonell funksjon kun er en proposisjon hvis alle variablene er bundet. Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
23 Mer om kvantorer Hvis vi negerer kvantorer får vi DeMorgans lover for kvantorer. Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
24 Mer om kvantorer Hvis vi negerer kvantorer får vi DeMorgans lover for kvantorer. Vi har disse to logiske ekvivalensene: xp(x) x P(x) xp(x) x P(x) Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
25 Mer om kvantorer Hvis vi negerer kvantorer får vi DeMorgans lover for kvantorer. Vi har disse to logiske ekvivalensene: xp(x) x P(x) xp(x) x P(x) Oversette fra dagligspråk til kvantifiserte utsagn. Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
26 Outline 1 Generell informasjon 2 Repetisjon Predikater og kvantorer Nøstede kvantorer Slutningsregler Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
27 Nøstede kvantorer To kvantorer er nøstet hvis variablene deres på en eller annen måte påvirker hverandre. Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
28 Nøstede kvantorer To kvantorer er nøstet hvis variablene deres på en eller annen måte påvirker hverandre. Merk: x yp(x, y) er ikke det samme som x yp)x, y). Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
29 Outline 1 Generell informasjon 2 Repetisjon Predikater og kvantorer Nøstede kvantorer Slutningsregler Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
30 Slutningsregler Definition (Teorem) Et teorem er et utsagn som kan vises å måtte være sant. Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
31 Slutningsregler Definition (Teorem) Et teorem er et utsagn som kan vises å måtte være sant. Hva betyr det å vise at noe er sant? At det kan konkluderes fra premissene via gyldig argumentasjon. Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
32 Slutningsregler Definition (Teorem) Et teorem er et utsagn som kan vises å måtte være sant. Hva betyr det å vise at noe er sant? At det kan konkluderes fra premissene via gyldig argumentasjon. Definition (Gyldig argumentasjon) En argumentasjon er gyldig hvis når hypotesene er sanne må konklusjonen være sann. Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
33 Slutningsregler Definition (Teorem) Et teorem er et utsagn som kan vises å måtte være sant. Hva betyr det å vise at noe er sant? At det kan konkluderes fra premissene via gyldig argumentasjon. Definition (Gyldig argumentasjon) En argumentasjon er gyldig hvis når hypotesene er sanne må konklusjonen være sann. Til dette har vi slutningsregler (side 66 i boka). Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
34 Slutningsregler Definition (Teorem) Et teorem er et utsagn som kan vises å måtte være sant. Hva betyr det å vise at noe er sant? At det kan konkluderes fra premissene via gyldig argumentasjon. Definition (Gyldig argumentasjon) En argumentasjon er gyldig hvis når hypotesene er sanne må konklusjonen være sann. Til dette har vi slutningsregler (side 66 i boka). Tre måter å vise at p q, en implikasjon, er sann: Direkte Indirekte Motsigelse Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
35 Neste gang: Avsnitt 2.1 og 2.2, kanskje litt av 2.3. Vi sees! Haaken Annfelt Moe (NTNU) TMA 4140 Diskret Matematikk, 2. forelesning / 16
TMA 4140 Diskret Matematikk, 3. forelesning
TMA 4140 Diskret Matematikk, 3. forelesning Haaken Annfelt Moe Department of Mathematical Sciences Norwegian University of Science and Technology (NTNU) September 5, 2011 Haaken Annfelt Moe (NTNU) TMA
TMA 4140 Diskret Matematikk, 1. forelesning
TMA 4140 Diskret Matematikk, 1. forelesning Haaken Annfelt Moe Department of Mathematical Sciences Norwegian University of Science and Technology (NTNU) August 29, 2011 Haaken Annfelt Moe (NTNU) TMA 4140
Ekvivalente utsagn. Eksempler: Tautologi : p V p Selvmotsigelse: p Λ p
Ekvivalente utsagn Definisjoner: Et sammensatt utsagn som ALLTID er SANT kalles for en TAUTOLOGI. Et sammensatt utsagn som ALLTID er USANT kalles for en SELVMOTIGELSE eller en KONTRADIKSJON (eng. contradiction).
TMA 4140 Diskret Matematikk, 4. forelesning
TMA 4140 Diskret Matematikk, 4. forelesning Haaken Annfelt Moe Department of Mathematical Sciences Norwegian University of Science and Technology (NTNU) September 9, 2011 Haaken Annfelt Moe (NTNU) TMA
Løsningsforslag for 1. obligatoriske oppgave høsten 2014
Løsningsforslag for 1 obligatoriske oppgave høsten 2014 Oppgave 1a) 1) Bruk av sannhetsverditabell: p q p p ( p ) p (( p ) S S U S U S S U U S U S U S S S S S U U S U U S Vi ser at (( p ) er en tautologi,
Emne 13 Utsagnslogikk
Emne 13 Utsagnslogikk Et utsagn er en erklæring som er entydig sann eller usann, men ikke begge deler. Noen eksempler på (ekte) utsagn: Utsagn : Gjøvik har bystatus er sann ( i alle fall pr. dags dato
Vi startet forelesningen med litt repetisjon fra forrige uke: Det omvendte, kontrapositive og inverse utsagnet. La p og q være to utsagn, og p -> q
Vi startet forelesningen med litt repetisjon fra forrige uke: Det omvendte, kontrapositive og inverse utsagnet. La p og q være to utsagn, og p -> q Begrepene «tilstrekkelig», «nødvendig» og «bare hvis».
MAT1030 Diskret Matematikk
MAT1030 Diskret Matematikk Forelesning 7: Logikk, predikatlogikk Roger Antonsen Institutt for informatikk, Universitetet i Oslo 10. februar 2009 (Sist oppdatert: 2009-02-11 01:52) Kapittel 4: Logikk (predikatlogikk)
Løsningsforslag til oblig 1 i DM 2018
Løsningsforslag til oblig 1 i DM 2018 Oppgave 2 p: «Det regner» q: «Det blåser» a) ikke p og ikke q blir: p q = ( p q) b) q hvis ikke p blir det samme som hvis ikke p så q: p q c) p bare hvis ikke q blir:
MAT1030 Diskret matematikk
MAT1030 Diskret matematikk Forelesning 7: Predikatlogikk Dag Normann Matematisk Institutt, Universitetet i Oslo 4. februar 2008 Oppsummering Vi har innført sannhetsverdiene T og F, begrepet utsagnsvariabel
Oppsummering. MAT1030 Diskret matematikk. Oppsummering. Oppsummering. Eksempel ((p q) r) Eksempel (p (q r))
Oppsummering MAT1030 Diskret matematikk Forelesning 7: Predikatlogikk Dag Normann Matematisk Institutt, Universitetet i Oslo 4. februar 2008 Vi har innført sannhetsverdiene T og F, begrepet utsagnsvariabel
FOL: syntaks og representasjon. 15. og 16. forelesning
FOL: syntaks og representasjon 15. og 16. forelesning Førsteordens logikk Førsteordens logikk: et formelt system som man bruker til å representere og studere argumenter. Som utsagnslogikk, men mer uttrykkskraftig,
Kapittel 4: Logikk (predikatlogikk)
MAT1030 Diskret Matematikk Forelesning 7: Logikk, predikatlogikk Dag Normann Matematisk Institutt, Universitetet i Oslo Kapittel 4: Logikk (predikatlogikk) 9. februar 2010 (Sist oppdatert: 2010-02-09 14:22)
Kapittel 4: Logikk (predikatlogikk)
MAT1030 Diskret Matematikk Forelesning 7: Logikk, predikatlogikk Roger Antonsen Institutt for informatikk, Universitetet i Oslo Kapittel 4: Logikk (predikatlogikk) 10. februar 2009 (Sist oppdatert: 2009-02-11
Det betyr igjen at det får verdien F nøyaktig når p = T, q = T og r = F.
Forelesning 7 Dag Normann - 4. februar 2008 Oppsummering Vi har innført sannhetsverdiene T og F, begrepet utsagnsvariabel og de utsagnslogiske bindeordene,,, og. Vi har sett hvordan vi kan undersøke egenskapene
Kapittel 4: Mer predikatlogikk
MAT1030 Diskret Matematikk Forelesning 8: Logikk, predikatlogikk, bevisteknikker Roger Antonsen Institutt for informatikk, Universitetet i Oslo Kapittel 4: Mer predikatlogikk 11. februar 009 (Sist oppdatert:
Kvantorer. MAT1030 Diskret matematikk. Kvantorer. Kvantorer. Eksempel. Eksempel (Fortsatt) Forelesning 8: Predikatlogikk, bevisføring
Kvantorer MAT1030 Diskret matematikk Forelesning 8: Predikatlogikk, bevisføring Dag Normann Matematisk Institutt, Universitetet i Oslo 6. februar 008 Mandag 04.0.008 introduserte vi predikatlogikk Vi innførte
MAT1030 Diskret matematikk
MAT1030 Diskret matematikk Forelesning 8: Predikatlogikk, bevisføring Dag Normann Matematisk Institutt, Universitetet i Oslo 6. februar 2008 Kvantorer Mandag 04.02.2008 introduserte vi predikatlogikk Vi
MAT1030 Forelesning 8
MAT1030 Forelesning 8 Logikk, predikatlogikk, bevisteknikker Roger Antonsen - 11. februar 009 (Sist oppdatert: 009-0-17 10:5) Kapittel 4: Mer predikatlogikk Oppsummering Læringsmålene for kapitlet om logikk
Kapittel 4: Logikk (utsagnslogikk)
MAT1030 Diskret Matematikk Forelesning 6: Logikk, predikatlogikk Roger Antonsen Institutt for informatikk, Universitetet i Oslo Kapittel 4: Logikk (utsagnslogikk) 28. januar 2009 (Sist oppdatert: 2009-01-28
MAT1030 Diskret Matematikk
MAT1030 Diskret Matematikk Forelesning 6: Logikk, predikatlogikk Roger Antonsen Institutt for informatikk, Universitetet i Oslo 28. januar 2009 (Sist oppdatert: 2009-01-28 12:23) Kapittel 4: Logikk (utsagnslogikk)
INF1800 Forelesning 20
INF1800 Forelesning 20 Førsteordens logikk Roger Antonsen - 22. oktober 2008 (Sist oppdatert: 2008-10-22 10:51) Mer om førsteordens logikk Tillukninger Vi har definert semantikk kun for lukkede formler.
INF1800 LOGIKK OG BEREGNBARHET
INF1800 LOGIKK OG BEREGNBARHET FORELESNING 20: FØRSTEORDENS LOGIKK Roger Antonsen Institutt for informatikk Universitetet i Oslo 22. oktober 2008 (Sist oppdatert: 2008-10-22 10:50) Mer om førsteordens
Mer om førsteordens logikk
INF1800 LOGIKK OG BEREGNBARHET FORELESNING 20: FØRSTEORDENS LOGIKK Roger Antonsen Mer om førsteordens logikk Institutt for informatikk Universitetet i Oslo 22. oktober 2008 (Sist oppdatert: 2008-10-22
Kapittel 4: Mer predikatlogikk
MAT1030 Diskret Matematikk Forelesning 8: Logikk, predikatlogikk, bevisteknikker Dag Normann Matematisk Institutt, Universitetet i Oslo Kapittel 4: Mer predikatlogikk 10. februar 010 (Sist oppdatert: 010-0-10
Kalles p for premissen og q for konklusjonen. Utsagnet kan uttrykkes på mange forskjellige måter:
Logisk implikasjon (eng: conditional statement) La p og q være to utsagn. Utsagnet leses som «p impliserer q». Utsagnet er usant hvis p er sant og q er usant, og er sant ellers. Huskeregel: «SUSS» Operatoren
Løsningsforslag til 1. obligatorisk oppgave i Diskret matematikk, høsten 2016
Løsningsforslag til 1. obligatorisk oppgave i Diskret matematikk, høsten 2016 Oppgave 1 a) b) r = p q p q s = p q q p q p t = p q p q c) Vi ser av sannehetsverditabellen at uttrykkene (p q) r og p (q r)
MAT1030 Forelesning 7
MAT1030 Forelesning 7 Logikk, predikatlogikk Dag Normann - 9. februar 2010 (Sist oppdatert: 2010-02-09 14:24) Kapittel 4: Logikk (predikatlogikk) Predikatlogikk Vi brukte hele forrige uke til å innføre
Et utsagn (eng: proposition) er en erklærende setning som enten er sann eller usann. Vi kaller det gjerne en påstand.
Utsagnslogikk. Et utsagn (eng: proposition) er en erklærende setning som enten er sann eller usann. Vi kaller det gjerne en påstand. Eksempler: Avgjør om følgende setninger er et utsagn, og i så fall;
Repetisjonsforelesning
Repetisjonsforelesning INF3170 Andreas Nakkerud Institutt for informatikk 24. november 2014 Institutt for informatikk Universitetet i Oslo Repetisjon 24. november 2014 1 / 39 Utsagnslogikk Utsagnslogikk
MAT1030 Diskret matematikk
MAT1030 Diskret matematikk Plenumsregning 5: Ukeoppgaver fra kapittel 4 Roger Antonsen Matematisk Institutt, Universitetet i Oslo 14. februar 2008 Oppgave 4.4 Skriv ned setninger som svarer til den konverse
MAT1030 Forelesning 6
MAT1030 Forelesning 6 Logikk, predikatlogikk Roger Antonsen - 28. januar 2009 (Sist oppdatert: 2009-01-28 12:23) Kapittel 4: Logikk (utsagnslogikk) Mer om parenteser Eksempel. (p q r) (p r) (q r) Her mangler
Kapittel 4: Logikk. MAT1030 Diskret Matematikk. Oppsummering. En digresjon. Forelesning 6: Utsagnslogikk og predikatlogikk.
MAT1030 Diskret Matematikk Forelesning 6: Utsagnslogikk og predikatlogikk Dag Normann Matematisk Institutt, Universitetet i Oslo Kapittel 4: Logikk 3. februar 2010 (Sist oppdatert: 2010-02-03 12:49) MAT1030
Sammensatte utsagn, sannhetsverditabeller. MAT1030 Diskret matematikk. Sammensatte utsagn, sannhetsverditabeller
Sammensatte utsagn, sannhetsverditabeller MAT1030 Diskret matematikk Forelesning 6: Logikk Dag Normann Matematisk Institutt, Universitetet i Oslo 30. januar 2008 Mandag 28/1 innførte vi bindeordene (konnektivene)
MAT1030 Forelesning 5
MAT1030 Forelesning 5 Utsagnslogikk Dag Normann - 2. februar 2010 (Sist oppdatert: 2010-02-02 14:10) Kapittel 4: Logikk (fortsettelse) Repetisjon Forrige gang snakket vi om utsagn og predikater, og vi
Karakteriseringen av like mengder. Mengder definert ved en egenskap.
Notat 2 for MAT1140 2 Bevis La oss si at vi er overbevist om at utsagn P er sant, og at vi ønsker å kommunisere denne innsikten. Eller la oss si vi er ganske sikre på at P er sant, men ønsker, overfor
Slides til 1.6 og 1.7. Andreas Leopold Knutsen
Slides til 1.6 og 1.7 Andreas Leopold Knutsen January 17, 2010 Begreper Matematiske resultater/utsagn som er sanne kalles gjerne: Teorem = viktig utsagn Proposisjon/Sats/Setning = litt mindre viktig utsagn
Vi var midt i et eksempel, som vi tar opp igjen her, da tiden var ute.
Forelesning 6 Logikk Dag Normann - 30. januar 2008 Sammensatte utsagn, sannhetsverditabeller Mandag 28/1 innførte vi bindeordene (konnektivene) for og, for eller og for ikke. Vi så hvordan vi kunne definere
Et utsagn (eng: proposition) er en erklærende setning som enten er sann eller usann. Vi kaller det gjerne en påstand.
Utsagnslogikk. Et utsagn (eng: proposition) er en erklærende setning som enten er sann eller usann. Vi kaller det gjerne en påstand. Eksempler: Avgjør om følgende setninger er et utsagn, og i så fall;
MAT1030 Forelesning 5
MAT1030 Forelesning 5 Logikk, utsagnslogikk Roger Antonsen - 27. januar 2009 (Sist oppdatert: 2009-01-28 09:12) Kapittel 4: Logikk (fortsettelse) Repetisjon Forrige gang snakket vi om utsagn og predikater,
Chapter 1 - Discrete Mathematics and Its Applications
Chapter 1 - Discrete Mathematics and Its Applications Løsningsforslag på utvalgte oppgaver Avsnitt 1.2 Oppgave 3 På norsk blir dette: Du kan velges til president i USA bare hvis du er minst 35 år, er født
INF1800 LOGIKK OG BEREGNBARHET
INF1800 LOGIKK OG BEREGNBARHET FORELESNING 5: UTSAGNSLOGIKK Roger Antonsen Institutt for informatikk Universitetet i Oslo 2. september 2008 (Sist oppdatert: 2008-09-04 17:26) Praktisk informasjon Endringer
Praktisk informasjon INF1800 LOGIKK OG BEREGNBARHET FORELESNING 5: UTSAGNSLOGIKK. Endringer i undervisningen. Spørreskjemaet.
INF1800 LOGIKK OG BEREGNBARHET FORELESNING 5: UTSAGNSLOGIKK Roger Antonsen Praktisk informasjon Institutt for informatikk Universitetet i Oslo 2. september 2008 (Sist oppdatert: 2008-09-04 17:26) Endringer
Oppgave 4.4 Skriv ned setninger som svarer til den konverse og den kontrapositive av følgende utsagn.
Plenumsregning 5 Ukeoppgaver fra kapittel 4 Roger Antonsen - 14. februar 2008 Oppgave 4.4 Skriv ned setninger som svarer til den konverse og den kontrapositive av følgende utsagn. Husk at hvis p q er påstanden,
Matematikk for IT, høsten 2015
Matematikk for IT, høsten 015 Oblig 5 Løsningsforslag 5. oktober 016 3.1.1 3.1.13 a) Modus ponens. b) Modus tollens. c) Syllogismeloven. a) Ikke gyldig. b) Gyldig. 3.1.15 a) Hvis regattaen ikke avlyses,
Semantikk Egenskaper ved predikatlogikk Naturlig deduksjon INF3170 / INF4171. Predikatlogikk: Semantikk og naturlig deduksjon.
INF3170 / INF4171 Predikatlogikk: Semantikk og naturlig deduksjon Andreas Nakkerud 3. september 2015 Eksempel Gitt en similaritetstype 0, 2; 1; 2 bygger vi en struktur (modell) hvor A = {c 1, c 2, a, b},
Faglig kontakt under eksamen: Haaken A. Moe Bokmål MIDTSEMESTERPRØVE I TMA4140/MA Oktober 2006 Tid:
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Faglig kontakt under eksamen: Haaken A. Moe 92650655 Bokmål MIDTSEMESTERPRØVE I TMA4140/MA0302 18.Oktober 2006 Tid:
MAT1030 Diskret Matematikk
MAT1030 Diskret Matematikk Plenumsregning 4: Ukeoppgaver Mathias Barra Matematisk institutt, Universitetet i Oslo 6. februar 2009 (Sist oppdatert: 2009-02-10 11:21) Plenumsregning 4 MAT1030 Diskret Matematikk
Forelesning 1: Introduksjon. Utsagnslogikk og sekventkalkyle Arild Waaler januar 2008
Forelesning 1: Introduksjon. Utsagnslogikk og sekventkalkyle Arild Waaler - 21. januar 2008 1 Praktisk informasjon 1.1 Forelesere og tid/sted Forelesere: Martin Giese (martingi@ifi.uio.no) Arild Waaler
MAT1030 Diskret matematikk
MAT30 Diskret matematikk Plenumsregning 6: Ukeoppgaver fra kapittel Roger Antonsen Matematisk Institutt, Universitetet i Oslo. februar 008 Oppgave. Skriv følgende mengder på listeform. (a) Mengden av alle
INF4170 { Logikk. Forelesning 1: Utsagnslogikk. Arild Waaler. 20. august Institutt for informatikk, Universitetet i Oslo
INF4170 { Logikk Forelesning 1: Utsagnslogikk Arild Waaler Institutt for informatikk, Universitetet i Oslo 20. august 2013 Dagens plan 1 Utsagnslogikk 2 Sekventkalkyle 3 Sunnhet 4 Kompletthet Institutt
MAT1030 Diskret matematikk
MAT1030 Diskret matematikk Plenumsregning 6: Ukeoppgaver fra kapittel 5 Roger Antonsen Matematisk Institutt, Universitetet i Oslo 21. februar 2008 Oppgave 5.1 Skriv følgende mengder på listeform. (a) Mengden
Oversettelse / Formalisering
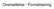Oversettelse / Formalisering P K + x (P(x) K(x)) Noen politikere er korrupte. Det fins en korrupt politiker. En politiker er korrupt. P - K x (P(x) K(x)) x (P(x) K(x)) x ( P(x) K(x)) x (P(x) K(x)) P K
INF3140 Modeller for parallellitet INF3140/4140: Programanalyse
INF3140/4140: Programanalyse Uke 4, side 1. Hvordan sjekke egenskaper ved programmer? Testing eller debugging øker tilliten til programmet ved prøving, men gir ingen garanti for korrekthet Operasjonell
MAT1030 Plenumsregning 5
MAT1030 Plenumsregning 5 Ukeoppgaver Mathias Barra - 13. februar 2009 (Sist oppdatert: 2009-03-06 18:29) Oppgave 4.18 Uttrykk følgende påstander i predikatlogikk, og finn deres sannhetsverdier. (a) Det
INF1800. Logikk og Beregnbarhet
INF1800 Logikk og Beregnbarhet Lærebok: Discrete Structures, Logic, and Computability Utdrag blir pensum. Obs: Første opplag inneholder mange feil, andre opplag inneholder noen feil. Har du kjøpt boken
MAT1030 Diskret Matematikk
MAT1030 Diskret Matematikk Plenumsregning 4: Ukeoppgaver Mathias Barra Matematisk institutt, Universitetet i Oslo 6. februar 2009 (Sist oppdatert: 2009-02-10 11:20) Plenumsregning 4 MAT1030 Diskret Matematikk
Dagens plan. INF3170 Logikk. Obliger og eksamen. Forelesning 1: Introduksjon. Utsagnslogikk og sekventkalkyle. Arild Waaler. 21.
INF3170 Logikk Dagens plan Forelesning 1: Introduksjon. og sekventkalkyle Arild Waaler Institutt for informatikk, Universitetet i Oslo 1 Praktisk informasjon 2 21. januar 2008 3 Institutt for informatikk
Faglig kontakt under eksamen: Haaken A. Moe Bokmål MIDTSEMESTERPRØVE I TMA Oktober 2007 Tid:
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Faglig kontakt under eksamen: Haaken A. Moe 92650655 Bokmål MIDTSEMESTERPRØVE I TMA4140 23.Oktober 2007 Tid: 18.15
INF1800 Forelesning 4
INF1800 Forelesning 4 Utsagnslogikk Roger Antonsen - 27. august 2008 (Sist oppdatert: 2008-09-03 12:39) Før vi begynner Praktiske opplysninger Kursets hjemmeside blir stadig oppdatert: http://www.uio.no/studier/emner/matnat/ifi/inf1800/
TMA4100 Matematikk 1, høst 2013
TMA4100 Matematikk 1, høst 2013 Teknostart Forelesning 3 www.ntnu.no TMA4100 Matematikk 1, høst 2013, Teknostart Forelesning 3 Tema Logikk Definisjoner og Teoremer Mengder og Egenskaper ved de Reelle Tall
Slides til 1.5. Andreas Leopold Knutsen
Slides til 1.5 Andreas Leopold Knutsen January 20, 2010 Argument Mål: korrekt resonnement (eks.:matematiske bevis) p 1 p 2. p n q Premisser/hypoteser/antagelser: p 1,..., p n (sammensatte prop.) Konklusjon/slutning/konsekvens:
Matematikk for IT, høsten 2017
Matematikk for IT, høsten 017 Oblig 5 Løsningsforslag 0. september 017 Oppgave 1 (eksamen desember 013) Gitt følgende logiske utsagn: ( p ( p q)) Benytt lovene i logikk til å finne hvilket av følgende
UNIVERSITETET I OSLO
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF1080 Logiske metoder for informatikk Eksamensdag: 26. november 2010 Tid for eksamen: 13:00 17:00 Oppgave 1 La A = { }. Mengdelære
INF1800 LOGIKK OG BEREGNBARHET
INF1800 LOGIKK OG BEREGNBARHET FORELESNING 4: UTSAGNSLOGIKK Roger Antonsen Institutt for informatikk Universitetet i Oslo 27. august 2008 (Sist oppdatert: 2008-09-03 12:39) Før vi begynner Praktiske opplysninger
Oppsummering av Kapittel 3. MAT1030 Diskret matematikk LOGIKK. Logikk. Forelesning 5: Logikk
Oppsummering av Kapittel 3 MAT1030 Diskret matematikk Forelesning 5: Logikk Dag Normann Matematisk Institutt, Universitetet i Oslo 28. januar 2008 I Kapittel 3 så vi på hvordan data, som hele tall og reelle
MAT1030 Diskret Matematikk
MAT1030 Diskret Matematikk Forelesning 4: Logikk Roger Antonsen Institutt for informatikk, Universitetet i Oslo 21. januar 2009 (Sist oppdatert: 2009-01-22 13:02) Kapittel 4: Logikk (fortsettelse) MAT1030
Kapittel 4: Logikk (fortsettelse)
MAT1030 Diskret Matematikk Forelesning 4: Logikk Roger Antonsen Institutt for informatikk, Universitetet i Oslo Kapittel 4: Logikk (fortsettelse) 21. januar 2009 (Sist oppdatert: 2009-01-22 13:03) MAT1030
INF1800 Forelesning 18
INF1800 Forelesning 18 Førsteordens logikk Roger Antonsen - 15. oktober 2008 (Sist oppdatert: 2008-10-15 23:50) Repetisjon og noen løse tråder Førsteordens språk Et førsteordens språk L består av: 1. Logiske
MAT1030 Diskret matematikk
MAT1030 Diskret matematikk Plenumsregning 4: Ukeoppgaver fra kapittel 3 & 4 Roger Antonsen Matematisk Institutt, Universitetet i Oslo 7. februar 2008 Oppgave 3.15 Forklar følgende påstand ved å vise til
INF1800 LOGIKK OG BEREGNBARHET
INF1800 LOGIKK OG BEREGNBARHET FORELESNING 18: FØRSTEORDENS LOGIKK Roger Antonsen Institutt for informatikk Universitetet i Oslo 15. oktober 2008 (Sist oppdatert: 2008-10-15 23:50) Repetisjon og noen løse
Repetisjon og noen løse tråder
INF1800 LOGIKK OG BEREGNBARHET FORELESNING 18: FØRSTEORDENS LOGIKK Roger Antonsen Repetisjon og noen løse tråder Institutt for informatikk Universitetet i Oslo 15. oktober 2008 (Sist oppdatert: 2008-10-15
v : T, kan bare ha verdi av typen T. n =0 slyfes alltid parentesene. Typet uttrykkssprak type representerer en verdimengde. variabel, deklarert funksjon, herunder karakteriseres syntaktisk ved a angi navn
I Kapittel 3 så vi på hvordan data, som hele tall og reelle tall, kan representeres som bitsekvenser
Forelesning 5 Logikk Dag Normann - 28. januar 2008 Oppsummering av Kapittel 3 I Kapittel 3 så vi på hvordan data, som hele tall og reelle tall, kan representeres som bitsekvenser i en datamaskin. Stoffet
Hvis Ole følger inf3170, så liker Ole logikk. Ole følger inf3170, og Ole følger ikke inf3170. Ole følger inf3170, eller Ole følger ikke inf3170.
Forelesning 4: Repetisjon og førsteordens logikk Christian Mahesh Hansen - 12. februar 2007 1 Repetisjon Motivasjon Er utsagnene sanne? Hvis Ole følger inf3170, så liker Ole logikk. Ole følger inf3170,
Dagens plan. INF3170 Logikk. Induktive definisjoner. Eksempel. Definisjon (Induktiv definisjon) Eksempel
INF3170 Logikk Dagens plan Forelesning 2: Induktive definisjoner, utsagnslogikk og sekventkalkyle Christian Mahesh Hansen Institutt for informatikk, Universitetet i Oslo 1 Induktive definisjoner 2 29.
Forelesning 2: Induktive definisjoner, utsagnslogikk og sekventkalkyle Christian Mahesh Hansen januar 2007
Forelesning 2: Induktive definisjoner, utsagnslogikk og sekventkalkyle Christian Mahesh Hansen - 29. januar 2007 1 Induktive definisjoner Induktive definisjoner Definisjon 1.1 (Induktiv definisjon). Å
Dagens plan. INF4170 Logikk. Modelleksistens for grunn LK repetisjon. Kompletthet av fri-variabel LK. Teorem (Kompletthet) Lemma (Modelleksistens)
INF4170 Logikk Dagens plan Forelesning 11: Automatisk bevissøk III fri-variabel kompletthet og repetisjon av sunnhet Martin Giese 1 Institutt for informatikk, Universitetet i Oslo 2 31. april 2008 Institutt
UNIVERSITETET I OSLO
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF1080 Logiske metoder for informatikk Eksamensdag: 28. november 2014 Tid for eksamen: 08.15 12.15 Oppgave 1 Mengdelære (10 poeng)
MAT1030 Diskret Matematikk
MAT1030 Diskret Matematikk Forelesning 4: Logikk Dag Normann Matematisk Institutt, Universitetet i Oslo 27. januar 2010 (Sist oppdatert: 2010-01-27 12:47) Kapittel 4: Logikk (fortsettelse) MAT1030 Diskret
3.1 Hva har mengdealgebra og utsagnslogikk felles?
Kapittel 3 Boolesk algebra 3.1 Hva har mengdealgebra og utsagnslogikk felles? I de to foregående kapitlene har vi innført mengdelære og utsagnslogikk. Den observante leser kan ikke ha ungått å se at det
Prøveeksamen 2016 (med løsningsforslag)
Prøveeksamen 2016 (med løsningsforslag 1 Grunnleggende mengdelære La A = {0, {0}} og B = {0, {0}, {0, {0}}}. Er følgende påstander sanne eller usanne? 1 {{0}} A 2 0 B 3 A B 4 A B 1 Usann 2 Usann 3 Sann
INF3170 Logikk. Ukeoppgaver oppgavesett 6
INF3170 Logikk Ukeoppgaver oppgavesett 6 Normalformer Negasjons normalform I dette oppgavesettet skal vi se nærmere på normalformer. Formelen (P Q) kan også skrives som P Q. Formlene er ekvivalente, dvs.
Databaser fra et logikkperspektiv
Databaser fra et logikkperspektiv Evgenij Thorstensen IFI, UiO Høst 2013 Evgenij Thorstensen (IFI, UiO) Databaser fra et logikkperspektiv Høst 2013 1 / 31 Outline 1 Logikk som verktøy 2 Relasjonsdatabaser
INF3170 Logikk. Forelesning 3: Utsagnslogikk, semantikk, sekventkalkyle. Roger Antonsen. Institutt for informatikk, Universitetet i Oslo
INF3170 Logikk Forelesning 3: Utsagnslogikk, semantikk, sekventkalkyle Roger Antonsen Institutt for informatikk, Universitetet i Oslo 9. februar 2010 (Sist oppdatert: 2010-02-09 15:10) Utsagnslogikk INF3170
EKSAMEN. Oppgavesettet består av 16 oppgaver. Ved sensur vil alle oppgaver telle like mye med unntak av oppgave 6 som teller som to oppgaver.
EKSAMEN Emnekode: ITF0705 Dato: 5. desember 204 Emne: Matematikk for IT Eksamenstid: kl 09.00 til kl 3.00 Hjelpemidler: To A4-ark med valgfritt innhold på begge sider. Kalkulator er ikke tillatt. Faglærer:
LF, KONTINUASJONSEKSAMEN TMA
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Faglig kontakt under eksamen: Haaken A. Moe 92650655 Bokmål LF, KONTINUASJONSEKSAMEN TMA4140 2008 Oppgave 1 (10%)
Forelesning 2 torsdag den 21. august
Forelesning 2 torsdag den 21 august 15 Flere eksempler på bevis ved induksjon Proposisjon 151 La n være et naturlig tall Da er 1 + 2 + 4 + + 2 n 1 = 2 n 1 Bevis Først sjekker vi om proposisjonen er sann
Hint til oppgavene. Uke 34. Uke 35. Fullstendige løsningsforslag finnes på emnesidene for 2017.
Hint til oppgavene Fullstendige løsningsforslag finnes på emnesidene for 2017. Uke 34 Oppgave 1, 2, 3 og 4 kan alle løses ved å tegne sannhetstabeller, men i flere tilfeller kan man like gjerne manipulere
Notat 1 for MAT1140 høsten 2017
Notat 1 for MAT1140 høsten 2017 0 Innledningsvis 0.1 Om kurset Vi begynner med å introdusere et fundament for matematikk. Hovedtemaene er: Logikk (utsagn, konnektiver, kvantorer, bevis). Mengder (aksiomer
UNIVERSITETET I OSLO
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i Eksamensdag: 28. november 2014 Tid for eksamen: 08.15 12.15 Oppgavesettet er på 6 sider. Vedlegg: Tillatte hjelpemidler: INF1080
MAT1030 Diskret matematikk
MAT1030 Diskret matematikk Forelesning 5: Logikk Dag Normann Matematisk Institutt, Universitetet i Oslo 28. januar 2008 Oppsummering av Kapittel 3 I Kapittel 3 så vi på hvordan data, som hele tall og reelle
X X X X X X X X X X X X X X. Generell informasjon - FIL Emenkode: FIL104 Emnenavn: Logikk og argumentasjonslære
Generell informasjon - FIL104 22.09.2017 Emenkode: FIL104 Emnenavn: Logikk og argumentasjonslære Dato: 22/09-2017 Tillatte hjelpemidler: Ingen Merknad: 7 av de følgende 9 oppgavene skal besvares. Noen
Dagens plan. INF4170 Logikk. Fri-variabel sekventkalkyle. Forelesning 10: Automatisk bevissøk II fri-variabel sekventkalkyle og sunnhet.
INF4170 Logikk Dagens plan Forelesning 10: fri-variabel sekventkalkyle og sunnhet Martin iese 1 Institutt for informatikk, Universitetet i Oslo 14. april 2008 Institutt for informatikk (UiO) INF4170 Logikk
Noen syntaktiske derivasjoner i den doxastiske predikatlogikken Kη og enkelte beslektede kalkyler.
Side 1 * Noen syntaktiske derivasjoner i den doxastiske predikatlogikken Kη og enkelte beslektede kalkyler. av Morten Rognes 2007 * Side 2 1 Innledning I det følgende notat skal jeg fremstille en rent
Dagens plan. INF3170 Logikk. Syntaks: Utsagnslogiske formler. Motivasjon
INF3170 Logikk Dagens plan Forelesning 4: og førsteordens logikk Christian Mahesh Hansen Institutt for informatikk, Universitetet i Oslo 1 2 12. februar 2007 3 Institutt for informatikk (UiO) INF3170 Logikk
Sekventkalkyle for første ordens predikatlogikk uten likhet
Sekventkalkyle for første ordens predikatlogikk uten likhet Tilleggslitteratur til INF1800 Versjon 29/9 07 Vi definerer sekventer for predikatlogikk på samme måte som i utsagnslogikk. En sekvent består
Øvingsforelesning 2. Mengdelære, funksjoner, rekurrenser, osv. TMA4140 Diskret Matematikk. 10. og 12. september 2018
Mengdelære, funksjoner, rekurrenser, osv. Øvingsforelesning 2 TMA4140 Diskret Matematikk 10. og 12. september 2018 Dagens øvingsforelesning Spørsmål til emnene i forrige uke Oppgaver fra midtsemesterprøver
Velkommen til MA Lineær algebra og geometri
Velkommen til MA1201 - Lineær algebra og geometri Benedikte Grimeland Institutt for matematiske fag 13. august 2014 2 Plan for forelesningen 1. informasjon om praktiske aspekt, samt øvingsopplegg 2. påmelding
MAT1030 Forelesning 4
MAT1030 Forelesning 4 Logikk Roger Antonsen - 21. januar 2009 (Sist oppdatert: 2009-01-22 13:02) Kapittel 4: Logikk (fortsettelse) Enda et eksempel (a) Jeg liker ikke Bamsemums. (b) Du liker alt jeg liker.