INF2220: Forelesning 3. Map og hashing Abstrakte datatyper (kapittel 3.1) Map (kapittel 4.8) Hashing (kapittel 5)
|
|
|
- Gunhild Didriksen
- 7 år siden
- Visninger:
Transkript
1 INF2220: Forelesning 3 Map og hashing Abstrakte datatyper (kapittel 3.1) Map (kapittel 4.8) Hashing (kapittel 5)
2 Map og hashing Ett minutt for deg selv: Hva vet du om maps/dictionarys og hashing fra tidligere? 2
3 ABSTRAKTE DATATYPER 3
4 Abstrakte datatyper En ADT består av: Et sett med objekter. Spesifikasjon av operasjoner på disse. Eksempler: ADT: binært søketre Operasjoner: innsetting, søking, fjerning, ADT: mengde Operasjoner: union, snitt, finn, ADT: map Operasjoner: containskey, get, put,
5 Hvorfor bruke ADTer? ADTer skiller det som er viktig (funksjonaliteten) fra detaljene (den konkrete implementasjonen). Dermed kan vi: Gjenbruke ADTen i andre programmer. Enklere overbevise oss om at programmet er riktig. Forandre innmaten (kodingen) av ADTen uten å forandre resten av programmet fordi grensesnittet er det samme. Lage modulære programmer. I Java er det naturlig å spesifisere en ADT som et interface. 5
6 MAP 6
7 Map ADT Samling (nøkkel,verdi)-par. Nøklene må være unike. Viktigste operasjoner: containskey(key): returnerer true hvis key finnes som nøkkel get(key): returnerer verdien assosiert med key put(key,value): legger til et nytt nøkkel/verdi-par keyset(): returnerer alle nøklene (som et sett) values(): returnerer alle verdiene SortedMap: Nøklene er organisert i sortert orden. 7
8 Maps To minutter sammen: Hvordan stemmer det du nå har hørt med det du trodde fra før? Hva lurer dere på nå? 8
9 HASHING 9
10 Hashing innledende eksempel Anta at en bilforhandler har 50 ulike modeller han ønsker å lagre data om. Hvis hver modell har et entydig nummer mellom 0 og 49 kan vi enkelt lagre dataene i en array som er 50 lang. Hva hvis numrene ligger mellom 0 og ? Array som er lang: Sløsing med plass! Array som er 50 lang: Søking tar lineær tid
11 Hashtabeller Ideen i hashing er å lagre elementene i en array (hashtabell). la verdien til elementet x (eller en del av x, da kalt nøkkelen til x), bestemme plasseringen (indeksen) til x i hashtabellen. Egenskaper til en god hash-funksjon: Rask å beregne. Kan gi alle mulige verdier fra 0 til tablesize - 1. Gir en god fordeling utover tabellindeksene. x hash(x) 0: 1: 2:... 11
12 Idealsituasjonen Perfekt situasjon: n elementer tabell med n plasser hash-funksjon slik at den er lett (rask) å beregne forskjellige nøkkelverdier gir forskjellige indekser Eksempel: Hvis modellene er nummerert 0, 1 000, 2 000,, , kan data om modell i lagres på indeks i/1 000 i en tabell som er 50 stor. Problem: Hva hvis modell får nytt nummer 3 999? 12
13 Eksempel: ideell situasjon Input: 0, 1, 4, 9, 16, 25, 36, 49, 64, 81 Hash-funksjon: hash(x,tablesize) = x 0: 0 0: 1: 2: 3: 4: 5: 6: Hva hvis hash-funksjonen hadde vært hash(x,tablesize) = x mod tablesize istedenfor? 1: 2: 3: 4: 5: 6: 7: 49 7: 8: 64 8: 9: 81 9: 13
14 Hashtabell ADT En hashtabell tilbyr innsetting sletting søking med konstant gjennomsnittstid. Men: operasjoner som finnminste og skrivsortert har ingen garantier. 14
15 Når bruker vi hashtabeller? Brukes gjerne når vi først og fremst ønsker et raskt svar på om et gitt element finnes i datastrukturen eller ikke. Eksempler: Kompilatorer: Er variabel y deklarert? Stavekontroller: Finnes ord x i ordlisten? Spill: Har jeg allerede vurdert denne stillingen via en annen trekkrekkefølge? XML parsering: Nøkler blir attributtnavn, verdi blir innhold. Nesten alle scriptspråk has hash som del av språket. (Perl, Python, Ruby, PHP, ) 15
16 Hashing: problemstillinger Hvordan velge hash-funksjon? Ofte er nøklene strenger. Hvordan håndtere kollisjoner? Hvor stor bør hash-tabellen være? 16
17 Hash-funksjoner Eksempel: Heltall som nøkler Begrenset antall tabellindekser La hash-funksjonen være hash(x,tablesize) = x mod tablesize Dette gir jevn fordeling for tilfeldige tall. Pass på at ikke nøklene har spesielle egenskaper: Hvis tablesize = 10 og alle nøklene slutter på 0 vil alle elementene havne på samme indeks! Huskeregel: La alltid tabellstørrelsen være et primtall. 17
18 Strenger som nøkler: funksjon 1 Vanlig strategi: ta utgangspunkt i ascii/unicodeverdiene til hver bokstav og gjør noe lurt. Funksjon 1: Summer verdiene til hver bokstav. int hash1(string key, int tablesize) { int hashval = 0; for (int i = 0; i < key.length(); i++) { hashval += key.charat(i); } } return (hashval % tablesize); Fordel: Enkel å implementere og beregne. Ulempe: Dårlig fordeling hvis tabellstørrelsen er stor. 18
19 Strenger som nøkler: funksjon 2 Funksjon 2: Bruk bare de tre første bokstavene og vekt disse. int hash2(string key, int tablesize) { int hashval = key.charat(0) + 27 * key.charat(1) + 729* key.charat(2); } return (hashval % tablesize); Fordel: Grei fordeling for tilfeldige strenger. Ulempe: Vanlig språk er ikke tilfeldig! 19
20 Strenger som nøkler: funksjon 3 Funksjon 3: i=0 keysize-1 key[keysize-i-1] * 37 i int hash3(string key, int tablesize) { int hashval = 0; for (int i = 0; i < key.length(); i++) { hashval = 37*hashVal + key.charat(i); } } return Math.abs(hashVal % tablesize); Fordel: Enkel og relativt rask å beregne. Stort sett bra nok fordeling. Ulempe: Beregningen tar lang tid for lange nøkler. 20
21 Hash-funksjoner: Oppsummering Må (i hvert fall teoretisk) kunne gi alle mulige verdier fra 0 til tablesize - 1. Må gi en god fordeling utover tabellindeksene. Tenk på hva slags data som skal brukes til nøkler. Fødselsår kan gi god fordeling i persondatabaser, men ikke for en skoleklasse! Generelt: Bør være mange ganger tablesize før man gjør mod-operasjonen. 21
22 hashcode i Java Alle Java-klasser er subklasser av java.lang.object, som inneholder metoden int hashcode() som typisk returnerer minneadresse konvertert til int. Men: Objekter vi regner som like (via equals) må ha samme hashverdi. 22
23 Kollisjonshåndtering Hva gjør vi når to elementer hashes til den samme indeksen? Åpen hashing: Elementer med samme hashverdi samles i en liste (eller annen passende struktur). Lukket hashing: Dersom en indeks er opptatt, prøver vi en annen indeks inntil vi finner en som er ledig. 23
24 Åpen hashing (Separate chaining) 0: 1: 2: Forventer at hashfunksjonen er god, slik at alle listene blir korte. 3: 4: 5: 6: 7: 8: 9: Load-faktoren er antall elementer i hashtabellen i forhold til tabellstørrelsen. For åpen hashing ønsker vi
25 Lukket hashing åpen adressering Prøver alternative indekser h 0 (x), h 1 (x), h 2 (x), inntil vi finner en som er ledig. h i er gitt ved h i (x) = (hash(x) + f(i)) mod tablesize slik at f(0) = 0. Merk at vi trenger en større tabell enn for åpen hashing generelt ønsker vi her 0.5 Skal se på tre mulige strategier (valg av f): Lineær prøving Kvadratisk prøving Dobbel hashing 25
26 Lineær prøving Velger f til å være en lineær funksjon av i, typisk f(i) = i Eksempel: Input: 89, 18, 49, 58, 69 Hash-funksjon: hash(x,tablesize) = x mod tablesize 0: 1: 2: 3: 4: 5: 6: 7: 8: 9: 26
27 Kvadratisk prøving Velger f til å være en kvadratisk funksjon av i, typisk f(i) = i 2 Eksempel: Input: 89, 18, 49, 58, 69 Hash-funksjon: hash(x,tablesize) = x mod tablesize 0: 1: 2: 3: 4: 5: 6: 7: 8: 9: 27
28 Dobbel hashing Bruker en ny hash-funksjon for å løse kollisjonene, typisk f(i) = i * hash 2 (x), med hash 2 (x) = R (x mod R) hvor R er et primtall mindre enn tablesize. Eksempel: Input: 89, 18, 49, 58, 69 Andre hash-funksjon: hash 2 (x) = 7 (x mod 7) 0: 1: 2: 3: 4: 5: 6: 7: 8: 9: 28
29 Rehashing Hvis tabellen blir for full, begynner operasjonene å ta veldig lang tid. Mulig løsning: Lag en ny hashtabell som er omtrent dobbelt så stor (men fortsatt primtall!). Gå gjennom hver element i den opprinnelige tabelln, beregn den nye hash-verdien og sett inn på rett plass i den nye hashtabellen. Dette er en dyr operasjon, O(n), men opptrer relativt sjelden (må ha hatt n/2 innsettinger siden forrige rehashing). 29
30 Utvidbar hashing Brukes spesielt når internminnet blir for lite, og det vesentligste blir antall diskoperasjoner. Anta at vi Skal lagre N elementer, der N varierer over tid. Kan lagre maksimalt M elementer i en diskblokk. Problemet med vanlig hashing er at Kollisjoner kan føre til at find(x) må undersøke mange diskblokker selv om hashfunksjonen distribuerer elementene godt. Rehashing blir veldig kostbart. 30
31 Løsning Lar hash-funksjonen via en katalog angi hvilken diskblokk et element x befinner seg i (hvis det finnes). Dermed trenger find(x) bare to diskaksesser (og bare en aksess dersom katalogen kan lagres i internminnet). 31
32 Utvidbar hashing: eksempel D = d = 2 d = 2 d = 2 d = 2 M = Forenklet tegning, hvor vi for hvert element bare lagrer hashverdien til elementet (som 6-sifret binærtall). 32
33 Utvidbar hashing Katalogen har 2 D indekser. Hver diskblokk har plass til M elementer. For hver diskblokk L lagrer vi et tall d L D. Invariant: Det garanteres at alle elementene i L har minst de d første bitene felles. Dersom d L = D vil nøyaktig en indeks i katalogen peke på diskblokk L. Dersom d L < D vil to eller flere indekser i katalogen peke på L. Over tid forventer vi at ca 69% av hver diskblokk er fylt opp. 33
34 Innsettingsalgoritme 1. Beregn hash(x) og finn riktig diskblokk L ved å slå opp i katalogen på de D første sifrene i hashverdien. 2. Hvis det er færre enn M elementer i L, sett x inn i L. 3. Hvis L derimot er full, sammenlign d L med D: a) Dersom d L < D splitter vi L i to blokker L 1 og L 2 : i. Sett d L 1 = d L2 = d L + 1. ii. Gå gjennom elementene i L og plasser dem i L 1 eller L 2 avhengig av verdien på de d L + 1 første sifrene. iii. Prøv igjen å sette inn x (gå til punkt 2). b) Dersom d L = D: i. Doble katalogstørrelsen ved å øke D med 1. ii. Fortsett som ovenfor (splitt L i to blokker osv.) 34
35 Innsetting: eksempel D = d = 1 d = 2 d = 2 M =
36 Java s HashMap Klassen java.util.hashmap: Implementerer en hashtabell som mapper nøkler til verdier. Implementerer grensesnittet Map (men ikke SortedMap). Bruker åpen hashing. Default tabellstørrelse 16. Default load faktor < 0.75 rehashing hvis denne overskrides. 36
37 Neste forelesning: 14. september PRIORITETSKØ OG HEAP HUFFMAN 37
INF2220: Forelesning 3
 INF2220: Forelesning 3 Map og hashing Abstrakte datatyper (kapittel 3.1) Map (kapittel 4.8) Hashing (kapittel 5) ABSTRAKTE DATATYPER 2 Abstrakte datatyper En ADT består av: Et sett med objekter. Spesifikasjon
INF2220: Forelesning 3 Map og hashing Abstrakte datatyper (kapittel 3.1) Map (kapittel 4.8) Hashing (kapittel 5) ABSTRAKTE DATATYPER 2 Abstrakte datatyper En ADT består av: Et sett med objekter. Spesifikasjon
... HASHING. Hashing. Hashtabeller. hash(x)
 HASHING Hashing Hashtabeller (kapittel.) Hash-funksjoner (kapittel.) Kollisjonshåndtering Åpen hashing (kapittel.) Lukket hashing (kapittel.) Anta at en bilforhandler har ulike modeller han ønsker å lagre
HASHING Hashing Hashtabeller (kapittel.) Hash-funksjoner (kapittel.) Kollisjonshåndtering Åpen hashing (kapittel.) Lukket hashing (kapittel.) Anta at en bilforhandler har ulike modeller han ønsker å lagre
INF2220: Forelesning 3
 INF2220: Forelesning 3 Map og hashing Abstrakte datatyper (kapittel 3.1) Map (kapittel 4.8) Hashing (kapittel 5) REPETISJON: ALGORITMER OG STOR O 2 REPETISJON RØD-SVARTE TRÆR 7 Rød-svarte trær Et rød-svart
INF2220: Forelesning 3 Map og hashing Abstrakte datatyper (kapittel 3.1) Map (kapittel 4.8) Hashing (kapittel 5) REPETISJON: ALGORITMER OG STOR O 2 REPETISJON RØD-SVARTE TRÆR 7 Rød-svarte trær Et rød-svart
Hashing. INF Algoritmer og datastrukturer HASHING. Hashtabeller
 Hashing INF2220 - Algoritmer og datastrukturer HØSTEN 200 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning : Hashing Hashtabeller (kapittel.) Hash-funksjoner (kapittel.2) Kollisjonshåndtering
Hashing INF2220 - Algoritmer og datastrukturer HØSTEN 200 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning : Hashing Hashtabeller (kapittel.) Hash-funksjoner (kapittel.2) Kollisjonshåndtering
INF1020 Algoritmer og datastrukturer
 Dagens plan Hashing Hashtabeller Hash-funksjoner Kollisjonshåndtering Åpen hashing (kap. 5.3) Lukket hashing (kap. 5.4) Rehashing (kap. 5.5) Sortering ut fra en hashing-ide (side 66-68) Bøttesortering
Dagens plan Hashing Hashtabeller Hash-funksjoner Kollisjonshåndtering Åpen hashing (kap. 5.3) Lukket hashing (kap. 5.4) Rehashing (kap. 5.5) Sortering ut fra en hashing-ide (side 66-68) Bøttesortering
Maps og Hashing. INF Algoritmer og datastrukturer. Map - ADT. Map vs Array
 Maps og Hashing INF0 - Algoritmer og datastrukturer HØSTEN 00 Institutt for informatikk, Universitetet i Oslo INF0, forelesning : Maps og Hashing Map - Abstrakt Data Type (kapittel.) Hash-funksjoner (kapittel..)
Maps og Hashing INF0 - Algoritmer og datastrukturer HØSTEN 00 Institutt for informatikk, Universitetet i Oslo INF0, forelesning : Maps og Hashing Map - Abstrakt Data Type (kapittel.) Hash-funksjoner (kapittel..)
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 3: Maps og Hashing Bjarne Holen (Ifi, UiO) INF2220 H2009, forelesning 3 1 / 25 Maps
INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 3: Maps og Hashing Bjarne Holen (Ifi, UiO) INF2220 H2009, forelesning 3 1 / 25 Maps
Maps og Hashing. INF Algoritmer og datastrukturer. Map - ADT. Map vs Array
 Maps og Hashing INF0 - Algoritmer og datastrukturer HØSTEN 00 Institutt for informatikk, Universitetet i Oslo INF0, forelesning : Maps og Hashing Map - Abstrakt Data Type Hash-funksjoner hashcode Kollisjonshåndtering
Maps og Hashing INF0 - Algoritmer og datastrukturer HØSTEN 00 Institutt for informatikk, Universitetet i Oslo INF0, forelesning : Maps og Hashing Map - Abstrakt Data Type Hash-funksjoner hashcode Kollisjonshåndtering
public interface Collec>on<V> { public void add(v value); public default V remove(v value) { return null;
 Hashing The term "hash" comes by way of analogy with its non-technical meaning, to "chop and mix". Indeed, typical hash func>ons, like the mod opera>on, "chop" the input domain into many sub-domains that
Hashing The term "hash" comes by way of analogy with its non-technical meaning, to "chop and mix". Indeed, typical hash func>ons, like the mod opera>on, "chop" the input domain into many sub-domains that
... Når internminnet blir for lite. Dagens plan: Løsning: Utvidbar hashing. hash(x) katalog. O modellen er ikke lenger gyldig ved
 Dagens plan: Utvidbar hashing (kapittel 5.6) B-trær (kap. 4.7) Abstrakte datatyper (kap. 3.1) Stakker (kap. 3.3) Når internminnet blir for lite En lese-/skriveoperasjon på en harddisk (aksesstid 7-12 millisekunder)
Dagens plan: Utvidbar hashing (kapittel 5.6) B-trær (kap. 4.7) Abstrakte datatyper (kap. 3.1) Stakker (kap. 3.3) Når internminnet blir for lite En lese-/skriveoperasjon på en harddisk (aksesstid 7-12 millisekunder)
Repetisjon: Binære. Dagens plan: Rød-svarte trær. Oppgave (N + 1)!
 Repetisjon: Binære søketrær Dagens plan: Rød-svarte trær (kap. 12.2) B-trær (kap. 4.7) bstrakte datatyper (kap. 3.1) takker (kap. 3.3) For enhver node i et binært søketre gjelder: lle verdiene i venstre
Repetisjon: Binære søketrær Dagens plan: Rød-svarte trær (kap. 12.2) B-trær (kap. 4.7) bstrakte datatyper (kap. 3.1) takker (kap. 3.3) For enhver node i et binært søketre gjelder: lle verdiene i venstre
INF1010 Hashing. Marit Nybakken 8. mars 2004
 INF1010 Hashing Marit Nybakken marnybak@ifi.uio.no 8. mars 2004 Til nå har vi trodd at en HashMap var en mystisk uendelig stor samleeske der vi på magisk vis kan putte inn objekter og ta ut objekter ved
INF1010 Hashing Marit Nybakken marnybak@ifi.uio.no 8. mars 2004 Til nå har vi trodd at en HashMap var en mystisk uendelig stor samleeske der vi på magisk vis kan putte inn objekter og ta ut objekter ved
Hashing: Håndtering av kollisjoner
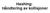 Hashing: Håndtering av kollisjoner Innsetting av dataelement i hashtabell Algoritme: 1. Bruk en hashfunksjon til å beregne hashverdi basert på dataelementets nøkkelverdi 2. Sett inn dataelementet i hashtabellen
Hashing: Håndtering av kollisjoner Innsetting av dataelement i hashtabell Algoritme: 1. Bruk en hashfunksjon til å beregne hashverdi basert på dataelementets nøkkelverdi 2. Sett inn dataelementet i hashtabellen
Hashfunksjoner. Hashfunksjonen beregner en indeks i hashtabellen basert på nøkkelverdien som vi søker etter
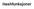 Hashfunksjoner Hashfunksjoner Hashfunksjonen beregner en indeks i hashtabellen basert på nøkkelverdien som vi søker etter Hash: «Kutte opp i biter og blande sammen» Perfekt hashfunksjon: Lager aldri kollisjoner
Hashfunksjoner Hashfunksjoner Hashfunksjonen beregner en indeks i hashtabellen basert på nøkkelverdien som vi søker etter Hash: «Kutte opp i biter og blande sammen» Perfekt hashfunksjon: Lager aldri kollisjoner
Hashtabeller. Lars Vidar Magnusson Kapittel 11 Direkte adressering Hashtabeller Chaining Åpen-adressering
 Hashtabeller Lars Vidar Magnusson 12.2.2014 Kapittel 11 Direkte adressering Hashtabeller Chaining Åpen-adressering Dictionaries Mange applikasjoner trenger dynamiske sett som bare har dictionary oparsjonene
Hashtabeller Lars Vidar Magnusson 12.2.2014 Kapittel 11 Direkte adressering Hashtabeller Chaining Åpen-adressering Dictionaries Mange applikasjoner trenger dynamiske sett som bare har dictionary oparsjonene
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i Eksamensdag: 12. desember 2008 Tid for eksamen: 9.00 12.00 Oppgavesettet er på 7 sider. Vedlegg: Tillatte hjelpemidler: INF2220
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i Eksamensdag: 12. desember 2008 Tid for eksamen: 9.00 12.00 Oppgavesettet er på 7 sider. Vedlegg: Tillatte hjelpemidler: INF2220
Søkeproblemet. Gitt en datastruktur med n elementer: Finnes et bestemt element (eller en bestemt verdi) x lagret i datastrukturen eller ikke?
 Søking Søkeproblemet Gitt en datastruktur med n elementer: Finnes et bestemt element (eller en bestemt verdi) x lagret i datastrukturen eller ikke? Effektiviteten til søkealgoritmer avhenger av: Om datastrukturen
Søking Søkeproblemet Gitt en datastruktur med n elementer: Finnes et bestemt element (eller en bestemt verdi) x lagret i datastrukturen eller ikke? Effektiviteten til søkealgoritmer avhenger av: Om datastrukturen
Ny/utsatt EKSAMEN. Dato: 6. januar 2017 Eksamenstid: 09:00 13:00
 Ny/utsatt EKSAMEN Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: 6. januar 2017 Eksamenstid: 09:00 13:00 Hjelpemidler: Alle trykte og skrevne Faglærer: Jan Høiberg Om eksamensoppgavene: Oppgavesettet
Ny/utsatt EKSAMEN Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: 6. januar 2017 Eksamenstid: 09:00 13:00 Hjelpemidler: Alle trykte og skrevne Faglærer: Jan Høiberg Om eksamensoppgavene: Oppgavesettet
Notater til INF2220 Eksamen
 Notater til INF2220 Eksamen Lars Bjørlykke Kristiansen December 13, 2011 Stor O notasjon Funksjon Navn 1 Konstant log n Logaritmisk n Lineær n log n n 2 Kvadratisk n 3 Kubisk 2 n Eksponensiell n! Trær
Notater til INF2220 Eksamen Lars Bjørlykke Kristiansen December 13, 2011 Stor O notasjon Funksjon Navn 1 Konstant log n Logaritmisk n Lineær n log n n 2 Kvadratisk n 3 Kubisk 2 n Eksponensiell n! Trær
Datastrukturer for rask søking
 Søking Søkeproblemet Gitt en datastruktur med n elementer: Finnes et bestemt element (eller en bestemt verdi) x lagret i datastrukturen eller ikke? Effektiviteten til søkealgoritmer avhenger av: Om datastrukturen
Søking Søkeproblemet Gitt en datastruktur med n elementer: Finnes et bestemt element (eller en bestemt verdi) x lagret i datastrukturen eller ikke? Effektiviteten til søkealgoritmer avhenger av: Om datastrukturen
Generelle Tips. INF Algoritmer og datastrukturer. Åpen og Lukket Hashing. Hashfunksjoner. Du blir bedømt etter hva du viser at du kan
 Generelle Tips INF2220 - lgoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo Du blir bedømt etter hva du viser at du kan Du må begrunne svar Du må ikke skrive av bøker
Generelle Tips INF2220 - lgoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo Du blir bedømt etter hva du viser at du kan Du må begrunne svar Du må ikke skrive av bøker
Dagens plan: INF2220 - Algoritmer og datastrukturer. Repetisjon: Binære søketrær. Repetisjon: Binære søketrær
 Dagens plan: INF2220 - lgoritmer og datastrukturer HØTEN 2007 Institutt for informatikk, Universitetet i Oslo (kap. 4.7) (kap. 12.2) Interface ollection og Iterator (kap. 3.3) et og maps (kap. 4.8) INF2220,
Dagens plan: INF2220 - lgoritmer og datastrukturer HØTEN 2007 Institutt for informatikk, Universitetet i Oslo (kap. 4.7) (kap. 12.2) Interface ollection og Iterator (kap. 3.3) et og maps (kap. 4.8) INF2220,
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 13: Eksamensgjennomgang Bjarne Holen (Ifi, UiO) INF2220 H2009, forelesning 13 1 /
INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 13: Eksamensgjennomgang Bjarne Holen (Ifi, UiO) INF2220 H2009, forelesning 13 1 /
Tillatte hjelpemidler: alle skrevne og trykte. Antall sider: 2 (+ 1 side vedlegg, bakerst). Oppgave 1 [25%]
![Tillatte hjelpemidler: alle skrevne og trykte. Antall sider: 2 (+ 1 side vedlegg, bakerst). Oppgave 1 [25%] Tillatte hjelpemidler: alle skrevne og trykte. Antall sider: 2 (+ 1 side vedlegg, bakerst). Oppgave 1 [25%]](/thumbs/62/47268453.jpg) Bokmål Det Matematisk-naturvitenskapelege fakultet UNIVERSITETET I BERGEN Eksamen i emnet INF101/INF101F Programmering II Tirsdag 28. september 2010, kl. 09-12. Tillatte hjelpemidler: alle skrevne og trykte.
Bokmål Det Matematisk-naturvitenskapelege fakultet UNIVERSITETET I BERGEN Eksamen i emnet INF101/INF101F Programmering II Tirsdag 28. september 2010, kl. 09-12. Tillatte hjelpemidler: alle skrevne og trykte.
INF2220: Forelesning 2
 INF2220: Forelesning 2 Mer om analyse av algoritmer Analyse av binære søketrær Balanserte søketrær Rød-svarte trær (kapittel12.2) B-trær (kapittel 4.7) ANALYSE AV ALGORITMER 2 Analyse av tidsforbruk Hvor
INF2220: Forelesning 2 Mer om analyse av algoritmer Analyse av binære søketrær Balanserte søketrær Rød-svarte trær (kapittel12.2) B-trær (kapittel 4.7) ANALYSE AV ALGORITMER 2 Analyse av tidsforbruk Hvor
Dagens tema. INF Algoritmer og datastrukturer. Binærtrær. Generelle trær
 Dagens tema INF2220 - Algoritmer og datastrukturer HØSTEN 2007 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 2: Binærtrær og abstrakte datatyper (ADT) Kort repetisjon Generelle trær
Dagens tema INF2220 - Algoritmer og datastrukturer HØSTEN 2007 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 2: Binærtrær og abstrakte datatyper (ADT) Kort repetisjon Generelle trær
O(log n) - søk. Søking i et balansert søketre med n elementer er alltid O(log n) Søkingen er basert på parvise sammenligninger av to og to verdier
 Hashing O(log n) - søk Søking i et balansert søketre med n elementer er alltid O(log n) Søkingen er basert på parvise sammenligninger av to og to verdier Er svært raskt uansett hvor stort søketreet er,
Hashing O(log n) - søk Søking i et balansert søketre med n elementer er alltid O(log n) Søkingen er basert på parvise sammenligninger av to og to verdier Er svært raskt uansett hvor stort søketreet er,
EKSAMEN. Dato: 28. mai 2018 Eksamenstid: 09:00 13:00
 EKSAMEN Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: 28. mai 2018 Eksamenstid: 09:00 13:00 Hjelpemidler: Alle trykte og skrevne Faglærer: Jan Høiberg Om eksamensoppgavene: Oppgavesettet
EKSAMEN Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: 28. mai 2018 Eksamenstid: 09:00 13:00 Hjelpemidler: Alle trykte og skrevne Faglærer: Jan Høiberg Om eksamensoppgavene: Oppgavesettet
Alg. Dat. Øvingsforelesning 3. Grafer, BFS, DFS og hashing. Børge Rødsjø rodsjo@stud.ntnu.no
 Alg. Dat Øvingsforelesning 3 Grafer, BFS, DFS og hashing Børge Rødsjø rodsjo@stud.ntnu.no Dagens tema Grafer Terminologi Representasjon av grafer Bredde først søk (BFS) Dybde først søk (DFS) Hashing Hashfunksjoner,
Alg. Dat Øvingsforelesning 3 Grafer, BFS, DFS og hashing Børge Rødsjø rodsjo@stud.ntnu.no Dagens tema Grafer Terminologi Representasjon av grafer Bredde først søk (BFS) Dybde først søk (DFS) Hashing Hashfunksjoner,
EKSAMENSOPPGAVE. INF-1101 Datastrukturer og algoritmer. Adm.bygget, rom K1.04 og B154 Ingen
 Fakultet for naturvitenskap og teknologi EKSAMENSOPPGAVE Eksamen i: Dato: 15.mai 2018 Klokkeslett: 09:00 13:00 Sted: Tillatte hjelpemidler: Adm.bygget, rom K1.04 og B154 Ingen Type innføringsark (rute/linje):
Fakultet for naturvitenskap og teknologi EKSAMENSOPPGAVE Eksamen i: Dato: 15.mai 2018 Klokkeslett: 09:00 13:00 Sted: Tillatte hjelpemidler: Adm.bygget, rom K1.04 og B154 Ingen Type innføringsark (rute/linje):
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF1010 Objektorientert programmering Eksamensdag: 9. juni 2011 Tid for eksamen: 09.00 15.00 Oppgavesettet er på 5 sider. Vedlegg:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF1010 Objektorientert programmering Eksamensdag: 9. juni 2011 Tid for eksamen: 09.00 15.00 Oppgavesettet er på 5 sider. Vedlegg:
PG4200 Algoritmer og datastrukturer Forelesning 9
 PG4200 Algoritmer og datastrukturer Forelesning 9 Lars Sydnes, NITH 2. april 2014 hash [hæs] hakke, skjære i stykker, ødelegge; hakkemat; lapskaus; hasj; virvar, rot, røre; Hvordan kan noe som kalles hashing
PG4200 Algoritmer og datastrukturer Forelesning 9 Lars Sydnes, NITH 2. april 2014 hash [hæs] hakke, skjære i stykker, ødelegge; hakkemat; lapskaus; hasj; virvar, rot, røre; Hvordan kan noe som kalles hashing
O(1) søking? Søking i sortert array og i søketrær: Optimalt søk som er O(1):
 Hashing O(1) søking? Søking i sortert array og i søketrær: Er basert på sammenligninger med verdier som allerede finnes i datastrukturen Effektiviteten er log n, avhenger av n (antall verdier i datastrukturen)
Hashing O(1) søking? Søking i sortert array og i søketrær: Er basert på sammenligninger med verdier som allerede finnes i datastrukturen Effektiviteten er log n, avhenger av n (antall verdier i datastrukturen)
Liste som abstrakt konsept/datatype
 Lister Liste som abstrakt konsept/datatype Listen er en lineær struktur (men kan allikevel implementeres ikke-lineært bak kulissene ) Hvert element har en forgjenger, unntatt første element i listen Hvert
Lister Liste som abstrakt konsept/datatype Listen er en lineær struktur (men kan allikevel implementeres ikke-lineært bak kulissene ) Hvert element har en forgjenger, unntatt første element i listen Hvert
EKSAMEN. Dato: 9. mai 2016 Eksamenstid: 09:00 13:00
 EKSAMEN Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: 9. mai 2016 Eksamenstid: 09:00 13:00 Hjelpemidler: Alle trykte og skrevne Faglærer: Jan Høiberg Om eksamensoppgavene: Oppgavesettet består
EKSAMEN Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: 9. mai 2016 Eksamenstid: 09:00 13:00 Hjelpemidler: Alle trykte og skrevne Faglærer: Jan Høiberg Om eksamensoppgavene: Oppgavesettet består
Pensum: fra boken (H-03)+ forelesninger
 Pensum: fra boken (H-03)+ forelesninger unntatt kursorisk tema KAP. 1 KAP. 2 KAP. 3 JAVA I-110 (ikke gjennomgått) OO + ABSTRAKSJON /GENERISK PROGRAMMERING REKURSJON ALGORITME-TIDSANALYSE; O-NOTASJON KAP.
Pensum: fra boken (H-03)+ forelesninger unntatt kursorisk tema KAP. 1 KAP. 2 KAP. 3 JAVA I-110 (ikke gjennomgått) OO + ABSTRAKSJON /GENERISK PROGRAMMERING REKURSJON ALGORITME-TIDSANALYSE; O-NOTASJON KAP.
UNIVERSITETET. Indeksering. Konvensjonelle indekser B-trær og hashing Flerdimensjonale indekser Hashliknende strukturer.
 UNIVERSITETET IOSLO Indeksering Konvensjonelle indekser B-trær og hashing Flerdimensjonale indekser Treliknende strukturer Hashliknende strukturer Bitmapindekser Institutt for Informatikk INF30 22.2.2011
UNIVERSITETET IOSLO Indeksering Konvensjonelle indekser B-trær og hashing Flerdimensjonale indekser Treliknende strukturer Hashliknende strukturer Bitmapindekser Institutt for Informatikk INF30 22.2.2011
Obligatorisk oppgave 1 INF1020 h2005
 Obligatorisk oppgave 1 INF1020 h2005 Frist: fredag 7. oktober Oppgaven skal løses individuelt, og må være godkjent for å kunne gå opp til eksamen. Før innlevering må retningslinjene Krav til innleverte
Obligatorisk oppgave 1 INF1020 h2005 Frist: fredag 7. oktober Oppgaven skal løses individuelt, og må være godkjent for å kunne gå opp til eksamen. Før innlevering må retningslinjene Krav til innleverte
UNIVERSITETET I OSLO
 Eksamen i UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamensdag: 15. desember 2010 Tid for eksamen: 14.30 18.30 Oppgavesettet er på 8 sider. Vedlegg: Tillatte hjelpemidler: INF2220
Eksamen i UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamensdag: 15. desember 2010 Tid for eksamen: 14.30 18.30 Oppgavesettet er på 8 sider. Vedlegg: Tillatte hjelpemidler: INF2220
Alg. Dat. Øvingsforelesning 3. Grafer, BFS, DFS og hashing
 Alg. Dat Øvingsforelesning 3 Grafer, BFS, DFS og hashing Dagens tema Grafer Terminologi Representasjon av grafer Bredde først søk (BFS) Dybde først søk (DFS) Hashing Hashfunksjoner, hashtabeller Kollisjonshåndtering
Alg. Dat Øvingsforelesning 3 Grafer, BFS, DFS og hashing Dagens tema Grafer Terminologi Representasjon av grafer Bredde først søk (BFS) Dybde først søk (DFS) Hashing Hashfunksjoner, hashtabeller Kollisjonshåndtering
Løsningsforslag for Obligatorisk Oppgave 3. Algoritmer og Datastrukturer ITF20006
 Løsningsforslag for Obligatorisk Oppgave 3 Algoritmer og Datastrukturer ITF20006 Lars Vidar Magnusson Frist 28.03.14 Den tredje obligatoriske oppgaven tar for seg forelesning 9 til 13, som dreier seg om
Løsningsforslag for Obligatorisk Oppgave 3 Algoritmer og Datastrukturer ITF20006 Lars Vidar Magnusson Frist 28.03.14 Den tredje obligatoriske oppgaven tar for seg forelesning 9 til 13, som dreier seg om
Pensum: fra boken (H-03)+ forelesninger
 Pensum: fra boken (H-03)+ forelesninger unntatt kursorisk tema KAP. 1 KAP. 2 KAP. 3 JAVA I-110 (ikke gjennomgått) OO + ABSTRAKSJON /GENERISK PROGRAMMERING REKURSJON ALGORITME-TIDSANALYSE; O-NOTASJON KAP.
Pensum: fra boken (H-03)+ forelesninger unntatt kursorisk tema KAP. 1 KAP. 2 KAP. 3 JAVA I-110 (ikke gjennomgått) OO + ABSTRAKSJON /GENERISK PROGRAMMERING REKURSJON ALGORITME-TIDSANALYSE; O-NOTASJON KAP.
Datastrukturer. Algoritmer og datastrukturer. Øvingsforelesning 2
 Datastrukturer Algoritmer og datastrukturer Øvingsforelesning 2 Datastrukturer Algoritmer og datastrukturer Øvingsforelesning 2 av Henrik Grønbech Datastrukturer Algoritmer og datastrukturer Øvingsforelesning
Datastrukturer Algoritmer og datastrukturer Øvingsforelesning 2 Datastrukturer Algoritmer og datastrukturer Øvingsforelesning 2 av Henrik Grønbech Datastrukturer Algoritmer og datastrukturer Øvingsforelesning
INF1000 HashMap. Marit Nybakken marnybak@ifi.uio.no 2. november 2003
 INF1000 HashMap Marit Nybakken marnybak@ifi.uio.no 2. november 2003 Dette dokumentet skal tas med en klype salt og forfatteren sier fra seg alt ansvar. Dere bør ikke bruke definisjonene i dette dokumentet
INF1000 HashMap Marit Nybakken marnybak@ifi.uio.no 2. november 2003 Dette dokumentet skal tas med en klype salt og forfatteren sier fra seg alt ansvar. Dere bør ikke bruke definisjonene i dette dokumentet
INF2220: Forelesning 2
 INF2220: Forelesning 2 Balanserte søketrær Rød-svarte trær (kapittel12.2) B-trær (kapittel 4.7) REPETISJON: BINÆRE SØKETRÆR 2 Binære søketrær 8 4 12 2 7 9 15 6 11 13 16 For enhver node i et binært søketre
INF2220: Forelesning 2 Balanserte søketrær Rød-svarte trær (kapittel12.2) B-trær (kapittel 4.7) REPETISJON: BINÆRE SØKETRÆR 2 Binære søketrær 8 4 12 2 7 9 15 6 11 13 16 For enhver node i et binært søketre
INF2220: Forelesning 2. Balanserte søketrær Rød-svarte trær (kapittel12.2) B-trær (kapittel 4.7)
 INF2220: Forelesning 2 Balanserte søketrær Rød-svarte trær (kapittel12.2) B-trær (kapittel 4.7) REPETISJON: BINÆRE SØKETRÆR 2 Binære søketrær 8 4 12 2 7 9 15 6 11 13 16 For enhver node i et binært søketre
INF2220: Forelesning 2 Balanserte søketrær Rød-svarte trær (kapittel12.2) B-trær (kapittel 4.7) REPETISJON: BINÆRE SØKETRÆR 2 Binære søketrær 8 4 12 2 7 9 15 6 11 13 16 For enhver node i et binært søketre
Hva er en liste? Hvert element har en forgjenger, unntatt første element i listen. Hvert element har en etterfølger, unntatt siste element i listen
 Lister Hva er en liste? Listen er en lineær datastruktur Hvert element har en forgjenger, unntatt første element i listen Hvert element har en etterfølger, unntatt siste element i listen I motsetning til
Lister Hva er en liste? Listen er en lineær datastruktur Hvert element har en forgjenger, unntatt første element i listen Hvert element har en etterfølger, unntatt siste element i listen I motsetning til
Heap og prioritetskø. Marjory the Trash Heap fra Fraggle Rock
 Heap og prioritetskø Marjory the Trash Heap fra Fraggle Rock Binær heap En heap er et komplett binært tre: Alle nivåene i treet, unntatt (muligens) det nederste, er alltid helt fylt opp med noder Alle
Heap og prioritetskø Marjory the Trash Heap fra Fraggle Rock Binær heap En heap er et komplett binært tre: Alle nivåene i treet, unntatt (muligens) det nederste, er alltid helt fylt opp med noder Alle
Oppgavesettet består av 7 sider, inkludert denne forsiden. Kontroll& at oppgaven er komplett før du begynner å besvare spørsmålene.
 Høgskoleni Østfold EKSAMEN Emnekode: Emnenavn: ITF20006 Algoritmer og datastrukturer Dato: Eksamenstid: 9. mai 2016 9.00 13.00 Hjelpemidler: Faglærer: Alle trykte og skrevne Jan Høiberg Om eksamensoppgaven
Høgskoleni Østfold EKSAMEN Emnekode: Emnenavn: ITF20006 Algoritmer og datastrukturer Dato: Eksamenstid: 9. mai 2016 9.00 13.00 Hjelpemidler: Faglærer: Alle trykte og skrevne Jan Høiberg Om eksamensoppgaven
IN Algoritmer og datastrukturer
 IN2010 - Algoritmer og datastrukturer HØSTEN 2018 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 3: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2010 H2018, forelesning
IN2010 - Algoritmer og datastrukturer HØSTEN 2018 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 3: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2010 H2018, forelesning
Innhold. Innledning 1
 Innhold Innledning 1 1 Kompleksitetsanalyse 7 1.1 Innledning.............................. 8 1.2 Hva vi beregner........................... 8 1.2.1 Enkle operasjoner...................... 8 1.2.2 Kompleksitet........................
Innhold Innledning 1 1 Kompleksitetsanalyse 7 1.1 Innledning.............................. 8 1.2 Hva vi beregner........................... 8 1.2.1 Enkle operasjoner...................... 8 1.2.2 Kompleksitet........................
Hva er en kø? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn først
 Køer Hva er en kø? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn først Et nytt element legges alltid til sist i køen Skal vi ta ut et element, tar vi alltid
Køer Hva er en kø? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn først Et nytt element legges alltid til sist i køen Skal vi ta ut et element, tar vi alltid
Kapittel 14, Hashing. Tema. Definere hashing Studere ulike hashfunksjoner Studere kollisjonsproblemet 17-1
 Kapittel 14, Hashing Tema Definere hashing Studere ulike hashfunksjoner Studere kollisjonsproblemet 17-1 Hashing Hashing er en effektiv metode ved lagring og gjenfinning (søking) av informasjon Søkemetoder
Kapittel 14, Hashing Tema Definere hashing Studere ulike hashfunksjoner Studere kollisjonsproblemet 17-1 Hashing Hashing er en effektiv metode ved lagring og gjenfinning (søking) av informasjon Søkemetoder
Hva er en kø? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn først
 Køer Hva er en kø? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn først Et nytt element legges alltid til sist i køen Skal vi ta ut et element, tar vi alltid
Køer Hva er en kø? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn først Et nytt element legges alltid til sist i køen Skal vi ta ut et element, tar vi alltid
Hva er en liste? Hvert element har en forgjenger, unntatt første element i listen. Hvert element har en etterfølger, unntatt siste element i listen
 Lister Hva er en liste? Listen er en lineær datastruktur Hvert element har en forgjenger, unntatt første element i listen Hvert element har en etterfølger, unntatt siste element i listen I motsetning til
Lister Hva er en liste? Listen er en lineær datastruktur Hvert element har en forgjenger, unntatt første element i listen Hvert element har en etterfølger, unntatt siste element i listen I motsetning til
Semantisk Analyse del III
 Semantisk Analyse del III Typesjekking Kapittel 6.4 08.03.2013 1 Datatyper og typesjekking Om typer generelt Hva er typer? Statisk og dynamisk typing Hvordan beskrive typer syntaktisk? Hvordan lagre dem
Semantisk Analyse del III Typesjekking Kapittel 6.4 08.03.2013 1 Datatyper og typesjekking Om typer generelt Hva er typer? Statisk og dynamisk typing Hvordan beskrive typer syntaktisk? Hvordan lagre dem
Array&ArrayList Lagring Liste Klasseparametre Arrayliste Testing Lenkelister
 Dagens tema Lister og generiske klasser, del I Array-er og ArrayList (Big Java 6.1 & 6.8) Ulike lagringsformer (Collection) i Java (Big Java 15.1) Klasser med typeparametre («generiske klasser») (Big Java
Dagens tema Lister og generiske klasser, del I Array-er og ArrayList (Big Java 6.1 & 6.8) Ulike lagringsformer (Collection) i Java (Big Java 15.1) Klasser med typeparametre («generiske klasser») (Big Java
INF2810: Funksjonell Programmering. Mer om verditilordning og muterbare data.
 INF2810: Funksjonell Programmering Mer om verditilordning og muterbare data. Erik Velldal Universitetet i Oslo 16. mars 2017 De siste ukene: destruktive operasjoner 2 set! endrer verditilordningen til
INF2810: Funksjonell Programmering Mer om verditilordning og muterbare data. Erik Velldal Universitetet i Oslo 16. mars 2017 De siste ukene: destruktive operasjoner 2 set! endrer verditilordningen til
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF2220 Algoritmer og datastrukturer Eksamensdag: 16. desember 2013 Tid for eksamen: 14.30 18.30 Oppgavesettet er på 8 sider.
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF2220 Algoritmer og datastrukturer Eksamensdag: 16. desember 2013 Tid for eksamen: 14.30 18.30 Oppgavesettet er på 8 sider.
b) 10 2 = 20 c) 5 1 = 5.
 INF1000 oppgavesett til teoritimer i undervisningsuke 11 (6-10 nov) 1) Hvor mange doubleverdier er det plass til i hver av disse arrayene? a) double[][] tabella = new double[9][9]; b) double[][] tabellb
INF1000 oppgavesett til teoritimer i undervisningsuke 11 (6-10 nov) 1) Hvor mange doubleverdier er det plass til i hver av disse arrayene? a) double[][] tabella = new double[9][9]; b) double[][] tabellb
UNIVERSITETET I OSLO. Indeksering. Hvordan finne et element raskt? Institutt for Informatikk. INF Ellen Munthe-Kaas
 UNIVERSITETET I OSLO Indeksering Hvordan finne et element raskt? Institutt for Informatikk INF3100 2.3.2010 Ellen Munthe-Kaas 1 Oversikt Konvensjonelle indekser B-trær og hashing Flerdimensjonale indekser
UNIVERSITETET I OSLO Indeksering Hvordan finne et element raskt? Institutt for Informatikk INF3100 2.3.2010 Ellen Munthe-Kaas 1 Oversikt Konvensjonelle indekser B-trær og hashing Flerdimensjonale indekser
Oppgave 1 a. INF1020 Algoritmer og datastrukturer. Oppgave 1 b
 Oppgave 1 1 a INF1020 Algoritmer og datastrukturer Forelesning 14: Gjennomgang av eksamen vår 2001 oppgave 1,2,4 Arild Waaler Institutt for informatikk, Universitetet i Oslo Oppgave 1 a Programmer en ikke-rekursiv
Oppgave 1 1 a INF1020 Algoritmer og datastrukturer Forelesning 14: Gjennomgang av eksamen vår 2001 oppgave 1,2,4 Arild Waaler Institutt for informatikk, Universitetet i Oslo Oppgave 1 a Programmer en ikke-rekursiv
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 5: Prioritetskø og Heap Bjarne Holen (Ifi, UiO) INF2220 H2009, forelesning 5 1 /
INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 5: Prioritetskø og Heap Bjarne Holen (Ifi, UiO) INF2220 H2009, forelesning 5 1 /
Binære søketrær. Et notat for INF1010 Stein Michael Storleer 16. mai 2013
 Binære søketrær Et notat for INF Stein Michael Storleer 6. mai 3 Dette notatet er nyskrevet og inneholder sikkert feil. Disse vil bli fortløpende rettet og datoen over blir oppdatert samtidig. Hvis du
Binære søketrær Et notat for INF Stein Michael Storleer 6. mai 3 Dette notatet er nyskrevet og inneholder sikkert feil. Disse vil bli fortløpende rettet og datoen over blir oppdatert samtidig. Hvis du
INF2810: Funksjonell Programmering. Mer om verditilordning og muterbare data.
 INF2810: Funksjonell Programmering Mer om verditilordning og muterbare data. Erik Velldal Universitetet i Oslo 16. mars 2017 De siste ukene: destruktive operasjoner 2 set! endrer verditilordningen til
INF2810: Funksjonell Programmering Mer om verditilordning og muterbare data. Erik Velldal Universitetet i Oslo 16. mars 2017 De siste ukene: destruktive operasjoner 2 set! endrer verditilordningen til
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2017 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2017, forelesning
INF2220 - Algoritmer og datastrukturer HØSTEN 2017 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2017, forelesning
Binær heap. En heap er et komplett binært tre:
 Heap Binær heap En heap er et komplett binært tre: Alle nivåene i treet, unntatt (muligens) det nederste, er alltid helt fylt opp med noder Alle noder på nederste nivå ligger så langt til venstre som mulig
Heap Binær heap En heap er et komplett binært tre: Alle nivåene i treet, unntatt (muligens) det nederste, er alltid helt fylt opp med noder Alle noder på nederste nivå ligger så langt til venstre som mulig
Ny/utsatt EKSAMEN. Dato: 5. januar 2018 Eksamenstid: 09:00 13:00
 Ny/utsatt EKSAMEN Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: 5. januar 2018 Eksamenstid: 09:00 13:00 Hjelpemidler: Alle trykte og skrevne Faglærer: Jan Høiberg Om eksamensoppgavene: Oppgavesettet
Ny/utsatt EKSAMEN Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: 5. januar 2018 Eksamenstid: 09:00 13:00 Hjelpemidler: Alle trykte og skrevne Faglærer: Jan Høiberg Om eksamensoppgavene: Oppgavesettet
Hva er en kø? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn først
 Køer Hva er en kø? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn først Et nytt element legges alltid til sist i køen Skal vi ta ut et element, tar vi alltid
Køer Hva er en kø? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn først Et nytt element legges alltid til sist i køen Skal vi ta ut et element, tar vi alltid
Definisjon: Et sortert tre
 Binære søketrær Definisjon: Et sortert tre For alle nodene i et binært søketre gjelder: Alle verdiene i nodens venstre subtre er mindre enn verdien i noden Alle verdiene i nodens høyre subtre er større
Binære søketrær Definisjon: Et sortert tre For alle nodene i et binært søketre gjelder: Alle verdiene i nodens venstre subtre er mindre enn verdien i noden Alle verdiene i nodens høyre subtre er større
Obligatorisk oppgave 4 i INF1010, våren 2014: "Leger og resepter" Versjon 1.1
 Obligatorisk oppgave 4 i INF1010, våren 2014: "Leger og resepter" Versjon 1.1 Denne oppgaven skal løses to og to vha. systemutviklingsmetoden Parprogrammering. For å få levere må alle registrere seg gjennom
Obligatorisk oppgave 4 i INF1010, våren 2014: "Leger og resepter" Versjon 1.1 Denne oppgaven skal løses to og to vha. systemutviklingsmetoden Parprogrammering. For å få levere må alle registrere seg gjennom
AlgDat 12. Forelesning 2. Gunnar Misund
 AlgDat 12 Forelesning 2 Forrige forelesning Følg med på hiof.no/algdat, ikke minst beskjedsida! Algdat: Fundamentalt, klassisk, morsomt,...krevende :) Pensum: Forelesningene, oppgavene (pluss deler av
AlgDat 12 Forelesning 2 Forrige forelesning Følg med på hiof.no/algdat, ikke minst beskjedsida! Algdat: Fundamentalt, klassisk, morsomt,...krevende :) Pensum: Forelesningene, oppgavene (pluss deler av
Indeksering. Konvensjonelle indekser B-trær og hashing Flerdimensjonale indekser Treliknende strukturer Hashliknende strukturer Bitmapindekser
 UNIVERSITETET I OSLO Indeksering Konvensjonelle indekser B-trær og hashing Flerdimensjonale indekser Treliknende strukturer Hashliknende strukturer Bitmapindekser Institutt for Informatikk INF30 3.3.2014
UNIVERSITETET I OSLO Indeksering Konvensjonelle indekser B-trær og hashing Flerdimensjonale indekser Treliknende strukturer Hashliknende strukturer Bitmapindekser Institutt for Informatikk INF30 3.3.2014
Innhold uke 4. INF 1000 høsten 2011 Uke 4: 13. september. Deklarasjon av peker og opprettelse av arrayobjektet. Representasjon av array i Java
 INF høsten 2 Uke 4: 3. september Grunnkurs i Objektorientert Programmering Institutt for Informatikk Universitetet i Oslo Siri Moe Jensen og Arne Maus Mål for uke 4: Innhold uke 4 Repetisjon m/ utvidelser:
INF høsten 2 Uke 4: 3. september Grunnkurs i Objektorientert Programmering Institutt for Informatikk Universitetet i Oslo Siri Moe Jensen og Arne Maus Mål for uke 4: Innhold uke 4 Repetisjon m/ utvidelser:
Flerveis søketrær og B-trær
 Flerveis søketrær og B-trær Flerveis (multi-way, n-ært) søketre Generalisering av binært søketre Binært søketre: Hver node har maksimalt 2 barn og 1 nøkkelverdi. Barna ligger sortert på verdi i forhold
Flerveis søketrær og B-trær Flerveis (multi-way, n-ært) søketre Generalisering av binært søketre Binært søketre: Hver node har maksimalt 2 barn og 1 nøkkelverdi. Barna ligger sortert på verdi i forhold
Eksamen iin115 og IN110, 15. mai 1997 Side 2 Oppgave 1 Trær 55 % Vi skal i denne oppgaven se på en form for søkestrukturer som er spesielt godt egnet
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i IN 115 og IN110 Algoritmer og datastrukturer Eksamensdag: 15. mai 1997 Tid for eksamen: 9.00 15.00 Oppgavesettet er på 8 sider.
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i IN 115 og IN110 Algoritmer og datastrukturer Eksamensdag: 15. mai 1997 Tid for eksamen: 9.00 15.00 Oppgavesettet er på 8 sider.
Uke 5 Disjunkte mengder
 Uke 5 Disjunkte mengder MAW, kap.. 8 September 19, 2005 Page 1 Hittil Forutsetninger for og essensen i faget Metodekall, rekursjon, permutasjoner Analyse av algoritmer Introduksjon til ADT er Den første
Uke 5 Disjunkte mengder MAW, kap.. 8 September 19, 2005 Page 1 Hittil Forutsetninger for og essensen i faget Metodekall, rekursjon, permutasjoner Analyse av algoritmer Introduksjon til ADT er Den første
UNIVERSITETET. Indeksering. Hvordan finne et element raskt? Vera Goebel, Ellen Munthe-Kaas
 UNIVERSITETET IOSLO Indeksering Hvordan finne et element raskt? Basert på foiler av Hector Garcia Molina Basert på foiler av Hector Garcia-Molina, Vera Goebel, Ellen Munthe-Kaas Oversikt Konvensjonelle
UNIVERSITETET IOSLO Indeksering Hvordan finne et element raskt? Basert på foiler av Hector Garcia Molina Basert på foiler av Hector Garcia-Molina, Vera Goebel, Ellen Munthe-Kaas Oversikt Konvensjonelle
Heap* En heap er et komplett binært tre: En heap er også et monotont binært tre:
 Heap Heap* En heap er et komplett binært tre: Alle nivåene i treet, unntatt (muligens) det nederste, er alltid helt fylt opp med noder Alle noder på nederste nivå ligger til venstre En heap er også et
Heap Heap* En heap er et komplett binært tre: Alle nivåene i treet, unntatt (muligens) det nederste, er alltid helt fylt opp med noder Alle noder på nederste nivå ligger til venstre En heap er også et
Definisjon. I et binært tre har hver node enten 0, 1 eller 2 barn
 Binære trær Definisjon I et binært tre har hver node enten 0, 1 eller 2 barn Rekursiv definisjon: Et binært tre er enten tomt, eller: Består av en rotnode og to binære trær som kalles venstre subtre og
Binære trær Definisjon I et binært tre har hver node enten 0, 1 eller 2 barn Rekursiv definisjon: Et binært tre er enten tomt, eller: Består av en rotnode og to binære trær som kalles venstre subtre og
Algoritmer og Datastrukturer IAI 21899
 Eksamen i Algoritmer og Datastrukturer IAI 21899 Høgskolen i Østfold Avdeling for informatikk og automatisering Torsdag 30. november 2000, kl. 09.00-14.00 LØSNINGSFORSLAG 1 Del 1, Binære søketrær Totalt
Eksamen i Algoritmer og Datastrukturer IAI 21899 Høgskolen i Østfold Avdeling for informatikk og automatisering Torsdag 30. november 2000, kl. 09.00-14.00 LØSNINGSFORSLAG 1 Del 1, Binære søketrær Totalt
Post-it spørsmål fra timen (Arv og subklasser)
 Post-it spørsmål fra timen 30.01 (Arv og subklasser) Tegning Spørsmål: Skjønte ikke tegningene Hater tegningene. Lær meg å tegne. Mvh frustrert elev. Spørsmål: Datastruktur-tegning, og hvor mye detaljer
Post-it spørsmål fra timen 30.01 (Arv og subklasser) Tegning Spørsmål: Skjønte ikke tegningene Hater tegningene. Lær meg å tegne. Mvh frustrert elev. Spørsmål: Datastruktur-tegning, og hvor mye detaljer
Algoritmer og Datastrukturer
 Eksamen i Algoritmer og Datastrukturer Høgskolen i Østfold Avdeling for informatikk og automatisering Torsdag 10. desember 1998, kl. 09.00-15.00 Hjelpemidler: Alle trykte og skrevne hjelpemidler. Kalkulator.
Eksamen i Algoritmer og Datastrukturer Høgskolen i Østfold Avdeling for informatikk og automatisering Torsdag 10. desember 1998, kl. 09.00-15.00 Hjelpemidler: Alle trykte og skrevne hjelpemidler. Kalkulator.
2 Om statiske variable/konstanter og statiske metoder.
 Litt om datastrukturer i Java Av Stein Gjessing, Institutt for informatikk, Universitetet i Oslo 1 Innledning Dette notatet beskriver noe av det som foregår i primærlageret når et Javaprogram utføres.
Litt om datastrukturer i Java Av Stein Gjessing, Institutt for informatikk, Universitetet i Oslo 1 Innledning Dette notatet beskriver noe av det som foregår i primærlageret når et Javaprogram utføres.
Litt om Javas class-filer og byte-kode
 Litt om Javas class-filer og byte-kode INF 5110, 11/5-2010, Stein Krogdahl (Dessverre litt få figurer) Disse formatene ble planlagt fra start som en del av hele Java-ideen Bt Byte-koden gir portabilitet
Litt om Javas class-filer og byte-kode INF 5110, 11/5-2010, Stein Krogdahl (Dessverre litt få figurer) Disse formatene ble planlagt fra start som en del av hele Java-ideen Bt Byte-koden gir portabilitet
INF120: Oblig 3. Yngve Mardal Moe
 Yngve Mardal Moe Mar 28, 2019 Contents 1 Hva trenger dere for denne oppgaven 3 2 Hvordan skal dere arbeide med denne oppgaven 5 3 En søkeindeks 7 4 Å slå opp i en søkeindeks 9 5 Å utvide en søkeindeks
Yngve Mardal Moe Mar 28, 2019 Contents 1 Hva trenger dere for denne oppgaven 3 2 Hvordan skal dere arbeide med denne oppgaven 5 3 En søkeindeks 7 4 Å slå opp i en søkeindeks 9 5 Å utvide en søkeindeks
Indeksering. Konvensjonelle indekser B-trær og hashing Flerdimensjonale indekser Trestrukturer Hashliknende strukturer Bitmapindekser
 UNIVERSITETET I OSLO Indeksering Konvensjonelle indekser B-trær og hashing Flerdimensjonale indekser Trestrukturer Hashliknende strukturer Bitmapindekser Institutt for Informatikk INF3100 V18 Evgenij Thorstensen
UNIVERSITETET I OSLO Indeksering Konvensjonelle indekser B-trær og hashing Flerdimensjonale indekser Trestrukturer Hashliknende strukturer Bitmapindekser Institutt for Informatikk INF3100 V18 Evgenij Thorstensen
KONTINUASJONSEKSAMEN
 Høgskolen i Gjøvik Avdeling for Teknologi KONTINUASJONSEKSAMEN FAGNAVN: FAGNUMMER: Algoritmiske metoder I L 189 A EKSAMENSDATO: 13. august 2001 KLASSE: 99HINDA / 99HINDB / 99HINEA / 00HDESY ( 2DA / 2DB
Høgskolen i Gjøvik Avdeling for Teknologi KONTINUASJONSEKSAMEN FAGNAVN: FAGNUMMER: Algoritmiske metoder I L 189 A EKSAMENSDATO: 13. august 2001 KLASSE: 99HINDA / 99HINDB / 99HINEA / 00HDESY ( 2DA / 2DB
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i IN 211 Programmeringsspråk Eksamensdag: 4. desember 2002 Tid for eksamen: 9.00 15.00 Oppgavesettet er på 10 sider. Vedlegg: Tillatte
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i IN 211 Programmeringsspråk Eksamensdag: 4. desember 2002 Tid for eksamen: 9.00 15.00 Oppgavesettet er på 10 sider. Vedlegg: Tillatte
Løsningsforslag til eksamen i PG4200 Algoritmer og datastrukturer 10. desember 2014
 Løsningsforslag Dette er et utbygd løsningsforslag. D.v.s at det kan forekomme feil og at løsningene er mer omfattende enn det som kreves av studentene på eksamen. Oppgavesettet består av 5 (fem) sider.
Løsningsforslag Dette er et utbygd løsningsforslag. D.v.s at det kan forekomme feil og at løsningene er mer omfattende enn det som kreves av studentene på eksamen. Oppgavesettet består av 5 (fem) sider.
Lenkelister, iteratorer, indre klasser. Repetisjonskurs våren 2018 kristijb
 Lenkelister, iteratorer, indre klasser Repetisjonskurs våren 2018 kristijb Lenket liste av objekter Vi lager en lenke ved at objekter refererer til hverandre. Vanlige er ofte å ha Node-objekter som har
Lenkelister, iteratorer, indre klasser Repetisjonskurs våren 2018 kristijb Lenket liste av objekter Vi lager en lenke ved at objekter refererer til hverandre. Vanlige er ofte å ha Node-objekter som har
INF1010 siste begreper før oblig 2
 INF1010 siste begreper før oblig 2 Sammenligning. Mer lenkede lister. Forskjellige listeimplementasjoner. Binære trær. Bittelitt om grensesnitt (interface). Dagens forelesning Flere temaer på grunn av
INF1010 siste begreper før oblig 2 Sammenligning. Mer lenkede lister. Forskjellige listeimplementasjoner. Binære trær. Bittelitt om grensesnitt (interface). Dagens forelesning Flere temaer på grunn av
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2016 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2016, forelesning
INF2220 - Algoritmer og datastrukturer HØSTEN 2016 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2016, forelesning
København 20 Stockholm
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i IN 115 Algoritmer og datastrukturer Eksamensdag: 26. mai 2001 Tid for eksamen: 9.00 15.00 Oppgavesettet er på 7 sider. Vedlegg:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i IN 115 Algoritmer og datastrukturer Eksamensdag: 26. mai 2001 Tid for eksamen: 9.00 15.00 Oppgavesettet er på 7 sider. Vedlegg:
Oppgave 1. Sekvenser (20%)
 Det matematisk-naturvitenskapelige fakultet UNIVERSITETET I BERGEN Eksamen i emnet I 20 - Algoritmer, datastrukturer og programmering Mandag 2.Mai 200, kl. 09-5. Ingen hjelpemidler tillatt. Oppgavesettet
Det matematisk-naturvitenskapelige fakultet UNIVERSITETET I BERGEN Eksamen i emnet I 20 - Algoritmer, datastrukturer og programmering Mandag 2.Mai 200, kl. 09-5. Ingen hjelpemidler tillatt. Oppgavesettet
PG4200 Algoritmer og datastrukturer Forelesning 7
 PG4200 Algoritmer og datastrukturer Forelesning 7 Lars Sydnes, NITH 19. mars 2014 I. TERMINOLOGI FOR TRÆR TRÆR Lister: Lineære Trær: Hierarkiske Modell / Språk: Bestanddeler: Noder, forbindelser. Forbindelse
PG4200 Algoritmer og datastrukturer Forelesning 7 Lars Sydnes, NITH 19. mars 2014 I. TERMINOLOGI FOR TRÆR TRÆR Lister: Lineære Trær: Hierarkiske Modell / Språk: Bestanddeler: Noder, forbindelser. Forbindelse
INF2220: Time 4 - Heap, Huffmann
 INF0: Time 4 - Heap, Huffmann Mathias Lohne mathialo Heap (prioritetskø) En heap (også kalt prioritetskø) er en type binært tre med noen spesielle struktur- og ordningskrav. Vi har to typer heap: min-
INF0: Time 4 - Heap, Huffmann Mathias Lohne mathialo Heap (prioritetskø) En heap (også kalt prioritetskø) er en type binært tre med noen spesielle struktur- og ordningskrav. Vi har to typer heap: min-
Array&ArrayList Lagring Liste Klasseparametre Arrayliste Testing Lenkelister Videre
 Dagens tema Lister og generiske klasser, del I Array-er og ArrayList (Big Java 6.1 & 6.8) Ulike lagringsformer (Collection) i Java (Big Java 15.1) Klasser med typeparametre («generiske klasser») (Big Java
Dagens tema Lister og generiske klasser, del I Array-er og ArrayList (Big Java 6.1 & 6.8) Ulike lagringsformer (Collection) i Java (Big Java 15.1) Klasser med typeparametre («generiske klasser») (Big Java
EKSAMENSOPPGAVE. IAI20102 Algoritmer og datastrukturer
 EKSAMENSOPPGAVE Fag: Lærer: IAI00 Algoritmer og datastrukturer André A. Hauge Dato:..005 Tid: 0900-00 Antall oppgavesider: 5 med forside Antall vedleggssider: 0 Hjelpemidler: Alle trykte og skrevne hjelpemidler,
EKSAMENSOPPGAVE Fag: Lærer: IAI00 Algoritmer og datastrukturer André A. Hauge Dato:..005 Tid: 0900-00 Antall oppgavesider: 5 med forside Antall vedleggssider: 0 Hjelpemidler: Alle trykte og skrevne hjelpemidler,
Mål. Pensum. TDT4110 Informasjonsteknologi grunnkurs: Tema: Unntak (exceptions) (Kap 6) Dictionaries (Kap. 9) Terje Rydland - IDI/NTNU
 1 Kunnskap for en bedre verden TDT4110 Informasjonsteknologi grunnkurs: Tema: Unntak (exceptions) (Kap 6) Dictionaries (Kap. 9) Terje Rydland - IDI/NTNU 2 Læringsmål og pensum Mål Lære å bruke unntak (Exceptions)
1 Kunnskap for en bedre verden TDT4110 Informasjonsteknologi grunnkurs: Tema: Unntak (exceptions) (Kap 6) Dictionaries (Kap. 9) Terje Rydland - IDI/NTNU 2 Læringsmål og pensum Mål Lære å bruke unntak (Exceptions)
