Flerveis søketrær og B-trær
|
|
|
- Hilmar Jensen
- 7 år siden
- Visninger:
Transkript
1 Flerveis søketrær og B-trær
2 Flerveis (multi-way, n-ært) søketre Generalisering av binært søketre Binært søketre: Hver node har maksimalt 2 barn og 1 nøkkelverdi. Barna ligger sortert på verdi i forhold til den ene nøkkelverdien. Flerveis søketre (av orden * m): Hver node har maksimalt m barn og m 1 sorterte nøkkelverdier. Barna ligger sortert på verdi «innimellom» de sortete nøkkelverdiene. Brukes oftest når vi ikke får plass til alle data i primærhukommelsen/ram: Må lese fra/skrive til (aksessere) sekundærhukommelsen (disk) Diskaksess er veldig mye langsommere RAM-aksess Filsystemer i operativsystemer og databaser bruker flerveis søketrær som er optimaliserte for diskaksess *: «orden» er ikke entydig definert i litteraturen
3 Definisjon: Flerveis søketre av orden m Alle noder i treet har maksimalt m subtrær/barn I en node med k subtrær, S 1, S 2,..., S k, er det slik at: Noden inneholder k 1 nøkkelverdier, v 1, v 2,..., v k 1 som er sorterte: v 1 v 2... v k 1 Verdiene i subtrærne, v(s i ), ligger sortert slik at v(s i ) < v i v(s i + 1 ), i = 1, 2,..., k 2 v k - 1 v(s k ) Merk at subtrærne til en node kan være tomme
4 Et flerveis søketre av orden m = 5
5 Et flerveis søketre av orden m = 4
6 Flerveis søketre av orden m = 5
7 Innsetting og søking i flerveis søketre Samme prinsipp som for binære søketrær: Følger en vei fra roten og nedover i treet I hver node sjekker vi om verdien vi søker/skal sette inn er lik, mindre eller større enn de sorterte nøkkelverdiene i noden Går videre fra en node til det subtreet der verdien skal ligge, hvis den finnes i treet Hvis treet har totalt n verdier og er balansert, er søking og innsetting meget raskt O(log n) Hvis treet blir svært ubalansert, og/eller nodene i liten grad er fylt opp med verdier, blir søking og innsetting langsomt O(n)
8 B-tre 1 Et flerveis søketre som alltid er perfekt balansert og minst halvveis fylt opp med verdier (Bayer/McCreight,1972) Garanterer O(log n) oppførsel for søking, innsetting og fjerning Antall verdier i hver node er gjerne svært stort (tilsvarende en diskblokk/page) B-trær (og varianter som B+-trær og B*-trær) brukes i de fleste filsystemer (Windows, Mac, Unix/Linux) og i store databasesystemer 1: B?
9 Definisjon av B-tre Et B-tre av orden m er et flerveis søketre der: Roten er enten et blad eller har minst to subtrær Alle noder (unntatt roten) inneholder minst m/2 verdier og maksimalt m - 1 verdier En node med k verdier (m/2 k m - 1) har enten 0 barn (en bladnode) eller k + 1 barn (indre node) Alle bladnoder ligger på samme nivå i treet
10 B-tre av orden m = 5
11 B-tre av orden m = 5
12
13 Effektivitet, B-tre av orden m = 201 Antall noder og verdier i hvert nivå i treet
14 Søking i B-trær «An algorithm for finding a key in B-tree is simple. Start at the root and determine which pointer to follow based on a comparison between the search value and key fields in the root node. Follow the appropriate pointer to a child node. Examine the key fields in the child node and continue to follow the appropriate pointers until the search value is found or a leaf node is reached that doesn't contain the desired search value» Er garantert O(log n)
15 Innsetting av ny verdi i B-tre Kravet om at alle blader skal være på samme nivå gir en karakteristisk oppførsel for B-trær: B-trær vokser ikke «nedover» ved at de får nye blader, som for binære søketrær Istedet vokser de «oppover» ved at de får ny rot Nye verdier settes inn i eksisterende bladnoder Når en bladnode er full deles den i to, og en verdi sendes «oppover» i treet YouTube: Demo av innsetting i B-tre av orden m = 3, med maksimalt 2 verdier og 3 barn per node Innsetting er alltid O(log n)
16 Algoritme for innsetting i B-tre Finn bladnoden der ny verdi skal settes inn Hvis bladnoden ikke er full: Sett inn ny verdi sortert i bladnoden Ellers, hvis bladnoden er full av verdier: Del bladnoden i to noder, med ~halvparten av verdiene i hver node Send midterste verdi et nivå oppover for innsetting i foreldernoden Hvis foreldernoden også blir full, fortsettes sending av verdi(er) oppover i treet på samme måte
17 Eksempel: Innsetting i B-tre av orden m = 5
18 Etter innsetting av 395
19 Etter innsetting av 382
20 Etter innsetting av 490
21 Fjerning av verdi i B-tre Kan resultere i noder med for få verdier (< m/2) Vil lage et «hull» i strukturen hvis verdien som fjernes er i en indre node Algoritmen for fjerning «reparerer» treet med: Flytting av verdier mellom noder (aka rotasjoner) Sammenslåinger (merging) av to noder til én ny node Fjerning av verdier er vist i læreboka for B-trær med orden m = 3 (se avsnitt 12.2) Fjerning i B-trær er relativt «fiklete», med flere spesialtilfeller, men er alltid O(log n)
22 Implementasjon/lagring av B-trær En node i et B-tre av orden m kan representeres med to arrayer av lengde hhv. m og m 1: En array med referanser til barna En sortert array med nøkkelverdier B-trær brukes mest når data må flyttes mellom primær og sekundær hukommelse: Pekere til barn (adresser i RAM) vil ikke virke Vanlig i stedet å representere hele treet som én lang array, der referansene til barna er arrayindekser og det er satt av like stor plass til alle noder virker både i RAM og på disk
23 B-trær og sekundærhukommelse Hvis dataene våre er for store til å få plass i RAM, må de flyttes frem og tilbake mellom RAM/disk (paging) Lesing og skriving til/fra disk (flytting av lese-/ skrivehode, rotasjon av disk, dataoverføring) er ofte flere tusen ganger tregere enn å lese/skrive RAM Disker leses og skrives i «blokker», typisk 4K bytes om gangen (Linux) B-treet kan minimalisere antall diskaksesser: Størrelsen på en node «tunes» til blokkstørrelsen, slik at alle dataene i noden håndteres med én read/write operasjon
24 B*-trær Utnytter plassen på hvert nivå i treet bedre B*-treet har alle egenskapene til et B-tre, men: I et B-tre av orden m har alle noder minst m/2 verdier I et B*-tre av orden m har alle noder minst 2 m/3 verdier Algoritmene for innsetting og fjerning er forskjellige: I stedet for å dele en node i to med en gang den er full, flyttes verdier over til søskennoder Når to søskennoder er fulle av verdier, deles de i tre nye noder
25 B+-trær Løser et problem forbundet med vanlige B-trær: Traversering av et B-tre (sekvensiell/sortert gjennomgang av dataene) er vanskelig å gjøre effektivt når vi må skyfle data til/fra sekundærhukommelsen Hver node må oppsøkes mange ganger i løpet av en traversering av B-treet B+-tre: Alle nøkkelverdier i indre noder lagres en gang til som sin egen inorder etterfølger i en bladnode Alle bladnodene lenkes sammen med «pekere» for å kunne gå gjennom alle dataene sekvensielt/sortert med minimalt antall diskaksesser Lagrer oftest bare nøkkelverdier i treet, sammen med et ekstra lag med noder på nederste nivå som inneholder pekere/ referanser til selve dataobjektene
26 Eksempel: B+-tre
27 Eksempel: B+-tre
Flerveis søketrær og B-trær
 Flerveis søketrær og B-trær Flerveis søketre * Generalisering av binært søketre Binært søketre: Hver node har maksimalt 2 subtrær/barn og 1 verdi Barna ligger sortert på verdi i forhold til den ene verdien
Flerveis søketrær og B-trær Flerveis søketre * Generalisering av binært søketre Binært søketre: Hver node har maksimalt 2 subtrær/barn og 1 verdi Barna ligger sortert på verdi i forhold til den ene verdien
Definisjon av binært søketre
 Binære søketrær Definisjon av binært søketre For alle nodene i et binært søketre gjelder: Alle verdiene i nodens venstre subtre er mindre enn verdien i noden Alle verdiene i nodens høyre subtre er større
Binære søketrær Definisjon av binært søketre For alle nodene i et binært søketre gjelder: Alle verdiene i nodens venstre subtre er mindre enn verdien i noden Alle verdiene i nodens høyre subtre er større
Definisjon: Et sortert tre
 Binære søketrær Definisjon: Et sortert tre For alle nodene i et binært søketre gjelder: Alle verdiene i nodens venstre subtre er mindre enn verdien i noden Alle verdiene i nodens høyre subtre er større
Binære søketrær Definisjon: Et sortert tre For alle nodene i et binært søketre gjelder: Alle verdiene i nodens venstre subtre er mindre enn verdien i noden Alle verdiene i nodens høyre subtre er større
Definisjon. I et binært tre har hver node enten 0, 1 eller 2 barn
 Binære trær Definisjon I et binært tre har hver node enten 0, 1 eller 2 barn Rekursiv definisjon: Et binært tre er enten tomt, eller: Består av en rotnode og to binære trær som kalles venstre subtre og
Binære trær Definisjon I et binært tre har hver node enten 0, 1 eller 2 barn Rekursiv definisjon: Et binært tre er enten tomt, eller: Består av en rotnode og to binære trær som kalles venstre subtre og
Selv-balanserende søketrær
 Selv-balanserende søketrær Georgy Maksimovich Adelson-Velsky Evgenii Mikhailovich Landis Søketrær og effektivitet O(log n) effektivitet av binære søketrær kan ikke garanteres Treet til venstre har høyde
Selv-balanserende søketrær Georgy Maksimovich Adelson-Velsky Evgenii Mikhailovich Landis Søketrær og effektivitet O(log n) effektivitet av binære søketrær kan ikke garanteres Treet til venstre har høyde
Et eksempel: Åtterspillet
 Trær Et eksempel: Åtterspillet To spillere som «trekker» annenhver gang I hvert trekk velges et av tallene 1, 2, 3, men ikke tallet som motspiller valgte i forrige trekk Valgte tall summeres fortløpende
Trær Et eksempel: Åtterspillet To spillere som «trekker» annenhver gang I hvert trekk velges et av tallene 1, 2, 3, men ikke tallet som motspiller valgte i forrige trekk Valgte tall summeres fortløpende
INF2220: Forelesning 2
 INF2220: Forelesning 2 Balanserte søketrær Rød-svarte trær (kapittel12.2) B-trær (kapittel 4.7) REPETISJON: BINÆRE SØKETRÆR 2 Binære søketrær 8 4 12 2 7 9 15 6 11 13 16 For enhver node i et binært søketre
INF2220: Forelesning 2 Balanserte søketrær Rød-svarte trær (kapittel12.2) B-trær (kapittel 4.7) REPETISJON: BINÆRE SØKETRÆR 2 Binære søketrær 8 4 12 2 7 9 15 6 11 13 16 For enhver node i et binært søketre
INF2220: Forelesning 2. Balanserte søketrær Rød-svarte trær (kapittel12.2) B-trær (kapittel 4.7)
 INF2220: Forelesning 2 Balanserte søketrær Rød-svarte trær (kapittel12.2) B-trær (kapittel 4.7) REPETISJON: BINÆRE SØKETRÆR 2 Binære søketrær 8 4 12 2 7 9 15 6 11 13 16 For enhver node i et binært søketre
INF2220: Forelesning 2 Balanserte søketrær Rød-svarte trær (kapittel12.2) B-trær (kapittel 4.7) REPETISJON: BINÆRE SØKETRÆR 2 Binære søketrær 8 4 12 2 7 9 15 6 11 13 16 For enhver node i et binært søketre
Binære trær: Noen algoritmer og anvendelser
 Binære trær: Noen algoritmer og anvendelser Algoritmer / anvendelser: Søking i usortert binært tre Telling av antall noder og nivåer i treet Traversering av binære trær Binære uttrykkstrær Kunstig intelligens(?):
Binære trær: Noen algoritmer og anvendelser Algoritmer / anvendelser: Søking i usortert binært tre Telling av antall noder og nivåer i treet Traversering av binære trær Binære uttrykkstrær Kunstig intelligens(?):
Repetisjon: Binære. Dagens plan: Rød-svarte trær. Oppgave (N + 1)!
 Repetisjon: Binære søketrær Dagens plan: Rød-svarte trær (kap. 12.2) B-trær (kap. 4.7) bstrakte datatyper (kap. 3.1) takker (kap. 3.3) For enhver node i et binært søketre gjelder: lle verdiene i venstre
Repetisjon: Binære søketrær Dagens plan: Rød-svarte trær (kap. 12.2) B-trær (kap. 4.7) bstrakte datatyper (kap. 3.1) takker (kap. 3.3) For enhver node i et binært søketre gjelder: lle verdiene i venstre
INF2220: Forelesning 2
 INF2220: Forelesning 2 Mer om analyse av algoritmer Analyse av binære søketrær Balanserte søketrær Rød-svarte trær (kapittel12.2) B-trær (kapittel 4.7) ANALYSE AV ALGORITMER 2 Analyse av tidsforbruk Hvor
INF2220: Forelesning 2 Mer om analyse av algoritmer Analyse av binære søketrær Balanserte søketrær Rød-svarte trær (kapittel12.2) B-trær (kapittel 4.7) ANALYSE AV ALGORITMER 2 Analyse av tidsforbruk Hvor
Heap og prioritetskø. Marjory the Trash Heap fra Fraggle Rock
 Heap og prioritetskø Marjory the Trash Heap fra Fraggle Rock Binær heap En heap er et komplett binært tre: Alle nivåene i treet, unntatt (muligens) det nederste, er alltid helt fylt opp med noder Alle
Heap og prioritetskø Marjory the Trash Heap fra Fraggle Rock Binær heap En heap er et komplett binært tre: Alle nivåene i treet, unntatt (muligens) det nederste, er alltid helt fylt opp med noder Alle
... Når internminnet blir for lite. Dagens plan: Løsning: Utvidbar hashing. hash(x) katalog. O modellen er ikke lenger gyldig ved
 Dagens plan: Utvidbar hashing (kapittel 5.6) B-trær (kap. 4.7) Abstrakte datatyper (kap. 3.1) Stakker (kap. 3.3) Når internminnet blir for lite En lese-/skriveoperasjon på en harddisk (aksesstid 7-12 millisekunder)
Dagens plan: Utvidbar hashing (kapittel 5.6) B-trær (kap. 4.7) Abstrakte datatyper (kap. 3.1) Stakker (kap. 3.3) Når internminnet blir for lite En lese-/skriveoperasjon på en harddisk (aksesstid 7-12 millisekunder)
Object [] element. array. int [] tall
![Object [] element. array. int [] tall Object [] element. array. int [] tall](/thumbs/104/163274132.jpg) Datastrukturer Object [] int [] tall array element 0 1 2 3 4 5 0 1 2 3 4 5 6 7 8 40 55 63 17 22 68 89 97 89 graf lenkeliste graf Object data Node neste Node neste Node neste Node neste Node Node neste
Datastrukturer Object [] int [] tall array element 0 1 2 3 4 5 0 1 2 3 4 5 6 7 8 40 55 63 17 22 68 89 97 89 graf lenkeliste graf Object data Node neste Node neste Node neste Node neste Node Node neste
Lars Vidar Magnusson
 Binære Søketrær Lars Vidar Magnusson 14.2.2014 Kapittel 12 Binære Søketrær Søking Insetting Sletting Søketrær Søketrær er datastrukturer som støtter mange dynamiske sett operasjoner. Kan bli brukt både
Binære Søketrær Lars Vidar Magnusson 14.2.2014 Kapittel 12 Binære Søketrær Søking Insetting Sletting Søketrær Søketrær er datastrukturer som støtter mange dynamiske sett operasjoner. Kan bli brukt både
Et eksempel: Åtterspillet
 Trær Et eksempel: Åtterspillet To spillere som «trekker» annenhver gang I hvert trekk velges et av tallene 1, 2, 3, men ikke tallet som motspiller valgte i forrige trekk Valgte tall summeres fortløpende
Trær Et eksempel: Åtterspillet To spillere som «trekker» annenhver gang I hvert trekk velges et av tallene 1, 2, 3, men ikke tallet som motspiller valgte i forrige trekk Valgte tall summeres fortløpende
INF2220: Gruppe me 2. Mathias Lohne Høsten 2017
 INF0: Gruppe me Mathias Lohne Høsten 0 1 Rød-svarte trær Vanlige binære søketrær blir fort veldig ubalanserte. røv å sett inn 1,,, 4, 5,, 7,... (i den rekkefølgen) i et binært søketre. Da vil vi i praksis
INF0: Gruppe me Mathias Lohne Høsten 0 1 Rød-svarte trær Vanlige binære søketrær blir fort veldig ubalanserte. røv å sett inn 1,,, 4, 5,, 7,... (i den rekkefølgen) i et binært søketre. Da vil vi i praksis
Lars Vidar Magnusson
 B-Trær Lars Vidar Magnusson 5.3.2014 Kapittel 18 B-trær Standard operasjoner Sletting B-Trær B-trær er balanserte trær som er designet for å fungere bra på sekundære lagringsmedium e.g. harddisk. Ligner
B-Trær Lars Vidar Magnusson 5.3.2014 Kapittel 18 B-trær Standard operasjoner Sletting B-Trær B-trær er balanserte trær som er designet for å fungere bra på sekundære lagringsmedium e.g. harddisk. Ligner
Trær. En datastruktur (og abstrakt datatype ADT)
 Trær Trær En datastruktur (og abstrakt datatype ADT) Trær En datastruktur (og abstrakt datatype ADT) En graf som 8lfredss8ller bestemte krav Object [] int [] tall array element 0 1 2 3 4 5 0 1 2 3 4 5
Trær Trær En datastruktur (og abstrakt datatype ADT) Trær En datastruktur (og abstrakt datatype ADT) En graf som 8lfredss8ller bestemte krav Object [] int [] tall array element 0 1 2 3 4 5 0 1 2 3 4 5
Dagens plan: INF2220 - Algoritmer og datastrukturer. Repetisjon: Binære søketrær. Repetisjon: Binære søketrær
 Dagens plan: INF2220 - lgoritmer og datastrukturer HØTEN 2007 Institutt for informatikk, Universitetet i Oslo (kap. 4.7) (kap. 12.2) Interface ollection og Iterator (kap. 3.3) et og maps (kap. 4.8) INF2220,
Dagens plan: INF2220 - lgoritmer og datastrukturer HØTEN 2007 Institutt for informatikk, Universitetet i Oslo (kap. 4.7) (kap. 12.2) Interface ollection og Iterator (kap. 3.3) et og maps (kap. 4.8) INF2220,
Binær heap. En heap er et komplett binært tre:
 Heap Binær heap En heap er et komplett binært tre: Alle nivåene i treet, unntatt (muligens) det nederste, er alltid helt fylt opp med noder Alle noder på nederste nivå ligger så langt til venstre som mulig
Heap Binær heap En heap er et komplett binært tre: Alle nivåene i treet, unntatt (muligens) det nederste, er alltid helt fylt opp med noder Alle noder på nederste nivå ligger så langt til venstre som mulig
Heap* En heap er et komplett binært tre: En heap er også et monotont binært tre:
 Heap Heap* En heap er et komplett binært tre: Alle nivåene i treet, unntatt (muligens) det nederste, er alltid helt fylt opp med noder Alle noder på nederste nivå ligger til venstre En heap er også et
Heap Heap* En heap er et komplett binært tre: Alle nivåene i treet, unntatt (muligens) det nederste, er alltid helt fylt opp med noder Alle noder på nederste nivå ligger til venstre En heap er også et
Binære søketrær. Et notat for INF1010 Stein Michael Storleer 16. mai 2013
 Binære søketrær Et notat for INF Stein Michael Storleer 6. mai 3 Dette notatet er nyskrevet og inneholder sikkert feil. Disse vil bli fortløpende rettet og datoen over blir oppdatert samtidig. Hvis du
Binære søketrær Et notat for INF Stein Michael Storleer 6. mai 3 Dette notatet er nyskrevet og inneholder sikkert feil. Disse vil bli fortløpende rettet og datoen over blir oppdatert samtidig. Hvis du
Kap.12. Flervegssøketre. Studerer 2-3 og 2-4 trær. Sist oppdatert
 Kap.12 Flervegssøketre Sist oppdatert 12.04.10 Studerer 2-3 og 2-4 trær Motivasjon n maks = antall elementer i et fullt binært tre med nivåer 0 k ; (en node har ett element) n maks = 2 0 + 2 1 + + 2 k
Kap.12 Flervegssøketre Sist oppdatert 12.04.10 Studerer 2-3 og 2-4 trær Motivasjon n maks = antall elementer i et fullt binært tre med nivåer 0 k ; (en node har ett element) n maks = 2 0 + 2 1 + + 2 k
PG4200 Algoritmer og datastrukturer Forelesning 7
 PG4200 Algoritmer og datastrukturer Forelesning 7 Lars Sydnes, NITH 19. mars 2014 I. TERMINOLOGI FOR TRÆR TRÆR Lister: Lineære Trær: Hierarkiske Modell / Språk: Bestanddeler: Noder, forbindelser. Forbindelse
PG4200 Algoritmer og datastrukturer Forelesning 7 Lars Sydnes, NITH 19. mars 2014 I. TERMINOLOGI FOR TRÆR TRÆR Lister: Lineære Trær: Hierarkiske Modell / Språk: Bestanddeler: Noder, forbindelser. Forbindelse
Fra Kap.10 Binære søketre (BS-tre) Sist oppdatert 20.03.10 Definere en abstrakt datastruktur binært søketre. Vise hvordan binær søketre kan brukes
 Fra Kap.10 Binære søketre (BS-tre) Sist oppdatert 20.03.10 Definere en abstrakt datastruktur binært søketre. Vise hvordan binær søketre kan brukes til å løse problemer. Undersøke ulike implementasjoner
Fra Kap.10 Binære søketre (BS-tre) Sist oppdatert 20.03.10 Definere en abstrakt datastruktur binært søketre. Vise hvordan binær søketre kan brukes til å løse problemer. Undersøke ulike implementasjoner
Liste som abstrakt konsept/datatype
 Lister Liste som abstrakt konsept/datatype Listen er en lineær struktur (men kan allikevel implementeres ikke-lineært bak kulissene ) Hvert element har en forgjenger, unntatt første element i listen Hvert
Lister Liste som abstrakt konsept/datatype Listen er en lineær struktur (men kan allikevel implementeres ikke-lineært bak kulissene ) Hvert element har en forgjenger, unntatt første element i listen Hvert
Binære søketrær. En ordnet datastruktur med raske oppslag. Sigmund Hansen
 Binære søketrær En ordnet datastruktur med raske oppslag Sigmund Hansen Lister og trær Rekke (array): 1 2 3 4 Lenket liste (dobbelt-lenket): 1 2 3 4 Binært søketre: 3 1 4 2 Binære
Binære søketrær En ordnet datastruktur med raske oppslag Sigmund Hansen Lister og trær Rekke (array): 1 2 3 4 Lenket liste (dobbelt-lenket): 1 2 3 4 Binært søketre: 3 1 4 2 Binære
Hashing: Håndtering av kollisjoner
 Hashing: Håndtering av kollisjoner Innsetting av dataelement i hashtabell Algoritme: 1. Bruk en hashfunksjon til å beregne hashverdi basert på dataelementets nøkkelverdi 2. Sett inn dataelementet i hashtabellen
Hashing: Håndtering av kollisjoner Innsetting av dataelement i hashtabell Algoritme: 1. Bruk en hashfunksjon til å beregne hashverdi basert på dataelementets nøkkelverdi 2. Sett inn dataelementet i hashtabellen
Hva er en liste? Hvert element har en forgjenger, unntatt første element i listen. Hvert element har en etterfølger, unntatt siste element i listen
 Lister Hva er en liste? Listen er en lineær datastruktur Hvert element har en forgjenger, unntatt første element i listen Hvert element har en etterfølger, unntatt siste element i listen I motsetning til
Lister Hva er en liste? Listen er en lineær datastruktur Hvert element har en forgjenger, unntatt første element i listen Hvert element har en etterfølger, unntatt siste element i listen I motsetning til
Balanserte binære søketrær
 Balanserte trær Balanserte binære søketrær Balanserte binære søketrær høyden (l treet er O(log 2 n) AVL trær rød-svarte trær svake AVL trær splaytrær heaps AVL trær rød-svarte trær svake AVL trær splaytrær
Balanserte trær Balanserte binære søketrær Balanserte binære søketrær høyden (l treet er O(log 2 n) AVL trær rød-svarte trær svake AVL trær splaytrær heaps AVL trær rød-svarte trær svake AVL trær splaytrær
Hva er en liste? Hvert element har en forgjenger, unntatt første element i listen. Hvert element har en etterfølger, unntatt siste element i listen
 Lister Hva er en liste? Listen er en lineær datastruktur Hvert element har en forgjenger, unntatt første element i listen Hvert element har en etterfølger, unntatt siste element i listen I motsetning til
Lister Hva er en liste? Listen er en lineær datastruktur Hvert element har en forgjenger, unntatt første element i listen Hvert element har en etterfølger, unntatt siste element i listen I motsetning til
Hva er en kø? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn først
 Køer Hva er en kø? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn først Et nytt element legges alltid til sist i køen Skal vi ta ut et element, tar vi alltid
Køer Hva er en kø? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn først Et nytt element legges alltid til sist i køen Skal vi ta ut et element, tar vi alltid
Et eksempel: Åtterspillet
 Trær Et eksempel: Åtterspillet To spillere som «trekker» annenhver gang I hvert trekk velges et av tallene 1, 2, 3, men ikke tallet som motspiller valgte i forrige trekk Valgte tall summeres fortløpende
Trær Et eksempel: Åtterspillet To spillere som «trekker» annenhver gang I hvert trekk velges et av tallene 1, 2, 3, men ikke tallet som motspiller valgte i forrige trekk Valgte tall summeres fortløpende
EKSAMEN. Dato: 28. mai 2018 Eksamenstid: 09:00 13:00
 EKSAMEN Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: 28. mai 2018 Eksamenstid: 09:00 13:00 Hjelpemidler: Alle trykte og skrevne Faglærer: Jan Høiberg Om eksamensoppgavene: Oppgavesettet
EKSAMEN Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: 28. mai 2018 Eksamenstid: 09:00 13:00 Hjelpemidler: Alle trykte og skrevne Faglærer: Jan Høiberg Om eksamensoppgavene: Oppgavesettet
Algoritmer og datastrukturer Kapittel 9 - Delkapittel 9.2
 Delkapittel 9.2 Rød-svarte og 2-3-4 trær side 1 av 21 Algoritmer og datastrukturer Kapittel 9 - Delkapittel 9.2 9.2 Rød-svarte og 2-3-4 trær 9.2.1 B-tre av orden 4 eller 2-3-4 tre Et rød-svart tre og et
Delkapittel 9.2 Rød-svarte og 2-3-4 trær side 1 av 21 Algoritmer og datastrukturer Kapittel 9 - Delkapittel 9.2 9.2 Rød-svarte og 2-3-4 trær 9.2.1 B-tre av orden 4 eller 2-3-4 tre Et rød-svart tre og et
Ny/utsatt EKSAMEN. Dato: 5. januar 2018 Eksamenstid: 09:00 13:00
 Ny/utsatt EKSAMEN Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: 5. januar 2018 Eksamenstid: 09:00 13:00 Hjelpemidler: Alle trykte og skrevne Faglærer: Jan Høiberg Om eksamensoppgavene: Oppgavesettet
Ny/utsatt EKSAMEN Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: 5. januar 2018 Eksamenstid: 09:00 13:00 Hjelpemidler: Alle trykte og skrevne Faglærer: Jan Høiberg Om eksamensoppgavene: Oppgavesettet
Hva er en kø? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn først
 Køer Hva er en kø? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn først Et nytt element legges alltid til sist i køen Skal vi ta ut et element, tar vi alltid
Køer Hva er en kø? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn først Et nytt element legges alltid til sist i køen Skal vi ta ut et element, tar vi alltid
Hva er en kø? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn først
 Køer Hva er en kø? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn først Et nytt element legges alltid til sist i køen Skal vi ta ut et element, tar vi alltid
Køer Hva er en kø? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn først Et nytt element legges alltid til sist i køen Skal vi ta ut et element, tar vi alltid
Filsystemet fra innsiden
 Filsystemet i Linux Filsystemet fra innsiden Har tidligere sett kommandoer for håndtering av filer i Linux filsystemet sett fra utsiden Skal nå se på filsystemet fra innsiden : Hvordan er filsystemet i
Filsystemet i Linux Filsystemet fra innsiden Har tidligere sett kommandoer for håndtering av filer i Linux filsystemet sett fra utsiden Skal nå se på filsystemet fra innsiden : Hvordan er filsystemet i
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 5: Prioritetskø og Heap Bjarne Holen (Ifi, UiO) INF2220 H2009, forelesning 5 1 /
INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 5: Prioritetskø og Heap Bjarne Holen (Ifi, UiO) INF2220 H2009, forelesning 5 1 /
Oppsummering. MAT1030 Diskret matematikk. Oppsummering. Oppsummering. Eksempel
 MAT1030 Diskret matematikk Forelesning 26: Trær Sist forelesning snakket vi i hovedsak om trær med rot, og om praktisk bruk av slike. rot Dag Normann Matematisk Institutt, Universitetet i Oslo barn barn
MAT1030 Diskret matematikk Forelesning 26: Trær Sist forelesning snakket vi i hovedsak om trær med rot, og om praktisk bruk av slike. rot Dag Normann Matematisk Institutt, Universitetet i Oslo barn barn
INF2220: Forelesning 1. Praktisk informasjon Analyse av algoritmer (kapittel 2) (Binær)trær (kapittel )
 INF2220: Forelesning 1 Praktisk informasjon Analyse av algoritmer (kapittel 2) (Binær)trær (kapittel 4.1-4.3 + 4.6) PRAKTISK INFORMASJON 2 Praktisk informasjon Kursansvarlige Ragnhild Kobro Runde (ragnhilk@ifi.uio.no)
INF2220: Forelesning 1 Praktisk informasjon Analyse av algoritmer (kapittel 2) (Binær)trær (kapittel 4.1-4.3 + 4.6) PRAKTISK INFORMASJON 2 Praktisk informasjon Kursansvarlige Ragnhild Kobro Runde (ragnhilk@ifi.uio.no)
Lars Vidar Magnusson Kapittel 13 Rød-Svarte (Red-Black) trær Rotasjoner Insetting Sletting
 Rød-Svarte Trær Lars Vidar Magnusson 21.2.2014 Kapittel 13 Rød-Svarte (Red-Black) trær Rotasjoner Insetting Sletting Rød-Svarte Trær Rød-Svarte trær (red-black trees) er en variasjon binære søketrær som
Rød-Svarte Trær Lars Vidar Magnusson 21.2.2014 Kapittel 13 Rød-Svarte (Red-Black) trær Rotasjoner Insetting Sletting Rød-Svarte Trær Rød-Svarte trær (red-black trees) er en variasjon binære søketrær som
Trær. Består av sammenkoblede noder Hver node har 0 eller flere barne-noder. Må være asyklisk. Et tre med n noder har n-1 kanter.
 Generelle trær: Trær Består av sammenkoblede noder Hver node har 0 eller flere barne-noder. Må være asyklisk. Et tre med n noder har n-1 kanter. løvnoder kant rotnode sub-tre 1 Generelle trær: Oppbygging
Generelle trær: Trær Består av sammenkoblede noder Hver node har 0 eller flere barne-noder. Må være asyklisk. Et tre med n noder har n-1 kanter. løvnoder kant rotnode sub-tre 1 Generelle trær: Oppbygging
INF2220: Forelesning 3
 INF2220: Forelesning 3 Map og hashing Abstrakte datatyper (kapittel 3.1) Map (kapittel 4.8) Hashing (kapittel 5) REPETISJON: ALGORITMER OG STOR O 2 REPETISJON RØD-SVARTE TRÆR 7 Rød-svarte trær Et rød-svart
INF2220: Forelesning 3 Map og hashing Abstrakte datatyper (kapittel 3.1) Map (kapittel 4.8) Hashing (kapittel 5) REPETISJON: ALGORITMER OG STOR O 2 REPETISJON RØD-SVARTE TRÆR 7 Rød-svarte trær Et rød-svart
INF110 Algoritmer og datastrukturer TRÆR. Vi skal i denne forelesningen se litt på ulike typer trær:
 TRÆR Vi skal i denne forelesningen se litt på ulike typer trær: Generelle trær (kap. 4.1) Binærtrær (kap. 4.2) Binære søketrær (kap. 4.3) Den siste typen trær vi skal behandle, B-trær (kap. 4.7) kommer
TRÆR Vi skal i denne forelesningen se litt på ulike typer trær: Generelle trær (kap. 4.1) Binærtrær (kap. 4.2) Binære søketrær (kap. 4.3) Den siste typen trær vi skal behandle, B-trær (kap. 4.7) kommer
Søkeproblemet. Gitt en datastruktur med n elementer: Finnes et bestemt element (eller en bestemt verdi) x lagret i datastrukturen eller ikke?
 Søking Søkeproblemet Gitt en datastruktur med n elementer: Finnes et bestemt element (eller en bestemt verdi) x lagret i datastrukturen eller ikke? Effektiviteten til søkealgoritmer avhenger av: Om datastrukturen
Søking Søkeproblemet Gitt en datastruktur med n elementer: Finnes et bestemt element (eller en bestemt verdi) x lagret i datastrukturen eller ikke? Effektiviteten til søkealgoritmer avhenger av: Om datastrukturen
EKSAMEN. Dato: 18. mai 2017 Eksamenstid: 09:00 13:00
 EKSAMEN Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: 18. mai 2017 Eksamenstid: 09:00 13:00 Hjelpemidler: Alle trykte og skrevne Kalkulator Faglærer: Jan Høiberg Om eksamensoppgavene: Oppgavesettet
EKSAMEN Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: 18. mai 2017 Eksamenstid: 09:00 13:00 Hjelpemidler: Alle trykte og skrevne Kalkulator Faglærer: Jan Høiberg Om eksamensoppgavene: Oppgavesettet
Eksamen i IN 110, 18. mai 1993 Side 2 Del 1 (15%) Vi skal se på prioritetskøer av heltall, der vi hele tiden er interessert i å få ut den minste verdi
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i Eksamensdag: 18. mai 1993 Tid for eksamen: 9.00 15.00 Oppgavesettet er på 7 sider. Vedlegg: Tillatte hjelpemidler: IN 110 Algoritmer
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i Eksamensdag: 18. mai 1993 Tid for eksamen: 9.00 15.00 Oppgavesettet er på 7 sider. Vedlegg: Tillatte hjelpemidler: IN 110 Algoritmer
Algoritmer og datastrukturer Kapittel 9 - Delkapittel 9.1
 Delkapittel 9.1 Generelt om balanserte trær Side 1 av 13 Algoritmer og datastrukturer Kapittel 9 - Delkapittel 9.1 9.1 Generelt om balanserte trær 9.1.1 Hva er et balansert tre? Begrepene balansert og
Delkapittel 9.1 Generelt om balanserte trær Side 1 av 13 Algoritmer og datastrukturer Kapittel 9 - Delkapittel 9.1 9.1 Generelt om balanserte trær 9.1.1 Hva er et balansert tre? Begrepene balansert og
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2015 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2015, forelesning
INF2220 - Algoritmer og datastrukturer HØSTEN 2015 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2015, forelesning
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2015 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2015, forelesning
INF2220 - Algoritmer og datastrukturer HØSTEN 2015 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2015, forelesning
IN Algoritmer og datastrukturer
 IN2010 - Algoritmer og datastrukturer HØSTEN 2018 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 3: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2010 H2018, forelesning
IN2010 - Algoritmer og datastrukturer HØSTEN 2018 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 3: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2010 H2018, forelesning
INF Algoritmer og datastrukturer
 INF0 - Algoritmer og datastrukturer HØSTEN 05 Institutt for informatikk, Universitetet i Oslo Forelesning 6: Grafer II Ingrid Chieh Yu (Ifi, UiO) INF0.09.05 / 8 Dagens plan: Minimale spenntrær Prim Kruskal
INF0 - Algoritmer og datastrukturer HØSTEN 05 Institutt for informatikk, Universitetet i Oslo Forelesning 6: Grafer II Ingrid Chieh Yu (Ifi, UiO) INF0.09.05 / 8 Dagens plan: Minimale spenntrær Prim Kruskal
Sist forelesning snakket vi i hovedsak om trær med rot, og om praktisk bruk av slike. rot. barn
 Forelesning 26 Trær Dag Normann - 28. april 2008 Oppsummering Sist forelesning snakket vi i hovedsak om trær med rot, og om praktisk bruk av slike. rot barn barn barnebarn barnebarn barn blad Her er noen
Forelesning 26 Trær Dag Normann - 28. april 2008 Oppsummering Sist forelesning snakket vi i hovedsak om trær med rot, og om praktisk bruk av slike. rot barn barn barnebarn barnebarn barn blad Her er noen
MAT1030 Diskret matematikk
 MAT1030 Diskret matematikk Forelesning 26: Trær Dag Normann Matematisk Institutt, Universitetet i Oslo 28. april 2008 Oppsummering Sist forelesning snakket vi i hovedsak om trær med rot, og om praktisk
MAT1030 Diskret matematikk Forelesning 26: Trær Dag Normann Matematisk Institutt, Universitetet i Oslo 28. april 2008 Oppsummering Sist forelesning snakket vi i hovedsak om trær med rot, og om praktisk
Algoritmer og datastrukturer Assignment 11 Side 1 av 5
 Assignment 11 Side 1 av 5 Oppgave 1 Utregning av ASCII summer, og hashfunksjon: Hashfunksjon: A(s) % n Nøkkel ASCII SUM (ASCII SUM) % 8 ANNE 290 2 PER 231 7 NINA 294 6 ANNI 294 6 ALI 214 6 KAREN 369 1
Assignment 11 Side 1 av 5 Oppgave 1 Utregning av ASCII summer, og hashfunksjon: Hashfunksjon: A(s) % n Nøkkel ASCII SUM (ASCII SUM) % 8 ANNE 290 2 PER 231 7 NINA 294 6 ANNI 294 6 ALI 214 6 KAREN 369 1
Datastrukturer for rask søking
 Søking Søkeproblemet Gitt en datastruktur med n elementer: Finnes et bestemt element (eller en bestemt verdi) x lagret i datastrukturen eller ikke? Effektiviteten til søkealgoritmer avhenger av: Om datastrukturen
Søking Søkeproblemet Gitt en datastruktur med n elementer: Finnes et bestemt element (eller en bestemt verdi) x lagret i datastrukturen eller ikke? Effektiviteten til søkealgoritmer avhenger av: Om datastrukturen
Generelt om permanent lagring og filsystemer
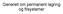 Generelt om permanent lagring og filsystemer Filsystem Den delen av OS som kontrollerer hvordan data lagres på og hentes frem fra permanente media Data deles opp i individuelle deler, filer, som får hvert
Generelt om permanent lagring og filsystemer Filsystem Den delen av OS som kontrollerer hvordan data lagres på og hentes frem fra permanente media Data deles opp i individuelle deler, filer, som får hvert
Kap 9 Tre Sist oppdatert 15.03
 Kap 9 Tre Sist oppdatert 15.03 Definere et tre som en datastruktur. Definere begreper knyttet til tre. Diskutere mulige implementasjoner av tre Analysere implementasjoner av tre som samlinger. Diskutere
Kap 9 Tre Sist oppdatert 15.03 Definere et tre som en datastruktur. Definere begreper knyttet til tre. Diskutere mulige implementasjoner av tre Analysere implementasjoner av tre som samlinger. Diskutere
Vi skal se på grafalgoritmer for:
 Grafalgoritmer Vi skal se på grafalgoritmer for: Traversering: Oppsøk alle nodene i grafen en og bare en gang, på en eller annen systematisk måte Nåbarhet: Finnes det en vei fra en node til en annen node?
Grafalgoritmer Vi skal se på grafalgoritmer for: Traversering: Oppsøk alle nodene i grafen en og bare en gang, på en eller annen systematisk måte Nåbarhet: Finnes det en vei fra en node til en annen node?
INF2220: Time 4 - Heap, Huffmann
 INF0: Time 4 - Heap, Huffmann Mathias Lohne mathialo Heap (prioritetskø) En heap (også kalt prioritetskø) er en type binært tre med noen spesielle struktur- og ordningskrav. Vi har to typer heap: min-
INF0: Time 4 - Heap, Huffmann Mathias Lohne mathialo Heap (prioritetskø) En heap (også kalt prioritetskø) er en type binært tre med noen spesielle struktur- og ordningskrav. Vi har to typer heap: min-
EKSAMENSOPPGAVE. INF-1101 Datastrukturer og algoritmer. Adm.bygget, rom K1.04 og B154 Ingen
 Fakultet for naturvitenskap og teknologi EKSAMENSOPPGAVE Eksamen i: Dato: 15.mai 2018 Klokkeslett: 09:00 13:00 Sted: Tillatte hjelpemidler: Adm.bygget, rom K1.04 og B154 Ingen Type innføringsark (rute/linje):
Fakultet for naturvitenskap og teknologi EKSAMENSOPPGAVE Eksamen i: Dato: 15.mai 2018 Klokkeslett: 09:00 13:00 Sted: Tillatte hjelpemidler: Adm.bygget, rom K1.04 og B154 Ingen Type innføringsark (rute/linje):
Vi skal se på grafalgoritmer for:
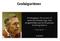 Grafalgoritmer Vi skal se på grafalgoritmer for: raversering: Nåbarhet: Oppsøk alle nodene i grafen en og bare en gang, på en eller annen systematisk måte innes det en vei fra en node til en annen node?
Grafalgoritmer Vi skal se på grafalgoritmer for: raversering: Nåbarhet: Oppsøk alle nodene i grafen en og bare en gang, på en eller annen systematisk måte innes det en vei fra en node til en annen node?
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2017 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2017, forelesning
INF2220 - Algoritmer og datastrukturer HØSTEN 2017 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2017, forelesning
INF1010 siste begreper før oblig 2
 INF1010 siste begreper før oblig 2 Sammenligning. Mer lenkede lister. Forskjellige listeimplementasjoner. Binære trær. Bittelitt om grensesnitt (interface). Dagens forelesning Flere temaer på grunn av
INF1010 siste begreper før oblig 2 Sammenligning. Mer lenkede lister. Forskjellige listeimplementasjoner. Binære trær. Bittelitt om grensesnitt (interface). Dagens forelesning Flere temaer på grunn av
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2016 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2016, forelesning
INF2220 - Algoritmer og datastrukturer HØSTEN 2016 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2016, forelesning
Dagens tema. INF Algoritmer og datastrukturer. Binærtrær. Generelle trær
 Dagens tema INF2220 - Algoritmer og datastrukturer HØSTEN 2007 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 2: Binærtrær og abstrakte datatyper (ADT) Kort repetisjon Generelle trær
Dagens tema INF2220 - Algoritmer og datastrukturer HØSTEN 2007 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 2: Binærtrær og abstrakte datatyper (ADT) Kort repetisjon Generelle trær
Notater til INF2220 Eksamen
 Notater til INF2220 Eksamen Lars Bjørlykke Kristiansen December 13, 2011 Stor O notasjon Funksjon Navn 1 Konstant log n Logaritmisk n Lineær n log n n 2 Kvadratisk n 3 Kubisk 2 n Eksponensiell n! Trær
Notater til INF2220 Eksamen Lars Bjørlykke Kristiansen December 13, 2011 Stor O notasjon Funksjon Navn 1 Konstant log n Logaritmisk n Lineær n log n n 2 Kvadratisk n 3 Kubisk 2 n Eksponensiell n! Trær
INF2220: Time 12 - Sortering
 INF0: Time 1 - Sortering Mathias Lohne mathialo Noen algoritmer Vi skal nå se på noen konkrete sorteringsalgoritmer. Gjennomgående i alle eksempler vil vi sortere tall etter tallverdi, men som diskutert
INF0: Time 1 - Sortering Mathias Lohne mathialo Noen algoritmer Vi skal nå se på noen konkrete sorteringsalgoritmer. Gjennomgående i alle eksempler vil vi sortere tall etter tallverdi, men som diskutert
Enkle datastrukturer. Lars Greger Nordland Hagen. Introduksjon til øvingsopplegget og gjennomgang av python
 1 Enkle datastrukturer Lars Greger Nordland Hagen algdat@idi.ntnu.no Introduksjon til øvingsopplegget og gjennomgang av python 2 I dag Stack Kø (queue) Lenkede lister (linked list) Trær Binære søketrær
1 Enkle datastrukturer Lars Greger Nordland Hagen algdat@idi.ntnu.no Introduksjon til øvingsopplegget og gjennomgang av python 2 I dag Stack Kø (queue) Lenkede lister (linked list) Trær Binære søketrær
Algoritmer og datastrukturer Kapittel 9 Delkapittel 9.2
 Delkapittel 9.2 Rød-svarte og 2-3-4 trær Side 1 av 24 Algoritmer og datastrukturer Kapittel 9 Delkapittel 9.2 9.2 Rød-svarte og 2-3-4 trær 9.2.1 B-tre av orden 4 eller 2-3-4 tre Et 2-3-4 tre (et B-tre
Delkapittel 9.2 Rød-svarte og 2-3-4 trær Side 1 av 24 Algoritmer og datastrukturer Kapittel 9 Delkapittel 9.2 9.2 Rød-svarte og 2-3-4 trær 9.2.1 B-tre av orden 4 eller 2-3-4 tre Et 2-3-4 tre (et B-tre
Pensum: fra boken (H-03)+ forelesninger
 Pensum: fra boken (H-03)+ forelesninger unntatt kursorisk tema KAP. 1 KAP. 2 KAP. 3 JAVA I-110 (ikke gjennomgått) OO + ABSTRAKSJON /GENERISK PROGRAMMERING REKURSJON ALGORITME-TIDSANALYSE; O-NOTASJON KAP.
Pensum: fra boken (H-03)+ forelesninger unntatt kursorisk tema KAP. 1 KAP. 2 KAP. 3 JAVA I-110 (ikke gjennomgått) OO + ABSTRAKSJON /GENERISK PROGRAMMERING REKURSJON ALGORITME-TIDSANALYSE; O-NOTASJON KAP.
KONTINUASJONSEKSAMEN
 Høgskolen i Gjøvik KONTINUASJONSEKSAMEN FAGNAVN: FAGNUMMER: Algoritmiske metoder I L 171 A EKSAMENSDATO: 19. august 1999 KLASSE: 97HINDA / 97HINDB ( 2DA / 2DB ) TID: 09.00-14.00 FAGLÆRER: Frode Haug ANT.
Høgskolen i Gjøvik KONTINUASJONSEKSAMEN FAGNAVN: FAGNUMMER: Algoritmiske metoder I L 171 A EKSAMENSDATO: 19. august 1999 KLASSE: 97HINDA / 97HINDB ( 2DA / 2DB ) TID: 09.00-14.00 FAGLÆRER: Frode Haug ANT.
Algoritmer og datastrukturer Kapittel 9 - Delkapittel 9.2
 Delkapittel 9.2 Rød-svarte og 2-3-4 trær Side 1 av 16 Algoritmer og datastrukturer Kapittel 9 - Delkapittel 9.2 9.2 Rød-svarte og 2-3-4 trær 9.2.1 B-tre av orden 4 eller 2-3-4 tre Et rød-svart tre og et
Delkapittel 9.2 Rød-svarte og 2-3-4 trær Side 1 av 16 Algoritmer og datastrukturer Kapittel 9 - Delkapittel 9.2 9.2 Rød-svarte og 2-3-4 trær 9.2.1 B-tre av orden 4 eller 2-3-4 tre Et rød-svart tre og et
Pensum: fra boken (H-03)+ forelesninger
 Pensum: fra boken (H-03)+ forelesninger unntatt kursorisk tema KAP. 1 KAP. 2 KAP. 3 JAVA I-110 (ikke gjennomgått) OO + ABSTRAKSJON /GENERISK PROGRAMMERING REKURSJON ALGORITME-TIDSANALYSE; O-NOTASJON KAP.
Pensum: fra boken (H-03)+ forelesninger unntatt kursorisk tema KAP. 1 KAP. 2 KAP. 3 JAVA I-110 (ikke gjennomgått) OO + ABSTRAKSJON /GENERISK PROGRAMMERING REKURSJON ALGORITME-TIDSANALYSE; O-NOTASJON KAP.
Sorteringsproblemet. Gitt en array A med n elementer som kan sammenlignes med hverandre:
 Sortering Sorteringsproblemet Gitt en array A med n elementer som kan sammenlignes med hverandre: Finn en ordning (eller permutasjon) av elementene i A slik at de står i stigende (evt. avtagende) rekkefølge
Sortering Sorteringsproblemet Gitt en array A med n elementer som kan sammenlignes med hverandre: Finn en ordning (eller permutasjon) av elementene i A slik at de står i stigende (evt. avtagende) rekkefølge
Dynamisk programmering Undervises av Stein Krogdahl
 Dynamisk programmering Undervises av Stein Krogdahl 5. september 2012 Dagens stoff er hentet fra kapittel 9 i læreboka, samt kapittel 20.5 (som vi «hoppet over» sist) Kapittel 9 er lagt ut på undervisningsplanen.
Dynamisk programmering Undervises av Stein Krogdahl 5. september 2012 Dagens stoff er hentet fra kapittel 9 i læreboka, samt kapittel 20.5 (som vi «hoppet over» sist) Kapittel 9 er lagt ut på undervisningsplanen.
Obligatorisk oppgave 1 INF1020 h2005
 Obligatorisk oppgave 1 INF1020 h2005 Frist: fredag 7. oktober Oppgaven skal løses individuelt, og må være godkjent for å kunne gå opp til eksamen. Før innlevering må retningslinjene Krav til innleverte
Obligatorisk oppgave 1 INF1020 h2005 Frist: fredag 7. oktober Oppgaven skal løses individuelt, og må være godkjent for å kunne gå opp til eksamen. Før innlevering må retningslinjene Krav til innleverte
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2016 Institutt for informatikk, Universitetet i Oslo Forelesning 6: Grafer II Ingrid Chieh Yu (Ifi, UiO) INF2220 28.09.2016 1 / 30 Dagens plan: Dijkstra fort.
INF2220 - Algoritmer og datastrukturer HØSTEN 2016 Institutt for informatikk, Universitetet i Oslo Forelesning 6: Grafer II Ingrid Chieh Yu (Ifi, UiO) INF2220 28.09.2016 1 / 30 Dagens plan: Dijkstra fort.
Datastrukturer. Stakker (Stacks) Hva er en datastruktur? Fordeler / Ulemper. Generelt om Datastrukturer. Stakker (Stacks) Elementære Datastrukturer
 Hva er en datastruktur? Datastrukturer Elementære Datastrukturer En datastruktur er en systematisk måte å lagre og organisere data på, slik at det er lett å aksessere og modifisere dataene Eksempler på
Hva er en datastruktur? Datastrukturer Elementære Datastrukturer En datastruktur er en systematisk måte å lagre og organisere data på, slik at det er lett å aksessere og modifisere dataene Eksempler på
PQ: HEAP. Heap. Er disse heap er? Hvordan implementere heap:
 PQ: HEAP Ingen sammenheng med memory heap Definisjon og data-invarianter for heap InsertKey og RemoveMin for heap Kompleksitet for operasjoner: O(log n) Prioritetskø impl vha Heap Heap En heap er et binært
PQ: HEAP Ingen sammenheng med memory heap Definisjon og data-invarianter for heap InsertKey og RemoveMin for heap Kompleksitet for operasjoner: O(log n) Prioritetskø impl vha Heap Heap En heap er et binært
Hvor raskt klarer vi å sortere?
 Sortering Sorteringsproblemet Gitt en array med n elementer som kan sammenlignes med hverandre: Finn en ordning (eller permutasjon) av elementene slik at de står i stigende (evt. avtagende) rekkefølge
Sortering Sorteringsproblemet Gitt en array med n elementer som kan sammenlignes med hverandre: Finn en ordning (eller permutasjon) av elementene slik at de står i stigende (evt. avtagende) rekkefølge
INF Algoritmer og datastrukturer. Hva er INF2220? Algoritmer og datastrukturer
 Praktiske opplysninger INF2220 - Algoritmer og datastrukturer HØSTEN 2007 Institutt for informatikk, Universitetet i Oslo Tid og sted: Mandag kl. 12:15-14:00 Store auditorium, Informatikkbygningen Kursansvarlige
Praktiske opplysninger INF2220 - Algoritmer og datastrukturer HØSTEN 2007 Institutt for informatikk, Universitetet i Oslo Tid og sted: Mandag kl. 12:15-14:00 Store auditorium, Informatikkbygningen Kursansvarlige
Binære Søketre. Egenskap. Egenskap : Grafisk. Egenskap : Kjøretid. Egenskap : Kjøretid. Egenskap : Oppsumering. Binære Søketre
 genskap inære Søketre inære Søketre t binært søketre er organisert som et binærtre, og har følgende egenskap a x være en node i et binært søketre. vis y er en node i x s venstre subtre, vil verdi[y] verdi[x]
genskap inære Søketre inære Søketre t binært søketre er organisert som et binærtre, og har følgende egenskap a x være en node i et binært søketre. vis y er en node i x s venstre subtre, vil verdi[y] verdi[x]
Hashing. INF Algoritmer og datastrukturer HASHING. Hashtabeller
 Hashing INF2220 - Algoritmer og datastrukturer HØSTEN 200 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning : Hashing Hashtabeller (kapittel.) Hash-funksjoner (kapittel.2) Kollisjonshåndtering
Hashing INF2220 - Algoritmer og datastrukturer HØSTEN 200 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning : Hashing Hashtabeller (kapittel.) Hash-funksjoner (kapittel.2) Kollisjonshåndtering
Anvendelser av grafer
 Grafer Anvendelser av grafer Passer for modeller/datastrukturer med usystematiske forbindelser Ikke-lineære og ikke-hierarkiske koblinger mellom dataobjektene Modellering av nettverk: Veisystemer/rutekart
Grafer Anvendelser av grafer Passer for modeller/datastrukturer med usystematiske forbindelser Ikke-lineære og ikke-hierarkiske koblinger mellom dataobjektene Modellering av nettverk: Veisystemer/rutekart
Algoritmer og Datastrukturer
 Eksamen i Algoritmer og Datastrukturer IAI 20102 Høgskolen i Østfold Avdeling for informatikk og automatisering Lødag 5. juni 2004, kl. 09.00-13.00 LØSNINGSFORSLAG 1 Del 1 60% Oppgave 1.1-10% Forklar kort
Eksamen i Algoritmer og Datastrukturer IAI 20102 Høgskolen i Østfold Avdeling for informatikk og automatisering Lødag 5. juni 2004, kl. 09.00-13.00 LØSNINGSFORSLAG 1 Del 1 60% Oppgave 1.1-10% Forklar kort
Dagens stoff er hentet fra kapittel 9 i læreboka, samt kapittel 20.5 (som vi «hoppet over» sist)
 Dynamisk programmering Undervises av Stein Krogdahl 5. september 2012 Dagens stoff er hentet fra kapittel 9 i læreboka, samt kapittel 20.5 (som vi «hoppet over» sist) Kapittel 9 er lagt ut på undervisningsplanen.
Dynamisk programmering Undervises av Stein Krogdahl 5. september 2012 Dagens stoff er hentet fra kapittel 9 i læreboka, samt kapittel 20.5 (som vi «hoppet over» sist) Kapittel 9 er lagt ut på undervisningsplanen.
EKSAMEN med løsningsforslag
 EKSAMEN med løsningsforslag Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: Eksamenstid: 20. mai 2009 kl 09.00 til kl 13.00 Hjelpemidler: 8 A4-sider (4 ark) med egne notater Kalkulator Faglærer:
EKSAMEN med løsningsforslag Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: Eksamenstid: 20. mai 2009 kl 09.00 til kl 13.00 Hjelpemidler: 8 A4-sider (4 ark) med egne notater Kalkulator Faglærer:
EKSAMEN. Dato: 9. mai 2016 Eksamenstid: 09:00 13:00
 EKSAMEN Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: 9. mai 2016 Eksamenstid: 09:00 13:00 Hjelpemidler: Alle trykte og skrevne Faglærer: Jan Høiberg Om eksamensoppgavene: Oppgavesettet består
EKSAMEN Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: 9. mai 2016 Eksamenstid: 09:00 13:00 Hjelpemidler: Alle trykte og skrevne Faglærer: Jan Høiberg Om eksamensoppgavene: Oppgavesettet består
Hva er en algoritme? INF HØSTEN 2006 INF1020. Kursansvarlige Ragnar Normann E-post: Dagens tema
 va er en algoritme? Vanlig sammenligning: Oppskrift. nput lgoritme NF1020 - ØSTEN 2006 Kursansvarlige Ragnar Normann E-post: ragnarn@ifi.uio.no Output Knuth : tillegg til å være et endelig sett med regler
va er en algoritme? Vanlig sammenligning: Oppskrift. nput lgoritme NF1020 - ØSTEN 2006 Kursansvarlige Ragnar Normann E-post: ragnarn@ifi.uio.no Output Knuth : tillegg til å være et endelig sett med regler
UNIVERSITETET I OSLO
 Eksamen i UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamensdag: 13. desember 2011 Tid for eksamen: 14.30 18.30 Oppgavesettet er på 7 sider. Vedlegg: INF2220 lgoritmer og datastrukturer
Eksamen i UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamensdag: 13. desember 2011 Tid for eksamen: 14.30 18.30 Oppgavesettet er på 7 sider. Vedlegg: INF2220 lgoritmer og datastrukturer
Filsystemet fra innsiden
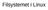 Filsystemet i Linux Filsystemet fra innsiden Tidligere sett brukerkommandoer for håndtering av filer filsystemet i Linux sett fra utsiden Skal nå se på filsystemet fra innsiden : Hvordan er filsystemet
Filsystemet i Linux Filsystemet fra innsiden Tidligere sett brukerkommandoer for håndtering av filer filsystemet i Linux sett fra utsiden Skal nå se på filsystemet fra innsiden : Hvordan er filsystemet
Eksamen iin115 og IN110, 15. mai 1997 Side 2 Oppgave 1 Trær 55 % Vi skal i denne oppgaven se på en form for søkestrukturer som er spesielt godt egnet
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i IN 115 og IN110 Algoritmer og datastrukturer Eksamensdag: 15. mai 1997 Tid for eksamen: 9.00 15.00 Oppgavesettet er på 8 sider.
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i IN 115 og IN110 Algoritmer og datastrukturer Eksamensdag: 15. mai 1997 Tid for eksamen: 9.00 15.00 Oppgavesettet er på 8 sider.
Løsningsforslag for Obligatorisk Oppgave 3. Algoritmer og Datastrukturer ITF20006
 Løsningsforslag for Obligatorisk Oppgave 3 Algoritmer og Datastrukturer ITF20006 Lars Vidar Magnusson Frist 28.03.14 Den tredje obligatoriske oppgaven tar for seg forelesning 9 til 13, som dreier seg om
Løsningsforslag for Obligatorisk Oppgave 3 Algoritmer og Datastrukturer ITF20006 Lars Vidar Magnusson Frist 28.03.14 Den tredje obligatoriske oppgaven tar for seg forelesning 9 til 13, som dreier seg om
Eksempel: Uttrykkstrær I uttrykkstrær inneholder bladnodene operander (konstanter, variable,... ), mens de interne nodene inneholder operatorer.
 TRÆR Generelle trær Dagens plan: Kort repetisjon Generelle trær Binærtrær Implementasjon Traversering Binære søketrær Definisjon Søking, innsetting og sletting Gjennomsnitts-analyse (!) Eksempel: Ibsens
TRÆR Generelle trær Dagens plan: Kort repetisjon Generelle trær Binærtrær Implementasjon Traversering Binære søketrær Definisjon Søking, innsetting og sletting Gjennomsnitts-analyse (!) Eksempel: Ibsens
Prioritetskøer. Binære heaper Venstrevridde heaper (Leftist) Binomialheaper Fibonacciheaper
 Prioritetskøer Binære heaper Venstrevridde heaper (Leftist) Binomialheaper Fibonacciheaper Prioritetskøer er viktige i bla. operativsystemer (prosesstyring i multitaskingssystemer), og søkealgoritmer (A,
Prioritetskøer Binære heaper Venstrevridde heaper (Leftist) Binomialheaper Fibonacciheaper Prioritetskøer er viktige i bla. operativsystemer (prosesstyring i multitaskingssystemer), og søkealgoritmer (A,
Løsnings forslag i java In115, Våren 1998
 Løsnings forslag i java In115, Våren 1998 Oppgave 1 // Inne i en eller annen klasse private char S[]; private int pardybde; private int n; public void lagalle(int i) if (i==n) bruks(); else /* Sjekker
Løsnings forslag i java In115, Våren 1998 Oppgave 1 // Inne i en eller annen klasse private char S[]; private int pardybde; private int n; public void lagalle(int i) if (i==n) bruks(); else /* Sjekker
