Alg. Dat. Øvingsforelesning 3. Grafer, BFS, DFS og hashing. Børge Rødsjø
|
|
|
- Alexandra Davidsen
- 8 år siden
- Visninger:
Transkript
1 Alg. Dat Øvingsforelesning 3 Grafer, BFS, DFS og hashing Børge Rødsjø rodsjo@stud.ntnu.no
2 Dagens tema Grafer Terminologi Representasjon av grafer Bredde først søk (BFS) Dybde først søk (DFS) Hashing Hashfunksjoner, hashtabeller Kollisjonshåndtering Øving 2: Redd Ratatosk Øving 3: Kobra lærer å stave
3 Terminologi: Grafer Node Kant Nabo Sykel Rettet graf DAGs Trær
4 Generelle grafer vs. trær Grafer er en overordnet, generell struktur Et tre er en graf som er sammenhengende, asyklisk og urettet I graftraversering er farging nyttig I en graf kan man oppdage grå eller svarte noder på nytt Vi må huske hvilke noder vi har sett
5 Representasjon av grafer En graf består av noder og relasjoner G = (V, E). V er alle nodene, E er relasjoner mellom nodene (i dagligtale: kanter)
6 Representasjon av grafer En graf består av noder og relasjoner G = (V, E). V er alle nodene, E er relasjoner mellom nodene (i dagligtale: kanter)
7 Representasjon av grafer En graf består av noder og relasjoner G = (V, E). V er alle nodene, E er relasjoner mellom nodene (i dagligtale: kanter)
8 Representasjon av grafer En graf består av noder og relasjoner G = (V, E). V er alle nodene, E er relasjoner mellom nodene (i dagligtale: kanter)
9 Nabolister Hver node har en liste over sine naboer Nyttigst hvis det er få kanter i forhold til antall noder (en sparse graf). Node a b c d e f Naboer c, d c, e d a f NIL
10 Nabomatrise En nxn matrise der en nabo er representert med en verdi Nyttig hvis grafen er tett (dense graf) a b c d e f a b c d e f
11 Bredde først søk (BFS) En enkel algoritme for å søke i en graf Har en kø over oppdagede (grå) elementer Vi har en mengde/liste av besøkte(ferdige) noder Se side 531 i Cormen
12 Bredde først søk (BFS) Begynn med å legge startnoden i kø Så lenge det finnes noder i køen: Plukk ut en node x fra starten av køen Legg alle naboer som ikke er besøkte eller oppdagede inn i køen (vi oppdager/gråfarger dem) Legg x inn i besøkt-mengden (farge den sort)
13 Kode for BFS def bfs(root): queue = Queue() queue.put(root) while len(queue) > 0: node = queue.get() # gjør noe fancy med noden her node.colour = Black for adj in node.adjacent: if adj.colour == White: adj.colour = Grey queue.add(adj)
14 Bruk av BFS Finne korteste vei fra en node til alle andre, i en uvektet graf Kan sjekke om en graf er bipartitt BFS er en viktig grunnstein for mer avanserte algoritmer
15 Kjøretid BFS Med naboliste: O(V + E) Må besøke alle noder (V), og sjekke alle kanter (E) Med nabomatrise: O(V 2 ) Må besøke alle noder (V), og sjekke alle kanter (V 2 )
16 Dybde først søk (DFS) Også en enkel algoritme for å søke i en graf Starter i en node og søker i dybden så langt det går Se side 541 i Cormen
17 Implementere DFS Kan implementeres via både rekursjon og iterasjon Med rekursjon så kaller metoden seg selv Dette er en treg måte å gjøre det på Med iterasjon har man nodene i en stakk Kjappere, behøver ikke rekursive kall
18 Kode for rekursiv DFS def dfs(node): node.colour = Grey for adj in node.adjacent: if adj.colour == White: dfs(adj) # gjør noe fancy med noden her node.colour = Black
19 Iterativ DFS Tar vare på nodene i en stakk. Alle noder er hvite før man oppdager dem Når en node blir oppdaget blir den fargelagt grå, og lagt til i stakken. En node er ferdig når alle dens barn er ferdigbehandlet; da taes noden ut av stakken og fargelegges svart
20 Bruk av DFS Brukes i mange andre algoritmer Strongly connected components (neste gang) Topologisk sortering (neste gang) Kjøretid: O(V + E) Alle noder(v) må besøkes, og alle kanter(e) må sjekkes
21 Hashing og hashtabeller Problemet vi søker en løsning på: Man har et lite/moderat antall elementer, i et stort verdiområde. Hvordan lagre og søke etter disse effektivt? Eks: Telefonnummer og navn på ansatte. Direkte-adressering vil kreve altfor stor plass.
22 Hvordan løser hashing dette? Hashing er en måte å konvertere verdier fra et stort utfallsrom til et som er mye mindre. Hashing gir en form for fingeravtrykk av en verdi. Vi kan bruke dette til å lagre og hente data effektivt fra en liten og kompakt tabell
23 Hashtabeller: Fordelene Oppslag i O(1) tid Innsetting i O(1) tid Sletting i O(1) tid O(1) betyr konstant tid Dvs. at hastigheten på operasjonene ikke er avhengig av antall elementer i tabellen NB! Dette er average-case, ikke worst case
24 Hashtabeller En tabell hvor vi får en hash av dataene til å beskrive hvor vi lagrer dem.
25 Hashing Hashfunksjon: h(k) = x h er hashfunksjonen vi har valgt oss k er hashnøkkelen, hele eller deler av dataene x er hashen av nøkkelen, dvs. posisjonen der vi plasserer dataene i en hashtabell
26 Valg av hashfunksjon Mål: transformere potensielt store data til en indeks i en tabell Påkrevd egenskap: Deterministisk Ønsket egenskap: Uniform fordeling Ønsket egenskap: Kjapp å utføre
27 Valg av hashfunksjon Noen eksempler på enkle, gode funksjoner (Se Cormen kap. 11): Divisjonsmetoden ( modulo-metoden ) h(k) = k mod m Multiplikasjonsmetoden h(k) = m (k A mod 1)
28 Valg av hashfunksjon Noen eksempler på dårlige hashfunksjoner: En konstant funksjon: h(k) = 20 Java 1.1 (før 1998): java.lang.string.hashcode() benyttet kun de første 16 bokstavene i en string til å generere hashen.
29 Håndtering av kollisjoner Kjeding ( chaining ) Lagrer en lenket liste i hver hash-bøtte Hvis vi får mange kollisjoner tar det tid å lete etter elementene Fordel: Enkelt å implementere Ulempe: Kan bli tregt, og kan bli en del overhead
30 Håndtering av kollisjoner Lineær søking Hvis det er en kollisjon, prøv neste plass i tabellen Ulempe: Primary clustering yter enda dårligere enn kjeding hvis man har mange kollisjoner
31 Håndtering av kollisjoner Kvadratisk søking Hvis det er en kollisjon, prøv å hoppe videre slik: For hopp i: Posisjon = (h(k) + a*i + b*i 2 ) mod m Fordel: Yter bedre enn de to forrige Ulempe: Secondary clustering kan fremdeles bli problemer hvis mange elementer hasher til samme posisjon
32 Håndtering av kollisjoner Dobbel hashing Bruker 2 hashfunksjoner, h 1 (k) og h 2 (k) Prøv først plass h 1 (k) i tabellen Hvis det oppstår kollisjon, prøv å hoppe h 2 (k) posisjoner videre helt til vi når en åpen plass Fordel: Enkel og kjapp å implementere
33 Øving 2: Redd Ratatosk Hvorfor vil BFS være bedre enn DFS her? Ratatosk har lik sjanse til å være på hvert nivå Færre noder per nivå nært roten av treet BFS sjekker da først de mest sannsynlige nodene Løsningsforslag ligger ute BFS bruker kø DFS bruker stakk
34 Øving 2: Redd Ratatosk Tweak-løsning Vi vet allerede hvilken node Ratatosk er i Trenger ikke å lese all input, og konstruere tre Husk koblinger barn->forelder, fremfor andre veien La Ratatosk klatre ned treet ved å følge koblingene Denne spesifikke løsningen er ikke eksamensrelevant
35 Øving 3: Kobra lærer å stave
36 Øving 3: Kobra lærer å stave def bygg(ordliste): Skal bygge et tre ut fra ei liste av (ord, posisjon) Skal returnere rot-noden def posisjoner(ord, indeks, node): Skal returnere ei liste av posisjoner der ord matcher Hvis man møter spørsmålstegn, må man sjekke alle subtrær rekursivt, ved å spesifisere indeks og node i nye kall til posisjoner
Alg. Dat. Øvingsforelesning 3. Grafer, BFS, DFS og hashing
 Alg. Dat Øvingsforelesning 3 Grafer, BFS, DFS og hashing Dagens tema Grafer Terminologi Representasjon av grafer Bredde først søk (BFS) Dybde først søk (DFS) Hashing Hashfunksjoner, hashtabeller Kollisjonshåndtering
Alg. Dat Øvingsforelesning 3 Grafer, BFS, DFS og hashing Dagens tema Grafer Terminologi Representasjon av grafer Bredde først søk (BFS) Dybde først søk (DFS) Hashing Hashfunksjoner, hashtabeller Kollisjonshåndtering
Øvingsforelesning 2 - TDT4120. Grafer og hashing. Benjamin Bjørnseth
 Øvingsforelesning 2 - TDT4120 Grafer og hashing Benjamin Bjørnseth Informasjon Studasser algdat@idi.ntnu.no Program Presentasjon av øving 2 Grafer og traverseringsalgoritmer BFS, DFS Hashing Gjennomgang
Øvingsforelesning 2 - TDT4120 Grafer og hashing Benjamin Bjørnseth Informasjon Studasser algdat@idi.ntnu.no Program Presentasjon av øving 2 Grafer og traverseringsalgoritmer BFS, DFS Hashing Gjennomgang
INF1020 Algoritmer og datastrukturer
 Dagens plan Hashing Hashtabeller Hash-funksjoner Kollisjonshåndtering Åpen hashing (kap. 5.3) Lukket hashing (kap. 5.4) Rehashing (kap. 5.5) Sortering ut fra en hashing-ide (side 66-68) Bøttesortering
Dagens plan Hashing Hashtabeller Hash-funksjoner Kollisjonshåndtering Åpen hashing (kap. 5.3) Lukket hashing (kap. 5.4) Rehashing (kap. 5.5) Sortering ut fra en hashing-ide (side 66-68) Bøttesortering
Grunnleggende Grafalgoritmer
 Grunnleggende Grafalgoritmer Lars Vidar Magnusson 19.3.2014 Kapittel 22 Representere en graf Bredde-først søk Grafer i Informatikken Problem med grafer går ofte igjen i informatikkens verden, så det å
Grunnleggende Grafalgoritmer Lars Vidar Magnusson 19.3.2014 Kapittel 22 Representere en graf Bredde-først søk Grafer i Informatikken Problem med grafer går ofte igjen i informatikkens verden, så det å
Hashtabeller. Lars Vidar Magnusson Kapittel 11 Direkte adressering Hashtabeller Chaining Åpen-adressering
 Hashtabeller Lars Vidar Magnusson 12.2.2014 Kapittel 11 Direkte adressering Hashtabeller Chaining Åpen-adressering Dictionaries Mange applikasjoner trenger dynamiske sett som bare har dictionary oparsjonene
Hashtabeller Lars Vidar Magnusson 12.2.2014 Kapittel 11 Direkte adressering Hashtabeller Chaining Åpen-adressering Dictionaries Mange applikasjoner trenger dynamiske sett som bare har dictionary oparsjonene
Grunnleggende Grafalgoritmer II
 Grunnleggende Grafalgoritmer II Lars Vidar Magnusson March 17, 2015 Kapittel 22 Dybde-først søk Topologisk sortering Relasjonen til backtracking Dybde-Først Søk Dybde-først søk i motsetning til et bredde-først
Grunnleggende Grafalgoritmer II Lars Vidar Magnusson March 17, 2015 Kapittel 22 Dybde-først søk Topologisk sortering Relasjonen til backtracking Dybde-Først Søk Dybde-først søk i motsetning til et bredde-først
Grunnleggende Grafteori
 Grunnleggende Grafteori 2. September, 2019 Institutt for Informatikk 1 Dagens plan Terminologi og definisjoner Hvordan representere grafer i datamaskinen Traversering Dybde-først-søk Bredde-først-søk Topologisk
Grunnleggende Grafteori 2. September, 2019 Institutt for Informatikk 1 Dagens plan Terminologi og definisjoner Hvordan representere grafer i datamaskinen Traversering Dybde-først-søk Bredde-først-søk Topologisk
Innhold. Innledning 1
 Innhold Innledning 1 1 Kompleksitetsanalyse 7 1.1 Innledning.............................. 8 1.2 Hva vi beregner........................... 8 1.2.1 Enkle operasjoner...................... 8 1.2.2 Kompleksitet........................
Innhold Innledning 1 1 Kompleksitetsanalyse 7 1.1 Innledning.............................. 8 1.2 Hva vi beregner........................... 8 1.2.1 Enkle operasjoner...................... 8 1.2.2 Kompleksitet........................
Algdat - øvingsforelesning
 Algdat - øvingsforelesning Topologisk sortering og minimale spenntrær Nils Barlaug Dagens plan 1. 2. 3. 4. 5. Praktisk og dagens plan Topologisk sortering Minimale spenntrær a. Kruskal b. Prim Tips til
Algdat - øvingsforelesning Topologisk sortering og minimale spenntrær Nils Barlaug Dagens plan 1. 2. 3. 4. 5. Praktisk og dagens plan Topologisk sortering Minimale spenntrær a. Kruskal b. Prim Tips til
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2016 Institutt for informatikk, Universitetet i Oslo Forelesning 6: Grafer II Ingrid Chieh Yu (Ifi, UiO) INF2220 28.09.2016 1 / 30 Dagens plan: Dijkstra fort.
INF2220 - Algoritmer og datastrukturer HØSTEN 2016 Institutt for informatikk, Universitetet i Oslo Forelesning 6: Grafer II Ingrid Chieh Yu (Ifi, UiO) INF2220 28.09.2016 1 / 30 Dagens plan: Dijkstra fort.
Øvingsforelesning 4. Topologisk sortering, Strongly Connected Components og Minimale spenntrær. Magnus Botnan
 Øvingsforelesning 4 Topologisk sortering, Strongly Connected Components og Minimale spenntrær Magnus Botnan botnan@stud.ntnu.no 09/10/09 1 I dag Topologisk Sortering Sterke Komponenter Minimale Spenntrær
Øvingsforelesning 4 Topologisk sortering, Strongly Connected Components og Minimale spenntrær Magnus Botnan botnan@stud.ntnu.no 09/10/09 1 I dag Topologisk Sortering Sterke Komponenter Minimale Spenntrær
Magnus Moan (Undertegnede) Enkle datastrukturer, trær, traversering og rekursjon
 1 Enkle datastrukturer, trær, traversering og rekursjon Magnus Moan (Undertegnede) algdat@idi.ntnu.no Enkle datastrukturer, trær, traversering og rekursjon 2 Dagens plan Praktisk Enkle datastrukturer Stack
1 Enkle datastrukturer, trær, traversering og rekursjon Magnus Moan (Undertegnede) algdat@idi.ntnu.no Enkle datastrukturer, trær, traversering og rekursjon 2 Dagens plan Praktisk Enkle datastrukturer Stack
Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer
 Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer Eksamensdato 14. desember 2011 Eksamenstid 1500 1900 Sensurdato 14. januar Språk/målform Bokmål Kontakt under eksamen Magnus Lie Hetland (tlf.
Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer Eksamensdato 14. desember 2011 Eksamenstid 1500 1900 Sensurdato 14. januar Språk/målform Bokmål Kontakt under eksamen Magnus Lie Hetland (tlf.
Maps og Hashing. INF Algoritmer og datastrukturer. Map - ADT. Map vs Array
 Maps og Hashing INF0 - Algoritmer og datastrukturer HØSTEN 00 Institutt for informatikk, Universitetet i Oslo INF0, forelesning : Maps og Hashing Map - Abstrakt Data Type Hash-funksjoner hashcode Kollisjonshåndtering
Maps og Hashing INF0 - Algoritmer og datastrukturer HØSTEN 00 Institutt for informatikk, Universitetet i Oslo INF0, forelesning : Maps og Hashing Map - Abstrakt Data Type Hash-funksjoner hashcode Kollisjonshåndtering
Maps og Hashing. INF Algoritmer og datastrukturer. Map - ADT. Map vs Array
 Maps og Hashing INF0 - Algoritmer og datastrukturer HØSTEN 00 Institutt for informatikk, Universitetet i Oslo INF0, forelesning : Maps og Hashing Map - Abstrakt Data Type (kapittel.) Hash-funksjoner (kapittel..)
Maps og Hashing INF0 - Algoritmer og datastrukturer HØSTEN 00 Institutt for informatikk, Universitetet i Oslo INF0, forelesning : Maps og Hashing Map - Abstrakt Data Type (kapittel.) Hash-funksjoner (kapittel..)
Hashing. INF Algoritmer og datastrukturer HASHING. Hashtabeller
 Hashing INF2220 - Algoritmer og datastrukturer HØSTEN 200 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning : Hashing Hashtabeller (kapittel.) Hash-funksjoner (kapittel.2) Kollisjonshåndtering
Hashing INF2220 - Algoritmer og datastrukturer HØSTEN 200 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning : Hashing Hashtabeller (kapittel.) Hash-funksjoner (kapittel.2) Kollisjonshåndtering
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 3: Maps og Hashing Bjarne Holen (Ifi, UiO) INF2220 H2009, forelesning 3 1 / 25 Maps
INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 3: Maps og Hashing Bjarne Holen (Ifi, UiO) INF2220 H2009, forelesning 3 1 / 25 Maps
Pensum: fra boken (H-03)+ forelesninger
 Pensum: fra boken (H-03)+ forelesninger unntatt kursorisk tema KAP. 1 KAP. 2 KAP. 3 JAVA I-110 (ikke gjennomgått) OO + ABSTRAKSJON /GENERISK PROGRAMMERING REKURSJON ALGORITME-TIDSANALYSE; O-NOTASJON KAP.
Pensum: fra boken (H-03)+ forelesninger unntatt kursorisk tema KAP. 1 KAP. 2 KAP. 3 JAVA I-110 (ikke gjennomgått) OO + ABSTRAKSJON /GENERISK PROGRAMMERING REKURSJON ALGORITME-TIDSANALYSE; O-NOTASJON KAP.
Pensum: fra boken (H-03)+ forelesninger
 Pensum: fra boken (H-03)+ forelesninger unntatt kursorisk tema KAP. 1 KAP. 2 KAP. 3 JAVA I-110 (ikke gjennomgått) OO + ABSTRAKSJON /GENERISK PROGRAMMERING REKURSJON ALGORITME-TIDSANALYSE; O-NOTASJON KAP.
Pensum: fra boken (H-03)+ forelesninger unntatt kursorisk tema KAP. 1 KAP. 2 KAP. 3 JAVA I-110 (ikke gjennomgått) OO + ABSTRAKSJON /GENERISK PROGRAMMERING REKURSJON ALGORITME-TIDSANALYSE; O-NOTASJON KAP.
Datastrukturer. Algoritmer og datastrukturer. Øvingsforelesning 2
 Datastrukturer Algoritmer og datastrukturer Øvingsforelesning 2 Datastrukturer Algoritmer og datastrukturer Øvingsforelesning 2 av Henrik Grønbech Datastrukturer Algoritmer og datastrukturer Øvingsforelesning
Datastrukturer Algoritmer og datastrukturer Øvingsforelesning 2 Datastrukturer Algoritmer og datastrukturer Øvingsforelesning 2 av Henrik Grønbech Datastrukturer Algoritmer og datastrukturer Øvingsforelesning
... HASHING. Hashing. Hashtabeller. hash(x)
 HASHING Hashing Hashtabeller (kapittel.) Hash-funksjoner (kapittel.) Kollisjonshåndtering Åpen hashing (kapittel.) Lukket hashing (kapittel.) Anta at en bilforhandler har ulike modeller han ønsker å lagre
HASHING Hashing Hashtabeller (kapittel.) Hash-funksjoner (kapittel.) Kollisjonshåndtering Åpen hashing (kapittel.) Lukket hashing (kapittel.) Anta at en bilforhandler har ulike modeller han ønsker å lagre
Ny/utsatt EKSAMEN. Dato: 6. januar 2017 Eksamenstid: 09:00 13:00
 Ny/utsatt EKSAMEN Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: 6. januar 2017 Eksamenstid: 09:00 13:00 Hjelpemidler: Alle trykte og skrevne Faglærer: Jan Høiberg Om eksamensoppgavene: Oppgavesettet
Ny/utsatt EKSAMEN Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: 6. januar 2017 Eksamenstid: 09:00 13:00 Hjelpemidler: Alle trykte og skrevne Faglærer: Jan Høiberg Om eksamensoppgavene: Oppgavesettet
IN Algoritmer og datastrukturer
 IN2010 - Algoritmer og datastrukturer HØSTEN 2018 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Grafer I Ingrid Chieh Yu (Ifi, UiO) INF2010 H2018, forelesning 4 1 / 54
IN2010 - Algoritmer og datastrukturer HØSTEN 2018 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Grafer I Ingrid Chieh Yu (Ifi, UiO) INF2010 H2018, forelesning 4 1 / 54
Studentnummer: Side 1 av 1. Løsningsforslag, Eksamen i TDT4120 Algoritmer og datastrukturer August 2005
 Studentnummer: Side 1 av 1 Løsningsforslag, Eksamen i TDT4120 Algoritmer og datastrukturer August 2005 Faglige kontakter under eksamen: Magnus Lie Hetland, Arne Halaas Tillatte hjelpemidler: Bestemt enkel
Studentnummer: Side 1 av 1 Løsningsforslag, Eksamen i TDT4120 Algoritmer og datastrukturer August 2005 Faglige kontakter under eksamen: Magnus Lie Hetland, Arne Halaas Tillatte hjelpemidler: Bestemt enkel
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2016 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 5: Grafer I Ingrid Chieh Yu (Ifi, UiO) INF2220 H2016, forelesning 5 1 / 49
INF2220 - Algoritmer og datastrukturer HØSTEN 2016 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 5: Grafer I Ingrid Chieh Yu (Ifi, UiO) INF2220 H2016, forelesning 5 1 / 49
Eksamen i tdt4120 Algoritmer og datastrukturer
 Norges teknisk naturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap Side 1 av 5 Oppgavestillere: Magnus Lie Hetland Jon Marius Venstad Kvalitetskontroll: Magnar Nedland Faglig
Norges teknisk naturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap Side 1 av 5 Oppgavestillere: Magnus Lie Hetland Jon Marius Venstad Kvalitetskontroll: Magnar Nedland Faglig
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 6: Grafer Bjarne Holen (Ifi, UiO) INF2220 H2009, forelesning 6 1 / 31 Dagens plan:
INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 6: Grafer Bjarne Holen (Ifi, UiO) INF2220 H2009, forelesning 6 1 / 31 Dagens plan:
Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer
 Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer Eksamensdato 3. desember 2012 Eksamenstid 0900 1300 Sensurdato 3. januar 2013 Språk/målform Bokmål Kontakt under eksamen Magnus Lie Hetland (tlf.
Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer Eksamensdato 3. desember 2012 Eksamenstid 0900 1300 Sensurdato 3. januar 2013 Språk/målform Bokmål Kontakt under eksamen Magnus Lie Hetland (tlf.
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf. 91851949 Eksamensdato 11. august 2014 Eksamenstid (fra til) 0900 1300 Hjelpemiddelkode D. Ingen
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf. 91851949 Eksamensdato 11. august 2014 Eksamenstid (fra til) 0900 1300 Hjelpemiddelkode D. Ingen
EKSAMEN. Dato: 28. mai 2018 Eksamenstid: 09:00 13:00
 EKSAMEN Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: 28. mai 2018 Eksamenstid: 09:00 13:00 Hjelpemidler: Alle trykte og skrevne Faglærer: Jan Høiberg Om eksamensoppgavene: Oppgavesettet
EKSAMEN Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: 28. mai 2018 Eksamenstid: 09:00 13:00 Hjelpemidler: Alle trykte og skrevne Faglærer: Jan Høiberg Om eksamensoppgavene: Oppgavesettet
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2015 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 5: Grafer I Ingrid Chieh Yu (Ifi, UiO) INF2220 H2015, forelesning 5 1 / 55
INF2220 - Algoritmer og datastrukturer HØSTEN 2015 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 5: Grafer I Ingrid Chieh Yu (Ifi, UiO) INF2220 H2015, forelesning 5 1 / 55
SIF8010 ALGORITMER OG DATASTRUKTURER
 SIF8010 ALGORITMER OG DATASTRUKTURER KONTINUASJONSEKSAMEN, 1999; LØSNINGSFORSLAG Oppgave 1 (12%) Anta at du skal lage et støtteprogram som umiddelbart skal varsle om at et ord blir skrevet feil under inntasting
SIF8010 ALGORITMER OG DATASTRUKTURER KONTINUASJONSEKSAMEN, 1999; LØSNINGSFORSLAG Oppgave 1 (12%) Anta at du skal lage et støtteprogram som umiddelbart skal varsle om at et ord blir skrevet feil under inntasting
Notater til INF2220 Eksamen
 Notater til INF2220 Eksamen Lars Bjørlykke Kristiansen December 13, 2011 Stor O notasjon Funksjon Navn 1 Konstant log n Logaritmisk n Lineær n log n n 2 Kvadratisk n 3 Kubisk 2 n Eksponensiell n! Trær
Notater til INF2220 Eksamen Lars Bjørlykke Kristiansen December 13, 2011 Stor O notasjon Funksjon Navn 1 Konstant log n Logaritmisk n Lineær n log n n 2 Kvadratisk n 3 Kubisk 2 n Eksponensiell n! Trær
Definisjon av binært søketre
 Binære søketrær Definisjon av binært søketre For alle nodene i et binært søketre gjelder: Alle verdiene i nodens venstre subtre er mindre enn verdien i noden Alle verdiene i nodens høyre subtre er større
Binære søketrær Definisjon av binært søketre For alle nodene i et binært søketre gjelder: Alle verdiene i nodens venstre subtre er mindre enn verdien i noden Alle verdiene i nodens høyre subtre er større
PG4200 Algoritmer og datastrukturer Forelesning 10
 PG4200 Algoritmer og datastrukturer Forelesning 10 Lars Sydnes, NITH 9. april 2014 NOE Å STUSSE PÅ? Quadratic probing i Hash-tabell: ( ) 2 i + 1 p = p + ( 1) i+1 2 Underforstått forutsetning: Heltallsaritmetikk
PG4200 Algoritmer og datastrukturer Forelesning 10 Lars Sydnes, NITH 9. april 2014 NOE Å STUSSE PÅ? Quadratic probing i Hash-tabell: ( ) 2 i + 1 p = p + ( 1) i+1 2 Underforstått forutsetning: Heltallsaritmetikk
GRAFER. Korteste vei i en vektet graf uten negative kanter. Korteste vei, en-til-alle, for: Minimale spenntrær
 IN Algoritmer og datastrukturer GRAER IN Algoritmer og datastrukturer Dagens plan: orteste vei, en-til-alle, for: ektet rettet graf uten negative kanter (apittel 9..) (Dijkstras algoritme) ektet rettet
IN Algoritmer og datastrukturer GRAER IN Algoritmer og datastrukturer Dagens plan: orteste vei, en-til-alle, for: ektet rettet graf uten negative kanter (apittel 9..) (Dijkstras algoritme) ektet rettet
Uretta grafar (1) Mengde nodar Mengde kantar som er eit uordna par av nodar
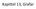 Kapittel 13, Grafar Uretta grafar (1) Ein uretta graf Mengde nodar Mengde kantar som er eit uordna par av nodar To nodar er naboar dersom dei er knytta saman med einkant Ein node kan ha kant til seg sjølv.
Kapittel 13, Grafar Uretta grafar (1) Ein uretta graf Mengde nodar Mengde kantar som er eit uordna par av nodar To nodar er naboar dersom dei er knytta saman med einkant Ein node kan ha kant til seg sjølv.
Uke 5 Disjunkte mengder
 Uke 5 Disjunkte mengder MAW, kap.. 8 September 19, 2005 Page 1 Hittil Forutsetninger for og essensen i faget Metodekall, rekursjon, permutasjoner Analyse av algoritmer Introduksjon til ADT er Den første
Uke 5 Disjunkte mengder MAW, kap.. 8 September 19, 2005 Page 1 Hittil Forutsetninger for og essensen i faget Metodekall, rekursjon, permutasjoner Analyse av algoritmer Introduksjon til ADT er Den første
Korteste vei i en vektet graf uten negative kanter
 Dagens plan: IN - Algoritmer og datastrukturer HØSTEN 7 Institutt for informatikk, Universitetet i Oslo IN, forelesning 7: Grafer II Korteste vei, en-til-alle, for: Vektet rettet graf uten negative kanter
Dagens plan: IN - Algoritmer og datastrukturer HØSTEN 7 Institutt for informatikk, Universitetet i Oslo IN, forelesning 7: Grafer II Korteste vei, en-til-alle, for: Vektet rettet graf uten negative kanter
IN Algoritmer og datastrukturer
 IN00 - Algoritmer og datastrukturer HØSTEN 08 Institutt for informatikk, Universitetet i Oslo Forelesning 5: Grafer II Ingrid Chieh Yu (Ifi, UiO) IN00 8.09.08 / Dagens plan: Korteste vei en-til-alle vektet
IN00 - Algoritmer og datastrukturer HØSTEN 08 Institutt for informatikk, Universitetet i Oslo Forelesning 5: Grafer II Ingrid Chieh Yu (Ifi, UiO) IN00 8.09.08 / Dagens plan: Korteste vei en-til-alle vektet
O, what a tangled. Fjerde forelesning. Robot-eksemplet som ikke ble gjennomgått sist blir frivillig selvstudium (ut fra foilene :-)
 Dagens oppvarming 1 O, what a tangled Fjerde forelesning Robot-eksemplet som ikke ble gjennomgått sist blir frivillig selvstudium (ut fra foilene :-) O, what a tangled web we weave / When first we practice
Dagens oppvarming 1 O, what a tangled Fjerde forelesning Robot-eksemplet som ikke ble gjennomgått sist blir frivillig selvstudium (ut fra foilene :-) O, what a tangled web we weave / When first we practice
Vi skal se på grafalgoritmer for:
 Grafalgoritmer Vi skal se på grafalgoritmer for: Traversering: Oppsøk alle nodene i grafen en og bare en gang, på en eller annen systematisk måte Nåbarhet: Finnes det en vei fra en node til en annen node?
Grafalgoritmer Vi skal se på grafalgoritmer for: Traversering: Oppsøk alle nodene i grafen en og bare en gang, på en eller annen systematisk måte Nåbarhet: Finnes det en vei fra en node til en annen node?
INF2220: Forelesning 3
 INF2220: Forelesning 3 Map og hashing Abstrakte datatyper (kapittel 3.1) Map (kapittel 4.8) Hashing (kapittel 5) REPETISJON: ALGORITMER OG STOR O 2 REPETISJON RØD-SVARTE TRÆR 7 Rød-svarte trær Et rød-svart
INF2220: Forelesning 3 Map og hashing Abstrakte datatyper (kapittel 3.1) Map (kapittel 4.8) Hashing (kapittel 5) REPETISJON: ALGORITMER OG STOR O 2 REPETISJON RØD-SVARTE TRÆR 7 Rød-svarte trær Et rød-svart
... Når internminnet blir for lite. Dagens plan: Løsning: Utvidbar hashing. hash(x) katalog. O modellen er ikke lenger gyldig ved
 Dagens plan: Utvidbar hashing (kapittel 5.6) B-trær (kap. 4.7) Abstrakte datatyper (kap. 3.1) Stakker (kap. 3.3) Når internminnet blir for lite En lese-/skriveoperasjon på en harddisk (aksesstid 7-12 millisekunder)
Dagens plan: Utvidbar hashing (kapittel 5.6) B-trær (kap. 4.7) Abstrakte datatyper (kap. 3.1) Stakker (kap. 3.3) Når internminnet blir for lite En lese-/skriveoperasjon på en harddisk (aksesstid 7-12 millisekunder)
Innledning. IN2010/INF Algoritmer og datastrukturer. Tirsdag 27. november 2018 Kl (4 timer)
 Innledning IN2010/INF2220 - Algoritmer og datastrukturer Tirsdag 27. november 2018 Kl. 14.30-18.30 (4 timer) Oppgavesettet består av totalt 15 oppgaver. Poengsum er angitt for hver oppgave. Maksimum poengsum
Innledning IN2010/INF2220 - Algoritmer og datastrukturer Tirsdag 27. november 2018 Kl. 14.30-18.30 (4 timer) Oppgavesettet består av totalt 15 oppgaver. Poengsum er angitt for hver oppgave. Maksimum poengsum
Løsningsforslag for eksamen i fag SIF8010 Algoritmer og datastrukturer Lørdag 9. august 2003, kl
 SIF8010 2003-08-09 Stud.-nr: Antall sider: 1 Løsningsforslag for eksamen i fag SIF8010 Algoritmer og datastrukturer Lørdag 9. august 2003, kl. 0900 1500 Faglig kontakt under eksamen: Arne Halaas, tlf.
SIF8010 2003-08-09 Stud.-nr: Antall sider: 1 Løsningsforslag for eksamen i fag SIF8010 Algoritmer og datastrukturer Lørdag 9. august 2003, kl. 0900 1500 Faglig kontakt under eksamen: Arne Halaas, tlf.
INF2220: Forelesning 3
 INF2220: Forelesning 3 Map og hashing Abstrakte datatyper (kapittel 3.1) Map (kapittel 4.8) Hashing (kapittel 5) ABSTRAKTE DATATYPER 2 Abstrakte datatyper En ADT består av: Et sett med objekter. Spesifikasjon
INF2220: Forelesning 3 Map og hashing Abstrakte datatyper (kapittel 3.1) Map (kapittel 4.8) Hashing (kapittel 5) ABSTRAKTE DATATYPER 2 Abstrakte datatyper En ADT består av: Et sett med objekter. Spesifikasjon
Trær. Består av sammenkoblede noder Hver node har 0 eller flere barne-noder. Må være asyklisk. Et tre med n noder har n-1 kanter.
 Generelle trær: Trær Består av sammenkoblede noder Hver node har 0 eller flere barne-noder. Må være asyklisk. Et tre med n noder har n-1 kanter. løvnoder kant rotnode sub-tre 1 Generelle trær: Oppbygging
Generelle trær: Trær Består av sammenkoblede noder Hver node har 0 eller flere barne-noder. Må være asyklisk. Et tre med n noder har n-1 kanter. løvnoder kant rotnode sub-tre 1 Generelle trær: Oppbygging
INF2220: Forelesning 1. Praktisk informasjon Analyse av algoritmer (kapittel 2) (Binær)trær (kapittel )
 INF2220: Forelesning 1 Praktisk informasjon Analyse av algoritmer (kapittel 2) (Binær)trær (kapittel 4.1-4.3 + 4.6) PRAKTISK INFORMASJON 2 Praktisk informasjon Kursansvarlige Ragnhild Kobro Runde (ragnhilk@ifi.uio.no)
INF2220: Forelesning 1 Praktisk informasjon Analyse av algoritmer (kapittel 2) (Binær)trær (kapittel 4.1-4.3 + 4.6) PRAKTISK INFORMASJON 2 Praktisk informasjon Kursansvarlige Ragnhild Kobro Runde (ragnhilk@ifi.uio.no)
Evt. forklar på tavla. Diskuter kjøretid (best-/ worst-case). Innsetting og søk. Rekursjon igjen. A C E G
 TLDR RTFM Innsetting og søk. Rekursjon igjen. Evt. forklar på tavla. Diskuter kjøretid (best-/ worst-case). D B F A C E G reduksjon! rekursjon dekomp. induksjon gjenbruk travers. Søk i søketre uten balansering
TLDR RTFM Innsetting og søk. Rekursjon igjen. Evt. forklar på tavla. Diskuter kjøretid (best-/ worst-case). D B F A C E G reduksjon! rekursjon dekomp. induksjon gjenbruk travers. Søk i søketre uten balansering
Løsningsforslag for Obligatorisk Oppgave 3. Algoritmer og Datastrukturer ITF20006
 Løsningsforslag for Obligatorisk Oppgave 3 Algoritmer og Datastrukturer ITF20006 Lars Vidar Magnusson Frist 28.03.14 Den tredje obligatoriske oppgaven tar for seg forelesning 9 til 13, som dreier seg om
Løsningsforslag for Obligatorisk Oppgave 3 Algoritmer og Datastrukturer ITF20006 Lars Vidar Magnusson Frist 28.03.14 Den tredje obligatoriske oppgaven tar for seg forelesning 9 til 13, som dreier seg om
INF2220: Forelesning 3. Map og hashing Abstrakte datatyper (kapittel 3.1) Map (kapittel 4.8) Hashing (kapittel 5)
 INF2220: Forelesning 3 Map og hashing Abstrakte datatyper (kapittel 3.1) Map (kapittel 4.8) Hashing (kapittel 5) Map og hashing Ett minutt for deg selv: Hva vet du om maps/dictionarys og hashing fra tidligere?
INF2220: Forelesning 3 Map og hashing Abstrakte datatyper (kapittel 3.1) Map (kapittel 4.8) Hashing (kapittel 5) Map og hashing Ett minutt for deg selv: Hva vet du om maps/dictionarys og hashing fra tidligere?
Innledning Grafer. Grafer / Nettverk. Hva er en graf? Hva er en graf? Eksempler på grafer? Hva er en graf? Elementære Graf-Algoritmer
 rafer / ettverk nnledning rafer lementære raf-lgoritmer ernt ngvald Sunde 1 ernt ngvald Sunde 2 va er en graf? e fleste applikasjoner involverer vanligvis ikke bare et sett elemeter, men også et sett med
rafer / ettverk nnledning rafer lementære raf-lgoritmer ernt ngvald Sunde 1 ernt ngvald Sunde 2 va er en graf? e fleste applikasjoner involverer vanligvis ikke bare et sett elemeter, men også et sett med
Binære søketrær. En ordnet datastruktur med raske oppslag. Sigmund Hansen
 Binære søketrær En ordnet datastruktur med raske oppslag Sigmund Hansen Lister og trær Rekke (array): 1 2 3 4 Lenket liste (dobbelt-lenket): 1 2 3 4 Binært søketre: 3 1 4 2 Binære
Binære søketrær En ordnet datastruktur med raske oppslag Sigmund Hansen Lister og trær Rekke (array): 1 2 3 4 Lenket liste (dobbelt-lenket): 1 2 3 4 Binært søketre: 3 1 4 2 Binære
Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer
 Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer Eksamensdato 3. desember 2012 Eksamenstid 0900 1300 Sensurdato 3. januar 2013 Språk/målform Bokmål Kontakt under eksamen Magnus Lie Hetland (tlf.
Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer Eksamensdato 3. desember 2012 Eksamenstid 0900 1300 Sensurdato 3. januar 2013 Språk/målform Bokmål Kontakt under eksamen Magnus Lie Hetland (tlf.
Hashing: Håndtering av kollisjoner
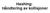 Hashing: Håndtering av kollisjoner Innsetting av dataelement i hashtabell Algoritme: 1. Bruk en hashfunksjon til å beregne hashverdi basert på dataelementets nøkkelverdi 2. Sett inn dataelementet i hashtabellen
Hashing: Håndtering av kollisjoner Innsetting av dataelement i hashtabell Algoritme: 1. Bruk en hashfunksjon til å beregne hashverdi basert på dataelementets nøkkelverdi 2. Sett inn dataelementet i hashtabellen
Dagens plan: INF Algoritmer og datastrukturer. Grafer vi har sett allerede. Det første grafteoretiske problem: Broene i Königsberg
 Dagens plan: INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 6: Grafer Definisjon av en graf Grafvarianter Intern representasjon
Dagens plan: INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 6: Grafer Definisjon av en graf Grafvarianter Intern representasjon
Oppgave 1. Sekvenser (20%)
 Det matematisk-naturvitenskapelige fakultet UNIVERSITETET I BERGEN Eksamen i emnet I 20 - Algoritmer, datastrukturer og programmering Mandag 2.Mai 200, kl. 09-5. Ingen hjelpemidler tillatt. Oppgavesettet
Det matematisk-naturvitenskapelige fakultet UNIVERSITETET I BERGEN Eksamen i emnet I 20 - Algoritmer, datastrukturer og programmering Mandag 2.Mai 200, kl. 09-5. Ingen hjelpemidler tillatt. Oppgavesettet
Enkle datastrukturer. Lars Greger Nordland Hagen. Introduksjon til øvingsopplegget og gjennomgang av python
 1 Enkle datastrukturer Lars Greger Nordland Hagen algdat@idi.ntnu.no Introduksjon til øvingsopplegget og gjennomgang av python 2 I dag Stack Kø (queue) Lenkede lister (linked list) Trær Binære søketrær
1 Enkle datastrukturer Lars Greger Nordland Hagen algdat@idi.ntnu.no Introduksjon til øvingsopplegget og gjennomgang av python 2 I dag Stack Kø (queue) Lenkede lister (linked list) Trær Binære søketrær
INF Algoritmer og datastrukturer
 INF0 - Algoritmer og datastrukturer HØSTEN 05 Institutt for informatikk, Universitetet i Oslo Forelesning 6: Grafer II Ingrid Chieh Yu (Ifi, UiO) INF0.09.05 / 8 Dagens plan: Minimale spenntrær Prim Kruskal
INF0 - Algoritmer og datastrukturer HØSTEN 05 Institutt for informatikk, Universitetet i Oslo Forelesning 6: Grafer II Ingrid Chieh Yu (Ifi, UiO) INF0.09.05 / 8 Dagens plan: Minimale spenntrær Prim Kruskal
IN Algoritmer og datastrukturer
 IN010 - Algoritmer og datastrukturer HØSTEN 018 Institutt for informatikk, Universitetet i Oslo Forelesning 6: Grafer III Ingrid Chieh Yu (Ifi, UiO) IN010 0.10.018 1 / 0 Dagens plan: Dybde-først søk Biconnectivity
IN010 - Algoritmer og datastrukturer HØSTEN 018 Institutt for informatikk, Universitetet i Oslo Forelesning 6: Grafer III Ingrid Chieh Yu (Ifi, UiO) IN010 0.10.018 1 / 0 Dagens plan: Dybde-først søk Biconnectivity
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2017 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 5: Grafer I Ingrid Chieh Yu (Ifi, UiO) INF2220 H2017, forelesning 5 1 / 53
INF2220 - Algoritmer og datastrukturer HØSTEN 2017 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 5: Grafer I Ingrid Chieh Yu (Ifi, UiO) INF2220 H2017, forelesning 5 1 / 53
Litt om grafer og traversering, og om hashing. Jeg gikk en tur i. Tredje forelesning
 Litt om grafer og traversering, og om hashing. Jeg gikk en tur i Tredje forelesning Ikke la dere lure av ordet reduksjon her! X? Det er jo bare å Y. Hvilken vei gir informasjon? Hvis jeg vil vise at A
Litt om grafer og traversering, og om hashing. Jeg gikk en tur i Tredje forelesning Ikke la dere lure av ordet reduksjon her! X? Det er jo bare å Y. Hvilken vei gir informasjon? Hvis jeg vil vise at A
Algoritmer og Datastrukturer IAI 21899
 Eksamen i Algoritmer og Datastrukturer IAI 21899 Høgskolen i Østfold Avdeling for informatikk og automatisering Torsdag 30. november 2000, kl. 09.00-14.00 LØSNINGSFORSLAG 1 Del 1, Binære søketrær Totalt
Eksamen i Algoritmer og Datastrukturer IAI 21899 Høgskolen i Østfold Avdeling for informatikk og automatisering Torsdag 30. november 2000, kl. 09.00-14.00 LØSNINGSFORSLAG 1 Del 1, Binære søketrær Totalt
Disjunkte mengder ADT
 Binære relasjoner A A = {(x, y) x, y A}: mengden av ordnede par over A. Disjunkte mengder ADT Weiss kap. 8.1 8.5 Løser ekvivalensproblemet Lett og rask implementasjon Vanskelig tidsforbrukanalyse Ark 1
Binære relasjoner A A = {(x, y) x, y A}: mengden av ordnede par over A. Disjunkte mengder ADT Weiss kap. 8.1 8.5 Løser ekvivalensproblemet Lett og rask implementasjon Vanskelig tidsforbrukanalyse Ark 1
INF1020 Algoritmer og datastrukturer GRAFER
 GRAFER Dagens plan: Definisjon av en graf (kapittel 9.1) Grafvarianter Intern representasjon av grafer (kapittel 9.1.1) Topologisk sortering (kapittel 9.2) Korteste vei, en-til-alle, for: uvektet graf
GRAFER Dagens plan: Definisjon av en graf (kapittel 9.1) Grafvarianter Intern representasjon av grafer (kapittel 9.1.1) Topologisk sortering (kapittel 9.2) Korteste vei, en-til-alle, for: uvektet graf
Kapittel 14, Hashing. Tema. Definere hashing Studere ulike hashfunksjoner Studere kollisjonsproblemet 17-1
 Kapittel 14, Hashing Tema Definere hashing Studere ulike hashfunksjoner Studere kollisjonsproblemet 17-1 Hashing Hashing er en effektiv metode ved lagring og gjenfinning (søking) av informasjon Søkemetoder
Kapittel 14, Hashing Tema Definere hashing Studere ulike hashfunksjoner Studere kollisjonsproblemet 17-1 Hashing Hashing er en effektiv metode ved lagring og gjenfinning (søking) av informasjon Søkemetoder
Algoritmer og Datastrukturer
 Eksamen i Algoritmer og Datastrukturer IAI 21899 Høgskolen i Østfold Avdeling for informatikk og automatisering Lørdag 15. desember 2001, kl. 09.00-14.00 Hjelpemidler: Alle trykte og skrevne hjelpemidler.
Eksamen i Algoritmer og Datastrukturer IAI 21899 Høgskolen i Østfold Avdeling for informatikk og automatisering Lørdag 15. desember 2001, kl. 09.00-14.00 Hjelpemidler: Alle trykte og skrevne hjelpemidler.
Eksamen i fag SIF8010 Algoritmer og datastrukturer Lørdag 9. august 2003, kl
 SIF8010 2003-08-09 Stud.-nr: Antall sider: 1 Eksamen i fag SIF8010 Algoritmer og datastrukturer Lørdag 9. august 2003, kl. 0900 1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 41661982; Magnus Lie
SIF8010 2003-08-09 Stud.-nr: Antall sider: 1 Eksamen i fag SIF8010 Algoritmer og datastrukturer Lørdag 9. august 2003, kl. 0900 1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 41661982; Magnus Lie
Det første grafteoretiske problem: Broene i Königsberg
 Dagens plan: INF0 - Algoritmer og datastrukturer HØSTEN 007 Institutt for informatikk, Universitetet i Oslo INF0, forelesning 6: Grafer Denisjon av en graf (kap. 9.1) Grafvarianter Intern representasjon
Dagens plan: INF0 - Algoritmer og datastrukturer HØSTEN 007 Institutt for informatikk, Universitetet i Oslo INF0, forelesning 6: Grafer Denisjon av en graf (kap. 9.1) Grafvarianter Intern representasjon
INF1010 Hashing. Marit Nybakken 8. mars 2004
 INF1010 Hashing Marit Nybakken marnybak@ifi.uio.no 8. mars 2004 Til nå har vi trodd at en HashMap var en mystisk uendelig stor samleeske der vi på magisk vis kan putte inn objekter og ta ut objekter ved
INF1010 Hashing Marit Nybakken marnybak@ifi.uio.no 8. mars 2004 Til nå har vi trodd at en HashMap var en mystisk uendelig stor samleeske der vi på magisk vis kan putte inn objekter og ta ut objekter ved
Anvendelser av grafer
 Grafer Anvendelser av grafer Passer for modeller/datastrukturer med usystematiske forbindelser Ikke-lineære og ikke-hierarkiske koblinger mellom dataobjektene Modellering av nettverk: Veisystemer/rutekart
Grafer Anvendelser av grafer Passer for modeller/datastrukturer med usystematiske forbindelser Ikke-lineære og ikke-hierarkiske koblinger mellom dataobjektene Modellering av nettverk: Veisystemer/rutekart
Søkeproblemet. Gitt en datastruktur med n elementer: Finnes et bestemt element (eller en bestemt verdi) x lagret i datastrukturen eller ikke?
 Søking Søkeproblemet Gitt en datastruktur med n elementer: Finnes et bestemt element (eller en bestemt verdi) x lagret i datastrukturen eller ikke? Effektiviteten til søkealgoritmer avhenger av: Om datastrukturen
Søking Søkeproblemet Gitt en datastruktur med n elementer: Finnes et bestemt element (eller en bestemt verdi) x lagret i datastrukturen eller ikke? Effektiviteten til søkealgoritmer avhenger av: Om datastrukturen
INF1020 Algoritmer og datastrukturer GRAFER
 GRAFER Dagens plan: Minimale spenntrær Prim Kapittel 9.5.1 Kruskal Kapittel 9.5.2 Dybde-først søk Kapittel 9.6.1 Løkkeleting Dobbeltsammenhengende grafer Kapittel 9.6.2 Å finne ledd-noder articulation
GRAFER Dagens plan: Minimale spenntrær Prim Kapittel 9.5.1 Kruskal Kapittel 9.5.2 Dybde-først søk Kapittel 9.6.1 Løkkeleting Dobbeltsammenhengende grafer Kapittel 9.6.2 Å finne ledd-noder articulation
Vi skal se på grafalgoritmer for:
 Grafalgoritmer Vi skal se på grafalgoritmer for: raversering: Nåbarhet: Oppsøk alle nodene i grafen en og bare en gang, på en eller annen systematisk måte innes det en vei fra en node til en annen node?
Grafalgoritmer Vi skal se på grafalgoritmer for: raversering: Nåbarhet: Oppsøk alle nodene i grafen en og bare en gang, på en eller annen systematisk måte innes det en vei fra en node til en annen node?
Eksamen iin115 og IN110, 15. mai 1997 Side 2 Oppgave 1 Trær 55 % Vi skal i denne oppgaven se på en form for søkestrukturer som er spesielt godt egnet
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i IN 115 og IN110 Algoritmer og datastrukturer Eksamensdag: 15. mai 1997 Tid for eksamen: 9.00 15.00 Oppgavesettet er på 8 sider.
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i IN 115 og IN110 Algoritmer og datastrukturer Eksamensdag: 15. mai 1997 Tid for eksamen: 9.00 15.00 Oppgavesettet er på 8 sider.
Lars Vidar Magnusson Kapittel 13 Rød-Svarte (Red-Black) trær Rotasjoner Insetting Sletting
 Rød-Svarte Trær Lars Vidar Magnusson 21.2.2014 Kapittel 13 Rød-Svarte (Red-Black) trær Rotasjoner Insetting Sletting Rød-Svarte Trær Rød-Svarte trær (red-black trees) er en variasjon binære søketrær som
Rød-Svarte Trær Lars Vidar Magnusson 21.2.2014 Kapittel 13 Rød-Svarte (Red-Black) trær Rotasjoner Insetting Sletting Rød-Svarte Trær Rød-Svarte trær (red-black trees) er en variasjon binære søketrær som
E K S A M E N. Algoritmiske metoder I. EKSAMENSDATO: 11. desember HINDA / 99HINDB / 99HINEA / 00HDESY ( 2DA / 2DB / 2EA / DESY )
 Høgskolen i Gjøvik Avdeling for Teknologi E K S A M E N FAGNAVN: FAGNUMMER: Algoritmiske metoder I L 189 A EKSAMENSDATO: 11. desember 2000 KLASSE: 99HINDA / 99HINDB / 99HINEA / 00HDESY ( 2DA / 2DB / 2EA
Høgskolen i Gjøvik Avdeling for Teknologi E K S A M E N FAGNAVN: FAGNUMMER: Algoritmiske metoder I L 189 A EKSAMENSDATO: 11. desember 2000 KLASSE: 99HINDA / 99HINDB / 99HINEA / 00HDESY ( 2DA / 2DB / 2EA
KONTINUASJONSEKSAMEN
 Høgskolen i Gjøvik KONTINUASJONSEKSAMEN FAGNAVN: FAGNUMMER: Algoritmiske metoder I L 171 A EKSAMENSDATO: 19. august 1999 KLASSE: 97HINDA / 97HINDB ( 2DA / 2DB ) TID: 09.00-14.00 FAGLÆRER: Frode Haug ANT.
Høgskolen i Gjøvik KONTINUASJONSEKSAMEN FAGNAVN: FAGNUMMER: Algoritmiske metoder I L 171 A EKSAMENSDATO: 19. august 1999 KLASSE: 97HINDA / 97HINDB ( 2DA / 2DB ) TID: 09.00-14.00 FAGLÆRER: Frode Haug ANT.
EKSAMEN. Dato: 18. mai 2017 Eksamenstid: 09:00 13:00
 EKSAMEN Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: 18. mai 2017 Eksamenstid: 09:00 13:00 Hjelpemidler: Alle trykte og skrevne Kalkulator Faglærer: Jan Høiberg Om eksamensoppgavene: Oppgavesettet
EKSAMEN Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: 18. mai 2017 Eksamenstid: 09:00 13:00 Hjelpemidler: Alle trykte og skrevne Kalkulator Faglærer: Jan Høiberg Om eksamensoppgavene: Oppgavesettet
INF Algoritmer og datastrukturer. Hva er INF2220? Algoritmer og datastrukturer
 Praktiske opplysninger INF2220 - Algoritmer og datastrukturer HØSTEN 2007 Institutt for informatikk, Universitetet i Oslo Tid og sted: Mandag kl. 12:15-14:00 Store auditorium, Informatikkbygningen Kursansvarlige
Praktiske opplysninger INF2220 - Algoritmer og datastrukturer HØSTEN 2007 Institutt for informatikk, Universitetet i Oslo Tid og sted: Mandag kl. 12:15-14:00 Store auditorium, Informatikkbygningen Kursansvarlige
Definisjon. I et binært tre har hver node enten 0, 1 eller 2 barn
 Binære trær Definisjon I et binært tre har hver node enten 0, 1 eller 2 barn Rekursiv definisjon: Et binært tre er enten tomt, eller: Består av en rotnode og to binære trær som kalles venstre subtre og
Binære trær Definisjon I et binært tre har hver node enten 0, 1 eller 2 barn Rekursiv definisjon: Et binært tre er enten tomt, eller: Består av en rotnode og to binære trær som kalles venstre subtre og
EKSAMEN med løsningsforslag
 EKSAMEN med løsningsforslag Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: Eksamenstid: 20. mai 2009 kl 09.00 til kl 13.00 Hjelpemidler: 8 A4-sider (4 ark) med egne notater Kalkulator Faglærer:
EKSAMEN med løsningsforslag Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: Eksamenstid: 20. mai 2009 kl 09.00 til kl 13.00 Hjelpemidler: 8 A4-sider (4 ark) med egne notater Kalkulator Faglærer:
INF2220: Forelesning 2
 INF2220: Forelesning 2 Mer om analyse av algoritmer Analyse av binære søketrær Balanserte søketrær Rød-svarte trær (kapittel12.2) B-trær (kapittel 4.7) ANALYSE AV ALGORITMER 2 Analyse av tidsforbruk Hvor
INF2220: Forelesning 2 Mer om analyse av algoritmer Analyse av binære søketrær Balanserte søketrær Rød-svarte trær (kapittel12.2) B-trær (kapittel 4.7) ANALYSE AV ALGORITMER 2 Analyse av tidsforbruk Hvor
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 13: Eksamensgjennomgang Bjarne Holen (Ifi, UiO) INF2220 H2009, forelesning 13 1 /
INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 13: Eksamensgjennomgang Bjarne Holen (Ifi, UiO) INF2220 H2009, forelesning 13 1 /
EKSAMEN. Dato: 9. mai 2016 Eksamenstid: 09:00 13:00
 EKSAMEN Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: 9. mai 2016 Eksamenstid: 09:00 13:00 Hjelpemidler: Alle trykte og skrevne Faglærer: Jan Høiberg Om eksamensoppgavene: Oppgavesettet består
EKSAMEN Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: 9. mai 2016 Eksamenstid: 09:00 13:00 Hjelpemidler: Alle trykte og skrevne Faglærer: Jan Høiberg Om eksamensoppgavene: Oppgavesettet består
EKSAMENSOPPGAVE. IAI20102 Algoritmer og datastrukturer
 EKSAMENSOPPGAVE Fag: Lærer: IAI00 Algoritmer og datastrukturer André A. Hauge Dato:..005 Tid: 0900-00 Antall oppgavesider: 5 med forside Antall vedleggssider: 0 Hjelpemidler: Alle trykte og skrevne hjelpemidler,
EKSAMENSOPPGAVE Fag: Lærer: IAI00 Algoritmer og datastrukturer André A. Hauge Dato:..005 Tid: 0900-00 Antall oppgavesider: 5 med forside Antall vedleggssider: 0 Hjelpemidler: Alle trykte og skrevne hjelpemidler,
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf.!! 91851949 Eksamensdato! 15. august 2013 Eksamenstid (fra til)! 0900 1300 Hjelpemiddelkode D.
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf.!! 91851949 Eksamensdato! 15. august 2013 Eksamenstid (fra til)! 0900 1300 Hjelpemiddelkode D.
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 10: Disjunkte Mengder Bjarne Holen (Ifi, UiO) INF2220 H2009, forelesning 10 1 / 27
INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 10: Disjunkte Mengder Bjarne Holen (Ifi, UiO) INF2220 H2009, forelesning 10 1 / 27
Algdat-ninja på 60 minutter: Et galskapsprosjekt. Magnus Lie Hetland
 Algdat-ninja på 60 minutter: Et galskapsprosjekt Magnus Lie Hetland 15. november, 2002 Advarsel: Tettpakkede og overfladiske foiler forut! 1 Algtdat i 6 punkter 1. Grunnbegreper og basisverktøy 2. Rekursjon
Algdat-ninja på 60 minutter: Et galskapsprosjekt Magnus Lie Hetland 15. november, 2002 Advarsel: Tettpakkede og overfladiske foiler forut! 1 Algtdat i 6 punkter 1. Grunnbegreper og basisverktøy 2. Rekursjon
Dagens plan: INF Algoritmer og datastrukturer. Eksempel. Binære Relasjoner
 Dagens plan: INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 10: Disjunkte Mengder Definisjon av binær relasjon Definisjon av ekvivalens
Dagens plan: INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 10: Disjunkte Mengder Definisjon av binær relasjon Definisjon av ekvivalens
GRAFER. Hva er en graf? Det første grafteoretiske problem: Broene i Königsberg. Grafer vi har sett allerede
 Dagens plan: GRAFER Definisjon av en graf (kapittel 9.) Grafvarianter Intern representasjon av grafer (kapittel 9..) Topologisk sortering (kapittel 9.) Korteste vei en-til-alle uvektet graf (kapittel 9..)
Dagens plan: GRAFER Definisjon av en graf (kapittel 9.) Grafvarianter Intern representasjon av grafer (kapittel 9..) Topologisk sortering (kapittel 9.) Korteste vei en-til-alle uvektet graf (kapittel 9..)
Øvingsforelesning 12 Maks flyt
 Øvingsforelesning 12 Maks flyt Ole Kristian Pedersen 9. november 2018 ] Plan for dagen Maksimal flyt og minimale snitt Maksimal bipartitt matching Tidligere eksamensoppgaver Introduksjon øving 12 Hva er
Øvingsforelesning 12 Maks flyt Ole Kristian Pedersen 9. november 2018 ] Plan for dagen Maksimal flyt og minimale snitt Maksimal bipartitt matching Tidligere eksamensoppgaver Introduksjon øving 12 Hva er
All good things. Fjortende forelesning
 All good things Fjortende forelesning Div notater finnes på http://www.idi.ntnu.no/~algdat Foiler finnes på http://www.idi.ntnu.no/~mlh/algdat/latitudinary Spørsmål? algdat@idi.ntnu.no Sjekkliste Dette
All good things Fjortende forelesning Div notater finnes på http://www.idi.ntnu.no/~algdat Foiler finnes på http://www.idi.ntnu.no/~mlh/algdat/latitudinary Spørsmål? algdat@idi.ntnu.no Sjekkliste Dette
Datastrukturer. Stakker (Stacks) Hva er en datastruktur? Fordeler / Ulemper. Generelt om Datastrukturer. Stakker (Stacks) Elementære Datastrukturer
 Hva er en datastruktur? Datastrukturer Elementære Datastrukturer En datastruktur er en systematisk måte å lagre og organisere data på, slik at det er lett å aksessere og modifisere dataene Eksempler på
Hva er en datastruktur? Datastrukturer Elementære Datastrukturer En datastruktur er en systematisk måte å lagre og organisere data på, slik at det er lett å aksessere og modifisere dataene Eksempler på
Binære trær: Noen algoritmer og anvendelser
 Binære trær: Noen algoritmer og anvendelser Algoritmer / anvendelser: Søking i usortert binært tre Telling av antall noder og nivåer i treet Traversering av binære trær Binære uttrykkstrær Kunstig intelligens(?):
Binære trær: Noen algoritmer og anvendelser Algoritmer / anvendelser: Søking i usortert binært tre Telling av antall noder og nivåer i treet Traversering av binære trær Binære uttrykkstrær Kunstig intelligens(?):
Hva er en algoritme? INF HØSTEN 2006 INF1020. Kursansvarlige Ragnar Normann E-post: Dagens tema
 va er en algoritme? Vanlig sammenligning: Oppskrift. nput lgoritme NF1020 - ØSTEN 2006 Kursansvarlige Ragnar Normann E-post: ragnarn@ifi.uio.no Output Knuth : tillegg til å være et endelig sett med regler
va er en algoritme? Vanlig sammenligning: Oppskrift. nput lgoritme NF1020 - ØSTEN 2006 Kursansvarlige Ragnar Normann E-post: ragnarn@ifi.uio.no Output Knuth : tillegg til å være et endelig sett med regler
Søk i tilstandsrom. Backtracking (Kap. 10) Branch-and-bound (Kap. 10) Iterativ fordypning. Dijkstras korteste sti-algoritme A*-søk (Kap.
 Søk i tilstandsrom Backtracking (Kap. 10) DFS i tilstandsrommet. Trenger lite lagerplass. Branch-and-bound (Kap. 10) BFS Trenger mye plass: må lagre alle noder som er «sett» men ikke studert. Kan også
Søk i tilstandsrom Backtracking (Kap. 10) DFS i tilstandsrommet. Trenger lite lagerplass. Branch-and-bound (Kap. 10) BFS Trenger mye plass: må lagre alle noder som er «sett» men ikke studert. Kan også
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i Eksamensdag: 12. desember 2008 Tid for eksamen: 9.00 12.00 Oppgavesettet er på 7 sider. Vedlegg: Tillatte hjelpemidler: INF2220
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i Eksamensdag: 12. desember 2008 Tid for eksamen: 9.00 12.00 Oppgavesettet er på 7 sider. Vedlegg: Tillatte hjelpemidler: INF2220
EKSAMENSOPPGAVE. INF-1101 Datastrukturer og algoritmer. Adm.bygget, rom K1.04 og B154 Ingen
 Fakultet for naturvitenskap og teknologi EKSAMENSOPPGAVE Eksamen i: Dato: 15.mai 2018 Klokkeslett: 09:00 13:00 Sted: Tillatte hjelpemidler: Adm.bygget, rom K1.04 og B154 Ingen Type innføringsark (rute/linje):
Fakultet for naturvitenskap og teknologi EKSAMENSOPPGAVE Eksamen i: Dato: 15.mai 2018 Klokkeslett: 09:00 13:00 Sted: Tillatte hjelpemidler: Adm.bygget, rom K1.04 og B154 Ingen Type innføringsark (rute/linje):
