Andre obligatoriske oppgave stk 1100
|
|
|
- Gunn Pia Hanssen
- 8 år siden
- Visninger:
Transkript
1 Andre obligatorise oppgave st 11 John Miael Modin 17. april 8 Oppgave 1 X er årsinteten til en tilfeldig valgt person i en befolningsgruppe. Sansynlighetstettheten til X er gitt ved { θ f X (x) = θ x θ 1 for x > ellers Hvor er minste inteten i befolningsgruppen og θ > avhenger av lønnsforsjellene. a) Den umulative fordelingen F X (x) til en ontinuerlig stoastis variabel X finner man ved å integrere tetthetsfunsjonen f X fra til x. F X (x) = = x f X (t)dt { x θθ t θ 1 dt for x > ellers x θ θ t θ 1 dt = θ x t θ 1 dt = θ [ t θ ] x θ = θ ( x θ θ) = 1 θ x θ For x < er f X = og dt = (c c) =. Dette betyr at F X(x) er gitt ved { 1 F X (x) = θ x θ for x > ellers La M være median årsintet. Da har vi at F X (M) = 1 M = F 1 X (1 ) 1
2 b) θ = F X (M) = 1 θ M θ = θ M θ = M θ θ log log = θ log M log + log θ = log M M = e log θ Den mediane årsinteten M er altså e log θ. Forventningen E(X) er gitt x f X(x) dx. Men siden f X (x) = for x < bruer jeg som nedre integrajsons grense. c) E(X) = x θ θ x θ 1 dx = θ θ x θ dx = lim b = lim b θ θ [ x θ+1 ] b 1 θ θ θ ( ) θ θ ( 1 θ b1 θ θ+1 ) 1 θ Siden θ > har vi at lim b b 1 θ = som gir ( ) θ θ ( θ+1 E(X) = ) = θ 1 θ θ 1 Vi har = roner og θ =.5. Median årsintet M er da e log.5 = Forventet årsintet E er da = Medianen ligger ganse nærme minsteinnteten, mens forventningen er en del større. Dette tyder på at mange har ganse lav inntet, mens noen har veldig høy. Derfor gir medianen et bedre uttry for den typise innteten i befolningen. d) Vi har at variansen til X er gitt ved Var(X) = E(X ) (E(X)). Jeg begynner med å finne E(X ).
3 E(X ) = x f X (x) dx b = lim θ θ x θ+1 dx b θ θ [ = lim x θ+ ] b b θ Har at θ > lim b b θ =. Sitter da igjenn med θθ θ θ+ = θ θ. Var(X) = ( ) θ θ θ θ 1 = θ θ θ (θ 1) ( ) = θ 1 θ θ (θ 1) ( θ = θ θ + 1 ( θ θ ) ) (θ )(θ 1) = θ (θ )(θ 1) Standardavviet til X er gitt σ = Var(X). Standandardavviet σ er da θ σ = (θ )(θ 1) θ = (θ )(θ 1) θ = θ 1 θ Der jeg har antatt at, siden er minste innteten i en befolning. e) Har gitt Y = θ log (X/). For å finne sansynlighetstettheten f Y finner jeg først F Y. F Y (y) = P(Y y) = P(θ log (X/) y). Siden θ > blir ie uliheten forandret av å dele på θ. Vi har da at F Y (y) = P(X e y θ ) = FX (e y θ ). For y er y θ e y θ 1 e y θ. For y har vi da F X (e y θ ) = 1 θ ( e y θ ) θ = 1 e y f Y (y) = (1 e y ) = e y 3
4 For y < er F X (e y θ ) =, f Y = () =. Altså er f Y (y) gitt { e y for y f Y (y) = ellers. Dette er er esponentialtettheten med λ = 1. Oppgave Har at X 1, X,..., X n er uavhengige identis fordelte stoastise variabler. Definerer µ = E(X i ) og σ = Var(X i ).Innfører gjennomsnittet X n = 1 n og det standardiserte gjennomsnittet n i=1 X i X Z n = n µ σ/ n Har også oppgitt at E( X n ) = µ, og Var( X n ) = σ n a) X Bruer at E(aX+b) = ae(x)+b. Det gir at E(Z n ) = E( n µ σ/ n ) = 1 σ/ n E( X n ) µ σ/ n = µ σ/ n µ σ/ n =. For å finne Var(X n) bruer jeg at Var(aX + b) = ( ) ( ) a X Var(X). Det gir at Var(Z n ) = Var( n µ σ/ 1 σ ( ) = Var( X) n σ / n = n ) n σ = 1. b) Sal se på det standardiserte gjennomsnittet når de stoastise variablene X 1, X,...X n har tre forsjellige fordelinger. Her sal jeg finne forventning, varians og standardavviet til de forsjellige fordelingene. 1) Jeg begynner med å se på X i når X i er uniformt fordelt. { 1 for x f Xi = ellers Var(X i ) = E(X i ) = 1 1 xdx = [ x ]1 = 1 x dx E(X i ) = = 1 1 σ = Var(X i ) = 1 1 = 1 3 4
5 ) Ser nå på X i når X i er esponensiellt fordelt. { e x for x f Xi = ellers E(X i ) = xe x dx = [ xe x e x ] = 1 E(Xi ) = x e x dx = [ x e x xe x e x ] = Var(X i ) = E(X i ) E(X i ) = 1 = 1 σ = Var(X i ) = 1 = 1 3) Til sist ser jeg på X i når X i er Bernoulli-fordelt. p Xi (x) = 1 for x =, 1 E(X i ) = = 1 Var(X i ) = ( 1 ) 1 + (1 1 ) 1 = = 1 4 c) σ = 1 4 = 1 Anta at vi har en stoastis variabel X som har en eller annen fordeling. Vi gjør m forsø der vi noterer utfallet. Arealet til bosene i det normerte histogramet til X, er bredden på intervallet ganger den relative frevensen av utfall i hver bos. Når m voser går den relative frevensen mot sansynligheten, og arealet av bosene vil gå mot arealet av en stripe av sansynlighetstettheten til X. Lar vi samtidig bredden på bosene rympe, vil stripene bli smalerere, og histogrammet vil gå mot sansynlighetestettheten til X. Dette gjelder også for Z n, og etter 1 forsø vil den relative frevensen være tilnærmet sansynligheten til Z n. d) Treer n=3 uniformt fordelte variable på (,1), 1 ganger, og tar gjennomsnittet. n = 3; X = unifrnd (,1,n,1); meanx = mean(x) ; Z = sqrt (3) (meanx.5) sqrt (3); Ser av figur 1 at histogrammet har en form som ligner på grafen til normalfordelingen. Flere treninger gjør ansje at den nærmer seg mer. 5
6 1 Figur 1: Z n uniformt fordelt, n = e) Sal finne sansynlighetene for at den standard-normalfordelte stoastise variabelen Z ligger i de forsjellige intervallene (,.5), [.5, ), [, 1.5), [ 1.5, 1), [ 1,.5), [.5, ), [,.5), [.5, 1), [1, 1.5), [1.5, ), [,.5), [.5, ). Jeg bruer at alle normalfordelinger er symmetrise om µ, dvs at fordelingen til Z er symmetris om. P( Z <.5)= =.1915 P(.5 Z < 1)= =.1498 P(1 Z < 1.5)= =.919 P(1.5 Z < )= =.44 P( Z <.5)= =.166 P(.5 Z < )= =.6 Tilsvarende sansynligheter gjelder da for de tilsvarende intervallene på den negative siden av. f) Finner de relative frevensene av verdiene til Z n e de samme intervallene som i e). n = 3; int = [ Inf,.5,, 1.5, 1,.5,,.5,1,1.5,,.5, Inf ] ; ant = histc (Z, int ) ; ant (1:1)/ Ser at de relative frevensene passer ganse bra med standardnormalfordelingen, men verdiene nærme er litt for lave, mens de er litt for høye halvveis ut til.5. g) Gjør d) og f) om igjenn med hhv. n=1 og n=3 uniformt fordelte variable på (,1). 6
7 1 Figur : Z n uniformt fordelt, n= Figur 3: Z n uniformt fordelt, n= n = 1; ant (1:1)/ n = 3; ant (1:1)/ De relatative frevensene nærmer seg sansynlighetene for stantardnormalfordelingen, men det er ie så stor forsjell fra n= 1, til n= 3. Ser av figur og figur 3 at histogrammet nærmer seg grafen til standardnormalfordelingen, men forandringen fra n= 1 til 3 er ie slående. Dette ommer no av at histogrammet var så nær allerede for n=3. h) Gjentar d), f) og g), men lar variablene være esponensiellt fordelt. 7
8 Figur 4: Z n esponentialfordelt, n= n = 3; X = exprnd (1,n,1); meanx = mean(x) ; Z = sqrt (3) (meanx 1)/1; hist (Z, 3:.5:3) print deps oppgave h exp n =3. eps int = [ Inf,.5,, 1.5, 1,.5,,.5,1,1.5,,.5, Inf ] ; ant = histc (Z, int ) ; ant (1:1)/ n = 1; ant (1:1)/ n = 3; ant (1:1)/ De relative frevensene går mot sansynlighetene til standarnormalfordelingen, men ie så fort. Vi an se både på de relative frevensene for n= 3, n=1 og figur 4 og 5, at histogrammet er struet ut mot høyre. Når n = 3 an man tydelig se de at relative frevensene går mot sansynlighetene til standardnormalfordelingen. Dette an også sees på figur 6, histogrammet har blit mere symmetris. i) Gjentar h), men lar variablene være Bernoulli-fordelt. 8
9 Figur 5: Z n esponentialfordelt, n= Figur 6: Z n esponentialfordelt, n= n = 3; X = binornd (1,.5,n,1); meanx = mean(x) ; Z = sqrt (n) (meanx.5)/.5; hist (Z, 3:.5:3) print deps oppgave i bino n =3. eps ant = histc (Z, int ) ; ant (1:1)/ n = 1; n = 3; Både på figur 7 og de relative frevensene for n=3, an vi se at det er mye hullrom mellom verdiene av de relative frevensene. Dette er pga. at gjennomsnittett, for n=3, bare an anta 4 forsjellige verdier, nemlig, 1 3, 3 og 1. Bortsett fra det stemmer de relative frevensene bra med sansynlighetene til standardnormalfordelingen. Det samme gjelder for n=1, og n=3, men hullrommene 9
10 4 Figur 7: Z n Bernoulli-fordelt, n= Figur 8: Z n Bernoulli-fordelt, n= blir stadig ferre siden gjennomsnittet an anta flere verdier. j) Vi an se av alle histogrammene at Bernoulli-fordelingen, og den uniforme fordelingen nærmer seg standardnormalfordelingen for lave n. Esponentialfordelingen derimot trenger større n før den nærmer seg. Dette an ha å gjøre med at symmetrien i både Bernoulli-fordelingen og den uniforme fordelingen, er helt fraværende i esponentialfordelingen. Esponentialfordelingen er mer avhengig av symmetrien i forventingen, som den får mer av, når n voser. 15 Figur 9: Z n Bernoulli-fordelt, n=
Oblig 1 i MAT2400. Oppgave 1. Tor Hedin Brønner. a) Vi tar integralet av f X (x) fra til x: = 1. Medianen, µ, finner vi ved å sette.
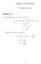 Oblig 1 i MAT24 Tor Hedin Brønner Oppgave 1. a) Vi tar integralet av f X (x) fra til x: x f X (x) dy = Medianen, µ, finner vi ved å sette.5 = µ dy + x = [ θ y θ] x = θ x θ + θ θ ( θ = 1 x) µ θ = θ.5 µ
Oblig 1 i MAT24 Tor Hedin Brønner Oppgave 1. a) Vi tar integralet av f X (x) fra til x: x f X (x) dy = Medianen, µ, finner vi ved å sette.5 = µ dy + x = [ θ y θ] x = θ x θ + θ θ ( θ = 1 x) µ θ = θ.5 µ
STK1100 Oblig 2. Øyvind Kolbu Gruppe februar 2007
 STK1100 Oblig 2 Øyvind Kolbu Gruppe 3 [email protected] 16. februar 2007 Oppgave A Vis at E(X n ) = µ: X n = 1 n n X i = 1 n (X 1 + X 2 +... + X n ) i=1 ( n ) E(X n ) = 1 n E X i = 1 n E (X 1 + X 2 +...
STK1100 Oblig 2 Øyvind Kolbu Gruppe 3 [email protected] 16. februar 2007 Oppgave A Vis at E(X n ) = µ: X n = 1 n n X i = 1 n (X 1 + X 2 +... + X n ) i=1 ( n ) E(X n ) = 1 n E X i = 1 n E (X 1 + X 2 +...
Forelesning 5: Kontinuerlige fordelinger, normalfordelingen. Jo Thori Lind
 Forelesning 5: Kontinuerlige fordelinger, normalfordelingen Jo Thori Lind [email protected] Oversikt 1. Kontinuerlige fordelinger 2. Uniform fordeling 3. Normal-fordelingen 1. Kontinuerlige fordelinger
Forelesning 5: Kontinuerlige fordelinger, normalfordelingen Jo Thori Lind [email protected] Oversikt 1. Kontinuerlige fordelinger 2. Uniform fordeling 3. Normal-fordelingen 1. Kontinuerlige fordelinger
(Det tas forbehold om feil i løsningsforslaget.) Oppgave 1
 ÅMA1 Sannsylighetsregning og statistikk Løsningsforslag til eksamen vår 2011, s. 1 (Det tas forbehold om feil i løsningsforslaget.) Oppgave 1 a) Data: x 1, x 2, x 3, x 4, x 5 Gjennomsnitt: x = 1 5 (x 1
ÅMA1 Sannsylighetsregning og statistikk Løsningsforslag til eksamen vår 2011, s. 1 (Det tas forbehold om feil i løsningsforslaget.) Oppgave 1 a) Data: x 1, x 2, x 3, x 4, x 5 Gjennomsnitt: x = 1 5 (x 1
Normalfordeling. Høgskolen i Gjøvik Avdeling for teknologi, økonomi og ledelse. Statistikk Ukeoppgaver uke 7
 Ueoppgaver i BtG207 Statisti, ue 7 : Normalfordeling. 1 Høgsolen i Gjøvi Avdeling for tenologi, øonomi og ledelse. Statisti Ueoppgaver ue 7 Normalfordeling. Oppgave 1 Anta Z N(0, 1), dvs. Z er standard
Ueoppgaver i BtG207 Statisti, ue 7 : Normalfordeling. 1 Høgsolen i Gjøvi Avdeling for tenologi, øonomi og ledelse. Statisti Ueoppgaver ue 7 Normalfordeling. Oppgave 1 Anta Z N(0, 1), dvs. Z er standard
Løsningsforslag, eksamen statistikk, juni 2015
 Løsningsforslag, eksamen statistikk, juni 0 Oppgave 1 Siden det spørres om tall fra et intervall, som oppgaven viser kan være et reelle, er det tydelig at tallene er tatt fra en kontinuerlig fordeling.
Løsningsforslag, eksamen statistikk, juni 0 Oppgave 1 Siden det spørres om tall fra et intervall, som oppgaven viser kan være et reelle, er det tydelig at tallene er tatt fra en kontinuerlig fordeling.
Bernoulli forsøksrekke og binomisk fordeling
 Bernoulli forsøksrekke og binomisk fordeling Bernoulli forsøksrekke i) gjentar et forsøk n ganger ii) hvert forsøk gir enten suksess eller fiasko iii) sannsynligheten for suksess er p i alle forsøkene
Bernoulli forsøksrekke og binomisk fordeling Bernoulli forsøksrekke i) gjentar et forsøk n ganger ii) hvert forsøk gir enten suksess eller fiasko iii) sannsynligheten for suksess er p i alle forsøkene
Løsningsforslag ECON 2130 Obligatorisk semesteroppgave 2017 vår
 Løsningsforslag ECON 130 Obligatorisk semesteroppgave 017 vår Andreas Myhre Oppgave 1 1. (i) Siden X og Z er uavhengige, vil den simultane fordelingen mellom X og Z kunne skrives som: f(x, z) = P(X = x
Løsningsforslag ECON 130 Obligatorisk semesteroppgave 017 vår Andreas Myhre Oppgave 1 1. (i) Siden X og Z er uavhengige, vil den simultane fordelingen mellom X og Z kunne skrives som: f(x, z) = P(X = x
STK1100 våren Kontinuerlige stokastiske variabler Forventning og varians Momentgenererende funksjoner
 STK1100 våren 2017 Kontinuerlige stokastiske variabler Forventning og varians Momentgenererende funksjoner Svarer til avsnittene 4.1 og 4.2 i læreboka Ørnulf Borgan Matematisk institutt Universitetet i
STK1100 våren 2017 Kontinuerlige stokastiske variabler Forventning og varians Momentgenererende funksjoner Svarer til avsnittene 4.1 og 4.2 i læreboka Ørnulf Borgan Matematisk institutt Universitetet i
TMA4240 Statistikk Høst 2016
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 9 Løsningsskisse Oppgave 1 a) Vi lar her Y være antall fugler som kolliderer med vindmølla i løpet av den gitte
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 9 Løsningsskisse Oppgave 1 a) Vi lar her Y være antall fugler som kolliderer med vindmølla i løpet av den gitte
Løsningsforslag statistikkeksamen desember 2014
 Løsningsforslag statistikkeksamen desember 2014 Oppgave 1 a i. To hendelser er disjunke hvis det er intet overlapp mellom hendelsene, altså hvis A B = Ø. Siden vi har en sannsynlighet for å finne A B som
Løsningsforslag statistikkeksamen desember 2014 Oppgave 1 a i. To hendelser er disjunke hvis det er intet overlapp mellom hendelsene, altså hvis A B = Ø. Siden vi har en sannsynlighet for å finne A B som
Forelesning 3. april, 2017
 Forelesning 3. april, 2017 APPENDIX TIL KAP. 6 Sentralgrenseteoremet AVSNITT 6.3 Anvendelser av sentralgrenseteoremet Histogrammer S-kurver Q-Q-plot Diverse eksempler MGF for følger av uavhengige identisk
Forelesning 3. april, 2017 APPENDIX TIL KAP. 6 Sentralgrenseteoremet AVSNITT 6.3 Anvendelser av sentralgrenseteoremet Histogrammer S-kurver Q-Q-plot Diverse eksempler MGF for følger av uavhengige identisk
Løsningsforslag oblig 1 STK1110 høsten 2014
 Løsningsforslag oblig STK høsten 4 Oppgave I forbindelse med en studie av antioksidanter og antocyanider, ble innholdet av antocyan i 5 beger med blåbær målt. De målte verdiene var (i mg per gram): 55
Løsningsforslag oblig STK høsten 4 Oppgave I forbindelse med en studie av antioksidanter og antocyanider, ble innholdet av antocyan i 5 beger med blåbær målt. De målte verdiene var (i mg per gram): 55
Binomisk sannsynlighetsfunksjon
 ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag 2 Binomisk sannsynlighetsfunksjon La det være n forsøk, sannsynlighet p for suksess og sannsynlighet q for fiasko. Den tilfeldige
ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag 2 Binomisk sannsynlighetsfunksjon La det være n forsøk, sannsynlighet p for suksess og sannsynlighet q for fiasko. Den tilfeldige
TMA4240 Statistikk Høst 2008
 TMA4240 Statistikk Høst 2008 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 7 Oppgave 1 Tippekonkurranse Denne oppgaven er ment som en kjapp test på hva du har
TMA4240 Statistikk Høst 2008 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 7 Oppgave 1 Tippekonkurranse Denne oppgaven er ment som en kjapp test på hva du har
ÅMA110 Sannsynlighetsregning med statistikk, våren 2006 Kp. 6, del 3
 ÅMA110 Sannsynlighetsregning med statistikk, våren 2006 Kp. 6, del 3 Bjørn H. Auestad Institutt for matematikk og naturvitenskap Universitetet i Stavanger 20. mars Bjørn H. Auestad Kp. 6: Hypotesetesting
ÅMA110 Sannsynlighetsregning med statistikk, våren 2006 Kp. 6, del 3 Bjørn H. Auestad Institutt for matematikk og naturvitenskap Universitetet i Stavanger 20. mars Bjørn H. Auestad Kp. 6: Hypotesetesting
Dagens tekst. Kap 7: Funksjonar av stokastiske variable Transformasjon av variable Moment Momentgenererande funksjon
 Dagens tekst Kap 7: Funksjonar av stokastiske variable Transformasjon av variable Moment Momentgenererande funksjon Notat: Ordningsvariable og ekstremvariable Ordnings variable Maksimum Minumum Transformasjon
Dagens tekst Kap 7: Funksjonar av stokastiske variable Transformasjon av variable Moment Momentgenererande funksjon Notat: Ordningsvariable og ekstremvariable Ordnings variable Maksimum Minumum Transformasjon
ÅMA110 Sannsylighetsregning og statistikk Løsningsforslag til eksamen høst 2010, s. 1. Oppgave 1. Histogram over frekvenser.
 ÅMA1 Sannsylighetsregning og statistikk Løsningsforslag til eksamen høst 0, s. 1 (Det tas forbehold om feil i løsningsforslaget.) a) Gjennomsnitt: x = 1 Emp. standardavvik: Median: 1 (1.33 + 1.) = 1.35
ÅMA1 Sannsylighetsregning og statistikk Løsningsforslag til eksamen høst 0, s. 1 (Det tas forbehold om feil i løsningsforslaget.) a) Gjennomsnitt: x = 1 Emp. standardavvik: Median: 1 (1.33 + 1.) = 1.35
TMA4240 Statistikk Høst 2015
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 8, blokk II Løsningsskisse Oppgave 1 Da komponentene danner et parallellsystem, vil systemet fungere dersom minst
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 8, blokk II Løsningsskisse Oppgave 1 Da komponentene danner et parallellsystem, vil systemet fungere dersom minst
ST0202 Statistikk for samfunnsvitere
 ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag Situasjonen er som i quiz-eksempelet: n = 4, p = 1/3 ( suksess betyr å gjette riktig alternativ), q = 2/3. Oppgave: Finn
ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag Situasjonen er som i quiz-eksempelet: n = 4, p = 1/3 ( suksess betyr å gjette riktig alternativ), q = 2/3. Oppgave: Finn
TMA4240 Statistikk 2014
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 9, blokk II Løsningsskisse Oppgave Scriptet run confds.m simulerer n data x,..., x n fra en normalfordeling med
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 9, blokk II Løsningsskisse Oppgave Scriptet run confds.m simulerer n data x,..., x n fra en normalfordeling med
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Deleksamen i: STK Sannsynlighetsregning og statistisk modellering Eksamensdag: Mandag 4. mars 26 Tid for eksamen: 5. 7. Oppgavesettet er
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Deleksamen i: STK Sannsynlighetsregning og statistisk modellering Eksamensdag: Mandag 4. mars 26 Tid for eksamen: 5. 7. Oppgavesettet er
Terningkast. Utfallsrommet S for et terningskast med en vanlig spillterning med 6 sider er veldefinert 1, 2, 3, 4, 5, 6
 Terningkast Halvor Aarnes, UiO, 2014 Innhold Ett terningkast og utfallsrom... 1 Union og snitt... 4 Betinget sannsynlighet... 5 Forventningsverdi E(X) og varianse Var(X)... 5 Konfidensintervall for proporsjoner...
Terningkast Halvor Aarnes, UiO, 2014 Innhold Ett terningkast og utfallsrom... 1 Union og snitt... 4 Betinget sannsynlighet... 5 Forventningsverdi E(X) og varianse Var(X)... 5 Konfidensintervall for proporsjoner...
TMA4240 Statistikk H2010 Kapittel 5: Diskrete sannsynlighetsfordelinger : Uniform, binomisk, hypergeometrisk fordeling
 TMA4240 Statistikk H2010 Kapittel 5: Diskrete sannsynlighetsfordelinger 5.1-5.4: Uniform, binomisk, hypergeometrisk fordeling Mette Langaas 2 Arbeidshverdag etter endt studium Studere et fenomen (f.eks.
TMA4240 Statistikk H2010 Kapittel 5: Diskrete sannsynlighetsfordelinger 5.1-5.4: Uniform, binomisk, hypergeometrisk fordeling Mette Langaas 2 Arbeidshverdag etter endt studium Studere et fenomen (f.eks.
Kap. 8: Utvalsfordelingar og databeskrivelse
 Kap. 8: Utvalsfordelingar og databeskrivelse Utvalsfordelingar Utvalsfordeling for gjennomsnitt (med kjent varians) ( X ) Sentralgrenseteoremet (SGT) Utvalsfordeling for varians (normalfordeling) Utvalfordeling
Kap. 8: Utvalsfordelingar og databeskrivelse Utvalsfordelingar Utvalsfordeling for gjennomsnitt (med kjent varians) ( X ) Sentralgrenseteoremet (SGT) Utvalsfordeling for varians (normalfordeling) Utvalfordeling
TMA4240 Statistikk Høst 2009
 TMA4240 Statistikk Høst 2009 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer b5 Løsningsskisse Oppgave 1 Vi ønsker å finne ut om et nytt serum kan stanse leukemi.
TMA4240 Statistikk Høst 2009 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer b5 Løsningsskisse Oppgave 1 Vi ønsker å finne ut om et nytt serum kan stanse leukemi.
Tyngdepunkt. Togforsinkelsen (Eksamen Des2003.1a) I denne oppgaven kan du bruke uten å vise det at. Kapittel 4
 3 Tyngdepunkt Kapittel 4 Forventningsverdi, varians, kovarians for én stokastisk variabel og funksjoner av stokastiske variabler TMA4240 H2006: Eirik Mo 2 4.1 Forventing til en stokastisk variabel DEF
3 Tyngdepunkt Kapittel 4 Forventningsverdi, varians, kovarians for én stokastisk variabel og funksjoner av stokastiske variabler TMA4240 H2006: Eirik Mo 2 4.1 Forventing til en stokastisk variabel DEF
Observatorer. STK Observatorer - Kap 6. Utgangspunkt. Eksempel høyde Oxford studenter
 Observatorer STK00 - Observatorer - Kap 6 Geir Storvik 4. april 206 Så langt: Sannsynlighetsteori Stokastiske modeller Nå: Data Knytte data til stokastiske modeller Utgangspunkt Eksempel høyde Oxford studenter
Observatorer STK00 - Observatorer - Kap 6 Geir Storvik 4. april 206 Så langt: Sannsynlighetsteori Stokastiske modeller Nå: Data Knytte data til stokastiske modeller Utgangspunkt Eksempel høyde Oxford studenter
Kap. 6, Kontinuerlege Sannsynsfordelingar
 Kapittel 6, Kontinuerlege Sannsynsfordelingar Sjå på eit utval av ofte brukte kontinuerlege sannsynsfordelingar Uniform Onsdag Normal Onsdag Eksponensial I dag Gamma I dag Kji-kvadrat I dag Student-T (Kap
Kapittel 6, Kontinuerlege Sannsynsfordelingar Sjå på eit utval av ofte brukte kontinuerlege sannsynsfordelingar Uniform Onsdag Normal Onsdag Eksponensial I dag Gamma I dag Kji-kvadrat I dag Student-T (Kap
Kap. 6, Kontinuerlege Sannsynsfordelingar
 Kapittel 6, Kontinuerlege Sannsynsfordelingar Sjå på eit utval av ofte brukte kontinuerlege sannsynsfordelingar Uniform I går Normal I går Eksponensial I dag Gamma I dag Kji-kvadrat I dag Nokre eigenskapar
Kapittel 6, Kontinuerlege Sannsynsfordelingar Sjå på eit utval av ofte brukte kontinuerlege sannsynsfordelingar Uniform I går Normal I går Eksponensial I dag Gamma I dag Kji-kvadrat I dag Nokre eigenskapar
Kap. 6, Kontinuerlege Sannsynsfordelingar
 Kapittel 6, Kontinuerlege Sannsynsfordelingar Sjå på eit utval av ofte brukte kontinuerlege sannsynsfordelingar Uniform I går Normal I går Eksponensial I dag Gamma I dag Kji-kvadrat I dag Nokre eigenskapar
Kapittel 6, Kontinuerlege Sannsynsfordelingar Sjå på eit utval av ofte brukte kontinuerlege sannsynsfordelingar Uniform I går Normal I går Eksponensial I dag Gamma I dag Kji-kvadrat I dag Nokre eigenskapar
Diskrete sannsynlighetsfordelinger som histogram. Varians. Histogram og kumulativ sannsynlighet. Forventning (gjennomsnitt) (X=antall mynt i tre kast)
 Diskret sannsynlighetsfordeling (kap 1.1-1.6) Oversikt Utfallsrom (sample space) Sannsynlighetsfordeling Forventning (expectation), E(X), populasjonsgjennomsnitt Bruk av figurer og histogram Binomialfordelingen
Diskret sannsynlighetsfordeling (kap 1.1-1.6) Oversikt Utfallsrom (sample space) Sannsynlighetsfordeling Forventning (expectation), E(X), populasjonsgjennomsnitt Bruk av figurer og histogram Binomialfordelingen
Eksamensoppgave i Løsningsskisse TMA4240 Statistikk
 Institutt for matematiske fag Eksamensoppgave i Løsningsskisse TMA440 Statistikk Faglig kontakt under eksamen: Håkon Tjelmeland a, Sara Martino b Tlf: a 48 18 96, b 99 40 33 30 Eksamensdato: 30. november
Institutt for matematiske fag Eksamensoppgave i Løsningsskisse TMA440 Statistikk Faglig kontakt under eksamen: Håkon Tjelmeland a, Sara Martino b Tlf: a 48 18 96, b 99 40 33 30 Eksamensdato: 30. november
Denne veka. Kap 7: Funksjonar av stokastiske variable Transformasjon av variable Moment Momentgenererande funksjon
 Denne veka Kap 7: Funksjonar av stokastiske variable Transformasjon av variable Moment Momentgenererande funksjon Notat: Ordningsvariable og ekstremvariable Ordnings variable Maksimum Minumum Transformasjon
Denne veka Kap 7: Funksjonar av stokastiske variable Transformasjon av variable Moment Momentgenererande funksjon Notat: Ordningsvariable og ekstremvariable Ordnings variable Maksimum Minumum Transformasjon
LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4240 STATISTIKK Mandag 12. desember 2011
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 10 LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4240 STATISTIKK Mandag 12. desember 2011 Oppgave 1 Oljeleting a) Siden P(A
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 10 LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4240 STATISTIKK Mandag 12. desember 2011 Oppgave 1 Oljeleting a) Siden P(A
ÅMA110 Sannsynlighetsregning med statistikk, våren 2006 Kp. 6, del 4
 ÅMA110 Sannsynlighetsregning med statistikk, våren 2006 Kp. 6, del 4 Bjørn H. Auestad Institutt for matematikk og naturvitenskap Universitetet i Stavanger 27. mars Bjørn H. Auestad Kp. 6: Hypotesetesting
ÅMA110 Sannsynlighetsregning med statistikk, våren 2006 Kp. 6, del 4 Bjørn H. Auestad Institutt for matematikk og naturvitenskap Universitetet i Stavanger 27. mars Bjørn H. Auestad Kp. 6: Hypotesetesting
Gammafordelingen og χ 2 -fordelingen
 Gammafordelingen og χ 2 -fordelingen Gammafunksjonen Gammafunksjonen er en funksjon som brukes ofte i sannsynlighetsregning. I mange fordelinger dukker den opp i konstantleddet. Hvis man plotter n-fakultet
Gammafordelingen og χ 2 -fordelingen Gammafunksjonen Gammafunksjonen er en funksjon som brukes ofte i sannsynlighetsregning. I mange fordelinger dukker den opp i konstantleddet. Hvis man plotter n-fakultet
ECON Statistikk 1 Forelesning 4: Stokastiske variable, fordelinger. Jo Thori Lind
 ECON2130 - Statistikk 1 Forelesning 4: Stokastiske variable, fordelinger Jo Thori Lind [email protected] Oversikt 1. Betinget sannsynlighet 2. Stokastiske variable 3. Forventning og varians 4. Regneregler
ECON2130 - Statistikk 1 Forelesning 4: Stokastiske variable, fordelinger Jo Thori Lind [email protected] Oversikt 1. Betinget sannsynlighet 2. Stokastiske variable 3. Forventning og varians 4. Regneregler
STK Oppsummering
 STK1100 - Oppsummering Geir Storvik 6. Mai 2014 STK1100 Tre temaer Deskriptiv/beskrivende statistikk Sannsynlighetsteori Statistisk inferens Sannsynlighetsregning Hva Matematisk verktøy for å studere tilfeldigheter
STK1100 - Oppsummering Geir Storvik 6. Mai 2014 STK1100 Tre temaer Deskriptiv/beskrivende statistikk Sannsynlighetsteori Statistisk inferens Sannsynlighetsregning Hva Matematisk verktøy for å studere tilfeldigheter
Forelening 1, kapittel 4 Stokastiske variable
 Forelening 1, kapittel 4 Stokastiske variable Eksempel X = "antall kron på kast med to mynter (før de er kastet)" Uniformt utfallsrom {MM, MK, KM, KK}. X = x beskriver hendelsen "antall kron på kast med
Forelening 1, kapittel 4 Stokastiske variable Eksempel X = "antall kron på kast med to mynter (før de er kastet)" Uniformt utfallsrom {MM, MK, KM, KK}. X = x beskriver hendelsen "antall kron på kast med
Løsningsforslag til obligatorisk oppgave i ECON 2130
 Andreas Mhre April 15 Løsningsforslag til obligatorisk oppgave i ECON 13 Oppgave 1: E(XY) = E(X(Z X)) Setter inn Y = Z - X E(XY) = E(XZ X ) E(XY) = E(XZ) E(X ) E(XY) = - E(X ) X og Z er uavhengige, så
Andreas Mhre April 15 Løsningsforslag til obligatorisk oppgave i ECON 13 Oppgave 1: E(XY) = E(X(Z X)) Setter inn Y = Z - X E(XY) = E(XZ X ) E(XY) = E(XZ) E(X ) E(XY) = - E(X ) X og Z er uavhengige, så
Kontinuerlige sannsynlighetsfordelinger.
 Kontinuerlige sannsynlighetsfordelinger. Dekkes av kap. 6 og deler av kap. 8.5 i boka. Husk: f(x er sannsynlighetstettheten til en kontinuerlig X dersom:. f(x 0 for alle x R 2. f(xdx = 3. P (a
Kontinuerlige sannsynlighetsfordelinger. Dekkes av kap. 6 og deler av kap. 8.5 i boka. Husk: f(x er sannsynlighetstettheten til en kontinuerlig X dersom:. f(x 0 for alle x R 2. f(xdx = 3. P (a
Econ 2130 Forelesning uke 10 (HG) Geometrisk og normal fordeling
 Econ 2130 Forelesning uke 10 (HG) Geometrisk og normal fordeling 1 Geometrisk fordeling Binomisk forsøks-serie En serie likeartete forsøk med to mulige utfall, S og F, i hvert. (Modell) forutsetninger
Econ 2130 Forelesning uke 10 (HG) Geometrisk og normal fordeling 1 Geometrisk fordeling Binomisk forsøks-serie En serie likeartete forsøk med to mulige utfall, S og F, i hvert. (Modell) forutsetninger
Siden vi her har brukt første momentet i fordelingen (EX = EX 1 ) til å konstruere estimatoren kalles denne metoden for momentmetoden.
 Estimeringsmetoder Momentmetoden La X, X 2,..., X n være uavhengige variable som er rektangulært fordelte på intervallet [0, θ]. Vi vet da at forventningsverdiene til hver observasjon og forventningen
Estimeringsmetoder Momentmetoden La X, X 2,..., X n være uavhengige variable som er rektangulært fordelte på intervallet [0, θ]. Vi vet da at forventningsverdiene til hver observasjon og forventningen
Forelesning 6: Punktestimering, usikkerhet i estimering. Jo Thori Lind
 Forelesning 6: Punktestimering, usikkerhet i estimering Jo Thori Lind [email protected] Oversikt 1. Trekke utvalg 2. Estimatorer og observatorer som stokastiske variable 3. Egenskapene til en estimator
Forelesning 6: Punktestimering, usikkerhet i estimering Jo Thori Lind [email protected] Oversikt 1. Trekke utvalg 2. Estimatorer og observatorer som stokastiske variable 3. Egenskapene til en estimator
Forslag til endringar
 Forslag til endringar Bakgrunn: Vi har ingen forelesningar veka etter påske. Eg skal bort 18. og 19. april. Eksamen er 30.mai Forslag til endringar: Ekstra forelesningar onsdag 16.mars og onsdag 30 mars
Forslag til endringar Bakgrunn: Vi har ingen forelesningar veka etter påske. Eg skal bort 18. og 19. april. Eksamen er 30.mai Forslag til endringar: Ekstra forelesningar onsdag 16.mars og onsdag 30 mars
ÅMA110 Sannsynlighetsregning med statistikk, våren
 ÅMA110 Sannsynlighetsregning med statistikk, våren 2006 Oppsummering Bjørn H. Auestad Institutt for matematikk og naturvitenskap Universitetet i Stavanger 24. april Bjørn H. Auestad Oppsummering våren
ÅMA110 Sannsynlighetsregning med statistikk, våren 2006 Oppsummering Bjørn H. Auestad Institutt for matematikk og naturvitenskap Universitetet i Stavanger 24. april Bjørn H. Auestad Oppsummering våren
Denne veka. Kap 7: Funksjonar av stokastiske variable Transformasjon av variable Moment Momentgenererande funksjon
 Denne veka Kap 7: Funksjonar av stokastiske variable Transformasjon av variable Moment Momentgenererande funksjon Notat: Ordningsvariable og ekstremvariable Ordnings variable Maksimum Minumum Transformasjon
Denne veka Kap 7: Funksjonar av stokastiske variable Transformasjon av variable Moment Momentgenererande funksjon Notat: Ordningsvariable og ekstremvariable Ordnings variable Maksimum Minumum Transformasjon
Bootstrapping og simulering Tilleggslitteratur for STK1100
 Bootstrapping og simulering Tilleggslitteratur for STK1100 Geir Storvik April 2014 (oppdatert April 2016) 1 Introduksjon Simulering av tilfeldige variable (stokastisk simulering) er et nyttig verktøy innenfor
Bootstrapping og simulering Tilleggslitteratur for STK1100 Geir Storvik April 2014 (oppdatert April 2016) 1 Introduksjon Simulering av tilfeldige variable (stokastisk simulering) er et nyttig verktøy innenfor
3.1 Stokastisk variabel (repetisjon)
 TMA4240 Statistikk H2010 3.3: Kontinuerlige sannsynlighetsfordelinger 4.1: Matematisk forventing (univariat del) Mette Langaas Foreleses mandag 6. september 2010 2 3.1 Stokastisk variabel (repetisjon)
TMA4240 Statistikk H2010 3.3: Kontinuerlige sannsynlighetsfordelinger 4.1: Matematisk forventing (univariat del) Mette Langaas Foreleses mandag 6. september 2010 2 3.1 Stokastisk variabel (repetisjon)
Bootstrapping og simulering
 Bootstrapping og simulering Tilleggslitteratur for STK1100 Geir Storvik April 2014 1 Introduksjon Simulering av tilfeldige variable (stokastisk simulering) er et nyttig verktøy innenfor statistikk, men
Bootstrapping og simulering Tilleggslitteratur for STK1100 Geir Storvik April 2014 1 Introduksjon Simulering av tilfeldige variable (stokastisk simulering) er et nyttig verktøy innenfor statistikk, men
6 x P (X = x) = x=1 = P (X 2 = 6)P (X 2 = 6)P (X 3 = 6) =
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalte oppgaver 4, blokk I Løsningsskisse Oppgave 1 a) Utfallsrommet til X 1 er {1, 2,, 4, 5, }. Sannsynlighetsfordelingen
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalte oppgaver 4, blokk I Løsningsskisse Oppgave 1 a) Utfallsrommet til X 1 er {1, 2,, 4, 5, }. Sannsynlighetsfordelingen
6.1 Kontinuerlig uniform fordeling
 Kapittel 6 Noen kontinuerlige sannsynlighetsfordelinger TMA4240 H2006: Eirik Mo 2 6.1 Kontinuerlig uniform fordeling Kontinuerlig uniform fordeling: Sannsynlighetstettheten til den kontinuerlige uniforme
Kapittel 6 Noen kontinuerlige sannsynlighetsfordelinger TMA4240 H2006: Eirik Mo 2 6.1 Kontinuerlig uniform fordeling Kontinuerlig uniform fordeling: Sannsynlighetstettheten til den kontinuerlige uniforme
Medisinsk statistikk Del I høsten 2009:
 Medisinsk statistikk Del I høsten 2009: Kontinuerlige sannsynlighetsfordelinger Pål Romundstad Beregning av sannsynlighet i en binomisk forsøksrekke generelt Sannsynligheten for at suksess intreffer X
Medisinsk statistikk Del I høsten 2009: Kontinuerlige sannsynlighetsfordelinger Pål Romundstad Beregning av sannsynlighet i en binomisk forsøksrekke generelt Sannsynligheten for at suksess intreffer X
Kontinuerlige sannsynlighetsfordelinger.
 Kontinuerlige sannsynlighetsfordelinger. Dekkes av kap. 6 og deler av kap. 8.5 i boka. Husk: f(x) er sannsynlighetstettheten til en kontinuerlig X dersom: 1. f(x) 0 for alle x R 2. f(x)dx =1 3. P (a
Kontinuerlige sannsynlighetsfordelinger. Dekkes av kap. 6 og deler av kap. 8.5 i boka. Husk: f(x) er sannsynlighetstettheten til en kontinuerlig X dersom: 1. f(x) 0 for alle x R 2. f(x)dx =1 3. P (a
Fasit for tilleggsoppgaver
 Fasit for tilleggsoppgaver Uke 5 Oppgave: Gitt en rekke med observasjoner x i (i = 1,, 3,, n), definerer vi variansen til x i som gjennomsnittlig kvadratavvik fra gjennomsnittet, m.a.o. Var(x i ) = (x
Fasit for tilleggsoppgaver Uke 5 Oppgave: Gitt en rekke med observasjoner x i (i = 1,, 3,, n), definerer vi variansen til x i som gjennomsnittlig kvadratavvik fra gjennomsnittet, m.a.o. Var(x i ) = (x
Diskrete sannsynlighetsfordelinger som histogram. Varians. Histogram og kumulativ sannsynlighet. Binomial-fordelingen
 Diskret sannsynlighetsfordeling (kap 1.1-1.6) Oversikt Utfallsrom (sample space) Sannsynlighetsfordeling Forventning (expectation), E(, populasjonsgjennomsnitt Bruk av figurer og histogram Binomialfordelingen
Diskret sannsynlighetsfordeling (kap 1.1-1.6) Oversikt Utfallsrom (sample space) Sannsynlighetsfordeling Forventning (expectation), E(, populasjonsgjennomsnitt Bruk av figurer og histogram Binomialfordelingen
TMA4240 Statistikk H2015
 TMA4240 Statistikk H2015 Kapittel 6: Kontinuerlige sannsynlighetsfordelinger 6.1 Uniform fordeling 6.2-6.3 Normalfordeling Mette Langaas Institutt for matematiske fag, NTNU wiki.math.ntnu.no/emner/tma4240/2015h/start/
TMA4240 Statistikk H2015 Kapittel 6: Kontinuerlige sannsynlighetsfordelinger 6.1 Uniform fordeling 6.2-6.3 Normalfordeling Mette Langaas Institutt for matematiske fag, NTNU wiki.math.ntnu.no/emner/tma4240/2015h/start/
Kapittel 6: Kontinuerlige sannsynlighetsfordelinger
 Kapittel 6: Kontinuerlige sannsynlighetsfordelinger TMA4240 Statistikk (F2 og E7) Foreleses 15. september, 2004. µ µ µ + Basert på slides av Mette Langås p.1/16 6.1 Kontinuerlig uniform fordeling Kontinuerlig
Kapittel 6: Kontinuerlige sannsynlighetsfordelinger TMA4240 Statistikk (F2 og E7) Foreleses 15. september, 2004. µ µ µ + Basert på slides av Mette Langås p.1/16 6.1 Kontinuerlig uniform fordeling Kontinuerlig
Statistikk 1 kapittel 4
 Statistikk 1 kapittel 4 Nico Keilman ECON 2130 Vår 2017 Kapittel 4 Stokastiske (tilfeldige) variabler Anta 1) Vi kjenner sannsynligheter for ulike utfall knyttet til et forsøk 2) Hvert utfall har en (meningsfull)
Statistikk 1 kapittel 4 Nico Keilman ECON 2130 Vår 2017 Kapittel 4 Stokastiske (tilfeldige) variabler Anta 1) Vi kjenner sannsynligheter for ulike utfall knyttet til et forsøk 2) Hvert utfall har en (meningsfull)
Oppfriskning av blokk 1 i TMA4240
 Oppfriskning av blokk 1 i TMA4240 Geir-Arne Fuglstad November 21, 2016 2 Hva har vi gjort i dette kurset? Vi har studert to sterkt relaterte grener av matematikk Sannsynlighetsteori: matematisk teori for
Oppfriskning av blokk 1 i TMA4240 Geir-Arne Fuglstad November 21, 2016 2 Hva har vi gjort i dette kurset? Vi har studert to sterkt relaterte grener av matematikk Sannsynlighetsteori: matematisk teori for
Kapittel 2: Hendelser
 Kapittel 2: Hendelser FENOMEN Eksperiment Utfall Utfallsrom Eksperiment. Utfall. Eksperiment Utfall Hendelse Sannsynlighet: egenskaper, gunstige vs. mulige, relativ frekvens Sannsynlighet for mer enn en
Kapittel 2: Hendelser FENOMEN Eksperiment Utfall Utfallsrom Eksperiment. Utfall. Eksperiment Utfall Hendelse Sannsynlighet: egenskaper, gunstige vs. mulige, relativ frekvens Sannsynlighet for mer enn en
TMA4245 Statistikk Eksamen desember 2016
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4245 Statistikk Eksamen desember 2016 Oppgave 1 En bedrift produserer elektriske komponenter. Komponentene kan ha to typer
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4245 Statistikk Eksamen desember 2016 Oppgave 1 En bedrift produserer elektriske komponenter. Komponentene kan ha to typer
Løsningsforslag Eksamen S2, høsten 2017 Laget av Tommy O. Sist oppdatert: 26. november 2017
 Løsningsforslag Eksamen S, høsten 017 Laget av Tommy O. Sist oppdatert: 6. november 017 Del 1 - uten hjelpemidler Oppgave 1 a) Vi skal derivere f(x) = x 4x 3. Vi bruker regelen samt regelen (x n ) = nx
Løsningsforslag Eksamen S, høsten 017 Laget av Tommy O. Sist oppdatert: 6. november 017 Del 1 - uten hjelpemidler Oppgave 1 a) Vi skal derivere f(x) = x 4x 3. Vi bruker regelen samt regelen (x n ) = nx
Høgskolen i Telemark. Institutt for økonomi og informatikk FORMELSAMLING Statistikk I. Til bruk ved eksamen. Per Chr. Hagen
 Høgskolen i Telemark Institutt for økonomi og informatikk FORMELSAMLING 6005 Statistikk I Til bruk ved eksamen Per Chr. Hagen . Sannsynlighetsregning. Regneregler Komplementsetningen: Addisjonssetningen:
Høgskolen i Telemark Institutt for økonomi og informatikk FORMELSAMLING 6005 Statistikk I Til bruk ved eksamen Per Chr. Hagen . Sannsynlighetsregning. Regneregler Komplementsetningen: Addisjonssetningen:
Regneregler for forventning og varians
 Regneregler for forventning og varians Det fins regneregler som er til hjelp når du skal finne forventningsverdier og varianser. Vi skal her se nærmere på disse reglene. Vi viser deg også hvordan reglene
Regneregler for forventning og varians Det fins regneregler som er til hjelp når du skal finne forventningsverdier og varianser. Vi skal her se nærmere på disse reglene. Vi viser deg også hvordan reglene
STK1100 våren Normalfordelingen. Normalfordelingen er den viktigste av alle sannsynlighetsfordelinger
 STK00 våren 206 Normalfordelingen Svarer til avsnitt 4.3 i læreboka Geir Storvik Matematisk institutt Universitetet i Oslo Normalfordelingen er den viktigste av alle sannsynlighetsfordelinger Normalfordelingen
STK00 våren 206 Normalfordelingen Svarer til avsnitt 4.3 i læreboka Geir Storvik Matematisk institutt Universitetet i Oslo Normalfordelingen er den viktigste av alle sannsynlighetsfordelinger Normalfordelingen
6.5 Normalapproksimasjon til. binomisk fordeling
 ....3.4.5..5..5..5...4.6.8....4.6.8....3.4..5..5 Kaittel 6: Kontinuerlige sannsynsfordelingar TMA445 Statistikk Ka 6.5-6.8. 6.5: Normal aroksimasjon til binomisk fordeling, 6.6-6.8: Eksonensialfordeling,
....3.4.5..5..5..5...4.6.8....4.6.8....3.4..5..5 Kaittel 6: Kontinuerlige sannsynsfordelingar TMA445 Statistikk Ka 6.5-6.8. 6.5: Normal aroksimasjon til binomisk fordeling, 6.6-6.8: Eksonensialfordeling,
Kapittel 4: Matematisk forventning
 Kapittel 4: Matematisk forventning TMA4240 Statistikk (F2 og E7) Multivariate tilfeller foreleses mandag 6.september, 2004 [email protected] p.1/16 Forventing til funksjon av flere stokastiske
Kapittel 4: Matematisk forventning TMA4240 Statistikk (F2 og E7) Multivariate tilfeller foreleses mandag 6.september, 2004 [email protected] p.1/16 Forventing til funksjon av flere stokastiske
ST0202 Statistikk for samfunnsvitere
 ST0202 Statistikk for samfunnsvitere Kapittel 7: Utvalgsfordeling Bo Lindqvist Institutt for matematiske fag 2 Fra kapittel 1: Populasjon Den mengden av individer/objekter som vi ønsker å analysere. Utvalg
ST0202 Statistikk for samfunnsvitere Kapittel 7: Utvalgsfordeling Bo Lindqvist Institutt for matematiske fag 2 Fra kapittel 1: Populasjon Den mengden av individer/objekter som vi ønsker å analysere. Utvalg
Tilfeldige variabler. MAT0100V Sannsynlighetsregning og kombinatorikk
 MAT0100V Sannsynlighetsregning og kombinatorikk Forventning, varians og standardavvik Tilnærming av binomiske sannsynligheter Konfidensintervall Ørnulf Borgan Matematisk institutt Universitetet i Oslo
MAT0100V Sannsynlighetsregning og kombinatorikk Forventning, varians og standardavvik Tilnærming av binomiske sannsynligheter Konfidensintervall Ørnulf Borgan Matematisk institutt Universitetet i Oslo
Togforsinkelsen (Eksamen Des2003.1a) I denne oppgaven kan du bruke uten å vise det at
 Kapittel 4 Forventningsverdi, varians, kovarians for én stokastisk variabel og funksjoner av stokastiske variabler TMA4245 V2007: Eirik Mo 2 4.1 Forventing til en stokastisk variabel DEF 4.1: La X være
Kapittel 4 Forventningsverdi, varians, kovarians for én stokastisk variabel og funksjoner av stokastiske variabler TMA4245 V2007: Eirik Mo 2 4.1 Forventing til en stokastisk variabel DEF 4.1: La X være
Kap. 7 - Sannsynlighetsfordelinger
 Oppgaver: Kap. 7 - Sannsynlighetsfordelinger Oppgaver fra kapitlet Lærebok: 7.0-0-0-,7.--7, 7.-, 7., 7., 7.7 Oppgavesamling: 7.00, 7.0, 7.09, 7., 7.9, 7., 7.0, 7.0, 7.0 7.0-0-0-0- Stokastisk variabel:
Oppgaver: Kap. 7 - Sannsynlighetsfordelinger Oppgaver fra kapitlet Lærebok: 7.0-0-0-,7.--7, 7.-, 7., 7., 7.7 Oppgavesamling: 7.00, 7.0, 7.09, 7., 7.9, 7., 7.0, 7.0, 7.0 7.0-0-0-0- Stokastisk variabel:
Regneøvelse 22/5, 2017
 Regneøvelse 22/5, 217 Arne Bang Huseby Eksamen STK11 212: oppgave 1 og 2 Eksamen STK11 28: oppgave 1) og 2 Eksamen 212, oppgave 1 Ved en bestemt butikk i en større dagligvarekjede viser langvarige data
Regneøvelse 22/5, 217 Arne Bang Huseby Eksamen STK11 212: oppgave 1 og 2 Eksamen STK11 28: oppgave 1) og 2 Eksamen 212, oppgave 1 Ved en bestemt butikk i en større dagligvarekjede viser langvarige data
ÅMA110 Sannsynlighetsregning med statistikk, våren 2006 Kp. 6, del 3
 ÅMA110 Sannsynlighetsregning med statistikk, våren 2006 Kp. 6, del 3 Bjørn H. Auestad Institutt for matematikk og naturvitenskap Universitetet i Stavanger 20. mars Bjørn H. Auestad Kp. 6: Hypotesetesting
ÅMA110 Sannsynlighetsregning med statistikk, våren 2006 Kp. 6, del 3 Bjørn H. Auestad Institutt for matematikk og naturvitenskap Universitetet i Stavanger 20. mars Bjørn H. Auestad Kp. 6: Hypotesetesting
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: ST101 Innføring i statistikk og sannsynlighetsregning. Eksamensdag: Mandag 29. november 1993. Tid for eksamen: 09.00 15.00. Oppgavesettet
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: ST101 Innføring i statistikk og sannsynlighetsregning. Eksamensdag: Mandag 29. november 1993. Tid for eksamen: 09.00 15.00. Oppgavesettet
TMA4240 Statistikk Høst 2015
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 0, blokk II Løsningsskisse Oppgave Surhetsgrad i ferskvann Eksamen august 00, oppgave av 3 a) En god estimator
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 0, blokk II Løsningsskisse Oppgave Surhetsgrad i ferskvann Eksamen august 00, oppgave av 3 a) En god estimator
ST0202 Statistikk for samfunnsvitere
 ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag 2 Fra første forelesning: Populasjon Den mengden av individer/objekter som vi ønsker å analysere. Utvalg En delmengde av
ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag 2 Fra første forelesning: Populasjon Den mengden av individer/objekter som vi ønsker å analysere. Utvalg En delmengde av
Seksjon 1.3 Tetthetskurver og normalfordelingen
 Seksjon 1.3 Tetthetskurver og normalfordelingen Har sett på ulike metoder for å plotte eller oppsummere data ved tall Vil nå starte på hvordan beskrive data ved modeller Hovedmetode er tetthetskurver Tetthetskurver
Seksjon 1.3 Tetthetskurver og normalfordelingen Har sett på ulike metoder for å plotte eller oppsummere data ved tall Vil nå starte på hvordan beskrive data ved modeller Hovedmetode er tetthetskurver Tetthetskurver
TMA4240 Statistikk Eksamen desember 2015
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4240 Statistikk Eksamen desember 15 Oppgave 1 La den kontinuerlige stokastiske variabelen X ha fordelingsfunksjon (sannsynlighetstetthet
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4240 Statistikk Eksamen desember 15 Oppgave 1 La den kontinuerlige stokastiske variabelen X ha fordelingsfunksjon (sannsynlighetstetthet
ÅMA110 Sannsynlighetsregning med statistikk, våren 2010 Oppsummering
 ÅMA110 Sannsynlighetsregning med statistikk, våren 2010 Oppsummering Bjørn H. Auestad Institutt for matematikk og naturvitenskap Universitetet i Stavanger 21. april Bjørn H. Auestad Oppsummering våren
ÅMA110 Sannsynlighetsregning med statistikk, våren 2010 Oppsummering Bjørn H. Auestad Institutt for matematikk og naturvitenskap Universitetet i Stavanger 21. april Bjørn H. Auestad Oppsummering våren
Løsningskisse for oppgaver til undervisningsfri uke 8 ( februar 2012)
 1 ECON 130 HG - februar 01 Løsningskisse for oppgaver til undervisningsfri uke 8 (0.-. februar 01) Oppg..1. Variabel: x = antall kundehenvendelser pr. dag 1. Antall observasjoner: n = 100 dager. I Excel
1 ECON 130 HG - februar 01 Løsningskisse for oppgaver til undervisningsfri uke 8 (0.-. februar 01) Oppg..1. Variabel: x = antall kundehenvendelser pr. dag 1. Antall observasjoner: n = 100 dager. I Excel
Kapittel 4.4: Forventning og varians til stokastiske variable
 Kapittel 4.4: Forventning og varians til stokastiske variable Forventning og varians til stokastiske variable Histogrammer for observerte data: Sannsynlighets-histogrammer og tetthetskurver for stokastiske
Kapittel 4.4: Forventning og varians til stokastiske variable Forventning og varians til stokastiske variable Histogrammer for observerte data: Sannsynlighets-histogrammer og tetthetskurver for stokastiske
Seksjon 1.3 Tetthetskurver og normalfordelingen
 Seksjon 1.3 Tetthetskurver og normalfordelingen Har sett på ulike metoder for å plotte eller oppsummere data Vil nå starte på hvordan beskrive data ved modeller Hovedmetode er tetthetskurver Tetthetskurver
Seksjon 1.3 Tetthetskurver og normalfordelingen Har sett på ulike metoder for å plotte eller oppsummere data Vil nå starte på hvordan beskrive data ved modeller Hovedmetode er tetthetskurver Tetthetskurver
Observatorar og utvalsfordeling. Torstein Fjeldstad Institutt for matematiske fag, NTNU
 Observatorar og utvalsfordeling Torstein Fjeldstad Institutt for matematiske fag, NTNU 08.10.2018 I dag Til no i emnet Observatorar Utvalsfordelingar Sentralgrenseteoremet 2 Til no i emnet definisjon av
Observatorar og utvalsfordeling Torstein Fjeldstad Institutt for matematiske fag, NTNU 08.10.2018 I dag Til no i emnet Observatorar Utvalsfordelingar Sentralgrenseteoremet 2 Til no i emnet definisjon av
x λe λt dt = 1 e λx for x > 0 uavh = P (X 1 v)p (X 2 v) = F X (v) 2 = (1 e λv ) 2 = 1 2e λv + e 2λv = 2 1 λ 1 2λ = 3
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 7 Løsningsskisse Oppgave 1 a) Regner først ut den kumulative fordelingsfunksjonen til X: F X (x) = x λe λt dt
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 7 Løsningsskisse Oppgave 1 a) Regner først ut den kumulative fordelingsfunksjonen til X: F X (x) = x λe λt dt
TMA4245 Statistikk Høst 2016
 TMA5 Statistikk Høst 6 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving Løsningsskisse Oppgave a) Den tilfeldige variabelen X er kontinuerlig fordelt med sannsynlighetstetthet
TMA5 Statistikk Høst 6 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving Løsningsskisse Oppgave a) Den tilfeldige variabelen X er kontinuerlig fordelt med sannsynlighetstetthet
TMA4240 Statistikk H2015
 TMA4240 Statistikk H2015 Funksjoner av stokastiske variabler (kapittel 7+notat) Fokus på start med kumulativ fordeling 7.2 Funksjon av en SV (inkludert en-entydighet). Fordeling til max/min (fra notat).
TMA4240 Statistikk H2015 Funksjoner av stokastiske variabler (kapittel 7+notat) Fokus på start med kumulativ fordeling 7.2 Funksjon av en SV (inkludert en-entydighet). Fordeling til max/min (fra notat).
Oppgave 1. a) Anlysetype: enveis variansanalyse (ANOVA). Modell for y ij = ekspedisjonstid nr. j for skrankeansatt nr. i:
 MOT310 tatistiske metoder 1 Løsningsforslag til eksamen høst 010, s 1 Oppgave 1 a) Anlysetype: enveis variansanalyse (ANOVA) Modell for y ij ekspedisjonstid nr j for skrankeansatt nr i: Y ij µ i + ε ij,
MOT310 tatistiske metoder 1 Løsningsforslag til eksamen høst 010, s 1 Oppgave 1 a) Anlysetype: enveis variansanalyse (ANOVA) Modell for y ij ekspedisjonstid nr j for skrankeansatt nr i: Y ij µ i + ε ij,
TMA4245 Statistikk. Innlevering 3. Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag
 TMA4245 Statistikk Vår 2017 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Innlevering 3 Dette er den første av to innleveringer i blokk 2 Denne øvingen skal oppsummere pensum
TMA4245 Statistikk Vår 2017 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Innlevering 3 Dette er den første av to innleveringer i blokk 2 Denne øvingen skal oppsummere pensum
Løsningsforslag til andre sett med obligatoriske oppgaver i STK1110 høsten 2010
 Løsningsforslag til andre sett med obligatoriske oppgaver i STK1110 høsten 2010 Oppgave 1 a Forventet antall dødsulykker i år i er E(X i λ i. Dermed er θ i λ i E(X i forventet antall dødsulykker per 100
Løsningsforslag til andre sett med obligatoriske oppgaver i STK1110 høsten 2010 Oppgave 1 a Forventet antall dødsulykker i år i er E(X i λ i. Dermed er θ i λ i E(X i forventet antall dødsulykker per 100
Inferens. STK Repetisjon av relevant stoff fra STK1100. Eksempler. Punktestimering - "Fornuftig verdi"
 Inferens STK1110 - Repetisjon av relevant stoff fra STK1100 Geir Storvik 12. august 2015 Data x 1,..., x n evt også y 1,..., y n Ukjente parametre θ kan være flere Vi ønsker å si noe om θ basert på data.
Inferens STK1110 - Repetisjon av relevant stoff fra STK1100 Geir Storvik 12. august 2015 Data x 1,..., x n evt også y 1,..., y n Ukjente parametre θ kan være flere Vi ønsker å si noe om θ basert på data.
