Løsningsforslag til obligatorisk oppgave i ECON 2130
|
|
|
- Unn Jensen
- 7 år siden
- Visninger:
Transkript
1 Andreas Mhre April 15 Løsningsforslag til obligatorisk oppgave i ECON 13 Oppgave 1: E(XY) = E(X(Z X)) Setter inn Y = Z - X E(XY) = E(XZ X ) E(XY) = E(XZ) E(X ) E(XY) = - E(X ) X og Z er uavhengige, så Cov(X, Z) =. Dermed er E(XZ) = E(X)E(Z) også lik, siden E(X) = E(Z) =. E(XY) = - (X) + (E(X)) ) Bruker formelen X) = E(X ) (E(X)) E(XY) = - X) E(XY) = -1 Har fått oppgitt i oppgaven at X er normalfordelt med forventning lik og standardavvik lik 1. Da er også X) = 1. Cov( X, Y ) σ x σ Cov( X, Y ) X )* Y ) X) = 1, og Var (Y) kan skrives som Z X): E( XY ) µ µ x Z X ) µ x = µ =, så dette leddet faller bort. E( XY ) 1* Z + ( 1) X ) 1 1 Z) + ( 1) X ) 1 Var ( Z) + X ) Z) og var(x) er begge lik 1. Så: 1 1
2 Oppgave : Her lot jeg først Excel til å trekke tall for variablene X og Z, der X og Z er normalfordelte med forventning og standardavvik 1. Deretter lagde jeg en tredje kolonne for Y, og satte Y lik Z - X. Først lagde jeg et punktdiagram for variablene X og Z, og fikk følgende resultat: 1,5 1, ,5 Series1-1 -1,5 - Her ser vi at det er stor spredning og liten sammenheng mellom variablene, X og Z virker å være uavhengige av hverandre. Korrelasjonen mellom X og Z er derfor i dette tilfellet liten (,17 i med disse tallene i Excel), da det ikke er noen tdelig lineær sammenheng. Den forventede korrelasjonen mellom X og Z er lik, så vårt estimat bommer noe på den sanne korrelasjonen. Dette skldes i hovedsak tilfeldigheter og at vi har få observasjoner. Deretter gjorde jeg akkurat det samme for variablene X og Y. Resultatet ble slik:,5,5 Series1 - -1,5-1 -,5 -,5,5 1 1,5 1, ,5 - Her ser vi en viss sammenheng mellom variablene, da det ikke er noen observasjoner av lav verdi på X som medfører lav verdi på Y, og ingen observasjoner av hø verdi for X som medfører en hø verdi for Y. Vi observerer derfor en negativ sammenheng mellom variablene. X og Y gir dermed et visst inntrkk av avhengighet, som forventet, da den teoretiske korrelasjonen mellom X og Y er -.77.
3 Oppgave 3: Først skal vi se at vi kan skrive korrelasjonen som a 1+ a Vi har Cov( X, Y ) σ σ x og Y = Z + ax Cov( X, Y ) X )* Y ) X) = 1, så vi kan skrive: E( XY ) µ x µ Y ) µ x = µ =, så dette leddet faller bort. Setter inn for Y: E( X ( Z + ax )) Z + ax ) E( XZ) + ae( X Z) + a a 1+ a ) X ) Siden X og Z er uavhengige er E(XZ) =. E(X ) = X) + (E(X)) = 1. X) = Z) = 1. Da kan vi skrive uttrkket som: Deretter kan vi løse denne likningen mhp a: ρ = a 1+ a ρ (1+a ) = a ρ +a ρ = a a (1-ρ ) = ρ a ρ = 1 ρ ρ a = ± 1 ρ 3
4 Da finner vi følgende verdi for a når ρ = -.: a = ±. 1 (.) = ±..96 = ±.4 Her blir a = -.4 fordi a og ρ må ha samme fortegn. Etter å ha simulert n = observasjoner for X og Z i Excel på samme måte som i oppgave, lager vi en tredje kolonne for Y, der vi setter Y = Z.4X. Deretter plotter vi X og Y-variablene i et punktdiagram. Der fikk jeg følgende resultat: 3,5 1,5 1,5 Series1 - -1,5-1 -,5 -,5,5 1 1,5-1 -1,5 Her ser vi at det er en svak negativ sammenheng mellom X og Y, omtrent som forventet, da ρ = -.. Og for ρ =.9: a = ± = ±.9.19 = ±.65 Her blir a =.65 fordi a og ρ må ha samme fortegn. Deretter gjør vi det samme som i sted, og får dette spredningsplottet: 4
5 Series Her ser vi at det er en tdelig lineær sammenheng mellom X og Y. Sammenhengen er positiv i likhet med fortegnet på ρ. Sammenhengen er også me tdeligere enn i sted, noe som skldes at absoluttverdien på ρ er større ved dette tilfellet. Oppgave 4: Her bruker vi tallene fra oppgave, og beregner korrelasjonen mellom X og Y ved hjelp av Excel. Resultatet jeg fikk, altså estimert korrelasjon mellom X og Y med mine observasjoner, ble r = Estimeringsfeilen er dermed (-.77) =.1355 Vi ser at korrelasjonen mellom X og Y for n = tilfeldige variabler er i nærheten av det forventede resultatet (-.77), men samtidig ikke helt nøaktig. Dette skldes i stor grad størrelsen på utvalget, da n = er et forholdsvis lite utvalg. Hadde vi økt n, og dermed fått et større utvalg, hadde sannsnligvis estimeringsfeilen vært mindre. Men størrelsen på estimeringsfeilen skldes også i stor grad tilfeldigheter. 5
6 Oppgave 5: Etter å ha fått 5 ulike observasjoner for r, lagde jeg et histogram med 6 intervaller og intervallbredde.5. Histogrammet mitt ble seende slik ut: Histogram Frekvens ,85 -,8 -,75 -,7 -,65 -,6 Mer Intervall Frekvens Til tross for relativt få observasjoner for r (5 observasjoner), gir histogrammet et visst inntrkk av at r er normalfordelt, da det er en klar tendens til at de fleste observasjonene samler seg rundt gjennomsnittet for de 5 observasjonene for r, som er -.74 (se histogram). Samtidig er flere av observasjonene for r er et stkke unna denne verdien. Dette kan forklares ved hjelp av størrelsen på standardavviket for r, som Excel beregnet til å være.67 med dette datasettet. Hadde standardavviket vært mindre, hadde sannsnligvis flere av observasjonene samlet seg rundt midten av histogrammet ved fast intervallbredde. Gjennomsnittet er beregnet til , og medianen til Vi ser her at begge disse verdiene treffer forholdsvis bra i forhold til forventningsverdien ρ (som er -.77), selv om treffsikkerheten nok kunne vært bedre. Gjennomsnittet bommer altså med.3357 på den forventete korrelasjonen. Standardavviket til gjennomsnittet er av Excel beregnet til å være.1364 (skal være lik standardavviket for r delt på n ). Et tpisk avvik for gjennomsnittet fra den forventete verdien ρ skal altså være ca Men gjennomsnittet bommer her med me mer, faktisk så me som.53 standardavvik (sjekk selv; ta gjennomsnittet av observasjonene for r minus forventningsverdien (ρ) delt på standardavviket til gjennomsnittet, kalt standardfeil i Excel). Dette er en forholdsvis stor bom også relativt til standardavviket, men samtidig ikke unaturlig stort. Hadde vi hatt flere observasjoner, hadde gjennomsnittet av observasjonene våre for r sannsnligvis truffet enda nærmere forventningsverdien ρ. Men me av årsaken til størrelsen på bommen skldes i dette tilfellet tilfeldigheter. Vår estimerte korrelasjon r virker å være en relativt pålitelig estimator for den sanne korrelasjonen ρ, vi må i alle fall være forsiktige med å konkludere med det motsatte. Største verdi for r var , og minste verdi Dette gir en differanse på.7647 mellom største og minste verdi. 6
7 Oppgave 6: Her gjør vi det samme som i oppgave 5, men øker n slik at n = 5 (for hver observasjon av r). Dette ga meg følgende histogram for observasjonene av r, med samme intervallbredde (.5) som i oppgave 5: Histogram Frekvens ,8 -,75 -,7 -,65 -,6 -,55 Mer Intervall Frekvens Dette histogrammet ser litt annerledes ut enn det jeg fikk i oppgave 5, men også her får vi inntrkket av at r er normalfordelt. Her ser histogrammet mer pålitelig ut, da ingen av intervallene skiller seg voldsomt ut med en veldig hø eller lav frekvens. Dette histogrammet gir også muligens et litt klarere inntrkk av at r er normalfordelt i forhold til i oppgave 5. Dette er helt forventet siden antallet observasjoner for hver av de 5 estimatorene for ρ (altså våre 5 observasjoner for r) har økt fra til 5. Men vær obs på at dette også i stor grad kan skldes tilfeldigheter, da et histogram kan se rimelig forskjellig ut avhengig av hvor man setter intervallgrensene. Det er begrenset for hvor bastante konklusjoner man kan trekke fra et histogram med så få observasjoner. Gjennomsnittet for våre 5 observasjoner for r er nå beregnet til å være -.714, og medianen er Disse verdiene treffer altså bedre enn verdiene i oppgave 5 på den forventede verdien ρ = Dette er i tråd med forventningene om at gjennomsnittet er en mer pålitelig estimator for den sanne verdien ρ når antallet observasjoner øker. Men som vi skal se, skldes dette her i stor grad tilfeldigheter. Standardavviket til r og standardavviket til gjennomsnittet til r (står som standardfeil i Excel) er henholdsvis.67 og.134, altså nesten akkurat det samme som i oppgave 5. Fordi vi har flere observasjoner for hver verdi av r, skulle en forvente at flere av verdiene samlet seg rundt midten av histogrammet ved samme intervallbredde, dvs. en skulle forvente at standardavviket for r var mindre enn i oppgave 5. Dette er dog ikke tilfellet her, så vi må konkludere med at dette skldes tilfeldigheter. Gjennomsnittet treffer likevel bedre enn i oppgave 5 (som ikke er gitt med tanke på at standardavviket for gjennomsnittet er omtrent det samme). For å komme med en litt mer generell konklusjon: Vi forventer at standardavviket for r, er mindre jo flere observasjoner vi har for hver verdi av r. Altså forventer vi også at standardavviket til gjennomsnittet for observasjonene av r, er mindre jo flere observasjoner vi har for hver verdi av r. Således forventer vi at gjennomsnittet treffer bedre på den sanne verdien ρ jo flere observasjoner vi har for hver verdi av r. Det gjorde det også i dette tilfellet, men ikke på grunn av lavere standardavvik. Her skldtes det i hovedsak tilfeldigheter. Men at standardavviket for r ikke var mindre selv om antall observasjoner økte, var ikke forventet, og således også tilfeldig. 7
8 Oppgave 7: Etter å ha simulert 5 observasjoner for X og Z, og satt Y = Z 3X fikk jeg følgende resultat: Series1 Deretter beregnet jeg korrelasjonen mellom X og Y i Excel, og fikk r(x, Y) =.783. Resultatet tder derfor på at det ikke er noen klar lineær sammenheng mellom X og Y, noe vi også ser i punktdiagrammet, at det ikke er. Vi observerer derimot at X og Y likevel virker å være stokastisk avhengige av hverandre, da observasjonene samler seg rundt det som ville vært en ikke-lineær kurve i diagrammet. Men denne effekten fanges ikke opp i beregningen av korrelasjonen. Dette er fordi korrelasjonsverdien r som vi beregner, beskriver den lineære sammenhengen mellom X og Y. I dette tilfellet er det heller ingen klar lineær sammenheng, men definitivt en sammenheng. Vi kan derfor konkludere med at r ikke nødvendigvis er egnet til å beskrive en sammenheng mellom to variabler som ikke er lineær. Her ser vi at selv om kovariansen mellom to variabler forventes å være lik (og derfor også korrelasjonen), trenger ikke nødvendigvis variablene å være uavhengige. Beregner også den sanne ρ: Cov( X, Y ) σ x σ Cov(X, Y) = E(XY) - µ x µ Forventningen til X og Y er lik. Cov(X, Y) = E(X(Z 3X )) Cov(X, Y) = E(XZ 3X 3 ) Cov(X, Y) = E(XZ) 3E(X 3 ) X og Z er uavhengige og E(XZ) er derfor lik. E(X 3 ) er også lik når X er normalfordelt med Cov(X, Y) = forventning. Og derfor må også korrelasjonen mellom X og Y, altså ρ(x, Y) være lik. Korrelasjon lik tilsier at det ikke er noen form for lineær sammenheng mellom X og Y, og eksperimentet gikk dermed omtrent som forventet, da estimeringsverdien r var svært liten, og ikke signifikant forskjellig fra. 8
9 Oppgave 8: (i) xx = = X sigarettkonsum per voksen per år. = = Y HKS-dødelighet per 1. 1 S x = S = Bruk formlene oppgitt i oppgave 4 for estimering av standardavviket til x og samt kovariansen. S x = Estimerer ρ: r(x, Y) = r(x, Y) = S x S S x * r(x, Y) = Sammenheng mellom sigarettkonsum og HKS-dødelighet HKS-dødelighet Series1 Linear (Series1) Sigarettkonsum 9
10 Vi ser at det er en relativt klar sammenheng mellom sigarettkonsum og HKS-dødelighet, uten at det forklarer alt. Korrelasjonskoeffisienten r =.795, gir r = Dermed forklares ca. 53 % av HKS-dødeligheten ut ifra sigarettkonsumet. Resten blir stående uforklart i vår modell. Denne uforklarte delen, er et resultat av at andre faktorer også spiller inn (som for eksempel landenes helsevesen), feilmargin (kommer an på størrelsen på utvalget) samt tilfeldigheter. Sammenhengen er likevel såpass klar at vi trolig kan slå fast at røking fører til en hppigere HKS-dødelighetsrate. Hvor sikkert vi kan slå fast dette, skal vi se nærmere på i oppgave 9. (ii) Hvis vi endrer benevningen for HKS-dødelighet til å omhandle hver 1, vil vi få følgende endringer: Estimator for standardavvik for X og Y: S x = S = uendret. 1/1 i forhold til i sted. Estimator for kovariansen: S x = /1 i forhold til i sted. Estimator for korrelasjonskoeffisienten: r(x, Y) = r(x, Y) = S x S S x * r(x, Y) =.795 uendret. Vi ser her at om vi endrer benevningen for HKS-dødeligheten til pr. 1, vil alle Y- verdiene bli 1 ganger mindre. Dette får konsekvenser for standardavviket til Y og kovariansen mellom X og Y, som begge får lavere verdier i forhold til i sted. Korrelasjonskoeffisienten, derimot, forblir uendret. Fordi alle Y-verdiene endres proporsjonalt med X, vil ikke den relative sammenhengen mellom X og Y bli påvirket. 1
11 Oppgave 9: (i) Ved å plotte en rad for verdiene av x for så å beregne verdiene for h(x), får vi følgende graf: 3 h(x) 1-1,5-1 -,5,5 1 1,5-1 h(x) - -3 Som vi ser er strengt voksende i x. Legg også merke til at funksjonen er kontinuerlig, dvs. det er ingen hopp. (ii) Legg merke til at Z = h(r), den samme funksjonen som i oppgave (i) bare med r som argument istedenfor x. Siden h(r) er en strengt voksende, kontinuerlig funksjon av r, vil h(r) være større enn eller lik h(r ) hvis og bare hvis r er større enn eller lik r. Å si at h(r) er større enn eller lik h(r ) er derfor ekvivalent med å si at r er større enn eller lik r. Dermed vil også sannsnligheten for at r er større enn eller lik r være den samme som sannsnligheten for at Z er større enn eller lik h(r ). Altså P(r r ) = P(Z h(r )). (iii) Vi har P(r r ) = P(Z h(r )). Vår observerte verdi for r fra oppgave 8, var r =.795. Så vi kan sette inn denne verdien i uttrkket: P(r.795) = P(Z h(.795)) = P(Z ln ) = P(Z 8.97) Siden vi vet at Z er tilnærmet normalfordelt med forventning og standardavvik 1, kan vi tolke dette uttrkket slik: Sannsnligheten for at vi observerer en verdi for r som er større enn vår verdi under antagelsen ρ =, er det samme som sannsnligheten for at en normalfordelt variabel er minst 8.97 standardavvik unna sin forventede verdi. Altså ekstremt usannsnlig. Hvor usannsnlig, kan vi finne ut ved hjelp av Excel, eller ved hjelp av tabell D.3 i Løvås. 11
12 For en normalfordelt variabel med forventning og standardavvik 1 gjelder følgende: P(Z z) = G(z) P(Z 8.97) = 1 - P(Z < 8.97) = 1 - P(Z 8.97) Siden Z er en kontinuerlig variabel. Så P(Z 8.97) = 1 - P(Z 8.97) = 1 - G(8.97) Ved å bruke Excel, finner vi G(8.97) 1. Altså er P(r.795) = P(Z 8.97). Vi observerer en p-verdi så liten at vi kan runde den av til. Dette betr at sannsnligheten for at vi observerer en verdi for r som er større enn vår verdi, er tilnærmet lik under antagelsen om at ρ =. Vi burde derfor vurdere om antagelsen vår er feil, og at det finnes en sammenheng mellom variablene, dvs. ρ. I dette tilfellet er resultatet svært signifikant, og vi kan fastslå nesten helt sikkert at ρ, og at det er en sammenheng mellom sigarettkonsum og HKS-dødelighet. En p-verdi nærme forteller oss at sannsnligheten for at ρ = er ekstremt liten, og konklusjonen vår om at ρ nesten alltid er sann. I dette tilfellet konkluderer vi med at ρ >, dvs. sammenhengen er positiv. Merk: Tabell D.3 i Løvås har bare verdier for G opp til ca. 3. Vi ser at allerede for G(3) er sannsnligheten veldig nærme 1. Altså er det ekstremt sjeldent en normalfordelt variabel er mer enn 3 standardavvik unna sin forventede verdi. Dermed er det enda sjeldnere at en normalfordelt variabel er så me som 8.97 standardavvik unna sin forventede verdi, og sannsnligheten for dette er veldig nærme. For verdier over 3 er vi derfor såpass sikre at vi i de fleste tilfeller kan runde sannsnligheten opp til 1. Men pass her på å si at sannsnligheten er tilnærmet lik 1, for helt 1 % sikkert er det ikke, men nesten! 1
Løsningsforslag til obligatorisk oppgave i ECON 2130
 Andres Mhre April 13 Løsningsforslg til obligtorisk oppgve i ECON 13 Oppgve 1: E(XY) = E(X(Z X)) Setter inn Y = Z - X E(XY) = E(XZ X ) E(XY) = E(XZ) E(X ) X og Z er uvhengige v hverndre, så Cov(X, Z) =.
Andres Mhre April 13 Løsningsforslg til obligtorisk oppgve i ECON 13 Oppgve 1: E(XY) = E(X(Z X)) Setter inn Y = Z - X E(XY) = E(XZ X ) E(XY) = E(XZ) E(X ) X og Z er uvhengige v hverndre, så Cov(X, Z) =.
Løsningsforslag ECON 2130 Obligatorisk semesteroppgave 2017 vår
 Løsningsforslag ECON 130 Obligatorisk semesteroppgave 017 vår Andreas Myhre Oppgave 1 1. (i) Siden X og Z er uavhengige, vil den simultane fordelingen mellom X og Z kunne skrives som: f(x, z) = P(X = x
Løsningsforslag ECON 130 Obligatorisk semesteroppgave 017 vår Andreas Myhre Oppgave 1 1. (i) Siden X og Z er uavhengige, vil den simultane fordelingen mellom X og Z kunne skrives som: f(x, z) = P(X = x
ECON2130 Kommentarer til oblig
 ECON2130 Kommentarer til oblig Her har jeg skrevet ganske utfyllende kommentarer til en del oppgaver som mange slet med. Har noen steder gått en del utover det som det strengt tatt ble spurt om i oppgaven,
ECON2130 Kommentarer til oblig Her har jeg skrevet ganske utfyllende kommentarer til en del oppgaver som mange slet med. Har noen steder gått en del utover det som det strengt tatt ble spurt om i oppgaven,
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 Øvelsesoppgave i: ECON30 Statistikk Dato for utlevering: Mandag 6. mars 009 Dato for innlevering: Tirsdag 3. mars 009 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Innleveringssted: Ved siden av SV-info-senter
Øvelsesoppgave i: ECON30 Statistikk Dato for utlevering: Mandag 6. mars 009 Dato for innlevering: Tirsdag 3. mars 009 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Innleveringssted: Ved siden av SV-info-senter
Kapittel 4: Matematisk forventning
 Kapittel 4: Matematisk forventning TMA4240 Statistikk (F2 og E7) Multivariate tilfeller foreleses mandag 6.september, 2004 Ole.Petter.Lodoen@math.ntnu.no p.1/16 Forventing til funksjon av flere stokastiske
Kapittel 4: Matematisk forventning TMA4240 Statistikk (F2 og E7) Multivariate tilfeller foreleses mandag 6.september, 2004 Ole.Petter.Lodoen@math.ntnu.no p.1/16 Forventing til funksjon av flere stokastiske
ECON2130 Obligatorisk Oppgave
 201303 ECON2130 Obligatorisk Oppgave Oppgave 1 Vi lar være uavhengige og normalfordelte,, setter og ønsker å vise at og at den teoretiske korrelasjonskoeffisienten mellom og er. Vi betrakter her en standard
201303 ECON2130 Obligatorisk Oppgave Oppgave 1 Vi lar være uavhengige og normalfordelte,, setter og ønsker å vise at og at den teoretiske korrelasjonskoeffisienten mellom og er. Vi betrakter her en standard
Tyngdepunkt. Togforsinkelsen (Eksamen Des2003.1a) I denne oppgaven kan du bruke uten å vise det at. Kapittel 4
 3 Tyngdepunkt Kapittel 4 Forventningsverdi, varians, kovarians for én stokastisk variabel og funksjoner av stokastiske variabler TMA4240 H2006: Eirik Mo 2 4.1 Forventing til en stokastisk variabel DEF
3 Tyngdepunkt Kapittel 4 Forventningsverdi, varians, kovarians for én stokastisk variabel og funksjoner av stokastiske variabler TMA4240 H2006: Eirik Mo 2 4.1 Forventing til en stokastisk variabel DEF
3.4: Simultanfordelinger (siste rest) 4.1,4.2,4.3: Multivariat del (ferdig med kapittel 3 og 4 etter denne forelesningen)
 TMA4240 Statistikk H200 3.4: Simultanfordelinger (siste rest) 4.,4.2,4.3: Multivariat del (ferdig med kapittel 3 og 4 etter denne forelesningen) Mette Langaas Foreleses mandag 3. september 200 2 f (x,
TMA4240 Statistikk H200 3.4: Simultanfordelinger (siste rest) 4.,4.2,4.3: Multivariat del (ferdig med kapittel 3 og 4 etter denne forelesningen) Mette Langaas Foreleses mandag 3. september 200 2 f (x,
Forelesning 13. mars, 2017
 Forelesning 13. mars, 217 AVSNITT 5.2 Kovariansen mellom to variable Korrelasjon mellom to variable AVSNITT 5.3 Betingede fordelinger Kovariansen mellom to stokastiske variable Kovariansen mellom to stokastiske
Forelesning 13. mars, 217 AVSNITT 5.2 Kovariansen mellom to variable Korrelasjon mellom to variable AVSNITT 5.3 Betingede fordelinger Kovariansen mellom to stokastiske variable Kovariansen mellom to stokastiske
Fasit for tilleggsoppgaver
 Fasit for tilleggsoppgaver Uke 5 Oppgave: Gitt en rekke med observasjoner x i (i = 1,, 3,, n), definerer vi variansen til x i som gjennomsnittlig kvadratavvik fra gjennomsnittet, m.a.o. Var(x i ) = (x
Fasit for tilleggsoppgaver Uke 5 Oppgave: Gitt en rekke med observasjoner x i (i = 1,, 3,, n), definerer vi variansen til x i som gjennomsnittlig kvadratavvik fra gjennomsnittet, m.a.o. Var(x i ) = (x
betyr begivenheten at det blir trukket en rød kule i første trekning og en hvit i andre, mens B1 B2
 ECON30: EKSAMEN 06v SENSORVEILEDNING. Det anbefales at de 9 deloppgavene merket med A, B, teller likt uansett variasjon i vanskelighetsgrad. Svarene er gitt i
ECON30: EKSAMEN 06v SENSORVEILEDNING. Det anbefales at de 9 deloppgavene merket med A, B, teller likt uansett variasjon i vanskelighetsgrad. Svarene er gitt i
Forelesning 6: Punktestimering, usikkerhet i estimering. Jo Thori Lind
 Forelesning 6: Punktestimering, usikkerhet i estimering Jo Thori Lind j.t.lind@econ.uio.no Oversikt 1. Trekke utvalg 2. Estimatorer og observatorer som stokastiske variable 3. Egenskapene til en estimator
Forelesning 6: Punktestimering, usikkerhet i estimering Jo Thori Lind j.t.lind@econ.uio.no Oversikt 1. Trekke utvalg 2. Estimatorer og observatorer som stokastiske variable 3. Egenskapene til en estimator
TMA4240 Statistikk Høst 2016
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 9 Løsningsskisse Oppgave 1 a) Vi lar her Y være antall fugler som kolliderer med vindmølla i løpet av den gitte
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 9 Løsningsskisse Oppgave 1 a) Vi lar her Y være antall fugler som kolliderer med vindmølla i løpet av den gitte
TMA4245 Statistikk Eksamen desember 2016
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4245 Statistikk Eksamen desember 2016 Oppgave 1 En bedrift produserer elektriske komponenter. Komponentene kan ha to typer
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4245 Statistikk Eksamen desember 2016 Oppgave 1 En bedrift produserer elektriske komponenter. Komponentene kan ha to typer
Forventning og varians.
 Forventning og varians. Dekkes av kapittel 4 i læreboka. Forventning (4.1) Forventningsverdi = gjennomsnitt i det lange løp. Defininsjon: Forventningsverdien til en stokastisk variabel X er: x xf(x),x
Forventning og varians. Dekkes av kapittel 4 i læreboka. Forventning (4.1) Forventningsverdi = gjennomsnitt i det lange løp. Defininsjon: Forventningsverdien til en stokastisk variabel X er: x xf(x),x
Forventning og varians.
 Forventning og varians. Dekkes av kapittel 4 i læreboka. Forventning (4.) Forventningsverdi gjennomsnitt i det lange løp. Defininsjon: Forventningsverdien til en stokastisk variabel X er: E(X) f(),x diskret
Forventning og varians. Dekkes av kapittel 4 i læreboka. Forventning (4.) Forventningsverdi gjennomsnitt i det lange løp. Defininsjon: Forventningsverdien til en stokastisk variabel X er: E(X) f(),x diskret
1.1.1 Rekke med konstante ledd. En rekke med konstante ledd er gitt som. a n (1) n=m
 Formelsamling og tabeller FO020E Matte 2000 for elektroprogrammet 1 Matematikk 1.1 Denisjoner av ulike typer polynomer og rekker 1.1.1 Rekke med konstante ledd En rekke med konstante ledd er gitt som a
Formelsamling og tabeller FO020E Matte 2000 for elektroprogrammet 1 Matematikk 1.1 Denisjoner av ulike typer polynomer og rekker 1.1.1 Rekke med konstante ledd En rekke med konstante ledd er gitt som a
Befolkning og velferd ECON 1730, H2016. Regresjonsanalyse
 Netto innfl. Befolkning og velferd ECON 1730, H2016 Regresjonsanalyse Problem: Gitt planer for 60 nye boliger i kommunen neste år, hvor mange innflyttere kan vi forvente? Tabell Vestby kommune Nye boliger
Netto innfl. Befolkning og velferd ECON 1730, H2016 Regresjonsanalyse Problem: Gitt planer for 60 nye boliger i kommunen neste år, hvor mange innflyttere kan vi forvente? Tabell Vestby kommune Nye boliger
Kapittel 4.4: Forventning og varians til stokastiske variable
 Kapittel 4.4: Forventning og varians til stokastiske variable Forventning og varians til stokastiske variable Histogrammer for observerte data: Sannsynlighets-histogrammer og tetthetskurver for stokastiske
Kapittel 4.4: Forventning og varians til stokastiske variable Forventning og varians til stokastiske variable Histogrammer for observerte data: Sannsynlighets-histogrammer og tetthetskurver for stokastiske
Løsningskisse seminaroppgaver uke 11 ( mars)
 HG Mars 008 Løsningskisse seminaroppgaver uke (0.-4. mars) ECON 0 EKSAMEN 004 VÅR Oppgave En gitt prøve er laget som en flervalgsprøve ( multiple choice test ). Prøven består av tre spørsmål. For hvert
HG Mars 008 Løsningskisse seminaroppgaver uke (0.-4. mars) ECON 0 EKSAMEN 004 VÅR Oppgave En gitt prøve er laget som en flervalgsprøve ( multiple choice test ). Prøven består av tre spørsmål. For hvert
Løsningsforslag Eksamen S2, våren 2016 Laget av Tommy Odland Dato: 29. januar 2017
 Løsningsforslag Eksamen S, våren 016 Laget av Tommy Odland Dato: 9. januar 017 Del 1 - uten hjelpemidler Oppgave 1 a) Vi skal derivere f(x) = e x. Den generelle regelen er at (e ax ) = ae ax, i vårt tilfelle
Løsningsforslag Eksamen S, våren 016 Laget av Tommy Odland Dato: 9. januar 017 Del 1 - uten hjelpemidler Oppgave 1 a) Vi skal derivere f(x) = e x. Den generelle regelen er at (e ax ) = ae ax, i vårt tilfelle
TMA4240 Statistikk 2014
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 9, blokk II Løsningsskisse Oppgave Scriptet run confds.m simulerer n data x,..., x n fra en normalfordeling med
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 9, blokk II Løsningsskisse Oppgave Scriptet run confds.m simulerer n data x,..., x n fra en normalfordeling med
Et lite notat om og rundt normalfordelingen.
 Et lite notat om og rundt normalfordelingen. Anta at vi har kontinuerlige data. Hva er likt og ulikt for histogrammer og fordelingskurver? Observasjoner Histogram Viser fordelingen av faktiske observerte
Et lite notat om og rundt normalfordelingen. Anta at vi har kontinuerlige data. Hva er likt og ulikt for histogrammer og fordelingskurver? Observasjoner Histogram Viser fordelingen av faktiske observerte
Løsningsforslag Eksamen S2, våren 2017 Laget av Tommy O. Sist oppdatert: 25. mai 2017
 Løsningsforslag Eksamen S, våren 17 Laget av Tommy O. Sist oppdatert: 5. mai 17 Del 1 - uten hjelpemidler Oppgave 1 a) Vi skal derivere f(x) = x /x = x x 1. Den eneste regelen vi trenger her er (kx n )
Løsningsforslag Eksamen S, våren 17 Laget av Tommy O. Sist oppdatert: 5. mai 17 Del 1 - uten hjelpemidler Oppgave 1 a) Vi skal derivere f(x) = x /x = x x 1. Den eneste regelen vi trenger her er (kx n )
Løsningskisse for oppgaver til undervisningsfri uke 8 ( februar 2012)
 1 ECON 130 HG - februar 01 Løsningskisse for oppgaver til undervisningsfri uke 8 (0.-. februar 01) Oppg..1. Variabel: x = antall kundehenvendelser pr. dag 1. Antall observasjoner: n = 100 dager. I Excel
1 ECON 130 HG - februar 01 Løsningskisse for oppgaver til undervisningsfri uke 8 (0.-. februar 01) Oppg..1. Variabel: x = antall kundehenvendelser pr. dag 1. Antall observasjoner: n = 100 dager. I Excel
HØGSKOLEN I STAVANGER
 HØGSKOLEN I STAVANGER Avdeling for TEKNISK NATURVITEN- EKSAMEN I: TE199 SANNSYNLIGHETSREGNING MED STATISTIKK SKAPELIGE FAG VARIGHET: 4 TIMER DATO: 5. JUNI 2003 TILLATTE HJELPEMIDLER: KALKULATOR OPPGAVESETTET
HØGSKOLEN I STAVANGER Avdeling for TEKNISK NATURVITEN- EKSAMEN I: TE199 SANNSYNLIGHETSREGNING MED STATISTIKK SKAPELIGE FAG VARIGHET: 4 TIMER DATO: 5. JUNI 2003 TILLATTE HJELPEMIDLER: KALKULATOR OPPGAVESETTET
Et lite notat om og rundt normalfordelingen. Anta at vi har kontinuerlige data. Hva er likt og ulikt for histogrammer og fordelingskurver?
 Et lite notat om og rundt normalfordelingen. Anta at vi har kontinuerlige data. Hva er likt og ulikt for histogrammer og fordelingskurver? Boka (Ch 1.4) motiverer dette ved å gå fra histogrammer til tetthetskurver.
Et lite notat om og rundt normalfordelingen. Anta at vi har kontinuerlige data. Hva er likt og ulikt for histogrammer og fordelingskurver? Boka (Ch 1.4) motiverer dette ved å gå fra histogrammer til tetthetskurver.
Formelsamling i medisinsk statistikk
 Formelsamling i medisinsk statistikk Versjon av 6. mai 208 Dette er en formelsamling til O. O. Aalen (red.): Statistiske metoder i medisin og helsefag, Gyldendal, 208. Gjennomsnitt x = n (x + x 2 + x 3
Formelsamling i medisinsk statistikk Versjon av 6. mai 208 Dette er en formelsamling til O. O. Aalen (red.): Statistiske metoder i medisin og helsefag, Gyldendal, 208. Gjennomsnitt x = n (x + x 2 + x 3
Mål på beliggenhet (2.6) Beregning av kvartilene Q 1, Q 2, Q 3. 5-tallssammendrag. ST0202 Statistikk for samfunnsvitere
 2 Mål på beliggenhet (2.6) Kvartiler: Deler de ordnede dataene inn i fire like store deler: ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag 1. kvartil Q 1 : 25% av dataene
2 Mål på beliggenhet (2.6) Kvartiler: Deler de ordnede dataene inn i fire like store deler: ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag 1. kvartil Q 1 : 25% av dataene
Beregning av kvartilen Q 1 (example 2.12) Mer repetisjon. ST0202 Statistikk for samfunnsvitere
 2 Beregning av kvartilen Q 1 (eample 2.12) Data: 76 74 82 96 66 76 78 72 52 68 86 84 62 76 78 92 82 74 88 84 Utvalgsstørrelse n = 20 Step 1: Ranger fra minste til største: 52 62 66 68 72 74 74 76 76 76
2 Beregning av kvartilen Q 1 (eample 2.12) Data: 76 74 82 96 66 76 78 72 52 68 86 84 62 76 78 92 82 74 88 84 Utvalgsstørrelse n = 20 Step 1: Ranger fra minste til største: 52 62 66 68 72 74 74 76 76 76
Merk at vi for enkelthets skyld antar at alle som befinner seg i Roma sentrum enten er italienere eller utenlandske turister.
 ECON230: EKSAMEN 20 VÅR - UTSATT PRØVE 2 TALLSVAR. Oppgave Da Anne var på besøk i Roma, fikk hun raskt problemer med språket. Anne snakker engelsk, men ikke italiensk, og kun av 5 italienere behersker
ECON230: EKSAMEN 20 VÅR - UTSATT PRØVE 2 TALLSVAR. Oppgave Da Anne var på besøk i Roma, fikk hun raskt problemer med språket. Anne snakker engelsk, men ikke italiensk, og kun av 5 italienere behersker
ST0202 Statistikk for samfunnsvitere
 ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag 2 Kap. 13: Lineær korrelasjons- og regresjonsanalyse Kap. 13.1-13.3: Lineær korrelasjonsanalyse. Disse avsnitt er ikke pensum,
ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag 2 Kap. 13: Lineær korrelasjons- og regresjonsanalyse Kap. 13.1-13.3: Lineær korrelasjonsanalyse. Disse avsnitt er ikke pensum,
Seksjon 1.3 Tetthetskurver og normalfordelingen
 Seksjon 1.3 Tetthetskurver og normalfordelingen Har sett på ulike metoder for å plotte eller oppsummere data Vil nå starte på hvordan beskrive data ved modeller Hovedmetode er tetthetskurver Tetthetskurver
Seksjon 1.3 Tetthetskurver og normalfordelingen Har sett på ulike metoder for å plotte eller oppsummere data Vil nå starte på hvordan beskrive data ved modeller Hovedmetode er tetthetskurver Tetthetskurver
Et lite notat om og rundt normalfordelingen.
 Et lite notat om og rundt normalfordelingen. Anta at vi har kontinuerlige data. Hva er likt og ulikt for histogrammer og fordelingskurver? Observasjoner Histogram Viser fordelingen av faktiske observerte
Et lite notat om og rundt normalfordelingen. Anta at vi har kontinuerlige data. Hva er likt og ulikt for histogrammer og fordelingskurver? Observasjoner Histogram Viser fordelingen av faktiske observerte
Ferdig før tiden 4 7 Ferdig til avtalt tid 12 7 Forsinket 1 måned 2 6 Forsinket 2 måneder 4 4 Forsinket 3 måneder 6 2 Forsinket 4 måneder 0 2
 Besvar alle oppgavene. Hver deloppgave har lik vekt. Oppgave I En kommune skal bygge ny idrettshall og vurderer to entreprenører, A og B. Begge gir samme pristilbud, men kommunen er bekymret for forsinkelser.
Besvar alle oppgavene. Hver deloppgave har lik vekt. Oppgave I En kommune skal bygge ny idrettshall og vurderer to entreprenører, A og B. Begge gir samme pristilbud, men kommunen er bekymret for forsinkelser.
6.2 Signifikanstester
 6.2 Signifikanstester Konfidensintervaller er nyttige når vi ønsker å estimere en populasjonsparameter Signifikanstester er nyttige dersom vi ønsker å teste en hypotese om en parameter i en populasjon
6.2 Signifikanstester Konfidensintervaller er nyttige når vi ønsker å estimere en populasjonsparameter Signifikanstester er nyttige dersom vi ønsker å teste en hypotese om en parameter i en populasjon
A. i) Sett opp en frekvenstabell over de fire mulige kombinasjonene av kjønn og røykestatus. Dvs. fyll inn. Ikke - røyker Sum Jente Gutt Sum 25
 1 ECON21: ESAEN 215v SENSORVEILEDNING. Det anbefales at de 9 deloppgavene merket med A, B, teller likt uansett variasjon i vanskelighetsgrad. Svarene er gitt i > Grensen til bestått bør ligge på ca
1 ECON21: ESAEN 215v SENSORVEILEDNING. Det anbefales at de 9 deloppgavene merket med A, B, teller likt uansett variasjon i vanskelighetsgrad. Svarene er gitt i > Grensen til bestått bør ligge på ca
Oppgave 1. . Vi baserer oss på at p 47 1 og p 2 er tilnærmet normalfordelte (brukbar tilnærming). Vi har tilnærmet at (n 1 = n 2 = 47)
 MOT310 tatistiske metoder 1 Løsningsforslag til eksamen vår 006, s. 1 Oppgave 1 a) En tilfeldig utvalgt besvarelse får F av sensor 1 med sannsynlighet p 1 ; resultatene for ulike besvarelser er uavhengige.
MOT310 tatistiske metoder 1 Løsningsforslag til eksamen vår 006, s. 1 Oppgave 1 a) En tilfeldig utvalgt besvarelse får F av sensor 1 med sannsynlighet p 1 ; resultatene for ulike besvarelser er uavhengige.
Løsningsforslag. n X. n X 1 i=1 (X i X) 2 og SY 2 = 1 ny S 2 X + S2 Y
 Statistiske metoder 1 høsten 004. Løsningsforslag Oppgave 1: a) Begge normalplottene gir punkter som ligger omtrent på ei rett linje så antagelsen om normalfordeling ser ut til å holde. Konfidensintervall
Statistiske metoder 1 høsten 004. Løsningsforslag Oppgave 1: a) Begge normalplottene gir punkter som ligger omtrent på ei rett linje så antagelsen om normalfordeling ser ut til å holde. Konfidensintervall
Eksamensoppgave i TMA4240 Statistikk
 Institutt for matematiske fag Eksamensoppgave i TMA4240 Statistikk Faglig kontakt under eksamen: Mette Langaas a, Ingelin Steinsland b, Geir-Arne Fuglstad c Tlf: a 988 47 649, b 926 63 096, c 452 70 806
Institutt for matematiske fag Eksamensoppgave i TMA4240 Statistikk Faglig kontakt under eksamen: Mette Langaas a, Ingelin Steinsland b, Geir-Arne Fuglstad c Tlf: a 988 47 649, b 926 63 096, c 452 70 806
Forelesning 7: Store talls lov, sentralgrenseteoremet. Jo Thori Lind
 Forelesning 7: Store talls lov, sentralgrenseteoremet Jo Thori Lind j.t.lind@econ.uio.no Oversikt 1. Estimering av variansen 2. Asymptotisk teori 3. Store talls lov 4. Sentralgrenseteoremet 1.Estimering
Forelesning 7: Store talls lov, sentralgrenseteoremet Jo Thori Lind j.t.lind@econ.uio.no Oversikt 1. Estimering av variansen 2. Asymptotisk teori 3. Store talls lov 4. Sentralgrenseteoremet 1.Estimering
Denne uken: kap : Introduksjon til statistisk inferens. - Konfidensintervall - Hypotesetesting - P-verdier - Statistisk signifikans
 Denne uken: kap. 6.1-6.2-6.3: Introduksjon til statistisk inferens - Konfidensintervall - Hypotesetesting - P-verdier - Statistisk signifikans VG 25/9 2011 Statistisk inferens Mål: Trekke konklusjoner
Denne uken: kap. 6.1-6.2-6.3: Introduksjon til statistisk inferens - Konfidensintervall - Hypotesetesting - P-verdier - Statistisk signifikans VG 25/9 2011 Statistisk inferens Mål: Trekke konklusjoner
TMA4245 Statistikk Eksamen desember 2016
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4245 Statistikk Eksamen desember 2016 Oppgave 1 Ei bedrift produserer elektriske komponentar. Komponentane kan ha to typar
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4245 Statistikk Eksamen desember 2016 Oppgave 1 Ei bedrift produserer elektriske komponentar. Komponentane kan ha to typar
La U og V være uavhengige standard normalfordelte variable og definer
 Binormalfordelingen Definisjon Noe av hensikten med å innføre begrepet betinget sannsynlighet er at kompliserte modeller ofte kan bygges ut fra enkle betingede modeller. Når man spesifiserer betingelser
Binormalfordelingen Definisjon Noe av hensikten med å innføre begrepet betinget sannsynlighet er at kompliserte modeller ofte kan bygges ut fra enkle betingede modeller. Når man spesifiserer betingelser
ÅMA110 Sannsylighetsregning og statistikk Løsningsforslag til eksamen høst 2010, s. 1. Oppgave 1. Histogram over frekvenser.
 ÅMA1 Sannsylighetsregning og statistikk Løsningsforslag til eksamen høst 0, s. 1 (Det tas forbehold om feil i løsningsforslaget.) a) Gjennomsnitt: x = 1 Emp. standardavvik: Median: 1 (1.33 + 1.) = 1.35
ÅMA1 Sannsylighetsregning og statistikk Løsningsforslag til eksamen høst 0, s. 1 (Det tas forbehold om feil i løsningsforslaget.) a) Gjennomsnitt: x = 1 Emp. standardavvik: Median: 1 (1.33 + 1.) = 1.35
Kapittel 2: Hendelser
 Kapittel 2: Hendelser FENOMEN Eksperiment Utfall Utfallsrom Eksperiment. Utfall. Eksperiment Utfall Hendelse Sannsynlighet: egenskaper, gunstige vs. mulige, relativ frekvens Sannsynlighet for mer enn en
Kapittel 2: Hendelser FENOMEN Eksperiment Utfall Utfallsrom Eksperiment. Utfall. Eksperiment Utfall Hendelse Sannsynlighet: egenskaper, gunstige vs. mulige, relativ frekvens Sannsynlighet for mer enn en
(Det tas forbehold om feil i løsningsforslaget.) Oppgave 1
 ÅMA1 Sannsylighetsregning og statistikk Løsningsforslag til eksamen vår 2011, s. 1 (Det tas forbehold om feil i løsningsforslaget.) Oppgave 1 a) Data: x 1, x 2, x 3, x 4, x 5 Gjennomsnitt: x = 1 5 (x 1
ÅMA1 Sannsylighetsregning og statistikk Løsningsforslag til eksamen vår 2011, s. 1 (Det tas forbehold om feil i løsningsforslaget.) Oppgave 1 a) Data: x 1, x 2, x 3, x 4, x 5 Gjennomsnitt: x = 1 5 (x 1
Seksjon 1.3 Tetthetskurver og normalfordelingen
 Seksjon 1.3 Tetthetskurver og normalfordelingen Har sett på ulike metoder for å plotte eller oppsummere data ved tall Vil nå starte på hvordan beskrive data ved modeller Hovedmetode er tetthetskurver Tetthetskurver
Seksjon 1.3 Tetthetskurver og normalfordelingen Har sett på ulike metoder for å plotte eller oppsummere data ved tall Vil nå starte på hvordan beskrive data ved modeller Hovedmetode er tetthetskurver Tetthetskurver
Løsningsforslag til obligatorisk oppgave i ECON2130 våren 2014 av Jonas Schenkel.
 Løsningsforslag til obligatorisk oppgave i ECON2130 våren 2014 av Jonas Schenkel. Det er i flere av oppgavene flere fremgangsmåter. Om din måte var riktig burde komme frem i rettingen. A Både X og Y tilfredsstiller
Løsningsforslag til obligatorisk oppgave i ECON2130 våren 2014 av Jonas Schenkel. Det er i flere av oppgavene flere fremgangsmåter. Om din måte var riktig burde komme frem i rettingen. A Både X og Y tilfredsstiller
Econ 2130 Forelesning uke 10 (HG) Geometrisk og normal fordeling
 Econ 2130 Forelesning uke 10 (HG) Geometrisk og normal fordeling 1 Geometrisk fordeling Binomisk forsøks-serie En serie likeartete forsøk med to mulige utfall, S og F, i hvert. (Modell) forutsetninger
Econ 2130 Forelesning uke 10 (HG) Geometrisk og normal fordeling 1 Geometrisk fordeling Binomisk forsøks-serie En serie likeartete forsøk med to mulige utfall, S og F, i hvert. (Modell) forutsetninger
QED 5 10. Matematikk for grunnskolelærerutdanningen. Bind 2. Fasit kapittel 4 Statistikk og kvantitativ metode
 QED 5 10 Matematikk for grunnskolelærerutdanningen Bind 2 Fasit kapittel 4 Statistikk og kvantitativ metode Kapittel 4 Oppgave 1. La x være antall øyne på terningen. a) Vi får følgende sannsynlighetsfordeling
QED 5 10 Matematikk for grunnskolelærerutdanningen Bind 2 Fasit kapittel 4 Statistikk og kvantitativ metode Kapittel 4 Oppgave 1. La x være antall øyne på terningen. a) Vi får følgende sannsynlighetsfordeling
STK1000 Uke 36, Studentene forventes å lese Ch 1.4 ( ) i læreboka (MMC). Tetthetskurver. Eksempel: Drivstofforbruk hos 32 biler
 STK1000 Uke 36, 2016. Studentene forventes å lese Ch 1.4 (+ 3.1-3.3 + 3.5) i læreboka (MMC). Tetthetskurver Eksempel: Drivstofforbruk hos 32 biler Fra histogram til tetthetskurver Anta at vi har kontinuerlige
STK1000 Uke 36, 2016. Studentene forventes å lese Ch 1.4 (+ 3.1-3.3 + 3.5) i læreboka (MMC). Tetthetskurver Eksempel: Drivstofforbruk hos 32 biler Fra histogram til tetthetskurver Anta at vi har kontinuerlige
Kapittel 3: Studieopplegg
 Oversikt over pensum Kapittel 1: Empirisk fordeling for en variabel o Begrepet fordeling o Mål for senter (gj.snitt, median) + persentiler/kvartiler o Mål for spredning (Standardavvik s, IQR) o Outliere
Oversikt over pensum Kapittel 1: Empirisk fordeling for en variabel o Begrepet fordeling o Mål for senter (gj.snitt, median) + persentiler/kvartiler o Mål for spredning (Standardavvik s, IQR) o Outliere
Løsningsforslag Eksamen S2, høsten 2016 Laget av Tommy Odland Dato: 27. januar 2017
 Løsningsforslag Eksamen S, høsten 016 Laget av Tommy Odland Dato: 7. januar 017 Del 1 - uten hjelpemidler Oppgave 1 a) Vi skal derivere f(x) = x 3 5x, og vi kommer til å få bruk for reglene (ax n ) = anx
Løsningsforslag Eksamen S, høsten 016 Laget av Tommy Odland Dato: 7. januar 017 Del 1 - uten hjelpemidler Oppgave 1 a) Vi skal derivere f(x) = x 3 5x, og vi kommer til å få bruk for reglene (ax n ) = anx
To-dimensjonale kontinuerlige fordelinger
 To-dimensjonale kontinuerlige fordelinger Noen resultater for diskrete fordelinger Vi har tidligere definert punktsannsynligheten p(x, y) for en todimensjonal variabel (X, Y ) som p(x, y) = P ({X = x}
To-dimensjonale kontinuerlige fordelinger Noen resultater for diskrete fordelinger Vi har tidligere definert punktsannsynligheten p(x, y) for en todimensjonal variabel (X, Y ) som p(x, y) = P ({X = x}
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 Eksamen i: ECON30 Statistikk UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamensdag: 03.06.06 Sensur kunngjøres: 4.06.06 Tid for eksamen: kl. 09:00 :00 Oppgavesettet er på 5 sider Tillatte hjelpemidler:
Eksamen i: ECON30 Statistikk UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamensdag: 03.06.06 Sensur kunngjøres: 4.06.06 Tid for eksamen: kl. 09:00 :00 Oppgavesettet er på 5 sider Tillatte hjelpemidler:
Hypotesetesting. Hvorfor og hvordan? Gardermoen 21. april 2016 Ørnulf Borgan. H. Aschehoug & Co Sehesteds gate 3, 0102 Oslo Tlf:
 Hypotesetesting Hvorfor og hvordan? Gardermoen 21. april 2016 Ørnulf Borgan H. Aschehoug & Co Sehesteds gate 3, 0102 Oslo Tlf: 22 400 400 www.aschehoug.no 1 Oversikt Sannsynlighetsregning og statistikk
Hypotesetesting Hvorfor og hvordan? Gardermoen 21. april 2016 Ørnulf Borgan H. Aschehoug & Co Sehesteds gate 3, 0102 Oslo Tlf: 22 400 400 www.aschehoug.no 1 Oversikt Sannsynlighetsregning og statistikk
Togforsinkelsen (Eksamen Des2003.1a) I denne oppgaven kan du bruke uten å vise det at
 Kapittel 4 Forventningsverdi, varians, kovarians for én stokastisk variabel og funksjoner av stokastiske variabler TMA4245 V2007: Eirik Mo 2 4.1 Forventing til en stokastisk variabel DEF 4.1: La X være
Kapittel 4 Forventningsverdi, varians, kovarians for én stokastisk variabel og funksjoner av stokastiske variabler TMA4245 V2007: Eirik Mo 2 4.1 Forventing til en stokastisk variabel DEF 4.1: La X være
EKSAMEN. TILLATTE HJELPEMIDLER: Kalkulator. Hornæs: Formelsamling statistikk HiG. John Haugan: Formler og tabeller.
 KANDIDATNUMMER: EKSAMEN FAGNAVN: FAGNUMMER: Statistikk. REA1081 EKSAMENSDATO: 11. juni 2007. KLASSE: Ingeniørklasser. TID: kl. 9.00 13.00. FAGLÆRER: Hans Petter Hornæs ANTALL SIDER UTLEVERT: 4 (innkl.
KANDIDATNUMMER: EKSAMEN FAGNAVN: FAGNUMMER: Statistikk. REA1081 EKSAMENSDATO: 11. juni 2007. KLASSE: Ingeniørklasser. TID: kl. 9.00 13.00. FAGLÆRER: Hans Petter Hornæs ANTALL SIDER UTLEVERT: 4 (innkl.
Siden vi her har brukt første momentet i fordelingen (EX = EX 1 ) til å konstruere estimatoren kalles denne metoden for momentmetoden.
 Estimeringsmetoder Momentmetoden La X, X 2,..., X n være uavhengige variable som er rektangulært fordelte på intervallet [0, θ]. Vi vet da at forventningsverdiene til hver observasjon og forventningen
Estimeringsmetoder Momentmetoden La X, X 2,..., X n være uavhengige variable som er rektangulært fordelte på intervallet [0, θ]. Vi vet da at forventningsverdiene til hver observasjon og forventningen
Verdens statistikk-dag.
 Verdens statistikk-dag http://unstats.un.org/unsd/wsd/ Signifikanstester Ønsker å teste hypotese om populasjon Bruker data til å teste hypotese Typisk prosedyre Beregn sannsynlighet for utfall av observator
Verdens statistikk-dag http://unstats.un.org/unsd/wsd/ Signifikanstester Ønsker å teste hypotese om populasjon Bruker data til å teste hypotese Typisk prosedyre Beregn sannsynlighet for utfall av observator
Løsningsforslag Eksamen i Statistikk SIF5060 Aug 2002
 Løsningsforslag Eksamen i Statistikk SIF5060 Aug 2002 Oppgave 1 a) En god estimator er forventningsrett og har liten varians. Vi tester forventningsretthet: E[ˆµ] E[Y ] µ E[ µ] E[ 1 2 X + 1 2 Y ] 1 2 E[X]
Løsningsforslag Eksamen i Statistikk SIF5060 Aug 2002 Oppgave 1 a) En god estimator er forventningsrett og har liten varians. Vi tester forventningsretthet: E[ˆµ] E[Y ] µ E[ µ] E[ 1 2 X + 1 2 Y ] 1 2 E[X]
A) B) 400 C) 120 D) 60 E) 10. Rett svar: C. Fasit: ( 5 6 = 60. Hvis A, B, C er en partisjon av utfallsrommet S, så er P (A B) lik.
 Oppgave 1 Det skal velges en komité bestående av 2 menn og 1 kvinne. Komitéen skal velges fra totalt 5 menn og 6 kvinner. Hvor mange ulike komitéer kan dannes? A) 86400 B) 400 C) 120 D) 60 E) 10 Rett svar:
Oppgave 1 Det skal velges en komité bestående av 2 menn og 1 kvinne. Komitéen skal velges fra totalt 5 menn og 6 kvinner. Hvor mange ulike komitéer kan dannes? A) 86400 B) 400 C) 120 D) 60 E) 10 Rett svar:
Observatorer. STK Observatorer - Kap 6. Utgangspunkt. Eksempel høyde Oxford studenter
 Observatorer STK00 - Observatorer - Kap 6 Geir Storvik 4. april 206 Så langt: Sannsynlighetsteori Stokastiske modeller Nå: Data Knytte data til stokastiske modeller Utgangspunkt Eksempel høyde Oxford studenter
Observatorer STK00 - Observatorer - Kap 6 Geir Storvik 4. april 206 Så langt: Sannsynlighetsteori Stokastiske modeller Nå: Data Knytte data til stokastiske modeller Utgangspunkt Eksempel høyde Oxford studenter
TMA4240 Statistikk H2010
 TMA4240 Statistikk H2010 Statistisk inferens: 8.1: Tilfeldig utvalg 9.1-9.3: Estimering Mette Langaas Foreleses uke 40, 2010 2 Utfordring Ved en bedrift produseres en elektrisk komponent. Komponenten må
TMA4240 Statistikk H2010 Statistisk inferens: 8.1: Tilfeldig utvalg 9.1-9.3: Estimering Mette Langaas Foreleses uke 40, 2010 2 Utfordring Ved en bedrift produseres en elektrisk komponent. Komponenten må
Utfordring. TMA4240 Statistikk H2010. Mette Langaas. Foreleses uke 40, 2010
 TMA4240 Statistikk H2010 Statistisk inferens: 8.1: Tilfeldig utvalg 9.1-9.3: Estimering Mette Langaas Foreleses uke 40, 2010 2 Utfordring Ved en bedrift produseres en elektrisk komponent. Komponenten må
TMA4240 Statistikk H2010 Statistisk inferens: 8.1: Tilfeldig utvalg 9.1-9.3: Estimering Mette Langaas Foreleses uke 40, 2010 2 Utfordring Ved en bedrift produseres en elektrisk komponent. Komponenten må
Snøtetthet. Institutt for matematiske fag, NTNU 15. august Notat for TMA4240/TMA4245 Statistikk
 Snøtetthet Notat for TMA424/TMA4245 Statistikk Institutt for matematiske fag, NTNU 5. august 22 I forbindelse med varsling av om, klimaforskning og særlig kraftproduksjon er det viktig å kunne anslå hvor
Snøtetthet Notat for TMA424/TMA4245 Statistikk Institutt for matematiske fag, NTNU 5. august 22 I forbindelse med varsling av om, klimaforskning og særlig kraftproduksjon er det viktig å kunne anslå hvor
LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4240 STATISTIKK Mandag 12. desember 2011
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 10 LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4240 STATISTIKK Mandag 12. desember 2011 Oppgave 1 Oljeleting a) Siden P(A
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 10 LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4240 STATISTIKK Mandag 12. desember 2011 Oppgave 1 Oljeleting a) Siden P(A
Bruk data fra tabellen over (utvalget) og opplysninger som blir gitt i oppgavene og svar på følgende spørsmål:
 Frafall fra videregende skole (VGS) er et stort problem. Bare ca 70% av elevene som begynner p VGS fullfører og bestr i løpet av 5 r. For noen elever er skolen s lite attraktiv at de velger slutte før
Frafall fra videregende skole (VGS) er et stort problem. Bare ca 70% av elevene som begynner p VGS fullfører og bestr i løpet av 5 r. For noen elever er skolen s lite attraktiv at de velger slutte før
Statistikk og dataanalyse
 Njål Foldnes, Steffen Grønneberg og Gudmund Horn Hermansen Statistikk og dataanalyse En moderne innføring Kapitteloversikt del 1 INTRODUKSJON TIL STATISTIKK Kapittel 1 Populasjon og utvalg 19 Kapittel
Njål Foldnes, Steffen Grønneberg og Gudmund Horn Hermansen Statistikk og dataanalyse En moderne innføring Kapitteloversikt del 1 INTRODUKSJON TIL STATISTIKK Kapittel 1 Populasjon og utvalg 19 Kapittel
Fasit og løsningsforslag STK 1110
 Fasit og løsningsforslag STK 1110 Uke 36: Eercise 8.4: a) (57.1, 59.5), b) (57.7, 58, 9), c) (57.5, 59.1), d) (57.9, 58.7) og e) n 239. (Hint: l(n) = 1 = 2z 1 α/2 σ/n 1/2 ). Eercise 8.10: a) (2.7, 7.5),
Fasit og løsningsforslag STK 1110 Uke 36: Eercise 8.4: a) (57.1, 59.5), b) (57.7, 58, 9), c) (57.5, 59.1), d) (57.9, 58.7) og e) n 239. (Hint: l(n) = 1 = 2z 1 α/2 σ/n 1/2 ). Eercise 8.10: a) (2.7, 7.5),
Denne uken: kap : Introduksjon til statistisk inferens. - Konfidensintervall - Hypotesetesting - P-verdier - Statistisk signifikans
 Denne uken: kap. 6.1-6.2-6.3: Introduksjon til statistisk inferens - Konfidensintervall - Hypotesetesting - P-verdier - Statistisk signifikans VG 25/9 2011 Statistisk inferens Mål: Trekke konklusjoner
Denne uken: kap. 6.1-6.2-6.3: Introduksjon til statistisk inferens - Konfidensintervall - Hypotesetesting - P-verdier - Statistisk signifikans VG 25/9 2011 Statistisk inferens Mål: Trekke konklusjoner
TMA4240 Statistikk 2014
 TMA4240 Statistikk 2014 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 12, blokk II Oppgave 1 På ein av vegane inn til Trondheim er UP interessert i å måle effekten
TMA4240 Statistikk 2014 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 12, blokk II Oppgave 1 På ein av vegane inn til Trondheim er UP interessert i å måle effekten
ST0202 Statistikk for samfunnsvitere
 ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag 2 Statistisk inferens (kap. 8) Statistisk inferens er å tolke/analysere resultater fra utvalget for å finne ut mest mulig
ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag 2 Statistisk inferens (kap. 8) Statistisk inferens er å tolke/analysere resultater fra utvalget for å finne ut mest mulig
Eksamen i. MAT110 Statistikk 1
 Avdeling for logistikk Eksamen i MAT110 Statistikk 1 Eksamensdag : Tirsdag 22. mai 2018 Tid : 09:00 13:00 (4 timer) Faglærer/telefonnummer : Molde + Kristiansund: Per Kristian Rekdal / 924 97 051 Hjelpemidler
Avdeling for logistikk Eksamen i MAT110 Statistikk 1 Eksamensdag : Tirsdag 22. mai 2018 Tid : 09:00 13:00 (4 timer) Faglærer/telefonnummer : Molde + Kristiansund: Per Kristian Rekdal / 924 97 051 Hjelpemidler
EKSAMEN. TILLATTE HJELPEMIDLER: Kalkulator. Hornæs: Formelsamling statistikk HiG. John Haugan: Formler og tabeller.
 KANDIDATNUMMER: EKSAMEN FAGNAVN: FAGNUMMER: Statistikk. BtG207 EKSAMENSDATO: 11. juni 2007. KLASSE: HIS 05 08. TID: kl. 8.00 13.00. FAGLÆRER: Hans Petter Hornæs ANTALL SIDER UTLEVERT: 5 (innkl. forside)
KANDIDATNUMMER: EKSAMEN FAGNAVN: FAGNUMMER: Statistikk. BtG207 EKSAMENSDATO: 11. juni 2007. KLASSE: HIS 05 08. TID: kl. 8.00 13.00. FAGLÆRER: Hans Petter Hornæs ANTALL SIDER UTLEVERT: 5 (innkl. forside)
Fordelinger, mer om sentralmål og variasjonsmål. Tron Anders Moger
 Fordelinger, mer om sentralmål og variasjonsmål Tron Anders Moger 20. april 2005 1 Forrige gang: Så på et eksempel med data over medisinerstudenter Lærte hvordan man skulle få oversikt over dataene ved
Fordelinger, mer om sentralmål og variasjonsmål Tron Anders Moger 20. april 2005 1 Forrige gang: Så på et eksempel med data over medisinerstudenter Lærte hvordan man skulle få oversikt over dataene ved
statistikk, våren 2011
 ÅMA110 Sannsynlighetsregning med statistikk, våren 011 Kp. 3 Diskrete tilfeldige variable 1 Diskrete tilfeldige variable, innledning Hva er en tilfeldig variabel (stokastisk variabel)? Diskret tilfeldig
ÅMA110 Sannsynlighetsregning med statistikk, våren 011 Kp. 3 Diskrete tilfeldige variable 1 Diskrete tilfeldige variable, innledning Hva er en tilfeldig variabel (stokastisk variabel)? Diskret tilfeldig
ÅMA110 Sannsynlighetsregning med statistikk, våren
 ÅMA110 Sannsynlighetsregning med statistikk, våren 2006 Oppsummering Bjørn H. Auestad Institutt for matematikk og naturvitenskap Universitetet i Stavanger 24. april Bjørn H. Auestad Oppsummering våren
ÅMA110 Sannsynlighetsregning med statistikk, våren 2006 Oppsummering Bjørn H. Auestad Institutt for matematikk og naturvitenskap Universitetet i Stavanger 24. april Bjørn H. Auestad Oppsummering våren
Datamatrisen: observasjoner, variabler og verdier. Variablers målenivå: Nominal Ordinal Intervall Forholdstall (ratio)
 Datamatrisen: observasjoner, variabler og verdier. Variablers målenivå: Nominal Ordinal Intervall Forholdstall (ratio) Beskrive fordelinger (sentraltendens, variasjon og form): Observasjon y i Sentraltendens
Datamatrisen: observasjoner, variabler og verdier. Variablers målenivå: Nominal Ordinal Intervall Forholdstall (ratio) Beskrive fordelinger (sentraltendens, variasjon og form): Observasjon y i Sentraltendens
Statistisk inferens (kap. 8) Hovedtyper av statistisk inferens. ST0202 Statistikk for samfunnsvitere
 2 Statistisk inferens (kap. 8) Statistisk inferens er å tolke/analysere resultater fra utvalget for å finne ut mest mulig om populasjonen. Konkret: Å analysere en utvalgsobservator for å trekke slutninger
2 Statistisk inferens (kap. 8) Statistisk inferens er å tolke/analysere resultater fra utvalget for å finne ut mest mulig om populasjonen. Konkret: Å analysere en utvalgsobservator for å trekke slutninger
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 Utsatt eksamen i: ECON2130 - Statistikk 1 Eksamensdag: 19.06.2014 Tid for eksamen: kl. 09:00 12:00 Oppgavesettet er på 4 sider UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Tillatte hjelpemidler: Alle trykte
Utsatt eksamen i: ECON2130 - Statistikk 1 Eksamensdag: 19.06.2014 Tid for eksamen: kl. 09:00 12:00 Oppgavesettet er på 4 sider UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Tillatte hjelpemidler: Alle trykte
Forelesning 5: Kontinuerlige fordelinger, normalfordelingen. Jo Thori Lind
 Forelesning 5: Kontinuerlige fordelinger, normalfordelingen Jo Thori Lind j.t.lind@econ.uio.no Oversikt 1. Kontinuerlige fordelinger 2. Uniform fordeling 3. Normal-fordelingen 1. Kontinuerlige fordelinger
Forelesning 5: Kontinuerlige fordelinger, normalfordelingen Jo Thori Lind j.t.lind@econ.uio.no Oversikt 1. Kontinuerlige fordelinger 2. Uniform fordeling 3. Normal-fordelingen 1. Kontinuerlige fordelinger
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Øvelsesoppgave i: ECON30- Statistikk Dato for utlevering: 5.03.06 Dato for innlevering: 05.04.06 innen kl. 5:00 Innleveringssted: Ekspedisjonen i. etasje ES hus
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Øvelsesoppgave i: ECON30- Statistikk Dato for utlevering: 5.03.06 Dato for innlevering: 05.04.06 innen kl. 5:00 Innleveringssted: Ekspedisjonen i. etasje ES hus
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 Øvelsesoppgave i: ECON2130 Statistikk 1 Dato for utlevering: Mandag 22. mars 2010 Dato for innlevering: Fredag 9. april 2010 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Innleveringssted: Ved siden av SV-info-senter
Øvelsesoppgave i: ECON2130 Statistikk 1 Dato for utlevering: Mandag 22. mars 2010 Dato for innlevering: Fredag 9. april 2010 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Innleveringssted: Ved siden av SV-info-senter
Illustrasjon av regel 5.19 om sentralgrenseteoremet og litt om heltallskorreksjon (som i eksempel 5.20).
 Econ 130 HG mars 017 Supplement til forelesningen 7. februar Illustrasjon av regel 5.19 om sentralgrenseteoremet og litt om heltallskorreksjon (som i eksempel 5.0). Regel 5.19 sier at summer, Y X1 X X
Econ 130 HG mars 017 Supplement til forelesningen 7. februar Illustrasjon av regel 5.19 om sentralgrenseteoremet og litt om heltallskorreksjon (som i eksempel 5.0). Regel 5.19 sier at summer, Y X1 X X
Oppgavesett nr. 5. MAT110 Statistikk 1, Et transportfirma har et varemottak for lastebiler med spesialgods, se figur 1.
 Innleveringsfrist: mandag 19. mars kl. 16:00 (version 01) Oppgavesett nr. 5 MAT110 Statistikk 1, 2018 Oppgave 1: ( logistikk ) Et transportfirma har et varemottak for lastebiler med spesialgods, se figur
Innleveringsfrist: mandag 19. mars kl. 16:00 (version 01) Oppgavesett nr. 5 MAT110 Statistikk 1, 2018 Oppgave 1: ( logistikk ) Et transportfirma har et varemottak for lastebiler med spesialgods, se figur
TMA4245 Statistikk. Innlevering 3. Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag
 TMA4245 Statistikk Vår 2017 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Innlevering 3 Dette er den første av to innleveringer i blokk 2 Denne øvingen skal oppsummere pensum
TMA4245 Statistikk Vår 2017 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Innlevering 3 Dette er den første av to innleveringer i blokk 2 Denne øvingen skal oppsummere pensum
Oblig 1 i MAT2400. Oppgave 1. Tor Hedin Brønner. a) Vi tar integralet av f X (x) fra til x: = 1. Medianen, µ, finner vi ved å sette.
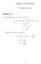 Oblig 1 i MAT24 Tor Hedin Brønner Oppgave 1. a) Vi tar integralet av f X (x) fra til x: x f X (x) dy = Medianen, µ, finner vi ved å sette.5 = µ dy + x = [ θ y θ] x = θ x θ + θ θ ( θ = 1 x) µ θ = θ.5 µ
Oblig 1 i MAT24 Tor Hedin Brønner Oppgave 1. a) Vi tar integralet av f X (x) fra til x: x f X (x) dy = Medianen, µ, finner vi ved å sette.5 = µ dy + x = [ θ y θ] x = θ x θ + θ θ ( θ = 1 x) µ θ = θ.5 µ
QED 1 7. Matematikk for grunnskolelærerutdanningen. Bind 2. Fasit kapittel 4 Statistikk og kvantitativ metode
 QED 1 7 Matematikk for grunnskolelærerutdanningen Bind 2 Fasit kapittel 4 Statistikk og kvantitativ metode Kapittel 4 Oppgave 1 La være antall øyne på terningen. a) Vi får følgende sannsynlighetsfordeling
QED 1 7 Matematikk for grunnskolelærerutdanningen Bind 2 Fasit kapittel 4 Statistikk og kvantitativ metode Kapittel 4 Oppgave 1 La være antall øyne på terningen. a) Vi får følgende sannsynlighetsfordeling
Eksamensoppgåve i TMA4240 Statistikk
 Institutt for matematiske fag Eksamensoppgåve i TMA4240 Statistikk Fagleg kontakt under eksamen: Mette Langaas a, Ingelin Steinsland b, Geir-Arne Fuglstad c Tlf: a 988 47 649, b 926 63 096, c 452 70 806
Institutt for matematiske fag Eksamensoppgåve i TMA4240 Statistikk Fagleg kontakt under eksamen: Mette Langaas a, Ingelin Steinsland b, Geir-Arne Fuglstad c Tlf: a 988 47 649, b 926 63 096, c 452 70 806
Oppgaven består av 10 delspørsmål som anbefales å veie like mye, Kommentarer og tallsvar er skrevet inn mellom <<, >>, Oppgave 1
 ECON 130 EKSAMEN 005 VÅR SENSORVEILEDNING Oppgaven består av 10 delspørsmål som anbefales å veie like mye, Kommentarer og tallsvar er skrevet inn mellom , Oppgave 1 I denne oppgaven kan du anta at
ECON 130 EKSAMEN 005 VÅR SENSORVEILEDNING Oppgaven består av 10 delspørsmål som anbefales å veie like mye, Kommentarer og tallsvar er skrevet inn mellom , Oppgave 1 I denne oppgaven kan du anta at
TMA4240 Statistikk Høst 2015
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 8, blokk II Løsningsskisse Oppgave 1 Da komponentene danner et parallellsystem, vil systemet fungere dersom minst
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 8, blokk II Løsningsskisse Oppgave 1 Da komponentene danner et parallellsystem, vil systemet fungere dersom minst
ST0202 Statistikk for samfunnsvitere Kapittel 13: Lineær regresjon og korrelasjon
 ST0202 Statistikk for samfunnsvitere Kapittel 13: Lineær regresjon og korrelasjon Bo Lindqvist Institutt for matematiske fag http://wiki.math.ntnu.no/st0202/2012h/start 2 Kap. 13: Lineær korrelasjons-
ST0202 Statistikk for samfunnsvitere Kapittel 13: Lineær regresjon og korrelasjon Bo Lindqvist Institutt for matematiske fag http://wiki.math.ntnu.no/st0202/2012h/start 2 Kap. 13: Lineær korrelasjons-
Tilfeldige variabler. MAT0100V Sannsynlighetsregning og kombinatorikk
 MAT0100V Sannsynlighetsregning og kombinatorikk Forventning, varians og standardavvik Tilnærming av binomiske sannsynligheter Konfidensintervall Ørnulf Borgan Matematisk institutt Universitetet i Oslo
MAT0100V Sannsynlighetsregning og kombinatorikk Forventning, varians og standardavvik Tilnærming av binomiske sannsynligheter Konfidensintervall Ørnulf Borgan Matematisk institutt Universitetet i Oslo
ØVINGER 2017 Løsninger til oppgaver. Øving 1
 ØVINGER 017 Løsninger til oppgaver Øving 1.1. Frekvenstabell For å lage en frekvenstabell må vi telle antall observasjoner av hvert antall henvendelser. Siden antall henvendelser på en gitt dag alltid
ØVINGER 017 Løsninger til oppgaver Øving 1.1. Frekvenstabell For å lage en frekvenstabell må vi telle antall observasjoner av hvert antall henvendelser. Siden antall henvendelser på en gitt dag alltid
Løsningsforslag Eksamen S2, høsten 2017 Laget av Tommy O. Sist oppdatert: 26. november 2017
 Løsningsforslag Eksamen S, høsten 017 Laget av Tommy O. Sist oppdatert: 6. november 017 Del 1 - uten hjelpemidler Oppgave 1 a) Vi skal derivere f(x) = x 4x 3. Vi bruker regelen samt regelen (x n ) = nx
Løsningsforslag Eksamen S, høsten 017 Laget av Tommy O. Sist oppdatert: 6. november 017 Del 1 - uten hjelpemidler Oppgave 1 a) Vi skal derivere f(x) = x 4x 3. Vi bruker regelen samt regelen (x n ) = nx
Statistisk inferens: 9.14: Sannsynlighetsmaksimeringsestimatoren 8.5: Fordeling til gjennomsnittet 9.4: Konfidensintervall for µ (σ kjent)
 TMA440 Statistikk H010 Statistisk inferens: 9.14: Sannsynlighetsmaksimeringsestimatoren 8.5: Fordeling til gjennomsnittet 9.4: Konfidensintervall for µ (σ kjent) Mette Langaas Foreleses mandag 11.oktober,
TMA440 Statistikk H010 Statistisk inferens: 9.14: Sannsynlighetsmaksimeringsestimatoren 8.5: Fordeling til gjennomsnittet 9.4: Konfidensintervall for µ (σ kjent) Mette Langaas Foreleses mandag 11.oktober,
Løsningsforslag, eksamen statistikk, juni 2015
 Løsningsforslag, eksamen statistikk, juni 0 Oppgave 1 Siden det spørres om tall fra et intervall, som oppgaven viser kan være et reelle, er det tydelig at tallene er tatt fra en kontinuerlig fordeling.
Løsningsforslag, eksamen statistikk, juni 0 Oppgave 1 Siden det spørres om tall fra et intervall, som oppgaven viser kan være et reelle, er det tydelig at tallene er tatt fra en kontinuerlig fordeling.
Eksamensoppgave i ST1201/ST6201 Statistiske metoder
 Institutt for matematiske fag Eksamensoppgave i ST1201/ST6201 Statistiske metoder Faglig kontakt under eksamen: Nikolai Ushakov Tlf: 45128897 Eksamensdato: 04. desember 2015 Eksamenstid (fra til): 09:00
Institutt for matematiske fag Eksamensoppgave i ST1201/ST6201 Statistiske metoder Faglig kontakt under eksamen: Nikolai Ushakov Tlf: 45128897 Eksamensdato: 04. desember 2015 Eksamenstid (fra til): 09:00
