Diskrete sannsynlighetsfordelinger.
|
|
|
- Sindre Lund
- 9 år siden
- Visninger:
Transkript
1 Diskrete sannsynlighetsfordelinger. Dekkes av kapittel 5 i læreboka. Husk: f() er punktsannsynligheten til en diskret X dersom: 1. f() 0 2. f() =1 3. f() =P (X = ) Vi skal nå sepå situasjoner der vi har en bestemt form på f() (f() gitt ved en kjent parametrisk funksjon). Diskret uniform fordeling (5.2) Dersom X har k mulige verdier 1,, k og alle er like sannsynlige sier vi at X er diskret uniform fordelt. Har da at f() =f(; k) = 1 k,= 1,, k Eksempel: Terningkast, k =6, 1 =1, 2 = 2,, 6 =6. Forventningogvarians: μ =E(X) = f() = 1 k = 1 k σ 2 =Var(X) = ( μ) 2 f() = 1 ( μ) 2 k Eksempel: Terningkast. E(X) = 1 6 Var(X) = =3.5 =1 6 ( 3.5) 2 =2.92 =1 1 2
2 Binomisk fordeling (5.3) I situasjoner karakterisert ved n uavhengige enkeltforsøk. Sjekker suksess eller ikke suksess i hvert enkeltforsøk (om en bestemt hendelse inntreffer eller ikke). Sannsynligheten for suksess er den samme i alle enkeltforsøk, p. har vi at X = antall suksesser i de n forsøkene er binomisk fordelt med parametre n og p. Vi skriver X B(n, p), og har at (se boka for detaljer) f() =b(; n, p) =( n )p (1 p) n, Det kan videre vises at: E(X) =np og Var(X) =np(1 p) =0, 1,...,n. Eksempler på ting som typisk er binomisk fordelt: Antall komponenter i en test som fungerer etter tid t. Antall personer for EU i et tilfeldig utvalg. Antall pasienter som får en infeksjon på en sykehusavdeling. Antall brønner hvor man finner olje. Antall 6ere i n terningkast. Multinomisk fordeling (5.3) Generalisering av binomisk fordeling til situasjoner der man har mer enn to mulige utfall. n uavhengige enkeltforsøk. Hvert enkeltforsøk har k mulige utfall. Sannsynlighetene, p 1,...,p k forhveravde k utfallene er de samme i alle enkeltforsøk. Da er simultanfordelingen til X 1,...,X k,derx j 3 4
3 representerer antall ganger utfall j inntreffer, j =1,...,k,enmultinomisk fordeling med parametre n og p 1,...,p k. Har da (kan vises): f( 1,..., k ; p 1,...,p k,n)= n! 1! k! p 1 1 p k k der k i=1 i = n og k i=1 p i = 1. Det kan også vises at E(X i )=np i, Var(X i )=np i (1 p i ), Cov(X i,x j )= np i p j for i j. Eksempel: En kafe selger tre sorter kaffe, vanlig, cappucino og espresso. De har registrert at 44% av kundene som bestiller kaffe bestiller vanlig kaffe, 32% cappucino og 24% bestiller espresso. 6 personer kommer til kafeen for åta en kaffe - hva er sannsynligheten for at tre av dem bestiller vanlig kaffe, to av dem cappucino og en av dem espresso? Vi har p 1 =0.44, p 2 =0.32 og p 3 =0.24, og får: f(3, 2, 1) = 6! 3!2!1! =0.13 Hypergeometrisk fordeling (5.4) Brukes i situasjoner karakterisert ved Totalt N enheter. k av de N enhetene er suksesser (og dermed N k ikke suksesser ). Trekker ut n enheter uten tilbakelegging. Har da at X = antall suksesser blant de n er hypergeometrisk fordelt med parametre N, k og n. f() = og E(X) = nk N ( k )( N k n ) ( N n ), =0, 1,...,min(k, n), N n og Var(X) = N 1 n k N (1 k N ). 5 6
4 Negativt binomisk fordeling (5.5) Dersom vi har: Eksempler på ting som er hypergeometrisk fordelt: Antall vinnerlodd man trekker ut i en loddtrekning. Antall spar i en korthånd. Antall defekte varer man avdekker i en stikkprøve. Merk: Trekker man med tilbakelegging blir X binomisk fordelt. Dersom N>>ner det liten forskjell på trekning med og uten tilbakelegging - kan da tilnærme hypergeometrisk med binomisk med parametre n = n og p = k/n. Uavhengige enkeltforsøk inntil k suksesser er observert. Sjekker suksess eller ikke suksess i hvert enkeltforsøk. Sannsynligheten for suksess er den samme i alle enkeltforsøk, p. og X = antall forsøk til kte suksess er X negativt binomisk fordelt med parametre k og p. Merk: Ved binomisk ser vi på antall suksesser i et gitt antall forsøk (antall suksesser stokastisk), mens ved negativt binomisk ser vi på antall forsøk som må gjøresforåfåetgittantall suksesser (antall forsøk stokastisk). Det kan vises ved et tilsvarende resonnement som for binomisk fordeling (se detaljer i boka) at: 7 8
5 f() =b (; k, p) =( 1 k 1 )pk (1 p) k, og at E(X) = k p, 1 p Var(X) =k p 2 Eksempler på ting som typisk er negativt binomisk fordelt: Antall komponenter man må produsere før man har k feilfrie komponenter. Antall hus en støvsugerselger må besøke før han har solgt k støvsugere. Antall personer man må spørre for åfå k underskrifter til en underskriftskampanje. Antall ganger man må kaste en terning før man har fått 6er k ganger. Eksempel: Ved en porselensfabrikk gjør man en kvalitetssjekk på alle ferdige produkt. Kun produkt klassifisert som A-vare sendes til vanlig salg. For en type tallerkener har man erfart at 91% av de ferdig produserte tallerkenene = k, k+1,.. klassifiseres til A-vare. Tallerkenene pakkes i esker med 6 stk. Hva er sannsynligheten for at man må sjekkes 8 eller flere tallerker før man har nok tallerker klassifisert til A-vare til å fylle en eske? Og hva er forventet antall tallerker man må sjekke? P (X 8) = 1 [P (X =6)+P (X =7)] =1 ( )0.916 (1 0.91) 6 6 ( )0.916 (1 0.91) 7 6 = = E(X)= k p = =6.6 Geometrisk fordeling (5.5) Spesialtilfelle av negativt binomisk der man ser på antall forsøk til første suksess, dvs k =1. F.eks. antall prøveboringer man må gjøre før første gang man finner olje. 9 10
6 Poisson-fordeling (5.6) Typisk for Poisson-forsøk er at vi ser på antall forekomster av en hendelse innenfor et tidsintervall eller et spesifisert område. Eksempler på ting som typisk er Poissonfordelt: Antall telefoner til et kontor i løpet av en time. Antall visninger av en webside per time. Antall trafikkulykker på enveistrekningi løpet av ett år. Antall utrykninger fra en brannstasjon per uke. Antall trykkfeil per side i en bok. Antall trær per mål i en skog. Forekomsten av hendelser følger en Poissonprosess dersom: 1. Antallene hendelser i ikke-overlappende intervaller er uavhengige. 2. For ethvert lite intervall [s, s + Δs] er P (en hendelse i [s, s +Δs]) λδs. 3. P (to eller flere hendelser i [s, s +Δs]) 0. Dersom dette er oppfylt er X= antall hendelser i[0,t] Poisson-fordelt med parameter μ = λt. Det kan da vises at: f() =p(; λt) = (λt) e λt, =0, 1, 2,...! og at E(X) =λt og Var(X) =λt. Parameteren λ representerer forventet antall hendelser per enhet og kalles intensiteten til prosessen. Vi skal lære mer om Poisson-prosesser senere i kurset
7 Poisson-fordeling som tilnærming til binomisk fordeling. Når n er stor og p nær 0 (eller 1) kan binomisk fordeling tilnærmes med Poisson-fordeling med μ = np. (Nyttig fordi det gir enklere regning). Eksempel: Antall vinnerrekker i lotto. Sanns. for at en rekke gir 7 rette er p =1/( 34 7 )= 1/ Antall innleverte rekker en uke er ca n = La X= antall rekker som har 7 rette. Vi har da at X B(n, p) Poisson(μ), der μ = np = / = Dvs: f(0) = P (X =0) e 4.37 = ! f(1) = P (X =1) e 4.37 = ! f() f()
Diskrete sannsynlighetsfordelinger.
 Diskrete sannsynlighetsfordelinger. Dekkes av kapittel 5 i læreboka. Husk: f(x) er punktsannsynligheten til en diskret X dersom: 1. f(x) 0 2. x f(x) =1 3. f(x) =P (X = x) Vi skal nå sepå situasjoner der
Diskrete sannsynlighetsfordelinger. Dekkes av kapittel 5 i læreboka. Husk: f(x) er punktsannsynligheten til en diskret X dersom: 1. f(x) 0 2. x f(x) =1 3. f(x) =P (X = x) Vi skal nå sepå situasjoner der
TMA4240/TMA4245 Statistikk Oppsummering diskrete sannsynlighetsfordelinger
 TMA4240/TMA4245 Statistikk Oppsummering diskrete sannsynlighetsfordelinger Binomisk fordeling* ( ) n b(x; n, p) = p x (1 p) n x = x ( ) n p x q n x, x x = 0, 1, 2,..., n Fenomén: i) n forsøk. ii) Suksess/fiasko
TMA4240/TMA4245 Statistikk Oppsummering diskrete sannsynlighetsfordelinger Binomisk fordeling* ( ) n b(x; n, p) = p x (1 p) n x = x ( ) n p x q n x, x x = 0, 1, 2,..., n Fenomén: i) n forsøk. ii) Suksess/fiasko
Bernoulli forsøksrekke og binomisk fordeling
 Bernoulli forsøksrekke og binomisk fordeling Bernoulli forsøksrekke i) gjentar et forsøk n ganger ii) hvert forsøk gir enten suksess eller fiasko iii) sannsynligheten for suksess er p i alle forsøkene
Bernoulli forsøksrekke og binomisk fordeling Bernoulli forsøksrekke i) gjentar et forsøk n ganger ii) hvert forsøk gir enten suksess eller fiasko iii) sannsynligheten for suksess er p i alle forsøkene
Kontinuerlige sannsynlighetsfordelinger.
 Kontinuerlige sannsynlighetsfordelinger. Dekkes av kap. 6 og deler av kap. 8.5 i boka. Husk: f(x) er sannsynlighetstettheten til en kontinuerlig X dersom: 1. f(x) 0 for alle x R 2. f(x)dx =1 3. P (a
Kontinuerlige sannsynlighetsfordelinger. Dekkes av kap. 6 og deler av kap. 8.5 i boka. Husk: f(x) er sannsynlighetstettheten til en kontinuerlig X dersom: 1. f(x) 0 for alle x R 2. f(x)dx =1 3. P (a
TMA4240 Statistikk Høst 2009
 TMA4240 Statistikk Høst 2009 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 5 Løsningsskisse Oppgave 1 En lottorekke kan oppfattes som et ikke-ordnet utvalg på
TMA4240 Statistikk Høst 2009 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 5 Løsningsskisse Oppgave 1 En lottorekke kan oppfattes som et ikke-ordnet utvalg på
Kontinuerlige sannsynlighetsfordelinger.
 Kontinuerlige sannsynlighetsfordelinger. Dekkes av kap. 6 og deler av kap. 8.5 i boka. Husk: f(x er sannsynlighetstettheten til en kontinuerlig X dersom:. f(x 0 for alle x R 2. f(xdx = 3. P (a
Kontinuerlige sannsynlighetsfordelinger. Dekkes av kap. 6 og deler av kap. 8.5 i boka. Husk: f(x er sannsynlighetstettheten til en kontinuerlig X dersom:. f(x 0 for alle x R 2. f(xdx = 3. P (a
TMA4240 Statistikk H2010 Kapittel 5: Diskrete sannsynlighetsfordelinger : Uniform, binomisk, hypergeometrisk fordeling
 TMA4240 Statistikk H2010 Kapittel 5: Diskrete sannsynlighetsfordelinger 5.1-5.4: Uniform, binomisk, hypergeometrisk fordeling Mette Langaas 2 Arbeidshverdag etter endt studium Studere et fenomen (f.eks.
TMA4240 Statistikk H2010 Kapittel 5: Diskrete sannsynlighetsfordelinger 5.1-5.4: Uniform, binomisk, hypergeometrisk fordeling Mette Langaas 2 Arbeidshverdag etter endt studium Studere et fenomen (f.eks.
5.2 Diskret uniform fordeling. Midtveiseksamen (forts.) Kapittel 5. Noen diskrete sannsynlighetsfordelinger. TMA4245 V2007: Eirik Mo
 Histogram of x 1 2 3 4 5 6 x 0 1 2 3 4 5 6 3 Midtveiseksamen oppg. 1a eksamen 06.08.2004 Kapittel 5 Noen diskrete sannsynlighetsfordelinger TMA4245 V2007: Eirik Mo Høsten 2004 ble det i TMA4240 bli innført
Histogram of x 1 2 3 4 5 6 x 0 1 2 3 4 5 6 3 Midtveiseksamen oppg. 1a eksamen 06.08.2004 Kapittel 5 Noen diskrete sannsynlighetsfordelinger TMA4245 V2007: Eirik Mo Høsten 2004 ble det i TMA4240 bli innført
Noen diskrete sannsynlighetsfordelinger. (utarbeidet av Mette Langaas), TMA4245 V2007
 Kapittel 5 Noen diskrete sannsynlighetsfordelinger TMA4245 V2007: Eirik Mo 2 5.2 Diskret uniform fordeling Diskret uniform fordeling: Hvis den stokastiske variabelen X antar verdiene x 1, x 2,..., x k
Kapittel 5 Noen diskrete sannsynlighetsfordelinger TMA4245 V2007: Eirik Mo 2 5.2 Diskret uniform fordeling Diskret uniform fordeling: Hvis den stokastiske variabelen X antar verdiene x 1, x 2,..., x k
TMA4240 Statistikk H2015
 TMA4240 Statistikk H2015 Kapittel 5: Noen diskrete sannsynlighetsfordelinger 5.4 Geometrisk og negativ binomisk fordeling 5.5 Poisson-prosess og -fordeling Mette Langaas Institutt for matematiske fag,
TMA4240 Statistikk H2015 Kapittel 5: Noen diskrete sannsynlighetsfordelinger 5.4 Geometrisk og negativ binomisk fordeling 5.5 Poisson-prosess og -fordeling Mette Langaas Institutt for matematiske fag,
ÅMA110 Sannsynlighetsregning med statistikk, våren Kp. 3 Diskrete tilfeldige variable. Diskrete tilfeldige variable, varians (kp. 3.
 ÅMA Sannsynlighetsregning med statistikk, våren 8 Kp. Diskrete tilfeldige variable Kp. Diskrete tilfeldige variable Har sett på (tidligere: begrep/definisjoner; tilfeldig (stokastisk variabel sannsynlighetsfordeling
ÅMA Sannsynlighetsregning med statistikk, våren 8 Kp. Diskrete tilfeldige variable Kp. Diskrete tilfeldige variable Har sett på (tidligere: begrep/definisjoner; tilfeldig (stokastisk variabel sannsynlighetsfordeling
Kap. 6, Kontinuerlege Sannsynsfordelingar
 Kapittel 6, Kontinuerlege Sannsynsfordelingar Sjå på eit utval av ofte brukte kontinuerlege sannsynsfordelingar Uniform I går Normal I går Eksponensial I dag Gamma I dag Kji-kvadrat I dag Nokre eigenskapar
Kapittel 6, Kontinuerlege Sannsynsfordelingar Sjå på eit utval av ofte brukte kontinuerlege sannsynsfordelingar Uniform I går Normal I går Eksponensial I dag Gamma I dag Kji-kvadrat I dag Nokre eigenskapar
Kap. 6, Kontinuerlege Sannsynsfordelingar
 Kapittel 6, Kontinuerlege Sannsynsfordelingar Sjå på eit utval av ofte brukte kontinuerlege sannsynsfordelingar Uniform Onsdag Normal Onsdag Eksponensial I dag Gamma I dag Kji-kvadrat I dag Student-T (Kap
Kapittel 6, Kontinuerlege Sannsynsfordelingar Sjå på eit utval av ofte brukte kontinuerlege sannsynsfordelingar Uniform Onsdag Normal Onsdag Eksponensial I dag Gamma I dag Kji-kvadrat I dag Student-T (Kap
Kap. 6, Kontinuerlege Sannsynsfordelingar
 Kapittel 6, Kontinuerlege Sannsynsfordelingar Sjå på eit utval av ofte brukte kontinuerlege sannsynsfordelingar Uniform I går Normal I går Eksponensial I dag Gamma I dag Kji-kvadrat I dag Nokre eigenskapar
Kapittel 6, Kontinuerlege Sannsynsfordelingar Sjå på eit utval av ofte brukte kontinuerlege sannsynsfordelingar Uniform I går Normal I går Eksponensial I dag Gamma I dag Kji-kvadrat I dag Nokre eigenskapar
ÅMA110 Sannsynlighetsregning med statistikk, våren 2011
 ÅMA0 Sannsynlighetsregning med statistikk, våren 0 Kp. 3 Diskrete tilfeldige variable Noen viktige sannsynlighetsmodeller Noen viktige sannsynlighetsmodeller ( Sanns.modell : nå betyr det klasse/type sanns.fordeling.
ÅMA0 Sannsynlighetsregning med statistikk, våren 0 Kp. 3 Diskrete tilfeldige variable Noen viktige sannsynlighetsmodeller Noen viktige sannsynlighetsmodeller ( Sanns.modell : nå betyr det klasse/type sanns.fordeling.
HØGSKOLEN I STAVANGER
 HØGSKOLEN I STAVANGER Avdeling for TEKNISK NATURVITEN- EKSAMEN I: TE199 SANNSYNLIGHETSREGNING MED STATISTIKK SKAPELIGE FAG VARIGHET: 4 TIMER DATO: 5. JUNI 2003 TILLATTE HJELPEMIDLER: KALKULATOR OPPGAVESETTET
HØGSKOLEN I STAVANGER Avdeling for TEKNISK NATURVITEN- EKSAMEN I: TE199 SANNSYNLIGHETSREGNING MED STATISTIKK SKAPELIGE FAG VARIGHET: 4 TIMER DATO: 5. JUNI 2003 TILLATTE HJELPEMIDLER: KALKULATOR OPPGAVESETTET
Oppgave 1 En ansatt skal overvåke et prosjekt der en lapp velges tilfeldig fra en boks som inneholder 10 lapper nummerert fra 1 til 10.
 TMA4245 Statistikk Vår 212 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving 4 blokk I Løsningsskisse Oppgave 1 En ansatt skal overvåke et prosjekt der en lapp velges tilfeldig
TMA4245 Statistikk Vår 212 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving 4 blokk I Løsningsskisse Oppgave 1 En ansatt skal overvåke et prosjekt der en lapp velges tilfeldig
TMA4240 Statistikk Høst 2015
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 6, blokk I Løsningsskisse Oppgave 1 Vi antar X er normalfordelt, X N(3315, 55 2. Ved bruk av formelheftet finner
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 6, blokk I Løsningsskisse Oppgave 1 Vi antar X er normalfordelt, X N(3315, 55 2. Ved bruk av formelheftet finner
TMA4240 Statistikk Høst 2008
 TMA4240 Statistikk Høst 2008 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 7 Oppgave 1 Tippekonkurranse Denne oppgaven er ment som en kjapp test på hva du har
TMA4240 Statistikk Høst 2008 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 7 Oppgave 1 Tippekonkurranse Denne oppgaven er ment som en kjapp test på hva du har
A) B) 400 C) 120 D) 60 E) 10. Rett svar: C. Fasit: ( 5 6 = 60. Hvis A, B, C er en partisjon av utfallsrommet S, så er P (A B) lik.
 Oppgave 1 Det skal velges en komité bestående av 2 menn og 1 kvinne. Komitéen skal velges fra totalt 5 menn og 6 kvinner. Hvor mange ulike komitéer kan dannes? A) 86400 B) 400 C) 120 D) 60 E) 10 Rett svar:
Oppgave 1 Det skal velges en komité bestående av 2 menn og 1 kvinne. Komitéen skal velges fra totalt 5 menn og 6 kvinner. Hvor mange ulike komitéer kan dannes? A) 86400 B) 400 C) 120 D) 60 E) 10 Rett svar:
Statistikk 1 kapittel 5
 Statistikk 1 kapittel 5 Nico Keilman ECON 2130 Vår 2016 Kapittel 5 Sannsynlighetsmodeller I kap. 4 så vi et eksempel med en s.v. X som hadde en uniform sannsynlighetsfordeling: alle verdier av x har like
Statistikk 1 kapittel 5 Nico Keilman ECON 2130 Vår 2016 Kapittel 5 Sannsynlighetsmodeller I kap. 4 så vi et eksempel med en s.v. X som hadde en uniform sannsynlighetsfordeling: alle verdier av x har like
Statistikk 1 kapittel 5
 Statistikk 1 kapittel 5 Nico Keilman ECON 2130 Vår 2017 Kapittel 5 Sannsynlighetsmodeller I kap. 4 så vi et eksempel med en s.v. X som hadde en uniform sannsynlighetsfordeling: alle verdier av x har like
Statistikk 1 kapittel 5 Nico Keilman ECON 2130 Vår 2017 Kapittel 5 Sannsynlighetsmodeller I kap. 4 så vi et eksempel med en s.v. X som hadde en uniform sannsynlighetsfordeling: alle verdier av x har like
TMA4240 Statistikk 2014
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 5, blokk I Løsningsskisse Oppgave 1 X og Y er uavhengige Poisson-fordelte stokastiske variable, X p(x;5 og Y p(y;1.
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 5, blokk I Løsningsskisse Oppgave 1 X og Y er uavhengige Poisson-fordelte stokastiske variable, X p(x;5 og Y p(y;1.
TMA4240 Statistikk H2010
 TMA4240 Statistikk H2010 Kapittel 5: Diskrete sannsynlighetsfordelinger 5.5-5.6: Negativ binomisk, geometrisk, Poisson Mette Langaas Foreleses mandag 20. september 2010 2 Kabel En kabel består av mange
TMA4240 Statistikk H2010 Kapittel 5: Diskrete sannsynlighetsfordelinger 5.5-5.6: Negativ binomisk, geometrisk, Poisson Mette Langaas Foreleses mandag 20. september 2010 2 Kabel En kabel består av mange
Regneøvelse 29/5, 2017
 Regneøvelse 29/5, 2017 Arne Bang Huseby Eksamen STK1100 2008: oppgave 3 Eksamen STK1100 2004: oppgave 2 Eksamen 2008, oppgave 3 Et vannverk tar prøver av drikkevannet for å kontrollere forekomsten av en
Regneøvelse 29/5, 2017 Arne Bang Huseby Eksamen STK1100 2008: oppgave 3 Eksamen STK1100 2004: oppgave 2 Eksamen 2008, oppgave 3 Et vannverk tar prøver av drikkevannet for å kontrollere forekomsten av en
Statistikk 1 kapittel 5
 Statistikk 1 kapittel 5 Nico Keilman ECON 2130 Vår 2015 Kapittel 5 Sannsynlighetsmodeller I kap. 4 så vi et eksempel om en s.v. X som hadde en uniform sannsynlighetsfordeling: alle verdier av x har like
Statistikk 1 kapittel 5 Nico Keilman ECON 2130 Vår 2015 Kapittel 5 Sannsynlighetsmodeller I kap. 4 så vi et eksempel om en s.v. X som hadde en uniform sannsynlighetsfordeling: alle verdier av x har like
Oppfriskning av blokk 1 i TMA4240
 Oppfriskning av blokk 1 i TMA4240 Geir-Arne Fuglstad November 21, 2016 2 Hva har vi gjort i dette kurset? Vi har studert to sterkt relaterte grener av matematikk Sannsynlighetsteori: matematisk teori for
Oppfriskning av blokk 1 i TMA4240 Geir-Arne Fuglstad November 21, 2016 2 Hva har vi gjort i dette kurset? Vi har studert to sterkt relaterte grener av matematikk Sannsynlighetsteori: matematisk teori for
Høgskolen i Telemark. Institutt for økonomi og informatikk FORMELSAMLING Statistikk I. Til bruk ved eksamen. Per Chr. Hagen
 Høgskolen i Telemark Institutt for økonomi og informatikk FORMELSAMLING 6005 Statistikk I Til bruk ved eksamen Per Chr. Hagen . Sannsynlighetsregning. Regneregler Komplementsetningen: Addisjonssetningen:
Høgskolen i Telemark Institutt for økonomi og informatikk FORMELSAMLING 6005 Statistikk I Til bruk ved eksamen Per Chr. Hagen . Sannsynlighetsregning. Regneregler Komplementsetningen: Addisjonssetningen:
Observatorer. STK Observatorer - Kap 6. Utgangspunkt. Eksempel høyde Oxford studenter
 Observatorer STK00 - Observatorer - Kap 6 Geir Storvik 4. april 206 Så langt: Sannsynlighetsteori Stokastiske modeller Nå: Data Knytte data til stokastiske modeller Utgangspunkt Eksempel høyde Oxford studenter
Observatorer STK00 - Observatorer - Kap 6 Geir Storvik 4. april 206 Så langt: Sannsynlighetsteori Stokastiske modeller Nå: Data Knytte data til stokastiske modeller Utgangspunkt Eksempel høyde Oxford studenter
Statistikk 1 kapittel 5
 Statistikk 1 kapittel 5 Nico Keilman ECON 2130 Vår 2014 Kapittel 5 Sannsynlighetsmodeller I kap. 4 så vi et eksempel om en s.v. X som hadde en uniform sannsynlighetsfordeling: alle verdier av x har like
Statistikk 1 kapittel 5 Nico Keilman ECON 2130 Vår 2014 Kapittel 5 Sannsynlighetsmodeller I kap. 4 så vi et eksempel om en s.v. X som hadde en uniform sannsynlighetsfordeling: alle verdier av x har like
Oppgave 1 Vi lar X være antall tankskip som ankommer havnen i løpet av en dag. Vi har fått oppgitt at X poisson(λ) med
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalte oppgaver 5, blokk I Løsningsskisse Oppgave 1 Vi lar X være antall tankskip som ankommer havnen i løpet av en dag.
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalte oppgaver 5, blokk I Løsningsskisse Oppgave 1 Vi lar X være antall tankskip som ankommer havnen i løpet av en dag.
TMA4240 Statistikk H2010
 TMA4240 Statistikk H2010 Statistisk inferens: 8.1: Tilfeldig utvalg 9.1-9.3: Estimering Mette Langaas Foreleses uke 40, 2010 2 Utfordring Ved en bedrift produseres en elektrisk komponent. Komponenten må
TMA4240 Statistikk H2010 Statistisk inferens: 8.1: Tilfeldig utvalg 9.1-9.3: Estimering Mette Langaas Foreleses uke 40, 2010 2 Utfordring Ved en bedrift produseres en elektrisk komponent. Komponenten må
µ = E(X) = Ʃ P(X = x) x
 Redigerte høydepunkt fra forrige episode 3.2: Punktsannsynlighet og kumulativ sannsynlighet punktsannsynlighet: sanns. for at en stok. var. X har en viss verdi x; P(X = x) kumulativ sannsynlighet: sanns.
Redigerte høydepunkt fra forrige episode 3.2: Punktsannsynlighet og kumulativ sannsynlighet punktsannsynlighet: sanns. for at en stok. var. X har en viss verdi x; P(X = x) kumulativ sannsynlighet: sanns.
ÅMA110 Sannsynlighetsregning med statistikk, våren
 ÅMA110 Sannsynlighetsregning med statistikk, våren 2006 Oppsummering Bjørn H. Auestad Institutt for matematikk og naturvitenskap Universitetet i Stavanger 24. april Bjørn H. Auestad Oppsummering våren
ÅMA110 Sannsynlighetsregning med statistikk, våren 2006 Oppsummering Bjørn H. Auestad Institutt for matematikk og naturvitenskap Universitetet i Stavanger 24. april Bjørn H. Auestad Oppsummering våren
1 Section 4-1: Introduksjon til sannsynlighet. 2 Section 4-2: Enkel sannsynlighetsregning. 3 Section 5-1: Introduksjon til sannsynlighetsfordelinger
 1 Section 4-1: Introduksjon til sannsynlighet 2 Section 4-2: Enkel sannsynlighetsregning 3 Section 5-1: Introduksjon til sannsynlighetsfordelinger 4 Section 5-2: Tilfeldige variable 5 Section 5-3: Binomisk
1 Section 4-1: Introduksjon til sannsynlighet 2 Section 4-2: Enkel sannsynlighetsregning 3 Section 5-1: Introduksjon til sannsynlighetsfordelinger 4 Section 5-2: Tilfeldige variable 5 Section 5-3: Binomisk
ÅMA110 Sannsynlighetsregning med statistikk, våren 2010 Oppsummering
 ÅMA110 Sannsynlighetsregning med statistikk, våren 2010 Oppsummering Bjørn H. Auestad Institutt for matematikk og naturvitenskap Universitetet i Stavanger 21. april Bjørn H. Auestad Oppsummering våren
ÅMA110 Sannsynlighetsregning med statistikk, våren 2010 Oppsummering Bjørn H. Auestad Institutt for matematikk og naturvitenskap Universitetet i Stavanger 21. april Bjørn H. Auestad Oppsummering våren
Emnenavn: Eksamenstid: 4 timer. Faglærer: Hans Kristian Bekkevard
 EKSAMEN Emnekode: SFB107111 Emnenavn: Metode 1, statistikk deleksamen Dato: 16. mai 2017 Hjelpemidler: Godkjent kalkulator og vedlagt formelsamling m/tabeller Eksamenstid: 4 timer Faglærer: Hans Kristian
EKSAMEN Emnekode: SFB107111 Emnenavn: Metode 1, statistikk deleksamen Dato: 16. mai 2017 Hjelpemidler: Godkjent kalkulator og vedlagt formelsamling m/tabeller Eksamenstid: 4 timer Faglærer: Hans Kristian
TMA4240 Statistikk. Øving nummer 7. Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag
 TMA4240 Statistikk Vår 2008 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 7 Oppgave Blandet drops a) Tippekupong På en tippekupong er det gitt 2 fotballkamper.
TMA4240 Statistikk Vår 2008 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 7 Oppgave Blandet drops a) Tippekupong På en tippekupong er det gitt 2 fotballkamper.
ECON Statistikk 1 Forelesning 4: Stokastiske variable, fordelinger. Jo Thori Lind
 ECON2130 - Statistikk 1 Forelesning 4: Stokastiske variable, fordelinger Jo Thori Lind [email protected] Oversikt 1. Betinget sannsynlighet 2. Stokastiske variable 3. Forventning og varians 4. Regneregler
ECON2130 - Statistikk 1 Forelesning 4: Stokastiske variable, fordelinger Jo Thori Lind [email protected] Oversikt 1. Betinget sannsynlighet 2. Stokastiske variable 3. Forventning og varians 4. Regneregler
Observatorar og utvalsfordeling. Torstein Fjeldstad Institutt for matematiske fag, NTNU
 Observatorar og utvalsfordeling Torstein Fjeldstad Institutt for matematiske fag, NTNU 08.10.2018 I dag Til no i emnet Observatorar Utvalsfordelingar Sentralgrenseteoremet 2 Til no i emnet definisjon av
Observatorar og utvalsfordeling Torstein Fjeldstad Institutt for matematiske fag, NTNU 08.10.2018 I dag Til no i emnet Observatorar Utvalsfordelingar Sentralgrenseteoremet 2 Til no i emnet definisjon av
Poissonprosesser og levetidsfordelinger
 Poissonprosesser og levetidsfordelinger Poissonfordeling som grensetilfelle for binomisk fordeling La X være binomisk fordelt med fordeling P (X = x) = ( ) n p x (1 p) n x, for x = 0, 1,... n. (1) x Forventningsverdien
Poissonprosesser og levetidsfordelinger Poissonfordeling som grensetilfelle for binomisk fordeling La X være binomisk fordelt med fordeling P (X = x) = ( ) n p x (1 p) n x, for x = 0, 1,... n. (1) x Forventningsverdien
Diskrete sannsynlighetsfordelinger som histogram. Varians. Histogram og kumulativ sannsynlighet. Forventning (gjennomsnitt) (X=antall mynt i tre kast)
 Diskret sannsynlighetsfordeling (kap 1.1-1.6) Oversikt Utfallsrom (sample space) Sannsynlighetsfordeling Forventning (expectation), E(X), populasjonsgjennomsnitt Bruk av figurer og histogram Binomialfordelingen
Diskret sannsynlighetsfordeling (kap 1.1-1.6) Oversikt Utfallsrom (sample space) Sannsynlighetsfordeling Forventning (expectation), E(X), populasjonsgjennomsnitt Bruk av figurer og histogram Binomialfordelingen
ST0103 Brukerkurs i statistikk Høsten Momentestimatoren og sannsynlighetsmaksimeringsestimatoren
 ST0103 Brukerkurs i statistikk Høsten 2016 Momentestimatoren og sannsynlighetsmaksimeringsestimatoren (SME) Boka har bare ett eksempel med sannsynlighetsmaksimeringsestimatoren. Vi gjengir dette nedenfor,
ST0103 Brukerkurs i statistikk Høsten 2016 Momentestimatoren og sannsynlighetsmaksimeringsestimatoren (SME) Boka har bare ett eksempel med sannsynlighetsmaksimeringsestimatoren. Vi gjengir dette nedenfor,
Midtveiseksamen i STK1100 våren 2017
 Midtveiseksamen i STK1100 våren 2017 Denne midtveiseksamenen består av 20 oppgaver. Det er ett riktig svaralternativ for hvert spørsmål. Hvis svaret er oppgitt som et desimaltall, er det rundet av til
Midtveiseksamen i STK1100 våren 2017 Denne midtveiseksamenen består av 20 oppgaver. Det er ett riktig svaralternativ for hvert spørsmål. Hvis svaret er oppgitt som et desimaltall, er det rundet av til
Utvalgsfordelinger. Utvalg er en tilfeldig mekanisme. Sannsynlighetsregning dreier seg om tilfeldige mekanismer.
 Utvalgsfordelinger Vi har sett at utvalgsfordelinger til en statistikk (observator) er fordelingen av verdiene statistikken tar ved mange gjenttatte utvalg av samme størrelse fra samme populasjon. Utvalg
Utvalgsfordelinger Vi har sett at utvalgsfordelinger til en statistikk (observator) er fordelingen av verdiene statistikken tar ved mange gjenttatte utvalg av samme størrelse fra samme populasjon. Utvalg
SFB LØSNING PÅ EKSAMEN HØSTEN 2018
 SFB107111 - LØSNING PÅ EKSAMEN HØSTEN 018 Eksamen høsten 018 Oppgave 1 Anta at 70% av studentene spiller fotball og at 0% ikke spiller fotball. Anta at av de som spiller fotball så er det 40% som spiller
SFB107111 - LØSNING PÅ EKSAMEN HØSTEN 018 Eksamen høsten 018 Oppgave 1 Anta at 70% av studentene spiller fotball og at 0% ikke spiller fotball. Anta at av de som spiller fotball så er det 40% som spiller
TMA4240 Statistikk 2014
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 6, blokk I Løsningsskisse Oppgave 1 Fremgangsmetode: P X 1 < 6.8 Denne kan finnes ved å sette opp integralet over
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 6, blokk I Løsningsskisse Oppgave 1 Fremgangsmetode: P X 1 < 6.8 Denne kan finnes ved å sette opp integralet over
Løsningskisse for oppgaver til undervisningsfri uke 14 (6.-9. april)
 HG April 010 Løsningskisse for oppgaver til undervisningsfri uke 14 (6.-9. april) Innledende merknad. De fleste oppgavene denne uka er øvelser i bruk av den viktige regel 5.0, som er sentral i dette kurset,
HG April 010 Løsningskisse for oppgaver til undervisningsfri uke 14 (6.-9. april) Innledende merknad. De fleste oppgavene denne uka er øvelser i bruk av den viktige regel 5.0, som er sentral i dette kurset,
FORMELSAMLING TIL STK1100 OG STK1110
 FORMELSAMLING TIL STK1100 OG STK1110 (Versjon av 16. november 2009) 1. Sannsynlighet La A, B, A 1, A 2,...,B 1, B 2,... være begivenheter, dvs. delmengder av et utfallsrom Ω. a) Aksiomene: Et sannsynlighetsmål
FORMELSAMLING TIL STK1100 OG STK1110 (Versjon av 16. november 2009) 1. Sannsynlighet La A, B, A 1, A 2,...,B 1, B 2,... være begivenheter, dvs. delmengder av et utfallsrom Ω. a) Aksiomene: Et sannsynlighetsmål
Forelesing 27 Oppsummering. Torstein Fjeldstad Institutt for matematiske fag, NTNU
 Forelesing 27 Oppsummering Torstein Fjeldstad Institutt for matematiske fag, NTNU 18.04.2018 I dag Lineær regresjon (sjekk av modellantagelser) Praktisk informasjon Andre statistikk-kurs Oversikt over
Forelesing 27 Oppsummering Torstein Fjeldstad Institutt for matematiske fag, NTNU 18.04.2018 I dag Lineær regresjon (sjekk av modellantagelser) Praktisk informasjon Andre statistikk-kurs Oversikt over
Hypergeometrisk modell
 Hpergeometrisk modell Tilnærming til binomisk fordeling - enklere å beregne binomiske sannsnligheter Dersom n er liten i forhold til N, er det tilnærmet uavhengighet mellom resultatene i ulike trekninger/
Hpergeometrisk modell Tilnærming til binomisk fordeling - enklere å beregne binomiske sannsnligheter Dersom n er liten i forhold til N, er det tilnærmet uavhengighet mellom resultatene i ulike trekninger/
Kapittel 9 og 10: Hypotesetesting
 Kapittel 9 og 1: Hypotesetesting Hypotesetesting er en standard vitenskapelig fremgangsmåte for å sjekke påstander. Generell problemstilling: Basert på informasjonen i data fra et tilfeldig utvalg ønsker
Kapittel 9 og 1: Hypotesetesting Hypotesetesting er en standard vitenskapelig fremgangsmåte for å sjekke påstander. Generell problemstilling: Basert på informasjonen i data fra et tilfeldig utvalg ønsker
ÅMA 110 SANNSYNLIGHETSREGNING MED STATISTIKK Løsningsforslag til regneøving nr. 12 (s. 34)
 ÅMA 110 SANNSYNLIGHETSREGNING MED STATISTIKK Løsningsforslag til regneøving nr. s. 34 Oppgave.1 Situasjon betraktes som 7 Bernoulliforsøk; Suksess: dyr velger belønning 1, motsatt fiasko. P suksess = p;
ÅMA 110 SANNSYNLIGHETSREGNING MED STATISTIKK Løsningsforslag til regneøving nr. s. 34 Oppgave.1 Situasjon betraktes som 7 Bernoulliforsøk; Suksess: dyr velger belønning 1, motsatt fiasko. P suksess = p;
TALLSVAR. Det anbefales at de 9 deloppgavene merket med A, B, teller likt uansett variasjon i vanskelighetsgrad. Svarene er gitt i <<< >>>.
 1 ECON213: EKSAMEN 217 VÅR - UTSATT PRØVE TALLSVAR. Det anbefales at de 9 deloppgavene merket med A, B, teller likt uansett variasjon i vanskelighetsgrad. Svarene er gitt i
1 ECON213: EKSAMEN 217 VÅR - UTSATT PRØVE TALLSVAR. Det anbefales at de 9 deloppgavene merket med A, B, teller likt uansett variasjon i vanskelighetsgrad. Svarene er gitt i
Løsningsforslag statistikkeksamen desember 2014
 Løsningsforslag statistikkeksamen desember 2014 Oppgave 1 a i. To hendelser er disjunke hvis det er intet overlapp mellom hendelsene, altså hvis A B = Ø. Siden vi har en sannsynlighet for å finne A B som
Løsningsforslag statistikkeksamen desember 2014 Oppgave 1 a i. To hendelser er disjunke hvis det er intet overlapp mellom hendelsene, altså hvis A B = Ø. Siden vi har en sannsynlighet for å finne A B som
Hypotesetesting. Formulere en hypotesetest: Når vi skal test om en parameter θ kan påstås å være større enn en verdi θ 0 skriver vi dette som:
 Hypotesetesting. 10 og fore- Dekkes av pensumsidene i kap. lesingsnotatene. Hypotesetesting er en systematisk fremgangsmåte for å undersøke hypoteser (påstander) knyttet til parametre i sannsynlighetsfordelinger.
Hypotesetesting. 10 og fore- Dekkes av pensumsidene i kap. lesingsnotatene. Hypotesetesting er en systematisk fremgangsmåte for å undersøke hypoteser (påstander) knyttet til parametre i sannsynlighetsfordelinger.
Kapittel 2: Hendelser
 Kapittel 2: Hendelser FENOMEN Eksperiment Utfall Utfallsrom Eksperiment. Utfall. Eksperiment Utfall Hendelse Sannsynlighet: egenskaper, gunstige vs. mulige, relativ frekvens Sannsynlighet for mer enn en
Kapittel 2: Hendelser FENOMEN Eksperiment Utfall Utfallsrom Eksperiment. Utfall. Eksperiment Utfall Hendelse Sannsynlighet: egenskaper, gunstige vs. mulige, relativ frekvens Sannsynlighet for mer enn en
TMA4240 Statistikk Høst 2009
 TMA4240 Statistikk Høst 2009 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer b5 Løsningsskisse Oppgave 1 Vi ønsker å finne ut om et nytt serum kan stanse leukemi.
TMA4240 Statistikk Høst 2009 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer b5 Løsningsskisse Oppgave 1 Vi ønsker å finne ut om et nytt serum kan stanse leukemi.
Formelsamling i medisinsk statistikk
 Formelsamling i medisinsk statistikk Versjon av 6. mai 208 Dette er en formelsamling til O. O. Aalen (red.): Statistiske metoder i medisin og helsefag, Gyldendal, 208. Gjennomsnitt x = n (x + x 2 + x 3
Formelsamling i medisinsk statistikk Versjon av 6. mai 208 Dette er en formelsamling til O. O. Aalen (red.): Statistiske metoder i medisin og helsefag, Gyldendal, 208. Gjennomsnitt x = n (x + x 2 + x 3
Kapittel 8: Tilfeldige utvalg, databeskrivelse og fordeling til observatorar, Kapittel 9: Estimering
 Kapittel 8: Tilfeldige utvalg, databeskrivelse og fordeling til observatorar, Kapittel 9: Estimering TMA4245 Statistikk Kapittel 8.1-8.5. Kapittel 9.1-9.3+9.15 [email protected] p.1/21 Har sett
Kapittel 8: Tilfeldige utvalg, databeskrivelse og fordeling til observatorar, Kapittel 9: Estimering TMA4245 Statistikk Kapittel 8.1-8.5. Kapittel 9.1-9.3+9.15 [email protected] p.1/21 Har sett
Forelening 1, kapittel 4 Stokastiske variable
 Forelening 1, kapittel 4 Stokastiske variable Eksempel X = "antall kron på kast med to mynter (før de er kastet)" Uniformt utfallsrom {MM, MK, KM, KK}. X = x beskriver hendelsen "antall kron på kast med
Forelening 1, kapittel 4 Stokastiske variable Eksempel X = "antall kron på kast med to mynter (før de er kastet)" Uniformt utfallsrom {MM, MK, KM, KK}. X = x beskriver hendelsen "antall kron på kast med
STK1100 våren 2019 Mere om konfidensintevaller
 STK1100 våren 2019 Mere om konfidensintevaller Svarer til avsnitt 8.2 i læreboka Ørnulf Borgan Matematisk institutt Universitetet i Oslo 1 Konfidensintervall for µ i store utvalg Anta at de stokastiske
STK1100 våren 2019 Mere om konfidensintevaller Svarer til avsnitt 8.2 i læreboka Ørnulf Borgan Matematisk institutt Universitetet i Oslo 1 Konfidensintervall for µ i store utvalg Anta at de stokastiske
Oppgaver fra 8.3, 8.4, , 8.51, 8.52, 8.231, 8.232, 8.250, 8.252
 Oppgaver fra 8.3, 8.4, 8.5 8.41, 8.51, 8.52, 8.231, 8.232, 8.250, 8.252 8.41 Populasjon: Tilfeldig variabel X : Trekke en tilfeldig flaske og måle volumet Ukjent sannsynlighetsfordeling, men forventning
Oppgaver fra 8.3, 8.4, 8.5 8.41, 8.51, 8.52, 8.231, 8.232, 8.250, 8.252 8.41 Populasjon: Tilfeldig variabel X : Trekke en tilfeldig flaske og måle volumet Ukjent sannsynlighetsfordeling, men forventning
Forelesning 5: Kontinuerlige fordelinger, normalfordelingen. Jo Thori Lind
 Forelesning 5: Kontinuerlige fordelinger, normalfordelingen Jo Thori Lind [email protected] Oversikt 1. Kontinuerlige fordelinger 2. Uniform fordeling 3. Normal-fordelingen 1. Kontinuerlige fordelinger
Forelesning 5: Kontinuerlige fordelinger, normalfordelingen Jo Thori Lind [email protected] Oversikt 1. Kontinuerlige fordelinger 2. Uniform fordeling 3. Normal-fordelingen 1. Kontinuerlige fordelinger
HØGSKOLEN I STAVANGER
 HØGSKOLEN I STAVANGER Avdeling for TEKNISK NATURVITEN- EKSAMEN I: TE199 SANNSYNLIGHETSREGNING MED STATISTIKK SKAPELIGE FAG VARIGHET: 4 TIMER DATO: 30. AUGUST 2003 TILLATTE HJELPEMIDLER: KALKULATOR OPPGAVESETTET
HØGSKOLEN I STAVANGER Avdeling for TEKNISK NATURVITEN- EKSAMEN I: TE199 SANNSYNLIGHETSREGNING MED STATISTIKK SKAPELIGE FAG VARIGHET: 4 TIMER DATO: 30. AUGUST 2003 TILLATTE HJELPEMIDLER: KALKULATOR OPPGAVESETTET
Diskrete sannsynlighetsfordelinger som histogram. Varians. Histogram og kumulativ sannsynlighet. Binomial-fordelingen
 Diskret sannsynlighetsfordeling (kap 1.1-1.6) Oversikt Utfallsrom (sample space) Sannsynlighetsfordeling Forventning (expectation), E(, populasjonsgjennomsnitt Bruk av figurer og histogram Binomialfordelingen
Diskret sannsynlighetsfordeling (kap 1.1-1.6) Oversikt Utfallsrom (sample space) Sannsynlighetsfordeling Forventning (expectation), E(, populasjonsgjennomsnitt Bruk av figurer og histogram Binomialfordelingen
Tilfeldige variable (5.2)
 Tilfeldige variable (5.) Dersom vi til hvert utfall av eksperimentet tilordner et tall, har vi laget en tilfeldig variabel. Tilfeldig variabel: En variabel som har en numerisk verdi for hvert utfall i
Tilfeldige variable (5.) Dersom vi til hvert utfall av eksperimentet tilordner et tall, har vi laget en tilfeldig variabel. Tilfeldig variabel: En variabel som har en numerisk verdi for hvert utfall i
Kapittel 5: Tilfeldige variable, forventning og varians.
 Kapittel 5: Tilfeldige variable, forventning og varians. Tilfeldige variable Tilfeldige variable kalles også stokastiske variable. En tilfeldig variabel er en variabel som får sin numeriske verdi bestemt
Kapittel 5: Tilfeldige variable, forventning og varians. Tilfeldige variable Tilfeldige variable kalles også stokastiske variable. En tilfeldig variabel er en variabel som får sin numeriske verdi bestemt
1.1.1 Rekke med konstante ledd. En rekke med konstante ledd er gitt som. a n (1) n=m
 Formelsamling og tabeller FO020E Matte 2000 for elektroprogrammet 1 Matematikk 1.1 Denisjoner av ulike typer polynomer og rekker 1.1.1 Rekke med konstante ledd En rekke med konstante ledd er gitt som a
Formelsamling og tabeller FO020E Matte 2000 for elektroprogrammet 1 Matematikk 1.1 Denisjoner av ulike typer polynomer og rekker 1.1.1 Rekke med konstante ledd En rekke med konstante ledd er gitt som a
STK1100 våren Kombinatorikk = = Uniform sannsynlighetsmodell. Et stokastisk forsøk har N utfall. Det er de mulige utfallene for forsøket.
 ST1100 våren 2017 ombinatorikk Uniform sannsynlighetsmodell Et stokastisk forsøk har N utfall. Det er de mulige utfallene for forsøket. Vi antar at de N utfallene er like sannsynlige. Svarer til avsnitt
ST1100 våren 2017 ombinatorikk Uniform sannsynlighetsmodell Et stokastisk forsøk har N utfall. Det er de mulige utfallene for forsøket. Vi antar at de N utfallene er like sannsynlige. Svarer til avsnitt
Løsning eksamen desember 2017
 Løsning eksamen desember 017 Oppgave 1 Innfører hendelsene D: enheten er defekt K: enheten blir kassert a i Disse sannsynlighetene kan leses ut av oppgaveteksten: P D = 0, 10 P K D = 0, 07 P K D = 0, 95
Løsning eksamen desember 017 Oppgave 1 Innfører hendelsene D: enheten er defekt K: enheten blir kassert a i Disse sannsynlighetene kan leses ut av oppgaveteksten: P D = 0, 10 P K D = 0, 07 P K D = 0, 95
STK1100 våren 2017 Kombinatorikk
 STK1100 våren 2017 Kombinatorikk Svarer til avsnitt 2.3 i læreboka Ørnulf Borgan Matematisk institutt Universitetet i Oslo 1 Uniform sannsynlighetsmodell Et stokastisk forsøk har N utfall. Det er de mulige
STK1100 våren 2017 Kombinatorikk Svarer til avsnitt 2.3 i læreboka Ørnulf Borgan Matematisk institutt Universitetet i Oslo 1 Uniform sannsynlighetsmodell Et stokastisk forsøk har N utfall. Det er de mulige
Løsningsforslag ECON 2130 Obligatorisk semesteroppgave 2017 vår
 Løsningsforslag ECON 130 Obligatorisk semesteroppgave 017 vår Andreas Myhre Oppgave 1 1. (i) Siden X og Z er uavhengige, vil den simultane fordelingen mellom X og Z kunne skrives som: f(x, z) = P(X = x
Løsningsforslag ECON 130 Obligatorisk semesteroppgave 017 vår Andreas Myhre Oppgave 1 1. (i) Siden X og Z er uavhengige, vil den simultane fordelingen mellom X og Z kunne skrives som: f(x, z) = P(X = x
Kap. 7 - Sannsynlighetsfordelinger
 Oppgaver: Kap. 7 - Sannsynlighetsfordelinger Oppgaver fra kapitlet Lærebok: 7.0-0-0-,7.--7, 7.-, 7., 7., 7.7 Oppgavesamling: 7.00, 7.0, 7.09, 7., 7.9, 7., 7.0, 7.0, 7.0 7.0-0-0-0- Stokastisk variabel:
Oppgaver: Kap. 7 - Sannsynlighetsfordelinger Oppgaver fra kapitlet Lærebok: 7.0-0-0-,7.--7, 7.-, 7., 7., 7.7 Oppgavesamling: 7.00, 7.0, 7.09, 7., 7.9, 7., 7.0, 7.0, 7.0 7.0-0-0-0- Stokastisk variabel:
TMA4245 Statistikk Eksamen desember 2016
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4245 Statistikk Eksamen desember 2016 Oppgave 1 En bedrift produserer elektriske komponenter. Komponentene kan ha to typer
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4245 Statistikk Eksamen desember 2016 Oppgave 1 En bedrift produserer elektriske komponenter. Komponentene kan ha to typer
Litt mer om eksponensialfordelingen
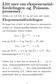 Litt mer om eksponensialfordelingen og Poissonprosesser. Dekkes av 5.6, 6.6, 6.7 og det som står under. Eksponensialfordelingen Så langt har vi lært at det finnes to parametriseringer av eksponensialfordelingen
Litt mer om eksponensialfordelingen og Poissonprosesser. Dekkes av 5.6, 6.6, 6.7 og det som står under. Eksponensialfordelingen Så langt har vi lært at det finnes to parametriseringer av eksponensialfordelingen
Eksamensoppgave i Løsningsskisse TMA4240 Statistikk
 Institutt for matematiske fag Eksamensoppgave i Løsningsskisse TMA440 Statistikk Faglig kontakt under eksamen: Håkon Tjelmeland a, Sara Martino b Tlf: a 48 18 96, b 99 40 33 30 Eksamensdato: 30. november
Institutt for matematiske fag Eksamensoppgave i Løsningsskisse TMA440 Statistikk Faglig kontakt under eksamen: Håkon Tjelmeland a, Sara Martino b Tlf: a 48 18 96, b 99 40 33 30 Eksamensdato: 30. november
Oppgave 1 a) La X være massen til et tilfeldig valgt egg, målt i gram. Sannsynligheten for at et tilfeldig valgt egg veier mer enn 60 g er
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 5 Løsningsskisse Oppgave 1 a La X være massen til et tilfeldig valgt egg, målt i gram. Sannsynligheten for at
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 5 Løsningsskisse Oppgave 1 a La X være massen til et tilfeldig valgt egg, målt i gram. Sannsynligheten for at
Kapittel 6: Kontinuerlige sannsynlighetsfordelinger 6.4-5.7: Normalfordelingen, normalapproksimasjon, eksponensial og gamma.
 TMA4240 Statistikk H2010 Kapittel 6: Kontinuerlige sannsynlighetsfordelinger 6.4-5.7: Normalfordelingen, normalapproksimasjon, eksponensial og gamma. Mette Langaas Foreleses mandag 27. september 2010 2
TMA4240 Statistikk H2010 Kapittel 6: Kontinuerlige sannsynlighetsfordelinger 6.4-5.7: Normalfordelingen, normalapproksimasjon, eksponensial og gamma. Mette Langaas Foreleses mandag 27. september 2010 2
Løsningskisse seminaroppgaver uke 15
 HG April 0 Løsningskisse seminaroppgaver uke 5 Oppg. 5.6 La X = antall barn i utvalget som har lærevansker. Andel barn med lærevansker i populasjonen av barn antas å være p = 0,5. Utvalgsstørrelsen er
HG April 0 Løsningskisse seminaroppgaver uke 5 Oppg. 5.6 La X = antall barn i utvalget som har lærevansker. Andel barn med lærevansker i populasjonen av barn antas å være p = 0,5. Utvalgsstørrelsen er
Tilfeldige variabler. MAT0100V Sannsynlighetsregning og kombinatorikk
 MAT0100V Sannsynlighetsregning og kombinatorikk Forventning, varians og standardavvik Tilnærming av binomiske sannsynligheter Konfidensintervall Ørnulf Borgan Matematisk institutt Universitetet i Oslo
MAT0100V Sannsynlighetsregning og kombinatorikk Forventning, varians og standardavvik Tilnærming av binomiske sannsynligheter Konfidensintervall Ørnulf Borgan Matematisk institutt Universitetet i Oslo
Da vil summen og gjennomsnittet være tilnærmet normalfordelte : Summen: X 1 +X X n ~N(nµ,nσ 2 ) Gjennomsnittet: X 1 +X
 Me me me me metallic hvit 4.4: Tilnærming til normalfordeling Tilnærming til normalfordeling: binomisk og Poisson kan tilnærmes v.h.a. normalfordeling under bestemte forhold (ved "mange" delforsøk/hendelser)
Me me me me metallic hvit 4.4: Tilnærming til normalfordeling Tilnærming til normalfordeling: binomisk og Poisson kan tilnærmes v.h.a. normalfordeling under bestemte forhold (ved "mange" delforsøk/hendelser)
EKSAMEN I EMNE TMA4265/SIF5072 STOKASTISKE PROSESSER Onsdag 10. august 2005 Tid: 09:00 13:00
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 6 Bokmål Faglig kontakt under eksamen: Håkon Tjelmeland 73 59 35 38 EKSAMEN I EMNE TMA4265/SIF5072 STOKASTISKE PROSESSER
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 6 Bokmål Faglig kontakt under eksamen: Håkon Tjelmeland 73 59 35 38 EKSAMEN I EMNE TMA4265/SIF5072 STOKASTISKE PROSESSER
STK1100 våren Kontinuerlige stokastiske variabler Forventning og varians Momentgenererende funksjoner
 STK1100 våren 2017 Kontinuerlige stokastiske variabler Forventning og varians Momentgenererende funksjoner Svarer til avsnittene 4.1 og 4.2 i læreboka Ørnulf Borgan Matematisk institutt Universitetet i
STK1100 våren 2017 Kontinuerlige stokastiske variabler Forventning og varians Momentgenererende funksjoner Svarer til avsnittene 4.1 og 4.2 i læreboka Ørnulf Borgan Matematisk institutt Universitetet i
Emnenavn: Deleksamen i Statistikk. Eksamenstid: Faglærer: Tore August Kro. Oppgaven er kontrollert:
 EKSAMEN Emnekode: IRB22515, IRBIO22013, IRE22518, IRM23116 Emnenavn: Deleksamen i Statistikk Dato: Sensurfrist: 03.01.19 24.01.19 Eksamenstid: 09.00 12.00 Antall oppgavesider: 6 Antall vedleggsider: 9
EKSAMEN Emnekode: IRB22515, IRBIO22013, IRE22518, IRM23116 Emnenavn: Deleksamen i Statistikk Dato: Sensurfrist: 03.01.19 24.01.19 Eksamenstid: 09.00 12.00 Antall oppgavesider: 6 Antall vedleggsider: 9
EKSAMEN I ST2101 STOKASTISK MODELLERING OG SIMULERING Onsdag 1. juni 2005 Tid: 09:00 14:00
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 6 Bokmål Faglig kontakt under eksamen: Håkon Tjelmeland 73 59 35 38 EKSAMEN I ST2101 STOKASTISK MODELLERING OG SIMULERING
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 6 Bokmål Faglig kontakt under eksamen: Håkon Tjelmeland 73 59 35 38 EKSAMEN I ST2101 STOKASTISK MODELLERING OG SIMULERING
TMA4240 Statistikk Høst 2016
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 9 Løsningsskisse Oppgave 1 a) Vi lar her Y være antall fugler som kolliderer med vindmølla i løpet av den gitte
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 9 Løsningsskisse Oppgave 1 a) Vi lar her Y være antall fugler som kolliderer med vindmølla i løpet av den gitte
Forventning og varians.
 Forventning og varians. Dekkes av kapittel 4 i læreboka. Forventning (4.) Forventningsverdi gjennomsnitt i det lange løp. Defininsjon: Forventningsverdien til en stokastisk variabel X er: E(X) f(),x diskret
Forventning og varians. Dekkes av kapittel 4 i læreboka. Forventning (4.) Forventningsverdi gjennomsnitt i det lange løp. Defininsjon: Forventningsverdien til en stokastisk variabel X er: E(X) f(),x diskret
Dekkes av pensumsidene i kap. lesingsnotatene. Hypotesetesting er en systematisk fremgangsmåte
 Hypotesetesting. 10 og fore- Dekkes av pensumsidene i kap. lesingsnotatene. Hypotesetesting er en systematisk fremgangsmåte for å undersøke hypoteser (påstander) knyttet til parametre i sannsynlighetsfordelinger.
Hypotesetesting. 10 og fore- Dekkes av pensumsidene i kap. lesingsnotatene. Hypotesetesting er en systematisk fremgangsmåte for å undersøke hypoteser (påstander) knyttet til parametre i sannsynlighetsfordelinger.
