INF 4130 / / Dagens foiler hovedsakelig laget av Petter Kristiansen Foreleser Stein Krogdahl Obliger:
|
|
|
- Annar Borgen
- 6 år siden
- Visninger:
Transkript
1 INF 4130 / / Dagens foiler hovedsakelig laget av Petter Kristiansen Foreleser Stein Krogdahl Obliger: Tre stykker, som må godkjennes. Frister: 21. sept, 26. okt, 16. nov Andre, «nærliggende» kurs: INF-MAT 3370 Lineær optimering INF-MAT 5360 Matematisk optimering INF 1080 Logiske metoder for informatikk (INF 1800) MAT-INF 3600 Mathematical Logic MAT 4630 Beregnbarhets-teori
2 Algoritmer, effektivitet, kompleksitet Litt repetisjon Problem-klasser Elementene (punktene i planet) er her «problemer», og hver bue angir en problem-klasse definert ut fra hva slags algoritmer som kan løse problemene under buen. Problem-klassen P består f.eks. av de problemer som kan løses med algoritmer som går i «polynomisk tid» (i worst case) Merk: Hvert. problem består igjen av et antall «instanser», og for at det skal være et interessant problem må det ha uendelig mange instanser. Uløsbare unsolvable Umedgjørlige intractable (NP-komplette) Lette (P) Og: Vi er i dag i P
3 Problem: Søk etter gitt substreng i «lang» streng Er blitt mer aktuelt i det siste, bl.a. på grunn av: Søk i DNA-strenger etter et gitt mønster (eller et «liknende» mønster) Google og liknende søker etter gitte strenger på alle nettsider Det å søke etter et liknende mønster er veldig aktuelt i genetikk De forskjellige gen-sekvensene forandrer seg litt over tid pga. mutasjoner Slike søk er behandlet i kap Vi tar det i forbindelse med dynamisk programmering (kap. 9, neste uke) Vi håper å få besøk av gruppa for Bio-informatikk som snakker om deres bruk av slike algoritmer.
4 Problem: Søk etter gitt substreng i «lang» streng Et alfabet er en endelig mengde symboler A = {a 1, a 2,, a k }. En streng S = S[0:n-1] av lengde n er en sekvens av symboler fra A. Vi kan se på strengen S både som en array S[0:n -1] og som en sekvens av symboler S = < s 0 s 1 s n-1 > Søkeproblemet: Gitt to strenger T (= Tekst) og P (=Pattern/mønster), der P ikke er lenger enn T (og gjerne er mye kortere) Avgjør om strengen P finnes som (sammenhengende) substreng i T, og i så fall hvor n -1 T [0:n -1] (Tekst) P [0:m -1] (Pattern)
5 Varianter av søking i strenger Naiv algoritme, ingen prebehandling av T eller P Anta lengden av T og P er hhv. n og m Gir allerede en polynomisk algoritme, med «worst case» tid O(n*m), som altså også er O(n 2 ). Prebehandling av P (mønsteret) for hver ny P Prefiks-søking Knuth-Morris-Pratt-algoritmen Suffiks-søking Boyer-Moore-algoritmen Hash-basert Karp-Rabin-algoritmen Om man skal søke i den samme teksten mange ganger: Prebehandling (indeksering) av teksten. Teksten kan da f.eks. gjøres om til: Trie-trær Suffiks-trær
6 Naiv algoritme Søker forover Vindu n -1 T [0:n -1] P [0:m -1]
7 Naiv algoritme n -1 T [0:n -1] P [0:m -1]
8 Naiv algoritme n -1 T [0:n -1] P [0:m -1]
9 Naiv algoritme n-m n -1 T [0:n -1] P [0:m -1]
10 Naiv algoritme n-m n -1 T [0:n -1] P [0:m -1] function NaiveStringMatcher (P [0:m -1], T [0:n -1]) for s 0 to n - m do if T [s :s + m -1] = P then return(s) endif endfor return(-1) end NaiveStringMatcher
11 Naiv algoritme n-m n -1 T [0:n -1] P [0:m -1] function NaiveStringMatcher (P [0:m -1], T [0:n -1]) for s 0 to n - m do if T [s :s + m -1] = P then}for-løkka eksekveres n m + 1 ganger. return(s) Hver sjekk inntil m symbolsammenlikninger. endif O(nm) kjøretid (worst case inntreffer om P ikke endfor finnes, eller P ligger helt på slutten i T) return(-1) end NaiveStringMatcher
12 Knuth-Morris-Pratt-algoritmen Det er rom for forbedringer av den naive algoritmen Den naive algoritmen flytter vinduet/patternet bare ett hakk i hvert steg Kan vi kanskje flytte mer enn bare ett hakk, ut fra hva vi vet pga. testene i forrige steg Vi ser på følgende eksempel:
13 Knuth-Morris-Pratt-algoritmen Søker forover
14 KMP-algoritmen
15 KMP-algoritmen Flytter ett hakk. Ikke match
16 KMP-algoritmen Flytter to hakk. Ikke match
17 KMP-algoritmen Flytter tre hakk. Her er det hvertfall match på den delen der de var like i forrige sammenlikning Vi kan altså flytte forbi alle situasjoner der det vi vet om T (ut fra den delen som stemte med P) ikke stemmer med det vi vet om P Det kan hende at vi aldri får slik match som på figuren over, og da kan vi flytte P slik at starten er der det ble forskjell i forrige søk. Dette, altså lange flytt, er det beste for effektiviteten av algoritmen.
18 KMP-algoritmen 0 1 i - d j i j -1 j j -2 j j - d j d j d j er lengden av lengste suffix av P [1 : j -1] som også er prefix av P [0 : j - 2] Vi vet nå at om vi flytter P mindre enn j - d j steg, så kan det ikke bli match. Og vi vet at etter flytting P [0: d j -1] matcher T, så vi kan starte å sammenlikne ved P [d j : m-1].
19 Knuth-Morris-Pratt-algoritmen Plan Vi vil lage en heltalls-tabell Next[0:m-1] som viser hvor langt vi kan flytte P når vi får en mismatch på stedet j i P, j = 0,1,2,, m-1 Men Next angir ikke dette direkte, men i stedet den nye (og mindre) verdien som j skal ha når vi fortsetter søket. Altså: Next[j] = j <antall steg P kan flyttes fram> Eller: Next[j] er det som er betegnet med d j på forrige foil Og etter flytting vil også de d j første som vi ser på i T stemme med de tilsvarende i P. Det var slik vi valgte d j. Og Next-arrayen kan altså beregnes ut fra bare innholdet i P
20 function KMPStringMatcher (P [0:m -1], T [0:n -1]) i 0 // indeks i T j 0 // indeks i P CreateNext(P [0:m -1], Next [n -1]) while i < n do if P [ j ] = T [ i ] then if j = m 1 then // sjekker om full match else endif i i +1 j j +1 return(i m + 1) j Next [ j ] if j = 0 then if T [ i ] P [0] then i i +1 endif endif endif endwhile return(-1) end KMPStringMatcher Worst case tid: O(n) Knuth-Morris-Pratt-algoritmen Denne if-setningen er med for å forhindre at algoritmen går i evig løkke. Om den ikke er med kan P bli «stående på samme sted» runde etter runde, uten at i blir øket.
21 Knuth-Morris-Pratt-algoritmen Vi må altså skrive en funksjon som finner Next ut fra P: function CreateNext (P [0:m -1], Next [0:m -1]) end CreateNext Denne kan skrives rett fram ved enkel søking, og vil da bruke tid O(m 2 ). Man kan imidlertid bruke noen av de samme triksene som når man går fra den naive søkealgoritmen, til KMP-algoritmen, og da kan man finne Next-arrayen i tid O(m). Det er den kompliserte som står i boka, men vi tar ikke den med som pensum.
22 Knuth-Morris-Pratt-algoritmen Eksempel Next-arrayen til P-en over : j = Next[j] =
23 Knuth-Morris-Pratt-algoritmen Next-arrayen til P-en over : j = Next[j] =
24 Knuth-Morris-Pratt-algoritmen Next-arrayen til P-en over : j = Next[j] =
25 Knuth-Morris-Pratt-algoritmen Next-arrayen til P-en over : j = Next[j] =
26 Knuth-Morris-Pratt-algoritmen Next-arrayen til P-en over : j = Next[j] = Lineær algoritme, O(n) kjøretid worst case.
27 Boyer-Moore-algoritmen (Horspool) Den naive algoritmen, og Knuth-Morris-Pratt er prefiksbaserte (fra venstre mot høyre). Boyer-Moore-algoritmen (og varianter) er suffixbasert (fra høyre mot venstre i patternet). Horspool laget en forenkling av Boyer-Moore, og det er den vi skal se på her Vi ser på følgende eksempel: B M m a t c h e r _ s h i f t _ c h a r a c t e r _ e x c h a r a c t e r
28 Boyer-Moore-algoritmen (Horspool) Sammenlikner bakfra i P B M m a t c h e r _ s h i f t _ c h a r a c t e r _ e x c h a r a c t e r
29 Boyer-Moore-algoritmen (Horspool) Den naive algoritmen, og Knuth-Morris-Pratt er prefiksbaserte (fra venstre mot høyre). Boyer-Moore-algoritmen (og varianter) er suffixbasert (fra høyre mot venstre i patternet). B M m a t c h e r _ s h i f t _ c h a r a c t e r _ e x c h a r a c t e r c h a r a c t e r
30 Boyer-Moore-algoritmen (Horspool) B M m a t c h e r _ s h i f t _ c h a r a c t e r _ e x c h a r a c t e r c h a r a c t e r c h a r a c t e r
31 Boyer-Moore-algoritmen (Horspool) B M m a t c h e r _ s h i f t _ c h a r a c t e r _ e x c h a r a c t e r c h a r a c t e r c h a r a c t e r c h a r a c t e r
32 Boyer-Moore-algoritmen (Horspool) B M m a t c h e r _ s h i f t _ c h a r a c t e r _ e x c h a r a c t e r c h a r a c t e r c h a r a c t e r c h a r a c t e r O(mn) kjøretid worst case (som den naive algoritmen). Sub-lineær ( n) i gjennomsnitt O(n (log A m) / m).
33 Boyer-Moore-algoritmen (Horspool) function HorspoolStringMatcher (P [0:m -1], T [0:n -1]) i 0 CreateShift(P [0:m -1], Shift [0: A - 1]) while i < n m do j m 1 while j 0 and T [ i+j]=p [ j ] do j j -1 endwhile if j = 0 then return( i ) endif i i + Shift[ T[ i + m -1] ] endwhile return(-1) end HorspoolStringMatcher
34 Funksjonen CreateShift Boyer-Moore-algoritmen (Horspool) function CreateShift (P [0:m -1], Shift [0: A - 1]) end HorspoolStringMatcher Vi må altså lage Shift-arrayen, som er like lang som alfabetet Vi leter da bakfra (ikke ta med helt bakerste tegn i P) og registrerer indeksen der de forskjellige tegnene opptrer første gang. For tegnene t som ikke opptrer i P setter vi Shift[t] = <lengden av P>. Det gir altså fult skift
35 Karp-Rabin-algoritmen Vi antar at strengene våre kommer fra et k-ært alfabet A = {0, 1, 2,, k -1}. Hvert symbol i A kan sees på som et siffer i k-tallssystemet. Hver streng S i A* kan sees på som tall S i k-tallssystemet. Eks: k = 10, og A = {0,1, 2,, 9} (Det vanlige 10-tallssystemet) Strengen kan sees på som tallet Gitt en streng P [0:m -1], kan vi beregne det korresponderende tallet P med m multiplikasjoner og m addisjoner (Horners regel): P = P [m -1]+k(P [m -2]+ +k(p [1] + kp [0])...)) Eks: 1234 = (3 + 10(2 + 10*1))
36 Karp-Rabin-algoritmen Gitt en tekststreng T [0:n -1], og et heltall s (start-index), bruker vi T s som en hash-verdi for delstrengen T [s: s + m -1]. (Vi antar at patternet vårt har lengde m.) En algoritme basert på Horners regel beregner T 0, T 1, T 2, og sammenlikner disse tallene med tallet P for patternet P. (Tilsvarende den naive algoritmen.)
37 Karp-Rabin-algoritmen Gitt en tekststreng T [0:n -1], og et heltall s (start-index), bruker vi T s som betegnelse på delstrengen T [s: s + m -1]. (Vi antar at patternet vårt har lengde m.) En algoritme basert på Horners regel beregner T 0, T 1, T 2, og sammenlikner disse tallene med tallet P for patternet P. (Tilsvarende den naive algoritmen.) Gitt T s -1 og k m 1, kan vi regne ut T s i konstant tid.
38 Karp-Rabin-algoritmen Gitt en tekststreng T [0:n -1], og et heltall s (start-index), bruker vi T s som betegnelse på delstrengen T [s: s + m -1]. (Vi antar at patternet vårt har lengde m.) En algoritme basert på Horners regel beregner T 0, T 1, T 2, og sammenlikner disse tallene med tallet P for patternet P. (Tilsvarende den naive algoritmen.) Gitt T s -1 og k m 1, kan vi regne ut T s i konstant tid s-1 s -1+ m -1 n -1 T [0:n -1] T s -1
39 Karp-Rabin-algoritmen Gitt en tekststreng T [0:n -1], og et heltall s (start-index), bruker vi T s som betegnelse på delstrengen T [s: s + m -1]. (Vi antar at patternet vårt har lengde m.) En algoritme basert på Horners regel beregner T 0, T 1, T 2, og sammenlikner disse tallene med tallet P for patternet P. (Tilsvarende den naive algoritmen.) Gitt T s -1 og k m 1, kan vi regne ut T s i konstant tid.! s-1 s s + m -1 n -1 T [0:n -1] T s
40 Karp-Rabin-algoritmen Grunnen til at vi kan beregne T s følgende rekurrensrelasjon: i konstant tid når vi har T s -1 og k m 1, er T s = k(t s -1 - k m 1 *T [s]) + T [s+m] s = 1,, n m Konstant, beregnes en gang, kan gjøres i tid O(log m) Eks: k = 10, A = {0,1, 2,, 9} (Det vanlige 10-tallssystemet) og m = 7. T s -1 = T s = T s = 10( ( * 7)) + 8 Kan gjøres i konstant tid. Bare multiplikasjon og addisjon, vi antar disse operasjonene kan gjøres i konstant tid. Dette blir jo hvertfall sant når vi senere går over til modulo-regning.
41 Karp-Rabin-algoritmen Kan beregne T s i konstant tid når vi har T s -1 og k m 1. Altså kan vi beregne de n m + 1 tallene T s, s = 0, 1,, n m og P itido(n). Vi kan altså, i teorien, implementere en søkealgoritme med kjøretid O(n). Dessverre vil tallene T s og P i praksis være for store til at algoritmen blir praktisk anvendbar. Trikset er å bruke modulo-aritmetikk. Vi gjør alle beregninger modulo q (q er valgt som et primtall, slik at kq akkurat passer i et 32/64 bits register). Primtall blir valgt fordi det fordeler hash-verdiene godt.
42 Vi beregner T (q) s og P (q), hvor Karp-Rabin-algoritmen T (q) s = T s mod q, P (q) = P mod q, } Resten i divisjonen, når vi deler på q: et tall i intervallet {0, 1,, q -1}. og sammenlikner. Vi kan ha T (q) s = P (q), selv om T s P, en såkalt spuriøs match. Har vi T (q) s = P (q), må vi altså gjøre en nøyaktig sjekk av T s og P. Med stor nok q, er sannsynligheten for spuriøse matcher lav.
43 Karp-Rabin-algoritmen function KarpRabinStringMatcher (P [0:m -1], T [0:n -1], k, q) c k m -1 mod q P (q) 0 T (q) s 0 for i 1 to m do P (q) (k * P (q) + P [ i ]) mod q T (q) 0 (k * T (q) 0 + T [ i ]) mod q endfor for s 0 to n - m do if s > 0 then T (q) s (k * ( T (q) s -1 -T[ s ] * c) + T [ s + m ]) mod q endif if T (q) s = P (q) then if T s = P then return(s) endif endif endfor return(-1) end KarpRabinStringMatcher
44 Karp-Rabin-algoritmen Lengste kjøretid for Karp-Rabin-algoritmen får vi når patternet P finnes helt i slutten av strengen T. Sannsynligheten for at T (q) s antar en spesifikk verdi i intervallet {0, 1,, q-1} er uniform 1/q. (Vi antar strengene er uniformt fordelte.) T (q) s, s = 0, 1,, n-m-1 vil for hver s altså gi opphav til en spuriøs match med sannsynlighet 1/q (altså at vi får like hash-verdier uten at strengene er like). La r være det forventede antall spuriøse matcher. Hver av disse innebærer inntil m sammenlikninger. I tillegg må vi sjekke T (q) n-m, hvor vi til slutt får ekte match. Kjøretiden blir altså: O( (r + 1)m + (n m + 1) )
45 Karp-Rabin-algoritmen (konklusjon) Om patternet P ikke finnes i T eller ligger helt på slutten av T (worst case) vil verdien av r med stor sannsynlighet ligge nær (n-m) * (1/q) Totalt får vi altså at max kjøretid blir: n m q O( 1 m ( n m 1) ) Slik vi valgte q er det rimelig å anta at q >> m, og da blir kjøretiden altså O(n).
46 Mange søk i samme strengen T Da kan det være lurt å preprosessere T Slik Google preprosserer de sidene den leser, for å kunne søke raskt i dem siden. Dette kalles også å «indeksere» en datamengde Vi gjør vår indeksering ved å lage et «suffiks-tre» Ofte er det slik at vi kan legge inn ny informasjon i datamengden (f.eks. forlenge T), og justere indekseringen etter forandringen. Dette gjøres typisk i Google etter hvert som den leser nye sider
47 Først: Trie-trær a i w Trykkfeil i boka l n e o g l t b r o e l r r d i t h m a l l n e t v l e w y
48 Trie-trær al inter w gorithm l n view eb orld ally et
49 Suffix-trær Suffix tre for babbage a b e ge bbage ge a bage bbage ge
50 Div.
Søking i strenger. Prefiks-søking Naiv algoritme Knuth-Morris-Pratt-algoritmen Suffiks-søking Boyer-Moore-algoritmen Hash-basert Karp-Rabin-algoritmen
 Søking i strenger Vanlige søkealgoritmer (on-line-søk) Prefiks-søking Naiv algoritme Knuth-Morris-Pratt-algoritmen Suffiks-søking Boyer-Moore-algoritmen Hash-basert Karp-Rabin-algoritmen Indeksering av
Søking i strenger Vanlige søkealgoritmer (on-line-søk) Prefiks-søking Naiv algoritme Knuth-Morris-Pratt-algoritmen Suffiks-søking Boyer-Moore-algoritmen Hash-basert Karp-Rabin-algoritmen Indeksering av
Turingmaskiner.
 Turingmaskiner http://www.youtube.com/watch?v=e3kelemwfhy http://www.youtube.com/watch?v=cyw2ewoo6c4 Søking i strenger Vanlige søkealgoritmer (on-line-søk) Prefiks-søking Naiv algoritme Knuth-Morris-Pratt-algoritmen
Turingmaskiner http://www.youtube.com/watch?v=e3kelemwfhy http://www.youtube.com/watch?v=cyw2ewoo6c4 Søking i strenger Vanlige søkealgoritmer (on-line-søk) Prefiks-søking Naiv algoritme Knuth-Morris-Pratt-algoritmen
Stein Krogdahl, Dino Karabeg, Petter Kristiansen. Kenneth A. Berman and Jerome L. Paul.
 Stein Krogdahl, Dino Karabeg, Petter Kristiansen steinkr at ifi.uio.no dino at ifi.uio.no pettkr at ifi.uio.no INF 4130 / 9135 Algoritmer: Design og effektivitet Algorithms: Sequential Parallel and Distributed
Stein Krogdahl, Dino Karabeg, Petter Kristiansen steinkr at ifi.uio.no dino at ifi.uio.no pettkr at ifi.uio.no INF 4130 / 9135 Algoritmer: Design og effektivitet Algorithms: Sequential Parallel and Distributed
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2015 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 10: Tekstalgoritmer 1 Ingrid Chieh Yu (Ifi, UiO) INF2220 H2015, forelesning 10 1
INF2220 - Algoritmer og datastrukturer HØSTEN 2015 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 10: Tekstalgoritmer 1 Ingrid Chieh Yu (Ifi, UiO) INF2220 H2015, forelesning 10 1
Tekstalgoritmer. Søk etter delstrenger i array
 Tekstalgoritmer Søk etter delstrenger i array Definisjoner Et alfabet er en endelig mengde tegn A = {a 1, a 2,, a k }. En (tekst)streng S = S [0: n -1] med lengde n er en sekvens av tegn fra A. Vi vil
Tekstalgoritmer Søk etter delstrenger i array Definisjoner Et alfabet er en endelig mengde tegn A = {a 1, a 2,, a k }. En (tekst)streng S = S [0: n -1] med lengde n er en sekvens av tegn fra A. Vi vil
Dynamisk programmering Undervises av Stein Krogdahl
 Dynamisk programmering Undervises av Stein Krogdahl 5. september 2012 Dagens stoff er hentet fra kapittel 9 i læreboka, samt kapittel 20.5 (som vi «hoppet over» sist) Kapittel 9 er lagt ut på undervisningsplanen.
Dynamisk programmering Undervises av Stein Krogdahl 5. september 2012 Dagens stoff er hentet fra kapittel 9 i læreboka, samt kapittel 20.5 (som vi «hoppet over» sist) Kapittel 9 er lagt ut på undervisningsplanen.
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet «Midterm» i: INF 4130: Algoritmer: Design og effektivitet Eksamensdag: 1. november 2011 Tid for «midterm»: Kl. 09:00 13:00 (4 timer) [124%,
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet «Midterm» i: INF 4130: Algoritmer: Design og effektivitet Eksamensdag: 1. november 2011 Tid for «midterm»: Kl. 09:00 13:00 (4 timer) [124%,
Notater til INF2220 Eksamen
 Notater til INF2220 Eksamen Lars Bjørlykke Kristiansen December 13, 2011 Stor O notasjon Funksjon Navn 1 Konstant log n Logaritmisk n Lineær n log n n 2 Kvadratisk n 3 Kubisk 2 n Eksponensiell n! Trær
Notater til INF2220 Eksamen Lars Bjørlykke Kristiansen December 13, 2011 Stor O notasjon Funksjon Navn 1 Konstant log n Logaritmisk n Lineær n log n n 2 Kvadratisk n 3 Kubisk 2 n Eksponensiell n! Trær
Pattern matching algorithms. INF Algoritmer og datastrukturer. Lokalisering av Substrenger. Brute force
 Pattern matching algorithms INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo Algoritmer for lokalisering av substrenger Brute force Enkleste tenkelige
Pattern matching algorithms INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo Algoritmer for lokalisering av substrenger Brute force Enkleste tenkelige
Dagens stoff er hentet fra kapittel 9 i læreboka, samt kapittel 20.5 (som vi «hoppet over» sist)
 Dynamisk programmering Undervises av Stein Krogdahl 5. september 2012 Dagens stoff er hentet fra kapittel 9 i læreboka, samt kapittel 20.5 (som vi «hoppet over» sist) Kapittel 9 er lagt ut på undervisningsplanen.
Dynamisk programmering Undervises av Stein Krogdahl 5. september 2012 Dagens stoff er hentet fra kapittel 9 i læreboka, samt kapittel 20.5 (som vi «hoppet over» sist) Kapittel 9 er lagt ut på undervisningsplanen.
Dynamisk programmering
 Dynamisk programmering Metoden ble formalisert av Richard Bellmann (RAND Corporation) på 50-tallet. Programmering i betydningen planlegge, ta beslutninger. (Har ikke noe med kode eller å skrive kode å
Dynamisk programmering Metoden ble formalisert av Richard Bellmann (RAND Corporation) på 50-tallet. Programmering i betydningen planlegge, ta beslutninger. (Har ikke noe med kode eller å skrive kode å
INF Stein Krogdahl. NB: Det som under forelesningen ble kalt et vitne er nå omdøpt til et sertifikat.
 INF 4130 15. oktober 2009 Stein Krogdahl NB: Det som under forelesningen ble kalt et vitne er nå omdøpt til et sertifikat. Dagens tema: NP-kompletthet Eller: hvilke problemer er umulig å løse effektivt?
INF 4130 15. oktober 2009 Stein Krogdahl NB: Det som under forelesningen ble kalt et vitne er nå omdøpt til et sertifikat. Dagens tema: NP-kompletthet Eller: hvilke problemer er umulig å løse effektivt?
INF oktober Stein Krogdahl. Altså: Hva kan ikke gjøres raskt (med mindre P = NP)
 INF 4130 22. oktober 2009 Stein Krogdahl Dagens tema: Mer om NP-kompletthet Altså: Hva kan ikke gjøres raskt (med mindre P = NP) Også her: Dette har blitt framstilt litt annerledes tidligere år Pensum
INF 4130 22. oktober 2009 Stein Krogdahl Dagens tema: Mer om NP-kompletthet Altså: Hva kan ikke gjøres raskt (med mindre P = NP) Også her: Dette har blitt framstilt litt annerledes tidligere år Pensum
INF 4130 Oppgavesett 3, 20/ m/løsningsforslag
 INF 4130 Oppgavesett 3, 20/09-2011 m/løsningsforslag Oppgave 1 1.1 Løs oppgave 20.19 (B&P), (a) er vist på forelesningen og kan vel bare repeteres, men løs (b). (a) er altså løst på forelesningen. (b)
INF 4130 Oppgavesett 3, 20/09-2011 m/løsningsforslag Oppgave 1 1.1 Løs oppgave 20.19 (B&P), (a) er vist på forelesningen og kan vel bare repeteres, men løs (b). (a) er altså løst på forelesningen. (b)
Hashtabeller. Lars Vidar Magnusson Kapittel 11 Direkte adressering Hashtabeller Chaining Åpen-adressering
 Hashtabeller Lars Vidar Magnusson 12.2.2014 Kapittel 11 Direkte adressering Hashtabeller Chaining Åpen-adressering Dictionaries Mange applikasjoner trenger dynamiske sett som bare har dictionary oparsjonene
Hashtabeller Lars Vidar Magnusson 12.2.2014 Kapittel 11 Direkte adressering Hashtabeller Chaining Åpen-adressering Dictionaries Mange applikasjoner trenger dynamiske sett som bare har dictionary oparsjonene
INF3/4130 PRØVE-EKSAMEN MED SVARFORSLAG Gjennomgås 1/ , (lille aud.)
 Oppgave 1 Uavgjørbarhet INF3/4130 PRØVE-EKSAMEN MED SVARFORSLAG Gjennomgås 1/12-2005, 14.15 (lille aud.) L = {(M 1, M 2 ) M 1 og M 2 er Turingmaskiner som er ekvivalente, dvs. gir samme output for samme
Oppgave 1 Uavgjørbarhet INF3/4130 PRØVE-EKSAMEN MED SVARFORSLAG Gjennomgås 1/12-2005, 14.15 (lille aud.) L = {(M 1, M 2 ) M 1 og M 2 er Turingmaskiner som er ekvivalente, dvs. gir samme output for samme
Dynamisk programmering
 Dynamisk programmering Metoden ble formalisert av Richard Bellmann (RAND Corporation) på 5-tallet. Programmering i betydningen planlegge, ta beslutninger. (Har ikke noe med kode eller å skrive kode å gjøre.)
Dynamisk programmering Metoden ble formalisert av Richard Bellmann (RAND Corporation) på 5-tallet. Programmering i betydningen planlegge, ta beslutninger. (Har ikke noe med kode eller å skrive kode å gjøre.)
INF2220: Forelesning 1. Praktisk informasjon Analyse av algoritmer (kapittel 2) (Binær)trær (kapittel )
 INF2220: Forelesning 1 Praktisk informasjon Analyse av algoritmer (kapittel 2) (Binær)trær (kapittel 4.1-4.3 + 4.6) PRAKTISK INFORMASJON 2 Praktisk informasjon Kursansvarlige Ragnhild Kobro Runde (ragnhilk@ifi.uio.no)
INF2220: Forelesning 1 Praktisk informasjon Analyse av algoritmer (kapittel 2) (Binær)trær (kapittel 4.1-4.3 + 4.6) PRAKTISK INFORMASJON 2 Praktisk informasjon Kursansvarlige Ragnhild Kobro Runde (ragnhilk@ifi.uio.no)
Datastrukturer for rask søking
 Søking Søkeproblemet Gitt en datastruktur med n elementer: Finnes et bestemt element (eller en bestemt verdi) x lagret i datastrukturen eller ikke? Effektiviteten til søkealgoritmer avhenger av: Om datastrukturen
Søking Søkeproblemet Gitt en datastruktur med n elementer: Finnes et bestemt element (eller en bestemt verdi) x lagret i datastrukturen eller ikke? Effektiviteten til søkealgoritmer avhenger av: Om datastrukturen
Søkeproblemet. Gitt en datastruktur med n elementer: Finnes et bestemt element (eller en bestemt verdi) x lagret i datastrukturen eller ikke?
 Søking Søkeproblemet Gitt en datastruktur med n elementer: Finnes et bestemt element (eller en bestemt verdi) x lagret i datastrukturen eller ikke? Effektiviteten til søkealgoritmer avhenger av: Om datastrukturen
Søking Søkeproblemet Gitt en datastruktur med n elementer: Finnes et bestemt element (eller en bestemt verdi) x lagret i datastrukturen eller ikke? Effektiviteten til søkealgoritmer avhenger av: Om datastrukturen
Kvalitetssikring ved Ifi. Undervisningsplan
 Forsr: Vkommn Dino Karabg, Stin Krogdah, Pttr Kristiansn dino@ifi.uio.no stinkr@ifi.uio.no pttkr@ifi.uio.no Gruppærr: Vkommn Dg? post@studnt.matnat.uio.no Lærbok: Agorithms: Squntia, Para, and Distributd,
Forsr: Vkommn Dino Karabg, Stin Krogdah, Pttr Kristiansn dino@ifi.uio.no stinkr@ifi.uio.no pttkr@ifi.uio.no Gruppærr: Vkommn Dg? post@studnt.matnat.uio.no Lærbok: Agorithms: Squntia, Para, and Distributd,
IN2010: Forelesning 11. Kombinatorisk søking Beregnbarhet og kompleksitet
 IN2010: Forelesning 11 Kombinatorisk søking Beregnbarhet og kompleksitet KOMBINATORISK SØKING Oversikt Generering av permutasjoner Lett: Sekvens-generering Vanskelig: Alle tallene må være forskjellige
IN2010: Forelesning 11 Kombinatorisk søking Beregnbarhet og kompleksitet KOMBINATORISK SØKING Oversikt Generering av permutasjoner Lett: Sekvens-generering Vanskelig: Alle tallene må være forskjellige
Hva er en algoritme? INF HØSTEN 2006 INF1020. Kursansvarlige Ragnar Normann E-post: Dagens tema
 va er en algoritme? Vanlig sammenligning: Oppskrift. nput lgoritme NF1020 - ØSTEN 2006 Kursansvarlige Ragnar Normann E-post: ragnarn@ifi.uio.no Output Knuth : tillegg til å være et endelig sett med regler
va er en algoritme? Vanlig sammenligning: Oppskrift. nput lgoritme NF1020 - ØSTEN 2006 Kursansvarlige Ragnar Normann E-post: ragnarn@ifi.uio.no Output Knuth : tillegg til å være et endelig sett med regler
INF Algoritmer: Design og effektivitet
 INF 4130 Algoritmer: Design og effektivitet Velkommen Forelesere: Stein Krogdahl, steinkr at ifi.uio.no Petter Kristiansen pettkr at ifi.uio.no Lærebok: Algorithms: Sequential, Parallel, and Distributed,
INF 4130 Algoritmer: Design og effektivitet Velkommen Forelesere: Stein Krogdahl, steinkr at ifi.uio.no Petter Kristiansen pettkr at ifi.uio.no Lærebok: Algorithms: Sequential, Parallel, and Distributed,
INF2220: Time 8 og 9 - Kompleksitet, beregnbarhet og kombinatorisk søk
 INF0: Time 8 og 9 - Kompleksitet, beregnbarhet og kombinatorisk søk Mathias Lohne mathialo Rekursjonseksempel Eksempel Finn kjøretid for følgende program: (Ex11 b) 1 float foo(a) { n = Alength; 3 4 if
INF0: Time 8 og 9 - Kompleksitet, beregnbarhet og kombinatorisk søk Mathias Lohne mathialo Rekursjonseksempel Eksempel Finn kjøretid for følgende program: (Ex11 b) 1 float foo(a) { n = Alength; 3 4 if
MAT1030 Forelesning 2
 MAT1030 Forelesning 2 Kontrollstrukturer, tallsystemer, basis Dag Normann - 20. januar 2010 (Sist oppdatert: 2010-01-20 12:31) Kapittel 1: Algoritmer (fortsettelse) Kontrollstrukturer I går innførte vi
MAT1030 Forelesning 2 Kontrollstrukturer, tallsystemer, basis Dag Normann - 20. januar 2010 (Sist oppdatert: 2010-01-20 12:31) Kapittel 1: Algoritmer (fortsettelse) Kontrollstrukturer I går innførte vi
INF oktober Stein Krogdahl. Kap 23.5: Trær og strategier for spill med to spillere
 INF 4130 1. oktober 2009 Stein Krogdahl Dagens program: Første time: Kap 23.5: Trær og strategier for spill med to spillere Andre time, gjesteforelesning: Rune Djurhuus: Om sjakkspillende programmer (Ikke
INF 4130 1. oktober 2009 Stein Krogdahl Dagens program: Første time: Kap 23.5: Trær og strategier for spill med to spillere Andre time, gjesteforelesning: Rune Djurhuus: Om sjakkspillende programmer (Ikke
MAT1030 Diskret Matematikk
 MAT1030 Diskret Matematikk Forelesning 2: Kontrollstrukturer, tallsystemer, basis Roger Antonsen Institutt for informatikk, Universitetet i Oslo 14. januar 2009 (Sist oppdatert: 2009-01-14 16:45) Kapittel
MAT1030 Diskret Matematikk Forelesning 2: Kontrollstrukturer, tallsystemer, basis Roger Antonsen Institutt for informatikk, Universitetet i Oslo 14. januar 2009 (Sist oppdatert: 2009-01-14 16:45) Kapittel
Programmering Høst 2017
 Programmering Høst 2017 Tommy Abelsen Ingeniørfag - Data Innledning Dette er et dokument med litt informasjon og eksempler om kontrollstrukturer, samt oppgaver til forskjellige kontrollstrukturer. Spør
Programmering Høst 2017 Tommy Abelsen Ingeniørfag - Data Innledning Dette er et dokument med litt informasjon og eksempler om kontrollstrukturer, samt oppgaver til forskjellige kontrollstrukturer. Spør
INF 4130. 8. oktober 2009. Dagens tema: Uavgjørbarhet. Neste uke: NP-kompletthet
 INF 4130 8. oktober 2009 Stein Krogdahl Dagens tema: Uavgjørbarhet Dette har blitt framstilt litt annerledes tidligere år Se Dinos forelesninger fra i fjor. I år: Vi tenker mer i programmer enn i Turing-maskiner
INF 4130 8. oktober 2009 Stein Krogdahl Dagens tema: Uavgjørbarhet Dette har blitt framstilt litt annerledes tidligere år Se Dinos forelesninger fra i fjor. I år: Vi tenker mer i programmer enn i Turing-maskiner
MAT1030 Diskret matematikk
 Oppgave 1.1 MAT1030 Diskret matematikk Plenumsregning 2: Ukeoppgaver fra kapittel 1 & 2 Roger Antonsen Matematisk Institutt, Universitetet i Oslo 24. januar 2008 Modifiser algoritmen fra 1.2.1 slik at
Oppgave 1.1 MAT1030 Diskret matematikk Plenumsregning 2: Ukeoppgaver fra kapittel 1 & 2 Roger Antonsen Matematisk Institutt, Universitetet i Oslo 24. januar 2008 Modifiser algoritmen fra 1.2.1 slik at
INF2220: Forelesning 2
 INF2220: Forelesning 2 Mer om analyse av algoritmer Analyse av binære søketrær Balanserte søketrær Rød-svarte trær (kapittel12.2) B-trær (kapittel 4.7) ANALYSE AV ALGORITMER 2 Analyse av tidsforbruk Hvor
INF2220: Forelesning 2 Mer om analyse av algoritmer Analyse av binære søketrær Balanserte søketrær Rød-svarte trær (kapittel12.2) B-trær (kapittel 4.7) ANALYSE AV ALGORITMER 2 Analyse av tidsforbruk Hvor
Stoff som i boka står i kap 4, men som er. 10. Februar Ifi, UiO
 INF5110 V2010 Stoff som i boka står i kap 4, men som er generelt stoff om grammatikker 10. Februar 2010 Stein Krogdahl Ifi, UiO Oppgaver som gjennomgås 16/2: - Spørsmålene på foil 35 og 36 fra 9/10 - Finn
INF5110 V2010 Stoff som i boka står i kap 4, men som er generelt stoff om grammatikker 10. Februar 2010 Stein Krogdahl Ifi, UiO Oppgaver som gjennomgås 16/2: - Spørsmålene på foil 35 og 36 fra 9/10 - Finn
MAT1030 Diskret matematikk
 MAT1030 Diskret matematikk Plenumsregning 2: Ukeoppgaver fra kapittel 1 & 2 Roger Antonsen Matematisk Institutt, Universitetet i Oslo 24. januar 2008 Oppgave 1.1 Modifiser algoritmen fra 1.2.1 slik at
MAT1030 Diskret matematikk Plenumsregning 2: Ukeoppgaver fra kapittel 1 & 2 Roger Antonsen Matematisk Institutt, Universitetet i Oslo 24. januar 2008 Oppgave 1.1 Modifiser algoritmen fra 1.2.1 slik at
INF 4130 Svarforslag til «Midterm», 01/
 INF 4130 Svarforslag til «Midterm», 01/11-2011 Oppgave 1 1.a Den generelle reglen blir: Dersom S[i] = [j]: Dersom S[i] [j]: true dersom B[i-1, j-1] = true eller om B[i-1, j-1] = true ellers: false true
INF 4130 Svarforslag til «Midterm», 01/11-2011 Oppgave 1 1.a Den generelle reglen blir: Dersom S[i] = [j]: Dersom S[i] [j]: true dersom B[i-1, j-1] = true eller om B[i-1, j-1] = true ellers: false true
INF2220: Time 12 - Sortering
 INF0: Time 1 - Sortering Mathias Lohne mathialo Noen algoritmer Vi skal nå se på noen konkrete sorteringsalgoritmer. Gjennomgående i alle eksempler vil vi sortere tall etter tallverdi, men som diskutert
INF0: Time 1 - Sortering Mathias Lohne mathialo Noen algoritmer Vi skal nå se på noen konkrete sorteringsalgoritmer. Gjennomgående i alle eksempler vil vi sortere tall etter tallverdi, men som diskutert
Oppsummering av Uke 3. MAT1030 Diskret matematikk. Binære tall. Oppsummering av Uke 3
 Oppsummering av Uke 3 MAT1030 Diskret matematikk Forelesning 3: Mer om representasjon av tall Dag Normann Matematisk Institutt, Universitetet i Oslo 21. januar 2008 Mandag 14.01 og delvis onsdag 16.01
Oppsummering av Uke 3 MAT1030 Diskret matematikk Forelesning 3: Mer om representasjon av tall Dag Normann Matematisk Institutt, Universitetet i Oslo 21. januar 2008 Mandag 14.01 og delvis onsdag 16.01
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF2220 Algoritmer og datastrukturer Eksamensdag: 16. desember 2013 Tid for eksamen: 14.30 18.30 Oppgavesettet er på 8 sider.
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF2220 Algoritmer og datastrukturer Eksamensdag: 16. desember 2013 Tid for eksamen: 14.30 18.30 Oppgavesettet er på 8 sider.
Kap. 4 del I Top Down Parsering INF5110 v2006. Stein Krogdahl Ifi, UiO
 Kap. 4 del I Top Down Parsering INF5110 v2006 Stein Krogdahl Ifi, UiO 1 Innhold First og Follow-mengder Boka ser på én parseringsmetode først, uten å se på First/Follow-mengder. Vi tar teorien først To
Kap. 4 del I Top Down Parsering INF5110 v2006 Stein Krogdahl Ifi, UiO 1 Innhold First og Follow-mengder Boka ser på én parseringsmetode først, uten å se på First/Follow-mengder. Vi tar teorien først To
INF Repetisjon: Hvordan bygge treet og analysere? 8. september Typisk situasjon. De problematiske syntaks-diagrammene
 Dagens tema: INF 2100 8. september 2004 Mer om strukturen i treet og hvordan bygge det Testing av at navn er deklarert og brukt riktig Arbeid i gruppene neste uke: Oppgaver relevant for dette stadiet i
Dagens tema: INF 2100 8. september 2004 Mer om strukturen i treet og hvordan bygge det Testing av at navn er deklarert og brukt riktig Arbeid i gruppene neste uke: Oppgaver relevant for dette stadiet i
MAT1030 Plenumsregning 1
 MAT1030 Plenumsregning 1 Kapittel 1 Mathias Barra - 16. januar 2009 (Sist oppdatert: 2009-02-02 14:21) Plenumsregning 1 Velkommen til plenumsregning for MAT1030 Fredager 12:15 14:00 Vi vil gjennomgå utvalgte
MAT1030 Plenumsregning 1 Kapittel 1 Mathias Barra - 16. januar 2009 (Sist oppdatert: 2009-02-02 14:21) Plenumsregning 1 Velkommen til plenumsregning for MAT1030 Fredager 12:15 14:00 Vi vil gjennomgå utvalgte
Plenumsregning 1. Kapittel 1. Roger Antonsen januar Velkommen til plenumsregning for MAT1030. Repetisjon: Algoritmer og pseudokode
 Plenumsregning 1 Kapittel 1 Roger Antonsen - 17. januar 2008 Velkommen til plenumsregning for MAT1030 Torsdager 10:15 12:00 Gjennomgang av ukeoppgaver Gjennomgang av eksempler fra boka Litt repetisjon
Plenumsregning 1 Kapittel 1 Roger Antonsen - 17. januar 2008 Velkommen til plenumsregning for MAT1030 Torsdager 10:15 12:00 Gjennomgang av ukeoppgaver Gjennomgang av eksempler fra boka Litt repetisjon
INF1020 Algoritmer og datastrukturer
 Dagens plan Hashing Hashtabeller Hash-funksjoner Kollisjonshåndtering Åpen hashing (kap. 5.3) Lukket hashing (kap. 5.4) Rehashing (kap. 5.5) Sortering ut fra en hashing-ide (side 66-68) Bøttesortering
Dagens plan Hashing Hashtabeller Hash-funksjoner Kollisjonshåndtering Åpen hashing (kap. 5.3) Lukket hashing (kap. 5.4) Rehashing (kap. 5.5) Sortering ut fra en hashing-ide (side 66-68) Bøttesortering
Euklids algoritmen. p t 2. 2 p t n og b = p s 1. p min(t 2,s 2 )
 For å finne største felles divisor (gcd) kan vi begrense oss til N, sidenfor alle a, b Z, harvi gcd(a, b) =gcd( a, b ). I prinsippet, dersom vi vet at a = p t 1 kan vi se at 1 p t 2 2 p t n og b = p s
For å finne største felles divisor (gcd) kan vi begrense oss til N, sidenfor alle a, b Z, harvi gcd(a, b) =gcd( a, b ). I prinsippet, dersom vi vet at a = p t 1 kan vi se at 1 p t 2 2 p t n og b = p s
LØSNINGSFORSLAG, EKSAMEN I ALGORITMER OG DATASTRUKTURER (IT1105)
 Norges teknisk naturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap Side 1 av 8 Faglig kontakt under eksamen: Magnus Lie Hetland LØSNINGSFORSLAG, EKSAMEN I ALGORITMER OG DATASTRUKTURER
Norges teknisk naturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap Side 1 av 8 Faglig kontakt under eksamen: Magnus Lie Hetland LØSNINGSFORSLAG, EKSAMEN I ALGORITMER OG DATASTRUKTURER
INF5110 V2013 Stoff som i boka står i kap 4, men som er generelt stoff om grammatikker
 INF5110 V2013 Stoff som i boka står i kap 4, men som er generelt stoff om grammatikker 29. januar 2013 Stein Krogdahl, Ifi, UiO NB: Ikke undervisning fredag 1. februar! Oppgaver som gjennomgås 5. februar
INF5110 V2013 Stoff som i boka står i kap 4, men som er generelt stoff om grammatikker 29. januar 2013 Stein Krogdahl, Ifi, UiO NB: Ikke undervisning fredag 1. februar! Oppgaver som gjennomgås 5. februar
Mer om representasjon av tall
 Forelesning 3 Mer om representasjon av tall Dag Normann - 21. januar 2008 Oppsummering av Uke 3 Mandag 14.01 og delvis onsdag 16.01 diskuterte vi hva som menes med en algoritme, og vi så på pseudokoder
Forelesning 3 Mer om representasjon av tall Dag Normann - 21. januar 2008 Oppsummering av Uke 3 Mandag 14.01 og delvis onsdag 16.01 diskuterte vi hva som menes med en algoritme, og vi så på pseudokoder
Forelesning 30: Kompleksitetsteori
 MAT1030 Diskret Matematikk Forelesning 30: Kompleksitetsteori Roger Antonsen Institutt for informatikk, Universitetet i Oslo Forelesning 30: Kompleksitetsteori 19. mai 2009 (Sist oppdatert: 2009-05-19
MAT1030 Diskret Matematikk Forelesning 30: Kompleksitetsteori Roger Antonsen Institutt for informatikk, Universitetet i Oslo Forelesning 30: Kompleksitetsteori 19. mai 2009 (Sist oppdatert: 2009-05-19
SIF8010 ALGORITMER OG DATASTRUKTURER
 SIF8010 ALGORITMER OG DATASTRUKTURER KONTINUASJONSEKSAMEN, 1999; LØSNINGSFORSLAG Oppgave 1 (12%) Anta at du skal lage et støtteprogram som umiddelbart skal varsle om at et ord blir skrevet feil under inntasting
SIF8010 ALGORITMER OG DATASTRUKTURER KONTINUASJONSEKSAMEN, 1999; LØSNINGSFORSLAG Oppgave 1 (12%) Anta at du skal lage et støtteprogram som umiddelbart skal varsle om at et ord blir skrevet feil under inntasting
MAT1030 Diskret Matematikk
 MAT1030 Diskret Matematikk Plenumsregning 1: Kapittel 1 Mathias Barra Matematisk institutt, Universitetet i Oslo 16. januar 2009 (Sist oppdatert: 2009-02-02 14:21) Plenumsregning 1 MAT1030 Diskret Matematikk
MAT1030 Diskret Matematikk Plenumsregning 1: Kapittel 1 Mathias Barra Matematisk institutt, Universitetet i Oslo 16. januar 2009 (Sist oppdatert: 2009-02-02 14:21) Plenumsregning 1 MAT1030 Diskret Matematikk
Alle hele tall g > 1 kan være grunntall i et tallsystem.
 Tallsystemer Heltall oppgis vanligvis i det desimale tallsystemet, også kalt 10-tallssystemet. Eksempel. Gitt tallet 3794. Dette kan skrives slik: 3 1000 + 7 100 + 9 10 + 4 = 3 10 3 + 7 10 2 + 9 10 1 +
Tallsystemer Heltall oppgis vanligvis i det desimale tallsystemet, også kalt 10-tallssystemet. Eksempel. Gitt tallet 3794. Dette kan skrives slik: 3 1000 + 7 100 + 9 10 + 4 = 3 10 3 + 7 10 2 + 9 10 1 +
INF Algoritmer og datastrukturer. Hva er INF2220? Algoritmer og datastrukturer
 Praktiske opplysninger INF2220 - Algoritmer og datastrukturer HØSTEN 2007 Institutt for informatikk, Universitetet i Oslo Tid og sted: Mandag kl. 12:15-14:00 Store auditorium, Informatikkbygningen Kursansvarlige
Praktiske opplysninger INF2220 - Algoritmer og datastrukturer HØSTEN 2007 Institutt for informatikk, Universitetet i Oslo Tid og sted: Mandag kl. 12:15-14:00 Store auditorium, Informatikkbygningen Kursansvarlige
Algoritmer og Datastrukturer IAI 21899
 Eksamen i Algoritmer og Datastrukturer IAI 21899 Høgskolen i Østfold Avdeling for informatikk og automatisering Torsdag 30. november 2000, kl. 09.00-14.00 LØSNINGSFORSLAG 1 Del 1, Binære søketrær Totalt
Eksamen i Algoritmer og Datastrukturer IAI 21899 Høgskolen i Østfold Avdeling for informatikk og automatisering Torsdag 30. november 2000, kl. 09.00-14.00 LØSNINGSFORSLAG 1 Del 1, Binære søketrær Totalt
Kap. 4: Ovenfra-ned (top-down) parsering
 Kap. 4: Ovenfra-ned (top-down) parsering Dette bør leses om igjen etter kapittelet: First og Follow-mengder Boka tar det et stykke uti kap 4, vi tok det først (forrige foilbunke) LL(1)-parsering og boka
Kap. 4: Ovenfra-ned (top-down) parsering Dette bør leses om igjen etter kapittelet: First og Follow-mengder Boka tar det et stykke uti kap 4, vi tok det først (forrige foilbunke) LL(1)-parsering og boka
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2017 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2017, forelesning
INF2220 - Algoritmer og datastrukturer HØSTEN 2017 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2017, forelesning
Modulo-regning. hvis a og b ikke er kongruente modulo m.
 Modulo-regning Definisjon: La m være et positivt heltall (dvs. m> 0). Vi sier at to hele tall a og b er kongruente modulo m hvis m går opp i (a b). Dette betegnes med a b (mod m) Vi skriver a b (mod m)
Modulo-regning Definisjon: La m være et positivt heltall (dvs. m> 0). Vi sier at to hele tall a og b er kongruente modulo m hvis m går opp i (a b). Dette betegnes med a b (mod m) Vi skriver a b (mod m)
INF5110 V2012 Kapittel 4: Parsering ovenfra-ned
 INF5110 V2012 Kapittel 4: Parsering ovenfra-ned (top-down) Tirsdag 7. februar Stein Krogdahl, Ifi, UiO Oppgaver som gjennomgås i morgen, onsdag: -Spørsmålene på de to siste foilene fra onsdag 1/2 (Bl.a.
INF5110 V2012 Kapittel 4: Parsering ovenfra-ned (top-down) Tirsdag 7. februar Stein Krogdahl, Ifi, UiO Oppgaver som gjennomgås i morgen, onsdag: -Spørsmålene på de to siste foilene fra onsdag 1/2 (Bl.a.
UNIVERSITETET I OSLO. Det matematisk-naturvitenskapelige fakultet
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: INF 4130: lgoritmer: Design og effektivitet Eksamensdag: 12. desember 2008 Tid for eksamen: Kl. 09:00 12:00 (3 timer) Oppgavesettet
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: INF 4130: lgoritmer: Design og effektivitet Eksamensdag: 12. desember 2008 Tid for eksamen: Kl. 09:00 12:00 (3 timer) Oppgavesettet
Python: Rekursjon (og programmering av algoritmer) Python-bok: Kapittel 12 + teoribok om Algoritmer
 Python: Rekursjon (og programmering av algoritmer) Python-bok: Kapittel 12 + teoribok om Algoritmer TDT4110 IT Grunnkurs Professor Guttorm Sindre Læringsmål og pensum Mål Forstå, og kunne bruke, algoritmer
Python: Rekursjon (og programmering av algoritmer) Python-bok: Kapittel 12 + teoribok om Algoritmer TDT4110 IT Grunnkurs Professor Guttorm Sindre Læringsmål og pensum Mål Forstå, og kunne bruke, algoritmer
Algoritmer - definisjon
 Algoritmeanalyse Algoritmer - definisjon En algoritme* er en beskrivelse av hvordan man løser et veldefinert problem med en presist formulert sekvens av et endelig antall enkle, utvetydige og tidsbegrensede
Algoritmeanalyse Algoritmer - definisjon En algoritme* er en beskrivelse av hvordan man løser et veldefinert problem med en presist formulert sekvens av et endelig antall enkle, utvetydige og tidsbegrensede
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 5: Prioritetskø og Heap Bjarne Holen (Ifi, UiO) INF2220 H2009, forelesning 5 1 /
INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 5: Prioritetskø og Heap Bjarne Holen (Ifi, UiO) INF2220 H2009, forelesning 5 1 /
To geometriske algoritmer, kap. 8.6
 INF 4130, 18. november 2010 To geometriske algoritmer, kap. 8.6 Computational Geometry Stein Krogdahl Hovedkapittelet t (kap. 8) dreier seg generelt om devide-and-conquer eller splitt og hersk : Splitt
INF 4130, 18. november 2010 To geometriske algoritmer, kap. 8.6 Computational Geometry Stein Krogdahl Hovedkapittelet t (kap. 8) dreier seg generelt om devide-and-conquer eller splitt og hersk : Splitt
INF / Kap. 5, Del 2 Stein Krogdahl, Ifi, UiO
 INF5110 12/2-2013 Kap. 5, Del 2 Stein Krogdahl, Ifi, UiO Dagens temaer: Noen foiler igjen fra forrige gang SLR(1), LR(1)- og LALR(1)-grammatikker NB: Oppgaver til kap 4 og 5 er lagt ut på undervisningsplanen
INF5110 12/2-2013 Kap. 5, Del 2 Stein Krogdahl, Ifi, UiO Dagens temaer: Noen foiler igjen fra forrige gang SLR(1), LR(1)- og LALR(1)-grammatikker NB: Oppgaver til kap 4 og 5 er lagt ut på undervisningsplanen
kap. 8.6 Computational Geometry Hovedkapittelet (kap. 8) dreier seg generelt om devide-and-conquer eller splitt og hersk :
 INF 4130, 17. november 2011 kap. 8.6 Computational Geometry Stein Krogdahl Hovedkapittelet (kap. 8) dreier seg generelt om devide-and-conquer eller splitt og hersk : Splitt problemet opp i mindre problemer.
INF 4130, 17. november 2011 kap. 8.6 Computational Geometry Stein Krogdahl Hovedkapittelet (kap. 8) dreier seg generelt om devide-and-conquer eller splitt og hersk : Splitt problemet opp i mindre problemer.
INF1010 notat: Binærsøking og quicksort
 INF1010 notat: Binærsøking og quicksort Ragnhild Kobro Runde Februar 2004 I dette notatet skal vi ta for oss ytterligere to eksempler der rekursjon har en naturlig anvendelse, nemlig binærsøking og quicksort.
INF1010 notat: Binærsøking og quicksort Ragnhild Kobro Runde Februar 2004 I dette notatet skal vi ta for oss ytterligere to eksempler der rekursjon har en naturlig anvendelse, nemlig binærsøking og quicksort.
Diskret matematikk tirsdag 13. oktober 2015
 Eksempler på praktisk bruk av modulo-regning. Tverrsum Tverrsummen til et heltall er summen av tallets sifre. a = 7358. Tverrsummen til a er lik 7 + 3 + 5 + 8 = 23. Setning. La sum(a) stå for tverrsummen
Eksempler på praktisk bruk av modulo-regning. Tverrsum Tverrsummen til et heltall er summen av tallets sifre. a = 7358. Tverrsummen til a er lik 7 + 3 + 5 + 8 = 23. Setning. La sum(a) stå for tverrsummen
7) Radix-sortering sekvensielt kode og effekten av cache
 ) Radix-sortering sekvensielt kode og effekten av cache Dels er denne gjennomgangen av vanlig Radix-sortering viktig for å forstå en senere parallell versjon. Dels viser den effekten vi akkurat så tilfeldig
) Radix-sortering sekvensielt kode og effekten av cache Dels er denne gjennomgangen av vanlig Radix-sortering viktig for å forstå en senere parallell versjon. Dels viser den effekten vi akkurat så tilfeldig
Algoritmer - definisjon
 Algoritmeanalyse Algoritmer - definisjon En algoritme er en beskrivelse av hvordan man løser et veldefinert problem med en presist formulert sekvens av et endelig antall enkle, utvetydige og tidsbegrensede
Algoritmeanalyse Algoritmer - definisjon En algoritme er en beskrivelse av hvordan man løser et veldefinert problem med en presist formulert sekvens av et endelig antall enkle, utvetydige og tidsbegrensede
Hashing: Håndtering av kollisjoner
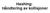 Hashing: Håndtering av kollisjoner Innsetting av dataelement i hashtabell Algoritme: 1. Bruk en hashfunksjon til å beregne hashverdi basert på dataelementets nøkkelverdi 2. Sett inn dataelementet i hashtabellen
Hashing: Håndtering av kollisjoner Innsetting av dataelement i hashtabell Algoritme: 1. Bruk en hashfunksjon til å beregne hashverdi basert på dataelementets nøkkelverdi 2. Sett inn dataelementet i hashtabellen
Stoff som i boka står i kap 4, men som er
 INF5110 V2011 Stoff som i boka står i kap 4, men som er generelt stoff om grammatikker 9. Februar 2011 Stein Krogdahl, Ifi, UiO Oppgaver som gjennomgås gå tirsdag 15/2: - Spørsmålene på de to siste foilene
INF5110 V2011 Stoff som i boka står i kap 4, men som er generelt stoff om grammatikker 9. Februar 2011 Stein Krogdahl, Ifi, UiO Oppgaver som gjennomgås gå tirsdag 15/2: - Spørsmålene på de to siste foilene
Velkommen til plenumsregning for MAT1030. MAT1030 Diskret matematikk. Repetisjon: Algoritmer og pseudokode. Eksempel fra boka. Eksempel
 Velkommen til plenumsregning for MAT1030 MAT1030 Diskret matematikk Plenumsregning 1: Kapittel 1 Roger Antonsen Matematisk Institutt, Universitetet i Oslo 17. januar 2008 Torsdager 10:15 12:00 Gjennomgang
Velkommen til plenumsregning for MAT1030 MAT1030 Diskret matematikk Plenumsregning 1: Kapittel 1 Roger Antonsen Matematisk Institutt, Universitetet i Oslo 17. januar 2008 Torsdager 10:15 12:00 Gjennomgang
Inf 1020 Algoritmer og datastrukturer
 Inf 1020 Algoritmer og datastrukturer Et av de mest sentrale grunnkursene i informatikkutdanningen... og et av de vanskeligste! De fleste 3000-kursene i informatikk bygger på Inf1020 Kurset hever programmering
Inf 1020 Algoritmer og datastrukturer Et av de mest sentrale grunnkursene i informatikkutdanningen... og et av de vanskeligste! De fleste 3000-kursene i informatikk bygger på Inf1020 Kurset hever programmering
Plenumsregning 1. MAT1030 Diskret Matematikk. Repetisjon: Algoritmer og pseudokode. Velkommen til plenumsregning for MAT1030
 MAT1030 Diskret Matematikk Plenumsregning 1: Kapittel 1 Mathias Barra Matematisk institutt, Universitetet i Oslo Plenumsregning 1 16. januar 2009 (Sist oppdatert: 2009-02-02 14:21) MAT1030 Diskret Matematikk
MAT1030 Diskret Matematikk Plenumsregning 1: Kapittel 1 Mathias Barra Matematisk institutt, Universitetet i Oslo Plenumsregning 1 16. januar 2009 (Sist oppdatert: 2009-02-02 14:21) MAT1030 Diskret Matematikk
Kap.4, del 2: Top Down Parsering Kap. 5, del 1: Bottom Up Parsing INF5110, 7/ Legger ut en oppgave til kap. 4 (se beskjed).
 Kap.4, del 2: Top Down Parsering Kap. 5, del 1: Bottom Up Parsing INF5110, 7/2-2008 Legger ut en oppgave til kap. 4 (se beskjed). tein Krogdahl Ifi, UiO Merk: Av de foilene som ble delt ut på papir på
Kap.4, del 2: Top Down Parsering Kap. 5, del 1: Bottom Up Parsing INF5110, 7/2-2008 Legger ut en oppgave til kap. 4 (se beskjed). tein Krogdahl Ifi, UiO Merk: Av de foilene som ble delt ut på papir på
Definisjon. I et binært tre har hver node enten 0, 1 eller 2 barn
 Binære trær Definisjon I et binært tre har hver node enten 0, 1 eller 2 barn Rekursiv definisjon: Et binært tre er enten tomt, eller: Består av en rotnode og to binære trær som kalles venstre subtre og
Binære trær Definisjon I et binært tre har hver node enten 0, 1 eller 2 barn Rekursiv definisjon: Et binært tre er enten tomt, eller: Består av en rotnode og to binære trær som kalles venstre subtre og
UNIVERSITETET I OSLO. Med svar-forslag
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: INF 3130/4130: Algoritmer: Design og effektivitet Eksamensdag: Fredag 14. desember 2007 Tid for eksamen: Kl. 09.00 til 12.00
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: INF 3130/4130: Algoritmer: Design og effektivitet Eksamensdag: Fredag 14. desember 2007 Tid for eksamen: Kl. 09.00 til 12.00
MAT1030 Plenumsregning 3
 MAT1030 Plenumsregning 3 Ukeoppgaver Mathias Barra - 30. januar 2009 (Sist oppdatert: 2009-02-02 14:26) Plenumsregning 3 Oppgave 2.7 - Horners metode (a) 7216 8 : 7 8+2 58 8+1 465 8+6 3726. Svar: 3726
MAT1030 Plenumsregning 3 Ukeoppgaver Mathias Barra - 30. januar 2009 (Sist oppdatert: 2009-02-02 14:26) Plenumsregning 3 Oppgave 2.7 - Horners metode (a) 7216 8 : 7 8+2 58 8+1 465 8+6 3726. Svar: 3726
INF2220: Forelesning 1
 INF2220: Forelesning 1 Praktisk informasjon Analyse av algoritmer (kapittel 2) (Binær)trær (kapittel 4.1-4.3 + 4.6) Praktisk informasjon 2 Praktisk informasjon Kursansvarlige Ingrid Chieh Yu de Vibe (ingridcy@ifi.uio.no)
INF2220: Forelesning 1 Praktisk informasjon Analyse av algoritmer (kapittel 2) (Binær)trær (kapittel 4.1-4.3 + 4.6) Praktisk informasjon 2 Praktisk informasjon Kursansvarlige Ingrid Chieh Yu de Vibe (ingridcy@ifi.uio.no)
UNIVERSITETET I OSLO
 Eksamen i UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamensdag: 13. desember 2011 Tid for eksamen: 14.30 18.30 Oppgavesettet er på 7 sider. Vedlegg: INF2220 lgoritmer og datastrukturer
Eksamen i UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamensdag: 13. desember 2011 Tid for eksamen: 14.30 18.30 Oppgavesettet er på 7 sider. Vedlegg: INF2220 lgoritmer og datastrukturer
Divide-and-Conquer. Lars Vidar Magnusson 13.1.2015
 Divide-and-Conquer Lars Vidar Magnusson 13.1.2015 Kapittel 4 Maximum sub-array problemet Matrix multiplikasjon Analyse av divide-and-conquer algoritmer ved hjelp av substitusjonsmetoden Divide-and-Conquer
Divide-and-Conquer Lars Vidar Magnusson 13.1.2015 Kapittel 4 Maximum sub-array problemet Matrix multiplikasjon Analyse av divide-and-conquer algoritmer ved hjelp av substitusjonsmetoden Divide-and-Conquer
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: INF 2220 Algoritmer og datastrukturer Eksamensdag: 8. desember 2016 Tid for eksamen: 09:00 13:00 (4 timer) Oppgavesettet er på:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: INF 2220 Algoritmer og datastrukturer Eksamensdag: 8. desember 2016 Tid for eksamen: 09:00 13:00 (4 timer) Oppgavesettet er på:
FASIT/LF FOR EKSAMEN TMA4140, H07
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 5 FASIT/LF FOR EKSAMEN TMA440, H07 Oppgave (0%) Benytt matematisk induksjon til å vise at for alle heltall n. n i i!
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 5 FASIT/LF FOR EKSAMEN TMA440, H07 Oppgave (0%) Benytt matematisk induksjon til å vise at for alle heltall n. n i i!
Introduksjon til Algoritmeanalyse
 Introduksjon til Algoritmeanalyse 26. August, 2019 Institutt for Informatikk 1 Hvordan skal vi tenke i IN2010? Effektive løsninger Hvordan skalérer problemet og løsningen? 2 Terminologi Betegnelse Problem
Introduksjon til Algoritmeanalyse 26. August, 2019 Institutt for Informatikk 1 Hvordan skal vi tenke i IN2010? Effektive løsninger Hvordan skalérer problemet og løsningen? 2 Terminologi Betegnelse Problem
Eksamen i IN 110, 18. mai 1993 Side 2 Del 1 (15%) Vi skal se på prioritetskøer av heltall, der vi hele tiden er interessert i å få ut den minste verdi
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i Eksamensdag: 18. mai 1993 Tid for eksamen: 9.00 15.00 Oppgavesettet er på 7 sider. Vedlegg: Tillatte hjelpemidler: IN 110 Algoritmer
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i Eksamensdag: 18. mai 1993 Tid for eksamen: 9.00 15.00 Oppgavesettet er på 7 sider. Vedlegg: Tillatte hjelpemidler: IN 110 Algoritmer
Kodegenerering, del 2: Resten av Kap. 8 pluss tilleggsnotat (fra kap. 9 i ASU ) INF5110 V2007
 Kodegenerering, del 2: Resten av Kap. 8 pluss tilleggsnotat (fra kap. 9 i ASU ) INF5110 V2007 Stein Krogdahl, Ifi UiO NB: Innfører noen begreper som først og fremst har mening om man skal gå videre med
Kodegenerering, del 2: Resten av Kap. 8 pluss tilleggsnotat (fra kap. 9 i ASU ) INF5110 V2007 Stein Krogdahl, Ifi UiO NB: Innfører noen begreper som først og fremst har mening om man skal gå videre med
MAT1030 Diskret matematikk
 MAT1030 Diskret matematikk Plenumsregning 1: Kapittel 1 Roger Antonsen Matematisk Institutt, Universitetet i Oslo 17. januar 2008 Velkommen til plenumsregning for MAT1030 Torsdager 10:15 12:00 Gjennomgang
MAT1030 Diskret matematikk Plenumsregning 1: Kapittel 1 Roger Antonsen Matematisk Institutt, Universitetet i Oslo 17. januar 2008 Velkommen til plenumsregning for MAT1030 Torsdager 10:15 12:00 Gjennomgang
KONTROLLSTRUKTURER. MAT1030 Diskret matematikk. Kontrollstrukturer. Kontrollstrukturer. Eksempel (Ubegrenset while-løkke)
 KONTROLLSTRUKTURER MAT1030 Diskret matematikk Forelesning 2: Flere pseudokoder. Representasjoner av tall. Dag Normann Matematisk Institutt, Universitetet i Oslo 16. januar 2008 Mandag innførte vi pseudokoder
KONTROLLSTRUKTURER MAT1030 Diskret matematikk Forelesning 2: Flere pseudokoder. Representasjoner av tall. Dag Normann Matematisk Institutt, Universitetet i Oslo 16. januar 2008 Mandag innførte vi pseudokoder
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 13: Eksamensgjennomgang Bjarne Holen (Ifi, UiO) INF2220 H2009, forelesning 13 1 /
INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 13: Eksamensgjennomgang Bjarne Holen (Ifi, UiO) INF2220 H2009, forelesning 13 1 /
6. oktober Dagens program: Første time: Andre time, gjesteforelesning: Uavgjørbarhet. Stein Krogdahl. (Ikke pensum, egne foiler legges ut)
 Dagens program: Første time: INF 4130 6. oktober 2011 Stein Krogdahl Kap 23.5: Spilltrær og strategier for spill med to spillere Andre time, gjesteforelesning: Rune Djurhuus: Om sjakkspillende programmer
Dagens program: Første time: INF 4130 6. oktober 2011 Stein Krogdahl Kap 23.5: Spilltrær og strategier for spill med to spillere Andre time, gjesteforelesning: Rune Djurhuus: Om sjakkspillende programmer
Forelesning 2. Flere pseudokoder. Representasjoner av tall. Dag Normann januar 2008 KONTROLLSTRUKTURER. Kontrollstrukturer. Kontrollstrukturer
 Forelesning 2 Flere pseudokoder. Representasjoner av tall. Dag Normann - 16. januar 2008 KONTROLLSTRUKTURER Mandag innførte vi pseudokoder og kontrollstrukturer. Vi hadde tre typer grunn-instruksjoner:
Forelesning 2 Flere pseudokoder. Representasjoner av tall. Dag Normann - 16. januar 2008 KONTROLLSTRUKTURER Mandag innførte vi pseudokoder og kontrollstrukturer. Vi hadde tre typer grunn-instruksjoner:
Kap.4 del I Top Down Parsering INF5110 v2005. Arne Maus Ifi, UiO
 Kap.4 del I Top Down Parsering INF5110 v2005 Arne Maus Ifi, UiO Innhold Motivering Boka gir først parsering uten First/Follow-mengder og så innfører dem. Vi tar teorien først First og Follow-mengder Fjerning
Kap.4 del I Top Down Parsering INF5110 v2005 Arne Maus Ifi, UiO Innhold Motivering Boka gir først parsering uten First/Follow-mengder og så innfører dem. Vi tar teorien først First og Follow-mengder Fjerning
INF5110, onsdag 19. februar, Dagens tema: Parsering ovenfra-ned (top-down)
 INF5110, onsdag 19. februar, 2014 Dagens tema: Kapittel 4 Parsering ovenfra-ned (top-down) Vi har med alle foilene til kap. 4 her, også de som ble gjennomgått mot slutten av forelesning 7. februar Pensum
INF5110, onsdag 19. februar, 2014 Dagens tema: Kapittel 4 Parsering ovenfra-ned (top-down) Vi har med alle foilene til kap. 4 her, også de som ble gjennomgått mot slutten av forelesning 7. februar Pensum
TDT4110 Informasjonsteknologi grunnkurs: Tema: Mer om strenger. - 3rd edition: Kapittel 8. Professor Alf Inge Wang
 1 TDT4110 Informasjonsteknologi grunnkurs: Tema: Mer om strenger - 3rd edition: Kapittel 8 Professor Alf Inge Wang 2 Læringsmål og pensum Mål Lære om Pensum Grunnleggende operasjoner på strenger Å skive/slice
1 TDT4110 Informasjonsteknologi grunnkurs: Tema: Mer om strenger - 3rd edition: Kapittel 8 Professor Alf Inge Wang 2 Læringsmål og pensum Mål Lære om Pensum Grunnleggende operasjoner på strenger Å skive/slice
Tallsystemer. Tallene x, y, z og u er gitt ved x = 2, y = 2, z = 4 og u = 2. Dermed blir =
 Tallsystemer Heltall oppgis vanligvis i det desimale tallsystemet, også kalt 10-tallssystemet. Eksempel. Gitt tallet 3794. Dette kan skrives slik: 3 1000 + 7 100 + 9 10 + 4 = 3 10 3 + 7 10 2 + 9 10 1 +
Tallsystemer Heltall oppgis vanligvis i det desimale tallsystemet, også kalt 10-tallssystemet. Eksempel. Gitt tallet 3794. Dette kan skrives slik: 3 1000 + 7 100 + 9 10 + 4 = 3 10 3 + 7 10 2 + 9 10 1 +
Algoritmer og Datastrukturer
 Eksamen i Algoritmer og Datastrukturer IAI 20102 Høgskolen i Østfold Avdeling for informatikk og automatisering Lødag 5. juni 2004, kl. 09.00-13.00 LØSNINGSFORSLAG 1 Del 1 60% Oppgave 1.1-10% Forklar kort
Eksamen i Algoritmer og Datastrukturer IAI 20102 Høgskolen i Østfold Avdeling for informatikk og automatisering Lødag 5. juni 2004, kl. 09.00-13.00 LØSNINGSFORSLAG 1 Del 1 60% Oppgave 1.1-10% Forklar kort
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2015 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2015, forelesning
INF2220 - Algoritmer og datastrukturer HØSTEN 2015 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2015, forelesning
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2016 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2016, forelesning
INF2220 - Algoritmer og datastrukturer HØSTEN 2016 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2016, forelesning
Introduksjon til DARK assembly
 Introduksjon til DARK assembly Magnus Jahre Institutt for datateknikk og informasjonsvitenskap 2 Plan Assembly vs. Java Dark stakkmaskin Oversikt over stakkmaskinen Dark stakkmaskin eksempel Dark Load-Store
Introduksjon til DARK assembly Magnus Jahre Institutt for datateknikk og informasjonsvitenskap 2 Plan Assembly vs. Java Dark stakkmaskin Oversikt over stakkmaskinen Dark stakkmaskin eksempel Dark Load-Store
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2015 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2015, forelesning
INF2220 - Algoritmer og datastrukturer HØSTEN 2015 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2015, forelesning
Løsningsforslag for eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 18. Desember 2000, kl
 Student nr.: Side 1 av 5 Løsningsforslag for eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 18. Desember 2000, kl 0900-1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 73 593442. Hjelpemidler:
Student nr.: Side 1 av 5 Løsningsforslag for eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 18. Desember 2000, kl 0900-1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 73 593442. Hjelpemidler:
