Datastrukturer og Algoritmer
|
|
|
- Holger Torgersen
- 8 år siden
- Visninger:
Transkript
1 TOD 063 Datastrukturer og Algoritmer Forside fra lærebokens Nord Amerikanske utgave Tar for seg praktisk problemstilling: Hvordan håndtere containere som blir lastet fra containerskip i en travel havn på best mulig vis Setter krav til: Effektiv lagringsstruktur Effektive algoritmer for å håndtere Kombinasjonen av de to som er noen av de problemstillingene vi skal se på i dette kurset
2 Timeplanen TOD :15 09:55 10:05 11:45 12:15 13:55 Mandag Tirsdag Onsdag Torsdag Fredag Felles foreles A 715au Felles foreles A 715au Data Klasse/Lab A622/Lab INF Klasse/Lab A627/Lab Data Klasse/Lab A622/Lab INF Klasse/Lab A627/Lab Lærere: Sven Olai Høyland Svein Ivar Lillehaug Harald Soleim + labassistenter
3 Faget på its Learning 1, 2 eller 3 sider.? Vi forsøker med en felles fagside for de to klassene (besluttet etter enighet blant studentene)
4 Først litt generelt om faget TOD 063 Fag nr. 2 i programmeringsutdanningen Utvikling av mindre programsystem Lage og analysere dt datastrukturer t og algoritmer for generelle problem Lære å implementere ulike datastrukturer (i Java) Lære å analysere effektivitet for algoritmer
5 Verktøy for programutviklere Maskinutstyr, nett Systemprogram (operativsystem, kompilatorer, editor/ide ) Krever kunnskap om (setter krav til dere ), må kjenne til / kunne beherske: Datastrukturer/algoritmer for generelle problem Metoder/teknikker for programutvikling (modularisering, OOP, topp ned, stegvis forfining, ADT, ) Programtesting/feilfinning
6 Presentasjon av høgnivå datastrukturer i boka Grensesnitt mot brukere (public metoder, interface ) Eksempel på bruk Implementering i Java (på en eller flere måter) Analyse av effektivitet (tidsbruk, plasskrav) Ev. sammenligning med tilsvarende ferdige klasser i Java API
7 Gruppering av stoffet ti boken det som kurset skal dekke Intro, analyse (kap. 1 og 2) Grunnleggende elementogteknikker: teknikker: Mengder, tabell, lenket struktur, rekursjon, søk/sorter (kap. 3, 4, 7, 8) Lineære høgnivå strukturer: Stabel, kø, lister (kap. 3, 5, 6,11) Ikkje lineære høgnivåstrukturar: Tre, haug, hash tabell, graf (kap. 9, 10, 11, 12, 13, 14) Gir grovt sett pensum: Det meste frem til og med kap. 14 Læreboken er helt fersk, så endelig pensum bestemmes underveis.
8 Bokas kapittel 1: Intro Identifisere forskjellige aspekt rundt programvare og kvalitet Motivere for bruk/valg av datastrukturer basert på kvalitative vurderinger Introduksjon av begrepet datastruktur og introduksjon av flere enkle datastrukturer
9 Utvikling av programvare (software development) Software Engineering i (Programvareutvikling) er studiet av de teknikker og teorier som støtter utviklingen av programvare av høy kvalitet Har som fokus å kontrollere utviklingsprosessen for til enhver til å oppnå gode resultat Vi skal etterstrebe å: tilfredsstille våre klienter de personer eller det firma/ organisasjon som har bestilt produktet møtebehovene til brukerne folket som skal bruke produktet
10 Mål med programvareutvikling Løse de rette problemene krever ofte litt å finne ut av hva disse er god kommunikasjon mot brukerne er et must husk: som oftest vanskeligere enn hva en først tror Levere løsninger i tide og i samsvar med budsjett alltid noen trade offs å ta stilling til Levere høy kvalitets løsninger må her også ta hensyn til forskjellige stakeholders og at alle disse skal komme best mulig ut av det hele (de med interesse i produktet: brukere, oppdragsgiver, investorer, osv )
11 Karakteristikker for god kvalitet i SW I bold: fokus TOD063 Korrekthet Pålitelighet Robusthet Brukervennlighet Lett å vedlikeholde Gjenbrukbarhet Plattformeruavh. Effektivitet Husk1: Pålitelig programvare feiler sjelden, og når den feiler minimaliseres følgene av feilen/avbruddet/programkræsjet Husk2: Kvalitet har forskjellig betydning for forskjellige folk
12 Et praktisk eksempel Problemstilling: Containere som losses i en havn Kunne kanskje laste disse direkte over på ventende trailere og tog? effektivt for de som jobber på kaien (får ting unna) menikkespesielt effektivt for befraktningsselskapene og jernbanen som kanskje ikke alltid er klar for å være der (ikke i korrespondanse med deres optimale logistikk)
13 eksempel forts. Hva vet vi om hver enkelt container? samme størrelse og form hver enkelt har sin unike ID ID gir en del informasjon, blant annet om hvor containeren skal havnearbeiderne har ikke behov for å vite hva som er i hver enkelt klcontainer
14 eksempel forts.. Containerne kan kanskje lastes rett av og settes på kaia? Effektivt med tanke på lossing av båt Ikke effektivt med tanke på å finne igjen containerne for å få dem på rette trailere/tog når disse er klare for å hente dem Krever i verste fll fall et lineært søk over hl hele ki kaiområdet når en container søkes for avhenting
15 eksempel forts Hva om vi maler et stort tabellsystem på kaien med nummerering og det hele slik at hver lagret container kan indekseres på dens ID? ID er unik for alle lagrede containere kaitabellen ville bli svært STOOOR (sannsynligvis ikke plass for den) kaitabellen ville være stort sett tom en betydelig sløsing med kaiplass!
16 eksempel forts. Hva om vi mekker om løsningen med ki kaitabell bllslik at denne kan ekspandere og trekke seg sammen for å unngå tomme plasser? vil alltid ha rekkefølge på IDer, og ingen tomme plasser enkelt å finne container etter ID MEN, vil tvinge containere til å flyttes flere ganger frem og tilbake ettersom nye containere kommer til og andre fjernes altså en hel masse overhead i arbeid!
17 eksempel forts.. På tide å tenke litt på hva vi vet om hver container ID nummeret gir oss også destinasjonen for hver container Hva om vi lager en kaitabell hvor hver celle i tabellen representerer en ny tabell med plass for containere?
18 eksempel forts Med vår nye løsning kan vi lagre containerne for hver destinasjon på en rekke forskjellige måter: lagre i den rekkefølge de lastes av med den første losset som den første som skal fraktes videre (kø) lagre i den rekkefølge de lestes med den siste it losset som den første som skal fraktes videre (stabel/stack) lagre på ID for hver destinasjon (ordnet liste) Eksempelet gir en liten pekepinn på hvordan forskjellige datastrukturer har sine fordeler/bakdeler for forskjellige problemstillinger
19 Algoritmer og effektivitetsanalyse Generelt: Finne tidsforbruk og krav til ekstra lagerplass l ved utføring av en algoritme Ofte: Ser bare på tidsforbruk df (nå: tid viktigere enn billig lagerplass) Ved analyse: Prøver å regne ut antall viktige/ dominerende operasjoner når en algoritme blir utført mest relevant ved store datamengder Ved testkjøring: Generer store mengder kunstige data og tar tiden ved kjøring av to eller flere alternative algoritmer for et problem på en bestemt PC.
20 Algoritmer og effektivitetsanalyse, forts. Ved analyse av kjøring av en metode på n data prøver en å finne en formel for tidsforbruk der konstanter og funksjoner av n inngår Eksempel: tid = k 1 + k 2 *n tid = k 1 + k 2 * n + k 3 * n 2 tid = k 1 + k 2 *log 2 n Det viktigste resultatet er størrelsesordenen på det største leddet når n blir svært stor. Eks.: O(1), O(n ), O(n 2 ), O(log 2 n )
21 Neste gang Mandag 11. januar Kap. 2. Effektivitetsnalyse av algoritmer (en intro) Se litt på første obligatoriske øvingsoppgave
INF2220: Forelesning 1. Praktisk informasjon Analyse av algoritmer (kapittel 2) (Binær)trær (kapittel )
 INF2220: Forelesning 1 Praktisk informasjon Analyse av algoritmer (kapittel 2) (Binær)trær (kapittel 4.1-4.3 + 4.6) PRAKTISK INFORMASJON 2 Praktisk informasjon Kursansvarlige Ragnhild Kobro Runde (ragnhilk@ifi.uio.no)
INF2220: Forelesning 1 Praktisk informasjon Analyse av algoritmer (kapittel 2) (Binær)trær (kapittel 4.1-4.3 + 4.6) PRAKTISK INFORMASJON 2 Praktisk informasjon Kursansvarlige Ragnhild Kobro Runde (ragnhilk@ifi.uio.no)
Liste som abstrakt konsept/datatype
 Lister Liste som abstrakt konsept/datatype Listen er en lineær struktur (men kan allikevel implementeres ikke-lineært bak kulissene ) Hvert element har en forgjenger, unntatt første element i listen Hvert
Lister Liste som abstrakt konsept/datatype Listen er en lineær struktur (men kan allikevel implementeres ikke-lineært bak kulissene ) Hvert element har en forgjenger, unntatt første element i listen Hvert
Velkommen til. IN1010 Objektorientert programmering Våren 2018
 Velkommen til IN1010 Objektorientert programmering Våren 2018 Idag: 1. time: Om IN1010 2. time (+ i morgen og neste uke): Om Java og objekter i Java 1 Stein Gjessing, Siri Jensen og Dag Langmyhr Universitetet
Velkommen til IN1010 Objektorientert programmering Våren 2018 Idag: 1. time: Om IN1010 2. time (+ i morgen og neste uke): Om Java og objekter i Java 1 Stein Gjessing, Siri Jensen og Dag Langmyhr Universitetet
Heap* En heap er et komplett binært tre: En heap er også et monotont binært tre:
 Heap Heap* En heap er et komplett binært tre: Alle nivåene i treet, unntatt (muligens) det nederste, er alltid helt fylt opp med noder Alle noder på nederste nivå ligger til venstre En heap er også et
Heap Heap* En heap er et komplett binært tre: Alle nivåene i treet, unntatt (muligens) det nederste, er alltid helt fylt opp med noder Alle noder på nederste nivå ligger til venstre En heap er også et
IN1010 Objektorientert programmering Våren 2019
 IN1010 Objektorientert programmering IN1010 Objektorientert programmering Våren 2019 Stein Gjessing Hva skjer de første to ukene? Forelesninger de to første ukene i dag 1. time: Info om IN1010 i dag 2.
IN1010 Objektorientert programmering IN1010 Objektorientert programmering Våren 2019 Stein Gjessing Hva skjer de første to ukene? Forelesninger de to første ukene i dag 1. time: Info om IN1010 i dag 2.
Pensum: fra boken (H-03)+ forelesninger
 Pensum: fra boken (H-03)+ forelesninger unntatt kursorisk tema KAP. 1 KAP. 2 KAP. 3 JAVA I-110 (ikke gjennomgått) OO + ABSTRAKSJON /GENERISK PROGRAMMERING REKURSJON ALGORITME-TIDSANALYSE; O-NOTASJON KAP.
Pensum: fra boken (H-03)+ forelesninger unntatt kursorisk tema KAP. 1 KAP. 2 KAP. 3 JAVA I-110 (ikke gjennomgått) OO + ABSTRAKSJON /GENERISK PROGRAMMERING REKURSJON ALGORITME-TIDSANALYSE; O-NOTASJON KAP.
Hva er en liste? Hvert element har en forgjenger, unntatt første element i listen. Hvert element har en etterfølger, unntatt siste element i listen
 Lister Hva er en liste? Listen er en lineær datastruktur Hvert element har en forgjenger, unntatt første element i listen Hvert element har en etterfølger, unntatt siste element i listen I motsetning til
Lister Hva er en liste? Listen er en lineær datastruktur Hvert element har en forgjenger, unntatt første element i listen Hvert element har en etterfølger, unntatt siste element i listen I motsetning til
Pensum: fra boken (H-03)+ forelesninger
 Pensum: fra boken (H-03)+ forelesninger unntatt kursorisk tema KAP. 1 KAP. 2 KAP. 3 JAVA I-110 (ikke gjennomgått) OO + ABSTRAKSJON /GENERISK PROGRAMMERING REKURSJON ALGORITME-TIDSANALYSE; O-NOTASJON KAP.
Pensum: fra boken (H-03)+ forelesninger unntatt kursorisk tema KAP. 1 KAP. 2 KAP. 3 JAVA I-110 (ikke gjennomgått) OO + ABSTRAKSJON /GENERISK PROGRAMMERING REKURSJON ALGORITME-TIDSANALYSE; O-NOTASJON KAP.
Velkommen til. INF våren 2017
 Velkommen til INF1010 - våren 2017 Idag: 1. time: Om INF1010 2.time: Om Objekter i Java 1 Stein Gjessing og Stein Michael Storleer Universitetet i Oslo 1 INF1010 Objektorientert programmering I INF1010
Velkommen til INF1010 - våren 2017 Idag: 1. time: Om INF1010 2.time: Om Objekter i Java 1 Stein Gjessing og Stein Michael Storleer Universitetet i Oslo 1 INF1010 Objektorientert programmering I INF1010
AlgDat 12. Forelesning 2. Gunnar Misund
 AlgDat 12 Forelesning 2 Forrige forelesning Følg med på hiof.no/algdat, ikke minst beskjedsida! Algdat: Fundamentalt, klassisk, morsomt,...krevende :) Pensum: Forelesningene, oppgavene (pluss deler av
AlgDat 12 Forelesning 2 Forrige forelesning Følg med på hiof.no/algdat, ikke minst beskjedsida! Algdat: Fundamentalt, klassisk, morsomt,...krevende :) Pensum: Forelesningene, oppgavene (pluss deler av
Hva er en liste? Hvert element har en forgjenger, unntatt første element i listen. Hvert element har en etterfølger, unntatt siste element i listen
 Lister Hva er en liste? Listen er en lineær datastruktur Hvert element har en forgjenger, unntatt første element i listen Hvert element har en etterfølger, unntatt siste element i listen I motsetning til
Lister Hva er en liste? Listen er en lineær datastruktur Hvert element har en forgjenger, unntatt første element i listen Hvert element har en etterfølger, unntatt siste element i listen I motsetning til
INF101 (kun et utvalg av kommentarene er med i denne rapporten)
 INF101 (kun et utvalg av kommentarene er med i denne rapporten) Respondenter Ny 0 0,0% Distribuert 59 71,1% Noen svar 0 0,0% Gjennomført 24 28,9% Frafalt 0 0,0% Prosent I alt 83 100,0% Er det første gang
INF101 (kun et utvalg av kommentarene er med i denne rapporten) Respondenter Ny 0 0,0% Distribuert 59 71,1% Noen svar 0 0,0% Gjennomført 24 28,9% Frafalt 0 0,0% Prosent I alt 83 100,0% Er det første gang
INF Algoritmer og datastrukturer. Hva er INF2220? Algoritmer og datastrukturer
 Praktiske opplysninger INF2220 - Algoritmer og datastrukturer HØSTEN 2007 Institutt for informatikk, Universitetet i Oslo Tid og sted: Mandag kl. 12:15-14:00 Store auditorium, Informatikkbygningen Kursansvarlige
Praktiske opplysninger INF2220 - Algoritmer og datastrukturer HØSTEN 2007 Institutt for informatikk, Universitetet i Oslo Tid og sted: Mandag kl. 12:15-14:00 Store auditorium, Informatikkbygningen Kursansvarlige
Algoritmeanalyse. (og litt om datastrukturer)
 Algoritmeanalyse (og litt om datastrukturer) Datastrukturer definisjon En datastruktur er den måten en samling data er organisert på. Datastrukturen kan være ordnet (sortert på en eller annen måte) eller
Algoritmeanalyse (og litt om datastrukturer) Datastrukturer definisjon En datastruktur er den måten en samling data er organisert på. Datastrukturen kan være ordnet (sortert på en eller annen måte) eller
Hva er en kø? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn først
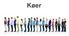 Køer Hva er en kø? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn først Et nytt element legges alltid til sist i køen Skal vi ta ut et element, tar vi alltid
Køer Hva er en kø? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn først Et nytt element legges alltid til sist i køen Skal vi ta ut et element, tar vi alltid
AlgDat 10. Forelesning 2. Gunnar Misund
 AlgDat 10 Forelesning 2 Oversikt Java repetisjon IDE eller teksteditor + kommandolinje? Java Collections and Generics Programvareutvikling En mengde mer eller mindre veldefinerte metoder (software engineering):
AlgDat 10 Forelesning 2 Oversikt Java repetisjon IDE eller teksteditor + kommandolinje? Java Collections and Generics Programvareutvikling En mengde mer eller mindre veldefinerte metoder (software engineering):
Hva er en kø? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn først
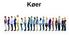 Køer Hva er en kø? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn først Et nytt element legges alltid til sist i køen Skal vi ta ut et element, tar vi alltid
Køer Hva er en kø? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn først Et nytt element legges alltid til sist i køen Skal vi ta ut et element, tar vi alltid
Hva er en kø? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn først
 Køer Hva er en kø? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn først Et nytt element legges alltid til sist i køen Skal vi ta ut et element, tar vi alltid
Køer Hva er en kø? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn først Et nytt element legges alltid til sist i køen Skal vi ta ut et element, tar vi alltid
Definisjon. I et binært tre har hver node enten 0, 1 eller 2 barn
 Binære trær Definisjon I et binært tre har hver node enten 0, 1 eller 2 barn Rekursiv definisjon: Et binært tre er enten tomt, eller: Består av en rotnode og to binære trær som kalles venstre subtre og
Binære trær Definisjon I et binært tre har hver node enten 0, 1 eller 2 barn Rekursiv definisjon: Et binært tre er enten tomt, eller: Består av en rotnode og to binære trær som kalles venstre subtre og
Python: Rekursjon (og programmering av algoritmer) Python-bok: Kapittel 12 + teoribok om Algoritmer
 Python: Rekursjon (og programmering av algoritmer) Python-bok: Kapittel 12 + teoribok om Algoritmer TDT4110 IT Grunnkurs Professor Guttorm Sindre Læringsmål og pensum Mål Forstå, og kunne bruke, algoritmer
Python: Rekursjon (og programmering av algoritmer) Python-bok: Kapittel 12 + teoribok om Algoritmer TDT4110 IT Grunnkurs Professor Guttorm Sindre Læringsmål og pensum Mål Forstå, og kunne bruke, algoritmer
Maps og Hashing. INF Algoritmer og datastrukturer. Map - ADT. Map vs Array
 Maps og Hashing INF0 - Algoritmer og datastrukturer HØSTEN 00 Institutt for informatikk, Universitetet i Oslo INF0, forelesning : Maps og Hashing Map - Abstrakt Data Type (kapittel.) Hash-funksjoner (kapittel..)
Maps og Hashing INF0 - Algoritmer og datastrukturer HØSTEN 00 Institutt for informatikk, Universitetet i Oslo INF0, forelesning : Maps og Hashing Map - Abstrakt Data Type (kapittel.) Hash-funksjoner (kapittel..)
Kompleksitetsanalyse Helge Hafting 25.1.2005 Opphavsrett: Forfatter og Stiftelsen TISIP Lærestoffet er utviklet for faget LO117D Algoritmiske metoder
 Helge Hafting 25.1.2005 Opphavsrett: Forfatter og Stiftelsen TISIP Lærestoffet er utviklet for faget LO117D Algoritmiske metoder Innhold 1 1 1.1 Hva er en algoritme?............................... 1 1.2
Helge Hafting 25.1.2005 Opphavsrett: Forfatter og Stiftelsen TISIP Lærestoffet er utviklet for faget LO117D Algoritmiske metoder Innhold 1 1 1.1 Hva er en algoritme?............................... 1 1.2
TDT4105 Informasjonsteknologi, grunnkurs
 1 TDT4105 Informasjonsteknologi, grunnkurs For BMAT, MTEL, MTENERG, MTING, MTIØT, MTMART og MTPROD Førsteamanuensis Roger Midtstraum Kontor: 206 i IT-bygget (Gløshaugen) Epost: roger@idi.ntnu.no Tlf: 735
1 TDT4105 Informasjonsteknologi, grunnkurs For BMAT, MTEL, MTENERG, MTING, MTIØT, MTMART og MTPROD Førsteamanuensis Roger Midtstraum Kontor: 206 i IT-bygget (Gløshaugen) Epost: roger@idi.ntnu.no Tlf: 735
Stack. En enkel, lineær datastruktur
 Stack En enkel, lineær datastruktur Hva er en stack? En datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn sist Et nytt element legges alltid på toppen av stakken Skal vi
Stack En enkel, lineær datastruktur Hva er en stack? En datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn sist Et nytt element legges alltid på toppen av stakken Skal vi
Hvor mye praktisk kunnskap har du tilegnet deg på dette emnet? (1 = ingen, 5 = mye)
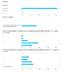 INF102 Er du? Er du? - Annet Hvor mye teoretisk kunnskap har du tilegnet deg på dette emnet? (1 = ingen, 5 = mye) Hvor mye praktisk kunnskap har du tilegnet deg på dette emnet? (1 = ingen, 5 = mye) Hvor
INF102 Er du? Er du? - Annet Hvor mye teoretisk kunnskap har du tilegnet deg på dette emnet? (1 = ingen, 5 = mye) Hvor mye praktisk kunnskap har du tilegnet deg på dette emnet? (1 = ingen, 5 = mye) Hvor
Definisjon av binært søketre
 Binære søketrær Definisjon av binært søketre For alle nodene i et binært søketre gjelder: Alle verdiene i nodens venstre subtre er mindre enn verdien i noden Alle verdiene i nodens høyre subtre er større
Binære søketrær Definisjon av binært søketre For alle nodene i et binært søketre gjelder: Alle verdiene i nodens venstre subtre er mindre enn verdien i noden Alle verdiene i nodens høyre subtre er større
Søkeproblemet. Gitt en datastruktur med n elementer: Finnes et bestemt element (eller en bestemt verdi) x lagret i datastrukturen eller ikke?
 Søking Søkeproblemet Gitt en datastruktur med n elementer: Finnes et bestemt element (eller en bestemt verdi) x lagret i datastrukturen eller ikke? Effektiviteten til søkealgoritmer avhenger av: Om datastrukturen
Søking Søkeproblemet Gitt en datastruktur med n elementer: Finnes et bestemt element (eller en bestemt verdi) x lagret i datastrukturen eller ikke? Effektiviteten til søkealgoritmer avhenger av: Om datastrukturen
Operativsystemer og grensesnitt
 Operativsystemer og grensesnitt Ulike måter å bruke OS'et på Application Program Interface (API) Applikasjoner (ofte C-programmer) som f.eks. emacs, som bruker tjenestene i OS ved å kalle på funksjoner
Operativsystemer og grensesnitt Ulike måter å bruke OS'et på Application Program Interface (API) Applikasjoner (ofte C-programmer) som f.eks. emacs, som bruker tjenestene i OS ved å kalle på funksjoner
Maps og Hashing. INF Algoritmer og datastrukturer. Map - ADT. Map vs Array
 Maps og Hashing INF0 - Algoritmer og datastrukturer HØSTEN 00 Institutt for informatikk, Universitetet i Oslo INF0, forelesning : Maps og Hashing Map - Abstrakt Data Type Hash-funksjoner hashcode Kollisjonshåndtering
Maps og Hashing INF0 - Algoritmer og datastrukturer HØSTEN 00 Institutt for informatikk, Universitetet i Oslo INF0, forelesning : Maps og Hashing Map - Abstrakt Data Type Hash-funksjoner hashcode Kollisjonshåndtering
INF109 (kun et utvalg av kommentarene er med i denne rapporten)
 INF109 (kun et utvalg av kommentarene er med i denne rapporten) Respondenter Prosent Ny 0 0,0% Distribuert 18 47,4% Noen svar 0 0,0% Gjennomført 19 50,0% Frafalt 1 2,6% I alt 38 100,0% Er det første gang
INF109 (kun et utvalg av kommentarene er med i denne rapporten) Respondenter Prosent Ny 0 0,0% Distribuert 18 47,4% Noen svar 0 0,0% Gjennomført 19 50,0% Frafalt 1 2,6% I alt 38 100,0% Er det første gang
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 3: Maps og Hashing Bjarne Holen (Ifi, UiO) INF2220 H2009, forelesning 3 1 / 25 Maps
INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 3: Maps og Hashing Bjarne Holen (Ifi, UiO) INF2220 H2009, forelesning 3 1 / 25 Maps
Ny 0 0,0% Distribuert 64 66,7% Noen svar 1 1,0% Gjennomført 31 32,3% Frafalt 0 0,0% I alt ,0%
 INF142 (kun et utvalg av kommentarene er med i denne rapporten) Respondenter Prosent Ny 0 0,0% Distribuert 64 66,7% Noen svar 1 1,0% Gjennomført 31 32,3% Frafalt 0 0,0% I alt 96 100,0% Er det første gang
INF142 (kun et utvalg av kommentarene er med i denne rapporten) Respondenter Prosent Ny 0 0,0% Distribuert 64 66,7% Noen svar 1 1,0% Gjennomført 31 32,3% Frafalt 0 0,0% I alt 96 100,0% Er det første gang
... Når internminnet blir for lite. Dagens plan: Løsning: Utvidbar hashing. hash(x) katalog. O modellen er ikke lenger gyldig ved
 Dagens plan: Utvidbar hashing (kapittel 5.6) B-trær (kap. 4.7) Abstrakte datatyper (kap. 3.1) Stakker (kap. 3.3) Når internminnet blir for lite En lese-/skriveoperasjon på en harddisk (aksesstid 7-12 millisekunder)
Dagens plan: Utvidbar hashing (kapittel 5.6) B-trær (kap. 4.7) Abstrakte datatyper (kap. 3.1) Stakker (kap. 3.3) Når internminnet blir for lite En lese-/skriveoperasjon på en harddisk (aksesstid 7-12 millisekunder)
Dagens plan: INF2220 - Algoritmer og datastrukturer. Repetisjon: Binære søketrær. Repetisjon: Binære søketrær
 Dagens plan: INF2220 - lgoritmer og datastrukturer HØTEN 2007 Institutt for informatikk, Universitetet i Oslo (kap. 4.7) (kap. 12.2) Interface ollection og Iterator (kap. 3.3) et og maps (kap. 4.8) INF2220,
Dagens plan: INF2220 - lgoritmer og datastrukturer HØTEN 2007 Institutt for informatikk, Universitetet i Oslo (kap. 4.7) (kap. 12.2) Interface ollection og Iterator (kap. 3.3) et og maps (kap. 4.8) INF2220,
Velkommen til MAT1030!
 MAT1030 Diskret Matematikk Forelesning 1: Algoritmer, pseudokoder, kontrollstrukturer Roger Antonsen Institutt for informatikk, Universitetet i Oslo Velkommen til MAT1030! 13. januar 2009 (Sist oppdatert:
MAT1030 Diskret Matematikk Forelesning 1: Algoritmer, pseudokoder, kontrollstrukturer Roger Antonsen Institutt for informatikk, Universitetet i Oslo Velkommen til MAT1030! 13. januar 2009 (Sist oppdatert:
MAT1030 Diskret Matematikk
 MAT1030 Diskret Matematikk Forelesning 1: Algoritmer, pseudokoder, kontrollstrukturer Roger Antonsen Institutt for informatikk, Universitetet i Oslo 13. januar 2009 (Sist oppdatert: 2009-01-14 16:44) Velkommen
MAT1030 Diskret Matematikk Forelesning 1: Algoritmer, pseudokoder, kontrollstrukturer Roger Antonsen Institutt for informatikk, Universitetet i Oslo 13. januar 2009 (Sist oppdatert: 2009-01-14 16:44) Velkommen
Heap og prioritetskø. Marjory the Trash Heap fra Fraggle Rock
 Heap og prioritetskø Marjory the Trash Heap fra Fraggle Rock Binær heap En heap er et komplett binært tre: Alle nivåene i treet, unntatt (muligens) det nederste, er alltid helt fylt opp med noder Alle
Heap og prioritetskø Marjory the Trash Heap fra Fraggle Rock Binær heap En heap er et komplett binært tre: Alle nivåene i treet, unntatt (muligens) det nederste, er alltid helt fylt opp med noder Alle
Fra Kap.10 Binære søketre (BS-tre) Sist oppdatert 20.03.10 Definere en abstrakt datastruktur binært søketre. Vise hvordan binær søketre kan brukes
 Fra Kap.10 Binære søketre (BS-tre) Sist oppdatert 20.03.10 Definere en abstrakt datastruktur binært søketre. Vise hvordan binær søketre kan brukes til å løse problemer. Undersøke ulike implementasjoner
Fra Kap.10 Binære søketre (BS-tre) Sist oppdatert 20.03.10 Definere en abstrakt datastruktur binært søketre. Vise hvordan binær søketre kan brukes til å løse problemer. Undersøke ulike implementasjoner
INF1020 Algoritmer og datastrukturer
 Dagens plan Hashing Hashtabeller Hash-funksjoner Kollisjonshåndtering Åpen hashing (kap. 5.3) Lukket hashing (kap. 5.4) Rehashing (kap. 5.5) Sortering ut fra en hashing-ide (side 66-68) Bøttesortering
Dagens plan Hashing Hashtabeller Hash-funksjoner Kollisjonshåndtering Åpen hashing (kap. 5.3) Lukket hashing (kap. 5.4) Rehashing (kap. 5.5) Sortering ut fra en hashing-ide (side 66-68) Bøttesortering
Hva er en stack? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn sist
 Stack Hva er en stack? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn sist Et nytt element legges alltid på toppen av stakken Skal vi ta ut et element, tar
Stack Hva er en stack? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn sist Et nytt element legges alltid på toppen av stakken Skal vi ta ut et element, tar
Hva er en stack? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn sist
 Stack Hva er en stack? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn sist Et nytt element legges alltid på toppen av stakken Skal vi ta ut et element, tar
Stack Hva er en stack? En lineær datastruktur der vi til enhver tid kun har tilgang til elementet som ble lagt inn sist Et nytt element legges alltid på toppen av stakken Skal vi ta ut et element, tar
Binær heap. En heap er et komplett binært tre:
 Heap Binær heap En heap er et komplett binært tre: Alle nivåene i treet, unntatt (muligens) det nederste, er alltid helt fylt opp med noder Alle noder på nederste nivå ligger så langt til venstre som mulig
Heap Binær heap En heap er et komplett binært tre: Alle nivåene i treet, unntatt (muligens) det nederste, er alltid helt fylt opp med noder Alle noder på nederste nivå ligger så langt til venstre som mulig
Kap 9 Tre Sist oppdatert 15.03
 Kap 9 Tre Sist oppdatert 15.03 Definere et tre som en datastruktur. Definere begreper knyttet til tre. Diskutere mulige implementasjoner av tre Analysere implementasjoner av tre som samlinger. Diskutere
Kap 9 Tre Sist oppdatert 15.03 Definere et tre som en datastruktur. Definere begreper knyttet til tre. Diskutere mulige implementasjoner av tre Analysere implementasjoner av tre som samlinger. Diskutere
Oversikt. Informatikk. INF1000: Grunnkurs i objektorientert programmering. Utenom INF1000 Informasjon & hjelp
 INF1000: Grunnkurs i objektorientert programmering Uke 0, høst 2014 Oversikt Informatikk - hva & hvorfor? Datasystemer, maskinvare, programmer Objektorientert programmering i INF1000 Programmeringsspråket
INF1000: Grunnkurs i objektorientert programmering Uke 0, høst 2014 Oversikt Informatikk - hva & hvorfor? Datasystemer, maskinvare, programmer Objektorientert programmering i INF1000 Programmeringsspråket
Algoritmer - definisjon
 Algoritmeanalyse Algoritmer - definisjon En algoritme er en beskrivelse av hvordan man løser et veldefinert problem med en presist formulert sekvens av et endelig antall enkle, utvetydige og tidsbegrensede
Algoritmeanalyse Algoritmer - definisjon En algoritme er en beskrivelse av hvordan man løser et veldefinert problem med en presist formulert sekvens av et endelig antall enkle, utvetydige og tidsbegrensede
Hashing. INF Algoritmer og datastrukturer HASHING. Hashtabeller
 Hashing INF2220 - Algoritmer og datastrukturer HØSTEN 200 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning : Hashing Hashtabeller (kapittel.) Hash-funksjoner (kapittel.2) Kollisjonshåndtering
Hashing INF2220 - Algoritmer og datastrukturer HØSTEN 200 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning : Hashing Hashtabeller (kapittel.) Hash-funksjoner (kapittel.2) Kollisjonshåndtering
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 6: Grafer Bjarne Holen (Ifi, UiO) INF2220 H2009, forelesning 6 1 / 31 Dagens plan:
INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 6: Grafer Bjarne Holen (Ifi, UiO) INF2220 H2009, forelesning 6 1 / 31 Dagens plan:
Datastrukturer for rask søking
 Søking Søkeproblemet Gitt en datastruktur med n elementer: Finnes et bestemt element (eller en bestemt verdi) x lagret i datastrukturen eller ikke? Effektiviteten til søkealgoritmer avhenger av: Om datastrukturen
Søking Søkeproblemet Gitt en datastruktur med n elementer: Finnes et bestemt element (eller en bestemt verdi) x lagret i datastrukturen eller ikke? Effektiviteten til søkealgoritmer avhenger av: Om datastrukturen
DRI 2001 Systemutviklingsarbeidet et overblikk Forelesning
 Systemutviklingsarbeidet et overblikk DRI2001 forelesning 21. sept. 05 Informasjonssystem og datasystem Hva er systemutvikling (SU) Et enkelt eksempel å bygge et hus Rammer og perspektiver for SU-arbeidet
Systemutviklingsarbeidet et overblikk DRI2001 forelesning 21. sept. 05 Informasjonssystem og datasystem Hva er systemutvikling (SU) Et enkelt eksempel å bygge et hus Rammer og perspektiver for SU-arbeidet
DRI 2001 Systemutviklingsarbeidet et overblikk Forelesning
 Systemutviklingsarbeidet et overblikk DRI2001 forelesning 12. sept. 06 Forholdet mellom informasjonssystemet og virkeligheten Hva innebærer utvikling av et IS (systemutvikling: SU) Å utvikle et IS det
Systemutviklingsarbeidet et overblikk DRI2001 forelesning 12. sept. 06 Forholdet mellom informasjonssystemet og virkeligheten Hva innebærer utvikling av et IS (systemutvikling: SU) Å utvikle et IS det
VELKOMMEN TIL MAT-INF1100(L) Knut Mørken knutm@ifi.uio.no Rom 1033, Niels Henrik Abels hus
 VELKOMMEN TIL MAT-INF1100(L) Knut Mørken knutm@ifi.uio.no Rom 1033, Niels Henrik Abels hus Forelesere Knut Mørken og Martin Reimers, Matematisk institutt, 10. etg i Niels Henrik Abels hus Arbeider med
VELKOMMEN TIL MAT-INF1100(L) Knut Mørken knutm@ifi.uio.no Rom 1033, Niels Henrik Abels hus Forelesere Knut Mørken og Martin Reimers, Matematisk institutt, 10. etg i Niels Henrik Abels hus Arbeider med
TDT4127 Programmering og Numerikk
 TDT4127 Programmering og Numerikk Torbjørn Ringholm, forsker, Institutt for matematiske fag Kontor: 1338 i Sentralbygg II (Gløshaugen) Epost: torbjorn.ringholm@ntnu.no Innhold i emnet Lære grunnleggende
TDT4127 Programmering og Numerikk Torbjørn Ringholm, forsker, Institutt for matematiske fag Kontor: 1338 i Sentralbygg II (Gløshaugen) Epost: torbjorn.ringholm@ntnu.no Innhold i emnet Lære grunnleggende
Dagens plan: INF Algoritmer og datastrukturer. Eksempel. Binære Relasjoner
 Dagens plan: INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 10: Disjunkte Mengder Definisjon av binær relasjon Definisjon av ekvivalens
Dagens plan: INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 10: Disjunkte Mengder Definisjon av binær relasjon Definisjon av ekvivalens
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 10: Disjunkte Mengder Bjarne Holen (Ifi, UiO) INF2220 H2009, forelesning 10 1 / 27
INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 10: Disjunkte Mengder Bjarne Holen (Ifi, UiO) INF2220 H2009, forelesning 10 1 / 27
Det første grafteoretiske problem: Broene i Königsberg
 Dagens plan: INF0 - Algoritmer og datastrukturer HØSTEN 007 Institutt for informatikk, Universitetet i Oslo INF0, forelesning 6: Grafer Denisjon av en graf (kap. 9.1) Grafvarianter Intern representasjon
Dagens plan: INF0 - Algoritmer og datastrukturer HØSTEN 007 Institutt for informatikk, Universitetet i Oslo INF0, forelesning 6: Grafer Denisjon av en graf (kap. 9.1) Grafvarianter Intern representasjon
Repetisjon: Binære. Dagens plan: Rød-svarte trær. Oppgave (N + 1)!
 Repetisjon: Binære søketrær Dagens plan: Rød-svarte trær (kap. 12.2) B-trær (kap. 4.7) bstrakte datatyper (kap. 3.1) takker (kap. 3.3) For enhver node i et binært søketre gjelder: lle verdiene i venstre
Repetisjon: Binære søketrær Dagens plan: Rød-svarte trær (kap. 12.2) B-trær (kap. 4.7) bstrakte datatyper (kap. 3.1) takker (kap. 3.3) For enhver node i et binært søketre gjelder: lle verdiene i venstre
Dagens plan: INF Algoritmer og datastrukturer. Grafer vi har sett allerede. Det første grafteoretiske problem: Broene i Königsberg
 Dagens plan: INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 6: Grafer Definisjon av en graf Grafvarianter Intern representasjon
Dagens plan: INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 6: Grafer Definisjon av en graf Grafvarianter Intern representasjon
DRI2001 Offentlige nettsteder. Litt om systemutvikling Torsdag 24 aug Arild Jansen, AFIN, UiO
 DRI 2001 13.9 : Introduksjon til systemutvikling. Introduksjon til systemutvikling Systemutvikling og nettstedsutvikling Om ulike typer offentlige nettsteder Kvalitetskrav til offentlige nettsteder Litt
DRI 2001 13.9 : Introduksjon til systemutvikling. Introduksjon til systemutvikling Systemutvikling og nettstedsutvikling Om ulike typer offentlige nettsteder Kvalitetskrav til offentlige nettsteder Litt
Uke 7. Magnus Li INF /
 Uke 7 Magnus Li magl@ifi.uio.no INF3290 17/18.10.2017 Innlevering 1 Innlevering 1 Gjør det enkelt for leser å følge med! - Struktur - Språk - Figurer - Tabeller Et mål er å vise at dere har lest og forstått
Uke 7 Magnus Li magl@ifi.uio.no INF3290 17/18.10.2017 Innlevering 1 Innlevering 1 Gjør det enkelt for leser å følge med! - Struktur - Språk - Figurer - Tabeller Et mål er å vise at dere har lest og forstått
... HASHING. Hashing. Hashtabeller. hash(x)
 HASHING Hashing Hashtabeller (kapittel.) Hash-funksjoner (kapittel.) Kollisjonshåndtering Åpen hashing (kapittel.) Lukket hashing (kapittel.) Anta at en bilforhandler har ulike modeller han ønsker å lagre
HASHING Hashing Hashtabeller (kapittel.) Hash-funksjoner (kapittel.) Kollisjonshåndtering Åpen hashing (kapittel.) Lukket hashing (kapittel.) Anta at en bilforhandler har ulike modeller han ønsker å lagre
Generelt om operativsystemer
 Generelt om operativsystemer Hva er problemet? Styring av maskinvare og ressurser tilknyttet en datamaskin er komplisert, detaljert og vanskelig Maskinvare, komponenter og programvare endres og forbedres
Generelt om operativsystemer Hva er problemet? Styring av maskinvare og ressurser tilknyttet en datamaskin er komplisert, detaljert og vanskelig Maskinvare, komponenter og programvare endres og forbedres
INF2220: Forelesning 1
 INF2220: Forelesning 1 Praktisk informasjon Analyse av algoritmer (kapittel 2) (Binær)trær (kapittel 4.1-4.3 + 4.6) Praktisk informasjon 2 Praktisk informasjon Kursansvarlige Ingrid Chieh Yu de Vibe (ingridcy@ifi.uio.no)
INF2220: Forelesning 1 Praktisk informasjon Analyse av algoritmer (kapittel 2) (Binær)trær (kapittel 4.1-4.3 + 4.6) Praktisk informasjon 2 Praktisk informasjon Kursansvarlige Ingrid Chieh Yu de Vibe (ingridcy@ifi.uio.no)
INF1000 Eksamensforberedelser og -tips. Høst 2014 Siri Moe Jensen
 INF1000 Eksamensforberedelser og -tips Høst 2014 Siri Moe Jensen Hva skal evalueres? Fra kurssidene Etter å ha tatt INF1000 Overordnet pensum kan du skrive små til middels store programmer oppdelt i klasser.
INF1000 Eksamensforberedelser og -tips Høst 2014 Siri Moe Jensen Hva skal evalueres? Fra kurssidene Etter å ha tatt INF1000 Overordnet pensum kan du skrive små til middels store programmer oppdelt i klasser.
Et eksempel: Åtterspillet
 Trær Et eksempel: Åtterspillet To spillere som «trekker» annenhver gang I hvert trekk velges et av tallene 1, 2, 3, men ikke tallet som motspiller valgte i forrige trekk Valgte tall summeres fortløpende
Trær Et eksempel: Åtterspillet To spillere som «trekker» annenhver gang I hvert trekk velges et av tallene 1, 2, 3, men ikke tallet som motspiller valgte i forrige trekk Valgte tall summeres fortløpende
Systemutvikling (Software Engineering) TDT 4110 IT Grunnkurs Professor Guttorm Sindre
 Systemutvikling (Software Engineering) TDT 4110 IT Grunnkurs Professor Guttorm Sindre Læringsmål og pensum Mål Lære å lage større og sammensatte programmer Pensum Pythonboka kap. 1-9, 12 Teorikapitlet
Systemutvikling (Software Engineering) TDT 4110 IT Grunnkurs Professor Guttorm Sindre Læringsmål og pensum Mål Lære å lage større og sammensatte programmer Pensum Pythonboka kap. 1-9, 12 Teorikapitlet
Lenkelister, iteratorer, indre klasser. Repetisjonskurs våren 2018 kristijb
 Lenkelister, iteratorer, indre klasser Repetisjonskurs våren 2018 kristijb Lenket liste av objekter Vi lager en lenke ved at objekter refererer til hverandre. Vanlige er ofte å ha Node-objekter som har
Lenkelister, iteratorer, indre klasser Repetisjonskurs våren 2018 kristijb Lenket liste av objekter Vi lager en lenke ved at objekter refererer til hverandre. Vanlige er ofte å ha Node-objekter som har
Velkommen til. INF våren 2016
 Velkommen til INF1010 - våren 2016 Denne uken (onsdag og torsdag): Om INF1010 Java datastrukturer Klasser med parametre i Java Stein Gjessing Institutt for informatikk Universitetet i Oslo 1 1 INF1010
Velkommen til INF1010 - våren 2016 Denne uken (onsdag og torsdag): Om INF1010 Java datastrukturer Klasser med parametre i Java Stein Gjessing Institutt for informatikk Universitetet i Oslo 1 1 INF1010
Definisjon: Et sortert tre
 Binære søketrær Definisjon: Et sortert tre For alle nodene i et binært søketre gjelder: Alle verdiene i nodens venstre subtre er mindre enn verdien i noden Alle verdiene i nodens høyre subtre er større
Binære søketrær Definisjon: Et sortert tre For alle nodene i et binært søketre gjelder: Alle verdiene i nodens venstre subtre er mindre enn verdien i noden Alle verdiene i nodens høyre subtre er større
VELKOMMEN TIL MAT-INF1100
 VELKOMMEN TIL MAT-INF1100 Foreleser Knut Mørken, Institutt for informatikk, CMA Rom nr. 1033 i Niels Henrik Abels hus E-post: knutm@ifi.uio.no Arbeider med numerisk analyse og representasjon av geometri.
VELKOMMEN TIL MAT-INF1100 Foreleser Knut Mørken, Institutt for informatikk, CMA Rom nr. 1033 i Niels Henrik Abels hus E-post: knutm@ifi.uio.no Arbeider med numerisk analyse og representasjon av geometri.
INF112(kun et utvalg av kommentarene er med i denne rapporten)
 INF112(kun et utvalg av kommentarene er med i denne rapporten) Respondenter Prosent Ny 0 0,0% Distribuert 20 46,5% Noen svar 1 2,3% Gjennomført 22 51,2% Frafalt 0 0,0% I alt 43 100,0% Er det første gang
INF112(kun et utvalg av kommentarene er med i denne rapporten) Respondenter Prosent Ny 0 0,0% Distribuert 20 46,5% Noen svar 1 2,3% Gjennomført 22 51,2% Frafalt 0 0,0% I alt 43 100,0% Er det første gang
PG4200 Algoritmer og datastrukturer Lab 1. 8.januar 2014. I dag skal vi undersøke en rekke velkjente databeholdere i Java:
 PG4200 Algoritmer og datastrukturer Lab 1 8.januar 2014 Innledning I dag skal vi undersøke en rekke velkjente databeholdere i Java: java.util.arraylist java.util.linkedlist java.util.hashset java.util.treeset
PG4200 Algoritmer og datastrukturer Lab 1 8.januar 2014 Innledning I dag skal vi undersøke en rekke velkjente databeholdere i Java: java.util.arraylist java.util.linkedlist java.util.hashset java.util.treeset
Alg. Dat. Øvingsforelesning 3. Grafer, BFS, DFS og hashing. Børge Rødsjø rodsjo@stud.ntnu.no
 Alg. Dat Øvingsforelesning 3 Grafer, BFS, DFS og hashing Børge Rødsjø rodsjo@stud.ntnu.no Dagens tema Grafer Terminologi Representasjon av grafer Bredde først søk (BFS) Dybde først søk (DFS) Hashing Hashfunksjoner,
Alg. Dat Øvingsforelesning 3 Grafer, BFS, DFS og hashing Børge Rødsjø rodsjo@stud.ntnu.no Dagens tema Grafer Terminologi Representasjon av grafer Bredde først søk (BFS) Dybde først søk (DFS) Hashing Hashfunksjoner,
Obligatorisk oppgave 1 INF1020 h2005
 Obligatorisk oppgave 1 INF1020 h2005 Frist: fredag 7. oktober Oppgaven skal løses individuelt, og må være godkjent for å kunne gå opp til eksamen. Før innlevering må retningslinjene Krav til innleverte
Obligatorisk oppgave 1 INF1020 h2005 Frist: fredag 7. oktober Oppgaven skal løses individuelt, og må være godkjent for å kunne gå opp til eksamen. Før innlevering må retningslinjene Krav til innleverte
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2016 Institutt for informatikk, Universitetet i Oslo Forelesning 6: Grafer II Ingrid Chieh Yu (Ifi, UiO) INF2220 28.09.2016 1 / 30 Dagens plan: Dijkstra fort.
INF2220 - Algoritmer og datastrukturer HØSTEN 2016 Institutt for informatikk, Universitetet i Oslo Forelesning 6: Grafer II Ingrid Chieh Yu (Ifi, UiO) INF2220 28.09.2016 1 / 30 Dagens plan: Dijkstra fort.
EKSAMENSOPPGAVE. IAI20102 Algoritmer og datastrukturer
 EKSAMENSOPPGAVE Fag: Lærer: IAI00 Algoritmer og datastrukturer André A. Hauge Dato:..005 Tid: 0900-00 Antall oppgavesider: 5 med forside Antall vedleggssider: 0 Hjelpemidler: Alle trykte og skrevne hjelpemidler,
EKSAMENSOPPGAVE Fag: Lærer: IAI00 Algoritmer og datastrukturer André A. Hauge Dato:..005 Tid: 0900-00 Antall oppgavesider: 5 med forside Antall vedleggssider: 0 Hjelpemidler: Alle trykte og skrevne hjelpemidler,
Obligatorisk oppgave 4: Lege/Resept
 Obligatorisk oppgave 4: Lege/Resept INF1010 Frist: mandag 27. mars 2017 kl. 12:00 Versjon 1.0 (111c894 ) Innhold 1 Innledning 1 1.1 Begreper................................ 2 2 Pasienter 2 3 Leger og lister
Obligatorisk oppgave 4: Lege/Resept INF1010 Frist: mandag 27. mars 2017 kl. 12:00 Versjon 1.0 (111c894 ) Innhold 1 Innledning 1 1.1 Begreper................................ 2 2 Pasienter 2 3 Leger og lister
Oppgave 1. Sekvenser (20%)
 Det matematisk-naturvitenskapelige fakultet UNIVERSITETET I BERGEN Eksamen i emnet I 20 - Algoritmer, datastrukturer og programmering Mandag 2.Mai 200, kl. 09-5. Ingen hjelpemidler tillatt. Oppgavesettet
Det matematisk-naturvitenskapelige fakultet UNIVERSITETET I BERGEN Eksamen i emnet I 20 - Algoritmer, datastrukturer og programmering Mandag 2.Mai 200, kl. 09-5. Ingen hjelpemidler tillatt. Oppgavesettet
AAR 6024 VITENSKAPLIGE METODER
 AAR 6024 VITENSKAPLIGE METODER 2014 Senter for Eiendomsutvikling og forvaltning AAR 6024 Vitenskaplige Metoder, EVU kull 2012 Vår 2014 Læringsmål Emnet skal gi studenten den metodekunnskap som er nødvendig
AAR 6024 VITENSKAPLIGE METODER 2014 Senter for Eiendomsutvikling og forvaltning AAR 6024 Vitenskaplige Metoder, EVU kull 2012 Vår 2014 Læringsmål Emnet skal gi studenten den metodekunnskap som er nødvendig
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2017 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2017, forelesning
INF2220 - Algoritmer og datastrukturer HØSTEN 2017 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2017, forelesning
Prioritetskøer. Prioritetskøer. Binære heaper (vanligst) Prioritetskøer
 Binære heaper (Leftist) Prioritetskøer Prioritetskøer er viktige i bla. operativsystemer (prosesstyring i multitaskingssystemer), og søkealgoritmer (A, A*, D*, etc.), og i simulering. Prioritetskøer Prioritetskøer
Binære heaper (Leftist) Prioritetskøer Prioritetskøer er viktige i bla. operativsystemer (prosesstyring i multitaskingssystemer), og søkealgoritmer (A, A*, D*, etc.), og i simulering. Prioritetskøer Prioritetskøer
INF1000 HashMap. Marit Nybakken marnybak@ifi.uio.no 2. november 2003
 INF1000 HashMap Marit Nybakken marnybak@ifi.uio.no 2. november 2003 Dette dokumentet skal tas med en klype salt og forfatteren sier fra seg alt ansvar. Dere bør ikke bruke definisjonene i dette dokumentet
INF1000 HashMap Marit Nybakken marnybak@ifi.uio.no 2. november 2003 Dette dokumentet skal tas med en klype salt og forfatteren sier fra seg alt ansvar. Dere bør ikke bruke definisjonene i dette dokumentet
Prioritetskøer. Binære heaper Venstrevridde heaper (Leftist) Binomialheaper Fibonacciheaper
 Prioritetskøer Binære heaper Venstrevridde heaper (Leftist) Binomialheaper Fibonacciheaper Prioritetskøer er viktige i bla. operativsystemer (prosesstyring i multitaskingssystemer), og søkealgoritmer (A,
Prioritetskøer Binære heaper Venstrevridde heaper (Leftist) Binomialheaper Fibonacciheaper Prioritetskøer er viktige i bla. operativsystemer (prosesstyring i multitaskingssystemer), og søkealgoritmer (A,
En snarvei til INF2100
 Et eksperiment En snarvei til INF2100 I år skal vi gjenta forsøket: Kan INF1000-studenter med ekstra programmeringsbakgrunn klare å gjennomføre INF2100? Hva lærer man i INF2100? INF2100 Prosjektoppgave
Et eksperiment En snarvei til INF2100 I år skal vi gjenta forsøket: Kan INF1000-studenter med ekstra programmeringsbakgrunn klare å gjennomføre INF2100? Hva lærer man i INF2100? INF2100 Prosjektoppgave
INF2220: Forelesning 1
 INF2220: Forelesning 1 Praktisk informasjon Analyse av algoritmer (kapittel 2) Rekursjon (kapittel 1.3) (Binær)trær (kapittel 4.1-4.3 + 4.6) Praktisk informasjon 2 Praktisk informasjon Kursansvarlige Ingrid
INF2220: Forelesning 1 Praktisk informasjon Analyse av algoritmer (kapittel 2) Rekursjon (kapittel 1.3) (Binær)trær (kapittel 4.1-4.3 + 4.6) Praktisk informasjon 2 Praktisk informasjon Kursansvarlige Ingrid
TMA4100 Matematikk 1. Høsten 2016
 TMA4100 Matematikk 1 Høsten 2016 Innhold Praktisk informasjon Læreboken Hjemmesiden Undervisningstilbud Digitale læringsressurser Krav for å få ta eksamen Mappevurdering Spørsmål og svar Faglig innhold
TMA4100 Matematikk 1 Høsten 2016 Innhold Praktisk informasjon Læreboken Hjemmesiden Undervisningstilbud Digitale læringsressurser Krav for å få ta eksamen Mappevurdering Spørsmål og svar Faglig innhold
Rekursiv programmering
 Rekursiv programmering Babushka-dukker En russisk Babushkadukke er en sekvens av like dukker inne i hverandre, som kan åpnes Hver gang en dukke åpnes er det en mindre utgave av dukken inni, inntil man
Rekursiv programmering Babushka-dukker En russisk Babushkadukke er en sekvens av like dukker inne i hverandre, som kan åpnes Hver gang en dukke åpnes er det en mindre utgave av dukken inni, inntil man
SIF8010 ALGORITMER OG DATASTRUKTURER
 SIF8010 ALGORITMER OG DATASTRUKTURER KONTINUASJONSEKSAMEN, 1999; LØSNINGSFORSLAG Oppgave 1 (12%) Anta at du skal lage et støtteprogram som umiddelbart skal varsle om at et ord blir skrevet feil under inntasting
SIF8010 ALGORITMER OG DATASTRUKTURER KONTINUASJONSEKSAMEN, 1999; LØSNINGSFORSLAG Oppgave 1 (12%) Anta at du skal lage et støtteprogram som umiddelbart skal varsle om at et ord blir skrevet feil under inntasting
MUSIKALSK TRIKKETUR 22.-30. APRIL
 Tirsdag. april 08:30 08:50 13:23 Grefsen vognhall 13:43 13:46 13:52 13:55 13:59 14:04 14:10 14:13 14:18 14:21 14:26 14:29 14:32 14:35 14:37 14:42 14:51 14:56 15:00 15:04 15:10 15:12 15:17 15: 15:26 15:28
Tirsdag. april 08:30 08:50 13:23 Grefsen vognhall 13:43 13:46 13:52 13:55 13:59 14:04 14:10 14:13 14:18 14:21 14:26 14:29 14:32 14:35 14:37 14:42 14:51 14:56 15:00 15:04 15:10 15:12 15:17 15: 15:26 15:28
Hva er en algoritme? INF HØSTEN 2006 INF1020. Kursansvarlige Ragnar Normann E-post: Dagens tema
 va er en algoritme? Vanlig sammenligning: Oppskrift. nput lgoritme NF1020 - ØSTEN 2006 Kursansvarlige Ragnar Normann E-post: ragnarn@ifi.uio.no Output Knuth : tillegg til å være et endelig sett med regler
va er en algoritme? Vanlig sammenligning: Oppskrift. nput lgoritme NF1020 - ØSTEN 2006 Kursansvarlige Ragnar Normann E-post: ragnarn@ifi.uio.no Output Knuth : tillegg til å være et endelig sett med regler
Grunnmal A uke 44 (partall) 10.trinn 2015-2016
 Grunnmal A uke 44 (partall) 10.trinn 2015-2016 Timer Mandag 26.20 Tirsdag 27.10. Onsdag 28.10. Torsdag 29.10. Fredag 30.10. 0 0810-0855 TEAM 1 0855-0940 NA em pl 0940-0955 2 0955-1040 NA NS (jhh) D1 AKF
Grunnmal A uke 44 (partall) 10.trinn 2015-2016 Timer Mandag 26.20 Tirsdag 27.10. Onsdag 28.10. Torsdag 29.10. Fredag 30.10. 0 0810-0855 TEAM 1 0855-0940 NA em pl 0940-0955 2 0955-1040 NA NS (jhh) D1 AKF
TMA4100 Matema,kk 1. Høsten 2014
 TMA4100 Matema,kk 1 Høsten 2014 Plan Prak0sk informasjon Læreboken Hjemmesiden Undervisnings0lbud Digitale læringsressurser Faglig innhold og læringsmål Kunnskap og ferdigheter Prak0sk informasjon om matema0kkdelen
TMA4100 Matema,kk 1 Høsten 2014 Plan Prak0sk informasjon Læreboken Hjemmesiden Undervisnings0lbud Digitale læringsressurser Faglig innhold og læringsmål Kunnskap og ferdigheter Prak0sk informasjon om matema0kkdelen
Øvingsforelesning i Python (TDT4110)
 Øvingsforelesning i Python (TDT4110) Tema: Introduksjon, Kalkulasjoner Vegard Hellem Velkommen! Litt om meg Vegard Hellem, 4. klasse datateknologi Øvingsforeleser i TDT4110 vegahel@stud.ntnu.no 2 Oversikt
Øvingsforelesning i Python (TDT4110) Tema: Introduksjon, Kalkulasjoner Vegard Hellem Velkommen! Litt om meg Vegard Hellem, 4. klasse datateknologi Øvingsforeleser i TDT4110 vegahel@stud.ntnu.no 2 Oversikt
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i Eksamensdag: 12. desember 2008 Tid for eksamen: 9.00 12.00 Oppgavesettet er på 7 sider. Vedlegg: Tillatte hjelpemidler: INF2220
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i Eksamensdag: 12. desember 2008 Tid for eksamen: 9.00 12.00 Oppgavesettet er på 7 sider. Vedlegg: Tillatte hjelpemidler: INF2220
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 13: Eksamensgjennomgang Bjarne Holen (Ifi, UiO) INF2220 H2009, forelesning 13 1 /
INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 13: Eksamensgjennomgang Bjarne Holen (Ifi, UiO) INF2220 H2009, forelesning 13 1 /
Om Kurset og Analyse av Algoritmer
 Om Kurset og Analyse av Algoritmer Lars Vidar Magnusson 8.1.2014 Praktisk informasjon om kurset Hva er en algoritme? (kapittel 1) Hvordan analysere en algoritme? (kapittel 2) Praktisk Informasjon Introduction
Om Kurset og Analyse av Algoritmer Lars Vidar Magnusson 8.1.2014 Praktisk informasjon om kurset Hva er en algoritme? (kapittel 1) Hvordan analysere en algoritme? (kapittel 2) Praktisk Informasjon Introduction
Systemutvikling. Universitetet i Oslo, Institutt for informatikk Vår 2017
 Systemutvikling Universitetet i Oslo, Institutt for informatikk Vår 2017 Dagens plan Introduksjon Emnets oppbygging Praktisk om ukesoppgaver og obligatoriske oppgaver Gjennomgang av ukesoppgaver Registrering
Systemutvikling Universitetet i Oslo, Institutt for informatikk Vår 2017 Dagens plan Introduksjon Emnets oppbygging Praktisk om ukesoppgaver og obligatoriske oppgaver Gjennomgang av ukesoppgaver Registrering
Hashing: Håndtering av kollisjoner
 Hashing: Håndtering av kollisjoner Innsetting av dataelement i hashtabell Algoritme: 1. Bruk en hashfunksjon til å beregne hashverdi basert på dataelementets nøkkelverdi 2. Sett inn dataelementet i hashtabellen
Hashing: Håndtering av kollisjoner Innsetting av dataelement i hashtabell Algoritme: 1. Bruk en hashfunksjon til å beregne hashverdi basert på dataelementets nøkkelverdi 2. Sett inn dataelementet i hashtabellen
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2016 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 5: Grafer I Ingrid Chieh Yu (Ifi, UiO) INF2220 H2016, forelesning 5 1 / 49
INF2220 - Algoritmer og datastrukturer HØSTEN 2016 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 5: Grafer I Ingrid Chieh Yu (Ifi, UiO) INF2220 H2016, forelesning 5 1 / 49
INF-MAT5370. Grafer og datastrukturer
 INF-MAT5370 Grafer og datastrukturer Øyvind Hjelle oyvindhj@simula.no, +47 67 82 82 75 Simula Research Laboratory, www.simula.no August 3, 2009 Innhold Kort om grafer Topologiske operatorer og operasjoner,
INF-MAT5370 Grafer og datastrukturer Øyvind Hjelle oyvindhj@simula.no, +47 67 82 82 75 Simula Research Laboratory, www.simula.no August 3, 2009 Innhold Kort om grafer Topologiske operatorer og operasjoner,
Velkommen til INF115
 Velkommen til INF115 Et helt nytt kurs!!! Høsten 2001 hadde vi siste gang et database kurs på instituttet - I126. Nå er vi tilbake ;-) Men INF115 skal allerede undervises i 2. semesteret. Det bringer med
Velkommen til INF115 Et helt nytt kurs!!! Høsten 2001 hadde vi siste gang et database kurs på instituttet - I126. Nå er vi tilbake ;-) Men INF115 skal allerede undervises i 2. semesteret. Det bringer med
