Kryptering og steganografi
|
|
|
- Henrik Berntsen
- 9 år siden
- Visninger:
Transkript
1 Kryptering og steganografi EJHJUBM SFQSFTFOUBTKPO FS FU LVMU GBH Jeg avlytter viktig informasjon, sa smarte Tor. Læreboka kapittel november 2007 INF1040-kryptering-1
2 HUSK Neste uke: Ingen forelesning. Gruppetimer og plenumsøvelser som vanlig. Frist oblig 3 onsdag 21. november! Kapittel 20 Digital representasjon av identitet Vil ikke bli forelest. ER PENSUM! INF1040-kryptering-2
3 Kryptologi fra gresk kryptos: hemmelig, gjemt -logi: læren om graphos: skriving kryptografi: studiet av hemmelig skrift kryptoanalyse: studiet av metoder og prinsipper for å kunne tyde en kryptert tekst uten kjennskap til krypteringsnøkkelen ( knekke koden krypteringsnøkkel: Data som brukes for å kryptere og dekryptere meldinger kryptologi: Kryptografi + kryptoanalyse INF1040-kryptering-3
4 Kryptering av data Krypteringsnøkkel Krypteringsnøkkel Data (klartekst Krypterte data (chiffertekst Krypteringsalgoritme Dekrypteringsalgoritme Data (klartekst Formål: Gjøre data som sendes eller lagres uleselige for uvedkommende. Utfordringer: Finne tilstrekkelig gode krypterings- og dekrypteringsalgoritmer. Gjøre det praktisk umulig å finne krypteringsnøkkelen ( knekke koden. Administrere krypteringsnøkler. INF1040-kryptering-4
5 Et enkelt eksempel: Cæsars kode Meget enkel krypteringsalgoritme: Bytt ut hver bokstav med en bokstav tre plasser lenger ut i alfabetet. (Ved slutten av alfabetet, wrap around. Eksempel: DIGITAL REPRESENTASJON ER ET KULT FAG GLJLWDO UHSUHVHQWDVMRQ HU HW NXOW IDJ Meget enkel dekrypteringsalgoritme: Bytt ut hver bokstav med bokstaven tre plasser tidligere i alfabetet. Cæsars kode er et eksempel på substitusjonsprinsippet med syklisk permutasjon. monoalfabetisk substitusjon samme nøkkel brukes for alle meldingene (bokstavene. symmetrisk kryptering samme nøkkel brukes både for kryptering og dekryptering. INF1040-kryptering-5
6 Generalisering av Cæsars kode Mer generell krypteringsalgoritme: Bytt ut hver bokstav med en bokstav k plasser lenger ut i alfabetet. Verdien av k er nøkkelen. Hvordan bryte koden når nøkkelen er ukjent? Brute force : Prøv alle N muligheter for k, der N er antall tegn i alfabetet, og se hvilken forskyvning som gir et forståelig resultat. ( Exhaustive search of the key space. 6 Frekvensanalyse: Lag et histogram for tegnene i den krypterte meldingen. (Hyppigste bokstaver i norsk: e r n t s i a d g l o D G H I J L M N O Q R S U V W X INF1040-kryptering-6
7 Kerckhoffs assumption Krypteringsnøkkel Data (klartekst Krypteringsalgoritme A. Kerckhoff, 1883: The security of a cipher must not depend on anything that cannot be easily changed The opponent is not to be underestimated. In particular, the opponent knows the encryption and decryption algorithms. So the strength of a cipher system depends on keeping the key information secret, not the algorithm se også INF1040-kryptering-7
8 Krypteringsprinsipper Krypteringsnøkkel Symmetrisk kryptering Samme nøkkel brukes for både kryptering og dekryptering Asymmetrisk kryptering To sammenhørende nøkler, den ene brukes for kryptering, den andre for dekryptering Håndtering av data Stream-kryptering Krypterer bitene eller bytene etter hvert som de kommer Blokk-kryptering Opererer på en blokk av biter typisk fra 64 til 384 ad gangen Algoritmer Substitusjonsprinsippet Bytte ut biter eller bytes med andre biter og bytes Transformasjonsprinsippet Endre rekkefølgen på biter eller bytes INF1040-kryptering-8
9 Symmetrisk kryptering Kryptering av klartekst P med nøkkel k gir chiffertekst C: E k (P C Dekryptering av chiffertekst C med samme nøkkel k gir klartekst P: D k (C P dvs. D k (E k (P P Kommunikasjonspartnerne deler en hemmelighet: Nøkkelen Fordel: Brukbar effektivitet Problem: Distribusjon (og hemmeligholdelse av nøkkelen INF1040-kryptering-9
10 Ligner Cæsars kryptering, men bruker en frase som nøkkel. Symmetrisk streamkryptering med polyalfabetisk substitusjon. Eksempel: nøkkel HEI REPRESENTASJON HEIHEIHEIHEIHE YIXYIALRBHWRVR Prøv for eksempel: Vigenère kryptering INF1040-kryptering-10
11 Enigma - Rotormaskin Brukt bl.a. av nazi-regimet under andre verdenskrig. Symmetrisk stream-kryptering som bygger på substitusjonsprinsippet. Hver rotor gjør en substitusjon. Rotorene er forskjellige og kan bytte plass. Et tastetrykk bevirker at tegnet sendes gjennom alle rotorene og tilbake (én rotor virker som reflektor. Rotorene dreies automatisk etter hvert tastetrykk. Nøkkelen er startposisjonen for rotorene. Tilsvarer en nøkkellengde på 380 biter (med plugboard. Flere detaljer på INF1040-kryptering-11
12 Hva medfører datateknologien? Mulighet for mer raffinerte krypterings- og dekrypteringsalgoritmer Vi krypterer biter og bytes, ikke tegn krypteringsalgoritmene ser altså ikke forskjell på tekst, bilder og lyd Kraftigere verktøy for kryptering men også kraftigere verktøy for kryptoanalyse ( knekking av kryptering Et enkelt regnestykke: Nøkkellengde 128 biter, antall mulige nøkler er La oss anta at det tar 0,001 sekund å sjekke ut en nøkkel da blir tidsforbruket i gjennomsnitt 0,5 * 0,001 * s = 1,7 * s = 5,4 * år INF1040-kryptering-12
13 Vernam-kryptering Den enkleste formen for symmetrisk stream-kryptering Oppfunnet av Gilbert Vernam i 1917 for telex se Nøkkelbitstrøm Nøkkelbitstrøm 0 0 = = = = 0 Klartekst bitstrøm bitwise exclusive or Kryptert bitstrøm bitwise exclusive or Klartekst bitstrøm Eksempel: to og to i UTF-8: 74 6F 20 6F F 20 = Tilfeldig valgt nøkkel: klartekst nøkkel chiffertekst nøkkel klartekst INF1040-kryptering-13
14 One-time-pad Vernam-kryptering med en tilfeldig nøkkel minst så lang som meldingen, og som brukes bare en gang Oppfunnet av Vernam og Mauborgne på 1920-tallet se Bevist av Shannon å være 100 % sikker Intuitivt: Enhver tekst med et gitt antall tegn kan genereres med en passende nøkkel One-time-pad One-time-pad Klartekst bitstrøm bitwise exclusive or Kryptert bitstrøm bitwise exclusive or Klartekst bitstrøm Når one-time-pad er 100 % sikker, hva er da problemet? INF1040-kryptering-14
15 Generert One-time-pad Problemet med one-time-pad er distribusjonen av et stort antall meget lange tilfeldige nøkler (men dette problemet er kanskje minkende? Et alternativ er å erstatte one-time-pad med en sekvens av pseudotilfeldige biter fra en random number generator (se neste lysark Nøkkelen blir da meget kort (består av seed og evt. konstanter Men gir ikke 100 % sikkerhet nøklene er ikke tilfeldige Seed etc. Random Number Generator Seed etc. Random Number Generator Brukes bl.a. i den populære RC4- krypteringen Klartekst bitstrøm bitwise exclusive or Kryptert bitstrøm bitwise exclusive or Klartekst bitstrøm INF1040-kryptering-15
16 Pseudotilfeldige tall Mange moderne krypteringsteknikker bygger på sekvenser av pseudotilfeldige tall Pseudotilfeldige tall ser ut som tilfeldige tall, men hvert tall i sekvensen er beregnet på grunnlag av det forrige. Det første tallet er beregnet på grunnlag av en startverdi ( seed. Nøkkelen består av seed og eventuelle konstanter (se neste lysark. Med denne nøkkelen og tilgang til algoritmen for beregning av de pseudotilfeldige tallene kan tallsekvensen regenereres av mottakeren av meldingen! Men: Robusthet mot knekking er ikke bevist. INF1040-kryptering-16
17 Algoritmer for pseudotilfeldige tall Eksempel på algoritme (ikke særlig velegnet for kryptering Linear Congruential Pseudo-number Generator x n+1 = (C*x n + D % M der C, D og M er konstanter valgt slik at: C og D er relativ prim (ingen felles faktorer C-1 er delbar med alle primfaktorer i M hvis M er delelig med 4, er også C-1 det. Da gir algoritmen alle tall fra 0 til M-1 i tilfeldig rekkefølge før sekvensen gjentas. Eksempel: C=5, D=3, M=16, seed=5 gir 12, 15, 14, 9, 0, 3, 2, 13, 4, 7, 6, 1, 8, 11, 10 For å få en noenlunde sikker nøkkel må M være stor! (> 128 biter se også INF1040-kryptering-17
18 Blokk-kryptering Blokk-kryptering opererer på en blokk av biter typisk fra 64 til 384 ad gangen Blokk-kryptering åpner for permutasjon av bitene i blokken To hovedprinsipper Confusion Sørge for en så komplisert sammenheng mellom nøkkel og chiffertekst at kryptoanalytikeren ikke kan få nyttig informasjon om nøkkelen ved statistisk analyse av chifferteksten Diffusion Skjule mønstre i klarteksten ved å spre blokkene over hele chifferteksten en endring av en bit i klarteksten bør gi endring i mange biter i chifferteksten. Løses med ombytting og xor ing av blokker se også INF1040-kryptering-18
19 Advanced Encryption Standard AES Vinner av en konkurranse utlyst av NIST (National Institute of Standards and Technology i USA vinneren kåret i oktober 2000 Konstruert av to belgiere, Joan Daemon og Vincent Rijmen, under navnet Rijndael Blokk- og nøkkellengde 128, 192 eller 256 biter Ingen patenter, kan benyttes av alle Motstandsdyktig mot alle kjente kryptoanalysemetoder Enkel, rask, lett å implementere i maskin- og/eller programvare Avløser DES Data Encryption Standard INF1040-kryptering-19
20 klartekstblokk nøkkelekspansjon forrunde substitusjon shiftrow mixcolumn keyaddition r<n-1 sluttrunde AES virkemåte (1 t 0,0 t 0,1 t 1,1 t 2,1 t 3,1 t 0,2 t 1,0 t 0,3 t 1,2 t 2,0 t 1,3 t 2,2 t 3,0 t 2,3 t 3,2 t 3,3 Klartekstblokken oppfattes som en 4 * 4 tabell (matrise med bytes (AES-standarden Generelt kan større blokker og matriser kan benyttes Antall runder (10, 12 eller 14 avhenger av blokkstørrelsen chifferblokk INF1040-kryptering-20
21 klartekstblokk AES virkemåte (2 nøkkelekspansjon forrunde substitusjon shiftrow ekspansjonsfunksjon (Rijandel s key schedule mixcolumn keyaddition pseudo-tilfeldig bitmønster av tilstrekkelig lengde r<n-1 sluttrunde chifferblokk INF1040-kryptering-21
22 klartekstblokk AES virkemåte (3 nøkkelekspansjon forrunde substitusjon shiftrow t 0,0 t 0,1 t 1,0 t 0,3 t 1,1 t 2,1 t 3,0 t 2,3 t 3,1 t 0,2 t 1,2 t 2,2 t 2,0 t 1,3 t 3,2 t 3,3 a 0,0 a 0,1 a 1,1 a 2,1 a 3,1 a 0,2 a 1,0 a 0,3 a 1,2 a 2,2 a 2,0 a 1,3 a 3,0 a 2,3 a 3,2 a 3,3 mixcolumn keyaddition r<n-1 sluttrunde chifferblokk k 0,0 k 0,1 k 1,0 k 0,3 k 1,1 k 2,1 k 3,0 k 2,3 k 3,1 k 0,2 k 1,2 k 2,2 k 2,0 k 1,3 k 3,2 k 3,3 Tilstandsmatrisen xor es med første del av den ekspanderte nøkkelen. INF1040-kryptering-22
23 klartekstblokk AES virkemåte (4 AES nøkkelekspansjon forrunde substitusjon a 0,0 a 0,1 a 1,0 a 0,3 a 1,1 a 2,1 a 3,0 a 2,3 a 3,1 a 0,2 a 1,2 a 2,2 a 2,0 a 1,3 a 3,2 a 3,3 S(a 0,0 S(a 1,0 S(a 2,0 S(a 3,0 S(a 0,1 S(a 1,1 S(a 2,1 S(a 3,1 S(a 0,2 S(a 1,2 S(a 2,2 S(a 3,2 S(a 0,3 S(a 1,3 S(a 2,3 S(a 3,3 shiftrow mixcolumn keyaddition r<n-1 sluttrunde chifferblokk Hver enkelt byte erstattes med en annen byte som finnes ved å slå opp i en tabell S med 2 8 elementer. Tabellen er konstruert slik at vi får best mulig confusion. S INF1040-kryptering-23
24 klartekstblokk AES virkemåte (5 AES nøkkelekspansjon S(a 0,0 S(a 0,1 S(a 0,2 S(a 0,3 Ingen endring forrunde S(a 1,0 S(a 2,0 S(a 1,1 S(a 2,1 S(a 1,2 S(a 2,2 S(a 1,3 S(a 2,3 Shift 1 Shift 2 substitusjon S(a 3,0 S(a 3,1 S(a 3,2 S(a 3,3 Shift 3 shiftrow S(a 0,0 S(a 0,1 S(a 0,2 S(a 0,3 mixcolumn S(a 1,1 S(a 1,2 S(a 1,3 S(a 1,0 keyaddition r<n-1 sluttrunde chifferblokk S(a 2,2 S(a 2,3 S(a 2,0 S(a 2,1 S(a 3,3 S(a 3,0 S(a 3,1 S(a 3,2 Linjene i tilstandsmatrisen roteres. Dette er første ledd i diffusion. INF1040-kryptering-24
25 klartekstblokk AES virkemåte (6 AES nøkkelekspansjon forrunde substitusjon S(a 0,0 S(a 1,1 S(a 2,2 S(a 3,3 S(a 0,1 S(a 1,2 S(a 2,3 S(a 3,0 S(a 0,2 S(a 1,3 S(a 2,0 S(a 3,1 S(a 0,3 S(a 1,0 S(a 2,1 S(a 3,2 A 0,0 A 0,1 A 1,1 A 2,1 A 3,1 A 0,2 A 1,0 A 0,3 A 1,2 A 2,0 A 1,3 A 2,2 A 3,0 A 2,3 A 3,2 A 3,3 shiftrow mixcolumn keyaddition r<n-1 sluttrunde chifferblokk c(x Kolonnene matrisemultipliseres med en fast vektor c(x. Det innebærer at innholdet i en S(a- byte påvirker innholdet i 4 A-bytes. Dette er andre ledd i diffusion. INF1040-kryptering-25
26 klartekstblokk AES virkemåte (7 AES nøkkelekspansjon forrunde substitusjon shiftrow A 0,0 A 0,1 A 1,0 A 0,3 A 1,1 A 2,1 A 3,0 A 2,3 A 3,1 A 0,2 A 1,2 A 2,2 A 2,0 A 1,3 A 3,2 A 3,3 b 0,0 b 0,1 b 1,1 b 2,1 b 3,1 b 0,2 b 1,0 b 0,3 b 1,2 b 2,2 b 2,0 b 1,3 b 3,0 b 2,3 b 3,2 b 3,3 mixcolumn keyaddition r<n-1 sluttrunde chifferblokk k 4,0 k 4,1 k 5,0 k 4,3 k 5,1 k 6,1 k 7,0 k 6,3 k 7,1 k 4,2 k 5,2 k 6,2 k 6,0 k 5,3 k 7,2 k 7,3 Tilstandsmatrisen xor es med neste del av den ekspanderte nøkkelen. INF1040-kryptering-26
27 klartekstblokk AES virkemåte (8 AES nøkkelekspansjon forrunde substitusjon shiftrow mixcolumn keyaddition r<n-1 sluttrunde chifferblokk Sluttrunden er som alle de andre, bortsett fra av skrittet mixcolumn er utelatt INF1040-kryptering-27
28 Bruksmåter ( modes of operation For å kryptere bitstrømmer lengre enn blokklengden, bakes blokkkrypteringen inn i ulike bruksmåter ( modes of operation : Electronic Code Book ECB Cipher feedback CFB Cipher Block Chaining CBC Derfor snakker vi for eksempel om AES-CBC Output feedback OFB Counter mode CTR Noen av disse utfører diffusion utenfor blokklengden. Ulike egenskaper med hensyn på sikkerhet og effektivitet. For detaljer, se de følgende lysark. se også INF1040-kryptering-28
29 Electronic Code Book - ECB Hver blokk krypteres for seg. Ulempe: Like klartekstblokker gir like chiffertekstblokker (dårlig diffusion. klartekstblokk 1 klartekstblokk 2 Kryptering: E k E k chiffertekstblokk 1 chiffertekstblokk 2 chiffertekstblokk 1 chiffertekstblokk 2 Dekryptering: E k E k klartekstblokk 1 klartekstblokk 2 INF1040-kryptering-29
30 Cipher Feedback - CFB Foregående chiffertekstblokk krypteres med nøkkelen første gang krypteres initialiseringsvektoren. Blokken xor es med resultatet. initialiseringsvektor E k E k klartekstblokk 1 klartekstblokk 2 chiffertekstblokk 1 initialiseringsvektor chiffertekstblokk 2 D k = E k D k D k chiffertekstblokk 1 chiffertekstblokk 2 klartekstblokk 1 klartekstblokk 2 INF1040-kryptering-30
31 Cipher Block Chaining CBC Klartekstsblokkene xor es med foregående chiffertekstblokk. Resultatet krypteres med nøkkelen. klartekstblokk 1 klartekstblokk 2 initialiseringsvektor E k E k chiffertekstblokk 1 chiffertekstblokk 1 chiffertekstblokk 2 chiffertekstblokk 2 D k D k initialiseringsvektor klartekstblokk 1 klartekstblokk 2 INF1040-kryptering-31
32 Output Feedback - OFB Ved første gjennomløp krypteres initialiseringsvektoren. Ved senere gjennomløp krypteres resultatet av foregående kryptering Klartekstblokken xor es med resultatet. initialiseringsvektor E k E k klartekstblokk 1 klartekstblokk 2 chiffertekstblokk 1 initialiseringsvektor chiffertekstblokk 2 D k = E k D k D k chiffertekstblokk 1 chiffertekstblokk 2 klartekstblokk 1 klartekstblokk 2 INF1040-kryptering-32
33 Counter mode CTR En nonce ( number used once etterfulgt av en teller krypteres med nøkkelen. Klartekstblokken xor es med resultatet. nonce, nonce, E k E k klartekstblokk 1 klartekstblokk 2 chiffertekstblokk 1 nonce, chiffertekstblokk 2 nonce, D k = E k D k D k chiffertekstblokk 1 chiffertekstblokk 2 klartekstblokk 1 klartekstblokk 2 INF1040-kryptering-33
34 Kvantekryptografi Symmetrisk kryptering har et stort problem: Oversending av nøkler på en sikker måte Her kan den såkalte kvantekryptografien komme til hjelp Bygger på at polariseringsretningen for fotoner i lys kan avleses bare én gang (BB84-protokollen Derfor er det umulig å lytte ubemerket på linjen Fungerer bra over opptil 50 km optisk linje Foreløpig få kommersielle anvendelser men mye forskning se f.eks. Tilfeldig krypteringsnøkkel Klartekst bitstrøm kvantekryptografisk forbindelse Kryptert bitstrøm Krypteringsalgoritme Dekrypteringsalgoritme Klartekst bitstrøm INF1040-kryptering-34
35 Asymmetrisk kryptering Asymmetrisk kryptering arbeider med et nøkkelpar k1 og k2 som er matematisk relatert til hverandre den ene nøkkelen brukes for kryptering, den andre for dekryptering Kryptering av klartekst P med nøkkel k1 gir chiffertekst C: E k1 (P C Dekryptering av chiffertekst C med nøkkel k2 gir klartekst P: D k2 (C P Asymmetrisk kryptering forenkler nøkkeladministrasjonen, men algoritmene er tunge! Klartekst bitstrøm Kryptert bitstrøm Krypteringsalgoritme Dekrypteringsalgoritme Klartekst bitstrøm INF1040-kryptering-35
36 Praktisk bruk av asymmetrisk kryptering (1 Alice vil sende en hemmelig melding til Bob På forhånd har Bob fått generert et nøkkelpar Bobk1 og Bobk2 Bobk1 offentliggjør han som sin offentlige nøkkel Bobk2 holder han strengt hemmelig som privat nøkkel Alice krypterer meldingen med Bobk1, altså Bobs offentlige nøkkel Bob er den eneste som kan dekryptere meldingen, fordi bare han er i besittelse av Bobk2, den tilhørende private nøkkelen INF1040-kryptering-36
37 Praktisk bruk av asymmetrisk kryptering (2 Alice vil sende en melding til Bob på en slik måte at Bob kan forsikre seg om at den virkelig er fra henne På forhånd har Alice fått generert et nøkkelpar Alicek1 og Alicek2 Alicek1 offentliggjør hun som sin offentlige nøkkel Alicek2 holder hun strengt hemmelig som privat nøkkel Alice krypterer meldingen med Alicek2, altså sin egen private nøkkel Bob ser at meldingen trolig kommer fra Alice, og dekrypter med Alicek1, dvs. hennes offentlige nøkkel. Går det bra, kan han gå ut fra at meldingen virkelig kommer fra Alice. INF1040-kryptering-37
38 Asymmetrisk krypteringsteknikk Vi ønsker at samme algoritme E brukes for både kryptering og dekryptering: dvs. E k2 (E k1 (P P Mest kjente algoritme: RSA (Rivest, Shamir & Adleman (se detaljer neste lysark RSA er basert på at det er lett å multiplisere to primtall, men vanskelig å faktorisere dem (bare empirisk vist! se også Multiplikasjon av to primtall er et eksempel på en matematisk enveisfunksjon: Det er enkelt å beregne y = f(x, og samtidig meget vanskelig å beregne x = f --1 (y Det er en matematisk utfordring å finne ut hvor enveis en gitt funksjon virkelig er! INF1040-kryptering-38
39 Virkemåte av RSA-algoritmen La meldingen P være et tall mindre enn N Kryptering: C = E k1 (P = P k1 % N Dekryptering: P = E k2 (C = C k2 % N N og k1 er den offentlige nøkkelen k2 er den private nøkkelen N, k1 og k2 må være omhyggelig valgt etter følgende regler: N = p * q, der p og q er store primtall k2 er et stort tall relativt prim til (p-1(q-1 (dvs. ingen andre felles faktorer enn 1 k1 er valgt slik at k1*k2 % (p-1(q-1 = 1 Eksempel: p = 3, q = 5, k2 = 7, k1 = 23, N = 15 Meldingen P er tallet 3: Kryptering: C = E 23 (3 = 3 23 % 15 = 12 Dekryptering: P = E 7 (12 = 12 7 % 15 = 3 Hvis p og q velges slik at N blir tilstrekkelig stor (mer enn 100 siffer, er det i praksis ikke mulig (selv med datamaskin å finne k2, selv om du kjenner k1 og N. INF1040-kryptering-39
40 Hvordan distribuere offentlige nøkler? En løsning: Digitale sertifikater (delegering av tillit Top Key Authority med kjent offentlig nøkkel (Verisign, Thawte, BT etc. Top Key Authority har som oppgave å sertifisere et underliggende nivå med Key Authorities x1, x2,... og så videre nedover i hierarkiet En Key Authority sender deg et sertifikat i form av en melding kryptert med Key Authority private nøkkel Sertifikatet bekrefter at bruker NN har offentlig nøkkel NNoff En mindre byråkratisk løsning: Web of trust INF1040-kryptering-40
41 Hvordan oppdage endring av meldinger Kryptering forhindrer at utenforstående kan lese dataene, men forhindrer ikke at utenforstående (inklusive støy på linjen ubemerket endrer dataene Mottiltak er å la en algoritme h beregne et såkalt digitalt segl eller message digest s ut fra meldingen P. Avsender beregner s = h(p og overfører s sammen med P Mottaker beregner s = h(p en gang til og sammenlikner med den overførte s INF1040-kryptering-41
42 Beregning av digitalt segl En hash-funksjon h kan beregne en tilsynelatende mystisk bit-sekvens (dvs. et tall fra enhver melding P h(p har alltid samme verdi for samme P Meldingen P kan bestå av navn, passord, dato, og selve klarteksten Ønskede egenskaper for en god hash-funksjon: Alle biter i P inngår i beregningen av h(p Uansett innholdet av de aktuelle P gir h(p en jevn fordeling over hele resultatområdet, dvs. alle verdier h(p er like sannsynlige Beregningen er rask INF1040-kryptering-42
43 Metode for sikker meldingsformidling Senderen må Beregne et digitalt segl for meldingen Kryptere seglet med egen privat nøkkel gir digital signatur Kryptere meldingen med en tilfeldig valgt nøkkel (sesjonsnøkkel Kryptere sesjonsnøkkelen med mottakerens offentlige nøkkel Mottakeren må Dekryptere sesjonsnøkkelen med egen privat nøkkel Dekryptere meldingen med sesjonsnøkkelen Dekryptere signaturen med avsenders offentlige nøkkel gir seglet Beregne seglet på nytt og sammenlikne med det oversendte seglet INF1040-kryptering-44
44 Steganografi fra gresk stegano: skjult, dekket, å dekke graphos: skriving Steganografi: A gjemme en representasjon av noe i en representasjon av noe annet et såkalt dekke ( cover Mitt ønske til mor er glemt, kan lillebror se etter katten selv? For et mer avansert eksempel (bilde skjult i bilde, se for eksempel INF1040-kryptering-45
45 Dekket Dekket er som oftest et bilde eller en lyd (mange biter! Den beste måten å holde noe hemmelig er å holde det hemmelig at det er noe å holde hemmelig dekket må ikke endres påfallende gjennom at noe er skjult Hemmelig melding Steganografiprogram Inverst steganografiprogram Hemmelig melding Dekke Stego-fil INF1040-kryptering-46
46 Et eksempel på steganografi Steganografi med Digital Invisible Ink Toolkit se Kart over modifiserte piksler Originalbilde 7 kb jpeg Dekke 40 kb jpeg Stegobilde 332 kb png Gjenvunnet bilde 7 kb jpeg INF1040-kryptering-47
47 Vannmerking Utvide en tekst-/bilde-/lydfil med ekstra data som ikke kan la seg fjerne uten å ødelegge originalen Deler av vannmerket kan være observerbart i teksten/bildet/lyden, men vanligvis er det ikke observerbart ved direkte observasjon Brukes for tilleggsopplysninger, som rettighetshaver, copyrightmarkering og eksemplarnummerering. Et vannmerke skal ikke kunne fjernes uten å ødelegge tekst/bilde/lyd Vannmerking ligner teknisk sett på steganografi, hovedforskjellen er intensjonen INF1040-kryptering-48
48 Hvordan gjemme data Trikset er å gjemme det hemmelige bitmønsteret på bestemte steder i bitmønsteret for dekket Eksempel: Et bilde (dekke er representert som en sekvens av RGBverdier, hver på 24 bit. Vi skal gjemme tegnet A, Unicode 41 (hex = Vi sørger for at den siste biten i for eksempel hver 64de RGBverdi har verdiene Av og til fører dette til at RGB-verdien blir endret, av og til ikke En eventuell endring i intensitet i blått hist og her vil antagelig ikke være synlig Variasjoner: Endre i R- eller G-verdi istedenfor Endre i de minst signifikante bitplanene i et bilde Endre hvor det allerede er store endringer (bildederivasjon! Endre i andre verdiområder (for eksempel frekvensdomenet Manipulere fargetabellen for bildeformater med fargetabell INF1040-kryptering-49
49 Stegoanalyse Å konstatere at et dekke inneholder et skjult budskap og eventuelt gjenvinne budskapet Vanskelig å gjøre ved direkte observasjon Analyseprogrammer er mye mer effektive er det noe uvanlig i teksten/bildefilen/lydfilen? Tilgang til dekket letter stegoanalysen betraktelig bruk ikke kjente digitale bilder som ligger på Internett som dekke! INF1040-kryptering-50
50 Oppsummering Data kan gjøres uleselige ved hjelp av kryptering (konfidensialitet. Urettmessig endring av data kan oppdages med digitale segl (integritet. Avsender kan verifiseres ved hjelp av asymmetrisk kryptering (autentisitet/ikke-benektbarhet. Kobling mellom individer og nøkler gjøres med sertifikater. Ved kryptering brukes oftest en kombinasjon av symmetriske og asymmetriske krypteringsteknikker. Vurderinger av sikkerheten mot knekking av krypteringer er kun basert på antagelser og empiri, intet er bevist. Steganografi brukes for å skjule en melding i et dekke. Vannmerker brukes for å gi tilleggsopplysninger som ikke kan fjernes uten å ødelegge dekket. INF1040-kryptering-51
Læringsmål kryptering og steganografi
 Kryptering og steganografi EJHJUBM SFQSFTFOUBTKPO FS FU LVMU GBH Jeg avlytter viktig informasjon, sa smarte Tor. Læreboka kapittel 19 12. november 2008 Læringsmål kryptering og steganografi Forstå ulike
Kryptering og steganografi EJHJUBM SFQSFTFOUBTKPO FS FU LVMU GBH Jeg avlytter viktig informasjon, sa smarte Tor. Læreboka kapittel 19 12. november 2008 Læringsmål kryptering og steganografi Forstå ulike
Kryptologi. Læringsmål kryptering og steganografi. Kryptering av data EJHJUBM SFQSFTFOUBTKPO FS FU LVMU GBH
 Læringsmål kryptering og steganografi Kryptering og steganografi Forstå ulike krypteringsprinsipper. Kunne sentrale begreper. Kjenne til en del sentrale teknikker. EJHJUBM SFQSFTFOUBTKPO FS FU LVMU GBH
Læringsmål kryptering og steganografi Kryptering og steganografi Forstå ulike krypteringsprinsipper. Kunne sentrale begreper. Kjenne til en del sentrale teknikker. EJHJUBM SFQSFTFOUBTKPO FS FU LVMU GBH
EJHJUBM SFQSFTFOUBTKPO FS FU LVMU GBH. Jeg avlytter viktig informasjon, sa smarte Tor. Læreboka kapittel 19
 Kryptering og steganografi EJHJUBM SFQSFTFOUBTKPO FS FU LVMU GBH Jeg avlytter viktig informasjon, sa smarte Tor. Læreboka kapittel 19 12. november 2008 Læringsmål kryptering og steganografi Forstå ulike
Kryptering og steganografi EJHJUBM SFQSFTFOUBTKPO FS FU LVMU GBH Jeg avlytter viktig informasjon, sa smarte Tor. Læreboka kapittel 19 12. november 2008 Læringsmål kryptering og steganografi Forstå ulike
Kryptering og steganografi
 Hemmeligholdelse av budskap Kryptering og steganografi EJHJUBM SFRSFTFOUBTKPM FS FU LVMU GBH Vi kan ofte være interessert i å gjøre data uleselig for uvedkommende, eller å gjemme dem slik at uvedkommende
Hemmeligholdelse av budskap Kryptering og steganografi EJHJUBM SFRSFTFOUBTKPM FS FU LVMU GBH Vi kan ofte være interessert i å gjøre data uleselig for uvedkommende, eller å gjemme dem slik at uvedkommende
Kryptering og steganografi
 Læringsmål kryptering og steganografi Kryptering og steganografi Forstå ulike krypteringsprinsipper Kunne sentrale begreper innen kryptering Kjenne til en del sentrale krypteringsteknikker Kjenne til steganografi
Læringsmål kryptering og steganografi Kryptering og steganografi Forstå ulike krypteringsprinsipper Kunne sentrale begreper innen kryptering Kjenne til en del sentrale krypteringsteknikker Kjenne til steganografi
Kryptering og steganografi
 Hemmeligholdelse av budskap Kryptering og steganografi EJHJUBM SFQSFTFOUBTKPO FS FU LVMU GBH Vi er ofte interessert i å gjøre data uleselig for uvedkommende, eller å gjemme dem slik at uvedkommende ikke
Hemmeligholdelse av budskap Kryptering og steganografi EJHJUBM SFQSFTFOUBTKPO FS FU LVMU GBH Vi er ofte interessert i å gjøre data uleselig for uvedkommende, eller å gjemme dem slik at uvedkommende ikke
Datasikkerhet. Datasikkerhet. Trusler mot sikkerheten. Kampen mellom det gode og det onde. Datasikkerhet dreier seg om
 Datasikkerhet Datasikkerhet dreier seg om At dataene er tilgjengelige for rette vedkommende (Tilgjengelighet) Datasikkerhet At dataene er utilgjengelig for uvedkommende (Konfidensialitet) At dataene er
Datasikkerhet Datasikkerhet dreier seg om At dataene er tilgjengelige for rette vedkommende (Tilgjengelighet) Datasikkerhet At dataene er utilgjengelig for uvedkommende (Konfidensialitet) At dataene er
Kryptografi og nettverkssikkerhet
 Kryptografi og nettverkssikkerhet Kapittel : Blokkchiffere og DES (the Data Encryption Standard) Moderne symmetrisk kryptografi Skal se på moderne blokkchiffere, en av de mest brukte kryptoalgoritmene.
Kryptografi og nettverkssikkerhet Kapittel : Blokkchiffere og DES (the Data Encryption Standard) Moderne symmetrisk kryptografi Skal se på moderne blokkchiffere, en av de mest brukte kryptoalgoritmene.
Kryptografi og nettverkssikkerhet
 Kryptografi og nettverkssikkerhet Kapittel : Blokkchiffere og DES (the Data Encryption Standard) Moderne symmetrisk kryptografi Skal se på moderne blokkchiffere, en av de mest brukte kryptoalgoritmene.
Kryptografi og nettverkssikkerhet Kapittel : Blokkchiffere og DES (the Data Encryption Standard) Moderne symmetrisk kryptografi Skal se på moderne blokkchiffere, en av de mest brukte kryptoalgoritmene.
Oppgaver til kapittel 19 - Kryptering og steganografi
 Oppgaver til kapittel 19 - Kryptering og steganografi Oppgave 1 - Cæsars kode (plenum) I symmetrisk kryptering brukes samme nøkkel både for å kryptere og dekryptere. Avhengig av hvordan nøkkelen utformes
Oppgaver til kapittel 19 - Kryptering og steganografi Oppgave 1 - Cæsars kode (plenum) I symmetrisk kryptering brukes samme nøkkel både for å kryptere og dekryptere. Avhengig av hvordan nøkkelen utformes
INF1040 Oppgavesett 14: Kryptering og steganografi
 INF1040 Oppgavesett 14: Kryptering og steganografi (Kapittel 19) Husk: De viktigste oppgavetypene i oppgavesettet er Tenk selv - og Prøv selv - oppgavene. Fasitoppgaver 1. Krypter følgende strenger ved
INF1040 Oppgavesett 14: Kryptering og steganografi (Kapittel 19) Husk: De viktigste oppgavetypene i oppgavesettet er Tenk selv - og Prøv selv - oppgavene. Fasitoppgaver 1. Krypter følgende strenger ved
1. Krypteringsteknikker
 Krypteringsteknikker Olav Skundberg Opphavsrett: Forfatter og Stiftelsen TISIP Lærestoffet er utviklet for faget 1. Krypteringsteknikker 1.1. Fire formål med sikker kommunikasjon Aller først, pålitelig
Krypteringsteknikker Olav Skundberg Opphavsrett: Forfatter og Stiftelsen TISIP Lærestoffet er utviklet for faget 1. Krypteringsteknikker 1.1. Fire formål med sikker kommunikasjon Aller først, pålitelig
Populærvitenskapelig foredrag Kryptering til hverdag og fest
 IN1020 - Introduksjon til datateknologi Populærvitenskapelig foredrag 18.10.2017 Kryptering til hverdag og fest Håkon Kvale Stensland & Andreas Petlund Plan for nettverksdelen av IN1020 18. oktober Populærvitenskapelig
IN1020 - Introduksjon til datateknologi Populærvitenskapelig foredrag 18.10.2017 Kryptering til hverdag og fest Håkon Kvale Stensland & Andreas Petlund Plan for nettverksdelen av IN1020 18. oktober Populærvitenskapelig
Kryptogra og elliptiske kurver
 Kryptogra og elliptiske kurver Eivind Eriksen Høgskolen i Oslo Gjesteforelesning, 7. november 2007 Eivind Eriksen (Høgskolen i Oslo) Kryptogra og elliptiske kurver 1 / 23 Plan: 1 Generelt om kryptogra
Kryptogra og elliptiske kurver Eivind Eriksen Høgskolen i Oslo Gjesteforelesning, 7. november 2007 Eivind Eriksen (Høgskolen i Oslo) Kryptogra og elliptiske kurver 1 / 23 Plan: 1 Generelt om kryptogra
Kryptografi, del 2. Aslak Bakke Buan, Ole Enge
 Aslak Bakke Buan, Ole Enge Kryptografi, del 2 Offentlig-nøkkel kryptografi Anta du vil handle på internett og blir bedt om å oppgi kredittkortnummeret ditt. Du stoler kanskje på at nettstedet du vil handle
Aslak Bakke Buan, Ole Enge Kryptografi, del 2 Offentlig-nøkkel kryptografi Anta du vil handle på internett og blir bedt om å oppgi kredittkortnummeret ditt. Du stoler kanskje på at nettstedet du vil handle
Elementær Kryptografi (Appendix A, Cryptography Basics, Building Secure Software)
 1 Elementær Kryptografi (Appendix A, Cryptography Basics, Building Secure Software) Mich ael Morten sen m ich aelm @ii.u ib.n o 10/ 10/ 05 INF329 Utviklin g av sikre ap p likasjon er 2 Elementær kryptografi
1 Elementær Kryptografi (Appendix A, Cryptography Basics, Building Secure Software) Mich ael Morten sen m ich aelm @ii.u ib.n o 10/ 10/ 05 INF329 Utviklin g av sikre ap p likasjon er 2 Elementær kryptografi
Eksamen i TMA4155 Kryptografi Intro Høst 2003 Løsningsskisse
 2004-10-25 Eksamen i TMA4155 Kryptografi Intro Høst 2003 Løsningsskisse 1 Et blokkchiffer med blokklengde l og nøkkellengde s består av to funksjoner Ẽ (krypteringsfunksjonen) og D (dekrypteringsfunksjonen)
2004-10-25 Eksamen i TMA4155 Kryptografi Intro Høst 2003 Løsningsskisse 1 Et blokkchiffer med blokklengde l og nøkkellengde s består av to funksjoner Ẽ (krypteringsfunksjonen) og D (dekrypteringsfunksjonen)
ECC i akademia vs. industrien
 Conax AS 2007 RSA ECC Utbredelse Kampen mellom ECC og RSA har pågått lenge. I akademia går ECC av som vinner, mens i industrien er det fortsatt RSA som gjelder. RSA RSA ECC Utbredelse I 1977 publiserte
Conax AS 2007 RSA ECC Utbredelse Kampen mellom ECC og RSA har pågått lenge. I akademia går ECC av som vinner, mens i industrien er det fortsatt RSA som gjelder. RSA RSA ECC Utbredelse I 1977 publiserte
VEDLEGG 7 SIKKERHET 1. KRAV TIL SIKRING AV DATAFILER VED OVERFØRING TIL/FRA BANKEN
 VEDLEGG 7 SIKKERHET 1. KRAV TIL SIKRING AV DATAFILER VED OVERFØRING TIL/FRA BANKEN 1.1 Sikkerhetskravene bygger på at det til enhver tid skal være et 1 til 1-forhold mellom det som er registrert i Virksomhetens
VEDLEGG 7 SIKKERHET 1. KRAV TIL SIKRING AV DATAFILER VED OVERFØRING TIL/FRA BANKEN 1.1 Sikkerhetskravene bygger på at det til enhver tid skal være et 1 til 1-forhold mellom det som er registrert i Virksomhetens
Koder. Kristian Ranestad. 8. Mars 2005
 i kryptering 8. Mars 2005 i kryptering i kryptering i kryptering En hemmelig melding Kari sender til Ole den hemmelige meldingen: J MPWF V siden responsen er litt treg prøver hun påny med: U EVOL I Nå
i kryptering 8. Mars 2005 i kryptering i kryptering i kryptering En hemmelig melding Kari sender til Ole den hemmelige meldingen: J MPWF V siden responsen er litt treg prøver hun påny med: U EVOL I Nå
Forelesning 2: Kryptografi
 Universitetet i Oslo IN2120 Informasjonssikkerhet Høst 2018 Workshop-spørsmål med svarforslag Forelesning 2: Kryptografi Spørsmål 1 a. For hvilke informasjonstilstander (lagring, overføring, behandling)
Universitetet i Oslo IN2120 Informasjonssikkerhet Høst 2018 Workshop-spørsmål med svarforslag Forelesning 2: Kryptografi Spørsmål 1 a. For hvilke informasjonstilstander (lagring, overføring, behandling)
OFFENTLIG-NØKKELKRYPTOGRAFI
 OFFENTLIG-NØKKELKRYPTOGRAFI S. O. SMALØ Abstract. I dette notatet, som skal inngå som pensum i etterog viderutdanningskurs i datasikkerhet, vil vi gi en kort innføring i oentlig-nøkkel-kryptogra med illustrasjoner
OFFENTLIG-NØKKELKRYPTOGRAFI S. O. SMALØ Abstract. I dette notatet, som skal inngå som pensum i etterog viderutdanningskurs i datasikkerhet, vil vi gi en kort innføring i oentlig-nøkkel-kryptogra med illustrasjoner
Sondre Granlund Moen
 Kryptering i sjøforsvaret Sondre Granlund Moen 27.06.17 Innhold Hva er kryptering?... 3 Symmetrisk kryptering... 3 Asymmetrisk kryptering... 3 Historie:... 3 Egypterne... 3 Cæsar- siffer (alfabetet)...
Kryptering i sjøforsvaret Sondre Granlund Moen 27.06.17 Innhold Hva er kryptering?... 3 Symmetrisk kryptering... 3 Asymmetrisk kryptering... 3 Historie:... 3 Egypterne... 3 Cæsar- siffer (alfabetet)...
Forelesning 2: Kryptografi
 Universitetet i Oslo IN2120 Informasjonssikkerhet Høst 2019 Workshop-oppgaver med løsningsforslag Forelesning 2: Kryptografi Oppgave 1 a. For hvilke informasjonstilstander (lagring, overføring, behandling)
Universitetet i Oslo IN2120 Informasjonssikkerhet Høst 2019 Workshop-oppgaver med løsningsforslag Forelesning 2: Kryptografi Oppgave 1 a. For hvilke informasjonstilstander (lagring, overføring, behandling)
Kryptering Kongruensregning Kongruensregning i kryptering Litteratur. Hemmelige koder. Kristian Ranestad. 9. Mars 2006
 i kryptering 9. Mars 2006 i kryptering i kryptering i kryptering En hemmelig melding Kari sender til Ole den hemmelige meldingen: J MPWF V siden responsen er litt treg prøver hun påny med: U EVOL I Nå
i kryptering 9. Mars 2006 i kryptering i kryptering i kryptering En hemmelig melding Kari sender til Ole den hemmelige meldingen: J MPWF V siden responsen er litt treg prøver hun påny med: U EVOL I Nå
Standardisering av krypto i offentlig sektor
 Direktoratet for forvaltning og IKT (Difi) Standardisering av krypto i offentlig sektor Vedlegg - Kryptografi og bruksområder Versjon 1.0 2011-07-22 Innhold 1 Teoretisk grunnlag 3 1.1 Kryptografi 3 1.2
Direktoratet for forvaltning og IKT (Difi) Standardisering av krypto i offentlig sektor Vedlegg - Kryptografi og bruksområder Versjon 1.0 2011-07-22 Innhold 1 Teoretisk grunnlag 3 1.1 Kryptografi 3 1.2
Selmersenteret. ACT - Prosjektet. Kryptografer lærer å tenke som kriminelle. Oversikt
 Kryptografer lærer å tenke som kriminelle - Litt om kappløpet i kryptografi - Rapport fra IKT - SOS prosjektet Advanced Cryptographic Techniques (ACT) ACT - Prosjektet Forskningsprosjekt under IKT - SOS
Kryptografer lærer å tenke som kriminelle - Litt om kappløpet i kryptografi - Rapport fra IKT - SOS prosjektet Advanced Cryptographic Techniques (ACT) ACT - Prosjektet Forskningsprosjekt under IKT - SOS
GigaCampus Mobilitetskurs Del 2. Sesjon 4. Torsdag 20.04.2006 [email protected]
 GigaCampus Mobilitetskurs Del 2 Sesjon 4 Torsdag 20.04.2006 [email protected] IEEE 802.1X En relativt gammel standard (godkjent 14. juni 2001) Definerer en standard for portbasert nettverks aksesskontroll
GigaCampus Mobilitetskurs Del 2 Sesjon 4 Torsdag 20.04.2006 [email protected] IEEE 802.1X En relativt gammel standard (godkjent 14. juni 2001) Definerer en standard for portbasert nettverks aksesskontroll
Kvantekryptografi. Hva er kryptografi? Symmetrisk kryptografi
 Kvantekryptografi Lars Lydersen og Johannes Skaar Institutt for elektronikk og telekommunikasjon, NTNU, og Universitetssenteret på Kjeller (UNIK). 26. mai 2014 Kvantekryptografi er kunsten å kommunisere
Kvantekryptografi Lars Lydersen og Johannes Skaar Institutt for elektronikk og telekommunikasjon, NTNU, og Universitetssenteret på Kjeller (UNIK). 26. mai 2014 Kvantekryptografi er kunsten å kommunisere
Eksamen i emne TTM4135 Informasjonssikkerhet Løsningsforslag.
 ksamen i emne TTM4135 Informasjonssikkerhet 2006-05-22. Løsningsforslag. Oppgave 1 1.1. (6 p.) Feltene i AH er som følger: - neste hode (8 bit): Identifiserer type hode som følger umiddelbart etter dette
ksamen i emne TTM4135 Informasjonssikkerhet 2006-05-22. Løsningsforslag. Oppgave 1 1.1. (6 p.) Feltene i AH er som følger: - neste hode (8 bit): Identifiserer type hode som følger umiddelbart etter dette
KODER I KLASSEROMMET
 KODER I KLASSEROMMET Kristian Ranestad 28.02.2001 Dette heftet er utarbeidet til klasseromsprosjektet ved Matematisk institutt, UiO. I dette prosjektet inngår det halvdags kurs for lærere i forskjellige
KODER I KLASSEROMMET Kristian Ranestad 28.02.2001 Dette heftet er utarbeidet til klasseromsprosjektet ved Matematisk institutt, UiO. I dette prosjektet inngår det halvdags kurs for lærere i forskjellige
Elektroniske spor. Innsynsrett, anonymitet. Personvernutfordringer. Innsynsrett. Informasjonsplikt og innsynsrett
 Elektroniske spor Innsynsrett, anonymitet Kirsten Ribu Kilde: Identity Management Systems (IMS): Identification and Comparison Study Independent Centre for Privacy Protection and Studio Notarile Genghini
Elektroniske spor Innsynsrett, anonymitet Kirsten Ribu Kilde: Identity Management Systems (IMS): Identification and Comparison Study Independent Centre for Privacy Protection and Studio Notarile Genghini
1. Cæsarchiffer er en av de enkleste krypteringsteknikkene. Hva går teknikken ut på?
 Prøve i kryptografi Navn: Karakter: Poeng: /30 Lykke til! Hjelpemidler: Viskelær og skrivesaker Teknologi i praksis, fre. 23. september Del 1 Flervalgsoppgaver Sett ring rundt alternativ A, B, C eller
Prøve i kryptografi Navn: Karakter: Poeng: /30 Lykke til! Hjelpemidler: Viskelær og skrivesaker Teknologi i praksis, fre. 23. september Del 1 Flervalgsoppgaver Sett ring rundt alternativ A, B, C eller
Teorem 10 (Z n, + n ) er en endelig abelsk gruppe. 8. november 2005 c Vladimir Oleshchuk 35. Teorem 11 (Z n, ) er en endelig abelsk gruppe.
 Endelige grupper Teorem 10 (Z n, + n ) er en endelig abelsk gruppe. En gruppe er en mengde S sammen med en binær operasjon definert på S, betegnes (S, ), med følgende egenskaper: 1. a, b S, a b S 2. det
Endelige grupper Teorem 10 (Z n, + n ) er en endelig abelsk gruppe. En gruppe er en mengde S sammen med en binær operasjon definert på S, betegnes (S, ), med følgende egenskaper: 1. a, b S, a b S 2. det
Offentlig nøkkel kryptografi og RSA
 Offentlig nøkkel kryptografi og RSA Jens Otto Hatlevold Jan Magne Tjensvold Oktober 2006 Sammendrag Utgangspunktet for prosjektet er offentlig nøkkel kryptografi og hvordan denne teknikken benyttes i praksis.
Offentlig nøkkel kryptografi og RSA Jens Otto Hatlevold Jan Magne Tjensvold Oktober 2006 Sammendrag Utgangspunktet for prosjektet er offentlig nøkkel kryptografi og hvordan denne teknikken benyttes i praksis.
Bevisbar sikkerhet. Kristian Gjøsteen. 2. mars 2005
 Bevisbar sikkerhet Kristian Gjøsteen 2. mars 2005 Oversikt Hvorfor bevisbar sikkerhet? Hva er bevisbar sikkerhet? Eksempel Hvorfor bevisbar sikkerhet? Mål Vi ønsker å lage kryptosystemer hvis sikkerhet
Bevisbar sikkerhet Kristian Gjøsteen 2. mars 2005 Oversikt Hvorfor bevisbar sikkerhet? Hva er bevisbar sikkerhet? Eksempel Hvorfor bevisbar sikkerhet? Mål Vi ønsker å lage kryptosystemer hvis sikkerhet
Vår referanse: A03 - G:17/173 Revisjon: 01 NASJONAL SIKKERHETSMYNDIGHET. Sikker informasjon i tiden etter en kvantedatamaskin KVANTERESISTENT KRYPTO
 Vår referanse: A03 - G:17/173 Revisjon: 01 NASJONAL SIKKERHETSMYNDIGHET Sikker informasjon i tiden etter en kvantedatamaskin KVANTERESISTENT KRYPTO INNHOLD 1. Introduksjon................................................................4
Vår referanse: A03 - G:17/173 Revisjon: 01 NASJONAL SIKKERHETSMYNDIGHET Sikker informasjon i tiden etter en kvantedatamaskin KVANTERESISTENT KRYPTO INNHOLD 1. Introduksjon................................................................4
INF1020 Algoritmer og datastrukturer
 Dagens plan Hashing Hashtabeller Hash-funksjoner Kollisjonshåndtering Åpen hashing (kap. 5.3) Lukket hashing (kap. 5.4) Rehashing (kap. 5.5) Sortering ut fra en hashing-ide (side 66-68) Bøttesortering
Dagens plan Hashing Hashtabeller Hash-funksjoner Kollisjonshåndtering Åpen hashing (kap. 5.3) Lukket hashing (kap. 5.4) Rehashing (kap. 5.5) Sortering ut fra en hashing-ide (side 66-68) Bøttesortering
6105 Windows Server og datanett
 6105 Windows Server og datanett Oppgave a: Installere Active Directory Certificate Services Bruk av kryptering i Windows forutsetter at brukerne får utstedt digitale sertifikater med krypteringsnøkler.
6105 Windows Server og datanett Oppgave a: Installere Active Directory Certificate Services Bruk av kryptering i Windows forutsetter at brukerne får utstedt digitale sertifikater med krypteringsnøkler.
6105 Windows Server og datanett
 6105 Windows Server og datanett Leksjon 12a Kryptering, digitale sertifikater og PKI Fire behov for sikker kommunikasjon Tegnorientert kryptering Symmetrisk og asymmetrisk kryptering Digital signatur Digitale
6105 Windows Server og datanett Leksjon 12a Kryptering, digitale sertifikater og PKI Fire behov for sikker kommunikasjon Tegnorientert kryptering Symmetrisk og asymmetrisk kryptering Digital signatur Digitale
Fire behov for sikker kommunikasjon
 6105 Windows Server og datanett Leksjon 12a Kryptering, digitale sertifikater og PKI Fire behov for sikker kommunikasjon Tegnorientert kryptering Symmetrisk og asymmetrisk kryptering Digital signatur Digitale
6105 Windows Server og datanett Leksjon 12a Kryptering, digitale sertifikater og PKI Fire behov for sikker kommunikasjon Tegnorientert kryptering Symmetrisk og asymmetrisk kryptering Digital signatur Digitale
Forelesning 24 mandag den 10. november
 Forelesning 24 mandag den 10. november 6.3 RSA-algoritmen Merknad 6.3.1. Én av de meste berømte anveldesene av tallteori er i kryptografi. Alle former for sikre elektroniske overføringer er avhengige av
Forelesning 24 mandag den 10. november 6.3 RSA-algoritmen Merknad 6.3.1. Én av de meste berømte anveldesene av tallteori er i kryptografi. Alle former for sikre elektroniske overføringer er avhengige av
Hvem er du? Autentisering og formelle metoder. Olav Andreas Hoemsnes. Universitetet i Oslo Institutt for lingvistiske fag
 Universitetet i Oslo Institutt for lingvistiske fag Hvem er du? Autentisering og formelle metoder Olav Andreas Hoemsnes Hovedfagsoppgave for graden Cand. Philol. i Språk, Logikk og Informasjon. 11. desember
Universitetet i Oslo Institutt for lingvistiske fag Hvem er du? Autentisering og formelle metoder Olav Andreas Hoemsnes Hovedfagsoppgave for graden Cand. Philol. i Språk, Logikk og Informasjon. 11. desember
Symmetrisk En hemmelig nøkkel ( passord ) som brukes både ved kryptering og dekryptering.
 1 Hva? Hva er informasjonssikkerhet? Information security encompasses the study of the concepts, techniques, technical measures, and administrative measures used to protect information assets from deliberate
1 Hva? Hva er informasjonssikkerhet? Information security encompasses the study of the concepts, techniques, technical measures, and administrative measures used to protect information assets from deliberate
KAPITTEL 10. EUKLIDS ALGORITME OG DIOFANTISKE LIGNINGER
 KAPITTEL 10. EUKLIDS ALGORITME OG DIOFANTISKE LIGNINGER Euklids algoritme Euklid s setning 1, divisjonslemmaet, fra Bok 7 Gitt to ulike tall. Det minste trekkes så fra det største så mange ganger dette
KAPITTEL 10. EUKLIDS ALGORITME OG DIOFANTISKE LIGNINGER Euklids algoritme Euklid s setning 1, divisjonslemmaet, fra Bok 7 Gitt to ulike tall. Det minste trekkes så fra det største så mange ganger dette
Autentiseringsløsninger i VPN og nøkkeldistribusjon
 IMT4051 Cryptology Autumn Term 2004 MSc in Information Security Autentiseringsløsninger i VPN og nøkkeldistribusjon Håvard Hasli, [email protected] Mats Erik Smestad, [email protected] Vidar Grønland, [email protected]
IMT4051 Cryptology Autumn Term 2004 MSc in Information Security Autentiseringsløsninger i VPN og nøkkeldistribusjon Håvard Hasli, [email protected] Mats Erik Smestad, [email protected] Vidar Grønland, [email protected]
Oversikt over kryptografi
 Oversikt over kryptografi Richard Williamson 3. desember 2014 Oppgave 1 Person A ønsker å sende meldingen Ha det! til person B, og ønsker å benytte RSAalgoritmen for å kryptere den. Den offentlige nøkkelen
Oversikt over kryptografi Richard Williamson 3. desember 2014 Oppgave 1 Person A ønsker å sende meldingen Ha det! til person B, og ønsker å benytte RSAalgoritmen for å kryptere den. Den offentlige nøkkelen
Steg 1: Regneoperasjoner på en klokke
 Diffie-Hellman nøkkelutveksling Skrevet av: Martin Strand Kurs: Python Tema: Tekstbasert, Kryptografi Fag: Matematikk, Programmering Klassetrinn: 8.-10. klasse, Videregående skole Introduksjon Du har tidligere
Diffie-Hellman nøkkelutveksling Skrevet av: Martin Strand Kurs: Python Tema: Tekstbasert, Kryptografi Fag: Matematikk, Programmering Klassetrinn: 8.-10. klasse, Videregående skole Introduksjon Du har tidligere
Vedlegg 1 HAN Personvern et tillegg til utredningen «AMS + HAN om å gjøre sanntid måledata tilgjengelig for forbruker»
 Vedlegg 1 HAN Personvern et tillegg til utredningen «AMS + HAN om å gjøre sanntid måledata tilgjengelig for forbruker» LILLEAKER 10.OKTOBER 2017 NORSK ELEKTROTEKNISK KOMITE LARS IHLER Oppsummering og konklusjon
Vedlegg 1 HAN Personvern et tillegg til utredningen «AMS + HAN om å gjøre sanntid måledata tilgjengelig for forbruker» LILLEAKER 10.OKTOBER 2017 NORSK ELEKTROTEKNISK KOMITE LARS IHLER Oppsummering og konklusjon
Kryptering med vigenere-metoden
 Kryptonøtt Skrevet av: Arve Seljebu Kurs: Python Tema: Tekstbasert Fag: Programmering Klassetrinn: 8.-10. klasse, Videregående skole Introduksjon Kryptering har lenge vært i bruk i kommunikasjon. Faktisk
Kryptonøtt Skrevet av: Arve Seljebu Kurs: Python Tema: Tekstbasert Fag: Programmering Klassetrinn: 8.-10. klasse, Videregående skole Introduksjon Kryptering har lenge vært i bruk i kommunikasjon. Faktisk
Forelesning 30. Kompleksitetsteori. Dag Normann mai Informasjon. Oppsummering
 Forelesning 30 Kompleksitetsteori Dag Normann - 14. mai 2008 Informasjon Det er lagt ut program for orakeltjenestene i MAT1030 denne våren på semestersiden. Det blir ikke ordinære gruppetimer fra og med
Forelesning 30 Kompleksitetsteori Dag Normann - 14. mai 2008 Informasjon Det er lagt ut program for orakeltjenestene i MAT1030 denne våren på semestersiden. Det blir ikke ordinære gruppetimer fra og med
HØGSKOLEN I SØR-TRØNDELAG
 HØGSKOLEN I SØR-TRØNDELAG AVDELING FOR INFORMATIKK OG E-LÆRING Kandidatnr: Eksamensdato: 9.mai 2005 Varighet: Fagnummer: Fagnavn: 3 timer LV 252 D Internett og sikkerhet Klasse(r): Studiepoeng: 6 Faglærer(e):
HØGSKOLEN I SØR-TRØNDELAG AVDELING FOR INFORMATIKK OG E-LÆRING Kandidatnr: Eksamensdato: 9.mai 2005 Varighet: Fagnummer: Fagnavn: 3 timer LV 252 D Internett og sikkerhet Klasse(r): Studiepoeng: 6 Faglærer(e):
Veiledning i kryptering med Open PGP
 Veiledning i kryptering med Open PGP GNU Privacy Guard for Windows (Gpg4win) er en gratis programvare for kryptering av tekst, filer og eposter ved hjelp av standarden OpenPGP for Windows-operativsystem.
Veiledning i kryptering med Open PGP GNU Privacy Guard for Windows (Gpg4win) er en gratis programvare for kryptering av tekst, filer og eposter ved hjelp av standarden OpenPGP for Windows-operativsystem.
Hashing: Håndtering av kollisjoner
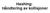 Hashing: Håndtering av kollisjoner Innsetting av dataelement i hashtabell Algoritme: 1. Bruk en hashfunksjon til å beregne hashverdi basert på dataelementets nøkkelverdi 2. Sett inn dataelementet i hashtabellen
Hashing: Håndtering av kollisjoner Innsetting av dataelement i hashtabell Algoritme: 1. Bruk en hashfunksjon til å beregne hashverdi basert på dataelementets nøkkelverdi 2. Sett inn dataelementet i hashtabellen
MAT1030 Diskret matematikk
 MAT1030 Diskret matematikk Forelesning 30: Kompleksitetsteori Dag Normann Matematisk Institutt, Universitetet i Oslo 14. mai 2008 Informasjon Det er lagt ut program for orakeltjenestene i MAT1030 denne
MAT1030 Diskret matematikk Forelesning 30: Kompleksitetsteori Dag Normann Matematisk Institutt, Universitetet i Oslo 14. mai 2008 Informasjon Det er lagt ut program for orakeltjenestene i MAT1030 denne
Tittel: Metode og enhet for randomisering av en hemmelig nøkkel for beskyttelse mot angrep fra supplerende kanaler
 V2199NO00 EP 2 99 26 B1 Tittel: Metode og enhet for randomisering av en hemmelig nøkkel for beskyttelse mot angrep fra supplerende kanaler 1 1 2 3 Beskrivelse [0001] Oppfinnelsen omfatter en metode og
V2199NO00 EP 2 99 26 B1 Tittel: Metode og enhet for randomisering av en hemmelig nøkkel for beskyttelse mot angrep fra supplerende kanaler 1 1 2 3 Beskrivelse [0001] Oppfinnelsen omfatter en metode og
Innføring i blokkjedeteknologi. Slobodan Petrović, NTNU Gjøvik 14/
 Innføring i blokkjedeteknologi Slobodan Petrović, NTNU Gjøvik 14/09-2018 Innhold Innledning Grunnkomponenter av en blokkjede (blockchain) Kryptografiske hash funksjoner (spredefunksjon, avtrykkfunksjon)
Innføring i blokkjedeteknologi Slobodan Petrović, NTNU Gjøvik 14/09-2018 Innhold Innledning Grunnkomponenter av en blokkjede (blockchain) Kryptografiske hash funksjoner (spredefunksjon, avtrykkfunksjon)
Hashing. INF Algoritmer og datastrukturer HASHING. Hashtabeller
 Hashing INF2220 - Algoritmer og datastrukturer HØSTEN 200 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning : Hashing Hashtabeller (kapittel.) Hash-funksjoner (kapittel.2) Kollisjonshåndtering
Hashing INF2220 - Algoritmer og datastrukturer HØSTEN 200 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning : Hashing Hashtabeller (kapittel.) Hash-funksjoner (kapittel.2) Kollisjonshåndtering
Database security. Kapittel 14 Building Secure Software. Inf329, Høst 2005 Isabel Maldonado [email protected]
 Database security Kapittel 14 Building Secure Software Inf329, Høst 2005 Isabel Maldonado [email protected] Kort introduksjon Database er en organisert samling av data. SQL(Structured Query Language)
Database security Kapittel 14 Building Secure Software Inf329, Høst 2005 Isabel Maldonado [email protected] Kort introduksjon Database er en organisert samling av data. SQL(Structured Query Language)
Forelesning 3: Nøkkelhåndtering og PKI
 Universitetet i Oslo IN2120 Informasjonssikkerhet Høst 2018 Workshop-spørsmål med svarforslag Forelesning 3: Nøkkelhåndtering og PKI Spørsmål 1 a. Hvorfor er god håndtering av kryptografiske nøkler essensiell
Universitetet i Oslo IN2120 Informasjonssikkerhet Høst 2018 Workshop-spørsmål med svarforslag Forelesning 3: Nøkkelhåndtering og PKI Spørsmål 1 a. Hvorfor er god håndtering av kryptografiske nøkler essensiell
Løsningsforslag til Eksamensoppgave i TDT4190 Distribuerte systemer
 Institutt for datateknikk og informasjonsvitenskap Løsningsforslag til Eksamensoppgave i TDT4190 Distribuerte systemer Faglig kontakt under eksamen: Jon Olav Hauglid Tlf.: 93 80 58 51 Eksamensdato: Lørdag
Institutt for datateknikk og informasjonsvitenskap Løsningsforslag til Eksamensoppgave i TDT4190 Distribuerte systemer Faglig kontakt under eksamen: Jon Olav Hauglid Tlf.: 93 80 58 51 Eksamensdato: Lørdag
Rapport Semesteroppgave i datasikkerhet Harald Dahle (795955) og Joakim L. Gilje (796196)
 Rapport Semesteroppgave i datasikkerhet Harald Dahle (795955) og Joakim L. Gilje (796196) Sammendrag Oppgaven går ut på å implementere RSA-krypteringen. Deloppgaver for denne krypteringen er å implementere
Rapport Semesteroppgave i datasikkerhet Harald Dahle (795955) og Joakim L. Gilje (796196) Sammendrag Oppgaven går ut på å implementere RSA-krypteringen. Deloppgaver for denne krypteringen er å implementere
INF 1040 Løsningsforslag til kapittel
 INF 040 Løsningsforslag til kapittel 8 Oppgave : Huffmankoding med kjente sannsynligheter Gitt en sekvens av symboler som er tilstrekkelig lang, og som inneholder de 6 symbolene A, B, C, D, E, F. Symbolene
INF 040 Løsningsforslag til kapittel 8 Oppgave : Huffmankoding med kjente sannsynligheter Gitt en sekvens av symboler som er tilstrekkelig lang, og som inneholder de 6 symbolene A, B, C, D, E, F. Symbolene
XBRL hva og hvorfor EDU - EDI. XBRL er. Svein A. Løken. Effektivt og pålitelig Alternativer å sende
 XBRL hva og hvorfor Svein A. Løken EDU - EDI Effektivt og pålitelig Alternativer å sende Regneark (formater?) Tradisjonelle filer (kolonner) Data og tolkningsinformasjon sammen EDI, dvs EDIFACT og lignende
XBRL hva og hvorfor Svein A. Løken EDU - EDI Effektivt og pålitelig Alternativer å sende Regneark (formater?) Tradisjonelle filer (kolonner) Data og tolkningsinformasjon sammen EDI, dvs EDIFACT og lignende
Maps og Hashing. INF Algoritmer og datastrukturer. Map - ADT. Map vs Array
 Maps og Hashing INF0 - Algoritmer og datastrukturer HØSTEN 00 Institutt for informatikk, Universitetet i Oslo INF0, forelesning : Maps og Hashing Map - Abstrakt Data Type (kapittel.) Hash-funksjoner (kapittel..)
Maps og Hashing INF0 - Algoritmer og datastrukturer HØSTEN 00 Institutt for informatikk, Universitetet i Oslo INF0, forelesning : Maps og Hashing Map - Abstrakt Data Type (kapittel.) Hash-funksjoner (kapittel..)
KRYPTOGRAFI, KRIMINALITET OG PERSONVERN
 KRYPTOGRAFI, KRIMINALITET OG PERSONVERN Copyright Bjørn Remseth og Thomas Gramstad Dette dokumentet er tilgjengelig under GNU Free Documentation License. 1. HVA ER KRYPTERING? 2. 'SVAK' KRYPTOGRAFI 3.
KRYPTOGRAFI, KRIMINALITET OG PERSONVERN Copyright Bjørn Remseth og Thomas Gramstad Dette dokumentet er tilgjengelig under GNU Free Documentation License. 1. HVA ER KRYPTERING? 2. 'SVAK' KRYPTOGRAFI 3.
Kryptering med Vigenère-metoden
 Kryptonøtt Skrevet av: Arve Seljebu Oversatt av: Stein Olav Romslo Kurs: Python Tema: Tekstbasert Fag: Programmering Klassetrinn: 8.-10. klasse, Videregående skole Introduksjon Kryptering har vore i bruk
Kryptonøtt Skrevet av: Arve Seljebu Oversatt av: Stein Olav Romslo Kurs: Python Tema: Tekstbasert Fag: Programmering Klassetrinn: 8.-10. klasse, Videregående skole Introduksjon Kryptering har vore i bruk
Legg bort skilpaddene dine, i dag skal vi lære hvordan vi kan sende hemmelige beskjeder!
 Level 1 Hemmelige koder All Code Clubs must be registered. Registered clubs appear on the map at codeclubworld.org - if your club is not on the map then visit jumpto.cc/ccwreg to register your club. Legg
Level 1 Hemmelige koder All Code Clubs must be registered. Registered clubs appear on the map at codeclubworld.org - if your club is not on the map then visit jumpto.cc/ccwreg to register your club. Legg
Løsningsforslag for Eksamensoppgave i TDT4190 Distribuerte systemer
 Institutt for datateknikk og informasjonsvitenskap Løsningsforslag for Eksamensoppgave i TDT4190 Distribuerte systemer Faglig kontakt under eksamen: Jon Olav Hauglid Tlf.: 93 80 58 51 Eksamensdato: Onsdag
Institutt for datateknikk og informasjonsvitenskap Løsningsforslag for Eksamensoppgave i TDT4190 Distribuerte systemer Faglig kontakt under eksamen: Jon Olav Hauglid Tlf.: 93 80 58 51 Eksamensdato: Onsdag
Vannmerking. Tradisjonell Vannmerking
 Vannmerking Et foredrag av Erlend Nilsen og Joakim Blomskøld Tradisjonell Vannmerking Teknologi fra så tidlig som på 1200-tallet. Kjemisk behandling av papir, bruk av usynlig blekk, liten skrift og lignende.
Vannmerking Et foredrag av Erlend Nilsen og Joakim Blomskøld Tradisjonell Vannmerking Teknologi fra så tidlig som på 1200-tallet. Kjemisk behandling av papir, bruk av usynlig blekk, liten skrift og lignende.
Forelesning 3: Nøkkelhåndtering og PKI
 Universitetet i Oslo IN2120 Informasjonssikkerhet Høst 2019 Workshop-oppgaver med løsningsforslag Forelesning 3: Nøkkelhåndtering og PKI Oppgave 1 a. Hvorfor er god håndtering av kryptografiske nøkler
Universitetet i Oslo IN2120 Informasjonssikkerhet Høst 2019 Workshop-oppgaver med løsningsforslag Forelesning 3: Nøkkelhåndtering og PKI Oppgave 1 a. Hvorfor er god håndtering av kryptografiske nøkler
Maps og Hashing. INF Algoritmer og datastrukturer. Map - ADT. Map vs Array
 Maps og Hashing INF0 - Algoritmer og datastrukturer HØSTEN 00 Institutt for informatikk, Universitetet i Oslo INF0, forelesning : Maps og Hashing Map - Abstrakt Data Type Hash-funksjoner hashcode Kollisjonshåndtering
Maps og Hashing INF0 - Algoritmer og datastrukturer HØSTEN 00 Institutt for informatikk, Universitetet i Oslo INF0, forelesning : Maps og Hashing Map - Abstrakt Data Type Hash-funksjoner hashcode Kollisjonshåndtering
Tall. Binære regnestykker. Binære tall positive, negative heltall, flytende tall
 Tall To måter å representere tall Som binær tekst Eksempel: '' i ISO 889-x og Unicode UTF-8 er U+ U+, altså Brukes eksempelvis ved innlesing og utskrift, i XML-dokumenter og i programmeringsspråket COBOL
Tall To måter å representere tall Som binær tekst Eksempel: '' i ISO 889-x og Unicode UTF-8 er U+ U+, altså Brukes eksempelvis ved innlesing og utskrift, i XML-dokumenter og i programmeringsspråket COBOL
Prosesslogg Hvordan klassen kom frem til problemstillingen November 2005 Desember 2005 Hvordan brukes kryptering.
 Samfundets Skole Kristiansand april 2006 Prosesslogg Hvordan klassen kom frem til problemstillingen November 2005 På høsten brukte vi mye tid for å komme frem til en god problemformulering. Vi startet
Samfundets Skole Kristiansand april 2006 Prosesslogg Hvordan klassen kom frem til problemstillingen November 2005 På høsten brukte vi mye tid for å komme frem til en god problemformulering. Vi startet
EN PRAKTISK INNFØRING I KRYPTERT E-POST FRA UDI
 EN PRAKTISK INNFØRING I KRYPTERT E-POST FRA UDI Asylavdelingen (ASA) i UDI forbereder seg til høsten 2010 der avdelingen skal begynne med fullelektronisk saksbehandling (esak). UDI har innført en løsning
EN PRAKTISK INNFØRING I KRYPTERT E-POST FRA UDI Asylavdelingen (ASA) i UDI forbereder seg til høsten 2010 der avdelingen skal begynne med fullelektronisk saksbehandling (esak). UDI har innført en løsning
Som en del av denne prosessen, når verten har startet og nøkkelfilene ikke er å finne, lages et nytt sett automatisk.
 De beste sikkerhetsrutiner for Symantec pcanywhere Dette dokumentet inneholder informasjon om forbedrede sikkerhetsendringer i pcanywhere 12.5 SP4 og pcanywhere Solution 12.6.7, hvordan viktige deler av
De beste sikkerhetsrutiner for Symantec pcanywhere Dette dokumentet inneholder informasjon om forbedrede sikkerhetsendringer i pcanywhere 12.5 SP4 og pcanywhere Solution 12.6.7, hvordan viktige deler av
Standardisering av krypto i offentlig sektor. Standardiseringsrådsmøte (beslutningssak)
 Standardisering av krypto i offentlig sektor Standardiseringsrådsmøte 14.09.11 (beslutningssak) Bakgrunn Det er lite hensiktsmessig at hvert prosjekt som skal ta i bruk krypteringsteknologi, selv skal
Standardisering av krypto i offentlig sektor Standardiseringsrådsmøte 14.09.11 (beslutningssak) Bakgrunn Det er lite hensiktsmessig at hvert prosjekt som skal ta i bruk krypteringsteknologi, selv skal
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 3: Maps og Hashing Bjarne Holen (Ifi, UiO) INF2220 H2009, forelesning 3 1 / 25 Maps
INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 3: Maps og Hashing Bjarne Holen (Ifi, UiO) INF2220 H2009, forelesning 3 1 / 25 Maps
MAT1030 Forelesning 13
 MAT1030 Forelesning 13 Funksjoner Dag Normann - 2. mars 2010 (Sist oppdatert: 2010-03-02 14:15) Kapittel 6: Funksjoner Forrige uke Forrige forelesning snakket vi om relasjoner. Vi snakket om ekvivalensrelasjoner
MAT1030 Forelesning 13 Funksjoner Dag Normann - 2. mars 2010 (Sist oppdatert: 2010-03-02 14:15) Kapittel 6: Funksjoner Forrige uke Forrige forelesning snakket vi om relasjoner. Vi snakket om ekvivalensrelasjoner
Backtracking som løsningsmetode
 Backtracking Backtracking som løsningsmetode Backtracking brukes til å løse problemer der løsningene kan beskrives som en sekvens med steg eller valg Kan enten finne én løsning eller alle løsninger Bygger
Backtracking Backtracking som løsningsmetode Backtracking brukes til å løse problemer der løsningene kan beskrives som en sekvens med steg eller valg Kan enten finne én løsning eller alle løsninger Bygger
Kapittel 6: Funksjoner
 MAT1030 Diskret Matematikk Forelesning 13: Funksjoner Dag Normann Matematisk Institutt, Universitetet i Oslo Kapittel 6: Funksjoner 2. mars 2010 (Sist oppdatert: 2010-03-02 14:14) MAT1030 Diskret Matematikk
MAT1030 Diskret Matematikk Forelesning 13: Funksjoner Dag Normann Matematisk Institutt, Universitetet i Oslo Kapittel 6: Funksjoner 2. mars 2010 (Sist oppdatert: 2010-03-02 14:14) MAT1030 Diskret Matematikk
PROSJEKT I KRYPTOLOGI IMT4051. Av: Ole Kasper Olsen Fredrik Skarderud Torkjel Søndrol Ole Martin Dahl
 PROSJEKT I KRYPTOLOGI IMT4051 Av: Ole Kasper Olsen Fredrik Skarderud Torkjel Søndrol Ole Martin Dahl Forord Vi har i denne oppgaven sett på kryptografiske hashfunksjoner. Vi starter rapporten med å se
PROSJEKT I KRYPTOLOGI IMT4051 Av: Ole Kasper Olsen Fredrik Skarderud Torkjel Søndrol Ole Martin Dahl Forord Vi har i denne oppgaven sett på kryptografiske hashfunksjoner. Vi starter rapporten med å se
6 Kryptografi Totienten Eulers teorem Et eksempel på et bevis hvor Eulers teorem benyttes RSA-algoritmen...
 Innhold 6 Kryptografi 3 6.1 Totienten.................................... 3 6.2 Eulers teorem.................................. 8 6.3 Et eksempel på et bevis hvor Eulers teorem benyttes............ 19
Innhold 6 Kryptografi 3 6.1 Totienten.................................... 3 6.2 Eulers teorem.................................. 8 6.3 Et eksempel på et bevis hvor Eulers teorem benyttes............ 19
... HASHING. Hashing. Hashtabeller. hash(x)
 HASHING Hashing Hashtabeller (kapittel.) Hash-funksjoner (kapittel.) Kollisjonshåndtering Åpen hashing (kapittel.) Lukket hashing (kapittel.) Anta at en bilforhandler har ulike modeller han ønsker å lagre
HASHING Hashing Hashtabeller (kapittel.) Hash-funksjoner (kapittel.) Kollisjonshåndtering Åpen hashing (kapittel.) Lukket hashing (kapittel.) Anta at en bilforhandler har ulike modeller han ønsker å lagre
Nasjonal sikkerhetsmyndighet
 Nasjonal sikkerhetsmyndighet IT-veiledning for ugradert nr 14 (U-14) Oppdatert: 2016-09-30 Transport Layer Security (TLS) Sikring av kommunikasjon med TLS Beskrivelse av grunnleggende tiltak for sikring
Nasjonal sikkerhetsmyndighet IT-veiledning for ugradert nr 14 (U-14) Oppdatert: 2016-09-30 Transport Layer Security (TLS) Sikring av kommunikasjon med TLS Beskrivelse av grunnleggende tiltak for sikring
Hashtabeller. Lars Vidar Magnusson Kapittel 11 Direkte adressering Hashtabeller Chaining Åpen-adressering
 Hashtabeller Lars Vidar Magnusson 12.2.2014 Kapittel 11 Direkte adressering Hashtabeller Chaining Åpen-adressering Dictionaries Mange applikasjoner trenger dynamiske sett som bare har dictionary oparsjonene
Hashtabeller Lars Vidar Magnusson 12.2.2014 Kapittel 11 Direkte adressering Hashtabeller Chaining Åpen-adressering Dictionaries Mange applikasjoner trenger dynamiske sett som bare har dictionary oparsjonene
Smartkort og Windows 2000
 Smartkort og Windows 2000 Hovedoppgave ved sivilingeniørutdanningen i informasjons- og kommunikasjonsteknologi, Høgskolen i Agder Terje Landa Våren 2000 Sammendrag Sikkerhet er et viktig tema innenfor
Smartkort og Windows 2000 Hovedoppgave ved sivilingeniørutdanningen i informasjons- og kommunikasjonsteknologi, Høgskolen i Agder Terje Landa Våren 2000 Sammendrag Sikkerhet er et viktig tema innenfor
Representasjon av tall på datamaskin Kort innføring for MAT-INF1100L
 Representasjon av tall på datamaskin Kort innføring for MAT-INF00L Knut Mørken 3. desember 204 Det er noen få prinsipper fra den første delen av MAT-INF00 om tall som studentene i MAT-INF00L bør kjenne
Representasjon av tall på datamaskin Kort innføring for MAT-INF00L Knut Mørken 3. desember 204 Det er noen få prinsipper fra den første delen av MAT-INF00 om tall som studentene i MAT-INF00L bør kjenne
