A new study has found that cockroaches are morons in the morning and geniuses in the evening in terms of their learning capacity.
|
|
|
- Halvard Lindberg
- 7 år siden
- Visninger:
Transkript
1 A new study has found that cockroaches are morons in the morning and geniuses in the evening in terms of their learning capacity. Previous studies suggest that the learning capacity of both people and rats are also affected by their internal biological clocks. But the effect is far more dramatic in cockroaches and it is the first time it has been found in insects. And, no, the researchers didn t try giving their cockroaches a sip of coffee to see if it revived them! slashdot.org, 28. sep 07 1
2 Choices, choices Tiende forelesning Dynamisk programmering: En serie med valg der valgmulighetene er avhengige av hva vi har valgt før. DAG- SP er erkeeksemplet (og den underliggende modellen for all DP). 2
3 Hva er et snitt? Eksempler på tavla: En sti s-x-y-z-t. To stier (noen kapasiteter 1, noen 2): s- x-y-t og s-u-v-t. Flere mulige snitt. Hva blir det minimale? Hva er kapasiteten til et snitt? Hvor mange snitt kan vi ha? Hva er et minimalt snitt? Hvorfor er min. snittkapasitet lik maks flyt? Eksempel på prosjektutvelgelse: Fire prosjekter: x, y, u og v. x er avhengig av y og u er avhengig av v, så vi har kanter xy og uv. x har verdi 4 og y har kostnad 2, mens u har verdi 10 og v har kostnad Diskuter endringer som f.eks. å redusere kostnaden til v fra 11 til 9, eller å legge til kantene xv eller uy.
4 Først, den abstrakte beskrivelsen av Floyd-Warshall (og Edmonds-Karp) Level 1 4
5 Finnes det en sti med ledig kapasitet fra s til t? Hver kant: Enten og f < c eller og f > 0 Øk flyt langs denne stien Bruk f.eks. BFS til å finne stien (E K) Ford-Fulkerson: 5 Generell metode. Ikke nødvendigvis polynomisk. Velger vi BFS får vi Edmonds-Karp, som har kjøretid på O(VE^2). (Det går an å gjøre det bedre.)
6 Det er to mulige tolkninger av dette: Vi «opphever» 5 av de 7 som går mot venstre ved å sende 5 til mot høyre. De 7 mot venstre tilsvarer 7 mot høyre, som kan økes opp mot 0. 4/9 7/8 Vi kan øke med 5 fra venstre til høyre Hva foregår «egentlig»? Ved å øke flyten inn i midt-noden fra venstre og å redusere flyten inn i noden fra høyre med samme mengde har noden samme flyt-sum, så vi ødelegger ingenting. 6
7 Eksempel Bruker ikke BFS her w 0/2 x 0/3 0/3 s 0/2 0/1 0/3 0/1 0/2 0/3 0/2 t y 0/3 z 7
8 Eksempel w 0/2 x 0/3 0/3 s 0/2 0/1 0/3 0/1 0/2 0/3 0/2 t y 0/3 z Alle kanter i stien går fremover, og minimums-kapasiteten er 2. 8
9 Eksempel Her er flyten økt med den maksimale ledige kapasiteten. w 2/2 x 0/3 0/3 s 2/2 0/1 2/3 0/1 2/2 0/3 2/2 t y 0/3 z 9
10 Eksempel Ny sti denne gangen med noen baklengskanter. I disse ser vi ikke etter ledig kapasitet, men flyt som kan kanselleres. w 2/2 x 0/3 0/3 s 2/2 0/1 2/3 0/1 2/2 0/3 2/2 t y 0/3 z Blant forover-kantene er minste ledige kapasitet 3. Blant bakover-kantene er minste flyt 2. Minimum blir altså 2. 10
11 Eksempel w 2/2 x 2/3 2/3 s 2/2 0/1 0/3 0/1 0/2 0/3 2/2 t y 2/3 z Igjen er flyten langs stien økt med det maksimale mulige (2). Flyt i fremoverkanter økes flyt i bakover-kanter reduseres. Totalt økes flyten fra s til t uten at vi bryter noen regler. 11
12 Eksempel w 2/2 x 2/3 2/3 s 2/2 0/1 0/3 0/1 0/2 0/3 2/2 t y 2/3 z Ikke mulig å finne noen flere flytforøkende stier, så vi er ferdige. 12
13 Eksempel w 2/2 x 2/3 2/3 s 2/2 0/1 0/3 0/1 0/2 0/3 2/2 t y 2/3 z Her er et minimalt snitt, med kapasitet lik maksflyten (4). Det er ikke mulig å presse mer flyt igjennom dette snittet. 13
14 Bokas implementasjon (veldig utbredt): Residualnett verk. Level 2a 14
15 I stedet for å tenke forover og bakover hver for seg så setter vi bare negativt fortegn på bakoverflyt. I boka opererer de med et eksplisitt «residualnett verk». Hvis det går flyt f går det flyt f Vi har bare kanter der vi kan få mer flyt Enten ved å øke f til c for eller ved å øke f til 0 for 15
16 En annen konkret implementasjon (den originale, mer eller mindre): «Merkelappmetoden» Level 2b 16
17 Under én iterasjon (BFS) I hver node vil vi huske hvor mye flyt vi har klart å transportere så langt og hvor den kom fra (og evt. om det var en «oppheving» av flyt som gikk ut). Y Flyt inn eller ut? +/X/8 Hvor mye? Hvor fra? 17
18 Kjør BFS Langs kanter der f < c Mot kanter der f > 0 Forgjengertabell bruker vi jo allerede i BFS (π). I tillegg trenger vi altså bare lagre hvor mye flyt vi får ført til noden (inkludert fortegn/retning). For hver node, lagre Hvor kom vi fra? Går flyten inn eller ut? Hvor mye flyt kan vi få hit? Hvis vi kom til slutten Oppdater flyten og begynn på nytt 18
19 Maks flyt I graf m kapasiteter Forøkende stier Bruk BFS Heltallsvekter: Gir oss heltallsflyt. (Selv om heltallsprogrammering generelt er NP-komplett.) Hvis vi kan bruke vilkårlig søk (og ikke BFS) så kan vi få eksponentiell kjøretid. Den generelle metoden (uten at vi bestemmer traverserings-metoden) heter Ford-Fulkerson. Edmonds Karp 19 O(VE 2 ) Hver sti: O(E). Fyller minst én av E kanter. Hver kant kan fylles flere ganger (ulike retninger), men avstanden til starten langs stien må øke. Kan maks øke V ganger.
20 Og så var det legeproblemet vårt, da. Sett på passende kapasiteter. Fridager Vi får likevel ikke begrenset oss til én dag per lege per ferieperiode Leger Kilde Sluk 20
21 Fridager Gadgets Leger Kilde Sluk Vi lager os ekstra-noder for å begrense flyten fra hver lege til hver ferie-periode! 21 Denne typen konstruksjoner er med på å gjøre maks-flyt til et svært allsidig verktøy.
22 Maks-flyt: Akkurat passe komplisert 22
23 Bellman-Ford BFS/DFS Binære søketrær Binærsøk Bubblesort Bucket sort Counting sort Dijkstra DAGshortest-path Edmonds- Karp Floyd- Warshall Hashing Heapsort Huffmankoding Insertion sort Kruskal Merge sort Prim Quicksort Radix sort Randomized Select Select Selection sort Sterke komponenter Topologisk sortering 23
24 Bellman-Ford BFS/DFS Binære søketrær Binærsøk Bubblesort Bucket sort Counting sort Dijkstra DAGshortest-path Edmonds- Karp Floyd- Warshall Hashing Heapsort Huffmankoding Insertion sort Kruskal Merge sort Prim Quicksort Radix sort Randomized Select Select Selection sort Sterke komponenter Topologisk sortering 24
25 D&C Bellman-Ford BFS/DFS Binære søketrær LP Binærsøk Bubblesort Bucket sort Counting sort Dijkstra DAGshortest-path Edmonds- Karp Floyd- Warshall Hashing Gr. Heapsort Huffmankoding Insertion sort NPC Flyt+ Kruskal Merge sort Prim Quicksort Radix sort En salig blanding av designmetoder, problemtyper med tilhørende algoritmer, kompleksitetsklasser Randomized for problemer og matematisk teori Select(Mye av dette er også knyttet opp mot de seks grunnverktøyene; D&C og dekomponering, f.eks.) Select Θ etc. DP er en designmetode. Sterke Splitt-og-hersk Topologisk Selection eller Divide sort & komponenter Conquer/D&C (eksemplifisert sortering ved f.eks. Mergesort og Quicksort) og grådighet ( Gr., eksemplifisert ved Huffman-koding) er to andre. 25 DP
26 D&C Bellman-Ford BFS/DFS Binære søketrær LP Binærsøk Bubblesort Bucket sort Counting sort Dijkstra DAGshortest-path Edmonds- Karp Floyd- Warshall Hashing Gr. Heapsort Huffmankoding Insertion sort NPC Flyt+ Kruskal Merge sort Prim Quicksort Radix sort Randomized Select Select Θ etc. Selection sort Sterke komponenter Topologisk sortering DP 26
27 D&C Bellman-Ford BFS/DFS Binære søketrær LP Binærsøk Bubblesort Bucket sort Counting sort Dijkstra DAGshortest-path Edmonds- Karp Floyd- Warshall Hashing Gr. Heapsort Huffmankoding Insertion sort NPC Flyt+ Kruskal Merge sort Prim Quicksort Radix sort Randomized Select Select Θ etc. Selection sort Sterke komponenter Topologisk sortering DP 27
28 Hvordan finner vi den lengste stigende subsekvensen?
29 w(q a, q b, s c, s d ) = is a scaling factor, used to account for es, and t(s i ) is the timestamp for the given note n a query q and a tune s can then be defined as d(q, s) = min i {d(q, s, i)}. ( a given alignment i, d(q, s, i) is minimized by choosing α as m j=2 α = (t(s i j ) t(s ))(t(q ij 1 j) t(q j 1 )) m i=2 (t(s. (4) i j ) t(s ij 1 ))2 Since the optimal value for α is given as a function of the alignment i, the optimization task in (3) becomes a matter of finding an optimal alignment. Assuming, for now, that the value of α is known, the optimization may be expressed recursively as follows: d(q 1:a, s 1:b ) = min Det finnes 2 n -1 mulige subsekvenser. Vi ønsker å finne den lengste stigende i polynomisk tid. Vi kan også f.eks. sette en maks-grense på «hoppene». (Dette minner bl.a. om en algoritme for musikksøk ) c {d(q 1:a 1, s 1:c ) + w(q a 1, q a, s c, s b ) 2 } 29 and s 1:b are prefixes of q and s, of length a and b, respectively. may be solved iteratively, by dynamic programming (Be simply consists of constructing a two-dimensi the partial solutions, and iterating over 1999) for examples of the same htein distance (edit dis ication of th
30 Dette er en enkel løsning men hvordan virker den egentlig? Vi kommer tilbake til saken (Det finnes også en mer effektiv løsning, med kjøretid O(n*log(n)) for i = 1 n for j = i 1 if A[i] > A[j] L[i] max(l[i], L[j]+1) 30
31 reduksjon! rekursjon dekomp. induksjon gjenbruk travers. Dynamisk programmering 31
32 reduksjon! rekursjon dekomp. induksjon gjenbruk travers. Dynamisk programmering 32
33 Ha DAG-SP i bakhodet! Relax inn fra forg jengere, i topologisk sortert rekkefølge. «Oppskrift» på dynamisk programmering. 1. Karakteriser strukturen til en optimal løsning. 2. Definér verdien til en optimal løsning rekursivt. 3. Beregn den optimale verdien «bottom-up», og ta vare på del-løsninger. struktur definisjon 4. Beregn løsningen som ga den optimale verdien. Memoisering (merk: bare én «r»): Kjør rekursjonen direkte, men lagre delløsninger (og bruk dem i stedet for rekursjon, om mulig). beregning løsning 33
34 Kjent? 34
35 Erke- Eksempel «DAG-Shortest-Path» 35
36 Erke- e s k E l e p m Dijkstra blir ganske likt, bare at vi har litt grådighet i tillegg (og at den topologiske ordningen må jukses til litt). forgjengere minimum topsort, relax tilbakesporing Tilbakesporingen g jøres ved at vi setter en forg jenger i en forg jentertabell hver gang vi endrer minimum i dollar-fasen. Standardløsning. «DAG-Shortest-Path» 36
37 Eksempel Floyd-Warshall 37
38 Ek s l e p em innom hvem? min(med, uten) innom 1, 2, tilbakesporing Floyd-Warshall 38
39 Noen nye Går ikke igjennom samlebåndseksemplet her. Viktig, på mange måter, siden det er «typisk DP» men det er egentlig bare DAG-SP, som vi jo har snakket om en del fra før. 39
40 Eksempel 0/1 Ryggsekkproblemet 40
41 $60 $100 $120 41
42 30 $ $ $ $ $60 10 $60 42
43 Delproblemparametre: Hvor stor plass har vi (igjen)? Hvor mange objekter har vi (igjen)? På sett og vis litt som Floyd-Warshall: Hvilke objekter får vi bruke? (Men også: Hvor mye plass får vi bruke?) 43
44 0 c[i, w] = c[i 1, w] max{vi + c[i 1, w wi ], c[i 1, w]} 44 if i = 0 or w = 0 if wi > w if i > 0 and w wi
45 DP-01K(v, w, n, W) for k 0 W c[0, k] 0 for i 1 n c[i, 0] 0 for k 1 W if w[i] k if v[i] + c[i 1, k w[i]] > c[i 1, k] c[i, k] v[i] + c[i 1, k w[i]] else c[i, k] c[i 1, k] else c[i, k] c[i 1, k] 45
46 Som før: Ta vare på valg i hver rute Nøst deg bakover fra siste rute 46
47 Pseudopolynomisk kjøretid: Polynomisk avhengig av verdien til et heltall som er en del av instansen altså egentlig eksponentiell som funksjon av problemstørrelsen (målt i lagringsplass). Dette er verdt å ha med seg når vi ser på NP-kompletthet. Problemet er NPkomplett, og ingen kjenner noen polynomiske løsninger på slike problemer så da hadde det jo vært rart om kjøretiden var polynomisk :-) Kjøretid: O(nW) Lett å gå seg bort i disse tingene. Pseudopolynomiske algoritmer kan faktisk være ganske effektive i praksis, f.eks. for rimelige verdier av W i dette tilfellet. Ikke polynomisk pseudopolynomisk! Hvis m = lg W er problemstørrelsen O(n + m) og kjøretiden O(n2 m ) 47
48 Ek s l e p em Optimale søketrær 48
49 Optimaliseringskriteriet blir den vektede (med vekt p_i) summen av dybdene (+1) til nøklene k_i. K = [k 1,, kn], k1 < k2 < < kn Vil bygge et binært søketre over K Sannsynlighet p i for søk etter ki Vil minimere forventet søkekostnad Antar at alle søk lykkes. 49
50 ; E Forventet søketid: ; 9 ; G ; F ; H 6 0,7#8 < (; 6 ) 0,7#8 < (; 6 ) EH E I I F E 19 G 9 1E H E 1J 919H 50
51 ;! ; " ; # Forventet søketid: (Optimalt.) ; $ Merk: Ikke sikkert vi vil ha minimal høyde. Heller ikke sikkert den høyeste sannsynligheten ender i rota. ; % 8 &'()* < (; 8 ) &'()* < (; 8 ) 2 8 " " +!#!,, % % +"# $! +$ # " +% "+", 51 Brute force: Bygg alle mulige binære søketrær (BST), og sett inn nøklene. Beregn forventet søkekostnad. Velg beste. Men det er Ω(4 n /n 3/2 ) BST-er med n noder.
52 Hvis T inneholder nøklene ki kj så må T være optimalt for disse nøklene vises lett ved selvmotsigelse.!!" 52
53 ! " Hvis vi antar at rota inneholder kr (som en hypotese) så vil alle k<kr være til venstre (og tilsv. for høyre). Begge deltrær må (som nevnt i forrige foil) være optimale for de gitte nøklene. Hvis vi undersøker alle k = ki kj som mulige røtter, og har (og løser problemet rekursivt) så er vi garantert å finne den optimale løsningen for ki kj!! #! "!"! "#"! $ 53
54 %&'()*& +,(&-.,* /012(&*!" ' 9*,:*17786:!"# w(8, ; ) = w(8, * $) + 2* + w(* + $, ; )% Hvis j = i 1 er treet tomt. &'()(*+)(, &-8, ;. = &-8, * $. + &-* + $, ;. + w(8, ; )% e[i, j] er forventet kostnad for optimalt BST over ki kj. &'/0 (1"2#/+3 200"4(0 #'2# 5( 26)( '/:' 9(8 /0 <* % ;( 7+3<#% &)8 266 :237/72#(0, 237 =/:9 #'( >(0# /* ; = 8 $, &-8, ;. = 4/3 {&-8, * $. + &-* + $, ;. + w(8, ; )} /* 8 ;. 8 * ; A+"67 5)/#( 2 )(:")0/B( 26C+)/#'4% % %!"#$%&'() *( "$&'#*+,"+%&'"( D0 E"0"26,F 5(<66 0#+)( #'( B26"(0 /3 2 #2>6(? Vi legger til w(i, j) (dvs. alle p-ene legges til én gang) fordi høyden til alle noder i deltrærne øker med én. w(i, j) er summen av pi pj &- "$.. #$ 6 + 6%. " #$ :23 0#+)( :23 0#+)( &-6 + $, 6. 54
55 [trekk pusten dypt] 55
56 !"#$%&'()*#(!, ", #)!"# $ + $" # + + %" %,$, $ +-. w,$, $ +-.!"# & + $" # %"!"# $ + $" # & + + %" ' $ + & + %,$, '- w,$, '- w,$, ' +- +! '!"# ( $ $" ' Kubisk kjøretid. /012/3 % 435 (**) l (liten L) i hovedløkken er størrelsen på deltrærne vi beregner. i er start og j er slutt for nøklene i det aktuelle deltreet. %" ) %,$, ( +- + %,( + +, '- + w,$, '- &! ) < %,$, '- $'() %,$, '- ) (**),$, '- ( 56
57 !"#$%&'!%(")%*+,-(.$%(!""#)!!""#/0, $ %8! 749 6:; 3<<68!"#$%&'!%(")%($'.%&==(0,! 0,!, 7>;?68,!""#)!"#$%&'!%(")%($'.%&==(! + 0, $,!, 734@:68,!""#)!"#$%&'!%(")%($'.%&==(&, ',!, (&!,!""#)!" & ' #$%& #!""#/&, ' %8 # 7498 (&! 7A:4>B <? %8!!"#$%&'!%(")%($'.%&==(&, # 0, #, 7>;?68,!""#)!"#$%&'!%(")%($'.%&==(# + 0, ', #, 734@:68,!""#) 57
58 Eksempel Longest Common Subsequence. Finner en felles subsekvens hos to sekvenser. Lengden kan brukes som et likhetsmål. Denne type algoritmer er vanlig i bioinformatikk og informasjonsg jenfinning. LCS 58
59 59 Dette er jo mer greatest common subset, også kjent som snitt/ intersection som det jo er trivielt å regne ut i lineær tid vha. f.eks. hashing :-)
60 60
61 Noen eksempler. En Brute Forceløsning vil ha en kjøretid på (n2^m) ser du hvorfor? s p r i n g t i m e h o r s e b a c k p i o n e e r s n o w f l a k e m a e l s t r o m h e r o i c a l l y b e c a l m Merk: John Stewarteksemplet ser bare på snittet av bokstavmengdene et mye enklere problem (som lett kan løses i lineær tid vha. f.eks. hashing). 61 s c h o l a r l y
62 X i = [x1,, xi], Yi = [y1,, yi] X = X m, Y = Yn Z = [z 1,, zk] er en LCS av X og Y 62
63 Hvis de ikke deler siste element kan LCS-en utvides en selvmotsigelse. Hvis x m = yn: z k = xm = yn og Z k 1 er en LCS av Xm 1 og Yn 1 Det samme gjelder her hvis Xm-1 og Yn-1 har en lenger felles subsekvens så kan vi finne en lenger total felles subsekvens enn Z igjen en selvmotsigelse. 63
64 Hvis xm yn og zk xm: I begge tilfeller må Z være en felles subsekvens. Hvis det eksisterte en som var lenger vil den også være lenger totalt en selvmotsigelse. Z er en LCS av X m 1 og Y Hvis xm yn og zk yn: Z er en LCS av X og Y n 1 64
65 !" #$%%&'()* '+," -'.&+ 0.&(&1+(& # +1 '7+ 8&9:&4*&8 *+4'3) ;(&!< 34 56# +1 ;(&!<&8 8&9:&4*&8" c[i,j] er lengden på en LCS av Xi og Yj.!"#$%&'(" )*%+$,-.'*/ =&!4& #>6, ;? +1 56# +1 <6 34B = ; " C& 734' #>5, 4?" )1 6 = D +( ; = D, D )1 6, ; > D 34B >6 = 3 ;, #>6, ;? = #>6 E, ; E? + E %3<(#>6 E, ;?, #>6, ; E?) )1 6, ; > D 34B >6 " = 3 ;. FA3)42 7& *+:@B 7()'& 3 (&*:(8)G& 3@A+()'.% H38&B +4 '.)8 1+(%:@3')+4" 0($ 7)'. H+I+2 H3'" J2!!2! 65 Enten er xi og yj like eller ikke. Hvis de er det skal xi=yj=zk være med. Ellers vil Z være en LCS enten av Xi-1 og Y eller av X og Yj-1. Vi vet ikke hvilken, men prøver begge og velger den største.!2!
66 Rekursjon? Enten vi gjør det rekursivt eller iterativt: Legg svarene i en tabell. J2!!2!!2!,2!!2,!2, J2E E2!,2,,2,!2E,2,!2E!2E J2D D2! E2, E2,,2E E2,,2E,2E!2D 66
67 !"#$!%&'()(!, ", #, $)!"# % * $" # %" &+%,,-,!"# ', $" $ %" &+,, '-,!"# % * $" # %"!"# ' * $" $ %" &! ( % = ) ' $'() &+%, '- &+% *, ' *- + * *+%, '-. / (*+( &! &+% *, '- &+%, ' *- $'() &+%, '- &+% *, '- *+%, '-. / (*+( &+%, '- &+%, ' *- *+%, '-. / #($,#) & 012 * I b-tabellen lagrer vi en referanse til hvor vi «kom fra». 67
68 K L L M M * K L L M M * L L L M M * L M M M M * L M M M M * M M M M M * * * * * * * * * * * * * * * * * * * * * * * * * * + &!, & -. * & /! # - # (. 0 - &! -. 68
69 X nedover til venstre, Y bortover på toppen. Nedoverpil: Dropp en bokstav fra X vekt 0. Bortoverpil: Dropp en bokstav fra Y vekt 0. Skråpil: Ta med bokstav fra X/Y: Vekt 1. Finn lengste vei fra øverst t.v. til nederst t.h. Dette er rett og slett DAG Shortest Path (eller Longest Path, da som jo blir like lett for DAG-er). 69
70 !"#$%&'()(!, ", #, $)!" # = * +, $ = * #$%& '%#('&!"!-#, $. = / 0 #$%&!"#$%&'()(!, ", # 1, $ 1) 2,345 % # %)*%!"!-#, $. = / 0 #$%&!"#$%&'()(!, ", # 1, $) %)*%!"#$%&'()(!, ", #, $ 1) 70
71 Egenskaper bak DP Optimal substruktur: En optimal løsning bygger på optimale løsninger på delproblemer Overlappende delproblemer: Fordi flere problemer deler delproblemer lønner det seg å lagre dem 71 Korteste vei? Har begge deler. Lengste vei (uten sykler)? Har ikke optimal substruktur Hvis vi ikke har overlappende delproblemer *kan* vi bruke DP, men det er egentlig ingen vits det blir bare splitt-og-hersk med unødvendig lagring av delproblemer.
72 ! 72
73 2 C 2 D < 2 Korteste vei oppdeling i delproblemer som må optimaliseres. Korteste veier består av korteste del-veier. 73
74 A * Lengste vei. Betrakt q-r-t, en maksimal sti fra q til t. Består den av lengste vei fra q til r og fra r til t? *Nei*! Vi kan ikke bruke DP (og har ingen annen god løsning heller). - ( 74
75 Og så var det denne, da
76 for i = 1 n for j = i 1 if A[i] > A[j] L[i] max(l[i], L[j]+1) A L For hvert element, let bakover etter lovlige forgjengere. (Å lete bakover er nyttig hvis vi vil begrense spranglengden.) Delproblemene er lengste subsekvens som slutter på en gitt posisjon, og det er disse vi bruker når vi leter bakover. (Vi kan også lagre hva vi valgte dvs. hva som er forgjengeren, altså pilene i figuren.) 76
77 Kan du finne en subkvadratisk løsning? Hint: Binærsøk 77
78 D&C Bellman-Ford BFS/DFS Binære søketrær LP Binærsøk Bubblesort Bucket sort Counting sort Dijkstra DAGshortest-path Edmonds- Karp Floyd- Warshall Hashing Gr. Heapsort Huffmankoding Insertion sort NPC Flyt+ Kruskal Merge sort Prim Quicksort Radix sort Randomized Select Select Θ etc. Selection sort Sterke komponenter Topologisk sortering DP 78
79 D&C Bellman-Ford BFS/DFS Binære søketrær LP Binærsøk Bubblesort Bucket sort Counting sort Dijkstra DAGshortest-path Edmonds- Karp Floyd- Warshall Hashing Gr. Heapsort Huffmankoding Insertion sort NPC Flyt+ Kruskal Merge sort Prim Mer Quicksort DP neste gang Radix :-) sort Randomized Select Select Θ etc. Selection sort Sterke komponenter Topologisk sortering DP 79
80 80
Choices, choices. Tiende forelesning. Dynamisk programmering: En serie med valg der valgmulighetene er avhengige av hva vi har valgt før.
 Choices, choices Tiende forelesning Dynamisk programmering: En serie med valg der valgmulighetene er avhengige av hva vi har valgt før. DAG- SP er erkeeksemplet (og den underliggende modellen for all DP).
Choices, choices Tiende forelesning Dynamisk programmering: En serie med valg der valgmulighetene er avhengige av hva vi har valgt før. DAG- SP er erkeeksemplet (og den underliggende modellen for all DP).
Choices, choices. Tiende forelesning. Dynamisk programmering: En serie med valg der valgmulighetene er avhengige av hva vi har valgt før.
 Choices, choices Tiende forelesning Dynamisk programmering: En serie med valg der valgmulighetene er avhengige av hva vi har valgt før. DAG- SP er erkeeksemplet (og den underliggende modellen for all DP).
Choices, choices Tiende forelesning Dynamisk programmering: En serie med valg der valgmulighetene er avhengige av hva vi har valgt før. DAG- SP er erkeeksemplet (og den underliggende modellen for all DP).
Live life and be merry
 Om grådighet og først litt mer DP. Live life and be merry Ellevte forelesning for tomorrow you may catch some disgusting skin disease. [Edmund Blackadder] D&C Bellman-Ford BFS/DFS Binære søketrær LP Binærsøk
Om grådighet og først litt mer DP. Live life and be merry Ellevte forelesning for tomorrow you may catch some disgusting skin disease. [Edmund Blackadder] D&C Bellman-Ford BFS/DFS Binære søketrær LP Binærsøk
Go with the. Niende forelesning. Mye matematikk i boka her ikke så komplisert, men mye å holde styr på.
 Go with the Niende forelesning Mye matematikk i boka her ikke så komplisert, men mye å holde styr på. Fokuserer på de viktigste ideene i dagens forelesning, så det forhåpentligvis blir lettere å skjønne
Go with the Niende forelesning Mye matematikk i boka her ikke så komplisert, men mye å holde styr på. Fokuserer på de viktigste ideene i dagens forelesning, så det forhåpentligvis blir lettere å skjønne
Go with the. Niende forelesning. Mye matematikk i boka her ikke så komplisert, men mye å holde styr på.
 Go with the Niende forelesning Mye matematikk i boka her ikke så komplisert, men mye å holde styr på. Fokuserer på de viktigste ideene i dagens forelesning, så det forhåpentligvis blir lettere å skjønne
Go with the Niende forelesning Mye matematikk i boka her ikke så komplisert, men mye å holde styr på. Fokuserer på de viktigste ideene i dagens forelesning, så det forhåpentligvis blir lettere å skjønne
Dijkstras algoritme. Her finnes det også (minst) en riktig rekkefølge for Relax, men den må vi oppdage litt etter hvert.
 Her finnes det også (minst) en riktig rekkefølge for Relax, men den må vi oppdage litt etter hvert. Tenk vann som sprer seg i rør: Vi behandler krysningspunktene i den rekkefølgen de fylles. Det må gi
Her finnes det også (minst) en riktig rekkefølge for Relax, men den må vi oppdage litt etter hvert. Tenk vann som sprer seg i rør: Vi behandler krysningspunktene i den rekkefølgen de fylles. Det må gi
Go with the. Niende forelesning. Mye matematikk i boka her ikke så komplisert, men mye å holde styr på.
 Go with the Niende forelesning Mye matematikk i boka her ikke så komplisert, men mye å holde styr på. Fokuserer på de viktigste ideene i dagens forelesning, så det forhåpentligvis blir lettere å skjønne
Go with the Niende forelesning Mye matematikk i boka her ikke så komplisert, men mye å holde styr på. Fokuserer på de viktigste ideene i dagens forelesning, så det forhåpentligvis blir lettere å skjønne
for bare trær Andre forelesning
 Formler eller bevis e.l. som er uklare? Si ifra, så kan jeg gå g jennom dem. Forelesningene er ment å være en hjelp til å forstå det man leser i boka ikke «spoon-feeding» av det samme som står der for
Formler eller bevis e.l. som er uklare? Si ifra, så kan jeg gå g jennom dem. Forelesningene er ment å være en hjelp til å forstå det man leser i boka ikke «spoon-feeding» av det samme som står der for
Pensum: 3. utg av Cormen et al. Øvingstime: I morgen, 14:15
 http://www.idi.ntnu.no/~algdat algdat@idi.ntnu.no Pensum: 3. utg av Cormen et al. Øvingstime: I morgen, 14:15 b c g a f d e h The pitch drop experiment. Foreløpig kjørt fra 1927 til nå. Åtte dråper har
http://www.idi.ntnu.no/~algdat algdat@idi.ntnu.no Pensum: 3. utg av Cormen et al. Øvingstime: I morgen, 14:15 b c g a f d e h The pitch drop experiment. Foreløpig kjørt fra 1927 til nå. Åtte dråper har
Live life and be merry
 Om grådighet og først litt mer DP. Live life and be merry Ellevte forelesning for tomorrow you may catch some disgusting skin disease. [Edmund Blackadder] 1 Litt repetisjon 2 Eksempel Longest Common Subsequence.
Om grådighet og først litt mer DP. Live life and be merry Ellevte forelesning for tomorrow you may catch some disgusting skin disease. [Edmund Blackadder] 1 Litt repetisjon 2 Eksempel Longest Common Subsequence.
Alle mot alle. Åttende forelesning. (eller eller Bellman-Ford, eller BFS, alt ettersom) fra alle noder.
 Enkel alle-til-allealgoritme: Kjør Dijkstra (eller eller Bellman-Ford, eller BFS, alt ettersom) fra alle noder. Kan fungere for spinkle grafer blir dyrt ellers. Alle mot alle Åttende forelesning 1 Dijkstra
Enkel alle-til-allealgoritme: Kjør Dijkstra (eller eller Bellman-Ford, eller BFS, alt ettersom) fra alle noder. Kan fungere for spinkle grafer blir dyrt ellers. Alle mot alle Åttende forelesning 1 Dijkstra
Rundt og rundt og. Trettende forelesning
 Nettverksalgoritmer. Anvendelser og generaliseringer. Sirkulasjonsproblemet/ lineær programmering. (Kap. 29.1-29.2) Rundt og rundt og Trettende forelesning 1 Merk: Ikke sikkert alt dette blir gjennomgått
Nettverksalgoritmer. Anvendelser og generaliseringer. Sirkulasjonsproblemet/ lineær programmering. (Kap. 29.1-29.2) Rundt og rundt og Trettende forelesning 1 Merk: Ikke sikkert alt dette blir gjennomgått
Algdat Eksamensforelesning. Nils Barlaug
 Algdat Eksamensforelesning Nils Barlaug Eksamen Pensum Eksamen Pensum Oppgaver du har gjort og ting du har lest Eksamen Pensum Oppgave på eksamen Oppgaver du har gjort og ting du har lest Eksamen Pensum
Algdat Eksamensforelesning Nils Barlaug Eksamen Pensum Eksamen Pensum Oppgaver du har gjort og ting du har lest Eksamen Pensum Oppgave på eksamen Oppgaver du har gjort og ting du har lest Eksamen Pensum
Dijkstras algoritme. Her finnes det også (minst) en riktig rekkefølge for Relax, men den må vi oppdage litt etter hvert.
 Her finnes det også (minst) en riktig rekkefølge for Relax, men den må vi oppdage litt etter hvert. Tenk vann som sprer seg i rør: Vi behandler krysningspunktene i den rekkefølgen de fylles. Det må gi
Her finnes det også (minst) en riktig rekkefølge for Relax, men den må vi oppdage litt etter hvert. Tenk vann som sprer seg i rør: Vi behandler krysningspunktene i den rekkefølgen de fylles. Det må gi
deeegimnoorrrsstt Sjette forelesning
 deeegimnoorrrsstt Sjette forelesning 1 2 Bellman-Ford BFS/DFS Binære søketrær Binærsøk Bubblesort Bucket sort Counting sort Dijkstra DAGshortest-path Edmonds- Karp Floyd- Warshall Hashing Heapsort Huffmankoding
deeegimnoorrrsstt Sjette forelesning 1 2 Bellman-Ford BFS/DFS Binære søketrær Binærsøk Bubblesort Bucket sort Counting sort Dijkstra DAGshortest-path Edmonds- Karp Floyd- Warshall Hashing Heapsort Huffmankoding
ALGORITMER OG DATASTRUKTURER
 Stud. nr: Side 1 av 6 NTNU Norges teknisk-naturvitenskapelige universitet BOKMÅL Fakultet for informasjonsteknologi, matematikk og elektroteknikk Institutt for datateknikk og informasjonsvitenskap LØSNINGSFORSLAG,
Stud. nr: Side 1 av 6 NTNU Norges teknisk-naturvitenskapelige universitet BOKMÅL Fakultet for informasjonsteknologi, matematikk og elektroteknikk Institutt for datateknikk og informasjonsvitenskap LØSNINGSFORSLAG,
O(V 2 ) bwfs(v, i=1) λ[v] = i for each neighbor u of v if 0 < λ[u] < i. bwfs(u, i+1) if λ[u] = 0
![O(V 2 ) bwfs(v, i=1) λ[v] = i for each neighbor u of v if 0 < λ[u] < i. bwfs(u, i+1) if λ[u] = 0 O(V 2 ) bwfs(v, i=1) λ[v] = i for each neighbor u of v if 0 < λ[u] < i. bwfs(u, i+1) if λ[u] = 0](/thumbs/64/51255941.jpg) O(V 2 ) bwfs(v, i=1) λ[v] = i for each neighbor u of v if 0 < λ[u] < i bwfs(u, i) for each neighbor u of v if λ[u] = 0 bwfs(u, i+1) Bacwards-first search; traverserer en graf med kvadratisk worst-casekjøretid.
O(V 2 ) bwfs(v, i=1) λ[v] = i for each neighbor u of v if 0 < λ[u] < i bwfs(u, i) for each neighbor u of v if λ[u] = 0 bwfs(u, i+1) Bacwards-first search; traverserer en graf med kvadratisk worst-casekjøretid.
Algdat - øvingsforelesning
 Algdat - øvingsforelesning Dynamisk programmering Nils Barlaug Dagens plan 1. 2. 3. 4. Praktisk og dagens plan LF øving 8 a. Teori b. Praksis Dynamisk programmering a. Introduksjon b. Rod Cutting c. Matrise-multiplikasjon
Algdat - øvingsforelesning Dynamisk programmering Nils Barlaug Dagens plan 1. 2. 3. 4. Praktisk og dagens plan LF øving 8 a. Teori b. Praksis Dynamisk programmering a. Introduksjon b. Rod Cutting c. Matrise-multiplikasjon
Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer
 Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer Eksamensdato 14. desember 2011 Eksamenstid 1500 1900 Sensurdato 14. januar Språk/målform Bokmål Kontakt under eksamen Magnus Lie Hetland (tlf.
Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer Eksamensdato 14. desember 2011 Eksamenstid 1500 1900 Sensurdato 14. januar Språk/målform Bokmål Kontakt under eksamen Magnus Lie Hetland (tlf.
Algdat-ninja på 60 minutter: Et galskapsprosjekt. Magnus Lie Hetland
 Algdat-ninja på 60 minutter: Et galskapsprosjekt Magnus Lie Hetland 15. november, 2002 Advarsel: Tettpakkede og overfladiske foiler forut! 1 Algtdat i 6 punkter 1. Grunnbegreper og basisverktøy 2. Rekursjon
Algdat-ninja på 60 minutter: Et galskapsprosjekt Magnus Lie Hetland 15. november, 2002 Advarsel: Tettpakkede og overfladiske foiler forut! 1 Algtdat i 6 punkter 1. Grunnbegreper og basisverktøy 2. Rekursjon
ALGORITMER OG DATASTRUKTURER
 Stud. nr: Side 1 av 7 NTNU Norges teknisk-naturvitenskapelige universitet BOKMÅL Fakultet for informasjonsteknologi, matematikk og elektroteknikk Institutt for datateknikk og informasjonsvitenskap AVSLUTTENDE
Stud. nr: Side 1 av 7 NTNU Norges teknisk-naturvitenskapelige universitet BOKMÅL Fakultet for informasjonsteknologi, matematikk og elektroteknikk Institutt for datateknikk og informasjonsvitenskap AVSLUTTENDE
All good things. Fjortende forelesning
 All good things Fjortende forelesning Div notater finnes på http://www.idi.ntnu.no/~algdat Foiler finnes på http://www.idi.ntnu.no/~mlh/algdat/latitudinary Spørsmål? algdat@idi.ntnu.no Sjekkliste Dette
All good things Fjortende forelesning Div notater finnes på http://www.idi.ntnu.no/~algdat Foiler finnes på http://www.idi.ntnu.no/~mlh/algdat/latitudinary Spørsmål? algdat@idi.ntnu.no Sjekkliste Dette
ALGORITMER OG DATASTRUKTURER
 Stud. nr: Side 1 av 6 NTNU Norges teknisk-naturvitenskapelige universitet BOKMÅL Fakultet for informasjonsteknologi, matematikk og elektroteknikk Institutt for datateknikk og informasjonsvitenskap AVSLUTTENDE
Stud. nr: Side 1 av 6 NTNU Norges teknisk-naturvitenskapelige universitet BOKMÅL Fakultet for informasjonsteknologi, matematikk og elektroteknikk Institutt for datateknikk og informasjonsvitenskap AVSLUTTENDE
Teoriøving 7 + litt om Ford-Fulkerson. Magnus Lie Hetland
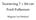 Teoriøving 7 + litt om Ford-Fulkerson Magnus Lie Hetland Oppgave 1 a s 7 t 3 x 4 2 2 8 2 u 6 v 3 w Bruk DIJKSTRA eller BELLMAN-FORD og finn minste avstand fra s til de andre nodene. Svar/utregning (DIJKSTRA):
Teoriøving 7 + litt om Ford-Fulkerson Magnus Lie Hetland Oppgave 1 a s 7 t 3 x 4 2 2 8 2 u 6 v 3 w Bruk DIJKSTRA eller BELLMAN-FORD og finn minste avstand fra s til de andre nodene. Svar/utregning (DIJKSTRA):
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Institutt for datateknikk og informasjonsvitenskap Eksamensoppgave i TDT0 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Telefon 98 5 99 Eksamensdato 7. desember, 06 Eksamenstid
Institutt for datateknikk og informasjonsvitenskap Eksamensoppgave i TDT0 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Telefon 98 5 99 Eksamensdato 7. desember, 06 Eksamenstid
Løsningsforslag for eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 18. Desember 2000, kl
 Student nr.: Side 1 av 5 Løsningsforslag for eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 18. Desember 2000, kl 0900-1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 73 593442. Hjelpemidler:
Student nr.: Side 1 av 5 Løsningsforslag for eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 18. Desember 2000, kl 0900-1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 73 593442. Hjelpemidler:
Kontinuasjonseksamen i fag SIF8010 Algoritmer og Datastrukturer Torsdag 9. August 2001, kl
 Student nr.: Side 1 av 5 Kontinuasjonseksamen i fag SIF8010 Algoritmer og Datastrukturer Torsdag 9. August 2001, kl 0900-1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 73 593442. Hjelpemidler: Alle
Student nr.: Side 1 av 5 Kontinuasjonseksamen i fag SIF8010 Algoritmer og Datastrukturer Torsdag 9. August 2001, kl 0900-1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 73 593442. Hjelpemidler: Alle
ALGORITMER OG DATASTRUKTURER
 Stud. nr: Side 1 av 6 NTNU Norges teknisk-naturvitenskapelige universitet BOKMÅL Fakultet for informasjonsteknologi, matematikk og elektroteknikk Institutt for datateknikk og informasjonsvitenskap AVSLUTTENDE
Stud. nr: Side 1 av 6 NTNU Norges teknisk-naturvitenskapelige universitet BOKMÅL Fakultet for informasjonsteknologi, matematikk og elektroteknikk Institutt for datateknikk og informasjonsvitenskap AVSLUTTENDE
Ekstra ark kan legges ved om nødvendig, men det er meningen at svarene skal få plass i rutene på oppgavearkene. Lange svar teller ikke positivt.
 Side 1 av 5 Noen viktige punkter: (i) (ii) (iii) (iv) Les hele eksamenssettet nøye før du begynner! Faglærer går normalt én runde gjennom lokalet. Ha evt. spørsmål klare! Skriv svarene dine i svarrutene
Side 1 av 5 Noen viktige punkter: (i) (ii) (iii) (iv) Les hele eksamenssettet nøye før du begynner! Faglærer går normalt én runde gjennom lokalet. Ha evt. spørsmål klare! Skriv svarene dine i svarrutene
Øvingsforelesning 12 Maks flyt
 Øvingsforelesning 12 Maks flyt Ole Kristian Pedersen 9. november 2018 ] Plan for dagen Maksimal flyt og minimale snitt Maksimal bipartitt matching Tidligere eksamensoppgaver Introduksjon øving 12 Hva er
Øvingsforelesning 12 Maks flyt Ole Kristian Pedersen 9. november 2018 ] Plan for dagen Maksimal flyt og minimale snitt Maksimal bipartitt matching Tidligere eksamensoppgaver Introduksjon øving 12 Hva er
August
 None of us truly understands the P versus NP problem, we have only begun to peel the layers around this increasingly complex question. Perhaps we will see a resolution of the P versus NP problem in the
None of us truly understands the P versus NP problem, we have only begun to peel the layers around this increasingly complex question. Perhaps we will see a resolution of the P versus NP problem in the
Pensum: fra boken (H-03)+ forelesninger
 Pensum: fra boken (H-03)+ forelesninger unntatt kursorisk tema KAP. 1 KAP. 2 KAP. 3 JAVA I-110 (ikke gjennomgått) OO + ABSTRAKSJON /GENERISK PROGRAMMERING REKURSJON ALGORITME-TIDSANALYSE; O-NOTASJON KAP.
Pensum: fra boken (H-03)+ forelesninger unntatt kursorisk tema KAP. 1 KAP. 2 KAP. 3 JAVA I-110 (ikke gjennomgått) OO + ABSTRAKSJON /GENERISK PROGRAMMERING REKURSJON ALGORITME-TIDSANALYSE; O-NOTASJON KAP.
Dynamisk programmering Undervises av Stein Krogdahl
 Dynamisk programmering Undervises av Stein Krogdahl 5. september 2012 Dagens stoff er hentet fra kapittel 9 i læreboka, samt kapittel 20.5 (som vi «hoppet over» sist) Kapittel 9 er lagt ut på undervisningsplanen.
Dynamisk programmering Undervises av Stein Krogdahl 5. september 2012 Dagens stoff er hentet fra kapittel 9 i læreboka, samt kapittel 20.5 (som vi «hoppet over» sist) Kapittel 9 er lagt ut på undervisningsplanen.
Algdat - Øvingsforelesning. Maks flyt
 Algdat - Øvingsforelesning Maks flyt Dagens plan 1. LF teoriøving 7 2. Maks flyt 3. Ford-Fulkerson 4. Maksimal bipartitt matching 5. Presentasjon av øving 9 2 Øving 7 4b) I hvilken rekkefølge velges noder
Algdat - Øvingsforelesning Maks flyt Dagens plan 1. LF teoriøving 7 2. Maks flyt 3. Ford-Fulkerson 4. Maksimal bipartitt matching 5. Presentasjon av øving 9 2 Øving 7 4b) I hvilken rekkefølge velges noder
Pensum: fra boken (H-03)+ forelesninger
 Pensum: fra boken (H-03)+ forelesninger unntatt kursorisk tema KAP. 1 KAP. 2 KAP. 3 JAVA I-110 (ikke gjennomgått) OO + ABSTRAKSJON /GENERISK PROGRAMMERING REKURSJON ALGORITME-TIDSANALYSE; O-NOTASJON KAP.
Pensum: fra boken (H-03)+ forelesninger unntatt kursorisk tema KAP. 1 KAP. 2 KAP. 3 JAVA I-110 (ikke gjennomgått) OO + ABSTRAKSJON /GENERISK PROGRAMMERING REKURSJON ALGORITME-TIDSANALYSE; O-NOTASJON KAP.
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 13: Dynamisk programmering (Ifi, UiO) INF2220 H2017, forelesning 13 1 / 30 Dagens plan Dynamisk
INF2220 - Algoritmer og datastrukturer Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 13: Dynamisk programmering (Ifi, UiO) INF2220 H2017, forelesning 13 1 / 30 Dagens plan Dynamisk
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf. 91851949 Eksamensdato 11. august 2014 Eksamenstid (fra til) 0900 1300 Hjelpemiddelkode D. Ingen
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf. 91851949 Eksamensdato 11. august 2014 Eksamenstid (fra til) 0900 1300 Hjelpemiddelkode D. Ingen
Dagens stoff er hentet fra kapittel 9 i læreboka, samt kapittel 20.5 (som vi «hoppet over» sist)
 Dynamisk programmering Undervises av Stein Krogdahl 5. september 2012 Dagens stoff er hentet fra kapittel 9 i læreboka, samt kapittel 20.5 (som vi «hoppet over» sist) Kapittel 9 er lagt ut på undervisningsplanen.
Dynamisk programmering Undervises av Stein Krogdahl 5. september 2012 Dagens stoff er hentet fra kapittel 9 i læreboka, samt kapittel 20.5 (som vi «hoppet over» sist) Kapittel 9 er lagt ut på undervisningsplanen.
Agenda. 1 Sortering, heap og select. 2 Binære trær. 3 Grafer, BFS og DFS. 4 Spenntrær og Korteste vei. 5 Maks flyt. 6 Dynamisk programmering
 Agenda 1 Sortering, heap og select Oppsummering Ola Natvig IDI - NTNU 23. november 2007 2 Binære trær 3 Grafer, BFS og DFS 4 Spenntrær og Korteste vei 5 Maks flyt 6 Dynamisk programmering 7 Grådighet 8
Agenda 1 Sortering, heap og select Oppsummering Ola Natvig IDI - NTNU 23. november 2007 2 Binære trær 3 Grafer, BFS og DFS 4 Spenntrær og Korteste vei 5 Maks flyt 6 Dynamisk programmering 7 Grådighet 8
Algdat Oppsummering, eksamen-ting. Jim Frode Hoff
 Algdat Oppsummering, eksamen-ting Jim Frode Hoff November 18, 2012 1 Definisjoner 1.1 Ordliste Problem Probleminstans Iterasjon Asymtpoisk notasjon O(x) kjøretid Ω(x) kjøretid Θ(x) kjøretid T (x) kjøretid
Algdat Oppsummering, eksamen-ting Jim Frode Hoff November 18, 2012 1 Definisjoner 1.1 Ordliste Problem Probleminstans Iterasjon Asymtpoisk notasjon O(x) kjøretid Ω(x) kjøretid Θ(x) kjøretid T (x) kjøretid
Longest increasing. subsequence Betingelser. Longest. common subsequence. Knapsack Grådig vs. DP Moro: 2D-Nim Spørsmål. Forside. Repetisjon.
 :: :: Dynamisk programmering Eksamenskurs Åsmund Eldhuset asmunde *at* stud.ntnu.no folk.ntnu.no/asmunde/algdat/dp.ppt Svært rask repetisjon Noen ganger (f.eks. ved utregning av Fibonaccitall) vil en rekursiv
:: :: Dynamisk programmering Eksamenskurs Åsmund Eldhuset asmunde *at* stud.ntnu.no folk.ntnu.no/asmunde/algdat/dp.ppt Svært rask repetisjon Noen ganger (f.eks. ved utregning av Fibonaccitall) vil en rekursiv
n/b log b n = (lg n) a log b n = n log b a
 Masterteoremet 1 T (n) = at (n/b) + f(n) Antall «barn»: Størrelse per «barn»: «Høyde»: a n/b log b n = (lg n) Rota har f(n) arbeid; hver løvnode har en konstant mengde arbeid. Hva vil dominere totalen?
Masterteoremet 1 T (n) = at (n/b) + f(n) Antall «barn»: Størrelse per «barn»: «Høyde»: a n/b log b n = (lg n) Rota har f(n) arbeid; hver løvnode har en konstant mengde arbeid. Hva vil dominere totalen?
Dynamisk programmering
 Dynamisk programmering Metoden ble formalisert av Richard Bellmann (RAND Corporation) på 5-tallet. Programmering i betydningen planlegge, ta beslutninger. (Har ikke noe med kode eller å skrive kode å gjøre.)
Dynamisk programmering Metoden ble formalisert av Richard Bellmann (RAND Corporation) på 5-tallet. Programmering i betydningen planlegge, ta beslutninger. (Har ikke noe med kode eller å skrive kode å gjøre.)
Lineær sortering. Radix sort
 Fra forrige gang 1 Lineær sortering Radix sort 2 Sorter hvert siffer for seg Bruk en stabil sortering (f.eks. CS) for å bevare arbeidet så langt Vi må begynne med minst signifikante siffer Konstant antall
Fra forrige gang 1 Lineær sortering Radix sort 2 Sorter hvert siffer for seg Bruk en stabil sortering (f.eks. CS) for å bevare arbeidet så langt Vi må begynne med minst signifikante siffer Konstant antall
Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer
 Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer Eksamensdato 3. desember 2012 Eksamenstid 0900 1300 Sensurdato 3. januar 2013 Språk/målform Bokmål Kontakt under eksamen Magnus Lie Hetland (tlf.
Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer Eksamensdato 3. desember 2012 Eksamenstid 0900 1300 Sensurdato 3. januar 2013 Språk/målform Bokmål Kontakt under eksamen Magnus Lie Hetland (tlf.
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf.!! 91851949 Eksamensdato! 15. august 2013 Eksamenstid (fra til)! 0900 1300 Hjelpemiddelkode D.
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf.!! 91851949 Eksamensdato! 15. august 2013 Eksamenstid (fra til)! 0900 1300 Hjelpemiddelkode D.
Innhold. Innledning 1
 Innhold Innledning 1 1 Kompleksitetsanalyse 7 1.1 Innledning.............................. 8 1.2 Hva vi beregner........................... 8 1.2.1 Enkle operasjoner...................... 8 1.2.2 Kompleksitet........................
Innhold Innledning 1 1 Kompleksitetsanalyse 7 1.1 Innledning.............................. 8 1.2 Hva vi beregner........................... 8 1.2.1 Enkle operasjoner...................... 8 1.2.2 Kompleksitet........................
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Institutt for datateknikk og informasjonsvitenskap Eksamensoppgave i TDT0 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Telefon 98 5 99 Eksamensdato 9. august, 07 Eksamenstid
Institutt for datateknikk og informasjonsvitenskap Eksamensoppgave i TDT0 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Telefon 98 5 99 Eksamensdato 9. august, 07 Eksamenstid
Live life and be merry
 Om grådighet og først litt mer DP. Live life and be merry Ellevte forelesning for tomorrow you may catch some disgusting skin disease. [Edmund Blackadder] 1 2 g i t k i s K o rt Grådighet All form for
Om grådighet og først litt mer DP. Live life and be merry Ellevte forelesning for tomorrow you may catch some disgusting skin disease. [Edmund Blackadder] 1 2 g i t k i s K o rt Grådighet All form for
Maks Flyt og NPkompletthet
 Maks Flyt og NPkompletthet Flyt - Intro Mange av oppgavene om flyt handler om å se at Dette kan vi løse som et flytproblem. Resten er som regel kortsvarsoppgaver, og går på grunnleggende forståelse av
Maks Flyt og NPkompletthet Flyt - Intro Mange av oppgavene om flyt handler om å se at Dette kan vi løse som et flytproblem. Resten er som regel kortsvarsoppgaver, og går på grunnleggende forståelse av
Evt. forklar på tavla. Diskuter kjøretid (best-/ worst-case). Innsetting og søk. Rekursjon igjen. A C E G
 TLDR RTFM Innsetting og søk. Rekursjon igjen. Evt. forklar på tavla. Diskuter kjøretid (best-/ worst-case). D B F A C E G reduksjon! rekursjon dekomp. induksjon gjenbruk travers. Søk i søketre uten balansering
TLDR RTFM Innsetting og søk. Rekursjon igjen. Evt. forklar på tavla. Diskuter kjøretid (best-/ worst-case). D B F A C E G reduksjon! rekursjon dekomp. induksjon gjenbruk travers. Søk i søketre uten balansering
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Institutt for datateknikk og informasjonsvitenskap Eksamensoppgave i TDT0 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Telefon 98 5 99 Eksamensdato 7. desember, 06 Eksamenstid
Institutt for datateknikk og informasjonsvitenskap Eksamensoppgave i TDT0 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Telefon 98 5 99 Eksamensdato 7. desember, 06 Eksamenstid
Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer
 Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer Eksamensdato 3. desember 2012 Eksamenstid 0900 1300 Sensurdato 3. januar 2013 Språk/målform Bokmål Kontakt under eksamen Magnus Lie Hetland (tlf.
Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer Eksamensdato 3. desember 2012 Eksamenstid 0900 1300 Sensurdato 3. januar 2013 Språk/målform Bokmål Kontakt under eksamen Magnus Lie Hetland (tlf.
Øvingsforelesning Korteste vei: Alle til alle
 Øvingsforelesning Korteste vei: Alle til alle TDT4120 Algoritmer og datastrukturer Ole Kristian Pedersen 02. november, 2018 IDI, NTNU Plan for dagen Løsninger teoriøving 10 Alle til alle med Dijkstra &
Øvingsforelesning Korteste vei: Alle til alle TDT4120 Algoritmer og datastrukturer Ole Kristian Pedersen 02. november, 2018 IDI, NTNU Plan for dagen Løsninger teoriøving 10 Alle til alle med Dijkstra &
Dynamisk programmering
 Dynamisk programmering Metoden ble formalisert av Richard Bellmann (RAND Corporation) på 50-tallet. Programmering i betydningen planlegge, ta beslutninger. (Har ikke noe med kode eller å skrive kode å
Dynamisk programmering Metoden ble formalisert av Richard Bellmann (RAND Corporation) på 50-tallet. Programmering i betydningen planlegge, ta beslutninger. (Har ikke noe med kode eller å skrive kode å
Fra A til B. Syvende forelesning
 Fra A til B Syvende forelesning 1 Amøbeproblemet nok en gang. Hva er 1+2+4+ +n/2? 2 Skal la være å trekke frem binærtrefiguren igjen ;-) La oss se på det på en litt annen måte, som passer dagens tema (fra
Fra A til B Syvende forelesning 1 Amøbeproblemet nok en gang. Hva er 1+2+4+ +n/2? 2 Skal la være å trekke frem binærtrefiguren igjen ;-) La oss se på det på en litt annen måte, som passer dagens tema (fra
Eksamen i tdt4120 Algoritmer og datastrukturer
 Norges teknisk naturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap Side 1 av 5 Oppgavestillere: Magnus Lie Hetland Jon Marius Venstad Kvalitetskontroll: Magnar Nedland Faglig
Norges teknisk naturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap Side 1 av 5 Oppgavestillere: Magnus Lie Hetland Jon Marius Venstad Kvalitetskontroll: Magnar Nedland Faglig
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf. 91851949 Eksamensdato 11. august 2014 Eksamenstid (fra til) 0900 1300 Hjelpemiddelkode D. Ingen
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf. 91851949 Eksamensdato 11. august 2014 Eksamenstid (fra til) 0900 1300 Hjelpemiddelkode D. Ingen
Løsningsforslag til eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 14. Desember 1999, kl
 Student nr.: Side 1 av 7 Løsningsforslag til eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 14. Desember 1999, kl 0900-1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 73 593442. Hjelpemidler:
Student nr.: Side 1 av 7 Løsningsforslag til eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 14. Desember 1999, kl 0900-1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 73 593442. Hjelpemidler:
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Institutt for datateknikk og informasjonsvitenskap Eksamensoppgave i TDT0 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Telefon 98 5 99 Eksamensdato 9. august, 07 Eksamenstid
Institutt for datateknikk og informasjonsvitenskap Eksamensoppgave i TDT0 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Telefon 98 5 99 Eksamensdato 9. august, 07 Eksamenstid
All good things. Fjortende forelesning
 All good things Fjortende forelesning 1 Reduksjons- Eksempler 2 Clique til Independent Set 3 Partition til Bin Packing 4 Partition til Subset Sum 5 CNF-SAT til Dir. Ham. Cycle 6 Dir. Ham. Cycle til Ham.
All good things Fjortende forelesning 1 Reduksjons- Eksempler 2 Clique til Independent Set 3 Partition til Bin Packing 4 Partition til Subset Sum 5 CNF-SAT til Dir. Ham. Cycle 6 Dir. Ham. Cycle til Ham.
Eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 18. Desember 2000, kl
 Student nr.: Side 1 av 5 Eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 18. Desember 2000, kl 0900-1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 73 593442. Hjelpemidler: Alle kalkulatortyper
Student nr.: Side 1 av 5 Eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 18. Desember 2000, kl 0900-1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 73 593442. Hjelpemidler: Alle kalkulatortyper
Longest. increasing. subsequence. Betingelser. Matrise- common. Grådig vs. DP. Forside. Intro. Fibonacci-tall. Memoisering DP
 og dynamisk Matrisemultiplikasjomultiplikasjon programmering Matrise- Åsmund Eldhuset og Dette er to ganske like teknikker for å lage algoritmer De kan brukes på svært mange tilsynelatende forskjellige
og dynamisk Matrisemultiplikasjomultiplikasjon programmering Matrise- Åsmund Eldhuset og Dette er to ganske like teknikker for å lage algoritmer De kan brukes på svært mange tilsynelatende forskjellige
deeegimnoorrrsstt Sjette forelesning
 deeegimnoorrrsstt Sjette forelesning 1 2 Rebus. Hva er dette? Svar: Kvadratiske sorteringsalgoritmer :-> Som vanlig relativt abstrakte beskrivelser her. Ta en titt på pseudokode i boka for mer detaljert
deeegimnoorrrsstt Sjette forelesning 1 2 Rebus. Hva er dette? Svar: Kvadratiske sorteringsalgoritmer :-> Som vanlig relativt abstrakte beskrivelser her. Ta en titt på pseudokode i boka for mer detaljert
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Institutt for datateknikk og informasjonsvitenskap Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Telefon 918 51 949 Eksamensdato 4. desember, 2017
Institutt for datateknikk og informasjonsvitenskap Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Telefon 918 51 949 Eksamensdato 4. desember, 2017
Notater til INF2220 Eksamen
 Notater til INF2220 Eksamen Lars Bjørlykke Kristiansen December 13, 2011 Stor O notasjon Funksjon Navn 1 Konstant log n Logaritmisk n Lineær n log n n 2 Kvadratisk n 3 Kubisk 2 n Eksponensiell n! Trær
Notater til INF2220 Eksamen Lars Bjørlykke Kristiansen December 13, 2011 Stor O notasjon Funksjon Navn 1 Konstant log n Logaritmisk n Lineær n log n n 2 Kvadratisk n 3 Kubisk 2 n Eksponensiell n! Trær
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 11: Huffman-koding & Dynamisk programmering (Ifi, UiO) INF2220 H2015, forelesning 11 1 / 32 Dagens
INF2220 - Algoritmer og datastrukturer Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 11: Huffman-koding & Dynamisk programmering (Ifi, UiO) INF2220 H2015, forelesning 11 1 / 32 Dagens
Eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 14. Desember 1999, kl
 Student nr.: Side 1 av 7 Eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 14. Desember 1999, kl 0900-1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 73 593442. Hjelpemidler: Alle kalkulatortyper
Student nr.: Side 1 av 7 Eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 14. Desember 1999, kl 0900-1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 73 593442. Hjelpemidler: Alle kalkulatortyper
IN Algoritmer og datastrukturer
 IN010 - Algoritmer og datastrukturer HØSTEN 018 Institutt for informatikk, Universitetet i Oslo Forelesning 6: Grafer III Ingrid Chieh Yu (Ifi, UiO) IN010 0.10.018 1 / 0 Dagens plan: Dybde-først søk Biconnectivity
IN010 - Algoritmer og datastrukturer HØSTEN 018 Institutt for informatikk, Universitetet i Oslo Forelesning 6: Grafer III Ingrid Chieh Yu (Ifi, UiO) IN010 0.10.018 1 / 0 Dagens plan: Dybde-først søk Biconnectivity
INF2220: Time 12 - Sortering
 INF0: Time 1 - Sortering Mathias Lohne mathialo Noen algoritmer Vi skal nå se på noen konkrete sorteringsalgoritmer. Gjennomgående i alle eksempler vil vi sortere tall etter tallverdi, men som diskutert
INF0: Time 1 - Sortering Mathias Lohne mathialo Noen algoritmer Vi skal nå se på noen konkrete sorteringsalgoritmer. Gjennomgående i alle eksempler vil vi sortere tall etter tallverdi, men som diskutert
45011 Algoritmer og datastrukturer Løsningsforslag eksamen 13. januar 1992
 45011 Algoritmer og datastrukturer Løsningsforslag eksamen 13. januar 12 Oppgave 1 Idé til algoritme Benytter S n som betegn på en tallmengde med n elementer. For at et tall m skal være et majoritetstall
45011 Algoritmer og datastrukturer Løsningsforslag eksamen 13. januar 12 Oppgave 1 Idé til algoritme Benytter S n som betegn på en tallmengde med n elementer. For at et tall m skal være et majoritetstall
Forelesningsplan. Grådighet. LF Øving 9. Hva er grådighet? Aktivitetsvelger En grådig strategi Grådig eller dynamisk? Knapsack Huffmankoding
 1 Grådighet 2 Forelesningsplan Grådighet Hva er grådighet? Aktivitetsvelger En grådig strategi Grådig eller dynamisk? Knapsack Huffmankoding LF Øving 9 Teori Praksis 3 Forelesningsplan Grådighet Hva er
1 Grådighet 2 Forelesningsplan Grådighet Hva er grådighet? Aktivitetsvelger En grådig strategi Grådig eller dynamisk? Knapsack Huffmankoding LF Øving 9 Teori Praksis 3 Forelesningsplan Grådighet Hva er
Avanserte flytalgoritmer
 Avanserte flytalgoritmer Magnus Lie Hetland, mars 2008 Stoff hentet fra: Network Flows av Ahua m.fl. (Prentice-Hall, 1993) Graphs, Networks and Algorithms, 2. utg., av Jungnickel (Springer, 2005) Repetisjon
Avanserte flytalgoritmer Magnus Lie Hetland, mars 2008 Stoff hentet fra: Network Flows av Ahua m.fl. (Prentice-Hall, 1993) Graphs, Networks and Algorithms, 2. utg., av Jungnickel (Springer, 2005) Repetisjon
Løsningsforslag for eksamen i fag SIF8010 Algoritmer og datastrukturer Lørdag 9. august 2003, kl
 SIF8010 2003-08-09 Stud.-nr: Antall sider: 1 Løsningsforslag for eksamen i fag SIF8010 Algoritmer og datastrukturer Lørdag 9. august 2003, kl. 0900 1500 Faglig kontakt under eksamen: Arne Halaas, tlf.
SIF8010 2003-08-09 Stud.-nr: Antall sider: 1 Løsningsforslag for eksamen i fag SIF8010 Algoritmer og datastrukturer Lørdag 9. august 2003, kl. 0900 1500 Faglig kontakt under eksamen: Arne Halaas, tlf.
Studentnummer: Side 1 av 1. Løsningsforslag, Eksamen i TDT4120 Algoritmer og datastrukturer August 2005
 Studentnummer: Side 1 av 1 Løsningsforslag, Eksamen i TDT4120 Algoritmer og datastrukturer August 2005 Faglige kontakter under eksamen: Magnus Lie Hetland, Arne Halaas Tillatte hjelpemidler: Bestemt enkel
Studentnummer: Side 1 av 1 Løsningsforslag, Eksamen i TDT4120 Algoritmer og datastrukturer August 2005 Faglige kontakter under eksamen: Magnus Lie Hetland, Arne Halaas Tillatte hjelpemidler: Bestemt enkel
LØSNINGSFORSLAG, EKSAMEN I ALGORITMER OG DATASTRUKTURER (IT1105)
 Norges teknisk naturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap Side 1 av 8 Faglig kontakt under eksamen: Magnus Lie Hetland LØSNINGSFORSLAG, EKSAMEN I ALGORITMER OG DATASTRUKTURER
Norges teknisk naturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap Side 1 av 8 Faglig kontakt under eksamen: Magnus Lie Hetland LØSNINGSFORSLAG, EKSAMEN I ALGORITMER OG DATASTRUKTURER
Algdat Redux. Fjortende forelesning. Repetisjon av utvalgte emner.
 Algdat Redux Fjortende forelesning Repetisjon av utvalgte emner. 1 Nå har vi en brukbar (om enn ikke helt intuitiv) definisjon av «alt» og nå ønsker vi å lage oss en liste med de problemene som er «verst
Algdat Redux Fjortende forelesning Repetisjon av utvalgte emner. 1 Nå har vi en brukbar (om enn ikke helt intuitiv) definisjon av «alt» og nå ønsker vi å lage oss en liste med de problemene som er «verst
Eksamen i fag SIF8010 Algoritmer og datastrukturer Lørdag 9. august 2003, kl
 SIF8010 2003-08-09 Stud.-nr: Antall sider: 1 Eksamen i fag SIF8010 Algoritmer og datastrukturer Lørdag 9. august 2003, kl. 0900 1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 41661982; Magnus Lie
SIF8010 2003-08-09 Stud.-nr: Antall sider: 1 Eksamen i fag SIF8010 Algoritmer og datastrukturer Lørdag 9. august 2003, kl. 0900 1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 41661982; Magnus Lie
Løsningsforslag for eksamen i fag TDT4120 Algoritmer og datastrukturer Tirsdag 9. desember 2003, kl
 TDT4120 2003-12-09 Stud.-nr: Antall sider: 1/7 Løsningsforslag for eksamen i fag TDT4120 Algoritmer og datastrukturer Tirsdag 9. desember 2003, kl. 0900 1500 Faglig kontakt under eksamen: Arne Halaas,
TDT4120 2003-12-09 Stud.-nr: Antall sider: 1/7 Løsningsforslag for eksamen i fag TDT4120 Algoritmer og datastrukturer Tirsdag 9. desember 2003, kl. 0900 1500 Faglig kontakt under eksamen: Arne Halaas,
Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer
 Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer Eksamensdato 14. desember 2011 Eksamenstid 1500 1900 Sensurdato 14. januar Språk/målform Bokmål Kontakt under eksamen Magnus Lie Hetland (tlf.
Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer Eksamensdato 14. desember 2011 Eksamenstid 1500 1900 Sensurdato 14. januar Språk/målform Bokmål Kontakt under eksamen Magnus Lie Hetland (tlf.
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2017 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2017, forelesning
INF2220 - Algoritmer og datastrukturer HØSTEN 2017 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2017, forelesning
Eksamenshefte TDT4120 Algoritmer og datastrukturer
 Eksamenshefte TDT4120 Algoritmer og datastrukturer Eirik Benum Reksten 1 SIF8010 august 2003 - Oppgave 1 I de følgende tre deloppgavene (1 a, b og c) skal du bruke den vektede, rettede grafen G = (V, E),
Eksamenshefte TDT4120 Algoritmer og datastrukturer Eirik Benum Reksten 1 SIF8010 august 2003 - Oppgave 1 I de følgende tre deloppgavene (1 a, b og c) skal du bruke den vektede, rettede grafen G = (V, E),
Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer
 Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer Eksamensdato 18. august 2011 Eksamenstid 0900 1300 Sensurdato 8. september Språk/målform Bokmål Kontakt under eksamen Magnus Lie Hetland (tlf.
Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer Eksamensdato 18. august 2011 Eksamenstid 0900 1300 Sensurdato 8. september Språk/målform Bokmål Kontakt under eksamen Magnus Lie Hetland (tlf.
EKSAMEN. Dato: 28. mai 2018 Eksamenstid: 09:00 13:00
 EKSAMEN Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: 28. mai 2018 Eksamenstid: 09:00 13:00 Hjelpemidler: Alle trykte og skrevne Faglærer: Jan Høiberg Om eksamensoppgavene: Oppgavesettet
EKSAMEN Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: 28. mai 2018 Eksamenstid: 09:00 13:00 Hjelpemidler: Alle trykte og skrevne Faglærer: Jan Høiberg Om eksamensoppgavene: Oppgavesettet
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf. 91851949 Eksamensdato 7. desember 2013 Eksamenstid (fra til) 0900 1300 Hjelpemiddelkode Målform/språk
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf. 91851949 Eksamensdato 7. desember 2013 Eksamenstid (fra til) 0900 1300 Hjelpemiddelkode Målform/språk
Øvingsforelesning 9. Flytnettverk, maksimum flyt og maksimum bipartitt matching. Jon Marius Venstad
 Øvingsforelesning 9 Flytnettverk, maksimum flyt og maksimum bipartitt matching Jon Marius Venstad venstad@idi.ntnu.no 1 Dagens tema Flytnettverk Terminologi Max-flow min-cut teoremet Ford-Fulkersons metode
Øvingsforelesning 9 Flytnettverk, maksimum flyt og maksimum bipartitt matching Jon Marius Venstad venstad@idi.ntnu.no 1 Dagens tema Flytnettverk Terminologi Max-flow min-cut teoremet Ford-Fulkersons metode
Grådige algoritmer. Lars Vidar Magnusson Kapittel 16. Aktivitetvelgingsproblemet Huffmankoder
 Grådige Algoritmer Lars Vidar Magnusson 12.3.2014 Kapittel 16 Grådige algoritmer Aktivitetvelgingsproblemet Huffmankoder Ideen bak Grådige Algoritmer Ideen bak grådige algoritmer er å løse optimaliseringsproblem
Grådige Algoritmer Lars Vidar Magnusson 12.3.2014 Kapittel 16 Grådige algoritmer Aktivitetvelgingsproblemet Huffmankoder Ideen bak Grådige Algoritmer Ideen bak grådige algoritmer er å løse optimaliseringsproblem
Grunnleggende Grafteori
 Grunnleggende Grafteori 2. September, 2019 Institutt for Informatikk 1 Dagens plan Terminologi og definisjoner Hvordan representere grafer i datamaskinen Traversering Dybde-først-søk Bredde-først-søk Topologisk
Grunnleggende Grafteori 2. September, 2019 Institutt for Informatikk 1 Dagens plan Terminologi og definisjoner Hvordan representere grafer i datamaskinen Traversering Dybde-først-søk Bredde-først-søk Topologisk
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf. 918 51 949 Eksamensdato 12. august, 2014 Eksamenstid (fra til) 0900 1300 Hjelpemiddelkode D.
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf. 918 51 949 Eksamensdato 12. august, 2014 Eksamenstid (fra til) 0900 1300 Hjelpemiddelkode D.
for bare trær Andre forelesning
 Formler eller bevis e.l. som er uklare? Si ifra, så kan jeg gå g jennom dem. Forelesningene er ment å være en hjelp til å forstå det man leser i boka ikke «spoon-feeding» av det samme som står der for
Formler eller bevis e.l. som er uklare? Si ifra, så kan jeg gå g jennom dem. Forelesningene er ment å være en hjelp til å forstå det man leser i boka ikke «spoon-feeding» av det samme som står der for
MAT1030 Diskret Matematikk
 MAT1030 Diskret Matematikk Forelesning 25: Trær Dag Normann Matematisk Institutt, Universitetet i Oslo 27. april 2010 (Sist oppdatert: 2010-04-27 14:15) Forelesning 25 MAT1030 Diskret Matematikk 27. april
MAT1030 Diskret Matematikk Forelesning 25: Trær Dag Normann Matematisk Institutt, Universitetet i Oslo 27. april 2010 (Sist oppdatert: 2010-04-27 14:15) Forelesning 25 MAT1030 Diskret Matematikk 27. april
SIF8010 ALGORITMER OG DATASTRUKTURER
 SIF8010 ALGORITMER OG DATASTRUKTURER KONTINUASJONSEKSAMEN, 1999; LØSNINGSFORSLAG Oppgave 1 (12%) Anta at du skal lage et støtteprogram som umiddelbart skal varsle om at et ord blir skrevet feil under inntasting
SIF8010 ALGORITMER OG DATASTRUKTURER KONTINUASJONSEKSAMEN, 1999; LØSNINGSFORSLAG Oppgave 1 (12%) Anta at du skal lage et støtteprogram som umiddelbart skal varsle om at et ord blir skrevet feil under inntasting
MAT1030 Forelesning 25
 MAT1030 Forelesning 25 Trær Dag Normann - 27. april 2010 (Sist oppdatert: 2010-04-27 14:16) Forelesning 25 Litt repetisjon Vi har snakket om grafer og trær. Av begreper vi så på var følgende: Eulerstier
MAT1030 Forelesning 25 Trær Dag Normann - 27. april 2010 (Sist oppdatert: 2010-04-27 14:16) Forelesning 25 Litt repetisjon Vi har snakket om grafer og trær. Av begreper vi så på var følgende: Eulerstier
Heapsort. Lars Vidar Magnusson Kapittel 6 Heaps Heapsort Prioritetskøer
 Heapsort Lars Vidar Magnusson 24.1.2014 Kapittel 6 Heaps Heapsort Prioritetskøer Sorterings Problemet Sorterings problemet er et av de mest fundementalske problemene innen informatikken. Vi sorterer typisk
Heapsort Lars Vidar Magnusson 24.1.2014 Kapittel 6 Heaps Heapsort Prioritetskøer Sorterings Problemet Sorterings problemet er et av de mest fundementalske problemene innen informatikken. Vi sorterer typisk
MAT1030 Diskret Matematikk
 MAT1030 Diskret Matematikk Forelesning 26: Trær Roger Antonsen Institutt for informatikk, Universitetet i Oslo 5. mai 2009 (Sist oppdatert: 2009-05-06 22:27) Forelesning 26 MAT1030 Diskret Matematikk 5.
MAT1030 Diskret Matematikk Forelesning 26: Trær Roger Antonsen Institutt for informatikk, Universitetet i Oslo 5. mai 2009 (Sist oppdatert: 2009-05-06 22:27) Forelesning 26 MAT1030 Diskret Matematikk 5.
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf.!! 91851949 Eksamensdato! 15. august 2013 Eksamenstid (fra til)! 0900 1300 Hjelpemiddelkode D.
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf.!! 91851949 Eksamensdato! 15. august 2013 Eksamenstid (fra til)! 0900 1300 Hjelpemiddelkode D.
HØGSKOLEN I BERGEN Avdeling for ingeniørutdanning
 HØGSKOLEN I BERGEN Avdeling for ingeniørutdanning EKSAMEN I KLASSE LVD525 Videregående algoritmer : 3DA og 3DB DATO :. april 2005 ANTALL OPPGAVER : 4 ANTALL SIDER : 4 VEDLEGG : side HJELPEMIDLER : ingen
HØGSKOLEN I BERGEN Avdeling for ingeniørutdanning EKSAMEN I KLASSE LVD525 Videregående algoritmer : 3DA og 3DB DATO :. april 2005 ANTALL OPPGAVER : 4 ANTALL SIDER : 4 VEDLEGG : side HJELPEMIDLER : ingen
Dagens plan. INF Algoritmer og datastrukturer. Koding av tegn. Huffman-koding
 Grafer Dagens plan INF2220 - Algoritmer og datastrukturer HØSTEN 2007 Institutt for informatikk, Universitetet i Oslo Avsluttende om grådige algoritmer (kap. 10.1.2) Dynamisk programmering Floyds algoritme
Grafer Dagens plan INF2220 - Algoritmer og datastrukturer HØSTEN 2007 Institutt for informatikk, Universitetet i Oslo Avsluttende om grådige algoritmer (kap. 10.1.2) Dynamisk programmering Floyds algoritme
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2016 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2016, forelesning
INF2220 - Algoritmer og datastrukturer HØSTEN 2016 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2016, forelesning
Spenntrær, oppsummert: Kruskal: Traverserer ikke. Plukker kanter i hytt og vær Prim: Legger alltid til den noden som er nærmest treet
 Spenntrær, oppsummert: Kruskal: Traverserer ikke. Plukker kanter i hytt og vær Prim: Legger alltid til den noden som er nærmest treet 1 A B D C Prim: Kruskal: AB, BD, DC DC, AB, BD 2 0 + 1 + + n 1; antall
Spenntrær, oppsummert: Kruskal: Traverserer ikke. Plukker kanter i hytt og vær Prim: Legger alltid til den noden som er nærmest treet 1 A B D C Prim: Kruskal: AB, BD, DC DC, AB, BD 2 0 + 1 + + n 1; antall
