Prosjektering av betongkonstruksjoner. Jan Arve Øverli. Institutt for konstruksjonsteknikk NTNU. Kursinnhold. Bruddgrensetilstand
|
|
|
- Hallvard Hagen
- 8 år siden
- Visninger:
Transkript
1 Eurokode 2: Prosjektering av betongkonstruksjoner Jan Arve Øverli Institutt for konstruksjonsteknikk NTNU 1 Kursinnhold Introduksjon Materialer og bestandighet Bruddgrensetilstand Moment og aksialkraft Skjærkraft og torsjon Slanke søyler Forankring Bruksgrensetilstand 2 1
2 Litteratur-hjelp-mm Svein Ivar Sørensen har skrevet lærebok Mye nyttig informasjon og litteratur finnes: Utenlandske lærebøker finnes NB! Alle land har sin egen måte å dimensjonere og tolke Eurokode på Eurokoder forutsetter bruk av nasjonalt bestemte parametere som bestemmes av hvert enkelt land Vær kritisk til bruk av dimensjoneringsprogram som er oppdatert til Eurokode 2 4 2
3 EUROKODER, hvorfor?? Eurokodene er primært laget av hensyn til fri flyt ved handel med byggevarer og dokumentasjon av Byggevaredirektivets essensielle krav Byggevarers egenskaper og dokumentasjon 1. Generelle krav Enhver byggevare som omfattes av Byggevaredirektivet, Rdir. 1989/106/EØF om tilnærming av medlemsstatenes lover og forskrifter vedrørende byggevarer, skal ha slike egenskaper som, når de er forsvarlig benyttet, medvirker til at byggverk tilfredsstiller de grunnleggende krav til -mekanisk motstandsevne og stabilitet brannsikring Eurokodene kan også brukes til prosjektering av byggverk, det er imidlertid ikke et vesentlig anliggende for kommisjonen, men for de fleste av oss andre 5 Eurokode historie 6 3
4 Norsk betongstandard historie 1893 Ingeniørkaptein Kolderups lærebok 1926 Forskrift for betongarbeider 1939 NS 427, Regler for utførelse av arbeider i armert betong 1963 NS 427 A, Del 1 til Del NS 3473, Første utgave 1974 NS 3474, Materialer, Utførelse og kontroll 1986 NS 3420 del L erstatter NS NS 3473, Hovedrevisjon, 3. utgave 2001 NS-EN 206-1, Betong med NA erstatter NS 3420 del L 2003 NS 3465, Utførelse av betongkonstruksjoner, erstatter NS3420 Del L 2003 NS 3473, 6. utgave 2008 NS-EN med NA 2010 NS 3473 og NS 3465 trekkes tilbake 2010 NS-EN Utførelse av betongkonstruksjoner med NA 7 Utvikling antall sider
5 Eurokoder 9 Betongstandarder Construction Products Directive (CPD) + National legislation Eurocode Actions on structures TC250/SC1 Eurocode Basis of structural design TC250 Eurocode Design of concrete structures TC250/SC2 EN Execution of concrete structures TC104/SC2 EN Concrete TC104/SC1 ISO 6934 or ETA Tendons & PT kits EN reinforcement EN xx or ETA Prefabricated elements TC229 Product and testing standards TC104/SCs and WGs Product and testing standards Product and testing standards Product and testing standards 10 5
6 NS-EN :2004+NA:2008 Eurokode 2: Prosjektering av betongkonstruksjoner Del 1-1: Allmenne regler og regler for bygninger NS-EN :2004+NA:2008 Del 1-2: Brannteknisk dimensjonering Del 2: Betong bruer Beregnings- og konstruksjonsregler Del 3: Siloer og beholdere 11 Innhold Eurokode 2: Del 1-1 (1) Kapittel 1: Generelt Kapittel 2: Grunnlag for prosjektering Kapittel 3: Materialer Kapittel 4: Bestandighet og overdekning for armering Kapittel 5: Konstruksjonsanalyse Kapittel 6: Bruddgrensetilstander Kapittel 7: Bruksgrensetilstander Kapittel 8: Armeringsregler for armering og spennarmering Kapittel 9: Konstruksjonsregler Kapittel 10: Tilleggsregler for prefabrikerte betongelementer Kapittel 11: Konstruksjoner av betong med lett tilslag Kapittel 12: Uarmerte og lett armerte betongkonstruksjoner 12 6
7 Innhold Eurokode 2: Del 1-1 (2) Tillegg A: Justering av partialfaktorer for materialer Tillegg B: Kryp og svinntøyning Tillegg C: Materialegenskaper for armering til bruk med denne Eurokoden Tillegg D: Detaljert beregningsmetode for relaksasjonstap i spennstål Tillegg E: Forventede fasthetsklasser for bestandighet Tillegg F: Uttrykk for beregning av strekkarmering i planet Tillegg G: Samvirke mellom grunn og konstruksjon k Tillegg H: Globale andre ordens effekter i konstruksjoner Tillegg I: Beregning av flatdekker og veggskiver Tillegg J: Konstruksjonsregler for spesielle eksempler 13 Prinsipper (P) og anvendelsesregler 14 7
8 Nasjonalt Tillegg (NA) som angir Nasjonalt Bestemte Parametre (NDP) Totalt 121 bestemmelser med nasjonale valg 15 Ordet bør i EK 2 I Prinsipper brukes skal (shall) I anvendelsesregler brukes bør (should) Når ordet bør brukes skal det leses som skal!! 16 8
9 Merknader (Notes) Anbefalte verdier for Nasjonalt Bestemte Parameter (NDP) Notest 17 Forskjeller EK2-NS3473 Materialfaktorer Trykk er gitt med positive verdier Andre betegnelser og notasjoner, indekser Krav til nedbøyning Ingen 50ø som forankringslengde Beregning av skjærarmering Beregning av slanke søyler Maks krav til armeringsmengde Ligner mer ei håndbok 18 9
10 Symboler for dimensjonerende verdier Laster: Lastvirkning: Kapasiteter: F d = f F rep = f F k N Ed,,V Ed,M Ed N Rd,,V Rd,M Rd (M M f M Ed ) (V cd V Rd ) p d M Ed
11 21 11
12 Eurokode 2: Materialer og bestandighet 1 Fasthetsklasser betong Fasthetsklasser er knyttet til sylindertrykkfasthet f ck med prefiks B EK2, 3.1.2, Tabell 3.1 f ck (MPa) f ck,cube (MPa) f cm (MPa) f ctm (MPa) 1,9 2,2 2,6 2,9 3,2 3,5 4,1 4,4 4,6 f ctk, 0,05 (MPa) 1,3 1,5 1,8 2,0 2,2 2,5 2,9 3,1 3,2 f ctk, 0,95 (MPa) 2,5 2,9 3,3 3,8 4,2 4,6 5,3 5,7 6,0 E cm (GPa) c1 ( ) 1,9 2,0 2,1 2,2 2,25 2,3 2,45 2,6 2,7 cu1 ( ) 3,5 3,0 2,8 c2 ( ) 2,0 2,3 2,4 cu2 ( ) 3,5 2,9 2,7 n 2,0 1,6 1,45 c3 ( ) 1,75 1,9 2,0 cu3 ( ) 3,5 2,9 2,7 2 1
13 Fasthet og deformasjonsegenskaper EK2, 3.1.2, og f f f f E cm ctm ctk,0,05 ctk,0,95 cm f ck 8(MPa) 2/3 0,30 fck B50 0,7 f 1, 3 f ctm ctm 0,31 c1 cm cm f 0,3 cm cm 22 /10 f i MPa 0,7 f f i MPa 3 Kryp EK2, cc c (, t0) E c Ligninger for utvikling av kryp over tid står i EK2, Tillegg B 4 2
14 Eksempel på kryptall etter lang tid B35, t 0 =5 døgn, h 0 =2A c /u=500mm B =2,3 5 Svinn EK2, 3.1.4(6) cs = cd + ca cd svinntøyning ved uttørkning ca autogene svinntøyning 6 3
15 Svinn EK2, Tabell 3.2 uttørkningssvinn [ ], cd0, cd = k h cd0 f ck /f ck,cube Relativ fuktighet RH (%) (MPa) / / / / / Ligninger for uttørkningssvinn og utvikling av svinn over tid står i EK2 og i Tillegg B 7 EK2, (1) Materialfaktorer Tabell NA.2.1.N Materialfaktorer for bruddgrensetilstand Dimensjonerende situasjoner Vedvarende og forbigående c for betong s for armeringsstål s for spennstål 1,5 1,15 1,15 Utmatting 1,5 1,15 1,15 Ulykkessituasjon 1,2 1,0 1,0 EK2, NA (2) Materialfaktorer for betong og armering i bruksgrensetilstand settes lik 1,0 der ikke annet er oppgitt i standarden 8 4
16 Dimensjonerende fastheter EK2, f f f / dimensjonerende trykkfasthet cd cc ck c f / dimensjonerende d strekkfasthet ctd ct ctk,0,05 c B35 f f cd ctd 0,8535 /1,5 19,8 MPa, NS3473: f =19,5 MPa 0,852,2 /1,5 1,25 MPa, NS3473: =1,43 MPa EK2, f / yd yk s s f E 200 GPa cd f td B500NC f yd 500 /1, MPa, NS3473: f =400 MPa sd 9 Arbeidsdiagram betong ved dimensjonering EK2, Figur 3.3 EK2, 3.1.7(1) n c c fcd 1 1 for 0 c c2 c2 f for c cd c2 c cu2 10 5
17 Forenklet arbeidsdiagram betong EK2, 3.1.7(2), Figur Arbeidsdiagram ved konstruksjonsanalyser EK2, 3.1.5(1), Figur
18 Betong med forhindret tverrutvidelse EK2, Fasthet og E-modul før 28 døgn EK2, f () t f () t 8 (MPa) 3t 28 døgn ck cm f ( t) f t 28 døgn ck ck f () t () t f cm cc cm 28 cc ( t) exp s1 s avhengig av sementtype t EK2, E () t ( f ()/ t f ) E 0,3 cm cm cm cm 14 7
19 Utvikling av fasthet og E-modul 1 (t)/fck Ecm(t)/Ecm fck( 0,8 0,6 0,4 02 0,2 Fasthet E-modul Dager 15 Arbeidsdiagram armering EK2, 3.2.7(2), Figur 3.8 yd =f yd /E s =2,17 EK2, NA, 3.2.7(2) B500NC ud = 3% og k=1,
20 EK2, 3.3.6(1), Figur 3.9 Spennstål - fasthet 17 Arbeidsdiagram spennstål EK2, 3.3.6(7), Figur 3.10 EK2, NA, 3.3.6(7) ud = max{ 0,01 ; 0,4 uk } 18 9
21 Spennstål - egenskaper EK2, 3.3.2(7), relaksasjonstap pr 5, e pi 0,75(1 ) 6,7 t 5 EK2, 3.3.6(2) og (3), Dimensjonerende E-modul E p = 205 GPa for tråd og stenger E p = 195 GPa for tau 19 Bestandighet EK2, 4.1(P) En bestandig konstruksjon skal oppfylle krav til brukbarhet, styrke gjennom dimensjonerende d levetid. Metode for påvisning går på overdekning, EK2, 4.4. EK2, (2) og (1) Nominell overdekning skal være angitt på tegningene. c nom = c min + c dev = c min + 10mm 20 10
22 Betongoverdekning Viderefører dagens krav i NS3473 som er avhengig av: Eksponeringsklasse (Bestandighetsklasse) Dimensjonerende levetid ( 50 år og 100 år) Ståltype (Vanlig stål og spennarmering) EK2, Minste overdekning c min Sikker overføring av krefter ved hjelp av heft Beskyttelse av stål mot korrosjon Tilfredsstillende brannmotstand (NS-EN ) c min =max{c min,b ; c min,dur +c dur, c dur,st - c dur,add ; 10mm} 21 Minste overdekning av hensyn til heft EK2, NA (3), Tabell NA
23 Minste overdekning av hensyn til bestandighet for armeringsstål EK2, NA (5), Tabell NA.4.4N 23 Minste overdekning av hensyn til bestandighet for spennstål EK2, NA (5), Tabell NA.4.5N 24 12
24 Eurokode 2: Bruddgrensetilstand Moment og aksialkraft 1 Lastfaktorer i bruddgrensetilstand NS-EN 1990 Eurokode: Grunnlag for prosjektering av konstruksjoner k Tabell NA.A.1.2(B) Dimensjonerende verdier for laster (STR/GEO) (Sett B) 1,35 1,0 1,05 1,05 1,2 1,0 1,5 1,05 2 1
25 Lastkombinasjoner i bruddgrensetilstand NS-EN 1990 Eurokode , Lastkombinasjoner for vedvarende eller forbigående situasjoner I Norge skal ligning (6.10a) og (6.10b) brukes G " " P" " Q " " Q G, j k, j p Q,1 0,1 k,1 Q, i 0, i k, i j1 i1 G " " P " " Q " " Q G, j k, j p Q,1 k,1 Q, i 0, i k, i j1 i1 3 Bøyning med eller uten aksialkraft EK2, 6.1.2(P) Plane tverrsnitt forblir plane Full heft mellom betong og armering Spennings- og tøyningsegenskaper etter EK2, (betong) og (armering) Det ses bort fra betongens strekkfasthet Minimum eksentrisitet e 0 =max( 20mm, h/30 ) 4 2
26 Tøyningsbegrensninger EK2, figur 6.1 A maksimal ståltøyning B maksimal kanttøyning i betong C maksimal trykktøyning i tyngdepunktet av tverrsnittet 5 Rektangulær spenningsfordeling EK2, ,8 1,0 Tøyninger for fasthetsklasser B50 Trykkspenningsforløp, EK2,3.1.7 Tilnærmet trykkspenningsforløp 0,8 ( fck -50)/400 for fasthetsklasser > B50 1,0 ( fck -50)/
27 Ren bøyning bjelker og plater Ingen endring i beregningsmodellene som brukes for kapasiteter og dimensjonering 2 M 0,8 10, 4 f bd for fasthetsklasser B20-B50 ( x/ d) Rd cd f bd E A E A 0, for overarmert tverrsnitt < 2 cd s s cu s s cu s yd f bd f A 0, for underarmert tverrsnitt cd yd s s yd Normalarmert tverrsnitt, = 2, fasthetsklasser B20-B45, B500NC M 0, 275 f bd Rd cd M Ed M Ed As, z 10,17 d fyd z MRd 2 s yk 7 Momentkapasitet (1) NS3473 vs EK 2 NS3473 EK2 f cd [MPa] 19,5 19,8 B35, B500NC underarmert tverrsnitt f yd [MPa] ,458 0,490 Rd [knm] 157,6 168,5 8 4
28 Momentkapasitet (2) NS3473 vs EK 2 NS3473 EK2 f cd [MPa] 19,5 19,8 B35, B500NC overarmert tverrsnitt f yd [MPa] ,618 0,654 Rd [knm] 196,0 206,5 9 Nødvendig armering NS3473 vs EK 2 NS3473 EK2 220 mm 180 mm f cd [MPa] 17,0 17,0 B30, B500NC normalarmert tverrsnitt f yd [MPa] z [mm] 169,9 169,9 M Ed =50,0 knm/m Rd [knm] 151,5 151,5 A s [mm 2 /m]
29 Konstruksjonsanalyse EK2, 5.1.1(6) Lineær elastisk oppførsel Lineær elastisk oppførsel med begrenset omfordeling Plastisk oppførsel Ikke-lineær oppførsel 11 Geometrisk avvik (1) EK2, 5.2 Generelt på konstruksjoner (1/ 200) H N N for virkning på avstivningssystem i h m i i b a 2 / l ; H N N /2 for virkning på dekkeskive h h i i b a 0, 5(1 1 m) m H i i N a Dekkeskive N b l i /2 N a H i i /2 N b 12 6
30 Geometrisk avvik (2) EK2, 5.2(7) På enkeltstående konstruksjonsdeler Som eksentrisitet e i = i l 0 /2 e i = l 0 /400 for vegger og enkeltstående søyler Som horisontallast: H i = i N for ikke-avstivede konstruksjonsdeler H i = 2 i N for avstivede konstruksjonsdeler ikkeavstivet avstivet 13 EK2, L eff = l n + a 1 + a 2 Effektiv spennvidde 14 7
31 Dimensjonerende snitt B A M Ed M A Ed M B Ed t F Ed,sup EK2, (3) og (4) Snitt A Dersom bjelke eller plate er monolittisk forbundet med oppleggene kan dimensjonerende moment settes ved kanten av opplegget Snitt B Over et opplegg som ikke gir rotasjonsmotstand kan støttemomentet reduseres med M Ed = F Ed,sup t/8 15 T-tverrsnitt effektiv flensbredde EK2, Effektiv flensbredde bør velges basert på avstanden l 0 mellom momentnullpunktene 16 8
32 Effektiv flensbredde b eff b eff,1 b w b eff,2 b 1 EK2, (3) b b b b eff eff, i w b 1 b w b 0, 2b 0,1l 0, 2l b eff, i i 0 0 eff, i b i b b 2 b 2 17 Effektiv flensbredde NS3473 vs EK 2 Eksempel fritt opplagt bjelke b w = 0,3 m b = 4,6 m L = 10 m = 0,2 m t f NS3473: b eff =2,3 m EK 2: b eff =3,2 m b eff =2,6 m kontinuerlig 18 9
33 Omfordeling av moment EK2, 5.5(4) I kontinuerlige bjelker eller plater der forholdet mellom nabofelt er mellom 0,5 og 2, kan omfordeling av lineær elastiske momenter foretas uten kontroll av rotasjonskapasitet. cu2 )x u /d 0,7 omfordelt moment / elastisk moment Ved dimensjonering av søyler benyttes elastiske momenter uten omfordeling 19 Grenseverdier for omfordeling 35 Omfordeling [%] f ck < 55 MPa B500NC 0 0,1 0,2 0,3 0,4 0,5 x/d 20 10
34 Omfordeling i kontinuerlig bjelker/dekker Momentomfordeling 21 Eksempel dimensjonering med omfordeling B25, B500NC M Ed =230 knm 20% omfordeling 0,44 1,25(0,6 0, / ) x / d 0,8 x u M 141 mm; =0,288 Rd cu 2 2 0,8 0, ,4 0,288 14, knm u 22 11
35 Eksempel forts. M Ed > M Rd må trykkarmere For å unngå trykkarmering er det mulig å omfordele: M Rd 2 0,8 10, 4 14, M 230 knm 0,383 x 188 mm u 0, 44 1,25 x / d 0, 44 1, 250,383 0,92 u Mulig å omfordele 8 % av momentet Ed 23 Spennarmerte konstruksjoner (1) Største spennkraft, EK2, (1)P P max A p p,max min{0,8 f ;0,9 f } p,max pk p0,1k Begrensning av trykkspenninger, EK2, (5) 0,6 f ( t) c ck 24 12
36 Spennarmerte konstruksjoner (2) Tap på grunn av elastisk deformasjon, EK2, (2) j () c t Pel Ap Ep Ecm () t Tap på grunn av friksjon, EK2, (1) P ( x) P 1e max ( kx) Tidsdavhengig tap, EK2, (2) P A csr p p, csr E E 0,8 ( t, t ) A p cs p pr 0 c, QP Ecm p Ep Ap Ac 2 1 (1 z cp )[10,8 ( t, t 0)] Ecm Ac Ic 25 Moment og aksialkraft Ingen endring i beregningsmodellene. EK2, 6.1: minste samlet eksentrisitet e min = max(20mm, h/30) Nye m-n diagram må utarbeides. Diagram kan lastes ned fra Bruk av disse diagrammene forutsetter: Karakteristisk fasthet f ck A s er total symmetrisk armeringsmengde i tverrsnittet d 2 /h 26 13
37 Eksempel m-n diagram 27 M-N diagram NS3473 vs EK NS EK N [kn] B30, B500NC A s1 =A s2 =4ø M [knm] 28 14
38 Aksialkraft og bøyning om to akser (1) EK2, 5.8.9(2) og (3) Det er ikke nødvendig å ta hensyn til biaksial bøyning dersom følgende 2 betingelser er oppfylt: 1) 2) y z 2 og 2 z y ey / heq ez / beq 0, 2 eller 0, 2 e / b e / h z eq y eq b, h i 12 for et ekvivalent rektangulært t tverrsnitt eq eq, - slankhet l / i y z i, i - treghetsradius = i y z e, e M / N y z Ed Ed 0 I A 29 Aksialkraft og bøyning om to akser (2) EK2, 5.8.9(4) a M M Edz Edy 1, 0 M Rdz M Rdy For rektangulære tverrsnitt: N Ed /N Rd 0,1 0,7 1,0 a 1,0 1,5 2,0 a N Rd =A c f cd + A s f yd For sirkulære tverrsnitt: a=2,
39 Biaksial bøyning for rektangulært tverrsnitt 31 Armeringsregler c nom a v c nom EK2, NA.8.2(2) a h a h max{ 2 ø; d g + 5 mm; 20 mm } a v max{ 1,5 ø; d g + 5 mm; 20 mm } < 32 mm 32 16
40 Konstruksjonsregler bjelker og plater EK2, 9.2 og 9.3 A s,min = 0,26 (f ctm /f yk ) b t d 0,0013 b t d A s,max = 0,04 A c Underkantarmering ved ende- og innvendige opplegg bør være 0,25 av armeringsareal i felt Delvis innspente opplegg som antas frie i beregningen skal dimensjoneres for et støttemoment 0,15 feltmoment for bjelker og 0,25 feltmoment for plater 33 Minimumsarmering i plater NS3473 vs EK Minimumsa armering [mm 2 /m] NS3473 h=500mm EK2, h=500mm NS3473, h=200mm EK2, h=200mm Betongfasthet, f ck 34 17
41 Konstruksjonsregler bjelker EK2, 9.2 Nødvendig di strekkarmering i flensen av et T-tverrsnitt skal fordeles i hele den effektive flensbredden Trykkarmering bør avstives med tverrarmering med s < 15ø trykk 35 EK2, 9.3 Konstruksjonsregler plater s max,slabs min{ 3h ; 400mm } for hovedarmering s max,slabs min{ 3,5h ; 450mm } for fordelingsarmering i Områder med konsentrerte laster og max moment: s max,slabs min{ 2h ; 250mm } for hovedarmering s max,slabs min{ 3h ; 400mm } for fordelingsarmering Tverrarmering i enveisplater 20% av hovedarmering I fritt opplagte plater bør halvparten av feltarmeringen fortsette frem til opplegget 36 18
42 Konstruksjonsregler søyler(1) EK2, 9.5 Ø h 4b min 10mm 0,01Ac As,min max N 0, 2 / 0,5 Ed Af c cd fyd f yd A,max 0,08 A inkludert skjøtt armering i omfarskjøter s c 37 Konstruksjonsregler søyler(2) EK2, s cl,max t 15ØØ lengde min hmin 400mm s cl,tmax s cl,tmax reduseres med en faktor 0,6 : I en høyde h over og under en bjelke eller plate Ved omfaringsskjøter dersom Ø>14mm. Minimum 3 bøyler fordelt langs omfaringslengden 150mm 38 19
43 Minimumsarmering i søyler NS3473 vs EK ] mumsarmering [mm 2 Mini NS EK2 NA 200 EK Betongfasthet, f ck 39 20
44 Eurokode 2: Bruddgrensetilstand Skjærkraft og torsjon 1 Skjær - bruddformer Bøyestrekkbrudd Trykkbrudd Hovedstrekkbrudd Flyt i skjærarmering 2 1
45 Skjærkapasitet, EK2, 6.2 Eurokode 2 skiller på konstruksjonsdeler med og uten beregningsmessig behov for skjærarmering V Rd,c V Rd,s V Rd,max - dimensjonerende kapasitet uten skjærarmering - dimensjonerende verdi av skjærkraften som kan opptas av skjærarmering ved flytning - dimensjonerende verdi av største skjærkraft som konstruksjonsdelen kan bære, begrenset av kapasiteten for trykkbrudd 3 Skjærstrekkapasitet EK2, 6.2.2(1) Konstruksjonsdeler uten behov for beregningsmessig skjærarmering 1/3 VRd, c CRd, c k (100 l fck ) bw d k1 cp bw d med en minste verdi VRd, c vmin bw d 3/2 1/2 vmin 0,035 k fck, NB! Trykkfeil i NA: k 1 2,0 d ASl l 0,02 bd w k2 CRd, c, k2 0,15 eller 0,18 avhengig av størrelse på tilslag c 4 2
46 Skjærkapasitet NS3473 vs EK 2 (1) Skjærkapasitet betongbidrag NS3473 EK2, k2=0,15 EK2, k2=0, Betongfasthet, f ck 5 Skjærkapasitet NS3473 vs EK 2 (2) Skjærkapasitet betongbidrag NS3473 EK2, k2=0,15 EK2, k2=0, ,005 0,01 0,015 0,02 0,025 Armeringsforhold 6 3
47 Skrårissbrudd EK2, 6.2.2(2) Forspente konstruksjonsdeler uten skjærarmering og bøyeriss fctd N N 2 4 V I Rd, c og N 1 cp Ibw Ib V f f S w 2 Rd, c ctd 1 cp ctd 7 Skjærtrykkapasitet EK2, 6.2.2(6) Konstruksjonsdeler uten beregningsmessig behov for skjærarmering V b d f Rd,max 0,5 w cd fck 0, B30 0,528 V 0,26b d f NS3473, V 0,3b z f ccd w cd Rd,max w cd 8 4
48 Konstruksjonsdeler med behov for skjærarmering (1) NS 3473 k a A s V 0,3 f bdk c bd fsd Asv Vsd z s cd td v V V V Rd cd sd 9 Konstruksjonsdeler med behov for skjærarmering (2) EK2, Dersom det er behov for skjærarmering, V Ed > V Rd,c, skal betongbidrag til skjærkapasiteten V Rd,c = 0, dvs at hele skjærkraften tas opp av skjærarmeringen Skjærkapasiteten med skjærarmering er V Rd = V Rd,s + V ccd + V td 10 5
49 Skjærarmering Dimensjonering med skjærarmering er basert på en fagverksmodell. Vinkelen på betongtrykkdiagonalen g velges innenfor EK2, NA6.3.2(2) 1,0 cot 2,5 ( 45 21,8 ) 11 Skjærstrekkapasitet EK2, 6.2.3(4) For konstruksjonsdeler med skrå skjærarmering er skjærkapasiteten Asw VRd, s z fywd (cot cot ) sin s z 0,9 d Skjærarmeringens kapasitet er størst for minst mulig vinkel på betongtrykkdiagonalen, cot = 2,5 ( 21,8 ) 12 6
50 Skjærtrykkapasitet EK2, 6.2.3(4) For konstruksjonsdeler med skrå skjærarmering er skjærtrykkapasiteten (cot cot ) VRd,max cw bw z1 fcd 2 (1 cot ) cw 1,0 når aksialkraft = 0, ellers gitt i NA.6.2.3(3) fck , Skjærtrykkapasiteten er størst for størst mulig vinkel på betongtrykkdiagonalen, cot = 1,0 ( = 45 ) 13 Nødvendig skjærarmering For konstruksjonsdeler med vertikal skjærarmering blir nødvendig skjærarmering og skjærtrykkapasiteten EK2, 6.3.2(3) Asw VEd s fywd zcot 1 VRd,max bw z 1 fcd 0,5bw z1 fcd sin 2 (cot tan ) 14 7
51 Begrensning av skjærarmering Det er en øvre begrensning på vinkelen til trykkdiagonalen på 45. Dette gir en begrensing på tverrsnittsarealet av skjærarmeringen. EK2, 6.3.2(3) A sw,max b w f s ywd f cd 15 Dimensjonering med fagverksmodell (1) Finn dimensjonerende skjærkraft V Ed I de fleste tilfeller ll er cot = 25 2,5, beregn V Rd,max = 0,31 b w d (1 f ck /250) f cd Hvis V Rd,max V Ed beregn nødvendig skjærarmering A sw / s = V Ed / ( 2,25 d f ywd ) Hvis V Rd,max V Ed beregn vinkelen for V Ed = 0,5 sin -1 [ V Ed / ( 0,27 d b w f cd (1-f ck /250))] 16 8
52 Dimensjonering med fagverksmodell (2) Hvis cot < 1 ( ) bør tverrsnittet endres, f ck økes eller lasten reduseres Hvis cot 1 beregn nødvendig skjærarmering A sw / s = V Ed / ( 0,9 d f ywd cot) 17 Skjærdimensjonering NS3473 vs EK 2 NS3473 EK2 cot V Rd,c [kn] V Rd,max [kn] B30, B500NC V Ed =179 kn sw /s [mm 2 /m]
53 Minimum skjærarmering for bjelker EK2, Krav til minimum skjærarmering i bjelker w,min 0,1 yk ck Asw A f sw ck w 0,1 sin sb sin s f w f f yk Krav til største senteravstand i lengderetning sl,max 0, 6 h'(1 cot ) 19 Minimum skjærarmering i bjelker NS3473 vs EK imumarerning [mm 2 /m] Min NS EK2 NA EK Betongfasthet, f ck 20 10
54 EK2, Skjærarmering for plater Ingen krav til minimum skjærarmering i plater, EK2621(4) EK2,6.2.1(4) Ved behov for skjærarmering gjelder formlene og minimum skjærarmering som for bjelker Plater med skjærarmering bør være minst 200mm Hvis V Ed 1/3 V Rd,max kan all skjærarmering være oppbøyde stenger Krav til største senteravstand i lengderetning s max = 0,75 d (1+cotfor bøyler i lengderetning s max = d for oppbøyde stenger i lengderetning s max = 1,5 d for skjærarmering i tverretning 21 Reduksjon av last nær opplegg EK2, 6.2.2(6) og 6.2.3(8) Når a v 2d kan bidraget fra lasten til skjærkraften reduseres med faktoren = a v / 2d innenfor en avstand 0,5d a v 2d fra oppleggskant for kontroll av skjærstrekkbrudd. For a v 0,5d brukes a v = 0,5d 22 11
55 Reduksjon av jevnt fordelt last nær opplegg q Ed 0,5d 2d q Ed VEd, red VEd VEd VEd 0,94qEd d EK2, 6.2.1(8), V Ed = q d 23 Skjærkraft fra konsentrerte laster EK2, 6.4 Kritisk kontrollsnitt er avstand 2 d fra belastet flate Kontrollsnitt har avrundende hjørner Skjærkapasiteten er summen av betongbidrag og skjærarmeringsbidrag Fagverksmodellen brukes ikke 24 12
56 25 Skjærkraft ved konsentrerte laster EK2, Kontroll av skjærkraftkapasitet påvises ved søylens kant og ved kritisk kontrollsnitt Ved behov for skjærarmering kontrolleres enda et snitt u out,ef der det ikke lenger er behov for skjærarmering Kapasiteten er basert på dimensjonerende skjærspenninger v Ed VEd u d M Ed u1 1k V W i Ed
57 Skjærkraft ved eksentrisk konsentrerte laster (1) EK2, 6.4.3(3) Innvendig rektangulær søyle 2 c1 2 W cc 4c d 16d 2 dc c 1 /c 2 0,5 1,0 2,0 3,0 K 0,45 0,60 0,70 0,80 27 Skjærkraft ved eksentrisk konsentrerte laster (2) EK2, 6.4.3(4) Kant og hjørne søyler u u 1 1 k epar u 1* W 1 1 u1* u 28 14
58 Skjærkraft ved eksentrisk konsentrerte laster(3) EK2, 6.4.3(6) For konstruksjoner der stabiliteten ikke er avhengig av rammevirkningen ik i mellom dekker og søyler og tilstøtende felt ikke avviker mer enn 25% i lengde, kan tilnærmes med 29 Skjærkapasitet uten skjærarmering ved konsentrerte laster EK2, v C k(100 f ) v 1/3 Rd, c Rd, c l ck min v 0,035k f min l lz ly 3/2 1/2 ck 30 15
59 Skjærkapasitet med skjærarmering ved konsentrerte laster EK2, Der det er behov for skjærarmering, v Ed v Rd.c, beregnes skjærkapasiteten etter vrd, cs 0,75vRd, c 1,5 ( d / sr ) Asw fywd, ef (1/ ( u1d) sin f 250 0, 25d f ywd, ef ywd v V Ed Ed u0 d v Rd,max v 0,4 f 1,6 v u / ( u ), EC2, NA Rd,max cd Rd, c Skjærarmering ved konsentrerte laster EK2, 6.4.5(4) Det ytterste snittet med skjærarmering plasseres i en avstand mindre enn d innenfor et kontrollsnitt u out (u out,ef ) u out,ef = V Ed / (v Rd,c d) 32 16
60 Minimum skjærarmering ved konsentrerte laster EK2, Asw,min (1, 5 sin cos ) / ( sr st ) 0, 08 Ytre snitt for skjærarmering Ytre kontrollsnitt d f f yk ck 1,5d (2d hvis >2d fra søyle) 0,5d 0,75d d Snitt A-A 33 Torsjon EK2, 6.3.1(1)P Der den statiske likevekten for en konstruksjon er avhenger av torsjonskapasiteten, skal det gjennomføres en fullstendig dimensjonering for torsjon. EK2, 6.3.1(3) Torsjonskapasiteten beregnes for et antatt lukket hulltverrsnitt. h u k t ef t ef A bh u 2( b h) b 34 17
61 Riss-torsjonsmoment Spenninger TEd 2 A t k ef T 2 f A t Rd, c ctd k ef Riss 35 Torsjon - trykkbrudd EK2, 6.3.2(4) Største kapasitet for en konstruksjonsdel utsatt for torsjon og skjærkraft er begrenset av betongtrykkstavens kapasitet TRd,max 2 fcd Ak tef sincos T T Ed Rd,max V V Ed Rd,max 1,
62 Torsjon nødvendig armering Torsjonsarmering er nødvendig når T Ed T, Rd c EK2, 6.3.2(3) Nødvendig lengdearmering for torsjon Asl fyd TEd u 2 A k k cot Nødvendig bøylearmering for torsjon Asw TEd tan s 2A f k ywd 37 Torsjonsdimensjonering NS3473 vs EK 2 B35, B500NC V Ed =100 kn T Ed =20 knm NS3473 EK2 cot T Rd,max [knm] V Rd,max [kn] T T Ed Rd,max V + V Ed Rd,max 0,55 0,52 T Rd,c [knm] 13,4 14,44 sl [mm 2 ] sw /s [mm 2 /m]
63 Torsjon - minimumsarmering EK2, 6.3.2(5) For rektangulære massive tverrsnitt kun minimumsarmering dersom TEd VEd 1, 0 T V Rd, c Rd, c EK2, Bestemmelsen for minimum skjærearmering gjelder. Vanligvis tilstrekkelig for torsjonsbøyler Største avstand i lengderetning: s < u/8 s < minste tverrsnittsdimensjon
64 Eurokode 2: Bruddgrensetilstand Slanke søyler 1 Første og andre ordens lastvirkning 2 1
65 Beregning av slanke søyler Basert på lineær 1.ordens teori Effekten av aksialkraften på momentet beregnes separat M total = M 0 + M 2 Egner seg for dimensjonering Lineær 2.ordens teori Tar hensyn til deformasjoner i likevektsberegningen Betong er lineært elastisk Må være samsvar mellom stivheten i beregningen av momenter og resultatet fra dimensjoneringen Ikke-lineær analyse Både geometri og materialer er ikke-lineært En kapasitetskontroll, dvs. må vite armeringsmengde 3 Slankhet 4 2
66 Normalisert slankhet EK2, NA n n k a i n 1 2k N f Ed yd As ; f A f A 2 a cd c cd c is i Ic ; A c ; k kan normalt settes lik 1,0 i s a Is A L0 ; L0 er knekklengden i s 5 Nedre slankhetsgrense (1) EK2, NA (1) Det kan ses bort fra effekten av 2.ordens lastvirkning dersom n n,lim For trykkstaver med en ende som er forskyvelig og for uforskyvelige staver med tverrlast er n,lim 13 A 1, 25 A 1 1 0,2 ef 6 3
67 Nedre slankhetsgrense (2) For trykkstaver uten tverrlast og uforskyvelige ender n,lim 13 2 r m A r m = M 01 /M 02 er forholdet mellom tallmessig største og minste stavendemoment r m = 1,0 hvis N Ed h / 20 > M 02 7 Øvre slankhetsgrense EK 2 gir ingen øvre slankhetsgrenser som ikke skal overskrides, for å unngå at trykkstaven blir så slank at det er risiko for stabilitetsbrudd (knekking) Bruk kravene fra NS3473 som en kontroll 45 n k a 8 4
68 EK2, 5.8.4(2) Kryp Kryp ivaretas på en forenklet måte ved hjelp av et effektiv kryptall ef t M M 0, t 0 M M 0Eqp 0Ed, er endelig kryp etter EK2, Eqp 0Ed er 1.ordens moment for tilnærmet permanent last i bruksgrensetilstand er 1.ordens bøyemoment i bruddgrensetilstand 9 Krypgrense EK2, 5.8.4(4) Det kan ses bort fra effekten av kryp, ef =0, dersom 2, t 0 75 M 0Ed h N Ed 10 5
69 Beregningsmetoder EK2, Generell metode basert på en andre ordens ikkelineær analyse, EK2, Metode basert på nominell stivhet, EK2, Metode basert på nominell krumning, EK2, Metode basert på nominell krumning EK2, M M M M N e N e Ed 0Ed 2 0Ed Ed 2 Ed min M 0Ed er første ordens moment inkludert formfeil e L 0 r c c = 10 for konstant tverrsnitt 12 6
70 N Nominelt moment Kapasitetskurve 1. ordens forløp Stabilitetsbrudd N Ed Ekvivalent stabilitetsbrudd M 2 M 0Ed M Ed M 13 EK2, Kr K r r 0 Nominell krumning 1 yd f ; yd r 0, 45d E K r nu n n n u bal 0 1 yd s N As f Ed yd n ; nu 1 ; ; nbal 0,4 f A A f K cd c c cd fck 1 ef 1 ; 0,
71 Krumningsvariasjon 1 1 Kr r r yd r 0, 45d 15 k r 16 8
72 Ekvivalent 1.ordens moment EK2, For søyler uten tverrlast M C M 0e m 02 M 01 Cm 0,6 0, 4 0, 4 ; M M M M M M M N e Ed 0Ed 2 0Ed Ed 2 17 Dimensjonerende totalmoment (1) Uforskyvelig søyle M 02 M 02 M Ed M Ed M 01 M 01 Enkeltkrum Dobbeltkrum 18 9
73 Dimensjonerende totalmoment (2) Forskyvelig søyle M 02 M 2 M Ed M Knekklengder enkeltstående søyler EK2, (2), Figur 5.7 l 0 = 0 l 20 10
74 Knekklengder rammer (1) EK2, Basert på relative rotasjonsfleksibiliteter Avstivede konstruksjonsdeler: k 1 k 2 0 0, , 45 k 0,45 k 1 2 Ikke-avstivede konstruksjonsdeler k1 k 2 k 1 k 2 0 max 110 ; 1 1 k1k2 1k1 1k2 21 Knekklengder rammer (2) k 1,2 EI L M 1,2 Søylestivhet Tilknyttete bjelke + søylestivheter 1,2 Søyle- og bjelkestivheter = c EI/L 22 11
75 Knekklengder rammer (3) NS3473 Basert på relative rotasjonsinnspenningsgrad S 1 j c K s Rj 1/ 1 ; j 1,2 EI c EI / L S 1 sk b b j c L S j Avstivede konstruksjonsdeler med c=4,8: 2 Lj Rj 0 ; ,1 11 R 0,90 9 R maks L R R Ikke-avstivede konstruksjonsdeler med c=2,4: j j R1R2 L R1R2 min L R R RR ; R 23 Eksempel B45 B500NC h = 0,8h N Ed =4173 kn 24 12
76 I bjelke I søyle 3 0, 40,5 4, , 4 3 2, ,13 / 6 Knekklengde 3 ka 0, ,54,17/5 2,13 / 6 kb 0, ,54,17/8 0, 283 0, , , 72 0, 45 0, 283 0,45 0, 454 L L0,728 5,76m 0 0 NS3473 gir 0 =0,70 25 Bestemmelse av kryptall etter lang tid B45, t 0 =5 døgn, h 0 =2A c /u=200mm B45 =2,
77 1. ordens momenter EK2, , Utilsiktet eksentrisitet e i = L 0 /400 = 5760/400 = 14,4 mm M i = ,0144 = 60 knm M 0A = M 1A + M i = 82 knm M 0B = M 1B + M i = 160 knm 27 L0 L ,9 i 0, 4 3 NEd n 1, 02 2 f A 25,5 400 cd c fyd As , 21 2 f A 25,5400 k a cd c 2 2 Slankhet is h'/2 i h / ,4 12 1, (EK2foreslår 1,0) 10) n 1, 02 n 49,9 37,4 12k 121,920,21 a 28 14
78 Slankhetsgrense M A ef 0Eqp, 0 2, 3 0, 5 1,15 t M 0Ed 1,25 1, 25 1, ,2 10,21,15 ef r M 82 0 A m M 0B 160 n,lim 0,51 r ,51 19, 4 m A 37, 4 søyla er slank n n,lim ordens utbøying 1 1 Kr K r r yd 0, ,3410 mm r 0,45d 0,45360 u bal 5 1 nu n 10,211,02 Kr 0,24, valgt 4Ø25 som armering n n 1, 21 0, ,9 K 1 ef 1 (0,35 ) 1,1515 1, ,241,281,3410 4,1210 mm r L e2 4, ,7 mm r
79 Dimensjonerende moment C M m 0,6 0, 0, ,4 0, M M C M M 0, , knm Ed m 02 2 M Ed 187 e d 45 mm > emin max{20mm; h/30} N 4173 Ed M ed 45 mm > e0 39 mm NEd Nødvendig armering N Ed = 4173 kn og M Ed = 187 knm gir nødvendig armering A S = 2880 mm 2 K r faktoren i 1/r ble beregnet med A S = 1964 mm 2 i n u Nytt dimensjonerende moment med A S =2880 mm 2 ny n u K r =0,32 1/r e 2 M 2 M Ed = 206 knm A S = 3168 mm 2 K r =0,
80 33 17
81 Eurokode 2: Bruddgrensetilstand Forankring 1 Forankringsbrudd 2 1
82 Forankring EK2, 8.4 Sørge for sikker overføring av krefter til betongen Unngå langsgående riss Unngå avskalling Forankringskapasiteten er avhengig av Overflateegenskaper til armeringsstangen Armeringsform Betongens strekkfasthet Overdekning Avstand mellom armeringsstenger Tverrarmering og trykk i tverretning 3 Forankring av lengdearmering, EK2 8.4 EK2, Figur 8.7, forankringsmetoder Kroker bidrar ikke til forankring av trykkarmering 4 2
83 Basis kraftinnføringslengde, EK2, F 0 L f 2 4 L 0, 25 / f x brqd, bd sd b, rqd sd bd 5 Dimensjonerende heftfasthet EK2, 8.4.2(2) For kamstenger: f bd = 2, f ctd f ctd = 0,85 f ctk,0,05 / c, begrenset til verdien for B avhengig av heftforhold, 1,0 eller 0,7 2 - avhengig ggav stangdiameter, 1,0 for ø 32 mm 2 Ved prosjektering betyr dette at: f bd = 2,25 f ctd 6 3
84 Heftbetingelser 7 Dimensjonerende forankringslengde (1) EK2, 8.4.4(1) l bd = l b,rqd l b,min ,7 l b,min max{0,3 l b,rqd ; 10ø; 100mm} forankringer i strekk l b,min max{0,6 l b,rqd ; 10ø; 100mm} forankringer i trykk Verdier av koeffisientene 1, 2, 3, 4 og 5 er gitt i EK2, Tabell 8.2 avhengig av om armeringsstangen er i trykk eller strekk. 8 4
85 Dimensjonerende forankringslengde (2) Påvirkningsfaktor Type forankring Armeringsstang Strekk Trykk 1 Stengenes form Rett 1,0 1,0 Ikke rett 0,7 1 1,0 2 Betong- overdekning Rett 0,7-1 1,0 Ikke rett 071 0, ,0 3 Tverrarmering Alle typer 0,7-1 1,0 4 Sveist tverrarmering Alle typer 0,7 0,7 5 Trykk i tverretning Alle typer 0, Dimensjonerende forankringslengde (3) EK2, 8.4.4(2) Forenklet kan forankringslengden i strekk settes lik: l b,eq = 1 l b,rqd EK2, Figur
86 Dimensjonerende forankringslengde (4) B30, overdekning 25mm forankringslengde l bd Heft betingelser Strekkarmering, diameter Trykkarmering Rett stang 2 < 1 2 God 30ø 36ø 39ø 41ø 42ø 42ø 43ø Dårlig 43ø 51ø 56ø 59ø 61ø 61ø 61ø B30, ø20, rett stang: Avhengig av overdekning og tverrarmering vil forankringslengden variere fra 30ø til 61ø 11 Forankringslengde NS3473 vs EK 2 Fo rankringslengde [mm] NS3473 EK2 strekk EK2 trykk Betongfasthet, f cck 12 6
87 Forankringslengde NS3473 vs EK 2 Fo orankringslengde [mm] B35 s=2ø NS3473 EK ,5 1 1,5 2 2,5 3 Overdekning [ *Ø] 13 Eksempel, endeopplegg bjelke T ø6 B30, B500NC c = 30 mm T = 113 kn Reaksjonskraft R Ed =90 kn ,0 B30 fbd 2,25 fctd 2, 250,85 2,55 MPa 1, 5 3 T T 113 kn sd 120 MPa A 3314 s 14 7
88 Eksempel forts. Nødvendig forankringslengde: l brqd, ø sd mm 4 f 4 2,55 bd Reduksjon av forankringslengde pga tverrtrykk: 3 REd 9010 p= 150MPa 1,50 bl ,04 p 10,041,50 0, Eksempel forts. Reduksjon av forankringslengde pga overdekning: 1 a (300 2 (30 6) mm 2 a 42 mm cd min 2 c 36 mm cd ø =1-0,15 =1-0,15 =0,88 ø 20 Dimensjonerende forankringslengde: l bd = l 0,880, mm < 200 mm OK 2 5 b, rqd 16 8
89 Eksempel, bjelke/søyle forbindelse Forankringslengde, l b,rqd ø16 c B30, B500NC c = 50 mm effektiv lengde 500 sd f yd 435 MPa 1,15 2,0 B30 fbd 2, 251 fctd 2, 250,7 0,85 1,79 MPa 1, 5 Nødvendig forankringslengde: l brqd, ø sd mm 4 f 4 1,79 bd 17 Eksempel forts. Reduksjon av forankringslengde pga vinkelkrok: c 50 mm 3 ø 48 mm d 0,7 1 Reduksjon av forankringslengde pga overdekning: cd 3ø =1-0,15 =1-0,15 =0,98 ø 16 Dimensjonerende forankringslengde: l bd = l 0,7 0, mm 1 2 b, rqd 18 9
90 Omfaringsskjøt EK2, Krav til avstander mellom armeringsstenger som skjøtes og avstand mellom tilgrensende omfaringsskjøter EK2, Figur Dimensjonerende omfaringslengde EK2, l 0 = l b,rqd l 0,min l 0,min max{0,3 6 l b,rqd ; 15ø; 200mm} 6 = ( 1 /25) 0,5 avhengig av andel som skjøtes, verdi 1-1,5 Verdier av koeffisientene 1, 2, 3, og 5 er som for forankringslengden
91 Dimensjonerende omfaringslengde EK2, figur Tverrarmering i omfaringsskjøt EK2, , stenger i strekk Dersom ø < 20mm eller prosentandel som omfarer hverandre er mindre en 25%, er tverrarmering eller bøyler som kreves av andre årsaker tilstrekkelig. Når ø 20mm skal A st A s 22 11
92 Tverrarmering i omfaringsskjøt EK2, , stenger med permanent trykk Samme krav som stenger i strekk, men én stang av tverrarmering plasseres utenfor enden av omfaringslengden 23 Buntet armering EK2, 8.9 Regler for enkeltstenger gjelder Ved dimensjonering erstattes bunten med en fiktiv diameter øn=ø nb 55 mm nb 4 for vertikale stenger i trykk og for stenger i omfaringsskjøt n 3 for alle andre tilfeller b Krav til senteravstand beregnes med ø n Fri avstand beregnes med faktisk utvendig omkrets 24 12
93 Forankring av underkantarmering ved opplegg EK2, og Underkantarmering ved opplegg bør være > 0,25 A s til feltarmeringen l bd er nødvendig fra der hvor opplegget starter Trykk i tverretning kan bare tas med ved direkte opplegg Fritt opplegg (indirekte) Fritt opplegg (direkte) 25 EK2, 8.3(2) Tillatt dordiameter (1) Generelt i EK er minste dordiameter m,min for å unngå m,min skade på armering 4ø når ø 16mm 7ø når ø > 16mm For armering etter NS3576, Tabell NA.8.1N.c 26 13
94 Tillatt dordiameter (2) EK2, 8.3(3) Minste dordiameter m,min for å unngå skade på betong m,min m,min F bt ((1/a b + 1/(2ø)) / f cd Ikke nødvendig å kontrollere brudd i betong når Forankringslengden som kreves av stangen ikke går mer enn 5 ø forbi bøyen Stangen ikke er plassert mot ytterkant, og det innenfor bøyen er en stang i tverretning med diameter ø 27 Kraft i strekkarmering pga skråriss Tilleggskraft i strekkarmering V cot / 2 M V xv zcot / 2 x zcot / 2 al 28 14
95 Avtrapping av lengdearmering (1) EK2, Virkning av skråriss på strekkraften må tas med For konstruksjonsdeler uten skjærarmering kan momentkurven forskyves en avstand a l = d, EK2, 6.2.2(5) For konstruksjonsdeler med skjærarmering kan momentkurven enten Forskyves en avstand a l = z (cot cot)/2 Beregne tilleggskraft i strekkarmeringen, EK2, 6.2.3(7) F td = 0,5 V Ed (cot cot) 29 Avtrapping av lengdearmering (2) Omhyllingskurve for (M ed /z + N ed ) Opptredende strekkraft F S Kapasitet i strekk F RS Forskyvningsregel 30 15
96 Eurokode 2: Bruksgrensetilstand Nedbøyning og rissvidder 1 Bruksgrensetilstand (SLS) EK2, 7.1 Spenningsbegrensning Rissviddebegrensning Nedbøyningsbegrensning EK2 omfatter ikke vibrasjoner Krav til nedbøyning Kan regne med tension stiffening 2 1
97 Lastfaktorer i bruksgrensetilstand NS-EN 1990 Eurokode: Grunnlag for prosjektering av konstruksjoner k Tabell A.1.4 Dimensjonerende verdier for laster for bruk i lastkombinasjoner 3 Kombinasjonsfaktorer i bruksgrensetilstand Tabell NA.1.1 Verdier for -faktorer for bygninger 4 2
98 Brukbarhetskriterier Eurokode NA.A Brukbarhetskriterier Nedbøyning der tidsavhengige effekter har betydning, beregnes for lastsituasjon tilnærmet t permanent, mens tilleggslasten for lastsituasjon karakteristisk eller ofte forekommende regnes som korttidslast Tabell NA.A1.1 (904) Krav til maksimal nedbøyning 5 EK2, 7.2 Spenningsbegrensning Begrensning av trykkspenninger i betongen for å unngå riss i lengderetning eller store krypdeformasjoner. For eksponeringsklasse XD, XF og XS er begrensningen c < 0,6 f ck NA.7.2(2) Begrensning av armeringsspenning for å unngå in- elastisk tøyning eller uakseptabel opprissing og deformasjon av hensyn til utseendet s < 0,8 f yk NA.7.2(5) 6 3
99 Tension stiffening (1) Betongen mellom riss tar strekk T stivheten i strekksonen er større en armeringsstivheten T Aksialbelastet stav s =T/A s Variasjon av stålspenning c Variasjon av betongspenning 7 Tension stiffening (2) M u Urisset respons Tension stiffening M riss Krumning 8 4
100 EK2, 7.3 Kontroll av rissvidder Rissviddebegrensning, EK2, Minimumsarmering, EK2, Rissviddebegrensning uten direkte beregning, EK2,7.3.3 Beregning av rissvidde, EK2, EK2, 7.3.1(P) Opprissing skal begrenses slik at ikke konstruksjonens egentlige funksjon eller bestandighet skades eller gir den et uakseptabelt utseende 9 Rissviddebegrensning Tabell NA.7.1N grenseverdier av w max (mm) Eksponeringsklasse Armerte konstruksjonsdeler Lastkombinasjon Grenseverdi X0 Tilnærmet permanent 0,40 XC1, XC2, XC3, XC4 Tilnærmet permanent 0,30 k c XD1, XD2, XS1, XS2 Tilnærmet permanent 0,30 k c XD3, XS3 Ofte forekommende 0,30 k c XSA Vurderes særskilt EK2, NA.7.3.1(5) Effekt av større overdekning enn kravet til c min,dur k c = c nom / c min,dur 1,3 10 5
101 EK2, Minimumsarmering Det kreves en minimumsarmering for å begrense opprissing A k k f A s,min c ct, eff ct / s k c - 0,4 for rektangulære bjelker utsatt for bøying A ct - betongareal av strekksonen før opprissing s - Armeringsspenning etter opprissing, vanligvis f yk Denne armeringsmengden må sees i sammenheng med det generelle kravet til minimumsarmering, EK2, kap.9 fctm As,min 0,26 bt d 0,0013bt d f yk 11 Rissviddebegrensning uten beregning (1) EK2, For dekker utsatt tt for bøyning er det ikke nødvendig di med tiltak for å begrense rissvidden dersom tverrsnittshøyden er 200 mm armering etter EK2, 9.2 velges Der det brukt en minimumsarmering etter EK2, kan begrensning av rissvidder idd kontrolleres med største stangdiameter, avhengig av armeringsspenning største senteravstand, avhengig av armeringsspenning 12 6
102 Rissviddebegrensning uten beregning (2) EK2, 7.3.3(2) Tabell 7.2N Armerings- Største stangdiameter [mm] spenning [MPa] w k = 0,4 mm w k = 0,3 mm w k = 0,2 mm Rissviddebegrensning uten beregning (3) EK2, 7.3.3(2) Tabell 7.3N Stålspenning Største senteravstand [mm] [MPa] w k = 04mm 0,4 w k = 03mm 0,3 w k = 02mm 0, Armeringsspenning i risset tverrsnitt: M (1 xc ) d s Es EI 14 7
103 Beregning av rissvidder (1) Armeringstøyning ws s r cm r sm Betongtøyning 15 EK2, w Beregning av rissvidder (2) s ( ) k r,max sm cm f 1 ct, eff s s kt peff, Ecm s ( sm cm) 0,6 E E s E s s r,max 34 3, c 0, 0425 k1 k2 / peff, senteravstand 5( c /2) 1,3 ( hxc ) senteravstand 5 ( c / 2) 16 8
104 Beregning av rissvidder (3) A A s s peff, Act, eff b hc, eff d x c h 2,5 ( h d) hceff, min ( hxc) / 3 h /2 hceff, ( hd 1,5 ) 17 Rissvidder NS3473 vs EK2 (1) NS 3473 vs. EN Steel stress s (N/mm 2 ) EC - Wk=0,4 EC - Wk=0 0,3 NS - Wk=0,4 NS - Wk=0, Bar diameter (mm) 18 9
105 Rissvidder NS3473 vs EK2 (2) NS 3473 vs. EN Steel stress s (N/mm 2 ) EC - ø20 - Wk=0,4 100 EC - ø20 - Wk=0,3 NS - ø20 - Wk=0,4 50 NS - ø20 - Wk=0, Concrete cover (mm) Armeringsspenning vs. betongoverdekning for ø20 & rissvidde 0,3 mm og 0,4 mm Tekna Side: Kontroll av nedbøyning EK2, 7.4 Nedbøyningsbegrensning, EK2, Kontroll av nedbøyning uten beregninger, EK2, Beregning av nedbøyning, EK2,
106 EK2, 7.4.1(1)P Nedbøyningsbegrensning Passende grenseverdier bør fastlegges for nedbøyning avhengig av Funksjon og type konstruksjon Tilstøtende konstruksjoner, delevegger, glassfasader EK2, 7.4.1(4) og (5) For kombinasjon tilnærmet permanente laster Maks nedbøyning spennvidde/250 Maks nedbøyning spennvidde/500 etter ferdig bygging 21 Nedbøyning av betongkonstruksjoner Last Beregnet uten opprissing Virkelig oppførsel Beregnet med null strekkfasthet ib betong Nedbøyning 22 11
107 Tilfeller der bergninger av nedbøyning kan utelates (1) EK2, Under normale forhold er det ikke nødvendig å beregne nedbøyninger, dvs krav i EK2, 7.4.1(4) og (5) er oppfylt dersom 3/2 l 0 0 K111,5 fck 3,2 fck 1 hvis 0 d l 1 ' 0 K 11 1,5 fck fck hvis 0 d ' 12 0 l er grenseverdi for spennvidde/høyde forholdet d er nødvendig strekkarmeringsforhold midt i feltet 23 Tilfeller der beregninger av nedbøyning kan utelates (2) EK2, Faktoren K tar hensyn til ulike statiske system, Tabell NA.7.4.N Bærende system Fritt opplagt bjelke, en- eller toveis fritt opplagt plate Endespenn for kontinuerlig bjelke eller kontinuerlig enveis dekke K 1,0 1,3 Innerfelt i bjelke eller enveis eller toveis dekk 1,5 Flatdekker 1,2 Utkraging 0,
108 Tilfeller der bergninger av nedbøyning kan utelates (3) Spennvidd de / høyde forhold l/d K=1,0 fritt opplagt Prosent nødvendig strekkarmering A s /bd 25 Kontroll av nedbøyning ved beregning EK2, 7.4.3(1)P og (2)P Deformasjoner skal beregnes for aktuelle belastningsforhold med en beregningsmetode som representerer konstruksjonens faktiske oppførsel Beregning er nødvendig når Estimat på nedbøyningen er nødvendig Grenseverdiene fra 7.4.1(4) og (5) ikke er egnet For å finne effekten på deformasjoner av å fjerne forskaling eller midlertidige laster i byggefasen Med tynne tverrsnitt gir en beregning av nedbøyninger en bedre økonomisk løsning 26 13
109 Virkning av kryp på nedbøyning EK2, 7.4.3(5) For laster med varighet som forårsaker kryp kan den totale deformasjonen medregnet kryp beregnes med en effektiv (langtids) elastisitetsmodul for betong Ecm Eceff, 1 (, t ) EK2 krever ikke at virkning av kryp på langtidslast påført før 28 døgn tas hensyn til Ecm () t Eceff, Ecm() t 1 (, t0) E 0 cm 27 Virkning av svinn på nedbøyning EK2, 7.4.3(6) Si Svinnkrumning i kan bestemmes av 1 S Es S cs e cs r I E I c c, eff 1 cs Es As e Ns e s r E I EI c c, eff 28 14
110 Beregning av bøyestivhet De gode gamle formler for bøyestivhet i stadium I og stadium II er fortsatt gyldig, for eksempel for rektangulære tverrsnitt ( EI) E I II c c2 1 x I x 1 b d c2 3 c2 c2 x c E E 2 ( ) 2 s c As b d ( EI) E I E I I c c1 s s1 3 2 bh h c1 c1 I b h x d 12 2 I A ( d x d) s1 s c1 x c1 Ac0,5h Ad s A A c s 2 29 EK2, 7.4.3(4) Risslast og strekkfasthet Det oppnås best estimat for nedbøyning når midlere strekkfasthet f ctm brukes, EK2, Tabell 3.1. Der det ikke er aksialspenninger kan bøyestrekkfastheten f ctm,fl gitt i EK2, brukes h f, max 1,6 f ; f 1000 ctm fl ctm ctm Rissmomentet er gitt som Ic 1Is1 1 2 M f bh f h x 6 riss ctm ctm c 30 15
111 Risset og uopprisset tverrsnitt EK2, 7.4.3(3) Det er i EK2 tillatt i beregning av nedbøyning å ta hensyn til graden av opprissing i tverrsnittet. (1 ) 2 2 sr M cr 1 1 s M Fordelingskoeffisient som tar hensyn til stivhetssøkning fra betong mellom rissene (tension stiffening) 31 Midlere elastisitetsmodul For laster som påføres ved forskjellig tidspunkt er det praktisk å regne med midlere elastisitetsmodul E c,middel total middel middel M i M1 M2 M 3 M4 E I E I E I E I E I E M i ( Mi / Ei ) 32 16
112 Tilnærmet beregning av nedbøyning EK2, 7.4.3(7) I de fleste tilfeller vil det være tilstrekkelig å beregne nedbøyninger ved å interpolere nedbøyning fra henholdsvis uopprisset og fullstendig opprisset tverrsnitt q L 1 E I r 4 2 k1 k2l ceff, (1 ) 33 Nøyaktig beregning av nedbøyning EK2, 7.4.3(7) Den mest nøyaktige metoden ved beregning av nedbøyninger er å beregne krumningen i flere snitt langs konstruksjonsdelen og deretter beregne nedbøyning ved numerisk integrasjon u M 1 1 dx u dx 2 2 x EI r r 1 M M (1 ) r EI EI 34 17
113
114 LYKKE TIL!!! 37 19
Statiske Beregninger for BCC 800
 Side 1 av 12 DEL 1 - GRUNNLEGGENDE FORUTSETNINGER OG ANTAGELSER 1.1 GENERELT Det er i disse beregningene gjort forutsetninger om dimensjoner og fastheter som ikke alltid vil være det man har i et aktuelt
Side 1 av 12 DEL 1 - GRUNNLEGGENDE FORUTSETNINGER OG ANTAGELSER 1.1 GENERELT Det er i disse beregningene gjort forutsetninger om dimensjoner og fastheter som ikke alltid vil være det man har i et aktuelt
Skjærdimensjonering av betong Hva venter i revidert utgave av Eurokode 2?
 Skjærdimensjonering av betong Hva venter i revidert utgave av Eurokode 2? Jan Arve Øverli Institutt for konstruksjonsteknikk NTNU 1 The never ending story of shear design Ritter, W., 1899, Die Bauweise
Skjærdimensjonering av betong Hva venter i revidert utgave av Eurokode 2? Jan Arve Øverli Institutt for konstruksjonsteknikk NTNU 1 The never ending story of shear design Ritter, W., 1899, Die Bauweise
Håndbok 185 Eurokodeutgave
 Håndbok 185 Eurokodeutgave Kapittel 5 Generelle konstruksjonskrav Kapittel 5.3 Betongkonstruksjoner Foredragsholder: Thomas Reed Thomas Reed Født i 1982 Utdannet sivilingeniør Begynte i Svv i 2007 Bruseksjonen
Håndbok 185 Eurokodeutgave Kapittel 5 Generelle konstruksjonskrav Kapittel 5.3 Betongkonstruksjoner Foredragsholder: Thomas Reed Thomas Reed Født i 1982 Utdannet sivilingeniør Begynte i Svv i 2007 Bruseksjonen
19.3.3 Strekkforankring av kamstål
 242 19.3.2.6 Armert betong Svært ofte vil senteravstander og kantavstander være så små at bruddkjeglene ikke gir nok utrivingskapasitet. Formlene her gir ingen addisjonseffekt av tilleggsarmering, så løsningen
242 19.3.2.6 Armert betong Svært ofte vil senteravstander og kantavstander være så små at bruddkjeglene ikke gir nok utrivingskapasitet. Formlene her gir ingen addisjonseffekt av tilleggsarmering, så løsningen
MEMO 812. Beregning av armering DTF/DTS150
 Side 1 av 7 INNHOLD GRUNNLEGGENDE FORUTSETNINGER OG ANTAGELSER... 2 GENERELT... 2 STANDARDER... 2 KVALITETER... 2 LAST... 3 ARMERINGSBEREGNING... 3 YTRE LIKEVEKT... 3 NØDVENDIG FORANKRINGSARMERING...3
Side 1 av 7 INNHOLD GRUNNLEGGENDE FORUTSETNINGER OG ANTAGELSER... 2 GENERELT... 2 STANDARDER... 2 KVALITETER... 2 LAST... 3 ARMERINGSBEREGNING... 3 YTRE LIKEVEKT... 3 NØDVENDIG FORANKRINGSARMERING...3
Statiske Beregninger for BCC 250
 Side 1 av 7 DEL 1 - GRUNNLEGGENDE FORUTSETNINGER OG ANTAGELSER 1.1 GENERELT Det er i disse beregningene gjort forutsetninger om dimensjoner og fastheter som ikke alltid vil være det man har i et aktuelt
Side 1 av 7 DEL 1 - GRUNNLEGGENDE FORUTSETNINGER OG ANTAGELSER 1.1 GENERELT Det er i disse beregningene gjort forutsetninger om dimensjoner og fastheter som ikke alltid vil være det man har i et aktuelt
Emnekode: IRB22013 Emnenavn: Konstruksjonsteknikk 2. Eksamenstid: kl
 EKSAMEN Emnekode: IRB22013 Emnenavn: Konstruksjonsteknikk 2 Dato: 02.01.2019 Eksamenstid: kl. 09.00 13.00 Sensurfrist: 23.01.2019 Antall oppgavesider: 4 Antall vedleggsider: 4 (inkl vedlegg for innlevering)
EKSAMEN Emnekode: IRB22013 Emnenavn: Konstruksjonsteknikk 2 Dato: 02.01.2019 Eksamenstid: kl. 09.00 13.00 Sensurfrist: 23.01.2019 Antall oppgavesider: 4 Antall vedleggsider: 4 (inkl vedlegg for innlevering)
Emnekode: IRB22013 Emnenavn: Konstruksjonsteknikk 2. Eksamenstid: kl Faglærer: Jaran Røsaker (betong) Siri Fause (stål)
 EKSAMEN Emnekode: IRB22013 Emnenavn: Konstruksjonsteknikk 2 Dato: 23.05.2019 Eksamenstid: kl. 09.00 13.00 Sensurfrist: 13.06.2019 Antall oppgavesider (inkludert forside): 5 Antall vedleggsider: 4 Faglærer:
EKSAMEN Emnekode: IRB22013 Emnenavn: Konstruksjonsteknikk 2 Dato: 23.05.2019 Eksamenstid: kl. 09.00 13.00 Sensurfrist: 13.06.2019 Antall oppgavesider (inkludert forside): 5 Antall vedleggsider: 4 Faglærer:
BWC 80 500. MEMO 724a. Søyler i front Innfesting i bærende vegg Eksempel
 INNHOLD BWC 80 500 Side 1 av 10 GRUNNLEGGENDE FORUTSETNINGER OG ANTAGELSER... GENERELT... LASTER... BETONG OG ARMERING... 3 VEGG OG DEKKETYKKELSER... 3 BEREGNINGER... 3 LASTER PÅ BWC ENHET... 3 DIMENSJONERING
INNHOLD BWC 80 500 Side 1 av 10 GRUNNLEGGENDE FORUTSETNINGER OG ANTAGELSER... GENERELT... LASTER... BETONG OG ARMERING... 3 VEGG OG DEKKETYKKELSER... 3 BEREGNINGER... 3 LASTER PÅ BWC ENHET... 3 DIMENSJONERING
Vedlegg 1.9 NS 3473 PROSJEKTERING AV BETONGKOPNSTRUKSJOENR
 Vedlegg 1.9 NS 3473 PROSJEKTERING AV BETONGKOPNSTRUKSJOENR Beregnings- og konstruksjonsregler Siri Fause Høgskolen i Østfold 1 NS 3473 Prosjektering av betongkonstruksjoner 6.utgave september 2003 Revisjonen
Vedlegg 1.9 NS 3473 PROSJEKTERING AV BETONGKOPNSTRUKSJOENR Beregnings- og konstruksjonsregler Siri Fause Høgskolen i Østfold 1 NS 3473 Prosjektering av betongkonstruksjoner 6.utgave september 2003 Revisjonen
D4 BRANNTEKNISK DIMENSJONERING AV ELEMENTER
 26 Innstøpningsgods av ubrennbart materiale kan benyttes i steget, forutsatt at avstanden mellom innstøpningsgods og armeringen ikke er mindre enn krav til armeringsdybde. Innstøpningsgods og sveiseplater
26 Innstøpningsgods av ubrennbart materiale kan benyttes i steget, forutsatt at avstanden mellom innstøpningsgods og armeringen ikke er mindre enn krav til armeringsdybde. Innstøpningsgods og sveiseplater
INNHOLDSFORTEGNELSE. BETONexpress - eksempler betongbjelker. 1. BJELKE-001, Bjelketverrsnitt med bøyningsmoment og skjærkraft
 - eksempler betongbjelker INNHOLDSFORTEGNELSE 1. BJELKE-001, Bjelketverrsnitt med bøyningsmoment og skjærkraft 1.1. Dimensjonering for bøyning i bruddgrensetilstand 1.2. Dimensjonering mot skjærbrudd 2.
- eksempler betongbjelker INNHOLDSFORTEGNELSE 1. BJELKE-001, Bjelketverrsnitt med bøyningsmoment og skjærkraft 1.1. Dimensjonering for bøyning i bruddgrensetilstand 1.2. Dimensjonering mot skjærbrudd 2.
5.2.2 Dimensjonering av knutepunkter
 92 Det er derfor tilstrekkelig å kontrollere hver av lastene sine hovedretninger. Se også punkt 2.1.4 her. E Edx + 0 E Edy 0 E Edx + E Edy 5.2.1.8 Kraftfordeling til veggskivene Tar utgangspunkt i taket
92 Det er derfor tilstrekkelig å kontrollere hver av lastene sine hovedretninger. Se også punkt 2.1.4 her. E Edx + 0 E Edy 0 E Edx + E Edy 5.2.1.8 Kraftfordeling til veggskivene Tar utgangspunkt i taket
C2 BJELKER. Fra figuren kan man utlede at fagverksmodellen kan bare benyttes når Ø (h h u 1,41 y 1 y 2 y 3 ) / 1,71
 32 C2 BJELKER 2.1.3 Dimensjonering for skjærkraft For å sikre bestandigheten bør spenningen f yd i armeringen ved ut - sparinger begrenses i henhold til tabell C 6.5. Små utsparinger Når utsparingen Ø
32 C2 BJELKER 2.1.3 Dimensjonering for skjærkraft For å sikre bestandigheten bør spenningen f yd i armeringen ved ut - sparinger begrenses i henhold til tabell C 6.5. Små utsparinger Når utsparingen Ø
Praktisk betongdimensjonering
 6. og 7. januar (7) Veggskiver Praktisk betongdimensjonering Magnus Engseth, Dr.techn.Olav Olsen www.betong.net www.rif.no 2 KORT OM MEG SELV > Magnus Engseth, 27 år > Jobbet i Dr.techn.Olav Olsen i 2.5
6. og 7. januar (7) Veggskiver Praktisk betongdimensjonering Magnus Engseth, Dr.techn.Olav Olsen www.betong.net www.rif.no 2 KORT OM MEG SELV > Magnus Engseth, 27 år > Jobbet i Dr.techn.Olav Olsen i 2.5
C8 BJELKER. 8.1 OPPLEGG MED RETT ENDE Dimensjonering
 180 I det følgende behandles typiske opplegg for bjelker. Dessuten gjennomgås dimensjonering av hylle for opplegg av dekker, mens dimensjonering av forbindelsen er vist i kapittel C11 for ribbeplater og
180 I det følgende behandles typiske opplegg for bjelker. Dessuten gjennomgås dimensjonering av hylle for opplegg av dekker, mens dimensjonering av forbindelsen er vist i kapittel C11 for ribbeplater og
Dimensjonering MEMO 54c Armering av TSS 41
 Side av 9 INNHOLD GUNNLEGGENDE FOUTSETNINGE OG ANTAGELSE... GENEELT... STANDADE... KVALITETE... 3 DIMENSJONE OG TVESNITTSVEDIE... 3 LASTE... 3 AMEINGSBEEGNING... 4 LIKEVEKT... 4 Side av 9 GUNNLEGGENDE
Side av 9 INNHOLD GUNNLEGGENDE FOUTSETNINGE OG ANTAGELSE... GENEELT... STANDADE... KVALITETE... 3 DIMENSJONE OG TVESNITTSVEDIE... 3 LASTE... 3 AMEINGSBEEGNING... 4 LIKEVEKT... 4 Side av 9 GUNNLEGGENDE
5.1.2 Dimensjonering av knutepunkter
 80 H5 DIMENSJONERINGSEKSEMPLER V (kn) og M (knm) 500 0 500 1000 5 10 15 20 25 30 35 40 45 50 x (m) 1500 Snitt 4 (33,7 m < x < 50,8 m): F y = 0; det vil si: V f + h fy x H y2 H y5 H y4 = 0 V f = 10,1 x
80 H5 DIMENSJONERINGSEKSEMPLER V (kn) og M (knm) 500 0 500 1000 5 10 15 20 25 30 35 40 45 50 x (m) 1500 Snitt 4 (33,7 m < x < 50,8 m): F y = 0; det vil si: V f + h fy x H y2 H y5 H y4 = 0 V f = 10,1 x
3T-MR - H over E1-32,8 kn 1. SiV - 5. btr - E2 Christiansen og Roberg AS BER
 3T-MR - H40-1-2 over E1-32,8 kn 1 Dataprogram: E-BJELKE versjon 6.5 Laget av Sletten Byggdata Beregningene er basert på NS-EN 1992-1-1 og NS-EN 1990:2002 + NA:2008 Data er lagret på fil: G:\SiV 5 - E2
3T-MR - H40-1-2 over E1-32,8 kn 1 Dataprogram: E-BJELKE versjon 6.5 Laget av Sletten Byggdata Beregningene er basert på NS-EN 1992-1-1 og NS-EN 1990:2002 + NA:2008 Data er lagret på fil: G:\SiV 5 - E2
HRC T-Hodet armering Fordeler for brukerne
 HIGH PERFORMANCE REINFORCEMENT PRODUCTS HRC T-Hodet armering Fordeler for brukerne HRC T-hodet armering har spesielle egenskaper som skiller den fra konvensjonell armering. HRC T-hoder forankrer den fulle
HIGH PERFORMANCE REINFORCEMENT PRODUCTS HRC T-Hodet armering Fordeler for brukerne HRC T-hodet armering har spesielle egenskaper som skiller den fra konvensjonell armering. HRC T-hoder forankrer den fulle
C3 DEKKER. Figur C 3.1. Skjæroverføring mellom ribbeplater. Figur C 3.2. Sveiseforbindelse for tynne platekanter.
 57 600 50 Figur C.1. Skjæroverføring mellom ribbeplater. punktlaster og linjelaster som overføres til naboelementene avhenger av konstruksjonens stivhet i tverretningen. Dette må beregnes basert på påstøpens
57 600 50 Figur C.1. Skjæroverføring mellom ribbeplater. punktlaster og linjelaster som overføres til naboelementene avhenger av konstruksjonens stivhet i tverretningen. Dette må beregnes basert på påstøpens
BSF ENHETER BEREGNING AV ARMERING
 Side 1 av 61 INNHOLD DEL 1 GUNNLEGGENDE FORUTSETNINGER OG ANTAGELSER... 4 1.1 GENERELT... 4 1. STANDARDER... 4 1.3 KVALITETER... 5 1.4 DIMENSJONER OG TVERRSNITTSVERDIER... 6 1.5 LAST... 8 1.6 TOLERANSER...
Side 1 av 61 INNHOLD DEL 1 GUNNLEGGENDE FORUTSETNINGER OG ANTAGELSER... 4 1.1 GENERELT... 4 1. STANDARDER... 4 1.3 KVALITETER... 5 1.4 DIMENSJONER OG TVERRSNITTSVERDIER... 6 1.5 LAST... 8 1.6 TOLERANSER...
Dato: ps DIMENSJONERING
 MEMO 812 Dato: 16.08.2012 Sign.: sss BEREGNING AV ARMERING Siste rev.: 13.05.2016 Sign.: sss DTF150/DTS150 Dok. nr.: K6-10/12 Kontr.: ps DIMENSJONERING BEREGNING AV ARMERING DTF150/DTS150 INNHOLD GRUNNLEGGENDE
MEMO 812 Dato: 16.08.2012 Sign.: sss BEREGNING AV ARMERING Siste rev.: 13.05.2016 Sign.: sss DTF150/DTS150 Dok. nr.: K6-10/12 Kontr.: ps DIMENSJONERING BEREGNING AV ARMERING DTF150/DTS150 INNHOLD GRUNNLEGGENDE
Vedlegg 1.5 SPENNBETONG SPENNBETONG 1
 Vedlegg 1.5 1 HVA ER FORSPENNING? SPENNARMERT BETONG/ Armert betong hvor all eller deler av armeringen av armeringen er forspent og dermed er gitt en strekktøyning i forhold til betongen. Kreftene som
Vedlegg 1.5 1 HVA ER FORSPENNING? SPENNARMERT BETONG/ Armert betong hvor all eller deler av armeringen av armeringen er forspent og dermed er gitt en strekktøyning i forhold til betongen. Kreftene som
Nye standarder. Eurokoder Andre standarder. Norske betongstandarder mer enn 80 års historie Eurokoder, 35 års historie
 Nye standarder Eurokoder Andre standarder Steinar Leivestad Standard Norge 2009-10-12 1 Norske betongstandarder mer enn 80 års historie Eurokoder, 35 års historie 1893 Ingeniørkaptein Kolderups Lærebok
Nye standarder Eurokoder Andre standarder Steinar Leivestad Standard Norge 2009-10-12 1 Norske betongstandarder mer enn 80 års historie Eurokoder, 35 års historie 1893 Ingeniørkaptein Kolderups Lærebok
HRC-produkter og NS-EN 1992-1-1 (Eurokode 2)
 HRC-produkter og NS-EN 1992-1-1 (Eurokode 2) HRC-produkter: T-hodet armering (HRC 100 Serie) T-hoder er en metode for å forankre armeringsstenger. HRC T-hodet armering forankrer armeringens fulle reelle
HRC-produkter og NS-EN 1992-1-1 (Eurokode 2) HRC-produkter: T-hodet armering (HRC 100 Serie) T-hoder er en metode for å forankre armeringsstenger. HRC T-hodet armering forankrer armeringens fulle reelle
4.4.5 Veiledning i valg av søyledimensjoner I det følgende er vist veiledende dimensjoner på søyler for noen typiske
 A HJELPEMIDLER TIL OVERSLAGSDIMENSJONERING Verdier for β er angitt for noen typiske søyler i figur A.. Verdier for β for andre avstivningsforhold for søyler er behandlet i bind B, punkt 1.2... Veiledning
A HJELPEMIDLER TIL OVERSLAGSDIMENSJONERING Verdier for β er angitt for noen typiske søyler i figur A.. Verdier for β for andre avstivningsforhold for søyler er behandlet i bind B, punkt 1.2... Veiledning
Focus 2D Konstruksjon
 Prosjekt: betongtal Beregning utført 01.04.2009 14:49:48 Focus 2D Konstruksjon BEREGNING AV PLANE KONSTRUKSJONER NTNU Student 3. Klasse 2008 14:49:48-01.04.2009 Side:1 1. KONSTRUKSJONSMODELL OG LASTER
Prosjekt: betongtal Beregning utført 01.04.2009 14:49:48 Focus 2D Konstruksjon BEREGNING AV PLANE KONSTRUKSJONER NTNU Student 3. Klasse 2008 14:49:48-01.04.2009 Side:1 1. KONSTRUKSJONSMODELL OG LASTER
C13 SKIVER 275. Tabell C Skjærkapasitet til svært glatt og urisset støpt fuge. Heft og øvre grense.
 C13 SKIER 275 Tabell C 13.12. Skjærkapasitet til svært glatt og urisset støpt fuge. Heft og øvre grense. Rd (kn/m) Fuge- B25, γ c = 1,8 B30, γ c = 1,8 B35, γ c = 1,8 bredde f cd = 11,8 MPa f cd = 14,2
C13 SKIER 275 Tabell C 13.12. Skjærkapasitet til svært glatt og urisset støpt fuge. Heft og øvre grense. Rd (kn/m) Fuge- B25, γ c = 1,8 B30, γ c = 1,8 B35, γ c = 1,8 bredde f cd = 11,8 MPa f cd = 14,2
168 C7 SØYLER. Figur C Komplett fagverksmodell ved konsoller. Figur C Eksentrisk belastet konsoll.
 168 C7 SØYLER Figur C 7.42. Komplett fagverksmodell ved konsoller. a) Sentrisk last over konsoll b) Eksentrisk last over konsoll Typiske prefabrikkerte søyler vil vanligvis ikke være maksimalt utnyttet
168 C7 SØYLER Figur C 7.42. Komplett fagverksmodell ved konsoller. a) Sentrisk last over konsoll b) Eksentrisk last over konsoll Typiske prefabrikkerte søyler vil vanligvis ikke være maksimalt utnyttet
BUBBLEDECK. Beregning, dimensjonering og utførelse av biaksiale hulldekkelementer. Veileder for Rådgivende ingeniører
 BUBBLEDECK Beregning, dimensjonering og utførelse av biaksiale hulldekkelementer Veileder for Rådgivende ingeniører 2009 Veileder for Rådgivende ingeniører Denne publikasjon er en uavhengig veileder for
BUBBLEDECK Beregning, dimensjonering og utførelse av biaksiale hulldekkelementer Veileder for Rådgivende ingeniører 2009 Veileder for Rådgivende ingeniører Denne publikasjon er en uavhengig veileder for
B19 FORANKRING AV STÅL 297
 B19 FORANKRING AV STÅL 297 19.11 FORANKRING AV ARMERING I denne sammenhengen betyr «armering» kamstål B500NC som støpes inn i elementer eller støpes inn i fuger på byggeplass. Sveising eller liming av
B19 FORANKRING AV STÅL 297 19.11 FORANKRING AV ARMERING I denne sammenhengen betyr «armering» kamstål B500NC som støpes inn i elementer eller støpes inn i fuger på byggeplass. Sveising eller liming av
Stavelement med tverrlast q og konstant aksialkraft N. Kombinert gir dette diff.ligningen for stavknekking 2EI 2EI
 DIMENSJONERING AV PLATER 1. ELASTISK STAVKNEKKING Stavelement med tverrlast q og konstant aksialkraft N Likevekt dv q x dx 0 vertikallikevekt ch e j e V dx dm N d 0 momentlikevekt Kombinert gir dette diff.ligningen
DIMENSJONERING AV PLATER 1. ELASTISK STAVKNEKKING Stavelement med tverrlast q og konstant aksialkraft N Likevekt dv q x dx 0 vertikallikevekt ch e j e V dx dm N d 0 momentlikevekt Kombinert gir dette diff.ligningen
B12 SKIVESYSTEM 141. Figur B Oppriss av veggskive. Plassering av skjøtearmering for seismisk påkjenning.
 12 KIVEYTEM 141 kjærkraft Den horisontale skjærkraften finnes som regel enkelt samtidig med moment og aksialkraft se figur 12.72. vært ofte vil skivene ha så stor aksiallast at friksjonseffekten µ N Ed
12 KIVEYTEM 141 kjærkraft Den horisontale skjærkraften finnes som regel enkelt samtidig med moment og aksialkraft se figur 12.72. vært ofte vil skivene ha så stor aksiallast at friksjonseffekten µ N Ed
5.5.5 Kombinasjon av ortogonale lastretninger Seismisk last på søylene Dimensjonering av innersøyle
 118 5.5.5 Kombinasjon av ortogonale lastretninger Da bygget er regulært i planet samt at det kun er søylene som er avstivende, kan det forutsettes at den seismiske påvirkningen virker separat og ikke behøver
118 5.5.5 Kombinasjon av ortogonale lastretninger Da bygget er regulært i planet samt at det kun er søylene som er avstivende, kan det forutsettes at den seismiske påvirkningen virker separat og ikke behøver
0,5 ν f cd [Tabell B 16.5, svært glatt, urisset]
![0,5 ν f cd [Tabell B 16.5, svært glatt, urisset] 0,5 ν f cd [Tabell B 16.5, svært glatt, urisset]](/thumbs/92/109097771.jpg) 12 KIVEYTEM kjærkraft Den horisontale skjærkraften finnes som regel enkelt samtidig med moment og aksialkraft se figur 12.72. vært ofte vil skivene ha så stor aksiallast at friksjonseffekten μ N Ed er
12 KIVEYTEM kjærkraft Den horisontale skjærkraften finnes som regel enkelt samtidig med moment og aksialkraft se figur 12.72. vært ofte vil skivene ha så stor aksiallast at friksjonseffekten μ N Ed er
Dato: sss DTF/DTS EKSEMPELBEREGNINGER. Siste rev.: Dok. nr.: BEREGNING AV ARMERING DTF150/DTS150
 MEMO 830 Dato: 19.09.013 Sign.: sss DTF/DTS EKSEMPELBEREGNINGER Siste rev.: 13.05.016 Sign.: sss DIMENSJONERING Dok. nr.: K6-10-30 Kontr.: ps BEREGNING AV ARMERING DTF150/DTS150 INNHOLD BEREGNING AV ARMERING
MEMO 830 Dato: 19.09.013 Sign.: sss DTF/DTS EKSEMPELBEREGNINGER Siste rev.: 13.05.016 Sign.: sss DIMENSJONERING Dok. nr.: K6-10-30 Kontr.: ps BEREGNING AV ARMERING DTF150/DTS150 INNHOLD BEREGNING AV ARMERING
Dato: Siste rev.: Dok. nr.: EKSEMPEL
 MEMO 74a Dato: 09.03.0 Sign.: sss BWC 80-500 - SØYLER I FRONT INFESTING I BÆRENDE VEGG EKSEMPEL Siste rev.: Dok. nr.: 8.05.06 K5-0/3 Sign.: Kontr.: sss ps EKSEMPEL INNHOLD GRUNNLEGGENDE FORUTSETNINGER
MEMO 74a Dato: 09.03.0 Sign.: sss BWC 80-500 - SØYLER I FRONT INFESTING I BÆRENDE VEGG EKSEMPEL Siste rev.: Dok. nr.: 8.05.06 K5-0/3 Sign.: Kontr.: sss ps EKSEMPEL INNHOLD GRUNNLEGGENDE FORUTSETNINGER
Høgskolen 1Østfold 1 Avdeling for ingeniørfag
 Høgskolen 1Østfold 1 EKSAMENSOPPGAVE Emne: IRB22013 Konstruksjonsteknikk 2 Lærer/telefon: Geir Flote Gru er: 2. B Dato: 04.01.2016 Tid: 09.00 13.00 Antall o avesider: 5 Antall vedle sider: 1 Sensurfrist:
Høgskolen 1Østfold 1 EKSAMENSOPPGAVE Emne: IRB22013 Konstruksjonsteknikk 2 Lærer/telefon: Geir Flote Gru er: 2. B Dato: 04.01.2016 Tid: 09.00 13.00 Antall o avesider: 5 Antall vedle sider: 1 Sensurfrist:
Prinsipper bak seismisk dimensjonering av betongkonstruksjoner
 Prinsipper bak seismisk dimensjonering av betongkonstruksjoner Max Milan Loo Innhold Generelle dimensjoneringsprinsipper Duktile/jordskjelvsikre betongkonstruksjoner Betongoppførsel under jordskjelvspåvirkning
Prinsipper bak seismisk dimensjonering av betongkonstruksjoner Max Milan Loo Innhold Generelle dimensjoneringsprinsipper Duktile/jordskjelvsikre betongkonstruksjoner Betongoppførsel under jordskjelvspåvirkning
Prosjekt/Project: Detaljhåndboka Beregningseksempel PF2 Prosjektnr: 513 00 75
 BA 013-05-7 Beregningseksempel PF Side 1 av 9 t.p HEA 00 S355 PL 0x30x380 S355J FUNDAMENTBOLTER 4x M4x600 8.8 BETONG B30 t.fc h.c Ø d.0 c.1 b.c t.wc c. c.1 b.1 e.1 m.0 e. d.1 Input Stålsort : "S355" f
BA 013-05-7 Beregningseksempel PF Side 1 av 9 t.p HEA 00 S355 PL 0x30x380 S355J FUNDAMENTBOLTER 4x M4x600 8.8 BETONG B30 t.fc h.c Ø d.0 c.1 b.c t.wc c. c.1 b.1 e.1 m.0 e. d.1 Input Stålsort : "S355" f
Brukonferansen Innføring av Eurokoder av Gunnar Egset, Johs. Holt as
 Innføring av Eurokoder av Gunnar Egset, Johs. Holt as 08.11.2011 Innføring av Eurokoder Eurokodene ble offisielt innført 31 mars 2010. I 2010 og fram til ca sommeren 2011 er det relativt få bruer som er
Innføring av Eurokoder av Gunnar Egset, Johs. Holt as 08.11.2011 Innføring av Eurokoder Eurokodene ble offisielt innført 31 mars 2010. I 2010 og fram til ca sommeren 2011 er det relativt få bruer som er
(8) Geometriske toleranser. Geometriske toleranser Pål Jacob Gjerp AF Gruppen Norge AS
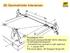 (8) Geometriske toleranser Geometriske toleranser Pål Jacob Gjerp AF Gruppen Norge AS Kursdagene 2011 Ny norsk standard NS-EN 13670: Utførelse av betongkonstruksjoner - konsekvenser og bruk av nytt regelverk
(8) Geometriske toleranser Geometriske toleranser Pål Jacob Gjerp AF Gruppen Norge AS Kursdagene 2011 Ny norsk standard NS-EN 13670: Utførelse av betongkonstruksjoner - konsekvenser og bruk av nytt regelverk
ISY Design. Brukerdokumentasjon. Betongtverrsnitt. Versjon 1.4
 ISY Design Brukerdokumentasjon Betongtverrsnitt Versjon 1.4 ISY Design Versjon 1.4 Programsystemet ISY Design er utarbeidet og eiet av: Norconsult Informasjonssystemer AS Vestfjordgaten 4 1338 SANDVIKA
ISY Design Brukerdokumentasjon Betongtverrsnitt Versjon 1.4 ISY Design Versjon 1.4 Programsystemet ISY Design er utarbeidet og eiet av: Norconsult Informasjonssystemer AS Vestfjordgaten 4 1338 SANDVIKA
Dato: Siste rev.: Dok. nr.: EKSEMPEL
 MEMO 744 Dato: 1.01.016 Sign.: sss BWC 30-U UTKRAGET BALKONG - INNSPENT I PLASSTØPT DEKKE EKSEMPEL Siste rev.: Dok. nr.: 3.05.016 K5-10-744 Sign.: Kontr.: sss nb EKSEMPEL INNHOLD EKSEMPEL... 1 GRUNNLEGGENDE
MEMO 744 Dato: 1.01.016 Sign.: sss BWC 30-U UTKRAGET BALKONG - INNSPENT I PLASSTØPT DEKKE EKSEMPEL Siste rev.: Dok. nr.: 3.05.016 K5-10-744 Sign.: Kontr.: sss nb EKSEMPEL INNHOLD EKSEMPEL... 1 GRUNNLEGGENDE
Dato: sss TSS 102. Siste rev.: sss ARMERING. ps DIMENSJONERING. Dok. nr.: ARMERING AV TSS 102
 MEMO 60 Dato: 04.10.011 Sign.: sss TSS 10 Siste rev.: 0.05.016 Sign.: sss ARMERING Dok. nr.: K3-10/60 Kontr.: ps DIMENSJONERING ARMERING AV TSS 10 INNHOLD GRUNNLEGGENDE FORUTSETNINGER OG ANTAGELSER...
MEMO 60 Dato: 04.10.011 Sign.: sss TSS 10 Siste rev.: 0.05.016 Sign.: sss ARMERING Dok. nr.: K3-10/60 Kontr.: ps DIMENSJONERING ARMERING AV TSS 10 INNHOLD GRUNNLEGGENDE FORUTSETNINGER OG ANTAGELSER...
B9 VERTIKALE AVSTIVNINGSSYSTEMER GEOMETRISKE AVVIK, KNEKKING, SLANKHET
 9.2.5 Slankhet og slankhetsgrenser Den geometriske slankheten defineres som λ = l 0 / i = l 0 / (I /A), det vil si l 0 = λ (I /A) der i er treghetsradien for urisset betongtverrsnitt (lineært elastisk).
9.2.5 Slankhet og slankhetsgrenser Den geometriske slankheten defineres som λ = l 0 / i = l 0 / (I /A), det vil si l 0 = λ (I /A) der i er treghetsradien for urisset betongtverrsnitt (lineært elastisk).
6. og 7. januar PRAKTISK BETONGDIMENSJONERING
 6. og 7. januar PRAKTISK BETONGDIMENSJONERING (9) Fundamentering- pelehoder www.betong.net Øystein Løset, Torgeir Steen, Dr. Techn Olav Olsen 2 KORT OM MEG SELV > 1974 NTH Bygg, betong og statikk > ->1988
6. og 7. januar PRAKTISK BETONGDIMENSJONERING (9) Fundamentering- pelehoder www.betong.net Øystein Løset, Torgeir Steen, Dr. Techn Olav Olsen 2 KORT OM MEG SELV > 1974 NTH Bygg, betong og statikk > ->1988
Dato: Siste rev.: Dok. nr.: ARMERING AV TSS 41
 MEMO 54c Dato: 26.04.2011 Sign.: sss ARMERING AV TSS 41 Siste rev.: 19.05.2016 Sign.: sss DIMENSJONERING Dok. nr.: K3-10/54c Kontr.: ps ARMERING AV TSS 41 INNHOLD GRUNNLEGGENDE FORUTSETNINGER OG ANTAGELSER...
MEMO 54c Dato: 26.04.2011 Sign.: sss ARMERING AV TSS 41 Siste rev.: 19.05.2016 Sign.: sss DIMENSJONERING Dok. nr.: K3-10/54c Kontr.: ps ARMERING AV TSS 41 INNHOLD GRUNNLEGGENDE FORUTSETNINGER OG ANTAGELSER...
SØYLER I FRONT INNFESTING I PLASSTØPT DEKKE, BEREGNING AV DEKKE OG BALKONGARMERING
 MEMO 711 Dato: 11.0.015 Sign.: sss SØYLER I FRONT INNFESTING I PLASSTØPT DEKKE, BEREGNING AV DEKKE OG BALKONGARMERING Siste rev.: Dok. nr.: 18.05.016 K5-10/711 Sign.: Kontr.: sss ps SØYLER I FRONT INNFESTING
MEMO 711 Dato: 11.0.015 Sign.: sss SØYLER I FRONT INNFESTING I PLASSTØPT DEKKE, BEREGNING AV DEKKE OG BALKONGARMERING Siste rev.: Dok. nr.: 18.05.016 K5-10/711 Sign.: Kontr.: sss ps SØYLER I FRONT INNFESTING
C11 RIBBEPLATER 231. Figur C Ribbeplater med strekkbånd. a) Strekkbånd i bjelken. b) Strekkbånd på opplegget. c) Strekkbånd på dekket
 C11 RIBBEPLATER 231 Lask a) Strekkbånd i bjelken b) Strekkbånd på opplegget c) Strekkbånd på dekket d) Armering og utstøping e) Innstøpt flattstål i plate res dette ofte med at den samme forbindelsen også
C11 RIBBEPLATER 231 Lask a) Strekkbånd i bjelken b) Strekkbånd på opplegget c) Strekkbånd på dekket d) Armering og utstøping e) Innstøpt flattstål i plate res dette ofte med at den samme forbindelsen også
BEREGNING AV SVEISEINNFESTNINGER OG BALKONGARMERING
 MEMO 732 Dato: 07.06.2012 Sign.: sss BWC 50-240 - SØYLER I FRONT INFESTING I STÅLSØYLE I VEGG, BEREGNING AV SVEISEINNFESTNINGER Siste rev.: Dok. nr.: 18.05.2016 K5-10/32 Sign.: Kontr.: sss ps OG BALKONGARMERING
MEMO 732 Dato: 07.06.2012 Sign.: sss BWC 50-240 - SØYLER I FRONT INFESTING I STÅLSØYLE I VEGG, BEREGNING AV SVEISEINNFESTNINGER Siste rev.: Dok. nr.: 18.05.2016 K5-10/32 Sign.: Kontr.: sss ps OG BALKONGARMERING
Bruk av HRC-produkter - eksempler
 Bruk av HRC-produkter - eksempler HRC-produkter: T-hodet armering (HRC 100 Serie) T-hoder er en metode for forankring av armeringsstenger. HRC T-hodet armering forankrer armeringens fulle reelle bruddstyrke
Bruk av HRC-produkter - eksempler HRC-produkter: T-hodet armering (HRC 100 Serie) T-hoder er en metode for forankring av armeringsstenger. HRC T-hodet armering forankrer armeringens fulle reelle bruddstyrke
EKSAMEN TKT 4122 MEKANIKK 2 Onsdag 4. desember 2013 Tid: kl
 L BD = 3 m side 1 av 5 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR KONSTRUKSJONSTEKNIKK Kontakt under eksamen Arne Aalberg (735) 94624, 976 42898 Tekst: Norsk EKSAMEN TKT 4122 MEKANIKK
L BD = 3 m side 1 av 5 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR KONSTRUKSJONSTEKNIKK Kontakt under eksamen Arne Aalberg (735) 94624, 976 42898 Tekst: Norsk EKSAMEN TKT 4122 MEKANIKK
MEMO 703a. Søyler i front - Innfesting i plasstøpt dekke Standard armering
 INNHOLD BWC 55-740 Dato: 15.05.2012 Side 1 av 19 FORUTSETNINGER...2 GENERELT... 2 TILLATT BRUDDLAST PÅ KOMPLETT ENHET... 2 TILLATT BRUDDLAST PÅ YTTERRØR BRUKT I KOMBINASJON MED TSS... 2 TILLATT BRUDDLAST
INNHOLD BWC 55-740 Dato: 15.05.2012 Side 1 av 19 FORUTSETNINGER...2 GENERELT... 2 TILLATT BRUDDLAST PÅ KOMPLETT ENHET... 2 TILLATT BRUDDLAST PÅ YTTERRØR BRUKT I KOMBINASJON MED TSS... 2 TILLATT BRUDDLAST
Dato: Siste rev.: Dok. nr.: ARMERING AV TSS 101
 MEMO 54d Dato: 6.04.011 Sign.: sss ARMERING AV TSS 101 Siste rev.: 19.05.016 Sign.: sss DIMENSJONERING Dok. nr.: K3-10/54d Kontr.: ps ARMERING AV TSS 101 INNHOLD ARMERING AV TSS 101... 1 GRUNNLEGGENDE
MEMO 54d Dato: 6.04.011 Sign.: sss ARMERING AV TSS 101 Siste rev.: 19.05.016 Sign.: sss DIMENSJONERING Dok. nr.: K3-10/54d Kontr.: ps ARMERING AV TSS 101 INNHOLD ARMERING AV TSS 101... 1 GRUNNLEGGENDE
4.3.4 Rektangulære bjelker og hyllebjelker
 66 Konstruksjonsdetaljer Oppleggsdetaljene som benyttes for IB-bjelker er stort sett de samme som for SIB-bjelker, se figurene A 4.22.a og A 4.22.b. 4.3.4 Rektangulære bjelker og yllebjelker Generelt Denne
66 Konstruksjonsdetaljer Oppleggsdetaljene som benyttes for IB-bjelker er stort sett de samme som for SIB-bjelker, se figurene A 4.22.a og A 4.22.b. 4.3.4 Rektangulære bjelker og yllebjelker Generelt Denne
7.3 SØYLETopp Grunnlaget finnes i bind B, punkt
 C7 SØYLER 159 Evt. shims Utstikkende søylejern Sentrisk gjengestang Utsparing (rør) gyses ved søylemontasje Figur C 7.28. Vanlig limeløsning. Illustrasjon til tabell C 7.6. u u a s Bjelke Korrugert rør
C7 SØYLER 159 Evt. shims Utstikkende søylejern Sentrisk gjengestang Utsparing (rør) gyses ved søylemontasje Figur C 7.28. Vanlig limeløsning. Illustrasjon til tabell C 7.6. u u a s Bjelke Korrugert rør
TSS 41 LOKAL DEKKEARMERING VERIFISERT MED TESTER
 Dato: 26.04.2011 Sign.: sss TSS 41 Siste rev.: 30.10.2018 Sign.: sss LOKAL DEKKEARMERING - Dok. nr.: K3-10/55c Kontr.: ps VERIFISERT MED TESTER DIMENSJONERING TSS 41 LOKAL DEKKEARMERING VERIFISERT MED
Dato: 26.04.2011 Sign.: sss TSS 41 Siste rev.: 30.10.2018 Sign.: sss LOKAL DEKKEARMERING - Dok. nr.: K3-10/55c Kontr.: ps VERIFISERT MED TESTER DIMENSJONERING TSS 41 LOKAL DEKKEARMERING VERIFISERT MED
C12 HULLDEKKER. Figur C Øvre grenselast. Ill. til tabell C 12.6.
 248 C12 HULLDEKKER Det er som regel bare vridningsforbindelser som kan kreve så store strekk-krefter som N maks2, se figur C 12.9.a. Dersom forbindelsen skal overføre skjærkrefter mellom hulldekke og vegg
248 C12 HULLDEKKER Det er som regel bare vridningsforbindelser som kan kreve så store strekk-krefter som N maks2, se figur C 12.9.a. Dersom forbindelsen skal overføre skjærkrefter mellom hulldekke og vegg
Beregning etter Norsok N-004. Platekonstruksjoner etter NORSOK N-004 / DNV-RP-C201
 Platekonstruksjoner etter ORSOK -004 / DV-RP-C201 orsk forening for stålkonstruksjoner Ingeniørenes Hus Oslo 19. mars 2009 Gunnar Solland, Det orske Veritas Beregning etter orsok -004 orsok -004 henviser
Platekonstruksjoner etter ORSOK -004 / DV-RP-C201 orsk forening for stålkonstruksjoner Ingeniørenes Hus Oslo 19. mars 2009 Gunnar Solland, Det orske Veritas Beregning etter orsok -004 orsok -004 henviser
9.2 TRE-ETASJES KONTOR- OG FORRETNINGSBYGG Dette beregningseksemplet viser praktisk beregning av knutepunktene i et kontor- og forretningsbygg.
 C9 BEREGNINGSEKSEMPLER FOR SØYLE- OG BJELKEFORBINDELSER 211 Et alternativ er å sveise bjelken til søyletoppen som vist i figur C 9.6.b. Kraft i sveis på grunn av tverrlastmomentet alene: S Ed = M Ed /
C9 BEREGNINGSEKSEMPLER FOR SØYLE- OG BJELKEFORBINDELSER 211 Et alternativ er å sveise bjelken til søyletoppen som vist i figur C 9.6.b. Kraft i sveis på grunn av tverrlastmomentet alene: S Ed = M Ed /
Eurokoder Dimensjonering av trekonstruksjoner
 Eurokoder Dimensjonering av trekonstruksjoner NS-EN 1995 NS-EN 1990 NS-EN 338 NS-EN 1194 NS-EN 1991 Ved Ingvar Skarvang og Arnold Sagen 1 Beregningseksempel 1 -vi skal beregne sperrene på dette huset laster
Eurokoder Dimensjonering av trekonstruksjoner NS-EN 1995 NS-EN 1990 NS-EN 338 NS-EN 1194 NS-EN 1991 Ved Ingvar Skarvang og Arnold Sagen 1 Beregningseksempel 1 -vi skal beregne sperrene på dette huset laster
Statiske beregninger og dimensjonering
 Fylke: Vest-Agder Vegnummer: E 39 Brunummer : Statiske beregninger og dimensjonering Dokument dato: 20.07.2012 Utført av: Hilde Solaas Signatur: Kontrollert: Trond Vabo Revidert dato: Kontrollert: Innhold
Fylke: Vest-Agder Vegnummer: E 39 Brunummer : Statiske beregninger og dimensjonering Dokument dato: 20.07.2012 Utført av: Hilde Solaas Signatur: Kontrollert: Trond Vabo Revidert dato: Kontrollert: Innhold
TSS 41 ANBEFALT ARMERINGSMØNSTER
 MEMO 55c Dato: 26.04.2011 Sign.: sss TSS 41 Siste rev.: 20.05.2016 Sign.: sss ANBEFALT ARMERINGSMØNSTER Dok. nr.: K3-10/55c Kontr.: ps DIMENSJONERING TSS 41 ANBEFALT ARMERINGSMØNSTER Figur 1: Anbefalt
MEMO 55c Dato: 26.04.2011 Sign.: sss TSS 41 Siste rev.: 20.05.2016 Sign.: sss ANBEFALT ARMERINGSMØNSTER Dok. nr.: K3-10/55c Kontr.: ps DIMENSJONERING TSS 41 ANBEFALT ARMERINGSMØNSTER Figur 1: Anbefalt
I! Emne~ode: j Dato: I Antall OPf9aver Antall vedlegg:
 -~ ~ høgskolen i oslo IEmne I Gruppe(r): I Eksamensoppgav en består av: Dimensjonering 2BA 288! Antall sider (inkl. 'forsiden): 4 I I! Emne~ode: LO 222 B I Faglig veileder:! F E Nilsen / H P Hoel j Dato:
-~ ~ høgskolen i oslo IEmne I Gruppe(r): I Eksamensoppgav en består av: Dimensjonering 2BA 288! Antall sider (inkl. 'forsiden): 4 I I! Emne~ode: LO 222 B I Faglig veileder:! F E Nilsen / H P Hoel j Dato:
Forankring av antennemast. Tore Valstad NGI
 Forankring av antennemast Tore Valstad NGI 40 Antennemast på 3960 berggrunn 1400 1400 1400 2800 0 40 Antennemast på 3960 jordgrunn 1400 1400 1400 2800 0 BRUDD I KRAFTLINJEMAT BRUDD I KRAFTLINJEMAT FUNDAMENTERING
Forankring av antennemast Tore Valstad NGI 40 Antennemast på 3960 berggrunn 1400 1400 1400 2800 0 40 Antennemast på 3960 jordgrunn 1400 1400 1400 2800 0 BRUDD I KRAFTLINJEMAT BRUDD I KRAFTLINJEMAT FUNDAMENTERING
SVEISTE FORBINDELSER NS-EN 1993-1-8 Knutepunkter
 SVEISTE FORBIDELSER S-E 1993-1-8 Knutepunkter I motsetning til S 347 er sveiser og skruer behandlet i S-E 1993-1-8, som i tillegg til orbindelsesmidlene også gir regler or knutepunkter (joints) Generelt
SVEISTE FORBIDELSER S-E 1993-1-8 Knutepunkter I motsetning til S 347 er sveiser og skruer behandlet i S-E 1993-1-8, som i tillegg til orbindelsesmidlene også gir regler or knutepunkter (joints) Generelt
122 C6 DIMENSJONERING AV FORBINDELSER
 122 C6 DIMENSJONERING AV FORBINDELSER Tabell C 6.1. Senteravstand på festemidler som gir kapasitet 20 kn/m. Kamstål (bind B, tabell B 19.11.2) B500NC Ø (mm): 8 10 12 16 20 25 N Rd,s = f yd A s (kn): 22
122 C6 DIMENSJONERING AV FORBINDELSER Tabell C 6.1. Senteravstand på festemidler som gir kapasitet 20 kn/m. Kamstål (bind B, tabell B 19.11.2) B500NC Ø (mm): 8 10 12 16 20 25 N Rd,s = f yd A s (kn): 22
Hovedpunkter fra pensum Versjon 12/1-11
 Hovedpunkter fra pensum Versjon 1/1-11 Kapittel 1 1 N = 1 kg m / s F = m a G = m g Haugan: s. 6 (Kap. 1.3, pkt. ) 1 kn = Tyngden (dvs. tyngdekraften G) fra en mann som veier 100 kg. Kapittel En kraft er
Hovedpunkter fra pensum Versjon 1/1-11 Kapittel 1 1 N = 1 kg m / s F = m a G = m g Haugan: s. 6 (Kap. 1.3, pkt. ) 1 kn = Tyngden (dvs. tyngdekraften G) fra en mann som veier 100 kg. Kapittel En kraft er
C1 GENERELT 15. Tilslag. Relativ fuktighet. Miljø. Temperatur. Svinn. Spennkraft Forspenningstap Kryp. Belastning Spennvidde
 C1 GENERELT 15 Langtidsdeformasjonene vil fortsette i konstruksjonens levetid, men endringene blir relativt raskt av ubetydelig størrelse. Figur C 1.4 illu - strerer tidsavhengigheten av langtidsdeformasjonene,
C1 GENERELT 15 Langtidsdeformasjonene vil fortsette i konstruksjonens levetid, men endringene blir relativt raskt av ubetydelig størrelse. Figur C 1.4 illu - strerer tidsavhengigheten av langtidsdeformasjonene,
TSS 101 LOKAL DEKKEARMERING VERIFISERT MED TESTER
 Dato: 26.04.2011 Sign.: sss TSS 101 Siste rev.: 30.10.2018 Sign.: sss LOKAL DEKKEARMERING Dok. nr.: K3-10/55d Kontr.: ps VERIFISERT MED TESTER DIMENSJONERING TSS 101 LOKAL DEKKEARMERING VERIFISERT MED
Dato: 26.04.2011 Sign.: sss TSS 101 Siste rev.: 30.10.2018 Sign.: sss LOKAL DEKKEARMERING Dok. nr.: K3-10/55d Kontr.: ps VERIFISERT MED TESTER DIMENSJONERING TSS 101 LOKAL DEKKEARMERING VERIFISERT MED
TSS 102 ANBEFALT ARMERINGSMØNSTER
 MEMO 57 Dato: 04.10.2011 Sign.: sss TSS 102 Siste rev.: 20.05.2016 Sign.: sss ANBEFALT ARMERINGSMØNSTER Dok. nr.: K3-10/57 Kontr.: ps DIMENSJONERING TSS 102 ANBEFALT ARMERINGSMØNSTER Figur 1: Anbefalt
MEMO 57 Dato: 04.10.2011 Sign.: sss TSS 102 Siste rev.: 20.05.2016 Sign.: sss ANBEFALT ARMERINGSMØNSTER Dok. nr.: K3-10/57 Kontr.: ps DIMENSJONERING TSS 102 ANBEFALT ARMERINGSMØNSTER Figur 1: Anbefalt
4.3. Statikk. Dimensjonerende kapasitet mot tverrlast og aksialkraft. 436 Gyproc Håndbok Gyproc Teknikk. Kapasiteten for Gyproc Duronomic
 Kapasiteten for Gyproc Duronomic Dimensjonerende kapasitet mot tverrlast og aksialkraft Forsterkningsstendere kan ta opp både tverrlaster og aksialkrefter. Dimensjoneringen er basert på partialkoeffisientmetoden.
Kapasiteten for Gyproc Duronomic Dimensjonerende kapasitet mot tverrlast og aksialkraft Forsterkningsstendere kan ta opp både tverrlaster og aksialkrefter. Dimensjoneringen er basert på partialkoeffisientmetoden.
Oppgavehefte i MEK2500 - Faststoffmekanikk
 Oppgavehefte i MEK2500 - Faststoffmekanikk av Henrik Mathias Eiding og Harald Osnes ugust 20 2 Oppgave 1 En kraft har - og y-komponentene F og F y. vstanden fra et gitt punkt til et punkt på kraftens angrepslinje
Oppgavehefte i MEK2500 - Faststoffmekanikk av Henrik Mathias Eiding og Harald Osnes ugust 20 2 Oppgave 1 En kraft har - og y-komponentene F og F y. vstanden fra et gitt punkt til et punkt på kraftens angrepslinje
Dato: ps DIMENSJONERING
 MEMO 55d Dato: 26.04.2011 Sign.: sss TSS 101 Siste rev.: 20.05.2016 Sign.: sss ANBEFALT ARMERINGSMØNSTER Dok. nr.: K3-10/55d Kontr.: ps DIMENSJONERING TSS 101 ANBEFALT ARMERINGSMØNSTER Figur 1: Anbefalt
MEMO 55d Dato: 26.04.2011 Sign.: sss TSS 101 Siste rev.: 20.05.2016 Sign.: sss ANBEFALT ARMERINGSMØNSTER Dok. nr.: K3-10/55d Kontr.: ps DIMENSJONERING TSS 101 ANBEFALT ARMERINGSMØNSTER Figur 1: Anbefalt
Strekkforankring av stenger med fot
 236 B19 FORAKRIG AV STÅL 19.3.2 Strekkforankring av stenger med fot 19.3.2.1 Generelt kjeglebrudd Anvisningene her baserer seg delvis på J. Hisdal, Masteroppgave \10\. Masteroppgaven analyserer hovedsakelig
236 B19 FORAKRIG AV STÅL 19.3.2 Strekkforankring av stenger med fot 19.3.2.1 Generelt kjeglebrudd Anvisningene her baserer seg delvis på J. Hisdal, Masteroppgave \10\. Masteroppgaven analyserer hovedsakelig
Eksempel 3.3, Limtredrager, taksperrer og opplegg
 Eksempel 3.3, Limtredrager, taksperrer og opplegg I huset nedenfor skal du regne ut egenlast og snølast på Røa i Oslo 105 meter over havet. Regn med at takets helning er 35 o. Regn ut både B1 og B2. Huset
Eksempel 3.3, Limtredrager, taksperrer og opplegg I huset nedenfor skal du regne ut egenlast og snølast på Røa i Oslo 105 meter over havet. Regn med at takets helning er 35 o. Regn ut både B1 og B2. Huset
BEREGNING AV SVEISINNFESTNINGER OG BALKONGARMERING
 MEMO 722b Dato: 09.03.2011 Sign.: sss BWC 40-500 - SØYLER I FRONT INFESTING I BÆRENDE VEGG BEREGNING AV SVEISINNFESTNINGER Siste rev.: Dok. nr.: 18.05.2016 K5-10/10 Sign.: Kontr.: sss ps OG BALKONGARMERING
MEMO 722b Dato: 09.03.2011 Sign.: sss BWC 40-500 - SØYLER I FRONT INFESTING I BÆRENDE VEGG BEREGNING AV SVEISINNFESTNINGER Siste rev.: Dok. nr.: 18.05.2016 K5-10/10 Sign.: Kontr.: sss ps OG BALKONGARMERING
D4 BRANNTEKNISK DIMENSJONERING AV ELEMENTER
 D4 BRANNTEKNISK DIMENSJONERING AV ELEMENTER 21 4.1 HULLDEKKER Hulldekker er enveis dekkekonstruksjoner, normalt med fritt dreibare opplegg. Slakkarmeringen som legges i fugene bidrar til å sikre dekkekonstruksjonens
D4 BRANNTEKNISK DIMENSJONERING AV ELEMENTER 21 4.1 HULLDEKKER Hulldekker er enveis dekkekonstruksjoner, normalt med fritt dreibare opplegg. Slakkarmeringen som legges i fugene bidrar til å sikre dekkekonstruksjonens
Dato: Siste rev.: Dok. nr.:
 MEMO 704 Dato: 8.0.0 Sign.: sss BWC 55-740 / BWC 55 LIGHT SØYLER I FRONT INNFESTING I PLASSTØPT DEKKE EKSEMPEL Siste rev.: Dok. nr.:.09.06 K5-4/5 Sign.: Kontr.: sss ps DIMENSJONERING INNHOLD GRUNNLEGGENDE
MEMO 704 Dato: 8.0.0 Sign.: sss BWC 55-740 / BWC 55 LIGHT SØYLER I FRONT INNFESTING I PLASSTØPT DEKKE EKSEMPEL Siste rev.: Dok. nr.:.09.06 K5-4/5 Sign.: Kontr.: sss ps DIMENSJONERING INNHOLD GRUNNLEGGENDE
7.1.4 Hylsefundament C7 SØYLER
 148 C7 SØYLER Tabell C 7.5. Forankring av limte stenger uten forankringsfot. Forutsetninger: Kamstål B500NC: f yd = 500 / 1,15 = 435 MPa l bd = nødvendig forankringslengde for oppgitt strekkapasitet l
148 C7 SØYLER Tabell C 7.5. Forankring av limte stenger uten forankringsfot. Forutsetninger: Kamstål B500NC: f yd = 500 / 1,15 = 435 MPa l bd = nødvendig forankringslengde for oppgitt strekkapasitet l
Dimensjonering MEMO 65 Armering av TSS 20 FA
 Dato: 10.04.2015 sss Side 1 av 9 INNHOLD DEL 1 GRUNNLEGGENDE FORUTSETNINGER OG ANTAGELSER... 2 GENERELT... 2 STANDARDER... 2 KVALITETER... 3 DIMENSJONER OG TVERRSNITTSVERDIER... 3 Rør: CFRHS 40x40x4, L=215mm.
Dato: 10.04.2015 sss Side 1 av 9 INNHOLD DEL 1 GRUNNLEGGENDE FORUTSETNINGER OG ANTAGELSER... 2 GENERELT... 2 STANDARDER... 2 KVALITETER... 3 DIMENSJONER OG TVERRSNITTSVERDIER... 3 Rør: CFRHS 40x40x4, L=215mm.
Schöck Isokorb type Q, QP, Q+Q, QP+QP
 Schöck Isokorb type, P, +, P+P Schöck Isokorb type 10 Innhold Side Eksempler på elementoppsett/tverrsnitt 60 Produktbeskrivelse/Kapasitetstabeller og tverrsnitt type 61 Planvisninger type 62 63 Beregningseksempel
Schöck Isokorb type, P, +, P+P Schöck Isokorb type 10 Innhold Side Eksempler på elementoppsett/tverrsnitt 60 Produktbeskrivelse/Kapasitetstabeller og tverrsnitt type 61 Planvisninger type 62 63 Beregningseksempel
Jernbaneverket BRUER Kap.: 8
 Stål- og samvirkekonstruksjoner Side: 1 av 12 1 HENSIKT OG OMFANG... 2 2 DIMENSJONERENDE MATERIALFASTHET... 3 2.1 Betongkonstruksjonsdelen... 3 2.1.1 Konstruksjonsfasthet...3 2.2 Stålkonstruksjonsdelen...
Stål- og samvirkekonstruksjoner Side: 1 av 12 1 HENSIKT OG OMFANG... 2 2 DIMENSJONERENDE MATERIALFASTHET... 3 2.1 Betongkonstruksjonsdelen... 3 2.1.1 Konstruksjonsfasthet...3 2.2 Stålkonstruksjonsdelen...
Pelefundamentering NGF Tekna kurs april 2014
 Pelefundamentering NGF Tekna kurs april 2014 Veiledning gjennom det greske alfabetet regelverket Astri Eggen, NGI 19 1 Agenda Regelverket peler Viktig standarder og viktige punkt i standardene Eksempler
Pelefundamentering NGF Tekna kurs april 2014 Veiledning gjennom det greske alfabetet regelverket Astri Eggen, NGI 19 1 Agenda Regelverket peler Viktig standarder og viktige punkt i standardene Eksempler
Seismisk dimensjonering av prefab. konstruksjoner
 Seismisk dimensjonering av prefab. konstruksjoner Geir Udahl Konstruksjonssjef Contiga Agenda DCL/DCM Modellering Resultater DCL vs DCM Vurdering mhp. prefab DCL Duktiltetsfaktoren q settes til 1,5 slik
Seismisk dimensjonering av prefab. konstruksjoner Geir Udahl Konstruksjonssjef Contiga Agenda DCL/DCM Modellering Resultater DCL vs DCM Vurdering mhp. prefab DCL Duktiltetsfaktoren q settes til 1,5 slik
Dimensjonering Memo 37. Standard armering av bjelke ender BCC
 Side 1 av 7 Standard armering for BCC 250 (NB! Dette er den totale armeringen i bjelke enden) For oversiktens skyld er bjelkens hovedarmering ikke tegnet inn på opprisset. Mellom de angitte bøyler i hver
Side 1 av 7 Standard armering for BCC 250 (NB! Dette er den totale armeringen i bjelke enden) For oversiktens skyld er bjelkens hovedarmering ikke tegnet inn på opprisset. Mellom de angitte bøyler i hver
INNHOLDSFORTEGNELSE. BETONexpress Rapport eksempel betongplater. 1. PLATE-001, Tverrsnitt av plate med bøyning
 Rapport eksempel betongplater INNHOLDSFORTEGNELSE 1. PLATE-001, Tverrsnitt av plate med bøyning 1.1. Dimensjonering for bøyning i bruddgrensetilstand 2. PLATE-002, Kontinuerlig plate 2.1. Tverrsnittsdimensjoner,
Rapport eksempel betongplater INNHOLDSFORTEGNELSE 1. PLATE-001, Tverrsnitt av plate med bøyning 1.1. Dimensjonering for bøyning i bruddgrensetilstand 2. PLATE-002, Kontinuerlig plate 2.1. Tverrsnittsdimensjoner,
C9 BEREGNINGSEKSEMPLER FOR SØYLE- OG BJELKEFORBINDELSER
 C9 BEREGNINGSEKSEMPLER FOR SØYLE- OG BJELKEFORBINDELSER 207 9.1 TO-SKIPS INDUSTRIHALL Dette beregningseksemplet viser praktisk beregning av knutepunk t - ene i en to-skips industrihall, ved hjelp av tabellene
C9 BEREGNINGSEKSEMPLER FOR SØYLE- OG BJELKEFORBINDELSER 207 9.1 TO-SKIPS INDUSTRIHALL Dette beregningseksemplet viser praktisk beregning av knutepunk t - ene i en to-skips industrihall, ved hjelp av tabellene
Varige konstruksjoner Konstruktive konsekvenser av alkalireaksjoner Fagdag 31 mai 2016
 Varige konstruksjoner Konstruktive konsekvenser av alkalireaksjoner Fagdag 31 mai 2016 Hans Stemland SINTEF Hans Stemland, SINTEF Eva Rodum, SVV Håvard Johansen, SVV 1 Alkalireaksjoner Skademekanisme for
Varige konstruksjoner Konstruktive konsekvenser av alkalireaksjoner Fagdag 31 mai 2016 Hans Stemland SINTEF Hans Stemland, SINTEF Eva Rodum, SVV Håvard Johansen, SVV 1 Alkalireaksjoner Skademekanisme for
C14 FASADEFORBINDELSER 323
 C14 FASADEFORBINDELSER 323 Elementet Når mellomlegget har tilnærmet samme bredde som bærende elementvange i et veggelement, blir spaltestrekk på tvers av elementet ubetydelig. Spaltestrekk i lengderetningen
C14 FASADEFORBINDELSER 323 Elementet Når mellomlegget har tilnærmet samme bredde som bærende elementvange i et veggelement, blir spaltestrekk på tvers av elementet ubetydelig. Spaltestrekk i lengderetningen
recostal type RSH Skjøtejernskassetter med trapesprofil
 recostal type RSH Eurokode 2 Geometrisk utformet trapesskjøt recostal trapesprofil møter de høyeste kravene gjeldende fortanning/skjærkraft I.h.h.t Eurokode 2 direktivene. Skjøtejernskassetter med trapesprofil
recostal type RSH Eurokode 2 Geometrisk utformet trapesskjøt recostal trapesprofil møter de høyeste kravene gjeldende fortanning/skjærkraft I.h.h.t Eurokode 2 direktivene. Skjøtejernskassetter med trapesprofil
3.2 DImENSjONERING Ribbeplater Hulldekker 3.3 DEKKER med AKSIALTRYKK Knekkingsberegning
 66 C3 DEKKER 3.2 DImENSjONERING Den generelle effekten av spennarmering i ribbeplater, forskalings - plater og hulldekker er beskrevet i innledningen til kapittel C3. 3.2.1 Ribbeplater Dimensjonering for
66 C3 DEKKER 3.2 DImENSjONERING Den generelle effekten av spennarmering i ribbeplater, forskalings - plater og hulldekker er beskrevet i innledningen til kapittel C3. 3.2.1 Ribbeplater Dimensjonering for
Steni 2. b eff. Øvre flens Steg h H Nedre flens
 FiReCo AS Dimensjonerings-diagram for BEET vegg Lastberegninger basert på NBI tester. Jørn Lilleborge Testdokument 1998 FiReCo AS 714-N-1 Side: 2 av 17 Innhold 1. DIMENSJONERINGSDIAGRAM FOR BEET VEGG...
FiReCo AS Dimensjonerings-diagram for BEET vegg Lastberegninger basert på NBI tester. Jørn Lilleborge Testdokument 1998 FiReCo AS 714-N-1 Side: 2 av 17 Innhold 1. DIMENSJONERINGSDIAGRAM FOR BEET VEGG...
BWC 30-U UTKRAGET BALKONG - INNSPENT I PLASSTØPT DEKKE BEREGNING AV FORANKRINGSPUNKT
 MEMO 742 Dato: 12.01.2016 Sign.: sss BWC 30-U UTKRAGET BALKONG - INNSPENT I PLASSTØPT DEKKE BEREGNING AV FORANKRINGSPUNKT Siste rev.: Dok. nr.: 23.05.2016 K5-10-742 Sign.: Kontr.: sss nb BWC 30-U UTKRAGET
MEMO 742 Dato: 12.01.2016 Sign.: sss BWC 30-U UTKRAGET BALKONG - INNSPENT I PLASSTØPT DEKKE BEREGNING AV FORANKRINGSPUNKT Siste rev.: Dok. nr.: 23.05.2016 K5-10-742 Sign.: Kontr.: sss nb BWC 30-U UTKRAGET
Forskjellige bruddformer Bruddformene for uttrekk av stål (forankring) innstøpt i betong kan deles i forskjellige bruddtyper som vist i figur B 19.
 B19 FORAKRIG AV STÅL 231 uttrykk i en lav verdi på sikkerhetsfaktoren. Er SF oppgitt til 3 eller mindre (for betongbrudd), kan det tyde på at det er denne modellen som er brukt. Det innebærer at: x d =
B19 FORAKRIG AV STÅL 231 uttrykk i en lav verdi på sikkerhetsfaktoren. Er SF oppgitt til 3 eller mindre (for betongbrudd), kan det tyde på at det er denne modellen som er brukt. Det innebærer at: x d =
Oppgave 1: Betong I oppgaven gjelder følgende forutsetninger: Betong: B35 Armering: B500NC Eksponeringsklasse XC1
 Høgskolen i Østfold 1 av 5 6/17 Avdeling for ingeniør og realfag KONT DESEMBER 2013 - EKSAMENSOPPGAVE Fag: IRB22013 Konstruksjonsteknikk 2 Lærere: Edin Mahmutcehajic, Siri Fause, Joachim Helgesen, Kjetil
Høgskolen i Østfold 1 av 5 6/17 Avdeling for ingeniør og realfag KONT DESEMBER 2013 - EKSAMENSOPPGAVE Fag: IRB22013 Konstruksjonsteknikk 2 Lærere: Edin Mahmutcehajic, Siri Fause, Joachim Helgesen, Kjetil
Beregning og dimensjonering av betongsøyler
 Beregning og dimensjonering av betongsøyler Kristoffer Brodshaug Knut Langehaug Bygg- og miljøteknikk (2-årig) Innlevert: juni 2014 Hovedveileder: Svein Ivar Sørensen, KT Norges teknisk-naturvitenskapelige
Beregning og dimensjonering av betongsøyler Kristoffer Brodshaug Knut Langehaug Bygg- og miljøteknikk (2-årig) Innlevert: juni 2014 Hovedveileder: Svein Ivar Sørensen, KT Norges teknisk-naturvitenskapelige
