NIO 1. runde eksempeloppgaver
|
|
|
- Camilla Øverland
- 8 år siden
- Visninger:
Transkript
1 NIO 1. runde eksempeloppgaver Oppgave 1 (dersom du ikke klarer en oppgave, bare gå videre vanskelighetsgraden er varierende) Hva må til for at hele det følgende uttrykket skal bli sant? NOT(a OR (b AND NOT a)) A: a er sann (likegyldig hva b er) B: a er usann og b er usann C: a er sann og b er sann D: Ingen av delene Oppgave 2 Hva gjør følgende programkode? (Husk at = ikke er et matematisk likhetstegn; det er en operasjon som legger verdien av høyre side inn i variabelen på venstre side.) (Divisjonene foregår med heltall; f.eks. er 24 / 10 lik 2, og 5 / 10 er lik 0) I = 0 while (A > 0) A = A / 10 I = I + 1 A: Regner ut A 10 B: Teller antall sifre i A C: Regner ut log A 10 D: Regner ut A 1/10 Oppgave 3 Vi har n øyer. Hva er det minste antall bruer som må bygges for at man skal kunne gå tørrskodd mellom alle øyene? (En bru går mellom to øyer, og bruer møtes aldri mellom øyene). A: n(n 1) B: n 2 1 C: n 1 D: n(n 1) / 2 E: n! Oppgave 4 Hvilken funksjon øker langsomst når n er stor? A: n! B: log(n) C: 2 n D: n 2 Oppgave 5 Mor i ekornfamilien lager middag. I matboden sin har hun 4 pinner med plass til 3 stykker mat på hver. For øyeblikket har 3 av dem 3 stykker mat hver, den første pinnen har nyper, den andre nøtter og den tredje tyttebær. Det går bare an å fjerne/legge til matstykker på toppen, og
2 hun kan bare flytte på et matstykke av gangen, dette for å unngå at stykker som ligger løst faller ned fra treet. Ekornmor vil gjerne flytte på matstykkene, slik at hun har 3 pinner med 3 forskjellige matstykker på hver (en av pinnene, samme hvilken, skal stå tom igjen etterpå). Hvor mange ganger må hun flytte et matstykke for å lage mat til familien? A: 8 B: 9 C: 10 Oppgave 6 Familien i nabotreet har også middag, men der er det to barn, og alle er kjempesultne, så nå må ekornmor lage 4 pinner med 4 forskjellige stykker mat på hver (nyper, nøtter, tranebær og blåbær). I tillegg har hun en annen tom pinne, også den med plass til 4 stykker mat. Til å begynne med har hun 4 pinner, hver med 4 stykker av den samme frukten. Hvor mange ganger må hun flytte et matstykke for å lage middag til familien? A: 15 B: 16 C: 17 D: 18 E: 19 Oppgave 7 Hvor mange forskjellige ord (inkl. dem som ikke betyr noe) kan man lage fra ordet OLYMPIADE hvis man bruker alle bokstaver nøyaktig én gang? A: 9 B: 27 C: 81 D: 729 E: 6561 F: G: H: I: Oppgave 8 Hva gjør følgende programkode? a = a + b; b = a - b; a = a - b; A: Regner ut omkrets av en trekant B: Legger absoluttverdi av differansen mellom a og b inn i a C: Bytter verdiene til variablene a og b D: Finner distansen mellom to punkter
3 Oppgave 9 Hva er resultatet av (binært)? A: B: C: D: Oppgave 10 1, 4, 9, 16, 25, 36,...? A: 45 B: 47 C: 49 D: 51 Oppgave 11 1, 2, 4, 8, 16, 32, 64, 128,...? A: 232 B: 244 C: 256 D: 268 Oppgave 12 0, 7, E, 15, 1C,...? A: 23 B: 25 C: 29 D: 2A Oppgave 13 Hvilken verdi returnerer følgende algoritme hvis a=42342 og b=23421, dvs. alg(42342,23421) =? alg(a, b) er lik a, når (b = 0), ellers er alg(a, b) lik alg(b, a mod b). (mod betyr resten etter divisjon - f.eks. er 39 mod 5 == 4 og 20 mod 4 == 0) A: 0 B: 1 C: 2 D: 3 Oppgave 14 Ola er på ferie i Manhattan og pleier å besøke Vegard, som bor der, og har kjøpt den nyeste humanoide roboten. Ola bor på hjørnet av 3rd avenue og 32nd street, og Vegard bor på hjørnet på av 8th avenue og 38th street. Ola skal kjøpe batterier for roboten på veien i en butikk som er på hjørnet av 6th avenue og 34th street. Hvor mange muligheter har Ola for å ta kortest mulig vei, hvis vi antar at gatene i Manhattan alle krysser hverandre med 90-graders vinkler? En av de mulige veiene er tegnet inn.
4 Ola Butikk A: 200 B: 150 C: 90 D: 2520 Vegard Oppgave 15 Ola er på vei tilbake, men nå vil han i alle fall unngå hjørnet av 34th street og 6th avenue (der butikken er), fordi han akkurat der traff to rare karer som var veldig interessert i hvorfor han kjøpte batterier, og er redd for at de er der fremdeles. Hvor mange korteste veier er tilgjengelige nå? A: 292 B: 312 C: 332 D: 352 Oppgave 16 Bokstaven a står skrevet på en tavle. Hvilket av følgende ord kan vi ikke få ved omskrivning av bokstavene på tavla med bruk av følgende regler? a -> aa a -> > > 10 F.eks. betyr regelen a -> aa at vi kan bytte ut en a med aa på samme plass. A: B: C: D:
5 Oppgave 17 Du har kanskje lekt den følgende gjetteleken før: Person A velger et tall mellom 1 og 1000 (inkludert), og person B skal gjette seg frem til dette tallet. Hver gang B gjetter et tall, forteller A om tallet var for stort eller for lite. Det kan for eksempel foregå slik: B: "100." A: "For lite." B: "200." A: "For stort." B: "190." A: "For lite." B: "192." A: "Riktig!" Nå var B temmelig heldig, da han traff tallet såpass raskt. Det lønner seg imidlertid å ha en god strategi for hvordan man gjetter, slik at man ikke er så avhengig av flaksen. Du skal spille dette med en kamerat og har selvfølgelig tenkt å imponere ham ved å gjette tallene raskt hvilken av de følgende strategiene er best? A: Starte på 1 og arbeide seg oppover til man treffer (1, 2, 3, 4,...) B: Starte på 1000 og arbeide seg nedover til man treffer (1000, 999, 998, 997,...) C: Prøve hvert 10. tall til man får vite at tallet er for høyt, og så gå nedover (f.eks. 10, 20, 30 (for høyt), 29, 28, 27,...) D: Hele tiden gjette på det midterste tallet (f.eks. 500 (for høyt), 250 (for lavt), 375 (for lavt), 437,...) E: Jobbe seg inn fra hver side (1, 1000, 2, 999, 3, 998,...)
6 Oppgave 18 Etter at du forhåpentligvis fant ut den beste metoden, bestemte kameraten din seg for å sørge for at du ville bruke veldig lang tid neste gang. Derfor sier han nå til deg: "jeg velger et tall mellom 1 og finn ut hva det er!" Før du går med på dette, vil du gjerne regne ut hvor mange gjetninger du i verste fall vil måtte trenge før du treffer. Hvor mange er det? A: B: C: D: E: 103 F: 42 G: 20 Oppgave 19 Denne programkoden kjøres på en liste array, som inneholder n elementer. toggle(i, j) bytter om elementene på plass i og plass j. Hva gjør koden, og hvor mange ganger vil toggle(i, j) bli brukt i verste fall? (Kryss av for en av de tre øverste og en av de fire nederste) for (int i = 0; i < n; ++i) for (int j = i + 1; j < n; ++j) if (array[i] > array[j]) toggle(i, j); For dem som ikke har vært borti programmeringsspråk er dette omtrentlig hva som skjer: - gå gjennom alle tallene i listen, og gjør det følgende en gang for hvert av dem: - gå gjennom alle tallene som står etter det tallet du står på i listen nå, og gjør følgende for hvert av dem: - sjekk om det første tallet er større enn det andre - bytt i så fall om på dem A: toggle(i, j) blir i verste fall startet n 2 ganger B: toggle(i, j) blir i verste fall startet n(n+1)/2 ganger C: toggle(i, j) blir i verste fall startet n(n-1)/2 ganger D: Koden sorterer tallene i stigende rekkefølge E: Koden sorterer tallene i synkende rekkefølge F: Koden stokker tallene tilfeldig G: Koden flytter ikke tallene i det hele tatt Hvis du likte å løse disse oppgavene og enten kan programmere eller har lyst til å begynne med det, ikke glem å gå inn på:
Norsk informatikkolympiade 2012 2013 1. runde
 Norsk informatikkolympiade 2012 2013 1. runde Uke 45, 2012 Tid: 90 minutter Tillatte hjelpemidler: Kun skrivesaker. Det er ikke tillatt med kalkulator eller trykte eller håndskrevne hjelpemidler. Instruksjoner:
Norsk informatikkolympiade 2012 2013 1. runde Uke 45, 2012 Tid: 90 minutter Tillatte hjelpemidler: Kun skrivesaker. Det er ikke tillatt med kalkulator eller trykte eller håndskrevne hjelpemidler. Instruksjoner:
Norsk informatikkolympiade runde
 Norsk informatikkolympiade 2015 2016 1. runde Sponset av Uke 46, 2015 Tid: 90 minutter Tillatte hjelpemidler: Kun skrivesaker. Det er ikke tillatt med kalkulator eller trykte eller håndskrevne hjelpemidler.
Norsk informatikkolympiade 2015 2016 1. runde Sponset av Uke 46, 2015 Tid: 90 minutter Tillatte hjelpemidler: Kun skrivesaker. Det er ikke tillatt med kalkulator eller trykte eller håndskrevne hjelpemidler.
Norsk informatikkolympiade runde
 Norsk informatikkolympiade 2016 2017 1. runde Sponset av Uke 46, 2016 Tid: 90 minutter Tillatte hjelpemidler: Kun skrivesaker. Det er ikke tillatt med kalkulator eller trykte eller håndskrevne hjelpemidler.
Norsk informatikkolympiade 2016 2017 1. runde Sponset av Uke 46, 2016 Tid: 90 minutter Tillatte hjelpemidler: Kun skrivesaker. Det er ikke tillatt med kalkulator eller trykte eller håndskrevne hjelpemidler.
Norsk informatikkolympiade 2012 2013 1. runde
 Norsk informatikkolympiade 2012 2013 1. runde Uke 45, 2012 Tid: 90 minutter Tillatte hjelpemidler: Kun skrivesaker. Det er ikke tillatt med kalkulator eller trykte eller håndskrevne hjelpemidler. Instruksjoner:
Norsk informatikkolympiade 2012 2013 1. runde Uke 45, 2012 Tid: 90 minutter Tillatte hjelpemidler: Kun skrivesaker. Det er ikke tillatt med kalkulator eller trykte eller håndskrevne hjelpemidler. Instruksjoner:
Norsk informatikkolympiade runde. Sponset av. Uke 46, 2015
 Norsk informatikkolympiade 2015 2016 1. runde Sponset av Uke 46, 2015 Tid: 90 minutter Tillatte hjelpemidler: Kun skrivesaker. Det er ikke tillatt med kalkulator eller trykte eller håndskrevne hjelpemidler.
Norsk informatikkolympiade 2015 2016 1. runde Sponset av Uke 46, 2015 Tid: 90 minutter Tillatte hjelpemidler: Kun skrivesaker. Det er ikke tillatt med kalkulator eller trykte eller håndskrevne hjelpemidler.
Norsk informatikkolympiade runde. Sponset av. Uke 46, 2016
 Norsk informatikkolympiade 2016 2017 1. runde Sponset av Uke 46, 2016 Tid: 90 minutter Tillatte hjelpemidler: Kun skrivesaker. Det er ikke tillatt med kalkulator eller trykte eller håndskrevne hjelpemidler.
Norsk informatikkolympiade 2016 2017 1. runde Sponset av Uke 46, 2016 Tid: 90 minutter Tillatte hjelpemidler: Kun skrivesaker. Det er ikke tillatt med kalkulator eller trykte eller håndskrevne hjelpemidler.
Norsk informatikkolympiade 2014 2015 1. runde
 Norsk informatikkolympiade 2014 2015 1. runde Sponset av Uke 46, 2014 Tid: 90 minutter Tillatte hjelpemidler: Kun skrivesaker. Det er ikke tillatt med kalkulator eller trykte eller håndskrevne hjelpemidler.
Norsk informatikkolympiade 2014 2015 1. runde Sponset av Uke 46, 2014 Tid: 90 minutter Tillatte hjelpemidler: Kun skrivesaker. Det er ikke tillatt med kalkulator eller trykte eller håndskrevne hjelpemidler.
Norsk informatikkolympiade runde
 Norsk informatikkolympiade 2017 2018 1. runde Sponset av Uke 46, 2017 Tid: 90 minutter Tillatte hjelpemidler: Kun skrivesaker. Det er ikke tillatt med kalkulator eller trykte eller håndskrevne hjelpemidler.
Norsk informatikkolympiade 2017 2018 1. runde Sponset av Uke 46, 2017 Tid: 90 minutter Tillatte hjelpemidler: Kun skrivesaker. Det er ikke tillatt med kalkulator eller trykte eller håndskrevne hjelpemidler.
Vi anbefaler at elevene blir introdusert for likninger via en praktisk problemstilling. Det kan for eksempel være:
 Likninger og algebra Det er større sprang fra å regne med tall til å regne med bokstaver enn det vi skulle tro. Vi tror at både likninger og bokstavregning (som er den algebraen elevene møter i grunnskolen)
Likninger og algebra Det er større sprang fra å regne med tall til å regne med bokstaver enn det vi skulle tro. Vi tror at både likninger og bokstavregning (som er den algebraen elevene møter i grunnskolen)
Norsk informatikkolympiade runde. Sponset av. Uke 46, 2017
 Norsk informatikkolympiade 2017 2018 1. runde Sponset av Uke 46, 2017 Tid: 90 minutter Tillatte hjelpemidler: Kun skrivesaker. Det er ikke tillatt med kalkulator eller trykte eller håndskrevne hjelpemidler.
Norsk informatikkolympiade 2017 2018 1. runde Sponset av Uke 46, 2017 Tid: 90 minutter Tillatte hjelpemidler: Kun skrivesaker. Det er ikke tillatt med kalkulator eller trykte eller håndskrevne hjelpemidler.
Norsk informatikkolympiade 2013 2014 1. runde
 Norsk informatikkolympiade 2013 2014 1. runde Sponset av Uke 46, 2013 Tid: 90 minutter Tillatte hjelpemidler: Kun skrivesaker. Det er ikke tillatt med kalkulator eller trykte eller håndskrevne hjelpemidler.
Norsk informatikkolympiade 2013 2014 1. runde Sponset av Uke 46, 2013 Tid: 90 minutter Tillatte hjelpemidler: Kun skrivesaker. Det er ikke tillatt med kalkulator eller trykte eller håndskrevne hjelpemidler.
Tall Vi på vindusrekka
 Tall Vi på vindusrekka Tall og siffer... 2 Dekadiske enheter... 3 Store tall... 4 Avrunding... 5 Tverrsum... 8 Partall og oddetall... 9 Primtall... 10 Sammensatte tall... 11 Faktorisering... 13 Negative
Tall Vi på vindusrekka Tall og siffer... 2 Dekadiske enheter... 3 Store tall... 4 Avrunding... 5 Tverrsum... 8 Partall og oddetall... 9 Primtall... 10 Sammensatte tall... 11 Faktorisering... 13 Negative
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO BOKMÅL Det matematisk-naturvitenskapelige fakultet Eksamen i : Eksamensdag : Torsdag 2. desember 2004 Tid for eksamen : 09.00 12.00 Oppgavesettet er på : Vedlegg : Tillatte hjelpemidler
UNIVERSITETET I OSLO BOKMÅL Det matematisk-naturvitenskapelige fakultet Eksamen i : Eksamensdag : Torsdag 2. desember 2004 Tid for eksamen : 09.00 12.00 Oppgavesettet er på : Vedlegg : Tillatte hjelpemidler
Algebra Vi på vindusrekka
 Algebra Vi på vindusrekka Utsagn... 2 Åpne utsagn... 3 Den ukjente... 4 Likhetstegnet... 5 Likninger... 6 Løs likninger... 7 Matematiske uttrykk... 8 Formel... 9 Tilordning... 10 Funksjon... 11 Koordinatsystem...
Algebra Vi på vindusrekka Utsagn... 2 Åpne utsagn... 3 Den ukjente... 4 Likhetstegnet... 5 Likninger... 6 Løs likninger... 7 Matematiske uttrykk... 8 Formel... 9 Tilordning... 10 Funksjon... 11 Koordinatsystem...
Kanter, kanter, mange mangekanter
 Kanter, kanter, mange mangekanter Nybegynner Processing PDF Introduksjon: Her skal vi se på litt mer avansert opptegning og bevegelse. Vi skal ta utgangspunkt i oppgaven om den sprettende ballen, men bytte
Kanter, kanter, mange mangekanter Nybegynner Processing PDF Introduksjon: Her skal vi se på litt mer avansert opptegning og bevegelse. Vi skal ta utgangspunkt i oppgaven om den sprettende ballen, men bytte
Norsk informatikkolympiade 2014 2015 1. runde. Sponset av. Uke 46, 2014
 Norsk informatikkolympiade 014 015 1. runde Sponset av Uke 46, 014 Tid: 90 minutter Tillatte hjelpemidler: Kun skrivesaker. Det er ikke tillatt med kalkulator eller trykte eller håndskrevne hjelpemidler.
Norsk informatikkolympiade 014 015 1. runde Sponset av Uke 46, 014 Tid: 90 minutter Tillatte hjelpemidler: Kun skrivesaker. Det er ikke tillatt med kalkulator eller trykte eller håndskrevne hjelpemidler.
Bygg et Hus. Steg 1: Prøv selv først. Sjekkliste. Introduksjon. Prøv selv
 Bygg et Hus Introduksjon I denne leksjonen vil vi se litt på hvordan vi kan få en robot til å bygge et hus for oss. Underveis vil vi lære hvordan vi kan bruke løkker og funksjoner for å gjenta ting som
Bygg et Hus Introduksjon I denne leksjonen vil vi se litt på hvordan vi kan få en robot til å bygge et hus for oss. Underveis vil vi lære hvordan vi kan bruke løkker og funksjoner for å gjenta ting som
Verden - Del 2. Steg 0: Oppsummering fra introduksjonsoppgaven. Intro
 Verden - Del 2 Nybegynner Processing Intro Denne oppgaven bygger på oppgaven med samme navn som ligger på introduksjonsnivå her i Processingoppgavene. Klikk her for å gå til introduksjonsoppgaven av verden.
Verden - Del 2 Nybegynner Processing Intro Denne oppgaven bygger på oppgaven med samme navn som ligger på introduksjonsnivå her i Processingoppgavene. Klikk her for å gå til introduksjonsoppgaven av verden.
Sprettball Erfaren ComputerCraft PDF
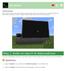 Sprettball Erfaren ComputerCraft PDF Introduksjon Nå skal vi lære hvordan vi kan koble en skjerm til datamaskinen. Med en ekstra skjerm kan vi bruke datamaskinen til å kommunisere med verden rundt oss.
Sprettball Erfaren ComputerCraft PDF Introduksjon Nå skal vi lære hvordan vi kan koble en skjerm til datamaskinen. Med en ekstra skjerm kan vi bruke datamaskinen til å kommunisere med verden rundt oss.
Utplukk og sortering. Innhold
 Innhold Utplukk og sortering... 2 Definering av utplukk... 2 Velge felter for utplukket... 2 Filtrering og søk på tilgjengelige databasefelter... 3 Endre databasekobling etter at felt er valgt... 7 Valg
Innhold Utplukk og sortering... 2 Definering av utplukk... 2 Velge felter for utplukket... 2 Filtrering og søk på tilgjengelige databasefelter... 3 Endre databasekobling etter at felt er valgt... 7 Valg
Kanter, kanter, mange mangekanter. Introduksjon: Steg 1: Enkle firkanter. Sjekkliste. Skrevet av: Sigmund Hansen
 Kanter, kanter, mange mangekanter Skrevet av: Sigmund Hansen Kurs: Processing Tema: Tekstbasert, Animasjon Fag: Matematikk, Programmering, Kunst og håndverk Klassetrinn: 8.-10. klasse, Videregående skole
Kanter, kanter, mange mangekanter Skrevet av: Sigmund Hansen Kurs: Processing Tema: Tekstbasert, Animasjon Fag: Matematikk, Programmering, Kunst og håndverk Klassetrinn: 8.-10. klasse, Videregående skole
Bli Kjent med Datamaskinen Introduksjon ComputerCraft PDF
 Bli Kjent med Datamaskinen Introduksjon ComputerCraft PDF Introduksjon Vi begynner med å bygge en enkel datamaskin. Etter å ha brukt litt tid på å bli kjent med hvordan datamaskinen virker, bruker vi den
Bli Kjent med Datamaskinen Introduksjon ComputerCraft PDF Introduksjon Vi begynner med å bygge en enkel datamaskin. Etter å ha brukt litt tid på å bli kjent med hvordan datamaskinen virker, bruker vi den
Start et nytt Scratch-prosjekt. Slett kattefiguren, for eksempel ved å høyreklikke på den og velge slett.
 Norgestur Introduksjon Bli med på en rundreise i Norge! Vi skal lage et spill hvor du styrer et helikopter rundt omkring et kart over Norge, mens du prøver å raskest mulig finne steder og byer du blir
Norgestur Introduksjon Bli med på en rundreise i Norge! Vi skal lage et spill hvor du styrer et helikopter rundt omkring et kart over Norge, mens du prøver å raskest mulig finne steder og byer du blir
Norsk informatikkolympiade runde. Sponset av. Uke 46, 2013
 Norsk informatikkolympiade 2013 2014 1. runde Sponset av Uke 46, 2013 Tid: 90 minutter Tillatte hjelpemidler: Kun skrivesaker. Det er ikke tillatt med kalkulator eller trykte eller håndskrevne hjelpemidler.
Norsk informatikkolympiade 2013 2014 1. runde Sponset av Uke 46, 2013 Tid: 90 minutter Tillatte hjelpemidler: Kun skrivesaker. Det er ikke tillatt med kalkulator eller trykte eller håndskrevne hjelpemidler.
Oversikt over det kinesiske restteoremet
 Oversikt over det kinesiske restteoremet Richard Williamson 3. desember 2014 Oppgave 1 Finn et heltall x slik at: (1) x 2 (mod 6); (2) x 3 (mod 11). Hvordan vet jeg at vi bør benytte det kinesiske restteoremet?
Oversikt over det kinesiske restteoremet Richard Williamson 3. desember 2014 Oppgave 1 Finn et heltall x slik at: (1) x 2 (mod 6); (2) x 3 (mod 11). Hvordan vet jeg at vi bør benytte det kinesiske restteoremet?
Likninger - en introduksjon på 8. trinn Hva er en likning og hva betyr å løse den?
 side 1 Detaljert eksempel om Likninger - en introduksjon på 8. trinn Hva er en likning og hva betyr å løse den? Dette er et forslag til undervisningsopplegg der utgangspunktet er sentrale problemstillinger
side 1 Detaljert eksempel om Likninger - en introduksjon på 8. trinn Hva er en likning og hva betyr å løse den? Dette er et forslag til undervisningsopplegg der utgangspunktet er sentrale problemstillinger
Mattespill Nybegynner Python PDF
 Mattespill Nybegynner Python PDF Introduksjon I denne leksjonen vil vi se litt nærmere på hvordan Python jobber med tall, og vi vil lage et enkelt mattespill. Vi vil også se hvordan vi kan gjøre ting tilfeldige.
Mattespill Nybegynner Python PDF Introduksjon I denne leksjonen vil vi se litt nærmere på hvordan Python jobber med tall, og vi vil lage et enkelt mattespill. Vi vil også se hvordan vi kan gjøre ting tilfeldige.
Hangman. Level. Introduksjon
 Level 2 Hangman All Code Clubs must be registered. Registered clubs appear on the map at codeclubworld.org - if your club is not on the map then visit jumpto.cc/ccwreg to register your club. Introduksjon
Level 2 Hangman All Code Clubs must be registered. Registered clubs appear on the map at codeclubworld.org - if your club is not on the map then visit jumpto.cc/ccwreg to register your club. Introduksjon
Robotinvasjon Introduksjon ComputerCraft PDF
 Robotinvasjon Introduksjon ComputerCraft PDF Introduksjon Vi har sett enkle datamaskiner. Nå skal vi leke oss med roboter, og finne ut hvordan vi kan få dem til å gjøre forskjellige ting for oss. Steg
Robotinvasjon Introduksjon ComputerCraft PDF Introduksjon Vi har sett enkle datamaskiner. Nå skal vi leke oss med roboter, og finne ut hvordan vi kan få dem til å gjøre forskjellige ting for oss. Steg
TDT4105 Informasjonsteknologi, grunnkurs
 1 TDT4105 Informasjonsteknologi, grunnkurs Matlab: Sortering og søking Anders Christensen (anders@idi.ntnu.no) Rune Sætre (satre@idi.ntnu.no) TDT4105 IT Grunnkurs 2 Pensum Matlab-boka: 12.3 og 12.5 Stoffet
1 TDT4105 Informasjonsteknologi, grunnkurs Matlab: Sortering og søking Anders Christensen (anders@idi.ntnu.no) Rune Sætre (satre@idi.ntnu.no) TDT4105 IT Grunnkurs 2 Pensum Matlab-boka: 12.3 og 12.5 Stoffet
DIANA Vil du hjelpe meg med matvarene? DAVID Okay. DIANA Tomatene ser fine ut... Har du sett dem? David? DAVID Hva er Gryphon?
 INDECENT PROPOSAL FORHISTORIE: Diana og David har gått langt for å ordne opp i økonomien sin. De har fått et tilbud: Diana har sex med en annen mann, mot en stor sum penger. I etterkant av dette er paret
INDECENT PROPOSAL FORHISTORIE: Diana og David har gått langt for å ordne opp i økonomien sin. De har fått et tilbud: Diana har sex med en annen mann, mot en stor sum penger. I etterkant av dette er paret
SINE Kris? Er du våken? KRISTOFFER. SINE (Jo, det er du vel.) Bli med meg til København. KRISTOFFER. SINE Jeg vil at du skal bli med.
 GOOD WILL HUNTING By Ben Affleck og Matt Damon WILL / SKYLAR/ Kris og Sine har hatt et forhold ei stund. Dette er en scene som gjenspeiler hvor vanskelig det kan være å ta det neste skrittet. Sine ønsker
GOOD WILL HUNTING By Ben Affleck og Matt Damon WILL / SKYLAR/ Kris og Sine har hatt et forhold ei stund. Dette er en scene som gjenspeiler hvor vanskelig det kan være å ta det neste skrittet. Sine ønsker
Verden. Steg 1: Vinduet. Introduksjon
 Verden Introduksjon Processing Introduksjon Velkommen til verdensspillet! Her skal vi lage begynnelsen av et spill hvor man skal gjette hvilke verdensdeler som er hvor. Så kan du utvide oppgava til å heller
Verden Introduksjon Processing Introduksjon Velkommen til verdensspillet! Her skal vi lage begynnelsen av et spill hvor man skal gjette hvilke verdensdeler som er hvor. Så kan du utvide oppgava til å heller
TDT4110 IT Grunnkurs Høst 2014
 TDT4110 IT Grunnkurs Høst 2014 Norges teknisk naturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap Øving 10 Denne øvingen er en to-ukers øving (prosjekt) og inneholder én
TDT4110 IT Grunnkurs Høst 2014 Norges teknisk naturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap Øving 10 Denne øvingen er en to-ukers øving (prosjekt) og inneholder én
Enkle generiske klasser i Java
 Enkle generiske klasser i Java Oslo, 7/1-13 Av Stein Gjessing, Institutt for informatikk, Universitetet i Oslo Del 1: Enkle pekere Før vi tar fatt på det som er nytt i dette notatet, skal vi repetere litt
Enkle generiske klasser i Java Oslo, 7/1-13 Av Stein Gjessing, Institutt for informatikk, Universitetet i Oslo Del 1: Enkle pekere Før vi tar fatt på det som er nytt i dette notatet, skal vi repetere litt
INT. BRYGGA. SENT Barbro har nettopp fått sparken og står og venter på brygga der Inge kommer inn med siste ferja. INGE BARBRO INGE BARBRO INGE
 I DAG OG I MORGEN av Liv Heløe Scene for mann og kvinne Manuset finnes til utlån på NSKI I DAG OG I MORGEN er et stykke som handler om Inge og Barbro som er et par, bosatt på en øy et sted i Norge. Inge
I DAG OG I MORGEN av Liv Heløe Scene for mann og kvinne Manuset finnes til utlån på NSKI I DAG OG I MORGEN er et stykke som handler om Inge og Barbro som er et par, bosatt på en øy et sted i Norge. Inge
Argumenter fra kommandolinjen
 Argumenter fra kommandolinjen Denne veiledningen er laget for å vise hvordan man kan overføre argumenter fra kommandolinjen til et program. Hvordan transportere data fra en kommandolinje slik at dataene
Argumenter fra kommandolinjen Denne veiledningen er laget for å vise hvordan man kan overføre argumenter fra kommandolinjen til et program. Hvordan transportere data fra en kommandolinje slik at dataene
Regler for: getsmart Grønn. Det anbefales at man først ser på powerpoint-reglene når man skal lære seg ulike spill med kortstokkene!
 -6 Regler for: getsmart Grønn Hele tall 3 4 Hele tall 8-6 -6 3-6 3 8 Hele tall Hele tall 3 4 Det anbefales at man først ser på powerpoint-reglene når man skal lære seg ulike spill med kortstokkene! Sjekk
-6 Regler for: getsmart Grønn Hele tall 3 4 Hele tall 8-6 -6 3-6 3 8 Hele tall Hele tall 3 4 Det anbefales at man først ser på powerpoint-reglene når man skal lære seg ulike spill med kortstokkene! Sjekk
Oversikt over kryptografi
 Oversikt over kryptografi Richard Williamson 3. desember 2014 Oppgave 1 Person A ønsker å sende meldingen Ha det! til person B, og ønsker å benytte RSAalgoritmen for å kryptere den. Den offentlige nøkkelen
Oversikt over kryptografi Richard Williamson 3. desember 2014 Oppgave 1 Person A ønsker å sende meldingen Ha det! til person B, og ønsker å benytte RSAalgoritmen for å kryptere den. Den offentlige nøkkelen
Trekanter på geobrettet. - oppgavene er hentet fra ressurspermen til Ingvill M. Stedøys Matematiske koffert
 G E O B R E T T Innledende tips- differensiering Når dere jobber med geobrettet kan det være fint å bruke bare en liten del av brettet, for at det ikke skal bli for vanskelig til å begynne med. Sett på
G E O B R E T T Innledende tips- differensiering Når dere jobber med geobrettet kan det være fint å bruke bare en liten del av brettet, for at det ikke skal bli for vanskelig til å begynne med. Sett på
INF1010 notat: Binærsøking og quicksort
 INF1010 notat: Binærsøking og quicksort Ragnhild Kobro Runde Februar 2004 I dette notatet skal vi ta for oss ytterligere to eksempler der rekursjon har en naturlig anvendelse, nemlig binærsøking og quicksort.
INF1010 notat: Binærsøking og quicksort Ragnhild Kobro Runde Februar 2004 I dette notatet skal vi ta for oss ytterligere to eksempler der rekursjon har en naturlig anvendelse, nemlig binærsøking og quicksort.
Oppsummering av Uke 3. MAT1030 Diskret matematikk. Binære tall. Oppsummering av Uke 3
 Oppsummering av Uke 3 MAT1030 Diskret matematikk Forelesning 3: Mer om representasjon av tall Dag Normann Matematisk Institutt, Universitetet i Oslo 21. januar 2008 Mandag 14.01 og delvis onsdag 16.01
Oppsummering av Uke 3 MAT1030 Diskret matematikk Forelesning 3: Mer om representasjon av tall Dag Normann Matematisk Institutt, Universitetet i Oslo 21. januar 2008 Mandag 14.01 og delvis onsdag 16.01
Her skal du lære å programmere micro:biten slik at du kan spille stein, saks, papir med den eller mot den.
 PXT: Stein, saks, papir Skrevet av: Bjørn Hamre Kurs: Microbit Introduksjon Her skal du lære å programmere micro:biten slik at du kan spille stein, saks, papir med den eller mot den. Steg 1: Velge tilfeldig
PXT: Stein, saks, papir Skrevet av: Bjørn Hamre Kurs: Microbit Introduksjon Her skal du lære å programmere micro:biten slik at du kan spille stein, saks, papir med den eller mot den. Steg 1: Velge tilfeldig
"Hjerneteppe!" er en huskelek hvor du skal huske stadig lengre rekker med bokstaver!
 PXT: Hjerneteppe! Skrevet av: Helene Isnes Kurs: Microbit Tema: Blokkbasert, Spill Fag: Programmering Klassetrinn: 5.-7. klasse, 8.-10. klasse Introduksjon "Hjerneteppe!" er en huskelek hvor du skal huske
PXT: Hjerneteppe! Skrevet av: Helene Isnes Kurs: Microbit Tema: Blokkbasert, Spill Fag: Programmering Klassetrinn: 5.-7. klasse, 8.-10. klasse Introduksjon "Hjerneteppe!" er en huskelek hvor du skal huske
Heap* En heap er et komplett binært tre: En heap er også et monotont binært tre:
 Heap Heap* En heap er et komplett binært tre: Alle nivåene i treet, unntatt (muligens) det nederste, er alltid helt fylt opp med noder Alle noder på nederste nivå ligger til venstre En heap er også et
Heap Heap* En heap er et komplett binært tre: Alle nivåene i treet, unntatt (muligens) det nederste, er alltid helt fylt opp med noder Alle noder på nederste nivå ligger til venstre En heap er også et
King Kong Erfaren Scratch PDF
 King Kong Erfaren Scratch PDF Introduksjon I dette spillet inspirert av historien om King Kong, skal vi se hvor lett det er å bruke grafikk som ikke allerede ligger i Scratchbiblioteket. I spillet styrer
King Kong Erfaren Scratch PDF Introduksjon I dette spillet inspirert av historien om King Kong, skal vi se hvor lett det er å bruke grafikk som ikke allerede ligger i Scratchbiblioteket. I spillet styrer
Steg 1: Hvordan styre figurer med piltastene
 Labyrint Skrevet av: Geir Arne Hjelle Kurs: Scratch Tema: Blokkbasert, Spill Fag: Programmering Klassetrinn: 1.-4. klasse, 5.-7. klasse, 8.-10. klasse Introduksjon I dette spillet vil vi kontrollere en
Labyrint Skrevet av: Geir Arne Hjelle Kurs: Scratch Tema: Blokkbasert, Spill Fag: Programmering Klassetrinn: 1.-4. klasse, 5.-7. klasse, 8.-10. klasse Introduksjon I dette spillet vil vi kontrollere en
EKSAMEN med løsningsforslag
 EKSAMEN med løsningsforslag Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: Eksamenstid: 20. mai 2009 kl 09.00 til kl 13.00 Hjelpemidler: 8 A4-sider (4 ark) med egne notater Kalkulator Faglærer:
EKSAMEN med løsningsforslag Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: Eksamenstid: 20. mai 2009 kl 09.00 til kl 13.00 Hjelpemidler: 8 A4-sider (4 ark) med egne notater Kalkulator Faglærer:
STEPH. GREG Hei, hva skjer? STEPH Kan jeg komme inn, eller? GREG Ja, faen, kom inn 'a Vil du ha en pils, eller? STEPH Pils nå? Nei takk.
 REASONS TO BE PRETTY Forkortet versjon ANIE Hei. Hei, hva skjer? Kan jeg komme inn, eller? Ja, faen, kom inn 'a Vil du ha en pils, eller? Pils nå? Nei takk. Nei eh juice, da? Ja. Det kan jeg ta. Vær så
REASONS TO BE PRETTY Forkortet versjon ANIE Hei. Hei, hva skjer? Kan jeg komme inn, eller? Ja, faen, kom inn 'a Vil du ha en pils, eller? Pils nå? Nei takk. Nei eh juice, da? Ja. Det kan jeg ta. Vær så
Bursdag i Antarktis Nybegynner Scratch PDF
 Bursdag i Antarktis Nybegynner Scratch PDF Introduksjon Bursdag i Antarktis er en interaktiv animasjon som forteller historien om en liten katt som har gått seg bort på bursdagen sin. Heldigvis treffer
Bursdag i Antarktis Nybegynner Scratch PDF Introduksjon Bursdag i Antarktis er en interaktiv animasjon som forteller historien om en liten katt som har gått seg bort på bursdagen sin. Heldigvis treffer
Hannametoden en finfin nybegynnermetode for å løse Rubik's kube, en såkalt "layer-by-layer" metode og deretter en metode for viderekommende.
 Hannametoden en finfin nybegynnermetode for å løse Rubik's kube, en såkalt "layer-by-layer" metode og deretter en metode for viderekommende. Olve Maudal (oma@pvv.org) Februar, 2012 Her er notasjonen som
Hannametoden en finfin nybegynnermetode for å løse Rubik's kube, en såkalt "layer-by-layer" metode og deretter en metode for viderekommende. Olve Maudal (oma@pvv.org) Februar, 2012 Her er notasjonen som
Det du skal gjøre i denne oppgava er først å sette opp bakgrunnen til spillet og så rett og slett å få firkanter til å falle over skjermen.
 Tetris Introduksjon Processing Introduksjon Lag starten på ditt eget tetris spill! Det du skal gjøre i denne oppgava er først å sette opp bakgrunnen til spillet og så rett og slett å få firkanter til å
Tetris Introduksjon Processing Introduksjon Lag starten på ditt eget tetris spill! Det du skal gjøre i denne oppgava er først å sette opp bakgrunnen til spillet og så rett og slett å få firkanter til å
TDT4102 Prosedyreog objektorientert programmering Vår 2016
 Norges teknisk naturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap TDT4102 Prosedyreog objektorientert programmering Vår 2016 Øving 4 Frist: 2016-02-12 Mål for denne øvingen:
Norges teknisk naturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap TDT4102 Prosedyreog objektorientert programmering Vår 2016 Øving 4 Frist: 2016-02-12 Mål for denne øvingen:
ToPlayer. Introduksjon: Skrevet av: Ruben Gjerstad Eide og Kine Gjerstad Eide
 ToPlayer Skrevet av: Ruben Gjerstad Eide og Kine Gjerstad Eide Kurs: Processing Tema: Tekstbasert Fag: Matematikk, Programmering Klassetrinn: 8.-10. klasse, Videregående skole Introduksjon: Nå skal vi
ToPlayer Skrevet av: Ruben Gjerstad Eide og Kine Gjerstad Eide Kurs: Processing Tema: Tekstbasert Fag: Matematikk, Programmering Klassetrinn: 8.-10. klasse, Videregående skole Introduksjon: Nå skal vi
ToPlayer. Steg 1: Kom i gang med metodene setup og draw. Gjør dette: Introduksjon:
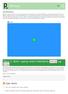 ToPlayer Introduksjon Processing Introduksjon: Nå skal vi lage et spill som to personer kan spille mot hverandre. Vi har kalt det ToPlayer, men du kan kalle det hva du vil. Målet er å dytte en figur, eller
ToPlayer Introduksjon Processing Introduksjon: Nå skal vi lage et spill som to personer kan spille mot hverandre. Vi har kalt det ToPlayer, men du kan kalle det hva du vil. Målet er å dytte en figur, eller
HUND BET MANN. Av kandidat 7
 HUND BET MANN Av kandidat 7 Innhold: 1 Innledning 2 Spillets start 2.0.1 Valgfri regel: Mysterier 2.1 Hovedpersoner 2.1.1 Valgfri regel: Saker uten hovedperson. 2.2 Spillederen 2.2.1 Valgfri regel: Fast
HUND BET MANN Av kandidat 7 Innhold: 1 Innledning 2 Spillets start 2.0.1 Valgfri regel: Mysterier 2.1 Hovedpersoner 2.1.1 Valgfri regel: Saker uten hovedperson. 2.2 Spillederen 2.2.1 Valgfri regel: Fast
Verden. Introduksjon. Skrevet av: Kine Gjerstad Eide og Ruben Gjerstad Eide
 Verden Skrevet av: Kine Gjerstad Eide og Ruben Gjerstad Eide Kurs: Processing Tema: Tekstbasert Fag: Matematikk, Programmering, Samfunnsfag Klassetrinn: 8.-10. klasse, Videregående skole Introduksjon Velkommen
Verden Skrevet av: Kine Gjerstad Eide og Ruben Gjerstad Eide Kurs: Processing Tema: Tekstbasert Fag: Matematikk, Programmering, Samfunnsfag Klassetrinn: 8.-10. klasse, Videregående skole Introduksjon Velkommen
Mer om representasjon av tall
 Forelesning 3 Mer om representasjon av tall Dag Normann - 21. januar 2008 Oppsummering av Uke 3 Mandag 14.01 og delvis onsdag 16.01 diskuterte vi hva som menes med en algoritme, og vi så på pseudokoder
Forelesning 3 Mer om representasjon av tall Dag Normann - 21. januar 2008 Oppsummering av Uke 3 Mandag 14.01 og delvis onsdag 16.01 diskuterte vi hva som menes med en algoritme, og vi så på pseudokoder
Hvor i All Verden? Del 3 Erfaren Scratch PDF
 Hvor i All Verden? Del 3 Erfaren Scratch PDF Introduksjon Hvor i All Verden? er et reise- og geografispill hvor man raskest mulig skal fly innom reisemål spredt rundt i Europa. Dette er den siste av tre
Hvor i All Verden? Del 3 Erfaren Scratch PDF Introduksjon Hvor i All Verden? er et reise- og geografispill hvor man raskest mulig skal fly innom reisemål spredt rundt i Europa. Dette er den siste av tre
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Side 1 Det matematisk-naturvitenskapelige fakultet Eksamen i: INF1010 Objektorientert programmering Eksamensdag: Tirsdag 12. juni 2012 Tid for eksamen: 9:00 15:00 Oppgavesettet er
UNIVERSITETET I OSLO Side 1 Det matematisk-naturvitenskapelige fakultet Eksamen i: INF1010 Objektorientert programmering Eksamensdag: Tirsdag 12. juni 2012 Tid for eksamen: 9:00 15:00 Oppgavesettet er
Binære søketrær. Et notat for INF1010 Stein Michael Storleer 16. mai 2013
 Binære søketrær Et notat for INF Stein Michael Storleer 6. mai 3 Dette notatet er nyskrevet og inneholder sikkert feil. Disse vil bli fortløpende rettet og datoen over blir oppdatert samtidig. Hvis du
Binære søketrær Et notat for INF Stein Michael Storleer 6. mai 3 Dette notatet er nyskrevet og inneholder sikkert feil. Disse vil bli fortløpende rettet og datoen over blir oppdatert samtidig. Hvis du
Fortell hva som skjuler seg under papiret uten å bruke det riktige ordet eller symbolet. Du finner noen ord/symboler som du kan bruke i rammen
 nederst på siden. Det kan være noen du ikke trenger der også! Be hjelperen nederst på siden. Det kan være noen du ikke trenger der også! Be hjelperen nederst på siden. Det kan være noen du ikke trenger
nederst på siden. Det kan være noen du ikke trenger der også! Be hjelperen nederst på siden. Det kan være noen du ikke trenger der også! Be hjelperen nederst på siden. Det kan være noen du ikke trenger
Tetris. Introduksjon. Skrevet av: Kine Gjerstad Eide. Lag starten på ditt eget tetris spill!
 Tetris Skrevet av: Kine Gjerstad Eide Kurs: Processing Introduksjon Lag starten på ditt eget tetris spill! Det du skal gjøre i denne oppgava er først å sette opp bakgrunnen til spillet og så rett og slett
Tetris Skrevet av: Kine Gjerstad Eide Kurs: Processing Introduksjon Lag starten på ditt eget tetris spill! Det du skal gjøre i denne oppgava er først å sette opp bakgrunnen til spillet og så rett og slett
Kapittel august Institutt for geofag Universitetet i Oslo. GEO En Introduksjon til MatLab. Kapittel 2.
 Institutt for geofag Universitetet i Oslo 28. august 2012 Kommandovinduet Det er gjennom kommandovinduet du først og fremst interagerer med MatLab ved å gi datamaskinen kommandoer når >> (kalles prompten
Institutt for geofag Universitetet i Oslo 28. august 2012 Kommandovinduet Det er gjennom kommandovinduet du først og fremst interagerer med MatLab ved å gi datamaskinen kommandoer når >> (kalles prompten
Kidsmonitor tutorials for mobil
 Kidsmonitor tutorials for mobil Hvordan sende en melding? Dette er for den typen melding som gjelder kun den ene dagen den sendes. Send disse samme dag som meldingen gjelder, FØR klokken 12.00. Sendes
Kidsmonitor tutorials for mobil Hvordan sende en melding? Dette er for den typen melding som gjelder kun den ene dagen den sendes. Send disse samme dag som meldingen gjelder, FØR klokken 12.00. Sendes
2.3 Delelighetsregler
 2.3 Delelighetsregler Begrepene multiplikasjon og divisjon og regneferdigheter med disse operasjonene utgjør sentralt lærestoff på barnetrinnet. Det er mange tabellfakta å huske og operasjonene skal kunne
2.3 Delelighetsregler Begrepene multiplikasjon og divisjon og regneferdigheter med disse operasjonene utgjør sentralt lærestoff på barnetrinnet. Det er mange tabellfakta å huske og operasjonene skal kunne
2 Om statiske variable/konstanter og statiske metoder.
 Litt om datastrukturer i Java Av Stein Gjessing, Institutt for informatikk, Universitetet i Oslo 1 Innledning Dette notatet beskriver noe av det som foregår i primærlageret når et Javaprogram utføres.
Litt om datastrukturer i Java Av Stein Gjessing, Institutt for informatikk, Universitetet i Oslo 1 Innledning Dette notatet beskriver noe av det som foregår i primærlageret når et Javaprogram utføres.
DYNAMISK KARTLEGGINGSPRØVE I MATEMATIKK
 DYNAMISK KARTLEGGINGSPRØVE I MATEMATIKK For elever fra 1. 5. trinn Del C: Notatark til kartleggingsleder Elev: Født: Skole: Klassetrinn: Kartleggingsleder: Andre til stede: Sted og dato for kartlegging:
DYNAMISK KARTLEGGINGSPRØVE I MATEMATIKK For elever fra 1. 5. trinn Del C: Notatark til kartleggingsleder Elev: Født: Skole: Klassetrinn: Kartleggingsleder: Andre til stede: Sted og dato for kartlegging:
Ida Festervoll 15.11.2010
 Brukerveiledning Legg inn portfolio Ida Festervoll 15.11.2010 Dette er en steg for steg veileder som hjelper deg å legge prosjekter i portfolioen Innhold Legg INN Portfolio... 2 Hvordan kan en portfolio
Brukerveiledning Legg inn portfolio Ida Festervoll 15.11.2010 Dette er en steg for steg veileder som hjelper deg å legge prosjekter i portfolioen Innhold Legg INN Portfolio... 2 Hvordan kan en portfolio
Hva er det? Steg 1: Få flere ting til å vise seg på tavlen. Sjekkliste. Test prosjektet. Introduksjon
 Hva er det? Introduksjon Et bilde av en tilfeldig ting vises på tavlen. Men bildet er forvrengt, slik at du må gjette hva det er ved å klikke på et av alternativene som vises under. Desto raskere du gjetter
Hva er det? Introduksjon Et bilde av en tilfeldig ting vises på tavlen. Men bildet er forvrengt, slik at du må gjette hva det er ved å klikke på et av alternativene som vises under. Desto raskere du gjetter
Matematisk julekalender for trinn, 2010
 Matematisk julekalender for 8. - 10. trinn, 2010 Årets julekalender for 8.-10. trinn består av 9 enkeltstående. Oppgavene kan løses uavhengig av hverandre, og alle svar tilsvarer en bokstav. Bokstavene
Matematisk julekalender for 8. - 10. trinn, 2010 Årets julekalender for 8.-10. trinn består av 9 enkeltstående. Oppgavene kan løses uavhengig av hverandre, og alle svar tilsvarer en bokstav. Bokstavene
Pedagogisk arbeid med tema tristhet og depresjon i småskolen
 Pedagogisk arbeid med tema tristhet og depresjon i småskolen (basert på «Rettleiingshefte for bruk i klasser og grupper») Undersøkelser har vist at for å skape gode vilkår for åpenhet og gode samtaler
Pedagogisk arbeid med tema tristhet og depresjon i småskolen (basert på «Rettleiingshefte for bruk i klasser og grupper») Undersøkelser har vist at for å skape gode vilkår for åpenhet og gode samtaler
Overslag FRA A TIL Å
 Overslag FRA A TIL Å VEILEDER FOR FORELDRE MED BARN I 5. 7. KLASSE EMNER Side 1 Innledning til overslag 2 2 Grunnleggende om overslag 2 3 Å gjøre overslag 6 4 Forsiktighetsregler 7 4.1 Når overslaget ikke
Overslag FRA A TIL Å VEILEDER FOR FORELDRE MED BARN I 5. 7. KLASSE EMNER Side 1 Innledning til overslag 2 2 Grunnleggende om overslag 2 3 Å gjøre overslag 6 4 Forsiktighetsregler 7 4.1 Når overslaget ikke
www.skoletorget.no Tall og algebra Matematikk Side 1 av 6
 Side 1 av 6 Hva = en ligning? Sist oppdatert: 15. november 2003 I dette kapittelet skal vi se på noen grunnregler for løsning av ligninger med én ukjent. Det viser seg at balanse er et helt sentralt prinsipp
Side 1 av 6 Hva = en ligning? Sist oppdatert: 15. november 2003 I dette kapittelet skal vi se på noen grunnregler for løsning av ligninger med én ukjent. Det viser seg at balanse er et helt sentralt prinsipp
Bjørn Ingvaldsen. Far din
 Bjørn Ingvaldsen Far din Far din, sa han. Det sto en svart bil i veien. En helt vanlig bil. Stasjonsvogn. Men den sto midt i veien og sperret all trafikk. Jeg var på vei hjem fra skolen, var sein, hadde
Bjørn Ingvaldsen Far din Far din, sa han. Det sto en svart bil i veien. En helt vanlig bil. Stasjonsvogn. Men den sto midt i veien og sperret all trafikk. Jeg var på vei hjem fra skolen, var sein, hadde
Programmering Høst 2017
 Programmering Høst 2017 Tommy Abelsen Ingeniørfag - Data Innledning Dette er et dokument med litt informasjon og eksempler om kontrollstrukturer, samt oppgaver til forskjellige kontrollstrukturer. Spør
Programmering Høst 2017 Tommy Abelsen Ingeniørfag - Data Innledning Dette er et dokument med litt informasjon og eksempler om kontrollstrukturer, samt oppgaver til forskjellige kontrollstrukturer. Spør
Forslag til opplegg for en foreldrekveld om matematikk (varighet: 2 timer) v/ Ingvill M. Stedøy-Johansen, 2007
 Forslag til opplegg for en foreldrekveld om matematikk (varighet: 2 timer) v/ Ingvill M. Stedøy-Johansen, 2007 Inviter foreldrene på matematisk aften (forslag til invitasjon nederst i dette dokumentet).
Forslag til opplegg for en foreldrekveld om matematikk (varighet: 2 timer) v/ Ingvill M. Stedøy-Johansen, 2007 Inviter foreldrene på matematisk aften (forslag til invitasjon nederst i dette dokumentet).
Øvingsforelesning 1 Python (TDT4110)
 Øvingsforelesning 1 Python (TDT4110) Introduksjon, Kalkulasjoner Ole-Magnus Pedersen Oversikt Praktisk Info Repetisjon fra sist Oppgaver for øving 2 2 Praktisk Info Last opp øvinger på Blackboard før godkjenning
Øvingsforelesning 1 Python (TDT4110) Introduksjon, Kalkulasjoner Ole-Magnus Pedersen Oversikt Praktisk Info Repetisjon fra sist Oppgaver for øving 2 2 Praktisk Info Last opp øvinger på Blackboard før godkjenning
Verden - Del 2. Intro. Skrevet av: Kine Gjerstad Eide
 Verden - Del 2 Skrevet av: Kine Gjerstad Eide Kurs: Processing Tema: Tekstbasert Fag: Matematikk, Programmering, Samfunnsfag Klassetrinn: 8.-10. klasse, Videregående skole Intro Denne oppgaven bygger på
Verden - Del 2 Skrevet av: Kine Gjerstad Eide Kurs: Processing Tema: Tekstbasert Fag: Matematikk, Programmering, Samfunnsfag Klassetrinn: 8.-10. klasse, Videregående skole Intro Denne oppgaven bygger på
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: INF 2220 Algoritmer og datastrukturer Eksamensdag: 8. desember 2016 Tid for eksamen: 09:00 13:00 (4 timer) Oppgavesettet er på:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: INF 2220 Algoritmer og datastrukturer Eksamensdag: 8. desember 2016 Tid for eksamen: 09:00 13:00 (4 timer) Oppgavesettet er på:
Kvinne 30, Berit eksempler på globale skårer
 Kvinne 30, Berit eksempler på globale skårer Demonstrasjon av tre stiler i rådgivning - Målatferd er ikke definert. 1. Sykepleieren: Ja velkommen hit, fint å se at du kom. Berit: Takk. 2. Sykepleieren:
Kvinne 30, Berit eksempler på globale skårer Demonstrasjon av tre stiler i rådgivning - Målatferd er ikke definert. 1. Sykepleieren: Ja velkommen hit, fint å se at du kom. Berit: Takk. 2. Sykepleieren:
Binær heap. En heap er et komplett binært tre:
 Heap Binær heap En heap er et komplett binært tre: Alle nivåene i treet, unntatt (muligens) det nederste, er alltid helt fylt opp med noder Alle noder på nederste nivå ligger så langt til venstre som mulig
Heap Binær heap En heap er et komplett binært tre: Alle nivåene i treet, unntatt (muligens) det nederste, er alltid helt fylt opp med noder Alle noder på nederste nivå ligger så langt til venstre som mulig
Tangram. Astrid Bondø NSMO
 Tangram Astrid Bondø NSMO T A N G R A M L E G E N D E N For lenge, lenge siden i det gamle Kina ville keiseren at tjeneren hans skulle bringe ham et kvadratisk stykke jade (bergart) Den uheldige tjeneren
Tangram Astrid Bondø NSMO T A N G R A M L E G E N D E N For lenge, lenge siden i det gamle Kina ville keiseren at tjeneren hans skulle bringe ham et kvadratisk stykke jade (bergart) Den uheldige tjeneren
Skilpaddekunst. Steg 1: Møt skilpadden. Sjekkliste. Introduksjon. Turtles
 Skilpaddekunst Introduksjon Skilpadder (turtles på engelsk) er en form for roboter som har vært i bruk innen programmering i lang tid. Vi vil bruke skilpadde-biblioteket i Python til å utforske flere programmeringskonsepter
Skilpaddekunst Introduksjon Skilpadder (turtles på engelsk) er en form for roboter som har vært i bruk innen programmering i lang tid. Vi vil bruke skilpadde-biblioteket i Python til å utforske flere programmeringskonsepter
MANN Jeg snakker om den gangen ved elva. MANN Den første gangen. På brua. Det begynte på brua.
 NATT En enakter av Harold Pinter INT. KJØKKEN. NATT Jeg snakker om den gangen ved elva. Hva for en gang? Den første gangen. På brua. Det begynte på brua. Jeg husker ikke. På brua. Vi stansa og så på vannet.
NATT En enakter av Harold Pinter INT. KJØKKEN. NATT Jeg snakker om den gangen ved elva. Hva for en gang? Den første gangen. På brua. Det begynte på brua. Jeg husker ikke. På brua. Vi stansa og så på vannet.
Oppgaver til julekalenderen 2005 for mellomtrinnet; 5. - 7.trinn
 Oppgaver til julekalenderen 2005 for mellomtrinnet; 5. - 7.trinn Løsningsord for kalenderen er RAKETTBASE PRESIS KLOKKA TO A B C D E F G H I J K L M N O 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 P Q R S T U
Oppgaver til julekalenderen 2005 for mellomtrinnet; 5. - 7.trinn Løsningsord for kalenderen er RAKETTBASE PRESIS KLOKKA TO A B C D E F G H I J K L M N O 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 P Q R S T U
PXT: Det regner mat! Introduksjon. Steg 1: Grunnlag. Sjekkliste. Skrevet av: Helene Isnes
 PXT: Det regner mat! Skrevet av: Helene Isnes Kurs: Microbit Tema: Elektronikk, Blokkbasert, Spill Fag: Matematikk, Programmering Klassetrinn: 5.-7. klasse, 8.-10. klasse, Videregående skole Introduksjon
PXT: Det regner mat! Skrevet av: Helene Isnes Kurs: Microbit Tema: Elektronikk, Blokkbasert, Spill Fag: Matematikk, Programmering Klassetrinn: 5.-7. klasse, 8.-10. klasse, Videregående skole Introduksjon
Kortryllekunst og matematikk.
 Kortryllekunst og matematikk. Innlevert av 7. trinn, Ulsmåg skole ved Ulsmåg skole (Bergen, Hordaland) Årets nysgjerrigper 201 Kjære leser Nå skal du få lese en rapport om et korttriks og mattematikk.
Kortryllekunst og matematikk. Innlevert av 7. trinn, Ulsmåg skole ved Ulsmåg skole (Bergen, Hordaland) Årets nysgjerrigper 201 Kjære leser Nå skal du få lese en rapport om et korttriks og mattematikk.
Spillet i korte trekk. Innhold. Forberedelser. Kristian r. a. Østby
 Kristian r. a. Østby Samoa. En vakker og tilsynelatende rolig øy i Stillehavet. Men i virkeligheten yrer det av liv: øya er et populært feriemål, og hver uke blir turister fløyet inn fra hele verden. De
Kristian r. a. Østby Samoa. En vakker og tilsynelatende rolig øy i Stillehavet. Men i virkeligheten yrer det av liv: øya er et populært feriemål, og hver uke blir turister fløyet inn fra hele verden. De
Maler som hjelper deg å få en relativt kald kontakt til å bli et hot leads.
 Maler som hjelper deg å få en relativt kald kontakt til å bli et hot leads. Om du føler at du trenger mer bakgrunn, gå tilbake å lytt til webinaropptaket # 3. Der forteller jeg mer om hvorfor og hva som
Maler som hjelper deg å få en relativt kald kontakt til å bli et hot leads. Om du føler at du trenger mer bakgrunn, gå tilbake å lytt til webinaropptaket # 3. Der forteller jeg mer om hvorfor og hva som
Hvor i All Verden? Del 2 Erfaren Scratch PDF
 Hvor i All Verden? Del 2 Erfaren Scratch PDF Introduksjon Hvor i All Verden? er et reise- og geografispill hvor man raskest mulig skal fly innom reisemål spredt rundt i Europa. Dette er den andre leksjonen
Hvor i All Verden? Del 2 Erfaren Scratch PDF Introduksjon Hvor i All Verden? er et reise- og geografispill hvor man raskest mulig skal fly innom reisemål spredt rundt i Europa. Dette er den andre leksjonen
LØSNINGSFORSLAG EKSAMEN VÅR07, MA0301
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 LØSNINGSFORSLAG EKSAMEN VÅR07, MA0301 Oppgave 1 Om mengder. a) (10%) Sett opp en medlemsskapstabell (membership
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 LØSNINGSFORSLAG EKSAMEN VÅR07, MA0301 Oppgave 1 Om mengder. a) (10%) Sett opp en medlemsskapstabell (membership
Algoritmer og datastrukturer Assignment 11 Side 1 av 5
 Assignment 11 Side 1 av 5 Oppgave 1 Utregning av ASCII summer, og hashfunksjon: Hashfunksjon: A(s) % n Nøkkel ASCII SUM (ASCII SUM) % 8 ANNE 290 2 PER 231 7 NINA 294 6 ANNI 294 6 ALI 214 6 KAREN 369 1
Assignment 11 Side 1 av 5 Oppgave 1 Utregning av ASCII summer, og hashfunksjon: Hashfunksjon: A(s) % n Nøkkel ASCII SUM (ASCII SUM) % 8 ANNE 290 2 PER 231 7 NINA 294 6 ANNI 294 6 ALI 214 6 KAREN 369 1
Lineære likningssystemer og matriser
 Kapittel 3 Lineære likningssystemer og matriser I dette kapittelet skal vi sette sammen Kapittel 1 og 2. 3.1 Den utvidede matrisen til et likningssystem Vi starter med et lineært likningssystem med m likninger
Kapittel 3 Lineære likningssystemer og matriser I dette kapittelet skal vi sette sammen Kapittel 1 og 2. 3.1 Den utvidede matrisen til et likningssystem Vi starter med et lineært likningssystem med m likninger
Heap og prioritetskø. Marjory the Trash Heap fra Fraggle Rock
 Heap og prioritetskø Marjory the Trash Heap fra Fraggle Rock Binær heap En heap er et komplett binært tre: Alle nivåene i treet, unntatt (muligens) det nederste, er alltid helt fylt opp med noder Alle
Heap og prioritetskø Marjory the Trash Heap fra Fraggle Rock Binær heap En heap er et komplett binært tre: Alle nivåene i treet, unntatt (muligens) det nederste, er alltid helt fylt opp med noder Alle
Hvorfor blir det færre og færre elever på noen skoler enn på andre?
 Konsvik skole 8752 Konsvikosen v/ 1.-4. klasse Hei alle 1.-4.klassinger ved Konsvik skole! Så spennende at dere er med i prosjektet Nysgjerrigper og for et spennende tema dere har valgt å forske på! Takk
Konsvik skole 8752 Konsvikosen v/ 1.-4. klasse Hei alle 1.-4.klassinger ved Konsvik skole! Så spennende at dere er med i prosjektet Nysgjerrigper og for et spennende tema dere har valgt å forske på! Takk
Anne-Cath. Vestly. Åtte små, to store og en lastebil
 Anne-Cath. Vestly Åtte små, to store og en lastebil Åtte små, to store og en lastebil Det var en gang en stor familie. Det var mor og far og åtte unger, og de åtte ungene het Maren, Martin, Marte, Mads,
Anne-Cath. Vestly Åtte små, to store og en lastebil Åtte små, to store og en lastebil Det var en gang en stor familie. Det var mor og far og åtte unger, og de åtte ungene het Maren, Martin, Marte, Mads,
Eventyr og fabler Æsops fabler
 Side 1 av 6 Den gamle mannen og døden Tekst: Eventyret er hentet fra samlingen «Storken og reven. 20 dyrefabler av Æsop» gjenfortalt av Søren Christensen, Aschehoug, Oslo 1985. Illustrasjoner: Clipart.com
Side 1 av 6 Den gamle mannen og døden Tekst: Eventyret er hentet fra samlingen «Storken og reven. 20 dyrefabler av Æsop» gjenfortalt av Søren Christensen, Aschehoug, Oslo 1985. Illustrasjoner: Clipart.com
Algoritmer og datastrukturer Eksamen 22. februar 2011
 Side 1 av 5 Algoritmer og datastrukturer Eksamen 22. februar 2011 Eksamenstid: 5 timer Hjelpemidler: Alle trykte og skrevne + håndholdt kalkulator som ikke kommuniserer. Faglærer: Ulf Uttersrud Råd og
Side 1 av 5 Algoritmer og datastrukturer Eksamen 22. februar 2011 Eksamenstid: 5 timer Hjelpemidler: Alle trykte og skrevne + håndholdt kalkulator som ikke kommuniserer. Faglærer: Ulf Uttersrud Råd og
Sprettende ball Introduksjon Processing PDF
 Sprettende ball Introduksjon Processing PDF Introduksjon: I denne modulen skal vi lære et programmeringsspråk som heter Processing. Det ble laget for å gjøre programmering lett for designere og andre som
Sprettende ball Introduksjon Processing PDF Introduksjon: I denne modulen skal vi lære et programmeringsspråk som heter Processing. Det ble laget for å gjøre programmering lett for designere og andre som
