Tutorial lectures on hydrodynamics instabilities
|
|
|
- Kåre Øverland
- 6 år siden
- Visninger:
Transkript
1 Tuoril leures o hdrodmis isiliies Leure oes preseed he Isiue of Lser Eieeri. Os Uiversi (4--6-(7--6 Jvier Sz Reio ETSI Aeroáuios. Uiversidd Poliéi de Mdrid
2 Coes Leure: The lssil Rleih-Tlor (RT isili. 3 Pheomeolo of he isili. Iompressile fluids: Heurisi derivio of he lier isili rowh re (Seod Newo Lw; lsis mehod (dispersio relio; Awood umer effes fiie hiess effes. Exmples. Compressile fluids. Dispersio relio. Iroduio o olier lssil RT isili. Pheomeolo. Lzer models pproh. Leure : Lier live RT isili 4 D lio fro sruure. Isori model d orol models.silizio mehisms. Heurisi derivio of he dispersio relio i shrp lio fros (Seod Newo Lw. Lier lsis mehod. Froude umer depedee. The riil surfe proximi effes (lo wveleh perurio d Ldu isili. Leure 3: No lier live RT isili 6 Shrp lio fro model: Therml equio momeum equio d ime evoluio equio of he ierfe. Sile mode perurios: surio mpliude iversio of spie ule smmer o lier uoff wve umer smpoi ule veloi. Referees: S. Boder Phs. Rev. Le (974. H. Te K. Mim L. Mohierh d R. Morse Phs Fluids (985. H. J. Kull Phs. Fluids B 7 (989. J. Sz Phs. Rev. Le (994. R. Bei e. l Phs. Plsms 3844 (995. A. Piriz J. Sz d L. Iñez Phs. Plsms 4 7 (997. J. Sz J. Rmirez R. Rmis R. Bei d R. P. J. Two Phs. Rev. Le (89 95 (. P. Clvi d L. Msse Phs. Plsms 69 (4.
3 THE CLASSICAL RT INSTABILITY 3
4 Pheomeolo of he isili (* η ( << λ = π η η γ η η e γ γ Visosi Surfe esio η η 3 loη.λ lo h α ( α.65 * - Lord Rleih Pro. Lodo Mh. So. 4 (883 7; G. Tlor Pro. R. So. A (95 9; D. J. Lewis Pro. R. So. A (95 8. Aelered fluid lers : P P > P 4
5 Rleih-Tlor isili Geophsis Asrophsis Teholoil ppliios: Ieril Cofieme Fusio (ICF x Iompressile fluids d uiform desi. ν = ( v v v + = p + 5
6 Seod Newo Lw: m = F λ = π ξ ξ = ξ + ξ + ξ 3 3 ξ = Ce γ ξ ξ Awood umer γ A T = AT = + > γ=± A T Usle. RT modes < γ=± i T A Sle. Grvi wves Mehod: ν = d ( v v v + = p + Equilirium soluio: v = p= p ( p + = Ierfes: Perured soluio: p v v v ix+ γ ix+ γ ( e = ( x e v + iv = x γ v = ip x γ v = p ix + j ξ e γ 6
7 Mehod: Soluio for eh fluid ler: p p = j+ j j d p = Ae + Be i vx = ( Ae + Be γ v = ( Ae Be γ Boudr odiios: = p + ξ p p + ξ oious j j j v oious d v = γξ j =± vriles mus eouded Compii odiio ->Dispersio relio : A B A D( γ = B ξ j How he sperum is?: For eh vlue we hve differe vlues of γ : γ γ. The umer of vlues m e ifiie u i se he sperum is disree. ( D de ( γ = Adved omme: Lple rsform i : Poles of K (disree sperum: e γ (*Brhe pois of K (oiuum sperum: α γ e (* E. O PRL 98 K( se s ds 7
8 Exmple : A+ ξ = B+ ξ A= B= γξ γ γ p = Ae p = Be ( A B = ξ γ γ A T = AT = + Exmple : d ξ ξ p Ae Be = + d d A+ B+ ξ = Ae + Be + ξ = d d ( A B = γξ ( Ae Be = γξ γ γ d d e e A γ B = ξ ξ d d γ e e 4 γ = γ =± γ =± i γ = ξ = ξ d e RT γ = ξ = ξ d e GW 8
9 Compressile fluids: p = d ξ p ξ Equilirium soluio: Perured soluio: = p + p / = os p = p ( + / d = ( + / d /( /( d = p/ = ( + / d = p ix+ γ ix+ γ = + e p = p + pe ix+ γ v = ( v v e x Equios: γ + ( v + iv = x γ v = p + γ v = ip x p = Boudr odiios: p + ξ = v = γξ ; = p + ξ = v = γξ ; = d Dispersio relio: γ ( + + ( = p p p γ ( + p p = = d p = A Hper( γ + B Lue( γ D( γ d = 9
10 Dispersio relio: γ ( + + ( = p p p We loo for iompressile modes! γ ( + p p = = d v ( v iv γ γ+ + + x = ( + p p = ( + / / ( / d γ p = C + d e d 4 γ = ( γ = γ = 4 ( γ D ( SM γ d = Nolier lssil RT isili p os Hrmois eerio (sri i he wel olier phse. Suhrmoi sde. Bules d spies show differe ime ehvior. Bule ompeiio.
11 v = φ r Δ φ = ( α x ξ r = φ ( φ = ξ φ + os Wel o-lier resuls ξ ( x η os x + η os x + η os3x η ξl ξl 4 η ξl ( ξl e γ γ = 3 η3 ξ 8 3 L mpliude 3...
12 Spie ule smmer s spie mpliude: ule mpliude: ξ + ξ s L L ξ ξ L L lo S lier heor lo Lo wveleh modes eerio = + γ ( γ + γ ξ = ξ ( ξ ( e γ γ ( γ+ γ γ ( +
13 Bule ompeiio. Aelerio of ule fro..8 h h h h = ( α.65 α v = φ x r Δ φ = ( α ξ r = φ ( φ = ξ φ + os 3
14 LINEAR ABLATIVE RT INSTABILITY 4
15 D lio fro sruure: re Lser d L v T L T v D lio fro sruure: Isori model T v v = v = m v v = p+ T T mt ( T = KT T 5 T T L / ( / / ( / L ( L 5 T KT mt = KT L = (..3 μm L 5m v v Fr = (.5 = << L M T / L T T ( + e ( L / L ( e Miimum desi rdie sle leh L = L + m + ( / 5
16 Cold ompressed re: α α P/ = P / = os + ( v = P+ O M ( ( d L L v T BC : P( = d( = P( = = P v ( = d ( = d ( v ( = = v α / = / ( + / α ( p p d p = α OM ( α d ( + ( v = v α d ( α d = d v α Lier live RTI: Silizio mehisms. Sli Lws π lio surfe ξ Δ m < Δ p < Δ m > Δ p > flow he ( << m = >> / V V m Δpd ξ 3 ( + ξ ( ξ Δ p d m ξ Hdrosi pressure Dmil pressure Alio: Fire polishisi. Vorii 6
17 Lier live RTI: silizio mehisms π ξ Δ m < Δ p < flow Δ m > Δ p > he ξ e γ lio surfe Therml pressure Roe effe 4V V γ + γ + AT + r r Fire polishi + Vorii V V γ = + + A VV + r + r T r = L / ( / A T r V = V = + r r uoff L F < /( r T v Lier lsis mehod: Isori model ( M << MF r << T v Equilirium soluio v= v = m v v= p+ T T mt ( T KT T 5 = Perured soluio Perured quiies re expded s ix e γ + 5h ODS γ + ( v + v + iv = γ x v + = p+ γ v + = ip ( T + T = x 5 ( ( vt KT T = = ouded modes = + 3 ouded modes Numeril eievlue prolem for γ γ L F( L Fr = v 7
18 v v Alil model: Isori model ( L << ξ e = ( / L v = v = Ve + φ ( + V v = p p + = x V = iae = Ae p = ( γ + V Ae / Q = p ( + ξ + V m Cold reio γ+ ix Ho reio ix+γ m e ix+γ Q e / Mss lio Momeum V γ + ( + f Vγ + q = ( L / Q ( L / q / V ξ m f V ξ q( γ f ( γ? Alil model: Isori model ( L << / ˆ γ( L / /( V << γ Sli: v T p / Normlized vriles: F = F( η + F ( η γ + ; η ˆ q q q = + ˆ γ + f = f + f γ + ˆ ( << v Eievlue prolem for: ( q f ( q f q f q / Γ (+ / ( < q < ξ e γ+ ix Ho reio ix+γ m e ix+γ Q e Momeum Mss lio re 5h ODS γ + ( v + v + iv = γ x v + = p+ γ v + = ip ( T + T = x 5 ( ( vt KT T = 8
19 Alil model: Dispersio relio ( L << V γ + ( + f Vγ + q = ( L / / q q q = + ˆ γ + f = f + V γ + ( + f + q V + = γ / ( L /( q / ( q Γ (+ / m ( V ξ f xq ( V ω r = Blow-off o lio desi rio Q p ( L / V ( ξ ( q q γ / + ˆ / iv L q + qˆ ω ( / ( ξ ( γ uoff: F ( L = ( > / r / q Fr Exesio of he lil model: (for ever F r vlue A T Awood umer effes r = + r ( = ( q / ( = r L Corol model = L Lerl he rspor he lio fro: (sed i SBM f + L ( + L ( + L + r LF r ( + L γ = AT V + r + r r + r Fr < < 9
20 Cuoff wveumer versus Froude umer V = F r Lerl he rsp. Sle leh desi- A umer orreios Roe effe-vor.ov. Fire polishi-vor.ov A umer orreios.. L = F r Cuoff wve umer versus Froude umer.5.. V β =.75.5 γ emp = βv + L m.5. β = F r
21 Ldu-Drrieus isili V Δ p < Δ p > < ( << γ γ LD LDRT V V + q V ( F / >> r >> γ / ( L Ldu-RT isili i ICF : M Criil surfe V T T I II III L Isori pproximio wih / d ever leh muh lrer h L. Reio I iompressile d poeil flow ( V = m. e. / Reio II : T = T ( / = ( / / u = u / ( / where ( / = L/. Reio III : = T = T u = u
22 Ldu-RT isili i ICF : Alio surfe Criil surfe M I II III x ξ e γ ix ξ e + γ ix+ V γ + ( + f Vγ + q = ( L / / i v V m x + ξ = ( + γξ Q ( QL ( / q = ξ ξ / / u( V ( m f V ( ξ qγ (? f( γ? Ldu-RT isili i ICF : Alio surfe Criil surfe M I II III x s ix ix ( ( ξ ξ e / ξe ξ e γ ix ξ e + γ ix+ + ( v = v + v v = p+ e Pv ( KT T = Iδ 5 ( m v ix+ γ ( v = θ + vr + γξe e ix I mv θ v r γξe e δ 5P + + ( + = ( = v r + = + v v v p e / ( θ = os. ( θ T
23 Ldu-RT isili i ICF : M Perured equios ( < s < : γ vr m (( ξ ξ/ θ/ s + ( ssθ θ+ ( s( ξ ξ/ + ξ = s γiv + v iv = rx s rx p (( s ξ ξ / + ξ ( + γu + γ uθ u ( ξ ξ / + u ( uθ s γv + v u + u v = p r r s s r s uθ uθ u ssθ u s ( u su sθ γu sθ γ + s s (( γs+ u su + + γu( ξ ξ / + γ ξ v + iv = s r rx Ldu-RT isili i ICF : M Boudr odiios: s + θ = sθ + = m / m + ( ξ ξ/ i m v r = vrx = ( + γξ p = Q θ = s θ = ( ξ ξ / s ( p ξ u v + = + u + iv r γξ ( ξ rx γ γ Q( γ m ( γ ξ ( γ 3
24 Ldu-RT isili i ICF : M Resoluio mehod: ( / ˆ = O ( F r = O( >> γ /( u >> ˆ/ Q q= q ˆ + qγ + u ( ξ m f = f ˆ + fγ + V ( ξ ˆ/ γ ˆ γ = u d ll perured quiies re perured i he sme w The ssem of ODE is ierivel solved q ( ˆ f ( ˆ q ( ˆ f ( ˆ Ldu-RT isili i ICF : M Dispersio relio: q= q + q ˆ γ + V γ + ( + f Vγ + q = / ( L / f = f + f ˆ γ + qv γ + + = ( + f+ q Vγ / ( L / Vorii: ω v + iγξ + iv rx r ˆ/ + iω ˆ ω( s = = q ˆ qγ + ( ξ u + xp = m ω( s = 4
25 Ldu-RT isili i ICF : qv γ + + = ( + f+ q Vγ / ( L /.5 q 5 L = 5/ = f 5.5 q Ldu isili Silizio F r / ˆ ˆ ˆ e e + + ˆ q ˆ = + ( ( ( / osh ˆ + osh ˆ Γ Γ = ξ f = h( q + h( = ξ osh( Ldu isili i ICF : ( F >> r γ V q ( ( L / / <.7 ( q < Ldu isili >.7 ( q > Osillios / ˆ ˆ ˆ e e + + ˆ q ˆ ( = + ( ( ( / osh ˆ + osh ˆ Γ Γ = q q / >> = = Γ (+ / (.67 = 5/ << q ( / 5
26 NONLINEAR ABLATIVE RAYLEIGH-TAYLOR INSTABILITY 6
27 Lier live RTI: silizio mehisms π ξ Δ m < Δ p < flow Δ m > Δ p > he lio surfe Therml pressure Roe effe d ξ d ξ 4 Vξ V ξ d d uoff L F < /( r Fire polishi + Vorii Nolier model 7
28 Cold reio Ve + φ Δ φ = r ( α x ξ m r = φ + V e m / Mss lio re ( p φ = ξ φ V φ p = q m q / Ho reio x ξ T = P 5 ( Pv KT T = + ( v = ( v v v + p v = + v (/5 K T r ( θ = KT /5 m m = + θ = θ ( r = θ ( l θ vr l θ θ ( x = = Mss lio re : m = m θ 8
29 Ho reio v = m θ + vr ( θ = KT /5 m ξ ( ω e z = vr ω+ ( m θ + vr ω = x v r = φ + Ve τ vr + φ ω( χ ( χ = HC.. of. θ Δ ψ = ω ( χ φ = ( ψ e ψ e x x e θ+ iχ dθ ωdχ = θ Coforml mp ( x ( χ θ d FT o χ φ ( i + τ θ Lier heor : ω = φ ξ = e iχ d ( x x x χ No-lier roe effe: Δ φ = Momeum flux : q= p + m / x ξ h h q flow Δ θ = h q m m m ω dχ = ( + h? 9
30 Resorifore x ξ flow v = m + v θ r ( v + p ω v v / m θ / L θ q p ( dθ + m ωdχ q p m m + m d ( l ω χ IFT o ( l = ( χ q ( m m + m ω Ali surfe equios: Δ φ = Ve + φ ξ x r = φ m / V e ( flow θ = θ = Δ θ = φ = ξ ( φ V φ m = m θ m m V ωdχ θ + iχ e dθ ω d χ = θ ( l φ ( i + τ iχ e d χ θ 3
31 Sile mode resuls Wel o-lier resuls Clssil RTI 3 η ξl ξl 4 η ξl 3 3 η3 ξl 8 ( /( 3 η ξl ξl 4( η ( ξl 3 3 η3 ( 4 ( 4 /3 ξl 8 ( < ξ ( x η os x + η os x + η os3x + 3 ( ( / / ( ξl e γ mpliude 3... / /4 3/4 < / < < < < 3/4 3
32 Iversio of spie ule smmer spie mpliude: ( (/ ξ ξ + s L L ule mpliude: ξ L( (/ ξ L < < < > / ( ( / / lier heor < / Nolier expoeil rowh. Surio mpliude. lssil 5 μm μm 4 μm F = 4.5 λ = μm r.5 λ..5 μm μm S (.5μm..5.5λ γ =.8 3
33 .86 No lier exp. rowh ( ξ. λ. < ξ. λ.. Simulios ART D I V II I V > V.λ. ( s. ( s V III > V II ξ λ...λ. ( s No lier isili for ξ ej >. Bifurio dirm ξe( x = ξej os( jx j= + 3 ξ ξ ( ξ ξ Lier heor shows: ξ ( x ξ os( x e e 33
34 No lier isili for >. Bifurio dirm ξe( x = ξej os( jx j=.. ξ ej π π / Full olier isili ( > =.5 ule 34
35 .86 No lier isili ( >. Simulios ART D ξ λ...λ. ( s ξ λ...λ Asmpoi ule veloi V /3 V super uoff V sv = = s = > 3V 3 35
36 Sili reios:.5 hs / λ F = 5 r / Muli mode resuls 36
37 Lo wveleh modes eerio / γ( γ+ γ ( ξ + = + ξ( ξ( ( γ+ γ γ γ( γ + γ ( e γ + γ γ = Lo wveleh modes eerio ξ = ξ( ξ ( G G = = op op = op / ART SIMUL. MULTI D SIMUL. Full olier heor Wel olier heor.5 Clssil: = / op
38 Bule ompeiio Aelerio of ule fro.4 λ = λ h h h h = α ( α.6 38
39 Aelerio of ule fro λ = λ h h h h = α ( α.6 Aelerio of ule fro λ = λ h.5 h h h = α ( α.3 39
40 Aelerio of ule fro α Fr=5 Fr= Fr=. Fr= h h =α / SC Aelerio of ule fro : ( α = α / SC.7 Fr=3.6 Fr=5 α h h = C V 3 ( h h =α Fr= Fr= C = 3α. / s
41 4
UNIVERSITETET I OSLO Det matematisk naturvitenskapelige fakultet
 UNIVERSITETET I OSLO Det matematisk naturvitenskapelige fakultet Eksamen i AST5220/9420 Kosmologi II Eksamensdag: Fredag 11. juni 2010 Tid for eksamen: 09.00 12.00 Oppgavesettet er på 4 sider. Vedlegg:
UNIVERSITETET I OSLO Det matematisk naturvitenskapelige fakultet Eksamen i AST5220/9420 Kosmologi II Eksamensdag: Fredag 11. juni 2010 Tid for eksamen: 09.00 12.00 Oppgavesettet er på 4 sider. Vedlegg:
HANDELSHØGSKOLEN I TROMSØ SENTRUM OG PERIFERI. Dixit-Stiglitz-Krugman modellen. Åge Haugslett. Vedlegg til Masteroppgave i - Samfunnsøkonomi (30 stp)
 HANDELSHØGSKOLEN I TROMSØ SENTRUM OG PERIFERI Dixit-Stiglitz-Krugman modellen Åge Haugslett Vedlegg til Masteroppgave i - Samfunnsøkonomi ( stp) Vedlegg kap,.. VEDLEGG KAPITTEL KapModATilf.mcd. Den enklestet
HANDELSHØGSKOLEN I TROMSØ SENTRUM OG PERIFERI Dixit-Stiglitz-Krugman modellen Åge Haugslett Vedlegg til Masteroppgave i - Samfunnsøkonomi ( stp) Vedlegg kap,.. VEDLEGG KAPITTEL KapModATilf.mcd. Den enklestet
Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
 Norges teknisk naturvitenskapelige universitet NTNU Side 1 av 9 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
Norges teknisk naturvitenskapelige universitet NTNU Side 1 av 9 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
EKSAMEN I FAG SIF4002 FYSIKK. Mandag 5. mai 2003 Tid: Sensur uke 23.
 side 1 av 5 (bokmål) NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET, INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Institutt for fysikk, Gløshaugen Professor Arnljot Elgsæter, 73940078 EKSAMEN I
side 1 av 5 (bokmål) NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET, INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Institutt for fysikk, Gløshaugen Professor Arnljot Elgsæter, 73940078 EKSAMEN I
7 Global Linkages and Economic Growth
 7 Global Linkages and Economic Growth Y t = F(K t,e t L t ), (1) Y t C t = S t = sf(k t, E t L t ). (2) K t+1 K t = sf(k t, E t L t ) δk t, (3) Foundations of International Macroeconomics (297) Chapter
7 Global Linkages and Economic Growth Y t = F(K t,e t L t ), (1) Y t C t = S t = sf(k t, E t L t ). (2) K t+1 K t = sf(k t, E t L t ) δk t, (3) Foundations of International Macroeconomics (297) Chapter
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ Ÿ Œ œ ˆ ˆ Š Œ. .. ³μ. μ ± Ë ²Ó Ò Ö Ò Í É Å ˆˆ Ô± ³ É ²Ó μ Ë ±, μ, μ Ö Œ Œ ˆˆ 79 ˆ Š ˆ
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 01.. 4.. 1 Ÿ Œ œ ˆ ˆ Š Œ ˆˆ ˆÄ ˆƒƒ Œˆ Œ Š.. ³μ μ ± Ë ²Ó Ò Ö Ò Í É Å ˆˆ Ô± ³ É ²Ó μ Ë ±, μ, μ Ö ˆ 70 Ÿ Œ œ ˆ ˆ Š Œ ˆˆ ˆÄ 7 ˆ ˆ IFW- ˆˆ ˆ Œ Œ Œ ˆˆ 79 Š ˆ 80 ˆ Š ˆ 81 E-mail: neznamov@vniief.ru
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 01.. 4.. 1 Ÿ Œ œ ˆ ˆ Š Œ ˆˆ ˆÄ ˆƒƒ Œˆ Œ Š.. ³μ μ ± Ë ²Ó Ò Ö Ò Í É Å ˆˆ Ô± ³ É ²Ó μ Ë ±, μ, μ Ö ˆ 70 Ÿ Œ œ ˆ ˆ Š Œ ˆˆ ˆÄ 7 ˆ ˆ IFW- ˆˆ ˆ Œ Œ Œ ˆˆ 79 Š ˆ 80 ˆ Š ˆ 81 E-mail: neznamov@vniief.ru
FORMELSAMLING TIL STK1100 OG STK1110
 FORMELSAMLING TIL STK1100 OG STK1110 (Versjon av 11. november 2017) 1. Sannsynlighet La A, B, A 1, A 2,..., B 1, B 2,... være begivenheter, dvs. delmengder av et utfallsrom Ω. a) Aksiomene: Et sannsynlighetsmål
FORMELSAMLING TIL STK1100 OG STK1110 (Versjon av 11. november 2017) 1. Sannsynlighet La A, B, A 1, A 2,..., B 1, B 2,... være begivenheter, dvs. delmengder av et utfallsrom Ω. a) Aksiomene: Et sannsynlighetsmål
Løsningsforslag, eksamen FY desember 2017
 1 Løsninsforsla, eksamen FY1001 14. desember 017 1 3 områder av t = 4 s, a konstant i hvert omrde. 1 : a 1 = 0; v 0 = 5m/s = x 1 = v 0 t; v 1 = v 0 : a = v/ t = 1.5 m/s = x = x 1 + v 1 t + a t = v 0 t
1 Løsninsforsla, eksamen FY1001 14. desember 017 1 3 områder av t = 4 s, a konstant i hvert omrde. 1 : a 1 = 0; v 0 = 5m/s = x 1 = v 0 t; v 1 = v 0 : a = v/ t = 1.5 m/s = x = x 1 + v 1 t + a t = v 0 t
Løsningsforslag til eksamen i TFY4205 Kvantemekanikk 12. august 2004
 NTNU Side 1 av 6 Institutt for fysi Faultet for naturvitensap og tenologi Løsningsforslag til esaen i TFY405 Kvanteeani 1. august 004 Dette løsningsforslaget er på 6 sider. Oppgave 1. To-diensjonal eletron-gass
NTNU Side 1 av 6 Institutt for fysi Faultet for naturvitensap og tenologi Løsningsforslag til esaen i TFY405 Kvanteeani 1. august 004 Dette løsningsforslaget er på 6 sider. Oppgave 1. To-diensjonal eletron-gass
Oppgave 1. ( xφ) φ x t, hvis t er substituerbar for x i φ.
 Oppgave 1 Beviskalklen i læreboka inneholder sluttningsregelen QR: {ψ φ}, ψ ( xφ). En betingelse for å anvende regelen er at det ikke finnes frie forekomste av x i ψ. Videre så inneholder beviskalklen
Oppgave 1 Beviskalklen i læreboka inneholder sluttningsregelen QR: {ψ φ}, ψ ( xφ). En betingelse for å anvende regelen er at det ikke finnes frie forekomste av x i ψ. Videre så inneholder beviskalklen
145± ±175 St 52 S ± ±225
 SNG V VKTG GNNG, DT, TB OG GU KP.. NNDNNG Pll: l o 5,, og. 5:, 6, 5,, 6,. :,.5, 6,, 5,.5,, 5, 6, 8,. :,..5,, 6, 8,,., 5, 8,.5, 5.5,, 5, 5, 56, 6, 7, 8, 9,. :,.6,.,.8,.5,.,, 5, 6, 7, 8, 9,,.,.,.6, 5, 6.5,
SNG V VKTG GNNG, DT, TB OG GU KP.. NNDNNG Pll: l o 5,, og. 5:, 6, 5,, 6,. :,.5, 6,, 5,.5,, 5, 6, 8,. :,..5,, 6, 8,,., 5, 8,.5, 5.5,, 5, 5, 56, 6, 7, 8, 9,. :,.6,.,.8,.5,.,, 5, 6, 7, 8, 9,,.,.,.6, 5, 6.5,
Løsningsforslag til eksamen i FY8306 KVANTEFELTTEORI Fredag 9. juni 2006
 NTNU Side av 3 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i FY836 KVANTEFELTTEORI Fredag 9. juni 6 Dette løsningsforslaget er på 3 sider, pluss et vedlegg
NTNU Side av 3 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i FY836 KVANTEFELTTEORI Fredag 9. juni 6 Dette løsningsforslaget er på 3 sider, pluss et vedlegg
Probema di Marek. (Problema dei quattro punti inaccessibili).
 ISTITUTO TECNICO STATALE COMMERCIALE E PER GEOMETRI "In Meoria dei Morti per La Patria" Viale Enrico Millo, 1-16043 Chiavari Laboratorio di Topografia - G.P.S. - G.I.S Anno scolastico 2009-2010 Soario
ISTITUTO TECNICO STATALE COMMERCIALE E PER GEOMETRI "In Meoria dei Morti per La Patria" Viale Enrico Millo, 1-16043 Chiavari Laboratorio di Topografia - G.P.S. - G.I.S Anno scolastico 2009-2010 Soario
Matematik, LTH Kontinuerliga system vt Formelsamling. q t. + j = k. u t. (Allmännare ρ 2 u. t2 Svängningar i gaser (ljud) t 2 c2 2 u
 Matematik, LH Kontinuerliga system vt 7 Formelsamling Formelsamligen utgör bara ett stöd för minnet. Beteckningar förklaras sålunda ej. Ej heller anges förutsättningar för formlernas giltighet. Fysikaliska
Matematik, LH Kontinuerliga system vt 7 Formelsamling Formelsamligen utgör bara ett stöd för minnet. Beteckningar förklaras sålunda ej. Ej heller anges förutsättningar för formlernas giltighet. Fysikaliska
Lipschitz Metrics for Non-smooth evolutions
 Lipschitz Metrics for Non-smooth evolutions Alberto Bressan Department of Mathematics, Penn State University bressan@math.psu.edu Alberto Bressan (Penn State) Nonsmooth evolutions 1 / 36 Well-posedness
Lipschitz Metrics for Non-smooth evolutions Alberto Bressan Department of Mathematics, Penn State University bressan@math.psu.edu Alberto Bressan (Penn State) Nonsmooth evolutions 1 / 36 Well-posedness
Faglig kontakt under eksamen: Ingjald Øverbø, tlf , eller
 NORSK TEKST Side 1 av 5 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 18 67, eller 9701355 EKSAMEN I TFY450 ATOM- OG MOLEKYLFYSIKK
NORSK TEKST Side 1 av 5 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 18 67, eller 9701355 EKSAMEN I TFY450 ATOM- OG MOLEKYLFYSIKK
Universitetet i Oslo Det matematisk-naturvitenskapelige fakultet
 Universitetet i Oslo Det matematisk-naturvitenskapelie fakultet Eksamen i: FYS4-Matematiske metoder i fysikk Dato: juni 9 Tid for eksamen: 9- Oppavesettet: sider Tillatte hjelpemidler: Elektronisk kalkulator,
Universitetet i Oslo Det matematisk-naturvitenskapelie fakultet Eksamen i: FYS4-Matematiske metoder i fysikk Dato: juni 9 Tid for eksamen: 9- Oppavesettet: sider Tillatte hjelpemidler: Elektronisk kalkulator,
Formelsamling Bølgefysikk Desember 2006
 Vedlegg 1 av 9 Formelsamling Bølgefysikk Desember 2006 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk
Vedlegg 1 av 9 Formelsamling Bølgefysikk Desember 2006 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk
Løsningsforslag til eksamen i TFY4170 Fysikk 2 Fysikk 2 Lørdag 8. august 2005
 NTNU Side 1 av 5 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i TFY4170 Fysikk Fysikk Lørdag 8. august 005 Merk: Hver del-oppgave teller like mye. Dette løsningsforslaget
NTNU Side 1 av 5 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i TFY4170 Fysikk Fysikk Lørdag 8. august 005 Merk: Hver del-oppgave teller like mye. Dette løsningsforslaget
Tegn og tekst. Et representert tegn kan vises på flere måter. Noen definisjoner. Enda noen definisjoner. \yvind og ]se N{rb}? a a a.
![Tegn og tekst. Et representert tegn kan vises på flere måter. Noen definisjoner. Enda noen definisjoner. \yvind og ]se N{rb}? a a a. Tegn og tekst. Et representert tegn kan vises på flere måter. Noen definisjoner. Enda noen definisjoner. \yvind og ]se N{rb}? a a a.](/thumbs/62/47219195.jpg) o o {rb} rprr på r år o prpp rpro r r rr rpro o r o or α r o or bor brp or b rr på ppr r r r r r rrr år på o oroooro o r or o br å r r pår r r orør p o b b år r å r o o o rprrr o p o rprrr o or op r r
o o {rb} rprr på r år o prpp rpro r r rr rpro o r o or α r o or bor brp or b rr på ppr r r r r r rrr år på o oroooro o r or o br å r r pår r r orør p o b b år r å r o o o rprrr o p o rprrr o or op r r
Tillegg om flateintegraler
 Kapittel 6 Tillegg om flateintegraler 6.1 Litt ekstra om flateintegraler I kompendiet har vi definert flateintegraler som grenseoverganger for diskretiseringer. Har vi en flate kan vi representere den
Kapittel 6 Tillegg om flateintegraler 6.1 Litt ekstra om flateintegraler I kompendiet har vi definert flateintegraler som grenseoverganger for diskretiseringer. Har vi en flate kan vi representere den
MEKANISK FYSIKK INKL SVINGNINGER. Newtons andre lov: F = dp/dt p = mv = mṙ. Konstant akselerasjon: v = v 0 + at x = x 0 + v 0 t at2
 TFY4106 Fysikk Eksamen 9. juni 2016 (Foreløpig versjon pr 7. mai 2016.) FORMLER: Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighetsområde og de ulike symbolenes
TFY4106 Fysikk Eksamen 9. juni 2016 (Foreløpig versjon pr 7. mai 2016.) FORMLER: Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighetsområde og de ulike symbolenes
Eksamen i fag RELATIVISTISK KVANTEMEKANIKK Fredag 26. mai 2000 Tid: 09:00 14:00
 Side 1 av 3 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Navn: Kåre Olaussen Telefon: 9 36 52 Eksamen i fag 74327 RELATIVISTISK KVANTEMEKANIKK Fredag
Side 1 av 3 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Navn: Kåre Olaussen Telefon: 9 36 52 Eksamen i fag 74327 RELATIVISTISK KVANTEMEKANIKK Fredag
UNIVERSITETET I OSLO
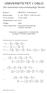 UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Eksamen i: Eksamensdag: Tid fo eksamen: 14.30 18.30 Oppgavesettet e på 5 side. Vedlegg: Tillatte hjelpemidle: MEK3230 Fluidmekanikk 6. Juni,
UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Eksamen i: Eksamensdag: Tid fo eksamen: 14.30 18.30 Oppgavesettet e på 5 side. Vedlegg: Tillatte hjelpemidle: MEK3230 Fluidmekanikk 6. Juni,
Solutions to selected problems from Exercise 5
 Soluions o seleced poblems om Execise 5 Po. Rakhesh Singh 1 Execise 5.1 Since j E E ˆ ˆ x + y e he diecion o wave popagaion k x ˆ + y ˆ x+ y he coesponding magneic ield can be obained om Maxwell s cul
Soluions o seleced poblems om Execise 5 Po. Rakhesh Singh 1 Execise 5.1 Since j E E ˆ ˆ x + y e he diecion o wave popagaion k x ˆ + y ˆ x+ y he coesponding magneic ield can be obained om Maxwell s cul
Eksponensielle klasser
 Eksponensielle klasser, de Jong & Heller, Kap. 3 Eksponensielle klasser STK3100-1. september 2008 Sven Ove Samuelsen En stokastisk variabel Y sies å ha fordeling i den eksponensielle fordelingsklasse dersom
Eksponensielle klasser, de Jong & Heller, Kap. 3 Eksponensielle klasser STK3100-1. september 2008 Sven Ove Samuelsen En stokastisk variabel Y sies å ha fordeling i den eksponensielle fordelingsklasse dersom
Løsningsforslag Eksamen 9. desember 2006 TFY4250 Atom- og molekylfysikk /FY2045 Kvantefysikk
 Eksamen TFY450/FY045 9. esember 006 - løsningsforslag 1 Løsningsforslag Eksamen 9. esember 006 TFY450 Atom- og molekylfysikk /FY045 Kvantefysikk Oppgave 1 a. Grunntilstanen ψ 1 (x) har ingen nullpunkter.
Eksamen TFY450/FY045 9. esember 006 - løsningsforslag 1 Løsningsforslag Eksamen 9. esember 006 TFY450 Atom- og molekylfysikk /FY045 Kvantefysikk Oppgave 1 a. Grunntilstanen ψ 1 (x) har ingen nullpunkter.
LØSNINGSFORSLAG TIL EKSAMEN I TEP4145 KLASSISK MEKANIKK Mandag 21. mai 2007 kl Løsningsforslaget er på i alt 9 sider.
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR ENERGI- OG PROSESSTEKNIKK Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I TEP4145
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR ENERGI- OG PROSESSTEKNIKK Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I TEP4145
2. Å R S B E R E T N I N G O G R E G N S K A P F O R A ) Å r s b e r e t n i n g o g r e g n s k a p f o r
 I N N K A L L I N G T I L O R D I N Æ R G E N E R A L F O R S A M L I N G 2 0 1 0 O r d i n æ r g e n e r a l f o r s a m l i n g i, a v h o l d e s m a n d a g 3. m ai 2 0 1 0, k l. 1 8 0 0 p å T r e
I N N K A L L I N G T I L O R D I N Æ R G E N E R A L F O R S A M L I N G 2 0 1 0 O r d i n æ r g e n e r a l f o r s a m l i n g i, a v h o l d e s m a n d a g 3. m ai 2 0 1 0, k l. 1 8 0 0 p å T r e
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag. Side 1 av 6. Faglig kontakt under eksamen: Navn: Brynjulf Owren (93518)
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren (93518) EKSAMEN I NUMERISK LØSNING AV DIFFERENISALLIGNINGER (75316)
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren (93518) EKSAMEN I NUMERISK LØSNING AV DIFFERENISALLIGNINGER (75316)
Løysingsframlegg øving 1
 FY6/TFY425 Innføring i kvantefysikk Løysingsframlegg øving Oppgåve Middelverdien er x = x Ω X xp (x) = 2 + 2 = 2. (.) Tilsvarande har vi x 2 = x Ω X x 2 P (x) = 2 2 + 2 2 = 2. (.2) Dette gjev variansen
FY6/TFY425 Innføring i kvantefysikk Løysingsframlegg øving Oppgåve Middelverdien er x = x Ω X xp (x) = 2 + 2 = 2. (.) Tilsvarande har vi x 2 = x Ω X x 2 P (x) = 2 2 + 2 2 = 2. (.2) Dette gjev variansen
Eksamensoppgave i TFY4115 FYSIKK
 Side 1 av 6. Institutt for fysikk Eksamensoppgave i TFY4115 FYSIKK for MTNANO, MTTK og MTEL Faglig kontakt under eksamen: Institutt for fysikk v/arne Mikkelsen Tlf.: 486 05 392 Eksamensdato: Torsdag 11.
Side 1 av 6. Institutt for fysikk Eksamensoppgave i TFY4115 FYSIKK for MTNANO, MTTK og MTEL Faglig kontakt under eksamen: Institutt for fysikk v/arne Mikkelsen Tlf.: 486 05 392 Eksamensdato: Torsdag 11.
Løsningsforslag for FYS2140 Kvantemekanikk, Torsdag 16. august 2018
 Løsningsforslag for FYS140 Kvantemekanikk, Torsdag 16. august 018 Oppgave 1: Materiens bølgeegenskaper a) De Broglie fikk Nobelprisen i 199 for sin hypotese. Beskriv med noen setninger hva den går ut på.
Løsningsforslag for FYS140 Kvantemekanikk, Torsdag 16. august 018 Oppgave 1: Materiens bølgeegenskaper a) De Broglie fikk Nobelprisen i 199 for sin hypotese. Beskriv med noen setninger hva den går ut på.
EKSAMEN I TFY4250 ATOM- OG MOLEKYLFYSIKK Lørdag 8. august 2009 kl
 NORSK TEKST Side av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 9702355 EKSAMEN I TFY4250 ATOM- OG MOLEKYLFYSIKK
NORSK TEKST Side av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 9702355 EKSAMEN I TFY4250 ATOM- OG MOLEKYLFYSIKK
TFY4102 Fysikk Eksamen 16. desember 2017 Foreløpig utgave Formelside 1 av 6
 TFY4102 Fysikk Eksamen 16. desember 2017 Foreløpig utgave Formelside 1 av 6 FORMLER: Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighetsområde og de ulike symbolenes
TFY4102 Fysikk Eksamen 16. desember 2017 Foreløpig utgave Formelside 1 av 6 FORMLER: Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighetsområde og de ulike symbolenes
Eksamensoppgave i TFY4115 FYSIKK
 Institutt for fysikk Eksamensoppgave i TFY4115 FYSIKK for MTNANO, MTTK og MTELSYS Faglig kontakt under eksamen: Institutt for fysikk v/jon Andreas Støvneng Tlf.: 454 55 533 Eksamensdato: Lørdag 16. desember
Institutt for fysikk Eksamensoppgave i TFY4115 FYSIKK for MTNANO, MTTK og MTELSYS Faglig kontakt under eksamen: Institutt for fysikk v/jon Andreas Støvneng Tlf.: 454 55 533 Eksamensdato: Lørdag 16. desember
Løsningsforslag Eksamen 27. mai 2005 FY2045 Kvantefysikk
 Eksamen FY2045 27. mai 2005 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 27. mai 2005 FY2045 Kvantefysikk a. Ifølge den tidsuavhengige Shrödingerligningen, Ĥψ = Eψ, har vi for x < 0 : E = Ĥψ ψ
Eksamen FY2045 27. mai 2005 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 27. mai 2005 FY2045 Kvantefysikk a. Ifølge den tidsuavhengige Shrödingerligningen, Ĥψ = Eψ, har vi for x < 0 : E = Ĥψ ψ
MEKANISK FYSIKK INKL SVINGNINGER. Newtons andre lov: F = dp/dt. p = mv = mṙ. Konstant akselerasjon: v = v 0 +at
 TFY4106 Fysikk Eksamen 17. desember 2014 FORMLER: Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighetsområde og de ulike symbolenes betydning antas forøvrig å
TFY4106 Fysikk Eksamen 17. desember 2014 FORMLER: Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighetsområde og de ulike symbolenes betydning antas forøvrig å
Formelsamling. ξ(r, t) = ξ 0 sin(k r ωt + φ) 2 ξ(x, t) = 1 2 ξ(x, t) t 2. 2 ξ. x ξ. z 2. y ξ. v = ω k. v g = dω dk
 Formelsamling Side 7 av 15 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk plan bølge: Bølgeligning:
Formelsamling Side 7 av 15 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk plan bølge: Bølgeligning:
Faglig kontakt under eksamen: Ingjald Øverbø, tlf , eller
 NORSK TEKST Side av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 9702355 EKSAMEN I TFY4250 ATOM- OG MOLEKYLFYSIKK
NORSK TEKST Side av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 9702355 EKSAMEN I TFY4250 ATOM- OG MOLEKYLFYSIKK
FY2045/TFY4250 Kvantemekanikk I, løsning øving 14 1 LØSNING ØVING 14. ψ 210 z ψ 100 d 3 r a.
 FY45/TFY45 Kvantemekanikk I, løsning øving 14 1 LØSNING ØVING 14 Løsning Oppgave 14 1 Fra oppg 3, eksamen august 1 a. Med Y = 1/ 4π og zy = ry 1 / 3 kan vi skrive matrise-elementene av z på formen (z)
FY45/TFY45 Kvantemekanikk I, løsning øving 14 1 LØSNING ØVING 14 Løsning Oppgave 14 1 Fra oppg 3, eksamen august 1 a. Med Y = 1/ 4π og zy = ry 1 / 3 kan vi skrive matrise-elementene av z på formen (z)
EKSAMEN I FY2045 KVANTEFYSIKK Onsdag 30. mai 2007 kl
 NORSK TEKST Side av 3 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 97355 EKSAMEN I FY45 KVANTEFYSIKK Onsdag 3.
NORSK TEKST Side av 3 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 97355 EKSAMEN I FY45 KVANTEFYSIKK Onsdag 3.
Løsningsforslag til eksamen i FY3404 RELATIVISTISK KVANTEMEKANIKK Tirsdag 30. november 2004
 NTNU Side av 7 Institutt for fysikk Løsningsforslag til eksamen i FY30 RELATIVISTISK KVANTEMEKANIKK Tirsdag 30. november 200 Dette løsningsforslaget er på 7 sider. Oppgave. Prosesser i QED Tegn, i de tilfeller
NTNU Side av 7 Institutt for fysikk Løsningsforslag til eksamen i FY30 RELATIVISTISK KVANTEMEKANIKK Tirsdag 30. november 200 Dette løsningsforslaget er på 7 sider. Oppgave. Prosesser i QED Tegn, i de tilfeller
INF3170 Logikk. Ukeoppgaver oppgavesett 7
 INF3170 Logikk Ukeoppgaver oppgavesett 7 Unifisering I forelesning 10 så vi på en unifiseringsalgoritme som finner en mest generell unifikator for to termer. I automatisk bevissøk har vi imidlertid bruk
INF3170 Logikk Ukeoppgaver oppgavesett 7 Unifisering I forelesning 10 så vi på en unifiseringsalgoritme som finner en mest generell unifikator for to termer. I automatisk bevissøk har vi imidlertid bruk
NORSK TEKST Side 1 av 4. Faglig kontakt under eksamen: Ingjald Øverbø, tlf , eller
 NORSK TEKST Side av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 972355 EKSAMEN I FY245/TFY425 KVANTEMEKANIKK
NORSK TEKST Side av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 972355 EKSAMEN I FY245/TFY425 KVANTEMEKANIKK
Hydrostatisk ligevægt
 Hyosaisk ligevæg F g F P Gaviy ynge Pesse yk F g F P Hyosaisk ligevæg P Gm. μ P k m m Gm P B π Sjene amosfæe μ P k m m Gm P B π Sjene amosfæe H P g GM B m g k H μ ~ konsan isoem ykskalahøjen 3 H h H h
Hyosaisk ligevæg F g F P Gaviy ynge Pesse yk F g F P Hyosaisk ligevæg P Gm. μ P k m m Gm P B π Sjene amosfæe μ P k m m Gm P B π Sjene amosfæe H P g GM B m g k H μ ~ konsan isoem ykskalahøjen 3 H h H h
EKSAMEN I EMNE SIE 4015 BØLGEFORPLANTNING
 NTNU Norges teknisk-naturvitenskapelige universitet Side 1 av 8 Fakultet for informatikk, matematikk og elektroteknikk Institutt for fysikalsk elektronikk Bokmål/Nynorsk Faglig/fagleg kontakt under eksamen:
NTNU Norges teknisk-naturvitenskapelige universitet Side 1 av 8 Fakultet for informatikk, matematikk og elektroteknikk Institutt for fysikalsk elektronikk Bokmål/Nynorsk Faglig/fagleg kontakt under eksamen:
LØSNINGSFORSLAG EKSAMEN, MAT 1001, HØSTEN (x + 1) 2 dx = u 2 du = u 1 = (x + 1) 1 = 1 x + 1. ln x
 LØSNINGSFORSLAG EKSAMEN, MAT 00, HØSTEN 06 DEL.. Hvilken av funksjonene gir en anti-derivert for f(x) = (x + )? Løsning. Vi setter u = x +, som gir du = dx, (x + ) dx = u du = u = (x + ) = x + a) x+ b)
LØSNINGSFORSLAG EKSAMEN, MAT 00, HØSTEN 06 DEL.. Hvilken av funksjonene gir en anti-derivert for f(x) = (x + )? Løsning. Vi setter u = x +, som gir du = dx, (x + ) dx = u du = u = (x + ) = x + a) x+ b)
Virvelfrihet, potensialer, Laplacelikningen
 Virvelfrihet, potensialer, Laplacelikningen Kap 10 og 9 Matematisk Institutt, UiO MEK1100, FELTTEORI OG VEKTORANALYSE Forelesninger NYTT TEMA Hvorfor snakker vi om virvelfri bevegelse? Forelesninger Todimensjonal
Virvelfrihet, potensialer, Laplacelikningen Kap 10 og 9 Matematisk Institutt, UiO MEK1100, FELTTEORI OG VEKTORANALYSE Forelesninger NYTT TEMA Hvorfor snakker vi om virvelfri bevegelse? Forelesninger Todimensjonal
Løsningsforslag til eksamen i SIF4022 Fysikk 2 Tirsdag 3. desember 2002
 NTNU Side 1 av 6 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i SIF40 Fysikk Tirsdag 3. desember 00 Dette løsningsforslaget er på 6 sider. Oppgave 1. a) Amplituden
NTNU Side 1 av 6 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i SIF40 Fysikk Tirsdag 3. desember 00 Dette løsningsforslaget er på 6 sider. Oppgave 1. a) Amplituden
Plan. I dag. Neste uke
 Plan I dag Referansegruppe... Ta opp igjen kurvelengde Areal bestemt av en kurve En annen måte å beskrive punkt i planet Kurver med denne beskrivelsen Tangenter, kurvelengde og areal Neste uke Kjeglesnitt
Plan I dag Referansegruppe... Ta opp igjen kurvelengde Areal bestemt av en kurve En annen måte å beskrive punkt i planet Kurver med denne beskrivelsen Tangenter, kurvelengde og areal Neste uke Kjeglesnitt
Formelsamling. ξ(r, t) = ξ 0 sin(k r ωt + φ) 2 ξ(x, t) = 1 2 ξ(x, t) t 2. 2 ξ. x ξ. z 2. y ξ. v = ω k. v g = dω dk
 Formelsamling Side 7 av 16 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk plan bølge: Bølgeligning:
Formelsamling Side 7 av 16 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk plan bølge: Bølgeligning:
FY1006/TFY4215 Innføring i kvantefysikk 26. mai 2016 Side 1 av 3
 FY16/TFY4215 Innføring i kvantefysikk 26. mai 216 Side 1 av 3 FLERVALGSOPPGAVER TRENING TIL EKSAMEN En partikkel med masse m beskrives av den stasjonære tilstanden Ψ(x,t) = ψ(x)e iωt, med e ikx + 1 3i
FY16/TFY4215 Innføring i kvantefysikk 26. mai 216 Side 1 av 3 FLERVALGSOPPGAVER TRENING TIL EKSAMEN En partikkel med masse m beskrives av den stasjonære tilstanden Ψ(x,t) = ψ(x)e iωt, med e ikx + 1 3i
LØSNINGSFORSLAG TIL EKSAMEN I TFY4160 BØLGEFYSIKK Mandag 3. desember 2007 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 7 59 6 6 / 45 45 55 LØSNINGSFORSLAG TIL EKSAMEN I TFY4160 BØLGEFYSIKK Mandag.
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 7 59 6 6 / 45 45 55 LØSNINGSFORSLAG TIL EKSAMEN I TFY4160 BØLGEFYSIKK Mandag.
Løsningsforslag Eksamen 14.desember 2011 FY2045/TFY4250 Kvantemekanikk I
 Eksamen FY2045/TFY4250 14. desember 2011 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 14.desember 2011 FY2045/TFY4250 Kvantemekanikk I a. For E < 3V 0 /4 er området x > a klassisk forbudt, og
Eksamen FY2045/TFY4250 14. desember 2011 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 14.desember 2011 FY2045/TFY4250 Kvantemekanikk I a. For E < 3V 0 /4 er området x > a klassisk forbudt, og
5) Tyngdens komponent langs skråplanet, mg sin β, lik maksimal statisk friksjonskraft, f max = µ s N =
 FY1001/TFY4145 Mekanisk Fysikk ksamen 9. august 2016 Løsningsforslag 1) Her har vi bevegelse med konstant akselerasjon: v = at = 9.81 0.5 m/s = 4.9 m/s. (Kula er fortsatt i fritt fall, siden h = at 2 /2
FY1001/TFY4145 Mekanisk Fysikk ksamen 9. august 2016 Løsningsforslag 1) Her har vi bevegelse med konstant akselerasjon: v = at = 9.81 0.5 m/s = 4.9 m/s. (Kula er fortsatt i fritt fall, siden h = at 2 /2
Qi-Wu-Zhang model. 2D Chern insulator. León Martin. 19. November 2015
 Qi-Wu-Zhang model 2D Chern insulator León Martin 19. November 2015 Motivation Repeat: Rice-Mele-model Bulk behavior Edge states Layering 2D Chern insulators Robustness of edge states Motivation topological
Qi-Wu-Zhang model 2D Chern insulator León Martin 19. November 2015 Motivation Repeat: Rice-Mele-model Bulk behavior Edge states Layering 2D Chern insulators Robustness of edge states Motivation topological
Flervalgsoppgave. Arbeid og energi. Energibevaring. Kollisjoner REP Konstant-akselerasjonslikninger. Vi har sett på:
 Arbeid og energi. Energibevaring. Arbeid = dw = F ds Kinetisk energi E k = ½ m v 2 Effekt = arbeid/tid = P = dw /dt Arbeid på legeme øker E k : dw = de k Potensiell energi E p (x,y,z) (Tyngdefelt: E p
Arbeid og energi. Energibevaring. Arbeid = dw = F ds Kinetisk energi E k = ½ m v 2 Effekt = arbeid/tid = P = dw /dt Arbeid på legeme øker E k : dw = de k Potensiell energi E p (x,y,z) (Tyngdefelt: E p
EKSAMEN I FY2045 KVANTEMEKANIKK I/ TFY4250 KVANTEMEKANIKK I Tirsdag 10. august 2010 kl
 NORSK TEKST Side 1 av 6 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk EKSAMEN I FY2045 KVANTEMEKANIKK I/ TFY4250 KVANTEMEKANIKK I Tirsdag 10. august 2010 kl. 09.00-13.00 Tillatte
NORSK TEKST Side 1 av 6 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk EKSAMEN I FY2045 KVANTEMEKANIKK I/ TFY4250 KVANTEMEKANIKK I Tirsdag 10. august 2010 kl. 09.00-13.00 Tillatte
EKSAMENSOPPGAVE. Eksamen i: FYS 0100 Generell fysikk Dato: Onsdag 26.feb 2014 Tid: Kl 09:00 13:00 Sted: Aud max.
 EKSAMENSOPPGAVE Eksamen i: FYS 0100 Generell fysikk Dato: Onsdag 26.feb 2014 Tid: Kl 09:00 13:00 Sted: Aud max. Tillatte hjelpemidler: Kalkulator med tomt dataminne Rottmann: Matematisk Formelsamling Oppgavesettet
EKSAMENSOPPGAVE Eksamen i: FYS 0100 Generell fysikk Dato: Onsdag 26.feb 2014 Tid: Kl 09:00 13:00 Sted: Aud max. Tillatte hjelpemidler: Kalkulator med tomt dataminne Rottmann: Matematisk Formelsamling Oppgavesettet
EKSAMENSOPPGAVE. Fys-1002 Elektromagnetisme. Adm.bygget B154 Kalkulator med tomt dataminne, Rottmann: Matematisk formelsamling
 Fakultet for naturvitenskap og teknologi EKSAMENSOPPGAE Eksamen i: Fys-1002 Elektromagnetisme Dato: Onsdag 26. september 2018 Klokkeslett: Kl. 9:00-13:00 Sted: Tillatte hjelpemidler: Adm.bygget B154 Kalkulator
Fakultet for naturvitenskap og teknologi EKSAMENSOPPGAE Eksamen i: Fys-1002 Elektromagnetisme Dato: Onsdag 26. september 2018 Klokkeslett: Kl. 9:00-13:00 Sted: Tillatte hjelpemidler: Adm.bygget B154 Kalkulator
Physical origin of the Gouy phase shift by Simin Feng, Herbert G. Winful Opt. Lett. 26, (2001)
 by Simin Feng, Herbert G. Winful Opt. Lett. 26, 485-487 (2001) http://smos.sogang.ac.r April 18, 2014 Introduction What is the Gouy phase shift? For Gaussian beam or TEM 00 mode, ( w 0 r 2 E(r, z) = E
by Simin Feng, Herbert G. Winful Opt. Lett. 26, 485-487 (2001) http://smos.sogang.ac.r April 18, 2014 Introduction What is the Gouy phase shift? For Gaussian beam or TEM 00 mode, ( w 0 r 2 E(r, z) = E
EKSAMEN I TFY4250 ATOM- OG MOLEKYLFYSIKK FY2045 KVANTEFYSIKK Tirsdag 1. desember 2009 kl
 NORSK TEKST Side 1 av 5 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 18 67, eller 97012355 EKSAMEN I TFY4250 ATOM- OG MOLEKYLFYSIKK
NORSK TEKST Side 1 av 5 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 18 67, eller 97012355 EKSAMEN I TFY4250 ATOM- OG MOLEKYLFYSIKK
10 6 (for λ 500 nm); minste størrelse av
 Sensorveiledning Eksamen FYS130 Oppgave 1 ( poeng) a) Brytningdeksen er forholdet mellom lyshastigheten i vakuum og lyshastigheten i mediet; siden lyshastigheten i et medium er alltid mindre enn i vakuum,
Sensorveiledning Eksamen FYS130 Oppgave 1 ( poeng) a) Brytningdeksen er forholdet mellom lyshastigheten i vakuum og lyshastigheten i mediet; siden lyshastigheten i et medium er alltid mindre enn i vakuum,
Konstanter og formelsamling finner du bakerst Merk: Figurene til oppgavene er ofte på en annen side en selve oppgaven
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Konteeksamen i AST1100, 8.januar 2009, 14.30 17.30 Oppgavesettet inkludert formelsamling er på 10 sider Tillatte hjelpemidler: medbrakt
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Konteeksamen i AST1100, 8.januar 2009, 14.30 17.30 Oppgavesettet inkludert formelsamling er på 10 sider Tillatte hjelpemidler: medbrakt
EKSAMENSOPPGAVE. Eksamen i: FYS 0100 Generell fysikk Dato: Fredag 13.des 2013 Tid: Kl 09:00 13:00 Sted: Administrasjonsbygget: Aud.
 EKSAMENSOPPGAVE Eksamen i: FYS 0100 Generell fysikk Dato: Fredag 13.des 013 Tid: Kl 09:00 13:00 Sted: Administrasjonsbygget: Aud.max og B154 Tillatte hjelpemidler: Kalkulator med tomt dataminne Rottmann:
EKSAMENSOPPGAVE Eksamen i: FYS 0100 Generell fysikk Dato: Fredag 13.des 013 Tid: Kl 09:00 13:00 Sted: Administrasjonsbygget: Aud.max og B154 Tillatte hjelpemidler: Kalkulator med tomt dataminne Rottmann:
v(t) = r (t) = (2, 2t) v(t) = t 2 T(t) = 1 v(t) v(t) = (1 + t 2 ), t 2 (1 + t 2 ) t = 2(1 + t 2 ) 3/2.
 NTNU Institutt for matematiske fag TMA40 Matematikk, øving, vår 0 Løsningsforslag Notasjon og merknader Hvis boken skriver en vektor som ai + bj + ck hender det at jeg skriver den som a, b, c). Jeg benytter
NTNU Institutt for matematiske fag TMA40 Matematikk, øving, vår 0 Løsningsforslag Notasjon og merknader Hvis boken skriver en vektor som ai + bj + ck hender det at jeg skriver den som a, b, c). Jeg benytter
Tillegg om strømfunksjon og potensialstrøm
 Kapittel 9 Tillegg om strømfunksjon og potensialstrøm 9.1 Divergensfri strøm 9.1.1 Strømfunksjonen I kompendiet, kap. 4.6 og kap. 9, er det påstått at dersom et todimensjonalt strømfelt v(x y) = v x (x
Kapittel 9 Tillegg om strømfunksjon og potensialstrøm 9.1 Divergensfri strøm 9.1.1 Strømfunksjonen I kompendiet, kap. 4.6 og kap. 9, er det påstått at dersom et todimensjonalt strømfelt v(x y) = v x (x
Oppgavene er hentet fra fagets lærebok, Hass, Weir og Thomas, samt gamle eksamener.
 NTNU Institutt for matematiske fag TMA45 Matematikk, øving, vår Løsningsforslag Notasjon og merknader Oppgavene er hentet fra fagets lærebok, Hass, Weir og Thomas, samt gamle eksamener. Oppgaver fra kapittel
NTNU Institutt for matematiske fag TMA45 Matematikk, øving, vår Løsningsforslag Notasjon og merknader Oppgavene er hentet fra fagets lærebok, Hass, Weir og Thomas, samt gamle eksamener. Oppgaver fra kapittel
MA2501 Numeriske metoder
 MA251 Numeriske metoder Løsningsforslag, Øving 3 Oppgave 1 a) Start med å tegne en skisse av funksjonen f(x) = x.99(e x 1). Vi oppdager fort at α må ligge svært nær, faktisk rundt.2. Newtons metode anvendt
MA251 Numeriske metoder Løsningsforslag, Øving 3 Oppgave 1 a) Start med å tegne en skisse av funksjonen f(x) = x.99(e x 1). Vi oppdager fort at α må ligge svært nær, faktisk rundt.2. Newtons metode anvendt
Løsningsforslag Eksamen 1. desember 2008 TFY4250 Atom- og molekylfysikk/fy2045 Kvantefysikk
 Eksamen TFY45/FY45. desember 8 - løsningsforslag Løsningsforslag Eksamen. desember 8 TFY45 Atom- og molekylfysikk/fy45 Kvantefysikk Oppgave a. For x og E = E B < har den tidsuavhengige Schrödingerligningen
Eksamen TFY45/FY45. desember 8 - løsningsforslag Løsningsforslag Eksamen. desember 8 TFY45 Atom- og molekylfysikk/fy45 Kvantefysikk Oppgave a. For x og E = E B < har den tidsuavhengige Schrödingerligningen
LØSNINGSFORSLAG TIL EKSAMEN I FY1002 og TFY4160 BØLGEFYSIKK Onsdag 20. desember 2006 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY1002 og TFY4160
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY1002 og TFY4160
K j æ r e b e b o e r!
 K j æ r e b e b o e r! D u h o l d e r n å i n nk a l l i n g e n t i l å r e t s g e n e r a l f o r s am l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s l a g et s å r s b e r e t n i
K j æ r e b e b o e r! D u h o l d e r n å i n nk a l l i n g e n t i l å r e t s g e n e r a l f o r s am l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s l a g et s å r s b e r e t n i
KONTINUASJONSEKSAMEN TFY4160 BØLGEFYSIKK Torsdag 9. august 2007 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 15 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 KONTINUASJONSEKSAMEN TFY4160 BØLGEFYSIKK
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 15 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 KONTINUASJONSEKSAMEN TFY4160 BØLGEFYSIKK
I N N K AL L I N G T I L O R D I N Æ R T S A M E I E R M Ø T E
 I N N K AL L I N G T I L O R D I N Æ R T S A M E I E R M Ø T E 2 0 0 9 O r d i næ r t s am e i e rm ø t e i S am b o b o l i g s a m ei e fi n n e r s t e d t o r s d ag 3 0. 0 4. 2 0 0 9 K l. 1 8. 3 0
I N N K AL L I N G T I L O R D I N Æ R T S A M E I E R M Ø T E 2 0 0 9 O r d i næ r t s am e i e rm ø t e i S am b o b o l i g s a m ei e fi n n e r s t e d t o r s d ag 3 0. 0 4. 2 0 0 9 K l. 1 8. 3 0
Løsningsforslag til øving 6
 1 FY100/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 01. Løsningsforslag til øving 6 Oppgave 1 a) Litt repetisjon: Generelt er hastigheten til mekaniske bølger gitt ved mediets elastiske modul
1 FY100/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 01. Løsningsforslag til øving 6 Oppgave 1 a) Litt repetisjon: Generelt er hastigheten til mekaniske bølger gitt ved mediets elastiske modul
Litt GRUPPETEORI for Fys4170
 Litt GRUPPETEORI for Fys4170 GRUPPER: Ei gruppe G = {g i } er ei samling element med disse egenskapene: * multiplikasjon slik at g i g j G ; * et enhetselement g 0 = 1 slik at g i g 0 = g 0 g i = g i ;
Litt GRUPPETEORI for Fys4170 GRUPPER: Ei gruppe G = {g i } er ei samling element med disse egenskapene: * multiplikasjon slik at g i g j G ; * et enhetselement g 0 = 1 slik at g i g 0 = g 0 g i = g i ;
Løysingsforslag (Skisse) Eksamen FY3452 Gravitasjon og Kosmologi Våren 2007
 Løysingsforslag (Skisse) Eksamen FY3452 Gravitasjon og Kosmologi Våren 2007 May 24, 2007 Oppgave 1 a) Lorentztransformasjonane er x = γ(x V t), t = γ(t V x), der γ = 1/ 1 V 2 Vi tar differensiala av desse
Løysingsforslag (Skisse) Eksamen FY3452 Gravitasjon og Kosmologi Våren 2007 May 24, 2007 Oppgave 1 a) Lorentztransformasjonane er x = γ(x V t), t = γ(t V x), der γ = 1/ 1 V 2 Vi tar differensiala av desse
Løsningsforslag til prøveeksamen i MAT1050, vår 2019
 Løsningsforslag til prøveeksamen i MT15, vår 19 Oppgave 1. a) Vi har sinx + y) d R cosx + y) sinx + π) + sin x siden alle fire leddene er. yπ y π dx sinx + y) dy dx cosx + π) + cos x) dx sin π + sin π)
Løsningsforslag til prøveeksamen i MT15, vår 19 Oppgave 1. a) Vi har sinx + y) d R cosx + y) sinx + π) + sin x siden alle fire leddene er. yπ y π dx sinx + y) dy dx cosx + π) + cos x) dx sin π + sin π)
On multigrid methods for the CahnHilliard equation with obstacle potential
 On multigrid methods for the CahnHilliard equation with obstacle potential ubomír Ba as Department of Mathematics Imperial College London Joint work with Robert Nürnberg http://www.ma.ic.ac.uk/~lubo lubo@imperial.ac.uk
On multigrid methods for the CahnHilliard equation with obstacle potential ubomír Ba as Department of Mathematics Imperial College London Joint work with Robert Nürnberg http://www.ma.ic.ac.uk/~lubo lubo@imperial.ac.uk
Rotasjon: Translasjon: F = m dv/dt = m a. τ = I dω/dt = I α. τ = 0 => L = konstant (N1-rot) stivt legeme om sym.akse: ω = konst
 Translasjon: Rotasjon: Bevegelsesmengde (linear momentum): p = m v Spinn (angular momentum): L = r m v L = I ω Stivt legeme om sym.akse N2-trans: F = dp/dt Stivt legeme (konst. m): F = m dv/dt = m a N2-rot
Translasjon: Rotasjon: Bevegelsesmengde (linear momentum): p = m v Spinn (angular momentum): L = r m v L = I ω Stivt legeme om sym.akse N2-trans: F = dp/dt Stivt legeme (konst. m): F = m dv/dt = m a N2-rot
a) Vis at startvolumet er V 0 = 1, 04m 3 Gassen presses deretter sammen til et volum på V 1 = 0, 80m 3 mens temperaturen i gassen holdes konstant.
 NB: Alle deloppgavene teller like mye i vurderingen. Dvs. oppgave 1a teller like mye som oppgave 4. Oppgave 1 I en beholder er 50,0 mol luft avstengt av et stempel som kan bevege seg uten friksjon mot
NB: Alle deloppgavene teller like mye i vurderingen. Dvs. oppgave 1a teller like mye som oppgave 4. Oppgave 1 I en beholder er 50,0 mol luft avstengt av et stempel som kan bevege seg uten friksjon mot
Løsningsforslag til eksamen i FY3404/FY8307 RELATIVISTISK KVANTEMEKANIKK Fredag 9. juni 2006
 NTNU Side 1 av 4 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i FY3404/FY8307 RELATIVISTISK KVANTEMEKANIKK Fredag 9. juni 2006 Dette løsningsforslaget
NTNU Side 1 av 4 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i FY3404/FY8307 RELATIVISTISK KVANTEMEKANIKK Fredag 9. juni 2006 Dette løsningsforslaget
FYS2140 Kvantefysikk. Løsningsforslag for Oblig 7
 FYS2140 Kvantefysikk Løsningsforslag for Oblig 7 Oppgave 2.23 Regn ut følgende intgral a) +1 3 (x 3 3x 2 + 2x 1)δ(x + 2) dx (1) Svar: For å løse dette integralet bruker vi Dirac deltafunksjonen (se seksjon
FYS2140 Kvantefysikk Løsningsforslag for Oblig 7 Oppgave 2.23 Regn ut følgende intgral a) +1 3 (x 3 3x 2 + 2x 1)δ(x + 2) dx (1) Svar: For å løse dette integralet bruker vi Dirac deltafunksjonen (se seksjon
Eksamen i emnet M117 - Matematiske metodar Mandag 29. mai 2000, kl Løysingsforslag:
 Eksamen i emnet M7 - Matematiske metodar Mandag 29. mai 2, kl. 9-5 Løysingsforslag: a Singulære punkt svarer til nullpunkta for x 2, dvs. x = og x =. Rekkeutvikler om x = : yx = a n x n y x = na n x n
Eksamen i emnet M7 - Matematiske metodar Mandag 29. mai 2, kl. 9-5 Løysingsforslag: a Singulære punkt svarer til nullpunkta for x 2, dvs. x = og x =. Rekkeutvikler om x = : yx = a n x n y x = na n x n
EKSAMENSOPPGAVE. Tillatte hjelpemidler: Kalkulator med tomt dataminne, Rottmann: Matematisk formelsamling.
 EKSAMENSOPPGAE Eksamen i: FYS-1002 Dato: Mandag 4. juni, 2018 Klokkeslett: 9:00 13:00 Sted: ADM B154 Tillatte hjelpemidler: Kalkulator med tomt dataminne, Rottmann: Matematisk formelsamling. Eksamenoppgaven
EKSAMENSOPPGAE Eksamen i: FYS-1002 Dato: Mandag 4. juni, 2018 Klokkeslett: 9:00 13:00 Sted: ADM B154 Tillatte hjelpemidler: Kalkulator med tomt dataminne, Rottmann: Matematisk formelsamling. Eksamenoppgaven
The Effects of an Extended Neutrino Sphere on Supernova Neutrino Oscillations
 The Effects of an Extended Neutrino Sphere on Supernova Neutrino Oscillations max-planck-institut für Kernphysik Heidelberg NDM 2018, IBS, Korea July 2, 2018 1 / 24 Janka et al. 2012 2 / 24 Impact of neutrino
The Effects of an Extended Neutrino Sphere on Supernova Neutrino Oscillations max-planck-institut für Kernphysik Heidelberg NDM 2018, IBS, Korea July 2, 2018 1 / 24 Janka et al. 2012 2 / 24 Impact of neutrino
HØGSKOLEN I NARVIK - SIVILINGENIØRUTDANNINGEN
 HØGSKOLEN I NARVIK - SIVILINGENIØRUTDANNINGEN EKSAMEN I FAGET STE 6243 MODERNE MATERIALER KLASSE: 5ID DATO: 7 Oktober 2005 TID: 900-200, 3 timer ANTALL SIDER: 7 (inklusiv Appendix: tabell og formler) TILLATTE
HØGSKOLEN I NARVIK - SIVILINGENIØRUTDANNINGEN EKSAMEN I FAGET STE 6243 MODERNE MATERIALER KLASSE: 5ID DATO: 7 Oktober 2005 TID: 900-200, 3 timer ANTALL SIDER: 7 (inklusiv Appendix: tabell og formler) TILLATTE
Arbeid og energi. Energibevaring.
 Arbeid og energi. Energibevaring. Arbeid = dw = F ds Kinetisk energi E k = ½ m v 2 Effekt = arbeid/tid = P = dw /dt Arbeid på legeme øker E k : Potensiell energi E p (x,y,z) dw = de k (Tyngdefelt: E p
Arbeid og energi. Energibevaring. Arbeid = dw = F ds Kinetisk energi E k = ½ m v 2 Effekt = arbeid/tid = P = dw /dt Arbeid på legeme øker E k : Potensiell energi E p (x,y,z) dw = de k (Tyngdefelt: E p
EKSAMEN I FY2045 KVANTEMEKANIKK I/ TFY4250 KVANTEMEKANIKK I Torsdag 20. desember 2012 kl
 NORSK TEKST Side av 5 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 972355 EKSAMEN I FY245 KVANTEMEKANIKK I/ TFY425
NORSK TEKST Side av 5 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 972355 EKSAMEN I FY245 KVANTEMEKANIKK I/ TFY425
LØSNINGSFORSLAG TIL EKSAMEN I FY1002 BØLGEFYSIKK Mandag 10. desember 2007 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY1002 BØLGEFYSIKK
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY1002 BØLGEFYSIKK
Differenslikninger. Inger Christin Borge. Matematisk institutt, UiO. Kompendium 2 i MAT1001 Matematikk 1. Våren 2009
 Differenslikninger Kompendium 2 i MAT1001 Matematikk 1 Våren 2009 Inger Christin Borge Matematisk institutt, UiO Forord Trilogien fortsetter, og du tar nå fatt på Kompendium 2 i MAT1001. Her skal vi ta
Differenslikninger Kompendium 2 i MAT1001 Matematikk 1 Våren 2009 Inger Christin Borge Matematisk institutt, UiO Forord Trilogien fortsetter, og du tar nå fatt på Kompendium 2 i MAT1001. Her skal vi ta
Løsningsforslag: Kurs TEP4195 TURBOMASKINER. NTNU Institutt for Energi- og Prosessteknikk FREDAG 21. MAI 2004 TID: 09:00 13:00
 NTNU Institutt for Energi- og Prosessteknikk Kontaktperson i løpet av eksamen Navn: Torbjørn K. Nielsen/ Lars Erik Bakken Tlf: (73 5) 9357/ Løsningsforslag: Kurs TEP495 TURBOMASKINER FREDAG. MAI 004 TID:
NTNU Institutt for Energi- og Prosessteknikk Kontaktperson i løpet av eksamen Navn: Torbjørn K. Nielsen/ Lars Erik Bakken Tlf: (73 5) 9357/ Løsningsforslag: Kurs TEP495 TURBOMASKINER FREDAG. MAI 004 TID:
9) Mhp CM er τ = 0 i selve støtet, slik at kula glir uten å rulle i starten. Dermed må friksjonskraften f virke mot venstre, og figur A blir riktig.
 TFY4115 Fysikk Eksamen 18. desember 2013 Løsningsforslag, kortversjon uten oppgavetekst og figurer 1) (4 0.264/0.164) (USD/USgal)(NOK/USD)(USg/L) = 6.44 NOK/L C) 6.44 2) N2: F = ma i a i = F/m B) a 1 =
TFY4115 Fysikk Eksamen 18. desember 2013 Løsningsforslag, kortversjon uten oppgavetekst og figurer 1) (4 0.264/0.164) (USD/USgal)(NOK/USD)(USg/L) = 6.44 NOK/L C) 6.44 2) N2: F = ma i a i = F/m B) a 1 =
Midtsemesterprøve Bølgefysikk Fredag 12. oktober 2007 kl
 Institutt for fysikk, NTNU FY1002/TFY4160 Bølgefysikk Høst 2007 Midtsemesterprøve Bølgefysikk Fredag 12. oktober 2007 kl 1215 1400. LØSNINGSFORSLAG 1) En masse er festet til ei fjær og utfører udempede
Institutt for fysikk, NTNU FY1002/TFY4160 Bølgefysikk Høst 2007 Midtsemesterprøve Bølgefysikk Fredag 12. oktober 2007 kl 1215 1400. LØSNINGSFORSLAG 1) En masse er festet til ei fjær og utfører udempede
Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Torsdag 8. august 2002
 NTNU Sie 1 av 7 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Torsag 8. august 2002 Eksamen gitt av Kåre Olaussen Dette løsningsforslaget
NTNU Sie 1 av 7 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Torsag 8. august 2002 Eksamen gitt av Kåre Olaussen Dette løsningsforslaget
NORSK TEKST Side 1 av 4. Faglig kontakt under eksamen: Ingjald Øverbø, tlf , eller
 NORSK TEKST Side 1 av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 18 67, eller 97012355 EKSAMEN I FY2045/TFY4250 KVANTEMEKANIKK
NORSK TEKST Side 1 av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 18 67, eller 97012355 EKSAMEN I FY2045/TFY4250 KVANTEMEKANIKK
Eksamen i FY8306 KVANTEFELTTEORI Fredag 9. juni :00 13:00
 NTNU Side av 3 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: 9 36 52 eller 45 43 7 70 Eksamen i FY8306 KVANTEFELTTEORI Fredag 9. juni 2006 09:00 3:00 Tillatte hjelpemidler:
NTNU Side av 3 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: 9 36 52 eller 45 43 7 70 Eksamen i FY8306 KVANTEFELTTEORI Fredag 9. juni 2006 09:00 3:00 Tillatte hjelpemidler:
EKSAMEN I EMNE TFY4125 FYSIKK. Lørdag 20. august 2005 Tid: kl
 Bokmål NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Institutt for fysikk, Gløshaugen Professor Tore Lindmo, mob. 911 47 844 Studentnummer: Studieretning:
Bokmål NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Institutt for fysikk, Gløshaugen Professor Tore Lindmo, mob. 911 47 844 Studentnummer: Studieretning:
