Estatistika POPULAZIOA ETA LAGINA ALDAGAI ESTATISTIKOAK MAIZTASUNAK ABSOLUTUAK ETA ERLATIBOAK ADIERAZPEN GRAFIKOAK ZENTRALIZAZIO-NEURRIAK
|
|
|
- Anne-Lise Gustavsen
- 6 år siden
- Visninger:
Transkript
1 Estatistika POPULAZIOA ETA LAGINA ALDAGAI ESTATISTIKOAK KUALITATIBOAK KUANTITATIBOAK DISKRETUAK JARRAITUAK MAIZTASUNAK ABSOLUTUAK ETA ERLATIBOAK METATUAK ADIERAZPEN GRAFIKOAK ZENTRALIZAZIO-NEURRIAK BATEZ BESTEKOA MEDIANA MODA SAKABANATZE-NEURRIAK IBILTARTEA ETA BATEZ BESTEKO DESBIDERATZEA BARIANTZA ETA DESBIDERATZE TIPIKOA ALDAKUNTZA- KOEFIZIENTEA 9
2 Jainkoak salba beza erregina! Sidney Herbert Gerrarako Estatuko Idazkariak karrera politikoko erabakirik arriskutsuena hartu zuen. Izan ere, haren lagun Florence Nightingale-ren esku utzi zuen aire zabaleko erizainen gorputza antolatzea, Krimeako Gerrako ospitaleak hobetzeko.. urtea zen eta bere etorkizun politikoa dama haren esku zegoen. Gatazka-gunera joateko prestatzen ari zela, herrialde osoa astindu zuen Brigada Arinaren deuseztapenak, errusiarren baterien aurkako eraso suizidaren ondoren. Ekintza hori ez zuten hondamen gisa zabaldu, ingelesen kemenaren eta ohorearen froga gisa baizik. Nightingale neurri higienikoak aplikatzen hasi zen, eta datuak bilduz eta grafikoen bidez antolatuz joan zen, errazago irakurtzeko. Txostena Gerrako Idazkariari bidali zioten, eta bertan laguntza eskatzen zen armadako buruzagiek jarritako oztopoak ezabatzeko. Amaieran, eskuizkribu bat ageri zen. Honela zioen eskuizkribuak: Urtarrilean,. bajetatik,. gaixotasun kutsakorrek eragin zituzten, gerrako zauriek eta beste arrazoi batzuek Gure ospitaleek etsaiaren kanoiek baino baja gehiago eragiten dituzte. Jauna, ez utzi Ingalaterraren ohorea ospitale bateko gela batean lurperatzen. Jainkoak salba beza erregina! Adierazi oharreko datuak grafiko egoki baten bidez. Datuak adierazteko, barra- edo sektore-diagrama erabil dezakegu; dena den, egokiena sektore-diagrama erabiltzea da. Bajak (pertsonak) BARRA-DIAGRAMA Kutsatuta Gudan Bestelakoak Arrazoiak SEKTORE-DIAGRAMA Bestelakoak Gudan F F Kutsatuta
3 Estatistika ARIKETAK 00 Ikastetxe bateko DBHko. mailako ikasleen oinetakoen neurriari buruzko azterketa estatistikoa egin nahi dugu. a) Zein da populazioa? b) Aukeratu lagin bat. Zer neurri du? a) Populazioa: ikastetxeko DBHko. mailako ikasle guztiak. b) Lagin bat: ikasgeletako bateko ikasleak. Neurria ikasgelako ikasle kopurua da. 00 Adierazi zer kasutan komeni den populazioa ala lagina aztertzea. a) Makina batek egiten dituen torlojuen luzera. b) Urte bateko turista guztien garaiera. c) Bost laguneko talde baten pisua. a) Lagina, ezin ditugu torloju guztiak neurtu. b) Lagina, turista asko daude-eta. c) Populazioa, talde txikia delako. 00 Hona hemen egunkari bateko izenburu bat. «ESPAINIARREN BATEZ BESTEKO PISUA 9 KG DA.» a) Zure ustez, nola lortzen da ondorio hori? Populazio osoa aztertu ote da? b) Zer ezaugarri izan behar ditu lagin osoak? Izan al litezke adin berekoak lagineko banako guztiak? Guztiak emakumeak badira, zuzena al litzateke lagina? a) Lagin esanguratsu bat hartu da, kontuan izanda zer taldetan bana daitekeen populazio osoa; inkesta egin eta batez bestekoa kalkulatu da. Ia ezinezkoa da espainiar guztiei galdetzea. b) Laginak esanguratsua izan behar du adin eta sexu guztietarako; populazioko proportzio berean ageri behar dute. 00 Pentsatu eta idatzi azterketa estatistikoa egiteko populazioaren adibide bat. Zer lagin har dezakegu? Adierazi zein diren banakoak eta zer neurri duen laginak. Populazioa: futbol-taldeetan inskribatutako hiri jakin bateko gazte guztiak. Lagina: futbol-talderen batean aritzen diren ikastetxeko gazte guztiak. Banakoak: aurreko lagineko gazte bakoitza. Laginaren neurria: aurreko lagineko gazte kopurua. 9
4 ERANTZUNAK 00 Adierazi kualitatiboak ala kuantitatiboak diren aldagai estatistiko hauek. a) Jaiotza-urtea. b) Ile-kolorea. c) Pertsona baten ogibidea. d) Perimetro torazikoa e) Egoera zibila. f) Gerriaren perimetroa. g) Zenbat aldiz bidaiatu den hegazkinez. Kualitatiboak: b), c) eta e). Kuantitatiboak: a), d), f) eta g). 00 Sailkatu aldagai hauek kualitatibotan eta kuantitatibotan; bigarren kasuan, bereizi diskretuak eta jarraituak. a) Norbera bizi den probintzia. b) Eraikin bateko auzotar kopurua. c) Aitaren ogibidea. d) Gasolina-kontsumoa 00 km-ko. Kuantitatiboak: b) eta d). Kualitatiboak: a) eta c). Diskretua: b) eta jarraitua: d). 00 Aldagai estatistiko kuantitatibo batek infinitu balio har baditzake, diskretua ala jarraitua da? Printzipioz, ez du zertan diskretua ala jarraitua izan. Esan dezakeguna hau da: aldagai bat jarraitua bada infinitu balio har ditzake. Aldagaia diskretua bada, tarte bakoitzean har dezakeen balio kopurua finitua da, baina aldagaiak infinitu balio har ditzake. Esate baterako, zenbaki arrunt gustukoena zein den galdetuz gero, printzipioz infinitu erantzun daude, zenbaki arrunt guztiak, hain zuzen ere. Hala ere, aldagaia diskretua da. 00 Hona hemen gazteren altuera (cm-tan): Egin tarteka antolatutako taula bat, zenbatu datuak eta lortu tarte bakoitzeko klase-markak. Tartea [0, 0) [0, 0) [0, 0) Klase-marka Zenbaketa 0 9
5 Estatistika lagunen ile-koloreak (B = beltzarana, I = ilehoria, G = ilegorria) hauek dira: B I G B B B B I I G G B B B B B B G I I I G B B B B I B B B Egin maiztasun-taula. Ile-kolorea h i F i H i Beltzarana 0, 0, Ilehoria 0, 0, Ilegorria 0, 0 Guztira 0 00 Zergatik dira tauletako tarteak alde batetik itxiak eta bestetik irekiak? Bi aldeetatik irekiak balira, puntu jakin bat ez zen tarte bakar batean ere egongo, eta bi tarteak itxiak balira, puntu jakin bat bi tartetan egongo litzateke. Eta bi egoera horiek ez dira zuzenak. 0 0 lagunek ordenagailuaren bidez lanean egunean ematen dituzten orduak: a) Zer motatako aldagai estatistikoa da? b) Egin maiztasun-taula. a) Aldagai kuantitatibo diskretua da. b) Orduak h i 0 0, 0, 0, 0, 0, 0, Guztira Hona hemen 0 laguni egindako adimen-test baten emaitzak: Egin maiztasun-taula, 0 zabalerako tarteak hartuta. Adina h i [, ) 0, [, ) 0, [, 9) 0, [9, 0) 0, [0, ) 0, [, ) 0, Guztira 0 9
6 ERANTZUNAK 0 Zer gertatzen da maiztasun absolutuen batura eta guztizko datu kopurua ez badira berdinak? Daturen bat ez dugu zenbatu edo bestela okertu egin gara kalkuluren bat egitean. 0 Hona hemen lagunen pisuak (kg-tan):,,, 9,, 9,,,,, 0,, 0, 0, 0, 0,, 9, 9,,, 0 a) Bildu 0 zabalerako tartetan eta egin maiztasun-taula. b) Zenbatek dute 0 kg-tik beherako pisua? c) Kalkulatu zer ehuneko adierazten duen guztizkoarekiko maiztasun absolutu handieneko tarteak. a) Tartea [0, 0) [0, 0) [0, 0) [0, 0) [0, 0) [0, 90) F i 9 0 h i / = 0, / = 0, / = 0, / = 0, / = 0, / = 0,0 H i 0, 0, 0, 0, 0,9 b) Maiztasun absolutu metatuen zutabeari, F i, erreparatuz, 9 lagunek 0 kg baino pisu txikiagoa dutela ikusten da. c) Maiztasun handieneko tartea [0, 0) da: = eta h i = 0, %. 0 Hona hemen 0 ikasleren egun bateko batez besteko ikasketa-orduak: Egin maiztasun-taula. Zer esanahi dute maiztasun metatuek? Orduak h i 0 0, 0, 0, 0, 0, 0, Guztira 0 F i 0 H i 0, 0, 0, 0, 0,9 Maiztasun metatuek egunean gehienez ordu kopuru jakin bat ikasten ematen duten ikasle kopurua edo ehunekoa adierazten dute. 99
7 Estatistika 0 Azaldu nola osatuko zenukeen maiztasun-taula bat, maiztasun absolutu metatuak soilik jakinda. Lehen maiztasun absolutu metatua eta lehen maiztasun absolutua berdinak dira. Gainerako maiztasun absolutuak kalkulatzeko, ondoz ondoko maiztasun absolutu metatuen kenketak egin behar dira. f = F = F i F i Laginaren neurria azken maiztasun absolutu metatua da, eta hortik abiatuta, maiztasun erlatiboak kalkulatzen dira. 0 Eraikin batean, etxebizitza daude. Etxebizitzetako telebista kopurua: 0 0 a) Egin maiztasun-taula. Zer aldagai mota da? Arrazoitu erantzuna. b) Egin datuen barra-diagrama eta maiztasun-poligonoa. c) Egin gauza bera maiztasun metatuekin. a) Aldagai kuantitatibo diskretua da. Telebistak h i 0 0, 0, 0, 0, Guztira F i H i 0, 0, 0, b) MAIZTASUN ABSOLUTUAK c) MAIZTASUN METATUAK Auzotarrak Auzotarrak 0 0 Telebistak 0 Telebistak 0 Aparkaleku publiko batean, auto gorri, 9 hori, zilar-koloreko 9, 0 zuri, berde, 0 urdin eta 0 beltz zeuden. a) Egin maiztasun-taula. c) Egin b) Kalkula al ditzakezu maiztasun metatuak? barra-diagrama. a) Kolorea Gorria Horia Zilar-kolorea Zuria Berdea Urdina Beltza h i /00 = 0, 9/00 = 0,09 9/00 = 0,9 0/00 = 0, /00 = 0, 0/00 = 0, 0/00 = 0,0 00
8 ERANTZUNAK b) Ezin dira maiztasun metatuak kalkulatu, aldagaia kualitatiboa delako. c) G H Zil. Z Ber. U Belt. 09 Egin aurreko ariketako grafikoak maiztasun erlatibo eta guzti. Zer hauteman duzu? 0, 0,0 0, 0,0 0, h i G H Zil. Z Ber. U Belt. Grafiko bera da, baina maiztasunen eskala aldatuta. 00 Hona hemen kilkerren luzera (cm-tan):,,9,,,,,9,,,,,,9,,, a) Egin tarteak eta idatzi maiztasun-taula. b) Adierazi datuak histograma eta maiztasun-poligono banaren bidez. c) Egin sektore-diagrama. Zure ustez, zer grafiko da egokiena? a) Tartea c) [,; ) [;,) [,; ) [,; ) [,; ) [;,) b),, Histograma da egokiena, datuak aldagai kuantitatibo batenak direlako. 0
9 Estatistika 0 Adierazi grafikoki datu hauek: 0 ikasleko gela batean; ikaslek ez dute irakasgaia gainditu; 0ek Nahiko atera dute; %k, Oso ongi; eta gainerakoek, Bikain. Notak Gutxiegi Nahiko Oso ongi Bikain 0 0 Bikain Gutxiegi Oso ongi Nahikoa 0 Egin grafikoari dagokion maiztasun-taula. Aldagaia h i [0, 0) 0,0 [0, 0) 0 0, [0, 0) 0, [0, 0) 0 0, [0, 0) 0, [0, 0) 0, Total Y X DBHko. mailako ikasleren altuerak (cm-tan) hauek dira: a) Bildu tartetan. b) Kalkulatu batez bestekoa, mediana eta moda. a). 90 Tartea x i x i b) x = [, 0),.0, =, [0, ) 9,., Me =, [, 0),.0,.90, Mo =, 0 Interpretatu ikasleren Gutxiegi kopuruen zentralizazio-neurriak Gutxiegi kopurua h i 0 0, 0, 0, 0, 0, F i 9 H i 0, 0, 0,0 0, 0
10 ERANTZUNAK x = = = Ikasle bakoitzak gutxiegi ditu, batez beste. Bi moda daude: Mo = eta Mo =. Me = denez, ikasleen erdiek irakasgaitan gutxiegi atera dute, gehienez. 0 Erantsi mediana aldatuko ez duen balio bat. 9 Mediana da eta edozein balio sartuta ere izango da. Izan ere, balio kopurua bikoitia da eta beste balio bat batzean, bakoitia izango da. Beraz, bi etako batek balio zentrala izaten jarraituko du. 0 Beheko datuek 0 langilek zenbat baja-egun izan dituzten erakusten dute. Kalkulatu datu multzoaren kuartilak Bajak F i Guztira 0 0 0, =, Q = , = Q = Me = =, 0 0, =, Q = 0 Interpretatu aurreko ariketan kalkulatutako kuartilak. Bajan egon ez diren langileak % dira, gutxienez; langileen erdiak gehienez egun bat egon dira bajan, eta langileen %, gehienez egun. 0 Oposizio-deialdia egin dute 0 lanpostu betetzeko eta 00 pertsona aurkeztu dira. Hona hemen emaitzak. Notak Oposiziogileak fi Zer nota behar da lanpostua lortzeko? 0 lanpostuak bat datoz hirugarren kuartilarekin, 0 pertsonak ez dituztelako lortu: % ek. Behar den nota da
11 Estatistika 09 Hona hemen torlojuen lagin bateko luzerak (mm-tan). Kalkulatu sakabanatze-neurriak, klase-markak erabiliz. Tartea [, ) [, ) [, ) [, ) Tartea [, ) [, ) [, ) [, ) x i,,,, 0 x i 0, 0,, 9, 90, x i x x i x (x i x) x = =, 0 BBD = = 0, σ = =, σ=, Ikasle batek nota hauek lortu ditu bost azterketatan:,,, eta. Eta beste batek, berriz, hauek:, 9,, eta. Zer ikaslek du sakabanatze handiena? Lehen ikaslea: H = = x i x i x i x x i x (x i x),, 0,,,,, 0,,,,,,9 0,,,,, x = =, BBD = =,,, σ= =, AK = = 0,, Bigarren ikaslea: H = 9 = x i 9 x i 9 x i x x i x (x i x),, 0,,,,, 0,,, 0,,,9 0,,,9 9,0 0, x = =, BBD = =,0 9,, σ= =, AK = = 0,, Beraz, bigarren ikasleak du sakabanatze handiena. 0
12 ERANTZUNAK 0 Galdetu adina eta altuera ikaskideri. Alderatu bi aldagaien sakabanatzea. Emaitzak laginaren araberakoak izango dira. ARIKETAK 0 Ikasleek irakurtzen ematen duten denborari buruzko azterketa egin nahi dugu. a) Aukeratu lagina, azterketa egiteko. b) Zer neurri du aukeratutako laginak? c) Zein da populazioa? a) Esate baterako, ikasgelako ikasleak. b) Ikasgelako ikasleen kopurua. c) Ikastetxeko ikasle guztiak. 0 Azaldu zer aldagai estatistiko mota ari garen aztertzen eta adierazi zer den onena kasu bakoitzean: lagina ala populazioa aztertzea. a) Zure familiako kideen programa gustukoena. b) Ikastetxe bateko ikasleen oinetakoen neurria. c) Zure probintziako eguneroko batez besteko tenperatura. d) Herrialde bateko biztanleen adina. e) Herri bateko biztanleen sexua. f) Zure lagunek astebetean gastatutako dirua. g) Sendagai berri baten eraginak gizakiarengan. h) Zure gelako ikaskideen ile-kolorea. a) Kualitatiboa. Populazioa. b) Kuantitatibo diskretua. Lagina. c) Kuantitatibo jarraitua. Populazioa. d) Kuantitatibo diskretua. Lagina. e) Kualitatiboa. Lagina. f) Kuantitatibo diskretua. Populazioa. g) Kualitatiboa. Lagina. h) Kualitatiboa. Populazioa. 0
13 Estatistika 0 Behean ageri diren aldagaietatik zein dira diskretuak? a) Maskota kopurua. b) Oinetakoen neurria. c) Burezurraren perimetroa. d) Fruta-denda bateko eguneroko diru-sarrerak. e) Astebetean ikastetxe bateko jangelan kontsumitutako okela-kilogramoak. Diskretuak: a) eta b). Jarraituak: c), d) eta e). 0 Atzerrira zenbat aldiz joan diren galdetu zaie 0 pertsonari. Hona hemen emaitzak: a) Egin zenbaketa eta antolatu datuak. b) Egin maiztasun-taula. a) Datuak ordenatuta:,,,,,,,,,,,,,,,,,,,. b) x i 0 F i 0 h i /0 = 0,0 /0 = 0, /0 = 0, /0 = 0,0 /0 = 0, /0 = 0,0 H i 0,0 0,0 0, 0, 0,90 % Hona hemen Gorputz Hezkuntzako 0 ikasleren oinetakoen neurria: Egin barra-diagrama eta maiztasun-poligonoa, eta adierazi maiztasun absolutuak eta maiztasun absolutu metatuak. MAIZTASUN ABSOLUTUAK MAIZTASUN METATUAK Ikasleak 0 Ikasleak Neurriak 9 0 Neurriak 0
14 ERANTZUNAK 0 Hona hemen gazteren altuerak (cm-tan): a) Erabili zabalerako tarteak, maiztasun-taula egiteko. b) Adierazi datuak histograma batean, maiztasun absolutuak eta maiztasun absolutu metatuak erabiliz. a) Tartea [0, ) [, 0) [0, ) [, 0) [0, ) [, 0) x i,,,,,, F i h i / = 0,0 / = 0, / = 0, / = 0, / = 0, / = 0, H i 0,0 0, 0, 0,9 0, b) MAIZTASUN ABSOLUTUAK MAIZTASUN METATUAK Gazteak Gazteak Altuera (cm) Altuera (cm) 0 Afari batera joan diren 0 lagunetatik, % 0k txahala jan zuen; % 0k, arkumea; eta gainerakoek, arraina. Adierazi aldagai estatistikoa eta antolatu emaitzak maiztasun-taula batean. Ondoren, adierazi datuak sektore-grafiko batean. Jatekoa h i Txahala 0, Arkumea 0, Arraina 0, 0 Arkumea () Txahala () Arraina () 0
15 Estatistika 09 Grafikoan, kiroldegi bateko teniseko pista hil bakoitzean zenbat aldiz alokatu den ageri da a) Kalkulatu maiztasun erlatiboak eta metatuak. b) Hilen zer ehunekotan alokatu zen pista 0 alditan baino gehiagotan? c) Adierazi maiztasun absolutu metatuen poligonoa. a) Hila Urt Ots Mar Api Mai Eka Uzt Abu Ira Urr Aza Abe U O M A M E U A I U A A b) Urtarrilean, maiatzean, ekainean, uztailean, urrian eta abenduan 0 aldiz alokatu zen pista, hilen % 0 baino gehiagoan. c).000 F i F i h i 0,09 0,0 0,0 0,00 0,09 0, 0,09 0,0 0,0 0, 0,0 0,0 H i 0,09 0, 0, 0, 0, 0,90 0, 0, 0, 0, 0, UOMAMEUA I UA A 00 Kalkulatu datu segida honen zentralizazio-neurriak x i 0 9 F i Batez best.: x = =,9 Mediana: Me = Moda: Mo = 0
16 ERANTZUNAK 0 Egin aurreko ariketa zabalerako tarteak hartuta. Emaitza berak lortu al dituzu? Zure ustez, zergatik gertatzen da hori? Aldagaia x i [0, ) 0 [, ) 0 [, ) [, ) [, 0) 9 F i Batez bestekoa: x = =, Mediana: Me = [, ) Moda: Mo = [, ) Emaitzak desberdinak dira. Hori gertatzen da datuak biltzean klase-markan daudel suposatzen dugulako, eta beraz, eragiketak aldatu egiten dira. 0 Kalkulatu datu hauen mediana. a) x i b) Bar. [0, 0) [0, 0) [0, 0) [0, 0) a) N = = denez, mediana. eta. lekuan dauden x i balioei dagokie. Kasu honetan: + x = eta x = Me = =, b) N = = denez eta F = 9 > Me = [0, 0) tarteko klase-marka = 0 Kalkulatu taula honetako datuen batez bestekoa, mediana, moda eta kuartilak. x i a) Taulako balio guztiak z biderkatuz gero, zenbatekoa litzateke batez bestekoa? Eta mediana? Eta moda? b) Aldagai baten balio guztiei zenbaki bera kendu edo haiek zenbaki beraz zatitzen baditugu, zenbatekoa izango da batez besteko berria? x = = =, 0 0 N = 0 denez, 0. eta. lekuetan dauden x i balioak dira mediana. Kasu honetan, Me =, Q = eta Q = 0. Gehien ageri den balioa hau da: Mo =. ( ) + ( ) + ( 0) + ( ) a) x = = 0 ( ) = = x aurrekoa 0 Kasu honetan, x berria =, =,. Beraz, Me = =, Q =, Q = 90 eta Mo =. b) Balio guztiei zenbaki bera kenduz gero, x berria = x zenbakia. Eta balio guztiak zenbaki beraz zatituz gero, x berria = x : zenbakia. 09
17 Estatistika 0 0,, a, 9,, b, datuen batez bestekoa, mediana eta moda 9 dira. Zenbatekoak dira a eta b? a b + x = = a + b = 9 = a + b = a b - a-k 9 (moda) izan behar duenez 9 + b = b =. 0 Demagun datuen multzo hau: 9 x y Jakinik batez bestekoa 0 eta moda direla, zenbatekoak dira x eta y? x + y + 0 = 0 = + x + y x + y = Moda Mo = bada, x-k edo y-k (edo biek) izan behar dute. x = y = balira x + y = + =. Beraz, x = y = =. 0 Hona hemen etxeetako irrati kopuruari buruzko inkesta bateko datuak. Irrati kopurua 0 Etxe kopurua...00 a) Zenbat irrati dituzte etxeen laurdenek? b) Eta etxeen % ek? c) Zer esanahi du medianak?. a) =., Q = Etxeen % ek irrati bat du edo bat ere ez.. b) =., Q = Etxeen % ek irrati edo gutxiago dituzte. c) Mediana bera baino datu handiagoen eta txikiagoen kopuru bera duen balioa da. X i F i Ebatzi ariketa hau, kalkulagailua erabiliz. Hilabetean, zortzi saltzailek aire girotuzko gailuen kopuru hauek saldu zituzten. Kalkulatu batez bestekoa, desbideratze tipikoa eta aldakuntza-koefizientea. 0
18 ERANTZUNAK Datuak ordenatuko ditugu: x = = = 0, σ = ( 0,) ( 0,) = = 0, +, + 0, +, + 0, =, = = 0, σ = 0, =, AK = 0, = 0, 0 Planetarioa bisitatu duten lehen 0 lagunen adinak (urtetan) hauek dira: Kalkulatu neurri estatistikoak. Datuak ordenatuko ditugu: x = = = 0, 0 0 Me = 0 Mo = 0 H = σ ( 0,) = (0 0,) = 0, σ =,9 σ =, 9 =, AK = = 0, 0, 09 EGIN HONELA NOLA ALDERATZEN DA BI ALDAGAI ESTATISTIKOREN SAKABANATZEA? Jaioberrien lagin bateko batez besteko pisua x =,-koa da, eta desbideratze tipikoa, σ= kg. Amen batez besteko pisua x = kg da, eta desbideratze tipikoa, σ= kg. Zer banaketatan da handiena sakabanatzea? LEHENA. Aldakuntza-koefizienteak kalkulatu. AK jaioberriak = = 0, = % AK amak = = 0, = %, BIGARRENA. Koefizienteak alderatu behar dira. 0, > 0, Sakabanatzea handiagoa da jaioberrien pisuan amen pisuan baino, desbideratze tipikoei erreparatuz gero aurkakoa dirudien arren: <.
19 Estatistika 00 Albertok nota hauek atera ditu azterketatan:,,, eta. Anek, berriz:,, 0, 0 eta. Bietatik zein da erregularrena errendimendu akademikoan? Albertoren kasuan, neurri estatistikoak hauek dira: x = =,, σ = = 0, σ = 0, 0, AK = = 0,, Aneren kasuan, neurri estatistikoak hauek dira: 0 x = = σ = =, σ =, 9 9, AK = = 0, Beraz, Ane da erregularrena errendimendu akademikoan. 0 Kalkulatu datu hauen batez bestekoa, mediana, moda eta desbideratze tipikoa. Pisua [, ) [, ) [, 9) [9, ) [, ) Ikasle kopurua Pisua [, ) [, ) [, 9) [9, ) [, ) x i 0 F i x i (x i x) (x i x),,,,,,, 00,, 0,.0, 90 x = =, Me = [, ) Mo = [, ) σ =. 0 =, 9 σ =,
20 ERANTZUNAK 0 Hona hemen 0 ikaslek Musikan lortu dituzten notak: Musika-gela Kalkulatu datuen batez bestekoa eta desbideratze tipikoa, aldagaia diskretu gisa hartuta, lehendabizi, eta ondoren, datuak tarte hauetan bilduz: [0, ), [, ), [, 9) eta [9, 0]. Zer alde hautematen da? Lehendabizi, datuak ordenatuko ditugu: x = =, 0 σ (0,) = (0,) =, 0, σ=, =, AK = = 0,0 0 Datuak tartetan bilduko ditugu: Tartea [0, ) [, ) [, 9) [9, 0] Klase-marka,,, 9, 0 x =, , = =, 0 0 σ = (,,) (9,,) 0 =, σ=,, =, AK = = 0,0 0 Batez bestekoa eta desbideratze tipikoa aldatu egin dira.
21 Estatistika 0 Taulan, etxebizitzen hileko alokairuen prezioak ageri dira. Prezioa ( ) Etxebizitza kopurua a) Zenbatekoa da batez besteko alokairua? b) Adierazi zer prezio ageri den gehien. c) Kalkulatu mediana. Zer esan nahi du? d) Kalkulatu bariantza eta desbideratze tipikoa. Zertarako dira zenbaki horiek? Prezioa ( ) F i x i (x i x) (x i x).00,00.00,00.900, ,00 9,.,9,,.,0.00,.0,0.90,.,9., 0.,. 00 a) x = =, b) Gehien ageri den prezioa moda da: Mo = 00. c) Mediana Me = 0 da eta prezio horren azpitik daude alokairuen erdiak. 0., d) σ = =., σ = 0, Zenbaki horiek datuen sakabanatzea ikusteko balio dute; kasu honetan, alokairu batzuen eta beste batzuen artean alde handia dagoen ikusteko, hau da, ea alokairuen prezioa homogeneoa den ala ez. 0 Grafiko hauetatik abiatuta, egin maiztasun-taula, eta kalkulatu datuen batez bestekoa, mediana, moda eta desbideratze tipikoa. a) Y 9 0 X
22 ERANTZUNAK b) Y 0 X 0 a) x i 9 0 b) x = =, N = denez, mediana. tokian dagoen balioa da Me =. Moda hau da: Mo =. σ = (,) (0,) =, σ=, =, Tartea [0, ) [, ) [, ) [, ) [, ) 0 x i 0,,,,, 0, , x = =, Me =, Mo =, σ = (0,,) (,,) =, σ=, =, 0 EGIN HONELA NOLA INTERPRETATZEN DIRA BATEZ BESTEKOA ETA DESBIDERATZE TIPIKOA BATERA? Saskibaloi-talde batek hegaleko bat behar du. Azken bost partidetan taulan adierazitako puntu kopurua lortu duten bi jokalariak aukeratu dira. Nor hautatuko zenuke? A jokalaria B jokalaria LEHENA. Batez bestekoa eta desbideratze tipikoa kalkulatu behar dira. x A = x B = A jokalaria B jokalaria σa =,09 σb =, BIGARRENA. Aurreko emaitzak aztertu behar dira. Batez bestekoak berdinak direnez, entrenatzaileak jokalari erregular bat nahi balu, A jokalaria aukeratuko luke (desbideratze tipiko txikiak antzeko datuak adierazten ditu). Baina pizgarri bat nahi izanez gero, B aukeratuko luke; izan ere, oso partida onak eta txarrak egiten ditu (desbideratze tipiko handiak datu desberdinak adierazten ditu). 0
23 Estatistika 0 proba egin ondoren taulan ageri diren emaitzak lortu dituzte bi ikaslek. Alderatu bien errendimendua. Jon Ane 0 9 Jon: batez bestekoa =, desbideratze tipikoa =,. Ane: batez bestekoa =, desbideratze tipikoa =,. Batez besteko bera izanda, Jon da konstanteena emaitzetan, desbideratze tipiko txikiena duelako. 0 Lehen ebaluazioan, gela bateko 0 ikasleetatik, % 0ek dena gainditu zuen, % 0k irakasgai bat suspenditu zuen; % 0ek bi irakasgai suspenditu zituen, eta gainerakoek, bi baino gehiago. Egin maiztasun-taula, datu horiek erabiliz. Bi irakasgai baino gutxiago zenbat ikaslek suspenditu zituzten galderari erantzuteko maiztasunik ba al dago? Arrazoitu erantzuna. Gutxiegi kopurua h i 0 0, 0, 0, baino gehiago 0, Guztira 0 F i 9 0 H i 0, 0, 0, Bi irakasgai baino gutxiago suspenditutako ikasleak adierazteko en maiztasun absolutu metatua erabiltzen da; hau da, 9 ikasle. 0 Lasterkari batek astelehenetik ostiralera egiten ditu entrenamenduak.,,, eta km egiten ditu, hurrenez hurren. Larunbatean ere entrenamendua egiten badu: a) Zenbat kilometro egin behar ditu batez bestekoa ez aldatzeko? b) Eta mediana ez aldatzeko? c) Eta moda ez aldatzeko? x = =,. Mediana:. Moda:. a) Larunbatean, km egin behar ditu. b) km edo handiagoa den edozein distantzia. c), edo km ez den edozein distantzia.
24 ERANTZUNAK 09 Buruzko kalkuluko (BK) proba eta psikomotrizitate-proba (P) bana egin zaie ikasgela bateko ikasleei. Emaitza hauek lortu dira: a) Zer probatan lortu dituzte emaitza onenak (batez besteko handiena)? b) Zer probatan izan da sakabanatze handiena? (Erabili aldakuntza-koefizientea.) a) Batez bestekoak kalkulatuko ditugu: x BK = = 90 x CM = =, x P = =. 00 x P = =, Psikomotrizitate-proban lortu dituzte emaitza onenak. b) σ (,) BK = (,) =. 9, σ CM = =,0 σ BK =,9 σ, 9 AK = AK = = 0, x, Puntu kopurua [0, 0) [0, 0) [0, 0) [0, 0) [0, 0) [0, 0) BK σ (,) P = (,) =.,, σ P = =, σ P =, AK = = 0,, Sakabanatzea ia bera izan da bi probetan. P 9 00 galderako proba bati erantzun zioten 0 ikasleetatik, % 0ek zuzen erantzun zien galderari; % 0ek, ri; % 0ek, 0i; eta gainerakoek, proba osoari. Kalkulatu datuen batez bestekoa, mediana eta moda. Kalkulatu desbideratze tipikoa. Lehendabizi, maiztasun-taula egingo dugu: x = = 0 Mediana. eta º posizioetako balioen batez bestekoa da, N = 0 baita; kasu honetan, Me =. handiena duen balioa Mo = da. σ ( ) = ( ) =, σ =, 0 x i 0 %0 0 = %0 0 = %0 0 = %0 0 =
25 Estatistika 0 Gestio-informatikan diplomadunek, lehen lanpostuan,.0 -ko batez besteko soldata dute. Desbideratze tipikoa 0 -koa da. Bestalde, sistemen informatikako diplomadunek.0 -ko batez besteko soldata dute eta 0 -ko desbideratze tipikoa. Gestio-informatikako diplomadun bati.00 -ko soldata eskaini diote, eta sistemen informatikako diplomadun bati,.0 -ko soldata: a) Nori egin diote eskaintza onena? b) Arrazoitu zergatik den hobea eskaintza bat..0.0 Erantzunak bistakoa dirudi,.00 >.0 baita. Beraz, itxuraz eskaintza onena gestio-informatikako diplomadunari egin diotena da. Hala ere, banako bakoitza zer populaziotakoa den aintzat hartuta alderatzeko, talde bakoitzeko batez besteko soldata eta sakabanatzea kontuan hartu beharko ditugu. Gestio-informatika:.00 irabazten dituzte eta sakabanatzea 0 -koa da taldeko batez bestekoaren gainetik (.0 ). Desbideratzea (0 ) eta talde horretan ageri den sakabanatzea alderatuko 0 ditugu: σ =0, = 0,, eta zenbat eta handiagoa izan zenbaki hori 0 orduan eta urrunago egongo da batez besteko soldatatik. Sistemen informatika:.0 irabazten dituzte eta sakabanatzea 0 -koa da taldeko batez bestekoaren gainetik (.0 ). Desbideratzea (0 ) eta taldeko sakabanatzea alderatuko ditugu: 0 σ=0, = 0,. 0 Beraz, eskaintza onena sistemen informatikako diplomadunari egin diotena da, 0, > 0, delako, eta horren ondorioz, egin dioten eskaintza gehiago urruntzen da taldeko batez besteko soldatatik. 0 Zenbaki oso positibo desberdinek osatutako datu multzo baten batez bestekoa da. Kontuan hartuta datu bat 9 dela eta datu guztien batura 9, zein da datu multzoan egon daitekeen zenbakirik handiena? 9 9 x = = N = = da datu kopurua. N Datu bat 9 denez, gainerakoek ahalik txikienak izan beharko dute:,,, eta. Zazpigarren zenbakia hau da: 9 ( ) =. Beraz, da egon daitekeen zenbakirik handiena.
26 ERANTZUNAK 0 Datu multzo hau dugu: x Kalkulatu x, datuen mediana eta batez bestekoa berdinak izan daitezen. x baino handiagoa bada, mediana izango da, eta batez bestekoa izatea nahi dugunez, bost gaien baturak 0 izan behar du. Beraz, x = 0 ( ) =. ez denez baino handiagoa, ezinezkoa da. x bada, mediana izango da, eta batez bestekoa izatea nahi dugunez, bost gaien baturak izan behar du. Beraz, x = ( ) = ; eta hori ezinezkoa da. x baino txikiagoa bada, mediana izango da, eta batez bestekoa izatea nahi dugunez, bost gaien baturak 0 izan behar du. Beraz, x = 0 ( ) =. Eta baino txikiagoa denez, ebazpena x = da. 0 Bost datuko multzo batean, batez bestekoa 0 da, eta mediana,. Zein da ibiltarteak har dezakeen baliorik txikiena? Mediana denez, edo handiagoak diren bi balio egon behar dute eta edo txikiagoak diren beste bi balio. Eta ibiltartea minimoa izan dadin, bi balio handienek ahalik txikienak izan behar dute (mediana batez bestekoa baino handiagoa denez), eta beraz, balioa izango dute. Bost gaien baturak 0 izan behar du eta hiru gairen batura da. Beraz, beste bi gaien baturak izan behar du. Ibiltartea minimoa izan dadin, balio txikienak ahalik handiena izan behar du, eta hori gertatzen da bi balio txikienak berdinak badira; beraz, balioa izango dute. Balioak,,,,, izango dira, eta ibiltartea,. 0 0,,,,,, x datu multzoaren batez bestekoa, mediana eta moda goranzko ordenan idazten baditugu, progresio aritmetiko bat lortuko dugu. Kalkulatu x aldagaiak har ditzakeen balio guztiak. Moda da, edozein kasutan. x baino txikiagoa bada, mediana izango da; beraz, progresio aritmetikoa izateko, batez bestekoak ere izan behar du, eta hori ezinezkoa da. x bada, mediana izango da; beraz, progresioa aritmetikoa izateko, batez bestekoak, edo izan behar du, eta hori ezinezkoa da. x edo handiagoa bada, mediana da; eta batez bestekoak baino balio handiagoak hartzen dituenez, progresio aritmetikoa izateko, batez bestekoak izan behar du. Beraz, gaien batura da: x = ( ) =. 9
27 Estatistika 0 Zazpi datuko multzo bat ordenatu ondoren, lehenengo lau datuak hartuz gero, batez bestekoa izango da; baina azken lau datuak hartuz gero, batez bestekoa izango da. Zenbaki guztien batez bestekoa bada, zenbatekoa da mediana? x = x + x + x + x + x + x + x = x + x + x + x = 0 = x + x + x + x + x + x + x + x = x + x + x + x = = + x x = Mediana da. EGUNEROKOAN 0 Ikasleen Matematikako errendimendua balioesten ari da Hezkuntza Saila. Hori dela-eta, iazko ikasturtean Bigarren Hezkuntzako ikasleek Matematikan izandako emaitzak erakusten dituen txostena egin du. Grafikoetan, txosten horren laburpena ikus daiteke. Sektore-diagrama egiteko, notarik handienak, OSO ONGI eta BIKAIN, bildu eta nota bakoitza % % lortu duten % ikasleen ehunekoak % sartu dira. % GUT NAH ONG OSO BIK GUT NAH ONG OSO + BIK Txostenaren arabera, NAHIKO nota atera duten ikasleak. izan dira. Grafikoei eta ehunekoei erreparatu, kalkulatu zenbat ikasle ebaluatu dituzten guztira eta zenbat ikaslek atera duten BIKAIN Ikasle guztien %. badira Guztira = =. 0 ikasle. 0 Ongi eta nahiko lortu dutenen kopurua = 0. 9 ikasle Oso ongi lortu dutenen kopurua 0 =. ikasle Bikain lortu dutenen kopurua =. 09 ikasle 00 0
28 ERANTZUNAK 0 Telebista-kate bateko ikusle kopuruaren araberakoa da kate horretan ematen den publizitatearen kostua. Horregatik, aldizka audientzia-indizeak jakinarazten dira. Audientzia-indize handieneko bi telebista-kateek urteko lehen lau hiletako emaitzak aurkeztu dituzte. Hona hemen zenbait komunikabidetan agertu diren grafikoak. Milakoak Milakoak MIRO TELEBISTA Urt. Ots. Mar. Api. Bi kateek gorakada handia izan dute, baina MIRO TELEBISTAko arduradunek diote haien telebistaren gorakada handiagoa izan dela. Zenbat ikusle irabazi ditu kate bakoitzak? Zer adierazpenek islatzen du ondoen egoera? FREE KATEA Urt. Ots. Mar. Api. Komunikabideetan argitaratutako grafikoetan ikus daitekeen moduan, Free Kateak baino gorakada handiagoa izan dugu. Bi grafikoen eskalak desberdinak dira, eta horregatik dirudi MIRO TELEBISTAren gorakada handiagoa dela; dena den, FREE KATEA telebistako audientziaren gorakada 0.000koa da, gutxi gorabehera. Beste kateko audientziaren gorakada, berriz, txikiagoa da: ikusentzule gehiago, gutxi gorabehera. Gorakada hobeto ikus daiteke MIRO TELEBISTAren grafikoan, eta adierazteko bi moduak baliozkoak diren arren, informazioa alderatzeko, eskala bera erabili behar genuke.
Ekuazioak eta inekuazioak
 Ekuazioak eta inekuazioak EKUAZIOAK LEHEN MAILAKOAK BIGARREN MAILAKOAK BIKARRATUAK BESTE MOTATAKO EKUAZIOAK ZATIKI ALJEBRAIKOEKIN ( a) ( b) 0 ERROKETADUN EKUAZIOAK INEKUAZIOAK Azken gaua Denbora-tarte
Ekuazioak eta inekuazioak EKUAZIOAK LEHEN MAILAKOAK BIGARREN MAILAKOAK BIKARRATUAK BESTE MOTATAKO EKUAZIOAK ZATIKI ALJEBRAIKOEKIN ( a) ( b) 0 ERROKETADUN EKUAZIOAK INEKUAZIOAK Azken gaua Denbora-tarte
Arantza Egurcegui MATEM DBH A 2 TIKA erein
 Arantza Egurcegui DBH 2 MATEMATIKA erein Obra honen edozein erreprodukzio modu, banaketa, komunikazio publiko edo aldaketa egiteko, nahitaezkoa da jabeen baimena, legeak aurrez ikusitako salbuespenezko
Arantza Egurcegui DBH 2 MATEMATIKA erein Obra honen edozein erreprodukzio modu, banaketa, komunikazio publiko edo aldaketa egiteko, nahitaezkoa da jabeen baimena, legeak aurrez ikusitako salbuespenezko
Ikuskorreko urdin eremutik gorri aldera igortzen duten BODIPY laser koloratzaile moldagarriak
 Gradu Amaierako Lana Kimikako Gradua Ikuskorreko urdin eremutik gorri aldera igortzen duten BODIPY laser koloratzaile moldagarriak Egilea: Edurne Avellanal Zaballa Zuzendaria: Jorge Bañuelos Prieto 2015,
Gradu Amaierako Lana Kimikako Gradua Ikuskorreko urdin eremutik gorri aldera igortzen duten BODIPY laser koloratzaile moldagarriak Egilea: Edurne Avellanal Zaballa Zuzendaria: Jorge Bañuelos Prieto 2015,
EUSKAL ELIZBARRUTI ARTEKO 'ITUN BERRIA' Itzulpen-xehetasunak historiaren argira
 EUSKAL ELIZBARRUTI ARTEKO 'ITUN BERRIA' Itzulpen-xehetasunak historiaren argira Donostia, 1980-x-31 Eustasio Etxezarreta Sarrera Euskal Herriko ak argitara eman berria du Itun Berria, liturgiarako egindako
EUSKAL ELIZBARRUTI ARTEKO 'ITUN BERRIA' Itzulpen-xehetasunak historiaren argira Donostia, 1980-x-31 Eustasio Etxezarreta Sarrera Euskal Herriko ak argitara eman berria du Itun Berria, liturgiarako egindako
AHT: Oraingoz ez. Bi hormetara Endrinak pardelean ohgi
 Nafarroako gehigarria / Ostirala,1995eko otsailaren 17a / VI. urtea /166. zenbakia Abiadura Handiko Trenak urteak beharko ditu Nafarroako tuneletatik sartu eta lautadak zeharkatzeko. Joan den abenduan
Nafarroako gehigarria / Ostirala,1995eko otsailaren 17a / VI. urtea /166. zenbakia Abiadura Handiko Trenak urteak beharko ditu Nafarroako tuneletatik sartu eta lautadak zeharkatzeko. Joan den abenduan
Antxitoneak. ehunurte. Hitzek neutralak behar dute izan. Bi hormetara. Egunsentiko bi aldeak
 Nafarroako gehigarria / Ostirala, 1994ko martxoak 18 / IV. urtea / 119. zenbakia Bi hormetara ~ JOSETXO AZKONA Antxitoneak Duela ehun urte, 1894an, Antxitonea deritzaion etxearen gibeleko aldean ehunurte
Nafarroako gehigarria / Ostirala, 1994ko martxoak 18 / IV. urtea / 119. zenbakia Bi hormetara ~ JOSETXO AZKONA Antxitoneak Duela ehun urte, 1894an, Antxitonea deritzaion etxearen gibeleko aldean ehunurte
BEKTOREAK ESPAZIOAN. Norabidea: A eta B puntuak dauden zuzenarena eta zuzen horren paralelo guztienari norabidea deitzen
 Bektoeak espaioak BEKTOREAK ESPAZIOAN. Eagiketak bektoeekin A jatoia eta B mta den bektoea honela adieaten da: AB Bektoe baten elementak haek dia: Modla: A-tik B-ako distantia, eta honela iendaten da:
Bektoeak espaioak BEKTOREAK ESPAZIOAN. Eagiketak bektoeekin A jatoia eta B mta den bektoea honela adieaten da: AB Bektoe baten elementak haek dia: Modla: A-tik B-ako distantia, eta honela iendaten da:
EUSKALTZAINDIAREN HIZTEGIA vs HIZTEGI BATUA
 EUSKALTZAINDIAREN HIZTEGIA vs HIZTEGI BATUA EZABATU BEHARREKO SARRERAK ZEIN AZPISARRERAK (HIZTEGI BATUAK ONARTUAK ZITUENAK): Hiztegi Batua Euskaltzaindiaren Hiztegia AZKEN ERABAKIA (HB) bizi-doia (AS s.u.
EUSKALTZAINDIAREN HIZTEGIA vs HIZTEGI BATUA EZABATU BEHARREKO SARRERAK ZEIN AZPISARRERAK (HIZTEGI BATUAK ONARTUAK ZITUENAK): Hiztegi Batua Euskaltzaindiaren Hiztegia AZKEN ERABAKIA (HB) bizi-doia (AS s.u.
itto! 650 zkia. EIBARKO ASTEKARIA 2008-X-3
 eta itto! 650 zkia. EIBARKO ASTEKARIA 2008-X-3 ELKARRIZKETA: Javier Jauregi ileapaintzailea Zinemaldian KIROLEZ KIROL: Carlos Pouso, Eibar KEko entrenatzailea FIRIN FARAN: Euskadiko Orkestra gaur Coliseoan
eta itto! 650 zkia. EIBARKO ASTEKARIA 2008-X-3 ELKARRIZKETA: Javier Jauregi ileapaintzailea Zinemaldian KIROLEZ KIROL: Carlos Pouso, Eibar KEko entrenatzailea FIRIN FARAN: Euskadiko Orkestra gaur Coliseoan
Aretxabaleta, Bergara eta Eskoriatzako udalerrietan 5. edukiontzia ezartzeko aurre proiektua, eta Elgetako sistemaren egokitzapena alboko kargara
 Aretxabaleta, Bergara eta Eskoriatzako udalerrietan 5. edukiontzia ezartzeko aurre proiektua, eta Elgetako sistemaren egokitzapena alboko kargara Nafarroa Etorbidea, 17. 20500 ARRASATE-MONDRAGON (GIPUZKOA)
Aretxabaleta, Bergara eta Eskoriatzako udalerrietan 5. edukiontzia ezartzeko aurre proiektua, eta Elgetako sistemaren egokitzapena alboko kargara Nafarroa Etorbidea, 17. 20500 ARRASATE-MONDRAGON (GIPUZKOA)
Egungo Euskararen Hiztegia T
 Egungo Euskararen Hiztegia T [bertsioa: 2014-07-14] tabakadi iz tabako saila. Txistu eta bozina joka jardun genuen, eguzkia tabakadi berdean hondoratzen ari zen bitartean. tabakismo iz tabakoa erretzeak
Egungo Euskararen Hiztegia T [bertsioa: 2014-07-14] tabakadi iz tabako saila. Txistu eta bozina joka jardun genuen, eguzkia tabakadi berdean hondoratzen ari zen bitartean. tabakismo iz tabakoa erretzeak
4. Aditz sintagma Aditzaren sailkapena formaren aldetik Aditzaren sailkapena moldeari begira. a. Adizki trinko edo sintetikoak
 4. Aditz sintagma 4.1. Aditz sintagmaren egitura 4.2. Aditza 4.2.1. Aditzaren sailkapena formaren aldetik a. Bakunak b. Eratorriak c. Elkartuak 4.2.2. Aditzaren sailkapena moldeari begira. 4.2.2.1. Aditz
4. Aditz sintagma 4.1. Aditz sintagmaren egitura 4.2. Aditza 4.2.1. Aditzaren sailkapena formaren aldetik a. Bakunak b. Eratorriak c. Elkartuak 4.2.2. Aditzaren sailkapena moldeari begira. 4.2.2.1. Aditz
So#ware Ingeniaritza. 3. Gaia: Diseinua. 3.3 Maila anitzeko so#ware arkitekturak. A. Goñi, J. Ibáñez, J. Iturrioz, J.A. Vadillo
 So#ware Ingeniaritza 3. Gaia: Diseinua 3.3 Maila anitzeko so#ware arkitekturak A. Goñi, J. Ibáñez, J. Iturrioz, J.A. Vadillo Aurkibidea Sarrera Maila anitzeko softwarearen arkitektura logikoa: aurkezpena,
So#ware Ingeniaritza 3. Gaia: Diseinua 3.3 Maila anitzeko so#ware arkitekturak A. Goñi, J. Ibáñez, J. Iturrioz, J.A. Vadillo Aurkibidea Sarrera Maila anitzeko softwarearen arkitektura logikoa: aurkezpena,
REPSOL BUTANO, SA AURKIBIDEA
 REPSOL BUTANO, SA AURKIBIDEA REPSOL BUTANO, SA... 1 A I.7.1.- Instalazioen deskribapena... 2 A I.1.7.1.1 Identifikazioa eta datu orokorrak... 2 A I.7.1.2. Instalazioen eta prozesuen deskribapena... 3 A
REPSOL BUTANO, SA AURKIBIDEA REPSOL BUTANO, SA... 1 A I.7.1.- Instalazioen deskribapena... 2 A I.1.7.1.1 Identifikazioa eta datu orokorrak... 2 A I.7.1.2. Instalazioen eta prozesuen deskribapena... 3 A
KALIFORNIA... KU-KU! Antonio Maria Labaien. Iturria: Teatro osoa euzkeraz (III), Antonio Labayen. La Gran Enciclopedia Vasca, 1976.
 Iturria: Teatro osoa euzkeraz (III), Antonio Labayen. La Gran Enciclopedia Vasca, 1976. Klasikoen Gordailuan: http://klasikoak.armiarma.com/idazlanak/l/labaienkalifornia.htm KALIFORNIA... KU-KU! Klasikoen
Iturria: Teatro osoa euzkeraz (III), Antonio Labayen. La Gran Enciclopedia Vasca, 1976. Klasikoen Gordailuan: http://klasikoak.armiarma.com/idazlanak/l/labaienkalifornia.htm KALIFORNIA... KU-KU! Klasikoen
( ) Euskaltzaindiaren arauak
 ( ) Ondoren, Euskaltzaindiak eman dituen arau nagusiak bildu ditugu laburbilduta. Tokirik ezean, hikako alokutiboa eta beste zenbait arau kanpoan utzi behar izan ditugu. Euskaltzaindiaren arauak ZENBAKIEN
( ) Ondoren, Euskaltzaindiak eman dituen arau nagusiak bildu ditugu laburbilduta. Tokirik ezean, hikako alokutiboa eta beste zenbait arau kanpoan utzi behar izan ditugu. Euskaltzaindiaren arauak ZENBAKIEN
Hurrengo aditzak nolakoak diren azaldu beharko bazenu, zein irizpideren arabera egingo zenuke?
 ditzk ditz motk ditz lokuziok dizki motk dizki joktu gbek dizkien osgik dizki ngusiko ezugrrik dizki lguntzileko ezugrrik Ezugrrik dizki trinkoetn dizki berezik ditz erk dizki lguntzileen errok dizki lguntzileetko
ditzk ditz motk ditz lokuziok dizki motk dizki joktu gbek dizkien osgik dizki ngusiko ezugrrik dizki lguntzileko ezugrrik Ezugrrik dizki trinkoetn dizki berezik ditz erk dizki lguntzileen errok dizki lguntzileetko
Mtl'l \ n SK VI MI/\HPs IIMOKI \\
 ELIZA Mtl'l \ n SK VI MI/\HPs IIMOKI \\ Elizak bere-berea duen adierazpen edo emaitza sortu du: artea eta bereziki arte erlijiosoa; eliz bizitzaren eta kristau-bizitzaren ageriko adierazpen iraunkorra.
ELIZA Mtl'l \ n SK VI MI/\HPs IIMOKI \\ Elizak bere-berea duen adierazpen edo emaitza sortu du: artea eta bereziki arte erlijiosoa; eliz bizitzaren eta kristau-bizitzaren ageriko adierazpen iraunkorra.
AURRENDAKO DOSTATZIA, DA OSASUNA BILATZIA
 Bertsio elektroniko honen egilea: Alberto Barandiaran. Iturria: Iruñeko Udalaren literatur lehiaketak (1882-1928), Alberto Barandiaran. Iruñeko Udala, 1996. Klasikoen Gordailuan: http://klasikoak.armiarma.com/idazlanak/g/garraldadostatzia.htm
Bertsio elektroniko honen egilea: Alberto Barandiaran. Iturria: Iruñeko Udalaren literatur lehiaketak (1882-1928), Alberto Barandiaran. Iruñeko Udala, 1996. Klasikoen Gordailuan: http://klasikoak.armiarma.com/idazlanak/g/garraldadostatzia.htm
GRADU AMAIERAKO LANA
 GRADU AMAIERAKO LANA INSTALAZIO ELEKTRIKO ADIMENTSU BATEN PROIEKTUA, AUTOKONTSUMORAKO SORKUNTZA ELEKTRIKOAREKIN, INDUSTRIAKO NABE BATENTZAT GIPUZKOAKO INGENIARITZA ESKOLA INGENIARITZA ELEKTRIKOKO GRADUA
GRADU AMAIERAKO LANA INSTALAZIO ELEKTRIKO ADIMENTSU BATEN PROIEKTUA, AUTOKONTSUMORAKO SORKUNTZA ELEKTRIKOAREKIN, INDUSTRIAKO NABE BATENTZAT GIPUZKOAKO INGENIARITZA ESKOLA INGENIARITZA ELEKTRIKOKO GRADUA
2016AN HIRUGARRENENTZAKO FAKTUREI EZARTZEKO PREZIOAK
 1/7 GOI MAILAN APLIKATU BEHARREKO PREZIOAK KONZEPTU PREZIOA UT Langileak Oficial Prezioa. Ohizko lan-ordutegia 43,46 /ord Enkargatua. Ohizko lan-ordutegia 61,15 /ord Antolakuntza buru/arduradun. Ohizko
1/7 GOI MAILAN APLIKATU BEHARREKO PREZIOAK KONZEPTU PREZIOA UT Langileak Oficial Prezioa. Ohizko lan-ordutegia 43,46 /ord Enkargatua. Ohizko lan-ordutegia 61,15 /ord Antolakuntza buru/arduradun. Ohizko
ZULO MADARIKATUAK! Jostirudia. Euzko oituraren ager-gaya. Bi egintza ta lau ager-alditan
 ZULO MADARIKATUAK! Jostirudia Euzko oituraren ager-gaya Bi egintza ta lau ager-alditan AGERLIAK EDO IRUDIGILLEAK... ardotegiko jabia... baserritar gaztia... baserritar gaztia AMORRATU... erariyak galdua...
ZULO MADARIKATUAK! Jostirudia Euzko oituraren ager-gaya Bi egintza ta lau ager-alditan AGERLIAK EDO IRUDIGILLEAK... ardotegiko jabia... baserritar gaztia... baserritar gaztia AMORRATU... erariyak galdua...
Hizkuntza-izenei glotonimo deritze. Grekotik dator termino hori, eta honako hitz hauek elkartuz sortua da:
 Hizkuntza-izenei glotonimo deritze. Grekotik dator termino hori, eta honako hitz hauek elkartuz sortua da:! γλῶττα (glôtta), «hizkuntza» esan nahi baitu.! ὄνομα (onoma), «izen» esan nahi baitu. Heteroglotonimoak
Hizkuntza-izenei glotonimo deritze. Grekotik dator termino hori, eta honako hitz hauek elkartuz sortua da:! γλῶττα (glôtta), «hizkuntza» esan nahi baitu.! ὄνομα (onoma), «izen» esan nahi baitu. Heteroglotonimoak
BITORIANO IRAOLA ARISTIGUIETA. O R O I T Z A K eta beste ipui asko AUSPOA LIBURUTEGIA
 BITORIANO IRAOLA ARISTIGUIETA O R O I T Z A K eta beste ipui asko AUSPOA LIBURUTEGIA OROITZAK ta beste ipui asko AUSPOA LIBURUTEGIA -9- Colección Auspoa - Plaza de Santa María, - Tolosa Ordaindu bearrak:
BITORIANO IRAOLA ARISTIGUIETA O R O I T Z A K eta beste ipui asko AUSPOA LIBURUTEGIA OROITZAK ta beste ipui asko AUSPOA LIBURUTEGIA -9- Colección Auspoa - Plaza de Santa María, - Tolosa Ordaindu bearrak:
Erakunde Publiko Finantzatzaileak. Erakunde Pribatu Finantzatzaileak
 2012 TXOSTENA 2 Erakude Publiko Fiatzatzaileak OSASUN ETA KONTSUMO SAILA DEPARTAMENTO DE SANIDAD Y CONSUMO ENPLEGU ETA GIZARTE GAIETAKO SAILA DEPARTAMENTO DE EMPLEO Y ASUNTOS SOCIALES Viviedas Etxebizitzak
2012 TXOSTENA 2 Erakude Publiko Fiatzatzaileak OSASUN ETA KONTSUMO SAILA DEPARTAMENTO DE SANIDAD Y CONSUMO ENPLEGU ETA GIZARTE GAIETAKO SAILA DEPARTAMENTO DE EMPLEO Y ASUNTOS SOCIALES Viviedas Etxebizitzak
GABON AV OSTATVBA!! ANTON KAIKU. AUSPOA LlBURUTEGIA
 MARCELINO SOROA LASA GABON AV OSTATVBA!! ANTON KAIKU AUSPOA LlBURUTEGIA js-i14 Jóh~.1.0 U bl (};~t;..h:r. 116 1- GASON AUOST ATUSA!! ANTON KAIKU AUSPOA liburutegia -~- Colecci6n Auspoa Plaza Santa María,
MARCELINO SOROA LASA GABON AV OSTATVBA!! ANTON KAIKU AUSPOA LlBURUTEGIA js-i14 Jóh~.1.0 U bl (};~t;..h:r. 116 1- GASON AUOST ATUSA!! ANTON KAIKU AUSPOA liburutegia -~- Colecci6n Auspoa Plaza Santa María,
MANUAL DEBOZIONEZKOA. Joanes Etxeberri «Ziburukoa»
 Iturria: Manual devotionezcoa edo ezperen oren oro escuetan errabilltçeco liburutchoa, Joannes Etxeberri (faksimilea). Hordago, 1978. Klasikoen Gordailuan: http://klasikoak.armiarma.com/idazlanak/e/etxebzibumanual.htm
Iturria: Manual devotionezcoa edo ezperen oren oro escuetan errabilltçeco liburutchoa, Joannes Etxeberri (faksimilea). Hordago, 1978. Klasikoen Gordailuan: http://klasikoak.armiarma.com/idazlanak/e/etxebzibumanual.htm
Kap. 8: Utvalsfordelingar og databeskrivelse
 Kap. 8: Utvalsfordelingar og databeskrivelse Utvalsfordelingar Utvalsfordeling for gjennomsnitt (med kjent varians) ( X ) Sentralgrenseteoremet (SGT) Utvalsfordeling for varians (normalfordeling) Utvalfordeling
Kap. 8: Utvalsfordelingar og databeskrivelse Utvalsfordelingar Utvalsfordeling for gjennomsnitt (med kjent varians) ( X ) Sentralgrenseteoremet (SGT) Utvalsfordeling for varians (normalfordeling) Utvalfordeling
P r in s ipp s ø k n a d. R egu l e r i ngsen d r i n g f o r S ands t a d gå r d gn r. 64 b n r. 4 i Å f j o r d ko mm un e
 P r in s ipp s ø k n a d R egu l e r i ngsen d r i n g f o r S ands t a d gå r d gn r. 64 b n r. 4 i Å f j o r d ko mm un e O pp d ra g s n r : 2 0 1 50 50 O pp d ra g s n a v n : Sa n d s ta d g å r d
P r in s ipp s ø k n a d R egu l e r i ngsen d r i n g f o r S ands t a d gå r d gn r. 64 b n r. 4 i Å f j o r d ko mm un e O pp d ra g s n r : 2 0 1 50 50 O pp d ra g s n a v n : Sa n d s ta d g å r d
Del I InDustrIutvIklIng: en fortelling om fornyelsen av luftfart... 15
 InnholD bak grunn... 11 h E n s i k t... 12 inn hold... 12 mo ti va sjon og takk... 13 Del I InDustrIutvIklIng: en fortelling om fornyelsen av luftfart... 15 o p p h E v E l s E n av t y n g d E k r a
InnholD bak grunn... 11 h E n s i k t... 12 inn hold... 12 mo ti va sjon og takk... 13 Del I InDustrIutvIklIng: en fortelling om fornyelsen av luftfart... 15 o p p h E v E l s E n av t y n g d E k r a
FAGKONFERANSE KONTROL L OG TILSYN GARDERMOEN JUNI A RSMØTE I FORU M FO R KONTROLL OG TILSYN 5. JUN I 2013
 FAGKONFERANSE KONTROL L OG TILSYN GARDERMOEN 5.- 6. JUNI 201 3 A RSMØTE I FORU M FO R KONTROLL OG TILSYN 5. JUN I 2013 09. 0 0 1 0. 0 0 R E G I S TR E R I NG N o e å b i t e i 10. 0 0 1 0. 15 Å p n i ng
FAGKONFERANSE KONTROL L OG TILSYN GARDERMOEN 5.- 6. JUNI 201 3 A RSMØTE I FORU M FO R KONTROLL OG TILSYN 5. JUN I 2013 09. 0 0 1 0. 0 0 R E G I S TR E R I NG N o e å b i t e i 10. 0 0 1 0. 15 Å p n i ng
Innhold. Ka pit tel 1 Inn led ning Barn og sam funn Bo kas opp byg ning... 13
 Innhold Ka pit tel 1 Inn led ning... 11 Barn og sam funn... 11 Bo kas opp byg ning... 13 Ka pit tel 2 So sia li se rings pro ses sen... 15 For hol det mel lom sam funn, kul tur og so sia li se ring...
Innhold Ka pit tel 1 Inn led ning... 11 Barn og sam funn... 11 Bo kas opp byg ning... 13 Ka pit tel 2 So sia li se rings pro ses sen... 15 For hol det mel lom sam funn, kul tur og so sia li se ring...
Levanger kommune, Foreløpig registrering, pr. 9. des. 2005
 240.001 Levanger og Frosta, PPT Klienter A F ca. 1964 ca. 1984 404.6.6 362 240.002 Levanger og Frosta, PPT Klienter G K ca. 1965 ca. 1985 404.6.6 363 240.003 Levanger og Frosta, PPT Klienter L R ca. 1966
240.001 Levanger og Frosta, PPT Klienter A F ca. 1964 ca. 1984 404.6.6 362 240.002 Levanger og Frosta, PPT Klienter G K ca. 1965 ca. 1985 404.6.6 363 240.003 Levanger og Frosta, PPT Klienter L R ca. 1966
[Skriv inn tekst]
![[Skriv inn tekst] [Skriv inn tekst]](/thumbs/96/128773473.jpg) [Skriv inn tekst] 22.08.2017 1 [Skriv inn tekst] 22.08.2017 2 Korrigert dato: 4 etasjer 8 1 33 1 34 520 etasjer 1 35 6 3 etasjer 1 32 Sandlekeplass 132 133 134 135 F RI O M RÅD E/F 132L OM VEI 133 KLATRETRÆR
[Skriv inn tekst] 22.08.2017 1 [Skriv inn tekst] 22.08.2017 2 Korrigert dato: 4 etasjer 8 1 33 1 34 520 etasjer 1 35 6 3 etasjer 1 32 Sandlekeplass 132 133 134 135 F RI O M RÅD E/F 132L OM VEI 133 KLATRETRÆR
Et lite notat om og rundt normalfordelingen.
 Et lite notat om og rundt normalfordelingen. Anta at vi har kontinuerlige data. Hva er likt og ulikt for histogrammer og fordelingskurver? Observasjoner Histogram Viser fordelingen av faktiske observerte
Et lite notat om og rundt normalfordelingen. Anta at vi har kontinuerlige data. Hva er likt og ulikt for histogrammer og fordelingskurver? Observasjoner Histogram Viser fordelingen av faktiske observerte
Innledning...16 Kapitlene Ano ny mi tet... 18
 Innhold Innledning...16 Kapitlene... 17 Ano ny mi tet... 18 Del I Innledning til mentoring KapIttel 1 Introduksjon til mentoring...20 Bak grunn...20 Be gre pe ne...22 Sponsorship og ut vik len de mentoring...23
Innhold Innledning...16 Kapitlene... 17 Ano ny mi tet... 18 Del I Innledning til mentoring KapIttel 1 Introduksjon til mentoring...20 Bak grunn...20 Be gre pe ne...22 Sponsorship og ut vik len de mentoring...23
STK1000 Uke 36, Studentene forventes å lese Ch 1.4 ( ) i læreboka (MMC). Tetthetskurver. Eksempel: Drivstofforbruk hos 32 biler
 STK1000 Uke 36, 2016. Studentene forventes å lese Ch 1.4 (+ 3.1-3.3 + 3.5) i læreboka (MMC). Tetthetskurver Eksempel: Drivstofforbruk hos 32 biler Fra histogram til tetthetskurver Anta at vi har kontinuerlige
STK1000 Uke 36, 2016. Studentene forventes å lese Ch 1.4 (+ 3.1-3.3 + 3.5) i læreboka (MMC). Tetthetskurver Eksempel: Drivstofforbruk hos 32 biler Fra histogram til tetthetskurver Anta at vi har kontinuerlige
Tegnforklaring. Bybanen fra sentrum til Fyllingsdalen. Mindemyren - Fyllingsdalen Teknisk forprosjekt - Veg Plan Kristianborg Rev.
 Gø t tu G a F ub akk tø Gø Ka a tø F u G a Lø b a u Ø F F j ø a Co Mo a k b a k E Lø b u u F F Ø F u a F u DE DE LSTR L S TR EK E K IG 2 I G3 Ø F u Lø b a M é é A Tfoka Stj po Bata a Bata tu Hopa Tumu
Gø t tu G a F ub akk tø Gø Ka a tø F u G a Lø b a u Ø F F j ø a Co Mo a k b a k E Lø b u u F F Ø F u a F u DE DE LSTR L S TR EK E K IG 2 I G3 Ø F u Lø b a M é é A Tfoka Stj po Bata a Bata tu Hopa Tumu
Et lite notat om og rundt normalfordelingen.
 Et lite notat om og rundt normalfordelingen. Anta at vi har kontinuerlige data. Hva er likt og ulikt for histogrammer og fordelingskurver? Observasjoner Histogram Viser fordelingen av faktiske observerte
Et lite notat om og rundt normalfordelingen. Anta at vi har kontinuerlige data. Hva er likt og ulikt for histogrammer og fordelingskurver? Observasjoner Histogram Viser fordelingen av faktiske observerte
Et lite notat om og rundt normalfordelingen. Anta at vi har kontinuerlige data. Hva er likt og ulikt for histogrammer og fordelingskurver?
 Et lite notat om og rundt normalfordelingen. Anta at vi har kontinuerlige data. Hva er likt og ulikt for histogrammer og fordelingskurver? Boka (Ch 1.4) motiverer dette ved å gå fra histogrammer til tetthetskurver.
Et lite notat om og rundt normalfordelingen. Anta at vi har kontinuerlige data. Hva er likt og ulikt for histogrammer og fordelingskurver? Boka (Ch 1.4) motiverer dette ved å gå fra histogrammer til tetthetskurver.
løsningsforslag - styrkeberegning grunnlag
 OPPGAVE Et tnnegget rør med tre diameter d = 00mm og eggtkkele t = 6mm er påkjent a en entrik irkende trekkraft F a = 00kN og et torjon(ride-)moment T = 50kNm. Betem, ed eregning og ed ruk a Mohr penningirkel:
OPPGAVE Et tnnegget rør med tre diameter d = 00mm og eggtkkele t = 6mm er påkjent a en entrik irkende trekkraft F a = 00kN og et torjon(ride-)moment T = 50kNm. Betem, ed eregning og ed ruk a Mohr penningirkel:
ESD SAMMENLEGGBARE KASSER ESD FBD 43/22
 ESD SAMMENLEGGBARE KASSER ESD FBD 43/22 ESD SAMMENLEGGBARE KASSER ESD FBD 43/22 Artikkelnr.: ESD FBD 43/22 : Høyde 40 x 30 x 22 cm 36,5 x 26,5 x 20 cm 21,5 cm 7,7 cm 7,2 cm 19 l 2,69 kg ESD SAMMENLEGGBARE
ESD SAMMENLEGGBARE KASSER ESD FBD 43/22 ESD SAMMENLEGGBARE KASSER ESD FBD 43/22 Artikkelnr.: ESD FBD 43/22 : Høyde 40 x 30 x 22 cm 36,5 x 26,5 x 20 cm 21,5 cm 7,7 cm 7,2 cm 19 l 2,69 kg ESD SAMMENLEGGBARE
Oppmerksomhet... 26 Emosjon og emosjonsregulering... 28 Relasjonen mellom emosjonsregulering og oppmerksomhet 36
 Innhold Kapittel 1 Innledning.............................................................. 15 Karl Ja cob sen og Bir git Svend sen Kapittel 2 Kunnskap om oppmerksomhet og emosjonsregulering 25 Karl Jacobsen
Innhold Kapittel 1 Innledning.............................................................. 15 Karl Ja cob sen og Bir git Svend sen Kapittel 2 Kunnskap om oppmerksomhet og emosjonsregulering 25 Karl Jacobsen
ÅMA110 Sannsylighetsregning og statistikk Løsningsforslag til eksamen høst 2010, s. 1. Oppgave 1. Histogram over frekvenser.
 ÅMA1 Sannsylighetsregning og statistikk Løsningsforslag til eksamen høst 0, s. 1 (Det tas forbehold om feil i løsningsforslaget.) a) Gjennomsnitt: x = 1 Emp. standardavvik: Median: 1 (1.33 + 1.) = 1.35
ÅMA1 Sannsylighetsregning og statistikk Løsningsforslag til eksamen høst 0, s. 1 (Det tas forbehold om feil i løsningsforslaget.) a) Gjennomsnitt: x = 1 Emp. standardavvik: Median: 1 (1.33 + 1.) = 1.35
2. Å R S B E R E T N I N G O G R E G N S K A P F O R A ) Å r s b e r e t n i n g o g r e g n s k a p f o r
 I N N K A L L I N G T I L O R D I N Æ R G E N E R A L F O R S A M L I N G 2 0 1 0 O r d i n æ r g e n e r a l f o r s a m l i n g i, a v h o l d e s m a n d a g 3. m ai 2 0 1 0, k l. 1 8 0 0 p å T r e
I N N K A L L I N G T I L O R D I N Æ R G E N E R A L F O R S A M L I N G 2 0 1 0 O r d i n æ r g e n e r a l f o r s a m l i n g i, a v h o l d e s m a n d a g 3. m ai 2 0 1 0, k l. 1 8 0 0 p å T r e
Medisinsk statistikk Del I høsten 2009:
 Medisinsk statistikk Del I høsten 2009: Kontinuerlige sannsynlighetsfordelinger Pål Romundstad Beregning av sannsynlighet i en binomisk forsøksrekke generelt Sannsynligheten for at suksess intreffer X
Medisinsk statistikk Del I høsten 2009: Kontinuerlige sannsynlighetsfordelinger Pål Romundstad Beregning av sannsynlighet i en binomisk forsøksrekke generelt Sannsynligheten for at suksess intreffer X
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Deleksamen i: STK1000 Innføring i avvendt statistikk Eksamensdag: Onsdag 7. oktober 2015 Tid for eksamen: 11.00 13.00 Oppgavesettet er på
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Deleksamen i: STK1000 Innføring i avvendt statistikk Eksamensdag: Onsdag 7. oktober 2015 Tid for eksamen: 11.00 13.00 Oppgavesettet er på
Il UNIVERSITETET I AGDER
 Il UNIVERSITETET I AGDER FAKULTETFOR TEKNOLOGIOG REALFAG EKSAMEN Emnekode: Emnenavn: MA913 Tall og algebra Dato: 7. desember 2011 Varighet: 09.00 15.00 Antall sider inkl. forside 7 Tillatte hjelpemidler:
Il UNIVERSITETET I AGDER FAKULTETFOR TEKNOLOGIOG REALFAG EKSAMEN Emnekode: Emnenavn: MA913 Tall og algebra Dato: 7. desember 2011 Varighet: 09.00 15.00 Antall sider inkl. forside 7 Tillatte hjelpemidler:
TFY4106 Fysikk Eksamen 17. august V=V = 3 r=r ) V = 3V r=r ' 0:15 cm 3. = m=v 5 = 7:86 g=cm 3
 TFY4106 Fysikk Eksamen 17. august 2018 Lsningsforslag 1) C: V = 4r 3 =3 = 5:575 cm 3 For a ansla usikkerheten i V kan vi regne ut V med radius hhv 11.1 og 10.9 mm. Dette gir hhv 5.729 og 5.425 cm 3, sa
TFY4106 Fysikk Eksamen 17. august 2018 Lsningsforslag 1) C: V = 4r 3 =3 = 5:575 cm 3 For a ansla usikkerheten i V kan vi regne ut V med radius hhv 11.1 og 10.9 mm. Dette gir hhv 5.729 og 5.425 cm 3, sa
w VTenor 2 ú ú ú ø ø ú ú
 Ter 1 E ggodt hu E ggodt hu VTer 1 2H 2 V H mel. ANCHORS AWEIGH H Komm Sange kom m mot to kom mot m to L san ge all L tid L san ge all tid mel. 2H E ggodt hu kom m mot to san ge all L tid Ter 1 2H kom
Ter 1 E ggodt hu E ggodt hu VTer 1 2H 2 V H mel. ANCHORS AWEIGH H Komm Sange kom m mot to kom mot m to L san ge all L tid L san ge all tid mel. 2H E ggodt hu kom m mot to san ge all L tid Ter 1 2H kom
Matematikk GS3 Temaer våren 2013 DEL 1: GEOMETRI. 1. Måleenheter. 1.1 Lengdeenheter. 1.2 Arealenheter. Eksempel 1: Gjør om 5 m til dm, cm og mm
 Matematikk GS3 Temaer våren 2013 DEL 1: GEOMETRI 1. Måleenheter 1.1 Lengdeenheter Eksempel 1: Gjør om 5 m til dm, cm og mm m dm 5 m = 5 10 dm = 50 dm m cm 5 m = 5 10 10 cm = 5 10 2 cm = 500 cm m mm 5 m
Matematikk GS3 Temaer våren 2013 DEL 1: GEOMETRI 1. Måleenheter 1.1 Lengdeenheter Eksempel 1: Gjør om 5 m til dm, cm og mm m dm 5 m = 5 10 dm = 50 dm m cm 5 m = 5 10 10 cm = 5 10 2 cm = 500 cm m mm 5 m
Invitasjon til elektro racing FE2 2015
 Invitasjon til elektro racing FE2 2015 Vi i Sørlandets modellbåtklubb har gleden av å invitere til race innen M seksjonen, elektro racing. Det vil bli lagt opp til løp i OTE1, OTE2, Mono 1 og Mono 2. Meld
Invitasjon til elektro racing FE2 2015 Vi i Sørlandets modellbåtklubb har gleden av å invitere til race innen M seksjonen, elektro racing. Det vil bli lagt opp til løp i OTE1, OTE2, Mono 1 og Mono 2. Meld
Innledning Veiledningsbegrepet og veiledningstradisjonene... 11
 INNHOLD Innledning Veiledningsbegrepet og veiledningstradisjonene... 11 Hva er veiledning?... 12 Veiledning er kontekstfølsom... 13 Teorikunnskap og personlig kunnskap...14 Hand lings- og refleksjonsmodellen
INNHOLD Innledning Veiledningsbegrepet og veiledningstradisjonene... 11 Hva er veiledning?... 12 Veiledning er kontekstfølsom... 13 Teorikunnskap og personlig kunnskap...14 Hand lings- og refleksjonsmodellen
2P, Statistikk Quiz. Test, 2 Statistikk
 Test, 2 Statistikk Innhold 1.1 Statistisk undersøkelse... 2 2.2 Presentasjon av tallmateriale... 2 2.3 Sentralmål... 8 2.4 Spredningsmål... 11 2.5 Gruppert datamateriale... 14 Grete Larsen 1 1.1 Statistisk
Test, 2 Statistikk Innhold 1.1 Statistisk undersøkelse... 2 2.2 Presentasjon av tallmateriale... 2 2.3 Sentralmål... 8 2.4 Spredningsmål... 11 2.5 Gruppert datamateriale... 14 Grete Larsen 1 1.1 Statistisk
Telefon 222 80 896 Fax 222 89 196. Operasasjonssakser. Kvalitet basert på erfaring. mail: firmapost@svas.no www.svas.no
 Operasasjonssakser 5 Kvalitet basert på erfaring Standardkutt: side 5-22 Superkutt: side 23-28 Bruk av utdannede spesialister, med erfaring fra fl ere tiår i bransjen, opplært til å behandle moderne maskineri
Operasasjonssakser 5 Kvalitet basert på erfaring Standardkutt: side 5-22 Superkutt: side 23-28 Bruk av utdannede spesialister, med erfaring fra fl ere tiår i bransjen, opplært til å behandle moderne maskineri
INNKALLING TIL ORDINÆRT SAMEIERMØTE 2010
 INNKALLING TIL ORDINÆRT SAMEIERMØTE 2010 O r d i n æ r t s am e i e rm øt e i S am B o B o l i g s am e i e, a v h o l d es o ns d a g 2 8. 04. 2 0 1 0, k l. 1 8. 3 0 i G r ef s e n m e n i g h e t s s
INNKALLING TIL ORDINÆRT SAMEIERMØTE 2010 O r d i n æ r t s am e i e rm øt e i S am B o B o l i g s am e i e, a v h o l d es o ns d a g 2 8. 04. 2 0 1 0, k l. 1 8. 3 0 i G r ef s e n m e n i g h e t s s
Oppgaver til Studentveiledning I MET 3431 Statistikk
 Oppgaver til Studentveiledning I MET 3431 Statistikk 20. mars 2012 kl 17.15-20.15 i B2 Handelshøyskolen BI 2 Oppgaver 1. Konfidensintervaller Vi ser på inntekten til en tilfeldig valgt person (i tusen
Oppgaver til Studentveiledning I MET 3431 Statistikk 20. mars 2012 kl 17.15-20.15 i B2 Handelshøyskolen BI 2 Oppgaver 1. Konfidensintervaller Vi ser på inntekten til en tilfeldig valgt person (i tusen
2P kapittel 3 Statistikk Løsninger til innlæringsoppgavene
 P kapittel 3 Statistikk Løsninger til innlæringsoppgavene 3. Frekvensen av hybelboere er 15 % av 10 elever, altså 10 0,15 = 18 elever. 3.3 Sier vi at det er N elever i Arams klasse, har vi fra opplysningene
P kapittel 3 Statistikk Løsninger til innlæringsoppgavene 3. Frekvensen av hybelboere er 15 % av 10 elever, altså 10 0,15 = 18 elever. 3.3 Sier vi at det er N elever i Arams klasse, har vi fra opplysningene
Eksamen MAT1005 Matematikk 2P-Y Va ren 2015
 Eksamen MAT1005 Matematikk 2P-Y Va ren 2015 Oppgave 1 (2 poeng) Dag Temperatur Mandag 4 C Tirsdag 10 C Onsdag 12 C Torsdag 5 C Fredag 6 C Lørdag Tabellen ovenfor viser hvordan temperaturen har variert
Eksamen MAT1005 Matematikk 2P-Y Va ren 2015 Oppgave 1 (2 poeng) Dag Temperatur Mandag 4 C Tirsdag 10 C Onsdag 12 C Torsdag 5 C Fredag 6 C Lørdag Tabellen ovenfor viser hvordan temperaturen har variert
Elvepark Nesttun Inspirasjonsbilder
 Inspirasjonsbilder.1.11 Inspirasjonsbilder.1.11 + 6,6 +,6 +,6 +,6 / / /1 +, +, +, 1 sti ek 6 /6 /1 x=66 Inn/utkjøring p-anlegg +16. -kjeller næring/ varelevering +16. esttunelva +16. +. +1. +1. +, +1,
Inspirasjonsbilder.1.11 Inspirasjonsbilder.1.11 + 6,6 +,6 +,6 +,6 / / /1 +, +, +, 1 sti ek 6 /6 /1 x=66 Inn/utkjøring p-anlegg +16. -kjeller næring/ varelevering +16. esttunelva +16. +. +1. +1. +, +1,
VEDLEGG 5. 1 Støy og skyggekast. 1.1 Resultater støy
 VEDLEGG 5 Ifølge regelverket skal støynivået ved helårsboliger og fritidsboliger ikke overstige den anbefalte grenseverdien på Lden 45 db. Dersom det vurderes som nødvendig for vindkraftverkets realiserbarhet
VEDLEGG 5 Ifølge regelverket skal støynivået ved helårsboliger og fritidsboliger ikke overstige den anbefalte grenseverdien på Lden 45 db. Dersom det vurderes som nødvendig for vindkraftverkets realiserbarhet
Innhold. Del I Selbukollektivets historie sett fra leders perspektiv Fakta Men nes ket bak ru sen ser vi hen ne og ham?...
 Innhold Fakta...15 Men nes ket bak ru sen ser vi hen ne og ham?...17 Inger Granby Unge rusmiddelavhengige bærere av en sammensatt problematikk...17 Rus re for men av 2004 et skritt fram el ler to til ba
Innhold Fakta...15 Men nes ket bak ru sen ser vi hen ne og ham?...17 Inger Granby Unge rusmiddelavhengige bærere av en sammensatt problematikk...17 Rus re for men av 2004 et skritt fram el ler to til ba
Last ned Minner fra Solferino - Henry Dunant. Last ned. Last ned e-bok ny norsk Minner fra Solferino Gratis boken Pdf, ibook, Kindle, Txt, Doc, Mobi
 Last ned Minner fra Solferino - Henry Dunant Last ned Forfatter: Henry Dunant ISBN: 9788292622995 Format: PDF Filstørrelse: 28.26 Mb «Minner fra Solferino» er Henry Dunants skildring av slaget ved Solferino
Last ned Minner fra Solferino - Henry Dunant Last ned Forfatter: Henry Dunant ISBN: 9788292622995 Format: PDF Filstørrelse: 28.26 Mb «Minner fra Solferino» er Henry Dunants skildring av slaget ved Solferino
R2 kapittel 8 Eksamenstrening Løsninger til oppgavene i læreboka
 R kapittel 8 Eksamenstrening Løsninger til oppgavene i læreboka E Bruker formelen cos 36 cos( 8 ) E sin 8 v og sin8 5 cos v sin sin8 5 5 6 5 5 8 5 5 8 6 5 8 6 5 8 8 3 5 5 5 a f ( ) sin 5 cos f ( ) 5cos
R kapittel 8 Eksamenstrening Løsninger til oppgavene i læreboka E Bruker formelen cos 36 cos( 8 ) E sin 8 v og sin8 5 cos v sin sin8 5 5 6 5 5 8 5 5 8 6 5 8 6 5 8 8 3 5 5 5 a f ( ) sin 5 cos f ( ) 5cos
Inn led ning...13 Bo kens inn hold og opp byg ning...16. For plik tel ses ba sert ver sus kon troll ori en tert HR... 23 Hva er så ef fek tiv HR?...
 Innhold Ka pit tel 1 Inn led ning...13 Bo kens inn hold og opp byg ning...16 Del 1 HR som kil de til lønn som het... 21 Ka pit tel 2 For plik tel ses ba sert ver sus kon troll ori en tert HR... 23 Hva
Innhold Ka pit tel 1 Inn led ning...13 Bo kens inn hold og opp byg ning...16 Del 1 HR som kil de til lønn som het... 21 Ka pit tel 2 For plik tel ses ba sert ver sus kon troll ori en tert HR... 23 Hva
2P eksamen høsten 2017
 2P eksamen høsten 2017 Tid: 2 timer Hjelpemidler: Vanlige skrivesaker, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (5 poeng) Tabellen nedenfor viser karakterfordelingen ved en skole ved
2P eksamen høsten 2017 Tid: 2 timer Hjelpemidler: Vanlige skrivesaker, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (5 poeng) Tabellen nedenfor viser karakterfordelingen ved en skole ved
Eksamen MAT1013 Matematikk 1T Va ren 2014
 Eksamen MAT1013 Matematikk 1T Va ren 2014 Oppgave 1 (1 poeng) Regn ut og skriv svaret på standardform 2,510 3,010 15 5 Oppgave 2 (2 poeng) Regn ut og skriv svaret så enkelt som mulig 1 2 0 1 3 2 9 6 4
Eksamen MAT1013 Matematikk 1T Va ren 2014 Oppgave 1 (1 poeng) Regn ut og skriv svaret på standardform 2,510 3,010 15 5 Oppgave 2 (2 poeng) Regn ut og skriv svaret så enkelt som mulig 1 2 0 1 3 2 9 6 4
Fotballturnering. Program. Østre Toten kunstgrasbane, Lena lørdag 29. september fra kl. 10.00
 Fotballturnering Østre Toten kunstgrasbane, Lena lørdag 29. september fra kl. 10.00 Program Kl. 10.00-12.30: Kamper Jenter 08, Jenter 09, Jenter 10, Jenter 11 Gutter 07, Gutter 08, Gutter 09, Kl. 12.30-13.00:
Fotballturnering Østre Toten kunstgrasbane, Lena lørdag 29. september fra kl. 10.00 Program Kl. 10.00-12.30: Kamper Jenter 08, Jenter 09, Jenter 10, Jenter 11 Gutter 07, Gutter 08, Gutter 09, Kl. 12.30-13.00:
Trymskvida. a d 2 l l l l. k t. k t. k k t t. k t. k t. k t. k t. k t. k t. k t. k t. tik t. k s k s k s k s k s k s k s k s. k s k s k s k s.
 Trmsvida Per Van G =80 d a 24 a d 2 4 b d 2 4 Sin va'n Tor hain ha b d 2 4 s s s s s Sin va'n Tor hain ha mes-a Sin va'n Tor hain ha mes-a s s s s s s s s mes-a Sin va'n Tor hain ha mes-a s s s s s 5 a
Trmsvida Per Van G =80 d a 24 a d 2 4 b d 2 4 Sin va'n Tor hain ha b d 2 4 s s s s s Sin va'n Tor hain ha mes-a Sin va'n Tor hain ha mes-a s s s s s s s s mes-a Sin va'n Tor hain ha mes-a s s s s s 5 a
INNKALLING TIL ORDINÆRT SAMEIERMØTE 2010
 INNKALLING TIL ORDINÆRT SAMEIERMØTE 2010 O r d i n æ r t s am e i e rm øt e i J o h a n n es B r u n s g at e 1 2 C S am e i e, a v h o l d e s T i r s d a g 2 3. m a r s 2 0 1 0, k l. 1 9 : 0 0 i l ok
INNKALLING TIL ORDINÆRT SAMEIERMØTE 2010 O r d i n æ r t s am e i e rm øt e i J o h a n n es B r u n s g at e 1 2 C S am e i e, a v h o l d e s T i r s d a g 2 3. m a r s 2 0 1 0, k l. 1 9 : 0 0 i l ok
PRISSTRATEGIER HOS NORSKE BEDRIFTER
 32 PRISSTRATEGIER HOS NORSKE BEDRIFTER RAGN HILD SIL KO SET før s te ama nu en sis dr.oecon, In sti tutt for mar keds fø ring, Han dels høy sko len BI PRIS OG BESLUTNINGER I BEDRIFTER Pris har til dels
32 PRISSTRATEGIER HOS NORSKE BEDRIFTER RAGN HILD SIL KO SET før s te ama nu en sis dr.oecon, In sti tutt for mar keds fø ring, Han dels høy sko len BI PRIS OG BESLUTNINGER I BEDRIFTER Pris har til dels
(Det tas forbehold om feil i løsningsforslaget.) Oppgave 1
 ÅMA1 Sannsylighetsregning og statistikk Løsningsforslag til eksamen vår 2011, s. 1 (Det tas forbehold om feil i løsningsforslaget.) Oppgave 1 a) Data: x 1, x 2, x 3, x 4, x 5 Gjennomsnitt: x = 1 5 (x 1
ÅMA1 Sannsylighetsregning og statistikk Løsningsforslag til eksamen vår 2011, s. 1 (Det tas forbehold om feil i løsningsforslaget.) Oppgave 1 a) Data: x 1, x 2, x 3, x 4, x 5 Gjennomsnitt: x = 1 5 (x 1
ILLUSTRASJON TIL REGULERING. Situasjonsplan 67,21 1,97 PARKERING/GRØNT NIVÅ MED OLE TJØTTAS VEI MEIERIGATA 22 Dato:
 12 13 14 15 16 17 18 19 20 21 22 x 164 = 3,600 m 11 9 8 7 6 5 4 3 2 1 A 67,21 +53,50 2,21 1,97 B 52,30 PARKERING TAKTERRASSE EKSISTERENDE NÆRING +50,70 PARKERING/GRØNT NIVÅ MED OLE TJØTTAS VEI +41,55 +53,20
12 13 14 15 16 17 18 19 20 21 22 x 164 = 3,600 m 11 9 8 7 6 5 4 3 2 1 A 67,21 +53,50 2,21 1,97 B 52,30 PARKERING TAKTERRASSE EKSISTERENDE NÆRING +50,70 PARKERING/GRØNT NIVÅ MED OLE TJØTTAS VEI +41,55 +53,20
Snøtetthet. Institutt for matematiske fag, NTNU 15. august Notat for TMA4240/TMA4245 Statistikk
 Snøtetthet Notat for TMA424/TMA4245 Statistikk Institutt for matematiske fag, NTNU 5. august 22 I forbindelse med varsling av om, klimaforskning og særlig kraftproduksjon er det viktig å kunne anslå hvor
Snøtetthet Notat for TMA424/TMA4245 Statistikk Institutt for matematiske fag, NTNU 5. august 22 I forbindelse med varsling av om, klimaforskning og særlig kraftproduksjon er det viktig å kunne anslå hvor
Sprang Competition 1, 1,10m (Individuell) Bedømming: Antall: Påmeldte = 35, Startende = 35 Info:
 Sprang Competition 1, 1,10m (Individuell) Antall: Påmeldte = 35, Startende = 35 Sprang Competition 2, 1,20m (Individuell) Antall: Påmeldte = 47, Startende = 47 Sprang Competition 3, 1,30m (Individuell)
Sprang Competition 1, 1,10m (Individuell) Antall: Påmeldte = 35, Startende = 35 Sprang Competition 2, 1,20m (Individuell) Antall: Påmeldte = 47, Startende = 47 Sprang Competition 3, 1,30m (Individuell)
En kamp på liv og død
 1 En kamp på liv og død Frank og Joe Har dy sto an sikt til an sikt på en øde klip pe. Ne den for slo bøl ge ne hardt inn mot land. Beg ge gut te ne holdt et syl skarpt sverd i hen de ne. De stir ret på
1 En kamp på liv og død Frank og Joe Har dy sto an sikt til an sikt på en øde klip pe. Ne den for slo bøl ge ne hardt inn mot land. Beg ge gut te ne holdt et syl skarpt sverd i hen de ne. De stir ret på
STUDIEÅRET 2011/2012. Utsatt individuell skriftlig eksamen. STA 200- Statistikk. Mandag 27. august 2012 kl. 10.00-12.00
 STUDIEÅRET 2011/2012 Utsatt individuell skriftlig eksamen STA 200- Statistikk i Mandag 27. august 2012 kl. 10.00-12.00 Hjelpemidler: kalkulator. Formelsamling blir delt ut på eksamen Eksamensoppgaven består
STUDIEÅRET 2011/2012 Utsatt individuell skriftlig eksamen STA 200- Statistikk i Mandag 27. august 2012 kl. 10.00-12.00 Hjelpemidler: kalkulator. Formelsamling blir delt ut på eksamen Eksamensoppgaven består
Fordelinger, mer om sentralmål og variasjonsmål. Tron Anders Moger
 Fordelinger, mer om sentralmål og variasjonsmål Tron Anders Moger 20. april 2005 1 Forrige gang: Så på et eksempel med data over medisinerstudenter Lærte hvordan man skulle få oversikt over dataene ved
Fordelinger, mer om sentralmål og variasjonsmål Tron Anders Moger 20. april 2005 1 Forrige gang: Så på et eksempel med data over medisinerstudenter Lærte hvordan man skulle få oversikt over dataene ved
42 elever sykler til skolen hver dag, mens 30 tar bussen. 26 går og 10 blir kjørt med bil. Da kan vi lage et diagram som gir en oversikt.
 elever sykler til skolen hver dag, mens 0 tar bussen. går og 10 blir kjørt med bil. Da kan vi lage et diagram som gir en oversikt. 7 Hm, er det så mange satellitter over år?! Statistikk MÅL I dette kapitlet
elever sykler til skolen hver dag, mens 0 tar bussen. går og 10 blir kjørt med bil. Da kan vi lage et diagram som gir en oversikt. 7 Hm, er det så mange satellitter over år?! Statistikk MÅL I dette kapitlet
ØVINGER 2017 Løsninger til oppgaver. Lineærkombinasjonen Z = 5X + 8Y har forventningsverdi
 ØVINGER 27 Løsninger til oppgaver Øving 6 4. (7). Fra oppgave 4.5 (øving 4) har vi forventningsverdien variansen til X, E[X] =.92, V ar[x] =.3. Lineærkombinasjonen Z = 5X + 8Y har forventningsverdi E[Z]
ØVINGER 27 Løsninger til oppgaver Øving 6 4. (7). Fra oppgave 4.5 (øving 4) har vi forventningsverdien variansen til X, E[X] =.92, V ar[x] =.3. Lineærkombinasjonen Z = 5X + 8Y har forventningsverdi E[Z]
(12) Oversettelse av europeisk patentskrift
 (12) Oversettelse av europeisk patentskrift (11) NO/EP 2114970 B1 (19) NO NORGE (51) Int Cl. C07F 9/58 (2006.01) A61K 31/44 (2006.01) A61P 1/00 (2006.01) A61P 11/06 (2006.01) A61P 19/02 (2006.01) A61P
(12) Oversettelse av europeisk patentskrift (11) NO/EP 2114970 B1 (19) NO NORGE (51) Int Cl. C07F 9/58 (2006.01) A61K 31/44 (2006.01) A61P 1/00 (2006.01) A61P 11/06 (2006.01) A61P 19/02 (2006.01) A61P
Faktor terminprøve i matematikk for 8. trinn
 Faktor terminprøve i matematikk for 8. trinn Våren 2009 nynorsk Namn: Gruppe: Informasjon Oppgåvesettet består av to delar der du skal svare på alle oppgåvene. Del 1 og del 2 blir delte ut samtidig, men
Faktor terminprøve i matematikk for 8. trinn Våren 2009 nynorsk Namn: Gruppe: Informasjon Oppgåvesettet består av to delar der du skal svare på alle oppgåvene. Del 1 og del 2 blir delte ut samtidig, men
ECON240 Høst 2017 Oppgaveseminar 1 (uke 35)
 ECON40 Høst 017 Oppgaveseminar 1 (uke 35) Oppgaver til prerequisites og kapittel 1 fra læreboken Example P.1, P.5, P.6, P.7, P.8, P.9, P.11, P.1, P.13, og P.14 Example 1.1, 1., 1.3, 1.4, 1.6, 1.7, 1.9,
ECON40 Høst 017 Oppgaveseminar 1 (uke 35) Oppgaver til prerequisites og kapittel 1 fra læreboken Example P.1, P.5, P.6, P.7, P.8, P.9, P.11, P.1, P.13, og P.14 Example 1.1, 1., 1.3, 1.4, 1.6, 1.7, 1.9,
Informasjon om våre produktstørrelser
 Informasjon om våre produktstørrelser Russeprofilering.no 1 INNHOLDSFORTEGNELSE 03 Standard hoodie unisex 04 Standard zip hoodie unisex 05 Standard zip hoodie dame 06 Standard college genser 07 Original
Informasjon om våre produktstørrelser Russeprofilering.no 1 INNHOLDSFORTEGNELSE 03 Standard hoodie unisex 04 Standard zip hoodie unisex 05 Standard zip hoodie dame 06 Standard college genser 07 Original
STK juni 2018
 Løsningsforslag til eksamen i STK. juni 8 Oppgave Tvillingpar kan være enten eneggede eller toeggede. Sannsynligheten for at det ved en tvillingfødsel blir født eneggede tvillinger er i Nord-Europa omtrent
Løsningsforslag til eksamen i STK. juni 8 Oppgave Tvillingpar kan være enten eneggede eller toeggede. Sannsynligheten for at det ved en tvillingfødsel blir født eneggede tvillinger er i Nord-Europa omtrent
Oblig 1 i MAT2400. Oppgave 1. Tor Hedin Brønner. a) Vi tar integralet av f X (x) fra til x: = 1. Medianen, µ, finner vi ved å sette.
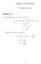 Oblig 1 i MAT24 Tor Hedin Brønner Oppgave 1. a) Vi tar integralet av f X (x) fra til x: x f X (x) dy = Medianen, µ, finner vi ved å sette.5 = µ dy + x = [ θ y θ] x = θ x θ + θ θ ( θ = 1 x) µ θ = θ.5 µ
Oblig 1 i MAT24 Tor Hedin Brønner Oppgave 1. a) Vi tar integralet av f X (x) fra til x: x f X (x) dy = Medianen, µ, finner vi ved å sette.5 = µ dy + x = [ θ y θ] x = θ x θ + θ θ ( θ = 1 x) µ θ = θ.5 µ
Sannsynlighetsregning og Statistikk.
 Sannsynlighetsregning og Statistikk. Leksjon Velkommen til dette kurset i sannsynlighetsregning og statistikk! Vi vil som lærebok benytte Gunnar G. Løvås:Statistikk for universiteter og høyskoler. I den
Sannsynlighetsregning og Statistikk. Leksjon Velkommen til dette kurset i sannsynlighetsregning og statistikk! Vi vil som lærebok benytte Gunnar G. Løvås:Statistikk for universiteter og høyskoler. I den
Sentralmål og spredningsmål
 Sentralmål og spredningsmål 3.1 Læreplanmål 1 3.1 Gjennomsnitt og typetall 2 3.2 Median 6 3.3 Variasjonsbredde og kvartilbredde 10 3.4 Varians og standardavvik 15 3.5 Digitale sentralmål og spredningsmål
Sentralmål og spredningsmål 3.1 Læreplanmål 1 3.1 Gjennomsnitt og typetall 2 3.2 Median 6 3.3 Variasjonsbredde og kvartilbredde 10 3.4 Varians og standardavvik 15 3.5 Digitale sentralmål og spredningsmål
Kapittel 9: Estimering
 Kapittel 9: Estimeing TMA445 Statistikk 9.8,9.9: Estimeing, to utvalg. 9.6: Pediksjonsintevall Tuid.Follestad@math.ntnu.no p.1/13 Repetisjon: Punkt-og intevall-estimeing, eitt utvalg La X 1, X,..., X n
Kapittel 9: Estimeing TMA445 Statistikk 9.8,9.9: Estimeing, to utvalg. 9.6: Pediksjonsintevall Tuid.Follestad@math.ntnu.no p.1/13 Repetisjon: Punkt-og intevall-estimeing, eitt utvalg La X 1, X,..., X n
ECON240 Vår 2018 Oppgaveseminar 1 (uke 6)
 ECON240 Vår 2018 Oppgaveseminar 1 (uke 6) Oppgaver til prerequisites og kapittel 1 fra læreboken Example P.1, P.5, P.6, P.7, P.8, P.9, P.11, P.12, P.13, og P.14 Example 1.1, 1.2, 1.3, 1.4, 1.6, 1.7, 1.9,
ECON240 Vår 2018 Oppgaveseminar 1 (uke 6) Oppgaver til prerequisites og kapittel 1 fra læreboken Example P.1, P.5, P.6, P.7, P.8, P.9, P.11, P.12, P.13, og P.14 Example 1.1, 1.2, 1.3, 1.4, 1.6, 1.7, 1.9,
Eksamen MAT1015 Matematikk 2P Våren 2013
 Eksamen MAT1015 Matematikk 2P Våren 2013 DEL 1 Uten hjelpemidler Oppgave 1 (5 poeng) En kveld kjørte en taxisjåfør 10 turer. Nedenfor ser du hvor mange passasjerer han hadde med på hver av turene. 1 5
Eksamen MAT1015 Matematikk 2P Våren 2013 DEL 1 Uten hjelpemidler Oppgave 1 (5 poeng) En kveld kjørte en taxisjåfør 10 turer. Nedenfor ser du hvor mange passasjerer han hadde med på hver av turene. 1 5
Malins favoritter - symønster Modell: Pimenta tunika
 Malins favoritter - symønster Modell: Pimenta tunika Mansjett A Mansjett B Fram Bak Stoff: elastisk Stofforbruk variant A: ca 180 cm på stoffbredde 150 cm. Stofforbruk variant B: ca 200 cm på stoffbredde
Malins favoritter - symønster Modell: Pimenta tunika Mansjett A Mansjett B Fram Bak Stoff: elastisk Stofforbruk variant A: ca 180 cm på stoffbredde 150 cm. Stofforbruk variant B: ca 200 cm på stoffbredde
1 Forutsetninger og rammebetingelser for fleksible organisasjonsformer
 Innhold Del 1 Forutsetninger og betingelser............................. 15 1 Forutsetninger og rammebetingelser for fleksible organisasjonsformer Rune Assmann og Tore Hil le stad............................
Innhold Del 1 Forutsetninger og betingelser............................. 15 1 Forutsetninger og rammebetingelser for fleksible organisasjonsformer Rune Assmann og Tore Hil le stad............................
Eksamen MAT1005 matematikk 2P-Y va ren 2015
 Eksamen MAT1005 matematikk 2P-Y va ren 2015 Oppgåve 1 (2 poeng) Dag Temperatur Måndag 4 C Tysdag 10 C Onsdag 12 C Torsdag 5 C Fredag 6 C Laurdag Tabellen over viser korleis temperaturen har variert i løpet
Eksamen MAT1005 matematikk 2P-Y va ren 2015 Oppgåve 1 (2 poeng) Dag Temperatur Måndag 4 C Tysdag 10 C Onsdag 12 C Torsdag 5 C Fredag 6 C Laurdag Tabellen over viser korleis temperaturen har variert i løpet
Klimabidrag fra byggsektoren
 Kmaak ambø kmagm E Økad, SFT, 6.jaua 2009 Kmabdag fa byggko 09.01.2009 Sd 1 Sa fougy (SFT) Kmamdg ju 2007 b Kmafok jaua 2008 09.01.2009 Sd 2 Sa fougy (SFT) K m a f o k Må Ovoppfy fopk Kyoopooko md 10%
Kmaak ambø kmagm E Økad, SFT, 6.jaua 2009 Kmabdag fa byggko 09.01.2009 Sd 1 Sa fougy (SFT) Kmamdg ju 2007 b Kmafok jaua 2008 09.01.2009 Sd 2 Sa fougy (SFT) K m a f o k Må Ovoppfy fopk Kyoopooko md 10%
Innbqld. Cppdrags 3 U a. 0.14.Rapportnr. 186, GeofysiskUndersdkelse. 11, juli- 11,august195u.
 á GEOFYSISKMALMLETING TTONOI 1 M Cppdrags 3 U a 0.14.Rapportnr. 186, GeofysiskUndersdkelse YOR A B KAB 11, juli- 11,august195u. UtfOrend sgeofysikerg.f. Sakshaug Asslaterende:Flåten,Davis,Frischknecht.
á GEOFYSISKMALMLETING TTONOI 1 M Cppdrags 3 U a 0.14.Rapportnr. 186, GeofysiskUndersdkelse YOR A B KAB 11, juli- 11,august195u. UtfOrend sgeofysikerg.f. Sakshaug Asslaterende:Flåten,Davis,Frischknecht.
Strømmålinger fra Rensøy Dybde: 5m Posisjon: 66*30.395'N, 12*04.574'Ø Dato: 29. juli 30. august 2011 Måler nr: s16
 Strømmålinger fra Rensøy Dybde: m Posisjon: *.', *.'Ø Dato:. juli. august Måler nr: s Rensøy m aug Tabell : Statistisk oversikt over strømforhold, Rensøy, meters dyp. STATISTICAL SUMMARY File name: rensøy
Strømmålinger fra Rensøy Dybde: m Posisjon: *.', *.'Ø Dato:. juli. august Måler nr: s Rensøy m aug Tabell : Statistisk oversikt over strømforhold, Rensøy, meters dyp. STATISTICAL SUMMARY File name: rensøy
Som laget for sørlandet
 Som laget for sørlandet Hvorfor kjøpe Adriatic rib Adriatic 330 4 Adriatic 360 6 Adriatic 390 8 Adriatic 430 10 Adriatic 470 12 Adriatic 520 14 Adriatic 580 16 Adriatic 660 18 Adriatic rib blir laget av
Som laget for sørlandet Hvorfor kjøpe Adriatic rib Adriatic 330 4 Adriatic 360 6 Adriatic 390 8 Adriatic 430 10 Adriatic 470 12 Adriatic 520 14 Adriatic 580 16 Adriatic 660 18 Adriatic rib blir laget av
