Forkurs i matematikk. Kompendium av Amir Hashemi, UiB. Notater, eksempler og oppgaver med fasit/løsningsforslag 1
|
|
|
- Fredrik Isaksen
- 8 år siden
- Visninger:
Transkript
1 Forkurs i mtemtikk Kompendium v Amir Hshemi, UiB. Notter, eksempler og oppgver med fsit/løsningsforslg Mtemtisk Institutt UiB Innhold Sist oppdtert 07. juni 0 i
2 Forord... Kpittel 0 Test deg selv... Oppgver Selvtest... Fsit Selvtest... Kpittel Grunnleggende emner Tllinjen og reelle tll Mengder og tllmengder Intervller Regnerekkefølge Bokstvregning og brøkregning Prentesregler Brøkregning og brudden brøk Fktorisering Fellesnevner Absoluttverdi Potenser med heltllige eksponenter Kvdrtsetningene Geometrisk rekke Summetegnet Aritmetisk rekke... 0 Oppgver Kpittel... Fsit Kpittel... Kpittel Funksjoner, ligninger og ulikheter Hv er en funksjon? Grfen til en funksjon Noen viktige begrep Noen funksjoner Førstegrdsfunksjoner f () b Ligninger Førstegrdsligninger Andregrdsligninger b c Andregrdsfunksjoner f () b c Inverse funksjoner.... Rsjonle ligninger.... Irrsjonle ligninger.... Ulikheter..... Enkle ulikheter Doble ulikheter Grfisk løsning Rsjonle ulikheter... 6 Oppgver Kpittel... 7 Fsit Kpittel... 9 Kpittel Eksponentielle funksjoner og logritmer.... Eksponentiell vekst.... Logritmer f log og f ln.... Regneregler for logritmer....4 Den nturlige logritmefunksjonen y e og y ln er inversfunksjoner... 4
3 .6 Eksponentile og logritmiske ligninger Ligningen b Noen eksponentilligninger Noen logritmiske ligninger... 5 Oppgver Kpittel... 6 Fsit Kpittel... 7 Kpittel 4 Trigonometri i grder og rdiner Vinkelmål: grder og rdiner Rettvinklet treknt Trekntberegninger Trigonometri i rdiner Noen kjente vinkler Grfene til sinus, cosinus og tngens Trekntberegninger (trigonometri i grder) Trigonometriske formler Beskrivelse v et periodisk fenomen ved hjelp v en cosinus- /sinuskurve Den periodiske funksjonen: f ( t) cost bsint Ligninger på formen: sin( ) b der Ligninger på formen: cos( ) c der Oppgver Kpittel Fsit Kpittel Kpittel 5 Grenseverdi og kontinuitet Grenseverdi f( ) 0 5. Grenseverdi lim g ( ) 0 5. Ensidig grense lim og lim Kontinuitetsbegrepet f( ) 5.5 Noen ord om grenseverdi når lim g ( ) 5.6 Asymptoter Tllet e Oppgver Kpittel Fsit Kpittel Kpittel 6 Derivsjon Vekstrte Definisjon, vekstrte Tolkninger Derivsjonsformler og derivsjonsregler Viktige derivsjonsregler Den deriverte til og r Den deriverte med hensyn til : d d 6.8 Oversikt over derivsjonsformler og -regler Derivert, nnenderivert og funksjonsdrøfting Mksimum og minimum Ligningen til tngenten og linerisering... 7 Oppgver Kpittel iii
4 Fsit Kpittel Kpittel 7 Integrsjon Det bestemte integrlet som rel Det bestemte integrlet Det ubestemte integrlet Integrsjonsformler Regneregler for bestemt og ubestemt integrl Integrsjon ved substitusjon Delvis integrsjon Noen nvendelser v det bestemte integrlet... 8 Oppgver Kpittel Fsit Kpittel Kpittel 8 Vektorer i rommet Hv er en vektor? Vektorlgebr Sklr produkt Vektor produkt Ligningen til en linje i rommet Ligningen til et pln i rommet Avstnden fr et punkt til et pln Projeksjonen v en vektor på en nnen vektor Noen kommentrer Oppgver Kpittel Fsit Kpittel Ikonbeskrivelser: Innhold Definisjon Eksempel Løsning Kommentr, hint, bemerk, husk Vnskelig oppgve
5 Forord Å lære mtemtikk er som å lære et nnet språk; ved første øyekst virker det uforståelig og vnskelig, men etter hvert vil du oppleve t det blir grdvis lettere. Mnge begreper i mtemtikken er forbundet og bygger på hverndre. Å forstå innholdet i et bestemt begrep, vil dermed hjelpe deg til å forstå mnge ndre. Å være usikker og frustrert i rbeidet med stoffet er en nturlig del v læringsprosessen. Husk t læring ikke bre skjer ved god innsts, men også ved intens konsentrsjon. Dette heftet er et oppsummeringsnott fr noen utvlgte grunnleggende emner i mtemtikk. Enkelte eksempler er ment som utfyllende forklring til lærestoffet og viser hvordn lærestoffet blir benyttet til å løse konkrete oppgver. For hvert kpittel finner du en oppgvedel etterfulgt v fsit/løsningsforslg. Når du skl lære et nytt emne er det ikke nok å få tk i hvordn ting skl gjøres. Det er like viktig å spørre seg hvorfor og prøve å forstå hvordn ting henger smmen. D blir det lettere å lære. Jo bedre du forstår mtemtikken, desto lettere er det å bruke den til å løse ktuelle problemer i ndre fgfelt. Det er svært viktig t du leser nøye gjennom oppgvene før du prøver å løse dem. Hvis du står fst i en oppgve, les heller gjennom lærestoffet enn å se på fsit/løsningsforslg. I kpittel 0 kn du teste og se om du innehr tilstrekkelig med bsisferdigheter i mtemtikk. Heftet er orgnisert på følgende måte: Kpittel 0: Test deg selv (elementære regneferdigheter) Del : Algebr Kpittel : Grunnleggende emner Del : Funksjonslære Kpittel : Funksjoner, inversfunksjoner, ligninger og ulikheter Kpittel : Eksponentielle funksjoner og logritmer Kpittel 5: Grenseverdi og kontinuitet Kpittel 6: Derivsjon, funksjonsdrøfting og en del nvendelser Del : Kpittel 4: Trigonometri Kpittel 7: Integrsjon og en del nvendelser Kpittel 8: Vektorlgebr Amir Mssoud Hshemi Mtemtisk institutt, UiB Juni 0 Copyright 0 Forftter
6 Kpittel 0: Test deg selv Kpittel 0 Test deg selv Før du begynner å lese nottene og t forkurset, kn du teste deg selv i grunnleggende emner. Oppgver Selvtest Oppgvene skl løses uten bruk v klkultor. Oppgve 0. Regn ut. 5 4 ) c) 5 4 Oppgve 0. Regn ut. ) 5 8 c) Oppgve d) 4 :6 7 Regn ut. 5 7 ) 8 5 Oppgve 0.4 c) : 5 5 Regn ut. 56 ) 5 64 c) Oppgve 0.5 Regn ut. ) c) 6 4 d) Oppgve 0.6 Multipliser og trekk smmen. b b b b ) b b ( d) b b ( b ) b( b ) b c)
7 Forkurs i mtemtikk - UiB (Amir.Hshemi@mth.uib.no) Oppgve 0.7 Skriv så enkelt som mulig. ) 6b b 6( 6b 9b 9b Oppgve 0.8 Bruk kvdrtsetningene og regn ut. ) c) Oppgve 0.9 d) Fktoriser uttrykkene. ) 4 8 c) t 8 d) Oppgve 0.0 Fktoriser uttrykkene ved hjelp v nullpunktene. ) 4 c) 5 d) y y 8 Oppgve 0. Forkort brøkene. ) 6 c) d) y 4y 4y Oppgve 0. ) Prisen til en vre gikk opp fr 0 til kr. Hvor mnge prosent vr prisstigningen? En fmilie på to voksne og to brn betlte til smmen 0 kroner for å komme inn på et rrngement. En nnen voksen og tre brn betlte til smmen 90 kroner. Hv koster én brnebillett, og hv koster én voksenbillett? c) En kinosl hr 80 seter. En voksenbillett koster 00 kroner og en brnebillett koster 60 kroner. Ved en forestilling vr slen fullstt. De smlede billettinntektene vr kroner. Hvor mnge voksne og hvor mnge brn vr til stede på forestillingen? d) Hvis y 00 og y 60, hv er d produktet y? e) Summen til to positive tll er 0 og summen v deres kvdrter er 5. Bestem disse.
8 Kpittel 0: Test deg selv Fsit Selvtest 0. ) 78 c) - 0. ) 4 5 c) 5 d) 0. ) 7 6 c) ) c) ) c) 6 9 d) 0.6 ) b 4 c) 6 b( b ) d) b b ( b b ) ( ( b ) 6( ( ( 6b 9b ( b 9b ( ( b 0.8 ) 0( 5) c) d) ) 99 c) tt d) 0.0 ) c) 5 d) y4 y7 0. ) c) y d) y 0. ) 0% 40kr og 70 kr. c) 0 voksne og 50 brn d) 0 e) 4 og 6.
9 Forkurs i mtemtikk - UiB (Amir.Hshemi@mth.uib.no) Kpittel Grunnleggende emner Dette kpittelet er en repetisjon v grunnleggende konsepter og prinsipper. Vi oppsummerer emner som: - Tllmengder, intervll - Bokstvregning og brøkregning - Regler for potensregning - Absoluttverdi - Geometriske og ritmetiske rekker. Tllinjen og reelle tll Reelle tll er mengden v de tll som tilsvrer lle punkter på en uendelig lng tllinje og betegnes eller R.. Mengder og tllmengder En mengde inneholder visse objekter, klt elementer. Elementene kn i prinsippet være hv som helst, for eksempel tll, personer, biler eller ndre mengder. M: er et element i mengden M M : et element er ikke i mengden M En mengde kn være tom. Den tomme mengden blir betegnet med Ø. Kjente tllmengder: Mengden v lle nturlige tll: N,,, { } { } Mengden v lle hele tll: Z,,,,0,,,, p Mengden v lle rsjonle tll: Q { p og q er hele tll, q 0} q Mengden v lle reelle tll: R inneholder lle tll på reelle tllinjen Et reelt tll som ikke er rsjonlt klles irrsjonlt, for eksempel: Eksempel. Noen rsjonle tll: 0,8,,, 5 7 Noen irrsjonle tll:, 4
10 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no). Intervller Intervller er deler v tllinjen. Et intervll kn være lukket eller åpent: Intervllet 0 er lukket og kn skrives som: 0, Intervllet 0 er åpent og kn skrives som: 0, Intervllet er hlvt lukket/hlvåpent og kn skrives som: [,, eller [, Åpent intervll Intervll notsjon Grfisk frmstilling, ( b, b ( ) b, ) R, ( tilhører reelle tll) Hlvt åpent intervll Intervll notsjon Grfisk frmstilling [, [ b [ b, [ ) b, ] ] Lukket intervll Intervll notsjon Grfisk frmstilling b [ b, ] [ ] b.4 Regnerekkefølge Kunnskper om smmenheng mellom regneopersjonene er svært viktig i lgebr. I smmenstte uttrykk kn mn regne ut uttrykket i følgende rekkefølge:. Regn ut lle prenteser. Regn ut potenser. Multipliser eller divider 4. Legg smmen eller trekk fr 4
11 Kpittel Eksempel. Regn ut uten klkultor: 5 7(5 ) ( ) ( ) Prenteser og potenser: Multipliser: Legg smmen: Bokstvregning og brøkregning Algebr er for mnge det smme som bokstvregning. I mtte brukes bokstver spesielt i formler, ligninger og ulikheter, identiteter og funksjonsuttrykk. Et ledd er et ledd, der er koeffisient, er vribel og er eksponent. To ledd tskilles fr hverndre med + eller : En fktor ( ) består v fktorer. To fktorer tskilles fr hverndre med gngetegn: y. Regneregler Kommuttiv lov Assositiv lov Distributiv lov Motstte og inverse tll Addisjon Multipliksjon b b b b ( b c) ( c ( b c) ( c ( ) 0 ( b c) b c der 0 Tllet 0 og : 0 0 5
12 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no).6 Prentesregler b c b c b( c d) c d bc bd.7 Brøkregning og brudden brøk b c b c Husk: b c b c c c Husk: b d b d b c b c : c d d Husk: : c d d d c c c d c c d c d d : Husk: b c d d : b d b c bc c b d b c bc d.8 Fktorisering Fktorisering er en prosess der mn deler opp et mtemtisk uttrykk som for eksempel en ligning eller et tll i mindre enheter (fktorer) som kn gnges smmen for å få det opprinnelige uttrykket. Eksempel : 5 6 ( ) Eksempel : 4 b b 8b 4b b b.9 Fellesnevner Fellesnevner Fellesnevner er det minste tllet som er delelig med lle nevnerne. Eksempel : Eksempel : ( ) En brudden brøk består v en brøk i telleren, en brøk i nevneren og en hovedbrøkstrek mellom dem. For mer info kn du lese her: 6
13 Kpittel.0 Absoluttverdi Absoluttverdien eller tllverdien til et reelt tll er den numeriske verdien til tllet uten hensyn til fortegnet. Den geometriske tolkningen v bsoluttverdi kn være vstnd på tllinjen. 0 0 Grfen til y : Husk: Absoluttverdien v kn tolkes som vstnden fr 0 til på tllinjen. Tilsvrende vil y bli vstnden mellom og y på tllinjen. Dermed hr vi t de som tilfredsstiller ligningen er lle tll slik. Noen regneregler som gjelder: 0 0 b b ( b 0) b b Det kn vises: b b b b Eksempel. ) Beregn: 7 Løs ligningen c) Tegn grfen til y ) c) y ( ). Grfen er vist her: Eksempel.4 Løs ligningene og ulikheten: ) 5 5 ) R 0 0 c) 0 eller R, 0 c) 7
14 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no). Potenser med heltllige eksponenter n klles potens (potensledd) og er definert som: n der er grunntll og n er et nturlig tll og klles eksponent. Hvis 0, kn vi skrive 0 n og n Regneregler n gnger n n n m n m n b b m n mn n m n m m n b n b p q p q n n Husk: 0 n n n n Kvdrtrot skrives slik: og. n te rot skrives n og kn noteres: n n Eksempel.5 Skriv så enkelt som mulig: ) ) 5 4 ( ). Kvdrtsetningene b b b (. og. kvdrtsetning) b b b (. kvdrtsetning). Geometrisk rekke Kjennetegnet til en geometrisk rekke er t forholdet mellom to påfølgende ledd er konstnt. n k (kvotient) n n Summen v de n første leddene i rekken er: S = + k + k + k n k og kn utledes som S, husk t n er ntll ledd i rekken. k 8
15 Kpittel Geometrisk rekke, ledd n n k n k er rekkens kvotient Summen v de n første leddene i en n k Gjelder for k. geometrisk rekke S k Hvis k = er, S n Summen v en uendelig Gjelder for k geometrisk rekke (konvergent) s k S = 0 når 0 Rentesrenteformelen p n Verdien K n om n år v et beløp K n K 0 ( ) 00 K 0 i dg Eksempel.6 Ved den første injeksjonen gir dosen 5 enheter. Psienten skl få 0 injeksjoner med en ukes mellomrom. ) Hvor mye skl injeksjonen økes slik t den siste dosen er enheter? Hvor mnge enheter mottr psienten i løpet v de 0 injeksjonene? ) ( p ) n Kn K0 00 p 9 p /9 00, 000 5( ) (0, 000), 684 p 0, 684 eller 68, 4 % Vi ønsker å bestemme summen til 0 ledd i en geometrisk rekke: 0 (, 684) S = (,684) + 5(,684) + 5(, 684) 5, 4590, enheter.. Summetegnet Summetegnet kn hjelpe oss til å omskrive en sum som følger en bestemt regel: n i i Eksempel.7 Skriv summen n () () () ved hjelp v summetegnet. Regn ut summen () () () () i eller i () () () () i Summen er d lik: () () () () 6096 i Bemerk: + k + k + k n n i ( k) i i ( n ) k k 9
16 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no) Eksempel.8 Bestem summen til den geometriske rekken: For å bestemme n (ntll ledd i rekken) kn vi benytte: n k n n n 7 n Summen er d lik: n Bemerk: + k + k + k n i i ( k) ( n k ) k i.4 Aritmetisk rekke Kjennetegnet til en ritmetisk rekke er t differnsen mellom lle to påfølgende ledd er konstnt. n n d Summen v de n første leddene i en ritmetisk rekke er gitt ved: n n n i ( d) ( d) ( ( n ) d) ( n) ( ( n ) d) i Eksempel.9 Bestem summen til den ritmetiske rekken: Differnsen d kn bestemmes: d For å bestemme n (ntll ledd i rekken) kn vi benytte: n ( n ) d 4( n ) 49 5 n n Summen er d lik: (5 49) 4 n n Bemerk: i ( d) ( d) ( ( n ) d) ( n) i 0
17 Kpittel Oppgver Kpittel Oppgvene skl løses uten bruk v klkultor. Oppgve. Regn ut ) c) 5 4 Oppgve. Regn ut. ) 6 5 c) Oppgve d) :6 Regn ut. ) 4 c) : Oppgve.4 Regn ut. ) 5 b b b b c) 5 5 Oppgve.5 Regn ut. ) c) 4 Oppgve.6 Multipliser og trekk smmen. ) b b b b( c) b b ( d) 4
18 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no) Oppgve.7 Skriv så enkelt som mulig: ) 4 4b b ( 4b 4b 4b Oppgve.8 Bruk kvdrtsetningene og regn ut. ) ( ) c) Oppgve.9 d) Fktoriser uttrykkene. ) 9 Oppgve c) 4t 9 d) 6 9 Fktoriser uttrykkene ved hjelp v nullpunktene. ) 5 4 c) d) b b 6 Oppgve. Forkort brøkene. 9 ) c) d) y 9y 9y Oppgve. Skriv så enkelt som mulig ( 0 ) : ) ( ) 4 c) 4 d) Oppgve. Bestem summene: 4 8 ) 9 7 der Oppgve.4 ) Løs ligningen: ( ). Tegn grfen til y. c) Bestem største verdien til f ( ) 5.
19 Kpittel Fsit Kpittel. ) 0 c). ) c) 6 7 d) 9. ) ) 5.5 ) ( ) b b b 9 b 5b 0 b.6 ) 4 c) c) c) 7 c) 4 b( d).7 ) b b b 4 c) 6 () d) ( ).8 ) 6.9 ) () (7)( 7) c) (t)(t) d) ( ).0 ) ( )( 4) ( )( ) c) ( 4)( ) d) ( (. ). ) c) d) ( ) 4 9 ( ) y y y y y 9y ( y)( y) y 94 ( ) ( ) ( ) c) d) n n ( ) 4 8 k. ) S S lim 9 7 k n n n ( ) k der S lim k n.4 ) y der n lim( ) 0 n c) Største verdien er 5 for.
20 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no) Kpittel Funksjoner, ligninger og ulikheter Her skl vi t for oss sentrle begreper knyttet til funksjoner og deretter studere ligninger og ulikheter.. Hv er en funksjon? En funksjon f er en regel som tilordner ethvert element,, fr en mengde klt definisjonsmengde, til et entydig bestemt element, y, i en mengde klt verdimengde: y f ( ) der D f og y V f og y klles henholdsvis uvhengig vribel og vhengig vribel. Krvet for t en relsjon y f () er en funksjon er: For enhver i definisjonsmengden finnes én og bre én y i verdimengden: y y Vertikllinjetesten: En linje prllell med y-ksen skjærer funksjonskurven høyst i ett punkt. Eksempel. y er en funksjon, mens y ikke tilfredsstiller definisjonen til en funksjon (grfen til y som er vist litt tykkere hr bre ett skjæringspunkt med en vertikl linje, mens y hr to).. Grfen til en funksjon L f være en funksjon. Mengden v lle tllpr (, f ( )) som vi får ved å l gjennomløpe definisjonsmengden til f, klles grfen til funksjonen y f (). Eksempel. Grfen til y f ( ) er vist her: Som vi ser, er denne relsjonen en funksjon. 4
21 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no). Noen viktige begrep Monotoni (i) En funksjon f er voksende dersom: f ( ) f ( ) (ii) En funksjon f er strengt voksende dersom: f ( ) f ( ) (iii) En funksjon f er vtgende dersom: f ( ) f ( ) (iv) En funksjon f er strengt vtgende dersom: f ( ) f ( ) Kontinuitet En funksjon y f ( ) er kontinuerlig dersom grfen er smmenhengende. I kpittel 5 skl vi studere kontinuitetsbegrepet nærmere. En entydig funksjon For enhver y i verdimengden finnes én og bre én i definisjonsmengden. Vi kn bruke den såklte horisontllinjetesten til å studere entydighet. Horisontllinjetesten En linje prllell med -ksen skjærer funksjonskurven høyst i ett punkt. Smmenstte funksjoner For eksempel: y kn nses som y g( ) der g ( ). Oppdelte funksjoner En funksjon som er uttrykt ved hjelp v flere funksjonsuttrykk i forskjellige intervller. For eksempel: 0 f( ) 0 Odde og jmne funksjoner, og symmetriegenskper (er foreløpig ikke pensum) 6
22 Kpittel.4 Noen funksjoner n Polynomfunksjoner: f ( ) 0 n (polynom v n te grd) (for eksempel førstegrds- og ndregrdsfunksjoner) f( ) Rsjonle funksjoner: y ( g ( ) 0 ), der f og g er polynomfunksjoner g ( ) Eksponentilfunksjoner: y, 0 Logritmefunksjoner: y log, der 0, 0. (for eksempel briggske logritmer, y log og nturlige logritmer, y ln ) Trigonometriske funksjoner: y sin, y cos, y tn, y c sin( ),.5 Førstegrdsfunksjoner f () b En førstegrdsfunksjon er en funksjon der funksjonsuttrykket er v første grd og kn skrives på formen: y b, der klles stigningstll og b er konstntleddet. Ettpunktsformelen: y y0 ( 0) (en rett linje med stigningstll som går gjennom punktet ( 0, y 0) ) y y0 y y0 Topunktsformelen: 0 0 (en rett linje gjennom punktene ( 0, y0) og (, y) der stigningstllet d blir Grfen til y b, der klles stigningstll og b konstnt ledd, er en rett linje. 0 funksjonen er strengt voksende. 0 funksjonen er strengt vtgende. 0 funksjonen er konstnt: y b. y y 0 0 ).6 Ligninger En ligning består v to mtemtiske uttrykk som er stt lik hverndre, der uttrykkene inneholder minst én ukjent. Den ukjente betegnes ofte. Når ett ledd (i en ligning) flyttes fr en side v likhetstegnet til den ndre, må vi skifte fortegn (, ) på leddet. En ligning som lltid er oppfylt, unsett vlg v den ukjente, klles en identitet. For eksempel ( ) ( ). 7
23 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no).7 Førstegrdsligninger Når vi skl løse førstegrdsligninger må vi prøve å smle -ene på en side og tllene på den ndre siden. Men for å få til det må vi legge til eller trekke fr det smme tllet på begge sider, eller multiplisere eller dividere lle ledd på begge sider med det smme tllet. Eksempel. Løs ligningene: ) c) ( ) 4 5 ) c) 0 ( ) ( ) ( ) Andregrdsligninger b c 0 Vi hr å gjøre med en ndregrdsligning når en ligning hr en ukjent som er opphøyd i. Den skrives ofte på denne formen: b c 0, der, b og c er reelle tll og 0. Løsningene til ndregrdsligningen: b c 0 kn skrives som:, b b 4c b c b Hvis b 0, kn ligningen Hvis c 0, kn ligningen b c 4 0 foskjellige reelle løsninger 4c 0 dobbel løsning 4 0 ingen reell løsninger c c 0 h løsningene, b b 0 h løsningene 0, En ndregrdsfunksjon nullpunkt(er): f ( ) b c som hr nullpunkt, kn fktoriseres med dens b c ( )( ), der og kn bestemmes ved:, b b 4c 8
24 Kpittel Det er hovedskelig tre tilfeller v ligningene: Ingen konstntledd 0 c Ingen førstegrdsledd b 0 0 ( 0 0 eller b 0 0 b c eller c c 0 c Generell b c 0 b b b 4c b 4c 0: reelle løsninger Eksempel 4 0 ( 4) 0 0 eller 0 eller ( ) 4 ( 6) 5 eller b 4c 0: en dobbel løsning Eksempel.4 Løs følgende ndregrdsligning SVAR: Bruker bc-formelen. Her er = 4, b = 0 og c = ( 4) , Dette gir de to løsningene 4 og 9
25 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no) Eksempel.5 Løs ligningene: ) 4 5 c) 5 0 ) ( 5) 0 4( 4) c) Andregrdsfunksjoner f () b c Dersom 0, smiler grfen, mens grfen er sur når 0. Skjæringspunkt med y-ksen er ( = 0, y = c ). b b 4c Nullpunktene til grfen (skjæringspunkt med -ksen) er (, y 0). Husk t ndregrdsfunksjonen kn fktoriseres hvis den hr løsning(er): b c ( )( ) Grfen er symmetrisk om linjen: b. For å tegne grfen til en ndregrdsfunksjon kn vi tenke slik: ) Er grfen sur eller smiler den? b b b b ) Bestem symmetrilinjen: og f ( ). Fktisk er punktet: (, y f ( ) ) koordintene til mksimumspunktet ( 0 ) eller minimumspunktet ( 0 ). ) Bestem eventuelle nullpunkt. 4) Bestem skjæringspunktet med y-ksen (0, c ). 0
26 Kpittel Eksempel.6 Tegn grfen til y 4 ) Nullpunktene : 4 0 og dermed er b 4 ) Symmetrilinjen:. ) 0 grfen smiler og dermed er (, f ()) (, 4() ) loklt minimum..0 Inverse funksjoner En invers funksjon til en funksjon y f ( ) der D f og y V f er en relsjon som tilordner y-verdien tilbke til -verdien. Dermed er: y f ( ) der D f V og f V f Df Krvet for t en funksjon hr en invers funksjon er t funksjonen er entydig (monoton). Husk: f ( f ( )) og f ( f ( )) Hvordn kn vi bestemme den inverse funksjonen til y f ( )? ) Bestem med hensyn til y. ) Bytt om og y. Eksempel.7 Bestem den inverse funksjonen til y f ( ) gitt 0 ) Finner uttrykt ved y: y og siden 0, får vi: y ) Bytter om og y: y dermed er: y f ( ) Bemerk: D Vf [, f og V Df [0, f.
27 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no). Rsjonle ligninger En brøk er ikke definert når nevneren er null. I rsjonle uttrykk må vi derfor psse på t nevneren ikke blir null. I uttrykket ( ) er nevneren null når 0og når. Det er ikke mulig å sette inn 0eller i uttrykket. Derfor må vi forutsette 0og når når vi regner med dette uttrykket. Slike forutsetninger er svært viktige når vi løser ligninger der den ukjente er med i nevneren. ( betyr ikke lik, i motsetning til =, som betyr lik ) Eksempel.8 Løs ligningene: ) ( ) ) ( ) 0 0 0, ( ) ( ) ( ) flyttes til venstre side og fellesnevneren er ( ) ( ) 0 ( ) ( ) ( ) ( ) 4 A Bemerk: 0 A 0 ( B 0) B. Irrsjonle ligninger Vi skl studere noen enkle irrsjonle ligninger på formen: b c d Eksempel.9 Løs ligningene: ) 5 ) Begge sider kvdreres: Mn får d ndregrdsligningen: 0 ( ) OK! 4( )
28 Kpittel Leddet med kvdrtroten ønsker vi å h lene på én side v ligningen. Ligningen må først skrives på formen: 5 Begge sider kvdreres: 5 Høyre side utvides ved hjelp v. kvdrtsetning: 0 5 Mn kn d sette opp ndregrdsligningen: 8 0 Ligningen hr reelle løsninger som må settes på prøve: Umulig ( 4)( 7) OK!. Ulikheter Ulikheter er et mtemtisk oppsett med opplysninger om hv som er større, mindre, større og lik, eller mindre og lik noe nnet. Minst ett v leddene består v en eller flere ukjente. Hv er de viktigste reglene ved løsing v en ulikhet? Reglene når du regner med ulikheter er nesten de smme som når du regner med ligninger. Det kn dderes og subtrheres med smme tll på begge sider. Det kn også multipliseres og divideres med et positivt tll på begge sider. Men hvis det skl multipliseres eller divideres med et negtivt tll, må ulikhetstegnet snus for t ulikheten skl stemme. Å løse en ulikhet er å finne de verdier v som gjør ulikheten snn. Hv må mn psse på når mn løser ulikheter? Når mn løser ulikheter må mn psse på å snu ulikhetstegnet når mn multipliserer eller dividerer med negtive tll. Regel : Legge til / trekke fr det smme tllet på begge sider. Eksempel: ulikhet 6 hr smme løsninger som ulikheten 8 (Den ndre ulikheten ble hentet fr den første ved å legge på begge sider.) Regel : Hvis vi bytter sidene i ulikhetene, endrer vi retningen på ulikhetstegnet. Eksempel: ulikhet hr smme løsninger som ulikheten. (Vi hr byttet side og vendte `` '' til en `` ''). Sist, men ikke minst, den opersjonen som er kilden til lle problemer med ulikheter: Regel : Multiplisere / dividere med smme positive tll på begge sider. Regel b: Multiplisere / dividere med smme negtive tll på begge sider og endre retningen på ulikhetstegnet. Betrkt ulikhetene med, b, og c der c 0 (c er negtiv): b c bc b c bc
29 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no) Her skl vi se på noen eksempler med Enkle ulikheter: p ( ),,, 0 Doble ulikheter m( ) p( ) n( ) Rsjonle ulikheter p( ) q( ),,, 0.. Enkle ulikheter Ulikheter der deler v (i første) inngår, løses som en ligning. Ulikheten settes på stndrdform slik t du hr 0 på den ene siden. Det vil si t lle ledd med smles på venstre side og trekkes smmen, og t lle tll smles på høyre side og trekkes smmen. Eksempel.0 Løs ulikhetene: ) 6 ) 6 Eksempel. Løs ulikheten: 4 0. Det trekkes 4 fr begge sider Begge sider deles med Løsningsmengden til ulikheten er d: { } eller [, ). - 4
30 Kpittel Eksempel. Løs ulikheten: 6 0 Andregrdsligningen kn fktoriseres: ( )( ) 0. Fortegnsskjem: ( )( ) Løsning Løsning Løsningsmengden til ulikheten er d: { },, eller.. Doble ulikheter En dobbel ulikhet på formen: A b B kn løses ved å gjøre lle prosesser i lle tre deler v ulikheten. Prosessene kn vnligvis gjøres i følgende rekkefølge: subtrksjon/ddisjon, multipliksjon/divisjon. Eksempel. Flersidige ulikheter Løs ulikheten: 8 Metode : Det dderes på begge sider 9 Metode : Deler i ulikheter og 8 9 Snittet mellom disse er : { } eller,. 5
31 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no).4 Grfisk løsning Ulikheten f ( ) g( ) kn omskrives som f ( ) g( ) 0. Løsningen er lle -verdier der y f ( ) g( ) 0, det vil si der grfen til y f ( ) g( ) er ovenfor y-ksen. Eksempel.4 - Grfisk løsning Løs 4 5 grfisk. Ulikheten skl først omskrives som Tegn grfen til y 4 5 og bestem mengden v -verdier der y 0: Løsning: { 5} eller, Rsjonle ulikheter Her skl vi se på noen eksempler der ulikheten hr én eller flere rsjonle uttrykk. En rsjonl ulikhet kn skrives på formen: P ( ) Q ( ) 0, P ( ) Q ( ) 0, P ( ) Q ( ) 0 eller P ( ) Q ( ) 0 der nevneren Qer ( ) forskjellig fr null ( Q ( ) 0) og hr en vribel. Eksempel.5 Løs ulikheten: 0. Fortegnsskiftepunkt: Nullpunkt fåes der telleren er lik null: 0. Bruddpunkt fåes der nevneren = 0, dvs Løsning Løsning: { } eller,,. 4 betegner bruddpunkt. 6
32 Kpittel Oppgver Kpittel Oppgve. Hvilken v følgende uttrykk for y f ( ) beskriver en funksjon? ) y 4 Oppgve. ) Gitt f ( ). Bestem f (0), f (), f ( ) og f( ) y c) y Gitt f ( ) og g( ) der. Bestem f ( g( )) og g( f ( )) 5. Hv kn vi si om f og g? 6 Oppgve. Gitt f ( ). Bestem definisjonsmengden og verdimengden til til f. Bestem Sett opp funksjonen g( ) f ( ). f ( ). Oppgve.4 Gitt f( ). Hv er definisjonsmengden til f? Tegn grfen til f( ). Oppgve.5 Grfen til en funksjon er vist her: ) Bestem f ( ) og f (). Er funksjonen kontinuerlig 7 i punktene og? Oppgve.6 Tegn grfen til f( ) der 0. Oppgve.7 Løs ligningene: ) Oppgve.8 Løs ligningene: ) b b b c) c) f ( g( )) og g( f ( )) klles smmenstt funksjon. Disse kn også skrives som f o g og go f. 6 Se kpittel.0 Inverse funksjoner. 7 Se kpittel 5.4 Kontinuitet. 0 7
33 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no) Oppgve.9 Løs ligningene: ) 6 c) 5 4 0,5 Oppgve.0 Løs ligningene: ) 5 0 ( ) 8 c) y 7y 0 Oppgve. Løs ligningene: ) 6 c) Oppgve. Løs ligningene ) 9 Oppgve. Løs ulikhetene: ) 5 4 c) 5 d) e) 5 f) g) h) Oppgve.4 Løs ulikhetene: ) c) 4 e) f) 8
34 Kpittel Fsit Kpittel Oppgver. ) J Nei. fordi y c) J ( ). f (0), f (), f ( ) og f ( ) f ( g( )) f ( ) og g( f ( )) g( ) tilsier t f og g er inverse funksjoner.. D { R } (lle reelle tll slik t er minst ) f V { y R y 0} (lle reelle tll y slik t er mer eller lik 0) f g( ) der. f ( )..4 D { R 0} lle reelle tll unnttt 0. f f ( ) (tegn grfen til linjen y der punktet (0, ) ikke ligger på grfen..5 f ( ) og f (). Funksjonen er kontinuerlig i men ikke i..6 0 f( ) 0.7 ).8 ) c).9 ),5 5 c),75.0 ) 5 4 c) y y 4. ) 0 c) c) b. ) Innsetting viser t løsningen 7 psser Det siste er åpenbrt umulig, siden Ligningen hr ingen løsning. )
35 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no) c) 4 8 d) e) f) g) h) i) j) ) Løsning: { 4} eller Løsning, 4, Løsning eller c) eller 0 0
36 Kpittel Tllinjedigrm: ( )( ) Løsning: eller 0 eller d) Her vet vi t er positiv siden ldri kn bli negtiv. Altså kn vi multiplisere begge sider v ulikheten med : Setter opp fortegnsskjem, og får eller. e) eller Vi bruker tllinjedigrm: Konklusjonen er t 0 4 f) 0 0. Her finner vi røttene i nnengrdspolynomet i telleren: 8, slik t. og. Tllinjedigrm: ( )( ) Løsning Løsning Konklusjonen er t betegner bruddpunkt.
37 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no) Kpittel Eksponentielle funksjoner og logritmer Her skl vi studere eksponentielle funksjoner som kn beskrive en eksponentiell vekst og lære oss hvordn vi kn benytte logritmer til å løse eksponentilligninger. Vi skl også oppsummere t y e og y ln er inverse funksjoner.. Eksponentiell vekst Når en størrelse øker/synker med en fst prosent over like store tidsrom, klles endringen en eksponentiell vekst/reduksjon. Eksponentiell vekst når For eksempel 5 f c y 0 Eksponentiell reduksjon når 0 For eksempel y 7 ( ) c 0 p der er vekstfktor og kn skrives om og p klles rentefot (gitt i %). 00 Eksempel: For en verdi som Vokser Vokser med 0% 0,, med 0% Synker Synker med 0% 0, 0,8 For en verdi som vokser med 00% Eksempel. Ved. jnur 980 vr jordens befolkning 4, millirder. Vi regner med t folketllet vokser med c. % pr. år. Sett opp en funksjon som beskriver folketllet t år etter året 980. f t c. Modellering ved hjelp v eksponentilfunksjonen: t Vi ønsker å bestemme c og. Vi kn betrkte året 980 som 0 f 0 4, f (0) c c 4, t og dermed er 0 Vekstfktoren er 0,0,0 og funksjonen blir: f t 4, (,0) t (millirder) som bestemmer folketllet t år etter året 980. I forrige eksempel, hvis vi skulle bestemme hvor lenge det tr før jordens befolkning hr blitt 4,9 millirder. Det vil si vi skl bestemme t når: t 4, (,0) 4,9 Her vi kn benytte logritmer. Jeg løser denne ligningen her, men du kn se på løsningen etter du hr lært om logritmer: t ln(4,9 4,) (, 0) 4,9 4, tln(, 0) ln(4,9 4,) t 9 ln(, 0)
38 Kpittel. Logritmer f log og ln f Logritmen til et tll med grunntll b er den eksponenten som grunntllet må opphøyes i for å få tllet b: b log der 0 og b 0 b Grunntllet b klles også bsis for logritmen. Tllet b er ntilogritmen. Logritmer med grunntll lik eulertllet klles nturlige logritmer, mens briggske logritmer bruker grunntllet 0. Dersom vi skl bestemme eksponenten i ligningen b, benytter vi logritmer. Senere skl vi se t b log b log ln b log (se oppgve.0) b log b ln b Når 0 gjelder: y log y Ti-logritmer (Briggske logritmer): y 0 log y Nturlige logritmer y e ln y log0, log 0, ln e, ln 0 Bemerk t 0 er vertikl symptote for log f ( lim log ). 0 Noen nyttige regler A log(0 ) A A ln( e ) A log 0 A A ln A e A. Regneregler for logritmer A n log A B log A log B log log A log B log A n log A B der A 0 og B 0
39 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no) Eksempel. Skriv så enkelt som mulig: ) log00 log000 c) log0,00 d) log 0 e) Fsit: ) c) d) 0,5 e) log7 7 log 00.4 Den nturlige logritmefunksjonen Dersom grunntllet i logritmen er e, klles logritmen den nturlige logritmen. y e og y ln er inversfunksjoner. lim e og lim e 0 ( y 0 er horisontl symptote for y e ) lim ln og ( 0 er vertikl symptote for y ln ) 0.5 y e og y ln er inversfunksjoner Når 0 gjelder: y log y og dette kn bety t y log er inversfunksjonen til y f ( ) 0 f ( ) log f ( ) e f ( ) ln.6 Eksponentile og logritmiske ligninger.6. Ligningen b Generelt Eksempel. b 7 ln( ) ln( ln ln b ln b ln ln( ) ln(7) ln ln7 ln 7 ln 4
40 Kpittel.6. Noen eksponentilligninger Her skl vi se på noen eksponentilligninger som kn løses ved hjelp v forskjellige frmgngsmåter. Eksempel.4 Løs ligningene: ) 5 e e e 0 ) e 5 5 e ln(5 / ) (ln(5 / ) ) e e 0 Velger hjelpevribelen: u e u e e u 0 som gir: u u ln 0 ln e be c 0 kn løses ved å velge u e : u bu c 0 (ndregrdsligning).6. Noen logritmiske ligninger Eksempel.5 Løs ligningene: ) ln( ) ln( ) ln( ) ln() c) ln( ) ln() 0 ) ln( ) e e ln( ) ln( ) ln(4) ln( ) ln(4) c) ln( ) ln() 0 ln( ()) 0 ( ) 0, Bemerk: kn ikke være løsning, fordi 0. 5
41 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no) Oppgver Kpittel Oppgve. Skriv så enkelt som mulig: ) e e e e 5e e Oppgve. k Eksponentilfunksjonen gitt ved: f ( ) c kn skrives som f ( ) c e. Bestem k. Oppgve. Folketllet i en bygd ved. jnur 000 vr 500. Vi regner med t bygdens befolkning vokser med c. % pr. år. ) Sett opp en funksjon som beskriver folketllet t år etter året 000. Hv er folketllet til bygd i slutten v 005 etter denne modellen. Oppgve.4 t år etter t en orgnisme døde, er ndelen v rdium redusert til p % v mengden i den levende orgnismen. Hlveringstiden er c.60 år. Sett opp en eksponentilfunksjon som beskriver pt () målt i %. Oppgve.5 Skriv så enkelt som mulig uten å bruke klkultor: ) ln e ln ln e c) ln ln ln d) ln ln ln 4 e) ln e f) ln ln ln Oppgve.6 Skriv så enkelt som mulig: ) ln e Oppgve.7 Løs ligningene: ln e c) e ln ln 5 ) e 5 5 e c) 5 e 7 0 6
42 Kpittel Oppgve.8 Løs ligningene: ) e e 0 e 0 e Oppgve.9 Løs ligningene: ) ln 0 ln ln 9 c) 6 d) 5 7 Oppgve.0 Vis t log ln b log. b log b ln b Fsit Kpittel. ) e ln. Vi vet t : e. ln ln ( e ) e dermed er k ln.. ) Nt ( ) 500 (,0) t t 60.4 t ln 6 N(6) 500 (,0) pt ( ) 00 ( ) eller p( t) 00 e.5 ) c) 0 d) ln e) f) 0.6 ) c) ) ln 5 ln c) ln ) 0 ln Hvis mn multipliserer begge sider med e, får mn smme ligning som i del ) 0 ln 9.9 ) e e 5 7 ln ln 6 c) d) 5 ln 7 ln 5 ln ln ln.0 b ln( ) ln( ln ln b ln b Def. b log b ln b log( ) log( log log b log b log 7
43 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no) Kpittel 4 Trigonometri i grder og rdiner Trigonometri (fr gresk trigonon = tre vinkler og metro = måling) er en gren innenfor mtemtikken som studerer forholdet mellom vinkler og sider i en rettvinklet treknt. Trigonometri nvendes i mtemtikk, stronomi og lndmåling, men også innen felter som ikke er direkte forbundet med dette, som meknikk og frekvensnlyse (lyd, lys, optikk, kvntemeknikk). Det er uenighet om trigonometrien er en egen mtemtisk gren eller om den er underlgt geometrien. I nturen gjentr det seg noen fenomener over en bestemt tidsperiode. Hr mn informsjon om fenomenet i denne tidsperioden, kn mn bruke trigonometriske funksjoner til å beskrive fenomenet over flere tidsperioder. 4. Vinkelmål: grder og rdiner Vinkelmålet rdin er en SI-enhet definert som buelengde delt på rdius. Det klles også for bsolutt vinkelmål. Andre vinkelmål er grder, som knskje er mest kjent. 60 grder tilsvrer π rdiner. Omregningsformelen er: 80 r d r d 80 der r er vinkelen regnet i rdien og d vinkelen regnet i grder (engelsk: degrees). Eksempel 4. Omgjør 0, 45, 60, 90 og 60 grder til rdiner. Vi vet t: 80 o rd, dermed er: 0 o rd, 45 6 o rd, 60 4 o rd,90 o rd o,60 rd 4. Rettvinklet treknt En rettvinklet treknt er en treknt hvor én v de tre vinklene er 90 grder, og hvor Pythgors setning gjelder: b c Forholdet mellom ktetene og hypotenusen kn defineres ved hjelp v sinus og cosinus: sin A c b cos A c sin A tn A b cos A 8
44 Kpittel 4 4. Trekntberegninger Cosinussetningen: b c bc cos( A) Sinussetningen: sin( A) sin( B) sin( C) b c Se oppgve Trigonometri i rdiner Enhetssirkel, sinus, cosinus og tngens sin cos (cos, sin ) Figuren til venstre viser de grunnleggende definisjonene v de trigonometriske funksjonene. Enhetssirkel (en sirkel med rdius med sentrum i origo) Cosinus-ksen (horisontlksen) Sinus-ksen (vertiklksen) Skjæringspunktet mellom denne linjen og enhetssirkelen hr d koordintene: cos, sin. sin tn. cos Med utgngspunkt i denne definisjonen (og Pytgors' setning) får vi t: sin cos Ved hjelp v enhetssirkelen kn vi sette opp følgende: sin sin cos cos tn tn sin sin cos cos tn tn Det gjelder også t: cos sin( ) sin cos( ) Det kn vises t grfen til en sinusfunksjon og en cosinusfunksjon hr fseforskjell. 9
45 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no) 4.5 Noen kjente vinkler Vinkel Rdiner sin cos tn 0 o o o o Grfene til sinus, cosinus og tngens Sinusfunksjon Cosinusfunksjon Tngensfunksjon y sin 0 y cos 0 y tn 0 Legg merke til t perioden til sin og cos er, mens for tn er den : sin sin( ), cos cos( ), tn tn( ) Husk: Grfen til en sinusfunksjon og en cosinusfunksjon hr fseforskjell: cos sin( ) eller sin cos( ) 40
46 Kpittel Trekntberegninger (trigonometri i grder) Cosinussetningen: b c bc cos( A) Sinussetningen: sin( A) sin( B) sin( C) b c 4.8 Trigonometriske formler Grunnleggende formler: sin cos tn sin cos cot tn Trigonometriske formler for y sin( y) sincos y cos sin y, cos( y) cos cos y sin siny tn tn y tn( y) tn tny Trigonometriske formler for sin sincos cos cos sin cos sin Andre formler: cosu cosv (cos(u v) cos(u v)) sinusin v (cos(u v) cos(u v)) sinu cosv (sin(u v) sin(u v)) Eksempel 4. Finn ekskte verdier for: ) sin 5 6 (Hint: Bruk tbell i delkpittel 4.5) ) c) tn 5 4 c) cos 5 4
47 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no) 4.9 Beskrivelse v et periodisk fenomen ved hjelp v en cosinus- /sinuskurve y C0 C cos ( t t0) og y C0 C sin ( t t0) T T der: C 0 er middelverdi (likevektslinje), er C mplitude, T er periode og sirkelfrekvens er gitt ved. t T 0 klles krofse. Noen eksempler for å studere disse prmetrene: y C0 C sin ( 0 ) C 0 = 0, C, T Amplitude C er fordoblet Sirkelfrekvens er fordoblet y sin y sin og y sin y sin og y sin C 0 Likevektslinje C0 Akrofse t 0 0 C =, C, og t 0 y sin og y sin y sin og ysin( ) y sin ( ) Eksempel 4. Grfen til en periodisk funksjon er tegnet her. Funksjonen kn uttrykkes ved: y C0 C sin ( 0 ) Bestem de ukjente prmetrene C 0, C, T og sirkelfrekvens ved T C 0 =, C =, og 0 0. T 4 cos( /) sin( ) eller sin( / ) cos( ) 4
48 Kpittel Den periodiske funksjonen: f ( t) cost bsint Omforming til funksjonen som en cosinusfunksjon: cos t bsin t C cos ( t t ) der C b og tn( t0) 0 b Husk t ( C, t 0 ) er polrkoordintene til punktet (,, og dermed hørert0 til smme kvdrnt som punktet (,. Eksempel 4.4 Gitt funksjonene: ) f ( t) cost sin t f ( t) cost sint Skriv dem på formen C cos ( t t0) og tegn grfen. ) C b og b tn( t0 ) t0 t0 6 f ( t) cos ( t ) og grfen blir d: C b og b tn( t0 ) t0 t0 f ( t) cos ( t ) og grfen blir d: 4
49 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no) 4. Ligninger på formen: sin( ) b der 0. Vi skl løse ligningen: sin( ) b eller sin( ) b b og dermed sin ( ) (Her kn du bre tste SHIFT SINUS( b ) eller INV SINUS( b ) på klkultoren. Du må først sjekke t klkultoren et innstilt på Rdin.) Vi må huske t sin( ) lltid sin( ) omløp ( 0 ), eller: b gir to vinkler og i første b og sin ( ) b sin ( ) De generelle løsningene med uendelig mnge vinkler er d: b b og n sin ( ) der n 0,,, n sin ( ) Ligningen sin( ) der som forklring løses på tilsvrende måte. Her er enhetssirkelen tegnet Eksempel 4.5 Løs ligningene når ) 6sin 7sin c) 7sin 44
50 Kpittel 4 ) 6sin sin 6 sin ( ) ( sin ( ) er en kjent vinkel. Se tbell i 4.5) Hvis det ikke vr ngitt 0, ville løsningene være: 5 n og n 6 6 7sin sin 7 7 0, 9,85 sin ( ) 0, 879 0, 9 Hvis det ikke vr ngitt 0, ville løsningene være: 0, 9 n og,85 n der n 0,,, c) 7sin 7 ( 0, 879), 4 sin ( ) 0, 879 ( 0, 879) 5,99 6 Hvis det ikke vr ngitt 0, ville løsningene være: 6 n og,4 n der n 0,,, 4. Ligninger på formen: cos( ) c der 0. c Vi skl løse ligningen: cos( ) c eller cos( ) c cos ( ) Her kn du bre tste SHIFT COSINUS( c ) eller INV COSINUS( c ) på klkultoren. Du må først sjekke t klkultoren er innstilt på Rdin. c Vi må huske t når cos( ) lltid cos( ) gir to vinkler i første omløp (0 ) c c cos ( ) og cos ( ) De generelle løsningene med uendelig mnge vinkler er d: c c og n cos ( ) der n 0,,, eller n cos ( ) c., n cos ( ) 45
51 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no) Eksempel 4.6 Løs ligningene når 0 ) 6cos 7cos c) 7cos ) 6cos cos 6 cos ( ) ( 5 cos ( ) er en kjent vinkel. Se tbell i 4.5) Hvis det ikke vr ngitt 0, ville løsningene være: 5 n og n 7cos cos 7 7 cos ( ), 79, 8, 8 5,5 Hvis det ikke vr ngitt 0, ville løsningene være:, 8 n og 5,5 n der n 0,,, c) 7cos 7 cos ( ), 04, 0,0 4, 7 4, Hvis det ikke vr ngitt 0, ville løsningene være: n og 4, n der n 0,,, 46
52 Kpittel 4 Oppgver Kpittel 4 Oppgve 4. L være en vinkel i. kvdrnt. Finn (uten å bruke klkultor) sin og cos når: ) tn tn c) tn 5 Oppgve 4. Løs ligningene: ) 5 cos = 0, [0, sin + = 0, [0, c) 4 tn + =, [0, Oppgve 4. ) 7 Gitt cos v og v [70, 60 ]. Bestem sin v og tn v. 5 Vis t cos ( ) 4 sin ( ) cos sin 6 c) 8 Gitt cos v og v [, ]. Bestem sin v og sin v, cos v og tn v. 7 Oppgve 4.4 I treknt ABC er vinkel B = 8.5, = 74.0 og b = 9.5 ) Finn de øvrige sidene og vinklene i treknten. Finn lengden v vinkelhlveringslinjen fr vinkel C. Oppgve 4.5 I en treknt ABC er følgende oppgitt. Du skl regne ut lle de tre sidene og de tre vinklene. ) = 4,7 cm, c=6,9 cm og C 56. c = 7, cm, A 5 og C 7 c) B 48, =8,0 cm og c= 6, cm Oppgve 4.6 I treknt ABC er AB =.9, BC = 6.4, vinkel C =.5, og vinkel A er stump. Bestem vinkelen A. 47
53 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no) Oppgve 4.7 Figuren viser treknt ABC, hvor vinkel C er stump. Målene fremgår v figuren. ) Bestem vinkel C. Bestem relet v treknten ABC. Oppgve 4.8 Figuren viser en treknt ABC, hvor vinkel A = 5.8 og AB = 5.5. Arelet v treknten er 4.4. Bestem AC og BC. Oppgve 4.9 En byggegrunn hr form som en firknt ABCD, hvor vinkel A = 80, vinkel B = 60, vinkel C = 05, AD = m og AB = 50 m. ) Tegn en modell v byggegrunnen, og bestem lengden f digonlen BD. Bestem relet v byggegrunnen. Oppgve 4.0 En treknt ABC er bestemt ved t = 9, b = og c = 0. ) Bestem størrelsen v vinkel A. Bestem relet v treknt ABC. Oppgve 4. I treknt ABC er vinkel A = 6., AC = 5.0 og BC =.0. Vinkel C er stump. ) Bestem vinklene B og C. Bestem AB. c) Bestem lengden v medinen m c. Oppgve 4. En byggegrunn hr form som en firknt ABCD. Tre v sidene hr følgende lengder: AB = 5.7 m, BC = 5. m og CD =.8 m. Lengden v digonlen AC er målt til 8. m. Endelig er vinkel D målt til 94. ) Bestem vinkel B. Bestem byggegrunnens rel. 48
54 Kpittel 4 Oppgve 4. På figuren ses en treknt ABC, hvor M er midtpunktet v siden AC. De kjente målene fremgår v figuren. Videre opplyses det t vinkel ABM er stump. ) Beregn vinkel ABM og AC. Beregn BC og vinkel B i treknten ABC. c) Beregn relet v treknt ABC. Oppgve 4.4 Figuren viser en skisse v en gvlkonstruksjon i et sommerhus. De kjente målene fremgår v figuren. ) Bestem lengden v bjelkene AB og BD. Bestem lengden v bjelken BC smt vinkel BCD. Oppgve 4.5 Figuren viser en firknt ABCD hvor digonlen BD er inntegnet. De kjente firkntens mål fremgår v figuren. ) Beregn BD Beregn vinkel D i treknt BDC. c) Beregn CD. d) Beregn AC. Oppgve 4.6 Gitt treknten på figuren til høyre.. Vis t bcos C ccos B b. Bruk så sinusproporsjonen til å vise t sin A sin Bcos C sin C cos B Oppgve 4.7 I treknten ABC er AB=7 cm, BC=4 cm og AC= 6 cm. Hlveringslinjen for vinkel C deler AB i stykkene og y. Beregn disse stykkene. Gjent utregningen når AB=c, BC= og AC=b. 49
55 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no) Oppgve 4.8 I treknten ABC er C 90, A 0 og AB=s. Hlveringslinjen for C deler AB i to stykker. Beregn disse stykkene uten å bruke tilnærmingsverdier. Oppgve 4.9 Gitt en treknt ABC med sidelengder 4, 5.5, og 8 enheter. Finn vinkelene til treknten. Oppgve 4.0 ) Bruk grfene til sin, cos og tn til å vise t: sin sin cos cos sin sin cos cos Vis de smme smmenhengene ved hjelp v enhetssirkelen og definisjonene v sin og cos. Oppgve 4. ) Benytt 45 o + 0 o = 75 o til å finne ekskte verdier for sin 75 o og cos 75 o. o o o Benytt 45 0 =5 til å finne ekskte verdier for sin 5 o og cos 5 o. Oppgve 4. ) Tegn grfen til funksjonen: f 4 cos( ), [0,4] Funksjonen forteller hvor høyt sol står på himmelen et sommerdøgn et sted nord for polrsirkelen. Vi kller denne høyden over horisonten for solhøyden og måler den i grder. Finn solhøyden kl og kl c) Når vr solhøyden o? d) Når stod sol på det høyeste? Hvor høyt stod sol d? Oppgve 4. Skriv funksjonene nedenfor på formen f C cos v : ) f sin 4cos f cos sin Oppgve 4.4 Grfen til en funksjon på formen y c sin( ( 0 )) er gitt: () ( Bestem c,, og 0. 50
56 Kpittel 4 Fsit Kpittel 4 4. ) Du kn tenke deg en rettvinklet treknt der lengden til kteten motstående for vinkelen er og hosliggende er, det vil si tn. Lengden til hypotenusen er d ( ). Vi få d sin og cos. Vi kn bruke smme metode for del og c) c) sin og cos. 5 sin og cos. 4. ) 5 cos = 0 5 cos cos 5 Vi bruker klkultoren og får frm den ene løsningen.,6 Den ndre løsningen finner vi ved å tegne enhetssirkelen. =,6 = 5, De to løsningene på ligningen er =,6 og = 5, 5
57 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no) sin + = 0, [0, sin sin Vi tegner enhetssirkelen og finner to løsninger.. Vi får to treknter der AOP = og BOP =. Av symmetrigrunner får vi d løsningene: De to løsningene på ligningen er 5 og eller c) 4 tn + =, [0, 4tn 9 tn 4 Klkultoren gir løsningen,5 Den generelle løsningen er d,5 n Ettersom løsningen skl være i første omløp, må [0,. n = =,5 +,4 =,99 n = =,5 +,4 = 5, Løsningene er d : =,99 og = 5, 5
58 Kpittel ) cos v og v [70, 60 ] 5 Enhetsformelen gir cos v sin v eller sin v cos v sin v Ettersom v [70, 60 ], er sin v negtiv. Det gir Definisjonen v tn v gir 4 sin v 5 4 sin v 5 c) sin v tn v = cos v cos ( ) 4 sin ( ) 6 (cos cos sin sin ) 4(sin cos cos sin ) 6 6 (cos ( ) sin ) 4(sin cos ) cos sin sin cos cos sin 8 cos v og v [, ] 7 cos v sin v eller sin v cos v sin v sin v Ettersom v [, ], er sin v positiv. Det gir 7 5 sin v sin v sin v cos v ( ) cos v sin v sin v tn v cos v
59 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no) 4-4 ) A = 5.5, C = 45., c = 66.0 v c = ) c sin C 4.7 sin A sin , A 4.4 sin C sin A c 6.9 B b c c 6.9cm b sin B sin cm sin B sin C sin C sin 56 c c 7,cm sin A sin cm sin A sin C sin C sin 7 B c sin B 7.cm sin 57 b 6.cm sin C sin 7 c) b c c cos B cos cm b sin B 8.0 sin 48 sin A 0.99, A 8 sin A sin B b 6.0 C b c Sinussetningen gir sin B sin, b c C. Dermed blir sin A sin B sin C sin A sin A sin B sin C ccos B bcos C cos C cos B. Vi dividerer denne likheten med sin A sin A og multipliserer sin A: sin A sin Bcos C sinc cos B. Siden sin( B C) sin(80 B C) sin A, følger t sin( B C) sin Bcos C sin C cos B 4.6 ) A = ) C = rel ) AC =.0, BC =
60 Kpittel ) BD = 50.8 m 00 m 4.0 ) A = 47. rel ) B = 47., C = 06.7 AB = 6.5 c) m c =.5 4. ) B = ) vinkel AMB = 6.5, AC =.9 BC = 5., B =.4 c) ) AB =.4 m, BD =.4 m BC = 5.5 m, vinkel BCD = ) BD = 7. vinkel BDC = 8.4 c) CD =.9 d) AC = ) Det er lett å vise ved hjelp v figuren bcos C ccos B c Det fremgår ved å dele begge sider b: cosc cos B b b sin sin sin Vi vet t sin A c sin C og dermed er: og. b c b sin B b sin B sin A sin C cos C cos B sin B sin B begge sider med sin B og får svret: sin A sin Bcos C sin C cos B 4.7 Se figuren til høyre. Ifølge setningen om delingsforhold og 6 hlveringslinje er y, vi får dermed 4 y. Vi hr også y 7. D må 7 y y, og vi får 5 7 y og dermed: 4 4 y, Når AB=c, BC= og AC=b, må y c og AC b og y BC c c b c og y,. b b b b y. D må b y c 55
61 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no) 4.8 I denne treknten er AB=s, BC s, AC s. Setningen om vinkelhlveringslinjenes deling v den motstående siden i en treknt gir d / AC AD AD og herv AD s AD, AD / BC BD s s AD 4.9 s AD s s BD AB AD s Vi setter = 5.5, b= 8, og c= 4, Vi finner vh cosinussetningen: Her lønner det seg å omforme b c bc cos slik t vi får lene på den ene b c 8 4 5,5 49,75 siden: cos bc cos (0,78) 8,74 Vi bruker sinusproporsjonen for å finne sin sin c sin 4sin(8, 74) sin 0, 46 c 5,5 sin 0, 46 sin 0,46 7,4 o og dermed: o o o 80 (8,74 7, 40 ), ) Det fremgår ved å tegne grfene og se t disse er like. Det fremgår ved å tegne enhetssirkelen og tegne inn vinklene og se t deres sin og cos er like. 4. ) sin 75 o 6 4 cos75 o 6 4 sin5 o 6 4 cos5 o ) o og 5 o Kl (kl. 4.00) c) Ved midntt (00.00), kl og kl d) Høyeste: kl ) C 5, v tn 0, 645, 49 4 C, 5 v tn 4.4 ) y5 sin y 5 sin ( 0,5) eller y5sin 56
62 Kpittel 5 Kpittel 5 Grenseverdi og kontinuitet 5. Grenseverdi L y f ( ) være en funksjon som er definert om et punkt, men ikke nødvendigvis i selve. Når vribelen går mot punktet, dersom funksjonen nærmer seg en verdi A, skriver mn: lim f ( ) A Noen regneregler for grenser Ant t lim f ( ) A, lim g ( ) B. D gjelder følgende: lim f ( ) g( ) A B lim ( ) ( ) f g AB f ( ) A lim ( B 0 ) g ( ) B 5. Grenseverdi f( ) 0 lim g ( ) 0 f( ) 0 I dette vsnittet skl vi se nærmere på tilfellet når lim og i delkpittel 4.5 når g ( ) 0 f( ) lim. Dersom det er mulig, kn vi fktorisere telleren og nevneren med ( ). g ( ) Ellers kn L'Hôpitls regel benyttes. 9 Nedenfor følger noen eksempler. Eksempel 5. Bestem grenseverdiene: 4 ) lim lim c) lim d) lim sin 5 9 e) lim f) lim 0 9 sin 5 sin 5 Fsit: ) 4 c) d) lim lim5 5 e) 6 f) sin lim 0 sin lim 0 b b tn lim 0 tn lim 0 b b sin sin lim lim 0 b 0 b b
63 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no) 5. Ensidig grense lim og lim For å undersøke kontinuitet til noen funksjoner som f( ) eller f( ) 4 er det nødvendig å studere grenseverdiene på høyre og venstre side. Eksempel 5. Bestem grenseverdiene: ) lim lim c) lim( ) 0 Fsit: ) Eksisterer ikke( ) c) Eksisterer ikke( ) 5.4 Kontinuitetsbegrepet En funksjon y f ( ) er kontinuerlig i punktet dersom grenseverdien eksisterer om dette punktet og er lik funksjonsverdien: lim f ( ) f ( ) Eksempel 5. Undersøk om følgende funksjoner er kontinuerlige i det ngitte punktet: 5 5 ) f( ) i g ( ) i 5 Fsit: ) J Nei (grenseverdi eksisterer ikke) 58
64 Kpittel Noen ord om grenseverdi når f( ) lim g ( ) n n 0 n n ( n ) n n n 0 lim lim m m b m bm b0 m bm b 0 ( bm ) m 0 n m n nm n lim n m bm bm nm når grenseverdien går mot, sier mn t grenseverdien ikke eksisterer. Eksempel 5.4 Bestem grenseverdiene: ) lim lim c) 5 lim 4 8 d) lim 9 Fsit: ) 0 c) d) 5.6 Asymptoter Asymptoter til grfen for y f ( ) er rette linjer, som ikke kn skjelnes fr grfen i det fjerne. Vi skl se nærmere på tre typer symptoter: y y Vertikl symptote: y Horisontl symptote: y Vertikl symptote: 0 y Skrå symptote: y 59
65 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no) Eksempel 5.5 Bestem eventuelle symptoter til: 5 ) y y c) y d) y 4 Fsit: ), y y c), y 0 d) 0, y Eksempel 5.6 Bestem grenseverdiene: 9 ) lim( ) ( ) lim c) lim d) lim( ) ( ) 7 5 n Fsit: ) (Eksisterer ikke) 0 c) d) 0 n n n 5.7 Tllet e Tllet e klles Eulers konstnt (Eulertllet) etter den sveitsiske mtemtikeren Leonhrd Euler og Npiers konstnt etter den skotske mtemtikeren John Npier. Konstnten e ble først omtlt i 68 i en tbell i tilleggsnottet til et verk om logritmer v John Npier. Selve konstnten vr ikke inkludert, men en rekke nturlige logritmer ble beregnet. Den første kjente nvendelsen v konstnten, d representert med en b, vr i en brevveksling mellom Gottfried Leibniz og Christin Huygens i 690 og 69. Noen mener t e står for "eksponentiell", siden tllet e er det nturlige vlget til grunntll i en eksponentilfunksjon. Leonhrd Euler strtet å bruke bokstven e om konstnten i 77, og den ble først brukt som e i Eulers Mechnic som ble publisert i 76 som er tilnærmet lik: e,788 Oppdgelsen v konstnten i seg selv krediteres Jkob Bernoulli, som forsøkte å finne verdien til det følgende uttrykket, som kn brukes som en definisjon v e: n lim e, 788 n n Euler-tllet kn også uttrykkes ved: e!! 60
66 Kpittel 5 Oppgver Kpittel 5 Oppgve 5. cos I) Bestem grenseverdiene: ) lim f( ) lim 0 II) For funksjonene f og g vet vi t lim f( ) og lim g ( ) 5. Bestem grenseverdiene: ) lim f ( ) g( ) lim f ( ) g( ) c) lim f( ) Oppgve 5. Bestem grenseverdiene: 9 ) lim d) lim lim e) lim 9 c) lim 9 f) lim g) lim 7 h) lim i) lim 5 j) sin lim 0 k) tn lim 0 sin l) lim Oppgve 5. Funksjonene f, g og h er gitt ved: f ( ) 5 7 g( ) h ( ) ) Vis t funksjonene f, g og h er kontinuerlige for. Vis t funksjonene f og g er kontinuerlige for lle punkter. c) Hvilke krv må vi stille for t h skl være kontinuerlig i? Oppgve 5.4 En funksjon er definert ved: sin når 0 f når 0 Beregn lim 0 f. Er f kontinuerlig for 0? Oppgve 5.5 Finn eventuelle vertikle symptoter til funksjonen. ) f( ) f( )
67 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no) Oppgve 5.6 Finn eventuelle horisontle symptoter til f når: 0 t 9 ) f( ) f() t t 7 Oppgve 5.7 For hver v funksjonene skl du bestemme: ) Nullpunktene ) De vertikle symptotene ) De horisontle symptotene ) 5 f( ) 5 4 f( ) 76 ( 56) Oppgve 5.8 Finn den skrå symptoten til funksjonene: ) y 8 7 y 8 Oppgve 5.9 Bestem det minste leddet i uttrykket når: n : f( n) (0,99) (,05) n n n Oppgve 5.0 Bestem grenseverdiene: 4 5 ) lim( ) ( ) 4 lim d) lim e) lim c) lim 5 7 f) lim( ) ( ) 5 n n n n Oppgve 5. En funksjon er definert ved: 9 når f når Beregn lim f. Bestem slik t f kontinuerlig i Oppgve 5. En funksjon er definert ved: Beregn lim f f når når. Er f kontinuerlig i? 6
68 Kpittel 5 Fsit Kpittel 5 5. I) ) II) ) 8 5 c) 9 5. ) 6 c) 6 d) e) 0 f) g) h) 0 i) Eksisterer ikke j) k) / l) 5. c) 5.4 J,. 5.5 ) 5, 5, ) y y ) , 6.,. 5.8 ) y y y 5 y 5.9 (,05) n er det minste leddet. Grenseverdi eksisterer ikke. 5.0 ) Eksisterer ikke 0 c) 8 5 d) 0 e) 0 f) , 6 5. Grenseverdi eksisterer ikke ( ): 0 ( )( ) lim = = lim lim ( ) ( ) 0 ( ) 0 ( )( ) lim = = lim lim ( ) ( ) 0 ( ) I nvendelsen v mtemtikk ønsker vi ofte å finne ut hvor rskt en størrelse er i ferd med å endre seg. Derivsjon hndler om endring v en vribel i forhold til en nnen vribel. I denne smmenhengen benyttes ofte begrepene momentn hstighet og vekstrte. Ved å finne den deriverte til en funksjon i et punkt på en kurve, finner du stigningstllet kkurt der, og denne kn klles vekstrten for dette punktet (momentn hstighet). 6
69 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no) Kpittel 6 Derivsjon 6. Vekstrte Den gjennomsnittlige vekstrten er definert ved forholdet mellom endringen til den y vhengige vribelen og den uvhengige vribelen: 6. Definisjon, vekstrte dy y f ( ) f ( ) y f ( ) lim lim d 0 0 Eksempel 6. Bestem den deriverte til y ved hjelp v definisjonen til derivsjon. ( ) ( ) ( ) y lim lim lim lim Tolkninger y f ( 0 h) f ( 0) Gjennomsnittsfrt: h Dette kn tolkes som stigningstllet til seknten 0 gjennom to punkter (P og Q) på grfen til f. På grfen er det vist noen seknter. Momentn frt: dy y f ( 0 h) f ( 0) y f ( ) lim lim d 0 h0 h Dette kn tolkes som stigningstllet til tngenten i et punkt (P) på grfen til f og kn beskrive hvor rsk funksjonen endrer seg i dette punktet. Tngenten er vist på grfen (linjen L). 0 Seknten til en kurve er en rett linje som går gjennom to punkter som ligger på kurven. Tngenten til en kurve er en rett linje som berører kurven bre i ett punkt. 64
70 Kpittel Derivsjonsformler og derivsjonsregler y f ( ) y f ( ) Konstntledd k 0 Potensfunksjon y r r r r r ( ) r ( ) Eksponentilfunksjon med k k e e ( e ) ke grunntllet e Eksponentilfunksjon ln med grunntllet y Logritmefunksjoner ln log ln0 Den deriverte til bsoluttverdifunksjonen: f ( ) f ( ) for Viktige derivsjonsregler Enkle regler: ( y) y ( u v) u v ( u bv) u bv Viktige kjente regler:. Produktregelen. Kvotientregelen. Kjerneregelen [ u v] uv u v u u v u v [ ] v v dy dy du y y( u( )) d du d. Produktregelen: Eksempel 6. y cos u v u v u v y cos ( sin ) (cos sin ) u u v u v v v. Kvotientregelen: Eksempel 6. cos ( sin ) (cos ) sin cos y y 65
71 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no). Kjerneregelen: dy dy du y y( u( )) d du d Eksempel 6.4 ucos y ln(cos ) y ln( u) y u ( sin ) tn u cos Eksempel 6.5 d Bestem (sin ) og d ( k cos t ) d dt d (sin ) cos d ( k cos t ) k sin t d dt r 6.6 Den deriverte til og Formel Generell (kjerneregelen) u u ( e ) e ( e ) e u r ( ) Eksempel ( e ) e r r r r ( u ) r u u ( ) ( ) 6( ) Den deriverte til : ( ) ln Vi kn først omskrive uttrykket: e ln Husk t: ln ln ( ) ( e ) ln e ln Eksempel 6.6 Deriver: ) y (cos ) y ( ) c) 7 e y d) y e) 5 y k Fsit ) 6 y 7cos sin d) y ln e) y k 5 ln5 y 45 ( ) c) y 7 e 66
72 Kpittel Den deriverte med hensyn til : d d df Uttrykket f( ) kn oppfttes som den deriverte til f med hensyn til : d df f y f ( ) lim d 0 Kjerneregelen kn formuleres slik: dy dy du y y( u( )) (Leibniz-notsjon) d du d Eksempel 6.7 d 4 Bestem ( r ) dr Løsning: d 4 ( r ) 4r dr Eksempel 6.8 d 4 Bestem ( r ) når rdien forndrer seg med tiden. dt d 4 dr ( r ) 4r (kjerneregelen) dt dt Eksempel 6.8 kn også formuleres: 4 Bestem endringshstigheten til volumet til en kule gitt ved V r der rdien r forndrer seg med tiden. dv dv dr 4 dr dr Løsning: V V ( r( t)) kjerneregelen: ( r ) 4r. dt dr dt dt dt Det vil si t volumendringen pr. tid vhenger v kulens overflterel S 4 r Eksempel 6.9 Gitt funksjonen: f ( ). ) Bestem f( ) og vgjør hvor funksjonen vtr og hvor den vokser. Bestem f( ) og vgjør hvor funksjonen krummer oppover og hvor den krummer nedover. c) Tegn grfen til denne funksjonen. 67
73 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no) f ( ) 0 f ( ) f( ) Øker Synker Øker Mks. pkt. Min. pkt. er mksimumspunkt og er mksimumsverdi ( f ( ) ). er minimumspunkt og er minimumsverdi ( f () ). f ( ) 6 f ( ) Vendepunkt: (0, 0) 0 f ( ) f( ) Krummer nedover Krummer oppover Mks. pkt. Min. pkt. c) Grfen til f ( ) Nullpunktene: 0 ( ) 0 0 c) Grfen: 68
74 Kpittel Oversikt over derivsjonsformler og -regler y f ( ) dy y f ( ) d k 0 n n e ln sin cos cos Kjerneregelen u n u u n n n 0 e u Eksempel e e u ln u u ln u sin tn tn cos u k e 5 4 sin 5 sin cos ke ln u u ln( u b sin u cos u u sin( cos( cos u sin u u cos( sin( tn tn u u u u cos u tn( k cos ( 6.9 Derivert, nnenderivert og funksjonsdrøfting Monotoniegenskpene L y f ( ) være en funksjon definert i intervllet I. f( ) 0 i intervllet I f( ) er voksende i intervllet I f( ) 0 i intervllet I f( ) er strengt voksende i intervllet I f( ) 0 i intervllet I f( ) er vtgende i intervllet I f( ) 0 i intervllet I f( ) er strengt vtgende i intervllet I For å finne de enkelte intervllene der funksjonen er voksende eller vtgende, kn det være nyttig å gjøre bruk v et fortegnsskjem: X f ( ) f( ) Synker Øker Synker Min. pkt. Mks. pkt. Av fortegnet til f ( ) kn vi bestemme de lokle ekstremlpunktene. Dersom funksjonen er definert i et lukket intervll, bør eksistensen v eventuelle bsolutte og lokle ekstremlpunkter undersøkes. 69
75 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no) 6.0 Mksimum og minimum Ekstrempunkt: L c være et ekstrempunkt for f. Hvis c ligger i definisjonsmengden til f og f() c eksisterer, er f( c) 0. Bemerk t c kn være et ekstrempunkt uten t f( c) 0. (globlt mksimum/minimum) Eksistens v mksimums- og minimumspunkt L f være definert og kontinuerlig i et lukket intervll [, b ]. D finnes det både et mksimumspunkt og et minimumspunkt i dette intervllet. Krkterisering v ekstrempunkt L y f ( ) være definert og kontinuerlig i et begrenset lukket intervll [, ].. Finn de punktene der f( ) 0 og bestem funksjonsverdien der f( ) 0. Angi de endepunktene der f er definert. Bestem funksjonsverdien i endepunktene.. Finn de punktene i intervllet der den deriverte ikke eksisterer. (For eksempel: den deriverte til f ( ) er f( ). f ( ) eksisterer ikke i = 0) Smmenlign disse verdiene for å bestemme eventuelle LOKALE /GLOBALE mksimums- og minimumspunkter. A er globlt mksimumspunkt, B er globlt minimumspunkt, C og E er lokle mksimumspunkter, D er loklt minimumspunkt. Eksempel 6.0 Betrkt funksjonen f ( ),,5 Bestem eventuelle ekstremlpunkt(er). I eksempel 6.9 fnt vi t: er mksimumspunkt og er mksimumsverdi( f ( ) ). er minimumspunkt og er minimumsverdi ( f () ). f (,5) 8,5 f () 8 70
76 Kpittel 6,5 globlt minimumspunkt (globl minimumsverdi er f (,5) 8,5 ) loklt minimumspunkt (lokl mksimumsverdi er f ( ) ) loklt minimumspunkt (lokl minimumsverdi er f () ) globlt minimumspunkt (globl mksimumsverdi er f () 8 ) Metode for funksjonsdrøftning ) Bestem eventuelle nullpunkter og skjæringspunkter med ksene. ) Bestem eventuelle symptoter. ) Finn f ( ). Finn eventuelle nullpunkter til f ( ) (ekstrempunkter) og sett opp fortegnsskjem. 4) Finn f ( ). Finn eventuelle nullpunkter til f ( ) (vendepunkter). Den ndrederiverte (krumning og vendepunkt) d f d df f ( ) klles den ndrederiverte til f : f( ) ( ) (Leibniz-notsjon) d d d L f være en dobbel deriverbr funksjon i. Dersom er et vendepunkt, er f( ) 0. X f ( ) f( ) Krumning Krumning Krumning nedover oppover nedover Vendepkt. Vendepkt. Eksempel 6. Vis t f ( ) hr ett vendepunkt. Grfen er vist her. f ( ) 0 (krummer oppover) f ( ) (0,0) er vendepunktet. 6. Ligningen til tngenten og linerisering Ligningen til tngenten for en funksjon y f ( ) i et punkt som ligger på grfen er: y f ( ) f ( )( ) Det å linerisere en deriverbr funksjon i et punkt = er å bruke tngentlinjen til funksjonen i dette punktet: f ( ) f ( ) f ( )( ) 7
77 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no) Eksempel 6. Bestem ligningen til tngentlinjen i det gitte punktet og lineriser funksjonene. ) f ( ) sin i 0 f ( ) e i 0 Grfen til funksjonen og tngenten for del er tegnet her: Fsit ) y y Tilvekstformelen Vi tr utgngspunkt i lineriseringne v y f ( ) : f ( ) f ( ) f ( )( ). Eller f ( ) f ( ) f ( )( ) Dette kn omskrives som f ( ) f ( ) f ( ) Eksempel 6. Bestem hvor mye volumet til en kule vokser hvis rdien øker fr 0 til 0, cm og fr 0 til 4 0,0 cm. Volumet til en kule med rdien r er gitt ved: V r. Ved å nvende tilvekstformelen for å bestemme en tilnærmet verdi for volumendringen: dv V r og derivere formelen for volumet v en kule med hensyn på r får vi: dr dv 4 ( ) 4 r r dr V 4r r 4 (0) 0, 5,7 cm V 4r r 4 (0) 0, 0, 57 cm Vi kunne eventuelt regne ut den ekskte endringen ved: 4 4 V V. V ( r r ) (0, 0 ) 6,9 cm 4 4 V V. V ( r r ) (0,0 0 ),58 cm Dette eksempelet bekrefter t jo mindre r blir, jo mer nøyktig blir svret fr tilvekstformelen. 7
78 Kpittel 6 Oppgver Kpittel 6 Oppgve 6. Deriver funksjonene. ) f ( ) 5 g ( ) 5 Oppgve 6. Deriver funksjonene. ) f ( ), f ( ),5 Oppgve 6. Deriver uttrykkene med hensyn til. ) c) Oppgve 6.4 Deriver funksjonene. ) f ( ) ( ) f ( ) ( ) c) f ( ) ( 5 ) Oppgve 6.5 Deriver funksjonene ved hjelp v produktregelen. ) 4 f ( ) ( ) f ( ) ( )cos Oppgve 6.6 dy Bestem y ' når d 5 sin ) y 7 y 5 cos c) y cos d) y ( )sin e) y f) y g) y h) y i) y(5) j) m) y k) 4 y 5 n) y l) y ln o) y 00 ( 5 ) 4 cos y Oppgve 6.7 dy Bestem y d når ) sin y y cos 7
79 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no) Oppgve 6.8 Deriver funksjonene. ) Oppgve f ( ) 4 5 f ( ) c) y ( ) 5 5 ) Bestem vekstfrten for funksjonen: f ( ) 4 i et punkt med. Bestem tngentlinjen til funksjonen: g( ) i et punkt med som ligger på kurven til funksjonen. Oppgve 6.0 ) Bestem eventuelle topp- eller bunnpunkter til funksjonen: Bestem vendepunktet. Bestem eventuelle topp- eller bunnpunkter til funksjonen: Bestem vendepunktet. y y 6 4 Oppgve 6. Finn y når: ) y y c) y 5 5 f f d) Bruk formelen lim til å bestemme den deriverte v 0 Oppgve 6. Bestem eventuelle grenseverdier: f 64 ) lim lim c) lim d) lim 9 Oppgve 6. ) Gitt funksjonen f ( ) e. Bestem lim f( ) Vis t f ( ) e og ( ) f e og lim f( ) c) Bestem eventuelle nullpunkter, ekstremlpunkter og vendepunkter. 74
80 Kpittel 6 Oppgve 6.4 Et kurvestykke f 0 4 er gitt. Punktet, f P ligger på kurven. ) Finn ligningen for tngenten ved dette punktet P. ) Denne tngenten skjærer -ksen ved punktet P. Finn koordintene til P. Oppgve 6.5 En funksjon y, 0,0 er gitt. ) Bestem eventuelle ekstremlpunkter på kurven. Bestem det punktet på kurven hvor vstnden mellom kurven og punktet (0, ) er minst mulig. Oppgve 6.6 mm En kuleformet snøbll smelter med en konstnt frt på og kuleformen beholdes min hele tiden. Hvor fort vtr rdien v snøbllen i det øyeblikket rdien er lik 6 mm? Hvor fort vtr overflten v snøbllen i det smme tidspunktet? Oppgve 6.7 Ligningen til en funksjon er gitt: f ( ) Bestem: ) Området hvor funksjonen vtr og øker Ekstremlverdier c) Eventuelle vendepunkter og konkviteten d) Skisser kurven. Oppgve 6.8 Ligningen til en funksjon er gitt: f ( ) 4 4 Bestem: ) Ekstremlverdier Området hvor funksjonen vokser og vtr c) Eventuelle vendepunkter og konkviteten d) Skisser grfen. 4 0 ; 5,5 75
81 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no) Fsit Kpittel 6 6. ) ) 0,,,5 7,5 6. ) c) 6.4 ) 6( ) 4 ( ) c) ( 5 )( 5) 6.5 ) 5 6 f ( ) cos ( )sin 4 cos sin 6.6 ) 5 5 sin c) sin cos d) sin ( ) cos e) f) 4 ( ) g) h) 99 i) 00( 5) ( ) j) 8 ( ) k) l) ( 5 ) m) 6.7 ) ( 5 ) cos sin y sin cos n) (ln ) o) cos sin cos sin y cos sin ) f ( ) 5 4 f( ) 4 c) y 5( ) ( ) ) f ( ) 5 8 og dermed er vekstfrt i : f ( ). Ligningen til tngenten i : f ( ) f ( ) f ( )( ) y f ( ) f ( )( ) y 4 y 5 f f ( ), ( ) 76
82 Kpittel ) Topp- og bunnpunkt: (, 8) (, 4) og vendepunkt: (0, ) Topp- og bunnpunkt: (0, 4) (4, 8) og vendepunkt: (, ) 6. 5 ) y 5 y 4 y y ( 5) c) y y ( 5) 5 ( 5 ) ( 5 ) ( 5) d) f( ) f ( ) f ( ) f ( ) f ( ) f ( ) f ' lim lim lim 0 0 ( )( ) 0 ( )( ) ( )( ) 6. Bemerk t mn kn også bruke L Hopitls regel ) lim lim lim lim lim lim lim 0 0 c) lim lim lim lim ( ) d)lim lim ( ) Dermed grenseverdi eksisterer ikke 6. ) 0, (ingen grenseverdi) Nullpunkt (0, 0) ekstremlpunkter (, ), vendepunkter (0, 0) (, ) og e e e f f ' y y 6.4 ) ) (, ) e e y 0 0, (, 0) (, ) e og 77
83 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no) 6.5 dy ) y ; 0,0 ; y 0 0; dette gir d y hr bsolutt minimum ved. Kontroll vh fortegnskjem. vstnd S ( 0) ( ) ( ) ( ) ( ) ( ) ds d Avstnden er minst ved O t do dt 6.7 ) 4 r r6 mm do dt 8 r 8 6 mm 4 dr dt mm 6 min mm min f f ( ) ; 5, 5, ( ) 4 0 0, 4 ( ) 0 0, vh fortegnsskjem finner vi t f vokser, 5 og vtr 5, f hr rel. min ved. f ( ) 4 0 ( ) 0 0,, ved fortegnsskjem finner vi krumning oppover 5, 0, krumning nedover 0,, vendepunkt : (0, 0) (, 6) 6.8 ( 4) ( ) 0 f ( ) f ( ) 0, 0 0, 0 4 ( 4) ( 4) f vokser, og, 0 vtr 0, og, rel. mks ved 0 ( 4) ( 0) 0 (( 4)( )) 0 4 ( ) 0, f får ingen reelle ( 4) ( 4) verdier, dermed ingen vendepunkter. Krumning oppover, og, krumning nedover,. 78
84 Kpittel 7 Kpittel 7 Integrsjon Integrsjonskonstnt f ( ) d F( ) C, og det gjelder: F( ) f ( ) Integrnd Anti-deriverte til f ( ) 7. Det bestemte integrlet som rel Arelet vgrenset v grfen til en funksjon og -ksen i et bestemt intervll [, b] kn beregnes ved hjelp v et bestemt integrl: f ( ) d. b RIEMANN-SUM Det bestemte integrlet kn skrives som grensen til en sum. Riemnn-sum hndler om å summere uendelig mnge uendelig små reler. Vi skl prøve å benytte summen til relene til mnge rektngler som en god tilnærming for relet under grfen til en begrenset kontinuerlig integrerbr funksjon. Integrsjonsintervllet [, b] deles i n deler:,,,,,, 0, b n, n der 0 n Delintervllene hr ikke nødvendigvis smme lengder. i i i, i,, n Vi kn sette opp øvre og nedre Riemnn-sum henholdsvis: n i * i S S Sup f ( ) * der ( i ) i Sup f er supremum til f( ) i delintervllet n i * i S S Inf f ( ) * der ( i ) i Inf f er infimum til f( ) i delintervllet i, i. i, i. n n i n n * * Sup f i i ( i ) lim ( ) lim n i Inf f Når denne grenseverdien eksisterer, skriver vi Riemnn-summen som bestemt integrl: i n S lim f ( ) f ( ) d F( ) F( F( ) i0 n i b b 79
85 Forkurs i mtemtikk UiB (Amir.Hshemi@mth.uib.no) 7. Det bestemte integrlet Som vist i forrige vsnitt, kn relet vgrenset v kurven til funksjonen y f ( ) og - ksen i intervllet b beregnes ved hjelp v det bestemte integrlet: Eksempel 7. b A f ( ) d F ( ) F( F( ) Bestem relet vgrenset v grfen til y, -ksen i intervllet [0,] d 7. Det ubestemte integrlet b Antideriverte til f ( ) Integrsjonskonstnt f ( ) d F( ) C og d gjelder: F( ) f ( ) Integrnd 7.4 Integrsjonsformler n n d C n, n cos d sin C d ln C sin d cos C e d e C tn d ln cos C d C d C ln tn cos 7.5 Regneregler for bestemt og ubestemt integrl Noen regler for bestemt integrl: b b b f ( ) d F( ) F( F( ) f ( ) d 0 f ( ) d f ( ) d b c c b f ( ) d f ( ) d f ( ) d der bc b Noen regler for ubestemt integrl: f ( ) d F( ) C Lineritetsegenskpen: k f ( ) d k f ( ) d der k er konstnt [ ( ) Bg( )] d A f ( ) d B g( Af ) d Uegentlig integrl: t f ( ) d lim f ( ) d (se oppgve 7.6 t Hvis grensen eksisterer, konvergerer integrlet, ellers er det divergent 80
Sammendrag kapittel 1 - Aritmetikk og algebra
 Smmendrg kpittel 1 - Aritmetikk og lgebr Regneregler for brøker Utvide brøk: Gng med smme tll i teller og nevner. b = k b k Forkorte brøk: del med smme tll i teller og nevner. b = : k b : k Summere brøker:
Smmendrg kpittel 1 - Aritmetikk og lgebr Regneregler for brøker Utvide brøk: Gng med smme tll i teller og nevner. b = k b k Forkorte brøk: del med smme tll i teller og nevner. b = : k b : k Summere brøker:
Oppfriskningskurs i matematikk Kompendium Notater, eksempler og oppgaver med fasit/løsningsforslag 1 Høsten 2017 Amir Massoud Hashemi
 Oppfriskningskurs i mtemtikk Kompendium Notter, eksempler og oppgver med fsit/løsningsforslg Høsten 07 Amir Mssoud Hshemi Sist oppdtert 5. ugust 07 i Innhold Forord... Kpittel 0 Test deg selv... Oppgver
Oppfriskningskurs i mtemtikk Kompendium Notter, eksempler og oppgver med fsit/løsningsforslg Høsten 07 Amir Mssoud Hshemi Sist oppdtert 5. ugust 07 i Innhold Forord... Kpittel 0 Test deg selv... Oppgver
Oppfriskningskurs i matematikk Kompendium Notater, eksempler og oppgaver med fasit/løsningsforslag 1 Høsten 2016 Amir Massoud Hashemi
 Oppfriskningskurs i mtemtikk Kompendium Notter, eksempler og oppgver med fsit/løsningsforslg Høsten 06 Amir Mssoud Hshemi Sist oppdtert. ugust 06 i Innhold Forord... Kpittel 0 Test deg selv... Oppgver
Oppfriskningskurs i mtemtikk Kompendium Notter, eksempler og oppgver med fsit/løsningsforslg Høsten 06 Amir Mssoud Hshemi Sist oppdtert. ugust 06 i Innhold Forord... Kpittel 0 Test deg selv... Oppgver
Oppfriskningskurs i matematikk 2007
 Oppfriskningskurs i mtemtikk 2007 Mrte Pernille Htlo Institutt for mtemtiske fg, NTNU 6.-11. ugust 2007 Velkommen! 2 Temer Algebr Trigonometri Funksjoner og derivsjon Integrsjon Eksponensil- og logritmefunksjoner
Oppfriskningskurs i mtemtikk 2007 Mrte Pernille Htlo Institutt for mtemtiske fg, NTNU 6.-11. ugust 2007 Velkommen! 2 Temer Algebr Trigonometri Funksjoner og derivsjon Integrsjon Eksponensil- og logritmefunksjoner
Brøkregning og likninger med teskje
 Brøkregning og likninger med teskje Dette heftet gir en uformell trinn for trinn gjennomgng v grunnleggende regler for brøkregning og likninger. Dette er sto som vi i FYS 000 egentlig forventer t dere
Brøkregning og likninger med teskje Dette heftet gir en uformell trinn for trinn gjennomgng v grunnleggende regler for brøkregning og likninger. Dette er sto som vi i FYS 000 egentlig forventer t dere
Eksamen våren 2016 Løsninger
 DEL Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med centimetermål og vinkelmåler Oppgve,8,8 (,8 ) 3,6 3, 6 3, 6,5 5, (5, ) Oppgve 3, 5 Vi ser på tllinj t,5 tilsvrer punkt F. Vi ser
DEL Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med centimetermål og vinkelmåler Oppgve,8,8 (,8 ) 3,6 3, 6 3, 6,5 5, (5, ) Oppgve 3, 5 Vi ser på tllinj t,5 tilsvrer punkt F. Vi ser
5: Algebra. Oppgaver Innhold Dato
 5: Alger Pln resten v året: - Kpittel 6: Ferur - Kpittel 7: Ferur/mrs - Kpittel 8: Mrs - Repetisjon: April/mi - Eventuell offentlig eksmen: Mi - Økter, prøver, prosjekter: Mi - juni For mnge er egrepet
5: Alger Pln resten v året: - Kpittel 6: Ferur - Kpittel 7: Ferur/mrs - Kpittel 8: Mrs - Repetisjon: April/mi - Eventuell offentlig eksmen: Mi - Økter, prøver, prosjekter: Mi - juni For mnge er egrepet
1T kapittel 8 Eksamenstrening Løsninger til oppgavene i læreboka
 T kpittel 8 Eksmenstrening Løsninger til oppgvene i lærebok Uten hjelpemidler E b c E b c Vi gnger vnlige tll med vnlige tll og tierpotenser med tierpotenser. Til slutt omformer vi svret så vi får et tll
T kpittel 8 Eksmenstrening Løsninger til oppgvene i lærebok Uten hjelpemidler E b c E b c Vi gnger vnlige tll med vnlige tll og tierpotenser med tierpotenser. Til slutt omformer vi svret så vi får et tll
Integrasjon Skoleprosjekt MAT4010
 Integrsjon Skoleprosjekt MAT4010 Tiin K. Kristinslund, Julin F. Rossnes og Torstein Hermnsen 19. mrs 2014 1 Innhold 1 Innledning 3 2 Integrsjon 3 3 Anlysens fundmentlteorem 7 4 Refernser 10 2 1 Innledning
Integrsjon Skoleprosjekt MAT4010 Tiin K. Kristinslund, Julin F. Rossnes og Torstein Hermnsen 19. mrs 2014 1 Innhold 1 Innledning 3 2 Integrsjon 3 3 Anlysens fundmentlteorem 7 4 Refernser 10 2 1 Innledning
1T kapittel 6 Geometri Løsninger til oppgavene i læreboka
 T kpittel 6 Geometri Løsninger til oppgvene i læreok Oppgve 6. Vi ruker pytgorssetningen. h 5 + 6 h 5 + 36 h 6 h ± 6 Hypotenusen er 6. Vi ruker pytgorssetningen. h, 4 + 6,7 h h 5, 076 + 45, 04 50, 047
T kpittel 6 Geometri Løsninger til oppgvene i læreok Oppgve 6. Vi ruker pytgorssetningen. h 5 + 6 h 5 + 36 h 6 h ± 6 Hypotenusen er 6. Vi ruker pytgorssetningen. h, 4 + 6,7 h h 5, 076 + 45, 04 50, 047
R2 - Heldagsprøve våren 2013
 Løsningsskisser HD R R - Heldgsprøve våren 0 Løsningsskisser Viktigste oppsummeringer: Må skrive med penn på eksmen! Slurv og regnefeil, både med tll og bokstver, er hovedproblemet. Beste måten å fikse
Løsningsskisser HD R R - Heldgsprøve våren 0 Løsningsskisser Viktigste oppsummeringer: Må skrive med penn på eksmen! Slurv og regnefeil, både med tll og bokstver, er hovedproblemet. Beste måten å fikse
R1 kapittel 1 Algebra
 Løsninger til oppgvene i ok R1 kpittel 1 Alger Løsninger til oppgvene i ok Oppgve 1.1 1 8 4 ( ) 15 5 (4 ) 7 1 7 ( ) d ( )( ) ( 4)( ) ( ) ( 4) ( )( 1) Oppgve 1. 49 7 ( 7)( 7) 5 5 5 5 1y 75 (4y 5) ( y) 5
Løsninger til oppgvene i ok R1 kpittel 1 Alger Løsninger til oppgvene i ok Oppgve 1.1 1 8 4 ( ) 15 5 (4 ) 7 1 7 ( ) d ( )( ) ( 4)( ) ( ) ( 4) ( )( 1) Oppgve 1. 49 7 ( 7)( 7) 5 5 5 5 1y 75 (4y 5) ( y) 5
Temahefte nr. 1. Hvordan du regner med hele tall
 1 ARBEIDSHEFTE I MATEMATIKK SNART MATTE EKSAMEN Hvordn du effektivt kn forberede deg til eksmen Temhefte nr. 1 Hvordn du regner med hele tll Av Mtthis Lorentzen mttegrisenforlg.com Opplysning: De nturlige
1 ARBEIDSHEFTE I MATEMATIKK SNART MATTE EKSAMEN Hvordn du effektivt kn forberede deg til eksmen Temhefte nr. 1 Hvordn du regner med hele tll Av Mtthis Lorentzen mttegrisenforlg.com Opplysning: De nturlige
1 Tallregning og algebra
 Tllregning og lger ØV MER. REGNEREKKEFØLGE Oppgve.0 6 d) ( : 6) Oppgve. ( ) ( ) ()() ( ) ( ) ( ) () (6 ) () d) ( ) 7() ( ) Oppgve. 6 ( ) d) Oppgve. Med ett ddisjonstegn, ett sutrksjonstegn, ett multipliksjonstegn
Tllregning og lger ØV MER. REGNEREKKEFØLGE Oppgve.0 6 d) ( : 6) Oppgve. ( ) ( ) ()() ( ) ( ) ( ) () (6 ) () d) ( ) 7() ( ) Oppgve. 6 ( ) d) Oppgve. Med ett ddisjonstegn, ett sutrksjonstegn, ett multipliksjonstegn
dx = 1 2y dy = dx/ x 3 y3/2 = 2x 1/2 + C 1
 NTNU Institutt for mtemtiske fg TMA Mtemtikk høsten Løsningsforslg - Øving 7 Avsnitt 6.5 ) En hr t y = e, så y + 3y = e + 3e = e. b) En hr t y = e 3 e (3/), så y + 3y = e 3e (3/) + 3e + 3e (3/) = e. c)
NTNU Institutt for mtemtiske fg TMA Mtemtikk høsten Løsningsforslg - Øving 7 Avsnitt 6.5 ) En hr t y = e, så y + 3y = e + 3e = e. b) En hr t y = e 3 e (3/), så y + 3y = e 3e (3/) + 3e + 3e (3/) = e. c)
2 Symboler i matematikken
 2 Symoler i mtemtikken 2.1 Symoler som står for tll og størrelser Nvn i geometri Nvn i mtemtikken enyttes på lignende måte som nvn på yer og personer, de refererer eller representerer et tll eller en størrelse,
2 Symoler i mtemtikken 2.1 Symoler som står for tll og størrelser Nvn i geometri Nvn i mtemtikken enyttes på lignende måte som nvn på yer og personer, de refererer eller representerer et tll eller en størrelse,
Eksamen R2, Va ren 2014, løsning
 Eksmen R, V ren 04, løsning Tid: timer Hjelpemidler: Vnlige skrivesker, psser, linjl med centimetermål og vinkelmåler er tilltt. Oppgve ( poeng) Deriver funksjonene ) f sin Vi bruker kjerneregelen på sin,
Eksmen R, V ren 04, løsning Tid: timer Hjelpemidler: Vnlige skrivesker, psser, linjl med centimetermål og vinkelmåler er tilltt. Oppgve ( poeng) Deriver funksjonene ) f sin Vi bruker kjerneregelen på sin,
Forkunnskaper i matematikk for fysikkstudenter. Trigonometri. Omregning mellom grader og radianer skjer etter formelen nedenfor:
 Forkunnskper i mtemtikk for fysikkstudenter.. Vinkelmål. Vinkler måles trdisjonelt i grder. Utgngspunktet er d t en hel sirkel deles i 6 like store deler, der her del klles en grd. En grd kn deles inn
Forkunnskper i mtemtikk for fysikkstudenter.. Vinkelmål. Vinkler måles trdisjonelt i grder. Utgngspunktet er d t en hel sirkel deles i 6 like store deler, der her del klles en grd. En grd kn deles inn
x 1, x 2,..., x n. En lineær funksjon i n variable er en funksjon f(x 1, x 2,..., x n ) = a 1 x 1 + a 2 x a n x n,
 Introduksjon Velkommen til emnet TMA45 Mtemtikk 3, våren 9 Disse nottene inneholder det vi gjennomgår i forelesningene, og utgjør, smmen med lle øvingene, pensum for emnet Læreoken nefles som støttelittertur
Introduksjon Velkommen til emnet TMA45 Mtemtikk 3, våren 9 Disse nottene inneholder det vi gjennomgår i forelesningene, og utgjør, smmen med lle øvingene, pensum for emnet Læreoken nefles som støttelittertur
Eksamen våren 2018 Løsninger
 DEL 1 Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med centimetermål og vinkelmåler Oppgve 1 5x+ y = 4 x+ 4y = 6 Vi multipliserer likningen 5x+ y = 4 med på egge sider og får 10x+ 4y
DEL 1 Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med centimetermål og vinkelmåler Oppgve 1 5x+ y = 4 x+ 4y = 6 Vi multipliserer likningen 5x+ y = 4 med på egge sider og får 10x+ 4y
... JULEPRØVE 9. trinn...
 .... JULEPRØVE 9. trinn.... Nvn: Gruppe: DELPRØVE 1 uten hjelpemidler ( 37 poeng) På denne delprøven kn du re ruke skrivesker, psser og linjl. Alle oppgvene i del 1 skl føres rett på rket. I noen oppgver
.... JULEPRØVE 9. trinn.... Nvn: Gruppe: DELPRØVE 1 uten hjelpemidler ( 37 poeng) På denne delprøven kn du re ruke skrivesker, psser og linjl. Alle oppgvene i del 1 skl føres rett på rket. I noen oppgver
M2, vår 2008 Funksjonslære Integrasjon
 M, vår 008 Funksjonslære Integrsjon Avdeling for lærerutdnning, Høgskolen i Vestfold. pril 009 1 Arelet under en grf Vi begynner vår diskusjon v integrsjon, på smme måte som vi begynte med derivsjon, ved
M, vår 008 Funksjonslære Integrsjon Avdeling for lærerutdnning, Høgskolen i Vestfold. pril 009 1 Arelet under en grf Vi begynner vår diskusjon v integrsjon, på smme måte som vi begynte med derivsjon, ved
3.7 Pythagoras på mange måter
 Oppgve 3.18 Vis t det er mulig å multiplisere og dividere linjestykker som vist i figur 3.. Bruk formlikhet. 3.7 Pythgors på mnge måter Grekeren Pythgors le født på Smos 569 og døde. år 500 f. Kr. Setningen
Oppgve 3.18 Vis t det er mulig å multiplisere og dividere linjestykker som vist i figur 3.. Bruk formlikhet. 3.7 Pythgors på mnge måter Grekeren Pythgors le født på Smos 569 og døde. år 500 f. Kr. Setningen
Integralregning. Mål. for opplæringen er at eleven skal kunne
 8 Integrlregning Mål for opplæringen er t eleven skl kunne gjøre rede for definisjonen v estemt integrl som grense for en sum og uestemt integrl som ntiderivert eregne integrler v de sentrle funksjonene
8 Integrlregning Mål for opplæringen er t eleven skl kunne gjøre rede for definisjonen v estemt integrl som grense for en sum og uestemt integrl som ntiderivert eregne integrler v de sentrle funksjonene
Kapittel 3. Potensregning
 Kpittel. Potensregning I potensregning skriver vi tll som potenser og forenkler uttrykk som inneholder potenser. Dette kpitlet hndler blnt nnet om: Betydningen v potenser som hr negtiv eksponent eller
Kpittel. Potensregning I potensregning skriver vi tll som potenser og forenkler uttrykk som inneholder potenser. Dette kpitlet hndler blnt nnet om: Betydningen v potenser som hr negtiv eksponent eller
1 Geometri KATEGORI 1. 1.1 Vinkelsummen i mangekanter. 1.2 Vinkler i formlike figurer
 Oppgver 1 Geometri KTGORI 1 1.1 Vinkelsummen i mngeknter Oppgve 1.110 ) I en treknt er to v vinklene 65 og 5. Finn den tredje vinkelen. b) I en firknt er tre v vinklene 0, 50 og 150. Finn den fjerde vinkelen.
Oppgver 1 Geometri KTGORI 1 1.1 Vinkelsummen i mngeknter Oppgve 1.110 ) I en treknt er to v vinklene 65 og 5. Finn den tredje vinkelen. b) I en firknt er tre v vinklene 0, 50 og 150. Finn den fjerde vinkelen.
1 Mandag 18. januar 2010
 Mndg 8. jnur 2 I denne første forelesningen skl vi friske opp litt rundt funksjoner i en vribel, se på hvordn de vokser/vtr, studere kritiske punkter og beskrive krumning og vendepunkter. Vi får ikke direkte
Mndg 8. jnur 2 I denne første forelesningen skl vi friske opp litt rundt funksjoner i en vribel, se på hvordn de vokser/vtr, studere kritiske punkter og beskrive krumning og vendepunkter. Vi får ikke direkte
1 Mandag 1. mars 2010
 Mndg. mrs Fundmentlteoremet sier t integrsjon og derivsjon er motstte opersjoner. Vi hr de siste ukene sett hvordn vi på ulike måter kn derivere funksjoner i flere vrible. Nå er turen kommet til den motstte
Mndg. mrs Fundmentlteoremet sier t integrsjon og derivsjon er motstte opersjoner. Vi hr de siste ukene sett hvordn vi på ulike måter kn derivere funksjoner i flere vrible. Nå er turen kommet til den motstte
Del 2. Alle oppgaver føres inn på eget ark. Vis tydelig hvordan du har kommet frem til svaret. Oppgave 2
 Del 2 Alle oppgver føres inn på eget rk. Vis tydelig hvordn du hr kommet frem til svret. Oppgve 1 Figuren viser sidefltene til et prisme. Grunnflten og toppflten mngler. ) Hvilken form må grunn- og toppflten
Del 2 Alle oppgver føres inn på eget rk. Vis tydelig hvordn du hr kommet frem til svret. Oppgve 1 Figuren viser sidefltene til et prisme. Grunnflten og toppflten mngler. ) Hvilken form må grunn- og toppflten
dy ycos 2 y = dx. Ved å integrere på begge sider av likhetstegnet får man ved å substituere u = y,du = dy dy ycos 2 y = 2du cos 2 u = x.
 NTNU Institutt for mtemtiske fg TMA Mtemtikk høsten 2 Løsningsforslg - Øving 7 Avsnitt 6.5 ) En hr t y = e, så 2y +y = 2e +e = e. b) En hr t y = e 2 e (/2), så 2y +y = 2e e (/2) +e +e (/2) = e. c) En hr
NTNU Institutt for mtemtiske fg TMA Mtemtikk høsten 2 Løsningsforslg - Øving 7 Avsnitt 6.5 ) En hr t y = e, så 2y +y = 2e +e = e. b) En hr t y = e 2 e (/2), så 2y +y = 2e e (/2) +e +e (/2) = e. c) En hr
Matematikk 1000. Øvingsoppgaver i numerikk leksjon 8 Numerisk integrasjon
 Mtemtikk 1000 Øvingsoppgver i numerikk leksjon 8 Numerisk integrsjon Som kjent kn vi regne ut (bestemte) integrler ved nti-derivsjon. Dette resulttet er et v de viktikgste innen klkulus; det heter tross
Mtemtikk 1000 Øvingsoppgver i numerikk leksjon 8 Numerisk integrsjon Som kjent kn vi regne ut (bestemte) integrler ved nti-derivsjon. Dette resulttet er et v de viktikgste innen klkulus; det heter tross
EKSAMEN. ANTALL SIDER UTLEVERT: 7 (innkl. forside og 2 sider formelark)
 KANDIDATNUMMER: EKSAMEN FAGNAVN: Mtemtikk FAGNUMMER: REA EKSAMENSDATO: 5. desember 6 KLASSE:. klssene, ingenørutdnning. TID: kl. 9... FAGLÆRER: Hns Petter Hornæs ANTALL SIDER UTLEVERT: 7 (innkl. forside
KANDIDATNUMMER: EKSAMEN FAGNAVN: Mtemtikk FAGNUMMER: REA EKSAMENSDATO: 5. desember 6 KLASSE:. klssene, ingenørutdnning. TID: kl. 9... FAGLÆRER: Hns Petter Hornæs ANTALL SIDER UTLEVERT: 7 (innkl. forside
1 Mandag 25. januar 2010
 Mndg 5. jnur Vi fortsetter med å se på det bestemte integrlet, bl.. på hvordn vi kn bruke numeriske beregninger til å bestemme verdien når vi ikke nødvendigvis kn finne en nti-derivert. Videre skl vi t
Mndg 5. jnur Vi fortsetter med å se på det bestemte integrlet, bl.. på hvordn vi kn bruke numeriske beregninger til å bestemme verdien når vi ikke nødvendigvis kn finne en nti-derivert. Videre skl vi t
Fag: Matematikk 1T-Y for yrkesfag for elever og privatisterr. Eksamensdato: 16. januar 2012
 Loklt gittt eksmen Eksmen Fg: Mtemtikk 1T-Y for yrkesfg for elever og privtisterr Fgkode: MAT1006 Eksmensdto: 16. jnur 2012 Antll sider i oppgven: 7 inklusiv forside og opplysningsside Del 1: oppgve 1-5
Loklt gittt eksmen Eksmen Fg: Mtemtikk 1T-Y for yrkesfg for elever og privtisterr Fgkode: MAT1006 Eksmensdto: 16. jnur 2012 Antll sider i oppgven: 7 inklusiv forside og opplysningsside Del 1: oppgve 1-5
S1 kapittel 6 Derivasjon Løsninger til oppgavene i boka
 S kpittel 6 Derivsjon Løsninger til oppgvene i ok 6. c y x y x = = = = y x 4 5 9 4 y 5 6 x 4 = = = = y x y x = = = = 7 ( 5) 6 ( ) 8 6. f( x ) f( x ) 5 7 x x ( ) 4 = = = = 6. T( x) = 0,x +,0 T T = + = (0)
S kpittel 6 Derivsjon Løsninger til oppgvene i ok 6. c y x y x = = = = y x 4 5 9 4 y 5 6 x 4 = = = = y x y x = = = = 7 ( 5) 6 ( ) 8 6. f( x ) f( x ) 5 7 x x ( ) 4 = = = = 6. T( x) = 0,x +,0 T T = + = (0)
DEL 1 Uten hjelpemidler
 DEL 1 Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med entimetermål og vinkelmåler Oppgve 1 f( ) + f + ( ) 4 g ( ) ln( ) 1 g ( ) h ( ) ( 1) h ( ) ( 1) 4 1 ( 1) Oppgve er en fktor i P
DEL 1 Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med entimetermål og vinkelmåler Oppgve 1 f( ) + f + ( ) 4 g ( ) ln( ) 1 g ( ) h ( ) ( 1) h ( ) ( 1) 4 1 ( 1) Oppgve er en fktor i P
ALTERNATIV GRUNNBOK BOKMÅL
 Anne Rsch-Hlvorsen Oddvr Asen Illustrtør: Bjørn Eidsvik 7B NY UTGAVE ALTERNATIV GRUNNBOK BOKMÅL CAPPELEN DAMM AS, 2011 Mterilet i denne publiksjonen er omfttet v åndsverklovens bestemmelser. Uten særskilt
Anne Rsch-Hlvorsen Oddvr Asen Illustrtør: Bjørn Eidsvik 7B NY UTGAVE ALTERNATIV GRUNNBOK BOKMÅL CAPPELEN DAMM AS, 2011 Mterilet i denne publiksjonen er omfttet v åndsverklovens bestemmelser. Uten særskilt
MAT 100A: Mappeeksamen 4
 . november, MAT A: Mppeeksmen Løsningsforslg Oppgve ) Vi bruker produktregelen: f (x) x rctn x + x + x Siden x og rctn x hr smme fortegn, og x ldri er negtiv, er f (x) positiv overlt, bortsett fr t f ().
. november, MAT A: Mppeeksmen Løsningsforslg Oppgve ) Vi bruker produktregelen: f (x) x rctn x + x + x Siden x og rctn x hr smme fortegn, og x ldri er negtiv, er f (x) positiv overlt, bortsett fr t f ().
Eksamen høsten 2016 Løsninger
 DEL 1 Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med centimetermål og vinkelmåler Oppgve 1 1: 5x y : x y 9 Fr likning : y x+ 9 Innstt i likning 1 gir det 5x (x+ 9) 5x 4x 18 9x 18 x
DEL 1 Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med centimetermål og vinkelmåler Oppgve 1 1: 5x y : x y 9 Fr likning : y x+ 9 Innstt i likning 1 gir det 5x (x+ 9) 5x 4x 18 9x 18 x
DEL 1 Uten hjelpemidler
 DEL Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med entimetermål og vinkelmåler Oppgve f = + f ( ) = 6 ( ) 3 g = ( ) e g = + = + ( ) e e e ( ) h = 3 ( ) ln( ) 3 h ( ) = 3 = 3 3 Oppgve
DEL Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med entimetermål og vinkelmåler Oppgve f = + f ( ) = 6 ( ) 3 g = ( ) e g = + = + ( ) e e e ( ) h = 3 ( ) ln( ) 3 h ( ) = 3 = 3 3 Oppgve
Mer øving til kapittel 2
 Mer øving til kpittel 2 KAPITTEL 2 GEOMETRI OG MÅLING Oppgve 1 Oppgve 2 Oppgve 3 Anne hr vært på ferie til sine esteforeldre fr 28. juni til 9. ugust. Hvor mnge dger hr hun vært på ferie? Fr hun kom hjem
Mer øving til kpittel 2 KAPITTEL 2 GEOMETRI OG MÅLING Oppgve 1 Oppgve 2 Oppgve 3 Anne hr vært på ferie til sine esteforeldre fr 28. juni til 9. ugust. Hvor mnge dger hr hun vært på ferie? Fr hun kom hjem
Kapittel 4 Tall og algebra Mer øving
 Kpittel 4 Tll og lger Mer øving Oppgve 1 d Oppgve 2 Se på uttrykket A = g h. Hv forteller de ulike okstvene? Se på uttrykket A = 2π. Hv står de ulike symolene for? Forklr hv vi mener med en vriel og en
Kpittel 4 Tll og lger Mer øving Oppgve 1 d Oppgve 2 Se på uttrykket A = g h. Hv forteller de ulike okstvene? Se på uttrykket A = 2π. Hv står de ulike symolene for? Forklr hv vi mener med en vriel og en
Heldagsprøve i matematikk. Svar og løsningsforslag
 Heldagsprøve i matematikk Svar og løsningsforslag Mandag 19. desember 005 Forkurset, Høgskolen i Oslo Tillatte hjelpemidler: Lommeregner. Formelsamling i matematikk. Tid: 5 klokketimer Alle svar må være
Heldagsprøve i matematikk Svar og løsningsforslag Mandag 19. desember 005 Forkurset, Høgskolen i Oslo Tillatte hjelpemidler: Lommeregner. Formelsamling i matematikk. Tid: 5 klokketimer Alle svar må være
1 k 2 + 1, k= 5. i=1. i = k + 6 eller k = i 6. m+6. (i 6) i=1
 TMA4 Høst 6 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Løsningsforslg Øving 5 5..6 Vi er gitt summen og ønsker å skrive den på formen m k=5 k +, f(i). i= Strtpunktene er henholdsvis
TMA4 Høst 6 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Løsningsforslg Øving 5 5..6 Vi er gitt summen og ønsker å skrive den på formen m k=5 k +, f(i). i= Strtpunktene er henholdsvis
YF kapittel 6 Lengder og vinkler Løsninger til oppgavene i læreboka
 YF kpittel 6 Lengder og vinkler Løsninger til oppgvene i læreok Oppgve 601 Vi skl gå ett hkk mot høyre, og gnger derfor med 10. 14 cm 14 10 mm 140 mm c Vi skl gå to hkk mot høyre, og gnger derfor med 10
YF kpittel 6 Lengder og vinkler Løsninger til oppgvene i læreok Oppgve 601 Vi skl gå ett hkk mot høyre, og gnger derfor med 10. 14 cm 14 10 mm 140 mm c Vi skl gå to hkk mot høyre, og gnger derfor med 10
1 dx cos 1 x =, 1 x 2 sammen med kjerneregelen for derivasjon. For å forenkle utregningen lar vi u = Vi regner først ut den deriverte til u,
 TMA0 Høst 205 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg 3.5.30: Vi bruker erivsjonsregelen for cos x, x cos x =, x 2 smmen me kjerneregelen for erivsjon. For å forenkle utregningen
TMA0 Høst 205 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg 3.5.30: Vi bruker erivsjonsregelen for cos x, x cos x =, x 2 smmen me kjerneregelen for erivsjon. For å forenkle utregningen
E K S A M E N. Matematikk 3MX. Elevar/Elever Privatistar/Privatister. AA6524/AA6526 8. desember 2004 UTDANNINGSDIREKTORATET
 E K S A M E N UTDANNINGSDIREKTORATET Mtemtikk 3MX Elevr/Elever Privtistr/Privtister AA654/AA656 8. desember 004 Vidregånde kurs II / Videregående kurs II Studieretning for llmenne, økonomiske og dministrtive
E K S A M E N UTDANNINGSDIREKTORATET Mtemtikk 3MX Elevr/Elever Privtistr/Privtister AA654/AA656 8. desember 004 Vidregånde kurs II / Videregående kurs II Studieretning for llmenne, økonomiske og dministrtive
Løsningsskisser til oppgaver i Kapittel 2: Trigonometri
 Løsningsskisser til oppgver i Kpittel : Trigonometri.07 Treknten i figuren hr: (Alle mål i cm.) grunnlinje: g 5 1 høyde: h Tilhørende sirkelsektor spenner over vinkelen v, der cosv 5 v 1.159 Arel Treknt
Løsningsskisser til oppgver i Kpittel : Trigonometri.07 Treknten i figuren hr: (Alle mål i cm.) grunnlinje: g 5 1 høyde: h Tilhørende sirkelsektor spenner over vinkelen v, der cosv 5 v 1.159 Arel Treknt
Faktorisering. 1 Hva er faktorisering? 2 Hvorfor skal vi faktorisere? Per G. Østerlie Senter for IKT i utdanningen 11.
 Fktorisering Per G. Østerlie Senter for IKT i utdnningen per@osterlie.no 11. mi 013 1 Hv er fktorisering? Vi må se på veret å fktorisere. Hv er det vi skl gjøre når vi fktoriserer? Svret er: å lge fktorer.
Fktorisering Per G. Østerlie Senter for IKT i utdnningen per@osterlie.no 11. mi 013 1 Hv er fktorisering? Vi må se på veret å fktorisere. Hv er det vi skl gjøre når vi fktoriserer? Svret er: å lge fktorer.
Oppfriskningskurs i matematikk 2008
 Oppfriskningskurs i matematikk 2008 Marte Pernille Hatlo Institutt for matematiske fag, NTNU 4.-9. august 2008 Velkommen! 2 Temaer Algebra Trigonometri Funksjoner og derivasjon Integrasjon Eksponensial-
Oppfriskningskurs i matematikk 2008 Marte Pernille Hatlo Institutt for matematiske fag, NTNU 4.-9. august 2008 Velkommen! 2 Temaer Algebra Trigonometri Funksjoner og derivasjon Integrasjon Eksponensial-
Formelsamling i matematikk
 Formelsmling i mtemtikk Algebr Aritmetiske opersjoner (b + c) b + c + c b Potensregler Polynom b + c b b + c d + bc d bc b c d b d c d bc x y x+y x x / x y x y n x x /n 0 x n x n ( x ) y xy (b) x x y (
Formelsmling i mtemtikk Algebr Aritmetiske opersjoner (b + c) b + c + c b Potensregler Polynom b + c b b + c d + bc d bc b c d b d c d bc x y x+y x x / x y x y n x x /n 0 x n x n ( x ) y xy (b) x x y (
Fag: Matematikk 1T-Y for elever og privatister. Antall sider i oppgaven: 8 inklusiv forside og opplysningsside
 Loklt gitt eksmen 2012 Eksmen Fg: Mtemtikk 1T-Y for elever og privtister Fgkode: MAT1006 Eksmensdto: 25. mi Antll sider i oppgven: 8 inklusiv forside og opplysningsside Eksmenstid: Hjelpemidler under eksmen:
Loklt gitt eksmen 2012 Eksmen Fg: Mtemtikk 1T-Y for elever og privtister Fgkode: MAT1006 Eksmensdto: 25. mi Antll sider i oppgven: 8 inklusiv forside og opplysningsside Eksmenstid: Hjelpemidler under eksmen:
a 2πf(x) 1 + (f (x)) 2 dx.
 MA 4: Anlyse Uke 44, http://home.hi.no/ svldl/m4 H Høgskolen i Agder Avdeling for relfg Institutt for mtemtiske fg Om lengde v kurver. Noen få formler der integrsjon brukes for å beregne lengder, reler
MA 4: Anlyse Uke 44, http://home.hi.no/ svldl/m4 H Høgskolen i Agder Avdeling for relfg Institutt for mtemtiske fg Om lengde v kurver. Noen få formler der integrsjon brukes for å beregne lengder, reler
Formelsamling i matematikk
 Formelsmling i mtemtikk Alger Aritmetiske opersjoner ( + c) = + c + c Potensregler Polynom = + c + c d + c = d c c d = d c = d c x y = x+y x = x / x y = x y n x = x /n 0 = x n = x n ( x ) y = xy () x =
Formelsmling i mtemtikk Alger Aritmetiske opersjoner ( + c) = + c + c Potensregler Polynom = + c + c d + c = d c c d = d c = d c x y = x+y x = x / x y = x y n x = x /n 0 = x n = x n ( x ) y = xy () x =
S1 kapittel 8 Eksamenstrening Løsninger til oppgavene i læreboka
 S1 kpittel 8 Eksmenstrening Løsninger til oppgvene i læreok E1 995 995 5 + 5 (995 5) (995 + 5) + 5 990 1000 + 5 990 000 + 5 990 05 E E (61+ 9) 51 49) (51+ 49) 61 9 (61 9) 51 49 ( 100 100 11 1997 00 199
S1 kpittel 8 Eksmenstrening Løsninger til oppgvene i læreok E1 995 995 5 + 5 (995 5) (995 + 5) + 5 990 1000 + 5 990 000 + 5 990 05 E E (61+ 9) 51 49) (51+ 49) 61 9 (61 9) 51 49 ( 100 100 11 1997 00 199
En (reell) funksjon f fra en (reell) mengde D er en regel som til hvert element x D tilordner en unik verdi y = f (x).
 Funksjoner En (reell) funksjon f fra en (reell) mengde D er en regel som til hvert element x D tilordner en unik verdi y = f (x). Mengden D kalles definisjonsmengden (eng.: domain) til f. Merknad Dersom
Funksjoner En (reell) funksjon f fra en (reell) mengde D er en regel som til hvert element x D tilordner en unik verdi y = f (x). Mengden D kalles definisjonsmengden (eng.: domain) til f. Merknad Dersom
TFY4104 Fysikk. Institutt for fysikk, NTNU. Lsningsforslag til ving 8. a =
 TFY414 Fysikk. Institutt for fysikk, NTNU. Lsningsforslg til ving 8. Oppgve 1. ) C F = E = m Newtons. lov. Her er = e, s elektronets kselersjon blir = e m E lts mot venstre. b) C Totlt elektrisk felt i
TFY414 Fysikk. Institutt for fysikk, NTNU. Lsningsforslg til ving 8. Oppgve 1. ) C F = E = m Newtons. lov. Her er = e, s elektronets kselersjon blir = e m E lts mot venstre. b) C Totlt elektrisk felt i
Fasit. Oppgavebok. Kapittel 4. Bokmål
 Fsit 9 Oppgvebok Kpittel 4 Bokmål Kpittel 4 Geometri og beregninger Arel og omkrets 4.1 54 m b 106 m 4.2 162 m2 b 484 m2 4.3 26,0 cm2 b 22,5 cm2 c 20,0 cm2 d De tre rektnglene hr lik omkrets, 21 cm 4.4
Fsit 9 Oppgvebok Kpittel 4 Bokmål Kpittel 4 Geometri og beregninger Arel og omkrets 4.1 54 m b 106 m 4.2 162 m2 b 484 m2 4.3 26,0 cm2 b 22,5 cm2 c 20,0 cm2 d De tre rektnglene hr lik omkrets, 21 cm 4.4
2x 3 4/x dx. 2 5 x 3 + LF: Vi utfører polynomdivisjon. 2x + 1 dx = + C = 5x8/ ln 2x C 4. πx 2 e 3x3 dx = π
 Innlevering ELFE KJFE MAFE Mtemtikk HIOA Obligtorisk innlevering 5 Innleveringsfrist Mndg 6. oktober 5 før forelesningen : Antll oppgver: Løsningsforslg Finn de ubestemte integrlene ) x 4/x dx LF: x 4/x
Innlevering ELFE KJFE MAFE Mtemtikk HIOA Obligtorisk innlevering 5 Innleveringsfrist Mndg 6. oktober 5 før forelesningen : Antll oppgver: Løsningsforslg Finn de ubestemte integrlene ) x 4/x dx LF: x 4/x
Fasit til utvalgte oppgaver MAT1100, uka 20-24/9
 Fsit til utvlgte oppgver MAT00, uk 20-24/9 Øyvind Ryn oyvindry@ifi.uio.no September 24, 200 Oppgve 5..5 år vi viser t f er kontinuerlig i ved et ɛ δ-bevis, er det lurt å strte med uttrykket fx f, og finne
Fsit til utvlgte oppgver MAT00, uk 20-24/9 Øyvind Ryn oyvindry@ifi.uio.no September 24, 200 Oppgve 5..5 år vi viser t f er kontinuerlig i ved et ɛ δ-bevis, er det lurt å strte med uttrykket fx f, og finne
Innledning. Kategori Regnerekkefølge. 1.2 Bokstavregning og parenteser
 Innledning Ktegori. Regnerekkefølge Oppgve.0 Regn uten lommeregner. b) ( ) d) ( ) Oppgve. Regn uten lommeregner. b) d) Oppgve. Regn ut med og uten lommeregner. b) ( ) d) ( 9) Oppgve. Regn ut med lommeregner.
Innledning Ktegori. Regnerekkefølge Oppgve.0 Regn uten lommeregner. b) ( ) d) ( ) Oppgve. Regn uten lommeregner. b) d) Oppgve. Regn ut med og uten lommeregner. b) ( ) d) ( 9) Oppgve. Regn ut med lommeregner.
Årsprøve 2014 10. trinn Del 2
 2 Årsprøve 2014 10. trinn Del 2 Informsjon for del 2 Prøvetid: Hjelpemidler på del 2: Vedlegg: Andre opplysninger: Fremgngsmåte og forklring: Veiledning om vurderingen: 5 timer totlt Del 2 skl du levere
2 Årsprøve 2014 10. trinn Del 2 Informsjon for del 2 Prøvetid: Hjelpemidler på del 2: Vedlegg: Andre opplysninger: Fremgngsmåte og forklring: Veiledning om vurderingen: 5 timer totlt Del 2 skl du levere
Eksamen høsten 2016 Løsninger
 DEL Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med centimetermål og vinkelmåler Oppgve f x x x f ( x) = 4x 5 ( ) = 5 6 gx ( ) = xln x Vi deriverer med produktregel: g ( x) = ln x+
DEL Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med centimetermål og vinkelmåler Oppgve f x x x f ( x) = 4x 5 ( ) = 5 6 gx ( ) = xln x Vi deriverer med produktregel: g ( x) = ln x+
Matematikk Øvingsoppgaver i numerikk leksjon 9 Numerisk integrasjon
 Mtemtikk 1000 Øvingsoppgver i numerikk leksjon 9 Numerisk integrsjon Forståelsen v integrlet som et rel ligger til grunn når vi skl beregne integrler numerisk. Litt mer presist: Når f(x) 0 for lle x i
Mtemtikk 1000 Øvingsoppgver i numerikk leksjon 9 Numerisk integrsjon Forståelsen v integrlet som et rel ligger til grunn når vi skl beregne integrler numerisk. Litt mer presist: Når f(x) 0 for lle x i
Løsningsforslag til Eksamen i fag MA1103 Flerdimensjonal analyse
 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Side 1 v 5 Løsningsforslg til Eksmen i fg MA113 Flerdimensjonl nlyse 2.5.6 Oppgve 1 Vi hr f(x, y) = (4 x 2 y 2 )e x+y. ) Kritiske
Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Side 1 v 5 Løsningsforslg til Eksmen i fg MA113 Flerdimensjonl nlyse 2.5.6 Oppgve 1 Vi hr f(x, y) = (4 x 2 y 2 )e x+y. ) Kritiske
Sammendrag R1. Sandnes VGS 19. august 2009
 Sammendrag R1 Sandnes VGS 19. august 2009 1 1 Notasjon Implikasjon Vi skriver A B hvis påstanden A impliserer B. Det vil si at hvis påstand A er riktig, så er påstand B riktig. Ekvivalens Vi skriver A
Sammendrag R1 Sandnes VGS 19. august 2009 1 1 Notasjon Implikasjon Vi skriver A B hvis påstanden A impliserer B. Det vil si at hvis påstand A er riktig, så er påstand B riktig. Ekvivalens Vi skriver A
DEL 1 Uten hjelpemidler
 Eksmen høsten 013 Løsninger Eksmen høsten 013 Løsninger DEL 1 Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med centimetermål og vinkelmåler Oppgve 1 150 sider Vi finner først hvor mnge
Eksmen høsten 013 Løsninger Eksmen høsten 013 Løsninger DEL 1 Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med centimetermål og vinkelmåler Oppgve 1 150 sider Vi finner først hvor mnge
Høgskolen i Bergen. Formelsamling. for. ingeniørutdanningen. FOA150 høsten 2006 fellespensum. 3.utgave
 Høgskolen i Bergen Formelsmling for ingeniørutdnningen FOA5 høsten 6 fellespensum. 3.utgve Funksjoner. Elementære regneregler og funksjoner: y = y, ( ) =, y y =,, =, = ) = ) = = log = ln ln c) ln y = y
Høgskolen i Bergen Formelsmling for ingeniørutdnningen FOA5 høsten 6 fellespensum. 3.utgve Funksjoner. Elementære regneregler og funksjoner: y = y, ( ) =, y y =,, =, = ) = ) = = log = ln ln c) ln y = y
Terminprøve Matematikk for 1P 1NA høsten 2014
 Terminprøve Mtemtikk for 1P 1NA høsten 2014 DEL 1 Vrer 1,5 time Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med entimetermål og vinkelmåler. Forsøk på lle oppgvene selv om du er usikker
Terminprøve Mtemtikk for 1P 1NA høsten 2014 DEL 1 Vrer 1,5 time Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med entimetermål og vinkelmåler. Forsøk på lle oppgvene selv om du er usikker
Analyse og metodikk i Calculus 1
 Analyse og metodikk i Calculus 1 Fredrik Göthner og Raymi Eldby Norges teknisk-naturvitenskapelige universitet 3. desember 01 1 Innhold Forord 3 1 Vurdering av grafer og funksjoner 4 1.1 Hva er en funksjon?.........................
Analyse og metodikk i Calculus 1 Fredrik Göthner og Raymi Eldby Norges teknisk-naturvitenskapelige universitet 3. desember 01 1 Innhold Forord 3 1 Vurdering av grafer og funksjoner 4 1.1 Hva er en funksjon?.........................
1T kapittel 3 Funksjoner Løsninger til oppgavene i læreboka
 1T kpittel 3 Funksjoner Løsninger til oppgvene i læreok Oppgve 3.1 Origo er skjæringspunktet mellom førsteksen og ndreksen. Koordintene til origo er ltså (0, 0). Førstekoordinten til punktet A er 15, og
1T kpittel 3 Funksjoner Løsninger til oppgvene i læreok Oppgve 3.1 Origo er skjæringspunktet mellom førsteksen og ndreksen. Koordintene til origo er ltså (0, 0). Førstekoordinten til punktet A er 15, og
OPPLÆRINGSREGION NORD. Skriftlig eksamen. MAT1001 Matematikk 1P-Y HØSTEN 2011. Privatister. Yrkesfag. Alle yrkesfaglige utdanningsprogrammer
 OPPLÆRINGSREGION NORD LK06 Finnmrk fylkeskommune Troms fylkeskommune Nordlnd fylkeskommune Nord-Trøndelg fylkeskommune Sør-Trøndelg fylkeskommune Møre og Romsdl fylke Skriftlig eksmen MAT1001 Mtemtikk
OPPLÆRINGSREGION NORD LK06 Finnmrk fylkeskommune Troms fylkeskommune Nordlnd fylkeskommune Nord-Trøndelg fylkeskommune Sør-Trøndelg fylkeskommune Møre og Romsdl fylke Skriftlig eksmen MAT1001 Mtemtikk
... JULEPRØVE
 Ashehoug JULEPRØVE 2014 9. trinn.... JULEPRØVE 2014.... Nvn: Gruppe: DELPRØVE 1 uten hjelpemidler ( 37 poeng) På denne delprøven kn du re ruke skrivesker, psser og linjl. Alle oppgvene i del 1 skl føres
Ashehoug JULEPRØVE 2014 9. trinn.... JULEPRØVE 2014.... Nvn: Gruppe: DELPRØVE 1 uten hjelpemidler ( 37 poeng) På denne delprøven kn du re ruke skrivesker, psser og linjl. Alle oppgvene i del 1 skl føres
FASIT, tips og kommentarer
 FASIT, tips og kommentrer JULEKALENDER 8.- 10- trinn Nivå 1 og Nivå 2. Tips til orgnisering: Kn jobbes med i gruppe, to og to eller individuelt. Spre rbeidet med klenderen i mttetimene i desember, eller
FASIT, tips og kommentrer JULEKALENDER 8.- 10- trinn Nivå 1 og Nivå 2. Tips til orgnisering: Kn jobbes med i gruppe, to og to eller individuelt. Spre rbeidet med klenderen i mttetimene i desember, eller
Numerisk derivasjon og integrasjon utledning av feilestimater
 Numerisk derivsjon og integrsjon utledning v feilestimter Knut Mørken 6 oktober 007 1 Innledning På forelesningen /10 brukte vi litt tid på å repetere inhomogene differensligninger og rkk dermed ikke gjennomgå
Numerisk derivsjon og integrsjon utledning v feilestimter Knut Mørken 6 oktober 007 1 Innledning På forelesningen /10 brukte vi litt tid på å repetere inhomogene differensligninger og rkk dermed ikke gjennomgå
RAMMER FOR SKRIFTLIG EKSAMEN I MATEMATIKK 1P-Y OG 1T-Y ELEVER 2015
 RAMMER FOR SKRIFTLIG EKSAMEN I MATEMATIKK 1P-Y OG 1T-Y ELEVER 015 Utdnningsrogrm: Yrkesfg Fgkoder: MAT1, MAT6 Årstrinn: Vg1 Ogveroduksjon: En lokl ogvenemnd lger ogver til ordinær eleveksmen og sommerskolen.
RAMMER FOR SKRIFTLIG EKSAMEN I MATEMATIKK 1P-Y OG 1T-Y ELEVER 015 Utdnningsrogrm: Yrkesfg Fgkoder: MAT1, MAT6 Årstrinn: Vg1 Ogveroduksjon: En lokl ogvenemnd lger ogver til ordinær eleveksmen og sommerskolen.
DEL 1 Uten hjelpemidler
 DEL 1 Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med centimetermål og vinkelmåler Oppgve 1 10 % v 60 er 0,1 60 = 6. Prisen øker d med 6 kr. Vren vil derfor koste 60 kr + 6 kr = 70
DEL 1 Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med centimetermål og vinkelmåler Oppgve 1 10 % v 60 er 0,1 60 = 6. Prisen øker d med 6 kr. Vren vil derfor koste 60 kr + 6 kr = 70
R1 kapittel 8 Eksamenstrening
 Løsninger til oppgvene i ok R kpittel 8 Eksmenstrening Løsninger til oppgvene i ok Uten hjelpemidler Oppgve E Hvis er et nullpunkt for De mulige nullpunktene for P, er konstntleddet 8 delelig med. P er
Løsninger til oppgvene i ok R kpittel 8 Eksmenstrening Løsninger til oppgvene i ok Uten hjelpemidler Oppgve E Hvis er et nullpunkt for De mulige nullpunktene for P, er konstntleddet 8 delelig med. P er
Kalkulus 2. Volum av et omdreiningslegeme. Rotasjon rundt x-aksen
 Klkulus Klkulus Volum v et omdreiningslegeme Rotsjon rundt x-ksen På figuren nedenfor hr vi skrvert området vgrenset v grfen til den kontinuerlige funksjonen y = f( x) og x-ksen fr x= til x=. Når vi roterer
Klkulus Klkulus Volum v et omdreiningslegeme Rotsjon rundt x-ksen På figuren nedenfor hr vi skrvert området vgrenset v grfen til den kontinuerlige funksjonen y = f( x) og x-ksen fr x= til x=. Når vi roterer
Sammendrag R1. 26. januar 2011
 Sammendrag R1 26. januar 2011 1 1 Notasjon Implikasjon Vi skriver A B hvis påstanden A impliserer B. Det vil si at hvis påstand A er riktig, så er påstand B riktig. Ekvivalens Vi skriver A B hvis to påstander
Sammendrag R1 26. januar 2011 1 1 Notasjon Implikasjon Vi skriver A B hvis påstanden A impliserer B. Det vil si at hvis påstand A er riktig, så er påstand B riktig. Ekvivalens Vi skriver A B hvis to påstander
Funksjoner (kapittel 1)
 Ukeoppgaver, uke 34 og 35, i Matematikk 0, Funksjoner og grenser. Høgskolen i Gjøvik Avdeling for ingeniørfag Matematikk 0 Ukeoppgaver uke 34 og 35 Funksjoner (kapittel ) Oppgave Figuren til øyre viser
Ukeoppgaver, uke 34 og 35, i Matematikk 0, Funksjoner og grenser. Høgskolen i Gjøvik Avdeling for ingeniørfag Matematikk 0 Ukeoppgaver uke 34 og 35 Funksjoner (kapittel ) Oppgave Figuren til øyre viser
2 Tallregning og algebra
 Tllregning og lger KATEGORI. Regnerekkefølge Oppgve.0 Regn uten digitlt hjelpemiddel. + ( + ) ( ) Oppgve. Regn uten digitlt hjelpemiddel. Oppgve. Regn ut med og uten digitlt hjelpemiddel. + (7 + ) ( 9)
Tllregning og lger KATEGORI. Regnerekkefølge Oppgve.0 Regn uten digitlt hjelpemiddel. + ( + ) ( ) Oppgve. Regn uten digitlt hjelpemiddel. Oppgve. Regn ut med og uten digitlt hjelpemiddel. + (7 + ) ( 9)
DEL 1 Uten hjelpemidler
 DEL 1 Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med entimetermål og vinkelmåler Oppgve 1 Melk: 2 14,95 2 15 30 Potet: 2,5 8,95 2,5 9 22,5 Ost: 0,5 89,95 0,5 90 45 Skinke: 0, 2 199
DEL 1 Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med entimetermål og vinkelmåler Oppgve 1 Melk: 2 14,95 2 15 30 Potet: 2,5 8,95 2,5 9 22,5 Ost: 0,5 89,95 0,5 90 45 Skinke: 0, 2 199
Projeksjon. Kapittel 11. Ortogonal projeksjon i R 2. Skalarproduktet i R n. w på v. Fra figuren ovenfor ser vi at komponenten til w ortogonalt på v er
 Kpittel Projeksjon En projeksjon er en lineærtrnsformsjon P som tilfredsstiller P x P x. for lle x. Denne ligningen sier t intet nytt skjer om du benytter lineærtrnsformsjonen for ndre gng, og mn kn tenke
Kpittel Projeksjon En projeksjon er en lineærtrnsformsjon P som tilfredsstiller P x P x. for lle x. Denne ligningen sier t intet nytt skjer om du benytter lineærtrnsformsjonen for ndre gng, og mn kn tenke
Integral Kokeboken. sin(πx 2 ) sinh 2 (πx) dx = 2. 1 log x. + log(log x) dx = x log(log x) + C. cos(x 2 ) + sin(x 2 ) dx = 2π. x s 1 e x 1 dx = Γ(s)
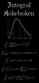 Integrl Kokeboken 4 3 4 6 8 log sinπ sinh π 4 + loglog loglog + C cos + sin π s e Γs n n s Γsζs π + sin +cos log + cos i Del I. Brøk................................... Trigonometriske funksjoner.....................
Integrl Kokeboken 4 3 4 6 8 log sinπ sinh π 4 + loglog loglog + C cos + sin π s e Γs n n s Γsζs π + sin +cos log + cos i Del I. Brøk................................... Trigonometriske funksjoner.....................
9 Potenser. Logaritmer
 9 Potenser. Logritmer Foret utregingene nedenfor: 5 5 c 6 7 d e 5 f g h i Regn ut og gjør svrene så enkle som mulige: c y y d e f g h i j y y + y + y + + y Prisen på en motorsg vr kr 56 i 99. Vi regner
9 Potenser. Logritmer Foret utregingene nedenfor: 5 5 c 6 7 d e 5 f g h i Regn ut og gjør svrene så enkle som mulige: c y y d e f g h i j y y + y + y + + y Prisen på en motorsg vr kr 56 i 99. Vi regner
EKSAMEN. 1. klassene, ingenørutdanning og Flexing. HansPetterHornæsogLarsNilsBakken. ANTALL SIDER UTLEVERT: 7 (innkl. forside og 4 sider formelark)
 KANDIDATNUMMER: EKSAMEN EMNENAVN: Mtemtikk EMNENUMMER: REA4 og REA4f EKSAMENSDATO: 9. desember 0 KLASSE:. klssene, ingenørutdnning og Flexing. TID: kl. 9.00 3.00. FAGANSVARLIG: HnsPetterHornæsogLrsNilsBkken
KANDIDATNUMMER: EKSAMEN EMNENAVN: Mtemtikk EMNENUMMER: REA4 og REA4f EKSAMENSDATO: 9. desember 0 KLASSE:. klssene, ingenørutdnning og Flexing. TID: kl. 9.00 3.00. FAGANSVARLIG: HnsPetterHornæsogLrsNilsBkken
1 Tall og variabler. Oppgave Regn ut uten lommeregner. Oppgave Sett inn symbolet eller i de tomme rutene. a) 9 N b) π Q c) 3 R
 Tll og vribler. TALL OG TALLREGNING Oppgve.0 Sett inn smbolet eller i de tomme rutene. ) N π Q R Oppgve. Sett inn smbolet eller i de tomme rutene. { } { π } ), 0,,,,,,, Oppgve. Skriv disse mengdene på
Tll og vribler. TALL OG TALLREGNING Oppgve.0 Sett inn smbolet eller i de tomme rutene. ) N π Q R Oppgve. Sett inn smbolet eller i de tomme rutene. { } { π } ), 0,,,,,,, Oppgve. Skriv disse mengdene på
Fasit. Grunnbok. Kapittel 2. Bokmål
 Fsit 9 Grunnbok Kpittel Bokmål Kpittel Lineære funksjoner rette linjer. ƒ(x) = 4x + 5 ƒ() = 3 ƒ(4) = ƒ(6) = 9.6 ƒ(x) = -x b ƒ(x) = x b ƒ(x) = (x + ) 3 ƒ() = ƒ(4) = 8 ƒ(6) = 4 ƒ(x) = x 4 ƒ() = - ƒ(4) =
Fsit 9 Grunnbok Kpittel Bokmål Kpittel Lineære funksjoner rette linjer. ƒ(x) = 4x + 5 ƒ() = 3 ƒ(4) = ƒ(6) = 9.6 ƒ(x) = -x b ƒ(x) = x b ƒ(x) = (x + ) 3 ƒ() = ƒ(4) = 8 ƒ(6) = 4 ƒ(x) = x 4 ƒ() = - ƒ(4) =
Tom Lindstrøm. Tilleggskapitler til. Kalkulus. 3. utgave. Universitetsforlaget,
 Tom Lindstrøm Tilleggskpitler til Klkulus 3. utgve Universitetsforlget, Oslo 3. utgve Universitetsforlget AS 2006 1. utgve 1995 2. utgve 1996 ISBN-13: 978-82-15-00977-3 ISBN-10: 82-15-00977-8 Mterilet
Tom Lindstrøm Tilleggskpitler til Klkulus 3. utgve Universitetsforlget, Oslo 3. utgve Universitetsforlget AS 2006 1. utgve 1995 2. utgve 1996 ISBN-13: 978-82-15-00977-3 ISBN-10: 82-15-00977-8 Mterilet
9.6 Tilnærminger til deriverte og integraler
 96 TILNÆRMINGER TIL DERIVERTE OG INTEGRALER 169 Figur 915 Bezier-kurve med kontrollpolygon som representerer bokstven S i Postscript-fonten Times-Romn De ulike Bezier-segmentene ser du mellom kontrollpunktene
96 TILNÆRMINGER TIL DERIVERTE OG INTEGRALER 169 Figur 915 Bezier-kurve med kontrollpolygon som representerer bokstven S i Postscript-fonten Times-Romn De ulike Bezier-segmentene ser du mellom kontrollpunktene
Sammendrag R2. www.kalkulus.no. 31. mai 2009
 Sammendrag R2 www.kalkulus.no 31. mai 2009 1 1 Trigonometri Definisjon av sinus og cosinus Sirkelen med sentrum i origo og radius 1 kalles enhetssirkelen. La v være en vinkel i grunnstilling, og la P være
Sammendrag R2 www.kalkulus.no 31. mai 2009 1 1 Trigonometri Definisjon av sinus og cosinus Sirkelen med sentrum i origo og radius 1 kalles enhetssirkelen. La v være en vinkel i grunnstilling, og la P være
Løsning av utvalgte øvingsoppgaver til Sigma R2 kapittel 1
 Løsning av utvalgte øvingsoppgaver til Sigma R kapittel A. c) tan + sin0 + d) sin60 tan0 A. B. A y sin0 0 sin0 cos0 y 0 y cos0 C 60 D cos AD 0 6 B AD 0 cos 0 CD AD B.6 A tan60 CD BD BD BD tan60 6 AB AD
Løsning av utvalgte øvingsoppgaver til Sigma R kapittel A. c) tan + sin0 + d) sin60 tan0 A. B. A y sin0 0 sin0 cos0 y 0 y cos0 C 60 D cos AD 0 6 B AD 0 cos 0 CD AD B.6 A tan60 CD BD BD BD tan60 6 AB AD
EKSAMEN. 1. klassene, ingenørutdanning og flexing. ANTALL SIDER UTLEVERT: 5(innkl. forside og 2 sider formelark)
 KANDIDATNUMMER: EKSAMEN EMNENAVN: Mtemtikk EMNENUMMER: REA4 og REA4f EKSAMENSDATO:. ugust 9 KLASSE:. klssene, ingenørutdnning og fleing. TID: kl. 9... FAGANSVARLIG: Hns Petter Hornæs ANTALL SIDER UTLEVERT:
KANDIDATNUMMER: EKSAMEN EMNENAVN: Mtemtikk EMNENUMMER: REA4 og REA4f EKSAMENSDATO:. ugust 9 KLASSE:. klssene, ingenørutdnning og fleing. TID: kl. 9... FAGANSVARLIG: Hns Petter Hornæs ANTALL SIDER UTLEVERT:
Fasit. Oppgavebok. Kapittel 2. Bokmål
 Fsit Oppgveok Kpittel 2 Bokmål Kpittel 2 Treknteregning 2.1 75 c 50 e 50 70 d 80 f 53 2.2 B og D er rettvinklet A og C er likeeint 2.3 8,9 m 2.4 J Nei c J 2.5 10,4 cm 6,4 cm c 8,9 cm 2.6 ---- 2.7 115 m
Fsit Oppgveok Kpittel 2 Bokmål Kpittel 2 Treknteregning 2.1 75 c 50 e 50 70 d 80 f 53 2.2 B og D er rettvinklet A og C er likeeint 2.3 8,9 m 2.4 J Nei c J 2.5 10,4 cm 6,4 cm c 8,9 cm 2.6 ---- 2.7 115 m
Numerisk matematikk. Fra Matematikk 3MX (2002) Side
 Numerisk mtemtikk Fr Mtemtikk 3MX (2002) Side 142 147 142 Kpittel 4: Integrlregning 47 NUMERISK MATEMATIKK pffiffiffiffiffi På lommeregneren finner du rskt t 71 er lik 8,426150, og t lg 5 er lik 0,698970
Numerisk mtemtikk Fr Mtemtikk 3MX (2002) Side 142 147 142 Kpittel 4: Integrlregning 47 NUMERISK MATEMATIKK pffiffiffiffiffi På lommeregneren finner du rskt t 71 er lik 8,426150, og t lg 5 er lik 0,698970
Bioberegninger - notat 3: Anvendelser av Newton s metode
 Bioberegninger - nott 3: Anvendelser v Newton s metode 20. februr 2004 1 Euler-Lotk ligningen L oss tenke oss en populsjon bestående v individer v ulik lder. L n være mksiml lder. L m i være ntll vkom
Bioberegninger - nott 3: Anvendelser v Newton s metode 20. februr 2004 1 Euler-Lotk ligningen L oss tenke oss en populsjon bestående v individer v ulik lder. L n være mksiml lder. L m i være ntll vkom
R2 eksamen våren 2014. (19.05.2014)
 R Eksmen V04 R eksmen våren 04. (9.05.04) Løsningsskisser (Versjon 3.0.4) Del - Uten hjelpemidler Oppgve ) fx sinu; u 3x Kjerneregel: f x f uu x cosu3 3 cos3x b) e x e x med kjerneregel som i ) Produktregel:
R Eksmen V04 R eksmen våren 04. (9.05.04) Løsningsskisser (Versjon 3.0.4) Del - Uten hjelpemidler Oppgve ) fx sinu; u 3x Kjerneregel: f x f uu x cosu3 3 cos3x b) e x e x med kjerneregel som i ) Produktregel:
R2 kapittel 4 Tredimensjonale vektorer
 Løsninger v oppgvene i ok R kpittel 4 Tredimensjonle vektorer Løsninger v oppgvene i ok 4. Vi tegner punket A i xy-plnet. Vi mrkerer plsseringen v A med linjestykker ut fr punktene (4,0,0) på x-ksen og
Løsninger v oppgvene i ok R kpittel 4 Tredimensjonle vektorer Løsninger v oppgvene i ok 4. Vi tegner punket A i xy-plnet. Vi mrkerer plsseringen v A med linjestykker ut fr punktene (4,0,0) på x-ksen og
