Løsning, eksamen TFY4205 Kvantemekanikk II Onsdag 8. desember 2010
|
|
|
- Siri Haaland
- 6 år siden
- Visninger:
Transkript
1 Løsning, eksamen TFY45 Kvantemekanikk II Onsdag 8. desember 1 1a) Det elektriske feltet er [ E = ωk Im ( e x a x + e y a y )e i(kz ωt)] [ = ωk Im ( e + a + + e a )e i(kz ωt)]. Et viktig poeng: E er reell, selv om amplitudene a x,a y,a ± og polarisasjonsvektorene e ± er komplekse. Sett først a y =, a x = 1. Vi kunne sette a x = ρe iα med en vilkårlig amplitude ρ og en vilkårlig fase α, men det ville ikke forandre noe vesentlig i argumentet. Vi får at E = ωk e x sin(kz ωt). Det elektriske feltet peker langs x-aksen, og oscillerer både som funksjon av z ved konstant t, for eksempel t = : E = ωk e x sin(kz), og som funksjon av t ved konstant z, for eksempel z = : E = ωk e x sin(ωt). Sett deretter a =, a + = 1, igjen er amplituden og fasen til a + uvesentlig. Vi får at E = ωk[ e x sin(kz ωt) + e y cos(kz ωt)]. Figur 1: E som funksjon av z ved t =, og som funksjon av t ved z =. Det elektriske feltet har nå konstant lengde, E = ωk, men har en retning som oscillerer. Som funksjon av z ved konstant t, for eksempel t =, er E = ωk [ e x sin(kz) + e y cos(kz)]. 1
2 Dette er formelen for en heliks med akse i z-retning, og heliksen er høyredreiende, som en høyreskrue. Som funksjon av t ved konstant z, for eksempel z =, er E = ωk [ e x sin(ωt) + e y cos(ωt)]. Vi ser altså det elektriske feltet rotere i retning med urviseren når vi ser mot bevegelsesretningen til bølgen. Denne rotasjonsretningen svarer til at z-komponenten av dreieimpulsen er negativ. Så da burde vi kanskje ha byttet navn på a + og a? 1b) Bevis for kommutasjonsrelasjonene: ([a x,a x ] i[a x,a y ] + i[a y,a x ] + [a y,a y ] ) [a +,a + ] = 1 [a x + ia y,a x ia y ] = 1 = 1 ( ) = 1. [a +,a ] = 1 [a x + ia y,a x + ia y ] = 1 ( ) [a x,a x] + + [a y,a y] =. Når det gjelder Hamilton-operatoren, kan vi for eksempel regne baklengs: a + a + + a a = 1 ( ) (a x ia y)(a x + ia y ) + (a x + ia y)(a x ia y ) = a xa x + a ya y. Derfor er H = ω(a xa x + a ya y + 1) = ω(a + a + + a a + 1). 1c) Beklager fortegnsfeil i en formel i den opprinnelige oppgaveteksten, korrekt versjon er: + = a + = 1 ( h i v ), = a = 1 ( h + i v ). Oppgaveteksten utlagt på nett er korrigert. Enda en kommentar: tilstandene h og v er ortogonale i Hilbertrommet, h v = a x a y = a ya x =. Og det svarer til at polarisasjonsvektorene e x og e y er ortogonale i vårt dagligdagse tredimensjonale rom. Vi så under 1a) at amplituden a + svarer til høyredreiende sirkulær polarisering. Fotonet i tilstanden + er altså høyredreiende sirkulært polarisert, mens fotonet i tilstanden er venstredreiende sirkulært polarisert. Tilsvarende til definisjonene e ± = 1 ( e x i e y ), a ± = 1 (a x ± ia y ) kan vi definere e f = 1 ( e x + e y ), e g = 1 ( e x e y ), a f = 1 (a x + a y ), a g = 1 (a x a y ),
3 slik at e x a x + e y a y = e f a f + e g a g. Amplituden a f svarer til polarisasjon langs vektoren e f, mens a g svarer til polarisasjon langs vektoren e g. Polarisasjonsvektorene e f og e g er dreid 45 i forhold til e x og e y. I tilstanden f = 1 ( h + v ) = 1 (a x + a y) = a f er altså fotonet lineært polarisert langs e f, og i tilstanden g = 1 ( h v ) = a g er fotonet lineært polarisert langs e g. Tilstandene + og er ortogonale i Hilbertrommet, og det svarer til at de komplekse polarisasjonsvektorene e + og e er ortogonale: ( e + ) e = 1 ( e x + i e y ) ( e x + i e y ) = 1 ( e x e x e y e y ) = 1 (1 1) =. På samme måte er tilstandene f og g ortogonale, akkurat som polarisasjonsvektorene e f og e g er ortogonale. 1d) For en generell tilstand ψ = ψ h h + ψ v v er sannsynligheten for å måle horisontal polarisasjon gitt som P(h ψ) = h ψ = ψ h, og sannsynligheten for å måle vertikal polarisasjon er P(v ψ) = v ψ = ψ v. De komplekse koeffisientene ψ h og ψ v er sannsynlighetsamplituder. Alle sannsynlighetene som det spørres etter, er 1/: P(h +) = P(v +) = P(h ) = P(v ) = P(h f) = P(v f) = P(h g) = P(v g) = 1. Det er altså umulig å se forskjell på de fire tilstandene dersom vi bare måler horisontal og vertikal polarisasjon. Skal vi kunne se forskjell, må vi måle noe som gir informasjon om fasene til sannsynlighetsamplitudene. 1e) Kommutatorrelasjonen [a x,a x] = 1 kan skrives slik: a x a x = a x a x + 1. Nedenfor bruker vi ellers at a x = a y = og at = 1. 3
4 Det er da rett fram å bevise at en-fotontilstanden h er normert (men det var det ikke spørsmål om i oppgaven): h h = a x a x = (a xa x + 1) = = 1. Det er like rett fram å bevise at to-fotontilstanden hv er normert: hv hv = a y a x a xa y = (a x a x)(a y a y) = (a xa x + 1)(a ya y + 1) Videre har vi at = (a x a x + 1) = = 1. (a x ) (a x) = a x (a x a x)a x = a x (a xa x + 1)a x = (a x a x) + a x a x = (a x a x + 1) + (a x a x + 1) = (a x a x) + 3a x a x +. Da kan vi bevise at to-fotontilstanden hh er normert: hh hh = 1 (a x) (a x) = 1 ((a xa x ) + 3a xa x + ) = = 1. Tilsvarende viser vi at tilstanden vv er normert. Dette er ikke den enkleste og mest systematiske måten å regne på. Vi kan bruke Leibnizregelen for kommutering, til å beregne kommutatoren Eller ganske generelt, [A,BC] = [A,B]C + B [A,C], [a x,(a x ) ] = [a x,a x a x ] = [a x,a x ]a x + a x [a x,a x ] = a x. Så bruker vi at a x =, det gir at [a x,(a x )k ] = k (a x )k 1. a x (a x) k = (a x (a x) k (a x) k a x ) = [a x,(a x) k ] = k (a x) k 1. Dermed har vi et mer gjennomskuelig bevis for at to-fotontilstanden hh er normert: hh hh = 1 (a x) (a x ) = 1 a xa x (a x ) = a x a x = = 1. Noen svarer på oppgaven omtrent slik: for en harmonisk oscillator er de normerte energiegentilstandene, 1,, osv., med a = 1 og a 1 = 1. Det er for så vidt korrekt, men er et ufullstendig svar på spørsmålet, vi påstår bare det vi skulle bevise. Fordi operatorene a x og a y kommuterer, har vi at + = a + a = 1 (a x ia y)(a x + ia y) = 1 ((a x) + (a y) ) = 1 ( hh + vv ). 4
5 I denne tilstanden er det følgelig 5 % sannsynlighet for å observere at begge fotonene er horisontalt polarisert, og 5 % sannsynlighet for å observere at begge fotonene er vertikalt polarisert. Vi vil aldri observere at det ene fotonet er horisontalt og det andre vertikalt polarisert. Hvis vi måler på to en-fotontilstander, først med fotonet i tilstanden + og etterpå med fotonet i tilstanden, så har vi hver gang 5 % sannsynlighet for å observere at fotonet er horisontalt polarisert og 5 % sannsynlighet for å observere at det er vertikalt polarisert. Og siden de to målingene er uavhengige av hverandre, har vi 5 % sannsynlighet for å observere at begge fotonene er horisontalt polarisert, 5 % sannsynlighet for å observere at begge er vertikalt polarisert, og 5 % sannsynlighet for å observere at det ene er horisontalt og det andre vertikalt polarisert. Vi må bare konstatere at en to-fotontilstand med de to fotonene i to ortogonale polarisasjonstilstander er noe helt annet enn to en-fotontilstander med de to fotonene i de samme to ortogonale polarisasjonstilstandene. Vi kan for eksempel spørre om de to fotonene har samme polarisasjon. Svaret avhenger, neppe helt uventet, av hva slags polarisasjon vi velger å måle. Hvis vi måler sirkulær polarisasjon, dvs., vi spør om polarisasjonstilstanden er + eller, så vil vi alltid få som svar at fotonene har motsatt polarisasjon. Naturlig nok, for det var jo slik vi preparerte dem før vi målte, og det gjelder både to-fotontilstanden og de to en-fotontilstandene. Hvis vi derimot måler lineær polarisasjon, hvis vi for eksempel spør om polarisasjonstilstanden er h eller v, så får vi totalt forskjellige svar for to-fotontilstanden og for en-fotontilstandene. Med to-fotontilstanden vil vi alltid få til svar at fotonene har samme polarisasjon, til tross for at vi preparerte dem med motsatt polarisasjon. Til gjengjeld er det helt tilfeldig om vi finner at begge har horisontal polarisasjon eller at begge har vertikal polarisasjon. Med en-fotontilstandene er det 5 % sannsynlighet for å måle samme polarisasjon og 5 % sannsynlighet for å måle motsatt polarisasjon, og det ligner kanskje mest på det vi ville vente oss intuitivt? Dette sitatet fra John Wheeler kan være en passende kommentar her: If you are not completely confused by quantum mechanics, you do not understand it. 1f) En 1-fotontilstand, der alle de 1 fotonene har samme impuls, har 11 mulige polarisasjonstilstander. Ortonormerte 1-fotontilstander er for eksempel r,s = 1 r!s! (a x )r (a y )s med r, s og r + s = 1. Vi skal ha 1 kreasjonsoperatorer, og hver av dem kan være enten a x eller a y. Men disse to operatorene kommuterer, slik at rekkefølgen av dem er likegyldig, bare antallet av a x og antallet av a y har betydning. At kreasjonsoperatorene a x og a y kommuterer, betyr at fotonene er bosoner: bølgefunksjonen for en mangefotontilstand er fullstendig symmetrisk. Det er denne symmetriegenskapen som reduserer antallet tilstander så drastisk. Uten den ville antallet tilstander ha vært 1 =
6 1g) Vi har at r fi = d 3 r (ψ f ( r)) r ψ i ( r) = 1 8πa 4 d 3 r e 3r a (x ex + y e y + z e z )(x + iy). Når vi multipliserer ut parentesene i integralet, får vi mange integral som blir null fordi integranden er antisymmetrisk. Som for eksempel d 3 r e 3r a xy = dz dy y dx e 3r a x =, der det innerste integralet er null fordi integranden er antisymmetrisk i x. Bare to av integralene blir ikke null, dem kan vi beregne enklest ved et lite knep: d 3 r e 3r a x = d 3 r e 3r a y = d 3 r e 3r a z = 1 d 3 r e 3r a r 3 = 4π 3 dr e 3r a r 4 = 4π 3 Ved delvis integrasjon finner vi, for λ > og k >, at 4!(a) = 14πa5 43. og følgelig dr e λr r k = 1 λ e λr r k dr e λr r 4 = 4! λ 4 + k λ dr e λr r k 1 = k λ dr e λr = 4! λ 5 e λr = 4! λ 5. dr e λr r k 1, En annen måte å regne ut det samme resultatet på er å starte med integralet dr e λr = 1 λ. Så opererer vi på denne ligningen fire ganger med d/dλ og får at dr e λr r = 1 λ, dr e λr r = λ 3, dr e λr r 3 = 3! λ 4, dr e λr r 4 = 4! λ 5. Alt i alt gir det at r fi = 18a 43 ( e x + i e y ). En grei kontroll er at r fi bør ha dimensjon lengde. Svaret på oppgaven er altså: C = 18a 43 = 7 a
7 Hvis fotonet sendes ut i (x, y)-planet, så kunne det tenkes å være lineært polarisert langs z-aksen, men i så fall blir overgangssannsynligheten null, fordi e = e z gir at ( e ) r fi = C e z ( e x + i e y ) =. Det betyr at dersom vi gjør et eksperiment der vi tester om fotonet er lineært polarisert i z-retningen, så får vi garantert negativt svar. Sagt med andre ord: fotonet er definitivt ikke lineært polarisert i z-retningen. Når vi vet det, så vet vi at tilstandsvektoren i Hilbertrommet må være ortogonal til den tilstanden der fotonet er lineært polarisert i z- retningen. Det er det samme som at polarisasjonsvektoren til fotonet må være ortogonal til e z. Den må dessuten være ortogonal til bevegelsesretningen til fotonet. La oss si at bølgetallsvektoren er k = k (cos α ex + sin α e y ), da må polarisasjonsvektoren være e = sinα e x + cos α e y, slik at k e =. Fotonet er altså lineært polarisert i denne retningen. Da er ( e ) r fi = C sin α + icos α = C. Overgangssannsynligheten er altså uavhengig av retningen på fotonet, så lenge fotonet sendes ut i (x,y)-planet: vinkelfordelingen av fotonene er isotrop i (x,y)-planet. Hvis fotonet sendes ut i positiv z-retning, så vil det være sirkulært polarisert. Vi ser at den komplekse polarisasjonsvektoren gir null overgangssannsynlighet, idet e + = 1 ( e x i e y ) ( e +) r fi = C ( e x + i e y ) ( e x + i e y ) = C e x e x + i e x e y + i e y e x e y e y = C =. Derfor må polarisasjonsvektoren være ortogonal til e +, og den eneste muligheten er e = 1 ( e x + i e y ). Den gir en overgangssannsynlighet ulik null, idet ( e ) r fi = C ( e x i e y ) ( e x + i e y ) = C e x e x + e y e y = C. Konklusjon: hvis fotonet kommer ut i positiv z-retning, er det i den sirkulære polarisasjonstilstanden. Merk at overgangssannsynligheten er proporsjonal med C for et foton som sendes ut i (x,y)-planet, og proporsjonal med C for et foton som sendes ut langs z-aksen. 7
8 Vinkelfordelingen av fotonene er ikke isotrop i alle tre dimensjonene: innenfor en gitt romvinkel kommer det ut dobbelt så mange fotoner langs z-aksen som i (x,y)-planet. Den sirkulære polarisasjonen til fotonene som sendes ut langs z-aksen kan vi forstå som en konsekvens av at dreieimpulsen er bevart. Atomet har en dreieimpuls langs z-aksen som er + i start-tilstanden ψ i og i slutt-tilstanden ψ f. Altså må fotonet ha overtatt z-komponenten av dreieimpulsen. Når impulsen til fotonet, p γ = k = k e z, peker langs den positive z-aksen, så kan ikke banedreieimpulsen til fotonet, L γ = r γ p γ, ha noen komponent langs z-aksen. Altså må spinnet til fotonet, Sγ, ha z-komponent lik +. Det stemmer med det vi fant ut ovenfor, under punkt 1a), at fotonet i den sirkulære polarisasjonstilstanden har positiv komponent av dreieimpulsen langs z-aksen. Spinnkomponenten langs impulsen, S γ k/k, kalles helisitet. Et foton kan ha helisitet enten + eller, hvis det da ikke er i en tilstand som er en superposisjon av de to helisitetsegentilstandene. Fotonet som hydrogenatomet sender ut langs den positive z- aksen, i vårt eksempel, har helisitet +, som en konsekvens av at z-komponenten av dreieimpulsen er bevart. a) Born-tilnærmingen gir spredningsamplituden f B som et integral, og når potensialet er kulesymmetrisk, kan vi utføre vinkelintegrasjonen. I integrasjonen bruker vi polarkoordinater med z-aksen langs q. Vi må skille mellom spredningsvinklene θ og φ og polarvinklene i integralet, la oss kalle dem α og β. Polarvinklene θ og φ bestemmer retningen til den utgående impulsen k i forhold til den innkommende impulsen k, og dermed retningen til q = k k, mens α og β bestemmer retningen til integrasjonsvariabelen r i forhold til q. Det gir at f B ( q) = m π = m π d 3 r V ( r) e i q r dr r 1 = m dr r V (r) = m 1 1 π d(cos α) 1 dr r V (r) sin(qr) qr iqr cos α dβ V (r) e du e iqru = m = m q dr r V (r) e iqru iqr dr r V (r)sin(qr). u=1 u= 1 b) Den viktigste forutsetningen for partialbølgeutviklingen er at potensialet er kulesymmetrisk, slik at banedreieimpulsen L = r p er bevart. Når vi kvantiserer L til verdien l(l+1), så er kvantetallet l bevart, og det eneste som kan skje med en innkommende bølge, er at den kommer ut igjen med en l-avhengig faseforskyving δ l. Siden asimutvinkelen φ ikke opptrer i partialbølgeutviklingen, er det lett å tenke (som mange eksamenskandidater gjør) at sylindersymmetri er tilstrekkelig, at full kulesymmetri ikke er nødvendig, men det er altså ikke korrekt. Det er også en forutsetning at det ikke finnes uelastisk spredning. Partialbølgeutviklingen på den formen som er gitt her, er gyldig for partikler uten spinn (eller for partikler med spinn når spredningen er uavhengig av spinnet). Anta at potensialet har en endelig rekkevidde R. I grensen når energien går mot null, bidrar da bare partialbølgene med lav l. Det kan vi forstå ut fra et klassisk resonnement: 8
9 dreieimpulsen L = r p til partikkelen som blir spredt, begrenses av ulikheten L = L l R p = Rk, altså l Rk. Ut fra Schrödingerligningen kan det vises, for eksempel for spredning på en hard kule, at δ l som k l+1 når k. Det er derfor en god tilnærming å bruke partialbølgeutviklingen med bare noen få ledd i summen når potensialet har endelig rekkevidde og energien er lav. Første ordens Born-tilnærming er bedre når energien er høy. Born-tilnærmingen blir generelt bedre når energien øker (i følge P.C. Hemmers lærebok). I motsetning til partialbølgeutviklingen med få ledd i summen, som blir dårligere når energien øker. c) Totaltverrsnittet, integrert over alle spredningsvinklene, er σ = dω dσ dω = = π 1 k d(cos θ) 1 = π k = 4π k l= l = 1 dω f(θ) = π l= l = 1 d(cos θ) f(θ)(f(θ)) (l + 1)(l + 1) e i(δ l δ ) l sin δ l sin δ l P l (cos θ)p l (cos θ) (l + 1)(l + 1) e i(δ l δ l ) sin δ l sin δ l (l + 1) sin δ l. l= δ ll l + 1 Når vi setter spredningsvinkelen lik null og tar imaginærdelen av spredningsamplituden, får vi at Im f() = 1 k (l + 1) (Im e iδ l )sin δ l P l (1) = 1 k l= Dette er det optiske teoremet. (l + 1) sin δ l = k 4π σ. Første ordens Born-tilnærming med et kulesymmetrisk potensial gir en rent reell spredningsamplitude, i følge formelen vi beviste under punkt a). Det resultatet er ikke konsistent med det optiske teoremet. l= 9
Løsning, eksamen TFY4205 Kvantemekanikk II Torsdag 8. desember 2011
 Løsning, eksamen TFY45 Kvantemekanikk II Torsdag 8. desember a) Et kort og fullgodt svar er at en stasjonær tilstand ψ er en løsning av den tidsuavhengige Schrödingerligningen H ψ E ψ, () der H er Hamilton-operatoren
Løsning, eksamen TFY45 Kvantemekanikk II Torsdag 8. desember a) Et kort og fullgodt svar er at en stasjonær tilstand ψ er en løsning av den tidsuavhengige Schrödingerligningen H ψ E ψ, () der H er Hamilton-operatoren
Eksamen i fag FY1004 Innføring i kvantemekanikk Tirsdag 22. mai 2007 Tid:
 Side 1 av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 51 72) Sensurfrist: Tirsdag 12. juni 2007
Side 1 av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 51 72) Sensurfrist: Tirsdag 12. juni 2007
Eksamen i fag TFY4205 Kvantemekanikk II Onsdag 8. desember 2010 Tid:
 Side 1 av 5 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53, mobil 90 07 51 7 Eksamen i fag TFY405 Kvantemekanikk
Side 1 av 5 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53, mobil 90 07 51 7 Eksamen i fag TFY405 Kvantemekanikk
FY2045/TFY4250 Kvantemekanikk I, løsning øving 14 1 LØSNING ØVING 14. ψ 210 z ψ 100 d 3 r a.
 FY45/TFY45 Kvantemekanikk I, løsning øving 14 1 LØSNING ØVING 14 Løsning Oppgave 14 1 Fra oppg 3, eksamen august 1 a. Med Y = 1/ 4π og zy = ry 1 / 3 kan vi skrive matrise-elementene av z på formen (z)
FY45/TFY45 Kvantemekanikk I, løsning øving 14 1 LØSNING ØVING 14 Løsning Oppgave 14 1 Fra oppg 3, eksamen august 1 a. Med Y = 1/ 4π og zy = ry 1 / 3 kan vi skrive matrise-elementene av z på formen (z)
Eksamen i fag FY1004 Innføring i kvantemekanikk Fredag 30. mai 2008 Tid: a 0 = 4πǫ 0 h 2 /(e 2 m e ) = 5, m
 Side av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 5 7 Sensurfrist: Fredag 0 juni 008 Eksamen
Side av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 5 7 Sensurfrist: Fredag 0 juni 008 Eksamen
Eksamen FY1004 Innføring i kvantemekanikk Tirsdag 22. mai 2007 Løsninger
 Eksamen FY1004 Innføring i kvantemekanikk Tirsdag. mai 007 Løsninger 1a Et hydrogenlikt atom har ett elektron med masse m og ladning e som er bundet til en atomkjerne med ladning Ze. Siden kjernen har
Eksamen FY1004 Innføring i kvantemekanikk Tirsdag. mai 007 Løsninger 1a Et hydrogenlikt atom har ett elektron med masse m og ladning e som er bundet til en atomkjerne med ladning Ze. Siden kjernen har
Løsningsforslag Eksamen 1. desember 2008 TFY4250 Atom- og molekylfysikk/fy2045 Kvantefysikk
 Eksamen TFY45/FY45. desember 8 - løsningsforslag Løsningsforslag Eksamen. desember 8 TFY45 Atom- og molekylfysikk/fy45 Kvantefysikk Oppgave a. For x og E = E B < har den tidsuavhengige Schrödingerligningen
Eksamen TFY45/FY45. desember 8 - løsningsforslag Løsningsforslag Eksamen. desember 8 TFY45 Atom- og molekylfysikk/fy45 Kvantefysikk Oppgave a. For x og E = E B < har den tidsuavhengige Schrödingerligningen
En samling av mer eller mindre relevante formler (uten nærmere forklaring) er gitt til slutt i oppgavesettet.
 Norges teknisk-naturvitenskapelige universitet NTNU Institutt for fysikk Lade EKSAMEN I: MNF FY 44 KVANTEMEKANIKK I DATO: Tirsdag 4. desember 999 TID: 9.00 5.00 Antall vekttall: 4 Antall sider: 3 Sensurdato:
Norges teknisk-naturvitenskapelige universitet NTNU Institutt for fysikk Lade EKSAMEN I: MNF FY 44 KVANTEMEKANIKK I DATO: Tirsdag 4. desember 999 TID: 9.00 5.00 Antall vekttall: 4 Antall sider: 3 Sensurdato:
A.3.e: Ortogonale egenfunksjonssett
 TFY4250/FY2045 Tillegg 2 1 Tillegg 2: A.3.e: Ortogonale egenfunksjonssett Ikke-degenererte egenverdier La oss først anta at en operator ˆF har et diskret og ikke-degeneret spektrum. Det siste betyr at
TFY4250/FY2045 Tillegg 2 1 Tillegg 2: A.3.e: Ortogonale egenfunksjonssett Ikke-degenererte egenverdier La oss først anta at en operator ˆF har et diskret og ikke-degeneret spektrum. Det siste betyr at
Løsningsforslag Eksamen 27. mai 2005 FY2045 Kvantefysikk
 Eksamen FY2045 27. mai 2005 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 27. mai 2005 FY2045 Kvantefysikk a. Ifølge den tidsuavhengige Shrödingerligningen, Ĥψ = Eψ, har vi for x < 0 : E = Ĥψ ψ
Eksamen FY2045 27. mai 2005 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 27. mai 2005 FY2045 Kvantefysikk a. Ifølge den tidsuavhengige Shrödingerligningen, Ĥψ = Eψ, har vi for x < 0 : E = Ĥψ ψ
Løsningsforslag Eksamen 8. august 2009 TFY4250 Atom- og molekylfysikk
 Eksamen TFY425 8. august 29 - løsningsforslag Oppgave Løsningsforslag Eksamen 8. august 29 TFY425 Atom- og molekylfysikk a. For β = har vi en ordinær boks fra x = til x = L. Energiegenfunksjonene har formen
Eksamen TFY425 8. august 29 - løsningsforslag Oppgave Løsningsforslag Eksamen 8. august 29 TFY425 Atom- og molekylfysikk a. For β = har vi en ordinær boks fra x = til x = L. Energiegenfunksjonene har formen
FY1006/TFY Løsning øving 8 1 LØSNING ØVING 8. a. (a1): Ved kontroll av egenverdiene kan vi se bort fra normeringsfaktorene.
 FY16/TFY415 - Løsning øving 8 1 Løsning oppgave 3 Vinkelfunksjoner, radialfunksjoner og orbitaler for hydrogenlignende system LØSNING ØVING 8 a. (a1: Ved kontroll av egenverdiene kan vi se bort fra normeringsfaktorene.
FY16/TFY415 - Løsning øving 8 1 Løsning oppgave 3 Vinkelfunksjoner, radialfunksjoner og orbitaler for hydrogenlignende system LØSNING ØVING 8 a. (a1: Ved kontroll av egenverdiene kan vi se bort fra normeringsfaktorene.
Løsningsforslag til øving 4
 1 FY100/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 01. Løsningsforslag til øving 4 Oppgave 1 a) D = D 0 [ cos (kx ωt) + sin (kx ωt) ] 1/ = D 0 for alle x og t. Med andre ord, vi har overalt
1 FY100/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 01. Løsningsforslag til øving 4 Oppgave 1 a) D = D 0 [ cos (kx ωt) + sin (kx ωt) ] 1/ = D 0 for alle x og t. Med andre ord, vi har overalt
Løsningsforslag Konte-eksamen 2. august 2003 SIF4048 Kjemisk fysikk og kvantemekanikk
 Konte-eksamen SIF448.aug. 3 - løsningsforslag 1 Oppgave 1 a. Hamilton-operatoren er Løsningsforslag Konte-eksamen. august 3 SIF448 Kjemisk fysikk og kvantemekanikk Ĥ = h m x + V (x), og den tidsuavhengige
Konte-eksamen SIF448.aug. 3 - løsningsforslag 1 Oppgave 1 a. Hamilton-operatoren er Løsningsforslag Konte-eksamen. august 3 SIF448 Kjemisk fysikk og kvantemekanikk Ĥ = h m x + V (x), og den tidsuavhengige
Løsningsforslag Eksamen 12. august 2004 TFY4215 Kjemisk fysikk og kvantemekanikk
 Eksamen TFY4215 12. august 2004 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 12. august 2004 TFY4215 Kjemisk fysikk og kvantemekanikk a. Den tidsuavhengige Schrödingerligningen, Ĥψ = Eψ, tar for
Eksamen TFY4215 12. august 2004 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 12. august 2004 TFY4215 Kjemisk fysikk og kvantemekanikk a. Den tidsuavhengige Schrödingerligningen, Ĥψ = Eψ, tar for
LØSNING EKSTRAØVING 2
 TFY415 - løsning Ekstraøving 1 Oppgave 9 LØSNING EKSTRAØVING hydrogenlignende atom a. For Z = 55 finner vi de tre målene for radien til grunntilstanden ψ 100 vha formlene side 110 i Hemmer: 1/r 1 = a =
TFY415 - løsning Ekstraøving 1 Oppgave 9 LØSNING EKSTRAØVING hydrogenlignende atom a. For Z = 55 finner vi de tre målene for radien til grunntilstanden ψ 100 vha formlene side 110 i Hemmer: 1/r 1 = a =
FY2045/TFY4250 Kvantemekanikk I, løsning øving 8 1 LØSNING ØVING 8
 FY045/TFY450 Kvantemekanikk I, løsning øving 8 1 Løsning oppgave 8 1 LØSNING ØVING 8 Koherente tilstander for harmonisk oscillator a. Utviklingen (3) er en superposisjon av stasjonære tilstander for oscillatoren,
FY045/TFY450 Kvantemekanikk I, løsning øving 8 1 Løsning oppgave 8 1 LØSNING ØVING 8 Koherente tilstander for harmonisk oscillator a. Utviklingen (3) er en superposisjon av stasjonære tilstander for oscillatoren,
Løsning, eksamen TFY4205 Kvantemekanikk II Mandag 13. august 2012
 Løsning, eksamen TFY4205 Kvantemekanikk II Mandag 13 august 2012 1a) Kravene at både ψ og ψ er kontinuerlige der potensialet er diskontinuerlig, følger av Schrödingerligningen 2 2m ψ x) + V x)ψx) = Eψx)
Løsning, eksamen TFY4205 Kvantemekanikk II Mandag 13 august 2012 1a) Kravene at både ψ og ψ er kontinuerlige der potensialet er diskontinuerlig, følger av Schrödingerligningen 2 2m ψ x) + V x)ψx) = Eψx)
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS14, Kvantefysikk Eksamensdag: 17. august 17 4 timer Lovlige hjelpemidler: Rottmann: Matematisk formelsamling, Øgrim og Lian:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS14, Kvantefysikk Eksamensdag: 17. august 17 4 timer Lovlige hjelpemidler: Rottmann: Matematisk formelsamling, Øgrim og Lian:
Løsningsforslag Konte-eksamen 13. august 2002 SIF4048 Kjemisk fysikk og kvantemekanikk
 ppgave Løsningsforslag Konte-eksamen 3. august SIF8 Kjemisk fysikk og kvantemekanikk a. Da sannsynlighetstettheten Ψ(x, ) mω/π h exp( mωx / h) er symmetrisk med hensyn på origo, er forventningsverdien
ppgave Løsningsforslag Konte-eksamen 3. august SIF8 Kjemisk fysikk og kvantemekanikk a. Da sannsynlighetstettheten Ψ(x, ) mω/π h exp( mωx / h) er symmetrisk med hensyn på origo, er forventningsverdien
Løsningsforslag Eksamen 1. desember 2009 TFY4250/FY2045
 Eksamen TFY45/FY45 1. desember 9 - løsningsforslag 1 Oppgave 1 a. For n = 3j er Løsningsforslag Eksamen 1. desember 9 TFY45/FY45 ψ () 3j (L/3) = A sin(jπ) = og ψ () 3j (L/3) = A sin(jπ) =. Vi kan da konstatere
Eksamen TFY45/FY45 1. desember 9 - løsningsforslag 1 Oppgave 1 a. For n = 3j er Løsningsforslag Eksamen 1. desember 9 TFY45/FY45 ψ () 3j (L/3) = A sin(jπ) = og ψ () 3j (L/3) = A sin(jπ) =. Vi kan da konstatere
TFY4215 Innføring i kvantefysikk - Løsning øving 1 1 LØSNING ØVING 1
 TFY425 Innføring i kvantefysikk - Løsning øving Løsning oppgave a. LØSNING ØVING Vi merker oss at sannsynlighetstettheten, Ψ(x, t) 2 = A 2 e 2λ x, er symmetrisk med hensyn på origo. For normeringsintegralet
TFY425 Innføring i kvantefysikk - Løsning øving Løsning oppgave a. LØSNING ØVING Vi merker oss at sannsynlighetstettheten, Ψ(x, t) 2 = A 2 e 2λ x, er symmetrisk med hensyn på origo. For normeringsintegralet
FY2045/TFY4250 Kvantemekanikk I, øving 6 1 ØVING 6. Fermi-impulser og -energier
 FY2045/TFY4250 Kvantemekanikk I, 2012 - øving 6 1 ØVING 6 Oppgave 6 1 Fermi-impulser og -energier a. Anta at en ideell gass av N (ikke-vekselvirkende) spinn- 1 -fermioner befinner seg i grunntilstanden
FY2045/TFY4250 Kvantemekanikk I, 2012 - øving 6 1 ØVING 6 Oppgave 6 1 Fermi-impulser og -energier a. Anta at en ideell gass av N (ikke-vekselvirkende) spinn- 1 -fermioner befinner seg i grunntilstanden
TFY4215 Kjemisk fysikk og kvantemekanikk - Øving 1 1 ØVING 1. En liten briefing om forventningsverdier, usikkerheter osv
 TFY4215 Kjemisk fysikk og kvantemekanikk - Øving 1 1 Frist for innlevering: mandag 26. januar ØVING 1 En liten briefing om forventningsverdier, usikkerheter osv Eksempel: Terningkast Ved terningkast er
TFY4215 Kjemisk fysikk og kvantemekanikk - Øving 1 1 Frist for innlevering: mandag 26. januar ØVING 1 En liten briefing om forventningsverdier, usikkerheter osv Eksempel: Terningkast Ved terningkast er
EKSAMENSOPPGAVE. Eksamen i: Fys-2000 Kvantemekanikk Dato: 5. juni 2013 Tid: Kl Sted: Åsgårdveien 9. og fysikk, lommekalkulator
 FAKUTET FOR NATURVITENSKAP OG TEKNOOGI EKSAMENSOPPGAVE Eksamen i: Fys-2000 Kvantemekanikk Dato: 5. juni 2013 Tid: Kl 09.00-13.00 Sted: Åsgårdveien 9 Tillatte hjelpemidler: Formelsamlinger i matematikk
FAKUTET FOR NATURVITENSKAP OG TEKNOOGI EKSAMENSOPPGAVE Eksamen i: Fys-2000 Kvantemekanikk Dato: 5. juni 2013 Tid: Kl 09.00-13.00 Sted: Åsgårdveien 9 Tillatte hjelpemidler: Formelsamlinger i matematikk
Løsningsforslag Eksamen 13. august 2011 FY1006/TFY4215 Innføring i kvantefysikk
 Eksamen FY1006/TFY415 13. august 011 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 13. august 011 FY1006/TFY415 Innføring i kvantefysikk a. Fra den tidsuavhengige Schrödingerligningen har vi for
Eksamen FY1006/TFY415 13. august 011 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 13. august 011 FY1006/TFY415 Innføring i kvantefysikk a. Fra den tidsuavhengige Schrödingerligningen har vi for
Løsningsforslag Eksamen 26. mai 2008 TFY4215 Kjemisk fysikk og kvantemekanikk
 Eksamen TFY4215 26. mai 2008 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 26. mai 2008 TFY4215 Kjemisk fysikk og kvantemekanikk a. Utenfor boksen, hvor V (x) =, er bølgefunksjonen lik null. Kontinuiteten
Eksamen TFY4215 26. mai 2008 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 26. mai 2008 TFY4215 Kjemisk fysikk og kvantemekanikk a. Utenfor boksen, hvor V (x) =, er bølgefunksjonen lik null. Kontinuiteten
A.5 Stasjonære og ikke-stasjonære tilstander
 TFY4250/FY2045 Tillegg 4 - Stasjonære og ikke-stasjonære tilstander 1 Tillegg 4: A.5 Stasjonære og ikke-stasjonære tilstander a. Stasjonære tilstander (Hemmer p 26, Griffiths p 21) Vi har i TFY4215 (se
TFY4250/FY2045 Tillegg 4 - Stasjonære og ikke-stasjonære tilstander 1 Tillegg 4: A.5 Stasjonære og ikke-stasjonære tilstander a. Stasjonære tilstander (Hemmer p 26, Griffiths p 21) Vi har i TFY4215 (se
Figur 1: Skisse av Franck-Hertz eksperimentet. Hentet fra Wikimedia Commons.
 Oppgave 1 Franck-Hertz eksperimentet Med utgangspunkt i skissen i figuren under, gi en konsis beskrivelse av Franck-Hertz eksperimentet, dets resultater og betydning for kvantefysikken. [ poeng] Figur
Oppgave 1 Franck-Hertz eksperimentet Med utgangspunkt i skissen i figuren under, gi en konsis beskrivelse av Franck-Hertz eksperimentet, dets resultater og betydning for kvantefysikken. [ poeng] Figur
Løsningsforslag for FYS2140 Kvantemekanikk, Torsdag 16. august 2018
 Løsningsforslag for FYS140 Kvantemekanikk, Torsdag 16. august 018 Oppgave 1: Materiens bølgeegenskaper a) De Broglie fikk Nobelprisen i 199 for sin hypotese. Beskriv med noen setninger hva den går ut på.
Løsningsforslag for FYS140 Kvantemekanikk, Torsdag 16. august 018 Oppgave 1: Materiens bølgeegenskaper a) De Broglie fikk Nobelprisen i 199 for sin hypotese. Beskriv med noen setninger hva den går ut på.
FY1006/TFY4215 Innføring i kvantefysikk - Øving 1 1 ØVING 1. En liten briefing om forventningsverdier, usikkerheter osv
 FY16/TFY4215 Innføring i kvantefysikk - Øving 1 1 Frist for innlevering: mandag 28. januar (jf Åre) ØVING 1 En liten briefing om forventningsverdier, usikkerheter osv Eksempel: Terningkast Ved terningkast
FY16/TFY4215 Innføring i kvantefysikk - Øving 1 1 Frist for innlevering: mandag 28. januar (jf Åre) ØVING 1 En liten briefing om forventningsverdier, usikkerheter osv Eksempel: Terningkast Ved terningkast
Løsningsforslag til eksamen i TFY4170 Fysikk august 2004
 NTNU Side 1av7 Institutt for fysikk Fakultet for naturvitenskap og teknologi Dette løsningsforslaget er på 7 sider. Løsningsforslag til eksamen i TFY4170 Fysikk 1. august 004 Oppgave 1. Interferens a)
NTNU Side 1av7 Institutt for fysikk Fakultet for naturvitenskap og teknologi Dette løsningsforslaget er på 7 sider. Løsningsforslag til eksamen i TFY4170 Fysikk 1. august 004 Oppgave 1. Interferens a)
Løsningsforslag Eksamen 20. desember 2012 FY2045/TFY4250 Kvantemekanikk I
 Eksamen FY045/TFY450 0. desember 0 - løsningsforslag Oppgave Løsningsforslag Eksamen 0. desember 0 FY045/TFY450 Kvantemekanikk I a. For x < 0 er potensialet lik null. (i) For E > 0 er da ψ E = (m e E/
Eksamen FY045/TFY450 0. desember 0 - løsningsforslag Oppgave Løsningsforslag Eksamen 0. desember 0 FY045/TFY450 Kvantemekanikk I a. For x < 0 er potensialet lik null. (i) For E > 0 er da ψ E = (m e E/
Løsningsforslag Eksamen 28. mai 2003 SIF4048 Kjemisk fysikk og kvantemekanikk
 Eksamen SIF4048 8.05.03 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 8. mai 003 SIF4048 Kjemisk fysikk og kvantemekanikk a. Da sannsynlighetstettheten Ψ(x, 0) = β/π exp( βx ) er symmetrisk med
Eksamen SIF4048 8.05.03 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 8. mai 003 SIF4048 Kjemisk fysikk og kvantemekanikk a. Da sannsynlighetstettheten Ψ(x, 0) = β/π exp( βx ) er symmetrisk med
EKSAMEN I TFY4250 ATOM- OG MOLEKYLFYSIKK FY2045 KVANTEFYSIKK Tirsdag 1. desember 2009 kl
 NORSK TEKST Side 1 av 5 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 18 67, eller 97012355 EKSAMEN I TFY4250 ATOM- OG MOLEKYLFYSIKK
NORSK TEKST Side 1 av 5 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 18 67, eller 97012355 EKSAMEN I TFY4250 ATOM- OG MOLEKYLFYSIKK
TFY Løsning øving 6 1 LØSNING ØVING 6. Grunntilstanden i hydrogenlignende atom
 TFY45 - Løsning øving 6 Løsning oppgave 8 LØSNING ØVING 6 Grunntilstanden i hydrogenlignende atom a. Vi merker oss først at vinkelderivasjonene i Laplace-operatoren gir null bidrag til ψ, siden ψ(r) ikke
TFY45 - Løsning øving 6 Løsning oppgave 8 LØSNING ØVING 6 Grunntilstanden i hydrogenlignende atom a. Vi merker oss først at vinkelderivasjonene i Laplace-operatoren gir null bidrag til ψ, siden ψ(r) ikke
TFY Løsning øving 5 1 LØSNING ØVING 5. Krumning og stykkevis konstante potensialer
 TFY4215 - Løsning øving 5 1 Løsning oppgave 16 LØSNING ØVING 5 Krumning og stykkevis konstante potensialer a. I et område hvor V er konstant (lik V 1 ), og E V 1 er positiv (slik at området er klassisk
TFY4215 - Løsning øving 5 1 Løsning oppgave 16 LØSNING ØVING 5 Krumning og stykkevis konstante potensialer a. I et område hvor V er konstant (lik V 1 ), og E V 1 er positiv (slik at området er klassisk
Løsning til øving 8 for FY1004, høsten 2007
 øsning til øving 8 for FY4, høsten 7 Vi tar for oss en partikkel med masse m i en endimensjonal boks med lengde For < x < gjelder den stasjonære Schrödingerligningen h m d ψ Eψ, ( dx der E er energien
øsning til øving 8 for FY4, høsten 7 Vi tar for oss en partikkel med masse m i en endimensjonal boks med lengde For < x < gjelder den stasjonære Schrödingerligningen h m d ψ Eψ, ( dx der E er energien
TFY Øving 7 1 ØVING 7. 3-dimensjonal isotrop harmonisk oscillator
 TFY4215 - Øving 7 1 Oppgave 20 ØVING 7 -dimensjonal isotrop harmonisk oscillator Vi har tidligere studert egenfunksjonen (orbitalen) for grunntilstanden i hydrogenlignende atomer, og skal senere sette
TFY4215 - Øving 7 1 Oppgave 20 ØVING 7 -dimensjonal isotrop harmonisk oscillator Vi har tidligere studert egenfunksjonen (orbitalen) for grunntilstanden i hydrogenlignende atomer, og skal senere sette
EKSAMEN I TFY4250 ATOM- OG MOLEKYLFYSIKK Lørdag 8. august 2009 kl
 NORSK TEKST Side av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 9702355 EKSAMEN I TFY4250 ATOM- OG MOLEKYLFYSIKK
NORSK TEKST Side av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 9702355 EKSAMEN I TFY4250 ATOM- OG MOLEKYLFYSIKK
Oppgave 1. NORSK TEKST Side 1 av 4. NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk
 NORSK TEKST Side 1 av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Margareth Nupen, tel. 7 55 96 4 Ingjald Øverbø, tel. 7 59 18 67 EKSAMEN I TFY415
NORSK TEKST Side 1 av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Margareth Nupen, tel. 7 55 96 4 Ingjald Øverbø, tel. 7 59 18 67 EKSAMEN I TFY415
Prøveeksamen i MAT 1100, H-03 Løsningsforslag
 Prøveeksamen i MAT, H- Løsningsforslag. Integralet cos x dx er lik: +sin x Riktig svar: c) arctan(sin x) + C. Begrunnelse: Sett u = sin x, da er du = cos x dx og vi får: cos x + sin x dx = du du = arctan
Prøveeksamen i MAT, H- Løsningsforslag. Integralet cos x dx er lik: +sin x Riktig svar: c) arctan(sin x) + C. Begrunnelse: Sett u = sin x, da er du = cos x dx og vi får: cos x + sin x dx = du du = arctan
TFY løsning øving 9 1 LØSNING ØVING 9
 TFY4215 - løsning øving 9 1 LØSNING ØVING 9 Løsning oppgave 25 Om radialfunksjoner for hydrogenlignende system a. (a1): De effektive potensialene Veff(r) l for l = 0, 1, 2, 3 er gitt av kurvene 1,2,3,4,
TFY4215 - løsning øving 9 1 LØSNING ØVING 9 Løsning oppgave 25 Om radialfunksjoner for hydrogenlignende system a. (a1): De effektive potensialene Veff(r) l for l = 0, 1, 2, 3 er gitt av kurvene 1,2,3,4,
En partikkel med masse m befinner seg i et éndimensjonalt, asymmetrisk brønnpotensial
 NORSK TEKST Side av 5 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tel. 7 59 8 67, eller 9755 EKSAMEN I TFY45 ATOM- OG MOLEKYLFYSIKK
NORSK TEKST Side av 5 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tel. 7 59 8 67, eller 9755 EKSAMEN I TFY45 ATOM- OG MOLEKYLFYSIKK
Midtsemesterprøve i FY3403 PARTIKKELFYSIKK Onsdag 22. oktober :15 16:00
 NTNU Side 1 av 6 Institutt for fysikk Midtsemesterprøve i FY3403 PARTIKKELFYSIKK Onsdag 22. oktober 2008 14:15 16:00 Tillatte hjelpemidler: Vanlig kalkulator Husk å skrive studentnummeret ditt på hvert
NTNU Side 1 av 6 Institutt for fysikk Midtsemesterprøve i FY3403 PARTIKKELFYSIKK Onsdag 22. oktober 2008 14:15 16:00 Tillatte hjelpemidler: Vanlig kalkulator Husk å skrive studentnummeret ditt på hvert
FY1006/TFY Øving 7 1 ØVING 7
 FY1006/TFY4215 - Øving 7 1 Frist for innlevering: 5. mars kl 17 ØVING 7 Den første oppgaven dreier seg om den tredimensjonale oscillatoren, som behandles i starten av Tillegg 5, og som vi skal gå gjennom
FY1006/TFY4215 - Øving 7 1 Frist for innlevering: 5. mars kl 17 ØVING 7 Den første oppgaven dreier seg om den tredimensjonale oscillatoren, som behandles i starten av Tillegg 5, og som vi skal gå gjennom
Løsningsforslag Eksamen 26. mai 2008 TFY4215 Kjemisk fysikk og kvantemekanikk
 Eksamen TFY415 6. mai 8 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 6. mai 8 TFY415 Kjemisk fysikk og kvantemekanikk a. Utenfor boksen, hvor V (x) =, er bølgefunksjonen lik null. Kontinuiteten
Eksamen TFY415 6. mai 8 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 6. mai 8 TFY415 Kjemisk fysikk og kvantemekanikk a. Utenfor boksen, hvor V (x) =, er bølgefunksjonen lik null. Kontinuiteten
TFY Løsning øving 7 1 LØSNING ØVING 7. 3-dimensjonal isotrop harmonisk oscillator
 TFY415 - Løsning øving 7 1 Løsning oppgave a. Med z = r cos θ har vi at LØSNING ØVING 7 3-dimensjonal isotrop harmonisk oscillator ψ 1 = C C 1 e mωr / h r cos θ, som er uavhengig av asimutvinkelen φ, dvs
TFY415 - Løsning øving 7 1 Løsning oppgave a. Med z = r cos θ har vi at LØSNING ØVING 7 3-dimensjonal isotrop harmonisk oscillator ψ 1 = C C 1 e mωr / h r cos θ, som er uavhengig av asimutvinkelen φ, dvs
FY2045/TFY4250 Kvantemekanikk I, løsning øving 13 1 LØSNING ØVING 13. V (x, t) = xf (t) = xf 0 e t2 /τ 2.
 FY045/TFY450 Kvantemekanikk I, løsning øving 13 1 Løsning Oppgave 13 1 LØSNING ØVING 13 Transient perturbasjon av harmonisk oscillator a. Med kraften F (t) = qe(t) = F 0 exp( t /τ ) og sammenhengen F (t)
FY045/TFY450 Kvantemekanikk I, løsning øving 13 1 Løsning Oppgave 13 1 LØSNING ØVING 13 Transient perturbasjon av harmonisk oscillator a. Med kraften F (t) = qe(t) = F 0 exp( t /τ ) og sammenhengen F (t)
Løsningsforslag Eksamen 14.desember 2011 FY2045/TFY4250 Kvantemekanikk I
 Eksamen FY2045/TFY4250 14. desember 2011 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 14.desember 2011 FY2045/TFY4250 Kvantemekanikk I a. For E < 3V 0 /4 er området x > a klassisk forbudt, og
Eksamen FY2045/TFY4250 14. desember 2011 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 14.desember 2011 FY2045/TFY4250 Kvantemekanikk I a. For E < 3V 0 /4 er området x > a klassisk forbudt, og
FY1006/TFY Øving 9 1 ØVING 9
 FY1006/TFY4215 - Øving 9 1 Frist for innlevering: 2. mars, kl 16 ØVING 9 Opgave 22 Om radialfunksjoner Figuren viser de effektive potensialene Veff(r) l for l = 0, 1, 2, for et hydrogenlignende atom, samt
FY1006/TFY4215 - Øving 9 1 Frist for innlevering: 2. mars, kl 16 ØVING 9 Opgave 22 Om radialfunksjoner Figuren viser de effektive potensialene Veff(r) l for l = 0, 1, 2, for et hydrogenlignende atom, samt
FY1006/TFY Løsning øving 3 1 LØSNING ØVING 3. Ikke-stasjonær bokstilstand
 FY006/TFY45 - Løsning øving 3 Løsning oppgave 8 LØSNING ØVING 3 Ikke-stasjonær bokstilstand a. For 0 < x < L er potensialet i boksen lik null, slik at Hamilton-operatoren har formen Ĥ = K + V (x) = ( h
FY006/TFY45 - Løsning øving 3 Løsning oppgave 8 LØSNING ØVING 3 Ikke-stasjonær bokstilstand a. For 0 < x < L er potensialet i boksen lik null, slik at Hamilton-operatoren har formen Ĥ = K + V (x) = ( h
Formelsamling Bølgefysikk Desember 2006
 Vedlegg 1 av 9 Formelsamling Bølgefysikk Desember 2006 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk
Vedlegg 1 av 9 Formelsamling Bølgefysikk Desember 2006 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk
EKSAMEN I FY2045 KVANTEMEKANIKK I/ TFY4250 KVANTEMEKANIKK I Tirsdag 10. august 2010 kl
 NORSK TEKST Side 1 av 6 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk EKSAMEN I FY2045 KVANTEMEKANIKK I/ TFY4250 KVANTEMEKANIKK I Tirsdag 10. august 2010 kl. 09.00-13.00 Tillatte
NORSK TEKST Side 1 av 6 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk EKSAMEN I FY2045 KVANTEMEKANIKK I/ TFY4250 KVANTEMEKANIKK I Tirsdag 10. august 2010 kl. 09.00-13.00 Tillatte
EKSAMEN I SIF4048 KJEMISK FYSIKK OG KVANTEMEKANIKK Tirsdag 13. august 2002 kl
 Side 1 av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Margareth Nupen, tel. 73 55 96 4 Ingjald Øverbø, tel. 73 59 18 67 EKSAMEN I SIF4048 KJEMISK
Side 1 av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Margareth Nupen, tel. 73 55 96 4 Ingjald Øverbø, tel. 73 59 18 67 EKSAMEN I SIF4048 KJEMISK
Løsningsforslag Eksamen 7. august 2006 TFY4215 Kjemisk fysikk og kvantemekanikk
 Eksamen TFY4215 7. august 2006 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 7. august 2006 TFY4215 Kjemisk fysikk og kvantemekanikk a. Bundne tilstander i et symmetrisk éndimensjonalt potensial
Eksamen TFY4215 7. august 2006 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 7. august 2006 TFY4215 Kjemisk fysikk og kvantemekanikk a. Bundne tilstander i et symmetrisk éndimensjonalt potensial
Løsningsforslag Eksamen 4. desember 2007 TFY4250 Atom- og molekylfysikk/fy2045 Kvantefysikk
 Eksamen TFY450/FY045 4. desember 007 - løsningsforslag Løsningsforslag Eksamen 4. desember 007 TFY450 Atom- og molekylfysikk/fy045 Kvantefysikk Oppgave a. For tilfellet α 0 har vi et ordinært bokspotensial
Eksamen TFY450/FY045 4. desember 007 - løsningsforslag Løsningsforslag Eksamen 4. desember 007 TFY450 Atom- og molekylfysikk/fy045 Kvantefysikk Oppgave a. For tilfellet α 0 har vi et ordinært bokspotensial
Løsningsforslag Eksamen 4. august 2008 TFY4250 Atom- og molekylfysikk
 Eksamen TFY450 4. auguast 008 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 4. august 008 TFY450 Atom- og molekylfysikk a. I områdene x < a og x > a har vi (med E V 0 ) at ψ m h [V (x) E ]ψ 0.
Eksamen TFY450 4. auguast 008 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 4. august 008 TFY450 Atom- og molekylfysikk a. I områdene x < a og x > a har vi (med E V 0 ) at ψ m h [V (x) E ]ψ 0.
Løsningsforslag til eksamen i TFY4170 Fysikk 2 Tirsdag 9. desember 2003
 NTNU Side 1av7 Institutt for fysikk Fakultet for naturvitenskap og teknologi Dette løsningsforslaget er på 7 sider. Løsningsforslag til eksamen i TFY4170 Fysikk Tirsdag 9. desember 003 Oppgave 1. a) Amplituden
NTNU Side 1av7 Institutt for fysikk Fakultet for naturvitenskap og teknologi Dette løsningsforslaget er på 7 sider. Løsningsforslag til eksamen i TFY4170 Fysikk Tirsdag 9. desember 003 Oppgave 1. a) Amplituden
FY1006/TFY4215 -øving 10 1 ØVING 10. Om radialfunksjoner for hydrogenlignende system. 2 ma. 1 r + h2 l(l + 1)
 FY1006/TFY4215 -øving 10 1 ØVING 10 Oppgave 25 Om radialfunksjoner for hydrogenlignende system De generelle formlene for energiene og de effektive potensialene for et hydrogenlignende system kan skrives
FY1006/TFY4215 -øving 10 1 ØVING 10 Oppgave 25 Om radialfunksjoner for hydrogenlignende system De generelle formlene for energiene og de effektive potensialene for et hydrogenlignende system kan skrives
Løsningsforslag til eksamen i FY3404 RELATIVISTISK KVANTEMEKANIKK Tirsdag 30. november 2004
 NTNU Side av 7 Institutt for fysikk Løsningsforslag til eksamen i FY30 RELATIVISTISK KVANTEMEKANIKK Tirsdag 30. november 200 Dette løsningsforslaget er på 7 sider. Oppgave. Prosesser i QED Tegn, i de tilfeller
NTNU Side av 7 Institutt for fysikk Løsningsforslag til eksamen i FY30 RELATIVISTISK KVANTEMEKANIKK Tirsdag 30. november 200 Dette løsningsforslaget er på 7 sider. Oppgave. Prosesser i QED Tegn, i de tilfeller
Eksamen i Klassisk feltteori, fag TFY 4270 Onsdag 26. mai 2004 Løsninger
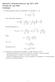 Eksamen i Klassisk feltteori, fag TFY 470 Onsdag 6. mai 004 Løsninger 1a) Sammenhengen mellom koordinattiden t og egentiden τ er at Den relativistiske impulsen er Hamiltonfunksjonen er Siden har vi at
Eksamen i Klassisk feltteori, fag TFY 470 Onsdag 6. mai 004 Løsninger 1a) Sammenhengen mellom koordinattiden t og egentiden τ er at Den relativistiske impulsen er Hamiltonfunksjonen er Siden har vi at
Løsningsforslag Eksamen 8. august 2011 FY2045/TFY4250 Kvantemekanikk I
 Eksamen FY45/TFY45 8. august - løsningsforslag Oppgave Løsningsforslag Eksamen 8. august FY45/TFY45 Kvantemekanikk I a. For E < V blir området x > klassisk forbudt, og den tidsuavhengige Schrödingerligningen
Eksamen FY45/TFY45 8. august - løsningsforslag Oppgave Løsningsforslag Eksamen 8. august FY45/TFY45 Kvantemekanikk I a. For E < V blir området x > klassisk forbudt, og den tidsuavhengige Schrödingerligningen
FYS2140 Kvantefysikk, Løsningsforslag Oblig 7
 FYS4 Kvantefysikk, Løsningsforslag Oblig 7 4. mars 8 Her finner dere løsningsforslag for Oblig 7 som bestod av Oppgave.,.45 og.46 fra Griffiths, og et løsningsforslag for Oppgave., som var tilleggsoppgave.
FYS4 Kvantefysikk, Løsningsforslag Oblig 7 4. mars 8 Her finner dere løsningsforslag for Oblig 7 som bestod av Oppgave.,.45 og.46 fra Griffiths, og et løsningsforslag for Oppgave., som var tilleggsoppgave.
EKSAMEN I FY2045 KVANTEFYSIKK Onsdag 30. mai 2007 kl
 NORSK TEKST Side av 3 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 97355 EKSAMEN I FY45 KVANTEFYSIKK Onsdag 3.
NORSK TEKST Side av 3 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 97355 EKSAMEN I FY45 KVANTEFYSIKK Onsdag 3.
Løsningsforslag Eksamen 1.juni 2004 TFY4215 Kjemisk fysikk og kvantemekanikk
 Eksamen TFY45. juni 004 - løsningsforslag Oppgave Løsningsforslag Eksamen.juni 004 TFY45 Kjemisk fysikk og kvantemekanikk a. Bundne energiegentilstander i et éndimensjonalt potensial er ikke-degenererte
Eksamen TFY45. juni 004 - løsningsforslag Oppgave Løsningsforslag Eksamen.juni 004 TFY45 Kjemisk fysikk og kvantemekanikk a. Bundne energiegentilstander i et éndimensjonalt potensial er ikke-degenererte
EKSAMEN I TFY4215 KJEMISK FYSIKK OG KVANTEMEKANIKK Torsdag 12. august 2004 kl
 NORSK TEKST Side 1 av 6 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Margareth Nupen, tel. 7 55 96 4 Ingjald Øverbø, tel. 7 59 18 67, eller 970155 EKSAMEN
NORSK TEKST Side 1 av 6 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Margareth Nupen, tel. 7 55 96 4 Ingjald Øverbø, tel. 7 59 18 67, eller 970155 EKSAMEN
Løsningsforslag Eksamen 27. mai 2011 FY1006/TFY4215 Innføring i kvantefysikk
 Eksamen FY1006/TFY4215 27. mai 2011 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 27. mai 2011 FY1006/TFY4215 Innføring i kvantefysikk a. For en energiegenfunksjon med energi E V 1 følger det fra
Eksamen FY1006/TFY4215 27. mai 2011 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 27. mai 2011 FY1006/TFY4215 Innføring i kvantefysikk a. For en energiegenfunksjon med energi E V 1 følger det fra
FY2045/TFY4250 Kvantemekanikk I, løsning øving 2 1 LØSNING ØVING 2
 FY2045/TFY4250 Kvantemekanikk I, løsning øving 2 1 LØSNING ØVING 2 Oppgave 2 1 LØSNING nesten en posisjonsegentilstand a Siden den Gaussiske sannsynlighetstettheten ψ(x) 2 = 2β/π exp( 2β(x a) 2 ) symmetrisk
FY2045/TFY4250 Kvantemekanikk I, løsning øving 2 1 LØSNING ØVING 2 Oppgave 2 1 LØSNING nesten en posisjonsegentilstand a Siden den Gaussiske sannsynlighetstettheten ψ(x) 2 = 2β/π exp( 2β(x a) 2 ) symmetrisk
Formelsamling. ξ(r, t) = ξ 0 sin(k r ωt + φ) 2 ξ(x, t) = 1 2 ξ(x, t) t 2. 2 ξ. x ξ. z 2. y ξ. v = ω k. v g = dω dk
 Formelsamling Side 7 av 15 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk plan bølge: Bølgeligning:
Formelsamling Side 7 av 15 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk plan bølge: Bølgeligning:
FY1006/TFY Løsning øving 9 1 LØSNING ØVING 9
 FY1006/TFY415 - Løsning øving 9 1 Løsning oppgave Numerisk løsning av den tidsuavhengige Schrödingerligningen LØSNING ØVING 9 a. Alle leddene i (1) har selvsagt samme dimensjon. Ved å dividere ligningen
FY1006/TFY415 - Løsning øving 9 1 Løsning oppgave Numerisk løsning av den tidsuavhengige Schrödingerligningen LØSNING ØVING 9 a. Alle leddene i (1) har selvsagt samme dimensjon. Ved å dividere ligningen
Løsningsforslag Eksamen 16. august 2008 TFY4215 Kjemisk fysikk og kvantemekanikk
 Eksamen TFY415 16. august 008 - løsningsforslag 1 Oppgave 1 (Teller 34 %) Løsningsforslag Eksamen 16. august 008 TFY415 Kjemisk fysikk og kvantemekanikk a. Siden potensialet V () er symmetrisk, er grunntilstanden
Eksamen TFY415 16. august 008 - løsningsforslag 1 Oppgave 1 (Teller 34 %) Løsningsforslag Eksamen 16. august 008 TFY415 Kjemisk fysikk og kvantemekanikk a. Siden potensialet V () er symmetrisk, er grunntilstanden
Formelsamling. ξ(r, t) = ξ 0 sin(k r ωt + φ) 2 ξ(x, t) = 1 2 ξ(x, t) t 2. 2 ξ. x ξ. z 2. y ξ. v = ω k. v g = dω dk
 Formelsamling Side 7 av 16 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk plan bølge: Bølgeligning:
Formelsamling Side 7 av 16 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk plan bølge: Bølgeligning:
Eksamen FY3403 Partikkelfysikk Onsdag 10. desember 2008 Løsninger
 Eksamen FY3403 Partikkelfysikk Onsdag 0. desember 008 Løsninger a) Den minste massesenterenergien vi kan ha, er E CM (m p + m Δ )c (938 + 3) MeV 70 MeV. Det er ikke noe poeng i å regne mer nøyaktig her,
Eksamen FY3403 Partikkelfysikk Onsdag 0. desember 008 Løsninger a) Den minste massesenterenergien vi kan ha, er E CM (m p + m Δ )c (938 + 3) MeV 70 MeV. Det er ikke noe poeng i å regne mer nøyaktig her,
B.1 Generelle egenskaper til energiegenfunksjoner
 TFY4250/FY2045 Tillegg 6 - Generelle egenskaper til energiegenfunksjoner 1 Tillegg 6: Noe av stoffet i dette Tillegget er repetisjon fra Tillegg 3 i TFY4215. B.1 Generelle egenskaper til energiegenfunksjoner
TFY4250/FY2045 Tillegg 6 - Generelle egenskaper til energiegenfunksjoner 1 Tillegg 6: Noe av stoffet i dette Tillegget er repetisjon fra Tillegg 3 i TFY4215. B.1 Generelle egenskaper til energiegenfunksjoner
Løsningsforslag Eksamen 11. august 2010 FY1006/TFY4215 Innføring i kvantefysikk
 Eksamen FY1006/TFY4215 11 august 2010 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 11 august 2010 FY1006/TFY4215 Innføring i kvantefysikk a Siden potensialet V (x) er symmetrisk med hensyn på
Eksamen FY1006/TFY4215 11 august 2010 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 11 august 2010 FY1006/TFY4215 Innføring i kvantefysikk a Siden potensialet V (x) er symmetrisk med hensyn på
Løsningsforslag for FYS2140 Kvantefysikk, Mandag 3. juni 2019
 Løsningsforslag for FYS210 Kvantefysikk, Mandag 3. juni 201 Oppgave 1: Stern-Gerlach-eksperimentet og atomet Stern-Gerlach-eksperimentet fra 122 var ment å teste Bohrs atommodell om at angulærmomentet
Løsningsforslag for FYS210 Kvantefysikk, Mandag 3. juni 201 Oppgave 1: Stern-Gerlach-eksperimentet og atomet Stern-Gerlach-eksperimentet fra 122 var ment å teste Bohrs atommodell om at angulærmomentet
LØSNINGSFORSLAG TIL EKSAMEN I FY1002 BØLGEFYSIKK Mandag 10. desember 2007 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY1002 BØLGEFYSIKK
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY1002 BØLGEFYSIKK
ψ(x) 2 dx = 1. (3) For det siste integralet har vi brukt fra Rottmann at
 Det er mulig å oppnå i alt 80 poeng på denne eksamen. Oppgave er inspirert av en tidligere eksamensoppgaver gitt ved NTNU, laget av Ingjald Øverbø og Jon Andreas Støvneng. Oppgave 1 En-dimensjonal harmonisk
Det er mulig å oppnå i alt 80 poeng på denne eksamen. Oppgave er inspirert av en tidligere eksamensoppgaver gitt ved NTNU, laget av Ingjald Øverbø og Jon Andreas Støvneng. Oppgave 1 En-dimensjonal harmonisk
Eksamen i fag RELATIVISTISK KVANTEMEKANIKK Fredag 26. mai 2000 Tid: 09:00 14:00
 Side 1 av 3 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Navn: Kåre Olaussen Telefon: 9 36 52 Eksamen i fag 74327 RELATIVISTISK KVANTEMEKANIKK Fredag
Side 1 av 3 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Navn: Kåre Olaussen Telefon: 9 36 52 Eksamen i fag 74327 RELATIVISTISK KVANTEMEKANIKK Fredag
Oppgave 2 Vi ser på et éndimensjonalt system hvor en av de stasjonære tilstandene ψ(x) er gitt som { 0 for x < 0, ψ(x) = Ne ax (1 e ax (1)
 Oppgave Gjør kort rede for hva den fotoelektriske effekt er, hva slags konklusjoner man kunne trekke fra observasjoner av denne i kvantefysikkens fødsel, og beskriv et eksperiment som kan observere og
Oppgave Gjør kort rede for hva den fotoelektriske effekt er, hva slags konklusjoner man kunne trekke fra observasjoner av denne i kvantefysikkens fødsel, og beskriv et eksperiment som kan observere og
Lfisningsforslag SIF4045 Kvantemekanikk Oppgave 1 a) Den tidsavhengige Schrödingerlikningen = c HΨ= Separable lfisninger av denn
 Lfisningsforslag SIF4045 Kvantemekanikk 0.08.00 Oppgave a) Den tidsavhengige Schrödingerlikningen er i @Ψ @t = c HΨ= Separable lfisninger av denne, 4 c ~p m + V (~r) 3 5 Ψ= Ψ(~r; t) =ψ(~r) e iet= ; er
Lfisningsforslag SIF4045 Kvantemekanikk 0.08.00 Oppgave a) Den tidsavhengige Schrödingerlikningen er i @Ψ @t = c HΨ= Separable lfisninger av denne, 4 c ~p m + V (~r) 3 5 Ψ= Ψ(~r; t) =ψ(~r) e iet= ; er
FY2045/TFY4250 Kvantemekanikk I, øving 2 1 ØVING 2. nesten en posisjonsegentilstand
 FY2045/TFY4250 Kvantemekanikk I, 2012 - øving 2 1 Oppgave 2 1 ØVING 2 nesten en posisjonsegentilstand Vi har sett at en posisjon ikke kan måles med en usikkerhet som er eksakt lik null. Derimot er det
FY2045/TFY4250 Kvantemekanikk I, 2012 - øving 2 1 Oppgave 2 1 ØVING 2 nesten en posisjonsegentilstand Vi har sett at en posisjon ikke kan måles med en usikkerhet som er eksakt lik null. Derimot er det
FY2045/TFY4250 Kvantemekanikk I, øving 5 1 LØSNING ØVING 5. Kvantekraft. L x. L 2 x. = A sin n xπx. sin n yπy. 2 y + 2.
 FY045/TFY450 Kvantemekanikk I, øving 5 1 øsning oppgave 5 1 a Med finner vi energien til egenfunksjonen ØSNING ØVING 5 Kvantekraft nπx sin = n xπ x x x ψ nx,n y,n z = A sin n xπx x sin nπx x, sin n yπy
FY045/TFY450 Kvantemekanikk I, øving 5 1 øsning oppgave 5 1 a Med finner vi energien til egenfunksjonen ØSNING ØVING 5 Kvantekraft nπx sin = n xπ x x x ψ nx,n y,n z = A sin n xπx x sin nπx x, sin n yπy
LØSNING ØVING 2. Løsning oppgave 5. TFY4215 Innføring i kvantefysikk - Løsning øving 2 1
 TFY4215 Innføring i kvantefysikk - Løsning øving 2 1 Løsning oppgave 5 LØSNING ØVING 2 Krumningsegenskaper for endimensjonale energiegenfunksjoner a. For oscillator-grunntilstanden i oppgave 3b har vi
TFY4215 Innføring i kvantefysikk - Løsning øving 2 1 Løsning oppgave 5 LØSNING ØVING 2 Krumningsegenskaper for endimensjonale energiegenfunksjoner a. For oscillator-grunntilstanden i oppgave 3b har vi
Løsningsforslag Eksamen 5. august 2009 TFY4215 Kjemisk fysikk og kvantemekanikk
 Eksamen TFY4215 5. august 29 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 5. august 29 TFY4215 Kjemisk fysikk kvantemekanikk a. Med ψ A (x) = C = konstant for x > har vi fra den tidsuavhengige
Eksamen TFY4215 5. august 29 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 5. august 29 TFY4215 Kjemisk fysikk kvantemekanikk a. Med ψ A (x) = C = konstant for x > har vi fra den tidsuavhengige
LØSNINGSFORSLAG TIL EKSAMEN I TFY4160 BØLGEFYSIKK Mandag 3. desember 2007 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 7 59 6 6 / 45 45 55 LØSNINGSFORSLAG TIL EKSAMEN I TFY4160 BØLGEFYSIKK Mandag.
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 7 59 6 6 / 45 45 55 LØSNINGSFORSLAG TIL EKSAMEN I TFY4160 BØLGEFYSIKK Mandag.
Faglig kontakt under eksamen: Ingjald Øverbø, tlf , eller
 NORSK TEKST Side 1 av 5 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 18 67, eller 9701355 EKSAMEN I TFY450 ATOM- OG MOLEKYLFYSIKK
NORSK TEKST Side 1 av 5 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 18 67, eller 9701355 EKSAMEN I TFY450 ATOM- OG MOLEKYLFYSIKK
NORSK TEKST Side 1 av 4. Faglig kontakt under eksamen: Ingjald Øverbø, tlf , eller
 NORSK TEKST Side 1 av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 18 67, eller 97012355 EKSAMEN I FY2045/TFY4250 KVANTEMEKANIKK
NORSK TEKST Side 1 av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 18 67, eller 97012355 EKSAMEN I FY2045/TFY4250 KVANTEMEKANIKK
FY1006/TFY4215 Innføring i kvantefysikk, - Ekstraøving 2 1. Ekstraøving 2. = 1 2 (3n2 l 2 l), = 1 n 2, 1 n 3 (l ), 1 n 3 l(l + 1.
 FY006/TFY45 Innføring i kvantefysikk, - Ekstraøving Frist for innlevering (Til I.Ø.): 7. mai kl 7 Oppgave 9 hydrogenlignende atom Ekstraøving I denne oppgaven ser vi på et hydrogenlignende atom, der et
FY006/TFY45 Innføring i kvantefysikk, - Ekstraøving Frist for innlevering (Til I.Ø.): 7. mai kl 7 Oppgave 9 hydrogenlignende atom Ekstraøving I denne oppgaven ser vi på et hydrogenlignende atom, der et
Oppgavene er hentet fra fagets lærebok, Hass, Weir og Thomas, samt gamle eksamener.
 NTNU Institutt for matematiske fag TMA45 Matematikk, øving, vår Løsningsforslag Notasjon og merknader Oppgavene er hentet fra fagets lærebok, Hass, Weir og Thomas, samt gamle eksamener. Oppgaver fra kapittel
NTNU Institutt for matematiske fag TMA45 Matematikk, øving, vår Løsningsforslag Notasjon og merknader Oppgavene er hentet fra fagets lærebok, Hass, Weir og Thomas, samt gamle eksamener. Oppgaver fra kapittel
TFY4215 Innføring i kvantefysikk - Øving 2 1 ØVING 2. Krumningsegenskaper for endimensjonale energiegenfunksjoner
 TFY415 Innføring i kvantefysikk - Øving 1 Oppgave 5 ØVING Krumningsegenskaper for endimensjonale energiegenfunksjoner En partikkel med masse m beveger seg i et endimensjonalt potensial V (x). Partikkelen
TFY415 Innføring i kvantefysikk - Øving 1 Oppgave 5 ØVING Krumningsegenskaper for endimensjonale energiegenfunksjoner En partikkel med masse m beveger seg i et endimensjonalt potensial V (x). Partikkelen
Løysingsframlegg øving 1
 FY6/TFY425 Innføring i kvantefysikk Løysingsframlegg øving Oppgåve Middelverdien er x = x Ω X xp (x) = 2 + 2 = 2. (.) Tilsvarande har vi x 2 = x Ω X x 2 P (x) = 2 2 + 2 2 = 2. (.2) Dette gjev variansen
FY6/TFY425 Innføring i kvantefysikk Løysingsframlegg øving Oppgåve Middelverdien er x = x Ω X xp (x) = 2 + 2 = 2. (.) Tilsvarande har vi x 2 = x Ω X x 2 P (x) = 2 2 + 2 2 = 2. (.2) Dette gjev variansen
Løsning til øving 17 for FY1004, våren 2008
 Løsning til øving 17 for FY1004, våren 2008 Her skal vi se på hvordan spinnet egenspinnet til et elektron påvirkes av et konstant magnetfelt B Merk: Det korrekte navnet på B er magnetisk flukstetthet,
Løsning til øving 17 for FY1004, våren 2008 Her skal vi se på hvordan spinnet egenspinnet til et elektron påvirkes av et konstant magnetfelt B Merk: Det korrekte navnet på B er magnetisk flukstetthet,
Løsning til øving 23 for FY1004, våren 2008
 Løsning til øving 23 for FY1004, våren 2008 Diracs δ-funksjon kan defineres ved at δ(x) = 0 for x 0, og dx δ(x) = 1. Vi vil bruke δ-funksjonen som et potensial for en partikkel i en dimensjon. Vi setter
Løsning til øving 23 for FY1004, våren 2008 Diracs δ-funksjon kan defineres ved at δ(x) = 0 for x 0, og dx δ(x) = 1. Vi vil bruke δ-funksjonen som et potensial for en partikkel i en dimensjon. Vi setter
EKSAMENSOPPGAVE. FYS 2000, Kvantemekanikk Dato: 7. Juni 2017 Klokkeslett: 9:00-13:00 Sted: Tillatte hjelpemidler: rute.
 EKSAMENSOPPGAVE Eksamen i: FYS 2000, Kvantemekanikk Dato: 7. Juni 2017 Klokkeslett: 9:00-13:00 Sted: Tillatte hjelpemidler: ett handskrevet A4-ark(2 sider med egne notater, samt K. Rottmann: Matematisk
EKSAMENSOPPGAVE Eksamen i: FYS 2000, Kvantemekanikk Dato: 7. Juni 2017 Klokkeslett: 9:00-13:00 Sted: Tillatte hjelpemidler: ett handskrevet A4-ark(2 sider med egne notater, samt K. Rottmann: Matematisk
EKSAMEN I FY1006 INNFØRING I KVANTEFYSIKK/ TFY4215 INNFØRING I KVANTEFYSIKK Onsdag 11. august 2010 kl
 NORSK TEKST Side 1 av 6 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Jon Andreas Støvneng, tel. 73 59 36 63, eller 45 45 55 33 EKSAMEN I FY1006 INNFØRING
NORSK TEKST Side 1 av 6 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Jon Andreas Støvneng, tel. 73 59 36 63, eller 45 45 55 33 EKSAMEN I FY1006 INNFØRING
SIF5005 Matematikk 2, 13. mai 2002 Løsningsforslag
 SIF55 Matematikk, 3. mai Oppgave Alternativ : At de to ligningene skjærer hverandre vil si at det finnes parameterverdier u og v som, innsatt i de to parametriseringene, gir samme punkt: Vi løser hver
SIF55 Matematikk, 3. mai Oppgave Alternativ : At de to ligningene skjærer hverandre vil si at det finnes parameterverdier u og v som, innsatt i de to parametriseringene, gir samme punkt: Vi løser hver
