Eksamen FY8104 Symmetri i fysikken Fredag 7. desember 2007 Løsninger
|
|
|
- Gunhild Simonsen
- 6 år siden
- Visninger:
Transkript
1 Eksamen FY8104 Symmetri i fysikken Fredag 7. desember 007 Løsninger 1a En konjugasjonskasse i SO(3 består av ae rotasjoner med en gitt rotasjonsvinke α og vikårig rotasjonsakse. En konjugasjonskasse i O(3 er enten identisk med en konjugasjonskasse i SO(3, eer den er het utenfor SO(3 og består av ae matriser S = R der R tihører en gitt konjugasjonskasse i SO(3. Når vi utvider gruppen fra SO(3 ti O(3, er det i prinsippet muig at noen konjugasjonskasser bir større, men det skjer atså ikke, fordi hee O(3 genereres av SO(3 med tiegg av ett nytt eement I, som kommuterer med hee SO(3. De nye gruppeeementene utenfor SO(3 må finne sin pass i nye konjugasjonskasser som igger het og hodent utenfor SO(3. En konjugasjonskasse i SU( består av ae SU(-matriser med en gitt rotasjonsvinke α og vikårig rotasjonsakse. 1b En SU(-matrise U som tihører sentret i SU(, må være et mutipum av identitetsmatrisen, i føge Schurs emma. Atså U = ai der a er et kompekst ta. At U SU( impiserer at detu = a = 1, atså a = ±1. Da er a = a 1, og U = ai er unitær, U = a I = U 1. Tisvarende gjeder for en SU(3-matrise U som tihører sentret i SU(3, at U = ai og detu = a 3 = 1, atså a = 1, a = ω eer a = ω der ω = e i π 3 = 1 + i 3. Også i dette tifeet er a = a 1, og føgeig er U unitær, U = a I = U 1. 1c Med U = cos I i sin er U = cos = cos I + isin I isin n σ = cos I isin (n 1 σ 1 + n σ + n 3 σ 3 ( ( α α n σ = cos I + i sin (n 1 σ 1 n σ + n 3 σ 3 m σ, der m 1 = n 1, m = n, m 3 = n 3. Atså m = R n, der R er en rotasjon med vinkeen π om y-aksen. Det gir at U = VUV 1 med ( V = exp i π ( 0 1 σ = iσ =. 1 0 V = σ fungerer nøyaktig ike bra. Riktignok er ikke σ SU(, men det er heer ikke noe krav at vi ska ha V SU(. 1
2 Det er et vesentig poeng her at V må kunne veges uavhengig av U. Vi kan kontroere svaret. Hvis vi foranger at en kompeks -matrise ( a c U = b d ska være unitær og ha determinant 1, finner vi at den mest generee øsningen er ( a b U = b a, der a og b er kompekse ta med a + b = 1. Da er ( U a b = b = VUV 1 a med V = V 1 = ( Av reasjonen U = VUV 1 føger at (TrU = Tr(U = Tr(VUV 1 = TrU. Det vi si at TrU er ree. Det ser vi forøvrig av den oppgitte formeen ( ( α α U = cos I isin n σ, som gir at TrU = cos. 1d Vi kan bruke karakterene χ 1 (U = Tr ρ 1 (U = TrU, χ (U = Tr ρ (U = Tr(U = (TrU = (χ 1 (U ti å vise at de to representasjonene er inekvivaente. Det er nok å finne en SU(3-matrise U sik at TrU ikke er ree, for da er χ 1 (U χ (U. Et eksempe er sentereementet U = ωi fra punkt b ovenfor, som har TrU = 3ω = 3(1 + i 3. 1e 1 og 1 utgjør sentret av kvaterniongruppen, de er sine egne konjugasjonskasser. Eers er f.eks. jij 1 = ijj 1 = i, sik at konjugasjonskassene er {i, i}, {j, j} og {k, k}. Karaktertabe:
3 1 1 i, i j, j k, k Her er noen hodepunkter for å konstruere karaktertabeen. Det er fem konjugasjonskasser og ike mange irredusibe representasjoner. Ae karakterene er reee, fordi, som vi ser, g og g 1 atid tihører samme konjugasjonskasse. Karakteren ti enhetseementet, χ(1, er dimensjonen ti representasjonen. Ortogonaitetsreasjon nr. gir at kvadratsummen av dimensjonene er N = 8, og det gir entydig dimensjonene 1, 1, 1, 1 og. En todimensjona representasjon var gitt i oppgaveteksten, nemig 1 I, i iσ 1, j iσ, k iσ 3. Den er irredusibe og gir siste inje i karaktertabeen. Irredusibiitet beviser vi ved hjep av ortogonaitetsreasjon nr. 1. En genere representasjon er en direkte sum av irredusibe representasjoner, med mutipisitet m µ av den irredusibe representasjonen µ, da har den karakter χ = m µ χ (µ, µ og ortogonaitetsreasjonen gir at N i χ i = m µ m ν N i (χ (µ i χ (ν i = N i µ,ν i µ m µ. Derfor vet vi at representasjonen er irredusibe (en m µ = 1, ae andre m µ = 0 når i N i χ i = N. For en endimensjona representasjon er det karakteren som er representasjonen, sik at χ(gh = χ(gχ(h. Og dimensjonen ti represntasjonen er χ(1 = 1. Siden ( 1 = 1, må (χ( 1 = χ(( 1 = χ(1 = 1, atså χ( 1 = ±1. Siden i = 1 og i 4 = 1, må (χ(i = χ(i = χ( 1 = ±1 og (χ(i 4 = χ(i 4 = χ(1 = 1, atså χ(i = ±1 eer χ(i = ±i. Videre er χ(i = χ( i, fordi i og i er konjugerte. Når samtidig χ( i = χ( 1χ(i, og χ(i 0, må vi ha χ( 1 = 1 og χ(i = ±1. Og så videre. Karakteren ti den todimensjonae irredusibe representasjonen kon vi forøvrig finne entydig ved hjep av ortogonaitetsreasjonene, etter at vi har funnet ae de endimensjonae. Her er enda et knep som viser at noen av karakterverdiene må være nu. Når χ 1 og χ er karakterene ti to representasjoner ρ 1 og ρ, av dimensjoner n 1 og n, så er χ 3 = χ 1 χ karakteren ti produktrepresentasjonen ρ 3 = ρ 1 ρ, av dimensjon n 3 = n 1 n. Hvis f.eks. ρ 1 er endimensjona og ρ er irredusibe, så er ρ 3 irredusibe (det kan vi bevise f.eks. ved hjep av ortogonaitetsreasjonen: vi har at χ 1 (g = 1 for ae g, og 3
4 derfor g χ 3 (g = g χ 1 (gχ (g = g χ (g = N. Videre, hvis det finnes et gruppeeement g sik at χ 1 (g 1, så er det to muigheter: enten er χ (g = 0, eer så har representasjonene ρ og ρ 3 samme dimensjon, men er inekvivaente. Kvaterniongruppen har bare en todimensjona irredusibe representasjon. Denne representasjonen må ha karakterverdi 0 for enhver konjugasjonskasse som har karakterverdi forskjeig fra 1 i en av de endimensjonae representasjonene. a Den fue tredimensjonae punktgruppen innehoder føgende transformasjoner. 6 rotasjoner om en akse vinkerett på panet, inkudert identitetstransformasjonen E (av noen kat I. Rotasjonsvinkene er kπ/6 med k = 0,1,,3,4,5. 6 såkate vertikae refeksjoner σ vj, j = 1,,3,4,5,6, om 6 pan som innehoder rotasjonsaksen. De 6 rotasjonene og 6 refeksjonene utgjør tisammen gruppen C 6v, som atså har orden 1. De 1 transformasjonene i C 6v er todimensjonae, de virker i det vi kaer horisontapanet og forandrer ikke den tredje koordinaten, angs rotasjonsaken. Derfor kommuterer de med refeksjonen om horisontapanet, σ h, som ikke gjør annnet enn å invertere den tredje koordinaten. At i at gir det 4 gruppeeementer, dette er den dihedrae gruppen D 6h, som er et direkte produkt, D 6h = C 6v {E,σ h } = C 6v {I,σ h }. Den er forøvrig et direkte produkt også på en annen måte: D 6h = D 6 {I, I}, der I er identitstransformasjonen r r og I er inversjonen r r. b Schurs emma sier at enhver operator som kommuterer med ae transformasjonene i en irredusibe representasjon, må være et mutipum av identitetsoperatoren. Transasjonsgruppen er kommutativ, og hvis vi har en irredusibe unitær representasjon av den, må enhver transasjonen være representert som et mutipum av identitetsoperatoren, atså som en fasefaktor. Men da må representasjonen være endimensjona, for eers vie den være redusibe. c Rotasjonen R (som mer generet også kan være en refeksjon transformerer r R r, mens transasjonen a transformerer r a + r. Hvis vi først roterer med R og etterpå transaterer med a, gir det at r R r a + R r = R(R 1 a + r. Samme resutat som om vi først transaterer med R 1 a og etterpå roterer med R. Vi har atså at U( aψ = U( au(rψ = U(RU(R 1 aψ = U(R(e i k (R 1 a ψ = e i(r k a U(Rψ = e i k a ψ. Fordi rotasjonen R bevarer skaarprodukt, har vi at k (R 1 a = (R k (RR 1 a = (R k a = k a. Atså er ψ og ψ egentistander for U( a med egenverdiene λ = e i k a og λ = e i k a. 4
5 Når U er unitær og har ψ og ψ som egenfunksjoner, Uψ = λψ og Uψ = λ ψ, så er egenverdiene λ og λ kompekse ta med absouttverdi 1, λ = λ = 1. Og hvis λ λ, så må ψ og ψ være ortogonae, (ψ,ψ = d 3 r (ψ( r ψ ( r = 0, fordi λ (ψ,ψ = (ψ,λ ψ = (ψ,uψ = (U ψ,ψ = (U 1 ψ,ψ = (λ 1 ψ,ψ = (λ 1 (ψ,ψ = λ(ψ,ψ. d Transformasjonene i punktgruppen permuterer de 1 bøgefunksjonene ψ 1 ti ψ 1, og kan representeres som 1 1-matriser der ae matriseeementene er enten 0 eer 1. Trasen ti en sik matrise er antaet enere på diagonaen, atså antaet bøgefunksjoner som transformeres over i seg sev. Karakteren ti identitetstransformasjonen er 1, nemig dimensjonen av matriserepresentasjonen. Ae andre transformasjoner har karakter 0, de transformerer ingen bøgefunksjon over i seg sev. Vi har atså en representasjon med føgende karakter: E C C 3 C 6 3σ d 3σ v χ Den er en ineærkombinasjon av de irredusibe karakterene, χ = m 1 A 1 + m A + m 3 B 1 + m 4 B + m 5 E 1 + m 6 E, med foreøpig ukjente mutipisiteter m 1,...,m 6. Vi har at 6 χ(g = 144 = 1 mi. g i=1 Det er nok ti å vise at representasjonen er redusibe, nemig i m i = 1. Hvis χ (µ er en irredusibe representasjon, så er (χ(g χ (µ (g = 1χ (µ (E. g Vår representasjon innehoder derfor den irredusibe representasjonen µ med mutipisitet χ (µ (E, som er dimensjonen ti den irredusibe representasjonen µ. Atså er de endimensjonae representasjonene A 1,A,B 1,B innehodt med mutipisitet 1, og de todimensjonae representasjonene E 1,E er innehodt med mutipisitet. e Den 1-dimensjonae matrisen T( a som representerer transasjonen r a + r har matriseeementene T m ( a = δ m e i k a. Hvis A er en 1-dimensjona matrise som kommuterer med T, så er A j T m ( a = A jm e i k m a = 5 T j ( aa m = A jm e i k j a.
6 Hvis j m her, så er k m k j (se Figur, og da finnes det en transasjonsvektor a sik at e i k m a e i k j a. Ligningen ovenfor kan da bare være oppfyt hvis A jm = 0. Det viser at A må være diagona. Anta nå at A er diagona, A jm = δ jm α j, og kommuterer med ae rotasjonene og refeksjonene. Se på to vikårige indekser j m. Hvis A kommuterer med en matrise B, så er A j B m = B jm α j = B j A m = B jm α m. Det finnes (minst en rotasjon eer refeksjon B i symmetrigruppen C 6v sik at Bψ m = ψ j. Da er B jm = 1, og fordi A og B kommuterer, må α j = α m. Konkusjon: α 1 = α =... = α 1 = α, og A er et mutipum av enhetsmatrisen, A = αi. Her har vi en gruppe som er uendeig og ikke-kompakt, fordi det ikke finnes noen begrensning på engden av en transasjonsvektor a. Men vi har en unitær representasjon av denne gruppen, og en unitær representasjon er atid enten irredusibe eer en direkte sum av irredusibe representasjoner. Da gjeder det omvendte Schurs emma, at representasjonen er irredusibe dersom bare matriser av formen αi kommuterer med ae transformasjonsmatrisene. Vi trekker den konkusjon at vår representasjon av romgruppen, med både transasjoner og rotasjoner (og refeksjoner, er irredusibe. f Transasjonen a 0 = M a 1 + N a i panet er identitetstransformasjonen på nanorøret. Transasjonene k a 0 i panet, med k = 0, ±1, ±,... er da også identitetstransformasjonen på nanorøret. For at en rotasjon eer refeksjon R C 6v ska tihøre punktgruppen ti nanorøret, er det nødvendig og tistrekkeig at enten R a 0 = a 0 eer R a 0 = a 0. Den triviee øsningen er identitetstransformasjonen R = E. En nesten ike trivie øsning er rotasjonen på 180, R = C. Disse to rotasjonene er atid symmetrier. Andre rotasjoner kan ikke være symmetrier. Om det finnes refeksjonssymmetrier, avhenger av hetaene M og N. Enten finnes det to refeksjonssymmetrier, refeksjon angs a 0 og refeksjon vinkerett på a 0, eer det finnes ingen. Vi ser av Figur 1 at det finnes refeksjonssymmetri i føgende tifeer: (i N = 0, (ii M = N, (iii M = 0, (iv M = N/, (v M = N, (vi M = N. g Bøgevektoren k ti en transasjon som er en symmetri på nanorøret, må oppfye betingesen e i k (M a 1 +N a = 1. Med k = k 1 b1 + k b gir det betingesen Mk 1 + Nk = nπ, n = 0, ±1, ±,.... Den definerer Briouin-sonen ti nanorøret som en mengde av paraee rette injer i Briouin-sonen ti det heksagonae gitteret. 6
Eksamen i fag FY8104 Symmetri i fysikken Fredag 7. desember 2007 Tid:
 Side 1 av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 51 72) Sensurfrist: Lørdag 22. desember
Side 1 av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 51 72) Sensurfrist: Lørdag 22. desember
Oppgaver MAT2500. Fredrik Meyer. 10. september 2014
 Oppgaver MAT500 Fredrik Meyer 0. september 04 Oppgave. Bruk forrige oppgave ti å vise at hvis m er orienteringsreverserende, så er m en transasjon. (merk: forrige oppgave sa at ae isometrier er på formen
Oppgaver MAT500 Fredrik Meyer 0. september 04 Oppgave. Bruk forrige oppgave ti å vise at hvis m er orienteringsreverserende, så er m en transasjon. (merk: forrige oppgave sa at ae isometrier er på formen
a) Bruk de Broglies relasjoner for energi og bevegelsesmengde til å vise at et relativistisk graviton har dispersjonsrelasjonen ω(k) = c λ g
 Oppgave Gravitasjonsbøger Gravitasjonsbøger be nyig oppdaget av LIGO-eksperimentet. Vi ska her anta at gravitasjon skydes en partikke, gjerne kat gravitonet, som har en masse m g. Under vi du få bruk for
Oppgave Gravitasjonsbøger Gravitasjonsbøger be nyig oppdaget av LIGO-eksperimentet. Vi ska her anta at gravitasjon skydes en partikke, gjerne kat gravitonet, som har en masse m g. Under vi du få bruk for
Eksamen i fag FY8104 Symmetri i fysikken Fredag 7. desember 2007 Tid:
 Side 1 av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 51 72) Sensurfrist: Lørdag 22. desember
Side 1 av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 51 72) Sensurfrist: Lørdag 22. desember
MEK Stabilitet og knekning av konstruksjoner. Høst Prosjektoppgave: Forslag til løsning (skisse)
 EK 50 tabiitet og knekning a konstruksjoner Høst 005 Prosjektoppgae: Forsag ti øsning (skisse). Hayman 0..005 - - Innedning Dette er kun en skisse ikke en fustendig rapport. Inndeingen i asnitt er bare
EK 50 tabiitet og knekning a konstruksjoner Høst 005 Prosjektoppgae: Forsag ti øsning (skisse). Hayman 0..005 - - Innedning Dette er kun en skisse ikke en fustendig rapport. Inndeingen i asnitt er bare
TMA4210 Numerisk løsning av part. diff.lign. med differansemetoder Vår 2005
 Norges teknisk naturvitenskapeige universitet Institutt for matematiske fag TMA420 Numerisk øsning av part diffign med differansemetoder Vår 2005 3 Crank Nicoson er en famiie metoder som fremkommer ved
Norges teknisk naturvitenskapeige universitet Institutt for matematiske fag TMA420 Numerisk øsning av part diffign med differansemetoder Vår 2005 3 Crank Nicoson er en famiie metoder som fremkommer ved
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Side 1 Det matematisk-naturvitenskapeige fakutet Eksamen i: FYS140 Kvantefysikk Eksamensdag: 10. juni Tid for eksamen: 09.00 (4 timer) Oppgavesettet er på fem (5) sider Vedegg: Ingen
UNIVERSITETET I OSLO Side 1 Det matematisk-naturvitenskapeige fakutet Eksamen i: FYS140 Kvantefysikk Eksamensdag: 10. juni Tid for eksamen: 09.00 (4 timer) Oppgavesettet er på fem (5) sider Vedegg: Ingen
Løsningsforslag til eksamen i klassisk mekanikk våren e N. R ρ m
 Løsningsforsag ti eksamen i kassisk mekanikk våren 010 Oppgave 1 ω v e T θ R ρ m e N Figure 1: a Lagrangefunksjonen er gitt ved: L = T V der T V er den kinetiske potensiee energien ti systemet. Finner
Løsningsforsag ti eksamen i kassisk mekanikk våren 010 Oppgave 1 ω v e T θ R ρ m e N Figure 1: a Lagrangefunksjonen er gitt ved: L = T V der T V er den kinetiske potensiee energien ti systemet. Finner
Musikkens fysikk. Johannes Skaar, NTNU. 9. januar 2010
 Musikkens fysikk Johannes Skaar, NTNU 9. januar 2010 I aboppgavene i TFE40 Eektromagnetisme ager du en eektrisk gitar, der den vibrerende strengen setter i gang vibrasjoner på en magnet, som videre induserer
Musikkens fysikk Johannes Skaar, NTNU 9. januar 2010 I aboppgavene i TFE40 Eektromagnetisme ager du en eektrisk gitar, der den vibrerende strengen setter i gang vibrasjoner på en magnet, som videre induserer
(θ,φ) er de sfæriske harmoniske. Her bruker vi sfæriske koordinater. x = rsinθcosφ, (2) y = rsinθsinφ, (3) z = rcosθ. (4)
 Oppgave 1 Hydrogenatom for kjemikere I denne oppgaven ska vi se på hydrogenatomet. Vrien i år er at vi ska skrive øsningen av Schrødingerigningen på en måte som kjemikere iker bedre. Vi ser bort fra spinn
Oppgave 1 Hydrogenatom for kjemikere I denne oppgaven ska vi se på hydrogenatomet. Vrien i år er at vi ska skrive øsningen av Schrødingerigningen på en måte som kjemikere iker bedre. Vi ser bort fra spinn
Løysingsforslag (Skisse) Eksamen FY3452 Gravitasjon og Kosmologi Våren 2007
 Løysingsforslag (Skisse) Eksamen FY3452 Gravitasjon og Kosmologi Våren 2007 May 24, 2007 Oppgave 1 a) Lorentztransformasjonane er x = γ(x V t), t = γ(t V x), der γ = 1/ 1 V 2 Vi tar differensiala av desse
Løysingsforslag (Skisse) Eksamen FY3452 Gravitasjon og Kosmologi Våren 2007 May 24, 2007 Oppgave 1 a) Lorentztransformasjonane er x = γ(x V t), t = γ(t V x), der γ = 1/ 1 V 2 Vi tar differensiala av desse
3.9 Symmetri GEOMETRI
 rektange der den ene siden er ik radius og den andre siden ik have omkretsen av sirkeen. Areaet kan da finnes ved å mutipisere sidekantene, noe som gir: A = r πr = πr 2. Oppgave 3.41 a) Konstruer en trekant
rektange der den ene siden er ik radius og den andre siden ik have omkretsen av sirkeen. Areaet kan da finnes ved å mutipisere sidekantene, noe som gir: A = r πr = πr 2. Oppgave 3.41 a) Konstruer en trekant
Litt GRUPPETEORI for Fys4170
 Litt GRUPPETEORI for Fys4170 GRUPPER: Ei gruppe G = {g i } er ei samling element med disse egenskapene: * multiplikasjon slik at g i g j G ; * et enhetselement g 0 = 1 slik at g i g 0 = g 0 g i = g i ;
Litt GRUPPETEORI for Fys4170 GRUPPER: Ei gruppe G = {g i } er ei samling element med disse egenskapene: * multiplikasjon slik at g i g j G ; * et enhetselement g 0 = 1 slik at g i g 0 = g 0 g i = g i ;
Løsning til øving 17 for FY1004, våren 2008
 Løsning til øving 17 for FY1004, våren 2008 Her skal vi se på hvordan spinnet egenspinnet til et elektron påvirkes av et konstant magnetfelt B Merk: Det korrekte navnet på B er magnetisk flukstetthet,
Løsning til øving 17 for FY1004, våren 2008 Her skal vi se på hvordan spinnet egenspinnet til et elektron påvirkes av et konstant magnetfelt B Merk: Det korrekte navnet på B er magnetisk flukstetthet,
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapeige fakutet Eksamen i: FYS-MEK 1110 Eksamensdag: 7 juni 016 Tid for eksamen: 14:30 18:30 (4 timer) Oppgavesettet er på 3 sider Vedegg: Formeark Tiatte
UNIVERSITETET I OSLO Det matematisk-naturvitenskapeige fakutet Eksamen i: FYS-MEK 1110 Eksamensdag: 7 juni 016 Tid for eksamen: 14:30 18:30 (4 timer) Oppgavesettet er på 3 sider Vedegg: Formeark Tiatte
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturitenskapeige fakutet Eksamen i: FYS1120 Eektromagnetisme Eksamensdag: 4. desember 2017 Tid for eksamen: 14.30 18.30 Oppgaesettet er på 9 sider. Vedegg: Tiatte hjepemider:
UNIVERSITETET I OSLO Det matematisk-naturitenskapeige fakutet Eksamen i: FYS1120 Eektromagnetisme Eksamensdag: 4. desember 2017 Tid for eksamen: 14.30 18.30 Oppgaesettet er på 9 sider. Vedegg: Tiatte hjepemider:
JEMISI(-TEKNISKE FISKERIDIRE TORATETS FORSKNINGSINSTITUTT BERGEN. Analyser av fett og tørrstoff Sammenlikning av analyseresultater ved 7 laboratorier
 FISKERIDIRE TORATETS FORSKNINGSINSTITUTT JEMISI(-TEKNISKE Anayser av fett og tørrstoff Sammenikning av anayseresutater ved 7 aboratorier ved Kåre Bakken og Gunnar Tertnes R.nr. 135/74 A. h. 44 BERGEN Anayser
FISKERIDIRE TORATETS FORSKNINGSINSTITUTT JEMISI(-TEKNISKE Anayser av fett og tørrstoff Sammenikning av anayseresutater ved 7 aboratorier ved Kåre Bakken og Gunnar Tertnes R.nr. 135/74 A. h. 44 BERGEN Anayser
Hall effekt. 3. Mål sammenhørende verdier mellom magnetfeltet og Hall-spenningen for to ulike kontrollstrømmer (I = 25 og 50 ma).
 FY1303 Eektrisitet og magnetisme nstitutt for fysikk, NTNU FY1303 Eektrisitet og magnetisme, høst 007 Laboratorieøvese 1 a effekt ensikt ensikten med øvesen er å gjøre seg kjent med a-effekten og måe denne
FY1303 Eektrisitet og magnetisme nstitutt for fysikk, NTNU FY1303 Eektrisitet og magnetisme, høst 007 Laboratorieøvese 1 a effekt ensikt ensikten med øvesen er å gjøre seg kjent med a-effekten og måe denne
Kortfattet løsningsforslag / fasit
 Kortfattet øsningsforsag / fasit Konteeksamen i FYS-MEK 1110 - Mekanikk / FYS-MEF 1110 - Mekanikk for MEF / FY-ME 100 Eksamensdag torsdag 18. august 005 (Versjon 19. august k 0840. En fei i øsningen av
Kortfattet øsningsforsag / fasit Konteeksamen i FYS-MEK 1110 - Mekanikk / FYS-MEF 1110 - Mekanikk for MEF / FY-ME 100 Eksamensdag torsdag 18. august 005 (Versjon 19. august k 0840. En fei i øsningen av
12.4 HORISONTALE SKIVER Virkemåte Generelt Vindlastene i skivebygg overføres fra ytterveggene til dekkekonstruksjonene,
 112 B12 SKIVESYSTEM Oppsummering av punkt 12.3 Enke, reguære bygg kan håndregnes etter former som er utedet. Føgende betingeser må være oppfyt. - Ae vertikae avstivende deer må ha hovedaksene i - og y-retning
112 B12 SKIVESYSTEM Oppsummering av punkt 12.3 Enke, reguære bygg kan håndregnes etter former som er utedet. Føgende betingeser må være oppfyt. - Ae vertikae avstivende deer må ha hovedaksene i - og y-retning
Permanentmagneter - av stål med konstant magnetisme. Elektromagneter- består av en spole som må tilkoples en spenning for å bli magnetiske.
 1 5.1 GEERELL MAGETSME - MAGETFELT Det skies meom to typer magnetisme: Permanentmagneter - av stå med konstant magnetisme. Eektromagneter- består av en spoe som må tikopes en spenning for å bi magnetiske.
1 5.1 GEERELL MAGETSME - MAGETFELT Det skies meom to typer magnetisme: Permanentmagneter - av stå med konstant magnetisme. Eektromagneter- består av en spoe som må tikopes en spenning for å bi magnetiske.
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapeige fakutet Eksamen i: MEK4550 Eementmetoden i faststoffmekanikk I. Eksamensdag: Mandag 15. desember 2008. Tid for eksamen: 14.30 17.30. Oppgavesettet
UNIVERSITETET I OSLO Det matematisk-naturvitenskapeige fakutet Eksamen i: MEK4550 Eementmetoden i faststoffmekanikk I. Eksamensdag: Mandag 15. desember 2008. Tid for eksamen: 14.30 17.30. Oppgavesettet
MA1201 Lineær algebra og geometri Løsningsforslag for eksamen gitt 3. desember 2007
 Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag MA101 Lineær algebra og geometri Løsningsforslag for eksamen gitt 3 desember 007 Oppgave 1 a) Vi ser på ligningssystemet x +
Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag MA101 Lineær algebra og geometri Løsningsforslag for eksamen gitt 3 desember 007 Oppgave 1 a) Vi ser på ligningssystemet x +
Relativitet og matematikk
 Reatiitet og matematikk Eementær agebra og igninger Beregning dersom rommet er absoutt og dersom det er reatit Horfor måingen i 887 ga det resutat man fant. At yset bruker ike ang tid ti å gå i ae retninger
Reatiitet og matematikk Eementær agebra og igninger Beregning dersom rommet er absoutt og dersom det er reatit Horfor måingen i 887 ga det resutat man fant. At yset bruker ike ang tid ti å gå i ae retninger
Løsningsforslag til eksamen i FY8306 KVANTEFELTTEORI Fredag 9. juni 2006
 NTNU Side av 3 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i FY836 KVANTEFELTTEORI Fredag 9. juni 6 Dette løsningsforslaget er på 3 sider, pluss et vedlegg
NTNU Side av 3 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i FY836 KVANTEFELTTEORI Fredag 9. juni 6 Dette løsningsforslaget er på 3 sider, pluss et vedlegg
Eksamen i Klassisk feltteori, fag TFY 4270 Onsdag 26. mai 2004 Løsninger
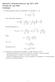 Eksamen i Klassisk feltteori, fag TFY 470 Onsdag 6. mai 004 Løsninger 1a) Sammenhengen mellom koordinattiden t og egentiden τ er at Den relativistiske impulsen er Hamiltonfunksjonen er Siden har vi at
Eksamen i Klassisk feltteori, fag TFY 470 Onsdag 6. mai 004 Løsninger 1a) Sammenhengen mellom koordinattiden t og egentiden τ er at Den relativistiske impulsen er Hamiltonfunksjonen er Siden har vi at
Eksamen TFY 4210 Kvanteteorien for mangepartikkelsystem, våren 2012
 NTNU Fakultet for Naturvitskap og Teknologi Institutt for fysikk Eksamen TFY 4210 Kvanteteorien for mangepartikkelsystem, våren 2012 Faglærar: Førsteamanuensis John Ove Fjærestad Institutt for fysikk Telefon:
NTNU Fakultet for Naturvitskap og Teknologi Institutt for fysikk Eksamen TFY 4210 Kvanteteorien for mangepartikkelsystem, våren 2012 Faglærar: Førsteamanuensis John Ove Fjærestad Institutt for fysikk Telefon:
Løsningsforslag til eksamen i FY3404/FY8307 RELATIVISTISK KVANTEMEKANIKK Fredag 9. juni 2006
 NTNU Side 1 av 4 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i FY3404/FY8307 RELATIVISTISK KVANTEMEKANIKK Fredag 9. juni 2006 Dette løsningsforslaget
NTNU Side 1 av 4 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i FY3404/FY8307 RELATIVISTISK KVANTEMEKANIKK Fredag 9. juni 2006 Dette løsningsforslaget
Eksamen i fag RELATIVISTISK KVANTEMEKANIKK Fredag 26. mai 2000 Tid: 09:00 14:00
 Side 1 av 3 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Navn: Kåre Olaussen Telefon: 9 36 52 Eksamen i fag 74327 RELATIVISTISK KVANTEMEKANIKK Fredag
Side 1 av 3 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Navn: Kåre Olaussen Telefon: 9 36 52 Eksamen i fag 74327 RELATIVISTISK KVANTEMEKANIKK Fredag
Oppgave 1 (25 %) - Flervalgsoppgaver
 Oppgaver og løsningsforslag for 4t eksamen 10.mai 006 i LO510D Lineær algebra med grafiske anvendelser. Fra og med oppgave skal alle svar begrunnes. Oppgave 1 (5 %) - Flervalgsoppgaver Denne oppgaven består
Oppgaver og løsningsforslag for 4t eksamen 10.mai 006 i LO510D Lineær algebra med grafiske anvendelser. Fra og med oppgave skal alle svar begrunnes. Oppgave 1 (5 %) - Flervalgsoppgaver Denne oppgaven består
KJM Radiokjemidelen
 Patikke i boks - en dimensjon KJM 1060 - Radiokjemideen Foeesning : Skamodeen d ψ m + E ψ 0 dx h n π h En V0 + m ψ n nπ( x + ) sin n 45 de n 1,,,... Sannsynigheten fo å finne patikkeen meom x og x+dx e:
Patikke i boks - en dimensjon KJM 1060 - Radiokjemideen Foeesning : Skamodeen d ψ m + E ψ 0 dx h n π h En V0 + m ψ n nπ( x + ) sin n 45 de n 1,,,... Sannsynigheten fo å finne patikkeen meom x og x+dx e:
DTL og universell utforming ikke godta diskriminering
 DISKRIMINERINGS- OG TILGJENGELIGHETSLOVEN UNIVERSELL UTFORMING ikke godta diskriminering DTL og universe utforming ikke godta diskriminering 1 DTL og universe utforming ikke godta diskriminering 1 DTL
DISKRIMINERINGS- OG TILGJENGELIGHETSLOVEN UNIVERSELL UTFORMING ikke godta diskriminering DTL og universe utforming ikke godta diskriminering 1 DTL og universe utforming ikke godta diskriminering 1 DTL
B4 TEMPERATURER, KRYP OG SVINN
 4.4 BEREGNING AV HORISONTAKREFTER I BJEKER OG DEKKER FRA TEMPERATUR, KRYP OG SVINN Summen av bevegeser fra temperaturendringer, kryp og svinn kaes kort for voumendringer. I dette kapitteet beregnes horisontae
4.4 BEREGNING AV HORISONTAKREFTER I BJEKER OG DEKKER FRA TEMPERATUR, KRYP OG SVINN Summen av bevegeser fra temperaturendringer, kryp og svinn kaes kort for voumendringer. I dette kapitteet beregnes horisontae
MA0002 Brukerkurs i matematikk B Vår 2014
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA0002 Brukerkurs i matematikk B Vår 2014 Løsningsforslag Øving 10 Oppgaver fra boken: 10.6 : 1, 8, 9, 12, 19, 26, 29,, 4 Det
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA0002 Brukerkurs i matematikk B Vår 2014 Løsningsforslag Øving 10 Oppgaver fra boken: 10.6 : 1, 8, 9, 12, 19, 26, 29,, 4 Det
LO510D Lin.Alg. m/graf. anv. Våren 2005
 TF Høgskolen i Sør Trøndelag Avdeling for informatikk og e læring LO5D Lin.Alg. m/graf. anv. Våren 5 Løsningsforslag Eksamen a) Setter α = og β = i ligningssystemet og gausseliminerer totalmatrisen til
TF Høgskolen i Sør Trøndelag Avdeling for informatikk og e læring LO5D Lin.Alg. m/graf. anv. Våren 5 Løsningsforslag Eksamen a) Setter α = og β = i ligningssystemet og gausseliminerer totalmatrisen til
Eksamen i fag FY1004 Innføring i kvantemekanikk Tirsdag 22. mai 2007 Tid:
 Side 1 av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 51 72) Sensurfrist: Tirsdag 12. juni 2007
Side 1 av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 51 72) Sensurfrist: Tirsdag 12. juni 2007
Løsningsforslag til eksamen i FY3404 RELATIVISTISK KVANTEMEKANIKK Tirsdag 30. november 2004
 NTNU Side av 7 Institutt for fysikk Løsningsforslag til eksamen i FY30 RELATIVISTISK KVANTEMEKANIKK Tirsdag 30. november 200 Dette løsningsforslaget er på 7 sider. Oppgave. Prosesser i QED Tegn, i de tilfeller
NTNU Side av 7 Institutt for fysikk Løsningsforslag til eksamen i FY30 RELATIVISTISK KVANTEMEKANIKK Tirsdag 30. november 200 Dette løsningsforslaget er på 7 sider. Oppgave. Prosesser i QED Tegn, i de tilfeller
MA0002 Brukerkurs i matematikk B Vår 2016
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA0002 Brukerkurs i matematikk B Vår 2016 Løsningsforslag Øving 11 Oppgaver fra boken: 10.6 : 1, 8, 9, 12, 19, 26, 29,, 4 Det
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA0002 Brukerkurs i matematikk B Vår 2016 Løsningsforslag Øving 11 Oppgaver fra boken: 10.6 : 1, 8, 9, 12, 19, 26, 29,, 4 Det
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS14, Kvantefysikk Eksamensdag: 17. august 17 4 timer Lovlige hjelpemidler: Rottmann: Matematisk formelsamling, Øgrim og Lian:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS14, Kvantefysikk Eksamensdag: 17. august 17 4 timer Lovlige hjelpemidler: Rottmann: Matematisk formelsamling, Øgrim og Lian:
Karakterer. Kapittel Homomorfier av grupper. 8.2 Representasjoner
 Kapittel 8 Karakterer 8. Homomorfier av grupper I forrige kapittel definerte vi begrepet abstrakt gruppe, som en abstrakt versjon av begrepet symmetrigruppe. For å studere forbindelsen mellom abstrakte
Kapittel 8 Karakterer 8. Homomorfier av grupper I forrige kapittel definerte vi begrepet abstrakt gruppe, som en abstrakt versjon av begrepet symmetrigruppe. For å studere forbindelsen mellom abstrakte
Eksamensoppgave i FY8104 / FY3105 Symmetrigrupper i fysikken
 Institutt for fysikk Eksamensoppgave i FY84 / FY35 Symmetrigrupper i fysikken Faglig kontakt under eksamen: Jan Myrheim Tlf.: 73 59 36 53 / 9 75 72 Eksamensdato: 5. desember 25 Eksamenstid: 9 3 Tillatte
Institutt for fysikk Eksamensoppgave i FY84 / FY35 Symmetrigrupper i fysikken Faglig kontakt under eksamen: Jan Myrheim Tlf.: 73 59 36 53 / 9 75 72 Eksamensdato: 5. desember 25 Eksamenstid: 9 3 Tillatte
Viktigheten av å kunne uttrykke seg skriftlig
 Innedning 1 Viktigheten av å kunne uttrykke seg skriftig Sik bir du bedre ti å skrive Det å skrive en oppgave er utfordrende og meningsfut. Når du skriver, egger du a din reevante kunnskap og forståese
Innedning 1 Viktigheten av å kunne uttrykke seg skriftig Sik bir du bedre ti å skrive Det å skrive en oppgave er utfordrende og meningsfut. Når du skriver, egger du a din reevante kunnskap og forståese
Oppgave 1: Blanda drops
 Fysikkprøve-0402-f.nb Oppgave : Banda drops a) En avgrenset mengde oksygen-gass HO 2 L ar temperaturen T = 300 K, trykket p = 0 kpa og voum V =0,00 m 3. Beregn massen ti den avgrensede gassen. Vi bruker
Fysikkprøve-0402-f.nb Oppgave : Banda drops a) En avgrenset mengde oksygen-gass HO 2 L ar temperaturen T = 300 K, trykket p = 0 kpa og voum V =0,00 m 3. Beregn massen ti den avgrensede gassen. Vi bruker
A.3.e: Ortogonale egenfunksjonssett
 TFY4250/FY2045 Tillegg 2 1 Tillegg 2: A.3.e: Ortogonale egenfunksjonssett Ikke-degenererte egenverdier La oss først anta at en operator ˆF har et diskret og ikke-degeneret spektrum. Det siste betyr at
TFY4250/FY2045 Tillegg 2 1 Tillegg 2: A.3.e: Ortogonale egenfunksjonssett Ikke-degenererte egenverdier La oss først anta at en operator ˆF har et diskret og ikke-degeneret spektrum. Det siste betyr at
Løsningsforslag Konte-eksamen 2. august 2003 SIF4048 Kjemisk fysikk og kvantemekanikk
 Konte-eksamen SIF448.aug. 3 - løsningsforslag 1 Oppgave 1 a. Hamilton-operatoren er Løsningsforslag Konte-eksamen. august 3 SIF448 Kjemisk fysikk og kvantemekanikk Ĥ = h m x + V (x), og den tidsuavhengige
Konte-eksamen SIF448.aug. 3 - løsningsforslag 1 Oppgave 1 a. Hamilton-operatoren er Løsningsforslag Konte-eksamen. august 3 SIF448 Kjemisk fysikk og kvantemekanikk Ĥ = h m x + V (x), og den tidsuavhengige
EKSAMEN I FY2045 KVANTEFYSIKK Mandag 2. juni 2008 kl
 NORSK TEKST Side av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 9702355 EKSAMEN I FY2045 KVANTEFYSIKK Mandag
NORSK TEKST Side av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 9702355 EKSAMEN I FY2045 KVANTEFYSIKK Mandag
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet
 NIVERSITETET I OSLO Det matematisk-naturvitenskapeige akutet Eksamen i: FYS 13 - Svingninger og bøger Eksamensdag: 4. mars 6 Tid or eksamen: K. 9-1 Godkjente hjepemider: Øgrim og Lian (eer Ange og Lian):
NIVERSITETET I OSLO Det matematisk-naturvitenskapeige akutet Eksamen i: FYS 13 - Svingninger og bøger Eksamensdag: 4. mars 6 Tid or eksamen: K. 9-1 Godkjente hjepemider: Øgrim og Lian (eer Ange og Lian):
En partikkel med masse m befinner seg i et éndimensjonalt, asymmetrisk brønnpotensial
 NORSK TEKST Side av 5 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tel. 7 59 8 67, eller 9755 EKSAMEN I TFY45 ATOM- OG MOLEKYLFYSIKK
NORSK TEKST Side av 5 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tel. 7 59 8 67, eller 9755 EKSAMEN I TFY45 ATOM- OG MOLEKYLFYSIKK
Klosters fileteringsmaskin. Rapport fra besøk
 - FISKE I!REKTORATETS JEMIS -TE NIS E FORSKNINGSINSTITUTT Kosters fieteringsmaskin. Rapport fra besøk 27.7.1959 ved Einar Soa. A-ugust 1959; R~nr; 56/59. A. h. 44. BERGEN Konkusjon. Der er ikke tvi om
- FISKE I!REKTORATETS JEMIS -TE NIS E FORSKNINGSINSTITUTT Kosters fieteringsmaskin. Rapport fra besøk 27.7.1959 ved Einar Soa. A-ugust 1959; R~nr; 56/59. A. h. 44. BERGEN Konkusjon. Der er ikke tvi om
En samling av mer eller mindre relevante formler (uten nærmere forklaring) er gitt til slutt i oppgavesettet.
 Norges teknisk-naturvitenskapelige universitet NTNU Institutt for fysikk Lade EKSAMEN I: MNF FY 44 KVANTEMEKANIKK I DATO: Tirsdag 4. desember 999 TID: 9.00 5.00 Antall vekttall: 4 Antall sider: 3 Sensurdato:
Norges teknisk-naturvitenskapelige universitet NTNU Institutt for fysikk Lade EKSAMEN I: MNF FY 44 KVANTEMEKANIKK I DATO: Tirsdag 4. desember 999 TID: 9.00 5.00 Antall vekttall: 4 Antall sider: 3 Sensurdato:
Fl S KE RIDIRE KTORATETS KJEMISK-TEKNISKE FORSKNINGSINSTITUTT
 F S KE RIDIRE KTORATETS KJEMISK-TEKNISKE FORSKNINGSINSTITUTT Betydningen av konsentratseparering i si~9je og sidemeindustrien. ved Einar Soa. R.nr 92/65. A,. h 56. BERGEN Betydningen av konsentratseparering
F S KE RIDIRE KTORATETS KJEMISK-TEKNISKE FORSKNINGSINSTITUTT Betydningen av konsentratseparering i si~9je og sidemeindustrien. ved Einar Soa. R.nr 92/65. A,. h 56. BERGEN Betydningen av konsentratseparering
a) Matrisen I uv T har egenverdier 1, med multiplisitet n 1 og 1 v T u, med multiplisitet 1. Derfor er matrisen inverterbar når v T u 1.
 Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Oppgave 1 a) Matrisen I uv T har egenverdier 1, med multiplisitet n 1 og 1 v T u, med multiplisitet 1. Derfor er
Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Oppgave 1 a) Matrisen I uv T har egenverdier 1, med multiplisitet n 1 og 1 v T u, med multiplisitet 1. Derfor er
EKSAMEN I NUMERISK LINEÆR ALGEBRA (TMA4205)
 Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag Side av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren 93064 EKSAMEN I NUMERISK LINEÆR ALGEBRA TMA405 Fredag 5 desember
Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag Side av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren 93064 EKSAMEN I NUMERISK LINEÆR ALGEBRA TMA405 Fredag 5 desember
MAT Grublegruppen Notat 11
 MAT1100 - Grublegruppen Notat 11 Jørgen O. Lye Matrisegrupper Den store gruppen vi skal se på er GL(n, K) = {inverterbare n n matriser med koesienter i K} Forkortelsen står for den generelle lineære gruppen
MAT1100 - Grublegruppen Notat 11 Jørgen O. Lye Matrisegrupper Den store gruppen vi skal se på er GL(n, K) = {inverterbare n n matriser med koesienter i K} Forkortelsen står for den generelle lineære gruppen
Løsningsforslag Eksamen 7. august 2006 TFY4215 Kjemisk fysikk og kvantemekanikk
 Eksamen TFY4215 7. august 2006 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 7. august 2006 TFY4215 Kjemisk fysikk og kvantemekanikk a. Bundne tilstander i et symmetrisk éndimensjonalt potensial
Eksamen TFY4215 7. august 2006 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 7. august 2006 TFY4215 Kjemisk fysikk og kvantemekanikk a. Bundne tilstander i et symmetrisk éndimensjonalt potensial
Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
 Norges teknisk naturvitenskapelige universitet NTNU Side 1 av 9 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
Norges teknisk naturvitenskapelige universitet NTNU Side 1 av 9 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
Løsningsforslag Eksamen 8. august 2009 TFY4250 Atom- og molekylfysikk
 Eksamen TFY425 8. august 29 - løsningsforslag Oppgave Løsningsforslag Eksamen 8. august 29 TFY425 Atom- og molekylfysikk a. For β = har vi en ordinær boks fra x = til x = L. Energiegenfunksjonene har formen
Eksamen TFY425 8. august 29 - løsningsforslag Oppgave Løsningsforslag Eksamen 8. august 29 TFY425 Atom- og molekylfysikk a. For β = har vi en ordinær boks fra x = til x = L. Energiegenfunksjonene har formen
Brukerundersøkelse for Aktivitetsskolen 2015/ 2016
 Brukerundersøkese for Aktivitetsskoen 2015/ 2016 Fakta om undersøkesen - Undersøkesen be hodt høsten 2015 på bestiing fra (UDE) - Samtige kommunae barneskoer med AKS er med i undersøkesen (99 stk.) - 56%
Brukerundersøkese for Aktivitetsskoen 2015/ 2016 Fakta om undersøkesen - Undersøkesen be hodt høsten 2015 på bestiing fra (UDE) - Samtige kommunae barneskoer med AKS er med i undersøkesen (99 stk.) - 56%
Oppgavesett. Kapittel Oppgavesett 1
 Kapittel 9 Oppgavesett Dette kapitlet består av fire oppgavesett med oppgaver fra alle deler av kompendiet. 9. Oppgavesett Oppgave. Et dynamisk system er gitt ved x n+ = M x n der M er -matrisen.6.. M
Kapittel 9 Oppgavesett Dette kapitlet består av fire oppgavesett med oppgaver fra alle deler av kompendiet. 9. Oppgavesett Oppgave. Et dynamisk system er gitt ved x n+ = M x n der M er -matrisen.6.. M
Fysikkolympiaden Norsk finale 2014
 Norsk fysikkærerforenin Fysikkoympiaden Norsk finae 01 3. uttakinsrunde Freda 8. mars k. 09.00 ti 11.30 Hjepemider: Tabe/formesamin, ommerener o utdet formeark Oppavesettet består av 6 oppaver på sider
Norsk fysikkærerforenin Fysikkoympiaden Norsk finae 01 3. uttakinsrunde Freda 8. mars k. 09.00 ti 11.30 Hjepemider: Tabe/formesamin, ommerener o utdet formeark Oppavesettet består av 6 oppaver på sider
EKSAMEN. Emne: Fysikk og datateknikk
 EKSAMEN Emnekode: ITD11006 Emne: Fysikk og datateknikk Dato: 05. Mai 010 Eksamenstid: k 9:00 ti k 13:00 Hjepemider: 4 sider (A4) ( ark) med egne notater. Kakuator. Gruppebesvarese, som bir det ut på eksamensdagen
EKSAMEN Emnekode: ITD11006 Emne: Fysikk og datateknikk Dato: 05. Mai 010 Eksamenstid: k 9:00 ti k 13:00 Hjepemider: 4 sider (A4) ( ark) med egne notater. Kakuator. Gruppebesvarese, som bir det ut på eksamensdagen
Vi viser denne ekvivalensen ved å vise begge implikasjoner. " "Anta at G virker trofast på X og anta at g, h G er slik at gx = hx for alle
 TMA4150 Algebra Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Seksjon 16 2 Fasit: G 1 = {ρ 0, δ 2 } = G 3 = G P1 = G P3 G S1 = {ρ 0, µ 1 } = G S3 G m1 = {ρ 0, ρ 2, µ 1, µ
TMA4150 Algebra Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Seksjon 16 2 Fasit: G 1 = {ρ 0, δ 2 } = G 3 = G P1 = G P3 G S1 = {ρ 0, µ 1 } = G S3 G m1 = {ρ 0, ρ 2, µ 1, µ
Løsningsforslag Eksamen 8. august 2011 FY2045/TFY4250 Kvantemekanikk I
 Eksamen FY45/TFY45 8. august - løsningsforslag Oppgave Løsningsforslag Eksamen 8. august FY45/TFY45 Kvantemekanikk I a. For E < V blir området x > klassisk forbudt, og den tidsuavhengige Schrödingerligningen
Eksamen FY45/TFY45 8. august - løsningsforslag Oppgave Løsningsforslag Eksamen 8. august FY45/TFY45 Kvantemekanikk I a. For E < V blir området x > klassisk forbudt, og den tidsuavhengige Schrödingerligningen
Faglig kontakt under eksamen: Ingjald Øverbø, tlf , eller
 NORSK TEKST Side av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 9702355 EKSAMEN I TFY4250 ATOM- OG MOLEKYLFYSIKK
NORSK TEKST Side av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 9702355 EKSAMEN I TFY4250 ATOM- OG MOLEKYLFYSIKK
Programvareløsninger for Lexmark Solutions Platform
 Lexmark Soutions Patform Programvareøsninger for Lexmark Soutions Patform Lexmark Soutions Patform er et rammeverk av programmer som er utformet av Lexmark med tanke på effektive og rimeige serverbaserte
Lexmark Soutions Patform Programvareøsninger for Lexmark Soutions Patform Lexmark Soutions Patform er et rammeverk av programmer som er utformet av Lexmark med tanke på effektive og rimeige serverbaserte
Eksamen i Ikkelineær dynamikk, fag TFY 4305 Onsdag 30. november 2005 Løsninger
 Eksamen i Ikkelineær ynamikk, fag TFY 4305 Onsag 30. november 2005 Løsninger 1) Den generelle løsningen av ligningen u t + cu x =0eru(x, t) =f(x ct), er f er en vilkårlig funksjon av en variabel. Hvoran
Eksamen i Ikkelineær ynamikk, fag TFY 4305 Onsag 30. november 2005 Løsninger 1) Den generelle løsningen av ligningen u t + cu x =0eru(x, t) =f(x ct), er f er en vilkårlig funksjon av en variabel. Hvoran
Løsningsforslag Eksamen 13. august 2011 FY1006/TFY4215 Innføring i kvantefysikk
 Eksamen FY1006/TFY415 13. august 011 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 13. august 011 FY1006/TFY415 Innføring i kvantefysikk a. Fra den tidsuavhengige Schrödingerligningen har vi for
Eksamen FY1006/TFY415 13. august 011 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 13. august 011 FY1006/TFY415 Innføring i kvantefysikk a. Fra den tidsuavhengige Schrödingerligningen har vi for
Papirprototyping. Opplegg for dagen. Hva er en prototyp (PT)
 Papirprototyping Oppegg for dagen 09:30-10:00: Om papirprototyping 10:00-10:15: Diskuter probemstiing 10:30-11:30: Lag PapirPT og tistandsdiagram for bruk i testen 12:00-13:30: Test PapirPT på andre (vi
Papirprototyping Oppegg for dagen 09:30-10:00: Om papirprototyping 10:00-10:15: Diskuter probemstiing 10:30-11:30: Lag PapirPT og tistandsdiagram for bruk i testen 12:00-13:30: Test PapirPT på andre (vi
EKSAMEN I FY2045 KVANTEFYSIKK Onsdag 30. mai 2007 kl
 NORSK TEKST Side av 3 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 97355 EKSAMEN I FY45 KVANTEFYSIKK Onsdag 3.
NORSK TEKST Side av 3 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 97355 EKSAMEN I FY45 KVANTEFYSIKK Onsdag 3.
Eksamen FY1004 Innføring i kvantemekanikk Tirsdag 22. mai 2007 Løsninger
 Eksamen FY1004 Innføring i kvantemekanikk Tirsdag. mai 007 Løsninger 1a Et hydrogenlikt atom har ett elektron med masse m og ladning e som er bundet til en atomkjerne med ladning Ze. Siden kjernen har
Eksamen FY1004 Innføring i kvantemekanikk Tirsdag. mai 007 Løsninger 1a Et hydrogenlikt atom har ett elektron med masse m og ladning e som er bundet til en atomkjerne med ladning Ze. Siden kjernen har
MØTEINNKALLING. Tillegg SAKLISTE HOVEDUTVALG FOR PLAN OG UTVIKLING. Utvalg: Møtested: Kommunehuset Møtedato: 28.01.
 Utvag: Møtested: Kommunehuset Møtedato: 28.01.2014 Tid: k1830 MØTEINNKALLING HOVEDUTVALG FOR PLAN OG UTVIKLING Forfa bes medt i god tid sik at vararepresentant kan bi innkat. Forfa ska medes ti servicekontoret,
Utvag: Møtested: Kommunehuset Møtedato: 28.01.2014 Tid: k1830 MØTEINNKALLING HOVEDUTVALG FOR PLAN OG UTVIKLING Forfa bes medt i god tid sik at vararepresentant kan bi innkat. Forfa ska medes ti servicekontoret,
Når en kraft angriper et stykke material fører det til påkjenninger som betegnes spenninger.
 Side 1 av 8 Mekanisk spenning i materiaer Tenk på et tungt egeme som ska bæres av en konstruksjon. Konstruksjonens må tåe kraften som går fra asten ti underaget. Denne kraften virker på konstruksjonen
Side 1 av 8 Mekanisk spenning i materiaer Tenk på et tungt egeme som ska bæres av en konstruksjon. Konstruksjonens må tåe kraften som går fra asten ti underaget. Denne kraften virker på konstruksjonen
Løysingsframlegg/skisse Eksamen TFY 4210 Kvanteteorien for mangepartikkelsystem 24. mai 2011
 Løysingsframlegg/skisse Eksamen TFY 4210 Kvanteteorien for mangepartikkelsystem 24. mai 2011 May 24, 2011 Oppgave 1 1) Ein global fasetransformasjon er på forma ψ ψe iα ψ ψ e iα, (1) der α er ein konstant.
Løysingsframlegg/skisse Eksamen TFY 4210 Kvanteteorien for mangepartikkelsystem 24. mai 2011 May 24, 2011 Oppgave 1 1) Ein global fasetransformasjon er på forma ψ ψe iα ψ ψ e iα, (1) der α er ein konstant.
Løsningsforslag Eksamen 20. desember 2012 FY2045/TFY4250 Kvantemekanikk I
 Eksamen FY045/TFY450 0. desember 0 - løsningsforslag Oppgave Løsningsforslag Eksamen 0. desember 0 FY045/TFY450 Kvantemekanikk I a. For x < 0 er potensialet lik null. (i) For E > 0 er da ψ E = (m e E/
Eksamen FY045/TFY450 0. desember 0 - løsningsforslag Oppgave Løsningsforslag Eksamen 0. desember 0 FY045/TFY450 Kvantemekanikk I a. For x < 0 er potensialet lik null. (i) For E > 0 er da ψ E = (m e E/
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MoD200 Eksamensdag: 15. desember 2003 Tid for eksamen: 14.30 17.30 Oppgavesettet er på 5 sider. Vedlegg: Tillatte hjelpemidler:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MoD200 Eksamensdag: 15. desember 2003 Tid for eksamen: 14.30 17.30 Oppgavesettet er på 5 sider. Vedlegg: Tillatte hjelpemidler:
Universitetet i Oslo Det matematisk-naturvitenskapelige fakultet
 Universitetet i Oslo Det matematisk-naturvitenskapelie fakultet Eksamen i: FYS4-Matematiske metoder i fysikk Dato: juni 9 Tid for eksamen: 9- Oppavesettet: sider Tillatte hjelpemidler: Elektronisk kalkulator,
Universitetet i Oslo Det matematisk-naturvitenskapelie fakultet Eksamen i: FYS4-Matematiske metoder i fysikk Dato: juni 9 Tid for eksamen: 9- Oppavesettet: sider Tillatte hjelpemidler: Elektronisk kalkulator,
Fasit TFY4215/FY1006 Innføring i kvantefysikk Vår 2015
 Fakultet for Naturvitskap og Teknologi Institutt for Fysikk Fasit TFY4215/FY1006 Innføring i kvantefysikk Vår 2015 Faglærar: Professor Jens O. Andersen Institutt for Fysikk, NTNU Mandag 27. mai 2015 kl.
Fakultet for Naturvitskap og Teknologi Institutt for Fysikk Fasit TFY4215/FY1006 Innføring i kvantefysikk Vår 2015 Faglærar: Professor Jens O. Andersen Institutt for Fysikk, NTNU Mandag 27. mai 2015 kl.
Vær OBS på at svarene på mange av oppgavene kan skrives på flere ulike måter!
 Vær OBS på at svarene på mange av oppgavene kan skrives på flere ulike måter! Oppgave.. a x y = x + y = r r r +r r x y = y fri x y = y fri Vi får én fri variabel, og løsningens har følgelig dimensjon.
Vær OBS på at svarene på mange av oppgavene kan skrives på flere ulike måter! Oppgave.. a x y = x + y = r r r +r r x y = y fri x y = y fri Vi får én fri variabel, og løsningens har følgelig dimensjon.
EKSAMEN I TFY4250 ATOM- OG MOLEKYLFYSIKK Onsdag 8. august 2007 kl
 NORSK TEKST Side 1 av 5 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: EKSAMEN I TFY4250 ATOM- OG MOLEKYLFYSIKK Onsdag 8. august 2007 kl. 09.00-13.00
NORSK TEKST Side 1 av 5 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: EKSAMEN I TFY4250 ATOM- OG MOLEKYLFYSIKK Onsdag 8. august 2007 kl. 09.00-13.00
FY2045 Kvantefysikk Løsningsforslag Eksamen 2. juni 2008
 Eksamen FY045. juni 008 - løsningsforslag Oppgave FY045 Kvantefysikk øsningsforslag Eksamen. juni 008 a. Fra den tidsuavhengige Schrödingerligningen, [ h ] m x + V x ψx Eψx, finner vi at den relative krumningen
Eksamen FY045. juni 008 - løsningsforslag Oppgave FY045 Kvantefysikk øsningsforslag Eksamen. juni 008 a. Fra den tidsuavhengige Schrödingerligningen, [ h ] m x + V x ψx Eψx, finner vi at den relative krumningen
Oppgaver MAT2500. Fredrik Meyer. 29. august 2014
 Oppgaver MAT500 Fredrik Meyer 9. august 04 Oppgave. Bruk cosinus-setningen til å se at definisjonen av vinkel i planet blir riktig. Løsning. Dette er en litt rar oppgave. Husk at cosinus-setningen sier
Oppgaver MAT500 Fredrik Meyer 9. august 04 Oppgave. Bruk cosinus-setningen til å se at definisjonen av vinkel i planet blir riktig. Løsning. Dette er en litt rar oppgave. Husk at cosinus-setningen sier
Økonomistyring for folkevalgte. Dan Lorentzen seniorrådgiver
 Økonomistyring for fokevagte Dan Lorentzen seniorrådgiver Hva er økonomistyring????? Forbedre Panegge Kontroere Gjennomføre Økonomistyring Bevigningsstyring God økonomistyring = Gode hodninger Roeavkaring
Økonomistyring for fokevagte Dan Lorentzen seniorrådgiver Hva er økonomistyring????? Forbedre Panegge Kontroere Gjennomføre Økonomistyring Bevigningsstyring God økonomistyring = Gode hodninger Roeavkaring
Valg 2011. Hurdal Arbeiderparti
 Vag 2011 Hurda Arbeiderparti Les dette før du bestemmer deg: Hurda Arbeiderparti har som overordnet føring at ae har ikt menneskeverd. Ae har ik rett ti utdanning, arbeid, boig og sosia trygghet. Derfor
Vag 2011 Hurda Arbeiderparti Les dette før du bestemmer deg: Hurda Arbeiderparti har som overordnet føring at ae har ikt menneskeverd. Ae har ik rett ti utdanning, arbeid, boig og sosia trygghet. Derfor
UNIVERSITET I BERGEN
 UNIVERSITET I BERGEN Det matematisk-naturvitenskapelige fakultet BOKMÅL Løsningsforslag eksamen MAT - Lineær algebra H Med forbehold om skrivefeil. Oppgave. Betrakt A = 6 5, b = 6 b (a) (b) Finn den reduserte
UNIVERSITET I BERGEN Det matematisk-naturvitenskapelige fakultet BOKMÅL Løsningsforslag eksamen MAT - Lineær algebra H Med forbehold om skrivefeil. Oppgave. Betrakt A = 6 5, b = 6 b (a) (b) Finn den reduserte
UNIVERSITETET I BERGEN
 BOKMÅL UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet. V.008. Løsningsforslag til eksamen i emnet MAT131 - Differensialligninger I 8. mai 008 kl. 0900-1400 Vi har ligningen der α er
BOKMÅL UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet. V.008. Løsningsforslag til eksamen i emnet MAT131 - Differensialligninger I 8. mai 008 kl. 0900-1400 Vi har ligningen der α er
Eksamen i fag FY1004 Innføring i kvantemekanikk Fredag 30. mai 2008 Tid: a 0 = 4πǫ 0 h 2 /(e 2 m e ) = 5, m
 Side av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 5 7 Sensurfrist: Fredag 0 juni 008 Eksamen
Side av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 5 7 Sensurfrist: Fredag 0 juni 008 Eksamen
Hvordan vurdere samtykkekompetanse?
 Geriatrisk avdeing Oso universitetssykehus Hvordan vurdere samtykkekompetanse? Torgeir Bruun Wyer Professor / overege Geriatrisk avdeing, Oso universitetssykehus Geriatrisk avdeing Oso universitetssykehus
Geriatrisk avdeing Oso universitetssykehus Hvordan vurdere samtykkekompetanse? Torgeir Bruun Wyer Professor / overege Geriatrisk avdeing, Oso universitetssykehus Geriatrisk avdeing Oso universitetssykehus
Forelesningsnotater SIF8039/ Grafisk databehandling
 Forelesningsnotater SIF839/ Grafisk databehandling Notater til forelesninger over: Kapittel 4: Geometric Objects and ransformations i: Edward Angel: Interactive Computer Graphics Vårsemesteret 22 orbjørn
Forelesningsnotater SIF839/ Grafisk databehandling Notater til forelesninger over: Kapittel 4: Geometric Objects and ransformations i: Edward Angel: Interactive Computer Graphics Vårsemesteret 22 orbjørn
Kjeglesnitt Harald Hanche-Olsen Versjon
 Kjegesnitt Hrd Hnche-Osen hnche@mth.ntnu.no Versjon 1.0 2013-01-25 Definisjon og grunneggende egenskper Et kjegesnitt er en pn kurve gitt v en styreinje, et brennpunkt B og et positivt t ε som vi ker eksentrisiteten
Kjegesnitt Hrd Hnche-Osen hnche@mth.ntnu.no Versjon 1.0 2013-01-25 Definisjon og grunneggende egenskper Et kjegesnitt er en pn kurve gitt v en styreinje, et brennpunkt B og et positivt t ε som vi ker eksentrisiteten
EKSAMEN I NUMERISK LØSNING AV DIFFERENSIALLIGNINGER MED DIFFERANSEMETODER (TMA4212)
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren (964) EKSAMEN I NUMERISK LØSNING AV DIFFERENSIALLIGNINGER MED DIFFERANSEMETODER
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren (964) EKSAMEN I NUMERISK LØSNING AV DIFFERENSIALLIGNINGER MED DIFFERANSEMETODER
MAUMAT644 ALGEBRA vår 2016 Første samling Runar Ile
 MAUMAT644 ALGEBRA vår 2016 Første samling Runar Ile 1 Introduksjon: Grupper og ringer Ringer En ring er et sted hvor du kan addere, subtrahere og multiplisere. Hvis du også kan dividere kalles ringen for
MAUMAT644 ALGEBRA vår 2016 Første samling Runar Ile 1 Introduksjon: Grupper og ringer Ringer En ring er et sted hvor du kan addere, subtrahere og multiplisere. Hvis du også kan dividere kalles ringen for
Oppgave 2 Vi ser på et éndimensjonalt system hvor en av de stasjonære tilstandene ψ(x) er gitt som { 0 for x < 0, ψ(x) = Ne ax (1 e ax (1)
 Oppgave Gjør kort rede for hva den fotoelektriske effekt er, hva slags konklusjoner man kunne trekke fra observasjoner av denne i kvantefysikkens fødsel, og beskriv et eksperiment som kan observere og
Oppgave Gjør kort rede for hva den fotoelektriske effekt er, hva slags konklusjoner man kunne trekke fra observasjoner av denne i kvantefysikkens fødsel, og beskriv et eksperiment som kan observere og
Løsningsforslag til eksamen i TFY4170 Fysikk 2 Fysikk 2 Lørdag 8. august 2005
 NTNU Side 1 av 5 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i TFY4170 Fysikk Fysikk Lørdag 8. august 005 Merk: Hver del-oppgave teller like mye. Dette løsningsforslaget
NTNU Side 1 av 5 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i TFY4170 Fysikk Fysikk Lørdag 8. august 005 Merk: Hver del-oppgave teller like mye. Dette løsningsforslaget
=,,,,, = det( A) a a a a a a a a a a + a a 0 1. a11 a12 a22 a12 a11 a22 a12 a21 a11a12 + a12 a11
 3.3 Oppgaver 3.3.1 1 2 3 1 2 3 2 0 1.La A,,,,, 3 4 B 2 1 C 0 1 a -1 b 1 c 2 Regn ut (a) A a, (b) B b, (c) C c, (d) A B, (e) A B C ( a) ( c) ( e) ( f ) 1-2 2 1 2 + ( 2) ( 1) 4 A a 3 4 1 3 2 + 4 ( 1 ( b)
3.3 Oppgaver 3.3.1 1 2 3 1 2 3 2 0 1.La A,,,,, 3 4 B 2 1 C 0 1 a -1 b 1 c 2 Regn ut (a) A a, (b) B b, (c) C c, (d) A B, (e) A B C ( a) ( c) ( e) ( f ) 1-2 2 1 2 + ( 2) ( 1) 4 A a 3 4 1 3 2 + 4 ( 1 ( b)
NORMALFORDELINGER, KOVARIANSMATRISER OG ELLIPSOIDER
 NORMALFORDELINGER, KOVARIANSMATRISER OG ELLIPSOIDER SIE 3080 STOKASTISKE OG ADAPTIVE SYSTEMER Oddvar Hallingstad 0. februar 00 Vi skal her utlede noen nyttige formler for arbeidet med kovariansmatriser
NORMALFORDELINGER, KOVARIANSMATRISER OG ELLIPSOIDER SIE 3080 STOKASTISKE OG ADAPTIVE SYSTEMER Oddvar Hallingstad 0. februar 00 Vi skal her utlede noen nyttige formler for arbeidet med kovariansmatriser
Q VISMK 25 MA! 2338 , « AVTALE OM SUPPLERINGSKJØP. Visma Unique AS (i avtalen kalt Leverandør) (i avtalen kalt Kunde) lnnhold. Kvinnherad kommune
 Why. MW f;.i i vi * - = ;=,d kommune 25 MA! 2338 I...,... c- r--, «*» = «' v,...,...j>.~.. --. "» i ~..._- : -' Å,..,...\.i. I...,. '». '. v. - '! - - za. t L du,, - ".-.i - - - ----' ' "" AVTALE OM SUPPLERINGSKJØP
Why. MW f;.i i vi * - = ;=,d kommune 25 MA! 2338 I...,... c- r--, «*» = «' v,...,...j>.~.. --. "» i ~..._- : -' Å,..,...\.i. I...,. '». '. v. - '! - - za. t L du,, - ".-.i - - - ----' ' "" AVTALE OM SUPPLERINGSKJØP
Løsningsforslag for FYS2140 Kvantemekanikk, Torsdag 16. august 2018
 Løsningsforslag for FYS140 Kvantemekanikk, Torsdag 16. august 018 Oppgave 1: Materiens bølgeegenskaper a) De Broglie fikk Nobelprisen i 199 for sin hypotese. Beskriv med noen setninger hva den går ut på.
Løsningsforslag for FYS140 Kvantemekanikk, Torsdag 16. august 018 Oppgave 1: Materiens bølgeegenskaper a) De Broglie fikk Nobelprisen i 199 for sin hypotese. Beskriv med noen setninger hva den går ut på.
12 Diagonalisering av matriser og operatorer (Ch. 5.1, 5.2 og 8.5)
 Diagonalisering av matriser og operatorer (Ch 5, 5 og 85) Motivasjon Det er veldig viktig å kunne beregne funksjonsverdier f (A) for kvadratiske matriser A I kalkulus (teori av differensiallikninger) er
Diagonalisering av matriser og operatorer (Ch 5, 5 og 85) Motivasjon Det er veldig viktig å kunne beregne funksjonsverdier f (A) for kvadratiske matriser A I kalkulus (teori av differensiallikninger) er
16 Ortogonal diagonalisering
 Ortogonal diagonalisering Ortogonale matriser Definisjon (Def 7) En n n matrise A kalles ortogonal dersom den er invertibel og A A T Denne betingelsen er ekvivalent til at der I n er n n identitesmatrisen
Ortogonal diagonalisering Ortogonale matriser Definisjon (Def 7) En n n matrise A kalles ortogonal dersom den er invertibel og A A T Denne betingelsen er ekvivalent til at der I n er n n identitesmatrisen
= 3 11 = = 6 4 = 1.
 MAT3000/4000 Eksamen V3 Løsningsforslag Oppgave [0 poeng] Sjekk at 3 er en kvadratisk rest i Z/(3) og finn løsningene av likningen x = 3 i Z/(3) (uten å lage en tabell for x ) Du får lov til å bruke at
MAT3000/4000 Eksamen V3 Løsningsforslag Oppgave [0 poeng] Sjekk at 3 er en kvadratisk rest i Z/(3) og finn løsningene av likningen x = 3 i Z/(3) (uten å lage en tabell for x ) Du får lov til å bruke at
