8 Kontinuumsmekanikk og elastisitetsteori
|
|
|
- Britt Borgen
- 6 år siden
- Visninger:
Transkript
1 8 Kontinuumsmekanikk og elastisitetsteori Innhold: Kontinuumsmekanikk Elastisitetsteori kontra klassisk fasthetslære Litteratur: Cook & Young, Advanced Mechanics of Materials, kap. 1.1 og 7.3 Irgens, Statikk, kap. 1 Bell, Konstruksjonsmekanikk Del I Likevektslære, kap. 1 Bell, Konstruksjonsmekanikk Del I Fasthetslære, kap. 1 TKT4124 Mekanikk 3, høst Kontinuumsmekanikk og elastisitetsteori
2 Fasthetslære Hittil i kurset (og i Mekanikk 1 + Mekanikk 2): Alle utledninger og resultater er basert på elementær fasthetslære (engelsk: mechanics of materials) I fasthetslæren idealiseres den virkelige oppførselen til systemet ved at det gjøres en del forenklinger og antagelser vedrørende spenningssituasjonen og/eller tøyningsfordeling. Eksempler: Teknisk (lineær) bjelketeori Naviers hypotese, dvs at tøyningene er lineære over høyden til tverrsnittet. OK for lange og slanke bjelker. St Venants torsjonsteori Antar at det kun er skjærdeformasjoner, dvs ingen hvelvning. OK for sirkuære tverrsnitt. Beholderteori Antar at spenningene i tykkelsesretningen kan neglisjeres. OK for tynnveggede beholdere. Typiske trinn i en fasthetslærebasert analyse: 1. Vurder geometrien i den deformerte komponenten 2. Hvilke tøyninger er relevante for aktuell deformert tilstand? 3. Bestem tilhørende spenninger (antar som regel Hookes lov) 4. Spenninger relateres til last (krefter, momenter, trykk etc) 5. Og dermed foreligger det en løsning som via trinnene forskyvning tøyning spenning belastning gir en relasjon mellom last og deformasjon TKT4124 Mekanikk 3, høst Kontinuumsmekanikk og elastisitetsteori
3 Kontinuumsmekanikk Kontinuumsmekanikken gir en formell og matematisk korrekt beskrivelse av materialoppførsel og -respons. Beskrivelsen er gyldig for faste stoffer (legemer), væsker og gasser. Utgangspunktet er kontinuumshypotesen: Stoffmengden forutsettes å være kontinuerlig fordelt i det rommet den opptar Hypotesen resulterer dermed i at vi fokuserer på de makroskopiske egenskapene til stoffmengden. Vi går ikke ned på atom- og molekylnivå. Eventuelle bruddflater eller glideflater behandles som diskontinuiteter i materialet. Et annet viktig utgangspunkt er at de kontinuumsmekaniske relasjonene skal være uavhengige av koordinatsystem. Matematisk håndteres dette med tensorer. Tensoralgebra er ikke pensum i TKT4124; vi velger oss et kartesisk koordinatsystem. Det matematiske formelverket i kontinuumsmekanikk etableres ved å anvende fysiske lover på infinitesimale utsnitt av et stoff. I dette utsnittet skal det være: Likevekt Kompatibilitet (sammenheng mellom tøyninger og ytre deformasjon) Konservering av masse, energi, bevegelsesmengde og spinn (bevaringslovene skal mao. være tilfredsstilt) Kontinuumsmekanikken tar utgangspunkt i en full tredimensjonal tilstand, og etablerer generelle uttrykk for spenning og tøyning. Så langt er betraktningen materialuavhengig. De spesifikke materialegenskapene (faste stoffer av ulike slag, væsker, gasser) beskrives ved hjelp av en materiallov, også kalt konstitutiv ligning, for det aktuelle materialet. TKT4124 Mekanikk 3, høst Kontinuumsmekanikk og elastisitetsteori
4 Kontinuumsmekanikk (forts.) Kontinuumsmekanikken i et nøtteskall: LIKEVEKT gir sammenheng mellom kraft (belastning) og spenninger. Behandles i kapittel 9. KINEMATISK KOMPATIBILITET gir sammenheng mellom forskyvning (deformasjon) og tøyninger. Behandles i kapittel 10. MATERIALLOV gir sammenheng mellom spenning og tøyning. Behandles i kapittel 11 (for elastiske materialer). Kraft Forskyvning Likevekt Kinematisk kompatibilitet Spenning Materiallov Tøyning VIKTIG: Likevekt og kinematisk kompatibilitet er fysisk, funderte ligninger med allmenn gyldighet. Materialloven er en empirisk sammenheng som er basert på observasjoner. En materiallov kan gi en presis eller mindre nøyaktig beskrivelse av observert oppførsel. TKT4124 Mekanikk 3, høst Kontinuumsmekanikk og elastisitetsteori
5 Ulike materiallover Hovedklasser av stoffer (aggregattilstander): Faste stoffer Bestemt volum og bestemt form Væsker Bestemt volum, men ingen bestemt form Gasser Verken volum eller form er bestemt En fellesbetegnelse for væsker og gasser er fluider. En karakteristisk egenskap for fluider er at de kun kan overføre normalspenninger når de er i ro. I en skjærspenningstilstand vil et fluid få en kontinuerlig deformasjon. En eventuell motstand mot denne skjærdeformasjonen kalles viskositet. De ulike egenskapene til faste stoffer, væsker og gasser leder til forskjellige materiallover for de tre aggregattilstandene. For faste stoffer gir fysiske observasjoner grunnlag for en ytterligere inndeling, eksempelvis Elastisitet Legemet gjenvinner sin opprinnelige geometri etter avlastning. De aller fleste materialer er elastiske ved små deformasjoner, og ofte er elastisiteten lineær. Plastisitet Legemet får permanente deformasjoner etter avlastning. Viskoelastisitet Tidsavhengig elastisitet, dvs at deformasjonen kommer gradvis etter pålastning. Typisk for polymerer. Trykkavhengighet Mange materialer har forskjellige egenskaper i trykk og strekk, f.eks betong, jord, tegl og stein. Kontinuumsmekanikk i TKT4124: Kun elastisitetsteori Mer om de øvrige i TKT4135 Materialmekanikk TKT4124 Mekanikk 3, høst Kontinuumsmekanikk og elastisitetsteori
6 Elastisitetsteori I klassisk elastisitetsteori forutsettes det at sammenhengen mellom spenning og tøyning er lineær og reversibel. Hvis materialet i tillegg er isotropt (samme egenskaper i alle retninger), vil den klassiske Hookes lov gi sammenhengen mellom spenning og tøyning. Her er det kun to uavhengige materialparametre, eksempelvis E og. For de fleste metaller kan den elastiske oppførselen med god nøyaktighet antas å være isotrop. I anisotrope materialer kreves det mer enn to elastiske parametre. I tre er det eksempelvis ulik E-modul i fiberretningen og på tvers av fiberretningen. Elastisitetsteorien kan i prinsippet gi en eksakt løsning for et vilkårlig problem i én, to eller tre dimensjoner. Likevekt og kinematisk kompatibilitet gir generelle sammenhenger (ligninger) som knytter sammen hhv. krefter og spenning, og forskyvning og tøyning. Hookes lov (forutsatt isotropt materiale) gir den siste relasjonen mellom spenning og tøyning. Men det er mange ukjente størrelser inne i bildet, og komplisert geometri/randbetingelser umuliggjør ofte en analytisk løsning. Likevel kan mange tilfeller løses analytisk. Dessuten kan Rayleigh-Ritz metode benyttes til å finne tilnærmede løsninger. I dag brukes elementmetoden for de aller fleste praktiske problemer. Denne er basert på en kontinuumsmekanisk beskrivelse av oppførselen til legemet. I tillegg deles legemet opp i et antall elementer (diskretisering), som alle har egenskaper definert med kontinuumsmekanikk. TKT4124 Mekanikk 3, høst Kontinuumsmekanikk og elastisitetsteori
11 Elastisk materiallov
 lastisk materiallov Innhold: lastisk materialoppførsel Isotrope og anisotrope materialer Generalisert Hookes lov Initialtøninger Hookes lov i plan spenning og plan tøning Volumtøning og kompresjonsmodul
lastisk materiallov Innhold: lastisk materialoppførsel Isotrope og anisotrope materialer Generalisert Hookes lov Initialtøninger Hookes lov i plan spenning og plan tøning Volumtøning og kompresjonsmodul
7 Rayleigh-Ritz metode
 7 Rayleigh-Ritz metode Innhold: Diskretisering Rayleigh-Ritz metode Essensielle og naturlige randbetingelser Nøyaktighet Hermittiske polynomer Litteratur: Cook & Young, Advanced Mechanics of Materials,
7 Rayleigh-Ritz metode Innhold: Diskretisering Rayleigh-Ritz metode Essensielle og naturlige randbetingelser Nøyaktighet Hermittiske polynomer Litteratur: Cook & Young, Advanced Mechanics of Materials,
6 Prinsippet om stasjonær potensiell energi
 6 Prinsippet om stasjonær potensiell energi Innhold: Konservative krefter Potensiell energi Prinsippet om stasjonær potensiell energi Stabil og ustabil likevekt rihetsgrader Litteratur: Irgens, Statikk,
6 Prinsippet om stasjonær potensiell energi Innhold: Konservative krefter Potensiell energi Prinsippet om stasjonær potensiell energi Stabil og ustabil likevekt rihetsgrader Litteratur: Irgens, Statikk,
MEK2500. Faststoffmekanikk 1. forelesning
 MEK2500 Faststoffmekanikk 1. forelesning MEK2500 Undervisning Foreleser: Frode Grytten Øvingslærer: NN Forelesninger: Tirsdag 10:15-12:00 B62 Torsdag 12:15-14:00 B91 Øvinger: Torsdag 14:15-16:00 B70 Øvinger
MEK2500 Faststoffmekanikk 1. forelesning MEK2500 Undervisning Foreleser: Frode Grytten Øvingslærer: NN Forelesninger: Tirsdag 10:15-12:00 B62 Torsdag 12:15-14:00 B91 Øvinger: Torsdag 14:15-16:00 B70 Øvinger
3 Tøyningsenergi. TKT4124 Mekanikk 3, høst Tøyningsenergi
 3 Tøningsenergi Innhold: Arbeid ved gradvis pålastning Tøningsenergitetthet og tøningsenergi Tøningsenergi som funksjon av lastvirkning,, T og V Skjærdeformasjoner Tøningsenergi som funksjon av aksialforskvning
3 Tøningsenergi Innhold: Arbeid ved gradvis pålastning Tøningsenergitetthet og tøningsenergi Tøningsenergi som funksjon av lastvirkning,, T og V Skjærdeformasjoner Tøningsenergi som funksjon av aksialforskvning
MEK2500 Faststoffmekanikk Forelesning 1: Generell innledning; statisk bestemte kraftsystemer
 MEK2500 Faststoffmekanikk Forelesning 1: Generell innledning; statisk bestemte kraftsystemer MEK2500-2014-1.1 MEK2500 Undervisning H2014 Forelesere: Brian Hayman, professor II Lars Brubak, amanuensis II
MEK2500 Faststoffmekanikk Forelesning 1: Generell innledning; statisk bestemte kraftsystemer MEK2500-2014-1.1 MEK2500 Undervisning H2014 Forelesere: Brian Hayman, professor II Lars Brubak, amanuensis II
10 Tøyninger og kinematisk kompatibilitet
 10 Tøninger og kinematisk kompatibilitet Innhold: Deformasjon kontra stivlegemebevegelse Normaltøning Skjærtøning Kinematikkligningene Plan tøningstilstand Kompatibilitetsbetingelsen Litteratur: Cook &
10 Tøninger og kinematisk kompatibilitet Innhold: Deformasjon kontra stivlegemebevegelse Normaltøning Skjærtøning Kinematikkligningene Plan tøningstilstand Kompatibilitetsbetingelsen Litteratur: Cook &
Statikk og likevekt. Elastisitetsteori
 Statikk og likevekt Elastisitetsteori 07.05.04 YS-MEK 0 07.05.04 man tir ons tor fre uke 9 0 3 5 9 6 forelesning: likevekt innlev. oblig 9 innlev. oblig 0 6 3 0 7 3 gruppe: gravitasjon+likevekt 7 4 8 4
Statikk og likevekt Elastisitetsteori 07.05.04 YS-MEK 0 07.05.04 man tir ons tor fre uke 9 0 3 5 9 6 forelesning: likevekt innlev. oblig 9 innlev. oblig 0 6 3 0 7 3 gruppe: gravitasjon+likevekt 7 4 8 4
Elastisitetens betydning for skader på skinner og hjul.ca.
 2. ARENA Narvik, 26. -27. november 2013 Elastisitetens betydning for skader på skinner og hjul.ca. Foreleser: Kjell Arne Skoglund Seniorforsker, dr.ing. jernbaneteknikk, Infrastruktur Kontakt: Kjell.Arne.Skoglund@sintef.no,
2. ARENA Narvik, 26. -27. november 2013 Elastisitetens betydning for skader på skinner og hjul.ca. Foreleser: Kjell Arne Skoglund Seniorforsker, dr.ing. jernbaneteknikk, Infrastruktur Kontakt: Kjell.Arne.Skoglund@sintef.no,
TKT4124 Mekanikk 3, høst Plastisk momentkapasitet og flyteledd
 2 Plastisk momentkapasitet og flyteledd Innhold: Elastisk kontra perfekt plastisk materiale Plastifisering av tverrsnitt utsatt for bøyning Plastisitetsmoment Plastisk motstandsmoment Flyteledd Kollaps
2 Plastisk momentkapasitet og flyteledd Innhold: Elastisk kontra perfekt plastisk materiale Plastifisering av tverrsnitt utsatt for bøyning Plastisitetsmoment Plastisk motstandsmoment Flyteledd Kollaps
Statikk og likevekt. Elastisitetsteori
 Statikk og likevekt Elastisitetsteori 08.05.017 YS-MEK 1110 08.05.017 1 uke 19 0 1 3 8 15 9 5 man forelesning: elastisitetsteori forelesning: spes. relativitet Eksamensverksted Pinse 9 16 3 30 6 tir ons
Statikk og likevekt Elastisitetsteori 08.05.017 YS-MEK 1110 08.05.017 1 uke 19 0 1 3 8 15 9 5 man forelesning: elastisitetsteori forelesning: spes. relativitet Eksamensverksted Pinse 9 16 3 30 6 tir ons
Statikk og likevekt. Elastisitetsteori
 Statikk og likevekt Elastisitetsteori.05.05 YS-MEK 0.05.05 man uke 0 3 forelesning: 8 5 elastisitetsteori gruppe: gravitasjon+likevekt innlev. oblig 0 forelesning: spes. relativitet gruppe: spes. relativitet
Statikk og likevekt Elastisitetsteori.05.05 YS-MEK 0.05.05 man uke 0 3 forelesning: 8 5 elastisitetsteori gruppe: gravitasjon+likevekt innlev. oblig 0 forelesning: spes. relativitet gruppe: spes. relativitet
Statikk og likevekt. Elastisitetsteori
 Statikk og likevekt Elastisitetsteori 9.05.06 YS-MEK 0 9.05.06 man tir uke 0 3 6 3 forelesning: 30 forelesning: 6 Pinse 7 4 3 7 7. mai spes. relativitet gruppe 5: gravitasjon+likevekt repetisjon gruppe
Statikk og likevekt Elastisitetsteori 9.05.06 YS-MEK 0 9.05.06 man tir uke 0 3 6 3 forelesning: 30 forelesning: 6 Pinse 7 4 3 7 7. mai spes. relativitet gruppe 5: gravitasjon+likevekt repetisjon gruppe
Last ned Ingeniørmekanikk - Fridtjov Irgens. Last ned. Forfatter: Fridtjov Irgens ISBN: Format: PDF Filstørrelse: 20.
 Last ned Ingeniørmekanikk - Fridtjov Irgens Last ned Forfatter: Fridtjov Irgens ISBN: 9788245016918 Format: PDF Filstørrelse: 20.66 Mb Ingeniørmekanikk er mekanikk tilpasset ingeniører og realister som
Last ned Ingeniørmekanikk - Fridtjov Irgens Last ned Forfatter: Fridtjov Irgens ISBN: 9788245016918 Format: PDF Filstørrelse: 20.66 Mb Ingeniørmekanikk er mekanikk tilpasset ingeniører og realister som
Symboler og forkortelser 1. INNLEDNING 1. 1.1 Hva er fasthetslære? 1. 1.2 Motivasjon 5. 1.3 Konvensjoner - koordinater og fortegn 7
 Innhold Forord Symboler og forkortelser v og vi xv 1. INNLEDNING 1 1.1 Hva er fasthetslære? 1 1.2 Motivasjon 5 1.3 Konvensjoner - koordinater og fortegn 7 1.4 Små forskyvninger og lineær teori 11 1.5 Omfang
Innhold Forord Symboler og forkortelser v og vi xv 1. INNLEDNING 1 1.1 Hva er fasthetslære? 1 1.2 Motivasjon 5 1.3 Konvensjoner - koordinater og fortegn 7 1.4 Små forskyvninger og lineær teori 11 1.5 Omfang
EKSAMEN I EMNE TKT 4100 FASTHETSLÆRE
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR KONSTRUKSJONSTEKNIKK Side 1 av 10.... Faglig kontakt under eksamen: Kjell Magne Mathisen, 73 59 46 74 Sensuren faller senest 10. januar (så
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR KONSTRUKSJONSTEKNIKK Side 1 av 10.... Faglig kontakt under eksamen: Kjell Magne Mathisen, 73 59 46 74 Sensuren faller senest 10. januar (så
MEK2500. Faststoffmekanikk 6. forelesning
 MEK2500 Faststoffmekanikk 6. forelesning Deformasjoner generelt Translasjon Rotasjon Stivlegemebevegelser Gir ikke tøyninger (eller spenninger) Ekspansjon/ Kontraksjon "formtro forandring" Skjærdeformasjon
MEK2500 Faststoffmekanikk 6. forelesning Deformasjoner generelt Translasjon Rotasjon Stivlegemebevegelser Gir ikke tøyninger (eller spenninger) Ekspansjon/ Kontraksjon "formtro forandring" Skjærdeformasjon
Last ned Ingeniørmekanikk - Fridtjov Irgens. Last ned. Last ned e-bok ny norsk Ingeniørmekanikk Gratis boken Pdf, ibook, Kindle, Txt, Doc, Mobi
 Last ned Ingeniørmekanikk - Fridtjov Irgens Last ned Forfatter: Fridtjov Irgens ISBN: 9788245016918 Format: PDF Filstørrelse:11.80 Mb Ingeniørmekanikk er mekanikk tilpasset ingeniører og realister som
Last ned Ingeniørmekanikk - Fridtjov Irgens Last ned Forfatter: Fridtjov Irgens ISBN: 9788245016918 Format: PDF Filstørrelse:11.80 Mb Ingeniørmekanikk er mekanikk tilpasset ingeniører og realister som
9 Spenninger og likevekt
 9 Spenninger og likevekt Innhold: Volumkrefter og flatekrefter Traksjonsvektoren Spenningsmatrisen Retningscosinuser Cauchs ligning Hovedspenninger og hovedspenningsretninger Spenningsinvarianter Hdrostatisk
9 Spenninger og likevekt Innhold: Volumkrefter og flatekrefter Traksjonsvektoren Spenningsmatrisen Retningscosinuser Cauchs ligning Hovedspenninger og hovedspenningsretninger Spenningsinvarianter Hdrostatisk
Eksamensoppgave i TKT4124 Mekanikk 3
 Institutt for konstruksjonsteknikk Eksamensoppgave i TKT4124 Mekanikk 3 Faglig kontakt under eksamen: Aase Reyes Tlf.: 73 59 45 24 Eksamensdato: 14. desember 2015 Eksamenstid (fra-til): 09.00 13.00 Hjelpemiddelkode/
Institutt for konstruksjonsteknikk Eksamensoppgave i TKT4124 Mekanikk 3 Faglig kontakt under eksamen: Aase Reyes Tlf.: 73 59 45 24 Eksamensdato: 14. desember 2015 Eksamenstid (fra-til): 09.00 13.00 Hjelpemiddelkode/
Kap. 16: Kontinuerlige systemer
 Kap. 16: Kontinuerlige systemer Har betraktet systemer med én frihetsgrad (avhengig av tiden) Partikler (med føringer) Stive legemer (med føringer) Ordinære differensiallikninger (ODE) Deformerbare legemer
Kap. 16: Kontinuerlige systemer Har betraktet systemer med én frihetsgrad (avhengig av tiden) Partikler (med føringer) Stive legemer (med føringer) Ordinære differensiallikninger (ODE) Deformerbare legemer
Hovedpunkter fra pensum Versjon 12/1-11
 Hovedpunkter fra pensum Versjon 1/1-11 Kapittel 1 1 N = 1 kg m / s F = m a G = m g Haugan: s. 6 (Kap. 1.3, pkt. ) 1 kn = Tyngden (dvs. tyngdekraften G) fra en mann som veier 100 kg. Kapittel En kraft er
Hovedpunkter fra pensum Versjon 1/1-11 Kapittel 1 1 N = 1 kg m / s F = m a G = m g Haugan: s. 6 (Kap. 1.3, pkt. ) 1 kn = Tyngden (dvs. tyngdekraften G) fra en mann som veier 100 kg. Kapittel En kraft er
E K S A M E N. MEKANIKK 1 Fagkode: ITE studiepoeng
 HiN TE 73 8. juni 0 Side av 8 HØGSKOLEN NRVK Teknologisk avdeling Studieretning: ndustriteknikk Studieretning: llmenn ygg Studieretning: Prosessteknologi E K S M E N MEKNKK Fagkode: TE 73 5 studiepoeng
HiN TE 73 8. juni 0 Side av 8 HØGSKOLEN NRVK Teknologisk avdeling Studieretning: ndustriteknikk Studieretning: llmenn ygg Studieretning: Prosessteknologi E K S M E N MEKNKK Fagkode: TE 73 5 studiepoeng
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MEK4550 Elementmetoden i faststoffmekanikk I. Eksamensdag: Mandag 17. desember 2007. Tid for eksamen: 14.0 17.0. Oppgavesettet
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MEK4550 Elementmetoden i faststoffmekanikk I. Eksamensdag: Mandag 17. desember 2007. Tid for eksamen: 14.0 17.0. Oppgavesettet
1 Virtuelt arbeid for stive legemer
 1 Vituelt abeid fo stive legeme Innhold: Abeidsbegepet i mekanikk Pinsippet om vituelt abeid fo stive legeme Litteatu: Igens, Statikk, kap. 10.1 10.2 Hibbele, Statics, kap. 11.1 11.3 Bell, Konstuksjonsmekanikk
1 Vituelt abeid fo stive legeme Innhold: Abeidsbegepet i mekanikk Pinsippet om vituelt abeid fo stive legeme Litteatu: Igens, Statikk, kap. 10.1 10.2 Hibbele, Statics, kap. 11.1 11.3 Bell, Konstuksjonsmekanikk
MEK4540/9540 Høsten 2008 Løsningsforslag
 MK454/954 Høsten 8 øsningsforslag Oppgave 1 a) Kan velge mellom følgende produksjonsmetoder: Spray-opplegg Håndopplegg Vakuum-bagging (i kombinasjon med håndopplegg eller andre metoder) Prepreg Vakuum-injisering
MK454/954 Høsten 8 øsningsforslag Oppgave 1 a) Kan velge mellom følgende produksjonsmetoder: Spray-opplegg Håndopplegg Vakuum-bagging (i kombinasjon med håndopplegg eller andre metoder) Prepreg Vakuum-injisering
Beregning av konstruksjon med G-PROG Ramme
 Side 1 av 11 Beregning av konstruksjon med G-PROG Ramme Introduksjon G-Prog Ramme er et beregningsprogram for plane (2-dimensjonale) ramme-strukturer. Beregningene har følgende fremgangsmåte: 1) Man angir
Side 1 av 11 Beregning av konstruksjon med G-PROG Ramme Introduksjon G-Prog Ramme er et beregningsprogram for plane (2-dimensjonale) ramme-strukturer. Beregningene har følgende fremgangsmåte: 1) Man angir
4 Energibalanse. TKT4124 Mekanikk 3, høst Energibalanse
 4 Energbalanse Innhold: Potensell energ Konservatve krefter Konserverng av energ Vrtuelt arbed for deformerbare legemer Vrtuelle forskvnngers prnspp Vrtuelle krefters prnspp Ltteratur: Irgens, Fasthetslære,
4 Energbalanse Innhold: Potensell energ Konservatve krefter Konserverng av energ Vrtuelt arbed for deformerbare legemer Vrtuelle forskvnngers prnspp Vrtuelle krefters prnspp Ltteratur: Irgens, Fasthetslære,
! EmnekOde: i SO 210 B. skriftlige kilder. Enkel ikkeprogrammerbar og ikkekommuniserbar kalkulator.
 l Alle ~ høgskolen oslo Emne: DIMENSJONER ~Gruppe(ry 3 BK NG II! EmnekOde: i SO 210 B - Dato: 19. februar -04 I I Fagiig veiled-e-r:-- Hoel/Harung/Nilsen Eksamenstid: 0900-1400 I Anttrlsldre~kI. forsiden):
l Alle ~ høgskolen oslo Emne: DIMENSJONER ~Gruppe(ry 3 BK NG II! EmnekOde: i SO 210 B - Dato: 19. februar -04 I I Fagiig veiled-e-r:-- Hoel/Harung/Nilsen Eksamenstid: 0900-1400 I Anttrlsldre~kI. forsiden):
EKSAMEN I EMNE TKT4124 MEKANIKK 3
 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR KONSTRUKSJONSTEKNIKK Side 1 av 7 Faglig kontakt under eksamen: NORSK Arild H. Clausen, 73 59 76 32 EKSAMEN I EMNE TKT4124 MEKANIKK 3 Torsdag
NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR KONSTRUKSJONSTEKNIKK Side 1 av 7 Faglig kontakt under eksamen: NORSK Arild H. Clausen, 73 59 76 32 EKSAMEN I EMNE TKT4124 MEKANIKK 3 Torsdag
Spenninger i bjelker
 N Teknologisk avd. R 1.0.1 Side 1 av 6 Rev Spenninger i bjelker rgens kap 18.1. ibbeler Sec. 1.1-1. En bjelke er et avlangt stkke materiale som utsettes for bøebelastning. Ren bøning bjelke b N 0 0 0 0
N Teknologisk avd. R 1.0.1 Side 1 av 6 Rev Spenninger i bjelker rgens kap 18.1. ibbeler Sec. 1.1-1. En bjelke er et avlangt stkke materiale som utsettes for bøebelastning. Ren bøning bjelke b N 0 0 0 0
EKSAMEN I EMNE TKT4116 MEKANIKK 1
 Faglig kontakt under eksamen: Jan Bjarte Aarseth 73 59 35 68 Aase Reyes 915 75 625 EKSAMEN I EMNE TKT4116 MEKANIKK 1 Fredag 3. juni 2011 Kl 09.00 13.00 Hjelpemidler (kode C): Irgens: Formelsamling mekanikk.
Faglig kontakt under eksamen: Jan Bjarte Aarseth 73 59 35 68 Aase Reyes 915 75 625 EKSAMEN I EMNE TKT4116 MEKANIKK 1 Fredag 3. juni 2011 Kl 09.00 13.00 Hjelpemidler (kode C): Irgens: Formelsamling mekanikk.
EKSAMEN I EMNE TKT 4100 FASTHETSLÆRE
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR KONSTRUKSJONSTEKNIKK Side 1 av 13.... Faglig kontakt under eksamen: Kjell Magne Mathisen, 73 59 46 74 Arild H. Clausen, 73 59 76 32 Sensuren
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR KONSTRUKSJONSTEKNIKK Side 1 av 13.... Faglig kontakt under eksamen: Kjell Magne Mathisen, 73 59 46 74 Arild H. Clausen, 73 59 76 32 Sensuren
Mandag 04.09.06. Institutt for fysikk, NTNU TFY4160/FY1002: Bølgefysikk Høsten 2006, uke 36
 Institutt for fsikk, NTNU TFY4160/FY1002: Bølgefsikk Høsten 2006, uke 36 Mandag 04.09.06 Del II: BØLGER Innledning Bølger er forplantning av svingninger. Når en bølge forplanter seg i et materielt medium,
Institutt for fsikk, NTNU TFY4160/FY1002: Bølgefsikk Høsten 2006, uke 36 Mandag 04.09.06 Del II: BØLGER Innledning Bølger er forplantning av svingninger. Når en bølge forplanter seg i et materielt medium,
KJ1042 Øving 3: Varme, arbeid og termodynamikkens første lov
 KJ1042 Øving 3: arme, arbeid og termodynamikkens første lov Ove Øyås Sist endret: 17. mai 2011 Repetisjonsspørsmål 1. Hvordan ser Ideell gasslov ut? Ideell gasslov kan skrives P nrt der P er trykket, volumet,
KJ1042 Øving 3: arme, arbeid og termodynamikkens første lov Ove Øyås Sist endret: 17. mai 2011 Repetisjonsspørsmål 1. Hvordan ser Ideell gasslov ut? Ideell gasslov kan skrives P nrt der P er trykket, volumet,
Beregning av konstruksjon med G-PROG Ramme
 Side 1 av 11 Beregning av konstruksjon med G-PROG Ramme Introduksjon G-Prog Ramme er et beregningsprogram for plane (2-dimensjonale) ramme-strukturer. Beregningene har følgende fremgangsmåte: 1) Man angir
Side 1 av 11 Beregning av konstruksjon med G-PROG Ramme Introduksjon G-Prog Ramme er et beregningsprogram for plane (2-dimensjonale) ramme-strukturer. Beregningene har følgende fremgangsmåte: 1) Man angir
Hydrodynamikk MAS 116 Vår 2019
 Hydrodynamikk (1600-1700 tallet): Vannbevegelse; læren om væskers (gassers) bevegelse Hydrodynamikk MAS 116 Vår 2019 Eksempel på virveldannelse bak et legeme i strømmende væske (Kármáns virvelgate). Thore
Hydrodynamikk (1600-1700 tallet): Vannbevegelse; læren om væskers (gassers) bevegelse Hydrodynamikk MAS 116 Vår 2019 Eksempel på virveldannelse bak et legeme i strømmende væske (Kármáns virvelgate). Thore
Oppgavehefte i MEK2500 - Faststoffmekanikk
 Oppgavehefte i MEK2500 - Faststoffmekanikk av Henrik Mathias Eiding og Harald Osnes ugust 20 2 Oppgave 1 En kraft har - og y-komponentene F og F y. vstanden fra et gitt punkt til et punkt på kraftens angrepslinje
Oppgavehefte i MEK2500 - Faststoffmekanikk av Henrik Mathias Eiding og Harald Osnes ugust 20 2 Oppgave 1 En kraft har - og y-komponentene F og F y. vstanden fra et gitt punkt til et punkt på kraftens angrepslinje
EKSAMEN I EMNE TKT4122 MEKANIKK 2
 INSTITUTT FOR KONSTRUKSJONSTEKNIKK Side 1 av 5 Faglig kontakt under eksamen: Bokmål Kjell Holthe, 951 12 477 / 73 59 35 53 Jan B. Aarseth, 73 59 35 68 EKSAMEN I EMNE TKT4122 MEKANIKK 2 Fredag 3. desember
INSTITUTT FOR KONSTRUKSJONSTEKNIKK Side 1 av 5 Faglig kontakt under eksamen: Bokmål Kjell Holthe, 951 12 477 / 73 59 35 53 Jan B. Aarseth, 73 59 35 68 EKSAMEN I EMNE TKT4122 MEKANIKK 2 Fredag 3. desember
13 Klassisk tynnplateteori
 13 Klassisk tnnplateteori Innhold: Forskjellige plateteorier Enveis- og toveisplater omenter og skjærkrefter i tnne plater Krumninger Platens likevektsligning og differensialligning Essensielle og naturlige
13 Klassisk tnnplateteori Innhold: Forskjellige plateteorier Enveis- og toveisplater omenter og skjærkrefter i tnne plater Krumninger Platens likevektsligning og differensialligning Essensielle og naturlige
FYS-MEK 1110 Løsningsforslag Eksamen Vår 2014
 FYS-MEK 1110 Løsningsforslag Eksamen Vår 2014 Oppgave 1 (4 poeng) Forklar hvorfor Charles Blondin tok med seg en lang og fleksibel stang når han balanserte på stram line over Niagara fossen i 1859. Han
FYS-MEK 1110 Løsningsforslag Eksamen Vår 2014 Oppgave 1 (4 poeng) Forklar hvorfor Charles Blondin tok med seg en lang og fleksibel stang når han balanserte på stram line over Niagara fossen i 1859. Han
EKSAMEN I EMNE TKT4116 MEKANIKK 1
 NORGES TEKNISK- NTURVITENSKPELIGE UNIVERSITET Institutt for konstruksjonsteknikk Faglig kontakt under eksamen: Førsteamanuensis rne alberg 73 59 46 24 EKSMEN I EMNE TKT4116 MEKNIKK 1 Mandag 2. juni 2008
NORGES TEKNISK- NTURVITENSKPELIGE UNIVERSITET Institutt for konstruksjonsteknikk Faglig kontakt under eksamen: Førsteamanuensis rne alberg 73 59 46 24 EKSMEN I EMNE TKT4116 MEKNIKK 1 Mandag 2. juni 2008
AST1010 En kosmisk reise. Forelesning 4: Fysikken i astrofysikk, del 1
 AST1010 En kosmisk reise Forelesning 4: Fysikken i astrofysikk, del 1 Innhold Mekanikk Termodynamikk Elektrisitet og magnetisme Elektromagnetiske bølger Mekanikk Newtons bevegelseslover Et legeme som ikke
AST1010 En kosmisk reise Forelesning 4: Fysikken i astrofysikk, del 1 Innhold Mekanikk Termodynamikk Elektrisitet og magnetisme Elektromagnetiske bølger Mekanikk Newtons bevegelseslover Et legeme som ikke
Varige konstruksjoner Konstruktive konsekvenser av alkalireaksjoner Fagdag 31 mai 2016
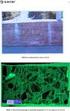 Varige konstruksjoner Konstruktive konsekvenser av alkalireaksjoner Fagdag 31 mai 2016 Hans Stemland SINTEF Hans Stemland, SINTEF Eva Rodum, SVV Håvard Johansen, SVV 1 Alkalireaksjoner Skademekanisme for
Varige konstruksjoner Konstruktive konsekvenser av alkalireaksjoner Fagdag 31 mai 2016 Hans Stemland SINTEF Hans Stemland, SINTEF Eva Rodum, SVV Håvard Johansen, SVV 1 Alkalireaksjoner Skademekanisme for
Forelesning nr.8 INF 1410
 Forelesning nr.8 INF 4 C og kretser 2.3. INF 4 Oversikt dagens temaer inearitet Opampkretser i C- og -kretser med kondensatorer Naturlig respons for - og C-kretser Eksponensiell respons 2.3. INF 4 2 Node
Forelesning nr.8 INF 4 C og kretser 2.3. INF 4 Oversikt dagens temaer inearitet Opampkretser i C- og -kretser med kondensatorer Naturlig respons for - og C-kretser Eksponensiell respons 2.3. INF 4 2 Node
Impuls, bevegelsesmengde, energi. Bevaringslover.
 Impuls, bevegelsesmengde, energi. Bevaringslover. Kathrin Flisnes 19. september 2007 Bevegelsesmengde ( massefart ) Når et legeme har masse og hastighet, viser det seg fornuftig å definere legemets bevegelsesmengde
Impuls, bevegelsesmengde, energi. Bevaringslover. Kathrin Flisnes 19. september 2007 Bevegelsesmengde ( massefart ) Når et legeme har masse og hastighet, viser det seg fornuftig å definere legemets bevegelsesmengde
C1 GENERELT 15. Tilslag. Relativ fuktighet. Miljø. Temperatur. Svinn. Spennkraft Forspenningstap Kryp. Belastning Spennvidde
 C1 GENERELT 15 Langtidsdeformasjonene vil fortsette i konstruksjonens levetid, men endringene blir relativt raskt av ubetydelig størrelse. Figur C 1.4 illu - strerer tidsavhengigheten av langtidsdeformasjonene,
C1 GENERELT 15 Langtidsdeformasjonene vil fortsette i konstruksjonens levetid, men endringene blir relativt raskt av ubetydelig størrelse. Figur C 1.4 illu - strerer tidsavhengigheten av langtidsdeformasjonene,
8. Elastisitet. Fysikk for ingeniører. 8. Elastisitet. Side 8-1
 8. Elastisitet. Side 8-1 8. Elastisitet. Når vi jobber med legemer i mekanikk, er det vanligvis underforstått at disse legemene ikke endrer form uansett hvilke påvirkninger de blir utsatt for. Vi snakker
8. Elastisitet. Side 8-1 8. Elastisitet. Når vi jobber med legemer i mekanikk, er det vanligvis underforstått at disse legemene ikke endrer form uansett hvilke påvirkninger de blir utsatt for. Vi snakker
Arbeid = kraft vei hvor kraft = masse akselerasjon. Hvis kraften F er konstant og virker i samme retning som forflytningen (θ = 0) får vi:
 Klassisk mekanikk 1.1. rbeid rbeid som utføres kan observeres i mange former: Mekanisk arbeid, kjemisk arbeid, elektrisk arbeid o.l. rbeid (w) kan likevel alltid beskrives som: rbeid = kraft vei hvor kraft
Klassisk mekanikk 1.1. rbeid rbeid som utføres kan observeres i mange former: Mekanisk arbeid, kjemisk arbeid, elektrisk arbeid o.l. rbeid (w) kan likevel alltid beskrives som: rbeid = kraft vei hvor kraft
KJ1042 Øving 5: Entalpi og entropi
 KJ1042 Øving 5: Entalpi og entropi Ove Øyås Sist endret: 17. mai 2011 Repetisjonsspørsmål 1. Hva er varmekapasitet og hva er forskjellen på C P og C? armekapasiteten til et stoff er en målbar fysisk størrelse
KJ1042 Øving 5: Entalpi og entropi Ove Øyås Sist endret: 17. mai 2011 Repetisjonsspørsmål 1. Hva er varmekapasitet og hva er forskjellen på C P og C? armekapasiteten til et stoff er en målbar fysisk størrelse
Institutt for konstruksjonsteknikk
 492 Institutt for konstruksjonsteknikk TKT4100 FASTHETSLÆRE Fasthetslære Strength of Materials Faglærer: Professor Kjell H. Holthe Uketimer: Høst: 4F+4Ø+4S = 7.50 SP F to 8-10 KJL5 Ø ti 8-12 KJL5 F fr
492 Institutt for konstruksjonsteknikk TKT4100 FASTHETSLÆRE Fasthetslære Strength of Materials Faglærer: Professor Kjell H. Holthe Uketimer: Høst: 4F+4Ø+4S = 7.50 SP F to 8-10 KJL5 Ø ti 8-12 KJL5 F fr
Forord. Jeg vil rette en takk til Torbjørn Hallgren for kyndig veiledning under arbeidet med denne oppgaven. Trondheim 15. juni 2005.
 Oppgave Deformasjon og manipulering av modeller av biologisk materiale i et haptisk system krever både god fysisk modellering og hurtige beregninger for å oppleves som realistiske. Behovet for rask oppdatering
Oppgave Deformasjon og manipulering av modeller av biologisk materiale i et haptisk system krever både god fysisk modellering og hurtige beregninger for å oppleves som realistiske. Behovet for rask oppdatering
EKSAMEN I MEK4550: Elementmetoden i faststoffmekanikk
 EKSAMEN I MEK4550: Elementmetoden i faststoffmekanikk Tillatte hjelpemidler: Ingen trykte eller håndskrevne hjelpemidler tillatt. Tid: Onsdag 14. januar 0900-1200. Oppgave 1 (ekt 1/3) a) Potensiell energi
EKSAMEN I MEK4550: Elementmetoden i faststoffmekanikk Tillatte hjelpemidler: Ingen trykte eller håndskrevne hjelpemidler tillatt. Tid: Onsdag 14. januar 0900-1200. Oppgave 1 (ekt 1/3) a) Potensiell energi
STREAMFLOW ROUTING. Estimere nedstrøms hydrogram, gitt oppstrøms. Skiller mellom. hydrologisk routing hydraulisk routing
 STREAMFLOW ROUTING Estimere nedstrøms hydrogram, gitt oppstrøms Skiller mellom hydrologisk routing hydraulisk routing Hydraulisk routing er basert på løsning av de grunnleggende differensial ligninger
STREAMFLOW ROUTING Estimere nedstrøms hydrogram, gitt oppstrøms Skiller mellom hydrologisk routing hydraulisk routing Hydraulisk routing er basert på løsning av de grunnleggende differensial ligninger
Løsningsforslag Eksamen i Fys-mek1110/Fys-mef1110 høsten 2007
 Løsningsforslag Eksamen i Fys-mek0/Fys-mef0 høsten 007 Side av 9 Oppgave a) En kule ruller med konstant hastighet bortover et horisontalt bord Gjør rede for og tegn inn kreftene som virker på kulen Det
Løsningsforslag Eksamen i Fys-mek0/Fys-mef0 høsten 007 Side av 9 Oppgave a) En kule ruller med konstant hastighet bortover et horisontalt bord Gjør rede for og tegn inn kreftene som virker på kulen Det
EKSAMEN I EMNE TKT4116 MEKANIKK 1
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET Institutt for konstruksjonsteknikk Faglig kontakt under eksamen: Førsteamanuensis Arne Aalberg 73 59 46 24 Førsteamanuensis Aase Gavina Reyes 73 59 45 24
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET Institutt for konstruksjonsteknikk Faglig kontakt under eksamen: Førsteamanuensis Arne Aalberg 73 59 46 24 Førsteamanuensis Aase Gavina Reyes 73 59 45 24
EKSAMEN I EMNE TKT4116 MEKANIKK 1
 INSTITUTT FOR KONSTRUKSJONSTEKNIKK Side 1 av 7 Faglig kontakt under eksamen: BOKMÅL Førsteamanuensis Arild H. Clausen, 482 66 568 Førsteamanuensis Erling Nardo Dahl, 917 01 854 Førsteamanuensis Aase Reyes,
INSTITUTT FOR KONSTRUKSJONSTEKNIKK Side 1 av 7 Faglig kontakt under eksamen: BOKMÅL Førsteamanuensis Arild H. Clausen, 482 66 568 Førsteamanuensis Erling Nardo Dahl, 917 01 854 Førsteamanuensis Aase Reyes,
Seismisk dimensjonering av pelefundamenter
 Seismisk dimensjonering av pelefundamenter Amir M. Kaynia Oversikt Jordskjelvpåvirkning i peler og EC8s krav Jord konsktruksjon samvirke (SSI) Beregning av stivheter Ikke lineære stivheter lateral kapasitet
Seismisk dimensjonering av pelefundamenter Amir M. Kaynia Oversikt Jordskjelvpåvirkning i peler og EC8s krav Jord konsktruksjon samvirke (SSI) Beregning av stivheter Ikke lineære stivheter lateral kapasitet
Tema i materiallære. HIN Allmenn Maskin RA 12.09.02 Side 1av7. Mekanisk spenning i materialer. Spenningstyper
 Side 1av7 Mekanisk spenning i materialer Tema i materiallære En kraft er et skyv eller drag som virker på et legeme og har sin årsak i et annet legeme. Eksempel: Et tungt legeme utgjør en last som skal
Side 1av7 Mekanisk spenning i materialer Tema i materiallære En kraft er et skyv eller drag som virker på et legeme og har sin årsak i et annet legeme. Eksempel: Et tungt legeme utgjør en last som skal
Faglig kontakt under eksamen: Navn: Anne Borg Tlf. 93413 BOKMÅL. EKSAMEN I EMNE TFY4115 Fysikk Elektronikk og Teknisk kybernetikk
 Side 1 av 10 NORGES TEKNISK NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Navn: Anne Borg Tlf. 93413 BOKMÅL EKSAMEN I EMNE TFY4115 Fysikk Elektronikk og Teknisk kybernetikk
Side 1 av 10 NORGES TEKNISK NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Navn: Anne Borg Tlf. 93413 BOKMÅL EKSAMEN I EMNE TFY4115 Fysikk Elektronikk og Teknisk kybernetikk
EKSAMEN I EMNE TKT4116 MEKANIKK 1 Onsdag 23. mai 2007 Kl
 Faglig kontakt under eksamen: Førsteamanuensis rne alberg 73 59 46 24 Førsteamanuensis Jan. arseth 73 59 35 68 EKSMEN I EMNE TKT4116 MEKNIKK 1 Onsdag 23. mai 2007 Kl 09.00 13.00 Hjelpemidler (kode ): Irgens:
Faglig kontakt under eksamen: Førsteamanuensis rne alberg 73 59 46 24 Førsteamanuensis Jan. arseth 73 59 35 68 EKSMEN I EMNE TKT4116 MEKNIKK 1 Onsdag 23. mai 2007 Kl 09.00 13.00 Hjelpemidler (kode ): Irgens:
Last ned Konstruksjonsmekanikk - Kolbein Bell. Last ned
 Last ned Konstruksjonsmekanikk - Kolbein Bell Last ned Forfatter: Kolbein Bell ISBN: 9788245018486 Format: PDF Filstørrelse:22.85 Mb Som DEL II er boken den naturlige fortsettelsen til DEL I (LIKEVEKTSLÆRE).
Last ned Konstruksjonsmekanikk - Kolbein Bell Last ned Forfatter: Kolbein Bell ISBN: 9788245018486 Format: PDF Filstørrelse:22.85 Mb Som DEL II er boken den naturlige fortsettelsen til DEL I (LIKEVEKTSLÆRE).
2. Termodynamikkens lover Termodynamikkens 1. lov Energiutveksling i form av varme og arbeid Trykk-volum arbeid
 Fysikk / Termodynamikk åren 2001 2. Termodynamikkens lover 2.1. Termodynamikkens 1. lov Termodynamikkens første lov kan formuleres å mange måter. En vanlig formulering er: Energien til et isolert system
Fysikk / Termodynamikk åren 2001 2. Termodynamikkens lover 2.1. Termodynamikkens 1. lov Termodynamikkens første lov kan formuleres å mange måter. En vanlig formulering er: Energien til et isolert system
EKSAMEN I EMNE TKT4122 MEKANIKK 2
 INSTITUTT FOR KONSTRUKSJONSTEKNIKK Side 1 av 7 Faglig kontakt under eksamen: NORSK Arild H. Clausen, 73 59 76 32 Kjell Holthe, 73 59 35 53 Jan B. Aarseth, 73 59 35 68 EKSAMEN I EMNE TKT4122 MEKANIKK 2
INSTITUTT FOR KONSTRUKSJONSTEKNIKK Side 1 av 7 Faglig kontakt under eksamen: NORSK Arild H. Clausen, 73 59 76 32 Kjell Holthe, 73 59 35 53 Jan B. Aarseth, 73 59 35 68 EKSAMEN I EMNE TKT4122 MEKANIKK 2
Newtons lover i én dimensjon
 Newtons lover i én dimensjon 6.01.017 YS-MEK 1110 6.01.017 1 Hva er kraft? Vi har en intuitivt idé om hva kraft er. Vi kan kvantifisere en kraft med elongasjon av en fjær. YS-MEK 1110 6.01.017 Bok på bordet
Newtons lover i én dimensjon 6.01.017 YS-MEK 1110 6.01.017 1 Hva er kraft? Vi har en intuitivt idé om hva kraft er. Vi kan kvantifisere en kraft med elongasjon av en fjær. YS-MEK 1110 6.01.017 Bok på bordet
Eksamensoppgave i TKT 4124 Mekanikk 3
 Institutt for konstruksjonsteknikk Eksamensoppgave i TKT 44 Mekanikk Faglig kontakt under eksamen: Aase Rees Tlf.: 7 5(9 45 4) / 95 75 65 Eksamensdato: 6. desember Eksamenstid (fra-til): 9 - Hjelpemiddelkode/Tillatte
Institutt for konstruksjonsteknikk Eksamensoppgave i TKT 44 Mekanikk Faglig kontakt under eksamen: Aase Rees Tlf.: 7 5(9 45 4) / 95 75 65 Eksamensdato: 6. desember Eksamenstid (fra-til): 9 - Hjelpemiddelkode/Tillatte
KJM Molekylmodellering. Introduksjon. Molekylmodellering. Molekylmodellering
 KJM3600 - Vebjørn Bakken Kjemisk institutt, UiO Introduksjon KJM3600 - p.1/29 Introduksjon p.2/29 Flere navn på moderne teoretisk kjemi: Theoretical chemistry (teoretisk kjemi) Quantum chemistry (kvantekjemi)
KJM3600 - Vebjørn Bakken Kjemisk institutt, UiO Introduksjon KJM3600 - p.1/29 Introduksjon p.2/29 Flere navn på moderne teoretisk kjemi: Theoretical chemistry (teoretisk kjemi) Quantum chemistry (kvantekjemi)
Statiske Beregninger for BCC 800
 Side 1 av 12 DEL 1 - GRUNNLEGGENDE FORUTSETNINGER OG ANTAGELSER 1.1 GENERELT Det er i disse beregningene gjort forutsetninger om dimensjoner og fastheter som ikke alltid vil være det man har i et aktuelt
Side 1 av 12 DEL 1 - GRUNNLEGGENDE FORUTSETNINGER OG ANTAGELSER 1.1 GENERELT Det er i disse beregningene gjort forutsetninger om dimensjoner og fastheter som ikke alltid vil være det man har i et aktuelt
Professor Elgarøy avslører: Hva DU bør repetere før AST1100-eksamen!
 Professor Elgarøy avslører: Hva DU bør repetere før AST1100-eksamen! Jeg burde starte med noen blomstrende ord om at målet med å ta et kurs er å lære mest mulig og å utvikle seg personlig, ikke å gjøre
Professor Elgarøy avslører: Hva DU bør repetere før AST1100-eksamen! Jeg burde starte med noen blomstrende ord om at målet med å ta et kurs er å lære mest mulig og å utvikle seg personlig, ikke å gjøre
Elastisitetsteori. Spesiell relativitetsteori
 lastisitetsteori Spesiell relativitetsteori 14.05.013 FYS-MK 1110 14.05.013 1 man tir uke 0 1 3 13 0 7 3 gruppe: elastisitet 14 1 8 4 forelesning: spes. relativitet Pinsemandag forelesning: repetisjon
lastisitetsteori Spesiell relativitetsteori 14.05.013 FYS-MK 1110 14.05.013 1 man tir uke 0 1 3 13 0 7 3 gruppe: elastisitet 14 1 8 4 forelesning: spes. relativitet Pinsemandag forelesning: repetisjon
Dette er en relativt stor oppgave, men en god oppsummering av hele kapittel 6. Tegningene finnes i større utgave på fagets hjemmeside.
 6.4.3 Eksempel 3 Spenningsanalyse av dobbeltbunn i tankskip (eksamen 07) Dette er en relativt stor oppgave, men en god oppsummering av hele kapittel 6. Tegningene finnes i større utgave på fagets hjemmeside.
6.4.3 Eksempel 3 Spenningsanalyse av dobbeltbunn i tankskip (eksamen 07) Dette er en relativt stor oppgave, men en god oppsummering av hele kapittel 6. Tegningene finnes i større utgave på fagets hjemmeside.
HiN Eksamen IST 1484 18.12.03 Side 4
 HiN Eksamen IST 1484 18.1.3 Side 4 Materialer og mekanikk. Teller 5% av eksamen Poengangivelsen viser kun vektingen mellom de fire oppgavene. Innenfor hver oppgave er det læringsmålene som avgjør vektingen.
HiN Eksamen IST 1484 18.1.3 Side 4 Materialer og mekanikk. Teller 5% av eksamen Poengangivelsen viser kun vektingen mellom de fire oppgavene. Innenfor hver oppgave er det læringsmålene som avgjør vektingen.
Elastisitetsteori. Spesiell relativitetsteori
 Elastisitetsteori Spesiell relativitetsteori 1.05.014 FYS-MEK 1110 1.05.014 1 man tir ons tor fre uke 0 1 3 1 19 6 forelesning: spes. relativitet innlev. olig 10 13 0 7 3 gruppe: spes. relativitet 14 1
Elastisitetsteori Spesiell relativitetsteori 1.05.014 FYS-MEK 1110 1.05.014 1 man tir ons tor fre uke 0 1 3 1 19 6 forelesning: spes. relativitet innlev. olig 10 13 0 7 3 gruppe: spes. relativitet 14 1
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK 1110 Eksamensdag: Tirsdag, 3. juni 2014 Tid for eksamen: kl. 9:00 13:00 Oppgavesettet omfatter 6 oppgaver på 4 sider
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK 1110 Eksamensdag: Tirsdag, 3. juni 2014 Tid for eksamen: kl. 9:00 13:00 Oppgavesettet omfatter 6 oppgaver på 4 sider
Eksamensoppgave i TKT4124 Mekanikk 3
 Eksamensoppgave i TKT4124 Mekanikk 3 Faglig kontakt under eksamen: Aase Reyes Tlf.: 73 59 45 24 Eksamensdato: 5. desember 2014 Eksamenstid (fra-til): 9.00 13.00 Hjelpemiddelkode/Tillatte hjelpemidler:
Eksamensoppgave i TKT4124 Mekanikk 3 Faglig kontakt under eksamen: Aase Reyes Tlf.: 73 59 45 24 Eksamensdato: 5. desember 2014 Eksamenstid (fra-til): 9.00 13.00 Hjelpemiddelkode/Tillatte hjelpemidler:
EKSAMENSOPPGAVE. Oppgavesettet er på 5 sider inklusiv forside Kontaktperson under eksamen: Stian Normann Anfinsen Telefon:
 EKSAMENSOPPGAVE Eksamen i: Fys-1001 Mekanikk Dato: Torsdag 4. desember 2014 Tid: Kl 09:00 13:00 Sted: Åsgårdvegen 9 Tillatte hjelpemidler: Fire A4-sider (to dobbeltsidige ark) med egne notater. Kalkulator
EKSAMENSOPPGAVE Eksamen i: Fys-1001 Mekanikk Dato: Torsdag 4. desember 2014 Tid: Kl 09:00 13:00 Sted: Åsgårdvegen 9 Tillatte hjelpemidler: Fire A4-sider (to dobbeltsidige ark) med egne notater. Kalkulator
(samme dreiemoment fra sider som støter opp til en kant). Formen må være en generalisering av definisjonsligningen
 & 99 Løsning G.1 En rigorøs utledning som må baseres på begreper fra tensoranalyse skal vi ikke kaste oss ut i. En standard utledning på intuitivt plan kan gå som følger: Definer spenningskomponent i -retning
& 99 Løsning G.1 En rigorøs utledning som må baseres på begreper fra tensoranalyse skal vi ikke kaste oss ut i. En standard utledning på intuitivt plan kan gå som følger: Definer spenningskomponent i -retning
KORT INTRODUKSJON TIL TENSORER
 KORT INTRODUKSJON TIL TENSORER Tensorer har vi allerede møtt i form av skalarer (tall) og vektorer. En skalar kan betraktes som en tensor av rang null (en komponent), mens en vektor er en tensor av rang
KORT INTRODUKSJON TIL TENSORER Tensorer har vi allerede møtt i form av skalarer (tall) og vektorer. En skalar kan betraktes som en tensor av rang null (en komponent), mens en vektor er en tensor av rang
Strøm av olje og vann i berggrunnen matematisk model, simulering og visualisering
 Strøm av olje og vann i berggrunnen matematisk model, simulering og visualisering Hans Fredrik Nordhaug Matematisk institutt Faglig-pedagogisk dag, 01.02.2000. Oversikt 1 Oversikt Introduksjon. Hva er
Strøm av olje og vann i berggrunnen matematisk model, simulering og visualisering Hans Fredrik Nordhaug Matematisk institutt Faglig-pedagogisk dag, 01.02.2000. Oversikt 1 Oversikt Introduksjon. Hva er
Likevekt STATISK LIKEVEKT. Når et legeme er i ro, sier vi at det er i statisk likevekt.
 Likevekt STATISK LIKEVEKT Når et legeme er i ro, sier vi at det er i statisk likevekt. Et legeme beveger seg i den retningen resultanten virker. Vi kan sette opp den første betingelsen for at et legeme
Likevekt STATISK LIKEVEKT Når et legeme er i ro, sier vi at det er i statisk likevekt. Et legeme beveger seg i den retningen resultanten virker. Vi kan sette opp den første betingelsen for at et legeme
Newtons lover i én dimensjon
 Newtons lover i én dimensjon 3.01.018 snuble-gruppe i dag, kl.16:15-18:00, Origo FYS-MEK 1110 3.01.018 1 Hva er kraft? Vi har en intuitivt idé om hva kraft er. Vi kan kvantifisere en kraft med elongasjon
Newtons lover i én dimensjon 3.01.018 snuble-gruppe i dag, kl.16:15-18:00, Origo FYS-MEK 1110 3.01.018 1 Hva er kraft? Vi har en intuitivt idé om hva kraft er. Vi kan kvantifisere en kraft med elongasjon
Kapittel 1:Introduksjon - Statikk
 1 - Introduksjon - Statikk Kapittel 1:Introduksjon - Statikk Studér: - Emnebeskrivelse - Emneinformasjon - Undervisningsplan 1.1 Oversikt over temaene Skjærkraft-, Moment- og Normalkraft-diagrammer Grunnleggende
1 - Introduksjon - Statikk Kapittel 1:Introduksjon - Statikk Studér: - Emnebeskrivelse - Emneinformasjon - Undervisningsplan 1.1 Oversikt over temaene Skjærkraft-, Moment- og Normalkraft-diagrammer Grunnleggende
Lecture 1 Phenomenology of plastic deformations LECTURES ON PLASTICITY THEORY. NTNU, Fall 2006
 LECTURES ON PLASTICITY THEORY NTNU, Fall 2006 Aase Reyes Based on lecture notes of Prof. Odd Sture Hopperstad Structural Impact Laboratory (SIMLab) Department of Structural Engineering Norwegian University
LECTURES ON PLASTICITY THEORY NTNU, Fall 2006 Aase Reyes Based on lecture notes of Prof. Odd Sture Hopperstad Structural Impact Laboratory (SIMLab) Department of Structural Engineering Norwegian University
Fag SIB7010 Konstruksjonsmekanikk 2 KURSPLAN. Vår Målsetting og omfang. Opplegg og gjennomføring. Focus Konstruksjon - studentversjon
 Norges teknisk-naturvitenskapelige universitet Institutt for konstruksjonsteknikk Fag SIB7010 Konstruksjonsmekanikk 2 KURSPLAN Vår 2000 Hvem og hvor Målsetting og omfang Opplegg og gjennomføring Forelesninger
Norges teknisk-naturvitenskapelige universitet Institutt for konstruksjonsteknikk Fag SIB7010 Konstruksjonsmekanikk 2 KURSPLAN Vår 2000 Hvem og hvor Målsetting og omfang Opplegg og gjennomføring Forelesninger
Newtons lover i én dimensjon (2)
 Newtons lover i én dimensjon () 0.0.015 oblig #1: innlevering: mandag, 9.feb. kl.1 papir: boks på ekspedisjonskontoret elektronisk: Devilry (ikke ennå åpen) YS-MEK 1110 0.0.015 1 Identifikasjon av kreftene:
Newtons lover i én dimensjon () 0.0.015 oblig #1: innlevering: mandag, 9.feb. kl.1 papir: boks på ekspedisjonskontoret elektronisk: Devilry (ikke ennå åpen) YS-MEK 1110 0.0.015 1 Identifikasjon av kreftene:
KONSTRUKSJONSSTÅL MATERIAL- EGENSKAPER
 KONSTRUKSJONSSTÅL MATERIAL- EGENSKAPER FASTHETER For dimensjoneringen benyttes nominelle fasthetsverdier for f y og f u - f y =R eh og f u =R m iht produkstandardene - verdier gitt i følgende tabeller
KONSTRUKSJONSSTÅL MATERIAL- EGENSKAPER FASTHETER For dimensjoneringen benyttes nominelle fasthetsverdier for f y og f u - f y =R eh og f u =R m iht produkstandardene - verdier gitt i følgende tabeller
Statiske Beregninger for BCC 250
 Side 1 av 7 DEL 1 - GRUNNLEGGENDE FORUTSETNINGER OG ANTAGELSER 1.1 GENERELT Det er i disse beregningene gjort forutsetninger om dimensjoner og fastheter som ikke alltid vil være det man har i et aktuelt
Side 1 av 7 DEL 1 - GRUNNLEGGENDE FORUTSETNINGER OG ANTAGELSER 1.1 GENERELT Det er i disse beregningene gjort forutsetninger om dimensjoner og fastheter som ikke alltid vil være det man har i et aktuelt
Repetisjonsoppgaver kapittel 0 og 1 løsningsforslag
 Repetisjonsoppgaver kapittel 0 og løsningsforslag Kapittel 0 Oppgave a) Gjennomsnittet er summen av måleverdiene delt på antallet målinger. Summen av målingene er,79 s. t sum av måleverdiene antallet målinger,79
Repetisjonsoppgaver kapittel 0 og løsningsforslag Kapittel 0 Oppgave a) Gjennomsnittet er summen av måleverdiene delt på antallet målinger. Summen av målingene er,79 s. t sum av måleverdiene antallet målinger,79
Newtons lover i én dimensjon (2)
 Newtons lover i én dimensjon () 1..16 YS-MEK 111 1..16 1 Identifikasjon av kreftene: 1. Del problemet inn i system og omgivelser.. Tegn figur av objektet og alt som berører det. 3. Tegn en lukket kurve
Newtons lover i én dimensjon () 1..16 YS-MEK 111 1..16 1 Identifikasjon av kreftene: 1. Del problemet inn i system og omgivelser.. Tegn figur av objektet og alt som berører det. 3. Tegn en lukket kurve
Ekstraordinær E K S A M E N. MATERIALLÆRE Fagkode: ILI 1269
 side 1 av 7 HØGSKOLEN I NARVIK Teknologisk Avdeling Studieretning: Allmenn Maskin Ekstraordinær E K S A M E N I MATERIALLÆRE Fagkode: ILI 1269 Tid: 21.08.01 kl 0900-1200 Tillatte hjelpemidler: Kalkulator
side 1 av 7 HØGSKOLEN I NARVIK Teknologisk Avdeling Studieretning: Allmenn Maskin Ekstraordinær E K S A M E N I MATERIALLÆRE Fagkode: ILI 1269 Tid: 21.08.01 kl 0900-1200 Tillatte hjelpemidler: Kalkulator
Seismisk dimensjonering av prefab. konstruksjoner
 Seismisk dimensjonering av prefab. konstruksjoner Geir Udahl Konstruksjonssjef Contiga Agenda DCL/DCM Modellering Resultater DCL vs DCM Vurdering mhp. prefab DCL Duktiltetsfaktoren q settes til 1,5 slik
Seismisk dimensjonering av prefab. konstruksjoner Geir Udahl Konstruksjonssjef Contiga Agenda DCL/DCM Modellering Resultater DCL vs DCM Vurdering mhp. prefab DCL Duktiltetsfaktoren q settes til 1,5 slik
Kapittel 2. 2 Case II: Plastkompositt
 Kapittel Case II: Plastkompositt -1 Kapittel Case II: Plastkompositt.1 Bakgrunn Gaute er revisor og deltidsbonde i et av norges utkantstrøk. Det har vært flere ulykker i bygda med gjødsel på avveie. Gautes
Kapittel Case II: Plastkompositt -1 Kapittel Case II: Plastkompositt.1 Bakgrunn Gaute er revisor og deltidsbonde i et av norges utkantstrøk. Det har vært flere ulykker i bygda med gjødsel på avveie. Gautes
Velkomen til TFY4108 Fysikk! Fagansvarlege. Fagleg innhald. Webside
 Klassisk mekanikk Velkomen til TFY4108 Fysikk! Kvantefysikk Fagansvarlege Forelesingar og øvingar: Førsteamanuensis John Ove Fjærestad john.fjaerestad@ntnu.no Laboratoriekurs: Førsteamanuensis Erik Wahlstrøm
Klassisk mekanikk Velkomen til TFY4108 Fysikk! Kvantefysikk Fagansvarlege Forelesingar og øvingar: Førsteamanuensis John Ove Fjærestad john.fjaerestad@ntnu.no Laboratoriekurs: Førsteamanuensis Erik Wahlstrøm
MEK likevektslære (statikk)
 MEK2500 - likevektslære (statikk) Tormod Landet Høst 2015 Mange konstruksjoner kan analyseres med tre enkle prinsipper 1. Saint-Venants prinsipp 2. Balanse i krefter 3. Balanse i momenter Denne forelesningen
MEK2500 - likevektslære (statikk) Tormod Landet Høst 2015 Mange konstruksjoner kan analyseres med tre enkle prinsipper 1. Saint-Venants prinsipp 2. Balanse i krefter 3. Balanse i momenter Denne forelesningen
Strøm av olje og vann i berggrunnen matematisk model, simulering og visualisering
 Strøm av olje og vann i berggrunnen matematisk model, simulering og visualisering Hans Fredrik Nordhaug Matematisk institutt Faglig-pedagogisk dag, 01.02.2000. Oversikt 1 Oversikt Introduksjon. Hva er
Strøm av olje og vann i berggrunnen matematisk model, simulering og visualisering Hans Fredrik Nordhaug Matematisk institutt Faglig-pedagogisk dag, 01.02.2000. Oversikt 1 Oversikt Introduksjon. Hva er
Klassifisering, modellering og beregning av knutepunkter
 Side 1 Konstruksjonsanalyse, klassifisering og beregning av knutepunkter 1 Konstruksjonsanalyse, klassifisering og beregning av knutepunkter Del 1 - Konstruksjonsanalyse og klassifisering av knutepunkter
Side 1 Konstruksjonsanalyse, klassifisering og beregning av knutepunkter 1 Konstruksjonsanalyse, klassifisering og beregning av knutepunkter Del 1 - Konstruksjonsanalyse og klassifisering av knutepunkter
Resultanten til krefter
 KRAFTBEGREPET Resultanten til krefter En kraft er en vektor. Kraften har måltall (størrelse), enhet(n) og retning (horisontalt mot høyre) Kraften virker langs en rett linje, kraftens angrepslinje Punktet
KRAFTBEGREPET Resultanten til krefter En kraft er en vektor. Kraften har måltall (størrelse), enhet(n) og retning (horisontalt mot høyre) Kraften virker langs en rett linje, kraftens angrepslinje Punktet
Newtons lover i én dimensjon
 Newtons lover i én dimensjon.01.014 Interessert å være studentrepresentant for YS-MEK kurset? ta kontakt med meg. YS-MEK 1110.01.014 1 Bok på bordet Gravitasjon virker på boken om den ligger på bordet
Newtons lover i én dimensjon.01.014 Interessert å være studentrepresentant for YS-MEK kurset? ta kontakt med meg. YS-MEK 1110.01.014 1 Bok på bordet Gravitasjon virker på boken om den ligger på bordet
Elastisitet, plastisitet og styrking av metaller
 Elastisitet, plastisitet og styrking av metaller Mål: Forstå hvilke mekanismer som gjør materialene sterke og harde eller duktile og formbare Frey Publishing 1 Introduksjon Hvorfor danner de to svake metallene
Elastisitet, plastisitet og styrking av metaller Mål: Forstå hvilke mekanismer som gjør materialene sterke og harde eller duktile og formbare Frey Publishing 1 Introduksjon Hvorfor danner de to svake metallene
Velkommen til MEK1100
 Velkommen til MEK1100 Seksjon for Mekanikk, Matematisk institutt, UiO MEK1100 FELTTEORI OG VEKTORANALYSE Våren 2018 Foreleser: Karsten Trulsen Gruppelærere: Susanne Støle Hentschel, Lars Magnus Valnes,
Velkommen til MEK1100 Seksjon for Mekanikk, Matematisk institutt, UiO MEK1100 FELTTEORI OG VEKTORANALYSE Våren 2018 Foreleser: Karsten Trulsen Gruppelærere: Susanne Støle Hentschel, Lars Magnus Valnes,
