En studie av sammenhengen mellom makroøkonomi og forsikring
|
|
|
- Dagfinn Børge Sletten
- 8 år siden
- Visninger:
Transkript
1 En studie av sammenhengen mellom makroøkonomi og forsikring Notatnr Forfattere SAMBA/41/07 Mathilde Wilhelmsen Xeni K. Dimakos Dato 6. november 2007
2 Norsk Regnesentral Norsk Regnesentral (NR) er en privat, uavhengig stiftelse som utfører oppdragsforskning for bedrifter og det offentlige i det norske og internasjonale markedet. NR ble etablert i 1952 og har kontorer i Informatikkbygningen ved Universitetet i Oslo. NR er et av Europas største miljøer innen anvendt statistikk. Det jobbes med svært mange forskjellige problemstillinger slik som estimering av torskebestanden, finansiell risiko, beskrivelse av geologien i petroleumsreservoarer og overvåking av klimaendringer. NR er også ledende i Norge innen utvalgte deler av informasjons- og kommunikasjonsteknologi. Problemstillinger kan være å overvåke inntrengning i datasystemer, e-læring i skole og næringsliv, bruk av datateknologi i markedsanalyser samt anvendelser av multimedia på forskjellige plattformer. NRs visjon er forskningsresultater som brukes og synes.
3 Tittel Forfattere En studie av sammenhengen mellom makroøkonomi og forsikring Mathilde Wilhelmsen Xeni K. Dimakos Dato 6. november 2007 Publikasjonsnummer SAMBA/41/07 Sammendrag I dette notatet har vi sett på tidsserier for CR for bolig, landbruk, yrkeskade, uførhet og motorvogn. Vi har forsøkt å se utviklingen i disse i sammenheng med utviklingen i de makroøkonomiske størrelsene KPI, BNP, lønn og arbeidsledighet. Gjensidiges tidsserier er korte og har grov oppløsning, noe som begrenser hvilke analyser som kan gjøres. Med utgangspunkt i dette datagrunnlaget finner vi at det ikke er mulig å trekke noen konklusjoner om sammenhengen mellom utviklingen hos Gjensidige og makroøkonomien. Emneord Målgruppe Tilgjengelighet Prosjekt Combined ratio, Korrelasjon, Konjunkturer, Makroøkonomi, Sykler Gjensidige Forsikring Åpen SFI P03 StatInsure Prosjektnummer Satsningsområde SFI Antall sider 45 Copyright Norsk Regnesentral 3
4
5 Innhold 1 Introduksjon Data Data fra Gjensidige Makroøkonomiske variable Glatting og interpolering Metode Autoregressive modeller Stasjonaritet Krysskorrelasjon Resultater Gjensidiges tidsrekker Makroøkonomiske størrelser Krysskorrelasjoner Fjerning av trend Laggede krysskorrelasjoner Oppsummering Appendiks A Mer metode A.1 Test av stasjonaritet A.2 Fjerning av trend Konjunkturer og sykler i forsikring 5
6 A.3 Fjerning av sesong A.4 Kointegrasjon Referanser Konjunkturer og sykler i forsikring
7 1 Introduksjon I dette notatet ser vi på tidsserier for combined ratio (CR, totalkostnadsprosent) for bolig, landbruk, yrkeskade, uførhet og motorvogn. Vi har forsøkt å se utviklingen i disse tidsseriene i sammenheng med utviklingen i de makroøkonomiske størrelsene KPI, BNP, lønn og arbeidsledighet. Vi ser på hvordan tidsseriene har utviklet seg over tid med hensyn på trend og svingninger (sykler). Videre studerer vi i hvilken grad CR samvarierer med makroøkonomien. Spesielt er vi interessert i om noen av de makroøkonomiske seriene er drivende for utviklingen i Gjensidige. Gjensidiges tidsserier er korte og har grov oppløsning, noe som begrenser hvilke analyser som kan gjøres. Notatet er organisert som følger. Kapittel 2 presenterer datagrunnlaget. Kapittel 3 beskriver metodene vi benytter, mens kapittel 4 presenterer resultatene. Tilslutt, i kapittel 5, beskriver vi hvilke analyser som kunne vært gjort dersom datagrunnlaget hadde vært større og bedre. Appendikset inneholder metodikk som i såfall er aktuell. 2 Data 2.1 Data fra Gjensidige Tabell 1 viser en oversikt over skadedata vi har mottatt fra Gjensidige. Alle tidsseriene er på årlig skala. Skadeprosenten angir hvor stor prosent erstatningskostnaden utgjør av premieinntekten. Kostnadsprosenten angir hvor stor prosent forsikringsrelaterte driftskostnader utgjør av forfalt premie. Combined ratio (CR) er summen av skadeprosent og kostnadsprosent, dvs. summen av erstatninger og driftskostnader i forhold til premien. CR blir også kalt totalkostnadsprosent. Dersom CR er større enn 100%, går Gjensidige i underskudd på denne skadetypen. Plottet øverst til venstre i figur 1, 2, 3, 4 og 5 viser CR for de fem skadetypene fra Gjensidige. Figurene viser at tidsseriene er for korte til at man kan identifisere flere sykler. For bolig, landbruk, yrkesskade og motorvogn inneholder seriene en periode med oppgang i CR og deretter en periode med nedgang. Mens tidsserien for uføre viser en reduksjon i CR over tid. Konjunkturer og sykler i forsikring 7
8 Bolig log(diff)) Tid Tid ACF(log(diff)) PACF(log(diff)) ACF Partial ACF Lag Lag Figur 1. Bolig CR. Øverst til venstre er den originale serien, øverst til høyre vises logaritmen til etterfølgende differanser, nederst til venstre er ACF til differansene plottet, og nederst til høyre vises PACF til differansene. 8 Konjunkturer og sykler i forsikring
9 Landbruk log(diff)) Tid Tid ACF(log(diff)) PACF(log(diff)) ACF Partial ACF Lag Lag Figur 2. Landbruk CR. Øverst til venstre er den originale serien, øverst til høyre vises logaritmen til etterfølgende differanser, nederst til venstre er ACF til differansene plottet, og nederst til høyre vises PACF til differansene. Konjunkturer og sykler i forsikring 9
10 Yrkesskade log(diff)) Tid Tid ACF(log(diff)) PACF(log(diff)) ACF Partial ACF Lag Lag Figur 3. Yrkesskade CR. Øverst til venstre er den originale serien, øverst til høyre vises logaritmen til etterfølgende differanser, nederst til venstre er ACF til differansene plottet, og nederst til høyre vises PACF til differansene. 10 Konjunkturer og sykler i forsikring
11 Uføre log(diff)) Q1 Q1 Q1 Q1 Q1 Q1 Q1 Q1 Q Tid Q1 Q1 Q1 Q1 Q1 Q1 Q1 Q Tid ACF(log(diff)) PACF(log(diff)) ACF Partial ACF Lag Lag Figur 4. Uførhet CR. Øverst til venstre er den originale serien, øverst til høyre vises logaritmen til etterfølgende differanser, nederst til venstre er ACF til differansene plottet, og nederst til høyre vises PACF til differansene. Konjunkturer og sykler i forsikring 11
12 Motor log(diff)) Tid Tid ACF(log(diff)) PACF(log(diff)) ACF Partial ACF Lag Lag Figur 5. Motorvogn CR. Øverst til venstre er den originale serien, øverst til høyre vises logaritmen til etterfølgende differanser, nederst til venstre er ACF til differansene plottet, og nederst til høyre vises PACF til differansene. 12 Konjunkturer og sykler i forsikring
13 Skadetype Tilgjengelige størrelser Oppløsning Tidsperiode Bolig Landbruk Yrkesskade Uførhet Motorvogn Skadeprosent Kostnadsprosent CR Skadeprosent Kostnadsprosent CR Skadeprosent Kostnadsprosent CR Skadeprosent Kostnadsprosent CR Antall skader Skadeprosent Kostnadsprosent CR Tabell 1. Tabell over skadedata fra Gjensidige Årlig Årlig Årlig Årlig Årlig Makroøkonomisk variabel Oppløsning Tidsperiode Kilde KPI Månedlig Januar juli 2007 SSB BNP Kvartalsvis 1. kvartal kvartal 2007 SSB Lønn Årlig SSB Arbeidsledighetsprosent Årlig NAV Tabell 2. Tabell over makroøkonomiske variable 2.2 Makroøkonomiske variable Vi har valgt ut fire makroøkonomiske variable; KPI (Konsumprisindeks), BNP (Brutto nasjonalprodukt), lønn og arbeidsledighetsprosent. Vi bruker en sesongjustert KPI, samt faste verdier for BNP og løpende verdier for lønn. Strengt tatt er det mer korrekt å se på faste verdier, men vi har kun fått tak i løpende verdier for lønn. For våre analyser overskygges dette av at usikkerheten som følger av at Gjensidiges data har så grov tidsoppløsning. Tabell 2 viser en oversikt over variablene. Plottet øverst til venstre i figur 6, 7, 8 og 9 viser tidsseriene for de fire makroøkonomiske variablene. Vi ser at KPI, BNP og lønn ikke overraskende har svært lik utvikling, med en jevn stigning i hele perioden. Arbeidsledigheten er mer varierende, med topper rundt 1985 og 1995, men også perioder med nedgang. Konjunkturer og sykler i forsikring 13
14 KPI sesong log(diff)) Tid Tid ACF(log(diff)) PACF(log(diff)) ACF Partial ACF Lag Lag Figur 6. KPI. Øverst til venstre er den originale serien, øverst til høyre vises logaritmen til etterfølgende differanser, nederst til venstre er ACF til differansene plottet, og nederst til høyre vises PACF til differansene. 14 Konjunkturer og sykler i forsikring
15 BNP fast log(diff)) Tid Tid ACF(log(diff)) PACF(log(diff)) ACF Partial ACF Lag Lag Figur 7. BNP. Øverst til venstre er den originale serien, øverst til høyre vises logaritmen til etterfølgende differanser, nederst til venstre er ACF til differansene plottet, og nederst til høyre vises PACF til differansene. Konjunkturer og sykler i forsikring 15
16 Lønn løpende log(diff)) Tid Tid ACF(log(diff)) PACF(log(diff)) ACF Partial ACF Lag Lag Figur 8. Lønn. Øverst til venstre er den originale serien, øverst til høyre vises logaritmen til etterfølgende differanser, nederst til venstre er ACF til differansene plottet, og nederst til høyre vises PACF til differansene. 16 Konjunkturer og sykler i forsikring
17 Arbeidsledighetsprosent log(diff)) Tid Tid ACF(log(diff)) PACF(log(diff)) ACF Partial ACF Lag Lag Figur 9. Arbeidsledighetsprosent. Øverst til venstre er den originale serien, øverst til høyre vises logaritmen til etterfølgende differanser, nederst til venstre er ACF til differansene plottet, og nederst til høyre vises PACF til differansene. Konjunkturer og sykler i forsikring 17
18 2.3 Glatting og interpolering Når man skal sammenligne to tidsserier, må de ha samme tidsoppløsning. Som vist i de forrige to avsnittene, er ikke dette tilfellet for tidsseriene vi skal studere. Man må da skalere en av tidsseriene slik at den får samme oppløsning som den andre. Vi har valgt å interpolere tidsserien med grovest oppløsning slik at den blir sammenlignbar med den med finest oppløsning. Vi beholder da den fine oppløsningen til den ene tidsserien, og unngår å korte ned lengden på tidsseriene. For å få en best mulig analyse, er det viktig at tidsseriene er lange. Det er mange måter å interpolere en tidsserie på. Tidsseriene med grovest oppløsning (årlig og kvartalsvis) i de forrige avsnittene består av gjennomsnittsverdier for hver periode. La oss si vi skal sammenligne tidsserie 1 på årlig oppløsning med tidsserie 2 på månedlig oppløsning. Ved å la de årlige gjennomsnittsverdiene være de samme for alle måneder, får vi på en enkel måte gjort om tidsserie 1 til månedlig skala. Denne tidsserien består nå av intervaller med konstante verdier av lengde 12. Det er også mulig å sette de årlige (eller kvartalsvise) gjennomsnittsverdiene til en spesifikk dato (typisk på starten, midten eller slutten av perioden). Splines, samt lineær eller konstant interpolasjon kan så brukes for å binde punktene sammen til en tidsserie med høyere oppløsning. I denne studien har vi gått videre og brukt rutinen MSmooth som glatter en slik serie på best mulig måte (Kåresen og Laading, 2000). Denne metoden lager en ny, glatt tidsserie med finere oppløsning enn den originale, ved å bevare gjennomsnittsverdiene i hver periode. Endringene påvirker egenskapene til den originale serien minst mulig. 3 Metode Det kapittelet presenterer metodikken vi benytter i analysene. Før vi forklarer ulike konsepter og metoder, starter vi i avsnitt 3.1 med å beskrive to vanlige måter å representere en tidsserie på. 3.1 Autoregressive modeller En autoregresjon av orden p, kalt AR(p), følger ligningen y t = c + φ 1 y t 1 + φ 2 y t 2 + φ p y t p + ɛ t, der ɛ t er hvit støy, se f.eks. Hamilton (1994). 18 Konjunkturer og sykler i forsikring
19 En ARMA(p,q) tidsserie er definert som y t = c + φ 1 y t 1 + φ 2 y t φ p y t p + ɛ t + θ 1 ɛ t θ q ɛ t q, se igjen Hamilton (1994). Dersom man må differensiere en ARMA(p,q) tidsserie d ganger for å få den stasjonær, sier vi at tidsserien er integrert av orden d, og vi har en ARIMA(p,d,q) modell. For nærmere beskrivelse av stasjonaritet og integrerte tidsserier, se henholdsvis avsnitt 3.2 og appendiks A Stasjonaritet La y t = {y t, t = 1,, T } være en tidsserie, dvs. en sekvens av tilfeldige tall med en tidsindeks t. Tidsserien y t er kovariansstasjonær hvis E[y t ] = µ for alle t og Cov(y t, y t j ) = E[(y t µ)(y t j µ)] = γ j for alle t og j, der E og Cov står for henholdsvis forventning og kovarians. Vi vil for enkelthets skyld kalle en kovariansstasjonær tidsserie for en stasjonær tidsserie. Parameteren γ j er autokovariansen til y t med orden (lag) j. Et plott av γ j for alle j blir kalt autokovariansfunksjonen. Autokorrelasjonene til y t er definert som ρ j = Cov(y t, y t j ) Var(yt )Var(y t j ) = γ j γ 0, der variansen Var(y t ) = Cov(y t, y t ) = γ 0 er den samme for alle t som følge av stasjonariteten. Et plott av ρ j for alle j blir kalt autokorrelasjonsfunksjonen (ACF). Et naturlig estimat for autokorrelasjonen ρ j er gitt ved ρ j = γ j / γ 0, der γ j = 1 T y = 1 T T (y t y)(y t j y) for j = 0, 1,..., T 1, t=j+1 T y t. t=1 En annen nyttig størrelse er den partielle autokorrelasjonsfunksjonen (PACF) a k,k = γ k k 1 i=1 a i,k 1 γ k i σk 1 2 der a i,k = a i,k 1 a k,k a k i,k 1 for 1 i k 1, Konjunkturer og sykler i forsikring 19
20 er et estimat av den ite autoregresjonskoeffisienten φ i i en AR(k) modell. Videre er σ 2 k = σ 2 k 1(1 a 2 k,k). Siden det kan vises at AR(p) koeffisientene φ 1, φ 2,..., φ p tilfredsstiller Yule-Walker ligningene γ m = p φ r γ m r for m = 1, 2,..., p, r=1 kan kvadratet av a k,k tolkes som et mål på nytten av å øke ordenen på AR prosessen fra k 1 til k. Sekvensen a k,k, k = 1,..., kan brukes for å sjekke om en serie er en AR prosess. Dersom serien er en AR(p) prosess, bør alle a k,k være nær null for k > p. Se for eksempel Hamilton (1994) og MathSoft (2000) for mer detaljer. 3.3 Krysskorrelasjon Korrelasjon er det enkleste målet på samvariasjon mellom to variable. Dersom man ser på tidsrekker, kalles ofte korrelasjonene mellom to tidsrekker for krysskorrelasjon. Dette er for å skille begrepet fra autokorrelasjon, som angir korrelasjonen mellom ulike tidspunkt i samme serie. For to tidsrekker x t = {x t, t = 1,, T } og y t = {y t, t = 1,, T } definerer vi (kryss)korrelasjonen som Corr(x t, y t ) = Cov(x t, y t )/ Var(x t )Var(y t ), som estimeres ved den empiriske korrelasjonskoeffisienten Ĉorr(x t, y t ) = T t=1 (x t x)(y t y) s x s y, der s x og s y angir empirisk standardavvik for tidsrekkene x t og y t. Dersom krysskorrelasjonen mellom to tidsrekker er positiv, kaller vi de to tidsrekkene pro-sykliske. Dersom den er negativ, sier vi at seriene er mot-sykliske, mens dersom korrelasjonen er nær 0, sier vi at de er asykliske. Denne terminologien er hentet fra Bjørnland (2000) som har gjort slike studier på restleddene etter at trend og sesong er fjernet. Korrelasjonene kan også studeres på ulike tidspunkt i de to tidsrekkene, dvs. når tidsrekkene er forskjøvet i forhold til hverandre. Hvis den høyeste korrelasjonen mellom en tidsrekke fra Gjensidige og en makroøkonomisk størrelse opptrer dersom serien forskyves forover i forhold til den makroøkonomiske størrelsen, sier 20 Konjunkturer og sykler i forsikring
21 vi at den makroøkonomiske variabelen er ledende for Gjensidiges variabel. Dersom vi lar m t angi den makroøkonmiske størrelsen og g t Gjensidiges størrelse tilsvarer dette at Corr(m t, g t+k ) er større for en positiv k, enn for k = 0. Negative verdier for k tilsvarer at Gjensidiges variabel er ledende for den makroøkonmiske variabelen, hvilket er svært lite sannsynlig. Studier av rullerende korrelasjoner viser hvordan korrelasjonen varierer over tid ved at man beregner korrelasjoner for et tidsvindu av en viss lengde og flytter dette vinduet stegvis fremover. Vi vil studere i hvilken grad tidsseriene fra Gjensidige samvarierer med de makroøkonomiske størrelsene. I slike sammenligninger bør man benytte sesongjusterte data dersom det er mulig. Når det gjelder tidsseriene fra Gjensidige, så har disse årlig oppløsning og sesongjusteringer er derfor ikke nødvendig. For SSB-dataene har vi benyttet sesongjusterte verdier der de har vært tilgjengelige. Dette samsvarer med hvilke variable SSB mener det er fornuftig å sesongjustere. Vi vil både se på samvariasjon av de originale tidsseriene og etter at trenden er fjernet fra seriene. Ved å fjerne trenden ser vi på hvordan utviklingen i tidsseriene utover trenden samvarierer. 4 Resultater 4.1 Gjensidiges tidsrekker Figur 1, 2, 3, 4 og 5 viser CR for de fem skadetypene fra Gjensidige. Plottene i øverste venstre hjørne viser selve tidsrekken. De fleste skadetypene har en periode med økning i CR og en periode med nedgang. Tidsrekkene inneholder altså maksimalt én sykel, noe som medfører at det ikke er mulig å etablere statistiske modeller for syklene. Plottene i øverste høyre hjørne viser differansen mellom logaritmen av tidsrekken på et tidspunkt og tidspunktet før, dvs. log y t log y t 1, og viser at det er relativt store variasjoner fra et tidspunkt til et annet på log-skala. De nederste plottene viser autokorrelasjonsfunksjonen og den partielle autokorrelasjonsfunksjonen for logdifferansene. Autokorrelasjonsfunksjonen viser at endringene i CR påfølgende år er svært lite korrelerte, noe som ikke er overraskende med en så grov oppløsning på dataene. De partielle autokorrelasjonene viser ikke noe entydig mønster og indikerer at usikkerheten er for stor til at man kan slutte noe om hvorvidt tidsrekkene kan beskrives som autoregressive prosesser. Konjunkturer og sykler i forsikring 21
22 4.2 Makroøkonomiske størrelser De makroøkonomiske størrelsene KPI, BNP, lønn og arbeidesledighet er plottet i hhv. figur 6, 7, 8 og 9. Figurene viser at KPI, BNP og lønn har hatt en jevn stigning, mens arbeidsledigheten har hatt både kraftige økninger og nedganger i perioden. Figurene viser at log-differansen for KPI, BNP og arbeidsledighet synes å være stasjonære prosesser, mens stasjonariteten for lønn er noe mer usikker. Autokorrelasjonsfunksjonene for KPI og lønn viser en positiv autokorrelasjon mellom verdier nær i tid, mens BNP har en negativ autokorrelasjon mellom påfølgende tidspunkter. Også for de makroøkonomiske variablene er de partielle autokorrelasjonene beheftet med en så stor usikkerhet at det ikke er mulig å trekke noen konklusjoner. 4.3 Krysskorrelasjoner Figur 10, 11, 12, 13 og 14 viser hver av tidsseriene til Gjensidige plottet mot hver av de makroøkonomiske variablene, samt tilhørende rullerende krysskorrelasjoner, uten at seriene er forskjøvet i forhold til hverandre. Tidsvinduene som er brukt ved beregning av rullerende krysskorrelasjoner varierer fra serie til serie, men det er typisk brukt et vindu på 3 5 år. Som det framgår av figurene, er det vanskelig å se et klart mønster i de rullerende krysskorrelasjonene. For de av Gjensidiges serier som består av en oppgang og en nedgang, blir korrelasjonen med makrovariablene nær null. Den rullerende korrelasjonen viser dette ved at den først er positiv (i oppgangsperioden) og deretter negativ (i nedgangsperioden). For uførhet, som har en nedadgående trend i hele perioden, blir korrelasjonen negativ. Endringene i Gjensidige CR data ble i tillegg sammenlignet med endringene i de makroøkonomiske dataene, men heller ikke disse viste et tydelig mønster i de rullerende krysskorrelasjonene. 4.4 Fjerning av trend Vi har også forsøkt å fjerne eventuelle trender i tidsseriene, og deretter sammenlignet de gjenstående residualene med hverandre. Den innebygde Splus funksjonen loess.smooth gjør en lokal polynomregresjon av dataene, som vi lar være trenden. Figur 15, 16, 17, 18 og 19 viser hver av CR tidsseriene (uten trend) plottet mot hver av de makroøkonomiske variablene (uten trend), samt de tilhørende krysskorrelasjonene, også her uten lag. Heller ikke nå er det lett å se et klart mønster i samvariasjonen mellom variablene. 22 Konjunkturer og sykler i forsikring
23 bolig.cr and kpi.sesong, months windowlength = 36 months bolig.cr kpi.sesong bolig.cr and bnp.fast, quarters windowlength = 12 quarters bolig.cr bnp.fast bolig.cr and lonnt, years windowlength = 5 years bolig.cr lonnt bolig.cr and arbledigt, years windowlength = 5 years bolig.cr arbledigt Figur 10. Bolig CR mot alle makroøkonomiske variable. Kolonnen til venstre viser Bolig CR data plottet mot hver av de makroøkonomiske variablene, mens kolonnen til høyre viser de tilhørende rullerende krysskorrelasjonene når seriene ikke er forskjøvet i forhold til hverandre. Konjunkturer og sykler i forsikring 23
24 landbruk.cr and kpi.sesong, months windowlength = 36 months landbruk.cr kpi.sesong landbruk.cr and bnp.fast, quarters windowlength = 12 quarters landbruk.cr bnp.fast landbruk.cr and lonnt, years windowlength = 5 years landbruk.cr lonnt landbruk.cr and arbledigt, years windowlength = 5 years landbruk.cr arbledigt Figur 11. Landbruk CR mot alle makroøkonomiske variable. Kolonnen til venstre viser Landbruk CR data plottet mot hver av de makroøkonomiske variablene, mens kolonnen til høyre viser de tilhørende rullerende krysskorrelasjonene når seriene ikke er forskjøvet i forhold til hverandre. 24 Konjunkturer og sykler i forsikring
25 yrkesskade.cr and kpi.sesong, months windowlength = 36 months yrkesskade.cr kpi.sesong yrkesskade.cr and bnp.fast, quarters windowlength = 12 quarters yrkesskade.cr bnp.fast yrkesskade.cr and lonnt, years windowlength = 5 years yrkesskade.cr lonnt yrkesskade.cr and arbledigt, years windowlength = 5 years yrkesskade.cr arbledigt Figur 12. Yrkesskade CR mot alle makroøkonomiske variable. Kolonnen til venstre viser Yrkesskade CR data plottet mot hver av de makroøkonomiske variablene, mens kolonnen til høyre viser de tilhørende rullerende krysskorrelasjonene når seriene ikke er forskjøvet i forhold til hverandre. Konjunkturer og sykler i forsikring 25
26 ufore.cr and kpi.sesong, months windowlength = 36 months ufore.cr kpi.sesong Q1 Q1 Q1 Q1 Q1 Q1 Q ufore.cr and bnp.fast, quarters windowlength = 12 quarters ufore.cr bnp.fast Q1 Q1 Q1 Q1 Q1 Q1 Q ufore.cr and lonnt, years windowlength = 5 years ufore.cr lonnt Q1 Q1 Q1 Q1 Q1 Q1 Q1 Q1 Q Q1 Q3 Q1 Q3 Q1 Q3 Q1 Q3 Q ufore.cr and arbledigt, years windowlength = 5 years ufore.cr arbledigt Q1 Q1 Q1 Q1 Q1 Q1 Q1 Q1 Q Q1 Q3 Q1 Q3 Q1 Q3 Q1 Q3 Q Figur 13. Uføre CR mot alle makroøkonomiske variable. Kolonnen til venstre viser Uføre CR data plottet mot hver av de makroøkonomiske variablene, mens kolonnen til høyre viser de tilhørende rullerende krysskorrelasjonene når seriene ikke er forskjøvet i forhold til hverandre. 26 Konjunkturer og sykler i forsikring
27 motor.cr and kpi.sesong, months windowlength = 36 months motor.cr kpi.sesong motor.cr and bnp.fast, quarters windowlength = 12 quarters motor.cr bnp.fast motor.cr and lonnt, years windowlength = 5 years motor.cr lonnt motor.cr and arbledigt, years windowlength = 5 years motor.cr arbledigt Figur 14. Motor CR mot alle makroøkonomiske variable. Kolonnen til venstre viser Motor CR data plottet mot hver av de makroøkonomiske variablene, mens kolonnen til høyre viser de tilhørende rullerende krysskorrelasjonene når seriene ikke er forskjøvet i forhold til hverandre. Konjunkturer og sykler i forsikring 27
28 bolig.cr and kpi.sesong, months windowlength = 36 months bolig.cr kpi.sesong bolig.cr and bnp.fast, quarters windowlength = 12 quarters bolig.cr bnp.fast bolig.cr and lonnt, years windowlength = 5 years bolig.cr lonnt bolig.cr and arbledigt, years windowlength = 5 years bolig.cr arbledigt Figur 15. Bolig CR mot alle makroøkonomiske variable, der trendene er tatt bort. Kolonnen til venstre viser Bolig CR data plottet mot hver av de makroøkonomiske variablene, alle uten trend, mens kolonnen til høyre viser de tilhørende rullerende krysskorrelasjonene når seriene ikke er forskjøvet i forhold til hverandre. 28 Konjunkturer og sykler i forsikring
29 landbruk.cr and kpi.sesong, months landbruk.cr kpi.sesong windowlength = 36 months landbruk.cr and bnp.fast, quarters windowlength = 12 quarters landbruk.cr bnp.fast landbruk.cr and lonnt, years windowlength = 5 years landbruk.cr lonnt landbruk.cr and arbledigt, years windowlength = 5 years landbruk.cr arbledigt Figur 16. Landbruk CR mot alle makroøkonomiske variable, der trendene er tatt bort. Kolonnen til venstre viser Landbruk CR data plottet mot hver av de makroøkonomiske variablene, alle uten trend, mens kolonnen til høyre viser de tilhørende rullerende krysskorrelasjonene når seriene ikke er forskjøvet i forhold til hverandre. Konjunkturer og sykler i forsikring 29
30 yrkesskade.cr and kpi.sesong, months windowlength = 36 months yrkesskade.cr kpi.sesong yrkesskade.cr and bnp.fast, quarters windowlength = 12 quarters yrkesskade.cr bnp.fast yrkesskade.cr and lonnt, years windowlength = 5 years yrkesskade.cr lonnt yrkesskade.cr and arbledigt, years windowlength = 5 years yrkesskade.cr arbledigt Figur 17. Yrkesskade CR mot alle makroøkonomiske variable, der trendene er tatt bort. Kolonnen til venstre viser Yrkesskade CR data plottet mot hver av de makroøkonomiske variablene, alle uten trend, mens kolonnen til høyre viser de tilhørende rullerende krysskorrelasjonene når seriene ikke er forskjøvet i forhold til hverandre. 30 Konjunkturer og sykler i forsikring
31 ufore.cr and kpi.sesong, months windowlength = 36 months ufore.cr kpi.sesong Q1 Q1 Q1 Q1 Q1 Q1 Q ufore.cr and bnp.fast, quarters windowlength = 12 quarters ufore.cr bnp.fast Q1 Q1 Q1 Q1 Q1 Q1 Q ufore.cr and lonnt, years windowlength = 5 years ufore.cr lonnt Q1 Q1 Q1 Q1 Q1 Q1 Q1 Q1 Q Q1 Q3 Q1 Q3 Q1 Q3 Q1 Q3 Q ufore.cr and arbledigt, years windowlength = 5 years ufore.cr arbledigt Q1 Q1 Q1 Q1 Q1 Q1 Q1 Q1 Q Q1 Q3 Q1 Q3 Q1 Q3 Q1 Q3 Q Figur 18. Uføre CR mot alle makroøkonomiske variable, der trendene er tatt bort. Kolonnen til venstre viser Uføre CR data plottet mot hver av de makroøkonomiske variablene, alle uten trend, mens kolonnen til høyre viser de tilhørende rullerende krysskorrelasjonene når seriene ikke er forskjøvet i forhold til hverandre. Konjunkturer og sykler i forsikring 31
Rekrutteringsfunksjoner for sild, torsk og lodde
 Rekrutteringsfunksjoner for sild, torsk og lodde Sild 0 50 100 150 200 250 300 Beverton-Holt Ricker linear regression paa log-skala 0 2 4 6 8 10 12 14 Gytebimoasse (millioner tonn) Torsk 0 5 10 15 20 25
Rekrutteringsfunksjoner for sild, torsk og lodde Sild 0 50 100 150 200 250 300 Beverton-Holt Ricker linear regression paa log-skala 0 2 4 6 8 10 12 14 Gytebimoasse (millioner tonn) Torsk 0 5 10 15 20 25
3.A IKKE-STASJONARITET
 Norwegian Business School 3.A IKKE-STASJONARITET BST 1612 ANVENDT MAKROØKONOMI MODUL 5 Foreleser: Drago Bergholt E-post: Drago.Bergholt@bi.no 11. november 2011 OVERSIKT - Ikke-stasjonære tidsserier - Trendstasjonaritet
Norwegian Business School 3.A IKKE-STASJONARITET BST 1612 ANVENDT MAKROØKONOMI MODUL 5 Foreleser: Drago Bergholt E-post: Drago.Bergholt@bi.no 11. november 2011 OVERSIKT - Ikke-stasjonære tidsserier - Trendstasjonaritet
Følsomme lusetellinger ved forslag til ny forskrift. Anders Løland
 Følsomme lusetellinger ved forslag til ny forskrift Notatnr Forfatter SAMBA/01/12 Anders Løland Dato 11. januar 2012 Norsk Regnesentral Norsk Regnesentral (NR) er en privat, uavhengig stiftelse som utfører
Følsomme lusetellinger ved forslag til ny forskrift Notatnr Forfatter SAMBA/01/12 Anders Løland Dato 11. januar 2012 Norsk Regnesentral Norsk Regnesentral (NR) er en privat, uavhengig stiftelse som utfører
EKSAMEN I TMA4285 TIDSREKKEMODELLER Fredag 7. desember 2012 Tid: 09:00 13:00
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 8 Bokmål Faglig kontakt under eksamen: John Tyssedal 73593534/41645376 EKSAMEN I TMA4285 TIDSREKKEMODELLER Fredag
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 8 Bokmål Faglig kontakt under eksamen: John Tyssedal 73593534/41645376 EKSAMEN I TMA4285 TIDSREKKEMODELLER Fredag
Matematisk statistikk og stokastiske prosesser B, høsten 2006 Oppgavesett 5, s. 1. Oppgave 1. Oppgave 2. Oppgave 3
 Matematisk statistikk og stokastiske prosesser B, høsten 2006 Oppgavesett 5, s. 1 Oppgave 1 For AR(2)-modellen: X t = 0.4X t 1 + 0.45X t 2 + Z t (der {Z t } er hvit søy med varians 1), finn γ(3), γ(4)
Matematisk statistikk og stokastiske prosesser B, høsten 2006 Oppgavesett 5, s. 1 Oppgave 1 For AR(2)-modellen: X t = 0.4X t 1 + 0.45X t 2 + Z t (der {Z t } er hvit søy med varians 1), finn γ(3), γ(4)
Appendiks 5 Forutsetninger for lineær regresjonsanalyse
 Appendiks 5 Forutsetninger for lineær regresjonsanalyse Det er flere krav til årsaksslutninger i regresjonsanalyse. En naturlig forutsetning er tidsrekkefølge og i andre rekke spiller variabeltype inn.
Appendiks 5 Forutsetninger for lineær regresjonsanalyse Det er flere krav til årsaksslutninger i regresjonsanalyse. En naturlig forutsetning er tidsrekkefølge og i andre rekke spiller variabeltype inn.
Falske positive i lusetellinger?
 Falske positive i lusetellinger? 50 % grense = 0,2 grense = 0,5 Sannsynlighet for en falsk positiv 40 % 30 % 20 % 10 % 0 % 0,0 0,1 0,2 0,3 0,4 0,5 Faktisk lusetall Notatnr Forfatter SAMBA/17/16 Anders
Falske positive i lusetellinger? 50 % grense = 0,2 grense = 0,5 Sannsynlighet for en falsk positiv 40 % 30 % 20 % 10 % 0 % 0,0 0,1 0,2 0,3 0,4 0,5 Faktisk lusetall Notatnr Forfatter SAMBA/17/16 Anders
Kort overblikk over kurset sålangt
 Kort overblikk over kurset sålangt Kapittel 1: Deskriptiv statististikk for en variabel Kapittel 2: Deskriptiv statistikk for samvariasjon mellom to variable (regresjon) Kapittel 3: Metoder for å innhente
Kort overblikk over kurset sålangt Kapittel 1: Deskriptiv statististikk for en variabel Kapittel 2: Deskriptiv statistikk for samvariasjon mellom to variable (regresjon) Kapittel 3: Metoder for å innhente
Matematisk statistikk og stokastiske prosesser B, høsten 2006 Løsninger til oppgavesett 5, s. 1. Oppgave 1
 Matematisk statistikk og stokastiske prosesser B, høsten 2006 Løsninger til oppgavesett 5, s AR2-modell: Oppgave X t φ X t φ 2 X t 2 Z t Antas å være kausal slik at X t ψ j Z t j er ukorrelert med Z t+,
Matematisk statistikk og stokastiske prosesser B, høsten 2006 Løsninger til oppgavesett 5, s AR2-modell: Oppgave X t φ X t φ 2 X t 2 Z t Antas å være kausal slik at X t ψ j Z t j er ukorrelert med Z t+,
SOS1120 Kvantitativ metode. Regresjonsanalyse. Lineær sammenheng II. Lineær sammenheng I. Forelesningsnotater 11. forelesning høsten 2005
 SOS1120 Kvantitativ metode Regresjonsanalyse Forelesningsnotater 11. forelesning høsten 2005 Per Arne Tufte Lineær sammenheng I Lineær sammenheng II Ukelønn i kroner 4000 3500 3000 2500 2000 1500 1000
SOS1120 Kvantitativ metode Regresjonsanalyse Forelesningsnotater 11. forelesning høsten 2005 Per Arne Tufte Lineær sammenheng I Lineær sammenheng II Ukelønn i kroner 4000 3500 3000 2500 2000 1500 1000
1.A INTRODUKSJON. Norwegian Business School. BST 1612 ANVENDT MAKROØKONOMI MODUL 5 Foreleser: Drago Bergholt E-post: Drago.Bergholt@bi.
 Norwegian Business School 1.A INTRODUKSJON BST 1612 ANVENDT MAKROØKONOMI MODUL 5 Foreleser: Drago Bergholt E-post: Drago.Bergholt@bi.no 10. november 2011 MOTIVASJON - I makroøkonomi er vi opptatt av spørsmål
Norwegian Business School 1.A INTRODUKSJON BST 1612 ANVENDT MAKROØKONOMI MODUL 5 Foreleser: Drago Bergholt E-post: Drago.Bergholt@bi.no 10. november 2011 MOTIVASJON - I makroøkonomi er vi opptatt av spørsmål
Løsningsforslag ECON 2130 Obligatorisk semesteroppgave 2017 vår
 Løsningsforslag ECON 130 Obligatorisk semesteroppgave 017 vår Andreas Myhre Oppgave 1 1. (i) Siden X og Z er uavhengige, vil den simultane fordelingen mellom X og Z kunne skrives som: f(x, z) = P(X = x
Løsningsforslag ECON 130 Obligatorisk semesteroppgave 017 vår Andreas Myhre Oppgave 1 1. (i) Siden X og Z er uavhengige, vil den simultane fordelingen mellom X og Z kunne skrives som: f(x, z) = P(X = x
Justering til gyldig korrelasjonsmatrise
 Absolute difference between original and adjusted matrix (major, with weights)...2.3.4.5.85.45.6 -.2. -. -.4.6.4.4.3.7 -.7 -.7. -.4.5.72.45 -.4 -.79.85.34.3 -.8.8.4 -. -.4..4.9.5 -.9 -.7 -.4 -.9.64.8.53.2
Absolute difference between original and adjusted matrix (major, with weights)...2.3.4.5.85.45.6 -.2. -. -.4.6.4.4.3.7 -.7 -.7. -.4.5.72.45 -.4 -.79.85.34.3 -.8.8.4 -. -.4..4.9.5 -.9 -.7 -.4 -.9.64.8.53.2
Analyse av data relatert til friksjonsmålinger og ulykkesfrekvens ved to veistrekninger i Oslo i perioden 2001-2009
 Analyse av data relatert til friksjonsmålinger og ulykkesfrekvens ved to veistrekninger i Oslo i perioden 2001-2009 Notatnr Forfattere SAMBA/15/10 Magne Aldrin Ragnar Bang Huseby Dato 26. mars 2010 Norsk
Analyse av data relatert til friksjonsmålinger og ulykkesfrekvens ved to veistrekninger i Oslo i perioden 2001-2009 Notatnr Forfattere SAMBA/15/10 Magne Aldrin Ragnar Bang Huseby Dato 26. mars 2010 Norsk
Eksamensoppgave i TMA4240 Statistikk
 Institutt for matematiske fag Eksamensoppgave i TMA4240 Statistikk Faglig kontakt under eksamen: Mette Langaas a, Ingelin Steinsland b, Geir-Arne Fuglstad c Tlf: a 988 47 649, b 926 63 096, c 452 70 806
Institutt for matematiske fag Eksamensoppgave i TMA4240 Statistikk Faglig kontakt under eksamen: Mette Langaas a, Ingelin Steinsland b, Geir-Arne Fuglstad c Tlf: a 988 47 649, b 926 63 096, c 452 70 806
I enkel lineær regresjon beskrev linja. μ y = β 0 + β 1 x
 Multiple regresjon Her utvider vi perspektivet for enkel lineær regresjon til også å omfatte flere forklaringsvariable.det er fortsatt en responsvariabel. Måten dette gjøre på er nokså naturlig. Prediktoren
Multiple regresjon Her utvider vi perspektivet for enkel lineær regresjon til også å omfatte flere forklaringsvariable.det er fortsatt en responsvariabel. Måten dette gjøre på er nokså naturlig. Prediktoren
Multippel regresjon. Her utvider vi perspektivet for enkel lineær regresjon til også å omfatte flere forklaringsvariable x 1, x 2,, x p.
 Multippel regresjon Her utvider vi perspektivet for enkel lineær regresjon til også å omfatte flere forklaringsvariable x 1, x 2,, x p. Det er fortsatt en responsvariabel y. Måten dette gjøre på er nokså
Multippel regresjon Her utvider vi perspektivet for enkel lineær regresjon til også å omfatte flere forklaringsvariable x 1, x 2,, x p. Det er fortsatt en responsvariabel y. Måten dette gjøre på er nokså
Inferens i regresjon
 Strategi som er fulgt hittil: Inferens i regresjon Deskriptiv analyse og dataanalyse først. Analyse av en variabel før studie av samvariasjon. Emne for dette kapittel er inferens når det er en respons
Strategi som er fulgt hittil: Inferens i regresjon Deskriptiv analyse og dataanalyse først. Analyse av en variabel før studie av samvariasjon. Emne for dette kapittel er inferens når det er en respons
Beregning av trafikkvolum for sykler basert på basiskurvemetoden
 Beregning av trafikkvolum for sykler basert på basiskurvemetoden Notatnr Forfattere SAMBA/08/05 Ola Haug Magne Aldrin Dato 12. april 2005 Forfatterne Magne Aldrin står bak ideen om bruk av såkalte basiskurver
Beregning av trafikkvolum for sykler basert på basiskurvemetoden Notatnr Forfattere SAMBA/08/05 Ola Haug Magne Aldrin Dato 12. april 2005 Forfatterne Magne Aldrin står bak ideen om bruk av såkalte basiskurver
TMA4245 Statistikk Eksamen desember 2016
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4245 Statistikk Eksamen desember 2016 Oppgave 1 En bedrift produserer elektriske komponenter. Komponentene kan ha to typer
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4245 Statistikk Eksamen desember 2016 Oppgave 1 En bedrift produserer elektriske komponenter. Komponentene kan ha to typer
+ S2 Y ) 2. = 6.737 6 (avrundet nedover til nærmeste heltall) n Y 1
 Løsningsforslag for: MOT10 STATISTISKE METODER 1 VARIGHET: 4 TIMER DATO: 6. november 007 TILLATTE HJELPEMIDLER: Kalkulator: HP0S, Casio FX8 eller TI-0 Tabeller og formler i statistikk (Tapir forlag) MERKNADER:
Løsningsforslag for: MOT10 STATISTISKE METODER 1 VARIGHET: 4 TIMER DATO: 6. november 007 TILLATTE HJELPEMIDLER: Kalkulator: HP0S, Casio FX8 eller TI-0 Tabeller og formler i statistikk (Tapir forlag) MERKNADER:
Oppgave 1. Det oppgis at dersom y ij er observasjon nummer j fra laboratorium i så er SSA = (y ij ȳ i ) 2 = 3.6080.
 EKSAMEN I: MOT310 STATISTISKE METODER 1 VARIGHET: 4 TIMER DATO: 28. FEBRUAR 2005 TILLATTE HJELPEMIDLER: KALKULATOR, TABELLER OG FORMLER I STATISTIKK (TAPIR FORLAG) OPPGAVESETTET BESTÅR AV 4 OPPGAVER PÅ
EKSAMEN I: MOT310 STATISTISKE METODER 1 VARIGHET: 4 TIMER DATO: 28. FEBRUAR 2005 TILLATTE HJELPEMIDLER: KALKULATOR, TABELLER OG FORMLER I STATISTIKK (TAPIR FORLAG) OPPGAVESETTET BESTÅR AV 4 OPPGAVER PÅ
Oppgave 1. X 1 B(n 1, p 1 ) X 2. Vi er interessert i forskjellen i andeler p 1 p 2, som vi estimerer med. p 1 p 2 = X 1. n 1 n 2.
 Løsningsforslag til eksamen i MOT310 STATISTISKE METODER 1 VARIGHET: 4 TIMER DATO: 17 november 2008 TILLATTE HJELPEMIDLER: Kalkulator: HP30S, Casio FX82 eller TI-30 Tabeller og formler i statistikk Tapir
Løsningsforslag til eksamen i MOT310 STATISTISKE METODER 1 VARIGHET: 4 TIMER DATO: 17 november 2008 TILLATTE HJELPEMIDLER: Kalkulator: HP30S, Casio FX82 eller TI-30 Tabeller og formler i statistikk Tapir
OPPGAVESETTET BESTÅR AV 3 OPPGAVER PÅ 6 SIDER MERKNADER: Alle deloppgaver vektlegges likt.
 EKSAMEN I: MOT310 STATISTISKE METODER 1 VARIGHET: 4 TIMER DATO: 08. mai 2008 TILLATTE HJELPEMIDLER: Kalkulator: HP30S, Casio FX82 eller TI-30 Tabeller og formler i statistikk (Tapir forlag) OPPGAVESETTET
EKSAMEN I: MOT310 STATISTISKE METODER 1 VARIGHET: 4 TIMER DATO: 08. mai 2008 TILLATTE HJELPEMIDLER: Kalkulator: HP30S, Casio FX82 eller TI-30 Tabeller og formler i statistikk (Tapir forlag) OPPGAVESETTET
Kontroller at oppgavesettet er komplett før du begynner å besvare spørsmålene. Ved sensuren teller alle delspørsmål likt.
 Eksamen i: MET040 Statistikk for økonomer Eksamensdag: 4 november 2008 Tid for eksamen: 09.00-13.00 Oppgavesettet er på 4 sider. Tillatte hjelpemidler: Alle trykte eller egenskrevne hjelpemidler og kalkulator.
Eksamen i: MET040 Statistikk for økonomer Eksamensdag: 4 november 2008 Tid for eksamen: 09.00-13.00 Oppgavesettet er på 4 sider. Tillatte hjelpemidler: Alle trykte eller egenskrevne hjelpemidler og kalkulator.
Oppgave 1. T = 9 Hypotesetest for å teste om kolesterolnivået har endret seg etter dietten: T observert = 2.16 0
 Løsningsforslag til eksamen i MOT310 STATISTISKE METODER 1 VARIGHET: 4 TIMER DATO: 08. mai 2008 TILLATTE HJELPEMIDLER: Kalkulator: HP30S, Casio FX82 eller TI-30 Tabeller og formler i statistikk (Tapir
Løsningsforslag til eksamen i MOT310 STATISTISKE METODER 1 VARIGHET: 4 TIMER DATO: 08. mai 2008 TILLATTE HJELPEMIDLER: Kalkulator: HP30S, Casio FX82 eller TI-30 Tabeller og formler i statistikk (Tapir
NOTAT. Feiing og salting i Strømsås-tunnelen mars innledende analyse. Norsk Regnesentral SAMBA/27/04. Magne Aldrin. 9.
 Feiing og salting i Strømsås-tunnelen mars 2004 - innledende analyse NR Norsk Regnesentral ANVENDT DATAFORSKNING NOTAT PM10, Stromsaas SAMBA/27/04 Magne Aldrin 9. november 2004 3 4 5 6 7 8 3 4 5 6 7 8
Feiing og salting i Strømsås-tunnelen mars 2004 - innledende analyse NR Norsk Regnesentral ANVENDT DATAFORSKNING NOTAT PM10, Stromsaas SAMBA/27/04 Magne Aldrin 9. november 2004 3 4 5 6 7 8 3 4 5 6 7 8
EKSAMEN I TMA4285 TIDSREKKJEMODELLAR Fredag 7. desember 2012 Tid: 09:00 13:00
 Noregs teknisk naturvitskaplege universitet Institutt for matematiske fag Side 1 av 8 Nynorsk Fagleg kontakt under eksamen: John Tyssedal 73593534/41645376 EKSAMEN I TMA4285 TIDSREKKJEMODELLAR Fredag 7.
Noregs teknisk naturvitskaplege universitet Institutt for matematiske fag Side 1 av 8 Nynorsk Fagleg kontakt under eksamen: John Tyssedal 73593534/41645376 EKSAMEN I TMA4285 TIDSREKKJEMODELLAR Fredag 7.
år i 1 2 3 4 5 6 7 8 9 alder x i 37 38 39 40 41 42 43 44 45 tid y i 45.54 41.38 42.50 38.80 41.26 37.20 38.19 38.05 37.45 i=1 (x i x) 2 = 60, 9
 TMA424 Statistikk Vår 214 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 11, blokk II Oppgave 1 Matlabkoden linearreg.m, tilgjengelig fra emnets hjemmeside, utfører
TMA424 Statistikk Vår 214 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 11, blokk II Oppgave 1 Matlabkoden linearreg.m, tilgjengelig fra emnets hjemmeside, utfører
HØGSKOLEN I STAVANGER
 HØGSKOLEN I STAVANGER Avdeling for TEKNISK NATURVITEN- EKSAMEN I: TE199 SANNSYNLIGHETSREGNING MED STATISTIKK SKAPELIGE FAG VARIGHET: 4 TIMER DATO: 5. JUNI 2003 TILLATTE HJELPEMIDLER: KALKULATOR OPPGAVESETTET
HØGSKOLEN I STAVANGER Avdeling for TEKNISK NATURVITEN- EKSAMEN I: TE199 SANNSYNLIGHETSREGNING MED STATISTIKK SKAPELIGE FAG VARIGHET: 4 TIMER DATO: 5. JUNI 2003 TILLATTE HJELPEMIDLER: KALKULATOR OPPGAVESETTET
Nedenfor er det vist hvordan statistikkprogrammet og programeringsmiljøet R (1) kan bli brukt til å analysere befolkningen i Norge.
 Norges befolkning Nedenfor er det vist hvordan statistikkprogrammet og programeringsmiljøet R (1) kan bli brukt til å analysere befolkningen i Norge. Innhold Mors alder ved fødsel av første barn... 1 Menneskepopulasjonen
Norges befolkning Nedenfor er det vist hvordan statistikkprogrammet og programeringsmiljøet R (1) kan bli brukt til å analysere befolkningen i Norge. Innhold Mors alder ved fødsel av første barn... 1 Menneskepopulasjonen
Profil Lavpris Supermarked Hypermarked Totalt. Coop Prix 4 4. Coop Extra 13 5. Coop Mega 7 7. Coop Obs 5 13. Rimi 24 24. Ica Supermarked 7 7
 Vedlegg 1 - Regresjonsanalyser 1 Innledning og formål (1) Konkurransetilsynet har i forbindelse med Vedtak 2015-24, (heretter "Vedtaket") utført kvantitative analyser på data fra kundeundersøkelsen. I
Vedlegg 1 - Regresjonsanalyser 1 Innledning og formål (1) Konkurransetilsynet har i forbindelse med Vedtak 2015-24, (heretter "Vedtaket") utført kvantitative analyser på data fra kundeundersøkelsen. I
6.2 Signifikanstester
 6.2 Signifikanstester Konfidensintervaller er nyttige når vi ønsker å estimere en populasjonsparameter Signifikanstester er nyttige dersom vi ønsker å teste en hypotese om en parameter i en populasjon
6.2 Signifikanstester Konfidensintervaller er nyttige når vi ønsker å estimere en populasjonsparameter Signifikanstester er nyttige dersom vi ønsker å teste en hypotese om en parameter i en populasjon
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 Eksamen i: ECON30 Statistikk UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamensdag: 03.06.06 Sensur kunngjøres: 4.06.06 Tid for eksamen: kl. 09:00 :00 Oppgavesettet er på 5 sider Tillatte hjelpemidler:
Eksamen i: ECON30 Statistikk UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamensdag: 03.06.06 Sensur kunngjøres: 4.06.06 Tid for eksamen: kl. 09:00 :00 Oppgavesettet er på 5 sider Tillatte hjelpemidler:
2. Hva er en sampelfordeling? Nevn tre eksempler på sampelfordelinger.
 H12 - Semesteroppgave i statistikk - sensurveiledning Del 1 - teori 1. Gjør rede for resonnementet bak ANOVA. Enveis ANOVA tester om det er forskjeller mellom gjennomsnittene i tre eller flere populasjoner.
H12 - Semesteroppgave i statistikk - sensurveiledning Del 1 - teori 1. Gjør rede for resonnementet bak ANOVA. Enveis ANOVA tester om det er forskjeller mellom gjennomsnittene i tre eller flere populasjoner.
Forventning og varians.
 Forventning og varians. Dekkes av kapittel 4 i læreboka. Forventning (4.) Forventningsverdi gjennomsnitt i det lange løp. Defininsjon: Forventningsverdien til en stokastisk variabel X er: E(X) f(),x diskret
Forventning og varians. Dekkes av kapittel 4 i læreboka. Forventning (4.) Forventningsverdi gjennomsnitt i det lange løp. Defininsjon: Forventningsverdien til en stokastisk variabel X er: E(X) f(),x diskret
Sentralverdi av dataverdi i et utvalg Vi tenker oss et utvalg med datapar. I vårt eksempel har vi 5 datapar.
 Statistisk behandling av kalibreringsresultatene Del 4. v/ Rune Øverland, Trainor Elsikkerhet AS Denne artikkelserien handler om statistisk behandling av kalibreringsresultatene. Dennne artikkelen tar
Statistisk behandling av kalibreringsresultatene Del 4. v/ Rune Øverland, Trainor Elsikkerhet AS Denne artikkelserien handler om statistisk behandling av kalibreringsresultatene. Dennne artikkelen tar
Snøtetthet. Institutt for matematiske fag, NTNU 15. august Notat for TMA4240/TMA4245 Statistikk
 Snøtetthet Notat for TMA424/TMA4245 Statistikk Institutt for matematiske fag, NTNU 5. august 22 I forbindelse med varsling av om, klimaforskning og særlig kraftproduksjon er det viktig å kunne anslå hvor
Snøtetthet Notat for TMA424/TMA4245 Statistikk Institutt for matematiske fag, NTNU 5. august 22 I forbindelse med varsling av om, klimaforskning og særlig kraftproduksjon er det viktig å kunne anslå hvor
Ferdig før tiden 4 7 Ferdig til avtalt tid 12 7 Forsinket 1 måned 2 6 Forsinket 2 måneder 4 4 Forsinket 3 måneder 6 2 Forsinket 4 måneder 0 2
 Besvar alle oppgavene. Hver deloppgave har lik vekt. Oppgave I En kommune skal bygge ny idrettshall og vurderer to entreprenører, A og B. Begge gir samme pristilbud, men kommunen er bekymret for forsinkelser.
Besvar alle oppgavene. Hver deloppgave har lik vekt. Oppgave I En kommune skal bygge ny idrettshall og vurderer to entreprenører, A og B. Begge gir samme pristilbud, men kommunen er bekymret for forsinkelser.
Tilleggsoppgaver for STK1110 Høst 2015
 Tilleggsoppgaver for STK0 Høst 205 Geir Storvik 22. november 205 Tilleggsoppgave Anta X,..., X n N(µ, σ) der σ er kjent. Vi ønsker å teste H 0 : µ = µ 0 mot H a : µ µ 0 (a) Formuler hypotesene som H 0
Tilleggsoppgaver for STK0 Høst 205 Geir Storvik 22. november 205 Tilleggsoppgave Anta X,..., X n N(µ, σ) der σ er kjent. Vi ønsker å teste H 0 : µ = µ 0 mot H a : µ µ 0 (a) Formuler hypotesene som H 0
LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4240 STATISTIKK Mandag 12. desember 2011
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 10 LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4240 STATISTIKK Mandag 12. desember 2011 Oppgave 1 Oljeleting a) Siden P(A
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 10 LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4240 STATISTIKK Mandag 12. desember 2011 Oppgave 1 Oljeleting a) Siden P(A
Fasit for tilleggsoppgaver
 Fasit for tilleggsoppgaver Uke 5 Oppgave: Gitt en rekke med observasjoner x i (i = 1,, 3,, n), definerer vi variansen til x i som gjennomsnittlig kvadratavvik fra gjennomsnittet, m.a.o. Var(x i ) = (x
Fasit for tilleggsoppgaver Uke 5 Oppgave: Gitt en rekke med observasjoner x i (i = 1,, 3,, n), definerer vi variansen til x i som gjennomsnittlig kvadratavvik fra gjennomsnittet, m.a.o. Var(x i ) = (x
Løsningsforslag til obligatorisk oppgave i ECON 2130
 Andreas Mhre April 15 Løsningsforslag til obligatorisk oppgave i ECON 13 Oppgave 1: E(XY) = E(X(Z X)) Setter inn Y = Z - X E(XY) = E(XZ X ) E(XY) = E(XZ) E(X ) E(XY) = - E(X ) X og Z er uavhengige, så
Andreas Mhre April 15 Løsningsforslag til obligatorisk oppgave i ECON 13 Oppgave 1: E(XY) = E(X(Z X)) Setter inn Y = Z - X E(XY) = E(XZ X ) E(XY) = E(XZ) E(X ) E(XY) = - E(X ) X og Z er uavhengige, så
Løsningsforslag til andre sett med obligatoriske oppgaver i STK1110 høsten 2010
 Løsningsforslag til andre sett med obligatoriske oppgaver i STK1110 høsten 2010 Oppgave 1 a Forventet antall dødsulykker i år i er E(X i λ i. Dermed er θ i λ i E(X i forventet antall dødsulykker per 100
Løsningsforslag til andre sett med obligatoriske oppgaver i STK1110 høsten 2010 Oppgave 1 a Forventet antall dødsulykker i år i er E(X i λ i. Dermed er θ i λ i E(X i forventet antall dødsulykker per 100
statistikk, våren 2011
 ÅMA110 Sannsynlighetsregning med statistikk, våren 011 Kp. 3 Diskrete tilfeldige variable 1 Diskrete tilfeldige variable, innledning Hva er en tilfeldig variabel (stokastisk variabel)? Diskret tilfeldig
ÅMA110 Sannsynlighetsregning med statistikk, våren 011 Kp. 3 Diskrete tilfeldige variable 1 Diskrete tilfeldige variable, innledning Hva er en tilfeldig variabel (stokastisk variabel)? Diskret tilfeldig
Temaartikkel. Statens pensjonsfond Norge, avkastningsutviklingen 1998 2008
 Temaartikkel Statens pensjonsfond Norge, avkastningsutviklingen 1998 2008 Denne temaartikkelen er hentet fra Folketrygdfondets årsrapport 2008 Haakon VIIs gate 2 Pb. 1845 Vika, 0123 Oslo Tlf: 23 11 72
Temaartikkel Statens pensjonsfond Norge, avkastningsutviklingen 1998 2008 Denne temaartikkelen er hentet fra Folketrygdfondets årsrapport 2008 Haakon VIIs gate 2 Pb. 1845 Vika, 0123 Oslo Tlf: 23 11 72
Forventning og varians.
 Forventning og varians. Dekkes av kapittel 4 i læreboka. Forventning (4.1) Forventningsverdi = gjennomsnitt i det lange løp. Defininsjon: Forventningsverdien til en stokastisk variabel X er: x xf(x),x
Forventning og varians. Dekkes av kapittel 4 i læreboka. Forventning (4.1) Forventningsverdi = gjennomsnitt i det lange løp. Defininsjon: Forventningsverdien til en stokastisk variabel X er: x xf(x),x
Løsningsforslag. n X. n X 1 i=1 (X i X) 2 og SY 2 = 1 ny S 2 X + S2 Y
 Statistiske metoder 1 høsten 004. Løsningsforslag Oppgave 1: a) Begge normalplottene gir punkter som ligger omtrent på ei rett linje så antagelsen om normalfordeling ser ut til å holde. Konfidensintervall
Statistiske metoder 1 høsten 004. Løsningsforslag Oppgave 1: a) Begge normalplottene gir punkter som ligger omtrent på ei rett linje så antagelsen om normalfordeling ser ut til å holde. Konfidensintervall
Ridge regresjon og lasso notat til STK2120
 Ridge regresjon og lasso notat til STK2120 Ørulf Borgan februar 2016 I dette notatet vil vi se litt nærmere på noen alternativer til minste kvadraters metode ved lineær regresjon. Metodene er særlig aktuelle
Ridge regresjon og lasso notat til STK2120 Ørulf Borgan februar 2016 I dette notatet vil vi se litt nærmere på noen alternativer til minste kvadraters metode ved lineær regresjon. Metodene er særlig aktuelle
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: STK2120 Statistiske metoder og dataanalyse 2. Eksamensdag: Fredag 7. juni 2013. Tid for eksamen: 14.30 18.30. Oppgavesettet er
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: STK2120 Statistiske metoder og dataanalyse 2. Eksamensdag: Fredag 7. juni 2013. Tid for eksamen: 14.30 18.30. Oppgavesettet er
Kapittel 3: Studieopplegg
 Oversikt over pensum Kapittel 1: Empirisk fordeling for en variabel o Begrepet fordeling o Mål for senter (gj.snitt, median) + persentiler/kvartiler o Mål for spredning (Standardavvik s, IQR) o Outliere
Oversikt over pensum Kapittel 1: Empirisk fordeling for en variabel o Begrepet fordeling o Mål for senter (gj.snitt, median) + persentiler/kvartiler o Mål for spredning (Standardavvik s, IQR) o Outliere
QED 5 10. Matematikk for grunnskolelærerutdanningen. Bind 2. Fasit kapittel 4 Statistikk og kvantitativ metode
 QED 5 10 Matematikk for grunnskolelærerutdanningen Bind 2 Fasit kapittel 4 Statistikk og kvantitativ metode Kapittel 4 Oppgave 1. La x være antall øyne på terningen. a) Vi får følgende sannsynlighetsfordeling
QED 5 10 Matematikk for grunnskolelærerutdanningen Bind 2 Fasit kapittel 4 Statistikk og kvantitativ metode Kapittel 4 Oppgave 1. La x være antall øyne på terningen. a) Vi får følgende sannsynlighetsfordeling
vekt. vol bruk
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: STK1110 Statistiske metoder og dataanalyse 1. Eksamensdag: 10. desember 2010. Tid for eksamen: 14.30 18.30. Oppgavesettet er
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: STK1110 Statistiske metoder og dataanalyse 1. Eksamensdag: 10. desember 2010. Tid for eksamen: 14.30 18.30. Oppgavesettet er
En tilnærmet sammenheng mellom rullerende tremånedersvekst og månedsvekst i Månedlig nasjonalregnskap
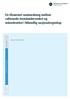 En tilnærmet sammenheng mellom rullerende tremånedersvekst og månedsvekst i Månedlig nasjonalregnskap Magnus Kvåle Helliesen NOTATER / DOCUMENTS 2019 / 23 I serien Notater publiseres dokumentasjon, metodebeskrivelser,
En tilnærmet sammenheng mellom rullerende tremånedersvekst og månedsvekst i Månedlig nasjonalregnskap Magnus Kvåle Helliesen NOTATER / DOCUMENTS 2019 / 23 I serien Notater publiseres dokumentasjon, metodebeskrivelser,
QED 1 7. Matematikk for grunnskolelærerutdanningen. Bind 2. Fasit kapittel 4 Statistikk og kvantitativ metode
 QED 1 7 Matematikk for grunnskolelærerutdanningen Bind 2 Fasit kapittel 4 Statistikk og kvantitativ metode Kapittel 4 Oppgave 1 La være antall øyne på terningen. a) Vi får følgende sannsynlighetsfordeling
QED 1 7 Matematikk for grunnskolelærerutdanningen Bind 2 Fasit kapittel 4 Statistikk og kvantitativ metode Kapittel 4 Oppgave 1 La være antall øyne på terningen. a) Vi får følgende sannsynlighetsfordeling
HØGSKOLEN I STAVANGER
 EKSAMEN I: MOT310 STATISTISKE METODER 1 VARIGHET: 4 TIMER DATO: 25. NOVEMBER 2003 TILLATTE HJELPEMIDLER: KALKULATOR, TABELLER OG FORMLER I STATISTIKK (TAPIR FORLAG) OPPGAVESETTET BESTÅR AV 3 OPPGAVER PÅ
EKSAMEN I: MOT310 STATISTISKE METODER 1 VARIGHET: 4 TIMER DATO: 25. NOVEMBER 2003 TILLATTE HJELPEMIDLER: KALKULATOR, TABELLER OG FORMLER I STATISTIKK (TAPIR FORLAG) OPPGAVESETTET BESTÅR AV 3 OPPGAVER PÅ
Oppgave N(0, 1) under H 0. S t n 3
 MOT310 Statistiske metoder 1, høsten 2011 Løsninger til regneøving nr 9 (s 1) Oppgave 1 Modell: Y i β 0 + β 1 x i + β 2 x 2 i + ε i der ε 1,, ε n uif N(0, σ 2 ) e) Y Xβ + ε der Y Y 1 Y n, X 1 x 1 x 2 1
MOT310 Statistiske metoder 1, høsten 2011 Løsninger til regneøving nr 9 (s 1) Oppgave 1 Modell: Y i β 0 + β 1 x i + β 2 x 2 i + ε i der ε 1,, ε n uif N(0, σ 2 ) e) Y Xβ + ε der Y Y 1 Y n, X 1 x 1 x 2 1
Gjør gjerne analysene under her selv, så blir dere mer fortrolige med utskriften fra Spss. Her har jeg sakset og klippet litt.
 Gjør gjerne analysene under her selv, så blir dere mer fortrolige med utskriften fra Spss. Her har jeg sakset og klippet litt. Data fra likelonn.sav og vi ser på variablene Salnow, Edlevel og Sex (hvor
Gjør gjerne analysene under her selv, så blir dere mer fortrolige med utskriften fra Spss. Her har jeg sakset og klippet litt. Data fra likelonn.sav og vi ser på variablene Salnow, Edlevel og Sex (hvor
Du skal besvare åtte av de tretten spørsmålene som er gitt nedenfor. a) Gi en kort beskrivelse av utsiktene for den norske pengepolitikken fremover.
 Skriftlig eksamen: BST 16121 Anvendt Makroøkonomi Eksamensdato: 11.12.2013 kl. 09.00-14.00 Totalt antall sider: 6 Tillatte hjelpemidler: BI-definert eksamenskalkulator TEXAS INSTRUMENTS BA II Plus Innføringsark:
Skriftlig eksamen: BST 16121 Anvendt Makroøkonomi Eksamensdato: 11.12.2013 kl. 09.00-14.00 Totalt antall sider: 6 Tillatte hjelpemidler: BI-definert eksamenskalkulator TEXAS INSTRUMENTS BA II Plus Innføringsark:
MOT310 Statistiske metoder 1, høsten 2006 Løsninger til regneøving nr. 8 (s. 1) Oppgaver fra boka:
 MOT30 Statistiske metoder, høsten 2006 Løsninger til regneøving nr. 8 (s. ) Oppgaver fra boka: Oppgave.5 (.3:5) ) Først om tolking av datautskriften. Sammendrag gir følgende informasjon: Multippel R =R,
MOT30 Statistiske metoder, høsten 2006 Løsninger til regneøving nr. 8 (s. ) Oppgaver fra boka: Oppgave.5 (.3:5) ) Først om tolking av datautskriften. Sammendrag gir følgende informasjon: Multippel R =R,
STK juni 2016
 Løsningsforslag til eksamen i STK220 3 juni 206 Oppgave a N i er binomisk fordelt og EN i np i, der n 204 Hvis H 0 er sann, er forventningen lik E i n 204/6 34 for i, 2,, 6 6 Hvis H 0 er sann er χ 2 6
Løsningsforslag til eksamen i STK220 3 juni 206 Oppgave a N i er binomisk fordelt og EN i np i, der n 204 Hvis H 0 er sann, er forventningen lik E i n 204/6 34 for i, 2,, 6 6 Hvis H 0 er sann er χ 2 6
TMA4240 Statistikk Høst 2009
 TMA4240 Statistikk Høst 2009 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer b6 Oppgave 1 Oppgave 11.5 fra læreboka. Oppgave 2 Oppgave 11.21 fra læreboka. Oppgave
TMA4240 Statistikk Høst 2009 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer b6 Oppgave 1 Oppgave 11.5 fra læreboka. Oppgave 2 Oppgave 11.21 fra læreboka. Oppgave
Generelt om sesongjustering
 Generelt om sesongjustering 1. Hva er sesongjustering?... 1 2. Prekorrigering... 3 2.1 Rådata... 3 2.2 Formål med prekorrigering... 3 2.3 Kalenderjusteringer... 3 2.4 Behandling av ekstreme verdier...
Generelt om sesongjustering 1. Hva er sesongjustering?... 1 2. Prekorrigering... 3 2.1 Rådata... 3 2.2 Formål med prekorrigering... 3 2.3 Kalenderjusteringer... 3 2.4 Behandling av ekstreme verdier...
Kap. 10: Løsningsforslag
 Kap. 10: Løsningsforslag 1 1.1 Markedets risikopremie (MP ) er definert som MP = (r m r f ). Ifølge oppsummeringen i læreboken (Strøm, 2017, side 199), er markedets risikopremie i området 5.0 8.0 prosent.
Kap. 10: Løsningsforslag 1 1.1 Markedets risikopremie (MP ) er definert som MP = (r m r f ). Ifølge oppsummeringen i læreboken (Strøm, 2017, side 199), er markedets risikopremie i området 5.0 8.0 prosent.
UNIVERSITETET I OSLO
 Deleksamen i: UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet STK1000 Innføring i anvendt statistikk. Eksamensdag: Onsdag 13. oktober 2010. Tid for eksamen: 15:00 17:00. Oppgavesettet
Deleksamen i: UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet STK1000 Innføring i anvendt statistikk. Eksamensdag: Onsdag 13. oktober 2010. Tid for eksamen: 15:00 17:00. Oppgavesettet
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: STK1110 Statistiske metoder og dataanalyse 1 Eksamensdag: Mandag 30. november 2015. Tid for eksamen: 14.30 18.00. Oppgavesettet
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: STK1110 Statistiske metoder og dataanalyse 1 Eksamensdag: Mandag 30. november 2015. Tid for eksamen: 14.30 18.00. Oppgavesettet
Statistikk og dataanalyse
 Njål Foldnes, Steffen Grønneberg og Gudmund Horn Hermansen Statistikk og dataanalyse En moderne innføring Kapitteloversikt del 1 INTRODUKSJON TIL STATISTIKK Kapittel 1 Populasjon og utvalg 19 Kapittel
Njål Foldnes, Steffen Grønneberg og Gudmund Horn Hermansen Statistikk og dataanalyse En moderne innføring Kapitteloversikt del 1 INTRODUKSJON TIL STATISTIKK Kapittel 1 Populasjon og utvalg 19 Kapittel
TMA4240 Statistikk Høst 2016
 TMA4240 Statistikk Høst 2016 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 12 Denne øvingen består av oppgaver om enkel lineær regresjon. De handler blant
TMA4240 Statistikk Høst 2016 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 12 Denne øvingen består av oppgaver om enkel lineær regresjon. De handler blant
Eksamensoppgåve i TMA4240 Statistikk
 Institutt for matematiske fag Eksamensoppgåve i TMA4240 Statistikk Fagleg kontakt under eksamen: Mette Langaas a, Ingelin Steinsland b, Geir-Arne Fuglstad c Tlf: a 988 47 649, b 926 63 096, c 452 70 806
Institutt for matematiske fag Eksamensoppgåve i TMA4240 Statistikk Fagleg kontakt under eksamen: Mette Langaas a, Ingelin Steinsland b, Geir-Arne Fuglstad c Tlf: a 988 47 649, b 926 63 096, c 452 70 806
HØGSKOLEN I STAVANGER
 EKSAMEN I: MOT0 STATISTISKE METODER VARIGHET: TIMER DATO:. NOVEMBER 00 TILLATTE HJELPEMIDLER: KALKULATOR, TABELLER OG FORMLER I STATISTIKK (TAPIR FORLAG) OPPGAVESETTET BESTÅR AV OPPGAVER PÅ 7 SIDER HØGSKOLEN
EKSAMEN I: MOT0 STATISTISKE METODER VARIGHET: TIMER DATO:. NOVEMBER 00 TILLATTE HJELPEMIDLER: KALKULATOR, TABELLER OG FORMLER I STATISTIKK (TAPIR FORLAG) OPPGAVESETTET BESTÅR AV OPPGAVER PÅ 7 SIDER HØGSKOLEN
ØVINGER 2017 Løsninger til oppgaver. Øving 1
 ØVINGER 017 Løsninger til oppgaver Øving 1.1. Frekvenstabell For å lage en frekvenstabell må vi telle antall observasjoner av hvert antall henvendelser. Siden antall henvendelser på en gitt dag alltid
ØVINGER 017 Løsninger til oppgaver Øving 1.1. Frekvenstabell For å lage en frekvenstabell må vi telle antall observasjoner av hvert antall henvendelser. Siden antall henvendelser på en gitt dag alltid
Beregning av trafikkvolum ved hjelp av basiskurvemetoden - En innføring
 Beregning av trafikkvolum ved hjelp av basiskurvemetoden - En innføring SAMBA/5/ Magne Aldrin Ola Haug Januar 2 NR Norsk Regnesentral ANVENDT DATAFORSKNING NR-notat/NR-Note Tittel/Title: Beregning av trafikkvolum
Beregning av trafikkvolum ved hjelp av basiskurvemetoden - En innføring SAMBA/5/ Magne Aldrin Ola Haug Januar 2 NR Norsk Regnesentral ANVENDT DATAFORSKNING NR-notat/NR-Note Tittel/Title: Beregning av trafikkvolum
Befolkning og velferd ECON 1730, H2016. Regresjonsanalyse
 Netto innfl. Befolkning og velferd ECON 1730, H2016 Regresjonsanalyse Problem: Gitt planer for 60 nye boliger i kommunen neste år, hvor mange innflyttere kan vi forvente? Tabell Vestby kommune Nye boliger
Netto innfl. Befolkning og velferd ECON 1730, H2016 Regresjonsanalyse Problem: Gitt planer for 60 nye boliger i kommunen neste år, hvor mange innflyttere kan vi forvente? Tabell Vestby kommune Nye boliger
Tillatte hjelpemidler: C3: alle typer kalkulator, alle andre hjelpemidler
 EKSAMENSOPPGAVER Institutt: Eksamen i: Tid: IKBM STAT100 Torsdag 13.des 2012 STATISTIKK 09.00-12.30 (3.5 timer) Emneansvarlig: Solve Sæbø ( 90065281) Tillatte hjelpemidler: C3: alle typer kalkulator, alle
EKSAMENSOPPGAVER Institutt: Eksamen i: Tid: IKBM STAT100 Torsdag 13.des 2012 STATISTIKK 09.00-12.30 (3.5 timer) Emneansvarlig: Solve Sæbø ( 90065281) Tillatte hjelpemidler: C3: alle typer kalkulator, alle
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 Eksamen: ECON2130 Statistikk 1 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamensdag: 29.05.2019 Sensur kunngjøres: 19.06.2019 Tid for eksamen: kl. 09:00 12:00 Oppgavesettet er på 5 sider Tillatte hjelpemidler:
Eksamen: ECON2130 Statistikk 1 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamensdag: 29.05.2019 Sensur kunngjøres: 19.06.2019 Tid for eksamen: kl. 09:00 12:00 Oppgavesettet er på 5 sider Tillatte hjelpemidler:
EKSAMEN I FAG TMA4260 INDUSTRIELL STATISTIKK
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 12 Faglig kontakt under eksamen: Bo Lindqvist Tlf. 975 89 418 EKSAMEN I FAG TMA4260 INDUSTRIELL STATISTIKK Onsdag
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 12 Faglig kontakt under eksamen: Bo Lindqvist Tlf. 975 89 418 EKSAMEN I FAG TMA4260 INDUSTRIELL STATISTIKK Onsdag
Eksamensoppgave i TMA4255 Anvendt statistikk
 Institutt for matematiske fag Eksamensoppgave i TMA4255 Anvendt statistikk Faglig kontakt under eksamen: Anna Marie Holand Tlf: 951 38 038 Eksamensdato: 30. mai 2014 Eksamenstid (fra til): 09:00-13:00
Institutt for matematiske fag Eksamensoppgave i TMA4255 Anvendt statistikk Faglig kontakt under eksamen: Anna Marie Holand Tlf: 951 38 038 Eksamensdato: 30. mai 2014 Eksamenstid (fra til): 09:00-13:00
Verdens statistikk-dag. Signifikanstester. Eksempel studentlån. http://unstats.un.org/unsd/wsd/
 Verdens statistikk-dag http://unstats.un.org/unsd/wsd/ Signifikanstester Ønsker å teste hypotese om populasjon Bruker data til å teste hypotese Typisk prosedyre Beregn sannsynlighet for utfall av observator
Verdens statistikk-dag http://unstats.un.org/unsd/wsd/ Signifikanstester Ønsker å teste hypotese om populasjon Bruker data til å teste hypotese Typisk prosedyre Beregn sannsynlighet for utfall av observator
Dato: Tirsdag 28. november 2006 Lengde på eksamen: 4 timer Tillatte hjelpemidler: Kun standard enkel kalkulator, HP 30S
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK130, Systemidentifikasjon Dato: Tirsdag 28. november 2006 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK130, Systemidentifikasjon Dato: Tirsdag 28. november 2006 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
Oppgave 1. a) Anlysetype: enveis variansanalyse (ANOVA). Modell for y ij = ekspedisjonstid nr. j for skrankeansatt nr. i:
 MOT310 tatistiske metoder 1 Løsningsforslag til eksamen høst 010, s 1 Oppgave 1 a) Anlysetype: enveis variansanalyse (ANOVA) Modell for y ij ekspedisjonstid nr j for skrankeansatt nr i: Y ij µ i + ε ij,
MOT310 tatistiske metoder 1 Løsningsforslag til eksamen høst 010, s 1 Oppgave 1 a) Anlysetype: enveis variansanalyse (ANOVA) Modell for y ij ekspedisjonstid nr j for skrankeansatt nr i: Y ij µ i + ε ij,
Kan vi stole på resultater fra «liten N»?
 Kan vi stole på resultater fra «liten N»? Olav M. Kvalheim Universitetet i Bergen Plan for dette foredraget Hypotesetesting og p-verdier for å undersøke en variabel p-verdier når det er mange variabler
Kan vi stole på resultater fra «liten N»? Olav M. Kvalheim Universitetet i Bergen Plan for dette foredraget Hypotesetesting og p-verdier for å undersøke en variabel p-verdier når det er mange variabler
EKSAMEN I TMA4240 Statistikk
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Faglig kontakt under eksamen: Henning Omre (909 37848) Mette Langaas (988 47649) EKSAMEN I TMA4240 Statistikk 18.
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Faglig kontakt under eksamen: Henning Omre (909 37848) Mette Langaas (988 47649) EKSAMEN I TMA4240 Statistikk 18.
EKSAMENSOPPGAVER STAT100 Vår 2011
 EKSAMENSOPPGAVER STAT100 Vår 2011 Løsningsforslag Oppgave 1 (Med referanse til Tabell 1) a) De 3 fiskene på 2 år hadde lengder på henholdsvis 48, 46 og 35 cm. Finn de manglende tallene i Tabell 1. Test
EKSAMENSOPPGAVER STAT100 Vår 2011 Løsningsforslag Oppgave 1 (Med referanse til Tabell 1) a) De 3 fiskene på 2 år hadde lengder på henholdsvis 48, 46 og 35 cm. Finn de manglende tallene i Tabell 1. Test
ting å gjøre å prøve å oppsummere informasjonen i Hva som er hensiktsmessig måter å beskrive dataene på en hensiktsmessig måte.
 Kapittel : Beskrivende statistikk Etter at vi har samlet inn data er en naturlig første ting å gjøre å prøve å oppsummere informasjonen i dataene på en hensiktsmessig måte. Hva som er hensiktsmessig måter
Kapittel : Beskrivende statistikk Etter at vi har samlet inn data er en naturlig første ting å gjøre å prøve å oppsummere informasjonen i dataene på en hensiktsmessig måte. Hva som er hensiktsmessig måter
Bruk data fra tabellen over (utvalget) og opplysninger som blir gitt i oppgavene og svar på følgende spørsmål:
 Frafall fra videregende skole (VGS) er et stort problem. Bare ca 70% av elevene som begynner p VGS fullfører og bestr i løpet av 5 r. For noen elever er skolen s lite attraktiv at de velger slutte før
Frafall fra videregende skole (VGS) er et stort problem. Bare ca 70% av elevene som begynner p VGS fullfører og bestr i løpet av 5 r. For noen elever er skolen s lite attraktiv at de velger slutte før
MOT310 Statistiske metoder 1, høsten 2011 Løsninger til regneøving nr. 7 (s. 1) Oppgaver fra boka: n + (x 0 x) 2 1. n + (x 0 x) 1 2 ) = 1 γ
 MOT310 Statistiske metoder 1, høsten 2011 Løsninger til regneøving nr. 7 (s. 1) Oppgaver fra boka: Oppgave 11.25 (11.27, 11.6:13) Modell: Y i = α + βx i + ε i der ε 1,..., ε n u.i.f. N(0, σ 2 ). Skal nne
MOT310 Statistiske metoder 1, høsten 2011 Løsninger til regneøving nr. 7 (s. 1) Oppgaver fra boka: Oppgave 11.25 (11.27, 11.6:13) Modell: Y i = α + βx i + ε i der ε 1,..., ε n u.i.f. N(0, σ 2 ). Skal nne
Kapittel 2: Hendelser
 Kapittel 2: Hendelser FENOMEN Eksperiment Utfall Utfallsrom Eksperiment. Utfall. Eksperiment Utfall Hendelse Sannsynlighet: egenskaper, gunstige vs. mulige, relativ frekvens Sannsynlighet for mer enn en
Kapittel 2: Hendelser FENOMEN Eksperiment Utfall Utfallsrom Eksperiment. Utfall. Eksperiment Utfall Hendelse Sannsynlighet: egenskaper, gunstige vs. mulige, relativ frekvens Sannsynlighet for mer enn en
Hvilke faktorer driver kursutviklingen på Oslo
 Hvilke faktorer driver kursutviklingen på Oslo Børs? Resultater for perioden 1980-2006 Randi Næs Norges Bank Johannes Skjeltorp Norges Bank Bernt Arne Ødegaard Handelshøyskolen BI og Norges Bank FIBE,
Hvilke faktorer driver kursutviklingen på Oslo Børs? Resultater for perioden 1980-2006 Randi Næs Norges Bank Johannes Skjeltorp Norges Bank Bernt Arne Ødegaard Handelshøyskolen BI og Norges Bank FIBE,
ÅMA110 Sannsynlighetsregning med statistikk, våren Kp. 3 Diskrete tilfeldige variable. Diskrete tilfeldige variable, varians (kp. 3.
 ÅMA Sannsynlighetsregning med statistikk, våren 8 Kp. Diskrete tilfeldige variable Kp. Diskrete tilfeldige variable Har sett på (tidligere: begrep/definisjoner; tilfeldig (stokastisk variabel sannsynlighetsfordeling
ÅMA Sannsynlighetsregning med statistikk, våren 8 Kp. Diskrete tilfeldige variable Kp. Diskrete tilfeldige variable Har sett på (tidligere: begrep/definisjoner; tilfeldig (stokastisk variabel sannsynlighetsfordeling
Løsningsforslag Eksamen S2, våren 2014 Laget av Tommy O. Sist oppdatert: 1. september 2018 Antall sider: 11
 Løsningsforslag Eksamen S, våren 014 Laget av Tommy O. Sist oppdatert: 1. september 018 Antall sider: 11 Finner du matematiske feil, skrivefeil, eller andre typer feil? Dette dokumentet er open-source,
Løsningsforslag Eksamen S, våren 014 Laget av Tommy O. Sist oppdatert: 1. september 018 Antall sider: 11 Finner du matematiske feil, skrivefeil, eller andre typer feil? Dette dokumentet er open-source,
betyr begivenheten at det blir trukket en rød kule i første trekning og en hvit i andre, mens B1 B2
 ECON30: EKSAMEN 06v SENSORVEILEDNING. Det anbefales at de 9 deloppgavene merket med A, B, teller likt uansett variasjon i vanskelighetsgrad. Svarene er gitt i
ECON30: EKSAMEN 06v SENSORVEILEDNING. Det anbefales at de 9 deloppgavene merket med A, B, teller likt uansett variasjon i vanskelighetsgrad. Svarene er gitt i
Eksamensoppgave i ST0103 Brukerkurs i statistikk
 Institutt for matematiske fag Eksamensoppgave i ST0103 Brukerkurs i statistikk Faglig kontakt under eksamen: Jarle Tufto Tlf: 99 70 55 19 Eksamensdato: 3. desember 2016 Eksamenstid (fra til): 09:00-13:00
Institutt for matematiske fag Eksamensoppgave i ST0103 Brukerkurs i statistikk Faglig kontakt under eksamen: Jarle Tufto Tlf: 99 70 55 19 Eksamensdato: 3. desember 2016 Eksamenstid (fra til): 09:00-13:00
Statistisk behandling av kalibreringsresultatene Del 3. v/ Rune Øverland, Trainor Elsikkerhet AS
 Statistisk behandling av kalibreringsresultatene Del 3. v/ Rune Øverland, Trainor Elsikkerhet AS Denne artikkelserien handler om statistisk behandling av kalibreringsresultatene. Denne artikkelen har kalibreringskurve
Statistisk behandling av kalibreringsresultatene Del 3. v/ Rune Øverland, Trainor Elsikkerhet AS Denne artikkelserien handler om statistisk behandling av kalibreringsresultatene. Denne artikkelen har kalibreringskurve
ST0202 Statistikk for samfunnsvitere
 ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag 2 Mål på beliggenhet (2.6) Kvartiler: Deler de ordnede dataene inn i fire like store deler: 1. kvartil Q 1 : 25% av dataene
ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag 2 Mål på beliggenhet (2.6) Kvartiler: Deler de ordnede dataene inn i fire like store deler: 1. kvartil Q 1 : 25% av dataene
TMA4245 Statistikk Eksamen desember 2016
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4245 Statistikk Eksamen desember 2016 Oppgave 1 Ei bedrift produserer elektriske komponentar. Komponentane kan ha to typar
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4245 Statistikk Eksamen desember 2016 Oppgave 1 Ei bedrift produserer elektriske komponentar. Komponentane kan ha to typar
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Underveiseksamen i: STK1000 Innføring i anvendt statistikk. Eksamensdag: Fredag 13.10.2006. Tid for eksamen: Kl. 09.00 11.00. Tillatte hjelpemidler:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Underveiseksamen i: STK1000 Innføring i anvendt statistikk. Eksamensdag: Fredag 13.10.2006. Tid for eksamen: Kl. 09.00 11.00. Tillatte hjelpemidler:
MOT 310 Statistiske metoder 1 Løsningsforslag til eksamen høst 2006, s. 1. Oppgave 1
 MOT 310 Statistiske metoder 1 Løsningsforslag til eksamen høst 2006, s. 1 Oppgave 1 a) Normalantakelse: Målingene x 1,..., x 21 og y 1,..., y 8 betraktes som utfall av tilfeldige variable X 1,..., X 21
MOT 310 Statistiske metoder 1 Løsningsforslag til eksamen høst 2006, s. 1 Oppgave 1 a) Normalantakelse: Målingene x 1,..., x 21 og y 1,..., y 8 betraktes som utfall av tilfeldige variable X 1,..., X 21
PSY2012 Forskningsmetodologi III: Statistisk analyse, design og måling Eksamen vår 2014
 Psykologisk institutt PSY2012 Forskningsmetodologi III: Statistisk analyse, design og måling Eksamen vår 2014 Skriftlig skoleeksamen fredag 2. mai, 09:00 (4 timer). Kalkulator uten grafisk display og tekstlagringsfunksjon
Psykologisk institutt PSY2012 Forskningsmetodologi III: Statistisk analyse, design og måling Eksamen vår 2014 Skriftlig skoleeksamen fredag 2. mai, 09:00 (4 timer). Kalkulator uten grafisk display og tekstlagringsfunksjon
Gruvedrift. Institutt for matematiske fag, NTNU. Notat for TMA4240/TMA4245 Statistikk
 Gruvedrift Notat for TMA/TMA Statistikk Institutt for matematiske fag, NTNU I forbindelse med planlegging av gruvedrift i et område er det mange hensyn som må tas når en skal vurdere om prosjektet er lønnsomt.
Gruvedrift Notat for TMA/TMA Statistikk Institutt for matematiske fag, NTNU I forbindelse med planlegging av gruvedrift i et område er det mange hensyn som må tas når en skal vurdere om prosjektet er lønnsomt.
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: STK1110 Løsningsforslag: Statistiske metoder og dataanalys Eksamensdag: Fredag 9. desember 2011 Tid for eksamen: 14.30 18.30
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: STK1110 Løsningsforslag: Statistiske metoder og dataanalys Eksamensdag: Fredag 9. desember 2011 Tid for eksamen: 14.30 18.30
