Litt GRUPPETEORI for Fys4170
|
|
|
- Snorre Hanssen
- 7 år siden
- Visninger:
Transkript
1 Litt GRUPPETEORI for Fys4170 GRUPPER: Ei gruppe G = {g i } er ei samling element med disse egenskapene: * multiplikasjon slik at g i g j G ; * et enhetselement g 0 = 1 slik at g i g 0 = g 0 g i = g i ; * g 1 g g 3 = g 1 g g 3 Assosiative lov * en invers g i 1 for alle g i G LIEGRUPPER I feltteori og partikkelfysikk har vi i hovedsak bruk for kontinuerlige grupper, kalt Lie-grupper. Ei Liegruppe er ei gruppe der elementa er en funksjon av kontinuerlige parametre: gα 1, α,..., α n, 1 der alle α i kan velges reelle. I feltteori og partikkelfysikk er de viktigste gruppene dvs. mengda av alle fasefaktorer, og U1 = { e iα ; α R }, SUn = { U = n n matrise n =, 3,.. ; U kl C, U U = 1, detu = 1 } 3 Her er R mengda av alle reelle tal, C er mengda av alle komplekse tal, og k, l løper fra 1 til n. Ei matrise U SUn har n komplekse, dvs. n reelle parametre. La oss betrakte matrisa M U U. Diagonalen har n element. Unitariteten, dvs. at M = 1, betyr at alle disse er lik 1. Det er derfor n n/ element over diagonalen. Unitariteten betyr at alle disse er lik 0 Da M = M er alle de n n/ elementa under diagonalen a priori gitt ved det komplekskonjugerte av sitt motstående element, dvs. for ledda under diagonalen får vi ingen nye likninger vilkår. Vi får derfor n n/ komplekse likninger, dvs n n reelle. Til slutt må vi utnytte kravet detu = 1. Fordi 1 = detm = detu U = detu detu = detu, 4 ser vi at detu må væra en fasefaktor, og at kravet detu = 1 bare gir ei ny likning. Dermed blir det: parametre i U SUn n n n n 1 = n 1 5 1
2 Lie- Algebra Gruppe-elementa i SUn kan skrives { U = exp i k α k L k }, 6 der α j ; j = 1,,..., n 1 er et sett av reelle parametre og generatorene L k = i U α k {α j =0} tilfredstiller en Lie-algebra sum over m er underforstått:, 7 [L k, L l ] = if klm L m, 8 der f klm er et sett av koeffisienter gruppas strukturkonstanter som er fullstendig antisymmetriske i indeksene klm. Dersom {L k } er et sett av generatorer for ei gruppe, kan vi få et nytt sett av generatorer {L k} -som altså også tilfredstiller Lie-algebraen i 8 ved hjelp av en similaritets-transformasjon: L k L k = S L k S 1, 9 der S er ei vilkårlig n n matrise med eksisterende invers. Da U = e A detu = e TrA, 10 får vi fra detu = 1 at for alle k = 1,,..., n 1. TrL k = 0, 11 Irredusible representasjoner For alle Lie-grupper vil en representasjon som kan transformeres til blokkdiagonal form ved en similaritets-transformasjon, dvs S U S 1 = U A 0 0 U B, 1 kalles redusibel. Fundamentalrepresentasjonene for SUn er irredusible, dvs de kan ikke transformeres til blokk-diagonal form. For SU er representasjonene tilsvarende s = 1/, 1, 3/,,... også kalt, 3, 4, 5,... irredusible. For SU3 er representasjonene 3, 6, 8, 10,... irredusible. Kontragrediente representasjoner La {M k } væra en reprentasjon av {L k }, slik at [M k, M l ] = if klm M m. For alle SUn grupper kan det vises at strukturkonstantene f klm er reelle, og
3 dermed vil også M k = Mk {U} og {U c } gitt ved tilfredstille Lie-algebraen. Representasjonene U = e iα k M k, U = e iα k M k = e iα k M k = U c 13 kalles innbyrdes kontragrediente. Det er et aksiom i partikkelfysikk at partikler og tilsvarende antipartikler transformerer etter innbyrdes kontragrediente representasjoner. For SU er de innbyrdes kontragrediente representasjonene ekvivalente -de er i verste fall relatert ved en similaritetstransformasjon. Gruppa SU: For U SU skriver vi U = a b c d ; a, b, c, d C. 14 For ei matrise definert ved 14 er den inverse gitt ved U 1 = 1 detu d b c a ; 15 der determinanten detu = ad bc. Kravet U U = 1 U 1 = U gir nå a b U = b a ; a + b = 1, 16 dvs. det er 3 uavhengige parametre i gruppa SU. I fundamentalrepresentasjonen av SU er L k = 1 σ k S 1/ k. 17 som svarer til spinn 1/. Høgere representasjoner s = 1, 3/,... har samme Lie-algebra [ s S k, S s ] l = i ǫklm S m s, 18 der ǫ klm er Levi-Civita tensoren. Men andre matriserelasjoner er forskjellige for forskjellig spinn,- for eksempel er σ k σ l = δ kl 1 + iǫ klm σ som impliserer σj = 1 for spinn 1/, mens Sj 3 = S j for spinn 1. Spinn 1 representasjonen av SU svarer til rotasjonsgruppa. Sammenhengen mellom SU og romlige rotasjoner Vi definerer S x σ dets = x 19 Determinanten finnes lett ved hjelp av standard-uttrykka for Paulimatrisene Vi lar så S transformere etter Uǫ SU : S S = USU. 0 3
4 Dermed blir S = x σ dets = x. 1 På den andre sida er dets = detu dets detu = detu dets = dets, slik at x = x 3 En rotasjon kan uttrykkes slik: x i x i = R ij x j. 4 Fra 19 og 1 og Trσ i σ j = δ ij finner vi da koeffisientene Dersom vi lar R ij = 1 Tr σ i Uσ j U. 5 U = exp i θ n σ = cosθ/ in σsinθ/, 6 representerer dette en rotasjon en vinkel θ omkring retninga n vi har n = 1. I dette tilfelle finner R ij = cosθ δ ij + 1 cosθ n i n j + sinθ ǫ ijk n k, 7 som er rotasjons-matrisa i tre romlige dimensjoner. Videre vil v χ σχ transformere som en vektor, dvs. og χ er en to-komponent spinor. v i v i = R ij v j når χ χ = Uχ 8 Lorentz-transformasjoner En Lorentz-transformasjon av en 4-vektor x µ = x 0, x er i analogi med 4 gitt ved x µ x µ = L µ ν x ν 9 der x x µ x µ = x µ x µ x L α µ L α ν = g µ ν L 1 µ ν = L ν µ 30 Lie-algebraen til Lorentz-gruppa er gitt ved [J k, J l ] = iǫ klm J m, [J k, K l ] = iǫ klm K m, [K k, K l ] = iǫ klm J m, 31 der J k er rotasjonsgeneratorene og K l er boost-generatorene. I Minkowskirepresentasjonen er rotasjons-generatorene i prinsippet 4x4 matriser, men med bare nuller for alle tidskomponentene komponenter der minst en indeks 4
5 er 0 og de vanlige 3x3 rotasjonsmatrisene i nedre høgre hjørne. For K x K 1 er K x 01 = K x 10 = i og resten av elementa lik 0. En rein boost langs enhetsvektoren e kan skrives der vi har brukt at L = e iψ e K = 1 i sinhψ e K coshψ 1e K 3 e K 3 = e K ; coshψ = 1 v /c 1/ 33 Sammenhengen mellom SLC og Lorentz-transformasjoner Gruppa SLC er definert ved SLC = {A = matrise ; A kl C, deta = 1} 34 Gruppa SLC forholder seg til Lorentz-gruppa på samme måte som SU forholder seg til rotasjonsgruppa. La der har vi definert T x µ σ µ dett = x µ x µ x, 35 σ µ = 1, σ og σ µ = 1, σ. 36 Vi lar så T transformere etter A SLC : T T = ATA. 37 Dermed blir T = x µσ µ dett = x. 38 På den andre sida er dett = deta dett deta = deta dett = dett, 39 slik at x = x. 40 Dermed finner vi analogt med 5 : L µ ν = 1 Tr σ µ Aσ ν A. 41 Videre vil v µ = χ σ µ χ transformere som en 4-vektor, dvs. v µ v µ = L µ ν v ν når χ χ = Aχ 4 og χ er en to-komponent spinor. I SLC-representasjonen er generatorene 5
6 gitt ved J = 1 σ og K = 1 i σ 43 En kan vise at en generell Lorentz-transformasjon kan skrives A = H U der H = H og U = U der H kan skrives analogt til U i 6: H = exp i iψ e σ = coshψ/ + e σsinhψ/ 45 Det er et poeng at matrisene i SLC er enklere å regne med enn 4 4 matrisene L i Minkowski-representasjonen. Dirac-representasjonen av Lorentz-gruppa Ved studiet av Lorentz-transformasjoner innafor Dirac-teori lønner det seg å bruke Kramer-Weyl representasjonen av Dirac-matrisene: γ µ = γ 0, γ = 0 σ µ σ µ 0 γ µ KW 46 Sammenhengen med den vanligst brukte Pauli-representasjonen er gitt ved γ µ KW = S 1 γ µ P S ; S = Transformasjonen for en Dirac-spinor Ψ er da gitt ved Ψ Ψ = ΛΨ ; Λ = A 0 0 A 1 48 Kramer-Weyl representasjonen kalles også chiral basis fordi høgre- og venstre- projeksjonene gitt ved Ψ R R Ψ, Ψ L L Ψ ; R γ 5, L 1 1 γ 5 49 har null for nedre og øvre to-komponent. Transformasjonen for Dirac-matrisene blir Λ 1 γ µ Λ = L µ ν γ ν 50 som impliserer tilsvarende relasjoner for A, σ µ, σ µ og L µ ν 6
Løsningsforslag til eksamen i FY8306 KVANTEFELTTEORI Fredag 9. juni 2006
 NTNU Side av 3 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i FY836 KVANTEFELTTEORI Fredag 9. juni 6 Dette løsningsforslaget er på 3 sider, pluss et vedlegg
NTNU Side av 3 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i FY836 KVANTEFELTTEORI Fredag 9. juni 6 Dette løsningsforslaget er på 3 sider, pluss et vedlegg
Eksamen i fag FY8104 Symmetri i fysikken Fredag 7. desember 2007 Tid:
 Side 1 av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 51 72) Sensurfrist: Lørdag 22. desember
Side 1 av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 51 72) Sensurfrist: Lørdag 22. desember
Eksamen i fag RELATIVISTISK KVANTEMEKANIKK Fredag 26. mai 2000 Tid: 09:00 14:00
 Side 1 av 3 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Navn: Kåre Olaussen Telefon: 9 36 52 Eksamen i fag 74327 RELATIVISTISK KVANTEMEKANIKK Fredag
Side 1 av 3 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Navn: Kåre Olaussen Telefon: 9 36 52 Eksamen i fag 74327 RELATIVISTISK KVANTEMEKANIKK Fredag
Løysingsforslag (Skisse) Eksamen FY3452 Gravitasjon og Kosmologi Våren 2007
 Løysingsforslag (Skisse) Eksamen FY3452 Gravitasjon og Kosmologi Våren 2007 May 24, 2007 Oppgave 1 a) Lorentztransformasjonane er x = γ(x V t), t = γ(t V x), der γ = 1/ 1 V 2 Vi tar differensiala av desse
Løysingsforslag (Skisse) Eksamen FY3452 Gravitasjon og Kosmologi Våren 2007 May 24, 2007 Oppgave 1 a) Lorentztransformasjonane er x = γ(x V t), t = γ(t V x), der γ = 1/ 1 V 2 Vi tar differensiala av desse
KORT INTRODUKSJON TIL TENSORER
 KORT INTRODUKSJON TIL TENSORER Tensorer har vi allerede møtt i form av skalarer (tall) og vektorer. En skalar kan betraktes som en tensor av rang null (en komponent), mens en vektor er en tensor av rang
KORT INTRODUKSJON TIL TENSORER Tensorer har vi allerede møtt i form av skalarer (tall) og vektorer. En skalar kan betraktes som en tensor av rang null (en komponent), mens en vektor er en tensor av rang
Eksamen TFY 4210 Kvanteteorien for mangepartikkelsystem, våren 2012
 NTNU Fakultet for Naturvitskap og Teknologi Institutt for fysikk Eksamen TFY 4210 Kvanteteorien for mangepartikkelsystem, våren 2012 Faglærar: Førsteamanuensis John Ove Fjærestad Institutt for fysikk Telefon:
NTNU Fakultet for Naturvitskap og Teknologi Institutt for fysikk Eksamen TFY 4210 Kvanteteorien for mangepartikkelsystem, våren 2012 Faglærar: Førsteamanuensis John Ove Fjærestad Institutt for fysikk Telefon:
Oppgaver MAT2500. Fredrik Meyer. 29. august 2014
 Oppgaver MAT500 Fredrik Meyer 9. august 04 Oppgave. Bruk cosinus-setningen til å se at definisjonen av vinkel i planet blir riktig. Løsning. Dette er en litt rar oppgave. Husk at cosinus-setningen sier
Oppgaver MAT500 Fredrik Meyer 9. august 04 Oppgave. Bruk cosinus-setningen til å se at definisjonen av vinkel i planet blir riktig. Løsning. Dette er en litt rar oppgave. Husk at cosinus-setningen sier
Eksamen FY8104 Symmetri i fysikken Fredag 7. desember 2007 Løsninger
 Eksamen FY8104 Symmetri i fysikken Fredag 7. desember 007 Løsninger 1a En konjugasjonskasse i SO(3 består av ae rotasjoner med en gitt rotasjonsvinke α og vikårig rotasjonsakse. En konjugasjonskasse i
Eksamen FY8104 Symmetri i fysikken Fredag 7. desember 007 Løsninger 1a En konjugasjonskasse i SO(3 består av ae rotasjoner med en gitt rotasjonsvinke α og vikårig rotasjonsakse. En konjugasjonskasse i
Løsningsforslag øving 6
 Løsningsforslag øving 6 7 Husk Teorem 79 i notatet: En delmengde U av et vektorrom V er et underrom hvis ) nullvektoren er i U, ) summen av to vektorer i U er i U igjen, og 3) et skalarmultiplum av en
Løsningsforslag øving 6 7 Husk Teorem 79 i notatet: En delmengde U av et vektorrom V er et underrom hvis ) nullvektoren er i U, ) summen av to vektorer i U er i U igjen, og 3) et skalarmultiplum av en
Forelesningsnotater SIF8039/ Grafisk databehandling
 Forelesningsnotater SIF839/ Grafisk databehandling Notater til forelesninger over: Kapittel 4: Geometric Objects and ransformations i: Edward Angel: Interactive Computer Graphics Vårsemesteret 22 orbjørn
Forelesningsnotater SIF839/ Grafisk databehandling Notater til forelesninger over: Kapittel 4: Geometric Objects and ransformations i: Edward Angel: Interactive Computer Graphics Vårsemesteret 22 orbjørn
Universitet i Bergen. Eksamen i emnet MAT121 - Lineær algebra
 Universitet i Bergen Det matematisk-naturvitenskapelige fakultet Bokmål Eksamen i emnet MAT2 - Lineær algebra Onsdag 29 mai, 20, kl. 09.00-4.00 Tillatte hjelpemidler. kalkulator, i samsvar med fakultetets
Universitet i Bergen Det matematisk-naturvitenskapelige fakultet Bokmål Eksamen i emnet MAT2 - Lineær algebra Onsdag 29 mai, 20, kl. 09.00-4.00 Tillatte hjelpemidler. kalkulator, i samsvar med fakultetets
MAT Grublegruppen Notat 11
 MAT1100 - Grublegruppen Notat 11 Jørgen O. Lye Matrisegrupper Den store gruppen vi skal se på er GL(n, K) = {inverterbare n n matriser med koesienter i K} Forkortelsen står for den generelle lineære gruppen
MAT1100 - Grublegruppen Notat 11 Jørgen O. Lye Matrisegrupper Den store gruppen vi skal se på er GL(n, K) = {inverterbare n n matriser med koesienter i K} Forkortelsen står for den generelle lineære gruppen
5.8 Iterative estimater på egenverdier
 5.8 Iterative estimater på egenverdier Det finnes ingen eksplisitt formel for beregning av egenverdiene til en kvadratisk matrise. Iterative metoder som finner (ofte) en (meget god) approksimasjon til
5.8 Iterative estimater på egenverdier Det finnes ingen eksplisitt formel for beregning av egenverdiene til en kvadratisk matrise. Iterative metoder som finner (ofte) en (meget god) approksimasjon til
Løsningsforslag til eksamen i FY3404/FY8307 RELATIVISTISK KVANTEMEKANIKK Fredag 9. juni 2006
 NTNU Side 1 av 4 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i FY3404/FY8307 RELATIVISTISK KVANTEMEKANIKK Fredag 9. juni 2006 Dette løsningsforslaget
NTNU Side 1 av 4 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i FY3404/FY8307 RELATIVISTISK KVANTEMEKANIKK Fredag 9. juni 2006 Dette løsningsforslaget
En rekke av definisjoner i algebra
 En rekke av definisjoner i algebra Martin Strand, martin.strand@math.ntnu.no 11. november 2010 Definisjonene som er gitt her, kommer i MA2201 Algebra og MA3201 Ringer og moduler. Forhåpentligvis blir det
En rekke av definisjoner i algebra Martin Strand, martin.strand@math.ntnu.no 11. november 2010 Definisjonene som er gitt her, kommer i MA2201 Algebra og MA3201 Ringer og moduler. Forhåpentligvis blir det
EKSAMEN I FY2045 KVANTEFYSIKK Onsdag 30. mai 2007 kl
 NORSK TEKST Side av 3 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 97355 EKSAMEN I FY45 KVANTEFYSIKK Onsdag 3.
NORSK TEKST Side av 3 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 97355 EKSAMEN I FY45 KVANTEFYSIKK Onsdag 3.
Eksamen i FY8306 KVANTEFELTTEORI Fredag 9. juni :00 13:00
 NTNU Side av 3 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: 9 36 52 eller 45 43 7 70 Eksamen i FY8306 KVANTEFELTTEORI Fredag 9. juni 2006 09:00 3:00 Tillatte hjelpemidler:
NTNU Side av 3 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: 9 36 52 eller 45 43 7 70 Eksamen i FY8306 KVANTEFELTTEORI Fredag 9. juni 2006 09:00 3:00 Tillatte hjelpemidler:
Karakterer. Kapittel Homomorfier av grupper. 8.2 Representasjoner
 Kapittel 8 Karakterer 8. Homomorfier av grupper I forrige kapittel definerte vi begrepet abstrakt gruppe, som en abstrakt versjon av begrepet symmetrigruppe. For å studere forbindelsen mellom abstrakte
Kapittel 8 Karakterer 8. Homomorfier av grupper I forrige kapittel definerte vi begrepet abstrakt gruppe, som en abstrakt versjon av begrepet symmetrigruppe. For å studere forbindelsen mellom abstrakte
Lineær algebra. H. Fausk 09.03.2015. i=1 a ix i. Her har vi oppgitt hva ledd nummer i skal være og hvilke indekser i vi summerer over.
 Lineær algebra H. Fausk 09.03.2015 Første utkast Linære likningsystem lar seg løse ved bruk av de elementære regneartene. Selv om løsningen av lineære likingsystem i prinsippet er elementært blir det fort
Lineær algebra H. Fausk 09.03.2015 Første utkast Linære likningsystem lar seg løse ved bruk av de elementære regneartene. Selv om løsningen av lineære likingsystem i prinsippet er elementært blir det fort
Løsningsforslag for FYS2140 Kvantefysikk, Mandag 3. juni 2019
 Løsningsforslag for FYS210 Kvantefysikk, Mandag 3. juni 201 Oppgave 1: Stern-Gerlach-eksperimentet og atomet Stern-Gerlach-eksperimentet fra 122 var ment å teste Bohrs atommodell om at angulærmomentet
Løsningsforslag for FYS210 Kvantefysikk, Mandag 3. juni 201 Oppgave 1: Stern-Gerlach-eksperimentet og atomet Stern-Gerlach-eksperimentet fra 122 var ment å teste Bohrs atommodell om at angulærmomentet
Oppgave 1 (25 %) - Flervalgsoppgaver
 Oppgaver og løsningsforslag for 4t eksamen 10.mai 006 i LO510D Lineær algebra med grafiske anvendelser. Fra og med oppgave skal alle svar begrunnes. Oppgave 1 (5 %) - Flervalgsoppgaver Denne oppgaven består
Oppgaver og løsningsforslag for 4t eksamen 10.mai 006 i LO510D Lineær algebra med grafiske anvendelser. Fra og med oppgave skal alle svar begrunnes. Oppgave 1 (5 %) - Flervalgsoppgaver Denne oppgaven består
Løsningsforslag øving 7
 Løsningsforslag øving 7 8 Husk at en funksjon er injektiv dersom x y gir f(x) f(y), men her ser vi at f(3) 9 f( 3), eller generelt at f(z) z f( z) for alle z C, som betyr at f ikke er injektiv Vi ser også
Løsningsforslag øving 7 8 Husk at en funksjon er injektiv dersom x y gir f(x) f(y), men her ser vi at f(3) 9 f( 3), eller generelt at f(z) z f( z) for alle z C, som betyr at f ikke er injektiv Vi ser også
TMA4110 Eksamen høsten 2018 EKSEMPEL 1 Løsning Side 1 av 8. Løsningsforslag. Vi setter opp totalmatrisen og gausseliminerer: x 1 7x 4 = 0
 TMA4 Eksamen høsten 28 EKSEMPEL Løsning Side av 8 Løsningsforslag Oppgave Vi setter opp totalmatrisen og gausseliminerer: 2 2 2 4 2 6 2 4 2 6 2 2 Dette gir likningene og 2 2 4 2 6 7 2. x 7x 4 = x 2 + 2x
TMA4 Eksamen høsten 28 EKSEMPEL Løsning Side av 8 Løsningsforslag Oppgave Vi setter opp totalmatrisen og gausseliminerer: 2 2 2 4 2 6 2 4 2 6 2 2 Dette gir likningene og 2 2 4 2 6 7 2. x 7x 4 = x 2 + 2x
FY2045/TFY4250 Kvantemekanikk I, løsning øving 10 1 LØSNING ØVING 10
 FY45/TFY45 Kvntemeknikk I, løsning øving LØSNING ØVING Løsning oppgve Spinn. D åde χ + og χ i likhet med lle ndre spinorer er egentilstnder til enhetsmtrisen med egenverdi lik, hr vi Videre finner vi t
FY45/TFY45 Kvntemeknikk I, løsning øving LØSNING ØVING Løsning oppgve Spinn. D åde χ + og χ i likhet med lle ndre spinorer er egentilstnder til enhetsmtrisen med egenverdi lik, hr vi Videre finner vi t
7.4 Singulærverdi dekomposisjonen
 7.4 Singulærverdi dekomposisjonen Singulærverdi dekomposisjon til en matrise A er en av de viktigste faktoriseringene av A (dvs. A skrives som et produkt av matriser). Den inneholder nyttig informasjon
7.4 Singulærverdi dekomposisjonen Singulærverdi dekomposisjon til en matrise A er en av de viktigste faktoriseringene av A (dvs. A skrives som et produkt av matriser). Den inneholder nyttig informasjon
Eksamen i fag FY8104 Symmetri i fysikken Fredag 7. desember 2007 Tid:
 Side 1 av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 51 72) Sensurfrist: Lørdag 22. desember
Side 1 av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 51 72) Sensurfrist: Lørdag 22. desember
A.3.e: Ortogonale egenfunksjonssett
 TFY4250/FY2045 Tillegg 2 1 Tillegg 2: A.3.e: Ortogonale egenfunksjonssett Ikke-degenererte egenverdier La oss først anta at en operator ˆF har et diskret og ikke-degeneret spektrum. Det siste betyr at
TFY4250/FY2045 Tillegg 2 1 Tillegg 2: A.3.e: Ortogonale egenfunksjonssett Ikke-degenererte egenverdier La oss først anta at en operator ˆF har et diskret og ikke-degeneret spektrum. Det siste betyr at
Vær OBS på at svarene på mange av oppgavene kan skrives på flere ulike måter!
 Vær OBS på at svarene på mange av oppgavene kan skrives på flere ulike måter! Oppgave.. a x y = x + y = r r r +r r x y = y fri x y = y fri Vi får én fri variabel, og løsningens har følgelig dimensjon.
Vær OBS på at svarene på mange av oppgavene kan skrives på flere ulike måter! Oppgave.. a x y = x + y = r r r +r r x y = y fri x y = y fri Vi får én fri variabel, og løsningens har følgelig dimensjon.
MAT1120 Notat 2 Tillegg til avsnitt 5.4
 MAT1120 Notat 2 Tillegg til avsnitt 54 Dette notatet utfyller bokas avsnitt 54 om matriserepresentasjonen (også kalt koordinatmatrisen) til en lineær avbildning mellom to endeligdimensjonale vektorrom
MAT1120 Notat 2 Tillegg til avsnitt 54 Dette notatet utfyller bokas avsnitt 54 om matriserepresentasjonen (også kalt koordinatmatrisen) til en lineær avbildning mellom to endeligdimensjonale vektorrom
Geometri på ikke-kommutative algebraer
 Geometri på ikke-kommutative algebraer Ski og matematikk 2011 Rondablikk Arne B. Sletsjøe Universitetet i Oslo January 4, 2012 Algebraiske varieteter k = k (f.eks. C), S = k[x 1,..., x n ] Affint algebraisk
Geometri på ikke-kommutative algebraer Ski og matematikk 2011 Rondablikk Arne B. Sletsjøe Universitetet i Oslo January 4, 2012 Algebraiske varieteter k = k (f.eks. C), S = k[x 1,..., x n ] Affint algebraisk
4.1 Vektorrom og underrom
 4.1 Vektorrom og underrom Vektorrom er en abstraksjon av R n. De kan brukes til å utlede egenskaper, resultater og metoder for tilsynelatende svært ulike klasser av objekter : n-tupler, følger, funksjoner,
4.1 Vektorrom og underrom Vektorrom er en abstraksjon av R n. De kan brukes til å utlede egenskaper, resultater og metoder for tilsynelatende svært ulike klasser av objekter : n-tupler, følger, funksjoner,
Løsninger for eksamen i MAT Lineær algebra og M102 - Lineær algebra, fredag 28. mai 2004, Oppgave 1. M s = = 1 2 (cofm 2) T.
 Løsninger for eksamen i MAT - Lineær algebra og M - Lineær algebra, fredag 8. mai 4, (a) Finn determinanten til matrisen M s = Oppgave s uttrykt ved s, og bruk dette til å avgjøre for hvilke s matrisen
Løsninger for eksamen i MAT - Lineær algebra og M - Lineær algebra, fredag 8. mai 4, (a) Finn determinanten til matrisen M s = Oppgave s uttrykt ved s, og bruk dette til å avgjøre for hvilke s matrisen
En partikkel med masse m befinner seg i et éndimensjonalt, asymmetrisk brønnpotensial
 NORSK TEKST Side av 5 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tel. 7 59 8 67, eller 9755 EKSAMEN I TFY45 ATOM- OG MOLEKYLFYSIKK
NORSK TEKST Side av 5 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tel. 7 59 8 67, eller 9755 EKSAMEN I TFY45 ATOM- OG MOLEKYLFYSIKK
Oppgave 14 til 9. desember: I polynomiringen K[x, y] i de to variable x og y over kroppen K definerer vi undermengdene:
![Oppgave 14 til 9. desember: I polynomiringen K[x, y] i de to variable x og y over kroppen K definerer vi undermengdene: Oppgave 14 til 9. desember: I polynomiringen K[x, y] i de to variable x og y over kroppen K definerer vi undermengdene:](/thumbs/64/52216522.jpg) HJEMMEOPPGAVER utgave av 8-12-2002): Oppgave 15 til 16 desember: La H være mengden av alle matriser på formen A = a 1 a 12 a 13 a 1n 0 a 2 0 0 0 0 a 3 0 0 0 a n der a 1 a 2 a n 0 Videre la SH være matrisene
HJEMMEOPPGAVER utgave av 8-12-2002): Oppgave 15 til 16 desember: La H være mengden av alle matriser på formen A = a 1 a 12 a 13 a 1n 0 a 2 0 0 0 0 a 3 0 0 0 a n der a 1 a 2 a n 0 Videre la SH være matrisene
Eksamen i fag FY1004 Innføring i kvantemekanikk Fredag 30. mai 2008 Tid: a 0 = 4πǫ 0 h 2 /(e 2 m e ) = 5, m
 Side av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 5 7 Sensurfrist: Fredag 0 juni 008 Eksamen
Side av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 5 7 Sensurfrist: Fredag 0 juni 008 Eksamen
MAT1120 Notat 2 Tillegg til avsnitt 5.4
 MAT1120 Notat 2 Tillegg til avsnitt 54 Dette notatet utfyller bokas avsnitt 54 om matriserepresentasjoner (også kalt koordinatmatriser) av lineære avbildninger mellom endeligdimensjonale vektorrom En slik
MAT1120 Notat 2 Tillegg til avsnitt 54 Dette notatet utfyller bokas avsnitt 54 om matriserepresentasjoner (også kalt koordinatmatriser) av lineære avbildninger mellom endeligdimensjonale vektorrom En slik
1 Gauss-Jordan metode
 Merknad I dette Kompendiet er det gitt referanser både til læreboka og til selve Kompendiet Hvordan å gjenkjenne dem? Referansene til boka er 3- tallede, som Eks 3 Vi kan også referere til 22, kap 22 eller
Merknad I dette Kompendiet er det gitt referanser både til læreboka og til selve Kompendiet Hvordan å gjenkjenne dem? Referansene til boka er 3- tallede, som Eks 3 Vi kan også referere til 22, kap 22 eller
NORMALFORDELINGER, KOVARIANSMATRISER OG ELLIPSOIDER
 NORMALFORDELINGER, KOVARIANSMATRISER OG ELLIPSOIDER SIE 3080 STOKASTISKE OG ADAPTIVE SYSTEMER Oddvar Hallingstad 0. februar 00 Vi skal her utlede noen nyttige formler for arbeidet med kovariansmatriser
NORMALFORDELINGER, KOVARIANSMATRISER OG ELLIPSOIDER SIE 3080 STOKASTISKE OG ADAPTIVE SYSTEMER Oddvar Hallingstad 0. februar 00 Vi skal her utlede noen nyttige formler for arbeidet med kovariansmatriser
FY2045 Kvantefysikk Løsningsforslag Eksamen 2. juni 2008
 Eksamen FY045. juni 008 - løsningsforslag Oppgave FY045 Kvantefysikk øsningsforslag Eksamen. juni 008 a. Fra den tidsuavhengige Schrödingerligningen, [ h ] m x + V x ψx Eψx, finner vi at den relative krumningen
Eksamen FY045. juni 008 - løsningsforslag Oppgave FY045 Kvantefysikk øsningsforslag Eksamen. juni 008 a. Fra den tidsuavhengige Schrödingerligningen, [ h ] m x + V x ψx Eψx, finner vi at den relative krumningen
Mer om kvadratiske matriser
 Kapittel 2 Mer om kvadratiske matriser Vi lader opp til anvendelser, og skal bli enda bedre kjent med matriser. I mange anvendelser er det ofte de kvadratiske matrisene som dukker opp, så fra nå skal vi
Kapittel 2 Mer om kvadratiske matriser Vi lader opp til anvendelser, og skal bli enda bedre kjent med matriser. I mange anvendelser er det ofte de kvadratiske matrisene som dukker opp, så fra nå skal vi
En samling av mer eller mindre relevante formler (uten nærmere forklaring) er gitt til slutt i oppgavesettet.
 Norges teknisk-naturvitenskapelige universitet NTNU Institutt for fysikk Lade EKSAMEN I: MNF FY 44 KVANTEMEKANIKK I DATO: Tirsdag 4. desember 999 TID: 9.00 5.00 Antall vekttall: 4 Antall sider: 3 Sensurdato:
Norges teknisk-naturvitenskapelige universitet NTNU Institutt for fysikk Lade EKSAMEN I: MNF FY 44 KVANTEMEKANIKK I DATO: Tirsdag 4. desember 999 TID: 9.00 5.00 Antall vekttall: 4 Antall sider: 3 Sensurdato:
Mer om kvadratiske matriser
 Kapittel 2 Mer om kvadratiske matriser Vi lader opp til anvendelser, og skal bli enda bedre kjent med matriser. I mange anvendelser er det ofte de kvadratiske matrisene som dukker opp, så fra nå skal vi
Kapittel 2 Mer om kvadratiske matriser Vi lader opp til anvendelser, og skal bli enda bedre kjent med matriser. I mange anvendelser er det ofte de kvadratiske matrisene som dukker opp, så fra nå skal vi
a) Matrisen I uv T har egenverdier 1, med multiplisitet n 1 og 1 v T u, med multiplisitet 1. Derfor er matrisen inverterbar når v T u 1.
 Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Oppgave 1 a) Matrisen I uv T har egenverdier 1, med multiplisitet n 1 og 1 v T u, med multiplisitet 1. Derfor er
Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Oppgave 1 a) Matrisen I uv T har egenverdier 1, med multiplisitet n 1 og 1 v T u, med multiplisitet 1. Derfor er
Dagens mål. Det matematiske fundamentet til den diskrete Fourier-transformen Supplement til forelesning 8 INF Digital bildebehandling
 Dagens mål Det matematiske fundamentet til den diskrete Fourier-transformen Supplement til forelesning 8 IF2310 - Digital bildebehandling Ole Marius Hoel Rindal, slides av Andreas Kleppe Dagens mål Forstå
Dagens mål Det matematiske fundamentet til den diskrete Fourier-transformen Supplement til forelesning 8 IF2310 - Digital bildebehandling Ole Marius Hoel Rindal, slides av Andreas Kleppe Dagens mål Forstå
Til enhver m n matrise A kan vi knytte et tall, rangen til A, som gir viktig informasjon.
 4.6 Rang Til enhver m n matrise A kan vi knytte et tall, rangen til A, som gir viktig informasjon. Definisjon: Rangen til en m n matrise A betegnes med rank A og er definert som dimensjonen til kolonnerommet
4.6 Rang Til enhver m n matrise A kan vi knytte et tall, rangen til A, som gir viktig informasjon. Definisjon: Rangen til en m n matrise A betegnes med rank A og er definert som dimensjonen til kolonnerommet
=,,,,, = det( A) a a a a a a a a a a + a a 0 1. a11 a12 a22 a12 a11 a22 a12 a21 a11a12 + a12 a11
 3.3 Oppgaver 3.3.1 1 2 3 1 2 3 2 0 1.La A,,,,, 3 4 B 2 1 C 0 1 a -1 b 1 c 2 Regn ut (a) A a, (b) B b, (c) C c, (d) A B, (e) A B C ( a) ( c) ( e) ( f ) 1-2 2 1 2 + ( 2) ( 1) 4 A a 3 4 1 3 2 + 4 ( 1 ( b)
3.3 Oppgaver 3.3.1 1 2 3 1 2 3 2 0 1.La A,,,,, 3 4 B 2 1 C 0 1 a -1 b 1 c 2 Regn ut (a) A a, (b) B b, (c) C c, (d) A B, (e) A B C ( a) ( c) ( e) ( f ) 1-2 2 1 2 + ( 2) ( 1) 4 A a 3 4 1 3 2 + 4 ( 1 ( b)
Pensum i lineæralgebra inneholder disse punktene.
 Pensum i lineæralgebra inneholder disse punktene. 1) Løsning av lineære ligningssystem. Finne løsning hvis den fins og også avgjøre om løsning ikke fins. Entydig, flertydig løsning. 2) Overføre en matrise
Pensum i lineæralgebra inneholder disse punktene. 1) Løsning av lineære ligningssystem. Finne løsning hvis den fins og også avgjøre om løsning ikke fins. Entydig, flertydig løsning. 2) Overføre en matrise
EKSAMEN I TMA4285 TIDSREKKJEMODELLAR Fredag 7. desember 2012 Tid: 09:00 13:00
 Noregs teknisk naturvitskaplege universitet Institutt for matematiske fag Side 1 av 8 Nynorsk Fagleg kontakt under eksamen: John Tyssedal 73593534/41645376 EKSAMEN I TMA4285 TIDSREKKJEMODELLAR Fredag 7.
Noregs teknisk naturvitskaplege universitet Institutt for matematiske fag Side 1 av 8 Nynorsk Fagleg kontakt under eksamen: John Tyssedal 73593534/41645376 EKSAMEN I TMA4285 TIDSREKKJEMODELLAR Fredag 7.
Eksamen i Klassisk feltteori, fag TFY 4270 Onsdag 26. mai 2004 Løsninger
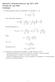 Eksamen i Klassisk feltteori, fag TFY 470 Onsdag 6. mai 004 Løsninger 1a) Sammenhengen mellom koordinattiden t og egentiden τ er at Den relativistiske impulsen er Hamiltonfunksjonen er Siden har vi at
Eksamen i Klassisk feltteori, fag TFY 470 Onsdag 6. mai 004 Løsninger 1a) Sammenhengen mellom koordinattiden t og egentiden τ er at Den relativistiske impulsen er Hamiltonfunksjonen er Siden har vi at
Egenverdier og egenvektorer
 Kapittel 9 Egenverdier og egenvektorer Det er ofte hensiktsmessig å tenke på en matrise ikke bare som en tabell med tall, men som en transformasjon av vektorer Hvis A er en m n-matrise, så gir A en transformasjon
Kapittel 9 Egenverdier og egenvektorer Det er ofte hensiktsmessig å tenke på en matrise ikke bare som en tabell med tall, men som en transformasjon av vektorer Hvis A er en m n-matrise, så gir A en transformasjon
Fasit eksamen Fys1000 vår 2009
 Fasit eksamen Fys1000 vår 2009 Oppgave 1 a) Klossen A er påvirka av tre krefter: 1) Tyngda m A g som peker loddrett nedover. Denne er det lurt å dekomponere i en komponent m A g sinθ langs skråplanet nedover
Fasit eksamen Fys1000 vår 2009 Oppgave 1 a) Klossen A er påvirka av tre krefter: 1) Tyngda m A g som peker loddrett nedover. Denne er det lurt å dekomponere i en komponent m A g sinθ langs skråplanet nedover
Universitet i Bergen. Eksamen i emnet MAT121 - Lineær algebra
 Universitet i Bergen Det matematisk-naturvitenskapelige fakultet Bokmål Eksamen i emnet MAT - Lineær algebra Onsdag 5 september, 0, kl. 09.00-4.00 Tillatte hjelpemidler. kalkulator, i samsvar med fakultetets
Universitet i Bergen Det matematisk-naturvitenskapelige fakultet Bokmål Eksamen i emnet MAT - Lineær algebra Onsdag 5 september, 0, kl. 09.00-4.00 Tillatte hjelpemidler. kalkulator, i samsvar med fakultetets
UNIVERSITET I BERGEN
 UNIVERSITET I BERGEN Det matematisk-naturvitenskapelige fakultet BOKMÅL Løsningsforslag eksamen MAT - Lineær algebra H Med forbehold om skrivefeil. Oppgave. Betrakt A = 6 5, b = 6 b (a) (b) Finn den reduserte
UNIVERSITET I BERGEN Det matematisk-naturvitenskapelige fakultet BOKMÅL Løsningsforslag eksamen MAT - Lineær algebra H Med forbehold om skrivefeil. Oppgave. Betrakt A = 6 5, b = 6 b (a) (b) Finn den reduserte
4.1 Vektorrom og underrom
 4.1 Vektorrom og underrom Vektorrom er en abstraksjon av R n. De kan brukes til å utlede egenskaper, resultater og metoder for tilsynelatende svært ulike klasser av objekter : n-tupler, følger, funksjoner,
4.1 Vektorrom og underrom Vektorrom er en abstraksjon av R n. De kan brukes til å utlede egenskaper, resultater og metoder for tilsynelatende svært ulike klasser av objekter : n-tupler, følger, funksjoner,
Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
 Norges teknisk naturvitenskapelige universitet NTNU Side 1 av 9 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
Norges teknisk naturvitenskapelige universitet NTNU Side 1 av 9 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
Kap. 5 Egenverdier og egenvektorer
 Kap. 5 Egenverdier og egenvektorer Egenverdier, egenvektorer og diagonaliserbarhet er sentrale begreper for kvadratiske matriser. Mye er kjent fra tidligere, skal repetere dette og gå videre. Sammenhengen
Kap. 5 Egenverdier og egenvektorer Egenverdier, egenvektorer og diagonaliserbarhet er sentrale begreper for kvadratiske matriser. Mye er kjent fra tidligere, skal repetere dette og gå videre. Sammenhengen
Løsning til øving 17 for FY1004, våren 2008
 Løsning til øving 17 for FY1004, våren 2008 Her skal vi se på hvordan spinnet egenspinnet til et elektron påvirkes av et konstant magnetfelt B Merk: Det korrekte navnet på B er magnetisk flukstetthet,
Løsning til øving 17 for FY1004, våren 2008 Her skal vi se på hvordan spinnet egenspinnet til et elektron påvirkes av et konstant magnetfelt B Merk: Det korrekte navnet på B er magnetisk flukstetthet,
OPPGAVER FOR FORUM
 OPPGAVER FOR FORUM 2006-2007 MERK!: Du skal først skrive hele oppgaveteksten for hver oppgave, og deretter svaret på oppgaven. Hvert svar skal være detajert, og skrevet i et klart og tydelig matematisk
OPPGAVER FOR FORUM 2006-2007 MERK!: Du skal først skrive hele oppgaveteksten for hver oppgave, og deretter svaret på oppgaven. Hvert svar skal være detajert, og skrevet i et klart og tydelig matematisk
Exam in FY3464 QUANTUM FIELD THEORY I Friday november 30th, :00 13:00
 NTNU Page 1 of 4 Institutt for fysikk Contact during the exam: Professor Kåre Olaussen Telephone: 9 36 52 or 45 43 71 70 Exam in FY3464 QUANTUM FIELD THEORY I Friday november 30th, 2007 09:00 13:00 Allowed
NTNU Page 1 of 4 Institutt for fysikk Contact during the exam: Professor Kåre Olaussen Telephone: 9 36 52 or 45 43 71 70 Exam in FY3464 QUANTUM FIELD THEORY I Friday november 30th, 2007 09:00 13:00 Allowed
j=1 (Y ij Ȳ ) 2 kan skrives som SST = i=1 (J i 1) frihetsgrader.
 FORMELSAMLING TIL STK2120 (Versjon av 30. mai 2012) 1 Enveis variansanalyse Anta at Y ij = µ + α i + ɛ ij ; j = 1, 2,..., J i ; i = 1, 2,..., I ; der ɛ ij -ene er uavhengige og N(0, σ 2 )-fordelte. Da
FORMELSAMLING TIL STK2120 (Versjon av 30. mai 2012) 1 Enveis variansanalyse Anta at Y ij = µ + α i + ɛ ij ; j = 1, 2,..., J i ; i = 1, 2,..., I ; der ɛ ij -ene er uavhengige og N(0, σ 2 )-fordelte. Da
DAFE ELFE Matematikk 1000 HIOA Obligatorisk innlevering 3 Innleveringsfrist Torsdag 26. mars 2015 Antall oppgaver: 10 + 3
 Innlevering DAFE ELFE Matematikk HIOA Obligatorisk innlevering 3 Innleveringsfrist Torsdag 26. mars 2 Antall oppgaver: + 3 For hver av matrisene nedenfor nn den ekvivalente matrisen som er på redusert
Innlevering DAFE ELFE Matematikk HIOA Obligatorisk innlevering 3 Innleveringsfrist Torsdag 26. mars 2 Antall oppgaver: + 3 For hver av matrisene nedenfor nn den ekvivalente matrisen som er på redusert
EKSAMEN I TMA4285 TIDSREKKEMODELLER Fredag 7. desember 2012 Tid: 09:00 13:00
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 8 Bokmål Faglig kontakt under eksamen: John Tyssedal 73593534/41645376 EKSAMEN I TMA4285 TIDSREKKEMODELLER Fredag
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 8 Bokmål Faglig kontakt under eksamen: John Tyssedal 73593534/41645376 EKSAMEN I TMA4285 TIDSREKKEMODELLER Fredag
EKSAMEN I FY2045 KVANTEFYSIKK Mandag 2. juni 2008 kl
 NORSK TEKST Side av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 9702355 EKSAMEN I FY2045 KVANTEFYSIKK Mandag
NORSK TEKST Side av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 9702355 EKSAMEN I FY2045 KVANTEFYSIKK Mandag
Lineærtransformasjoner
 Kapittel 8 Lineærtransformasjoner I forrige kapittel begynte vi å formulere lineær algebra på en generell måte, ved å gi en abstrakt definisjon av vektorrom For å beskrive sammenhenger mellom forskjellige
Kapittel 8 Lineærtransformasjoner I forrige kapittel begynte vi å formulere lineær algebra på en generell måte, ved å gi en abstrakt definisjon av vektorrom For å beskrive sammenhenger mellom forskjellige
OBLIG 2 - MAT 1120 Høsten 2005
 > with(linearalgebra): with(linalg):with(plots): Warning, the name GramSchmidt has been rebound Warning, the protected names norm and trace have been redefined and unprotected Warning, the name changecoords
> with(linearalgebra): with(linalg):with(plots): Warning, the name GramSchmidt has been rebound Warning, the protected names norm and trace have been redefined and unprotected Warning, the name changecoords
12 Diagonalisering av matriser og operatorer (Ch. 5.1, 5.2 og 8.5)
 Diagonalisering av matriser og operatorer (Ch 5, 5 og 85) Motivasjon Det er veldig viktig å kunne beregne funksjonsverdier f (A) for kvadratiske matriser A I kalkulus (teori av differensiallikninger) er
Diagonalisering av matriser og operatorer (Ch 5, 5 og 85) Motivasjon Det er veldig viktig å kunne beregne funksjonsverdier f (A) for kvadratiske matriser A I kalkulus (teori av differensiallikninger) er
Komplekse tall. Kapittel 2. Den imaginære enheten. Operasjoner på komplekse tall
 Kapittel Komplekse tall Oppfinnelsen av nye tallsystemer henger gjerne sammen med polynomligninger x + 4 0 har ingen positiv løsning, selv om koeffisientene er positive tall Vi må altså inn med negative
Kapittel Komplekse tall Oppfinnelsen av nye tallsystemer henger gjerne sammen med polynomligninger x + 4 0 har ingen positiv løsning, selv om koeffisientene er positive tall Vi må altså inn med negative
Vi viser denne ekvivalensen ved å vise begge implikasjoner. " "Anta at G virker trofast på X og anta at g, h G er slik at gx = hx for alle
 TMA4150 Algebra Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Seksjon 16 2 Fasit: G 1 = {ρ 0, δ 2 } = G 3 = G P1 = G P3 G S1 = {ρ 0, µ 1 } = G S3 G m1 = {ρ 0, ρ 2, µ 1, µ
TMA4150 Algebra Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Seksjon 16 2 Fasit: G 1 = {ρ 0, δ 2 } = G 3 = G P1 = G P3 G S1 = {ρ 0, µ 1 } = G S3 G m1 = {ρ 0, ρ 2, µ 1, µ
MAUMAT644 ALGEBRA vår 2016 Første samling Runar Ile
 MAUMAT644 ALGEBRA vår 2016 Første samling Runar Ile 1 Introduksjon: Grupper og ringer Ringer En ring er et sted hvor du kan addere, subtrahere og multiplisere. Hvis du også kan dividere kalles ringen for
MAUMAT644 ALGEBRA vår 2016 Første samling Runar Ile 1 Introduksjon: Grupper og ringer Ringer En ring er et sted hvor du kan addere, subtrahere og multiplisere. Hvis du også kan dividere kalles ringen for
Løsningsforslag til eksamen i FY3404 RELATIVISTISK KVANTEMEKANIKK Tirsdag 30. november 2004
 NTNU Side av 7 Institutt for fysikk Løsningsforslag til eksamen i FY30 RELATIVISTISK KVANTEMEKANIKK Tirsdag 30. november 200 Dette løsningsforslaget er på 7 sider. Oppgave. Prosesser i QED Tegn, i de tilfeller
NTNU Side av 7 Institutt for fysikk Løsningsforslag til eksamen i FY30 RELATIVISTISK KVANTEMEKANIKK Tirsdag 30. november 200 Dette løsningsforslaget er på 7 sider. Oppgave. Prosesser i QED Tegn, i de tilfeller
TMA4110 Matematikk 3 Eksamen høsten 2018 Løsning Side 1 av 9. Løsningsforslag. Vi setter opp totalmatrisen og gausseliminerer:
 TMA4 Matematikk 3 Eksamen høsten 8 Løsning Side av 9 Løsningsforslag Oppgave Vi setter opp totalmatrisen og gausseliminerer: 8 5 4 8 3 36 8 4 8 8 8 Den siste matrisen her er på redusert trappeform, og
TMA4 Matematikk 3 Eksamen høsten 8 Løsning Side av 9 Løsningsforslag Oppgave Vi setter opp totalmatrisen og gausseliminerer: 8 5 4 8 3 36 8 4 8 8 8 Den siste matrisen her er på redusert trappeform, og
Eksamensoppgave i TMA4110/TMA4115 Calculus 3
 Institutt for matematiske fag Eksamensoppgave i TMA4110/TMA4115 Calculus 3 Faglig kontakt under eksamen: Markus Szymik Tlf: 411 16 793 Eksamensdato: August 2018 Eksamenstid (fra til): 09:00 13:00 Hjelpemiddelkode/Tillatte
Institutt for matematiske fag Eksamensoppgave i TMA4110/TMA4115 Calculus 3 Faglig kontakt under eksamen: Markus Szymik Tlf: 411 16 793 Eksamensdato: August 2018 Eksamenstid (fra til): 09:00 13:00 Hjelpemiddelkode/Tillatte
Oppgaver MAT2500 høst 2011
 Oppgaver MAT2500 høst 2011 31. oktober 2011 Oppgaver avsnitt 1 Oppgave 1. Bruk cosinussetningen til å se at definisjonen av vinkel i planet blir riktig. Oppgave 2. Vis at d(x, y) = 0 hvis og bare hvis
Oppgaver MAT2500 høst 2011 31. oktober 2011 Oppgaver avsnitt 1 Oppgave 1. Bruk cosinussetningen til å se at definisjonen av vinkel i planet blir riktig. Oppgave 2. Vis at d(x, y) = 0 hvis og bare hvis
Oppgavesett. Kapittel Oppgavesett 1
 Kapittel 9 Oppgavesett Dette kapitlet består av fire oppgavesett med oppgaver fra alle deler av kompendiet. 9. Oppgavesett Oppgave. Et dynamisk system er gitt ved x n+ = M x n der M er -matrisen.6.. M
Kapittel 9 Oppgavesett Dette kapitlet består av fire oppgavesett med oppgaver fra alle deler av kompendiet. 9. Oppgavesett Oppgave. Et dynamisk system er gitt ved x n+ = M x n der M er -matrisen.6.. M
Diagonalisering. Kapittel 10
 Kapittel Diagonalisering I te kapitlet skal vi anvende vår kunnskap om egenverdier og egenvektorer til å analysere matriser og deres tilsvarende lineærtransformasjoner Eksempel Vi begynner med et eksempel
Kapittel Diagonalisering I te kapitlet skal vi anvende vår kunnskap om egenverdier og egenvektorer til å analysere matriser og deres tilsvarende lineærtransformasjoner Eksempel Vi begynner med et eksempel
Midtsemesterprøve i FY3403 PARTIKKELFYSIKK Onsdag 22. oktober :15 16:00
 NTNU Side 1 av 6 Institutt for fysikk Midtsemesterprøve i FY3403 PARTIKKELFYSIKK Onsdag 22. oktober 2008 14:15 16:00 Tillatte hjelpemidler: Vanlig kalkulator Husk å skrive studentnummeret ditt på hvert
NTNU Side 1 av 6 Institutt for fysikk Midtsemesterprøve i FY3403 PARTIKKELFYSIKK Onsdag 22. oktober 2008 14:15 16:00 Tillatte hjelpemidler: Vanlig kalkulator Husk å skrive studentnummeret ditt på hvert
Løsningsforslag for FYS2140 Kvantemekanikk, Tirsdag 29. mai 2018
 Løsningsforslag for FYS40 Kvantemekanikk, Tirsdag 9. mai 08 Oppgave : Fotoelektrisk effekt Millikan utførte følgende eksperiment: En metallplate ble bestrålt med monokromatisk lys. De utsendte fotoelektronene
Løsningsforslag for FYS40 Kvantemekanikk, Tirsdag 9. mai 08 Oppgave : Fotoelektrisk effekt Millikan utførte følgende eksperiment: En metallplate ble bestrålt med monokromatisk lys. De utsendte fotoelektronene
Lineær algebra. 0.1 Vektorrom
 Lineær algebra Siden dette temaet er alt for stort til å kunne gjennomgås på en halvtime, med alle de teoremene og denisjonene som skal til, har jeg laget dette notatet. Det bygger hovedsakelig på notatene
Lineær algebra Siden dette temaet er alt for stort til å kunne gjennomgås på en halvtime, med alle de teoremene og denisjonene som skal til, har jeg laget dette notatet. Det bygger hovedsakelig på notatene
Løsning til øving 23 for FY1004, våren 2008
 Løsning til øving 23 for FY1004, våren 2008 Diracs δ-funksjon kan defineres ved at δ(x) = 0 for x 0, og dx δ(x) = 1. Vi vil bruke δ-funksjonen som et potensial for en partikkel i en dimensjon. Vi setter
Løsning til øving 23 for FY1004, våren 2008 Diracs δ-funksjon kan defineres ved at δ(x) = 0 for x 0, og dx δ(x) = 1. Vi vil bruke δ-funksjonen som et potensial for en partikkel i en dimensjon. Vi setter
I dette kapittelet skal vi studerer noen matematiske objekter som kalles matriser. Disse kan blant annet brukes for å løse lineære likningssystemer.
 Kapittel 2 Matriser I dette kapittelet skal vi studerer noen matematiske objekter som kalles matriser. Disse kan blant annet brukes for å løse lineære likningssystemer. 2.1 Definisjoner og regneoperasjoner
Kapittel 2 Matriser I dette kapittelet skal vi studerer noen matematiske objekter som kalles matriser. Disse kan blant annet brukes for å løse lineære likningssystemer. 2.1 Definisjoner og regneoperasjoner
Obligatorisk innleveringsoppgave, løsning Lineær algebra, Våren 2006
 Obligatorisk innleveringsoppgave, løsning Lineær algebra, Våren 006 Oppgave I hele oppgaven bruker vi I = 0 0 0 0. 0 0 a) Matrisen A har størrelse og B har størrelse slik at matriseproduktet A B er en
Obligatorisk innleveringsoppgave, løsning Lineær algebra, Våren 006 Oppgave I hele oppgaven bruker vi I = 0 0 0 0. 0 0 a) Matrisen A har størrelse og B har størrelse slik at matriseproduktet A B er en
MAT Grublegruppen Notat 9
 MAT1100 - Grublegruppen Notat 9 Jørgen O. Lye Gruppeteori Oppvarmingseksempel La oss som vanlig ta en historisk vinkling. En klassisk måte grupper (som jeg straks skal denere) oppstod er gjennom å lete
MAT1100 - Grublegruppen Notat 9 Jørgen O. Lye Gruppeteori Oppvarmingseksempel La oss som vanlig ta en historisk vinkling. En klassisk måte grupper (som jeg straks skal denere) oppstod er gjennom å lete
Repetisjon: Om avsn og kap. 3 i Lay
 Repetisjon: Om avsn. 2.1-2.4 og kap. 3 i Lay Matrisemultiplikasjon. La A = [a ij ] være en m n matrise og B = [b kl ] være en n p matrise. ] Skriv B = [b 1 b 2 b p. Produktet AB er m p matrisen definert
Repetisjon: Om avsn. 2.1-2.4 og kap. 3 i Lay Matrisemultiplikasjon. La A = [a ij ] være en m n matrise og B = [b kl ] være en n p matrise. ] Skriv B = [b 1 b 2 b p. Produktet AB er m p matrisen definert
NORSK TEKST Side 1 av 4. Faglig kontakt under eksamen: Ingjald Øverbø, tlf , eller
 NORSK TEKST Side av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 972355 EKSAMEN I FY245/TFY425 KVANTEMEKANIKK
NORSK TEKST Side av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 972355 EKSAMEN I FY245/TFY425 KVANTEMEKANIKK
Løysingsframlegg/skisse Eksamen TFY 4210 Kvanteteorien for mangepartikkelsystem 24. mai 2011
 Løysingsframlegg/skisse Eksamen TFY 4210 Kvanteteorien for mangepartikkelsystem 24. mai 2011 May 24, 2011 Oppgave 1 1) Ein global fasetransformasjon er på forma ψ ψe iα ψ ψ e iα, (1) der α er ein konstant.
Løysingsframlegg/skisse Eksamen TFY 4210 Kvanteteorien for mangepartikkelsystem 24. mai 2011 May 24, 2011 Oppgave 1 1) Ein global fasetransformasjon er på forma ψ ψe iα ψ ψ e iα, (1) der α er ein konstant.
Siden vi her har brukt første momentet i fordelingen (EX = EX 1 ) til å konstruere estimatoren kalles denne metoden for momentmetoden.
 Estimeringsmetoder Momentmetoden La X, X 2,..., X n være uavhengige variable som er rektangulært fordelte på intervallet [0, θ]. Vi vet da at forventningsverdiene til hver observasjon og forventningen
Estimeringsmetoder Momentmetoden La X, X 2,..., X n være uavhengige variable som er rektangulært fordelte på intervallet [0, θ]. Vi vet da at forventningsverdiene til hver observasjon og forventningen
13 Oppsummering til Ch. 5.1, 5.2 og 8.5
 3 Oppsummering til Ch. 5. 5. og 8.5 3. Motivasjon Det er veldig viktig å kunne beregne funksjonsverdier f (A) for kvadratiske matriser A. I kalkulus (teori av differensiallikninger) er det viktig å beregne
3 Oppsummering til Ch. 5. 5. og 8.5 3. Motivasjon Det er veldig viktig å kunne beregne funksjonsverdier f (A) for kvadratiske matriser A. I kalkulus (teori av differensiallikninger) er det viktig å beregne
Løsningsforslag Eksamen 1. desember 2008 TFY4250 Atom- og molekylfysikk/fy2045 Kvantefysikk
 Eksamen TFY45/FY45. desember 8 - løsningsforslag Løsningsforslag Eksamen. desember 8 TFY45 Atom- og molekylfysikk/fy45 Kvantefysikk Oppgave a. For x og E = E B < har den tidsuavhengige Schrödingerligningen
Eksamen TFY45/FY45. desember 8 - løsningsforslag Løsningsforslag Eksamen. desember 8 TFY45 Atom- og molekylfysikk/fy45 Kvantefysikk Oppgave a. For x og E = E B < har den tidsuavhengige Schrödingerligningen
Lineære likningssystemer
 Lineære likningssystemer Mange fysiske problemer kan formuleres som lineære likningssystemer i vektorrommet, 1/19 Lu = f Lineær: betyr at virkningen av L på u + v er L(u + v) = Lu + Lv, og skaleres som
Lineære likningssystemer Mange fysiske problemer kan formuleres som lineære likningssystemer i vektorrommet, 1/19 Lu = f Lineær: betyr at virkningen av L på u + v er L(u + v) = Lu + Lv, og skaleres som
FY2045/TFY4250 Kvantemekanikk I, øving 10 1 ØVING 10
 FY45/TFY45 Kvntemeknikk I, - øving ØVING Mesteprten v denne øvingen går ut på å gjøre seg kjent med spinn, men øvingen inneholder også en oppgve om koherente tilstnder. Denne er en fortsettelse v oppgve
FY45/TFY45 Kvntemeknikk I, - øving ØVING Mesteprten v denne øvingen går ut på å gjøre seg kjent med spinn, men øvingen inneholder også en oppgve om koherente tilstnder. Denne er en fortsettelse v oppgve
UNIVERSITETET I OSLO
 Side av 5 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK Eksamensdag: Onsdag. juni 2 Tid for eksamen: Kl. 9-3 Oppgavesettet er på 5 sider + formelark Tillatte hjelpemidler:
Side av 5 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK Eksamensdag: Onsdag. juni 2 Tid for eksamen: Kl. 9-3 Oppgavesettet er på 5 sider + formelark Tillatte hjelpemidler:
Transformasjoner av stokastiske variabler
 Transformasjoner av stokastiske variabler Notasjon merkelapper på fordelingene Sannsynlighetstettheten og den kumulative fordelingen til en stokastisk variabel X betegnes hhv. f X og F X. Indeksen er altså
Transformasjoner av stokastiske variabler Notasjon merkelapper på fordelingene Sannsynlighetstettheten og den kumulative fordelingen til en stokastisk variabel X betegnes hhv. f X og F X. Indeksen er altså
Lineær algebra-oppsummering
 Kapittel 9 Lineær algebra-oppsummering Matriser 1 Matriser er et rektangulært sett av elementer ordnet i rekker og kolonner: a 11 a 12 a 1n a 21 a 22 a 2n A = = [a ij m n a m1 a n2 a mn 2 Kvadratisk matrise:
Kapittel 9 Lineær algebra-oppsummering Matriser 1 Matriser er et rektangulært sett av elementer ordnet i rekker og kolonner: a 11 a 12 a 1n a 21 a 22 a 2n A = = [a ij m n a m1 a n2 a mn 2 Kvadratisk matrise:
Løsningsforslag for FYS2140 Kvantemekanikk, Torsdag 16. august 2018
 Løsningsforslag for FYS140 Kvantemekanikk, Torsdag 16. august 018 Oppgave 1: Materiens bølgeegenskaper a) De Broglie fikk Nobelprisen i 199 for sin hypotese. Beskriv med noen setninger hva den går ut på.
Løsningsforslag for FYS140 Kvantemekanikk, Torsdag 16. august 018 Oppgave 1: Materiens bølgeegenskaper a) De Broglie fikk Nobelprisen i 199 for sin hypotese. Beskriv med noen setninger hva den går ut på.
LO118D Forelesning 5 (DM)
 LO118D Forelesning 5 (DM) Relasjoner 03.09.2007 1 Relasjoner 2 Ekvivalensrelasjoner 3 Matriser av relasjoner 4 Relasjonsdatabaser Relasjon Relasjoner er en generalisering av funksjoner En relasjon er en
LO118D Forelesning 5 (DM) Relasjoner 03.09.2007 1 Relasjoner 2 Ekvivalensrelasjoner 3 Matriser av relasjoner 4 Relasjonsdatabaser Relasjon Relasjoner er en generalisering av funksjoner En relasjon er en
Repetisjon: om avsn og kap. 3 i Lay
 Repetisjon: om avsn. 2.1-2.4 og kap. 3 i Lay Matrisemultiplikasjon La A = [a ij ] være en m n matrise og B = [b kl ] være en n p matrise. ] Skriv B = [b 1 b 2 b p der b j -ene er i R n for hver j. Produktet
Repetisjon: om avsn. 2.1-2.4 og kap. 3 i Lay Matrisemultiplikasjon La A = [a ij ] være en m n matrise og B = [b kl ] være en n p matrise. ] Skriv B = [b 1 b 2 b p der b j -ene er i R n for hver j. Produktet
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT 1120 Lineær algebra Eksamensdag: 9. desember 2014. Tid for eksamen: 14.30 18.30. Oppgavesettet er på 6 sider. Vedlegg: Tillatte
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT 1120 Lineær algebra Eksamensdag: 9. desember 2014. Tid for eksamen: 14.30 18.30. Oppgavesettet er på 6 sider. Vedlegg: Tillatte
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS14, Kvantefysikk Eksamensdag: 17. august 17 4 timer Lovlige hjelpemidler: Rottmann: Matematisk formelsamling, Øgrim og Lian:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS14, Kvantefysikk Eksamensdag: 17. august 17 4 timer Lovlige hjelpemidler: Rottmann: Matematisk formelsamling, Øgrim og Lian:
MAUMAT644 ALGEBRA vår 2016 Fjerde samling Runar Ile
 MAUMAT644 ALGEBRA vår 2016 Fjerde samling Runar Ile 1 Kroppsutvidelser og geometriske konstruksjoner 1.1 Hva har kroppsutvidelser med geometriproblemer å gjøre? Avsnitt 29: Kroppsutvidelser Stoff: Utvidelseskropper
MAUMAT644 ALGEBRA vår 2016 Fjerde samling Runar Ile 1 Kroppsutvidelser og geometriske konstruksjoner 1.1 Hva har kroppsutvidelser med geometriproblemer å gjøre? Avsnitt 29: Kroppsutvidelser Stoff: Utvidelseskropper
Felt i naturen, skalar- og vektorfelt, skalering
 Kapittel 1 Felt i naturen, skalar- og vektorfelt, skalering Oppgave 1 To vektorer u og v er parallelle hvis vi kan skrive u = cv, der c er en skalar. 2a 1 6 b = c 1 4 b 3a a2+3c+b 16 14 c = 0. Dette gir
Kapittel 1 Felt i naturen, skalar- og vektorfelt, skalering Oppgave 1 To vektorer u og v er parallelle hvis vi kan skrive u = cv, der c er en skalar. 2a 1 6 b = c 1 4 b 3a a2+3c+b 16 14 c = 0. Dette gir
