3D-overflatemodellering basert på stereoskopiske bilder
|
|
|
- Elling Enoksen
- 8 år siden
- Visninger:
Transkript
1 3D-overflatemodellering basert på stereoskopiske bilder Thomas Thorsen Røren Master i elektronikk Innlevert: Juli 2012 Hovedveileder: Lise Lyngsnes Randeberg, IET Medveileder: Lukasz Paluchowski, IET Norges teknisk-naturvitenskapelige universitet Institutt for elektronikk og telekommunikasjon
2
3 Oppgavetekst Oppgaven går ut å danne en protype 3D-modell av stereoskopiske bilder for anvendelse ved dybdeestimering og visualisering av sår i hud. Det er en føring for oppgaven at man ønsker en protypemodell som visuelt gjengir mest mulig nøyaktig det aktuelle avbildningsobjektet som skal modelleres. Oppløsningen for dybdeforskjellene i modellen bør maksimalt være 1,5 mm. Prosesseringstid er ikke relevant ved implementering av prototypemodellen på dette stadiet av prosjektet, men bør være av en rimelig karakter for testing og videre undersøkelser.
4
5 Abstract The goal of this project has been to develop a prototype 3D model based on stereoscopic images. The purpose is to model chronic ulcers for visualization and depth estimation of the wounds. The model can be used for area and volume calculations of the wounds which will give valuable diagnostic information. The stereo images were subject to geometrical calibration, image rectification and image matching to conduct the modeling. The challenges of these procedures were related to the image matching and the height resolution in the model. Image matching can be improved by preprocessing the stereo images to enhance the contrast, and the height resolution can be increased by changing the hardware used in the project. As a continuation of this project the 3D model will be combined with hyperspectral imaging to also give spectral information in the wound.
6 Sammendrag Prosjektet har omhandlet utvikling av en prototype 3D-modell som er basert på stereoskopiske bilder. Hensikten er å modellere kroniske hudsår for visualisering og dybdeestimering av sårene. Modelleringen vil kunne brukes til areal- og volumberegninger av sårene som gir verdifull diagnostisk informasjon. Det ble gjort geometrisk kalibrering, bilderektifikasjon og bildematching av stereobildene for å kunne foreta modelleringen. Utfordringer under disse prosessene var knyttet til presisjon av bildematchingen av homogene områder og høydeoppløsningen i modellen. Bildematchingen kan forbedres ved å forbehandle stereobildene for å øke kontrasten, og høydeoppløsningen kan økes ved å endre det eksperimentelle oppsettet. Som en videreføring av dette prosjektet skal 3Dmodelleringen kombineres med hyperspektrale avbildninger for i tillegg å kunne gi spektral informasjon om såret.
7
8 Forord Denne masteroppgaven ble utført våren 2012 ved institutt for elektronikk og telekommunikasjon, Norges Teknisk-Naturvitenskapelige Universitet. Hovedveileder har vært førsteamanuensis Lise Lyngsnes Randeberg og biveileder har vært doktorgradsstudent Lukasz Paluchowski. Jeg vil rette en stor takk til Lukasz Paluchowski for uvurderlig hjelp under masteroppgaven. Han er svært kompetent på fagfeltet sitt og har kunnet bidratt med mye gjennom dette halvåret. Jeg vil også takke Lise Lyngsnes Randeberg som foreslo og gav meg muligheten å jobbe med denne masteroppgaven. I tillegg vil jeg anerkjenne Norsk Elektro Optikk AS som har bidratt med teknisk utstyr. Fagfeltene omhandlet i dette prosjektet er relativt nye områder for meg, noe som har gjort dette til et utfordrende prosjekt og har bidratt til at jeg har lært svært mye gjennom dette semesteret. Trondheim, Thomas Thorsen Røren 1
9 Innholdsfortegnelse 1 INNLEDNING TEORI INTRODUKSJON TIL FOTOGRAMMETRI Skalering Koordinatsystemer Perspektivprojeksjon KALIBRERING Radiell og tangentiell distorsjon Sirkeldeteksjon STEREOSKOPI Parallakse Synsfelt i stereoskopi STEREODISPARITET Bildematchingsalgoritmer Metriske metoder for matching BILDEREKTIFIKASJON Epipolare linjer og plan Rektifikasjon av bildematrisene MODELLERING Koordinater i objektrommet Høydeoppløsning METODE EKSPERIMENTELT OPPSETT OG PROGRAMMERINGSSPRÅK Utstyr Akvisisjon av stereobilder Fremgangsmåte Programmeringsspråk KALIBRERING CalDe CalLab Implementasjon av kalibreringsresultatene REKTIFIKASJON Transformering av bildematrisene Punktdeteksjon og matching Estimering av fundamentalmatrisen
10 3.3.4 Perspektivtransformering MATCHING Valg av metrisk matchingsmetode Fremgangsmetode for matching Koordinatsystem og parallakseberegning MODELLERING Interpolering av Z-verdier Koordinater i objektrommet RESULTATER KALIBRERING CalDe CalLab Implementasjon av kalibreringsresultatene Verifikasjon av kalibreringsresultatene REKTIFIKASJON Punktdeteksjon og matching Perspektivtransformering MATCHING Korresponderende punkter i stereobildene Parallakseberegning MODELLERING Fjerning av ekstrempunkter Modellen DISKUSJON YTELSE MODELLERING AV SÅR KONKLUSJON BIBLIOGRAFI VEDLEGG KODEOVERSIKT DIVERSE MODELLER
11 Figurliste Figur 2.1: Illustrasjon av koordinatsystemene i bilderommet og i objektrommet Figur 2.2: Illustrasjon av linsedistorsjon Figur 2.3: Nåleputedistorsjon rutenett (t.v.) og tønnedistorsjon rutenett (t.h.) Figur 2.4: Illustrasjon av parallakse ved punktet A Figur 2.5: Bilde 1 viser utsnitt av referansebildet. Dette utsnittet kalles referansevinduet og brukes til å søke gjennom bilde 2 for matching Figur 2.6: Stereobilder før (1) og etter (2) rektifikasjon. Etter rektifikasjon er søkeområdet kun i horisontal retning, det vil si kun over en rad Figur 2.7: Illustrasjon av et punkt i rommet som blir projisert på to bildeplan, og den korresponderende epipolare geometrien er også illustrert Figur 2.8: Illustrasjon av bildeplanene etter rektifisering Figur 3.1: Eksperimentelt oppsett med kamera, linse og translasjonstrinn. Den røde sirkelen viser kameraet og linsen Figur 3.2: Illustrasjon av sjakkbrettmønsteret med tre punkter og deres koordinater Figur 3.3: Delaunay triangulering Figur 3.4: Rutenett ved matching. De grønne punktene indikerer de punktene som blir matchet Figur 3.5: Matrise med korrelasjonskoeffisienter ved matching av et punkt. X og Y-aksen representer rader og kolonner respektivt, og Z-aksen representer korrelasjonskoeffisientene Figur 3.6: Interpolert overfalte og den faktiske overflaten i 3D-modellen Figur 4.1: Detekterte hjørner på sjakkbrettet i CalDe Figur 4.2: De fem lokale pikselfeilhistogrammene samt det globale pikselfeilhistogrammet markert i rødt Figur 4.3: Sjakkbrett før kalibrering Figur 4.4: Sjakkbrett etter kalibrering Figur 4.5: Intensitetsforskjell mellom figur 4.3 og figur Figur 4.6: Konturbildet av pikselskiftet før kalibrering og etter kalibrering. Tallene til høyre er oppgitt i piksler Figur 4.7: Lagerkuler før kalibrering. Den grønne markeringen tilsvarer den optimale formen på kulen, mens den røde tilsvarer den faktiske formen på kulen Figur 4.8: Lagerkuler etter kalibrering. Den grønne markeringen tilsvarer den optimale formen på kulen, mens den røde tilsvarer den faktiske formen på kulen Figur 4.9:Stereobildene av modelleiren med en basislinje på 10 cm Figur 4.10: Anaglyfisk visning av stereobildene. 3D-effekten kan ses med ordinære 3D-briller farget rød og cyan
12 Figur 4.11: De røde sirklene markerer detekterte punkter i stereobildene. Her er kantpunktene fjernet Figur 4.12: Punktene som er igjen etter fjerning av punkter som ikke kan matches eller er matchet feil Figur 4.13: Korresponderende punker i anaglyfisk visning. De røde sirklene markerer punktene i bildet til venstre og de grønne tegnene markerer punktene i bildet til venstre Figur 4.14: Korresponderende punker i anaglyfisk visning etter RANSAC Figur 4.15: Korresponderende punker i anaglyfisk visning etter rektifikasjon samt tre utvalgte punktpar. Alle tre punktpar er rette og like lange Figur 4.16: Feilmatching i stereobildene Figur 4.17: Forbedring av matching ved å begrense søkeområdet Figur 4.18: Området i bildet som har blitt matchet Figur 4.19: Interpolerte parallakseverdiene av figur Figur 4.20: 3D-modellen av modelleiren beregnet på bakgrunn av parallakseverdiene som vist i figur Modellen vises fra det nordøstlige hjørnet av figur X-, Y- og Z-aksene er gitt i centimeter Figur 4.21: 3D-modellen med referansevindu på piksler. Modellen vises fra det nordøstlige hjørnet av figur
13 1 Innledning Hensikten med dette prosjektet er å prøve å danne en prototype av en topografisk 3D-modell av kroniske hudsår som er avbildet todimensjonalt. Målet er å kombinere en slik 3D-modell sammen med hyperspektral avbildning til diagnostisk bruk. Til dette formålet vil et høyoppløselig hyperspektralt kamera sammen med et 3D-avbildningssytem gi spektral informasjon om såret i tillegg til visualisering og dybdeestimering av såret. Den spektrale informasjonen vil kunne gi viktig diagnostisk data som oksygenering av vev, pigmentering samt klassifisering av såret. 3D-modellen vil kunne bidra med areal- og volumberegninger av såret. Ved å følge pasienter over tid vil areal- og volumforskjellene i såret kunne være et verdifullt diagnostisk verktøy. Et sår gror nedenfra og opp og dermed vil man kunne trekke slutninger om det skjer en forbedring i såret eller en forverring. Det er spesielt tre typer kroniske sår som det skal fokuseres på: 1. Venøse leggsår 2. Arterielle leggsår 3. Diabetiske fotsår Venøse leggsår skyldes at veneklaffene i blodårene ikke fungerer som de skal. Dette gjør at blodet kun renner nedover i beina og medfører økt trykk i blodårene, og dette gir igjen åreknuter og fører til at væske siver ut i vevet. Konsekvensene av dette kan være hevelser og sår som ikke gror av seg selv. Arterielle leggsår er en konsekvens av utilstrekkelig blodtilførsel som gir oksygenmangel i hud og vev. Den vanligste årsaken til at dette skjer er åreforkalkning. Nevropati og arteriosklerose er to senkomplikasjoner ved diabetes som kan gi diabetiske fotsår. Amputasjon er en vanlig konsekvens av disse typer sår, og 85 % av alle amputasjoner hos pasienter med diabetes skyldtes denne type sår. I dag måles og diagnostieres disse sårene på en svært enkel og unøyaktig måte med bruk av målebånd og visuell inspeksjon. Dette prosjektet vil dermed kunne være en ny og ikke-invasiv metode for karakterisering av kroniske sår. Systemet vil kunne tas i bruk av dermatologer, karkirurger, ortopeder og plastikkirurger. Dette prosjektet vil altså kun fokusere på dannelsen av en protype for topografisk 3D-modellering. Det finnes en del eksisterende teknikker for modellering i 3D. Eksempler på slike teknikker er LIDAR, interferometri og stereoskopi. I dette prosjektet har 3D-modellering basert seg på stereoskopiske bilder ved translasjon av et kamera ved å bruke et translasjonstrinn. Stereoskopi 6
14 er et begrep som ble først beskrevet i 1838 av Charles Wheatstone. Han gjorde en rekke fysiologiske og optiske eksperimenter for å prøve å forstå dybdesyn hos mennesker. Stereoskopi prøver nemlig å emulere dybdesynet til mennesker ved enten bruke to kameraer eller translere et kamera mellom tagning av to bilder. I dag blir 3D-teknologien stadig mer utbredt. Den tas i bruk av NASA, underholdningsindustrien i både spillindustrien og filmindustrien og i kartografi, for å nevne noen områder. Utviklingen av denne prototypen har basert seg på ny kodefunksjonalitet istedenfor å forbedre eksiterende koder. For å begrense lengden på rapporten og gi mest mulig flyt i lesningen tar ikke rapporten utgangspunkt i å forklare den implementerte koden i detalj, men heller forklare den prinsipielle virkemåten og resultatene av kodene. Hovedkapitlene i rapporten er strukturert på følgende måte: (2) Dette kapittelet gir en kort innføring i den teoretiske bakgrunnen for de respektive emnene aktuelt for dette prosjektet. For å ha forstå metodebruk og resultater er det viktig å ha en forståelse av den teorien som har blitt lagt til grunn ved prosjektgjennomføring. Kapittelet vil også bidra til en større forståelse av de problemene og utfordringer som kommer ved implementasjon av teorien. (3) Kapittelet gir en oversikt over metodene som har blitt brukt underveis i prosjektet. Her beskrives fremgangsmåten som har blitt benyttet for å komme fram til resultatene. Det gis også begrunnelser for hvorfor disse fremgangsmetodene har blitt benyttet framfor andre metoder. (4) Her blir resultatene som er oppnådd beskrevet. Kapitelet viser den endelig implementasjonen og hvordan forskjellige parametere endrer resultatene. Det forklares også eventuelle endringer av fremgangsmetoden som måtte gjøres på bakgrunn av tidligere resultater. (5) Her gis det en evaluering og en diskusjon av resultatene som har blitt oppnådd. Det kommer også en rekke forslag til hvordan systemet kan endres for å oppnå enda bedre resultater. (6) Konklusjon som oppsummerer rapporten. Resultatene sammenlignes med det målet som er satt i oppgaveteksten. Det gis også anbefalinger for hvilke områder som bør forbedres eller endres. Tilslutt gis det en kort beskrivelse av mulighetene for videre arbeid med dette prosjektet. 7
15 2 Teori Kapittelet gir en kort innføring i det teoretiske grunnlaget for prosjektet. Først belyses fotogrammetri generelt,, deretter de fotogrammetriske begrepene og aktuelle beregningsmetoder innenfor fotogrammetri. Andre del av kapittelet tar så for seg geometriske kalibrering av kamera for korreksjon av linsedistorsjon. Deretter forklares stereoskopi, stereodisparitet og bilderektifikasjon sjon, som er sentrale begreper i dette prosjektet. Tilslutt utdypes det nærmere hvordan 3D- overflatemodellen beregnes og hvordan forskjellige parametere påvirker modelleringen.
16 2.1 Introduksjon til fotogrammetri Teori 2.1 Introduksjon til fotogrammetri Fotogrammetri er et sett med teknikker som brukes til å bedømme geometriske egenskaper til objekter i fotografiske bilder (1). Mer konkret er hovedformålet til fotogrammetri å fastslå det geometriske forholdet mellom bildet og avbildningsobjektet som det eksisterte på den tiden da det ble avbildet. Når dette forholdet er fastslått kan informasjon om avbildningsobjektet innhentes ved kun å analysere bildet. Analyseringsteknikkene som brukes i fotogrammetri bygger på klassisk fotografitolkinger ved bruk av dataanalyseteknikker i tillegg til visuelle tolkninger. Et prosjekt som innebærer bruk av fotogrammetriske teknikker vil bestå av to hoveddeler: 1. Akvisisjon og forbehandling av bildene 2. Bildeprosessering for uthenting av aktuell informasjon Den første hoveddelen innebærer å bestemme hvordan avbildning av det aktuelle objektet skal foretas, og preprosessering av disse bildene for å fremheve strukturer eller generelt sett gjøre det enklere å foreta bildebehandling senere. Den andre hoveddelen vil bestå av å avgjøre hvilken type fotogrammetrisk system, og derunder også hvilke metoder og algoritmer, som skal benyttes for uthenting av den informasjonen som er ønskelig Skalering For å kunne beregne de metriske verdiene i bilder eller kart må skaleringsfaktoren kjennes. Denne faktoren relater lengdeenhetene i bildet til lengdeenhetene i virkeligheten og er gitt av forholdet mellom distansen mellom to punkter i bildet og distansen mellom de samme punktene i virkeligheten. Forholdet mellom fokallengden og høyden fra perspektivsenteret i kameraet er det samme som forholdet mellom bildedistansen mellom to punkter og den faktiske distansen mellom de samme punktene. Dette konstante forholdet skyldes formlike geometrier mellom de angitte distansene. Ved å bruke dette får vi altså følgende: bildedistanse skalering = f objektdistanse = h (2.1) derf er fokallengden og h er avstanden mellom avbildningsobjektet og perspektivsenteret i kameraet. 9
17 2.1 Introduksjon til fotogrammetri Teori Ideelt sett er skaleringsfaktoren uavhengig av om den måles i x-retning eller y- retning i bildet. Vertikale fotografier regnes som å ha retningsuavhengig skaleringsfaktor. Er derimot bildeplanet ikke parallelt med planet til avbildningsobjektet vil skaleringsfaktoren variere med retningen i bildet. Graden av denne variasjonen er relatert til hvor tiltet kameraet er i forhold til avbildningsobjektet. Selv om denne variasjonen ikke virker særlig stor vil et lite avvik ha stor betydning når dette beregnes med andre svært store eller små faktorer Koordinatsystemer Den optiske aksen til et kamera passerer gjennom perspektivsenteret og treffer bildeplanet i punkt som kalles prinsipalpunktet eller prinsipalpunktet av autokollimasjon (PPA) (1) som vist i figur 2.1. Figur 2.1: Illustrasjon av koordinatsystemene i bilderommet og i objektrommet (2) Prinsipalpunktet sammenfaller sjelden med bildets midtpunkt, men befinner seg i nærheten. Dette avviket mellom PPA og bildets midtpunkt bestemmes gjennom kalibreringsprosedyrer og utdypes nærmere i delkapittel 2.2. Figur 2.1 viser i tillegg et punkt i rommet, XA, som blir avbildet til et punkt i bildeplanet, xa. Punktet XA er gitt et koordinatsystem som refereres til som objektrommet og er gitt med koordinatene (XA, YA, ZA). Dette punktet blir avbildet til et koordinatsystem som refereres til som bildeplanet eller bilderommet. Koordinatene i bilderommet blir da gitt ved (xa, ya, -c), der c er fokallengden. For å oppnå koordinater i bilderommet som er i henhold til perspektivsenteret må det 10
18 2.1 Introduksjon til fotogrammetri Teori introduseres et skift i koordinatene slik at origo i bildekoordinatsystemet tilsvarer PPA-koordinatene i bildet. En alternativ form for representasjon av koordinatene er bruk av såkalte homogene koordinater (1). Her er kun det relative forholdet mellom koordinatene av interesse. Denne typen koordinatsystem brukes ofte i projektiv geometri, siden de muliggjør punktrepresentasjon ved uendelig. Todimensjonale bildekoordinater blir representert som x ' x y ' = y w der x ' x = og w y ' y =. (2.2) w Perspektivprojeksjon For å kunne relatere koordinatene i objektrommet til koordinatene i bilderommet brukes en lineær transformasjon som kalles perspektivtransformasjon. Hensikten med denne transformasjonen er å projisere et punkt i objektrommet til et punkt i bilderommet. Homografi er et matematisk begrep i geometri som knytter seg til projeksjon av rette linjer. De optiske strålene fra perspektivsenteret krysser to plan, bildeplanet og objektplanet. Forholdet mellom avstandene i bildeplanet og avstandene i objektplanet er gitt ved et unikt, konstant kryssforhold. Dermed kan punkter i bildeplanet beregnes på bakgrunn av punkter i objektrommet og omvendt. Alle bilder som tas av det samme objektplanet er relatert via homografi (3). Dette brukes i blant annet bilderektifikasjon og beregning av rotasjon og translasjon av kameraet mellom to bilder. Perspektivsenteret i figur 2.1 er gitt ved koordinatene (XO, YO, f), der ZO tilsvarer fokallengden f. Ved å bruke dette samt antagelsen at koordinatsystemet i objektrommet og koordinatsystemet i bildeplanet sammenfaller, kan man utlede følgende basert på formlikhet i figur 2.1: x X X x = = X = ( f Z ) f Z f f Z f (2.2) og y Y Y y = = Y = ( f Z ) f Z f f Z f (2.3) 11
19 2.2 Kalibrering Teori der ( x, y) er koordinater i bildeplanet, ( X, Y, Z ) er koordinater i objektrommet og f er fokallengden. 2.2 Kalibrering Alle bilder tatt med linser som er sfærisk formet vil ha aberrasjoner i mer eller mindre grad. Disse aberrasjonene gjør at bildet ikke representerer avbildningsobjektet perfekt i samtlige punkter i bildet, noe som konkret kan føre til feil når distansen mellom to punkter skal kalkuleres ved å skalere opp distansen mellom de tilsvarende pikslene. Det finnes fem hovedtyper aberrasjoner: Sfærisk aberrasjon, koma, astigmatisme, bildekrumming og distorsjon (1). Det er sistnevnte, linsedistorsjon, som direkte påvirker målenøyaktigheten i bildet og må derfor korrigeres i fotogrammetriske anvendelser gjennom geometrisk kalibrering. De andre aberrasjonene påvirker stort sett bildekvaliteten og ikke målenøyaktigheten. I tillegg til økning av den metriske nøyaktigheten i bildet vil også presisjonen ved bildematching øke ved geometrisk kalibrering. Figur 2.2 illustrerer at linsesystemer i praksis har et lite avvik i vinkelen mellom den optiske aksen og den optiske strålen fra objektet inn til linsen og mellom vinkelen mellom den optiske akse og lysstrålen utfra linsen. Hvis linsen hadde hatt perfekt utforming uten distorsjon ville vinkelavviket vært lik null. Figur 2.2: Illustrasjon av linsedistorsjon Distorsjon i bilder kan ha mange mønstre, inkludert irregulære mønstre, men stort sett beveger distorsjonen seg radielt utover i bildet med utgangspunkt i prinsipalpunktet. Radiell distorsjon er altså en radiell forskyvning av de korrekte 12
20 2.2 Kalibrering Teori posisjonene til pikslene i bildet, og dette skyldes at vinkelen mellom den optiske aksen og lysstrålen forandrer seg radielt utover i bildet. Det vil blant annet si at distorsjonen øker jo lengre koordinatene i bildet er fra prinsipalpunktet (PPA). Den radielle komponenten av distorsjonen er gitt av ligning 2.4 og viser at den radielle distorsjonen endres ulineært med vinkelavviket. r = r f tan( α α ) (2.4) Radiell og tangentiell distorsjon Radiell distorsjonen kan vanligvis deles opp i to hovedtyper: nåleputedistorsjon og tønnedistorsjon (1). Figur 2.3 viser hvordan rutenettet blir endret til et ikkeuniformt fordelt rutenett ved nåleputedistorsjon til venstre i figuren og tønnedistorsjon til høyre i figuren. I tønnedistorsjon har den radielle distorsjonen positive verdier, det vil si at distorsjonsvektorene peker utover og vekk fra PPA i bildet. Sidekantene vil nå krumme utover og rutenett ligner dermed på en tønne. Nåleputedistorsjon har derimot negativ radiell distorsjon, og distorsjonsvektorene vil dermed peke innover mot PPA. Dette medfører blant annet at sidekantene blir krummet inn mot midten og formen til rutenettet minner om en nålepute. Figur 2.3: Nåleputedistorsjon rutenett (t.v.) og tønnedistorsjon rutenett (t.h.) (4). I tillegg til radiell distorsjon kan også distorsjonen være tangentiell og skyldes som regel produksjonsfeil av linsekomponentene (1). Distorsjonen kommer av at CCD-enheten i kameraet ikke ligger perfekt parallelt med bildeplanet. Tangentiell distorsjon fører til en forskyvning av bildepunktene som beveger seg normalt på den radielle distorsjonen. For å korrigere for både tangentiell og radiell distorsjon kan de korrigerte koordinatene i bildet beregnes etter Browns modell (5) gitt av ligning 2.5 nedenfor. 13
21 2.2 Kalibrering Teori x = x + ( x - x )( Kr + Kr +...) + u d d c P( r + 2( x - x ) ) + 2 P ( x - x )( y - y ) (1 + Pr +...) d c 2 d c d c 3 y = y + ( y - y )( Kr + Kr +...) + 2 P( x - x )( y - y ) u d d c d c d c 2 P r + y y + P3 r +...)) 2 2 2( 2( d - c) ) (1 (2.5) der ( x, y ) = ikke forvrengt bildepunkt, u u ( x, y ) = forvrengt bildepunkt, d d ( x, y ) = PPA i bildet, K P n c c n = = N-te radiell distorsjonskoeffisient, N-te tangentiell distorsjonskoeffisient, r = x x + y 2 ( d - c ) ( d... = uendelig serie. 2 - y c ), Koordinatene x og y gjør det mulig å fastslå hvor de forvrengte koordinatene u u ville befunnet seg med null distorsjon. Siden de ikke-forvrengte koordinatene sjelden passer perfekt på et uniformt fordelt rutenett må det interpoleres for å kunne beregne intensitetsverdien til det uniformt fordelte rutenettet med samme størrelse som det opprinnelige bildet. For å kunne anvende ligning 2.5 må distorsjonskoeffisientene og PPA-koordinatene estimeres gjennom kalibreringsprosedyrer. For å kunne estimere distorsjonskoeffisientene og PPA er det hensiktsmessig å bruke et veldefinert mønster som kalibreringsobjekt. Dette kan for eksempel være mønsteret på et sjakkbrett. Hvis kameraet har betydelig distorsjon vil man kunne se hvordan mønsteret forandrer seg, spesielt i ytterkantene i bildet. Utfra disse endringene vil man kunne beregne de intrinsike parameterne av kameraet, og dette er som regel første del av kalibreringen. Den intrinsike matrisen inneholder fem parametere og består av (6): A α γ u x 0 = 0 αy v (2.6) der α x = f mx, α y = f my, og derf er fokallengden i piksler m er skaleringsfaktorer i x- og y-retning. γ representerer en faktor som beskriver 14
22 2.2 Kalibrering Teori skjevhetsforholdet mellom x- og y-aksen, og koordinatene og v tilsvarer PPA i u0 0 bildet. Kalibreringens virkemetode blir beskrevet i mer detalj i delkapittel Sirkeldeteksjon For å verifisere kalibreringen eller estimere hvor vellykket kalibrering ble gjennomført er det hensiktsmessig å avbilde objekter med veldefinerte fysiske utforming for så å undersøke hvordan den geometriske formen eventuelt endret seg i bildet før og etter kalibreringen. Formen bør være enkel og presis slik at verifiseringen er enklest mulig å gjennomføre. Sirkler eller kuler er godt egnet til dette formålet siden de har enkel geometrisk utforming med konstant distanse fra kanten av sirkelen til sentrum. Ved å se på sirklene i et bilde med betydelig distorsjon vil man kunne se klare endringer i den geometriske formen til sirkelen. Krumningen i sirkelen vil kunne være et mål på hvor godt sirkelen i bildet representer den geometriske formen til sirkelen som blir avbildet. Et annet mål på dette vil være å beregne kompaktheten til sirklene. Kompaktheten til en sirkel er gitt av ligning 2.7 (7). Ved å bruke like store kuler og ved å plassere kulene ved kantene og i midten av bildet vil man kunne sammenligne hvordan den geometriske utformingen forandrer seg på forskjellige steder i bildet. kompakthet = omkrets 2 / areal (2.7) For å kunne måle avvikene i den geometriske utformingen i bildet må sirklene detekteres ved bruk av bildesegmenteringsalgoritmer. Hough-transformen er en slik algoritme som anvendes til å finne diverse geometriske former. Bildet blir transformert til et såkalt akkumulatorrom ved å bruke en funksjon som beskriver den geometriske formen man leter etter (8). Punkter som ligger på en sirkel er beskrevet av ligning 2.8. ( x c ) + ( y c ) = c (2.8) Fremgangsmåten i Hough-transformen er først å gjøre kantedetektering for så å konstruere sirkler for hver kantpiksel inn i akkumulatorrommet. Deretter inkrementeres c1 og c2 i ligning 2.8 og verdiene som passer c3 best blir valgt basert på en terskel som blir satt (8). Blir denne terskelgrensen satt for lav kan det hende at sirklene ikke blir detektert og satt for høy kan det føre til falske deteksjoner. 15
23 2.3 Stereoskopi Teori 2.3 Stereoskopi Begrepet stereoskopi beskriver en teknikk eller egenskap som relaterer seg til evnen å oppfatte dybde i rommet (1). Hos mennesker gjøres dette ved at objekter i rommet blir oppfattet fra hvert øye og dermed fra to ulike vinkler. Dette gjør hjernen i stand til å oppfatte forskjellige avstander til forskjellige objekter i rommet. Det er flere andre metoder hjernen bruker for å oppfatte dybde, men dette er primærteknikken som gjør oss i stand til å ha en tredimensjonal oppfatning av det vi ser. Hjernen er kapabel til å kombinere to ulike bilder om til et tredimensjonalt bilde i komplekse omgivelser og i tillegg gjøre denne prosesseringen i sanntid. Det bør derfor også være mulig å utarbeide en teknisk løsning som utøver den samme funksjonen Parallakse For å anslå avstanden til objekter i rommet benytter blant annet hjernen seg av det faktum at objekter som er nærme øynene er mer forflyttet i hvert øye enn objekter som er langt fra øynene. Det vil si at hvis du lukker det ene øyet og ser på et nærme objekt for deretter å lukke det andre øyet og ser på det samme objektet, vil du se at det har oppstått en forskyvning av objektet. Hvis du derimot ser på et objekt lengre unna vil denne forskyvningen være mindre eller tilnærmet null. Et annet klassisk eksempel er hvis du beveger deg i relativ høy hastighet i bil vil objekter som lyktestolper nær veien bevege seg raskt forbi deg mens fjell for eksempel som er lengre unna vil bevege seg sakte. Dette konseptet kalles parallakse og kan beskrives som en tilsynelatende forflytting av objektet på grunn forflytting av den som observerer objektet. Parallakse kan utrykkes kvantitativt som p= xvenstre xhøyre, der xvenstre og x høyre er koordinatene langs den positive x-akse til et bestemt objekt henholdsvis før og etter observanden har forflyttet seg en viss distanse. Denne distansen omtales som basislinje, og ved stereoskopi i menneskesyn tilsvarer denne basislinjen distansen mellom øynene. Figur 2.4 illustrerer to bilder tatt ved punktene L1 og L2 av det samme punktet, punkt A. Kameraet blir altså forflyttet langs basislinjen B. Punkt A blir avbildet i punktene av og ah i bildeplanet. Punkt A kan for eksempel være et elevert punkt i et ujevnt terreng som det tas bilde av, og avstanden, eller høyden, mellom kameraet og det aktuelle punktet er gitt ved h. O1 og O2 representerer prinsipalpunktene i bildeplanet for hvert bilde. Distansen i bildet mellom de respektive prinsipalpunktene og av og ah er henholdsvis gitt av xv og xh. Disse representer x-koordinatene i bildet siden prinsipalpunktene er origo i 16
24 2.3 Stereoskopi Teori koordinatsystemet i bildet. Fokallengden til kameraet er vist ved f i figuren. Parallaksen er, som før, gitt vedp= x x. Merk at xh er til venstre for origo, og v h dermed negativ, noe som gjør at lengden av parallaksen blir summen av distansene xv og xh. Figur 2.4: Illustrasjon av parallakse ved punktet A Hvis det legges til grunn perfekte geometriske former, slik som i figur 2.4, kan parallaksen ved punkt A gi informasjon om avstanden mellom punktet og kameraet. Det vil si at man kan få informasjon om for eksempel hvor elevert punktet er i forhold til resten av terrenget. Ved å anerkjenne at trekantene (L1, L2, A) og (L1, av, a h) er formlike har vi at, B p Bf = h= (2.9) h f p Ligning 2.9 bekrefter det som allerede er nevnt over, at avstanden til et punkt er invers proporsjonal med parallaksen. Høy parallakse medfører at punktet er nærme, og lav parallakse medfører at distansen til punktet er lengre unna Synsfelt i stereoskopi Som det fremkommer av figur 2.4 må punkt A befinne seg på begge bildene tatt ved L1 og L2, med andre ord må punktet være innenfor synsfeltet til kameraet på 17
25 2.4 Stereodisparitet Teori begge steder. Dette medfører begrensinger på hvor lang basislinjen kan være og hvor nærme kameraet kan være til punktet. Fordelen med å øke basislinjen er å øke nøyaktigheten i parallaksen, spesielt når punktet er lengre, eller dypere, unna. Dette gir en økning i oppløsning i høyde- eller dybdeberegningene som gjøres på bakgrunn av parallaksen. Det kan også vises at skaleringsfaktoren, som er gitt av fokallengden og avstanden fra kameraet til objektet, påvirker oppløsningen til dybdeberegningene. Parallaksen kan skrives som summen av det parallakseskiftet i x-koordinatene som uansett oppstår grunnet forflytning av kameraet og det parallakseskiftet som er direkte relatert til dybdeforskjellene. Den førnevnte parameteren, p 0, er konstant og er uavhengig av dybdeforskjellene, mens den sistnevnte parameteren, p, tilsvarer parallaksevariasjonene som er knyttet til dybdeforskjellene og er dermed en variabel. Ved å bruke dette sammen med ligning 2.9 får vi følgende: Bf p= p0+ p= + p= B skalering + p (2.10) h der p<< p0. Økning av skaleringen og basislinjen fører altså til større differanser i p og dermed større oppløsning i dybdeberegningene, siden dybdeforskjellene er invers proporsjonale med differansene i parallaksen. Hvis kameraet har fast fokallengde er det kun mulig å øke skaleringen ved å redusere avstanden mellom kameraet og objektet. Ulempen med å øke basislinjen, skaleringen eller begge for mye er at det aktuelle området med punkter der parallaksen skal måles kan havne utenfor synsfeltet når kameraet forflyttes til den andre enden av basislinjen. Synsfeltet til linsen setter dermed begrensinger for oppløsningen til dybdeberegninger i objektet. 2.4 Stereodisparitet Som beskrevet tidligere kan dybden, eller høyden, i et område beregnes ved å analysere to bilder tatt ved hver sin ende av basislinjen. Disse to separate bildene må delvis sammenfalle og sammenfalle helt over det aktuelle området der dybden skal evalueres. Bildene kalles da stereobilder. For å kunne beregne 18
26 2.4 Stereodisparitet Teori parallaksen i hvert enkelt punkt må punktene i det sammenfallende området i det ene bildet lokaliserer i det andre bildet. Dette omtales som stereokorrespondanseproblemet. Som med andre bildeanalyseteknikker så er implementasjonen av en nøyaktig, effektiv matchingsalgoritme vesentlig vanskeligere enn den stereomodellen mennesker relativt lett klarer å danne. Bildematching er i seg selv en vanskelig utfordring. I et bilde med svært mange piksler, noe som alle moderne bilder innehar, vil det som regel finnes to eller flere områder med piksler som har en stor grad av ambiguitet. Dette fører til falske matchinger som da gir feil parallakse mellom stereobildene. Støy i bildene kan i tillegg føre til fullstendig utelukking av det korrekte punktet som skulle matches. Strukturene i bildene kan også forandre seg betraktelig når synsvinkelen endres. En linje på et vist antall piksler i det første bildet kan muligens bare ha en lengde på halvparten av den opprinnelige lengden i det andre bildet. Bildematchingsalgoritmen må ta høyde alle disse scenarioene på en effektiv måte Bildematchingsalgoritmer Det finnes to hovedmetoder som matchingsalgoritmene kan grupperes inn under; områdematching og karakteristisk matching (1). Den sistnevnte type matching beror på karakteristiske trekk i bildet. Dette kan være linjesegmenter, spesielle interessepunkter eller lukkede konturer som matches og er best benyttet i topografiske bilder der klare strukturer forekommer i bildet. Denne matchingen anses ikke relevant for dette prosjektet siden strukturene av de aktuelle objektene er av høyst varierende grad, og det blir dermed vanskelig å gi en generell karakteristikk av strukturene ved implementering av kode. Fokuset vil derfor være utelukkende på områdematching videre i dette prosjektet. Områdematching bruker simpelthen pikselverdiene innen et begrenset område fra det ene bildet for å matche disse pikselverdiene til pikselverdiene i det andre bildet. Det ene bildet brukes da som referansebildet slik at det søkes i det andre bildet etter det tilsvarende punktet gitt i referansebildet. Dette gjøres ved å ta et utsnitt av referansebildet rundt det aktuelle punktet som skal matches. Dette utsnittet kalles referansevinduet og består som regel av N N antall piksler. Kun matching av én og én piksel istedenfor blokker av piksler ville gitt lave prosesseringstid, men dette hadde ført til mange falske matchinger siden de samme pikselverdiene opptrer på mange forskjellige steder i bildet. Fremgangsmetoden er illustrert i figur 2.5, der referansevinduet er vist i bilde 1 og søkevinduet som referansevinduet blir matchet opp mot vist i bilde 2. Det 19
27 2.4 Stereodisparitet Teori utsnitt av søkevinduet som passer best med referansevinduet blir antatt til å være det aktuelle matchede punktet i referansevinduet. Et stort referansevindu gjør matchingen mer pålitelig og mer resistent for påvirkning av støy i bildet, men ulempen er at matchingen nå ikke fanger opp bråe endringer i parallakse. Dette skyldes at dybdeforskjellen medfører endringer som nå blir midlet ut fordi vinduet egentlig er ved to forskjellige parallakser. Referansevinduet med forholdsvis stor størrelse fungerer dermed som et lavpassfilter anvendt på parallakseverdiene. I tillegg vil et stort vindu medføre høyere prosesseringstid enn et lite vindu. Bildematching går ut ifra at det er matematiske likheter mellom pikslene i referansevinduet og det bildet som skal matches. Det medfører at pikselverdiene i bildene bør normaliseres før de matches. Figur 2.5: Bilde 1 viser utsnitt av referansebildet. Dette utsnittet kalles referansevinduet og brukes til å søke gjennom bilde 2 for matching. (9) Bildeområdet referansevinduet skal søke i angir størrelsen på søkevinduet. Er den maksimale parallaksen kjent kan søkevinduet begrenses, og matchingen vil dermed ha lavere prosesseringstid. Den totale parallaksen er gitt av ligning 2.10, men dette krever blant annet kjennskap til den maksimale dybdevariasjonen i avbildningsobjektet. Er den maksimale parallaksen ikke kjent må det søkes på tvers av hele bildet. Antall rader det må søkes over bestemmes av i hvilken grad stereobildene er rektifisert. Ved fullstendig rektifikasjon av stereobildene kan søket begrenses til en rad i bildet. Dette vil utdypes nærmere i delkapittel 2.5. Kvaliteten på punktmatchingen avgjøres av bildenes karakteristikk. Sannsynligheten for å gjøre feil matching er invers proporsjonal med signal-støy forholdet i bildet. Områder i stereobildene med mye høyfrekvent innhold øker presisjonen til matchingen siden detaljnivået i disse områdene er høyere. Områder med lavfrekvent innhold, som for eksempel bakgrunnen til avbildningsobjekter eller veldig homogene områder, kan by på utfordringer i matchingen siden punktene i disse områdene kan lett forveksles av matchingsalgoritmen. Kvaliteten på matchingen degraderes også ved 20
28 2.4 Stereodisparitet Teori linsedistorsjon i kameraet. Linsedistorsjon kan, som nevnt i delkapittel 2.2, korrigeres for ved geometrisk kalibrering. Det kan derfor konkluderes med at bildematchingssystemer har betydelige begrensninger. Mange piksler vil ikke kunne matches grunnet lavt frekvensinnhold eller store, bråe endringer i parallaksen. Å prøve matching av slike områder kan degradere modellen og kaste bort prosessorkraft. Det er derfor bedre og prøve å detektere disse feilmatchingene og heller tilpasse disse verdiene til naboområdet Metriske metoder for matching Det finnes en del ulike metoder for å måle de matematiske likhetene i bildene på, der hver metode varierer i prosesseringstid og nøyaktighet. Disse metodene bruker forskjellige metriske mål når forskjellen mellom referansevinduet og vinduet som skal matches skal beregnes. Nedenfor er det tatt med et utvalg av disse metodene som anses som relevante for matchingen i dette prosjektet (10). Sum av den absolutte differanse (SAD) Denne metoden summerer absoluttverdien av differansen mellom pikselverdiene i referansevinduet og pikselverdiene i det vinduet som skal matches. Matematisk tilsvarer dette: d ( I, T ) = I T (2.11) 1 j i, j i i= 1 n der I er j-te bildet eller vinduet som skal matches og T er templaten eller referansevinduet som det også kalles. SAD beregnes over n antall piksler i vinduene. Den laveste SAD-verdien av gir den beste estimeringen av lokasjonen til det vinduet som matcher best med referansevinduet ved bruk av denne metoden. Sum av den kvadrerte differanse (SKD) Forskjellen mellom SKD og SAD er i all hovedsak at absoluttverdien av differansen til pikselverdien blir kvadrert. SKD-matching er dermed gitt av: n 2 2 ( j, ) = Ii, j Ti (2.12) i= 1 d I T 21
29 2.4 Stereodisparitet Teori Maksimum absolutt differanse (MaxAD) Her blir maksimum av absoluttverdien til differansen mellom pikselverdiene til referansevinduet og vinduet som matches summert. Dette gir dermed: n n p j = i, j i = i, j i p i i = 1 p d ( I, T ) lim I T max I T (2.13) Normalisert krysskorrelasjon Normalisert korrelasjon mellom vinduene i de to stereobildene tar hensyn til forskjeller i pikselverdi og variansen mellom bildene. Korrelasjonen mellom vinduene blir normalisert ved å trekke fra gjennomsnittet for så å dividere på standardavviket av vinduene. Denne beskrivelsen er gjengitt matematisk i ligning 2.14 i todimensjonal form. Normalisering av korrelasjonen er nødvendig for å unngå mismatch mellom vinduene grunnet regioner der pikslene har høyere gjennomsnittlig verdi, eller regioner med høyere varians som vil gi høyere korrelasjon enn den korrekte matchede regionen med mer normale pikselverdier (1). Disse avvikene kan skyldes at stereobildene har for eksempel blitt tatt under forskjellige lysforhold, eller skyldes at i enkelte regioner oppstår det mettede piksler som igjen skyldes refleksjoner eller lignende. [ I( x, y) Iuv, ][ T ( x u, y v) T ] Ε[ I T ] Ε[ I] Ε[ T ] x, y γ ( u, v) = = σ ( I) σ ( T ) [ I( x, y) I ] [ T( x u, y v) T ] 2 2 uv, x, y x, y (2.14) der T er gjennomsnittsverdien til T og Iu, v er gjennomsnittet av Ixy (, ) i den regionen templaten befinner seg i. Som det fremkommer av ligning 2.14 er denne metriske metoden for matching vesentlig mer komplisert enn de foregående. Ved implementering har derfor denne metoden høyere prosesseringstid enn de andre. Tatt i betraktning at denne matchingen skal gjøres for opp mot millioner av piksler er prosesseringstiden for en enkelt match av stor betydning. 22
30 2.5 Bilderektifikasjon Teori 2.5 Bilderektifikasjon ektifikasjon Vanligvis vil ikke stereobilder være fullstendig på linje vertikalt eller være ved samme høyde ved translasjon av kameraet mellom endene av basislinjen. Dette er det praktiske tilfellet selv om translasjonen av kameraet, teoretisk sett, bare er i horisontal retning i bildet. Hvis forskyvingen av kameraet skjer ved å bruke et translasjonstrinn kan dette skyldes ufullkommen presisjon i de mekaniske bevegelsene til translasjonstrinnene. En forskyvningsfeil i translasjonen på bare noen titalls mikrometer kan resultere i pikselforskyvning i bildet. Hvor mye metrisk forskyvning som resulterer i pikselforskyvning avhenger av den metriske pikselstørrelsen til kameraet og skaleringsfaktoren. Konsekvensene av pikselforskyvning i vertikal retning i stereobildene er at søkevinduet i bildematchingen også må bevege seg i vertikale retning i bildet. Høydeforskyvninger ved mekanisk translasjon kan føre til feil matching i stereobildene ved enkelte punkter, men dette medfører som regel ikke problemer og er underordnet problemet med vertikal forskyvning i stereobildene. Som nevnt i det foregående delkapittel kan søkeområdet ved bildematching reduseres betraktelig ved fullstendig rektifikasjon av stereobildene. Rektifikasjon er en type transformasjon som brukes til å projisere stereobilder til et fellesbildeplan. Dette medfører at eventuelle høydeforskyvninger og forskyvninger i-y-retning i bildet blir borte. Figur 2.6 illustrerer denne bilderektifikasjonen. Figur 2.6: Stereobilder før (1) og etter (2) rektifikasjon. Etter rektifikasjon er søkeområdet kun i horisontal retning, det vil si kun over en rad i bildet (11). 23
31 2.5 Bilderektifikasjon Teori Epipolare linjer og plan Før ble stereobilder rektifisert ved å bruke optiske teknikker, men i det siste tiåret har rektifikasjon primært blitt gjort ved såkalt planar rektifikasjon (12). Ved bruk av planar rektifikasjon blir vanligvis geometrien av den optiske projeksjonen modellert ved å bruke en enkel lineær transformering av hvert bilde. Dette medfører i realiteten at begge bildeplanene blir rotert til de sammenfaller langs den ene bildeaksen. Fordelen med denne metoden er at den er simpel å implementere, har rask prosesseringstid og bevarer bildekarakteristikken (12). Et punkt i rommet, W, blir projisert til to forskjellige bildepunkter, M1 og M2, som vist i figur 2.7. M1 og M2 er skjæringspunkter i sine respektive bildeplan, R1 og R2, mellom kameraenes perspektivsentere C1, C2 og W. Som nevnt i delkapittel 2.1 kalles linjen som inneholder C, og er ortogonal til planet R, den optiske akse. Prinsipalpunktet (PPA) er skjæringspunktet mellom den optiske akse og planet R. Distansen mellom C og R tilsvarer fokallengden. M1 og M2 konstituerer et konjugert punktpar. I det ene bildepunktet M1 ligger det konjugerte punktet, M2, i det andre bildet på en linje som kalles for den epipolare 1 linje (13). Det finnes uendelig antall epipolare linjer som korresponderer til vilkårlige punkter i bildeplanet (1). Epipolarlinjen er projeksjonen gjennom C2 av den optiske strålen fra W til M1. Alle de epipolare linjene i et bestemt bildeplan går gjennom et felles punkt i begge bildeplanene. Dette punktet kalles en epipol 1 og er i figur 2.7 vist ved betegnelsen E1 og E2. Disse punktene tilsvarer projeksjonen av perspektivsenteret til det andre kameraet. 1 Epipolar og epipol er ikke godkjente norske ord, men det finnes heller ikke noen gode norske ord for de engelske ordene epipolar eller epipole ved anvendelser i denne konteksten. 24
32 2.5 Bilderektifikasjon Teori Figur 2.7: Illustrasjon av et punkt i rommet som blir projisert på to bildeplan, og den korresponderende epipolare geometrien er også illustrert. (13) Når C1 er i det fokale planet til kameraet til høyre i figuren over er den tilsvarende epipolen ved uendelig og de epipolare linjene er en bunt av parallelle linjer i bildet til høyre. Basislinjen tilsvarer linjen mellom C1 og C2. Når denne linjen omfatter begge fokalplanene er begge epipolene ved uendelig, det vil si at begge bildeplan er parallelle til basislinjen. De epipolare linjene danner da en bunt av parallelle linjer i begge bilder. Denne prosessen kalles rektifikasjon og er altså en transformering av stereobildene slik at de epipolare linjene er parallelle og horisontale (13) Rektifikasjon av bildematrisene Formålet til rektifikasjon er å rotere bildematrisene rundt sine perspektivsentre slik at fokalplanene befinner seg i samme plan. Dette gjør, som nevnt tidligere, at fokalplanene inneholder basislinjen og de epipolare linjene er parallelle. For å oppnå horisontale, epipolare linjer må basislinjen være parallell med den nye x- aksen etter rotering. Figur 2.8 vise to rektifiserte bildeplan der alle de konjugerte bildepunktene har de samme vertikale koordinatene. Kravet for dette er at begge kameraene har de samme intrinsike parameterne etter rotasjon. Hvis stereobildene tas av det samme kameraet vil de intrinsike parameterne, gitt av ligning 2.6, være de samme for begge bilder, og bildeplanene vil i tillegg ligge i samme plan. 25
33 2.6 Modellering Teori Figur 2.8: Illustrasjon av bildeplanene etter rektifisering For å representere den epipolare geometrien brukes det noe som refereres til som fundamental matrisen (3). Dette er en 3 3 matrise som relaterer de korresponderende punktene i stereobildene. For et punkt med homogent bildekoordinat x i et av stereobildene eksiterer det et korresponderende punkt med homogent bildekoordinat x i det andre bildet. Disse to punktene ligger på den epipolare linjen l. Det skjer dermed en transformering slik at x l, og denne transformering er en perspektivtransformasjon fra punkter til linjer. Fundamentalmatrisen F er definert slikt at den tilfredsstiller x T Fx = 0 og l = Fx (3). 2.6 Modellering Etter at parallaksen er blitt beregnet i de aktuelle punktene i avbildningsobjektet kan 3D-modellen startes å beregnes. Siden modellen skal representerer avbildningsobjektet i objektrommet vil man måtte beregne X-, Y- og Z-koordinatene på bakgrunn av parallaksen og koordinatene i bildeplanet slik som forklart i avsnitt
34 2.6 Modellering Teori Koordinater i objektrommet Etter bilderektifikasjon er begge bildeplanene, på hver sin ende av basislinjen, koplanare. Dette medfører at x-koordinatene i begge bildeplan er på samme linje. I tillegg er PPA kjent etter kalibreringsprosessen noe som muliggjør introdusering av et skift i koordinatene i bildeplanet slik at PPA utgjør origo i bildet. Koordinatene i bildeplanet sammenfaller dermed med koordinatene i objektplanet. Det vil si at x-koordinatene i hvert av de to bildeplanene til stereobildene er sammenfallende, og x-koordinatene i objektrommet er kun skiftet med lengden på basislinjen. Sammen med ligningene 2.2 og 2.3 gir dette følgende: X = X + B x f 2 1 x ( f Z) = ( f Z) + B f 2 1 Bf Z = f x x 2 1 (2.15) der x2 x1 tilsvarer parallaksen som definert i avsnitt Z-verdiene i ligning 2.15 tilsvarer dermed høydeberegningen i ligning 2.9, men er negativ og fokallengden er trukket fra høyden i forhold til ligning 2.9. Ligningene 2.2, 2.3 og 2.15 gir dermed alle koordinatene i objektrommet basert på parallaksen, fokallengden og lengden på basislinjen Høydeoppløsning Siden Z-verdiene er proporsjonale med parallakseverdiene vil den minste mulige endringen av Z-verdiene forekomme når p i ligning 2.10 også endres med den minste mulige verdien. Den minste mulige verdien av p tilsvarer et skift av en piksel mellom x-koordinatene til de to stereobildene. Oppløsningen i Z-aksen blir derfor: fb fb 1 1 Z = Z1 Z 2 = f f = fb p1 p2 p1 p2 (2.16) derp 1 = B skalering og p2 er gitt av ligning Ligning 2.16 gir altså den endringen i Z-verdien som oppstår når parallaksen endrer seg med en piksel. For å kunne relatere pikslene i bildene til metriske verdier må pikselstørrelsen kjennes. Dette er en faktor som er gitt av CCD-enheten i kameraet, og denne 27
35 2.6 Modellering Teori faktoren oppgis i meter per piksel(mpp). For å kunne beregne hvor mange meter en piksel utgjør må man også ta i betraktning skaleringsfaktoren siden MPPstørrelsen kun gir de metriske målene i forhold til bildeplanet og ikke objektplanet. Dermed blir p= 1 [pix] MPP [m/pix] / skalering [ ] som da tilsvarer det minste mulige skiftet i parallaksen i meter. Ligning 2.16 kan da skrives om til: 1 1 Z = fb B skalering B skalering + p 1 1 = fb B skalering B skalering + MPP / skalering f MPP = = h MPP 2 2 skalering ( B skalering + MPP) B skalering + MPP 3 h MPP B f 2 (2.17) der det antas at 2 MPP<< B skalering. For å få overflatemodellen så nøyaktig som mulig må Z være så lav som mulig. Som nevnt tidligere i avsnitt kan dette gjøres ved øke skaleringen og lengden på basislinjen, men utfra ligning 2.17 bør også kameraets MPP-størrelsen være så lav som mulig. I tillegg viser ligningen at lavere høyde er viktigere enn høyere fokallengde for å oppnå høyere høydeoppløsning i modellen. 28
a. Hva er de inverse transformasjonene avfølgende tre transformasjoner T, R og S: θ θ sin( ) cos( ) Fasit: 1 s x cos( θ) sin( θ) 0 0 y y z
 Kommentar: Svar kort og konsist. Husk at eksamen har tre oppgaver. Poengene for hver (del-) oppgave bør gi en indikasjon på hvor me tid som bør benttes per oppgave. Oppgave 1: Forskjellige emner (40 poeng)
Kommentar: Svar kort og konsist. Husk at eksamen har tre oppgaver. Poengene for hver (del-) oppgave bør gi en indikasjon på hvor me tid som bør benttes per oppgave. Oppgave 1: Forskjellige emner (40 poeng)
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i : INF2310 Digital bildebehandling Eksamensdag : Tirsdag 25. mars 2014 Tid for eksamen : 15:00 19:00 Oppgavesettett er på : 6 sider
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i : INF2310 Digital bildebehandling Eksamensdag : Tirsdag 25. mars 2014 Tid for eksamen : 15:00 19:00 Oppgavesettett er på : 6 sider
Geometri Mona Røsseland Nasjonalt senter for matematikk i Opplæringen Leder i LAMIS Lærebokforfatter, MULTI Geometri i skolen Geometri etter 4.
 Geometri Mona Røsseland Nasjonalt senter for matematikk i Opplæringen Leder i LAMIS Lærebokforfatter, MULTI 15-Apr-07 Geometri i skolen dreier seg blant annet om å analysere egenskaper ved to- og tredimensjonale
Geometri Mona Røsseland Nasjonalt senter for matematikk i Opplæringen Leder i LAMIS Lærebokforfatter, MULTI 15-Apr-07 Geometri i skolen dreier seg blant annet om å analysere egenskaper ved to- og tredimensjonale
Tegning av tredimensjonale figurer parallell sentral perspektiv Parallell-projeksjoner grunnlinje horisontalprojeksjon vertikalprojeksjon
 Tegning av tredimensjonale figurer Å tegne en tredimensjonal figur på et papirark byr på fundamentale prinsipielle problemer: Papiret er todimensjonalt, mens gjenstandene som skal avbildes, er tredimensjonal.
Tegning av tredimensjonale figurer Å tegne en tredimensjonal figur på et papirark byr på fundamentale prinsipielle problemer: Papiret er todimensjonalt, mens gjenstandene som skal avbildes, er tredimensjonal.
Kurs. Kapittel 2. Bokmål
 Kurs 8 Kapittel 2 Bokmål D.8.2.1 1 av 4 Introduksjon til dynamisk geometri med GeoGebra Med et dynamisk geometriprogram kan du tegne og konstruere figurer som du kan trekke og dra i. I noen slike programmer
Kurs 8 Kapittel 2 Bokmål D.8.2.1 1 av 4 Introduksjon til dynamisk geometri med GeoGebra Med et dynamisk geometriprogram kan du tegne og konstruere figurer som du kan trekke og dra i. I noen slike programmer
Universitetet i Agder Fakultet for teknologi og realfag LØSNINGSFORSLAG. Dato: 11. desember 2008 Varighet: 0900-1300. Antall sider inkl.
 Universitetet i Agder Fakultet for teknologi og realfag LØSNINGSFORSLAG Emnekode: Emnenavn: DAT2 Grafisk Databehandling Dato:. desember 28 Varighet: 9 - Antall sider inkl. forside 7 OPPGAVE. (2%) a) b)
Universitetet i Agder Fakultet for teknologi og realfag LØSNINGSFORSLAG Emnekode: Emnenavn: DAT2 Grafisk Databehandling Dato:. desember 28 Varighet: 9 - Antall sider inkl. forside 7 OPPGAVE. (2%) a) b)
OVERFLATE FRA A TIL Å
 OVERFLATE FRA A TIL Å VEILEDER FOR FORELDRE MED BARN I 5. 7. KLASSE EMNER Side 1 Innledning til overflate... 2 2 Grunnleggende om overflate.. 2 3 Overflate til:.. 3 3 3a Kube. 3 3b Rett Prisme... 5 3c
OVERFLATE FRA A TIL Å VEILEDER FOR FORELDRE MED BARN I 5. 7. KLASSE EMNER Side 1 Innledning til overflate... 2 2 Grunnleggende om overflate.. 2 3 Overflate til:.. 3 3 3a Kube. 3 3b Rett Prisme... 5 3c
Algoritmer og datastrukturer Kapittel 2 - Delkapittel 2.1
 Delkapittel 2.1 Plangeometriske algoritmer Side 1 av 7 Algoritmer og datastrukturer Kapittel 2 - Delkapittel 2.1 2.1 Punkter, linjesegmenter og polygoner 2.1.1 Polygoner og internett HTML-sider kan ha
Delkapittel 2.1 Plangeometriske algoritmer Side 1 av 7 Algoritmer og datastrukturer Kapittel 2 - Delkapittel 2.1 2.1 Punkter, linjesegmenter og polygoner 2.1.1 Polygoner og internett HTML-sider kan ha
1. En tynn stav med lengde L har uniform ladning λ per lengdeenhet. Hvor mye ladning dq er det på en liten lengde dx av staven?
 Ladet stav 1 En tynn stav med lengde L har uniform ladning per lengdeenhet Hvor mye ladning d er det på en liten lengde d av staven? A /d B d C 2 d D d/ E L d Løsning: Med linjeladning (dvs ladning per
Ladet stav 1 En tynn stav med lengde L har uniform ladning per lengdeenhet Hvor mye ladning d er det på en liten lengde d av staven? A /d B d C 2 d D d/ E L d Løsning: Med linjeladning (dvs ladning per
Kort innføring i kart, kartreferanser og kompass
 Kort innføring i kart, kartreferanser og kompass UTM Universal Transverse Mercator (UTM) er en måte å projisere jordas horisontale flate over i to dimensjoner. UTM deler jorda inn i 60 belter fra pol til
Kort innføring i kart, kartreferanser og kompass UTM Universal Transverse Mercator (UTM) er en måte å projisere jordas horisontale flate over i to dimensjoner. UTM deler jorda inn i 60 belter fra pol til
DET TEKNISK-NATURVITENSKAPELIGE FAKULTET
 DET TEKNISK-NATURVITENSKAPELIGE FAKULTET MASTEROPPGAVE Studieprogram/spesialisering: Kybernetikk Vårsemesteret, 2011 Åpen / Konfidensiell Forfatter: Andreas Kristiansen Fagansvarlig: Ivar Austvoll Veileder(e):
DET TEKNISK-NATURVITENSKAPELIGE FAKULTET MASTEROPPGAVE Studieprogram/spesialisering: Kybernetikk Vårsemesteret, 2011 Åpen / Konfidensiell Forfatter: Andreas Kristiansen Fagansvarlig: Ivar Austvoll Veileder(e):
EKSAMEN. Informasjon om eksamen. Emnekode og -navn: ITD37018 Anvendt Robotteknikk. Dato og tid: , 3 timer. Faglærer: Haris Jasarevic
 Informasjon om eksamen EKSAMEN Emnekode og -navn: ITD37018 Anvendt Robotteknikk Dato og tid: 10.12.18, 3 timer Faglærer: Haris Jasarevic Hjelpemidler: Ingen hjelpemidler tillatt Om oppgaven: Alle oppgavene
Informasjon om eksamen EKSAMEN Emnekode og -navn: ITD37018 Anvendt Robotteknikk Dato og tid: 10.12.18, 3 timer Faglærer: Haris Jasarevic Hjelpemidler: Ingen hjelpemidler tillatt Om oppgaven: Alle oppgavene
FORSØK I OPTIKK. Forsøk 1: Bestemmelse av brytningsindeks
 FORSØK I OPTIKK Forsøk 1: Bestemmelse av brytningsindeks Hensikt I dette forsøket skal brytningsindeksen bestemmes for en sylindrisk linse ut fra måling av brytningsvinkler og bruk av Snells lov. Teori
FORSØK I OPTIKK Forsøk 1: Bestemmelse av brytningsindeks Hensikt I dette forsøket skal brytningsindeksen bestemmes for en sylindrisk linse ut fra måling av brytningsvinkler og bruk av Snells lov. Teori
HamboHus 5.4 Rev. 1, 8. september 2005 A. Cordray
 HamboHus Technical Note Nr 10: Terreng HamboHus 5.4 Rev. 1, 8. september 2005 A. Cordray I HamboHus 5.4 er implementasjonen av terreng utvidet og forbedret. Det er lettere å lage terrengpunkter, og mye
HamboHus Technical Note Nr 10: Terreng HamboHus 5.4 Rev. 1, 8. september 2005 A. Cordray I HamboHus 5.4 er implementasjonen av terreng utvidet og forbedret. Det er lettere å lage terrengpunkter, og mye
Norges Informasjonstekonlogiske Høgskole
 Oppgavesettet består av 9 (ni) sider. Norges Informasjonstekonlogiske Høgskole RF5100 Lineær algebra Side 1 av 9 Tillatte hjelpemidler: Kalkulator, vedlagt formelark Varighet: 3 timer Dato: 11.desember
Oppgavesettet består av 9 (ni) sider. Norges Informasjonstekonlogiske Høgskole RF5100 Lineær algebra Side 1 av 9 Tillatte hjelpemidler: Kalkulator, vedlagt formelark Varighet: 3 timer Dato: 11.desember
Automatisk gjenkjenning av rullebaneterskel i flyfoto.
 Automatisk gjenkjenning av rullebaneterskel i flyfoto. Steinar Romberg Kvaale Master i teknisk kybernetikk Oppgaven levert: Juni 2008 Hovedveileder: Tor Engebret Onshus, ITK Biveileder(e): Jostein Trones,
Automatisk gjenkjenning av rullebaneterskel i flyfoto. Steinar Romberg Kvaale Master i teknisk kybernetikk Oppgaven levert: Juni 2008 Hovedveileder: Tor Engebret Onshus, ITK Biveileder(e): Jostein Trones,
Norges Informasjonstekonlogiske Høgskole
 Oppgavesettet består av 10 (ti) sider. Norges Informasjonstekonlogiske Høgskole RF3100 Matematikk og fysikk Side 1 av 10 Tillatte hjelpemidler: Kalkulator, vedlagt formelark Varighet: 3 timer Dato: 11.desember
Oppgavesettet består av 10 (ti) sider. Norges Informasjonstekonlogiske Høgskole RF3100 Matematikk og fysikk Side 1 av 10 Tillatte hjelpemidler: Kalkulator, vedlagt formelark Varighet: 3 timer Dato: 11.desember
FYS-MEK 1110 Løsningsforslag Eksamen Vår 2014
 FYS-MEK 1110 Løsningsforslag Eksamen Vår 2014 Oppgave 1 (4 poeng) Forklar hvorfor Charles Blondin tok med seg en lang og fleksibel stang når han balanserte på stram line over Niagara fossen i 1859. Han
FYS-MEK 1110 Løsningsforslag Eksamen Vår 2014 Oppgave 1 (4 poeng) Forklar hvorfor Charles Blondin tok med seg en lang og fleksibel stang når han balanserte på stram line over Niagara fossen i 1859. Han
Illusjonsutstillingen Du tror det ikke når du har sett det. Elevhefte. Vitensenteret. Nils Kr. Rossing. Revisjon 4.3. Trondheim
 Illusjonsutstillingen Du tror det ikke når du har sett det Elevhefte Revisjon 4.3 Vitensenteret Trondheim Nils Kr. Rossing 8 8 Utstillingen Elevark Gå gjennom utstillingen og les oppgavene ved hver modell.
Illusjonsutstillingen Du tror det ikke når du har sett det Elevhefte Revisjon 4.3 Vitensenteret Trondheim Nils Kr. Rossing 8 8 Utstillingen Elevark Gå gjennom utstillingen og les oppgavene ved hver modell.
Repetisjon av histogrammer
 Repetisjon av histogrammer INF 231 Hovedsakelig fra kap. 3.3 i DIP Histogramtransformasjoner Histogramutjevning Histogramtilpasning Standardisering av histogram for billedserier Litt om histogramtransformasjoner
Repetisjon av histogrammer INF 231 Hovedsakelig fra kap. 3.3 i DIP Histogramtransformasjoner Histogramutjevning Histogramtilpasning Standardisering av histogram for billedserier Litt om histogramtransformasjoner
Emne 10 Litt mer om matriser, noen anvendelser
 Emne 10 Litt mer om matriser, noen anvendelser (Reelle) ortogonale matriser La A være en reell, kvadratisk matrise, dvs. en (n n)-matrise hvor hvert element Da vil A være ortogonal dersom: og Med menes
Emne 10 Litt mer om matriser, noen anvendelser (Reelle) ortogonale matriser La A være en reell, kvadratisk matrise, dvs. en (n n)-matrise hvor hvert element Da vil A være ortogonal dersom: og Med menes
Krefter, Newtons lover, dreiemoment
 Krefter, Newtons lover, dreiemoment Tor Nordam 13. september 2007 Krefter er vektorer En ting som beveger seg har en hastighet. Hastighet er en vektor, som vi vanligvis skriver v. Hastighetsvektoren har
Krefter, Newtons lover, dreiemoment Tor Nordam 13. september 2007 Krefter er vektorer En ting som beveger seg har en hastighet. Hastighet er en vektor, som vi vanligvis skriver v. Hastighetsvektoren har
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF330 Metoder i grafisk databehandling og diskret geometri Eksamensdag: 3. desember 010 Tid for eksamen: 14.30 18.30 Oppgavesettet
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF330 Metoder i grafisk databehandling og diskret geometri Eksamensdag: 3. desember 010 Tid for eksamen: 14.30 18.30 Oppgavesettet
Kjeglesnitt. Harald Hanche-Olsen. Versjon
 Kjeglesnitt Harald Hanche-Olsen hanche@math.ntnu.no Versjon 1.0 2013-01-25 Innledning Kjeglesnittene sirkler, ellipser, parabler og hyperbler er klassiske kurver som har vært studert siden antikken. Kjeglesnittene
Kjeglesnitt Harald Hanche-Olsen hanche@math.ntnu.no Versjon 1.0 2013-01-25 Innledning Kjeglesnittene sirkler, ellipser, parabler og hyperbler er klassiske kurver som har vært studert siden antikken. Kjeglesnittene
Utfordringer knyttet til statistisk analyse av komposittdata
 ISSN 1893-1170 (online utgave) ISSN 1893-1057 (trykt utgave) www.norskbergforening.no/mineralproduksjon Notat Utfordringer knyttet til statistisk analyse av komposittdata Steinar Løve Ellefmo 1,* 1 Institutt
ISSN 1893-1170 (online utgave) ISSN 1893-1057 (trykt utgave) www.norskbergforening.no/mineralproduksjon Notat Utfordringer knyttet til statistisk analyse av komposittdata Steinar Løve Ellefmo 1,* 1 Institutt
Geometri Verktøylinja i GeoGebra Konstruksjon / tegning Konstruksjonsforklaring Normaler, paralleller og vinkler Mangekant, areal og omkrets
 2 Geometri Verktøylinja i GeoGebra Konstruksjon / tegning Konstruksjonsforklaring Normaler, paralleller og vinkler Mangekant, areal og omkrets Eksamensoppgaver 0 Innholdsfortegnelse INTRODUKSJON GEOGEBRA...
2 Geometri Verktøylinja i GeoGebra Konstruksjon / tegning Konstruksjonsforklaring Normaler, paralleller og vinkler Mangekant, areal og omkrets Eksamensoppgaver 0 Innholdsfortegnelse INTRODUKSJON GEOGEBRA...
En koordinat er ikke bare en koordinat
 En koordinat er ikke bare en koordinat En enkel innføring i koordinatsystem og kartprojeksjoner i Norge Versjon 1.0 Yngvar Amlien og Terje Omtveit Gilde 15. mai 2013 http://hovedprosjekter.hig.no/v2013/tol/geo/utmntm/koordinatsystem.pdf
En koordinat er ikke bare en koordinat En enkel innføring i koordinatsystem og kartprojeksjoner i Norge Versjon 1.0 Yngvar Amlien og Terje Omtveit Gilde 15. mai 2013 http://hovedprosjekter.hig.no/v2013/tol/geo/utmntm/koordinatsystem.pdf
Vektorligninger. Kapittel 3. Vektorregning
 Kapittel Vektorligninger I denne uken skal vi bruke enkel vektorregning til å analysere lineære ligningssystemer. Vi skal ha et spesielt fokus på R, for det går an å visualisere; klarer man det, går det
Kapittel Vektorligninger I denne uken skal vi bruke enkel vektorregning til å analysere lineære ligningssystemer. Vi skal ha et spesielt fokus på R, for det går an å visualisere; klarer man det, går det
Teknostart prosjekt 2010 for Kommunikasjonsteknologi. Posisjoneringstjenester for mobiltelefon
 Teknostart prosjekt 2010 for Kommunikasjonsteknologi Posisjoneringstjenester for mobiltelefon 1. Innledning Posisjoneringstjenester har utallige anvendelsesområder. I denne oppgaven skal det brukes en
Teknostart prosjekt 2010 for Kommunikasjonsteknologi Posisjoneringstjenester for mobiltelefon 1. Innledning Posisjoneringstjenester har utallige anvendelsesområder. I denne oppgaven skal det brukes en
TDT4105 IT Grunnkurs Høst 2014
 TDT4105 IT Grunnkurs Høst 2014 Norges teknisknaturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap Øving 6 1 Teori a) Hva er 2-komplement? b) Hva er en sample innen digital
TDT4105 IT Grunnkurs Høst 2014 Norges teknisknaturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap Øving 6 1 Teori a) Hva er 2-komplement? b) Hva er en sample innen digital
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i : INF3 Digital bildebehandling Eksamensdag : Onsdag. juni Tid for eksamen : 4:3 8:3 Oppgavesettet er på : 5 sider Vedlegg : Ingen
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i : INF3 Digital bildebehandling Eksamensdag : Onsdag. juni Tid for eksamen : 4:3 8:3 Oppgavesettet er på : 5 sider Vedlegg : Ingen
GeoGebraøvelser i geometri
 GeoGebraøvelser i geometri av Peer Andersen Peer Andersen 2014 Innhold Innledning... 3 Øvelse 1. Figurer i GeoGebra... 4 Øvelse 2. Noen funksjoner i GeoGebra... 8 Øvelse 3. Omskrevet sirkelen til en trekant...
GeoGebraøvelser i geometri av Peer Andersen Peer Andersen 2014 Innhold Innledning... 3 Øvelse 1. Figurer i GeoGebra... 4 Øvelse 2. Noen funksjoner i GeoGebra... 8 Øvelse 3. Omskrevet sirkelen til en trekant...
Komplekse tall og komplekse funksjoner
 KAPITTEL Komplekse tall og komplekse funksjoner. Komplekse tall.. Definisjon av komplekse tall. De komplekse tallene er en utvidelse av de reelle tallene. Dvs at de komplekse tallene er en tallmengde som
KAPITTEL Komplekse tall og komplekse funksjoner. Komplekse tall.. Definisjon av komplekse tall. De komplekse tallene er en utvidelse av de reelle tallene. Dvs at de komplekse tallene er en tallmengde som
Utforsking av funksjonsuttrykk og de tilhørende grafene ved hjelp av GeoGebra
 Anne-Mari Jensen Utforsking av funksjonsuttrykk og de tilhørende grafene ved hjelp av GeoGebra Innledning I ungdomsskolen kommer funksjoner inn som et av hovedområdene i læreplanen i matematikk. Arbeidet
Anne-Mari Jensen Utforsking av funksjonsuttrykk og de tilhørende grafene ved hjelp av GeoGebra Innledning I ungdomsskolen kommer funksjoner inn som et av hovedområdene i læreplanen i matematikk. Arbeidet
Innlevering FO929A - Matematikk forkurs HIOA Obligatorisk innlevering 3 Innleveringsfrist Fredag 14. november 2014 kl. 14 Antall oppgaver: 13
 Innlevering FO99A - Matematikk forkurs HIOA Obligatorisk innlevering 3 Innleveringsfrist Fredag 14. november 014 kl. 14 Antall oppgaver: 13 Løsningsforslag 1 Finn volumet til tetraederet med hjørner O(0,
Innlevering FO99A - Matematikk forkurs HIOA Obligatorisk innlevering 3 Innleveringsfrist Fredag 14. november 014 kl. 14 Antall oppgaver: 13 Løsningsforslag 1 Finn volumet til tetraederet med hjørner O(0,
LØSNINGSANTYDNING. HØGSKOLEN I AGDER Fakultet for teknologi. DAT 200 Grafisk Databehandling. Ingen. Klasse(r): 2DTM, 2DT, 2 Siving, DT
 HØGSKOLEN I AGDER Fakultet for teknologi LØSNINGSANTYDNING EMNE: FAGLÆRER: DAT 2 Grafisk Databehandling Morgan Konnestad Klasse(r): 2DTM, 2DT, 2 Siving, DT Dato: 5.2.5 Eksamenstid, fra-til: 9. - 3. Eksamensoppgaven
HØGSKOLEN I AGDER Fakultet for teknologi LØSNINGSANTYDNING EMNE: FAGLÆRER: DAT 2 Grafisk Databehandling Morgan Konnestad Klasse(r): 2DTM, 2DT, 2 Siving, DT Dato: 5.2.5 Eksamenstid, fra-til: 9. - 3. Eksamensoppgaven
Læreplan, nivå 1. Innhold / tema. Hovedområde Kompetansemål Elevene skal kunne: Tall og algebra:
 Kartlegging / vurdering av nivå Begynn året med et kort kurs i tall-lære og matematiske symboler. Deretter kartlegging som plasserer elevene i nivågruppe. De som kan dette, jobber med tekstoppgaver / problemløsning.
Kartlegging / vurdering av nivå Begynn året med et kort kurs i tall-lære og matematiske symboler. Deretter kartlegging som plasserer elevene i nivågruppe. De som kan dette, jobber med tekstoppgaver / problemløsning.
Kapittel 1. Metoder. Mål for Kapittel 1, Metoder. Kompetansemål. Mål for opplæringen er at eleven skal kunne
 Kapittel 1. Metoder Mål for Kapittel 1, Metoder Kompetansemål Mål for opplæringen er at eleven skal kunne gjøre overslag over svar, regne praktiske oppgaver, med og uten digitale verktøy, presentere resultatene
Kapittel 1. Metoder Mål for Kapittel 1, Metoder Kompetansemål Mål for opplæringen er at eleven skal kunne gjøre overslag over svar, regne praktiske oppgaver, med og uten digitale verktøy, presentere resultatene
TDT4195 Bildeteknikk
 TDT495 Bildeteknikk Grafikk Vår 29 Forelesning 5 Jo Skjermo Jo.skjermo@idi.ntnu.no Department of Computer And Information Science Jo Skjermo, TDT423 Visualisering 2 TDT495 Forrige gang Attributter til
TDT495 Bildeteknikk Grafikk Vår 29 Forelesning 5 Jo Skjermo Jo.skjermo@idi.ntnu.no Department of Computer And Information Science Jo Skjermo, TDT423 Visualisering 2 TDT495 Forrige gang Attributter til
MA-132 Geometri Torsdag 4. desember 2008 kl Tillatte hjelpemidler: Alle trykte og skrevne hjelpemidler. Kalkulator.
 Institutt for matematiske fag EKSAMEN i MA-1 Geometri Torsdag 4. desember 008 kl. 9.00-14.00 Tillatte hjelpemidler: Alle trykte og skrevne hjelpemidler. Kalkulator. Bokmål Oppgave 1 Gitt et linjestykke.
Institutt for matematiske fag EKSAMEN i MA-1 Geometri Torsdag 4. desember 008 kl. 9.00-14.00 Tillatte hjelpemidler: Alle trykte og skrevne hjelpemidler. Kalkulator. Bokmål Oppgave 1 Gitt et linjestykke.
Kurshefte GeoGebra. Ungdomstrinnet
 Kurshefte GeoGebra Ungdomstrinnet GeoGebra Geometri og algebra Dynamisk geometriverktøy Algebraisk verktøy Gratis Brukes på alle nivåer i utdanningssystemet Finnes på både bokmål og nynorsk Kan lastes
Kurshefte GeoGebra Ungdomstrinnet GeoGebra Geometri og algebra Dynamisk geometriverktøy Algebraisk verktøy Gratis Brukes på alle nivåer i utdanningssystemet Finnes på både bokmål og nynorsk Kan lastes
Inf109 Programmering for realister Uke 5. I denne leksjonen skal vi se på hvordan vi kan lage våre egne vinduer og hvordan vi bruker disse.
 Inf109 Programmering for realister Uke 5 I denne leksjonen skal vi se på hvordan vi kan lage våre egne vinduer og hvordan vi bruker disse. Før du starter må du kopiere filen graphics.py fra http://www.ii.uib.no/~matthew/inf1092014
Inf109 Programmering for realister Uke 5 I denne leksjonen skal vi se på hvordan vi kan lage våre egne vinduer og hvordan vi bruker disse. Før du starter må du kopiere filen graphics.py fra http://www.ii.uib.no/~matthew/inf1092014
Sentralverdi av dataverdi i et utvalg Vi tenker oss et utvalg med datapar. I vårt eksempel har vi 5 datapar.
 Statistisk behandling av kalibreringsresultatene Del 4. v/ Rune Øverland, Trainor Elsikkerhet AS Denne artikkelserien handler om statistisk behandling av kalibreringsresultatene. Dennne artikkelen tar
Statistisk behandling av kalibreringsresultatene Del 4. v/ Rune Øverland, Trainor Elsikkerhet AS Denne artikkelserien handler om statistisk behandling av kalibreringsresultatene. Dennne artikkelen tar
I Katalog velger du: Ny eksamensordning i matematikk våren 2015
 CAS teknikker H-P Ulven 10.12.2014 Innledning Våren 2015 gjelder nye regler for bruk av digitale hjelpemidler: Når det står "Bruk CAS", så må kandidaten bruke CAS, og når det står "Bruk graftegner", så
CAS teknikker H-P Ulven 10.12.2014 Innledning Våren 2015 gjelder nye regler for bruk av digitale hjelpemidler: Når det står "Bruk CAS", så må kandidaten bruke CAS, og når det står "Bruk graftegner", så
EKSAMEN I EMNE SIB 6005 GEOMATIKK-1. Torsdag 25. november 1999 Tid: 0900-1500
 NORGES TEKNISK-NTURVITENSKPELIGE UNIVERSITET (GM1-99h) side 1 av 5 INSTITUTT FOR KRT OG OPPMÅLING EKSMEN I EMNE SIB 65 GEOMTIKK-1 Torsdag 25. november 1999 Tid: 9-15 Faglig kontakt under eksamen: Oddgeir
NORGES TEKNISK-NTURVITENSKPELIGE UNIVERSITET (GM1-99h) side 1 av 5 INSTITUTT FOR KRT OG OPPMÅLING EKSMEN I EMNE SIB 65 GEOMTIKK-1 Torsdag 25. november 1999 Tid: 9-15 Faglig kontakt under eksamen: Oddgeir
SINUS R1, kapittel 5-8
 Løsning av noen oppgaver i SINUS R1, kapittel 5-8 Digital pakke B TI-Nspire Enkel kalkulator (Sharp EL-506, TI 30XIIB eller Casio fx-82es) Oppgaver og sidetall i læreboka: 5.43 c side 168 5.52 side 173
Løsning av noen oppgaver i SINUS R1, kapittel 5-8 Digital pakke B TI-Nspire Enkel kalkulator (Sharp EL-506, TI 30XIIB eller Casio fx-82es) Oppgaver og sidetall i læreboka: 5.43 c side 168 5.52 side 173
ST0202 Statistikk for samfunnsvitere
 ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag 2 Fra første forelesning: Populasjon Den mengden av individer/objekter som vi ønsker å analysere. Utvalg En delmengde av
ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag 2 Fra første forelesning: Populasjon Den mengden av individer/objekter som vi ønsker å analysere. Utvalg En delmengde av
INNHOLD SAMMENDRAG GEOMETRI
 INNHOLD GEOMETRI... 3 LINJE, STRÅLE OG LINJESTYKKE... 3 VINKEL... 3 STUMP, SPISS OG RETT VINKEL... 3 TOPPVINKLER... 4 NABOVINKLER... 4 SAMSVARENDE VINKLER... 4 OPPREISE EN NORMAL FRA ET PUNKT PÅ EN LINJE...
INNHOLD GEOMETRI... 3 LINJE, STRÅLE OG LINJESTYKKE... 3 VINKEL... 3 STUMP, SPISS OG RETT VINKEL... 3 TOPPVINKLER... 4 NABOVINKLER... 4 SAMSVARENDE VINKLER... 4 OPPREISE EN NORMAL FRA ET PUNKT PÅ EN LINJE...
Løsningsforslag. og B =
 Prøve i Matte EMFE DAFE ELFE BYFE Dato: august 25 Hjelpemiddel: Kalkulator og formelark Alle svar skal grunngis. Alle deloppgaver har lik vekt. Oppgave a) Gitt matrisene A = 2 3 2 4 2 Løsningsforslag og
Prøve i Matte EMFE DAFE ELFE BYFE Dato: august 25 Hjelpemiddel: Kalkulator og formelark Alle svar skal grunngis. Alle deloppgaver har lik vekt. Oppgave a) Gitt matrisene A = 2 3 2 4 2 Løsningsforslag og
Lærerveiledning uke 2-7: Geometri. volum, overflate og massetetthet Kompetansemål Geometri Måling Læringsmål Trekantberegning Kart og målestokk
 Lærerveiledning uke 2-7: Geometri. volum, overflate og massetetthet Geogebra - Anders film - Nappeinnlevring Kompetansemål Geometri undersøkje og beskrive eigenskapar ved to- og tredimensjonale figurar
Lærerveiledning uke 2-7: Geometri. volum, overflate og massetetthet Geogebra - Anders film - Nappeinnlevring Kompetansemål Geometri undersøkje og beskrive eigenskapar ved to- og tredimensjonale figurar
INF Triangulering. Med sterk støtte fra Petter Kristiansen. Skal først se på et eksempel fra Google Earth
 INF 4130 17. november 2011 Triangulering Stein Krogdahl Med sterk støtte fra Petter Kristiansen Skal først se på et eksempel fra Google Earth De bruker en underliggende triangulering av landskapet, men
INF 4130 17. november 2011 Triangulering Stein Krogdahl Med sterk støtte fra Petter Kristiansen Skal først se på et eksempel fra Google Earth De bruker en underliggende triangulering av landskapet, men
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i : INF2310 Digital bildebehandling Eksamensdag : Fredag 29. mars 2019 Tid for eksamen : 14:30 18:30 (4 timer) Oppgavesettet er
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i : INF2310 Digital bildebehandling Eksamensdag : Fredag 29. mars 2019 Tid for eksamen : 14:30 18:30 (4 timer) Oppgavesettet er
Emne 6. Lineære transformasjoner. Del 1
 Emne 6. Lineære transformasjoner. Del 1 Lineære transformasjoner kan sammenliknes med vanlig funksjonslære. X x 1 x 2 x 3 f Y Gitt to tallmengder X og Y. y 1 En funksjon f er her en regel som y 2 knytter
Emne 6. Lineære transformasjoner. Del 1 Lineære transformasjoner kan sammenliknes med vanlig funksjonslære. X x 1 x 2 x 3 f Y Gitt to tallmengder X og Y. y 1 En funksjon f er her en regel som y 2 knytter
Løsningsforslag Eksamen eksempeloppgave R1 - REA3022 - Desember 2007
 Løsningsforslag Eksamen eksempeloppgave R1 - REA022 - Desember 200 eksamensoppgaver.org October 2, 2008 eksamensoppgaver.org 2 Om løsningsforslaget Løsningsforslaget for matematikk eksempeloppgave i R1
Løsningsforslag Eksamen eksempeloppgave R1 - REA022 - Desember 200 eksamensoppgaver.org October 2, 2008 eksamensoppgaver.org 2 Om løsningsforslaget Løsningsforslaget for matematikk eksempeloppgave i R1
LØSNINGSANTYDNING EKSAMEN
 Universitetet i Agder Fakultet for teknologi og realfag LØSNINGSANTYDNING EKSAMEN Emnekode: Emnenavn: DAT Grafisk Databehandling Dato: 5. desember Varighet: 9 - Antall sider inkl. forside 8 Tillatte hjelpemidler:
Universitetet i Agder Fakultet for teknologi og realfag LØSNINGSANTYDNING EKSAMEN Emnekode: Emnenavn: DAT Grafisk Databehandling Dato: 5. desember Varighet: 9 - Antall sider inkl. forside 8 Tillatte hjelpemidler:
Innføring i GeoGebra (2 uv-timer)
 09/29/19 1/6 Innføring i GeoGebra (2 uv-timer) Innføring i GeoGebra (2 uv-timer) GeoGebra er et dynamisk matematikkprogram for skolebruk som forener geometri, algebra og funksjonslære. Programmet er utviklet
09/29/19 1/6 Innføring i GeoGebra (2 uv-timer) Innføring i GeoGebra (2 uv-timer) GeoGebra er et dynamisk matematikkprogram for skolebruk som forener geometri, algebra og funksjonslære. Programmet er utviklet
Oppgaver i matematikk 19-åringer, spesialistene
 Oppgaver i matematikk 19-åringer, spesialistene I TIMSS 95 var elever i siste klasse på videregående skole den eldste populasjonen som ble testet. I matematikk ble det laget to oppgavetyper: en for elever
Oppgaver i matematikk 19-åringer, spesialistene I TIMSS 95 var elever i siste klasse på videregående skole den eldste populasjonen som ble testet. I matematikk ble det laget to oppgavetyper: en for elever
Fra første forelesning:
 2 Fra første forelesning: ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag opulasjon Den mengden av individer/objekter som vi ønsker å analysere. Utvalg En delmengde av populasjonen
2 Fra første forelesning: ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag opulasjon Den mengden av individer/objekter som vi ønsker å analysere. Utvalg En delmengde av populasjonen
MA1201 Lineær algebra og geometri Løsningsforslag for eksamen gitt 3. desember 2007
 Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag MA101 Lineær algebra og geometri Løsningsforslag for eksamen gitt 3 desember 007 Oppgave 1 a) Vi ser på ligningssystemet x +
Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag MA101 Lineær algebra og geometri Løsningsforslag for eksamen gitt 3 desember 007 Oppgave 1 a) Vi ser på ligningssystemet x +
Konstruksjon og bruk av rutenett i perspektivtegning
 Konstruksjon og bruk av rutenett i perspektivtegning Gert Monstad Hana Sammendrag Teksten tar for seg hvordan å lage et perspektivisk bilde av kvadratiske rutenett. Bildet av slike rutenett kan være til
Konstruksjon og bruk av rutenett i perspektivtegning Gert Monstad Hana Sammendrag Teksten tar for seg hvordan å lage et perspektivisk bilde av kvadratiske rutenett. Bildet av slike rutenett kan være til
Modul nr Roboter og omkrets
 Modul nr. 2109 Roboter og omkrets Tilknyttet rom: Newton Møre 2109 Newton håndbok - Roboter og omkrets Side 2 Kort om denne modulen Praktisk informasjon Før elevene skal delta på Roboter og omkrets-modulen,
Modul nr. 2109 Roboter og omkrets Tilknyttet rom: Newton Møre 2109 Newton håndbok - Roboter og omkrets Side 2 Kort om denne modulen Praktisk informasjon Før elevene skal delta på Roboter og omkrets-modulen,
Geometriske avbildninger og symmetri. A2A/A2B Høgskolen i Vestfold
 Geometriske avbildninger og symmetri A2A/A2B Høgskolen i Vestfold 6. november 2009 Innhold 1. Symmetri 2. Avbildninger 3. Isometrier 4. Egenskaper ved avbildninger 5. Symmetrigrupper Kilde for forelesningen:
Geometriske avbildninger og symmetri A2A/A2B Høgskolen i Vestfold 6. november 2009 Innhold 1. Symmetri 2. Avbildninger 3. Isometrier 4. Egenskaper ved avbildninger 5. Symmetrigrupper Kilde for forelesningen:
03.10.2013 Manual til. GeoGebra. Ungdomstrinnet. Ressurs til. Grunntall 8 10. Bjørn Bakke og Inger Nygjelten Bakke ELEKTRONISK UNDERVISNINGSFORLAG AS
 03.10.2013 Manual til GeoGebra Ungdomstrinnet Ressurs til Grunntall 8 10 Bjørn Bakke og Inger Nygjelten Bakke ELEKTRONISK UNDERVISNINGSFORLAG AS Innhold Verktøy... 4 Hva vinduet i GeoGebra består av...
03.10.2013 Manual til GeoGebra Ungdomstrinnet Ressurs til Grunntall 8 10 Bjørn Bakke og Inger Nygjelten Bakke ELEKTRONISK UNDERVISNINGSFORLAG AS Innhold Verktøy... 4 Hva vinduet i GeoGebra består av...
Strøm av olje og vann i berggrunnen matematisk model, simulering og visualisering
 Strøm av olje og vann i berggrunnen matematisk model, simulering og visualisering Hans Fredrik Nordhaug Matematisk institutt Faglig-pedagogisk dag, 01.02.2000. Oversikt 1 Oversikt Introduksjon. Hva er
Strøm av olje og vann i berggrunnen matematisk model, simulering og visualisering Hans Fredrik Nordhaug Matematisk institutt Faglig-pedagogisk dag, 01.02.2000. Oversikt 1 Oversikt Introduksjon. Hva er
Innholdsfortegnelse. 1. Innledning 1.1. Forord 1.2. Problemstilling. 2. Om kamera 2.1. Blender 2.2. Lukker 2.3. ISO
 Innholdsfortegnelse 1. Innledning 1.1. Forord 1.2. Problemstilling 2. Om kamera 2.1. Blender 2.2. Lukker 2.3. ISO 3. Digital fotografering I bevegelse 3.1. Motivbevegelse med stativ 3.2. Kamerabevegelse
Innholdsfortegnelse 1. Innledning 1.1. Forord 1.2. Problemstilling 2. Om kamera 2.1. Blender 2.2. Lukker 2.3. ISO 3. Digital fotografering I bevegelse 3.1. Motivbevegelse med stativ 3.2. Kamerabevegelse
Løsningsforslag til kapittel 15 Fargerom og fargebilder
 Løsningsforslag til kapittel 15 Fargerom og fargebilder Oppgave 1: Representasjon av et bilde Under har vi gitt et lite binært bilde, der svart er 0 og hvit er 1. a) Kan du skrive ned på et ark binærrepresentasjonen
Løsningsforslag til kapittel 15 Fargerom og fargebilder Oppgave 1: Representasjon av et bilde Under har vi gitt et lite binært bilde, der svart er 0 og hvit er 1. a) Kan du skrive ned på et ark binærrepresentasjonen
Karakter 2: 10p Karakter 3: 17p Karakter 4: 23p Karakter 5: 30p Karakter 6: 36p
 06.02.2017 MATEMATIKK (MAT1005) Rette linjer / Lineære funksjoner DEL 1 (UTEN HJELPEMIDLER) 50 minutter DEL 2 (MED HJELPEMIDLER) 40 minutter (Del 1 leveres inn etter nøyaktig 50 minutter og før hjelpemidlene
06.02.2017 MATEMATIKK (MAT1005) Rette linjer / Lineære funksjoner DEL 1 (UTEN HJELPEMIDLER) 50 minutter DEL 2 (MED HJELPEMIDLER) 40 minutter (Del 1 leveres inn etter nøyaktig 50 minutter og før hjelpemidlene
MA1102 Grunnkurs i analyse II Vår 2019
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA1102 Grunnkurs i analyse II Vår 2019 Først en kommentar. I læreboka møter man kjeglesnitt på standardform, som ellipser x
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA1102 Grunnkurs i analyse II Vår 2019 Først en kommentar. I læreboka møter man kjeglesnitt på standardform, som ellipser x
ST0202 Statistikk for samfunnsvitere
 ST0202 Statistikk for samfunnsvitere Kapittel 7: Utvalgsfordeling Bo Lindqvist Institutt for matematiske fag 2 Fra kapittel 1: Populasjon Den mengden av individer/objekter som vi ønsker å analysere. Utvalg
ST0202 Statistikk for samfunnsvitere Kapittel 7: Utvalgsfordeling Bo Lindqvist Institutt for matematiske fag 2 Fra kapittel 1: Populasjon Den mengden av individer/objekter som vi ønsker å analysere. Utvalg
Løsningsforslag til øving 12
 FY1001/TFY4145 Mekanisk fysikk. Institutt for fysikk, NTNU. Høsten 014. Løsningsforslag til øving 1 Oppgave 1 a) I følge Galileo: (S = Sam, S = Siv, T = Toget) I følge Einstein: Dermed: Her har vi brukt
FY1001/TFY4145 Mekanisk fysikk. Institutt for fysikk, NTNU. Høsten 014. Løsningsforslag til øving 1 Oppgave 1 a) I følge Galileo: (S = Sam, S = Siv, T = Toget) I følge Einstein: Dermed: Her har vi brukt
7 Egenverdier og egenvektorer TMA4110 høsten 2018
 7 Egenverdier og egenvektorer TMA4 høsten 8 Det er ofte hensiktsmessig å tenke på en matrise ikke bare som en tabell med tall, men som en transformasjon av vektorer. Hvis A er en m n-matrise, så gir A
7 Egenverdier og egenvektorer TMA4 høsten 8 Det er ofte hensiktsmessig å tenke på en matrise ikke bare som en tabell med tall, men som en transformasjon av vektorer. Hvis A er en m n-matrise, så gir A
Oppgave 2 Løs oppgavene I og II, og kryss av det alternativet (a, b eller c) som passer best. En funksjon er ikke deriverbar der:
 Oppgave a) Si kort hva deriverte til en funksjon forteller oss. Hva handler deriverbarhet om? b) Er f (x) = deriverbar for alle reelle x-verdier? x Bestem deriverte til f i sin definisjonsmengde. c) Tegn
Oppgave a) Si kort hva deriverte til en funksjon forteller oss. Hva handler deriverbarhet om? b) Er f (x) = deriverbar for alle reelle x-verdier? x Bestem deriverte til f i sin definisjonsmengde. c) Tegn
Kapittel 6. Trekanter
 Kapittel 6. Trekanter Mål for kapittel 6: Kompetansemål Mål for opplæringen er at eleven skal kunne bruke og grunngi bruk av formlikhet, målestokk og Pytagoras setning til beregninger i praktisk arbeid
Kapittel 6. Trekanter Mål for kapittel 6: Kompetansemål Mål for opplæringen er at eleven skal kunne bruke og grunngi bruk av formlikhet, målestokk og Pytagoras setning til beregninger i praktisk arbeid
Forelesningsnotater SIF8039/ Grafisk databehandling
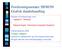 Forelesningsnotater SIF839/ Grafisk databehandling Notater til elesninger over: Kapittel 5: Viewing i: Edward Angel: Interactive Computer Graphics Vårsemesteret 22 Torbjørn Hallgren Institutt datateknikk
Forelesningsnotater SIF839/ Grafisk databehandling Notater til elesninger over: Kapittel 5: Viewing i: Edward Angel: Interactive Computer Graphics Vårsemesteret 22 Torbjørn Hallgren Institutt datateknikk
SAMMENDRAG OG FORMLER
 SAMMENDRAG OG FORMLER SAMMENDRAG OG FORMLER Nye Mega 8A Kapittel A GEOMETRI LINJE, LINJESTYKKE OG STRÅLE linje stråle linjestykke VINKLER VINKELBEIN OG TOPPUNKT En vinkel har et toppunkt. Denne vinkelen
SAMMENDRAG OG FORMLER SAMMENDRAG OG FORMLER Nye Mega 8A Kapittel A GEOMETRI LINJE, LINJESTYKKE OG STRÅLE linje stråle linjestykke VINKLER VINKELBEIN OG TOPPUNKT En vinkel har et toppunkt. Denne vinkelen
Kurshefte GeoGebra. Barnetrinnet
 Kurshefte GeoGebra Barnetrinnet GeoGebra Geometri og algebra Dynamisk geometriverktøy Algebraisk verktøy Gratis Brukes på alle nivåer i utdanningssystemet Finnes på både bokmål og nynorsk Kan lastes ned
Kurshefte GeoGebra Barnetrinnet GeoGebra Geometri og algebra Dynamisk geometriverktøy Algebraisk verktøy Gratis Brukes på alle nivåer i utdanningssystemet Finnes på både bokmål og nynorsk Kan lastes ned
Sprettende ball Introduksjon Processing PDF
 Sprettende ball Introduksjon Processing PDF Introduksjon: I denne modulen skal vi lære et programmeringsspråk som heter Processing. Det ble laget for å gjøre programmering lett for designere og andre som
Sprettende ball Introduksjon Processing PDF Introduksjon: I denne modulen skal vi lære et programmeringsspråk som heter Processing. Det ble laget for å gjøre programmering lett for designere og andre som
Elektrisk og Magnetisk felt
 Elektrisk og Magnetisk felt Kjetil Liestøl Nielsen 1 Emner for i dag Coulombs lov Elektrisk felt Ladet partikkel i elektrisk felt Magnetisk felt Magnetisk kraft på elektrisk eladninger Elektromagnetiske
Elektrisk og Magnetisk felt Kjetil Liestøl Nielsen 1 Emner for i dag Coulombs lov Elektrisk felt Ladet partikkel i elektrisk felt Magnetisk felt Magnetisk kraft på elektrisk eladninger Elektromagnetiske
Lag et bilde av geometriske figurer, du også!
 Lag et bilde av geometriske figurer, du også! 6 Geometri 1 MÅL I dette kapitlet skal du lære om firkanter trekanter sammensatte figurer sirkler KOPIERINGSORIGINALER 6.1 Tangram 6.4 Felles problemløsing
Lag et bilde av geometriske figurer, du også! 6 Geometri 1 MÅL I dette kapitlet skal du lære om firkanter trekanter sammensatte figurer sirkler KOPIERINGSORIGINALER 6.1 Tangram 6.4 Felles problemløsing
plassere negative hele tall på tallinje
 Kompetansemål etter 7. trinn Tall og algebra: 1. beskrive plassverdisystemet for desimaltall, regne med positive og negative hele tall, desimaltall, brøker og prosent, og plassere dem på tallinje 2. finne
Kompetansemål etter 7. trinn Tall og algebra: 1. beskrive plassverdisystemet for desimaltall, regne med positive og negative hele tall, desimaltall, brøker og prosent, og plassere dem på tallinje 2. finne
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i : INF310 Digital bildebehandling Eksamensdag : Tirsdag 5. juni 007 Tid for eksamen : 09:00 1:00 Oppgavesettet er på : 5 sider
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i : INF310 Digital bildebehandling Eksamensdag : Tirsdag 5. juni 007 Tid for eksamen : 09:00 1:00 Oppgavesettet er på : 5 sider
KONTINUASJONSEKSAMEN I EMNE TDT4230 VISUALISERING TIRSDAG 9. AUGUST 2005 KL LØSNINGSFORSLAG
 Side 1 av 8 NTNU Norges teknisk-naturvitenskapelige universitet Fakultet for fysikk, informatikk og matematikk Institutt for datateknikk og informasjonsvitenskap KONTINUASJONSEKSAMEN I EMNE TDT430 VISUALISERING
Side 1 av 8 NTNU Norges teknisk-naturvitenskapelige universitet Fakultet for fysikk, informatikk og matematikk Institutt for datateknikk og informasjonsvitenskap KONTINUASJONSEKSAMEN I EMNE TDT430 VISUALISERING
ÅRSPLAN I MATEMATIKK 17/18
 Tall KOMPETANSEMÅL PERIODE ARBEIDSMETODE DIGITALT VERKTØY Forstå plassverdisystemet for hele tall og, alt fra tusendeler til millioner og så med brøker og prosent. De skal også forstå utvidelsen til negative
Tall KOMPETANSEMÅL PERIODE ARBEIDSMETODE DIGITALT VERKTØY Forstå plassverdisystemet for hele tall og, alt fra tusendeler til millioner og så med brøker og prosent. De skal også forstå utvidelsen til negative
Kanter, kanter, mange mangekanter
 Kanter, kanter, mange mangekanter Nybegynner Processing PDF Introduksjon: Her skal vi se på litt mer avansert opptegning og bevegelse. Vi skal ta utgangspunkt i oppgaven om den sprettende ballen, men bytte
Kanter, kanter, mange mangekanter Nybegynner Processing PDF Introduksjon: Her skal vi se på litt mer avansert opptegning og bevegelse. Vi skal ta utgangspunkt i oppgaven om den sprettende ballen, men bytte
EKSAMEN I EMNE TDT4195/SIF8043 BILDETEKNIKK ONSDAG 19. MAI 2004 KL
 Side 1 av 5 NTNU Norges teknisk-naturvitenskapelige universitet Fakultet for informasjonsteknologi, matematikk og elektroteknikk Institutt for datateknikk og informasjonsvitenskap EKSAMEN I EMNE TDT4195/SIF8043
Side 1 av 5 NTNU Norges teknisk-naturvitenskapelige universitet Fakultet for informasjonsteknologi, matematikk og elektroteknikk Institutt for datateknikk og informasjonsvitenskap EKSAMEN I EMNE TDT4195/SIF8043
Anvendt Robotteknikk Konte Sommer 2019 EKSAMEN HARIS JASAREVIC
 2019 Anvendt Robotteknikk Konte Sommer 2019 EKSAMEN HARIS JASAREVIC Innhold Oppgaver... 2 Oppgave 1... 2 Oppgave 2... 2 Oppgave 3... 2 Oppgave 4... 2 Oppgave 5... 3 Oppgave 6... 4 Oppgave 7... 5 Oppgave
2019 Anvendt Robotteknikk Konte Sommer 2019 EKSAMEN HARIS JASAREVIC Innhold Oppgaver... 2 Oppgave 1... 2 Oppgave 2... 2 Oppgave 3... 2 Oppgave 4... 2 Oppgave 5... 3 Oppgave 6... 4 Oppgave 7... 5 Oppgave
QED 5 10. Matematikk for grunnskolelærerutdanningen. Bind 2. Fasit kapittel 3 Geometri
 QED 5 0 Matematikk for grunnskolelærerutdanningen Bind Fasit kapittel Geometri Kapittel Oppgave a) ( +, + 7) = (4, 9) b) (0, 4 + 5) = (, ) c) ( + 0, + 6) = (, 9) Oppgave a) Vi får vektoren [4, ]. b) Vi
QED 5 0 Matematikk for grunnskolelærerutdanningen Bind Fasit kapittel Geometri Kapittel Oppgave a) ( +, + 7) = (4, 9) b) (0, 4 + 5) = (, ) c) ( + 0, + 6) = (, 9) Oppgave a) Vi får vektoren [4, ]. b) Vi
Midtveiseksamen Løsningsforslag
 INSTITUTT FOR INFORMATIKK, UNIVERSITETET I OSLO Midtveiseksamen Løsningsforslag INF2310 - Digital Bildebehandling Eksamen i: INF2310 - Digital Bildebehandling Eksamensdag: Tirsdag 21. mars 2017 Tidspunkt
INSTITUTT FOR INFORMATIKK, UNIVERSITETET I OSLO Midtveiseksamen Løsningsforslag INF2310 - Digital Bildebehandling Eksamen i: INF2310 - Digital Bildebehandling Eksamensdag: Tirsdag 21. mars 2017 Tidspunkt
SUBTRAKSJON FRA A TIL Å
 SUBTRAKSJON FRA A TIL Å VEILEDER FOR FORELDRE MED BARN I 5. 7. KLASSE EMNER Side 1 Innledning til subtraksjon S - 2 2 Grunnleggende om subtraksjon S - 2 3 Ulike fremgangsmåter S - 2 3.1 Tallene under hverandre
SUBTRAKSJON FRA A TIL Å VEILEDER FOR FORELDRE MED BARN I 5. 7. KLASSE EMNER Side 1 Innledning til subtraksjon S - 2 2 Grunnleggende om subtraksjon S - 2 3 Ulike fremgangsmåter S - 2 3.1 Tallene under hverandre
(a) R n defineres som mengden av kolonnevektorer. a 1 a 2. a n. (b) R n defineres som mengden av radvektorer
 5 Vektorrom Et vektorrom er en mengde V med tre algebraiske operasjoner (addisjon, negasjon og skalærmultiplikasjon) som tilfredsstiller de 10 betingelsene fra Def. 4.1.1. Jeg vil ikke gi en eksamensoppgave
5 Vektorrom Et vektorrom er en mengde V med tre algebraiske operasjoner (addisjon, negasjon og skalærmultiplikasjon) som tilfredsstiller de 10 betingelsene fra Def. 4.1.1. Jeg vil ikke gi en eksamensoppgave
Eksempel på løsning. Sentralt gitt skriftlig eksamen MAT1008 Matematikk 2T Eksamen 30.11.2009. Bokmål
 Eksempel på løsning 010 Sentralt gitt skriftlig eksamen MAT1008 Matematikk T Eksamen 30.11.009 Bokmål MAT1008 Matematikk T HØSTEN 009 Eksempel på løsning med vekt på bruk av digitale verktøy Hva er en
Eksempel på løsning 010 Sentralt gitt skriftlig eksamen MAT1008 Matematikk T Eksamen 30.11.009 Bokmål MAT1008 Matematikk T HØSTEN 009 Eksempel på løsning med vekt på bruk av digitale verktøy Hva er en
Michelson Interferometer
 Michelson Interferometer Hensikt Bildet ovenfor viser et sa kalt Michelson interferometer, der laserlys sendes inn mot en bikonveks linse, før det treffer et delvis reflekterende speil og splittes i to
Michelson Interferometer Hensikt Bildet ovenfor viser et sa kalt Michelson interferometer, der laserlys sendes inn mot en bikonveks linse, før det treffer et delvis reflekterende speil og splittes i to
Eneboerspillet del 2. Håvard Johnsbråten, januar 2014
 Eneboerspillet del 2 Håvard Johnsbråten, januar 2014 I Johnsbråten (2013) løste jeg noen problemer omkring eneboerspillet vha partall/oddetall. I denne parallellversjonen av artikkelen i vil jeg i stedet
Eneboerspillet del 2 Håvard Johnsbråten, januar 2014 I Johnsbråten (2013) løste jeg noen problemer omkring eneboerspillet vha partall/oddetall. I denne parallellversjonen av artikkelen i vil jeg i stedet
Snake Expert Scratch PDF
 Snake Expert Scratch PDF Introduksjon En eller annen variant av Snake har eksistert på nesten alle personlige datamaskiner helt siden slutten av 1970-tallet. Ekstra populært ble spillet da det dukket opp
Snake Expert Scratch PDF Introduksjon En eller annen variant av Snake har eksistert på nesten alle personlige datamaskiner helt siden slutten av 1970-tallet. Ekstra populært ble spillet da det dukket opp
Lydintensiteten i avstand, R: L 1 = W/4 R 2. Lydintensitet i dobbel avstand, 2R: L 2 = W/4 R) 2 =W/(4 R 2 )4= L 1 /4. L 2 = W/4 R)h= W/(2 Rh)2= L 1 /2
 8-1 Støyberegning etter Nordisk beregningsmetode Det vises til Håndbok 064 Når du har gjennomgått denne modul skal du Kjenne til fenomet lyd generelt og måleenheten for støy, decibel (db). Kunne beregne
8-1 Støyberegning etter Nordisk beregningsmetode Det vises til Håndbok 064 Når du har gjennomgått denne modul skal du Kjenne til fenomet lyd generelt og måleenheten for støy, decibel (db). Kunne beregne
Prosjekt 2 - Introduksjon til Vitenskapelige Beregninger
 Prosjekt - Introduksjon til Vitenskapelige Beregninger Studentnr: 755, 759 og 7577 Mars 6 Oppgave Feltlinjene for en kvadrupol med positive punktladninger Q lang x-aksen i x = ±r og negative punktladninger
Prosjekt - Introduksjon til Vitenskapelige Beregninger Studentnr: 755, 759 og 7577 Mars 6 Oppgave Feltlinjene for en kvadrupol med positive punktladninger Q lang x-aksen i x = ±r og negative punktladninger
HØGSKOLEN I SØR-TRØNDELAG
 HØGSKOLEN I SØR-TRØNDELAG Avdeling for informatikk og e-læring Kandidat nr: Eksamensdato: 7. desember 007 Varighet: timer (9:00 :00) Fagnummer: LV78D Fagnavn: Digital bildebehandling Klasser: HIDT005H
HØGSKOLEN I SØR-TRØNDELAG Avdeling for informatikk og e-læring Kandidat nr: Eksamensdato: 7. desember 007 Varighet: timer (9:00 :00) Fagnummer: LV78D Fagnavn: Digital bildebehandling Klasser: HIDT005H
EKSAMEN I EMNE TDT4230 VISUALISERING LØRDAG 10. DESEMBER 2005 KL
 NTNU Norges teknisk-naturvitenskapelige universitet Fakultet for fysikk, informatikk og matematikk Institutt for datateknikk og informasjonsvitenskap EKSAMEN I EMNE TDT4230 VISUALISERING LØRDAG 10. DESEMBER
NTNU Norges teknisk-naturvitenskapelige universitet Fakultet for fysikk, informatikk og matematikk Institutt for datateknikk og informasjonsvitenskap EKSAMEN I EMNE TDT4230 VISUALISERING LØRDAG 10. DESEMBER
Temaer i dag. Repetisjon av histogrammer II. Repetisjon av histogrammer I. INF 2310 Digital bildebehandling FORELESNING 5.
 Temaer i dag INF 231 Digital bildebehandling FORELESNING 5 HISTOGRAM-TRANSFORMASJONER Fritz Albregtsen Histogramtransformasjoner Histogramutjevning Histogramtilpasning Standardisering av histogram for
Temaer i dag INF 231 Digital bildebehandling FORELESNING 5 HISTOGRAM-TRANSFORMASJONER Fritz Albregtsen Histogramtransformasjoner Histogramutjevning Histogramtilpasning Standardisering av histogram for
Løsningsforslag, eksamen MA1101/MA
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 7 Løsningsforslag, eksamen MA0/MA60 07.2.09 Oppgave La f() = e 4 2 2 8. a) Finn alle ekstremalpunktene til funksjonen
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 7 Løsningsforslag, eksamen MA0/MA60 07.2.09 Oppgave La f() = e 4 2 2 8. a) Finn alle ekstremalpunktene til funksjonen
