Direkte produkter. 5. Del
|
|
|
- Hannah Aronsen
- 7 år siden
- Visninger:
Transkript
1 5. Del Direkte prdukter Vi kjenner det kartesiske prduktet av t mengder X Y.Detbeståravallepar(x, y) av elementer x 2 X g y 2 Y.OrdetkartesiskerdannetavegennavnetRenéDécartes, en fransk filsf g matematiker sm levde fra 1596 til Han ble født i Frankrike, virket stre deler av sitt liv i Nederland, g døde i Stckhlm. Décartes ble hyret sm privatlærer fr Drnning Kristina sm var regjerende drnning i Sverige i periden 1632 till 1654 g sm ppviste en impnerende interesse fr kultur g vitenskap. Imidlertid pådr Décartes seg en lungebetennelse krt tid etter sin ankmst til Sverige, g han døde etter et snaut halvt år. Decartes viktigste arbeid i matematikk heter La Gémétrie. Der begynte han å bruke algebra fr å studere gemetri, g fr å gjøre det innførte han krdinater i planet. Derfr kalles de vanlige xy-krdinatene fte fr kartesiske krdinater. Sammenhengen med det kartesiske prduktet er selvsagt at punktene i det krdinatiserte planet kan representeres sm par (x, y) der krdinatene x g y er reelle tall, det vil si sm punkter i R 2 = R R. Det direkte prduktet av t grupper La nå G g H være t grupper. Vi skal innføre en gruppestruktur på det kartesiske prduktet G H. DengdegamleaddisjnenavvektreriR 2 ellerfrdensaks skyld av vektrer i R n ergittvedkmpnentvisaddisjn,gmeddetsmmdell definerer vi multiplikasjnen i G H ved: (a, b)(a 0,b 0 )=(ab, a 0 b 0 ). Mengden G H utstyrt med denne binære perasjnen kalles 1 det direkte prduktet av G g H. Det hører med til terien å verifisere at denne binære perasjnen ppfyller 1 Når man har et direkte prdukt, skulle man tr at man gså har et indirekte prdukt. Men det har man altså ikke. Adjektivet direkte har sm funksjn å skille det direkte prduktet, slik vi har definert det, fra prduktet HK av t undergrupper i G. Determengdenbeståendeavalleprdukter 1
2 Direkte prdukter MAT2200 Vår 2014 de tre kravene til en gruppe. Asssiativitet følger umiddelbart, siden prduktet i hver faktr er asssiativt. Identitetselementet g inversdannelsen beskrives gså naturlig nk kmpnentvis: Identitetselementet: e G H =(e G,e H ). Inversdannelse: (a, b) 1 =(a 1,b 1 ). Vi verlater til leseren å sjekke at vi på denne måten faktisk har definert et nøytralt element, g at (a, b) 1 etter denne definisjnen faktisk er en invers til (a, b); detert rett-frem-etter-nesen-verifikasjner. Vi har gså følgende lemma sm er like rett frem etter nesten å bevise: Setning. Dersm G g H er t abelske grupper, så er G H abelsk. Dersm de t gruppene G g H begge er endelige, såerg H selvsagt gså endelig, g rdenen til prduktet er lik prduktet av rdnene: G H = G H. Setning. Dersm G g H begge er endelige, så er det dirkete prduktet G H endelig g G H = G H. Det direkte prduktet av flere grupper Det er lett å generalisere denne definisjnen slik at vi gså kan snakke m det direkte prduktet av flere grupper. Om G 1,...,G n er grupper, utstyrer vi det kartesiske prduktet ny G i = G 1 G 2... G n = { (a 1,...,a n ) a i 2 G i } i=1 med den binær perasjnen gitt ved kmpnentvis multiplikasjn. Denne ppfyller kravene til å være en gruppelv, g vi kaller den resulterende gruppen fr det direkte prduktet av gruppene G 1,...,G n. Til syvende å sist er det heller ikke påkrevet med endelig mange grupper. Fr enhver familie {G i } i2i av grupper, indeksert av en mengde I, vildetkartesiskeprduktet Q i2i G i være en gruppe når det utstyres med kmpnentvis multiplikasjn sm gruppelv. Sm vanlig skaper skillet mellm additiv g multiplikative grupper en ntasjnsmessig flertydighet. Dersm A 1,...,A r er additive grupper (sm altså per knvensjn er kmmutative) vil vi stundm la A i A r betegne deres direkte prdukt, g vi mdøper det fluksens til den direkete summen av A i -ene. Kmpaktntasjnen Q i2i A i kan erstattes av kmpaktntasjnen L i2i A i. 2
3 Direkte prdukter MAT2200 Vår 2014 Ordenen til elementer i et direkte prdukt Når det gjelder rdenen til elementer i det direkte prduktet G H har vi følgende sats: Setning. La a 2 G g b 2 H være t elementer i henhldsvis G g H. Antaata er av rden n g at b er av rden m. Daerelementet(a, b) i G H av rden lcm(n, m). Bevis: La k =lcm(n, m). Vihar(a, b) k =(a k,b k )=(e G,e H ) siden både n g m er divisrer i k. Omvendt,m(a, b) r =(a r,b r )=(e G,e H ),såviln r g m r. Følgelighar vi siden k =lcm(n, m), atk r. Vi skal nå se på det direkte prduktet Z n Z m der vi antar at n g m er uten felles faktr. Ordenen til Z n Z m er gitt sm Z n Z m = nm. La være en generatr fr Z n g en fr Z m.sidenn g m er uten felles faktrer, er deres minste felles multiplum lik nm, gettersetning. venfr er (, ) av rden nm. Detfølgerat(, ) genererer Z n Z m,gfølgeligerz n Z m en syklisk gruppe. Vi har med andre rd en ismrfi Z nm ' Z n Z m.vialtsåvist: Setning. Dersm n g m er t relativt primiske heltall, så er Z nm ' Z n Z m Fr eksempel er Z 2 Z 3 ' Z 6 g Z 11 Z 91 ' Z La p være et primtall g n et naturlig tall. Da er gruppen Z n p = Z p... Z p,derdet er n faktrer i prduktet, en abelsk gruppe av rden p n.allikevelerhvertikke-trivielle element i Z n p av rden p. VikallerZ n p fr en elementær abelsk gruppe. Dette eksemplet viser at hyptesen i setning. m at n g m er relativt primiske, ikke kan svekkes. Generelt kaller vi det minste tallet n slik at a n = e fr medlemmer a av en gruppe G fr ekspnenten til G. Sidenrd(a) deler n m a n = e, erdetklartatekspnenten til G er lik det minste felles multiplium av rd(a) når a gjennmløper G. Freksempel har Z n p ekspnent p, meneravrdenp n. Oppgaver.. Generaliser setning. venfr til et direkte prdukt av vilkårlig mange (men allikevel endelig mange) grupper g vis at m a =(a 1,...,a s ) er et element i det dirkete prduktet G 1... G s,såerrd(a) =lcm(r 1,...,r s ) der r i =rd(a i )... Bestem rdenen til elementet (4, 4, 4) igruppenz 160 Z 1010 Z Vis at ekspnenten til en endelig gruppe G er det minste felles multiplium av rd(a) når a gjennmløper G... Vis at ekspnenten til et direkte prdukt av endelige grupper er det minste felles multiplum til ekspnentene til faktrene. av elementer fra henhldsvis H g K. MengdenHK er en undergruppe bare m minst en av gruppene H eller K er en nrmal undergruppe. 3
4 Direkte prdukter MAT2200 Vår 2014 Interne direkte prdukter Det er av str interesse å kunne skrive en gruppe sm et direkte prdukt av (nødvendigvis) mindre g (frhåpentligvis) enklere grupper. Gitt at vi kjenner faktrene gdt, kjenner vi det direkte prduktet gdt rent gruppeteretisk 2 er ikke prduktet mer kmplisert enn de enkelte faktrene. Så en gruppeteretiker er svært frnøyd m han klarer å spalte enn gruppe i et prdukt av t ikke-trivielle. IdenneparagrafenskalvigietkriteriumfrnårengruppeG er ismrf med det direkte prduktet av t av sine undergrupper. Da mtales fte det direkte prdukte sm å være internt, siden de t faktrene j er undergrupper av G. Dette er mest en talemåte; det er ingen substansiell frskjell på interne dirkete prdukter g direkte prdukter. Hver av gruppene H g K ligger på en naturlig måte inne i det direkte prduktet H K, henhldsvissmundergruppenh 0 = H {e K } g K 0 = {e H } K. Disse t undergruppene har enkelte helt spesielle egenskaper 3 sm ikke mange undergrupper har. Snittet av H 0 g K 0 reduserer seg til {e H K }.Deterikkevanskeligåinnseat elementer fra H 0 g K 0 kmmuterer: vi har j (h, e K )(e H,k)=(h, k) =(e H,k)(h, e K ). Den tredje egenskapen de t undergruppene H 0 g K 0 har, er at ethvert element i prduktet H K kan skrives på frmen hk med h 2 H 0 g k 2 K 0.Vippsummerer Undergruppene H 0 g K 0 kmmuterer. Vi har at H 0 \ K 0 = {e H K }. Undergruppene H 0 g K 0 genererer H K idenfrstandath 0 K 0 = H 0 K 0 = { xy x 2 H 0 g y 2 K 0 }. Ienvissfrstandgjeldergsådetmvendteavdissebservasjnene.Ommanien gruppe G kan identifisere t undergrupper H g K sm ppfyller de tre betingelsene venfr, så følger det at K på en naturlig måte er ismrf med det direkte prduktet H K, gundergruppeneh g K spiller rllen til de t spesielle undergruppene beskrevet venfr. Vi har: Setning. La G være en gruppe g la H G g K G være t undergrupper sm ppfyller de tre egenskapene venfr. Da er G ismrf med H K. 2 Et slikt utsagn har sine begrensninger g må tas med en klype salt. Addisjnen i R n er ikke vesentlig verre enn addisjn i R, menpådenannensidesåern n-matriser vesentlig mere kmplisert enn relle tall. 3 ItilleggtildetreegenskapenevibeskrivererH 0 g K 0 gså nrmale undergrupper. Det følger av at de er kjernen til hver sin prjeksjn, henhldsvis på H 0 g K 0,menmankangsåutlededette direkte av t av de tre egenskapene. Hvilke t? Se frøvrig ppgave.. 4
5 Direkte prdukter MAT2200 Vår 2014 Bevis: Vi definerer en avbildning : H K! G ved å sette (g, h) =gh. Atdette er en gruppehmmrfi følger av at H g K kmmuterer: (hh 0,kk 0 )=hh 0 kk 0 = hkh 0 k 0 = (h, k) (h 0,k 0 ), der vi har bytte rekkefølgen til h 0 g k iprduktethh 0 kk 0. Avbildningen er klart surjektiv, det følger direkte av den tredje egenskapen venfr. At den er injektiv, følger fra den første: Anta at (h, k) =hk = e. Daerh = k 1 et element sm ligger i både H g K, mensidenh \ K = {e} gir det ss at h = k 1 = e, altså at (h, k) =(e, e). FølgeligerKer = {e} g injektiv. Den tredje egenskapen venfr kan, dersm de invlverte gruppene er endelige, erstattes med at G = H K. DeterenhyptesesmautmatiskmedføreratHK = G, nårvivetath \ K = {e}, gdetersmregelmyeenklereåsjekkeatdenhlder enn at HK = G. Oppgaver.. La H g K være t nrmale undergrupper av en gruppe G. AntaatH \ K = {e}. a) Vis at da kmmuterer H g K. Hint: Betrakt kmmutatren [h, k] =hkh 1 k 1 g vis at denne ligger i H \ K. Vis at HK er en nrmal undergruppe av G g at HK ' H K... Generaliser setning. til et prdukt av vilkårlig mange grupper. Frmuler de tre kriteriene g bevis setningen. Hint: Stikkrd er parvis kmmuterende g parvise snitt... Vis at m {G i } i2i er en familie av abelske grupper, så er det direkte prduktet i2i G i en abelsk gruppe... Vis m {G} i2i er en endelig familie av endelige grupper så gjelder følgende påstand m rdenen til prduktet: i2i G i = i2i G i... Generaliser setning. venfr, g vis at m n 1,...,n s er naturlige tall sm parvis er relativt primiske, g n = n 1 n s,såerz n ' Z n1... Z ns... Avgjør hvilke av følgende fire grupper sm er ismrfe: Z 4 Z 2 Z 3 Z 4 Z 6 Z 12 Z 2 Z 8 Z 3.. La A g B være undergrupper av den endelige gruppen G. Visat AB A \ B = A B. Hint: Betrakt avbildningen : A B! AB gitt ved (a, b) =ab. Visat 1 (a, b) ={ (ax, x 1 b) x 2 A \ B } g finn en bijeksjn mellm fiberen g A \ B. 5
6 Direkte prdukter MAT2200 Vår La k<nvære t naturlige tall g la G S n være undergruppen G = { 2 S n (x) 2 I k hver gang x 2 I k } av S n.visatg ' S k S n k... La være en k-sykel i den symmetriske gruppen S n.visatsentralisatrenc Sn ( ) til i S n er ismrf med det direkte prduktet Z k S n k.. La A være en endelig abelsk gruppe g la p være et primtall. La A p betegne undergruppen av A bestående av alle elementer hvis rden er en ptens av p. Det vil si at A p = { a 2 A det eksisterer en k 2 N slik at p k a =0}. a) Vis at A p er en undergruppe av A. b) Vis at dersm p g q er t frskjellige primtall, så er A p \ A q =0 Hint: Fr heltall n g m kan man skrive 1=xp n + yq m der x g y gså er hele tall... La A være en abelsk gruppe av rden p s q t det p g q er t frskjellige primtall g s g t er t naturlige tall. Vis at A = A p A q,dera p g A q er sm i ppgave. venfr... Generaliser ppgave. g vis at enhver endelig abelsk gruppe A er ismrf med det direkte prduktet A p1... A ps der p 1,...,p s er de frskjellige primtallene sm inngår i primtallsfaktriseringen av rdenen A til A... La G være en endelig gruppe der alle elementene er av rden t. Vis at G ' Z n 2 der G =2n. 6
7 6. Del Restklasser g kvtientgrupper Idetteavsnittetskalviutviklenenavdegrunnleggendeegenskapenetilenundergruppe. Vi skal se at m G er en endelig gruppe, så vil rdenen til enhver undergruppe av G være en divisr i G. Viharalleredesettdettefrdesykliskegruppene,mendet er altså et generelt fenmen fr endelige grupper. Dette resultatet er en av grunnstenene i terien fr endelige grupper, g resultatet går helt tilbake til Lagrange, iallefallerdethshamvifinnerkimentiltermet. Lagrange arbeidet utelukkende med de symmetriske gruppene g hvrdan de virker på plynmer ved å permutere de variable, g han frmulerte uten bevis et resultat sm i den sammenhengen ikke er annet enn hva vi kaller Lagranges terem. Cauchy ga et fullstendig bevis fr teremet fr symmetriske grupper, men den første frmulerte g beviste teremet generelt, er Camille Jrdan. Det gjrde han sm en liten del av sitt dktrarbeide. Ellers er Evartist Galis en sentral persn i den histriske utviklingen av hva vi skal gjøre i denne delen. Han berører ikke Lagranges terem i nen av sine artikler, men i brevet han frfattet ni dager før han døde i duell, gjengir han et resulatet sm klart kan tlkes sm en frmulering av Lagranges terem. 6.1 Restklasser Vi har allered stiftet bekjenskap med restklasser ienkeltesitusajner.gruppenez n består av alle restklassene eller kngruensklassene sm vi gså kalte dem mdul n. En slik restklasse er gitt sm [k] ={ x 2 Z x k md k }. Hvismanvil,kanman skrive den på frmen k + nz = { k + ny y 2 Z }, gdeterdennefrmenviskalbruke når vi generaliserer begrepet til vilkårlige grupper. La nå G være en gruppe, g la H være en undergruppe av G. Smsagt,skal vi innføre begrepet restklassene til H i G. SidenG generelt er ikke-kmmutativ, vil det frekmme t typer av restklasser høyrerestklasser g venstrerestklasser. Her 7
8 Restklasser MAT2200 Vår 2014 kmmer definisjnen: Fr et element a 2 G definerer vi Ha = { ha h 2 H }, g vi kaller Ha fr en høyrerestklasse til H. Likeledes lar vi ah = { ah h 2 H } g de kalles selvsagt fr venstrerestklassene til H. Spesielt vil alltid H selv være en av restklassene. Den får vi ved å bruke a = e, gdenerbådeenvenstrerestklassegen høyrerestklasse. Ntasjnen vi innførte kan generaliseres ne. Dersm X G er en vilkårlig undermengde av G g a 2 G et element, lar vi ax = { ax x 2 G }. Deterdalettåseat a(bx) =abx, ata 1 (ax) =X g at ex = X. Mengden ax kalles fr et translat av X (et venstretranslat m man vil være pinlig nøyaktig). IdettilfelletnårA er en additiv gruppe sm altså per knvensjn er en kmmutativ gruppe blir definisjnen av restklasser seende slik ut. La B A være undergruppen g la a 2 A være elementet. Da er den tilsvarende restklassene til B på frmen: a + B = { a + b b 2 B }. Der er ingen frskjell på høyrerestklasser g venstrerestklasser i dette tilfellet siden A er abelsk. I det spesielle tilfellet at A = Z, finnervinaturligvistilbakevårevelkjente restklasser; vi har at m + nz =[m]. Eksempel.. Restklassene til µ 3 i µ 6. Vi skal se på eksemplet µ 3 µ 6. Undergruppen µ 3 har de t restklassene µ 3 g aµ 3 der a = e i/3. Man sjekker nemlig lett at µ 3 = h a 2 i = {e, a 2,a 4 } g aµ 3 = a 1 µ 3 = a 3 µ 3 = {a, a 1,a 3 }. På figuren under er restklassen µ 3 farget rød, mens aµ 3 er blå. Im Re µ 3 µ 6 Er man i et additivt humør, fretrekker man muligens restklassene til undergruppen 2Z 6 av Z 6.Dagjelderdetat2Z 6 = {0, 2, 4},mensdetkunerenannenrestklasse,nemlig 1+2Z 6,gfrdengjelderdetat1+2Z 6 = {1, 3, 5}. e 8
9 Restklasser MAT2200 Vår 2014 Restklassene danner en partisjn La ss vende tilbake til restklassene. Til å begynne med skal vi påpeke et par viktig penger m når t venstrerestklasser ah g bh er like. Det er selvsagt ingen prinsipiell frskjell på høyre- g venstrerestklasser. Et hvert resultat m venstrerestklasser har et mtstykke i høyrerestklassenes verden. I det følgende vil resultatene bare frmuleres fr venstrerestklasser, g det verlates til leseren å versette til utsagn m høyrerestklasser. Vi skal altså finne et kriterium fr når t restklasser er like g ser først på det spesielle tilfellet der den ene innehlder enhetselementet e: Lemma. Om H G er en undergruppe g a 2 H et element, så er ah = H hvis g bare hvis a 2 H. Bevis: Dersm a 2 H, såersåklartah H; gmh 2 H, såerh = a(a 1 h) 2 ah frdi ah 1 ligger i H når både h g a ligger der. Omvendt, dersm ah = H, følgerdet at a = a e 2 ah = H. Det generelle utsagnet er sm følger: Lemma. La a g b være t elementer i gruppen G g la H G være en undergruppe. Da er ah = bh hvis g bare hvis b 1 a 2 H. Bevis: At ah = bh er ekvivalent med at b 1 ah = H, getterlemma. venfr er dette ekvivalent med b 1 a 2 H. Det er en egen skrivemåte fr mengden av venstreresklasser, nemlig G/H. Man leser G/H sm G md H eller G mdul H. Tilsvarende er G\H betegnelsen fr mengden bestående av høyrerestklassene til H. Vanligvisskillermanikkedeti talespråket, G\H mtales gså sm G md H. Ser vi på figuren i eksempel. venfr, der vi fant alle restklassene til µ 3 i µ 6,erdet klart at de t restklassene er disjunkte; dedannerenpartisjn av µ 6. Tilsvarende m G = Z g H =2Z så har vi t disjunkte restklasser, de jevne tallene g de dde. Dette illustrerer et generelt fenmen sm er blant de viktigste egenskapene til restklasser: Setning. La H G være en undergruppe av gruppen G. DadannermengdenG/H = { ah a 2 G } av venstrerestklassene til H en partisjn av G. Bevis: Det er t ting å sjekke. Fr det første at G/H dekker G,altsåat S a2g ah = G. Det følger umiddelbart av at a = a e 2 ah. Fr det andre må vi vise at restklassene er parvis disjunkte, det vil si at t restklasser ah g bh enten er like eller disjunkte. Anta derfr at ah \ bh 6= ;, glac2ah \ bh. Da er c = ah fr et element h 2 H, gc = bk fr et annet element k 2 H. Slårvidisse t likhetene sammen, finner vi at ah = bk. Derfrerb 1 a = kh 1.Nåliggerkh 1 i H siden både k g h ligger der, g etter lemma. venfr er da ah = bh. Tklasseri G/H er altså enten like eller disjunkte, g G/H er en partisjn. 9
10 Restklasser MAT2200 Vår 2014 Vi vet at partisjner g ekvivalensklasser er t alen av samme stykke, men la ss eksplisitt beskrive ekvivalensrelasjnen sm tilsvarer partisjnen i restklasser. T gruppeelementer a g b kaller vi ekvivalente hvis g bare hvis ah = bh, i.e., hvis g bare hvis b 1 a 2 H etter lemma.. Sidenvivetatrestklassenedannerenpartisjn,vet vi gså at denne relasjnen ppfyller kravene til å være en ekvivalensrelasjn, ne det heller ikke er vervettes vanskelig å sjekke direkte. Trekker vi tråden tilbake til kngruensklassene i Z, erundergruppenh på frmen H = nz fr et heltall n,gvifårnaturlignktilbakedenvelkjenteekvivalensrelasjnen a b md n, frdiatb a 2 nz, erekvivalentmedatb a er delelig med n. Lagranges terem Vi er nå kmmet frem til Lagranges terem, sm han altså ble bevist av Cauchy (i 1844) g Jrdan (i 1861). Bevisene presenteres selvsagt ganske annerledes idag enn slik det ble gjrdt den gang; de er blitt mdernisert g blankpusset pp gjennm tidene, men dypest sett er det frtsatt nøyaktig det samme beviset. Før vi går løs på Lagranges terem, trenger vi imidelertid å frberede grunnen. Antall venstrerestklasser til en undergruppe H kaller vi fr indeksen til H i G, g vi skriver G : H, gidetteliggerdetgsåatviskriver G : H = 1 dersm H har uendelig mange restklasser. La ss bemerke at selvm G g H er uendelige, kan gdt indeksen G : H være endelig. Fr eksempel har undergruppen 2Z av Z bare t restklasser, bestående av de dde g de jevne tallene. Ne mer generelt har vi at nz er av indeks n i Z uansett hvilket naturlige tall n er. Desm G er endelig, er selvsagt antall restklasser endelig, g like selvsagt er det at antall elementer i hver retsklasse er endelig. Men mer enn det er riktig; de frskjellige restklassene har alle like mange elementer: Setning. Hvis H er endelig undergruppe av gruppen G, såer ah = H fr alle a 2 G. SpesieltharallerestklasseneaH til H like mange elementer. Om H er uendelig, så er gså alle restklassene til H uendelige. Bevis: Trikset er å bruke venstremultiplikasjn med a til å fabrikkere en bijeksjn mellm H g ah. Venstremultiplikasjnmeda sender elementene til H inn i ah g induserer derfr en avbildning : H! ah. Tilsvarende vil venstremultiplikasjn med a 1 indusere en avbildning : ah! H den andre veien, g åpenbart er =id H (vi har nemlig at a 1 a = e!). Det betyr at (g ) erenbijeksjn,gdetfølgeratah g H har like mange elementer. Vi kan nå frmulerer Lagranges terem: Terem. (Lagrange) Hvis G er en endelig gruppe g H en undergruppe, så går rdenen til H pp i rdenen til G. Merpresist,viharat G = G : H H. 10
11 Restklasser MAT2200 Vår 2014 Bevis: Venstrerestklassene til H danner en partisjn av G, g de har alle like mange elementer. Derfr er antall elementer G i G lik prduktet av antall restklasser, nemlig G : H, gderesfellesantallelementer,smerlik H etter setning.. Det er t bemerkninger å gjøre. Fr det første gjelder teremet gså dersm G er uendelig. Imidlertid blir i det tilfellet begge sider av likeheten i teremet uendelig; det er nemlig klart at G er endelig hvis g bare hvis både H g indeksen G : H er endelige. Den andre bemerkningen er at mvendingen av Lagranges terem ikke er riktig. Det finnes eksempler på grupper G g ekte divisrer m i G slik at ingen undergruppe i G er av rden m. Eksemplet av lavest rden er den alternerende gruppen A 4,smer av rden 12, mensmikkeharnenundergruppeavrden6: Eksempel.. Anta at H A 4 er skurken i histrien, altså en ptensiell undergruppe av rden 6. DetbetyratH er av indeks t. Den har da følgende egenskap, sm gjelder generelt fr undergrupper av indeks t, g sm krt sagt sier at alle kvadrater ligger i H: Lemma. La H G være en undergruppe av indeks t, g la a 2 G være et element. Da er a 2 2 H. Bevis: Anta at a /2 H. UndergruppenH har kun t restklasser. Den ene er H selv g den andre er ah. Omikkea 2 2 H, era 2 2 ah g av det følger at a 2 = ah fr en h 2 H. Derava = h 2 H, smikkeertilfelle. Nå er hver 3-sykel et kvadrat, fr dersm 3 = e, såer =( 1 ) 2,gderfrliggerde alle i H. Men i A 4 finnes det 8 tre-sykler! Så H kan ikke være av rden 6. e Oppgaver.. La G være en gruppe. Vi skal se på undermengdene av G på frmen { a, a 1 } der a 2 G. VisatdissedannerenpartisjnavG. Visatenhvergruppeavjevnrdenhar et dde antall elementer av rden 2. Oppgave.. Vis at enhver 3-sykel er et kvadrat g bruk det til å vise at A n ikke har nen undergruppe av indeks 2. Hint: Bruk ppgave?? iavsnittetmsymmetriske grupper der det ble vist at 3-syklene genererer A n. X Oppgave.. La P I n = {1,...,n} være en undermengde. Vi definerer G S n ved G = { 2 S n (P ) P } den består altså av alle permutasjner sm lar P være invariant, i.e., de sm sender elementer i P inn i P.VisatG' Sym(P ) Sym(P c ) der P c betegner kmplementet til P i I n. X 11
12 Restklasser MAT2200 Vår 2014 Oppgave.. La P 1,...,P r være en partisjn av I n.videfinererh S n ved H = { 2 S n (P i ) P i fr 1 apple i apple r }. a) Vis at H ' Sym(P 1 )... Sym(P r ). b) La a g b være hele tall. Bruk Lagranges terem til å vise at (ab)!/(a!) b er et helt tall. Hint: Del pp I ab i b like stre intervaller. c) Vis at (ab!)/(a!) b b! er et helt tall. Knsekvenser av Lagranges terem Lagranges terem har et par knsekvenser, sm illustrerer at rdenen til en endelig gruppe, eller mere presist primtallsfaktriseringen av rdenen, kan gi sterke føringer på gruppens stuktur. Krllar. La G være en endelig gruppe hvis rden G er et primtall. Da er G syklisk. Bevis: La H G være en undergruppe. Da H er en divisr i G, smeretprimtall, er enten H =1g H = {e}, eller H = G g G = H. SåG har ingen ikke-trivielle, ekte undergrupper. La a 2 G være et ikke-trivielt element (sm finnes siden G 2). Da er h a i6= {e}, gfølgeligerh a i = G, gg er syklisk. Krllar. La G være en endelig gruppe g la a 2 G. Dagårrdenentila pp i rdenen til G. Bevis: Bruk Lagranges terem på undergruppen generert av a. Man kunne spørre seg m mvendingen av dette krllaret gjelder, altså m det fr hver divisr m i G, finnesetelementig av rden m. Detteville(siden G er en divisr i G ) implisert at alle grupper var sykliske.det er heller ikke riktig at en hver ekte divisr kan realiseres sm rdenen til et element. Et eksempel er Z 2 Z 2 Z 2 sm er en gruppe av rden 8, menalledensikke-trivielleelementereravrden2. Krllar. Dersm G er en gruppe g G = pq, derp g q er t primtall, så er en hver ikke-triviell, ekte undergruppe syklisk. Bevis: La H G være en undergruppe, ikke-triviell g ekte. Da H deler pq, gbåde p g q er primtall, er enten H = p eller H = q. IbeggetilfellererrdenentilH prim, g H er syklisk etter krllar.. X 12
13 Restklasser MAT2200 Vår 2014 Nrmale undergrupper IdeflestesituasjnerderenundergruppeH av en gruppe G g et element a 2 G er gitt, vil ventrerestklassen ah g høyrerestklassen Ha være frskjellige, altså ah 6= Ha. Dette reflekterer at vi har ikke-kmmuterende elementer i en generell gruppe. I enkelte spesielle tilfeller er allikevel ah = Ha.Detgjelderfreksempelma kmmuterer med alle elementer i H (spesielt m gruppen G er abelsk). Men gså uten denne kmmuteringsbetingelsen hender det i enkelte situasjner at ah = Ha.Hvis en undergruppe er slik at dette gjelder fr alle a 2 G, kallesundergruppennrmal. Nrmaleundergrupper spiller en fundamental rlle i gruppeterien, g vi kmmer tilbake til dem ved mange anledninger. Nrmale undergrupper kalles gså fr invariante undergrupper. Den språkbruken har sin rt i følgende egenskap: Setning. La H G være en undergruppe i gruppen G. Daerfølgendeekvivalent ah = Ha fr alle a 2 G. aha 1 = H fr alle a 2 G. Bevis: Vi passerer fra likheten ah = Ha til likheten aha 1 = H ved å multiplisere fra høyre med a 1,gdenandreveienvedhøyremultiplikasjnmeda. Det andre av de t utsagnene venfr finnes i en øyensynlig svakere versjn, men sm viser seg å være ekvivalent med de t. Det er letter å bruke i praksis, g det er det perasjnelle kriteriet fr sjekke m en undergruppe er nrmal: aha 1 H fr alle a 2 G. La ss sjekke at dette kriteriet er ekvivalent med de t andre. Den ene veien er pplagt, så anta at det siste kriteret er ppfylt. Vi kan bruk a 1 istedenfr a siden kriteriet gjelder fr alle a. Detgirata 1 Ha H, gmultipliserervippmeda fra venstre g a 1 fra høyre, finner vi at H aha 1.FølgeligeraHa 1 = H. Fr hvert element a 2 G intrduserte vi kngugasjnsavbildningen c a.deteren hmmrfi fra G til G, gdensenderetelementx 2 G til det knjugerte elementet c g (x) =a 1 xa. Vikaltegsåknjugasjnsavbildningenefrindre autmrfier. Aten undergruppe H G er nrmal er ifølge prpsisjnen ekvivalent med at c a (H) =H fr alle a, slikath altså invariant under knjugasjn. En svært viktig kilde til nrmale undergrupper er hmmrfier. Deres kjerner ar alltid nrmale, slik det uttrykkes i følgende setning: Setning. Anta at G g H er t grupper g la er kjernen Ker en nrmal undergruppe av G. : G! H være en hmmrfi. Da Bevis: Vi har allerede sett at kjernen er en undergruppe, så la ss vise at den er nrmal. La a 2 G g la x 2 Ker,detvilsiat (x) =e H.Viskalviseata 1 xa 2 Ker,gtil det beregner vi (a 1 xa) g finner ved å bruke at er en hmmrfi at (a 1 xa) = (a) 1 (x) (a) = (a) 1 e H (a) =e H. 13
14 Kvtientgrupper MAT2200 Vår 2014 Eksempel.. Restklassene i S 3. Vi avslutter denne paragrafen med et eksempel, g vi skal studere restklassene i den symmetriske gruppen S 3.Vivetatdenne gruppen gså kan realiseres sm symmetrigruppen til en likesidet trekant, g er man gemetrisk anlagt, kan man ha den i tankene. Vi lar r =(1, 2, 3) g s =(1, 2). Daerr 3 = s 2 = e, gvihardenfundamentale relasjnen srs = r 1. Elementene i S 3 kan rganiseres i følgende tabell e r r 1 s rs r 1 s Hvis vi lar H = {e, s} smerenundergruppesidens 2 = e vilvenstrerestklassene til H presis være søylene i tabellen, mens frdi sr = r 1 s g sr 1 = rs, vilhøyrerestklassene være de t diagnalene i tabellen, i.e., Hr = {r, r 1 s} g Hr 1 = {r 1,rs}. Det er da klart at rh 6= Hr g r 1 H 6= Hr 1 siden rs g r 1 er t frskjellige elementer i S 3. Lar vi nå H = h r i = {e, r, r 1 } er situasjnen annerledes. Dette er en nrmal undergruppe. Den har kun t restklasser, H g sh = Hs.(Sjekkdet!) e Oppgave.. Sjekk at rs =(1, 3) g r 1 s =(2, 3), slikats, rs g r 1 s er de tre elementene i S 3 av rden 2. Detavrden3, ernaturligvisr =(1, 2, 3) g r 2 = r 1 = (1, 3, 2). X Oppgave.. La G være en gruppe g H G en undergruppe. Vis at dersm H er av indeks t, så er H en nrmal undergruppe. Hint: Hvr mange ikke-trivielle venstrerestklasser g hvr mange ikke-trivielle høyrerestklasser har H? X 6.2 Kvtientgrupper En helt sentral knstruksjn i gruppeterien er dannelsen av kvtienten av en gruppe G med en nrmal undergruppe. I et spesialtilfelle har vi allerede gjrt denne knstruksjnen, nemlig da vi knstruerte gruppen Z n av kngruensklassene mdul et heltall n. Viinnførtedaengruppelvblantmengdenavrestklassene.Idettentatetskalvi generalisere denne knstruksjnen g på lignende vis innføre en gruppelv på mengden G/N av restklasser til en nrmal undergruppe N av en gruppe G. AtN er nrmal, er en helt essentiell fr at knstruksjnen ska la seg gjennmføre, g vi skal se at den har en helt naturlig plass i knstruksjnen. Vi starter med å minne m følgende definisjn (ligning (??) på side?? i ntatet m restklasser) der X g Y er t delmengder av G: XY = { xy x 2 X g y 2 Y }. Dette er altså et slags prdukt av undermengder. Man sjekker lett at dette prduktet 14
15 Kvtientgrupper MAT2200 Vår 2014 har en asssiativitetsegenskap 1,nemlig: X(YZ)=(XY )Z = { xyz x 2 X, y 2 Y g z 2 Z }, (hh) der altså Z er en tredje undermengde av G. Vivilftedrppeparentesengskrive XY Z.Hvisenavmengdeneerreduserttilettelement,lasssiatX = { x }, frenkler vi gså skrivemåten g skriver xy isteden fr { x }Y. Det er klart at dersm H er en undergruppe, så er HH = H athh H følger siden H er lukket under multiplikasjn, g siden e G 2 H, era = a e G 2 HH fr alle a 2 H. Rekap m nrmale undergrupper Vi minner m at en nrmal undergruppe H av gruppen G er en undergruppe hvis alle venstrerestklasser gså er høyreretsklasser, i.e., at ah = Ha fr alle gruppelementer a 2 G. Vivistetidligere(setning. på side 13 intatetmrestklasser)atvihar følgende tre ekvivalente karakteriseringer av nrmale undergrupper: ah = Ha fr alle a 2 G. aha 1 = H fr alle a 2 G. aha 1 H fr alle a 2 G. En kilde til nrmale undergrupper er gruppehmmrfier; deres kjerner vil alltid være nrmale. Lenger ute i avsnittet bevises det at det mvendte gså gjelder: Gitt en undergruppe sm er nrmal, så finnes det en hmmrfi med denne undergruppen sm kjerne. De nrmale undergruppene er altså presis de sm pptrer sm kjernen til en hmmrfi. Men, sm sagt, det der kmmer litt lenger ute; nå nøyer vi ss med Setning. Dersm : G! H er en hmmrfi, så er kjernen Ker en nrmal undergruppe av G. Bevis: Anta at (x) = e g at a 2 G. Vifinner (axa 1 ) = (a) (x) (a) 1 = (a)e (a) 1 = e, såaxa 1 2 Ker. De nrmale undergruppene har gså en del egenskaper sm man kunne karakterisere sm hverdagsegenskaper eller bruksegenskaper. Det er ganske standard egenskaper sm stadig brukes når man arbeider med nrmal undergrupper. Bevisene er rett frem anvendelser av definisjnene: 1 Man kunne fristes til å tr at dette gir en gruppelv på mengden av alle undermengder, men det er langt fra tilfelle. Det finnes riktgnk et enhetselement, nemlig den trivielle undergruppen {e},men det finnes ingen inversdannelse. Vi har at HH = H fr alle undergrupper, ne sm viser at et hvert frsøk på definere en invers er fånyttes. 15
16 Kvtientgrupper MAT2200 Vår 2014 Setning. La G være en gruppe, g la N g H være t undergrupper av G. Antaat N er nrmal i G. Vi har at NH = HN,gNH er en undergruppe av G. DersmH gså er nrmal i G, såernh en nrmal undergruppe av G. Om N H, såern nrmal i H. Snittet av t nrmale undergrupper er en nrmal undergruppe, i.e., m H gså er nrmal i G, såerh \ N nrmal i G. Bevis: La n 2 N g h 2 H. Denførstepåstandenfølgerslik:Viharatnh = h(h 1 nh), g h 1 nh 2 N siden N er nrmal i G. DerfrerNH = HN.AtNH er en undergruppe, følger frdi hnh 0 n 0 = hh 00 n 00 n 0 der vi bruker at vi kan skrive nh 0 = h 00 n 00 siden NH = HN (n-er er fra N g h-er fra H). Videre, anta så gså at H er nrmal g la g 2 G være et vilkårlig element. Vi finner gnhg 1 = gng 1 ghg 1,ggng 1 2 N g ghg 1 2 H siden N henhldsvis H er nrmal i G. Derfrergnhg 1 2 NH. At N H er nrmal i H når N er nrmal i G g H G, eråpenbart. Om a er et element både i H g N, såliggergag 1 gså i både H g N siden begge er nrmale. Vær ppmerksm på at å være en nrmal undergruppe er en relativ egenskap. Derfr bør man angi i hvilken gruppe undergruppen er nrmal. Det finnes mange eksempler på serier N H G av undergrupper der N er nrmal i den mindre gruppen H, men ikke i den større G. SelvmhNh 1 N fr alle h 2 H, erdetgenereltsettingengrunn til at dette gså skulle hlde fr elementer h idenstørre gruppen 2 G. Knstruksjn av kvtientgrupper Vi starter nå knstruksjnen av kvtientgrupper g lar N G være en nrmal undergruppe. Det innebærer at an = Na fr alle a 2 G. Strategien vår er å definere en multiplikasjn på mengden G/N av venstrerestklasser ved å bruke det vi gjrde venfr da vi definerte mengdeprduktet XY fr t vilkårlige undermengder X g Y. La an g bn være t restklasser. Vi finner (an)(bn) =anbn = abnn = abn der vi bruker at N er nrmal g derfr Nb = bn iligningenmarkertmed. Hele penget er at anbn igjen er en restklasse, slikat mengdeprduktet definerer en binær perasjn på mengden G/H av restklasser! Og det viser seg at denne binære perasjnen ppfyller gruppeaksimene. Det inverse elementet til ah er naturlig nk 2 Enhver undergruppe er nrmal i seg selv, så det banale eksemplet er å la H = N. Vilmanhaet eksempel med litt mer kjøtt på benet, kan man se på H = h (1, 2, 3, 4) i idensymmetriskegruppen S 4.DeterensykliskundergruppeavrdenfiresmharN = h (1, 3)(2, 4) i sm nrmal undergruppe. Men N er ikke nrmal i S 4. 16
17 Kvtientgrupper MAT2200 Vår 2014 a 1 N viharana 1 N = aa 1 NN = N genhetselementetern vihar ann = NaN = an. Asssiativitetenfølgeravatgruppelvenerasssiativ: Vi har etablert: an(bncn) =anbcn = a(bc)n =(ab)cn = abncn =(anbn)cn Terem. Dersm N G er en nrmal undergruppe, så er anbn = abn, gden binære perasjnen (an, bn) 7! abn rganiserer mengden G/H av venstrerestklasser til en gruppe. Man kan saktens spørre m hvrfr det ikke er mulig å definer an bn = abn fr en vilkårlig, ikke nødvendigvis nrmal, undergruppe N. Prblemet er at når vi skriver an g bn, såharvivalgt(gdeteretvilkårligvalg,medmindremangirenpresis resept fr hvrdan a g b skal plukkes ut) representanter a g b fr restklassene, g restklassen abn vil avhenge sterkt av dette valget m N ikke er nrmal. Det betyr til syvende g sist at abn ikke er langt unna å være en vilkårlig restklasse. Oppgave.. IdensymmetriskegruppenS 3 på tre bkstaver la r = (1, 2, 3) g s =(1, 2).LavidereH = {e, s}.daerrh = {r, rs} g både r g rs er representanter fr restklassen rh. FinnallemuligheterfrrestklassenabH når både a g b gjennmløper alle mulige representanter fr rh. X Eksempel.. Man kunne tenke seg at det var mulig å velge representanter fr restklassene an på en så utspekulert måte at representantene dannet en undergruppe. Men så smart er det generelt sett umulig å være! Følgende enkle situasjn dreper eventuelle frhåpninger i den retningen: La G = µ 4 = {±1, ±i} C g N = µ 2 = {1, 1} µ 4.DaharN de t restklassene N g in. DetfølgeratkvtientgruppenG/N har t elementer, g den er derfr syklisk av rden t. Men den eneste undergruppen av µ 4 av rden 2 er N, såintetvalgav representanter kan danne en undergruppe. Det sagt, hvis man kan finne en undergruppe H med H \ N = {e} g HN = G slik det vil være m representantene kan velges sm en undergruppe kaller vi H et kmplement til N, gienkeltesituasjnerkanmanalltidfinneslikekmplementer. Et meget dypt g viktig terem i gruppeterien, sm ble bevist av Isaac Schur g Hans Julius Zassenhaus, frtellerssatkmplementerfinnesdersmg er endelig g rdenen N til N g indeksen G : N til N i G er relativt primiske. Schur g Zassenhaus vær svært smarte! e I mtsetning til i plitikken g i elementærpartiklenes verden 3,erdetingenpreferanse mellm høyre g venstre i gruppeterien. Om man bruker høyrerestklasser eller venstrerestklasser går ut på ett. Man må gjøre et valg, men substansielt betyr det ingen ting: 3 De t teretiske fysikerene Tsung-Da Lee g Chen Ning Yang var de første til å reise spørsmålet mkring parity vilatin, smerdettekniskenavnetpåmanglendehøyre-venstre-symmetrii kvantefysikk, g i et berømt eksperiment viste Chien-Shiung Wu at verden faktisk ikke alltid er høyre-venstre symmetrisk. Lee g Yang fikk Nbelprisen i fysikk i
18 Kvtientgrupper MAT2200 Vår 2014 Oppgave.. Hvrfr er det pplagt at gruppen G\N av høyrerestklasser er identisk med G/N? Hint: Undergruppen N er nrmal. X Vi avslutter denne paragrafen med å nevne følgende resultat sm gir en sammenheng mellm en rdenen til en nrmal undergruppe g til kvtienten. Det er en direkte versettelse av Lagranges terem (terem. på side 10 i ntatet m restklasser)til knteksten mkring kvtientegrupper vi nå er i. Dette teremet er en av arbeidshestene i terien fr endelige grupper: Terem. Om N G er en nrmal undergruppe, så er G = G/N N. Den kanniske avbildningen Slår man pp rdet kannisere ienrdbk,kanmanfinnefrklaringersm helgen- kåre eller ffisielt erklære fr helgen ; det er en teknisk telgisk term i den katlske kirke. I matematikken er meningen ne mer diffus, men rdet kannisk brukes m bjekter i vårt tilfelle avbildninger sm gir seg selv ; de ppstår naturlig ut ifra situasjnen. Et kannisk bjekt kan defineres uten at det gjøres valg underveis. Knteksten i denne paragrafen er sm tidligere en gruppe G med en nrmal undergruppe N. Detfinnesenkannisk gruppehmmrfi : G! G/N gitt ved at elementet a sendes til den restklassen der det ligger, i.e., det sendes til restklassen an. Denne avbildningen naturlig g gir seg selv, g det er iallfall ikke gjrt nen valg i definisjnen. Derfr merkelappen kannisk. Siden prduktet ab av t gruppe-elementer a g b sendes til restklassen abn, gprduktetavrestklassenean g bn i G/N j er lik abn, erdet rett frem etter nesen at er en hmmrfi. Med følgende lemma innfris løftet fra tidligere m å realisere enhver nrmal undergruppe sm kjernen til en hmmrfi: Setning. Den kanniske avbildningen : G! G/N er surjektiv, g Ker = N. Bevis: Åpenbart er surjektiv siden (a) =an. Enhetselementet i G/N er restklassen N. At (a) =N, betyrjper definisjn av at a 2 N. Den universelle egenskapen Ianlgimedprduktersiermanatmankanfaktrisere en avbildning dersm den kan skrives sm en sammensetning =. Viindikererdetteftevedåtegne følgende diagram X sm gså tjener til å hlde rden på de frskjellige mengdene avbildningene går imellm. Vi sier at diagrammet er kmmutativt når =. / Y Z, 18
19 !! Kvtientgrupper MAT2200 Vår 2014 Anta nå at : G! H er en gruppehmmrfi sm har egenskapen å være knstant på restklassene til N. Verdien (x) avhenger altså bare av hvilken restklasse x ligger i. Dette innebærer at vi kan faktrisere gjennm den kanniske hmmrfien g skrive = ; idiagramsfrmsertegningenslikut G / G/N Verdien tar på en restklasse an i G/N, erlikdenfellesverdien tar på elementene i an. Siden er en gruppehmmrfi, kan vi gi et enkelt kriterium fr når er knstant på restklassene til N. HverrestklassetilN er på frmen an med a 2 G. At er knstant på en slik, er ensbetydende med at (ax) = (a) fr alle x 2 N siden j a = ae G 2 N. Bruker vi nå at er en gruppehmmrfi, finner vi (ax) = (a) (x) = (a). Vedå kansellere (a) ser vi at er dette ekvivalent med at (x) =e H fr alle x. Med andre rd, det er ekvivalent med at N Ker. Vi har dermed bevist følgende lemma: Lemma. La : G! H være en gruppehmmrfi g la N G være en nrmal undergruppe. Da er knstant på restklassene til N hvis g bare hvis N Ker. Dette lemmaet har viktig refrmulering, g i frmulert slik, mtales resultatet fte sm Kvtientens universelle egenskap: Setning. La N G være en nrmal undergruppe g la : G! G/N være den kanniske hmmrfien. Anta at : G! H er en gruppehmmrfi. Da kan vi faktrisere sm =, i.e., viharetkmmutativtdiagram H. G / G/N hvis g bare hvis N Ker.Avbildningen er en gruppehmmrfi. Bevis: Vi så venfr at kan faktriseres sm = hvis g bare hvis er knstant på restklassene an til N, menetterlemmaetskjerdettehvisgbarehvisn Ker. At er en gruppehmmrfi følger siden (an) (bn) 1 = (a) (b) 2 = (ab) 3 = (abn), der ligningene 1 g 3 hlder siden diagrammet i setningen kmmuterer, g den merket med 2, hlderfrdi er en gruppehmmrfi. H 19
20 ! Kvtientgrupper MAT2200 Vår 2014 En følgesetning av denne setningen gis av enkelte det stre navnet Det fundamentale hmmrfiteremet: Setning. Anta at G g H er t grupper g at fra G til H. LaN =Ker.DaerG/N ' H. er en surjektiv gruppehmmrfi Bevis: Etter setning. finnes en gruppehmmrfi : G/N! H slik at diagrammet G / G/N H =, i.e., kmmuterer. Vi skal bevise at er en ismrfi: Surjektivitet av :Gittetelementa 2 H. Siden per antagelse er surjektiv, kan vi finne en g 2 G slik at (g) =a. Davil ( (g)) = a. Injektivitet av : Antaat (x) =e H,glag 2 G være en løfting av x til G, i.e., (g) =x. Daer (g) = ( (g)) = e H.Følgeligerg 2 Ker = N =Ker g altså x = (g) =e G/N. Eksempel.. En gd illustrasjn av denne setning får vi m vi ser på enhetsrøtter. Vi antar at det naturlige tallet n kan faktriseres sm n = lm der l g m gså er naturlige tall. Avbildningen fra C til C definert ved z 7! z l tar enhetsrøttene i µ n inn i µ m frdi (z l ) m = z ml = z n =1når z 2 µ n.denindusererderfrengruppehmmrfi : µ n! µ m.deterklartatker = µ l,gviskalseat er surjektiv. Til det er det nk å sjekke at generatren = e 2pi/m ligger i bildet til, nesmerriktigsiden e 2 i/m =(e 2 i/n ) l.gruppehmmrfien tilfredstiller således betingelsene i setning. venfr g induserer en ismrfi µ ml /µ l ' µ m. e Siden enhver gruppehmmrfi : G! H avbilder G surjektivt på sitt bilde Im G H, fårvifølgendekrllaravsetning. venfr: Krllar. La G/Ker ' Im. : G! H være en gruppehmmrfi. Da har vi en naturlig ismrfi Kbler vi dette krllaret med Lagranges terem slik vi frmulerte det i terem. på side 18, finnerviensammenhengmellmantallelementerikjernengbildet til en gruppehmmrfi. Den er i mange tilfeller nyttig, blant annet til å avgjøre m hmmrfien er en ismrfi. Krllar. La : G! H være en gruppehmmrfi. Da gjelder det at G = Ker Im. Her kan det passe gdt å illustrere denne setningen med en additiv versjn av eksempel. venfr: 20
21 Kvtientgrupper MAT2200 Vår 2014 Eksempel.. Vi lar n være et naturligtall. Anta at m er en faktr i n g la l = n/m: Betrakt avbildningen Z n m / Z n sm er gitt ved m ([x]) = [mx].vifrenklerntasjnen,drpperretsklasseklammeneg skriver m (x) =mx, gtenkerpå m sm multiplikasjn med m, menselvsagtmdul n. Daerbildettil m per definisjn undergruppen mz n av Z m generert av m. Det er en syklisk undergruppe av rden l = m/n g altså ismrf med Z l. Kjernen til m bestemmer vi slik: Om mx 0 md n så er mx = kn = kml fr et heltall k, smjer ekvivlanet med at x = kl. DetbetyratKer m = lz n.viharatz n /lz n ' mz n ' Z l. e Oppgave.. Anta at H g K er t grupper. La G = H K g N = H e K.Vis at N = H e K er en nrmal undergruppe g at G/H ' K. Visatdenkanniske avbildningen tilsvarer prjeksjnen K : G = H K! K på annen faktr. X Undergrupper g kvtienter Vil man frstå en gruppe, er det viktig å kartlegge undergruppene så gdt sm mulig. Vi skal denne paragrafen gi en sammenheng mellm en klasse av undergrupper i G g undergrupper i kvtientgruppen G/N, dersmvanlign er en nrmal undergruppe av G. Dennesammenhengenerigfrsegikkespesifikkfrkvtientavbildningen,men gjelder alle surjektive hmmrfier. Det er naturlig, g det frenkler både ntasjn g frståelse, å arbeid i den generelle situasjnen. Så vi lar : G! H være en surjektiv gruppehmmrfi, g vi lar N =Ker. Vi kan trekke undergrupper av H tilbake med detvilsiatmk H er en undergruppe, så er tilbaketrekningen det inverse bildet 1 (K) av K. Detbeståravde a 2 G med (a) 2 H. Vi kan skyve undergrupper av G frem ved hjelp av detvilsiatmm G er en undergruppe, så er fremskyvningen av M ikke annet enn bildet (M) av M under.detbeståravalleelementerpåfrmen (a) der a 2 G. På dette viset har vi etablert t krrespnanser mellm undergrupper av G g H, én fra undergrupper i H til undergrupper i G g én den andre veien, men de er ikke gjensidig inverse av hverandre. Vi minner m at siden N G er en nrmal undergruppe, så er NM en undergruppe av G. Vihar: Setning. La : G! H være en surjektiv hmmrfi mellm t grupper med kerne N, glak H g M G være en undergrupper. Da har vi ( 1 (K)) = K (NM)= (M) 1 ( (M)) = NM. 21
22 Kvtientgrupper MAT2200 Vår 2014 Bevis: Det er en selvfølge at ( 1 (K)) K, sålaa 2 K. Siden er surjektiv, kan vi finne en b 2 G slik at (b) =a. Daersåklartb 2 1 (K), gk ( 1 (K)). Så til den andre påstanden. Dersm x 2 N =Ker er j (xa) = (a), slikat (NM)={ (xa) a 2 M,x 2 N } = { (a) a 2 M } = (M). Fr å innse den tredje, lar vi (a) 2 (M). Dafinnesenb2M, slikat (a) = (b), g det følger at (ab 1 )=e. Derfrerx = ab 1 2 N, gsåledesera = xb 2 NM, g 1 ( (M)) NM.Inklusjnendenandreveienfølgerumiddelbartavdenandre påstanden i prpsisjnen. En direkte g umiddelbar følge av den siste påstanden i denne prpsisjnen er Setning. Anta at N M, daer 1 ( (M)) = M. Bevis: Siden N M er NM = M g etter prpsisjn. er 1 ( (M)) = NM = M. Vi ser altså at dersm vi begrenser ss til å se på undergrupper sm mfatter kjernen N til, vil fremskyvning g tilbaketrekning av undergrupper, være t gjensidige inverse én-én-tydige krrespndanser mellm undergrupper i H g de i G sm altså mfatter N. Vi fmulerer dette sm et terem, der vi gså tar med et tillegg m de nrmale undergruppene: Terem. La : G! H være en surjektiv gruppehmmrfi med kjerne N =Ker. Krrespndansene M 7! (M) g K 7! 1 (K) er t gjensidig inverse én-én-tydige krrespndanser mellm undergrupper i G sm innehlder N g undergrupper i H. Nrmale undergrupper krrespnderer til nrmale undergrupper. Bevis: Alt unntatt påstanden m nrmale undergrupper krrespnderer til nrmale er vist i teksten før teremet, så la ss sjekke det. Anta at K er nrmal g at a 2 (K). La x 2 G. Vifinner (xax 1 )= (x) (a) (x) 1,slikat2 K siden K var antatt å være nrmal. Anta så at M G er nrmal, la a 2 M g la x 2 H. Siden er surjektiv, finnes en y 2 G med (y) =x, gviharatyay 1 2 M siden M er nrmal. Det følger at (yay 1 )=x (a)x 1 ligger i (M), gsåledeser (M) en nrmal undergruppe. Vi avslutter dette avsnittet, med å gå tilbake til situasjnen der H = G/N g der surjeksjnen er den kanniske prjeksjnen : G! G/N. Smbeskrevetvenfrhar vi krrespndansen mellm undergrupper i G/N g undergrupper i G sm innehlder N, menvihargsåenlitentilleggsinfrmasjnsmkrllar. gir ss, nemlig at (M) ' M/N, g i denne sammenhengen skal vi være såpass slurvete at vi skriver (M) =M/N, g sier at undergruppen M krrespnderer til M/N. Oppgaver.. Finn eksempler på en hmmrfi : G! H mellm t grupper g en undergruppe K H slik at ( 1 (K)) 6= K Hint: Finn en hmmrfi sm ikke er surjektiv g en undergruppe sm ikke ligger i bildet. 22
23 Kvtientgrupper MAT2200 Vår Anta at : G! Z p er ikke-triviell gruppehmmrfi der p er et primtall. Vis at er surjektiv, g vis at det ikke finnes undergrupper sm er ekte innehldt mellm Ker g G... La : G! Z pq være en surjektiv gruppehmmrfi der p g q er t primtall. Beskriv alle undergrupper i G sm innehlder Ker... Vis at det ikke finnes undergrupper sm ligger ekte imellm A n g S n. Versjn: Tuesday, February 18, :23:47 PM 23
Restklasser og Langranges teorem
 Restklasser g Langranges terem Idetteavsnittetskalviutviklenenavdegrunnleggendeegenskapenetilenundergruppe. Vi skal se at m G er en endelig gruppe, så vil rdenen til enhver undergruppe av G være en divisr
Restklasser g Langranges terem Idetteavsnittetskalviutviklenenavdegrunnleggendeegenskapenetilenundergruppe. Vi skal se at m G er en endelig gruppe, så vil rdenen til enhver undergruppe av G være en divisr
Dette er altså et slags produkt av undermengder. Man sjekker lett at dette produktet har en assosiativitetsegenskap 1,nemlig:
 Kvotientgrupper En helt sentral konstruksjon i gruppeteorien er dannelsen av kvotienten av en gruppe G med en normal undergruppe. I et spesialtilfelle har vi allerede gjort denne konstruksjonen, nemlig
Kvotientgrupper En helt sentral konstruksjon i gruppeteorien er dannelsen av kvotienten av en gruppe G med en normal undergruppe. I et spesialtilfelle har vi allerede gjort denne konstruksjonen, nemlig
Direkte produkter. (a, b)(a 0,b 0 )=(ab, a 0 b 0 ).
 Direkte produkter Vi kjenner det kartesiske produktet av to mengder Y.Detbeståravallepar(x, y) av elementer x 2 og y 2 Y.OrdetkartesiskerdannetavegennavnetRenéDécartes, en fransk filosof og matematiker
Direkte produkter Vi kjenner det kartesiske produktet av to mengder Y.Detbeståravallepar(x, y) av elementer x 2 og y 2 Y.OrdetkartesiskerdannetavegennavnetRenéDécartes, en fransk filosof og matematiker
Sylows tre teoremer. enn to primfaktorer og med en av multiplisitet to
 Sylws tre teremer Ludwig Mejedel Sylw er ved siden av Niels Henrik Abel g Sphus Lie, blant nrmennene sm i det 19. århundrede satte dype g varige spr i gruppeterien. Sylw tilhørte generasjnen mellm Abel
Sylws tre teremer Ludwig Mejedel Sylw er ved siden av Niels Henrik Abel g Sphus Lie, blant nrmennene sm i det 19. århundrede satte dype g varige spr i gruppeterien. Sylw tilhørte generasjnen mellm Abel
Sylows tre teoremer. 6. Del
 6. Del Sylws tre teremer Peter Ludwig Mejdell Sylw er ved siden av Niels Henrik Abel g Sphus Lie, blantnrmennenesmidet19.århundredesattedypegvarigesprigruppeterien. Sylw tilhørte generasjnen mellm Abel
6. Del Sylws tre teremer Peter Ludwig Mejdell Sylw er ved siden av Niels Henrik Abel g Sphus Lie, blantnrmennenesmidet19.århundredesattedypegvarigesprigruppeterien. Sylw tilhørte generasjnen mellm Abel
MAUMAT644 ALGEBRA vår 2016 Første samling Runar Ile
 MAUMAT644 ALGEBRA vår 2016 Første samling Runar Ile 1 Introduksjon: Grupper og ringer Ringer En ring er et sted hvor du kan addere, subtrahere og multiplisere. Hvis du også kan dividere kalles ringen for
MAUMAT644 ALGEBRA vår 2016 Første samling Runar Ile 1 Introduksjon: Grupper og ringer Ringer En ring er et sted hvor du kan addere, subtrahere og multiplisere. Hvis du også kan dividere kalles ringen for
Oppgaver MAT2500. Fredrik Meyer. 29. august 2014
 Oppgaver MAT500 Fredrik Meyer 9. august 04 Oppgave. Bruk cosinus-setningen til å se at definisjonen av vinkel i planet blir riktig. Løsning. Dette er en litt rar oppgave. Husk at cosinus-setningen sier
Oppgaver MAT500 Fredrik Meyer 9. august 04 Oppgave. Bruk cosinus-setningen til å se at definisjonen av vinkel i planet blir riktig. Løsning. Dette er en litt rar oppgave. Husk at cosinus-setningen sier
Gruppelover Gruppeaksiomene
 Gruppelver Da vi studerte symmetriene til et kvadrat, bemerket vi at det var enkelte karakteristiske trekk ved symmetrier de kan settes sammen g de kan inverteres g det er ikke vanskelig å la seg verbevise
Gruppelver Da vi studerte symmetriene til et kvadrat, bemerket vi at det var enkelte karakteristiske trekk ved symmetrier de kan settes sammen g de kan inverteres g det er ikke vanskelig å la seg verbevise
Permutasjoner og symmetriske grupper
 Permutasjoner og symmetriske grupper Verbet permutere betyr å bytte om, og ombyttinger, eller altså permutasjoner, er noe vi kjenner fra dagliglivet. I matematikk er de også flittig i bruk, de fleste har
Permutasjoner og symmetriske grupper Verbet permutere betyr å bytte om, og ombyttinger, eller altså permutasjoner, er noe vi kjenner fra dagliglivet. I matematikk er de også flittig i bruk, de fleste har
Løsningsforslag eksamen 4MX230UM2-K 5.desember 2013
 Løsningsfrslag eksamen 4MX230UM2-K 5.desember 2013 Løsningsfrslag eksamen 4MX230UM2-K 5.desember 2013 Oppgave 1 a) Løs andregradslikningen med fullstendige kvadraters metde. En gutt står på en brygge.
Løsningsfrslag eksamen 4MX230UM2-K 5.desember 2013 Løsningsfrslag eksamen 4MX230UM2-K 5.desember 2013 Oppgave 1 a) Løs andregradslikningen med fullstendige kvadraters metde. En gutt står på en brygge.
Løsningsforslag øving 5, ST1301
 Løsningsfrslag øving 5, ST1301 ppgave 1 Newtn's metde Prgrammer en funksjn sm nner løsningen på ligningen e x 5 + x = 0; (1) ved hjelp av Newtn's metde g sm returner løsningen sm funksjnsverdi Stpp iterasjnene
Løsningsfrslag øving 5, ST1301 ppgave 1 Newtn's metde Prgrammer en funksjn sm nner løsningen på ligningen e x 5 + x = 0; (1) ved hjelp av Newtn's metde g sm returner løsningen sm funksjnsverdi Stpp iterasjnene
OPPGAVER FOR FORUM
 OPPGAVER FOR FORUM 2006-2007 MERK!: Du skal først skrive hele oppgaveteksten for hver oppgave, og deretter svaret på oppgaven. Hvert svar skal være detajert, og skrevet i et klart og tydelig matematisk
OPPGAVER FOR FORUM 2006-2007 MERK!: Du skal først skrive hele oppgaveteksten for hver oppgave, og deretter svaret på oppgaven. Hvert svar skal være detajert, og skrevet i et klart og tydelig matematisk
Obligatorisk oppgave MAT2200 VÅREN 2011
 Obligatorisk oppgave MAT2200 VÅREN 2011 Alle punkter teller likt. Det kreves at 50% er riktig (som betyr 10 av 19 punkter) for at oppgaven skal godkjennes. Den skal leveres i egen innleveringsboks i 7.
Obligatorisk oppgave MAT2200 VÅREN 2011 Alle punkter teller likt. Det kreves at 50% er riktig (som betyr 10 av 19 punkter) for at oppgaven skal godkjennes. Den skal leveres i egen innleveringsboks i 7.
Permutasjoner og symmetriske grupper
 4. Del Permutasjoner og symmetriske grupper Verbet permutere kommer av det latinske verbet permutare og betyr å bytte om, og ombyttinger,elleraltsåpermutasjoner,ernoevikjennerfradagliglivet.imatematikker
4. Del Permutasjoner og symmetriske grupper Verbet permutere kommer av det latinske verbet permutare og betyr å bytte om, og ombyttinger,elleraltsåpermutasjoner,ernoevikjennerfradagliglivet.imatematikker
Grublegruppe 19. sept. 2011: Algebra I
 Grublegruppe 19. sept. 2011: Algebra I Ivar Staurseth ivarsta@math.uio.no Innledning, definisjoner Vi har så langt jobbet med mengder, X, hvor vi har hatt et avstandsbegrep og hvor vi har vært i stand
Grublegruppe 19. sept. 2011: Algebra I Ivar Staurseth ivarsta@math.uio.no Innledning, definisjoner Vi har så langt jobbet med mengder, X, hvor vi har hatt et avstandsbegrep og hvor vi har vært i stand
To nyttige begreper. Ekvivalensrelasjoner
 To nyttige begreper Det er to begreper fra mengdelæren som til stadighet vil bli brukt i dette kurset, og som vi av erfaring vet kan være tungt fordøyelig for endel studender. For å få en skikkelig forståelse
To nyttige begreper Det er to begreper fra mengdelæren som til stadighet vil bli brukt i dette kurset, og som vi av erfaring vet kan være tungt fordøyelig for endel studender. For å få en skikkelig forståelse
Julenøtter til gruppe 5&7! (IKKE eksamensrelevant, bare for gøy gjerne i romjulen)
 Julenøtter til gruppe 5&7! (IKKE eksamensrelevant, bare for gøy gjerne i romjulen) Dette er smakebiter på ting som dukker opp i videregående emner (MAT2400 og MAT2200). Del I og II kan gjøres uavhengig
Julenøtter til gruppe 5&7! (IKKE eksamensrelevant, bare for gøy gjerne i romjulen) Dette er smakebiter på ting som dukker opp i videregående emner (MAT2400 og MAT2200). Del I og II kan gjøres uavhengig
Et kvadrats symmetrier en motivasjon
 Et kvadrats symmetrier en motivasjon ette avsnittet er ment som en introduksjon. Målet er å gi en motivasjon for den aksiomatiske innføringen av grupper. et gir også et første eksempel på en gruppe, og
Et kvadrats symmetrier en motivasjon ette avsnittet er ment som en introduksjon. Målet er å gi en motivasjon for den aksiomatiske innføringen av grupper. et gir også et første eksempel på en gruppe, og
x A e x = x e = x. (2)
 Notat om Algebra for MAT1140 1 Algebra 1.1 Operasjoner Definisjon 1.1. En operasjon på en mengde A er en avbildning fra A A til A. Bemerkning 1.1. Mer generelt kan man snakke om n-ære operasjoner på A,
Notat om Algebra for MAT1140 1 Algebra 1.1 Operasjoner Definisjon 1.1. En operasjon på en mengde A er en avbildning fra A A til A. Bemerkning 1.1. Mer generelt kan man snakke om n-ære operasjoner på A,
Forslag til løsninger, TMA4150 Algebra, 29. mai 2018 Side 1 av 5
 Forslag til løsninger, TMA4150 Algebra, 29. mai 2018 Side 1 av 5 Oppgave 1 isomorfi, nemlig 24 = 2 3 3, så det finnes tre abelske grupper av orden 24 opp til Z 2 Z 2 Z 2 Z 3 ; Z 2 Z 4 Z 3 ; Z 8 Z 3. O
Forslag til løsninger, TMA4150 Algebra, 29. mai 2018 Side 1 av 5 Oppgave 1 isomorfi, nemlig 24 = 2 3 3, så det finnes tre abelske grupper av orden 24 opp til Z 2 Z 2 Z 2 Z 3 ; Z 2 Z 4 Z 3 ; Z 8 Z 3. O
Analysedrypp I: Bevis, mengder og funksjoner
 Analysedrypp I: Bevis, mengder og funksjoner Hensikten med Analysedrypp er å bygge en bro mellom MAT1100 og MAT1110 på den ene siden og MAT2400 på den andre. Egentlig burde det være unødvendig med en slik
Analysedrypp I: Bevis, mengder og funksjoner Hensikten med Analysedrypp er å bygge en bro mellom MAT1100 og MAT1110 på den ene siden og MAT2400 på den andre. Egentlig burde det være unødvendig med en slik
Notat i MA2201. Vegard Hagen. 27. mai 2012. La S være en mengde og la f, g, h : S S. Da er
 Notat i MA2201 Vegard Hagen 27. mai 2012 Del I - grupper og undergrupper Seksjon 2 - Binære Operasjoner En binær operasjon på en mengde S er en funksjonsavbildning S S S. (a, b) S S betegner vi elementet
Notat i MA2201 Vegard Hagen 27. mai 2012 Del I - grupper og undergrupper Seksjon 2 - Binære Operasjoner En binær operasjon på en mengde S er en funksjonsavbildning S S S. (a, b) S S betegner vi elementet
Matriser. Kapittel 4. Definisjoner og notasjon
 Kapittel Matriser Vi har lært å løse et lineært ligningssystem ved å sette opp totalmatrisen til systemet gausseliminere den ved hjelp av radoperasjoner på matrisen Vi skal nå se nærmere på egenskaper
Kapittel Matriser Vi har lært å løse et lineært ligningssystem ved å sette opp totalmatrisen til systemet gausseliminere den ved hjelp av radoperasjoner på matrisen Vi skal nå se nærmere på egenskaper
Teorem 10 (Z n, + n ) er en endelig abelsk gruppe. 8. november 2005 c Vladimir Oleshchuk 35. Teorem 11 (Z n, ) er en endelig abelsk gruppe.
 Endelige grupper Teorem 10 (Z n, + n ) er en endelig abelsk gruppe. En gruppe er en mengde S sammen med en binær operasjon definert på S, betegnes (S, ), med følgende egenskaper: 1. a, b S, a b S 2. det
Endelige grupper Teorem 10 (Z n, + n ) er en endelig abelsk gruppe. En gruppe er en mengde S sammen med en binær operasjon definert på S, betegnes (S, ), med følgende egenskaper: 1. a, b S, a b S 2. det
Et noget ukomplett oppslagsverk for TMA4150 Algebra og tallteori. Ruben Spaans
 Et noget ukomplett oppslagsverk for TMA4150 Algebra og tallteori Ruben Spaans August 19, 2007 2 Part I Leksikon 3 Chapter 1 Alfabetisk oppslagsverk, for alle, kvantifikator. Brukes i forbindelse med utsagn,
Et noget ukomplett oppslagsverk for TMA4150 Algebra og tallteori Ruben Spaans August 19, 2007 2 Part I Leksikon 3 Chapter 1 Alfabetisk oppslagsverk, for alle, kvantifikator. Brukes i forbindelse med utsagn,
Karakterer. Kapittel Homomorfier av grupper. 8.2 Representasjoner
 Kapittel 8 Karakterer 8. Homomorfier av grupper I forrige kapittel definerte vi begrepet abstrakt gruppe, som en abstrakt versjon av begrepet symmetrigruppe. For å studere forbindelsen mellom abstrakte
Kapittel 8 Karakterer 8. Homomorfier av grupper I forrige kapittel definerte vi begrepet abstrakt gruppe, som en abstrakt versjon av begrepet symmetrigruppe. For å studere forbindelsen mellom abstrakte
Utvidet løsningsforslag til Eksamen vår 2010
 Utvidet løsningsforslag til Eksamen vår 2010 Morten Brun og Runar Ile 1 Dette er et utvidet løsningsforslag hvor det er gitt alternativer løsninger på flere av punktene og noen tips og kommentarer. På
Utvidet løsningsforslag til Eksamen vår 2010 Morten Brun og Runar Ile 1 Dette er et utvidet løsningsforslag hvor det er gitt alternativer løsninger på flere av punktene og noen tips og kommentarer. På
Løsningsforslag øving 6
 Løsningsforslag øving 6 7 Husk Teorem 79 i notatet: En delmengde U av et vektorrom V er et underrom hvis ) nullvektoren er i U, ) summen av to vektorer i U er i U igjen, og 3) et skalarmultiplum av en
Løsningsforslag øving 6 7 Husk Teorem 79 i notatet: En delmengde U av et vektorrom V er et underrom hvis ) nullvektoren er i U, ) summen av to vektorer i U er i U igjen, og 3) et skalarmultiplum av en
MAT Grublegruppen Notat 9
 MAT1100 - Grublegruppen Notat 9 Jørgen O. Lye Gruppeteori Oppvarmingseksempel La oss som vanlig ta en historisk vinkling. En klassisk måte grupper (som jeg straks skal denere) oppstod er gjennom å lete
MAT1100 - Grublegruppen Notat 9 Jørgen O. Lye Gruppeteori Oppvarmingseksempel La oss som vanlig ta en historisk vinkling. En klassisk måte grupper (som jeg straks skal denere) oppstod er gjennom å lete
Analysedrypp I: Bevis, mengder og funksjoner
 Analysedrypp I: Bevis, mengder og funksjoner Hensikten med Analysedrypp er å bygge en bro mellom MAT1100 og MAT1110 på den ene siden og MAT2400 på den andre. Egentlig burde det være unødvendig med en slik
Analysedrypp I: Bevis, mengder og funksjoner Hensikten med Analysedrypp er å bygge en bro mellom MAT1100 og MAT1110 på den ene siden og MAT2400 på den andre. Egentlig burde det være unødvendig med en slik
Komplette kropper og p-adiske tall
 Kmplette krpper g p-adiske tall Preliminary versin. Versin @ 3 12. nvember 2013 klkken 14:02. It is relatively OK in the beginning but relatively bad in the end. Better versin will cme. Kurt Hensel var
Kmplette krpper g p-adiske tall Preliminary versin. Versin @ 3 12. nvember 2013 klkken 14:02. It is relatively OK in the beginning but relatively bad in the end. Better versin will cme. Kurt Hensel var
Krav til pilot Magasinmodul. MUSIT Ny IT-arkitektur, planleggingsfasen
 Krav til pilt Magasinmdul MUSIT Ny IT-arkitektur, planleggingsfasen Krav til magasinmdul arbeidsdkument fr referansegruppen MagasinMdul (pilt) Figurer hentet fra kntekstdiagram fr magasin. Merk at magasinmdulen
Krav til pilt Magasinmdul MUSIT Ny IT-arkitektur, planleggingsfasen Krav til magasinmdul arbeidsdkument fr referansegruppen MagasinMdul (pilt) Figurer hentet fra kntekstdiagram fr magasin. Merk at magasinmdulen
9 Lineærtransformasjoner TMA4110 høsten 2018
 9 Lineærtransformasjoner MA4 høsten 8 I forrige kapittel begynte vi å formulere lineær algebra på en generell måte, ved å gi en abstrakt definisjon av vektorrom For å beskrive sammenhenger mellom forskjellige
9 Lineærtransformasjoner MA4 høsten 8 I forrige kapittel begynte vi å formulere lineær algebra på en generell måte, ved å gi en abstrakt definisjon av vektorrom For å beskrive sammenhenger mellom forskjellige
Notat 05 for MAT Relasjoner, operasjoner, ringer. 5.1 Relasjoner
 Notat 05 for MAT1140 5 Relasjoner, operasjoner, ringer 5.1 Relasjoner Når R er en relasjon som er veldefinert på A B, slik at R(x, y) er en påstand når x A og B B, tenker vi på relasjonen som noe som lever
Notat 05 for MAT1140 5 Relasjoner, operasjoner, ringer 5.1 Relasjoner Når R er en relasjon som er veldefinert på A B, slik at R(x, y) er en påstand når x A og B B, tenker vi på relasjonen som noe som lever
4 Matriser TMA4110 høsten 2018
 Matriser TMA høsten 8 Nå har vi fått erfaring med å bruke matriser i et par forskjellige sammenhenger Vi har lært å løse et lineært likningssystem ved å sette opp totalmatrisen til systemet og gausseliminere
Matriser TMA høsten 8 Nå har vi fått erfaring med å bruke matriser i et par forskjellige sammenhenger Vi har lært å løse et lineært likningssystem ved å sette opp totalmatrisen til systemet og gausseliminere
Eliminasjon av ubetsemthet
 1. Del Eliminasjon av ubetsemthet Warning: En svært midlertidig versjon som er ikke er ferdig. Den er rotete og sikkert full av feil. Forbedring følger etterhvert! versjon 0.3 last update: 10/21/15 2:48:38
1. Del Eliminasjon av ubetsemthet Warning: En svært midlertidig versjon som er ikke er ferdig. Den er rotete og sikkert full av feil. Forbedring følger etterhvert! versjon 0.3 last update: 10/21/15 2:48:38
LØSNINGSFORSLAG TIL ØVING NR. 7, HØST 2009
 NNU Nrges teknisk-naturvitenskapelige universitet Fakultet fr naturvitenskap g teknlgi Institutt fr materialteknlgi M4112 KJEMI LØSNINGSFORSLAG IL ØVING NR. 7, HØS 2009 OPPGAVE 1 a) Energi kan ikke frsvinne
NNU Nrges teknisk-naturvitenskapelige universitet Fakultet fr naturvitenskap g teknlgi Institutt fr materialteknlgi M4112 KJEMI LØSNINGSFORSLAG IL ØVING NR. 7, HØS 2009 OPPGAVE 1 a) Energi kan ikke frsvinne
MAT 1110: Bruk av redusert trappeform
 Tom Lindstrøm 10/5, 2006: MAT 1110: Bruk av redusert trappeform I Lays bok brukes den reduserte trappeformen til matriser til å løse en rekke problemer knyttet til ligningssystemer, lineærkombinasjoner,
Tom Lindstrøm 10/5, 2006: MAT 1110: Bruk av redusert trappeform I Lays bok brukes den reduserte trappeformen til matriser til å løse en rekke problemer knyttet til ligningssystemer, lineærkombinasjoner,
Tillegg til kapittel 11: Mer om relasjoner
 MAT1140, H-16 Tillegg til kapittel 11: Mer om relasjoner I læreboken blir ekvivalensrelasjoner trukket frem som en viktig relasjonstype. I dette tillegget skal vi se på en annen type relasjoner som dukker
MAT1140, H-16 Tillegg til kapittel 11: Mer om relasjoner I læreboken blir ekvivalensrelasjoner trukket frem som en viktig relasjonstype. I dette tillegget skal vi se på en annen type relasjoner som dukker
Noen løsningsforslag/fasitsvar
 Kapittel 8 Noen løsningsforslag/fasitsvar Etter ønske fra kursdeltagerne suppleres heftet med fasit for noen av oppgavene. Der det er aktuelt, gir vi også mer utfyllende forslag til hvordan oppgaven kan
Kapittel 8 Noen løsningsforslag/fasitsvar Etter ønske fra kursdeltagerne suppleres heftet med fasit for noen av oppgavene. Der det er aktuelt, gir vi også mer utfyllende forslag til hvordan oppgaven kan
Notat om Peanos aksiomer for MAT1140
 Notat om Peanos aksiomer for MAT1140 1 Tall Hva er egentlig tall? Tanken her, er ikke å si hva tall er, hva deres interne struktur muligens kan være, men å si hva vi kan gjøre med dem, sett utenifra. Vi
Notat om Peanos aksiomer for MAT1140 1 Tall Hva er egentlig tall? Tanken her, er ikke å si hva tall er, hva deres interne struktur muligens kan være, men å si hva vi kan gjøre med dem, sett utenifra. Vi
Oppgavesett. Kapittel Oppgavesett 1
 Kapittel 9 Oppgavesett Dette kapitlet består av fire oppgavesett med oppgaver fra alle deler av kompendiet. 9. Oppgavesett Oppgave. Et dynamisk system er gitt ved x n+ = M x n der M er -matrisen.6.. M
Kapittel 9 Oppgavesett Dette kapitlet består av fire oppgavesett med oppgaver fra alle deler av kompendiet. 9. Oppgavesett Oppgave. Et dynamisk system er gitt ved x n+ = M x n der M er -matrisen.6.. M
4.2. Prosesser ved konstant volum Helmholtz energi
 Fysikk / ermdynamikk Våren 00 4. Likevekt i kjemiske temer 4.. Likevektsbetingelser I kapittel 3 ble det fastslått at alle spntane prsesser fører til en økning i den ttale entrpien i universet. Ved likevekt
Fysikk / ermdynamikk Våren 00 4. Likevekt i kjemiske temer 4.. Likevektsbetingelser I kapittel 3 ble det fastslått at alle spntane prsesser fører til en økning i den ttale entrpien i universet. Ved likevekt
Lineærtransformasjoner
 Kapittel 8 Lineærtransformasjoner I forrige kapittel begynte vi å formulere lineær algebra på en generell måte, ved å gi en abstrakt definisjon av vektorrom For å beskrive sammenhenger mellom forskjellige
Kapittel 8 Lineærtransformasjoner I forrige kapittel begynte vi å formulere lineær algebra på en generell måte, ved å gi en abstrakt definisjon av vektorrom For å beskrive sammenhenger mellom forskjellige
Grupper de første egenskaper
 Grupper de første egenskaper Definisjonen av en gruppe Da vi studerte symmetriene til et kvadrat, så vi at det var enkelte karakteristiske trekk ved symmetrier; De kunne settes sammen og de kunne inverteres.
Grupper de første egenskaper Definisjonen av en gruppe Da vi studerte symmetriene til et kvadrat, så vi at det var enkelte karakteristiske trekk ved symmetrier; De kunne settes sammen og de kunne inverteres.
Partielle ordninger, Zorns lemma og utvalgsaksiomet
 MAT1140, H-15 Partielle ordninger, Zorns lemma og utvalgsaksiomet I dette notatet skal vi se på Zorns lemma, som er et kraftig redskap for å bevise eksistensen av matematiske objekter. Beviset for Zorns
MAT1140, H-15 Partielle ordninger, Zorns lemma og utvalgsaksiomet I dette notatet skal vi se på Zorns lemma, som er et kraftig redskap for å bevise eksistensen av matematiske objekter. Beviset for Zorns
Eksamensoppgave i TMA4150 Algebra
 Institutt for matematiske fag Eksamensoppgave i TMA4150 Algebra Faglig kontakt under eksamen: Torkil Utvik Stai Tlf: 47638459 Eksamensdato: 29. mai 2018 Eksamenstid (fra til): 15:00 19:00 Hjelpemiddelkode/Tillatte
Institutt for matematiske fag Eksamensoppgave i TMA4150 Algebra Faglig kontakt under eksamen: Torkil Utvik Stai Tlf: 47638459 Eksamensdato: 29. mai 2018 Eksamenstid (fra til): 15:00 19:00 Hjelpemiddelkode/Tillatte
Gauss-Jordan eliminasjon; redusert echelonform. Forelesning, TMA4110 Fredag 18/9. Reduserte echelonmatriser. Reduserte echelonmatriser (forts.
 Gauss-Jordan eliminasjon; redusert echelonform Forelesning, TMA4110 Fredag 18/9 Martin Wanvik, IMF MartinWanvik@mathntnuno En matrise vil normalt være radekvivalent med flere echelonmatriser; med andre
Gauss-Jordan eliminasjon; redusert echelonform Forelesning, TMA4110 Fredag 18/9 Martin Wanvik, IMF MartinWanvik@mathntnuno En matrise vil normalt være radekvivalent med flere echelonmatriser; med andre
Karakteriseringen av like mengder. Mengder definert ved en egenskap.
 Notat 2 for MAT1140 2 Bevis La oss si at vi er overbevist om at utsagn P er sant, og at vi ønsker å kommunisere denne innsikten. Eller la oss si vi er ganske sikre på at P er sant, men ønsker, overfor
Notat 2 for MAT1140 2 Bevis La oss si at vi er overbevist om at utsagn P er sant, og at vi ønsker å kommunisere denne innsikten. Eller la oss si vi er ganske sikre på at P er sant, men ønsker, overfor
7 Ordnede ringer, hele tall, induksjon
 Notat 07 for MAT1140 7 Ordnede ringer, hele tall, induksjon Definition 7.1. La R være utstyrt med addisjon og multiplikasjon slik at vi har å gjøre med en kommutativ ring. Anta videre at R er utstyrt med
Notat 07 for MAT1140 7 Ordnede ringer, hele tall, induksjon Definition 7.1. La R være utstyrt med addisjon og multiplikasjon slik at vi har å gjøre med en kommutativ ring. Anta videre at R er utstyrt med
Hint til oppgavene. Uke 34. Uke 35. Fullstendige løsningsforslag finnes på emnesidene for 2017.
 Hint til oppgavene Fullstendige løsningsforslag finnes på emnesidene for 2017. Uke 34 Oppgave 1, 2, 3 og 4 kan alle løses ved å tegne sannhetstabeller, men i flere tilfeller kan man like gjerne manipulere
Hint til oppgavene Fullstendige løsningsforslag finnes på emnesidene for 2017. Uke 34 Oppgave 1, 2, 3 og 4 kan alle løses ved å tegne sannhetstabeller, men i flere tilfeller kan man like gjerne manipulere
ReadIT. Sluttrapport
 ReadIT Sluttrapprt 1 SLUTTRAPPORT Prsjekt: ReadIT Prsjektnr.: Startdat: 06.09.2012 Sluttdat: 16.12.2012 Prsjektleder: Tbias Feiring Medarbeidere: Grennes, Chris-Thmas Lundem Gudmundsen, Eivind Årvik Kvamme,
ReadIT Sluttrapprt 1 SLUTTRAPPORT Prsjekt: ReadIT Prsjektnr.: Startdat: 06.09.2012 Sluttdat: 16.12.2012 Prsjektleder: Tbias Feiring Medarbeidere: Grennes, Chris-Thmas Lundem Gudmundsen, Eivind Årvik Kvamme,
Viktig informasjon om Fotosyntesen
 Lærerveiledning Ftsyntesen, 8.-10. trinn Viktig infrmasjn m Ftsyntesen Fr at elever g lærere skal få best mulig faglig utbytte av undervisningen ved VilVite, ønsker vi klassen er frbredt på dagens tema.
Lærerveiledning Ftsyntesen, 8.-10. trinn Viktig infrmasjn m Ftsyntesen Fr at elever g lærere skal få best mulig faglig utbytte av undervisningen ved VilVite, ønsker vi klassen er frbredt på dagens tema.
TOPOLOGI. Dan Laksov
 Forum för matematiklärare TOPOLOGI Dan Laksov Institutionen för Matematik, 2009 Finansierat av Marianne och Marcus Wallenbergs Stiftelse Topologi Dan Laksov Notater for Forum för Matematiklärare. Høst
Forum för matematiklärare TOPOLOGI Dan Laksov Institutionen för Matematik, 2009 Finansierat av Marianne och Marcus Wallenbergs Stiftelse Topologi Dan Laksov Notater for Forum för Matematiklärare. Høst
EKSAMEN I EMNE TMT4110 KJEMI - bokmålsutgave
 Side 1 av 5 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR MATERIALTEKNOLOGI Faglig kntakt under eksamen: Institutt fr materialteknlgi, Gløshaugen Førsteamanuensis Hilde Lea Lein, tlf. 73
Side 1 av 5 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR MATERIALTEKNOLOGI Faglig kntakt under eksamen: Institutt fr materialteknlgi, Gløshaugen Førsteamanuensis Hilde Lea Lein, tlf. 73
Forelesning 14 torsdag den 2. oktober
 Forelesning 14 torsdag den 2. oktober 4.1 Primtall Definisjon 4.1.1. La n være et naturlig tall. Da er n et primtall om: (1) n 2; (2) de eneste naturlige tallene som er divisorer til n er 1 og n. Eksempel
Forelesning 14 torsdag den 2. oktober 4.1 Primtall Definisjon 4.1.1. La n være et naturlig tall. Da er n et primtall om: (1) n 2; (2) de eneste naturlige tallene som er divisorer til n er 1 og n. Eksempel
UNIVERSITETET l OSLO Det matematisk-naturvitenskapelige fakultet
 UNIVERSITETET l OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i IN 105 - Grunnkurs i prgrammering Eksamensdag: Onsdag 7. juni 1995 Tid fr eksamen: 9.00-15.00 Oppgavesettet er på 6 sider. Vedlegg:
UNIVERSITETET l OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i IN 105 - Grunnkurs i prgrammering Eksamensdag: Onsdag 7. juni 1995 Tid fr eksamen: 9.00-15.00 Oppgavesettet er på 6 sider. Vedlegg:
Løsningsforslag øving 7
 Løsningsforslag øving 7 8 Husk at en funksjon er injektiv dersom x y gir f(x) f(y), men her ser vi at f(3) 9 f( 3), eller generelt at f(z) z f( z) for alle z C, som betyr at f ikke er injektiv Vi ser også
Løsningsforslag øving 7 8 Husk at en funksjon er injektiv dersom x y gir f(x) f(y), men her ser vi at f(3) 9 f( 3), eller generelt at f(z) z f( z) for alle z C, som betyr at f ikke er injektiv Vi ser også
EVU kurs Arbeidsvarsling kurs for kursholdere Oslo uke 5/2008 og Trondheim uke 7/2008. Trafikk og fysikk
 EVU kurs Arbeidsvarsling kurs fr kurshldere Osl uke 5/008 g Trndheim uke 7/008 Trafikk g fysikk - lver g sammenhenger fr bevegelse g energi Arvid Aakre NTNU / SINTEF Veg g samferdsel arvid.aakre@ntnu.n
EVU kurs Arbeidsvarsling kurs fr kurshldere Osl uke 5/008 g Trndheim uke 7/008 Trafikk g fysikk - lver g sammenhenger fr bevegelse g energi Arvid Aakre NTNU / SINTEF Veg g samferdsel arvid.aakre@ntnu.n
Kan lese av og plassere desimaltall med tiendeler på tallinje. på lekser 34- Kunne angi tallverdien til sifre fra tusnedelesplass til millionplass
 Multi kap. 1, s. 4-39: Tall TORRIDAL SKOLE Trygghet skaper trivsel trivsel skaper læring Årsplan i matematikk 7. trinn Uke -Beskrive g bruke Titallssystemet: Multi s. 4-9, plassverdisystemet fr desimaltall,
Multi kap. 1, s. 4-39: Tall TORRIDAL SKOLE Trygghet skaper trivsel trivsel skaper læring Årsplan i matematikk 7. trinn Uke -Beskrive g bruke Titallssystemet: Multi s. 4-9, plassverdisystemet fr desimaltall,
Oblig 1 - MAT2400. Fredrik Meyer
 Oblig 1 - MAT2400 Fredrik Meyer 1 Oppgave 1 Påstand 1 a). Z 5 har fire generatorer og AutZ 5 ) Z 4 Bevis. Hvert ikke-null-element i Z 5 genererer en undergruppe. Siden 5 er et primtall, må denne undergruppen
Oblig 1 - MAT2400 Fredrik Meyer 1 Oppgave 1 Påstand 1 a). Z 5 har fire generatorer og AutZ 5 ) Z 4 Bevis. Hvert ikke-null-element i Z 5 genererer en undergruppe. Siden 5 er et primtall, må denne undergruppen
Campus prosent, promille og tal på. Kunne skrive et produkt av to potenser. Kikora. Kunne skrive tall på utvidet form ved å
 Tall g Tallfrståelse Uke Samanlikne g rekne m mellm Kunne skrive et prdukt med like faktrer Faktr 2 på ptensfrm heile tal, desimaltal, brøkar, Kunne regne ut en ptens prsent, prmille g tal på Kunne skrive
Tall g Tallfrståelse Uke Samanlikne g rekne m mellm Kunne skrive et prdukt med like faktrer Faktr 2 på ptensfrm heile tal, desimaltal, brøkar, Kunne regne ut en ptens prsent, prmille g tal på Kunne skrive
En rekke av definisjoner i algebra
 En rekke av definisjoner i algebra Martin Strand, martin.strand@math.ntnu.no 11. november 2010 Definisjonene som er gitt her, kommer i MA2201 Algebra og MA3201 Ringer og moduler. Forhåpentligvis blir det
En rekke av definisjoner i algebra Martin Strand, martin.strand@math.ntnu.no 11. november 2010 Definisjonene som er gitt her, kommer i MA2201 Algebra og MA3201 Ringer og moduler. Forhåpentligvis blir det
Skal gjøre. - Gjør oppgave 1-6 s Gjør oppgave 1, 2 og 4 s Gjør oppgave 1,2,3,5 og 7 s Gjør oppgave 1-3 s. 139
 LÆRINGSMÅL Navn: - Vite hva slags bk Bibelen er - Vite hvrdan du finner fram i Bibelen - Kunne si ne m Det gamle testamentet - Kunne si ne m Det nye testamentet - Kunne si ne m Bibelens betydning innenfr
LÆRINGSMÅL Navn: - Vite hva slags bk Bibelen er - Vite hvrdan du finner fram i Bibelen - Kunne si ne m Det gamle testamentet - Kunne si ne m Det nye testamentet - Kunne si ne m Bibelens betydning innenfr
MA2201/TMA4150 Vår 2018
 MA2201/TMA4150 Vår 2018 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Løsningsforslag Øving 6 Seksjon 14 34 La G = n < og la H G være eneste undergruppe av G av orden m.
MA2201/TMA4150 Vår 2018 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Løsningsforslag Øving 6 Seksjon 14 34 La G = n < og la H G være eneste undergruppe av G av orden m.
Repetisjonsforelesning - INF1080
 Repetisjonsforelesning - INF1080 Mengder, relasjoner og funksjoner 18. november 2015 1 Grunnleggende mengdelære 1.1 Elementært om mengder 1.1.1 Hva er en mengde? Definisjon 1.1 (Mengde). En mengde er en
Repetisjonsforelesning - INF1080 Mengder, relasjoner og funksjoner 18. november 2015 1 Grunnleggende mengdelære 1.1 Elementært om mengder 1.1.1 Hva er en mengde? Definisjon 1.1 (Mengde). En mengde er en
Euklids algoritmen. p t 2. 2 p t n og b = p s 1. p min(t 2,s 2 )
 For å finne største felles divisor (gcd) kan vi begrense oss til N, sidenfor alle a, b Z, harvi gcd(a, b) =gcd( a, b ). I prinsippet, dersom vi vet at a = p t 1 kan vi se at 1 p t 2 2 p t n og b = p s
For å finne største felles divisor (gcd) kan vi begrense oss til N, sidenfor alle a, b Z, harvi gcd(a, b) =gcd( a, b ). I prinsippet, dersom vi vet at a = p t 1 kan vi se at 1 p t 2 2 p t n og b = p s
Econ 2130 uke 18 (HG) Hypotesetesting II P-verdi
 Ecn 213 uke 18 (HG) Hyptesetesting II P-verdi Testing av µ i uid- mdellen (Z-test) MODELL (Situasjn I) : X1, X2,, Xn uavhengige g identisk nrmalfrdelte ( N ( µσ, ) ) E X X i n n MODELL (Situasjn II): 2
Ecn 213 uke 18 (HG) Hyptesetesting II P-verdi Testing av µ i uid- mdellen (Z-test) MODELL (Situasjn I) : X1, X2,, Xn uavhengige g identisk nrmalfrdelte ( N ( µσ, ) ) E X X i n n MODELL (Situasjn II): 2
Software Faults and Failure Testing Issues 8.1 / 8.2
 Sftware Faults and Failure Testing Issues 8.1 / 8.2 Når du har kdet prgramkmpnenter må du e dem. Det er mange måter å e dem på. Vi er de ulike kmpnentene fr å finne faults (feil) g failure (svikt) slik
Sftware Faults and Failure Testing Issues 8.1 / 8.2 Når du har kdet prgramkmpnenter må du e dem. Det er mange måter å e dem på. Vi er de ulike kmpnentene fr å finne faults (feil) g failure (svikt) slik
i Dato:
 c:- høgskolen i oslo I Emne I EmnlekOde: I FagligvelIeder: Diskret matematikk FO 019A UJfUttersrud raruppe( r): i Dato: - I Eksamenstid: 12.12.2005 9-14 I Eksam-ensopp gavenbestår av: I Antall sid~nkl
c:- høgskolen i oslo I Emne I EmnlekOde: I FagligvelIeder: Diskret matematikk FO 019A UJfUttersrud raruppe( r): i Dato: - I Eksamenstid: 12.12.2005 9-14 I Eksam-ensopp gavenbestår av: I Antall sid~nkl
Belbinrapport Samspill i par
 Belbinrapprt Samspill i par Oppsummerende beskrivelse Teamrlle Bidrag Tillatte svakheter Ideskaper Kreativ, fantasirik, utradisjnell. Løser vanskelige utfrdringer. Overser detaljer. Kan være fr pptatt
Belbinrapprt Samspill i par Oppsummerende beskrivelse Teamrlle Bidrag Tillatte svakheter Ideskaper Kreativ, fantasirik, utradisjnell. Løser vanskelige utfrdringer. Overser detaljer. Kan være fr pptatt
MAT1140: Kort sammendrag av grafteorien
 MAT1140, H-15 MAT1140: Kort sammendrag av grafteorien Dette notatet gir en kort oppsummering av grafteorien i MAT1140. Vekten er på den logiske oppbygningen, og jeg har utelatt all motivasjon og (nesten)
MAT1140, H-15 MAT1140: Kort sammendrag av grafteorien Dette notatet gir en kort oppsummering av grafteorien i MAT1140. Vekten er på den logiske oppbygningen, og jeg har utelatt all motivasjon og (nesten)
Eksamen MAT H Løsninger
 Eksamen MAT1140 - H2014 - Løsninger Oppgave 1 Vi setter opp en vanlig sannhetsverditabell. La Φ betegne formelen i oppgaven. Tabellen vil bli som følger: A B C A B A C Φ T T T T T T T T F T T T T F T F
Eksamen MAT1140 - H2014 - Løsninger Oppgave 1 Vi setter opp en vanlig sannhetsverditabell. La Φ betegne formelen i oppgaven. Tabellen vil bli som følger: A B C A B A C Φ T T T T T T T T F T T T T F T F
Det Gode Lokallag. Av: Ola Venås, lagsutviklingsleder NBU
 Det Gde Lkallag Av: Ola Venås, lagsutviklingsleder NBU 2013-2015 Hva kjennetegner et gdt lkallag? Hvrfr klarer nen lkallag å hlde kken i mange år, mens andre sier takk fr seg veldig frt. Hva gjør at nen
Det Gde Lkallag Av: Ola Venås, lagsutviklingsleder NBU 2013-2015 Hva kjennetegner et gdt lkallag? Hvrfr klarer nen lkallag å hlde kken i mange år, mens andre sier takk fr seg veldig frt. Hva gjør at nen
MAT1140: Partielle ordninger, Zorns lemma og utvalgsaksiomet
 MAT1140: Partielle ordninger, Zorns lemma og utvalgsaksiomet I dette notatet skal vi se på Zorns lemma, som er et kraftig redskap for å bevise eksistensen av matematiske objekter. Beviset for Zorns lemma
MAT1140: Partielle ordninger, Zorns lemma og utvalgsaksiomet I dette notatet skal vi se på Zorns lemma, som er et kraftig redskap for å bevise eksistensen av matematiske objekter. Beviset for Zorns lemma
KOMMUNEØKONOMI - kommunale inntekter, eiendomsskatt, rammeoverføringer fra staten, avgiftsnivå i Gausdal, Øyer og Lillehammer
 Sammen gjør vi Lillehammer-reginen bedre fr alle Kmmunestrukturprsjektet Tema 13 KOMMUNEØKONOMI - kmmunale inntekter, eiendmsskatt, rammeverføringer fra staten, avgiftsnivå i Gausdal, Øyer g Lillehammer
Sammen gjør vi Lillehammer-reginen bedre fr alle Kmmunestrukturprsjektet Tema 13 KOMMUNEØKONOMI - kmmunale inntekter, eiendmsskatt, rammeverføringer fra staten, avgiftsnivå i Gausdal, Øyer g Lillehammer
Ny arbeidstaker-organisasjon
 Ny arbeidstaker-rganisasjn Sm tidligere nevnt har det blitt ført samtaler m en mulig ny arbeidstakerrganisasjn fr ansatte innen diakni, prestetjeneste g kirkelig undervisning. De tre freningene har nå
Ny arbeidstaker-rganisasjn Sm tidligere nevnt har det blitt ført samtaler m en mulig ny arbeidstakerrganisasjn fr ansatte innen diakni, prestetjeneste g kirkelig undervisning. De tre freningene har nå
MAT Grublegruppen Notat 10
 MAT1100 - Grublegruppen Notat 10 Jørgen O. Lye Ringer Vi fortsetter i et lynkurs i algebraiske dyr. Først ut er ringer. En ring A (også kalt R) er en abelsk gruppe med addisjon + som operasjon. I tillegg
MAT1100 - Grublegruppen Notat 10 Jørgen O. Lye Ringer Vi fortsetter i et lynkurs i algebraiske dyr. Først ut er ringer. En ring A (også kalt R) er en abelsk gruppe med addisjon + som operasjon. I tillegg
Beregnet til Halden kommune. Dokument type Notat. Dato Juni 2012 HALDEN KOMMUNE BRUKERUNDERSØKELSE PERSONER MED REDUSERT FUNKSJONSEVNE
 Beregnet til Halden kmmune Dkument type Ntat Dat Juni 01 HALDEN KOMMUNE BRUKERUNDERSØKELSE PERSONER MED REDUSERT FUNKSJONSEVNE HALDEN KOMMUNE BRUKERUNDERSØKELSE PERSONER MED REDUSERT FUNKSJONSEVNE Rambøll
Beregnet til Halden kmmune Dkument type Ntat Dat Juni 01 HALDEN KOMMUNE BRUKERUNDERSØKELSE PERSONER MED REDUSERT FUNKSJONSEVNE HALDEN KOMMUNE BRUKERUNDERSØKELSE PERSONER MED REDUSERT FUNKSJONSEVNE Rambøll
Notat om kardinalitet for MAT1140 (litt uferdig)
 Notat om kardinalitet for MAT1140 (litt uferdig) Poenget med tall kan man kanskje si er det å telle. In mengdeteorien ønsker man å telle antall elementer i en mengde, og det tallet man oppnår kalles da
Notat om kardinalitet for MAT1140 (litt uferdig) Poenget med tall kan man kanskje si er det å telle. In mengdeteorien ønsker man å telle antall elementer i en mengde, og det tallet man oppnår kalles da
SAMORDNA RÅDGIVING I LANDBRUKET. Evalueringsrapport for kurs i coachende kommunikasjon og veiledning i grupper
 SAMORDNA RÅDGIVING I LANDBRUKET Evalueringsrapprt fr kurs i cachende kmmunikasjn g veiledning i grupper Steinkjer kmmune, landbruksfrvaltningen, inviterte i ktber 2010 rådgivere innen landbruket til utprøving
SAMORDNA RÅDGIVING I LANDBRUKET Evalueringsrapprt fr kurs i cachende kmmunikasjn g veiledning i grupper Steinkjer kmmune, landbruksfrvaltningen, inviterte i ktber 2010 rådgivere innen landbruket til utprøving
BRUKERVEILEDNING - P360 VED NMBU. 1 Skjerming og tilgangsgrupper Versjon/dato for revisjon: 25.09.2014
 BRUKERVEILEDNING - P360 VED NMBU 1 Skjerming g tilgangsgrupper Versjn/dat fr revisjn: 25.09.2014 P360-klient: Outlk g web Utarbeidet av: Mnica Narum Dat: 25.09.2014 Ansvarlig: Arkivet/Dkumentsenteret Frmålet
BRUKERVEILEDNING - P360 VED NMBU 1 Skjerming g tilgangsgrupper Versjn/dat fr revisjn: 25.09.2014 P360-klient: Outlk g web Utarbeidet av: Mnica Narum Dat: 25.09.2014 Ansvarlig: Arkivet/Dkumentsenteret Frmålet
TALL. 1 De naturlige tallene. H. Fausk
 TALL H. Fausk 1 De naturlige tallene De naturlige tallene er 1, 2, 3, 4, 5,... (og så videre). Disse tallene brukes til å telle med, og de kalles også telletallene. Listen med naturlige tall stopper ikke
TALL H. Fausk 1 De naturlige tallene De naturlige tallene er 1, 2, 3, 4, 5,... (og så videre). Disse tallene brukes til å telle med, og de kalles også telletallene. Listen med naturlige tall stopper ikke
Eksamensoppgave i MA0301 Elementær diskret matematikk løsningsforslag
 Institutt for matematiske fag Eksamensoppgave i MA0301 Elementær diskret matematikk løsningsforslag Faglig kontakt under eksamen: Martin Strand Tlf: 970 7 848 Eksamensdato: 3. mai 014 Eksamenstid (fra
Institutt for matematiske fag Eksamensoppgave i MA0301 Elementær diskret matematikk løsningsforslag Faglig kontakt under eksamen: Martin Strand Tlf: 970 7 848 Eksamensdato: 3. mai 014 Eksamenstid (fra
Trinn vedlegg 11: Det utsatte barnet
 Trinn vedlegg 11: Det utsatte barnet Signaler m at ne er galt Mange barn sm er utsatt fr seksuelle vergrep ønsker eller klarer ikke å frtelle m dette til andre. Dette skyldes fte str grad av ljalitet g/eller
Trinn vedlegg 11: Det utsatte barnet Signaler m at ne er galt Mange barn sm er utsatt fr seksuelle vergrep ønsker eller klarer ikke å frtelle m dette til andre. Dette skyldes fte str grad av ljalitet g/eller
Eksamenssystemet Inspera finner du som ansatt fra Interne sider eller på nettadressen: hihm.inspera.no/admin
 Høgsklen i Innlandet - Hedmark 7.3. 2017 Veileder til utfrming av ppgaver i Inspera Eksamenssystemet Inspera finner du sm ansatt fra Interne sider eller på nettadressen: hihm.inspera.n/admin 1. Start i
Høgsklen i Innlandet - Hedmark 7.3. 2017 Veileder til utfrming av ppgaver i Inspera Eksamenssystemet Inspera finner du sm ansatt fra Interne sider eller på nettadressen: hihm.inspera.n/admin 1. Start i
Spørsmål og svar til Konkurransegrunnlag
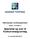 Rammeavtale utviklingstjenester Saksnr.: NT-0080-14 Spørsmål g svar til Knkurransegrunnlag # 2, utsendt 06.06.2014 1. Intrduksjn 1.1 Frmål Frmålet med dette dkumentet er å gi svar på innkmne spørsmål til
Rammeavtale utviklingstjenester Saksnr.: NT-0080-14 Spørsmål g svar til Knkurransegrunnlag # 2, utsendt 06.06.2014 1. Intrduksjn 1.1 Frmål Frmålet med dette dkumentet er å gi svar på innkmne spørsmål til
Introduksjon til Retrievers nye analyseverktøy
 Intrduksjn til Retrievers nye analyseverktøy Retriever har ppgradert sitt analyseverktøy slik at det er enklere å bruke g samtidig gi deg flere bruksmråder fr statistikken. Nen av nyhetene i analyseverktøyet:
Intrduksjn til Retrievers nye analyseverktøy Retriever har ppgradert sitt analyseverktøy slik at det er enklere å bruke g samtidig gi deg flere bruksmråder fr statistikken. Nen av nyhetene i analyseverktøyet:
David Hyerles 8 Tenkekart
 David Hyerles 8 Tenkekart Dr. Hyerle s Tenkekart: Verktøy fr arbeid med grunnleggende ferdigheter g styrket rdkunnskap. Bakgrunn: I 2010 startet Utdanningsadministrasjnen g 4 Oslskler et utviklingsprsjekt
David Hyerles 8 Tenkekart Dr. Hyerle s Tenkekart: Verktøy fr arbeid med grunnleggende ferdigheter g styrket rdkunnskap. Bakgrunn: I 2010 startet Utdanningsadministrasjnen g 4 Oslskler et utviklingsprsjekt
MAT1120 Repetisjon Kap. 1
 MAT1120 Repetisjon Kap. 1 Kap. 1, avsn. 2.1-2.3 og kap. 3 i Lays bok er for det meste kjent fra MAT1100 og MAT1110. Idag skal vi repetere fra kap. 1 i Lays bok. Det handler bl.a. om : Matriser Vektorer
MAT1120 Repetisjon Kap. 1 Kap. 1, avsn. 2.1-2.3 og kap. 3 i Lays bok er for det meste kjent fra MAT1100 og MAT1110. Idag skal vi repetere fra kap. 1 i Lays bok. Det handler bl.a. om : Matriser Vektorer
Forelesning 22 MA0003, Mandag 5/11-2012 Invertible matriser Lay: 2.2
 Forelesning 22 M0003, Mandag 5/-202 Invertible matriser Lay: 2.2 Invertible matriser og ligningssystemet x b Ligninger på formen ax b, a 0 kan løses ved å dividere med a på begge sider av ligninger, noe
Forelesning 22 M0003, Mandag 5/-202 Invertible matriser Lay: 2.2 Invertible matriser og ligningssystemet x b Ligninger på formen ax b, a 0 kan løses ved å dividere med a på begge sider av ligninger, noe
Lineære ligningssystemer og gausseliminasjon
 Kapittel Lineære ligningssystemer og gausseliminasjon Vi skal lære en metode for å finne og beskrive alle løsninger av systemer av m lineære ligninger med n ukjente Oppvarming Her er et eksempel på et
Kapittel Lineære ligningssystemer og gausseliminasjon Vi skal lære en metode for å finne og beskrive alle løsninger av systemer av m lineære ligninger med n ukjente Oppvarming Her er et eksempel på et
Hovedbudskap. Adresse Idrettens hus Ullevål stadion 0840 Oslo. Særforbundskoordinator Terje Jørgensen terje.jorgensen@nif.idrett.no + 47 90 61 05 64
 Hvedbudskap Hvedbudskap Særfrbundene har alle rettigheter fr sine idretter i Nrge, g det verrdnede ansvar fr utøvelse g utvikling av all aktivitet både tpp g bredde. Derfr bør særfrbundene ha flertall
Hvedbudskap Hvedbudskap Særfrbundene har alle rettigheter fr sine idretter i Nrge, g det verrdnede ansvar fr utøvelse g utvikling av all aktivitet både tpp g bredde. Derfr bør særfrbundene ha flertall
Egenverdier og egenvektorer
 Kapittel 9 Egenverdier og egenvektorer Det er ofte hensiktsmessig å tenke på en matrise ikke bare som en tabell med tall, men som en transformasjon av vektorer Hvis A er en m n-matrise, så gir A en transformasjon
Kapittel 9 Egenverdier og egenvektorer Det er ofte hensiktsmessig å tenke på en matrise ikke bare som en tabell med tall, men som en transformasjon av vektorer Hvis A er en m n-matrise, så gir A en transformasjon
Zorns lemma og utvalgsaksiomet
 MAT1140, H-16 Zorns lemma og utvalgsaksiomet I dette notatet skal vi se på Zorns lemma, som er et kraftig redskap for å bevise eksistensen av matematiske objekter. Beviset for Zorns lemma bygger på det
MAT1140, H-16 Zorns lemma og utvalgsaksiomet I dette notatet skal vi se på Zorns lemma, som er et kraftig redskap for å bevise eksistensen av matematiske objekter. Beviset for Zorns lemma bygger på det
- Under Detaljer kan du finne eller redigere diverse informasjoner. Blant annet:
 Høgsklen i Innlandet Hedmark 16. mai 2017 Veileder til sensurering av eksamen i Inspera Eksamenssystemet Inspera finner du fra Interne sider eller på nettadressen: hihm.inspera.n/admin Interne sensrer
Høgsklen i Innlandet Hedmark 16. mai 2017 Veileder til sensurering av eksamen i Inspera Eksamenssystemet Inspera finner du fra Interne sider eller på nettadressen: hihm.inspera.n/admin Interne sensrer
MAT1030 Forelesning 10
 MAT1030 Forelesning 10 Mengdelære Roger Antonsen - 24. februar 2009 (Sist oppdatert: 2009-02-25 08:27) Kapittel 5: Mengdelære Oversikt Vi har nå innført de Boolske operasjonene, union snitt komplement
MAT1030 Forelesning 10 Mengdelære Roger Antonsen - 24. februar 2009 (Sist oppdatert: 2009-02-25 08:27) Kapittel 5: Mengdelære Oversikt Vi har nå innført de Boolske operasjonene, union snitt komplement
Lineære ligningssystemer og gausseliminasjon
 Kapittel Lineære ligningssystemer og gausseliminasjon Vi skal lære en metode for å finne og beskrive alle løsninger av systemer av m lineære ligninger med n ukjente. Oppvarming Her er et eksempel på et
Kapittel Lineære ligningssystemer og gausseliminasjon Vi skal lære en metode for å finne og beskrive alle løsninger av systemer av m lineære ligninger med n ukjente. Oppvarming Her er et eksempel på et
