Kap. 2. Ragnar Soleng. August 27, Oppgave Oppgave 8 side 120. Oppgave 9 side 120
|
|
|
- Astri Jacobsen
- 7 år siden
- Visninger:
Transkript
1 Kap. Ragnar Soleng August 7, 01 Oppgave.1. a) Vi har {0,3,6,9,1} = {3x x er et heltall mellom 0 og 4}. b) Vi har { 3,, 1,0,1,,3} = {x x Z x 3}. c) Vi har {m,n,o,p} = {x x er et bokstav mellom m og p}. Oppgave 8 side { }, True. {, { }}, True 3. { } { }, False, { } 4. { } {{ }}, True 5. { } {, { }}, True 6. {{ }} {, { }}, True, x A,x B, thus A B 7. {{ }} {{ }, { }}, True Oppgave 9 side 10 a) x {x} True b) {x} {x} True ( a A,a B, thus A B) c){x} {x} False (x {x}) d){x} {{x}}true e) {x} True f) {x} False 1
2 Oppgave.1.15 Vi minner definisjonen av A B: og A B x A, x B. Siden vi har A B og B C, vi har a A, a B b B, b C. La nå x være et vilkårlig element i A. A B medfører altså at a er et element i B. Men B C medfører at a også er et element i C. Vi har derfor sett at dvs at A C. Oppgave.1.16 a A, a C, Betrakt mengdene A = {1} og B = {{1},1}. Da har vi at A B naturligvis (det er det første elementen i deskripsjonen til B), og A B siden x A, x = 1 og 1 B. Oppgave.1.19 a) Vi har b) Vi har c) Vi har P({a}) = {, {a}}. P({a,b}) = {, {a}, {b}, {a,b}}. P({, { }}) = {, { }, {{ }}, {, { }}}. Oppgave.1.0 Dette er sant. Nemlig, siden A A, A P(A) = P(B), og det betyr altså at A B. På det samme måte, vi finner at B A. Men A B B A A = B.
3 Oppgave 1 side 10 Let a b a) P({a,b, {a,b}}) has 3 = 8 elements. We can list them: P({a,b, {a,b}}) = {, {a}, {b}, {{a,b}}, {a,b}, {a, {a,b}}, {b, {a,b}}, {a,b, {a, b}}} b)p({,a, {a}, {{a}}}) has 4 = 16 elements. {, { }, {a}, {{a}}, {{{a}}}, {,a}, {, {a}}, {, {{a}}}, {a, {a}}, {a, {{a}}}, {{a}, {{a}}}, {,a, {a}}, {,a, {{a}}}, {, {a}, {{a}}}, {a, {a}, {{a}}}, {, a, {a}, {{a}}}} c)p(p( )) = P({ }) = {, { }} has 0 = 1 = elements Oppgave.1.8 a) Vi har b) Da er A B C = C B A = c) Vi har C A B = { (a,x,0),(a,x,1),(a,y,0),(a,y,1),(b,x,0),(b,x,1), (b,y,0),(b,y,1),(c,x,0),(c,x,1),(c,y,0),(c,y,1) { (0,x,a),(0,x,b),(0,x,c),(0,y,a),(0,y,b),(0,y,c), (1,x,a),(1,x,b),(1,x,c),(1,y,a),(1,y,b),(1,y,c) { (0,a,x),(0,a,y),(0,b,x),(0,b,y),(0,c,x),(0,c,y), (1,a,x),(1,a,y),(1,b,x),(1,b,y),(1,c,x),(1,c,y) }. }. }. d) Vi har B B B = { (x,x,x),(x,x,y),(x,y,x),(x,y,y), (y,x,x),(y,x,y),(y,y,x),(y,y,y) }. Oppgave 38 side 11 Let S be the set that contains all the set that do not belong to themselves. In mathematical words, S = {x x / x}. a)suppose that S S. Then it means that S (left) satisfy the property of being an element of S. Thus S / S and we have our contradiction with our hypothesis. b)we now suppose that S / S. Thus it means that S satisfy the property of being a member of S! Thus S S and we obtain a new contradiction! Thus after question a) and b), we get that S / S and S S. And thus it means that our first definition of S is not correct to define a new object. 3
4 Oppgave 4 side 130 Let A = {a,b,c,d,e} and B = {a,b,c,d,e,f,g,h} 1. A B = {a,b,c,d,e} {a,b,c,d,e,f,g,h} = {a,b,c,d,e,f,g,h}. A B = {a,b,c,d,e} {a,b,c,d,e,f,g,h} = {a,b,c,d,e} 3. A B = elements in A but not in B = 4. B A = elements in B but not in A = {f,g,h} Oppgave..1 Vi skal vise en dobbel inklusjon. Vi har selvfølgelig, og derfor x A, x A (A B) A A (A B). Omvendt, la x A (A B). Det betyr at enten x A eller x A B A. I alle tilfeller, x A og derfor har vi bevist at Når vi setter alt sammen får vi A (A B) A. A = A (A B). Oppgave 16 side 131 Let A and B be two sets. a)let x A B, then x A and x B, thus x A, and then we have A B A ( x A B,x A) b)let x A, then x A or x B thus x A B and A A B c)let x A B, then x A and x / B, thus x A and A B A d)let x A (B A), then x A and x B A thus, x A and x B and x / A. There is no such x, thus A (B A) = e)let x A (B A). According to c), x A or x B, thus x A B. Then A (B A) A B Let x A B, then x A or x B If x A, then x A (B A). If not, then x B A and then x A (B A) too. Finally we have A (B A) = A B 4
5 Oppgave 5 side 131 Let A = {0,,4,6,8,10}, B = {0,1,,3,4,5,6} and C = {4,5,6,7,8,9,10}. a) A B C = {4,6} b) A B C = {0,1,,3,4,5,6,7,8,9,10} c) (A B) C = {4,5,6,8,10} d) (A B) C = {4,6} Oppgave..30ab a) A C = B C medfører ikke at A = B. Vi viser et moteksempel. La oss ta A = og B = C = {1}. Da har vi men A B. A C = {1} = B C b) Det er feil igjen. La denne gangen A = C = og B = {1}. Da har vi men A B. Oppgave..34 A C = = B C Det mørke arealet er den symmetriske differansen. 5
6 Oppgave..44 Betrakt mengdene X = A og Y = B C. Da har vi A B C = X Y = X + Y X Y = A + B C A (B C). Men X Y = A (B C) = (A B) (A C). Betrakt da mengdene T = A B og U = A C. Da har vi A (B C) = T U = T + U T U = A B + A C (A B) (A C). Vi vet også at B C = B + C B C. Når vi setter alt tilsammen får vi: A B C = A + B C A (B C) = A + ( B + C B C ) A (B C) = A + B + C B C ( A B + A C (A B) (A C) ) = A + B + C A B A C B C + (A B) (A C) Til slutt, siden (A B) (A C) = A B C, vi får: A B C = A + B + C A B A C B C + A B C. Oppgave 45 side 131 Let A i = {1,,3,,i} i N a) n i=1 A i = A n = {1,,,n} b) n i=1 A i = A 1 = {1} Oppgave 46 side 131 Let A i = {,, 1,0,1,,3,,i} i N a) n i=1 A i = A n = {,, 1,0,1,,,n} b) n i=1 A i = A 1 = {,, 1,0,1} 6
7 Oppgave 51 side 13 Let U = {1,,3,4,5,6,7,8,9,10} a) corresponds to {1,, 3, 4, 7, 8, 9, 10} b) corresponds to {,4,5,6,7} c) corresponds to {1,10} Oppgave 1 side 146 a) f(x) = 1 x is not a function from R to R because f is not defined at x = 0 b) f(x) = x is not a function from R to R because f is not defined x < 0 c) f(x) = ± x + 1 is not a function from R to R because f(x) has two different values for any x! f(x) is never defined Oppgave.3. a) Dette er ikke en funksjon fra Z til R, fordi vi kan få to verdier for n 0. Nemlig, f(1) er ikke veldig bra definert (kan være enten 1 eller 1). b) Dette er en funksjon fra Z til R. For enhver n Z, vi får et unik element i R. c) Dette er ikke en funksjon. Nemlig, f(±) er ikke definert. Oppgave.3.6 a) Dette er funksjonen f : Z + Z + Z + (a, b) a og det er veldig lett å se at domain er Z + Z + mens codomain er Z +. b) Dette er funksjonen g : Z + {1,,9} a 1...a n max(a 1,,a n ). Da er det lett å se en gang til at domain er Z +, og litt vanskeligere å se at codomain er {1,,9} (at det er en undermengde av {0,,9} er lett, å finne et eksempel for alle bortsett fra 0 er lett, og hvis f(n)=0 medfører at n = 0, som ikke er positiv. c) Her er selvfølgelig domain alle bitstringer, mens codomain er Z (jeg tar altså som definisjon for differanse: antall nuller - antall ener). 7
8 d) Da har vi selvfølgelig at domain er Z +. Codomain er litt mer vanskelig, men den er Z +. At det er en undermengde av Z + er openbar. Nå hvis n Z +, da har vi at n = n, og derfor alle elementene i Z + er i codomain. e) Dette er en selvfølge: domain er alle bitstring, mens codomain er N. Oppgave.3.8 a) 1.1 = 1. b) 1.1 =. c) 0.1 = 1. d) 0.1 = 0. e).99 = 3. f).99 =. g) = = 3 = 1. h) = = 3 =. Oppgave 10 side 146 We are looking for one-to-one functions from {a,b,c,d} to itself: Definition: A function f is said to be one to one if and only if f(a) = f(b) implies that a = b for all a and b in the domain of f. Or equivalently, a, b,(a b, f(a) f(b)) 1. f(a) = b,f(b) = a,f(c) = c,f(d) = d The condition a, b,(a b, f(a) f(b)) is true for a,b,c and d and thus f is injective. f(a) = b,f(b) = b,f(c) = d,f(d) = c f(a) = f(b) but a b thus f is not one-to-one. 3. f(a) = d,f(b) = b,f(c) = c,f(d) = d f(a) = f(d) but a d thus f is not one-to-one. Oppgave.3.14 a) f er openbart surjektiv. Nemlig, n Z,f(0, n) = n. 8
9 b) f er ikke surjektiv. Nemlig, det finnes ikke noe par (m,n) Z slik at f(m,n) =. Det ser vi nå, med å bevise at hvis m,n 0, og m ± n, da er m n 3. Vi kan først anta at både m,n > 0, siden m = ( m). Siden problemet vårt er symmetirsk i m,n og at m n, så kan vi anta at m > n. La da l Z + være slik at m = n + l. Da har vi m n = m n = (n + l) n = n + l + ln n = l + ln Siden l,n er begge to positive heltall så får vi se at m n 3. Nå kan vi se at f(m,n) (m,n) Z. Nemlig, hvis det fantes slike tall, så ved hjelp av det vi nettopp har sett, at enten m = 0, eller n = 0 eller m = ±n. Men hvis m = ±n, så ser vi at f(m,n) = 0. Hvis m = 0, så ser vi at f(0,n) 0. Til slutt, hvis n = 0, så ser vi at m =, og dette er kjent til å ikke være mulig siden m er et heltall. c) f er surjektiv. Nemlig, n Z, f(0,n 1) = 0 + n = n. d) f er surjekiv. Nemlig, la n Z. Hvis n 0, da har vi mens hvis n 0, da har vi f(0,n) = 0 n = ( n) = n f(n,0) = n 0 = n. e) f er ikke surjektiv: det finnes ikke noe (m,n) Z slike at f(m,n) = 5, fordi hvis det fantes, da ville vi ha m 4 = 5 m = 1 og dette er kjent til å ikke være snat for heltall. Oppgave 15 side 147 Let f : Z Z Z a)f(m,n) = m+n is onto. n Z, (m 0,n 0 ) = (0,n) such that f(m 0,n 0 ) = n b)f(m,n) = m + n is not onto. (m,n) Z Z such that f(m,n) = 1 c)f(m,n) = m is onto. n Z, (m 0,n 0 ) = (n,0) such that f(m 0,n 0 ) = n d)f(m,n) = n is not onto. (m,n) Z Z such that f(m,n) = 1 e)f(m,n) = m n is onto. n Z, (m 0,n 0 ) = (n,0) such that f(m 0,n 0 ) = n 9
10 Oppgave 16 side 146 a) f : N N, f(n) = n + 1 f is one-to-one: f(n) = f(m) n + 1 = m + 1 n = m f is not onto, because f(n) = 0 has no solution in N b) f : N N, f(0) = 0, f(n) = n 1 f is onto: n N, m = n + 1, such that f(m) = n f is not one-to-one because f(0) = f(1) and 0 1 { n + 1 if n is even c)f : N N, f(n) = n 1 if n is odd f is one-to-one : f(n) = f(m) = k k is odd n + 1 = m + 1 n = m k is even n 1 = m 1 n = m and onto: let n N if n is odd, then it exists m = n 1 such that f(m) = n else n is even, and then it exists m = n + 1 such that f(m) = n d) f : N N, f(n) = 0 f is neither onto (f(n) = 1 has no solution in N)nor one-to-one (f(0) = f(1) = 0, and 0 1) Oppgave.3.18 a) Dette er en bijeksjon. Først er dette en injeksjon, fordi hvis f(x 1 ) = f(x ), så har vi 3x = 3x + 4 x 1 = x. Men dette er også en surjeksjon, fordi ( ) 4 x x R,f = 3 4 x + 4 = x
11 b) Dette er ikke en bijeksjon, fordi det er ikke en injeksjon. Nemlig vi har f(1) = 4 = f( 1). Legg merke til at dette ikke var en surjeksjon heller, men vi trenger ikke det. c) f( ) er ikke definert, så det kan ikke være en bijeksjon (ikke en funksjon en gang). d) Dette er en bijeksjon. f er surjektiv, fordi x R, f( 5 x 1) = x = x. f er også injektiv fordi hvis f(x 1 ) = f(x ), medfører det at x 5 1 = x 5, men dette er ekvivalent til x 1 = x. Oppgave 19 side 147 Let f : R R a)f(x) = x + 1. f is one-to-one: f(a) = f(b) a + 1 = b + 1 a = b f is onto: y R, x = y 1 R such that f(x) = y. And thus f is a bijection b)f(x) = x + 1 is not onto and thus not a bijection because x R such that f(x) = 0 c)f(x) = x 3 is one-to-one: f(a) = f(b) a 3 = b 3 a = b f is onto: y R, x = 3 y R such that f(x) = y. Thus f is a bijection d) f(x) = x + 1 x + = x + 1 x = x + 1 f is not onto and thus not a bijection. There is no x such that f(x) = 0 11
12 Oppgave 6 side 147 Let S = { 1,0,,4,7} a)f(x) = 1, thus f(s) = {1} b)f(x) = x + 1, thus f(s) = { 1,1,5,9,15} c)f(x) = x 5, thus f(s) = {0,1,} d)f(x) = x +1 3, thus f(s) = {0,1,5,16} Oppgave.3.36 a) Vi viser egenskapen med dobbel inklusjon: la først x f(s T). Det vil si at det finnes et element y S T slik at x = f(y). Men siden y S T, så vet vi at enten y S eller y T. I det første tilfelle er x = f(y) f(s) f(s) f(t), mens i det andre tilfelle x = f(y) f(t) f(s) f(t). Vi ser at uansett, x = f(y) f(s) f(t) og vi har derfor bevist at f(s T) f(s) f(t). Omvendt, la x f(s) f(t). Det betyr at enten x f(s) eller x f(t). I den første tilfelle, så finnes det y S S T slik at x = f(y), mens i den andre tilfelle kan vi finne et element y T S T slik at f(y) = x. I begge tilfellene har vi at x f(s T) og vi har derfor bevist at f(s) f(t) f(s T). Hvis vi legger sammen begge resultatene så ser vi at f(s T) = f(s) f(t). b) La nå x f(s T). Da finnes det y S T slik at x = f(y). men y S T S medfører at x = f(y) f(s), og tilsvarende for x f(t). Siden x er element i både f(s) og f(t), så har vi at x f(s) f(t), og vi har derfor bevist at f(s T) f(s) f(t). Bemerkning: De to mengdene kan være ulike. Nemlig, la A = B = R, S = R, T = R + og f(x) = x. Da har vi at S T = {0}, og derfor f(s T) = {0}. Men f(s) = f(t) = R + f(s) f(t) = R +. 1
13 Oppgave 46 side 148 x = Ceiling function of x = smaller integer that is greater than or equal to x x = n where n N and n 1 < x n Let k be the integer such that x + m = k thus we have And thus k 1 < x + m k k m 1 < x k m x = k m because k m is an integer k = x + m = x + m Oppgave.3.54 En byte korresponderer til 8 bits av data. Vi ser altså at for å kodere n bits av data, så trenger man n 8 bytes. Vi trenger derfor a) 4 8 = 1 byte for å kodere 4 bits b) 10 8 = bytes for å kodere 10 bits c) = 63 bytes for å kodere 500 bits d) = 375 bytes for å kodere 3000 bits Oppgave 56 side 148 The ATM system described in Example 6 is organized into cells of 53 bytes. Thus each cells is 53 8 = 44 bits long. a) The connection is 18 kilobits per second. Thus, in 10s, this connection can transmitted 18, = 1,80,000 bits. The number of cells that can be transmitted is the largest integer not exceeding the quotient of 1,80,000 divided by 44. Then 1,80,000/44 = 3018 ATM cells can be transmitted in 10s over a 18 kilobit per second connection. b) The connection is 300 kilobits per second. Thus, in 10s, this connection can transmitted 300, = 3, 000, 000 bits. The number of ATM cells that can be transmitted in 10s over a 300 kilobit per second connection is 3, 000, 000/44 = c) The connection is 1 megabits per second. Thus, in 10s, this connection can transmitted 1,000, = 10,000,000 bits. The number of ATM cells that can be transmitted in 10s over a 1 megabit per second connection is 10,000,000/44 = 3,
14 Oppgave 65 side 148 We consider the function f(x) = x This function is a bijection from R to R. f is an injection: f(a) = f(b) a = b a 3 = b 3 a = b f is a surjection: b R, a = 3 b 1 R such that f(a) = ( 3 b 1) = b Then f 1 exists! By using the relation f(a) = b and f 1 (b) = a, we obtain f(f 1 (b)) = b. Then f 1 (b) = b and f 1 (b) = 3 b 1 Oppgave.3.66 Man burde først bevise at f g er invertible, mao at f g er en bijektiv funksjon. La oss gjøre det først. La x 1,x X slike at f g(x 1 ) = f g(x ). Siden f er injektiv får vi g(x 1 ) = g(x ), og siden g er injektiv, x 1 = x, og f g er derfor injektiv. f g er også surjektiv. Nemlig, la z Z. Siden f er surjektiv, det finnes et y Y slik at f(y) = z. Men siden g er surjektiv, finnes det et element x X slik at g(x) = y. Nå, f g(x) = f(g(x)) = f(y) = z og f er også surjektiv. La z Z. Vi vet x = (f g) 1 (z) hvis og bare hvis f g(x) = z. Men da skriver vi f g(g 1 f 1 (x)) = f(g(g 1 (f 1 (x)))) = f(f 1 (x)) = x og derfor har vi (f g) 1 = g 1 f 1. Oppgave.3.68 La n = A = B. For b B, definer N b = {a A f(a) = b} og n b = #N b. Vi har at b B n b = n, 14
15 f er surjektiv hvis og bare hvis b B, n b 1, f er injektiv hvis og bare hvis b B, n b 1. Nemlig, A N b fordi hvis a A, a N f(a). Vi har også selvfølgelig at b B N b A siden alle n b er delmengder til A. Dessuten, hvis b 1 b, så b B er n b1 N b =. Hvis ikke, så finnes det et element x i begge to. Men per definisjon har vi da b 1 = f(x) = b, og dette er absurd. A er derfor en ditinkt union av alle de mengdene N b, og vi har derfor n = #A = b B #N b = b B n b. Anta først at f er surjektiv. La b B. Da vet vi at det finnes et element a A slik at f(a) = b. Med andre ord, N b n b 1. Omvendt, anta at b B, n b 1. La b B. Siden n b 1, N b og derfor det finnes et element a N b A slik at f(a) = b. f er derfor surjektiv. Anta at f er injektiv. La b B. Hvis n b > 1, så finnes det to forskjellige elementer a 1,a i A slike at f(a 1 ) = f(a ) = b Men dette motsier antaglesen at f er injektiv. Anta nå at b B, n b 1. La a 1,a slike at f(a 1 ) = f(a ). Da er begge elementene a 1,a i N b der b = f(a 1 ). Men siden det finnes maksimum et element i N b, så vet vi at a 1 = a. Vi er da klare for å bevise at f er surjektiv hvis og bare hvis den er injektiv. Anta først at den er surjektiv. Da vet vi at b B, n b 1. Hvis for en b 0 B, n b > 1, da ville vi ha fått n = n b = n b0 + n b > 1+ n b 1+ 1 = 1+(n 1) = n b B b B, b b 0 b B, b b 0 b B, b b 0 men dette er absurd. Derfor, b B, n b 1 og f er injektiv. Anta nå at f er injektiv. Da vet vi at b B, n b 1. Hvis for en b 0 B, n b < 1, da ville vi ha fått n = n b = n b0 + n b < 1+ n b 1+ 1 = 1+(n 1) = n b B b B, b b 0 b B, b b 0 b B, b b 0 men dette er absurd. Derfor, b B, n b 1 og f er sujektiv. Oppgave.4.8 Vi kan først ha u n = n + 3 for n N. Med andre ord, u i er den i te odde tall større enn 1. Vi kan ellers si at u i er den i-te odde primtall. Vi kan også ha u 0 = 3, u 1 = 5 og i, u i = u i + u i
16 Oppgave.4.9 a) Vi kan ha for eksempel. { 0 hvis i i u i = < i 1 ellers b) Vi kan ha u 3i = i + 1, mens u 3i+1 = u 3i+ = i + for eksempel. c) Vi kan ha for eksempel. u i = d) Vi kan ha u i = 3 i for eksempel. e) Vi kan ha u i = 15 7i for eksempel. { i hvis i er par 0 ellers f) Vi kan ha u 0 = 3 og u i = u i i for eksempel. g) Vi kan ha u i = (i + 1) 3 og u i+1 = 4 (i + 1) 3 for eksempel. h) Vi kan ha u i = 1 + (i + 1)! for eksempel. Oppgave.4.10 a) Vi kan ha u 0 = 3 og u i+1 = u i + i + 1 for eksempel. b) Vi kan ha u i = 7 + 4i for eksempel. c) Vi kan ha u i er den i + 1-te tall skrevet i binar for eksempel. d) Det ser ut til å være en komplisert Fibonacci sekvens. Da fant jeg ut at vi kunne ta ( u i = ) i ( ) i for eksempel. e) Vi kan ha u i = 3 i+1 1 for eksempel. f) Vi kan ha u i = (i+1)! i i! for eksempel. g) Vi kan ha for eksempel. u i = { 0 hvis 1+ 8i+1 1 ellers h) Vi kan ha u i = i+1 for eksempel. er et partall, 16
17 Oppgave.4.1 Boken sier selvfølgelig at en sekvens begynner med indeks 1, mens det er vanlig at det begynner med indeks 0. Men OK... Vi vet at hvis i Z +, antall i-er er i, så det første i kommer på plass nummer ( i 1 k=1 k) + 1, og den siset i plass nummer i k=1 k. Vi vet dessuten at i Z +, i k = k=1 i(i + 1). Det første sted med i er altså i(i 1), mens det siste er i(i+1). Så vi vet at a n = i i(i 1) + 1 n i(i + 1). La da n Z + og betrakt t = n+ 1 t(t 1). Hvis vi bevise at +1 n t(t+1), så skal vi ha bevist at a n = t. Men definisjonen til t er at t er det eneste heltall slik at t n + 1 < t + 1. Da får vi med en gang at t 1 n 1 < t. Og siden t 1 (lett å se), så kan vi multiplisere ulikhetene, nemlig mens t(t 1) + 1 n = n n 1 8 t(t + 1) <. Men siden t(t 1) + 1, n og t(t+1) er heltall, vi kan bare glemme de 7 8 og 1 8 (hvis man tar ikke streng ulikheter lengre), nemlig, Da har vi bevist at t(t 1) + 1 n t(t + 1). a n = t = n
18 Oppgave.4.16 a) 8 ( 1 + ( 1) j ) = 10. j=0 b) 8 ( 3 j j) = (1 1) + (3 ) + (9 4) + (7 8) + (81 16) j=0 +(43 3) + (79 64) + (187 18) + ( ) = c) 8 ( 3 j + 3 j) = ( + 3) + (6 + 6) + (18 + 1) + (54 + 4) + ( ) j=0 +( ) + ( ) + ( ) + ( ) = 115. d) 8 ( j+1 j ) = 9 0 = 51 1 = 511. j=0 Oppgave.4.18 a) Vi har 3 3 (i j) = (i 1 + i ) i=1 j=1 i=1 3 = (i 3) i=1 = = 3 18
19 b) Vi har 3 3 (3i + j) = (3i + 3i + + 3i + 4) i=0 j=0 i=0 3 = (9i + 6) i=0 = = 78 c) Vi har 3 3 j = ( ) i=1 j=0 i=1 3 = 3 i=1 = = 9 d) Vi har 3 1 i j 3 = (i + 8i + 7i ) i=0 j=0 i=0 3 = 36i i=0 = = 180 Oppgave.4.7 a) Det må være 0 siden en av termene, nemlig i = 0 er 0. Derfor har vi 10 i=0 i = 0. b) Vi har 8 i = = i=5 19
20 c) Vi har 100 ( 1) i = i = 1 50 ( 1) i i = 1 50 ( 1) i 1 i=1 = i = i = 1 50 ( 1) = ( 1) 50 = 1 d) Vi har 10 i=1 = 10 = 104. Oppgave.4.31 a) Z er tellbar siden vi har en bijeksjon f : N Z gitt ved f(n) = 1 n. b) Mengden av partall, P er tellbar siden vi har en bijeksjon f : N P gitt ved f(n) = n hvis n er et partall, og f(n) = n ellers. c) Dette er ikke tellbar. Mengden er i bijeksjon med R ved hjelp av funksjonen tan(πx π ), og vi vet at R ikke er tellbar. b) Mengden av partall, M 7 er tellbar siden vi har en bijeksjon f : N M 7 gitt ved f(n) = 7n hvis n er et partall, og f(n) = 7n ellers. Oppgave.3.34 a) Mengden S 3 er tellbar. Nemlig, vi har en bijeksjon f : Z S 3 gitt ved f(n) = 3n 3(n 1) + 1 hvis n er et partall, og f(n) = + hvis n er et odde tall. Men vi vet også at det finnes en bijeksjon g : N Z, og da er f g en bijeksjon mellom N og S 3. b) Mengden D er tellbar også. Vi kan bevise at mengden S 7 av heltall som ikke er delelig med / er tellbar: la f : Z S 7, definert ved f(6k + i) = 7k + i + 1 for k Z, i {0,1,,3,4,5}. Dette gir en bijeksjon mellom Z og S 7. Kombinert med g definert i a), f g : N S 7 er en bijeksjon. Betrakt da bijeksjonene h : S 7 D gitt ved h(n) = 5n. Da ser vi at h f g : N D er en bijeksjon, og D er derfor tellbar. c) Her tar jeg med utgangspunktet at 0, ikke bare skrives med 1, siden det er en 0 foran. Det spiller faktisk ingen rolle, men vi må bli 0
21 klar over dette. Mengden U er tellbar. Jeg skal gi,uten å bevise dette, en bijeksjon. Først, la f : N N N\{(0,0)} gitt ved: hvis 9 + 8t 1 δ(t) =, da er ( δ(t)(δ(t) + 3) f(t) = t 1,t + 1 ) δ(t)(δ(t) + 1). f er en bijeksjon. La nå g : N N\{(0,0)} U 1 } {{ 1 },1 1 }{{} hvis a 0 a (a, b) b 1 } {{ 1 },1 1 hvis a = 0 b g f er da en bijeksjon mellom N og U. d) Det er ikke tellbar, me det er litt vanskelig å se. Jeg skal gjøre den samme oppgaven med å erstatte 9 med 8, og da blir det mye enklere. Vi skal vise at det finnes en delmengde som ikke er tellbar, og derfor blir hele mengden ikke tellbar (ganske lett å se, siden en undermengde av N er enten endelig, eller tellbar) Vi betrakter den uendelig delmengden I som er formert av alle tall som har en uendelig desimal ekspansjon, og som heldelen er lik 1. Anta at det finnes en bijeksjon f : N I. For enhver i N, betrakt d i den i + 1-te desimal siffer. Betrakt da tallet x = 1,(9 d 0 )(9 d 1 )(9 d ) (9 d n ) Det er lett å se at x I. Da må det finnes et tall j slik at x = f(j). Men, den j + 1-te siffer i x er per definisjon d j, som er også 9 d j. Dette er umulig. Bemerkning: Jeg ville ikke gjøre oppgaven med 9, for da risikerer du å få x = 1,hva som helst199999, som er lik x = 1,hva som helst, og derfor er ikke i I. Det finnes forresten mer tall med 8 enn med 9 (hvis man erstatter 9 med 8), men forskjellen er en tellbar mengde, og da kommer vi tilbake til vår oppgaven. Oppgave.4.4 Dette er en vanskelig oppgave hvis man skal gjøre alt matematisk. La t N. Vi definerer følgende funksjoner: 3 + 8t + 1 δ(t) =, 1
22 og δ(t)(δ(t) 1) a(t) = t, (δ(t) 1)(δ(t) ) b(t) = δ(t) a(t) = t + 1 I tillegg, hvis (a,b) Z +,, vi definerer g(a,b) = f(t) = (a(t),b(t)). (a + b )(a + b 1) + b 1. Det første vi gjør er å bevise at g(a,b) N. Men dette er klart siden a,b 1 og er heltall. Vi må nå se at a(t),b(t) Z +. At de er i Z er en selvfølge, siden t N og δ(t) Z. Men, definisjon til gjør slik at og δ(t) 3 + 8t + 1 δ(t) t + 1 < δ(t) + 1, < δ(t) δ(t) 1 + 8t + 1 < δ(t) 1. Siden δ(t) δ(0) =, alle disse ulikhetene medfører og δ(t)(δ(t) 1)) Da får vi veldig enkelt at og δ(t)(δ(t) 1)) 0 < a(t) 1 > t t + 1 8t t + 1 b(t) = δ(t) a(t) > 0. Vi har derfor bevist at vi har to funksjoner f : N Z + og g : Z + N. Vi skal bevise at f g = Id og g f = Id, og da skal f og g være bijeskjoner, inverse fra hverandre. Vi begynner med det enkleste, nemlig at t N,g f(t) = t.
23 Nemlig, vi har g f(t) = g(a(t),b(t)) = g(a(t),δ(t) a(t)) (δ(t) )(δ(t) 1) = + δ(t) a(t) 1 ( (δ(t) )(δ(t) 1) δ(t)(δ(t) 1) = + δ(t) = t. Den andre delen er mye mer vanskelig, og vi skal først bevise at Vi har nemlig δ(g(a,b)) = = δ(g(a,b)) = a + b g(a,b) a + b + ab + 3a b + ) t 1 Men siden a 1, 3a a + 1, 3a + a + 1 og derfor a + b + ab 3a b + (a + b 1) = a + b 1. og vi får at 3 + (a + b 1) δ(g(a,b)) = a + b. Omvendt, siden b 1, 3b b + og derfor a + b 3 a + b + ab 3a b + og vi får at 3 + (a + b 3 δ(g(a,b)) = a + b. Vi har derfor bevist at δ(g,a,b)) = a + b. Til slutt får vi a(g(a,b)) = δ(g(a,b))(δ(g(a,b)) 1) g(a,b) = (a + b)(a + b 1) (a + b 1)(a + b ) b + 1 = (a + b 1)(a + b a b + ) b 1 = a + b 1 b + 1 = a 3
24 og Dette gir oss b(g(a,b)) = δ(g(a,b)) a(g(a,b)) = a + b a = b. f(g(a,b)) = (a,b). 4
Øvingsforelesning 2. Mengdelære, funksjoner, rekurrenser, osv. TMA4140 Diskret Matematikk. 10. og 12. september 2018
 Mengdelære, funksjoner, rekurrenser, osv. Øvingsforelesning 2 TMA4140 Diskret Matematikk 10. og 12. september 2018 Dagens øvingsforelesning Spørsmål til emnene i forrige uke Oppgaver fra midtsemesterprøver
Mengdelære, funksjoner, rekurrenser, osv. Øvingsforelesning 2 TMA4140 Diskret Matematikk 10. og 12. september 2018 Dagens øvingsforelesning Spørsmål til emnene i forrige uke Oppgaver fra midtsemesterprøver
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT2400 Analyse 1. Eksamensdag: Onsdag 15. juni 2011. Tid for eksamen: 09.00 13.00 Oppgavesettet er på 6 sider. Vedlegg: Tillatte
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT2400 Analyse 1. Eksamensdag: Onsdag 15. juni 2011. Tid for eksamen: 09.00 13.00 Oppgavesettet er på 6 sider. Vedlegg: Tillatte
Trigonometric Substitution
 Trigonometric Substitution Alvin Lin Calculus II: August 06 - December 06 Trigonometric Substitution sin 4 (x) cos (x) dx When you have a product of sin and cos of different powers, you have three different
Trigonometric Substitution Alvin Lin Calculus II: August 06 - December 06 Trigonometric Substitution sin 4 (x) cos (x) dx When you have a product of sin and cos of different powers, you have three different
Unit Relational Algebra 1 1. Relational Algebra 1. Unit 3.3
 Relational Algebra 1 Unit 3.3 Unit 3.3 - Relational Algebra 1 1 Relational Algebra Relational Algebra is : the formal description of how a relational database operates the mathematics which underpin SQL
Relational Algebra 1 Unit 3.3 Unit 3.3 - Relational Algebra 1 1 Relational Algebra Relational Algebra is : the formal description of how a relational database operates the mathematics which underpin SQL
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF 3230 Formell modellering og analyse av kommuniserende systemer Eksamensdag: 4. april 2008 Tid for eksamen: 9.00 12.00 Oppgavesettet
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF 3230 Formell modellering og analyse av kommuniserende systemer Eksamensdag: 4. april 2008 Tid for eksamen: 9.00 12.00 Oppgavesettet
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF 3230 Formell modellering og analyse av kommuniserende systemer Eksamensdag: 4. juni 2010 Tid for eksamen: 9.00 12.00 Oppgavesettet
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF 3230 Formell modellering og analyse av kommuniserende systemer Eksamensdag: 4. juni 2010 Tid for eksamen: 9.00 12.00 Oppgavesettet
Databases 1. Extended Relational Algebra
 Databases 1 Extended Relational Algebra Relational Algebra What is an Algebra? Mathematical system consisting of: Operands --- variables or values from which new values can be constructed. Operators ---
Databases 1 Extended Relational Algebra Relational Algebra What is an Algebra? Mathematical system consisting of: Operands --- variables or values from which new values can be constructed. Operators ---
TMA4329 Intro til vitensk. beregn. V2017
 Norges teknisk naturvitenskapelige universitet Institutt for Matematiske Fag TMA439 Intro til vitensk. beregn. V17 ving 4 [S]T. Sauer, Numerical Analysis, Second International Edition, Pearson, 14 Teorioppgaver
Norges teknisk naturvitenskapelige universitet Institutt for Matematiske Fag TMA439 Intro til vitensk. beregn. V17 ving 4 [S]T. Sauer, Numerical Analysis, Second International Edition, Pearson, 14 Teorioppgaver
1 Aksiomatisk definisjon av vanlige tallsystemer
 Notat XX for MAT1140 1 Aksiomatisk definisjon av vanlige tallsystemer 1.1 Aksiomer Vi betrakter en mengde R, utstyrt med to avbild- Algebraiske aksiomer. ninger: addisjon { R R R, (x, y) x + y. { R R R,
Notat XX for MAT1140 1 Aksiomatisk definisjon av vanlige tallsystemer 1.1 Aksiomer Vi betrakter en mengde R, utstyrt med to avbild- Algebraiske aksiomer. ninger: addisjon { R R R, (x, y) x + y. { R R R,
Slope-Intercept Formula
 LESSON 7 Slope Intercept Formula LESSON 7 Slope-Intercept Formula Here are two new words that describe lines slope and intercept. The slope is given by m (a mountain has slope and starts with m), and intercept
LESSON 7 Slope Intercept Formula LESSON 7 Slope-Intercept Formula Here are two new words that describe lines slope and intercept. The slope is given by m (a mountain has slope and starts with m), and intercept
Oppgave 1. ( xφ) φ x t, hvis t er substituerbar for x i φ.
 Oppgave 1 Beviskalklen i læreboka inneholder sluttningsregelen QR: {ψ φ}, ψ ( xφ). En betingelse for å anvende regelen er at det ikke finnes frie forekomste av x i ψ. Videre så inneholder beviskalklen
Oppgave 1 Beviskalklen i læreboka inneholder sluttningsregelen QR: {ψ φ}, ψ ( xφ). En betingelse for å anvende regelen er at det ikke finnes frie forekomste av x i ψ. Videre så inneholder beviskalklen
Dette krever ikke noe nytt aksiom. Hvorfor? Og hvorfor må vi anta at A ikke er tom? Merk at vi har:
 Notat 4 for MAT1140 4 Mer om mengder 4.1 Familier av mengder Union og snitt. Aksiom 4.1. Dersom A er en mengde bestående av mengder, kan de sistnevnte føyes sammen til en stor mengde, kalt unionen til
Notat 4 for MAT1140 4 Mer om mengder 4.1 Familier av mengder Union og snitt. Aksiom 4.1. Dersom A er en mengde bestående av mengder, kan de sistnevnte føyes sammen til en stor mengde, kalt unionen til
Hint til oppgavene. Uke 34. Uke 35. Fullstendige løsningsforslag finnes på emnesidene for 2017.
 Hint til oppgavene Fullstendige løsningsforslag finnes på emnesidene for 2017. Uke 34 Oppgave 1, 2, 3 og 4 kan alle løses ved å tegne sannhetstabeller, men i flere tilfeller kan man like gjerne manipulere
Hint til oppgavene Fullstendige løsningsforslag finnes på emnesidene for 2017. Uke 34 Oppgave 1, 2, 3 og 4 kan alle løses ved å tegne sannhetstabeller, men i flere tilfeller kan man like gjerne manipulere
Eksempel. La A = {a, b, c, d} og B = {1, 2, 3} La f være gitt ved: f(a) = 1, f(b) = 3, f(c) = 2, f(d) = 1. Dette kan illustreres slik:
 Funksjoner La A og B være to mengder. En funksjon f fra A til B betegnes med f: A -> B og er en tilordning (regel) som til ethvert element a A tilordner ett og bare ett element b B. Elementet b kalles
Funksjoner La A og B være to mengder. En funksjon f fra A til B betegnes med f: A -> B og er en tilordning (regel) som til ethvert element a A tilordner ett og bare ett element b B. Elementet b kalles
Dynamic Programming Longest Common Subsequence. Class 27
 Dynamic Programming Longest Common Subsequence Class 27 Protein a protein is a complex molecule composed of long single-strand chains of amino acid molecules there are 20 amino acids that make up proteins
Dynamic Programming Longest Common Subsequence Class 27 Protein a protein is a complex molecule composed of long single-strand chains of amino acid molecules there are 20 amino acids that make up proteins
Eksempel. La A = {a, b, c, d} og B = {1, 2, 3} La f være gitt ved: f(a) = 1, f(b) = 3, f(c) = 2, f(d) = 1. Dette kan illustreres slik:
 Funksjoner La A og B være to mengder. En funksjon f fra A til B betegnes med f: A -> B og er en tilordning (regel) som til ethvert element a A tilordner ett og bare ett element b B. Elementet b kalles
Funksjoner La A og B være to mengder. En funksjon f fra A til B betegnes med f: A -> B og er en tilordning (regel) som til ethvert element a A tilordner ett og bare ett element b B. Elementet b kalles
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS
 UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Postponed exam: ECON420 Mathematics 2: Calculus and linear algebra Date of exam: Tuesday, June 8, 203 Time for exam: 09:00 a.m. 2:00 noon The problem set covers
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Postponed exam: ECON420 Mathematics 2: Calculus and linear algebra Date of exam: Tuesday, June 8, 203 Time for exam: 09:00 a.m. 2:00 noon The problem set covers
Physical origin of the Gouy phase shift by Simin Feng, Herbert G. Winful Opt. Lett. 26, (2001)
 by Simin Feng, Herbert G. Winful Opt. Lett. 26, 485-487 (2001) http://smos.sogang.ac.r April 18, 2014 Introduction What is the Gouy phase shift? For Gaussian beam or TEM 00 mode, ( w 0 r 2 E(r, z) = E
by Simin Feng, Herbert G. Winful Opt. Lett. 26, 485-487 (2001) http://smos.sogang.ac.r April 18, 2014 Introduction What is the Gouy phase shift? For Gaussian beam or TEM 00 mode, ( w 0 r 2 E(r, z) = E
Mathematics 114Q Integration Practice Problems SOLUTIONS. = 1 8 (x2 +5x) 8 + C. [u = x 2 +5x] = 1 11 (3 x)11 + C. [u =3 x] = 2 (7x + 9)3/2
![Mathematics 114Q Integration Practice Problems SOLUTIONS. = 1 8 (x2 +5x) 8 + C. [u = x 2 +5x] = 1 11 (3 x)11 + C. [u =3 x] = 2 (7x + 9)3/2 Mathematics 114Q Integration Practice Problems SOLUTIONS. = 1 8 (x2 +5x) 8 + C. [u = x 2 +5x] = 1 11 (3 x)11 + C. [u =3 x] = 2 (7x + 9)3/2](/thumbs/77/75859899.jpg) Mathematics 4Q Name: SOLUTIONS. (x + 5)(x +5x) 7 8 (x +5x) 8 + C [u x +5x]. (3 x) (3 x) + C [u 3 x] 3. 7x +9 (7x + 9)3/ [u 7x + 9] 4. x 3 ( + x 4 ) /3 3 8 ( + x4 ) /3 + C [u + x 4 ] 5. e 5x+ 5 e5x+ + C
Mathematics 4Q Name: SOLUTIONS. (x + 5)(x +5x) 7 8 (x +5x) 8 + C [u x +5x]. (3 x) (3 x) + C [u 3 x] 3. 7x +9 (7x + 9)3/ [u 7x + 9] 4. x 3 ( + x 4 ) /3 3 8 ( + x4 ) /3 + C [u + x 4 ] 5. e 5x+ 5 e5x+ + C
Grublegruppe 19. sept. 2011: Algebra I
 Grublegruppe 19. sept. 2011: Algebra I Ivar Staurseth ivarsta@math.uio.no Innledning, definisjoner Vi har så langt jobbet med mengder, X, hvor vi har hatt et avstandsbegrep og hvor vi har vært i stand
Grublegruppe 19. sept. 2011: Algebra I Ivar Staurseth ivarsta@math.uio.no Innledning, definisjoner Vi har så langt jobbet med mengder, X, hvor vi har hatt et avstandsbegrep og hvor vi har vært i stand
Graphs similar to strongly regular graphs
 Joint work with Martin Ma aj 5th June 2014 Degree/diameter problem Denition The degree/diameter problem is the problem of nding the largest possible graph with given diameter d and given maximum degree
Joint work with Martin Ma aj 5th June 2014 Degree/diameter problem Denition The degree/diameter problem is the problem of nding the largest possible graph with given diameter d and given maximum degree
Kneser hypergraphs. May 21th, CERMICS, Optimisation et Systèmes
 Kneser hypergraphs Frédéric Meunier May 21th, 2015 CERMICS, Optimisation et Systèmes Kneser hypergraphs m, l, r three integers s.t. m rl. Kneser hypergraph KG r (m, l): V (KG r (m, l)) = ( [m]) l { E(KG
Kneser hypergraphs Frédéric Meunier May 21th, 2015 CERMICS, Optimisation et Systèmes Kneser hypergraphs m, l, r three integers s.t. m rl. Kneser hypergraph KG r (m, l): V (KG r (m, l)) = ( [m]) l { E(KG
Oppgaver MAT2500. Fredrik Meyer. 29. august 2014
 Oppgaver MAT500 Fredrik Meyer 9. august 04 Oppgave. Bruk cosinus-setningen til å se at definisjonen av vinkel i planet blir riktig. Løsning. Dette er en litt rar oppgave. Husk at cosinus-setningen sier
Oppgaver MAT500 Fredrik Meyer 9. august 04 Oppgave. Bruk cosinus-setningen til å se at definisjonen av vinkel i planet blir riktig. Løsning. Dette er en litt rar oppgave. Husk at cosinus-setningen sier
SVM and Complementary Slackness
 SVM and Complementary Slackness David Rosenberg New York University February 21, 2017 David Rosenberg (New York University) DS-GA 1003 February 21, 2017 1 / 20 SVM Review: Primal and Dual Formulations
SVM and Complementary Slackness David Rosenberg New York University February 21, 2017 David Rosenberg (New York University) DS-GA 1003 February 21, 2017 1 / 20 SVM Review: Primal and Dual Formulations
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON3120/4120 Mathematics 2: Calculus an linear algebra Exam: ECON3120/4120 Mathematics 2: Calculus an linear algebra Eksamensag: Tirsag 3. juni 2008
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON3120/4120 Mathematics 2: Calculus an linear algebra Exam: ECON3120/4120 Mathematics 2: Calculus an linear algebra Eksamensag: Tirsag 3. juni 2008
Speed Racer Theme. Theme Music: Cartoon: Charles Schultz / Jef Mallett Peanuts / Frazz. September 9, 2011 Physics 131 Prof. E. F.
 September 9, 2011 Physics 131 Prof. E. F. Redish Theme Music: Speed Racer Theme Cartoon: Charles Schultz / Jef Mallett Peanuts / Frazz 1 Reading questions Are the lines on the spatial graphs representing
September 9, 2011 Physics 131 Prof. E. F. Redish Theme Music: Speed Racer Theme Cartoon: Charles Schultz / Jef Mallett Peanuts / Frazz 1 Reading questions Are the lines on the spatial graphs representing
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF 3230/4230 Formell modellering og analyse av kommuniserende systemer Eksamensdag: 24. mars 2006 Tid for eksamen: 13.30 16.30
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF 3230/4230 Formell modellering og analyse av kommuniserende systemer Eksamensdag: 24. mars 2006 Tid for eksamen: 13.30 16.30
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON30/40 Matematikk : Matematisk analyse og lineær algebra Exam: ECON30/40 Mathematics : Calculus and Linear Algebra Eksamensdag: Tirsdag 0. desember
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON30/40 Matematikk : Matematisk analyse og lineær algebra Exam: ECON30/40 Mathematics : Calculus and Linear Algebra Eksamensdag: Tirsdag 0. desember
Universitetet i Bergen Det matematisk-naturvitenskapelige fakultet Eksamen i emnet Mat131 - Differensiallikningar I Onsdag 25. mai 2016, kl.
 1 MAT131 Bokmål Universitetet i Bergen Det matematisk-naturvitenskapelige fakultet Eksamen i emnet Mat131 - Differensiallikningar I Onsdag 25. mai 2016, kl. 09-14 Oppgavesettet er 4 oppgaver fordelt på
1 MAT131 Bokmål Universitetet i Bergen Det matematisk-naturvitenskapelige fakultet Eksamen i emnet Mat131 - Differensiallikningar I Onsdag 25. mai 2016, kl. 09-14 Oppgavesettet er 4 oppgaver fordelt på
Maple Basics. K. Cooper
 Basics K. Cooper 2012 History History 1982 Macsyma/MIT 1988 Mathematica/Wolfram 1988 /Waterloo Others later History Why? Prevent silly mistakes Time Complexity Plots Generate LATEX This is the 21st century;
Basics K. Cooper 2012 History History 1982 Macsyma/MIT 1988 Mathematica/Wolfram 1988 /Waterloo Others later History Why? Prevent silly mistakes Time Complexity Plots Generate LATEX This is the 21st century;
Oppgaver med et odde nummer har fasit bakerst i læreboken. Her er løsningsforslag med mellomregninger for de gitte øvingsoppgavene.
 Diskret matematikk - Høgskolen i Oslo Løsningsforslag for en del oppgaver fra boken Discrete Mathematics and Its Applications Forfatter: Kenneth H. Rosen Oppgaver med et odde nummer har fasit bakerst i
Diskret matematikk - Høgskolen i Oslo Løsningsforslag for en del oppgaver fra boken Discrete Mathematics and Its Applications Forfatter: Kenneth H. Rosen Oppgaver med et odde nummer har fasit bakerst i
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Utsatt ksamen i: ECON3120/4120 Matematikk 2: Matematisk analyse og lineær algebra Postponed exam: ECON3120/4120 Mathematics 2: Calculus and linear algebra Eksamensdag:
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Utsatt ksamen i: ECON3120/4120 Matematikk 2: Matematisk analyse og lineær algebra Postponed exam: ECON3120/4120 Mathematics 2: Calculus and linear algebra Eksamensdag:
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Exam: ECON320/420 Mathematics 2: Calculus and Linear Algebra Eksamen i: ECON320/420 Matematikk 2: Matematisk analyse og lineær algebra Date of exam: Friday, May
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Exam: ECON320/420 Mathematics 2: Calculus and Linear Algebra Eksamen i: ECON320/420 Matematikk 2: Matematisk analyse og lineær algebra Date of exam: Friday, May
STILLAS - STANDARD FORSLAG FRA SEF TIL NY STILLAS - STANDARD
 FORSLAG FRA SEF TIL NY STILLAS - STANDARD 1 Bakgrunnen for dette initiativet fra SEF, er ønsket om å gjøre arbeid i høyden tryggere / sikrere. Både for stillasmontører og brukere av stillaser. 2 Reviderte
FORSLAG FRA SEF TIL NY STILLAS - STANDARD 1 Bakgrunnen for dette initiativet fra SEF, er ønsket om å gjøre arbeid i høyden tryggere / sikrere. Både for stillasmontører og brukere av stillaser. 2 Reviderte
Repetisjonsforelesning - INF1080
 Repetisjonsforelesning - INF1080 Mengder, relasjoner og funksjoner 18. november 2015 1 Grunnleggende mengdelære 1.1 Elementært om mengder 1.1.1 Hva er en mengde? Definisjon 1.1 (Mengde). En mengde er en
Repetisjonsforelesning - INF1080 Mengder, relasjoner og funksjoner 18. november 2015 1 Grunnleggende mengdelære 1.1 Elementært om mengder 1.1.1 Hva er en mengde? Definisjon 1.1 (Mengde). En mengde er en
Notat med oppgaver for MAT1140
 Notat med oppgaver for MAT1140 1 Injeksjon, surjeksjon Oppgave 1.1. La f : A B være en avbildning. Vis at da er f injektiv hvis og bare hvis følgende holder: for hver mengde C og for hver g, h : C A hvis
Notat med oppgaver for MAT1140 1 Injeksjon, surjeksjon Oppgave 1.1. La f : A B være en avbildning. Vis at da er f injektiv hvis og bare hvis følgende holder: for hver mengde C og for hver g, h : C A hvis
Oppgave 1a Definer følgende begreper: Nøkkel, supernøkkel og funksjonell avhengighet.
 TDT445 Øving 4 Oppgave a Definer følgende begreper: Nøkkel, supernøkkel og funksjonell avhengighet. Nøkkel: Supernøkkel: Funksjonell avhengighet: Data i en database som kan unikt identifisere (et sett
TDT445 Øving 4 Oppgave a Definer følgende begreper: Nøkkel, supernøkkel og funksjonell avhengighet. Nøkkel: Supernøkkel: Funksjonell avhengighet: Data i en database som kan unikt identifisere (et sett
Øving 5 - Fouriertransform - LF
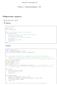 Øving 5 - Fouriertransform - LF Obligatoriske oppgaver See the notes Matlab: %x og t aksen x=:.:pi; t=:pi/:*pi; %sette opp funksjon og plotte hver frame for j=:length(t) %funksjonsverdier p innev rende
Øving 5 - Fouriertransform - LF Obligatoriske oppgaver See the notes Matlab: %x og t aksen x=:.:pi; t=:pi/:*pi; %sette opp funksjon og plotte hver frame for j=:length(t) %funksjonsverdier p innev rende
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON320/420 Matematikk 2: Matematisk analyse og lineær algebra Exam: ECON320/420 Mathematics 2: Calculus and Linear Algebra Eksamensdag: Mandag 8. desember
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON320/420 Matematikk 2: Matematisk analyse og lineær algebra Exam: ECON320/420 Mathematics 2: Calculus and Linear Algebra Eksamensdag: Mandag 8. desember
MAT1030 Forelesning 14
 MAT1030 Forelesning 14 Mer om funksjoner Roger Antonsen - 10. mars 2009 (Sist oppdatert: 2009-03-10 11:34) Kapittel 6: Funksjoner Surjektive funksjoner Den neste gruppen av funksjoner vi skal se på er
MAT1030 Forelesning 14 Mer om funksjoner Roger Antonsen - 10. mars 2009 (Sist oppdatert: 2009-03-10 11:34) Kapittel 6: Funksjoner Surjektive funksjoner Den neste gruppen av funksjoner vi skal se på er
Oppgave: Avgjør om følgende to mengder er like: 1) (A B) C 2) A (B C)
 Mengder, fortsettelse. Tre mengder Venndiagram for tre mengder A, B og C må tegnes slik at alle muligheter blir dekket. For å få dette til må de overlappe hverandre: Oppgave: Avgjør om følgende to mengder
Mengder, fortsettelse. Tre mengder Venndiagram for tre mengder A, B og C må tegnes slik at alle muligheter blir dekket. For å få dette til må de overlappe hverandre: Oppgave: Avgjør om følgende to mengder
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON3120/4120 Matematikk 2: Matematisk analyse og lineær algebra Exam: ECON3120/4120 Mathematics 2: Calculus and Linear Algebra Eksamensdag: Tirsdag
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON3120/4120 Matematikk 2: Matematisk analyse og lineær algebra Exam: ECON3120/4120 Mathematics 2: Calculus and Linear Algebra Eksamensdag: Tirsdag
Neural Network. Sensors Sorter
 CSC 302 1.5 Neural Networks Simple Neural Nets for Pattern Recognition 1 Apple-Banana Sorter Neural Network Sensors Sorter Apples Bananas 2 Prototype Vectors Measurement vector p = [shape, texture, weight]
CSC 302 1.5 Neural Networks Simple Neural Nets for Pattern Recognition 1 Apple-Banana Sorter Neural Network Sensors Sorter Apples Bananas 2 Prototype Vectors Measurement vector p = [shape, texture, weight]
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON320/420 Matematikk 2: Matematisk analyse og lineær algebra Exam: ECON320/420 Mathematics 2: Calculus and Linear Algebra Eksamensdag: Onsdag 6. desember
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON320/420 Matematikk 2: Matematisk analyse og lineær algebra Exam: ECON320/420 Mathematics 2: Calculus and Linear Algebra Eksamensdag: Onsdag 6. desember
Løsningsforslag oblig. innlevering 1
 Løsningsforslag oblig. innlevering 1 IN1150 Logiske metoder Høsten 2017 Oppgave 1 - Mengdelære (10 poeng) a) Ut fra opplysningene under, angi hvilke mengder A og B er. A B = {1, 2, 3, 4, 5, 6} A B = {2,
Løsningsforslag oblig. innlevering 1 IN1150 Logiske metoder Høsten 2017 Oppgave 1 - Mengdelære (10 poeng) a) Ut fra opplysningene under, angi hvilke mengder A og B er. A B = {1, 2, 3, 4, 5, 6} A B = {2,
UNIVERSITETET I OSLO. Det matematisk-naturvitenskapelige fakultet
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF1080 Logiske metoder for informatikk Eksamensdag: 10. desember 2013 Tid for eksamen: 09.00 13.00 Oppgave 1 Mengdelære (10 poeng)
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF1080 Logiske metoder for informatikk Eksamensdag: 10. desember 2013 Tid for eksamen: 09.00 13.00 Oppgave 1 Mengdelære (10 poeng)
Kapittel 6: Funksjoner
 MAT1030 Diskret Matematikk Forelesning 14: Mer om funksjoner Roger Antonsen Institutt for informatikk, Universitetet i Oslo Kapittel 6: Funksjoner 10. mars 2009 (Sist oppdatert: 2009-03-10 11:34) MAT1030
MAT1030 Diskret Matematikk Forelesning 14: Mer om funksjoner Roger Antonsen Institutt for informatikk, Universitetet i Oslo Kapittel 6: Funksjoner 10. mars 2009 (Sist oppdatert: 2009-03-10 11:34) MAT1030
Løsningsførslag i Matematikk 4D, 4N, 4M
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 6 Løsningsførslag i Matematikk 4D, 4N, 4M Oppgave (Kun før 4D Vi har f(x, y x + y x y, for x y. Dette gir For (x, y
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 6 Løsningsførslag i Matematikk 4D, 4N, 4M Oppgave (Kun før 4D Vi har f(x, y x + y x y, for x y. Dette gir For (x, y
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON20/420 Matematikk 2: Matematisk analyse og lineær algebra Exam: ECON20/420 Mathematics 2: Calculus and Linear Algebra Eksamensdag: Fredag 2. mai
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON20/420 Matematikk 2: Matematisk analyse og lineær algebra Exam: ECON20/420 Mathematics 2: Calculus and Linear Algebra Eksamensdag: Fredag 2. mai
Notat om Peanos aksiomer for MAT1140
 Notat om Peanos aksiomer for MAT1140 1 Tall Hva er egentlig tall? Tanken her, er ikke å si hva tall er, hva deres interne struktur muligens kan være, men å si hva vi kan gjøre med dem, sett utenifra. Vi
Notat om Peanos aksiomer for MAT1140 1 Tall Hva er egentlig tall? Tanken her, er ikke å si hva tall er, hva deres interne struktur muligens kan være, men å si hva vi kan gjøre med dem, sett utenifra. Vi
TMA 4140 Diskret Matematikk, 4. forelesning
 TMA 4140 Diskret Matematikk, 4. forelesning Haaken Annfelt Moe Department of Mathematical Sciences Norwegian University of Science and Technology (NTNU) September 9, 2011 Haaken Annfelt Moe (NTNU) TMA
TMA 4140 Diskret Matematikk, 4. forelesning Haaken Annfelt Moe Department of Mathematical Sciences Norwegian University of Science and Technology (NTNU) September 9, 2011 Haaken Annfelt Moe (NTNU) TMA
Løsningsforslag øving 7
 Løsningsforslag øving 7 8 Husk at en funksjon er injektiv dersom x y gir f(x) f(y), men her ser vi at f(3) 9 f( 3), eller generelt at f(z) z f( z) for alle z C, som betyr at f ikke er injektiv Vi ser også
Løsningsforslag øving 7 8 Husk at en funksjon er injektiv dersom x y gir f(x) f(y), men her ser vi at f(3) 9 f( 3), eller generelt at f(z) z f( z) for alle z C, som betyr at f ikke er injektiv Vi ser også
Obligatorisk oppgave 1 i MAT1140, Høst Løsninger med kommentarer
 Obligatorisk oppgave 1 i MAT1140, Høst 2014. Oppgave 1 er med kommentarer En funksjon f : R R er en polynomfunksjon hvis f kan defineres som f(x) = a 0 + a 1 x + + a n x n hvor n 0 og a 0,..., a n er reelle
Obligatorisk oppgave 1 i MAT1140, Høst 2014. Oppgave 1 er med kommentarer En funksjon f : R R er en polynomfunksjon hvis f kan defineres som f(x) = a 0 + a 1 x + + a n x n hvor n 0 og a 0,..., a n er reelle
Verifiable Secret-Sharing Schemes
 Aarhus University Verifiable Secret-Sharing Schemes Irene Giacomelli joint work with Ivan Damgård, Bernardo David and Jesper B. Nielsen Aalborg, 30th June 2014 Verifiable Secret-Sharing Schemes Aalborg,
Aarhus University Verifiable Secret-Sharing Schemes Irene Giacomelli joint work with Ivan Damgård, Bernardo David and Jesper B. Nielsen Aalborg, 30th June 2014 Verifiable Secret-Sharing Schemes Aalborg,
FYS2140 Kvantefysikk. Løsningsforslag for Oblig 7
 FYS2140 Kvantefysikk Løsningsforslag for Oblig 7 Oppgave 2.23 Regn ut følgende intgral a) +1 3 (x 3 3x 2 + 2x 1)δ(x + 2) dx (1) Svar: For å løse dette integralet bruker vi Dirac deltafunksjonen (se seksjon
FYS2140 Kvantefysikk Løsningsforslag for Oblig 7 Oppgave 2.23 Regn ut følgende intgral a) +1 3 (x 3 3x 2 + 2x 1)δ(x + 2) dx (1) Svar: For å løse dette integralet bruker vi Dirac deltafunksjonen (se seksjon
Notat 05 for MAT Relasjoner, operasjoner, ringer. 5.1 Relasjoner
 Notat 05 for MAT1140 5 Relasjoner, operasjoner, ringer 5.1 Relasjoner Når R er en relasjon som er veldefinert på A B, slik at R(x, y) er en påstand når x A og B B, tenker vi på relasjonen som noe som lever
Notat 05 for MAT1140 5 Relasjoner, operasjoner, ringer 5.1 Relasjoner Når R er en relasjon som er veldefinert på A B, slik at R(x, y) er en påstand når x A og B B, tenker vi på relasjonen som noe som lever
Sammensetningen h = f g er en funksjon fra A til C, h: A -> C og er definert ved h(a) = f(g(a)) Viktig: f g g f
 Sammensetningen av to funksjoner. Gitt mengdene A, B og C. La f og g være funksjonene der g: A -> B f: B -> C Da kan vi lage sammensetningen h av f og g. Den betegnes som h = f g (lese som «f ring g»).
Sammensetningen av to funksjoner. Gitt mengdene A, B og C. La f og g være funksjonene der g: A -> B f: B -> C Da kan vi lage sammensetningen h av f og g. Den betegnes som h = f g (lese som «f ring g»).
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON320/420 Matematikk 2: Matematisk analyse og lineær algebra Exam: ECON320/420 Mathematics 2: Calculus and Linear Algebra Eksamensdag: Tirsdag 7. juni
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON320/420 Matematikk 2: Matematisk analyse og lineær algebra Exam: ECON320/420 Mathematics 2: Calculus and Linear Algebra Eksamensdag: Tirsdag 7. juni
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON360/460 Samfunnsøkonomisk lønnsomhet og økonomisk politikk Exam: ECON360/460 - Resource allocation and economic policy Eksamensdag: Fredag 2. november
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON360/460 Samfunnsøkonomisk lønnsomhet og økonomisk politikk Exam: ECON360/460 - Resource allocation and economic policy Eksamensdag: Fredag 2. november
12 Lineære transformasjoner
 2 Lineære transformasjoner 2 Funksjoner Definisjon 2 En funksjon ( a function) f : A B er en regel, som tilordner en entydig bestemt verdi f (a) B til ethvert element a A Mengden A kalles domenet til f
2 Lineære transformasjoner 2 Funksjoner Definisjon 2 En funksjon ( a function) f : A B er en regel, som tilordner en entydig bestemt verdi f (a) B til ethvert element a A Mengden A kalles domenet til f
Analysedrypp I: Bevis, mengder og funksjoner
 Analysedrypp I: Bevis, mengder og funksjoner Hensikten med Analysedrypp er å bygge en bro mellom MAT1100 og MAT1110 på den ene siden og MAT2400 på den andre. Egentlig burde det være unødvendig med en slik
Analysedrypp I: Bevis, mengder og funksjoner Hensikten med Analysedrypp er å bygge en bro mellom MAT1100 og MAT1110 på den ene siden og MAT2400 på den andre. Egentlig burde det være unødvendig med en slik
IN2010: Algoritmer og Datastrukturer Series 2
 Universitetet i Oslo Institutt for Informatikk S.M. Storleer, S. Kittilsen IN2010: Algoritmer og Datastrukturer Series 2 Tema: Grafteori 1 Publisert: 02. 09. 2019 Utvalgte løsningsforslag Oppgave 1 (Fra
Universitetet i Oslo Institutt for Informatikk S.M. Storleer, S. Kittilsen IN2010: Algoritmer og Datastrukturer Series 2 Tema: Grafteori 1 Publisert: 02. 09. 2019 Utvalgte løsningsforslag Oppgave 1 (Fra
MA2501 Numerical methods
 MA250 Numerical methods Solutions to problem set Problem a) The function f (x) = x 3 3x + satisfies the following relations f (0) = > 0, f () = < 0 and there must consequently be at least one zero for
MA250 Numerical methods Solutions to problem set Problem a) The function f (x) = x 3 3x + satisfies the following relations f (0) = > 0, f () = < 0 and there must consequently be at least one zero for
5 E Lesson: Solving Monohybrid Punnett Squares with Coding
 5 E Lesson: Solving Monohybrid Punnett Squares with Coding Genetics Fill in the Brown colour Blank Options Hair texture A field of biology that studies heredity, or the passing of traits from parents to
5 E Lesson: Solving Monohybrid Punnett Squares with Coding Genetics Fill in the Brown colour Blank Options Hair texture A field of biology that studies heredity, or the passing of traits from parents to
Noen løsningsforslag/fasitsvar
 Kapittel 8 Noen løsningsforslag/fasitsvar Etter ønske fra kursdeltagerne suppleres heftet med fasit for noen av oppgavene. Der det er aktuelt, gir vi også mer utfyllende forslag til hvordan oppgaven kan
Kapittel 8 Noen løsningsforslag/fasitsvar Etter ønske fra kursdeltagerne suppleres heftet med fasit for noen av oppgavene. Der det er aktuelt, gir vi også mer utfyllende forslag til hvordan oppgaven kan
Gradient. Masahiro Yamamoto. last update on February 29, 2012 (1) (2) (3) (4) (5)
 Gradient Masahiro Yamamoto last update on February 9, 0 definition of grad The gradient of the scalar function φr) is defined by gradφ = φr) = i φ x + j φ y + k φ ) φ= φ=0 ) ) 3) 4) 5) uphill contour downhill
Gradient Masahiro Yamamoto last update on February 9, 0 definition of grad The gradient of the scalar function φr) is defined by gradφ = φr) = i φ x + j φ y + k φ ) φ= φ=0 ) ) 3) 4) 5) uphill contour downhill
Ole Isak Eira Masters student Arctic agriculture and environmental management. University of Tromsø Sami University College
 The behavior of the reindeer herd - the role of the males Ole Isak Eira Masters student Arctic agriculture and environmental management University of Tromsø Sami University College Masters student at Department
The behavior of the reindeer herd - the role of the males Ole Isak Eira Masters student Arctic agriculture and environmental management University of Tromsø Sami University College Masters student at Department
Moving Objects. We need to move our objects in 3D space.
 Transformations Moving Objects We need to move our objects in 3D space. Moving Objects We need to move our objects in 3D space. An object/model (box, car, building, character,... ) is defined in one position
Transformations Moving Objects We need to move our objects in 3D space. Moving Objects We need to move our objects in 3D space. An object/model (box, car, building, character,... ) is defined in one position
TMA4100 Matematikk 1, høst 2013
 TMA4100 Matematikk 1, høst 2013 Teknostart Forelesning 3 www.ntnu.no TMA4100 Matematikk 1, høst 2013, Teknostart Forelesning 3 Tema Logikk Definisjoner og Teoremer Mengder og Egenskaper ved de Reelle Tall
TMA4100 Matematikk 1, høst 2013 Teknostart Forelesning 3 www.ntnu.no TMA4100 Matematikk 1, høst 2013, Teknostart Forelesning 3 Tema Logikk Definisjoner og Teoremer Mengder og Egenskaper ved de Reelle Tall
ECON3120/4120 Mathematics 2, spring 2004 Problem solutions for the seminar on 5 May Old exam problems
 Department of Economics May 004 Arne Strøm ECON0/40 Mathematics, spring 004 Problem solutions for the seminar on 5 May 004 (For practical reasons (read laziness, most of the solutions this time are in
Department of Economics May 004 Arne Strøm ECON0/40 Mathematics, spring 004 Problem solutions for the seminar on 5 May 004 (For practical reasons (read laziness, most of the solutions this time are in
Vi skal se på lambda-uttrykk. Følgende er definerte og vil bli brukt gjennom oppgaven
 SLI 230 - side 2 av 8 EKSAMENSOPPGAVE - SLI 230 - VÅR 2000 Nedenfor følger eksamensoppgaver i SLI 230. Først om oppgavene Bakerst følger to sider med hjelp slik det er avtalt - liste over primitiver fra
SLI 230 - side 2 av 8 EKSAMENSOPPGAVE - SLI 230 - VÅR 2000 Nedenfor følger eksamensoppgaver i SLI 230. Først om oppgavene Bakerst følger to sider med hjelp slik det er avtalt - liste over primitiver fra
TMA4240 Statistikk Høst 2013
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 6, blokk I Løsningsskisse Oppgave 1 Vi antar X er normalfordelt, X N(3315, 575 2 ). Ved bruk av tabell A.3 finner
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 6, blokk I Løsningsskisse Oppgave 1 Vi antar X er normalfordelt, X N(3315, 575 2 ). Ved bruk av tabell A.3 finner
MAT1030 Diskret Matematikk
 MAT1030 Diskret Matematikk Plenumsregning 10: Ukeoppgaver Mathias Barra Matematisk institutt, Universitetet i Oslo 20. mars 2009 (Sist oppdatert: 2009-03-30 09:38) Oppgave 6.1 Avgjør hvorvidt følgende
MAT1030 Diskret Matematikk Plenumsregning 10: Ukeoppgaver Mathias Barra Matematisk institutt, Universitetet i Oslo 20. mars 2009 (Sist oppdatert: 2009-03-30 09:38) Oppgave 6.1 Avgjør hvorvidt følgende
MAT1030 Forelesning 13
 MAT1030 Forelesning 13 Funksjoner Dag Normann - 2. mars 2010 (Sist oppdatert: 2010-03-02 14:15) Kapittel 6: Funksjoner Forrige uke Forrige forelesning snakket vi om relasjoner. Vi snakket om ekvivalensrelasjoner
MAT1030 Forelesning 13 Funksjoner Dag Normann - 2. mars 2010 (Sist oppdatert: 2010-03-02 14:15) Kapittel 6: Funksjoner Forrige uke Forrige forelesning snakket vi om relasjoner. Vi snakket om ekvivalensrelasjoner
MAT1140 Strukturer og argumenter
 12. november 2018 MAT1140 Strukturer og argumenter Innleveringsfrist Obligatorisk oppgave 2 av 2 Torsdag 8. november 2018, klokken 14:30 i Devilry (devilry.ifi.uio.no). Instruksjoner Du velger selv om
12. november 2018 MAT1140 Strukturer og argumenter Innleveringsfrist Obligatorisk oppgave 2 av 2 Torsdag 8. november 2018, klokken 14:30 i Devilry (devilry.ifi.uio.no). Instruksjoner Du velger selv om
OPPGAVER FOR FORUM
 OPPGAVER FOR FORUM 2006-2007 MERK!: Du skal først skrive hele oppgaveteksten for hver oppgave, og deretter svaret på oppgaven. Hvert svar skal være detajert, og skrevet i et klart og tydelig matematisk
OPPGAVER FOR FORUM 2006-2007 MERK!: Du skal først skrive hele oppgaveteksten for hver oppgave, og deretter svaret på oppgaven. Hvert svar skal være detajert, og skrevet i et klart og tydelig matematisk
Kapittel 6: Funksjoner
 MAT1030 Diskret Matematikk Forelesning 13: Funksjoner Dag Normann Matematisk Institutt, Universitetet i Oslo Kapittel 6: Funksjoner 2. mars 2010 (Sist oppdatert: 2010-03-02 14:14) MAT1030 Diskret Matematikk
MAT1030 Diskret Matematikk Forelesning 13: Funksjoner Dag Normann Matematisk Institutt, Universitetet i Oslo Kapittel 6: Funksjoner 2. mars 2010 (Sist oppdatert: 2010-03-02 14:14) MAT1030 Diskret Matematikk
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF1080 Logiske metoder for informatikk Eksamensdag: 26. november 2010 Tid for eksamen: 13:00 17:00 Oppgave 1 La A = { }. Mengdelære
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF1080 Logiske metoder for informatikk Eksamensdag: 26. november 2010 Tid for eksamen: 13:00 17:00 Oppgave 1 La A = { }. Mengdelære
TDT4110 IT Grunnkurs Høst 2015
 TDT4110 IT Grunnkurs Høst 2015 Norges teknisk naturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap Løsningsforlag Auditorieøving 1 1 Teori Løsning er skrevet med uthevet tekst
TDT4110 IT Grunnkurs Høst 2015 Norges teknisk naturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap Løsningsforlag Auditorieøving 1 1 Teori Løsning er skrevet med uthevet tekst
TFY4170 Fysikk 2 Justin Wells
 TFY4170 Fysikk 2 Justin Wells Forelesning 5: Wave Physics Interference, Diffraction, Young s double slit, many slits. Mansfield & O Sullivan: 12.6, 12.7, 19.4,19.5 Waves! Wave phenomena! Wave equation
TFY4170 Fysikk 2 Justin Wells Forelesning 5: Wave Physics Interference, Diffraction, Young s double slit, many slits. Mansfield & O Sullivan: 12.6, 12.7, 19.4,19.5 Waves! Wave phenomena! Wave equation
Hvor mye teoretisk kunnskap har du tilegnet deg på dette emnet? (1 = ingen, 5 = mye)
 Emneevaluering GEOV325 Vår 2016 Kommentarer til GEOV325 VÅR 2016 (emneansvarlig) Forelesingsrommet inneholdt ikke gode nok muligheter for å kunne skrive på tavle og samtidig ha mulighet for bruk av power
Emneevaluering GEOV325 Vår 2016 Kommentarer til GEOV325 VÅR 2016 (emneansvarlig) Forelesingsrommet inneholdt ikke gode nok muligheter for å kunne skrive på tavle og samtidig ha mulighet for bruk av power
MAT1030 Plenumsregning 10
 MAT1030 Plenumsregning 10 Ukeoppgaver Mathias Barra - 20. mars 2009 (Sist oppdatert: 2009-03-30 09:38) Oppgave 6.1 Avgjør hvorvidt følgende funksjoner er veldefinerte. For de som er veldefinerte, gi definisjonsområdet,
MAT1030 Plenumsregning 10 Ukeoppgaver Mathias Barra - 20. mars 2009 (Sist oppdatert: 2009-03-30 09:38) Oppgave 6.1 Avgjør hvorvidt følgende funksjoner er veldefinerte. For de som er veldefinerte, gi definisjonsområdet,
TMA4240 Statistikk 2014
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 6, blokk I Løsningsskisse Oppgave 1 Fremgangsmetode: P X 1 < 6.8 Denne kan finnes ved å sette opp integralet over
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 6, blokk I Løsningsskisse Oppgave 1 Fremgangsmetode: P X 1 < 6.8 Denne kan finnes ved å sette opp integralet over
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF1080 Logiske metoder for informatikk Eksamensdag: 27. desember 2015 Tid for eksamen: 08.15 12:15 Oppgave 1 Grunnleggende mengdelære
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF1080 Logiske metoder for informatikk Eksamensdag: 27. desember 2015 Tid for eksamen: 08.15 12:15 Oppgave 1 Grunnleggende mengdelære
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSIEE I OSLO ØKONOMISK INSIU Eksamen i: ECON320/420 Mathematics 2: Calculus and Linear Algebra Exam: ECON320/420 Mathematics 2: Calculus and Linear Algebra Eksamensdag:. desember 207 Sensur kunngjøres:
UNIVERSIEE I OSLO ØKONOMISK INSIU Eksamen i: ECON320/420 Mathematics 2: Calculus and Linear Algebra Exam: ECON320/420 Mathematics 2: Calculus and Linear Algebra Eksamensdag:. desember 207 Sensur kunngjøres:
Eksamensoppgave i MA0301 Elementær diskret matematikk løsningsforslag
 Institutt for matematiske fag Eksamensoppgave i MA0301 Elementær diskret matematikk løsningsforslag Faglig kontakt under eksamen: Martin Strand Tlf: 970 27 848 Eksamensdato:. august 2014 Eksamenstid (fra
Institutt for matematiske fag Eksamensoppgave i MA0301 Elementær diskret matematikk løsningsforslag Faglig kontakt under eksamen: Martin Strand Tlf: 970 27 848 Eksamensdato:. august 2014 Eksamenstid (fra
INF2810: Funksjonell Programmering. Mer om strømmer
 INF2810: Funksjonell Programmering Mer om strømmer Stephan Oepen & Erik Velldal Universitetet i Oslo 19. april 2013 Tema 2 Forrige uke Repetisjon: parallelitet Noe helt nytt: strømmer Noe quizzaktivitet
INF2810: Funksjonell Programmering Mer om strømmer Stephan Oepen & Erik Velldal Universitetet i Oslo 19. april 2013 Tema 2 Forrige uke Repetisjon: parallelitet Noe helt nytt: strømmer Noe quizzaktivitet
Oppgåvesettet er på 3 sider med oppgåvene Engelsk omsetjing på sidene 4-6.
 UNIVERSITETET I BERGEN Det matematisk-naturvitskaplege fakultet Eksamen i emnet MNF130 Diskrete strukturar Fredag 21. mai 2010, kl. 09-12, altså 3 timar. NYNORSK Ingen tillatne hjelpemiddel. Oppgåvesettet
UNIVERSITETET I BERGEN Det matematisk-naturvitskaplege fakultet Eksamen i emnet MNF130 Diskrete strukturar Fredag 21. mai 2010, kl. 09-12, altså 3 timar. NYNORSK Ingen tillatne hjelpemiddel. Oppgåvesettet
MAT1030 Diskret matematikk
 MAT1030 Diskret matematikk Plenumsregning 2: Ukeoppgaver fra kapittel 1 & 2 Roger Antonsen Matematisk Institutt, Universitetet i Oslo 24. januar 2008 Oppgave 1.1 Modifiser algoritmen fra 1.2.1 slik at
MAT1030 Diskret matematikk Plenumsregning 2: Ukeoppgaver fra kapittel 1 & 2 Roger Antonsen Matematisk Institutt, Universitetet i Oslo 24. januar 2008 Oppgave 1.1 Modifiser algoritmen fra 1.2.1 slik at
Hvordan føre reiseregninger i Unit4 Business World Forfatter:
 Hvordan føre reiseregninger i Unit4 Business World Forfatter: dag.syversen@unit4.com Denne e-guiden beskriver hvordan du registrerer en reiseregning med ulike typer utlegg. 1. Introduksjon 2. Åpne vinduet
Hvordan føre reiseregninger i Unit4 Business World Forfatter: dag.syversen@unit4.com Denne e-guiden beskriver hvordan du registrerer en reiseregning med ulike typer utlegg. 1. Introduksjon 2. Åpne vinduet
Endelig ikke-røyker for Kvinner! (Norwegian Edition)
 Endelig ikke-røyker for Kvinner! (Norwegian Edition) Allen Carr Click here if your download doesn"t start automatically Endelig ikke-røyker for Kvinner! (Norwegian Edition) Allen Carr Endelig ikke-røyker
Endelig ikke-røyker for Kvinner! (Norwegian Edition) Allen Carr Click here if your download doesn"t start automatically Endelig ikke-røyker for Kvinner! (Norwegian Edition) Allen Carr Endelig ikke-røyker
UNIVERSITETET I OSLO. Det matematisk-naturvitenskapelige fakultet
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF1080 Logiske metoder for informatikk Eksamensdag: 10. desember 2012 Tid for eksamen: 09.00 13.00 Innledning La U være mengden
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF1080 Logiske metoder for informatikk Eksamensdag: 10. desember 2012 Tid for eksamen: 09.00 13.00 Innledning La U være mengden
Ingen hjelpemiddel er tillatne. Ta med all mellomrekning som trengst for å grunngje svaret. Oppgåve 1... (4%) = = 10 =
 Eksamen. desember 205 Eksamenstid 4 timar IR2072 Diskret Matematikk Ingen hjelpemiddel er tillatne. Ta med all mellomrekning som trengst for å grunngje svaret. Oppgåve.......................................................................................
Eksamen. desember 205 Eksamenstid 4 timar IR2072 Diskret Matematikk Ingen hjelpemiddel er tillatne. Ta med all mellomrekning som trengst for å grunngje svaret. Oppgåve.......................................................................................
INF2810: Funksjonell Programmering. Mer om strømmer
 INF2810: Funksjonell Programmering Mer om strømmer Stephan Oepen & Erik Velldal Universitetet i Oslo 19. april 2013 Tema 2 Forrige uke Repetisjon: parallelitet Noe helt nytt: strømmer Noe quizzaktivitet
INF2810: Funksjonell Programmering Mer om strømmer Stephan Oepen & Erik Velldal Universitetet i Oslo 19. april 2013 Tema 2 Forrige uke Repetisjon: parallelitet Noe helt nytt: strømmer Noe quizzaktivitet
Ma Linær Algebra og Geometri Øving 5
 Ma20 - Linær Algebra og Geometri Øving 5 Øistein søvik 7. oktober 20 Excercise Set.5.5 7, 29,.6 5,, 6, 2.7, A = 0 5 B = 0 5 4 7 9 0-5 25-4 C = 0 5 D = 0 0 28 4 7 9 0-5 25 F = 6 2-2 0-5 25 7. Find an elementary
Ma20 - Linær Algebra og Geometri Øving 5 Øistein søvik 7. oktober 20 Excercise Set.5.5 7, 29,.6 5,, 6, 2.7, A = 0 5 B = 0 5 4 7 9 0-5 25-4 C = 0 5 D = 0 0 28 4 7 9 0-5 25 F = 6 2-2 0-5 25 7. Find an elementary
To mengder S og T er like, S = T, hvis de inneholder de samme elementene. Notasjon. Mengden med elementene a, b, c og d skrives ofte {a, b, c, d}.
 Forelesning 0: Mengdelære, Induksjon Martin Giese - 23. januar 2008 1 Mengdelære 1.1 Mengder Mengder Definisjon 1.1. En mengde er en endelig eller uendelig samling objekter der innbyrdes rekkefølge og
Forelesning 0: Mengdelære, Induksjon Martin Giese - 23. januar 2008 1 Mengdelære 1.1 Mengder Mengder Definisjon 1.1. En mengde er en endelig eller uendelig samling objekter der innbyrdes rekkefølge og
Dagens plan. INF3170 Logikk. Mengder. Definisjon. Notasjon. Forelesning 0: Mengdelære, Induksjon. Martin Giese. 23. januar 2008.
 INF3170 Logikk Dagens plan Forelesning 0:, Induksjon Martin Giese 1 Institutt for informatikk, Universitetet i Oslo 2 23. januar 2008 Institutt for informatikk (UiO) INF3170 Logikk 23.01.2008 2 / 47 1
INF3170 Logikk Dagens plan Forelesning 0:, Induksjon Martin Giese 1 Institutt for informatikk, Universitetet i Oslo 2 23. januar 2008 Institutt for informatikk (UiO) INF3170 Logikk 23.01.2008 2 / 47 1
Han Ola of Han Per: A Norwegian-American Comic Strip/En Norsk-amerikansk tegneserie (Skrifter. Serie B, LXIX)
 Han Ola of Han Per: A Norwegian-American Comic Strip/En Norsk-amerikansk tegneserie (Skrifter. Serie B, LXIX) Peter J. Rosendahl Click here if your download doesn"t start automatically Han Ola of Han Per:
Han Ola of Han Per: A Norwegian-American Comic Strip/En Norsk-amerikansk tegneserie (Skrifter. Serie B, LXIX) Peter J. Rosendahl Click here if your download doesn"t start automatically Han Ola of Han Per:
Stationary Phase Monte Carlo Methods
 Stationary Phase Monte Carlo Methods Daniel Doro Ferrante G. S. Guralnik, J. D. Doll and D. Sabo HET Physics Dept, Brown University, USA. danieldf@het.brown.edu www.het.brown.edu Introduction: Motivations
Stationary Phase Monte Carlo Methods Daniel Doro Ferrante G. S. Guralnik, J. D. Doll and D. Sabo HET Physics Dept, Brown University, USA. danieldf@het.brown.edu www.het.brown.edu Introduction: Motivations
TALLÆRE UKE 34. Rest. Hvis vi deler a med b og det ikke går opp har vi rest som er mindre enn b.
 TALLÆRE UKE 34. Faktor. Hva er en faktor i et heltall? Vi fant ut at hvis et heltall b er med i et regnestykke med kun multiplikasjon som gir heltallet a som svar da er b faktor i a. Eksempel: 3 8=24 og
TALLÆRE UKE 34. Faktor. Hva er en faktor i et heltall? Vi fant ut at hvis et heltall b er med i et regnestykke med kun multiplikasjon som gir heltallet a som svar da er b faktor i a. Eksempel: 3 8=24 og
