Korteste-vei problemet Nettverksflyt med øvre begrensninger Maksimum-flyt problemet Teorem: Maksimum-flyt Minimum-kutt
|
|
|
- Ingrid Aronsen
- 7 år siden
- Visninger:
Transkript
1 Lekson 11
2 Korteste-ve problemet Nettverksflyt med øvre begrensnnger Maksmum-flyt problemet Teorem: Maksmum-flyt Mnmum-kutt MoD233 - Ger Hasle - Lekson 11 2
3 Heltallsprogrammerng Tdsplanleggng (skedulerng, schedulng) Handelsresende-problemet (TSP) Mer generelle kostnadsfunksoner Forgrenngs- og begrensnngsmetoden (Branch&Bound) MoD233 - Ger Hasle - Lekson 11 3
4 !! Oppgave: fnne korteste (raskeste, bllgste,...) ve fra A tl B gtt nettverk (rettet graf) Postv lengde (kostnad) på hver lenke er gtt Respektere enveskørng, fnne bllgste rettede st Eksempel: korteste rettede st fra a tl b nettverket tl høyre (a,e,b) kostnad 17 a c 18 f d b e 19 g Mange anvendelser MoD233 - Ger Hasle - Lekson 11 4
5 " # Fnn korteste ve fra alle noder dgraf tl gtt node r (rotnoden) Kan formuleres som mnmum kostnad nettverksflytproblem Hvordan? MoD233 - Ger Hasle - Lekson 11 5
6 $#%# Tlgang lk 1 på alle noder unntatt rotnoden Behov lk summen av tlgang (negert) rotnoden Kostnad lk lengden (eller resetd, - kostnad) på hver kant Mnmum kostnad flyt vl g flyt på 1 ut fra hver node Korteste ve fra vlkårlg node lgger langs et optmalt spenntre Lengden på korteste ve fra en gtt node er forskellen dual verd mellom rotnoden og denne noden 1 1 f a MoD233 - Ger Hasle - Lekson 11 6 c d b e g -6
7 Nettverksflyt-formulerng og løsnng med Nettverks Smpleksmetoden er kke den mest effektve beregnngsmessg Merkelapp (label)-baserte algortmer merkelapp-settng merkelapp-korrgerng MoD233 - Ger Hasle - Lekson 11 7
8 &%! Merkelapp på hver node (verdfunkson) avstand for korteste ve tl rotnoden: v, V må ha, for vlkårlg merkelapp: v r = { } { } v = mn c + v : (, ) r Bellman s lgnng Prnsppet om Dynamsk programmerng Rekurson! v f v a a 56 f c 28 v c 48 v d d b 33 7 v b v e e 19 g v g MoD233 - Ger Hasle - Lekson 11 8
9 v r = { } { } v = mn c + v : (, ) r Korteste ve fra node tl rotnoden er karaktersert ved: {(, ) : v c v } = = + Ikke alltd tre f a c 28 d b 33 e 19 g MoD233 - Ger Hasle - Lekson 11 9
10 ' ' vr = a 1 v = mn { c + v : (, ) } { r} d 48 Getter på løsnng: v () r () = { } v =, r Itererer fram bedre tlnærmnger, helt tl ngen endrng sker: v ( k + 1) r = ( k + 1) ( ) { k } { } v = mn c + v : (, ) r f 18 c b Antall terasoner: O( ) e 19 g MoD233 - Ger Hasle - Lekson 11 1
11 ( Vktge datastrukturer: v, noder som har fått rktg merkelapp ( ferdge ) h, merkelapper neste node korteste ve a c 28 d b 7 e 19 Intalserng: v () r () = { } v =, r f g MoD233 - Ger Hasle - Lekson 11 11
12 ( Så lenge ås { k } { } { } arg mn v : k for alle : (, ) rof hvs c + v < v så shv v c + v h 24 f a c d O( log ( )) 15 b e 19 g MoD233 - Ger Hasle - Lekson 11 12
13 $#%') Kapastetsbegrensnnger på kanter mn (, ) k k k :(, k ) :( k, ) c slk at = b, k, (, ) Nye førnger: u, (, ) 9 f MoD233 - Ger Hasle - Lekson a c d Kan løses drekte med modfsert Nettverks Smpleks Kan reduseres tl Nettverksflyt uten begrensnnger! Skal vse Maksmal-flyt Mnmalt-kutt teoremet 38 b e g 5
14 ? $#%') Kant (,) med øvre skranke: u, (, ) Kan omskrves ved bruk av slakkvarabel: Flytbalanse og øvre skranke: = b + = b + t = u = b t = b u + t = u b k + t = u c u, t b Fås ved å subtrahere sste lgnng b u k b c = k k = t + u MoD233 - Ger Hasle - Lekson 11 14
15 $#%') * # Ser på optmal løsnng for transformerte. 1. Dersom k = er dualslakken kkenegatv og k lk u : b u k b c = k k = t + u = z = y + c y = u > z = y y = k k k k k k y + c y 2. Dersom k =u er dualslakken og k lk : ( = u > = ) ( z = y + c y = z = y y ) k k k k k k y + c y MoD233 - Ger Hasle - Lekson 11 15
16 $#%') +!,) 3. Dersom < k <u er det postv flyt på begge kanter: ( ) < < u > z = y + c y = z = y y = k y + c = y k k k k k Gelder også motsatt ve! For optmal løsnng på orgnalt problem har v: b c = y + c y = u y + c y < < u y + c = y b u MoD233 - Ger Hasle - Lekson k b c = u k k = t b Vl bruke dette teorem for Maksmum-flyt problem + u
17 #% Vktg problem Delproblem mange Nettverksflyt-problemer Svært effektve algortmer fns V skal se på vktg teorem for dette problemet: Maksmum-flyt Mnmum-kutt teoremet MoD233 - Ger Hasle - Lekson 11 17
18 #% # =, ( ) b s = s { s, d} b d = d u,(, ) Nettverk Klde s og sluk d Øvre begrensnnger på (noen) kanter Mål: Presse så mye flyt som mulg gennom fra klde tl sluk! MoD233 - Ger Hasle - Lekson 11 18
19 #% * # $- s { s, d} d Kan omformes tl Mnmum-kostnad Nettverks Flyt med øvre begrensnnger { d s } c =, (, ) (, (, ) ) = c ds = 1 u ds = b =, MoD233 - Ger Hasle - Lekson 11 19
20 # Et kutt er en partsonerng av nodemengden to delmengder slk at klden er den ene delmengden og sluket den andre. Kuttet representeres av den delmengden som nneholder klden. s d Et kutt C MoD233 - Ger Hasle - Lekson 11 2
21 # Kapasteten tl et kutt (kuttkapastet) defneres som den samlete kapasteten tl de kanter som spenner over kuttet rktg retnng. κ ( C) = u C C C C s d MoD233 - Ger Hasle - Lekson 11 21
22 -% C C s d = κ ( C) ds C C C C Brukbar flyt MoD233 - Ger Hasle - Lekson 11 22
23 #% C C s d Teorem 14.1: Maksmum-flyt Mnmum kutt Maksmum flyt er lk mnmal kuttkapastet for nettverket. ds = mn κ ( C) alle C MoD233 - Ger Hasle - Lekson 11 23
24 #%. C C s d ds = mn κ ( C) alle C For vlkårlg kutt C og brukbar flyt har v: = u = κ ( C) ds C C C C C C C C Nok å fnne kutt C* og brukbar flyt slk at: ds = κ * ( C ) MoD233 - Ger Hasle - Lekson 11 24
25 #%. C C s d ds = mn κ ( C) alle C * Vl fnne kutt C* og brukbar flyt slk at: = κ C I optmal flyt har v følge tdlgere resultat: Ser på kant fra sluk tl klde: * * * * * ds ds d = s d s < < u = y + ( 1) y y > y ( ) MoD233 - Ger Hasle - Lekson ds * * * = + y c y * * * = + u y c y * * * < < u y + c = y
26 #%. s C C d ds = mn κ ( C) alle C Vl fnne kutt C* og brukbar flyt slk at: * * Defner kutt C* slk at: C { k : y * * } k ys * * * = + y c y * * * = + u y c y ds = κ ( C ) = Gyldg kutt? * * * < < u y + c = y Kanter som spenner rktg ve: = {(, ) : C * C * } Kanter som spenner fel ve: = {(, ) : C * C * } * * * * s (, ) y y < y = u c = * * * * s (, ) y y < y = c = MoD233 - Ger Hasle - Lekson 11 26
27 #%./ C C s d ds = mn κ ( C) alle C Vl fnne kuttsett C* og brukbar flyt slk at: * ds = κ ( C ) { : * * } k s * C = k y y * * * * s (, ) y y < y = u c = * * * * s (, ) y y < y = c = * * * * ds = = = κ (, ) (, ) (, ) (, ) u ( C ) QED! MoD233 - Ger Hasle - Lekson 11 27
28 1 Mange oppgaver den vrkelge verden kan modelleres som LP med heltallghetsførnger Dskrete valg, sekvenserng, kombnatorkk, logkk Tds- og ressursplanleggng, operasonsanalyse LP med heltallsførnger kalles Heltallsprogrammer Heltallsprogrammer er generelt langt vanskelgere å løse beregnngsmessg enn ordnære LP V skal se på: noen eksempler Generell løsnngsmetode: Forgrenng og begrensnng (Branch & Bound) MoD233 - Ger Hasle - Lekson 11 28
29 n = 1 n ma ζ = c slk at = 1 a b = 1,,m = 1,, n n = 1 n ma ζ = c slk at = 1 a b = 1,,m = 1,, n { } + I 1,,n Blandete heltallsprogrammer (Med Integer Programs MIP) Rene heltallsprogrammer (Pure Integer Programs IP, PIP) -1 programmer { } I 1,,n { } I = 1,,n { },1 MoD233 - Ger Hasle - Lekson 11 29
30 *' & Handelsresendeproblemet (TSP) Ruteplanleggngsproblemet (Vehcle Routng Problem, VRP) Produksonsplanleggng verksted (Job Shop Schedulng, JSS) Fly- og mannskapsplanleggng flyselskap (Arplane and crew rotaton) MoD233 - Ger Hasle - Lekson 11 3
31 -% Flyselskap ønsker god ressursutnyttelse Gtt rutetabell med flyvnnger (legs) ploter og kabnansatte - mannskap flyene som flyselskapet dsponerer - flåten Oppgave Lage turer, dvs. sekvenser av flyvnnger som starter og stopper på basen For flyene, slk at hver flyvnng får ett fly For mannskapene slk at hver flyvnng får ett mannskap (plot- og kabn) Sette sammen turer for fly og mannskap tl plan (for en uke) Tlfredsstller lover, avtaler, ressurstlgang Mnmere kostnader for planen MoD233 - Ger Hasle - Lekson 11 31
32 -% Rotasonsplan for fly/mannskap Deler opp problemet 1. Lager et stort utvalg (alle) lovlge turer 2. Setter sammen alternatve turer tl lovlg plan med mnmal kostnad MoD233 - Ger Hasle - Lekson 11 32
33 -% '# ##% m flyvnnger skal dekkes Har laget n alternatve tllatte flyturer Tlhørende kostnad for hver tur Koeffsenter som ser om flyvnng dekkes av tur Mengdedelngsproblemet (Set Parttonng Problem) 1 hvs flyvnng er med rute a = ellers Beslutnngsvarable 1 hvs rute brukes planen = ellers mn { } n = 1 1,,m { } { 1,,n} MoD233 - Ger Hasle - Lekson n = 1 c c a = 1, = 1,, m,1
34 -% / '# # + ' m flyvnnger skal dekkes 1,,m 1,,n Har laget n mulge tllatte flyturer Tlhørende kostnad for hver tur Koeffsenter som ser om flyvnng dekkes av tur Mengdedeknngsproblemet (Set Coverng Problem) 1 hvs flyvnng er med rute a = ellers Beslutnngsvarable 1 hvs rute brukes planen = ellers mn n = 1 { } { } { } MoD233 - Ger Hasle - Lekson n = 1 c c a 1, = 1,, m,1
35 -% 2 Mengdedelngs- og Mengdedeknngsproblemene er beregnngsmessg harde Lkevel kan ganske store nstanser løses eksakt Approksmasonsmetoder og heurstkker Verktøyleverandører tl flyselskap MoD233 - Ger Hasle - Lekson 11 35
36 1 ' '*! Handelsresende n byer 3 mnmal rundtur der hver by besøkes en og kun en gang kente resekostnader 5 NP-komplett problem 6 Lar seg uttrykke som (rent) heltallsprogram MoD233 - Ger Hasle - Lekson 11 36
37 *! n byer {,, n 1} kent resekostnad ( avstand ) mellom byer c, =,, n 1, =,, n 1, tur fullstendg bestemt ved permutason: n 1 s = s =, s,, s ( ) ( ) = antall mulge turer: ( n 1)! 1 n 1 MoD233 - Ger Hasle - Lekson 11 37
38 #) ! ! ! ! MoD233 - Ger Hasle - Lekson 11 38
39 *! Beslutnngsvarable (-1 varable):, =,, n 1, =,, n 1 1 dersom by nr. følger rett etter by turen = ellers Obektfunkson: mn n 1 n 1 = = c MoD233 - Ger Hasle - Lekson 11 39
40 *! Førnger må skre rundtur der alle byer besøkes en og kun en gang: n 1 = n 1 = = 1 =,, n 1 = 1 =,, n 1 For hver by skal det være en og kun en utgående kant For hver by skal det være en og kun en nngående kant MoD233 - Ger Hasle - Lekson 11 4
41 *! / Formulerng: mn n 1 = n 1 = n 1 n 1 = = = 1 =,, n 1 = 1 =,, n 1 c mn = 1 = 1 { } slk at,1,, c Har v sett en lgnende formulerng før? Tlordnngsproblemet, som o er beregnngsmessg enkelt! Noe er galt... MoD233 - Ger Hasle - Lekson 11 41
42 *! / Formulerng: mn n 1 = n 1 = n 1 n 1 = = = 1 =,, n 1 = 1 =,, n 1 c 1 Førngene hndrer kke dsunkte subturer! Er førngene tlstrekkelge for å skre en rundtur der alle byer besøkes en og kun en gang (Hamlton-tur)? MoD233 - Ger Hasle - Lekson 11 42
43 *! 2 Må legge tl subtur-ødeleggende førnger mn n 1 = n 1 = n 1 n 1 = = = 1 =,, n 1 = 1 =,, n 1 c La ( t n 1 ) = ( t =, t,, t ) = 1 n = 1, = 1, = 1, = 1, = 1, = 1, = ( s ) 6 = ( ) = 4 6,3,1, 2,5, 4,6 g possonen tl by nr. (nvers permutason tl s) t = s = s t MoD233 - Ger Hasle - Lekson ( t ) 6 = ( ) =, 2,3,1,5, 4,6
44 *! 3 Possonen tl by nr. ( t n 1 ) = ( t =, t,, t ) = 1 n For en lovlg tur må v ha: = 1 t = t + 1 t t + 1 = t t + 1 n 5 6 Dette kan sammenfattes tl: t t + 1 (1 ) n Nødvendg betngelse for å unngå subturer. Tlstrekkelg? MoD233 - Ger Hasle - Lekson 11 44
45 *! 4 mn n 1 = n 1 = n 1 n 1 = = = 1 =,, n 1 = 1 =,, n 1 t t + 1 (1 ) n,, =,, n 1, c Anta det fns subturer. Se på en av subturene. La r>1 være antall kanter subturen. Summerer sste førng over alle kanter subturen. V får, ved å subtrahere t for alle nodene subturen: r MoD233 - Ger Hasle - Lekson 11 45
46 *! 5 mn n 1 = n 1 = n 1 n 1 = = = 1 =,, n 1 = 1 =,, n 1 t t + 1 (1 ) n,, =,1,, n 1 { } + t =, t,,1 c n 2 +n varable n 2 +2n førnger 6 4 MoD233 - Ger Hasle - Lekson 11 46
47 '# LP krever utgangspunktet lneær kostnadsfunkson Ofte er en lneær kostnadsmodell lte adekvat V skal se på to utvdelser fast ntalkostnad stykkevs lneær kostnad Dsse kan løses med heltallsutvdelser MoD233 - Ger Hasle - Lekson 11 47
48 - ' Ser på kostnadsfunkson av typen: hvs = Fast ntalkostnad c( ) = K + c hvs > Innfører bnær varabel og modfserer problemet: c( ) = Ky + c Øvre grense for! uy y {,1} Trkset brukes for hver ntalkostnad! MoD233 - Ger Hasle - Lekson 11 48
49 % ' Approksmerer kostnadskurve stykkevs lneært, k segmenter Dekomponerer ved å nnføre en varabel for hvert av de k lnestykker: = k Følgende heltallsbeskranknnger skrer rktg dekomponerng: L w L w = 1,, k 1 { } w = 1, w,1 = 1,, k = 1,, k 3 L 3 Ny kostnadsfunkson: c( ) = K + c + + c 1 1 k MoD233 - Ger Hasle - Lekson k
50 % ' L w L w = 1,, k 1 { } w = 1, w,1 = 1,, k = 1,, k w w = 1,, k 1 w = w = 1 L L, = 1,, k 1 w = w =, = 2,, k 1 w =, w = 1 L, = 2,, k 1 3 L 3 MoD233 - Ger Hasle - Lekson 11 5
51 T ma c slk at A b, har heltallge komponenter Generell, eksakt metode for løsnng: forgrenng og begrensnng (Branch & Bound) Genererer LP på en systematsk måte Løser LP-relaksason Forgrener to tlfeller Enumererngstre Avskærng Kan ta laaang td MoD233 - Ger Hasle - Lekson 11 51
52 - Forgrenng 1 =1 2 =4 ζ=64 Bladnode LP1 MIP1 MIP 1 1 MIP LP 1 = =3.33 ζ=68.33 MIP2 MIP 1 2 LP2 1 =2 2 =2.86 ζ= =2.6 2 =2 ζ=63.89 LP3 MIP3 MIP2 2 2 MIP4 MIP2 2 3 LP4 Inkonsstent! Begrensnng MoD233 - Ger Hasle - Lekson 11 52
53 - Generell, eksakt metode for løsnng av MIP Genererer LP på en systematsk måte et tre - enumererngstreet Løser LP-relaksasonen (LPR) av et MIP hver node Hvs LPR-løsnngen er heltallg, har v en brukbar løsnng og underestmat (maksmerng) for optmal løsnng Hvs kke heltallg løsnng, velges en kke-heltallg varabel og v forgrener to ved å legge på gensdg utelukkende ulkhetsførnger Hvs v får dårlgere verd på LP-relaksasonen enn beste heltallge løsnng funnet, kan v foreta avskærng (prunng) Ikke-tllatt løsnng en node gr også avskærng Enumererngstreet kan utforskes på mange måter bredde først dybde først (stort sett bedre, se boka sde 391) Det fnnes heurstkker (uformelle regler) for hvlke varabler det kan lønne seg å forgrene på MoD233 - Ger Hasle - Lekson 11 53
54 - Kan ta svært lang td (eksponenselt antall noder) Vktg å få fram brukbar (heltallg) løsnng tdlg søket Tdlg brukbar løsnng kan g tdlgere avskærng LPene treet fra roten og nedover er svært lke tllegg/endrng av spesell type førng: grense på varabel Kan bruke løsnng fra LPen overlggende node tl å løse LPen nneværende node raskere Læreboka sde 391 MoD233 - Ger Hasle - Lekson 11 54
55 Heltallsprogrammerng (M)IP Mange problemer kan formuleres som MIP Operasonsanalyse Tdsplanleggng (skedulerng, schedulng) Handelsresende-problemet (TSP) Mer generelle kostnadsfunksoner Forgrenngs- og begrensnngsmetoden (Branch&Bound) MoD233 - Ger Hasle - Lekson 11 55
MoD233 - Geir Hasle - Leksjon 10 2
 Leksjon 10 Anvendelser nettverksflyt Transportproblemet Htchcock-problemet Tlordnngsproblemet Korteste-ve problemet Nettverksflyt med øvre begrensnnger Maksmum-flyt problemet Teorem: Maksmum-flyt Mnmum-kutt
Leksjon 10 Anvendelser nettverksflyt Transportproblemet Htchcock-problemet Tlordnngsproblemet Korteste-ve problemet Nettverksflyt med øvre begrensnnger Maksmum-flyt problemet Teorem: Maksmum-flyt Mnmum-kutt
Mål. MoD233 - Geir Hasle - Repetisjon 2
 Repetson Mål teoretsk forståelse, grunnleggende optmerng løsnngsmetoder LP og utvdelser algortmsk forståelse anvendelser LP og utvdelser modellerng og løsnng v.h.a. verktøy Innhold og forelesnngsplan Eksempler
Repetson Mål teoretsk forståelse, grunnleggende optmerng løsnngsmetoder LP og utvdelser algortmsk forståelse anvendelser LP og utvdelser modellerng og løsnng v.h.a. verktøy Innhold og forelesnngsplan Eksempler
Simpleksmetoden. Initiell basistabell Fase I for å skaffe initiell, brukbar løsning. Fase II: Iterativ prosess for å finne optimal løsning Pivotering
 Lekson 3 Smpleksmetoden generell metode for å løse LP utgangspunkt: LP på standardform Intell basstabell Fase I for å skaffe ntell, brukbar løsnng løse helpeproblem hvs optmale løsnng gr brukbar løsnng
Lekson 3 Smpleksmetoden generell metode for å løse LP utgangspunkt: LP på standardform Intell basstabell Fase I for å skaffe ntell, brukbar løsnng løse helpeproblem hvs optmale løsnng gr brukbar løsnng
Dynamisk programmering. Hvilke problemer? Overlappende delproblemer. Optimalitetsprinsippet
 Dynamsk programmerng Hvlke problemer? Metoden ble formalsert av Rchard Bellmann (RAND Corporaton) på -tallet. Har ngen tng med programmerng å gøre. Dynamsk er et ord som kan aldr brukes negatvt. Skal v
Dynamsk programmerng Hvlke problemer? Metoden ble formalsert av Rchard Bellmann (RAND Corporaton) på -tallet. Har ngen tng med programmerng å gøre. Dynamsk er et ord som kan aldr brukes negatvt. Skal v
IT1105 Algoritmer og datastrukturer
 Løsnngsforslag, Eksamen IT1105 Algortmer og datastrukturer 1 jun 2004 0900-1300 Tllatte hjelpemdler: Godkjent kalkulator og matematsk formelsamlng Skrv svarene på oppgavearket Skrv studentnummer på alle
Løsnngsforslag, Eksamen IT1105 Algortmer og datastrukturer 1 jun 2004 0900-1300 Tllatte hjelpemdler: Godkjent kalkulator og matematsk formelsamlng Skrv svarene på oppgavearket Skrv studentnummer på alle
Dynamisk programmering. Hvilke problemer? Overlappende delproblemer. Optimalitetsprinsippet
 Dynamsk programmerng Metoden ble formalsert av Rchard Bellmann (RAND Corporaton på -tallet. Programmerng betydnngen planlegge, ta beslutnnger. (Har kke noe med kode eller å skrve kode å gøre. Dynamsk for
Dynamsk programmerng Metoden ble formalsert av Rchard Bellmann (RAND Corporaton på -tallet. Programmerng betydnngen planlegge, ta beslutnnger. (Har kke noe med kode eller å skrve kode å gøre. Dynamsk for
Del A: Diskret optimering og heuristiske metoder Leksjon 8
 Del A: Dskret optmerg og heurstske metoder Lekso 8 Sefsforsker Ger Hasle SINTEF Avedt matematkk, Oslo!"# Kategorserg av metaheurstkker Kostruktve heurstkker Mult-start baserte metaheurstkker Tlfeldg Restart
Del A: Dskret optmerg og heurstske metoder Lekso 8 Sefsforsker Ger Hasle SINTEF Avedt matematkk, Oslo!"# Kategorserg av metaheurstkker Kostruktve heurstkker Mult-start baserte metaheurstkker Tlfeldg Restart
i B maksimal b Fundamentalteoremet for lineærprogrammering Den leksikografiske metode Blands pivoteringregel MoD233 - Geir Hasle - Leksjon 4 2
 Lekso 4 ( k ) a ( k ) I ( k ) U ( k) B maksmal ( k ) b Sste spesaltlfelle - valg av utgåede Degeerert basstabell, degeererert pvoterg Degeerert pvoterg ka g syklsk pvoterg Eeste tlfelle der Smpleksmetode
Lekso 4 ( k ) a ( k ) I ( k ) U ( k) B maksmal ( k ) b Sste spesaltlfelle - valg av utgåede Degeerert basstabell, degeererert pvoterg Degeerert pvoterg ka g syklsk pvoterg Eeste tlfelle der Smpleksmetode
Forelesning nr.3 INF 1410
 Forelesnng nr. INF 40 009 Node og mesh-analyse 6.0.009 INF 40 Oerskt dagens temaer Bakgrunn Nodeanalyse og motasjon Meshanalyse 009 Supernode Bruksområder og supermesh for node- og meshanalyse 6.0.009
Forelesnng nr. INF 40 009 Node og mesh-analyse 6.0.009 INF 40 Oerskt dagens temaer Bakgrunn Nodeanalyse og motasjon Meshanalyse 009 Supernode Bruksområder og supermesh for node- og meshanalyse 6.0.009
Automatisk koplingspåsats Komfort Bruksanvisning
 Bruksanvsnng System 2000 Art. Nr.: 0661 xx /0671 xx Innholdsfortegnelse 1. rmasjon om farer 2. Funksjon 2.1. Funksjonsprnspp 2.2. Regstrerngsområde versjon med 1,10 m lnse 2.3. Regstrerngsområde versjon
Bruksanvsnng System 2000 Art. Nr.: 0661 xx /0671 xx Innholdsfortegnelse 1. rmasjon om farer 2. Funksjon 2.1. Funksjonsprnspp 2.2. Regstrerngsområde versjon med 1,10 m lnse 2.3. Regstrerngsområde versjon
EKSAMEN I FAG SIF5040 NUMERISKE METODER Tirsdag 15. mai 2001 Tid: 09:00 14:00
 Norges teknsk naturvtenskapelge unverstet Insttutt for matematske fag Sde 1 av 9 Faglg kontakt under eksamen: Enar Rønqust, tlf. 73 59 35 47 EKSAMEN I FAG SIF5040 NUMERISKE METODER Trsdag 15. ma 2001 Td:
Norges teknsk naturvtenskapelge unverstet Insttutt for matematske fag Sde 1 av 9 Faglg kontakt under eksamen: Enar Rønqust, tlf. 73 59 35 47 EKSAMEN I FAG SIF5040 NUMERISKE METODER Trsdag 15. ma 2001 Td:
Veiledning til obligatorisk oppgave i ECON 3610/4610 høsten N. Vi skal bestemme den fordeling av denne gitte arbeidsstyrken som
 Jon sle; oktober 07 Ogave a. elednng tl oblgatorsk ogave ECO 60/60 høsten 07 har nå at samlet arbedskraftmengde er gtt lk, slk at ressurskravet er. skal bestemme den fordelng av denne gtte arbedsstyrken
Jon sle; oktober 07 Ogave a. elednng tl oblgatorsk ogave ECO 60/60 høsten 07 har nå at samlet arbedskraftmengde er gtt lk, slk at ressurskravet er. skal bestemme den fordelng av denne gtte arbedsstyrken
Illustrasjon av regel 5.19 om sentralgrenseteoremet og litt om heltallskorreksjon (som i eksempel 5.18).
 Econ 2130 HG mars 2012 Supplement tl forelesnngen 19. mars Illustrasjon av regel 5.19 om sentralgrenseteoremet og ltt om heltallskorreksjon (som eksempel 5.18). Regel 5.19 ser at summer, Y = X1+ X2 + +
Econ 2130 HG mars 2012 Supplement tl forelesnngen 19. mars Illustrasjon av regel 5.19 om sentralgrenseteoremet og ltt om heltallskorreksjon (som eksempel 5.18). Regel 5.19 ser at summer, Y = X1+ X2 + +
MA1301 Tallteori Høsten 2014
 MA1301 Tallteor Høsten 014 Rchard Wllamson 3. desember 014 Innhold Forord 1 Induksjon og rekursjon 7 1.1 Naturlge tall og heltall............................ 7 1. Bevs.......................................
MA1301 Tallteor Høsten 014 Rchard Wllamson 3. desember 014 Innhold Forord 1 Induksjon og rekursjon 7 1.1 Naturlge tall og heltall............................ 7 1. Bevs.......................................
Anvendelser. Kapittel 12. Minste kvadraters metode
 Kapttel Anvendelser I dette kaptlet skal v se på forskjellge anvendelser av teknkke v har utvklet løpet av de sste ukene Avsnttene og eksemplene v skal se på er derfor forholdsvs uavhengge Mnste kvadraters
Kapttel Anvendelser I dette kaptlet skal v se på forskjellge anvendelser av teknkke v har utvklet løpet av de sste ukene Avsnttene og eksemplene v skal se på er derfor forholdsvs uavhengge Mnste kvadraters
Appendiks 1: Organisering av Riksdagsdata i SPSS. Sannerstedt- og Sjölins data er klargjort for logitanalyse i SPSS filen på følgende måte:
 Appendks 1: Organserng av Rksdagsdata SPSS Sannerstedt- og Sjölns data er klargjort for logtanalyse SPSS flen på følgende måte: Enhet År SKJEBNE BASIS ANTALL FARGE 1 1972 1 0 47 1 0 2 1972 1 0 47 1 0 67
Appendks 1: Organserng av Rksdagsdata SPSS Sannerstedt- og Sjölns data er klargjort for logtanalyse SPSS flen på følgende måte: Enhet År SKJEBNE BASIS ANTALL FARGE 1 1972 1 0 47 1 0 2 1972 1 0 47 1 0 67
(iii) Når 5 er blitt trukket ut, er det tre igjen som kan blir trukket ut til den siste plassen, altså:
 A-besvarelse ECON2130- Statstkk 1 vår 2009 Oppgave 1 A) () Antall kke-ordnede utvalg: () P(Arne nummer 1) = () Når 5 er bltt trukket ut, er det tre gjen som kan blr trukket ut tl den sste plassen, altså:
A-besvarelse ECON2130- Statstkk 1 vår 2009 Oppgave 1 A) () Antall kke-ordnede utvalg: () P(Arne nummer 1) = () Når 5 er bltt trukket ut, er det tre gjen som kan blr trukket ut tl den sste plassen, altså:
TMA4240/4245 Statistikk Eksamen august 2016
 Norges teknsk-naturvtenskapelge unverstet Insttutt for matematske fag TMA44/445 Statstkk Eksamen august 6 Løsnngssksse Oppgave a) Ved kast av to ternnger er det 36 mulge utfall: (, ),..., (6, 6). La Y
Norges teknsk-naturvtenskapelge unverstet Insttutt for matematske fag TMA44/445 Statstkk Eksamen august 6 Løsnngssksse Oppgave a) Ved kast av to ternnger er det 36 mulge utfall: (, ),..., (6, 6). La Y
TALLSVAR. Det anbefales at de 9 deloppgavene merket med A, B, teller likt uansett variasjon i vanskelighetsgrad. Svarene er gitt i <<< >>>.
 ECON30: EKSAMEN 05 VÅR - UTSATT PRØVE TALLSVAR. Det anbefales at de 9 deloppgavene merket med A, B, teller lkt uansett varasjon vanskelghetsgrad. Svarene er gtt
ECON30: EKSAMEN 05 VÅR - UTSATT PRØVE TALLSVAR. Det anbefales at de 9 deloppgavene merket med A, B, teller lkt uansett varasjon vanskelghetsgrad. Svarene er gtt
Del A: Diskret optimering og heuristiske metoder Leksjon 2
 Del A: Dskret optmerg og heurstske metoder Leksjo 2 Sjefsforsker Ger Hasle SINTEF Avedt matematkk, Oslo! Kursformasjo Motvasjo Operasjosaalyse Kustg tellges Optmergsproblemer (dskrete) Matematsk program
Del A: Dskret optmerg og heurstske metoder Leksjo 2 Sjefsforsker Ger Hasle SINTEF Avedt matematkk, Oslo! Kursformasjo Motvasjo Operasjosaalyse Kustg tellges Optmergsproblemer (dskrete) Matematsk program
Balanserte søketrær. AVL-trær. AVL-trær. AVL-trær høyde AVL AVL. AVL-trær (Adelson-Velskii og Landis, 1962) Splay-trær (Sleator og Tarjan, 1985)
 alanserte søketrær VL-trær Et bnært tre er et VL-tre hvs ølgende holder: VL-trær delson-velsk og Lands, 96 play-trær leator og Tarjan, 98. orskjellen høyde mellom det høyre og det venstre deltreet er maksmalt,
alanserte søketrær VL-trær Et bnært tre er et VL-tre hvs ølgende holder: VL-trær delson-velsk og Lands, 96 play-trær leator og Tarjan, 98. orskjellen høyde mellom det høyre og det venstre deltreet er maksmalt,
Alternerende rekker og absolutt konvergens
 Alternerende rekker og absolutt konvergens Forelest: 0. Sept, 2004 Sst forelesnng så v på rekker der alle termene var postve. Mange av de kraftgste metodene er utvklet for akkurat den typen rekker. I denne
Alternerende rekker og absolutt konvergens Forelest: 0. Sept, 2004 Sst forelesnng så v på rekker der alle termene var postve. Mange av de kraftgste metodene er utvklet for akkurat den typen rekker. I denne
Eksamen ECON 2200, Sensorveiledning Våren Deriver følgende funksjoner. Deriver med hensyn på begge argumenter i e) og f).
 Eksamen ECON 00, Sensorvelednng Våren 0 Oppgave (8 poeng ) Derver følgende funksjoner. Derver med hensyn på begge argumenter e) og f). (Ett poeng per dervasjon, dvs, poeng e og f) a) f( x) = 3x x + ln
Eksamen ECON 00, Sensorvelednng Våren 0 Oppgave (8 poeng ) Derver følgende funksjoner. Derver med hensyn på begge argumenter e) og f). (Ett poeng per dervasjon, dvs, poeng e og f) a) f( x) = 3x x + ln
Løsningsforslag ST2301 Øving 8
 Løsnngsforslag ST301 Øvng 8 Kapttel 4 Exercse 1 For tre alleler, fnn et sett med genfrekvenser for to populasjoner, som gr flere heterozygoter enn forventa utfra Hardy-Wenberg-andeler for mnst én av de
Løsnngsforslag ST301 Øvng 8 Kapttel 4 Exercse 1 For tre alleler, fnn et sett med genfrekvenser for to populasjoner, som gr flere heterozygoter enn forventa utfra Hardy-Wenberg-andeler for mnst én av de
Forelesning 17 torsdag den 16. oktober
 Forelesnng 17 torsdag den 16. oktober 4.12 Orden modulo et prmtall Defnsjon 4.12.1. La p være et prmtall. La x være et heltall slk at det kke er sant at x 0 Et naturlg tall t er ordenen tl a modulo p dersom
Forelesnng 17 torsdag den 16. oktober 4.12 Orden modulo et prmtall Defnsjon 4.12.1. La p være et prmtall. La x være et heltall slk at det kke er sant at x 0 Et naturlg tall t er ordenen tl a modulo p dersom
ØVINGER 2017 Løsninger til oppgaver
 ØVINGER 017 Løsnnger tl oppgaver Øvng 1 7.1. Med utgangspunkt de n 5 observasjonsparene (x 1, y 1 ), (x, y ),..., (x 5, y 5 ) beregner v først mddelverdene x 1 5 Estmert kovarans blr x 3. ȳ 1 5 s XY 1
ØVINGER 017 Løsnnger tl oppgaver Øvng 1 7.1. Med utgangspunkt de n 5 observasjonsparene (x 1, y 1 ), (x, y ),..., (x 5, y 5 ) beregner v først mddelverdene x 1 5 Estmert kovarans blr x 3. ȳ 1 5 s XY 1
Forelesning nr.3 INF 1411 Elektroniske systemer. Parallelle og parallell-serielle kretser Kirchhoffs strømlov
 Forelesnng nr.3 INF 4 Elektronske systemer Parallelle og parallell-serelle kretser Krchhoffs strømlov Dagens temaer Parallelle kretser Kretser med parallelle og serelle ster Effekt parallelle kretser Krchhoffs
Forelesnng nr.3 INF 4 Elektronske systemer Parallelle og parallell-serelle kretser Krchhoffs strømlov Dagens temaer Parallelle kretser Kretser med parallelle og serelle ster Effekt parallelle kretser Krchhoffs
Sparing gir mulighet for å forskyve forbruk over tid; spesielt kan ujevne inntekter transformeres til jevnere forbruk.
 ECON 0 Forbruker, bedrft og marked Forelesnngsnotater 09.0.07 Nls-Henrk von der Fehr FORBRUK OG SPARING Innlednng I denne delen skal v anvende det generelle modellapparatet for konsumentens tlpasnng tl
ECON 0 Forbruker, bedrft og marked Forelesnngsnotater 09.0.07 Nls-Henrk von der Fehr FORBRUK OG SPARING Innlednng I denne delen skal v anvende det generelle modellapparatet for konsumentens tlpasnng tl
Oppgaver. Multiple regresjon. Forelesning 3 MET3592 Økonometri ved David Kreiberg Vår 2011
 Forelesnng 3 MET359 Økonometr ved Davd Kreberg Vår 0 Oppgaver Alle oppgaver er merket ut fra vanskelghetsgrad på følgende måte: * Enkel ** Mddels vanskelg *** Vanskelg Multple regresjon Oppgave.* Ta utgangspunkt
Forelesnng 3 MET359 Økonometr ved Davd Kreberg Vår 0 Oppgaver Alle oppgaver er merket ut fra vanskelghetsgrad på følgende måte: * Enkel ** Mddels vanskelg *** Vanskelg Multple regresjon Oppgave.* Ta utgangspunkt
Eksamen i emne SIB8005 TRAFIKKREGULERING GRUNNKURS
 Sde 1 av 5 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Fakultet for bygg- og mljøteknkk INSTITUTT FOR SAMFERDSELSTEKNIKK Faglg kontakt under eksamen: Navn Arvd Aakre Telefon 73 59 46 64 (drekte) / 73
Sde 1 av 5 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Fakultet for bygg- og mljøteknkk INSTITUTT FOR SAMFERDSELSTEKNIKK Faglg kontakt under eksamen: Navn Arvd Aakre Telefon 73 59 46 64 (drekte) / 73
EKSAMEN ny og utsatt løsningsforslag
 8.. EKSAMEN n og utsatt løsnngsorslag Emnekode: ITD Dato:. jun Hjelpemdler: - To A-ark med valgrtt nnhold på begge sder. Emnenavn: Matematkk ørste deleksamen Eksamenstd: 9.. Faglærer: Chrstan F Hede -
8.. EKSAMEN n og utsatt løsnngsorslag Emnekode: ITD Dato:. jun Hjelpemdler: - To A-ark med valgrtt nnhold på begge sder. Emnenavn: Matematkk ørste deleksamen Eksamenstd: 9.. Faglærer: Chrstan F Hede -
X ijk = µ+α i +β j +γ ij +ǫ ijk ; k = 1,2; j = 1,2,3; i = 1,2,3; i=1 γ ij = 3. i=1 α i = 3. j=1 β j = 3. j=1 γ ij = 0.
 UNIVERSITETET I OSLO Det matematsk-naturvtenskapelge fakultet Eksamen : Eksamensdag: 7. jun 2013. Td for eksamen: 14.30 18.30. Oppgavesettet er på 8 sder. Vedlegg: Tllatte hjelpemdler: STK2120 LØSNINGSFORSLAG
UNIVERSITETET I OSLO Det matematsk-naturvtenskapelge fakultet Eksamen : Eksamensdag: 7. jun 2013. Td for eksamen: 14.30 18.30. Oppgavesettet er på 8 sder. Vedlegg: Tllatte hjelpemdler: STK2120 LØSNINGSFORSLAG
Forelesning nr.3 INF 1411 Elektroniske systemer
 Forelesnng nr.3 INF 4 Elektronske systemer 009 04 Parallelle og parallell-serelle kretser Krchhoffs strømlov 30.0.04 INF 4 Dagens temaer Parallelle kretser Kretser med parallelle og serelle ster Effekt
Forelesnng nr.3 INF 4 Elektronske systemer 009 04 Parallelle og parallell-serelle kretser Krchhoffs strømlov 30.0.04 INF 4 Dagens temaer Parallelle kretser Kretser med parallelle og serelle ster Effekt
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematsk-naturvtenskapelge fakultet Deleksamen MAT-INF Modellerng og beregnnger. Eksamensdag: Onsdag 7. oktober 29. Td for eksamen: 5: 7:. Oppgavesettet er på 6 sder. Vedlegg:
UNIVERSITETET I OSLO Det matematsk-naturvtenskapelge fakultet Deleksamen MAT-INF Modellerng og beregnnger. Eksamensdag: Onsdag 7. oktober 29. Td for eksamen: 5: 7:. Oppgavesettet er på 6 sder. Vedlegg:
Løsningskisse for oppgaver til uke 15 ( april)
 HG Aprl 01 Løsnngsksse for oppgaver tl uke 15 (10.-13. aprl) Innledende merknad. Flere oppgaver denne uka er øvelser bruk av den vktge regel 5.0, som er sentral dette kurset, og som det forventes at studentene
HG Aprl 01 Løsnngsksse for oppgaver tl uke 15 (10.-13. aprl) Innledende merknad. Flere oppgaver denne uka er øvelser bruk av den vktge regel 5.0, som er sentral dette kurset, og som det forventes at studentene
TMA4265 Stokastiske prosesser
 orges teknsk-naturvtenskapelge unverstet Insttutt for matematske fag TMA4265 Stokastske prosesser Våren 2004 Løsnngsforslag - Øvng 6 Oppgaver fra læreboka 4.56 X n Antallet hvte baller urna Trekk tlf.
orges teknsk-naturvtenskapelge unverstet Insttutt for matematske fag TMA4265 Stokastske prosesser Våren 2004 Løsnngsforslag - Øvng 6 Oppgaver fra læreboka 4.56 X n Antallet hvte baller urna Trekk tlf.
Vekst i skjermet virksomhet: Er dette et problem? Trend mot større andel sysselsetting i skjermet
 Forelesnng NO kapttel 4 Skjermet og konkurranseutsatt vrksomhet Det grunnleggende formål med eksport: Mulggjøre mport Samfunnsøkonomsk balanse mellom eksport og mportkonkurrerende: Samme valutanntjenng/besparelse
Forelesnng NO kapttel 4 Skjermet og konkurranseutsatt vrksomhet Det grunnleggende formål med eksport: Mulggjøre mport Samfunnsøkonomsk balanse mellom eksport og mportkonkurrerende: Samme valutanntjenng/besparelse
NA Dok. 52 Angivelse av måleusikkerhet ved kalibreringer
 Sde: av 7 orsk akkredterng Dok.d.: VII..5 A Dok. 5: Angvelse av måleuskkerhet ved kalbrernger Utarbedet av: Saeed Behdad Godkjent av: ICL Versjon:.00 Mandatory/Krav Gjelder fra: 09.05.008 Sdenr: av 7 A
Sde: av 7 orsk akkredterng Dok.d.: VII..5 A Dok. 5: Angvelse av måleuskkerhet ved kalbrernger Utarbedet av: Saeed Behdad Godkjent av: ICL Versjon:.00 Mandatory/Krav Gjelder fra: 09.05.008 Sdenr: av 7 A
Sorterings- Algoritmer
 Hva er sorterng? Sorterngs- Algortmer Algortmer og Datastrukturer Input: en sekvens av N nummer Output: reorganserng nput-sekvensen slk at: a < a < a... < a n- < a n V søker algortmer som gjør dette på
Hva er sorterng? Sorterngs- Algortmer Algortmer og Datastrukturer Input: en sekvens av N nummer Output: reorganserng nput-sekvensen slk at: a < a < a... < a n- < a n V søker algortmer som gjør dette på
Regler om normalfordelingen
 1 HG mars 2009 Notat tl kapttel 5 Løvås Regler om ormalfordelge Kjeskap tl reglee for ormalfordelge er gruleggede for de statstske aalyse kapttel 6 Løvås, og studetee må kue beherske dsse skkkelg dette
1 HG mars 2009 Notat tl kapttel 5 Løvås Regler om ormalfordelge Kjeskap tl reglee for ormalfordelge er gruleggede for de statstske aalyse kapttel 6 Løvås, og studetee må kue beherske dsse skkkelg dette
Tillegg 7 7. Innledning til FY2045/TFY4250
 FY1006/TFY4215 Tllegg 7 1 Dette notatet repeterer noen punkter fra Tllegg 2, og dekker detalj målng av degenererte egenverder samt mpulsrepresentasjonen av kvantemekankk. Tllegg 7 7. Innlednng tl FY2045/TFY4250
FY1006/TFY4215 Tllegg 7 1 Dette notatet repeterer noen punkter fra Tllegg 2, og dekker detalj målng av degenererte egenverder samt mpulsrepresentasjonen av kvantemekankk. Tllegg 7 7. Innlednng tl FY2045/TFY4250
EKSAMEN Ny og utsatt Løsningsforslag
 . jun 0 EKSAMEN Ny og utsatt Løsnngsorslag Emnekode: ITD50 Dato:. jun 0 Emne: Matematkk, deleksamen Eksamenstd: 09.00.00 Hjelpemdler: To A-ark med valgrtt nnhold på begge sder. Formelhete. Kalkulator er
. jun 0 EKSAMEN Ny og utsatt Løsnngsorslag Emnekode: ITD50 Dato:. jun 0 Emne: Matematkk, deleksamen Eksamenstd: 09.00.00 Hjelpemdler: To A-ark med valgrtt nnhold på begge sder. Formelhete. Kalkulator er
Regler om normalfordelingen
 1 HG Revdert mars 013 Notat tl kapttel 5 Løvås Regler om ormalfordelge Kjeskap tl reglee for ormalfordelge er gruleggede for de statstske aalyse kapttel 6 Løvås, og studetee må kue beherske dsse skkkelg
1 HG Revdert mars 013 Notat tl kapttel 5 Løvås Regler om ormalfordelge Kjeskap tl reglee for ormalfordelge er gruleggede for de statstske aalyse kapttel 6 Løvås, og studetee må kue beherske dsse skkkelg
Regler om normalfordelingen
 HG mars 0 Notat tl kapttel 5 Løvås Regler om ormalfordelge Kjeskap tl reglee for ormalfordelge er gruleggede for de statstske aalyse kapttel 6 Løvås, og studetee må kue beherske dsse skkkelg dette kurset.
HG mars 0 Notat tl kapttel 5 Løvås Regler om ormalfordelge Kjeskap tl reglee for ormalfordelge er gruleggede for de statstske aalyse kapttel 6 Løvås, og studetee må kue beherske dsse skkkelg dette kurset.
Innkalling til andelseiermøte
 Tl andelseerne Holberg Global og Holberg Rurk Bergen, 24. november 2017 Innkallng tl andelseermøte Vedtektsendrnger verdpaprfondene Holberg Global og Holberg Rurk Forvaltnngsselskapet Holberg Fondsforvaltnng
Tl andelseerne Holberg Global og Holberg Rurk Bergen, 24. november 2017 Innkallng tl andelseermøte Vedtektsendrnger verdpaprfondene Holberg Global og Holberg Rurk Forvaltnngsselskapet Holberg Fondsforvaltnng
EKSAMEN Løsningsforslag
 . desember 6 EKSAMEN Løsnngsorslag Emnekode: ITD Emnenavn: Matematkk ørste deleksamen Dato:. desember 6 Hjelpemdler: - To A-ark med valgrtt nnold på begge sder. - Formelete. - Kalkulator som deles ut samtdg
. desember 6 EKSAMEN Løsnngsorslag Emnekode: ITD Emnenavn: Matematkk ørste deleksamen Dato:. desember 6 Hjelpemdler: - To A-ark med valgrtt nnold på begge sder. - Formelete. - Kalkulator som deles ut samtdg
Formler og regler i statistikk ifølge lærebok Gunnar Løvås: Statistikk for universiteter og høgskoler
 Formler og regler statstkk følge lærebok Guar Løvås: tatstkk for uversteter og høgskoler Kap. Hva er fakta om utvalget etralmål Meda: mdterste verd etter sorterg Modus: hyppgst forekommede verd Gjeomstt:
Formler og regler statstkk følge lærebok Guar Løvås: tatstkk for uversteter og høgskoler Kap. Hva er fakta om utvalget etralmål Meda: mdterste verd etter sorterg Modus: hyppgst forekommede verd Gjeomstt:
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 Utsatt eksamen : ECON130 Statstkk 1 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamensdag: 15.0.015 Sensur kunngjøres senest: 0.07.015 Td for eksamen: kl. 09:00 1:00 Oppgavesettet er på 4 sder Tllatte hjelpemdler:
Utsatt eksamen : ECON130 Statstkk 1 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamensdag: 15.0.015 Sensur kunngjøres senest: 0.07.015 Td for eksamen: kl. 09:00 1:00 Oppgavesettet er på 4 sder Tllatte hjelpemdler:
Statistikk og økonomi, våren 2017
 Statstkk og økonom, våren 7 Oblgatorsk oppgave Løsnngsforslag Oppgave Anta at forbruket av ntrogen norsk landbruk årene 987 99 var følgende målt tonn: 987: 9 87 988: 8 989: 8 99: 8 99: 79 99: 87 99: 9
Statstkk og økonom, våren 7 Oblgatorsk oppgave Løsnngsforslag Oppgave Anta at forbruket av ntrogen norsk landbruk årene 987 99 var følgende målt tonn: 987: 9 87 988: 8 989: 8 99: 8 99: 79 99: 87 99: 9
Auksjoner og miljø: Privat informasjon og kollektive goder. Eirik Romstad Handelshøyskolen Norges miljø- og biovitenskapelige universitet
 Auksjoner og mljø: Prvat nformasjon og kollektve goder Erk Romstad Handelshøyskolen Auksjoner for endra forvaltnng Habtatvern for bologsk mangfold Styresmaktene lyser ut spesfserte forvaltnngskontrakter
Auksjoner og mljø: Prvat nformasjon og kollektve goder Erk Romstad Handelshøyskolen Auksjoner for endra forvaltnng Habtatvern for bologsk mangfold Styresmaktene lyser ut spesfserte forvaltnngskontrakter
Arbeid og potensiell energi
 Arbed og potensell energ 4.3.5 Mdtveseksamen: 6.3. Pensum: Kap. boken flere lærer på data-lab YS-MEK 4.3.5 Konservatve krefter: v kan fnne en potensalfunksjon slk at: d d energbevarng vertkal kast: mg
Arbed og potensell energ 4.3.5 Mdtveseksamen: 6.3. Pensum: Kap. boken flere lærer på data-lab YS-MEK 4.3.5 Konservatve krefter: v kan fnne en potensalfunksjon slk at: d d energbevarng vertkal kast: mg
system 16 mm / 25 mm / 32 mm MONTERINGSVEILEDNING
 16 mm / 25 mm / 32 mm MONTERINGSVEILEDNING Sdoprofl Monterngsprofl Murprofl (tllval) (A) (B) 1000 mm 20 mm mn. 50 mm Klck! Før du starter monterngen av dtt nye tak, bør du kontrollere at du har motatt
16 mm / 25 mm / 32 mm MONTERINGSVEILEDNING Sdoprofl Monterngsprofl Murprofl (tllval) (A) (B) 1000 mm 20 mm mn. 50 mm Klck! Før du starter monterngen av dtt nye tak, bør du kontrollere at du har motatt
Magnetisk nivåregulering. Prosjektoppgave i faget TTK 4150 Ulineære systemer. Gruppe 4: Rune Haugom Pål-Jørgen Kyllesø Jon Kåre Solås Frode Efteland
 Magnetsk nvåregulerng Prosjektoppgave faget TTK 45 Ulneære systemer Gruppe 4: Rune Haugom Pål-Jørgen Kyllesø Jon Kåre Solås Frode Efteland Innholdsfortegnelse Innholdsfortegnelse... Innlednng... Oppgave
Magnetsk nvåregulerng Prosjektoppgave faget TTK 45 Ulneære systemer Gruppe 4: Rune Haugom Pål-Jørgen Kyllesø Jon Kåre Solås Frode Efteland Innholdsfortegnelse Innholdsfortegnelse... Innlednng... Oppgave
Rapportere kraftsystemdata i Fosweb
 Rapportere kraftsystemdata Fosweb Brukervelednng Sst oppdatert 03.04.2019 Rapportere kraftsystemdata Fosweb Innholdsoverskt Om denne brukervelednngen Introduksjon tl Fosweb Organserng av Fosweb Organserng
Rapportere kraftsystemdata Fosweb Brukervelednng Sst oppdatert 03.04.2019 Rapportere kraftsystemdata Fosweb Innholdsoverskt Om denne brukervelednngen Introduksjon tl Fosweb Organserng av Fosweb Organserng
Trykkløse rørsystemer
 Trykkløse rørsystemer har kabel- og avløpsrørsystemer PVC, PP og PE med komplette delespektre. PE benyttes trykkrør som utslppslednnger, som lednng dårlge masser (myr) og ved høy overdeknng og/eller høy
Trykkløse rørsystemer har kabel- og avløpsrørsystemer PVC, PP og PE med komplette delespektre. PE benyttes trykkrør som utslppslednnger, som lednng dårlge masser (myr) og ved høy overdeknng og/eller høy
Seleksjon og uttak av alderspensjon fra Folketrygden
 ato: 07.01.2008 aksbehandler: DH Seleksjon og uttak av alderspensjon fra Folketrygden Dette notatet presenterer en enkel framstllng av problemet med seleksjon mot uttakstdpunkt av alderspensjon av folketrygden.
ato: 07.01.2008 aksbehandler: DH Seleksjon og uttak av alderspensjon fra Folketrygden Dette notatet presenterer en enkel framstllng av problemet med seleksjon mot uttakstdpunkt av alderspensjon av folketrygden.
må det justeres for i avkastningsberegningene. se nærmere nedenfor om valg av beregningsmetoder.
 40 Metoder for å måle avkastnng Totalavkastnngen tl Statens petroleumsfond blr målt med stor nøyaktghet. En vktg forutsetnng er at det alltd beregnes kvaltetsskret markedsverd av fondet når det kommer
40 Metoder for å måle avkastnng Totalavkastnngen tl Statens petroleumsfond blr målt med stor nøyaktghet. En vktg forutsetnng er at det alltd beregnes kvaltetsskret markedsverd av fondet når det kommer
Terrasser TRAPPER OG REKKVERK LAG DIN EGEN UTEPLASS! VÅRE PRODUKTER HAR LANG LEVETID OG DU VIL HA GLEDE I DET DU HAR BYGGET I MANGE ÅR FREMOVER
 Terrasser TRAPPER OG REKKVERK LAG DIN EGEN UTEPLASS! VÅRE PRODUKTER HAR LANG LEVETID OG DU VIL HA GLEDE I DET DU HAR BYGGET I MANGE ÅR FREMOVER Malmfuru terrasse Malmfuru er den mest mljøvennlge terrassen
Terrasser TRAPPER OG REKKVERK LAG DIN EGEN UTEPLASS! VÅRE PRODUKTER HAR LANG LEVETID OG DU VIL HA GLEDE I DET DU HAR BYGGET I MANGE ÅR FREMOVER Malmfuru terrasse Malmfuru er den mest mljøvennlge terrassen
UNIVERSITETET I OSLO
 Løsnngsforslag UNIVERSITETET I OSLO Det matematsk-naturvtenskapelge fakultet Eksamen : INF3 Dgtal bldebehandlng Eksamensdag : Trsdag 9. mars 3 Td for eksamen : 5: 9: Løsnngsforslaget er på : sder Vedlegg
Løsnngsforslag UNIVERSITETET I OSLO Det matematsk-naturvtenskapelge fakultet Eksamen : INF3 Dgtal bldebehandlng Eksamensdag : Trsdag 9. mars 3 Td for eksamen : 5: 9: Løsnngsforslaget er på : sder Vedlegg
Løsningsforslag øving 10 TMA4110 høsten 2018
 Løsnngsforslag øvng TMA4 høsten 8 [ + + Projeksjonen av u på v er: u v v u v v v + ( 5) [ + u v v u [ 8/5 6/5 For å fnne ut om en matrse P representerer en projeksjon, må v sjekke om P P a) b) c) [ d)
Løsnngsforslag øvng TMA4 høsten 8 [ + + Projeksjonen av u på v er: u v v u v v v + ( 5) [ + u v v u [ 8/5 6/5 For å fnne ut om en matrse P representerer en projeksjon, må v sjekke om P P a) b) c) [ d)
Tema for forelesningen var Carnot-sykel (Carnot-maskin) og entropibegrepet.
 FORELESNING I ERMOYNMIKK ONSG 29.03.00 ema for forelesnngen var arnot-sykel (arnot-maskn) og entropbegrepet. En arnot-maskn produserer arbed ved at varme overføres fra et sted med en øy temperatur ( )
FORELESNING I ERMOYNMIKK ONSG 29.03.00 ema for forelesnngen var arnot-sykel (arnot-maskn) og entropbegrepet. En arnot-maskn produserer arbed ved at varme overføres fra et sted med en øy temperatur ( )
Adaptivt lokalsøk for boolske optimeringsproblemer
 Adaptvt lokalsøk for boolske optmerngsproblemer Lars Magnus Hvattum Høgskolen Molde Lars.M.Hvattum@hmolde.no Arne Løkketangen Høgskolen Molde Arne.Lokketangen@hmolde.no Fred Glover Leeds School of Busness,
Adaptvt lokalsøk for boolske optmerngsproblemer Lars Magnus Hvattum Høgskolen Molde Lars.M.Hvattum@hmolde.no Arne Løkketangen Høgskolen Molde Arne.Lokketangen@hmolde.no Fred Glover Leeds School of Busness,
TALLSVAR. Det anbefales at de 9 deloppgavene merket med A, B, teller likt uansett variasjon i vanskelighetsgrad. Svarene er gitt i << >>.
 ECON13: EKSAMEN 14V TALLSVAR. Det anbefales at de 9 deloppgavene merket med A, B, teller lkt uansett varasjon vanskelghetsgrad. Svarene er gtt >. Oppgave 1 Innlednng. Rulett splles på en rekke kasnoer
ECON13: EKSAMEN 14V TALLSVAR. Det anbefales at de 9 deloppgavene merket med A, B, teller lkt uansett varasjon vanskelghetsgrad. Svarene er gtt >. Oppgave 1 Innlednng. Rulett splles på en rekke kasnoer
Geometriske operasjoner
 Geometrske operasjoner INF 23 27.2.27 Kap. 9 (samt 5.5.2) Geometrske operasjoner Affne transformer Interpolasjon Samregstrerng av blder Endrer på pkslenes possjoner ransformerer pkselkoordnatene (x,) tl
Geometrske operasjoner INF 23 27.2.27 Kap. 9 (samt 5.5.2) Geometrske operasjoner Affne transformer Interpolasjon Samregstrerng av blder Endrer på pkslenes possjoner ransformerer pkselkoordnatene (x,) tl
ingen Fase I nødvendig konvergerer dersom LP er begrenset og konsistent skifter mellom primal og dual pivotering MoD233 - Geir Hasle - Leksjon 8 2
 Leksjon 8 Ofte behov for å løse mange relaterte LP Regnetid kan spares ved å bruke informasjon fra tidligere løsninger Parametrisk analyse homotopi-metoden Den Parametriske Selv-duale Simpleksmetoden ingen
Leksjon 8 Ofte behov for å løse mange relaterte LP Regnetid kan spares ved å bruke informasjon fra tidligere løsninger Parametrisk analyse homotopi-metoden Den Parametriske Selv-duale Simpleksmetoden ingen
DEN NORSKE AKTUARFORENING
 DEN NORSKE AKTUARFORENING _ MCft% Fnansdepartementet Postboks 8008 Dep 0030 OSLO Dato: 03.04.2009 Deres ref: 08/654 FM TME Horngsuttalelse NOU 2008:20 om skadeforskrngsselskapenes vrksomhet. Den Norske
DEN NORSKE AKTUARFORENING _ MCft% Fnansdepartementet Postboks 8008 Dep 0030 OSLO Dato: 03.04.2009 Deres ref: 08/654 FM TME Horngsuttalelse NOU 2008:20 om skadeforskrngsselskapenes vrksomhet. Den Norske
Seminaroppgaver for uke 13 (Oppgave (1), (2), og (3))
 1 ECON 2130 2017 vår Semarpla fra og med uke 13 Semaroppgaver for uke 13 (Oppgave (1), (2), og (3)) (1) Fra eksame Eco 2130, 2004 høst: Oppgave 3: (Fel oppgave på ststuttets overskt over gamle eksamesoppgaver)
1 ECON 2130 2017 vår Semarpla fra og med uke 13 Semaroppgaver for uke 13 (Oppgave (1), (2), og (3)) (1) Fra eksame Eco 2130, 2004 høst: Oppgave 3: (Fel oppgave på ststuttets overskt over gamle eksamesoppgaver)
Seminaroppgaver for uke 13
 1 ECON 2130 2016 vår Semarpla fra og med uke 13 Semaroppgaver for uke 13 1) Fra eksame Eco 2130, 2004 høst: Oppgave 3: (Fel oppgave på ststuttets overskt over gamle eksamesoppgaver) La X og Y være to uavhegge
1 ECON 2130 2016 vår Semarpla fra og med uke 13 Semaroppgaver for uke 13 1) Fra eksame Eco 2130, 2004 høst: Oppgave 3: (Fel oppgave på ststuttets overskt over gamle eksamesoppgaver) La X og Y være to uavhegge
NA Dok. 52 Angivelse av måleusikkerhet ved kalibreringer
 Sde: av 7 NA Dok. 5 Angvelse av måleuskkerhet ved kalbrernger Dokument kategor: Krav Fagområde: Kalbrerngslaboratorer Dette dokumentet er en oversettelse av EA-4/0 European Cooperaton for Accrédtaton of
Sde: av 7 NA Dok. 5 Angvelse av måleuskkerhet ved kalbrernger Dokument kategor: Krav Fagområde: Kalbrerngslaboratorer Dette dokumentet er en oversettelse av EA-4/0 European Cooperaton for Accrédtaton of
Innkalling til andelseiermøter
 Bergen, 27. aprl 2018 Innkallng tl andelseermøter Vedtektsendrnger verdpaprfondene Holberg Norge, Holberg Norden, Holberg Trton, Holberg Global, Holberg Rurk, Holberg Kredtt, Holberg Oblgasjon Norden,
Bergen, 27. aprl 2018 Innkallng tl andelseermøter Vedtektsendrnger verdpaprfondene Holberg Norge, Holberg Norden, Holberg Trton, Holberg Global, Holberg Rurk, Holberg Kredtt, Holberg Oblgasjon Norden,
NO kapittel 3.5 Næringsstruktur og faktoravlønning, Stolper Samuelson, Rybczynski
 1 Frelesnng 10 NO kapttel 3.5 Nærngsstruktur g faktravlønnng, Stlper Samuelsn, Rybczynsk 3.5 Lang skt Lkevekt arbeds g kaptalmarkeder Relevansen av langtdslkevekt Ikke skkert v får knvergens, en dynamsk
1 Frelesnng 10 NO kapttel 3.5 Nærngsstruktur g faktravlønnng, Stlper Samuelsn, Rybczynsk 3.5 Lang skt Lkevekt arbeds g kaptalmarkeder Relevansen av langtdslkevekt Ikke skkert v får knvergens, en dynamsk
NÆRINGSSTRUKTUR OG INTERNASJONAL HANDEL
 NÆRINGSSTRUKTUR OG INTERNASJONAL HANDEL Norman & Orvedal, kap. 1-5 Bævre & Vsle Generell lkevekt En lten, åpen økonom Nærngsstruktur Skjermet versus konkurranseutsatt vrksomhet Handel og komparatve fortrnn
NÆRINGSSTRUKTUR OG INTERNASJONAL HANDEL Norman & Orvedal, kap. 1-5 Bævre & Vsle Generell lkevekt En lten, åpen økonom Nærngsstruktur Skjermet versus konkurranseutsatt vrksomhet Handel og komparatve fortrnn
Arbeid og potensiell energi
 Arbed og potensell energ 5.3.4 YS-MEK 5.3.4 Konservatve krefter: v kan fnne en potensalfunksjon slk at: d d energbevarng vertkal kast: mg d d mg fjær: k d k d atom krstall: b cos b b d d sn b YS-MEK 5.3.4
Arbed og potensell energ 5.3.4 YS-MEK 5.3.4 Konservatve krefter: v kan fnne en potensalfunksjon slk at: d d energbevarng vertkal kast: mg d d mg fjær: k d k d atom krstall: b cos b b d d sn b YS-MEK 5.3.4
DET KONGELIGE FISKERI- OG KYSTDEPARTEMENT. prisbestemmelsen
 DET KONGELIGE FISKERI- OG KYSTDEPARTEMENT Fskebãtredernes forbund Postboks 67 6001 ALESUND Deres ref Var ref Dato 200600063- /BSS Leverngsplkt for torsketrálere - prsbestemmelsen V vser tl Deres brev av
DET KONGELIGE FISKERI- OG KYSTDEPARTEMENT Fskebãtredernes forbund Postboks 67 6001 ALESUND Deres ref Var ref Dato 200600063- /BSS Leverngsplkt for torsketrálere - prsbestemmelsen V vser tl Deres brev av
C(s) + 2 H 2 (g) CH 4 (g) f H m = -74,85 kj/mol ( angir standardtilstand, m angir molar størrelse)
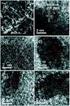 Fyskk / ermodynamkk Våren 2001 5. ermokjem 5.1. ermokjem I termokjemen ser v på de energendrnger som fnner sted kjemske reaksjoner. Hver reaktant og hvert produkt som nngår en kjemsk reaksjon kan beskrves
Fyskk / ermodynamkk Våren 2001 5. ermokjem 5.1. ermokjem I termokjemen ser v på de energendrnger som fnner sted kjemske reaksjoner. Hver reaktant og hvert produkt som nngår en kjemsk reaksjon kan beskrves
COLUMBUS. Lærerveiledning Norge og fylkene. ved Rolf Mikkelsen. Cappelen Damm
 COLUMBUS Lærervelednng Norge og fylkene ved Rolf Mkkelsen Cappelen Damm Innlednng Columbus Norge er et nteraktvt emddel som nneholder kart over Norge, fylkene og Svalbard, samt øvelser og oppgaver. Det
COLUMBUS Lærervelednng Norge og fylkene ved Rolf Mkkelsen Cappelen Damm Innlednng Columbus Norge er et nteraktvt emddel som nneholder kart over Norge, fylkene og Svalbard, samt øvelser og oppgaver. Det
Bruk av tabusøk og critical event memory på set partitioning-problemet
 Bruk av tabusøk og crtcal event memory på set parttonng-problemet Chrstan Magnus Berg Insttutt for Informatkk, Unverstetet Bergen chrsta@.ub.no Arne Løkketangen Insttutt for Informatkk, Høgskolen Molde
Bruk av tabusøk og crtcal event memory på set parttonng-problemet Chrstan Magnus Berg Insttutt for Informatkk, Unverstetet Bergen chrsta@.ub.no Arne Løkketangen Insttutt for Informatkk, Høgskolen Molde
Notater. Bjørn Gabrielsen, Magnar Lillegård, Berit Otnes, Brith Sundby, Dag Abrahamsen, Pål Strand (Hdir)
 2009/48 Notater Bjørn Gabrelsen, Magnar Lllegård, Bert Otnes, Brth Sundby, Dag Abrahamsen, Pål Strand (Hdr) Notater Indvdbasert statstkk for pleeog omsorgstjenesten kommunene (IPLOS) Foreløpge resultater
2009/48 Notater Bjørn Gabrelsen, Magnar Lllegård, Bert Otnes, Brth Sundby, Dag Abrahamsen, Pål Strand (Hdr) Notater Indvdbasert statstkk for pleeog omsorgstjenesten kommunene (IPLOS) Foreløpge resultater
SIF5072 Stokastske prosesser Sde 2 av 6 b) Hva vl det s at en Markov-kjede er rredusbel? Er Markov-kjeden fx n g denne oppgaven rredusbel? Er den aper
 Norges teknsk naturvtenskapelge unverstet Insttutt for matematske fag Sde 1 av 6 Faglg kontakt under eksamen: Bo Lndqvst 73 59 35 20 EKSAMEN I FAG SIF5072 STOKASTISKE PROSESSER Mandag 13. august 2001 Td:
Norges teknsk naturvtenskapelge unverstet Insttutt for matematske fag Sde 1 av 6 Faglg kontakt under eksamen: Bo Lndqvst 73 59 35 20 EKSAMEN I FAG SIF5072 STOKASTISKE PROSESSER Mandag 13. august 2001 Td:
Fourieranalyse. Fourierrekker på reell form. Eksempel La. TMA4135 Matematikk 4D. En funksjon sies å ha periode p > 0 dersom
 TMA435 Matematkk 4D Foureranalyse Fourerrekker på reell form En funksjon ses å ha perode p > dersom f(x + p) = f(x) () for alle x defnsjonsmengden tl f. Den mnste p slk at () holder, kalles fundamentalperoden
TMA435 Matematkk 4D Foureranalyse Fourerrekker på reell form En funksjon ses å ha perode p > dersom f(x + p) = f(x) () for alle x defnsjonsmengden tl f. Den mnste p slk at () holder, kalles fundamentalperoden
Alderseffekter i NVEs kostnadsnormer. - evaluering og analyser
 Alderseffekter NVEs kostnadsnormer - evaluerng og analyser 2009 20 06 20 10 20 10 20 10 21 2011 20 10 20 10 20 10 20 10 20 10 20 10 20 10 20 10 20 10 R A P P O R T 20 10 20 10 20 10 20 10 20 10 20 10 20
Alderseffekter NVEs kostnadsnormer - evaluerng og analyser 2009 20 06 20 10 20 10 20 10 21 2011 20 10 20 10 20 10 20 10 20 10 20 10 20 10 20 10 20 10 R A P P O R T 20 10 20 10 20 10 20 10 20 10 20 10 20
Klassisk Mekanikk IVER H. BREVIK. KOMPENDIUM i faget TEP4145 Til L A TEXved Simen Ellingsen
 Klasssk Mekankk IVER H. BREVIK KOMPENDIUM faget TEP4145 Tl L A TEXved Smen Ellngsen Insttutt for Energ og Prosessteknkk, Norges Teknsk Naturvtenskapelge Unverstet Mars 2006 Klasssk Mekankk Iver H. Brevk
Klasssk Mekankk IVER H. BREVIK KOMPENDIUM faget TEP4145 Tl L A TEXved Smen Ellngsen Insttutt for Energ og Prosessteknkk, Norges Teknsk Naturvtenskapelge Unverstet Mars 2006 Klasssk Mekankk Iver H. Brevk
STK desember 2007
 Løsnngsfrslag tl eksamen STK0 5. desember 2007 Oppgave a V antar at slaktevektene tl kalkunene fra Vrgna er bserverte verder av stkastske varabler X, X 2, X, X 4 sm er uavhengge g Nµ, σ 2 -frdelte, g at
Løsnngsfrslag tl eksamen STK0 5. desember 2007 Oppgave a V antar at slaktevektene tl kalkunene fra Vrgna er bserverte verder av stkastske varabler X, X 2, X, X 4 sm er uavhengge g Nµ, σ 2 -frdelte, g at
Ambulanseflystruktur og operativ/teknisk kravspesifikasjon. Høringsuttalelser (ajour 26.01.2007) Kommentarer beredskap
 Ambulanseflystruktur og operatv/teknsk kravspesfkasjon. Hørngsuttalelser (ajour 26.01.2007) Hørngsnstans Kommentar basestruktur Kommentarer beredskap Kommentarer tlbudsdok/ kravspek Andre kommentarer RHF:
Ambulanseflystruktur og operatv/teknsk kravspesfkasjon. Hørngsuttalelser (ajour 26.01.2007) Hørngsnstans Kommentar basestruktur Kommentarer beredskap Kommentarer tlbudsdok/ kravspek Andre kommentarer RHF:
Tretak VARIG, MILJØVENNLIG OG TRADISJONELT
 Tretak VARIG, MILJØVENNLIG OG TRADISJONELT ROYAL FARGER BRUN med UV-beskyttelse Alvdal Royal tretak Et varg og formstablt furu tretak CU-mpregnert klasse AB og Royal behandlet. KLAR uten UV-pgment, vl
Tretak VARIG, MILJØVENNLIG OG TRADISJONELT ROYAL FARGER BRUN med UV-beskyttelse Alvdal Royal tretak Et varg og formstablt furu tretak CU-mpregnert klasse AB og Royal behandlet. KLAR uten UV-pgment, vl
EKSAMEN I TFY4210 ANVENDT KVANTEMEKANIKK Torsdag 11. august, Tillatte hjelpemidler : K.Rottman, Matematisk formelsamling
 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglg kontakt under eksamen: Professor Asle Sudbø, tlf 93403 EKSAMEN I TFY4210 ANVENDT KVANTEMEKANIKK Torsdag 11. august, 2005 09.00-13.00
NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglg kontakt under eksamen: Professor Asle Sudbø, tlf 93403 EKSAMEN I TFY4210 ANVENDT KVANTEMEKANIKK Torsdag 11. august, 2005 09.00-13.00
Oppgave 3, SØK400 våren 2002, v/d. Lund
 Oppgave 3, SØK400 våren 00, v/d. Lnd En bonde bonde dyrker poteter. Hvs det blr mldvær, blr avlngen 0. Hvs det blr frost, blr avlngen. Naboen bonde, som vl være tsatt for samme vær, dyrker også poteter,
Oppgave 3, SØK400 våren 00, v/d. Lnd En bonde bonde dyrker poteter. Hvs det blr mldvær, blr avlngen 0. Hvs det blr frost, blr avlngen. Naboen bonde, som vl være tsatt for samme vær, dyrker også poteter,
Fleksibelt arbeidsliv. Befolkningsundersøkelse utført for Manpower September 2015
 Fleksbelt arbedslv Befolknngsundersøkelse utført for Manpower September 015 Antall dager med hjemmekontor Spørsmål: Omtrent hvor mange dager jobber du hjemmefra løpet av en gjennomsnttsmåned (n=63) Prosent
Fleksbelt arbedslv Befolknngsundersøkelse utført for Manpower September 015 Antall dager med hjemmekontor Spørsmål: Omtrent hvor mange dager jobber du hjemmefra løpet av en gjennomsnttsmåned (n=63) Prosent
Samfunnsøkonomi andre avdeling, mikroøkonomi, Diderik Lund, 18. mars 2002
 Samfunnsøkonom andre avdelng, mkroøkonom, Dderk Lund, 8. mars 00 Markeder under uskkerhet Uskkerhet vktg mange (de fleste? markeder Uskkerhet omkrng framtdge prser og leverngsskkerhet (f.eks. om leverandør
Samfunnsøkonom andre avdelng, mkroøkonom, Dderk Lund, 8. mars 00 Markeder under uskkerhet Uskkerhet vktg mange (de fleste? markeder Uskkerhet omkrng framtdge prser og leverngsskkerhet (f.eks. om leverandør
Alvdal Royal kledning
 Klednng STORT UTVALG AV KLEDNINGSPRODUKTER UNIK BEHANDLING AV HVERT PROSJEKT FOKUS PÅ MILJØVENNLIGE LØSNINGER Alvdal Royal klednng Vår bestselger når det gjelder kvaltet, levetd og prs. Lang levetd Begrenset
Klednng STORT UTVALG AV KLEDNINGSPRODUKTER UNIK BEHANDLING AV HVERT PROSJEKT FOKUS PÅ MILJØVENNLIGE LØSNINGER Alvdal Royal klednng Vår bestselger når det gjelder kvaltet, levetd og prs. Lang levetd Begrenset
14 Systemer av differensiallikninger TMA4110 høsten 2018
 Systemer v fferensllknnger TMA høsten 8 I ette kptlet skl v ruke et v hr lært om lneær lger tl å løse fferensllknnger Det fnnes fferensllknnger for nesten lt, men et er kun e ller enkleste som er mulg
Systemer v fferensllknnger TMA høsten 8 I ette kptlet skl v ruke et v hr lært om lneær lger tl å løse fferensllknnger Det fnnes fferensllknnger for nesten lt, men et er kun e ller enkleste som er mulg
Bente Halvorsen, Bodil M. Larsen og Runa Nesbakken
 2005/8 Rapporter Reports Bente Halvorsen, Bodl M. Larsen og Runa Nesbakken Prs- og nntektsfølsomet ulke usoldnngers etterspørsel etter elektrstet, fyrngsoler og ved Statstsk sentralbyrå Statstcs Norway
2005/8 Rapporter Reports Bente Halvorsen, Bodl M. Larsen og Runa Nesbakken Prs- og nntektsfølsomet ulke usoldnngers etterspørsel etter elektrstet, fyrngsoler og ved Statstsk sentralbyrå Statstcs Norway
TMA4300 Mod. stat. metoder
 TMA4300 Mod stat metoder Norges teknsk-naturvtenskapelge unverstet Insttutt for matematske fag Løsnngsforslag - Eksamen jun 2007 Oppgave Pseudokode for å evaluere θ: Generer uavhengge realsasjoner x,,x
TMA4300 Mod stat metoder Norges teknsk-naturvtenskapelge unverstet Insttutt for matematske fag Løsnngsforslag - Eksamen jun 2007 Oppgave Pseudokode for å evaluere θ: Generer uavhengge realsasjoner x,,x
TMA4265 Stokastiske prosesser
 Norges teknsk-naturvtenskapelge unverstet Insttutt for matematske fag TMA65 Stokastske prosesser Våren Løsnngsforslag - Øvng Oppgaver fra læreboka.6 P er dobbelt stokastsk P j j La en slk kjede være rredusbel,
Norges teknsk-naturvtenskapelge unverstet Insttutt for matematske fag TMA65 Stokastske prosesser Våren Løsnngsforslag - Øvng Oppgaver fra læreboka.6 P er dobbelt stokastsk P j j La en slk kjede være rredusbel,
EKSAMEN I FAG SIF8052 VISUALISERING MANDAG 21. MAI 2001 KL LØSNINGSFORSLAG
 Sde 1 av 5 NTNU Norges teknsk-naturvtenskapelge unverstet Fakultet for fyskk, nformatkk og matematkk Insttutt for datateknkk og nformasjonsvtenskap EKSAMEN I FAG SIF8052 VISUALISERING MANDAG 21. MAI 2001
Sde 1 av 5 NTNU Norges teknsk-naturvtenskapelge unverstet Fakultet for fyskk, nformatkk og matematkk Insttutt for datateknkk og nformasjonsvtenskap EKSAMEN I FAG SIF8052 VISUALISERING MANDAG 21. MAI 2001
De normalfordelte: x og sd for hver gruppe. De skjevfordelte og de ekstremt skjevfordelte: Median og kvartiler for hver gruppe.
 STK H-26 Løsnngsforslag Alle deloppgaver teller lkt vurderngen av besvarelsen. Oppgave I et tlfeldg utvalg på normalvektge personer, og overvektge personer, måles konsentrasjonen av 2 ulke protener blodet.
STK H-26 Løsnngsforslag Alle deloppgaver teller lkt vurderngen av besvarelsen. Oppgave I et tlfeldg utvalg på normalvektge personer, og overvektge personer, måles konsentrasjonen av 2 ulke protener blodet.
Arbeid og potensiell energi
 Arbed og potensell energ.3.7 YS- MEK.3.7 Konservatve krefter: v kan fnne en potensalfunksjon slk at: d energbevarng vertkal kast: mg d mg fjær: k k d atom krstall: b π cos π b b d π sn b YS- MEK.3.7 kraft
Arbed og potensell energ.3.7 YS- MEK.3.7 Konservatve krefter: v kan fnne en potensalfunksjon slk at: d energbevarng vertkal kast: mg d mg fjær: k k d atom krstall: b π cos π b b d π sn b YS- MEK.3.7 kraft
Dynamisk programmering. Hvilke problemer? Optimalitetsprinsippet. Overlappende delproblemer
 ynask prograerng Metoden ble foralsert av Rchard Bellann (RAN Corporaton på -tallet. Prograerng betydnngen planlegge, ta beslutnnger. (Har kke noe ed kode eller å skrve kode å gøre. ynask for å ndkere
ynask prograerng Metoden ble foralsert av Rchard Bellann (RAN Corporaton på -tallet. Prograerng betydnngen planlegge, ta beslutnnger. (Har kke noe ed kode eller å skrve kode å gøre. ynask for å ndkere
Heltallighetsteoremet for nettverksflyt Königs teorem Denne gang: Anvendelser nettverksflyt
 Leksjon 9 Begreper nettverk / grafteori Minimum-kost nettverksflyt Moellering Spesialvariant av Simpleksmetoen Heltallighetsteoremet for nettverksflyt Königs teorem Denne gang: Anvenelser nettverksflyt
Leksjon 9 Begreper nettverk / grafteori Minimum-kost nettverksflyt Moellering Spesialvariant av Simpleksmetoen Heltallighetsteoremet for nettverksflyt Königs teorem Denne gang: Anvenelser nettverksflyt
