Løsningsforslag Utvalgte eksamensoppgaver i uiddynamikk
|
|
|
- Terje Aamodt
- 7 år siden
- Visninger:
Transkript
1 HØGSKOLEN I STAVANGER Institutt fo matematikk og natuvitenskap Løsningsfoslag Utvalgte eksamensoppgave i uiddynamikk Løsningsfoslag til de este oppgave i kuset TE 6349 Fluiddynamikk ved HiS/HSR fo tiden tidligee numme 4349 og TE 349). Fo noen oppgave henvises det til løsningsfoslag fo paktisk talt identiske oppgave i Jan Finjods Fluiddynamikk fo millione efeet til som Finjod). Fo to oppgave, som ikke falle innenfo dagens pensum, foeligge intet løsningsfoslag. Læebok i kuset e D. J. Titton: Physical Fluid Dynamics, som efeees til som Titton. Stavange, Pe A Amundsen 1
2 1992 V: Se 1996V, oppgave 2, nedenfo. Oppgave 2 Tilsvae stot sett 1995V, oppgave 2, nedenfo. Oppgave 3 Dette tilsvae oppgave 8.1 hos Finjod, som skissee løsningen på sidene Oppgave 4 Se 1995H, oppgave 4 nedenfo V: NavieStokes ligning lyde ρ Du Dt = p + µ 2 u Fo R 1 kypende støm) kan vi neglisjee det dynamiske leddet Du Dt, så vi ha tilnæmet p µ 2 u. Fo et kvalitativt esultat må det væe nok å betakte én-dimensjonal støm, og dimensjonsanalyse gi da tykkfallet som: x = u µ 2 x 2 p L µ U L 2 p µu L Desom dette tykkfallet skal balansees av kompesjon av uidet, må vi ha dvs.: p ρ ρ = c2 s, p ρ ρ = c2 s ρ µu L Desom uidet skal betaktes som inkompessibelt må den elative kompesjonen væe liten: ρ ρ 1 µu ρlc 2 s = νu Lc 2 s 1 U 2 c 2 s = M 2 LU ν = R, de M e Mach-tallet. Oppgave 2 Denne oppgaven e ligge utenfo dagens pensum. 2
3 Oppgave 3 Siden vi hele tiden betakte to-dimensjonal laminæ støm, avhenge alle vaiable kun av x, y, og t. a) Hvis u, t) = u,, ), edusee kontinuitetsligningen seg til: u = u = u = uy, t). x Dette medføe: Du Dt u u + u )u = t t + u u x = u t. y- og z-komponentene til NavieStokes ligning edusee seg til = y og = z så p = px, t). Vi stå da igjen med x-komponenten av NavieStokes ligning, som kan skives: 1 ρ x = Du Dt ν 2 u = u t ν 2 u y 2 Siden u = uy, t), e høye side av denne ligningen uavhengig av x, så x helle ikke avhenge av x, må vi ha: så Gt) = p L = Gt) dvs. p = Gt) i x L L p = x dx = Gt) dx = Gt)L.. Ligningen fo uy, t) bli da: må væe det. Da denne u t ν 2 u y 2 = Gt) ρ ) som e en inhomogen) lineæ patiell dieensialligning. Gensebetingelsene andbetingelsene) e u a, t) = ua, t) = ; uy, ) = u y), de u y) e hastighetsfeltet ved t = [som ikke e oppgitt]. b) Vi må he anta at ω e en sikelfekvens nedenfo kalt Ω). I så fall e dimensjonen til poduktet yω en hastighet: [yω] = U. Følgelig e [ωy 2 /ν] = UL/ν, dimensjonen til et eynoldstall, som e dimensjonsløst. c) Hvis Gt) = G, ha vi den stasjonæ løsning u t som µ = νρ) = ) av ν 2 u y 2 = G ρ uy) = G 2µ y2 + Ay + B Integasjonskonstantene A og B bestemmes av u±a) = som A =, B = G 2µ a2, så vi ha standad Poiseuille-Hagen løsning u = G 2µ a2 y 2 ) Fo µ = ν = ha vi = G /p, som kun e mulig hvis tykkfallet fosvinne. Fo µ ha vi paabolsk pol sml g 2.5 i Titton fo x = ). Fo µ = e ethvet hastighetspol mulig. 3
4 d) Siden ligningen fo uy, t) e lineæ, e den eelle og også den imaginæe) delen av en kompleks løsning en løsning. Vi søke defo en løsning på kompleks fom: Gt) = G cosωt) = Re G e iωt og u = Re Uy)e iωt. Innsatt i *) gi dette iωe iωt Uy) νe iωt 2 U y 2 = 1 ρ G e iωt U + i Ω ν U = G µ, ) hvo meket angi deivasjon med hensyn på y. Denne ligningen ha en løsning Uy) = U = i G. Til Ωρ denne kan vi legge til en vilkålig løsning av den tilsvaende homogene ligning U + i Ω ν U =. Denne ligning ha løsninge av fomen Ae κy, de κ må tilfedsstille de k = Ω 2ν κ 2 + i Ω ν = κ = iω ν Den geneelle løsning av **) bli altså: Ω = ± 1 + i) 2ν = ± 1 + i)k, Uy) = Ae κy + Be κy + U = Ae ky e iky + Be ky e iky + i G Ωρ Randkavet Ua) = U a) gi A = B, dvs Ua) = bestemme så A som så den fysiske løsningen bli: Uy) = 2A [cosky) coshky) i sinky) sinhky)] + i G Ωρ A = i G 2Ωρ uy, t) = Re Uy)e iωt = Re 1 coska) coshka) i sinka) sinhka), Vi skal ikke fosøke å foenkle dette uttykket ytteligee. Fo et ikke-viskøst uid ν = ) kan vi skive **) som så { [ ]} ig cosky) coshky) i sinky) sinhky) Ωρ e iωt 1. coska) coshka) i sinka) sinhka) iωu = G ρ uy, t) = Re Vi se at gensen Ω statisk tykk) e entydig: Uy) = i G Ωρ { } ig Ωρ e iωt = G Ωρ sinωt) G G t sinωt) uy, t) lim sinωt) = lim = G t Ω Ωρ Ω ρ Ωt ρ, så hastigheten øke lineæt med tiden. Siden, i favæ av viskositet, en konstant tykkaft nettopp må føe til en hastighet som øke lineæt med tiden, e dette den fysisk koekte løsning. Dette foklae hvofo vi ikke fant noen stasjonæ løsning fo denne situasjonen i c) ovenfo. 1 sml. b) ovenfo), bø stømmen bli laminæ, dvs. Poiseuille-, så: e) Fo langsom bevegelse, Ωy2 ν Ωa2 ν lignende. I gensen Ω vil k = Ω 2ν cosky) k2 y 2, coshky) k2 y 2, sinky) ky, sinhky) ky, 4
5 med tilsvaende uttykk fo funksjone av ka. Dette gi husk at geneelt e 1 + x) 1 1 x fo små x): så Uy) ig Ωρ [ k2 y 2 ) k2 y 2 ) ik 2 y 2 ] G k k2 a 2 ) k2 a 2 ) ik 2 a 2 Ωρ a2 y 2 ) = G 2µ a2 y 2 ). uy, t) Re G 2µ a2 y 2 ) e iωt = G cosωt) a 2 y 2 ) Ω ). 2µ Dette e ligningen fo Poiseuille-Hage støm, med tidsavhengig tykk-gadient, Gt) = G cosωt). f) Fo alle vedie av Ω e hastigheten midt mellom platene, y =, gitt som: u, t) = Re Fo stoe Ω, dvs. stoe k, ha vi da { [ ]} ig 1 Ωρ e iωt 1 coska) coshka) i sinka) sinhka) Dette gi u, t) Re coshka) = 1 2 e ka + e ka) 1 2 eka, sinhka) = 1 2 e ka e ka) 1 2 eka. ) { [ ig 2e ka ]} Ωρ e iωt 1 Re ig coska) i sin ka Ωρ e iωt = G sinωt) = G cosωt π 2 ) Ωρ Ωρ Dette esultatet e uavhengig av µ [i oppgaven må ω estattes med Ω]. Det e tilstekkelig å betakte stømmen næ den øve veggen, y a. Fo stoe k kan vi he også benytte ***), eventuelt med ka estattet med ky. Dette gi uy, t) Re { ig Ωρ e iωt [ 1 e ka y) e ika y)]} Fo å foenkle ytteligee, må vi vite om vi e så næ veggen at k a y 1, dvs om elle ei samtidig som Ωa2 ν og nne Ω 2ν a y 2 1 1). Hvis dette e tilfellet, kan vi ekkeutvikle eksponentialfunksjonene, { } { ig uy, t) Re Ων e iωt [1 1 1 i)ka y))] = Re 1 + i) G } k a y)e iωt Ωρ { } 2G k = Re a y)e i Ωt+ π 4 ) = G cosωt π 4 ) a y). Ωρ νωρ He ha vi bukt at e i π 4 = 1 + i)/ 2. Siden vi ha y 2 a 2 = y + a)y a) 2ay a) næ veggen, ligne dette på en Poiseuille-støm, men med modiset amplitude og en fasefoskyvning på π/4. [Lenge vekk fa veggen, de k 2 a y) 2 = Ω 2ν a y)2 1, kan vi neglisjee leddene med eksponentialfunksjone, og nne som e samme esultat som midt i øet.] uy, t) Re ig Ωρ e iωt = G Ωρ sinωt) Abeidmengden i denne oppgaven kan synes ufoholdsmessig sto. 5
6 1994 V: Dette tilsvae stot sett 1996V, oppgave 1 se nedenfo). Oppgave 2 Se løsningsfoslag til oppgave 4.1 hos Finjod s. 2123). Sml. også avsnitt 9.3 i Titton foeleses fo tiden ikke). Oppgave 3 Fo tiden utenfo pensum. Oppgave 4 Dette tilsvae stot sett oppgave 1.3 hos Finjod løsningsfoslag på s. 229) V: Det e oppgitt at u = u, v, w) = Ωy, Ωx, w ). Ligningene fo stømlinjene, gi da f. eks. dx u = dy v = dz w, dx u = dy v dx Ωy = dy Ωx Ωx dx + y dy) = Ω 2 dx2 + y 2 ) =, så x 2 + y 2 = a 2, de a e en vilkålig integasjonskonstant. Dette e ligningen fo en sikulæ sylinde om z-aksen, med adius a. Altenativt kunne vi ha skevet nest siste ligning ovenfo som y dy dx = x, og integet denne sepaable dieensialligningen på vanlig måte). En annen, uavhengig, ligning bli da: dx u = dz w dx Ωy = dz w dz dx = w Ω a 2 x 2, med løsning x w z = Ω a 2 x = w 2 Ω acsin x a + z, de z e en integasjonskonstant. Denne ligning kan invetees til å gi z = a sin w + α), de α e en annen vilkålig) konstant, gitt ved henholdsvis α = Ωz w og α = Ωz w + π fo de to valgene av fotegn. Ωz 6
7 Oppgave 2 I løsningsfoslaget følges Tittons fotegnskonvensjon med u = Φ. a) De betingelsene som må oppfylles e: 1) Siden u = Φ = divegensen til en cul fosvinne alltid), e stømmens vivelfi. Hastighetskomponentene i sylindekoodinate bli: u = Φ = u 1 a2 2 u φ = 1 Φ φ = u 1 + a2 2 u z = Φ z = ) cos φ ) sin φ Stømmen e altså to-dimensjonal, og vi vil neglisjee z-komponenten i det følgende. Vi nne da: u = 1 u ) + 1 u φ φ = u [1 + a2 2 ) cos φ 1 + a2 2 ) ] sin φ = Følgelig oppfylle stømmen kontinuitetsligningen fo et inkompessibelt uid. Dette bety at u = 2 Φ =, som e ekvivalent med Eule-ligningen fo vivelfi støm. [At hastighetspotensialet fo slik støm oppfylle Laplaces ligning, e pensum, og anses kjent]. 2) Diekte innsetting gi koekt gensebetingelse på sylindeen, u a, φ, z) =. 3) Gensebetingelsen nå bli: u u cos φ, u φ u sin φ, som e støm med konstant hastighet u i etningen cos φ e + sin φ e φ ) = i, dvs i negativ x-etning. b) Stømmen i denne del av oppgaven, u b e den samme som i a), som vi nå kalle u a, botsett fa et tillegg u = Γ 2π e φ u φ e φ, dvs u b = u a + u. Utenfo sylindeen > a) ha vi u) = u φ z = u) φ = u) z = 1 u φ ) = 1 ) Γ =, 2π så u b = u a =, og stømmen e vivelfi, og kan defo avledes av et nytt hastighetspotensial, Φ b. Siden u = 1 u φ φ =, og defo 2 Φ b =, beskive også u b vivelfi inkompessibel Eulestøm. Videe e andbetingelsene uendede: På sylindeen siden u b a, φ) = og likeledes nå, Γ siden lim 2π =. Sikulasjonen undt sylindeen bli: S = a u b dl = a u a dl + a Γ 2π 2π e φ dl = Φ dl + a siden linjeintegalet av en gadient undt en lukket kuve alltid fosvinne. Γ 2π dφ = + Γ = Γ c) Siden stømmen e vivelfi, e stagnasjonstykket det samme fo alle stømlinje. Vi benytte Benoullis ligning fo en stømlinje i det uendelige og en annen på sylindeoveaten: p ρu2 = pa, φ) ρu φa, φ) 2 7
8 elle p = p p = 1 2 ρ [u 2 u 2 2 sin φ + Γ ) ] 2 = 1 [ 2πau 2 ρu2 1 4 sin 2 φ 2Γ Γ 2 ] sin φ πau 2πau ) 2. Tykket e ettet vinkelett mot sylindeoveaten, og egnes positivt innove mot denne. Løftet pe lengdeenhet i z-etningen e gitt som: L = F L l = 2π = 1 2 aρu2 pa, φ) sin φ a dφ 2π [ sin φ 1 4 sin 2 φ 2Γ Γ 2 ] sin φ πau 2πau ) 2 dφ Leddene som inneholde odde potense av sin φ fosvinne ved integasjon ove en hel peiode, så L = 1 2Γ 2 aρu2 πau 2π i oveensstemmelse med Kutta-Joukowskis teoem. Oppgave 3 sin 2 φ dφ = ρu Γ, Dette tilsvae oppgave 8.1 hos Finjod, som skissee løsningen på sidene H: Se 1996V, oppgave 2, nedenfo. Oppgave 2 a) Beegne sikulasjonen undt en sikel med adius > R og samme sentum som sylindeen d = d e + dφ e φ ): 2π 2π u d = dφ = Γ. ) 2π u φ dφ = u 1 + R2 2 sin φ dφ Γ 2π At fotegnet e negativt bety at sikulasjonen e i negativ deieetning med uviseen). b) Hastighetsfeltet avhenge ikke av viskositeten, og fo vivelfi ikke-viskøs støm gjelde Benoullis ligning med samme konstant stagnasjonstykk) fo alle stømlinje. Hvis tykket på sylindeveggen og uendelig langt vekk fa denne betegnes med henholdsvis pφ) og p, ha vi: p ρu2 = pφ) ρu2 pφ) p = 1 2 ρu2 2 sin φ Γ 2πR ) 2, 1 4 sin 2 φ 2Γ πru sin φ Γ 2 ) 4π 2 R 2 u 2. Løftet pe lengdeenhet vinkelett på stømetningen, L, nnes ved å ta pojeksjonen av tykk-kaften i denne etningen pass på fotegn, tykket vike i negativ -etning!), og integee ove sylindeoveaten. Beegningen foenkles ved å meke seg at tykkfoskjellen mellom to diametalt motsatte punkte på sylindeen e pφ) pφ + π) = 2Γρu πr sin φ. L = 2π pφ)r sin φ dφ = R = ρu Γ = ρu Γ), i henhold til Kutta-Joukowskis teoem. π pφ) pφ + π)) sin φ dφ = 2Γρu π 8 π sin 2 φ dφ
9 Oppgave 3 Dette tilsvae oppgave 8.1 hos Finjod, som skissee løsningen på sidene Oppgave 4 Det e oppgitt at laminæe gensesjikt e stabile fo R = UL/ν 1 6. a) R = : Intet laminæt gensesjikt. b) R = 1 6 : Maginalt stabilt laminæt gensesjikt, i alle fall den foe delen e nok. c) R = km/h = 1 m/s): Intet signikant laminæt gensesjikt V: a) Nå u = u z =, edusee vivlingen seg til w =,, ω z ), de ω z = u φ + u φ. Med u φ = A nne vi da ω z = A + A/ = 2A. Vivlingen fosvinne altså ikke noe sted, og konstanten i Benoullis ligning stagnasjonstykket) e foskjellig fo alle stømlinje. b) Med u φ = B/ bli ω z = B/ 2 + B/ 2 = fo / ). Vivlingen fosvinne altså utenfo oigo, og stagnasjonstykket e det samme fo alle stømlinje. c) d) Siden u = u φ e φ få vi med dl = dφ e φ få sikulasjonen om en sikelkuve med adius som Γ = u dl = 2π u φ dφ = 2π B dφ = 2πB Siden vivlingen fosvinne utenfo = e sikulasjonen den samme fo alle lukkede kuve, uavhengig av fom og støelse, som omslutte oigo i samme etning) en gang. 9
10 Oppgave 2 a) Fo ikke-viskøs støm gjelde u θ = u [ ) ] 3 R sin θ så u θ u = u sin θ bemek u θ > u ). Følgelig ha vi 1% avvik fa asymptotisk hastighet nå: u θ u = R 3 ) = 1.1 dvs =.2) 1/3 R 3.7R. b) Nå e u θ = u [ R 1 4 ) ] 3 R sin θ så i dette tilfellet e u θ < u ): u θ = u [ R 1 4 Fo å løse den siste ligningen anta vi at R, så R som e konsistent med antagelsen om at ) R 3 R. Oppgave 3 Se 1997V, oppgave 2 a, c og d nedenfo. Oppgave 4 ) ] 3 R =.99 3 R ) 3 R + =.4 ) 3 R. I så fall bli 3 R.4, elle 75R, a) Den tubulente skjæspenningen på veggen e τ w = ρu 2 τ. Da bli den viskøse fiksjons bidag til dag-kaften F µ husk at vingene ha to side!) F µ = 2Lcτ w = 2Lcρ uτ u ) 2 u 2 = 2 4 N b) Foat vingene skal egnes som glatte, må støelsen på oveateujevnhetene væe betydelig minde enn tykkelsen på det viskøse undesjiktet. Det siste ha tykkelse omtent δ L 8 ν u τ = 8 u µu ρu τ 5 µm 1997 V: I hele oppgaven e u z =, og vi ha ingen z-avhengighet, så u, φ) = u, φ) e + u φ, φ) e φ. a) Fo viskøs støm må hastigheten til væsken på sylindeoveaten væe lik hastigheten til oveaten selv: u R, φ) =, u φ R, φ) = ωr. 1
11 Hastigheten uendelig langt vekk fa sylindeen fosvinne: u, φ), u φ, φ) as. Siden dl = R dφ e φ, bli sikulasjonen undt oveaten: Γ = u dl = 2π =R u φ R dφ = 2πωR 2. b) På gunn av sylindesymmeti e alle etninge likevedige, så u = u ), u φ = u φ ). Kontinuitetsligningen dvs. massebevaelse) gi at den adielle hastigheten da må fosvinne, u ) = : Det må gå like mye uid inn og ut av ethvet sylindisk skall som e koaksialt med sylindeen, men det e ingen støm ut av sylindeen. Altenativt kan dette sees av kontinuitetsligningen: u = u + u = med løsning u ) = C. C bestemmes ved andbetingelsen u R) = C /R =, dvs. C =. Fa φ-komponenten av NavieStokes ligning ha vi da 2 u φ = µ u φ u ) φ 2 med løsning u φ ) = C/ siden dette e en annen odens dieensialligning, ha den geneelle løsningen også et ledd u φ = C, som imidletid hveken e av oppgitt fom, elle tilfedsstille andkavet nå ). Konstanten C bestemmes ved å folange andkavet i = R oppfylt: u φ R) = C R = ωr C = ωr2 = Γ 2π. c) Skjæspenning langs sylindeoveaten A = 2πRL e aealet av sylindeaten): uφ F φ = τ φ A = µ u ) φ =R 2πRL = µγ 2πRL = 4πµωRL = 2.5 N. πr2 Eekten bli da P = F u φ R) = 4πµω 2 R 2 L = 5 W. d) Av -komponenten av NavieStokes ligning ha vi: som ved integasjon gi: p = p = ρu2 φ = ργ2 4π 2 3 ργ2 8π 2 2 = p 1 R4 ρω2 2 2 Siden u as, edusee Benoullis ligning seg til: p p = 1 2 ρu2 = 1 2 ρu2 φ = 1 R4 ρω som gi samme svaet. Åsaken til at svaene e identiske i dette tilfellet e at vi ha 2 u =, så NavieStokes ligning og Eule-ligningen ha samme løsning. Videe e denne løsningen vivelfi u =, så Benoullis ligning ha samme konstant fo alle stømlinje disse danne sikle undt sylindeen). 11
12 Oppgave 2 a) Siden vi anta todimensjonal støm som e uavhengig av x, u = uy), vy), ), gi kontinuitetsligningen: = u = v y med løsning vy) = v, de v e en konstant. Siden v) e hastigheten på den poøse veggen, e v > ) hastigheten væsken stømme inn i veggen med. b) Fo todimensjonal støm lyde x-komponenten av NavieStokes ligning: u u x + v u y = 1 ρ x + ν 2 ) u x u y 2 Hvis stømmen vaiee på en lengdeskala L i x-etningen og på en skala δ gensesjikttykkelsen) i y-etningen, med δ L, ha vi 2 u x 2 U L 2 2 u y 2 U δ 2 hvoav esultatet følge. c) Fodi gensesjiktet e tynt, kan stømmen de ikke balansee noen sto tykkfoskjell, så vi må ha x, de x p x) e tykket i favæ av gensesjikt tykket fo den ikke-viskøse Eule-løsningen). Fo en fomaliset diskusjon, se Titton Siden u = uy), kan helle ikke Eule-løsningen u avhenge av x, siden u må gå kontinuelig ove i u på anden av gensesjiktet. Dvs.: og gensesjiktligningen edusee seg til: x x = ρ u x = u v y = ν 2 u y 2 2 u y 2 + v u ν y som e en odinæ annen odens dieensialligning fo uy) med konstante koesiente. Gensebetingelsen i y = e den vanlige, u) =. d) Hvis vi innføe hjelpefunksjonen fy) = u y, ha vi med løsning f y = v ν u fy) = u y = B e v y ν, de B e en integasjonskonstant. Vi nne da uy) ved å integee en gang til: uy) = u +Be v y/ν, de B = νb /v. Gensebetingelsen u) = gi u + B =, så uy) = u 1 e vy/ν ). Det e lett å se at u e hastigheten til Eule-) stømmen uendelig langt vekk fa veggen. 12
13 Oppgave 3 a) Leddet ρdu/dt i NavieStokes ligning e teghets-kaften pe volumenhet), / x e tykkaften og µ 2 u gi den viskøse kaften på et uidelement. Med L som lengdeskala, U som hastighetsskala og T = U/L som tidsskala ha vi: u t U 2 2 U, u )u L L, ν 2 u ν U L 2 Altså e R = teghetsledd viskøst ledd = LU ν = ρlu µ b) Hvis vi sette inn de oppgitte identitete samt u = i NavieStokes ligning, få vi: u t u2 u w = 1 p ν w. ρ Fo inkompessibel vivelfi støm, w =, edusee defo NavieStokes ligning seg til Euleligningen. [Bemekning: Siden gensebetingelsene fo de to ligningene e foskjellige, så e de fysiske omstendighete som gi opphav til vivelfi støm ikke de samme! Men hvis vi ha viskøs vivelfi støm, så gi dette også en løsning av Eule-ligningen sml. oppgave 1d ovenfo)]. c) w = u =,, ζ), de så stømmen e ikke vivelfi. ζ = u y = p Lµ y, 1998 V: a) Fodi u = Φ [Tittons fotegnskonvensjon], fosvinne vivlingen: ω = u = Φ =. Kontinuitetsligningen fo stasjonæ inkompessibel støm edusee seg da til 2 Φ =. Med oppgitt Φ, φ) nne vi 2 Φ = 2 Φ Φ Φ 2 φ 2 = u 2 a a2 3 1 ) a2 3 cos φ =. Da vil u = Φ også væe en løsning av Eule-ligningen, med den vedi av tykket som følge av Benoullis ligning. b) Av den oppgitte Φ nne vi: u = Φ = u ) 1 a2 cos φ, u φ = u 1 + a2 2 2 ) sin φ, u z =. Gensebetingelsene e u = fo = a og u = fo φ =, π på sjøbunnen), samt u u cos φ, u φ u sin φ nå, som alle e oppfylt. c) Siden vi ha ikke-viskøs vivelfi støm, kan vi nne tykket av Benoullis ligning: 1 2 ρu2 = 1 2 u2 a, φ) + pa, φ). 13
14 Siden u a, φ) =, u φ a, φ) = 2u sin φ, ha vi: pa, φ) = 1 2 ρ u 2 u 2 φa, φ) ) = 1 2 ρu2 1 4 sin 2 φ ). Da p, φ) = p, π φ), e tykk-fodelingen symmetisk oppstøms og nedstøms, og vi ha ingen netto dag-kaft, D = d'alembets paadoks). d) Med de angitte vedie: R = 2au /ν = 2 1 6, som e altfo sto fo laminæ støm. e) Kaftkomponenten i y-etningen bli z e et vilkålig lengdestykke i z-etningen): df y φ) = pa, φ) sin φ da = 1 2 ρu2 1 4 sin 2 φ ) sin φ za dφ. Dette gi løftet pe lengdeenhet av sylindeen som: L = F y z = 1 2 ρu2 a = 1 2 ρu2 a π 1 4 sin 2 φ ) sin φ dφ [ cos φ 4 3 cos3 φ + 4 cos φ f) R Stømningsmønste 1/2 Kypende støm 4 Laminæ støm > 4 Vivel evje) bak sylindeen > 1 Veldenet laminæt gensesjikt, vivelavløsning > 2 von Kaman-gate bak øet > 4 Tedimensjonale ustabilitete > Tubulent viveldannelse > Tubulent gensesjikt med laminæt undesjikt Oppgave 2 Se 2V, oppgave 3 a-e), nedenfo. ] π = 5 3 ρu2 a = 167 N/m 1998 H: Punktene a)-d) e identiske med eksamen 1997 V, oppgave 1. e) Hvis vi sette inn de oppgitte identitete samt u = i NavieStokes ligning, få vi: u t u2 u w = 1 p ν w. ρ Fo inkompessibel vivelfi støm, w =, edusee defo NavieStokes ligning seg til Euleligningen. Siden gensebetingelsene fo den føste inneholde en tilleggsbetingelse i fohold til den siste ingen tangentiell komponent av hastighetsfeltet på veggene), vil løsninge av NavieStokes ligning også gi løsninge av Euleligningen, men ikke omvendt. 14
15 Oppgave 2 a) Leddet ρdu/dt i NavieStokes ligning e teghets-kaften pe volumenhet), / x e tykkaften og µ 2 u gi den viskøse kaften på et uidelement. Dimensjonsanalyse gi at foholdet R x = ρlu/µ, de L e en lengdeskala i x-etningen, angi foholdet mellom teghetskaften og den viskøse kaften. b) Fo fi støm dominee den viskøse kaften ved lave hastighete lave eynoldstall), mens tegheten dominee ved høye. På gunn av gensebetingelsen u = ved veggen, vil hastigheten alltid væe lav næ denne, og viskositeten kan aldi neglisjees he. Dette e åsaken til at vi alltid ha et gensesjikt nå viskositeten kan neglisjees i esten av stømmen. c) Kontinuitetsligningen gi u x + v y = = v y = ax) x = a så, siden v x, ) = : Fo tykk-gadienten nne vi: v x, y) = a y dy = ay. x = ρu u x = ρa2 x < som bety gunstig tykkgadient. d) Ligningene fo stømlinjene e: dx = dy = u v dx ax = dy ay som e en sepaabel føste odens dieensialligning, med løsning xy = C de C e en konstant. Stømlinjene e altså gene av en likesidet hypebel. [Man tenke seg he en passende gu]. e) Tykkelsen av gensesjiktet mot veggen må involvee viskositeten µ elle ν = µ/ρ). Fo små y fosvinne v, så den elevante hastighetsskalaen e satt av u. Vi ha da kun muligheten δ = νx ν = u a som e uavhengig av x. Gensesjiktets tykkelse e altså uavhengig av x. f) Nå R x vokse, bli gensesjiktet ustabilt. Ved R x 15 fo nøytal tykk-gadient) få vi en enkel ustabil bølge-modus Tollmien-Schlichting bølge). Deette vil vi få et fekvensbånd av ustabile mode. Den videe posess e kjent som en K-type ovegang, en få føst te-dimensjonale tansveselle) ustabilitete og så stige kompleksiteten i mønsteet stadig, i det ustabilitetene selv bli ustabile, til en få en situasjon med fullt utviklet tubulens, føst i begensede omåde tubulente ekke). Tubulente gensesjiktet e todelte, med et inde viskøst undesjikt og utenfo dette et sjikt med et logaitmisk hastighetspol. Fullt utviklede tubulente gensesjikt oppstå fo eynoldstall av støelsesoden 3 til 3. 15
16 1999 V: Punktene a-c) e identiske med de i oppgave 1 fo 2 H, se nedenfo. d) Volumstøm: Φ = Dvs.: Middelstømmen bli a p u da = 2π 4µL a2 2 )d = 2π p [ 1 4µL 2 a2 2 1 ] a 4 4 = π pa4 8µL ū = p = 8µLΦ πa 4 =.41 Pa. Φ πa 2 = pa2 = 1.3 cm/s 8µL e) Den viskøse spenningen på øveggen, τ v e motsatt lik spenningen i det ytteste væskesjiktet. Altså: ) u τ v = τ z = µ = pa 2L = Pa. Samlet kaft på veggen, F v e da: =a F v = τ v 2πaL = pπa 2 = paø = Fø = N de Fø e den samlede tykk-kaften ove tvesnittet av øet. f) Reynoldstallet e R = ρū2a µ = 1 3 som e unde selv den laveste vedien som gi ustabil støm, R c = 1 8 3, så stømmen e laminæ. g) Velge vi R c = 2 ha vi, siden ρ, a og µ ikke ende seg, at stømmen slutte å væe laminæ nå R c R = ūc ū = Φ c Φ Φ c = R c Φ =.15 l/s R [Sva baset på ande imelige valg av R c godkjennes selvsagt]. Det videe foløp e typisk som følge: R > 2 : Dannelse av tubulente slugge plugge) R > 5 : Spontant pulseende støm R > 1 : Ustabil støm, ikke fullstendig tubulent R > 1 : Innløpet indusee tubulent støm Lineæ stabilitetsteoi gi at Poiseuille-støm e stabil fo alle vedie av R. h) Siden symmetien i poblemet e den samme som fø, e også den geneelle løsningen av poblemet ufoandet. Defo e pz) som fø, mens andbetingelsen fo NavieStokes ligning nå e ua) = ub) =. Dvs u) = A ln + B + C 2, med C = p/4µl. A og B bestemmes av ua) = A ln a + B + Ca 2 = ub) = A ln b + B + Cb 2 = Dette e to lineæe ligninge fo de 2 ukjente A og B. Løsningen nnes, f. eks. ved eliminasjon, som Følgelig bli A = C a2 b 2 ln a ln b = p a2 b2 4µL ln ) a b B = Ca 2 p A ln a = 4µL ln ) a b 2 ln a a 2 ln b ) b u) = p 4µL a 2 ln b 16 ) b 2 ln ) ) a ln ) a 2. b
17 Oppgave 2 a) Leddene i NavieStokes ligning kan kaakteisees som følge: ρ u/ t: akseleasjonsledd; ρu )u: teghetsledd; p: tykkledd; µ 2 u: viskøst ledd. Reynoldstallet R x = ρux/µ = Ux/ν, de U e hastighetsskalaen. Dimensjonsanalyse gi [ρu )u] = [ρ]u 2 /L og [µ 2 u] = [µ]u/l 2, så siden [x] = L, e R x = teghetsledd viskøst ledd = ρlu µ b) Ved lave R x dominee det viskøse leddet, ved høye teghetsleddet. Næ veggen vil u, så det viskøse leddet e alltid viktig he, og vi få gensesjikt desom R x e sto i esten av stømmen. c) Hvis ux, y) = a/x, vx, y), ) gi kontinuitetsligningen som kan integees til Tykk-gadienten i x-etningen bli u = u x + v y = v y = u x = a x 2 x = ρu a a x = ρ x vx, y) = ay x 2 a x x + ay x 2 y ) a = ρ a2 x x 3 > fo x >. Dvs tykk-gadienten e ugunstig i x-etningen fo x < e iktignok x <, men også u = a/x <, og tykk-gadienten e fotsatt ugunstig). = ρu ay y x 2 = ρ som også gi ugunstig tykk-gadient. d) Ligningen fo stømlinjene e: med løsning dx u = dy v a x x xdx a ay x 2 + ay x 2 = x2 dy ay y ) ay x 2 = ρ a2 y x 4 > ln x = ln y + C x = Ky dx x = dy y de K = e C e en integasjonskonstant. Stømlinjene e altså ette linje ut fa spalten [skisse mangle]. e) Siden vi alleede vet at u) oppfylle kontinuitetsligningen, gjenstå) det å bestemme p og a fa NavieStokes ligning. I x-etningen ha vi, siden u = a x x + y x y som gi I y-etningen nne vi tilsvaende ρ u ) a x = x + µ 2 x 2 a x ρ u ) ay x 2 = y + µ px, y) = ρa 2 + µ ) a x 2 + p y) 2 ) x ay y 2 x 2 x = 2µ + ρa) a x 3 = 6µ + aρ)ay y x 4 Dette gi px, y) = p 1 x) + 3µ + aρ ) ay 2 2 x 4 Disse to uttykkene fo px, y) e konsistente bae hvis p y) = p, en konstant. I så fall må 3µ = aρ/2, elle a = 6µ/ρ = 6ν, og vi ha px, y) = px) = p 12µ 2 /ρx 2. f) Næ x = divegee u, og demed det eektive lokale eynoldstallet. Stømmen he e defo sikket tubulent, og den funne løsningen ustabil. Den eksakte tykk-gadienten e også ustabil i x-etningen, nøytal i y-etningen, x = 24µ2 ρx 3 > ; y =, så bevegelsen i x-etningen e geneelt potensielt ustabil. 17
18 1999 H: Denne oppgaven e lik oppgave 1 fo 1998 V, botsett fa at punktene d) og e) e byttet om, at hastigheten u e endet, så R = , og at det i d) e sput ette løft-koesienten d = 2a e diameteen): Oppgave 2 a) Identisk med eksamen 1999 V, oppgave 2a b) Identisk med eksamen 1999 V, oppgave 2b C L = L 1 2 ρu2 d = 5 3 = c) Av oppgitt fomel fo u nne vi vivlingen: ω = u) z = u φ + u φ = c 2 sin ψ + c 2 sin ψ =, fo > uttykket e singulæt fo = ). Sikulasjonen, beegnet fo en sikulæ skive med sentum i oigo og adius e da: Γ = ω n da = = u d = 2π 2π u φ dφ = c sin ψ dφ = 2πc sin ψ, som ikke fosvinne, unntatt hvis ψ =, π. Vivlingen ω må altså væe singulæ i oigo, siden ateintegalet av ω n ikke fosvinne, selvom ω = fo >. d) Av de oppgitte fomlene kontollee vi at kontinuitetsligningen e oppfylt: Eule-ligningen gi da i -etningen: u = u + u + 1 u φ φ = c 2 cos ψ + c 2 cos ψ + =. u [u )u] = u u2 φ = c2 3 = 1 ρ, med løsning fo p, φ): I φ-etningen få vi tilsvaende: p, φ) = p φ) ρc2 2 2, u φ [u )u] φ = u + u u φ = = 1 ρ φ, slik at p må væe uavhengig av φ, dvs p = p) = ρc [Dette kunne vi ha funnet like lett av Benoullis ligning.] e) Diekte innsetting i den oppgitte fomelen vise at 2 u =. Siden u også oppfylle Eule-ligningen oppfylle den også NavieStokes ligning: Du Dt = 1 ρ p + ν 2 u. Siden også kontinuitetsligningen e oppfylt, e u også løsning fo viskøs støm. Siden løsningen e den samme fo alle ν elle µ), kan den ikke avhenge av Reynoldstallet R = LU/ν. 18
19 f) Fo et innitesimalt tidsintevall dt gjelde d = u dt og dφ = u φ dt. Dvs.: som e den oppgitte ligning. Innsatt dt = d u = dφ u φ, d c cos ψ = 2 dφ c sin ψ dφ d = tan ψ, med løsning ) φ = tan ψ ln + φ = tan ψ ln. Den fysiske tolkningen av integasjonskonstanten e den vedien av de φ) ha nullpunkt, φ ) =. Dette e én av en uendelig mengde punkte de stømlinjen kysse x-aksen. Stømlinjene e logaitmiske spiale, som deie seg utove med uviseen fo ψ π/2, med uviseen fo π/2 < ψ < π. Fo ψ < gå stømmen innove mot oigo. Løsningen kan også skives: = e φ cot ψ. 2 V: a) Fo to-dimensjonal støm i sylindekoodinate, φ lyde kontinuitetsligningen u = u + u + 1 u φ φ =. Med sylindesymmeti avhenge ikke u av φ alle etninge e likevedige), så dette edusee seg til u + u =, med løsning u ) = c/. Med c > stømme vannet inn mot sluket, slik foutsatt i oppgaven. b) Siden [u] = L/T, e [c] = [u][] = L 2 /T, hvilket e samme dimensjon som fo kinematisk viskositet, ν. Siden aealet til oveaten til en sylinde med adius og høyde H e A = 2πH, bli volumstømmen innove: V = Au = 2πHc, uavhengig av. Følgelig: c = V 2πH = m 2 /s. c) Med de gitte antagelse bli Navie-Stokes ligning i φ-etningen / φ = på gunn av sylindesymmeti): u φ u + u u φ 2 u φ = ν u φ u ) φ 2 Diekte innsetting vise at de oppgitte uttykk fo u φ ) løse ligningen. d) Fo en akseptabel fysisk løsning må u φ ) fosvinne, elle til nød fobli endelig, nå. Dette bety at 1 c/ν, elle c c k = ν. Det logaitmiske leddet ln )/ fo c = 2ν tilfedsstille også denne betingelsen. Fo c < c k = ν må altså B =. 19
20 e) Vivlingen fo > bli ω = ωe z ): ω = u φ + u φ = B { ) 2 c ν c/ν c, ν 2 1 c, 2 ν = 2. Siden B = fo c < c k, e stømmen vivelfi i dette tilfellet. Da hveken u elle u φ avhenge av ν, e løsningen den det samme som fo ikke-viskøs, vivelfi støm i dette tilfellet. Tykket kan da nnes av Benoulli's ligning, med samme konstant stagnasjonstykk) fo alle stømlinje. Siden p p, u og u φ nå, få vi: p) + ρ 2 u 2 ) + u 2 φ) ) = p = p) = p c2 + A 2 )ρ 2 2. f) Fo et tynt, paktisk talt todimensjonalt, sjikt må tykket væe det samme i som ett ove sjiktet, siden tykket må væe kontinuelig. Fo c < c k se vi av esultatet i foegående punkt at vi i så fall må ha A = c =, som e en litt gov foenkling [I vikeligheten e vannoveaten ikke plan!.] Fo c > c k gi -komponenten til Navie-Stokes ligning, innsatt de fundne uttykk fo u og u φ : u u u2 φ = c2 3 1 ) A AB c/ν + B 2 2 2c/ν =, med et tilsvaende uttykk fo tilfellet c = 2ν. Også denne ligningen ha kun løsningen A = B = c =. Vi se defo at betingelsen om at p) skal væe konstant e fo steng fo å få en akseptabel løsning. g) Fo et innitesimalt vilkålig kot) tidsintevall dt gjelde: d = u dt og dφ = u φ dt. Dvs.: dt = d u = dφ u φ, som e den oppgitte ligning. Dette gi videe, fo c 2ν: med løsning: dφ d = u φ u = A c B c 1 c/ν, φ = A c ln ) de e en integasjonskonstant. Fo c = 2ν få vi i stedet: 1 B 2 c/ν c 2 c/ν, dφ d = A c B ln), c med løsningen: φ = A ) c ln B )) 2 ln. 2c I alle tilfelle edusee løsningen fo B = seg til en logaitmisk spial, = e cφ/a 2
21 Oppgave 2 a) På veggen fosvinne alle hastighete heftebetingelsen), så vi ha både U = V = og u = v = he, dvs. uv =. Dette bety at næ nok veggen edusee Reynolds-ligningen seg til den laminæe genssjiktligningen. Den inde delen av et tubulent gensesjikt e altså laminæt. b) Akkuat som Navie-Stokes ligning, som den e utledet fa, inneholde Reynolds-ligningen på dimensjonsløs fom kun den dimensjonsløse paameteen R = u L/ν med standad notasjon). Følgelig må u τ /u = fr). Siden [ν] = LU, e [ν/u τ ] = L, slik at δ L u τ /ν = cr) e en dimensjonsløs støelse. c) Med u = 36 km/h = 1 m/s ha vi skinn-fiksjonen Lc e tilnæmet) vingeaalet og faktoen 2 skyldes at vingene ha både undeside og oveside): F µ = 2τ W Lc = 2Lcρu 2 τ = 2Lcρ Eekten av fiksjonskaften F µ e P µ = F µ u, så uτ u ) 2 u 2 = 2 6 N F µ D = P µ P = F µu P =.13 = 13% d) Fo at vi skal ha et laminæt undesjikt, må uheten,, væe tydelig minde enn tykkelsen på undesjiktet, δ L : δ L = 8ν = 8µ u = 32 µm u τ ρu uτ e) Siden U = u = på veggen vil et uidelement som bevege seg utove fa denne, og defo ha v >, komme til et omåde de det bevege seg langsommee i x-etningen enn den omkingliggende væsken, så det vil ha u <, og defo bli uv <. Det motsatte skje fo et uidelement som bevege seg inn mot veggen, så v <. Dette vil bevege seg askee i x-etningen enn den omkingliggende væsken, så u >, og igjen bli uv <. Av dette følge det at et tubulent gensesjiktet oppføe seg som om det ha en skjæspenning som e eektivt støe enn den viskøse skjæspenningen: τ e = µ U y ρuv > µ U y = τ. f) I sjiktet umiddelbat utenfo det viskøse undesjiktet e skjæspenningen fotsatt paktisk talt τ W, så u τ sette fotsatt hastighetsskalaen. Dimensjonsanalyse gi da at vi tilnæmet må ha Denne ligningen ha løsningen U y = 1 u τ K y. Uy) = u τ dy K y = u τ K ln y + C) = u [ τ yuτ ) ] ln + A, K ν de C e en integasjonskonstant, og vi ha innføt en ny konstant A = C + ln ν/u τ ), fo å gjøe agumentet til logaitmen dimensjonsløs ande skivemåte e mulige, men kombinasjonen yu τ /ν e et bekvemt dimensjonsløst eynoldstall). 21
22 2 H: a) På gunn av sylindesymmeti e u) = u, z). Kontinuitetsligningen gi da: så u e uavhengig av z, u = u). b) Siden u = u z =, u )u = u u z =, edusee NavieStokes ligning i z-etningen seg til z = µ 2 u. I - og φ-etningene gi ligningen at p ikke avhenge av og φ.) Deivee vi denne ligningen med hensyn på z og buke u/ z =, få vi 2 p u = µ 2 z2 z =, som ha løsning pz) = Az + p, med p = p). Med p = p pl) = AL ha vi A = p/l og pz) = p p z L. c) Fa foegående punkt få vi 2 u = 2 u u = 1 µ z = p µl. Hvis vi anta en løsning av den oppgitte fomen, nne vi u ) = A + 2C og u ) = A 2 + 2C. Innsatt i ligningen gi dette A 2 + 2C + A + 2C = p 2 µl C = p 4µL. [Vi se at vi ha løsning fo alle vedie av A og B, så u ) = A ln + B e den geneelle løsning av den homogene ligningen u ) + u)/ =, mens u p ) = C 2 e en patikulæ løsning av den inhomogene ligningen.] I tillegg til andkavet ua) = heftebetingelsen) ha vi kavet u) < fo < a inne i øet), og spesielt fo =. Dette gi at A =. Vi nne da ua) = B + Ca 2 B = Ca 2 og d) Volumstøm: Φ = Dvs.: u) = C 2 a 2 ) = p 4µL a2 2 ). a p u da = 2π 4µL a2 2 )d = 2π p [ 1 4µL 2 a2 2 1 ] a 4 4 = π pa4 8µL. p = 8µLΦ πa 4 = 2. Pa. 22
23 Middelhastigheten bli ū = Φ πa 2 = pa2 = 2. cm/s. 8µL e) Reynoldstallet e R = ρū2a µ = 1 6. Stømmen slutte å væe laminæ fo R ). f) Sammenholde vi det oppgitte uttykket fo p med det fa d) og utnytte e), nne vi: p = f Lū2 ρ 4a = 8µLū a 2 = f = 32µ aūl = 64 R. g) Nå stømmen slutte å væe laminæ, dannes det små omåde med tubulent, elle tilnæmet tubulent, støm, såkalte tubulente "slugge". Dette edusee gjennomstømningshastigheten, dvs ū synke desom p e ufoandet. Av uttykket i f) se vi at dette bety at f øke. h) Den viskøse kaften på øveggen aeal A W = 2πaL) må balansees av foskjellen i tykk-kefte mellom øets ende, siden vannet ikke akseleees: Dette gi τ W A W = pπa 2 A W = p = τ W πa 2 = τ 2L W a. τ W = a p 2L = 2. mpa. i) Ved å kombinee denisjonen av u τ, utykket fo p i foige punkt og denisjonen av f fa f), nne vi: p = 2L a ρu2 τ = f Lū2 ρ 8 = ū = 4a f u τ. Oppgave 2 a) Siden vi anta todimensjonal støm som e uavhengig av x slik at u = uy), vy), ), gi kontinuitetsligningen: = u = v y, med løsning vy) = v, de v e en konstant. Siden v) e hastigheten på den poøse veggen, e v > ) hastigheten væsken stømme inn i veggen med. b) Fo todimensjonal støm lyde x-komponenten av NavieStokes ligning: u u x + v u y = 1 ρ x + ν 2 ) u x u y 2. Hvis stømmen ha en hastighetsskala U og vaiee på en lengdeskala L i x-etningen og på en skala δ gensesjikttykkelsen) i y-etningen, de δ L, ha vi hvoav esultatet følge. 2 u x 2 U L 2 2 u y 2 U δ 2, c) Siden gensesjiktet e tynt, kan ikke tykket væe svæt foskjellig fa tykket utenfo, hvo vi ha ikke-viskøs støm, så px, y) p x, y) fo ee detalje, se Titton 11.2). Vi ha videe x { > ugunstig tykk-gadient = nøytal tykk-gadient < gunstig tykk-gadient 23.
24 En gunstig tykk-gadient vike stabiliseende på stømmen, en ugunstig vike destabiliseende. d) Med px, y) = p x, y) = og u som i a), edusee gensesjiktligningen seg til: u v y = ν 2 u y 2 2 u y 2 + v u ν y =, som e en odinæ annen odens dieensialligning med konstante koesiente fo uy). Gensebetingelsen i y = e den vanlige heftebetingelsen u) =, mens fo y må uy) u. e) Med notasjonen fy) = u y, ha vi f med løsning y = v ν u, fy) = u y = B e v y ν, de B e en integasjonskonstant. Dette kan integees en gang til til å gi uy) = u + Be vy/ν, de B = νb /v. Betingelsen u) = gi da u + B =, så uy) = u 1 e v y/ν ), som oppgitt. f) Ligningen fo stømlinjene bli: dx u = dy v dx u 1 e vy/ν ) = dy v dx dy = u v 1 e v y/ν ), med løsning xy) = u ) 1 e v y/ν dy = u y + ν ) e v y/ν + K, v v v de K e en integasjonskonstant. Hvis vi folange x) = x, nne vi K = x + νu, og v 2 xy) = x u y + νu v v 2 1 e vy/ν). g) Langt vekk fa veggen e stømlinjene skå ette linje, y = v u x + y ; vannet stømme langsomt, hvis v u ) mot veggen. Ved veggen e u =, mens v = v, så stømlinjene stå vinkelett på veggen tegning mangle). 24
Løsningsforslag Eksamen i fag TEP4110 Fluidmekanikk
 Oppgave Løsningsfoslag Eksamen i fag TEP40 Fluidmekanikk Onsdag 8 desembe 00 kl 500 900 Hastighetspotensialet fo en todimensjonal potensialstømning av en inkompessibel fluid e gitt som: (, ) Acos ln ()
Oppgave Løsningsfoslag Eksamen i fag TEP40 Fluidmekanikk Onsdag 8 desembe 00 kl 500 900 Hastighetspotensialet fo en todimensjonal potensialstømning av en inkompessibel fluid e gitt som: (, ) Acos ln ()
Løsningsforslag TEP 4110 FLUIDMEKANIKK 18.desember ρ = = = m / s m / s 0.1
 Løsningsfoslag TEP 40 FLUIDMEKNIKK 8.desembe 007 Oppgave a) Foskjellen i vekt e oppdiftskaften på kula nå den e neddykket i olje (oppdiften i luft neglisjees). Oppdift =ρ Volum g olje π =ρvann SGolje d
Løsningsfoslag TEP 40 FLUIDMEKNIKK 8.desembe 007 Oppgave a) Foskjellen i vekt e oppdiftskaften på kula nå den e neddykket i olje (oppdiften i luft neglisjees). Oppdift =ρ Volum g olje π =ρvann SGolje d
ρ = = = m / s m / s Ok! 0.1
 Løsningsfoslag TEP 00 FLUIDMEKNIKK.juni 007 Oppgave a) Foskjellen i vekt e oppdiftskaften på kula nå den e neddykket i olje (oppdiften i luft neglisjees). Oppdift =ρ Volum g olje π =ρvann SGolje d g 6
Løsningsfoslag TEP 00 FLUIDMEKNIKK.juni 007 Oppgave a) Foskjellen i vekt e oppdiftskaften på kula nå den e neddykket i olje (oppdiften i luft neglisjees). Oppdift =ρ Volum g olje π =ρvann SGolje d g 6
UNIVERSITETET I OSLO
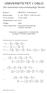 UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Eksamen i: Eksamensdag: Tid fo eksamen: 14.30 18.30 Oppgavesettet e på 5 side. Vedlegg: Tillatte hjelpemidle: MEK3230 Fluidmekanikk 6. Juni,
UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Eksamen i: Eksamensdag: Tid fo eksamen: 14.30 18.30 Oppgavesettet e på 5 side. Vedlegg: Tillatte hjelpemidle: MEK3230 Fluidmekanikk 6. Juni,
EKSAMEN FAG TFY4160 BØLGEFYSIKK OG FAG FY1002/MNFFY101 GENERELL FYSIKK II Lørdag 6. desember 2003 kl Bokmål
 ide av 0 NORGE TEKNIK- NATURVITENKAPELIGE UNIVERITET INTITUTT FOR FYIKK Faglig kontakt unde eksamen: Føsteamanuensis Knut Ane tand Telefon: 73 59 34 6 EKAMEN FAG TFY460 ØLGEFYIKK OG FAG FY00/MNFFY0 GENERELL
ide av 0 NORGE TEKNIK- NATURVITENKAPELIGE UNIVERITET INTITUTT FOR FYIKK Faglig kontakt unde eksamen: Føsteamanuensis Knut Ane tand Telefon: 73 59 34 6 EKAMEN FAG TFY460 ØLGEFYIKK OG FAG FY00/MNFFY0 GENERELL
Γ = u dl = u φ adφ = 2πωa 2 = 6.28m 2 /s. r = 1 (ru r )
 À ËÃÇÄ Æ Á ËÌ Î Æ Ê ÁÒ Ø ØÙØØ ÓÖ Ñ Ø Ñ Ø Ó Ò ØÙÖÚ Ø Ò Ô Ä Ò Ò ÓÖ Ð Ñ Ò Ì ÐÙ ÝÒ Ñ ¾¼¼½ Î ÇÔÔ Ú ½ I hele oppgaven er u z = 0, og vi har ingen z-avhengighet, så u(r,φ) = u r (r,φ)e r +u φ (r,φ)e φ. a) For
À ËÃÇÄ Æ Á ËÌ Î Æ Ê ÁÒ Ø ØÙØØ ÓÖ Ñ Ø Ñ Ø Ó Ò ØÙÖÚ Ø Ò Ô Ä Ò Ò ÓÖ Ð Ñ Ò Ì ÐÙ ÝÒ Ñ ¾¼¼½ Î ÇÔÔ Ú ½ I hele oppgaven er u z = 0, og vi har ingen z-avhengighet, så u(r,φ) = u r (r,φ)e r +u φ (r,φ)e φ. a) For
Om bevegelsesligningene
 Inst. fo Mekanikk, Temo- og Fluiddynamikk Om bevegelsesligningene (Repetisjon av utledninge fa IO 1008 Fluidmekanikk) P.-Å. Kogstad I det ettefølgende epetees kot utledningene av de fundamentale bevegelsesligninge,
Inst. fo Mekanikk, Temo- og Fluiddynamikk Om bevegelsesligningene (Repetisjon av utledninge fa IO 1008 Fluidmekanikk) P.-Å. Kogstad I det ettefølgende epetees kot utledningene av de fundamentale bevegelsesligninge,
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Eksamen i: MEK3220/MEK4220 Kontinuumsmekanikk Eksamensdag: Onsdag 2. desembe 2015. Tid fo eksamen: 09.00 13.00. Oppgavesettet e på 7 side.
UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Eksamen i: MEK3220/MEK4220 Kontinuumsmekanikk Eksamensdag: Onsdag 2. desembe 2015. Tid fo eksamen: 09.00 13.00. Oppgavesettet e på 7 side.
Newtons lover i to og tre dimensjoner
 Newtons love i to og te dimensjone 7..13 innleveing: buk iktige boks! FYS-MEK 111 7..13 1 Skått kast kontaktkaft: luftmotstand langtekkende kaft: gavitasjon initialbetingelse: () v() v v cos( α ) iˆ +
Newtons love i to og te dimensjone 7..13 innleveing: buk iktige boks! FYS-MEK 111 7..13 1 Skått kast kontaktkaft: luftmotstand langtekkende kaft: gavitasjon initialbetingelse: () v() v v cos( α ) iˆ +
Forelesning 9/ ved Karsten Trulsen
 Foelesning 9/2 218 ved Kasten Tulsen Husk fa sist våe to spøsmål om kuveintegale: Desom vi skal beegne et kuveintegal som state i et punkt og ende opp i et annet punkt 1, så kan det væe mange veie fo å
Foelesning 9/2 218 ved Kasten Tulsen Husk fa sist våe to spøsmål om kuveintegale: Desom vi skal beegne et kuveintegal som state i et punkt og ende opp i et annet punkt 1, så kan det væe mange veie fo å
Notat i FYS-MEK/F 1110 våren 2006
 1 Notat i FYS-MEK/F 1110 våen 2006 Rulling og skliing av kule og sylinde Foelest 24. mai 2006 av Ant Inge Vistnes Geneelt Rotasjonsdynamikk e en svæt viktig del av mekanikkuset våt. Dette e nytt stoff
1 Notat i FYS-MEK/F 1110 våen 2006 Rulling og skliing av kule og sylinde Foelest 24. mai 2006 av Ant Inge Vistnes Geneelt Rotasjonsdynamikk e en svæt viktig del av mekanikkuset våt. Dette e nytt stoff
Eksamensoppgave i TEP4105 FLUIDMEKANIKK
 Institutt fo enegi- og posessteknikk Eksamensoppgave i TEP45 FLUIDMEKANIKK Faglig kontakt unde eksamen: Ive Bevik Tlf.: 7359 3555 Eksamensdato: 7. august 23 Eksamenstid : 9. 3. Hjelpemiddelkode/Tillatte
Institutt fo enegi- og posessteknikk Eksamensoppgave i TEP45 FLUIDMEKANIKK Faglig kontakt unde eksamen: Ive Bevik Tlf.: 7359 3555 Eksamensdato: 7. august 23 Eksamenstid : 9. 3. Hjelpemiddelkode/Tillatte
Mandag E = V. y ŷ + V ẑ (kartesiske koordinater) r sin θ φ ˆφ (kulekoordinater)
 Institutt fo fysikk, NTNU TFY4155/FY13: Elektisitet og magnetisme Vå 26, uke 6 Mandag 6.2.6 Beegning av E fa V [FGT 24.4; YF 23.5; TM 23.3; F 21.1; LHL 19.9; DJG 2.3.1, 1.2.2] Gadientopeatoen : V = V V
Institutt fo fysikk, NTNU TFY4155/FY13: Elektisitet og magnetisme Vå 26, uke 6 Mandag 6.2.6 Beegning av E fa V [FGT 24.4; YF 23.5; TM 23.3; F 21.1; LHL 19.9; DJG 2.3.1, 1.2.2] Gadientopeatoen : V = V V
( 6z + 3z 2 ) dz = = 4. (xi + zj) 3 i + 2 ) 3 x x 4 9 y. 3 (6 2y) (6 2y)2 4 y(6 2y)
 TMA415 Matematikk 2 Vå 215 Noges teknisk natuvitenskapelige univesitet Institutt fo matematiske fag Løsningsfoslag Øving 11 Alle oppgavenumme efeee til 8. utgave av Adams & Essex Calculus: A Complete Couse.
TMA415 Matematikk 2 Vå 215 Noges teknisk natuvitenskapelige univesitet Institutt fo matematiske fag Løsningsfoslag Øving 11 Alle oppgavenumme efeee til 8. utgave av Adams & Essex Calculus: A Complete Couse.
Eksamen TFY 4240: Elektromagnetisk teori
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt unde eksamen: Ola Hundei, tlf. 93411 (mobil: 95143671) Eksamen TFY 4240: Elektomagnetisk teoi 8 desembe 2007 kl. 09.00-13.00
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt unde eksamen: Ola Hundei, tlf. 93411 (mobil: 95143671) Eksamen TFY 4240: Elektomagnetisk teoi 8 desembe 2007 kl. 09.00-13.00
Løsningsforslag til ukeoppgave 11
 Oppgave FYS1001 Vå 2018 1 Løsningsfoslag til ukeoppgave 11 Oppgave 23.04 B F m qv = F m 2eV = 6, 3 10 3 T Kaft, magnetfelt og fat stå vinkelett på hveande. Se læebok s. 690. Oppgave 23.09 a) F = qvb =
Oppgave FYS1001 Vå 2018 1 Løsningsfoslag til ukeoppgave 11 Oppgave 23.04 B F m qv = F m 2eV = 6, 3 10 3 T Kaft, magnetfelt og fat stå vinkelett på hveande. Se læebok s. 690. Oppgave 23.09 a) F = qvb =
c) etingelsen fo at det elektiske feltet E e otasjonsinvaiant om x-aksen e, med E og ee som denet ovenfo, at e E = E. Dette skal gjelde fo en vilkalig
 Eksamen i klassisk feltteoi, fag 74 5, 4. august 995 Lsninge a) Koodinatene x; y; z tansfomees slik x 7 bx = x; y 7 by = y cos, z sin ; z 7 by = y sin + z cos Den invese tansfomasjonen e en otasjon en
Eksamen i klassisk feltteoi, fag 74 5, 4. august 995 Lsninge a) Koodinatene x; y; z tansfomees slik x 7 bx = x; y 7 by = y cos, z sin ; z 7 by = y sin + z cos Den invese tansfomasjonen e en otasjon en
KONTINUASJONSEKSAMEN I EMNE TFE 4120 ELEKTROMAGNETISME
 Noges teknisk natuvitenskapelige univesitet Institutt fo elektonikk og telekommunikasjon ide 1 av 8 Bokmål/Nynosk Faglig/fagleg kontakt unde eksamen: Jon Olav Gepstad 41044764) Hjelpemidle: C - pesifisete
Noges teknisk natuvitenskapelige univesitet Institutt fo elektonikk og telekommunikasjon ide 1 av 8 Bokmål/Nynosk Faglig/fagleg kontakt unde eksamen: Jon Olav Gepstad 41044764) Hjelpemidle: C - pesifisete
b) 3 MATEMATISKE METODER I 1 ( ) ( ) ( ) ( ) ( ) ( ) Repetisjonsoppgaver Bruk av regneregler: 1 Regn ut: e) 0 x ) 4 3 d) 4 x f) 5y
 MATEMATISKE METODER I Buk av egneegle: Regn ut: a ( ( b 7 c ( 7 y 8 d 8 e f 5y y Regn ut og tekk sammen: a 5a b a b a + b b y + y + + y c t t + 6 ( 6t t + 8 d s+ s + s ( s + s Multiplise ut og odne a (
MATEMATISKE METODER I Buk av egneegle: Regn ut: a ( ( b 7 c ( 7 y 8 d 8 e f 5y y Regn ut og tekk sammen: a 5a b a b a + b b y + y + + y c t t + 6 ( 6t t + 8 d s+ s + s ( s + s Multiplise ut og odne a (
NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKALSK ELEKTRONIKK
 Side 1 av 8 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKALSK ELEKTRONIKK Faglig/fagleg kontakt unde eksamen: Navn: Helge E. Engan Tlf.: 944 EKSAMEN I EMNE SIE415 BØLGEFORPLANTNING
Side 1 av 8 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKALSK ELEKTRONIKK Faglig/fagleg kontakt unde eksamen: Navn: Helge E. Engan Tlf.: 944 EKSAMEN I EMNE SIE415 BØLGEFORPLANTNING
Matematikk 3MX AA6524 / AA6526 Elever / privatister Oktober 2002
 E K S A M E N LÆRINGSSENTERET Matematikk 3MX AA6524 / AA6526 Eleve / pivatiste Bokmål Eksempeloppgave ette læeplan godkjent juli 2000 Videegående kus II Studieetning fo allmenne, økonomiske og administative
E K S A M E N LÆRINGSSENTERET Matematikk 3MX AA6524 / AA6526 Eleve / pivatiste Bokmål Eksempeloppgave ette læeplan godkjent juli 2000 Videegående kus II Studieetning fo allmenne, økonomiske og administative
Newtons lover i én dimensjon
 Newtons love i én dimensjon 4.01.013 kaft akseleasjon hastighet posisjon YS-MEK 1110 4.01.013 1 Hva e kaft? Vi ha en intuitivt idé om hva kaft e. Vi kan kvantifisee en kaft med elongasjon av en fjæ. Hva
Newtons love i én dimensjon 4.01.013 kaft akseleasjon hastighet posisjon YS-MEK 1110 4.01.013 1 Hva e kaft? Vi ha en intuitivt idé om hva kaft e. Vi kan kvantifisee en kaft med elongasjon av en fjæ. Hva
Oppgave 8.12 Gitt en potensialhvirvel med styrke K i origo. Bestem sirkulasjonen ' langs kurven C. Sirkulasjonen er definert som: ' /
 Løsning øving 3 Oppgve 8. Gitt en potensilhvivel med styke i oigo. Bestem sikulsjonen ' lngs kuven C. C y (I oppgven stå det t vi skl gå med klokk, men he h vi gått mot klokk i oveensstemmelse med definisjonen
Løsning øving 3 Oppgve 8. Gitt en potensilhvivel med styke i oigo. Bestem sikulsjonen ' lngs kuven C. C y (I oppgven stå det t vi skl gå med klokk, men he h vi gått mot klokk i oveensstemmelse med definisjonen
Magnetisk hysterese. 1. Beregn magnetfeltet fra en strømførende spole med kjent vindingstall.
 FY33 Elektisitet og magnetisme II Institutt fo fysikk, TU FY33 Elektisitet og magnetisme II, høst 7 Laboatoieøvelse Magnetisk hysteese Hensikt Hensikten med oppgave å gjøe seg kjent med opphavet til magnetiske
FY33 Elektisitet og magnetisme II Institutt fo fysikk, TU FY33 Elektisitet og magnetisme II, høst 7 Laboatoieøvelse Magnetisk hysteese Hensikt Hensikten med oppgave å gjøe seg kjent med opphavet til magnetiske
FAG: MA-209 Matematikk 3 LÆRER: Per Henrik Hogstad KANDIDATEN MÅ SELV KONTROLLERE AT OPPGAVESETTET ER FULLSTENDIG
 UNIVERITETET I AGDER Gimstad E K A M E N O P P G A V E : FAG: MA-9 Matematikk ÆRER: Pe enik ogstad Klasse: Dato:.6. Eksamenstid fa-til: 9.. Eksamensoppgaven bestå av følgende Antall side: 5 inkl. foside
UNIVERITETET I AGDER Gimstad E K A M E N O P P G A V E : FAG: MA-9 Matematikk ÆRER: Pe enik ogstad Klasse: Dato:.6. Eksamenstid fa-til: 9.. Eksamensoppgaven bestå av følgende Antall side: 5 inkl. foside
Midtsemesterprøve onsdag 7. mars 2007 kl
 Institutt fo fysikk, NTNU FY1003 lektisitet og magnetisme I TFY4155 lektomagnetisme Vå 2007 Midtsemestepøve onsdag 7. mas 2007 kl 1300 1500. Svatabellen stå på side 11. Sett tydelige kyss. Husk å skive
Institutt fo fysikk, NTNU FY1003 lektisitet og magnetisme I TFY4155 lektomagnetisme Vå 2007 Midtsemestepøve onsdag 7. mas 2007 kl 1300 1500. Svatabellen stå på side 11. Sett tydelige kyss. Husk å skive
b) C Det elektriske feltet går radielt ut fra en positivt ladd partikkel.
 Løsningsfoslag Fysikk 2 Høst 203 Løsningsfoslag Fysikk 2 Høst 203 Opp Sva Foklaing gave a) B Fomelen fo bevegelsesmengde p = mv gi enheten kg m. s Dette kan igjen skives som: kg m = kg m s s2 s = Ns b)
Løsningsfoslag Fysikk 2 Høst 203 Løsningsfoslag Fysikk 2 Høst 203 Opp Sva Foklaing gave a) B Fomelen fo bevegelsesmengde p = mv gi enheten kg m. s Dette kan igjen skives som: kg m = kg m s s2 s = Ns b)
Eksamen i TFY4205 Kvantemekanikk Mandag 8. august :00 13:00
 NTNU Side 1 av 9 Institutt fo fysikk Faglig kontakt unde eksamen: Pofesso Ane Bataas Telefon: 73593647 Eksamen i TFY405 Kvantemekanikk Mandag 8. august 005 9:00 13:00 Tillatte hjelpemidle: Altenativ C
NTNU Side 1 av 9 Institutt fo fysikk Faglig kontakt unde eksamen: Pofesso Ane Bataas Telefon: 73593647 Eksamen i TFY405 Kvantemekanikk Mandag 8. august 005 9:00 13:00 Tillatte hjelpemidle: Altenativ C
Pytagoreiske tripler og Fibonacci-tall
 Johan F. Aanes Pytagoeiske tiple og Fibonai-tall Pytagoas og Fibonai siamesiske tvillinge? Me enn 700 å skille dem i tid, men matematisk e de på en måte uadskillelige. Pytagoas (a. 585 500 f.k.) og Leonado
Johan F. Aanes Pytagoeiske tiple og Fibonai-tall Pytagoas og Fibonai siamesiske tvillinge? Me enn 700 å skille dem i tid, men matematisk e de på en måte uadskillelige. Pytagoas (a. 585 500 f.k.) og Leonado
Løsningsforslag for eksamen i FY101 Elektromagnetisme torsdag 12. desember 2002
 Løsningsfoslag fo eksamen i FY Elektomagnetisme tosdag. desembe Ved sensueing vil alle delspøsmål i utgangspunktet bli gitt samme vekt (uavhengig av oppgavenumme), men vi fobeholde oss etten til justeinge.
Løsningsfoslag fo eksamen i FY Elektomagnetisme tosdag. desembe Ved sensueing vil alle delspøsmål i utgangspunktet bli gitt samme vekt (uavhengig av oppgavenumme), men vi fobeholde oss etten til justeinge.
Newtons lover i to og tre dimensjoner
 Newtons love i to og te dimensjone 9..17 Oblig e lagt ut. Innleveing: Mandag,.. FYS-MEK 111 9..17 1 Skått kast med luftmotstand F net F D G D v v mg ˆj hoisontal og vetikal bevegelse ikke lenge uavhengig:
Newtons love i to og te dimensjone 9..17 Oblig e lagt ut. Innleveing: Mandag,.. FYS-MEK 111 9..17 1 Skått kast med luftmotstand F net F D G D v v mg ˆj hoisontal og vetikal bevegelse ikke lenge uavhengig:
Øving 8. Dersom ikke annet er oppgitt, antas det at systemet er i elektrostatisk likevekt.
 Institutt fo fysikk, NTNU TFY455/FY003: lektisitet og magnetisme Vå 2008 Øving 8 Veiledning: 04.03 i R2 25-400, 05.03 i R2 25-400 Innleveingsfist: Fedag 7. mas kl. 200 (Svatabell på siste side.) Opplysninge:
Institutt fo fysikk, NTNU TFY455/FY003: lektisitet og magnetisme Vå 2008 Øving 8 Veiledning: 04.03 i R2 25-400, 05.03 i R2 25-400 Innleveingsfist: Fedag 7. mas kl. 200 (Svatabell på siste side.) Opplysninge:
Newtons lover i én dimensjon (2)
 Newtons love i én dimensjon () 9.1.13 husk: data lab fedag 1-16 FYS-MEK 111 9.1.13 1 Identifikasjon av keftene: 1. Del poblemet inn i system og omgivelse.. Tegn figu av objektet og alt som beøe det. 3.
Newtons love i én dimensjon () 9.1.13 husk: data lab fedag 1-16 FYS-MEK 111 9.1.13 1 Identifikasjon av keftene: 1. Del poblemet inn i system og omgivelse.. Tegn figu av objektet og alt som beøe det. 3.
Sammendrag, uke 14 (5. og 6. april)
 Institutt fo fysikk, NTNU TFY4155/FY1003: Elektisitet og magnetisme Vå 2005 Sammendag, uke 14 (5. og 6. apil) Magnetisk vekselvikning [FGT 28, 29; YF 27, 28; TM 26, 27; AF 22, 24B; H 23; DJG 5] Magnetisme
Institutt fo fysikk, NTNU TFY4155/FY1003: Elektisitet og magnetisme Vå 2005 Sammendag, uke 14 (5. og 6. apil) Magnetisk vekselvikning [FGT 28, 29; YF 27, 28; TM 26, 27; AF 22, 24B; H 23; DJG 5] Magnetisme
Fysikk-OL Norsk finale 2005
 Univesitetet i Oslo Nosk Fysikklæefoening Fysikk-OL Nosk finale 005 3. uttakingsunde Tid: Fedag 5. apil kl 09.00.00 Hjelpemidle: Tabell/fomelsamling, gafisk lommeegne Oppgavesettet bestå av 7 oppgave på
Univesitetet i Oslo Nosk Fysikklæefoening Fysikk-OL Nosk finale 005 3. uttakingsunde Tid: Fedag 5. apil kl 09.00.00 Hjelpemidle: Tabell/fomelsamling, gafisk lommeegne Oppgavesettet bestå av 7 oppgave på
Laboratorieøvelse i MNFFY1303-Elektromagnetisme Institutt for Fysikk, NTNU MAGNETISK HYSTERESE
 Laboatoieøvelse i MNFFY33-Elektomagnetisme Institutt fo Fysikk, NTNU Hensikten med oppgave å gjøe seg kjent med opphavet til magnetiske felte og målinge av slike. Det innebæe måling av magnetfelt fa enkle
Laboatoieøvelse i MNFFY33-Elektomagnetisme Institutt fo Fysikk, NTNU Hensikten med oppgave å gjøe seg kjent med opphavet til magnetiske felte og målinge av slike. Det innebæe måling av magnetfelt fa enkle
Problemet. Datamaskinbaserte doseberegninger. Usikkerheter i dose konsekvenser 1 Usikkerheter i dose konsekvenser 2
 Poblemet Datamaskinbasete dosebeegninge Beegne dosefodeling i en pasient helst med gunnlag i CT-bilde Eiik Malinen Sentale kilde: T. Knöös (http://www.clin.adfys.lu.se/downloads.htm) A. Ahnesjö (div. publikasjone)
Poblemet Datamaskinbasete dosebeegninge Beegne dosefodeling i en pasient helst med gunnlag i CT-bilde Eiik Malinen Sentale kilde: T. Knöös (http://www.clin.adfys.lu.se/downloads.htm) A. Ahnesjö (div. publikasjone)
Betinget bevegelse
 Betinget bevegelse 1.0.013 innleveing på fonte FYS-MEK 1110 1.0.013 1 Innleveinge aksenavn! enhete! kommente esultatene utegninge: skitt fo skitt, ikke bae esultatet vi tenge å fostå hva du ha gjot sett
Betinget bevegelse 1.0.013 innleveing på fonte FYS-MEK 1110 1.0.013 1 Innleveinge aksenavn! enhete! kommente esultatene utegninge: skitt fo skitt, ikke bae esultatet vi tenge å fostå hva du ha gjot sett
Utvalg med tilbakelegging
 Utvalg med tilbakelegging Gitt n foskjellige objekte. Vi skal velge objekte på en slik måte at fo hvet objekt vi velge, notee vi hvilket det e og legge det tilbake. Det bety at vi kan velge det samme objektet
Utvalg med tilbakelegging Gitt n foskjellige objekte. Vi skal velge objekte på en slik måte at fo hvet objekt vi velge, notee vi hvilket det e og legge det tilbake. Det bety at vi kan velge det samme objektet
UNIVERSITETET I OSLO
 Side av 5 UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Eksamen i: FYS-MEK Eksamensdag: Mandag 9. juni 28 Tid fo eksamen: Kl. 9-2 Oppgavesettet e på 5 side inkludet fomelaket. Tillatte
Side av 5 UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Eksamen i: FYS-MEK Eksamensdag: Mandag 9. juni 28 Tid fo eksamen: Kl. 9-2 Oppgavesettet e på 5 side inkludet fomelaket. Tillatte
Oppgave 1 a)1 b)3 c)2 d)3 e)3 f)2 g)3 h)2 i)1 j)2 k)1 l)2
 1 Løsningsfoslag EMC-eksamen 24.5. Oppgave 1 a)1 b)3 c)2 d)3 e)3 f)2 g)3 h)2 i)1 j)2 k)1 l)2 Oppgave 2 a) En geneisk standad e en geneell standad som bukes nå det ikke foeligge en poduktstandad. EN581
1 Løsningsfoslag EMC-eksamen 24.5. Oppgave 1 a)1 b)3 c)2 d)3 e)3 f)2 g)3 h)2 i)1 j)2 k)1 l)2 Oppgave 2 a) En geneisk standad e en geneell standad som bukes nå det ikke foeligge en poduktstandad. EN581
Løsningsforslag Fysikk 2 Høst 2014
 Løsningsfoslag Fysikk Høst 014 Løsningsfoslag Fysikk Høst 014 Opp Sva Foklaing gave a) D Det elektiske feltet gå adielt ut fa en positivt ladet patikkel. Til høye fo elektonet lage elektonet en feltstyke
Løsningsfoslag Fysikk Høst 014 Løsningsfoslag Fysikk Høst 014 Opp Sva Foklaing gave a) D Det elektiske feltet gå adielt ut fa en positivt ladet patikkel. Til høye fo elektonet lage elektonet en feltstyke
Eksamen 16. des Løsningsforslag
 Institutt fo fysikk TFY44/FY Mekanisk fysikk Eksamen 6. des.. Løsningsfoslag Dette løsningsfoslaget e spesielt fyldig med flee altenative løsninge, som ukt av flee studente i eksamensesvaelsen. Det e også
Institutt fo fysikk TFY44/FY Mekanisk fysikk Eksamen 6. des.. Løsningsfoslag Dette løsningsfoslaget e spesielt fyldig med flee altenative løsninge, som ukt av flee studente i eksamensesvaelsen. Det e også
Løsningsforslag sist oppdatert
 Løsningsfoslag sist oppdatet.. BOKMÅL Oppgave En funksjon f e definet i intevallet ved f ( ) ( ) e a) Finn f ( ). Avgjø hvo funksjonen e stigende og hvo funksjonen e avtagende. Bestem funksjonens eventuelle
Løsningsfoslag sist oppdatet.. BOKMÅL Oppgave En funksjon f e definet i intevallet ved f ( ) ( ) e a) Finn f ( ). Avgjø hvo funksjonen e stigende og hvo funksjonen e avtagende. Bestem funksjonens eventuelle
EKSAMEN I EMNE SIE 4015 BØLGEFORPLANTNING
 NTNU Noges teknisk-natuvitenskapelige univesitet Side 1 av 8 Fakultet fo infomatikk, matematikk og elektoteknikk Institutt fo fysikalsk elektonikk Bokmål/Nynosk Faglig/fagleg kontakt unde eksamen: Navn:
NTNU Noges teknisk-natuvitenskapelige univesitet Side 1 av 8 Fakultet fo infomatikk, matematikk og elektoteknikk Institutt fo fysikalsk elektonikk Bokmål/Nynosk Faglig/fagleg kontakt unde eksamen: Navn:
Spørretime TEP Våren Spørretime TEP Våren 2008
 Søetime EP 4115 - Våen 28 Fotegnskonvensjonen og Ka.9 (& OB s slides) Q: ilsynelatende uoveensstemmelse mellom det Olav Bolland esentete fo Otto/Diesel og det som stå i læeboka nå det gjelde fotegn i likninge.
Søetime EP 4115 - Våen 28 Fotegnskonvensjonen og Ka.9 (& OB s slides) Q: ilsynelatende uoveensstemmelse mellom det Olav Bolland esentete fo Otto/Diesel og det som stå i læeboka nå det gjelde fotegn i likninge.
EKSAMEN i. MA-132 Geometri. Torsdag 3. desember 2009 kl Tillatte hjelpemidler: Alle trykte og skrevne hjelpemidler. Kalkulator.
 Institutt fo matematiske fag EKSAMEN i MA-1 Geometi Tosdag. desembe 009 kl. 9.00-14.00 Tillatte hjelpemidle: Alle tykte og skevne hjelpemidle. Kalkulato. Bokmål Oppgave 1 I oppgaven nedenfo skal du oppgi
Institutt fo matematiske fag EKSAMEN i MA-1 Geometi Tosdag. desembe 009 kl. 9.00-14.00 Tillatte hjelpemidle: Alle tykte og skevne hjelpemidle. Kalkulato. Bokmål Oppgave 1 I oppgaven nedenfo skal du oppgi
a) C Det elektriske feltet går radielt ut fra en positivt ladet partikkel og radielt innover mot en negativt ladd partikkel.
 Løsningsfoslag Fysikk 2 Vå 2015 Løsningsfoslag Fysikk 2 Vå 2015 Oppgav e Sva Foklaing a) C Det elektiske feltet gå adielt ut fa en positivt ladet patikkel og adielt innove mot en negativt ladd patikkel.
Løsningsfoslag Fysikk 2 Vå 2015 Løsningsfoslag Fysikk 2 Vå 2015 Oppgav e Sva Foklaing a) C Det elektiske feltet gå adielt ut fa en positivt ladet patikkel og adielt innove mot en negativt ladd patikkel.
Løsning midtveiseksamen H12 AST1100
 Løsning midtveiseksamen H AST00 Aleksande Seland Setembe 5, 04 Ogave Vi se at kuven fo adiell hastighet e eiodisk og minne om en hamonisk funksjon. Vi kan defo anta at denne stjenen gå i bane undt et felles
Løsning midtveiseksamen H AST00 Aleksande Seland Setembe 5, 04 Ogave Vi se at kuven fo adiell hastighet e eiodisk og minne om en hamonisk funksjon. Vi kan defo anta at denne stjenen gå i bane undt et felles
Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 6. august 2003
 Noges teknisk natuvitenskapelige univesitet NTNU Side av 9 Institutt fo fysikk Fakultet fo natuvitenskap og teknologi Løsningsfoslag til eksamen i SIF47 KLASSISK FELTTEORI Onsdag 6. august 3 Dette løsningsfoslaget
Noges teknisk natuvitenskapelige univesitet NTNU Side av 9 Institutt fo fysikk Fakultet fo natuvitenskap og teknologi Løsningsfoslag til eksamen i SIF47 KLASSISK FELTTEORI Onsdag 6. august 3 Dette løsningsfoslaget
Utvalg med tilbakelegging
 Utvalg med tilbakelegging Gitt n foskjellige objekte. Vi skal velge objekte på en slik måte at fo hvet objekt vi velge, notee vi hvilket det e og legge det tilbake. Det bety at vi kan velge det samme objektet
Utvalg med tilbakelegging Gitt n foskjellige objekte. Vi skal velge objekte på en slik måte at fo hvet objekt vi velge, notee vi hvilket det e og legge det tilbake. Det bety at vi kan velge det samme objektet
LØSNINGSFORSLAG TIL EKSAMEN I FAG TEP4170 VARME- OG FORBRENNINGSTEKNIKK 18. mai 2007 Tid:
 av 4 Noges teknisk-natuvitenskapelige univesitet Initutt fo enegi- og poseseknikk Kontakt unde eksamen: Toleif Weydahl, tlf. 7359634 / 945 ØSNINGSFORSAG TI EKSAMEN I FAG TEP47 VARME- OG FORBRENNINGSTEKNIKK
av 4 Noges teknisk-natuvitenskapelige univesitet Initutt fo enegi- og poseseknikk Kontakt unde eksamen: Toleif Weydahl, tlf. 7359634 / 945 ØSNINGSFORSAG TI EKSAMEN I FAG TEP47 VARME- OG FORBRENNINGSTEKNIKK
EKSAMEN I FY1001 og TFY4145 MEKANISK FYSIKK: LØSNINGSFORSLAG
 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK EKSAMEN I FY1001 og TFY4145 MEKANISK FYSIKK: LØSNINGSFORSLAG Tisdag 18. desembe 01 kl. 0900-100 Oppgave 1. Ti flevalgsspøsmål. (Telle
NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK EKSAMEN I FY1001 og TFY4145 MEKANISK FYSIKK: LØSNINGSFORSLAG Tisdag 18. desembe 01 kl. 0900-100 Oppgave 1. Ti flevalgsspøsmål. (Telle
EKSAMENSOPPGAVE - Skoleeksamen. Institutt for Samfunnsøkonomi. Utlevering: 17.12.2014 Kl. 09.00 Innlevering: 17.12.2014 Kl. 14.00
 EKSAMENSOPPGAVE - Skoleeksamen MET 11803 Matematikk Institutt fo Samfunnsøkonomi Utleveing: 17122014 Kl 0900 Innleveing: 17122014 Kl 1400 Vekt: 70% av MET 1180 Antall side i oppgaven: Antall vedleggsfile:
EKSAMENSOPPGAVE - Skoleeksamen MET 11803 Matematikk Institutt fo Samfunnsøkonomi Utleveing: 17122014 Kl 0900 Innleveing: 17122014 Kl 1400 Vekt: 70% av MET 1180 Antall side i oppgaven: Antall vedleggsfile:
KONTINUASJONSEKSAMEN I EMNE TFE 4120 ELEKTROMAGNETISME
 Noges teknisk natuitenskapelige uniesitet Institutt fo elektonikk og telekommunikasjon ide 1 a 7 Faglæe: Johannes kaa KONTINUAJONEKAMEN I EMNE TFE 4120 ELEKTROMAGNETIME Tosdag 15. august 2013 Oppgae 1
Noges teknisk natuitenskapelige uniesitet Institutt fo elektonikk og telekommunikasjon ide 1 a 7 Faglæe: Johannes kaa KONTINUAJONEKAMEN I EMNE TFE 4120 ELEKTROMAGNETIME Tosdag 15. august 2013 Oppgae 1
Midtsemesterprøve fredag 10. mars kl
 Institutt fo fysikk, NTNU FY1003 lektisitet og magnetisme I TFY4155 lektomagnetisme Vå 006 Midtsemestepøve fedag 10. mas kl 0830 1130. Svatabellen stå på et eget ak. Sett tydelige kyss. Husk å skive på
Institutt fo fysikk, NTNU FY1003 lektisitet og magnetisme I TFY4155 lektomagnetisme Vå 006 Midtsemestepøve fedag 10. mas kl 0830 1130. Svatabellen stå på et eget ak. Sett tydelige kyss. Husk å skive på
KJM Radiokjemidelen
 Patikke i boks - en dimensjon KJM 1060 - Radiokjemideen Foeesning : Skamodeen d ψ m + E ψ 0 dx h n π h En V0 + m ψ n nπ( x + ) sin n 45 de n 1,,,... Sannsynigheten fo å finne patikkeen meom x og x+dx e:
Patikke i boks - en dimensjon KJM 1060 - Radiokjemideen Foeesning : Skamodeen d ψ m + E ψ 0 dx h n π h En V0 + m ψ n nπ( x + ) sin n 45 de n 1,,,... Sannsynigheten fo å finne patikkeen meom x og x+dx e:
EKSAMEN I FAG SIF 4008 FYSIKK Mandag 7. mai 2001 kl Bokmål. K. Rottmann: Matematisk formelsamling
 Side 1 av 1 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt unde eksamen: Føsteamanuensis Knut Ane Stand Telefon: 73 59 34 61 EKSAMEN I FAG SIF 48 FYSIKK Mandag 7. mai
Side 1 av 1 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt unde eksamen: Føsteamanuensis Knut Ane Stand Telefon: 73 59 34 61 EKSAMEN I FAG SIF 48 FYSIKK Mandag 7. mai
FFI RAPPORT FORDAMPING FRA OVERFLATER OG DRÅPER. BUSMUNDRUD Odd FFI/RAPPORT-2005/03538
 FFI RAPPORT FORDAMPING FRA OVERFLATER OG DRÅPER BUSMUNDRUD Odd FFI/RAPPORT-5/58 FORDAMPING FRA OVERFLATER OG DRÅPER BUSMUNDRUD Odd FFI/RAPPORT-5/58 FORSVARETS FORSKNINGSINSTITUTT Nowegian Defence Reseach
FFI RAPPORT FORDAMPING FRA OVERFLATER OG DRÅPER BUSMUNDRUD Odd FFI/RAPPORT-5/58 FORDAMPING FRA OVERFLATER OG DRÅPER BUSMUNDRUD Odd FFI/RAPPORT-5/58 FORSVARETS FORSKNINGSINSTITUTT Nowegian Defence Reseach
Løsningsforslag Fysikk 2 Vår 2013 Oppgav e
 Løsningsfoslag Fysikk 2 Vå 203 Løsningsfoslag Fysikk 2 Vå 203 Oppgav e Sva Foklaing a) B Feltet E gå adielt ut fa en positivt ladning. Siden ladning og 2 e like stoe, og ligge like langt unna P vil E væe
Løsningsfoslag Fysikk 2 Vå 203 Løsningsfoslag Fysikk 2 Vå 203 Oppgav e Sva Foklaing a) B Feltet E gå adielt ut fa en positivt ladning. Siden ladning og 2 e like stoe, og ligge like langt unna P vil E væe
At energi ikke kan gå tapt, må bety at den er bevart. Derav betegnelsen bevaringslov.
 Side av 8 LØSNINGSFORSLAG KONINUASJONSEKSAMEN 006 SMN694 VARMELÆRE DAO: 04. Mai 007 ID: KL. 09.00 -.00 OPPGAVE (Vekt: 40%) a) emodynamikkens. hovedsats:. hovedsetning: Enegi kan hveken oppstå elle fosvinne,
Side av 8 LØSNINGSFORSLAG KONINUASJONSEKSAMEN 006 SMN694 VARMELÆRE DAO: 04. Mai 007 ID: KL. 09.00 -.00 OPPGAVE (Vekt: 40%) a) emodynamikkens. hovedsats:. hovedsetning: Enegi kan hveken oppstå elle fosvinne,
Fysikkolympiaden 1. runde 25. oktober 5. november 2004
 Nosk Fysikklæefoening Nosk Fysisk Selskaps fagguppe fo undevisning Fysikkolympiaden 1. unde 5. oktobe 5. novembe 004 Hjelpemidle: abell og fomelsamlinge i fysikk og matematikk Lommeegne id: 100 minutte
Nosk Fysikklæefoening Nosk Fysisk Selskaps fagguppe fo undevisning Fysikkolympiaden 1. unde 5. oktobe 5. novembe 004 Hjelpemidle: abell og fomelsamlinge i fysikk og matematikk Lommeegne id: 100 minutte
Eksamen i MA-104 Geometri Løsningsforslag
 Eksamen i M-04 Geometi 4.0.007 Løsningsfoslag Oppgave Et kvadat ha side lik s, som du velge selv. E e midtpunktet på og F e midtpunktet på. iagonalen skjæe F i H. E skjæe F i G. I oppgaven skal du buke
Eksamen i M-04 Geometi 4.0.007 Løsningsfoslag Oppgave Et kvadat ha side lik s, som du velge selv. E e midtpunktet på og F e midtpunktet på. iagonalen skjæe F i H. E skjæe F i G. I oppgaven skal du buke
Betraktninger rundt det klassiske elektronet.
 Betaktninge undt det klassiske elektonet. Kistian Beland Matteus Häge - 1 - - - Innholdsfotegnelse: 1. Sammendag - 5 -. Innledning - 6 -. Innledende betaktninge - 7-4. Vå elektonmodell - 8-5. Enegi i feltene
Betaktninge undt det klassiske elektonet. Kistian Beland Matteus Häge - 1 - - - Innholdsfotegnelse: 1. Sammendag - 5 -. Innledning - 6 -. Innledende betaktninge - 7-4. Vå elektonmodell - 8-5. Enegi i feltene
Klossen beveger seg med konstant fart, så Newtons 1.lov gir at friksjonskraften R er like stor som parallellkomponenten til tyngden G 2
 Løsningsfoslag Fysikk 2 H2017 Oppgave 1 Oppgave Sva Foklaing a) B Magnetisk fluks måles i Webe (Wb), som foøvig e det samme som Teslakvadatmete (T m & ). b) B Klossen bevege seg ikke nomalt på bakkeplanet,
Løsningsfoslag Fysikk 2 H2017 Oppgave 1 Oppgave Sva Foklaing a) B Magnetisk fluks måles i Webe (Wb), som foøvig e det samme som Teslakvadatmete (T m & ). b) B Klossen bevege seg ikke nomalt på bakkeplanet,
Øving nr. 7. LØSNINGSFORSLAG
 FAG 4 PÅLITELIGHET I ELKRAFTSYSTEMER - GRUNNKURS. Øving n. 7. LØSNINGSFORSLAG Tilstandsdiagam: : Begge enhete i funksjon µ : En av enhetene feile Mek: seiell epaasjon innebæe at ovegangsintensiteten µ,
FAG 4 PÅLITELIGHET I ELKRAFTSYSTEMER - GRUNNKURS. Øving n. 7. LØSNINGSFORSLAG Tilstandsdiagam: : Begge enhete i funksjon µ : En av enhetene feile Mek: seiell epaasjon innebæe at ovegangsintensiteten µ,
1 Virtuelt arbeid for stive legemer
 1 Vituelt abeid fo stive legeme Innhold: Abeidsbegepet i mekanikk Pinsippet om vituelt abeid fo stive legeme Litteatu: Igens, Statikk, kap. 10.1 10.2 Hibbele, Statics, kap. 11.1 11.3 Bell, Konstuksjonsmekanikk
1 Vituelt abeid fo stive legeme Innhold: Abeidsbegepet i mekanikk Pinsippet om vituelt abeid fo stive legeme Litteatu: Igens, Statikk, kap. 10.1 10.2 Hibbele, Statics, kap. 11.1 11.3 Bell, Konstuksjonsmekanikk
RAPPORT. Endring E014 Flomvurdering eksisterende E6 STATENS VEGVESEN OPPDRAGSNUMMER [ R01] 29/05/2015 SWECO NORGE AS
![RAPPORT. Endring E014 Flomvurdering eksisterende E6 STATENS VEGVESEN OPPDRAGSNUMMER [ R01] 29/05/2015 SWECO NORGE AS RAPPORT. Endring E014 Flomvurdering eksisterende E6 STATENS VEGVESEN OPPDRAGSNUMMER [ R01] 29/05/2015 SWECO NORGE AS](/thumbs/62/46972182.jpg) RAPPORT STATENS VEGVESEN Ending E014 Flomvudeing eksisteende E6 OPPDRAGSNUMMER 12143214 [12143214-R01] 29/05/2015 SWECO NORGE AS SAMUEL VINGERHAGEN epo002.docx 2013-06-14 Sweco epo002.docx 2013-06-14
RAPPORT STATENS VEGVESEN Ending E014 Flomvudeing eksisteende E6 OPPDRAGSNUMMER 12143214 [12143214-R01] 29/05/2015 SWECO NORGE AS SAMUEL VINGERHAGEN epo002.docx 2013-06-14 Sweco epo002.docx 2013-06-14
Kap 28: Magnetiske kilder. Kap 28: Magnetiske kilder. Kap 28. Rottmann integraltabell (s. 137) μ r. μ r. μ r. μ r
 Kap 8 Kap 8: Magnetiske kilde Elektostatikk: Ladning q påvikes av kaft qe Definisjon E-felt E-feltet skapes fa ladninge (Coulombs lov) (Coulombs lov) Magnetostatikk: Ladning q i bevegelse påvikes av kaft
Kap 8 Kap 8: Magnetiske kilde Elektostatikk: Ladning q påvikes av kaft qe Definisjon E-felt E-feltet skapes fa ladninge (Coulombs lov) (Coulombs lov) Magnetostatikk: Ladning q i bevegelse påvikes av kaft
Løsning øving 12 N L. Fra Faradays induksjonslov får vi da en indusert elektromotorisk spenning:
 nstitutt fo fysikk, NTNU Fg SF 4 Elektognetise og MNFFY 3 Elektisitet og gnetise Høst øsning øving Oppgve Mgnetfeltet inne i solenoiden e : ( H( (N/) ( (dvs fo < R). Utenfo solenoiden: ( > R) Fo å eegne
nstitutt fo fysikk, NTNU Fg SF 4 Elektognetise og MNFFY 3 Elektisitet og gnetise Høst øsning øving Oppgve Mgnetfeltet inne i solenoiden e : ( H( (N/) ( (dvs fo < R). Utenfo solenoiden: ( > R) Fo å eegne
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MEK 1100 Feltteori og vektoranalyse. Eksamensdag: Fredag 29 mai 2009. Tid for eksamen: 14:30 17:30. Oppgavesettet er på 6 sider.
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MEK 1100 Feltteori og vektoranalyse. Eksamensdag: Fredag 29 mai 2009. Tid for eksamen: 14:30 17:30. Oppgavesettet er på 6 sider.
Konstanter og formelsamling for kurset finner du bakerst Merk: Figurene til oppgavene er ofte på en annen side enn selve oppgaven
 UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Avsluttende eksamen i AST2000, 17. desembe 2018, 09.00 13.00 Oppgavesettet inkludet fomelsamling e på 8 side Tillatte hjelpemidle: 1) Angel/Øgim
UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Avsluttende eksamen i AST2000, 17. desembe 2018, 09.00 13.00 Oppgavesettet inkludet fomelsamling e på 8 side Tillatte hjelpemidle: 1) Angel/Øgim
TFE4120 Elektromagnetisme
 NTNU IET, IME-fkultetet, Noge teknisk-ntuvitenskpelige univesitet TFE4120 Elektomgnetisme Løsningsfoslg øving 5 Oppgve 1 ) Pg. symmeti h vi E = E()ˆ gjennom hele oppgven. i) Vi l Gussflten S væe oveflten
NTNU IET, IME-fkultetet, Noge teknisk-ntuvitenskpelige univesitet TFE4120 Elektomgnetisme Løsningsfoslg øving 5 Oppgve 1 ) Pg. symmeti h vi E = E()ˆ gjennom hele oppgven. i) Vi l Gussflten S væe oveflten
KONTINUASJONSEKSAMEN I EMNE TFE 4120 ELEKTROMAGNETISME
 Noges teknisk natuitenskapelige uniesitet Institutt fo elektoniske systeme ide 1 a 7 Faglæe: Johannes kaa KONTINUAJONEKAMEN I EMNE TFE 4120 ELEKTROMAGNETIME August 2017 Alle anlige deloppgae telle 4 poeng.
Noges teknisk natuitenskapelige uniesitet Institutt fo elektoniske systeme ide 1 a 7 Faglæe: Johannes kaa KONTINUAJONEKAMEN I EMNE TFE 4120 ELEKTROMAGNETIME August 2017 Alle anlige deloppgae telle 4 poeng.
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MEK 11 Feltteori og vektoranalyse. Eksamensdag: Torsdag 1 desember 29. Tid for eksamen: 14:3 17:3. Oppgavesettet er på 7 sider.
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MEK 11 Feltteori og vektoranalyse. Eksamensdag: Torsdag 1 desember 29. Tid for eksamen: 14:3 17:3. Oppgavesettet er på 7 sider.
Mot 5: Støy i bipolare transistorer
 1/34 Mot 5: Støy i bipolae tansistoe Vi ha tidligee unnet Eni, En, og n o en osteke. Vi vil nå gjøe dette o en bipola tansisto. Vi vil se at støyen e både avhengig av opeasjonspunktet (støm og spenning)
1/34 Mot 5: Støy i bipolae tansistoe Vi ha tidligee unnet Eni, En, og n o en osteke. Vi vil nå gjøe dette o en bipola tansisto. Vi vil se at støyen e både avhengig av opeasjonspunktet (støm og spenning)
Kapittel 2: Krumlinjet bevegelse
 Kapittel : Kumlinjet bevegelse Vannett kast v = v v = gt x 0 1 x = vt 0 y= gt y Skått kast v = v v = v gt x 0x y 0y 1 x = v0 t y = v x 0 t gt y Sving uten dosseing U+ G = ma N = G v R = m R = μn = μmg
Kapittel : Kumlinjet bevegelse Vannett kast v = v v = gt x 0 1 x = vt 0 y= gt y Skått kast v = v v = v gt x 0x y 0y 1 x = v0 t y = v x 0 t gt y Sving uten dosseing U+ G = ma N = G v R = m R = μn = μmg
Løsning, eksamen 3FY juni 1999
 Løsning, eksamen 3FY juni 1999 Oppgae 1 km/s a) Hubbles lo sie at H, de H. 10 lyså Faten til galaksen e: 3 10 m/s H 5,0 10 7 lyså 1,10 10 m/s 10 lyså b) Dopplefomelen gi oss λ, de c e lysfaten og λ 0 e
Løsning, eksamen 3FY juni 1999 Oppgae 1 km/s a) Hubbles lo sie at H, de H. 10 lyså Faten til galaksen e: 3 10 m/s H 5,0 10 7 lyså 1,10 10 m/s 10 lyså b) Dopplefomelen gi oss λ, de c e lysfaten og λ 0 e
sosiale behov FASE 2: Haug barnehage 2011-2012
 : Hva kjennetegne bana i denne fasen? De voksnes olle Banemøte Påkledning Samlinge Måltid Posjekte Uteleik Konfliktløsning Vudeing Haug banehage 2011-2012 «Omsog, oppdagelse og læing i banehagen skal femme
: Hva kjennetegne bana i denne fasen? De voksnes olle Banemøte Påkledning Samlinge Måltid Posjekte Uteleik Konfliktløsning Vudeing Haug banehage 2011-2012 «Omsog, oppdagelse og læing i banehagen skal femme
8 Eksamens trening. E2 (Kapittel 1) På figuren er det tegnet grafene til funksjonene f og g gitt ved
 84 8 Eksamenstening 8 Eksamens tening Uten hjelpemidle E1 (Kapittel 1) Polynomfunksjonen P e gitt ved P ( ) = 7 + 14 8, DP = R. a Det kan vises at alle heltallige løsninge av P() = 0 gå opp i konstantleddet
84 8 Eksamenstening 8 Eksamens tening Uten hjelpemidle E1 (Kapittel 1) Polynomfunksjonen P e gitt ved P ( ) = 7 + 14 8, DP = R. a Det kan vises at alle heltallige løsninge av P() = 0 gå opp i konstantleddet
Fysikk 2 Eksamen høsten Løsningsforslag
 Fysikk - Løsninsfosla Oppave a) D Tesla b) B Tyndeakseleasonen e det samme som feltstyken til avitasonsfeltet, som e itt ved m m Siden e en konstant (avitasonskonstanten), vil oså bee planetene. væe likt
Fysikk - Løsninsfosla Oppave a) D Tesla b) B Tyndeakseleasonen e det samme som feltstyken til avitasonsfeltet, som e itt ved m m Siden e en konstant (avitasonskonstanten), vil oså bee planetene. væe likt
FAG: MA-209 Matematikk 3 LÆRER: Per Henrik Hogstad KANDIDATEN MÅ SELV KONTROLLERE AT OPPGAVESETTET ER FULLSTENDIG
 UNIVERITETET I GDER Gimstad E K M E N O P P G V E : G: M-9 Matematikk LÆRER: Pe Henik Hogstad Klasse: Dato: 8..8 Eksamenstid fa-til: 9.. Eksamensoppgaven bestå av følgende ntall side: 6 inkl. foside vedlegg
UNIVERITETET I GDER Gimstad E K M E N O P P G V E : G: M-9 Matematikk LÆRER: Pe Henik Hogstad Klasse: Dato: 8..8 Eksamenstid fa-til: 9.. Eksamensoppgaven bestå av følgende ntall side: 6 inkl. foside vedlegg
Kap 28: Magnetiske kilder
 : Magnetiske kilde Elektostatikk: Ladning q påvikes av kaft qe Definisjon E-felt E-feltet skapes fa ladninge (Coulombs lov) (Coulombs lov) Magnetostatikk: Ladning q i bevegelse påvikes av kaft qv x B Definisjon
: Magnetiske kilde Elektostatikk: Ladning q påvikes av kaft qe Definisjon E-felt E-feltet skapes fa ladninge (Coulombs lov) (Coulombs lov) Magnetostatikk: Ladning q i bevegelse påvikes av kaft qv x B Definisjon
Tillatte hjelpemidler: Lærebok og kalkulator i samsvar med fakultetet sine regler Oppgave 1 En funksjon f er gitt ved f ( x) ( x 2) e x.
 UNIVERSITETET I BERGEN De maemaisk-nauvienskapelige fakule Eksamen i emne MAT Bukekus i maemaikk Fedag 8 febua, kl 9-4 BOKMÅL Tillae hjelpemidle: Læebok og kalkulao i samsva med fakulee sine egle Oppgave
UNIVERSITETET I BERGEN De maemaisk-nauvienskapelige fakule Eksamen i emne MAT Bukekus i maemaikk Fedag 8 febua, kl 9-4 BOKMÅL Tillae hjelpemidle: Læebok og kalkulao i samsva med fakulee sine egle Oppgave
FYSIKK-OLYMPIADEN Andre runde: 4/2 2010
 Nosk Fysikklæefoening Nosk Fysisk Selskaps fagguppe fo undevisning FYSIKK-OLYMPIADEN 009 010 Ande unde: / 010 Skiv øvest: Navn, fødselsdato, e-postadesse og skolens navn Vaighet:3 klokketime Hjelpemidle:abell
Nosk Fysikklæefoening Nosk Fysisk Selskaps fagguppe fo undevisning FYSIKK-OLYMPIADEN 009 010 Ande unde: / 010 Skiv øvest: Navn, fødselsdato, e-postadesse og skolens navn Vaighet:3 klokketime Hjelpemidle:abell
Hesteveddeløp i 8. klasse
 Andeas Loange Hesteveddeløp i 8. klasse Spillbettet. Gå det an å ha det gøy, utfoske algebaens mysteie og samtidig læe noe? Vi befinne oss i 8. klasse på Kykjekinsen skole i Begen. Jeg ha nettopp blitt
Andeas Loange Hesteveddeløp i 8. klasse Spillbettet. Gå det an å ha det gøy, utfoske algebaens mysteie og samtidig læe noe? Vi befinne oss i 8. klasse på Kykjekinsen skole i Begen. Jeg ha nettopp blitt
Energi Norge v/ingvar Solberg og Magne Fauli THEMA Consulting Group v/åsmund Jenssen og Jacob Koren Brekke 5. februar 2019
 Til: Enegi Noge v/ingva Solbeg og agne Fauli Fa: v/åsmund Jenssen og Jacob Koen Bekke Dato: 5. febua 219 Refeanse: ENO-18-1 Analyse av povenyvikninge av skatteendinge siden 27 Noske vannkaftvek ha siden
Til: Enegi Noge v/ingva Solbeg og agne Fauli Fa: v/åsmund Jenssen og Jacob Koen Bekke Dato: 5. febua 219 Refeanse: ENO-18-1 Analyse av povenyvikninge av skatteendinge siden 27 Noske vannkaftvek ha siden
Oppgavene er hentet fra fagets lærebok, Hass, Weir og Thomas, samt gamle eksamener.
 NTNU Institutt for matematiske fag TMA45 Matematikk, øving, vår Løsningsforslag Notasjon og merknader Oppgavene er hentet fra fagets lærebok, Hass, Weir og Thomas, samt gamle eksamener. Oppgaver fra kapittel
NTNU Institutt for matematiske fag TMA45 Matematikk, øving, vår Løsningsforslag Notasjon og merknader Oppgavene er hentet fra fagets lærebok, Hass, Weir og Thomas, samt gamle eksamener. Oppgaver fra kapittel
TFY4104 Fysikk. Institutt for fysikk, NTNU. Høsten Øving 9. Veiledning: 18. oktober. Innleveringsfrist: 23. oktober kl 14.
 TFY404 Fysikk. Institutt fo fysikk, NTNU. Høsten 203. Øving 9. Veiledning: 8. oktobe. Innleveingsfist: 23. oktobe kl 4. Oppgve ) Figuen vise et unifomt elektisk felt (heltukne linje). Lngs hvilken stiplet
TFY404 Fysikk. Institutt fo fysikk, NTNU. Høsten 203. Øving 9. Veiledning: 8. oktobe. Innleveingsfist: 23. oktobe kl 4. Oppgve ) Figuen vise et unifomt elektisk felt (heltukne linje). Lngs hvilken stiplet
Oppgave 1 a) I det generelle tilfelle kan man ta utgangspunkt i uttrykket D( E)
 Løsigsfoslag, eksae 8. desebe 998 Oppgave a) I det geeelle tilfelle ka a ta utgagspukt i uttykket D ( ) d k ( ( k) ) ( π) δ Me ut fa geoetiske betaktige av atall tilstade ello og + d se vi at di: πk D(
Løsigsfoslag, eksae 8. desebe 998 Oppgave a) I det geeelle tilfelle ka a ta utgagspukt i uttykket D ( ) d k ( ( k) ) ( π) δ Me ut fa geoetiske betaktige av atall tilstade ello og + d se vi at di: πk D(
Midtsemesterprøve onsdag 7. mars 2007 kl Versjon A
 Institutt fo fysikk, NTNU FY1003 lektisitet og mgnetisme I TFY4155 lektomgnetisme Vå 2007 Midtsemestepøve onsdg 7. ms 2007 kl 1300 1500. Løsningsfoslg. Vesjon 1) Hvilken påstnd om elektisk potensil e feil?
Institutt fo fysikk, NTNU FY1003 lektisitet og mgnetisme I TFY4155 lektomgnetisme Vå 2007 Midtsemestepøve onsdg 7. ms 2007 kl 1300 1500. Løsningsfoslg. Vesjon 1) Hvilken påstnd om elektisk potensil e feil?
Fysikkolympiaden Norsk finale 2010
 Uniesitetet i Oslo Nosk Fysikklæefoening Fysikkolympiaden Nosk finale. ttakingsnde Fedag 6. mas kl 9. til. Hjelpemidle: abell/fomelsamling, lommeegne og tdelt fomelak Oppgaesettet bestå a 6 oppgae på side
Uniesitetet i Oslo Nosk Fysikklæefoening Fysikkolympiaden Nosk finale. ttakingsnde Fedag 6. mas kl 9. til. Hjelpemidle: abell/fomelsamling, lommeegne og tdelt fomelak Oppgaesettet bestå a 6 oppgae på side
Formelsamling. ξ(r, t) = ξ 0 sin(k r ωt + φ) 2 ξ(x, t) = 1 2 ξ(x, t) t 2. 2 ξ. x ξ. z 2. y ξ. v = ω k. v g = dω dk
 Formelsamling Side 7 av 15 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk plan bølge: Bølgeligning:
Formelsamling Side 7 av 15 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk plan bølge: Bølgeligning:
Formelsamling Bølgefysikk Desember 2006
 Vedlegg 1 av 9 Formelsamling Bølgefysikk Desember 2006 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk
Vedlegg 1 av 9 Formelsamling Bølgefysikk Desember 2006 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk
Tips for prosjektoppgaven i FYS-MEK/F 1110 V2006
 1 Tips fo posjektoppgaven i FYS-MEK/F 1110 V2006 Utfosking av et telegeme-system Ant Inge Vistnes, vesjon 0605141330 Det e ikke nødvendig å lese dette skivet fo å løse posjektoppgaven, men de fleste vil
1 Tips fo posjektoppgaven i FYS-MEK/F 1110 V2006 Utfosking av et telegeme-system Ant Inge Vistnes, vesjon 0605141330 Det e ikke nødvendig å lese dette skivet fo å løse posjektoppgaven, men de fleste vil
Løsningsforslag. FY-ME100 eksamen 13. juni 2003
 1 Løsningsfoslag FY-ME100 eksamen 13. juni 003 Oppgaveteksten e gjengitt fo at løsningsfoslaget skal kunne leses uten at den oiginale oppgaveteksten e tilgjengelig samtidig. I en nomal studentbesvaelse
1 Løsningsfoslag FY-ME100 eksamen 13. juni 003 Oppgaveteksten e gjengitt fo at løsningsfoslaget skal kunne leses uten at den oiginale oppgaveteksten e tilgjengelig samtidig. I en nomal studentbesvaelse
Løsningsforslag eksamen 2. august 2003 SIF 4005 Fysikk for kjemi og materialteknologi
 Løsningsfslag eksamen. august SF 5 Fysikk f kjemi g mateialteknlgi Oppgave lektstatikk a) Sylineens ttale laning pe lengeenhet finnes ve å integee laningsfelingen ( ) ve aealelementet A= e sylineens aius
Løsningsfslag eksamen. august SF 5 Fysikk f kjemi g mateialteknlgi Oppgave lektstatikk a) Sylineens ttale laning pe lengeenhet finnes ve å integee laningsfelingen ( ) ve aealelementet A= e sylineens aius
Kap. 22. Gauss lov. Gauss lov skjematisk. Eks.1: Homogent ladd kule =Y&F Ex = LHL Vi skal se på: Fluksen til elektrisk felt E Gauss lov
 Kap.. Gauss lov Vi skal se på: Fluksen til elektisk felt E Gauss lov Integalfom og diffeensialfom Elektisk ledee. Efelt fa Coulombs lov: q E = k E = k å n q n n n dq E= k ò tot. ladn. Punktladn Flee punktladn.
Kap.. Gauss lov Vi skal se på: Fluksen til elektisk felt E Gauss lov Integalfom og diffeensialfom Elektisk ledee. Efelt fa Coulombs lov: q E = k E = k å n q n n n dq E= k ò tot. ladn. Punktladn Flee punktladn.
LØSNINGSFORSLAG TIL EKSAMEN I FY1003 ELEKTRISITET OG MAGNETISME I TFY4155 ELEKTROMAGNETISME Fredag 8. juni 2007 kl
 NOGES TEKNISK- NATUVITENSKAPELIGE UNIVESITET INSTITUTT FO FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFOSLAG TIL EKSAMEN I FY1003 ELEKTISITET OG
NOGES TEKNISK- NATUVITENSKAPELIGE UNIVESITET INSTITUTT FO FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFOSLAG TIL EKSAMEN I FY1003 ELEKTISITET OG
Konstanter og formelsamling for kurset finner du bakerst Merk: Figurene til oppgavene er ofte på en annen side enn selve oppgaven
 UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Avsluttende eksamen i AST1100, 13. desembe 2016, 9.00 13.00 Oppgavesettet inkludet fomelsamling e på 7 side Tillatte hjelpemidle: 1) Angel/Øgim
UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Avsluttende eksamen i AST1100, 13. desembe 2016, 9.00 13.00 Oppgavesettet inkludet fomelsamling e på 7 side Tillatte hjelpemidle: 1) Angel/Øgim
