Rasjonell spekulasjon i eksperimentelle. aksjemarked
|
|
|
- Alfhild Holm
- 8 år siden
- Visninger:
Transkript
1 Rasjonell spekulasjon i eksperimentelle aksjemarked av Tobias Erevik Masteroppgave Masteroppgaven er levert for å fullføre graden Master i samfunnsøkonomi Universitetet i Bergen, Institutt for økonomi September 2010
2
3 Sammendrag Sammendrag Rasjonell spekulasjon i eksperimentelle aksjemarked av Tobias Erevik, Master i samfunnsøkonomi Universitetet i Bergen, 2010 Veileder: Sigve Tjøtta Denne oppgaven hadde som formål å undersøke tilstedeværelsen av rasjonell spekulasjon i eksperimentelle aksjemarkeder. For å se på tilstedeværelsen av rasjonell spekulasjon, gjennomføres to eksperimentelle aksjemarkeder ved bruk av Z-tree programvaren. Feil i eksperimentdesignet gjør imidlertid at resultatene fra de eksperimentelle aksjemarkedene ikke kan belyse spørsmålet om rasjonell spekulasjon. Regresjonsarbeidet ble foretatt i STATA. iii
4 Innholdsfortegnelse Innholdsfortegnelse Forord...ii Sammendrag...iii Innholdsfortegnelse...iv Tabeller...v Figurer...vi Innledning Teori Rasjonelle forventinger hypotesen Effisienshypotesen Nyklassiske teori modeller for aktivapriser Forskningsprogrammet til Smith, Suchanek og Williams Eksperimentoppsettet Forskningsprogrammet Analysen av forskningsprogramemts datasett Hovedfunnene fra forskningsprogrammet Eksperimentene Eksperimentdesignet Eksperimentenes oppsett Utførelsen av eksperimentene Resultater Oppsummering...70 Appendix A...72 Appendix B...88 Appendix C...89 Appendix D Referanser iv
5 Tabeller Tabeller Tabell 2.1 Eksperimentoppsettene i forskningsprogrammet...13 Tabell 3.1 Prisboblemål...50 Tabell 3.2 Forventingsrettheten til enkeltdeltakernes prognoser i det uinformerte eksperimentet...52 Tabell 3.3 Forventingsrettheten til enkeltdeltakernes prognoser i det informerte eksperimentet...53 Tabell 3.4 Prognosene til deltaker 3 i det informerte eksperimentet...54 Tabell 3.5 Adaptive forventningermodellen med dummy variabler - det informerte...60 Tabell 3.6 Adaptive forventingermodellen med dummy variabler - det informerte...61 Tabell 3.7 Statisitkk over x t,i = F t,i E( D t )...63 v
6 Figurer Figurer Figur 3.1 Handelsskjermen...36 Figur 3.2 Oppsummeringsskjermen...39 Figur 3.3 Handelen i det uinformerte eksperimentet...43 Figur 3.4 Prognosegjennomsnittet i det uinformerte eksperimentet...45 Figur 3.5 Handelen i det informerte eksperimentet...46 Figur 3.6 Prisboblen i det informerte eksperimentet...47 Figur 3.7 Prognosegjennomsnittet i det informerte eksperimentet...48 Figur 3.8 Prisboblesammenligningen...49 Figur 3.9 Frekvensdigram over prognoseavvikene i det uinformerte eksperimentet...55 Figur 3.10 Frekvensdigram over prognoseavvikene i det informerte eksperimentet...56 Figur 3.11 Adaptive forventinger i det informerte eksperimentet...58 Figur 3.12 Deltakernes endelige fortjeneste og kumulative prognoseavvik i det uinformerte eksperimentet...64 Figur 3.13 Deltakernes endelige fortjeneste og kumulative prognoseavvik mellom prognosene og gjennomsnittspris i det informerte eksperimentet...65 vi
7 ! Innledning Innledning Denne oppgaven hadde som formål å undersøke tilstedeværelsen av rasjonell spekulasjon i eksperimentelle aksjemarkeder. En aktiv litteratur innen eksperimentell økonomi har konsistent produsert prisbobler i eksperimentelle aksjemarkeder hvor den forventede verdien til aksjenes fremtidige dividendeutbetalinger tydelig fremkommer (Noussair og Tucker 2006). Prisbobler er hendelser hvor handelsprisene overgår forventet verdi av fremtidige utbetalinger. Smith, Suchanek og Williams (1988) hypotiserer at det er rasjonell spekulasjon som produserer prisboblene i de eksperimentelle aksjemarkedene. For å se på tilstedeværelsen av rasjonell spekulasjon, gjennomføres to eksperimentelle aksjemarkeder. Det ene aksjemarkedet er et kontrolleksperiment, som får navnet det informerte eksperimentet. Det informerte eksperimenet er tilnærmet likt tidligere eksperimentelle aksjemarkeder. Det andre eksperimentet kalles det uinformerte eksperimentet, fordi dividendeutfallenes sannsynlighetsfordelingen ikke opplyses. Idéen var at en mindre prisboble i det uinformerte eksperimentet sammenlignet med det informerte eksperimentet, ville være uforenelig med rasjonell spekulasjon. Designet ble begrunnet med at forskjellen i informasjon ville gjøre rasjonelle deltakeres preferanse for spekulasjon større i det uinformerte eksperimentet. Begrunnelsen er imidlertid feilaktig, slik at prisboblesammenligningen ikke gir grunnlag for å si noe om rasjonell spekulasjon. På grunn av forskjellen i utgitt informasjon kan ikke to identiske deltakeres preferanser for spekulasjon sammenlignes på tvers av de to eksperimentene, slik det var tiltenkt. Eksperimentene gir allikevel noen nye resultater. Det informerte eksperimentet viser seg å støtte en ny prisdynamikkhypotese og en ny prisforventningerhypotese. Tidligere studier har funnet støtte for at interperiode prisforventnignene er adaptive og at endringen i interperiodegjennomsnittsprisen kommer som følge av budoverskudd. Det informerte eksperimentet støtter hypoteser om endring i gjennomsnittsprisen og forventningene basert på de periodevise dividendeutbetalingene. 1
8 ! Teori Kapittel 1 presenterer teori som tar for seg prisbobler i finansmarkeder. Kapittel 2 presenterer forskningsprogrammet som fant tilstedeværelsen av prisbobler i eksperimentelle aksjemarkeder hvor forventet fremtidig dividendeverdi fremkommer tydelig. Kapittel 3 presenterer gjennomførelsen av, og resultatene fra, det uinformerte og det informerte eksperimentet. 1. Teori I dette kapittelet gjennomgås teoriene som forekommer i fremstillingen og utredningen av de eksperimentelle aksjemarkedene. Kapittelet er på ingen måte ment som en utømmende fremstilling av teorier som tar for seg prisbobler i finansmarkeder. Først forklares begrepet prisbobler. Deretter gjennomgås rasjonelle forventninger hypotesen til Muth. Hypotesen til Muth gjennomgås for å kunne presentere effisienshypotesen, som er en rasjonelle forventninger modell. Effisienshypotesen sier at finansmarkedene er effisiente og at prisbobler dermed ikke kan forekomme. Til slutt gjennomgås prisbobler i det nyklassiske modelloppsettet. Prisbobler Prisbobler forklares vanligvis som tilfeller hvor prisen på aktiva overgår fundamentalverdi (Brunnermeier 2008)(King et. al. 1993)(Camerer 1989). Prisningsteori sier at priser skal tendere mot fundamentalverdien (Hiorta og Sunder 2002). Standard prisningsteori, «the fundamenal theorem of asset pricing», sier at fundamentalverdien i en usikker verden er lik summen av risikojusterte neddiskonterte forventninger til fremtidige dividendeutbetalinger (Santos og Woodford 1997). Forutsetningen for dette er at det ikke eksisterer arbitrasjemuligheter i markedet (Skiadas 2009). Teorien begrunnes i baklengs induksjon (Hiorta og Sunder 2002). 1.1 Rasjonelle forventninger hypotesen Fremstillingen nedenfor baseres på Sheffrin (1996). 2
9 ! Teori Rasjonelle forventninger hypotesens motivasjon Rasjonelle forventninger hypotesen ble framsatt av John Muth i Hypotesen ble motivert av et problem knyttet til interaksjonen mellom forventninger og virkelighet. Det finnes mange eksempler på slike problem i økonomisk litteratur. Et eksempel er forholdet mellom forventningene til prisen og den realiserte prisen på avlignene i landbruket. Bønder bestemmer hvor mye å så på bakgrunn av hva de forventer prisen vil bli i neste periode. Forventningene til prisen blir derfor avgjørende for den faktiske prisen. Prisdynamikken i et slikt market vil avhenge av måten forventningene dannes. Dersom bøndene forventer samme pris som i foregående periode, kan markedsprisen flukturere dramatisk over tid. Sett at dårlig vær ødelegger mye av avlingene et år. Prisen vil da bli høy, siden mindre avlinger selges i markedet. Dersom bøndene forventer denne høye prisen også i neste periode, vil de så en større mengde. Resultatet blir en lav pris i den påfølgende perioden. Forventningene til lav pris vil føre til at bøndene sår i små mengder osv. Avhengig av helningen på tilbuds- og etterspørselskurven vil fluktasjonene i prisen avta eller tilta. En annen forventningsdannelse vil gi en annen prisdynamikk. Dynamiske modeller, som for eksempel en modell av prisdynamikken i det ovenfor forklarte markedet, vil avhenge av forutsetningene om forventningsdannelsen. Forventningsdannelsen var som regel faste formler i dynamiske modeller. Ifølge Muth kan ikke økonomer være tilfreds med slike faste formler for forventningsdannelsen. Formlene tillater ikke endringer i forventningene ved endring i den underliggende økonomiske strukuren. Muth mente at det ofte var endrignene i forventningene økonomene var opptatt av. Rasjonelle forventninger hypotesen Rasjonelle forventninger hypotesen forklarer hvordan økonomiske aktører utarbeider sine forventninger til stokastiske økonomiske variabler. Hypotesen bygger på at økonomiske aktører er rasjonelle og informerte. Ifølge hypotesen tar aktørene i bruk all relevant økonomisk teori når de utarbeider sine forventninger. Ved å ta i bruk relevant økonomisk teori vil aktørenes egne subjektive forventninger på tidspunkt t-1, E t 1 [X t ], til stokastiske økonomiske variabler i periode t, X t, i 3
10 ! Teori gjennomsnitt være lik den objektivt betingede forventningen, E[X t I t 1 ], til de samme variablene. Altså ; E t 1 [X t ]=E[X t I t 1 ] (1.1) I t 1 er her informasjon, herunder relevant teori, rådende forhold, osv., tilgjengelig ved tidspunkt t-1. Rasjonelle forventninger hypotesen sier altså at de økonomiske aktørene i snitt har den rette forventningen til stokastiske økonomiske variabeler og at den faktiske verdien på variabelene blir lik aktørenes snittforventning så fremt noe uforusett ikke skjer. Individenes forventningsdannelse Friedman påpekte at økonomiske aktører kun trenger å oppføre seg som om de maksimerer nytte eller profitt for at teorier skal fungere (Sheffrin 1996). På samme måte påpekte Muth at rasjonelle forventninger hypotesen ikke impliserer at alle økonomiske aktører kan all relevant økonomisk teori og utnytter kunnskapen i sin forventningsdannelse. Hypotesen er ikke avhengig av at alle har den samme forventningen. Individenes forventninger må bare være fordelt rundt den objektive forventningen. På denne måten blir gjennomsnittet av forventningene lik den objektive forventningen. Antagelsen om at aktørenes forventninger er fordelt rundt den objektive forventningen, har vært gjenstand for kritikk. For at inidvidenes forventninger skal være fordelt rundt den objektivt forventede verdien, må aktørene vite variabelens sanne fordeling. Hadde aktørenes tatt utgangspunkt i feil priorsfordeling, ville forventningene bli fordelt rundt et vilkårlig punkt. Et svar til kritikken er at individene «lærer» den sanne fordelingen etter hvert. Det er blitt vist at selv ved grove tommelfingerregler i forventningsdannelsen, kan forventningene bli lik rasjonlle forventninger løsningen. Et eksempel på en slik tommelfingerregel er forventninger om at neste periodes pris blir lik inneværende periodes pris i landbrukseksempelet. Med en slik forventningsdannelse vil forventningene etterhvert konvergere mot den rasjonelle forventningen. 1.2 Effisienshypotesen 4
11 ! Teori Effisienshypotesen er en rasjonelle forventninger modell. Hypotesen fremholder at finansmarkeder er informasjonseffisiente. Det vil si at prisene til en hver tid reflekterer all tilgjenglig informasjon. Informasjonseffisiens innebærer at det ikke er mulig å konsekvent tjene mer enn den risikojusterte markedsavkasntingen (Barberis og Thaler 2003). Informasjonseffisente priser sikerer at prisbobler ikke forekommer. Hypotesens historie presenteres i neste avsnitt. Avsnittet er med for å fasilitere forklaringen av hypotesen. Det påfølgende avsnittet gir en intuitiv forklaring av hypotesen. Siste avsnitt i dette underkapittelet gir en intuitiv forklaring av hypotesens avvisning av prisbobler. Effisienshypotesens motivasjon. Fra midten av 1950-tallet til tidlig 1960-tallet forekom en akkumulasjon av empiriske støtte for at oppførselen til aktivapriser kunne approksimeres ved random walk (Fama 1970). Med opphopningen av empirisk støtte begynte økonomer å prøve å forklare fenomenet. En forklaring ble fremsatt av Paul A. Samuelson i 1965 i artikkelen «Proof That Properly Anticipated Prices Fluctuate Randomly». Her viste Samuelson at futurespriser (priser på fremtidige handler/transaksjoner) følger en random walk dersom prisen er lik den objektive betingede forventningen til spotprisen på datoen til den fremtidige handelen/ transaksjonen (Sheffrin 1996). Antakelsen stilte imidlertid nye spørsmål som Samuelson selv ikke hadde svaret på. Han kunne ikke si hvor den objektive sannsynlighetsfordelingen, som den betingede forventningen bygde på, skulle komme fra (Sheffrin 1996). «I have not asked where the basic probability distributions are supposed to come from. In whose mind are they ex ante?» (Samuelson 1965). Effisienshypotesen Svaret på Samuelsons spørsmål gav Eugene F. Fama (1970). Fama løste spørsmålet ved å anvende rasjonelle forventninger hypotesen. Rasjonelle økonomiske aktører vil bruke relevant økonomisk teori samt all tilgjengelig informasjon til å danne seg en forventning til aktivaverdien. Som rasjonelle forventninger hypotesen sier, så vil forventningene i gjennomsnitt være lik den objektive 5
12 ! Teori matematiske sannsynligheten. De økonomiske aktørene vil handle på sine forventninger og markedsprisen vil justeres inntil den reflekterer den objektive forventningen til aktivaverdien. I frikonkurranse finansmarkeder skjer justeringen momentant slik at markedsprisene til enhver tid fullt ut reflekterer all tilgjengelig informasjon (Fama 1970). Hypotesen forutsetter; - Et Velfungerende frikonkurranse finansmarket som har dybde og likviditet (Shiller 2008). - Alle aktører har tilgang til samme informasjon på samme tidspunkt (Schouw-Hansen 2007) - Aktørene er rasjonelle og verdsetter aktiva rasjonelt. Rasjonelle innebærer her at aktørene oppdaterer sin subjektive forventede nytte korrekt jamnfør Bayes lov ( Barberis og Thaler 2003) - Irrasjonelle aktører vil oppføre seg tilfeldig. Virkningene fra deres handlinger vil derfor kansellere hverandre ut (Schouw-Hansen 2007) Effisienshypotesen og prisbobler At markedsprisene til en hver tid gjenspeiler all tilgjengelig informasjon, impliserer at markedet er informasjonseffisient. Konsekvensen av informasjonseffisiens er at at markedsprisen er lik fundamentalverdien (Beechey et. al. 2000). Effisienshypotesen avviser dermed muligheten for prisbobler. 1.3 Nyklassiske teorimodeller for aktivapriser. Nyklassisk teori utelukker eksistensen av prisbobler ved symmetrisk informasjon både i endelig tid modeller og i uendelig tid modeller. Dette underkapittelet presenterer to nyklassiske modeller. En med endelig tidshorisont, og en med uendelig tidshorisont. Den matematiske fremstillingen er basert på LeRoy (2004). Endelig tidshorisont Avkastningensraten, r t+1, til et aktivum eller en portefølje fra tid t til t + 1, defineres; 6
13 ! Teori r t+1 = d t+1 + p t+1 p t 1 (1.2) d t er dividendeutbetalingen på tidspunkt t. p t er prisen på aktivumet eller porteføljen på tidspunkt t. Tar forventningen til (1.2) gitt informasjonen tilgjenglig på tidspunkt t. Løser så uttrykket for p t og får; p t = E t(d t+1 + p t+1 ) 1+E t (r t+1 ) (1.3) E t (...) er her kort for E t (... I t ), hvor I t er informasjonen tilgjenglig på tidspunkt t. Ingen forskjeller gjøres mellom subjektive og objektive forventninger, så modellen impliserer her rasjonelle forventnigner og symmetrisk informasjon. Det forutsettes at forventningen til avkastningen er lik konstanten r. Likningen kan skrives på følgende måte; p t =(1+r) 1 E t (d t+1 + p t+1 ) (1.4) På samme måte vil prisen ved tidspunkt t + 1, p t+1 kunne skrives som; p t+1 =(1+r) 1 E t+1 (d t+2 + p t+2 ) (1.5) Innsetting av (1.5) i (1.4) gir; p t =(1+r) 1 E t (d t+1 )+(1+r) 2 E t (d t+2 + p t+2 ) (1.6) Ved å gjenta denne innsettingen n ganger får en; 7
14 ! Teori p t = n (1 + r) i E t (d t+i )+(1+r) n E t (p t+n ) (1.7) i=1 (1.7) uttrykker prisen til et aktiva eller en portefølje på tidspunkt t. Fundamentalprisen er tidligere definert som nåverdien av de fremtidige utbetalignene til et aktivum. De fremtidige utbetalingene i (1.7) forkortes til; F t = n (1 + r) 1 E t (d t+i ) (1.8) i=1 Likning (1.8) gir her fundamentalverdien til aktivumet eller porteføljen (Hiorta og Sunder 2002). Likning (1.7) kan nå skrives; p t = F t + n (1 + r) n E t (p t+n ) (1.9) i=1 I en endelig tidshorisont modell gir aktivumet eller porteføljen siste utbetaling ved tidspunkt t+n; E t (p t+n )=E t (d t+n ) (1.10) Likning (1.10) inn i likning (1.9) gir; p t = n (1 + r) i E t (d t+i )=F t (1.11) i=1 På grunn av den endelig tidshorisonten kan aktørene foreta baklengs induksjon. Det sikrer at prisen blir lik fundamentalverdien som i (1.13). Uendelig tidshorisont 8
15 ! Teori Likning (1.7) gir aktivaprismodellen med uendelig tidshorisont på aktivumet eller porteføljen, ved å la n gå mot uendelig; p t = i=1 (1 + r) i E t (d t+i )+ lim n (1 + r) n E t (p t+n ) (1.12) Det første leddet på høyre side i (1.12) forkortes igjen til fundamentalverdien F; p t = F t +lim n (1 + r) n E t (p t+n ) (1.13) Det andre leddet på høyre side av (1.13) kalles den rasjonelle boble komponenten av prisen. Så lenge dette leddet er forskjellig fra null, hindres prisen i å være lik fundamentalverdien. Boble komponenten er en del av prisen og kan ikke fjernes ved arbitrasje (Gurkaynak 2005). Boblen komponenten oppstår i modellen forutsetter rasjonelle aktører. Den intuitive forklaringen er at de rasjonelle akøterene kjøper til en pris høyere en fundamentalprisen fordi de forventer å tjene på videresalg til irrasonelle aktører eller til rasjonelle aktører som forventer å tjene på videresalg (Lei et al. 2001). Eliminering av rasjonelle bobler Santos og Woodford (1997) presenterer et spesialtilfelle av aktivaprismodellen med uendelig tidshorisont (Gurkaynak 2005). Santos og Woodford s modell setter det andre leddet på høyre side i (1.13) lik null. Santos og Woodford s modell eliminerer dermed muligheten for en rasjonell boble. Den intuitive forklaringen på resultatet er følgende; Sett at en aktør med uendelig liv selger aktivumet. Den tapte nytten fra didivendeutbetalingene vil da være mindre enn nytten fra betalingen for salget. Dette kan umulig være en likevekt ettersom alle aktørene vil selge i en slik situasjon og prisen faller til fundamentalverdien (Gurkaynak 2005). 9
16 ! Forskningsprogrammet til Smith, Suchanek og Williams 2. Forskningsprogrammet til Smith, Suchanek og Williams Prisbobler gav Smith, Suchanek og Williams (1988) idéen om å konstruere et «gjennomsiktig» aksjemarket hvor aksjenes funamentalverdi var klart synlig. De designet et aksjemarked hvor markedsdeltakerene fikk vite dividendefordelingen og den forventede dividendeverdien. Resultatene fra eksperimentet skulle brukes som kontrolleksperiment i deres forskningsprogram. Formålet med forsknings-programmet var å fremkalle prisbobler ved å manipulere forskjellige parametre i kontroll-eksperimetet. Kontrolleksperimentet produserte imidlertid overraskende resultat. Det oppstod prisbobler i det «gjennomsiktige» aksjemarkedet. Prisbobler i kontrolleksperimentet var en overraskelse fordi det stod i kontrast til resultatene i nyklassisk teori (Sunder 1995). Ved symmetrisk informasjon og en endelig tidshorisont skal baklengs induksjon sikre at prisen følger fundamentalverdien. Etter de overraskende resultatene ble forskningsprogrammets formål endret. Fra å fremkalle prisbobler, ble formålet å redusere og eliminere prisboblene i kontrolleksperimentet (Plott og Smith 2008). I løpet av forskningsprogrammet oppstod det prisbobler i 14 av 22 eksperiment. Prisboblene tok mange forskjellige former og langt i fra alle fikk påfølgende priskrasj. Smith, Suchanek og Williams finner at deltakere med erfaring fra tidligere eksperiment, er den eneste faktoren som reduserer sannsynligheten for prisbobler. Deltakere med erfaring fra eksperiment med den samme deltakergruppen, var den eneste faktoren som så ut til å kunne eliminere prisbobler. Ifølge Smith, Suchanek og Williams oppstår prisboblene i de eksperimentelle aksjemarkedene på grunn av mangelen på rasjonelle forventninger. Ex ante kan deltakerene være usikre på hvorvidt de øvrige deltakerene vil oppføre seg rasjonelt. Usikkerheten gjør at en rasjonell løsning av maksimeringsproblemet kan være forskjellig fra en ex-ante baklengs induksjon. 10
17 ! Forskningsprogrammet til Smith, Suchanek og Williams Smith, Suchanek og Williams hypotiserer at det er usikkerheten rundt øvrige deltakeres rasjonalitet som fører til prisbobler. Usikkerheten til øvrige deltakeres rasjonalitet, gjør at deltakerene forventer fortjeneste ved å selge aksjer til en pris over fundamentalverdi. Spekulasjon, det vil si kjøpe aksjer til priser over fundamentalverdi, er rasjonelt så lenge en forventer å videreselge til en enda høyere pris. Spekulasjonen fører til prisboblene i de eksperimentelle markedene. Erfaring reduserer og eliminerer prisbobler, fordi usikkerheten til øvrige deltakeres rasjonalitet forsvinner. Når deltakerene deltar på flere eksperiment, erfarer de at de øvrige deltakerene oppfører seg rasjonelt. Tvilen om øvrige deltakeres atferd vil da forsvinne, slik at spekulasjon ikke lenger er rasjonelt. Smith, Suchanek og Williams hypotese beskriver hvordan markedet når likevekt, slik likevekt beskrives av nyklassisk teori og effisienshypotesen. Rasjonell spekulasjon kan dermed ses som en slags ulikevektshypotese, som beskriver hvordan markedet kommer i likevekt. Basert på artikkelen til Smith, Suchanek og Williams følger en gjennomgang av; eksperimentoppsettet, variasjonene av eksperimentet, analysen av dataen forskningsprogrammet produserte og til slutt en oppsummering av forskningsprogrammets funn. 2.1 Eksperimentoppsettet I det eksperimentelle aksjemarkedet handler deltakerene på et fiktivt aksjemarked. Aksjemarkedet er åpent i 15 perioder på 240 sekunder. Aksjene har en dividendefordeling på null, x1, x2 eller x3 med 25% sannsynlighet for hvert utfall. Dividende trekkes og utbetales etter handelen i hver periode. For risikonøytrale deltakere vil dividendeutbetalingen for en periode ha forventningsverdien E( d) = 3 i=1 x i 4 11
18 ! Forskningsprogrammet til Smith, Suchanek og Williams For en risikonøytral deltaker vil dividendens forventningsverdi i periode t, vil være E( D t )=16E( d) te( d) Før hver periode blir deltakerene påminnet om dividendefordelingen. På dette tidspunktet blir deltakerene verbalt påminnet om at dividendefordelingen og faktisk dividendeutbetaling er den samme for alle i eksperimentet. Etter hver periode får deltakerene vite samlet verdi av gjenværende dividendeutbetalinger dersom de resterende utbetalinger blir lik; minimumsutbetalingen, maksimumsutbetalingen eller gjennomsnittsutbetalingen. I begynnelsen av eksperimentet får hver deltaker utdelt en startmengde av aksjer og kapital. Underveis vil kapitalen til en deltaker avvike fra startmengden med: i) Samlet gevinst eller tap fra kjøp og salg av aksjer i markedet. ii) Samlet dividende utbetalt til aksjer på deltakerens hånd. Etter eksperimentets slutt får deltakerene utbetalt sluttverdien av kapitalen. Handel Deltakerene står fritt til å bestemme om og når de vil handle i markedet. Deltakerene kan kjøpe og selge etter egen vilje. Handelen skjer ved dobbelauksjon hvor kjøpere (selgere) står fritt til å gi bud (tilbud) ( Ketcham et. al. 1984). Et bud (tilbud) angir prisen kjøperen (selgeren) vil kjøpe (selge) én aksje for. Deltakerene får til en hver tid vite det beste budet og det beste tilbudet på markedet. Det beste budet er den høyeste prisen en deltaker vil betale for én aksje. Det beste tilbudet er den laveste prisen en deltaker i markedet godtar for å selge én aksje. Alle bud (tilbud) som ikke overgår beste kjøpspris (salgspris) settes i en usynlig kø. Køen sorteres etter pris. Jo høyere (lavere) prisen på budet (tilbudet) er, jo lenger fremme i køen er budet (tilbudet). Hvis en handel, hvor en selger (kjøper) aksepterer det beste budet (tilbudet), intreffer, vil budet (tilbudet) som er først i køen bli det nye beste budet (tilbudet). 12
19 ! Forskningsprogrammet til Smith, Suchanek og Williams Hver deltaker sitter ved en datamaskin og all handel og informasjonsformidling foregår på datamaskiner. På datamaskinen kan deltakerene gi og godta bud og tilbud. Under handelen får deltakerene informasjon på dataskjermen. Skjermenbildet viser deltakerens kapital- og askjebeholdning og beste bud og tilbud. Forskjellige opplysninger om aksjene deltakeren besitter, vises i et slags regnskapsoppsett. I oppsettet opplyses kostprisen, kjøpstidspunkt og samlet dividendeutbetaling til hver aksje. Startbeholdning I hvert av de 26 eksperimentene blir deltakerene delt opp i tre grupper. De tre gruppene får forskjellig startmengde aksjer og kapital. Gruppene er på 3 eller 4 deltakere, avhengig av om eksperimentet består av 9 eller 12 deltakere. Ifølge Smith, Suchanek og Williams så tillater et slikt oppsett ekspansjon av markedet uten å endre per capita strukturen. I løpet av de 26 eksperimentene blir det brukt 5 forskjellige oppsett. Oppsettene er forskjellige i; gruppenes startmengde aksjer og kapital, dividendeutfallene og dermed også forventningsverdien til dividendefordelingen. Tabell 2.1 fremstiller de forskjellige oppsettene som blir brukt, samt hvilke eksperiment de forskjellige oppsettene blir brukt i. INITIELL MENGE Oppsett Gruppe 1 Gruppe 2 Gruppe 3 Dividendeutfall Forventet dividende -verdi aksjeverdien i 1. periode Eksperiment 1 ($2,80;4) ($7,60;2) ($10,00;1) (0,4,8,20) 8 $2,40 m/ oppkjøp 2 ($2,25;3) ($5,85;2) ($9,45;1) (0,4,14,30) 12 $3,60 m/ oppkjøp (5;12)(7;12)(12xn;9,3c) (17;12)(23pc;12) (6x;9)(9x;9)(10;9)(16;9) (18;9)(19x;9)(20xpc;9) 3 ($2,80;4) ($7,60;2) ($10,00;1) (0,8,16,40) 16 $2,40 (26;12)(41f;12) 4 ($2,25;3) ($5,85;2) ($9,45;1) (0,8,28,60) 24 $3,60 (25x;9)(28x;9)(30xsf;9) (36xx;9)(39xsf;9) (43xnf;9)(46f;9) (48xnf;9)(49xnf;9) (50xxf;9) (90f;9) (124xxf;9) 5 ($2,25;3) ($5,85;2) ($9,45;1) (0,8,28,60) 24 $7,20 (42xf;9) 13
20 ! Forskningsprogrammet til Smith, Suchanek og Williams Tabell 2.1 Eksperimentoppsettene i forskningsprogrammet. Notasjonen i de tre gruppe kolonnene er; ( startkapital; starmengde aksjer). Forventet dividendeverdi kolonnen oppgir fortentningsverdien for én divideneutbetaling. Dividendeutfallene oppgis i cents. Verdien i kolonnen oppgis i cents. Notasjonen i eksperiment kolonnen er ( navn på eksperiment; antall deltakere). Fra tabell 2.1 ser man at oppsett 4, blir brukt flest ganger som eksperimentoppsett. Oppkjøpsfunksjon Det «gjennomsiktige» markedet gav Smith, Suchanek og Williams en a priori bekymring for at deltakerenes prisforventninger ville bli for like, slik at handel ikke forekom. Eksperimentet ble derfor designet med en oppkjøpsfunksjon i siste periode. Oppkjøpsprisen på en aksje er summen av tidligere perioders dividendeutbetalinger pluss en konstant. Konstanten blir trukket fra en uniform fordeling med to mulige utfall. Det ene utfallet er en negativ konstant, det andre utfallet er en positiv konstant. Oppkjøpsfunksjonen hindrer den forventede verdien i å falle ned til E( d) i 15. periode. Ex ante bekymringen for fravær av handel, viste seg å være uberettiget og oppkjøpsfunksjonen ble etterhvert fjernet fra eksperimentet. Ved bruk av oppkjøpsfunksjonen ble opplysningene om maximumsverdi, minimumsverdi og forventet verdi av resterende dividendeutbetalinger, automatisk justert. Prognoser I forskningsprogrammets 10 siste eksperimenter blir deltakerene bedt om å gi sin prognose for kommende periodes gjennomsnittspris. Deltakerene gir sine prognoser for periodene 2 til 15. Etter handelen i hver periode får deltakerene se; alle sine tidligere prognoser, tidligere perioders faktiske gjennomsnittspriser og avvik mellom prognosene og faktiske gjennomsnittspriser. Deltakerene har kun tilgang til sine egne prognoser. For å unngå prismanipulering ved jevne konkurranser, får ikke deltakerene vite hvordan deres prognoser er i forhold til andres prognoser. 14
21 ! Forskningsprogrammet til Smith, Suchanek og Williams Deltakeren med det minste kumulative avviket mellom sine prognoser og faktisk gjennomsnittspris vinner 1 dollar. Tidligere studier gir støtte til at premiesummen motiverer til seriøs innsats, uten å samtidig gi insentiv til prismanipulering. 2.2 Forskningsprogrammet Dette underkapittelet presenterer som Smith Suchanek og Williams (1988) kom frem til i løpet av forskningsprogrammet. Sentrale funn er: i) Deltakerenes initelle prisforventninger er heterogene ii) Deltakerenes prisforventninger er endogene og vanskelige å påvirke gjennom eksperimentparametre. iii) Erfaring fra tidligere eksperiment reduserer sannsynligheten for- og størrelsen på, prisbobler i et market. iv) Erfaring fra den samme deltakergruppen over flere eksperiment, er den eneste faktoren som kan fjerne prisbobler helt. I løpet av forskningsprogrammet ble det utført mange eksperimentvariasjoner. Variasjonene ble implementer for å undersøke hypoteser som ble utarbeidet underveis. Funnene vil bli presentert i lys av eksperimentvariasjonene. Smith, Suchanek og Williams ble oppmerksomme på effekten av erfaring på prisbobler, allerede etter de to første eksperimentene i forskningsprogrammet. Eksperimentene ble navngitt 5 og 6x. Eksperiment 5 bestod av tolv deltakere. I eksperiment 6x deltok ni av tolv deltakerene fra eksperiment 5. X en i navnet 6x, indikerer at deltakerene har erfaring fra et tildligere eksperiment. Eksperiment 5 produserte betydelige avvik mellom gjennomsnittsprisen og fundamentalverdi. I første periode ble gjennomsnittsprisen litt over 4 dollar, mens fundamentalverdien for perioden var 2,40 dollar. Gjennomsnittsprisen ble liggende rundt 4 dollar helt frem til periode 11. I siste del av eksperimentet sank gjennomsnittsprisen ned til fundamentalverdi. I eksperiment 6x, hvor deltakerene hadde erfaring, ble utfallet et helt annet. Gjennomsnittsprisen fulgte fundamentalverdien mye tettere, uten å konvergere helt. På bakgrunn av eksperiment 5 og 6x hypotiserte Smith, Suchanek og Williams at erfaring gav en reduksjon i avviket mellom handelspris og fundamentalverdi. For å teste sin hypotese ble det 15
Kap. 10: Løsningsforslag
 Kap. 10: Løsningsforslag 1 1.1 Markedets risikopremie (MP ) er definert som MP = (r m r f ). Ifølge oppsummeringen i læreboken (Strøm, 2017, side 199), er markedets risikopremie i området 5.0 8.0 prosent.
Kap. 10: Løsningsforslag 1 1.1 Markedets risikopremie (MP ) er definert som MP = (r m r f ). Ifølge oppsummeringen i læreboken (Strøm, 2017, side 199), er markedets risikopremie i området 5.0 8.0 prosent.
Løsningsforslag ECON 2130 Obligatorisk semesteroppgave 2017 vår
 Løsningsforslag ECON 130 Obligatorisk semesteroppgave 017 vår Andreas Myhre Oppgave 1 1. (i) Siden X og Z er uavhengige, vil den simultane fordelingen mellom X og Z kunne skrives som: f(x, z) = P(X = x
Løsningsforslag ECON 130 Obligatorisk semesteroppgave 017 vår Andreas Myhre Oppgave 1 1. (i) Siden X og Z er uavhengige, vil den simultane fordelingen mellom X og Z kunne skrives som: f(x, z) = P(X = x
MAT4010 PROSJEKTOPPGAVE: Statistikk i S2. Olai Sveine Johannessen, Vegar Klem Hafnor & Torstein Mellem
 MAT400 PROSJEKTOPPGAVE: Statistikk i S2 Olai Sveine Johannessen, Vegar Klem Hafnor & Torstein Mellem 20. mai 205 Innhold. Stokastisk Variabel.. Stokastiske variable som funksjoner 3 2. Forventningsverdi
MAT400 PROSJEKTOPPGAVE: Statistikk i S2 Olai Sveine Johannessen, Vegar Klem Hafnor & Torstein Mellem 20. mai 205 Innhold. Stokastisk Variabel.. Stokastiske variable som funksjoner 3 2. Forventningsverdi
Litt om forventet nytte og risikoaversjon. Eksempler på økonomisk anvendelse av forventning og varians.
 H. Goldstein Revidert januar 2008 Litt om forventet nytte og risikoaversjon. Eksempler på økonomisk anvendelse av forventning og varians. Dette notatet er ment å illustrere noen begreper fra Løvås, kapittel
H. Goldstein Revidert januar 2008 Litt om forventet nytte og risikoaversjon. Eksempler på økonomisk anvendelse av forventning og varians. Dette notatet er ment å illustrere noen begreper fra Løvås, kapittel
Forelesning 7: Store talls lov, sentralgrenseteoremet. Jo Thori Lind
 Forelesning 7: Store talls lov, sentralgrenseteoremet Jo Thori Lind j.t.lind@econ.uio.no Oversikt 1. Estimering av variansen 2. Asymptotisk teori 3. Store talls lov 4. Sentralgrenseteoremet 1.Estimering
Forelesning 7: Store talls lov, sentralgrenseteoremet Jo Thori Lind j.t.lind@econ.uio.no Oversikt 1. Estimering av variansen 2. Asymptotisk teori 3. Store talls lov 4. Sentralgrenseteoremet 1.Estimering
TALLSVAR. Det anbefales at de 9 deloppgavene merket med A, B, teller likt uansett variasjon i vanskelighetsgrad. Svarene er gitt i <<< >>>.
 1 ECON213: EKSAMEN 217 VÅR - UTSATT PRØVE TALLSVAR. Det anbefales at de 9 deloppgavene merket med A, B, teller likt uansett variasjon i vanskelighetsgrad. Svarene er gitt i
1 ECON213: EKSAMEN 217 VÅR - UTSATT PRØVE TALLSVAR. Det anbefales at de 9 deloppgavene merket med A, B, teller likt uansett variasjon i vanskelighetsgrad. Svarene er gitt i
= 5, forventet inntekt er 26
 Eksempel på optimal risikodeling Hevdet forrige gang at i en kontrakt mellom en risikonøytral og en risikoavers person burde den risikonøytrale bære all risiko Kan illustrere dette i en enkel situasjon,
Eksempel på optimal risikodeling Hevdet forrige gang at i en kontrakt mellom en risikonøytral og en risikoavers person burde den risikonøytrale bære all risiko Kan illustrere dette i en enkel situasjon,
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 Utsatt eksamen i: ECON130 Statistikk 1 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamensdag: 1306017 Sensur kunngjøres senest: 3006017 Tid for eksamen: kl 09:00 1:00 Oppgavesettet er på 5 sider Tillatte
Utsatt eksamen i: ECON130 Statistikk 1 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamensdag: 1306017 Sensur kunngjøres senest: 3006017 Tid for eksamen: kl 09:00 1:00 Oppgavesettet er på 5 sider Tillatte
3.A IKKE-STASJONARITET
 Norwegian Business School 3.A IKKE-STASJONARITET BST 1612 ANVENDT MAKROØKONOMI MODUL 5 Foreleser: Drago Bergholt E-post: Drago.Bergholt@bi.no 11. november 2011 OVERSIKT - Ikke-stasjonære tidsserier - Trendstasjonaritet
Norwegian Business School 3.A IKKE-STASJONARITET BST 1612 ANVENDT MAKROØKONOMI MODUL 5 Foreleser: Drago Bergholt E-post: Drago.Bergholt@bi.no 11. november 2011 OVERSIKT - Ikke-stasjonære tidsserier - Trendstasjonaritet
Forskningsmetoder i menneske-maskin interaksjon
 Forskningsmetoder i menneske-maskin interaksjon Kapittel 2- Eksperimentell forskning Oversikt Typer atferdsforskning Forskningshypoteser Grunnleggende om eksperimentell forskning Signifikanstesting Begrensninger
Forskningsmetoder i menneske-maskin interaksjon Kapittel 2- Eksperimentell forskning Oversikt Typer atferdsforskning Forskningshypoteser Grunnleggende om eksperimentell forskning Signifikanstesting Begrensninger
TMA4245 Statistikk Eksamen desember 2016
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4245 Statistikk Eksamen desember 2016 Oppgave 1 En bedrift produserer elektriske komponenter. Komponentene kan ha to typer
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4245 Statistikk Eksamen desember 2016 Oppgave 1 En bedrift produserer elektriske komponenter. Komponentene kan ha to typer
Modeller med skjult atferd
 Modeller med skjult atferd I dag og neste gang: Kap. 6 i GH, skjult atferd Ser først på en situasjon med fullstendig informasjon, ikke skjult atferd, for å vise kontrasten i resultatene En prinsipal, en
Modeller med skjult atferd I dag og neste gang: Kap. 6 i GH, skjult atferd Ser først på en situasjon med fullstendig informasjon, ikke skjult atferd, for å vise kontrasten i resultatene En prinsipal, en
6.2 Signifikanstester
 6.2 Signifikanstester Konfidensintervaller er nyttige når vi ønsker å estimere en populasjonsparameter Signifikanstester er nyttige dersom vi ønsker å teste en hypotese om en parameter i en populasjon
6.2 Signifikanstester Konfidensintervaller er nyttige når vi ønsker å estimere en populasjonsparameter Signifikanstester er nyttige dersom vi ønsker å teste en hypotese om en parameter i en populasjon
Forelesning 23 og 24 Wilcoxon test, Bivariate Normal fordeling
 Forelesning 23 og 24 Wilcoxon test, Bivariate Normal fordeling Wilcoxon Signed-Rank Test I uke, bruker vi Z test eller t-test for hypotesen H:, og begge tester er basert på forutsetningen om normalfordeling
Forelesning 23 og 24 Wilcoxon test, Bivariate Normal fordeling Wilcoxon Signed-Rank Test I uke, bruker vi Z test eller t-test for hypotesen H:, og begge tester er basert på forutsetningen om normalfordeling
Oppgaven består av 10 delspørsmål som anbefales å veie like mye. Kommentarer og tallsvar er skrevet inn mellom <<. >>. Oppgave 1
 ECON 0 EKSAMEN 004 VÅR SENSORVEILEDNING Oppgaven består av 0 delspørsmål som anbefales å veie like mye. Kommentarer og tallsvar er skrevet inn mellom
ECON 0 EKSAMEN 004 VÅR SENSORVEILEDNING Oppgaven består av 0 delspørsmål som anbefales å veie like mye. Kommentarer og tallsvar er skrevet inn mellom
ST0202 Statistikk for samfunnsvitere Kapittel 9: Inferens om én populasjon
 ST0202 Statistikk for samfunnsvitere Kapittel 9: Inferens om én populasjon Bo Lindqvist Institutt for matematiske fag 2 Kap. 9: Inferens om én populasjon Statistisk inferens har som mål å tolke/analysere
ST0202 Statistikk for samfunnsvitere Kapittel 9: Inferens om én populasjon Bo Lindqvist Institutt for matematiske fag 2 Kap. 9: Inferens om én populasjon Statistisk inferens har som mål å tolke/analysere
EKSAMEN I FAG 75510/75515 STATISTIKK 1 Tirsdag 20. mai 1997 Tid: 09:00 14:00
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Faglig kontakt under eksamen: Håvard Rue 73 59 35 20 Håkon Tjelmeland 73 59 35 20 Bjørn Kåre Hegstad 73 59 35 20
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Faglig kontakt under eksamen: Håvard Rue 73 59 35 20 Håkon Tjelmeland 73 59 35 20 Bjørn Kåre Hegstad 73 59 35 20
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 Eksamen i: ECON30 Statistikk UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamensdag: 03.06.06 Sensur kunngjøres: 4.06.06 Tid for eksamen: kl. 09:00 :00 Oppgavesettet er på 5 sider Tillatte hjelpemidler:
Eksamen i: ECON30 Statistikk UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamensdag: 03.06.06 Sensur kunngjøres: 4.06.06 Tid for eksamen: kl. 09:00 :00 Oppgavesettet er på 5 sider Tillatte hjelpemidler:
Kontroller at oppgavesettet er komplett før du begynner å besvare spørsmålene. Ved sensuren teller alle delspørsmål likt.
 Eksamen i: MET040 Statistikk for økonomer Eksamensdag: 4. juni 2008 Tid for eksamen: 09.00-13.00 Oppgavesettet er på 5 sider. Tillatte hjelpemidler: Alle trykte eller egenskrevne hjelpemidler og kalkulator.
Eksamen i: MET040 Statistikk for økonomer Eksamensdag: 4. juni 2008 Tid for eksamen: 09.00-13.00 Oppgavesettet er på 5 sider. Tillatte hjelpemidler: Alle trykte eller egenskrevne hjelpemidler og kalkulator.
Oversikt over kap. 19 i Gravelle og Rees. Sett i forhold til resten av pensum:
 Oversikt over kap. 19 i Gravelle og Rees Først et forbehold: Disse forelesningene er svært kortfattede i forhold til pensum og vil ikke dekke alt. Dere må lese selv! Sett i forhold til resten av pensum:
Oversikt over kap. 19 i Gravelle og Rees Først et forbehold: Disse forelesningene er svært kortfattede i forhold til pensum og vil ikke dekke alt. Dere må lese selv! Sett i forhold til resten av pensum:
TMA4240 Statistikk Eksamen desember 2015
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4240 Statistikk Eksamen desember 15 Oppgave 1 La den kontinuerlige stokastiske variabelen X ha fordelingsfunksjon (sannsynlighetstetthet
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4240 Statistikk Eksamen desember 15 Oppgave 1 La den kontinuerlige stokastiske variabelen X ha fordelingsfunksjon (sannsynlighetstetthet
Oppgavesett nr. 5. MAT110 Statistikk 1, Et transportfirma har et varemottak for lastebiler med spesialgods, se figur 1.
 Innleveringsfrist: mandag 19. mars kl. 16:00 (version 01) Oppgavesett nr. 5 MAT110 Statistikk 1, 2018 Oppgave 1: ( logistikk ) Et transportfirma har et varemottak for lastebiler med spesialgods, se figur
Innleveringsfrist: mandag 19. mars kl. 16:00 (version 01) Oppgavesett nr. 5 MAT110 Statistikk 1, 2018 Oppgave 1: ( logistikk ) Et transportfirma har et varemottak for lastebiler med spesialgods, se figur
Seminaroppgave 10. (a) Definisjon: En estimator θ. = θ, der n er et endelig antall. observasjoner. Forventningsretthet for β: Xi X ) Z i.
 Seminaroppgave 0 a Definisjon: En estimator θ n er forventningsrett hvis E θn observasjoner. Forventningsretthet for β: θ, der n er et endelig antall β Xi X Y i Xi X Xi X α 0 + βx i + n Xi X Xi X β + Xi
Seminaroppgave 0 a Definisjon: En estimator θ n er forventningsrett hvis E θn observasjoner. Forventningsretthet for β: θ, der n er et endelig antall β Xi X Y i Xi X Xi X α 0 + βx i + n Xi X Xi X β + Xi
ECON2130 Kommentarer til oblig
 ECON2130 Kommentarer til oblig Her har jeg skrevet ganske utfyllende kommentarer til en del oppgaver som mange slet med. Har noen steder gått en del utover det som det strengt tatt ble spurt om i oppgaven,
ECON2130 Kommentarer til oblig Her har jeg skrevet ganske utfyllende kommentarer til en del oppgaver som mange slet med. Har noen steder gått en del utover det som det strengt tatt ble spurt om i oppgaven,
Arbitrasje og finansielle beslutninger. Kapittel 3
 Arbitrasje og finansielle beslutninger Kapittel 3 Arbitrasje og loven om en pris Konkurranse og verdsetting Holdning til risiko Arbitrasje og konkurranse Arbitrasje er å utnytte prisforskjeller. Nordmenn
Arbitrasje og finansielle beslutninger Kapittel 3 Arbitrasje og loven om en pris Konkurranse og verdsetting Holdning til risiko Arbitrasje og konkurranse Arbitrasje er å utnytte prisforskjeller. Nordmenn
Utvalgsfordelinger. Utvalg er en tilfeldig mekanisme. Sannsynlighetsregning dreier seg om tilfeldige mekanismer.
 Utvalgsfordelinger Vi har sett at utvalgsfordelinger til en statistikk (observator) er fordelingen av verdiene statistikken tar ved mange gjenttatte utvalg av samme størrelse fra samme populasjon. Utvalg
Utvalgsfordelinger Vi har sett at utvalgsfordelinger til en statistikk (observator) er fordelingen av verdiene statistikken tar ved mange gjenttatte utvalg av samme størrelse fra samme populasjon. Utvalg
Eksamensoppgave i TMA4240 Statistikk
 Institutt for matematiske fag Eksamensoppgave i TMA4240 Statistikk Faglig kontakt under eksamen: Mette Langaas a, Ingelin Steinsland b, Geir-Arne Fuglstad c Tlf: a 988 47 649, b 926 63 096, c 452 70 806
Institutt for matematiske fag Eksamensoppgave i TMA4240 Statistikk Faglig kontakt under eksamen: Mette Langaas a, Ingelin Steinsland b, Geir-Arne Fuglstad c Tlf: a 988 47 649, b 926 63 096, c 452 70 806
Skjulte egenskaper (hidden characteristics)
 Skjulte egenskaper (hidden characteristics) Ny klasse av situasjoner, kap. 7 i Hendrikse (Se bort fra avsnitt 7.5; ikke kjernepensum) Forskjellig fra skjult handling (hidden action) (kap. 6) Men her: Skjulte
Skjulte egenskaper (hidden characteristics) Ny klasse av situasjoner, kap. 7 i Hendrikse (Se bort fra avsnitt 7.5; ikke kjernepensum) Forskjellig fra skjult handling (hidden action) (kap. 6) Men her: Skjulte
Oppgave 1. T = 9 Hypotesetest for å teste om kolesterolnivået har endret seg etter dietten: T observert = 2.16 0
 Løsningsforslag til eksamen i MOT310 STATISTISKE METODER 1 VARIGHET: 4 TIMER DATO: 08. mai 2008 TILLATTE HJELPEMIDLER: Kalkulator: HP30S, Casio FX82 eller TI-30 Tabeller og formler i statistikk (Tapir
Løsningsforslag til eksamen i MOT310 STATISTISKE METODER 1 VARIGHET: 4 TIMER DATO: 08. mai 2008 TILLATTE HJELPEMIDLER: Kalkulator: HP30S, Casio FX82 eller TI-30 Tabeller og formler i statistikk (Tapir
OPPGAVEHEFTE I STK1000 TIL KAPITTEL 5 OG 6. a b
 OPPGAVEHEFTE I STK1000 TIL KAPITTEL 5 OG 6 1. Regneoppgaver til kapittel 5 6 Oppgave 1. Mange som kommer til STK1000 med dårlige erfaringer fra tidligere mattefag er livredd ulikheter, selv om man har
OPPGAVEHEFTE I STK1000 TIL KAPITTEL 5 OG 6 1. Regneoppgaver til kapittel 5 6 Oppgave 1. Mange som kommer til STK1000 med dårlige erfaringer fra tidligere mattefag er livredd ulikheter, selv om man har
Mulige sammenhenger for plassering på samfunnsstigen
 Mulige sammenhenger for plassering på samfunnsstigen - blokkvis multippel regresjonsanalyse - Utarbeidet av Ronny Kleiven Antall ord (ekskludert forside og avsnitt 7) 2163 1. SAMMENDRAG Oppgaven starter
Mulige sammenhenger for plassering på samfunnsstigen - blokkvis multippel regresjonsanalyse - Utarbeidet av Ronny Kleiven Antall ord (ekskludert forside og avsnitt 7) 2163 1. SAMMENDRAG Oppgaven starter
HØGSKOLEN I STAVANGER
 HØGSKOLEN I STAVANGER Avdeling for TEKNISK NATURVITEN- EKSAMEN I: TE199 SANNSYNLIGHETSREGNING MED STATISTIKK SKAPELIGE FAG VARIGHET: 4 TIMER DATO: 5. JUNI 2003 TILLATTE HJELPEMIDLER: KALKULATOR OPPGAVESETTET
HØGSKOLEN I STAVANGER Avdeling for TEKNISK NATURVITEN- EKSAMEN I: TE199 SANNSYNLIGHETSREGNING MED STATISTIKK SKAPELIGE FAG VARIGHET: 4 TIMER DATO: 5. JUNI 2003 TILLATTE HJELPEMIDLER: KALKULATOR OPPGAVESETTET
ECON2200 Matematikk 1/Mikroøkonomi 1 Diderik Lund, 22. februar Monopol
 Monopol Forskjellige typer atferd i produktmarkedet Forrige gang: Prisfast kvantumstipasser I dag motsatt ytterlighet: Monopol, ØABL avsn. 6.1 Fortsatt prisfast kvantumstilpasser i faktormarkedene Monopol
Monopol Forskjellige typer atferd i produktmarkedet Forrige gang: Prisfast kvantumstipasser I dag motsatt ytterlighet: Monopol, ØABL avsn. 6.1 Fortsatt prisfast kvantumstilpasser i faktormarkedene Monopol
ECON1810 Organisasjon, strategi og ledelse Forelesning ved Diderik Lund 15.03.04
 Opsjoner En finansiell opsjon er en type kontrakt med to parter Utstederen (the issuer eller writer) (som kan være en person eller et selskap) påtar seg en forpliktelse Opsjonen gir motparten (som blir
Opsjoner En finansiell opsjon er en type kontrakt med to parter Utstederen (the issuer eller writer) (som kan være en person eller et selskap) påtar seg en forpliktelse Opsjonen gir motparten (som blir
Løsningsforslag Eksamen S2, våren 2017 Laget av Tommy O. Sist oppdatert: 25. mai 2017
 Løsningsforslag Eksamen S, våren 17 Laget av Tommy O. Sist oppdatert: 5. mai 17 Del 1 - uten hjelpemidler Oppgave 1 a) Vi skal derivere f(x) = x /x = x x 1. Den eneste regelen vi trenger her er (kx n )
Løsningsforslag Eksamen S, våren 17 Laget av Tommy O. Sist oppdatert: 5. mai 17 Del 1 - uten hjelpemidler Oppgave 1 a) Vi skal derivere f(x) = x /x = x x 1. Den eneste regelen vi trenger her er (kx n )
Kap. 10: Inferens om to populasjoner. Eksempel. ST0202 Statistikk for samfunnsvitere
 Kap. 10: Inferens om to populasjoner Situasjon: Vi ønsker å sammenligne to populasjoner med populasjonsgjennomsnitt henholdsvis μ 1 og μ. Vi trekker da ett utvalg fra hver populasjon. ST00 Statistikk for
Kap. 10: Inferens om to populasjoner Situasjon: Vi ønsker å sammenligne to populasjoner med populasjonsgjennomsnitt henholdsvis μ 1 og μ. Vi trekker da ett utvalg fra hver populasjon. ST00 Statistikk for
Fasit for tilleggsoppgaver
 Fasit for tilleggsoppgaver Uke 5 Oppgave: Gitt en rekke med observasjoner x i (i = 1,, 3,, n), definerer vi variansen til x i som gjennomsnittlig kvadratavvik fra gjennomsnittet, m.a.o. Var(x i ) = (x
Fasit for tilleggsoppgaver Uke 5 Oppgave: Gitt en rekke med observasjoner x i (i = 1,, 3,, n), definerer vi variansen til x i som gjennomsnittlig kvadratavvik fra gjennomsnittet, m.a.o. Var(x i ) = (x
+ S2 Y ) 2. = 6.737 6 (avrundet nedover til nærmeste heltall) n Y 1
 Løsningsforslag for: MOT10 STATISTISKE METODER 1 VARIGHET: 4 TIMER DATO: 6. november 007 TILLATTE HJELPEMIDLER: Kalkulator: HP0S, Casio FX8 eller TI-0 Tabeller og formler i statistikk (Tapir forlag) MERKNADER:
Løsningsforslag for: MOT10 STATISTISKE METODER 1 VARIGHET: 4 TIMER DATO: 6. november 007 TILLATTE HJELPEMIDLER: Kalkulator: HP0S, Casio FX8 eller TI-0 Tabeller og formler i statistikk (Tapir forlag) MERKNADER:
Kapittel 3: Studieopplegg
 Oversikt over pensum Kapittel 1: Empirisk fordeling for en variabel o Begrepet fordeling o Mål for senter (gj.snitt, median) + persentiler/kvartiler o Mål for spredning (Standardavvik s, IQR) o Outliere
Oversikt over pensum Kapittel 1: Empirisk fordeling for en variabel o Begrepet fordeling o Mål for senter (gj.snitt, median) + persentiler/kvartiler o Mål for spredning (Standardavvik s, IQR) o Outliere
UNIVERSITETET I OSLO
 Deleksamen i: UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet STK1000 Innføring i anvendt statistikk. Eksamensdag: Onsdag 13. oktober 2010. Tid for eksamen: 15:00 17:00. Oppgavesettet
Deleksamen i: UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet STK1000 Innføring i anvendt statistikk. Eksamensdag: Onsdag 13. oktober 2010. Tid for eksamen: 15:00 17:00. Oppgavesettet
Hypotesetesting av λ og p. p verdi.
 Forelesning 7, kapittel 6 Hypotesetesting av λ og p. p verdi. Det som gjøres i denne forelesningen er nær opptil det vi gjorde da vi konstruerte z test for µ, og styrkefunksjon for denne. I tillegg til
Forelesning 7, kapittel 6 Hypotesetesting av λ og p. p verdi. Det som gjøres i denne forelesningen er nær opptil det vi gjorde da vi konstruerte z test for µ, og styrkefunksjon for denne. I tillegg til
Verdens statistikk-dag. Signifikanstester. Eksempel studentlån. http://unstats.un.org/unsd/wsd/
 Verdens statistikk-dag http://unstats.un.org/unsd/wsd/ Signifikanstester Ønsker å teste hypotese om populasjon Bruker data til å teste hypotese Typisk prosedyre Beregn sannsynlighet for utfall av observator
Verdens statistikk-dag http://unstats.un.org/unsd/wsd/ Signifikanstester Ønsker å teste hypotese om populasjon Bruker data til å teste hypotese Typisk prosedyre Beregn sannsynlighet for utfall av observator
Statistikk og dataanalyse
 Njål Foldnes, Steffen Grønneberg og Gudmund Horn Hermansen Statistikk og dataanalyse En moderne innføring Kapitteloversikt del 1 INTRODUKSJON TIL STATISTIKK Kapittel 1 Populasjon og utvalg 19 Kapittel
Njål Foldnes, Steffen Grønneberg og Gudmund Horn Hermansen Statistikk og dataanalyse En moderne innføring Kapitteloversikt del 1 INTRODUKSJON TIL STATISTIKK Kapittel 1 Populasjon og utvalg 19 Kapittel
Oppsummering av forelesningen 10.11.04 Spillteori (S & W kapittel 12 og 19) Fangens dilemma
 Økonomisk Institutt, november 004 Robert G. Hansen, rom 08 Oppsummering av forelesningen 0..04 Spillteori (S & W kapittel og 9) Fangens dilemma Spillteori er et effektivt verktøy for analyse av strategisk
Økonomisk Institutt, november 004 Robert G. Hansen, rom 08 Oppsummering av forelesningen 0..04 Spillteori (S & W kapittel og 9) Fangens dilemma Spillteori er et effektivt verktøy for analyse av strategisk
Mer om hypotesetesting
 Mer om hypotesetesting I underkapittel 36 i læreboka gir vi en kort innføring i tankegangen ved hypotesetesting Vi gir her en grundigere framstilling av temaet Problemstilling Vi forklarer problemstillingen
Mer om hypotesetesting I underkapittel 36 i læreboka gir vi en kort innføring i tankegangen ved hypotesetesting Vi gir her en grundigere framstilling av temaet Problemstilling Vi forklarer problemstillingen
Kort overblikk over kurset sålangt
 Kort overblikk over kurset sålangt Kapittel 1: Deskriptiv statististikk for en variabel Kapittel 2: Deskriptiv statistikk for samvariasjon mellom to variable (regresjon) Kapittel 3: Metoder for å innhente
Kort overblikk over kurset sålangt Kapittel 1: Deskriptiv statististikk for en variabel Kapittel 2: Deskriptiv statistikk for samvariasjon mellom to variable (regresjon) Kapittel 3: Metoder for å innhente
1 Section 4-1: Introduksjon til sannsynlighet. 2 Section 4-2: Enkel sannsynlighetsregning. 3 Section 5-1: Introduksjon til sannsynlighetsfordelinger
 1 Section 4-1: Introduksjon til sannsynlighet 2 Section 4-2: Enkel sannsynlighetsregning 3 Section 5-1: Introduksjon til sannsynlighetsfordelinger 4 Section 5-2: Tilfeldige variable 5 Section 5-3: Binomisk
1 Section 4-1: Introduksjon til sannsynlighet 2 Section 4-2: Enkel sannsynlighetsregning 3 Section 5-1: Introduksjon til sannsynlighetsfordelinger 4 Section 5-2: Tilfeldige variable 5 Section 5-3: Binomisk
Verdens statistikk-dag.
 Verdens statistikk-dag http://unstats.un.org/unsd/wsd/ Signifikanstester Ønsker å teste hypotese om populasjon Bruker data til å teste hypotese Typisk prosedyre Beregn sannsynlighet for utfall av observator
Verdens statistikk-dag http://unstats.un.org/unsd/wsd/ Signifikanstester Ønsker å teste hypotese om populasjon Bruker data til å teste hypotese Typisk prosedyre Beregn sannsynlighet for utfall av observator
Tallfølger er noe av det første vi treffer i matematikken, for eksempel når vi lærer å telle.
 Kapittel 1 Tallfølger 1, 2, 3, 4, 5, 6, 7, 8,... Det andre temaet i kurset MAT1001 er differenslikninger. I en differenslikning er den ukjente en tallfølge. I dette kapittelet skal vi legge grunnlaget
Kapittel 1 Tallfølger 1, 2, 3, 4, 5, 6, 7, 8,... Det andre temaet i kurset MAT1001 er differenslikninger. I en differenslikning er den ukjente en tallfølge. I dette kapittelet skal vi legge grunnlaget
Løsningsforslag Eksamen S2, våren 2014 Laget av Tommy O. Sist oppdatert: 1. september 2018 Antall sider: 11
 Løsningsforslag Eksamen S, våren 014 Laget av Tommy O. Sist oppdatert: 1. september 018 Antall sider: 11 Finner du matematiske feil, skrivefeil, eller andre typer feil? Dette dokumentet er open-source,
Løsningsforslag Eksamen S, våren 014 Laget av Tommy O. Sist oppdatert: 1. september 018 Antall sider: 11 Finner du matematiske feil, skrivefeil, eller andre typer feil? Dette dokumentet er open-source,
ST0202 Statistikk for samfunnsvitere
 ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag 2 Inferens om varians og standardavvik for ett normalfordelt utvalg (9.4) Inferens om variansen til en normalfordelt populasjon
ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag 2 Inferens om varians og standardavvik for ett normalfordelt utvalg (9.4) Inferens om variansen til en normalfordelt populasjon
Eksamen i. MAT110 Statistikk 1
 Avdeling for logistikk Eksamen i MAT110 Statistikk 1 Eksamensdag : Tirsdag 22. mai 2018 Tid : 09:00 13:00 (4 timer) Faglærer/telefonnummer : Molde + Kristiansund: Per Kristian Rekdal / 924 97 051 Hjelpemidler
Avdeling for logistikk Eksamen i MAT110 Statistikk 1 Eksamensdag : Tirsdag 22. mai 2018 Tid : 09:00 13:00 (4 timer) Faglærer/telefonnummer : Molde + Kristiansund: Per Kristian Rekdal / 924 97 051 Hjelpemidler
Fire kort. Mål. Gjennomføring. Film. Problemløsing Fire kort Planleggingsdokument
 Fire kort Mål Generelt: Søke etter mønster og sammenhenger. Gjennomføre undersøkelse og begrunne resultat. Utfordre elevene på å resonnere og kommunisere. Spesielt: Finne alle kombinasjoner når de adderer
Fire kort Mål Generelt: Søke etter mønster og sammenhenger. Gjennomføre undersøkelse og begrunne resultat. Utfordre elevene på å resonnere og kommunisere. Spesielt: Finne alle kombinasjoner når de adderer
Faktor. Eksamen vår 2002 SV SØ 206: Næringsøkonomi og finansmarkeder Besvarelse nr 1: -en eksamensavis utgitt av Pareto
 Faktor -en eksamensavis utgitt av Pareto Eksamen vår 2002 SV SØ 206: Næringsøkonomi og finansmarkeder Besvarelse nr 1: OBS!! Dette er en eksamensbevarelse, og ikke en fasit. Besvarelsene er uten endringer
Faktor -en eksamensavis utgitt av Pareto Eksamen vår 2002 SV SØ 206: Næringsøkonomi og finansmarkeder Besvarelse nr 1: OBS!! Dette er en eksamensbevarelse, og ikke en fasit. Besvarelsene er uten endringer
Løsningsforslag, eksamen statistikk, juni 2015
 Løsningsforslag, eksamen statistikk, juni 0 Oppgave 1 Siden det spørres om tall fra et intervall, som oppgaven viser kan være et reelle, er det tydelig at tallene er tatt fra en kontinuerlig fordeling.
Løsningsforslag, eksamen statistikk, juni 0 Oppgave 1 Siden det spørres om tall fra et intervall, som oppgaven viser kan være et reelle, er det tydelig at tallene er tatt fra en kontinuerlig fordeling.
Sannsynlighetsbegrepet
 Sannsynlighetsbegrepet Notat til STK1100 Ørnulf Borgan Matematisk institutt Universitetet i Oslo Januar 2004 Formål Dette notatet er et supplement til kapittel 1 i Mathematical Statistics and Data Analysis
Sannsynlighetsbegrepet Notat til STK1100 Ørnulf Borgan Matematisk institutt Universitetet i Oslo Januar 2004 Formål Dette notatet er et supplement til kapittel 1 i Mathematical Statistics and Data Analysis
Terningkast. Utfallsrommet S for et terningskast med en vanlig spillterning med 6 sider er veldefinert 1, 2, 3, 4, 5, 6
 Terningkast Halvor Aarnes, UiO, 2014 Innhold Ett terningkast og utfallsrom... 1 Union og snitt... 4 Betinget sannsynlighet... 5 Forventningsverdi E(X) og varianse Var(X)... 5 Konfidensintervall for proporsjoner...
Terningkast Halvor Aarnes, UiO, 2014 Innhold Ett terningkast og utfallsrom... 1 Union og snitt... 4 Betinget sannsynlighet... 5 Forventningsverdi E(X) og varianse Var(X)... 5 Konfidensintervall for proporsjoner...
ETISK RÅD AVGJØRELSE I SAK NR. 2013/3
 ETISK RÅD AVGJØRELSE I SAK NR. 2013/3 Klager: X Innklaget: SpareBank 1 Nord-Norge Markets Saken gjelder: Saken gjelder klage på megler, som angivelig ga misvisende opplysning vedrørende klagers ubenyttede
ETISK RÅD AVGJØRELSE I SAK NR. 2013/3 Klager: X Innklaget: SpareBank 1 Nord-Norge Markets Saken gjelder: Saken gjelder klage på megler, som angivelig ga misvisende opplysning vedrørende klagers ubenyttede
Oppgave 1. X 1 B(n 1, p 1 ) X 2. Vi er interessert i forskjellen i andeler p 1 p 2, som vi estimerer med. p 1 p 2 = X 1. n 1 n 2.
 Løsningsforslag til eksamen i MOT310 STATISTISKE METODER 1 VARIGHET: 4 TIMER DATO: 17 november 2008 TILLATTE HJELPEMIDLER: Kalkulator: HP30S, Casio FX82 eller TI-30 Tabeller og formler i statistikk Tapir
Løsningsforslag til eksamen i MOT310 STATISTISKE METODER 1 VARIGHET: 4 TIMER DATO: 17 november 2008 TILLATTE HJELPEMIDLER: Kalkulator: HP30S, Casio FX82 eller TI-30 Tabeller og formler i statistikk Tapir
Faktorer på Oslo Børs
 Faktorer på Oslo Børs Bernt Arne Ødegaard Professor, Universitetet i Stavanger Presentasjon hos folketrygdfondet, Januar 2010 Oversikt Oppsummere studien Hvilke faktorer driver kursutviklingen på Oslo
Faktorer på Oslo Børs Bernt Arne Ødegaard Professor, Universitetet i Stavanger Presentasjon hos folketrygdfondet, Januar 2010 Oversikt Oppsummere studien Hvilke faktorer driver kursutviklingen på Oslo
Snøtetthet. Institutt for matematiske fag, NTNU 15. august Notat for TMA4240/TMA4245 Statistikk
 Snøtetthet Notat for TMA424/TMA4245 Statistikk Institutt for matematiske fag, NTNU 5. august 22 I forbindelse med varsling av om, klimaforskning og særlig kraftproduksjon er det viktig å kunne anslå hvor
Snøtetthet Notat for TMA424/TMA4245 Statistikk Institutt for matematiske fag, NTNU 5. august 22 I forbindelse med varsling av om, klimaforskning og særlig kraftproduksjon er det viktig å kunne anslå hvor
Eksempler: Nasjonalt forsvar, fyrtårn, gatelys, kunst i det offentlige rom, kunnskap, flokkimmunitet (ved vaksine), et bærekraftig klima
 Eksamen in ECON1210 V15 Oppgave 1 (vekt 25 %) Forklart kort følgende begreper (1/2-1 side på hver): Lorenz-kurve: Definisjon Kollektivt gode c) Nåverdi Sensorveiledning: Se side 386 i læreboka: «..the
Eksamen in ECON1210 V15 Oppgave 1 (vekt 25 %) Forklart kort følgende begreper (1/2-1 side på hver): Lorenz-kurve: Definisjon Kollektivt gode c) Nåverdi Sensorveiledning: Se side 386 i læreboka: «..the
Systematisk usikkerhet
 Kvalitetssikring av konseptvalg, samt styringsunderlag og kostnadsoverslag for valgt prosjektalternativ Systematisk usikkerhet Basert på et utkast utarbeidet under ledelse av Dovre International AS Versjon
Kvalitetssikring av konseptvalg, samt styringsunderlag og kostnadsoverslag for valgt prosjektalternativ Systematisk usikkerhet Basert på et utkast utarbeidet under ledelse av Dovre International AS Versjon
Test, 3 Sannsynlighet og statistikk
 Test, 3 Sannsynlighet og statistikk Innhold 3. Stokastiske variabler og sannsynlighetsfordelinger... 3. Forventningsverdi, varians og standardavvik... 5 3.3 Normalfordelingen... 4 3.4 Sentralgrensesetningen...
Test, 3 Sannsynlighet og statistikk Innhold 3. Stokastiske variabler og sannsynlighetsfordelinger... 3. Forventningsverdi, varians og standardavvik... 5 3.3 Normalfordelingen... 4 3.4 Sentralgrensesetningen...
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 Øvelsesoppgave i: ECON30 Dato for utlevering: 7.03.04 Dato for innlevering: 07.04.04 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Innleveringssted: Ekspedisjonen, etasje innen kl 5:00 Øvrig informasjon: Denne
Øvelsesoppgave i: ECON30 Dato for utlevering: 7.03.04 Dato for innlevering: 07.04.04 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Innleveringssted: Ekspedisjonen, etasje innen kl 5:00 Øvrig informasjon: Denne
LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4240 STATISTIKK Mandag 12. desember 2011
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 10 LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4240 STATISTIKK Mandag 12. desember 2011 Oppgave 1 Oljeleting a) Siden P(A
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 10 LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4240 STATISTIKK Mandag 12. desember 2011 Oppgave 1 Oljeleting a) Siden P(A
QED 1 7. Matematikk for grunnskolelærerutdanningen. Bind 2. Fasit kapittel 4 Statistikk og kvantitativ metode
 QED 1 7 Matematikk for grunnskolelærerutdanningen Bind 2 Fasit kapittel 4 Statistikk og kvantitativ metode Kapittel 4 Oppgave 1 La være antall øyne på terningen. a) Vi får følgende sannsynlighetsfordeling
QED 1 7 Matematikk for grunnskolelærerutdanningen Bind 2 Fasit kapittel 4 Statistikk og kvantitativ metode Kapittel 4 Oppgave 1 La være antall øyne på terningen. a) Vi får følgende sannsynlighetsfordeling
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 Øvelsesoppgave i: ECON2130 Statistikk 1 Dato for utlevering: Mandag 22. mars 2010 Dato for innlevering: Fredag 9. april 2010 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Innleveringssted: Ved siden av SV-info-senter
Øvelsesoppgave i: ECON2130 Statistikk 1 Dato for utlevering: Mandag 22. mars 2010 Dato for innlevering: Fredag 9. april 2010 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Innleveringssted: Ved siden av SV-info-senter
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Øvelsesoppgave i: ECON30- Statistikk Dato for utlevering: 5.03.06 Dato for innlevering: 05.04.06 innen kl. 5:00 Innleveringssted: Ekspedisjonen i. etasje ES hus
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Øvelsesoppgave i: ECON30- Statistikk Dato for utlevering: 5.03.06 Dato for innlevering: 05.04.06 innen kl. 5:00 Innleveringssted: Ekspedisjonen i. etasje ES hus
HØGSKOLEN I STAVANGER
 EKSAMEN I: MOT0 STATISTISKE METODER VARIGHET: TIMER DATO:. NOVEMBER 00 TILLATTE HJELPEMIDLER: KALKULATOR, TABELLER OG FORMLER I STATISTIKK (TAPIR FORLAG) OPPGAVESETTET BESTÅR AV OPPGAVER PÅ 7 SIDER HØGSKOLEN
EKSAMEN I: MOT0 STATISTISKE METODER VARIGHET: TIMER DATO:. NOVEMBER 00 TILLATTE HJELPEMIDLER: KALKULATOR, TABELLER OG FORMLER I STATISTIKK (TAPIR FORLAG) OPPGAVESETTET BESTÅR AV OPPGAVER PÅ 7 SIDER HØGSKOLEN
Løsningsforslag Til Statlab 5
 Løsningsforslag Til Statlab 5 Jimmy Paul September 6, 007 Oppgave 8.1 Vi skal se på ukentlige forbruk av søtsaker blant barn i et visst område. En pilotstudie gir at standardavviket til det ukentige forbruket
Løsningsforslag Til Statlab 5 Jimmy Paul September 6, 007 Oppgave 8.1 Vi skal se på ukentlige forbruk av søtsaker blant barn i et visst område. En pilotstudie gir at standardavviket til det ukentige forbruket
ST0202 Statistikk for samfunnsvitere
 ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag 2 Statistisk inferens (kap. 8) Statistisk inferens er å tolke/analysere resultater fra utvalget for å finne ut mest mulig
ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag 2 Statistisk inferens (kap. 8) Statistisk inferens er å tolke/analysere resultater fra utvalget for å finne ut mest mulig
Lineære likningssystemer og matriser
 Kapittel 3 Lineære likningssystemer og matriser I dette kapittelet skal vi sette sammen Kapittel 1 og 2. 3.1 Den utvidede matrisen til et likningssystem Vi starter med et lineært likningssystem med m likninger
Kapittel 3 Lineære likningssystemer og matriser I dette kapittelet skal vi sette sammen Kapittel 1 og 2. 3.1 Den utvidede matrisen til et likningssystem Vi starter med et lineært likningssystem med m likninger
Notasjon og Tabell 8. ST0202 Statistikk for samfunnsvitere
 2 Inferens om varians og standardavvik for ett normalfordelt utvalg (9.4) Inferens om variansen til en normalfordelt populasjon bruker kjikvadrat-fordelingen ( chi-square distribution ) (der kji er den
2 Inferens om varians og standardavvik for ett normalfordelt utvalg (9.4) Inferens om variansen til en normalfordelt populasjon bruker kjikvadrat-fordelingen ( chi-square distribution ) (der kji er den
TMA4240 Statistikk Høst 2016
 TMA4240 Statistikk Høst 2016 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 11 Oppgavene i denne øvingen dreier seg om hypotesetesting og sentrale begreper
TMA4240 Statistikk Høst 2016 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 11 Oppgavene i denne øvingen dreier seg om hypotesetesting og sentrale begreper
BESLUTNINGER UNDER USIKKERHET
 24. april 2002 Aanund Hylland: # BESLUTNINGER UNDER USIKKERHET Standard teori og kritikk av denne 1. Innledning En (individuell) beslutning under usikkerhet kan beskrives på følgende måte: Beslutningstakeren
24. april 2002 Aanund Hylland: # BESLUTNINGER UNDER USIKKERHET Standard teori og kritikk av denne 1. Innledning En (individuell) beslutning under usikkerhet kan beskrives på følgende måte: Beslutningstakeren
Hypotesetesting. Hvorfor og hvordan? Gardermoen 21. april 2016 Ørnulf Borgan. H. Aschehoug & Co Sehesteds gate 3, 0102 Oslo Tlf:
 Hypotesetesting Hvorfor og hvordan? Gardermoen 21. april 2016 Ørnulf Borgan H. Aschehoug & Co Sehesteds gate 3, 0102 Oslo Tlf: 22 400 400 www.aschehoug.no 1 Oversikt Sannsynlighetsregning og statistikk
Hypotesetesting Hvorfor og hvordan? Gardermoen 21. april 2016 Ørnulf Borgan H. Aschehoug & Co Sehesteds gate 3, 0102 Oslo Tlf: 22 400 400 www.aschehoug.no 1 Oversikt Sannsynlighetsregning og statistikk
ST0202 Statistikk for samfunnsvitere
 ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag 2 Statistisk inferens (kap. 8) Statistisk inferens er å tolke/analysere resultater fra utvalget for å finne ut mest mulig
ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag 2 Statistisk inferens (kap. 8) Statistisk inferens er å tolke/analysere resultater fra utvalget for å finne ut mest mulig
Forelesning 6: Punktestimering, usikkerhet i estimering. Jo Thori Lind
 Forelesning 6: Punktestimering, usikkerhet i estimering Jo Thori Lind j.t.lind@econ.uio.no Oversikt 1. Trekke utvalg 2. Estimatorer og observatorer som stokastiske variable 3. Egenskapene til en estimator
Forelesning 6: Punktestimering, usikkerhet i estimering Jo Thori Lind j.t.lind@econ.uio.no Oversikt 1. Trekke utvalg 2. Estimatorer og observatorer som stokastiske variable 3. Egenskapene til en estimator
Introduksjon til inferens
 Introduksjon til inferens Hittil: Populasjon der verdien til et individ/enhet beskrives med en fordeling. Her inngår vanligvis ukjente parametre, μ, p,... Enkelt tilfeldig utvalg (SRS), observator p =
Introduksjon til inferens Hittil: Populasjon der verdien til et individ/enhet beskrives med en fordeling. Her inngår vanligvis ukjente parametre, μ, p,... Enkelt tilfeldig utvalg (SRS), observator p =
1 Sammendrag. Skattyternes etterlevelse ved salg av aksjer
 Innholdsfortegnelse 1 Sammendrag... 2 2 Innledning hvordan måle skattyternes etterlevelse ved salg av aksjer... 3 2.1 Analysepopulasjonen... 3 2.2 Vurdering av skattyters etterlevelse... 4 3 Utvikling
Innholdsfortegnelse 1 Sammendrag... 2 2 Innledning hvordan måle skattyternes etterlevelse ved salg av aksjer... 3 2.1 Analysepopulasjonen... 3 2.2 Vurdering av skattyters etterlevelse... 4 3 Utvikling
En tilnærmet sammenheng mellom rullerende tremånedersvekst og månedsvekst i Månedlig nasjonalregnskap
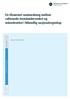 En tilnærmet sammenheng mellom rullerende tremånedersvekst og månedsvekst i Månedlig nasjonalregnskap Magnus Kvåle Helliesen NOTATER / DOCUMENTS 2019 / 23 I serien Notater publiseres dokumentasjon, metodebeskrivelser,
En tilnærmet sammenheng mellom rullerende tremånedersvekst og månedsvekst i Månedlig nasjonalregnskap Magnus Kvåle Helliesen NOTATER / DOCUMENTS 2019 / 23 I serien Notater publiseres dokumentasjon, metodebeskrivelser,
Konfidensintervall for µ med ukjent σ (t intervall)
 Forelesning 3, kapittel 6 Konfidensintervall for µ med ukjent σ (t intervall) Konfidensintervall for µ basert på n observasjoner fra uavhengige N( µ, σ) fordelinger når σ er kjent : Hvis σ er ukjent har
Forelesning 3, kapittel 6 Konfidensintervall for µ med ukjent σ (t intervall) Konfidensintervall for µ basert på n observasjoner fra uavhengige N( µ, σ) fordelinger når σ er kjent : Hvis σ er ukjent har
Vurdering av kvaliteten på undersøkelser om virkninger av trafikksikkerhetstiltak
 Sammendrag: Vurdering av kvaliteten på undersøkelser om virkninger av trafikksikkerhetstiltak TØI-rapport 984/2008 Forfatter(e): Rune Elvik Oslo 2008, 140 sider Denne rapporten presenterer en undersøkelse
Sammendrag: Vurdering av kvaliteten på undersøkelser om virkninger av trafikksikkerhetstiltak TØI-rapport 984/2008 Forfatter(e): Rune Elvik Oslo 2008, 140 sider Denne rapporten presenterer en undersøkelse
betyr begivenheten at det blir trukket en rød kule i første trekning og en hvit i andre, mens B1 B2
 ECON30: EKSAMEN 06v SENSORVEILEDNING. Det anbefales at de 9 deloppgavene merket med A, B, teller likt uansett variasjon i vanskelighetsgrad. Svarene er gitt i
ECON30: EKSAMEN 06v SENSORVEILEDNING. Det anbefales at de 9 deloppgavene merket med A, B, teller likt uansett variasjon i vanskelighetsgrad. Svarene er gitt i
Matematisk induksjon
 Matematisk induksjon 1 Innledning Dette er et nytt forsøk på å forklare induksjon. Strategien min i forelesning var å prøve å unngå å få det til å se ut som magi, ved å forklare prinsippet fort ved hjelp
Matematisk induksjon 1 Innledning Dette er et nytt forsøk på å forklare induksjon. Strategien min i forelesning var å prøve å unngå å få det til å se ut som magi, ved å forklare prinsippet fort ved hjelp
Profil Lavpris Supermarked Hypermarked Totalt. Coop Prix 4 4. Coop Extra 13 5. Coop Mega 7 7. Coop Obs 5 13. Rimi 24 24. Ica Supermarked 7 7
 Vedlegg 1 - Regresjonsanalyser 1 Innledning og formål (1) Konkurransetilsynet har i forbindelse med Vedtak 2015-24, (heretter "Vedtaket") utført kvantitative analyser på data fra kundeundersøkelsen. I
Vedlegg 1 - Regresjonsanalyser 1 Innledning og formål (1) Konkurransetilsynet har i forbindelse med Vedtak 2015-24, (heretter "Vedtaket") utført kvantitative analyser på data fra kundeundersøkelsen. I
Dersom spillerne ønsker å notere underveis: penn og papir til hver spiller.
 "FBI-spillet" ------------- Et spill for 4 spillere av Henrik Berg Spillmateriale: --------------- 1 vanlig kortstokk - bestående av kort med verdi 1 (ess) til 13 (konge) i fire farger. Kortenes farger
"FBI-spillet" ------------- Et spill for 4 spillere av Henrik Berg Spillmateriale: --------------- 1 vanlig kortstokk - bestående av kort med verdi 1 (ess) til 13 (konge) i fire farger. Kortenes farger
Oppgave 11: Oppgave 12: Oppgave 13: Oppgave 14:
 Oppgave 11: Ved produksjon på 100 000 enheter pr periode har en bedrift marginalkostnader på 1 000, gjennomsnittskostnader på 2 500, variable kostnader på 200 000 000 og faste kostnader på 50 000 000.
Oppgave 11: Ved produksjon på 100 000 enheter pr periode har en bedrift marginalkostnader på 1 000, gjennomsnittskostnader på 2 500, variable kostnader på 200 000 000 og faste kostnader på 50 000 000.
Fire kort. Mål. Gjennomføring. Film. Problemløsing Fire kort
 Fire kort Mål Generelt: Søke etter mønster og sammenhenger. Gjennomføre undersøkelse og begrunne resultat. Utfordre elevene på å resonnere og kommunisere. Spesielt: Finne alle kombinasjoner når de adderer
Fire kort Mål Generelt: Søke etter mønster og sammenhenger. Gjennomføre undersøkelse og begrunne resultat. Utfordre elevene på å resonnere og kommunisere. Spesielt: Finne alle kombinasjoner når de adderer
Ferdig før tiden 4 7 Ferdig til avtalt tid 12 7 Forsinket 1 måned 2 6 Forsinket 2 måneder 4 4 Forsinket 3 måneder 6 2 Forsinket 4 måneder 0 2
 Besvar alle oppgavene. Hver deloppgave har lik vekt. Oppgave I En kommune skal bygge ny idrettshall og vurderer to entreprenører, A og B. Begge gir samme pristilbud, men kommunen er bekymret for forsinkelser.
Besvar alle oppgavene. Hver deloppgave har lik vekt. Oppgave I En kommune skal bygge ny idrettshall og vurderer to entreprenører, A og B. Begge gir samme pristilbud, men kommunen er bekymret for forsinkelser.
ST0202 Statistikk for samfunnsvitere
 ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag 2 Kap. 10: Inferens om to populasjoner Situasjon: Vi ønsker å sammenligne to populasjoner med populasjonsgjennomsnitt henholdsvis
ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag 2 Kap. 10: Inferens om to populasjoner Situasjon: Vi ønsker å sammenligne to populasjoner med populasjonsgjennomsnitt henholdsvis
Fire kort. Mål. Gjennomføring. Film. Problemløsing Fire kort
 Fire kort Mål Generelt: Søke etter mønster og sammenhenger. Gjennomføre undersøkelse og begrunne resultat. Utfordre elevene på å resonnere og kommunisere. Spesielt: Finne alle kombinasjoner når de adderer
Fire kort Mål Generelt: Søke etter mønster og sammenhenger. Gjennomføre undersøkelse og begrunne resultat. Utfordre elevene på å resonnere og kommunisere. Spesielt: Finne alle kombinasjoner når de adderer
OPPGAVEHEFTE I STK1000 TIL KAPITTEL Regneoppgaver til kapittel 7. X 1,i, X 2 = 1 n 2. D = X 1 X 2. På onsdagsforelesningen påstod jeg at da må
 OPPGAVEHEFTE I STK000 TIL KAPITTEL 7 Regneoppgaver til kapittel 7 Oppgave Anta at man har resultatet av et randomisert forsøk med to grupper, og observerer fra gruppe, mens man observerer X,, X,2,, X,n
OPPGAVEHEFTE I STK000 TIL KAPITTEL 7 Regneoppgaver til kapittel 7 Oppgave Anta at man har resultatet av et randomisert forsøk med to grupper, og observerer fra gruppe, mens man observerer X,, X,2,, X,n
Kapittel 4.4: Forventning og varians til stokastiske variable
 Kapittel 4.4: Forventning og varians til stokastiske variable Forventning og varians til stokastiske variable Histogrammer for observerte data: Sannsynlighets-histogrammer og tetthetskurver for stokastiske
Kapittel 4.4: Forventning og varians til stokastiske variable Forventning og varians til stokastiske variable Histogrammer for observerte data: Sannsynlighets-histogrammer og tetthetskurver for stokastiske
Eksempeloppgave REA3028 Matematikk S2. Bokmål
 Eksempeloppgave 2008 REA3028 Matematikk S2 Bokmål Bokmål Eksamensinformasjon Eksamenstid: Hjelpemidler på Del 1: Hjelpemidler på Del 2: Bruk av kilder: Vedlegg: Framgangsmåte: Veiledning om vurderingen:
Eksempeloppgave 2008 REA3028 Matematikk S2 Bokmål Bokmål Eksamensinformasjon Eksamenstid: Hjelpemidler på Del 1: Hjelpemidler på Del 2: Bruk av kilder: Vedlegg: Framgangsmåte: Veiledning om vurderingen:
Opplæring i korrekt bruk og tilpasning av ørepropper
 Opplæring i korrekt bruk og tilpasning av ørepropper Innledning Støy er en den vanligste innrapporterte arbeidsbetingede skaden og utgjør et alvorlig problem for de som blir rammet. Hver dag bruker tusenvis
Opplæring i korrekt bruk og tilpasning av ørepropper Innledning Støy er en den vanligste innrapporterte arbeidsbetingede skaden og utgjør et alvorlig problem for de som blir rammet. Hver dag bruker tusenvis
Kap 13 Opsjonsprising: Løsninger
 Kap 13 Opsjonsprising: Løsninger 1 Prising med arbitrasje Oppgave 1 For å finne opsjonens verdi, bruker vi følgende fremgangsmåte: 1. Definer aksjens prisprosess. Gitt dagens pris, kan aksjen ha en av
Kap 13 Opsjonsprising: Løsninger 1 Prising med arbitrasje Oppgave 1 For å finne opsjonens verdi, bruker vi følgende fremgangsmåte: 1. Definer aksjens prisprosess. Gitt dagens pris, kan aksjen ha en av
Illustrasjon av regel 5.19 om sentralgrenseteoremet og litt om heltallskorreksjon (som i eksempel 5.20).
 Econ 130 HG mars 017 Supplement til forelesningen 7. februar Illustrasjon av regel 5.19 om sentralgrenseteoremet og litt om heltallskorreksjon (som i eksempel 5.0). Regel 5.19 sier at summer, Y X1 X X
Econ 130 HG mars 017 Supplement til forelesningen 7. februar Illustrasjon av regel 5.19 om sentralgrenseteoremet og litt om heltallskorreksjon (som i eksempel 5.0). Regel 5.19 sier at summer, Y X1 X X
Denne uken: kap : Introduksjon til statistisk inferens. - Konfidensintervall - Hypotesetesting - P-verdier - Statistisk signifikans
 Denne uken: kap. 6.1-6.2-6.3: Introduksjon til statistisk inferens - Konfidensintervall - Hypotesetesting - P-verdier - Statistisk signifikans VG 25/9 2011 Statistisk inferens Mål: Trekke konklusjoner
Denne uken: kap. 6.1-6.2-6.3: Introduksjon til statistisk inferens - Konfidensintervall - Hypotesetesting - P-verdier - Statistisk signifikans VG 25/9 2011 Statistisk inferens Mål: Trekke konklusjoner
