Opsjoner. R. Øystein Strøm. 14. april 2004
|
|
|
- Hannah Pettersen
- 7 år siden
- Visninger:
Transkript
1 Opsjoner R. Øystein Strøm 14. april 2004 Slide 1 1. Innledning 2. Definisjoner 3. Salgs-kjøps-pariteten 4. En en-periodisk binomisk opsjonsformel 5. De generelle modellene 1 Innledning Opsjoner er å finne overalt: Slide 2 En opsjon er som en billett til kino. Er det fint vær vil du kanskje heller finne på noe annet. Billetten kastes og er verdiløs, hvis du ikke får solgt den før forestillingen starter. Stein Erik Hagen har en opsjon til å selge aksjene sine i Ahold 26. april. Direktører blir belønnet med opsjoner knyttet til aksjekursen på selskapets aksjer for å stimulere til økt verdiskaping. Opsjoner finnes på alt i finansmarkeder, på aksjer, varer (for eksempel vin), hendelser, slik som jordskjelv i Japan.
2 2 Definisjoner Opsjonen avleder sin verdi fra den underliggende eiendel. Opsjonen, for eksempel en aksjeopsjon Slide 3 avleder sin verdi fra Den underliggende eiendel, for eksempel en aksje Figur 1: Opsjonen som et avledet instrument, et derivat Opsjonen er skrevet på en bestemt eiendel som er underliggende. Det er to slag opsjoner, en kjøpsopsjon og en salgsopsjon. DEFINISJON 1 En kjøpsopsjon er en rett, men ikke en plikt, til å kjøpe et bestemt antall aksjer på et bestemt tidspunkt eller før, til en på forhånd avtalt pris (utøvelsesprisen). Slide 4 DEFINISJON 2 En salgsopsjon er en rett, men ikke en plikt, til å selge et bestemt antall aksjer på et bestemt tidspunkt eller før, til en på forhånd avtalt pris (utøvelsesprisen). Hagen har en salgsopsjon! Opsjonen er slik at den kan brukes, hvis eieren ser seg tjent med det. Hvis ikke, kan eieren la være å bruke den.
3 2.1 Et eksempel Slide 5 Når vil opsjonen brukes? EKSEMPEL 1 Du vurderer å kjøpe en kjøpsopsjon på en aksje. Utøvelseskursen er 100. Premien er 5. Opsjonen kan bare utøves på en bestemt dag. Anta kursen kan være fra 80 til 130 på utøvelsestidspunktet. Når vil opsjonen benyttes? Tabell 1: Verdien av opsjonen i eksempel 1. Utøvelseskurs = 100 Slide 6 Kurs Premie Opsjon Er kursen over 100, vil opsjonen benyttes. Er kursen under 100, er det billigere å kjøpe aksjen på børsen.
4 Vi trenger noen definisjoner: Slide 7 K T S T I A t B t r f Kjøpsopsjon på forfallstidspunktet T Salgsopsjon ved T Innløsningskurs (utøvelseskurs) Aksje på tidspunkt t Risikofri obligasjon Risikofri rente Vi skal nå se på de fire grunnleggende kontantstrømmer for opsjoner. K T Slide 8 Premie I A T Ved forfall: Figur 2: Kontantstrøm for en kjøpt kjøpsopsjon K T = max [0, (A T I)] (1)
5 K T Slide 9 Premie I A T Figur 3: Kontantstrøm for en solgt kjøpsopsjon Slide 10 K T Premie I A T Figur 4: Kontantstrøm for en kjøpt salgsopsjon Ved forfall: K T = max [0, (I A T )] (2)
6 K T Slide 11 Premie I A T Figur 5: Kontantstrøm for en solgt salgsopsjon 3 Sikring og spekulasjon De ulike typer opsjoner kan kombineres med hverandre eller med eie eller salg av aksjer. Slike kombinasjoner kalles porteføljer. Vi ser på et par spekulasjonsstrategier og et par sikringsstrategier. Slide Spekulasjon EKSEMPEL 2 Anta at du venter at prisen på aksjen vil holde seg stabil i tiden fremover. Hvordan kan en spekulant tjene på dette? Svar: Sett sammen en portefølje av en solgt kjøpsopsjon og en solgt salgsopsjon på samme innløsningskurs.
7 K T Slide 13 KJØP SALG I A T Portefølje Figur 6: Kontantstrøm for en solgt salgsopsjon og en solgt kjøpsopsjon Slide 14 EKSEMPEL 3 Anta i stedet at du venter at aksjen vil være svært urolig i fremtiden, men du vet ikke om den vil gå opp eller ned. Hvilken spekulasjonsstrategi ville du anbefale? Svar: Kjøp både en salgsopsjon og en kjøpsopsjon på samme utøvelseskurs.
8 K T Slide 15 Portefølje KJØP I SALG A T Figur 7: Kontantstrøm for en kjøpt salgsopsjon og en kjøpt kjøpsopsjon 3.2 Sikring Slide 16 EKSEMPEL 4 Anta nå at du eier en aksje. Går kursen på aksjen i været, tjener du penger. Går kursen ned i kjelleren, taper du. Du ønsker å sikre deg mot kjellertilværelsen. Hva kan gjøres? Svar: Kjøp en salgsopsjon med samme innløsningskurs som dagens kurs.
9 K T Portefølje Slide 17 I SALG A T Aksje Figur 8: Kontantstrøm for en kjøpt salgsopsjon og eie av aksjen 4 Salg-kjøp-pariteten Slide 18 PROPOSISJON 1 Forskellen mellom prisen på en kjøpsopsjon og en salgsopsjon på samme aksje og med samme innløsningskurs og tid til forfall, er lik prisen på den underliggende aksje minus nåverdien av innløsningskursen. 1 K 0 S 0 = A 0 (1 + r f ) T I (3) Denne sammenhengen gjelder for en europeisk opsjon som ikke betaler utbytte før forfall. Alternativt kunne vi bruke en obligasjon med pålydende lik innløsningskursen. Vi skal bevise proposisjon 1. For enkelthets skyld droppes fotskrift.
10 4.1 K S-pariteten: Del A Anta at pariteten ikke holder, dvs. i første omgang: Slide 19 Hva om K S > A 1 (1+r f ) T I Da er K S A + 1 (1+r f ) T I > 0 Hvis dette er tilfellet, kan man altså tjene penger på å kjøpe aksjen A, selge den overvurderte kjøpsopsjonen +K og kjøpe den undervurderte salgsopsjonen S, og ved å låne +I (1 + r f ) T. Dette er et eksempel på en risikofri arbitrasje. Tabell 2: Salgs-kjøpspariteten hvis aksjens pris er høyere enn innløsningskurs Ved forfall Slide 20 I dag A T < I A T > I Selg KJØP K 0 (A T I) Kjøp SALG S + (I A T ) 0 Kjøp aksje A +A T +A T Lån + 1 (1+r f ) T I I I > 0 0 0
11 4.2 K S-pariteten: Del B Slide 21 Hva om K S < A 1 (1+r f ) T I Da er K S A + 1 (1+r f ) T I < 0 eller K + S + A 1 (1+r f ) T I > 0 Tabell 3: Salgs-kjøpspariteten hvis aksjens pris er lavere enn innløsningskurs Ved forfall Slide 22 I dag A T < I A T > I Kjøp KJØP K 0 + (A T I) Selg SALG +S (I A T ) 0 Selg aksje +A A T A T Lån ut - 1 (1+r f ) T I +I +I > 0 0 0
12 4.2.1 Et enkelt eksempel Slide 23 EKSEMPEL 5 Anta at en kjøpsopsjon på selskapet D med forfall om 39 dager til en innløsningskurs på 45,000 er til salgs for 4,875. Aksjekursen på D s aksjer er for tiden på 47,000. Salgsopsjonen på samme innløsningskurs og samme forfallstidspunkt selges for 2,875. Risikofri rente er på årsbasis 6%. Stemmer disse opsjonsprisene med salgs-kjøps-pariteten? Slide 24 Vi vil altså vente, generelt, at K S = A Her har vi at 1 (1 + r f ) T I T = 39 = 0, Venstre side gir: K S = 4, 875 2, 875 = 2, 000 Høyre side er: 1 A (1 + r f ) T I = = 2, 287 1, 060,10685 Salgs-kjøpspariteten er ikke oppfylt!
13 Utnytt mangel på paritet til å tjene penger via arbitrasje: Tabell 4: Beregning av arbitrasjefortjeneste pr. opsjon i eksempel 5 Slide 25 Handling Symbol Verdi Kjøp KJØP K -4,875 Selg SALG +S +2,875 Selg aksje +A +47,000 Lån ut I(1 + r) T -44,713 Fortjeneste 0,287 5 Prising av opsjoner Prisen på en kjøpsopsjon avhenger av følgende forhold: Aksjens pris Slide 26 Innløsningskurs Rentenivået Volatilitet, eller aksjens flyktighet Tid til forfall Vi kan illustrere disse forholdene i en enkel binomisk modell. I denne modellen forutsettes det at prisen på aksjen enten øker eller avtar, og med samme størrelse.
14 Slide Figur 9: Effekten av høyere aksjepris, innløsningskurs = 100. Opsjonen er mer verdt når prisen på aksjen er ved 110 enn ved 100. Mulighet for å nå Slide Figur 10: Effekten av høyere innløsningskurs, innløsningskurs = 110. Opsjonen er mindre verdt når innløsningskursen øker.
15 Slide Figur 11: Effekten av lengre tid til forfall. Innløsningskurs = 100. Lengre tid til forfall betyr flere sjanser til å nå høye verdier. Opsjonens tidsverdi Slide Figur 12: Effekten av høyere volatilitet, innløsningskurs = 100. Høyere volatilitet innebærer større sannsynlighet for å oppnå høy pris på aksjen.
16 5.1 En en-periodisk binomisk opsjonsmodell En binomisk opsjonsmodell forutsetter at aksjekursen går enten opp med en prosent u eller ned med en prosent d. Slide 31 Alternativet er en opsjonsmodell i kontinuerlig tid, hvor aksjekursen er fordelt normalt (eller log-normalt). Fordelene med en binomisk modell: Prinsippene for opsjonsprising kan vises med enkel matematikk. Flere spesifikasjoner er mulige, for eksempel at endringene fra en periode til neste er ulike. Den binomiske modellen har den kontinuerlige som grense. 5.2 Forutsetninger Slide Markedene er perfekte og komplette, dvs. det er ingen arbitrasjemuligheter og alle eiendeler prises. Videre: Ingen transaksjonskostnader, ingen krav til delinnbetaling og ingen skatter. Andeler av eiendeler kan kjøpes. 2. Hver periodes rente r og hver periodes positive endring u og negative endring d er kjent.
17 5.3 Fremgangsmåte 1. Definer aksjens prisprosess. Gitt dagens pris, aksjen kan ha en av to verdier neste periode, enten A(1 + u) eller A(1 + d). Slide Bestem verdien av kjøpsopsjonen ved forfall. Det vil bare være to mulig priser på kjøpsopsjonen ved forfall. 3. Sett verdien av en ukjent likeverdig portefølje av aksjen og lån lik med kontantstrømmen av kjøpsopsjonen. Dette gir to ligninger med to ukjente. 4. Benytt loven om en pris: hvis to eiendeler har samme kontantstrømmer på et fremtidig tidspunkt, må de to eiendelene være like mye verdt. Siden porteføljen og kjøpsopsjonen har samme kontantstrømmer, må de være like mye verdt. 5.4 Utledning av modellen Vi har to perioder, 0 og 1. Slide 34 A 0 A 1,u = (1 + u)a 0 A 1,d = (1 + d)a 0 Figur 13: Aksjens prisprosess: To sluttverdier er mulige.
18 K 1,u = max [0, A 1,u I] = max [0, (1 + u)a 0 I] Slide 35 K 0 K 1,d = max [0, A 1,d I] = max [0, (1 + d)a 0 I] Figur 14: Verdien av en kjøpsopsjon: To sluttverdier er mulige. Nå kommer det tredje steget. Kjøp en andel av aksjen, kall andelen h. Invester samtidig et beløp B i en obligasjon med risikofri rente (eller lån ut til risikofri rente). Denne ukjente porteføljen vil ha samme kontantstrøm som kjøpsopsjonen. Slide 36 h vil alltid være enten positiv eller null. B vil alltid være enten negativ eller null. Den risikofrie renten er slik at d < r < u for å fjerne muligheter for arbitrasje.
19 ha 1,u + (1 + r f ) B = h(1 + u)a 0 + (1 + r f ) B Slide 37 ha 0 + B ha 1,d + (1 + r f ) B = h(1 + d)a 0 + (1 + r f ) B Figur 15: Verdien av en porteføljen: To sluttverdier er mulige. Fjerde steget: Sett verdien av kjøpsopsjonen lik verdien av portefølgen i de to tilstandene: Slide 38 h(1 + u)a 0 + (1 + r f )B = K 1,u h(1 + d)a 0 + (1 + r f )B = K 1,d dvs. To ligninger og to ukjente, h og B.
20 Løsning for de to ukjente gir: h = K 1,u K 1,d (u d)a 0 = K 1,u K 1,d A 1,u A 1,d h 0 (4) Slide 39 B = (1 + u)k 1,d (1 + d)k 1,u (u d)(1 + r f ) B 0 (5) Verdien av h forteller hvor stor andel av aksjen man må anskaffe for å etterligne en kjøpsopsjon, dvs. 0, 0 h 1, 0. h kalles sikringsforholdet. Verdien av B forteller hvor mye som må lånes for å finansiere investeringen i aksjen. Når kjøpsopsjonen og obligasjons-aksje-porteføljen er like mye verdt i år 1, må de være like mye verdt også i år 0: K 0 = ha 0 + B (6) Slide 40 Flytt uttrykkene for h og B fra ligning (4) og ligning (5) inn i siste ligning (6). Det gir: K 0 = 1 [ rf d 1 + r f u d K 1,u + u r ] f u d K 1,d (7) I hakeparentesen finner vi de to sluttverdiene til kjøpsopsjonen. Dagens verdi K 0 avhenger altså av disse to mulige fremtidige verdiene. Betydningen av de to sluttverdiene er veid med to brøker, hvor endringer og risikofri rente inngår. Brøkene er en slags sannsynligheter. Det hele er så diskontert med risikofri rente.
21 Slide 41 Alternativt kan uttrykket skrives: K 0 = r f [qk 1,u + (1 q)k 1,d ] (8) der q = r f d u d og 1 q = u r f u d q kalles sikringssannsynligheten. q omdanner de to mulige utfallene for opsjonens verdi i hakeparentesen i ligning (8) til en sikkerhetsekvivalent kontantstrøm. En sikker kontantstrøm skal videre diskonteres med risikofri rente. 5.5 Lærdommer fra modellen Kjøpsopsjonens verdi er uavhengig av investorenes risikoholdning. Kjøpsopsjonens verdi er uavhengig av sannsynligheten for at aksjeprisen stiger eller faller. Slide 42 Siden hverken sannsynligheter for prisøkning eller risikoholdning spiller noen rolle, har heller ikke forventninger noen rolle i prissettingen. Basert på (8) kan kjøpsopsjonens verdi sees på som den forventede verdien av kjøpsopsjonen ved forfall, diskontert med risikofri rente og sannsynligheten for kursøkning er gitt av q. Kjøpsopsjonens verdi avhenger bare av u, d, r f, I og A 0.
22 6 De generelle modellene For referansens skyld, her er den binomiske modellen for n perioder og Black-Scholes-formelen for kontinuerlig tid. Slide Den generelle binomiske formelen K 0 = 1 (1 + r f ) n n n j j=0 q j (1 q) n j max [ 0, (1 + u) j (1 + d) n j A T n I ] (9) der j er tallet på økninger. Slide 44 Ignorer alle utfall som gir kjøpsopsjonens verdi ved T lik null. Dermed: 1 n K 0 = n (1 + r f ) n q j (1 q) n j j j=0 [ (1 + u) j (1 + d) n j A T n I ] (10)
23 6.2 Black-Scholes-formelen Her brukes kontinuerlig tid, dvs.: K 0 = A 0 N (d 1 ) I e r f T N (d 2 ) (11) Slide 45 der d 1 = ln ( A 0 I ) + ( rf σ2) T σ T og (12) d 2 = d 1 σ T (13) Tabell 5: Symbolforklaringer til Black-Scholes-modellen Slide 46 σ Standardavvik til aksjen ln(a 0 /I) Den naturlige logaritmen til A 0 /I e r f T N( ) Nåverdi-faktoren når r f beregnes i kontinuerlig tid Arealet av den normaliserte normalfordelingen opp til verdien i parentesen Modellen krever bare beregning av den underliggende eiendels standardavvik. Alle andre størrelser er gitt i markedet. Markedsrisiko inngår ikke, heller ikke risikoholdning.
Kap 13 Opsjonsprising: Løsninger
 Kap 13 Opsjonsprising: Løsninger 1 Prising med arbitrasje Oppgave 1 For å finne opsjonens verdi, bruker vi følgende fremgangsmåte: 1. Definer aksjens prisprosess. Gitt dagens pris, kan aksjen ha en av
Kap 13 Opsjonsprising: Løsninger 1 Prising med arbitrasje Oppgave 1 For å finne opsjonens verdi, bruker vi følgende fremgangsmåte: 1. Definer aksjens prisprosess. Gitt dagens pris, kan aksjen ha en av
Nåverdi og pengenes tidsverdi
 Nåverdi og pengenes tidsverdi Arne Rogde Gramstad Universitetet i Oslo 9. september 2014 Versjon 1.0 Ta kontakt hvis du finner uklarheter eller feil: a.r.gramstad@econ.uio.no 1 Innledning Anta at du har
Nåverdi og pengenes tidsverdi Arne Rogde Gramstad Universitetet i Oslo 9. september 2014 Versjon 1.0 Ta kontakt hvis du finner uklarheter eller feil: a.r.gramstad@econ.uio.no 1 Innledning Anta at du har
Kap 13 Opsjonsprising: Løsninger
 Kap 3 Opsjonsprising: Løsninger Grunnleggende sammenhenger. Tabell viser gevinsten for opsjonen ved ulike utøvelseskurser. Tabell Verdien av opsjonen i eksempel.. Utøvelseskurs = 00 Utøvelses- Kurs kurs
Kap 3 Opsjonsprising: Løsninger Grunnleggende sammenhenger. Tabell viser gevinsten for opsjonen ved ulike utøvelseskurser. Tabell Verdien av opsjonen i eksempel.. Utøvelseskurs = 00 Utøvelses- Kurs kurs
Løsningsforslag F-oppgaver i boka Kapittel 2
 Løsningsforslag F-oppgaver i boka Kapittel OPPGAVE. Produsenten maksimerer overskuddet ved å velge det kvantum som gir likhet mellom markedsprisen og grensekostnaden. Begrunnelsen er slik: (i) Hvis prisen
Løsningsforslag F-oppgaver i boka Kapittel OPPGAVE. Produsenten maksimerer overskuddet ved å velge det kvantum som gir likhet mellom markedsprisen og grensekostnaden. Begrunnelsen er slik: (i) Hvis prisen
Under noen av oppgavene har jeg lagt inn et hint til hvordan dere kan går frem for å løse dem! Send meg en mail om dere finner noen feil!
 Under noen av oppgavene har jeg lagt inn et hint til hvordan dere kan går frem for å løse dem! Send meg en mail om dere finner noen feil! 1. Husk at vi kan definere BNP på 3 ulike måter: Inntektsmetoden:
Under noen av oppgavene har jeg lagt inn et hint til hvordan dere kan går frem for å løse dem! Send meg en mail om dere finner noen feil! 1. Husk at vi kan definere BNP på 3 ulike måter: Inntektsmetoden:
Tallet 0,04 kaller vi prosentfaktoren til 4 %. Prosentfaktoren til 7 % er 0,07, og prosentfaktoren til 12,5 % er 0,125.
 Prosentregning Når vi skal regne ut 4 % av 10 000 kr, kan vi regne slik: 10 000 kr 4 = 400 kr 100 Men det er det samme som å regne slik: 10 000 kr 0,04 = 400 kr Tallet 0,04 kaller vi prosentfaktoren til
Prosentregning Når vi skal regne ut 4 % av 10 000 kr, kan vi regne slik: 10 000 kr 4 = 400 kr 100 Men det er det samme som å regne slik: 10 000 kr 0,04 = 400 kr Tallet 0,04 kaller vi prosentfaktoren til
Fasit - Oppgaveseminar 1
 Fasit - Oppgaveseminar Oppgave Betrakt konsumfunksjonen = z + (Y-T) - 2 r 0 < 0 Her er Y bruttonasjonalproduktet, privat konsum, T nettoskattebeløpet (dvs skatter og avgifter fra private til det
Fasit - Oppgaveseminar Oppgave Betrakt konsumfunksjonen = z + (Y-T) - 2 r 0 < 0 Her er Y bruttonasjonalproduktet, privat konsum, T nettoskattebeløpet (dvs skatter og avgifter fra private til det
Forelesning 9 mandag den 15. september
 Forelesning 9 mandag den 15. september 2.6 Største felles divisor Definisjon 2.6.1. La l og n være heltall. Et naturlig tall d er den største felles divisoren til l og n dersom følgende er sanne. (1) Vi
Forelesning 9 mandag den 15. september 2.6 Største felles divisor Definisjon 2.6.1. La l og n være heltall. Et naturlig tall d er den største felles divisoren til l og n dersom følgende er sanne. (1) Vi
Mer om likninger og ulikheter
 Mer om likninger og ulikheter Studentene skal kunne utføre polynomdivisjon anvende nullpunktsetningen og polynomdivisjon til faktorisering av polynomer benytte polynomdivisjon til å løse likninger av høyere
Mer om likninger og ulikheter Studentene skal kunne utføre polynomdivisjon anvende nullpunktsetningen og polynomdivisjon til faktorisering av polynomer benytte polynomdivisjon til å løse likninger av høyere
1015 kr 1,015 1000 kr 1,015 1,015 1000 kr 1,015 1030 kr. Vi ganger med vekstfaktoren 2 ganger.
 7.9 Kredittkort I Norge bruker de fleste betalingskort ved kjøp av varer og tjenester. Betalingskortene kan vi dele i to typer: debetkort og kredittkort. Når vi bruker et debetkort, trekker vi pengene
7.9 Kredittkort I Norge bruker de fleste betalingskort ved kjøp av varer og tjenester. Betalingskortene kan vi dele i to typer: debetkort og kredittkort. Når vi bruker et debetkort, trekker vi pengene
NORCAP Markedsrapport
 NORCAP Markedsrapport Juni 2009 Bratt oppgang! Mai: Oslo børs: +15,8% S&P 500: +2,3% FTSE World: +6,9% FTSE Emerging: +14,9% Oljepris: +24,7% Oppgangen fortsatte i mai Historisk bratt oppgang Primært drevet
NORCAP Markedsrapport Juni 2009 Bratt oppgang! Mai: Oslo børs: +15,8% S&P 500: +2,3% FTSE World: +6,9% FTSE Emerging: +14,9% Oljepris: +24,7% Oppgangen fortsatte i mai Historisk bratt oppgang Primært drevet
Disclaimer / ansvarsfraskrivelse:
 Viktig informasjon Dette er et mindre utdrag av TotalRapport_Norge. Den inneholder kun korte sammendrag. For å få tilgang til den fullstendige rapporten må du være en registrert kunde eller investor hos
Viktig informasjon Dette er et mindre utdrag av TotalRapport_Norge. Den inneholder kun korte sammendrag. For å få tilgang til den fullstendige rapporten må du være en registrert kunde eller investor hos
Løsningsforslag til F-oppgavene i kapittel 2
 Løsningsforslag til F-oppgavene i kapittel 2 Oppgave 1 Noen eksempler på ulike markeder: Gatekjøkkenmat i Bergen gatekjøkken produserer mat, folk i Bergen kjøper Aviser i Norge avisene (VG, Dagbladet,
Løsningsforslag til F-oppgavene i kapittel 2 Oppgave 1 Noen eksempler på ulike markeder: Gatekjøkkenmat i Bergen gatekjøkken produserer mat, folk i Bergen kjøper Aviser i Norge avisene (VG, Dagbladet,
I n f o r m a s j o n o m a k s j e o p s j o n e r
 I n f o r m a s j o n o m a k s j e o p s j o n e r Her kan du lese om aksjeopsjoner, og hvordan de kan brukes. Du vil også finne eksempler på investeringsstrategier. Aksjeopsjoner kan være tatt opp til
I n f o r m a s j o n o m a k s j e o p s j o n e r Her kan du lese om aksjeopsjoner, og hvordan de kan brukes. Du vil også finne eksempler på investeringsstrategier. Aksjeopsjoner kan være tatt opp til
BØK311 Bedriftsøkonomi 2b. Løsningsforslag
 BØK311 Bedriftsøkonomi 2b Løsningsforslag Eksamen 31 mai 2012 Oppgave 1 Kjøpe TV på avbetaling Sammenligne kontantstrømmer a) Hvor stor er årlig effektiv rente EKSAMEN I BØK311 BEDRIFTSØKONOMI 2B 31 MAI
BØK311 Bedriftsøkonomi 2b Løsningsforslag Eksamen 31 mai 2012 Oppgave 1 Kjøpe TV på avbetaling Sammenligne kontantstrømmer a) Hvor stor er årlig effektiv rente EKSAMEN I BØK311 BEDRIFTSØKONOMI 2B 31 MAI
Endringer i DNB Aktiv fondene Spørsmål og svar
 Hva skjer? 1. september endres referanseindeksene og dermed innholdet i DNB Aktiv fondene. Andelen internasjonale aksjer økes noe på bekostning av norske aksjer og vil fremover også inkludere fremvoksende
Hva skjer? 1. september endres referanseindeksene og dermed innholdet i DNB Aktiv fondene. Andelen internasjonale aksjer økes noe på bekostning av norske aksjer og vil fremover også inkludere fremvoksende
Innhold Innledning Eierskap og kontroll Arbitrasjefrie markeder
 Innhold 1 Innledning 13 1.1 Hva er foretaksfinans?...................... 14 1.2 Foretakets eierform........................ 15 1.2.1 Aksjeselskapets fordeler................. 16 1.3 Finansielle beslutninger
Innhold 1 Innledning 13 1.1 Hva er foretaksfinans?...................... 14 1.2 Foretakets eierform........................ 15 1.2.1 Aksjeselskapets fordeler................. 16 1.3 Finansielle beslutninger
En beskrivelse af de norske regler for beskatning af finansielle instrumenter
 En beskrivelse af de norske regler for beskatning af finansielle instrumenter Notat af Ingebjørg Vamråk, Norges Handelshøjskole Udarbejdet til brug i projekt Anvendelse af finansielle instrumenter i primærproduktionen
En beskrivelse af de norske regler for beskatning af finansielle instrumenter Notat af Ingebjørg Vamråk, Norges Handelshøjskole Udarbejdet til brug i projekt Anvendelse af finansielle instrumenter i primærproduktionen
Oppgave 6 (4 poeng) La X være utbyttet til kasinoet ved en spilleomgang. a) Forklar at. b) Skriv av og fyll ut tabellen nedenfor.
 Oppgave 6 (4 poeng) I et terningspill på et kasino kastes to terninger. Det koster i utgangspunktet ikke noe å delta i spillet. Dersom summen av antall øyne blir 2 eller 12, får spilleren 200 kroner. Blir
Oppgave 6 (4 poeng) I et terningspill på et kasino kastes to terninger. Det koster i utgangspunktet ikke noe å delta i spillet. Dersom summen av antall øyne blir 2 eller 12, får spilleren 200 kroner. Blir
Gjennomgang / utvidet løsning, semesteroppgave ECON2310 Høst 14 Even CH
 Gjennomgang / utvidet løsning, semesteroppgave ECON2310 Høst 14 Even CH Hvis du oppdager eventuelle feil og mangler, si ifra på evenhvinden(at)yahoo.no Oppgave 1 a) «En statskasseveksel («treasury bill»)
Gjennomgang / utvidet løsning, semesteroppgave ECON2310 Høst 14 Even CH Hvis du oppdager eventuelle feil og mangler, si ifra på evenhvinden(at)yahoo.no Oppgave 1 a) «En statskasseveksel («treasury bill»)
S1 Eksamen våren 2009 Løsning
 S1 Eksamen, våren 009 Løsning S1 Eksamen våren 009 Løsning Del 1 Oppgave 1 a) Skriv så enkelt som mulig 1) x 1 x 1 x 1 x 1 1 x 1 x 1 x x 1 x 1 x 1 1 x 1 x 1 ) a b 3 a b 3 a 4a b 1 3 4a b 3 b 1 b) Løs likningene
S1 Eksamen, våren 009 Løsning S1 Eksamen våren 009 Løsning Del 1 Oppgave 1 a) Skriv så enkelt som mulig 1) x 1 x 1 x 1 x 1 1 x 1 x 1 x x 1 x 1 x 1 1 x 1 x 1 ) a b 3 a b 3 a 4a b 1 3 4a b 3 b 1 b) Løs likningene
VEKSTSERTIFIKAT VINN-VINN NORGE
 CRÉDIT AGRICOLE VEKSTSERTIFIKAT VINN-VINN NORGE Tjen penger når børsen går opp og når den går ned. Norge < Løpetid 2 år < Investeringsbeløp 13 500 kr per vekstsertifikat < Pålydende beløp 100 000 kr per
CRÉDIT AGRICOLE VEKSTSERTIFIKAT VINN-VINN NORGE Tjen penger når børsen går opp og når den går ned. Norge < Løpetid 2 år < Investeringsbeløp 13 500 kr per vekstsertifikat < Pålydende beløp 100 000 kr per
I n f o r m a s j o n o m v a l u t a o p s j o n s f o r r e t n i n g e r
 I n f o r m a s j o n o m v a l u t a o p s j o n s f o r r e t n i n g e r Her finner du generell informasjon om valutaopsjonsforretninger som kan handles i Danske Bank. Valutaopsjoner kan inngås som
I n f o r m a s j o n o m v a l u t a o p s j o n s f o r r e t n i n g e r Her finner du generell informasjon om valutaopsjonsforretninger som kan handles i Danske Bank. Valutaopsjoner kan inngås som
Obligasjonsbaserte futures, terminer og opsjoner
 Obligasjonsbaserte futures, terminer og opsjoner Her kan du lese om obligasjonsbaserte futures, terminer og opsjoner og hvordan de brukes. Du vil også finne en rekke eksempler på investeringsstrategier.
Obligasjonsbaserte futures, terminer og opsjoner Her kan du lese om obligasjonsbaserte futures, terminer og opsjoner og hvordan de brukes. Du vil også finne en rekke eksempler på investeringsstrategier.
for opplæringen er at eleven skal kunne regne med forhold, prosent, prosentpoeng og vekst faktor
 46 2 Forhold og prosent MÅL for opplæringen er at eleven skal kunne regne med forhold, prosent, prosentpoeng og vekst faktor behandle proporsjonale og omvendt proporsjonale størrelser i praktiske sammenhenger
46 2 Forhold og prosent MÅL for opplæringen er at eleven skal kunne regne med forhold, prosent, prosentpoeng og vekst faktor behandle proporsjonale og omvendt proporsjonale størrelser i praktiske sammenhenger
Sensorveiledning obligatorisk øvelsesoppgave ECON 1310, høsten 2013
 Sensorveiledning obligatorisk øvelsesoppgave ECON 30, høsten 203 Ved sensuren skal oppgave og 3 telle 25 prosent, og oppgave 2 telle 50 prosent. Alle oppgaver skal besvares. Det er lov å samarbeide når
Sensorveiledning obligatorisk øvelsesoppgave ECON 30, høsten 203 Ved sensuren skal oppgave og 3 telle 25 prosent, og oppgave 2 telle 50 prosent. Alle oppgaver skal besvares. Det er lov å samarbeide når
TMA4140 Diskret matematikk Høst 2011 Løsningsforslag Øving 7
 Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag Side 1 av?? TMA4140 Diskret matematikk Høst 011 Løsningsforslag Øving 7 7-1-10 a) Beløpet etter n 1 år ganges med 1.09 for å
Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag Side 1 av?? TMA4140 Diskret matematikk Høst 011 Løsningsforslag Øving 7 7-1-10 a) Beløpet etter n 1 år ganges med 1.09 for å
SKAGEN Høyrente Statusrapport april 2016
 SKAGEN Høyrente Statusrapport april 2016 Nøkkeltall pr 29. april Nøkkeltall SKAGEN Høyrente Referanseindeks* Avkastning april 0,25 % -0,01 % 0,08 % Avkastning siste 12 mnd. 1,44 % 0,84 % 1,17 % 3 mnd.
SKAGEN Høyrente Statusrapport april 2016 Nøkkeltall pr 29. april Nøkkeltall SKAGEN Høyrente Referanseindeks* Avkastning april 0,25 % -0,01 % 0,08 % Avkastning siste 12 mnd. 1,44 % 0,84 % 1,17 % 3 mnd.
Handelshøyskolen BI Institutt for regnskap, revisjon og jus. med beslutningsverktøy. Eksamensdato: 16.06.2000 kl. 09.00-14.00
 Handelshøyskolen BI Institutt for regnskap, revisjon og jus Sensorveiledning i: MAN89981 Bedriftsøkonomisk analyse med beslutningsverktøy Eksamensdato: 16.06.2000 kl. 09.00-14.00 Tillatte hjelpemidler:
Handelshøyskolen BI Institutt for regnskap, revisjon og jus Sensorveiledning i: MAN89981 Bedriftsøkonomisk analyse med beslutningsverktøy Eksamensdato: 16.06.2000 kl. 09.00-14.00 Tillatte hjelpemidler:
Masteroppgave. Opsjoner vs. Warranter på Oslo Børs. Jon Sverre Monsen & Kjetil Wiger
 Masteroppgave Opsjoner vs. Warranter på Oslo Børs Av Jon Sverre Monsen & Kjetil Wiger Masteroppgaven er gjennomført som et ledd i utdanningen ved Universitetet i Agder og er godkjent som sådan. Denne godkjenningen
Masteroppgave Opsjoner vs. Warranter på Oslo Børs Av Jon Sverre Monsen & Kjetil Wiger Masteroppgaven er gjennomført som et ledd i utdanningen ved Universitetet i Agder og er godkjent som sådan. Denne godkjenningen
IFRS 2. Verdsettelse av opsjoner til ansatte. Jan Erling Nilsen. Veileder: Professor Atle Johnsen. Utredning i profilen: Økonomisk Styring
 NORGES HANDELSHØYSKOLE Bergen, våren 2006 IFRS 2 Verdsettelse av opsjoner til ansatte Jan Erling Nilsen Veileder: Professor Atle Johnsen Utredning i profilen: Økonomisk Styring NORGES HANDELSHØYSKOLE Denne
NORGES HANDELSHØYSKOLE Bergen, våren 2006 IFRS 2 Verdsettelse av opsjoner til ansatte Jan Erling Nilsen Veileder: Professor Atle Johnsen Utredning i profilen: Økonomisk Styring NORGES HANDELSHØYSKOLE Denne
Terminprøve i matematikk for 8. trinn
 Terminprøve i matematikk for 8. trinn Høsten 2005 bokmål Til noen av oppgavene skal du bruke opplysninger fra informasjonsheftet. Disse oppgavene er merket med dette symbolet: DELPRØVE 1 Maks. poengsum:
Terminprøve i matematikk for 8. trinn Høsten 2005 bokmål Til noen av oppgavene skal du bruke opplysninger fra informasjonsheftet. Disse oppgavene er merket med dette symbolet: DELPRØVE 1 Maks. poengsum:
2010-025 Kjøp av tre borettslagsleiligheter, finansavtaleloven 47
 2010-025 Kjøp av tre borettslagsleiligheter, finansavtaleloven 47 Saken gjaldt spørsmålet om banken hadde en frarådningsplikt i 2006, da banken utstedte et finansieringsbevis på kr 1.345.000,- for å finansiere
2010-025 Kjøp av tre borettslagsleiligheter, finansavtaleloven 47 Saken gjaldt spørsmålet om banken hadde en frarådningsplikt i 2006, da banken utstedte et finansieringsbevis på kr 1.345.000,- for å finansiere
Forelesning 22 MA0003, Mandag 5/11-2012 Invertible matriser Lay: 2.2
 Forelesning 22 M0003, Mandag 5/-202 Invertible matriser Lay: 2.2 Invertible matriser og ligningssystemet x b Ligninger på formen ax b, a 0 kan løses ved å dividere med a på begge sider av ligninger, noe
Forelesning 22 M0003, Mandag 5/-202 Invertible matriser Lay: 2.2 Invertible matriser og ligningssystemet x b Ligninger på formen ax b, a 0 kan løses ved å dividere med a på begge sider av ligninger, noe
Innledning. Mål. for opplæringen er at eleven skal kunne
 8 1 Innledning Mål for opplæringen er at eleven skal kunne løse likninger, ulikheter og likningssystemer av første og andre grad og enkle likninger med eksponential- og logaritme funksjoner, både ved regning
8 1 Innledning Mål for opplæringen er at eleven skal kunne løse likninger, ulikheter og likningssystemer av første og andre grad og enkle likninger med eksponential- og logaritme funksjoner, både ved regning
Repetisjon: høydepunkter fra første del av MA1301-tallteori.
 Repetisjon: høydepunkter fra første del av MA1301-tallteori. Matematisk induksjon Binomialteoremet Divisjonsalgoritmen Euklids algoritme Lineære diofantiske ligninger Aritmetikkens fundamentalteorem Euklid:
Repetisjon: høydepunkter fra første del av MA1301-tallteori. Matematisk induksjon Binomialteoremet Divisjonsalgoritmen Euklids algoritme Lineære diofantiske ligninger Aritmetikkens fundamentalteorem Euklid:
Vekst av planteplankton - Skeletonema Costatum
 Vekst av planteplankton - Skeletonema Costatum Nivå: 9. klasse Formål: Arbeid med store tall. Bruke matematikk til å beskrive naturfenomen. Program: Regneark Referanse til plan: Tall og algebra Arbeide
Vekst av planteplankton - Skeletonema Costatum Nivå: 9. klasse Formål: Arbeid med store tall. Bruke matematikk til å beskrive naturfenomen. Program: Regneark Referanse til plan: Tall og algebra Arbeide
Oppgave 1 (40 %) a) Produktvalgproblemet kan formuleres slik: Maks DB = 200A + 75B + 100C. gitt at:
 Oppgave 1 (40 %) a) Produktvalgproblemet kan formuleres slik: Maks DB 200A + 75B + 100C gitt at: 3A + 2B + 3C < 1 000 7A + 2B + 3C < 2 000 10A + 5B + 10C < 4000 4A < 600 b) Initialtablået er vist under:
Oppgave 1 (40 %) a) Produktvalgproblemet kan formuleres slik: Maks DB 200A + 75B + 100C gitt at: 3A + 2B + 3C < 1 000 7A + 2B + 3C < 2 000 10A + 5B + 10C < 4000 4A < 600 b) Initialtablået er vist under:
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Sensorveiledning 1310, H12
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Sensorveiledning 30, H Ved sensuren tillegges oppgave vekt /4, oppgave vekt ½, og oppgave 3 vekt /4. For å bestå eksamen, må besvarelsen i hvert fall: gi minst
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Sensorveiledning 30, H Ved sensuren tillegges oppgave vekt /4, oppgave vekt ½, og oppgave 3 vekt /4. For å bestå eksamen, må besvarelsen i hvert fall: gi minst
DEL 1 Uten hjelpemidler
 DEL 1 Uten hjelpemidler Oppgave 1 (1 poeng) Prisen på en vare er satt ned med 30 %. I dag koster varen 280 kroner. Hvor mye kostet varen før prisen ble satt ned? Oppgave 2 (1 poeng) Regn ut og skriv svaret
DEL 1 Uten hjelpemidler Oppgave 1 (1 poeng) Prisen på en vare er satt ned med 30 %. I dag koster varen 280 kroner. Hvor mye kostet varen før prisen ble satt ned? Oppgave 2 (1 poeng) Regn ut og skriv svaret
Oppgave 1 (25 %) N = 0.95 = ( ) = a) Antall kontrakter som skal shortes er:
 Oppgave 1 (25 %) a) Antall kontrakter som skal shortes er: * 1 N =.95 = 188.12 22 25 Vi avrunder til nærmeste hele tall og shorter dermed 188 kontrakter. b) Tabellen under viser at strategien sikrer en
Oppgave 1 (25 %) a) Antall kontrakter som skal shortes er: * 1 N =.95 = 188.12 22 25 Vi avrunder til nærmeste hele tall og shorter dermed 188 kontrakter. b) Tabellen under viser at strategien sikrer en
Oppgaver i MM1 og MM2 (uten skatt)
 Oppgaver i MM1 og MM2 (uten skatt) 1 MM-proposisjonene De første proposisjonene utviklet Miller og Modigliani for en tenkt verden uten skatt. 1.1 Første proposisjon I første proposisjon ier MM at verdien
Oppgaver i MM1 og MM2 (uten skatt) 1 MM-proposisjonene De første proposisjonene utviklet Miller og Modigliani for en tenkt verden uten skatt. 1.1 Første proposisjon I første proposisjon ier MM at verdien
7 av 10 nordmenn tror at vi ikke er over det verste i gjeldskrisen enda
 Pressemelding 2011-11-30 7 av 10 nordmenn tror at vi ikke er over det verste i gjeldskrisen enda Nettbanken Nordnet har gjennomført en undersøkelse blant nordmenn om gjeldskrisen. Resultatet støtter opp
Pressemelding 2011-11-30 7 av 10 nordmenn tror at vi ikke er over det verste i gjeldskrisen enda Nettbanken Nordnet har gjennomført en undersøkelse blant nordmenn om gjeldskrisen. Resultatet støtter opp
Undersøkelse om svart arbeid. Oktober 2011
 Undersøkelse om svart arbeid Oktober 2011 Om undersøkelsen Undersøkelsen er gjennomført som en webundersøkelse i Opinion sitt befolkningspanel. Undersøkelsen er gjennomført som en del av en web-omnibus
Undersøkelse om svart arbeid Oktober 2011 Om undersøkelsen Undersøkelsen er gjennomført som en webundersøkelse i Opinion sitt befolkningspanel. Undersøkelsen er gjennomført som en del av en web-omnibus
Kapittel 1. Potensregning
 Kapittel. Potensregning I potensregning skriver vi tall som potenser og forenkler uttrykk som inneholder potenser. Dette kapitlet handler blant annet om: Betydningen av potenser som har negativ eksponent
Kapittel. Potensregning I potensregning skriver vi tall som potenser og forenkler uttrykk som inneholder potenser. Dette kapitlet handler blant annet om: Betydningen av potenser som har negativ eksponent
Modifisering av Black & Scholes opsjonsprising ved bruk av NIG-fordelingen
 Modifisering av Black & Scholes opsjonsprising ved bruk av NIG-fordelingen Prosjektoppgave STK-MAT2011 Sindre Froyn Salgsopsjon A B K S 0 T S 0 : porteføljeprisen ved tiden t = 0. K: garantert salgspris
Modifisering av Black & Scholes opsjonsprising ved bruk av NIG-fordelingen Prosjektoppgave STK-MAT2011 Sindre Froyn Salgsopsjon A B K S 0 T S 0 : porteføljeprisen ved tiden t = 0. K: garantert salgspris
Informasjon om Equity Options
 Informasjon om Equity Options Her kan du lese generell informasjon om equity options som kan handles med Danske Bank. Equity options kan handels på en regulert markedsplass eller OTC med banken som motpart.
Informasjon om Equity Options Her kan du lese generell informasjon om equity options som kan handles med Danske Bank. Equity options kan handels på en regulert markedsplass eller OTC med banken som motpart.
a) Ved avlesning på graf får man. Dermed er hastighet ved tid sekund lik.
 Løsningsforslag utsatt eksamen Matematikk 2, 4MX25-10 (GLU2 5-10) 5.desember 2013 Oppgave 1 a) Ved avlesning på graf får man. Dermed er hastighet ved tid sekund lik. Ved å bruke tangentlinja i punktet
Løsningsforslag utsatt eksamen Matematikk 2, 4MX25-10 (GLU2 5-10) 5.desember 2013 Oppgave 1 a) Ved avlesning på graf får man. Dermed er hastighet ved tid sekund lik. Ved å bruke tangentlinja i punktet
I n f o r m a s j o n o m r å v a r e o p s j o n e r
 Danske Bank A/S. Org.nr. D 61 12 62 28 - øbenhavn I n f o r m a s j o n o m r å v a r e o p s j o n e r Her finner du generell informasjon om råvareopsjoner som kan handles gjennom Danske Bank. Råvarer
Danske Bank A/S. Org.nr. D 61 12 62 28 - øbenhavn I n f o r m a s j o n o m r å v a r e o p s j o n e r Her finner du generell informasjon om råvareopsjoner som kan handles gjennom Danske Bank. Råvarer
Renter og oljepriser og konsekvenser for kommuneøkonomi og pensjon. Per Richard Johansen, Kommuneøkonomikonferansen 29. mai 2015
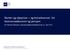 Renter og oljepriser og konsekvenser for kommuneøkonomi og pensjon Per Richard Johansen, Kommuneøkonomikonferansen 29. mai 2015 Oljepris og renter har vært på historiske unntaksnivåer Lave renter og høye
Renter og oljepriser og konsekvenser for kommuneøkonomi og pensjon Per Richard Johansen, Kommuneøkonomikonferansen 29. mai 2015 Oljepris og renter har vært på historiske unntaksnivåer Lave renter og høye
Første kvartal 2012 * Balanse, Resultat og Noter
 Første kvartal 2012 * Balanse, Resultat og Noter EnterCard Norge AS EnterCard Norge AS BALANSE PR. 31. MARS 2012 OG 2011 OG 31. DESEMBER 2011 NOK 1000 EIENDELER Note 1. KVT 2012 1. KVT 2011 2011 Utlån
Første kvartal 2012 * Balanse, Resultat og Noter EnterCard Norge AS EnterCard Norge AS BALANSE PR. 31. MARS 2012 OG 2011 OG 31. DESEMBER 2011 NOK 1000 EIENDELER Note 1. KVT 2012 1. KVT 2011 2011 Utlån
er et er et heltall. For eksempel er 2, 3, 5, 7 og 11 primtall, mens 4 = 2 2, 6 = 2 3 og 15 = 3 5 er det ikke.
 . Primtall og primtallsfaktorisering Definisjon Et primtall p er et heltall, større enn, som ikke er delelig med andre tall enn og seg selv, altså bare delelig med og p (og egentlig også og p) At et tall
. Primtall og primtallsfaktorisering Definisjon Et primtall p er et heltall, større enn, som ikke er delelig med andre tall enn og seg selv, altså bare delelig med og p (og egentlig også og p) At et tall
Stud.nr: 0899975 Runar Søndersrød Brøvig. Anvendt økonomi og ledelse. Del E BudsjetteringFinans
 Publiseringsoppgave: 1) Budsjetter resultat og kontantstrøm for årene 2009 til 2013. Arbeidskapitalen løses opp i 2014. Beregn nåverdien. Bruk et avkastningskrav på 12% etter skatt. Basismodellen historikk
Publiseringsoppgave: 1) Budsjetter resultat og kontantstrøm for årene 2009 til 2013. Arbeidskapitalen løses opp i 2014. Beregn nåverdien. Bruk et avkastningskrav på 12% etter skatt. Basismodellen historikk
ECON2200 Matematikk 1/Mikroøkonomi 1 Diderik Lund, 2. mars 2010
 Etterspørsel etter arbeidskraft på kort sikt Slutten av avsn. 2.3 i ØABL: Maks dekningsbidrag med n som valgvariabel (tidl.: med x) Siden x = F (n) er enentydig: Nøyaktig samme problem max n [pf (n) wn]
Etterspørsel etter arbeidskraft på kort sikt Slutten av avsn. 2.3 i ØABL: Maks dekningsbidrag med n som valgvariabel (tidl.: med x) Siden x = F (n) er enentydig: Nøyaktig samme problem max n [pf (n) wn]
Prop. 26 S. (2014 2015) Proposisjon til Stortinget (forslag til stortingsvedtak) Endringer i statsbudsjettet 2014 under Klima- og miljødepartementet
 Prop. 26 S (2014 2015) Proposisjon til Stortinget (forslag til stortingsvedtak) Endringer i statsbudsjettet 2014 under Klima- og miljødepartementet Tilråding fra Klima- og miljødepartementet 21. november
Prop. 26 S (2014 2015) Proposisjon til Stortinget (forslag til stortingsvedtak) Endringer i statsbudsjettet 2014 under Klima- og miljødepartementet Tilråding fra Klima- og miljødepartementet 21. november
Arbitrasje og finansielle beslutninger. Kapittel 3
 Arbitrasje og finansielle beslutninger Kapittel 3 Arbitrasje og loven om en pris Konkurranse og verdsetting Holdning til risiko Arbitrasje og konkurranse Arbitrasje er å utnytte prisforskjeller. Nordmenn
Arbitrasje og finansielle beslutninger Kapittel 3 Arbitrasje og loven om en pris Konkurranse og verdsetting Holdning til risiko Arbitrasje og konkurranse Arbitrasje er å utnytte prisforskjeller. Nordmenn
Fortsettelses kurs i Word
 Fortsettelses kurs i Word Lynkurs fra Kristiansand folkebibliotek Innholdsfortegnelse Formål med dagens kurs... 2 Sette inn forsider... 2 Sette inn tabeller... 2 Topptekst Bunntekst Sidetall... 2 Sett
Fortsettelses kurs i Word Lynkurs fra Kristiansand folkebibliotek Innholdsfortegnelse Formål med dagens kurs... 2 Sette inn forsider... 2 Sette inn tabeller... 2 Topptekst Bunntekst Sidetall... 2 Sett
Resonnerende oppgaver
 Resonnerende oppgaver Oppgavene på de påfølgende sidene inneholder flere påstander eller opplysninger. Opplysningene bygger på eller utfyller hverandre, og de stiller visse krav eller betingelser. Når
Resonnerende oppgaver Oppgavene på de påfølgende sidene inneholder flere påstander eller opplysninger. Opplysningene bygger på eller utfyller hverandre, og de stiller visse krav eller betingelser. Når
5 TIPS - FÅ RÅD TIL DET DU ØNSKER DEG
 5 TIPS - FÅ RÅD TIL DET DU ØNSKER DEG Du vil lære... Hvorfor du skal ta kontroll på økonomien De 5 stegene til hvordan du får råd til det du drømmer om Hvorfor det er så smart å begynne før sommeren, dette
5 TIPS - FÅ RÅD TIL DET DU ØNSKER DEG Du vil lære... Hvorfor du skal ta kontroll på økonomien De 5 stegene til hvordan du får råd til det du drømmer om Hvorfor det er så smart å begynne før sommeren, dette
(1) Naturlig monopol (S & W kapittel 12 i både 3. og 4. utgave) (2) Prisdiskriminering (S & W kapittel 12 i både 3. og 4. utgave)
 Økonomisk Institutt, oktober 2006 Robert G. Hansen, rom 1207 Oppsummering av forelesningen 27.10 Hovedtemaer: (1) Naturlig monopol (S & W kapittel 12 i både 3. og 4. utgave) (2) Prisdiskriminering (S &
Økonomisk Institutt, oktober 2006 Robert G. Hansen, rom 1207 Oppsummering av forelesningen 27.10 Hovedtemaer: (1) Naturlig monopol (S & W kapittel 12 i både 3. og 4. utgave) (2) Prisdiskriminering (S &
Samarbeidsmodell med utbyggere for å skaffe kommunen utleieboliger
 Samarbeidsmodell med utbyggere for å skaffe kommunen utleieboliger Særutskrift Utvalg Utvalgssak Møtedato Utvalg for levekår 44/16 07.06.2016 Utvalg for teknikk og miljø 188/16 10.06.2016 Formannskapet
Samarbeidsmodell med utbyggere for å skaffe kommunen utleieboliger Særutskrift Utvalg Utvalgssak Møtedato Utvalg for levekår 44/16 07.06.2016 Utvalg for teknikk og miljø 188/16 10.06.2016 Formannskapet
Treningsavgifter 2015-2016:
 Klubbens økonomi Treningsavgifter og salgsdugnader et stadig tilbakevennende tema blant foreldre. Det snakkes mye om dette, og hvis det er noe det klages på så er det først og fremst disse to tingene det
Klubbens økonomi Treningsavgifter og salgsdugnader et stadig tilbakevennende tema blant foreldre. Det snakkes mye om dette, og hvis det er noe det klages på så er det først og fremst disse to tingene det
Utkast til løsningsforslag til eksamen i emnet MAT 121 - Lineær algebra Utan ansvar for feil og mangler Mandag 31. mai 2010, kl. 09-14.
 Utkast til løsningsforslag til eksamen i emnet MAT 2 - Lineær algebra Utan ansvar for feil og mangler Mandag 3. mai 2, kl. 9-4. Oppgave En bisverm flyr mellom to kuber, A og B, på dagtid, og hver bi blir
Utkast til løsningsforslag til eksamen i emnet MAT 2 - Lineær algebra Utan ansvar for feil og mangler Mandag 3. mai 2, kl. 9-4. Oppgave En bisverm flyr mellom to kuber, A og B, på dagtid, og hver bi blir
Uendelige rekker. Konvergens og konvergenskriterier
 Uendelige rekker. Konvergens og konvergenskriterier : Et absolutt nødvendig, men ikke tilstrekkelig vilkår for konvergens er at: lim 0 Konvergens vha. delsummer :,.,,,. I motsatt fall divergerer rekka.
Uendelige rekker. Konvergens og konvergenskriterier : Et absolutt nødvendig, men ikke tilstrekkelig vilkår for konvergens er at: lim 0 Konvergens vha. delsummer :,.,,,. I motsatt fall divergerer rekka.
Beskrivelse av handel med CFD.
 Side 1 av 5 Beskrivelse av handel med CFD. Hva er en CFD?...2 Gearing... 3 Prising.... 4 Markeder som stiger.... 5 Markeder som faller... 5 Side 2 av 5 Hva er en CFD? CFD er en forkortelse for Contract
Side 1 av 5 Beskrivelse av handel med CFD. Hva er en CFD?...2 Gearing... 3 Prising.... 4 Markeder som stiger.... 5 Markeder som faller... 5 Side 2 av 5 Hva er en CFD? CFD er en forkortelse for Contract
Løsningsforslag til underveisvurdering i MAT111 vår 2005
 Løsningsforslag til underveisvurdering i MAT111 vår 5 Beregn grenseverdien Oppgave 1 (x 1) ln x x x + 1 Svar: Merk at nevneren er lik (x 1), så vi kan forkorte (x 1) oppe og nede og får (x 1) ln x ln x
Løsningsforslag til underveisvurdering i MAT111 vår 5 Beregn grenseverdien Oppgave 1 (x 1) ln x x x + 1 Svar: Merk at nevneren er lik (x 1), så vi kan forkorte (x 1) oppe og nede og får (x 1) ln x ln x
Sideordnede spesifikasjoner
 Norsk bokføringsstandard NBS 8 (April 2015) Innhold 1. Innledning og virkeområde... 2 2. Lov og forskrift... 3 3. Forutsetninger for bruk av sideordnede spesifikasjoner... 4 3.1 Konsolidering av spesifikasjoner...
Norsk bokføringsstandard NBS 8 (April 2015) Innhold 1. Innledning og virkeområde... 2 2. Lov og forskrift... 3 3. Forutsetninger for bruk av sideordnede spesifikasjoner... 4 3.1 Konsolidering av spesifikasjoner...
Leseveiledning til 27.02.12
 Leseveiledning til 7.0. Litt repetisjon av hva vi gjennomgikk om konsumentens valg: Hva er det beste valget for konsumenten gitt at hun må holde seg på budsjettbetingelsen? Indifferenskurvene (IK) bestemmer
Leseveiledning til 7.0. Litt repetisjon av hva vi gjennomgikk om konsumentens valg: Hva er det beste valget for konsumenten gitt at hun må holde seg på budsjettbetingelsen? Indifferenskurvene (IK) bestemmer
Løsningsforslag til obligatorisk oppgave i MAT 1100, H-04
 Løsningsforslag til obligatorisk oppgave i MAT 00, H-04 Oppgave : a) Vi har zw ( + i )( + i) + i + i + i i og + i + i ( ) + i( + ) z w + i + i ( + i )( i) ( + i)( i) i + i i i ( i ) ( + ) + i( + ) + +
Løsningsforslag til obligatorisk oppgave i MAT 00, H-04 Oppgave : a) Vi har zw ( + i )( + i) + i + i + i i og + i + i ( ) + i( + ) z w + i + i ( + i )( i) ( + i)( i) i + i i i ( i ) ( + ) + i( + ) + +
Vedtekter Verdipapirfondet Danske Invest Norsk Obligasjon Institusjon
 Vedtekter for verdipapirfondet Danske Invest Norsk Obligasjon Institusjon 1 Verdipapirfondets navn m.v. Verdipapirfondet Danske Invest Norsk Obligasjon Institusjon er en selvstendig formuesmasse oppstått
Vedtekter for verdipapirfondet Danske Invest Norsk Obligasjon Institusjon 1 Verdipapirfondets navn m.v. Verdipapirfondet Danske Invest Norsk Obligasjon Institusjon er en selvstendig formuesmasse oppstått
QED 5 10. Matematikk for grunnskolelærerutdanningen. Bind 2. Fasit kapittel 2 Tallenes hemmeligheter
 QED 5 10 Matematikk for grunnskolelærerutdanningen Bind Fasit kapittel Tallenes hemmeligheter Kapittel Oppgave 5. Nei Oppgave 7. Addisjon og multiplikasjon Oppgave 8. b) Hvis vi ser på hele tall er {1},
QED 5 10 Matematikk for grunnskolelærerutdanningen Bind Fasit kapittel Tallenes hemmeligheter Kapittel Oppgave 5. Nei Oppgave 7. Addisjon og multiplikasjon Oppgave 8. b) Hvis vi ser på hele tall er {1},
Avhending av tidligere Ankerskogen videregående skole, Hamar kommune, gårds- og bruksnummer 1/2262
 Saknr. 14/4245-1 Saksbehandler: Kristin Bjerkli Avhending av tidligere Ankerskogen videregående skole, Hamar kommune, gårds- og bruksnummer 1/2262 Innstilling til vedtak: Fylkesrådet legger saken fram
Saknr. 14/4245-1 Saksbehandler: Kristin Bjerkli Avhending av tidligere Ankerskogen videregående skole, Hamar kommune, gårds- og bruksnummer 1/2262 Innstilling til vedtak: Fylkesrådet legger saken fram
Styrets beretning 2013. Forsknings- og undervisningsfondet i Trondheim
 Styrets beretning 2013 Stiftelsens formål er gjennom avkastning på stiftelsens kapital å yte bidrag i forbindelse med tilrettelegging av forsknings- og undervisningsaktivitet ved NTNU. Fondet kan også
Styrets beretning 2013 Stiftelsens formål er gjennom avkastning på stiftelsens kapital å yte bidrag i forbindelse med tilrettelegging av forsknings- og undervisningsaktivitet ved NTNU. Fondet kan også
ÅRSREGNSKAPET 2015. Solastranden Golfklubb Org.nr 974 467 569. Årsberetning Resultatregnskap Balanse Noter Revisjonsberetning
 ÅRSREGNSKAPET 2015 Solastranden Golfklubb Org.nr 974 467 569 Årsberetning Resultatregnskap Balanse Noter Revisjonsberetning Resultatregnskap Driftsinntekter og driftskostnader Note 2015 2014 Driftsinntekter
ÅRSREGNSKAPET 2015 Solastranden Golfklubb Org.nr 974 467 569 Årsberetning Resultatregnskap Balanse Noter Revisjonsberetning Resultatregnskap Driftsinntekter og driftskostnader Note 2015 2014 Driftsinntekter
DE VIKTIGSTE SELSKAPSFORMENE. Velg riktig selskapsform
 Velg riktig selskapsform 1 2015 Miniforetak AS Send gjerne dette e-heftet til andre, blogg om det eller del det i sosiale medier men pass på ikke å endre noe av innholdet før du gjør det. miniforetak.no
Velg riktig selskapsform 1 2015 Miniforetak AS Send gjerne dette e-heftet til andre, blogg om det eller del det i sosiale medier men pass på ikke å endre noe av innholdet før du gjør det. miniforetak.no
DnB Aksjeindeksobligasjon Europa/Japan 2000/2006: En sammenligning med Røeggen produktene
 Petter Bjerksund, professor NHH dr.oecon. Aller siste versjon: 0.0.04 DnB Aksjeindeksobligasjon Europa/Japan 000/006: En sammenligning med Røeggen produktene. Introduksjon Undertegnede var sakkyndig vitne
Petter Bjerksund, professor NHH dr.oecon. Aller siste versjon: 0.0.04 DnB Aksjeindeksobligasjon Europa/Japan 000/006: En sammenligning med Røeggen produktene. Introduksjon Undertegnede var sakkyndig vitne
Oversikt. Trond Kristoffersen. Totalkapitalrentabilitet. Totalkapitalrentabilitet. Finansregnskap. Regnskapsanalyse (del 3) Beregning av nøkkeltall:
 Oversikt Trond Kristoffersen Finansregnskap Regnskapsanalyse (del 3) Utvidet analyse av lønnsomhet Generelt Likviditet Bedriftens betalingssituasjon Finansiering Anskaffelse og anvendelse av kapital Soliditet
Oversikt Trond Kristoffersen Finansregnskap Regnskapsanalyse (del 3) Utvidet analyse av lønnsomhet Generelt Likviditet Bedriftens betalingssituasjon Finansiering Anskaffelse og anvendelse av kapital Soliditet
Aksjekupong DNB/Hydro/Yara. Norse Securities
 Aksjekupong DNB/Hydro/Yara Norse Securities 1 Aksjekupong DNB/Hydro/Yara Hva er en aksjekupong? En aksjekupong er et produkt som tilbyr en kupongutbetaling gitt at forhåndsbestemte kriterier inntreffer
Aksjekupong DNB/Hydro/Yara Norse Securities 1 Aksjekupong DNB/Hydro/Yara Hva er en aksjekupong? En aksjekupong er et produkt som tilbyr en kupongutbetaling gitt at forhåndsbestemte kriterier inntreffer
Regnskapsanalyse med risikovurdering integrert i Maestro Årsoppgjør
 Din guide til EFFEKTIV styring og utvikling av bedriften Regnskapsanalyse med risikovurdering integrert i Maestro Årsoppgjør Anders Thoresen Gründer og daglig leder, Lederkilden.no 900 35 938 anders@lederkilden.no
Din guide til EFFEKTIV styring og utvikling av bedriften Regnskapsanalyse med risikovurdering integrert i Maestro Årsoppgjør Anders Thoresen Gründer og daglig leder, Lederkilden.no 900 35 938 anders@lederkilden.no
Høringsnotat - unntak fra reglene om beskatning av lån fra selskap til aksjonær
 Saksnr. 15/2037 17.11.2015 Høringsnotat - unntak fra reglene om beskatning av lån fra selskap til aksjonær Innhold 1 Innledning og sammendrag... 3 2 Bakgrunn... 3 3 Departementets vurderinger og forslag...
Saksnr. 15/2037 17.11.2015 Høringsnotat - unntak fra reglene om beskatning av lån fra selskap til aksjonær Innhold 1 Innledning og sammendrag... 3 2 Bakgrunn... 3 3 Departementets vurderinger og forslag...
Prosent. Det går likare no! Svein H. Torkildsen, NSMO
 Prosent Det går likare no! Svein H. Torkildsen, NSMO Enkelt opplegg Gjennomført med ei gruppe svakt presterende elever etter en test som var satt sammen av alle prosentoppgavene i Alle Teller uansett nivå.
Prosent Det går likare no! Svein H. Torkildsen, NSMO Enkelt opplegg Gjennomført med ei gruppe svakt presterende elever etter en test som var satt sammen av alle prosentoppgavene i Alle Teller uansett nivå.
VELFERDSSTATEN ET OPPSLAG I LEKSIKON
 FAKTAHEFTE VELFERDSSTATEN ET OPPSLAG I LEKSIKON Velferdsstat er betegnelsen på en stat som, i tillegg til å sørge for sine borgeres sikkerhet, yter dem en rekke grunnleggende goder som for eksempel støtte
FAKTAHEFTE VELFERDSSTATEN ET OPPSLAG I LEKSIKON Velferdsstat er betegnelsen på en stat som, i tillegg til å sørge for sine borgeres sikkerhet, yter dem en rekke grunnleggende goder som for eksempel støtte
Fasit og løsningsforslag til Julekalenderen for mellomtrinnet
 Fasit og løsningsforslag til Julekalenderen for mellomtrinnet 01.12: Svaret er 11 For å få 11 på to terninger kreves en 5er og en 6er. Siden 6 ikke finnes på terningen kan vi altså ikke få 11. 02.12: Dagens
Fasit og løsningsforslag til Julekalenderen for mellomtrinnet 01.12: Svaret er 11 For å få 11 på to terninger kreves en 5er og en 6er. Siden 6 ikke finnes på terningen kan vi altså ikke få 11. 02.12: Dagens
Preken 14. august 2016 13. s i treenighet Kapellan Elisabeth Lund. Tekst: Joh. 15, 13-17
 Preken 14. august 2016 13. s i treenighet Kapellan Elisabeth Lund Tekst: Joh. 15, 13-17 I dag har vi fått høre en prekentekst som handler om kjærlighet, om å bli kalt venner og om å bære frukt. Den er
Preken 14. august 2016 13. s i treenighet Kapellan Elisabeth Lund Tekst: Joh. 15, 13-17 I dag har vi fått høre en prekentekst som handler om kjærlighet, om å bli kalt venner og om å bære frukt. Den er
2 Likningssett og ulikheter
 Likningssett og ulikheter KATEGORI 1.1 Grafisk løsning av lineære likningssett Oppgave.110 Et lineært likningssett består av likningene for to rette linjer. De to rette linjene er tegnet i koordi natsystemet
Likningssett og ulikheter KATEGORI 1.1 Grafisk løsning av lineære likningssett Oppgave.110 Et lineært likningssett består av likningene for to rette linjer. De to rette linjene er tegnet i koordi natsystemet
PROSJEKTOPPGAVE. (våren 2009) Fag: STATISTIKK OG ØKONOMI (ITD20106) 2. klasse dataingeniører. Tidsfrister: Utdelt: onsdag 25. mars.
 Avdeling for informasjonsteknologi Remmen, Halden Høgskolen i Østfold Fag: STATISTIKK OG ØKONOMI (ITD20106) 2. klasse dataingeniører PROSJEKTOPPGAVE (våren 2009) Tidsfrister: Utdelt: onsdag 25. mars. Innleveringsfrist:
Avdeling for informasjonsteknologi Remmen, Halden Høgskolen i Østfold Fag: STATISTIKK OG ØKONOMI (ITD20106) 2. klasse dataingeniører PROSJEKTOPPGAVE (våren 2009) Tidsfrister: Utdelt: onsdag 25. mars. Innleveringsfrist:
Styrets beretning 2013. Norsk Fond for Klinisk Kjemi
 Styrets beretning 2013 Stiftelsens formål er å gi økonomisk støtte til virksomhet som kan styrke faget medisinsk biokjemi i Norge. Stiftelsen har ingen ansatte og virksomheten forurenser ikke det ytre
Styrets beretning 2013 Stiftelsens formål er å gi økonomisk støtte til virksomhet som kan styrke faget medisinsk biokjemi i Norge. Stiftelsen har ingen ansatte og virksomheten forurenser ikke det ytre
Global Skipsholding 2 AS. Kvartalsrapport desember 2014
 Global Skipsholding 2 AS Kvartalsrapport desember 2014 innhold Hovedpunkter 3 Nøkkeltall 3 Aksjekurs og utbetalinger 4 Drift, forvaltning og finansiering 5 Generelt om selskapet 6 2 Kvartalsrapport desember
Global Skipsholding 2 AS Kvartalsrapport desember 2014 innhold Hovedpunkter 3 Nøkkeltall 3 Aksjekurs og utbetalinger 4 Drift, forvaltning og finansiering 5 Generelt om selskapet 6 2 Kvartalsrapport desember
Smådriftsulemper og sammenslåingsnøytralitet betydningen av nytt gradert basistilskudd Strategikonferanse Telemark 10.2.2016 Trond Erik Lunder
 Smådriftsulemper og sammenslåingsnøytralitet betydningen av nytt gradert basistilskudd Strategikonferanse Telemark 10.2.2016 Trond Erik Lunder 1 Foreløpige innspill om strukturkriteriet Strukturkriteriet
Smådriftsulemper og sammenslåingsnøytralitet betydningen av nytt gradert basistilskudd Strategikonferanse Telemark 10.2.2016 Trond Erik Lunder 1 Foreløpige innspill om strukturkriteriet Strukturkriteriet
OVERSIKT OVER GODTGJØRELSESPLANEN FOR NORGE
 OVERSIKT OVER GODTGJØRELSESPLANEN FOR NORGE WorldVentures Marketing, LLC Revidert 1. februar 2015. Gyldig 1. februar 2015 2. mai 2015 Representanter for WorldVentures får ikke verve nye representanter
OVERSIKT OVER GODTGJØRELSESPLANEN FOR NORGE WorldVentures Marketing, LLC Revidert 1. februar 2015. Gyldig 1. februar 2015 2. mai 2015 Representanter for WorldVentures får ikke verve nye representanter
Eksamen 2012 ECON 1310
 Eksamen 2012 ECON 1310 Oppgave 1. (i) Hvilken funksjon har penger? Penger fungerer som et middel for verdsetting av varer. Før pengene måtte man verdsette ting i enheter av andre ting, eks. 2sau = 1 gris,
Eksamen 2012 ECON 1310 Oppgave 1. (i) Hvilken funksjon har penger? Penger fungerer som et middel for verdsetting av varer. Før pengene måtte man verdsette ting i enheter av andre ting, eks. 2sau = 1 gris,
Politisk økonomi. Individuell etterspørsel etter offentlige goder avhenger av: Produksjon av private goder Bestemmes gjennom prismekanismen.
 Hva handler dette kapittelet om? Hvordan går vi fra individuelle preferanser til kollektive beslutninger? Politisk økonomi J. S. Kapittel 7 Hvorfor eksisterer det ikke alltid et veldefinert utfall når
Hva handler dette kapittelet om? Hvordan går vi fra individuelle preferanser til kollektive beslutninger? Politisk økonomi J. S. Kapittel 7 Hvorfor eksisterer det ikke alltid et veldefinert utfall når
Interpellasjon v/jann Atle Jensen (DEM) - Salg av fryselager Isbjørn Is. Utvalg Utvalgssak Møtedato Kommunestyret 55/16 28.04.2016
 Interpellasjon v/jann Atle Jensen (DEM) - Salg av fryselager Isbjørn Is Saksfremlegg Utvalg Utvalgssak Møtedato Kommunestyret 55/16 28.04.2016 Saksbehandler: Ordfører Arkivsaknr.: 2016/2715-2 Ordføreren
Interpellasjon v/jann Atle Jensen (DEM) - Salg av fryselager Isbjørn Is Saksfremlegg Utvalg Utvalgssak Møtedato Kommunestyret 55/16 28.04.2016 Saksbehandler: Ordfører Arkivsaknr.: 2016/2715-2 Ordføreren
Median: Det er 20 verdier. Median blir da gjennomsnittet av verdi nr. 10 og nr. 11. Begge disse verdiene er 2, så median er 2.
 2P 2013 høst LØSNING DEL EN Oppgave 1 Rangerer verdiene i stigende rekkefølge: 0, 0, 0, 0, 0, 0, 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 7, 11, 28, 32 Median: Det er 20 verdier. Median blir da gjennomsnittet av
2P 2013 høst LØSNING DEL EN Oppgave 1 Rangerer verdiene i stigende rekkefølge: 0, 0, 0, 0, 0, 0, 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 7, 11, 28, 32 Median: Det er 20 verdier. Median blir da gjennomsnittet av
Terminprøve Sigma 1T Våren 2008 m a t e m a t i k k
 Terminprøve Sigma 1T Våren 2008 Prøvetid 5 klokketimer for Del 1 og Del 2 til sammen. Vi anbefaler at du ikke bruker mer enn to klokketimer på Del 1. Du må levere inn Del 1 før du tar fram hjelpemidler.
Terminprøve Sigma 1T Våren 2008 Prøvetid 5 klokketimer for Del 1 og Del 2 til sammen. Vi anbefaler at du ikke bruker mer enn to klokketimer på Del 1. Du må levere inn Del 1 før du tar fram hjelpemidler.
ARBEIDSHEFTE I MATEMATIKK
 ARBEIDSHEFTE I MATEMATIKK Temahefte nr Hvordan du regner med brøk Detaljerte forklaringer Av Matthias Lorentzen mattegrisenforlag.com Opplysning: Et helt tall er delelig på et annet helt tall hvis svaret
ARBEIDSHEFTE I MATEMATIKK Temahefte nr Hvordan du regner med brøk Detaljerte forklaringer Av Matthias Lorentzen mattegrisenforlag.com Opplysning: Et helt tall er delelig på et annet helt tall hvis svaret
