Grunnleggende Excel Tor Espen Kristensen
|
|
|
- Hallgeir Mortensen
- 8 år siden
- Visninger:
Transkript
1 Grunnleggende Excel 2010 Tor Espen Kristensen
2
3 Innhold iii Innhold 1 Litt om Excel Formler i regneark Grafisk framstilling i Excel Sektordiagram Søyle/stolpediagram Innebygde funksjoner Middelverdi Median tilfeldig, tilfeldigmellom og antall.hvis Trendlinje Andre funksjoner Verktøy i Excel Sortering og lister Målsøking Oppgaver
4
5 Litt om Excel 1 1 Litt om Excel Det er vanlig å bruke Excel og regneark som to synonyme ord. Excel er et av flere programmer i Microsofts Office. De senere årene har derimot Open- Office blitt stadig mer aktuelt. Dette heftet er basert på Excel Vår strategi er å gå gjennom en del eksempler som illustrerer hvordan oppgaver kan løses ved hjelp av regneark. Figur 1 Excel Et regneark kan vi tenke på som et stort rutenett. I rutene (cellene) kan vi skrive inn tekst ➍, tall ➎ eller formler ➏. Vi henviser til en bestemt celle på samme måte som i et sjakkbrett; ved å bruke bokstaven for kolonnen og tallet for raden. På figur 1 står teksten «Spenning» i celle B3. Vi kan be Excel om å utføre regnestykker ved å skive inn formler. I celle C7 har vi beregnet forholdet Spenning/strøm ved å skrive formelen =B7/A7. Når vi så trykker (enter) vil Excel utføre operasjonen og gi svaret (0,41) i cellen. Vi kan se hvilken formel som er utført i formellinjen ➊. Vi kan velge hvilket format vi ønsker tallene våre i ved å klikke på knappene ved ➌. Dersom vi vil endre bakgrunnsfarge i en eller flere celler kan vi gjøre dette ved å bruke knappene ved ➐. (se også figure 8) 2 Formler i regneark Mange praktiske problemstillinger kan være nokså krevende å løse med papir og blyant. Det kan være mange tall som skal legges sammen eller mange størrelser som varierer. I slike tilfeller kan regneark være til god hjelp. Eksempel 1 Vi ønsker å lage en valutakalkulator som regner ut hva du får når du veksler fra norske kroner til amerikanske dollar. Siden kursen
6 2 Regneark med Excel Figur 2 En enkel valutakalkulator stadig forandres, må denne lett kunne justeres. På figur 2 ser du et eksempel på hvordan en slik kalkulator kan lages. I kolonne A er det skrevet inn tekst som forklarer hva som skal stå i kolonne B. I B4 har vi ført inn den gjeldende valutakurs, mens i B6 føres inn hvor mange norske kroner som skal veksles inn. I B8 skriver vi inn hva svaret skal bli uttrykt ved rutenavna. Vi vet at svaret skal være antall norske kroner delt på kursen. Det vil si B5/B4. Når vi skriver inn en slik formel, må vi alltid starte med likhetstegnet =. Det vil si at vi i B8 skriver «=B6/B4». I eksempelet over brukte vi en formel for å gjøre om til USD (=B5/B4). Excel har også innebygd en del «ferdige» formler eller funksjoner som vi kan bruke. Eksempel 2 Lisa har sommerjobb på butikken. Hun tjener 122 kroner i timen. Her er timelisten hennes: Uke Mandag Tirsdag Onsdag Torsdag Fredag Lørdag a) Hvor mye tjener hun i hver uke? b) Hvor mye tjener hun til sammen? Løsning: Vi skriver tallene inn i et regneark. Pass på å skrive nok forklarende tekst (figur 3). Før vi går løs på selve oppgaven, merker vi oss hvordan cellene er formatert i regnearket (figur 3). En vanlig feil er å skrive «kr 62,00» i celle B2. Excel vil da tolke dette som tekst og ikke som et tall (på grunn av de to bokstavene «kr»). Vi skal heller
7 Formler i regneark 3 Figur 3 Timelisten i Excel. Pass på å skrive forklarende tekst i regneark. formatere cellen riktig for å få fram kr og riktig antall desimaltall. For å gjøre det klikker vi på ikonet (ved ➌ på figur 1 side 1). For å regne ut hvor mye Lisa tjener hver uke, er det lurt a summere timene. Vi kan skrive formelen =B5+C5+D5+E5+F5+G5 i for eksempel H5, men det blir litt tungvint i lengden, spesielt når antall ledd som skal summeres blir mange. I stedet kan vi bruke en innbygget funksjon i Excel som summerer for oss. Denne har ikonet. Gå til den cellen du vil ha summen i (i vårt tilfelle H5). Klikk på og marker det området du vil summere ved å klikke ned venstre musetast i B5 og dra markøren bort til G5 mens du hele tiden holder venstre museknapp nede. Da vil du få noe slik som i figur 4. Figur 4 i Excel. Autosummer Figur 5 Autokopiering: Klikk i cellen du vil kopiere nedover (eller bort- over), flytt markøren til den lille firkanten i nedre høyre hjørne. Ta tak i denne ved å holde venstre musetast nede og dra.
8 4 Regneark med Excel Trykk så Enter og du får svaret i celle H5, nemlig 32. Gjenta dette for alle de tre ukene. For å gjøre dette behøver du egentlig ikke å gå gjennom hele prosessen beskrevet ovenfor. Det er nok å klikke på celle H5, klikke i nedre høyre hjørne og dra nedover de to cellene mens du hele tiden holder museknappen nede. (Se figur 5.) Nå har vi regnet ut antall timer Lisa har jobbet hver uke. Neste steg er da å regne ut hvor mye hun tjente hver uke ved å multiplisere timetallet med timelønnen. Dette gjør vi i kolonne I. Vi bruker da formelen =H5*B2 (timelønnen har vi skrevet inn i B2). Der er lurt å skrive inn timelønnen i en egen celle. Da vil det være lett å gjøre utregningene om igjen om vi oppdager at lønnen var for eksempel 72 kr/time. Vi vil få et regneark som på figur 6 når vi har løst hele oppgaven. Figur 6 løst! Oppgaven Merk at du ikke sånn uten videre kan bruke trikset med å dra cellene nedover når det gjelder lønnen. Dette fordi du da vil få formelen =B3*H6 i I6 og altså ikke =B2*H6. Vi sier at cellehenvisningen er relativ. For å løse dette problemet kan vi bruke absolutt henvisning. I I5 skriver vi formelen =B$2*H5. Dollartegnet forteller programmet at det ikke skal endre tallet bak dollartegnet når du autokopierer formler. Du får tak i dollartegnet ved å trykke på AltGr og 4 $ (men du holder inne AltGr ). En annen måte å få fram dollartegnet i Excel er å trykke på F4 like etter at du har skrevet inn B2. Oppgave 1 Hansen har 9000 kr i banken Han er interessert i å finne ut hvor mye innskuddet vil vokse i løpet av en tiårsperiode. Hansen regner med å få 4 % p.a. rente i denne perioden. Sett regnestykket opp i et regneark. Begynn gjerne slik som i figur 7. a) Hvor mye har Hansen stående i banken etter 5 år? b) Hvor mange år vil det gå før han har kr i banken? c) Hvor mange år går det før startkapitalen er fordoblet? d) Hvor mye har Hansen stående i banken etter 10 år?
9 Formler i regneark 5 A B C D 1 Oversikt over sparepengene til Hansen 2 3 Startkapital kr 9 000, 00 4 Rentefot 4 % 5 6 År Kapital Rente Kapital =B Figur 7 Hansens lønn Oppgave 2 I følge en persisk legende, ble sjakkbrettet oppfunnet av en tjener til den persiske kongen. Kongen ble så begeistret for spillet at han ville belønne tjeneren, og ba ham ønske seg noe. Tjeneren tenkte seg om og ba om at han måtte få ett hvetekorn for den første ruten på sjakkbrettet, to for den andre, fire for den tredje osv. For hver ny rute på brettet fordoblet han antall korn. Kongen ble forundret over det han trodde var et beskjedent ønske. Var det beskjedent? Hvor mye korn fikk tjeneren? I margen ser du starten på en tabell som førere regnskap med antall riskorn. Gjør tabellen ferdig. Oppgave 3 Lise setter opp et budsjett over utgifter til bilhold i løpet av ett år. Hun regner med en kjørelengde på km, og Lise opererer med følgende utgiftsposter: Rute nr. Antall riskorn Bensinutgiftene regnes ut fra 14,00 kr per liter og et forbruk på 0,85 liter per mil Årsavgift til staten er på kr Forsikringspremien er på kr, men hun får 70 % rabatt på dette beløpet Verksteds- og vedlikeholdsutgifter settes til kr Garasjeleien er 250 kr per måned a) Hva antar Lise at utgiftene vil bli i løpet av ett år? Ved årets slutt viste deg seg at Lise hadde kjørt km. b) Hva ble Lises utgifter til bilhold dette året? (De andre utgiftspostene er slik som oppgitt ovenfor)
10 6 Regneark med Excel Oppgave 4 Lag et regneark som gjør om fra grader Celsius til grader Fahrenheit. Sammenhengen mellom disse er gitt ved: Grader Fahrenheit = 1, 8 grader Celsius + 32 Figur 8 Vi kan også formatere celler etter behov ved å markere de aktuelle cellene, trykke ned høyre musetast og velge «Formater celler». Du vil da få opp dette vinduet. 3 Grafisk framstilling i Excel Å framstille data grafisk ved hjelp av Excel kan være motiverende! Med noen enkle klikk, og vips så er diagrammet tegnet! Dette har selvsagt sine ulemper. Vet du egentlig hva det er du framstiller? Kan du tolke diagrammene du så pent får framstilt? Dette er noe vi må være bevisst på når vi jobber med grafisk framstilling i Excel. Sektordiagram Eksempel 3 En gruppe studenter undersøkte hvilke treningsformer som ble foretrukket i klassen de gikk i. Resultatene er ført opp i tabellen under. Aearobic: 5 Svømming: 4 Sykling: 10 squash: 2 ski: 9 Tabell 1 Studentenes treningsvalg
11 Søyle/stolpediagram 7 Dette fører vi inn i et regneark: Figur 9 Du setter inn diagrammer, grafer og liknende ved å velge fanen «Sett inn» Marker så A2 B5 og klikk så på fanen «Sett inn» og velg så «Sektor». Du får da opp et sektordiagram som du kan jobbe videre med. Hvor vil du ha forklaringene? Hvilke farger vil du at diagrammet skal ha? Se figur 10 Figur 10 Du får flere alternativer når du klikker på ønsket diagramtype. Merk at disse går vekk dersom du klikker i regnearket. Figur 11 Sektordiagram tegnet med Excel Søyle/stolpediagram Vi kaster en terning 100 ganger og får følgende frekvenstabell:
12 8 Regneark med Excel Antall øyne Hyppighet Sum: 100 Vi ønsker å vise resultatet i et stolpediagram. Vi skriver da dataene inn i et regneark og markerer kolonnen med verdiene i (se figur 12). Vi klikker på fanen «Sett inn» og velger stolpediagram. Klikk til slutt på «Fullfør». Du vil da få et diagram som på figur 13. Figur 12 Vi markere («svarter») de cellene som vi vil illustrere med søylediagram Figur 13 Søylediagram laget i Excel Figur 14 Studentenes treningsvalg Oppgave 5 Lag et søylediagram som illustrerer studentenes treningsvalg på side 6. Du skal få noe slikt som diagrammet i figur 14. Hvilke type diagram synes du best illustrerer studentenes valg? Vi kan også plotte grafer til funksjoner i Excel. Eksempel 4 Vi måler temperaturen et døgn og får følgende resultat: Tid (kl) Temp ( C)
13 Søyle/stolpediagram 9 Vi skriver dette inn i et regneark, markerer det vi har skrevet inn og klikker på fanen «Sett inn» og velger deretter punktdiagram som vist på figur 15. Figur 15 Punktdiagram i Excel 2010 Du kan velge om du vil plotte bare punktene, om det skal være linjediagram eller utglattet; om punktene skal være med eller ikke. Når du har klikket på ett av disse alternativene, vil du få tegnet inn diagrammet i regnearket. Dette diagrammet kan være greit nok slik det står, men det hender ofte at vi ønsker å endre verdien på aksene (for eksempel om de er noe annet enn 1, 3, 4, osv). Da klikker du på «Merk data» og velger «rediger» i vinduet du da får opp. Klikk så i feltet med «Serie X-verdier» og marker deretter det som er x-verdiene i regnearket ditt. Se figur 17. Etter at du har gjort dine valg kan du få et diagram som vist på figur 16 Figur 16 Temperaturen som funksjon av tiden.
14 10 Regneark med Excel Figur 17 Du kan endre verdiene på x-aksen ved å høyreklikke på et av punkta (1) og velge «Rediger» (2) og området i regnearket (3). Eksempel 5 Plott grafen til funksjonen y = x 2 + 2x 3. Løsning: Vi er nødt til å lage en tabell over en del verdier for funksjonen. Vi lager derfor et regneark der vi skriver inn en del verdier for x og regner ut de tilhørende verdiene for y: Legg merke til at x 2 + 2x 3 skrives inn som =A2ˆ2+2*A2-3 i celle B2. Denne formelen autokopierer vi nedover og får på den måten en verditabell for funksjonen. Så markerer vi tallene og klikker på Sett inn Diagram. Vi velger punktdiagram og alternativet «Punktdiagram med utjevnede linjer». Etter litt pynting og fikling får vi følgende diagram:
15 Innebygde funksjoner 11 Oppgave 6 Vi har målt høyden til et tre i årene 1972 til 2004 og fått følgende målinger: År Høyde (m) 1,0 1,6 2,6 3,8 5,9 7,5 8,6 9,1 9,5 Plott høyden som en funksjon av årstallet (årstallene på x-aksen og høyden på y-aksen). Figur 18 Du kan formatere aksene slik du måtte ønske. Klikk på grafikken og velg deretter «Oppsett» på båndet. 4 Innebygde funksjoner Vi har sett at vi kan lage enkle formler i Excel. Det kan være å multiplisere tallene i to celler. Formelen vi da skriver kan for eksempel være =A2*B5. Vi har også summert tall i rekker/rader ved å bruke autosummer ( ). I Excel finnes det mange slike innebygde funksjoner, og vi skal her bli kjent med noen av disse. I Excel er det innebygget en egen funksjonsveiviser. Denne finner du ved å klikke på ikonet (➊ på figur 1 side 1. Se også figur 19)
16 12 Regneark med Excel Middelverdi Figur 19 Når du skal få Excel til å regne ut noe ved hjelp av de innebygde funksjonene klikker du i den ruten du vil ha svaret (i dette tilfellet B15), klikker på f x -knappen (1), velger kategori (2) og finner funksjonen du vil bruke (3). Vi vil nå bruke funksjonsveiviseren til å regne ut middelverdien (også kalt gjennomsnittet) for et datasett. Middelverdien regner vi ut ved å summere sammen alle tallene vi skal regne ut middelverdien til og dele på antall tall i datasettet. Dette er noe vi lett kan la programmet gjøre for oss. Eksempel 6 Vi skal ved hjelp av Excel regne ut middelverdien til tallene 1,3,4,3,4,2,4, 3, 2, 3,4,3. Vi førere da tallene inn i et regneark og går til den cellen vi vil at svaret skal stå i: Vi klikker så på for å sette i gang funksjonsveiviseren (figur 19 og 20). Velg gjennomsnitt i listen til venstre. For å redusere antall funksjoner, kan det være lurt å velge kategorien statistikk. Klikk så ok. Da er det på tide å spesifisere hvilke tall som det skal regnes ut gjennomsnitt av. I stedet for å skrive dette manuelt inn i ruten ved siden av tall 1, kan vi gå i regnearket vårt direkte og markere de aktuelle tallene (se figur 20). Så er det bare å klikke på OK og gjennomsnittet er regnet ut! (Det ble 3). Oppgave 7 Regn ut medianen til tallene i eksempelet over. (Gjør det samme som vi gjorde for middelverdi, men velg median i stedet for gjennomsnitt. Svaret er 3. ) Median Eksempel 7 Nedenfor er alderen til studentene i klasse 1f på lærerskolen ført inn:
17 tilfeldig, tilfeldigmellom og antall.hvis 13 Figur 20 Vi markerer de cellene vi skal regne ut gjennomsnittet av (A2-A13) Vi ønsker å finne medianene, som er definert som den observasjonen som ligger i midten etter at observasjonene er ordnet i stigende rekkefølge. Her er det lett å se at svaret er 19, men når antall observasjoner øker blir det en slitsom og kanskje litt kjedelig jobb å ordne dem etter rekkefølge. Da kan det være greit å bruke en egen funksjon som heter median. Denne finner du under statistikk på funksjonslisten. Oppgave 8 Regn ut medianen til observasjonene ovenfor ved å bruke Excel. Hva om en av studentene på 18 år sluttet. Hva blir medianen da? tilfeldig, tilfeldigmellom og antall.hvis To andre nyttige innebygd funksjoner i Excel er tilfeldig og tilfeldigmellom(;). La oss si at du ønsker å simulere et terningkastforsøk. Du vil med andre ord at Excel skal generere et tilfeldig helt tall mellom 1 og 6. Du skriver da i en celle formelen =tilfeldigmellom(1;6). Når vi har skrevet inn denne formelen, kan vi utvide forsøket ved å autokopiere cellen til andre celler (se figur 5 side 3). På den måten får vi gjort forsøket så mange ganger vi måtte ønske (Figur 21). Trykk F9 for å oppdatere regnearket ditt, slik at du kan få nye tall. Neste utfordring blir så å plassere resultatene i en frekvenstabell. Det er selvsagt en håpløs jobb å gjøre dette manuelt. Hva om vi ønsker å gjøre forsøket på nytt? Vi bruker derfor funksjonen antall.hvis. Med denne kan du spesifisere området du vil telle fra og hva som skal telles. I figur 22 har vi laget en frekvenstabell ved å bruke antall.hvis-funksjonen. I celle D3 har vi skrevet inn formelen =antall.hvis(a:a;c3). Det betyr at vi skal telle antall celler i kolonne A som har samme verdi som C3. Vi bruker så autokopier og lager hele frekvenstabellen.
18 14 Regneark med Excel Figur 21 Vi kan simulere mange terningkastforsøk i Excel ved å autokopiere formelen i celle A1. Figur 22 Funksjonen antall.hvis. Legg merke til at vi har valgt området til å være A:A. Det vil si at vi skal telle i hele kolonne A. Vilkåret er C3. Det vil si at vi teller antall forekomster i kolonne A som er lik det som står i celle C3 (det vil si lik 1) Oppgave 9 Gjør forsøket over. Presenter resultatet ved hjelp av søylediagram. Oppdater regnearket og se hva som skjer. Hvor mange terningkast bør vi ha før det resultatet begynner å bli relativt nok så jevnt (det vil si til det er omtrent like mange av hvert slag)?
19 Trendlinje 15 Trendlinje Vi har sett at det går an å plotte en kurve ved bruke diagramveiviseren. En annen mulighet som finnes i Excel er å finne linjen som best passer til et sett med punkter. Eksempel 8 I et forsøk måler elevene spenning og strøm for en motstand. De fikk følgende måleserie: I (A) 0,4 0,8 1,2 1,6 2,0 U (V) 0,3 0,4 0,5 0,7 0,9 Når vi plotter disse punktene i et diagram får vi: 1,2 y 0,8 0,4 0,4 0,8 1,2 1,6 2,0 2,4 x Vi ser at punktene ligger så godt som på en linje. Vi ønsker å finne linjen som passer best de gitte punktene (i en eller annen forstand som vi ikke kommer inn på her). Vi fører dataene inn i et regneark, markerer dataene, klikker på fanen «Sett inn» og velger punktdiagram. Når vi har plottet punktene i et diagram, høyreklikker vi på ett av punktene. Da vil vi få opp et vindu hvor vi kan velge «Legg til trendlinje...» (se figur 23) Du vil da få opp et nytt vindu Figur 23 Vi kan legge til trendlinjen til et sett med punkter. hvor du kan velge hvilke type kurve du vil tilpasse datasettet med. Du kan også velge om kurven skal gå gjennom ett gitt punkt (for eksempel origo) og om du vil at funksjonsuttrykket skal være med i diagrammet. Se figur 23. Dersom vi velger «Lineær» (for rett linje) og haker av for «Vis
20 16 Regneark med Excel Figur 24 Valg for trendlinjen. Du kan velge hvilke type trendlinje (1) og andre alternativer (2) formel i diagram» så får vi y = 0,375x + 0,11. Men vi vet at dersom det ikke er spenning over en motstand, så kan det heller ikke gå strøm gjennom den. Det vil si at den rette linjen må gå gjennom (0,0). Vi velger derfor å hake av for «Angi skjæringspunkt» og velger 0 i feltet til høyre (se figur 24). Vi får da at formelen er y = 0,45x. et vil si at vi har Ohms lov: Det vil si at motstanden R er 0,45 Ω. U = 0,45 ċ I. Andre funksjoner Det er fint om du tar deg litt tid til å lete og leke med Excel. Da vil du snart finne ut at det er en rekke ting den kan regne ut, som for eksempel typetall (modus), skjevhet, varians og standardavvik. Prinsippet for bruken av disse
21 Verktøy i Excel 17 er den samme. Marker ruten du vil ha svaret i, klikk på den funksjonen du vil bruke og marker datamaterialet ditt. 5 Verktøy i Excel Sortering og lister Dersom du har laget en liste med en del data, så kan Excel sortere listen for deg. Det er mulig å sortere på tre nivå. Eksempel 9 I tabell 2 er resultatene etter en prøve i matematikk ført opp. A B C D E F 1 Navn Poeng 2 Lise 23 3 Anne M 21 4 Geir 12 5 Trine 14 6 Truls 11 7 Tor 19 8 Tabell 2 Resultater fra en prøve Vi ønsker nå å kunne sortere denne listen alfabetisk og etter poeng. Marker alle cellene og klikk på fanen «Data». Du vil da kunne velge «Sorter» i menyene som vist på figur 25. Klikk på OK og listen er sortert! Figur 25 Sorteringskriterier i Excel. Her sorterer vi først etter poeng og deretter navn. Begge i stigende rekkefølge.
22 18 Regneark med Excel Eksempel 10 Det finnes en annen måte å få orden på lister på. Vi kan legge et filter på listen. Marker alle kolonnene du vil legge et filter på. Velg Data-fanen og klikk på «Filtrer» (se figur 26). Du kan nå enkelt filtrere ut Figur 26 Excel. Autofilter i enkelte data ved å klikke på kanppen for å velge for eksempel Jens. Målsøking Hva skal du gjøre om du vet hva resultatet av en formel skal være, men vet ikke hva som må stå i en annen celle for å få dette resultatet? La oss vise ved hjelp av noen eksempler hvordan slike oppgaver kan løses med Excel. Eksempel 11 Hvor mye penger må du sette inn i banken for at det skal stå 2000 kr på konto etter ti år når rentefoten er 3,3 %? Vi setter opp et regneark som på figur 27. I celle A3 har skrevet 1000 kr (som ikke gir det ønskede resultat). Vi går så til celle E12 (hvor vi ønsker det skal stå 2000 kr etter at vi har endret beløpet i calle A3.) Velger vi «Målsøking» under «Hvaskjer-hvis-analyse» vil vi få opp et dialogvindu som spør hvilke verdi du ønsker å sette cellen til og hvilke celle som skal endres. Skriv inn 2000 og A3 i feltene (som vist på figur 27) og klikk så på Ok. Da vil du få beskjed om hva resultatet av målsøkingen ble. Eksempel 12 Vi kan bruke «Målsøking» til å løse likninger. La oss se på likningen x 2 5x + 1 = 0 (1) Vi lager da et regneark der vi velger en eller annen verdi i celle A1, for eksempel 1, og skriver inn formelen =A1ˆ2-5*A1+1 i celle A2. (Merk at vi bruker tegnet ˆ for å lage potenser i Excel.) Du vil da få 3 som svar i A2.
23 Målsøking 19 Figur 27 Tilpass verdien til en celle ved å bruke «Målsøking». For å løse likning (1) vil vi at det skal stå 0 i celle A2. Vi går derfor til denne cellen, velger «Målsøking...» og skriver inn 0 som «Til verdi» og A1 som cellen som skal endres. Klikk ok og få 0,21 som en løsning. Merknad: Slike kvadratiske likninger kan ha to løsninger. Excel vil da velge den løsningen som er nærmest den verdien vi startet med i celle A1. Gjenta prosedyren ovenfor, men velg nå A1 lik 10. Da skal du få den andre løsningen av (1), nemlig 4,79. Oppgave 10 Løs likningene ved å bruke metoden over: a) 2x + 4 = 10 b) x 2 4x 5 = 0 c) x 2 x + 4 = 10 d) ċ 1,02 x = e) 2x x 3 = x 2 + 1
24 20 Regneark med Excel 6 Oppgaver Oppgave 11 Ole har fått seg ekstrajobb. I oppsettet nedenfor finner du opplysninger om Oles skatteprosent og inntekt i januar Lønn Skatteprosent 20 Januar 2003 Bruttoinntekt (kr) 5000 Skatt (kr) 1000 Nettoinntekt (kr) 4000 Bruk regneark når du løser disse oppgavene: a) Hvilken formel må du bruke for å regne ut skatten? b) Hvilken formel må du bruke for å regne ut nettoinntekt? c) I februar har Ole en bruttoinntekt på 7800 kr. Hva blir nettoinntekten hans denne måneden? Oppgave 12 Liv jobber på i et grossistlager og har mottatt følgende bestilling: 1 offroad-sykkel til 1990 kr 3 sykler til 2550 kr per stykk 2 sykler til 3990 kr per stykk Kunden må betale 25% i merverdiavgift (mva). Hva må kunden betale? Bruk regneark når du løser oppgaven. Begynn gjerne slik som figuren ved siden av. Salg av sykler MVA (%) 25 Tekst Antall Enhetspris i kr Pris i kr Offroadsykkel Oppgave 13 (Tatt fra skolenettet.no) I juni 1970 tok Svein ut 100 kr fra Postsparebanken. Det stod da igjen 1 kr på kontoen. Svein glemte det hele inntil han i 1992 fikk beskjed om at han hadde 33 kr i banken. I løpet av de 22 årene hadde kontoen vokst med 32 kr! Hvor mange prosent rente hadde Svein fått hvert år? Her er plan for et regneark som kan brukes for å finne rentefoten:
25 Oppgaver 21 A B C 1 Rentefot p 2 3 År: Beløp Rente: =B4*$B$1 5 1 =B4+C4 Tabell 3 Kopier formlene nedover ved å bruke autokopiering Oppgave 14 Gunnar har fått sommerjobb som jordbærplukker hos Pettersen. Han får 8 kr for hver liter han plukker. I tillegg får han 70 kr per dag. Tabellen viser hvor mye han plukker den første uka. Mandag Tirsdag Onsdag Torsdag Fredag 90 liter 85 liter 70 liter 80 liter 95 liter a) Hvor mye tjener han de forskjellige dagene, og hvor mye får han i ukelønn? Bruk regneark når du løser oppgaven. Begynn gjerne slik: Lønn for jordbærplukking Fast lønn per dag 70 Lønn per liter i kr 8 Dag Mandag Tirsdag Onsdag Torsdag Fredag Ukelønn Antall liter Lønn i kr per dag Trond har sommerjobb som jordbærplukker hos Andersen. Han får 10 kr for hver liter han plukker, men ikke noe fast beløp per dag. Hver dag den første uka plukker Trond akkurat like mye som Gunnar. b) Bruk regneark og finn ut hvor mye Trond tjener hver av dagene, og hvor mye han får i ukelønn. c) Lag et diagram som viser både hva Gunnar og hva Trond tjener hver av dagene. Hvem ville du helst ha jobbet for, Pettersen eller Andersen?
26 22 Regneark med Excel Oppgave 15 Per, Anders og Line eier en hytte sammen. De skal betale utgiftene til strøm i forhold til hvor mange kilowattimer (kwh) hver av dem bruker. De leser av målerstanden hver gang de kommer til hytta og hver gang de reiser fra hytta. På den måten finner de ut hvor mange kwh hver av dem har brukt. Første halvår 2003 ble forbruket slik: Navn Målerstand ankomst Målerstand avreise Strømforbruk (kwh) (kwh) (kwh) Per Line Anders Line Prisen på en kilowattime (kwh) er 78 øre. Bruk regneark til å finne ut hvor mye hver av de tre skal betale. Oppgave 16 Kari satte for 10 år siden 9000 kr i banken. I dag har dette forrentet seg til kroner. a) Hva er rentefoten? (vi antar at det er fast rente på denne kontoen) b) Hvor mange år går det før startkapitalen er fordoblet? c) Turid satte kroner i banken samtidig med Kari. Hvor mye har hun i dag? d) Hvor lang tid tar det før Turid har kroner på konto? Oppgave 17 (Lønn til avisbud (fra skolenettet.no)) Arild går med avisen «Gladnytt». Han betaler ikke skatt. Derfor får han utbetalt hele lønna. Slik beregner «Gladnytt» Arilds lønn for en måned: Sykkelpenger: Grunnlønn: Aviser: Slett rute: Bakkete rute: Minstelønn: 115,00 kr 148,00 kr 4,30 kr per avis (gjennomsnitt per dag) 45,50 kr per km 55,50 kr per km 650,00 kr per måned Arilds budrute er 4 km på slett vei og 1,3 km i bakke.
27 Oppgaver 23 a) En måned hadde Arild 97 aviser i gjennomsnitt per dag. Hvor mye fikk han utbetalt denne måneden? b) En måned kom avisen ut bare 22 dager. Hver dag noterte Arild hvor mange aviser han hadde: Hvor mange aviser hadde Arild i gjennomsnitt per dag? c) Hvor stor var lønna denne måneden? d) Lag plan for et regneark som beregner lønn for avisbud. Bruk regnearket og prøv deg fram: Et avisbud fikk 1020 kr lønn. Lag et par forslag til antall aviser og lengde på denne budruta. Vurdér Hva synes du om denne måten å beregne lønna på? Er alle tallene enkle å bestemme? Kan du lage en bedre modell for beregning av lønn? Oppgave 18 (Tatt fra skolenettet.no) Elevene ved Lie skole skal på klassetur sammen med tre lærere. De ber om pristilbud fra tre selskap. Ryenruta: 1100 kr i fast avgift 5,50 kr per kilometer Elevene vurderer tre mulige turer: Hagenruta: 4000 kr for turer opp til 800 km Lie turservice: 9 kr per kilometer Sted km én vei Kristiansand Dyrepark ca 200 Tusenfryd ca 140 Hunderfossen ca 320 Gjør overslag Hvilket av tilbudene er best til hvert av de tre reisemålene? Hvor langt kan elevene komme for 3500 kr? Tabell i regneark Bruk et regneark og lag en tabell som viser pris for ulike avstander. Regnearket kan for eksempel se slik ut:
28 24 Regneark med Excel A B C D 1 Antall km Ryenruta Lie turservice Hagenruta 2 200?? =A2* =D Tabell 4 Kopier formlene nedover ved å bruke autokopiering Hvilken formel kan du bruke rute B2? Viser tabellen nøyaktig hvor mange km en må kjøre for at det skal bli lik pris med Ryenruta og Lie turservice? Hva om du sammenlikner Lie turservice og Hagenruta? Sammenlikn også Hagenruta og Ryenruta. Bruk kurvetegningsprogram Lag et funksjonsuttrykk som viser prisen (y kr) for ulike avstander (x km) med hvert av de tre selskapene? Tegn alle tre kurvene i samme koordinatsystem. Bruk programmet til å finne koordinatene for skjæringspunktene mellom kurvene. Hvilken informasjon gir koordinatene for skjæringspunktene? Vurdér Kunne du funnet svar på spørsmålene over uten å bruke dataverktøy? Hvilke fordeler og ulemper ser du med å bruke dataverktøy på slike problem? En ekstra utfordring Hvor mye tar hver av selskapene per km? Oppgave 19 Lag et regnearkoppsett til følgende oppgave: Plasser tallene fra 1 til 9 i rektanglene under slik at summene av de fire tallene langs hver av sidene i trekanten blir like. Du bør med andre ord lage et regneark hvor du kan skrive inn tallene i rektanglene og hvor regnearket regner ut summen langs de tre sidene i tall-trekanten. Regnearket kan se slik ut:
29 Oppgaver 25 Figur 28 Løsing av oppgave 19 på regneark Ekstra utfordring: Bruk hvis (eller dersom i Calc på nynorsk) til å sette opp regnearket slik at det står «Bingo!» i en celle dersom alle tre summene er like. Oppgave 20 Studer oppstillingen: A B C D E F Tallene 1,..., 9 er satt inn i hver sin rute i området A1:C3. I noen ruter i kolonne E er det skrevet formler. Det står for eksempel =A1*C1 i E1 og =E1+E3+A5+C5 i E5. Finn ut hvordan oppstillingen er og lag det på regnearket. Finn ut hvordan tallene i området A1:C3 må stå for å få summen i rute E5 størst mulig og minst mulig. Prøv å lage tilsvarende oppgaver av denne typen. Oppgave 21 (Spillet Blink, Tatt fra Breiteig and Fuglestad (2000)) Arbeid to og to sammen. Velg et tall som skal være mål, for eksempel 100. Skriv det inn i rute B3. Velg et tall til å starte med, for eksempel 17. Sett det i rute B5. Oppgaven videre er å sette inn tall i kolonne C, slik at det multiplisert med nabotallet i B-kolonna blir så nære 100 som mulig. Den som først treffer (eller kommer nær nok) målet, vinner.
Vet du hva vi kan bruke et regneark på pc-en til?
 Vet du hva vi kan bruke et regneark på pc-en til? 14 Vi starter med blanke regneark! Regneark MÅL I dette kapitlet skal du lære om hva et regneark er budsjett og regnskap hvordan du kan gjøre enkle utregninger
Vet du hva vi kan bruke et regneark på pc-en til? 14 Vi starter med blanke regneark! Regneark MÅL I dette kapitlet skal du lære om hva et regneark er budsjett og regnskap hvordan du kan gjøre enkle utregninger
13.03.2013 Manual til Excel. For ungdomstrinnet ELEKTRONISK UNDERVISNINGSFORLAG AS
 13.03.2013 Manual til Excel 2010 For ungdomstrinnet ELEKTRONISK UNDERVISNINGSFORLAG AS Innholdsfortegnelse Huskeliste... 3 Lage en formel... 3 Når du får noe uønsket som f.eks. en dato i en celle... 3
13.03.2013 Manual til Excel 2010 For ungdomstrinnet ELEKTRONISK UNDERVISNINGSFORLAG AS Innholdsfortegnelse Huskeliste... 3 Lage en formel... 3 Når du får noe uønsket som f.eks. en dato i en celle... 3
Øgrim Bakken Pettersen Skrindo Dypbukt Mustaparta Thorstensen Thorstensen. Digitalt verktøy for Sigma 2P. Microsoft Excel
 Øgrim Bakken Pettersen Skrindo Dypbukt Mustaparta Thorstensen Thorstensen Digitalt verktøy for Microsoft Excel Innhold 1 Om Excel 4 2 Regning 4 2.1 Tallregning................................... 4 2.2
Øgrim Bakken Pettersen Skrindo Dypbukt Mustaparta Thorstensen Thorstensen Digitalt verktøy for Microsoft Excel Innhold 1 Om Excel 4 2 Regning 4 2.1 Tallregning................................... 4 2.2
Øgrim Bakken Pettersen Skrindo Dypbukt Mustaparta Thorstensen Thorstensen. Digitalt verktøy for Sigma 2P. Microsoft Excel
 Øgrim Bakken Pettersen Skrindo Dypbukt Mustaparta Thorstensen Thorstensen Digitalt verktøy for Microsoft Excel Innhold 1 Om Excel 4 2 Regning 4 2.1 Tallregning................................... 4 2.2
Øgrim Bakken Pettersen Skrindo Dypbukt Mustaparta Thorstensen Thorstensen Digitalt verktøy for Microsoft Excel Innhold 1 Om Excel 4 2 Regning 4 2.1 Tallregning................................... 4 2.2
Bruk SUMMER-funksjonen i formelen i G9. Oppgave 14. H. Aschehoug & Co Side 1
 Repetisjon fra kapittel 2: Summere mange tall, funksjonen SUMMER() Regnearket inneholder en mengde innebygde funksjoner. Vi skal her se på en av de funksjonene vi oftest bruker. Funksjonen SUMMER() legger
Repetisjon fra kapittel 2: Summere mange tall, funksjonen SUMMER() Regnearket inneholder en mengde innebygde funksjoner. Vi skal her se på en av de funksjonene vi oftest bruker. Funksjonen SUMMER() legger
18.07.2013 Manual til Excel. For mellomtrinnet. Inger Nygjelten Bakke ELEKTRONISK UNDERVISNINGSFORLAG AS
 18.07.2013 Manual til Excel 2010 For mellomtrinnet Inger Nygjelten Bakke ELEKTRONISK UNDERVISNINGSFORLAG AS Innhold Husk... 2 1. Det kan bare være tall i cellene som skal brukes i formelen.... 2 2. En
18.07.2013 Manual til Excel 2010 For mellomtrinnet Inger Nygjelten Bakke ELEKTRONISK UNDERVISNINGSFORLAG AS Innhold Husk... 2 1. Det kan bare være tall i cellene som skal brukes i formelen.... 2 2. En
På reise Nivå: Formål: Program: Henvisning til plan: 8. klasse Matematikk i dagliglivet: Tall og algebra: Grafer og funksjoner:
 På reise Nivå: 8. og 9. klasse Formål: Arbeide med lineære funksjoner og verktøyprogram Program: Regneark, kurvetegningsprogram Henvisning til plan: 8. klasse Matematikk i dagliglivet: registrere og formulere
På reise Nivå: 8. og 9. klasse Formål: Arbeide med lineære funksjoner og verktøyprogram Program: Regneark, kurvetegningsprogram Henvisning til plan: 8. klasse Matematikk i dagliglivet: registrere og formulere
Skriv teksten «Ukelønn» i celle A1 (kolonne A, rad 1) og 60 i celle B1 (kolonne B, rad 1). Løsning
 Hva er et regneark? Vi bruker regneark til å sortere data, gjøre beregninger og lage diagrammer. I denne manualen finner du veiledning til hvordan du kan bruke regneark. Et regneark består av celler som
Hva er et regneark? Vi bruker regneark til å sortere data, gjøre beregninger og lage diagrammer. I denne manualen finner du veiledning til hvordan du kan bruke regneark. Et regneark består av celler som
Simulering på regneark
 Anne Berit Fuglestad Simulering på regneark Trille terninger eller kaste mynter er eksempler som går igjen i sannsynlighetsregningen. Ofte kunne vi trenge flere forsøk for å se en klar sammenheng og få
Anne Berit Fuglestad Simulering på regneark Trille terninger eller kaste mynter er eksempler som går igjen i sannsynlighetsregningen. Ofte kunne vi trenge flere forsøk for å se en klar sammenheng og få
2P-Y eksamen våren 2016 løsningsforslag
 2P-Y eksamen våren 2016 løsningsforslag Tid: 2 timer Hjelpemidler: Vanlige skrivesaker, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (3 poeng) Dato Temperatur 01.03 2 C 02.03 0 C 03.03
2P-Y eksamen våren 2016 løsningsforslag Tid: 2 timer Hjelpemidler: Vanlige skrivesaker, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (3 poeng) Dato Temperatur 01.03 2 C 02.03 0 C 03.03
Etter å ha gjennomgått dette «kurset», bør du ha fått et innblikk i hva et regneark er, og
 Ei innføring i Calc 1 Innledning Etter å ha gjennomgått dette «kurset», bør du ha fått et innblikk i hva et regneark er, og noe av hva det kan brukes til. OpenOffice Calc er brukt som mønster her, men
Ei innføring i Calc 1 Innledning Etter å ha gjennomgått dette «kurset», bør du ha fått et innblikk i hva et regneark er, og noe av hva det kan brukes til. OpenOffice Calc er brukt som mønster her, men
2P-Y eksamen våren 2016
 2P-Y eksamen våren 2016 Tid: 2 timer Hjelpemidler: Vanlige skrivesaker, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (3 poeng) Dato Temperatur 01.03 2 C 02.03 0 C 03.03 --4 C 04.03 --6
2P-Y eksamen våren 2016 Tid: 2 timer Hjelpemidler: Vanlige skrivesaker, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (3 poeng) Dato Temperatur 01.03 2 C 02.03 0 C 03.03 --4 C 04.03 --6
Innføring i OOcalc Side 1. OOcalc
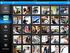 Innføring i OOcalc Side 1 OOcalc Hva er et regneark? Et regneark kan sammenlignes med et vanlig ruteark, hvor tall skrives inn og beregninger utføres. På et vanlig ruteark må man selv utføre beregningen.
Innføring i OOcalc Side 1 OOcalc Hva er et regneark? Et regneark kan sammenlignes med et vanlig ruteark, hvor tall skrives inn og beregninger utføres. På et vanlig ruteark må man selv utføre beregningen.
Radene har løpenummer nedover og kolonner navnes alfabetisk. Dermed får hver celle (rute) et eget "navn", eksempelvis A1, B7, D3 osv.
 Excel grunnkurs Skjermbilde/oppbygging Radene har løpenummer nedover og kolonner navnes alfabetisk. Dermed får hver celle (rute) et eget "navn", eksempelvis A1, B7, D3 osv. I hver celle kan vi skrive Tekst
Excel grunnkurs Skjermbilde/oppbygging Radene har løpenummer nedover og kolonner navnes alfabetisk. Dermed får hver celle (rute) et eget "navn", eksempelvis A1, B7, D3 osv. I hver celle kan vi skrive Tekst
2P eksamen våren 2016 løsningsforslag
 2P eksamen våren 2016 løsningsforslag Tid: 2 timer Hjelpemidler: Vanlige skrivesaker, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (3 poeng) Dato Temperatur 01.03 2 C 02.03 0 C 03.03 --4
2P eksamen våren 2016 løsningsforslag Tid: 2 timer Hjelpemidler: Vanlige skrivesaker, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (3 poeng) Dato Temperatur 01.03 2 C 02.03 0 C 03.03 --4
DEL 1 Uten hjelpemidler
 DEL 1 Uten hjelpemidler Oppgave 1 (3 poeng) Dato Temperatur 01.03 2 02.03 0 03.03 4 04.03 6 05.03 2 06.03 6 Guro målte temperaturen utenfor hytta de seks første dagene i mars. Se tabellen ovenfor. Bestem
DEL 1 Uten hjelpemidler Oppgave 1 (3 poeng) Dato Temperatur 01.03 2 02.03 0 03.03 4 04.03 6 05.03 2 06.03 6 Guro målte temperaturen utenfor hytta de seks første dagene i mars. Se tabellen ovenfor. Bestem
2P eksamen våren 2016
 2P eksamen våren 2016 Tid: 2 timer Hjelpemidler: Vanlige skrivesaker, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (3 poeng) Dato Temperatur 01.03 2 C 02.03 0 C 03.03 --4 C 04.03 --6 C
2P eksamen våren 2016 Tid: 2 timer Hjelpemidler: Vanlige skrivesaker, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (3 poeng) Dato Temperatur 01.03 2 C 02.03 0 C 03.03 --4 C 04.03 --6 C
Bruk av Google Regneark
 Bruk av Google Regneark DIM-konferanse 21. mars Mini-foredrag Kort om Google Disk Google Regneark Mye likt som Excel Engelske kommandoer Ikke makroer, men mulig å scripte gjennom Google Apps Script (Javascript-basert)
Bruk av Google Regneark DIM-konferanse 21. mars Mini-foredrag Kort om Google Disk Google Regneark Mye likt som Excel Engelske kommandoer Ikke makroer, men mulig å scripte gjennom Google Apps Script (Javascript-basert)
DEL 1 Uten hjelpemidler
 DEL 1 Uten hjelpemidler Oppgave 1 (3 poeng) Dato Temperatur 01.03 2 02.03 0 03.03 4 04.03 6 05.03 2 06.03 6 Guro målte temperaturen utenfor hytta de seks første dagene i mars. Se tabellen ovenfor. Bestem
DEL 1 Uten hjelpemidler Oppgave 1 (3 poeng) Dato Temperatur 01.03 2 02.03 0 03.03 4 04.03 6 05.03 2 06.03 6 Guro målte temperaturen utenfor hytta de seks første dagene i mars. Se tabellen ovenfor. Bestem
Eksamen MAT1015 Matematikk 2P Va ren 2015
 Eksamen MAT1015 Matematikk P Va ren 015 Oppgave 1 ( poeng) Dag Temperatur Mandag 4 C Tirsdag 10 C Onsdag 1 C Torsdag 5 C Fredag 6 C Lørdag Tabellen ovenfor viser hvordan temperaturen har variert i løpet
Eksamen MAT1015 Matematikk P Va ren 015 Oppgave 1 ( poeng) Dag Temperatur Mandag 4 C Tirsdag 10 C Onsdag 1 C Torsdag 5 C Fredag 6 C Lørdag Tabellen ovenfor viser hvordan temperaturen har variert i løpet
Eksamen MAT1005 Matematikk 2P-Y Høsten 2014
 Eksamen MAT1005 Matematikk P-Y Høsten 014 Oppgave 1 (1 poeng) Regn ut og skriv svaret på standardform 0,0003 500000000 0,00,0 10,0 4 8 3,0 10 5,0 10 3,0 5,0 4 8 ( 3) 7 3 10 7,5 10 Oppgave (1 poeng) Prisen
Eksamen MAT1005 Matematikk P-Y Høsten 014 Oppgave 1 (1 poeng) Regn ut og skriv svaret på standardform 0,0003 500000000 0,00,0 10,0 4 8 3,0 10 5,0 10 3,0 5,0 4 8 ( 3) 7 3 10 7,5 10 Oppgave (1 poeng) Prisen
Kommentarer til boka Regneark for barnetrinnet 1
 Kommentarer til boka Regneark for barnetrinnet (Ideen er den samme, men skjermbildene noe forskjellige i ulike versjoner av Excel) Arket Om regneark Endre cellebredden Plasser markøren midt mellom to kolonner.
Kommentarer til boka Regneark for barnetrinnet (Ideen er den samme, men skjermbildene noe forskjellige i ulike versjoner av Excel) Arket Om regneark Endre cellebredden Plasser markøren midt mellom to kolonner.
Faktor REGNEARK & GRAFTEGNER ØVINGSOPPGAVER FOR. Bokmål. Flere oppgaver finns i Faktor Fordypningshefte og Faktor Eksamensforberedende hefte.
 Bokmål Faktor ØVINGSOPPGAVER FOR REGNEARK & GRAFTEGNER Flere oppgaver finns i Faktor Fordypningshefte og Faktor Eksamensforberedende hefte. Cappelen Damm AS 1 Oppgaver for REGNEARK Oppgavene er hentet
Bokmål Faktor ØVINGSOPPGAVER FOR REGNEARK & GRAFTEGNER Flere oppgaver finns i Faktor Fordypningshefte og Faktor Eksamensforberedende hefte. Cappelen Damm AS 1 Oppgaver for REGNEARK Oppgavene er hentet
Excel. Excel. Legge inn tall eller tekst i en celle. Merke enkeltceller
 Excel Hva er et regneark? Vi bruker regneark til å sortere data, gjøre beregninger og lage diagrammer. I denne manualen finner du veiledning til hvordan du kan bruke regneark. Et regneark består av celler
Excel Hva er et regneark? Vi bruker regneark til å sortere data, gjøre beregninger og lage diagrammer. I denne manualen finner du veiledning til hvordan du kan bruke regneark. Et regneark består av celler
INNHOLD. Matematikk for ungdomstrinnet
 INNHOLD STATISTIKK... 2 FREKVENS... 2 RELATIV FREKVENS... 2 FREKVENSTABELL... 2 KLASSEDELING... 3 SØYLEDIAGRAM (STOLPEDIAGRAM)... 3 LINJEDIAGRAM... 4 SEKTORDIAGRAM... 4 HISTOGRAM... 4 FRAMSTILLING AV DATA...
INNHOLD STATISTIKK... 2 FREKVENS... 2 RELATIV FREKVENS... 2 FREKVENSTABELL... 2 KLASSEDELING... 3 SØYLEDIAGRAM (STOLPEDIAGRAM)... 3 LINJEDIAGRAM... 4 SEKTORDIAGRAM... 4 HISTOGRAM... 4 FRAMSTILLING AV DATA...
ENT3R. Oppgavehefte. Basert på tidligere eksamener for 10. klasse. Tommy Odland 2/4/2014
 ENT3R Oppgavehefte Basert på tidligere eksamener for 10. klasse Tommy Odland 2/4/2014 Dette er et oppgavehefte med oppgaver inspirert fra tidligere eksamener for 10. klassinger. Målet er at heftet skal
ENT3R Oppgavehefte Basert på tidligere eksamener for 10. klasse Tommy Odland 2/4/2014 Dette er et oppgavehefte med oppgaver inspirert fra tidligere eksamener for 10. klassinger. Målet er at heftet skal
Øgrim Bakken Pettersen Skrindo Thorstensen Thorstensen. Digitalt verktøy for Sigma 1P. Microsoft Excel
 Øgrim Bakken Pettersen Skrindo Thorstensen Thorstensen Digitalt verktøy for Microsoft Excel Innhold 1 Om Excel 4 1.1 Utvide området kopiere celler....................... 4 1.2 Vise formler i regnearket...........................
Øgrim Bakken Pettersen Skrindo Thorstensen Thorstensen Digitalt verktøy for Microsoft Excel Innhold 1 Om Excel 4 1.1 Utvide området kopiere celler....................... 4 1.2 Vise formler i regnearket...........................
Oppgaver der du bruker regneark Forslag på oppgaver: 8.trinn
 Oppgave 1: Lotte har satt opp utstyr som hun kan måle nedbørsmengden med. Hun målte nedbøren hver dag en uke i april. Resultatet av målingene ser du nedenfor. Ukedag Nedbør (mm) Søndag 10 Mandag 15 Tirsdag
Oppgave 1: Lotte har satt opp utstyr som hun kan måle nedbørsmengden med. Hun målte nedbøren hver dag en uke i april. Resultatet av målingene ser du nedenfor. Ukedag Nedbør (mm) Søndag 10 Mandag 15 Tirsdag
Eksamen 1P, Høsten 2011
 Eksamen 1P, Høsten 2011 Del 1 Tid: 2 timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (18 poeng) a) Bjørn skal lage havregrøt. Han har 6 dl
Eksamen 1P, Høsten 2011 Del 1 Tid: 2 timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (18 poeng) a) Bjørn skal lage havregrøt. Han har 6 dl
Eksamen MAT1005 Matematikk 2P-Y Høsten 2013
 Eksamen MAT1005 Matematikk 2P-Y Høsten 2013 DEL 1 Uten hjelpemidler Oppgave 1 (2 poeng) I en klasse er det 20 elever. Nedenfor ser du hvor mange dager hver av elevene var borte fra skolen i løpet av et
Eksamen MAT1005 Matematikk 2P-Y Høsten 2013 DEL 1 Uten hjelpemidler Oppgave 1 (2 poeng) I en klasse er det 20 elever. Nedenfor ser du hvor mange dager hver av elevene var borte fra skolen i løpet av et
Eksamen 2P MAT1015 Vår 2012 Løsning
 Eksamen 2P MAT1015 Vår 2012 Oppgave 1 (14 poeng) a) 20 elever blir spurt om hvor mange datamaskiner de har hjemme. Se tabellen ovenfor. Finn variasjonsbredden, typetallet, medianen og gjennomsnittet. Variasjonsbredden
Eksamen 2P MAT1015 Vår 2012 Oppgave 1 (14 poeng) a) 20 elever blir spurt om hvor mange datamaskiner de har hjemme. Se tabellen ovenfor. Finn variasjonsbredden, typetallet, medianen og gjennomsnittet. Variasjonsbredden
Eksamen MAT1005 Matematikk 2P-Y Va ren 2015
 Eksamen MAT1005 Matematikk P-Y Va ren 015 Oppgave 1 ( poeng) Dag Temperatur Mandag 4 C Tirsdag 10 C Onsdag 1 C Torsdag 5 C Fredag 6 C Lørdag Tabellen ovenfor viser hvordan temperaturen har variert i løpet
Eksamen MAT1005 Matematikk P-Y Va ren 015 Oppgave 1 ( poeng) Dag Temperatur Mandag 4 C Tirsdag 10 C Onsdag 1 C Torsdag 5 C Fredag 6 C Lørdag Tabellen ovenfor viser hvordan temperaturen har variert i løpet
DEL 1 Uten hjelpemidler
 DEL 1 Uten hjelpemidler Hjelpemidler: vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler Oppgave 1 Variasjonsredden: 6 C ( 6 C) = 6 C+ 6 C= 12 C Gjennomsnittet: 2 C+ 0 C + ( 4 C) + (
DEL 1 Uten hjelpemidler Hjelpemidler: vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler Oppgave 1 Variasjonsredden: 6 C ( 6 C) = 6 C+ 6 C= 12 C Gjennomsnittet: 2 C+ 0 C + ( 4 C) + (
Verdens korteste grunnkurs i Excel (2007-versjonen)
 Verdens korteste grunnkurs i Excel (2007-versjonen) NB! Vær oppmerksom på at Excel kan se annerledes ut hos dere enn det gjør på bildene under. Her er det tatt utgangspunkt i programvaren fra 2007, mens
Verdens korteste grunnkurs i Excel (2007-versjonen) NB! Vær oppmerksom på at Excel kan se annerledes ut hos dere enn det gjør på bildene under. Her er det tatt utgangspunkt i programvaren fra 2007, mens
Lineære funksjoner - Elevark
 Lineære funksjoner - Elevark -Navn: Oppgave 1 a) Hva koster det å reise for to personer? b) Hvor mange kan reise for 160 kr? c) Hva koster en billett? d) Vi kaller antall personer for x, og utgiftene for
Lineære funksjoner - Elevark -Navn: Oppgave 1 a) Hva koster det å reise for to personer? b) Hvor mange kan reise for 160 kr? c) Hva koster en billett? d) Vi kaller antall personer for x, og utgiftene for
Matematikk GS3 Temaer våren 2013 DEL 1: GEOMETRI. 1. Måleenheter. 1.1 Lengdeenheter. 1.2 Arealenheter. Eksempel 1: Gjør om 5 m til dm, cm og mm
 Matematikk GS3 Temaer våren 2013 DEL 1: GEOMETRI 1. Måleenheter 1.1 Lengdeenheter Eksempel 1: Gjør om 5 m til dm, cm og mm m dm 5 m = 5 10 dm = 50 dm m cm 5 m = 5 10 10 cm = 5 10 2 cm = 500 cm m mm 5 m
Matematikk GS3 Temaer våren 2013 DEL 1: GEOMETRI 1. Måleenheter 1.1 Lengdeenheter Eksempel 1: Gjør om 5 m til dm, cm og mm m dm 5 m = 5 10 dm = 50 dm m cm 5 m = 5 10 10 cm = 5 10 2 cm = 500 cm m mm 5 m
Terminprøve i matematikk for 9. trinn
 Terminprøve i matematikk for 9. trinn Våren 2006 bokmål Til noen av oppgavene skal du bruke opplysninger fra informasjonsheftet. Disse oppgavene er merket med dette symbolet: Navn: DELPRØVE 1 Maks. poengsum:
Terminprøve i matematikk for 9. trinn Våren 2006 bokmål Til noen av oppgavene skal du bruke opplysninger fra informasjonsheftet. Disse oppgavene er merket med dette symbolet: Navn: DELPRØVE 1 Maks. poengsum:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
 Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
QED 5 10. Matematikk for grunnskolelærerutdanningen. Bind 1 og 2. Grunnleggende Excel-øvelser (2010-versjon) Av Peer Sverre Andersen
 QED 5 10 Matematikk for grunnskolelærerutdanningen Bind 1 og 2 Grunnleggende Excel-øvelser (2010-versjon) Av Peer Sverre Andersen Innhold INNLEDNING... 3 KORT INNFØRING OM REGNEARK... 4 ØVELSE 1. PRESENTASJON
QED 5 10 Matematikk for grunnskolelærerutdanningen Bind 1 og 2 Grunnleggende Excel-øvelser (2010-versjon) Av Peer Sverre Andersen Innhold INNLEDNING... 3 KORT INNFØRING OM REGNEARK... 4 ØVELSE 1. PRESENTASJON
Grunnleggende kurs i Excel. Langnes skole
 Grunnleggende kurs i Excel Langnes skole Noen viktige begreper Kolonne Celler - Alle cellene har egne navn, f.eks A1 Kolonner Rader Arkfaner rad - start hver oppgave i en ny fane - kan velge så ark du
Grunnleggende kurs i Excel Langnes skole Noen viktige begreper Kolonne Celler - Alle cellene har egne navn, f.eks A1 Kolonner Rader Arkfaner rad - start hver oppgave i en ny fane - kan velge så ark du
Terminprøve i matematikk for 9. trinn
 Terminprøve i matematikk for 9. trinn Høsten 2006 bokmål Til noen av oppgavene skal du bruke opplysninger fra informasjonsheftet. Disse oppgavene er merket med dette symbolet: Navn: DELPRØVE 1 Maks. poengsum:
Terminprøve i matematikk for 9. trinn Høsten 2006 bokmål Til noen av oppgavene skal du bruke opplysninger fra informasjonsheftet. Disse oppgavene er merket med dette symbolet: Navn: DELPRØVE 1 Maks. poengsum:
99 matematikkspørsma l
 99 matematikkspørsma l TALL 1. Hva er et tall? Et tall er symbol for en mengde. Et tall forteller om antallet i en mengde. 5 sauer eller 5 epler eller 5.. 2. Hvilket siffer står på eneplassen i tallet
99 matematikkspørsma l TALL 1. Hva er et tall? Et tall er symbol for en mengde. Et tall forteller om antallet i en mengde. 5 sauer eller 5 epler eller 5.. 2. Hvilket siffer står på eneplassen i tallet
Eksamen MAT1015 Matematikk 2P Va ren 2015
 Eksamen MAT1015 Matematikk 2P Va ren 2015 Oppgave 1 (2 poeng) Dag Temperatur Mandag 4 C Tirsdag 10 C Onsdag 12 C Torsdag 5 C Fredag 6 C Lørdag Tabellen ovenfor viser hvordan temperaturen har variert i
Eksamen MAT1015 Matematikk 2P Va ren 2015 Oppgave 1 (2 poeng) Dag Temperatur Mandag 4 C Tirsdag 10 C Onsdag 12 C Torsdag 5 C Fredag 6 C Lørdag Tabellen ovenfor viser hvordan temperaturen har variert i
QED 1 7. Matematikk for grunnskolelærerutdanningen. Bind 1 og 2. Grunnleggende Excel-øvelser (2013-versjon) Av Peer Sverre Andersen
 QED 1 7 Matematikk for grunnskolelærerutdanningen Bind 1 og 2 Grunnleggende Excel-øvelser (2013-versjon) Av Peer Sverre Andersen Innhold INNLEDNING... 3 KORT INNFØRING OM REGNEARK... 4 ØVELSE 1. PRESENTASJON
QED 1 7 Matematikk for grunnskolelærerutdanningen Bind 1 og 2 Grunnleggende Excel-øvelser (2013-versjon) Av Peer Sverre Andersen Innhold INNLEDNING... 3 KORT INNFØRING OM REGNEARK... 4 ØVELSE 1. PRESENTASJON
Eksamen MAT1005 Matematikk 2P-Y Va ren 2014
 Eksamen MAT1005 Matematikk 2P-Y Va ren 2014 Oppgave 1 (2 poeng) Nedenfor ser du hvor mange snegler Astrid har plukket i hagen hver kveld de ti siste kveldene. 10 5 22 28 2 8 50 15 40 10 Bestem gjennomsnittet
Eksamen MAT1005 Matematikk 2P-Y Va ren 2014 Oppgave 1 (2 poeng) Nedenfor ser du hvor mange snegler Astrid har plukket i hagen hver kveld de ti siste kveldene. 10 5 22 28 2 8 50 15 40 10 Bestem gjennomsnittet
DEL 1 Uten hjelpemidler
 DEL 1 Uten hjelpemidler Oppgave 1 ( poeng) Dag Temperatur Mandag 4 ºC Tirsdag 10 ºC Onsdag 1 ºC Torsdag 5 ºC Fredag 6 ºC Lørdag Tabellen ovenfor viser hvordan temperaturen har variert i løpet av noen dager.
DEL 1 Uten hjelpemidler Oppgave 1 ( poeng) Dag Temperatur Mandag 4 ºC Tirsdag 10 ºC Onsdag 1 ºC Torsdag 5 ºC Fredag 6 ºC Lørdag Tabellen ovenfor viser hvordan temperaturen har variert i løpet av noen dager.
DEL 1 Uten hjelpemidler
 DEL 1 Uten hjelpemidler Oppgave 1 (1 poeng) Regn ut og skriv svaret på standardform 0,0003 500000000 0,00 Oppgave (1 poeng) Prisen for en vare er satt opp med 5 %. Nå koster varen 50 kroner. Hva kostet
DEL 1 Uten hjelpemidler Oppgave 1 (1 poeng) Regn ut og skriv svaret på standardform 0,0003 500000000 0,00 Oppgave (1 poeng) Prisen for en vare er satt opp med 5 %. Nå koster varen 50 kroner. Hva kostet
Kvalifiseringstjenesten Tentamen matematikk GS3 22. 04. 2013
 Tentamen matematikk GS3 Mandag 22. april 2013 DEL 1 Excel Oppgave 1. Hans låner 90 000 kr i banken til 4 % rente pr år. Nedbetalingstiden for lånet er 6 år. a) Lag tabellen nedenfor i Excel. År % rente
Tentamen matematikk GS3 Mandag 22. april 2013 DEL 1 Excel Oppgave 1. Hans låner 90 000 kr i banken til 4 % rente pr år. Nedbetalingstiden for lånet er 6 år. a) Lag tabellen nedenfor i Excel. År % rente
Løsningsforslag til utsatt eksamen 2. desember 2015
 Løsningsforslag til utsatt eksamen 2. desember 2015 Oppgave 1 (vekt 20 %) a) Løs ligningen 3x 2 7x + 2 = 0 ved å bruke formelen for løsning av andregradsligninger. Løsning. 3x 2 7x + 2 = 0 x = ( 7) ( 7)2
Løsningsforslag til utsatt eksamen 2. desember 2015 Oppgave 1 (vekt 20 %) a) Løs ligningen 3x 2 7x + 2 = 0 ved å bruke formelen for løsning av andregradsligninger. Løsning. 3x 2 7x + 2 = 0 x = ( 7) ( 7)2
Delprøve 1. 2) Per kjøper 17 skruer à kr 11,70 og 17 muttere à kr 8,20. Hvor mye betaler han?
 Delprøve 1 OPPGAVE 1 a) 1) Hvor mye er 3 delt på 1 2? 2) Per kjøper 17 skruer à kr 11,70 og 17 muttere à kr 8,20. Hvor mye betaler han? b) Når temperaturen i Rjukan er 16 o C, kan temperaturen x meter
Delprøve 1 OPPGAVE 1 a) 1) Hvor mye er 3 delt på 1 2? 2) Per kjøper 17 skruer à kr 11,70 og 17 muttere à kr 8,20. Hvor mye betaler han? b) Når temperaturen i Rjukan er 16 o C, kan temperaturen x meter
Eksamen MAT1005 Matematikk 2P-Y Va ren 2015
 Eksamen MAT1005 Matematikk 2P-Y Va ren 2015 Oppgave 1 (2 poeng) Dag Temperatur Mandag 4 C Tirsdag 10 C Onsdag 12 C Torsdag 5 C Fredag 6 C Lørdag Tabellen ovenfor viser hvordan temperaturen har variert
Eksamen MAT1005 Matematikk 2P-Y Va ren 2015 Oppgave 1 (2 poeng) Dag Temperatur Mandag 4 C Tirsdag 10 C Onsdag 12 C Torsdag 5 C Fredag 6 C Lørdag Tabellen ovenfor viser hvordan temperaturen har variert
Algebra Vi på vindusrekka
 Algebra Vi på vindusrekka Utsagn... 2 Åpne utsagn... 3 Den ukjente... 4 Likhetstegnet... 5 Likninger... 6 Løs likninger... 7 Matematiske uttrykk... 8 Formel... 9 Tilordning... 10 Funksjon... 11 Koordinatsystem...
Algebra Vi på vindusrekka Utsagn... 2 Åpne utsagn... 3 Den ukjente... 4 Likhetstegnet... 5 Likninger... 6 Løs likninger... 7 Matematiske uttrykk... 8 Formel... 9 Tilordning... 10 Funksjon... 11 Koordinatsystem...
Eksamen 23.11.2011. MAT1011 Matematikk 1P. Nynorsk/Bokmål
 Eksamen 23.11.2011 MAT1011 Matematikk 1P Nynorsk/Bokmål Bokmål Eksamensinformasjon Eksamenstid: Hjelpemidler på Del 1: Hjelpemidler på Del 2: Framgangsmåte: 5 timer: Del 1 skal leveres inn etter 2 timer.
Eksamen 23.11.2011 MAT1011 Matematikk 1P Nynorsk/Bokmål Bokmål Eksamensinformasjon Eksamenstid: Hjelpemidler på Del 1: Hjelpemidler på Del 2: Framgangsmåte: 5 timer: Del 1 skal leveres inn etter 2 timer.
16 Excel triks det er smart å kunne
 16 Excel triks det er smart å kunne Viste du at: Det er mer en 300 funksjoner i Excel. Den første versjonen av Excel ble laget til Macintosh i 1985 Det er mer en 200 hurtigtaster i Excel ProCloud sammen
16 Excel triks det er smart å kunne Viste du at: Det er mer en 300 funksjoner i Excel. Den første versjonen av Excel ble laget til Macintosh i 1985 Det er mer en 200 hurtigtaster i Excel ProCloud sammen
Excel. Kursopplegg for SKUP-skolen 2010
 Excel Kursopplegg for SKUP-skolen 2010 1 Excel: Basisfunksjoner Konseptet bak Excel er referansepunkter bestående av ett tall og en bokstav. Et regneark består av loddrette kolonner (bokstav) og vannrette
Excel Kursopplegg for SKUP-skolen 2010 1 Excel: Basisfunksjoner Konseptet bak Excel er referansepunkter bestående av ett tall og en bokstav. Et regneark består av loddrette kolonner (bokstav) og vannrette
Eksamen 2P MAT1015 Høsten 2012 Løsning
 Eksamen 2P MAT1015 Høsten 2012 Oppgave 1 (4 poeng) Alle som går tur til Pollfjell, skriver navnet sitt i boka som ligger i postkassen på toppen av fjellet. Nedenfor ser du hvor mange som har skrevet seg
Eksamen 2P MAT1015 Høsten 2012 Oppgave 1 (4 poeng) Alle som går tur til Pollfjell, skriver navnet sitt i boka som ligger i postkassen på toppen av fjellet. Nedenfor ser du hvor mange som har skrevet seg
Eksamen 2P, Våren 2011
 Eksamen 2P, Våren 2011 Del 1 Tid: 2 timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (20 poeng) a) Skriv på standardform 1) 36 200 36200 3,62
Eksamen 2P, Våren 2011 Del 1 Tid: 2 timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (20 poeng) a) Skriv på standardform 1) 36 200 36200 3,62
Årsplan i matematikk 6.trinn 2015/2016
 Årsplan i matematikk 6.trinn 2015/2016 Tidspunkt Kompetansemål: (punkter fra K-06) Delmål: Arbeidsmetode: Vurderingsmetode: Uke 36 /37 Tall og tallforståelse -siffer og tall -beskrive plassverdisystemet
Årsplan i matematikk 6.trinn 2015/2016 Tidspunkt Kompetansemål: (punkter fra K-06) Delmål: Arbeidsmetode: Vurderingsmetode: Uke 36 /37 Tall og tallforståelse -siffer og tall -beskrive plassverdisystemet
Simulering - Sannsynlighet
 Simulering - Sannsynlighet Når regnearket skal brukes til simulering, er det et par grunninnstillinger som må endres i Excel. Hvis du får feilmelding om 'sirkulær programmering', betyr det vanligvis at
Simulering - Sannsynlighet Når regnearket skal brukes til simulering, er det et par grunninnstillinger som må endres i Excel. Hvis du får feilmelding om 'sirkulær programmering', betyr det vanligvis at
Excel. Kursopplegg for SKUP-konferansen 2015. Laget av trond.sundnes@dn.no
 Excel Kursopplegg for SKUP-konferansen 2015 Laget av trond.sundnes@dn.no 1 Konseptet bak Excel er referansepunkter bestående av ett tall og en bokstav. Et regneark består av loddrette kolonner (bokstav)
Excel Kursopplegg for SKUP-konferansen 2015 Laget av trond.sundnes@dn.no 1 Konseptet bak Excel er referansepunkter bestående av ett tall og en bokstav. Et regneark består av loddrette kolonner (bokstav)
Eksamen 25.05.2011. MAT1015 Matematikk 2P. Nynorsk/Bokmål
 Eksamen 25.05.2011 MAT1015 Matematikk 2P Nynorsk/Bokmål Bokmål Eksamensinformasjon Eksamenstid: Hjelpemidler på Del 1: Hjelpemidler på Del 2: Framgangsmåte: 5 timer: Del 1 skal leveres inn etter 2 timer.
Eksamen 25.05.2011 MAT1015 Matematikk 2P Nynorsk/Bokmål Bokmål Eksamensinformasjon Eksamenstid: Hjelpemidler på Del 1: Hjelpemidler på Del 2: Framgangsmåte: 5 timer: Del 1 skal leveres inn etter 2 timer.
Oppgaver. Innhold. Funksjoner Vg1P
 Oppgaver Innhold Innhold... 1 Modul 1. Funksjonsbegrepet... Modul. Lineære funksjoner... 6 Modul 3. Mer om lineær vekst... 10 Modul 4. Andregradsfunksjoner... 13 Modul 5. Andre funksjoner... 16 Polynomfunksjoner...
Oppgaver Innhold Innhold... 1 Modul 1. Funksjonsbegrepet... Modul. Lineære funksjoner... 6 Modul 3. Mer om lineær vekst... 10 Modul 4. Andregradsfunksjoner... 13 Modul 5. Andre funksjoner... 16 Polynomfunksjoner...
Statistikk. Forkurs 2018
 Statistikk Forkurs 2018 Hva er statistikk? Undersøke Registrere Lage oversikt Presentasjon av informasjon Formidle Arbeidet med statistikk kan vi dele inn i to hovedområder: Samle inn og ordne opplysninger
Statistikk Forkurs 2018 Hva er statistikk? Undersøke Registrere Lage oversikt Presentasjon av informasjon Formidle Arbeidet med statistikk kan vi dele inn i to hovedområder: Samle inn og ordne opplysninger
GeoGebra 4.2 for Sinus 1P. av Sigbjørn Hals
 GeoGebra 4.2 for Sinus 1P av Sigbjørn Hals Innhold Litt om GeoGebra... 3 GeoGebra som kalkulator. Eksempel side 55... 3 Omforming av formler. Side 82 i læreboka... 4 Rette linjer. Side 89 i læreboka...
GeoGebra 4.2 for Sinus 1P av Sigbjørn Hals Innhold Litt om GeoGebra... 3 GeoGebra som kalkulator. Eksempel side 55... 3 Omforming av formler. Side 82 i læreboka... 4 Rette linjer. Side 89 i læreboka...
Eksempel på løsning. Sentralt gitt skriftlig eksamen MAT1003 Matematikk 2P Eksamen 30.11.2009. Bokmål
 Eksempel på løsning 010 Sentralt gitt skriftlig eksamen MAT1003 Matematikk P Eksamen 30.11.009 Bokmål MAT1003 Matematikk P HØSTEN 009 Eksempel på løsning med vekt på bruk av digitale verktøy Hva er en
Eksempel på løsning 010 Sentralt gitt skriftlig eksamen MAT1003 Matematikk P Eksamen 30.11.009 Bokmål MAT1003 Matematikk P HØSTEN 009 Eksempel på løsning med vekt på bruk av digitale verktøy Hva er en
Eksamen våren 2016 Løsninger
 DEL 1 Uten hjelpemidler Hjelpemidler: vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler Oppgave 1 Variasjonsbredde = 6 C ( 6 C) = 1 C Gjennomsnitt: + 0 + ( 4) + ( 6) + + 6 0 x = = =
DEL 1 Uten hjelpemidler Hjelpemidler: vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler Oppgave 1 Variasjonsbredde = 6 C ( 6 C) = 1 C Gjennomsnitt: + 0 + ( 4) + ( 6) + + 6 0 x = = =
Eksamen MAT 1011 Matematikk 1P Våren 2013
 Eksamen MAT 1011 Matematikk 1P Våren 01 Oppgave 1 ( poeng) Hilde skal kjøpe L melk,5 kg poteter 0,5 kg ost 00 g kokt skinke Gjør et overslag og finn ut omtrent hvor mye hun må betale. L melk:14,95 kr 15
Eksamen MAT 1011 Matematikk 1P Våren 01 Oppgave 1 ( poeng) Hilde skal kjøpe L melk,5 kg poteter 0,5 kg ost 00 g kokt skinke Gjør et overslag og finn ut omtrent hvor mye hun må betale. L melk:14,95 kr 15
QED Matematikk for grunnskolelærerutdanningen. Bind 1 og 2. Grunnleggende Excel-øvelser (2013-versjon) Av Peer Sverre Andersen
 QED 5 10 Matematikk for grunnskolelærerutdanningen Bind 1 og 2 Grunnleggende Excel-øvelser (2013-versjon) Av Peer Sverre Andersen Innhold INNLEDNING... 3 KORT INNFØRING OM REGNEARK... 4 ØVELSE 1. PRESENTASJON
QED 5 10 Matematikk for grunnskolelærerutdanningen Bind 1 og 2 Grunnleggende Excel-øvelser (2013-versjon) Av Peer Sverre Andersen Innhold INNLEDNING... 3 KORT INNFØRING OM REGNEARK... 4 ØVELSE 1. PRESENTASJON
Bokmål. Eksamensinformasjon. Del 2 skal leveres etter 5 timer.
 Eksamen 02.12.2008 MAT1003 Matematikk 2P Nynorsk/Bokmål Bokmål Eksamensinformasjon Eksamenstid: Hjelpemidler på del 1: Hjelpemidler på del 2: Vedlegg: Andre opplysninger: Framgangsmåte og forklaring: 5
Eksamen 02.12.2008 MAT1003 Matematikk 2P Nynorsk/Bokmål Bokmål Eksamensinformasjon Eksamenstid: Hjelpemidler på del 1: Hjelpemidler på del 2: Vedlegg: Andre opplysninger: Framgangsmåte og forklaring: 5
SIGBJØRN HALS TORE OLDERVOLL. GeoGebra 6 for Sinus 2P
 SIGBJØRN HALS TORE OLDERVOLL GeoGebra 6 for Sinus 2P Sinus 2P ble skrevet med utgangspunkt i GeoGebra 5. I boka er det også lagt opp til at elevene har en enkel lommeregner i tillegg til datamaskin. I
SIGBJØRN HALS TORE OLDERVOLL GeoGebra 6 for Sinus 2P Sinus 2P ble skrevet med utgangspunkt i GeoGebra 5. I boka er det også lagt opp til at elevene har en enkel lommeregner i tillegg til datamaskin. I
1P eksamen våren 2017 løsningsforslag
 1P eksamen våren 017 løsningsforslag Tid: timer Hjelpemidler: Vanlige skrivesaker, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (1 poeng) Du har 15 L saft. Du skal helle saften over i
1P eksamen våren 017 løsningsforslag Tid: timer Hjelpemidler: Vanlige skrivesaker, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (1 poeng) Du har 15 L saft. Du skal helle saften over i
Statistikk. Forkurs 2017
 Statistikk Forkurs 2017 Hva er statistikk? Undersøke Registrere Lage oversikt Presentasjon av informasjon Formidle Arbeidet med statistikk kan vi dele inn i to hovedområder: Samle inn og ordne opplysninger
Statistikk Forkurs 2017 Hva er statistikk? Undersøke Registrere Lage oversikt Presentasjon av informasjon Formidle Arbeidet med statistikk kan vi dele inn i to hovedområder: Samle inn og ordne opplysninger
Funksjoner, likningssett og regning i CAS
 Funksjoner, likningssett og regning i CAS MKH, TUS 2014, GeoGebra 4.4 Innholdsfortegnelse Funksjoner og likningssett i GeoGebra... 2 Introduksjon til lineære funksjoner... 2 Oppgave om mobilabonnement...
Funksjoner, likningssett og regning i CAS MKH, TUS 2014, GeoGebra 4.4 Innholdsfortegnelse Funksjoner og likningssett i GeoGebra... 2 Introduksjon til lineære funksjoner... 2 Oppgave om mobilabonnement...
Eksamen våren 2015 Løsninger
 DEL 1 Uten hjelpemidler Hjelpemidler: vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler Oppgave 1 For et utvalg der antall observasjoner er et partall, slik som her, er medianen gjennomsnittet
DEL 1 Uten hjelpemidler Hjelpemidler: vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler Oppgave 1 For et utvalg der antall observasjoner er et partall, slik som her, er medianen gjennomsnittet
Eksamen 02.05.2008. VG1340 Matematikk 1MX Privatistar/Privatister. Nynorsk/Bokmål
 Eksamen 02.05.2008 VG1340 Matematikk 1MX Privatistar/Privatister Nynorsk/Bokmål Nynorsk Eksamensinformasjon Eksamenstid: Hjelpemiddel: Vedlegg: Andre opplysningar: Framgangsmåte og forklaring: 5 timar
Eksamen 02.05.2008 VG1340 Matematikk 1MX Privatistar/Privatister Nynorsk/Bokmål Nynorsk Eksamensinformasjon Eksamenstid: Hjelpemiddel: Vedlegg: Andre opplysningar: Framgangsmåte og forklaring: 5 timar
Kurs. Kapittel 2. Bokmål
 Kurs 9 Kapittel 2 Bokmål 1 av 9 Kurs i GeoGebra Funksjoner og grafer I dette kurset skal vi se nærmere på hvordan vi kan bruke GeoGebra som en graftegner. Grunnleggende innstillinger Når vi skal bruke
Kurs 9 Kapittel 2 Bokmål 1 av 9 Kurs i GeoGebra Funksjoner og grafer I dette kurset skal vi se nærmere på hvordan vi kan bruke GeoGebra som en graftegner. Grunnleggende innstillinger Når vi skal bruke
Faktor terminprøve i matematikk for 10. trinn
 Faktor terminprøve i matematikk for 10. trinn Høsten 201 Bokmål Navn: Gruppe: Prøveinformasjon Prøvetid: Hjelpemidler på Del 1 og 2: Framgangsmåte og forklaring: 5 timer totalt. Del 1 og Del 2 blir utdelt
Faktor terminprøve i matematikk for 10. trinn Høsten 201 Bokmål Navn: Gruppe: Prøveinformasjon Prøvetid: Hjelpemidler på Del 1 og 2: Framgangsmåte og forklaring: 5 timer totalt. Del 1 og Del 2 blir utdelt
Excel Dan S. Lagergren
 Excel 2007 Dan S. Lagergren 1 Temaer for dagen Automatiske lister Formatering av regneark Sortering og filtrering Formelbruk Grafer Utskrift 2 Har du hentet eksempelfila? Gå til: http://www.ntnu.no/lynkurs/09/excel
Excel 2007 Dan S. Lagergren 1 Temaer for dagen Automatiske lister Formatering av regneark Sortering og filtrering Formelbruk Grafer Utskrift 2 Har du hentet eksempelfila? Gå til: http://www.ntnu.no/lynkurs/09/excel
Eksempeloppgave 2014. MAT1010 Matematikk 2T-Y Ny eksamensordning våren 2015. Ny eksamensordning. Del 1: 3 timer (uten hjelpemidler)
 Eksempeloppgave 2014 MAT1010 Matematikk 2T-Y Ny eksamensordning våren 2015 Ny eksamensordning Del 1: 3 timer (uten hjelpemidler) Del 2: 2 timer (med hjelpemidler) Minstekrav til digitale verktøy på datamaskin:
Eksempeloppgave 2014 MAT1010 Matematikk 2T-Y Ny eksamensordning våren 2015 Ny eksamensordning Del 1: 3 timer (uten hjelpemidler) Del 2: 2 timer (med hjelpemidler) Minstekrav til digitale verktøy på datamaskin:
Eksamen MAT1015 Matematikk 2P Va ren 2014
 Eksamen MAT1015 Matematikk 2P Va ren 2014 Oppgave 1 (3 poeng) Nedenfor ser du hvor mange snegler Astrid har plukket i hagen hver kveld de ti siste kveldene. 10 5 22 28 2 8 50 15 40 10 Bestem gjennomsnittet,
Eksamen MAT1015 Matematikk 2P Va ren 2014 Oppgave 1 (3 poeng) Nedenfor ser du hvor mange snegler Astrid har plukket i hagen hver kveld de ti siste kveldene. 10 5 22 28 2 8 50 15 40 10 Bestem gjennomsnittet,
Eksempelsett 2P, Høsten 2010
 Eksempelsett 2P, Høsten 2010 Del 1 Tid: 2 timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (4 poeng) Grete og Per fyller etanol i et beger.
Eksempelsett 2P, Høsten 2010 Del 1 Tid: 2 timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (4 poeng) Grete og Per fyller etanol i et beger.
Sandefjordskolen BREIDABLIKK UNGDOMSSKOLE ÅRSPLAN FOR FORESATTE MATTE 10.TRINN SKOLEÅR 2015-2016. Side 1 av 9
 Sandefjordskolen BREIDABLIKK UNGDOMSSKOLE ÅRSPLAN FOR FORESATTE MATTE 10.TRINN SKOLEÅR 2015-2016 Side 1 av 9 Periode 1: UKE 34-UKE 39 Tall og Algebra Analysere sammensatte problemstillinger, identifisere
Sandefjordskolen BREIDABLIKK UNGDOMSSKOLE ÅRSPLAN FOR FORESATTE MATTE 10.TRINN SKOLEÅR 2015-2016 Side 1 av 9 Periode 1: UKE 34-UKE 39 Tall og Algebra Analysere sammensatte problemstillinger, identifisere
Eksempeloppgave 2014. MAT1015 Matematikk 2P Ny eksamensordning våren 2015. Ny eksamensordning. Del 1: 2 timer (uten hjelpemidler)
 Eksempeloppgave 2014 MAT1015 Matematikk 2P Ny eksamensordning våren 2015 Ny eksamensordning Del 1: 2 timer (uten hjelpemidler) Del 2: 3 timer (med hjelpemidler) Minstekrav til digitale verktøy på datamaskin:
Eksempeloppgave 2014 MAT1015 Matematikk 2P Ny eksamensordning våren 2015 Ny eksamensordning Del 1: 2 timer (uten hjelpemidler) Del 2: 3 timer (med hjelpemidler) Minstekrav til digitale verktøy på datamaskin:
Øgrim Bakken Pettersen Skrindo Thorstensen Thorstensen. Digitalt verktøy for Sigma 1P. Geogebra
 Øgrim Bakken Pettersen Skrindo Thorstensen Thorstensen Digitalt verktøy for Geogebra Innhold 1 Om Geogebra 4 1.1 Innstillinger................................... 5 2 Regning 5 2.1 Tallregning...................................
Øgrim Bakken Pettersen Skrindo Thorstensen Thorstensen Digitalt verktøy for Geogebra Innhold 1 Om Geogebra 4 1.1 Innstillinger................................... 5 2 Regning 5 2.1 Tallregning...................................
Sandefjordskolen BREIDABLIKK UNGDOMSSKOLE ÅRSPLAN I MATEMATIKK 10. TRINN SKOLEÅR 2014-2015
 Sandefjordskolen BREIDABLIKK UNGDOMSSKOLE ÅRSPLAN I MATEMATIKK 10. TRINN SKOLEÅR 2014-2015 Periode 1: UKE 34 UKE 39 Tema: Tall og algebra Kunne skrive tall på ulike måter. Skrive veldig store og små tall
Sandefjordskolen BREIDABLIKK UNGDOMSSKOLE ÅRSPLAN I MATEMATIKK 10. TRINN SKOLEÅR 2014-2015 Periode 1: UKE 34 UKE 39 Tema: Tall og algebra Kunne skrive tall på ulike måter. Skrive veldig store og små tall
Formellinje. Nytt ark
 1 Bli kjent med regnearket Et regnearkdokument er bygd opp som ei arbeidsbok med flere ark. Du gir arbeidsboka navn når du lagrer filen. Du kan legge til flere ark og du kan gi arkene navn som sier noe
1 Bli kjent med regnearket Et regnearkdokument er bygd opp som ei arbeidsbok med flere ark. Du gir arbeidsboka navn når du lagrer filen. Du kan legge til flere ark og du kan gi arkene navn som sier noe
DEL 1 Uten hjelpemidler
 DEL 1 Uten hjelpemidler Oppgave 1 (3 poeng) Lotte har spurt ti medelever om hvor mange ganger de handler i kantina i løpet av en uke. Resultatene ser du nedenfor. 1 5 1 3 3 1 4 2 4 0 Bestem medianen, gjennomsnittet,
DEL 1 Uten hjelpemidler Oppgave 1 (3 poeng) Lotte har spurt ti medelever om hvor mange ganger de handler i kantina i løpet av en uke. Resultatene ser du nedenfor. 1 5 1 3 3 1 4 2 4 0 Bestem medianen, gjennomsnittet,
Løsningsforslag, eksamen i matematikk 1, modul 2, for 2NGLU(ss) våren 2012
 Løsningsforslag, eksamen i matematikk 1, modul 2, for 2NGLU(ss) våren 2012 OPPGAVE 1 (8 %) a) 2 b) Totalt areal: (a + b)² Areal av rektanglene: a², b², ab og ab. c) 5 25 10 d) OPPGAVE 2 (15 %) a) 7 11
Løsningsforslag, eksamen i matematikk 1, modul 2, for 2NGLU(ss) våren 2012 OPPGAVE 1 (8 %) a) 2 b) Totalt areal: (a + b)² Areal av rektanglene: a², b², ab og ab. c) 5 25 10 d) OPPGAVE 2 (15 %) a) 7 11
Eksempel på løsning. Sentralt gitt skriftlig eksamen MAT1008 Matematikk 2T Eksamen 30.11.2009. Bokmål
 Eksempel på løsning 010 Sentralt gitt skriftlig eksamen MAT1008 Matematikk T Eksamen 30.11.009 Bokmål MAT1008 Matematikk T HØSTEN 009 Eksempel på løsning med vekt på bruk av digitale verktøy Hva er en
Eksempel på løsning 010 Sentralt gitt skriftlig eksamen MAT1008 Matematikk T Eksamen 30.11.009 Bokmål MAT1008 Matematikk T HØSTEN 009 Eksempel på løsning med vekt på bruk av digitale verktøy Hva er en
Løsningsforslag for 2P våren 2015
 Del 1 Oppgave 1 Sortert i stigende rekkefølge blir det: 4 5 6? 10 12 Medianen, som er 7, skal ligge midt mellom de to midterste tallene 6 og det ukjente tallet, som derfor må være 8. Oppgave 2 Opprinnelig
Del 1 Oppgave 1 Sortert i stigende rekkefølge blir det: 4 5 6? 10 12 Medianen, som er 7, skal ligge midt mellom de to midterste tallene 6 og det ukjente tallet, som derfor må være 8. Oppgave 2 Opprinnelig
Plassere positive og negative tall på tallinjen KOPIERINGSORIGINAL 2.1. Navn: KAPITTEL 2 Tall og tallforståelse. Oppgave 4a. Oppgave 4b.
 KOPIERINGSORIGINAL 2.1 KAPITTEL 2 Tall og tallforståelse Plassere positive og negative tall på tallinjen Navn: Oppgave 4a 0 1 Oppgave 4b 40 0 40 Oppgave 4c 20 0 20 Oppgave 5a 6 3 0 1 4 Oppgave 5b 2 1 0
KOPIERINGSORIGINAL 2.1 KAPITTEL 2 Tall og tallforståelse Plassere positive og negative tall på tallinjen Navn: Oppgave 4a 0 1 Oppgave 4b 40 0 40 Oppgave 4c 20 0 20 Oppgave 5a 6 3 0 1 4 Oppgave 5b 2 1 0
ØVINGSPRØVE TIL ÅRSPRØVEN 10. trinn. Oppgave 1 (2 poeng) Regn ut. a) 34, ,3 = c) 1,1 2,9 = b) 3,06 1,28 = d) 33 : 2,2 =
 ØVINGSPRØVE TIL ÅRSPRØVEN 10. trinn Del 1: 2 timer. Maks 30,5 poeng. Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler. Bruk sort eller blå penn når du fører inn svar eller
ØVINGSPRØVE TIL ÅRSPRØVEN 10. trinn Del 1: 2 timer. Maks 30,5 poeng. Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler. Bruk sort eller blå penn når du fører inn svar eller
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
 Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Faktor terminprøve i matematikk for 9. trinn
 Faktor terminprøve i matematikk for 9. trinn Våren 2013 bokmål Navn: Gruppe: Informasjon Oppgavesettet består av to deler hvor alle oppgaver skal besvares. Del 1 og del 2 blir delt ut samtidig, men del
Faktor terminprøve i matematikk for 9. trinn Våren 2013 bokmål Navn: Gruppe: Informasjon Oppgavesettet består av to deler hvor alle oppgaver skal besvares. Del 1 og del 2 blir delt ut samtidig, men del
16 Excel triks det er smart å kunne
 16 Excel triks det er smart å kunne Viste du at: Det er mer en 300 funksjoner i Excel. Den første versjonen av Excel ble laget til Macintosh i 1985 Det er mer en 200 hurtigtaster i Excel Du kan dele regneark
16 Excel triks det er smart å kunne Viste du at: Det er mer en 300 funksjoner i Excel. Den første versjonen av Excel ble laget til Macintosh i 1985 Det er mer en 200 hurtigtaster i Excel Du kan dele regneark
Sandefjordskolen BREIDABLIKK UNGDOMSSKOLE ÅRSPLAN FOR FORESATTE MATTE 10.TRINN SKOLEÅR Side 1 av 8
 Sandefjordskolen BREIDABLIKK UNGDOMSSKOLE ÅRSPLAN FOR FORESATTE MATTE 10.TRINN SKOLEÅR 2017-2018 Side 1 av 8 Periode 1: UKE 33-39 Tall og Algebra Analysere sammensatte problemstillinger, identifisere faste
Sandefjordskolen BREIDABLIKK UNGDOMSSKOLE ÅRSPLAN FOR FORESATTE MATTE 10.TRINN SKOLEÅR 2017-2018 Side 1 av 8 Periode 1: UKE 33-39 Tall og Algebra Analysere sammensatte problemstillinger, identifisere faste
SINUS R1, kapittel 5-8
 Løsning av noen oppgaver i SINUS R1, kapittel 5-8 Digital pakke B TI-Nspire Enkel kalkulator (Sharp EL-506, TI 30XIIB eller Casio fx-82es) Oppgaver og sidetall i læreboka: 5.43 c side 168 5.52 side 173
Løsning av noen oppgaver i SINUS R1, kapittel 5-8 Digital pakke B TI-Nspire Enkel kalkulator (Sharp EL-506, TI 30XIIB eller Casio fx-82es) Oppgaver og sidetall i læreboka: 5.43 c side 168 5.52 side 173
Oppgaver i matematikk, 9-åringer
 Oppgaver i matematikk, 9-åringer Her er gjengitt de frigitte oppgavene fra TIMSS 95. Oppgavene fra TIMSS 2003 ventes frigitt i løpet av sommeren 2004 og vil bli lagt ut kort tid etter dette. Oppgavene
Oppgaver i matematikk, 9-åringer Her er gjengitt de frigitte oppgavene fra TIMSS 95. Oppgavene fra TIMSS 2003 ventes frigitt i løpet av sommeren 2004 og vil bli lagt ut kort tid etter dette. Oppgavene
Sandefjordskolen BREIDABLIKK UNGDOMSSKOLE ÅRSPLAN FOR FORESATTE I MATEMATIKK 9.TRINN SKOLEÅR 2015-2016. Side 1 av 9
 Sandefjordskolen BREIDABLIKK UNGDOMSSKOLE ÅRSPLAN FOR FORESATTE I MATEMATIKK 9.TRINN SKOLEÅR 2015-2016 Side 1 av 9 Periode 1: UKE 34-UKE 39 Tema: Statistikk gjennomføre undersøkelser og bruke databaser
Sandefjordskolen BREIDABLIKK UNGDOMSSKOLE ÅRSPLAN FOR FORESATTE I MATEMATIKK 9.TRINN SKOLEÅR 2015-2016 Side 1 av 9 Periode 1: UKE 34-UKE 39 Tema: Statistikk gjennomføre undersøkelser og bruke databaser
Du skal svare på alle oppgavene i Del 1 og 2. Skriv med sort eller blå penn når du krysser av eller fører inn svar.
 Høsten 2014 Bokmål Navn: Gruppe: Prøveinformasjon Prøvetid: Hjelpemidler på Del 1 og Del 2: Framgangsmåte og forklaring: 5 timer totalt. Del 1 og Del 2 blir utdelt samtidig. Del 1 skal du levere innen
Høsten 2014 Bokmål Navn: Gruppe: Prøveinformasjon Prøvetid: Hjelpemidler på Del 1 og Del 2: Framgangsmåte og forklaring: 5 timer totalt. Del 1 og Del 2 blir utdelt samtidig. Del 1 skal du levere innen
