Universitetet i Oslo Institutt for geofag. Flomrisikoanalyse for Hamar og Lillestrøm. Helge Bakkehøi. Candidatus Scientiarum
|
|
|
- Carl Iversen
- 8 år siden
- Visninger:
Transkript
1 Uiversitetet i Oslo Istitutt for geofag Flomrisikoaalse for Hamar og Lillestrøm Helge Bakkehøi Cadidatus Scietiarum 1. september 2003
2
3 ABSTRACT 2 Abstract This work focuses o the two tows most exposed for floodig i Norwa: Lillestrøm which lies alogside Lake Øere, ad Hamar which is situated ear Norwa s largest lake, Mjøsa. The mai objective of this work is to produce damage curves for roads, railwas ad detached houses for these tows. However, i the Lillestrøm area, with fewer sigificat data, damage curves were produced ol for roads ad railwas. A risk aalses was made b coectig a flood frequec aalsis, geographical iformatio ad cost data from the big flood i Due to the lack of sufficiet cost data, more focus was give to the ucertaities of the aalses rather tha the actual results. The results showed that the expected damage (risk from floodig for all the detached houses i the Hamar regio was 12 millio NOK. The expected damage (risk from floodig railwas ad roads are NOK ad NOK, respectivel. I Lillestrøm the expected damage (risk from floodig railwas ad roads was equall to ero, due to the huge flood protectio works i this area. The results from the ucertait aalses showed that more work eeds to be performed to better estimate the total risk.
4
5 INNHOLD 4 Ihold INNHOLD INNLEDNING BAKGRUNN MÅL OPPGAVENS UTFORMING DATA GEOGRAFISKE INFORMASJONSSYSTEMER (GIS Sosi-filer GIS-verktø HYDROLOGISKE DATA Mjøsa Øere SKADE TEORI LITT GENERELL STATISTIKK De uiforme fordelige Estimerig av de kumulative fordeligsfuksjoe F(x Kjeretetthetsestimerig FLOMFREKVENSANALYSE Bruk av L-mometer til Parameterestimerig GEV (Geeralied Extreme Value-fordelige Reduced Gumbel plott Autokorrelasjosplott Gjetaksitervall Tredtest USIKKERHETSANALYSE Bootstrappig Stokastisk simulerig Kofidesitervall Kofidesbåd til de kumulative fordeligsfuksjoe RISIKO Skadefuksjoe... 26
6 5 INNHOLD 4 METODE FLOMFREKVENSANALYSE RISIKOBEREGNING SKADEFUNKSJON FOR VEI/JERNBANE SKADEFUNKSJONEN FOR BYGNINGER RESULTATER OG DISKUSJON INNLEDENDE FLOMFREKVENSANALYSE Mjøsa Øere Regioal flomfrekvesaalse USIKKERHETSBEREGNINGER Usikkerhet fra kostadberegiger Usikkerhete fra flomfrekvesaalse Usikkerhet fra GIS-aalse Geerelt om usikkerhetsberegigee RISIKOANALYSE Lillestrøm Hamar KONKLUSJON TILLEGG A BYGNINGSFORDELING FOR HAMAR, KONSTRUERT PÅ BAKGRUNN AV SOSI-DATA TILLEGG B ARCINFO KOMMANDOER: KILDELISTE STIKKORDREGISTER... 68
7 1.1 BAKGRUNN 6 1 Iledig 1.1 Bakgru Etter flomme på Østladet i 1995 ble det satt i gag me arbeid for å ugå at skadee blir like store ved framtidige flommer. Me det vil uasett kue oppstå ligede situasjoer igje, slik at beregiger av evetuelle skader fortsatt er aktuelt. Risikoaalse er et relativ tt felt iefor hdrologie, me økede fordi det etter hvert har blitt tilgjegelig me ttig iformasjo digitalt som ka behadles i geografiske iformasjos sstemer (GIS. Det er ofte e del uklarheter i hva som ligger i begrepet risiko. I hdrologie opereres det med i hvert fall tre forskjellige defiisjoer på risiko. I dette arbeidet vil risiko bli sett på som de forvetede skade, slik som det er defiert i baesiask statistikk (Berger (1985. Mer kokret for dette arbeidet vil risikoe bli sett på som gjeomsittlig årlig skade agitt i orske kroer. I dette arbeidet er det valgt å se på de to bee Lillestrøm og Hamar som grulag for risikoaalse. Disse to bee ligger heholdsvis ved Øere og Mjøsa. Lillestrøm ble sterk berørt av storflommee i 1966 og 67, etter dette ble det gjort me arbeid med å ugå slike igje, og skadee etter flomme i 1995 ble me midre e e tilsvarede flom 30 år før. Likevel ga dee flomme skader for 100 millioer kroer. På bakgru av dette har Skedsmo kommue og NVE satt opp flomvoller og pumpestasjoer til 70 millioer kroer som besktter hele be mot i hvert fall e 300 års flom (106 m. o. h.. Hamar har ikke blitt utsatt for flom på samme måte som Lillestrøm, me ble oe berørt uder flomme i 1995 som var de sjette største registrerte flomme i Mjøsa side måligee begte på 1800-tallet. Fordi avreige fra Mjøsa er e av de to store tilførslee til Øere, ka e storflom i Øere bli ugått hvis ma fller opp Mjøsa. Det blir da et spørsmål hvilke av disse to bee som er viktigst, me det er et me større potesielt skadeområde rudt Lillestrøm og sørover e hva det er lags Mjøsa. Oppgave bgger på aalser gjort etter flomme i Det har ikke vært mulig å få tak i så me data på skadetall, slik at det i dette arbeidet vil bli fokusert på skade på veier, jerbae og bolighus. Metodikke brukt i dee oppgave bgger på Gottschalk og Krasovskaia (1999. I tillegg er det iført oe usikkerhetsberegiger, samt skadefuksjo for veier og jerbae. Usikkerhetsberegigee er kosetrert rudt flomrisikoaalse, da det er lite bakgrusdata for kostader. All iformasjo om kostader er tatt fra Wathe m. flere (1999. Det fies mer iformasjo om kostader fra flomme i 1995 hos
8 7 1. INNLEDNING forsikrigsselskaper og takstme, me å få tak i dee iformasjoe krever et omfattede arbeid. 1.2 Mål Oppgaves mål er å udersøke skadee som ka oppstå uder e evetuell flom ved to av de mest flomutsatte bee i Norge. Det vil bli gjort forsøk på å etablere skadekurver med Mjøsa og Øere som grulag. Det teoretiske vil få e setral rolle i oppgave, da det er begreset med data tilgjegelig for å si oe om skade på aet e veier, jerbaer og bolighus. Videre vil usikkerhetsaalse bli viktig, dee vil bli utført på bakgru av bootstrappig. Det vil da være usikkerhete fra de iledede flomfrekvesaalse som vil stå mest setralt. Det vil bli utarbeidet skadekurver for de bgigstper der kostadsdata er lett tilgjegelig. Veier og jerbae vil også bli sett på, i tillegg utarbeides skadekurver for disse. Det vil bli implemetert usikkerhet i alle skadekurvee. Tilsvarede aalser gjort etter flomme i 1995 bgger på vaførigsdata, mes det i dette arbeidet blir brukt vastadsdata fra Mjøsa og Øere. 1.3 Oppgaves utformig Oppave er delt i i 6. kapitler. Kapittel 2 vil ta for seg de data som er brukt i oppgave. Der vil de tre hovedkompoete i oppgave bli presetert, som er vastadsdata, skadetall og GIS-data. Videre vil det i kapittel 3 bli presetert de statistiske bakgrusteorie til dette arbeidet, og hvorda dette blir brukt i oppgave vil bli presetert uder kapittel 4 som blir kalt metode. Resultatee blir først presetert i kapittel 5, som er delt i i 3 uderkapitler. Det er iledede aalse, usikkerhetsberegiger og til slutt risikoaalse. E oppsummerig kommer uder koklusjoe i kapittel 6. Til slutt er det to vedleggskapitler, hvor det første er e tabell over berørte bgiger uder tidligere storflommer og det adre er e oversikt over kommadoer som er brukt i GIS-verktøet Arcifo.
9 2.1 GEOGRAFISKE INFORMASJONSSYSTEMER (GIS 8 2 Data 2.1 Geografiske iformasjossstemer (GIS For å kue gjeomføre e flomrisikoaalse kreves det e detaljert iformasjo om beliggehete til de evetuelt oversvømte objektee. Til dette er det brukt kartdata som ete er oppmålt av kommuee eller States kartverk, og deretter digitalisert. Disse dataee er samlet i igjeom Skedsmo kommue og NVE. Dataee fra NVE er brukt i aalse for Hamar. Det var ikke mulig å få tak i ere kartgrulag e fra For Lillestrøm fates det data, me dataee var lite differesierte, slik at det ikke var mulig å skille mellom forskjellige tper hus. Derfor vil det her ku bli utarbeidet e skadekurve for veier og jerbae. Disse dataee er tilveiebrakt fra Skedsmo kommue. Kartdataee for både Hamar og Lillestrøm har NGO akse III som koordiatsstem. Adre kart brukt i oppgave kommer fra States kartverk. Figur 1: Oversiktskart over områdee sett på i dette arbeidet. Kartee er fra States kartverk, N50 serie.
10 9 2. DATA Sosi-filer Sosi-stadarde er e orsk stadard for å presetere kartdata digitalt, og står for Samordet opplegg for stedfestet iformasjo. De ble første gag itrodusert i 1987, og har seere blitt foradret for å tilpasse seg e mer iterasjoal stadard. Sosi-filer deles ofte opp i objekter som kommer i forskjellige filer. De objektee som er brukt i oppgave er: TERR - Hødeiformasjo BYGG - Bgiger VANN - Isjøer og vassdrag VSIT - Veisituasjo BANE - Jerbaedata I e sosi-fil ligger det flere egeskaper til dataee. Alle tper kartteg har hver si temakode, slik at det går greit å skille de forskjellige elemetee fra hveradre. Hvis vi for eksempel tar for oss veier, så har veikat temakode 7002, mes veies midtlije har Når det gjelder bgiger, så er ofte disse både presetert som flater og lijer. Flater til bgiger har temakode Objekter har ofte ege uike elemeter. Bgiger har et elemet som står meget setralt i oppgave, det er BYGGTYP_NBR. Dee gir iformasjo om hva slags tpe bgig vi har med å gjøre. De fleste digitale kart ieholder dee iformasjoe, og det gjør arbeidet med e flomrisikoaalse me eklere. Hvis ma da vet skadefuksjoe for de forskjellige boligtpee, så går det este automatisk å rege ut totalskade. Hvis dee iformasjoe derimot ikke er implemetert, må ma sfare området og samle i dee iformasjoe på egehåd, før ma ka kjøre e flomrisikoaalse. E alterativ løsig til dee meget tidkrevede prosesse er å ata at to bgiger med omtret like stort areal påføres omtret de samme skade. Arealet er ofte implemetert i sosi-dataee, me det er uasett greit å rege ut i et GIS-verktø (for eksempel Arcifo.
11 2.2 HYDROLOGISKE DATA 10 Tpe Bgg BYGGTYP_NBR Eebolig 111 Garasje, uthus aeks til bolig 181 Lagerhall 231 Verkstedsbgig 212 Tabell 2.1.1: Tabelle viser BYGGTYP_NBR for oe av de mest flomutsatte bgigstpee i Hamar kommue, e total oversikt fies i vedlegg A GIS-verktø Sosi-filee har blitt kovertert, og videre bearbeidet i GIS-verktøet Arcifo 8.1. Programmet Arcview har blitt brukt til ekel visualiserig. Dataee har videre blitt eksportert til statistikkpakke R, som er et kraftig, gratis statistikkprogram. R er e kloe av det kommersielle programmet S-plus, me det går me raskere å rege ut for-løkker her! S-plus har også blitt brukt til ekelte ekle beregiger. 2.2 Hdrologiske data Vastadsdata som er brukt i oppgave er fra NVE, og går fra for Mjøsa og for Øere. Målestasjoee som er brukt er for Øere Mørkfoss og for Mjøsa 2.10 Hamar. Vastadsdataee er presetert som daglige maksimumsverdier. Når vastade i Mjøsa og Øere er 0, ligger vaet heholdsvis 117,694 og 96,538 m. o. h. på bakgru av States kartverks hødesstem NN Mjøsa Mjøsa er Norges største isjø, og har Gudbradsdalslåge som si viktigste tilførselselv. I løpet av 1800 og 1900-tallet har Mjøsa blitt regulert 5 gager. Det var i 1854, 1907, 1940, 1947 og Det ble i 1854 oppført e demig sør for Eidsvoll, dee ble revet i I 1909 ble det satt opp e demig litt leger ed i Vorma, ved Svafoss. Her er det gjort foradriger utover på 1900-tallet, de siste store regulerigee ble gjort i Regulerigee har ført til høere vastad på høst og viter og lavere vastad reste av året, mes flomvastade har blitt lavere. Oppstrøms er det gjort e god del reguleriger i det forrige århudre i forbidelse
12 11 2. DATA med kraftverksutbggige, me ige større vassdrag er regulert etter Aursjø i Det vil si at det er gjort miimalt med regulerig etter 1962, og det er aturlig at vassdraget i framtide oppfører seg okså likt som i periode fra 1962 og fram til i dag. Tegforklarig Veier Jerbae Vakat N Meters Figur 2: Kartet over viser veier og jerbae brukt i aalse for Hamar Øere Øere er Norges iede største isjø, og får si tilførsel først og fremst fra Glomma og Vorma. Lillestrøm ligger ord for tilløpet fra Glomma i e bukt kalt Svellet, her får Øere tilførsel fra to midre elver, Leira og Nittelva. Leira og Nittelva dreerer store deler av Romerike, og Nittelva dreerer også betdelige områder av Nord- og Østmarka. Utløpet av Øere ligger ved Mørkfoss, hvor Glomma fortsetter ed mot Fredrikstad.
13 2.3 SKADE 12 Lillestrøm N Tegforklarig Veier Jerbae Elv Flomvoller Meters Figur 3: Kart over de veiee og jerbaee i Lillestrøm som er aalsert. Det har vært gjort oe forsøk på sekigsarbeid av Øere på midte av tallet, me det var først etter at Solbergfoss kraftverk ble bgget på 1920-tallet at det ble oe forbedriger. Flomme i 1966 og 1967 gjorde stor skade i Lillestrøm, og det ble satt i gag tterligere flomreduserede tiltak, som ble ferdig i Etter flomme i 1995 er bare driftsikkerhete i kraftverket blitt utbedret. I dag skjer regulerige av Øere ved Solbergfoss kraftverk, 5 km sør for Øeres utløp. Oppstrøms får Øere si tilførsel både fra Låge- og Glommavassdraget, me det er ku gjort små reguleriger her etter siste regulerig av Øere. Det vil si at vaførige har stabilisert seg etter Skade Som grulag for beregige av kostader er det brukt tall utarbeidet av Wathe, m.flere(1999. Når det gjelder bgiger har det ku blitt gjort aalser for bolighus,
14 13 2. DATA da dette er de eeste bgigstpe det fies data lett tilgjegelig for. Det er brukt følgede regresjoslikig som stadard for å berege idividuelle boligkostader: skade i 1000 kr = 1,2405* vahøde fra grumur(cm (1 Likig 1 er fuet ved å plotte skade på hvert hus etter 1995-flomme mot hvor høt vastade kom på de forskjellige husee, og tilpasset dette med e lieær regresjosaalse. Det er atatt at et bolighus blir påført skade fra og med år vaet er i kotakt med grumure. 2,5 meter er satt som et stadardmål på grumures høde. For vei og jerbae er det brukt følgede tall: Vei: kr/km Jerbae: kr/km Prisee over er tatt fra Wathe, m. flere(1999. Alle kostadsberegiger som er brukt i dee aalse bgger på data som ble samlet i etter 1995-flomme. Det er ikke tatt hes til evetuelle prisstigiger i beregigee. Likevel ka det være greit å være klar over at det har vært e geerell prisstigig i løpet av dee periode, som blir bereget som kosumprisidekse. Kosumprisidekse lå i 1995 på 94,2 %, å ligger de på ca. 111%. Det vil si at prisøkige fra 1995 til i dag er på ca. 17,8 %.
15 3.1 LITT GENERELL STATISTIKK 14 3 Teori 3.1 Litt geerell statistikk I statistikk opererer ma med to forskjellig hovedmetoder å presetere data på: 1. Saslighetstetthete, som sier oe om hvor de forskjellige datae ligger i forhold til hveradre, på samme måte som et histogram. 2. Kumulativ fordeligsfuksjo, som sier oe om saslighete for at data er lavere e e x verdi. 1. Saslighetstetthet: 2. Kumulativ fordeligsfuksjo: + df( x f ( x = der dx f ( x dx = 1 (2 b P ( a < X > b = f ( x dx (3 a x F ( x = f ( t dt (4 P ( X < x = F( x (5 f(x F(x x x Figur 4: Stadard ormalfordelig presetert som e tetthetsfuksjo. Figur 5: Stadard ormalfordelig presetert som e kumulativ fordeligsfuksjo.
16 15 3. TEORI X er e tilfeldig variabel, og x er e gitt verdi. Det vil si at P(X<x blir saslighete for at e tilfeldig verdi i populasjoe er midre e verdie x. P ( a < X < b blir da saslighete for at e tilfeldig variabel X ligger iefor a,. itervallet ( b Formlee beskrevet over er for teoretiske fordeliger, og krever først at ma fier e tilpasig til de opprielige data. Det fies også metoder for å fie fram til dette empirisk. Dette vil bli behadlet seiere. Noe valige fordeligsfuksjoer er ormalfordelige, logormalfordelige, og for ekstremverdier GEV-fordelige. Metoder for å tilpasse slike fordeliger vil bli ærmere forklart i kapitel De uiforme fordelige De ekleste kotiuerlige fordeligsfuksjoe som er mulig er de uiforme fordelige, ofte også kalt rektagelfordelige: f ( x = 1 år a < x < b (6 b a b + a E( x = 2 2 ( b a Var( X = (7 12 I e uiform fordelig vil f(x være kostat for ehver x, altså i teorie skal alle verdier forekomme like mage gager Estimerig av de kumulative fordeligsfuksjoe F(x. Et problem som ofte dukket opp i dette arbeidet, var at det var gitt e x-verdi, og så skal ma fie F(x fra de kumulative fordeligsfuksjoe. E grei måte å løse dette problemet på, er å fie atall verdier som er midre e x, for så å dele på atall verdier totalt, matematisk blir det slik: F X 1 ( x = PX ( X < x = I{ X < x}, (8 i= 1 der I { X < x} er idikatorfuksjoe som er defiert som I{ X < x} 1 = 0 hvis hvis ( X < x ( X > x
17 3.2 FLOMFREKVENSANALYSE Kjeretetthetsestimerig For å sammelige opprielige data med e fordeligsfuksjo, er det valig å bruke et histogram. Me dette blir ofte okså uøaktig, og det ka være greit å bruke e mer avasert metode. Kjeretetthetsestimerig er e metode for å estimere f basert på data x 1,,x uif ~ f, og det er gaske tug teori som ligger bak som ikke tas med her. Nærmere ifo fies i Veables og Riple(1999. Tetthet Histogram Kjerepuktsestimerig eksempel Figur 6: Kjeretetthetsestimerig sammeliget med histogram 3.2 Flomfrekvesaalse Flomfrekvesaalse er me brukt i hdrologie til å fie gjetaksitervall, og vil i dette arbeidet ha e setral posisjo som bakgru for risikoberegigee. I e flomfrekvesaalse plukker ma ut ekstremverdiee fra vaførigsseriee, og så tilpasses disse e fordelig ved hjelp av e esitmerigsmetode (beskrevet i kapittel Det fies to hovedmetoder å plukke ut ekstremverdiee på. Ma ka ete plukke ut de høeste årlige verdiee (AM, eller plukke ut verdier over e viss terskel (POT. Dette vil bli ærmere beskrevet i kapittel 4.1. To viktige atagelser i flomfrekvesaalse er at data er uavhegig idetiske fordelte variable (uif og at de ikke foradres med tide (stasjoære. I tillegg er det viktig at alle data kommer fra de samme fordelige, altså at data er homogee. Et autokorrelasjosplot ka brukes til å si oe om uavhegighet til dataee, mes e tredtest (lieær regresjo ka brukes til å kotrollere for stasjoæritet. Hvis det er flere vastadsmåliger tilgjegelig i det samme område er det e fordel å ormalisere data og kjøre e regioal flomfrekvesaalse. Da vil datagrulaget bli større og ma vil oppå e mer robust aalse. Dette krever homogeitet i data. Mer iformasjo om dette ka fies i Gottschalk og Krasovskaia ( Bruk av L-mometer til Parameterestimerig L-mometer er e metode som brukes til å estimere parametere i e teoretisk fordelig slik at de blir best mulig tilpasset til data. L-mometer ble første gag
18 17 3. TEORI itrodusert av Hoskig (1990, og er defiert som lieære kombiasjoer av data, ordet i stigede rekkefølge. Disse har de seere år begt å erstatte bruke av ordiære mometer. Noe av grue til dette er at ordiære mometer gir stor vekt på outliers (data som avviker fra reste, og gir store variasjoer av parametere for små datasett. L-mometer fugerer bra til parameterestimerig av fordeliger med lage haler, for eksempel ekstremverdifordeliger. L-mometer er utarbeidet av hdrologer, me er å også på vei i i de ordiære statistikke. Ordiere mometer er defiert slik: ( X E. Forvetige E (X er første ordes momet. I tillegg er det oe som heter setralmomet som er defiert slik: E[ ( X m ]. Adre ordes setralmomet er defiert som variase, og tredje ordes setralmomet er defiert som skjevhete. Dette er verdier som både ka fies teoretisk og empirisk, slik at det er mulig å estimere parametere, ut i fra løsig av et likigssstem. Hoskig m. flere viste i 1985 at maximum likelihood estimerig av små dataserier ga veldig ustabile svar, og abefalt å bruke PWM (probabilit weigthed momets til estimerige. L-mometer er e videreutviklig av PWM, som har større øaktighet og er eklere å bruke. L-mometer ka skrives som lieære kombiasjoer av PWM. For mer iformasjo om maximum likelihood estimerig se for eksempel Larse og Marx (1986 L-momet er defiert slik: λ = E( X 1 1:1 1 λ1 = E( X 2 1 λ3 = E( X 3 1 λ4 = E( X 4 2:2 3:3 4:4 X 1:2 2X 3X 2:3 3:4 + X 1:3 + 3X 2:4 X 1:4 (9 L-mometee sitt forholdstall, som er aalogt til ordiære mometer er defiert slik : τ r = λr / λ 2, r = 3,4,. (10 τ 3 er et mål på skjevhet og τ 4 er et mål på kurtosis GEV (Geeralied Extreme Value-fordelige GEV-fordelige ble først itrodusert av Jekiso (1955. Det er e 3-parameters geeraliserig av de tre ekstremverdifordeligee weibull (k>0, frechet (k<0 og gumbel (k 0. GEV-fordelige brukes i hdrologie til tilpasig av årlig maksimal vastad. De har også e tedes til å passe godt for adre tper
19 3.2 Flomfrekvesaalse 18 hdrologiske data, selv om dette ikke stemmer overes med teorie. For e dpere iførig i GEV-fordelige hevises det til Kot og Nadarajah (2000. Tetthetsfuksjoe til GEV-fordelige er på dee forme: f ( x = 1 x u 1 k a α 1/ k 1 e 1 / k x u 1 k α (11 der k er formparameter, u er lokasjosparameter og α er skalaparameter. De kumulative fuksjoe blir da slik: k( x u F( x = exp 1 α 1/ k (12 Det ka ekelte gager også være iteressat å fie de iverse til F, F 1 ( x : k [ 1 ( l( F ] α F 1 ( x = u + k (13 F 1 ( x er ofte ttig til simulerig og for å kue operere med kotiuerlige verdier. Det har i dee oppgave blitt brukt L-mometer som parameterestimerigsmetode, så de teoretiske L-mometee (defiert i kapittel til GEV-fordelige er: α λ1 = u + [ 1 Γ(1 + k ] k α k λ2 = (1 2 Γ(1 + k k k 2( 1 3 τ 3 = 3 k 1 2 ( (14 (15 (16 Dette likigssstemet er det ikke mulig å løse, så vi må gjøre følgede tilærmig fra Hoskig m. flere (1985: k c c, (17 2 c = τ log 2 log3 (18 De adre parametere blir da som følger: λ 2 k α, (19 = k ( 1 2 Γ( 1+ k
20 19 3. TEORI { 1 Γ(1 + k } α u = λ 1, (20 k der Γ er gammafuksjoe, som ligger iebgd i de fleste statistikkprogram. Bakgru for GEV Bakgrue for at ma som oftest bruker GEV-fordelige år ma tilpasser e fordeligsfuksjo til ekstremverdier, er aalogt med det velkjete setralgreseteoremet, bare at ma her bruker M = Max X,..., X, mes ma i ( 1 = X X. setralgreseteoremet bruker e sum S ( + Teorem(Fisher og Tippett (1928: Ata at ( X,..., 1 X er uavhegige, idetisk fordelte og tilfeldige variable med e fordeligsfuksjo F. Hvis det fies e kostat a > 0 og b R slik at M a b Y,, (21 der Y er e tilfeldig variabel med fordeligsfuksjo G, så er G e av de tre ekstremverdifordeligee frechet, weibull eller gumbel Reduced Gumbel plott Dette er e måte å plotte ekstremverdifordeliger på, itrodusert av Gumbel (1958. I et reduced gumbelplot, plotter ma E[X] = -LN(-LN(F(x mot x. Blir kurve diagoal, har vi e gumbelfordelig. For empirisk plottig av F(x til data er det greit å bruke Grigortes-plotteformel: r 0.44 F ( x =, der r = {1, }, og er atall verdier. ( For å få mer forståelse av kurve er det greit å kombiere Gjetaksitervallet med dette plottet. Sammehege mellom disse to blir fra Gumbel (1958 som følger: 1 - LN(-LN(F(x = log( T der T er gjetaksitervallet. (23 2T
21 3.2 Flomfrekvesaalse 20 x Weibull, k > 0 Frechet, k < 0 Gumbel, k = Reduced Gumbel variate Figur 7: Figure viser et reduced gumbel plot over GEV-fordelige, med forskjellige verdier for formparametere k. Figur 7 viser at gumbelfordelige i et slikt plott følger e rett lije, og weibullfordelige kokav, mes frechetfordelige er koveks. Av dette følger det da at weibull er oppad begreset, mes frechet er edad begreset Autokorrelasjosplott Et autokorrelasjosplott sier oe om avhegighete mellom verdier over tid. Et slikt plott krever at det er kostat avstad mellom de målte data Y, for eksempel tidsserier. Hver posisjo i tidsserie blir idetifisert med t, og t+τ og er referert som et lag med legde τ. Autokovariase er defiert slik: 1 cov = t (24 τ τ τ t= + t t YtY 1 τ τ Autokorrelasjoe er ormalisert autokovarias og blir da som følger:
22 21 3. TEORI r τ = cov τ vary = ( ( /( = 1+ Y Y t t t τ τ τ t t τ 2 ( ( t Y /( 1 t= 1 τ 1 (25 E bredere iførig i dette temaet ka fies i Davis ( Gjetaksitervall Vi har de geometriske fordelige som er defiert slik: p( = p(1-p, =1,2 (26 p er saslighete for at e hedelse A skal itreffe. De tilfeldige variabele Y er defiert som atall gager vi må gjeta forsøket før e hedelse A itreffer. Forvetige til Y blir som følger: [ ] E Y = 1 p (27 Gjetaksitervallet ka å fies ved å iføre følgede: A: overstige vastade x F[X] = P(X < x, som er fordeligsfuksjo for vastade X, som vil si saslighet for at e tilfeldig vastad X er midre e e gitt vastad x. p er saslighete for at vastade x overstiges. er atall år det tar før x overstiges.. Videre har ma følgede: p = P(X > x = 1- P(X < x = 1-F[X] (28 De geometriske fordelige i dette tilfellet blir da: p( = p(1-p = (1-F(x(1-(1-F(x, =1,2 (29 Det forvetede atall år det tar før x er oversteget er da: 1 1 E [ ] = = = T ( x (30 p 1 F( x
23 3.3 USIKKERHETSANALYSE 22 Det er dette som i hdrologie brukes som defiisjoe på gjetaksitervallet, og F(x fier ma ut fra e flomfrekvesaalse. Med adre ord blir da gjetaksitervallet gjeomsittlig atall år det tar før e gitt flom blir oversteget. Hvis ma har POT-data blir dette mer komplisert, og ma må først kovertere data til AM. Mer ifo om dette fies i Gottschalk og Krasovskaia ( Tredtest E tredtest er e test der det blir gjort e lieær regresjosaalse av data. E lije som følger dee likige: i = a x i + b, blir tilpasset data ved miste kvadraters metode. Hvis a er sigifikat forskjellig fra 0, så ka ma ata at det er tred i data, side a er stigigstallet. Dette ka udersøkes ved og kjøre e såkalt t-test. T a 0 =, (31 s / Da har vi at a er sigifikat forskjellig fra ull hvis T-verdie ligger utefor følgede itervall: t (0.05 < T < t (0.95. Der t( er (100* -kvatile til e stadard t-fordelig. 3.3 Usikkerhetsaalse Bootstrappig Bootstrappig ble itrodusert i 1979 av Efro. Bootsrappig er e måte å fie usikkerhete til parametere θ, ut i fra simulerig eller resamplig. Metode krever stor regekraft, og har først blitt mulig å uttte fullt ut i de seere åra. Gruidee bak bootstrappig er som følger: Vi kjeer ikke F, me la oss iføre et estimat på F kalt Fˆ, og se på egeskapee til parametere θˆ uder Fˆ Bakgrue for bruk av bootstrappig ligger i store talls lov: Hvis X 1,X 2,X 3,.,X trekkes uif ~ G så gjelder følgede X 1 = X i=1 i E[ X ] år (32 Forvetigsskjevhete, eller Bias som det ofte kalles, er defiert slik:
24 23 3. TEORI Bias = E Fˆ [] ˆ θ θ ( Fˆ ˆ ˆ ˆ 1 θ ˆ i (33 F * der E [ ] = θ. i= 1 Bias er altså gjeomsittet av bootstrappsamplee θ estimatet Det er to mulige framgagsmåter i bootstrapp-verdee, det er parametrisk og ikkeparametrisk bootstrappig. I parametrisk bootstrappig utfører ma e simulerig av fordeligsfuksjoe, mes i ikke-parametrisk bootstrappig resampler ma data, med tilbakeleggig. Når vi har e korrekt parametrisk modell, ka det vises at ikke-parametrisk bootstrappig har dobbelt så stor varias som parametrisk bootstrappig. Til å kotrollere om e modell er korrekt, ka vi bruke e såkalt goodess-of-fit test, eller sammelige kjeretetthetsestimatee til parametere. Simulerig har utviklet seg til å bli et stort område iefor statistikk, og det har blitt utarbeidet metoder for å simulere fra de fleste kjete fordeligsfuksjoee, også GEV-fordelige, e mer detaljert beskrivelse fies i kapittel Framgasmåte for bootstrappig for GEV-fordelige blir da som følger: 1. Simuler datasampler fra GEV-fordelige med iverterigsmetode. 2. Fi parametere ved hjelp av L-mometer til alle de datasamplee. 3. Nå ka de datasamplee brukes til beregig av f.eks stadardavvik, bias og kofidesitervall til parametere. E ae metode som har blitt brukt til usikkerhetsestimerig er jackkifig. Dee metode er raskere, me ikke så god. Jackkifig brukes også til å lage kofidesitervall uder BC a -metode. Mer iformasjo om jackkifig fies i Efro og Tibshirai( Stokastisk simulerig Iverterigsmetode: Iverterigsmetode er e simulerigsmetode for iverterbare fordeligsfuksjoer. Det er e metode som er grei å implemetere, og fugerer bra i de fleste situasjoer. De fleste fuksjoer er iverterbare, me det er også mulig å tilærme fuksjoe slik at iverterigsmetode fortsatt fugerer. GEV-fordelige er e iverterbar fuksjo. Fremgagsmåte for å simulere fra GEV-fordelige blir da som følger: 1. Geerer data fra dee uiforme fordelige, U [ 0,1]
25 3.3 USIKKERHETSANALYSE Sett så X = F 1 ( U, der F er de kumulative fordeligsfuksjoe for GEV. 3. X ee vil da bli GEV-fordelte. For mer iformasjo om simulerigsmetoder se Liestøl og Storvik (2001. Resamplig: Dette er e metode der ma trekker tilfeldige data fra dataserie, og legger tallee tilbake etter hver gag. Metode brukes me iefor bootstrappigsverdee, og fugerer i de fleste situasjoer. De brukes til ikke-parametrisk bootstrappig Kofidesitervall Når ma skal fie kofidesitervallet til e parameter θ, er ma iteressert i å P A θ B er de øskete dekigsgrade, for eksempel 95%. fie A og B der { } Det fies flere måter å fie kofidesitervaller fra bootstrappig på. Geerelt har vi de klassiske metodee som ormaltilærmige, og bruk av percetil-metode. Disse metodee er ikke korrigert for skjevhet i fordelige, og ka bli litt uøaktige. E ae mer avasert metode er BC a -metode. BC a metode, ofte kalt ABCmetode(Acceleratio & Bias Corrected, er e adre ordes korrekt måte å fie kofidesitervallet på. De er geerelt sett på som e av de mest sikre metodee, og er defiert slik: α α Φ a ( α 1 = 0 Φ a 0 ( α ( + 0 (1 α = (1 α ( + 0, (34, (35 her er Φ ( stadard kumulativ ormalfordelige med forvetig 0 og (α stadardavvik 1. er (100 * α-kvatile til stadard ormalfordelige. Parametere 0 og a er ikke helt greie å fie, me de ka fies på blat aet følgede måte: 1 atall{ θ * ( b < θ } = Φ 0, der B er atall bootstrappsampler. (36 B
26 25 3. TEORI a = 6 1= 1 1= 1 ( θ θ ( ( θ θ ( ( i ( i / 2 ˆ i, der θ ( er jackkifesampler. (37 ˆ θ ( = i= 1 ˆ θ ( i (38 Kofidesitervallet blir da som følger: KI = *( α *( 2 [ 1, α θ θ ] (39 *( θ er (100* -kvatile til de simulerte parameterverdiee, Mer iformasjo om dee metode fies i Efro og Tibshirai (1998. * θ Kofidesbåd til de kumulative fordeligsfuksjoe Det fies flere mulige fremgagsmåter for å fie et kofidesbåd til de kumulative fordeligsfuksjo. De viktigste metodee er delt i i globale og puktvise kofidesbåd. Puktvise båd blir laget ved å plukke ut e god del x-verdier og fie kofidesitervallet til F(x, for hver av disse x-verdiee. Dee treger simulerig. Globale båd er samtidige båd som er kostruert med hele fordelige som grulag for alle verdier. Dee metode ka klare seg ute simuleriger. E tradisjoell fremgagsmåte for å utarbeide kofidesbåd er basert på Kolmogorov-Smirov test. De er global og ikke-parametrisk. Dee metode har e tedes til å gi for stort kofidesitervall i hale, og bådet vil få e kostat bredde år F ( x 1. Dette passer dårlig i e flomfrekvesaalse, der vi ofte er iteressert i de høe F(x verdiee. Selv om dee metode er forholdsvis ekel å implemetere, så er det bedre å bruke et puktvist kofidesbåd i dee oppgave. Adre forbedrede globale metoder hvor ma for eksempel bootstrapper fies, me de fleste bgger på maximum likelihood estimerigsmetode, se Jeg og Meeker(2000 Et puktvist kofidesbåd er lettest å lage, og det kostrueres ved hjelp av bootstrappig. Det er viktig at dette kostrueres ut i fra F 1 ( x, da F(x ka gi
27 3.4 RISIKO 26 udefierte verdier. Ma kjører 1000 simuleriger, og plukker ut øvre og edre kvatil. Ulempee med et puktvist kofidesbåd kotra et globalt, er at de statistiske egeskapee til fordelige ikke blir bevart i hvert pukt. Et globalt kofidesbåd tar hes til dette. Når ma har kostruert et kofidesbåd til de kumulative fordeligsfuksjoe, er det rimelig greit å overføre dette til e skadekurve 3.4 Risiko Fra Baesiask statistikk (Berger (1985 er risiko defiert som forvetige til e skadefuksjo, l(d(x,θ. Det ka da skrives slik: [ l( d( X, θ ] = l( d( x, θ f x ( x dx R( d, θ = E θ. (40 X Poeget er å velge e hadlig a=d(x fra et område A ieholdt alle mulige hadliger, basert på observasjoer av e tilfeldig variabel X. Saslighetsfordelige til X er basert på e parameter θ, som ofte blir kalt aturtilstade. Hvis vi skriver om risikoe til å passe med otasjoee i dette arbeidet, ser det ut som følger : [ l(, d( x ] = l(, d( x f x ( x dx R(, d( = E (41 X Skadefuksjoe Det å fie skadefuksjoe (totale kostader er gaske rett fram ved å bruke elemetær matematikk og statistikk: De totale kostade = atall objekter oversvømt * skade pr. objekt mer matematisk blir dette: l (, = ( ( l'( (42 l ( er skade for hvert ekelt objekt, og ( er atall objekter oversvømt. Vaivået i e bgig ka defierers slik, = -h, der h er høde over havet til hvert ekelt objekt og er e gitt vastad(m.o.h. De maksimale vaivået ma
28 27 3. TEORI da ka få blir max = - h 0, der h 0 er høde over havet til det lavest beliggede objektet. ( er da alle objekter som ligger iefor og max, det er da det samme som: atall objekter * saslighete for at et objekt ligger iefor og max som matematisk ka skrives slik: ( c = N * P( < Y < = N f ( d (43 c max max c Y der N er totalt atall objekter. Det vil da si at ma er iteressert i å fie ( som er ukjet. Det fies i hvert fall to mulige fremgagsmåter å fie f Y ( på, de ee er ku å estimere f Y ( ved hjelp av kjeretetthetsestimerigsmetoder. Dette er e ekel tilærmigsmetode, og det blir da kurat å implemetere kofidesitervall. Side ma er iteressert i å fie e statistisk fremstillig av skadefuksjoe, så er de adre fremgagsmåte å foretrekke, som er e aaltisk metode kostruert ved hjelp av elemetær matematikk og statistikk utarbeidet av Gottshalk og Kraskovskaia (1999: Fra elemetær statistikk har vi kovolverige mellom f Z og f H som er defiert slik: f Y f Y f Z ( f H ( ( = d år = + h (44 For = h ka ma skrive om kovolverigsformele litt: f Y ( f Z ( f H ( = d (45 det ka videre skrives at f Z ( har e uiform fordelig: f Z 1 ( = (46 a b der a og b er heholdsvis øvre og edre grese for kofidesitervallet til vastade( ut i fra usikkerhete i hødemodelle. De vil fugere som e glattigsparameter, der stor avstad mellom a og b gir e glattere kurve. 1 1 f = Y ( = f Z ( f H ( d = f H ( d f H ( d (47 a b a b
29 3.4 RISIKO 28 Videre er defiisjoe av de kumulative fordeligsfuksjoe (skrevet om for å passe i i uttrkket over: = d f F H a H ( ( (48 Dette itegralet ka da settes i i likig 43, og ma får følgede: ( 1 ( F f a H b a Y =, 0 0 h h b a < (49 Dette ka igje skrives slik: [ ] ( ( 1 ( F F f b H a H b a Y =, 0 h b < (50 Dermed er f Y ( beskrevet med et uttrkk ma ka fie, og ma ka da plotte ( f Y ved hjelp av likig 50. Plottig av e slik likig ka virke litt vriet, me det gjøres på følgede måte med å skrive om uttrkket for ( f Y litt: [ ]= = ( ( 1 ( F F f b H a H b a Y { } { } < < = = i b i a b a H I H I 1 1 ( 1 ( 1 1 (51 { } = < = < = i a a H a H H I H P F 1 ( 1 ( ( ( (52 { } = < = < = i b b H b H H I H P F 1 ( 1 ( ( ( (53 der I er e idikatorfuksjo som er 1 år iholdet er sat, og 0 år det er usat. Når ma å har fuet ( f Y er ma videre iteressert i hvor mage objekter som blir oversvømt, det er gitt ved ligig 43. Side ma ikke opererer med kotiuerlige data må vi skrive de slik: = m f N c c Y c max ( ( (54 der m er atall -verdier ma har. Nå har ma alt ma treger for å berege skadefuksjoe, som er slik: ( ' (, ( l l = (55
30 29 3. TEORI Vi er å videre iteressert i å fie, ( l f L, og et me brukt teorem i statistikk sier at fra likig 55 så ka vi skrive, ( l f L slik:, (, (, ( (, ( ' (, ( ' ' l f l f l f L L L = = (56 Videre følger da forvetige til dee fuksjoe: [ ] d l f l L E L =, (, (, ( ( ' (57 Empirisk ka forvetige skrives slik: [ ] [ ] = = = 1, ( 1 i i l l L E (58 Det er viktig år ma skal plotte disse data at ma hele tide passer på at ma bruker de samme vastadsdataee for skadefuksjoe og frekvesfordelige.
31 4.1 FLOMFREKVENSANALYSE 30 4 Metode 4.1 Flomfrekvesaalse Flomfrekvesaalse er e viktig del av risikoaalse, og årsake til dette vil bli beskrevet ærmere i kapittel 4.2. Det er alltid greiest å bege med dee aalse, me fordi dataee som ligger til gru er forholdsvis lette å få tak i, og det er viktig å ta seg god tid med å studere vastadsdataee får ma setter i gag. Det er viktig å ata at dataee er uavhegig før ma går i gag med e flomfrekvesaalse, da all bakgrusteori krever at data er uavhegige idetiske fordelte variable. I e flomfrekvesaalse er ma ikke iteressert i alle de opprielige vastadsdataee, me ma plukker ut ku de ekstreme hedelsee og aalserer disse. Dette ka gjøres på to forskjellige måter: 1. Plukke ut de høeste verdie for hvert år, de såkalt AM-metode. 2. Plukke ut alle verdier over e viss terskel, POT-metode. POT er e mer kompleks metode e AM, og krever mer arbeid og aalse fra brukere. Det kreves også i e POT-aalse at dataee er uavhegige av hveradre. Det kreves for så vidt også for AM-metode, me side ma bare plukker ut e verdi per år så ka vi ata uavhegighet. POT er sett på som e mer robust metode e AM fordi de tillater mer data, så hvis det er mulig å bruke dee bør de brukes. AM ka i teorie gå glipp av de est høest verdie. I følge Rao og Hamed (2000 er AM mer statistisk effektiv e POT år λ er lite (λ<1.65. λ er årlig gjeomsittlig atall verdier som er over terskele. Et aet problem med POT er at e verdi over terskele ofte kommer dage etter e ae som også er over terskele. Det betr at disse dataee er avhegige av hveradre, og de laveste må fjeres mauelt. Dette ka løses med å bruke e form for clusteraalse hvor ma ku tar vare på de største verdie iefor et gitt itervall. POT-data pleier å følge e geeralied parreto fordelig i motsetig til AM, som følger e GEV-fordelig. Valg av begge disse fordeligee samsvarer meget godt overes med teorie, slik at det ikke er oe gru til å prøve å tilpasse data til adre fordeliger.
32 31 4. METODE 4.2 Risikoberegig Flomrisikoaalse tar utgagspukt i to forskjellige aalser, e valig flomfrekvesaalse og e skadefuksjosaalse. Disse to aalsee ka til slutt kombieres og ma får et plott som i Figur 25. E geerell fremgagsmåte blir da å alltid ta utgagspuktet i et overskridelsessaslighetplott og et vastadskadeplott som vist i Figur 8. Side vastade er represetert i begge de to plottee (a og (b, ka da e skadekurve ekelt kostrueres ut i fra dette. Fra dette følger det at ma ka skrive følgede: F ( = F ( l( F ( l Z L = L (59 r = lf ( l dl = l( f ( d L 0 0 Z (60 der l( er skadefuksjoe og f ( er frekvesfordelige til flommee. Risikoe r er forvetige til skadefuksjoe l, eller gjeomsittlig årlig skade. (a (b Vastad Vastad Overskridelsessaslighet Figur 8: Figure viser fremgagsmåte for å kostruere e skadekurve ved å kombiere et overskridelsessaslighetsplott (a fra flomfrekvesaalse og et vastad-skadeplott (b fra risikoaalse.
33 4.3 SKADEFUNKSJON FOR VEI/JERNBANE 32 Dee fremgagsmåte gjelder for alle skadeberegiger i dette arbeidet. Det er ku skadefuksjoe som ligger til gru for plott (b som varierer om det er vei, jerbaer eller bolighus ma studerer. 4.3 Skadefuksjo for vei/jerbae. For veier og jerbae er det blitt brukt e skadefuksjo som ikke bgger på statistiske beregiger. Metodee brukt for disse aalsee er ekle og rett fram. De er helt forskjellig fra skadefuksjoe presetert i 4.2. Framgagsmåte for å fie de total kostade blir da: 1. Plukke ut midtlije til veiee fra e sosi-fil. Dette er kaskje ikke implemetert i de este sosi-stadarde. 2. Koverter disse til gridceller på for eksempel 5x5 meter, eller helst så lite som mulig 3. Tilorde hødeverdier til gridet ut i fra e hødemodell 4. Plukke ut e god del aktuelle hødeverdier, og tell opp atall gridceller som ligger lavere e disse hødeverdiee. 5. Nå ka disse hødeverdiee multipliseres med gridstørrelse, og vi får atall kilometer oversvømt for gitte vastader. 6. Side vi vet kostade pr. kilometer har vi ok til å etablere e vastadskadekurve for vei eller jerbae. 7. I tillegg treger ma å kostruerer e overskridelsessaslighetskurve fra flomfrekvesaalse. 8. Skadekurve ka å kostrueres ut i fra overskridelsessaslighetsplottet og vastad-skadeplottet slik som Figur 8 viser. Dette er e veldig ekel fremgagsmåte, og det er her blitt brukt e god del tilærmiger. Det er ikke tatt hes til at skade blir større ved e lagvarig flom, og det er ku brukt et kostadskille: oversvømt eller ikke-oversvømt. Det ka også oppstå skade, selv om flomme ikke år helt opp til objektet. For jerbae er det foreslått av Wathe m. flere(1999 at ma skal dele opp i 3 lag: Formasjosplaet, overbgig og skier. Skadee vil da bege cirka e meter uder bakke, og øke med høde.
34 33 4. METODE E flom som er så stor at de gir store flomskader i Lillestrøm og Hamar, er ofte forelig med at små sideelver også går over sie bredder og forsterker flomme. Det er ofte slike sideelver som gjør de største skadee på veier og jerbaer. I kostadsdataee presetert i kapittel 2.3 er de totale skade tatt med, iklusiv skade fra sideelver. Disse kostadee vil da trolig bli litt for høe i forhold til det reelle tallet. Det er jo veier/jerbae oversvømt av isjøe som er iteressat i oppgave. 4.4 Skadefuksjoe for bgiger For å fie skadefuksjoe til bgiger, er det brukt e mer detaljert beregig e de for vei/jerbae. Her er det fulgt teorie fra kapittel Begresede megder data medførte at bolighus var de eeste bgigsforme som ble sett på i oppgave. Me det er viktig å merke seg at akkurat de samme metode ka brukes til hvilke som helst ae bgigstpe. E ekel beskrivelse på hvorda dette ka gjøres i praksis: 1. Gjør e flomfrekvesaalse for det aktuelle området. E regioal flomfrekvesaalse er å foretrekke hvis det er oppåelig. 2. Importer Sosi-file i Arcifo 3. Plukk ut alle flater med temakode 5001 (bgiger og ku de tper bgiger hvor skadefuksjoe er kjet, fra e sosi-fil. 4. Tilorde disse flatee hødeverdier ved hjelp av e terregmodell 5. Eksporter dette i i et statistikkprogram, og gjør reste av aalse der. 6. For så videre å kue lage e vastad-skadekurve ka ma følge metode for skadefuksjoe beskrevet i kapittel I tillegg treger ma å kostruerer e overskridelsessaslighetskurve fra flomfrekvesaalse. 8. Skadekurve ka å kostrueres ut i fra overskridelsessaslighetsplottet og vastad-skadeplottet slik som Figur 8 viser. Terregmodelle er i oppgave kostruert ut i fra hødekurver med 1 og 5 meters ekvidistase. Iterpolasjosmetode som er brukt til dette er topogrid. Nærmere beskrivelse av dee metode ka fies i Hutchiso(1989.
35 5.1 INNLEDENDE FLOMFREKVENSANALYSE 34 5 Resultater og diskusjo 5.1 Iledede flomfrekvesaalse Som bakgru for risikoaalse kreves det at det gjøres e flomfrekvesaalse. E viktig forutsetig for å kue utføre e slik er at data er uavhegige idetiske fordelte variable. Det er ofte vaskelig å få data som tilfredsstiller dette kravet, så det kreves e tilærmig. Series : Hamar Series : Lillestrøm ACF ACF Lag Lag Figur 9: Figure over viser et autokorrelasjosplot over vastad fra Hamar og Lillestrøm (Mørkfoss som sier oe om avhegighete fra et gjeomsittlig tidspukt og framover i tid. 1 lag er i dette tilfellet e dag. Autokorrelasjoesplottet fra Figur 9 viser at dataee er sterkt avhegig av hveradre. Selv etter 45 dager er det e korrelasjo på ca Fra dette er det da tdelig at flere av de høeste verdiee kommer fra samme hedelse. For POTaalse krever dette at ma bruker e kluster-metode for å luke bort de dataee som er fra samme hedelse. Bruk av POT-data er ok mer aktuelt for vaførigsdata e i dette tilfellet hvor det er brukt vastadsdata, fordi det er me tregere respos i e isjø som Mjøsa e i for eksempel Glomma. Det ble gjort oe forsøk på å plukke ut POT-data, me λ-verdiee (atall verdier per år over e bestemt terskel var tett opptil 1, altså este ekvivalet med AM. Så i oppgave er det brukt AM-verdier til de videre aalse, selv om bruk av POT er
36 35 5. RESULTATER OG DISKUSJON sett på som e mer robuste metode. Det hadde vært e stor fordel å kue brukt POTdata her side de pålitelige måleseriee er så korte. Petterso(1997 har også brukt AM-data til e likede aalse for både Øere og Mjøsa. Mjøsa Øere Vastad(meter Vastad(meter år år Figur 10: Tredplott for vastade for målestasjoee på Mørkfoss og i Hamar Det er verdt å merke seg at de fleste AM verdiee kommer fra vårflomme. De største flommee i disse vassdragee kommer som regel som vårflommer. E vårflom oppstår i hovedsak pga. søsmeltig, mes e høstflom som oftest er forårsaket av reg. I Mjøsa er høstflomme som regel også et resultat av vårflomme, da det tar lag tid før vastade går ed etter vårflomme. Det ka være lurte å ikke blade data fra høst og vår, fordi de kommer fra to forskjellige populasjoer. Hvis det er e ormal flom i vassdraget, sker vastade sakte. Er det derimot e storflom, går vastade fort ed til det ivået e ormalflom ligger på. Figur 10 viser at det er e markat egativ tred i data både for Mjøsa og Øere. E tred ka ete skldes at vassdraget har blitt regulert eller at det har skjedd klimaedriger. I disse to tilfellee er det ok mest saslig at trede skldes reguleriger Mjøsa Fra Figur 10 ser vi at det er e markat tred i data, t-verdie bekrefter også dette. Side vi er iteressert i e flomfrekvesaalse for dages forhold er det e for stor tred i data til å bruke måleserie i si helhet.
37 5.2 USIKKERHETSBEREGNINGER vastad Februar April 100 Jui 200August Oktober 300 Desember Dato Figur 11: Vastadskurve for Hamar i Det ka se ut som at vastade i Mjøsa først stabiliserer seg på et fast ivå etter siste regulerigsedrig i Det beste hadde da vært å bare brukt data etter 1961 i de videre aalse. Me det er ikke så lett, da de teoretisk tilpasige ikke blir særlig robust med et så lite datagrulag. Et alterativ hadde vært å fjere trede fra dataseriee, ved å trekke fra regresjoslija fra Figur 10. Dette er litt skummelt da oppførsele til dataee egetlig er mer trappetriformet. Da måtte ma evetuelt fjeret trede for periode frem til 1961 og koblet dette samme med de resterede data. Det er mulig dette hadde gitt et mer reelt resultat, me ma må være veldig forsiktig med å maipulere slik med data. Det ble dermed valgt å dele opp serie i to, e periode fram til 1961 og e fra 1962 og utover, og kjøre aalse parallelt for disse to med hovedtgde på de seere periode.
38 37 5. RESULTATER OG DISKUSJON Gjetaksitervall i år Gjetaksitervall i år Vastad Fra 1909 Til % kofidestitervall F(x Data Vastad Fra 1962 Til % kofidestitervall F(x Data Reduced Gumbel variate Reduced Gumbel variate Figur 12: Reduced gumbel-plott for Hamar for periode , og for periode Fra Figur 12 ser vi at plottet blir aerledes om vi plukker ut data fram til regulerige av Svafoss i 1961, e etter regulerige. Vi ka også legge merke til at de høre kurve følger e weibullfordelig mes de vestre følger frechetfordelige. Det ka da tde på at det har skjedd e edrig i oppførsele til vassdraget, og ma bør dermed være forsiktig med å bruke data fra før For å fie de teoretiske fordeligsfuksjoe til data ble GEV-fordelige brukt, da teorie i kapittel idikerer at det ka være lurt å bruke dee fordelige til maksimumsverdier. Det er like viktig med e god teoretisk bakgru, som at fordelige er godt tilpasset til data Øere På samme måte som for Mjøsa ser vi av Figur 10 at det er e tdelig tred i data, faktisk større e for Mjøsa. I motsetig til Mjøsa ka ma fra Figur 13 se at reguleriger har gjort store utslag på gjetaksitervallet. Det er også verdt å merke seg at i periode fra har det vært hele 8 flommer som har ådd høere e hva flomme gjorde i For dee periode er de teoretiske fordelige godt tilpasset data, mes for de seiere periode passer det ikke fullt så bra. Flomme i 1995 er ok de største årsake til dee dårlige tilpasige i tillegg til at 24 år er et lite datagrulag. E bedre tilpasig ka ma oppå ved å ata at 1995 er e såkalt outlier, og fjere dee. I så tilfelle vil trolig gjetaksitervallet bli uderestimert, side det da ikke bgger på oe ekstreme hedelser. Petterso(2002 har brukt periode til å fie lave gjetaksitervall, og periode for å fie høe gjetaksitervall for Øere. E flomfrekvesaalse for periode 1962-
39 5.2 USIKKERHETSBEREGNINGER gir me større flom for høe gjetaksitervall e periode , selv om det meste av regulerige i vassdraget skal være gjort ie da. Side det er først etter 1973 at det ikke er e egativ tred i data, er det i dette arbeidet valgt å bruke periode istedefor Det er i tillegg valgt å se på periode Da det er este 3 meters forskjell på et 50 års gjetaksitervall i de to aalsee fra Figur 13, ka dette tde på at ma bør være meget forsiktig med hva ma gjør. Selv om dataee fra er dårlig tilpasset GEV-fordelige, er det ok det beste utgagspuktet for e videre flomrisikoaalse, side vassdraget trolig vil oppføre seg ligede i framtide. Det er også mulig å foreta e såkalt goodess of fit test for å verifisere om tilpasige er god ok. E slik test vil rimelig sikkert kokludere med at tilpasige for periode ikke er god ok. Et eksempel på e slik test som fugerer greit for ekstremverdier er Aderso-Darlig test. Det er også mulig å se på kjeretetthetsplott for simulerig av parametere, oe som er ærmere beskrevet i kapittel Gjetaksitervall i år Gjetaksitervall i år Vastad Fra 1909 Til % kofidestitervall F(x Data + Vastad Fra 1974 Til Reduced Gumbel variate Reduced Gumbel variate Figur 13: Plottet viser flomfrekvesaalse for Mørkfoss, delt opp før og etter siste regulerig. Det er også videre i riskoaalse tatt med data fra før og etter 1974 for å sammelige, selv om data etter siste regulerig trolig er mer å stole på. Det hadde også for Øere vært e mulighet å fjeret trede vist i Figur 10, og basert de videre aalse på dette. For Øere hadde dette vært mer aktuelt å gjøre e for Hamar, da periode er kortere og det er usikkert hvor me ma ka stole på beregige fra flomfrekvesaalse for
40 39 5. RESULTATER OG DISKUSJON Regioal flomfrekvesaalse De opprielige plae for dette arbeidet var å kjøre e regioal flomfrekvesaalse for data fra Mjøsa og Øere, og deretter å skape skadekurver ut fra dette. Øere blir påvirket av både Mjøsa- og Glomma-vassdraget, slik at forholdee i Øere blir så forskjellig fra Mjøsa at e regioal flomfrekvesaalse blir vaskelig. Uder store flommer er det valig at ma holder igje vaet i Mjøsa, slik at flomtoppe fra Vorma og Glomma ikke skal møtes samtidig og skape problemer i Øere Det ble gjort oe forsøk med e slik regioal aalse, me resultatet viste seg å bli for sprikede. E evetuell fordel med e regioal aalse hadde vært at ma hadde fått et større datagrulag, og kue miimert usikkerhete. Gjetaksitervall i år Normalisert vastad % kofidestitervall Teoretisk tilpassig Data for Mjøsa Data for Øere Reduced Gumbel variate Figur 14: Et reduced Gumbel plott over regioal flomfrekvesaalse for Mjøsa og Øere for periode Figur 14 viser at de regioale tilpassige, som også er med AM-data, ikke er helt bra og seriee spriker litt for me fra hveradre. Det er tdelig å se at de ikke følger de samme fordelige. I e regioal flomfrekvesaalse er det også e fordel å bruke så mage målestasjoer som mulig, to stasjoer ka være litt lite hvis data ikke passer godt overes.
Mer om utvalgsundersøkelser
 Mer om utvalgsudersøkelser I uderkapittel 3.6 i læreboka gir vi e kort iførig i takegage ved utvalgsudersøkelser. Vi gir her e grudigere framstillig av temaet. Populasjo og utvalg Ved e utvalgsudersøkelse
Mer om utvalgsudersøkelser I uderkapittel 3.6 i læreboka gir vi e kort iførig i takegage ved utvalgsudersøkelser. Vi gir her e grudigere framstillig av temaet. Populasjo og utvalg Ved e utvalgsudersøkelse
LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4245 STATISTIKK 6.august 2004
 Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Side av 0 LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4245 STATISTIKK 6.august 2004 Oppgave Midtveiseksame a) X er e stokastisk variabel
Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Side av 0 LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4245 STATISTIKK 6.august 2004 Oppgave Midtveiseksame a) X er e stokastisk variabel
ÅMA110 Sannsynlighetsregning med statistikk, våren 2010 Kp. 6, del 5
 ÅMA110 Sasylighetsregig med statistikk, våre 2010 Kp. 6, del 5 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 12. april Bjør H. Auestad Kp. 6: Hypotesetestig del 4 1/ 59
ÅMA110 Sasylighetsregig med statistikk, våre 2010 Kp. 6, del 5 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 12. april Bjør H. Auestad Kp. 6: Hypotesetestig del 4 1/ 59
Introduksjon. Hypotesetesting / inferens (kap 3) Populasjon og utvalg. Populasjon og utvalg. Populasjonsvarians
 Hypotesetestig / iferes (kap ) Itroduksjo Populasjo og utvalg Statistisk iferes Utvalgsfordelig (samplig distributio) Utvalgsfordelige til gjeomsittet Itroduksjo Vi øsker å få iformasjo om størrelsee i
Hypotesetestig / iferes (kap ) Itroduksjo Populasjo og utvalg Statistisk iferes Utvalgsfordelig (samplig distributio) Utvalgsfordelige til gjeomsittet Itroduksjo Vi øsker å få iformasjo om størrelsee i
ÅMA110 Sannsynlighetsregning med statistikk, våren 2007 Kp. 6, del 4. Hypotesetesting, del 4
 ÅMA11 Sasylighetsregig med statistikk, våre 27 Kp. 6, del 4 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 19. mars Bjør H. Auestad Kp. 6: Hypotesetestig del 4 1/ 27 Bjør
ÅMA11 Sasylighetsregig med statistikk, våre 27 Kp. 6, del 4 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 19. mars Bjør H. Auestad Kp. 6: Hypotesetestig del 4 1/ 27 Bjør
Forelesning 4 og 5 Transformasjon, Weibull-, lognormal, beta-, kji-kvadrat -, t-, F- fordeling
 STAT (V6) Statistikk Metoder Yushu.Li@uib.o Forelesig 4 og 5 Trasformasjo, Weibull-, logormal, beta-, kji-kvadrat -, t-, F- fordelig. Oppsummerig til Forelesig og..) Momet (momet about 0) og setral momet
STAT (V6) Statistikk Metoder Yushu.Li@uib.o Forelesig 4 og 5 Trasformasjo, Weibull-, logormal, beta-, kji-kvadrat -, t-, F- fordelig. Oppsummerig til Forelesig og..) Momet (momet about 0) og setral momet
Løsningsforslag for andre obligatoriske oppgave i STK1100 Våren 2007 Av Ingunn Fride Tvete og Ørnulf Borgan
 Løsigsforslag for adre obligatoriske oppgave i STK11 Våre 27 Av Igu Fride Tvete (ift@math..uio.o) og Ørulf Borga (borga@math.uio.o). NB! Feil ka forekomme. NB! Sed gjere e mail hvis du fier e feil! Oppgave
Løsigsforslag for adre obligatoriske oppgave i STK11 Våre 27 Av Igu Fride Tvete (ift@math..uio.o) og Ørulf Borga (borga@math.uio.o). NB! Feil ka forekomme. NB! Sed gjere e mail hvis du fier e feil! Oppgave
Påliteligheten til en stikkprøve
 Pålitelighete til e stikkprøve Om origiale... 1 Beskrivelse... 2 Oppgaver... 4 Løsigsforslag... 4 Didaktisk bakgru... 5 Om origiale "Zuverlässigkeit eier Stichprobe" på http://www.mathe-olie.at/galerie/wstat2/stichprobe/dee
Pålitelighete til e stikkprøve Om origiale... 1 Beskrivelse... 2 Oppgaver... 4 Løsigsforslag... 4 Didaktisk bakgru... 5 Om origiale "Zuverlässigkeit eier Stichprobe" på http://www.mathe-olie.at/galerie/wstat2/stichprobe/dee
Econ 2130 uke 15 (HG) Poissonfordelingen og innføring i estimering
 Eco 130 uke 15 (HG) Poissofordelige og iførig i estimerig 1 Poissofordelige (i) Tilærmig til biomialfordelige. Regel. ( Poissotilærmelse ) Ata Y ~ bi(, p) E( Y ) = p og var( Y ) = p(1 p). Hvis er stor
Eco 130 uke 15 (HG) Poissofordelige og iførig i estimerig 1 Poissofordelige (i) Tilærmig til biomialfordelige. Regel. ( Poissotilærmelse ) Ata Y ~ bi(, p) E( Y ) = p og var( Y ) = p(1 p). Hvis er stor
Konfidensintervall. Notat til STK1110. Ørnulf Borgan, Ingrid K. Glad og Anders Rygh Swensen Matematisk institutt, Universitetet i Oslo.
 Kofidesitervall Notat til STK1110 Ørulf Borga, Igrid K. Glad og Aders Rygh Swese Matematisk istitutt, Uiversitetet i Oslo August 2007 Formål E valig metode for å agi usikkerhete til et estimat er å berege
Kofidesitervall Notat til STK1110 Ørulf Borga, Igrid K. Glad og Aders Rygh Swese Matematisk istitutt, Uiversitetet i Oslo August 2007 Formål E valig metode for å agi usikkerhete til et estimat er å berege
Repetisjon; 9.1, 9.2, 9.3, 9.4, 9.5, og Repetisjon; 9.1, 9.2, 9.3, 9.4, 9.5, og 9.10
 Repetisjo; 9.1, 9.2, 9.3, 9.4, 9.5, og 9.10 og Geerell defiisjo av : Situasjo: Data x 1,...,x ;utfallav:x 1,...,X ; u.i.f. tilfeldige variable Ukjet parameter i fordelige til X i ee: θ Dersom L og U L
Repetisjo; 9.1, 9.2, 9.3, 9.4, 9.5, og 9.10 og Geerell defiisjo av : Situasjo: Data x 1,...,x ;utfallav:x 1,...,X ; u.i.f. tilfeldige variable Ukjet parameter i fordelige til X i ee: θ Dersom L og U L
MOT310 Statistiske metoder 1, høsten 2011
 MOT310 Statistiske metoder 1, høste 2011 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 24. august, 2011 Bjør H. Auestad Itroduksjo og repetisjo 1 / 32 Repetisjo; 9.1,
MOT310 Statistiske metoder 1, høste 2011 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 24. august, 2011 Bjør H. Auestad Itroduksjo og repetisjo 1 / 32 Repetisjo; 9.1,
Løsningsforsalg til første sett med obligatoriske oppgaver i STK1110 høsten 2018
 Løsigsforsalg til første sett med obligatoriske oppgaver i STK1110 høste 2018 Oppgave 1 (a Et 100(1 α% kofidesitervall for forvetigsverdie µ er gitt ved formel (8.15 på side 403 i læreboka. For situasjoe
Løsigsforsalg til første sett med obligatoriske oppgaver i STK1110 høste 2018 Oppgave 1 (a Et 100(1 α% kofidesitervall for forvetigsverdie µ er gitt ved formel (8.15 på side 403 i læreboka. For situasjoe
Utvidet løsningsforslag Eksamen i TMA4100 Matematikk 1, 16/12 2008
 Utvidet løsigsforslag Eksame i TMA4 Matematikk, 6/ 8 Oppgave i) Vi gjør substitusjoe u = si θ og får π/ [ u si θ cos θ dθ = u du = E ae løsigsmetode er π/ si θ cos θ dθ = π/ ] si θ dθ = 4 = 4 ( ( ) ( ))
Utvidet løsigsforslag Eksame i TMA4 Matematikk, 6/ 8 Oppgave i) Vi gjør substitusjoe u = si θ og får π/ [ u si θ cos θ dθ = u du = E ae løsigsmetode er π/ si θ cos θ dθ = π/ ] si θ dθ = 4 = 4 ( ( ) ( ))
TALLSVAR. Det anbefales at de 9 deloppgavene merket med A, B, teller likt uansett variasjon i vanskelighetsgrad. Svarene er gitt i << >>.
 1 ECON130: EKSAMEN 013 VÅR - UTSATT PRØVE TALLSVAR. Det abefales at de 9 deloppgavee merket med A, B, teller likt uasett variasjo i vaskelighetsgrad. Svaree er gitt i
1 ECON130: EKSAMEN 013 VÅR - UTSATT PRØVE TALLSVAR. Det abefales at de 9 deloppgavee merket med A, B, teller likt uasett variasjo i vaskelighetsgrad. Svaree er gitt i
ÅMA110 Sannsynlighetsregning med statistikk, våren 2010. Noen viktige sannsynlighetsmodeller. Binomisk modell. Kp. 3 Diskrete tilfeldige variable
 ÅMA Saslighetsregig med statistikk, våre K. 3 Diskrete tilfeldige variable Noe viktige saslighetsmodeller Noe viktige saslighetsmodeller ( Sas.modell : å betr det klasse/te sas.fordelig.) Biomisk modell
ÅMA Saslighetsregig med statistikk, våre K. 3 Diskrete tilfeldige variable Noe viktige saslighetsmodeller Noe viktige saslighetsmodeller ( Sas.modell : å betr det klasse/te sas.fordelig.) Biomisk modell
X = 1 5. X i, i=1. som vil være normalfordelt med forventningsverdi E( X) = µ og varians Var( X) = σ 2 /5. En rimelig estimator for variansen er
 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Abefalte oppgaver 11, blokk II Løsigsskisse Oppgave 1 a) E rimelig estimator for forvetigsverdie µ er gjeomsittet X = 1 X i, som
Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Abefalte oppgaver 11, blokk II Løsigsskisse Oppgave 1 a) E rimelig estimator for forvetigsverdie µ er gjeomsittet X = 1 X i, som
ARBEIDSHEFTE I MATEMATIKK
 ARBEIDSHEFTE I MATEMATIKK Temahefte r Hvorda du reger med poteser Detaljerte forklariger Av Matthias Loretze mattegriseforlag.com Opplsig: E potes er e forkortet skrivemåte for like faktorer. E potes består
ARBEIDSHEFTE I MATEMATIKK Temahefte r Hvorda du reger med poteser Detaljerte forklariger Av Matthias Loretze mattegriseforlag.com Opplsig: E potes er e forkortet skrivemåte for like faktorer. E potes består
TMA4245 Statistikk Eksamen mai 2017
 TMA445 Statistikk Eksame mai 07 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Løsigsskisse Oppgave a Når vi reger ut disse tre sasylighetee må ma huske på at de mulige verdiee
TMA445 Statistikk Eksame mai 07 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Løsigsskisse Oppgave a Når vi reger ut disse tre sasylighetee må ma huske på at de mulige verdiee
Løsningsforsalg til første sett med obligatoriske oppgaver i STK1110 høsten 2015
 Løsigsforsalg til første sett med obligatoriske oppgaver i STK1110 høste 2015 Oppgave 1 (a Et 100(1 α% kofidesitervall for forvetigsverdie µ er gitt ved formel (8.15 på side 403 i læreboka. For situasjoe
Løsigsforsalg til første sett med obligatoriske oppgaver i STK1110 høste 2015 Oppgave 1 (a Et 100(1 α% kofidesitervall for forvetigsverdie µ er gitt ved formel (8.15 på side 403 i læreboka. For situasjoe
Estimering og hypotesetesting. Estimering og hypotesetesting. Estimering og hypotesetesting. Kapittel 10. Ett- og toutvalgs hypotesetesting
 3 Estimerig og hypotesetestig Kapittel 10 Ett- og toutvalgs hypotesetestig TMA445 V007: Eirik Mo Feome Bilkjørig Høyde til studeter Estimator ˆp = X, X atall ˆµ = X gjeomsittlig høyde. som syes de er flikere
3 Estimerig og hypotesetestig Kapittel 10 Ett- og toutvalgs hypotesetestig TMA445 V007: Eirik Mo Feome Bilkjørig Høyde til studeter Estimator ˆp = X, X atall ˆµ = X gjeomsittlig høyde. som syes de er flikere
KLMED8004 Medisinsk statistikk. Del I, høst Estimering. Tidligere sett på. Eksempel hypertensjon
 Tidligere sett på KLMED8004 Medisisk statistikk Del I, høst 008 Estimerig Hvorda kjete sasylighetsfordeliger (biomialfordelig, ormalfordelig) med kjete populasjosparametrer (forvetig, varias osv.) ka gi
Tidligere sett på KLMED8004 Medisisk statistikk Del I, høst 008 Estimerig Hvorda kjete sasylighetsfordeliger (biomialfordelig, ormalfordelig) med kjete populasjosparametrer (forvetig, varias osv.) ka gi
TMA4240 Statistikk Høst 2016
 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Abefalt øvig 11 Løsigsskisse Oppgave 1 a) E rimelig estimator for forvetigsverdie µ er gjeomsittet X = 1 X i, som vil være ormalfordelt
Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Abefalt øvig 11 Løsigsskisse Oppgave 1 a) E rimelig estimator for forvetigsverdie µ er gjeomsittet X = 1 X i, som vil være ormalfordelt
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-aturviteskapelige fakultet Eksame i: STK2100 Løsigsforslag Eksamesdag: Torsdag 14. jui 2018. Tid for eksame: 14.30 18.30. Oppgavesettet er på 6 sider. Vedlegg: Tillatte
UNIVERSITETET I OSLO Det matematisk-aturviteskapelige fakultet Eksame i: STK2100 Løsigsforslag Eksamesdag: Torsdag 14. jui 2018. Tid for eksame: 14.30 18.30. Oppgavesettet er på 6 sider. Vedlegg: Tillatte
Høgskolen i Telemark Avdeling for estetiske fag, folkekultur og lærerutdanning BOKMÅL 12. desember 2008
 Høgskole i Telemark Avdelig for estetiske fag, folkekultur og lærerutdaig BOKMÅL. desember 8 EKSAMEN I MATEMATIKK, Utsatt røve Modul 5 studieoeg Tid: 5 timer Ogavesettet er å sider (ikludert formelsamlig).
Høgskole i Telemark Avdelig for estetiske fag, folkekultur og lærerutdaig BOKMÅL. desember 8 EKSAMEN I MATEMATIKK, Utsatt røve Modul 5 studieoeg Tid: 5 timer Ogavesettet er å sider (ikludert formelsamlig).
Kap. 9: Inferens om én populasjon. Egenskaper ved t-fordelingen. ST0202 Statistikk for samfunnsvitere. I Kapittel 8 brukte vi observatoren
 2 Kap. 9: Iferes om é populasjo I Kapittel 8 brukte vi observatore z = x μ σ/ for å trekke koklusjoer om μ. Dette krever kjet σ (urealistisk). ST0202 Statistikk for samfusvitere Bo Lidqvist Istitutt for
2 Kap. 9: Iferes om é populasjo I Kapittel 8 brukte vi observatore z = x μ σ/ for å trekke koklusjoer om μ. Dette krever kjet σ (urealistisk). ST0202 Statistikk for samfusvitere Bo Lidqvist Istitutt for
Kapittel 8: Estimering
 Kaittel 8: Estimerig Estimerig hadler kort sagt om hvorda å aslå verdie å arametre som,, og dersom disse er ukjete. like arametre sier oss oe om oulasjoe vi studerer (dvs om alle måliger av feomeet som
Kaittel 8: Estimerig Estimerig hadler kort sagt om hvorda å aslå verdie å arametre som,, og dersom disse er ukjete. like arametre sier oss oe om oulasjoe vi studerer (dvs om alle måliger av feomeet som
Metoder for politiske meningsmålinger
 Metoder for politiske meigsmåliger AV FORSKER IB THOMSE STATISTISK SETRALBYRÅ Beregigsmetodee som brukes i de forskjellige politiske meigsmåliger har vært gjestad for mye diskusjo i dagspresse det siste
Metoder for politiske meigsmåliger AV FORSKER IB THOMSE STATISTISK SETRALBYRÅ Beregigsmetodee som brukes i de forskjellige politiske meigsmåliger har vært gjestad for mye diskusjo i dagspresse det siste
LØSNINGSFORSLAG TILEKSAMEN I FAG TMA4240/TMA4245 STATISTIKK 10. august 2005
 Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Side av 8 LØSNINGSFORSLAG TILEKSAMEN I FAG TMA440/TMA445 STATISTIKK 0. august 005 Oppgave Smeltepuktsbestemmelse a) Vi jobber i dette
Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Side av 8 LØSNINGSFORSLAG TILEKSAMEN I FAG TMA440/TMA445 STATISTIKK 0. august 005 Oppgave Smeltepuktsbestemmelse a) Vi jobber i dette
Oppgaver fra boka: X 2 X n 1
 MOT30 Statistiske metoder, høste 00 Løsiger til regeøvig r 3 (s ) Oppgaver fra boka: 94 (99:7) X,, X uif N(µ, σ ) og X,, X uif N(µ, σ ) og alle variable er uavhegige Atar videre at σ = σ = σ og ukjet Kodesitervall
MOT30 Statistiske metoder, høste 00 Løsiger til regeøvig r 3 (s ) Oppgaver fra boka: 94 (99:7) X,, X uif N(µ, σ ) og X,, X uif N(µ, σ ) og alle variable er uavhegige Atar videre at σ = σ = σ og ukjet Kodesitervall
LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4240 STATISTIKK 5.august 2004
 Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Side av 0 LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4240 STATISTIKK 5.august 2004 Oppgave Foruresig X er e stokastisk variabel som agir
Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Side av 0 LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4240 STATISTIKK 5.august 2004 Oppgave Foruresig X er e stokastisk variabel som agir
ÅMA110 Sannsynlighetsregning med statistikk, våren 2008 Kp. 6, del 5
 ÅMA110 Sasylighetsregig med statistikk, våre 2008 Kp. 6, del 5 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 26. mars Bjør H. Auestad Kp. 6: Hypotesetestig del 5 1/ 53
ÅMA110 Sasylighetsregig med statistikk, våre 2008 Kp. 6, del 5 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 26. mars Bjør H. Auestad Kp. 6: Hypotesetestig del 5 1/ 53
ÅMA110 Sannsynlighetsregning med statistikk, våren Estimering. Målemodellen. Sannsynlighetsregning med statistikk. Kp. 5 Estimering.
 ÅMA asylighetsregig med statistikk våre 008 Kp. 5 Estimerig Estimerig. Målemodelle. Ihold:. (ukt)estimerig i biomisk modell (kp. 5.). Målemodelle... (kp. 5.3) 3. (ukt)estimerig i målemodelle (kp. 5.3)
ÅMA asylighetsregig med statistikk våre 008 Kp. 5 Estimerig Estimerig. Målemodelle. Ihold:. (ukt)estimerig i biomisk modell (kp. 5.). Målemodelle... (kp. 5.3) 3. (ukt)estimerig i målemodelle (kp. 5.3)
5 y y! e 5 = = y=0 P (Y < 5) = P (Y 4) = 0.44,
 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Abefalte oppgaver 9, blokk II Løsigsskisse Oppgave a) Vi lar her Y være atall fugler som kolliderer med vidmølla i løpet av de gitte
Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Abefalte oppgaver 9, blokk II Løsigsskisse Oppgave a) Vi lar her Y være atall fugler som kolliderer med vidmølla i løpet av de gitte
ÅMA110 Sannsynlighetsregning med statistikk, våren 2011
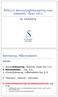 ÅMA110 asylighetsregig med statistikk våre 011 Kp. 5 Estimerig 1 Estimerig. Målemodelle. Ihold: 1. (ukt)estimerig i biomisk modell (kp. 5.). Målemodelle... (kp. 5.3) 3. (ukt)estimerig i målemodelle (kp.
ÅMA110 asylighetsregig med statistikk våre 011 Kp. 5 Estimerig 1 Estimerig. Målemodelle. Ihold: 1. (ukt)estimerig i biomisk modell (kp. 5.). Målemodelle... (kp. 5.3) 3. (ukt)estimerig i målemodelle (kp.
8 (inkludert forsiden og formelsamling) Tegne- og skrivesaker, kalkulator, formelsamling (se vedlagt).
 Eksamesoppgave våre 011 Ordiær eksame Bokmål Fag: Matematikk Eksamesdato: 10.06.011 Studium/klasse: GLU 5-10 Emekode: MGK00 Eksamesform: Skriftlig Atall sider: 8 (ikludert forside og formelsamlig) Eksamestid:
Eksamesoppgave våre 011 Ordiær eksame Bokmål Fag: Matematikk Eksamesdato: 10.06.011 Studium/klasse: GLU 5-10 Emekode: MGK00 Eksamesform: Skriftlig Atall sider: 8 (ikludert forside og formelsamlig) Eksamestid:
Econ 2130 Forelesning uke 11 (HG)
 Eco 130 Forelesig uke 11 (HG) Mer om ormalfordelige og setralgreseteoremet Uke 1 1 Fra forrige gag ~ betyr er fordelt som. ~ N( µσ, ) E( ) = µ, og var( ) = σ Normalfordelige er symmetrisk om μ og kotiuerlig
Eco 130 Forelesig uke 11 (HG) Mer om ormalfordelige og setralgreseteoremet Uke 1 1 Fra forrige gag ~ betyr er fordelt som. ~ N( µσ, ) E( ) = µ, og var( ) = σ Normalfordelige er symmetrisk om μ og kotiuerlig
Numeriske metoder: Euler og Runge-Kutta Matematikk 3 H 2016
 Numeriske metoder: Euler og Ruge-Kutta Matematikk 3 H 06 Iledig Differesiallikiger spiller e setral rolle i modellerigsproblemer i igeiør viteskap, matematikk, fsikk, aeroautikk, astroomi, damikk, elastisitet,
Numeriske metoder: Euler og Ruge-Kutta Matematikk 3 H 06 Iledig Differesiallikiger spiller e setral rolle i modellerigsproblemer i igeiør viteskap, matematikk, fsikk, aeroautikk, astroomi, damikk, elastisitet,
TMA4245 Statistikk Vår 2015
 TMA4245 Statistikk Vår 2015 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Øvig ummer 12, blokk II Oppgave 1 Kari har ylig kjøpt seg e y bil. Nå øsker hu å udersøke biles besiforbruk
TMA4245 Statistikk Vår 2015 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Øvig ummer 12, blokk II Oppgave 1 Kari har ylig kjøpt seg e y bil. Nå øsker hu å udersøke biles besiforbruk
ÅMA110 Sannsynlighetsregning med statistikk, våren 2007
 ÅMA Sasylighetsregig med statistikk, våre 27 Kp. 6 (kp. 6) Tre deler av faget/kurset:. Beskrivede statistikk 2. Sasylighetsteori, sasylighetsregig 3. Statistisk iferes estimerig kofidesitervall hypotesetestig
ÅMA Sasylighetsregig med statistikk, våre 27 Kp. 6 (kp. 6) Tre deler av faget/kurset:. Beskrivede statistikk 2. Sasylighetsteori, sasylighetsregig 3. Statistisk iferes estimerig kofidesitervall hypotesetestig
n 2 +1) hvis n er et partall.
 TMA445 Statistikk Vår 04 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Øvig ummer, blokk II Oppgave Mediae til et datasett, X, er de midterste verdie. Hvis vi har stokastiske
TMA445 Statistikk Vår 04 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Øvig ummer, blokk II Oppgave Mediae til et datasett, X, er de midterste verdie. Hvis vi har stokastiske
Forelesning Moment og Momentgenererende funksjoner
 ushu.li@uib.o Forelesig + 3 Momet og Mometgeererede fuksjoer 1. Oppsummerig til Forelesig 1 1.1) Fuksjoe av S.V: hvis variabele er e fuksjo (trasformasjo) av S.V. : g( ), da er også e S.V.: til ethvert
ushu.li@uib.o Forelesig + 3 Momet og Mometgeererede fuksjoer 1. Oppsummerig til Forelesig 1 1.1) Fuksjoe av S.V: hvis variabele er e fuksjo (trasformasjo) av S.V. : g( ), da er også e S.V.: til ethvert
Kap. 9: Inferens om én populasjon
 2 ST0202 Statistikk for samfusvitere Bo Lidqvist Istitutt for matematiske fag Ka. 9: Iferes om é oulasjo Hvis σ er ukjet bytter vi ut σ med s i Ny observator blir t = x μ s/ z = x μ σ/ der s = Σx 2 (Σx)
2 ST0202 Statistikk for samfusvitere Bo Lidqvist Istitutt for matematiske fag Ka. 9: Iferes om é oulasjo Hvis σ er ukjet bytter vi ut σ med s i Ny observator blir t = x μ s/ z = x μ σ/ der s = Σx 2 (Σx)
EKSAMEN Løsningsforslag
 ..4 EKSAMEN Løsigsforslag Emekode: ITF75 Dato: 6. desember Eme: Matematikk for IT Eksamestid: kl 9. til kl. Hjelpemidler: To A4-ark med valgfritt ihold på begge sider. Kalkulator er ikke tillatt. Faglærer:
..4 EKSAMEN Løsigsforslag Emekode: ITF75 Dato: 6. desember Eme: Matematikk for IT Eksamestid: kl 9. til kl. Hjelpemidler: To A4-ark med valgfritt ihold på begge sider. Kalkulator er ikke tillatt. Faglærer:
Statistikk og økonomi, våren 2017
 Statistikk og økoomi, våre 07 Obligatorisk oppgave 6 Løsigsforslag Oppgave E terig kastes 0 gager, og det registreres hvor mage 6-ere som oppås i løpet av disse 0 kastee. Vi ka kalle atall 6-ere i løpet
Statistikk og økoomi, våre 07 Obligatorisk oppgave 6 Løsigsforslag Oppgave E terig kastes 0 gager, og det registreres hvor mage 6-ere som oppås i løpet av disse 0 kastee. Vi ka kalle atall 6-ere i løpet
Estimering 1 -Punktestimering
 Estimerig 1 -Puktestimerig Dekkes av kap. 8, 9.1-9.3 og 9.15/9.14. Vi har til å settpå e rekke forskjellige sasylighetsfordeliger og sett hvorda disse ka brukes til å modellere mage forskjellige typer
Estimerig 1 -Puktestimerig Dekkes av kap. 8, 9.1-9.3 og 9.15/9.14. Vi har til å settpå e rekke forskjellige sasylighetsfordeliger og sett hvorda disse ka brukes til å modellere mage forskjellige typer
ECON240 Statistikk og økonometri
 ECON240 Statistikk og økoometri Arild Aakvik, Istitutt for økoomi 1 Mellomregig MKM Model: Y i = a i + bx i + e i MKM-estimator for b: b = = Xi Y i 1 Xi Yi Xi 1 ( X i ) 2 (Xi X)(Y i Ȳi) (Xi X) 2 hvor vi
ECON240 Statistikk og økoometri Arild Aakvik, Istitutt for økoomi 1 Mellomregig MKM Model: Y i = a i + bx i + e i MKM-estimator for b: b = = Xi Y i 1 Xi Yi Xi 1 ( X i ) 2 (Xi X)(Y i Ȳi) (Xi X) 2 hvor vi
Eksamen REA3028 S2, Våren 2011
 Eksame REA08 S, Våre 0 Del Tid: timer Hjelpemidler: Valige skrivesaker, passer, lijal med cetimetermål og vikelmåler er tillatt. Oppgave (8 poeg) a) Deriver fuksjoee ) f 5 f 6 5 ) g g ) h l 9 9 6 4 h l
Eksame REA08 S, Våre 0 Del Tid: timer Hjelpemidler: Valige skrivesaker, passer, lijal med cetimetermål og vikelmåler er tillatt. Oppgave (8 poeg) a) Deriver fuksjoee ) f 5 f 6 5 ) g g ) h l 9 9 6 4 h l
STK1100 våren 2017 Estimering
 STK1100 våre 017 Estimerig Svarer til sidee 331-339 i læreboka Ørulf Borga Matematisk istitutt Uiversitetet i Oslo 1 Politisk meigsmålig Spør et tilfeldig utvalg på 1000 persoer hva de ville ha stemt hvis
STK1100 våre 017 Estimerig Svarer til sidee 331-339 i læreboka Ørulf Borga Matematisk istitutt Uiversitetet i Oslo 1 Politisk meigsmålig Spør et tilfeldig utvalg på 1000 persoer hva de ville ha stemt hvis
ÅMA110 Sannsynlighetsregning med statistikk, våren 2007 Kp. 6, del 5. Hypotesetesting, del 5
 ÅMA11 Sasylighetsregig med statistikk, våre 7 Kp. 6, del 5 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 26. mars Bjør H. Auestad Kp. 6: Hypotesetestig del 5 1/ 59 Bjør
ÅMA11 Sasylighetsregig med statistikk, våre 7 Kp. 6, del 5 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 26. mars Bjør H. Auestad Kp. 6: Hypotesetestig del 5 1/ 59 Bjør
3MX 2007/8 - Kapittel 5: 8. januar 5. februar 2008
 3MX 00/8 - Kapittel : 8. jauar. februar 008 Pla for skoleåret 00/008: Kapittel 6: 6/ /. Kapittel : / /3. Prøver på eller skoletime etter hvert kapittel. É heildagsprøve i hver termi. Repetisjo, prøver,
3MX 00/8 - Kapittel : 8. jauar. februar 008 Pla for skoleåret 00/008: Kapittel 6: 6/ /. Kapittel : / /3. Prøver på eller skoletime etter hvert kapittel. É heildagsprøve i hver termi. Repetisjo, prøver,
ÅMA110 Sannsynlighetsregning med statistikk, våren 2008 Kp. 6, del 5
 ÅMA110 Sasylighetsregig med statistikk, våre 2008 Kp. 6, del 5 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 3. april Bjør H. Auestad Kp. 6: Hypotesetestig del 5 1/ 56
ÅMA110 Sasylighetsregig med statistikk, våre 2008 Kp. 6, del 5 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 3. april Bjør H. Auestad Kp. 6: Hypotesetestig del 5 1/ 56
TMA4240 Statistikk Høst 2009
 TMA440 Statistikk Høst 009 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Øvig ummer b4 Løsigsskisse Oppgave Øsker å fie 99% kofidesitervall for µ µ år vi atar ormalfordeliger
TMA440 Statistikk Høst 009 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Øvig ummer b4 Løsigsskisse Oppgave Øsker å fie 99% kofidesitervall for µ µ år vi atar ormalfordeliger
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 Eksame i: ECON130 Statistikk 1 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamesdag: 6.05.017 Sesur kugøres: 16.06.017 Tid for eksame: kl. 14:30 17:30 Oppgavesettet er på 6 sider Tillatte helpemidler: Alle
Eksame i: ECON130 Statistikk 1 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamesdag: 6.05.017 Sesur kugøres: 16.06.017 Tid for eksame: kl. 14:30 17:30 Oppgavesettet er på 6 sider Tillatte helpemidler: Alle
ÅMA110 Sannsynlighetsregning med statistikk, våren 2006 Kp. 6, del 5
 ÅMA110 Sasylighetsregig med statistikk, våre 2006 Kp. 6, del 5 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 3. april Bjør H. Auestad Kp. 6: Hypotesetestig del 5 1 / 56
ÅMA110 Sasylighetsregig med statistikk, våre 2006 Kp. 6, del 5 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 3. april Bjør H. Auestad Kp. 6: Hypotesetestig del 5 1 / 56
Løsning eksamen R1 våren 2010
 Løsig eksame R våre 00 Oppgave a) ) f ( ) l f ( ) ' l l l l f ( ) (l ) ) g( ) 4e g( ) 4 e ( ) 4 e ( ) g( ) 4( ) e b) ( ) 4 4 6 P ) P() 4 4 6 8 6 8 6 0 Divisjo med ( ) går opp. 4 4 6 : ( ) 8 4 4 8 6 8 6
Løsig eksame R våre 00 Oppgave a) ) f ( ) l f ( ) ' l l l l f ( ) (l ) ) g( ) 4e g( ) 4 e ( ) 4 e ( ) g( ) 4( ) e b) ( ) 4 4 6 P ) P() 4 4 6 8 6 8 6 0 Divisjo med ( ) går opp. 4 4 6 : ( ) 8 4 4 8 6 8 6
Hypotesetesting, del 5
 Oversikt, del 5 Kofidesitervall p-verdi Kofidesitervall E (tosidig test ka gjeomføres vha. av et kofidesitervall. For eksempel, dersom vi i målemodell 1 vil teste: H 0 : μ = μ 0 mot H 1 : μ μ 0, ka vi
Oversikt, del 5 Kofidesitervall p-verdi Kofidesitervall E (tosidig test ka gjeomføres vha. av et kofidesitervall. For eksempel, dersom vi i målemodell 1 vil teste: H 0 : μ = μ 0 mot H 1 : μ μ 0, ka vi
TMA4240 Statistikk Høst 2015
 TMA4240 Statistikk Høst 2015 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Øvig ummer 12, blokk II I dee siste øvige fokuserer vi på lieær regresjo, der vi har kjete kovariater
TMA4240 Statistikk Høst 2015 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Øvig ummer 12, blokk II I dee siste øvige fokuserer vi på lieær regresjo, der vi har kjete kovariater
Kommentarer til oppgaver;
 Kapittel - Algebra Versjo: 11.09.1 - Rettet feil i 0, 1 og 70 og lagt i litt om GeoGebra-bruk Kommetarer til oppgaver; 0, 05, 10, 13, 15, 5, 9, 37, 5,, 5, 59, 1, 70, 7, 78, 80,81 0 a) Trykkfeil i D-koloe
Kapittel - Algebra Versjo: 11.09.1 - Rettet feil i 0, 1 og 70 og lagt i litt om GeoGebra-bruk Kommetarer til oppgaver; 0, 05, 10, 13, 15, 5, 9, 37, 5,, 5, 59, 1, 70, 7, 78, 80,81 0 a) Trykkfeil i D-koloe
Modeller og parametre. STK Punktestimering - Kap 7. Eksempel støtfangere. Statistisk inferens. Binomisk fordeling. p X (x) = p x (1 p) n x
 STK1100 - Puktestimerig - Kap 7 Geir Storvik Modeller og parametre Biomisk fordelig ( ) p X (x) = p x (1 p) x x Parameter: p Normalfordelig f X (x) = 1 2πσ e 1 2σ 2 (x µ) 2 11. april 2016 Parametre: µ,
STK1100 - Puktestimerig - Kap 7 Geir Storvik Modeller og parametre Biomisk fordelig ( ) p X (x) = p x (1 p) x x Parameter: p Normalfordelig f X (x) = 1 2πσ e 1 2σ 2 (x µ) 2 11. april 2016 Parametre: µ,
Oppgave 1. (i) Hva er sannsynligheten for at det øverste kortet i bunken er et JA-kort?
 ECON EKSAMEN 8 VÅR TALLSVAR Oppgave Vi har e kortstokk beståede av 6 kort. På av disse står det skrevet JA på forside mes det står NEI på forside av de adre kortee. Hvis ma får se kortet med bakside vedt
ECON EKSAMEN 8 VÅR TALLSVAR Oppgave Vi har e kortstokk beståede av 6 kort. På av disse står det skrevet JA på forside mes det står NEI på forside av de adre kortee. Hvis ma får se kortet med bakside vedt
ÅMA110 Sannsynlighetsregning med statistikk, våren Kontinuerlige tilfeldige variable, intro. Kontinuerlige tilfeldige variable, intro.
 ÅMA Sasylighetsregig med statistikk, våre 6 Kp. 4 Kotiuerlige tilfeldige variable og ormaldelige Kotiuerlige tilfeldige variable, itro. (eller: Kotiuerlige sasylighetsdeliger) Vi har til å sett på diskrete
ÅMA Sasylighetsregig med statistikk, våre 6 Kp. 4 Kotiuerlige tilfeldige variable og ormaldelige Kotiuerlige tilfeldige variable, itro. (eller: Kotiuerlige sasylighetsdeliger) Vi har til å sett på diskrete
ÅMA110 Sannsynlighetsregning med statistikk, våren Kontinuerlige tilfeldige variable, intro. Kontinuerlige tilfeldige variable, intro.
 ÅMA Sasylighetsregig med statistikk, våre Kp. 4 Kotiuerlige tilfeldige variable; Normalfordelig Kotiuerlige tilfeldige variable, itro. (eller: Kotiuerlige sasylighetsfordeliger) Vi har til å sett på diskrete
ÅMA Sasylighetsregig med statistikk, våre Kp. 4 Kotiuerlige tilfeldige variable; Normalfordelig Kotiuerlige tilfeldige variable, itro. (eller: Kotiuerlige sasylighetsfordeliger) Vi har til å sett på diskrete
H 1 : µ 1 µ 2 > 0. t = ( x 1 x 2 ) (µ 1 µ 2 ) s p. s 2 p = s2 1 (n 1 1) + s 2 2 (n 2 1) n 1 + n 2 2
 TMA4245 Statistikk Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Øvig ummer b4 Løsigsskisse Oppgave 1 Vi øsker å fie ut om et ytt serum ka stase leukemi. 5 mus får serumet, 4
TMA4245 Statistikk Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Øvig ummer b4 Løsigsskisse Oppgave 1 Vi øsker å fie ut om et ytt serum ka stase leukemi. 5 mus får serumet, 4
2T kapittel 3 Modellering og bevis Utvalgte løsninger oppgavesamlingen
 T kapittel 3 Modellerig og bevis Utvalgte løsiger oppgavesamlige 301 a Sitthøyde i 1910 blir 170,0 171, 4 170,7. I 1970 blir de 177,1 179, 4 178,3. b Med som atall år etter 1900 og y som sitthøyde i cetimeter
T kapittel 3 Modellerig og bevis Utvalgte løsiger oppgavesamlige 301 a Sitthøyde i 1910 blir 170,0 171, 4 170,7. I 1970 blir de 177,1 179, 4 178,3. b Med som atall år etter 1900 og y som sitthøyde i cetimeter
Estimering 1 -Punktestimering
 Estimerig 1 -Puktestimerig Dekkes av kap. 8, 9.1-9.3 og 9.15/9.14. Vi har til å settpå e rekke forskjellige sasylighetsfordeliger og sett hvorda disse ka brukes til å modellere mage forskjellige typer
Estimerig 1 -Puktestimerig Dekkes av kap. 8, 9.1-9.3 og 9.15/9.14. Vi har til å settpå e rekke forskjellige sasylighetsfordeliger og sett hvorda disse ka brukes til å modellere mage forskjellige typer
Fagdag 2-3mx 24.09.07
 Fagdag 2-3mx 24.09.07 Jeg beklager at jeg ikke har fuet oe ye morsomme spill vi ka studere, til gjegjeld skal dere slippe prøve/test dee gage. Istruks: Vi arbeider som valig med 3 persoer på hver gruppe.
Fagdag 2-3mx 24.09.07 Jeg beklager at jeg ikke har fuet oe ye morsomme spill vi ka studere, til gjegjeld skal dere slippe prøve/test dee gage. Istruks: Vi arbeider som valig med 3 persoer på hver gruppe.
TMA4240 Statistikk Høst 2016
 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Abefalt øvig 8 Løsigsskisse Oppgave 1 a) Simuler 1000 datasett i MATLAB. Hvert datasett skal bestå av 100 utfall fra e ormalfordelig
Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Abefalt øvig 8 Løsigsskisse Oppgave 1 a) Simuler 1000 datasett i MATLAB. Hvert datasett skal bestå av 100 utfall fra e ormalfordelig
Estimering 2. -Konfidensintervall
 Estimerig 2 -Kofidesitervall Dekkes av kap. 9.4-9.5, 9.10, 9.12 og forelesigsotatee. Dersom forsøket gjetas mage gager vil (1 α)100% av itervallee [ ˆΘ L, ˆΘ U ] ieholde de ukjete parametere θ (som er
Estimerig 2 -Kofidesitervall Dekkes av kap. 9.4-9.5, 9.10, 9.12 og forelesigsotatee. Dersom forsøket gjetas mage gager vil (1 α)100% av itervallee [ ˆΘ L, ˆΘ U ] ieholde de ukjete parametere θ (som er
Noen vanlige. Indikatorfordeling: 1, dersom suksess. I mange situasjoner kan fenomenet vi ser på. 0, dersom ikke suksess
 Kapittel 5: Noe valige sasylighetsfordeliger I mage situasjoer ka feomeet vi ser på beskrives med e bestemt type sasylighets- fordelig (e sasylighetsfordelig gitt ved e bestemt formel. Vi skal se på oe
Kapittel 5: Noe valige sasylighetsfordeliger I mage situasjoer ka feomeet vi ser på beskrives med e bestemt type sasylighets- fordelig (e sasylighetsfordelig gitt ved e bestemt formel. Vi skal se på oe
Løsningsforslag ST1101/ST6101 kontinuasjonseksamen 2018
 Løsigsforslag ST/ST6 kotiuasjoseksame Oppgave a Defier hedelsee R, B, B rød kule i første trekig, blå kule i adre trekig, blå kule i tredje trekig. Vi skal fie PR B B for to ulike situasjoer. Geerelt vet
Løsigsforslag ST/ST6 kotiuasjoseksame Oppgave a Defier hedelsee R, B, B rød kule i første trekig, blå kule i adre trekig, blå kule i tredje trekig. Vi skal fie PR B B for to ulike situasjoer. Geerelt vet
Oversikt over konfidensintervall i Econ 2130
 1 HG Revidert april 014 Oversikt over kofidesitervall i Eco 130 Merk at dee oversikte ikke er met å leses istedefor framstillige i Løvås, me som et supplemet. De ieholder tabeller med formler for kofidesitervaller
1 HG Revidert april 014 Oversikt over kofidesitervall i Eco 130 Merk at dee oversikte ikke er met å leses istedefor framstillige i Løvås, me som et supplemet. De ieholder tabeller med formler for kofidesitervaller
Høgskolen i Telemark Avdeling for estetiske fag, folkekultur og lærerutdanning BOKMÅL 20. mai 2008
 Høgskole i Telemark Avdelig for estetiske fag, folkekultur og lærerutdaig BOKMÅL. mai 8 EKSAMEN I MATEMATIKK Modul 5 studieoeg Tid: 5 timer Ogavesettet er å sider (ikludert formelsamlig). Hjelemidler:
Høgskole i Telemark Avdelig for estetiske fag, folkekultur og lærerutdaig BOKMÅL. mai 8 EKSAMEN I MATEMATIKK Modul 5 studieoeg Tid: 5 timer Ogavesettet er å sider (ikludert formelsamlig). Hjelemidler:
Ukeoppgaver i BtG207 Statistikk, uke 4 : Binomisk fordeling. 1
 Ukeoppgaver i BtG20 Statistikk, uke 4 : Biomisk fordelig. 1 Høgskole i Gjøvik Avdelig for tekologi, økoomi og ledelse. Statistikk Ukeoppgaver uke 4 Biomisk fordelig. Oppgave 1 La de stokastiske variable
Ukeoppgaver i BtG20 Statistikk, uke 4 : Biomisk fordelig. 1 Høgskole i Gjøvik Avdelig for tekologi, økoomi og ledelse. Statistikk Ukeoppgaver uke 4 Biomisk fordelig. Oppgave 1 La de stokastiske variable
TMA4240 Statistikk Eksamen desember 2015
 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag TMA20 Statistikk Eksame desember 205 Løsigsskisse Oppgave a) De kumulative fordeligsfuksjoe til X, F (x) P (X x): F (x) P (X x) x
Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag TMA20 Statistikk Eksame desember 205 Løsigsskisse Oppgave a) De kumulative fordeligsfuksjoe til X, F (x) P (X x): F (x) P (X x) x
Forkunnskaper i matematikk for fysikkstudenter. Derivasjon.
 Defiisjo av derivert Vi har stor ytte av å vite hvor raskt e fuksjo vokser eller avtar Mer presist: Vi øsker å bestemme stigigstallet til tagete til fuksjosgrafe P Q Figure til vestre viser hvorda vi ka
Defiisjo av derivert Vi har stor ytte av å vite hvor raskt e fuksjo vokser eller avtar Mer presist: Vi øsker å bestemme stigigstallet til tagete til fuksjosgrafe P Q Figure til vestre viser hvorda vi ka
Løsningsforslag Oppgave 1
 Løsigsforslag Oppgave 1 a X i µ 0 σ X i µ 0 2 σ 2, i 1,..., er uavhegige og stadard N0, 1 fordelte. Da er, i 1,..., uavhegige og χ 2 -fordelte med e frihetsgrad. Da er summe χ 2 -fordelt med atall frihetsgrader
Løsigsforslag Oppgave 1 a X i µ 0 σ X i µ 0 2 σ 2, i 1,..., er uavhegige og stadard N0, 1 fordelte. Da er, i 1,..., uavhegige og χ 2 -fordelte med e frihetsgrad. Da er summe χ 2 -fordelt med atall frihetsgrader
Oversikt over konfidensintervall i Econ 2130
 1 HG Revidert april 011 Oversikt over kofidesitervall i Eco 130 Merk at dee oversikte ikke er met å leses istedefor framstillige i Løvås, me som et supplemet. Løvås ieholder mage verdifulle kommetarer
1 HG Revidert april 011 Oversikt over kofidesitervall i Eco 130 Merk at dee oversikte ikke er met å leses istedefor framstillige i Løvås, me som et supplemet. Løvås ieholder mage verdifulle kommetarer
ÅMA110 Sannsynlighetsregning med statistikk, våren 2007
 ÅMA0 Sasylighetsregig med statistikk, våre 007 Kp. 4 Kotiuerlige tilfeldige variable; Normalfordelig Kotiuerlige tilfeldige variable, itro. (eller: Kotiuerlige sasylighetsfordeliger) Vi har til å sett
ÅMA0 Sasylighetsregig med statistikk, våre 007 Kp. 4 Kotiuerlige tilfeldige variable; Normalfordelig Kotiuerlige tilfeldige variable, itro. (eller: Kotiuerlige sasylighetsfordeliger) Vi har til å sett
TMA4240 Statistikk Høst 2015
 Høst 205 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Øvig ummer, blokk II Løsigsskisse Oppgave a) X bi(, p) fordi: Udersøker uavhegige delar av DNA-strukture. Fi for kvar del
Høst 205 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Øvig ummer, blokk II Løsigsskisse Oppgave a) X bi(, p) fordi: Udersøker uavhegige delar av DNA-strukture. Fi for kvar del
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-aturviteskapelige fakultet Eksame i STK2120 Statistiske metoder og dataaalyse 2 Eksamesdag: Madag 6. jui 2011. Tid for eksame: 09.00 13.00. Oppgavesettet er på 5 sider.
UNIVERSITETET I OSLO Det matematisk-aturviteskapelige fakultet Eksame i STK2120 Statistiske metoder og dataaalyse 2 Eksamesdag: Madag 6. jui 2011. Tid for eksame: 09.00 13.00. Oppgavesettet er på 5 sider.
ÅMA110 Sannsynlighetsregning med statistikk, våren Kontinuerlige tilfeldige variable, intro. Kontinuerlige tilfeldige variable, intro.
 ÅMA0 Sasylighetsregig med statistikk, våre 008 Kp. 4 Kotiuerlige tilfeldige variable; Normalfordelig Kotiuerlige tilfeldige variable, itro. (eller: Kotiuerlige sasylighetsfordeliger) Vi har til å sett
ÅMA0 Sasylighetsregig med statistikk, våre 008 Kp. 4 Kotiuerlige tilfeldige variable; Normalfordelig Kotiuerlige tilfeldige variable, itro. (eller: Kotiuerlige sasylighetsfordeliger) Vi har til å sett
ÅMA110 Sannsynlighetsregning med statistikk, våren 2007 Kp. 6, del 2
 ÅMA11 Sasylighetsregig med statistikk, våre 27 Kp. 6, del 2 Bjør H. Auestad Istitutt for matematikk og aturviteskap 5. mars 21 Bjør H. Auestad Kp. 6: del 1/2 1/ 42 Bjør H. Auestad Kp. 6: del 1/2 2/ 42
ÅMA11 Sasylighetsregig med statistikk, våre 27 Kp. 6, del 2 Bjør H. Auestad Istitutt for matematikk og aturviteskap 5. mars 21 Bjør H. Auestad Kp. 6: del 1/2 1/ 42 Bjør H. Auestad Kp. 6: del 1/2 2/ 42
ÅMA110 Sannsynlighetsregning med statistikk, våren 2010 Kp. 6, del 4
 ÅMA11 Sasylighetsregig med statistikk, våre 21 Kp. 6, del 4 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 22. mars Bjør H. Auestad Kp. 6: Hypotesetestig del 4 1/ 29 Bjør
ÅMA11 Sasylighetsregig med statistikk, våre 21 Kp. 6, del 4 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 22. mars Bjør H. Auestad Kp. 6: Hypotesetestig del 4 1/ 29 Bjør
Oppgave 1 a) Minste kvadraters metode tilpasser en linje til punktene ved å velge den linja som minimerer kvadratsummen. x i (y i α βx i ) = 0, SSE =
 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Abefalte oppgaver 2, blokk II Løsigsskisse Oppgave a Miste kvadraters metode tilpasser e lije til puktee ved å velge de lija som
Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Abefalte oppgaver 2, blokk II Løsigsskisse Oppgave a Miste kvadraters metode tilpasser e lije til puktee ved å velge de lija som
Tema. Statistikk og prøvetakning. Hvorfor måle mer enn en gang? Fordelinger en innledning. Hvorfor måle mer enn en gang
 Tema Statistikk og prøvetakig Marti Veel Svedse Trodheim, 31. jauar 017 Hvorfor måle mer e e gag praktisk tilærmig til statistikk Basis statistiske begreper Best. r 450 krav/veiledig til måliger Eksempler
Tema Statistikk og prøvetakig Marti Veel Svedse Trodheim, 31. jauar 017 Hvorfor måle mer e e gag praktisk tilærmig til statistikk Basis statistiske begreper Best. r 450 krav/veiledig til måliger Eksempler
Forventningsverdi. MAT0100V Sannsynlighetsregning og kombinatorikk
 MAT0100V Sasylighetsregig og kombiatorikk Forvetigsverdi Sasylighetsfordelige til e tilfeldig variabel X gir sasylighete for de ulike verdiee X ka ata Forvetig, varias og stadardavvik Tilærmig av biomiske
MAT0100V Sasylighetsregig og kombiatorikk Forvetigsverdi Sasylighetsfordelige til e tilfeldig variabel X gir sasylighete for de ulike verdiee X ka ata Forvetig, varias og stadardavvik Tilærmig av biomiske
2. Hypotesetesting i ulike sitausjoner: i. for forventingen, μ, i målemodellen med normalantakelse og kjent varians, σ 2.
 Oversikt 1. Hva er hypotesetestig? 2. i ulike sitausjoer: i. for forvetige, μ, med ormalatakelse og kjet varias, σ 2. ii. for forvetige, μ, med stor og ormaltilærmig (variase, σ 2, ukjet). iii. for suksessasylighete,
Oversikt 1. Hva er hypotesetestig? 2. i ulike sitausjoer: i. for forvetige, μ, med ormalatakelse og kjet varias, σ 2. ii. for forvetige, μ, med stor og ormaltilærmig (variase, σ 2, ukjet). iii. for suksessasylighete,
IN3030 Uke 12, v2019. Eric Jul PSE, Inst. for informatikk
 IN3030 Uke 12, v2019 Eric Jul PSE, Ist. for iformatikk 1 Hva skal vi se på i Uke 12 Review Radix sort Oblig 4 Text Program Parallellizig 2 Oblig 4 Radix sort Parallelliser Radix-sorterig med fra 1 5 sifre
IN3030 Uke 12, v2019 Eric Jul PSE, Ist. for iformatikk 1 Hva skal vi se på i Uke 12 Review Radix sort Oblig 4 Text Program Parallellizig 2 Oblig 4 Radix sort Parallelliser Radix-sorterig med fra 1 5 sifre
Deskriptiv statistikk for sentrum og spredning i fordelingen. Gjennomsnitt og standardavvik. eller
 Eksempel : tall dager i sykehus. Ikke-parametriske tester versus parametriske tester Stia Lyderse Presetert på Regioal forskigskoferase for psykiatri og rusfeltet Ålesud 4 jui 03 Behadlig : 6, 5, 37,,
Eksempel : tall dager i sykehus. Ikke-parametriske tester versus parametriske tester Stia Lyderse Presetert på Regioal forskigskoferase for psykiatri og rusfeltet Ålesud 4 jui 03 Behadlig : 6, 5, 37,,
) = P(Z > 0.555) = > ) = P(Z > 2.22) = 0.013
 TMA4240 Statistikk Vår 2008 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Øvig ummer b5 Løsigsskisse Oppgave 1 a) X 1,...,X 16 er u.i.f. N(80,18 2 ). Setter Y = X. i) P(X 1 >
TMA4240 Statistikk Vår 2008 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Øvig ummer b5 Løsigsskisse Oppgave 1 a) X 1,...,X 16 er u.i.f. N(80,18 2 ). Setter Y = X. i) P(X 1 >
ÅMA110 Sannsynlighetsregning med statistikk, våren 2006
 ÅMA110 Sasylighetsregig med statistikk, våre 2006 Kp. 6, del 2 Bjør H. Auestad Kp. 6: Hypotesetesig del 2 1/ 38 Bjør H. Auestad Kp. 6: Hypotesetesig del 2 2/ 38 Oversikt 1. Hva er hypotesetestig? 2. Hypotesetestig
ÅMA110 Sasylighetsregig med statistikk, våre 2006 Kp. 6, del 2 Bjør H. Auestad Kp. 6: Hypotesetesig del 2 1/ 38 Bjør H. Auestad Kp. 6: Hypotesetesig del 2 2/ 38 Oversikt 1. Hva er hypotesetestig? 2. Hypotesetestig
«Uncertainty of the Uncertainty» Del 4 av 6
 «Ucertaity of the Ucertaity» Del 4 av 6 v/rue Øverlad, Traior Elsikkerhet AS Iledig Dette er del fire i artikkelserie om «Ucertaity of the Ucertaity». I dag skal jeg vise deg utledige av formele: σ m s,
«Ucertaity of the Ucertaity» Del 4 av 6 v/rue Øverlad, Traior Elsikkerhet AS Iledig Dette er del fire i artikkelserie om «Ucertaity of the Ucertaity». I dag skal jeg vise deg utledige av formele: σ m s,
MA1101 Grunnkurs Analyse I Høst 2017
 Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag MA0 Grukurs Aalyse I Høst 07 Løsigsforslag Øvig..b) Vi skriver om 7 = 4 4 7 Korollar.. gir at 7 4 er irrasjoal (side vi vet 7 4 er
Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag MA0 Grukurs Aalyse I Høst 07 Løsigsforslag Øvig..b) Vi skriver om 7 = 4 4 7 Korollar.. gir at 7 4 er irrasjoal (side vi vet 7 4 er
Hypotesetesting, del 4
 Oversikt, del 4 t-fordelig t-test t-itervall Del 5 Kofidesitervall vs. test p-verdi t-fordelig Rett på defiisjo: Utgagspuktet er målemodelle med ormalatakelse: X 1,...,X,u.i.f.tilf.var.derX i Nμ, σ 2 ).La
Oversikt, del 4 t-fordelig t-test t-itervall Del 5 Kofidesitervall vs. test p-verdi t-fordelig Rett på defiisjo: Utgagspuktet er målemodelle med ormalatakelse: X 1,...,X,u.i.f.tilf.var.derX i Nμ, σ 2 ).La
Løsningsforslag ST2301 øving 3
 Løsigsforslag ST2301 øvig 3 Kapittel 1 Exercise 11 Et utvalg på 100 idivider trekkes fra e populasjo med tilfeldig parrig. Det ble observert AA 63 idivider av geotype AA, Aa 27, og aa 10. Lag et 95 % kofidesitervall
Løsigsforslag ST2301 øvig 3 Kapittel 1 Exercise 11 Et utvalg på 100 idivider trekkes fra e populasjo med tilfeldig parrig. Det ble observert AA 63 idivider av geotype AA, Aa 27, og aa 10. Lag et 95 % kofidesitervall
Kapittel 7: Noen viktige sannsynlighetsfordelinger
 Kapittel 7: Noe viktige sasylighetsfordeliger I mage situasjoer ka feomeet vi ser på beskrives med e bestemt type sasylighetsfordelig e sasylighetsfordelig gitt ved e bestemt formel. Vi skal se på oe av
Kapittel 7: Noe viktige sasylighetsfordeliger I mage situasjoer ka feomeet vi ser på beskrives med e bestemt type sasylighetsfordelig e sasylighetsfordelig gitt ved e bestemt formel. Vi skal se på oe av
Løsningsforslag til prøveeksamen i MAT1110, våren 2012
 Løsigsforslag til prøveeksame i MAT, våre Oppgave : Vi har A = 3 III+I I+II 3 ( )II 3 3 Legg merke til at A er de utvidede matrise til ligigssystemet. Vi ser at søyle 3 og 4 i de reduserte trappeforme
Løsigsforslag til prøveeksame i MAT, våre Oppgave : Vi har A = 3 III+I I+II 3 ( )II 3 3 Legg merke til at A er de utvidede matrise til ligigssystemet. Vi ser at søyle 3 og 4 i de reduserte trappeforme
Oppgave 1 Hardheten til en bestemt legering er undersøkt med åtte målinger og resultatene ble (i kg/mm 2 ) som i tabellen til høyre.
 EKSAMEN I: ÅMA110 SANNSYNLIGHETSREGNING MED STATISTIKK VARIGHET: 4 TIMER DATO: 28. AUGUST 2010 BOKMÅL TILLATTE HJELPEMIDLER: KALKULATOR: HP30S, Casio FX82 eller TI-30 OPPGAVESETTET BESTÅR AV 3 OPPGAVER
EKSAMEN I: ÅMA110 SANNSYNLIGHETSREGNING MED STATISTIKK VARIGHET: 4 TIMER DATO: 28. AUGUST 2010 BOKMÅL TILLATTE HJELPEMIDLER: KALKULATOR: HP30S, Casio FX82 eller TI-30 OPPGAVESETTET BESTÅR AV 3 OPPGAVER
LØSNING, EKSAMEN I STATISTIKK, TMA4240, DESEMBER Anta at sann porøsitet er r. Måling med utstyret gir da X n(x; r, 0,03).
 LØSNING, EKSAMEN I STATISTIKK, TMA440, DESEMBER 006 OPPGAVE 1 Ata at sa porøsitet er r. Målig med utstyret gir da X (x; r, 0,03). a) ( ) X r P(X > r) P 0,03 > 0 P(Z > 0) 0,5. ( X r P(X r > 0,05) P 0,03
LØSNING, EKSAMEN I STATISTIKK, TMA440, DESEMBER 006 OPPGAVE 1 Ata at sa porøsitet er r. Målig med utstyret gir da X (x; r, 0,03). a) ( ) X r P(X > r) P 0,03 > 0 P(Z > 0) 0,5. ( X r P(X r > 0,05) P 0,03
