Sampling, kvantisering og lagring av lyd
|
|
|
- Jan Ansgar Nilssen
- 8 år siden
- Visninger:
Transkript
1 Litteratur : Temaer i dag: Neste uke : Sampling, kvantisering og lagring av lyd Cyganski kap Merk: trykkfeilliste legges på web-siden Sampling av lyd Kvantisering av lyd Avspilling av samplet og kvantisert lyd Formater for lagring av lyd Bilder, Cyganski kap 5 Generelle lydsignaler Et resultat fra Fourier-teori sier at vi kan uttrykke et vilkårlig periodisk signal som en endelig sum av sinussignaler med ulik frekvens Hver komponent av sinussignalet vektes med en tilsvarende amplitide A i (A i beskriver hvor sterk komponent i er sammenlinget med de andre komponentene) Alle lydsignaler vi hører, kan beskrives som signaler som inneholder ulik frekvensinformasjon (frekvensene kan endre seg med tiden, men i et kort øyeblikk hører vi en lyd som består av svingninger med et antall ulike frekvenser) Ved å se på frekvensspekteret til signalet, kan vi se hvilke frekvenser det inneholder (lærer mer om dette i INF 2400 Stikkordet er Digital Signalbehandling) frekvensinformasjon Dette kan hjelpe oss når vi skal representere lyd INF1040-Lyd2-1 INF1040-Lyd2-2 Sum av harmoniske sinus-komponenter Mer om sum av sinuser Skarpe endringer i kurveform, som feks en firkantpuls, trenger man mange sinuskomponenter for å representere Slike lyder dekker derfor mange frekvenser i frekvensspekteret 4/πcos(2πft), f=2 4/π(cos(2πft)+ 1/3cos(2π3ft) 4/π(cos(2πft)+ 1/3cos(2π3ft)+1/5*cos(2π5ft) Sum av 3 harmoniske sinuser 4/π(cos(2πft)+ 1/3cos(2π3ft)++1/13*cos(2π13ft) Sum av 7 harmoniske sinuser INF1040-Lyd2-3 INF1040-Lyd2-4
2 Frekvensinnhold og båndbredde Eksempel båndbredde Alle lydsignaler kan betraktes som å inneholde et endelig sett av ulike frekvenser lyd30wav Odd Børretzen med full CD-kvalitet, frekvenser opp til Hz Begrepet båndbredde referer til ulike frekvensbånd Hvis vi skal spille signaler opp til Hz må vi ha en båndbredde på Hz lyd31wav Odd Børretzen - kun frekvenser opp til Hz Dette må vi ta hensyn til når vi skal lagre lyd feks på en CD lyd32wav Odd Børretzen - kun frekvenser opp til Hz Vi kan også utnytte informasjon om at mennesket hører frekvenser mellom 20 og Hz lyd33wav Odd Børretzen - kun frekvenser opp til Hz Ulike lydsignaler inneholder ulike bånd av frekvensspekteret: Musikk, feks orkestermusikk, setter store krav til båndbredde (20000 Hz) Tale ligger på max Hz lyd34wav lyd35wav Odd Børretzen - kun frekvenser opp til Hz Odd Børretzen - kun frekvenser opp til Hz Dette brukes i telefonoverføringer (max Hz) Det mest sentrale er den maksimale frekvensen vi ønsker å representere INF1040-Lyd2-5 INF1040-Lyd2-6 Sampling av lyd Sampling Alle lydsignaler må samples og kvantiseres for å kunne lagres digitalt Sampling representerer overgang fra et signal som er kontinuerlig i tid til et signal som er diskret i tid Prosessen som gjør signalet diskret i tid kalles sampling Å sample et signal vil si å plukke ut verdien til signalet på tidspunkter med gitte intervaller Lydstyrken ved tiden t, x(t) må så kvantiseres for å kunne lagres (feks til un-signed byte som gir verdiene 0-255) Vi kan ikke lagre uendelig mange punkter på denne kurven, vi må velge et endelig antall tidspunkter og plukke ut bare en verdi pr tidspunkt Vi lagrer lydstyrken bare for de svarte punktene INF1040-Lyd2-7 INF1040-Lyd2-8
3 Mer om sampling Dette er den kontinuerlige kurven vi skal sample Tidspunktene som vi skal sample på Sampling gjøres av AD-konverteren ved at en Lydstyrke / spenning holdes i et lite tidsintervall (samplingsintervallet) Samplingsintervall og samplingsfrekvens Hvor ofte må vi sample et lydsignal, dvs hvor tett må tidssamplene ligge? Vi antar at vi sampler uniformt, dvs med like lange tidsintervaller Avstanden i tid mellom samplene kalles samplingsintervallet T s (måles i sekunder) Fra samplingsintervallet finner vi samplingsfrekvensen f s f s =1/T s (måles i Hertz) Hvor ofte vi må sample avhenger av hvor fort signalet varierer, dvs hvilke frekvenser signalet består av Det mest kritiske er signalets høyeste frekvens En kvinnestemme må samples med høyere frekvens enn en mannsstemme ( Figurene 1013 og 1015 i boka er byttet om) INF1040-Lyd2-9 INF1040-Lyd2-10 Oversampling og undersampling Anta at vi har et sinus-signal med en frekvens f=125 Hz Hvis vi sampler dette signalet med en samplingsfrekvens f s =1 khz = Hz, så får vi f s /f = 1 000/125 sampler = 8 sampler pr periode T Dette er en oversampling Se plansje 26 i boka (Perioden T ble forklart i Lyd1, foil 15) Sampler vi med f s = 250 Hz, får vi f s /f = 250/125 = 2 sampler pr periode T Dette er det minste antall sampler pr periode som vil gi en korrekt rekonstruksjon av en sinusoid NB! Plansje 27 er feil, den er identisk med 26! Undersampling, f s = 187,5 Hz (ikke 187,5kHz som i figurteksten til plansje 28!) gir f s /f=187,5/125=12/8 sampler pr periode, altså 12 sampler på 8 perioder, som i plansje 28 Men det rekonstruerte signalet er på 625 Hz, ikke 125 Hz! Vi har fått en forvrenging av frekvensinnholdet, aliasing Mer om sampling La oss si at vi har samplet bare for de 3 røde punktene Hvordan ser kurven ut mellom punktene? INF1040-Lyd2-11 INF1040-Lyd2-12
4 Fra samplede punkter til avspilling Mer om avspilling Når lydsignalet skal spilles av, må det konverteres til et kontinuerlig / analogt signal igjen Avspillingsprogrammet må også fylle ut med lydverdier mellom hvert sampel, dvs feks mellom tidspunkt og tidpunkt Denne konverteringen kalles DA-konvertering (Digital -> Analog) og gjøres feks i CD-spilleren (eller i programmet play) For å spille av lydsignalet, må vi vite samplingsraten Vi må vite tidsintervallet mellom et sampel og det neste Avspillingsprogrammet vet at på tidspunkt var lydstyrken l 1, og på tidspunkt var lydstyrken l 2 Dette kan gjøres på flere måter (algoritmer), feks ved Sette inn nuller Sette inn kopier av forrige sampel Lineær interpolasjon Høyere-ordens interpolasjon l 0 l 1 l 2 l 3 l 4 l 5 l 6 INF1040-Lyd2-13 INF1040-Lyd2-14 Avspilling ved å sette inn nuller Denne algoritmen sier at lydsignalet har lydstyrke 0 på alle tidspunkt mellom samplene, feks mellom tidspunkt og tidpunkt Avspilling ved å sette inn kopier av sampel Denne algoritmen sier at lydsignalet har samme lydstyrke på alle tidspunkt mellom samplene, feks mellom tidspunkt og tidpunkt Mellom tidspunktene og tidpunkt ligger det uendelig mange punkter med lydstyrke 0 Dette gjøres vanligvis ved at vi sier vi skifter fra lydstyre l 0 til l 1 på et tidspunkt midt mellom sampel og, osv Med denne metoden skifter signalet brått fra en verdi til en annen Brå skifter gir ikke alltid god lyd! Husk at for å representere slike brå skift trengs det mange frekvenskomponenter, helt opp til de mest høyfrekvente (foil 3&4)! INF1040-Lyd2-15 INF1040-Lyd2-16
5 Avspilling ved lineær interpolasjon Algoritmen sier at lydsignalet har endrer seg gradvis fra den lydstyrken det hadde på tidspunkt til den lydstyrken det skal ha på tidspunkt Avspilling ved høyere-ordens interpolasjon Algoritmen antar at lydsignalet har endrer seg gradvis fra den lydstyrken det hadde på tidspunkt til den lydstyrken det skal ha på tidspunkt Lydstyrken på tidspunkt mellom til finnes ved å legge en rett linje mellom verdien på tidspunkt og verdien på tidspunkt Med denne måten blir det ikke så brå skifter i lydstyrke Den avspilte lyden vil ikke inneholde så høye frekvenser som i forrige algoritme Lydstyrken på tidspunkt mellom til finnes ved å tilpasse en glatt kurve (feks et polynom) mellom verdiene på tidspunkt og verdien på tidspunkt, osv Kurven skal gå gjennom alle punktene,,,,, t g og, og den skal være glatt i skjøtene (for eksempel en spline-kurve) Med denne måten blir det glatte overganger i lydstyrke INF1040-Lyd2-17 INF1040-Lyd2-18 Kommentar til de spesielt interesserte I virkeligheten er det som skjer i en moderne CD-spiller en kombinasjon av både digital og analog signalbehandling Lydsignalet oppsamples, og filteres både med software (digitale filtere) og i elektronikken (analoge filtere) Nyquist-teoremet Anta at et analogt signal er bånd-begrenset, dvs at det ikke har sinuskomponenter med frekvenser over et maksimum f max Signalet kan da rekonstrueres eksakt fra de samplene vi har, hvis samplingsfrekvensen f s = 1/T s er større enn 2f max 2f max kalles Nyquist raten Hvis vi sampler med samplingsfrekvens f s lik 2f max, så sampler vi i henhold til Nyquist-teoremet Anta at vi skal sample lyd slik at vi kan rekonstruere alle hørbare frekvenser (opp til Hz) uten noen feil eller forvrenging Hvor mange sampler må vi da minst ha per sekund? INF1040-Lyd2-19 INF1040-Lyd2-20
6 Sampling med Nyquist-raten Diskret til analog rekonstruksjon gir som resultat den kombinasjon av sinusoider som er kompatibelt med det diskrete signal Vi antar at signalet er samplet med f s =2f max har de lavest mulige frekvenser Sampler vi under Nyquist raten og senere forsøker å rekonstruere det analoge signalet får vi rekonstruert feil signal I praksis oversampler vi med en faktor for å få god rekonstruksjon Aliasing, undersampling og oversampling Aliasing betegner fenomenet at en sinusoid ved for lav samplingsrate gir opphav til samme diskrete signal som en sinusoid med lavere frekvens Undersampling betyr at vi sampler med lavere samplingsrate enn 2f max Da får vi forvrenginger i frekvensinnholdet/aliasing Oversampling betyr at vi sampler med en høyere samplingsrate enn 2f max I rekonstruksjon gjøres en filtrering/prosessering for å få det analoge signalet Denne filtreringen blir enklere, og kan gjøres raskere, hvis vi oversampler Dersom vi oversampler med for høy faktor, øker lagringsbehovet mye Det er ikke dette 4xoversampling på CD-spilleren betyr! INF1040-Lyd2-21 INF1040-Lyd2-22 Kvantisering - antall bit pr sampel På tidspunkt t skal vi lagre verdien til det kontinuerlige lydsignalet x(t) Vi minner om: Hvor mange bit trenger vi pr lydsampel? Lyden vi skal sample er feks en elektrisk spenning som varierer mellom V min og V max Tenk at vi deler området mellom V min og V max i N ulike nivåer Nivåene har som regel lik bredde (uniform kvantisering) V min V max Antall nivåer vi trenger gir oss hva slags datatype vi må velge 8 bit: 2 8 = 256 nivåer 12 bit: 2 12 =4 096 nivåer 16 bit: 2 16 = nivåer 32 bit: 2 32 = nivåer INF1040-Lyd2-23 INF1040-Lyd2-24
7 Mer om kvantisering Antall bit pr sampel kalles ordlengde Med 8 bits ordlengde kan vi lagre verdiene eller -128 til 127 Med heltall deler vi inn intervallet mellom v min og v max i N nivåer med bredde v=(v max -v min )/N Alle verdier for x(t) som ligger i samme celle representerer vi med samme verdi (kalles rekonstruksjonsnivå) Vi finner verdier x(t) skal representeres med som x( t) v v out = min N vmax vmin Hvor mange bits trenger vi for å få så mange nivåer som vi vil? Output Rekonstruksjonsnivå Input Mer kvantisering Anta at x(t) rekonstrueres til verdien f Da får vi en kvantiseringsfeil e = x(t)-f La oss si at vi velger f slik at den ligger midt i kvantiseringscellen Den største kvantiseringsfeilen vi kan få for et sampel er gitt ved bredden på en kvantiseringscelle: f x(t) Alle verdier i dette intervallet kvantiseres til samme verdi f Kvantiseringsfeilen e INF1040-Lyd2-25 INF1040-Lyd2-26 Hvor mange nivåer trenger vi for lyd? Når vi skal velge antall nivåer og dermed ordlengden, kan vi bruke det vi vet om hva øret kan oppfatte Kvantiseringsfeil kalles også kvantiseringsstøy Et mål på hvor stor feilen er, er SNR-raten (Signal-to-noise ratio) Kvantiseringsfeil som er så små at vi ikke kan høre dem, er OK Samtidig kan vi velge ulike nivåer for tale, musikk og telefoner Musikk-CD: 16 bit ( nivåer), samplingsrate Hz Digital telefon: 8 bit, samplingsrate Hz Merk: i tillegg kommer smart koding og kompresjon Kvantisering med 4 vs 16 bit Diskretisert variabel Kvantiserings nivåer 16 bit 4 bit Kontinuerlig variabel INF1040-Lyd2-27 INF1040-Lyd2-28
8 Beethovens 9 symfoni Effekten av ordlengde Bethovens 9, samplet med 441 khz 16 bit kvantisering 4 bit kvantisering Musikk på CD-er ligger med 16 bit pr sampel Prøv programmet DACSimulator med ulike musikkstykker og taleeksempler Varier mellom 1 og 16 bit pr sampel 0 Amplitude bit kvantisering lyd36wav Tid 4 bit kvantisering (dum og dårlig) lyd37wav INF1040-Lyd2-29 INF1040-Lyd2-30 Lagring av digital lyd Anta at vi har samplet med samplingsraten f s, og at vi har samplet minst i henhold til Nyquist raten Vi må lagre f s Da kan vi regne ut T s, dvs hvor lang tid hvert sampel skal spilles av med Hvis lydsignalet varer i N sekunder, må vi lagre N*f s sampler Hvert sampel lagres med valgt datatype (vanligvis 16 bit integer) Hvis vi lagrer i stereo, lagrer vi 2 kanaler (hver med feks 16 bit) Skal vi lagre 1 time musikk som er samplet med samplingsfrekvens Hz, blir lagringsbehovet *3 600*16 bit = bit = byte = 144 MB i mono eller 288 MB i stereo Fra artist via CD til ditt øre ADconverter Sample med Hz Kvantisere til 16 bit Filtering Interpolasjon DA-converter 8xOversampling: legg til 7 kopier av hvert sampel før DA-konvertering for å få bedre rekonstruksjon INF1040-Lyd2-31 INF1040-Lyd2-32
9 Hva ligger på en musikk-cd? Data lagres som bitmønstre i spesielle posisjonsceller/bins Lagringsmedium Lagring og kapasitet Kapasitet Kassett 016 MB Standard for CD audio kalles Red Book Audio-CD er deles inn i følgende enheter: 5 1/4 diskett 12 MB Frame (24 bytes data) 3 1/2 diskett 14 MB En blokk består av 98 frames (24 x 98 = bytes data) Enheten sekund har 75 blokker Harddisk MB-> MB->?? Minutt består av 60 sekunder Kapasiteten er 74 minutter CD-ROM 600 MB Avspilling skjer ved at rotasjonshastigheten varieres (innenfra og utover) slik at 75 blokker leses pr sekund med data rate: DVD MB R = samples/s*2 byte*2 kanaler = bps INF1040-Lyd2-33 INF1040-Lyd2-34 Noen kjente lydformater MP3 (En del av Motion Picture Experts Group (MPEG), layer3, ~64 Kb/s (ukomprimert CD 705 Kb/s)) AU (Sun s lydformat, 8-12 bit, endel brukt på internett) WAV (Microsoft/IBM, offisiell standard for PC) MID (For MIDI koder, ikke all slags lyd) MOD (Krysning mellom WAV og MID) Smakebiter fra signalbehandling Hvordan skal vi best interpolere i DA-konverteringen? Hvordan forsterker vi bassen? Hvordan fjerner vi høyfrekvens støy? Hvordan mikser vi sammen ulike instrumenter? Kan vi spille av med annen hastighet? Hvordan legger vi til ekko/romklang? Kan jeg lage min egen synth? Hvordan lager jeg en sonar eller ultralydscanner? Lær mer i INF Digital signalbehandling Krever MAT 1100 og MAT 1110 INF1040-Lyd2-35 INF1040-Lyd2-36
Analog. INF 1040 Sampling, kvantisering og lagring av lyd. Kontinuerlig. Digital
 INF 14 Sampling, kvantisering og lagring av lyd Temaer i dag : 1. Analog eller digital, kontinuerlig eller diskret 2. Sampling, kvantisering, digitalisering 3. Nyquist-Shannon teoremet 4. Oversampling,
INF 14 Sampling, kvantisering og lagring av lyd Temaer i dag : 1. Analog eller digital, kontinuerlig eller diskret 2. Sampling, kvantisering, digitalisering 3. Nyquist-Shannon teoremet 4. Oversampling,
Tema nr 2: Analog eller digital, kontinuerlig eller diskret. Eksempel på ulike båndbredder. Frekvensinnhold og båndbredde. Analog
 INF 1040 Sampling, kvantisering og lagring av lyd Temaer i dag : 1. Frekvensinnhold og båndbredde 2. Analog eller digital, kontinuerlig eller diskret 3. Sampling, kvantisering, digitalisering 4. Nyquist-Shannon
INF 1040 Sampling, kvantisering og lagring av lyd Temaer i dag : 1. Frekvensinnhold og båndbredde 2. Analog eller digital, kontinuerlig eller diskret 3. Sampling, kvantisering, digitalisering 4. Nyquist-Shannon
INF 1040 Sampling, kvantisering og lagring av lyd
 INF 1040 Sampling, kvantisering og lagring av lyd Temaer i dag : 1. Analog eller digital, kontinuerlig eller diskret 2. Sampling, kvantisering, digitalisering 3. Nyquist-Shannon teoremet 4. Oversampling,
INF 1040 Sampling, kvantisering og lagring av lyd Temaer i dag : 1. Analog eller digital, kontinuerlig eller diskret 2. Sampling, kvantisering, digitalisering 3. Nyquist-Shannon teoremet 4. Oversampling,
Analog. INF 1040 Sampling, kvantisering og lagring av lyd. Kontinuerlig. Digital
 INF 14 Sampling, kvantisering og lagring av lyd Temaer i dag : 1 Analog eller digital, kontinuerlig eller diskret 2 Sampling, kvantisering, digitalisering 3 Nyquist-Shannon teoremet 4 Oversampling, undersampling,
INF 14 Sampling, kvantisering og lagring av lyd Temaer i dag : 1 Analog eller digital, kontinuerlig eller diskret 2 Sampling, kvantisering, digitalisering 3 Nyquist-Shannon teoremet 4 Oversampling, undersampling,
Analog. INF 1040 Sampling, kvantisering og lagring av lyd. Kontinuerlig. Digital
 INF 14 Sampling, kvantisering og lagring av lyd Temaer i dag : 1. Analog eller digital, kontinuerlig eller diskret 2. Sampling, kvantisering, digitalisering 3. Nyquist-Shannon teoremet 4. Oversampling,
INF 14 Sampling, kvantisering og lagring av lyd Temaer i dag : 1. Analog eller digital, kontinuerlig eller diskret 2. Sampling, kvantisering, digitalisering 3. Nyquist-Shannon teoremet 4. Oversampling,
INF 1040 Sampling, kvantisering og lagring av lyd
 INF 1040 Sampling, kvantisering og lagring av lyd Temaer i dag : 1. Analog eller digital, kontinuerlig eller diskret 2. Sampling, kvantisering, digitalisering 3. Nyquist-Shannon teoremet 4. Oversampling,
INF 1040 Sampling, kvantisering og lagring av lyd Temaer i dag : 1. Analog eller digital, kontinuerlig eller diskret 2. Sampling, kvantisering, digitalisering 3. Nyquist-Shannon teoremet 4. Oversampling,
INF 1040 høsten 2008: Oppgavesett 9 Sampling og kvantisering av lyd (kapittel 11)
 INF 1040 høsten 2008: Oppgavesett 9 Sampling og kvantisering av lyd (kapittel 11) Fasitoppgaver Denne seksjonen inneholder innledende oppgaver hvor det finnes en enkel fasit bakerst i oppgavesettet. Det
INF 1040 høsten 2008: Oppgavesett 9 Sampling og kvantisering av lyd (kapittel 11) Fasitoppgaver Denne seksjonen inneholder innledende oppgaver hvor det finnes en enkel fasit bakerst i oppgavesettet. Det
Repetisjon: Sampling. Repetisjon: Diskretisering. Repetisjon: Diskret vs kontinuerlig. Forelesning, 12.februar 2004
 Repetisjon: Diskret vs kontinuerlig Forelesning,.februar 4 Kap. 4.-4. i læreboken. Anta variabelen t slik at a < t < b, (a, b) R sampling og rekonstruksjon, i tids- og frekvensdomenet Nyquist-Shannons
Repetisjon: Diskret vs kontinuerlig Forelesning,.februar 4 Kap. 4.-4. i læreboken. Anta variabelen t slik at a < t < b, (a, b) R sampling og rekonstruksjon, i tids- og frekvensdomenet Nyquist-Shannons
Lyd. Litt praktisk informasjon. Litt fysikk. Lyd som en funksjon av tid. Husk øretelefoner på øvelsestimene denne uken og en stund framover.
 Lyd Hva er lyd? Sinuser, frekvenser, tidssignaler Hvordan representere lydsignaler matematisk? Litt praktisk informasjon Husk øretelefoner på øvelsestimene denne uken og en stund framover. Lydeksemplene
Lyd Hva er lyd? Sinuser, frekvenser, tidssignaler Hvordan representere lydsignaler matematisk? Litt praktisk informasjon Husk øretelefoner på øvelsestimene denne uken og en stund framover. Lydeksemplene
Sampling av bilder. Romlig oppløsning, eksempler. INF Ukens temaer. Hovedsakelig fra kap. 2.4 i DIP
 INF 2310 22.01.2008 Ukens temaer Hovedsakelig fra kap. 2.4 i DIP Romlig oppløsning og sampling av bilder Kvantisering Introduksjon til pikselmanipulasjon i Matlab (i morgen på onsdagstimen) Naturen er
INF 2310 22.01.2008 Ukens temaer Hovedsakelig fra kap. 2.4 i DIP Romlig oppløsning og sampling av bilder Kvantisering Introduksjon til pikselmanipulasjon i Matlab (i morgen på onsdagstimen) Naturen er
Temaer i dag. Mer om romlig oppløsning. Optisk avbildning. INF 2310 Digital bildebehandling
 Temaer i dag INF 2310 Digital bildebehandling Forelesning II Sampling og kvantisering Fritz Albregtsen Romlig oppløsning i bilder Sampling av bilder Kvantisering i bilder Avstandsmål i bilder Pensum: Kap.
Temaer i dag INF 2310 Digital bildebehandling Forelesning II Sampling og kvantisering Fritz Albregtsen Romlig oppløsning i bilder Sampling av bilder Kvantisering i bilder Avstandsmål i bilder Pensum: Kap.
Forelesning, 23.februar INF2400 Sampling II. Øyvind Ryan. Februar 2006
 INF2400 Februar 2006 INF2400 Innhold Delkapitlene 4.4-4.6 fra læreboken, 4.3 er til selvstudium. Repetisjon om sampling og aliasing Diskret-til-kontinuerlig omforming Interpolasjon med pulser Oversamling
INF2400 Februar 2006 INF2400 Innhold Delkapitlene 4.4-4.6 fra læreboken, 4.3 er til selvstudium. Repetisjon om sampling og aliasing Diskret-til-kontinuerlig omforming Interpolasjon med pulser Oversamling
Forelesning, 17.februar INF2400 Sampling II. Øyvind Ryan. Februar 2005
 INF2400 Februar 2005 INF2400 Innhold Delkapitlene 4.4-4.6 fra læreboken, 4.3 er til selvstudium. Repetisjon om sampling og aliasing Diskret-til-kontinuerlig omforming Interpolasjon med pulser Oversamling
INF2400 Februar 2005 INF2400 Innhold Delkapitlene 4.4-4.6 fra læreboken, 4.3 er til selvstudium. Repetisjon om sampling og aliasing Diskret-til-kontinuerlig omforming Interpolasjon med pulser Oversamling
INF januar 2017 Ukens temaer (Kap med drypp fra kap. 4. i DIP)
 25. januar 2017 Ukens temaer (Kap 2.3-2.4 med drypp fra kap. 4. i DIP) Romlig oppløsning Sampling av bilder Kvantisering av pikselintensiteter 1 / 27 Sampling av bilder Naturen er kontinuerlig (0,0) j
25. januar 2017 Ukens temaer (Kap 2.3-2.4 med drypp fra kap. 4. i DIP) Romlig oppløsning Sampling av bilder Kvantisering av pikselintensiteter 1 / 27 Sampling av bilder Naturen er kontinuerlig (0,0) j
Løsningsforslag til kapittel 11 sampling, kvantisering og lagring av lyd
 Løsningsforslag til kapittel 11 sampling, kvantisering og lagring av lyd Sampling og samplingsrate Hvis vi har et lydsignal som inneholder frekvenser fra 100 til 500 Hz, hvilken samplingsrate og samplingsintervall
Løsningsforslag til kapittel 11 sampling, kvantisering og lagring av lyd Sampling og samplingsrate Hvis vi har et lydsignal som inneholder frekvenser fra 100 til 500 Hz, hvilken samplingsrate og samplingsintervall
Introduksjon til lyd. Det ytre øret. Fra lydbølger til nerveimpulser. INF1040 - Digital representasjon 23.09.2009: Introduksjon til lyd.
 Foreleser: INF1040 - Digital representasjon 23.09.2009: Introduksjon til lyd Martin Giese Kontakt: martingi@ifi.uio.no, 22852737 Det blir en del stoff per forelesning Er det matematikk eller praktisk regning?
Foreleser: INF1040 - Digital representasjon 23.09.2009: Introduksjon til lyd Martin Giese Kontakt: martingi@ifi.uio.no, 22852737 Det blir en del stoff per forelesning Er det matematikk eller praktisk regning?
Temaer i dag. Mer om romlig oppløsning. Optisk avbildning. INF 2310 Digital bildebehandling
 Temaer i dag INF 231 Digital bildebehandling Forelesning II Sampling og kvantisering Fritz Albregtsen Romlig oppløsning i bilder Sampling av bilder Kvantisering i bilder Avstandsmål i bilder Pensum: Kap.
Temaer i dag INF 231 Digital bildebehandling Forelesning II Sampling og kvantisering Fritz Albregtsen Romlig oppløsning i bilder Sampling av bilder Kvantisering i bilder Avstandsmål i bilder Pensum: Kap.
INF 2310 Digital bildebehandling
 INF 2310 Digital bildebehandling Forelesning II Sampling og kvantisering Fritz Albregtsen 27.01.2014 INF2310 1 Temaer i dag Romlig oppløsning i bilder Sampling av bilder Kvantisering i bilder Avstandsmål
INF 2310 Digital bildebehandling Forelesning II Sampling og kvantisering Fritz Albregtsen 27.01.2014 INF2310 1 Temaer i dag Romlig oppløsning i bilder Sampling av bilder Kvantisering i bilder Avstandsmål
INF 2310 Digital bildebehandling
 Temaer i dag INF 231 Digital bildebehandling Forelesning II Sampling og kvantisering Fritz Albregtsen Romlig oppløsning i bilder Sampling av bilder Kvantisering i bilder Avstandsmål i bilder Pensum: Kap.
Temaer i dag INF 231 Digital bildebehandling Forelesning II Sampling og kvantisering Fritz Albregtsen Romlig oppløsning i bilder Sampling av bilder Kvantisering i bilder Avstandsmål i bilder Pensum: Kap.
INF 2310 Digital bildebehandling
 Temaer i dag INF 231 Digital bildebehandling Forelesning II Sampling og kvantisering Fritz Albregtsen Romlig oppløsning i bilder Sampling av bilder Kvantisering i bilder Avstandsmål i bilder Pensum: Kap.
Temaer i dag INF 231 Digital bildebehandling Forelesning II Sampling og kvantisering Fritz Albregtsen Romlig oppløsning i bilder Sampling av bilder Kvantisering i bilder Avstandsmål i bilder Pensum: Kap.
Forkunnskapskrav. Hva handler kurset om. Kontaktinformasjon. Kurset er beregnet på en student som kan
 Velkommen til INF4, Digital signalbehandling Hilde Skjevling (Kursansvarlig) Svein Bøe (Java) INSTITUTT FOR INFORMATIKK Kontaktinformasjon E-post: hildesk@ifi.uio.no Telefon: 85 4 4 Kontor: 4 i 4.etasje,
Velkommen til INF4, Digital signalbehandling Hilde Skjevling (Kursansvarlig) Svein Bøe (Java) INSTITUTT FOR INFORMATIKK Kontaktinformasjon E-post: hildesk@ifi.uio.no Telefon: 85 4 4 Kontor: 4 i 4.etasje,
INF 2310 Digital bildebehandling
 Temaer i dag INF 231 Digital bildebehandling Forelesning II Sampling og kvantisering Fritz Albregtsen Romlig oppløsning i bilder Sampling av bilder Kvantisering i bilder Avstandsmål i bilder Pensum: Kap.
Temaer i dag INF 231 Digital bildebehandling Forelesning II Sampling og kvantisering Fritz Albregtsen Romlig oppløsning i bilder Sampling av bilder Kvantisering i bilder Avstandsmål i bilder Pensum: Kap.
Lyd på datamaskiner. Knut Mørken. November 17, 2008
 Lyd på datamaskiner Knut Mørken November 17, 2008 1 Digital lyd Svært mye av informasjonen som omgir oss i dag er lagret digitalt og blir overført digitalt. Vi har digital lyd på CD-plater, på internet
Lyd på datamaskiner Knut Mørken November 17, 2008 1 Digital lyd Svært mye av informasjonen som omgir oss i dag er lagret digitalt og blir overført digitalt. Vi har digital lyd på CD-plater, på internet
04.04.2013. Lektor 2 for Stovner VGS 12. februar 2013
 Lektor 2 for Stovner VGS 12. februar 2013 Født i Sandefjord for 54 år siden Døpt Bjørn Aarseth Utdannet elektronikkingeniør Ansatt i NRK i 1981 5. september 2004 = halve livet i NRK! Interesser: musikk
Lektor 2 for Stovner VGS 12. februar 2013 Født i Sandefjord for 54 år siden Døpt Bjørn Aarseth Utdannet elektronikkingeniør Ansatt i NRK i 1981 5. september 2004 = halve livet i NRK! Interesser: musikk
6DPSOLQJ DY NRQWLQXHUOLJH VLJQDOHU
 TE6146 ignalbehandling 6DPOLQJ DY NRQWLQXHUOLJH VLJQDOHU,QWURGXNVMRQ Mest vanlige måte å oppnå diskrete signaler på er ved sampling av kontinuerlige signaler Under gitte forutsetninger kan kontinuerlige
TE6146 ignalbehandling 6DPOLQJ DY NRQWLQXHUOLJH VLJQDOHU,QWURGXNVMRQ Mest vanlige måte å oppnå diskrete signaler på er ved sampling av kontinuerlige signaler Under gitte forutsetninger kan kontinuerlige
TDT4105/TDT4110 Informasjonsteknologi grunnkurs:
 1 TDT4105/TDT4110 Informasjonsteknologi grunnkurs: Uke 38 Digital representasjon, del 2 - Representasjon av lyd og bilder - Komprimering av data Rune Sætre satre@idi.ntnu.no 2 Digitalisering av lyd Et
1 TDT4105/TDT4110 Informasjonsteknologi grunnkurs: Uke 38 Digital representasjon, del 2 - Representasjon av lyd og bilder - Komprimering av data Rune Sætre satre@idi.ntnu.no 2 Digitalisering av lyd Et
Digitalisering av lyd
 Digitalisering av lyd Denne øvelsen er basert på materiale som Tore A. Danielsen utviklet som del av sin masteroppgave i fysikkdidaktikk. Arnt Inge Vistnes har også bidratt med ideer og diskusjoner. Hva
Digitalisering av lyd Denne øvelsen er basert på materiale som Tore A. Danielsen utviklet som del av sin masteroppgave i fysikkdidaktikk. Arnt Inge Vistnes har også bidratt med ideer og diskusjoner. Hva
3UDNWLVN DQYHQGHOVH DY ')7
 TE6146 ignalbehandling 3UDNWLVN DQYHQGHOVH DY ')7,QWURGXNVMRQ Kjenner DFT og FFT for effektiv numerisk beregning av DFT. Finnes ferdige funksjoner for FFT- algoritmer implementert i C/C og andre programmeringsspråk.
TE6146 ignalbehandling 3UDNWLVN DQYHQGHOVH DY ')7,QWURGXNVMRQ Kjenner DFT og FFT for effektiv numerisk beregning av DFT. Finnes ferdige funksjoner for FFT- algoritmer implementert i C/C og andre programmeringsspråk.
Kap 7: Digital it prosessering av analoge signaler
 Kap 7: Digital it prosessering av analoge signaler Sverre Holm Temaer 1. Sampling og rekonstruksjon 2. Finne spektret til samplet signal 3. Gjenvinning med forskjellige interpolasjoner 4. Nullinnsetting
Kap 7: Digital it prosessering av analoge signaler Sverre Holm Temaer 1. Sampling og rekonstruksjon 2. Finne spektret til samplet signal 3. Gjenvinning med forskjellige interpolasjoner 4. Nullinnsetting
Konvolusjon og filtrering og frevensanalyse av signaler
 Høgskolen i Østfold Avdeling for informasjonsteknologi Fag IAD33505 Bildebehandling og mønstergjenkjenning Laboppgave nr 2 Konvolusjon og filtrering og frevensanalyse av signaler Sarpsborg 21.01.2005 20.01.05
Høgskolen i Østfold Avdeling for informasjonsteknologi Fag IAD33505 Bildebehandling og mønstergjenkjenning Laboppgave nr 2 Konvolusjon og filtrering og frevensanalyse av signaler Sarpsborg 21.01.2005 20.01.05
f(t) F( ) f(t) F( ) f(t) F( )
 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR PETROLEUMSTEKNOLOGI OG ANVENDT GEOFYSIKK Oppgave SIG4045 Geofysisk Signalanalyse Lsningsforslag ving 3 a) ' xy (t) = x()y(t + )d : La oss, for
NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR PETROLEUMSTEKNOLOGI OG ANVENDT GEOFYSIKK Oppgave SIG4045 Geofysisk Signalanalyse Lsningsforslag ving 3 a) ' xy (t) = x()y(t + )d : La oss, for
INF 1040 høsten 2009: Oppgavesett 8 Introduksjon til lyd (kapittel 9 og 10)
 INF 1040 høsten 2009: Oppgavesett 8 Introduksjon til lyd (kapittel 9 og 10) Vi regner med at decibelskalaen og bruk av logaritmer kan by på enkelte problemer. Derfor en kort repetisjon: Absolutt lydintensitet:
INF 1040 høsten 2009: Oppgavesett 8 Introduksjon til lyd (kapittel 9 og 10) Vi regner med at decibelskalaen og bruk av logaritmer kan by på enkelte problemer. Derfor en kort repetisjon: Absolutt lydintensitet:
1.8 Binære tall EKSEMPEL
 1.8 Binære tall Når vi regner, bruker vi titallssystemet. Hvordan det virker, finner vi ut ved å se på for eksempel tallet 2347. 2347 = 2 1000 + 3 100 + 4 10 + 7 Hvis vi bruker potenser, får vi 2347 =
1.8 Binære tall Når vi regner, bruker vi titallssystemet. Hvordan det virker, finner vi ut ved å se på for eksempel tallet 2347. 2347 = 2 1000 + 3 100 + 4 10 + 7 Hvis vi bruker potenser, får vi 2347 =
KAPITTEL 4 Følger og differensligninger
 KAPITTEL 4 Følger og differensligninger Følger er et sentralt begrep i matematikk som dukker opp i mange ulike sammenhenger Samtidig er det mange naturlige prosesser som kan beskrives ved hjelp av følger,
KAPITTEL 4 Følger og differensligninger Følger er et sentralt begrep i matematikk som dukker opp i mange ulike sammenhenger Samtidig er det mange naturlige prosesser som kan beskrives ved hjelp av følger,
LØSNINGSFORSLAG TIL SIGNALBEHANDLING 1 JUNI 2010
 LØSNINGSFORSLAG TIL SIGNALBEHANDLING JUNI Løsningsforslag til eksamen i Signalbehandling, mai Side av 5 Oppgave a) Inngangssignalet x(t) er gitt som x( t) = 5cos(π t) + 8cos(π 4 t). Bruker Eulers formel
LØSNINGSFORSLAG TIL SIGNALBEHANDLING JUNI Løsningsforslag til eksamen i Signalbehandling, mai Side av 5 Oppgave a) Inngangssignalet x(t) er gitt som x( t) = 5cos(π t) + 8cos(π 4 t). Bruker Eulers formel
For J kvantiseringsnivåer er mean square feilen:
 Slide 1 Slide 2 Kap. 6 Bilde kvantisering Kap. 6.1 Skalar kvantisering Desisons og rekonstruksonsnivåer velges ved å minimalisere et gitt kvantiseringsfeilmål mellom f og ˆf. Kvantisering: Prosessen som
Slide 1 Slide 2 Kap. 6 Bilde kvantisering Kap. 6.1 Skalar kvantisering Desisons og rekonstruksonsnivåer velges ved å minimalisere et gitt kvantiseringsfeilmål mellom f og ˆf. Kvantisering: Prosessen som
INF1040 Digital representasjon
 INF1040 Digital representasjon av tekster, tall, former, lyd, bilder og video Forelesere: Gerhard Skagestein Fritz Albregtsen Første forelesning: Onsdag 23. august 12:15 14:00, Sophus Lies Auditorium.
INF1040 Digital representasjon av tekster, tall, former, lyd, bilder og video Forelesere: Gerhard Skagestein Fritz Albregtsen Første forelesning: Onsdag 23. august 12:15 14:00, Sophus Lies Auditorium.
Den analoge verden blir digitalisert
 Den analoge verden blir digitalisert Lindem 4. mai 2008 Med bestemte tidsintervall går vi inn og avleser (digitaliserer) den analoge verdien til signalet. Nyquist Shannon sampling theorem: Skal vi beholde
Den analoge verden blir digitalisert Lindem 4. mai 2008 Med bestemte tidsintervall går vi inn og avleser (digitaliserer) den analoge verdien til signalet. Nyquist Shannon sampling theorem: Skal vi beholde
y(t) t
 Løsningsforslag til eksamen i TE 559 Signaler og Systemer Høgskolen i Stavanger Trygve Randen, t.randen@ieee.org 3. mai 999 Oppgave a) Et tidsinvariant system er et system hvis egenskaper ikke endres med
Løsningsforslag til eksamen i TE 559 Signaler og Systemer Høgskolen i Stavanger Trygve Randen, t.randen@ieee.org 3. mai 999 Oppgave a) Et tidsinvariant system er et system hvis egenskaper ikke endres med
BRUKERMANUAL Digispiller
 BRUKERMANUAL Digispiller INNHOLDSFORTEGNELSE 3. Ved første gangs bruk 4. Hvitt kort med et? Husk alltid dette 5. Skru PÅ/AV Bytte digikort 6. Lade digispiller 7. Funksjonsknapper 8. - 9. Hovedmeny 10.
BRUKERMANUAL Digispiller INNHOLDSFORTEGNELSE 3. Ved første gangs bruk 4. Hvitt kort med et? Husk alltid dette 5. Skru PÅ/AV Bytte digikort 6. Lade digispiller 7. Funksjonsknapper 8. - 9. Hovedmeny 10.
Digital sampling og analog estetikk
 Digital sampling og analog estetikk UiO, Institutt for Musikkvitenskap MUS4830 Musikk, Teknologi og Produksjon Kristian Nymoen, 2014 Tellef Kvifte (2007): "Digital sampling and analogue aesthetics" i A.
Digital sampling og analog estetikk UiO, Institutt for Musikkvitenskap MUS4830 Musikk, Teknologi og Produksjon Kristian Nymoen, 2014 Tellef Kvifte (2007): "Digital sampling and analogue aesthetics" i A.
UTVIDET TEST AV PROGRAM
 Tid : 16.2.99, kl. 153 Til : Ole Meyer og prøvenemda Fra : Anders Sak : Fagprøve våren 1999, utvidet test av program Denne oppgaven var tre-delt. UTVIDET TEST AV PROGRAM Først skulle jeg påtrykke AD-kortet
Tid : 16.2.99, kl. 153 Til : Ole Meyer og prøvenemda Fra : Anders Sak : Fagprøve våren 1999, utvidet test av program Denne oppgaven var tre-delt. UTVIDET TEST AV PROGRAM Først skulle jeg påtrykke AD-kortet
Fysisk Lag. Overføringskapasitet. Olav Lysne med bidrag fra Kjell Åge Bringsrud, Pål Spilling og Carsten Griwodz
 Fysisk Lag Olav Lysne med bidrag fra Kjell Åge Bringsrud, Pål Spilling og Carsten Griwodz Fysisk Lag 1 Overføringskapasitet r Faktorer som påvirker kvalitet og kapasitet: m Forvrengning av signal gjennom
Fysisk Lag Olav Lysne med bidrag fra Kjell Åge Bringsrud, Pål Spilling og Carsten Griwodz Fysisk Lag 1 Overføringskapasitet r Faktorer som påvirker kvalitet og kapasitet: m Forvrengning av signal gjennom
DV - CODEC. Introduksjon
 DV - CODEC EN KORT PRESENTASJON I INF 5080 VED RICHARD MAGNOR STENBRO EMAIL: rms@stenbro.net 21. April 2004 Introduksjon Dv-codecen ble utviklet spesielt for bruk i både profesjonelle og konsumer kamera.
DV - CODEC EN KORT PRESENTASJON I INF 5080 VED RICHARD MAGNOR STENBRO EMAIL: rms@stenbro.net 21. April 2004 Introduksjon Dv-codecen ble utviklet spesielt for bruk i både profesjonelle og konsumer kamera.
INF Digital representasjon : Introduksjon til lyd
 INF1040 - Digital representasjon 23.09.2009: Introduksjon til lyd Foreleser: Martin Giese Kontakt: martingi@ifi.uio.no, 22852737 Det blir en del stoff per forelesning Er det matematikk eller praktisk regning?
INF1040 - Digital representasjon 23.09.2009: Introduksjon til lyd Foreleser: Martin Giese Kontakt: martingi@ifi.uio.no, 22852737 Det blir en del stoff per forelesning Er det matematikk eller praktisk regning?
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Side 1 Det matematisk-naturvitenskapelige fakultet Eksamen i: INF1411 Eksamensdag: mandag 3.juni 2013 Tid for eksamen: 14.30-18.30 Oppgavesettet er på 6 sider Vedlegg: Ingen Tillatte
UNIVERSITETET I OSLO Side 1 Det matematisk-naturvitenskapelige fakultet Eksamen i: INF1411 Eksamensdag: mandag 3.juni 2013 Tid for eksamen: 14.30-18.30 Oppgavesettet er på 6 sider Vedlegg: Ingen Tillatte
Fourier-analyse. Hittil har vi begrenset oss til å se på bølger som kan beskrives ved sinus- eller cosinusfunksjoner
 Fourier-analyse Hittil har vi begrenset oss til å se på bølger som kan beskrives ved sinus- eller cosinusfunksjoner som yxt (, ) = Asin( kx ωt+ ϕ) En slik bølge kan karakteriseres ved en enkelt frekvens
Fourier-analyse Hittil har vi begrenset oss til å se på bølger som kan beskrives ved sinus- eller cosinusfunksjoner som yxt (, ) = Asin( kx ωt+ ϕ) En slik bølge kan karakteriseres ved en enkelt frekvens
Lydproduksjon. t.no. ww ww.hin. Forelesning 6 Signaler Digital audioteknologi MMT205 - F6 1
 MMT205 Lydproduksjon t.no ww ww.hin Forelesning 6 Signaler Digital audioteknologi MMT205 - F6 1 F6 - Innhold MMT205 - F6 2 Elektrisitet hva er det? Elektroner som vandrer i ei lukka sløyfe (krets). Grunnstørrelser:
MMT205 Lydproduksjon t.no ww ww.hin Forelesning 6 Signaler Digital audioteknologi MMT205 - F6 1 F6 - Innhold MMT205 - F6 2 Elektrisitet hva er det? Elektroner som vandrer i ei lukka sløyfe (krets). Grunnstørrelser:
Det fysiske laget, del 2
 Det fysiske laget, del 2 Kjell Åge Bringsrud (med foiler fra Pål Spilling) 1 Pulsforvrengning gjennom mediet Linje g(t) innsignal Dempning A(f) v(t) utsignal A(f) 0% 50% Frekvensresponsen Ideell Frekv.
Det fysiske laget, del 2 Kjell Åge Bringsrud (med foiler fra Pål Spilling) 1 Pulsforvrengning gjennom mediet Linje g(t) innsignal Dempning A(f) v(t) utsignal A(f) 0% 50% Frekvensresponsen Ideell Frekv.
Sampling ved Nyquist-raten
 Samplingsteoremet Oppgavegjennomgang, 7.mai Oversikt Presisering av samplingsteoremet Løse utsendt oppgave om sampling Løse oppgave, V Løse oppgave 3, V If a function f (t contains no frequencies higher
Samplingsteoremet Oppgavegjennomgang, 7.mai Oversikt Presisering av samplingsteoremet Løse utsendt oppgave om sampling Løse oppgave, V Løse oppgave 3, V If a function f (t contains no frequencies higher
Introduksjon til lyd. Litt praktisk informasjon. Det ytre øret. Fra lydbølger til nerveimpulser
 Introduksjon til lyd Temaer i dag: Hvordan kan vi høre lyd? Lyd og lydbølger Sinuser, frekvenser, tidssignaler Litt praktisk informasjon Husk øretelefoner på øvelsestimene denne uken og en stund framover.
Introduksjon til lyd Temaer i dag: Hvordan kan vi høre lyd? Lyd og lydbølger Sinuser, frekvenser, tidssignaler Litt praktisk informasjon Husk øretelefoner på øvelsestimene denne uken og en stund framover.
INF1040 Digital representasjon Oppsummering 2008 del II
 INF040 Digital representasjon Oppsummering 2008 del II Fritz Albregtsen INF040-Oppsum-FA- Lydintensitet Vi kan høre lyder over et stort omfang av intensiteter: fra høreterskelen, I 0 = 0-2 W/m 2,tilSmerteterskelen,0
INF040 Digital representasjon Oppsummering 2008 del II Fritz Albregtsen INF040-Oppsum-FA- Lydintensitet Vi kan høre lyder over et stort omfang av intensiteter: fra høreterskelen, I 0 = 0-2 W/m 2,tilSmerteterskelen,0
Løsningsforslag til kapittel 10 - Lydbølger
 Løsningsforslag til kapittel - Lydbølger Oppgaver til plenum: Vi regner med at decibelskalaen og bruk av logaritmer kan by på enkelte problemer. Derfor en kort repetisjon: Absolutt lydintensitet: Vi betegner
Løsningsforslag til kapittel - Lydbølger Oppgaver til plenum: Vi regner med at decibelskalaen og bruk av logaritmer kan by på enkelte problemer. Derfor en kort repetisjon: Absolutt lydintensitet: Vi betegner
MAT-INF 2360: Obligatorisk oppgave 1
 6. februar, MAT-INF 36: Obligatorisk oppgave Oppgave I denne oppgaven skal vi sammenligne effektiviteten av FFT-algoritmen med en mer rett frem algoritme for DFT. Deloppgave a Lag en funksjon y=dftimpl(x)
6. februar, MAT-INF 36: Obligatorisk oppgave Oppgave I denne oppgaven skal vi sammenligne effektiviteten av FFT-algoritmen med en mer rett frem algoritme for DFT. Deloppgave a Lag en funksjon y=dftimpl(x)
UNIVERSITETET I OSLO.
 UNIVERSITETET I OSLO. Det matematisk - naturvitenskapelige fakultet. Eksamen i : Eksamens dag : Tid for eksamen : Oppgavesettet er på 6 sider Vedlegg : Tillatte hjelpemidler : FYS1210-Elektronikk med prosjektoppgaver
UNIVERSITETET I OSLO. Det matematisk - naturvitenskapelige fakultet. Eksamen i : Eksamens dag : Tid for eksamen : Oppgavesettet er på 6 sider Vedlegg : Tillatte hjelpemidler : FYS1210-Elektronikk med prosjektoppgaver
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i Eksamensdag: Oppgavesettet er på 9 sider. Vedlegg: Tillatte hjelpemidler: INF2400 Digital signalbehandling 16. 23. april 2004,
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i Eksamensdag: Oppgavesettet er på 9 sider. Vedlegg: Tillatte hjelpemidler: INF2400 Digital signalbehandling 16. 23. april 2004,
INF1040 Digital representasjon Oppsummering 2008 del II
 INF igital representasjon Oppsummering 8 del II Lydintensitet Vi kan høre lyder over et stort omfang av intensiteter: fra høreterskelen, I - W/m,tilSmerteterskelen, W/m Oftest angir vi ikke absolutt lydintensitet
INF igital representasjon Oppsummering 8 del II Lydintensitet Vi kan høre lyder over et stort omfang av intensiteter: fra høreterskelen, I - W/m,tilSmerteterskelen, W/m Oftest angir vi ikke absolutt lydintensitet
Noen presiseringer mhp Diskret Fourier Transform. Relevant for oblig 1.
 FYS2130 Våren 2008 Noen presiseringer mhp Diskret Fourier Transform. Relevant for oblig 1. Vi har på forelesning gått gjennom foldingsfenomenet ved diskret Fourier transform, men ikke vært pinlig nøyaktige
FYS2130 Våren 2008 Noen presiseringer mhp Diskret Fourier Transform. Relevant for oblig 1. Vi har på forelesning gått gjennom foldingsfenomenet ved diskret Fourier transform, men ikke vært pinlig nøyaktige
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i : INF2310 Digital bildebehandling Eksamensdag : Onsdag 28. mars 2007 Tid for eksamen : 13:30 16:30 Oppgavesettet er på : 4 sider
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i : INF2310 Digital bildebehandling Eksamensdag : Onsdag 28. mars 2007 Tid for eksamen : 13:30 16:30 Oppgavesettet er på : 4 sider
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF3470 Digital signalbehandling Eksamensdag: 1. desember 013 Tid for eksamen: 14.30 18.30 Oppgavesettet er på 15 sider. Vedlegg:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF3470 Digital signalbehandling Eksamensdag: 1. desember 013 Tid for eksamen: 14.30 18.30 Oppgavesettet er på 15 sider. Vedlegg:
FFT. Prosessering i frekvensdomenet. Digital signalprosessering Øyvind Brandtsegg
 FFT Prosessering i frekvensdomenet Digital signalprosessering Øyvind Brandtsegg Representasjonsmåter Tidsdomene: Amplityde over tid Frekvensdomene: Amplityde over frekvens Hvorfor? Prosessering i frekvensdomenet
FFT Prosessering i frekvensdomenet Digital signalprosessering Øyvind Brandtsegg Representasjonsmåter Tidsdomene: Amplityde over tid Frekvensdomene: Amplityde over frekvens Hvorfor? Prosessering i frekvensdomenet
INF 1040 Digital representasjon 2007 Utkast til - Obligatorisk oppgave nr 2
 INF 40 Digital representasjon 2007 Utkast til - Obligatorisk oppgave nr 2 Utlevering: onsdag 17. oktober 2007, kl. 17:00 Innlevering: fredag 2. november 2007, kl. 23:59:59 Formaliteter Besvarelsen skal
INF 40 Digital representasjon 2007 Utkast til - Obligatorisk oppgave nr 2 Utlevering: onsdag 17. oktober 2007, kl. 17:00 Innlevering: fredag 2. november 2007, kl. 23:59:59 Formaliteter Besvarelsen skal
Ved bruk av 5.1 høyttaleroppsett: - Veksler midtre høyttaler og subwoofer
 Produktinformasjon Tilkobling Beskrivelse A 1 Jumperbryter for: - Midtre/Subwoofer - Linje inn: V/H Ved bruk av 5.1 høyttaleroppsett: - Veksler midtre høyttaler og subwoofer Ved bruk av 2 4 høyttaleroppsett:
Produktinformasjon Tilkobling Beskrivelse A 1 Jumperbryter for: - Midtre/Subwoofer - Linje inn: V/H Ved bruk av 5.1 høyttaleroppsett: - Veksler midtre høyttaler og subwoofer Ved bruk av 2 4 høyttaleroppsett:
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF347/447 Digital signalbehandling Eksamensdag: 1. desember 16 Tid for eksamen: 14.3 18.3 Oppgavesettet er på 8 sider. Vedlegg:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF347/447 Digital signalbehandling Eksamensdag: 1. desember 16 Tid for eksamen: 14.3 18.3 Oppgavesettet er på 8 sider. Vedlegg:
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i : INF2310 Digital bildebehandling Eksamensdag : Onsdag 2. juni 2010 Tid for eksamen : 09:00 12:00 Oppgavesettet er på : XXX sider
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i : INF2310 Digital bildebehandling Eksamensdag : Onsdag 2. juni 2010 Tid for eksamen : 09:00 12:00 Oppgavesettet er på : XXX sider
Tips til arbeidet med obligatorisk oppgave 2 i MAT-INF 1100 høsten 2004
 Tips til arbeidet med obligatorisk oppgave 2 i MAT-INF 1100 høsten 2004 Knut Mørken 3. november 2004 Etter samtale med noen av dere de siste dagene skjønner jeg at noen strever med del 2 av oblig2. Problemene
Tips til arbeidet med obligatorisk oppgave 2 i MAT-INF 1100 høsten 2004 Knut Mørken 3. november 2004 Etter samtale med noen av dere de siste dagene skjønner jeg at noen strever med del 2 av oblig2. Problemene
IT1101 Informatikk basisfag 4/9. Praktisk. Oppgave: tegn kretsdiagram. Fra sist. Representasjon av informasjon binært. Ny oppgave
 IT Informatikk basisfag 4/9 Sist gang: manipulering av bits I dag: Representasjon av bilde og lyd Heksadesimal notasjon Organisering av data i hovedminne og masselager (elektronisk, magnetisk og optisk
IT Informatikk basisfag 4/9 Sist gang: manipulering av bits I dag: Representasjon av bilde og lyd Heksadesimal notasjon Organisering av data i hovedminne og masselager (elektronisk, magnetisk og optisk
KAPITTEL 10 Flerskala-analyse og kompresjon av lyd
 KAPITTEL 10 Flerskala-analyse og kompresjon av lyd Vi kan lagre dokumenter av mange forskjellige typer på en datamaskin. Vi kan for eksempel ha en datafil der innholdet er tall, vi kan ha en tekstfil,
KAPITTEL 10 Flerskala-analyse og kompresjon av lyd Vi kan lagre dokumenter av mange forskjellige typer på en datamaskin. Vi kan for eksempel ha en datafil der innholdet er tall, vi kan ha en tekstfil,
Uke 9: Diskret Fourier Transform, I
 Uke 9: Diskret Fourier Transform, I Jo Inge Buskenes Institutt for informatikk, Universitetet i Oslo INF3470/4470, høst 2011 2/23 Dagens temaer Sampling og periodisitet DFT DFT og DTFT 3/23 Tema Sampling
Uke 9: Diskret Fourier Transform, I Jo Inge Buskenes Institutt for informatikk, Universitetet i Oslo INF3470/4470, høst 2011 2/23 Dagens temaer Sampling og periodisitet DFT DFT og DTFT 3/23 Tema Sampling
Hjelpemidler: D Ingen trykte eller håndskrevne hjelpemidler tillatt. Bestemt, enkel kalkulator tillatt.
 Side av 5 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR ELEKTRONIKK OG TELEKOMMUNIKASJON Faglig kontakt under eksamen: Navn: John Torjus Flåm Tlf.: 957602 EKSAMEN I EMNE TTT40 INFORMASJONS-
Side av 5 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR ELEKTRONIKK OG TELEKOMMUNIKASJON Faglig kontakt under eksamen: Navn: John Torjus Flåm Tlf.: 957602 EKSAMEN I EMNE TTT40 INFORMASJONS-
SUB640 02 BRUKERMANUAL 05 ILLUSTRASJONER 07 SPESIFIKASJONER 07 FEILSØKING. www.argonaudio.com 1
 02 BRUKERMANUAL 05 ILLUSTRASJONER 07 SPESIFIKASJONER 07 FEILSØKING www.argonaudio.com 1 Brukermanual SUB640 Kjære kunde Kvalitet har alltid vært drivkraften for oss, og grunnleggelsen av Argon Audio er
02 BRUKERMANUAL 05 ILLUSTRASJONER 07 SPESIFIKASJONER 07 FEILSØKING www.argonaudio.com 1 Brukermanual SUB640 Kjære kunde Kvalitet har alltid vært drivkraften for oss, og grunnleggelsen av Argon Audio er
Datakonvertering. analog til digital og digital til analog
 Datakonvertering analog til digital og digital til analog Komparator Lindem 29.april. 2014 Signalspenningene ut fra en sensor kan variere sterkt. Hvis vi bare ønsker informasjon om når signal-nivået overstiger
Datakonvertering analog til digital og digital til analog Komparator Lindem 29.april. 2014 Signalspenningene ut fra en sensor kan variere sterkt. Hvis vi bare ønsker informasjon om når signal-nivået overstiger
HØGSKOLEN I SØR-TRØNDELAG Avdeling for teknologi
 HØGSKOLEN I SØR-TRØNDELAG Avdeling for teknologi Målform: Bokmål Eksamensdato: 7.mai 24 Varighet/eksamenstid: 5 timer Emnekode: TELE 23 Emnenavn: Signalbehandling Klasse(r): 2EI 2EE Studiepoeng: Faglærer(e):
HØGSKOLEN I SØR-TRØNDELAG Avdeling for teknologi Målform: Bokmål Eksamensdato: 7.mai 24 Varighet/eksamenstid: 5 timer Emnekode: TELE 23 Emnenavn: Signalbehandling Klasse(r): 2EI 2EE Studiepoeng: Faglærer(e):
Om obligatoriske oppgave 2 Bakgrunn og tips
 Kompresjon p.1/14 Om obligatoriske oppgave 2 Bakgrunn og tips Forelesning 31/10, 2005 MAT-INF1100 Kompresjon p.2/14 Oblig 2 Hovedelementer 1. Dekomponering og interpolasjon 2. Kompresjon Siktemål Gi eksempler
Kompresjon p.1/14 Om obligatoriske oppgave 2 Bakgrunn og tips Forelesning 31/10, 2005 MAT-INF1100 Kompresjon p.2/14 Oblig 2 Hovedelementer 1. Dekomponering og interpolasjon 2. Kompresjon Siktemål Gi eksempler
SPEKTALANALYSATORER. Fig. 1 Illustrasjon av sammenhengen tidsfunksjon - frekvensspektrum
 SPEKTALANALYSATORER Fig. 1 Illustrasjon av sammenhengen tidsfunksjon - frekvensspektrum Vi har ofte nytte av å kunne veksle mellom de to grafiske presentasjonsmåtene for et elektrisk signal, tidsfunksjon
SPEKTALANALYSATORER Fig. 1 Illustrasjon av sammenhengen tidsfunksjon - frekvensspektrum Vi har ofte nytte av å kunne veksle mellom de to grafiske presentasjonsmåtene for et elektrisk signal, tidsfunksjon
MPEG-1 lag 1, 2 og lag 3
 MPEG-1 lag 1, 2 og lag 3 Sverre Holm Basert på presentasjon laget av Torbjörn Ekman, 2005 (nå på NTNU) INSTITUTT FOR INFORMATIKK August 2009-1 MPEG audiokoding Motivasjon for de fleste kapitlene i Ambardar,
MPEG-1 lag 1, 2 og lag 3 Sverre Holm Basert på presentasjon laget av Torbjörn Ekman, 2005 (nå på NTNU) INSTITUTT FOR INFORMATIKK August 2009-1 MPEG audiokoding Motivasjon for de fleste kapitlene i Ambardar,
Datakonvertering. analog til digital og digital til analog
 Datakonvertering analog til digital og digital til analog Komparator Signalspenningene ut fra en sensor kan variere sterkt. Hvis vi bare ønsker informasjon om når signal-nivået overstiger en bestemt terskelverdi
Datakonvertering analog til digital og digital til analog Komparator Signalspenningene ut fra en sensor kan variere sterkt. Hvis vi bare ønsker informasjon om når signal-nivået overstiger en bestemt terskelverdi
Semesteroppgave for interaktiv musikk
 ESPEN AURE MUS 2830 HØST 2013 Semesteroppgave for interaktiv musikk «STEP SEQUENCING» Hensikten med denne oppgaven er å belyse de mulighetene som finnes innenfor et interaktivt system med fokus på step
ESPEN AURE MUS 2830 HØST 2013 Semesteroppgave for interaktiv musikk «STEP SEQUENCING» Hensikten med denne oppgaven er å belyse de mulighetene som finnes innenfor et interaktivt system med fokus på step
STE 6146 Digital signalbehandling. Løsningsforslag til eksamen avholdt
 HØGSKOLEN I NARVIK Institutt for data-, elektro-, og romteknologi Sivilingeniørstudiet EL/RT STE 6146 Digital signalbehandling Løsningsforslag til eksamen avholdt 06.02.03 Oppgaver 1. Forklar hva som er
HØGSKOLEN I NARVIK Institutt for data-, elektro-, og romteknologi Sivilingeniørstudiet EL/RT STE 6146 Digital signalbehandling Løsningsforslag til eksamen avholdt 06.02.03 Oppgaver 1. Forklar hva som er
UNIVERSITETET I OSLO.
 UNIVERSITETET I OSLO. Det matematisk - naturvitenskapelige fakultet. Eksamen i : Eksamens dag : Tid for eksamen : Oppgavesettet er på 6 sider Vedlegg : Tillatte hjelpemidler : FYS1210-Elektronikk med prosjektoppgaver
UNIVERSITETET I OSLO. Det matematisk - naturvitenskapelige fakultet. Eksamen i : Eksamens dag : Tid for eksamen : Oppgavesettet er på 6 sider Vedlegg : Tillatte hjelpemidler : FYS1210-Elektronikk med prosjektoppgaver
Løsningsforslag, Ukeoppgaver 10 INF2310, våren 2011 kompresjon og koding del II
 Løsningsforslag, Ukeoppgaver 10 INF2310, våren 2011 kompresjon og koding del II 1. En fax-oppgave: a. Et ark med tekst og enkle strektegninger skal sendes pr digital fax over en modemlinje med kapasitet
Løsningsforslag, Ukeoppgaver 10 INF2310, våren 2011 kompresjon og koding del II 1. En fax-oppgave: a. Et ark med tekst og enkle strektegninger skal sendes pr digital fax over en modemlinje med kapasitet
INF 4130. 8. oktober 2009. Dagens tema: Uavgjørbarhet. Neste uke: NP-kompletthet
 INF 4130 8. oktober 2009 Stein Krogdahl Dagens tema: Uavgjørbarhet Dette har blitt framstilt litt annerledes tidligere år Se Dinos forelesninger fra i fjor. I år: Vi tenker mer i programmer enn i Turing-maskiner
INF 4130 8. oktober 2009 Stein Krogdahl Dagens tema: Uavgjørbarhet Dette har blitt framstilt litt annerledes tidligere år Se Dinos forelesninger fra i fjor. I år: Vi tenker mer i programmer enn i Turing-maskiner
Fourier-Transformasjoner II
 Fourier-Transformasjoner II Lars Vidar Magnusson February 27, 2017 Resten av Delkapittel 4.2 Preliminary Concepts Delkapittel 4.3 Sampling and the Fourier Transform of Sampled Functions Delkapittel 4.4
Fourier-Transformasjoner II Lars Vidar Magnusson February 27, 2017 Resten av Delkapittel 4.2 Preliminary Concepts Delkapittel 4.3 Sampling and the Fourier Transform of Sampled Functions Delkapittel 4.4
SUB840 02 BRUKERMANUAL 05 ILLUSTRASJONER 07 SPESIFIKASJONER 07 FEILSØKING. www.argonaudio.com 1
 02 BRUKERMANUAL 05 ILLUSTRASJONER 07 SPESIFIKASJONER 07 FEILSØKING www.argonaudio.com 1 Brukermanual SUB840 Kjære kunde Kvalitet har alltid vært drivkraften for oss, og grunnleggelsen av Argon Audio er
02 BRUKERMANUAL 05 ILLUSTRASJONER 07 SPESIFIKASJONER 07 FEILSØKING www.argonaudio.com 1 Brukermanual SUB840 Kjære kunde Kvalitet har alltid vært drivkraften for oss, og grunnleggelsen av Argon Audio er
Tittel: Design av FSK-demodulator. Forfattere: Torstein Mellingen Langan. Versjon: 1.0 Dato: Innledning 1
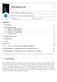 Designnotat Innhold Tittel: Design av FSK-demodulator Forfattere: Torstein Mellingen Langan Versjon: 1.0 Dato: 13.11.17 1 Innledning 1 2 Prinsipiell løsning 2 2.1 Analyse av inngangssignal.............................
Designnotat Innhold Tittel: Design av FSK-demodulator Forfattere: Torstein Mellingen Langan Versjon: 1.0 Dato: 13.11.17 1 Innledning 1 2 Prinsipiell løsning 2 2.1 Analyse av inngangssignal.............................
Kollektivassignment i EMMA og VISUM
 Kollektivassignment i EMMA og VISUM Odd I. Larsen Høgskolen i Molde Stockholm 15.12.2010 Algoritmene VISUM Random Departure Time (RDT) (Hasselström, 1981) EMMA Optimal Strategy (OS) (Spiess & Florian,
Kollektivassignment i EMMA og VISUM Odd I. Larsen Høgskolen i Molde Stockholm 15.12.2010 Algoritmene VISUM Random Departure Time (RDT) (Hasselström, 1981) EMMA Optimal Strategy (OS) (Spiess & Florian,
Obligatorisk oppgave nr 4 FYS Lars Kristian Henriksen UiO
 Obligatorisk oppgave nr 4 FYS-213 Lars Kristian Henriksen UiO 18. februar 215 Diskusjonsoppgaver: Oppgave 1 Hvordan kan vi ved å ta utgangspunkt i et frekvensspekter lage en syntstisk lyd? Vil en slik
Obligatorisk oppgave nr 4 FYS-213 Lars Kristian Henriksen UiO 18. februar 215 Diskusjonsoppgaver: Oppgave 1 Hvordan kan vi ved å ta utgangspunkt i et frekvensspekter lage en syntstisk lyd? Vil en slik
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i Eksamensdag: 29. mars 2007 Tid for eksamen: 09.00 2.00 Oppgavesettet er på 5 sider. Vedlegg: INF 3470 / INF 4470 Digital Signalbehandling
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i Eksamensdag: 29. mars 2007 Tid for eksamen: 09.00 2.00 Oppgavesettet er på 5 sider. Vedlegg: INF 3470 / INF 4470 Digital Signalbehandling
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i Eksamensdag: 11. juni 27 Tid for eksamen: 14.3 17.3 Oppgavesettet er på 5 sider. Vedlegg: INF 347 / INF 447 Digital Signalbehandling
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i Eksamensdag: 11. juni 27 Tid for eksamen: 14.3 17.3 Oppgavesettet er på 5 sider. Vedlegg: INF 347 / INF 447 Digital Signalbehandling
Installering Før installering: Hvis du har et internt lydkort, deaktiverer du det på hovedkort-bios og fjerner tilknyttet programvare og drivere.
 Produktinformasjon A: Analoge innganger og utganger B: Digital S/PDIF-inngang og utgang C: Intern analog inngang C A B Installering Før installering: Hvis du har et internt lydkort, deaktiverer du det
Produktinformasjon A: Analoge innganger og utganger B: Digital S/PDIF-inngang og utgang C: Intern analog inngang C A B Installering Før installering: Hvis du har et internt lydkort, deaktiverer du det
Løsning av øvingsoppgaver, INF2310, 2005, kompresjon og koding
 Løsning av øvingsoppgaver, INF230, 2005,. Vi har gitt følgende bilde: kompresjon og koding 0 2 2 2 3 3 3 2 3 3 3 0 2 2 2 3 3 2 2 2 3 2 3 4 4 2 2 3 2 2 3 4 4 2 2 2 3 3 3 4 3 4 a. Finn Huffman-kodingen av
Løsning av øvingsoppgaver, INF230, 2005,. Vi har gitt følgende bilde: kompresjon og koding 0 2 2 2 3 3 3 2 3 3 3 0 2 2 2 3 3 2 2 2 3 2 3 4 4 2 2 3 2 2 3 4 4 2 2 2 3 3 3 4 3 4 a. Finn Huffman-kodingen av
INF1040 Digital representasjon. Oppsummering. Glyfer og tegn. Den endelige løsning UNICODE og ISO bit ulike tegn!
 INF040 Digital representasjon Oppsummering Glyfer og tegn Tegn: Det bakenforliggende begrep for bestemte visualiseringer ( strektegninger ) på papir, skjerm, steintavler Et tegn kan vises fram med ulike
INF040 Digital representasjon Oppsummering Glyfer og tegn Tegn: Det bakenforliggende begrep for bestemte visualiseringer ( strektegninger ) på papir, skjerm, steintavler Et tegn kan vises fram med ulike
INF1400 Kap 0 Digitalteknikk
 INF1400 Kap 0 Digitalteknikk Binære tall (ord): Digitale signaler: Hva betyr digital? Tall som kun er representert ved symbolene 0 og 1 (bit s). Nøyaktighet gitt av antall bit. (avrundingsfeil) Sekvenser
INF1400 Kap 0 Digitalteknikk Binære tall (ord): Digitale signaler: Hva betyr digital? Tall som kun er representert ved symbolene 0 og 1 (bit s). Nøyaktighet gitt av antall bit. (avrundingsfeil) Sekvenser
7.3 Samplerate-konvertering
 7.3 Samplerate-konvertering Ultralyd kommunikasjonssystem for kombinasjon med drfid Signal 40 khz ± 2-4 khz B = 4-8 khz Anti-aliasing filter transducers båndpasskarakteristikk f s 17.7 khz: Båndpass sampling
7.3 Samplerate-konvertering Ultralyd kommunikasjonssystem for kombinasjon med drfid Signal 40 khz ± 2-4 khz B = 4-8 khz Anti-aliasing filter transducers båndpasskarakteristikk f s 17.7 khz: Båndpass sampling
Oblig 1 FYS2130. Elling Hauge-Iversen
 Oblig 1 FYS2130 Elling Hauge-Iversen February 9, 2009 Oppgave 1 For å estimere kvalitetsfaktoren til basilarmembranen for ulike frekvenser har jeg laget et program som generer et rent sinussignal. Ideen
Oblig 1 FYS2130 Elling Hauge-Iversen February 9, 2009 Oppgave 1 For å estimere kvalitetsfaktoren til basilarmembranen for ulike frekvenser har jeg laget et program som generer et rent sinussignal. Ideen
INF109 - Uke 1b 20.01.2016
 INF109 - Uke 1b 20.01.2016 1 Variabler Et program er ikke til stor hjelp hvis det er statisk. Statisk betyr at programmet bare bearbeider faste data som er lagt inn i programkoden. For å gjøre programmer
INF109 - Uke 1b 20.01.2016 1 Variabler Et program er ikke til stor hjelp hvis det er statisk. Statisk betyr at programmet bare bearbeider faste data som er lagt inn i programkoden. For å gjøre programmer
Vedlegg B; Nedbøralgoritme.
 Vedlegg B til Teknisk kravspesifikasjon; Nedbøralgoritme Godkjent: Author: R Brækkan Side: 1 av 6 Vedlegg B; Nedbøralgoritme. Met.no geonor-algoritme (oppdatert 30/04-2009): Formålet med å lage en algoritme
Vedlegg B til Teknisk kravspesifikasjon; Nedbøralgoritme Godkjent: Author: R Brækkan Side: 1 av 6 Vedlegg B; Nedbøralgoritme. Met.no geonor-algoritme (oppdatert 30/04-2009): Formålet med å lage en algoritme
Introduksjon til lyd. Litt praktisk informasjon. Fra lydbølger til nerveimpulser. Det ytre øret
 Introduksjon til lyd Temaer i dag: Hvordan kan vi høre lyd? Lyd og lydbølger Amplitude, frekvens, periode og bølgelengde Hvordan representere lydsignaler matematisk? Hvordan illustrere lydsignaler grafisk?
Introduksjon til lyd Temaer i dag: Hvordan kan vi høre lyd? Lyd og lydbølger Amplitude, frekvens, periode og bølgelengde Hvordan representere lydsignaler matematisk? Hvordan illustrere lydsignaler grafisk?
Hvorfor? Læreplanen. Læreplanen MUSISERE KOMPONERE LYTTE. Digitale verktøy kommer inn som en naturlig del i alle hovedområdene.
 Hvorfor? Mestring på alle nivåer - tilpasset opplæring. Egnede arbeidsmetoder, bl.a. for læring og øving. Nye klanger. Noen ganger kan vi hoppe over den vanskelige øveprosessen - rett på lyd som klinger
Hvorfor? Mestring på alle nivåer - tilpasset opplæring. Egnede arbeidsmetoder, bl.a. for læring og øving. Nye klanger. Noen ganger kan vi hoppe over den vanskelige øveprosessen - rett på lyd som klinger
