Aksepter, ta skuld og iverksett!
|
|
|
- Edgar Mikalsen
- 8 år siden
- Visninger:
Transkript
1 Godt nyttår til alle dere som leser TANGEN- TEN. Det er kjekt å vite at det er langt over 3000 abonnenter nå som leser bladet. Like kjekt er det å se at vi også har mange engasjerte lesere som sender stoff til oss og som også påtar seg skriveoppgaver når redaksjonen ber om det. Vi kan være stolte av en slik dugnadsånd og et slikt felleskap. I desember skylte en ny bølge med resultater fra PISA- og TIMSS-undersøkelsen over oss, og mange er oppgitt over manglende fremgang trass iherdig innsats. Igjen ser Norge seg forbigått av Finland og mange andre land. Mange spør hvorfor? I analysen nå i etterkant ser vi stadig oftere at reformtempo, nye arbeidsformer, skolens og lærernes autoritetstap blir nevnt som mulige forklaringer. Reformene har bidratt til en endring av elev- og lærerrollen som enkelte hevder har ført til dårligere matematikkunnskaper. Oppsummering og forklaring i timene gjennom en formidlende lærer er undervisningselementer på vikende front. Kan der være en sammenheng med dette og elevers manglende evne til å kunne strukturere isolerte kunnskapsbiter til et meningsfullt hele? Ut fra det finske utdanningssystemet kan det se ut til at en autoritetsheving gjennom større faglighet og større fagkompetanse hos lærerne kan være en vei å gå. Men hvordan får vi engasjerte, dyktige, kvalifiserte og interesserte lærere? Rune Herheim, som er nytt medlem i redaksjonen for TANGENTEN, kommer med noen egne betraktninger omkring PISA- og TIMSSstudienes resultater og deres konsekvenser for vårt utdanningssystem. (Les side 2.) Også i dette heftet finner du en del bakgrunnsstoff om de nasjonale prøvene i matematikk. Kompetansebegrepet innen matematikk dannet en del av det didaktiske grunnlaget for utviklingen av prøvene. Mona Røsseland gir oss bakteppet for tenkningen bak de nasjonale prøvene i to artikler. Den første finner du i dette heftet. I neste hefte fortsetter hennes artikkel. År 2005 er også det første året Holmboeprisen deles ut. Holmboeprisen er på sett og vis en spin-off -effekt av Abelprisen. Prisen skal hedre stor innsats for matematikkfaget i skolen og premiere gode lærere eller gode lærerteam. Det er naturlig at Abel-komiteen ikke bare setter fokus på de store vitenskapelige, matematiske bragder, men også har undervisning og opplæringsdimensjonen med. Vi vet alle at vi kan lære mye av gode forbilder, og det gjelder selvsagt også vårt fag. Det blir spennende å (fortsettes side 4) tangenten 1/2005 1
2 Rune Herheim Aksepter, ta skuld og iverksett! PISA/TIMSS sett frå sidelina Torsdag 16. desember var det fagkonferanse om resultata frå TIMSS 2003 og PISA PISAundersøkinga, der OECD har eit overordna koordineringsansvar, har sett på 10. klassingar sine evner til å nytta kunnskap i matematikk, naturfag, lesing og problemløysing. TIMSSundersøkinga har sett på 4. og 8. klassingar sine skulekunnskapar i matematikk og naturfag. I begge undersøkingane har norske elevar oppnådd svake resultat i matematikk og naturfag, både samanlikna med andre land, men òg samanlikna med kva norske elevar tidlegare har prestert i tilsvarande testar. Eit av dei viktigaste poenga frå prosjektleiarane for PISA og TIMSS og fleire av innleiarane på konferansen, mellom anna Per Aahlin frå utdanningsforbundet, var at utdanningssystemet må akseptera desse resultata. Ein ynskte ikkje at det no skulle brukast energi på å debattera om undersøkingsresultata er gyldige og pålitelege, men at kreftene skulle fokuserast mot å løysa den norske realfagskrisa. At det er 2 Rune Herheim er høgskolelektor i matematikk fagdidaktikk ved Høgskolen i Bergen, rher@hib.no lagt mykje arbeid ned i desse undersøkingane er det ikkje tvil om. Ein har kvalitetssikra oppgåvetypar, oversetjingar, korrektur, søkt representative utval av elevar og skular osv. Men skal ein få med seg personar i ulike roller i utdanningssystemet er ein avhengig av at alle dreg i same retning. Oppnår ein dette ved å unngå ein debatt om sjølve undersøkingane? Ein risikerer at folk sit med spørsmål og kritikk mot undersøkingane som dei ikkje har fått svar på. For å nytta filosofen Hans Skjervheim [1] sine omgrep; skal lærarar, foreldre og andre verta samde om at ein bør justera realfagsundervisinga må dei overtydast om at det er naudsynt, ikkje overtalast. I det norske utdanningssystemet har ein underleg trend utvikla seg. Studentar og elevar har manglar i sin realfagskunnskap, men det einaste som er sikkert er at det ikkje er vår skuld På universitet og høgskular skuldar ein på dårlege førekunnskapar frå vidaregåande trinn, på vidaregåande trinn skuldar ein på ungdomstrinnet, medan på ungdomstrinnet skuldar ein på barnetrinnet. Og så skuldar me alle på L97. Eit signal som kom tydeleg fram under konferansen var at alle må ta skuld, anten ein er utdanningsminister, lærarutdannar eller lærar. Det er meir fruktbart å sjå kva 1/2005 tangenten
3 Figur side 149 i Hva i all verden har skjedd i realfagene? ein sjølv kan gjera betre, enn å konstatera at det ein annan stad er gjort for dårleg arbeid. Me har ein systemfeil vart det sagt fleire gonger på konferansen. Systemfeil er eit omgrep det kan vera vanskeleg å knyta noko presist innhald til. Langt viktigare enn å strø om seg med vide omgrep er det å sjå på kva konkret som bør gjerast for å styrka realfagsundervisinga. På konferansen vart barne-, ungdoms- og vidaregåande trinn trekt fram som satsingsområde. Det er bra, men kva med førskuletrinnet? Det er vel ingen som trur at elevar fyrst startar oppbygginga av sin matematiske kompetanse den dagen dei byrjar på skulen? Tiltak må setjast i verk. Det vil ikkje seia at alt må endrast, og undervisingsmetodar må forkastast. Svært mykje av det arbeidet som vert gjort i skulen er bra. Professor Svein Lie kom i sitt innlegg under konferansen inn på at det kan vera verdt å sjå på nokon av konsekvensane av L97. Det har vorte lagt opp til nye roller i skulen, der lærar har gått frå formidlar til rettleiar, og elevar har fått ansvar for eiga læring. Formidling har nesten vorte uglesett, og det har vore lagt føringar der mellom anna tema- og prosjektarbeid har fått ei dominerande rolle. Lie sa at ein slik metodetvang ikkje legg til rette for at ein lærar kan nytta sine beste sider. Gjennom leik og tema- og prosjektarbeid kan elevar oppnå viktige læringsmål, men som Lie var inne på så kan ein spørje seg om det har vore mindre læringsutbyte av desse metodane enn det som har vore tenkt? Har lærarar ikkje vore medvitne nok i å leggja til rette for læring, eller sikra at elevar får eit læringsutbyte, i desse metodane? Men konsekvensar av L97 treng ikkje i seg sjølv vera forklaring til svak utvikling innan realfag. Ein kan faktisk spørja seg om L97 eigentleg har vorte realisert i den grad at det er meining i å vurdera konsekvensane av denne planen? I ein evalueringsrapport av L97 [2] har ein funne at det langt på veg ikkje er tilfelle. Under klasseromsobservasjonar har dei funne at det er to arbeidsformer som er dominerande. Den eine er der lærar er forelesande og den andre er når elevar arbeider individuelt med lærebøkene. Norske elevar ligg i verdstoppen når ein ser på tiltru til eigne realfaglege evner. Som det står i [3] kan dette forklarast med kulturelle skilnadar, men det kan òg sjåast i høve til tangenten 1/2005 3
4 meistringsaspektet. Har me i Noreg fokusert så mykje på at elevar skal lukkast og utvikla sjølvtillit i faget at dei ikkje har fått varierte og store nok utfordringar? Har frykta for at elevar ikkje skal lukkast ført til at me heller har slakka litt av på dei faglege krava? Når ein derimot snakkar om det å ha interesse for faget og det å lika å arbeida med det, ligg norske elevar igjen langt ned på lista. Her kan det vera ein samanheng. Motivasjon får ein ved å lukkast, og dess meir krevjande utfordringar ein løyser, dess større vert gleda og gnisten til å arbeida vidare i faget. Det handlar såleis ikkje berra om å løysa ei oppgåve, ein må òg få strekkja seg. Under konferansen kom det fram sterke signal om at ein ynskte fagleg sterkare lærarar. I figuren på førre sida kan ein sjå noko av bakgrunnen for dette. Av norske lærarar som underviser i matematikk i 8. klasse har svært få fordjuping i matematikk, og nesten ingen har fordjuping i matematikk didaktikk. Dette bilete er hakket verre for 4. klasse, og i tillegg har norske lærarar lite relevant etterutdanning for matematikkundervising. I den norske skulen har me såleis eit sterkt behov for ei større fagleg tyngde i matematikk. For å utdanna lærarar med fagleg djupn bør ein kanskje vurdera å ta oppatt dei linedelte lærarhøgskuleutdanningane, eller syta for å ha fordjupingsfag i matematikk som er aktuelle og tilgjengelege for allmennlærarstudentane. Då kan ein få ein gunstigare kombinasjon av allmennutdanna lærarar og lærar med større fagleg tyngde. Men då må det presiserast at på same vis som ein skiskyttar må meistra både langrenn og skyting, må ein lærar ha både fagleg og fagdidaktisk kompetanse. Så viss ein aksepterer at arbeidet med realfaga i skulen har eit utviklingspotensiale og er sjølv viljug til å forbetra seg, kan tiltak setjast i verk for å snu 4 den negative trenden for realfaga. Men det mest grunnleggjande grepet ein bør gjera er å syta for at dei som faktisk har kompetanse i matematikkundervising òg underviser i faget. Referansar [1] Skjervheim (2001): Eit grunnproblem i pedagogisk filosofi. I: Hans Skjervheim, Deltakar og tilskodar og andre essays, (pp ). Oslo: Aschehoug & Co, Idé og tanke [2] Brekke, Breiteig og Alseth (2003): Synteserapport. Endringer og utvikling ved R97 som bakgrunn for videre planlegging og justering matematikkfaget som kasus. uploaded/nedlasting/brekke.doc [3] Grønmo, Bergem, Kjærnsli, Lie og Turmo (2004): Hva i all verden har skjedd i realfagene? Norske elevers prestasjoner i matematikk og naturfag i TIMSS (fortsatt fra side 1) se hvem som vinner årets Holmboepris. Tangenten skal presentere vinneren så snart han eller hun er utpekt. Tangenten håper denne prisen kan være med å skape blest rundt faget og matematikk som undervisningsfag. Fristen for nominasjon av kandidater er nettopp gått ut, så har du noen kandidater: ikke nøl med å foreslå dem til neste års Holmboepris! 1/2005 tangenten
5 Sindre Haugstad Torp Eksponentielle tallfølger og geometriske figurer Hallo, jeg har funnet ut en formel for hvordan man kan finne neste kvadrattall i rekken av kvadrattall. Jeg lurer på om dette er en kjent formel? y = x + kvadratroten av x ganger der x = et kvadrattall y = neste kvadrattall i rekken av kvadrattall 1 1 = 1, 2 2 = 4, 3 3 = 9, 4 4 = 16, 5 5 = 25, 6 6 = 36 For eksempel: = 5625 Det neste kvadrattallet i rekken blir da: x + (kvadratroten av x) ganger 2 + 1, det vil si ganger = 5776 kvadratroten av 5776 = 76 Dette ble skrevet til Newtonredaksjonen av 12 år gamle Sindre Haugstad Torp nå elev ved Solvang Ungdomsskole i Asker, men elev ved Jansløkka grunnskole da utforskningen startet. Nils Kr. Rossing fra Vitensenteret i Trondheim oppfordret Sindre til å skrive hvordan han tenkte da han kom fram til regelen. Resultatet sees her hvor Sindre viser hvordan han undersøkte videre og fant løsning for kubikktall, tallfølger i fjerde potens og en generell løsning. Tallfølgen i annen potens Jeg satt på rommet mitt og studerte rekken av kvadrattall (1, 4, 9, 16, 25 ) Lagde kvadrater som illustrasjon til tallene. For hvert kvadrat illustrerte jeg også det foregående som et mindre kvadrat inni det neste. Y = 4 2 Y = 5 2 På tegningen kommer økningen for hvert kvadrattall tydelig fram. Det så ut som økningen tangenten 1/2005 5
6 fulgte et mønster. Jeg gikk ned til stua og viste tallene og kvadratene til faren min som sa: Kall det lille kvadratet for X og det store for Y og lag en regel. En stund etter hadde jeg formelen skrevet på et papir. Y = X + X Tallfølgen i tredje potens En annen gang satt jeg med en ny oppgave. Hvordan blir det for kubikkrekka (1, 8, 27, 64, 125 )? Hva er sammenhengen mellom et kubikktall Y og det foregående X? I hodet forestilte jeg meg kuber som illustrerte tallene. Hva måtte jeg legge til kuben X for å få kuben Y? Jeg skjønte at det ville blitt alt for komplisert å finne formelen direkte ved bare å bruke X og Y. Jeg innførte derfor Z (se figuren under). = (X + 3Z 2 + 3Z) = (X + 3Z 2 + 3Z + 1) Formelen blir da: 2 Y = X + ( Z 3) + Z der Z = et helt tall, X = Z 3 og Y = ( Z + 1) 3. Løser vi ut Z får vi formelen: = Z = X = (X + 3Z 2 ) 3 Y = X + 3 X + 3 X + 1. Tallfølgen i fjerde potens Jeg prøvde av og til å få til i fjerde-rekka. Jeg hadde nå brukt flateinnhold for å finne formelen for kvadrattallene og kuber for kubikktallene, men nå var det ikke flere dimensjoner å bruke. Men en dag kom jeg til å tenke på en ting: Tre i fjerde betyr jo bare tre ganger tre ganger tre ganger tre. Tre i fjerde blir da tre tre i tredje kuber. Z i fjerde blir Z antall Z i tredje kuber, der Z har samme betydning som før. For å finne formelen må man være nøyaktig med antall kuber og det som skal legges på (fortsettes side 18) /2005 tangenten
7 Per Arne Birkeland, Ole Mydland På leting etter mønster Hvordan klarer elever å oppdage mønstre og se generelle trekk ved dem? Greier de å bruke algebra til å uttrykke slike trekk med utgangspunkt i en praktisk tilnærming? Av og til sier lærere at å generalisere blir for vanskelig for elevene. De klarer sjelden å oppdage generelle sammenhenger selv. Og hvis de skal bruke algebra, blir det ekstra vanskelig. Samtidig vet vi at L97 [1] gir klare beskjeder til oss lærere om hva målet for elevene er: De skal kunne tolke og bruke bokstaver som symboler for ukjente og variable størrelser og til å generalisere og bevise. Elevene skal kunne bruke tall som et utgangspunkt for fordypning og generalisering av ideer og metoder. (L97, s. 166) Som lærere i allmennlærerutdanningen ved Høgskolen i Agder og med mange års erfaring fra undervisning i ungdomsskolen, ville vi Per Arne Birkeland er høgskolelektor i matematikk fagdidaktik ved Høgskolen i Agder, per.a.birkeland@hia.no Ole Mydland er pensjonert høgskolelektor i matematikk. undersøke i hvilken grad ungdomsskoleelever ved samarbeid i grupper greier å oppdage generelle mønstre. Vi fant en egnet oppgave fra et tidligere nummer av Tangenten ([4], se farget boks neste side), og allierte oss med Inger Margrethe Haanes, som er matematikklærer i en 9- klasse ved en skole i Kristiansand. Utprøvingen skjedde i en dobbelttime en maidag i Klassen ble delt inn i 5 grupper. Et lokalt snekkerfirma hadde tatt utfordingen med å lage terninger med mål 2 cm 2 cm 2 cm slik at hver av gruppene hadde 125 småterninger hver. På forhånd var vi litt usikre på om gutter og jenter i 14- til 15-årsalderen ville synes det var for barnslig å bygge med klosser, og om de kunne ha noen hjelp av denne konkretiseringen. Derfor sa vi på forhånd at klossene kunne brukes hvis elevene hadde lyst til det. Lærerne skulle observere, stille spørsmål og gi hint etter behov. Etter noen minutters informasjon i starten, satte elevene i gang. Når de skulle finne hvor mange sider som var synlige eller ikke, startet alle gruppene med å bygge en 3-terning og telle de ulike kategoriene. Det virket som ingen av elevene så løsningen umiddelbart uten den konkrete 3-terningen. Diskusjonen gikk imidlertid livlig om hvordan småterningene i tangenten 1/2005 7
8 Oppgaven vi gav I denne oppgaven skal dere arbeide med en terning som er satt sammen av små-terninger. På figuren under ser dere en terning som er satt sammen av 3 terninger i hver retning. En slik sammensatt terning kaller vi en 3-terning. hvert tilfelle kunne telles opp. Det var spesielt interessant å merke at ganske tidlig i prosessen begynte elever å lete etter mønster. Da ei av gruppene skulle til å studere 4-terningen, utbryter en gutt spontant: «Nå må vi til med et mønster! Kan vi ikke ta sånn en tabell, en sånn skala som passer til alle de andre?» Resten av gruppa er enig. Og så begynner den mer eller mindre bevisste letingen etter mønster, skritt for skritt. I posen dere har fått på gruppa, er det nok småterninger til å bygge en 5-terning. Hvor mange småterninger består en 3-terning av? en 4-terning? en 5-terning? en 10-terning? en n-terning? Sidene på noen av småterningene er synlige, det vil si at de enten vender ut i lufta eller ned i bordet, og noen sider er skjulte. I en 3-terning fins småterninger der 3 sider er synlige, 2 sider er synlige, 1 side er synlig, og 0 sider er synlige. Hvor mange av småterningene i en 3-terning har: 0 sider synlige? 1 side synlig? 2 sider synlige? 3 sider synlige? Her leter elever etter et system. «Det er 4 klosser som har null sider synlig, det er de fire der, de som er heilt inni der,» mener ei jente og peker engasjert. Gutten er enig: «Ja, for du har en der, en der,, en, to, tre, fire». Men plutselig sier han: «Det er 8! Se der! En, to, tre, fire ikke sant? De fire i det laget der, Finn ut det samme på en 4-terning og en 5-terning. Dere har ikke nok terninger til å bygge en 6-terning. Men kan dere likevel finne ut hvor mange småterninger dere har av hver type i en slik terning? Kan dere finne ut det samme om en 10-terning? Har dere funnet et mønster slik at dere kan si med et tall eller et bokstavuttrykk hvor mange dere har av hver type småterning i en n-terning? 8 1/2005 tangenten
9 og fire i det laget der». Heile gruppa dras med i prosessen, og gutten prøver å overbevise de andre ved å lage en 2-terning: «Det er sånn en terning som er gjemt inni der». Tilsvarende arbeider gruppa med å finne 1 og 2 sider som er synlige på 4-terningen, og kommer i begge tilfellene til at dette antallet blir 4 ganger 6. Det kan virke som elevene bare teller, men et noe uklart mønster avtegner seg snart. Da de like etter studerer 5-terningen, går det mye kjappere med å finne antall synlige og usynlige sider på småterningene. Ikke fordi elevene teller fortere, men fordi de har funnet spesielle måter å telle på, eller tenke på. Lærer oppmuntrer dem til å skrive ned regnestykket som viser hvordan de tenker. opp: «Det er 12 ganger 1, 12 ganger 2, 12 ganger 3,», men så stopper det opp. Mønsteret som de mener å ha funnet, passer ikke på 6- og 7- terningen. Lærer spør elevene om hvordan en kan kontrollere at tallene i tabellen stemmer. De finner feilen, og letingen etter mønster kan fortsette. Dette lille hintet hjelper elevene i den videre letingen etter mønster: «Å var det vi ganga her med? Vi kan bare se på den», sier ei jente. Elevene går tilbake til 3-terningen og velger å lage en tabell, en matrise. Kombinert med å telle, tar de til å resonnere seg fram til hvert enkelt tall i tabellen. En interessant og noe uventet uttalelse fra en av guttene innleder denne viktige tankeprosessen: «Jeg vet ikke om jeg klarer å føre det ned, men jeg vet i alle fall åssen en tenker»! Sammen begynner gruppa med 3 synlig : «Det blir 8 her uansett», skyter ei jente raskt inn, «og der plusser vi bare på 12», fortsetter hun. De er kommet til 2 synlig. En gutt følger Gruppa er i ferd med å knekke koden Ved 2-synlig finner elevene en fast differanse, 12, mellom tallene i de forskjellige terningene. Det er derfor ganske logisk at de også leter etter en fast forskjell mellom tallene i rekka ved 1- synlig. Men her må de tenke i andre baner. «Har du funne systemet, det som var der?», spør en av guttene. «Jaaa, det var 6 ganger» Det er antall småterninger med 1 synlig side i en 6-terning elevene leter etter. De finner at tallet 16 er sentralt her, men diskuterer ivrig hvilket tall dette skal ganges med. Lenge holder de på 4, men til slutt ender de opp med 16 ganger 6. Lærer spør elevene om hvordan de kom fram til 16, om dette tallet også er et gangestykke. «4 ganger 4», svarer ei jente kjapt. «Åssen kom dere fram til tallet 4 da», spør lærer videre. Etter hvert oppdager elevene at i en slik sammensatt terning er det «to utenfor», som de sier. Da står en igjen med: «4 i en 6-terning og 8 i en 10-terning. Og i en 20-terning 18». «I en n-terning da», spør lærer? «n minus 2» svarer ei jente fort og ler, som om hun ville si: Så enkelt! tangenten 1/2005 9
10 Til ei gruppe som hadde funnet at det er 96 småterninger som har 1 side synlig i en 6-terning, spør lærer: «Åssen fant du 96?». Et svar kommer kontant og overbevisende: «Jeg må tenke meg at det er en 6-terning vi holder på med. Så da blir det 4. 4 på den sida, 4 på den, 4 på den, 4 på den, 4 på den og 4 på den eller, ja ikke sant, det blir 16 på alle samma. 16 ganger 6 er 96». Fra 6-terning går gruppa over til 10-terning, og tar også med 23-terning og 64-terning. De fyller ut tabellen og kontrollerer hver linje i den ved addisjon. En av guttene på gruppa har allerede i hodet et løsningsmønster for de ulike kategoriene. Lærer utfordrer ham til å forklare dette for de andre. «På null blir det n 2 i tredje». «Du må forklare hvorfor det blir n 2». «Fordi du må ta vekk 2 for å få det midterste». «Hvorfor tar du vekk 2?» «De ytterste, de ytterste lagene, så får vi bare den siden som er i midten, der som ingen sider vil være ut». De tenkte på 10 at de måtte skrelle av et lag ytterst. Etter at elevene på dette tidspunktet hadde jobbet med oppgaven i en god klokketime, var alle gruppene kommet godt i gang med å skrive et algebraisk uttrykk for antall terninger i de ulike kategoriene. En viktig bit av denne dobbelttimen var oppsummeringen. Vi hadde snakket på forhånd om hvor viktig det er for elevenes læringsutbytte at elevene blir hjulpet til å se tilbake på det de har gjort. Vi ønsket også å spørre dem om hvordan de selv opplevde å arbeide på denne måten. Tilbakemeldingen vi fikk fra elevene, var udelt positive. «Dette var gøy», sa de. Læreren var også meget godt fornøyd, og syntes elevene hadde klart mer enn hun hadde trodd på forhånd. Elevene viste i denne oppgaven at de i stor grad var i stand til å oppdage generelle mønstre. Men de var ikke overlatt helt til seg selv. Lærerens funksjon vurderer vi som meget viktig. Hvis ikke det hadde vært en voksen til stede som kunne stille de rette spørsmålene, og som kunne gi de nødvendige puff videre der det stoppet litt opp, ville nok noen elever «stått fast» og mistet interessen. At lærer gir hint, er ikke ensbetydende med å frata elevene følelsen av å mestre oppgaven selv. Her er det selvfølgelig en balansegang. Man må unngå å gi elevene hele løsningen. Men erfaringer fra dette og tilsvarende arbeid, viser tydelig at elevene selv med viktige hint, ikke fratas følelsen av og gleden ved å ha oppdaget ting selv. Tidligere forskning støtter også opp om de erfaringene vi gjorde i dette lille prosjektet. Det er liten tvil om at elevene strever i deres møte med algebra. Furinghetti og Paola [2] grupperte vanskelighetene slik: vanskeligheter med å sette opp formler vanskeligheter med å forstå formler og å 1/2005 tangenten
11 kontrollere dem vanskeligheter med å individualisere problemteksten vanskeligheter med å representere tankegangen gjennom algebraisk manipulasjon vanskeligheter med å tolke foreslåtte utsagn. Men det er flere som har rapportert om gode erfaringer med å tilnærme seg algebra ved å studere mønstre i tilknytning til konkrete materialer. Pegg og Redden [3] gjorde dette med barn i 12-årsalderen, hvor de arbeidet med å lage trekanter ved hjelp av fyrstikker. Etter en lang erfaringsøkt med fyrstikkene der tallene etter hvert ble satt inn i tabeller, vokste bokstavbehovet gradvis frem ved at antall fyrstikker ble kalt f. Dette ble barna etter hvert fortrolige med. Påstanden om at elevene må ha nådd et visst modenhetsnivå, er heller ikke et entydig resultat fra forskningen. Mulig det kan vises dersom forutsetningen er en undervisning uten bruk av mønsterbasert innfallsvinkel. Men Zack [5] rapporterer om at åringer kan nå ganske langt i evnen til å løse generaliseringsproblemer når problemløsning er en viktig del av undervisningen, og der det skjer i en oppmuntrende atmosfære gjennom samarbeid. Behovet for å bruke algebra vokste her frem som et resultat av studier med mønstre tilknyttet situasjoner som elevene kunne etterprøve og forstå. Litteratur [1] Det kongelige kirke-, utdannings- og forskningsdepartement.(1996). Læreplanverket for den 10-årige grunnskolen. Oslo, Norway: Nasjonalt læremiddelsenter. [2] Furinghetti, F. & Paola, D. (1995). A different approach to algebra and proof: Behaviours observed in classroom. In L. Meira & D. Carraher (Eds.): Proceedings of the Nineteenth International Conference of the International Group for the Psychology of Mathematics Education (Vol. 1, p. 202). Recife, Brazil: Universidade Federal de Pernambuco. [3] Pegg, J. & Redden, E. (1990). Procedures for, and experiences in, introducing algebra in New South Wales. Mathematics Teacher, 83, [4] Torkildsen, Ole E. (1995). Klasseoppgave. Tangenten 2, [5] Zack, V. (1995). Algebraic thinking in the upper elementary school: The role of collaboration in making meaning of generalisation. In L. Meira & D. Carraher (Eds.): Proceedings of the Nineteenth International Conference of the International Group for the Psychology of Mathematics Education (Vol. 2, pp ). Recife, Brazil: Universidade Federal de Pernambuco. tangenten 1/
12 Mona Røsseland Hva er matematisk kompetanse? Norge har nok en gang kommet dårlig ut i undersøkelser som viser elevers kompetanse i matematikk. Vi leter etter årsaker, og vi prøver å finne den riktige veien framover. Før vi kan enes om en hensiktsmessig strategi for å gjøre norske barn og unge bedre i matematikk, bør vi diskutere hva det innebærer å ha matematisk kompetanse. Noen mener at bare elevene kan de fire regningsartene (les algoritmene) når de går ut barneskolen, må vi være fornøyde. Andre mener at det viktigste er at elevene er kreative og klarer å finne løsninger på problemløsningsoppgaver uten tanke på en riktig fremgangsmåte. Heldigvis er det mange som mener at det er viktig at elevene behersker flere ulike kompetanser i matematikk, men da trenger vi en bevisstgjøring omkring hva det vil si å ha matematiske kompetanse. I Danmark har de kommet et stykke på vei i dette arbeidet. I 2000 satte de i gang prosjektet Kompetenceudvikling og Matematiklæring, der målet var å prøve å skape en felles forståelse for hva det vil si å beherske matematikk. Mona Røsseland er nettverkskoordinator ved Matematikksenteret, mona.rosseland@hjemme.no 12 matematikkbeherskelse, og hvordan dette kan påvirke matematikkundervisningen og gjøre den bedre. Arbeidet ble ledet av Mogens Niss, professor ved Roskilde Universitetssenter, og i 2002 kom rapporten Kompetancer og matematiklæring [5] fra det danske Undervisningsministeriet. Rapporten er grunnlag for min beskrivelse av de matematiske kompetansene. Det har også vært inspirasjonskilde til de nasjonale prøvene i matematikk i Norge. I disse prøvene blir elevene testet i ulike oppgavetyper, og de blir vurdert ut i fra en beskrivelse av matematiske kompetanser. Etter prøvene skal lærerne lage en profil over hver elev og for klassen som helhet. Profilen beskriver hvilket nivå elevene har i de ulike kompetansene. Kompetansebegrepene jeg gjør rede for her ligger til grunn for arbeid med de nasjonale prøvene. Den danske rapporten vender seg bort fra den tradisjonelle, pensumbaserte beskrivelsen av matematikkfaget. I stedet foreslår den at hensikt og utbytte med undervisning karakteriseres ved hjelp av åtte kompetanser som en ønsker at elevene skal utvikle. De åtte kompetansene er: Tankegang-, Resonnement-, Kommunikasjon-, Problembehandling-, Modellering-, Representasjon-, Symbol og 1/2005 tangenten
13 formalisme- og Hjelpemiddelkompetansen. Denne kompetansebaserte beskrivelsen av matematikkfaget ønsker jeg å belyse gjennom to artikler her i Tangenten. Den siste artikkelen kommer i Tangenten nr 2 (2005). Jeg velger å knytte beskrivelsen av kompetansene opp mot undervisning gjennom å vise hvilke type aktiviteter og situasjoner som kan være med å stimulere utviklingen av kompetansene hos elevene. Skal de nasjonale prøvene bli et hjelpemiddel for lærerne, vil det være helt vesentlig at lærerne har en god forståelse for hva de ulike kompetansene står for. Det vil også være av betydning at lærerne tar kompetansebeskrivelsene med inn i klasserommet, som grunnlag for undervisningen slik at det får praktiske konsekvenser i norsk skole. I denne artikkelen tar jeg for meg tankegangs-, resonnements- og kommunikasjonskompetansen. I den siste artikkelen beskriver jeg problembehandlings-, modellerings-, hjelpemiddel-, representasjons-, symbol- og formalismekompetansen. Der belyser jeg noen problemstillinger i forhold til å bruke kompetansebeskrivelsene som grunnlag for vurdering, slik det blir gjort i forbindelse med de nasjonale prøvene i matematikk. En kompetansebeskrivelse av matematisk faglighet Hvorfor er det så nødvendig å forandre på vår tradisjonelle måte å se matematikkfaget på? Hvorfor lage de nasjonale prøvene så kompliserte, der en må forholde seg til mange nye begreper, som disse matematiske kompetansene? Skolematematikken har vært preget av et fokus på produktet og den riktige fremgangsmåten, og en har arbeidet for å få større fokus på prosessdimensjonen i faget. Vi ser det tydelig at L97 understreker betydningen av elevaktivitet, der elevene skal konstruere sin egen kunnskap. Vi er nå blitt mer opptatte av hvordan elevene bruker sin matematiske kompetanse, hvilke strategier de velger for å løse oppgaver og problemer og hvilken begrepsforståelse de har. Også i PISA-undersøkelsen (Programme for Internastional Student Assessment) har prosessdimensjonen i faget grunnleggende betydning. Her blir det understreket at det kreves ulik matematisk kompetanse for å løse forskjellige typer matematiske problemer. PISA fokuserer altså i langt større grad på et mer integrert spektrum av kunnskaper, ferdigheter og holdninger enn det som har vært vanlig i tester til nå. En legger vekt på elevenes evne til å tolke informasjon og trekke slutninger på basis av kunnskap og ferdigheter som de har, og på hvordan elevene bruker kunnskaper og ferdigheter i gitte sammenhenger (Bergem [1]). I PISA brukes tre kompetanseklasser Oppgavene er delt inn i tre kategorier etter hvilke kompetanser de krever: Reproduksjonsklassen: Oppgavene er knyttet til elevers bruk av faktakunnskaper og standardalgoritmer. En kan også finne enkle problemløsningsoppgaver her, men konteksten er matematisk og fremgangsmåten (algoritmen) gitt. Forbindelsesklassen: Her skal elevene se forbindelser og kunne sette sammen informasjon som grunnlag for problemløsningen. Elevene må da ha evne til å se sammenhenger mellom ulike deler av matematikken for å løse oppgavene, og de skal kunne bruke ulike representasjoner. tangenten 1/
14 Refleksjonsklassen: Her er oppgavetypene mer sammensatte enn ved forrige klasse og krever at elevene i tillegg har evne til å utvikle originale løsningsstrategier. Kompetansen kjennetegnes ved at elevene selv må finne fram til hva som er oppgavens matematiske problem, og vise evne til kritisk tenkning, analyse og refleksjon (Lie m.fl. [2]). Når de overordnede målene i matematikk kun tydeliggjør hvilke matematiske emneområder som skal læres, er det vanskelig å klargjøre hva matematikkundervisning skal gå ut på. Vi vet at det er langt mer gjennomgripende forhold enn pensumbeherskelse som gjør seg gjeldende i matematisk faglighet. Faren blir at en reduserer matematisk faglighet til rette og feile svar, noe som igjen fører til et for lavt ambisjonsnivå for undervisningen. En kompetansebeskrivelse av faget går langt mer direkte på selve undervisningen, for da vil en også sette fokus på ferdigheter som vanskelig lar seg teste i en skriftlig prøve. Lærerne bør dermed sette flere krav til sin undervisning, for eksempel bruke mer tid på kommunikasjon, der elevene får forklare hvordan de tenker og forstår. En slik reduksjon av matematikkompetanse kan sammenlignes med å identifisere språkbeherskelse med en liste over ordforråd og grammatiske regler en skal gjenkjenne og kunne. Norsklærere har større ambisjoner for undervisningen enn at elevene bare lærer dette. De ønsker at elevene skal forstå stoffets oppbygging og indre sammenheng, og ikke minst være skapende og analyserende i faget i forhold til et mangfold av sjangrer og stilarter. En kan selvsagt understreke at dette ikke går uten et ordforråd og grammatikk, men ingen vil heller mene at det i seg selv er nok for språkbeherskelse (Niss [4]). På samme måte blir det med matematikken. 14 Å ha matematisk kompetanse kjennetegnes ved å ha viten om, å forstå, utøve, anvende og kunne ta stilling til matematikk og matematisk virksomhet i et mangfold av sammenhenger. Dette impliserer naturligvis en mangfoldighet av konkret viten og konkrete ferdigheter innen forskjellige matematiske områder, men matematisk kompetanse kan ikke reduseres til disse forutsetningene. Beskrivelse av kompetansene Tankegangskompetansen Denne kompetansen består først og fremt i det å være klar over hvilke typer spørsmål som er karakteristisk for matematikk, selv å kunne stille slike spørsmål og ha blikk for hvilke typer av svar som kan forventes. Matematisk tankegang omfatter bevissthet rundt hvilke spørsmål som er karakteristiske for matematikk. Det vil også si å kjenne, forstå og kunne bruke matematiske begreper, kunne abstrahere og generalisere og kunne skille mellom påstander, antagelser og bevis. For grunnskolen vil dette gjelde elementær matematikk, det vil si grunnbegrepene for størrelse, tall og rom som det er naturlig at de respektive aldersgrupper befatter seg med (se NSMO [3]). Denne kompetansen vil komme til syne gjennom dialog mellom elevene og mellom elevene og lærer. Elever med god tankegangskompetanse kan stille spørsmål som Finnes det et tall som både er partall og oddetall? Hva betyr brøk egentlig? Hvorfor blir svaret større enn det vi deler med når en deler med et tall mindre enn 1? Denne kompetansen henger nøye sammen med resonnementskompetansen, og til tider kan det være vanskelig å skille dem fra hverandre. Disse to kompetansene, sammen med kommunikasjonskompetansen blir også slått sammen til en kompetanseprofil i de nasjonale prøvene fra /2005 tangenten
15 Slik jeg ser det, vil denne kompetansen være en betydningsfull lærerkompetanse. Det er viktig at lærerne har evne til å stille gode spørsmål til elevene, spørsmål som får elevene til å reflektere. Ved hjelp av lærerens ledende spørsmål klarer elevene selv å resonnere seg frem til svar som gir innsikt og forståelse. Her tror jeg vi har mye å lære, for vi har ofte en higen etter å gi elevene svarene med en gang de spør. Kanskje vi langt oftere skulle stille spørsmål tilbake til elevene, og så la dem få tid til å tenke og gjerne komme med nye mer reflekterte spørsmål? Eksempelet med figurtall (nedenfor) viser lærerens tankegangskompetanse i sin dialog med elevene. Resonnementkompetansen Kompetanse i matematisk resonnement inneholder å kunne tenke ut og gjennomføre uformelle og formelle resonnementer, kunne omforme resonnementer og antagelser til gyldige bevis og kunne følge og bedømme matematiske resonnementer og forstå hva et bevis er (Niss m.fl. [5], s. 54). Denne kompetansen er aktiv når en elev klarer å bedømme holdbarheten av en matematisk påstand, det innebærer også å overbevise seg selv og andre om eventuell gyldighet av denne. Det dreier seg både om regler og setningers riktighet, men også avgjørelsen om at gitte svar på spørsmål, oppgaver eller problemer er korrekte og tilstrekkelige. Resonnementskompetansen er den som aktiverer hvilke operasjoner en skal bruke i en regneoppgave, hvis denne aktiveringen stiller krav til oppfinnsomhet, analyseevne eller overblikk. Denne kompetansen henger nøye sammen med både modellerings- og problemløsningskompetansen, og vi kan si at resonneringskompetansen er disse kompetansenes juridiske side, den som vurderer om svaret er rett eller galt (ibid. s. 210). Å forstå et resonnement er for eksempel å kunne forstå utsagn som: Tone har flere dukker enn Kine, og Kine har flere dukker en Marit. Da har Tone flere dukker enn Marit. Eksempel på å kunne følge og forholde seg til et elementært matematisk resonnement er: Utsagn: Berit og Anne bor henholdsvis 1,5 og 2 km fra skolen, så de må bo 3,5 km fra hverandre. Resonnement: Nei, det trenger de ikke. Det kan jo være de bor på samme vei til skolen, og da vil det bare være 0,5 km mellom dem. På barnetrinnet vil elevenes resonnementer være intuitive og uformelle eller konkrete, basert på spesifikke opptellinger, utregninger eller tegninger. Det er derfor ikke forventet at de skal gjennomføre noen bevisførsel i en streng betydning av begrepet. Eksempelet som følger viser både tankegangs- og resonnementskompetansen gjennom en aktivitet med figurtall. Arbeid med figurtall et undervisningsopplegg som legger til rette for utvikling av tankegang- og resonnementskompetanse. En fjerde klasse arbeider med figurtall. Læreren har satt elevene i gang med å lage ulike figurer ved hjelp av små kvadratiske brikker. Først skal elevene lage en figur der de ikke får bruke mer enn 8 biter. Neste steg blir å lage en noenlunde tilsvarende figur, men den skal være større. Det innebærer at de må bruke flere brikker. Så skal de lage en tredje figur, som igjen er større enn de forrige, men lik i form. Læreren ber elevene finne ut hvor mange brikker de har brukt i hver figur. Kari og Lucie har funnet ut at de har brukt tangenten 1/
16 8 biter i første figur, 25 biter i andre figur og 52 biter i tredje figur. Læreren observerer jentene i arbeidet, og kommer nå med noen spørsmål: Kan dere finne ut hvor mange biter dere trenger til fjerde figuren, uten å legge den med biter? Nei, går det an? svarer jentene tvilende. Jo, jeg tror det! sier læreren og går et stykke unna jentene for å se hvordan de griper problemet an alene. Jentene diskuterer en stund seg i mellom før de spør: Kan vi få tegne figuren i stedet? Jentene får ruteark og tegner den fjerde figuren. De teller antall biter og kommer til 89. Så kommer læreren igjen med nye spørsmål: Kan dere nå finne ut hvor mange biter dere trenger til den femte figuren, og denne gangen uten å tegne den? Jentene ser rådville ut, så læreren kommer med et nytt tips: Hvis dere skriver ned alle tallene dere har funnet til nå i et skjema, blir det litt mer oversiktelig. Læreren hjelper jentene i gang med å lage en tabell: 16 Figur nr Antall biter Vokser med Hva forteller tallene dere? Kan dere finne noe mønster i dem? Læreren trekker seg nok en gang litt i bakgrunnen, og lar jentene resonnere seg frem på egenhånd. Jentene begynner å studere tallene: Hvor mye større blir tallene fra figur til figur? Kan det være at figurene hele tiden vokser med 10 mer enn forrige gang? Det går ikke så veldig lang tid før de kommer med en hypotese: Mon tro om ikke det neste figuren vokser med 47? Lærer, vi tror at den femte figuren vil ha 136 biter. De klarer nesten ikke sitte stille på stolene, og de nesten roper ut. Kan vi få tegne nå? Læreren synes det er en glimrende ide, og berømmer jentene for deres fremragende matematiske resonnement og fremgangsmåte. Det tar heller ikke lang tid før de fornøyd kan konstatere at femte figur virkelig består av 136 biter. Går det an å finne ut hvor mange brikker dere trenger til den 10. figuren? spør læreren. Lucie stønner litt: Da trenger vi store ark til å tegne på. Trenger vi å fortsette å tegne, tro? spør Kari. Hvis vi vet hvordan figurene vokser, kan vi kanskje regne det ut uten å tegne? Jentene finner seg en kalkulator og går i gang med å fylle ut tabellen. Timen er over for lengst og deres medelever er gått ut, og læreren går til lunsj. Da hun kommer tilbake, sitter jentene med store smil, og de kan fortelle at den tiende figuren vil ha 521 biter! 1/2005 tangenten
17 Kommunikasjonskompetanse Kompetanse i kommunikasjon inneholder det å kunne sette seg inn i og tolke andres matematikkholdige skriftlige, muntlige eller visuelle utsagn og tekster. Det er å kunne uttrykke seg om matematiske forhold på ulike måter og på forskjellig nivå av teoretisk og teknisk nøyaktighet, både skriftlig, muntlig og visuelt for forskjellige kategorier av mottakere (ibid., s. 60). Vi kan gjerne si at denne kompetansen er todelt, i og med at kommunikasjonen skjer mellom avsendere og mottakere. På denne måten består denne kompetansen dels i å forstå og tolke andre sine matematikkholdige tekster, både visuelle, skriftlige (f. eks.i bøker og i oppgaver) og muntlige (eks. læreren gir en grublis muntlig). Dette vil da betegne den mottakende siden av kommunikasjonskompetansen. I tillegg trenger elevene denne kompetansen når de selv skal formidle sine matematiske kunnskaper, for eksempel når de skal gjøre rede for et matematisk resonnement, Hvordan tenkte du nå? Hvordan kom du frem til svaret? og dette kan de gjøre skriftlig, muntlig eller visuelt gjennom f. eks. tegninger. Dette viser uttrykkssiden av kommunikasjonskompetansen. Eksempler på vurdering av kommunikasjonskompetansen hos to 4. klassinger Klassen jobber med problemløsningsoppgaver, såkalte grubliser, og læreren går rundt og snakker med elevene. Hun prøver å få elevene til å formidle hvordan de forstår oppgavene og hva de tenker når de løser dem. Sissel klarer til en viss grad å forklare hva hun tenker, men det er i et enkelt og dagligdags språk. Hun bruker lite et matematisk språk, som for eksempel sier hun ikke enere og tiere, men ord som begynne bakerst når hun skal forklare hvordan hun tenker i addisjonsstykker. Hun er også i stor grad avhengig av konkreter for å forstå og forklare hva hun gjør. Hun viser dårlig begrepsforståelse, noe som igjen reduserer hennes muligheter til å forstå og sette seg inn i de matematiske tekstene. Se eksempel fra dialogen mellom henne og lærer da hun arbeider med oppgaven: Du har 80 kr og så kjøper du to flasker brus til 15 kr stykk. Hvor mye penger har du igjen? Sissel resonnerer: Jeg tar en tikroning, og så en til og så Hun er veldig usikker og lærer spør hvor mange tiere det er i 80. Det er , nei, Hun tegner nå 8 sirkler på papiret. Lærer hjelper videre og gjentar oppgaven med at hun skal kjøpe to brus til 15 kr. Nå er hun veldig usikker, men sier forsiktig: Da kan jeg i hvert fall ta bort en tikroning Og så, ja, nå må jeg tenke tror du det går an til å ta kroner også? Nei, jeg forstår ikke hvordan jeg skal gjøre dette, sier hun fortvilt. Jeg klarer det ikke! Lærer hjelper henne videre, med å gjenta oppgaven. Du har 80 kr og så skal du kjøpe deg brus. Hvor mye må du betale i kiosken for brusen? Jeg må betale 20 kr eller blir det mer? Nå forslår lærer at hun tegner ned pengene. Hun tegner ned en tier og fem kronestykker og sier videre: så tar jeg en tier til Kan jeg veksle en tikroning, tror du? Til slutt klarer hun å finne frem til at det blir 30 kr, og teller seg frem til at hun da vil ha 50 kr igjen av de 80. Lars på sin side viser stor kompetanse i kommunikasjon. Han forklarer løsningene sine på en tydelig måte, og han bruker et matematisk språk i sine forklaringer. Han sier blant annet hundreplass, og han bruker helt naturlig tiere og enere. Lars har heller ingen problemer med å forstå innholdet i problemløsningsoppgavene, og han viser god begrepsforståelse. På oppgaven Du har 4 poser med kjærligheter. tangenten 1/
18 Det er 8 kjærligheter i hver pose. Hvor mange kjærligheter har du? viser han at han både har flere mulige løsningsmetoder og at han klarer å formidle hvordan han tenker: Han sier: er 32! Han skriver ned 8 4 = 32 mens han forklarer: Det er 8 i hver pakke og så er det 4 pakker, det blir 32. Jeg kunne også ha skrevet det slik: = 32. Men jeg tenkte slik: (8 + 8 = 16) = 32. Eksemplene illustrerer at dialogen med lærer er verdifull når vi skal vurdere elevene sin matematiske kompetanse. For å få et fullgodt bilde av kompetansene til elevene våre, er det ikke tilstrekkelig med en to timers prøve. Men dette vil jeg komme nærere inn på i den neste artikkelen. Litteraturliste [1] Bergem, O. C. (2002) Utvikling av matematikkoppgaver i PISA. Hovedfagsoppgave levert til Institutt for læreutdanning og skoleutvikling ved UiO. [2] Lie, S, Kjærnsli, M, Roe, A og Turmo, A; Nasjonal hovedrapport PISA 2000: Godt rustet for framtida? Norske 15-åringers kompetanse i lesing og realfag i et internasjonalt perspektiv. Acta Didactica 4/2001 [3] Nasjonalt senter for matematikk i opplæringen (NSMO); Informasjon om de Nasjonale Prøver i matematikk. [4] Niss, M (1999). Kompetencer og uddannelsesbeskrivelse, Uddannelse 9: Danmark [5] Niss, M, Jensen, T. H. (2002) Utdannelsesstyrelsens temahefter nr ; Kompetancer og matematiklæring. Undervisningsministeriet, København (fortsatt fra side 6) kubene. Følger ellers samme prinsipp som for i tredje rekka. Setter X = Z 4, Y = ( Z + 1) 4. Formelen blir da: Y = X + 3Z Z + 3Z Z + Z + Z + 3Z + 3Z Y = X + 4Z + 6Z + 4Z + 1 Løser vi ut Z får vi formelen: Y = X + 4( X ) + 6( X ) + 4( X ) + 1. En generell løsning Etter hvert begynte jeg å undre meg om det fantes en generell løsning for tall opphøyd i hva som helst. Jeg hadde begynt å tenke på det allerede når jeg holdt på med kubikkrekka, men nå så jeg en viss likhet mellom denne og formelen for tall opphøyd i fjerde potens. Jeg prøvde med mange generelle uttrykk uten å lykkes. Til slutt innså jeg at løsningen var enklere enn jeg hadde trodd. Ved å bruke de samme definisjoner for Y og Z som tidligere, og når n er naturlige tall, får vi: 2 n Y = ( Z + 1 ). Da X = blir Z = X. Får da den generelle likningen: Z n n n n Y = ( X + 1 ). 18 1/2005 tangenten
19 Per Storfossen Lag et regnestykke med 25 som svar På barnetrinnet møter elevene tallregningen eller aritmetikken. Addisjon eller addisjonsoppgaver blir først presentert. Deretter følger ofte de andre basisregningsartene i rekkefølgen subtraksjon, multiplikasjon og divisjon. Kanskje det er mulig og fruktbart samtidig å ta i bruk alle de fire basisregningsartene for å hjelpe elever til å se sammenhengen mellom dem når tallene som oftest er små? Hvilken oppgavetype kan i så fall stimulere til en slik elevaktivitet? En slik problemstilling ga grunnlag for at elevene i en fjerdeklasse ved Lovisenberg skole i Hamar arbeidet med å løse oppgaven «Lag et regnestykke med 25 som svar». Senere har vi oppdaget at den samme oppgavetypen er gitt i Nasjonale Prøver med oppgaveteksten «Lag fem forskjellige regnestykker med 24 til svar». Fokus var å se hvordan elever opplever møtet med regningsartene. Elevene hadde ikke tidligere erfaring med den oppgavetypen. Vi var spente på hvordan de ville reagere på selve oppgaveformuleringen, og hvordan de ville komme i gang med å løse en slik åpen oppgave. Ville de for eksempel lage kun ett regnestykke som de Per Storfossen er høgskolelektor i matematikk fagdidaktikk ved Høgskolen i Hamar, studiested Elverum, per.storfossen@hihm.no ble bedt om, eller mange regnestykker hvor alle de fire basisregneartene kom i betraktning? Vi prøvde å unngå presentasjon og bruk av standardalgoritmer (effektive, rigide og abstrakte regnemaskiner ) når tallene er små, og når elever selv foretrekker å bruke egne metoder. Elevene gikk til verket Læreren skrev bare oppgaveteksten på tavla, og ga dem ikke veiledning eller forklaring. Hensikten var å gi elevene en reell sjanse til å prøve seg på utfordringene oppgaven ga. Elevene gikk til verket. Responsen til oppgaveteksten uteble ikke. Noen satt som spørsmålstegn og spurte «Hva skal jeg gjøre, jeg forstår ikke noe? Skal jeg gange eller legge sammen?» Andre uttalte etter en kort stund «Hei, det går ikke an å stoppe, det er jo ørthen måter å gjøre dette på». Den sistnevnte kommentaren reflekterte til opplevelsen av å se den store mengden av regnestykker. De så for seg uendelig av muligheter. Vi lærere fikk oppleve å se barns naturlige nysgjerrighet og kreativitet komme til syne. Den umiddelbare friheten ved det å komponere noe og å kaste seg ut i et undersøkelseslandskap var noe nytt og spennende for dem. Det var også konkurranse mellom noen av elevene om å lage flest mulig regnestykker. Her ble det mye regnetrening! tangenten 1/
20 Den andre gruppen av elever hadde problemer med å komme i gang med oppgaven. Det så ikke ut til at de fikk tak i hva som var meningen med den, eller hva de skulle gjøre. Etter en stund fikk de hjelp av læreren som foreslo hvordan de kunne arbeide. I etterkant snakket vi med noen elever for å få nærmere kjennskap til framgangsmåtene deres. Vi så spor av flere mulige tankemodeller. I elevbesvarelse nr. 1 er det første regnestykket 100 : 4 = 25, mens det siste er : = 25. I linjen under dobles både dividend og divisor slik at en får 200 : 8 = 25. Neste regnestykke, 300 : 12 = 25, kan være en transformasjon av 100 : 4 = 25 ved at dividend og divisor er multiplisert med : 120 = 25 kan være framkommet ved å multiplisere med 10 i både teller og nevner i det tidligere regnestykket 300 : 12, eller ved å multiplisere med 30 i både teller og nevner i regnestykket 100 : 4. Det er også mulig å komme fram til det samme resultatet ved å addere (kombinere resultater fra tidligere regnestykker) tellerne og nevnerne hver for seg i regnestykkene 100 : 4 og 200 : 8 ved at ( ) :(4 + 8 ) = 25. Resultatet er gyldig fordi = = ( 1+ 2) og = = 25 ved at kvotienten (konstanten) er den samme (25). Resultatet er gener ( 1+ 2) aliserbart eller allmenngyldig fordi når a = k a = b k b kvotient, vil a + ka = a( 1+ k) = a = kvotient. Å nytte b+ kb b( 1+ k) b at kvotienten er den samme krever en innsikt i brøkbegrepet. Et nytt regnestykke kan framkomme ved å ta utgangspunkt i et tidligere regnestykke, for deretter å multiplisere teller og nevner med en ønsket konstant. Et eksempel er regnestykket 7000 : 280 = 25 som kan utledes fra det tidligere regnestykket 1000 : 40, hvor den valgte konstanten er 7. Flere regnestykker indikerer at eleven kan ha en oppfattelse av multiplikasjon og divisjon som motsatte regneoperasjoner. Vi får bekreftelser på dette når vi gjen- 20 Tre eksempler på elevarbeider Elevbesvarelse nr. 1 Elevbesvarelse nr. 2 Elevbesvarelse nr. 3 1/2005 tangenten
Hva er matematisk kompetanse?
 Mona Røsseland Hva er matematisk kompetanse? Norge har nok en gang kommet dårlig ut i undersøkelser som viser elevers kompetanse i matematikk. Vi leter etter årsaker, og vi prøver å finne den riktige veien
Mona Røsseland Hva er matematisk kompetanse? Norge har nok en gang kommet dårlig ut i undersøkelser som viser elevers kompetanse i matematikk. Vi leter etter årsaker, og vi prøver å finne den riktige veien
Matematisk samtale og undersøkingslandskap
 Matematisk samtale og undersøkingslandskap En visuell representasjon av de ulike matematiske kompetansene 5-Mar-06 5-Mar-06 2 Tankegang og resonnementskompetanse Tankegang og resonnementskompetansen er
Matematisk samtale og undersøkingslandskap En visuell representasjon av de ulike matematiske kompetansene 5-Mar-06 5-Mar-06 2 Tankegang og resonnementskompetanse Tankegang og resonnementskompetansen er
Hva er god matematikkundervisning?
 Hva er god matematikkundervisning? Astrid Bondø Nasjonalt Senter for Matematikk i Opplæringen 22-Feb-08 Ny læreplan, nye utfordringer for undervisninga i matematikk? Hva vil det si å ha matematiske kompetanse?
Hva er god matematikkundervisning? Astrid Bondø Nasjonalt Senter for Matematikk i Opplæringen 22-Feb-08 Ny læreplan, nye utfordringer for undervisninga i matematikk? Hva vil det si å ha matematiske kompetanse?
ADDISJON FRA A TIL Å
 ADDISJON FRA A TIL Å VEILEDER FOR FORELDRE MED BARN I 5. 7. KLASSE EMNER Side 1 Innledning til addisjon 2 2 Grunnleggende om addisjon 3 3 Ulike tenkemåter 4 4 Hjelpemidler i addisjoner 9 4.1 Bruk av tegninger
ADDISJON FRA A TIL Å VEILEDER FOR FORELDRE MED BARN I 5. 7. KLASSE EMNER Side 1 Innledning til addisjon 2 2 Grunnleggende om addisjon 3 3 Ulike tenkemåter 4 4 Hjelpemidler i addisjoner 9 4.1 Bruk av tegninger
Emnekode: LGU 51014 Emnenavn: Matematikk 1 (5 10), emne 1. Semester: VÅR År: 2016 Eksamenstype: Skriftlig
 Sensurveiledning Emnekode: LGU 51014 Emnenavn: Matematikk 1 (5 10), emne 1 Semester: VÅR År: 2016 Eksamenstype: Skriftlig Oppgave 1 Figuren viser hvordan en nettside forklarer en metode for addisjon og
Sensurveiledning Emnekode: LGU 51014 Emnenavn: Matematikk 1 (5 10), emne 1 Semester: VÅR År: 2016 Eksamenstype: Skriftlig Oppgave 1 Figuren viser hvordan en nettside forklarer en metode for addisjon og
REGNEPLAN FOR LANDÅS SKOLE
 1 REGNEPLAN FOR LANDÅS SKOLE På Landås skole har alle lærere, i alle fag, på alle trinn ansvar for elevenes regneutvikling. Å kunne regne er å bruke matematikk på en rekke livsområder. Å kunne regne innebærer
1 REGNEPLAN FOR LANDÅS SKOLE På Landås skole har alle lærere, i alle fag, på alle trinn ansvar for elevenes regneutvikling. Å kunne regne er å bruke matematikk på en rekke livsområder. Å kunne regne innebærer
Posisjonsystemet FRA A TIL Å
 Posisjonsystemet FRA A TIL Å VEILEDER FOR FORELDRE MED BARN I 5. 7. KLASSE EMNER Side 1 Innledning til posisjonsystemet P - 2 2 Grunnleggende om posisjonsystemet P - 2 3 Titallsystemet P - 3 4 Posisjonsystemet
Posisjonsystemet FRA A TIL Å VEILEDER FOR FORELDRE MED BARN I 5. 7. KLASSE EMNER Side 1 Innledning til posisjonsystemet P - 2 2 Grunnleggende om posisjonsystemet P - 2 3 Titallsystemet P - 3 4 Posisjonsystemet
Læreplanene for Kunnskapsløftet
 Læreplanene for Kunnskapsløftet Hvordan få samsvar mellom intensjon og praksis? Mona Røsseland Nasjonalt senter for matematikk i opplæringen Leder i Lamis Lærebokforfatter; MULTI 21-Mar-06 Intensjoner
Læreplanene for Kunnskapsløftet Hvordan få samsvar mellom intensjon og praksis? Mona Røsseland Nasjonalt senter for matematikk i opplæringen Leder i Lamis Lærebokforfatter; MULTI 21-Mar-06 Intensjoner
Sensurveiledning til skriftlig eksamen i Matematikk 1, 1-7
 Sensurveiledning til skriftlig eksamen i Matematikk 1, 1-7 24. mai 2011 Oppgavesettet besto av 3 oppgaver. Alle oppgavene skulle besvares og svarene begrunnes. Oppgavene telte i utgangspunktet som vist
Sensurveiledning til skriftlig eksamen i Matematikk 1, 1-7 24. mai 2011 Oppgavesettet besto av 3 oppgaver. Alle oppgavene skulle besvares og svarene begrunnes. Oppgavene telte i utgangspunktet som vist
Forfatterne bak Multi: Multi i praksis. 5.-7.trinn. En bred matematisk kompetanse. Oppbyggingen av Multi. Grunntanken bak Multi
 Forfatterne bak Multi: Multi i praksis 5.-7.trinn Bjørnar Alseth Universitetet i Oslo Henrik Kirkegaard, Flisnes skole, Ålesund Mona Røsseland, Matematikksenteret Gunnar Nordberg, Høgskolen i Oslo Grunntanken
Forfatterne bak Multi: Multi i praksis 5.-7.trinn Bjørnar Alseth Universitetet i Oslo Henrik Kirkegaard, Flisnes skole, Ålesund Mona Røsseland, Matematikksenteret Gunnar Nordberg, Høgskolen i Oslo Grunntanken
Elevaktiv matematikk. hvorfor og hvordan? Retningslinjer for undervisningen. Intensjoner med ny læreplan. Hvilke utfordringer gir dette lærerne?
 Elevaktiv matematikk Hvordan får vi aktive, engasjerte og motiverte elever og lærere i matematikk? hvorfor og hvordan? Mona Røsseland Leder i Lamis Nasjonalt senter for matematikk i opplæringen Lærebokforfatter
Elevaktiv matematikk Hvordan får vi aktive, engasjerte og motiverte elever og lærere i matematikk? hvorfor og hvordan? Mona Røsseland Leder i Lamis Nasjonalt senter for matematikk i opplæringen Lærebokforfatter
10.03.2011. Hvorfor får elevene problemer med tekstoppgaver? Hva kan vi gjøre for at elevene skal mestre tekstoppgaver bedre?
 Hvorfor får elevene problemer med tekstoppgaver? Hva kan vi gjøre for at elevene skal mestre tekstoppgaver bedre? Mona Røsseland Matematikksenteret (for tiden i studiepermisjon) Lærebokforfatter, MULTI
Hvorfor får elevene problemer med tekstoppgaver? Hva kan vi gjøre for at elevene skal mestre tekstoppgaver bedre? Mona Røsseland Matematikksenteret (for tiden i studiepermisjon) Lærebokforfatter, MULTI
Kvikkbilde 8 6. Mål. Gjennomføring. Planleggingsdokument Kvikkbilde 8 6
 Kvikkbilde 8 6 Mål Generelt: Sammenligne og diskutere ulike måter å se et antall på. Utfordre elevene på å resonnere omkring tallenes struktur og egenskaper, samt egenskaper ved regneoperasjoner. Spesielt:
Kvikkbilde 8 6 Mål Generelt: Sammenligne og diskutere ulike måter å se et antall på. Utfordre elevene på å resonnere omkring tallenes struktur og egenskaper, samt egenskaper ved regneoperasjoner. Spesielt:
Telle i kor steg på 120 frå 120
 Telle i kor steg på 120 frå 120 Erfaringer fra utprøving Erfaringene som er beskrevet i det følgende er gjort med lærere og elever som gjennomfører denne typen aktivitet for første gang. Det var fire erfarne
Telle i kor steg på 120 frå 120 Erfaringer fra utprøving Erfaringene som er beskrevet i det følgende er gjort med lærere og elever som gjennomfører denne typen aktivitet for første gang. Det var fire erfarne
2.3 Delelighetsregler
 2.3 Delelighetsregler Begrepene multiplikasjon og divisjon og regneferdigheter med disse operasjonene utgjør sentralt lærestoff på barnetrinnet. Det er mange tabellfakta å huske og operasjonene skal kunne
2.3 Delelighetsregler Begrepene multiplikasjon og divisjon og regneferdigheter med disse operasjonene utgjør sentralt lærestoff på barnetrinnet. Det er mange tabellfakta å huske og operasjonene skal kunne
Nummer 8-10. H. Aschehoug & Co Sehesteds gate 3, 0102 Oslo Tlf: 22 400 400. www.aschehoug.no
 Nummer 8-10 H. Aschehoug & Co Sehesteds gate 3, 0102 Oslo Tlf: 22 400 400 www.aschehoug.no Hvorfor styrker man algebra i skolen? Det klages over at begynnerstudenter ved ulike høgskoler/universiteter har
Nummer 8-10 H. Aschehoug & Co Sehesteds gate 3, 0102 Oslo Tlf: 22 400 400 www.aschehoug.no Hvorfor styrker man algebra i skolen? Det klages over at begynnerstudenter ved ulike høgskoler/universiteter har
Matematikk 1, 4MX15-10E1 A
 Skriftlig eksamen i Matematikk 1, 4MX15-10E1 A 15 studiepoeng ORDINÆR EKSAMEN 19. desember 2011. BOKMÅL Sensur faller innen onsdag 11. januar 2012. Resultatet blir tilgjengelig på studentweb første virkedag
Skriftlig eksamen i Matematikk 1, 4MX15-10E1 A 15 studiepoeng ORDINÆR EKSAMEN 19. desember 2011. BOKMÅL Sensur faller innen onsdag 11. januar 2012. Resultatet blir tilgjengelig på studentweb første virkedag
Etterutdanningskurs "Mestre Ambisiøs Matematikkundervisning" høst 2015 - vår 2016
 Etterutdanningskurs "Mestre Ambisiøs Matematikkundervisning" høst 2015 - vår 2016 Om kurset Prosjektet "Mestre Ambisiøs Matematikkundervisning" (MAM) er et treårig prosjekt ved Matematikksenteret med oppstart
Etterutdanningskurs "Mestre Ambisiøs Matematikkundervisning" høst 2015 - vår 2016 Om kurset Prosjektet "Mestre Ambisiøs Matematikkundervisning" (MAM) er et treårig prosjekt ved Matematikksenteret med oppstart
Lese og skrive seg til forståelse. Svein H. Torkildsen
 Lese og skrive seg til forståelse Svein H. Torkildsen Fra media Muntlig Munnlege ferdigheiter i matematikk inneber å skape meining gjennom å lytte, tale og samtale om matematikk. Det inneber å gjere seg
Lese og skrive seg til forståelse Svein H. Torkildsen Fra media Muntlig Munnlege ferdigheiter i matematikk inneber å skape meining gjennom å lytte, tale og samtale om matematikk. Det inneber å gjere seg
Utdrag fra Beate Børresen og Bo Malmhester: Filosofere i barnehagen, manus mars 2008.
 Utdrag fra Beate Børresen og Bo Malmhester: Filosofere i barnehagen, manus mars 2008. Hvorfor skal barn filosofere? Filosofiske samtaler er måte å lære på som tar utgangspunkt i barnets egne tanker, erfaring
Utdrag fra Beate Børresen og Bo Malmhester: Filosofere i barnehagen, manus mars 2008. Hvorfor skal barn filosofere? Filosofiske samtaler er måte å lære på som tar utgangspunkt i barnets egne tanker, erfaring
Argumentasjon og regnestrategier
 Ole Enge, Anita Valenta Argumentasjon og regnestrategier Undersøkelser (se for eksempel Boaler, 2008) viser at det er en stor forskjell på hvilke oppfatninger matematikere og folk flest har om matematikk.
Ole Enge, Anita Valenta Argumentasjon og regnestrategier Undersøkelser (se for eksempel Boaler, 2008) viser at det er en stor forskjell på hvilke oppfatninger matematikere og folk flest har om matematikk.
Alle teller. - en introduksjon. Ny GIV 1. samling 2012/2013 Anne-Gunn Svorkmo Astrid Bondø Svein Hallvard Torkildsen
 Alle teller - en introduksjon Ny GIV 1. samling 2012/2013 Anne-Gunn Svorkmo Astrid Bondø Svein Hallvard Torkildsen Håndbok - for lærere som underviser i matematikk i grunnskolen Forfatteren: Professor
Alle teller - en introduksjon Ny GIV 1. samling 2012/2013 Anne-Gunn Svorkmo Astrid Bondø Svein Hallvard Torkildsen Håndbok - for lærere som underviser i matematikk i grunnskolen Forfatteren: Professor
ÅRSPLAN I MATEMATIKK 1. KLASSE BREIVIKBOTN SKOLE 2014-2015. Lærer: Turid Nilsen
 ÅRSPLAN I MATEMATIKK 1. KLASSE BREIVIKBOTN SKOLE 2014-2015 Lærer: Turid Nilsen Matematikkverket består av: Grunntall 1a + 1b Ressursperm Nettsted med oppgaver Grunnleggende ferdigheter Grunnleggjande ferdigheiter
ÅRSPLAN I MATEMATIKK 1. KLASSE BREIVIKBOTN SKOLE 2014-2015 Lærer: Turid Nilsen Matematikkverket består av: Grunntall 1a + 1b Ressursperm Nettsted med oppgaver Grunnleggende ferdigheter Grunnleggjande ferdigheiter
Forfatterne bak Multi!
 Multi i praktisk bruk Forfatterne bak Multi! Tilpasset opplæring Forfatterteam: Bjørnar Alseth Universitetet i Oslo Henrik Kirkegaard, Flisnes skole, Ålesund Mona Røsseland, Matematikksenteret Gunnar Nordberg,
Multi i praktisk bruk Forfatterne bak Multi! Tilpasset opplæring Forfatterteam: Bjørnar Alseth Universitetet i Oslo Henrik Kirkegaard, Flisnes skole, Ålesund Mona Røsseland, Matematikksenteret Gunnar Nordberg,
God matematikkundervisning... - Kva er det? Hva er matematisk kompetanse? Oversikt
 God matematikkundervisning... - Kva er det? Mona Røsseland Matematikksenteret, NTNU Leder i Lamis Lærebokforfatter, MULTI 12-Apr-07 Oversikt Noen tanker om hva som kan være kjennetegn på god matematikkundervisning..
God matematikkundervisning... - Kva er det? Mona Røsseland Matematikksenteret, NTNU Leder i Lamis Lærebokforfatter, MULTI 12-Apr-07 Oversikt Noen tanker om hva som kan være kjennetegn på god matematikkundervisning..
Gjett tre kort. Foreldrene betyr all verden! Grunntanken bak Multi. Mastermind. Faglig fokus og tydelige læringsmål. En bred matematisk kompetanse
 Foreldrene betyr all verden! Gjett tre kort Mona Røsseland Lærebokforfatter, MULTI Matematikksenteret, NTNU 10-Oct-10 2 Mastermind Grunntanken bak Multi Faglig fokus og tydelige læringsmål Elevene skal
Foreldrene betyr all verden! Gjett tre kort Mona Røsseland Lærebokforfatter, MULTI Matematikksenteret, NTNU 10-Oct-10 2 Mastermind Grunntanken bak Multi Faglig fokus og tydelige læringsmål Elevene skal
Undervisning som stimulerer barns evne til matematiske tenkning «russisk matematikk» i norsk skole
 Undervisning som stimulerer barns evne til matematiske tenkning «russisk matematikk» i norsk skole Novemberkonferansen 26. 27. november 2014 Kjersti Melhus Disposisjon for presentasjonen Litt om bakgrunnen
Undervisning som stimulerer barns evne til matematiske tenkning «russisk matematikk» i norsk skole Novemberkonferansen 26. 27. november 2014 Kjersti Melhus Disposisjon for presentasjonen Litt om bakgrunnen
Foreldrene betyr all verden!
 Foreldrene betyr all verden! Gjett tre kort Mona Røsseland Doktorgradsstipendiat, Universitetet i Agder Lærebokforfatter, MULTI www.fiboline.no 29-Oct-4 2 Hvilken rolle har foreldrene? Formell notation
Foreldrene betyr all verden! Gjett tre kort Mona Røsseland Doktorgradsstipendiat, Universitetet i Agder Lærebokforfatter, MULTI www.fiboline.no 29-Oct-4 2 Hvilken rolle har foreldrene? Formell notation
ÅRSPLAN I MATEMATIKK 2. KLASSE BREIVIKBOTN SKOLE 2013-2014
 ÅRSPLAN I MATEMATIKK 2. KLASSE BREIVIKBOTN SKOLE 2013-2014 Lærer: Turid Nilsen Matematikkverket består av: - Ressursperm - Grunntall 2a + 2b - CD-rom Forfattere: Bjørn Bakke og Inger Nygjelten Bakke Grunnleggende
ÅRSPLAN I MATEMATIKK 2. KLASSE BREIVIKBOTN SKOLE 2013-2014 Lærer: Turid Nilsen Matematikkverket består av: - Ressursperm - Grunntall 2a + 2b - CD-rom Forfattere: Bjørn Bakke og Inger Nygjelten Bakke Grunnleggende
Ny Giv. Grunnleggende regneferdighet. Tone Skori Stavanger 270213. Ditt navn og årstall
 Ny Giv Grunnleggende regneferdighet Tone Skori Stavanger 270213 Ditt navn og årstall Læringspartner (Kilde: Hilde Ødegaard Olsen, Skøyen skole) Hva er en læringspartner? En du sitter sammen med en viss
Ny Giv Grunnleggende regneferdighet Tone Skori Stavanger 270213 Ditt navn og årstall Læringspartner (Kilde: Hilde Ødegaard Olsen, Skøyen skole) Hva er en læringspartner? En du sitter sammen med en viss
Nysgjerrigper. Forskningsrådets tilbud til barneskolen. Annette Iversen Aarflot Forskningsrådet, 13.november 2015 Nysgjerrigperkonferansen 2015.
 Nysgjerrigper Forskningsrådets tilbud til barneskolen Annette Iversen Aarflot Forskningsrådet, 13.november 2015 Nysgjerrigperkonferansen 2015 Side Mål for kurset: Du har fått god kunnskap om Nysgjerrigpermetoden.
Nysgjerrigper Forskningsrådets tilbud til barneskolen Annette Iversen Aarflot Forskningsrådet, 13.november 2015 Nysgjerrigperkonferansen 2015 Side Mål for kurset: Du har fått god kunnskap om Nysgjerrigpermetoden.
Inspirasjon og motivasjon for matematikk
 Inspirasjon og motivasjon for matematikk Mona Røsseland Nasjonalt senter for matematikk i Opplæringen 13-Oct-06 Kursinnhald Hva er matematisk kompetanse? Hvordan styrke den hos elevene på en slik måte
Inspirasjon og motivasjon for matematikk Mona Røsseland Nasjonalt senter for matematikk i Opplæringen 13-Oct-06 Kursinnhald Hva er matematisk kompetanse? Hvordan styrke den hos elevene på en slik måte
Sensurveiledning Matematikk 1, 5-10, emne 1 Høsten 2013
 Sensurveiledning Matematikk 1, 5-10, emne 1 Høsten 2013 Oppgave 1 a) =2 = 5 2 =5 2 = = 25 4 = 25 8 Full uttelling gis for arealet uttrykt over. Avrundinger gis noe uttelling. b) DC blir 5 cm og bruk av
Sensurveiledning Matematikk 1, 5-10, emne 1 Høsten 2013 Oppgave 1 a) =2 = 5 2 =5 2 = = 25 4 = 25 8 Full uttelling gis for arealet uttrykt over. Avrundinger gis noe uttelling. b) DC blir 5 cm og bruk av
Refleksjoner omkring hverdagsmatematikk
 Reidar Mosvold Refleksjoner omkring hverdagsmatematikk Matematikk i dagliglivet kom inn som eget emne i norske læreplaner med L97. En undersøkelse av tidligere læreplaner viser at en praktisk tilknytning
Reidar Mosvold Refleksjoner omkring hverdagsmatematikk Matematikk i dagliglivet kom inn som eget emne i norske læreplaner med L97. En undersøkelse av tidligere læreplaner viser at en praktisk tilknytning
Meningsfylt matematikk
 Meningsfylt matematikk - også for elever som strever med faget Geir Botten Høgskolen i Sør-Trøndelag, Trondheim København 28.04.15 Eksempler på motiverende opplegg i matematikk Hva koster ei ukes ferie
Meningsfylt matematikk - også for elever som strever med faget Geir Botten Høgskolen i Sør-Trøndelag, Trondheim København 28.04.15 Eksempler på motiverende opplegg i matematikk Hva koster ei ukes ferie
Multiplikation och division av bråk
 Geir Martinussen & Bjørn Smestad Multiplikation och division av bråk Räkneoperationer med bråk kan visualiseras för att ge stöd åt resonemang som annars kan upplevas som abstrakta. I denna artikel visar
Geir Martinussen & Bjørn Smestad Multiplikation och division av bråk Räkneoperationer med bråk kan visualiseras för att ge stöd åt resonemang som annars kan upplevas som abstrakta. I denna artikel visar
Spill "Til topps" - transkripsjon av samtalen
 Spill "Til topps" - transkripsjon av samtalen Elevene på 6. trinn sitter to og to ved pultene. Thomas er læreren og sier at de skal ha et spill i dag. 1 Thomas Det er slik at dere skal være på lag med
Spill "Til topps" - transkripsjon av samtalen Elevene på 6. trinn sitter to og to ved pultene. Thomas er læreren og sier at de skal ha et spill i dag. 1 Thomas Det er slik at dere skal være på lag med
Dagens tall i mange varianter
 Dagens tall i mange varianter Alle klassetrinn Hensikt: Å bruke dagens tall som innfallsport kan gi mange muligheter, på ulike alderstrinn, innenfor ulike faglige temaer som klassen holder på med. I mange
Dagens tall i mange varianter Alle klassetrinn Hensikt: Å bruke dagens tall som innfallsport kan gi mange muligheter, på ulike alderstrinn, innenfor ulike faglige temaer som klassen holder på med. I mange
Presentasjon av Multi
 Presentasjon av Multi Mellomtrinnet Eksempler på Multi i praktisk bruk Faglig fokus og tydelige læringsmål Nettstedet Tilpasset opplæring Ulike oppgavetyper og aktivitetsformer Faglig fokus og tydelige
Presentasjon av Multi Mellomtrinnet Eksempler på Multi i praktisk bruk Faglig fokus og tydelige læringsmål Nettstedet Tilpasset opplæring Ulike oppgavetyper og aktivitetsformer Faglig fokus og tydelige
Hva kan bidra til å styrke vår emosjonelle utvikling, psykiske helse og positive identitet?
 Hva kan bidra til å styrke vår emosjonelle utvikling, psykiske helse og positive identitet? Hva trenger vi alle? Hva trenger barn spesielt? Hva trenger barn som har synsnedsettelse spesielt? Viktigste
Hva kan bidra til å styrke vår emosjonelle utvikling, psykiske helse og positive identitet? Hva trenger vi alle? Hva trenger barn spesielt? Hva trenger barn som har synsnedsettelse spesielt? Viktigste
GODE ALGORITMER. Mekanisk regneferdighet. Forskningens konklusjon. Hva kreves i læreplanen? Var alt bedre før? 17.09.2012
 Mekanisk regneferdighet GODE ALGORITMER IKKE SØRGELIG SUBTRAKSJON OG DYSTER DIVISJON Bjørnar Alseth Multi i Vest 2012 Forskningens konklusjon Hva kreves i læreplanen? Forskerne er enige om 1. Vi må ikke
Mekanisk regneferdighet GODE ALGORITMER IKKE SØRGELIG SUBTRAKSJON OG DYSTER DIVISJON Bjørnar Alseth Multi i Vest 2012 Forskningens konklusjon Hva kreves i læreplanen? Forskerne er enige om 1. Vi må ikke
Livet til det lykkelige paret Howie og Becca blir snudd på hodet når deres fire år gamle sønn dør i en ulykke.
 RABBIT HOLE av David Lyndsay-Abaire Scene for mann og kvinne. Rabbit hole er skrevet både for scenen og senere for film, manuset til filmen ligger på nettsidene til NSKI. Det andre manuset kan du få kjøpt
RABBIT HOLE av David Lyndsay-Abaire Scene for mann og kvinne. Rabbit hole er skrevet både for scenen og senere for film, manuset til filmen ligger på nettsidene til NSKI. Det andre manuset kan du få kjøpt
Hva er matematisk kompetanse?
 Kursinnhald Hva er matematisk kompetanse? Mona Røsseland Nasjonalt senter for matematikk i Opplæringen Leder i LAMIS (landslaget for matematikk i skolen) Lærebokforfatter, MULTI Hva er matematisk kompetanse
Kursinnhald Hva er matematisk kompetanse? Mona Røsseland Nasjonalt senter for matematikk i Opplæringen Leder i LAMIS (landslaget for matematikk i skolen) Lærebokforfatter, MULTI Hva er matematisk kompetanse
Regn i hodet: 46 + 28. Å uttrykke tall. Ulike uttrykksmåter. Det vesentlige er utvikling. Hvordan jobbe med dette? Hvordan jobbe med dette? 10.09.
 Hva er Hvorfor Singaporematematikk er folk interesserte i Singapore-matematikk Fordi elevene i Singapore stadig får best resultat på En samling undervisningsstrategier vanlig i Singapore internasjonale
Hva er Hvorfor Singaporematematikk er folk interesserte i Singapore-matematikk Fordi elevene i Singapore stadig får best resultat på En samling undervisningsstrategier vanlig i Singapore internasjonale
EVALUERING AV FORSØK MED ANONYME PRØVER 2013
 HORDALAND FYLKESKOMMUNE Opplæringsavdelinga Arkivsak 200903324-51 Arkivnr. 520 Saksh. Farestveit, Linda Saksgang Møtedato Opplærings- og helseutvalet 17.09.2013 EVALUERING AV FORSØK MED ANONYME PRØVER
HORDALAND FYLKESKOMMUNE Opplæringsavdelinga Arkivsak 200903324-51 Arkivnr. 520 Saksh. Farestveit, Linda Saksgang Møtedato Opplærings- og helseutvalet 17.09.2013 EVALUERING AV FORSØK MED ANONYME PRØVER
Addisjon og subtraksjon i fire kategorier
 Mona Røsseland Nasjonalt senter for matematikk i Opplæringen 7-Feb-07 Addisjon og subtraksjon i fire kategorier Problemstillinger som inkluderer addisjon og subtraksjon kan ha svært varierende strukturer.
Mona Røsseland Nasjonalt senter for matematikk i Opplæringen 7-Feb-07 Addisjon og subtraksjon i fire kategorier Problemstillinger som inkluderer addisjon og subtraksjon kan ha svært varierende strukturer.
Ordenes makt. Første kapittel
 Første kapittel Ordenes makt De sier et ord i fjernsynet, et ord jeg ikke forstår. Det er en kvinne som sier det, langsomt og tydelig, sånn at alle skal være med. Det gjør det bare verre, for det hun sier,
Første kapittel Ordenes makt De sier et ord i fjernsynet, et ord jeg ikke forstår. Det er en kvinne som sier det, langsomt og tydelig, sånn at alle skal være med. Det gjør det bare verre, for det hun sier,
Etterarbeid til forestillingen «stor og LITEN»
 Etterarbeid til forestillingen «stor og LITEN» Beate Børresen har laget dette opplegget til filosofisk samtale og aktivitet i klasserommet i samarbeid med utøverne. Det er en fordel at klassen arbeider
Etterarbeid til forestillingen «stor og LITEN» Beate Børresen har laget dette opplegget til filosofisk samtale og aktivitet i klasserommet i samarbeid med utøverne. Det er en fordel at klassen arbeider
7.4 Eksempler på misoppfatninger/mistolkinger
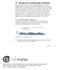 Verdier som parvis hører sammen. Nedbør som samsvarer med dagen vi velger. Utviklingen eller forandringen. Har nedbørsmengden steget eller sunket, har det gått opp og ned? Måleverdien har forandret seg
Verdier som parvis hører sammen. Nedbør som samsvarer med dagen vi velger. Utviklingen eller forandringen. Har nedbørsmengden steget eller sunket, har det gått opp og ned? Måleverdien har forandret seg
Leker gutter mest med gutter og jenter mest med jenter? Et nysgjerrigpersprosjekt av 2. klasse, Hedemarken Friskole 2016
 Leker gutter mest med gutter og jenter mest med jenter? Et nysgjerrigpersprosjekt av 2. klasse, Hedemarken Friskole 2016 1 Forord 2. klasse ved Hedemarken friskole har hatt mange spennende og morsomme
Leker gutter mest med gutter og jenter mest med jenter? Et nysgjerrigpersprosjekt av 2. klasse, Hedemarken Friskole 2016 1 Forord 2. klasse ved Hedemarken friskole har hatt mange spennende og morsomme
Læringsfellesskap i matematikk utvikling og forskning i samarbeid.
 Anne Berit Fuglestad og Barbara Jaworski Anne.B.Fuglestad@hia.no Barbara.Jaworski@hia.no Høgskolen i Agder Læringsfellesskap i matematikk utvikling og forskning i samarbeid. En onsdag ettermiddag kommer
Anne Berit Fuglestad og Barbara Jaworski Anne.B.Fuglestad@hia.no Barbara.Jaworski@hia.no Høgskolen i Agder Læringsfellesskap i matematikk utvikling og forskning i samarbeid. En onsdag ettermiddag kommer
Hjemmet og matematikkundervisningen. (Uavhengig av de voksnes tidligere erfaringer med matematikk?!)
 Foreldre teller!! Hjemmet og matematikkundervisningen. (Uavhengig av de voksnes tidligere erfaringer med matematikk?!) Denne økten: Hva kan vi gjøre hjemme for at matematikk skal bli et spennende fag?
Foreldre teller!! Hjemmet og matematikkundervisningen. (Uavhengig av de voksnes tidligere erfaringer med matematikk?!) Denne økten: Hva kan vi gjøre hjemme for at matematikk skal bli et spennende fag?
DEN GODE HYRDE / DEN GODE GJETEREN
 DEN GODE HYRDE / DEN GODE GJETEREN TIL DENNE LEKSJONEN Fokus: Gjeteren og sauene hans Tekster: Matteus 18:12-14; Lukas 15:1-7 (Salme 23; Joh.10) Lignelse Kjernepresentasjon Materiellet: Plassering: Lignelseshylla
DEN GODE HYRDE / DEN GODE GJETEREN TIL DENNE LEKSJONEN Fokus: Gjeteren og sauene hans Tekster: Matteus 18:12-14; Lukas 15:1-7 (Salme 23; Joh.10) Lignelse Kjernepresentasjon Materiellet: Plassering: Lignelseshylla
Reviderte læreplaner konsekvenser for undervisningen?
 Reviderte læreplaner konsekvenser for undervisningen? Multiaden 2013 Innhold Kompetanse i matematikk Den reviderte læreplanen Hva skal elevene lære? Grunnleggende ferdigheter i matematikk Konsekvenser
Reviderte læreplaner konsekvenser for undervisningen? Multiaden 2013 Innhold Kompetanse i matematikk Den reviderte læreplanen Hva skal elevene lære? Grunnleggende ferdigheter i matematikk Konsekvenser
Oppgaver til julekalenderen 2005 for mellomtrinnet; 5. - 7.trinn
 Oppgaver til julekalenderen 2005 for mellomtrinnet; 5. - 7.trinn Løsningsord for kalenderen er RAKETTBASE PRESIS KLOKKA TO A B C D E F G H I J K L M N O 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 P Q R S T U
Oppgaver til julekalenderen 2005 for mellomtrinnet; 5. - 7.trinn Løsningsord for kalenderen er RAKETTBASE PRESIS KLOKKA TO A B C D E F G H I J K L M N O 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 P Q R S T U
Hva er god matematikkundervisning?
 Hva er god matematikkundervisning? Astrid Bondø Nasjonalt Senter for Matematikk i Opplæringen 22-Feb-08 Ny læreplan, nye utfordringer for undervisninga i matematikk? Hva vil det si å ha matematiske kompetanse?
Hva er god matematikkundervisning? Astrid Bondø Nasjonalt Senter for Matematikk i Opplæringen 22-Feb-08 Ny læreplan, nye utfordringer for undervisninga i matematikk? Hva vil det si å ha matematiske kompetanse?
OBLIGATORISKE SPØRSMÅL I ELEVUNDERSØKELSEN
 OBLIGATORISKE SPØRSMÅL I ELEVUNDERSØKELSEN Nr Kategori/spørsmål Trivsel 1 Trives du på skolen? Svaralternativ: Trives svært godt Trives godt Trives litt Trives ikke noe særlig Trives ikke i det hele tatt
OBLIGATORISKE SPØRSMÅL I ELEVUNDERSØKELSEN Nr Kategori/spørsmål Trivsel 1 Trives du på skolen? Svaralternativ: Trives svært godt Trives godt Trives litt Trives ikke noe særlig Trives ikke i det hele tatt
Matematisk julekalender for 5. - 7. trinn, fasit
 Matematisk julekalender for 5. - 7. trinn, fasit DAG 1 (1. desember) (...) Klokka er nå 15.55. Toget de har billetter til går klokka 19.30. Kampstart er klokka 1700. For å være ute i god tid til å få billetter,
Matematisk julekalender for 5. - 7. trinn, fasit DAG 1 (1. desember) (...) Klokka er nå 15.55. Toget de har billetter til går klokka 19.30. Kampstart er klokka 1700. For å være ute i god tid til å få billetter,
Arbeid med sosiometrisk undersøkelse.
 Arbeid med sosiometrisk undersøkelse. Arbeid med sosiometrisk kartlegging gir innsikt i vennestruktur i klassen, den enkelte elevs sosiale posisjon, popularitet, innflytelse, positiv og negativ kommunikasjon
Arbeid med sosiometrisk undersøkelse. Arbeid med sosiometrisk kartlegging gir innsikt i vennestruktur i klassen, den enkelte elevs sosiale posisjon, popularitet, innflytelse, positiv og negativ kommunikasjon
Den gretne marihøna. Mål med undervisningsopplegget: Elevene skal kunne:
 Den gretne marihøna Dette undervisningsopplegget kan gjennomføres mot slutten av skoleåret på 1. trinn. Da har elevene lært seg alle bokstavene, og de har erfaring med å skrive tekster. Opplegget kan også
Den gretne marihøna Dette undervisningsopplegget kan gjennomføres mot slutten av skoleåret på 1. trinn. Da har elevene lært seg alle bokstavene, og de har erfaring med å skrive tekster. Opplegget kan også
Undring provoserer ikke til vold
 Undring provoserer ikke til vold - Det er lett å provosere til vold. Men undring provoserer ikke, og det er med undring vi møter ungdommene som kommer til Hiimsmoen, forteller Ine Gangdal. Side 18 Ine
Undring provoserer ikke til vold - Det er lett å provosere til vold. Men undring provoserer ikke, og det er med undring vi møter ungdommene som kommer til Hiimsmoen, forteller Ine Gangdal. Side 18 Ine
Løft matematikkundervisningen. med Multi 01.05.2010. Gruppere ulike mengder. Telling. Lineær modell
 Løft matematikkundervisningen med Multi 1. 1.trinnsboka har vært for lite utfordrende for mange elever. Revidert Multi 1 består nå av to grunnbøker Elevene får med dette bedre tid til å utvikle grunnleggende
Løft matematikkundervisningen med Multi 1. 1.trinnsboka har vært for lite utfordrende for mange elever. Revidert Multi 1 består nå av to grunnbøker Elevene får med dette bedre tid til å utvikle grunnleggende
Legg merke til at summen av sannsynlighetene for den gunstige hendelsen og sannsynligheten for en ikke gunstig hendelse, er lik 1.
 Sannsynlighet Barn spiller spill, vedder og omgir seg med sannsynligheter på andre måter helt fra de er ganske små. Vi spiller Lotto og andre spill, og håper vi har flaks og vinner. Men hvor stor er sannsynligheten
Sannsynlighet Barn spiller spill, vedder og omgir seg med sannsynligheter på andre måter helt fra de er ganske små. Vi spiller Lotto og andre spill, og håper vi har flaks og vinner. Men hvor stor er sannsynligheten
BRUKARUNDERSØKING 2008 - MOTTAK AV FLYKTNINGAR MOTTAK AV FLYKTNINGAR
 TIME KOMMUNE Arkiv: K1-070, K3-&32 Vår ref (saksnr.): 08/1355-6 JournalpostID: 08/14810 Saksbeh.: Helge Herigstad BRUKARUNDERSØKING 2008 - MOTTAK AV FLYKTNINGAR MOTTAK AV FLYKTNINGAR Saksgang: Utval Saksnummer
TIME KOMMUNE Arkiv: K1-070, K3-&32 Vår ref (saksnr.): 08/1355-6 JournalpostID: 08/14810 Saksbeh.: Helge Herigstad BRUKARUNDERSØKING 2008 - MOTTAK AV FLYKTNINGAR MOTTAK AV FLYKTNINGAR Saksgang: Utval Saksnummer
Guri A. Nortvedt Institutt for lærerutdanning og skoleforskning. Revidert læreplan i matematikk
 Guri A. Nortvedt Institutt for lærerutdanning og skoleforskning Revidert læreplan i matematikk Læreplan i matematikk Skoleforordningen 1734 Regning og matematikk Dagliglivets matematikk Grunnleggende ferdigheter
Guri A. Nortvedt Institutt for lærerutdanning og skoleforskning Revidert læreplan i matematikk Læreplan i matematikk Skoleforordningen 1734 Regning og matematikk Dagliglivets matematikk Grunnleggende ferdigheter
PROGRESJONS DOKUMENT. Barnehagens fagområder. Barns læringsprosesser
 PROGRESJONS DOKUMENT Barnehagene i SiT jobber ut fra en felles pedagogisk plattform. Den pedagogiske plattformen er beskrevet i barnehagenes årsplaner. Dette dokumentet viser mer detaljer hvordan vi jobber
PROGRESJONS DOKUMENT Barnehagene i SiT jobber ut fra en felles pedagogisk plattform. Den pedagogiske plattformen er beskrevet i barnehagenes årsplaner. Dette dokumentet viser mer detaljer hvordan vi jobber
Hva er matematisk kompetanse?
 Hva er matematisk kompetanse? Mona Røsseland Nasjonalt senter for matematikk i Opplæringen Leder i LAMIS (landslaget for matematikk i skolen) Lærebokforfatter, MULTI 9-Jan-07 Kursinnhald Hva er matematisk
Hva er matematisk kompetanse? Mona Røsseland Nasjonalt senter for matematikk i Opplæringen Leder i LAMIS (landslaget for matematikk i skolen) Lærebokforfatter, MULTI 9-Jan-07 Kursinnhald Hva er matematisk
Tenke, lytte og samtale i matematikktimen.
 Tenke, lytte og samtale i matematikktimen. Verksted Novemberkonferansen i Trondheim 24.november 2015 Barne- og ungdomstrinnet Svein Anders Heggem «Hei og velkommen inn til et klasserom..» for å dele dagligdagse
Tenke, lytte og samtale i matematikktimen. Verksted Novemberkonferansen i Trondheim 24.november 2015 Barne- og ungdomstrinnet Svein Anders Heggem «Hei og velkommen inn til et klasserom..» for å dele dagligdagse
LIKESTILLING OG LIKEVERD
 LIKESTILLING OG LIKEVERD Oppsummering Kroppanmarka barnehagers Interne prosjekter 2009 2011 Resultatene er basert på egne observasjoner som utgangspunkt for våre antagelser Er det forskjeller i samspill
LIKESTILLING OG LIKEVERD Oppsummering Kroppanmarka barnehagers Interne prosjekter 2009 2011 Resultatene er basert på egne observasjoner som utgangspunkt for våre antagelser Er det forskjeller i samspill
Hva er matematisk kompetanse? del 2
 Mona Røsseland Hva er matematisk kompetanse? del 2 Dette er andre del av en artikkel som tar for seg de matematiske kompetansene som ligger til grunn for de nasjonale prøvene i matematikk. Den første delen
Mona Røsseland Hva er matematisk kompetanse? del 2 Dette er andre del av en artikkel som tar for seg de matematiske kompetansene som ligger til grunn for de nasjonale prøvene i matematikk. Den første delen
Nye læreplaner, nye utfordringer i matematikk!
 Oversikt Nye læreplaner, nye utfordringer i matematikk! Mona Røsseland Nasjonalt senter for matematikk i Opplæringen Leder i LAMIS Lærebokforfatter, MULTI Ny læreplan, nye utfordringer for undervisningen
Oversikt Nye læreplaner, nye utfordringer i matematikk! Mona Røsseland Nasjonalt senter for matematikk i Opplæringen Leder i LAMIS Lærebokforfatter, MULTI Ny læreplan, nye utfordringer for undervisningen
«Litterasitetsutvikling i en tospråklig kontekst»
 «Litterasitetsutvikling i en tospråklig kontekst» Hvordan opplever minoritetsspråklige voksne deltakere i norskopplæringen å kunne bruke morsmålet når de skal lære å lese og skrive? Masteroppgave i tilpasset
«Litterasitetsutvikling i en tospråklig kontekst» Hvordan opplever minoritetsspråklige voksne deltakere i norskopplæringen å kunne bruke morsmålet når de skal lære å lese og skrive? Masteroppgave i tilpasset
Tor Fretheim. Kjære Miss Nina Simone
 Tor Fretheim Kjære Miss Nina Simone FAMILIEN De trodde det ikke. De klarte ikke å forstå at det var sant. Ingen hadde noen gang kunnet tenke seg at noe slikt skulle skje. Sånt hender andre steder. Det
Tor Fretheim Kjære Miss Nina Simone FAMILIEN De trodde det ikke. De klarte ikke å forstå at det var sant. Ingen hadde noen gang kunnet tenke seg at noe slikt skulle skje. Sånt hender andre steder. Det
To likninger med to ukjente
 To likninger med to ukjente 1. En skisse av undervisningsopplegget Mål Målet er at elevene skal lære seg addisjonsmetoden til å løse lineære likningssett med to ukjente. I stedet for å få metoden forklart
To likninger med to ukjente 1. En skisse av undervisningsopplegget Mål Målet er at elevene skal lære seg addisjonsmetoden til å løse lineære likningssett med to ukjente. I stedet for å få metoden forklart
Matematisk samtale og undersøkelseslandskap i matematikk
 Mona Røsseland Nasjonalt senter for matematikk i opplæringen Leder i LAMIS Lærebokforfatter; MULTI Matematisk samtale og undersøkelseslandskap i matematikk 16-Nov-06 Oversikt kursinnhold 1.gang: Generell
Mona Røsseland Nasjonalt senter for matematikk i opplæringen Leder i LAMIS Lærebokforfatter; MULTI Matematisk samtale og undersøkelseslandskap i matematikk 16-Nov-06 Oversikt kursinnhold 1.gang: Generell
Forfatterne bak Multi:
 Multi i praksis Tilpasset opplæring Program for dagen 12.00 13.30: Tankene bak Multi Varierte uttrykksformer gir differensiering og god læring 13.30 14.10: Mat 14.10 15.00: Varierte uttrykksformer gir
Multi i praksis Tilpasset opplæring Program for dagen 12.00 13.30: Tankene bak Multi Varierte uttrykksformer gir differensiering og god læring 13.30 14.10: Mat 14.10 15.00: Varierte uttrykksformer gir
Nynorsk. Institutt for lærerutdanning og skoleutvikling Universitetet i Oslo. 4. klasse
 Nynorsk Institutt for lærerutdanning og skoleutvikling Universitetet i Oslo Hovudtest Skolespørjeskjema 4. klasse Rettleiing Skolen din har sagt seg villig til å vere med i TIMSS 2003, ein stor internasjonal
Nynorsk Institutt for lærerutdanning og skoleutvikling Universitetet i Oslo Hovudtest Skolespørjeskjema 4. klasse Rettleiing Skolen din har sagt seg villig til å vere med i TIMSS 2003, ein stor internasjonal
Molde Domkirke 2016. Konfirmasjonspreike
 Molde Domkirke 2016 Konfirmasjonspreike Så er altså dagen her. Den store dagen. Dagen eg trur mange av dykk har gleda seg til lenge. Og det er lov å kjenne litt sommarfuglar i magen og både glede og grue
Molde Domkirke 2016 Konfirmasjonspreike Så er altså dagen her. Den store dagen. Dagen eg trur mange av dykk har gleda seg til lenge. Og det er lov å kjenne litt sommarfuglar i magen og både glede og grue
Vi anbefaler at elevene blir introdusert for likninger via en praktisk problemstilling. Det kan for eksempel være:
 Likninger og algebra Det er større sprang fra å regne med tall til å regne med bokstaver enn det vi skulle tro. Vi tror at både likninger og bokstavregning (som er den algebraen elevene møter i grunnskolen)
Likninger og algebra Det er større sprang fra å regne med tall til å regne med bokstaver enn det vi skulle tro. Vi tror at både likninger og bokstavregning (som er den algebraen elevene møter i grunnskolen)
Tallinjen FRA A TIL Å
 Tallinjen FRA A TIL Å VEILEDER FOR FORELDRE MED BARN I 5. 7. KLASSE EMNER Side 1 Innledning til tallinjen T - 2 2 Grunnleggende om tallinjen T - 2 3 Hvordan vi kan bruke en tallinje T - 4 3.1 Tallinjen
Tallinjen FRA A TIL Å VEILEDER FOR FORELDRE MED BARN I 5. 7. KLASSE EMNER Side 1 Innledning til tallinjen T - 2 2 Grunnleggende om tallinjen T - 2 3 Hvordan vi kan bruke en tallinje T - 4 3.1 Tallinjen
Kengurukonkurransen 2008 > Et sprang inn i matematikken <
 Kengurukonkurransen 2008 > Et sprang inn i matematikken < Benjamin (6. 8. trinn) Hefte for læreren Kengurukonkurransen 2008 Velkommen til Kengurukonkurransen! I år arrangeres den for fjerde gang i Norge.
Kengurukonkurransen 2008 > Et sprang inn i matematikken < Benjamin (6. 8. trinn) Hefte for læreren Kengurukonkurransen 2008 Velkommen til Kengurukonkurransen! I år arrangeres den for fjerde gang i Norge.
Det er frivillig å delta i spørreundersøkelsen, ingen skal vite hvem som svarer hva, og derfor skal du ikke skrive navnet ditt på skjemaet.
 7 Vedlegg 4 Spørreskjema for elever - norskfaget Spørsmålene handler om forhold som er viktig for din læring. Det er ingen rette eller gale svar. Vi vil bare vite hvordan du opplever situasjonen på din
7 Vedlegg 4 Spørreskjema for elever - norskfaget Spørsmålene handler om forhold som er viktig for din læring. Det er ingen rette eller gale svar. Vi vil bare vite hvordan du opplever situasjonen på din
Forslag til opplegg for en foreldrekveld om matematikk (varighet: 2 timer) v/ Ingvill M. Stedøy-Johansen, 2007
 Forslag til opplegg for en foreldrekveld om matematikk (varighet: 2 timer) v/ Ingvill M. Stedøy-Johansen, 2007 Inviter foreldrene på matematisk aften (forslag til invitasjon nederst i dette dokumentet).
Forslag til opplegg for en foreldrekveld om matematikk (varighet: 2 timer) v/ Ingvill M. Stedøy-Johansen, 2007 Inviter foreldrene på matematisk aften (forslag til invitasjon nederst i dette dokumentet).
Hvis dere vil bli profesjonelle matematikklærere
 Hvis dere vil bli profesjonelle matematikklærere Rammebetingelser. Tilrettelegging. Motivasjon. Finnmark, mars 2007 Ingvill Merete Stedøy-Johansen 7-Mar-07 Vil vi? JA! Vi gjør det!!! Ledelsen Personalet
Hvis dere vil bli profesjonelle matematikklærere Rammebetingelser. Tilrettelegging. Motivasjon. Finnmark, mars 2007 Ingvill Merete Stedøy-Johansen 7-Mar-07 Vil vi? JA! Vi gjør det!!! Ledelsen Personalet
Vurdering FOR læring. Fra mål og kriterier til refleksjon og læring. Line Tyrdal. 24.september
 Vurdering FOR læring Fra mål og kriterier til refleksjon og læring Line Tyrdal 24.september Sarah Hva gjør Sarah i stand til å snakke slik hun gjør? Hvordan? Når? Hvem? VURDERINGS- KULTUR Hvorfor? Hvordan
Vurdering FOR læring Fra mål og kriterier til refleksjon og læring Line Tyrdal 24.september Sarah Hva gjør Sarah i stand til å snakke slik hun gjør? Hvordan? Når? Hvem? VURDERINGS- KULTUR Hvorfor? Hvordan
Uteliv kombinert med kunst, kultur og kreativitet
 PROSJEKTTITTEL «Uteliv kombinert med kunst, kultur og kreativitet» - Samarbeid med eksterne fagpersoner fra Universitetet i Nordland. FORANKRING I RAMMEPLANEN «Barnehagen skal formidle verdier og kultur,
PROSJEKTTITTEL «Uteliv kombinert med kunst, kultur og kreativitet» - Samarbeid med eksterne fagpersoner fra Universitetet i Nordland. FORANKRING I RAMMEPLANEN «Barnehagen skal formidle verdier og kultur,
Likninger - en introduksjon på 8. trinn Hva er en likning og hva betyr å løse den?
 side 1 Detaljert eksempel om Likninger - en introduksjon på 8. trinn Hva er en likning og hva betyr å løse den? Dette er et forslag til undervisningsopplegg der utgangspunktet er sentrale problemstillinger
side 1 Detaljert eksempel om Likninger - en introduksjon på 8. trinn Hva er en likning og hva betyr å løse den? Dette er et forslag til undervisningsopplegg der utgangspunktet er sentrale problemstillinger
Inspirasjon og motivasjon for matematikk
 Inspirasjon og motivasjon for matematikk Hvordan får vi aktive, engasjerte og motiverte elever og lærere i matematikk? Bjørnar Alseth Høgskolen i Oslo Styremedlem i Lamis Lærebokforfatter; MULTI Mona Røsseland
Inspirasjon og motivasjon for matematikk Hvordan får vi aktive, engasjerte og motiverte elever og lærere i matematikk? Bjørnar Alseth Høgskolen i Oslo Styremedlem i Lamis Lærebokforfatter; MULTI Mona Røsseland
Vi har alle et ansvar for å bidra til å endre slike holdninger. REGNING FOR ALLE LÆRERE EN FAMILIE PÅ FEM
 EN FAMILIE PÅ FEM REGNING FOR ALLE LÆRERE Mysen, 27.09.13 gretof@ostfoldfk.no DIGITAL Jeg har aldri forstått matematikk hatet faget på skolen. Ikke har jeg hatt bruk for det heller, det har gått helt fint
EN FAMILIE PÅ FEM REGNING FOR ALLE LÆRERE Mysen, 27.09.13 gretof@ostfoldfk.no DIGITAL Jeg har aldri forstått matematikk hatet faget på skolen. Ikke har jeg hatt bruk for det heller, det har gått helt fint
Kengurukonkurransen 2013
 Kengurukonkurransen 2013 «Et sprang inn i matematikken» ECOLIER (4. 5. trinn) Hefte for læreren Kengurukonkurransen 2013 Velkommen til Kengurukonkurransen! I år arrangeres den for niende gang i Norge.
Kengurukonkurransen 2013 «Et sprang inn i matematikken» ECOLIER (4. 5. trinn) Hefte for læreren Kengurukonkurransen 2013 Velkommen til Kengurukonkurransen! I år arrangeres den for niende gang i Norge.
Lesing i matematikk - med modelltegning som hjelp til å løse oppgavene. Ann-Christin Arnås ann-christin.arnas@gyldendal.no
 Lesing i matematikk - med modelltegning som hjelp til å løse oppgavene Ann-Christin Arnås ann-christin.arnas@gyldendal.no Hva sier læreplanen om lesing i matematikk? Å kunne lese i matematikk inneber å
Lesing i matematikk - med modelltegning som hjelp til å løse oppgavene Ann-Christin Arnås ann-christin.arnas@gyldendal.no Hva sier læreplanen om lesing i matematikk? Å kunne lese i matematikk inneber å
NY GIV I REGNING. Brynhild Farbrot Foosnæs Brynhild.foosnas@baerum.kommune.no @BrynhildFF
 NY GIV I REGNING Brynhild.foosnas@baerum.kommune.no @BrynhildFF Hva er grunnleggende regneferdighet? Hvorfor strever elevene? Hva gjør vi med det? Hva menes med grunnleggende regneferdighet? Hva skiller
NY GIV I REGNING Brynhild.foosnas@baerum.kommune.no @BrynhildFF Hva er grunnleggende regneferdighet? Hvorfor strever elevene? Hva gjør vi med det? Hva menes med grunnleggende regneferdighet? Hva skiller
Da Askeladden kom til Haugsbygd i 2011
 Da Askeladden kom til Haugsbygd i 2011 Nå skal jeg fortelle dere om en merkelig ting som hendte meg en gang. Det er kanskje ikke alle som vil tro meg, men du vil uansett bli forundret. Jeg og den kule
Da Askeladden kom til Haugsbygd i 2011 Nå skal jeg fortelle dere om en merkelig ting som hendte meg en gang. Det er kanskje ikke alle som vil tro meg, men du vil uansett bli forundret. Jeg og den kule
24.11.2010. Hvorfor får elevene problemer med tekstoppgaver? Hva kan vi gjøre for at elevene skal mestre tekstoppgaver bedre?
 Hvorfor får elevene problemer med tekstoppgaver? Hva kan vi gjøre for at elevene skal mestre tekstoppgaver bedre? Mona Røsseland Matematikksenteret (for tiden i studiepermisjon) Lærebokforfatter, MULTI
Hvorfor får elevene problemer med tekstoppgaver? Hva kan vi gjøre for at elevene skal mestre tekstoppgaver bedre? Mona Røsseland Matematikksenteret (for tiden i studiepermisjon) Lærebokforfatter, MULTI
Pressemelding. Kor mykje tid brukar du på desse media kvar dag? (fritid)
 Mikkel, Anders og Tim Pressemelding I årets Kvitebjørnprosjekt valde me å samanlikna lesevanane hjå 12-13 åringar (7. og 8.klasse) i forhold til lesevanane til 17-18 åringar (TVN 2. og 3.vgs). Me tenkte
Mikkel, Anders og Tim Pressemelding I årets Kvitebjørnprosjekt valde me å samanlikna lesevanane hjå 12-13 åringar (7. og 8.klasse) i forhold til lesevanane til 17-18 åringar (TVN 2. og 3.vgs). Me tenkte
ÅRSPLAN I MATTE 2. TRINN BREIVIKBOTN SKOLE 2011-2012
 ÅRSPLAN I MATTE 2. TRINN BREIVIKBOTN SKOLE 2011-2012 Lærer: Knut Brattfjord Læreverk: Grunntall 2 a og b, av Bakke og Bakke, Elektronisk Undervisningsforlag AS Målene er fra Lærerplanverket for kunnskapsløftet
ÅRSPLAN I MATTE 2. TRINN BREIVIKBOTN SKOLE 2011-2012 Lærer: Knut Brattfjord Læreverk: Grunntall 2 a og b, av Bakke og Bakke, Elektronisk Undervisningsforlag AS Målene er fra Lærerplanverket for kunnskapsløftet
I følge Kunnskapsløftet er formålet med matematikkfaget å dekke følgende behov: (se s.57)
 Kunnskapsløftet-06 Grunnlag og mål for planen: Den lokale læreplanen skal være en kvalitetssikring i matematikkopplæringen ved Haukås skole, ved at den bli en bruksplan, et redskap i undervisningshverdagen.
Kunnskapsløftet-06 Grunnlag og mål for planen: Den lokale læreplanen skal være en kvalitetssikring i matematikkopplæringen ved Haukås skole, ved at den bli en bruksplan, et redskap i undervisningshverdagen.
Førskolebarnets matematikk-kunnskaper
 Førskolebarnets matematikk-kunnskaper Vad kan förskolebarn om tal? Hur löser de problem? Lärarstuderande Grethe Midtgård, Bergen, berättar om Marit, 6 år och hennes sätt att hantera situationer med matematik.
Førskolebarnets matematikk-kunnskaper Vad kan förskolebarn om tal? Hur löser de problem? Lärarstuderande Grethe Midtgård, Bergen, berättar om Marit, 6 år och hennes sätt att hantera situationer med matematik.
Samansette tekster og Sjanger og stil
 MAPPEOPPGÅVE 5 Samansette tekster og Sjanger og stil Skreve av Kristiane, Renate, Espen og Marthe Glu 5-10, vår 2011 I denne oppgåva skal me først forklare kva ein samansett tekst er, og kvifor samansette
MAPPEOPPGÅVE 5 Samansette tekster og Sjanger og stil Skreve av Kristiane, Renate, Espen og Marthe Glu 5-10, vår 2011 I denne oppgåva skal me først forklare kva ein samansett tekst er, og kvifor samansette
