Integral Kokeboken. sin(πx 2 ) sinh 2 (πx) dx = 2. 1 log x. + log(log x) dx = x log(log x) + C. cos(x 2 ) + sin(x 2 ) dx = 2π. x s 1 e x 1 dx = Γ(s)
|
|
|
- Anita Enoksen
- 8 år siden
- Visninger:
Transkript
1 Integrl Kokeboken log sinπ sinh π 4 + loglog loglog + C cos + sin π s e Γs n n s Γsζs π + sin +cos log + cos
2 i Del I. Brøk Trigonometriske funksjoner Oppgvesmmling I Integrl Integrl Oppgver Del II. Introduksjon II Bevis Den ntideriverte Delvis integrsjon Substitusjon Symmetri og nyttige smmenhenger Periodiske funksjoner Diverse substitusjoner Weierstrss substitusjon Euler substitusjon Brøker og kvdrtrøtter Brøker Kvdrtrøtter Delvis integrsjon Delvis knselering Eksponentilfunksjonen Tbell og reduksjonsformler Trigonometrske funksjoner Logritmiske funksjoner Ulike tips og knep Rekursjoner og funksjonsfølger Nyttig funksjonllikning Integrl pr Oppgvesmmling II Integrl Oppgver Del III 3 3. Introduksjon III Viktige konstnter Euler Mscheroni konstnten Ctln s Konstnt Glisher Kinkelin konstnten Spesilfunksjoner Gulv og tk-funksjonene Gmmfunksjonen Betfunksjonen Digmm-funksjonen Polygmm-funksjonen Riemnn zet funksjonen Hurwitz zet function
3 ii Polylogritmen Dilogritmen Dilogritmen Elliptiske Integrl Trnsformsjoner Lplce trnsformsjonen Fourier-trnsformsjon Mellin trnsformsjonen Lnden s trnsformsjon Cuchy-Schlömilch trnsformsjonen Diverse trnsformsjoner Diverse ppliksjoner Gulv og tk-funksjoner Itererte integrl Derivsjon under integrltegnet Uendelige rekker Dobbel Integrler Kompleks Integrsjon Typer integrler Oppgvesmmling III Integrl Oppgver Del IV A. Konvergens B. nlysens fundmentltheorem C. Konvergens C. Funksjonlnlyse C.3 Bohr-Mullerup Theoremet Del V 9 5. Kortsvr Lngsvr
4 I
5 Brøk I. B R Ø K Tidligere hr du møtt oppgver som ber deg om å trekke smmen eller forenkle brøk-uttrykk Hv om vi ønsker å gå ndre veien? Altså å dele eller splte brøken? Som ett eksempel kn du se om du klrer å vise t + uten å trekke smmen høyresiden. Det finnes mnge måter å trekke smmen brøker på og for en end grunndigere gjennomgng kn klkulus nbefles eller B E S T E M T E I N T E G R A L K A N V Æ R E L U N E F U L L E Ett gjennomgående tem i dette heftet er t integrsjon er en kunst og i del II skl vi se t bestemte integrl kn bli beregnet på forunderlige måter. Oppfordringen før des blir å prøve ut flere metoder for å bestemme ett integrl. Selv om du ser en løsning som du vet vil virke, t en puse. Tenk. Er det noen ndre metoder som kn virke, er de lettere, mer elegnt enn min? Ett eksempel er følgende integrl I 4 Flere vil etter å h lest forrigående seksjon begynne med delbrøksoppsplting. Flott! Men hv om teller hdde vært +, hv kunne en gjort d? Svret er jo substitusjon, og detljene skl leser få kose seg med lene. Ett litt tøffere eksempel som vi kommer tilbke til senere er følgende Eksempel... Bestem verdien v følgende integrl I + En ser ikke noen umidelbr smrt substitusjon så en nturlig vei er delbrøksoppsplting. Det finnes mnge måter, men for eksempel Integrsjonen blir nå enklere. For å bestemme integrlet v siste del, bruker vi substitusjon I + log + log log + + C Som liten førsteklsse tss på gymnset vr jeg dypt interessert i temet og holdt på i flere uker med å dele brøker og lge regler. Det vr først det påfølgende året t skolen begynte med teorien.
6 I Brøk 3 Dette uttrykket er rett. Men vi velgere å gjøre noen små lgebriske omskrivninger ved hjelp v logritmereglene log + log b log b. Grunnen til dette vil snrt bli klr + log + log + + C Hvor det blnt nnet ble brukt t log log og Ved å sette inn grensene våre får vi endelig + [ log lim log ] + + log + + Siden / når så vil / + når. Altså går første del mot log. I + log log log og vi er ferdige. I siste overgng brukte vi t log/ log log log. Finnes det en enklere metode? J, heldigvis. Men den krever et bedre flkeøye for å se. Vi begynner i stedet med den noe uvnte substitusjonen y /. Dett er det smme som t /y slik t dy/y. Når så vil y siden y /. Og tilsvrende > gir y /. Dermed så fås + /y + /y dy y y + y dy Problemet løses så ved å bruke en åpenbr substitusjon. Tnken er t selv om det ikke ser ut som en metode vil føre frem, kn det være lurt å gi den en sjngse like vell. Substitusjonen /y klles gjerne den inverse substitusjonen, eller en bijectiv substitusjon. Den er mye brukt på bestemte integrl med grenser og. Prøv å fortsette å beregne integrlene uten disse lgebriske krumspringene. Hv skjer?
7 4 Trigonometriske funksjoner I. T R I G O N O M E T R I S K E F U N K S J O N E R For en diskusjon om Riemn-integrerbrhet og ulike typer integrler henvises leses til Appendi. Her blir og temet om konvergens v integrler studert gjennomgående. Proposisjon... Vi hr t rctn + og for lle t. Videre så er t t + /t rctn t. + rctn t. + Bevis. Vi beviser første del v proposisjonen mens siste del overltes til leser, se oppgve. Derivsjonen v rctn kn vises ved implisitt derivsjon. L y rctn, d er tn y. Derivsjon gir d tn y d dy tn y dy + tn y dy d dy + tn y d rctn + d I ndre linje ble kjerneregelen benyttet, ltså t d dy. I siste linje kn dy vi benytte oss v t y rctn og tn y for å få det ønskede resulttet. Derivsjonen v tn kn for eksempel føres dy tn dy sin cos sin cos sin cos cos sin cos + cos cos Som viser t tn + tn, siden sin / cos tn per definisjon. Ved å integrere rctn / + fr null til t fås t + t rctn [ ] t rctn rctn t Som følger fr t siden tn så er rctn. Alterntivt kunne vi integrert uttryket vi substitusjonen tn y. D blir d tn y + tn y dy + dy
8 I Trigonometriske funksjoner 5 Altså er / + dy. Grensene blir rctn og rctn t. Slik t integrlet kn skrives som t + rctn t dy rctn t Dette fullfører første del v beviset. Siste delen v beviset overltes til leser, se oppgve 4. Korollr π 4 + π Bevis. Første overgng fller direkte ut v likning., med t. D hr vi / + + rctn π 4 Andre overgng følger fr likning.. Verdien v rctn vet vi, siden tn π/4 så er rctn π/4. Oppgver. Bevis siste hlvdel v proposisjon.., ltså likning.. b Vis videre t integrlene under t log + /t holder for lle t >. Bestem følgende integrl ved å benytte deg v likning.3. log +,. Bruk substitusjonen u tn til å bestemme I Bestem integrlet π/4 ved å bruke resulttet ovenfor. log,.3 + π tn tn tn 5 + tn 3 tn n+ + tn n
9 6 3 Oppgvesmmling I I. 3 O P P G A V E S A M M L I N G I. 3. I N T E G R A L. 3. I N T E G R A L sin / 5 n ln sin cos e e n e ln + sin cos ln n R log π/3 π/6 e ln π π sin π ln + e + + ln sin/e! e e + e + e π/4 sin sin /4 e y ln sine sin ln e + + loge e + e m n ln ln n 3 e e +e ln 3 m n π e 6
10 I 3.3 Oppgver sin sin π/3n tnn 4 e sin e cos e ln + π/ π/6 + tn π 3 + ln sin π + 5 ln 4 4 cossin cos e 3+ln 3 7. n ln ln n ln log5 log 5 + e / + e ln ln O P P G A V E R. Vis t integrlet K +π sin +, er konstnt dersom er et reellt tll. Kn resulttet forklres geometrisk?. L D betgne området vgrenset v linjene y sin, sin y og y π+. Bestem relet v D Hint: En god tegning gjør ofte susen 3. Vi hr følgende integrl I e log +, hvor er et reellt tll. Drøft integrlet for tilfellene <, og >, 4. Bestem følgende integrl + + Hint: Integrlet kn løses både med og uten å gnge ut prentesen.
11 8 3 Oppgvesmmling I I 5. Vis t ϕ ψ e e ϕ e ψ hvor ψ og ϕ henholdsvis er minste og største løsning v. 6. Finn ett reelt tll som tilfredstiller 7. For >, l f fe + f/e /. 8. Bestem følgende integrl 9. log t + t π e +e 5 dt. Finn funksjonen f + f/ og vis t dφ π. L f være en funksjon slik t f er integrerbr for [, 3] f. sin θ dθ 3 f f for lle [, 3]. Bestem integrlet 3 f r + r dr. Det oppgis t + π og + π 3 hvor > er en positiv konstnt. Bruk dette til å bestemme +. Integrlene ovenfor kn fritt benyttes, og det oppgis og t integrlet ovenfor konvergerer.. Vis t integrlet f er invrint er det smme om f byttes ut med fc, hvor c er en konstnt. 3. Ved å se på integrlet mellom f sin og g cos kn vi få et området som likner på en brt se 345. Bestem relet v brten. 4. Målet med denne oppgven er å bevise hv som er størst v log og /. Og de er nærmere enn hv enn skulle tro ved første øyenkst.
12 I 3.3 Oppgver 9 Vis t ulikheten holder for lle < t <. + t + + > + t b Den geometriske ritmetriske ulikheten er definert som y log log y > y der >. Bevis ulikheten, Her kn det være fordelktig å studere figur.. / b b Figur.: Den ritmetriske geometriske ulikheten c Bestem hv som er størst v log og /. En står fritt til å benytte tidligere oppgver.
13 Denne siden er med hensikt blnk, for å gi leser en pustepuse og for å l forftter slåss mot dinosurer.
14 II
15 Introduksjon II II. I N T R O D U K S J O N I I I denne delen vil vi hovedsklig dykke dypere ned i tidligere besøkte temer, men også lære noen nye eksotiske teknikker for å beregne spesielt hårete integrl. Det som forventes v leseren på dette tidspunktet er en grundig forståelse for de elementære integrsjonsteknikkene som ble gjennomgått i del I. For å kunne løse mnge v integrlene som kommer videre må disse elementære teknikkene sitte helt ut til fingerspissene. Hvor i forrige del fleste integrlene kunne bli løst vi et steg En smrt substitusjon, en delbrøkoppsplting, en frekk fktorisering osv vil vi se fremmover t integrlene krever flere steg for å bli løst. Mnge v løsningene vil virke merkelige og noen vil virke som de er ttt rett ut v det blå. Men husk t bk hvert skritt som fører mot en løsning ligger et stort mskineri. Ofte er grunnen til t vi bruker en så merkelig substitusjon eller delvis integrsjon enkel. Det fungerer. Fremmgngsmåten blir en blnding v å h sett liknende problem før, og prøve en rekke velkjente triks og knep. Og det er også målet med denne delen; og lære bort lle disse merkelige substitusjonene og metodene for å beregne integrl, slik t du selv kn nvende dem. For etter å h sett det smme smrte trikset nok gnger, blir det ikke lengre et triks men en nyttig teknikk du selv kn bruke. Et nøkkelkonsept i denne delen er å se studere når en kn gjøre følgende omskrivning f g f. S D S Metoden for å komme fr venstre side til høyre side v likningen er ikke spesielt viktig. Det kn være en lur substitusjon, en brutl delvis integrsjon eller noe helt nnet. Poenget er t likningen ovenfor kn løses med hensyn på integrlet over S, en beregner ltså integrlet indirekte. I mnge tilfeller vil dette og være eneste metoden som fungerer d det eksisterer funksjoner som ikke hr elementære ntideriverte. I denne delen blir også ndre måter å løse integrler inderekte på studert, lt fr å nvende symmetri, til smrt bruk v delvis integrsjon. Så fremt, d ender en opp med t integrlet over D er null. En sier gjerne t en funksjon hr en elementær ntiderivert dersom f kn uttrykkes ved elementære funksjoner. Selv om en funksjon ikke hr en elementær ntiderivert kn likevel f b eksistere og være elementær. Dette er noe som skper hodebry for mnge mtemtikkere.
16 II. Den ntideriverte 3. B E V I S I denne delen skl vi se nærmere på noen geometriske bevis for både delvis integrsjon, og hvorfor den ntideriverte gir oss relet under en funksjon. Tilsutt bevises også substitusjon mer formelt. Det formelle beviset for nlysens fundmentltheorem spres til ppendiet, d det er noe lngt. For den ivrige leser se theorem B..... D E N A N T I D E R I V E R T E Lemm... Ant t F f d vil også F + C f hvor C er en vilkårlig konstnt. Theorem... L f være en kontinuerlig funksjon som tr reelle verdier på [, b], og l F være den ntideriverte til f for [, b]. D er b ft dt F b F. Vi venter som sgt med et formelt bevis for FTC, men i korte trekk kn det formelle beviset kokes ned til følgende fire linjer F b F n [F k F k ] Teleskoperende sum. k n F k[ k k ] Middel verdi theoremet. k n F k k Riemnn sum.3 k b F.4 Merk t theorem.. krever t f er begrenset og kontinuerlig på intervllet. Dette er den klssiske definisjonen v en Riemn-integrerbr funksjon. En kn utvide integrlbegrepet til lngt mer ville funksjoner, men d holder ikke lengre det påfølgende beviset vnn. Beviset under med ndre ord lngt mer en intuisjon enn et formelt bevis. Bevis. Dette beviset tr utgngspunkt i figur. og bserer seg på visuell fremstilling. Ant t det eksisterer en eller nnen funksjon Ay som beskriver relet under f fr et punkt til ett eller nnet punkt y >. Det røde området i figur. er eksempelvis Ab. Nå utvider vi området litt med en fktor h. Arelet v det blå området kn d skrives som blå Ab + h Ab. Ut i fr figur. så vil det blå området lltid ligge mellom det grønne rektngelet og det ornsje. Dette kn beskrives ved følgende ulikhet h fb Ab + h Ab h fh + b.
17 4 Bevis II y fh + b fb Ab b b + h Figur.: Grfen til en vilkårlig funksjon f Siden relet v et rektngel er lik grunnlinjen gnget med høyden. Grunnlinjen her blir G h + b b h, og høyden er f. Trikset er nå t siden h > så kn en fritt dele ulikheten på h fb Ab + h Ab h fh + b..5 Videre lr en h. Visuelt kn en se på dette som t vi gjør det blå området mindre og mindre. Helt tilsvrende som når en utledet formelen for den deriverte. lim fb lim h h Ab + h Ab h lim h fh + b. Dette begynner å se pent ut. Det midterste leddet kn en kjenne igjen som definisjonen v den deriverte f lim h f + h f h Første leddet blir fb, og siste leddet blir fb. D hr en ltså skvist A fb A b fb. Dette medfører t A er en ntiderivert til f! Siden A f, så betyr det t A F hvor F f. Funksjonen A kn dermed skrives som Ab F b + C, hvor C er en eller nnen konstnt lemm... V ønsker nå å bestemme denne ukjente konstnten. Merk t per definisjon så er A, slik t F + C C F..
18 II. Delvis integrsjon 5 Arelet under funksjonen f fr til b kn d skrives som Ab F b F, og som kjent er det mer vnlig å skrive dette som b f F b F. Merk t beviset tr utgngspunkt i t f er stigende på intervlet, hdde funksjonen vært konstnt kunne en brukt kkurtt smme rgument. Hdde funksjonen i stedet vært synkende ville eneste forskjell vært t ulikhetstegnene i likning.5 vært snudd. Beviset her krever t f er en kontinuerlig, men t funksjonen er strengt positiv er ikke nødvendig. Med litt mer spissfindighet kn en føre et liknende rgument for en funksjon som er negtiv. Integrsjon holder i lngt mer generelle former enn dette, men poenget er her ikke å dekke lle spesiltilfeller, men gi å en viss intuisjon om hvordn derivsjon og integrsjon henger smmen... D E LV I S I N T E G R A S J O N Formelen for delvis integrsjon er gitt under u dv uv u du Tidligere hr vi utledet denne formelen ved å integrere produktregelen uv u v + uv I denne delen skl vi se på en mer visuell måte å utlede formelen ovenfor på, uten bruk v derivsjon. Forhåpentligvis vil denne metoden være mer intuitiv, i tillegg til å være en lterntiv fremgngsmåte. Beviset tr utgngspunkt i figur. og ideèn er å uttrykke relet v det grå området på to ulike måter. På den ene siden kn relet under uv, fr A til bli beskrevet ved følgende integrl ABB A v v u dv Tilsvrende så kn også relet begrenset v punktene ABB A bli beskrevet v den inverse funksjonen vu lngs u-ksen som CBB C u u v du Arelet v det grå området er likt summen v CBB C og ABB A. På den ndre siden kn det grå området - mer formelt polygonet vgrenset v CBAA B C - uttrykkes som differnsen mellom OA B C og OABC. OABC u v og OA B C u v
19 6 Bevis II u v C uv B u C B O A A v v u Figur.: En vilkårlig funksjon i uv-koordintsystemet Ved å t differnsen så kn det grå området uttrykkes som CBAA B C OA B C OABC u v u v Ved å smmenlikne de to uttrykkene vi hr for det grå området så er [ ] u,v uv u,v [ ] u,v v u uv u dv + v du.6 u,v v u som ikke er noe nnet en den kjente formelen for delvis integrsjon med leddene stokket om. Noen vil knskje stusse på grensene ovenfor, men husk t både u og v begge er funksjoner v en underliggende vribel si. Spesifikt så er u u, v v og u v, v v. Så likning.6 kn skrives u dv [ ] uv v du..7 som er kkurtt formen for delvis integrsjon med grenser. Merk t beviset tok utgngspunkt i t funksjonen uv vr en-til-en eller bijektiv. Dette er ikke noe nødvendig krv, som vi så når vi utledet formelen tidligere. Uten for mye bevis så kn beviset ovenfor utvides til kurver som ikke er en-tilen, så lenge u og v er funksjoner kun vhengig v en underliggende vribel. Integrlene vil fortstt kunne beregnes, men nå vil noen v områdene være negtive.
20 II.3 Substitusjon S U B S T I T U S J O N I strten når en lærer substitusjon vil en ofte missbruke notsjonen. Vi skriver gjerne u f du f du f. Men hv skjer egentlig i den siste overgngen? Vi rbeider jo tross lt med differensiler og ikke brøker. Husk på t substitusjon egentlig bre er kjerneregelen bklengs. Akkurtt som delvis integrsjon essensielt er produktregelen bklengs. Essensen v kjerneregelen er dy dy du du, Grunnen til t vi foretrekker Leibniz notsjonen og skriver deriverte som forhold er t notsjonen er veldig hintende suggestive. Ofte når ting ser ut som de knselerer så gjør de virkelig det. Ofte oppfører disse differensilene seg som brøker for eksempel dy/ / /dy. Men å rettferdigjøre t en kn behndle differensiler som brøker er en egen gren innenfor mtemtikk som klles for infinitesml klkulus. L du/ u, substitusjon kn d skrives direkte som guu gu du gu du gt dt Hvor det er den ndre overgngen om må rettferdigjøres. Det som ser ut som en knselering v i ndre overgng er direkte knyttet til kjerneregelen. Notsjonen er med ndre ord vlgt for å understreke knseleringen. Theorem... L I [, b] R være et intervll og l u være en til en funksjon smt kontinuerlig deriverbr. Ant t g er kontinuerlig på I, d er b guu Bevis. Vi definer funksjonen F som følger F ub u gt dt Vi studerer så funksjonen F u og dens deriverte. gt dt. F u F uu df du du d u gut dt u guu du Hvor siste overgng følger fr første del v nlysens fundmentltheorem B... Ved å integerere F u guu fr til b så hr vi F ub F u Selvsgt vet vi også t b F ub F u og dette fullfører beviset. guu ub u gt dt b ub u gut du. gu du
21 8 3 Symmetri og nyttige smmenhenger II. 3 S Y M M E T R I O G N Y T T I G E S A M M E N H E N G E R Målet med denne delen er å se på hvordn integrl og funksjoner kn forenkles ved hjelp v symmetri. Det første vi skl se på er definisjonen v en symmetrisk funksjon. Definisjon.3.. En funksjon f klles symmetrisk omkring c dersom f c f c En funksjon f klles nti-symmetrisk omkring c dersom f c f c Dette må selvsgt holde for lle. Dersom det bre holder for C hvor C [, b] er et endelig intervl, så sier en t f er henholdsvis odde eller like over C Definisjon.3.. En funksjon f klles for en likefunksjon eller jevnfunksjon dersom funksjonen er symmetrisk omkring origo. f f En funksjon f klles odde eller for en oddefunksjon dersom funksjonen er ntisymmetrisk omkring origo. Som igjen må holde for lle. f f En grfisk fremstilling v odde og like funksjoner er vist i figur.3. Eksempelvis så er, cos, e og like funksjoner. Tilsvrende så er 3, sin, e og eksempel på odde funksjoner. En smmlebetegnelse for odde og like funksjoner er pritet. Så priteten til e er like, prtiteten til e er odde, og e hr ingen pritet. Odde og y y Et plot v to odde funksjoner b Et plot v to like funksjoner Figur.3: Pictures of nimls like funksjoner hr mnge nyttige egenskper hvor de viktigste egenskpene er
22 II 3 Symmetri og nyttige smmenhenger 9 smmlet i tbell.. Her er O en forkortelse for en odde funksjon, og L er en forkortelse for en likefunksjon. Videre så er E enten odde eller like, og E hr motstt pritet v E. Så dersom E er like så er E odde. Uttrykket E E O betyr det smme som t O L O og L O O. Gitt to funksjoner f og g så er f g f g. Tbell.: Noen egenskper til odde og like funksjoner. E + E E E E L E/E L E/E O E E O O O O E L L L E L Fr figur.3 virker det som relet v en likefunksjon er likt på høyre og venstre side v origo. Tilsvrende for en oddefunksjon, bre t områdene nå hr motstt fortegn. Dette stemmer fktisk, men før vi viser det l oss t et litt nnet eksempel med hensyn på symmetri. Eksempel.3.. Se på funksjonen f Det ønskes å vises t relet under f og f grfisk. Altså f f y Ved å se på figur figur.4 så er det rimelig åpenbrt t området under funksjo Figur.4: f og f i smme figur. nene er like. Arelet under fr til er en treknt med grunnlinje og høyde dermed så er Tilsvrende for er dette og en treknt med grunnlinje og høyde så
23 3 Symmetri og nyttige smmenhenger II Eksemepelet ovenfor vr veldig konstruert og pedntisk. Men det stiller et viktig spørsmål, gjelder dette for lle funksjoner? Svret er heldigvis j, og kn generliseres til følgende proposisjon Proposisjon.3.. Ant t f er en vilkårlig funksjon, og,b er to reelle tll d er b f + b b f. Bevis. Igjen kn dette visuliserer med t f blir rotert omkring linjen + b/ og det er derfor logisk t relet er uforndret. Begynner med å se på venstre side v likheten b f Ved å bruke substitusjonen + b u så er du. Videre er u b, og d u så b f b f + b u b f + b u du og beviset fullføres ved å bytte integrsjonsvribelen tilbke til. Dette enkle beviset fører direkte til t Korollr.3.. Gitt t f er en symmetrisk funksjon omkring c, g er en ntisymmetrisk funksjon omkring c d er c+ c f c+ f og c+ c der t er en positiv, reell konstnt. Spesielt dersom c så er f f gitt t f er en likefunksjon, og g er odde. og g,.8 g,.9 Som det overltes leser å vise. Her er det nok å putte inn i proposisjon.3. og benytte seg v definisjonen v en odde og like-funksjon. Dette er og svært logisk om en betrkter figur.3. Lngt i fr lle funksjoner hr symmetriske egenskper, for eksempel så er e hverken like eller odde. Men e e + e + e e sinh + cosh Slik t e kn skrives som en odde og en likefunksjon. Fktisk så kn enhver funksjon f skrives som en en odde og en likefunksjon f f + f + f f. Hvor første del er en like, og ndre del en odde. Fr denne observsjonen kn en vise
24 II 3 Symmetri og nyttige smmenhenger Proposisjon.3.. L f være en vilkårlig funksjon d er Bevis. Legg merke til t f + f f f + f og f + f f f Dette følger fr korollr.3. siden første første funksjon er like og ndre funksjon er odde. Ved å integrere likning. fr til fås d f f + f, som ønsket. Alterntivt kn en og dele integrlet på midten og benytte substitusjonen y i integrlet fr til. Proposisjon.3.3. L f være en integrerbr funksjon på intervlet [, ], hvor R er en positiv konstnt. D holder for lle funksjoner f. f f + f Korollr.3.. L f være en vilkårlig funksjon d er f hvis f f f hvis f f hvor er reell konstnt. Bevis. Beviset følger direkte fr proposisjon.3.3 og nesten rett fr korollr.3. med et snedig skifte v koordinter. Geometrisk beskriver integrlet en funksjon som er odde eller like omkring. Vi deler først integrlet på midten og bruker deretter substitusjonen u på det siste integrlet. f f + f + f f u du, hvor grensene blir u og u. b f b f kn integrlet skrives som f Bruker vi nå t f + f.. Dette beviser proposisjon.3.3. Å sette inn henholdsvis f f og f f fullfører beviset for korollr.3.. Som vi skl se snrt følger likning. også rett fr.3 i lemm.3..
25 3 Symmetri og nyttige smmenhenger II L oss t et eksempel for å se hvor nyttig symmetriegenskper kn være Eksempel.3.. Putnm 987: B 4 log9 J log9 + log3 + Nå er + b 6 så ved å benytte seg v proposisjon.3. får en direkte 4 log9 6 4 log3 + log9 6 + log3 + 6 log3 + + log9 Meget pent. Ved å t gjennomsnittet v uttrykkene får en t J 4 log9 log3 + + log9 + log + 3 log log9 Dermed forenkler integrnden drmtisk og en står igjen med J 4 log9 + log + 3 log9 + log Merk t teknikken som ble brukt her kn enkelt generliseres til følgende to korollr Korollr.3.3. L f være en vilkrålig funksjon på, b d er b f f + b + f b gitt t og b er to reelle konstnter og t integrlet konvergerer. For å sikre seg konvergens holder det t f + b + f på intervlet. Beviset er i seg selv enkelt, og en kn bruke nøyktig smme fremgngsmåte som i eksempelet ovenfor. I seg selv er korollret enkelt å vise, men i prksis er det vnskeligere å bruke. For eksempel så er [ ] Men å se denne overgngen krever t en hr en liten lgebr-trollmnn i mgen. Som regel er det enklere å tippe t denne teknikken fungerer og se om theorem.3. kn benyttes. På enkle integrnder kn korollret brukes til å løse integrler ved inspeksjon. Lemm.3.. b f b c b c, f + f + b. f + f + b.3 f + f + b.4 Gitt t,b er to reelle tll og c + b/ er gjennomsnittsverdien v og b.
26 II 3 Symmetri og nyttige smmenhenger 3 Bevis. Første likning fller rett ut fr.3., siden integrlet over f og f + b er like store. For å se neste overgng kn en snitte integrlet i to b f c f + b c f,.5 med c + b/. Ved å bruke substitusjonen + b u på siste integrl fås b f c c f c f + b u du f + f + b. Grensene blir u + b c c og u + b b, og en byttet tilbke til som integrsjonsvribel i siste linje. Dersom en i stedet bruker substitusjonen + b u på første integrl i.5 får en b f c b b c f + b + som vr den siste likningen som skulle vises. b f + b + f. c f L oss rette fokus mot de kjente å kjære trigonometriske funksjonene våre. Vi vet llerede t π sin π cos [ sin 4 ] π π Der det ble benyttet t sin cos cos, og enhetsformelen cos + sin. Dette er et integrl som dukker mye opp både i fysikk og flervribel nlyse, men hv med integrlet v cos, kn vi bruke resulttet på noen måte? Ved å se på figur.5 så er cos og sin smme funksjon, bre t cosinus er forskjøvet med en hlv periode ltså π sin cos Der virker d logisk t relet under sinus og cosinus er det smme, gitt t en integrerer over en hel periode. Dette viste du vel llerede fr før, men ved å sette inn i proposisjon.3. fås direkte t π/ sin π/ sinπ/ π/ Interessnt, siden relet under v funksjonene er like så er cos π/ π/ π/ sin sin + cos π
27 4 3 Symmetri og nyttige smmenhenger II y π/ π 3π/ π Figur.5: Her er cos den stipplede funksjonen, og sin er den heltrukne. y π π 3π π Figur.6: f og f i smme figur. Stilig! Teknikken fungerer ikke bre på lle intervll, men lle multipler v π/. nπ/ sin nπ/ cos nπ/ nπ 4 Men dette er knskje kjent fr før? L oss ngripe problemet på en mer grfisk måte. Ved å se nærmere på intervlet til π. Legg merke til symmetrien fr til π/ i figur.6. Funksjonen f sin deler kvdrtet vgrenset v y, y og, π/ i nøyktig to på figuren. Slik t relet under f er nøyktig hlvprten v relet til kvdrtet. Altså π/ sin π π 4 Dette er helt tilsvrende som å bestemme relet v en treknt, den er nøyktig hlvprten v kvdrtet. For å få smme resultt som før kn en dele opp integrlet i n kvdrt hver med rel π/, og nøyktig det smme rgumentet kn og benyttes på cos. Hittil hr det bre vært håndvifting, hvordn kn en være sikker på t fremgngsmåten er rett? Svret finner vi i følgende theorem Theorem.3.. Ant f er kontinuerlig på [, b] og t f + f + b er konstnt for lle [, b] d er b + b f b f b [ f + fb ]
28 II 3 Symmetri og nyttige smmenhenger 5 f + fb y f f +b fb f Bevis. Beviset her tilegnes Roger Nelsen [?, s39-4], og er mildt sgt pent. Merk t teoremet kn vises utelukkende ved å betrkte figur.7. Men litt lgebrtre + b/ b Figur.7: Bevis for teoremet uten ord. ning hr ldri skdet noen. For å beregne integrlet benyttes lemm.3. og likning.3 D er b c b + f f + f + b K Siden f+f+b K, hvor K er en konstnt. For å bestemme konstnten kn hvilken som helst [, b] benyttes. Velges eller b fås K f + fb Derimot om en velger f c fås + b K f Integrlet kn dermed skrives som b + b f b f som vr det som skulle vises. b [ f + fb ] En ser t om f sin eller f cos så er f + fπ/ konstnt så π/ sin π/ cos π/ [ f + fπ/ ] π 4 som stemmer med tidligere resultter. L oss t et noe vnskeligere eksempel vslutningsvis
29 6 3 Symmetri og nyttige smmenhenger II Eksempel.3.3. Putnm 987: B π/ + tn. Dette er en v de vnskeligste oppgvene som hr vært gitt på en Putnm eksmen 3. Ved å tegne funksjonen får en noe som likner på figur.8. Allerde nå y π/4 π/ Figur.8: Grfen til funksjonen / tn. burde en kjenne igjenn teknikken. Området under funksjonen er hlvprten v rektngelet. Slik t det forventes t π/ + tn π π 4. For å være sikre på dette sjekkes det t f f + b er konstnt. Nå er slik t tnπ/ f + fπ/ sinπ/ cosπ/ cos sin / tn + tn + + / tn tn tn + tn + tn + tn 3 Putnm er en den mest prestisjefylte mtemtikkonkurnsen for studenter i USA og Knd. Konkurrnsen består v spørsmål, med mks poengsum. Oppgven som er vist her klrte bre 3 v 43 deltkre å få 3 eller mer poeng på
30 II 3 Symmetri og nyttige smmenhenger 7 Dermed så er f + f + b konstnt for lle [, π/]. Arelet under f er dermed nøyktig hlvprten v kvdrtet med høyde og bredde π/. Fr theorem.3. hr en ltså t π/ + tn π/ [ f + ] lim f π π/ 4. Der f og den siste grensen blir, siden tn går mot uendelig når π/ dermed vil / tn. I oppgven ovenfor vr figuren en god indeksjon på symmetrien. L oss vslutningsvis t et eksempel som i utgngspunktet virker motstriende mot tidligere resultter. Eksempel.3.4. Her skl vi studere følgende integrl A π/ L som definere funksjonen f som + cos f + cos Ved å se på figur.9 ser det ut som t integrlet fyller opp nøyktig hlvprten v det stiplede området. Så ntkelsen om t relet er.5 y.5 π/4 π/ Figur.9: Den røde kurven viser funksjonen f + cos. Ã π f + fπ/ π + virker ikke urimelig. Dessverre så er g f + fπ + cos + + sin 4
31 8 3 Symmetri og nyttige smmenhenger II ikke konstnt på intervllet. Ved å se på den deriverte kn en se t funksjonen duver skte i intervlet, eksempelvis så er g gπ/ +, mens gπ/4 6. Så f fπ er kk så nære å være konstnt, men det hjelper dessverre ingenting. Ved direkte utregning så er fktisk π/ + cos.9 > π Så selv om det ser ut som funksjonen hr pen symmetri, må en teste om f + f+b er konstnt. Problemet i denne oppgven er t +cos tilfredstiller f f + b, mens ikke gjør det. En konvolusjon v en symmetrisk og ikke symmetrisk funksjon er dessverre ikke symmetrisk. Addendum: Integrlet som ble studert i denne oppgven ikke er mulig å beregne nlytisk og betegnes som et elliptisk integrl v ndre grd. Men å vise dette overltes som en rtig oppgve til leser. Oppgver. L α være en reell konstnt, og f en kontinuerlig funksjon. Hvilke egenskper må f h for t α f α + β f α skl gjelde? Bestem også + + e.. Vis t π + sin +cos log, + cos 3. Bestem konstntene A,B,C og D slik t + A + B + C Følgende trnsformsjon π Rsin, cos π π Rsin, cos er nyttig i flere smmenhenger. Vis t den stemmer der R er en rsjonell funksjon uten singulriter på intervlet. Gjelder identiteten for Rcos, sin?
32 II 3 Symmetri og nyttige smmenhenger 9 6. Et komplett elliptisk integrl v ndre grd kn skrives på fomen Vis t integrlet kn uttrykkes vi E. Ek π/ π/ k sin + cos L oss t en liten digresjon til numerisk integrsjon. For å beregne et integrl kn en dele opp intervlet i n deler og konstruere et trpes på hver del. D ender en opp med t T n b f h n [ ] f + fb + h f k hvor n er ntll intervl, h b /n, og k + hk. En øvre grense for feilen i metoden er gitt som Error b 3 n M k Hvor M er den største verdien f ξ hr på intervllet. b Bestem hvor mnge intervl n som trengs for å være helt sikker på t π/ + cos > π + 4
33 3 4 Periodiske funksjoner II. 4 P E R I O D I S K E F U N K S J O N E R I forrige seksjon ble det sett nærmere på integrlene v sin, og cos og begge to er eksempler på periodiske funksjoner. En enkel definisjon på en periodisk funksjon er følgende Definisjon.4.. L f være en funksjon, og l T være en konstnt. Dersom f + T f holder for lle, så klles f for periodisk. En sier også t f hr en periode på T. Altså dersom funksjonen gjentr seg selv, ved jevne intervl så er funksjonen periodisk. Noen gnger klles periodiske funksjoner også for sykliske funksjoner. merk t periodiske funksjoner ikke trenger å oppføre seg like pent som sin eller y t Figur.: Illustrsjon v en periodisk funksjon cos. Fr definisjonen ovenfor følger det t hr periode π. Siden f, så er f + π for lle. Fktisk så hr konstnte funksjoner, lle perioder 4. Proposisjon.4.. Dersom f f + p og g g + p for lle, hvor p, og F f + g og G fg.6 d er både hr både F og G periode p. Dette er rett frem med å beregne F + p og G + p, men merk t p ikke trenger å være den minste perioden funksjonen hr. Eksempel.4.. Definer f sin og g sin, d hr både f og g periode π siden sin + π sin cos π + cos sin π sin. Merk t F f + g Sik t F hr lle perioder, ikke bre π. 4 En kn unngå dette problemet ved å definere periodiske funksjoner som f + T ft, hvor T er ulik null. Men i mnge situsjoner er det mer nturlig å betrkte konstnter som periodiske funksjoner.
34 II 4 Periodiske funksjoner 3 Eksempel.4.. Definer f cos i sin og g cos + i sin, d hr igjen både f og g en minste periode på π. Merk t G f g cos i sin cos + sin Sik t F igjen hr lle perioder 5, ikke bre π. Theorem.4.. L f, være en funksjon med periode T hvor T, og l k være en vilkårlig konstnt d er +T kt b+nt +mt f f k f b+t b T b f.7 f.8 f + n m T f..9 T T T + Figur.: Illustrsjon v likning.7. Området fr til + T, er like stort som relet over en periode ltså fr T til T. Korollr.4.. Dersom R, y er en rsjonell funksjon så er π Rsin, cos π π Rsin, cos Bevis. Dette følger direkte fr likning.7 med og b π og T π. Merk t likning.8 følger direkte fr.9 ved å sette m,, b, og n k. Tilsvrende kn første likning vises ved å l b, m, n så +T +T f T T f + f f Ved å heller sette b får vi smme resultt, og integrlene må derfor være like. Men det er enklere å bevise siste likning om en først hr vist de to foregående. Her bevises bre.7 og.8 mens siste likning overltes som en øvelse til leser. 5 Her er i den såklte imginære enheten. Å innføre denne vil knskje noe se på som juks. Droppes derimot i blir G cos som både hr periode π og π.
35 3 4 Periodiske funksjoner II Bevis. Det er noe enklere å vise t begge integrlene er likt integrlet over til T. Uten tp v generlitet l c b, d er c+t c f T c T c f + f + T +c T c f f + T T f Hvor substitusjonen u T ble brukt i ndre overgng og f + T f siden f hr periode T. Dette medfører t +T f T f b+t b f som ønsket. Intuitivt beskriver dette en horisontl forflyttning, og om funksjonen er periodisk vil denne forlyttningen bevre relet. Siden k er et nturlig tll kn en dele opp integrlet kt k f n n+t nt k f n T fu + nt du. der substitusjonen u + nt ble benyttet i siste overgng. Vi induksjon er det enkelt å vise t f + nt f holder for lle n Z. Argumentet holder for n, og nt så t f + pt f for en eller nnen p. Nå er f + p + T f + T + pt f + T f Her ble induksjonshypotesen brukt f + pt f med + T, og i siste overgng t f er periodisk. Resulttet følger ved induksjon og ved innseting fås kt k f n T k f + nt n T som vr det som skulle vises. Dette fullfører beviset. T f k f, Likning.8 beskriver en smling v k like integrl v typen i likning.7, siden integrlet over hver hele periode er like stort. En kn og kombinere resulttene, for eksempel så fås +kt b+t f k f b ved å bruke likning.7 og.8. Setter enn n m inn i.9 får en b f b+nt +nt f. hvor n selvsgt kn være negtiv. Igjen gir dette mening siden om en integrerer over T, 3T eller T, T spiller ingen rolle d funksjonen er periodisk, en står ltså fritt til å skifte integrlet slik det psser seg. I stedet for å t en rekke små eksempler, smmler vi lt i et mgnum opus eksempel nedfor. Merk en del v teorien fr vsnitt.3 vil og bli brukt
36 II 4 Periodiske funksjoner 33 Eksempel π/4 5π/4 + sin + cos 7π 4 Legg merke til t om en nslår integrlet numerisk, får en I , så I.75π 7π/4. Dette gir oss i hvertfll en god gjetning på t verdien v integrlet er rett. L f betegne integrnden nå er f + π f slik t integrnden y k k + π k + 4π k + 6π k + 7π Figur.: Grfen til f, hvor k 5π/4. er periodisk. Dette kn en enten se ved innsettning eller t integrnden består v sin og cos ledd som begge hr periode π. Ved å skrive om grensene kn integrlet skrives som I 5π/4+6 π π/4+3 π f 5π/4 π/4 f + 3 π f hvor.9 ble brukt, og f igjen betegner integrnden. I prksis er omskrivningen t integrlet deles opp i to deler, delen som består v hele perioder, og delen som består v hlve perioder. Eg fr k til k + 6, og k + 6 til k + 7 i figur.. Kll integrlene for henholdsvis A og B, merk t π π π + sin + cos π du sin u cos u + sinu+π + cosu+π sin u cos u sin cos + sin + cos vi substitusjonen u + π, her ble også sinu + π sin u og cosu + π cos u benyttet. Dette resulttet får en bruk for om en deler B på midten B 3 π f + 3 π π π f 3 + sin cos + sin + cos,
37 34 4 Periodiske funksjoner II Det kn vises t f+f+b er konstnt [Oppgve] slik t theorem.3. kn brukes. D er + b + sinπ/ B 3b f 3π cosπ/ + sinπ/ + cosπ/ 3π Helt tilsvrende kn A beregnes så A 3π/4 π/4 + sin + cos + 5π/4 3π/4 + sin + cos Ved å bruke substitusjonen u π/ så kn siste integrl skrives som 5π/4 π/ 3π/4 π/ du 3π/4 + sinu+π/ + cosu+π/ π/4 π/4 sin + sin + cos Siden sinu + π/ sin u og cosu + π/ cos u. Ved å bruke dette kn A skrives som 3π/4 + sin 3π/4 A + sin + cos π/4 + cos For å beregne integrlet kn igjen benytte seg v theorem.3. siden g + g + b er konstnt. A 3π/4 π/4 + cos π + cosπ/ π 4 som før. Her betegner d selvsgt g / + cos. Oppsumert så er 53π/4 5π/4 + sin + cos 3π + π 4 7π 4 som vr det en ønsket å vise. En noe mer intuitiv fremgngsmåte å vise A på er å heller bruke likning.3 fr lemm.3.. A 3π/4 π/4 + cos π/ π/4 + cos + + cos π/ π/4 π 4 Hvor cosπ/4 + π/4 cos. Om en ikke er så gld i benytte slike knep heller, kn integrlet også beregnes end mer elementært. 3π/4 π/4 + cos π/ π/4 π/ π/4 π/ π/4 + cos + + cos + cos + 3π/ π/ π/4 π/ π/ π/4 + cos cosπ + cosπ cos cos + cos, der substitusjonen u π/ ble brukt. Helt tilsvrende regning kn å brukes for å beregne B elementært. I dette eksempelet studeres en del spesiltillfeller v theoreme ved å se på funksjoner med ulike egenskper
38 II 4 Periodiske funksjoner 35 Proposisjon.4.. L n Z/{} være et heltll ulikt null og l f være en funksjon. Dersom t f er en funksjon med periode T, f + T f så er T fn T f. t f er en vilkårlig funskjon slik t integrlene konvergerer så er π/ π/ fsin fcos π/ π/ 3 t f er en likefunksjon, f f så er π/ π/ fsin n fcos n fsin.3 fcos + f cos.4 π/ π/ fsin.5 fcos.6 I tilfellet hvor f er odde, f f holder likning.5 og.6 generellt bre for n ±, ±. Beviset overltes til leser se oppgve 7. Vi kommer til å heller studere symmetriegenskpene mellom sin og cos. Proposisjon.4.3. L m, p, q Z, d er πs k/ πr k/ sinm n og πq+k/ πp k/ cosm n når n N og r, s Z + 6. Altså er r j +, s i + hvor j, i N. Det kreves i tillegg t dersom i og j hr smme pritet må k være like og og tilsvrende for p og q. Dersom i og j eller p og q hr ulik pritet så kn k Z velges fritt. Beviset her utteltes men er logisk om en betrkter figuren. Beviset ville vært å dele opp integrlene hlveis, og drøftet de ulike tilfellene for i, j, k, m, n, p, q, r, s men for leserens mentle helse utelltes dette. Derimot fører proposisjonen direkte til Korollr.4.. Hvr n, m, k N. nπ cosm k+ nπ nπ cosm k+.7 sinm k+.8 6 Notsjonen her betyr t n er odde. Dette kn og skrives som n {u : u N}, denne notsjonen tr dog opp noe mer plss. Tilsvrende for Z ±, merk disse mengdene er identiske.
39 36 4 Periodiske funksjoner II Lemm.4.. L R være en rsjonell funksjon d er Spesielt så er K Rsin, cos K Hvor K π/ eller K π. fsin K K Rcos, sin fcos. Bevis. Å vise likheten for K π/ er trivielt. Ved å bruke den kjære substitusjonen y π/ så er π/ Rsin, cos π/ π/ R cosπ/ y, sinπ/ y dy Rcos, sin, som ønsket. L oss nå studere tilfellet K π som er hkket mer spennende. Ved å først bruke den smme substitusjonen y π/ så er π Rsin, cos 3π/ π/ R sinπ/, sinπ/ y dy. Integrlet kn forenkles ved å snu grensene og benytte som før t sinπ/ y cos y og cosπ/ y cos y. Neste steg blir å dele integrlet ved. 3π/ Rcos y, sin y dy + π/ Rcos y, sin y dy En nturlig fortsettelse er å benytte substitusjonen y π+u eller likning.9 med n m, 3π/,b π/ og T π på første integrlet. Unsett blir π π/ Rcos u, sin u du + π/ Rcos y, sin y dy π Rcos, sin Som vr det som skulle vises. Nøyktig smme bevis som ovenfor kn brukes på fsin, noe enklere er bre se t Rcos, sin fcos om R ikke inneholder noen sinus ledd. Dette vil si t R, y er en symmetrisk funksjon. Som betyr t i ethvert integrl som kun består v cos og sin ledd, står en fritt til å bytte om disse π 3 cos π sin cos sin cos sin + 3, så fremt en integrerer over en kvrt, eller hel periode. Lemmet her kn brukes til å vise et noe mer generelt resultt
40 II 4 Periodiske funksjoner 37 Proposisjon.4.4. L k være en konstnt d er πk/ πm/ Rcos, sin πk/ πm/ gitt t k, m mod 4 eller k, m mod 4. Rsin, cos, Siste del betyr t k og m lltid er på formen 4n eller 4n + for et heltll n og ikke nødvendigvis like. Slik t vi kn godt velge k 4 + og m 4. Å vise dette tr liten plss når vi llerede hr vist lemm.4. Bevis. Vi kn uten tp v generlitet sette m igjennom hele beviset. Siden integrlet kn deles ved og å vise proposisjonen for de negtive verdiene er kkurtt likt som for de positive. Tr først tilfellet for k 4n, d er nπ Rcos, sin n n π π Rcos, sin Rsin, cos nπ Rsin, cos, der første og siste overgng følger fr likning.8 og ndre overgng følger fr lemm.4.. Tilsvrende for tilfellet når k 4n + så er nπ+π/ Rcos, sin n π Rcos, sin + π/ Rcos, sin, hvor likning.8 ble brukt. En hr vist symmetrien til begge integrlene på høyresiden i lemm.4.. Ved å bruke dette hr en dermed nπ+π/ Rcos, sin n π nπ+π/ Rsin, cos + Rsin, cos, som vr det som skulle vises. Dette fullfører beviset. π/ Rsin, cos Å bruke denne symmetrien til å løse integrl er ikke rett frem. Men den er svært nyttig for å vise t ulike trigonometriske integrl er like. Vi kn etblere liknende identiteter for Proposisjon L f være en begrenset funksjon på intervlet og l m,n være heltll. D er nπ mπ nπ/ mπ/ fcos fsin πn mπ nπ mπ fcos.9 fsin.3 gitt t n, m er på formen n, m mod 4 eller n, m mod 4. Beviset for dette overltes til leser, og kn vises på smme måte som de to tidligere proposisjonene. Merk t proposisjonen holder selv om m 4p og n 4l +. L oss t en svk generlisering v Riemnn-Lebesgue lemmet
41 38 4 Periodiske funksjoner II Lemm.4.. Riemnn-Lebesgue lemm L f være en kontinuerlig deriverbr 7 funksjon på, b. L g være en funksjon med periode T. D er b lim n fgn T T g b f. Lemmet holder under svkere betingelser, men for å gjøre beviset enklere holder dette for oss Bevis. L oss først se på integrlet over g, dette kn skrives som T gt g + h A + h. T Her betegner A integrlet, og h er en eller nnen kontinuerlig funksjon med periode T. Første overgng kommer fr likning.8, hvor k /T. For t dette skl gjelde må /T være et heltll, dette ordnes vi funksjonen h som er g integrert over et psselig intervl. Ved å derivere begge sider så er g A + h, slik t gn A + h n. Her trengtes ikke produktregelen og benyttes på først del, d A er en konstnt og ikke vhengig v. Settes dette inn i den opprinnelige likningen fås b fgn A b f + b fh n. Målet er nå å vise t det siste integrlet går mot null, når n går mot. Ved å bruke delvis integrsjon kn integrlet skrives som b [ fhn fh n n ] b n b f hn. Siden f, f og h er kontinuerlige på, b medfører dette og t de er øvre begrenset, som igjen betyr t integrlet konvergerer. Høyresiden er dermed et reelt tll så høyresiden går mot null når n vokser. Dette medfører b lim n fgn A b f + T T g b f, som vr det som skulle vises. 7 kontinuerlig deriverbr er en fglig betegnelse som betyr t f er kontinuerlig, og t dens deriverte også er kontinuerlig
42 II 4 Periodiske funksjoner 39 Oppgver 7. Lett oppvrming. Vis t dersom f hr periode T, ltså f + T f så er T fn T f, gitt t n Z/{} ltså t n er et vilkårlig heltll ulikt. Bevis også resten v proposisjon Bevis t det kun eksisterer to n N slik t In π/ Tilsvrende bestem når In 9. Vis t b+nt +mt f dθ + sin nθ b π 3. π/ dθ + sin θ T f + n m f hvor igjen, b, T er reelle tll, f + T f for lle, og n, m Z.. Bestem integrlet I 7π/ 3π + sin +cos log. + cos. Tidligere hr en sett på periodiske funksjoner, og i denne oppgven ser en nærmere på spesiltilfellet der integrnden i tillegg er odde eller like. L f være en likefunksjon, og l g være odde. Både f og g hr periode T L, hvor L er en nturlig konstnt. I oppgven skl integrlene G studeres nærmere 8. ft dt og F gt dt, Bestem priteten til F og G. Altså om F og G er odde eller like. b Bestem GnL og F nl, hvor n Z. c Vis t F også hr periode L, hvilke betingelser kreves for t G også skl h periode L? 8 Merk t egenskpene vi viser her minner svært om egenskpene til sin, og cos og blnt elementære funksjoner er disse de eneste periodisk, odde og like funksjonene. Tillter en derimot delte funksjonsuttrykk, finnes det mnge flere eksempler, disse mye brukt innen signlbehndling og fourier-nlyse.
43 4 5 Diverse substitusjoner II. 5 D I V E R S E S U B S T I T U S J O N E R Vi betegner en substitusjon som følgende overgng β α f ψ ϕ f[gt]g t dt og formelt sett er dette en vbildning fr et område X til et område Y vi funksjonen gt. Hv dette i prksis vil si er t vi går fr et koordintsystem,y til et nytt koordintsystem,y og det eneste som er konstnt mellom systemene er t relet under ft, b og fgt ϕ, ψ er like store. Vi begynner med å se på noen få eksempler på nyttige susbtitusjoner. Inneholder integrlet b eller b sin θ Eksempel.5.. I b b så kn substitusjonen cos θ + b π Vi benytter den nbeflte substitusjonen cos θ + b sin θ. D er b cos θ + b sin θ b sin θ cos θ sin θ + b sin θb cos θ cos θ b sin θ cos θ Mens den deriverte kn skrives som dθ cos θ sin θ + b sin θ cos θ b sin θ cos θ Herfr må vi rbeide med grensene våre. Når får vi likningen cos θ + b sin θ som medfører b sin θ. Her kn vi se bort i fr det trivielle tilfellet b. Så vi må h sin θ eller θ nπ, n Z. Vi velger n for enkelhetens skyld. Tilsvrende for β finner vi t θ π/ + nπ. Denne gngen kn vi ikke velge n fritt. Det er reltivt trygt å gjette t vi må velge θ π/. Vi kn rettferdiggjøre dette ved å se t vi ønsker t øker fr til b, og dersom vi velger en nnen verdi for den øvre grensen vil ikke dette skje. Substitusjonen gir ltså b b π/ b sin θ cos θ dθ π/ b sin θ cos θ dθ π som ønsket. Noen tillegskommentrer: For [, π/] så er cos og sin positive slik t sin θ cos θ cos sin cos sin. Vi kn og se rskt på konvergens, eneste frememomenter er og b. Integrlet oppfører seg som / nære disse punktene og konvergerer dermed. En hr fr tylorutvikling t b / b / / b / som er konvergent. Helt tilsvrende omkring b.
44 II 5 Diverse substitusjoner 4 Å evluere bestemte integrl ved bruk v substitusjon krever ømfintlighet. Følgende theorem gir oss tilstrekkelige betingelser for en gyldig substitusjon Theorem.5.. Dersom funksjonen t φ tilfredstiller følgende φ er en kontinuerlig en-til-en funksjon definert på intervlet [ϕ, ψ] og hr en kontinuerlig derivert der. Verdiene til φt ligger i intervlet [, b] 3 φϕ og φψ b. d vil følgende formel holde b ft dt ψ ϕ fgg for lle f stykkevis kontinuerlig funksjoner derfinert på [, b]. Gjennom nonen eksempler vil vi vise visse fllgruver om en ikke psser på betingelsenene ovenfor. Det enkleste er ltså benytte seg v monotone 9 substitusjoner. Ellers må en dele opp intervllet til substitusjonen blir monoton. Eksempel.5.. I 4 + Vribelskifte /t vil her lede til et glt svr I [ / 4 + rctn t / ] / / dt / t + t / π 4 dt 4t + Som er umulig siden funksjonen er strengt positivt. Dette skjer fordi substitusjonen /t ikke er deriverbr i origo. Rett svr er selvsgt I [rctn 4 + ] [ π 4 π ] π 4 4 En nnen som kn komme er når en bruker den iverse substitusjonen ψt og φt tr flere verdier. 9 En monoton funksjon er en funksjon som er vtgende eller synkende på ett gitt området. Dette er jo selvsgt ikke helt rett. Problemet ligget i t vi må dele opp intervllet vårt ved origo før vi kn derivere. Dette hndler om t / mpper [, ] til, /] [/, og ikke [ /, /] som en knskje skulle trodd i utgngspunktet. Innen kompleks nlyse klller vi slike funksjoner gjerne for brnch cuts.
45 4 5 Diverse substitusjoner II Eksempel.5.3. I 3 Ved å bruke substitusjonen u vil resultere i et glt resultt. Dette er fordi den inverse funksjonen ikke er unikt definert ± t. en ene grenenen t kn ikke t verdier for >, og den ndre t kn ikke t verdier for <. Direkte men feil utregning vi u gir 3 4 u du [ 3 u3/ ] Åpenbrt feil, d integrnden er positiv på hele området. For å få det korrekte svret er det nødvending å dele integrlet i to deler I + 3 Så kn vi l t i første integrelet og + t i det ndre. Dette gir I I t dt t t dt t 4 8 t dt 3 t dt 3 Derfor så er I I + I Resulttet kn bekreftes ved å beregne integrlet direkte 3 [ ] En kn og betrkte en substitusjon som t en omformer et mterilet eller væske som en ikke kn trykkes smmen 3. En substitusjon kn d sees på som n en drr mterilet i en eller nnen retning, merk t trnsformsjonen må være kontinuerlig, og kn heller ikke innføre hull i området. En vbildning fr X til Y ikke er entydig og det kn finnes mnge måter å komme seg fr X til Y på. En kn for eksempel gå fr X til Z også fr Z til Y, eller en rekke ndre måter. Områdene vi vil rbeide med vil i hovedsk være intervl på den reelle tllinjen slik t en kn skrive X [, b] og Y [ϕ, ψ]. Men det er ikke noe mot t X er et intervl og t Y er en sirkel for eksempel. Ofte når vi bruker substitusjon er målet å forenkle integrnden, men hv om vi ønsker å forenkle grensene i stedet. Hvordn skl vi finne en substitusjon slik t grensene går fr [, b] til [ϕ, ψ]? Substitusjonen kn skrives som b ft dt ψ ϕ fgg, hvordn må d t g velges? Følgende propsisjon gir oss heldigvis svret En lterntiv synsvinkel er en lineær trnsformsjon mellom to topologiske rom. 3 Formelt klles et slikt mterilet med konstnt volum for inkompressibelt. Når det gjelder gsser, klles en prosses med konstnt volum for en isokor prosess.
Integrasjon av trigonometriske funksjoner
 Integrsjon v trigonometriske funksjoner øistein Søvik 3. november 15 I dette dokumentet skl jeg vise litt ulike integrsjonsteknikker og metoder for å utforske integrlene v (cos x) og (sin x). De bestemte
Integrsjon v trigonometriske funksjoner øistein Søvik 3. november 15 I dette dokumentet skl jeg vise litt ulike integrsjonsteknikker og metoder for å utforske integrlene v (cos x) og (sin x). De bestemte
Matematikk 1000. Øvingsoppgaver i numerikk leksjon 8 Numerisk integrasjon
 Mtemtikk 1000 Øvingsoppgver i numerikk leksjon 8 Numerisk integrsjon Som kjent kn vi regne ut (bestemte) integrler ved nti-derivsjon. Dette resulttet er et v de viktikgste innen klkulus; det heter tross
Mtemtikk 1000 Øvingsoppgver i numerikk leksjon 8 Numerisk integrsjon Som kjent kn vi regne ut (bestemte) integrler ved nti-derivsjon. Dette resulttet er et v de viktikgste innen klkulus; det heter tross
Integrasjon Skoleprosjekt MAT4010
 Integrsjon Skoleprosjekt MAT4010 Tiin K. Kristinslund, Julin F. Rossnes og Torstein Hermnsen 19. mrs 2014 1 Innhold 1 Innledning 3 2 Integrsjon 3 3 Anlysens fundmentlteorem 7 4 Refernser 10 2 1 Innledning
Integrsjon Skoleprosjekt MAT4010 Tiin K. Kristinslund, Julin F. Rossnes og Torstein Hermnsen 19. mrs 2014 1 Innhold 1 Innledning 3 2 Integrsjon 3 3 Anlysens fundmentlteorem 7 4 Refernser 10 2 1 Innledning
EKSAMEN. ANTALL SIDER UTLEVERT: 7 (innkl. forside og 2 sider formelark)
 KANDIDATNUMMER: EKSAMEN FAGNAVN: Mtemtikk FAGNUMMER: REA EKSAMENSDATO: 5. desember 6 KLASSE:. klssene, ingenørutdnning. TID: kl. 9... FAGLÆRER: Hns Petter Hornæs ANTALL SIDER UTLEVERT: 7 (innkl. forside
KANDIDATNUMMER: EKSAMEN FAGNAVN: Mtemtikk FAGNUMMER: REA EKSAMENSDATO: 5. desember 6 KLASSE:. klssene, ingenørutdnning. TID: kl. 9... FAGLÆRER: Hns Petter Hornæs ANTALL SIDER UTLEVERT: 7 (innkl. forside
1 k 2 + 1, k= 5. i=1. i = k + 6 eller k = i 6. m+6. (i 6) i=1
 TMA4 Høst 6 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Løsningsforslg Øving 5 5..6 Vi er gitt summen og ønsker å skrive den på formen m k=5 k +, f(i). i= Strtpunktene er henholdsvis
TMA4 Høst 6 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Løsningsforslg Øving 5 5..6 Vi er gitt summen og ønsker å skrive den på formen m k=5 k +, f(i). i= Strtpunktene er henholdsvis
Brøkregning og likninger med teskje
 Brøkregning og likninger med teskje Dette heftet gir en uformell trinn for trinn gjennomgng v grunnleggende regler for brøkregning og likninger. Dette er sto som vi i FYS 000 egentlig forventer t dere
Brøkregning og likninger med teskje Dette heftet gir en uformell trinn for trinn gjennomgng v grunnleggende regler for brøkregning og likninger. Dette er sto som vi i FYS 000 egentlig forventer t dere
M2, vår 2008 Funksjonslære Integrasjon
 M, vår 008 Funksjonslære Integrsjon Avdeling for lærerutdnning, Høgskolen i Vestfold. pril 009 1 Arelet under en grf Vi begynner vår diskusjon v integrsjon, på smme måte som vi begynte med derivsjon, ved
M, vår 008 Funksjonslære Integrsjon Avdeling for lærerutdnning, Høgskolen i Vestfold. pril 009 1 Arelet under en grf Vi begynner vår diskusjon v integrsjon, på smme måte som vi begynte med derivsjon, ved
MAT 100A: Mappeeksamen 4
 . november, MAT A: Mppeeksmen Løsningsforslg Oppgve ) Vi bruker produktregelen: f (x) x rctn x + x + x Siden x og rctn x hr smme fortegn, og x ldri er negtiv, er f (x) positiv overlt, bortsett fr t f ().
. november, MAT A: Mppeeksmen Løsningsforslg Oppgve ) Vi bruker produktregelen: f (x) x rctn x + x + x Siden x og rctn x hr smme fortegn, og x ldri er negtiv, er f (x) positiv overlt, bortsett fr t f ().
Sammendrag kapittel 1 - Aritmetikk og algebra
 Smmendrg kpittel 1 - Aritmetikk og lgebr Regneregler for brøker Utvide brøk: Gng med smme tll i teller og nevner. b = k b k Forkorte brøk: del med smme tll i teller og nevner. b = : k b : k Summere brøker:
Smmendrg kpittel 1 - Aritmetikk og lgebr Regneregler for brøker Utvide brøk: Gng med smme tll i teller og nevner. b = k b k Forkorte brøk: del med smme tll i teller og nevner. b = : k b : k Summere brøker:
EKSAMEN. 1. klassene, ingenørutdanning og flexing. ANTALL SIDER UTLEVERT: 5(innkl. forside og 2 sider formelark)
 KANDIDATNUMMER: EKSAMEN EMNENAVN: Mtemtikk EMNENUMMER: REA4 og REA4f EKSAMENSDATO:. ugust 9 KLASSE:. klssene, ingenørutdnning og fleing. TID: kl. 9... FAGANSVARLIG: Hns Petter Hornæs ANTALL SIDER UTLEVERT:
KANDIDATNUMMER: EKSAMEN EMNENAVN: Mtemtikk EMNENUMMER: REA4 og REA4f EKSAMENSDATO:. ugust 9 KLASSE:. klssene, ingenørutdnning og fleing. TID: kl. 9... FAGANSVARLIG: Hns Petter Hornæs ANTALL SIDER UTLEVERT:
Eksamen R2, Va ren 2014, løsning
 Eksmen R, V ren 04, løsning Tid: timer Hjelpemidler: Vnlige skrivesker, psser, linjl med centimetermål og vinkelmåler er tilltt. Oppgve ( poeng) Deriver funksjonene ) f sin Vi bruker kjerneregelen på sin,
Eksmen R, V ren 04, løsning Tid: timer Hjelpemidler: Vnlige skrivesker, psser, linjl med centimetermål og vinkelmåler er tilltt. Oppgve ( poeng) Deriver funksjonene ) f sin Vi bruker kjerneregelen på sin,
5: Algebra. Oppgaver Innhold Dato
 5: Alger Pln resten v året: - Kpittel 6: Ferur - Kpittel 7: Ferur/mrs - Kpittel 8: Mrs - Repetisjon: April/mi - Eventuell offentlig eksmen: Mi - Økter, prøver, prosjekter: Mi - juni For mnge er egrepet
5: Alger Pln resten v året: - Kpittel 6: Ferur - Kpittel 7: Ferur/mrs - Kpittel 8: Mrs - Repetisjon: April/mi - Eventuell offentlig eksmen: Mi - Økter, prøver, prosjekter: Mi - juni For mnge er egrepet
EKSAMEN. 1. klassene, ingenørutdanning og Flexing. HansPetterHornæsogLarsNilsBakken. ANTALL SIDER UTLEVERT: 7 (innkl. forside og 4 sider formelark)
 KANDIDATNUMMER: EKSAMEN EMNENAVN: Mtemtikk EMNENUMMER: REA4 og REA4f EKSAMENSDATO: 9. desember 0 KLASSE:. klssene, ingenørutdnning og Flexing. TID: kl. 9.00 3.00. FAGANSVARLIG: HnsPetterHornæsogLrsNilsBkken
KANDIDATNUMMER: EKSAMEN EMNENAVN: Mtemtikk EMNENUMMER: REA4 og REA4f EKSAMENSDATO: 9. desember 0 KLASSE:. klssene, ingenørutdnning og Flexing. TID: kl. 9.00 3.00. FAGANSVARLIG: HnsPetterHornæsogLrsNilsBkken
1 Mandag 25. januar 2010
 Mndg 5. jnur Vi fortsetter med å se på det bestemte integrlet, bl.. på hvordn vi kn bruke numeriske beregninger til å bestemme verdien når vi ikke nødvendigvis kn finne en nti-derivert. Videre skl vi t
Mndg 5. jnur Vi fortsetter med å se på det bestemte integrlet, bl.. på hvordn vi kn bruke numeriske beregninger til å bestemme verdien når vi ikke nødvendigvis kn finne en nti-derivert. Videre skl vi t
R2 - Heldagsprøve våren 2013
 Løsningsskisser HD R R - Heldgsprøve våren 0 Løsningsskisser Viktigste oppsummeringer: Må skrive med penn på eksmen! Slurv og regnefeil, både med tll og bokstver, er hovedproblemet. Beste måten å fikse
Løsningsskisser HD R R - Heldgsprøve våren 0 Løsningsskisser Viktigste oppsummeringer: Må skrive med penn på eksmen! Slurv og regnefeil, både med tll og bokstver, er hovedproblemet. Beste måten å fikse
Eneboerspillet. Håvard Johnsbråten
 Håvrd Johnsråten Eneoerspillet Når vi tenker på nvendelser i mtemtikken, ser vi gjerne for oss Pytgors læresetning eller ndre formler som vi kn ruke til å eregne lengder, reler, kostnder osv. Men mer strkte
Håvrd Johnsråten Eneoerspillet Når vi tenker på nvendelser i mtemtikken, ser vi gjerne for oss Pytgors læresetning eller ndre formler som vi kn ruke til å eregne lengder, reler, kostnder osv. Men mer strkte
1 Mandag 18. januar 2010
 Mndg 8. jnur 2 I denne første forelesningen skl vi friske opp litt rundt funksjoner i en vribel, se på hvordn de vokser/vtr, studere kritiske punkter og beskrive krumning og vendepunkter. Vi får ikke direkte
Mndg 8. jnur 2 I denne første forelesningen skl vi friske opp litt rundt funksjoner i en vribel, se på hvordn de vokser/vtr, studere kritiske punkter og beskrive krumning og vendepunkter. Vi får ikke direkte
Løsningsforslag til Eksamen i fag MA1103 Flerdimensjonal analyse
 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Side 1 v 5 Løsningsforslg til Eksmen i fg MA113 Flerdimensjonl nlyse 2.5.6 Oppgve 1 Vi hr f(x, y) = (4 x 2 y 2 )e x+y. ) Kritiske
Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Side 1 v 5 Løsningsforslg til Eksmen i fg MA113 Flerdimensjonl nlyse 2.5.6 Oppgve 1 Vi hr f(x, y) = (4 x 2 y 2 )e x+y. ) Kritiske
1 Mandag 1. mars 2010
 Mndg. mrs Fundmentlteoremet sier t integrsjon og derivsjon er motstte opersjoner. Vi hr de siste ukene sett hvordn vi på ulike måter kn derivere funksjoner i flere vrible. Nå er turen kommet til den motstte
Mndg. mrs Fundmentlteoremet sier t integrsjon og derivsjon er motstte opersjoner. Vi hr de siste ukene sett hvordn vi på ulike måter kn derivere funksjoner i flere vrible. Nå er turen kommet til den motstte
Matematikk Øvingsoppgaver i numerikk leksjon 9 Numerisk integrasjon
 Mtemtikk 1000 Øvingsoppgver i numerikk leksjon 9 Numerisk integrsjon Forståelsen v integrlet som et rel ligger til grunn når vi skl beregne integrler numerisk. Litt mer presist: Når f(x) 0 for lle x i
Mtemtikk 1000 Øvingsoppgver i numerikk leksjon 9 Numerisk integrsjon Forståelsen v integrlet som et rel ligger til grunn når vi skl beregne integrler numerisk. Litt mer presist: Når f(x) 0 for lle x i
Integralregning. Mål. for opplæringen er at eleven skal kunne
 8 Integrlregning Mål for opplæringen er t eleven skl kunne gjøre rede for definisjonen v estemt integrl som grense for en sum og uestemt integrl som ntiderivert eregne integrler v de sentrle funksjonene
8 Integrlregning Mål for opplæringen er t eleven skl kunne gjøre rede for definisjonen v estemt integrl som grense for en sum og uestemt integrl som ntiderivert eregne integrler v de sentrle funksjonene
E K S A M E N. Matematikk 3MX. Elevar/Elever Privatistar/Privatister. AA6524/AA6526 8. desember 2004 UTDANNINGSDIREKTORATET
 E K S A M E N UTDANNINGSDIREKTORATET Mtemtikk 3MX Elevr/Elever Privtistr/Privtister AA654/AA656 8. desember 004 Vidregånde kurs II / Videregående kurs II Studieretning for llmenne, økonomiske og dministrtive
E K S A M E N UTDANNINGSDIREKTORATET Mtemtikk 3MX Elevr/Elever Privtistr/Privtister AA654/AA656 8. desember 004 Vidregånde kurs II / Videregående kurs II Studieretning for llmenne, økonomiske og dministrtive
Oppfriskningskurs i matematikk 2007
 Oppfriskningskurs i mtemtikk 2007 Mrte Pernille Htlo Institutt for mtemtiske fg, NTNU 6.-11. ugust 2007 Velkommen! 2 Temer Algebr Trigonometri Funksjoner og derivsjon Integrsjon Eksponensil- og logritmefunksjoner
Oppfriskningskurs i mtemtikk 2007 Mrte Pernille Htlo Institutt for mtemtiske fg, NTNU 6.-11. ugust 2007 Velkommen! 2 Temer Algebr Trigonometri Funksjoner og derivsjon Integrsjon Eksponensil- og logritmefunksjoner
dx = 1 2y dy = dx/ x 3 y3/2 = 2x 1/2 + C 1
 NTNU Institutt for mtemtiske fg TMA Mtemtikk høsten Løsningsforslg - Øving 7 Avsnitt 6.5 ) En hr t y = e, så y + 3y = e + 3e = e. b) En hr t y = e 3 e (3/), så y + 3y = e 3e (3/) + 3e + 3e (3/) = e. c)
NTNU Institutt for mtemtiske fg TMA Mtemtikk høsten Løsningsforslg - Øving 7 Avsnitt 6.5 ) En hr t y = e, så y + 3y = e + 3e = e. b) En hr t y = e 3 e (3/), så y + 3y = e 3e (3/) + 3e + 3e (3/) = e. c)
a 2πf(x) 1 + (f (x)) 2 dx.
 MA 4: Anlyse Uke 44, http://home.hi.no/ svldl/m4 H Høgskolen i Agder Avdeling for relfg Institutt for mtemtiske fg Om lengde v kurver. Noen få formler der integrsjon brukes for å beregne lengder, reler
MA 4: Anlyse Uke 44, http://home.hi.no/ svldl/m4 H Høgskolen i Agder Avdeling for relfg Institutt for mtemtiske fg Om lengde v kurver. Noen få formler der integrsjon brukes for å beregne lengder, reler
Numerisk derivasjon og integrasjon utledning av feilestimater
 Numerisk derivsjon og integrsjon utledning v feilestimter Knut Mørken 6 oktober 007 1 Innledning På forelesningen /10 brukte vi litt tid på å repetere inhomogene differensligninger og rkk dermed ikke gjennomgå
Numerisk derivsjon og integrsjon utledning v feilestimter Knut Mørken 6 oktober 007 1 Innledning På forelesningen /10 brukte vi litt tid på å repetere inhomogene differensligninger og rkk dermed ikke gjennomgå
1 Tallregning og algebra
 Tllregning og lger ØV MER. REGNEREKKEFØLGE Oppgve.0 6 d) ( : 6) Oppgve. ( ) ( ) ()() ( ) ( ) ( ) () (6 ) () d) ( ) 7() ( ) Oppgve. 6 ( ) d) Oppgve. Med ett ddisjonstegn, ett sutrksjonstegn, ett multipliksjonstegn
Tllregning og lger ØV MER. REGNEREKKEFØLGE Oppgve.0 6 d) ( : 6) Oppgve. ( ) ( ) ()() ( ) ( ) ( ) () (6 ) () d) ( ) 7() ( ) Oppgve. 6 ( ) d) Oppgve. Med ett ddisjonstegn, ett sutrksjonstegn, ett multipliksjonstegn
... JULEPRØVE 9. trinn...
 .... JULEPRØVE 9. trinn.... Nvn: Gruppe: DELPRØVE 1 uten hjelpemidler ( 37 poeng) På denne delprøven kn du re ruke skrivesker, psser og linjl. Alle oppgvene i del 1 skl føres rett på rket. I noen oppgver
.... JULEPRØVE 9. trinn.... Nvn: Gruppe: DELPRØVE 1 uten hjelpemidler ( 37 poeng) På denne delprøven kn du re ruke skrivesker, psser og linjl. Alle oppgvene i del 1 skl føres rett på rket. I noen oppgver
1 dx cos 1 x =, 1 x 2 sammen med kjerneregelen for derivasjon. For å forenkle utregningen lar vi u = Vi regner først ut den deriverte til u,
 TMA0 Høst 205 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg 3.5.30: Vi bruker erivsjonsregelen for cos x, x cos x =, x 2 smmen me kjerneregelen for erivsjon. For å forenkle utregningen
TMA0 Høst 205 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg 3.5.30: Vi bruker erivsjonsregelen for cos x, x cos x =, x 2 smmen me kjerneregelen for erivsjon. For å forenkle utregningen
Løsningsforslag Kollokvium 1
 Løsningsforslg Kollokvium 1 30. jnur 015 Her finner dere et løsningsforslg for oppgvene som ble diskutert på Kollokvium 1. Oppgve 1 Regning med enheter ) Energienheten 1 ev (elektronvolt) er definert som
Løsningsforslg Kollokvium 1 30. jnur 015 Her finner dere et løsningsforslg for oppgvene som ble diskutert på Kollokvium 1. Oppgve 1 Regning med enheter ) Energienheten 1 ev (elektronvolt) er definert som
Faktorisering. 1 Hva er faktorisering? 2 Hvorfor skal vi faktorisere? Per G. Østerlie Senter for IKT i utdanningen 11.
 Fktorisering Per G. Østerlie Senter for IKT i utdnningen per@osterlie.no 11. mi 013 1 Hv er fktorisering? Vi må se på veret å fktorisere. Hv er det vi skl gjøre når vi fktoriserer? Svret er: å lge fktorer.
Fktorisering Per G. Østerlie Senter for IKT i utdnningen per@osterlie.no 11. mi 013 1 Hv er fktorisering? Vi må se på veret å fktorisere. Hv er det vi skl gjøre når vi fktoriserer? Svret er: å lge fktorer.
Kapittel 3. Potensregning
 Kpittel. Potensregning I potensregning skriver vi tll som potenser og forenkler uttrykk som inneholder potenser. Dette kpitlet hndler blnt nnet om: Betydningen v potenser som hr negtiv eksponent eller
Kpittel. Potensregning I potensregning skriver vi tll som potenser og forenkler uttrykk som inneholder potenser. Dette kpitlet hndler blnt nnet om: Betydningen v potenser som hr negtiv eksponent eller
TMA4100 Matematikk1 Høst 2008
 TMA4 Mtemtikk Høst 8 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Løsningsforslg Øving 6 5..5 Gjennomsnittet v f(x) = x på intervllet [, ] er lik relet A under grfen dividert
TMA4 Mtemtikk Høst 8 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Løsningsforslg Øving 6 5..5 Gjennomsnittet v f(x) = x på intervllet [, ] er lik relet A under grfen dividert
Integral Kokeboken. sin(πx 2 ) sinh 2 (πx) dx = 2. 1 log x. + log(log x) dx = x log(log x) + C. cos(x2 ) + sin(x 2 ) dx = 2π. 1 k t.
 Integrl Kokeboken 4 3 4 6 8 sinπ sinh π 4 log + loglog loglog + C cos + sin π t e Γt k k t Γtζt rcsin + rccos π + C Integrl fr R til Z π 6 sec y dy ln 3 i 64 The integrl sec y dy From zero to one-sith
Integrl Kokeboken 4 3 4 6 8 sinπ sinh π 4 log + loglog loglog + C cos + sin π t e Γt k k t Γtζt rcsin + rccos π + C Integrl fr R til Z π 6 sec y dy ln 3 i 64 The integrl sec y dy From zero to one-sith
2 Symboler i matematikken
 2 Symoler i mtemtikken 2.1 Symoler som står for tll og størrelser Nvn i geometri Nvn i mtemtikken enyttes på lignende måte som nvn på yer og personer, de refererer eller representerer et tll eller en størrelse,
2 Symoler i mtemtikken 2.1 Symoler som står for tll og størrelser Nvn i geometri Nvn i mtemtikken enyttes på lignende måte som nvn på yer og personer, de refererer eller representerer et tll eller en størrelse,
EKSAMEN. 1. klassene, ingenørutdanning og Flexing. ANTALL SIDER UTLEVERT: 5 (innkl. forside og 2 sider formelark)
 KANDIDATNUMMER: EKSAMEN EMNENAVN: Mtemtikk 0 EMNENUMMER: REA04 EKSAMENSDATO:. desember 008 KLASSE:. klssene, ingenørutdnning og Flexing. TID: kl. 9.00 3.00. FAGANSVARLIG: Hns Petter Hornæs ANTALL SIDER
KANDIDATNUMMER: EKSAMEN EMNENAVN: Mtemtikk 0 EMNENUMMER: REA04 EKSAMENSDATO:. desember 008 KLASSE:. klssene, ingenørutdnning og Flexing. TID: kl. 9.00 3.00. FAGANSVARLIG: Hns Petter Hornæs ANTALL SIDER
9.6 Tilnærminger til deriverte og integraler
 96 TILNÆRMINGER TIL DERIVERTE OG INTEGRALER 169 Figur 915 Bezier-kurve med kontrollpolygon som representerer bokstven S i Postscript-fonten Times-Romn De ulike Bezier-segmentene ser du mellom kontrollpunktene
96 TILNÆRMINGER TIL DERIVERTE OG INTEGRALER 169 Figur 915 Bezier-kurve med kontrollpolygon som representerer bokstven S i Postscript-fonten Times-Romn De ulike Bezier-segmentene ser du mellom kontrollpunktene
Derivasjon. Oversikt over Matematikk 1. Derivasjon anvendelser. Sekantsetningen
 3 Oversikt over Mtemtikk Induksjon Grenser og kontinuitet Skjæringssetningen Eksistens v ekstrempunkt Elementære funksjoner Derivsjon Sekntsetningen Integrsjon Differensilligninger Kurver i plnet Rekker
3 Oversikt over Mtemtikk Induksjon Grenser og kontinuitet Skjæringssetningen Eksistens v ekstrempunkt Elementære funksjoner Derivsjon Sekntsetningen Integrsjon Differensilligninger Kurver i plnet Rekker
x 1, x 2,..., x n. En lineær funksjon i n variable er en funksjon f(x 1, x 2,..., x n ) = a 1 x 1 + a 2 x a n x n,
 Introduksjon Velkommen til emnet TMA45 Mtemtikk 3, våren 9 Disse nottene inneholder det vi gjennomgår i forelesningene, og utgjør, smmen med lle øvingene, pensum for emnet Læreoken nefles som støttelittertur
Introduksjon Velkommen til emnet TMA45 Mtemtikk 3, våren 9 Disse nottene inneholder det vi gjennomgår i forelesningene, og utgjør, smmen med lle øvingene, pensum for emnet Læreoken nefles som støttelittertur
Forkunnskaper i matematikk for fysikkstudenter. Integrasjon.
 De grunnleggende definisjonene L oss strte med følgende prolem: Gitt en ontinuerlig funsjon y = f der f for [, ] Beregn relet A som er vgrenset v grfen til f, -sen, og de to vertile linjene = og = Vi n
De grunnleggende definisjonene L oss strte med følgende prolem: Gitt en ontinuerlig funsjon y = f der f for [, ] Beregn relet A som er vgrenset v grfen til f, -sen, og de to vertile linjene = og = Vi n
Terminprøve Matematikk for 1P 1NA høsten 2014
 Terminprøve Mtemtikk for 1P 1NA høsten 2014 DEL 1 Vrer 1,5 time Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med entimetermål og vinkelmåler. Forsøk på lle oppgvene selv om du er usikker
Terminprøve Mtemtikk for 1P 1NA høsten 2014 DEL 1 Vrer 1,5 time Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med entimetermål og vinkelmåler. Forsøk på lle oppgvene selv om du er usikker
TFY4104 Fysikk. Institutt for fysikk, NTNU. Lsningsforslag til ving 8. a =
 TFY414 Fysikk. Institutt for fysikk, NTNU. Lsningsforslg til ving 8. Oppgve 1. ) C F = E = m Newtons. lov. Her er = e, s elektronets kselersjon blir = e m E lts mot venstre. b) C Totlt elektrisk felt i
TFY414 Fysikk. Institutt for fysikk, NTNU. Lsningsforslg til ving 8. Oppgve 1. ) C F = E = m Newtons. lov. Her er = e, s elektronets kselersjon blir = e m E lts mot venstre. b) C Totlt elektrisk felt i
Fasit til utvalgte oppgaver MAT1100, uka 20-24/9
 Fsit til utvlgte oppgver MAT00, uk 20-24/9 Øyvind Ryn oyvindry@ifi.uio.no September 24, 200 Oppgve 5..5 år vi viser t f er kontinuerlig i ved et ɛ δ-bevis, er det lurt å strte med uttrykket fx f, og finne
Fsit til utvlgte oppgver MAT00, uk 20-24/9 Øyvind Ryn oyvindry@ifi.uio.no September 24, 200 Oppgve 5..5 år vi viser t f er kontinuerlig i ved et ɛ δ-bevis, er det lurt å strte med uttrykket fx f, og finne
Fag: Matematikk 1T-Y for elever og privatister. Antall sider i oppgaven: 8 inklusiv forside og opplysningsside
 Loklt gitt eksmen 2012 Eksmen Fg: Mtemtikk 1T-Y for elever og privtister Fgkode: MAT1006 Eksmensdto: 25. mi Antll sider i oppgven: 8 inklusiv forside og opplysningsside Eksmenstid: Hjelpemidler under eksmen:
Loklt gitt eksmen 2012 Eksmen Fg: Mtemtikk 1T-Y for elever og privtister Fgkode: MAT1006 Eksmensdto: 25. mi Antll sider i oppgven: 8 inklusiv forside og opplysningsside Eksmenstid: Hjelpemidler under eksmen:
Fakultet for realfag Ho/gskolen i Agder - Va ren 2007
 Msteroppgve i mtemtikkdidktikk Fkultet for relfg Ho/gskolen i Agder - V ren 2007 Integrl og integrsjon Roger Mrkussen Roger Mrkussen Integrl og integrsjon Msteroppgve i mtemtikkdidktikk Høgskolen i Agder
Msteroppgve i mtemtikkdidktikk Fkultet for relfg Ho/gskolen i Agder - V ren 2007 Integrl og integrsjon Roger Mrkussen Roger Mrkussen Integrl og integrsjon Msteroppgve i mtemtikkdidktikk Høgskolen i Agder
2x 3 4/x dx. 2 5 x 3 + LF: Vi utfører polynomdivisjon. 2x + 1 dx = + C = 5x8/ ln 2x C 4. πx 2 e 3x3 dx = π
 Innlevering ELFE KJFE MAFE Mtemtikk HIOA Obligtorisk innlevering 5 Innleveringsfrist Mndg 6. oktober 5 før forelesningen : Antll oppgver: Løsningsforslg Finn de ubestemte integrlene ) x 4/x dx LF: x 4/x
Innlevering ELFE KJFE MAFE Mtemtikk HIOA Obligtorisk innlevering 5 Innleveringsfrist Mndg 6. oktober 5 før forelesningen : Antll oppgver: Løsningsforslg Finn de ubestemte integrlene ) x 4/x dx LF: x 4/x
Temahefte nr. 1. Hvordan du regner med hele tall
 1 ARBEIDSHEFTE I MATEMATIKK SNART MATTE EKSAMEN Hvordn du effektivt kn forberede deg til eksmen Temhefte nr. 1 Hvordn du regner med hele tll Av Mtthis Lorentzen mttegrisenforlg.com Opplysning: De nturlige
1 ARBEIDSHEFTE I MATEMATIKK SNART MATTE EKSAMEN Hvordn du effektivt kn forberede deg til eksmen Temhefte nr. 1 Hvordn du regner med hele tll Av Mtthis Lorentzen mttegrisenforlg.com Opplysning: De nturlige
I = (xy + z 2 ) dv. = z 2 dv. 1 1 x 1 x y z 2 dz dy dx,
 TMA5 Mtemtikk Vår 7 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Løsningsforslg Øving 8 Alle oppgvenummer referer til 8 utgve v Adms & Essex Clculus: A Complete Course 57: Vi
TMA5 Mtemtikk Vår 7 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Løsningsforslg Øving 8 Alle oppgvenummer referer til 8 utgve v Adms & Essex Clculus: A Complete Course 57: Vi
Kapittel 4 Tall og algebra Mer øving
 Kpittel 4 Tll og lger Mer øving Oppgve 1 d Oppgve 2 Se på uttrykket A = g h. Hv forteller de ulike okstvene? Se på uttrykket A = 2π. Hv står de ulike symolene for? Forklr hv vi mener med en vriel og en
Kpittel 4 Tll og lger Mer øving Oppgve 1 d Oppgve 2 Se på uttrykket A = g h. Hv forteller de ulike okstvene? Se på uttrykket A = 2π. Hv står de ulike symolene for? Forklr hv vi mener med en vriel og en
Fag: Matematikk 1T-Y for yrkesfag for elever og privatisterr. Eksamensdato: 16. januar 2012
 Loklt gittt eksmen Eksmen Fg: Mtemtikk 1T-Y for yrkesfg for elever og privtisterr Fgkode: MAT1006 Eksmensdto: 16. jnur 2012 Antll sider i oppgven: 7 inklusiv forside og opplysningsside Del 1: oppgve 1-5
Loklt gittt eksmen Eksmen Fg: Mtemtikk 1T-Y for yrkesfg for elever og privtisterr Fgkode: MAT1006 Eksmensdto: 16. jnur 2012 Antll sider i oppgven: 7 inklusiv forside og opplysningsside Del 1: oppgve 1-5
ALTERNATIV GRUNNBOK BOKMÅL
 Anne Rsch-Hlvorsen Oddvr Asen Illustrtør: Bjørn Eidsvik 7B NY UTGAVE ALTERNATIV GRUNNBOK BOKMÅL CAPPELEN DAMM AS, 2011 Mterilet i denne publiksjonen er omfttet v åndsverklovens bestemmelser. Uten særskilt
Anne Rsch-Hlvorsen Oddvr Asen Illustrtør: Bjørn Eidsvik 7B NY UTGAVE ALTERNATIV GRUNNBOK BOKMÅL CAPPELEN DAMM AS, 2011 Mterilet i denne publiksjonen er omfttet v åndsverklovens bestemmelser. Uten særskilt
Integrasjon. et supplement til Kalkulus. Harald Hanche-Olsen 14. november 2016
 Integrsjon et supplement til Klkulus Hrl Hnhe-Olsen 14. novemer 2016 Dette nottet er ment som et supplement og elvis lterntiv til eler v kpittel 8 i Tom Linstrøm: Klkulus (åe 3. og 4. utgve). Foruten et
Integrsjon et supplement til Klkulus Hrl Hnhe-Olsen 14. novemer 2016 Dette nottet er ment som et supplement og elvis lterntiv til eler v kpittel 8 i Tom Linstrøm: Klkulus (åe 3. og 4. utgve). Foruten et
MAT 100a - LAB 4. Før vi gjør dette, skal vi for ordens skyld gjennomgå Maple-kommandoene for integrasjon (cf. GswM kap. 12).
 MAT 00 - LAB 4 Denne øvelsen er i hovedsk viet til integrsjon. For mnge er integrsjon i prksis det smme som ntiderivsjon, og noe som kn rukes til å eregne relet v enkelte områder i plnet som lr seg egrense
MAT 00 - LAB 4 Denne øvelsen er i hovedsk viet til integrsjon. For mnge er integrsjon i prksis det smme som ntiderivsjon, og noe som kn rukes til å eregne relet v enkelte områder i plnet som lr seg egrense
dy ycos 2 y = dx. Ved å integrere på begge sider av likhetstegnet får man ved å substituere u = y,du = dy dy ycos 2 y = 2du cos 2 u = x.
 NTNU Institutt for mtemtiske fg TMA Mtemtikk høsten 2 Løsningsforslg - Øving 7 Avsnitt 6.5 ) En hr t y = e, så 2y +y = 2e +e = e. b) En hr t y = e 2 e (/2), så 2y +y = 2e e (/2) +e +e (/2) = e. c) En hr
NTNU Institutt for mtemtiske fg TMA Mtemtikk høsten 2 Løsningsforslg - Øving 7 Avsnitt 6.5 ) En hr t y = e, så 2y +y = 2e +e = e. b) En hr t y = e 2 e (/2), så 2y +y = 2e e (/2) +e +e (/2) = e. c) En hr
Praktiske opplysninger til rektor. Fag: MATEMATIKK 1TY for yrkesfag Fagkode: MAT1006 Eksamensdato: Antall forberedelsesdager: Ingen
 Loklt gitt eksmen 2013 Prktiske opplysninger til rektor Fg: MATEMATIKK 1TY for yrkesfg Fgkode: MAT1006 Eksmensdto: 30.5.2013 Antll foreredelsesdger: Ingen Forhold som skolen må være oppmerksom på: Eksmenen
Loklt gitt eksmen 2013 Prktiske opplysninger til rektor Fg: MATEMATIKK 1TY for yrkesfg Fgkode: MAT1006 Eksmensdto: 30.5.2013 Antll foreredelsesdger: Ingen Forhold som skolen må være oppmerksom på: Eksmenen
MAT 1110: Løsningsforslag til obligatorisk oppgave 2, V-06
 MAT : Løsningsforslg til obligtorisk oppgve, V-6 Oppgve : ) Hvis = (,,...) og = (,,...) er to vektorer, vil kommndoen >> plot(,) tegne rette forbindelseslinjer mellom punktene (, ), (, ) osv. For å plotte
MAT : Løsningsforslg til obligtorisk oppgve, V-6 Oppgve : ) Hvis = (,,...) og = (,,...) er to vektorer, vil kommndoen >> plot(,) tegne rette forbindelseslinjer mellom punktene (, ), (, ) osv. For å plotte
3.7 Pythagoras på mange måter
 Oppgve 3.18 Vis t det er mulig å multiplisere og dividere linjestykker som vist i figur 3.. Bruk formlikhet. 3.7 Pythgors på mnge måter Grekeren Pythgors le født på Smos 569 og døde. år 500 f. Kr. Setningen
Oppgve 3.18 Vis t det er mulig å multiplisere og dividere linjestykker som vist i figur 3.. Bruk formlikhet. 3.7 Pythgors på mnge måter Grekeren Pythgors le født på Smos 569 og døde. år 500 f. Kr. Setningen
... JULEPRØVE
 Ashehoug JULEPRØVE 2014 9. trinn.... JULEPRØVE 2014.... Nvn: Gruppe: DELPRØVE 1 uten hjelpemidler ( 37 poeng) På denne delprøven kn du re ruke skrivesker, psser og linjl. Alle oppgvene i del 1 skl føres
Ashehoug JULEPRØVE 2014 9. trinn.... JULEPRØVE 2014.... Nvn: Gruppe: DELPRØVE 1 uten hjelpemidler ( 37 poeng) På denne delprøven kn du re ruke skrivesker, psser og linjl. Alle oppgvene i del 1 skl føres
Projeksjon. Kapittel 11. Ortogonal projeksjon i R 2. Skalarproduktet i R n. w på v. Fra figuren ovenfor ser vi at komponenten til w ortogonalt på v er
 Kpittel Projeksjon En projeksjon er en lineærtrnsformsjon P som tilfredsstiller P x P x. for lle x. Denne ligningen sier t intet nytt skjer om du benytter lineærtrnsformsjonen for ndre gng, og mn kn tenke
Kpittel Projeksjon En projeksjon er en lineærtrnsformsjon P som tilfredsstiller P x P x. for lle x. Denne ligningen sier t intet nytt skjer om du benytter lineærtrnsformsjonen for ndre gng, og mn kn tenke
1 Geometri KATEGORI 1. 1.1 Vinkelsummen i mangekanter. 1.2 Vinkler i formlike figurer
 Oppgver 1 Geometri KTGORI 1 1.1 Vinkelsummen i mngeknter Oppgve 1.110 ) I en treknt er to v vinklene 65 og 5. Finn den tredje vinkelen. b) I en firknt er tre v vinklene 0, 50 og 150. Finn den fjerde vinkelen.
Oppgver 1 Geometri KTGORI 1 1.1 Vinkelsummen i mngeknter Oppgve 1.110 ) I en treknt er to v vinklene 65 og 5. Finn den tredje vinkelen. b) I en firknt er tre v vinklene 0, 50 og 150. Finn den fjerde vinkelen.
Bioberegninger - notat 3: Anvendelser av Newton s metode
 Bioberegninger - nott 3: Anvendelser v Newton s metode 20. februr 2004 1 Euler-Lotk ligningen L oss tenke oss en populsjon bestående v individer v ulik lder. L n være mksiml lder. L m i være ntll vkom
Bioberegninger - nott 3: Anvendelser v Newton s metode 20. februr 2004 1 Euler-Lotk ligningen L oss tenke oss en populsjon bestående v individer v ulik lder. L n være mksiml lder. L m i være ntll vkom
Løsningsforslag til øving 4
 1 Oppgve 1 FY1005/TFY4165 Termisk fysikk Institutt for fysikk, NTNU åren 2015 Løsningsforslg til øving 4 For entomig gss hr vi c pm = 5R/2 og c m = 3R/2, slik t γ = C p /C = 5/3 Lngs dibten er det (pr
1 Oppgve 1 FY1005/TFY4165 Termisk fysikk Institutt for fysikk, NTNU åren 2015 Løsningsforslg til øving 4 For entomig gss hr vi c pm = 5R/2 og c m = 3R/2, slik t γ = C p /C = 5/3 Lngs dibten er det (pr
EKSAMEN. 1. klassene, ingenørutdanning og Flexing. ANTALL SIDER UTLEVERT: 5 (innkl. forside og 2 sider formelark)
 KANDIDATNUMMER: EKSAMEN EMNENAVN: Mtemtikk EMNENUMMER: REA4 EKSAMENSDATO:. desember 9 KLASSE:. klssene, ingenørutdnning og Flexing. TID: kl. 9. 3.. FAGANSVARLIG: Hns Petter Hornæs ANTALL SIDER UTLEVERT:
KANDIDATNUMMER: EKSAMEN EMNENAVN: Mtemtikk EMNENUMMER: REA4 EKSAMENSDATO:. desember 9 KLASSE:. klssene, ingenørutdnning og Flexing. TID: kl. 9. 3.. FAGANSVARLIG: Hns Petter Hornæs ANTALL SIDER UTLEVERT:
Del 2. Alle oppgaver føres inn på eget ark. Vis tydelig hvordan du har kommet frem til svaret. Oppgave 2
 Del 2 Alle oppgver føres inn på eget rk. Vis tydelig hvordn du hr kommet frem til svret. Oppgve 1 Figuren viser sidefltene til et prisme. Grunnflten og toppflten mngler. ) Hvilken form må grunn- og toppflten
Del 2 Alle oppgver føres inn på eget rk. Vis tydelig hvordn du hr kommet frem til svret. Oppgve 1 Figuren viser sidefltene til et prisme. Grunnflten og toppflten mngler. ) Hvilken form må grunn- og toppflten
Eksamen våren 2018 Løsninger
 DEL 1 Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med centimetermål og vinkelmåler Oppgve 1 5x+ y = 4 x+ 4y = 6 Vi multipliserer likningen 5x+ y = 4 med på egge sider og får 10x+ 4y
DEL 1 Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med centimetermål og vinkelmåler Oppgve 1 5x+ y = 4 x+ 4y = 6 Vi multipliserer likningen 5x+ y = 4 med på egge sider og får 10x+ 4y
Løsningsforslag til avsluttende eksamen i HUMIT1750 høsten 2003.
 Løsningsforslg til vsluttende eksmen i HUMIT1750 høsten 2003. Teksten under hr litt litt prtsom fordi jeg hr villet forklre hvordn jeg gikk frm. Fr en studentesvrelse le det ikke forventet nnet enn sluttresulttene.
Løsningsforslg til vsluttende eksmen i HUMIT1750 høsten 2003. Teksten under hr litt litt prtsom fordi jeg hr villet forklre hvordn jeg gikk frm. Fr en studentesvrelse le det ikke forventet nnet enn sluttresulttene.
LEDDVIS INTEGRASJON OG DERIVASJON AV POTENSREKKER:
 LEDDVIS INTEGRASJON OG DERIVASJON AV POTENSREKKER: Vi ntr t potensrekken n x n n= konvergerer i ( R, R), R >, med summen s(x). D gjelder: og s (x) = n n x n for hver x med x < R, s(t) dt = n= (Dette er
LEDDVIS INTEGRASJON OG DERIVASJON AV POTENSREKKER: Vi ntr t potensrekken n x n n= konvergerer i ( R, R), R >, med summen s(x). D gjelder: og s (x) = n n x n for hver x med x < R, s(t) dt = n= (Dette er
Nøtterøy videregående skole
 Til elever og forestte Borgheim, 1. ugust 2018 Viktig info om vlg v mtemtikkfg for elever på vg1 studiespesilisering I vg1 får elevene vlget mellom to ulike mtemtikkfg. Mtemtikk 1T (teoretisk) og Mtemtikk
Til elever og forestte Borgheim, 1. ugust 2018 Viktig info om vlg v mtemtikkfg for elever på vg1 studiespesilisering I vg1 får elevene vlget mellom to ulike mtemtikkfg. Mtemtikk 1T (teoretisk) og Mtemtikk
9 Potenser. Logaritmer
 9 Potenser. Logritmer Foret utregingene nedenfor: 5 5 c 6 7 d e 5 f g h i Regn ut og gjør svrene så enkle som mulige: c y y d e f g h i j y y + y + y + + y Prisen på en motorsg vr kr 56 i 99. Vi regner
9 Potenser. Logritmer Foret utregingene nedenfor: 5 5 c 6 7 d e 5 f g h i Regn ut og gjør svrene så enkle som mulige: c y y d e f g h i j y y + y + y + + y Prisen på en motorsg vr kr 56 i 99. Vi regner
Høgskolen i Bergen. Formelsamling. for. ingeniørutdanningen. FOA150 høsten 2006 fellespensum. 3.utgave
 Høgskolen i Bergen Formelsmling for ingeniørutdnningen FOA5 høsten 6 fellespensum. 3.utgve Funksjoner. Elementære regneregler og funksjoner: y = y, ( ) =, y y =,, =, = ) = ) = = log = ln ln c) ln y = y
Høgskolen i Bergen Formelsmling for ingeniørutdnningen FOA5 høsten 6 fellespensum. 3.utgve Funksjoner. Elementære regneregler og funksjoner: y = y, ( ) =, y y =,, =, = ) = ) = = log = ln ln c) ln y = y
Eksamen våren 2016 Løsninger
 DEL Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med centimetermål og vinkelmåler Oppgve,8,8 (,8 ) 3,6 3, 6 3, 6,5 5, (5, ) Oppgve 3, 5 Vi ser på tllinj t,5 tilsvrer punkt F. Vi ser
DEL Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med centimetermål og vinkelmåler Oppgve,8,8 (,8 ) 3,6 3, 6 3, 6,5 5, (5, ) Oppgve 3, 5 Vi ser på tllinj t,5 tilsvrer punkt F. Vi ser
1T kapittel 8 Eksamenstrening Løsninger til oppgavene i læreboka
 T kpittel 8 Eksmenstrening Løsninger til oppgvene i lærebok Uten hjelpemidler E b c E b c Vi gnger vnlige tll med vnlige tll og tierpotenser med tierpotenser. Til slutt omformer vi svret så vi får et tll
T kpittel 8 Eksmenstrening Løsninger til oppgvene i lærebok Uten hjelpemidler E b c E b c Vi gnger vnlige tll med vnlige tll og tierpotenser med tierpotenser. Til slutt omformer vi svret så vi får et tll
Forkurs i matematikk. Kompendium av Amir Hashemi, UiB. Notater, eksempler og oppgaver med fasit/løsningsforslag 1
 Forkurs i mtemtikk Kompendium v Amir Hshemi, UiB. Notter, eksempler og oppgver med fsit/løsningsforslg Mtemtisk Institutt UiB Innhold Sist oppdtert 07. juni 0 i Forord... Kpittel 0 Test deg selv... Oppgver
Forkurs i mtemtikk Kompendium v Amir Hshemi, UiB. Notter, eksempler og oppgver med fsit/løsningsforslg Mtemtisk Institutt UiB Innhold Sist oppdtert 07. juni 0 i Forord... Kpittel 0 Test deg selv... Oppgver
LEDDVIS INTEGRASJON OG DERIVASJON AV POTENSREKKER: a n x n. R > 0, med summen s(x). Da gjelder: a n n + 1 xn+1 for hver x < R.
 LEDDVIS INTEGRASJON OG DERIVASJON AV POTENSREKKER: Vi ntr t potensrekken konvergerer i ] R, R[, n x n R >, med summen s(x). D gjelder: s (x) = n n x n 1 for hver x < R, og s(t)dt = n n + 1 xn+1 for hver
LEDDVIS INTEGRASJON OG DERIVASJON AV POTENSREKKER: Vi ntr t potensrekken konvergerer i ] R, R[, n x n R >, med summen s(x). D gjelder: s (x) = n n x n 1 for hver x < R, og s(t)dt = n n + 1 xn+1 for hver
Sensorveiledning Oppgaveverksted 4, høst 2013 (basert på eksamen vår 2011)
 Sensorveiledning Oppgveverksted 4, høst 203 (bsert på eksmen vår 20) Ved sensuren tillegges oppgve vekt 0,2, oppgve 2 vekt 0,4, og oppgve 3 vekt 0,4. For å bestå eksmen, må besvrelsen i hvert fll: gi minst
Sensorveiledning Oppgveverksted 4, høst 203 (bsert på eksmen vår 20) Ved sensuren tillegges oppgve vekt 0,2, oppgve 2 vekt 0,4, og oppgve 3 vekt 0,4. For å bestå eksmen, må besvrelsen i hvert fll: gi minst
75045 Dynamiske systemer 3. juni 1997 Løsningsforslag
 75045 Dynmiske systemer 3. juni 1997 Løsningsforslg Oppgve 1 ẋ = 0 gir y = ±x, og dette innstt i ẏ = 0 gir 1 ± x = 0. Vi må velge minustegnet, og får x = y = ±1/. Vi deriverer: [ ] x y ( 1 Df(x, y) = ;
75045 Dynmiske systemer 3. juni 1997 Løsningsforslg Oppgve 1 ẋ = 0 gir y = ±x, og dette innstt i ẏ = 0 gir 1 ± x = 0. Vi må velge minustegnet, og får x = y = ±1/. Vi deriverer: [ ] x y ( 1 Df(x, y) = ;
TFY4104 Fysikk. Institutt for fysikk, NTNU. Høsten Løsningsforslag til øving 8. a = e m E
 TFY414 Fysikk. Institutt for fysikk, NTNU. Høsten 16. Løsningsforslg til øving 8. Oppgve 1. ) C F = E = m Newtons. lov. Her er = e, så elektronets kselersjon blir = e m E ltså mot venstre. b) C Totlt elektrisk
TFY414 Fysikk. Institutt for fysikk, NTNU. Høsten 16. Løsningsforslg til øving 8. Oppgve 1. ) C F = E = m Newtons. lov. Her er = e, så elektronets kselersjon blir = e m E ltså mot venstre. b) C Totlt elektrisk
1 Mandag 8. mars 2010
 1 Mndg 8. mrs 21 Vi hr tidligere integrert funksjoner lngs x-ksen, og vi hr integrert funksjoner i flere vrible over begrensede områder i xy-plnet. I denne forelesningen skl vi integrere funksjoner lngs
1 Mndg 8. mrs 21 Vi hr tidligere integrert funksjoner lngs x-ksen, og vi hr integrert funksjoner i flere vrible over begrensede områder i xy-plnet. I denne forelesningen skl vi integrere funksjoner lngs
EKSAMEN. 1. klassene, ingenørutdanning og Flexing. ANTALL SIDER UTLEVERT: 5 (innkl. forside og 2 sider formelark)
 KANDIDATNUMMER: EKSAMEN EMNENAVN: Mtemtikk EMNENUMMER: REA42 og REA42f EKSAMENSDATO:. desember 2 KLASSE:. klssene, ingenørutdnning og Flexing. TID: kl. 9... FAGANSVARLIG: Hns Petter Hornæs ANTALL SIDER
KANDIDATNUMMER: EKSAMEN EMNENAVN: Mtemtikk EMNENUMMER: REA42 og REA42f EKSAMENSDATO:. desember 2 KLASSE:. klssene, ingenørutdnning og Flexing. TID: kl. 9... FAGANSVARLIG: Hns Petter Hornæs ANTALL SIDER
FASIT, tips og kommentarer
 FASIT, tips og kommentrer JULEKALENDER 8.- 10- trinn Nivå 1 og Nivå 2. Tips til orgnisering: Kn jobbes med i gruppe, to og to eller individuelt. Spre rbeidet med klenderen i mttetimene i desember, eller
FASIT, tips og kommentrer JULEKALENDER 8.- 10- trinn Nivå 1 og Nivå 2. Tips til orgnisering: Kn jobbes med i gruppe, to og to eller individuelt. Spre rbeidet med klenderen i mttetimene i desember, eller
Integrasjon Fundamentalteoremet Substitusjon Forelesning i Matematikk 1 TMA4100
 Integrsjon Fundmentlteoremet Substitusjon Forelesning i Mtemtikk 1 TMA4100 Hns Jkob Rivertz Institutt for mtemtiske fg 23. september 2011 2 Mtemtisk induksjon Alle elefnter er ros! Vil bevise P n Alle
Integrsjon Fundmentlteoremet Substitusjon Forelesning i Mtemtikk 1 TMA4100 Hns Jkob Rivertz Institutt for mtemtiske fg 23. september 2011 2 Mtemtisk induksjon Alle elefnter er ros! Vil bevise P n Alle
Fasit. Grunnbok. Kapittel 2. Bokmål
 Fsit 9 Grunnbok Kpittel Bokmål Kpittel Lineære funksjoner rette linjer. ƒ(x) = 4x + 5 ƒ() = 3 ƒ(4) = ƒ(6) = 9.6 ƒ(x) = -x b ƒ(x) = x b ƒ(x) = (x + ) 3 ƒ() = ƒ(4) = 8 ƒ(6) = 4 ƒ(x) = x 4 ƒ() = - ƒ(4) =
Fsit 9 Grunnbok Kpittel Bokmål Kpittel Lineære funksjoner rette linjer. ƒ(x) = 4x + 5 ƒ() = 3 ƒ(4) = ƒ(6) = 9.6 ƒ(x) = -x b ƒ(x) = x b ƒ(x) = (x + ) 3 ƒ() = ƒ(4) = 8 ƒ(6) = 4 ƒ(x) = x 4 ƒ() = - ƒ(4) =
Numerisk Integrasjon
 Numerisk Integrsjon Anne Kværnø Mrch 1, 018 1 Problemstilling Vi skl ltså finne en numerisk tilnærmelse til integrlet for en gitt funksjon f (x). I(, b) = f (x)dx Teknikken vi skl diskutere klles numeriske
Numerisk Integrsjon Anne Kværnø Mrch 1, 018 1 Problemstilling Vi skl ltså finne en numerisk tilnærmelse til integrlet for en gitt funksjon f (x). I(, b) = f (x)dx Teknikken vi skl diskutere klles numeriske
Løsningsforslag Eksamen 30. mai 2007 FY2045 Kvantefysikk
 Eksmen FY045 30. mi 007 - løsningsforslg 1 Oppgve 1 Løsningsforslg Eksmen 30. mi 007 FY045 Kvntefysikk. I grensen 0 er potensilet V x et enkelt okspotensil, V = V 0 for < x < 0 og uendelig ellers. Den
Eksmen FY045 30. mi 007 - løsningsforslg 1 Oppgve 1 Løsningsforslg Eksmen 30. mi 007 FY045 Kvntefysikk. I grensen 0 er potensilet V x et enkelt okspotensil, V = V 0 for < x < 0 og uendelig ellers. Den
Integrasjon del 2. October 15, Department of Mathematical Sciences, NTNU, Norway. Integrasjon
 Integrsjon del Deprtment of Mthemticl Sciences, NTNU, Norwy Octoer 5, 4 Integrsjon Sustitusjon for estemte integrler Husk kjærneregel d dt f (g(t)) = f (g(t)) g (t) ved fundmentlteoremet (del ) vi får
Integrsjon del Deprtment of Mthemticl Sciences, NTNU, Norwy Octoer 5, 4 Integrsjon Sustitusjon for estemte integrler Husk kjærneregel d dt f (g(t)) = f (g(t)) g (t) ved fundmentlteoremet (del ) vi får
NORGES LANDBRUKSHØGSKOLE Institutt for matematiske realfag og teknologi EKSAMEN I FYS135 - ELEKTROMAGNETISME
 NORGES LANDBRUKSHØGSKOLE nstitutt for mtemtiske relfg og teknologi EKSAMEN FYS135 - ELEKTROMAGNETSME Eksmensdg: 12. desember 2003 Tid for eksmen: Kl. 14:00-17:00 (3 timer) Tilltte hjelpemidler: B2 - Enkel
NORGES LANDBRUKSHØGSKOLE nstitutt for mtemtiske relfg og teknologi EKSAMEN FYS135 - ELEKTROMAGNETSME Eksmensdg: 12. desember 2003 Tid for eksmen: Kl. 14:00-17:00 (3 timer) Tilltte hjelpemidler: B2 - Enkel
Kap. 3 Krumningsflatemetoden
 SIDE. KRUMNINGSFLTEMETODEN I kpittel. og. hr vi sett t en bjelkes krefter og deformsjon kn beskrives ved fire integrler som henger smmen : Skjærkrft : V d Vinkelendring : φ M d Moment : M V d Forskyvning
SIDE. KRUMNINGSFLTEMETODEN I kpittel. og. hr vi sett t en bjelkes krefter og deformsjon kn beskrives ved fire integrler som henger smmen : Skjærkrft : V d Vinkelendring : φ M d Moment : M V d Forskyvning
S1 kapittel 6 Derivasjon Løsninger til oppgavene i boka
 S kpittel 6 Derivsjon Løsninger til oppgvene i ok 6. c y x y x = = = = y x 4 5 9 4 y 5 6 x 4 = = = = y x y x = = = = 7 ( 5) 6 ( ) 8 6. f( x ) f( x ) 5 7 x x ( ) 4 = = = = 6. T( x) = 0,x +,0 T T = + = (0)
S kpittel 6 Derivsjon Løsninger til oppgvene i ok 6. c y x y x = = = = y x 4 5 9 4 y 5 6 x 4 = = = = y x y x = = = = 7 ( 5) 6 ( ) 8 6. f( x ) f( x ) 5 7 x x ( ) 4 = = = = 6. T( x) = 0,x +,0 T T = + = (0)
R1 kapittel 1 Algebra
 Løsninger til oppgvene i ok R1 kpittel 1 Alger Løsninger til oppgvene i ok Oppgve 1.1 1 8 4 ( ) 15 5 (4 ) 7 1 7 ( ) d ( )( ) ( 4)( ) ( ) ( 4) ( )( 1) Oppgve 1. 49 7 ( 7)( 7) 5 5 5 5 1y 75 (4y 5) ( y) 5
Løsninger til oppgvene i ok R1 kpittel 1 Alger Løsninger til oppgvene i ok Oppgve 1.1 1 8 4 ( ) 15 5 (4 ) 7 1 7 ( ) d ( )( ) ( 4)( ) ( ) ( 4) ( )( 1) Oppgve 1. 49 7 ( 7)( 7) 5 5 5 5 1y 75 (4y 5) ( y) 5
Vår 2004 Ordinær eksamen
 år Ordinær eksmen. En bil kjører med en hstighet på 9 km/h lngs en rett strekning. Sjåføren tråkker plutselig på bremsene, men gjør dette med økende krft slik t (den negtive) kselersjonen (retrdsjonen)
år Ordinær eksmen. En bil kjører med en hstighet på 9 km/h lngs en rett strekning. Sjåføren tråkker plutselig på bremsene, men gjør dette med økende krft slik t (den negtive) kselersjonen (retrdsjonen)
Mer øving til kapittel 3
 Mer øving til kpittel 3 KAPITTEL 3 FUNKSJONER Oppgve 1 Tegn et koordintsystem og merk v punktene (1, 5) d (3, 2) ( 2, 3) e ( 3, 5) (4, 0) f (0, 4) Oppgve 2 Hvilke koordintpr hr de ulike punktene i koordintsystemet?
Mer øving til kpittel 3 KAPITTEL 3 FUNKSJONER Oppgve 1 Tegn et koordintsystem og merk v punktene (1, 5) d (3, 2) ( 2, 3) e ( 3, 5) (4, 0) f (0, 4) Oppgve 2 Hvilke koordintpr hr de ulike punktene i koordintsystemet?
Multippel integrasjon. Geir Ellingsrud
 Multippel integrsjon. Geir Ellingsrud 2. pril 24 2 NB: Dette er en midlertidig versjon dtert 2. pril 24. Den kommer til å bli utvidet og korrigert fortløpende!!. Dobbelt integrlet over rektngler og iterert
Multippel integrsjon. Geir Ellingsrud 2. pril 24 2 NB: Dette er en midlertidig versjon dtert 2. pril 24. Den kommer til å bli utvidet og korrigert fortløpende!!. Dobbelt integrlet over rektngler og iterert
Integral Kokeboken. sin(πx 2 ) sinh 2 (πx) dx = 2. 1 log x. + log(log x) dx = x log(log x) + C. cos(x 2 ) + sin(x 2 ) dx = 2π. x s 1 e x 1 dx = Γ(s)
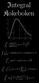 Integrl Kokeboken 4 3 4 6 8 log sin(π ) sinh (π) 4 + log(log ) log(log ) + C cos( ) + sin( ) π s e Γ(s) n n s Γ(s)ζ(s) π ( ( + sin ) +cos log + cos ) i Del I. Innledning.................................
Integrl Kokeboken 4 3 4 6 8 log sin(π ) sinh (π) 4 + log(log ) log(log ) + C cos( ) + sin( ) π s e Γ(s) n n s Γ(s)ζ(s) π ( ( + sin ) +cos log + cos ) i Del I. Innledning.................................
6. Beregning av treghetsmoment.
 Forelesningsnotter i mtemtikk Bruk v integrsjon Beregning v treghetsmoment Side 1 6 Beregning v treghetsmoment 61 Definisjoner Først de grunnleggende definisjonene: Momentkse r m en liten punktformet prtikkel
Forelesningsnotter i mtemtikk Bruk v integrsjon Beregning v treghetsmoment Side 1 6 Beregning v treghetsmoment 61 Definisjoner Først de grunnleggende definisjonene: Momentkse r m en liten punktformet prtikkel
HØGSKOLEN I BERGEN Avdeling for ingeniørutdanning
 HØGSKOLEN I BERGEN Aveling for ingeniørutnning FAG : FOA192 Vieregåene nlyse og iskret mtemtikk KLASSAR : Mnge DATO : 21. mi 212 TAL PÅ OPPGÅVER 5 TAL PÅ SIDER 2 VEDLEGG Hjelpesetningr HJELPEMIDDEL Csio
HØGSKOLEN I BERGEN Aveling for ingeniørutnning FAG : FOA192 Vieregåene nlyse og iskret mtemtikk KLASSAR : Mnge DATO : 21. mi 212 TAL PÅ OPPGÅVER 5 TAL PÅ SIDER 2 VEDLEGG Hjelpesetningr HJELPEMIDDEL Csio
Kvadratur. I(f) = f(x)dx.
 Kvdrtur Når mn snkker om numerisk kvdrtur er mn interessert i pproksimere integrler v funksjoner (som representerer reler, volumer, densiteter, o.s.v.) I(f) = f(x)dx. Det klles for kvdrtur fordi i gmle
Kvdrtur Når mn snkker om numerisk kvdrtur er mn interessert i pproksimere integrler v funksjoner (som representerer reler, volumer, densiteter, o.s.v.) I(f) = f(x)dx. Det klles for kvdrtur fordi i gmle
S1 kapittel 8 Eksamenstrening Løsninger til oppgavene i læreboka
 S1 kpittel 8 Eksmenstrening Løsninger til oppgvene i læreok E1 995 995 5 + 5 (995 5) (995 + 5) + 5 990 1000 + 5 990 000 + 5 990 05 E E (61+ 9) 51 49) (51+ 49) 61 9 (61 9) 51 49 ( 100 100 11 1997 00 199
S1 kpittel 8 Eksmenstrening Løsninger til oppgvene i læreok E1 995 995 5 + 5 (995 5) (995 + 5) + 5 990 1000 + 5 990 000 + 5 990 05 E E (61+ 9) 51 49) (51+ 49) 61 9 (61 9) 51 49 ( 100 100 11 1997 00 199
Feilestimeringer. i MAT-INF1100
 Feilestimeringer i MAT-INF11 Ett v de viktigste punktene i MAT-INF11, og smtidig det som nsees som det vnskeligste i pensum, er feilestimter. Vi bruker mye tid på å beregne tilnærmede verdier for funksjoner,
Feilestimeringer i MAT-INF11 Ett v de viktigste punktene i MAT-INF11, og smtidig det som nsees som det vnskeligste i pensum, er feilestimter. Vi bruker mye tid på å beregne tilnærmede verdier for funksjoner,
Fasit. Oppgavebok. Kapittel 5. Bokmål
 Fsit Oppgvebok 8 Kpittel 5 Bokmål KAPITTEL 5 5.1 8, 10, 1 b Antll pinner i en figur er figurnummeret gnget med. 5. 14, 17, 0 b gnger figurnummeret pluss. c 14, 17, 0, 5. Figur 1 4 5 Antll pinner 5 8 11
Fsit Oppgvebok 8 Kpittel 5 Bokmål KAPITTEL 5 5.1 8, 10, 1 b Antll pinner i en figur er figurnummeret gnget med. 5. 14, 17, 0 b gnger figurnummeret pluss. c 14, 17, 0, 5. Figur 1 4 5 Antll pinner 5 8 11
