a(x) b(x) a(x) X=1 a(1) W1
|
|
|
- Ivar Langeland
- 5 år siden
- Visninger:
Transkript
1 Or-Parallelism within Tabling Ricardo Rocha Fernando Silva Vtor Santos Costa? DCC-FC & LIACC, University of Porto, Rua do Campo Alegre, Porto, Portugal Abstract. One important advantage of logic programming is that it allows the implicit exploitation of parallelism. Towards this goal, we suggest that or-parallelism can be eciently exploited in tabling systems and propose two alternative approaches, Or-Parallelism within Tabling (OPT) and Tabling within Or-Parallelism (TOP). We concentrate on the fundamental concepts of an environment copying based model to implement the OPT approach and introduce the data structures and algorithms necessary to extend the YapOr Or-Parallel system, in order to obtain a parallel tabling system. Keywords: Parallel Logic Programming, Or-Parallelism, Tabling. 1 Introduction Prolog is an extremely popular and powerful logic programming language. Prolog execution is based on SLD resolution for Horn clauses. This strategy allows ecient implementation, but suers from fundamental limitations, such as in dealing with innite loops and redundant subcomputations. SLG resolution [3] is a tabling based method of resolution that overcomes some limitations of traditional Prolog. The method evaluates programs by storing newly found answers of current subgoals in a table. The method then uses this table to verify for repeated subgoals. Whenever such a repeated subgoal is found, the subgoal's answers are recalled from the table instead of being resolved against the program clauses. SLG resolution can thus reduce the search space for logic programs and in fact it has been proven that it can avoid looping and thus terminate for all programs that construct bounded depth terms. The XSB-Prolog system [11] was the rst Prolog system to implement SLG resolution. One important advantage of logic programming is that it allows the implicit exploitation of parallelism. This is true for SLD-based systems, and should also apply for SLG-based systems. A rst proposal on how to exploit implicit parallelism in tabling systems was Freire's table-parallelism [6]. In this model, each tabled subgoal is associated with a new computational thread, a generator thread, that will produce and add the answers into the table. Threads that call a tabled? The rst author is thankful to PRAXIS and Fundac~ao para a Ci^encia e Tecnologia for their nancial support. This work was partially funded by the Melodia project (JNICT PBIC/C/TIT/2495/95).
2 subgoal will asynchronously consume answers as they are added to the table. This model is limitative in that it restricts exploitation of parallelism to just one implicit form of parallelism present in logic programs. Ideally, we would like to exploit maximum parallelism and take maximum advantage of current technology for parallel and tabling systems. We observe that tabling is still about exploiting alternatives to nd solutions for goals, and that or-parallel systems have precisely been designed to achieve this goal eciently. We therefore propose two computational models, the OPT and TOP models, that combine or-parallelism and tabling by considering all open alternatives to subgoals as being amenable to parallel exploitation, be they from tabled or non-tabled subgoals. The OPT approach considers that tabling is the base component of the system, this is, each worker can be considered like a full sequential tabling engine. The or-parallel component of the system is only triggered when a worker runs out of alternatives to exploit. The TOP model unies or-parallel suspension and suspension due to tabling. A suspended subgoal can wake up for several reasons, such as new alternatives having been found for the subgoal, the subgoal becoming leftmost, or just for lack of non speculative work in the search tree. The TOP approach considers that each worker can be considered like a sequential WAM engine, hence only managing a logical branch of the search tree, and not several branches. In this paper we compare both models and focus on the design and implementation of the OPT model for combining or-parallelism and tabling. We chose the OPT model mainly because we believe it gives the highest degree of orthogonality between or-parallelism and tabling, thus simplifying initial implementation issues. The implementation framework is based on YapOr [9], an or-parallel system that extends Yap's sequential execution model to exploit implicit orparallelism in Prolog programs. YapOr is based on the environment copy model, as rst implemented in Muse [1]. We describe the main issues that arise in supporting tabling and its parallelization through copying. The implementation of tabling is largely based on the XSB engine, the SLG-WAM, however substantial dierences exist in particular on the algorithms for restoring a computation, determining the leader node and completion operation. All these and the extended data structures already take into account the support of combined tabling and or-parallelism. In summary, we briey introduce the implementation of tabling. Next, we discuss the fundamental issues in supporting or-parallelism for SLG resolution and propose two alternative approaches. Then, we present the new data structures and algorithms required to extend YapOr to support tabling and to allow for a combined exploitation of or-parallelism and tabling. This corresponds to the implementation work already done and terminate by outlining some conclusions. 2 Tabling Concepts and the SLG-WAM The SLG evaluation process can be modeled by a SLG-forest [10]. Whenever a tabled subgoal S is called for the rst time, a new tree with root S is added to the
3 SLG-forest. Simultaneously, an entry for S is allocated in the table space. This entry will collect all the answers generated for S. Repeated calls to variants of S are resolved by consuming the answers already stored in the table. Meanwhile, as new answers are generated to S, they are inserted into the table and returned to all variant subgoals. Within this model, the nodes in the search tree are classied as either generator nodes, that is, rst calls to tabled subgoals, consumer nodes, that consumer answers from the table space, and interior nodes, that are evaluated by the standard SLD resolution. Space for a tree can be reclaimed when its root subgoal has been completely evaluated. A subgoal is said to be completely evaluated when all possible resolutions for it have been made, that is, when no more answers can be generated and the variant subgoals have consumed all the available answers. Note that a number of root subgoals may be mutually dependent, forming a strongly connected component (or SCC ), and therefore can only be completed together. The completion operation is thus performed by the leader of the SCC, that is, by the oldest root subgoal in the SCC, when all possible resolutions have been made for all root subgoals in the SCC. Hence, in order to eciently evaluate programs one needs an ecient and dynamic detection scheme to determine when both the subgoals in an SCC and the SCC itself have been completely evaluated. For denite programs, tabling based evaluation has four main types of operations: (i) Tabled Subgoal Call, creates a generator node; (ii) New Answer, veries whether a newly generated answer is already in the table, and if not, inserts it; (iii) Answer Return, consumes an answer from the table; and Completion determines whether an SCC is completely evaluated, and if not, schedules a possible resolution to continue the execution. The implementation of tabling in XSB was attained by extending the WAM into the SLG-WAM, with minimal overhead. In short, the SLG-WAM introduces special instructions to deal with the operations above and two new memory areas: a table space, used to save the answers for tabled subgoals; and a completion stack, used to detect when a set of subgoals is completely evaluated. Further, whenever a consumer node gets to a point in which it has consumed all available answers, but the correspondent tabled subgoal has not yet completed and new answers may still be generated, it must suspend its computation. In the SLG-WAM the suspension mechanism is implemented through a new set of registers, the freeze registers, which freeze the WAM stacks at the suspension point and prevent all data belonging to the suspended branch from being erased. A suspended consumer is resumed by restoring the registers saved in the corresponding node and by using an extension of the standard trail, the forward trail, to restore the bindings of the suspended branch. The resume operation is implemented by setting the failure continuation eld of the consumer nodes to a special answer return instruction. This instruction is responsible for resuming the computation, guaranteeing that all answers are given once and just once to every variant subgoal. Through failure and backtracking to a consumer node, the answer return instruction gets executed and resuming takes place.
4 It is upon the leader of an SCC to detect its completion. This operation is executed dynamically and must be eciently implemented in order to minimize overheads. To achieves this, the SLG-WAM sets the failure continuation eld of a generator node to a special completion instruction whenever it resolves the last applicable program clause for the correspondent subgoal. The completion instruction thus ensures the total and correct evaluation of the subgoal search space. This instruction is executed through backtracking. In the default XSB scheduling strategy (batched scheduling [7]), it resumes the consumer node corresponding to the deeper variant subgoal with unconsumed answers. The computation will consume all the newly found answers, backtrack to other consumer nodes (higher up in the chain of consumer nodes) with unconsumed answers, and fail to the generator node, until no more answers are left to consume. At this point, if that node is the leader of its SCC, a xpoint is reached, all dependent subgoals are completed, and the subgoal can be marked completed. Otherwise, the computation will fail back to the previous node and the xpoint check will later be executed in an upper generator node. 3 Parallel Execution of Tabled Programs Ideally, we would like to exploit maximum parallelism and take maximum advantage of current technology for tabling systems. We propose that all alternatives to subgoals should be amenable to parallel exploitation, be they from normal or tabled subgoals, and that or-parallel frameworks can be used as the basis to do so. This gives an unied approach with two major advantages. First, it does not restrict parallelism to tabled subgoals and, second, it can draw from the very successful body of work in implementing or-parallel systems. We believe that this approach can result in ecient models for the exploitation of parallelism in tabling-based systems. We envisage two dierent models to combine or-parallelism and tabling: Or-Parallelism within Tabling (OPT) In this approach, parallelism is exploited between independent tabling engines, that share alternatives. Tabling is the base component of the system, this is, each worker can be considered a full sequential tabling engine and should spend most of its computation time exploiting the search tree involved in such an evaluation. It thus can allocate all three types of nodes, fully implement suspension of tabled subgoals, and resume subcomputations to consume newly found answers. Or-parallelism is triggered when a worker runs out of alternatives to exploit. In the OPT approach, unexploited alternatives should be made available for parallel execution, regardless of whether they originate from a generator, consumer or interior node. Therefore, parallelism can and should stem from both tabled and non-tabled subgoals. From the viewpoint of or-parallelism, the OPT approach generalizes Warren's multi-sequential engine framework for the exploitation of or-parallelism. Or-parallelism now stems from having several engines that implement SLGresolution, instead of implementing Prolog's SLD-resolution.
5 Fig. 1 gives an example of this approach for the following small program and the query?-. We assume two workers, W1 and W2. :- table a/1. b(1). :-. b(x) :- :- b(x). b(x) :- Consider that worker W1 executes the query goal. It rst inserts an entry for the tabled subgoal into the table and creates a generator node for it. The execution of the rst alternative leads to a recursive call for a/1, thus the worker creates a consumer node for a/1 and backtracks. The next alternative nds a non-tabled subgoal b/1 for which an interior node is created. The rst alternative for b/1 succeeds and an answer for is therefore found (a(1)). The worker inserts the newly found answer in the table and then starts exploiting the next alternative of b/1. Generator Node Consumer Node Interior Node Private Branch b(x) b(x) Completed Branch X=1 X=1 Shared Branch New Answer a(1) W1 a(1) W1 W2 One Worker (W1) Two workers (W1 and W2) Fig. 1. Sharing work in a SLG tree. At this point, worker W2 moves in to share work. Consider that worker W1 decides to share work up to its last private node (that is, the interior node for b/1). The two workers will share three nodes: the generator node for a/1, the consumer node for a/1 and the interior node for b/1. Worker W2 takes the next unexploited alternative of b/1 and from now on, both workers can quickly nd further answers for and any of them can restart the shared consumer node. Tabling Unied with Or-Parallelism (TOP) We have seen that in tabling based systems subgoals need to suspend on other subgoals obtaining the full set of answers. Or-parallel systems also need to suspend, either while waiting for leftmostness in the case of side-eects, or to avoid speculative execution. The need for suspending introduces an important similarity between tabling and orparallelism. The TOP approach unies or-parallel suspensions and suspensions due to tabling. When exploiting parallelism between branches in the search tree, some branches may be suspended, say, because they are speculative or not leftmost nodes, or because they are consumer nodes waiting for more solutions, while others are available for parallel execution.
6 Fig. 2 shows parallel execution for the previous program under this approach. The left gure shows that as soon as W1 suspends on consumer node for a/1, it makes the current branch of the search tree public and backtracks to the upper node. The consumer node for a/1 can only be resumed after answers to are found. In the left gure an answer for subgoal was found. So, worker W2 can choose whether to resume the consumer node with the newly found answer or to ask worker W1 to share his private nodes. In this case we represent the situation where worker W2 resumes the consumer node. Generator Node Consumer Node Interior Node Private Branch b(x) b(x) Completed Branch X=1 a(1) X=1 Shared Branch New Answer a(1) W1 W2 a(1) W1 One Worker (W1) Two workers (W1 and W2) Fig. 2. Unifying suspension in parallelized tabling execution. Comparing the Two Models The TOP model is a very attractive model, as it provides a clean and systematic unication of tabling and or-parallel suspensions. Workers have a clearly dened position, because a worker always occupies the tip of a single branch in the search tree. Everything else is shared work. It also has practical advantages, such as the fact that in this approach we can guarantee a suspended branch will only appear once, instead of possibly several times for several workers. On the other hand, as suspended nodes are always shared in or-parallel systems, the unied suspension may result in having a larger public part of the tree which may increase overheads. Besides, to support all forms of suspension with minimal overhead, the unied suspension mechanism must be implemented eciently. Moreover, support for the tabling component in the TOP approach requires a slightly dierent tabling engine than SLG-WAM. The recently proposed CAT model [4] seems to fulll best the requirements of the TOP approach, since it assumes a linear stack for the current branch and uses an auxiliary area to save the suspended nodes. Therefore, in order to implement the TOP approach using CAT, we should adopt, for the or-parallel component, an environment copying model (such as used in Muse) as it ts best with the kind of operations CAT introduces. In this regard, the OPT approach oers some interesting advantages. It enables dierent combinations for or-parallelism and tabling, giving implementors the highest degree of freedom. For instance, one can use the SLG-WAM for
7 tabling, and environment copying [1] or binding arrays [5] for or-parallelism. Moreover, the OPT approach reduces to a minimum the overlap between orparallelism and tabling, as we only have a tabling system extended with an or-parallel component. In TOP, we have a standard Prolog system extended with a tabling/or-parallel component. In this work, we focus on the design and implementation of the OPT approach, adopting the SLG-WAM for tabling and environment copying for orparallelism. Our choice seems the most natural as we believe the OPT approach gives the highest degree of orthogonality between or-parallelism and tabling. The hierarchy of or-parallelism within tabling results in a property that one can take advantage of to structure, and thus simplify, scheduler design and initial implementation issues. Overview of the Model In our model, a set of workers, will execute a tabled program by traversing its search tree, whose nodes are entry points for parallelism. Each worker physically owns a copy of the environment (that is, the stacks) and shares a large area related to tabling and scheduling. During execution, the search tree is implicitly divided in public and private regions. Workers in the private region execute nearly as in sequential tabling. A worker with excess of work (that is, with private nodes with unexploited alternatives or unconsumed answers) when prompted for work by other workers, shares some of their private nodes. When a worker shares work with another worker, the incremental copy technique is used to set the environment for the requesting worker. Whenever a worker backtracks to a public node it synchronizes to perform the usual actions that are executed in sequential tabling. For the generator and interior nodes it takes the next alternative, and for the consumer nodes it takes the next unconsumed answer. If there are no alternatives or no unconsumed answers left, then the worker executes the public completion 1 operation. 4 Extending YapOr to Support Tabling We next discuss the main data structures to extend YapOr to support parallel tabling. In the initial design, we will only consider table predicates without any kind of negative calls. Data Areas The data areas necessary to implement the complete or-parallel tabling system are shown in the memory layout depicted in Fig. 3. The memory is divided into a global shared area and into a number of logically private areas, each owned by a single worker in the system. The private areas contains the standard WAM stacks, as required for each worker. The global shared area includes four main sub-areas, that we describe next. The or-frame space is required by the or-parallel component in order to synchronize access to shared nodes [1] and to store scheduling information. The table space is required by the tabling component. It contains the table structure 1 A public completion operation is a completion operation executed in a shared node.
8 Shared Memory Or-Frames Space Table Space Dependency Frames Space Private Memory (Worker X) WAM Stacks Private Memory (Worker Y) Saved Stacks Space WAM Stacks Fig. 3. Memory layout for the proposed OPT approach. and has to be stored in shared memory for fast access to tabled subgoals by all the workers. The dependency frames space is a novel data structure, designed to support or-parallel tabling. Dependency frames extend consumer nodes by holding supplementary information about a suspension point. They must be implemented in shared memory in order to permit synchronization among workers in the management of the suspension points, and in order to avoid unnecessary copying of information when a consumer node is shared between workers. This data structure is discussed in more detail below. The saved stacks space preserves stacks of suspended branches. This space is required by a purely or-parallel implementation to save worker's suspension on builtins that require to be leftmost, or voluntarily abandon speculative work in favor of work that is not likely to be pruned [2]. In both cases, workers suspend their current work by copying their stacks into the saved stacks space, and start searching for other work. When we execute tabling in parallel, workers that share nodes can have dependencies between them. Thus, sometimes it may be necessary to delay the execution of a public completion operation until no more dependencies exist. On the other hand, in order to allow the parallel exploitation of other alternatives, as required by the environment copy model, it is necessary to maintain the stacks coherent with those of the workers that share the same nodes. These two objectives can be achieved by saving in the saved stacks space the parts of the stacks that correspond to the branches in the range of the public completion operation. Table Space The design and implementation of the data structures and algorithms to eciently access the table space is one of the critical issues in the design of a tabling system. Next, we provide a brief description of our implementation. It uses tries as the basis for tables as proposed in [8]. Tries provide complete discrimination for terms and permit a lookup and possible insertion to be performed in a single pass through a term. Tries are also easily parallelizable. The table space can be accessed in dierent ways during the course of an evaluation: to look up if a subgoal is in the table, and if not insert it; to verify whether a newly found answer is already in the table, and if not insert it; to pick up answers from the table to consumer nodes; and nally to mark subgoals as completed during a completion operation.
9 Fig. 4 presents the table data structures for a particular predicate t/2 after the execution of some tabled subgoal call and new answer instructions. code for t/2 table entry for t/2 tabled_subgoal_call t(x,a) new_answer t(x,a) -> X = h(i) tabled_subgoal_call t(y,z) new_answer t(y,z) -> Y = b; Z = c new_answer t(y,z) -> Y = b; Z = d new_answer t(y,z) -> Y = e; Z = f var 0 var 1 a subgoal trie nodes subgoal frame for call t(var 0,var 1) subgoal frame for call t(var 0,a) e b h/1 answer trie nodes last_answer f d c i first_answer Fig. 4. Using tries to organize the table space. The subgoal frames delimit the subgoal and answer trie nodes space. They are used to easily access the answers found for a particular subgoal and to eciently check if new answers have been found for a particular consumer node, through its last answer pointer. The subgoal frames are also used by the completion operation to mark a subgoal as completed. Each invocation of the tabled subgoal call instruction leads to either nding a path through the subgoal trie nodes, always starting from the table entry, until reaching a matching subgoal frame, or to creating the correspondent path of subgoal trie nodes, otherwise. Each invocation of the new answer instruction corresponds to the denition of a path through the answer trie nodes, starting from the corresponding subgoal frame. In the example, the subgoal trie node with value var 0 and the answer trie nodes with value b belong to several paths. This design property merges the paths that have the same rst arguments. Note also that each trie node can only hold atoms, variables, or functors. Thus we need two nodes to represent the answer h(i), one for the functor h/1 and the other for the argument i. Accessing and updating the table space must be carefully controlled in a parallel system. We want to maximize parallelism, whilst minimizing overheads. Read/write locks are the ideal data structure for this purpose. One can have a single lock for the table, thus only enabling a single writer for the whole table, one lock per table entry allowing one writer per procedure, one lock per path
10 allowing one writer per call, or one lock per every trie node to attain most parallelism. Experimental evaluation is required to nd the best solution. Dependency Frames The dependency frame is the key data structure required to control suspension, resumption and completion of subcomputations. This data structure serves to: save information about the suspension point; connect consumer nodes with the table space, to search for and to pick up new answers; and form a dependency graph between consumer nodes, to eciently check for leader nodes and perform completion. Fig. 5 shows an example of an evaluation involving dependency frames. The sub-gure to the left presents the dependencies between the predicates involved. t(x) table_trust_me generator node for first t(x) call fail_cont dfn = 1 sg_fr_ptr table_retry_me subgoal frame for call t(var 0) v(y) table_retry_me generator node for first v(y) call fail_cont dfn = 2 sg_fr_ptr completion subgoal frame for call v(var 0) v(y) t(x) tabled_subgoal_call t(x) tabled_subgoal_call v(y) tabled_subgoal_call v(y) tabled_subgoal_call t(x) consumer node for second v(y) call consumer node for second t(x) call fail_cont dfn = 3 dep_fr_ptr fail_cont dfn = 4 dep_fr_ptr answer_return answer_return previous_dep_fr leader_dfn = 2 subgoal_frame consumer_node last_answer freeze_registers previous_dep_fr leader_dfn = 1 subgoal_frame consumer_node last_answer freeze_registers top_dep_fr Fig. 5. Table data structures dependencies. The rst instance of tabled subgoal call searches the table space for the corresponding subgoal t(x). Supposing this is the rst call to the subgoal, it must allocate a subgoal frame and create a generator choice point. In our scheme, a generator choice point is simply a standard choice point plus a new sg fr ptr eld, pointing to the newly allocated subgoal frame. The pointer is used to add new solutions and to check for completion. In order to mark the precedence between choice points in the left-to-right, top-down search, we introduce an extra eld, dfn (depth rst number), in all choice points. This eld is not strictly necessary in the implementation because we can achieve the same goal by using the addresses of the choice points, however it simplies the description of the model. Following the example, an analogous situation occurs with the rst call to subgoal v(y). The repeated call to subgoal v(y) allocates a dependency frame and creates a consumer choice point. A consumer choice point is a standard
11 choice point plus an extra dep fr ptr eld, pointing to the newly allocated dependency frame. A dependency frame contains six elds. The previous dep fr eld points to the previous allocated dependency frame. The last dependency frame is pointed by the global variable top dep fr. The leader dfn eld stores the dfn of the bottommost leader node (details are presented next). The subgoal frame eld is a pointer to the correspondent subgoal frame. The consumer node eld is a back pointer to the consumer node. The last answer eld is a pointer to the last consumed answer, and is used in conjunction with the subgoal frame eld to check if new answers have been found for the subgoal call. The freeze registers elds stores the current top positions of each of the stacks. When a completion instruction is executed with success, we consult the freeze registers of the resulting top dependency frame to restore the top positions of each stack and release space. Note that in the SLG-WAM these registers are kept at the nodes were completion may take place, that is the generator nodes. In our case, this solution is not adequate as we may execute completion in any node. Finally, the second call to t(x) implies an analogous situation to the previous one. A dependency frame and a consumer choice point are allocated and the top dep fr is updated. 5 The Flow of Control A tabling evaluation can be seen as a sequence of suspension and resumptions of subcomputations. A computation suspends every time a consumer node has consumed all available answers and resumes when new solutions are found. Restoring a Computation Every time a consumer node is allocated, its failure continuation pointer is made to point to an answer return instruction. The instruction is executed through failure to the node, and guarantees that every answer is consumed once and just once. Before resuming a computation, it is necessary to restore the WAM registers and the variable bindings at the suspension point. The WAM register values are saved in the consumer node and the variable bindings are saved in the forward trail. The forward trail is an extension of the standard WAM trail that includes variable bindings in trail operations. The SLG-WAM uses a forward trail with three elds per each frame. They record the address of the trailed variable (as the standard WAM trail), the value to which the variable was bound and a pointer to the parent trail frame which permits to chain correctly the variables through the current branch, hence jumping across the frozen segments (see [10] for more details). In our approach we only use the rst two elds to implement the forward trail, thus spending less space in the trail stack. As Yap already uses the trail to store information beyond the normal variable trailing (to control dynamic predicates and multi-assignment variables), we extend this information to also control the chain between the different frozen segments. In terms of computational complexity the two approaches are equivalent. The main advantage of our scheme is that Yap already tests the
12 trail frames to check if they are of a special type, and so we do not introduce further overheads in the system. It would be the case if we had chosen to implement the SLG-WAM approach. Leader Nodes In sequential tabling, only generator nodes can be leader nodes, hence only they perform completion. In our design any node can be a leader. We must therefore check for leader nodes whenever we backtrack to a private generator node or to any shared node. If the node is leader we perform completion, otherwise we simply fail and backtrack. We designed our algorithms to quickly determine whether a node is a leader. find_bottommost_leader_node () { leader_dfn = direct_dependency_dfn(); aux_dep_fr = top_dep_fr; while (aux_dep_fr!= NULL && leader_dfn < DependencyFrame_consumer_dfn(aux_dep_fr)) { if (leader_dfn >= DependencyFrame_leader_dfn(aux_dep_fr)) return DependencyFrame_leader_dfn(aux_dep_fr); aux_dep_fr = DependencyFrame_previous_dep_fr(aux_dep_fr); } return leader_dfn; } Fig. 6. Pseudo-code for find bottommost leader node(). Fig. 6 presents the pseudo-code to initialize the leader dfn eld when we allocate a new dependency frame. The direct dependency dfn() function returns the dfn of the depth-most node that contains in one of the branches below it, the generator node of the variant subgoal call. In sequential tabling, as we have all nodes, the depth-most node that contains the generator node for a particular subgoal call, is the generator node itself. Hence, the dfn returned is the value of the dfn eld within the generator node. Fig. 7 illustrates the dependencies between the several depth rst numbers involved in the find bottommost leader node() algorithm, in the case of a parallel evaluation. In order for a worker to test if a certain node, of its own branch, is leader or not, it has to check if the dfn eld of the node is equal to the leader dfn eld found in the top dep fr register. In Fig. 7, workers 1 and 2 have leader nodes at generator node a and interior node b respectively. Public Completion The correctness and eciency of the completion algorithm appears to be one of the most important points in the implementation of a combined tabling/or-parallel system. Next we present a design for our OPTbased implementation. If a leader node is shared and contains consumer nodes below it, this means that it depends on branches explored by other workers. Thus, even after a worker having backtracked to a leader node, it may not execute the completion operation
13 a b dfn = 1 dfn = 2 shared branch interior node generator node consumer node dfn = 3 c d dfn = 3 dfn = 4 direct_dependency_dfn = 1 leader_dfn = 1 a c dfn = 4 direct_dependency_dfn = 2 leader_dfn = 2 dfn = 5 direct_dependency_dfn = 2 leader_dfn = 1 d worker 2 worker 1 Fig. 7. Depth rst number dependencies. immediately. The reason for this is that the other workers can still inuence the leader branch. As a result, it becomes necessary to suspend 2 the leader branch, and therefore, allow the current worker to continue execution. This suspension mechanism includes, saving the correspondent part of the stacks to the save stacks space (putting the respective reference in the leader node) and readjusting the freeze registers. The save stacks space resides in a shared area to allow any other worker to complete a suspended branch. This scheme also enables the current worker to proceed its execution. If the worker would not suspend the leader branch, hence not saving the stacks in the shared space, then a future sharing work operation would damage the stack areas related to the leader branch and therefore would make the completion operation unworkable. An alternative would be for the worker responsible for the leader branch to wait until no one else could inuence it and only then complete the branch. Obviously, this is not an ecient strategy and besides it may carry us into a deadlock situation. Fig. 8 shows the pseudo-code for the public completion() operation. This operation is executed when a worker backtracks to a shared interior/generator node with no more alternatives left, or to a shared consumer node without unconsumed answers. The last worker leaving a node is responsible for checking and collecting all the suspension branches that have unconsumed answers. To resume a suspension branch a worker needs to copy the saved stacks to the correct position in its own stacks. Thus, for a worker to resume immediately a suspension branch, it has rst to suspend its current branch and only later restart it. This has the disadvantage that the worker has to make two suspensions and resumptions instead of just one. Hence, we adopted the strategy of resuming the collected branches only when the worker nds itself in a leader node position. Here, a worker either completes the correspondent branch or suspends it. In both 2 The notion of suspension in this context is obviously dierent from the one presented for tabling.
14 public_completion (node N) { if (last worker in node N) for all suspension branches SB stored in node N if (exists unconsumed answers for any consumer node in SB) collect (SB) /* to be resumed later */ if (N is a leader node) if (exists unconsumed answers for any consumer node below node N) backtrack_through_new_answers() /* as in SLG-WAM */ if (suspension branches collected) suspend_current_branch() resume (a suspension branch) else if (not last worker in node N) suspend_current_branch() else if (hidden workers in node N) suspend_current_branch() else complete_all() else /* not leader */ if (consumer nodes below node N) increment hidden workers in node N backtrack } Fig. 8. Pseudo-code for public completion(). situations, the stacks do not contain frozen segments below the leader node and therefore we do not have to pay extra overheads to resume a collected branch. Whenever a node nds that it is a leader, it starts to check if there are no consumer nodes with unconsumed answers below. If there is such a node, it resumes the computation to the deeper consumer node with unconsumed answers. To check if there is a node with unconsumed answers, we can follow the dependency frames chain corresponding to the consumer nodes below, and check for one such that the last answer pointer is dierent from the one stored on the subgoal frame pointed by the subgoal frame eld. When a worker backtracks from a node and that node stays preserved in its stacks, the worker has to increment the hidden workers counter of the node. This counter indicates the number of workers that are executing in upper nodes and still contain the node. These workers can inuence the node, if a resume operation takes place and it includes the node. In this public completion algorithm, a worker only completes a leader node when there is nothing that can inuence its branches. This only happens, when there are no suspended branches collected and there are no workers in the node, be they physically present or hidden. Completing a node includes marking the tabled subgoals involved as completed, releasing memory space and readjusting the freeze registers. The public completion scheme proposed has two major advantages. One is that there is no communication or explicit synchronization between workers, therefore it reduces signicantly possible overheads. The second advantage is that the leader nodes are the only points where we suspend branches. This is very important, since it reduces the number of check points we have to make
15 in order to ensure that all answers are consumed in a suspended branch, to just one. This check point is executed by the last worker that leaves a node. Besides, in upper nodes we do not need to care about the uncollected suspended branches stored in the bottom nodes because we know that no upper branches can inuence them. 6 Conclusions In this paper we presented two approaches to combine or-parallelism and tabling, and focused on the design of data structures and algorithms to implement the OPT approach. These new structures and algorithms were built from within the environment copying based system, YapOr, in order to obtain a parallel tabling system. Currently, we have sequential tabling and or-parallelism functioning separately within the same system. However, we already have in the system all the data structures necessary to combine their execution and conforming with the description given in this paper. We are now working on adjusting the system for parallel execution of tabling. This will require changes to the current scheduler in order to eciently and correctly execute tabled logic programs in parallel. References 1. K. A. M. Ali and R. Karlsson. Full Prolog and Scheduling OR-Parallelism in Muse. Intern. Journal of Parallel Programming, 19(6), Dec K. A. M. Ali and R. Karlsson. Scheduling Speculative Work in Muse and Performance Results. Intern. Journal of Parallel Programming, 21(6), Dec W. Chen and D. S. Warren. Query Evaluation under the Well Founded Semantics. In Proc. of PODS'93, pages 168{179, B. Demoen and K. Sagonas. CAT: the Copying Approach to Tabling. In Proc. of PLILP/ALP'98. Springer-Verlag, Sep E. Lusk et. al. The Aurora Or-parallel Prolog System. In Proc. of FGCS'88, pages 819{830. ICOT, Nov J. Freire, R. Hu, T. Swift, and D. S. Warren. Exploiting Parallelism in Tabled Evaluations. In Proc. of PLILP'95, pages 115{132. Springer-Verlag, J. Freire, T. Swift, and D. S. Warren. Beyond Depth-First: Improving Tabled Logic Programs through Alternative Scheduling Strategies. In Proc. of PLILP'96, pages 243{258. Springer-Verlag, Sep I. V. Ramakrishnan, P. Rao, K. Sagonas, T. Swift, and D. S. Warren. Ecient Tabling Mechanisms for Logic Programs. In Proc. of ICLP'95, pages 687{711. The MIT Press, June R. Rocha, F. Silva, and V. S. Costa. YapOr: an Or-Parallel Prolog System based on Environment Copying. Technical Report DCC-97-14, DCC-FC & LIACC, University of Porto, Dec K. Sagonas and T. Swift. An Abstract Machine for Tabled Execution of Fixed- Order Stratied Logic Programs. Journal of ACM Transactions on Programming Languages and Systems, To appear. 11. K. Sagonas, T. Swift, and D. S. Warren. XSB as an Ecient Deductive Database Engine. In Proc. of ACM SIGMOD International Conference on the Management of Data, pages 442{453, May 1994.
Slope-Intercept Formula
 LESSON 7 Slope Intercept Formula LESSON 7 Slope-Intercept Formula Here are two new words that describe lines slope and intercept. The slope is given by m (a mountain has slope and starts with m), and intercept
LESSON 7 Slope Intercept Formula LESSON 7 Slope-Intercept Formula Here are two new words that describe lines slope and intercept. The slope is given by m (a mountain has slope and starts with m), and intercept
Unit Relational Algebra 1 1. Relational Algebra 1. Unit 3.3
 Relational Algebra 1 Unit 3.3 Unit 3.3 - Relational Algebra 1 1 Relational Algebra Relational Algebra is : the formal description of how a relational database operates the mathematics which underpin SQL
Relational Algebra 1 Unit 3.3 Unit 3.3 - Relational Algebra 1 1 Relational Algebra Relational Algebra is : the formal description of how a relational database operates the mathematics which underpin SQL
Emneevaluering GEOV272 V17
 Emneevaluering GEOV272 V17 Studentenes evaluering av kurset Svarprosent: 36 % (5 av 14 studenter) Hvilket semester er du på? Hva er ditt kjønn? Er du...? Er du...? - Annet PhD Candidate Samsvaret mellom
Emneevaluering GEOV272 V17 Studentenes evaluering av kurset Svarprosent: 36 % (5 av 14 studenter) Hvilket semester er du på? Hva er ditt kjønn? Er du...? Er du...? - Annet PhD Candidate Samsvaret mellom
Call function of two parameters
 Call function of two parameters APPLYUSER USER x fµ 1 x 2 eµ x 1 x 2 distinct e 1 0 0 v 1 1 1 e 2 1 1 v 2 2 2 2 e x 1 v 1 x 2 v 2 v APPLY f e 1 e 2 0 v 2 0 µ Evaluating function application The math demands
Call function of two parameters APPLYUSER USER x fµ 1 x 2 eµ x 1 x 2 distinct e 1 0 0 v 1 1 1 e 2 1 1 v 2 2 2 2 e x 1 v 1 x 2 v 2 v APPLY f e 1 e 2 0 v 2 0 µ Evaluating function application The math demands
Information search for the research protocol in IIC/IID
 Information search for the research protocol in IIC/IID 1 Medical Library, 2013 Library services for students working with the research protocol and thesis (hovedoppgaven) Open library courses: http://www.ntnu.no/ub/fagside/medisin/medbiblkurs
Information search for the research protocol in IIC/IID 1 Medical Library, 2013 Library services for students working with the research protocol and thesis (hovedoppgaven) Open library courses: http://www.ntnu.no/ub/fagside/medisin/medbiblkurs
Databases 1. Extended Relational Algebra
 Databases 1 Extended Relational Algebra Relational Algebra What is an Algebra? Mathematical system consisting of: Operands --- variables or values from which new values can be constructed. Operators ---
Databases 1 Extended Relational Algebra Relational Algebra What is an Algebra? Mathematical system consisting of: Operands --- variables or values from which new values can be constructed. Operators ---
Neural Network. Sensors Sorter
 CSC 302 1.5 Neural Networks Simple Neural Nets for Pattern Recognition 1 Apple-Banana Sorter Neural Network Sensors Sorter Apples Bananas 2 Prototype Vectors Measurement vector p = [shape, texture, weight]
CSC 302 1.5 Neural Networks Simple Neural Nets for Pattern Recognition 1 Apple-Banana Sorter Neural Network Sensors Sorter Apples Bananas 2 Prototype Vectors Measurement vector p = [shape, texture, weight]
Dynamic Programming Longest Common Subsequence. Class 27
 Dynamic Programming Longest Common Subsequence Class 27 Protein a protein is a complex molecule composed of long single-strand chains of amino acid molecules there are 20 amino acids that make up proteins
Dynamic Programming Longest Common Subsequence Class 27 Protein a protein is a complex molecule composed of long single-strand chains of amino acid molecules there are 20 amino acids that make up proteins
HONSEL process monitoring
 6 DMSD has stood for process monitoring in fastening technology for more than 25 years. HONSEL re- rivet processing back in 990. DMSD 2G has been continuously improved and optimised since this time. All
6 DMSD has stood for process monitoring in fastening technology for more than 25 years. HONSEL re- rivet processing back in 990. DMSD 2G has been continuously improved and optimised since this time. All
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF 3230 Formell modellering og analyse av kommuniserende systemer Eksamensdag: 4. juni 2010 Tid for eksamen: 9.00 12.00 Oppgavesettet
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF 3230 Formell modellering og analyse av kommuniserende systemer Eksamensdag: 4. juni 2010 Tid for eksamen: 9.00 12.00 Oppgavesettet
Dagens tema: Eksempel Klisjéer (mønstre) Tommelfingerregler
 UNIVERSITETET I OSLO INF1300 Introduksjon til databaser Dagens tema: Eksempel Klisjéer (mønstre) Tommelfingerregler Institutt for informatikk Dumitru Roman 1 Eksempel (1) 1. The system shall give an overview
UNIVERSITETET I OSLO INF1300 Introduksjon til databaser Dagens tema: Eksempel Klisjéer (mønstre) Tommelfingerregler Institutt for informatikk Dumitru Roman 1 Eksempel (1) 1. The system shall give an overview
Level-Rebuilt B-Trees
 Gerth Stølting Brodal BRICS University of Aarhus Pankaj K. Agarwal Lars Arge Jeffrey S. Vitter Center for Geometric Computing Duke University August 1998 1 B-Trees Bayer, McCreight 1972 Level 2 Level 1
Gerth Stølting Brodal BRICS University of Aarhus Pankaj K. Agarwal Lars Arge Jeffrey S. Vitter Center for Geometric Computing Duke University August 1998 1 B-Trees Bayer, McCreight 1972 Level 2 Level 1
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT2400 Analyse 1. Eksamensdag: Onsdag 15. juni 2011. Tid for eksamen: 09.00 13.00 Oppgavesettet er på 6 sider. Vedlegg: Tillatte
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT2400 Analyse 1. Eksamensdag: Onsdag 15. juni 2011. Tid for eksamen: 09.00 13.00 Oppgavesettet er på 6 sider. Vedlegg: Tillatte
Endelig ikke-røyker for Kvinner! (Norwegian Edition)
 Endelig ikke-røyker for Kvinner! (Norwegian Edition) Allen Carr Click here if your download doesn"t start automatically Endelig ikke-røyker for Kvinner! (Norwegian Edition) Allen Carr Endelig ikke-røyker
Endelig ikke-røyker for Kvinner! (Norwegian Edition) Allen Carr Click here if your download doesn"t start automatically Endelig ikke-røyker for Kvinner! (Norwegian Edition) Allen Carr Endelig ikke-røyker
Moving Objects. We need to move our objects in 3D space.
 Transformations Moving Objects We need to move our objects in 3D space. Moving Objects We need to move our objects in 3D space. An object/model (box, car, building, character,... ) is defined in one position
Transformations Moving Objects We need to move our objects in 3D space. Moving Objects We need to move our objects in 3D space. An object/model (box, car, building, character,... ) is defined in one position
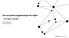
Graphs similar to strongly regular graphs
 Joint work with Martin Ma aj 5th June 2014 Degree/diameter problem Denition The degree/diameter problem is the problem of nding the largest possible graph with given diameter d and given maximum degree
Joint work with Martin Ma aj 5th June 2014 Degree/diameter problem Denition The degree/diameter problem is the problem of nding the largest possible graph with given diameter d and given maximum degree
Evaluating Call-by-need on the Control Stack
 Evaluating Call-by-need on the Control Stack Stephen Chang, David Van Horn, Matthias Felleisen Northeastern University 1 Lazy Abstract Machines Sharing implemented with: heap 2 Lazy Abstract Machines Sharing
Evaluating Call-by-need on the Control Stack Stephen Chang, David Van Horn, Matthias Felleisen Northeastern University 1 Lazy Abstract Machines Sharing implemented with: heap 2 Lazy Abstract Machines Sharing
TMA4329 Intro til vitensk. beregn. V2017
 Norges teknisk naturvitenskapelige universitet Institutt for Matematiske Fag TMA439 Intro til vitensk. beregn. V17 ving 4 [S]T. Sauer, Numerical Analysis, Second International Edition, Pearson, 14 Teorioppgaver
Norges teknisk naturvitenskapelige universitet Institutt for Matematiske Fag TMA439 Intro til vitensk. beregn. V17 ving 4 [S]T. Sauer, Numerical Analysis, Second International Edition, Pearson, 14 Teorioppgaver
Kartleggingsskjema / Survey
 Kartleggingsskjema / Survey 1. Informasjon om opphold i Norge / Information on resident permit in Norway Hvilken oppholdstillatelse har du i Norge? / What residence permit do you have in Norway? YES No
Kartleggingsskjema / Survey 1. Informasjon om opphold i Norge / Information on resident permit in Norway Hvilken oppholdstillatelse har du i Norge? / What residence permit do you have in Norway? YES No
Hvordan føre reiseregninger i Unit4 Business World Forfatter:
 Hvordan føre reiseregninger i Unit4 Business World Forfatter: dag.syversen@unit4.com Denne e-guiden beskriver hvordan du registrerer en reiseregning med ulike typer utlegg. 1. Introduksjon 2. Åpne vinduet
Hvordan føre reiseregninger i Unit4 Business World Forfatter: dag.syversen@unit4.com Denne e-guiden beskriver hvordan du registrerer en reiseregning med ulike typer utlegg. 1. Introduksjon 2. Åpne vinduet
5 E Lesson: Solving Monohybrid Punnett Squares with Coding
 5 E Lesson: Solving Monohybrid Punnett Squares with Coding Genetics Fill in the Brown colour Blank Options Hair texture A field of biology that studies heredity, or the passing of traits from parents to
5 E Lesson: Solving Monohybrid Punnett Squares with Coding Genetics Fill in the Brown colour Blank Options Hair texture A field of biology that studies heredity, or the passing of traits from parents to
IN 211 Programmeringsspråk. Dokumentasjon. Hvorfor skrive dokumentasjon? For hvem? «Lesbar programmering» Ark 1 av 11
 Dokumentasjon Hvorfor skrive dokumentasjon? For hvem? «Lesbar programmering» Ark 1 av 11 Forelesning 8.11.1999 Dokumentasjon Med hvert skikkelig program bør det komme følgende dokumentasjon: innføring
Dokumentasjon Hvorfor skrive dokumentasjon? For hvem? «Lesbar programmering» Ark 1 av 11 Forelesning 8.11.1999 Dokumentasjon Med hvert skikkelig program bør det komme følgende dokumentasjon: innføring
Andrew Gendreau, Olga Rosenbaum, Anthony Taylor, Kenneth Wong, Karl Dusen
 Andrew Gendreau, Olga Rosenbaum, Anthony Taylor, Kenneth Wong, Karl Dusen The Process Goal Definition Data Collection Data Preprocessing EDA Choice of Variables Choice of Method(s) Performance Evaluation
Andrew Gendreau, Olga Rosenbaum, Anthony Taylor, Kenneth Wong, Karl Dusen The Process Goal Definition Data Collection Data Preprocessing EDA Choice of Variables Choice of Method(s) Performance Evaluation
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS
 UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Postponed exam: ECON420 Mathematics 2: Calculus and linear algebra Date of exam: Tuesday, June 8, 203 Time for exam: 09:00 a.m. 2:00 noon The problem set covers
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Postponed exam: ECON420 Mathematics 2: Calculus and linear algebra Date of exam: Tuesday, June 8, 203 Time for exam: 09:00 a.m. 2:00 noon The problem set covers
GEOV219. Hvilket semester er du på? Hva er ditt kjønn? Er du...? Er du...? - Annet postbachelor phd
 GEOV219 Hvilket semester er du på? Hva er ditt kjønn? Er du...? Er du...? - Annet postbachelor phd Mener du at de anbefalte forkunnskaper var nødvendig? Er det forkunnskaper du har savnet? Er det forkunnskaper
GEOV219 Hvilket semester er du på? Hva er ditt kjønn? Er du...? Er du...? - Annet postbachelor phd Mener du at de anbefalte forkunnskaper var nødvendig? Er det forkunnskaper du har savnet? Er det forkunnskaper
Hvor mye praktisk kunnskap har du tilegnet deg på dette emnet? (1 = ingen, 5 = mye)
 INF247 Er du? Er du? - Annet Ph.D. Student Hvor mye teoretisk kunnskap har du tilegnet deg på dette emnet? (1 = ingen, 5 = mye) Hvor mye praktisk kunnskap har du tilegnet deg på dette emnet? (1 = ingen,
INF247 Er du? Er du? - Annet Ph.D. Student Hvor mye teoretisk kunnskap har du tilegnet deg på dette emnet? (1 = ingen, 5 = mye) Hvor mye praktisk kunnskap har du tilegnet deg på dette emnet? (1 = ingen,
Exercise 1: Phase Splitter DC Operation
 Exercise 1: DC Operation When you have completed this exercise, you will be able to measure dc operating voltages and currents by using a typical transistor phase splitter circuit. You will verify your
Exercise 1: DC Operation When you have completed this exercise, you will be able to measure dc operating voltages and currents by using a typical transistor phase splitter circuit. You will verify your
REMOVE CONTENTS FROM BOX. VERIFY ALL PARTS ARE PRESENT READ INSTRUCTIONS CAREFULLY BEFORE STARTING INSTALLATION
 2011-2014 FORD EXPLORER PARTS LIST Qty Part Description Qty Part Description 1 Bull Bar 2 12mm x 35mm Bolt Plates 1 Passenger/Right Mounting Bracket 2 12mm Nut Plate 1 Driver/Left Mounting Bracket 2 12mm
2011-2014 FORD EXPLORER PARTS LIST Qty Part Description Qty Part Description 1 Bull Bar 2 12mm x 35mm Bolt Plates 1 Passenger/Right Mounting Bracket 2 12mm Nut Plate 1 Driver/Left Mounting Bracket 2 12mm
Estimating Peer Similarity using. Yuval Shavitt, Ela Weinsberg, Udi Weinsberg Tel-Aviv University
 Estimating Peer Similarity using Distance of Shared Files Yuval Shavitt, Ela Weinsberg, Udi Weinsberg Tel-Aviv University Problem Setting Peer-to-Peer (p2p) networks are used by millions for sharing content
Estimating Peer Similarity using Distance of Shared Files Yuval Shavitt, Ela Weinsberg, Udi Weinsberg Tel-Aviv University Problem Setting Peer-to-Peer (p2p) networks are used by millions for sharing content
Den som gjør godt, er av Gud (Multilingual Edition)
 Den som gjør godt, er av Gud (Multilingual Edition) Arne Jordly Click here if your download doesn"t start automatically Den som gjør godt, er av Gud (Multilingual Edition) Arne Jordly Den som gjør godt,
Den som gjør godt, er av Gud (Multilingual Edition) Arne Jordly Click here if your download doesn"t start automatically Den som gjør godt, er av Gud (Multilingual Edition) Arne Jordly Den som gjør godt,
Oppgave 1a Definer følgende begreper: Nøkkel, supernøkkel og funksjonell avhengighet.
 TDT445 Øving 4 Oppgave a Definer følgende begreper: Nøkkel, supernøkkel og funksjonell avhengighet. Nøkkel: Supernøkkel: Funksjonell avhengighet: Data i en database som kan unikt identifisere (et sett
TDT445 Øving 4 Oppgave a Definer følgende begreper: Nøkkel, supernøkkel og funksjonell avhengighet. Nøkkel: Supernøkkel: Funksjonell avhengighet: Data i en database som kan unikt identifisere (et sett
MID-TERM EXAM TDT4258 MICROCONTROLLER SYSTEM DESIGN. Wednesday 3 th Mars Time:
 Side 1 av 8 Norwegian University of Science and Technology DEPARTMENT OF COMPUTER AND INFORMATION SCIENCE MID-TERM EXAM TDT4258 MICROCONTROLLER SYSTEM DESIGN Wednesday 3 th Mars 2010 Time: 1615-1745 Allowed
Side 1 av 8 Norwegian University of Science and Technology DEPARTMENT OF COMPUTER AND INFORMATION SCIENCE MID-TERM EXAM TDT4258 MICROCONTROLLER SYSTEM DESIGN Wednesday 3 th Mars 2010 Time: 1615-1745 Allowed
Trigonometric Substitution
 Trigonometric Substitution Alvin Lin Calculus II: August 06 - December 06 Trigonometric Substitution sin 4 (x) cos (x) dx When you have a product of sin and cos of different powers, you have three different
Trigonometric Substitution Alvin Lin Calculus II: August 06 - December 06 Trigonometric Substitution sin 4 (x) cos (x) dx When you have a product of sin and cos of different powers, you have three different
FIRST LEGO League. Härnösand 2012
 FIRST LEGO League Härnösand 2012 Presentasjon av laget IES Dragons Vi kommer fra Härnosänd Snittalderen på våre deltakere er 11 år Laget består av 4 jenter og 4 gutter. Vi representerer IES i Sundsvall
FIRST LEGO League Härnösand 2012 Presentasjon av laget IES Dragons Vi kommer fra Härnosänd Snittalderen på våre deltakere er 11 år Laget består av 4 jenter og 4 gutter. Vi representerer IES i Sundsvall
IN2010: Algoritmer og Datastrukturer Series 2
 Universitetet i Oslo Institutt for Informatikk S.M. Storleer, S. Kittilsen IN2010: Algoritmer og Datastrukturer Series 2 Tema: Grafteori 1 Publisert: 02. 09. 2019 Utvalgte løsningsforslag Oppgave 1 (Fra
Universitetet i Oslo Institutt for Informatikk S.M. Storleer, S. Kittilsen IN2010: Algoritmer og Datastrukturer Series 2 Tema: Grafteori 1 Publisert: 02. 09. 2019 Utvalgte løsningsforslag Oppgave 1 (Fra
Verifiable Secret-Sharing Schemes
 Aarhus University Verifiable Secret-Sharing Schemes Irene Giacomelli joint work with Ivan Damgård, Bernardo David and Jesper B. Nielsen Aalborg, 30th June 2014 Verifiable Secret-Sharing Schemes Aalborg,
Aarhus University Verifiable Secret-Sharing Schemes Irene Giacomelli joint work with Ivan Damgård, Bernardo David and Jesper B. Nielsen Aalborg, 30th June 2014 Verifiable Secret-Sharing Schemes Aalborg,
Maple Basics. K. Cooper
 Basics K. Cooper 2012 History History 1982 Macsyma/MIT 1988 Mathematica/Wolfram 1988 /Waterloo Others later History Why? Prevent silly mistakes Time Complexity Plots Generate LATEX This is the 21st century;
Basics K. Cooper 2012 History History 1982 Macsyma/MIT 1988 Mathematica/Wolfram 1988 /Waterloo Others later History Why? Prevent silly mistakes Time Complexity Plots Generate LATEX This is the 21st century;
EMPIC MEDICAL. Etterutdanningskurs flyleger 21. april Lars (Lasse) Holm Prosjektleder Telefon: E-post:
 EMPIC MEDICAL Etterutdanningskurs flyleger 21. april 2017 Lars (Lasse) Holm Prosjektleder Telefon: +47 976 90 799 E-post: Lrh@caa.no it-vakt@caa.no Luftfartstilsynet T: +47 75 58 50 00 F: +47 75 58 50
EMPIC MEDICAL Etterutdanningskurs flyleger 21. april 2017 Lars (Lasse) Holm Prosjektleder Telefon: +47 976 90 799 E-post: Lrh@caa.no it-vakt@caa.no Luftfartstilsynet T: +47 75 58 50 00 F: +47 75 58 50
Server-Side Eclipse. Bernd Kolb Martin Lippert it-agile GmbH
 Server-Side Eclipse Bernd Kolb b.kolb@kolbware.de Martin Lippert it-agile GmbH lippert@acm.org 2006 by Martin Lippert, lippert@acm.org; made available under the EPL v1.0 Outline Introduction Why Eclipse?
Server-Side Eclipse Bernd Kolb b.kolb@kolbware.de Martin Lippert it-agile GmbH lippert@acm.org 2006 by Martin Lippert, lippert@acm.org; made available under the EPL v1.0 Outline Introduction Why Eclipse?
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF 3230 Formell modellering og analyse av kommuniserende systemer Eksamensdag: 4. april 2008 Tid for eksamen: 9.00 12.00 Oppgavesettet
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF 3230 Formell modellering og analyse av kommuniserende systemer Eksamensdag: 4. april 2008 Tid for eksamen: 9.00 12.00 Oppgavesettet
Capturing the value of new technology How technology Qualification supports innovation
 Capturing the value of new technology How technology Qualification supports innovation Avanserte Marine Operasjoner - Fra operasjon til skip og utstyr Dag McGeorge Ålesund, 1 Contents Introduction - Cheaper,
Capturing the value of new technology How technology Qualification supports innovation Avanserte Marine Operasjoner - Fra operasjon til skip og utstyr Dag McGeorge Ålesund, 1 Contents Introduction - Cheaper,
EN Skriving for kommunikasjon og tenkning
 EN-435 1 Skriving for kommunikasjon og tenkning Oppgaver Oppgavetype Vurdering 1 EN-435 16/12-15 Introduction Flervalg Automatisk poengsum 2 EN-435 16/12-15 Task 1 Skriveoppgave Manuell poengsum 3 EN-435
EN-435 1 Skriving for kommunikasjon og tenkning Oppgaver Oppgavetype Vurdering 1 EN-435 16/12-15 Introduction Flervalg Automatisk poengsum 2 EN-435 16/12-15 Task 1 Skriveoppgave Manuell poengsum 3 EN-435
Elektronisk innlevering/electronic solution for submission:
 VIKINGTIDSMUSEET Plan- og designkonkurranse/design competition Elektronisk innlevering/electronic solution for submission: Det benyttes en egen elektronisk løsning for innlevering (Byggeweb Anbud). Dette
VIKINGTIDSMUSEET Plan- og designkonkurranse/design competition Elektronisk innlevering/electronic solution for submission: Det benyttes en egen elektronisk løsning for innlevering (Byggeweb Anbud). Dette
TEKSTER PH.D.-VEILEDERE FREMDRIFTSRAPPORTERING DISTRIBUSJONS-E-POST TIL ALLE AKTUELLE VEILEDERE:
 TEKSTER PH.D.-VEILEDERE FREMDRIFTSRAPPORTERING DISTRIBUSJONS-E-POST TIL ALLE AKTUELLE VEILEDERE: Kjære , hovedveileder for Den årlige fremdriftsrapporteringen er et viktig tiltak som gjør
TEKSTER PH.D.-VEILEDERE FREMDRIFTSRAPPORTERING DISTRIBUSJONS-E-POST TIL ALLE AKTUELLE VEILEDERE: Kjære , hovedveileder for Den årlige fremdriftsrapporteringen er et viktig tiltak som gjør
Gir vi de resterende 2 oppgavene til én prosess vil alle sitte å vente på de to potensielt tidskrevende prosessene.
 Figure over viser 5 arbeidsoppgaver som hver tar 0 miutter å utføre av e arbeider. (E oppgave ka ku utføres av é arbeider.) Hver pil i figure betyr at oppgave som blir pekt på ikke ka starte før oppgave
Figure over viser 5 arbeidsoppgaver som hver tar 0 miutter å utføre av e arbeider. (E oppgave ka ku utføres av é arbeider.) Hver pil i figure betyr at oppgave som blir pekt på ikke ka starte før oppgave
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON1910 Poverty and distribution in developing countries Exam: ECON1910 Poverty and distribution in developing countries Eksamensdag: 1. juni 2011 Sensur
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON1910 Poverty and distribution in developing countries Exam: ECON1910 Poverty and distribution in developing countries Eksamensdag: 1. juni 2011 Sensur
0:7 0:2 0:1 0:3 0:5 0:2 0:1 0:4 0:5 P = 0:56 0:28 0:16 0:38 0:39 0:23
 UTKAST ENGLISH VERSION EKSAMEN I: MOT100A STOKASTISKE PROSESSER VARIGHET: 4 TIMER DATO: 16. februar 2006 TILLATTE HJELPEMIDLER: Kalkulator; Tabeller og formler i statistikk (Tapir forlag): Rottman: Matematisk
UTKAST ENGLISH VERSION EKSAMEN I: MOT100A STOKASTISKE PROSESSER VARIGHET: 4 TIMER DATO: 16. februar 2006 TILLATTE HJELPEMIDLER: Kalkulator; Tabeller og formler i statistikk (Tapir forlag): Rottman: Matematisk
Han Ola of Han Per: A Norwegian-American Comic Strip/En Norsk-amerikansk tegneserie (Skrifter. Serie B, LXIX)
 Han Ola of Han Per: A Norwegian-American Comic Strip/En Norsk-amerikansk tegneserie (Skrifter. Serie B, LXIX) Peter J. Rosendahl Click here if your download doesn"t start automatically Han Ola of Han Per:
Han Ola of Han Per: A Norwegian-American Comic Strip/En Norsk-amerikansk tegneserie (Skrifter. Serie B, LXIX) Peter J. Rosendahl Click here if your download doesn"t start automatically Han Ola of Han Per:
Justeringsanvisninger finnes på de to siste sidene.
 d Montering av popup spredere Justeringsanvisninger finnes på de to siste sidene. Link til monteringsfilm på youtube: http://youtu.be/bjamctz_kx4 Hver spreder har montert på en "svinkobling", det vil si
d Montering av popup spredere Justeringsanvisninger finnes på de to siste sidene. Link til monteringsfilm på youtube: http://youtu.be/bjamctz_kx4 Hver spreder har montert på en "svinkobling", det vil si
Den europeiske byggenæringen blir digital. hva skjer i Europa? Steen Sunesen Oslo,
 Den europeiske byggenæringen blir digital hva skjer i Europa? Steen Sunesen Oslo, 30.04.2019 Agenda 1. 2. CEN-veileder til ISO 19650 del 1 og 2 3. EFCA Guide Oppdragsgivers krav til BIMleveranser og prosess.
Den europeiske byggenæringen blir digital hva skjer i Europa? Steen Sunesen Oslo, 30.04.2019 Agenda 1. 2. CEN-veileder til ISO 19650 del 1 og 2 3. EFCA Guide Oppdragsgivers krav til BIMleveranser og prosess.
Dokumentasjon. Hvorfor skrive dokumentasjon? For hvem? Javas dokumentasjon «Lesbar programmering» («Literate programming») IN 211 Programmeringsspråk
 Dokumentasjon Hvorfor skrive dokumentasjon? For hvem? Javas dokumentasjon «Lesbar programmering» («Literate programming») Ark 1 av 13 Forelesning 6.11.2000 Dokumentasjon Med hvert skikkelig program bør
Dokumentasjon Hvorfor skrive dokumentasjon? For hvem? Javas dokumentasjon «Lesbar programmering» («Literate programming») Ark 1 av 13 Forelesning 6.11.2000 Dokumentasjon Med hvert skikkelig program bør
TEKSTER PH.D.-KANDIDATER FREMDRIFTSRAPPORTERING
 TEKSTER PH.D.-KANDIDATER FREMDRIFTSRAPPORTERING DISTRIBUSJONS-E-POST TIL ALLE KANDIDATER: (Fornavn, etternavn) Den årlige fremdriftsrapporteringen er et viktig tiltak som gjør instituttene og fakultetene
TEKSTER PH.D.-KANDIDATER FREMDRIFTSRAPPORTERING DISTRIBUSJONS-E-POST TIL ALLE KANDIDATER: (Fornavn, etternavn) Den årlige fremdriftsrapporteringen er et viktig tiltak som gjør instituttene og fakultetene
Instructions for the base (B)-treatment and the elicitation (E)-treatment of the experiment
 Appendix Instructions for the base (B)-treatment and the elicitation (E)-treatment of the experiment We here provide the instructions given to the participants at the beginning of the session and throughout
Appendix Instructions for the base (B)-treatment and the elicitation (E)-treatment of the experiment We here provide the instructions given to the participants at the beginning of the session and throughout
Perpetuum (im)mobile
 Perpetuum (im)mobile Sett hjulet i bevegelse og se hva som skjer! Hva tror du er hensikten med armene som slår ut når hjulet snurrer mot høyre? Hva tror du ordet Perpetuum mobile betyr? Modell 170, Rev.
Perpetuum (im)mobile Sett hjulet i bevegelse og se hva som skjer! Hva tror du er hensikten med armene som slår ut når hjulet snurrer mot høyre? Hva tror du ordet Perpetuum mobile betyr? Modell 170, Rev.
Independent Inspection
 Independent Inspection Odd Ivar Johnsen Vidar Nystad Independent Inspection Mål: Felles forståelse og utøvelse av "Independent Inspection" i forbindelse med "Critical Maintenance Task". Independent Inspection
Independent Inspection Odd Ivar Johnsen Vidar Nystad Independent Inspection Mål: Felles forståelse og utøvelse av "Independent Inspection" i forbindelse med "Critical Maintenance Task". Independent Inspection
STILLAS - STANDARD FORSLAG FRA SEF TIL NY STILLAS - STANDARD
 FORSLAG FRA SEF TIL NY STILLAS - STANDARD 1 Bakgrunnen for dette initiativet fra SEF, er ønsket om å gjøre arbeid i høyden tryggere / sikrere. Både for stillasmontører og brukere av stillaser. 2 Reviderte
FORSLAG FRA SEF TIL NY STILLAS - STANDARD 1 Bakgrunnen for dette initiativet fra SEF, er ønsket om å gjøre arbeid i høyden tryggere / sikrere. Både for stillasmontører og brukere av stillaser. 2 Reviderte
Forecast Methodology September LightCounting Market Research Notes
 Forecast Methodology September 2015 LightCounting Market Research Notes Vladimir Market Kozlov Forecast Methodology, September, September, 2015 2015 1 Summary In summary, the key assump=on of our forecast
Forecast Methodology September 2015 LightCounting Market Research Notes Vladimir Market Kozlov Forecast Methodology, September, September, 2015 2015 1 Summary In summary, the key assump=on of our forecast
Server-Side Eclipse. Martin Lippert akquinet agile GmbH
 Server-Side Eclipse Martin Lippert akquinet agile GmbH martin.lippert@akquinet.de 2006 by Martin Lippert, martin.lippert@akquinet.de; made available under the EPL v1.0 Outline Introduction Why Eclipse?
Server-Side Eclipse Martin Lippert akquinet agile GmbH martin.lippert@akquinet.de 2006 by Martin Lippert, martin.lippert@akquinet.de; made available under the EPL v1.0 Outline Introduction Why Eclipse?
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON360/460 Samfunnsøkonomisk lønnsomhet og økonomisk politikk Exam: ECON360/460 - Resource allocation and economic policy Eksamensdag: Fredag 2. november
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON360/460 Samfunnsøkonomisk lønnsomhet og økonomisk politikk Exam: ECON360/460 - Resource allocation and economic policy Eksamensdag: Fredag 2. november
Emnedesign for læring: Et systemperspektiv
 1 Emnedesign for læring: Et systemperspektiv v. professor, dr. philos. Vidar Gynnild Om du ønsker, kan du sette inn navn, tittel på foredraget, o.l. her. 2 In its briefest form, the paradigm that has governed
1 Emnedesign for læring: Et systemperspektiv v. professor, dr. philos. Vidar Gynnild Om du ønsker, kan du sette inn navn, tittel på foredraget, o.l. her. 2 In its briefest form, the paradigm that has governed
Du må håndtere disse hendelsene ved å implementere funksjonene init(), changeh(), changev() og escape(), som beskrevet nedenfor.
 6-13 July 2013 Brisbane, Australia Norwegian 1.0 Brisbane har blitt tatt over av store, muterte wombater, og du må lede folket i sikkerhet. Veiene i Brisbane danner et stort rutenett. Det finnes R horisontale
6-13 July 2013 Brisbane, Australia Norwegian 1.0 Brisbane har blitt tatt over av store, muterte wombater, og du må lede folket i sikkerhet. Veiene i Brisbane danner et stort rutenett. Det finnes R horisontale
Level Set methods. Sandra Allaart-Bruin. Level Set methods p.1/24
 Level Set methods Sandra Allaart-Bruin sbruin@win.tue.nl Level Set methods p.1/24 Overview Introduction Level Set methods p.2/24 Overview Introduction Boundary Value Formulation Level Set methods p.2/24
Level Set methods Sandra Allaart-Bruin sbruin@win.tue.nl Level Set methods p.1/24 Overview Introduction Level Set methods p.2/24 Overview Introduction Boundary Value Formulation Level Set methods p.2/24
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF 3230/4230 Formell modellering og analyse av kommuniserende systemer Eksamensdag: 24. mars 2006 Tid for eksamen: 13.30 16.30
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF 3230/4230 Formell modellering og analyse av kommuniserende systemer Eksamensdag: 24. mars 2006 Tid for eksamen: 13.30 16.30
Multimedia in Teacher Training (and Education)
 Multimedia in Teacher Training (and Education) Bodo Eckert, Stefan Altherr, Hans-Jörg Jodl Second International GIREP Seminar 1-6 September 2003 University of Udine, Italy Content Training courses for
Multimedia in Teacher Training (and Education) Bodo Eckert, Stefan Altherr, Hans-Jörg Jodl Second International GIREP Seminar 1-6 September 2003 University of Udine, Italy Content Training courses for
EXAM TTM4128 SERVICE AND RESOURCE MANAGEMENT EKSAM I TTM4128 TJENESTE- OG RESSURSADMINISTRASJON
 Side 1 av 5 NTNU Norges teknisk-naturvitenskapelige universitet Institutt for telematikk EXAM TTM4128 SERVICE AND RESOURCE MANAGEMENT EKSAM I TTM4128 TJENESTE- OG RESSURSADMINISTRASJON Contact person /
Side 1 av 5 NTNU Norges teknisk-naturvitenskapelige universitet Institutt for telematikk EXAM TTM4128 SERVICE AND RESOURCE MANAGEMENT EKSAM I TTM4128 TJENESTE- OG RESSURSADMINISTRASJON Contact person /
On Capacity Planning for Minimum Vulnerability
 On Capacity Planning for Minimum Vulnerability Alireza Bigdeli Ali Tizghadam Alberto Leon-Garcia University of Toronto DRCN - October 2011 Kakow - Poland 1 Outline Introduction Network Criticality and
On Capacity Planning for Minimum Vulnerability Alireza Bigdeli Ali Tizghadam Alberto Leon-Garcia University of Toronto DRCN - October 2011 Kakow - Poland 1 Outline Introduction Network Criticality and
Physical origin of the Gouy phase shift by Simin Feng, Herbert G. Winful Opt. Lett. 26, (2001)
 by Simin Feng, Herbert G. Winful Opt. Lett. 26, 485-487 (2001) http://smos.sogang.ac.r April 18, 2014 Introduction What is the Gouy phase shift? For Gaussian beam or TEM 00 mode, ( w 0 r 2 E(r, z) = E
by Simin Feng, Herbert G. Winful Opt. Lett. 26, 485-487 (2001) http://smos.sogang.ac.r April 18, 2014 Introduction What is the Gouy phase shift? For Gaussian beam or TEM 00 mode, ( w 0 r 2 E(r, z) = E
Mathematics 114Q Integration Practice Problems SOLUTIONS. = 1 8 (x2 +5x) 8 + C. [u = x 2 +5x] = 1 11 (3 x)11 + C. [u =3 x] = 2 (7x + 9)3/2
![Mathematics 114Q Integration Practice Problems SOLUTIONS. = 1 8 (x2 +5x) 8 + C. [u = x 2 +5x] = 1 11 (3 x)11 + C. [u =3 x] = 2 (7x + 9)3/2 Mathematics 114Q Integration Practice Problems SOLUTIONS. = 1 8 (x2 +5x) 8 + C. [u = x 2 +5x] = 1 11 (3 x)11 + C. [u =3 x] = 2 (7x + 9)3/2](/thumbs/77/75859899.jpg) Mathematics 4Q Name: SOLUTIONS. (x + 5)(x +5x) 7 8 (x +5x) 8 + C [u x +5x]. (3 x) (3 x) + C [u 3 x] 3. 7x +9 (7x + 9)3/ [u 7x + 9] 4. x 3 ( + x 4 ) /3 3 8 ( + x4 ) /3 + C [u + x 4 ] 5. e 5x+ 5 e5x+ + C
Mathematics 4Q Name: SOLUTIONS. (x + 5)(x +5x) 7 8 (x +5x) 8 + C [u x +5x]. (3 x) (3 x) + C [u 3 x] 3. 7x +9 (7x + 9)3/ [u 7x + 9] 4. x 3 ( + x 4 ) /3 3 8 ( + x4 ) /3 + C [u + x 4 ] 5. e 5x+ 5 e5x+ + C
E-Learning Design. Speaker Duy Hai Nguyen, HUE Online Lecture
 E-Learning Design Speaker Duy Hai Nguyen, HUE Online Lecture Design Educational Design Navigation Design Educational Design Some Important Considerations: 1. Authentic learning environment: For effective
E-Learning Design Speaker Duy Hai Nguyen, HUE Online Lecture Design Educational Design Navigation Design Educational Design Some Important Considerations: 1. Authentic learning environment: For effective
The regulation requires that everyone at NTNU shall have fire drills and fire prevention courses.
 1 The law The regulation requires that everyone at NTNU shall have fire drills and fire prevention courses. 2. 3 Make your self familiar with: Evacuation routes Manual fire alarms Location of fire extinguishers
1 The law The regulation requires that everyone at NTNU shall have fire drills and fire prevention courses. 2. 3 Make your self familiar with: Evacuation routes Manual fire alarms Location of fire extinguishers
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON20 Forbruker, bedrift og marked, høsten 2004 Exam: ECON20 - Consumer behavior, firm behavior and markets, autumn 2004 Eksamensdag: Onsdag 24. november
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON20 Forbruker, bedrift og marked, høsten 2004 Exam: ECON20 - Consumer behavior, firm behavior and markets, autumn 2004 Eksamensdag: Onsdag 24. november
Start Here USB *CC * *CC * USB USB
 1 USB Start Here USB 11 USB WARNING: To ensure that the software is installed correctly, do not connect the USB cable until step 11. 11 USB 2 a. b. Lower both the paper tray and the print cartridge door.
1 USB Start Here USB 11 USB WARNING: To ensure that the software is installed correctly, do not connect the USB cable until step 11. 11 USB 2 a. b. Lower both the paper tray and the print cartridge door.
SVM and Complementary Slackness
 SVM and Complementary Slackness David Rosenberg New York University February 21, 2017 David Rosenberg (New York University) DS-GA 1003 February 21, 2017 1 / 20 SVM Review: Primal and Dual Formulations
SVM and Complementary Slackness David Rosenberg New York University February 21, 2017 David Rosenberg (New York University) DS-GA 1003 February 21, 2017 1 / 20 SVM Review: Primal and Dual Formulations
SAS FANS NYTT & NYTTIG FRA VERKTØYKASSA TIL SAS 4. MARS 2014, MIKKEL SØRHEIM
 SAS FANS NYTT & NYTTIG FRA VERKTØYKASSA TIL SAS 4. MARS 2014, MIKKEL SØRHEIM 2 TEMA 1 MULTIPROSESSERING MED DATASTEGET Multiprosessering har lenge vært et tema i SAS Stadig ny funksjonalitet er med på
SAS FANS NYTT & NYTTIG FRA VERKTØYKASSA TIL SAS 4. MARS 2014, MIKKEL SØRHEIM 2 TEMA 1 MULTIPROSESSERING MED DATASTEGET Multiprosessering har lenge vært et tema i SAS Stadig ny funksjonalitet er med på
Norsk (English below): Guide til anbefalt måte å printe gjennom plotter (Akropolis)
 Norsk (English below): Guide til anbefalt måte å printe gjennom plotter (Akropolis) 1. Gå til print i dokumentet deres (Det anbefales å bruke InDesign til forberedning for print) 2. Velg deretter print
Norsk (English below): Guide til anbefalt måte å printe gjennom plotter (Akropolis) 1. Gå til print i dokumentet deres (Det anbefales å bruke InDesign til forberedning for print) 2. Velg deretter print
PATIENCE TÅLMODIGHET. Is the ability to wait for something. Det trenger vi når vi må vente på noe
 CARING OMSORG Is when we show that we care about others by our actions or our words Det er når vi viser at vi bryr oss om andre med det vi sier eller gjør PATIENCE TÅLMODIGHET Is the ability to wait for
CARING OMSORG Is when we show that we care about others by our actions or our words Det er når vi viser at vi bryr oss om andre med det vi sier eller gjør PATIENCE TÅLMODIGHET Is the ability to wait for
Stationary Phase Monte Carlo Methods
 Stationary Phase Monte Carlo Methods Daniel Doro Ferrante G. S. Guralnik, J. D. Doll and D. Sabo HET Physics Dept, Brown University, USA. danieldf@het.brown.edu www.het.brown.edu Introduction: Motivations
Stationary Phase Monte Carlo Methods Daniel Doro Ferrante G. S. Guralnik, J. D. Doll and D. Sabo HET Physics Dept, Brown University, USA. danieldf@het.brown.edu www.het.brown.edu Introduction: Motivations
Guidance. CBEST, CSET, Middle Level Credential
 Guidance CBEST, CSET, Middle Level Credential Liberal Studies for Teachers, 2009 CBEST California Basic Educational Skills Test Measures basic educational skills needed for teachers Reading Writing Math
Guidance CBEST, CSET, Middle Level Credential Liberal Studies for Teachers, 2009 CBEST California Basic Educational Skills Test Measures basic educational skills needed for teachers Reading Writing Math
Virginia Tech. John C. Duke, Jr. Engineering Science & Mechanics. John C. Duke, Jr.
 A New Paradigm for Health Management of Bridges Presentation Overview Introduction AASHTO Grand Challenges SAFETEA-LU LTBP Is the Problem Unique? RCM A New Paradigm Design, Build, Maintain---Asset Management
A New Paradigm for Health Management of Bridges Presentation Overview Introduction AASHTO Grand Challenges SAFETEA-LU LTBP Is the Problem Unique? RCM A New Paradigm Design, Build, Maintain---Asset Management
Chapter 7: Deadlocks
 Chapter 7: Deadlocks Chapter 7: Deadlocks The Deadlock Problem System Model Deadlock Characterization Methods for Handling Deadlocks Deadlock Prevention Deadlock Avoidance Deadlock Detection Recovery from
Chapter 7: Deadlocks Chapter 7: Deadlocks The Deadlock Problem System Model Deadlock Characterization Methods for Handling Deadlocks Deadlock Prevention Deadlock Avoidance Deadlock Detection Recovery from
Elektronisk termostat med spareprogram. Lysende LCD display øverst på ovnen for enkel betjening.
 Elektronisk termostat med spareprogram. Lysende LCD display øverst på ovnen for enkel betjening. 27.5 LCD Electronic thermostat with program setting. Bright LCD display placed at the top of the heater
Elektronisk termostat med spareprogram. Lysende LCD display øverst på ovnen for enkel betjening. 27.5 LCD Electronic thermostat with program setting. Bright LCD display placed at the top of the heater
32.2. Linear Multistep Methods. Introduction. Prerequisites. Learning Outcomes
 Linear Multistep Methods 32.2 Introduction In the previous Section we saw two methods (Euler and trapezium) for approximating the solutions of certain initial value problems. In this Section we will see
Linear Multistep Methods 32.2 Introduction In the previous Section we saw two methods (Euler and trapezium) for approximating the solutions of certain initial value problems. In this Section we will see
GEO231 Teorier om migrasjon og utvikling
 U N I V E R S I T E T E T I B E R G E N Institutt for geografi Emnerapport høsten 2013: GEO231 Teorier om migrasjon og utvikling Innhold: 1. Informasjon om emnet 2. Statistikk 3. Egenevaluering 4. Studentevaluering
U N I V E R S I T E T E T I B E R G E N Institutt for geografi Emnerapport høsten 2013: GEO231 Teorier om migrasjon og utvikling Innhold: 1. Informasjon om emnet 2. Statistikk 3. Egenevaluering 4. Studentevaluering
Appendix B, not for publication, with screenshots for Fairness and family background
 Appendix B, not for publication, with screenshots for Fairness and family background Ingvild Almås Alexander W. Cappelen Kjell G. Salvanes Erik Ø. Sørensen Bertil Tungodden This document shows screenshots
Appendix B, not for publication, with screenshots for Fairness and family background Ingvild Almås Alexander W. Cappelen Kjell G. Salvanes Erik Ø. Sørensen Bertil Tungodden This document shows screenshots
GLOBALCOMSERVER HP 9100C DIGITAL SENDER GATEWAY ADMINISTRATOR S GUIDE 1998 AVM INFORMATIQUE (UPDATED: AUGUST 22, 2006)
 PAGE 1 / 13 GLOBALCOMSERVER HP 9100C DIGITAL SENDER GATEWAY ADMINISTRATOR S GUIDE 1998 AVM INFORMATIQUE (UPDATED: AUGUST 22, 2006) PAGE 2 / 13 LICENSE LICENSE Information in this document is subject to
PAGE 1 / 13 GLOBALCOMSERVER HP 9100C DIGITAL SENDER GATEWAY ADMINISTRATOR S GUIDE 1998 AVM INFORMATIQUE (UPDATED: AUGUST 22, 2006) PAGE 2 / 13 LICENSE LICENSE Information in this document is subject to
Education 436. September 14, 2011
 Education 436 September 14, 2011 Outline Review of Class 2 The Program Planning Process: The Basics The Program Planning Process: Putting Theory into Action Working with Program Assistants The Program
Education 436 September 14, 2011 Outline Review of Class 2 The Program Planning Process: The Basics The Program Planning Process: Putting Theory into Action Working with Program Assistants The Program
Endringer i neste revisjon av EHF / Changes in the next revision of EHF 1. October 2015
 Endringer i neste revisjon av / Changes in the next revision of 1. October 2015 INFORMASJON PÅ NORSK 2 INTRODUKSJON 2 ENDRINGER FOR KATALOG 1.0.3 OG PAKKSEDDEL 1.0.2 3 ENDRINGER FOR ORDRE 1.0.3 4 ENDRINGER
Endringer i neste revisjon av / Changes in the next revision of 1. October 2015 INFORMASJON PÅ NORSK 2 INTRODUKSJON 2 ENDRINGER FOR KATALOG 1.0.3 OG PAKKSEDDEL 1.0.2 3 ENDRINGER FOR ORDRE 1.0.3 4 ENDRINGER
Prosjektet Digital kontaktinformasjon og fullmakter for virksomheter Digital contact information and mandates for entities
 Prosjektet Digital kontaktinformasjon og fullmakter for virksomheter Digital contact information and mandates for entities Nordisk Adressemøte / Nordic Address Forum, Stockholm 9-10 May 2017 Elin Strandheim,
Prosjektet Digital kontaktinformasjon og fullmakter for virksomheter Digital contact information and mandates for entities Nordisk Adressemøte / Nordic Address Forum, Stockholm 9-10 May 2017 Elin Strandheim,
Jacob Nielsens 10 heuristikker. Dansk Guru med 10 Tommelfingerregler en_(usability_consultant)
 Jacob Nielsens 10 heuristikker Dansk Guru med 10 Tommelfingerregler http://en.wikipedia.org/wiki/jakob_niels en_(usability_consultant) Jacob Nilsens heuristikker - 1 Visibility of system status The system
Jacob Nielsens 10 heuristikker Dansk Guru med 10 Tommelfingerregler http://en.wikipedia.org/wiki/jakob_niels en_(usability_consultant) Jacob Nilsens heuristikker - 1 Visibility of system status The system
Examination paper for TDT4252 and DT8802 Information Systems Modelling Advanced Course
 Department of Computer and Information Science Examination paper for TDT4252 and DT8802 Information Systems Modelling Advanced Course Academic contact during examination: Phone: Examination date: Examination
Department of Computer and Information Science Examination paper for TDT4252 and DT8802 Information Systems Modelling Advanced Course Academic contact during examination: Phone: Examination date: Examination
How Bridges Work Sgrad 2001
 How Bridges Work Sgrad 2001 The Basic s There are three major types of bridges: The beam bridge The arch bridge The suspension bridge prepared by Mr.S.Grad 2 The biggest difference between the three is
How Bridges Work Sgrad 2001 The Basic s There are three major types of bridges: The beam bridge The arch bridge The suspension bridge prepared by Mr.S.Grad 2 The biggest difference between the three is
Disjoint Sets. Chapter 21. CPTR 430 Algorithms Disjoint Sets 1
 Disjoint Sets Chapter 21 CPTR 430 Algorithms Disjoint Sets 1 S2 Disjoint Sets A disjoint-set data structure maintains a collection S 1 S k of disjoint dynamic sets Each set has a designated representative
Disjoint Sets Chapter 21 CPTR 430 Algorithms Disjoint Sets 1 S2 Disjoint Sets A disjoint-set data structure maintains a collection S 1 S k of disjoint dynamic sets Each set has a designated representative
Bruk av ALARP analyse for beslutningstaking på behovet for sikkerhetssystemer / barrierer
 Bruk av ALARP analyse for beslutningstaking på behovet for sikkerhetssystemer / barrierer Morten Sørum, Senior Advisor Safety, Statoil Classification: Internal 2014-11-16 ALARP prinsippet ALARP (As Low
Bruk av ALARP analyse for beslutningstaking på behovet for sikkerhetssystemer / barrierer Morten Sørum, Senior Advisor Safety, Statoil Classification: Internal 2014-11-16 ALARP prinsippet ALARP (As Low
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT BOKMÅL Eksamen i: ECON1210 - Forbruker, bedrift og marked Eksamensdag: 26.11.2013 Sensur kunngjøres: 18.12.2013 Tid for eksamen: kl. 14:30-17:30 Oppgavesettet er
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT BOKMÅL Eksamen i: ECON1210 - Forbruker, bedrift og marked Eksamensdag: 26.11.2013 Sensur kunngjøres: 18.12.2013 Tid for eksamen: kl. 14:30-17:30 Oppgavesettet er
Hvor mye teoretisk kunnskap har du tilegnet deg på dette emnet? (1 = ingen, 5 = mye)
 INF234 Er du? Er du? - Annet Hvor mye teoretisk kunnskap har du tilegnet deg på dette emnet? (1 = ingen, 5 = mye) Hvor mye praktisk kunnskap har du tilegnet deg på dette emnet? (1 = ingen, 5 = mye) Hvor
INF234 Er du? Er du? - Annet Hvor mye teoretisk kunnskap har du tilegnet deg på dette emnet? (1 = ingen, 5 = mye) Hvor mye praktisk kunnskap har du tilegnet deg på dette emnet? (1 = ingen, 5 = mye) Hvor
Western Alaska CDQ Program. State of Alaska Department of Community & Economic Development
 Western Alaska State of Alaska Department of Community & Economic Development The CDQ program was formally approved in 1992 by the North Pacific Fishery Management Council and implemented by Governor
Western Alaska State of Alaska Department of Community & Economic Development The CDQ program was formally approved in 1992 by the North Pacific Fishery Management Council and implemented by Governor
Innovasjonsvennlig anskaffelse
 UNIVERSITETET I BERGEN Universitetet i Bergen Innovasjonsvennlig anskaffelse Fredrikstad, 20 april 2016 Kjetil Skog 1 Universitetet i Bergen 2 Universitetet i Bergen Driftsinntekter på 4 milliarder kr
UNIVERSITETET I BERGEN Universitetet i Bergen Innovasjonsvennlig anskaffelse Fredrikstad, 20 april 2016 Kjetil Skog 1 Universitetet i Bergen 2 Universitetet i Bergen Driftsinntekter på 4 milliarder kr
Vurderingsveiledning SPR3008 Internasjonal engelsk Eleven gir stort sett greie og relevante svar på oppgavene i samsvar med oppgaveordlyden.
 Answering Exam Tasks Currently the exam for this course has two tasks. Task 1 is referred to as the short task and task 2 is referred to as the long task. There are sometimes two parts to Task 1, a and
Answering Exam Tasks Currently the exam for this course has two tasks. Task 1 is referred to as the short task and task 2 is referred to as the long task. There are sometimes two parts to Task 1, a and
Public roadmap for information management, governance and exchange. 2015-09-15 SINTEF david.norheim@brreg.no
 Public roadmap for information management, governance and exchange 2015-09-15 SINTEF david.norheim@brreg.no Skate Skate (governance and coordination of services in egovernment) is a strategic cooperation
Public roadmap for information management, governance and exchange 2015-09-15 SINTEF david.norheim@brreg.no Skate Skate (governance and coordination of services in egovernment) is a strategic cooperation
